Второй закон Ньютона: формула, определение, применение
В «Математических началах натуральной философии» Ньютона сформулирован закон, который в двадцатом веке охарактеризован Эйнштейном как главный постулат механики и считается фундаментом теоретической физики.
Второй закон Ньютона формулировка
Ньютон, формулируя постулат, связывал движущую силу и изменение количества движения.
второй закон Ньютона
Современная трактовка использует более привычные для восприятия термины, сегодня 2-й закон Ньютона звучит как:
В системах отсчёта, называемых инерциальными, материальная точка приобретает ускорение, сонаправленное силе или равнодействующей сил, являющихся возбудителями движения, и находящееся в прямо пропорциональной зависимости от неё. Также упомянутое ускорение обратно пропорционально массе движущейся материальной точки.
Трактовать постулат динамики можно через импульс – меру движения тела, численно равную результату умножения массы на скорость:
расчет импульса
где p, m, v – импульс, масса, скорость тела или точки.
Вторая формулировка второго закона Ньютона гласит:
В системах отсчёта, называемых инерциальными, скорость изменения импульса, имеющего также название «количество движения», численно равно силе или равнодействующей сил, являющихся возбудителями движения материальной точки.
ВНИМАНИЕ: инерциальные – системы, в которых тела покоятся или движутся равномерно, прямолинейно.
Область применения
2-й закон Ньютона применяют к материальным точкам – объектам массой, сосредоточенной в точке, и размерами, которыми допустимо пренебречь. Логичен вывод, что постулат механики работает в случаях, где масса тела остаётся постоянной. Также формулу свободно применяют в задачах движения центра масс системы, используя одноимённую теорему.
Формулировки отмечают ограниченность применимости закона инерциальными системами отсчёта. Однако, если внести силы инерции в равнодействующую, уравнение движения, составленное на основе постулата Ньютона, допустимо использовать в неинерциальных системах.
Вывод закона на основании проведённых опытов
Изучаемый фундамент динамики (динамика – наука, изучающая движение) не удастся вывести путём математических вычислений, формулу доказывают опытом, представленным рисунком.
эксперимент по выводу формулы второго закона Ньютона
Тележка массой m взаимодействует с пружиной, растянутой на длину l. Если тянуть конец пружины, соблюдая выбранное значение деформации, тележка покатится по направлению воздействия, обладая ускорением a. Увеличим вес, добавив тележку, идентичную используемой, и снова потянем свободный конец пружины, следя за постоянностью удлинения. Зафиксируем уменьшение ускорения. Для полноты эксперимента, добавив третью тележку, повторим опыт и заметим, что значение ускорения меньше.
В эксперименте прикладываемая нагрузка оставалась неизменной, что контролировалось путём использования одной пружины, деформированной на величину l.
Рассмотрим произведение массы на ускорение тележки:
То есть, рассмотренное произведение одинаково и зависит от меры оказанного воздействия :
,Вывод формулы второго закона Ньютона — видео.
Зависимость между массой и ускорением
Согласно проиллюстрированному опыту, ускорение объекта уменьшается настолько, насколько увеличивается масса. Результаты эксперимента для наглядности приведём в табличный вид:
| Значение (единицы измерения условные) | Значение (единицы измерения условные) |
|---|---|
| 1 | 1 |
| 2 | 1/2 |
| 3 | 1/3 |
Вывод: ускорение обратно пропорционально массе.
Зависимость между силой и ускорением
Для отражения связи между ускорением и силой придадим продемонстрированному опыту другую форму. К тележке массой m приложим силу, увеличивающуюся по модулю. Изменение нагрузки фиксируется за счёт возрастающей деформации пружины, тянущей тележку. В качестве эталонного проведём знакомый эксперимент: будем тянуть тележку массой m при помощи пружины с удлинением l и зафиксируем ускорение системы, равное a. Далее воздействуем на объект в два раза сильнее, растянув пружину до значения деформации 2l, и заметим, увеличение ускорения тележки до 2a. Для закрепления результата снова увеличим усилие, под действием которого растягивается пружина. По закону Гука, деформация пружины напрямую зависит от меры воздействия. Увеличив значение удлинения до 3l, увидим, что тележка двинется с ускорением 3a.
Изменение нагрузки фиксируется за счёт возрастающей деформации пружины, тянущей тележку. В качестве эталонного проведём знакомый эксперимент: будем тянуть тележку массой m при помощи пружины с удлинением l и зафиксируем ускорение системы, равное a. Далее воздействуем на объект в два раза сильнее, растянув пружину до значения деформации 2l, и заметим, увеличение ускорения тележки до 2a. Для закрепления результата снова увеличим усилие, под действием которого растягивается пружина. По закону Гука, деформация пружины напрямую зависит от меры воздействия. Увеличив значение удлинения до 3l, увидим, что тележка двинется с ускорением 3a.
Анализируя эксперимент, делаем вывод: ускорение прямо пропорционально действующей силе.
вывод зависимости между силой и ускорением
Единица измерения силы
Международная система единиц, в привычном обозначении СИ – система интернациональная, называет ньютоны в качестве единиц, в которых измеряется сила. Ньютоны – производные единицы, выраженные основными (к ним относится семь наименований) путём умножения или деления последних друг на друга:
Ньютоны – производные единицы, выраженные основными (к ним относится семь наименований) путём умножения или деления последних друг на друга:
Справка: Фамилия Ньютон пишется с заглавной буквы, одноимённое название единиц измерений записывается со строчной.
Формула второго закона Ньютона
Формулу, выражающую закон Ньютона, записывают различными формами, в зависимости от системы координат. Стандартная запись:
формула второго закона Ньютона
в декартовой прямоугольной системе координат выглядит следующим образом:
,где
,– орты или единичные векторы.В сферической и цилиндрической системах запись усложнена, однако все виды формулы выражают одну взаимосвязь силы, ускорения и массы.
Равнодействующая сила
Интуитивно значение силы, действующей на тело, ясно, однако второй закон Ньютона определении вносит незнакомый термин – «равнодействующая», и изначально сложно уверенно утверждать, о каком воздействии говорится.
равнодействующая сила
Мало кто способен назваться гением по физике, однако каждому понятно, что любое тело испытывает воздействие нескольких сил одновременно. Сюда относятся, например, силы тяжести, сопротивления воздуха или упругости, реакция опоры. Для удобства расчётов прикладываемые к объекту воздействия сформировывают в одно – равнодействующую.
Совместное действие находят суммированием векторов внешних сил, приложенных к телу:
.На практике подобное осуществляется проецированием векторов на координатные оси:
суммирование векторов сил по координатам
Если присутствует воздействие пары сил, действующих вдоль одной прямой, равнодействующая определяется как:
ВНИМАНИЕ: равнодействующая равна нулю, если тело движется равномерно.
Таким образом, больше не возникнет вопроса, как читается выражение
, и изученный закон сразу будет формулироваться в мыслях.Законы Ньютона
Законы Ньютона являются основополагающими в классической механике и однозначно, поворотным моментом в физике. Это своего рода объединение накопленных к тому времени знаний о физических телах и их движении в законы.
Это своего рода объединение накопленных к тому времени знаний о физических телах и их движении в законы.
Закон Ньютона первый выдвигает в качестве исходного положения инерцию тела. Именно в связи с этим данный закон иногда трактуют как Закон Инерции. Что же подразумевает данная сила. Под инерцией понимается, сохранение скорости движения тела, при условии что на тело не воздействуют силы. Для изменения скорости движения тел, нужно воздействие на него силой. Действие одной и той же силы на разные тела будет различное, из чего следует что различное тело имеет свою инертность. А значит инертность тела – это сопротивление тела к изменениям их прежнего состояния. Значение инертности зависит от массы тела.
Определение первого закона Ньютона в наши дни:
Второй закон Ньютона отличительный закон о движении, раскрывающий связь приложенной силы и полученного ускорения. Используя массу тела в виде меры означающей инертность мат.
 точки в конкретной ИСО.
точки в конкретной ИСО.Определение второго закона Ньютона с наши дни:
Закон Ньютона формула
а = F /m
в которой а ? – приходиться ускорением; F ? – постоянная всех сил; m -приходиться массой.
Для ИСО изменение скорости импульсов тела равняется постоянной от всех сил.
dp /dt = F
в которой p – приходится импульсом, t – время.
Третий закон Ньютона дает описание взаимодействия двух материальных точек. Рассмотрим две точки находящиеся в замкнутой системе. Одна из которых воздействует на другую с силой F ?1?2, а другая в обратную с силой F ?2?1. Из чего следует, сила действия равна силе противодействия.
Добавление: При воздействии на одно тело несколькими силами, данный закон записывается как:
либо
Для второго закона Ньютона, существует только для передвижения тел, меньшей чем скорость света.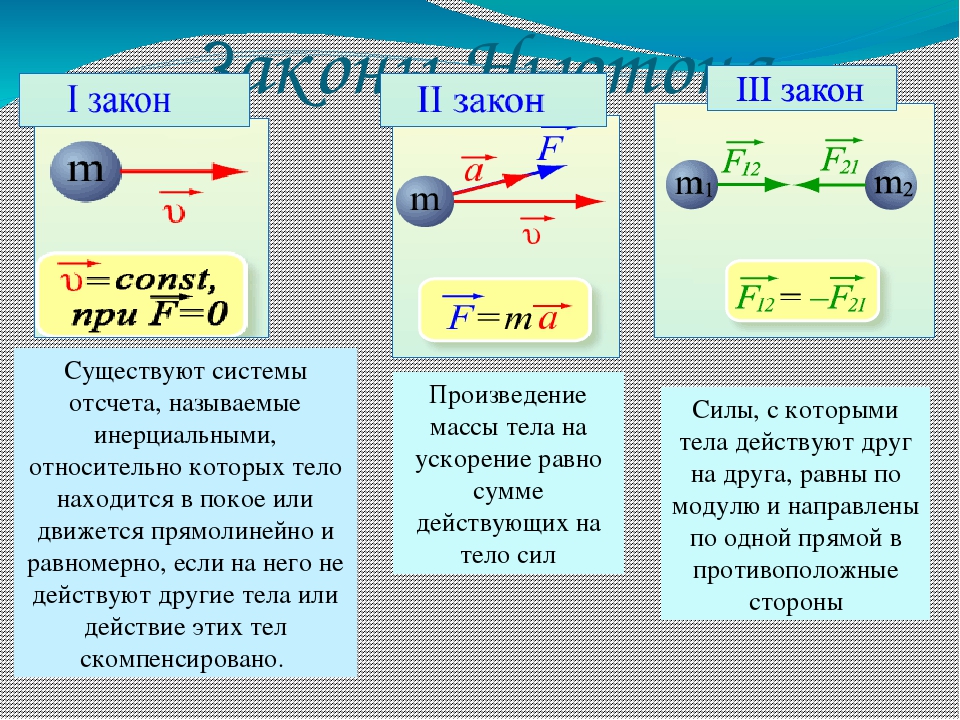
Определение второго закона Ньютона с наши дни:
Третий закон дает понять, силы возникают только парно, при этом появление каждой из них будет благодаря другой. Другими словами. Появление сил самостоятельно, не имеющих взаимодействия с другими телами, не является возможным.
Первой публикацией (более приближен к первому закону) был Галилей, который говорил о свободном продвижении и по линии и по кругу (астрономия). Тем самым положив начало всем законам Ньютона.
Заметка: Любите фотографировать, но на качественное и дорогое оборудование не хватает денег? Это не беда! Ведь есть аренда объективов (http://zoom-prokat.ru/) и не только. Перейдя по ссылке Вы найдете все что вам нужно.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Закон Гука и второй Закон механики Ньютона
(Тер.Инк. N47-01, 23/11/2001)Вадим Прибытков
В 1676 году Роберт Гук открыл закон растяжения
пружин.
Закон Гука гласит: каково удлинение, такова и сила. Т.е. при растяжении пружины с помощью силы удлинение пружины изменяется прямо пропорционально величине силы. Это соотношение выдерживается для стальных пружин с идеальной точностью в широком диапазоне удлинений.
Закон Гука сыграл важную роль в физике и технике, хотя он является по существу одним из проявлений второго закона движения Ньютона. Но при этом Гук сформулировал его раньше Ньютона.
И действительно, три величины: сила, масса и ускорение связаны между собой основным законом механики–вторым законом Ньютона–в следующей всеобъемлющей формуле: приложенная сила равна массе, умноженной на ускорение. Из этого закона следует, что величина ускорения (а также движения, удлинения, растяжения, сжатия и т.д.) приобретаемого телом, прямо пропорционально приложенной силе.
Масса тела, а также способность пружины к растяжению и т.д. не меняется и играет в приводимом равенстве роль коэффициента.
Следовательно, и закон Гука можно записать через приводимое равенство, понимая под массой физические свойства пружины.
В механике широко пользуются статистическим измерением сил с помощью пружин. С поведением тел по закону Гука мы имеем место во многих случаях растяжения, сжатия, изгиба, прогиба, кручения и вообще упругой деформации любого вида. Такой же последовательности подчиняются колебания груза на пружине, вибрации камертона и пр.
Доказывая, что все эти виды движения происходят на основании второго закона механики Ньютона, мы объединяем все существующие виды движений в единую систему.
Как известно Гук оспаривал у Ньютона приоритет в установлении закона всемирного тяготения. Здесь он был явно не прав. Но он мог бы оспаривать первенство в установлении приоритета по второму закону механики. Однако Гук ограничился лишь растяжением пружин. Ему не хватило широты охвата, включения в данный закон всех явлений. Если бы Гук не совершил этой оплошности, то вся история науки могла бы быть несколько иной.
Ньютон смотрел дальше и сформулировал закон, охвативший все виды движения. Такова правда и сложная коллизия исторического развития науки.
Второй закон Ньютона
Ньютон в своем знаменитом труде «Математические начала натуральной философии» определяет силу следующими словами:
Другими словами, сила есть причина ускорения. Второй же закон движения Ньютон формулирует так:
Слова «изменение движения», несомненно, означают изменение скорости движения, так как именно скорость – главная количественная характеристика движения, а направление вектора скорости и есть направление движения. Таким образом, второй закон Ньютона сводится к утверждению, что ускорение (которое непосредственно связано с изменением скорости) тела пропорционально приложенной к нему силе и направлено так же, как сила.
Таким образом, чтобы найти, как изменилась скорость тела, нам надо знать, какая сила действует на тело.
Масса тела напрямую связана с ускорением, приобретаемым телом в результате воздействия силы.
Более полная формулировка второго закона Ньютона:
Второй закон Ньютона выполняется в инерциальных системах отсчета.
Важно понять: из второго закона Ньютона следует, что сила определяет направление ускорения, а не направление скорости: ${\overrightarrow{a}} \upuparrows {\overrightarrow{F}}$.
Так, например, под действием силы тяжести тело может двигаться вертикально вниз (рис. 1, а) и по параболе (рис. 1, б), в зависимости от наличия и направления его начальной скорости. Однако ускорение тела в этом случае совпадает с направлением силы тяжести.
Рисунок 1. Движение тела под действием силы тяжести
Если направление скорости тела совпадает с направлением действия приложенной к телу силы, то оно движется равноускоренно по прямой линии, совпадающей с линией действия силы (рис. 2 а, в).
Рисунок 2
а) скорость сонаправлена ускорению и силе, движение равноускоренное; б) скорость противонаправлена ускорению и силе, движение равнозамедленное; в) скорость перпендикулярна ускорению и силе – движение по окружности; г) скорость направлена под острым углом к линии действия силы – движение по криволинейной траектории.
Если скорость по направлению противоположна силе – тело движется по прямой равнозамедленно (рис. 2 б).
Если вектор скорости тела перпендикулярен направлению вектора силы, тело движется по дуге окружности (рис. 2 г).
Во втором законе Ньютона заключен, как частный случай, первый закон, или закон инерции. Действительно, если F = 0, то и a = 0, т. е. если на тело не действуют силы (или силы действуют, но их равнодействующая равна нулю), то и ускорение равно нулю, и значит, тело сохраняет состояние покоя или равномерного прямолинейного движения. Однако первый закон Ньютона имеет более глубокое физическое содержание — он постулирует существование инерциальных систем отсчета.
Задача 2
Футболист, ударяя мяч массой 700 г, сообщает ему горизонтальную скорость 15 м/с. Считая продолжительность удара равной 0,02 с, определите среднюю силу удара.
Решение
Дано:
$m$ = 700 г = 0,7 кг
$v_x$ = 15 м/c
$t$ = 0,02 c
$F$ – ?
По 2 закону Ньютона, $\overrightarrow{F}=m\overrightarrow{a}$. Ускорение, приобретённое телом в результате взаимодействия, пропорционально времени взаимодействия и приращению его скорости: $\overrightarrow{a}=\left(v-v_0\right)t$.
Ускорение, приобретённое телом в результате взаимодействия, пропорционально времени взаимодействия и приращению его скорости: $\overrightarrow{a}=\left(v-v_0\right)t$.
Считая, что до удара мяч покоился, и направив ось ОХ горизонтально, по линии действия силы, получим:
\[a=\ \frac{v}{t};\ F=ma=m\frac{v}{t}=0,7\cdot \frac{15}{0,02}=525\ H\]Ответ: сила удара по мячу была 525 ньютонов.
Второй закон Ньютона и «Три богатыря» Васнецова
Статьи
Линия УМК А. В. Грачева. Физика (7-9)
Физика
Как думаете, какая связь существует между картиной Васнецова «Три богатыря» и вторым законом Ньютона?
27 августа 2019
Ответ на загадку найдете в конце статьи, а пока давайте вспомним вклад Ньютона в классическую физику.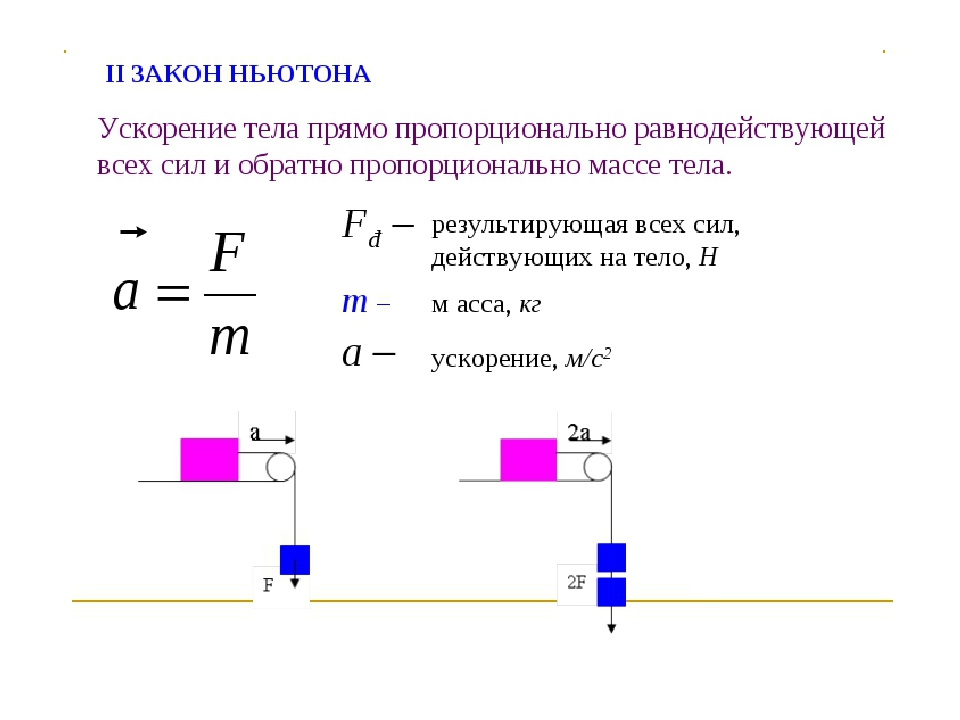
Галилей, Гюйгенс, Кеплер, множество других исследователей, чьи имена остались похоронены под слоем пыли в темных библиотеках средневековых замков, проводили опыты и эксперименты, пытаясь открыть законы движения предметов в окружающей среде.
Исаак Ньютон, опираясь на знания и эксперименты предшественников и собственные наблюдения, смог подытожить накопленный колоссальный опыт и сформулировать законы, по которым движутся физические тела.
В 1867 году увидел свет его научный труд: «Математические начала натуральной философии», где английский физик представил известные законы механики и закон всемирного тяготения.С того времени классическая механика базируется на законах Ньютона.
Физика. 8 класс. Учебник.
Учебнипк рассчитан на учащихся общеобразовательных организаций. Настоящее издание вместе с рабочими тетрадями, тетрадью для лабораторных работ и методическим пособием для учителей составляет учебно-методический комплект по физике для 8 класса. В учебнике представлены разделы «Тепловые явления» и «Электромагнитные явления».
В учебнике представлены разделы «Тепловые явления» и «Электромагнитные явления».
Первый закон, или закон инерции гласит: «Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.» Подробно данный закон разбирается в учебнике «Физика 9 класс» под редакцией Л.С. Хижнякова и А.А. Синявина
Цель нашей статьи — второй закон Ньютона.
Как вы заметили, первый закон определяет, что происходит с телом в покое, т.е. когда на него не действуют силы. Но в реальном мире движение повсюду.Играете ли вы в футбол, нога футболиста с силой ударяет по мячу, придавая нужное ускорение и траекторию, чтобы забить победный гол. Отбивает ли мама на кухне мясо — рука передает кухонному молотку также определенную силу, чтобы получился вкусный стейк.
И именно эти взаимодействия объясняет второй закон Ньютона, который звучит так: «Величина силы, действующая на тело, равна произведению массы тела на ускорение, которое получает тело, когда на него начинает действовать сила. »
»
Если представить этот закон математически, формула второго закона Ньютона выглядит следующим образом:
F=m*a, где:
- m- масса тела,
- а — ускорение, которое получает тело под воздействием приложенной силы,
- F — Это результирующая всех сил приложенных к телу (велосипедисту, паровозу, самолету и т.д.)
Однако, эта формула вводит в небольшое заблуждение, потому что глядя на нее, кажется, что ускорение вызывает силу, а такого в живой природе быть не может.
Преобразовав уравнение таким образом:
а=F/m
приходим к выводу, что сила определяет ускорение, а не наоборот.
Чем большая сила действует на тело, тем больше ускорение он получит, и наоборот, чем больше масса, тем меньше ускорит свое движение тело.
Физика. 9 класс. Учебник.
Настоящее издание является завершением линии учебников для учащихся 7-9 классов общеобразовательных организаций (авт. А.В.Грачёв, В.А. Погожев и др.). Учебник рассматривает разделы «Механические явления», «Электромагнитные явления», «Оптические явления» и «Квантовые явления». В учебник включены материалы для учащихся, интересующихся физикой, задания для внеклассной работы.
А.В.Грачёв, В.А. Погожев и др.). Учебник рассматривает разделы «Механические явления», «Электромагнитные явления», «Оптические явления» и «Квантовые явления». В учебник включены материалы для учащихся, интересующихся физикой, задания для внеклассной работы.
А сейчас ответим на вопрос, заданный в начале статьи, о том, что общего между богатырями с картины Васнецова и вторым законом Ньютона.
Представьте: ратное поле и три красавца коня ноздря в ноздрю бьют копытом землю. Как думаете, чья силушка богатырская будет больше, если кони сорвутся в бой с одинаковым ускорением? Конечно у того богатыря, чья масса больше.
А вот и ответ. Картина Васнецова напоминает простое мнемоническое правило для лучшего запоминания второго закона Ньютона: сила богатыря равна богатырской массе умноженной на богатырское ускорение.
Что ещё почитать?
#ADVERTISING_INSERT#Законы Нью́тона — законы классической механики, позволяющие записать уравнения движения для любой механической системы. Первый закон Ньютона
По сути, этот закон постулирует инерцию тел, что сегодня кажется очевидным. Но это было далеко не так на заре исследования природы. Аристотель вот утверждал, что причиной всякого движения является сила, т. е. движения по инерции для него не существовало. [источник?] Второй закон НьютонаВторой закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и её ускорением. Второй закон Ньютона утверждает, что
При подходящем выборе единиц измерения этот закон можно записать в виде формулы: где — ускорение тела; — сила, приложенная к телу; m — масса тела. Или в более известном виде: Если на тело действуют несколько сил, то второй закон Ньютона записывается: или где — импульс тела. В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется в общем виде: скорость изменения импульса точки равна действующей на неё силе. где — импульс (количество движения) точки; t — время; — производная по времени. Второй закон Ньютона действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта. Нельзя рассматривать частный случай (при) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО. Третий закон НьютонаЭтот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой, а второе — на первое с силой. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются. Сам закон:
ВыводыИз законов Ньютона сразу же следуют некоторые интересные выводы. Так, третий закон Ньютона говорит, что, как бы тела ни взаимодействовали, они не могут изменить свой суммарный импульс: возникает закон сохранения импульса. Далее, надо потребовать, чтобы потенциал взаимодействия двух тел зависел только от модуля разности координат этих тел U( | r1 − r2 | ). Тогда возникает закон сохранения суммарной механической энергии взаимодействующих тел: Важно Законы Ньютона являются основными законами механики. Из них могут быть выведены все остальные законы механики. Источник: http://fizika.my1.ru/index/0-28 Законы НьютонаЗаконы Ньютона являются основополагающими в классической механике и однозначно, поворотным моментом в физике. Это своего рода объединение накопленных к тому времени знаний о физических телах и их движении в законы. Закон Ньютона первый выдвигает в качестве исходного положения инерцию тела. Именно в связи с этим данный закон иногда трактуют как Закон Инерции. Что же подразумевает данная сила. Под инерцией понимается, сохранение скорости движения тела, при условии что на тело не воздействуют силы. Для изменения скорости движения тел, нужно воздействие на него силой. Действие одной и той же силы на разные тела будет различное, из чего следует что различное тело имеет свою инертность. А значит инертность тела – это сопротивление тела к изменениям их прежнего состояния. Значение инертности зависит от массы тела. Определение первого закона Ньютона в наши дни:
Определение второго закона Ньютона с наши дни: Закон Ньютона формула а = F /m в которой а ? – приходиться ускорением; F ? – постоянная всех сил; m -приходиться массой. Для ИСО изменение скорости импульсов тела равняется постоянной от всех сил. в которой p – приходится импульсом, t – время. Третий закон Ньютона дает описание взаимодействия двух материальных точек. Рассмотрим две точки находящиеся в замкнутой системе. Одна из которых воздействует на другую с силой F ?1?2, а другая в обратную с силой F ?2?1. Из чего следует, сила действия равна силе противодействия. Добавление: При воздействии на одно тело несколькими силами, данный закон записывается как: либо Для второго закона Ньютона, существует только для передвижения тел, меньшей чем скорость света. Определение второго закона Ньютона с наши дни: Третий закон дает понять, силы возникают только парно, при этом появление каждой из них будет благодаря другой. Другими словами. Появление сил самостоятельно, не имеющих взаимодействия с другими телами, не является возможным. Первой публикацией (более приближен к первому закону) был Галилей, который говорил о свободном продвижении и по линии и по кругу (астрономия). Тем самым положив начало всем законам Ньютона. Заметка: Любите фотографировать, но на качественное и дорогое оборудование не хватает денег? Это не беда! Ведь есть аренда объективов (http://zoom-prokat.ru/) и не только. Перейдя по ссылке Вы найдете все что вам нужно. Источник: http://reshit.ru/Zakony-Nyutona Оценка статьи: Загрузка…Поделиться с друзьями: Законы ньютона для чайников: первый, второй, третий закон кратко с объяснением, формулами Ссылка на основную публикацию |
2.2. Динамика. Законы Ньютона. Механика. Физика. Курс лекций
2.2.1. Динамические характеристики поступательного движения. Сила. Масса. Импульс
2.2.2. Виды сил
2.2.3. Первый закон Ньютона
2.2.4. Второй закон Ньютона
2.2.5. Третий закон Ньютона
2.2.6. Закон сохранения импульса
2.2.7. Динамические характеристики вращательного движения
2.2.8. Основное уравнение динамики вращательного движения
2.2.9. Закон сохранения момента импульса
2.2.1. Динамические характеристики поступательного движения. Сила. Масса. Импульс
До сих пор мы рассматривали перемещение тел в зависимости от времени без выяснения причин, вызывающих эти перемещения. Законы динамики устанавливают связь между движением тел и причинами, которые вызвали или изменили то или иное движение.
Рассмотрим поступательное движение материальной точки, для этого введем динамические характеристики, с помощью которых будем описывать такое движение. К таким характеристикам относятся понятие силы, массы, импульса. Начнем рассмотрение с движений тел в системах отсчета, которые называются инерциальными, и определение которых будет дано позднее.
1. Движение любого тела в инерциальной системе отсчета вызывается или изменяется только при взаимодействии с другими телами. Для описания взаимодействия между телами вводится понятие силы, которая дает количественную меру этого взаимодействия.
Физическая природа взаимодействия может быть различной, существуют гравитационные, электрические, магнитные и другие взаимодействия (см. Таблицу 1). В механике физическая природа сил несущественна, вопрос об их происхождении не выясняется. Но для всех видов взаимодействий их количественная мера должна быть выбрана единым образом. Измерять силы различной природы надо с помощью одних и тех же эталонов и единиц измерений. Законы механики универсальны, т.е. они описывают движение тел под действием силы любой природы. Для взаимодействий, которые рассматриваются в механике, сила может быть определена следующим образом.
Силой называется векторная величина F, являющаяся мерой механического воздействия одного тела на другое.
Механическое взаимодействие может осуществляться как между непосредственно контактирующими телами (сила трения, сила реакции опоры и т.д.), так и между удаленными телами.
Особая форма материи, связывающая частицы вещества в единые системы и передающая с конечной скоростью действие одних частиц на другие, называется физическим полем, или просто полем.
Взаимодействия между удаленными телами осуществляется посредством гравитационных (сила тяжести) или электромагнитных полей.
Механическое действие силы может вызвать ускорение тела или его деформацию. Сила – результат взаимодействия двух тел. Для правильного определения сил, действующих на тело, можно воспользоваться литературой [7,9], где приведены многочисленные примеры.
Сила F – вектор – полностью определена, если заданы ее модуль (величина), направление в пространстве и точка приложения. Прямая, вдоль которой направлен вектор F, называется линией действия силы.
Если говорить о силе, приложенной не к материальной точке, а к твердому телу и вызывающей его поступательное движение, то воздействие на тело не изменится при переносе точки действия силы вдоль линии ее действия.
Одновременное действие на материальную точку С нескольких сил F1,F2….. Fn эквивалентно действию одной силы, равной их геометрической (векторной) сумме и называемой результирующей или равнодействующей силой (см. Рисунок 7):
Fрез. = F1 +F2 + ….. +Fn.
Рисунок 7 – Векторное сложение сил.
Силы, действующие на тело или систему тел, можно разделить на внешние и внутренние. Тела, не входящие в состав исследуемой механической системы, называются внешними и силы, действующие с их стороны, – внешние. Внутренние силы – силы, действующие на точку или тело со стороны точек или тел, входящих в рассматриваемую систему.
Система, на которую не действуют внешние силы, называется изолированной или замкнутой.
2. Основополагающим понятием в динамике является понятие массы m, о котором в кинематике даже не упоминалось, не было необходимости. Любой материальный объект (тела, элементарные частицы, поля) обладает массой. Масса выступает как многосторонняя характеристика тела.
Она определяет его гравитационные свойства, т.е. силы, с которыми тело притягивается к другим телам, в частности, к Земле.
Масса характеризует инерционные свойства тела, т.е. способность тела сохранить состояние покоя или равномерного прямолинейного движения, или изменить скорость.
Масса тела m определяет количество вещества в данном теле и равна произведению плотности вещества ρ на объем V тела:
m = ρ∙V.
Масса тела вместе с его скоростью определяет импульс и кинетическую энергию тела.
В классической механике для понятия массы характерно следующее:
- m = const, она не зависит от состояния движения тела,
- масса – величина аддитивная, т.е. масса системы равна арифметической сумме масс тел, входящих в систему,
- масса замкнутой системы остается неизменной при любых процессах, происходящих внутри системы (закон сохранения массы).
Итак, для массы можно дать следующее определение.
Масса – мера инертности тела или мера гравитационного взаимодействия.
3. Импульсом материальной точки называется векторная величина, равная произведению ее массы на ее скорость P = mv.
Импульсом системы материальных точек называется вектор, равный геометрической (векторной) сумме импульсов всех материальных точек системы:
P = P1 + P2 +…..+ Pn = Pi
Используя понятие массы, импульс системы равен произведению массы всей системы на скорость ее центра масс P = mvц.
Импульс P – вектор, по направлению совпадающий с направлением скорости.
Импульс – одна из фундаментальных характеристик физической системы. И масса, и скорость были определены ранее, но только импульс обладает уникальным свойством. Для него сформулирован закон сохранения импульса, который является универсальным законом. Он выполняется и в микромире (на уровне элементарных частиц, атомов и молекул), и в макромире (мир вокруг нас), и в мегамире (на уровне планет, Вселенной, Галактики). До сих пор не открыто явлений, в которых бы нарушался закон сохранения импульса.
2.2.2. Виды сил
1. В настоящее время понятия основных взаимодействий, известных в природе, связано с понятием основных полей. Понятие физического поля мы определили ранее. Вообще понятие поля более широкое. Всякую физическую величину, плавно изменяющуюся в пространстве и однозначно определенную во всех его точках, можно рассматривать как поле. Поля бывают векторные и скалярные. Примерами скалярных полей является поле температур вблизи нагретой пластины или поле давлений около поверхности Земли. Примерами векторных полей является электрические и магнитные поля, гравитационное поле Земли и т.д. В Таблице 1 приведены характеристики различных взаимодействий, известных к настоящему времени в природе. Соответственно название физических полей совпадает с названием взаимодействий.
Таблица 1 (данные взяты из [1], том 3, стр263).| Взаимодействие/ Поле | Радиус взаимодействия | Const взаимодействия | Время взаимодействия |
| Гравитационное | ¥ | 10 –39 | – |
| Электромагнитное | ¥ | ≈10 -2 | 10-16 -10-20 с |
| Ядерное (сильное) | 10 –15 м | 10 | 10-23 с |
| Слабое (распадное) | 10 –15 м | 10 –14 | 10 -9 с |
Интенсивность взаимодействия принято характеризовать с помощью безразмерной величины, пропорциональной вероятности процессов, обусловленных данным видом взаимодействия. Гравитационное взаимодействие является универсальным, ему подвержены все без исключения элементарные частицы, но оно обладает предельно малой интенсивностью. Понятие времени взаимодействия является весьма условным. Эмпирически его можно ввести как минимальное время жизни частиц, подверженных распадам за счет данного взаимодействия. Прочерк в соответствующей графе для гравитационного взаимодействия стоит потому, что предполагаемый переносчик гравитационного взаимодействия – гравитон – экспериментально пока не обнаружен.
2. Силы в механике. Наиболее фундаментальные силы, лежащие в основе всех механических явлений, это силы гравитационные и электрические. Сила тяжести относится к гравитационному взаимодействию, сила трения и силы упругости – к электромагнитному взаимодействию.
Сила тяжести F = mg , где m – масса тела, g – ускорение силы тяжести. Заметим, что вес тела P – это сила, с которой тело действует на опору или подвес P = m (g – a), где a – ускорение тела (и опоры) относительно Земли. Если а = g, то вес тела равен нулю Р = 0 (состояние невесомости).
Упругая сила – сила, пропорциональная смещению точки из положения равновесия и направленная к положению равновесия. Примером такой силы может быть сила упругой деформации при растяжении (сжатии) пружины или стержня. В соответствии с законом Гука эта сила определяется так:
Fупр. = – k∙∆l, где k – коэффициент жесткости пружины (стержня), ∆l – величина упругой деформации. Знак минус означает, что противоположны направления смещения точки и силы упругости, возникающей при этом смещении и действующей на смещенную точку.
Величина силы трения скольжения, возникающая при скольжении одного тела по поверхности другого, равна Fтр. = μN, где μ – коэффициент трения, зависящий от соприкасающихся поверхностей, N – сила реакции опоры.
Сила трения направлена в сторону противоположную направлению движения данного тела относительно другого. Есть другие виды сил трения – силы трения покоя и сила трения качения.
Сила сопротивления, действующая на тело при его поступательном движении в газе или жидкости определяется зависимостью Fсопр. = αv, где v – скорость тела относительно среды, α – положительный коэффициент, характерный для данного тела и данной среды, при малых скоростях практически постоянен. Сила сопротивления всегда направлена противоположно вектору скорости тела.
Выталкивающая сила Архимеда равна весу вытесненной жидкости или газа: FАрх. = gρсрV, где ρср. – плотность среды, V – объем тела, g – ускорение свободного падения.
2.2.3. Первый закон Ньютона
Законы Ньютона представляют собой обобщение опытных данных (фактов). Эти законы устанавливались на основании наблюдений медленных по сравнению со скоростью света в вакууме движений.
1-й закон Ньютона
Всякая материальная точка или тело сохраняет состояние покоя или равномерного прямолинейного движения, пока на них не действуют силы или действие сил скомпенсировано.
Этот закон называется законом инерции, а движение точки или тела, свободных от внешних воздействий, называется движением по инерции.
Покой – частный случай равномерного прямолинейного движения, когда а = 0 и v = const, или v = 0.
Любое механическое движение – относительное движение, его характер зависит от системы отсчета. Закон инерции справедлив не во всех системах отсчета.
Системы, в которых выполняется первый закон Ньютона, называются инерциальными.
Системы, в которых не выполняется первый закон Ньютона, называются неинерциальными.
Инерциальных систем бесконечно много. Любая система, движущаяся относительно данной инерциальной системы равномерно и прямолинейно, является также инерциальной системой.
2.2.4. Второй закон Ньютона
Первый закон Ньютона говорит о состоянии тел, если на них не действуют силы. Каким будет движение, если на точку или тело действуют силы? Ответ на этот вопрос дает второй закон Ньютона, он связывает три величины – силу, массу и ускорение.
Второй закон Ньютона
Произведение массы материальной точки (тела) на ее ускорение равно действующей на нее силе F = ma.
Если на тело действует несколько сил, то в формулировке 2-ого закона используется равнодействующая сила (см. Рисунок 7)
Fрез = ma.
Это является следствием независимости действия сил на тело (точку) или говорят, что силы подчиняются принципу суперпозиции. Такое утверждение надо рассматривать как обобщение опытных фактов.
Так как в классической механике а = dv/dt и m = const, то второй закон можно переписать в виде:
И еще один вид уравнения 2-ого закона:
F∙dt = dP
Величина F∙dt называется вектором импульса силы, а величина dP – вектор изменение импульса тела под действием данной силы.
Основное уравнение динамики (второй закон Ньютона в векторном виде) можно записать в проекциях на касательное направление и нормаль к траектории в данной точке, используя полученные ранее выражения для нормального и тангенциального ускорений (§2.1.4):
,
.
Если тело (или точка) вращается по окружности, то можно записать уравнение для силы, действующей по касательной к траектории , и для силы, действующей по радиусу окружности (Рисунок 8) .
Рисунок 8 – Разложение вектора F на составляющие Fτ и Fn, R – радиус окружности, по которой вращается тело (или точка).
2.2.5. Третий закон Ньютона
В первом и во втором законах Ньютона речь идет о силах, действующих на данное тело, и его движении под действием этих сил, но нет упоминания о других телах, со стороны которых эти силы действуют. Роль второго тела во взаимодействии отражена в третьем законе Ньютона.
3-й закон Ньютона
Силы, с которыми два тела действуют друг на друга, равны по величине, направлены в противоположные стороны F12 = – F21.
F12 – сила, действующая со стороны второго тела на первое, приложена к первому телу, F21 – сила, действующая на второе тело со стороны первого, приложена ко второму телу (Рисунок 9).
Рисунок 9 – Взаимодействие двух тел.
2.2.6. Закон сохранения импульса
1. Совокупность тел, частиц (например, в газе) или отдельное твердое можно рассматривать как систему материальных точек. Если система с течением времени изменяется, то это означает, что изменяется ее состояние. Зная законы действующих на частицы системы сил и состояние системы в начальный момент времени, можно с помощью уравнений движения рассчитать состояние системы в любой момент времени. Но в некоторых случаях это может быть задачей достаточно сложной (сложна сама система или неизвестны законы действующих сил, или детальное рассмотрение поведения отдельных частиц системы не имеет смысла, например, в газе).
Возникает вопрос: нет ли каких-либо общих принципов, которые позволили бы иначе подойти к решению задач и обойти возникшие трудности? Оказалось, такие принципы есть. Это законы сохранения энергии, импульса и момента импульса (см. [7], стр. 52-57).
Эти законы справедливы не только в рамках классической механики. Все они являются универсальными законами природы, выполняются и в макромире, и в микромире, и во всей Вселенной. В настоящее время неизвестно ни одного эксперимента и ни одного физического явления, в котором упомянутые универсальные законы сохранения нарушались бы.
Закон сохранения импульса выполняется для замкнутых систем (см. 2.2.1. Динамические характеристики поступательного движения. Сила. Масса. Импульс, п.1).
2. Справедливость закона сохранения импульса можно показать для замкнутой системы, состоящей из двух тел, применяя второй и третий законы Ньютона. Пусть первое тело, имеющее массу m1, движется со скоростью , второе тело, масса которого m2, движется со скоростью 2.
При столкновении тела взаимодействуют друг с другом, и, согласно Третьему закону Ньютона, сила 12 = – 21. По второму закону Ньютона сила F12, действующая на первое тело, изменит импульс первого тела, можно записать 12= , Точно так же можно записать, что сила F21 изменит импульс второго тела: 21= . Подставим значения F12 и F21 в третий закон Ньютона: = – , Т.к. время взаимодействия – одно и то же, то: = – или + = .
Рассматриваемая нами замкнутая система состояла из двух тел, полный вектор импульса этой системы = + ,
+ = – это изменение вектора полного импульса. При взаимодействии двух тел получили, что изменение вектора полного импульса = 0, следовательно, полный вектор импульса системы при взаимодействии не изменился: если = 0, то P = const.
Если система состоит из N тел, то P = m1∙ v1 + m2∙ v2 + ……..+ mN∙ v N есть полный вектор импульса замкнутой системы, и P = const.
Закон сохранения импульса (ЗСИ).
Полный вектор импульса замкнутой системы есть величина постоянная при любых взаимодействиях внутри данной системы. Только внешние силы изменяют импульс системы.
3. Если векторная сумма внешних сил не равна нулю, то надо посмотреть, нет ли такого направления, вдоль которого внешние силы не действуют или сумма их проекций на это направление равна нулю. Если такое направление в движении тел, входящих в систему, есть, то можно применять закон сохранения для проекции полного вектора импульса системы на выделенное направление.
2.2.7. Динамические характеристики вращательного движения. Момент силы. Момент импульса
При поступательном движении системы все ее точки проходят одинаковые пути, имеют в данный момент времени одинаковые скорости и ускорения. При вращательном движения твердого тела все эти характеристики различны для разных точек вращающегося тела, поэтому и математическая форма 2-го закона Ньютона будет иной. При вращательном движении существенно изменяются сами понятия причины, вызывающей вращение, и величины, определяющей инертность тела.
При поступательном движении динамическими характеристиками являются сила, масса, импульс. При вращательном движении динамическими характеристиками являются момент силы, момент инерции, момент импульса. Эти характеристики можно рассматривать относительно точки вращения (полюса) и относительно оси вращения. В дальнейшем будем рассматривать эти характеристики относительно оси вращения. Определим эти характеристики.
1. Момент силы, действующей на материальную точку, относительно оси вращения
а) Пусть материальная точка массы m вращается относительно оси ОО ΄. Обозначим r – радиус-вектор, проведенный от оси вращения до точки приложения силы F (Рисунок 10).
Рисунок 10. Вращение материальной точки
Моментом силы F относительно оси вращения называется вектор M, равный векторному произведению радиус-вектора на вектор силы M = [ r∙ F] и направленный по оси вращения в сторону, определяемую по правилу правого буравчика Модуль вектора момента силы равен M = F∙r∙sinα, где α – угол между векторами rи F.
2. Момент импульса
Моментом импульса материальной точки относительно оси вращения называется вектор L, равный векторному произведению радиуса-вектора r на вектор импульса P: L = [ r∙P] = [ r∙ mv], где m, v – соответственно масса и вектор скорости точки. Направление Lопределяется по правилу правого буравчика. Модуль вектора L = mv∙ r∙ sinα, где α – угол между векторами r и v.
3. Момент инерции материальной точки относительно оси вращения
Моментом инерции материальной точки относительно оси вращения называется физическая величина, численно равная произведению массы точки на квадрат расстояния точки до оси вращения (Рисунок 10).
I = mr2
Момент инерции – величина скалярная.
Моментом инерции механической системы относительно неподвижной оси называется физическая величина, равная сумме произведений масс всех точек системы на квадраты их расстояний до оси вращения.
I = mi∙ ri2
Для твердого тела, разбитого на элементарные массы ∆ mi, момент инерции относительно оси равен I = ∆ mi∙ ri2.
Моменты инерции тел правильной геометрической формы могут быть легко вычислены. В Таблице 2 приведены результаты расчетов моментов инерции для тел правильной формы относительно оси вращения ОО’, проходящей через их центр масс.
Для расчета моментов инерции вращающихся тел вокруг оси, не проходящей через центр масс тела, можно использовать теорему Штейнера.
4. Теорема Штейнера
Момент инерции тела относительно произвольной оси АА’ равен сумме момента инерции тела относительно оси ОО’, проходящей через центр масс тела и параллельной данной оси АА’, и произведения массы тела как целого на квадрат расстояния d между осями АА’ и ОО’ (Рисунок 11).
IАА’ = IОО’ + md2
Рисунок 11.
Пример. Применение теоремы Штейнера для расчета момента инерции стержня длины l и массы m (см. Таблицу 2), если ось вращения проходит не через центр масс, а через конец стержня, приводит к следующему:
IАА’ = IОО’ + md2 = .
Рисунок 12. Вращение стержня вокруг оси
2.2.8. Основное уравнение динамики вращательного движения
1. В разделе “Кинематика” при рассмотрении поступательного и вращательного движений мы показали, что кинематические уравнения обоих движений имеют одинаковый вид, но при поступательном движении мы используем линейные характеристики (путь, скорость, ускорение), а при вращательном – угловые характеристики (угловое перемещение, угловую скорость, угловое ускорение). Используем эту аналогию и в динамике. При поступательном движении уравнение второго закона Ньютона имеет вид dP/dt = F.
Для вращательного движения: dL/dt = M.
Это уравнение называется уравнением моментов или основным законом вращательного движения. Вид уравнения не изменится и для системы материальных точек и для вращения твердого тела, только L определяется как момент импульса для системы точек.
2. Еще один вид уравнения второго закона Ньютона для вращательного движения имеет вид:
M∙ dt = dL,
где величина M∙ dt называется импульс момента сил, а dL – изменение момента импульса системы.
2.2.9. Закон сохранения момента импульса
Обратимся к уравнению моментов dL/ dt = M, где M – главный вектор момента внешних сил.
Если M = 0, то и L = const.
Если относительно некоторой точки О выбранной системы отсчета момент всех сил, действующих на систему материальных точек, равен нулю, то относительно этой точки вектор момента импульса системы не изменяется с течением времени (закон сохранения момента импульса относительно полюса).
Примеры.
а) Человек стоит на скамье Жуковского, представляющей массивный, диск, который может вращаться вокруг оси, проходящей через его центр, с пренебрежимо малым трением. Момент импульса системы “человек – диск” равен нулю. Человек начинает идти вдоль обода диска. Диск начинает вращаться в обратную ходу человека сторону.
б) Фигурист выполняет “волчок”, его руки раскинуты в стороны, его момент инерции относительно вертикальной оси вращения I1, угловая скорость ω1. Затем он резко прижимает руки к груди, его момент инерции уменьшается и становится I2, а угловая скорость ω2 увеличивается. При этом выполняется закон сохранения момента импульса относительно вертикальной неподвижной оси, проходящей через линию симметрии тела фигуриста I1∙ ω1 = I2∙ω2.
Веб-сайт класса физики
Законы движения Ньютона: обзор набора задач
Этот набор из 30 задач нацелен на вашу способность различать массу и вес, определять чистую силу по значениям отдельных сил, связывать ускорение с чистой силой и массой, анализировать физические ситуации, чтобы нарисовать диаграмму свободного тела и решить неизвестная величина (ускорение или значение индивидуальной силы) и объединить анализ второго закона Ньютона с кинематикой для определения неизвестной величины (кинематической величины или значения силы).Проблемы варьируются по сложности от очень простых и простых до очень сложных и сложных. Более сложные задачи обозначены цветом , синие задачи .
Масса против веса
Этот набор из 30 задач нацелен на вашу способность различать массу и вес, определять чистую силу по значениям отдельных сил, связывать ускорение с чистой силой и массой, анализировать физические ситуации, чтобы нарисовать диаграмму свободного тела и решить неизвестная величина (ускорение или индивидуальное значение силы), масса – это величина, которая зависит от количества вещества, присутствующего в объекте; обычно выражается в килограммах.Масса материи, которой обладает объект, не зависит от его местоположения во Вселенной. С другой стороны, вес – это сила тяжести, с которой Земля притягивает к себе объект. Поскольку гравитационные силы меняются в зависимости от местоположения, вес объекта на поверхности Земли отличается от его веса на Луне. Вес, как сила, чаще всего выражается в метрических единицах измерения в ньютонах. Каждое место во Вселенной характеризуется постоянной гравитационного поля, представленной символом g (иногда называемое ускорением свободного падения).Вес (или F grav ) и масса ( м ) связаны уравнением:
F грав = m • g
Второй закон движения Ньютона
Второй закон движения Ньютона гласит, что ускорение ( a ), испытываемое объектом, прямо пропорционально чистой силе ( F net ), испытываемой объектом, и обратно пропорционально массе объекта.В форме уравнения можно сказать, что a = F net / m . Чистая сила – это векторная сумма всех индивидуальных значений силы. Если величина и направление отдельных сил известны, то эти силы могут быть добавлены как векторы для определения результирующей силы. Следует обратить внимание на векторную природу силы. Направление важно. Поднимающую силу и прижимающую силу можно добавить, присвоив прижимной силе отрицательное значение, а восходящей силе положительное значение. Аналогичным образом, сила, направленная вправо, и сила, направленная влево, могут быть добавлены путем присвоения левой силе отрицательного значения и правой силы положительного значения.
Уравнение a = F net / m можно использовать как формулу для решения проблем и как руководство к размышлениям. При использовании уравнения в качестве формулы для решения проблемы важно, чтобы числовые значения двух из трех переменных в уравнении были известны, чтобы найти неизвестную величину. При использовании уравнения в качестве руководства к размышлениям необходимо учитывать прямые и обратные отношения между ускорением и чистой силой и массой. Двукратное или трёхкратное увеличение чистой силы вызовет такое же изменение ускорения, удвоение или утроение его значения.Увеличение массы в два или три раза вызовет обратное изменение ускорения, уменьшив его значение в два или три раза.
Диаграммы свободного тела
Диаграммы свободного тела представляют силы, которые действуют на объект в данный момент времени. Отдельные силы, действующие на объект, представлены векторными стрелками. Направление стрелок указывает направление силы, а приблизительная длина стрелки представляет относительную величину силы.Силы обозначены в соответствии с их типом. Схема свободного тела может оказаться полезным подспорьем в процессе решения проблем. Он обеспечивает визуальное представление сил, действующих на объект. Если величины всех отдельных сил известны, диаграмму можно использовать для определения чистой силы. И если ускорение и масса известны, то можно рассчитать чистую силу, и диаграмму можно использовать для определения значения единственной неизвестной силы.
Коэффициент трения
Объект, который движется (или событие, пытающееся двигаться) по поверхности, встречает силу трения.Сила трения возникает из-за того, что две поверхности плотно прижаты друг к другу, вызывая межмолекулярные силы притяжения между молекулами разных поверхностей. Таким образом, трение зависит от природы двух поверхностей и от степени их прижатия друг к другу. Силу трения можно рассчитать по формуле:
F frict = µ • F norm
Символ µ (произносится как «мью») представляет коэффициент трения и будет отличаться для разных поверхностей.
Смешение законов Ньютона и кинематических уравнений
Кинематика относится к описанию движения объекта и фокусируется на вопросах, как далеко?, Как быстро?, Сколько времени? а с каким ускорением? Чтобы помочь ответить на такие вопросы, в модуле «Одномерная кинематика» были представлены четыре кинематических уравнения. Четыре уравнения перечислены ниже.
- d = v o • t + 0.5 • а • т 2
- v f = v o + a • t
- v f 2 = v o 2 + 2 • a • d
- d = (v o + v f ) / 2 • t
где
- d = рабочий объем
- t = время
- a = ускорение
- v o = исходная или начальная скорость
- v f = конечная скорость
Законы Ньютона и кинематика разделяют один из этих общих вопросов: с каким ускорением? Ускорение (a) F net = m • a уравнение – это то же ускорение, что и в кинематических уравнениях.Таким образом, общие задачи включают:
- использование кинематической информации для определения ускорения, а затем использование ускорения в анализе законов Ньютона, или
- использование информации о силе и массе для определения значения ускорения, а затем использование ускорения в кинематическом анализе.
При анализе словесной проблемы физики целесообразно идентифицировать известные величины и систематизировать их либо как кинематические величины, либо как величины типа F-m-a.
Привычки эффективно решать проблемы
Эффективный решатель проблем по привычке подходит к физической проблеме таким образом, который отражает набор дисциплинированных привычек. Хотя не все эффективные специалисты по решению проблем используют один и тот же подход, все они имеют общие привычки. Эти привычки кратко описаны здесь. Эффективное решение проблем …
- …. внимательно читает задачу и создает мысленную картину физической ситуации. При необходимости они набрасывают простую схему физической ситуации, чтобы помочь визуализировать ее.
- … определяет известные и неизвестные величины в организованном порядке, часто записывая их на диаграмме. Они приравнивают заданные значения к символам, используемым для представления соответствующей величины (например, v o = 0 м / с, a = 2,67 м / с / с, v f = ???).
- …построит стратегию решения неизвестной величины; стратегия, как правило, сосредоточена вокруг использования физических уравнений и во многом зависит от понимания физических принципов.
- … определяет подходящую (ые) формулу (ы) для использования, часто записывая их. При необходимости они выполняют необходимое преобразование количеств в правильные единицы.
- … выполняет подстановки и алгебраические манипуляции, чтобы найти неизвестную величину.
Подробнее …
Дополнительная литература / Учебные пособия:
Следующие страницы из учебного пособия по физике могут быть полезны для понимания концепций и математики, связанных с этими проблемами.
Набор задач о законах движения Ньютона
Просмотреть набор задач
Законы Ньютона о движении Решения с аудиосистемой
Ознакомьтесь с аудиогидом решения проблемы:1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30
Второй закон движения Ньютона: концепция системы
Цели обучения
К концу этого раздела вы сможете:
- Определите чистую силу, внешнюю силу и систему.
- Поймите второй закон движения Ньютона.
- Примените второй закон Ньютона для определения веса объекта.
Второй закон движения Ньютона тесно связан с первым законом движения Ньютона. Он математически устанавливает причинно-следственную связь между силой и изменениями в движении. Второй закон движения Ньютона является более количественным и широко используется для расчета того, что происходит в ситуациях, связанных с действием силы. Прежде чем мы сможем записать второй закон Ньютона в виде простого уравнения, дающего точное соотношение силы, массы и ускорения, нам необходимо отточить некоторые идеи, которые уже упоминались.
Во-первых, что мы подразумеваем под изменением движения? Ответ заключается в том, что изменение движения эквивалентно изменению скорости. Изменение скорости по определению означает наличие ускорения . Первый закон Ньютона гласит, что чистая внешняя сила вызывает изменение движения; таким образом, мы видим, что чистая внешняя сила вызывает ускорение .
Сразу возникает еще один вопрос. Что мы подразумеваем под внешней силой? Интуитивное представление о внешнем является правильным – внешняя сила действует извне из интересующей системы .Например, на рис. 1 (а) интересующей системой является вагон плюс ребенок в нем. Две силы, действующие со стороны других детей, – это внешние силы. Между элементами системы действует внутренняя сила. Снова посмотрев на рисунок 1 (а), сила, которую ребенок в повозке прикладывает, чтобы повиснуть на повозке, представляет собой внутреннюю силу между элементами интересующей системы. Согласно первому закону Ньютона, только внешние силы влияют на движение системы. (Внутренние силы фактически отменяются, как мы увидим в следующем разделе.) Вы должны определить границы системы, прежде чем сможете определить, какие силы являются внешними . Иногда система очевидна, тогда как в других случаях определение границ системы более тонкое. Концепция системы является фундаментальной для многих областей физики, как и правильное применение законов Ньютона. Эта концепция будет неоднократно пересматриваться в нашем путешествии по физике.
Рис. 1. Различные силы, действующие на одну и ту же массу, вызывают разное ускорение.а) Двое детей толкают тележку с ребенком в ней. Показаны стрелки, представляющие все внешние силы. Интересующая система – это повозка и ее водитель. Вес w системы и опора земли N также показаны для полноты и, как предполагается, компенсируются. Вектор f представляет трение, действующее на вагон, и действует влево, противодействуя движению вагона. (b) Все внешние силы, действующие на систему, в сумме образуют чистую силу, F net .На диаграмме свободного тела показаны все силы, действующие на интересующую систему. Точка представляет собой центр масс системы. Каждый вектор силы простирается от этой точки. Поскольку справа действуют две силы, мы рисуем векторы коллинеарно. (c) Большая чистая внешняя сила вызывает большее ускорение ( a ‘> a ), когда взрослый толкает ребенка.
Теперь кажется разумным, что ускорение должно быть прямо пропорционально и в том же направлении, что и чистая (полная) внешняя сила, действующая на систему.Это предположение было проверено экспериментально и показано на рисунке 1. В части (а) меньшая сила вызывает меньшее ускорение, чем большая сила, показанная в части (с). Для полноты картины также показаны вертикальные силы; предполагается, что они отменяются, поскольку нет ускорения в вертикальном направлении. Вертикальные силы – это вес w и опора на землю N , а горизонтальная сила f представляет собой силу трения. Они будут обсуждаться более подробно в следующих разделах.На данный момент мы определим трение как силу, которая противодействует движению объектов, которые соприкасаются друг с другом. На рисунке 1 (b) показано, как векторы, представляющие внешние силы, складываются вместе, чтобы получить результирующую силу,
.F net .
Чтобы получить уравнение для второго закона Ньютона, сначала запишем соотношение ускорения и чистой внешней силы как пропорциональность
[латекс] \ text {a} \ propto {\ text {F} _ {net}} \\ [/ latex]
, где символ ∝ означает «пропорционально», а F net – это чистая внешняя сила .(Чистая внешняя сила представляет собой векторную сумму всех внешних сил и может быть определена графически, используя метод “голова к хвосту”, или аналитически, используя компоненты. Методы такие же, как и для сложения других векторов, и рассматриваются в двумерной кинематике.) Эта пропорциональность выражает то, что мы сказали словами: ускорение прямо пропорционально чистой внешней силе . После выбора интересующей системы важно определить внешние силы и игнорировать внутренние.Это огромное упрощение – не учитывать многочисленные внутренние силы, действующие между объектами внутри системы, такие как мышечные силы в теле ребенка, не говоря уже о мириадах сил между атомами в объектах, но, делая это, мы можем легко решить некоторые очень сложные проблемы с минимальной ошибкой благодаря нашему упрощению.
Теперь также кажется разумным, что ускорение должно быть обратно пропорционально массе системы. Другими словами, чем больше масса (инерция), тем меньше ускорение, создаваемое данной силой.И действительно, как показано на рисунке 2, та же самая чистая внешняя сила, приложенная к автомобилю, вызывает гораздо меньшее ускорение, чем при приложении к баскетбольному мячу. Пропорциональность записывается как
.[латекс] \ text {a} \ propto {\ frac {1} {m}} \\ [/ latex]
, где м – масса системы. Эксперименты показали, что ускорение прямо обратно пропорционально массе, точно так же, как оно прямо линейно пропорционально чистой внешней силе.
Рис. 2. Одна и та же сила, действующая на системы разной массы, вызывает разное ускорение.(a) Баскетболист толкает баскетбольный мяч, чтобы сделать передачу. (Влияние силы тяжести на мяч игнорируется.) (B) Тот же игрок оказывает идентичную силу на остановившийся внедорожник и производит гораздо меньшее ускорение (даже если трение незначительно). (c) Диаграммы свободного тела идентичны, что позволяет напрямую сравнить две ситуации. По мере того, как вы будете решать больше задач, появится серия паттернов для диаграммы свободного тела.
Было обнаружено, что ускорение объекта зависит только от чистой внешней силы и массы объекта.Объединение двух только что приведенных пропорциональностей дает второй закон движения Ньютона.
Второй закон движения Ньютона
Ускорение системы прямо пропорционально чистой внешней силе, действующей на систему, и в том же направлении, и обратно пропорционально ее массе. В форме уравнения второй закон движения Ньютона равен
.[латекс] {\ text {a}} = \ frac {{{\ text {F}}} _ {\ text {net}}} {m} \\ [/ latex].
Это часто записывается в более знакомой форме
F нетто = м a .
Если рассматривать только величину силы и ускорения, это уравнение просто
F net = ma.
Хотя эти последние два уравнения на самом деле одинаковы, первое дает больше понимания того, что означает второй закон Ньютона. Закон – причинно-следственная связь между тремя величинами, которая не просто основана на их определениях. Справедливость второго закона полностью основана на экспериментальной проверке.
F net = м a используется для определения единиц силы в терминах трех основных единиц массы, длины и времени. Единица силы в системе СИ называется ньютон (сокращенно Н) и представляет собой силу, необходимую для ускорения системы массой 1 кг со скоростью 1 м / с 2 . То есть, поскольку F net = м a ,
1 Н = 1 кг ⋅ м / с 2 .
В то время как почти весь мир использует ньютон в качестве единицы силы, в Соединенных Штатах наиболее известной единицей силы является фунт (фунт), где 1 N = 0.225 фунтов
Вес и сила тяжести
Когда объект падает, он ускоряется к центру Земли. Второй закон Ньютона гласит, что общая сила, действующая на объект, отвечает за его ускорение. Если сопротивление воздуха незначительно, результирующая сила, действующая на падающий объект, – это сила тяжести, обычно называемая его весом Вт. Вес можно обозначить как вектор w, потому что он имеет направление; вниз – это, по определению, направление силы тяжести, и, следовательно, вес – это сила, направленная вниз.Величина веса обозначается как w . Галилей показал, что при отсутствии сопротивления воздуха все объекты падают с одинаковым ускорением g . Используя результат Галилея и второй закон Ньютона, мы можем вывести уравнение для веса.
Рассмотрим объект массой м , падающий на Землю. Он испытывает только направленную вниз силу тяжести, величина которой составляет w . Второй закон Ньютона гласит, что величина чистой внешней силы, действующей на объект, составляет F net = ма .Поскольку объект испытывает только направленную вниз силу тяжести, F net = w . Мы знаем, что ускорение объекта под действием силы тяжести составляет g , или a = g . Подставляя их во второй закон Ньютона, получаем
МассаЭто уравнение для веса – силы тяжести, действующей на массу m:
w = мг
Так как g = 9,80 м / с 2 на Земле, вес 1.0 кг объекта на Земле составляет 9,8 Н, как мы видим:
w = мг = (1,0 кг) (9,80 м / с 2 ) = 9,8 Н.
Напомним, что g может принимать положительное или отрицательное значение в зависимости от положительного направления в системе координат. Обязательно учтите это при решении задач с весом.
Когда чистая внешняя сила, действующая на объект, равна его весу, мы говорим, что оно находится в пределах свободного падения . То есть единственная сила, действующая на объект, – это сила тяжести.В реальном мире, когда объекты падают вниз к Земле, они никогда не находятся в состоянии свободного падения, потому что на объект всегда действует некоторая восходящая сила из воздуха.
Ускорение свободного падения g незначительно меняется по поверхности Земли, поэтому вес объекта зависит от местоположения и не является внутренним свойством объекта. Вес резко меняется, если человек покидает поверхность Земли. На Луне, например, ускорение свободного падения всего 1.67 м / с 2 . Таким образом, масса в 1,0 кг имеет вес 9,8 Н на Земле и всего около 1,7 Н на Луне.
Самое широкое определение веса в этом смысле состоит в том, что вес объекта – это сила тяжести, действующая на него со стороны ближайшего большого тела , такого как Земля, Луна, Солнце и так далее. Это наиболее распространенное и полезное определение веса в физике. Однако оно кардинально отличается от определения веса, используемого НАСА и популярными СМИ в отношении космических путешествий и исследований.Когда они говорят о «невесомости» и «микрогравитации», они на самом деле имеют в виду явление, которое мы называем «свободным падением» в физике. Мы будем использовать приведенное выше определение веса и проведем тщательное различие между свободным падением и фактической невесомостью.
Важно знать, что вес и масса – очень разные физические величины, хотя они тесно связаны. Масса – это количество материи (сколько «вещества») и не изменяется в классической физике, тогда как вес – это сила тяжести, которая зависит от силы тяжести.Заманчиво приравнять эти два понятия, поскольку большинство наших примеров имеет место на Земле, где вес объекта лишь немного зависит от его местоположения. Кроме того, в повседневном языке термины масса и масса используются взаимозаменяемо; например, в наших медицинских записях наш «вес» часто указывается в килограммах, но никогда в правильных единицах – ньютонах.
Распространенные заблуждения: масса против весаВ повседневной речи масса и вес часто используются как синонимы.Однако в науке эти термины существенно отличаются друг от друга. Масса – это мера количества вещества в объекте. Типичной мерой массы является килограмм (или «пуля» в английских единицах измерения). С другой стороны, вес – это мера силы тяжести, действующей на объект. Вес равен массе объекта (м), умноженной на ускорение свободного падения (g). Как и любая другая сила, вес измеряется в ньютонах (или фунтах в английских единицах). Предполагая, что масса объекта остается неизменной, она остается неизменной независимо от его местоположения.Однако, поскольку вес зависит от ускорения свободного падения, вес объекта может измениться на , когда объект входит в область с более сильной или слабой гравитацией. Например, ускорение свободного падения на Луне составляет 1,67 м / с 2 (что намного меньше ускорения свободного падения на Земле, 9,80 м / с 2 ). Если вы измерили свой вес на Земле, а затем измерили свой вес на Луне, вы бы обнаружили, что «весите» намного меньше, хотя и не выглядите худее.Это потому, что сила тяжести на Луне слабее. Фактически, когда люди говорят, что они «худеют», они на самом деле имеют в виду, что они теряют «массу» (что, в свою очередь, заставляет их весить меньше).
Эксперимент на вынос: масса и вес
Что измеряют весы для ванной? Когда вы стоите на весах в ванной, что происходит с весами? Слегка угнетает. Весы содержат пружины, которые сжимаются пропорционально вашему весу – подобно резиновым лентам, расширяющимся при натяжении.Пружины позволяют измерить ваш вес (для объекта, который не ускоряется). Это сила в ньютонах (или фунтах). В большинстве стран результат делится на 9,80, чтобы получить значение в килограммах. Весы измеряют вес, но откалиброваны для предоставления информации о массе. Стоя на весах в ванной, нажмите на соседний стол. Что происходит с чтением? Почему? Будет ли ваша шкала измерять ту же «массу» на Земле, что и на Луне?
Пример 1.Какое ускорение может дать человек, толкая газонокосилку?
Предположим, что чистая внешняя сила (толчок минус трение), действующая на газонокосилку, составляет 51 Н (около 11 фунтов) параллельно земле. Масса косилки 24 кг. Какое у него ускорение?Рис. 3. Сила полезного действия на газонокосилку справа составляет 51 Н. С какой скоростью газонокосилка ускоряется вправо?
СтратегияПоскольку даны F net и m, ускорение можно рассчитать непосредственно из второго закона Ньютона, как указано в F net = m a .{2} \\ [/ латекс].
ОбсуждениеНаправление ускорения совпадает с направлением результирующей силы, параллельной земле. В этом примере нет информации об отдельных внешних силах, действующих на систему, но мы можем кое-что сказать об их относительных величинах. Например, сила, прикладываемая человеком, толкающим косилку, должна быть больше, чем трение, препятствующее движению (поскольку мы знаем, что косилка движется вперед), а вертикальные силы должны нейтрализоваться, если не должно быть ускорения в вертикальном направлении ( косилка движется только горизонтально).Обнаруженное ускорение достаточно мало, чтобы быть приемлемым для человека, толкающего косилку. Такое усилие не будет длиться слишком долго, потому что человек скоро достигнет максимальной скорости.
Пример 2. Какая ракетная тяга разгоняет салазки?
До пилотируемых космических полетов ракетные сани использовались для испытания самолетов, ракетного оборудования и физиологических воздействий на людей на высоких скоростях. Они состояли из платформы, которая была установлена на одной или двух направляющих и приводилась в движение несколькими ракетами.Вычислите величину силы, прилагаемой каждой ракетой, которая называется ее тягой T, для четырехракетной двигательной установки, показанной на рисунке 4. Начальное ускорение салазок составляет 49 м / с2, масса системы – 2100 кг, а сила трения. противодействие движению, как известно, составляет 650 Н.Рис. 4. Салазки испытывают ракетную тягу, которая ускоряет их вправо. Каждая ракета создает одинаковую тягу T. Как и в других ситуациях, когда есть только горизонтальное ускорение, вертикальные силы нейтрализуются.Земля оказывает на систему направленную вверх силу N, равную по величине и противоположную по направлению ее весу w. Система здесь – сани, его ракеты и всадник, поэтому никакие силы между этими объектами не учитываются. Стрелка, обозначающая трение (f), нарисована крупнее шкалы.
СтратегияНесмотря на то, что существуют силы, действующие вертикально и горизонтально, мы предполагаем, что вертикальные силы компенсируются, поскольку нет вертикального ускорения. Это оставляет нам только горизонтальные силы и более простую одномерную задачу.Направления указываются знаками плюс или минус, при этом вправо принимается за положительное направление. См. Диаграмму свободного тела на рисунке.
РешениеПоскольку ускорение, масса и сила трения даны, мы начнем со второго закона Ньютона и ищем способы найти тягу двигателей. Поскольку мы определили направление силы и ускорения как действующие «вправо», нам нужно учитывать в расчетах только величины этих величин.Следовательно, мы начинаем с
F net = ma,
, где F net – чистая сила в горизонтальном направлении. Из рисунка 4 видно, что тяга двигателя увеличивается, а трение противодействует тяги. В форме уравнения чистая внешняя сила равна
.Подставляя это во второй закон Ньютона, получаем
Используя небольшую алгебру, мы решаем общую тягу 4 T :
Подстановка известных значений дает
[латекс] 4T = \ text {ma} + f = \ left (\ text {2100 кг} \ right) \ left ({\ text {49 м / с}} ^ {2} \ right) + \ text { 650 Н} \ [/ латекс]
[латекс] 4Т = 1.{4} \ text {N} \\ [/ латекс].
ОбсуждениеЦифры довольно большие, поэтому результат может вас удивить. Подобные эксперименты проводились в начале 1960-х годов для проверки пределов человеческой выносливости и установки, предназначенной для защиты людей при аварийных выбросах реактивных истребителей. Была получена скорость 1000 км / ч с ускорением 45 g. (Напомним, что g, ускорение свободного падения, составляет 9,80 м / с 2 . Когда мы говорим, что ускорение составляет 45 g, это 45 × 9.80 м / с 2 , что составляет примерно 440 м / с 2 .) Хотя живые предметы больше не используются, с помощью ракетных саней была получена сухопутная скорость 10 000 км / ч. В этом примере, как и в предыдущем, интересующая система очевидна. В последующих примерах мы увидим, что выбор интересующей системы имеет решающее значение, и этот выбор не всегда очевиден.
Второй закон движения Ньютона – это больше, чем определение; это соотношение между ускорением, силой и массой.Это может помочь нам делать прогнозы. Каждую из этих физических величин можно определить независимо, поэтому второй закон говорит нам что-то основное и универсальное о природе. В следующем разделе представлен третий и последний закон движения.
Сводка раздела
- Ускорение, a , определяется как изменение скорости, то есть изменение ее величины или направления, или и того, и другого.
- Внешняя сила – это сила, действующая на систему извне, в отличие от внутренних сил, которые действуют между компонентами внутри системы.
- Второй закон движения Ньютона гласит, что ускорение системы прямо пропорционально и в том же направлении, что и чистая внешняя сила, действующая на систему, и обратно пропорционально ее массе.
- В форме уравнения второй закон движения Ньютона выглядит так: [latex] {\ text {a}} = \ frac {{{\ text {F}}} _ {\ text {net}}} {m} \\ [/ латекс].
- Это часто записывается в более привычной форме: F net = m a .
- Вес объекта w определяется как сила тяжести, действующая на объект массой м .Объект испытывает ускорение свободного падения g :
w = м г .
- Если единственная сила, действующая на объект, вызвана гравитацией, объект находится в свободном падении.
- Трение – это сила, которая препятствует движению соприкасающихся объектов друг за другом.
Концептуальные вопросы
1. Какое утверждение верно? (а) Чистая сила вызывает движение. (b) Чистая сила вызывает изменение движения. Объясните свой ответ и приведите пример.
2. Почему мы можем пренебрегать такими силами, как силы, удерживающие тело вместе, когда мы применяем второй закон движения Ньютона?
3. Объясните, как выбор «интересующей системы» влияет на то, какие силы необходимо учитывать при применении второго закона движения Ньютона.
4. Опишите ситуацию, в которой чистая внешняя сила, действующая на систему, не равна нулю, но ее скорость остается постоянной.
5. Система может иметь ненулевую скорость, в то время как чистая внешняя сила, действующая на нее , равна нулю.Опишите такую ситуацию.
6. Камень брошен вверх. Какая чистая внешняя сила действует на скалу, когда она находится на вершине своей траектории?
7. (a) Приведите пример различных чистых внешних сил, действующих на одну и ту же систему, вызывая разные ускорения. (b) Приведите пример одной и той же чистой внешней силы, действующей на системы разной массы, вызывая разные ускорения. (c) Какой закон точно описывает оба эффекта? Сформулируйте это словами и в виде уравнения.
8. Если ускорение системы равно нулю, не действуют ли на нее внешние силы? А как насчет внутренних сил? Объясни свои ответы.
9. Если к объекту приложена постоянная ненулевая сила, что вы можете сказать о скорости и ускорении объекта?
10. Сила тяжести, действующая на баскетбольный мяч на рисунке 2, игнорируется. Когда сила тяжести принимается во внимание , каково направление чистой внешней силы на баскетбольный мяч – выше горизонтали, ниже горизонтали или все еще горизонтально?
Задачи и упражнения
Вы можете предположить, что данные, взятые с иллюстраций, имеют точность до трех цифр.
1. Спринтер весом 63,0 кг начинает забег с ускорением 4,20 м / с. 2 . Какая чистая внешняя сила действует на него?
2. Если спринтер из предыдущей задачи разгоняется с такой скоростью на 20 м, а затем сохраняет эту скорость до конца 100-метрового рывка, сколько у него времени для забега?
3. Пылесос толкает тележку для белья весом 4,50 кг таким образом, чтобы чистая внешняя сила, действующая на нее, составляла 60,0 Н. Вычислите величину ее ускорения.
4. Поскольку астронавты на орбите явно невесомые, необходим умный метод измерения их массы, чтобы отслеживать прирост или потерю массы для корректировки диеты. Один из способов сделать это – приложить известную силу к космонавту и измерить возникающее ускорение. Предположим, что действует чистая внешняя сила 50,0 Н и измеренное ускорение астронавта составляет 0,893 м / с 2 . (а) Рассчитайте ее массу. (b) При приложении силы к космонавту, аппарат, в котором он движется по орбите, испытывает равную и противоположную силу.Обсудите, как это повлияет на измерение ускорения космонавта. Предложите метод, позволяющий избежать отдачи автомобиля.
5. На рис. 3 чистая внешняя сила на газонокосилке 24 кг заявлена равной 51 Н. Если сила трения, препятствующая движению, равна 24 Н, то какая сила F (в ньютонах) – это сила, действующая на человека. косилка? Предположим, косилка движется со скоростью 1,5 м / с при снятии усилия F . Как далеко уйдет косилка до остановки?
6.Те же ракетные салазки, изображенные на рисунке 5, замедляются со скоростью 196 м / с 2 . Какая сила необходима, чтобы вызвать это замедление? Предположим, что ракеты выключены. Масса системы 2100 кг.
Рисунок 5.
7. (a) Если салазки ракеты, показанные на рисунке 6, запускаются с горящей только одной ракетой, какова величина ее ускорения? Предположим, что масса системы составляет 2100 кг, тяга T составляет 2,4 × 10 4 Н, а сила трения, препятствующая движению, известна как 650 Н.б) Почему ускорение не в четыре раза меньше, чем у всех горящих ракет?
Рисунок 6.
8. Какое замедление у ракетных саней, если они останавливаются за 1,1 с со скорости 1000 км / ч? (Из-за такого замедления один испытуемый потерял сознание и временно потерял сознание.)
9. Предположим, двое детей толкаются горизонтально, но в противоположных направлениях, на третьего ребенка в повозке. Первый ребенок прикладывает силу 75,0 Н, второй – 90.{2} \\ [/ latex] при скорости 90,0 км / ч. На этой скорости силы, противодействующие движению, включая трение и сопротивление воздуха, составляют в сумме 400 Н. (Сопротивление воздуха аналогично трению воздуха. Оно всегда противодействует движению объекта.) Какова величина силы, которую мотоцикл оказывает на мотоцикл в обратном направлении. земля, чтобы произвести его ускорение, если масса мотоцикла с водителем составляет 245 кг?
11. Ракетные салазки, показанные на рисунке 8, ускоряются со скоростью 49,0 м / с. 2 . Его пассажирский вес 75.0 кг. (а) Рассчитайте горизонтальную составляющую силы, которую сиденье оказывает на его тело. Сравните это с его весом, используя соотношение. (b) Рассчитайте направление и величину общей силы, которую сиденье оказывает на его тело.
Рисунок 8.
12. Повторите предыдущую задачу для ситуации, когда салазки ракеты замедляются со скоростью 201 м / с. 2 . В этой задаче силы прилагаются к сиденью и удерживающим ремням.
13. Вес космонавта вместе с его скафандром на Луне составляет всего 250 Н.Сколько они весят на Земле? Какая масса на Луне? На земле?
14. Предположим, масса полностью загруженного модуля, в котором космонавты взлетают с Луны, составляет 10 000 кг. Тяга его двигателей составляет 30 000 Н. (а) Рассчитайте величину ускорения при вертикальном взлете с Луны. б) Может ли он взлететь с Земли? Если нет, то почему? Если бы это было возможно, вычислите величину его ускорения.
Глоссарий
- ускорение:
- скорость, с которой скорость объекта изменяется за период времени
- свободное падение:
- ситуация, в которой единственной силой, действующей на объект, является сила тяжести
- трение:
- – сила соприкасающихся объектов друг с другом; примеры включают шероховатую поверхность и сопротивление воздуха
- чистая внешняя сила:
- векторная сумма всех внешних сил, действующих на объект или систему; заставляет массу ускоряться
- Второй закон движения Ньютона:
- чистая внешняя сила F net на объект с массой m пропорциональна и в том же направлении, что и ускорение объекта, a , и обратно пропорциональна массе; математически определяется как [latex] \ mathbf {\ text {a}} = \ frac {{\ mathbf {\ text {F}}} _ {\ text {net}}} {m} \\ [/ latex]
- система
- определяется границами наблюдаемого объекта или набора объектов; все силы, возникающие извне системы, считаются внешними силами
- вес
- сила w за счет силы тяжести, действующей на объект массой [латекс] м [/ латекс]; математически определяется как: w = mg , где g – величина и направление ускорения свободного падения
Избранные решения проблем и упражнения
1.265 N
3. 13,3 м / с 2
7. (a) 12 м / с 2 (b) Ускорение не в четверть от того, что было при горящих ракетах, потому что сила трения все еще такая же большая, как при всех горящих ракетах.
9. (a) Система – это ребенок в вагоне плюс вагон.
Рисунок 9
(б)
(c) a = 0,130 м / с 2 в направлении толчка второго ребенка.
(г) a = 0,00 м / с 2
11.(а) 3,68 × 10 3 Н. Эта сила в 5,00 раз превышает его вес. (b) 3750 Н; 11,3º над горизонтом
13. 1,5 × 10 3 Н, 150 кг, 150 кг
Как использовать формулы законов Ньютона – Видео и стенограмма урока
Первый закон Ньютона
Первый закон Ньютона – это закон инерции. Он гласит, что любой объект в состоянии покоя или в движении будет оставаться в покое или в движении, если на него не действует другая сила. Другими словами, скорость объекта остается постоянной, если на него не действует другая сила.В отличие от того, что вы увидите, когда мы перейдем ко второму и третьему законам, с первым законом Ньютона нет конкретной формулы. Однако это не делает его менее важным, чем два других.
Из трех законов этот может быть самым легким для людей, не знакомых с физикой, для повседневной жизни. Например, вы чувствуете действие первого закона Ньютона всякий раз, когда путешествуете в транспортном средстве: автомобиле, автобусе, поезде, самолете и т. Д. закон инерции в действии.Ваше тело было в состоянии покоя, и когда автомобиль начал движение, ваше тело хотело оставаться в покое. Вы чувствуете силу, прилагаемую к вам автомобилем, заставляющую вас двигаться.
На вводном уроке физики вы все время будете работать с первым законом Ньютона. Каждый раз, когда объект меняет скорость, вы знаете, что действует первый закон Ньютона. Хотя вы, возможно, не зацикливаетесь на этом напрямую, первый закон Ньютона будет работать повсеместно на протяжении всего вашего изучения классической механики в физике.
Второй закон Ньютона
В то время как первый закон Ньютона смотрит на то, как сила влияет на движение объектов, второй закон углубляется в то, как мы определяем саму силу. Второй закон Ньютона гласит, что ускорение объекта (или a ) прямо пропорционально чистой силе (или F ), действующей на него, и обратно пропорционально его массе (или м ). В отличие от первого закона Ньютона, у этого нет сокращенного названия, но он более известен своей математической формулой, которую вы можете увидеть:
Однако гораздо чаще можно увидеть, что это написано в форме, где оно имеет знак равенства вместо знака пропорциональности, который вы можете увидеть:
Эта формула говорит нам, что сила, действующая на объект, равна массе этого объекта, умноженной на ускорение, вызванное силой.Вы обнаружите, что эта формула постоянно используется во время изучения вводной физики.
Отличным примером действия второго закона Ньютона в нашей жизни является наш вес. Обычно вы можете не думать об этом таким образом, но ваш вес на самом деле является гравитационной силой земли, действующей на вас. Ваш вес равен вашей массе, умноженной на ускорение свободного падения, 9,81 м / с.
Теперь давайте воспользуемся этой информацией, чтобы найти силу гравитации, действующую на человека массой 81 килограмм:
Обратите внимание, что мы дали наш ответ в Ньютонах ( N ).Это стандартная международная единица силы. 1 N равно силе, необходимой для ускорения массы 1 кг со скоростью 1 метр в секунду. Эта формула работает не только для силы тяжести. Если вы знаете ускорение и массу любого объекта, вы можете найти действующую на него чистую силу с помощью второго закона Ньютона.
Третий закон Ньютона
Третий закон Ньютона , вероятно, тот, о котором большинство людей слышало раньше. В нем говорится, что «на каждое действие есть равное и противоположное противодействие.Это означает, что когда один объект создает силу для другого объекта, этот второй объект будет создавать равную силу в обратном направлении на первый объект. Математически мы можем записать это, поскольку сила объекта A на объекте B равна отрицательному значению силы объекта B на объект A:
FAB = -FBA
Решение, какая сила получает отрицательный знак в проблема произвольная; это просто показывает, что силы действуют в противоположных направлениях.
Эта формула показывает нам, что силы всегда приходят парами.Когда вы ударяете по бейсбольному мячу битой, бита оказывает на мяч силу ( Fbat ), но мяч также воздействует на биту назад ( Fball ).
Этот закон распространяется не только на движущиеся объекты, но и на неподвижные. Когда вы сидите на земле, земля прикладывает к вам силу тяжести ( Fg ) вниз, в то время как земля прикладывает равную нормальную силу ( FN ) вверх. Обычная сила – это то, что не дает вам провалиться в землю.
Краткое содержание урока
Сэр Исаак Ньютон – один из самых известных ученых, когда-либо живших в области физики, и его три закона движения являются одними из выдающихся его многочисленных открытий.
Первый закон Ньютона гласит, что любой объект в состоянии покоя или в движении будет оставаться в покое или в движении, если на него не действует другая сила. Это означает, что объект будет сохранять постоянную скорость, если на него не действует сила. У этого закона нет формулы, связанной с ним, но он будет использоваться постоянно, когда вы работаете с силами.
Второй закон Ньютона гласит, что ускорение объекта (или a ) прямо пропорционально действующей на него чистой силе (или F ) и обратно пропорционально его массе (или м ).Чаще всего это записывается как сила, равная массе, умноженной на ускорение.
F = ma
Наконец, третий закон Ньютона гласит, что «на каждое действие есть равная и противоположная реакция». Итак, если объект A создает силу на объект B ( FAB ), этот закон говорит нам, что объект B должен создавать равную силу на объект A ( FBA ) в противоположном направлении.
FAB = -FBA
Это закон, который позволяет нам знать, что силы всегда действуют парами.
5.3 Второй закон Ньютона – Университетская физика, том 1
Какая ракетная тяга ускоряет этот снегоход?
До космических полетов с участием космонавтов ракетные сани использовались для проверки самолетов, ракетного оборудования и физиологических воздействий на людей на высоких скоростях. Они состояли из платформы, которая была установлена на одной или двух направляющих и приводилась в движение несколькими ракетами.Рассчитайте величину силы, прилагаемой каждой ракетой, которая называется ее тягой T , для четырехракетной двигательной установки, показанной на рисунке 5.14. Начальное ускорение салазок составляет 49 м / с 249 м / с 2, масса системы 2100 кг, сила трения, препятствующая движению, составляет 650 Н.
Фигура 5,14 Салазки испытывают ракетную тягу, разгоняющую их вправо. Каждая ракета создает одинаковую тягу Т . Система здесь – это сани, его ракеты и его всадник, поэтому никакие силы между этими объектами не учитываются. Стрелка, обозначающая трение (f →) (f →), нарисована больше масштаба.Стратегия
Хотя силы действуют как вертикально, так и горизонтально, мы предполагаем, что вертикальные силы компенсируются, потому что нет вертикального ускорения.Это оставляет нам только горизонтальные силы и более простую одномерную задачу. Направления указываются знаками плюс или минус, при этом вправо принимается за положительное направление. См. Диаграмму свободного тела на рис. 5.14.Решение
Поскольку ускорение, масса и сила трения даны, мы начнем со второго закона Ньютона и ищем способы найти тягу двигателей. Мы определили направление силы и ускорения как действующее «вправо», поэтому в расчетах нам нужно учитывать только величины этих величин.Следовательно, мы начинаем с, где FnetFnet – чистая сила в горизонтальном направлении. Из рисунка видно, что тяга двигателя увеличивается, а трение противодействует тяге. В форме уравнения чистая внешняя сила равна
.Подставляя это во второй закон Ньютона, получаем
Fnet = ma = 4T − f. Fnet = ma = 4T − f.Используя небольшую алгебру, мы решаем общую тягу 4 T :
Подстановка известных значений дает
4T = ma + f = (2100 кг) (49 м / с2) + 650N.4T = ma + f = (2100 кг) (49 м / с2) + 650N.Следовательно, общая тяга
4T = 1.0 × 105N, 4T = 1.0 × 105N,и индивидуальные тяги
T = 1.0 × 105N4 = 2.5 × 104N, T = 1.0 × 105N4 = 2.5 × 104N.Значение
Цифры довольно большие, поэтому результат может вас удивить. Подобные эксперименты проводились в начале 1960-х годов, чтобы проверить пределы человеческой выносливости, и установка была разработана для защиты людей при аварийных выбросах реактивных истребителей. Была получена скорость 1000 км / ч с ускорением 45 g ’s.(Напомним, что g , ускорение свободного падения составляет 9,80 м / с 29,80 м / с2. Когда мы говорим, что ускорение составляет 45 g , это 45 × 9,8 м / с2,45 × 9,8 м / с2. , что составляет примерно 440 м / с – 2440 м / с2.) Хотя живые предметы больше не используются, с помощью ракетных саней была получена сухопутная скорость 10 000 км / ч.В этом примере, как и в предыдущем, интересующая система очевидна. В последующих примерах мы увидим, что выбор интересующей системы имеет решающее значение, и этот выбор не всегда очевиден.
Второй закон Ньютона – это больше, чем определение; это соотношение между ускорением, силой и массой. Это может помочь нам делать прогнозы. Каждую из этих физических величин можно определить независимо, поэтому второй закон говорит нам что-то основное и универсальное о природе.
4.3: Второй закон движения Ньютона – концепция системы
Цели обучения
К концу этого раздела вы сможете:
- Определите чистую силу, внешнюю силу и систему.
- Поймите второй закон движения Ньютона.
- Примените второй закон Ньютона для определения веса объекта.
Второй закон движения Ньютона тесно связан с первым законом движения Ньютона. Он математически устанавливает причинно-следственную связь между силой и изменениями в движении. Второй закон движения Ньютона является более количественным и широко используется для расчета того, что происходит в ситуациях, связанных с действием силы. Прежде чем мы сможем записать второй закон Ньютона в виде простого уравнения, дающего точное соотношение силы, массы и ускорения, нам необходимо отточить некоторые идеи, которые уже упоминались.
Во-первых, что мы подразумеваем под изменением движения? Ответ заключается в том, что изменение движения эквивалентно изменению скорости. Изменение скорости по определению означает наличие ускорения . Первый закон Ньютона гласит, что чистая внешняя сила вызывает изменение движения; таким образом, мы видим, что чистая внешняя сила вызывает ускорение .
Сразу возникает еще один вопрос. Что мы подразумеваем под внешней силой? Интуитивное представление о внешнем является правильным – внешняя сила , действует извне из интересующей системы .Например, на рисунке \ (\ PageIndex {1a} \) интересующей системой является вагон плюс его дочерний элемент. Две силы, действующие со стороны других детей, – это внешние силы. Между элементами системы действует внутренняя сила. Снова посмотрев на рисунок \ (\ PageIndex {1a} \), можно увидеть, что сила, которую ребенок в тележке прикладывает, чтобы повиснуть на тележке, является внутренней силой между элементами интересующей системы. Согласно первому закону Ньютона, только внешние силы влияют на движение системы. (Внутренние силы фактически отменяются, как мы увидим в следующем разделе.) Вы должны определить границы системы, прежде чем сможете определить, какие силы являются внешними . Иногда система очевидна, тогда как в других случаях определение границ системы более тонкое. Концепция системы является фундаментальной для многих областей физики, как и правильное применение законов Ньютона. Эта концепция будет неоднократно пересматриваться в нашем путешествии по физике.
Рисунок \ (\ PageIndex {1} \): Различные силы, действующие на одну и ту же массу, вызывают разное ускорение.а) Двое детей толкают тележку с ребенком в ней. Показаны стрелки, представляющие все внешние силы. Интересующая система – это повозка и ее водитель. Вес \ (w \) системы и опора основания \ (N \) также показаны для полноты и, как предполагается, сокращаются. Вектор \ (f \) представляет трение, действующее на вагон, и действует влево, противодействуя движению вагона. (b) Все внешние силы, действующие на систему, складываются вместе, образуя результирующую силу, \ (F_ {net} \).На диаграмме свободного тела показаны все силы, действующие на интересующую систему. Точка представляет собой центр масс системы. Каждый вектор силы простирается от этой точки. Поскольку справа действуют две силы, мы рисуем векторы коллинеарно. (c) Большая чистая внешняя сила вызывает большее ускорение \ ((al> a) \), когда взрослый толкает ребенка.Теперь кажется разумным, что ускорение должно быть прямо пропорционально и в том же направлении, что и чистая (полная) внешняя сила, действующая на систему.Это предположение было проверено экспериментально и показано на рисунке. В части (а) меньшая сила вызывает меньшее ускорение, чем большая сила, показанная в части (с). Для полноты картины также показаны вертикальные силы; предполагается, что они отменяются, поскольку нет ускорения в вертикальном направлении. Вертикальные силы – это вес \ (w \) и опора на землю \ (N \), а горизонтальная сила \ (f \) представляет собой силу трения. Они будут обсуждаться более подробно в следующих разделах.На данный момент мы определим трение как силу, которая противодействует движению мимо друг друга соприкасающихся объектов. На рисунке \ (\ PageIndex {1b} \) показано, как векторы, представляющие внешние силы, складываются вместе, образуя чистую силу, \ (F_ {net} \).
Чтобы получить уравнение для второго закона Ньютона, сначала запишем соотношение ускорения и чистой внешней силы как пропорциональность
\ [a \ propto F_ {net} \]
, где символ \ (\ propto \) означает «пропорционально», а \ (F_ {net} \) – чистая внешняя сила .(Чистая внешняя сила представляет собой векторную сумму всех внешних сил и может быть определена графически, используя метод “голова к хвосту”, или аналитически, используя компоненты. Методы такие же, как и для сложения других векторов, и рассматриваются в главе, посвященной двумерной кинематике.) Эта пропорциональность выражает то, что мы сказали словами – ускорение прямо пропорционально чистой внешней силе . После выбора интересующей системы важно определить внешние силы и игнорировать внутренние.Это огромное упрощение – не учитывать многочисленные внутренние силы, действующие между объектами внутри системы, такие как мышечные силы в теле ребенка, не говоря уже о мириадах сил между атомами в объектах, но, делая это, мы можем легко решить некоторые очень сложные задачи с минимальной ошибкой благодаря нашему упрощению
Теперь также кажется разумным, что ускорение должно быть обратно пропорционально массе системы. Другими словами, чем больше масса (инерция), тем меньше ускорение, создаваемое данной силой.И действительно, как показано на рисунке, та же самая чистая внешняя сила, приложенная к автомобилю, вызывает гораздо меньшее ускорение, чем при приложении к баскетбольному мячу. Пропорциональность записывается как
.\ [a \ propto \ dfrac {1} {m}, \]
где \ (m \) – масса системы. Эксперименты показали, что ускорение прямо обратно пропорционально массе, точно так же, как оно прямо линейно пропорционально чистой внешней силе.
Рисунок \ (\ PageIndex {2} \): Одна и та же сила, действующая на системы разной массы, вызывает разное ускорение.(a) Баскетболист толкает баскетбольный мяч, чтобы сделать передачу. (Влияние силы тяжести на мяч игнорируется.) (B) Тот же игрок оказывает идентичную силу на остановившийся внедорожник и производит гораздо меньшее ускорение (даже если трение незначительно). (c) Диаграммы свободного тела идентичны, что позволяет напрямую сравнить две ситуации. По мере того, как вы будете решать больше задач, появится серия паттернов для диаграммы свободного тела.Было обнаружено, что ускорение объекта зависит только от чистой внешней силы и массы объекта.Комбинирование двух только что приведенных пропорциональностей дает второй закон движения Ньютона.
Второй закон движения Ньютона
Ускорение системы прямо пропорционально чистой внешней силе, действующей на систему, и в том же направлении, и обратно пропорционально ее массе. В форме уравнения второй закон движения Ньютона равен
.\ [a = \ dfrac {F_ {net}} {m} \]
Это часто записывается в более знакомой форме
\ [F_ {net} = ma.\]
Если рассматривать только величину силы и ускорения, это уравнение просто
\ [F_ {net} = ma. \]
Хотя эти последние два уравнения на самом деле одинаковы, первое дает больше понимания того, что означает второй закон Ньютона. Закон – причинно-следственная связь между тремя величинами, которая не просто основана на их определениях. Справедливость второго закона полностью основана на экспериментальной проверке.
Единицы силы
\ (F_ {net} = ma \) используется для определения единиц силы в терминах трех основных единиц массы, длины и времени.2 \]
В то время как почти весь мир использует ньютон в качестве единицы силы, в Соединенных Штатах наиболее известной единицей силы является фунт (фунт), где 1 Н = 0,225 фунта.
Вес и сила тяжести
Когда объект падает, он ускоряется к центру Земли. Второй закон Ньютона гласит, что общая сила, действующая на объект, отвечает за его ускорение. Если сопротивление воздуха незначительно, результирующая сила, действующая на падающий объект, – это сила тяжести, обычно называемая его весом \ (w \).Вес можно обозначить как вектор \ (w \), потому что он имеет направление; Вниз по определению является направлением силы тяжести, и, следовательно, вес – это сила, направленная вниз. Величина веса обозначается как \ (w \). Галилей сыграл важную роль в демонстрации того, что при отсутствии сопротивления воздуха все объекты падают с одинаковым ускорением \ (w \). Используя результат Галилея и второй закон Ньютона, мы можем вывести уравнение для веса.
Рассмотрим объект с массой \ (m \), падающий вниз к Земле. Он испытывает только направленную вниз силу тяжести, величина которой равна \ (w \).Второй закон Ньютона гласит, что величина чистой внешней силы, действующей на объект, равна \ (F_ {net} = ma \).
Поскольку на объект действует только сила тяжести, направленная вниз, \ (F_ {net} = w \). Мы знаем, что ускорение объекта под действием силы тяжести равно \ (g \) или \ (a = g \). Подставляя их во второй закон Ньютона, получаем
ВЕС
Это уравнение веса – силы тяжести, действующей на массу \ (m \):
\ [w = мг \]
Так как вес \ (g = 9.2) = 9,8 Н. \]
Напомним, что \ (g \) может принимать положительное или отрицательное значение, в зависимости от положительного направления в системе координат. Обязательно учтите это при решении задач с весом.
Когда чистая внешняя сила, действующая на объект, равна его весу, мы говорим, что он находится в состоянии свободного падения . То есть единственная сила, действующая на объект, – это сила тяжести. В реальном мире, когда объекты падают вниз к Земле, они никогда не находятся в состоянии свободного падения, потому что на объект всегда действует некоторая восходящая сила из воздуха.2 \). Таким образом, масса в 1,0 кг имеет вес 9,8 Н на Земле и всего около 1,7 Н на Луне.
Самое широкое определение веса в этом смысле состоит в том, что вес объекта – это сила тяжести, действующая на него со стороны ближайшего большого тела , такого как Земля, Луна, Солнце и так далее. Это наиболее распространенное и полезное определение веса в физике. Однако оно кардинально отличается от определения веса, используемого НАСА и популярными СМИ в отношении космических путешествий и исследований.Когда они говорят о «невесомости» и «микрогравитации», они на самом деле имеют в виду явление, которое мы называем «свободным падением» в физике. Мы будем использовать приведенное выше определение веса и проведем тщательное различие между свободным падением и фактической невесомостью.
Важно знать, что вес и масса – очень разные физические величины, хотя они тесно связаны. Масса – это количество материи (сколько «вещества») и не изменяется в классической физике, тогда как вес – это сила тяжести, которая зависит от силы тяжести.Заманчиво приравнять эти два понятия, поскольку большинство наших примеров имеет место на Земле, где вес объекта лишь немного зависит от его местоположения. Кроме того, в повседневном языке термины масса и масса используются взаимозаменяемо; например, в наших медицинских записях наш «вес» часто указывается в килограммах, но никогда в правильных единицах – ньютонах.
РАСПРОСТРАНЕННЫЕ Заблуждения: МАССА VS. ВЕС
Масса и вес в повседневной речи часто используются как синонимы.Однако в науке эти термины существенно отличаются друг от друга. Масса – это мера количества вещества в объекте. Типичной мерой массы является килограмм (или «пуля» в английских единицах измерения). С другой стороны, вес – это мера силы тяжести, действующей на объект. Вес равен массе объекта \ ((m) \), умноженной на ускорение свободного падения \ ((g) \). Как и любая другая сила, вес измеряется в ньютонах (или фунтах в английских единицах).
Предполагая, что масса объекта остается неизменной, она останется неизменной независимо от его местоположения.2 \)). Если вы измерили свой вес на Земле, а затем измерили свой вес на Луне, вы бы обнаружили, что «весите» намного меньше, хотя и не выглядите худее. Это потому, что сила тяжести на Луне слабее. Фактически, когда люди говорят, что они «худеют», они на самом деле имеют в виду, что они теряют «массу» (что, в свою очередь, заставляет их весить меньше)
ЭКСПЕРИМЕНТ НА ДОМУ: МАССА И ВЕС
Что измеряют весы для ванной? Когда вы стоите на весах в ванной, что происходит с весами? Слегка угнетает.Весы содержат пружины, которые сжимаются пропорционально вашему весу – подобно резиновым лентам, расширяющимся при натяжении. Пружины позволяют измерить ваш вес (для объекта, который не ускоряется). Это сила в ньютонах (или фунтах). В большинстве стран результат делится на 9,80, чтобы получить значение в килограммах. Весы измеряют вес, но откалиброваны для предоставления информации о массе. Стоя на весах в ванной, нажмите на соседний стол. Что происходит с чтением? Почему? Будет ли ваша шкала измерять ту же «массу» на Земле, что и на Луне?
Пример \ (\ PageIndex {1} \): какое ускорение может дать человек, толкая газонокосилку?
Предположим, что чистая внешняя сила (толчок минус трение), действующая на газонокосилку, составляет 51 Н (около 11 фунтов) параллельно земле.Масса косилки 24 кг. Какое у него ускорение?
Рисунок \ (\ PageIndex {3} \): Чистое усилие на газонокосилке составляет 51 Н. вправо. С какой скоростью газонокосилка ускоряется вправо?Стратегия
Поскольку даны \ (F_ {net} \) и \ (m \), ускорение можно вычислить непосредственно из второго закона Ньютона, как указано в \ (F_ {net} = ma \).
Решение
Величина ускорения \ (a \) равна \ (a = \ frac {F_ {net}} {m} \).2 \]
Обсуждение
Направление ускорения совпадает с направлением результирующей силы, параллельной земле. В этом примере нет информации об отдельных внешних силах, действующих на систему, но мы можем кое-что сказать об их относительных величинах. Например, сила, прикладываемая человеком, толкающим косилку, должна быть больше, чем трение, препятствующее движению (поскольку мы знаем, что косилка движется вперед), а вертикальные силы должны нейтрализоваться, если не должно быть ускорения в вертикальном направлении ( косилка движется только горизонтально).Обнаруженное ускорение достаточно мало, чтобы быть приемлемым для человека, толкающего косилку. Такое усилие не будет длиться слишком долго, потому что человек скоро достигнет максимальной скорости.
Пример \ (\ PageIndex {2} \): Какая ракетная тяга ускоряет этот снегоход?
До пилотируемых космических полетов ракетные сани использовались для испытания самолетов, ракетного оборудования и физиологических воздействий на людей на высоких скоростях. Они состояли из платформы, которая была установлена на одной или двух направляющих и приводилась в движение несколькими ракетами.2 \) масса системы 2100 кг, а сила трения, препятствующая движению, известна как 650 Н.
Рисунок 4.4.4. Салазки испытывают ракетную тягу, разгоняющую их вправо. Каждая ракета создает одинаковую тягу \ (T \). Как и в других ситуациях, когда есть только горизонтальное ускорение, вертикальные силы нейтрализуются. Земля оказывает на систему направленную вверх силу \ (N \), равную по величине и противоположную по направлению ее весу, \ (w \). Система здесь – сани, его ракеты и всадник, поэтому никакие силы между этими объектами не учитываются.Стрелка, обозначающая трение \ ((f) \), нарисована больше масштаба.Стратегия
Несмотря на то, что существуют силы, действующие вертикально и горизонтально, мы предполагаем, что вертикальные силы компенсируются, поскольку нет вертикального ускорения. Это оставляет нам только горизонтальные силы и более простую одномерную задачу. Направления указываются знаками плюс или минус, при этом вправо принимается за положительное направление. См. Диаграмму свободного тела на рисунке.
Решение
Поскольку ускорение, масса и сила трения даны, мы начнем со второго закона Ньютона и ищем способы найти тягу двигателей.Поскольку мы определили направление силы и ускорения как действующие «вправо», нам нужно учитывать в расчетах только величины этих величин. Следовательно, мы начинаем с \ [F_ {net} = ma. \], где \ (F_ {net} \) – чистая сила в горизонтальном направлении. Из рисунка видно, что тяга двигателя увеличивается, а трение противодействует тяге. В форме уравнения чистая внешняя сила равна \ [F_ {net} = 4T – f. \]
Подставляя это во второй закон Ньютона, получаем \ [F_ {net} = ma = 4T – f.2 \)). Пока живые предметы больше не используются, с помощью ракетных саней была получена сухопутная скорость 10 000 км / ч. В этом примере, как и в предыдущем, интересующая система очевидна. В последующих примерах мы увидим, что выбор интересующей системы имеет решающее значение, и этот выбор не всегда очевиден.
Второй закон движения Ньютона – это больше, чем определение; это соотношение между ускорением, силой и массой. Это может помочь нам делать прогнозы. Каждую из этих физических величин можно определить независимо, поэтому второй закон говорит нам что-то основное и универсальное о природе.В следующем разделе представлен третий и последний закон движения.
Сводка
- Ускорение, \ (a \), определяется как изменение скорости, то есть изменение ее величины или направления, или того и другого.
- Внешняя сила – это сила, действующая на систему извне, в отличие от внутренних сил, которые действуют между компонентами внутри системы.
- Второй закон движения Ньютона гласит, что ускорение системы прямо пропорционально и в том же направлении, что и чистая внешняя сила, действующая на систему, и обратно пропорционально ее массе.
- В форме уравнения второй закон движения Ньютона: \ (a = \ frac {F_ {net}} {m} \)
- Это часто записывается в более знакомой форме: \ (F_ {net} = ma. \)
- Вес \ (w \) объекта определяется как сила тяжести, действующая на объект массы \ (m. \). Этот объект испытывает ускорение силы тяжести \ (g \): \ [w = mg. \]
- Если единственная сила, действующая на объект, вызвана гравитацией, объект находится в свободном падении.
- Трение – это сила, которая препятствует движению соприкасающихся объектов друг за другом.
Авторы и авторство
Пол Питер Урон (почетный профессор Калифорнийского государственного университета, Сакраменто) и Роджер Хинрикс (Государственный университет Нью-Йорка, колледж в Освего) с участвующими авторами: Ким Диркс (Оклендский университет) и Манджула Шарма (Сиднейский университет). Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Второй закон движения Ньютона
Второй закон Ньютона устанавливает связь между силой \ (\ mathbf {F} \), действующей на тело массы \ (m \), и ускорением \ (\ mathbf {a} \), вызываемым этой силой.2}}}.} \]
Эта формулировка действительна для систем с постоянной массой. При изменении массы (например, в случае релятивистского движения) второй закон Ньютона принимает вид
\ [\ mathbf {F} = \ frac {{d \ mathbf {p}}} {{dt}}, \]
где \ (\ mathbf {p} \) – импульс (импульс) тела.
В общем случае сила \ (\ mathbf {F} \) может зависеть от координат тела, то есть от радиус-вектора \ (\ mathbf {r}, \) его скорости \ (\ mathbf {v}, \ ) и время \ (t: \)
\ [\ mathbf {F} = \ mathbf {F} \ left ({\ mathbf {r}, \ mathbf {v}, t} \ right).t {v \ left (\ tau \ right) d \ tau}, \]
где \ ({x_0} \) – начальная координата тела, \ (\ tau \) – переменная интегрирования.
Сила зависит от скорости: \ (\ mathbf {F} = \ mathbf {F} \ left ({\ mathbf {v}} \ right) \)
Когда твердое тело движется в жидкой или газовой среде, на него действует сила сопротивления (или сила трения). 2}}} = m \ frac {{dv}} {{dt}} = – кв.{- {\ large \ frac {k} {m} \ normalsize} t}}} \ right).}
\]
Последняя формула показывает, что путь, пройденный телом до полной остановки, равен \ (\ large \ frac {{m {v_0}}} {k} \ normalsize, \), то есть пропорционален начальному импульсу тело \ (m {v_0}. \)
По мере увеличения скорости тела изменяется физика процесса. Кинетическая энергия тела начинает тратиться не только на трение между слоями жидкости, но и на движение жидкости перед телом.2}, \]
где \ (\ mu \) – коэффициент пропорциональности, \ (S \) – площадь поперечного сечения тела, \ (\ rho \) – плотность среды.
Описанный выше нелинейный режим возникает при условиях
\ [\ mathbf {\ text {Re}} = \ frac {{\ rho vL}} {\ eta}> 100, \]
где \ (\ mathbf {\ text {Re}} \) – безразмерное число Рейнольдса, \ (\ eta \) – вязкость среды, \ (L \) – характерный размер поперечного сечения, например, радиус тела.t {d \ tau}.}
\]
Здесь \ (u \) и \ (\ tau \) снова обозначают переменные интегрирования. За время \ (t, \) скорость тела уменьшится от начального значения \ ({v_0} \) до конечного значения \ (v. \) В результате получим
\ [
{- \ left ({\ frac {1} {v} – \ frac {1} {{{v_0}}}} \ right) = – \ frac {{\ mu \ rho S}} {m } t, \; \;} \ Rightarrow
{\ frac {1} {v} = \ frac {1} {{{v_0}}} + \ frac {{\ mu \ rho S}} {m} t, \; \;} \ Rightarrow
{v \ left (t \ right) = \ frac {1} {{\ frac {1} {{{v_0}}}} + \ frac {{\ mu \ rho S}} { m} t}}} = {\ frac {{{v_0}}} {{1 + \ frac {{\ mu \ rho S {v_0}}} {m} t}}.t} \ right]}
= {\ frac {m} {{\ mu \ rho S}} \ ln \ left ({1 + \ frac {{\ mu \ rho S {v_0}}}} {m} t} \ right).}
\]
Важно иметь в виду, что эти формулы справедливы для достаточно больших значений скорости: при меньших скоростях эта модель физически некорректна, так как сила сопротивления начинает линейно зависеть от скорости (этот случай рассматривался ранее).
Сила зависит от позиции: \ (\ mathbf {F} = \ mathbf {F} \ left (x \ right) \)
Примеры сил, которые зависят только от координаты, в частности:
- Сила упругости \ (F = -kx; \)
- Сила гравитационного притяжения \ (F = – G \ large \ frac {{{m_1} {m_2}}} {{{x ^ 2}}} \ normalsize. 2}}}} = m \ frac {{dv}} {{dt}}} = {mv \ frac {{dv }} {{dx}}} = {F \ left (x \ right).L {F \ left (x \ right) dx}.}
\]Последнее уравнение выражает закон сохранения энергии. Левая часть описывает изменение кинетической энергии, а правая часть соответствует работе переменной силы \ ({F \ left (x \ right)} \) при перемещении тела на расстояние \ (L. \)
Последующее интегрирование функции \ ({v \ left (t \ right)} \) позволяет найти закон движения \ ({x \ left (t \ right)}. \) К сожалению, это не всегда возможно из-за громоздких аналитических выражений для \ ({v \ left (t \ right)}.\)
Решенные проблемы
Щелкните или коснитесь проблемы, чтобы увидеть решение.
Пример 1
Тело начинает падать с высоты \ (H \) под действием силы тяжести. При падении он испытывает сопротивление, пропорциональное скорости. Определите время падения.Пример 2
В начальный момент цепочка длиной \ (L \) свешивается над краем стола, так что сила тяжести уравновешивается силой трения (рис. \ (3 \)).В результате небольшого сдвига \ (\ varepsilon \) цепочка начинает скользить. Определите время \ (T, \), за которое цепь полностью соскользнет со стола. Коэффициент трения между цепью и поверхностью стола равен \ (\ mu. \)Второй закон Ньютона – Силы, ускорение и законы движения Ньютона – Eduqas – GCSE Combined Science Revision – Eduqas
Сила, масса и ускорение
Второй закон движения Ньютона можно описать следующим уравнением:
- результирующая сила = масса × ускорение
- F = ma
Это когда:
- результирующая сила (F) измеряется в ньютонах (Н)
- масса (м) измеряется в килограммах (кг)
- измеряется ускорение (a) в метрах в секунду в квадрате (м / с²)
Уравнение показывает, что ускорение объекта:
- пропорционально результирующей силе, действующей на объект
- , обратно пропорционально массе объекта
Другими словами Другими словами, ускорение объекта увеличивается, если результирующая сила, действующая на него, увеличивается, и уменьшается, если масса объекта увеличивается.
Второй закон Ньютона может быть выражен как «результирующая сила = масса × ускорение» или «Ускорение объекта прямо пропорционально результирующей (или суммарной) силе в том же направлении, что и сила, и обратно пропорционально масса объекта “.
Инерционная масса – Высшая
Отношение силы к ускорению – это определение инертной массы. Инерционная масса – это мера того, насколько сложно изменить скорость объекта. Он определяется как «отношение силы к ускорению».Объекты с большей массой имеют большую инерцию, поэтому для того же ускорения потребуется большая результирующая сила.
Пример
Рассчитайте силу, необходимую для ускорения 22-килограммового гепарда со скоростью 15 м / с².
\ [F = m \ a \]
\ [F = 22 \ times 15 \]
\ [\ underline {F = 330 \ N} \]
- Вопрос
Рассчитайте усилие, необходимое для разогнать газель массой 15 кг со скоростью 10 м / с².
- Показать ответ
\ [F = m \ a \]
\ [F = 15 \ times 10 \]
\ [\ underline {F = 150 \ N} \]
Оценка скорости , ускорения и силы
Важно уметь оценивать скорость, ускорения и силы, задействованные в дорожных транспортных средствах.Символ ~ используется для обозначения приблизительного значения или ответа. В таблице приведены некоторые примеры.
Автомобиль Максимальная разрешенная скорость на одинарной проезжей части в м / с Масса в кг Ускорение в м / с2 Семейный автомобиль ~ 27 ~ 1,600 3 Грузовик ~ 22 ~ 36 000 ~ 0,4 Пример
Оценить силу, необходимую для разгона семейного автомобиля до максимальной скорости на одинарной проезжей части.Используя значения ~ 1600 кг и ~ 3 м / с 2 , и F = m a:
- \ [1600 \ times 3 = \ underline {\ sim 4800 \ N} \]
- Вопрос
Оцените силу, необходимую для разгона грузовика до максимальной скорости на одной проезжей части.
- Показать ответ
Используя значения ~ 36 000 кг и ~ 0,4 м / с 2 , и F = ma:
\ [\ underline {Force (F) \ is \ sim 14400 \ N} \]

 Сегодня с ними знаком каждый школьник, но во времена великого ученого подобные открытия считались революционными. Законы Ньютона, кратко и понятно будут описаны ниже, они помогают не только понять основу механики и взаимодействия объектов, но и помогают записать данные в качестве уравнения.
Сегодня с ними знаком каждый школьник, но во времена великого ученого подобные открытия считались революционными. Законы Ньютона, кратко и понятно будут описаны ниже, они помогают не только понять основу механики и взаимодействия объектов, но и помогают записать данные в качестве уравнения.
 Что означает данное определение и как его понять?
Что означает данное определение и как его понять?







 Он утверждает, что существуют такие системы отсчета, в которых любое тело, что не подверглось воздействию внешних сил, сохраняет состояние покоя или прямолинейного равномерного движения.
Он утверждает, что существуют такие системы отсчета, в которых любое тело, что не подверглось воздействию внешних сил, сохраняет состояние покоя или прямолинейного равномерного движения. В обратном случае используется формула.
В обратном случае используется формула. История их открытия известна всем. Согласно легенде, Ньютон сидел в своем саду и обратил внимание на падающее с дерева яблоко.
История их открытия известна всем. Согласно легенде, Ньютон сидел в своем саду и обратил внимание на падающее с дерева яблоко.
 Но возможно ли изменение скорости тела без непосредственного действия на него сил? И казалось бы правильный ответ нет, но… Тут нужно вспомнить тот факт, что движение относительно, соответственно, очень важна система отсчета, которую мы выбрали, а что если она начнет двигаться с ускорением?
Но возможно ли изменение скорости тела без непосредственного действия на него сил? И казалось бы правильный ответ нет, но… Тут нужно вспомнить тот факт, что движение относительно, соответственно, очень важна система отсчета, которую мы выбрали, а что если она начнет двигаться с ускорением?
 Поэтому иногда говорят, что масса является мерой инертности тела, то есть характеризует его способность сохранять скорость постоянной.
Поэтому иногда говорят, что масса является мерой инертности тела, то есть характеризует его способность сохранять скорость постоянной.

 И потяните за колечко второго безмена. Проследите за показаниями обоих приборов. Каждый из них покажет силу, с которой на него воздействует другой безмен.
И потяните за колечко второго безмена. Проследите за показаниями обоих приборов. Каждый из них покажет силу, с которой на него воздействует другой безмен. Этот закон справедлив как для случая, когда одно тело тянет другое, так и для случая, когда тела отталкиваются. Все тела во Вселенной взаимодействуют друг с другом, подчиняясь этому закону.
Этот закон справедлив как для случая, когда одно тело тянет другое, так и для случая, когда тела отталкиваются. Все тела во Вселенной взаимодействуют друг с другом, подчиняясь этому закону.

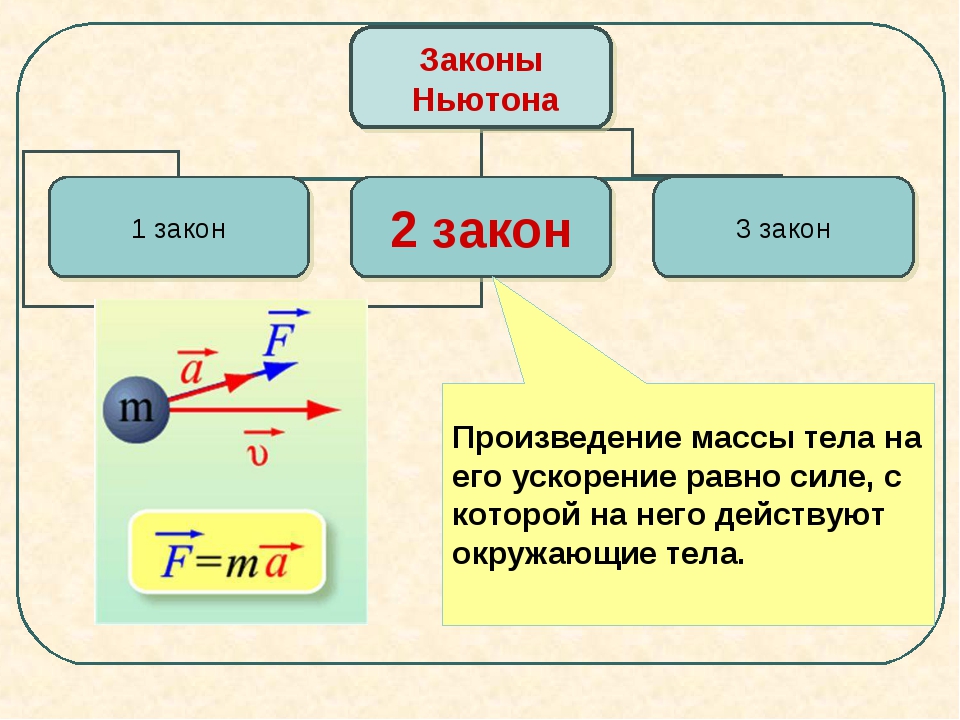 На фундамент действуют две одинаковые, но направленные в противоположные стороны силы, о чем говорит третий закон Ньютона.
На фундамент действуют две одинаковые, но направленные в противоположные стороны силы, о чем говорит третий закон Ньютона.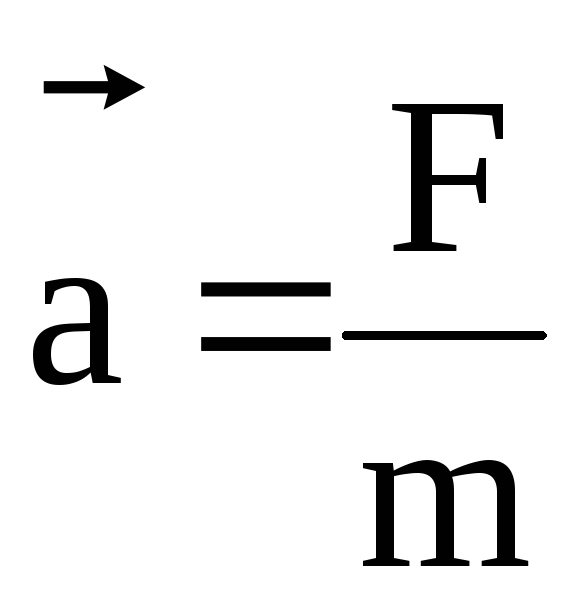 Парашютист падает на Землю, а Земля «падает» на парашютиста. Но масса парашютиста по сравнению с массой Земли ничтожна, и потому его движение быстро, а масса Земли огромна, и ее ответное и встречное движение совершенно неуловимо.
Парашютист падает на Землю, а Земля «падает» на парашютиста. Но масса парашютиста по сравнению с массой Земли ничтожна, и потому его движение быстро, а масса Земли огромна, и ее ответное и встречное движение совершенно неуловимо.