Тест “Формулы за 7 класс”
Главная / Старшие классы / Физика
Скачать
304.36 КБ, 472042.pptx Автор: Алексеева Людмила Петровна, 21 Мар 2015
Интерактивный тест на проверку формул по физике для 7 класса.
Автор: Алексеева Людмила Петровна
Похожие материалы
| Тип | Название материала | Автор | Опубликован |
|---|---|---|---|
| презентация | Тест “Формулы за 7 класс” | Алексеева Людмила Петровна | 21 Мар 2015 |
| документ | Тест по алгебре 7 класс: “Формулы сокращенного умножения” | Двойнова Марина Валерьевна | 21 Мар 2015 |
| документ | Тест по алгебре для обучающихся 7 класса по теме “Формулы сокращенного умножения” | Дегтярева Наталья Николаевна | 21 Мар 2015 |
| документ | Тест по теме “Формулы тригонометрии “10 класс | Лапкина Ольга Адольфовна | 21 Мар 2015 |
| документ | тест по теме “Тригонометрические формулы”, 10 класс | Кандыба Светлана Борисовна | 4 Апр 2015 |
| презентация, документ | Конспект урока “Формулы сокращенного умножения” 7 класс | Агринская Любовь Федоровна | 21 Мар 2015 |
| презентация | Видеоурок “Формулы сокращенного умножения”, математика, 7 класс | Нукеева Гульмайра Укиметовна | 21 Мар 2015 |
| документ | Конспект урока “Формулы сокращенного умножения” 7 класс | Никитина Ирина Николаевна | 21 Мар 2015 |
| документ | Урок “Формулы сокращенного умножения” 7 класс | Павлова Ольга Геннадьевна | 1 Апр 2015 |
| презентация | Презентация “Формулы сокращенного умножения” 7 класс | Мишарина Альбина Геннадьевна | 1 Апр 2015 |
| презентация | Урок алгебры 7 класс”Формулы сокращенного умножения” | Кузьмина Елена Владимировна | 31 Июл 2015 |
| документ | Урок алгебры 7 класс “Формулы сокращенного умножения” | Козлова Анна Александровна | 6 Дек 2015 |
| документ | Урок “Формулы сокращенного умножения” 7 класс | Шукшина Надежда Владимировна | 8 Фев 2016 |
| документ | Урок алгебры 7 класс “Формулы сокращенного умножения” | Козлова Надежда Владимировна | 8 Апр 2016 |
| презентация | Интерактивный кроссворд “Основы композиции в конструктивных искусствах”, итоговый тест для 7 класса за 1 четверть | Вязникова Наталья Викторовна | 20 Ноя 2015 |
| документ | Итоовый тест по русскому за 7 класс | Резаева Елена Юрьевна | 20 Мар 2015 |
| документ | Тест по ОБЖ за 1 полугодие 7 класс | Горпенюк Станислав Владимирович | 20 Мар 2015 |
| документ | Итоговый тест за курс истории России. 7 класс | Равина Светлана Михайловна | 11 Апр 2016 |
| документ | 7 класс. Тест по физике за 1 четверть. | Лаврова Наталья Владимировна | 21 Мар 2015 |
| документ | Итоговый тест по литературе за 1 полугодие 7 класс | Шамсутдинова Светлана Николаевна | 20 Мар 2015 |
| документ | тест по физике 7 класс за 1 полугодие | Лезневская Елена Юрьевна | 21 Мар 2015 |
| документ | Итоговый тест по экологии животных за 7 класс. | Сторожилова Дина Александровна | 6 Апр 2015 |
| документ | Итоговый тест за 7 класс | Хлюпина Елена Михайловна | 11 Апр 2015 |
| разное | Тест ” Сила. Плотность” 7 класс | Митрофанова Надежда Михайловна | |
| презентация | тест по теме: “Формулы сокращённого умножения” | Берчук Татьяна Васильевна | 21 Мар 2015 |
| разное | Тест “Формулы в Excel” | Пигарева Ирина Анатольевна | 21 Мар 2015 |
| презентация | Интерактивный тест по теме “Формулы сокращенного умножения”. | Горбачёва Ольга Владимировна | 8 Фев 2016 |
| разное | Тест По теме “Формулы двойного аргумента” | Щукина Ольга Александровна | 8 Фев 2016 |
| разное | Тест по теме “Формулы приведения” | Щукина Ольга Александровна | 30 Янв 2016 |
| разное | Разработка урока “Формулы приведения” 10 класс | Мелихова Анна Геннадьевна | 7 Июл 2015 |
| документ | “Формулы приведения. ” 10 класс. | Антропова Эльза Валерьевна | 7 Июл 2015 |
| разное | тест “Уход за одеждой” | Коновалова Ирина Валериевна | 27 Апр 2015 |
| документ | Контрольный тест по теме “Повторение пройденного за курс 5 класса” | Грачева Наталья Александровна | 7 Фев 2016 |
| документ | Контрольный тест за I полугодие природоведение 5 класс | Антипина Елена Вячеславовна | 7 Апр 2015 |
| документ | Итоговый тест по русскому языку за 6 класс | Кадиева Ирина Константиновна | 7 Апр 2015 |
| документ | Итоговый тест по Музыке за 6 класс | Елена Геннадьевна Дегтярева | 7 Июн 2015 |
| документ | Итоговый тест по русск. яз. за 2 класс | Комарова Инна Анатольевна | 7 Дек 2015 |
| документ | Урок в 7 классе “Формулы сокращенного умножения” | Астахова Вера Григорьевна | 1 Апр 2015 |
| документ | урок математики 7 класса “Формулы сокращённого умножения” | Семёнова Татьяна Ивановна | 11 Апр 2015 |
| презентация | Тест формулы по теме “Электрические явления” – 8 класс Диск | Алексеева Людмила Петровна | 4 Апр 2015 |
Школьные формулы по физике 7-11 классы
- формат docx
- размер 97.
99 КБ - добавлен 07 декабря 2009 г.
99 КБВсе школьные формулы по механике, молекулярной физике, термодинамике, электродинамике, оптике, квантовой физике и т. д.
Смотрите также
Шпаргалка
- формат pdf
- размер 1.58 МБ
- добавлен 21 января 2012 г.
М.: РИОР, 2009. – 32 с. В шпаргалке приведены все основные формулы и определения по физике. Рекомендуется всем изучающим и сдающим физику в школах, средних и высших учебных заведениях.
Шпаргалка
- формат jpg
- размер 149. 22 КБ
- добавлен 14 января 2011 г.
22 КБЗдесь представлены самые основные формулы, которые могут понадобиться студенту при сдачи экзамена по физике. Разделы: кинематика, динамика, электростатика, квантовая физика, ядерная физика и другие. Один этот самый лист.
software
- формат exe
- размер 91.13 КБ
- добавлен 12 июля 2010 г.
Программа, выводящая на экран формулы по физике. Бета-версия. Доступна только кинематика. NNSoft, 2006 г. Разработки для Pocket PC. Разделы: Кинематика; Динамика, Законы Сохранения; Статика, гидростатика; Мех. Колебания. Волны.; МКТ; термодинамика.rn
- формат pdf
- размер 1. 95 МБ
- добавлен 06 октября 2011 г.
95 МБНа 10 страницах приведены всё основные формулы по физике. Может пригодиться студенту при подготовке к экзамену, контрольной работе или просто для освежения памяти по следующим разделам: Кинематика. Динамика. Законы сохранения. Работа и мощность. Статика и гидростатика. Тепловые явления. Электростатика. Постоянный ток. Магнитные явления. Колебания и волны. Оптика.
Шпаргалка
- формат doc
- размер 128.54 КБ
- добавлен 30 октября 2011 г.
Выписки на 9 листах из книги “Краткий справочник по физике” Гридасов А.Ю. Новосибирск 1997 г. Файл содержит формулы из курса физики, которые будут полезны учащимся старших классов школ и младших курсов вузов.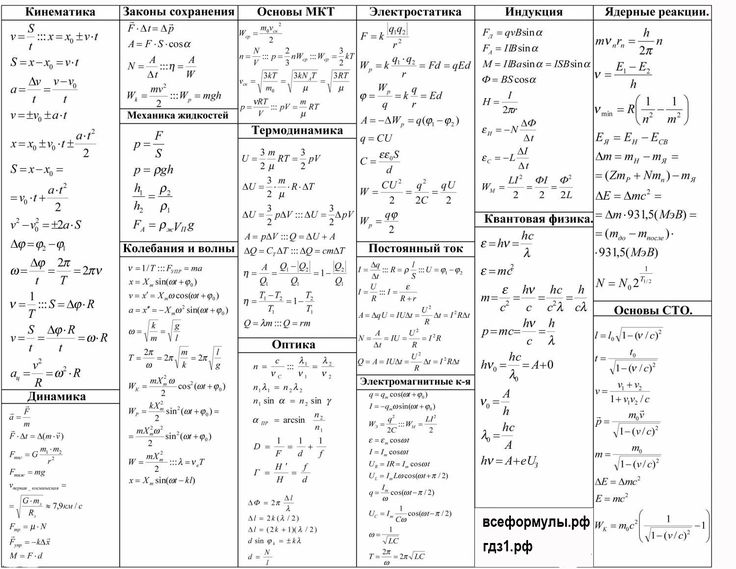
Все формулы изложены в компактном виде с небольшими комментариями. Файл также содержит полезные константы и прочую информацию.
Шпаргалка
- формат doc
- размер 136.87 КБ
- добавлен 24 января 2009 г.
Формулы по курсу физики: Механике, молекулярной физике и термодинамике, электричеству и магнетизму, колебаниям и волнам, оптике, квантовой природе излучения, элементам квантовой физики атомов, молекул и твёрдых тел, элементам физики атомного ядра и элементарных частиц.
- формат jpg
- размер 1.15 МБ
- добавлен 27 мая 2009 г.
Формулы – Шпоры по физике сделаны специально для мобильного телефона или графического калькулятора.
(калькулятор должен иметь флешь память и читать jpg формат) Есть формулы по: Кинематике. Динамике. Законах сохранения энергии. Механика жидкостей. Основах МКТ. Термодинамике. Колебаниях и волнах. Электростатике. Постоянном электрическом токе. Индукции. Электромагнитным колебаниям. Оптике. Ядерным реакциям. Квантовой физике. Основам СТО.rn
- формат doc
- размер 120.56 КБ
- добавлен 11 декабря 2007 г.
Шпора по физике. Готова к распечатке. Содержит формулы по темам: кинематика, движение под углом к горизонту, криволинейное движение, механика жидкостей и газов, свойства газов, молекулярно-кинетическая теория, электричество и магнетизм и так далее.
Шпаргалка
- формат doc
- размер 2.24 МБ
- добавлен
22 февраля 2011 г.
Полный сборник по физике, включающий в себя основные формулы, законы и определения. Данный сборник(глоссарий предназначен для студентов технического факультета). Рассмотрены следующие темы: Механика. Динамика. Молекулярный физика и термодинамика. Электричество и магнетизм. Оптика.
- формат jpg, htm
- размер 17.33 МБ
- добавлен 22 октября 2009 г.
Шпоры по Физике. Буквы, используемые для обозначения величин Методика решения задач по физике Векторы Основные положения, законы и формулы Механика Кинематика Динамика Статика Простые механизмы Жидкости и газы Молекулярная физика Термодинамика Электростатика Электричество Магнитное поле Колебания и волны Оптика Элементы теории относительности Квантовая физика Атомная и ядерная физика Приложения Шкала электромагнитных волн.
..
простых гармонических движений | Формула, примеры и факты
- Связанные темы:
- вибрация колебание
Просмотреть весь связанный контент →
Резюме
Прочтите краткий обзор этой темы
простое гармоническое движение , в физике повторяющееся движение вперед и назад через положение равновесия или центральное положение, при котором максимальное смещение с одной стороны этого положения равно максимальному смещению с другой стороны. Интервал времени каждой полной вибрации одинаков. Сила, ответственная за движение, всегда направлена к положению равновесия и прямо пропорциональна расстоянию от него. то есть F = − kx , где F — сила, x — перемещение, а k — постоянная. Это соотношение называется законом Гука.
Конкретным примером простого гармонического осциллятора является колебание массы, прикрепленной к вертикальной пружине, другой конец которой закреплен на потолке.
При максимальном смещении – х, пружина находится под наибольшим напряжением, которое толкает массу вверх. При максимальном водоизмещении + х, пружина достигает наибольшего сжатия, что заставляет массу снова опускаться. В любом положении максимального смещения сила наибольшая и направлена к положению равновесия, скорость ( v ) массы равна нулю, ее ускорение максимально, и масса меняет направление. В положении равновесия скорость максимальна, а ускорение ( a ) упало до нуля. Простое гармоническое движение характеризуется этим изменяющимся ускорением, которое всегда направлено к положению равновесия и пропорционально смещению от положения равновесия. При этом интервал времени для каждого полного колебания постоянен и не зависит от величины максимального смещения. Таким образом, в той или иной форме простое гармоническое движение лежит в основе хронометража.
Тест “Британника”
Физика и законы природы
Какая сила замедляет движение? Каждому действию есть равное и противоположное что? В этом викторине по физике нет ничего, что E = mc было бы квадратным.
Чтобы выразить, как смещение массы изменяется со временем, можно использовать второй закон Ньютона, F = ma , и установить ma = − kx . Ускорение a есть вторая производная от x по времени t , и можно решить полученное дифференциальное уравнение с x = A cos ω t , где A — максимальное перемещение, а ω — угловая частота в радианах в секунду. Время, которое требуется массе, чтобы переместиться от A к − A и обратно, равно времени, которое требуется ω t для перемещения на 2π. Следовательно, период T , необходимый для перемещения массы от A до − A и обратно, равен ω Т = 2π или Т = 2π/ω. Частота вибрации в циклах в секунду составляет 1/ T или ω/2π.
Многие физические системы демонстрируют простое гармоническое движение (при условии отсутствия потерь энергии): колеблющийся маятник, электроны в проводе с переменным током, вибрирующие частицы среды в звуковой волне и другие совокупности, включающие относительно небольшие колебания относительно положения устойчивого равновесия.
Движение называется гармоническим, потому что музыкальные инструменты производят такие колебания, которые в свою очередь вызывают соответствующие звуковые волны в воздухе. Музыкальные звуки на самом деле представляют собой комбинацию многих простых гармонических волн, соответствующих множеству способов, которыми вибрирующие части музыкального инструмента колеблются в наборах наложенных друг на друга простых гармонических движений, частоты которых кратны самой низкой основной частоте. В самом деле, любое регулярно повторяющееся движение и любая волна, какой бы сложной ни была ее форма, можно рассматривать как сумму ряда простых гармонических движений или волн. Это открытие впервые было опубликовано в 1822 году французским математиком Жозефом Фурье.
Редакторы Британской энциклопедии Эта статья была недавно отредактирована и обновлена Эриком Грегерсеном.
1.2: Энергия связи и полуэмпирическая формула массы
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 25690
- Паола Капелларо
- Массачусетский технологический институт через MIT OpenCourseWare
Энергия связи
Два важных свойства ядра, которые мы хотим изучить, — это энергия связи ядра и масса нуклидов.
Вы можете подумать, что, поскольку мы знаем массы протона и нейтрона, мы можем просто найти массы всех нуклидов по простой формуле:
\[m_{N} \stackrel{?}{=} Z m_{p }+N m_{n}.\] 92\). Тогда, если мы просто суммируем массы всех составляющих ядра, мы получим, сколько энергии они представляют. Масса ядра также связана с его внутренней энергией. Таким образом, имеет смысл, что это не только сумма составляющих его энергий, поскольку мы ожидаем, что какая-то другая энергия тратится на сохранение целостности ядра. Если бы энергии были равны, то иметь связанные ядра было бы невыгодно, и все ядра были бы нестабильны, постоянно переходя из своего связанного состояния в сумму протонов и нейтронов. 9{A-1} X_{N}\right)
\end{aligned}\]
, которые являются аналогами энергий ионизации в атомной физике, отражая энергии валентных нуклонов. Мы увидим, что эти энергии показывают признаки оболочечной структуры ядер.
Полуэмпирическая массовая формула
Энергия связи обычно изображается как B/A или энергия связи на нуклон.
Это показывает, что энергия связи в целом просто пропорциональна A, поскольку B/A в основном постоянна.
Однако в эту тенденцию внесены коррективы. Зависимость B/A от A (и Z) фиксируется полуэмпирической формулой массы . Эта формула основана на соображениях первого принципа (модель ядерной силы) и на экспериментальных данных, позволяющих найти точные параметры, определяющие ее. В этой модели, так называемой жидкокапельной модели , все нуклоны равномерно распределены внутри ядра и связаны между собой ядерными силами, а кулоновское взаимодействие вызывает отталкивание протонов. Характеристики ядерной силы (ее малый радиус действия) и кулоновского взаимодействия частично объясняют полуэмпирическую массовую формулу. Однако были введены другие (меньшие) поправки, учитывающие вариации энергии связи, возникающие из-за ее квантово-механической природы (и приводящие к 9{2} \nonumber\]
, где энергия связи B(Z, A) определяется следующей формулой:
Теперь мы изучим каждый член SEMF.
Объемный член
Первый член – это объемный член a v A, который описывает, как энергия связи в основном пропорциональна A. Почему это так?
Помните, что энергия связи является мерой взаимодействия между нуклонами. Поскольку нуклоны плотно упакованы в ядре, а ядерная сила имеет очень малый радиус действия, каждый нуклон в конечном итоге взаимодействует только с несколькими соседями. Это означает, что независимо от общего числа нуклонов каждый из них вносит одинаковый вклад. Таким образом, сила не пропорциональна A(A − 1)/2 ∼ A 2 (общее количество нуклонов, с которыми может взаимодействовать один нуклон), но оно просто пропорционально A. Константа пропорциональности — это подгоночный параметр, который экспериментально определен как v = 15,5 МэВ.
Эта величина меньше, чем энергия связи нуклонов с их соседями, определяемая силой ядерного (сильного) взаимодействия. Установлено (и мы изучим это позже), что энергия связи одного нуклона с другими нуклонами составляет порядка 50 МэВ.
Вместо этого полная энергия связи представляет собой разницу между взаимодействием нуклона с его соседом и кинетической энергией самого нуклона. Что касается электронов в атоме, то нуклоны — это фермионы, поэтому они не могут все находиться в одном и том же состоянии с нулевой кинетической энергией, но они будут заполнять все уровни кинетической энергии в соответствии с принципом запрета Паули. Эта модель, учитывающая энергию связи ядер и кинетическую энергию за счет заполнения оболочек, действительно дает точную оценку для 9{2 / 3}\), также основанный на сильной силе, является поправкой к объемному члену. Мы объяснили, что объемный член возникает из-за того, что каждый нуклон взаимодействует с постоянным числом нуклонов, не зависящим от A. Хотя это верно для нуклонов глубоко внутри ядра, у этих нуклонов на поверхности ядра меньше ближайших соседей. Этот термин аналогичен поверхностным силам, возникающим, например, в каплях жидкости, механизму, создающему поверхностное натяжение в жидкостях.
{2}}{R} \номер\] 9{2}}{4 \pi \epsilon_{0} R_{0}}\), где R 0 = 1,25 фм, составляет c ≈ 0,691 МэВ, что недалеко от экспериментального значения.
Член симметрии
Член Кулона, по-видимому, указывает на то, что было бы лучше иметь меньше протонов в ядре и больше нейтронов. Однако это не так, и мы должны прибегнуть к чему-то помимо жидкокапельной модели, чтобы объяснить тот факт, что у нас есть примерно одинаковое количество нейтронов и протонов в стабильных ядрах. Таким образом, в SEMF есть поправочный член, который пытается учесть симметрию протонов и нейтронов. Эту поправку (и следующую) можно объяснить только более сложной моделью ядра, 9{2}}{А}\). Это легче понять, если учесть тот факт, что этот член стремится к нулю при A = 2Z и его влияние меньше при больших A (в то время как для меньших ядер эффект симметрии более важен).
Коэффициент равен симм = 23 МэВ.
Термин спаривания
Последний термин связан с физическим доказательством того, что одноименные нуклоны имеют тенденцию образовывать пары. Тогда это означает, что энергия связи больше (δ > 0), если мы имеем четно-четное ядро, где все нейтроны и все протоны спарены. Если у нас есть ядро с нечетным числом нейтронов и протонов, то, таким образом, выгодно преобразовать один из протонов в нейтроны или наоборот (конечно, принимая во внимание другие указанные выше ограничения). Таким образом, при всех остальных постоянных факторах мы должны вычесть (δ < 0) член из энергии связи для нечетно-нечетных конфигураций. Наконец, для четно-нечетных конфигураций мы не ожидаем никакого влияния этой энергии спаривания (δ = 0). Тогда срок сопряжения равен 9.{2 / 3} \frac{a_{c}}{a_{s y m}}\right) \end{align*}\]
, что дает \(Z \приблизительно \frac{A}{2} \) в малое A, но имеет поправку на большее A, так что Z ≈ 0,41A для тяжелых ядер. [Обратите внимание, что аппроксимация и расширение ряда взяты, потому что \(a_c \ll a_{sym}\)]
Если мы построим зависимость \(Z/A\) от \(A\), то нуклиды лежат между 1/2 и 0,41 .
Существует линия стабильности, следующая за стабильными изотопами (красная на рисунке \(\PageIndex{4}\) и черная на рисунке \(\PageIndex{3}\)). Затем изотопы по-разному маркируются, например, здесь по времени их жизни. Интерактивная информация доступна на сайте www.nndc.bnl.gov/chart/.
Эта страница под названием 1.2: Энергия связи и полуэмпирическая формула массы распространяется под лицензией CC BY-NC-SA 4.
0 и была создана, изменена и/или курирована Паолой Каппелларо (MIT OpenCourseWare) через исходный контент, который был отредактирован к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Паола Капелларо
- Лицензия
- СС BY-NC-SA
- Версия лицензии
- 4,0
- Программа OER или Publisher
- MIT OpenCourseWare
- Показать оглавление
- нет
- Теги
- энергия связи
- жидкостно-капельная модель
- полуэмпирическая формула массы
- модель корпуса
- источник@https://ocw.
