в чем измеряется, обозначение, формула нахождения через частоту
Содержание:
- Что такое длина волны
- Физические характеристики волны
-
Виды волн, какие бывают
- Продольные волны
- Поперечные волны
- Стоячие волны
- Бегущие волны
-
Формулы длины волны
- Длина стоячей и бегущей волны
- Длина электромагнитной волны
- Длина звуковой волны
- Расчет длины волны через энергию фотона
- Примеры решения задач
Содержание
- Что такое длина волны
- Физические характеристики волны
-
Виды волн, какие бывают
- Продольные волны
- Поперечные волны
- Стоячие волны
- Бегущие волны
- Длина стоячей и бегущей волны
- Длина электромагнитной волны
- Длина звуковой волны
- Расчет длины волны через энергию фотона
- Примеры решения задач
Что такое длина волны
Волна — изменение характеристик физического поля или среды, способное удаляться от места возникновения или колебаться внутри ограниченной области пространства.
Длина волны — расстояние между точками, которое волна проходит за одно колебание.
Если точки отстоят на расстояние \(\lambda\) друг от друга, их смещения из положений равновесия будут одинаковы, и колебания в них будут происходить в одинаковой фазе.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В системе СИ длина волны измеряется в метрах.
Чем меньше длина волны, тем легче сконцентрировать ее энергию в заданном направлении. Поэтому, например, в эхолокации используют ультразвук. Поскольку ультразвуковые волны в воде затухают гораздо слабее, чем в воздухе, эхолокацию особенно широко используют в гидроакустике.
Физические характеристики волны
Два главных параметра волны — частота колебаний f (число полных циклов колебаний в секунду) и длина волны \(\lambda\) — зависят друг от друга.
Зная эти параметры, можно произвести вычисления, чтобы выяснить период повторения колебаний Т и скорость распространения волны v.
Интенсивность волны описывается такими параметрами, как:
- амплитуда;
- плотность энергии;
- плотность потока мощности.
Геометрически волна состоит из гребней и ложбин.
Для продольных волн чаще используют понятия точек максимального сжатия и максимального растяжения.
Для стоячих волн — понятия пучности и узла, характеризующие участки с максимальной и минимальной амплитудой колебаний.
Виды волн, какие бывают
Продольные волны
Продольные волны — волны, при которых частицы вещества колеблются перпендикулярно направлению распространения.
Они возникают при сопротивлении среды изменению ее объема, их причина — деформация сжатия/растяжения (в твердой среде) или уплотнения/разрежения (в газах и жидкостях).
Продольная волна заставляет частицы среды колебаться у своих положений равновесия, и этот процесс перемещается параллельно направлению распространения волны. Частицы сдвигаются строго по одной линии.
Частицы сдвигаются строго по одной линии.
Чтобы узнать длину волны, нужно измерить расстояние между ближайшими точками сжатия или растяжения. Продольные волны могут распространяться в любой среде: твердой, жидкой, газообразной. Во время этого процесса непрерывно изменяется давление в каждой точке среды.
Примечание
В твердых телах продольные волны распространяются быстрее, чем поперечные. Для сравнения: продольная волна движется в стали со скоростью около 5900 м/с, поперечная — примерно 3250 м/с.
Поперечные волны
Поперечные волны — волны, при которых частицы вещества колеблются перпендикулярно направлению распространения.
Они возникают при сдвиге слоев среды относительно друг друга. В поперечной волне колебания элементов происходят в направлениях, перпендикулярных направлению распространения волны. Среда стремится вернуть деформированные частицы на место, при этом на несмещенные частицы рядом со смещенными воздействуют силы упругости и отклоняют их от положения равновесия.
Длина поперечной волны — расстояние между двумя ближайшими ее впадинами или горбами.
Примечание
И продольные, и поперечные волны относятся к упругим — возникающим только в упругой среде, обладающей свойством после деформации возвращаться к прежней форме.
Стоячие волны
Стоячие волны — волновые процессы в распределенных колебательных системах с устойчивым в пространстве расположением участков с максимальной и минимальной амплитудой.
Самую простую одномерную стоячую волну можно возбудить, запустив колебательный процесс с одного конца стержня или гибкой струны. Добравшись до конца стержня или струны, волна отразится, что вызовет наложение.
Бегущие волны
Бегущие волны — процессы последовательного изменения (с определенным запаздыванием) состояния взаимодействующих тел, когда они друг за другом приходят в движение.
Ее можно запустить, например, в системе из косточек домино, выстроенных строго друг за другом на ровной поверхности. Если осторожно толкнуть первую, она, падая, уронит вторую, та — следующую, и в результате такого последовательного падения по ряду побежит волна.
Формулы длины волны
Длина стоячей и бегущей волны
\(\lambda_{}\;=\;v\;\times\;T\;=\;\frac vf\;=\;\frac{2\mathrm{πv}}\omega\)
v здесь — фазовая скорость волны, Т — период колебаний, f — частота, \(\omega\) — круговая частота.
Длина стоячей волны — это расстояние между двумя пучностями или двумя узлами, которое можно рассчитать с помощью формулы:
\(\lambda_{ст}\;=\;\frac\lambda2.\)
Длина стоячей волны равна половине длины соответствующей бегущей волны, так как возникает при наложении двух волн, падающей и отраженной, и сумма их амплитуд равна нулю.
Длина электромагнитной волны
Электромагнитная волна — это электрическое и магнитное поля, взаимно превращающиеся друг в друга. 8\;\frac мс.\)
8\;\frac мс.\)
Длина звуковой волны
Колебания частотой от 16 до 20 000 Гц воспринимаются ухом человека. Колебания источников звуковых волн, например, струн или голосовых связок, создают в среде последовательно сменяющие друг друга сжатия и разрежения.
Когда периодические изменения давления достигают барабанной перепонки, она совершает вынужденные колебания. Эти колебания анализирует по амплитуде и частоте внутреннее ухо, имеющее форму улитки, рецепторы которого настроены на различные звуковые частоты. Затем колебания передаются в мозг по слуховому нерву и воспринимаются как слышимые звуки.
Длину звуковой волны вычисляют по общей формуле:
\(\lambda\;=\;v\;\times\;T\;.\)
Расчет длины волны через энергию фотона
Электромагнитное излучение испускается не непрерывно, а отдельными порциями, которые называют квантами или фотонами. Их энергия пропорциональна частоте и высчитывается по формуле:
\(E\;=\;h\times\nu\)
Где h — постоянная Планка, равная \(6,6\;\times\;10^{-34}\;Дж\times с. {-19}\;Дж.\)
{-19}\;Дж.\)
Кванты видимого излучения обладают энергиями 2–3 эВ и занимают лишь небольшую область исследуемого в астрофизике электромагнитного спектра, который простирается от значений энергии порядка миллионных долей электронвольта для метровых радиоволн до миллионов электронвольт для гамма-излучения.
Так как частота равна скорости распространения излучения, деленной на длину волны, длину волны можно вычислить, зная энергию фотона и частоту.
\(\lambda\;=\frac{\;h\times\;c\;}E\)
Примеры решения задач
Задача № 1
Найдите длину волны при звучании ноты «ля», если известно, что частота ее колебаний равна 440 Гц, а скорость распространения звука в воздухе — 340 м/с.
Решение:
\(\lambda\;=\;v\;\times\;T\;\)
Для нахождения периода Т воспользуемся формулой \(Т\;=\frac{\;1\;}f. \)
\)
Следовательно, \(\lambda\;=\;\frac{v\;}f.\)
Подставив известные данные, получим \(\lambda\;=\;\frac{340\;}{440}\;=\;0,78\;м.\)
Ответ: 78 см.
Задача № 2
Найдите длину волны, если известно, что ее скорость 8 м/с, а период — 1 час.
Решение:
\(\lambda\;=\;v\;\times\;T\;\)
1 час = 3600 секунд
Подставив известные данные, получим \(\lambda\;=\;8\;\times\;3600\;=\;28800\;м.\)
Ответ: 28800 м.
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Поиск по содержимому
Все формулы окружности. Длина окружности формула через диаметр. Площадь круга через диаметр.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы “Альфа”. Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку “Записаться” принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Оксана Александровна Латтеган
Репетитор по математике
Стаж (лет)
Образование:
Новосибирский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Камо Аркадьевич Филипосян
Репетитор по математике
Стаж (лет)
Образование:
Самаркандский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Наталья Анатольевна Люфт
Репетитор по математике
Стаж (лет)
Образование:
Новосибирскй педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Подготовка к ЕГЭ по математике (базовый уровень)
- Репетитор по химии для подготовки к ОГЭ
- Репетитор для подготовки к ЕГЭ по физике
- Репетитор по русскому языку для подготовки к ЕГЭ
- Репетитор для подготовки к сочинению ЕГЭ по русскому
- Подготовка к олимпиадам по английскому языку
- Разговорный английский язык
- ВПР по физике
- Репетитор для подготовки к ЕГЭ по обществознанию
- Подготовка к ЕГЭ по информатике
Похожие статьи
- Признаки делимости (Часть 1)
- Объем и площадь параллелепипеда
- Свойства скалярного произведения
- Как легко умножить на 0,5
- Как вычислить 50 процентов от числа?
- Бизнес-информатика (РУДН)
- Теорема косинусов
- Учимся оказывать первую помощь себе и друзьям
Нажимая кнопку “Записаться” принимаю условия Пользовательского соглашения и Политики конфиденциальности
Текст с ошибкой:
Расскажите, что не так
1.
 4 Анализ размерностей – University Physics Volume 1
4 Анализ размерностей – University Physics Volume 11 Единицы и измерения
Цели обучения
К концу этого раздела вы сможете:
- Находить размерности математического выражения, включающего физические величины.
- Определить, является ли размерно-согласованным уравнение, включающее физические величины.
Размерность любой физической величины выражает ее зависимость от основных величин как произведение символов (или степеней символов), представляющих основные величины. На рисунке перечислены основные величины и символы, используемые для их измерения. Например, говорят, что измерение длины имеет размерность L или L 1 , измерение массы имеет размерность M или M 1 , а измерение времени имеет размерность T или T 1 . Как и единицы, измерения подчиняются правилам алгебры. Таким образом, площадь является произведением двух длин и поэтому имеет размерность L 2 , или длину в квадрате. Точно так же объем является произведением трех длин и имеет размерность L 3 , или длину в кубе. Скорость имеет размерность длины во времени, L/T или LT –1 . Объемная массовая плотность имеет размерность M/L .{0}[/latex]) называется безразмерным (или иногда «размерностью 1», потому что все, что возведено в нулевую степень, равно единице). Физики часто называют безразмерные величины чистыми числами .
Точно так же объем является произведением трех длин и имеет размерность L 3 , или длину в кубе. Скорость имеет размерность длины во времени, L/T или LT –1 . Объемная массовая плотность имеет размерность M/L .{0}[/latex]) называется безразмерным (или иногда «размерностью 1», потому что все, что возведено в нулевую степень, равно единице). Физики часто называют безразмерные величины чистыми числами .
| Базовое количество | Символ размера |
|---|---|
| Длина | л |
| Масса | М |
| Время | Т |
| Текущий | я |
| Термодинамическая температура | Θ |
| Количество вещества | Н |
| Сила света | Дж |
Физики часто используют квадратные скобки вокруг символа физической величины, чтобы представить размеры этой величины. Например, если [latex]r[/latex] — это радиус цилиндра, а [latex]h[/latex] — его высота, то мы пишем [latex][r]=\text{L}[/latex] и [latex][h]=\text{L}[/latex], чтобы указать, что размеры радиуса и высоты совпадают с размерами длины или L. Точно так же, если мы используем символ [latex]A[/latex] для площади поверхности цилиндра и [латекс]V[/латекс] для его объема, то [ 9{-3}.[/латекс]
Например, если [latex]r[/latex] — это радиус цилиндра, а [latex]h[/latex] — его высота, то мы пишем [latex][r]=\text{L}[/latex] и [latex][h]=\text{L}[/latex], чтобы указать, что размеры радиуса и высоты совпадают с размерами длины или L. Точно так же, если мы используем символ [latex]A[/latex] для площади поверхности цилиндра и [латекс]V[/латекс] для его объема, то [ 9{-3}.[/латекс]
Важность концепции размерности возникает из-за того факта, что любое математическое уравнение, связывающее физические величины, должно быть размерно-согласованным, что означает, что уравнение должно подчиняться следующим правилам:
- Каждый термин в выражении должен иметь одинаковые размеры; нет смысла прибавлять или вычитать количества разной размерности (вспомните старую поговорку: «Нельзя складывать яблоки и апельсины»). В частности, выражения по обе стороны равенства в уравнении должны иметь одинаковые размерности.
- Аргументы любых стандартных математических функций, таких как тригонометрические функции (такие как синус и косинус), логарифмы или экспоненциальные функции, которые появляются в уравнении, должны быть безразмерными.
 Эти функции требуют чистых чисел в качестве входных данных и дают чистые числа в качестве выходных данных.
Эти функции требуют чистых чисел в качестве входных данных и дают чистые числа в качестве выходных данных.
Если какое-либо из этих правил нарушается, уравнение не является размерно-согласованным и не может быть правильной формулировкой физического закона. Этот простой факт можно использовать для проверки опечаток или алгебраических ошибок, чтобы помочь вспомнить различные законы физики и даже предложить форму, которую могут принять новые законы физики. Это последнее использование измерений выходит за рамки этого текста, но вы, несомненно, узнаете об этом позже в своей академической карьере. 9{2}[/latex] и [latex]2\pi r.[/latex] Одно выражение — это длина окружности круга радиусом r , а другое — его площадь. Но что есть что?
Стратегия
Естественная стратегия — искать информацию, но это может занять время, чтобы найти информацию из авторитетного источника. Кроме того, даже если мы считаем источник авторитетным, мы не должны доверять всему, что читаем. {2},[/латекс], то размерные анализ не поможет), но помогает нам запомнить правильную основную форму уравнений. 9{2}\text{/}s).[/latex]
{2},[/латекс], то размерные анализ не поможет), но помогает нам запомнить правильную основную форму уравнений. 9{2}\text{/}s).[/latex]
Стратегия
В соответствии с определением размерной согласованности нам нужно проверить, что каждый член в данном уравнении имеет те же размерности, что и другие члены в этом уравнении, и что аргументы любых стандартных математических функций безразмерны.
Решение
- В этом уравнении нет ни тригонометрических, ни логарифмических, ни экспоненциальных функций, поэтому нам достаточно посмотреть на размеры каждого члена, входящего в уравнение. Есть три термина, один в левом выражении и два в выражении справа, поэтому мы рассмотрим каждый по очереди: 9{2}}{s})\right ]=1.}\hfill \end{массив}[/latex]
Два термина имеют разные размерности — это означает, что уравнение не является размерно-согласованным. Это уравнение — еще один пример «бессмыслицы».
Значение
Если мы доверяем людям, эти виды размерных проверок могут показаться ненужными. Но, будьте уверены, любой учебник по количественному предмету, такому как физика (включая этот), почти наверняка содержит некоторые уравнения с опечатками. Регулярная проверка уравнений с помощью размерного анализа избавляет нас от необходимости использовать неверное уравнение. Кроме того, проверка размерностей уравнения, которое мы получаем с помощью алгебраических манипуляций, — отличный способ убедиться, что мы не допустили ошибку (или обнаружить ошибку, если она была допущена).
Но, будьте уверены, любой учебник по количественному предмету, такому как физика (включая этот), почти наверняка содержит некоторые уравнения с опечатками. Регулярная проверка уравнений с помощью размерного анализа избавляет нас от необходимости использовать неверное уравнение. Кроме того, проверка размерностей уравнения, которое мы получаем с помощью алгебраических манипуляций, — отличный способ убедиться, что мы не допустили ошибку (или обнаружить ошибку, если она была допущена).
Проверьте свое понимание
Является ли уравнение v = при размерно-согласованным?
Показать решениеда
Еще один момент, о котором следует упомянуть, — это влияние операций исчисления на размерности. Мы видели, что размеры подчиняются правилам алгебры, как и единицы, но что происходит, когда мы берем производную одной физической величины по отношению к другой или интегрируем физическую величину по другой? Производная функции — это просто наклон линии, касательной к ее графику, а наклоны — это отношения, поэтому для физических величин v и t , мы имеем, что размерность производной v по отношению к t есть просто отношение размерности v к размерности t :
[латекс][\frac{dv}{dt}]=\frac{[v]}{[t]}. [/latex]
[/latex]
Точно так же, поскольку интегралы представляют собой просто суммы произведений, размерность интеграла v по отношению к t — это просто размерность v , умноженная на размерность t :
[латекс][\int vdt]=[v]\cdot [т].[/латекс]
По тем же рассуждениям аналогичные правила справедливы для единиц физических величин, полученных из других величин интегрированием или дифференцированием.
Резюме
- Размерность физической величины — это просто выражение основных величин, из которых она получена.
- Все уравнения, выражающие физические законы или принципы, должны быть согласованы по размерам. Этот факт можно использовать как помощь в запоминании физических законов, как способ проверить, возможны ли заявленные соотношения между физическими величинами, и даже для вывода новых физических законов. 9{2};[/latex] (c) [latex]v=s\text{/}t;[/latex] (d) [latex]a=v\text{/}t.[/latex] Показать Решение
а.
 Да, оба члена имеют размерность L 2 T -2 b. № с. Да, оба термина имеют размерность LT -1 d. Да, оба члена имеют размерность LT -2
Да, оба члена имеют размерность L 2 T -2 b. № с. Да, оба термина имеют размерность LT -1 d. Да, оба члена имеют размерность LT -2 Рассмотрим физические величины [латекс]м,[/латекс] [латекс]с,[/латекс] [латекс]в,[/латекс] [латекс]а,[/латекс] и [латекс]т[/латекс] с размерами [ м ] = M, [ s ] = L, [ v ] = LT –1 , [ a ] = LT –2 и [ t ] = T. Предполагая, что каждое из следующих уравнений размерностно согласовано, найдите размерность величины в левой части уравнение: (а) F = мА ; б) К = 0,5 mv 2 ; в) р = mv ; (г) Вт = мсек. дуги ; (e) L = mvr .
Предположим, что количество [latex]s[/latex] — это длина, а количество [latex]t[/latex] — это время. Предположим, что величины [латекс]v[/латекс] и [латекс]а[/латекс] определены как 9{–3},[/latex] и [t] = T.
 (a) Какова размерность [latex]\int \rho dV?[/latex] (b) Какова размерность dV / дт ? (c) Какова размерность [латекс]\ро (dV\текст{/}dt)?[/латекс]
(a) Какова размерность [latex]\int \rho dV?[/latex] (b) Какова размерность dV / дт ? (c) Какова размерность [латекс]\ро (dV\текст{/}dt)?[/латекс]Формула длины дуги говорит длину [латекс]s[/латекс] дуги, опирающейся на угол [ латекс]Ɵ[/латекс] в окружности радиуса [латекс]r[/латекс] задается уравнением [латекс]s=rƟ.[/латекс] Каковы размеры (а) s , (b ) r и (c) [латекс]\текст{Ɵ?}[/латекс] 9{0}=1;[/latex] также называется количеством измерения 1 или чистым числом.
Длина дуги (расчет)
Использование вычислений для определения длины кривой .
(Сначала прочтите о производных и интегралах)Представьте, что мы хотим найти длину кривой между двумя точками. И кривая гладкая (производная непрерывна).
Сначала мы разбиваем кривую на маленькие отрезки и используем формулу расстояния между 2 точками для каждого отрезка, чтобы получить приблизительный ответ:
Расстояние от x 0 до x 1 составляет:
S 1 = √ (х 1 – х 0 ) 2 + (у 1 – у 0 ) 2
И давайте использовать Δ (дельта) для обозначения разницы между значениями, так что получается:
S 1 = √ (Δx 1 ) 2 + (Δy 1 ) 2
Теперь нам нужно намного больше:
S 2 = √ (Δx 2 ) 2 + (Δy 2 ) 2
S 3 = √ (Δx 3 ) 9 29998 2 2 2 2 2 2 2 2 2 2 2 2 . 2
2
…
…
S n = √(Δx n ) 2 + (Δy n ) 2Мы можем записать все эти строки всего за одну строку используя Sum:
С ≈
√(Δx i ) 2 + (Δy i ) 2
Но мы все равно обречены на большое количество вычислений!
Может быть, мы можем сделать большую электронную таблицу или написать программу для вычислений… но давайте попробуем что-нибудь еще.
У нас есть хитрый план:
- все Δx i будут одинаковыми , поэтому мы можем извлечь их из квадратного корня
- , а затем превратить сумму в интеграл.
Поехали:
Сначала разделите и , умножьте Δy i на Δx i :
С ≈
√(Δx i ) 2 + (Δx i ) 2 (Δy i /Δx i ) 2
Теперь вычтите (Δx i ) 2 :
С ≈
√(Δx i ) 2 (1 + (Δy i /Δx и ) 2 )
Возьмем (Δx i ) 2 из квадратного корня:
С ≈
√1 + (Δy i /Δx i ) 2 Δx i
Теперь, когда n приближается к бесконечности (по мере того, как мы приближаемся к бесконечному количеству срезов, и каждый срез становится меньше), мы получаем:
С =
lim
n→∞
√1 + (Δy i /Δx i ) 2 ∆x i
Теперь у нас есть интеграл, и мы пишем dx , чтобы обозначить, что Δx срезов приближаются к нулю по ширине (аналогично для dy) :
С =
√1+(dy/dx) 2 dx
И dy/dx является производной функции f(x), которую также можно записать как f’(x) :
С =
√1+(f’(x)) 2 dx
Формула длины дугиА теперь вдруг мы в гораздо лучшем месте, нам не нужно складывать множество срезов, мы можем вычислить точный ответ (если мы сможем решить дифференциал и интеграл).

Примечание: интеграл также работает по y, полезно, если мы знаем x=g(y):
С =
√1+(g’(y)) 2 dy
Итак, наши шаги:
- Найдите производную от f’(x)
- Решите интеграл от √1 + (f’(x)) 2 дх
Несколько простых примеров для начала:
Пример: Найдите длину f(x) = 2 между x=2 и x=3
f(x) — это просто горизонтальная линия, поэтому ее производная равна f'(x) = 0
Начните с:
S =
√1+(f’(x)) 2 dx
Введите f’(x) = 0 :
S =
√1+0 2 дх
Упрощение:
С =
dx
Вычислить интеграл:
S = 3 − 2 = 1
Таким образом, длина дуги между 2 и 3 равна 1.
 Конечно, это так, но приятно, что мы нашли правильный ответ!
Конечно, это так, но приятно, что мы нашли правильный ответ!Интересный момент: часть «(1 + …)» формулы длины дуги гарантирует, что мы получим по крайней мере расстояние между значениями x, например, в этом случае, когда f’(x) равно нулю.
Пример: Найдите длину f(x) = x между x=2 и x=3
Производная f’(x) = 1
Начните с:S =
√1+(f’(x)) 2 dx
Введите f’(x) = 1 :
S =
√1+(1) 2 дх
Упрощение:
S =
√2 дх
Вычислить интеграл:
S = (3−2)√2 = √2
А диагональ единичного квадрата действительно равна квадратному корню из 2, верно?
Хорошо, теперь о более сложном.
 Пример реального мира.
Пример реального мира.Пример: Металлические столбы установлены
на расстоянии 6 м друг от друга через ущелье.Найдите длину висячего моста, следующего за кривой:
f(x) = 5 ch(x/5)
Вот реальная кривая:
Сначала решим общий случай!
Висячий трос образует кривую, называемую контактной сетью :
f(x) = a cosh(x/a)
Большие значения и имеют меньший прогиб посередине
И “cosh” – это функция гиперболического косинуса.Производная равна f'(x) = sh(x/a)
Кривая симметрична, поэтому легче работать только с половиной контактной сети, от центра до конца в точке “b”:
Начните с:
S =
√1+(f’(x)) 2 dx
Введите f’(x) = sh(x/a) :
S =
√1 + sin 2 (x/a) dx
Используйте идентификатор 1 + sinh 2 (x/a) = cosh 2 (x/a):
S =
√кош 2 (x/a) dx
Упрощение:
S =
кош(х/а) дх
Вычислить интеграл:
S = a sh(b/a)
Теперь, помня о симметрии, перейдем от −b к +b:
S = 2a sh(b/a)
В нашем конкретный случай a=5 и 6-метровый пролет меняется от −3 до +3
S = 2×5 sh(3/5)
= 6,367 м (с точностью до миллиметра)Это важно знать! Если мы построим его ровно 6 м в длину, то никоим образом не сможем тянуть его достаточно сильно, чтобы он соответствовал стойкам.
 Но на 6,367 м он будет работать прекрасно.
Но на 6,367 м он будет работать прекрасно.Пример: Найдите длину y = x
(3/2) от x = 0 до x = 4.)
Начать с:
С =
√1+(f’(x)) 2 dx
Вставить (3/2)x (1/2) :
S =
√1+((3/2)x (1/2) ) 2 дх
Упрощение:
S =
√1+(9/4)х дх
Мы можем использовать интегрирование путем замены:
- u = 1 + (9/4)x
- ду = (9/4) дх
- (4/9)ду = дх
- Границы: u(0)=1 и u(4)=10
Получаем:
С =
(4/9)√у ду
Интегрировать:
S = (8/27) u (3/2) от 1 до 10
Вычислить:
S = (8/27) (10 (3/2) − 9 1 9001 (3/2) ) = 9,073.


 Эти функции требуют чистых чисел в качестве входных данных и дают чистые числа в качестве выходных данных.
Эти функции требуют чистых чисел в качестве входных данных и дают чистые числа в качестве выходных данных. Да, оба члена имеют размерность L 2 T -2 b. № с. Да, оба термина имеют размерность LT -1 d. Да, оба члена имеют размерность LT -2
Да, оба члена имеют размерность L 2 T -2 b. № с. Да, оба термина имеют размерность LT -1 d. Да, оба члена имеют размерность LT -2  (a) Какова размерность [latex]\int \rho dV?[/latex] (b) Какова размерность dV / дт ? (c) Какова размерность [латекс]\ро (dV\текст{/}dt)?[/латекс]
(a) Какова размерность [latex]\int \rho dV?[/latex] (b) Какова размерность dV / дт ? (c) Какова размерность [латекс]\ро (dV\текст{/}dt)?[/латекс] 2
2 
 Конечно, это так, но приятно, что мы нашли правильный ответ!
Конечно, это так, но приятно, что мы нашли правильный ответ!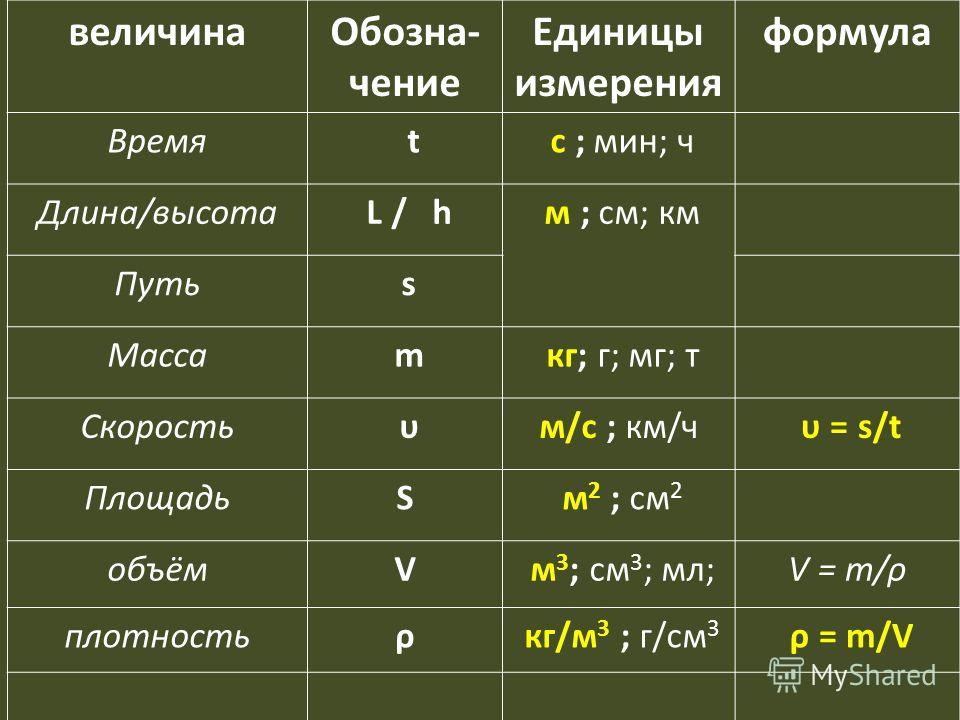 Пример реального мира.
Пример реального мира. Но на 6,367 м он будет работать прекрасно.
Но на 6,367 м он будет работать прекрасно.