Формулы энергии в физике: Ошибка: 404 Материал не найден

Закон сохранения энергии, общая форма. Полная энергия: механическая, кинетическая, потенциальная. Формулировка, формулы

Тестирование онлайн

Закон сохранения энергии

Полная механическая энергия замкнутой системы тел остается неизменной

Закон сохранения энергии можно представить в виде

Если между телами действуют силы трения, то закон сохранения энергии видоизменяется. Изменение полной механической энергии равно работе сил трения

Рассмотрим свободное падение тела с некоторой высоты h2. Тело еще не движется (допустим, мы его держим), скорость равна нулю, кинетическая энергия равна нулю. Потенциальная энергия максимальная, так как сейчас тело находится выше всего от земли, чем в состоянии 2 или 3.

В состоянии 2 тело обладает кинетической энергией (так как уже развило скорость), но при этом потенциальная энергия уменьшилась, так как h3 меньше h2. Часть потенциальной энергии перешло в кинетическую.

Состояние 3 – это состояние перед самой остановкой. Тело как бы только-только дотронулось до земли, при этом скорость максимальная. Тело обладает максимальной кинетической энергией. Потенциальная энергия равна нулю (тело находится на земле).

Полные механические энергии равны между собой , если пренебрегать силой сопротивления воздуха. Например, максимальная потенциальная энергия в состоянии 1 равна максимальной кинетической энергии в состоянии 3.

А куда потом исчезает кинетическая энергия? Исчезает бесследно? Опыт показывает, что механическое движение никогда не исчезает бесследно и никогда оно не возникает само собой. Во время торможения тела произошло нагревание поверхностей. В результате действия сил трения кинетическая энергия не исчезла, а превратилась во внутреннюю энергию теплового движения молекул.

При любых физических взаимодействиях энергия не возникает и не исчезает, а только превращается из одной формы в другую.

Главное запомнить

1) Суть закона сохранения энергии

Закон сохранения механической энергии: определение, формулы

Майер предположил, что кровь не меняет цвет, поскольку организму в тропическом климате нет необходимости тратить кислород на поддержание

температуры тела.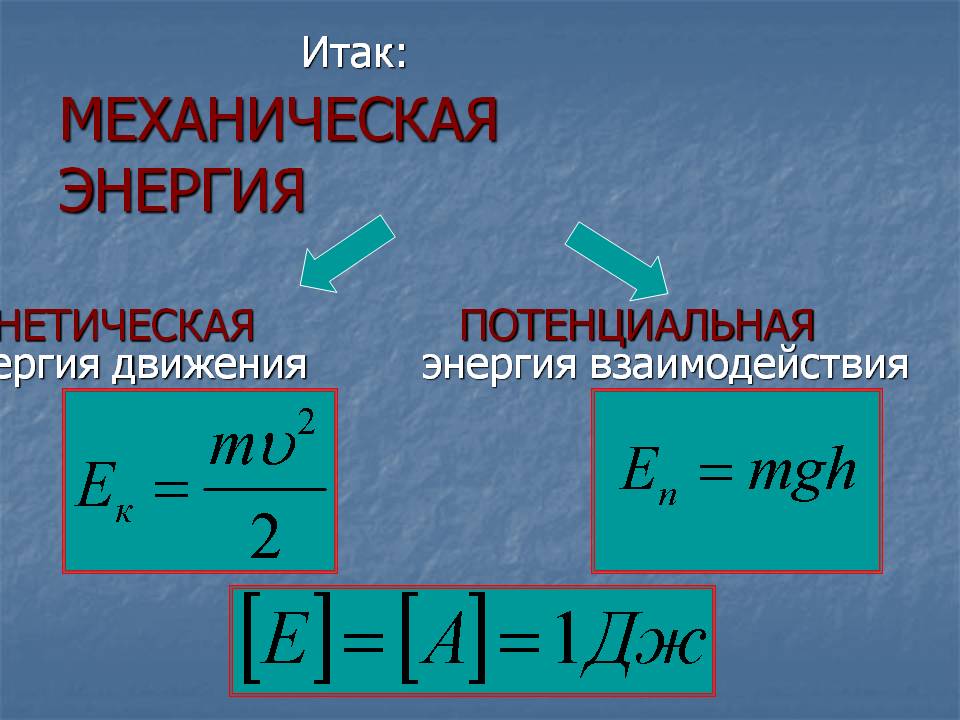 Вернувшись на родину, перед тем как сформулировать закон сохранения механической энергии, Майер продолжил опыты с открытыми на то время разновидностями энергии:

• кинетической,
• потенциальной,
• внутренней,
• механической;
  

…и смог определить, в чем заключается закон сохранения механической энергии.

«Тепло, электричество и перемещение представляют собою феномены, которые могут быть сведены к одной силе, измеряются друг другом и переходят друг в друга по определенным законам» — излагал в своей научной работе Майер.

Английский физик Джеймс Джоуль, чье имя носит единица измерения энергии, и германский естествоиспытатель Герман Гельмгольц несколькими годами позже также
описали закон сохранения энергии.

Физика. 8 класс. Учебник.

Учебник соответствует Федеральному государственному образовательному стандарту основного общего образования. Большое количество красочных иллюстраций, разнообразные вопросы и задания, а также дополнительные сведения и любопытные факты способствуют эффективному усвоению учебного материала.

Купить

Кинетическая и потенциальная энергия

Энергия тела — физическая величина, определяющая работу наблюдаемого тела или системы тел за бесконечно долгое время.

В изучении механических явлений рассматривают

потенциальную и кинетическую энергии.

• Единица энергии в СИ 1 Джоуль (Дж).

Кинетическая энергия — энергия, которой обладает тело в движении (вращении, перемещении в пространстве).

Футбольный мяч, летящий в ворота, летящая в цель стрела, выпущенная метким лучником, едущие с горы сани с сидящим в них хохочущим ребенком — все они во время движения характеризуются кинетической энергией.

Кинетическая энергия напрямую зависит от массы тела и скорости перемещения.

Формула кинетической энергии Е_к = mv

2/2

Где где m — масса объекта;

v  — скорость перемещения объекта в конкретной точке.

Потенциальная энергия. Само по себе тело потенциальной энергией не обладает.  Этот вид энергии характеризует взаимосвязь элементов объекта или двух отдельных тел в пространстве.

Стоящие на вершине холма санки, стрела, вложенная лучником в натянутую тетиву, ядро в стволе средневековой пушки — пример объекта, обладающего потенциальной энергией.

Потенциальная энергия бывает положительной или отрицательной относительно определенного условного нулевого уровня, принятого для системы координат:

• сила тяжести,
• сила упругости,
• архимедова сила

Потенциальная энергия объекта зависит от приложенных к нему сил.

Если оценивать расположение объекта в отношении уровня Земли, то потенциальная энергия объекта на поверхности планеты принимается за ноль.

Уравнение Е_п = mɡh поможет рассчитать потенциальную энергию на высоте h:
где m — масса тела;
ɡ – ускорение свободного падения;
h — высота центров масс объектов относительно поверхности планеты;
ɡ = 9,8 м/с²

Потенциальная энергия упруго деформированного объекта (пружины) рассчитывается согласно уравнению:

Е_п = k·(∆x)²/2,
где k — коэффициент жёсткости,
∆x — изменение длины объекта вследствие его сжатия или растяжения.

Подробно различные виды потенциальной энергии разбираются на странице 131 учебника «Физика 10 кл. под редакцией Касьянова В. А.»

Физика. 9 класс. Учебник.

Учебник отличаются качественным современным оформлением, в нём приводятся многочисленные слайды и микрофотографии. Выполняя проблемные, поисковые и исследовательские задания, школьники не только активно усваивают материал, но и учатся мыслить, искать и анализировать информацию из разных источников, в том числе из интернета.

Особое внимание уделяется практическим заданиям: ученикам предлагается проводить опыты, конструировать модели, разрабатывать проекты.

Купить Закон превращения и сохранения энергии

Суммарное число значений потенциальной и кинетической энергий объекта обозначают как механическая энергия. Для каждого конкретного объекта механическая энергия определяется не выбором системы отсчета, в которой рассчитывают скорость движения исследуемого объекта, а установлением уровня условного нуля для всех видов потенциальных энергий, определенных у данного объекта.

Механическая энергия определяет свойство объекта (системы объектов) совершать работу за счет изменения скорости перемещения объекта или изменения расположения взаимодействующих объектов относительно друг друга.

Что ещё почитать?

Сформулируем закон сохранения механической энергии с помощью математического уравнения:

Е_k1 + Е_п1 = Е_k2 + Е_п2

Глядя на представленную формулу видно, что энергия не появляется из ниоткуда и не исчезает в неизвестном направлении; лишь происходит преобразование одной разновидности в другую или переход между взаимодействующими объектами.

В изолированной или закрытой системе, т.е. системе, на которую не оказывают влияния силы извне или их возможно игнорировать, энергетический обмен с внешней средой не происходит, и внутренняя энергия объекта не изменяется. В ней могут происходить лишь превращения потенциальной энергии в кинетическую и наоборот. В учебнике «Физика. 10 класс» под редакцией В. А. Касьянова на портале LECTA разобраны примеры задач на закон сохранения энергии.

#ADVERTISING_INSERT#

Формула кинетической энергии в физике

Содержание:

Определение и формула кинетической энергии

Определение

Кинетическую энергию тела определяют при помощи работы, которая совершается телом при его торможении от начальной скорости, до скорости, равной нулю.

Кинетическая энергия тела – мера механического движения тела. Она зависит от относительной скорости тел.

Встречаются следующие обозначения кинетической энергии: E_k,W_k,T. {2}}{2 J}=\frac{L \omega}{2}(4)$$

где J – момент инерции тела по отношению к оси вращения, ?–модуль угловой скорости вращения тела, r – расстояние от элементарного участка тела до оси вращения, L – проекция момента импульса вращающегося тела на ось во круг которой идет вращение.

Если твердое тело совершает вращение относительно неподвижной точки (например, точки O), то его кинетическую энергию находят как:

$$E_{k}=\frac{\bar{L} \bar{\omega}}{2}(5)$$ $\bar{L}$ – момент импульса рассматриваемого тела относительно точки О.

Единицы измерения кинетической энергии

Основной единицей измерения кинетической энергии (как и любого другого вида энергии) в системе СИ служит:

[E_k]=Дж (джоуль),

в системе СГС –[E_k]= эрг.

При этом: 1 дж= 10⁷ эрг.

Теорема Кенига

Для самого общего случая при расчете кинетической энергии применяют теорему Кенига. В соответствии с которой, кинетическая энергия совокупности материальных точек есть сумма кинетической энергии поступательного перемещения системы со скоростью центра масс (v_c) и кинетической энергии (E’_k) системы при ее относительном движении к поступательному перемещению системы отсчета. {2}}+1}$

Читать дальше: Формула массы тела.

Масса, энергия, импульс и закон сохранения / Хабр

Множество непонятных свойств мира связаны с природой массы и энергии (а также импульса). Все мы слышали эти слова и у многих из нас есть туманное представление об их значении. Конечно, значений у слов «масса» и «энергия» в английском и других языках довольно много. К сожалению, ни одно из них не совпадает с теми, что имеют в виду физики. Попробуйте отставить в сторону эти значения слов и поработать с точными физическими понятиями – иначе вы полностью запутаетесь.

Необходимо отметить, что не стоит при словосочетании «масса и энергия» вспоминать другую популярную пару, «вещество и энергия». Многие люди упоминают последнее словосочетания так, будто вещество и энергия – это две стороны одной медали. Но это не так. Вещество и энергия относятся к разным категориям, как яблоки и орангутанги. Вещество, не важно, как его определять – это класс объектов, существующих во Вселенной, а масса и энергия – это не объекты, а свойства, которыми эти объекты обладают. Масса и энергия глубоко переплетены друг с другом, и заслуживают общего объяснения.

Чтобы понять массу и энергию, необходимо добавить к ним импульс и обсудить различия и связи этих величин.

Энергия

У слова «энергия» есть множество значений. Когда мы заболеваем, то говорим о том, что у нас не осталось энергии, имея в виду силу и мотивацию. Когда мы говорим, что у кого-то полно энергии, мы имеем в виду его высокую активность. Мы жалуемся на рост цен на энергию, имея в виду топливо. Мы говорим о духовной энергии как о чём-то неизмеримом, но важном, возможно, о некоей форме харизмы. И все эти понятия перекликаются друг с другом, поэтому мы и выбираем одно слово для их описания. Но в физике энергия – это совсем другое. С точки зрения физики ошибочно будет смешивать одно из этих определений с физическим. В физике нужно придерживаться физического термина, чтобы не получить неправильные ответы и не запутаться вконец.

К несчастью, понятие «энергии» в физике очень сложно описать так, как это делают словари – короткой содержательной фразой. Но не подумайте плохого – всё дело в несовершенстве естественного языка, а не в том, что понятие энергии в физике расплывчато. В любой заданной физической системе совершенно понятно, какова её энергия, как в смысле её экспериментального измерения, так и в смысле расчётов (при наличии описывающих систему уравнений).

Одна из причин, по которым энергию так сложно описать – она может принимать множество форм, и не все из них просто понять. Вот три наиболее часто встречающихся разновидности:

1. Энергия может быть заключена в массе объекта. Здесь я называю такой вариант «энергией массы» (благодаря известному уравнению E=mc² энергия связывается с массой. Также она называется «энергия покоя», поскольку это энергия объекта, находящегося в покое, то есть, без движения).

2. Во-вторых, энергия бывает связанной с движением объекта. Здесь я называю её «энергией движения», а технический термин для этого – кинетическая энергия. Этот вариант интуитивно легко воспринять, поскольку у быстро движущихся объектов энергия больше, чем у медленно движущихся.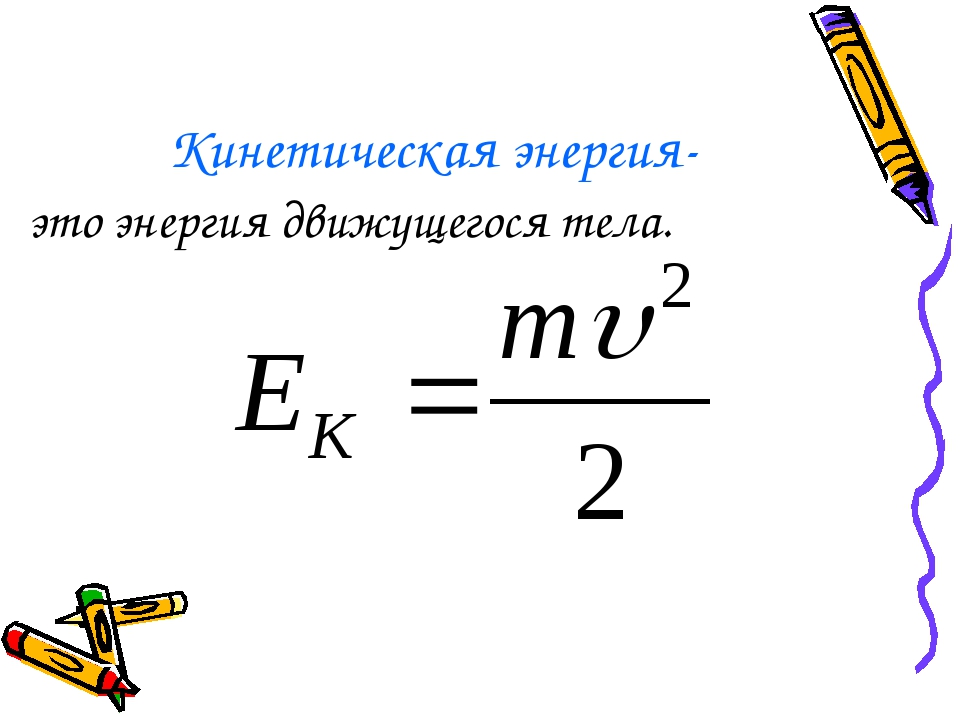 Кроме того, у тяжёлого объекта энергия движения больше, чем у лёгкого, движущегося с той же скоростью.

3. Энергия может храниться во взаимоотношении объектов (и обычно называется «потенциальной»). Она хранится в растянутой пружине, в воде за дамбой, в гравитационном взаимодействии Земли и Солнца, во взаимодействиях атомов в молекуле. Существует множество способов хранения энергии. Звучит расплывчато, но в этом виноват язык. В любом из перечисленных случаев существуют точные формулы, описывающие сохранённую в системе энергию и хорошо определённые пути её измерения.

С третьим типом энергии связано то, что я буду называть энергией взаимодействия, и это наиболее запутанное понятие из всех. В отличие от энергии массы и энергии движения, которые всегда больше или равны нулю, энергия взаимодействий может быть положительной и отрицательной. Пока я оставлю эту тему, но мы к ней ещё вернёмся.

Энергия – это особая величина огромной важности для физики. Причина такой важности – в том, что она «сохраняется». Что же это означает?

Если вы начнёте наблюдение с объекта или с набора объектов – назовём их «системой объектов» – обладающих определённым количеством энергии в начальный момент (не забудьте подсчитать всю энергию – массы, движения, сохранённую энергию всех типов, и т.п.), а затем части системы будут взаимодействовать только друг с другом и более ни с чем, тогда в конце наблюдения общее количество энергии, которым обладают эти объекты, будет тем же, что и в начале. Общая энергия системы сохраняется – её общее количество не меняется. Она может менять форму, но если отслеживать все разновидности, то в конце её будет столько же, сколько и в начале.

Это правило работает, даже если некоторые объекты будут исчезать и уступать место другим, к примеру, если одна частица в системе распадётся на две других, вливающихся в систему.

Почему энергия сохраняется? Из-за математического принципа, соотносящего тот факт, что законы природы со временем не меняются, с существованием сохраняющейся величины, которую мы по определению называем «энергией».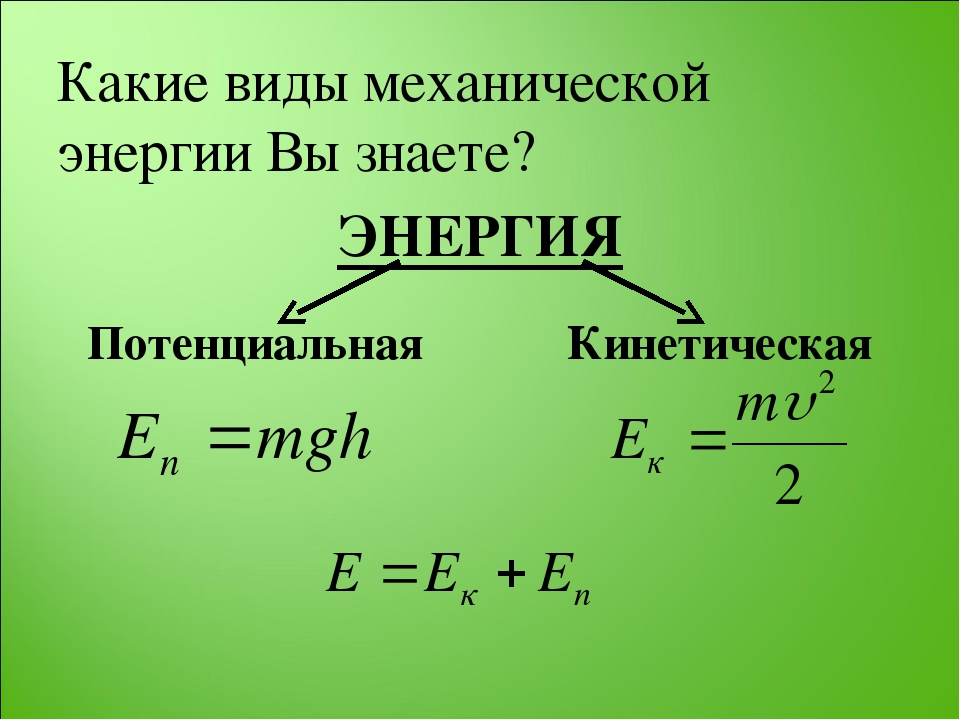

Самым известным и общим определением этого принципа мы обязаны Эмми Нётер, одной из величайших математических физиков предыдущего столетия, современнице Эйнштейна. Некоторые члены физического и математического сообщества относились к ней с глубоким уважением, но в то время в своей родной Германии она страдала от дискриминации по половому и национальному признаку (там блокировали попытки присвоить ей звание профессора в Гёттингене, и оттуда ей пришлось бежать после того, как к власти пришли нацисты). Эмигрировав в США, всего после двух лет преподаваний в колледже Брин-Мар (который по сию пору принимает для обучения только женщин), она умерла от онкологического заболевания.

Знаменитая теорема Нётер (реально это две тесно связанных теоремы) говорит нам, что если в законах природы существует симметрия – в нашем случае это значит, что законы природы одинаковы в любой момент времени – то из этого следует сохранение некоей величины – в нашем случае, энергии.

Более того, теорема в точности сообщает нам, что это за величина – каковы различные формы энергии, для заданной системы объектов, которые необходимо сложить, чтобы получить общую энергию. Именно поэтому физики всегда точно знают, что такое энергия, и почему её легче получить при помощи уравнений, чем определить словами.

Импульс

С импульсом дело обстоит примерно таким же образом, что и с энергией. Законы природы везде одинаковые. Грубо говоря, эксперименты дают одни и те же ответы, проводите ли вы их к северу или к югу отсюда, к западу или востоку, на вершине здания или в глубокой шахте. Выберите любое направление в пространстве. Тогда, согласно Нётер, импульс вдоль этого направления сохраняется. Поскольку в пространстве есть три измерения, то можно двигаться в трёх разных независимых направлениях и существуют три независимых закона сохранения. Выбрать можно три любых направления, при условии, что они разные. К примеру, можно выбрать в качестве трёх законов сохранения импульсы в направлениях север-юг, запад-восток и вверх-вниз. Или можно выбрать три других – по направлению к и от Солнца, вдоль орбиты Земли в обе стороны, и вверх и вниз по отношению к плоскости Солнечной системы.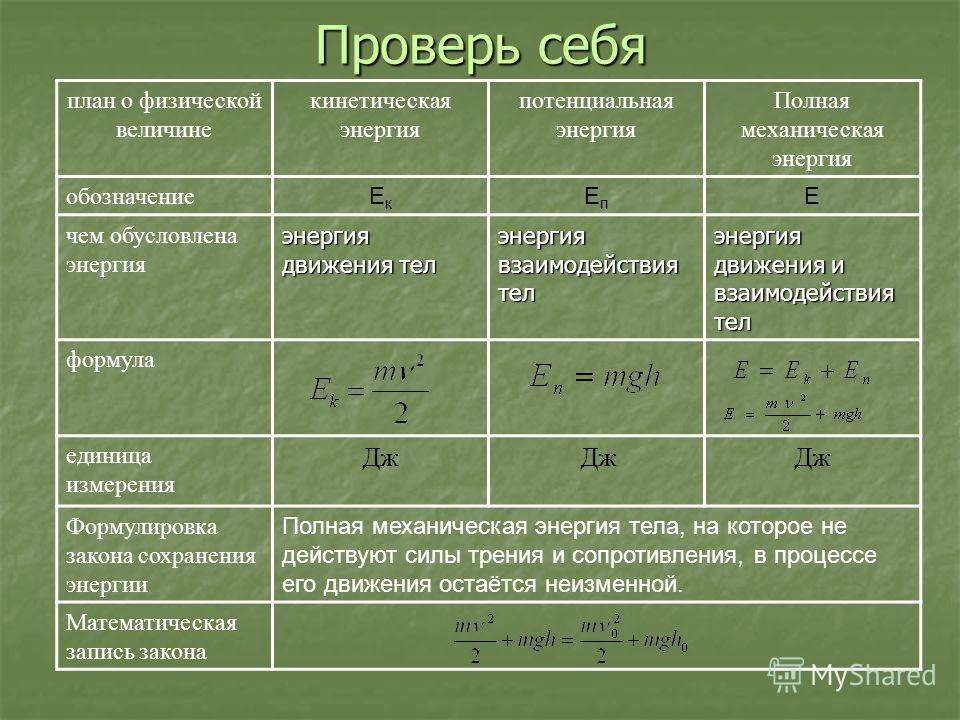 Ваш выбор не имеет значения, ибо импульс сохраняется вдоль любого направления.

Простейшая форма импульса возникает благодаря простому движению объектов, и это примерно то, что можно представить себе интуитивно: если объект двигается в определённом направлении, то у него есть импульс в этом направлении, и чем быстрее он двигается, тем больше этот импульс. А у более тяжёлого объекта импульс больше, чем у лёгкого, если они двигаются с одинаковыми скоростями.

Одно из интересных следствий этого сохранения: если у вас имеется неподвижная система из объектов (то есть, система в целом не двигается, если усреднить все движения составляющих её объектов), тогда она будет оставаться неподвижной, если только ей не придаст движение какое-либо внешнее воздействие. Причина в том, что у неподвижной системы суммарный импульс равен нулю, и поскольку импульс сохраняется, он останется равным нулю навсегда, если только не вмешается что-либо извне системы.

Масса, и её связь с энергией и импульсом

Теперь обратимся к массе

К сожалению, с массой связано много путаницы – после выхода работы Эйнштейна по теории относительности некоторое время существовало два понятия массы. И только одно из них (то, на котором остановился сам Эйнштейн, и которое иногда называют «инвариантной массой» или «массой покоя», чтобы отличить её от уже ставшего архаичным термина «релятивистская масса»), до сих пор используют в физике частиц. В отдельной статье я поясню это более подробно.

Рис. 1

Под массой m, которую я использую в статьях, подразумевается та масса, что непосредственно связывает энергию и импульс. Для объекта, двигающегося без воздействия внешних сил (не взаимодействующего значительно с другими объектами), Эйнштейн предположил (и это было подтверждено экспериментами), что его энергия E, импульс p и масса m удовлетворяют простому пифагорову равенству:

Помните старика Пифагора, утверждавшего, что для прямоугольного треугольника со сторонами A и B и гипотенузой C выполняется равенство ? Это связь того же типа – см. рис. 1. У нас с – постоянная скорость, которая, как мы увидим, служит универсальным пределом скорости. Также мы увидим, почему её называют «скоростью света».

Согласно уравнениям Эйнштейна, скорость объекта, делённая на предел скорости с, это просто отношение pc к Е:

То есть отношение горизонтального катета к гипотенузе. Оно также равно синусу угла α на рис. 1. Вот так вот, граждане. А поскольку катеты прямоугольного треугольника всегда короче гипотенузы (синус любого угла всегда меньше или равен 1), скорость любого объекта не может превышать с, универсальный предел скорости. С увеличением скорости объекта фиксированной массы p и E становятся очень большими (рис. 2), но E всегда больше pc, поэтому v всегда меньше c!

Рис. 2

Теперь обратите внимание, что если объект не двигается, то его импульс p равен нулю, и отношение в уравнении 1 сводится к:

Знаменитая формула Эйнштейна, связь массы с фиксированным количеством энергии (то, что я называю энергией массы), это просто утверждение, соответствующее тому, что когда треугольник вырождается в вертикальную линию, как на рис. 3 слева, его гипотенуза становится такой же длины, как вертикальный катет. При этом оно не означает, что энергия всегда равна массе, помноженной на квадрат с. Это работает только для покоящегося объекта с нулевым импульсом.

Рис. 3

Ещё одно интересное наблюдение: для безмассовой частицы вертикальный катет треугольника нулевой, а гипотенуза и горизонтальный катет совпадают, как на рис. 3. В таком случае E равняется pc, что означает, что v/c = 1, или v = c. Видно, что безмассовая частица (к примеру, фотон, частица света) неизбежно перемещается со скоростью с. Поэтому скорость света такая же, как универсальный предел скорости, с.

С другой стороны, если взять обладающую массой частицу, как на рис. 4, то неважно, насколько большим вы делаете импульс и энергию, E всегда будет немного больше, чем p*c, поэтому скорость всегда будет меньше с. Безмассовые частицы обязаны перемещаться с максимальной скоростью. Скорость массивных частиц должна быть меньше.

Рис. 4. Здесь “>>” означает «гораздо больше»

Представьте себе другой пограничный случай, медленно (по сравнению со скоростью света) движущийся массивный объект, к примеру, автомобиль. Поскольку его скорость v гораздо меньше с, его импульс p умноженный на c будет гораздо меньше E, и, как видно из рис. 5, E будет немногим больше, чем mc². Поэтому энергия движения медленного объекта E — mc² гораздо меньше, чем энергия его массы mc², а у быстрого объекта энергию движения можно сделать сколь угодно большой, как мы видели на рис. 4.

Один тонкий момент: импульс – это не только число, но и вектор. У него есть величина и направление. Он направлен в сторону движения частицы. Когда я пишу «p», я указываю только величину. Во многих случаях необходимо отслеживать и направление импульса, хотя в уравнении №1, связывающем импульс с энергией и массой, этого делать не нужно.

Рис. 5

Ещё один тонкий момент: я использовал треугольники и простейшую тригонометрию, поскольку она известна всем из школы. Экспертам же нужно быть осторожнее – правильно понять уравнения Эйнштейна можно, используя гиперболические функции, обычно не встречающиеся дилетантам, но крайне важные для понимания структуры теории, и делающие более понятными такие вещи, как сложение скоростей, сжатие расстояний и т. п. Не претендующие на экспертизу люди могут это игнорировать.

Но скорость же относительна?..

Если вы внимательно читали текст, вас уже может кое-что удивить. Вы знаете, что скорость частицы – или чего угодно, движущегося медленнее света – зависит от точки зрения.

Если вы сидите дома и читаете книгу, вы скажете, что скорость книги нулевая (и относительно вас она действительно покоится), следовательно, у неё нет импульса и энергии движения, только энергия массы. Но если бы я стоял на Луне, то я напомнил бы вам, что Земля вертится, поэтому это вращение увлекает и вас, и двигает вас относительно меня со скоростью в сотни километров в час. Так что вы с вашей книгой обладали бы импульсом с моей точки зрения.

Кто же прав?

Вариант относительности согласно Галилею – первый принцип относительности – утверждает, что правы мы оба. Вариант относительности Эйнштейна соглашается с точкой зрения Галилея в том, что правы оба, но вносит важные корректировки в то, как обозначили бы последователи Галилея энергию, импульс и массу книги, помещая эти величины в пифагорово соотношение уравнения №1.

Но если правы все, какую E и какой p мне нужно подставить в соотношение энергии/импульса/массы, ? Подставить E и p, измеренные вами, читающим книгу, то есть E = mc² и p = 0? Или подставить E и p, которыми обладает книга с моей точки зрения, когда вы двигаетесь вместе с Землёй?

В ответе на этот вопрос содержится вся суть уравнения Эйнштейна №1. Каждый наблюдатель измерит разные величины E и p для книги, в зависимости от того, как быстро книга будет двигаться относительно него. Но для всех наблюдателей уравнение будет верным!

Магия! А на самом деле, гениальность – мысль, пришедшая в 1905 году, о том, как можно заменить набор уравнений, предложенных Ньютоном и его последователями, новым удивительным набором уравнений, всё ещё совпадающим со всеми предыдущими экспериментами, но оказавшимся более точным представлением реальности. Сложно представить, как сильно нужно было изменить образ мышления, чтобы додуматься до этого, пока не разберёшься с тем, сколько всего во время формирования новой теории могло пойти не так, и сколько других различных уравнений, содержащих противоречия с математикой или с предыдущими экспериментами, можно было бы предложить (а люди их предлагали). Мне, к примеру, постоянно приходят работы начинающих физиков, пытающихся «исправить» уравнения Эйнштейна, но я никогда не видел, чтобы кто-нибудь из них проверил свои уравнения на внутреннюю непротиворечивость. Это очень сложная задача и причина неудачи большинства теорий.

Но как тогда могут сохраняться энергия и импульс?

Погодите-ка, – скажете вы, когда ваша голова уже готова будет взорваться и забрызгать всё вокруг мозгами (я и сам помню это ощущение), – но энергия и импульс должны сохраняться! Так как же могут разные наблюдатели не соглашаться с тем, что они собой представляют?

Тут есть ещё больше магии, которая, кстати, была ещё до Эйнштейна. Поверьте мне, Вселенная – очень, очень хитроумный бухгалтер, и, несмотря на то, что разные наблюдатели не будут соглашаться по поводу энергии, имеющейся у объекта или системы объектов, они все согласятся, что эта энергия не меняется со временем. То же касается и импульса.

А вот масса очень сильно отличается от энергии и импульса. Во-первых, масса не сохраняется. В природе есть множество процессов, изменяющих общую массу системы: к примеру, массивная частица Хиггса может распадаться на два безмассовых фотона. С массой не связана симметрия, и поэтому у Нётер нет для нас закона сохранения. Во-вторых, в отличие от энергии и импульса, чьи величины зависят от наблюдателя (в частности, от его скорости по отношению к измеряемым объектам), все наблюдатели согласятся с величиной массы m объекта. А это вовсе не очевидно, и происходит так оттого, как ужасно хитроумно работают уравнения Эйнштейна.

Итак, что мы имеем

На текущий момент у нас несколько, на первый взгляд, противоречивых знаний. Мы знаем, что:

• Энергия и импульс изолированной физической системы сохраняются (общая энергия и общий импульс изолированной системы не меняются со временем) с точки зрения любого наблюдателя.
• Разные наблюдатели, движущиеся относительно друг друга, по-разному оценят величины энергии и импульса системы!
• Сумма масс объектов, составляющих систему, не сохраняется, она может меняться.
• Но все наблюдатели согласятся с величиной массы объекта.

К этому списку нужно добавить ещё два факта и два вывода:

Масса физической системы объектов не равна сумме масс объектов, составляющих эту систему.

Вместо этого масса физической системы, по поводу которой согласятся все наблюдатели, определяется её энергией и импульсом, и удовлетворяет своему варианту уравнения №1:

Получается, что дополнительный закон сохранения не нужен, и что хотя сумма масс объектов, составляющих систему, не сохраняется, масса системы сохраняется, поскольку она связана через уравнение №1′ с энергией и импульсом системы, которые сохраняются.

Масса системы объектов – это единственный пункт нашего списка, одновременно и сохраняющийся, и не являющийся предметом споров наблюдателей.

Нужно лишь помнить, что масса системы объектов – это не сумма масс объектов, составляющих систему, а то, что задано уравнением №1′.

Чем пытаться объяснить это, просто посмотрим, как это работает. Яркий пример стоит тысячи слов. Давайте в качестве примера системы рассмотрим самую модную штуку, а именно, частицу Хиггса (обладающую массой в 126 ГэВ/с²), и посмотрим, как различные утверждения, сделанные выше, работают при её распаде на два фотона.

Одна частица Хиггса, два фотона и три наблюдателя

Рис. 6. Три наблюдателя смотрят на частицу Хиггса. По отношению к ней Петя (Peter) не двигается, Маша (Marie) двигается вниз, а Костя (Chris) двигается влево.

Давайте посмотрим на то, как частица Хиггса распадается на два фотона, с точки зрения трёх разных наблюдателей. Они изображены на рис. 6 вместе с частицей Хиггса, на которую они смотрят. Конечно, они не могут увидеть её глазами, ибо она существует слишком малый отрезок времени и она слишком мала. Им необходимо использовать какое-либо научное оборудование. Для Пети частица Хиггса не двигается. Маша двигается вниз относительно Пети. Костя двигается влево относительно Пети. Значит, для Маши частица Хиггса двигается вверх, а для Кости – вправо. Три наблюдателя видят, как частица распадается согласно рис. 7. Петя видит, что Хиггс распадается на два фотона одинаковых энергий, один из которых двигается вверх, а другой – вниз. Маша видит, что Хиггс распадается на два фотона различных энергий, и у двигающегося вверх энергии больше, чем у двигающегося вниз. Костя видит, как Хиггс распадается на два фотона, направляющихся вправо вверх и вправо вниз. Давайте посчитаем, какие энергии и импульсы присвоят Хиггсу и двум фотонам наблюдатели, и как каждый из них придёт к выводу о сохранении энергии и импульса в процессе распада.

Распад неподвижной частицы Хиггса

Для начала разберём частицу Хиггса с точки зрения Пети. Петя смотрит (при помощи измерительных приборов) на частицу Хиггса, и что же он видит? (Я буду ставить чёрточку над всем, что видит Петя, и потом мы сравним это с наблюдениями Маши и Кости). Хиггс не двигается, значит, его импульс

равен нулю, и согласно уравнению №1 у него, с его массой m = 126 ГэВ/c

²

энергия будет

Теперь, согласно сохранению энергии и импульса, система, состоящая из частицы Хиггса, сохранит всю энергию и импульс после распада. И это будет так, пока никакая внешняя сила не будет воздействовать на Хиггса. Вы можете спросить, нужно ли нам волноваться по поводу земного притяжения, ведь гравитация и будет внешним воздействием, способным менять импульс. Отвечу, что за то краткое время, которое нужно Хиггсу на распад, влияние гравитации будет столько малым, что если бы я рассказал вам, какое оно на самом деле мелкое, вы бы захихикали. Забудьте об этом.

Итак, когда Хиггс распадается, энергии частиц, составляющих его остатки, должны в сумме дать 126 ГэВ, а импульс частиц (учитывая, что импульс – это не только величина, но и направление — вектор) в сумме даст ноль.

Два безмассовых фотона, на которые распадается Хиггс, могут разлететься в любых направлениях, но чтобы упростить пример, представим, что они разлетятся вертикально – один вверх, а другой, отскочив от него, вниз. (Чуть позже обсудим, почему они должны разлетаться в противоположных направлениях).

Каким импульсом обладают фотоны? Это просто. Во-первых, общий импульс системы – сумма импульсов двух фотонов – должен быть нулевым, поскольку у Хиггса до распада был нулевой импульс (с точки зрения Пети). Теперь у каждого из фотонов есть импульс определённой величины и направления. В сумме они могут давать ноль только одним способом – если они равной величины и противоположного направления. Если один идёт вверх, другой должен идти вниз, и величина их должна быть одинаковой.

Рис. 8: что видит Петя

Во-вторых, общая энергия системы – это сумма энергий двух фотонов. Это происходит потому, что между ними нет никакой энергии взаимодействия (кроме крайне малого гравитационного притяжения, о котором можно забыть). Конечно, раз у них нет масс, то вся их энергия заключается в энергии движения. Кроме того, в случае для безмассовой частицы уравнение №1 говорит о том, что E = p c, где p – величина импульса. Из-за этого два фотона с одинаковыми импульсами должны обладать и одинаковыми энергиями. А поскольку две эти энергии в сумме должны дать энергию частицы Хиггса, то энергия каждого фотона должна равняться половине энергии частицы Хиггса.

А поскольку для безмассовой частицы p = E/c, то

И это отображено на рис. 8.

Энергия и импульс сохраняются, а масса – нет, поскольку у фотонов нет массы, а у Хиггса была. А что по поводу массы системы? Какова масса системы из двух фотонов? Ненулевая. Очевидно, какая она. Точно так же, как и для самого Хиггса (из которого и состояла изначально вся система), система из двух фотонов обладает той же энергией и импульсом, что были у Хиггса:

А поскольку для Пети ,

Что и есть масса Хиггса. Масса системы не изменилась за время распада, как и ожидалось.

Наблюдатель, для которого Хиггс движется вверх

Маша движется вниз по отношению к Пете, так что с её точки зрения Петя и Хиггс двигаются вверх. Допустим, что Хиггс двигается со скоростью v = 0,8 c, то есть 4/5 скорости света, относительно неё. В отличие от Пети, с точки зрения Маши Хиггс обладает ненулевым импульсом, а импульсы у фотонов оказываются разными по величине, но по-прежнему разнонаправленными – в результате чего сумма их импульсов будет ненулевой.

Рис. 9: как Маша видит распад частицы Хиггса

Как посчитать, какими импульсом и энергией обладает Хиггса и два фотона, на которые он распадается, с точки зрения Маши? Для этого нам понадобится ещё один набор простых уравнений Эйнштейна. Допустим, с точки зрения некоего наблюдателя объект обладает импульсом p и энергией E. Тогда с точки зрения другого наблюдателя, движущегося со скоростью v по направлению движения объекта (или против него), импульс и энергия объекта будут выражаться следующим образом:

Где γ удовлетворяет ещё одному пифагорову уравнению:

согласно Эйнштейну. Это позволяет нам выполнять преобразования между тем, что видит Петя, и тем, что видит Маша (или любой другой наблюдатель, двигающийся со скоростью v). То, что мы обнаружим, показано на рис. 9.

Чтобы сравнить наблюдения Маши с наблюдениями Пети, нам понадобятся v и γ. Я утверждаю, что если v=4/5 c, то γ = 5/3.

Проверим, используя уравнение №5: 1 = (4/5)2 + (3/5)2 = 16/25 + 9/25 = 25/25

Петя говорит, что у Хиггса .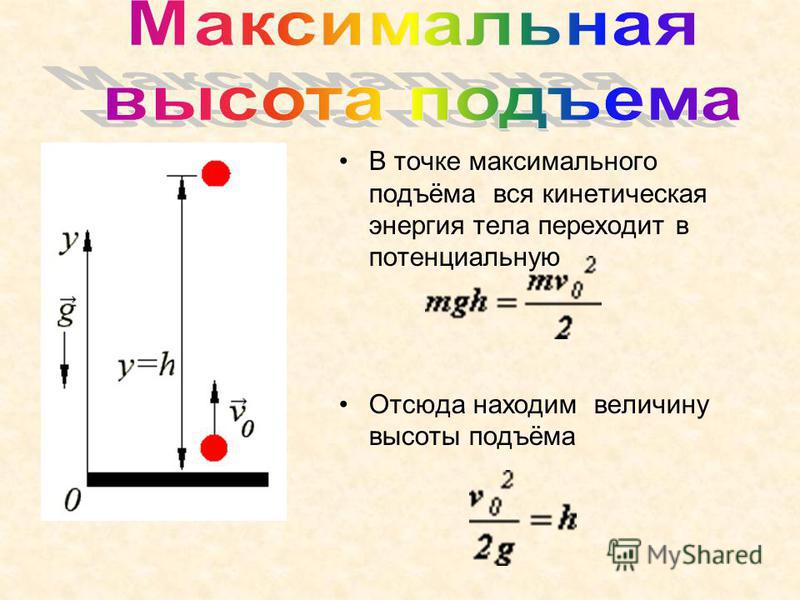 Что насчёт Маши? Она говорит, что:

Петя утверждает, что у двух фотонов , и для каждого из них E = p c. Теперь мы можем подсчитать, что видит Маша, используя уравнения №4 и №4.

Работает! Энергия сохраняется и с точки зрения Марии, ибо

Импульс тоже сохраняется:

Масса системы совпадает с массой Хиггса до и после распада, поскольку до и после распада

Что, согласно уравнению №1′, приводит массу системы вновь к , как и у Пети, поскольку

Наблюдатель, с точки зрения которого Хиггс движется вправо

Что у нас с Костей? Костя двигается влево относительно Пети, допустим, со скоростью v=4/5 c, так что относительно Кости Хиггс (и Петя) двигаются вправо со скоростью v=4/5 c. Те же расчёты, что мы делали для Маши, показывают, что энергия Хиггса

, но, в отличие от Маши, для которой Хиггс двигается вверх, для Кости импульс Хиггса направлен вправо. Это изображено на рис. 10.

Рис. 10

Хиггс распадается на два фотона. Если с точки зрения Пети фотоны двигаются вверх и вниз, то для Кости, наблюдающего, как Хиггс и Петя двигаются вправо, один из фотонов двигается вправо вверх, а другой – вправо вниз. Какие у них тогда будут импульс и энергия?

Через уравнения №4 и №5 нам этого не узнать, поскольку они предназначаются для случаев, когда частица и наблюдатель двигаются в одном направлении. Для нашего случая уравнения будут такими:

Эти уравнения будут проще, чем кажутся, поскольку с точки зрения Пети, у p нет компоненты, двигающейся слева направо, и весь импульс идёт вверх или вниз. Так что Костя наблюдает следующие величины для Хиггса:

А у фотона, идущего вверх

Для второго фотона формулы те же, только его вертикальная составляющая направлена вниз. Заметьте, что для обоих фотонов E = p c, согласно теореме Пифагора для размера p у каждого из импульсов – согласно врезке на рис. 10

И вновь Костя наблюдает другие величины энергии и импульса, по сравнению с Петей и Машей. Но и для Кости энергия и импульс всё равно сохраняются. Также Костя наблюдает, что у системы с двумя фотонами масса совпадает с массой Хиггса. Почему? Общая вертикальная часть импульса системы нулевая, она взаимно уничтожается. Горизонтальная часть импульса системы равна 168 ГэВ/с. Общая энергия системы 210 ГэВ. Это то же, что наблюдала Маша, за исключением того, что у неё импульс системы шёл вверх, а не вправо. Но направление импульса не влияет на уравнение №1′. Там играет роль только его величина. Так что, как и Маша, Костя видит, что масса системы из двух протонов получается , равной массе первичной частицы Хиггса.

Итог

Итак, мы видим, что наблюдают три разных наблюдателя. Их наблюдения:

• разнятся по поводу того, какие у Хиггса энергия и импульс,
• разнятся в части энергии и импульса обоих фотонов,
• согласуются по поводу сохранения энергии и импульса при распаде,
• следовательно, они согласны, что при этом сохраняется масса системы,
• соглашаются, что масса системы равна 126 ГэВ/c²,
• и более того, что сумма масс объектов системы не сохраняется, а уменьшается с 126 ГэВ/c² до нуля.

И это не случайно. Эйнштейн из предыдущих экспериментов знал, что энергия и импульс сохраняются, поэтому он искал и нашёл уравнения, сохраняющие эту особенность мира. Также в процессе он обнаружил, что масса системы должна удовлетворять уравнению №1′.

Бонус: как это используется в поисках частицы Хиггса

Учёные:

• наблюдают столкновения протонов, в результате которых рождается два фотона;
• подсчитывают массу системы из двух фотонов (на техническом жаргоне это называется инвариантная масса пары фотонов).

Когда в результате эксперимента получается частица Хиггса, распадающаяся на два фотона, то вне зависимости от того, в каком направлении и с какой скоростью двигается частица по отношению к лаборатории, система из двух фотонов, на которую она распадётся, всегда будет обладать массой, равной массе частицы Хиггса, произведшей их на свет! Поэтому, в отличие от случайных процессов, в результате которых получается система из двух фотонов случайной массы, частицы Хиггса всегда будут порождать систему из двух фотонов одной и той же массы. Поэтому, если в результатах эксперимента появятся частицы Хиггса, и если они иногда будут распадаться на два фотона, то мы увидим пик от распадов Хиггса, возвышающийся над гладким фоном из других случайных процессов. Так и произошло в эксперименте на БАК!

Энергия как физическая величина. Виды энергии. Физика, 7 класс: уроки, тесты, задания.

1.	Кинетическая энергия велосипедиста Сложность: лёгкое	2
2.	Определение, свойства, единицы измерения энергии Сложность: лёгкое	2
3.	Словесные определения формул Сложность: лёгкое	1
4.	Единицы величин Сложность: лёгкое	2
5.	Формулы (выражение переменных) Сложность: лёгкое	1
6.	Превращение одного вида энергии в другой Сложность: лёгкое	1
7.	Кинетическая энергия метеорита Сложность: среднее	4
8.	Изменение кинетической энергии Сложность: среднее	4
9.	Потенциальная энергия, определение совершённой работы Сложность: среднее	3
10.	Изменение потенциальной энергии Сложность: среднее	3
11.	Потенциальная энергия камня Сложность: среднее	4
12.	Механическая энергия Сложность: среднее	1
13.	Неизвестная высота Сложность: среднее	2
14.	Потенциальная энергия тела относительно земли или крыши Сложность: среднее	3
15.	Изменение кинетической энергии (скорости) Сложность: среднее	4
16.	Неизвестная скорость Сложность: среднее	3
17.	Превращение одной энергии в другую Сложность: среднее	4
18.	Неизвестная высота дирижабля Сложность: сложное	4
19.	Потенциальная энергия коробок относительно пола Сложность: сложное	5
20.	Сравнение энергий Сложность: сложное	3

материалы для подготовки к ЕГЭ по Физике

 

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: работа силы, мощность, кинетическая энергия, потенциальная энергия, закон сохранения механической энергии.

Мы приступаем к изучению энергии – фундаментального физического понятия. Но предварительно нужно разобраться с другой физической величиной – работой силы.

Работа.

 

Пусть на тело действует постоянная сила и тело, двигаясь прямолинейно по горизонтальной поерхности, совершило перемещение . Сила не обязательно является непосредственной причиной перемещения (так, сила тяжести не является непосредственной причиной перемещения шкафа, который передвигают по комнате).

Предположим сначала, что векторы силы и перемещения сонаправлены (рис. 1; остальные силы, действующие на тело, не указаны)

Рис. 1.A=Fs

 

В этом простейшем случае работа определяется как произведение модуля силы на модуль перемещения:

. (1)

Единицей измерения работы служит джоуль (Дж): Дж=Н м. Таким образом, если под действием силы 1 Н тело перемещается на 1 м, то сила совершает работу 1 Дж.

Работа силы, перпендикулярной перемещению, по определению считается равной нулю. Так, в данном случае сила тяжести и сила реакции опоры не совершают работы.

Пусть теперь вектор силы образует с вектором перемещения острый угол (рис. 2).

Рис. 2. A=Fs cos

 

Разложим силу на две составляющие: (параллельную перемещению) и (перпендикулярную перемещению). Работу совершает только . Поэтому для работы силы получаем:

. Итак,

. (2)

Если вектор силы образует с вектором перемещения тупой угол , то работа по-прежнему определяется формулой (2). В этом случае работа оказывается отрицательной.

Например, работа силы трения скольжения, действующей на тело в рассмотренных ситуациях, будет отрицательной, так как сила трения направлена противоположно перемещению. В этом случае имеем:

, и для работы силы трения получаем:

,

где – масса тела, – коэффициент трения между телом и опорой.

Соотношение (2) означает, что работа является скалярным произведением векторов силы и перемещения:

.

Это позволяет вычислять работу через координаты данных векторов:

.

Пусть на тело действуют несколько сил и – равнодействующая этих сил. Для работы силы имеем:

,

или

,

где – работы сил . Итак, работа равнодействующей приложенных к телу сил равна сумме работ каждой силы в отдельности.

Мощность.

 

Часто имеет значение быстрота, с которой совершается работа. Скажем, на практике важно знать, какую работу сможет выполнить данное устройство за фиксированное время.

Мощность – это величина, характеризующая скорость совершения работы. Мощность есть отношение работы ко времени , за которое эта работа совершена:

.

Мощность измеряется в ваттах (Вт). 1 Вт = 1 Дж/с, то есть 1 Вт – это такая мощность, при которой работа в 1 Дж совершается за 1 с.

Предположим, что силы, действующие на тело, уравновешены, и тело движется равномерно и прямолинейно со скоростью . В этом случае существует полезная формула для мощности, развиваемой одной из действующих сил .

За время тело совершит перемещение . Работа силы будет равна:

.

Отсюда получаем мощность:

,

или

,

где -угол между векторами силы и скорости.

Наиболее часто эта формула используется в ситуации, когда – сила “тяги” двигателя автомобиля (которая на самом деле есть сила трения ведущих колёс о дорогу). В этом случае , и мы получаем просто:

.

Механическая энергия.

 

Энергия является мерой движения и взаимодействия любых объектов в природе. Имеются различные формы энергии: механическая, тепловая, электромагнитная, ядерная. . .

Опыт показывает, что энергия не появляется ниоткуда и не исчезает бесследно, она лишь переходит из одной формы в другую. Это самая общая формулировка закона сохранения энергии.

Каждый вид энергии представляет собой некоторое математическое выражение. Закон сохранения энергии означает, что в каждом явлении природы определённая сумма таких выражений остаётся постоянной с течением времени.

Измеряется энергия в джоулях, как и работа.

Механическая энергия является мерой движения и взаимодействия механических объектов (материальных точек, твёрдых тел).

Мерой движения тела является кинетическая энергия. Она зависит от скорости тела. Мерой взаимодействия тел является потенциальная энергия. Она зависит от взаимного расположения тел.

Механическая энергия системы тел равна сумме кинетической энергии тел и потенциальной энергии их взаимодействия друг с другом.

Кинетическая энергия.

 

Кинетической энергией тела (принимаемого за материальную точку) называется величина

,

где – масса тела, – его скорость.

Кинетической энергией системы из тел называется сумма кинетических энергий каждого тела:

.

Если тело движется под действием силы , то кинетическая энергия тела, вообще говоря, меняется со временем. Оказывается, именение кинетической энергии тела за некоторый промежуток времени равно работе силы . Покажем это для случая прямолинейного равноускоренного движения.

Пусть – начальная скорость, – конечная скорость тела. Выберем ось вдоль траектории тела (и, соответственно, вдоль вектора силы ). Для работы силы получаем:

.

(мы воспользовались формулой для , выведенной в статье “Равноускоренное движение”). Заметим теперь, что в данном случае проекция скорости отличается от модуля скорости разве что знаком; поэтому и . В результате имеем:

,

что и требовалось.

На самом деле соотношение справедливо и в самом общем случае криволинейного движения под действием переменной силы.

Теорема о кинетической энергии. Изменение кинетической энергии тела равно работе, совершённой приложенными к телу внешними силами за рассматриваемый промежуток времени.

Если работа внешних сил положительна, то кинетическая энергия увеличивается (, тело разгоняется).

Если работа внешних сил отрицательна, то кинетическая энергия уменьшается (, тело замедляет движение). Пример – торможение под действием силы трения, работа которой отрицательна.

Если же работа внешних сил равна нулю, то кинетическая энергия тела за это время не меняется. Нетривиальный пример – равномерное движение по окружности, совершаемое грузом на нити в горизонтальной плоскости. Сила тяжести, сила реакции опоры и сила натяжения нити всегда перпендикулярны скорости, и работа каждой из этих сил равна нулю в течение любого промежутка времени. Соответственно, кинетическая энергия груза (а значит, и его скорость) остаётся постоянной в процессе движения.

Задача. Автомобиль едет по горизонтальной дороге со скоростью и начинает резко тормозить. Найти путь , пройденный автомобилем до полной остановки, если коэффициент трения шин о дорогу равен .

Решение. Начальная кинетическая энергия автомобиля , конечная кинетическая энергия . Изменение кинетической энергии .

На автомобиль действуют сила тяжести , реакция опоры и сила трения . Сила тяжести и реакция опоры, будучи перпендикулярны перемещению автомобиля, работы не совершают. Работа силы трения:

.

Из теоремы о кинетической энергии теперь получаем:

.

Потенциальная энергия тела вблизи поверхности Земли.

 

Рассмотрим тело массы , находящееся на некоторой высоте над поверхностью Земли. Высоту считаем много меньше земного радиуса. Изменением силы тяжести в процессе перемещения тела пренебрегаем.

Если тело находится на высоте , то потенциальная энергия тела по определению равна:

где – ускорение свободного падения вблизи поверхности Земли.

Высоту не обязательно отсчитывать от поверхности Земли. Как мы увидим ниже (формулы (3), (4)), физическим смыслом обладает не сама по себе потенциальная энергия, но её изменение. А изменение потенциальной энергии не зависит от уровня отсчёта. Выбор нулевого уровня потенциальной энергии в конкретной задаче диктуется исключительно соображениями удобства.

Найдём работу, совершаемую силой тяжести при перемещении тела. Предположим, что тело перемещается по прямой из точки , находящейся на высоте , в точку , находящуюся на высоте (рис. 3).

Рис. 3.A=mg(h2-h3)[/math]

 

Угол между силой тяжести и перемещением тела обозначим . Для работы силы тяжести получим:

.

Но, как видно из рис. 3, . Поэтому

,

или

. (3)

Учитывая, что , имеем также:

. (4)

Можно доказать, что формулы (3) и (4) справедливы для любой траектории, по которой тело перемещается из точки в точку , а не только для прямолинейного отрезка.

Работа силы тяжести не зависит от формы траектории, по которой перемещается тело, и равна разности значений потенциальной энергии в начальной и конечной точках траектории. Иными словами, работа силы тяжести всегда равна изменению потенциальной энергии с противоположным знаком. В частности, работа силы тяжести по любому замкнутому пути равна нулю.

Сила называется консервативной, если при перемещении тела работа этой силы не зависит от формы траектории, а определяется только начальным и конечным положением тела. Сила тяжести, таким образом, является консервативной. Работа консервативной силы по любому замкнутому пути равна нулю. Только в случае консервативной силы возможно ввести такую величину, как потенциальная энергия.

Потенциальна яэнергия деформированной пружины.

 

Рассмотрим пружину жёсткости . Начальная деформация пружины равна . Предположим,
что пружина деформируется до некоторой конечной величины деформации . Чему равна при этом работа силы упругости пружины?

В данном случае силу на перемещение не умножишь, так как сила упругости меняется в процессе деформации пружины. Для нахождения работы переменной силы требуется интегрирование. Мы не будем приводить здесь вывод, а сразу выпишем конечный результат.

Оказывается, сила упругости пружины также является консервативной. Её работа зависит лишь от величин и и определяется формулой:

.

Величина

называется потенциальной энергией деформированной пружины (x – величина деформации).

Следовательно,

,

что полностью аналогично формулам (3) и (4).

Закон сохранения механической энергии.

 

Консервативные силы называются так потому, что сохраняют механическую энергию замкнутой системы тел.

Механическая энергия тела равна сумме его кинетической и потенциальной энергий:

.

Механическая энергия системы тел равна сумме их кинетических энергий и потенциальной энергии их взаимодействия друг с другом.

Предположим, что тело совершает движение под действием силы тяжести и/или силы упругости пружины. Будем считать, что трения нет. Пусть в начальном положении кинетическая и потенциальная энергии тела равны и , в конечном положении – и . Работу внешних сил при перемещении тела из начального положения в конечное обозначим .

По теореме о кинетической энергии

.

Но работа консервативных сил равна разности потенциальных энергий:

.

Отсюда получаем:

,

или

.

Левая и правая части данного равенства представляют собой механическую энергию тела в начальном и конечном положении:

.

Следовательно, при движении тела в поле силы тяжести и/или на пружине механическая энергия тела остаётся неизменной при отсутствии трения. Справедливо и более общее утверждение.

Закон сохранения механической энергии. Если в замкнутой системе действуют только консервативные силы, то механическая энергия системы сохраняется.

При этих условиях могут происходить лишь превращения энергии: из кинетической в потенциальную и наоборот. Общий запас механической энергии системы остаётся постоянным.

Закон изменения механической энергии.

 

Если между телами замкнутой системы имеются силы сопротивления (сухое или вязкое трение), то механическая энергия системы будет уменьшаться. Так, автомобиль останавливается в результате торможения, колебания маятника постепенно затухают и т. д. Силы трения неконсервативны: работа силы трения очевидным образом зависит от пути, по которому перемещается тело между данными точками. В частности, работа силы трения по замкнутому пути не равна нулю.

Снова рассмотрим движение тела в поле силы тяжести и/или на пружине. Вдобавок на тело действует сила трения, которая за рассматриваемый промежуток времени совершает отрицательную работу . Работу консервативных сил (тяжести и упругости) по-прежнему обозначаем .

Изменение кинетической энергии тела равно работе всех внешних сил:

.

Но , следовательно

.

Отсюда

,

или

.

В левой части стоит величина – изменение механической энергии тела:

.

Итак,при движении тела в поле силы тяжести и/или на пружине изменение механической энергии тела равно работе силы трения. Так как работа силы трения отрицательна,изменение механической энергии также отрицательно: механическая энергия убывает.
Справедливо и более общее утверждение.

Закон изменения механической энергии. Изменение механической энергии замкнутой системы равно работе сил трения, действующих внутри системы.

Ясно, что закон сохранения механической энергии является частным случаем данного утверждения.

Конечно, убыль механической энергии не противоречит общефизическому закону сохранения энергии. В данном случае механическая энергия превращается в энергию теплового движения частиц вещества и их потенциальную энергию взаимодействия друг с другом, т. е. переходит во внутреннюю энергию тел системы.

 

Энергия | Физика

Термин «энергия» был введен в 1807 г. английским ученым Т. Юнгом. В переводе с греческого это слово означает «действие, деятельность».

Современная наука немыслима без этого понятия. Оно присутствует во всех разделах физики. Это и электрическая энергия, магнитная энергия, атомная энергия и т. д.

Энергия, изучаемая в механике, называется механической. Именно с нее мы и начнем знакомство с этим важнейшим понятием.

Механическая энергия обозначается буквой Е и измеряется в тех же единицах, что и работа, т. е. в джоулях (Дж).

Поскольку в механике изучают движение тел и их взаимодействие друг с другом, то принято различать два вида механической энергии — энергию, обусловленную движением тел, и энергию, обусловленную их взаимодействием. Первая из них обозначается E_к и называется кинетической энергией, вторая обозначается E_п и называется потенциальной энергией.

Для расчета и той и другой энергии существует общее правило. Чтобы определить энергию, которой обладает тело, надо найти работу, необходимую для перевода этого тела из нулевого состояния в данное (нулевое состояние — это то, в котором соответствующая энергия тела считается равной нулю). Чем больше эта работа, тем большей энергией обладает тело в данном состоянии.

Воспользуемся этим правилом для расчета каждой из энергий.

1. Кинетическая энергия. Найдем кинетическую энергию тела массой т, движущегося со скоростью, равной и. Кинетическая энергия — это энергия, обусловленная движением. Поэтому нулевым состоянием для нее является то, в котором тело покоится. Найдя работу, необходимую для сообщения телу данной скорости, мы найдем и его кинетическую энергию.

Воспользовавшись определением работы (A = Fs), вторым законом Ньютона (F = ma), а также формулами (2.1) и (4.2), получаем (рис. 25)

Последнее из написанных здесь выражений и является кинетической энергий тела:

Итак, кинетическая энергия тела равна половине произведения массы тела на квадрат его скорости.

2. Потенциальная энергия. Найдем потенциальную энергию тела, взаимодействующего с Землей. Нулевым будем считать положение тела на поверхности Земли. Тогда потенциальная энергия тела, находящегося на некоторой высоте h, будет равна работе, необходимой для перемещения этого тела с поверхности Земли на заданную высоту. При равномерном подъеме, когда прикладываемая к телу сила совпадает по величине с силой тяжести (рис. 26), эта работа может быть найдена следующим образом:

A = Fs = F_тh = mgh.

Это и есть потенциальная энергия тела на высоте h:

   E_п = mgh.         (14.2)

Итак, потенциальная энергия тела, взаимодействующего с Землей, равна произведению массы этого тела, ускорению свободного падения и высоты, на которой находится тело.

За нулевое положение тела при расчете его потенциальной энергии необязательно выбирать то, которое расположено на поверхности Земли. Это может быть и уровень пола в помещении, и поверхность стола и т. д. Нулевое положение, от которого отсчитывается высота тела h, выбирают произвольно, руководствуясь обычно лишь соображениями удобства и простоты.

По формуле (14.2) находится потенциальная энергия тела, взаимодействующего с Землей. Потенциальная энергия других взаимодействий находится по другим формулам.

От энергии, которой обладает тело, зависит работа, которую оно может совершить. Чем больше энергия тела, тем большая работа будет совершена при переходе тела из данного состояния в нулевое. Проиллюстрируем это простыми опытами.

Возьмем составной желоб, имеющий наклонную и горизонтальную части, и поместим на его сгибе алюминиевый цилиндр (рис. 27). Пуская по наклонной части желоба шарики разной массы с одинаковой высоты и шарики одинаковой массы с разных высот, можно заметить, что, чем большей потенциальной энергией наверху желоба и кинетической энергией внизу обладал шарик, тем на большее расстояние он передвинет металлический цилиндр.

1. Чем обусловлена кинетическая энергия? 2. Чему равна кинетическая энергия тела? 3. Чем обусловлена потенциальная энергия? 4. Чему равна потенциальная энергия тела, взаимодействующего с Землей? 5. Как называется единица энергии? 6. В каком случае кинетическая энергия тела равна нулю? 7. Какой энергией — кинетической, потенциальной или обеими вместе — обладает летящий в небе самолет? 8. Какой энергией обладает вода, удерживаемая плотиной, и какой энергией обладает вода, падающая с плотины? 9. Как изменяются потенциальная и кинетическая энергии мяча, брошенного вертикально вверх, в процессе его полета?

Кинетическая и потенциальная энергия – Веб-формулы

Энергия:
Объект обладает энергией, когда он способен выполнять работу. Такие занятия, как приготовление еды, танцы под музыку, пение песен, требуют энергии. Жизнь невозможна без энергии. Солнце – самый большой естественный источник бесплатной энергии.
Объект, обладающий энергией, может воздействовать на другой объект, и энергия передается от первого к второму. Второй объект движется, поскольку он получает энергию и, следовательно, выполняет некоторую работу.Это означает, что любой объект, обладающий энергией, может работать.
Единица энергии = джоуль

Формы энергии:
Различные формы энергии включают
· Механическая энергия – Кинетическая энергия и потенциальная энергия
· Тепловая энергия
· Химическая энергия
· Электроэнергия
· Световая энергия

Кинетическая энергия:
Когда объект находится в движении, он обладает энергией, которая называется кинетической энергией. Такие виды деятельности, как верховая езда, вождение автомобиля, катящийся камень, летающий самолет, являются примерами кинетической энергии.Кинетическая энергия объекта увеличивается с его скоростью.
Рассмотрим объект массы m, движущийся с равномерной скоростью u. Пусть теперь перемещается на расстояние s, когда на него действует постоянная сила F в направлении его перемещения. Теперь проделанная работа над объектом составляет

W = F s ——————- (1)

Работа, проделанная над объектом, вызывает изменение его скорости v и ускорение объекта равно a, тогда

………………………… (2)

Теперь сила F = ma ……………………… (3)

Применяя 2 и 3 в уравнении 1:

ЕСЛИ объект стартует из своего стационарного положения, то есть u = 0, тогда

Уравнение показывает, что выполненная работа равна изменению кинетической энергии объекта (E _k ).

Потенциальная энергия:
Потенциальная энергия, которой обладает объект, – это энергия, присутствующая в нем в силу его положения или конфигурации, что означает, что потенциальная энергия сохраняется в объекте, когда с ним выполняется работа, но скорость или скорость объекта не изменяется. .
Гравитационная потенциальная энергия – это энергия, которой обладает объект, когда он поднимается против силы тяжести. Он определяется как работа, выполняемая при поднятии его с земли в эту точку против силы тяжести.
Рассмотрим объект массы m, поднятый на высоту h от земли. Для этого требуется сила. Минимальная сила, необходимая для поднятия объекта, равна весу объекта mg. Объект получает энергию, равную проделанной над ним работе. Пусть работа, проделанная с объектом против силы тяжести, тогда будет w,

Сделанная работа w = сила x смещение
w = mg x h

Поскольку работа, выполняемая над объектом, равна mgh, объект получает энергию, равную mgh единиц.Это потенциальная энергия (Ep) объекта.
E _p = mgh

Уравнение показывает, что работа, выполняемая силой тяжести, зависит от разницы вертикальных высот начального и конечного положений объекта, а не от пути, по которому объект перемещается

Закон сохранения энергии:
Общая энергия системы остается неизменной при преобразовании энергии. Энергия не может быть ни создана, ни уничтожена, а только преобразована из одной формы в другую.Общая энергия до и после преобразования остается неизменной. Это называется законом сохранения энергии.

Предположим, что объект массы m вынужден свободно падать с высоты h.
Вначале потенциальная энергия = mgh, а кинетическая энергия = ноль, потому что его скорость равна нулю.
Полная энергия объекта = mgh.
При падении его потенциальная энергия превратится в кинетическую. Если v – скорость объекта в данный момент, кинетическая энергия = 1 / 2mv ² .
По мере продолжения падения объекта потенциальная энергия будет уменьшаться, а кинетическая – увеличиваться.
Когда объект приближается к земле, h = 0 и v будет самым высоким. Следовательно, кинетическая энергия будет наибольшей, а потенциальная – наименьшей. Однако сумма потенциальной энергии и кинетической энергии объекта будет одинаковой во всех точках.

Потенциальная энергия + кинетическая энергия = константа
мг · ч + ½ мв ² = константа

Сумма кинетической энергии и потенциальной энергии объекта является его полной механической энергией.

Расчеты:
Пример-1: Если объект, имеющий массу m, движется со скоростью v, то кинетическая энергия объекта равна …… ..
a) mv b) 1/2 mv c) 1 / 2 мв ² г) мв ²

Ответ: кинетическая энергия объекта зависит от его движения. Проделанная работа равна изменению кинетической энергии объекта. Здесь объект движется со скоростью v и массой m, поэтому кинетическая энергия объекта составляет 1/2 мв ² .

Пример-2: Сумма кинетической энергии и потенциальной энергии называется ……………
а) Тепловая энергия
б) Химическая энергия
в) Механическая энергия
г) Нет

Ответ: объект обладает энергией, когда он способен выполнять работу.

Ex-3: Объект массой 12 кг находится на определенной высоте над землей. Если потенциальная энергия объекта 480 Дж, найдите высоту объекта относительно земли.Учитывая g = 10 м / с.
а) 5 м б) 10 м в) 4 м г) 40 м
Ответ:
м = 12 кг
Ep = 480 Дж
Ep = m g h
в = 480
12 x 10
h = 4 м

Кинетическая энергия – Гипертекст по физике

Обсуждение

Кинетическая энергия – это простая концепция с простым уравнением, которое легко вывести. Сделаем это дважды.

Вывод с использованием только алгебры (и в предположении постоянного ускорения).Начните с теоремы о работе-энергии, затем добавьте второй закон движения Ньютона.

∆ K = W = F ∆ s = ma ∆ s

Возьмите соответствующее уравнение кинематики и немного измените его.

v 2 = v 0 2 + 2 a ∆ s

a ∆ с =	v 2 – v 0 2
	2

Объедините два выражения.

∆ K = м	⎛ ⎜ ⎝	v 2 – v 0 2	⎞ ⎟ ⎠
		2

А теперь кое-что необычное. Расширять.

∆ К =	1	мв 2 –	1	мв 0 2
	2		2

Если кинетическая энергия – это энергия движения, то, естественно, кинетическая энергия покоящегося объекта должна быть равна нулю.Следовательно, второй член нам не нужен, и кинетическая энергия объекта составляет всего…

K = ½ мв ²

Вывод с использованием исчисления (но теперь нам не нужно ничего предполагать об ускорении). Опять же, начните с теоремы о работе-энергии и добавьте второй закон движения Ньютона (расчетная версия).

∆ K = ⌠ ⌡ F ( r ) · d r

∆ K = ⌠ ⌡ м a · d r

∆ K = м ⌠ ⌡ d v · d r дт

Переставьте дифференциальные члены, чтобы получить интеграл и функцию в соглашение.

∆ K = м ⌠ ⌡ d v · d r дт

∆ K = м ⌠ ⌡ d r · d v дт

∆ K = м ⌠ ⌡ v · d v

Интеграл которого довольно просто вычислить за пределы начальной скорости ( v ) до конечной скорости ( v ₀ ).

∆ К =	1	мв 2 –	1	мв 0 2
	2		2

Естественно, кинетическая энергия покоящегося объекта должна быть равна нулю. Таким образом, кинетическая энергия объекта математически определяется следующим уравнением…

K = ½ мв ²

Томас Янг (1773–1829) вывел аналогичную формулу в 1807 году, хотя он не стал добавлять ½ к началу и не использовал слова «масса» и «вес» с той же точностью, что и сейчас.Он также был первым, кто использовал слово энергия в его нынешнем значении в лекции о столкновениях, прочитанной перед Королевским институтом.

Термин энергия может быть применен с большим уместным к произведению массы или веса тела на квадрат числа, выражающего его скорость. Таким образом, если вес в одну унцию движется со скоростью ноги в секунду, мы можем назвать его энергию 1; если второе тело весом в две унции имеет скорость три фута в секунду, его энергия будет вдвое больше квадрата трех, или 18.

Томас Янг, 1807

Янг просто назвал это энергией. Уильям Томсон, лорд Кельвин (1824–1907) добавил прилагательное «кинетическая», чтобы отделить ее от «потенциальной энергии», названной Уильямом Рэнкином (1820–1872) в 1853 году.

Кинетическая энергия иногда обозначается буквой T . Вероятно, это происходит от французского travail mécanique (механическая работа) или Quantité de travail (количество работы).

Потенциальная и кинетическая энергия

Энергия

Энергия – это способность выполнять работу .

Единица энергии – Дж (Джоуль), что также равно кг · м ² / с ² (килограмм-метр в квадрате на секунду в квадрате)

Энергия может быть во многих формах! Здесь мы смотрим на потенциальную энергию (PE) и кинетическую энергию (KE).

Потенциальная энергия и кинетическая энергия

Молоток:

• в поднятом состоянии имеет потенциал энергию (энергия положения или состояния)
• при падении имеет кинетическую энергию (энергия движения)

Потенциальная энергия (PE) –

накопленная энергия из-за положения или состояния

• поднятый молот имеет PE под действием силы тяжести.
• топливо и взрывчатые вещества имеют Химический ПЭ
• витая пружина или натянутая дуга также имеют PE из-за их состояния

Кинетическая энергия (КЭ) – энергия движения

У движущегося автомобиля много кинетической энергии

От PE до KE

Эти парашютисты обладают потенциальной энергией из-за того, что они находятся высоко.
После прыжка эта потенциальная энергия
преобразуется в кинетической энергии (и тепла) по мере того, как они ускоряются.

Гравитационная потенциальная энергия

Когда PE возникает из-за высоты объекта, тогда:

PE под действием силы тяжести = m g h

Где:

• м – масса объекта (кг)
• г – «напряженность гравитационного поля» 9,8 м / с ² у поверхности Земли
• h высота (м)

Пример: Этот молоток весом 2 кг имеет высоту 0,4 м. Что это такое?

PE = m g h

= 2 кг × 9.8 м / с ² × 0,4 м

= 7,84 кг · м ² / с ²

= 7,84 Дж

Кинетическая энергия

Формула:

KE = ½ м v ²

Где

• м – масса объекта (кг)
• v – скорость объекта (м / с)

Пример: каков KE автомобиля массой 1500 кг, движущегося на пригородной скорости

14 м / с (около 50 км / ч или 30 миль в час)?

KE = ½ м v ²

KE = ½ × 1500 кг × (14 м / с) ²

KE = 147000 кг · м ² / с ²

KE = 147 кДж

Давайте удвоим скорость!

Пример: тот же автомобиль сейчас движется со скоростью

28 м / с (около 100 км / ч или 60 миль / ч)?

KE = ½ м v ²

KE = ½ × 1500 кг × (28 м / с) ²

KE = 588000 кг · м ² / с ²

KE = 588 кДж

Ух ты! это большой прирост энергии! Скорость по шоссе намного опаснее.

Удвойте скорость и KE увеличивается на четыре раза. Очень важно знать

Метеорит весом 1 кг падает на Луну со скоростью 11 км / с. Сколько это KE?

KE = ½ м v ²

KE = ½ × 1 кг × (11000 м / с) ²

KE = 60 500 000 Дж

КЭ = 60,5 МДж

Это в 100 раз больше энергии, чем у автомобиля, движущегося по шоссе.

От PE до KE

При падении PE объекта из-за силы тяжести преобразуется в KE , а также тепла из-за сопротивления воздуха.

Давай что-нибудь уроним!

Пример: мы бросаем это 0,1 кг яблока на 1 метр. С какой скоростью он ударяется о землю?

На высоте 1 м над землей его потенциальная энергия

PE = m g h

PE = 0,1 кг × 9,8 м / с ² × 1 м

PE = 0,98 кг · м ² / с ²

Игнорируя сопротивление воздуха (которое в любом случае мало для этого маленького падения), PE преобразуется в KE:

KE = ½ м v ²

Поменять местами и переставить:

½ м v ² = KE

v ² = 2 × KE / м

v = √ (2 × KE / м)

Теперь поместите PE в KE, и мы получим:

v = √ (2 × 0.98 кг м ² / с ² / 0,1 кг)

v = √ (19,6 м ² / с ² )

v = 4,427 … м / с

Примечание: для скорости мы можем комбинировать формулы следующим образом:

Скорость от KE:		v = √ (2 × KE / м)
Введите формулу для полиэтилена:		v = √ (2 × мг-час / м)
Отмена м / м:		v = √ (2gh)

Масса значения не имеет! Все дело в высоте и гравитации.Для нашего предыдущего примера:

v = √ (2gh)

v = √ (2 × 9,8 м / с ² × 1 м)

v = 4,427 … м / с

Сводка

Расчет кинетической энергии – Высшая школа физики

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Механическая энергия – Видео по физике от Brightstorm

Способность объекта выполнять работу измеряется его механической энергией , или суммой кинетической энергии объекта и потенциальной энергии. Механическая энергия возникает из-за положения или движения объекта. Формула для механической энергии: механическая энергия = кинетическая энергия + потенциальная энергия .

Механическая энергия, механическая энергия – это энергия, обусловленная положением или движением объекта в порядке. И есть 2 большие формы механической энергии, кинетической энергии и потенциальной энергии.Итак, давайте рассмотрим несколько примеров, когда у меня есть мяч для скашивания, и если я подниму его высоко, он получит потенциальную энергию, верно? Я могу отпустить это, и что произойдет? Что ж, потенциальная энергия правильно преобразуется в кинетическую. Прямо здесь, когда он падает на пол, он не имеет потенциальной энергии, и я остановил кинетическую энергию прямо здесь, так что снова эти типы энергии можно передавать, и вы часто увидите много проблем, когда вам нужно что-то преобразовать из определенное количество кинетической энергии в потенциальную энергию, скажем, с маятником, который движется там, где у него есть максимальное количество кинетической энергии, а затем эта кинетическая энергия медленно преобразуется в потенциальную энергию.Итак, давайте быстро посмотрим, что такое кинетическая и потенциальная энергия. Итак, кинетическая энергия, которая представляет собой энергию движения, равна половине массы объекта, умноженной на квадрат скорости. Итак, одна половина мв в квадрате – это формула, которую мы используем для кинетической энергии.

Потенциальная энергия Когда мы говорим о позиционной энергии, нам нужно знать массу, затем силу тяжести g, а затем высоту, на которую мы поднимаем ее. Итак, умножение массы на силу тяжести, умноженную на высоту, дает нам потенциальную энергию и помните, что сила тяжести равна 9.Там 8 метров в секунду в квадрате силы ускорения. Итак, это 2 типа механической энергии, и часто мы будем решать что-то, исходя из определенного количества потенциальной энергии, и выясним, сколько кинетической энергии она имеет в самой низкой точке, и мы снова используем эти 2 уравнения для решения задач с механической энергией. энергия.

Практика применения формул скорости и энергии

Расчет скорости

Скорость – это скорость (в секундах, минутах или часах), с которой мы преодолеем заданное расстояние (в метрах, милях или футах).Чтобы вычислить скорость, мы берем изменение расстояния ( x ), разделенное на изменение во времени ( t ):

Допустим, вы ехали к дому своего друга. Вы начали в 9:30 и пришли в 9:50. И вы знаете, что это в 15 милях отсюда. Какая средняя скорость была у вас?

Итак, вы ехали в среднем со скоростью 50 миль в час (миль в час).

Теперь давайте посмотрим на это уравнение немного иначе. Предположим, вы знаете, что ограничение скорости на автостраде составляет 75 миль в час, и вы склонны в среднем выходить за его пределы. У вас есть еще 50 миль до выхода. Сколько времени вам понадобится, чтобы добраться до выхода?

Чтобы решить это уравнение, нам нужно немного изменить формулу:

Теперь мы можем вставить информацию, которая у нас есть:

Дорога до выхода займет 40 минут.

Кинетическая энергия

Теперь, когда мы знаем, как вычислить скорость, мы можем лучше понять, как вычислять задачи кинетической энергии. Формула для кинетической энергии ( KE ) – это половина массы ( м ), умноженная на скорость ( v ) в квадрате:

Обычно кинетическая энергия измеряется в джоулях (Дж) , что равно одному килограмму, умноженному на один метр в квадрате, деленному на одну секунду в квадрате:

Это говорит нам о том, что нам нужно, чтобы наши единицы измерения были в килограммах и метрах.Если масса не в килограммах, обязательно переводите ее в килограммы. И не забудьте перевести скорость в метры в секунду (м / с).

Теперь давайте возьмем приведенный выше пример с автомобилем и определим кинетическую энергию автомобиля, движущегося по автостраде. Он разгоняется до 75 миль в час, что составляет 34 м / с, а средний вес автомобиля составляет около 1800 килограммов.

Итак, кинетическая энергия этого автомобиля составляет 1,0 мДж (мегаджоуль, мДж, равен одному миллиону джоулей).

Потенциальная энергия

Другой тип энергии называется потенциальной энергией или энергией, обусловленной положением объекта. Лучший способ подумать о потенциальной энергии – это представить себе, как вы держите камень из окна большого небоскреба. Если вы уроните этот камень, он упадет (кинетическая энергия), но в настоящее время не движется. Поскольку энергия никогда не создается и не разрушается, откуда берется эта кинетическая энергия? Прежде чем камень уронят, он находится в форме потенциальной энергии.2, то можно рассчитать потенциальную энергию:

Потенциальная энергия этой породы составляет 12 кДж (килоджоуль, кДж, равен 1000 джоулей).

Потенциальная и кинетическая энергия

Изменение потенциальной энергии плюс кинетическая энергия всегда равно нулю. Другими словами, начальная кинетическая энергия плюс начальная потенциальная энергия равна конечной кинетической энергии плюс конечная потенциальная энергия. Давайте еще раз взглянем на этот камень.Мы хотим знать, какой будет скорость камня перед тем, как он упадет на землю, в этот момент вся потенциальная энергия превратилась в кинетическую.

Мы можем изменить формулу кинетической энергии, использованную ранее, чтобы найти скорость вместо кинетической энергии:

Затем мы можем решить для скорости:

Скорость камня к моменту падения на землю превышает 100 метров в секунду!

Мы также можем определить скорость камня в определенных местах вдоль падения.Какая будет скорость скалы на полпути вниз по небоскребу или на высоте 275 метров?

Сначала нам нужно определить потенциальную энергию в этой точке:

Потенциальная энергия 6,2 кДж.

Затем мы можем найти окончательную кинетическую энергию, используя формулу начальной и конечной кинетической и потенциальной энергии:

Мы можем изменить эту формулу, чтобы найти окончательную кинетическую энергию:

Кинетическая энергия на полпути вниз по небоскребу равна 5.8 кДж. Отсюда мы можем определить скорость, как и раньше:

Скорость камня на полпути вниз по небоскребу составляет 71 м / с.

Резюме урока

Мы можем вычислить скорость , или скорость объекта, разделив изменение расстояния на изменение во времени. Затем это можно использовать для вычисления кинетической энергии объекта, взяв квадрат скорости, умноженный на массу, умноженный на половину.

Потенциальная энергия – это энергия, обусловленная положением. К концу вся потенциальная энергия превратится в кинетическую.

Импульс и энергия

Импульс и энергия

Импульс и энергия

Пожалуй, самое известное уравнение в физике это

E = m c ² .

Он выражает тот факт, что объект в состоянии покоя обладает большим количеством энергии благодаря своей массе м .Эта энергия имеет значение в ситуациях, когда масса изменяется, например, в ядерно-физических взаимодействиях, где ядра создаются или уничтожаются.

Энергия движущегося объекта, конечно, еще больше – в ньютоновской физике на количество, определяемое известной формулой кинетической энергии (1/2) m v ² . Правильное выражение согласно теории относительности:

E = г м c ²

для полной энергии, и, следовательно,

E = (г – 1) м c ²

для кинетической энергии, где г – тот же коэффициент относительности, который использовался ранее:

Импульс, который в ньютоновской физике задается соотношением м против , определяется выражением

p = г м v

согласно теории относительности.

Если скорость v мала по сравнению с c , формулы относительности для импульса и кинетическая энергия становится эквивалентны их ньютоновским (нерелятивистским) аналогам.

Если скорость v приближается с , и импульс, и энергия приближаются к бесконечности. Таким образом, скорость объект, который вообще имеет какую-либо массу, всегда должен быть меньше, чем с .Однако в принципе нет предела насколько большим может быть импульс или энергия объекта.

Формулы энергии и импульса также могут быть использованы для понимания случая частиц, подобных фотону, которые имеют нулевую массу. Чтобы энергия и импульс оставались конечными в пределе т -> 0, это должно быть так грамм -> бесконечность , а значит, v -> c. Таким образом, частиц с нулевая масса всегда движется со скоростью c . Энергия и импульс формулы подразумевают p / E = v / c ² , и, следовательно, p = E / c для частиц с нулевой массой.