Формулы физических величин: Такой страницы нет – Инженерный справочник DPVA.ru / Технический справочник ДПВА / Таблицы для инженеров (ex DPVA-info)

Обозначения физических величин, система СИ – Физика – Теория, тесты, формулы и задачи

• Главная –
• Формулы и прочее –
• Физика: Система СИ

Обозначения физических величин и другие сведения о системе СИ приводятся здесь в качестве справочного материала, так как они требуются при решении многих задач по физике. И хотя на большинстве экзаменов, в том числе и на ЦТ или ЕГЭ, все физические величины указываются вместе со своими единицами измерения, тем не менее очень важно всегда точно знать и хорошо уметь переводить любые единицы измерения любых физических величин в систему СИ, так как в большинстве задач корректно рассчитать ответ можно только выполняя расчеты именно в системе СИ.

 

Изучать обозначения физических величин и систему СИ онлайн:

• Назад
• Вперёд

 

Как успешно подготовиться к ЦТ по физике и математике?

Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:

1. Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
2. Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
3. Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.

Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.

 

Нашли ошибку?

Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.

01-е. Единицы физических величин

• Главная
• Справочник
• Физика
• Физические величины
• Книги, лекции и конспекты по физике
• Физика 7 класс
• 01-е. Единицы физических величин

      § 01-е. Единицы физических величин

С давних времён для измерения различных величин люди применяют множество единиц. Например, длину полотна ткани когда-то измеряли локтями, потому что ткань удобно наматывать на руку между ладонью и локтем. Расстояние между городами и деревнями измеряли милями (от лат. «милле» – тысяча). Тысяча двойных шагов, шаг левой и шаг правой ногой, составляли одну милю. Существовали и другие единицы, причём в каждой стране и, порой, местности внутри страны – свои.

С 1918 г. в России используется так называемая метрическая система мер. Она принята в большинстве стран Европы и во многих неевропейских государствах. В её основу положен так называемый десятичный принцип: в каждой крупной единице содержится десять следующих по значению меньших единиц. Например, в метре – десять дециметров, в дециметре – десять сантиметров, в сантиметре – десять миллиметров.

Значения приставок, служащих для образования кратных и дольных единиц согласно десятичному принципу.

мега = 1 000 000 кило = 1 000 гекто = 100 дека = 10

деци = 0,1 санти = 0,01 милли = 0,001 микро = 0,000 001

Взгляните на равенства в рамке. В левой их части – так называемые десятичные приставки. Они служат для образования больших и меньших единиц величин, называемых кратными и дольными единицами. В правом столбце перечислены числовые значения приставок, их также называют десятичными множителями. Существуют и другие приставки и множители.

Название каждой приставки и её значение всегда взаимозаменяемы.

Рассмотрим некоторые примеры взаимозаменяемости:

5 километров   =   5 · 1000 метров   =   5000 метров,

200 миллиграммов   =   200 · 0,001 грамма   =   0,2 грамма,

5 дм³ = 5 (деци · метр)³ = 5 · деци³ · метр³ = 5 · 0,1³ · м³ = 0,005 м³.

Изучая физику, вы будете сталкиваться с самыми разными величинами, выраженными в различных единицах. Поэтому перед началом вычислений по формулам значения всех величин желательно выразить в согласующихся друг с другом единицах.

Рассмотрим пример. Пусть длина поверхности стола 1,5 м, ширина 80 см.

По формуле S = l·b вычислим площадь поверхности стола:

S_ст = 1,5 м · 80 см = 120 м·см.

Этот ответ правильный. Однако площадь не принято выражать в таких единицах. Рассмотрим, как принято поступать.

Решение расчетных задач в физике принято оформлять в виде двух-трех столбцов. Слева записывают данные условия задачи. Справа записывают формулы и вычисления.

Допустимый вариант – выразить значения в сантиметрах:
l = 1,5 м = 150 см b = 80 см	S = l · b	Sст = 150 см · 80 см Sст = 150 · 80 см·см
Sст = ?		Sст = 12000 см2
Рекомендуемый вариант – выразить все значения в метрах:
l = 1,5 м b = 80 см = 0,8 м	S = l · b	Sст = 1,5 м · 0,8 м Sст = 1,5 · 0,8 м·м
Sст = ?		Sст = 1,2 м2

Итак, мы получили три значения для одной и той же величины – площади поверхности стола: 120 м·см, 12000 см² и 1,2 м².

Покажем, что все эти значения равны друг другу. Для этого выразим их в одинаковых единицах – квадратных метрах:

120 м·см = 120 м · (санти)метр = 120 м · (0,01) м = 1,2 м²

12000 см² = 12000 (см)² = 12000 · (0,01 м)² = 12000 · 0,0001 м² = 1,2 м²

Эти равенства подтверждают верность трёх рассмотренных нами вариантов вычисления площади поверхности стола:

120 м·см   =   1,2 м²   =   12000 см²

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Физические величины Формулы Физика Теория 7 класс 2564

Источник

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

Работа с физическими величинами в математических формулах

Введение

На уроках математики и особенно естественных наук (физика, химия и т. д.) вы выполняете вычисления, которые используют физические величины в качестве входных данных и дают физическую величину в качестве ответа. 2\)). Но этот упрощенный метод работы с единицами измерения в лучшем случае вводит в заблуждение, а в худшем — опасен. Поскольку единицы не участвуют в расчетах и ​​добавляются задним числом, труднее обнаружить ошибки вычислений из-за использования несоответствующих единиц, и можно использовать неправильную формулу, не заметив этого (например, используя формулу объема вместо формула площади).

На самом деле, с физическими величинами/единицами удобно обращаться строго, и в этой статье я объясню и проиллюстрирую, как это сделать. Вам нужно знать только основы алгебры, чтобы понять основную концепцию работы с единицами измерения. Кроме того, все физические единицы (например, метр, секунда, грамм и т. д.) будут рассматриваться как непрозрачные положительные переменные, подчиняющиеся всем правилам алгебры.

Преобразование единиц измерения

В этом мире есть много способов измерить одно и то же количество. Например, длину можно измерять в метрах (обозначение: м) или футах (обозначение: футы). Поскольку эти единицы измеряют одни и те же вещи, их можно приравнять к коэффициенту преобразования.

Например, 1 фут равен 0,3048 метра. Мы можем записать это как уравнение: \(1\text{ft} = 0,3048\text{m}\).
Мы можем взять уравнение и преобразовать его, чтобы получить следующее: \(\frac{1\text{ft}}{0,3048\text{m}} = 1\).
Это может выглядеть необычно, но через мгновение это будет полезно.
Точно так же мы можем переставить по-другому, чтобы получить: \(\frac{0,3048\text{ m}}{1\text{ ft}} = 1\).

Другой пример: \(1000\text{ м} = 1\text{ км}\), следовательно, \(\frac{1000\text{ м}}{1\text{ км}} = 1 = \frac{ 1\text{ км}}{1000\text{ м}}\).

Вооружившись этими дробями, равными единице, мы умножаем на любую из них, чтобы выполнить преобразование единиц измерения.
Например, что такое 3125 футов в километрах? Займемся алгеброй:

\(\require{cancel} 3125\text{ футов} \:=\: 3125\text{ футов} × 1 × 1 \:=\: 3125\text{ футов} ×\! \frac{0.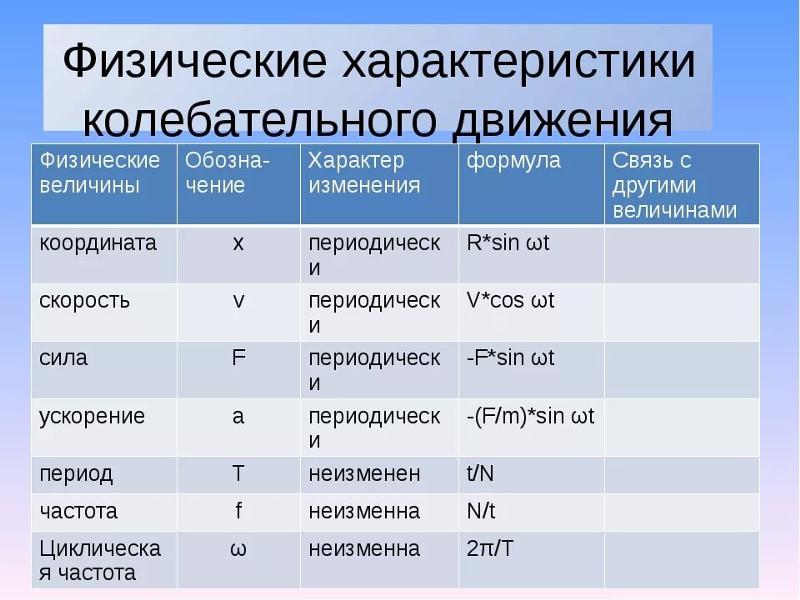 3048\text{ м}}{1\текст{ фут}} \!×\!\frac{1\text{ км}}{1000\text{ м}} \:=\: \frac{3125 \,×\, 0,3048 \ ,×\, 1\, \cancel{\text{ft}} \cdot \cancel{\text{m}} \cdot\, \text{км}}{1 \,×\, 1000\, \cancel{ \text{ft}} \cdot \cancel{\text{m}}} \:=\: 0,92\).

Это простой случай, когда все единицы согласуются друг с другом. Большинство учебников не превышают этот уровень сложности.

Прямоугольник с \(l = 74\text{m}, w = 81\text{км}\):

Таким образом, \(A = (74\text{м})(81\текст{км}) = 5994\текст{м} \cdot \text{км} = 5994\текст{м} \cdot \text{км} × \frac{1\text{км}}{1000\text{м}} = \frac{5994\, \cancel{\text{м}} \cdot\, \text{км} \,\cdot\, \text{км}}{1000\, \cancel{\text{м}}} = 5,92\).

Здесь мы получили промежуточный результат, выраженный в метрах-в-километрах (что является мерой площади). Технически это правильно, но некрасиво, поэтому мы умножили на коэффициент преобразования, чтобы получить ответ в квадратных километрах.

Прямоугольник с \(l = 3\text{ми}, w = 2\текст{км}\):

Таким образом, \(A \:=\: (3\text{мили})(2\text{км}) \:=\: 6\text{мили} \cdot \text{км} \:\приблизительно\: 6\text{ миль} \cdot \text{км} × \frac{1,6092 + 8t + 3\), где \(t\) в секундах, а \(h(t)\) в метрах.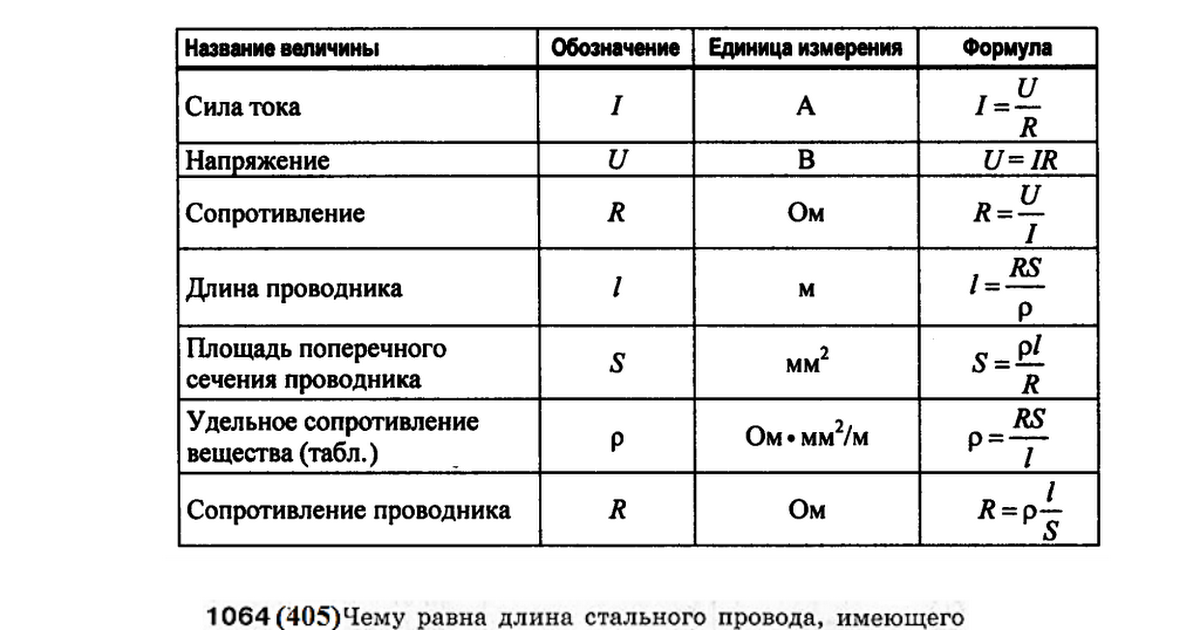

Чтобы вычислить эту функцию при \(t = 2\text{ s}\), вам нужно убедиться, что \(t\) задано в секундах (или преобразовать, чтобы удовлетворить этому требованию), а затем убрать единицу измерения, чтобы вы получаете безразмерное число 2, оцениваете формулу, чтобы получить -0,6, и добавляете единицу, чтобы получить -0,6 метра.

Более правильный, но громоздкий способ выглядел бы так:
Мяч, выпущенный из пушки, имеет высоту \(h(t) = (-4,92\text{m}) + (8 × 2\text{m}) + (3\text{m}) \:=\: -0,6\text{m}\).

Исчисление

Производные и интегралы — полезные понятия в физике. Например, скорость — это производная от смещения, а площадь — это интеграл от длин линий. Хорошая новость заключается в том, что взятие производной или интеграла функции автоматически учитывает единицы измерения.

В качестве примера в предыдущем разделе была описана функция, вычисляющая высоту пушечного ядра по заданному времени. Если взять производную от функции, то получим: \(\frac{d}{dt} h(t) \:=\: (-4,92) \, t + (8\text{ m}/\text{s})\).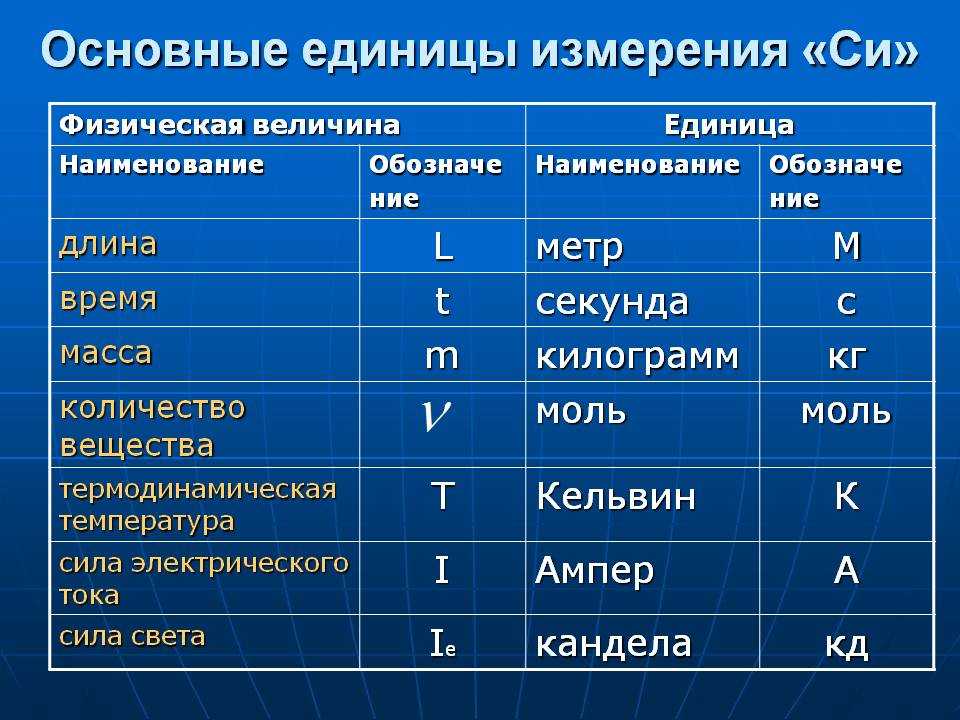 Мы ожидаем, что это будет формулой скорости. Действительно, когда мы подставляем значение для \(t\), мы получаем ответ, который выражается в \(\text{m}/\text{s}\).

Обнаружение ошибки

При расчете с явными единицами измерения любые несоответствующие единицы будут отображаться в конечном результате. Например:

• Длина прямоугольника измеряется в километрах, а ширина — в милях. Затем умножение двух чисел даст площадь, правильно измеренную в километрах на мили. Если бы при вычислении не использовались единицы измерения, было бы ошибкой считать, что ответ дается в квадратных километрах или квадратных милях. 92\) (или просто \(\text{N}\)), и вы заметите несоответствие. Если бы вы производили расчет без единиц измерения, было бы легко не заметить несоответствие единиц, потому что есть 3 переменные с разными единицами и одна константа с довольно сложной составной единицей.

При выборе формулы для использования вы можете исключить кандидатов, если они дают бессмысленные единицы измерения.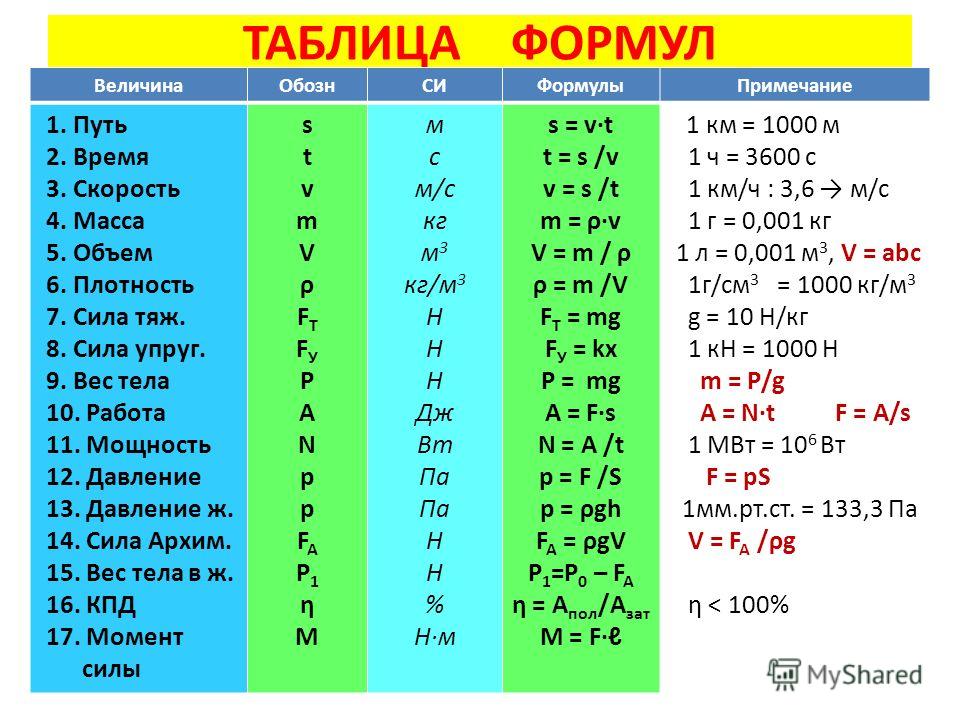 2 \, /\, R\) на самом деле верно. 92}} = \text{W}\). Эта формула проходит базовую проверку единиц.

Выполняя размерный анализ, мы можем отказаться от бессмысленных расчетов, прежде чем потратим время, пытаясь применить их результаты.

Категории: Математика, Письмо

Последнее обновление: 09.09.2015

Анализ размерности: формула и уравнение

В этой статье вы узнаете о размерностях и формуле размерности физических величин с помощью примеров.

Начнем с определений.

Каковы размеры?

Размерность физической величины определяется как степень, в которую возводятся фундаментальные величины для выражения физической величины. Например, размерность скорости 0, 1, -1 в Масса , Длина , Время соответственно.

Если поначалу это кажется запутанным, не волнуйтесь, мы рассмотрим вычисления размеров позже в этой статье.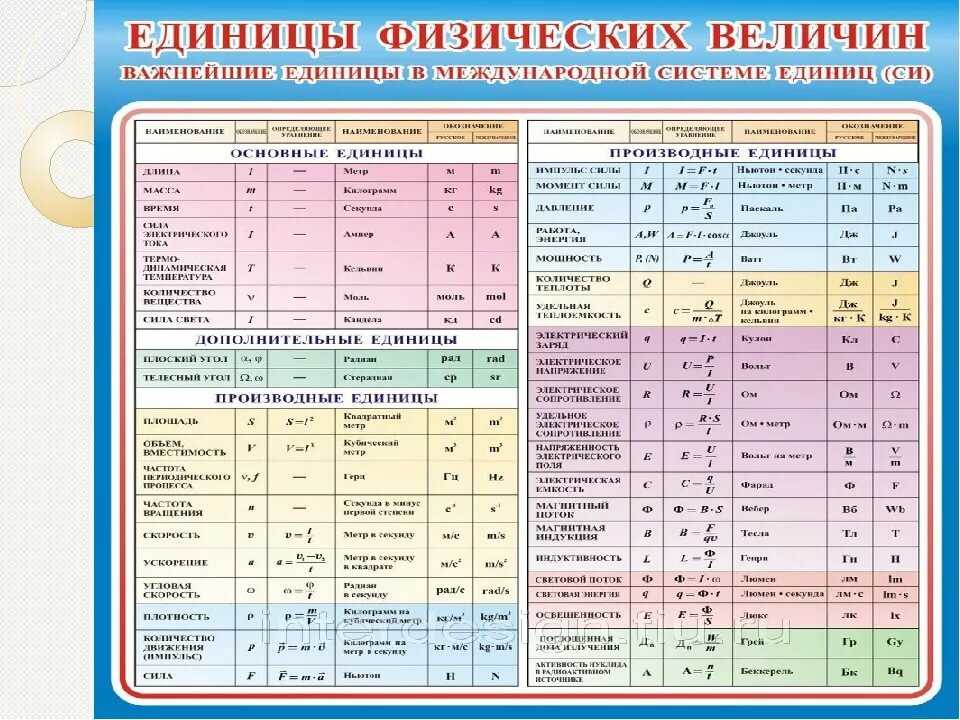

---

Что такое формула измерения?

Размерная формула определяется как выражение физической величины через ее основную единицу (фундаментальную величину) с соответствующими размерами. Например,

Размерная формула скорости [ M ⁰ L ¹ T ^-1 ]

0, 1, -1 — размеры

Обычно мы используем 3 фундаментальные величины: массу, длину и время, чтобы вывести размерные формулы различных физических величин.

Сначала давайте рассмотрим размерный символ этих фундаментальных величин.

Размерная формула фундаментальных величин

• МАССА [M]
• Длина [L]
• Время [Т.]
• – . ?

  Теперь, когда мы знаем, что такое размерная формула, давайте посмотрим, как мы можем вычислить размерную формулу физической величины.

  Мы можем вычислить формулу размерности физической величины, если известна ее связь с другими физическими величинами. 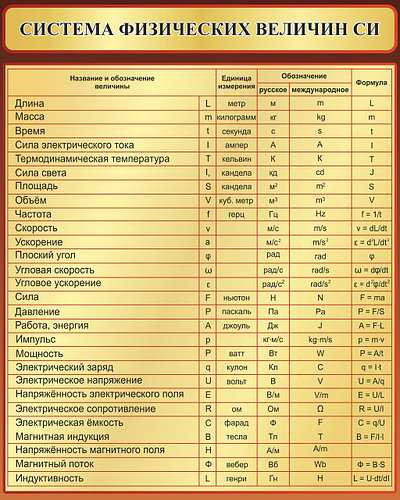Например, предположим, что мы хотим вычислить размерную формулу плотности.

  Мы знаем, что плотность связана с массой и объемом, то есть плотность = масса/объем. Теперь воспользуемся этим соотношением для расчета размерной формулы плотности:

    Плотность = масса/объем
            = масса / (длина * ширина * объем)
   

  Мы можем использовать основную величину

  • [L] (Длина) – для длины, ширины и объема
  • [M] (Масса) – для массы

  Следовательно, наша формула становится 9000 Плотность = [M] / ([L] * [L] * [L] = [М] / [Д ³ ] = [М ¹ ] * [Л ^-3 ]

  И, так как время не упоминается в плотности, мы можем написать

  Dimensional Formula of Density = [ M ¹ L ^-3 T ⁰  ]

  In this way, we can calculate the dimensional formula of physical количества.

  ---

  Размерная формула и единица СИ

  Мы также можем получить единицы СИ, используя размерную формулу и наоборот. Давайте посмотрим пример.

  1. Размерная формула для преобразования единиц СИ

  Dimensional Formula of density = [ M ¹ L ^-3 T ⁰  ] .

  Мы знаем единицу СИ

  • [М] кг (килограмм)
  • [л] м (метр)
  • [Т] сейчас 0 90,90 90,9057 секунд если перевести формулу в единицы СИ, то будет [ кг ¹ м ^-3 с ⁰ ] . Следовательно,

    единица плотности СИ равна кг·м ^-3 .

    2. Блок SI в размерную преобразование формулы

    Блок плотности SI составляет кг M ^-3

    Здесь, мы знаем, что

    9008

  • .

  • м единица длины в системе СИ

  Итак, наша формула будет выглядеть так: [M L ^-3 ] .

  Поскольку время здесь не упоминается, мы можем использовать 0 для времени.

  Dimensional formula of density = [M ¹ L ^-3 T ⁰ ]

  ---

  Dimensional Formula of Physical Quantity

  Now that we know размерная формула, давайте посмотрим размерную формулу различных физических величин.

  Размерная формула различных физических величин

  ---

  Размерное уравнение

  Уравнение, содержащее физические величины с размерной формулой, известно как размерное уравнение. Размерное уравнение получается приравниванием размерной формулы в правой и левой частях уравнения. Например,

  Уравнение размерности v = u + at равно

  [ M  0  L  1  T  -1  ] = [ M  0  L  1  T  -1  ] + [ M  0  L  1  Т  -1  ] * [ М  0  Л  0  Т  1  ]
   

  ---

  Принцип однородности размерного уравнения

  В соответствии с этим принципом размерности фундаментальных величин в левой части уравнения должны быть равны размерностям фундаментальных величин в правой части этого уравнения.

  Рассмотрим три величины A , B и C, такие, что C = A + B . Следовательно, согласно этому принципу, размеры C равны размерам A и B.

  Рассмотрим пример. Здесь у нас есть наше раннее размерное уравнение v = u + at :

  [M  0  L  1  T  -1 ] = [M  0  L  1  T  -1 ] + [M  0  L  1 ] + [M  0  L  1 ] + [M  0  L  1 ].  0  Л  0  Т  1  ]
   

  1. Решение правой части

   RHS = [M  0  L  1  T  -1  ] + [M  0  L T  -1  ] X [M  0  L  0  T]
       = [M  0  L  1  T  -1  ] + [M  0  L  1  T  0  ]
   RHS = [M  0  L  1  T  -1  ] = LHS
   

  Здесь уравнение правой части теперь совпадает с уравнением левой части. 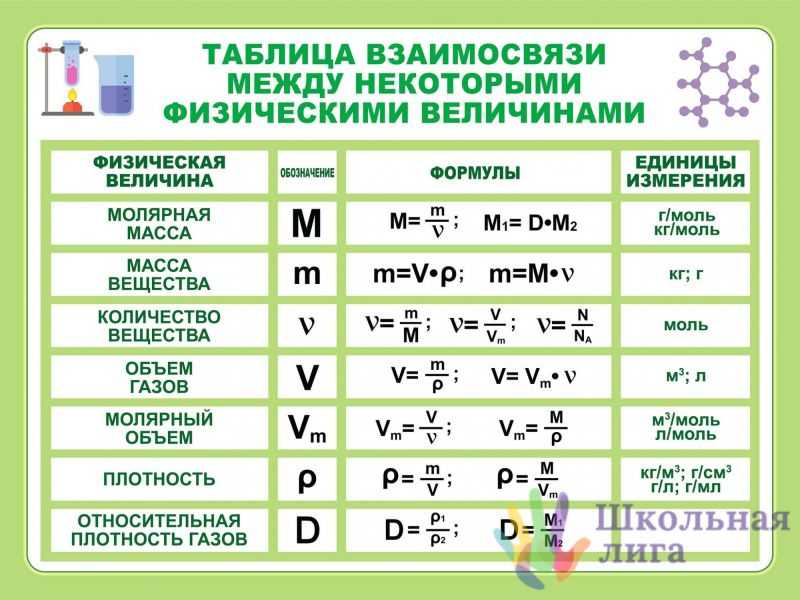Таким образом, принцип однородности размерных уравнений доказан.

  ---

  Для чего используются уравнения размерности?

  Вот некоторые примеры использования размерного уравнения:

  • Мы можем использовать размерные уравнения для проверки правильности физических соотношений.
  • Это также помогает нам установить соотношение между различными физическими величинами.
  • Мы можем преобразовать значение физической величины из одной системы единиц в другую, используя уравнение размерности.
  • Находит размерность констант в заданном отношении.

  ---

  Каковы ограничения размерного анализа?

  Ниже приведены ограничения размерного анализа.

  • Мы не можем получить информацию о размерной константе, используя размерный анализ.
  • Если величина зависит от более чем трех факторов, имеющих размерность, Мы не можем вывести формулу размерности.
  • Мы не можем вывести формулу, содержащую тригонометрические, экспоненциальные, логарифмические функции и т.