Обобщающий урок по физике в 10 классе на тему “Динамика материальной точки”
Повторение и обобщение темы “Динамика материальной точки”
Цели урока:
Образовательная: повторить и систематизировать материал по теме «Основы динамики»- основные законы, определения, формулы; научить определять логическую связь между понятиями и явлениями;
Воспитательная: повторить формирование навыков коллективной работы, повышение познавательной деятельности и активности учащихся;
Развивающая: развитие интереса к физике, развитие речи учащихся, развитие умения видеть в окружающих процессах физические явления и уметь их обобщать.
Тип урока: Урок обобщения и систематизации знаний.
Оборудование: опорные обобщающие конспекты, карточки-задания, раздаточный материал (тесты), обобщающие таблицы, бланки для ответов, мультипроектор, презентация к уроку
Ум заключается не только в знаниях, но и в умении применять знания на деле
Аристотель (384-322гг. до н.э.). древнегреческий философ
до н.э.). древнегреческий философ
I. Организация начала урока . Вступительное слово учителя.
Мы изучили весь курс физики средней школы и сегодня продолжаем повторять изученный материал. Тема нашего урока «Динамика материальной точки» Эпиграфом сегодняшнего урока я выбрала слова древнегреческого философа Аристотеля. Какова будет цель нашего урока?
Учитель уточняет цели и задачи урока, знакомит учащихся с этапами урока
Учитель: Целью нашего урока будет систематизация знаний по теме «Динамика материальной точки». Результатом работы будет схема со структурой этой темы .
Что называется материальной точкой?
Что изучает динамика? (Динамика изучает причину изменения скорости, причину ускорения).
Прежде всего, нужно напомнить, что динамика – логическое продолжение кинематики. Динамика изучает причины, которыми обусловлено движение
Динамика изучает причины, которыми обусловлено движение
Человек не только стремится к знаниям, не только их получает, но и их систематизирует. Ньютон создавал механику, как попытку создать систему, объясняющую мир, и это ему удалось.
Ожидаемый результат: после повторения и систематизации пройденного материала, успешно выполнить, предлагаемый тест
II. Актуализация знаний учащихся.
1. Повторение понятия – Силы.Учитель:
Что называется силой? (Сила – величина, характеризующая взаимодействие тел.)
Какие две силы считаются равными?
Как измерить силу?
Как складываются силы, действующие на тело?
Назовите единицу измерения силы
Как измерить силу? а) эталонная пружина (динамометр) б) через ускорение (расчет )
На каком принципе основано применение динамометра?
Учитель: Давайте вспомним, какие силы мы знаем?
Учащиеся:
сила упругости,
сила трения,
архимедова сила,
сила всемирного тяготения,
вес тела.

Работа в группах
Систематизация знаний по теме «Виды сил». Раздаются группам обобщающие таблицы «Виды сил» Каждая группа выполняет определённую часть таблицы
Взаимопроверка и оценка работы одноклассников.
Сила тяжести
Как направлена сила тяжести?
От чего зависит сила тяжести?
На чем основано измерение массы тел?
От чего зависит ускорение свободного падения?
Что называется весом тела?
Как направлен вес тела?
От чего зависит вес тела?
Что называется невесомостью?
Как изменится вес тела при перемещении с полюса на экватор? А масса тела?
Почему тела падают с одинаковыми ускорениями?
Всегда ли вес тела равен силе тяжести?
Сила всемирного тяготения
Где проявляются силы тяготения
Как направлены силы тяготения?
Что общего в движении падающего яблока и Луны?
Почему не приближаются друг к другу предметы, находящиеся в комнате, хотя они взаимно притягиваются?
Сила трения
Когда возникает сила трения? Как она направлена ?
Назовите виды силы трения
Когда возникает сила трения скольжения?
От чего зависит сила трения скольжения?
От чего зависит коэффициент трения?
Как уменьшить силу трения скольжения?
Чему равна сила трения, если тело движется равномерно?
Почему ящик труднее сдвинуть с места, чем сохранять движение?
Какие санки скатятся с горы быстрее: с одним или двумя седоками?
Может ли автомобиль двигаться равномерно по горизонтальному участку с выключенным двигателем?
Сила упругости
Что называется деформацией?
В чем причина силы упругости?
Как направлена сила упругости?
Почему возникает сила реакции опоры?
Как движется тело под действием силы упругости?
На каком принципе работает динамометр?
Зачем у динамометров делают ограничитель растяжения пружины?
 Повторение законов динамики.
Повторение законов динамики.Учитель: На какие законы опирается динамика?
Учащиеся: Основные законы по теме «Динамика»
I закон Ньютона.
II закон Ньютона.
III закон Ньютона.
Закон Гука.
Закон всемирного тяготения.
Учитель: Сформулируйте первый закон Ньютона
Учащиеся: ( варианты )
Существуют такие СО, относительно которых свободные тела движутся равномерно и прямолинейно
прямолинейно, пока действие со стороны других тел не выведет его из этого состояния
В инерциальной СО тело, не подверженное внешним воздействиям, находится в покое или движется равномерно и прямолинейно
2. Что называется инерцией? Примеры
Что называется инерцией? Примеры
Какая СО называется инерциальной?
В каком случае тело движется равномерно?
Почему споткнувшийся человек падает вперед, а поскользнувшийся – назад?
Почему парашютист по истечении некоторого времени падения с раскрытым парашютом, падает равномерно, а не ускоренно? 7.Заяц, спасаясь от преследуемой его собаки, делает резкие прыжки в сторону. Почему собаке трудно поймать зайца, хотя она бегает быстрее?
Как движется тело, если F = 0?
Объясните опыт. Пустой стакан сверху накрыт открыткой, на которой лежит монета. При резком ударе по открытке монета падает в стакан. (Рисунок)
Учитель: Первый закон Ньютона выполняется для изолированных тел. Но в реальном мире, который нас окружает, практически не встречается изолированных тел.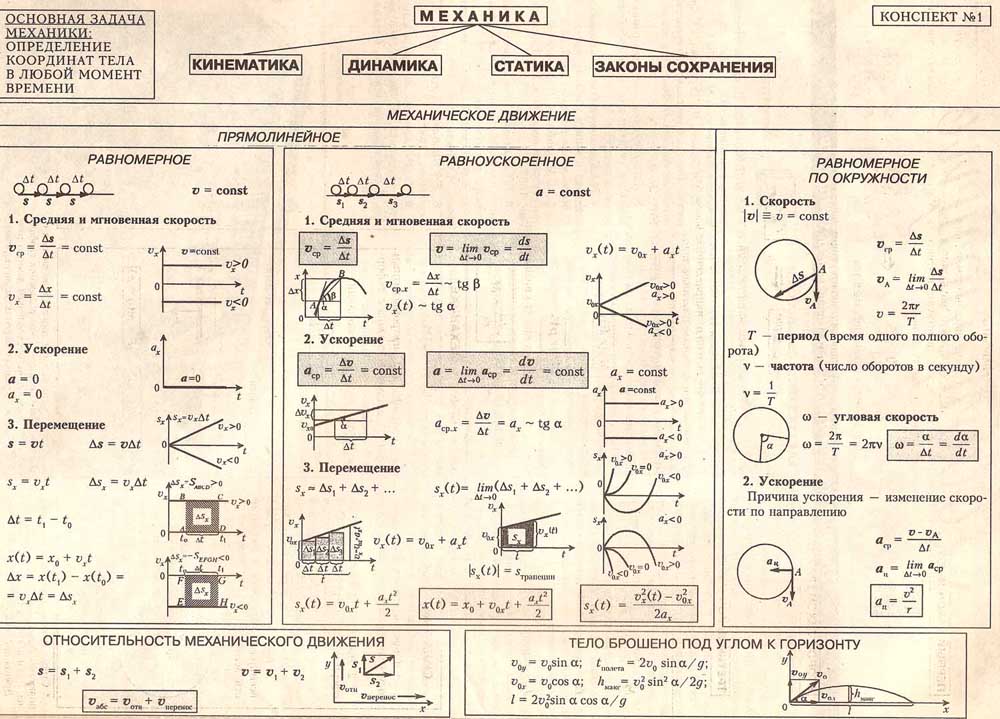
Сформулируйте второй закон Ньютона
Ускорение, с которым двигается тело пропорционально равнодействующей сил, действующей на тело, и обратно пропорционально массе этого тела
Особенности второго закона Ньютона:
Для любых сил
F – причина а, определяет а
Вектор а сонаправлен F
Если действуют несколько сил, то берется результирующая сила
ma = F1 + F2 + F3 + . . .
5. Если F = 0 , то а = 0 ( первый закон Ньютона )
Как этот закон записать?
Как ускорение связано с силой?
Как направлено ускорение тела?
Учитель: Первые два закона Ньютона объясняют поведение тел во многих ситуациях, но как выглядит взаимодействие двух тел между собой?
Сформулируйте третий закон Ньютона
силы, с которыми взаимодействуют два тела, равны по модулю и противоположны по направлению. Здесь нужно отметить особенности сил:
Здесь нужно отметить особенности сил:
Действуют только парами.
Всегда при взаимодействии.
Силы одной природы.
не уравновешиваются
для сил любой природы
Учитель: Следует заметить, что силы, с которыми взаимодействуют два тела, никогда себя не уравновешивают, так как они приложены к разным телам
Как этот закон записать?
В чем заключены особенности этого закона?
Почему в III законе силы не уравновешивают друг друга?
Почему нельзя поднять себя за волосы?
Если топор застрял в бревне, как лучше его извлечь ударяя о
твердую опору: вниз поленом или вниз обухом топора?
Почему при прыжке в момент приземления нужно сгибать колени?
Тело брошено под углом к горизонту.
 Куда направлено ускорениетела, если сопротивление воздуха не учитывать?
Куда направлено ускорениетела, если сопротивление воздуха не учитывать?Почему сорняки не рекомендуется вырывать рывком?
Учитель:
Сформулируйте закон всемирного тяготения
Между всеми телами действуют силы взаимного притяжения – гравитационные силы.
Учащиеся: Закон всемирного тяготения гласит:
Все тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.
G – коэффициент пропорциональности, который назвали гравитационной постоянной. Численно она равна:
Как называется коэффициент пропорциональности в формуле ЗВТ?
Как опытным путем было установлено значение G?
Как был использован ЗВТ для открытия новых планет?
Почему закон получил название «всемирного»?
Учитель:
Сформулируйте закон Гука
Учащиеся: Закон всемирного тяготения гласит:
сила упругости, возникающая при деформации тела, пропорциональна удлинению тела и направлена в сторону, противоположную направлению перемещений частиц тела при деформации:
(Fупр)х = -кх
4.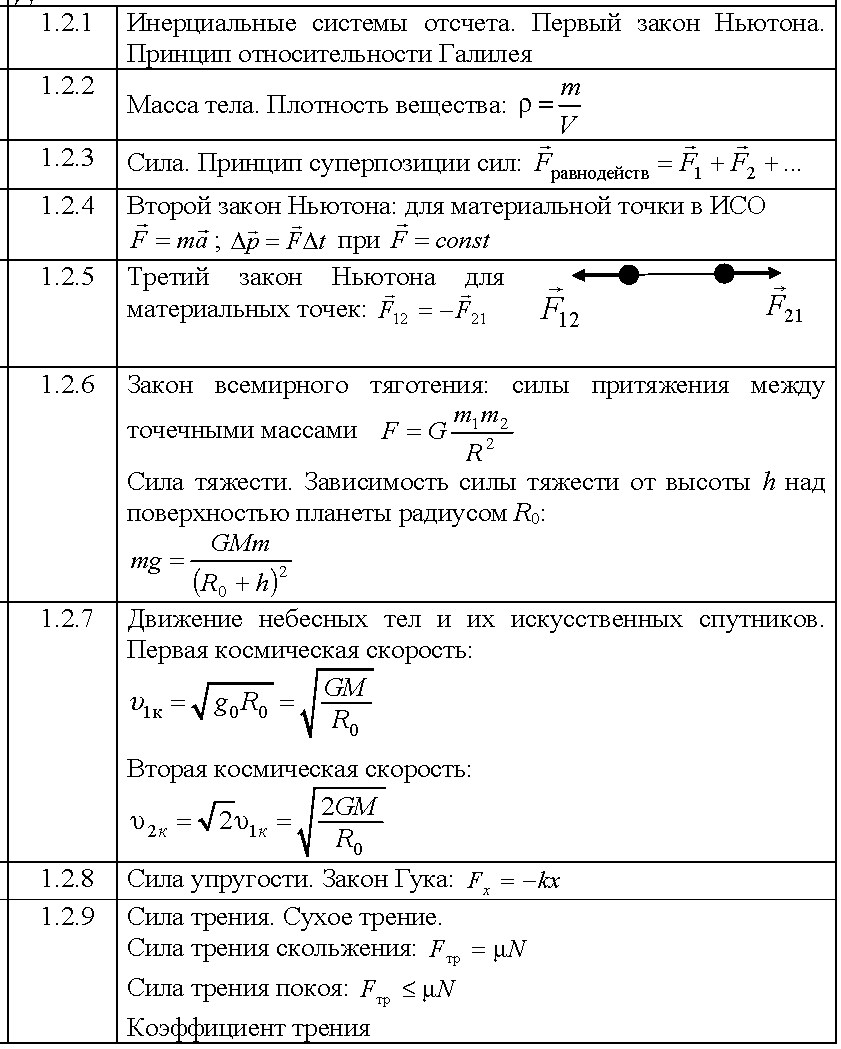 При каких условиях выполняется закон Гука?
При каких условиях выполняется закон Гука?
5. Что называется коэффициентом жесткости? Единицы измерения.
6. От чего зависит коэффициент жесткости?
III. Проверь себя (тест) IV. Подведение итогов урока.Учитель: Наш урок подошёл к концу. Все о чем мы с вами сегодня говорили можно обобщить в виде схемы.( СМ приложение)
V. Рефлексия.Учитель: Наш урок я хотела бы закончить словами Исаака Ньютона, которые он написал перед смертью:
«Не знаю, чем я могу казаться миру, но самому себе я кажусь мальчиком, играющим у моря, которому удалось найти более красивый камушек, чем другим: но океан неизвестного лежит передо мной».
Возьмите листочки, не подписывая их, напишите три существительных, которые пришли вам в голову после этого урока.
VI. Домашнее задание: повторение темы «Законы сохранения», п.п. 28-36, выписать и повторить формулы
Официальный сайт – Ученикам- учитесь!
1. Физика
1.1 Формулы по физике
Формулы по кинематике
Формулы по динамике, законам сохранения в механике
Формулы по молекулярной физике
Формулы по электростатике и постоянному току
Формулы по магнитному полю, механическим колебаниям
Формулы по электромагнитным колебаниям, оптике,ТО
Формулы по квантовой и атомной физике. жидкостям
1.2 Приблизительные вычисления и погрешности
О приближенных вычислениях
О погрешностях
Погрешности и построения графиков
1.3 Задания для дополнительной работы
7-9 классы
Механическое движение. Плотность
Механическая работа и мощность
Давление твердых тел, жидкостей и газов
Архимедова сила Кинематика Динамика
Законы сохранения механической энергии и импульса
Механические колебания и волны
Внутренняя энергия Изменение агрегатных состояний вещества
Электрический ток Работа и мощность тока
Оптические явления Гравитационные явления
Ответы 7кл Ответы 8 кл Ответы 9 кл-1 Ответы 9 кл-2
Справочные данные
2. Английский язык
Сайт для родителей второклашек, изучающих английский язык
1.2 Формулы по физике
Формулы по кинематике
Формулы по динамике, законам сохранения в механике
Формулы по молекулярной физике
Формулы по электростатике и постоянному току
Формулы по магнитному полю, механическим колебаниям
Формулы по электромагнитным колебаниям, оптике,ТО
Формулы по квантовой и атомной физике. жидкостям
жидкостям
1.3 Приблизительные вычисления и погрешности
О приближенных вычислениях
О погрешностях
Погрешности и построения графиков
Физика
1.1 Сдаем ЕГЭ
Демонстрационный вариант -2013
Тренировочные варианты ЕГЭ-2013
Тренировочные варианты ЕГЭ-2012
1.2 Формулы по физике
Формулы по кинематике
Формулы по динамике, законам сохранения в механике
Формулы по молекулярной физике
Формулы по электростатике и постоянному току
Формулы по магнитному полю, механическим колебаниям
Формулы по электромагнитным колебаниям, оптике,ТО
Формулы по квантовой и атомной физике.жидкостям
1.3 Приблизительные вычисления и погрешности
О приближенных вычислениях
О погрешностях
Погрешности и построения графиков
Формулы по физике основные. Формулы по физике для егэ. Работа, мощность, энергия
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.

- Выучить все формулы и законы в физике, и формулы и методы в математике . На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.

Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов , позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика , термодинамика и молекулярная физика , электричество . Их и возьмем!
Основные формулы по физике динамика, кинематика, статика
Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.
Формулы кинематики:
Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.
После динамики самое время рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику
Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!
Основные формулы молекулярной физики и термодинамики
Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.
Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева – все эти милые сердцу формулы собраны ниже.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы .
Основные формулы по физике: электричество
Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.
И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.
На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
Обращайтесь, и вскоре любая задача будет вам «по зубам».
Абсолютно необходимы для того, чтобы человек, решивший изучать эту науку, вооружившись ими, мог чувствовать себя в мире физики как рыба в воде. Без знания формул немыслимо решение задач по физике. Но все формулы запомнить практически невозможно и важно знать, особенно для юного ума, где найти ту или иную формулу и когда ее применить.
Расположение физических формул в специализированных учебниках распределяется обычно по соответствующим разделам среди текстовой информации, поэтому их поиск там может отнять довольно-таки много времени, а тем более, если они вдруг понадобятся Вам срочно!
Представленные ниже шпаргалки по физике содержат все основные формулы из курса физики , которые будут полезны учащимся школ и вузов.
Все формулы школьного курса по физике с сайта http://4ege.ru
I. Кинематика скачать
1. Основные понятия
2. Законы сложения скоростей и ускорений
3. Нормальное и тангенциальное ускорения
Нормальное и тангенциальное ускорения
4. Типы движений
4.1. Равномерное движение
4.1.1. Равномерное прямолинейное движение
4.1.2. Равномерное движение по окружности
4.2. Движение с постоянным ускорением
4.2.1. Равноускоренное движение
4.2.2. Равнозамедленное движение
4.3. Гармоническое движение
II. Динамика скачать
1. Второй закон Ньютона
2. Теорема о движении центра масс
3. Третий закон Ньютона
4. Силы
5. Гравитационная сила
6. Силы, действующие через контакт
III. Законы сохранения. Работа и мощность скачать
1. Импульс материальной точки
2. Импульс системы материальных точек
3. Теорема об изменении импульса материальной точки
4. Теорема об изменении импульса системы материальных точек
5. Закон сохранения импульса
6. Работа силы
7. Мощность
8. Механическая энергия
9. Теорема о механической энергии
10. Закон сохранения механической энергии
11. Диссипативные силы
12. Методы вычисления работы
13. Средняя по времени сила
Средняя по времени сила
IV. Статика и гидростатика скачать
1. Условия равновесия
2. Вращающий момент
3. Неустойчивое равновесие, устойчивое равновесие, безразличное равновесие
4. Центр масс, центр тяжести
5. Сила гидростатического давления
6. Давлением жидкости
7. Давление в какой-либо точке жидкости
8, 9. Давление в однородной покоящейся жидкости
10. Архимедова сила
V. Тепловые явления скачать
1. Уравнение Менделеева-Клапейрона
2. Закон Дальтона
3. Основное уравнение МКТ
4. Газовые законы
5. Первый закон термодинамики
6. Адиабатический процесс
7. КПД циклического процесса (теплового двигателя)
8. Насыщенный пар
VI. Электростатика скачать
1. Закон Кулона
2. Принцип суперпозиции
3. Электрическое поле
3.1. Напряженность и потенциал электрического поля, созданного одним точечным зарядом Q
3.2. Напряженность и потенциал электрического поля, созданного системой точечных зарядов Q1, Q2, …
3. 3. Напряженность и потенциал электрического поля, созданного равномерно заряженным по поверхности шаром
3. Напряженность и потенциал электрического поля, созданного равномерно заряженным по поверхности шаром
3.4. Напряженность и потенциал однородного электрического поля, (созданного равномерно заряженной плоскотью или плоским конденсатором)
4. Потенциальная энергия системы электрических зарядов
5. Электроемкость
6. Свойства проводника в электрическом поле
VII. Постоянный ток скачать
1. Упорядоченная скорость
2. Сила тока
3. Плотность тока
4. Закон Ома для участка цепи, не содержащего ЭДС
5. Закон Ома для участка цепи, содержащего ЭДС
6. Закон Ома для полной (замкнутой) цепи
7. Последовательное соединение проводников
8. Параллельное соединение проводников
9. Работа и мощность электрического тока
10. КПД электрической цепи
11. Условие выделения максимальной мощности на нагрузке
12. Закон Фарадея для электролиза
VIII. Магнитные явления скачать
1. Магнитное поле
2. Движение зарядов в магнитном поле
3. Рамка с током в магнитном поле
4. Магнитные поля, создаваемые различными токами
Магнитные поля, создаваемые различными токами
5. Взаимодействие токов
6. Явление электромагнитной индукции
7. Явление самоиндукции
IX. Колебания и волны скачать
1. Колебания, определения
2. Гармонические колебания
3. Простейшие колебательные системы
4. Волна
X. Оптика скачать
1. Закон отражения
2. Закон преломления
3. Линза
4. Изображение
5. Возможные случаи расположения предмета
6. Интерференция
7. Дифракция
Большая шпаргалка по физике . Все формулы изложены в компактном виде с небольшими комментариями. Шпаргалка также содержит полезные константы и прочую информацию. Файл содержит следующие разделы физики:
Механика (кинематика, динамика и статика)
Молекулярная физика. Свойства газов и жидкостей
Термодинамика
Электрические и электромагнитные явления
Электродинамика. Постоянный ток
Электромагнетизм
Колебания и волны. Оптика. Акустика
Квантовая физика и теория относительности
Маленькая шпора по физике . Все самое необходимое для экзамена. Нарезка основных формул по физике на одной странице. Не очень эстетично, зато практично. 🙂
Все самое необходимое для экзамена. Нарезка основных формул по физике на одной странице. Не очень эстетично, зато практично. 🙂
Размер: px
Начинать показ со страницы:
Транскрипт1
Формулы по физике, которые рекомендуется выучить и хорошо освоить для успешной сдачи ЕГЭ. Версия: 0.92 β. Составитель: Ваулин Д.Н. Литература: 1. Пёрышкин А.В. Физика 7 класс. Учебник для общеобразовательных учреждений. 13-е издание, стереотипное. Москва. Дрофа Пёрышкин А.В. Физика 8 класс. Учебник для общеобразовательных учреждений. 12-е издание, стереотипное. Москва. Дрофа Пёрышкин А.В., Гутник Е.М. Физика 9 класс. Учебник для общеобразовательных учреждений. 14-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я. и др. Физика. Механика 10 класс. Профильный уровень. Учебник для общеобразовательных учреждений. 11-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я., Синяков А.З. Физика. Молекулярная физика. Термодинамика 10 класс. Профильный уровень. Учебник для общеобразовательных учреждений. 13-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я., Синяков А.З., Слободсков Б.А. Физика. Электродинамика классы. Профильный уровень. Учебник для общеобразовательных учреждений. 11-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я., Синяков А.З. Физика. Колебания и волны 11 класс. Профильный уровень. Учебник для общеобразовательных учреждений. 9-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я., Синяков А.З. Физика. Оптика. Квантовая физика 11 класс. Профильный уровень. Учебник для общеобразовательных учреждений. 9-е издание, стереотипное. Москва. Дрофа Жирным выделены формулы, которые стоит учить, когда уже отлично освоены не выделенные жирным формулы. 7 класс. 1. Средняя скорость: 2. Плотность: 3. Закон Гука: 4. Сила тяжести:
13-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я., Синяков А.З., Слободсков Б.А. Физика. Электродинамика классы. Профильный уровень. Учебник для общеобразовательных учреждений. 11-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я., Синяков А.З. Физика. Колебания и волны 11 класс. Профильный уровень. Учебник для общеобразовательных учреждений. 9-е издание, стереотипное. Москва. Дрофа Мякишев Г.Я., Синяков А.З. Физика. Оптика. Квантовая физика 11 класс. Профильный уровень. Учебник для общеобразовательных учреждений. 9-е издание, стереотипное. Москва. Дрофа Жирным выделены формулы, которые стоит учить, когда уже отлично освоены не выделенные жирным формулы. 7 класс. 1. Средняя скорость: 2. Плотность: 3. Закон Гука: 4. Сила тяжести:
2
5. Давление: 6. Давление столба жидкости: 7. Архимедова сила: 8. Механическая работа: 9. Мощность совершения работы: 10. Момент силы: 11. Коэффициент полезного действия (КПД) механизма: 12. Потенциальная энергия при постоянном: 13. Кинетическая энергия: 8 класс.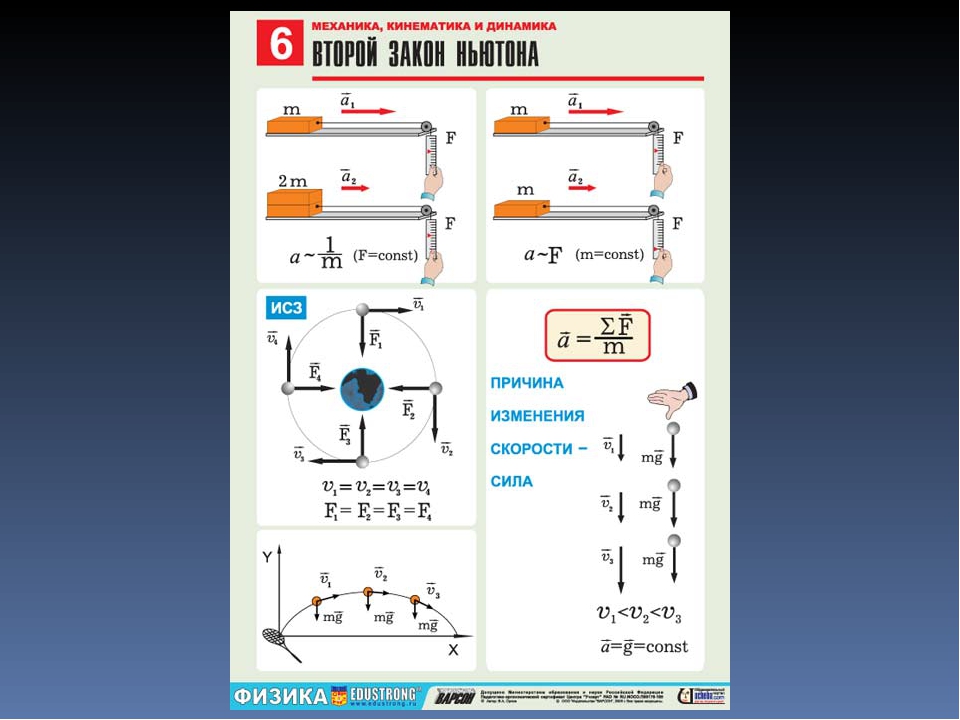 14. Количество теплоты необходимое для нагревания: 15. Количество теплоты, выделяемое при сгорании: 16. Количество теплоты необходимое для плавления:
14. Количество теплоты необходимое для нагревания: 15. Количество теплоты, выделяемое при сгорании: 16. Количество теплоты необходимое для плавления:
3 17. Относительная влажность воздуха: 18. Количество теплоты необходимое для парообразования: 19. КПД теплового двигателя: 20. Полезная работа теплового двигателя: 21. Закон сохранения заряда: 22. Сила тока: 23. Напряжение: 24. Сопротивление: 25. Общее сопротивление последовательного соединения проводников: 26. Общее сопротивление параллельного соединения проводников: 27. Закон Ома для участка цепи:
4 28. Мощность электрического тока: 29. Закон Джоуля-Ленца: 30. Закон отражения света: 31. Закон преломления света: 32. Оптическая сила линзы: 9 класс. 33. Зависимость скорости от времени при равноускоренном движении: 34. Зависимость радиус вектора от времени при равноускоренном движении: 35. Второй закон Ньютона: 36. Третий закон Ньютона: 37. Закон всемирного тяготения:
5
38. Центростремительное ускорение: 39. Импульс: 40.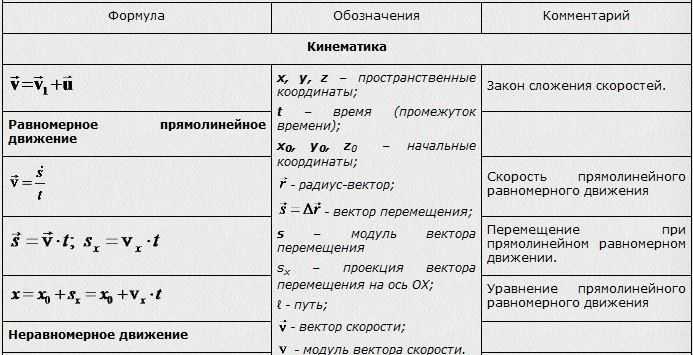 Закон изменения энергии: 41. Связь периода и частоты: 42. Связь длинны волны и частоты: 43. Закон изменения импульса: 44. Закон Ампера: 45. Энергия магнитного поля тока: 46. Формула трансформатора: 47. Действующее значение тока: 48. Действующее значение напряжения:
Закон изменения энергии: 41. Связь периода и частоты: 42. Связь длинны волны и частоты: 43. Закон изменения импульса: 44. Закон Ампера: 45. Энергия магнитного поля тока: 46. Формула трансформатора: 47. Действующее значение тока: 48. Действующее значение напряжения:
6 49. Заряд конденсатора: 50. Электроёмкость плоского конденсатора: 51. Общая ёмкость параллельно соединённых конденсаторов: 52. Энергия электрического поля конденсатора: 53. Формула Томпсона: 54. Энергия фотона: 55. Поглощение фотона атомом: 56. Связь массы и энергии: 1. Поглощённая доза излучения: 2. Эквивалентная доза излучения:
7 57. Закон радиоактивного распада: 10 класс. 58. Угловая скорость: 59. Связь скорости с угловой: 60. Закон сложения скоростей: 61. Сила трения скольжения: 62. Сила трения покоя: 3. Сила сопротивления среды: [ 63. Потенциальная энергия растянутой пружины: 4. Радиус вектор центра масс:
8
64. Количество вещества: 65. Уравнение Менделеева-Клапейрона: 66. Основное уравнение молекулярно кинетической теории: 67. Концентрация частиц: 68. Связь между средней кинетической энергией частиц и температурой газа: 69. Внутренняя энергия газа: 70. Работа газа: 71. Первое начало термодинамики: 72. КПД машины Карно: 5. Тепловое линейное расширение: 6. Тепловое объёмное расширение:
Концентрация частиц: 68. Связь между средней кинетической энергией частиц и температурой газа: 69. Внутренняя энергия газа: 70. Работа газа: 71. Первое начало термодинамики: 72. КПД машины Карно: 5. Тепловое линейное расширение: 6. Тепловое объёмное расширение:
9 73. Закон Кулона: 74. Напряжённость электрического поля: 75. Напряжённость электрического поля точечного заряда: 7. Поток напряжённости электрического поля: 8. Теорема Гаусса: 76. Потенциальная энергия заряда при постоянном: 77. Потенциальная энергия взаимодействия тел: 78. Потенциальная энергия взаимодействия зарядов: 79. Потенциал: 80. Разность потенциалов: 81. Связь напряжённости однородного электрического поля и напряжения:
10
82. Общая электроёмкость последовательно соединённых конденсаторов: 83. Зависимость удельного сопротивления от температуры: 84. Первое правило Кирхгофа: 85. Закон Ома для полной цепи: 86. Второе правило Кирхгофа: 87. Закон Фарадея: 11 класс. 9. Закон Био-Савара-Лапласа: 10. Магнитная индукция бесконечного провода: 88.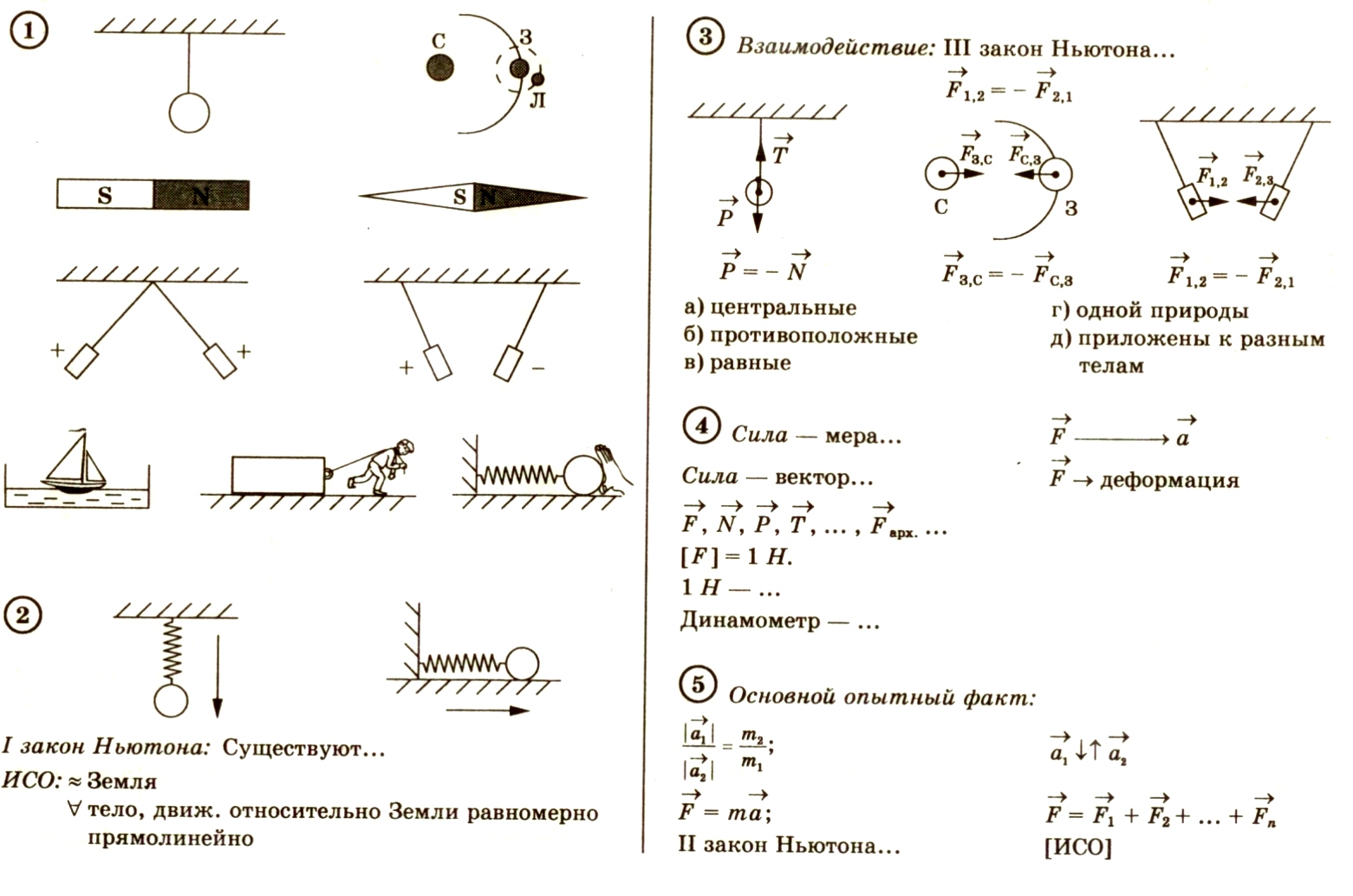 Сила Лоренца:
Сила Лоренца:
11 89. Магнитный поток: 90. Закон электромагнитной индукции: 91. Индуктивность: 92. Зависимость величины, изменяющейся по гармоническому закону от времени: 93. Зависимость скорости изменения величины, изменяющейся по гармоническому закону от времени: 94. Зависимость ускорения изменения величины, изменяющейся по гармоническому закону от времени: 95. Период колебаний нитяного маятника: 96. Период колебаний пружинного маятника: 11. Емкостное сопротивление: 12. Индуктивное сопротивление:
12 13. Сопротивление для переменного тока: 97. Формула тонкой линзы: 98. Условие интерференционного максимума: 99. Условие интерференционного минимума: 14. Преобразования Лоренца координат: 15. Преобразования Лоренца времени: 16. Релятивистский закон сложения скоростей: 100. Зависимость массы тела от скорости: 17. Релятивистская связь между энергией и импульсом:
13 101. Уравнение фотоэффекта: 102. Красная граница фотоэффекта: 103. Длина волны Де Бройля:
Программа вступительных испытаний по учебному предмету «Физика» для лиц, имеющих общее среднее образование, для получения высшего образования І ступени, 2018 год 1 УТВЕРЖДЕНО Приказ Министра образования
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «АНГАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» УТВЕРЖДАЮ “чебной работе II. В. Истомина 2016 г. ПРОГРАММА ВСТУПИТЕЛЬНОГО
В. Истомина 2016 г. ПРОГРАММА ВСТУПИТЕЛЬНОГО
2 6. Количество заданий в одном варианте теста 30. Часть А 18 заданий. Часть В 12 заданий. 7. Структура теста Раздел 1. Механика 11 заданий (36,7 %). Раздел 2. Основы молекулярно-кинетической теории и
УТВЕРЖДЕНО Приказ Министра образования Республики Беларусь от 30.10.2015 817 Программы вступительных испытаний в учреждения образования для лиц, имеющих общее среднее образование, для получения высшего
1/5 ПРОГРАММА ВСТУПИТЕЛЬНЫХ ИСПЫТАНИЙ ФИЗИКА 1. МЕХАНИКА КИНЕМАТИКА Механическое движение и его виды. Относительность механического движения. Скорость. Ускорение. Равномерное движение. Прямолинейное равноускоренное
1. Общие положения Программа предназначена для подготовки к вступительному испытанию по физике для поступающих на факультет физики и ИКТ Чеченского государственного университета. Вступительный экзамен
Код: Содержание: 1. МЕХАНИКА 1.1. КИНЕМАТИКА 1.1.1. Механическое движение и его виды 1.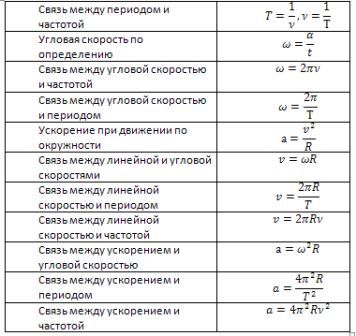 1.2. Относительность механического движения 1.1.3. Скорость 1.1.4. Ускорение 1.1.5. Равномерное движение 1.1.6. Прямолинейное
1.2. Относительность механического движения 1.1.3. Скорость 1.1.4. Ускорение 1.1.5. Равномерное движение 1.1.6. Прямолинейное
ПРОГРАММА ЭЛЕМЕНТОВ СОДЕРЖАНИЯ И ТРЕБОВАНИЙ К УРОВНЮ ПОДГОТОВКИ ВЫПУСКНИКОВ ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЙ ДЛЯ ПРОВЕДЕНИЯ В 2014 ГОДУ ВСТУПИТЕЛЬНЫХ ИСПЫТАНИЙ ПО ФИЗИКЕ Программа элементов содержания по
ПРОГРАММА СОБЕСЕДОВАНИЯ ПО ДИСЦИПЛИНЕ «ФИЗИКА» Физика и методы научного познания Предмет физики. Физика как наука. Научные методы познания окружающего мира и их отличия от других методов познания. Физика
СПЕЦИФИКАЦИЯ теста по учебному предмету «Физика» для проведения централизованного тестирования в 2017 году 1. Назначение теста объективное оценивание уровня подготовки лиц, имеющих общее среднее образование
СПЕЦИФИКАЦИЯ теста по учебному предмету «Физика» для проведения централизованного тестирования в 2018 году 1. Назначение теста объективное оценивание уровня подготовки лиц, имеющих общее среднее образование
Оглавление Основные положения. .. 3 1. МЕХАНИКА… 3 2. МОЛЕКУЛЯРНАЯ ФИЗИКА. ТЕПЛОВЫЕ ЯВЛЕНИЯ… 4 3. ОСНОВЫ ЭЛЕКТРОДИНАМИКИ… 4 4. КОЛЕБАНИЯ И ВОЛНЫ… 5 5. ОПТИКА… 5 6. КВАНТОВАЯ ФИЗИКА… 6 СПИСОК
.. 3 1. МЕХАНИКА… 3 2. МОЛЕКУЛЯРНАЯ ФИЗИКА. ТЕПЛОВЫЕ ЯВЛЕНИЯ… 4 3. ОСНОВЫ ЭЛЕКТРОДИНАМИКИ… 4 4. КОЛЕБАНИЯ И ВОЛНЫ… 5 5. ОПТИКА… 5 6. КВАНТОВАЯ ФИЗИКА… 6 СПИСОК
1 Общие положения Настоящая программа составлена на основе действующих учебных программ для средней школы, колледжа и техникума. При проведении собеседования основное внимание обращается на понимание абитуриентами
Спецификация теста по предмету физика для Единого национального тестирования и комплексного тестирования (Утвержден для использования в Едином национальном тестировании и комплексном тестировании с 2018
ПРОГРАММА ВСТУПИТЕЛЬНЫХ ИСПЫТАНИЙ (БАКАЛАВРИАТ/СПЕЦИАЛИТЕТ) ПО ОБЩЕОБРАЗОВАТЕЛЬНОЙ ДИСЦИПЛИНЕ «ФИЗИКА» Программа составлена на основе Федерального государственного образовательного стандарта среднего общего
«УТВЕРЖДАЮ» Руководитель Федеральной службы по надзору в сфере образования и науки «СОГЛАСОВАНО» Председатель Научнометодического совета ФИПИ по физике Единый государственный экзамен по ФИЗИКЕ Кодификатор
По предмету: Физика, 11 класс 2017 г. СОДЕРЖАНИЕ 1. Перечень диагностических работ 2. Количественные показатели 3. Общие результаты 3.1. Результаты на уровне региона 3.2. Распределение по баллам 3.3. Результаты
СОДЕРЖАНИЕ 1. Перечень диагностических работ 2. Количественные показатели 3. Общие результаты 3.1. Результаты на уровне региона 3.2. Распределение по баллам 3.3. Результаты
НЕКОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ «АССОЦИАЦИЯ МОСКОВСКИХ ВУЗОВ» ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОДЕЗИИ И КАРТОГРАФИИ НАУЧНО-ОБРАЗОВАТЕЛЬНЫЙ
УТВЕРЖДЕНО Приказ Министра образования Республики Беларусь 03.12.2018 836 Билеты для проведения экзамена в порядке экстерната при освоении содержания образовательной программы среднего образования по учебному
ПРОГРАММА ВСТУПИТЕЛЬНЫХ ЭКЗАМЕНОВ ПО ФИЗИКЕ В первом столбце указан код раздела, которому соответствуют крупные блоки содержания. Во втором столбце приводится код элемента содержания, для которого создаются
ПРОГРАММА ВСТУПИТЕЛЬНЫХ ИСПЫТАНИЙ ПО ФИЗИКЕ САНКТ-ПЕТЕРБУРГ 2014 ГОД 1. Механическое движение. Относительность движения. Системы отсчета. Материальная точка. 2. Траектория. Путь и перемещение. 3. Равномерное
Материальная точка. 2. Траектория. Путь и перемещение. 3. Равномерное
Министерство образования и науки Краснодарского края государственное бюджетное профессиональное образовательное учреждение Краснодарского края “Краснодарский информационно- технологический техникум” Тематический
Подготовка к ЕГЭ по физике (4 месяца) Перечень лекций, тестов и заданий. Дата начала Дата завершения Блок 0 Введение В.1 Скалярные и векторные величины. В.2 Сложение и вычитание векторов. В.3 Умножение
Введение………………………………. 8 Руководство по использованию диска…………….. 8 Установка программы……………………. 8 Работа с программой……………………. 11 От издательства…………………………
Негосударственное образовательное учреждение высшего образования «Кубанский социально-экономический институт (КСЭИ)» ПРОГРАММА ВСТУПИТЕЛЬНЫХ ИСПЫТАНИЙ ПО ФИЗИКЕ для абитуриентов, поступающих в вуз Рассмотрено
ПРОГРАММА ВСТУПИТЕЛЬНОГО ИСПЫТАНИЯ ПО ФИЗИКЕ В ФГБОУ ВО «ПГУ» В 2016 ГОДУ СОДЕРЖАНИЕ ПРОГРАММЫ 1 МЕХАНИКА 1. 1 КИНЕМАТИКА 1.1.1 Механическое движение и его виды 1.1.2 Относительность механического движения
1 КИНЕМАТИКА 1.1.1 Механическое движение и его виды 1.1.2 Относительность механического движения
ПРОГРАММА ВСТУПИТЕЛЬНОГО ИСПЫТАНИЯ ПО ФИЗИКЕ для поступающих в Московский государственный университет геодезии и картографии. Программа составлена в соответствии с типовой программой по физике средней
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Московский государственный строительный университет»
Вопросы к экзаменационным билетам по дисциплине Физика Билет 1 1. Физика и метод научного познания. Современная физическая картина мира. 2. Магнитное поле. Магнитное взаимодействие. Вектор магнитной индукции.
«УТВЕРЖДАЮ» Директор Федерального института педагогических измерений «СОГЛАСОВАНО» Председатель Научнометодического совета ФИПИ по физике Единый государственный экзамен по ФИЗИКЕ Кодификатор элементов
Тематика тестовых задач по физике для 11 класса Механика Кинематика: 1.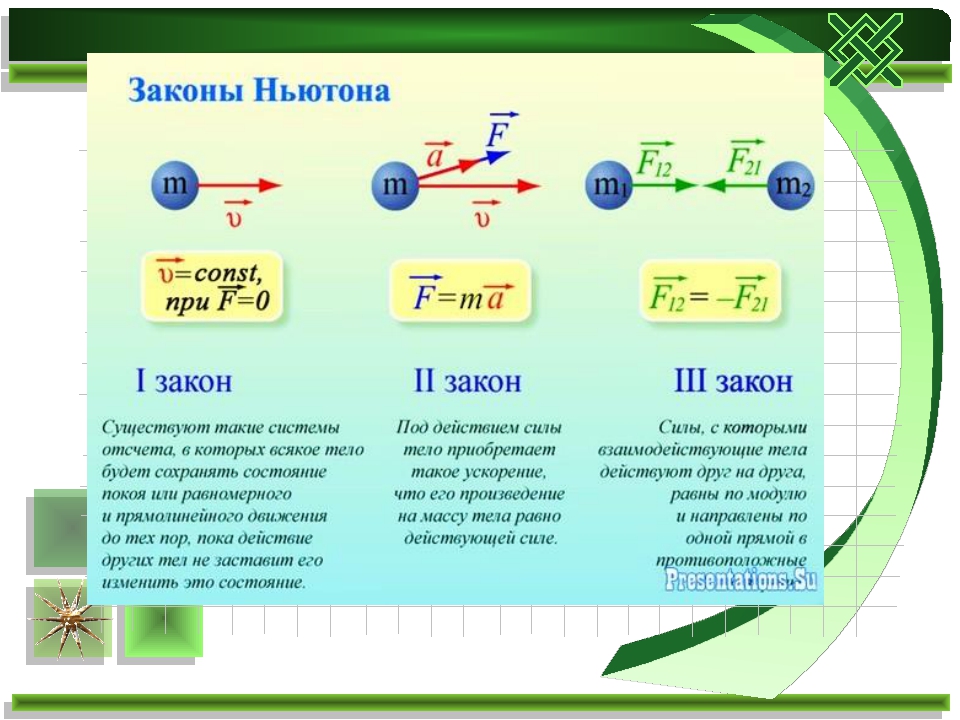 Кинематика прямолинейного движения материальной точки. Путь и перемещение. Скорость и ускорение. Сложение скоростей. Прямолинейное
Кинематика прямолинейного движения материальной точки. Путь и перемещение. Скорость и ускорение. Сложение скоростей. Прямолинейное
ÓÄÊ 373:53 ÁÁÊ 22.3ÿ72 Í34 Макет подготовлен при содействии ООО «Айдиономикс» В оформлении обложки использованы элементы дизайна: Tantoon Studio, incomible / Istockphoto / Thinkstock / Fotobank.ru Í34
ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПРОГРАММА ВСТУПИТЕЛЬНОГО ЭКЗАМЕНА ПО ФИЗИКЕ Составитель: Профессор, к.т.н. Першенков П.П. Пенза 2014 Механика 1. Прямолинейное равномерное движение. Вектор. Проекции
МИНИСТЕРСТВО ОБОРОНЫ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное казённое военное образовательное учреждение высшего образования Краснодарское высшее военное авиационное училище лётчиков имени Героя
189 УТВЕРЖДЕНО Приказ Министра образования Республики Беларусь от 30.10.2018 765 Программа вступительных испытаний по учебному предмету «Физика» для лиц, имеющих общее среднее образование, для получения
Программа вступительных испытаний по учебному предмету «Физика» для лиц, имеющих общее среднее образование, для получения высшего образования І ступени или среднего специального образования, 2019 год ПОЯСНИТЕЛЬНАЯ
Контрольные работы по физике 29 группа 4 семестр Решаем один из предложенных вариантов в каждой контрольной работе. Контрольная работа 11 Механические колебания. Упругие волны. Вариант 1 1. Материальная
Контрольная работа 11 Механические колебания. Упругие волны. Вариант 1 1. Материальная
Программа к вступительному испытанию по общеобразовательному предмету «Физика» при поступлении в Сыктывкарский лесной институт Программа предназначена для подготовки к массовой письменной проверке знаний
Федеральное государственное автономное учреждение высшего профессионального образования Национальный исследовательский университет «Высшая школа экономики» Программа вступительного испытания по физике
Пояснительная записка Программный материал рассчитан для учащихся 11 классов на 1 учебный час в неделю, всего 34 часа. Настоящая программа позволяет более глубоко и осмысленно изучать практические и теоретические
ФГБОУ ВПО «Петербургский государственный университет путей сообщения Императора Александра I» Программа вступительного испытания по физике для поступающих на обучение по программам бакалавриата и специалитета
ПРОГРАММА ВСТУПИТЕЛЬНОГО ЭКЗАМЕНА ПО ФИЗИКЕ для абитуриентов, поступающих в ФГБОУ ВО Смоленскую ГСХА в 2017 году Программа для вступительного испытания по физике Раздел 1. Перечень элементов содержания,
Перечень элементов содержания,
Занят ия Наименование разделов и дисциплин 1 Механическое движение. Относительность механического движения. Система отсчёта. Материальная точка. Траектория. Путь. Вектор перемещения и его проекции. Прямолинейное
Аннотация к рабочей программе по физике 7 класс (базовый уровень) Рабочая программа по физике 7 класса составлена на основании ФЗ РФ 273 от компонента государственного стандарта основного общего образования
1 семестр Введение. 1 Основные науки о природе. Естественнонаучный метод познания. Раздел 1. Механика. Тема 1.1. Кинематика твёрдого тела 2 Относительность механического движения. Системы отсчета. Характеристики
2 ификатор элементов содержания и требований к уровню подготовки выпускников общеобразовательных учреждений для проведения единого государственного экзамена по ФИЗИКЕ Единый государственный экзамен по
ПРОГРАММА ПО ФИЗИКЕ При проведении экзаменов по физике основное внимание должно быть обращено на понимание экзаменующимся сущности физический явлений и законов, на умение истолковать смысл физических величин
Программа по физике для поступающих в ОАНО ВПО ВУиТ Вступительные испытания по физике проводятся в форме письменной работы (тестирования) и собеседования, с помощью которой проверяются знания учащихся,
Министерство образования и науки Российской Федерации федеральное государственное автономное образовательное учреждение высшего образования «Санкт-Петербургский политехнический университет Петра Великого»
ЭКЗАМЕНАЦИОННЫЕ БИЛЕТЫ ГОСУДАРСТВЕННОЙ ИТОГОВОЙ АТТЕСТАЦИИ ПО ФИЗИКЕ ПО ОБРАЗОВАТЕЛЬНЫМ ПРОГРАММАМ ОСНОВНОГО ОБЩЕГО ОБРАЗОВАНИЯ Билет 1 1.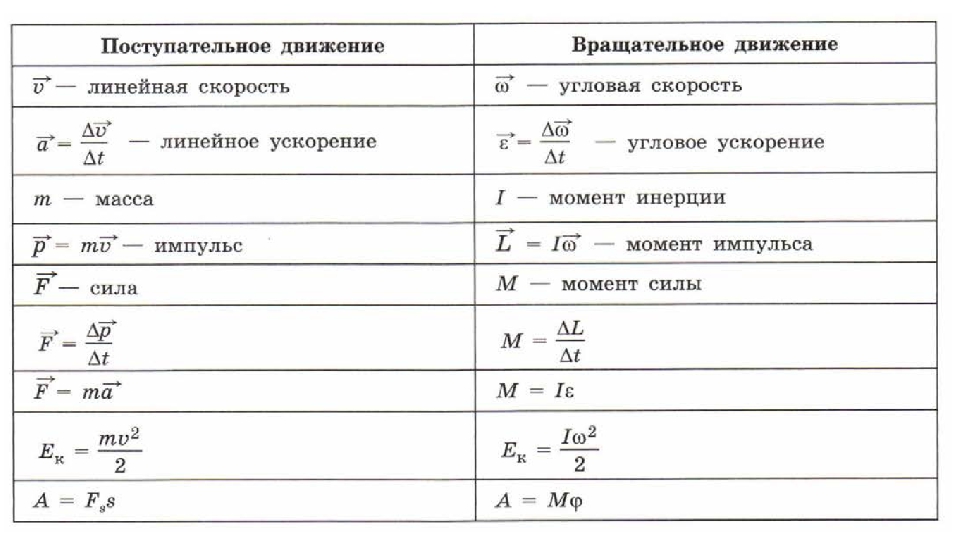 Что изучает физика. Физические явления. Наблюдения, опыты. 2.
Что изучает физика. Физические явления. Наблюдения, опыты. 2.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ Учреждение образования «Брестский государственный технический университет» ПРОГРАММА собеседования для иностранных абитуриентов по предмету «ФИЗИКА» Разработана:
Аннотация к рабочим программам по физике Класс: 10 Уровень изучения учебного материала: базовый. УМК, учебник: Рабочая программа по физике для 10-11 классов составлена на основе Федерального компонента
Методы научного познания Эксперимент и теория в процессе познания мира. Моделирование явлений. Физические законы и пределы их применения. Роль математики в физике. Принципы причинности и соответствия.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «ОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»
Аннотация к контрольно-оценочному средству по учебному предмету «Физика» 1.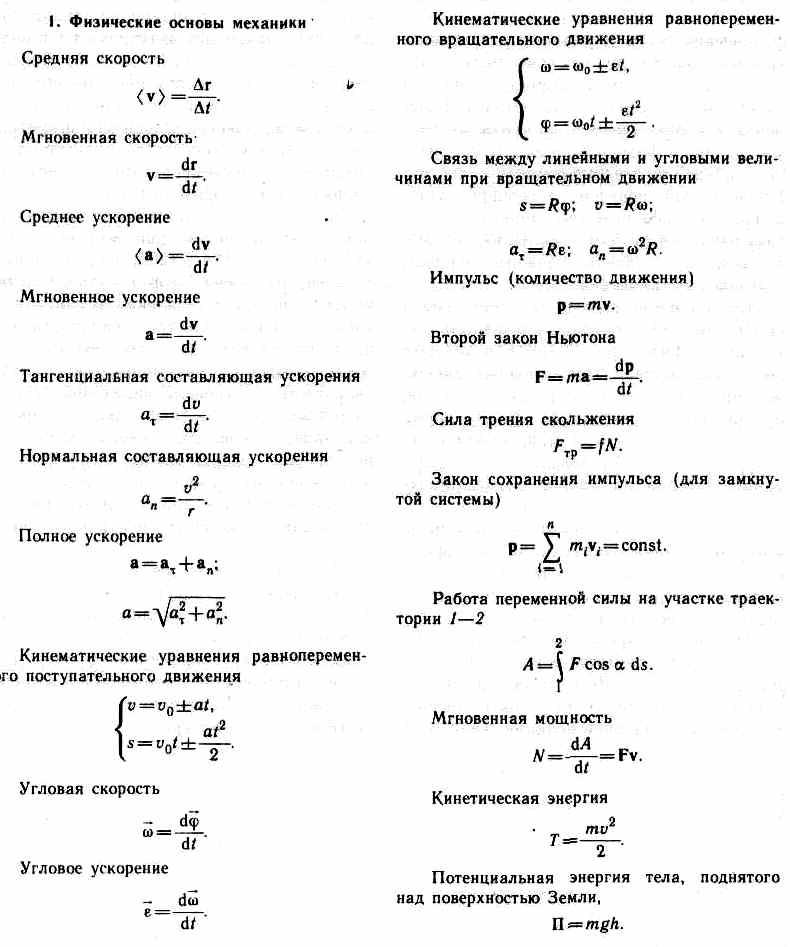 Общие положения. Контрольно-оценочные средства (КОС) предназначены для контроля и оценки образовательных достижений обучающихся,
Общие положения. Контрольно-оценочные средства (КОС) предназначены для контроля и оценки образовательных достижений обучающихся,
При составлении программы следующие правовые документы 10-11классы были использованы федеральный компонент государственного стандарта среднего (полного) общего образования по физике, утвержденный в 2004
Раздел 1. Планируемые результаты. Личностные: в ценностно-ориентированной сфере чувство гордости за российскую физическую науку, отношение к физике как элементу общечеловеческой культуры, гуманизм, положительное
Е.Н. Бурцева, В.А. Пивень, Т.Л. Шапошникова, Л.Н. Терновая ОСНОВЫ ЭЛЕМЕНТАРНОЙ ФИЗИКИ (базовый уровень) Учебное пособие Краснодар 2012 УДК 53 ББК 22.3 Б91 Рецензенты: Е.Н. Тумаев, доктор физико-математических
0 Пояснительная записка. Программа по физике для 10 11 классов составлена на основе авторской программы: Физика 10 11 класс Г.Я. Мякишев М.:Дрофа,-2010г. и ориентирована на использование учебно-методического
Тема Дата Количество часов Календарно-тематическое планирование По физике 10 класс (профильный уровень) Требования к знаниям Форма контроля ФИЗИКА И МЕТОДЫ НАУЧНОГО ПОЗНАНИЯ 1 ФИЗИЧЕСКИЕ ЗАКОНЫ И ТЕОРИИ
Как правило, именно математику, а не физику принято считать королевой точных наук. Мы полагаем, что это утверждение спорно, ведь технический прогресс невозможен без знания физики и её развития. Из-за своей сложности она вряд ли когда-либо будет включена в список обязательных государственных экзаменов, но, так или иначе, абитуриентам технических специальностей приходится сдавать её в обязательном порядке. Труднее всего запомнить многочисленные законы и формулы по физике для ЕГЭ, именно о них мы расскажем в этой статье.
Мы полагаем, что это утверждение спорно, ведь технический прогресс невозможен без знания физики и её развития. Из-за своей сложности она вряд ли когда-либо будет включена в список обязательных государственных экзаменов, но, так или иначе, абитуриентам технических специальностей приходится сдавать её в обязательном порядке. Труднее всего запомнить многочисленные законы и формулы по физике для ЕГЭ, именно о них мы расскажем в этой статье.
Секреты подготовки
Возможно, это связано с кажущейся сложностью предмета или популярностью профессий гуманитарного и управленческого профиля, но в 2016 году только 24 % всех абитуриентов приняли решение сдавать физику, в 2017 – лишь 16 %. Такие статистические данные невольно заставляют задуматься, не слишком ли завышены требования или просто уровень интеллекта в стране падает. Почему-то не верится, что так мало школьников 11 класса желают стать:
- инженерами;
- ювелирами;
- авиаконструкторами;
- геологами;
- пиротехниками;
- экологами,
- технологами на производстве и т.
 д.
д.
Знание формул и законов физики в равной степени необходимо для разработчиков интеллектуальных систем, вычислительной техники, оборудования и вооружения. При этом всё взаимосвязано. Так, например, специалисты, производящие медицинское оборудование, в своё время изучали углубленный курс атомной физики, ведь без разделения изотопов, у нас не будет ни рентгенологической аппаратуры, ни лучевой терапии. Поэтому создатели ЕГЭ постарались учесть все темы школьного курса и, кажется, не пропустили ни одной.
Те ученики, которые исправно посещали все уроки физики вплоть до последнего звонка, знают, что в период с 5 по 11 класс изучается около 450 формул. Выделить из этих четырех с половиной сотен хотя бы 50 крайне сложно, поскольку все они важны. Подобного мнения, очевидно, также придерживаются разработчики Кодификатора. Тем не менее, если вы одарены необыкновенно и не ограничены во времени, вам хватит 19 формул, ведь при желании из них можно вывести все остальные. За основу мы решили взять главные разделы:
- механику;
- физику молекулярную;
- электромагнетизм и электричество;
- оптику;
- физику атомную.

Очевидно, что подготовка к ЕГЭ должна быть ежедневной, но если по каким-то причинам вы приступили к изучению всего материала лишь сейчас, настоящее чудо может совершить экспресс-курс, предлагаемый нашим центром. Надеемся, эти 19 формул также будут вам полезны:
Вы, наверное, заметили, что некоторые формулы по физике для сдачи ЕГЭ остались без пояснений? Мы предоставляем вам самим их изучить и открыть для себя законы, по которым абсолютно всё вершится в этом мире.
Картинки формулы по физике (58 фото)
Знания формул по физике часто необходимы при ремонте техники. С помощью них можно управлять током, температурой и различными видами энергий. Для каждой величины в формулах по физике даются развернутые определения. Также при расчетах стоит внимательно отнестись к единицам измерения. Представляем вам красивые картинки про формулы по физике, которые тут можно посмотреть.
Кинематика, динамика, гидростатика.
Вычисление количества теплоты.
Формула силы трения в физике.
Потенциальная энергия, длина волны.
Таблица с единицами измерения.
Картинка формулы по физике.
Коэффициент полезного действия.
Законы Ньютона, изучаемые в школе.
Формулы физики для мощности.
Сила трения качения.
Расчет скорости движения.
Сложные формулы по физике.
Равноускоренное прямолинейное движение.
Давление на дно и боковую грань.
Прикольная картинка формул по физике.
Колебания, вращение, конденсатор.
Термодинамика, индукция, оптика.
Формулы физики для периода.
Ускорение свободного падения.
Удельная теплоемкость при нагревании.
Кинематика в формулах по физике.
Расчет объемной плотности энергии.
Теорема для материальных точек.
Основы электродинамики в формулах по физике.
Колонка с определениями величин.
Частота при движении по окружности.
Формулы по физике на картинке.
Молекулярная масса и количество вещества.
Потенциальная энергия в джоулях.
Сила и давление в формулах по физике.
Единица измерения в метрах.
Учебный материал девятого класса.
Формулы физики для колебаний.
Работа силы упругости.
Закон Кулона, напряженность.
Основа квантовой физики в формулах.
Охлаждение, плавление, сгорание.
Расчет массы тела.
Цветная картинка формул по физике.
Величина, обозначение, примечание.
Сообщающиеся сосуды.
Формулы по физике из 10 класса.
Количество теплоты во время плавления.
Величина полезной работы.
Механика в формулах по физике.
Скорость деленная на время.
Равенство для гидравлического пресса.
Формулы электрических явлений физики.
Влажность, тепловой баланс.
Колонка с базовыми параметрами.
Занимательные формулы по физике.
Частота математического маятника.
Памятка для изотермического закона.
Синяя таблица с формулами по физике.
Скорость тела в уравнениях.
Плотность водяного пара.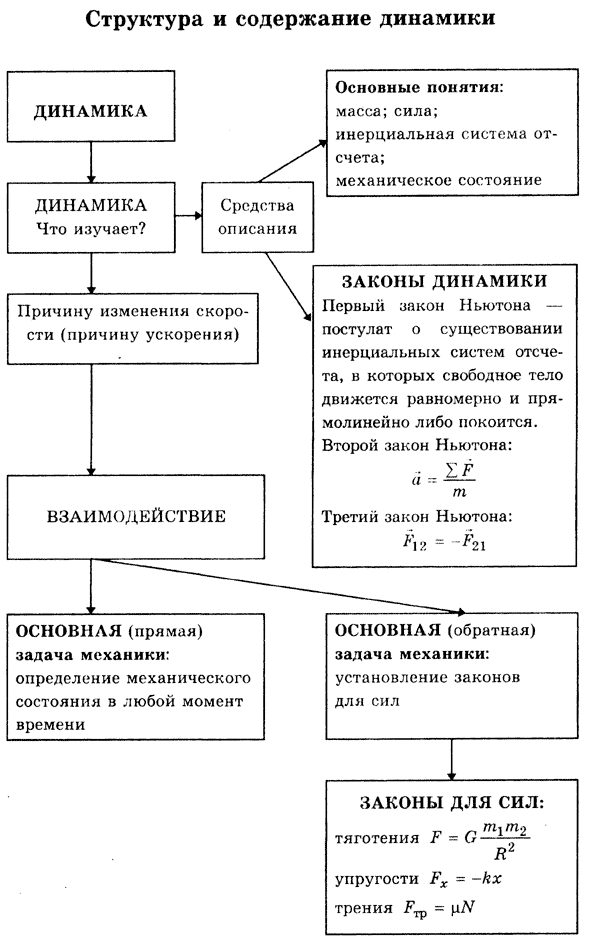
Изучаем электродинамику.
Понравился пост? Оцените его:
Рейтинг: 5,00/5 (голосов: 3)
Поделитесь с друзьями!
Wolfram | Alpha Примеры: Физика
Другие примеры
МеханикаИзучите физические законы, которые описывают поведение одного или нескольких тел под действием системы сил.
Вычислить центростремительное ускорение:
Сделайте расчет гравитации:
Другие примеры
Другие примеры
Колебания и волны Исследуйте колебательные движения, от маятников до электромагнитных волн.
Проанализируйте гармонический осциллятор:
Проанализируйте движение пружинного маятника:
Другие примеры
Другие примеры
Статистическая физика Исследуйте движение жидкостей с помощью статистических методов.
Найдите распределение Максвелла скорости газа:
Вычислите энтропию с помощью уравнения Сакура – Тетрода:
Другие примеры
Другие примеры
Термодинамика Изучите тепло, энергию и энтропию и их связь с термодинамическими системами.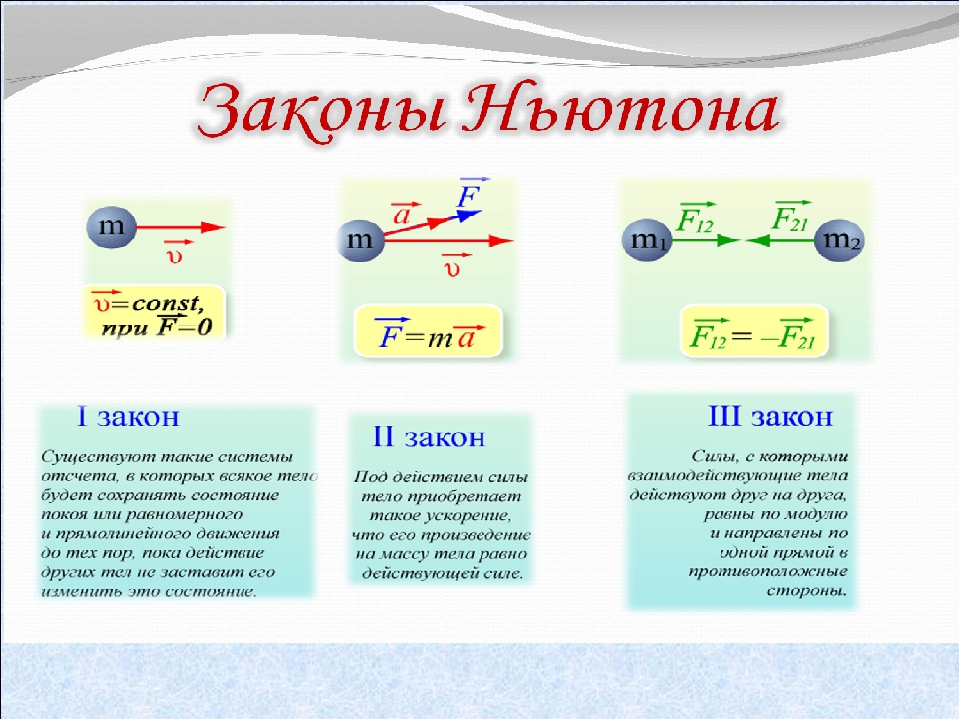
Проведите вычисления по закону Джоуля:
Проанализируйте адиабатический процесс:
Выполните расчет закона идеального газа:
Проанализируйте цикл Аткинсона:
Другие примеры
Другие примеры
Электричество и магнетизм Изучите физику электромагнитной силы.
Используйте поля ввода, чтобы указать данные для вычисления закона Ома:
Найдите уравнения, связанные с намагниченным объектом:
Выполните вычисление по закону Кулона:
Другие примеры
Другие примеры
Оптика Изучите свойства и поведение света.
Выполните вычисления, используя уравнение тонкой линзы:
Вычислите дифракционную картину для круглой апертуры:
Вычислите дифракционную картину для одной щели:
Используйте формулу Ридберга для вычисления спектральных линий:
Другие примеры
Другие примеры
Относительность Изучите теории Эйнштейна специальной и общей теории относительности и то, как они связаны с гравитацией, временем и пространством.
Сделайте релятивистское сложение скоростей:
Вычислите релятивистский импульс:
Определите гравитационное замедление времени возле массивных объектов:
Другие примеры
Другие примеры
Ядерная физика Исследуйте аспекты ядерной физики, включая радиацию и ядерную энергетику.
Вычислите тормозную способность материала:
Получить информацию об изотопе:
Вычислите характеристики излучения Черенкова:
Другие примеры
Другие примеры
Квантовая физика Исследуйте квантовые явления, такие как рассеяние и квантовые состояния.
Вычислите энергию фотона с учетом его длины волны:
Вычислите длину волны Комптона:
Другие примеры
Другие примеры
Физика частиц Получите информацию о частицах и их взаимодействиях.
Получить информацию о частице:
Выполните расчет со свойствами частицы:
Сравните значения свойства для класса частиц:
Другие примеры
Другие примеры
Астрофизика Исследуйте природу небесных объектов, включая черные дыры, звезды и планеты.
Вычислите период обращения массивного тела вокруг другого:
Вычислите космологические свойства Вселенной:
Вычислите свойства черной дыры:
Другие примеры
Другие примеры
Физические константы Изучите детали, значения и определения для различных физических констант.
Получите значение физической постоянной:
Выполните вычисления с использованием констант:
Другие примеры
Другие примеры
Физические принципы Изучите физические законы, принципы и эффекты.
Узнайте о законах Ньютона:
Узнайте о броуновском движении:
Узнайте о парадоксе в квантовой механике:
Другие примеры
Другие примеры
Физические эффекты Получите информацию о физических эффектах и сравните их.
Изучите физические эффекты:
Сравните физические эффекты:
Другие примеры
Другие примеры
Механика жидкости Исследуйте поведение жидкостных систем и движущихся через них объектов.
Рассчитайте расход через трубу:
Определите изменение скорости жидкости по изменению давления:
Вычислить поток жидкости вокруг объекта:
Другие примеры
Язык физики, язык математики: дисциплинарная культура и динамическая эпистемология
Идеи в разд. 3 хорошо сочетается со структурой ресурсов , разрабатываемой сообществом Physics Education Research (PER) для анализа мышления студентов в области физики (diSessa 1993; Hammer 2000; Hammer et al. 2005; Redish 2004; Redish 2014). Footnote 10 В этой структуре рассуждение человека моделируется как результат активации подмножества когнитивных ресурсов (тесно связанных структур когнитивного знания), активируемых в ответ на восприятие и интерпретацию как внешнего, так и внутреннего контекстов (фрейминг).
3 хорошо сочетается со структурой ресурсов , разрабатываемой сообществом Physics Education Research (PER) для анализа мышления студентов в области физики (diSessa 1993; Hammer 2000; Hammer et al. 2005; Redish 2004; Redish 2014). Footnote 10 В этой структуре рассуждение человека моделируется как результат активации подмножества когнитивных ресурсов (тесно связанных структур когнитивного знания), активируемых в ответ на восприятие и интерпретацию как внешнего, так и внутреннего контекстов (фрейминг).
Эта структура, используемая в PER для понимания динамики того, как учащиеся конструируют значение в физике, разделяет многие ключевые особенности структур, используемых для понимания динамики того, как люди конструируют значение в языке.
Воплощенное познание: Феноменологические примитивы связывают основные физические рассуждения с воплощенным опытом.
Энциклопедические знания : Многообразие производственных ресурсов используется динамически.
Контекстуализация : Активация зависит от концептуальных, эпистемологических и аффективных факторов.
Здесь мы приводим примеры того, как структура ресурсов использует те же основные идеи, чтобы помочь нам описать несколько способов, которыми студенты-физики могут придавать смысл уравнениям, а также понять динамику того, как студенты могут переходить от одного значения к другому. и как концептуальные, эпистемологические и аффективные реакции могут сложным образом взаимодействовать.
Воплощенное познание: феноменологические примитивы, связывающие основы физики с воплощенным опытом
Структура ресурсов ставит «ноги на землю» аналогично когнитивной лингвистике – через воплощенный опыт. ДиСесса (1993) идентифицировал основные воплощенные элементы физического мышления как феноменологических примитивов («p-примитивов»). Это элементы знаний о том, как устроен мир, часто в очень раннем возрасте. Два из их основных аспектов – это очевидность , и несводимость . – p-prims активируются легко и напрямую, и, насколько известно пользователю, они не имеют структуры.«Так и есть». Два примера [из многих, процитированных в классической статье ДиСесса (1993)] – это «динамическое уравновешивание» (два влияния в конфликте, которые уравновешивают друг друга) и «п-прим Ома» (агент или стимул действует через сопротивление, создавая результат). Например, думая о том, насколько тяжелый объект будет двигаться в ответ на толчок, ученик может использовать в своих рассуждениях свою физическую интуицию через p-prim Ома, а не формальные принципы физики.
Аналогичным образом Шерин (2001) обнаружил, что студенты старших курсов физики обычно создают новые уравнения для моделирования физических ситуаций посредством своего интуитивного понимания, а не применения формальных правил или принципов физики.При описании сил, действующих на объект, падающий с предельной скоростью, пара студентов сразу перешла к написанию уравнения вида \ (F _ {\ text {gravity}} = F _ {{{\ text {air}} \, {\ текст {сопротивление}}}} \). Этот одноэтапный вывод исключает формальный вывод из законов Ньютона, где общая сила оказывается равной \ (F _ {\ text {net}} = F _ {\ text {gravity}} – F _ {\ text {air \, сопротивление} } \), который вставляется во второй закон Ньютона, чтобы получить \ (F _ {\ text {net}} = F _ {\ text {gravity}} – F _ {\ text {air \, сопротивление}} = ma \).Поскольку a принимается равным нулю для предельной скорости, это приводит к \ (F _ {\ text {gravity}} – F _ {{{\ text {air}} \, {\ text {сопротивление}}}} = 0 \), что означает \ (F _ {\ text {gravity}} = F _ {{{\ text {air}} \, {\ text {сопротивление}}}} \).
Вместо этого Шерин моделирует решение этих студентов как опирающееся на символическую форму , уравновешивающую , чтобы связать интуитивные идеи двух влияний в противовес шаблону символа □ = □. Этот способ использования физической интерпретации ситуации, чтобы повлиять на то, как генерируются, используются и интерпретируются математические уравнения, отражает физический дисциплинарный опыт и отличается от простой формальной обработки математического синтаксиса.
Энциклопедические знания: множество производственных ресурсов используются динамически
P-prims образуют подмножество знаний, которые люди могут использовать для понимания физических ситуаций. В структуре ресурсов индивидуальные знания состоят из детализированных ресурсов знаний. Подобно тому, как некоторая часть наших дополнительных энциклопедических знаний применяется для придания значения языку, люди привносят некоторую часть своих ресурсов для придания значения физике. Различные подмножества этих ресурсов могут быть применены к одной и той же ситуации для образования разных значений (точно так же, как «безопасный пляж» может пониматься как подразумевающий либо безопасность посетителя пляжа, либо безопасность пляжа от застройки).Из-за множества возможных значений изучение физики включает в себя уточнение моделей активации и связи с нашей энциклопедической базой знаний для построения согласованной и стабильной структуры знаний, которая согласуется с каноническими знаниями и рассуждениями дисциплины физики.
Хотя эти активации чрезвычайно ценны для повседневной жизни, иногда, когда они отображаются в учебных ситуациях, они могут быть активированы несоответствующим образом или неверно истолкованы. Один из примеров этого обсуждается в Redish (2014), (Frank 2009, Frank and Scherr 2012).Студентам выдается набор бумажных лент с точками. (См. Рис. 5.) Точки создаются путем присоединения объекта к бумажной ленте и приведения объекта в движение. Лента проходит через машину (Pasco Tape Timer), которая ударяет булавкой с фиксированной скоростью по бумажной ленте через копировальную бумагу, делая точку каждый раз, когда булавка ударяет вниз, как показано слева на рис. 5. Если объект движется быстро, лента много перемещается между точками, а между точками есть большие промежутки, как показано в образце в правом верхнем углу рис.5. Если объект движется медленно, лента мало перемещается между касаниями, а точки находятся близко друг к другу, как показано в правом нижнем углу рис. 5.
Рис. 5Устройство для отображения скорости движения с помощью точек с разнесением и два примера
Аппарат был показан в начале раздела декламации, а его механизм объяснил ассистент аспиранта. Студенты работали в группах, и каждой группе из четырех студентов были даны четыре ленты разной длины, содержащие шесть точек (как показано на рис.5). Первый вопрос в их рабочем листе: «На создание какой ленты ушло больше времени?» Поскольку штифт постукивает с фиксированной скоростью, на изготовление любой ленты с шестью точками потребуется то же время. Было замечено, что несколько групп студентов быстро переходят от одной интерпретации к другой. В ответ на первый вопрос урока, задавая вопрос: «Какая лента изготовляла больше времени?», Многие студенты сказали что-то вроде: «Очевидно, что для создания более короткой ленты [более близко расположенных точек] требуется меньше времени… потому что она короче.«Мы интерпретируем этих студентов как применяющих легко доступный интуитивно понятный ресурс, который« большее расстояние означает больше времени »(неявно предполагая, что скорость не меняется). Спустя некоторое время, в ответ на подсказку, в которой им задали более подробный вопрос (чтобы найти скорость), эти группы переосмыслили длину полос как пропорциональную тому, как быстро лента была протянута через машину, опираясь на интуитивную идею о том, что «Большее расстояние означает большую скорость» (неявное предположение – правильно – отсутствие изменения во времени).
Из этой общей траектории рассуждений следует отметить две важные особенности. Во-первых, в разные моменты группа студентов может подключать разные когнитивные ресурсы для достижения разных интерпретаций того, что означают разные длины. Во-вторых, группы используют разные части своих энциклопедических знаний в зависимости от того, как они контекстуализировали задачу в ответ на различные сигналы в разных частях урока, чтобы придать два разных (и взаимоисключающих) значения одних и тех же объектов.
Важнейшей частью структуры ресурсов является наблюдение, что ресурсы являются общими – ни правильными, ни неправильными, пока не будут определены контекст и использование. Хотя одно из выводов студентов о длине тикерных лент здесь было неверным, их интуитивные ресурсы знаний не могут быть определены как правильные или неправильные независимо от контекста. В лингвистике было бы неправильно интерпретировать предложение «Сэм сломал руку, значит, он в гипсе уже 6 недель», как означающее, что Сэм играл в театральном представлении с учетом контекста.Тем не менее, было бы также неверно утверждать, что «актерский состав» может означать «группу актеров в одной постановке». Что касается тикерных лент, хотя интуиция «большее расстояние означает больше времени» неверна при интерпретации этих тикерных лент, она была бы правильной в других контекстах, таких как сравнение времени полета авиакомпаний между разными городами.
В следующем разделе мы приводим пример двух способов, которыми студенты-физики могут использовать ресурсы энциклопедических знаний для использования и интерпретации уравнения \ (v = v_ {0} + at \).Мы утверждаем, что, хотя оба значения являются правильными способами интерпретации уравнения в физике, оппортунистическое и продуктивное сочетание физического смысла с математическим синтаксисом свидетельствует о более экспертных рассуждениях в области физики.
Пример # 1: Смешение физического смысла с математической структурой
Понимание уравнения в физике не ограничивается соединением символов с физическими переменными и возможностью выполнять операции с этим уравнением.Важным компонентом является возможность связать математические операции в уравнении с их физическим смыслом и интегрировать уравнение с его последствиями в физическом мире. В этом разделе мы проиллюстрируем различия в способах придания значения уравнению, проанализировав отрывки из двух клинических интервью со студентами вводного курса физики для инженеров (Kuo et al. 2013). Оба отрывка сосредоточены на понимании учащимися уравнения скорости объекта, движущегося с постоянным ускорением: \ (v = v_ {0} + at \), [Eq.(7)] где v – скорость объекта в момент времени t , v 0 – это скорость объекта при t = 0, а a – постоянное ускорение. Оба студента могут удовлетворительно использовать уравнение для решения задач, но энциклопедический смысл, приписываемый уравнению Алексом, отличается от того, который приписывает Пат.
В интервью Алекс, когда ее просили объяснить уравнение скорости, она сосредоточилась на математическом значении символов:
I: Вот уравнение; Хорошо, вы наверняка это видели.
Алекс: Ага.
I: Верно. Предположим, вам пришлось объяснить это уравнение другу из класса. Как бы вы это сделали?
Алекс: Умм, ладно, ну, я думаю, во-первых, ну, это уравнение скорости. Умм, ну, я бы сказал им, что это интеграл ускорения, производная от положения { борозды, брови }, верно? Так вот как они могли это понять, я не знаю.Я не совсем { смеется }, я не совсем уверен, что еще я мог бы сказать об этом. Вы можете найти скорость. Типа, я думаю, это интересно, потому что вы можете найти скорость в любое время, если у вас есть начальная скорость, ускорение и время …
Ответ Алекс предполагает, что она думает об уравнении как о чем-то, что позволяет вычислить скорость объекта в любой момент. Она действительно называет скорость производной от положения и интеграла ускорения, но ее комментарий не отражает, имеют ли для нее те математические операции, связывающие скорость с положением и скорость с ускорением, более глубокий физический смысл.
В интервью Пэт она также ссылается на физический смысл символов в уравнении, но ее объяснение не ограничивается их названиями. Ее объяснение, кажется, требует ее физических знаний о движении, единицах и процессах изменения:
Я: Хорошо. Итак, вот, вероятно, уравнение, которое вы видели раньше, не так ли? И гм, если бы вы объяснили это уравнение другу из класса, как бы вы это объяснили?
Пэт: Ну, я думаю, что первое, что вам нужно было бы пройти, это определения каждой переменной и то, что каждая из них означает, и я думаю, чтобы получить часть интуиции, я не совсем уверен, что начну с размерный анализ или попытайтесь объяснить каждый термин перед этим.Потому что я имею в виду, если вы посмотрите на это со стороны устройства, станет ясно, что ускорение, умноженное на время, – это скорость, но может быть проще, если вы подумаете о том, что вы начинаете с начальной скорости, а затем ускорение в течение определенного периода времени увеличивается. это или уменьшает эту скорость.
Пэт также рассматривает физический смысл каждого символа в уравнении и то, как они связаны. Она рассказывает о единицах измерения и о том, как размеры в уравнении должны согласовываться между терминами.Но она придает уравнению более глубокий смысл, привнося дополнительные знания о физическом процессе ускорения, который изменяет начальную скорость. Дальнейшие отрывки из ее интервью показывают, что для Пэт математическая формулировка уравнения (7) стабильно связан с концептуальной схемой base + change , где вы начинаете с начального количества, а затем что-то его меняет. Термин « at» для нее отражает общую сумму, на которую изменяется начальное значение.Мы моделируем ее рассуждения как соединение символической формы основания + изменение с отношениями между физическими переменными скорости и ускорения, чтобы придать смысл этому уравнению.
В разд. 2, мы утверждаем, что культурные нормы дисциплины физики включают оппортунистическое смешение физического смысла при использовании и интерпретации уравнений. Из-за этого мы утверждаем, что использование Патом базы + замены для объединения в общую концептуальную историю, связывающую скорость и ускорение с уравнением скорости, отражает более похожую на эксперта физическую практику.
Кроме того, мы видим, что такая интерпретация уравнения влияет на его использование при решении задач. Позже в интервью Алекс и Пэт используют это уравнение для решения задачи о разнице в скоростях двух мячей, одновременно брошенных из здания с разными начальными скоростями. Алекс использует уравнение как инструмент для вычисления конечных скоростей с учетом начальной скорости, времени и ускорения. Пэт, с другой стороны, использует уравнение гораздо больше, чем мог бы опытный физик, находя ответ без необходимости подставлять числа и проводить арифметические вычисления, и она демонстрирует экспертное понимание того, почему результат должен быть таким, какой он есть, на основе от значения, которое она придает структуре уравнения.
Контекстуализация: активация зависит от концептуальных, эпистемологических и аффективных факторов
Человеческий разум содержит огромное количество знаний о многих вещах, но имеет ограниченные возможности доступа к этим знаниям в любой момент времени. (Miller 1956) Как отмечают специалисты по когнитивной семантике, контекст имеет большое значение в том, как интерпретируются стимулы, и это так же верно как на уроках физики, так и в повседневной жизни. Иногда это означает, что структурные особенности контекста проблемы указывают на знания, связанные с физическими концепциями – проблема с блоком на пандусе указывает на концептуальные знания о силах и движении, а не на концептуальные знания, связанные с магнитными полями.Тем не менее, контекст выходит за рамки физического содержания конкретных представленных проблем. Он включает в себя контекст, в котором учащийся на уроке физики общается с учителями и другими учениками. Учащиеся приносят на уроки физики множество ресурсов, связанных с «способами познания», разработанными в результате многолетнего опыта школьного обучения и накопления знаний. Поскольку «эпистемология» означает науку познания знаний, мы называем их эпистемологическими ресурсами .
Элби и Хаммер (2001) и Хаммер и Элби (2002, 2003) исследуют, какие основные идеи используют люди, чтобы решить, что они что-то знают.Некоторые основные эпистемологические ресурсы, которые имеют отношение к нашему рассмотрению использования математики в науке, включают (Bing and Redish 2009, 2012):
Воплощенная физическая интуиция: Знания, основанные на опыте и восприятии (например, p-prims), надежны.
Автор: Информации из авторитетного источника можно доверять.
Расчет: Шаги алгоритмических вычислений приводят к достоверному результату.
Физическое сопоставление с математикой: Математическое символическое представление точно характеризует некоторые особенности физических или геометрических систем, которые оно предназначено для представления.
Математическая согласованность: Математические представления имеют регулярность и надежность, согласованные в разных ситуациях.
Мы можем моделировать энциклопедические знания, которые люди используют для создания контекстуального значения, в виде скоординированных совокупностей ресурсов – координации, включая, среди прочего, концептуальные, эпистемологические и аффективные факторы.В результате опыта учащихся как в их повседневной жизни, так и в процессе обучения мы отмечаем, что часто такая координация ресурсов может развиваться в регулярные, согласованные модели. Например, если математическая обработка часто активируется с негативным и стрессовым аффектом – это очень сложно, – они могут иметь тенденцию активироваться вместе.
Хотя до сих пор мы подчеркивали множество возможных моделей активации ресурсов, мы также считаем, что иногда ожидания в отношении знаний и обучения могут быть довольно стабильными и надежными.Согласованность может стать сильной, по крайней мере, на время и в обычных условиях. На вопрос, как преобразовать T ( x , y ) в T ( r , θ ), мы ожидаем, что специалисты по физике и математике будут отвечать в соответствии с правилами их конкретной дисциплины. контексты. По физике учащиеся могут потратить 15 минут или больше, застряв, используя непродуктивные методы накопления знаний для решения проблемы. (Bing and Redish 2008) Более того, ученик на уроке физики может использовать способы осмысления физики – решение проблем или изучение стратегий, – которые неизменно оказываются бесполезными, даже если есть свидетельства того, что у них есть ресурсы для большего продуктивные стратегии (Hammer et al.2005). Примат и стабильность определенных паттернов согласованных активаций могут препятствовать переходу к другим, потенциально более продуктивным.
Однако было бы ошибкой предполагать, что кажущаяся стабильность одной линии рассуждений не предполагает никаких альтернатив. Как и в случае с языком, осмысление в физике – это динамический процесс, часто реагирующий на изменение социальных ситуаций и сигналов. В следующем тематическом исследовании мы подчеркиваем, что даже очевидно стабильные способы рассуждений могут быть переоценены и изменены интервьюером, предлагающим соответствующие подсказки.
Пример # 2: Как сдвиги в эпистемологии подтверждают сдвиги в значении уравнений
В качестве примера роли, которую эпистемология может играть в динамике смыслообразования в физике, мы представляем тематическое исследование меняющейся интерпретации одного студента двух «изоморфных» уравнений (Kuo 2013).
Девон дал интервью летом после его первого семестра курса физики. Его интервью началось с той же подсказки, на которую ответили Алекс и Пэт: объясните уравнение \ (v = v_ {0} + at \).Объяснение Девон, предназначенное для ученика средней школы, было похоже на объяснение Алекса, сосредоточив внимание на значении переменных ровно столько, сколько требуется для использования уравнения в качестве вычислительного инструмента.
Тем не менее, мы ожидаем, что Девон, бакалавр инженерной специальности, обладает ресурсами для понимания уравнений с основанием , + , изменением и другими символическими формами. После подсказки скорости Девон попросили придумать изоморфное уравнение для денег:
Вы начинаете с м 0 долларов, а вы зарабатываете р доллара в день.Сколько долларов ( м ) у вас будет в конце d рабочих дней? Не могли бы вы выразить количество долларов ( м ) в уравнении?
Девон быстро приходит к правильному уравнению: \ (m = m_ {0} + rd \). Когда его попросили объяснить ученику средней школы, как он получил это уравнение, он объясняет через базовое изменение + , начиная с более конкретного примера того, сколько денег вы заработаете за 1 неделю:
Девон: Итак, если вы работаете пять дней и получаете столько денег каждый день, что вы делаете, чтобы рассчитать свой общий заработок за эти пять дней? И я думаю, что к двенадцати они будут знать, о, просто умножьте на то, сколько вы получаете в день, хорошо, и это позаботится об этом, r умножить на d, и тогда вы знаете, чтобы получить общее количество, они уже знают, что вы начните с того, чтобы они знали, что нужно добавить к этому.
I: Зачем добавлять?
Девон: Поскольку вы хотите получить общую сумму, например, для, вы начинаете с определенной суммы и хотите знать, сколько у вас будет после недели, поэтому ваша начальная сумма плюс то, сколько вы заработали на этой неделе, равняется общая сумма денег, которая у вас есть.
Как и в объяснении Пэта \ (v = v_ {0} + at \), объяснение Девона денежного уравнения определяет количество базового («вы начинаете с определенной суммы»), изменения («сколько вы заработали на этой неделе »), а также общую историю, которая связывает базовую сумму и изменение с окончательной суммой (« ваша начальная сумма плюс то, сколько вы заработали на этой неделе, равняется общей сумме денег, которая у вас есть »).Существует множество концептуальных различий в задачах, которые способствуют тому, что Девон по-разному интерпретирует эти два уравнения. Здесь мы подчеркиваем эпистемологическое различие. В интервью Девон рассматривает понимание уравнений в физике как запоминание, а понимание уравнений в математике – как понимание того, почему эти уравнения работают:
I: Когда вы действительно чувствуете себя комфортно с уравнением, когда вы чувствуете, что действительно понимаете уравнение?
Девон: Что ж, в физике я чувствую себя комфортно, когда запоминаю вещь, и я знаю все единицы, которые к ней прикреплены.“ Потому что, как я уже сказал, мне нравится, я конкретный последовательный парень в математике, поэтому, если я знаю, если бы я мог видеть, что единицы имеют смысл, тогда я знаю, что то, что я делаю, должно быть правильным, я Нет, мне просто не нравится думать о концепциях, лежащих в основе этого, я не люблю думать о гравитации, понимаете. Другие люди думают, что из-за этого, из-за гравитации, она будет делать то-то и то-то, а я нет, вы знаете, мне нравится просто сосредотачиваться на единицах и просто, если это имеет смысл, и я просто запоминаю уравнение, я имею в виду, другие люди могут вывести уравнения, я не знаю, с помощью второго закона Ньютона или построения диаграмм свободного тела, и они могут вывести уравнение или определенную кинематику, но я этого не делаю, я просто думаю о том, что имеет смысл Я полагаю, что это разумно.
I: А как насчет математики? Когда вы чувствуете, что действительно понимаете математическое уравнение?
Девон: Ну, в математике, ну вроде, есть так много доказательств, и они имеют смысл, я не знаю, как производные, интегралы и преобразования Якоби. Для меня все это имеет смысл, потому что есть причина, по которой это работает, и это только одна причина. На самом деле это не похоже на физику, где существует так много разных случаев, как я уже говорил.В математике, например, если я понимаю доказательства того, почему это так, и тогда мне удобно пользоваться этим уравнением.
Здесь возникают две явные, актуальные эпистемологические позиции по отношению к уравнениям. В физике Девон предпочитает сосредотачиваться на единицах измерения и запоминать уравнения, а не думать о концепциях, лежащих в основе уравнений. Он признает, что другие люди могут рассуждать о концепциях (например, гравитации) или выводить уравнения из более основных принципов (например, второго закона Ньютона), но он явно предпочитает не делать этого.
Напротив, для Девона математические уравнения имеют смысл. В отличие от множества различных случаев в физике, математика для Девона проще и унифицирована («Есть одна причина, по которой она работает, и это всего одна причина»). Возможно, из-за кажущейся относительной простоты Девон стремится к пониманию математических уравнений, тогда как распространение уравнений и понятий в физике делает такое понимание слишком трудным для достижения.
Позже в интервью Девон возвращается в область физики, чтобы объяснить уравнение скорости автомобиля с базой + изменение .Это говорит о том, что объяснение денежного уравнения не только показало, как Девон понимает смысл уравнений в контексте математических задач, но и задействовало производительный ресурс, который затем, без особых усилий, можно было применить для придания смысла уравнению в контексте физики.
Рассуждения Девона приводят примеры двух ключевых особенностей структуры ресурсов. Во-первых, его первоначальная неспособность использовать базу + изменение не означает дефицита знаний. Рассуждения Девона с уравнениями зависят от контекста, и другой контекст проблемы показывает, как он может использовать на основе + изменение , чтобы интерпретировать подобное уравнение.Во-вторых, эпистемологическая позиция Девон по отношению к уравнениям в математике и физике согласуется с различными способами рассуждения с помощью уравнений и поддерживает их.
Контекстуализация: как аффектные сдвиги наряду со сдвигами в концептуальном значении и эпистемологии
До сих пор мы обсуждали, как динамика рассуждений студентов в физике зависит от знания, как концептуального, так и эпистемологического. Тем не менее, как учителя, мы знаем, что аффективные состояния учащихся так же важны, как и знания, которыми они обладают, для определения того, как они понимают проблемы физики.Например, как учителя, мы интуитивно знаем, что не следует преподавать новый материал в день экзамена, потому что негативное влияние на результаты будет препятствовать глубокому взаимодействию с новыми темами.
Тем не менее, несмотря на эту учебную интуицию, а также исследования, показывающие корреляцию между эмоциями и обучением, исследования концептуальных знаний и эпистемологии студентов-физиков по-прежнему значительно превосходят по количеству исследования, изучающие роль аффекта и эмоций в динамике этих студентов ». рассуждения.Мы не должны рассматривать детальную спецификацию концептуальных и эпистемологических ресурсов в структуре ресурсов, чтобы подразумевать, что другие факторы, такие как аффект, не играют никакой роли в контекстуализации и смыслообразовании. Далее мы обсуждаем тематическое исследование, показывающее, как аффект сочетается с концептуальными и эпистемологическими ресурсами в сдвигах в рассуждениях учащихся.
Пример # 3: Реакция ученика на математику динамична и может быть опосредована воздействием
Гупта и Элби (2011) сообщают об чрезвычайно интересном интервью со студентом вводного курса физики для инженеров, которое иллюстрирует динамическую реакцию ученика. студент пытается понять математику на уроке физики и демонстрирует взаимодействие концептуальных, эпистемологических и аффективных факторов.
Интервью проводилось в первом семестре по физике для инженеров. Интервьюер не участвовал в обучении или оценке класса. После обсуждения уравнения. (7), тема, которая обсуждалась в классе, интервьюер обратился к теме, которая еще не обсуждалась: давление в жидкостях. Он представляет уравнение:
$$ p \, = \, p_ {0} + \, \ rho gh $$
(8)
, где p представляет давление под поверхностью озера, p 0 – давление в верхней части озера, ρ – плотность воды, г, – гравитационное поле, и h – глубина под поверхностью воды.Затем он спрашивает испытуемого, Джима, видел ли он это уравнение раньше, и Джим отвечает, что не видел. Затем интервьюер спрашивает, больше ли давление на глубине 7 м под поверхностью озера, равно или меньше давления на глубине 5 м ниже поверхности.
Джим сначала склоняется к использованию этого уравнения, и, после некоторого колебания, он решает, что h должно быть отрицательным под поверхностью и, следовательно, что давление на 7 м ниже поверхности должно быть меньше, чем это в 5 м.Ему это несколько неудобно, поскольку это противоречит его интуиции и опыту. Он совершил ошибку, приняв h за отрицательное значение (положительное как восходящее), но не приняв g за отрицательное значение (гравитация указывает вниз).
На вопрос, как друг из класса английского мог бы рассуждать о проблеме (Я: «Предположим, был ваш друг, говорящий по-английски, [который] на самом деле не знает физику и вопросы, вроде того. Могли бы они ответить на это вопрос? »), Джим демонстрирует, что он обладает хорошей физической интуицией относительно ситуации.
Джим: Например, если они действительно были под водой, значит, давление, они могли бы немного знать о давлении под водой… Как грубая оценка. Давление было выше, когда я был глубже. [I: Хорошо] Давление было ниже, когда я был выше на поверхности … Они могли спорить, исходя из своего личного опыта, например, однажды я нырял с аквалангом и находился примерно на 30 футов ниже воды, и давление было такое, давление было очень высоким. . Как будто я просто плавал, я был всего в паре футов ниже воды, и давление было не таким сильным.
Но он твердо верит в уравнение. Он объясняет, что находится на уроке физики, заявляет, что «это сложно», и выражает позицию, согласно которой на экзамене он будет доверять своему анализу уравнения, а не своей интуиции.
Джим: Чтобы уравнение было дано вам, оно должно быть похоже на теорию и должно содержать факты. Итак, факт применим ко всему. Это похоже на закон. Это применимо ко всем ситуациям, в которых вы можете оказаться.Но, например, иногда ваш опыт или восприятие просто другое – или у вас нет знаний об этом курсе или о чем-то еще. Итак, я пойду с людьми, которые исполнили закон, и он работал раз за разом.
Хотя Джим может эффективно и правильно использовать свой воплощенный опыт, его аффект – его неуверенность в своих интуициях и ощущение, что «физика трудна» – заставляет его подавлять эпистемологический ресурс, поддерживающий «знание, построенное на восприятии», и вместо этого полагаться на на знании, основанном на авторитете, и знании, построенном на математических манипуляциях.Это показано на фиг. 6а линиями со стрелками, указывающими активацию, и линиями с кружками на конце, указывающими ингибирование. Похоже, он активно отверг свою интуицию. (Хотя детали этого рисунка отличаются от Gupta and Elby (2011), мы согласны с ними в той степени, в какой наша диаграмма направлена на моделирование того, как две разные эпистемологические позиции могут совместно использовать определенные эпистемологические ресурсы, и показать механизм того, как контекстный сигнал может сместить одну местную эпистемологическую позицию на другую.)
I: Как вы думаете, уравнение [гидростатического давления] связано с [физическим ощущением давления]?
Джим: Возможно, так или иначе, но не напрямую. Я думаю, что есть какой-то способ, который просто полностью связывает их вместе, но не совсем ясно, что это за связь.
Чуть позже интервьюер намекает, что, возможно (если он будет настаивать на том, что вниз – это отрицательное направление), он мог бы рассмотреть знак g .
I: Что вы думаете о г в уравнении [гидростатического давления]? Это должно быть минус десять или плюс десять?
Джим: Ой! минус десять… Итак, это дает вам положительный результат. [I: Хорошо.] Я бы сказал, что негатив больше не имеет значения. Ооо! Понятно. Чем выше вы опускаетесь под воду, э-э, чем ниже вы опускаетесь под воду, тем выше ваше давление, потому что отрицательное и отрицательное взаимно компенсируются … Итак, чем больше вы под водой, тем выше будет ваше давление, я думаю сейчас .Я забыл разложить на множитель г . Я так думаю.
I: Хорошо. Это удобнее или менее комфортно?
Джим: Так удобнее, потому что теперь это имеет для меня больше смысла. И теперь ваш опыт действительно работает, потому что, находясь под водой, вы почувствовали большее давление, чем на поверхности. Если принять во внимание оба отрицательных момента, это просто положительный момент, они просто складываются.
Эпистемологическая позиция Джима резко изменилась вместе с его аффектом.Теперь его расчет (привязанный к эпистемологическим ресурсам «знание, построенное на математических манипуляциях» и «знание от авторитета») согласуется с его интуицией («знание, построенное на восприятии»), как показано на рис. 6b.
Рис. 6Взаимодействие аффекта Джима и эпистемологических ресурсов с физическим контекстом. a До сверки; б после сверки. Блеклые узлы временно неактивны. (После Гупты и Элби 2011)
В целом, тематические исследования, которые мы представили в этой статье, демонстрируют, что рассмотрение смыслообразования с помощью математики через призму воплощенного познания, энциклопедических ресурсов и контекстуализации, уточненной эпистемологическим анализом, дает нам понимание того, как студенты могут не использовать в их фонды продуктивного знания, как можно изменить контекст, чтобы раскрыть это продуктивное знание, и как аффект играет интерактивную роль в динамике создания смысла.
Модуль 03: Динамика – AP Physics 1 Online
Цели:
Понятия силы и чистой силы
- Студент должен уметь (а) соотносить силу с движением и (б ) объясните, что подразумевается под чистой или неуравновешенной силой.
- Учащийся должен уметь (а) сформулировать и объяснить закон Ньютона инерции (1-й закон движения) и, (б) описывают инерцию и ее отношение к массе.
- Учащиеся должны уметь анализировать ситуации, в которых частица остается в покое, или движется с постоянной скоростью под действием нескольких сил.
- Учащийся должен уметь (а) сформулировать и объяснить закон Ньютона ускорения (2-й закон движения), (б) применить его к физическому ситуации и (c) различать вес и массу.
- Учащиеся должны понимать взаимосвязь между силой, действующей на объект, и результирующим изменением скорости объекта, чтобы они могли:
- Рассчитать, для объекта, движущегося в одном измерении, изменение скорости, которое приводит к когда постоянная сила F действует в течение заданного интервала времени.
- Определить, для объекта, движущегося в плоскости, вектор скорости которого испытывает указанное изменение за указанный интервал времени, средняя сила, которая действовали на объект.
- Студенты должны понимать, как Второй закон Ньютона , F = ma , применяется к объекту, подверженному таким силам, как гравитация, натяжение струн или контактные силы, чтобы они могли:
- Нарисовать колодец- маркированная диаграмма свободного тела, показывающая все действительные силы, действующие на объект.
- Запись вниз по векторному уравнению, полученному в результате применения Второго закона Ньютона к объекту, и возьмите компоненты этого уравнения вдоль соответствующих топоры.
- Студенты должны уметь анализировать ситуации в объект движется с заданным ускорением под действием одна или несколько сил, чтобы они могли определить величину и направление чистая сила или одна из сил, составляющих чистую силу, например, движение вверх или вниз с постоянным ускорением.
- Учащиеся должны уметь (а) сформулировать и объяснить закон действия-противодействия (3-й закон движения), и (б) определить пары сила действия-противодействия.
- Студенты должны понимать Третий закон Ньютона так что для данной системы они могут идентифицировать пары сил и объекты, на которые они действуют, и указывают величину и направление каждого сила.
- Студенты должны уметь применять третий закон Ньютона при анализе силы контакта между двумя объектами, которые вместе ускоряются по горизонтали или вертикальной линией или между двумя скользящими поверхностями.
- Студенты должны уметь решать задачи в котором применение законов Ньютона приводит к двум или трем совместные линейные уравнения, включающие неизвестные силы или ускорения.
- Учащиеся должны уметь (а) применять законы Ньютона в анализ различных ситуаций с использованием диаграмм свободного тела, и (б) понять концепцию поступательного равновесия.
- Студенты должны знать, что напряжение постоянна в легкой струне, которая проходит через безмассовый шкив и должны уметь использовать этот факт при анализе движения системы два объекта, соединенных строкой.
- Учащиеся должны уметь объяснять (а) причины трение, и (б) как трение описывается с помощью коэффициентов трение.
- Учащиеся должны понимать значение коэффициента трения , чтобы они могли:
- Записать соотношение между нормальными силами и силами трения на поверхности.
- Проанализируйте ситуации, в которых объект движется по неровной наклонной плоскости или горизонтальной поверхности.
- Проанализируйте, при каких обстоятельствах объект начнет скользить, или вычислите величину силы статического трения.
- Учащиеся должны понимать влияние силы сопротивления на движение объекта, чтобы они могли:
- Найти конечную скорость объекта, движущегося вертикально под действием замедляющей силы, зависящей от скорости.
Постоянное понимание 1.C:
Объекты и системы обладают свойствами инертной массы и гравитационной массы, которые экспериментально подтверждены, чтобы быть одинаковыми и которые удовлетворяют принципам сохранения.
Essential Knowledge 1.C.1:
Инерционная масса – это свойство объекта или системы, которое определяет, как изменяется его движение при взаимодействии с другими объектами или системами.
Цель обучения (1.C.1.1):
Учащийся может разработать эксперимент по сбору данных, чтобы определить взаимосвязь между чистой силой, действующей на объект, его инерционной массой и его ускорением.
[См. Научную практику 4.2]
Основные знания 1.C.3:
Объекты и системы обладают
свойствами инертной массы и гравитационной массы, которые экспериментально подтверждены как одинаковые и удовлетворяют принципам сохранения.
Цель обучения (1.C.3.1):
Учащийся может разработать план сбора данных для измерения гравитационной массы и измерения инертной массы, а также провести различие между двумя экспериментами.
[См. Научную практику 4.2]
Векторы силы
Постоянное понимание 3.A:
Все силы обладают некоторыми общими характеристиками, если их рассматривать наблюдателями в инерциальных системах отсчета.
Essential Knowledge 3.A.2:
Силы описываются векторами.
- Силы обнаруживаются по их влиянию на движение объекта.
- Силы имеют величин и направление .
Цель обучения (3.A.2.1): Нарисуйте и рассчитайте
Учащийся может представить силы на диаграммах или математически , используя соответствующим образом обозначенные векторы с величиной, направлением и единицами измерения во время анализа ситуации .
[См. Научную практику 1.1]
Силы заставляют вещи ускоряться
Основные знания 3.A.3:
Сила , действующая на объект, всегда возникает из-за взаимодействия этого объекта с другим объектом.
- Объект не может оказывать на себя силу.
- Даже если объект находится в состоянии покоя, на него могут действовать силы со стороны других объектов.
- Ускорение объекта, но не обязательно его скорость, всегда происходит в направлении результирующей силы, прикладываемой к объекту другими объектами.
Цель обучения (3.A.3.1):
Учащийся может анализировать сценарий и выдвигать утверждения (развивать аргументы, обосновывать утверждения) о силах, действующих на объект другими объектами для различных типов сил. или
составляющих сил.
[См. Научные практики 6.4 и 7.2]
Цель обучения (3.A.3.2):
Учащийся может оспорить утверждение о том, что объект может оказывать на себя силу.
[См. Научную практику 6.1]
Цель обучения (3.A.3.3):
Учащийся может описать силу как взаимодействие между двумя объектами и идентифицировать оба объекта для любой силы.
[См. Научную практику 1.4]
Третий закон движения Ньютона
Основные знания 3.A.4:
Если один объект оказывает силу на второй объект, второй объект всегда оказывает силу равной величины на первом объекте в обратном направлении
.
Цель обучения (3.A.4.1):
Учащийся может построить объяснения физических ситуаций, связанных с взаимодействием тел, используя третий закон Ньютона и представление пар сил действие-противодействие.
[См. Научные практики 1.4 и 6.2]
Цель обучения (3.A.4.2):
Учащийся может использовать третий закон Ньютона, чтобы выдвигать утверждения и предсказывать о парах действие-реакция сил при взаимодействии двух объектов.
[См. Научные практики 6.4 и 7.2]
Цель обучения (3.A.4.3):
Учащийся может анализировать ситуации , включающие взаимодействие между несколькими объектами , используя диаграммы свободного тела , которые включают приложение третьего закона Ньютона для определения сил.
[См. Научную практику 1.4]
Второй закон движения Ньютона
Постоянное понимание 3.B:
Классически ускорение объекта, взаимодействующего с другими объектами, можно предсказать, используя ΣF = ma .
Essential Knowledge 3.B.1:
Если интересующий объект взаимодействует с несколькими другими объектами, чистая сила является векторной суммой отдельных сил.
Цель обучения (3.B.1.1):
Учащийся может предсказать движение объекта с учетом сил, действующих со стороны нескольких объектов, используя второй закон Ньютона в различных физических ситуациях с ускорением в одно измерение.
[См. Научную практику 6.4 и 7.2]
Цель обучения (3.B.1.2):
Учащийся может разработать план сбора и анализа данных движения (статического, постоянного или ускоряющегося) на основе измерений силы и переноса. провести анализ, чтобы определить взаимосвязь между чистой силой и векторной суммой отдельных сил.
[См. Научные практики 4.2 и 5.1]
Цель обучения (3.B.1.3):
Учащийся может преобразовать диаграмму свободного тела в математическое представление и решить математическое представление для ускорения объекта.
[См. Научные практики 1.5 и 2.2]
Диаграммы свободного тела
Основные знания 3.B.2: Диаграммы свободного тела – полезные инструменты для визуализации сил, действующих на отдельный объект, и написания уравнений которые представляют физическую ситуацию.
- Объект можно нарисовать так, как если бы он был извлечен из его среды, и взаимодействия с ней идентифицированы.
- Сила, действующая на объект, может быть представлена в виде стрелки, длина которой представляет величину силы, а направление показывает направление силы.
- Система координат с одной осью, параллельной направлению ускорения, упрощает переход от диаграммы свободного тела к алгебраическому представлению.
Цель обучения (3.B.2.1):
Ученик может создавать и использовать диаграммы свободного тела, чтобы анализировать физические ситуации решать задачи с движением качественно и количественно .
[См. Научную практику 1.1, 1.4 и 2.2]
Откуда берутся силы?
Постоянное понимание 3.C:
На макроскопическом уровне силы можно разделить на дальнодействующих (действие на расстоянии) сил или контактных сил .
Essential Knowledge 3.C.4:
Контактные силы возникают в результате взаимодействия одного объекта, касающегося другого объекта, и возникают из межатомных электрических сил . Эти силы включают натяжение, трение, нормальные, пружинные (Физика 1) и плавучие (Физика 2).
Цель обучения (3.C.4.1):
Учащийся может утверждать о различных контактах сил между объектами на основе микроскопической причины этих сил.
[См. Научную практику 6.1]
Цель обучения (3.C.4.2):
Учащийся может объяснить контактные силы (натяжение, трение, нормальное давление, пружина), возникающие из-за межатомных электрических сил и что они поэтому есть определенные направления.
[См. Научную практику 6.2]
Фундаментальные силы
Постоянное понимание 3.G:
Определенные типы сил считаются фундаментальными.
Essential Knowledge 3.G.1:
Гравитационные силы действуют во всех масштабах и преобладают на самых больших масштабах расстояний и масс.
Цель обучения (3.G.1.1):
Учащийся может сформулировать ситуации , когда сила тяжести является доминирующей силой, а электромагнитные, слабые и сильные силы можно игнорировать.
[См. Научную практику 7.1]
Центр масс
Постоянное понимание 4.A:
Ускорение центра масс системы связано с чистой силой, действующей на систему, где ΣF = ma .
Границы:
Физика 1 не включает вычислений центров масс; уравнение не предоставляется до Физики 2. Однако, без проведения расчетов, студенты Физики 1, как ожидается, смогут определить центр масс высокосимметричных распределений масс, таких как однородный стержень или куб с однородной плотностью, или две сферы равная масса.
Essential Knowledge 4.A.1:
Линейное движение системы можно описать с помощью смещения, скорости и ускорения ее центра масс.
Цель обучения (4.A.1.1):
Учащийся может использовать представления центра масс изолированной двухобъектной системы для качественного и полуколичественного анализа движения системы.
[См. Научные практики 1.2, 1.4, 2.3 и 6.4]
Основные знания 4.A.2:
Ускорение равно скорости изменения скорости во времени, а скорость равна скорости изменения положения во времени.
- Ускорение центра масс системы прямо пропорционально чистой силе, прилагаемой к нему всеми объектами, взаимодействующими с системой, и обратно пропорционально массе системы.
- Сила и ускорение являются векторами с ускорением в том же направлении, что и результирующая сила.
Цель обучения (4.A.2.1):
Ученик может делать прогнозы о движении системы на основании того факта, что ускорение равно изменению скорости в единицу времени, а скорость равна изменению положения на единицу. время.
[См. Научную практику 6.4]
Цель обучения (4.A.2.2):
Учащийся может оценить, используя данные , были ли задействованы все силы в системе или все части системы идентифицированы.
[См. Научную практику 5.3]
Цель обучения (4.A.2.3):
Учащийся может создавать математические модели и анализировать графических взаимосвязей для ускорения, скорости и положения центра масс системы и используйте их для вычисления
свойств движения центра масс системы.
[См. Научные практики 1.4 и 2.2]
Кинематические уравнения
Основные знания 4.A.3:
Силы, которые системы оказывают друг на друга, возникают из-за взаимодействия между объектами в системах. Если взаимодействующие объекты являются частями одной и той же системы, скорость центра масс этой системы не изменится.
Цель обучения (4.A.3.1):
Учащийся может применить второй закон Ньютона к системам, чтобы вычислить изменение скорости центра масс при воздействии на систему внешней силы .
[См. Научную практику 2.2]
Цель обучения (4.A.3.2):
Учащийся может использовать визуальные или математические представления сил между объектами в системе, чтобы предсказать, произойдет ли изменение в центре. массовой скорости этой системы.
[См. Научную практику 1.4]
Силы или Динамика. Часть 1. Множественный выбор. 11 класс. Физика.
. Этот продукт содержит 30 страниц вопросов по физике с множественным выбором по законам Ньютона, Fnet = ma, закону инерции, силам действия-противодействия, сила тяжести, вес, сила трения, коэффициент трения, нормальная сила, чистая сила и приложенные силы.Существуют теоретические вопросы с несколькими вариантами ответов и вопросы с несколькими вариантами ответов на основе расчетов. Эти вопросы с несколькими вариантами ответов подходят для тестов по физике или викторин для 11 класса.
Все вопросы с несколькими вариантами ответов набраны 12 шрифтом (новый латинский шрифт), без текстовых полей и сжаты до минимально возможного места. Все вопросы с несколькими вариантами ответов, вопросы с короткими ответами, PowerPoint, рабочие листы, викторины, лабораторные работы и тесты, которые я публикую, правильно отформатированы и готовы к печати.Проверены на ошибки и опечатки!
Меня зовут Даррин Мэтьюсон, я доктор органической химии. Я преподаю физику и химию более 15 лет.
У меня есть более 140 очков Power Point на продажу в моем магазине, 40 пакетов рабочих листов, 100 тестовых пакетов, 100 пакетов с множественным выбором и 70 пакетов с короткими ответами. У меня есть Power Points, тесты, викторины, вопросы с несколькими вариантами ответов, вопросы с короткими ответами и рабочие листы по каждой теме, охваченной естественными науками 10 класса, химией 11 класса, физикой 11 класса и химией 12 класса!
ПОИСКОВ КЛЮЧЕВЫХ СЛОВ ДЛЯ НАВИГАЦИИ МОЙ МАГАЗИН:
типа «точка силы физики 11 класса» для просмотра точек силы физики 11 класса
тип «точка силы химии 11 класса» взгляд 11 точка силы химии
тип «точка силы химии 12 класса» вид точки силы химии 12 класса
тип «оценка 10 очков силы науки »для просмотра 10 очков силы наукивведите «пакет тестов по физике 11 класса» для просмотра тестов по физике 11 класса
введите «пакет тестов по химии 11 класса» для просмотра тестов по химии 11 класса
введите «пакет тестов по химии 12 класса» для просмотра тестов по химии 12 класса
введите «пакет тестов» естественные науки 10-го класса », чтобы просмотреть тесты 10-го классавведите «рабочие листы по физике 11 класса», чтобы просмотреть рабочие листы по физике 11 класса.
введите «рабочие листы по химии 11 класса», чтобы просмотреть рабочие листы по химии 11 класса.
введите «рабочие листы по химии 12 класса», чтобы просмотреть рабочие листы по химии 12 класса.
введите «рабочие листы 10 класса по естествознанию» для просмотра заданий по естествознанию за 10 классвведите «краткий ответ для 11 класса по физике», чтобы просмотреть короткий ответ по физике для 11 класса.
введите «краткий ответ для 11 класса по химии» просмотрите короткий ответ по химии для 11 класса
введите «краткий ответ для 12 класса по химии» просмотрите краткий ответ по химии для 12 класса
введите «короткий ответ» ответ 10 класс по естествознанию »для просмотра 10 класса по естествознанию короткий ответтип «множественный выбор для 11 класса физики» просмотр 11-го класса физика множественный выбор
тип «множественный выбор для 10-го класса естествознание» просмотр 10-й класс естествознания множественный выбор
тип «множественный выбор для 11-го класса химии» для просмотра 11-го класса химия множественный выбор
выбор
тип « множественный выбор по химии для 12-го класса »для просмотра 12-го класса по химии, множественный выбор
выбор
AP Physics 1 Видео с физикой
Точек привязки для этой страницы:
Вводные понятия для физики, основанной на алгебреAP Physics 1 Free Response Exam Вопросы, которые вы должны уметь решать на этом этапе учебной программы:
- (7:56) 2015 # 1 – Короткий ответ
- (4:55) 2015 # 4 – Paragraph Argument Short Answer
- (10:30) 2016 № 3 – Количественный / качественный перевод
- (12:36) 2017 # 2 – Вопрос экспериментального дизайна
- (11:19) 2019 # 2 – Количественный / качественный перевод
- (12:44) 2015 # 3 – Количественный / качественный перевод
- (6:55) 2017 # 4 – Краткий ответ
- (11:38) 2019 # 3 – Вопрос об экспериментальном дизайне
- (8:30) 2016 # 2 – Experimental Design Question
- (10:10) 2016 # 1 – Краткий ответ
- (10:54) 2017 # 3 – Количественный / качественный перевод
- (10:19) 2018 # 3 – Количественный / качественный перевод
- (10:29) 2019 # 1 – Краткий ответ
- (11:06) 2018 # 1 – Краткий ответ
- (9:42) 2018 # 5 – Paragraph Argument Short Answer
AP Physics 1 Free Response Exam Вопросы, которые вы должны уметь решать на этом этапе учебной программы:
- (6:15) 2015 # 5 – Краткий ответ
- (4:08) 2016 # 5 – Абзац Аргумент Краткий ответ
- (6:33) 2017 # 5 – Краткий ответ
- (8:00) 2018 # 4 – Краткий ответ
- (8:08) 2019 # 5 – Краткий ответ
- (7:54) 2015 # 2 – Вопрос экспериментального дизайна
- (12:11) 2016 # 4 – Количественный / качественный перевод
- (6:28) 2017 # 1 – Краткий ответ на аргумент абзаца
- (11:11) 2018 # 2 – Вопрос экспериментального проектирования
- (4:58) 2019 # 4 – Краткий ответ на аргумент абзаца
Все видео ниже этого пункта предназначены для учебной программы AP Physics 2 и представляют собой лекции в классе.В какой-то момент я планирую переделать их в видео по «Перелистывание физики», однако сейчас я концентрируюсь на других программах.
Электрический заряд, электрическая сила и электрическое поле
Все лекции и ссылка на плейлист YouTube для электрического заряда, электрической силы и электрического поляВведение в силу Кулона или электрическую силу: видео
- Определение коэффициента трения между пробкой и столом – Проблема силы Кулона: видео
- Введение в электрическое поле: видео
- Таблица друзей – заряд, электрическая сила и электрическое поле: видео
- Проблема определения электрического поля из-за двухточечных зарядов: видео
Энергия электрического потенциала и разность электрических потенциалов
Все лекции и ссылка на плейлист YouTube для определения электрической потенциальной энергии и разности электрических потенциалов
- Введение в электрическую потенциальную энергию в постоянном электрическом поле: видео
- Проблема определения изменения электрической потенциальной энергии в постоянном поле: видео
- Введение в электрическую потенциальную энергию между двумя точечными зарядами: видео
- Введение в разность электрических потенциалов в постоянном электрическом поле: видео
- Введение в разность электрических потенциалов из-за точечного заряда: видео
- Проблема определения разницы электрических потенциалов из-за точечного заряда: видео
- Проблема определения разницы электрических потенциалов из-за двухточечных зарядов: видео
- Проблема определения изменения электрической потенциальной энергии в постоянном электрическом поле: видео
- Таблица друзей – электрическая потенциальная энергия и разность электрических потенциалов: видео 9071 4
- Нахождение эквивалентного сопротивления и разности электрических потенциалов в цепи с последовательно включенными резисторами: видео
- Нахождение эквивалентного сопротивления и электрической мощности в цепи с последовательными и параллельными резисторами: видео
- Цепь сложного резистора: Часть a) Рисование Принципиальная схема и поиск эквивалентного сопротивления: видео Цепь сложного резистора
- A: часть b) Определение мощности, рассеиваемой одним резистором: видео
- Введение в магнитные полюса и закон полюсов: видео
- Введение в магнитное поле и магнитные полюса Земли: видео
- Введение в магнитное поле Сила и Теслас: видео
- Введение в правило правой руки для направления магнитной силы с примерами: видео
- Примеры правил правой руки с магнитной силой с использованием основных направлений (север, юг, восток, запад): видео
- Введение в Магнитная сила на проводе, проводящем ток: Видео
- Введение в путь заряженной частицы в постоянном магнитном поле: Видео
- Пример – Электрон, движущийся в постоянном магнитном поле: Часть a) Поиск скорости: Видео
- Пример – Электрон, движущийся в постоянном магнитном поле: Часть б) Определение периода: Видео Пример
- – Электрон, движущийся в постоянном магнитном поле d: Часть c) Определение разницы электрических потенциалов: видео
- Введение в свет, видимый свет, электромагнитные волны и скорость света: видео
- Введение в отражение света – зеркальное и диффузное: видео
- Обзор электромагнитного спектра: видео
- Зеркальное отражение от плоского зеркала – падающие и отраженные лучи: видео
- Основы отражения от вогнутого сферического зеркала: видео
- Введение в характеристики расстояния, увеличения и изображения до объекта и объекта: Видео
- (часть a) Пример – обучение рисованию лучевой диаграммы вогнутого сферического зеркала – только диаграмма: видео
- (часть b) Пример – обучение рисованию лучевой диаграммы вогнутого сферического зеркала – использование математики: Видео
- Определение характеристик изображения в вогнутом сферическом зеркале с помощью видео: Видео
- Определение характеристик изображения в Выпуклое сферическое зеркало с помощью видео: видео
- (часть a) Пример – обучение рисованию лучевой диаграммы выпуклого сферического зеркала – использование математики: видео
- (часть b) Пример – обучение рисованию лучевой диаграммы Выпуклое сферическое зеркало – лучевая диаграмма: видео
- Таблица друзей – зеркала: видео
- Обзор основ зеркал, характеристик изображений и лучевых диаграмм: видео
- Я зеркало – Песня о физике зеркал – Исполняется вживую in Class !: Тексты песен с аккордами, mp3 и видео
- Введение в преломление света и показатель преломления: видео
- Введение в дисперсию, закон Снеллиуса с примером задачи: видео
- Понимание того, как работает мираж – преломление света: видео
- Введение в сходящиеся линзы (или Bi-Convex), линзы Френеля и характеристики изображения: видео Пример
- – обучение рисованию лучевой диаграммы сходящейся линзы (или Bi-Convex) включает в себя математику: видео Пример
- – обучение рисованию лучевой диаграммы Расходящаяся линза (или двояковогнутая) включает Математику: Видео
- Введение в преломление света и Индекс преломления: Видео
- Основное объяснение оптики человеческого глаза: Видео
- Введение в полное внутреннее отражение и критический угол: видео
- Пример – полное внутреннее отражение, критический угол и построение лучевой диаграммы: видео
- Добавление в список друзей – Объективы: видео
- Введение в конструктивное и деструктивное вмешательство света и дифракцию: видео
- Введение в эксперимент Томаса Юнга 1801 с двойной щелью: видео
- Выведение уравнений максимума интерференции и минимумы в эксперименте с двойной щелью: видео
- Задача – определение угла для максимума интерференции в эксперименте с двойной щелью: видео
- Задача – определение угла для минимума интерференции в эксперименте с двойной щелью: видео
- Введение к дифракционной решетке и максимумам и минимумам интерференции: видео
- # 1 Проблема – определение количества линий на сантиметр на дифракционной решетке: видео
- (часть 1) Электростатика, электрическое поле, разность электрических потенциалов: видео
- (часть 2) Ток, сопротивление и схемы: видео
- (часть 3) Магнетизм, Магнитная сила: видео
- (часть 4) Свет, оптика, зеркала, линзы, помехи: видео
- Введение в лекцию по современной физике: видео
- Что такое свет? Объяснение эксперимента Майкельсона Морли: поиск эфира: видео
- Введение в относительность одновременности: видео
- Доказательство замедления времени – часть специальной теории относительности Эйнштейна: видео
- Пример двойного парадокса – замедление времени Задача: видео
- Обсуждение последствий специальной теории относительности: видео
- Обсуждение черных дыр, как их найти и спагеттификация: видео
- Обсуждение нашей Галактики, Вселенной и того, насколько мы незначительны: Видео
- Определение частот, создаваемых велосипедной шиной с использованием эффекта Доплера: видео
- Введение в интенсивность звука и человеческий слух: видео
- Введение в сверхзвуковой Скорости и звуковой удар: видео
- Введение в физику музыкальной теории: видео
- Основы физики гитары: видео
- Butterfly Face – Песня, не имеющая ничего общего с физикой, извините: видео
- Опишите характеристики потока
- Расчет расхода
- Опишите взаимосвязь между расходом и скоростью
- Объясните последствия уравнения неразрывности для сохранения массы
- в шланге и
- в насадке.
Магнитные поля и магнитные силы
Все лекции и ссылка на плейлист YouTube для магнитных полей и магнитных сил
Зеркала, отражение и диаграммы лучей
Все лекции и ссылка на плейлист YouTube для зеркал, отражений и диаграмм лучей
Все лекции и ссылка на плейлист YouTube по интерференции и дифракции света
Обзор всего со времени последнего обзора (Электричество через оптику)
Все лекции и ссылка на плейлист YouTube для этого обзораВсе лекции и ссылка на плейлист YouTube по физике звука и музыки
14.7. Гидродинамика – Physics LibreTexts
Цели обучения
Первая часть этой главы посвящена статике жидкости, изучению жидкости в состоянии покоя. Остальная часть этой главы посвящена гидродинамике, изучению движущихся жидкостей.Даже самые простые формы движения жидкости могут быть довольно сложными. По этой причине мы ограничиваем наше исследование идеальными жидкостями во многих примерах. Идеальная жидкость – это жидкость с пренебрежимо малой вязкостью . Вязкость – это мера внутреннего трения в жидкости; мы исследуем его более подробно в разделе «Вязкость и турбулентность». На нескольких примерах мы исследуем несжимаемую жидкость – ту, для которой требуется чрезвычайно большая сила для изменения объема – поскольку плотность в несжимаемой жидкости постоянна на всем протяжении.
Характеристики потока
Векторы скорости часто используются для иллюстрации движения жидкости в таких приложениях, как метеорология. Например, ветер – жидкое движение воздуха в атмосфере – может быть представлен векторами, указывающими скорость и направление ветра в любой заданной точке на карте. На рисунке \ (\ PageIndex {1} \) показаны векторы скорости, описывающие ветры во время урагана Артур в 2014 году.
Рисунок \ (\ PageIndex {1} \): Векторы скорости показывают поток ветра во время урагана Артур.Обратите внимание на циркуляцию ветра вокруг очага урагана. Самые высокие скорости ветра у глаз. Цвета представляют относительную завихренность, меру вращения или вращения воздуха.Другой метод представления движения жидкости – это линия тока . Линия тока представляет путь небольшого объема жидкости, когда она течет. Скорость всегда тангенциальна к линии тока. Диаграммы на рисунке \ (\ PageIndex {2} \) используют линии тока, чтобы проиллюстрировать два примера движения жидкости по трубе.Первая жидкость демонстрирует ламинарный поток (иногда описываемый как устойчивый поток), представленный плавными параллельными линиями тока. Обратите внимание, что в примере, показанном в части (а), скорость жидкости наибольшая в центре и уменьшается у стенок трубы из-за вязкости жидкости и трения между стенками трубы и жидкостью. Это особый случай ламинарного потока, когда трение между трубой и жидкостью велико, что известно как граничные условия отсутствия проскальзывания. Вторая диаграмма представляет турбулентный поток , в котором линии тока нерегулярны и меняются со временем.В турбулентном потоке пути потока жидкости нерегулярны, поскольку разные части жидкости смешиваются вместе или образуют небольшие круглые области, напоминающие водовороты. Это может произойти, когда скорость жидкости достигает определенной критической скорости.
Рисунок \ (\ PageIndex {2} \): (a) Ламинарный поток можно представить как слои жидкости, движущиеся параллельными регулярными путями. (б) В турбулентном потоке области жидкости движутся по нерегулярным, сталкивающимся траекториям, что приводит к перемешиванию и завихрению.Расход и его связь со скоростью
Объем жидкости, проходящей через заданное место через область в течение периода времени, называется расходом \ (Q \), или, точнее, объемным расходом.В символах это записывается как
.\ [Q = \ frac {dV} {dt} \ label {14.13} \]
где \ (V \) – объем, а \ (t \) – прошедшее время. На рисунке \ (\ PageIndex {3} \) объем цилиндра равен \ (Ax \), поэтому расход равен
.\ [Q = \ frac {dV} {dt} = \ frac {d} {dt} (Ax) = A \ frac {dx} {dt} = Av \ ldotp \]
В системе СИ для расхода используется м 3 / с, но обычно используются несколько других единиц для \ (Q \), например, литры в минуту (л / мин). Обратите внимание, что литр (L) равен 1/1000 кубического метра или 1000 кубических сантиметров (10 −3 м 3 или 10 3 см 3 ).
Рисунок \ (\ PageIndex {3} \): Скорость потока – это объем жидкости, протекающей мимо точки через область \ (A \) в единицу времени. Здесь заштрихованный цилиндр жидкости обтекает точку \ (P \) по однородной трубе во времени \ (t \).Расход и скорость связаны, но совершенно разными физическими величинами. Чтобы сделать различие ясным, рассмотрим скорость течения реки. Чем больше скорость воды, тем больше скорость течения реки. Но скорость потока также зависит от размера и формы реки.Стремительный горный ручей несет гораздо меньше воды, чем, например, река Амазонка в Бразилии. На рисунке \ (\ PageIndex {3} \) показан объемный расход. Объемный расход равен \ (Q = \ frac {dV} {dt} = Av \), где A – площадь поперечного сечения трубы, а v – величина скорости.
Точное соотношение между расходом \ (Q \) и средней скоростью \ (v \) составляет
\ [Q = Av, \]
где \ (A \) – площадь поперечного сечения, а \ (v \) – средняя скорость. Это соотношение говорит нам, что скорость потока прямо пропорциональна средней скорости жидкости и площади поперечного сечения реки, трубы или другого водовода.Чем больше размер трубы, тем больше площадь его поперечного сечения. На рисунке \ (\ PageIndex {3} \) показано, как получается это отношение. Заштрихованный цилиндр имеет объем \ (V = Ad \), который проходит мимо точки \ (P \) за время \ (t \). Разделив обе стороны этого отношения на \ (t \), получим
\ [\ frac {V} {t} = \ frac {Ad} {t} \ ldotp \ label {eq14.14A} \]
Отметим, что \ (Q = \ frac {V} {t} \), а средняя скорость равна \ (v = \ frac {d} {t} \). Таким образом, уравнение \ ref {eq14.14A} становится
\ [Q = Av.\]
На рисунке \ (\ PageIndex {4} \) показана несжимаемая жидкость, текущая по трубе с уменьшающимся радиусом. Поскольку жидкость несжимаема, то же количество жидкости должно пройти через любую точку трубы за заданное время, чтобы обеспечить непрерывность потока. Поток является непрерывным, поскольку они не являются источниками или стоками, которые добавляют или удаляют массу, поэтому масса, текущая в трубу, должна быть равна массе, вытекающей из трубы. В этом случае, поскольку площадь поперечного сечения трубы уменьшается, скорость обязательно должна увеличиваться.Эту логику можно расширить, чтобы сказать, что скорость потока должна быть одинаковой во всех точках трубы. В частности, для произвольных точек 1 и 2
\ [\ begin {split} Q_ {1} & = Q_ {2}, \\ A_ {1} v_ {1} & = A_ {2} v_ {2} \ ldotp \ end {split} \ label {14.14 } \]
Это называется уравнением неразрывности и справедливо для любой несжимаемой жидкости (с постоянной плотностью). Следствия уравнения непрерывности можно наблюдать, когда вода течет из шланга в узкую форсунку: она выходит с большой скоростью – это и есть цель форсунки.И наоборот, когда река впадает в один конец водохранилища, вода значительно замедляется, возможно, снова набирая скорость, когда она покидает другой конец водохранилища. Другими словами, скорость увеличивается, когда площадь поперечного сечения уменьшается, и скорость уменьшается, когда увеличивается площадь поперечного сечения.
Рисунок \ (\ PageIndex {4} \): Когда труба сужается, тот же объем занимает большую длину. Для того, чтобы тот же объем проходил через точки 1 и 2 за заданное время, скорость должна быть больше в точке 2. Процесс в точности обратим.Если жидкость течет в обратном направлении, ее скорость уменьшается при расширении трубки. (Обратите внимание, что относительные объемы двух цилиндров и соответствующие стрелки вектора скорости не в масштабе.)Поскольку жидкости по существу несжимаемы, уравнение неразрывности справедливо для всех жидкостей. Однако газы сжимаемы, поэтому уравнение следует применять с осторожностью к газам, если они подвергаются сжатию или расширению.
Пример 14.5: Расчет скорости жидкости через сопло
Сопло диаметром 0.500 см крепится к садовому шлангу радиусом 0,900 см. Скорость потока через шланг и сопло составляет 0,500 л / с. Рассчитайте скорость воды:
Стратегия
Мы можем использовать соотношение между расходом и скоростью, чтобы найти обе скорости. {2}} \ ldotp $$ Подстановка значений и использование соответствующих преобразований единиц дает $$ v = \ frac {(0.{2}} (1,96 \; м / с) = 25,5 \; м / с \ ldotp $$
Значение
Скорость 1,96 м / с примерно подходит для воды, выходящей из шланга с форсункой. Сопло создает значительно более быстрый поток, просто сужая поток до более узкой трубки.
Решение последней части примера показывает, что скорость обратно пропорциональна квадрату радиуса трубы, что дает большие эффекты при изменении радиуса. Мы можем задуть свечу на большом расстоянии, например, поджав губы, тогда как задувание свечи с широко открытым ртом совершенно неэффективно.
Сохранение массы
Скорость потока жидкости также может быть описана массовым расходом или массовым расходом. Это скорость, с которой масса жидкости движется мимо точки. Еще раз обратитесь к рисунку \ (\ PageIndex {3} \), но на этот раз рассмотрите массу в заштрихованном объеме. Масса определяется по плотности и объему:
\ [m = \ rho V = \ rho Ax \ ldotp \]
Тогда массовый расход будет
\ [\ frac {dm} {dt} = \ frac {d} {dt} (\ rho Ax) = \ rho A \ frac {dx} {dt} = \ rho Av, \]
где \ (\ rho \) – плотность, A – площадь поперечного сечения, а v – величина скорости.Массовый расход является важной величиной в гидродинамике и может использоваться для решения многих задач. Рассмотрим рисунок \ (\ PageIndex {5} \). Труба на рисунке начинается у входа с площадью поперечного сечения A 1 и сужается до выхода с меньшей площадью поперечного сечения A 2 . Масса жидкости, поступающей в трубу, должна быть равна массе жидкости, покидающей трубу. По этой причине скорость на выходе (v 2 ) больше, чем скорость на входе (v 1 ).Используя тот факт, что масса жидкости, поступающей в трубу, должна быть равна массе жидкости, покидающей трубу, мы можем найти связь между скоростью и площадью поперечного сечения, взяв скорость изменения массы в трубе и массы из:
\ [\ begin {split} \ left (\ dfrac {dm} {dt} \ right) _ {1} & = \ left (\ dfrac {dm} {dt} \ right) _ {2} \\ \ rho_ {1} A_ {1} v_ {1} & = \ rho_ {2} A_ {2} v_ {2} \ ldotp \ end {split} \ label {14.15} \]
Уравнение \ ref {14.15} также известно как уравнение неразрывности в общем виде.Если плотность жидкости остается постоянной из-за сужения, то есть жидкость несжимаема, тогда плотность сокращается из уравнения неразрывности,
\ [A_ {1} v_ {1} = A_ {2} v_ {2} \ ldotp \]
Уравнение сокращается, чтобы показать, что объемный расход в трубе равен объемному расходу из трубы.
Рисунок \ (\ PageIndex {5} \): Геометрия для вывода уравнения неразрывности. Количество жидкости, поступающей в площадь поперечного сечения (заштрихованную), должно равняться количеству жидкости, покидающей площадь поперечного сечения, если жидкость несжимаема.Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Динамика кругового движения – объяснения и важные часто задаваемые вопросы
Что такое круговое движение?
Говорят, что тело, движущееся по окружности с постоянной скоростью, совершает круговое движение.
Например, автомобиль, совершающий круговое движение со скоростью 8 м / с по окружности 24 метра.
При одинаковой скорости он выполнит один цикл за 3 секунды.
Это означает, что в каждом круге на 24-метровой окружности тело будет занимать одно и то же время в 4 секунды.
Итак, эту взаимосвязь между длиной окружности, временем на один оборот и скоростью тела можно описать в терминах средней скорости.
Итак, Средняя скорость = расстояние / время = окружность / время = 2 * π * r / T
Как длина окружности = 2 * π * r
Динамика кругового движения
Рассмотрим тело, движущееся по круговой траектории радиус r по часовой стрелке в плоскости бумаги.
Допустим, ось кругового движения проходит через центр O перпендикулярно плоскости бумаги.
Как вы видите на рисунке 1 ниже:
(Изображение будет добавлено в ближайшее время)
Угол, проведенный от P до Q, называется угловым смещением, определяемым как:
Ө = PQ / r = S / r
Это векторная величина.
Его направление может быть задано правилом правой руки.
Правило правой руки
(Изображение будет добавлено в ближайшее время)
В нем говорится, что если пальцы согнуты в направлении движения, как будто они сжимают ось вращения. Большой палец, который удерживается перпендикулярно изгибу пальцев, представляет направление вектора углового смещения.
Поскольку он демонстрирует круговое движение, он также имеет скорость, и эта скорость является угловой скоростью.
Угловая скорость – это скорость изменения углового смещения. Это символизируется ω.
Где ω = v / r
(изображение будет добавлено в ближайшее время).
Это векторная величина.
По правилу правой руки большой палец представляет направление угловой скорости.
(Изображение будет добавлено в ближайшее время)
Для тела, вращающегося против часовой стрелки, по правилу правой руки направление ω находится вдоль оси круговой траектории и направлено вверх, а при вращении по часовой стрелке ω направлено вниз .
Динамика равномерного кругового движения
Естественная тенденция тела – равномерно двигаться по прямой линии.
Когда мы прикладываем к нему центростремительную силу, он вынужден двигаться по окружности.
Рассмотрим тело, равномерно движущееся по окружности под действием псевдосилы.
(Изображение будет добавлено в ближайшее время)
Псевдосила, действующая по радиусу и направленная к центру круга, называется центростремительной силой.
Согласно первому закону движения Ньютона, тело не может изменить свое направление движения, для поддержания его кругового движения требуется внешняя сила.
Однако это тело само по себе непрерывно меняет направление своего движения, при этом изменяется и скорость, поэтому оно испытывает ускорение, называемое радиальным центростремительным ускорением.
a = v2 / r
Мы знаем, что F = ma
F = mv2 / r
Динамика равномерного кругового движения
При движении по окружности тело имеет постоянную тенденцию восстанавливать свой естественный линейный путь.Эта тенденция порождает центробежную силу.
Мы можем рассматривать центростремительную силу как реакцию центростремительной силы.
Это означает, что центробежная сила всегда равна центростремительной силе и противоположна ей.
Итак, центробежная сила = mv2 / r, и она действует по радиусу, но вдали от центра окружности.
Центростремительная и центробежная силы – это силы действия и противодействия соответственно.
Допустим, к одному концу веревки привязан камень, а другой конец вращается по кругу.
(Изображение будет добавлено в ближайшее время)
Как видно на рисунке.
Когда центростремительная сила F1 приложена к камню рукой. Его вытягивает наружу центробежная сила F2, действующая на него, потому что он стремится восстановить свое естественное линейное движение.
(Изображение будет добавлено в ближайшее время)
Динамика неравномерного кругового движения
Рассмотрим тело, движущееся с угловой скоростью ω.

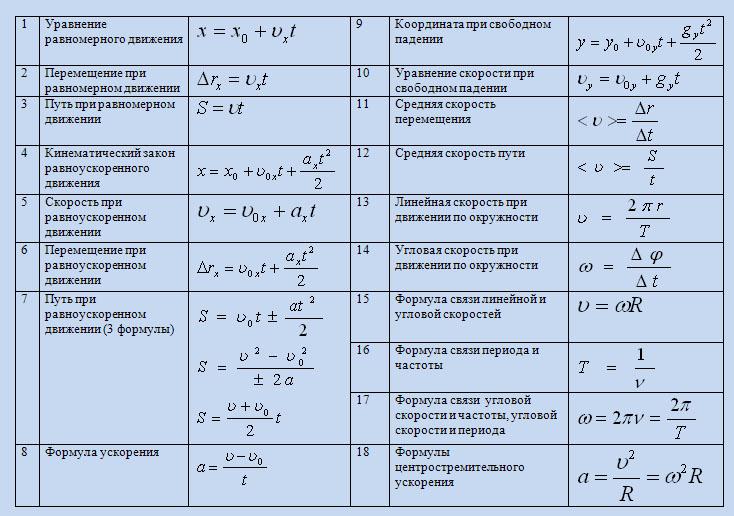
 Куда направлено ускорениетела, если сопротивление воздуха не учитывать?
Куда направлено ускорениетела, если сопротивление воздуха не учитывать? 3 Задания для дополнительной работы
3 Задания для дополнительной работы жидкостям
жидкостям 
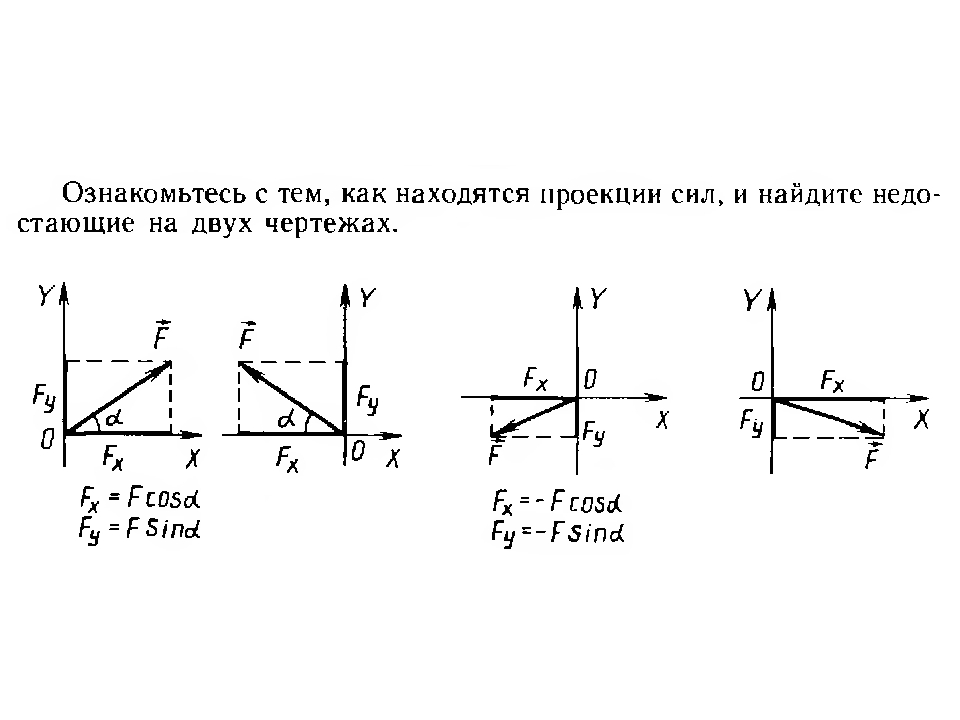
 д.
д.