9 уравнений, которые изменили мир
Математические уравнения открывают уникальные окна в мир. Они придают смысл реальности и помогают нам увидеть вещи, которые раньше не замечались. Поэтому неудивительно, что новые достижения в математике часто идут рука об руку с достижениями в нашем понимании Вселенной. Здесь мы рассмотрим девять уравнений из истории, которые произвели революцию в нашем взгляде на все, от крошечных частиц до огромного космоса.
Теорема Пифагора 92, и известно
по меньшей мере 3700 лет , со времен древних вавилонян. Греческому математику Пифагору приписывают запись версии уравнения, используемого сегодня, по данным Университета Сент-Эндрюс в Шотландии. Наряду с нахождением применения в строительстве, навигации, составлении карт и других важных процессах, теорема Пифагора помогла расширить само понятие чисел. В пятом веке до нашей эры математик Гиппас из Метапонта заметил, что у равнобедренного прямоугольного треугольника, длина двух сторон которого равна 1 единице, гипотенуза равна квадратному корню из 2, что равно 9.
0009 иррациональное число . (До этого момента никто в письменной истории не встречал таких чисел.) Говорят, что за свое открытие Гиппас был брошен в море, потому что последователи Пифагора (включая Гиппаса) были настолько обеспокоены возможностью чисел, что продолжался вечно после запятой без повторения, в соответствии со статьей Кембриджского университета.
F = ма и закон всемирного тяготения
(Изображение предоставлено: Фон: Эскай Лим / EyeEm через Getty Images) 92, где m1 и m2 — массы двух объектов, r — расстояние между ними. G — фундаментальная константа, значение которой должно быть обнаружено экспериментальным путем. С тех пор эти концепции использовались для понимания многих физических систем, включая движение планет в Солнечной системе и средства перемещения между ними с помощью ракет.Волновое уравнение
(Изображение предоставлено: Фон: Эскай Лим / EyeEm через Getty Images) Используя относительно новые законы Ньютона, ученые 18-го века начали анализировать все вокруг себя.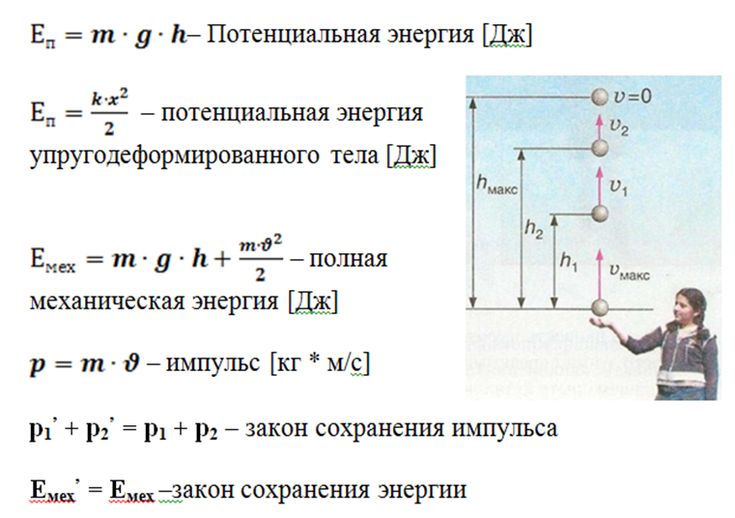
Согласно статье, опубликованной в 2020 году в журнале 9, в 1743 году французский эрудит Жан-Батист ле Ронд д’Аламбер вывел уравнение, описывающее колебания колеблющейся струны или движение волны.2
В этом уравнении v — скорость волны, а остальные части описывают смещение волны в одном направлении. Волновое уравнение, расширенное до двух или более измерений, позволяет исследователям предсказывать движение воды, сейсмических и звуковых волн и является основой для таких вещей, как уравнение Шредингера квантовой физики, которое лежит в основе многих современных компьютерных устройств.
Уравнения Фурье
(Изображение предоставлено: Neslihan Gorucu/istock/Getty Images Plus) Даже если вы не слышали о французском бароне Жане-Батисте Жозефе Фурье, его работа повлияла на вашу жизнь. Это потому, что математические уравнения, которые он записал в 1822 году, позволили исследователям разбить сложные и беспорядочные данные на комбинации простых волн, которые гораздо легче анализировать.
Преобразование Фурье, как известно, было радикальным понятием в свое время, и многие ученые отказывались верить, что сложные системы могут быть сведены к такой элегантной простоте, согласно статье в журнале 9.0009 Йельский научный . Но преобразования Фурье — рабочие лошадки во многих современных областях науки, включая обработку данных, анализ изображений, оптику, связь, астрономию и инженерию.
Уравнения Максвелла
(Изображение предоставлено: ClaudeLux/istock/Getty Image Plus) Электричество и магнетизм были еще новыми понятиями в 1800-х годах, когда ученые исследовали, как поймать и использовать эти странные силы. Шотландский ученый Джеймс Клерк Максвелл значительно расширил наше понимание обоих явлений в 1864 году, когда он опубликовал список из 20 уравнений, описывающих, как электричество и магнетизм функционируют и взаимосвязаны. Уравнения Максвелла, позже доведенные до четырех, теперь преподаются первокурсникам студентов-физиков в колледжах и служат основой для всего электронного в нашем современном технологическом мире.
92, мы бы не поняли, как работают звезды или Вселенная, и не знали бы, как построить гигантские ускорители частиц, такие как Большой адронный коллайдер , чтобы исследовать природу субатомного мира.
Уравнения Фридмана
(Изображение предоставлено Минди Вайсбергер)Кажется высокомерием думать, что вы можете создать набор уравнений, которые определяют весь космос, но это именно то, что русский физик Александр Фридман сделал в 1920-х годах. Используя теорию относительности Эйнштейна, Фрейдман показал, что характеристики расширяющейся Вселенной можно выразить, начиная с Большого взрыва, с помощью двух уравнений.
Они сочетают в себе все важные аспекты космоса, включая его кривизну, количество вещества и энергии, которые он содержит, и скорость его расширения, а также ряд важных констант, таких как скорость света, гравитационная постоянная и постоянная Хаббла , отражающая ускоряющееся расширение Вселенной. Известно, что Эйнштейну не нравилась идея расширяющейся или сжимающейся Вселенной, которая, как предполагала его общая теория относительности, происходила из-за эффектов гравитации.
Он попытался добавить к результату переменную , обозначенную греческой буквой лямбда, которая действовала против гравитации, делая космос статичным. Хотя позже он назвал это своей величайшей ошибкой, десятилетия спустя эта идея была развеяна, и было показано, что она существует в форме таинственной субстанции темной энергии , которая вызывает ускоренное расширение Вселенной.
Большинство людей знакомы с 0 и 1, которые составляют компьютерные биты. Но эта важная концепция не стала бы популярной без новаторской работы американского математика и инженера Клода Шеннона. В важном 19В статье 48 Шеннон изложил уравнение, показывающее максимальную эффективность, с которой может передаваться информация, часто определяемое как C = B * 2log(1+S/N). В формуле C — достижимая пропускная способность конкретного информационного канала, B — ширина полосы пропускания линии, S — средняя мощность сигнала и N — средняя мощность шума.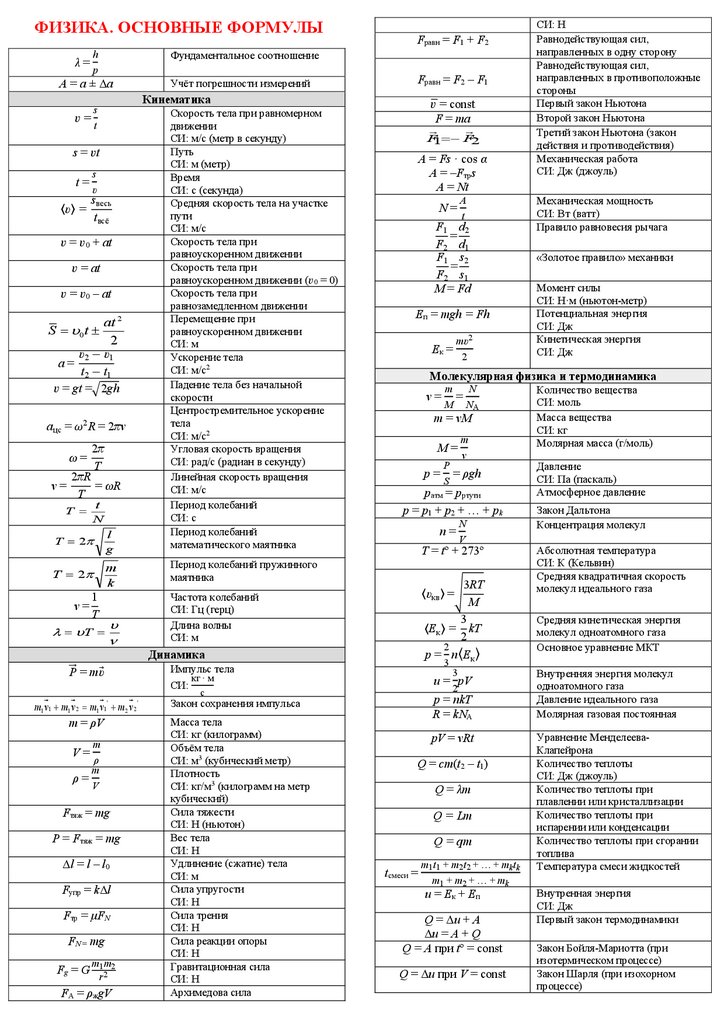
(Отношение S к N дает знаменитое отношение сигнал/шум в системе.) Результат уравнения выражается в битах в секунду. В статье 1948 года Шеннон приписывает идею бита математику Джону У. Тьюки как сокращению фразы «двоичная цифра».
Логистическая карта мая
(Изображение предоставлено фоном: Eskay Lim / EyeEm через Getty Images) Иногда очень простые вещи могут привести к невообразимо сложным результатам. Этот трюизм может показаться не таким уж радикальным, но только в середине 20-го века ученые полностью оценили важность этой идеи. Когда в то время бурно развивалась область теории хаоса, исследователи начали разбираться в том, как системы, в которых всего несколько частей, которые имеют обратную связь сами с собой, могут производить случайное и непредсказуемое поведение. Австралийский физик, математик и эколог Роберт Мэй написал статью, опубликованную в журнале 
Xn представляет некоторую величину в системе в настоящее время, которая возвращается сама к себе через часть, обозначенную (1 – xn). K — константа, а xn+1 показывает систему в следующий момент времени. Несмотря на то, что это довольно просто, различные значения k приведут к сильно отличающимся результатам, в том числе со сложным и хаотичным поведением. Карта Мэя использовалась для объяснения динамики популяций в экологических системах и для генерации случайных чисел для компьютерного программирования.
Адам Манн — независимый журналист с десятилетним стажем, специализирующийся на астрономии и физике. Он имеет степень бакалавра астрофизики Калифорнийского университета в Беркли. Его работы публиковались в New Yorker, New York Times, National Geographic, Wall Street Journal, Wired, Nature, Science и многих других изданиях. Он живет в Окленде, штат Калифорния, где любит кататься на велосипеде.
Формулы стандартного отклонения
Отклонение просто означает, насколько далеко от нормы
Стандартное отклонениеСтандартное отклонение является мерой
Вы могли бы прочитать эту более простую страницу о стандартном отклонении в первую очередь.
Но здесь мы объясняем формулы .
Стандартное отклонение обозначается символом σ (греческая буква сигма).
Это формула стандартного отклонения:
Что сказать? Пожалуйста, объясните!
ОК. Давайте объясним это шаг за шагом.
Скажем, у нас есть набор чисел вроде 9, 2, 5, 4, 12, 7, 8, 11.
- 1. Определите среднее (простое среднее из номеров)
- 2. Затем для каждого числа: вычтите среднее значение и возведите результат в квадрат
- 3. Затем определите среднее значение эти разностей в квадрате.
- 4. Извлеките из этого квадратный корень, и готово!
Формула на самом деле говорит все это, и я покажу вам, как это сделать.
Объяснение формулы
Во-первых, давайте поработаем с несколькими примерами значений:
Пример: у Сэма 20 кустов роз.
Количество цветков на каждом кусте
9, 2, 5, 4, 12, 7, 8, 11, 9, 3, 7, 4, 12, 5, 4, 10, 9, 6, 9, 4
Расчет стандартного отклонения.
Шаг 1. Вычислите среднее значение
В приведенной выше формуле μ (греческая буква «мю») — это среднее значение всех наших значений…
Пример: 9, 2, 5, 4, 12, 7, 8, 11, 9, 3, 7, 4, 12, 5, 4, 10, 9, 6, 9, 4
Среднее значение:
9+2+5+4+12+7+8+11+9+3+7+4+12+5+4+10+9+6+9+4 20
= 140 20 = 7
Итак, μ = 7
Шаг 2. Затем для каждого числа: вычтите среднее значение и возведите результат в квадрат
Это часть формулы, которая говорит:
Так что же такое
д….Другими словами х 1 = 9, х 2 = 2, х 3 = 5 и т. д.
Итак, он говорит: «для каждого значения вычтите среднее значение и возведите результат в квадрат», вот так
Пример (продолжение):
(9 – 7) 2 = (2) 2 = 4
(2 – 7) 2 = (-5) 2 = 25
9 9000 397 7 9000 37 9000 37 9000 3(5 – 7) 2 = (-2) 2 = 4
(4 – 7) 2 = (-3) 2 = 9 5 2 = (5) 2 = 25
(7 – 7) 2 = (0) 2 = 0
(8 – 7) 2 = (1) 2 = 1
… etc …
И получаем такие результаты:
4, 25, 4, 9, 25, 0, 1, 16, 4, 16, 0, 9, 25, 4, 9, 9, 4, 1, 4, 9
Шаг 3.
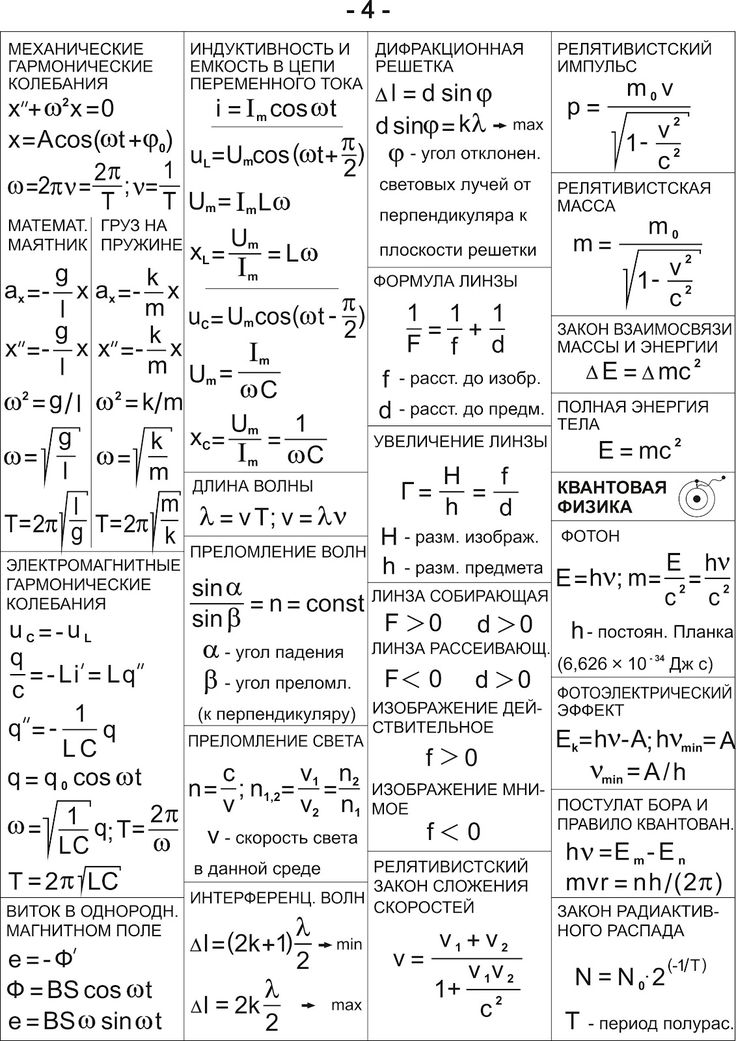Затем вычислите среднее значение этих квадратов разностей.Чтобы вычислить среднее значение, сложите все значения , затем разделите на сколько .
Сначала сложите все значения из предыдущего шага.
Но как мы говорим «сложить их все» в математике? Используем “Сигму”: Σ
Удобная сигма-нотация предлагает суммировать столько терминов, сколько мы хотим:
Сигма-нотация
Мы хотим сложить все значения от 1 до N, где в нашем случае N=20, потому что значений 20:
Пример (продолжение):
Что означает: Сумма всех значений из (x 1 -7) 2 to (x N -7) 2
Мы уже вычислили (x 1 -7) 2 =4 и т. д. на предыдущем шаге, так что просто суммируйте их3
: = 4+25+4+9+25+0+1+16+4+16+0+9+25+4+9+9+4+1+4+9 =
178Но это еще не среднее, нам нужно
Пример (продолжение):
Среднее квадратов разностей = (1/20) × 178 = 8,9
(Примечание: это значение называется «дисперсией»)
Шаг 4.
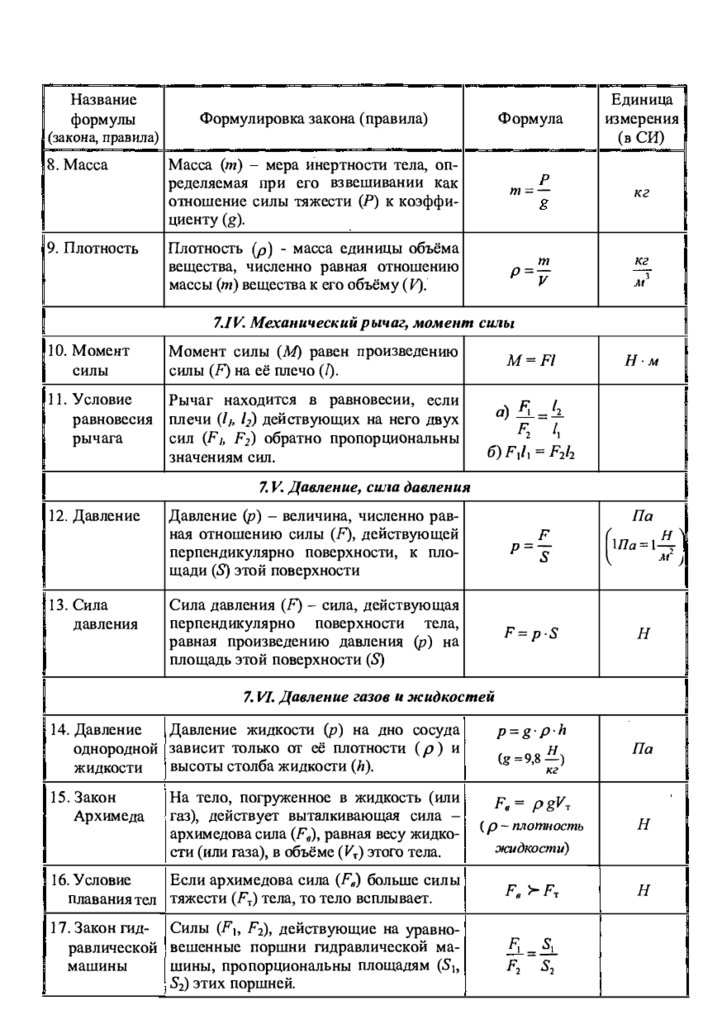Извлеките из этого квадратный корень:Пример (завершение):
σ = √(8.9) = 2,983…
ГОТОВО!
Стандартное отклонение выборки
Но подождите, есть еще…
…иногда наши данные всего лишь выборка всего населения.
Пример: у Сэма есть
20 кустов роз, но насчитали только цветы на 6 из них !«Население» — это все 20 розовых кустов,
, а «образец» — это 6 кустов, у которых Сэм насчитал цветы.
Скажем, количество цветов Сэма:
9, 2, 5, 4, 12, 7
Мы все еще можем оценить стандартное отклонение.
Но когда мы используем выборку как оценку всего населения , формула стандартного отклонения меняется на это:
Формула для Стандартное отклонение выборки :
Важным изменением является “N-1” вместо “N” (что называется “поправкой Бесселя”).
Символы также изменяются, чтобы отразить, что мы работаем с выборкой, а не со всей совокупностью:
- Среднее значение теперь равно x (называемому «x-bar») для выборочного среднего вместо μ для совокупности среднее,
- И ответ s (для стандартного отклонения выборки) вместо о .
Но на расчеты не влияют. Только N-1 вместо N меняет расчеты.
Хорошо, давайте теперь воспользуемся стандартным отклонением образца :
Шаг 1. Вычислите среднее значение
Пример 2: Использование выборочных значений 9, 2, 5, 4, 12, 7
Среднее значение равно (9+2+5+4+12+7) / 6 = 39/6 = 6,5
Итак:
х = 6,5
Шаг 2. Затем для каждого числа: вычтите среднее значение и возведите результат в квадрат
Пример 2 (продолжение):
(9 – 6,5) 2 = (2,5) 2 = 6,25
(2 – 6,5) 2 = (-4,5) 2 = 20,25
(50236 2 = 20,25
(50236 2 = 20,25
(-4,5) 2 . – 6.5) 2 = (-1.5)
(4 – 6.5) 2 = (-2.5) 2 = 6.25
(12 – 6.5) 2 = (5.
5) 2 = 30,25
(7 – 6,5) 2 = (0,5) 2 = 0,25
Шаг 3. Затем вычислите среднее значение этих квадратов разностей.
Чтобы вычислить среднее значение, сложите все значения , затем разделите на сколько .
Но подождите… мы вычисляем стандартное отклонение выборки , поэтому вместо деления на сколько (N) мы будем делить на N-1
Example 2 (continued):
Sum = 6.25 + 20.25 + 2.25 + 6.25 + 30.25 + 0.25 = 65.5
( Это значение называется «выборочной дисперсией»)
Шаг 4. Извлеките из этого квадратный корень:
Пример 2 (завершение):
s = √(13.1) = 3,619…
ГОТОВО!
Сравнение
Используя всю совокупность , мы получили: Среднее значение = 7 , Стандартное отклонение = 2,983.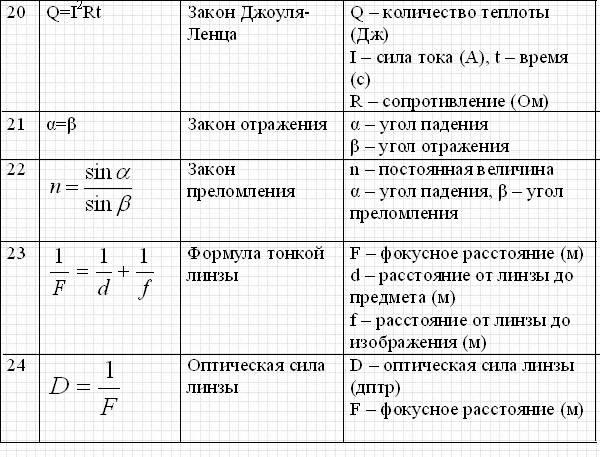
..
Используя образец , мы получили: Среднее значение выборки = 6,5 , Стандартное отклонение выборки = 3,619…
Наше выборочное среднее было ошибочным на 7%, а наше выборочное стандартное отклонение было ошибочным на 21%.
Зачем брать пробу?
В основном потому, что это проще и дешевле.
Представьте, что вы хотите знать, что думает вся страна… вы не можете спросить миллионы людей, поэтому вместо этого вы спросите, может быть, 1000 человек.
Есть хорошая цитата (возможно, Сэмюэля Джонсона):
“Не обязательно есть животное целиком, чтобы понять, что мясо жесткое.”
Это основная идея выборки. Чтобы узнать информацию о популяции (например, среднее значение и стандартное отклонение), нам не нужно смотреть на все человек населения; нам нужен только образец.
Но когда мы берем образец, мы теряем некоторую точность.
Поиграйте с этим в симуляторе нормального распространения.