Формулы физика магнитное поле: формулы для расчета, используемые обозначения / Справочник :: Бингоскул

формулы для расчета, используемые обозначения / Справочник :: Бингоскул

Электромагнитное поле: формулы для расчета, используемые обозначения

добавить в закладки удалить из закладок

Содержание:

Вокруг проводника, по которому проходит электрический ток, возникает магнитное поле. Оно вызывает проявление физических явлений, например, механических сил: изменяет сопротивление металлов, сплавов, размеры тел. Рассмотрим напряженность магнитного поля, формулы для её вычисления.

Теория

Электромагнитное поле – аналог механической силы, проявляется воздействием на перемещающиеся носители электрического заряда, тела с магнитным моментом. Характеризуется механической силой, которое поле оказывает на проводники либо магниты.

Опыты показывают, что магнитное поле пытается сориентировать магнитную стрелку, развернуть её относительно плоскости витка, в направлении, которое называется направлением поля. Для планеты его принимают за линию, направленную с географического севера на юг. Электрическое поле характеризуется векторной величиной E – напряженностью. Для описания магнитного воздействия применяют величину B, названную магнитной индукцией.

Во избежание путаницы характеристики носят разные названия.

Направлением B считают то, куда укажет магнитная стрелка относительно витка с электрическим током. Его модуль определяют по максимальному значению вращающего момента Mmax, действующего на стрелку. При одинаковом значении индукции в каждой точке пространства поле называется однородным, когда его величина проявляется в веществе в разной степени – неоднородным.

Магнитное поле: все формулы

В однородное поле помещают плоские контуры – изготовленные из точнейшей проволоки замкнутые проводники – с током. Измерения пикового вращающего момента показывает, что он:

1. прямо пропорционален силе протекающего через контур электрического тока I;
2. зависит от площади контура S;
3. не зависит от формы замкнутого проводника при равной площади.

Магнитный момент контура с током равен:

p_m = IS.

Рассмотрим остальные формулы, позволяющие рассчитать электромагнитное поле.

Вращающий и магнитный моменты характеризуют электромагнитную индукцию, по модулю она равняется:

B= M_max : p_m.

Измеряется в теслах (Тл), названа в честь величайшего сербского учёного XX века Николы Теслы. 

При расчётах неоднородных полей в них помещают маленькие контуры, по габаритам сравнимые с расстояниями, на которых наблюдаются изменения.

Магнитное полевое образование характеризуется напряжённостью H, пропорциональной индукции в вакууме:

B = μ₀H,

μ₀ = 4π*10^-7 Гн/м или Тл*м/А.

При вычислениях для вещества добавляется коэффициент магнитной проницаемости μ, для вакуума он равен единице.

B = μ μ₀H.

Магнитная индукция соленоида:

B = μ₀nI, здесь:

• n = N : l, N – число витков катушки, l – её длина;
• I – сила протекающего тока.

Формула энергии W магнитного поля для соленоида:

W = LI² : 2 = ФI : 2

• L – индуктивность катушки;
• I – сила тока;
• Ф – магнитный поток.

Сила взаимодействия между проводниками с электрическим током:

F = μ μ0I₁I₂l : 2πr, здесь:

• I₁, I₂ – сила тока в обоих проводниках;
• l – их длина;
• r – расстояние между проводами с током.

Наибольший момент:

M_max= BIS;

S – площадь контура.

Электромагнитное поле образуется вокруг намагниченных тел и проводников с током.

Поделитесь в социальных сетях:

18 октября 2021, 18:15

Физика

Could not load xLike class!

Определение индукции магнитного поля и проверка формулы Ампера контрольная по физике | Экзамены Физика

Скачай Определение индукции магнитного поля и проверка формулы Ампера контрольная по физике и еще Экзамены в формате PDF Физика только на Docsity! Определение индукции магнитного поля и исследование формулы Ампера Введение В последнее время физики вновь обратились к необходимости использования различных экспериментальных работ для более углубленного и осмысленного изучения физики. Данная экспериментальная работа не представлена в учебниках, как лабораторная, поэтому мы предлагаем ее учителям для использования в лабораторном практикуме и для более углубленного изучения теории по теме «Действие магнитного поля на проводник с током. Сила Ампера». Целью данной работы является определение индукции магнитного поля подковообразного магнита, действие данного поля на проводник с током, а также исследование прямой пропорциональной зависимости силы Ампера от длины проводника, силы тока в цепи и индукции магнитного поля. Главной задачей данной исследовательской работы является изготовление установки для проведения всех измерений по данной теме, а также разработка методического пособия в помощь для учителей и учащихся, которые заинтересуются углубленным изучением данной темы. Теория по данной теме основывается на изучении учебников под редакцией Г.С. Ландсберга «Элементарный учебник физики. т. 2», Б.И. Спасского «Хрестоматия по физике 8–10», учебника «Физика 10» авторов Г.Я. Мякишева, Б.Б. Буховцева, учебник по физике Л. Эллиота, У. Уилкокса, а также статьи автора И.И. Гейнбихнера в журнале «Физика в школе». Так как важнейшим применением силы Ампера является ее использование в электрических двигателях, то данная работа позволяет учащимся познать их принцип действия, а в будущем, возможно, подтолкнет на создание более мощных электрических приборов. пока плоскость ее не установится перпендикулярно к линии, соединяющей полюсы магнита. Таким образом, магнитное поле оказывает на рамку с ток ориентирующее действие. 1.2 Вектор магнитной индукции Величина, характеризующая магнитное поле количественно называется вектором магнитной индукции и обозначают Ориентирующее действие магнитного поля на магнитную стрелку или рамку с током можно использовать для определения направления вектора магнитной индукции. За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле. Это направление совпадает с направлением положительной нормали к замкнутому контуру с током. рис. 4 Положительная нормаль направлена в ту сторону, куда перемещается буравчик, если вращать его по направлению тока в рамке. Располагая рамкой с током или магнитной стрелкой, можно определить направление вектора магнитной индукции в любой точке поля. В магнитном поле прямолинейного проводника с током магнитная стрелка в каждой точке устанавливается по касательной к окружности. Плоскость окружности перпендикулярна проводу, а центр ее лежит на оси провода. Направление вектора магнитной индукции устанавливают с помощью правила буравчика: если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции. 1.3 Линии магнитной индукции Наглядную картину магнитного поля можно получить, если построить линии магнитной индукции. Линиями магнитной индукции называют линии, касательные к которым направлены так же, как и вектор в данной точке поля. Для прямолинейного проводника с током линии магнитной индукции представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной этому проводнику с током. Центр окружностей находится на оси проводника. Стрелки на линиях указывают, в какую сторону направлен вектор магнитной индукции, касательный к данной линии. Для катушки с током картина линий магнитной индукции, построенная с помощью магнитных стрелок или малых контуров с током, показана на рис. 6. Если длина соленоида много больше его диаметра, то магнитное поле внутри! соленоида можно считать однородным. Линии магнитной индукции такого поля параллельны. Картину линий магнитной индукции можно сделать видимой, воспользовавшись мелкими железными опилками. В магнитном поле каждый кусочек железа, насыпанный на лист картона, намагничивается и ведет себя как маленькая магнитная стрелка. Наличие большого количестве таких стрелок позволяет в большее числе точек определить направление магнитного поля и, следовательно более точно выяснить расположение линий магнитной индукции. Важная особенность линий магнитной индукции состоит в том, что они не имеют ни начала, ни конца. Они всегда замкнуты. Поля с замкнутыми силовыми линиями называют вихревыми. Магнитное поле – вихревое поле. Замкнутость линий магнитной индукции представляет собой фундаментальное свойство магнитного поля. Оно заключается в том, что магнитное поле не имеет источников. Магнитных зарядов, подобных электрическим в природе нет. 2.2 Модуль вектора магнитной индукции Свободно подвешенный горизонтально проводник находится в поле постоянного подковообразного магнита. Поле магнита сосредоточено в основном между его полюсами, поэтому магнитная сила действует практически только на часть проводника длиной , расположенную непосредственно между полюсами. Сила измеряется с помощью специальных весов, связанных с проводником двумя стерженьками. Она направлена горизонтально перпендикулярно проводнику и линиям магнитной индукции. Увеличивая силу тока в 2 раза, можно заметить, что и действующая на проводник сила также увеличивается в 2 раза. Прибавив еще один магнит, в 2 раза увеличив размеры области, где существует магнитное поле, и тем самым в 2 раза увеличив длину части проводника, на которую действует магнитное поле. угла, образованного вектором В с проводником. В этом можно убедиться, меняя наклон подставки, на которой находятся магниты, так, чтобы изменялся угол между проводником и линиями магнитной индукции. Сила достигает максимального значения Рт, когда магнитная индукция перпендикулярна проводнику. Итак, максимальная сила, действующая на участок проводника длиной А/, по которому идет ток, прямо пропорциональна произведению силы тока / на длину участка Д/: /7т~/Л/. Модулем вектора магнитной индукции назовем отношение максимальной силы, действующей со стороны магнитного поля на участок проводника с током, к произведению силы тока на длину этого участка: Магнитное поле полностью характеризуется вектором магнитной индукции В. В каждой точке магнитного поля могут быть определены направление вектора магнитной индукции и его модуль с помощью измерения силы, действующей на участок проводника с током. 2.3 Модуль силы Ампера Пусть вектор магнитной индукции В составляет угол с направлением отрезка проводника с током. Опыт показывает, что магнитное поле, вектор индукции которого направлен вдоль проводника с током, не оказывает никакого действия на ток. Поэтому модуль силы зависит лишь от модуля составляющей вектора В, перпендикулярной проводнику, т.е. от , и не зависит от параллельной составляющей вектора В, направленной вдоль проводника. Максимальная сила Ампера равна: ей соответствует . При произвольном значении угла сила пропорциональна не , а составляющей . Поэтому выражение для модуля силы F, действующей на малый отрезок проводника , по которому течет ток I, со стороны магнитного поля с индукцией , составляющей с элементом тока угол , имеет вид: Это выражение называют законом Ампера. Сила Ампера равна произведению вектора магнитной индукции на силу тока, длину участка проводника и на синус угла между магнитной индукцией и участком проводника. 2.4 Направление силы Ампера В рассмотренном выше опыте вектор перпендикулярен элементу тока и вектору . Его направление определяется правилом левой руки: если левую руку расположить так, чтобы перпендикулярная к проводнику составляющая вектора магнитной индукции В входила в ладонь а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90° большой палец покажет направление силы, действующей на отрезок проводника За единицу магнитной индукции можно принять магнитную индукцию однородного поля, в котором на участок проводника длиной 1 м при силе тока в нем 1 А действует со стороны поля максимальная сила Fm=1 Н. Единица магнитной индукции получила название тесла в честь югославского ученого-электротехника Н. Тесла. Опираясь на измерение силы, действующей со стороны магнитного поля на участок проводника с током, можно определить модуль вектора магнитной индукции. исследование силы Ампера Опытный закон Ампера устанавливает зависимость величины силы, действующей на прямолинейный участок проводника с током, помещенный в магнитное поле, от основной характеристики магнитного поля – вектора индукции магнитного поля: где l – длина активной части прямолинейного участка проводника, по которому протекает ток силой I, В-численное значение вектора индукции магнитного поля в месте расположения проводника, – угол между направлением оси проводника и направлением вектора, Если проводник расположить так, чтобы = 90°, то Таким образом, измерив действующую силу в ньютонах, величину тока в амперах и длину активной части проводника в метрах, легко определить величину индукции магнитного поля. В данной экспериментальной работе необходимо определить индукцию магнитного поля В между полюсами различных подковообразных магнитов, а также экспериментально проверить прямую пропорциональную зависимость силы F от величины тока, длины активной части проводника и индукции магнитного поля: Оставляя поочередно две величины, входящие в формулу, постоянными, можно установить зависимость силы, с которой магнитное поле действует на проводник с током, от третьей величины. Поскольку в формулу входят три величины, от которых зависит величина силы, то и нужно провести три серии измерений. 3.1. Описание и принцип действия установки Для работ используется следующее оборудование: электродинамическая рамка, штатив с принадлежностями, лабораторные весы с разновесками, лабораторные амперметр и реостат, источник постоянного напряжения на 4–6 В, два или три подковообразных магнита. Собирают установку как показано на рисунке 13, а также на фотографиях в приложении №1 и уравновешивают весы. Самодельную рамку с отводами включают в цепь по схеме рисунка 14. Магнит для устойчивости устанавливают либо на немагнитной коробке, соответствующего размера, либо на специальной подставке из дерева. Все применяемые в работах магниты целесообразно предварительно перенумеровать несмываемой краской. На проводник с током, помещенный в магнитное постоянного подковообразного магнита поле действует сила Ампера. Следовательно, замыкая электрическую цепь, равновесие весов нарушается за счет действия силы Ампера со стороны магнитного поля. Уравновешивая весы с помощью разновесов, можно определить значение силы тяжести, а следовательно и силы Ампера. Зная длину активной части проводника, силу тока в цепи, можно вычислить индукцию магнитного поля данного подковообразного магнита. При изменении силы тока, а также длины проводника, сила Ампера также будет изменяться. Эти свойства и использовались в ходе данной исследовательской работы. 3.2 Этапы и результаты проведения работы Для измерений были взяты 3 магнита: два одинаковой длины в поперечнике и один в два раза уже. Выполняют серии измерений с магнитом №1 при включении рамки на 15 витков. Указанные измерения проводят для различных токов: 0,18А, 0,2 А, 0,3 А, 0,4 А и 0,5 А. Такие же измерения выполняют с магнитом №2 и №3. Затем измерения проводят с двумя магнитами №2 и №3, а также с магнитами №1 и №2, скрепленными между собой одинаковыми полюсами. Все результаты заносим в таблицу. Для каждого случая измерений вычисляем значение силы Ампера, а также индукции магнитного поля каждого подковообразного магнита с вычислением значений абсолютной и относительной погрешности. По данным результатам строим графики зависимости силы Ампера от силы приложенного тока и от длины проводника. По полученным графикам убеждаемся в прямой зависимости данных величин и в выполнении закона Ампера. В приложении №6 представлена разработка лабораторной работы по данной теме.

Магнитное поле | Физические формулы

Магнитная сила между параллельными проводниками

Находить

Известно, что:

Fμμ0I1I2lπr =

Рассчитать F

Магнитная сила между параллельными проводниками

Находить

Известно, что:

FμI1I2lr =

Рассчитать F

Магнитная постоянная

Находить

Известно, что:

μ0π =

Рассчитать ‘μ0’

Интенсивность магнитного поля

Находить

Известно, что:

HI =

Рассчитать ‘H’

Индукция магнитного поля

Находить

Известно, что:

Bμ0μH =

Рассчитать ‘B’

Максимальный силовой момент магнитного поля

Находить

Известно, что:

M_maxBIS =

Расчет ‘M_max’

Магнитная индукция

Находить

Известно, что:

МИСБа =

Рассчитать ‘M’

Момент однородного магнитного поля

Находить

Известно, что:

p_mIS =

Вычислить ‘p_m’

Магнитное поле (индукция) из-за тока в конечном прямолинейном проводнике (проводе)

Находить

Известно, что:

Bμμ0Ia1a2πr =

Рассчитать ‘B’

Магнитное поле (индукция) из-за тока в бесконечном прямолинейном проводнике (проводе)

Находить

Известно, что:

Bμμ0Iπr =

Вычислить ‘B’

Магнитное поле, вызванное током в круглом проводе (витке)

Находить

Известно, что:

Bμμ0IR =

Рассчитать ‘B’

Интенсивность магнитного поля (сила): бесконечный прямой провод

Находить

Известно, что:

HIπr =

Рассчитать ‘H’

Напряженность магнитного поля (сила) в центре круглого провода (витка)

Находить

Известно, что:

ИР =

Рассчитать ‘H’

Магнитная индукция соленоида

Находить

Известно, что:

Bμμ0NIl =

Рассчитать ‘B’

Напряженность магнитного поля (сила) соленоида

Находить

Известно, что:

HNIl =

Рассчитать ‘H’

Магнитный поток и угол

Находить

Известно, что:

ФБСа =

Рассчитать ‘Φ’

Магнитный поток (поток)

Находить

Известно, что:

ФБС =

Вычислить ‘Φ’

Сила Ампера

Находить

Известно, что:

ФИлБа =

Рассчитать F

Магнитная индукция и сила Ампера

Находить

Известно, что:

BF_maxIl =

Рассчитать B

Сила Лоренца

Находить

Известно, что:

FqvBa =

Рассчитать F

Сила Лоренца и сила Ампера

Находить

Известно, что:

F_LF_AN =

Рассчитать ‘F_L’

Сила электромагнитного поля

Находить

Известно, что:

FqEvBa =

Рассчитать ‘F’

Радиосвязь траектории движения заряженной частицы в магнитном поле

Находить

Известно, что:

rmvqB =

Рассчитать ‘r’

Период обращения заряженной частицы в магнитном поле

Находить

Известно, что:

TπmqB =

Расчет ‘T’

Формулы магнетизма для класса – 12 Физика |Физика Wallah

Формулы физики

Магнетизм относится к группе природных явлений, в которых определенные металлы указывают на магнитное поле.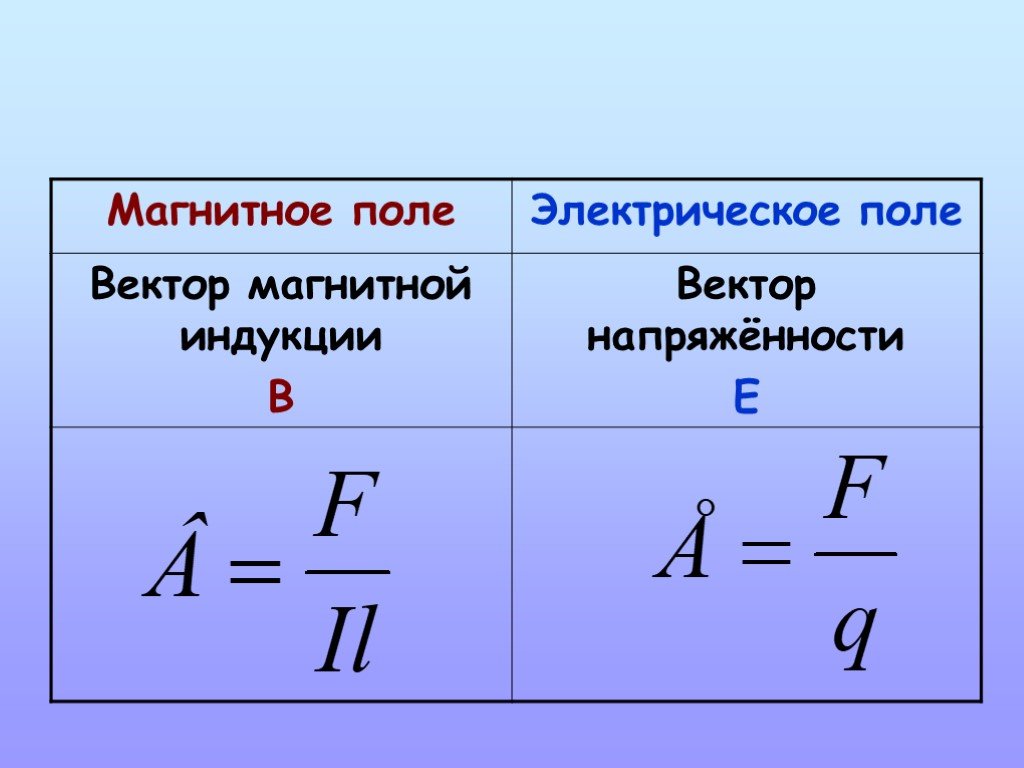 Эти металлы встречаются в природе в горных породах, а также в электрических и ядерных приложениях. Эти магниты обычно состоят из проволочной катушки, надежно закрепленной на металлическом объекте, подключенной к другому источнику питания. Этот тип магнита называется электромагнетизм . Электромагниты также используются во многих устройствах связи.

Мы можем рассмотреть магнитное поле вокруг магнита. Магнит стягивает куски металла вместе, чтобы образовать определенное расстояние. Следовательно, магнитные поля, такие как электрический ток и магнитное поле, действуют на расстоянии. Эта концепция энергии включает в себя идею магнитного поля.

Магнитное поле, которое один магнит воздействует на магнитное поле, можно рассматривать как часть магнитного поля. Простой способ описать магнитное поле вокруг магнита — нарисовать линии поля вокруг него. Следовательно, магнитное поле является результатом магнитного поля и вызвано движением зарядов. Мы можем назвать их движущимися зарядами вокруг магнитного поля.

Магнетизм относится к группе природных явлений, в которых определенные металлы указывают на магнитное поле. Эти металлы естественным образом встречаются в горных породах, а также в электротехнике и атомной энергии. Магнитные элементы были впервые обнаружены и записаны примерно в 20 году нашей эры.

Однако Аристотель описывал магнетические свойства своего времени, не имея собственных имен за наукой. Есть два основных источника магнитного поведения, оба из которых используются для создания «постоянных» магнитов. Эти магниты обычно состоят из проволочной катушки, надежно прикрепленной к металлическому предмету, подключенному к другому источнику питания.

Этот тип магнита называется электромагнетизмом. Электромагниты также используются во многих устройствах связи. Мы можем рассмотреть магнитное поле вокруг магнита. Магнит стягивает куски железа вместе, чтобы образовать определенное расстояние.

Следовательно, магнитные поля, такие как электрический ток и магнитное поле, действуют на расстоянии. Эта концепция энергии включает в себя идею магнитного поля. Магнитное поле одного магнита на магнитном поле можно считать частью магнитного поля.

Простой способ описать магнитное поле вокруг интереса — нарисовать линии его площади. Следовательно, магнитное поле является результатом электромагнитной силы и вызвано движением зарядов. Мы можем назвать их движущимися зарядами с магнитным полем.

Сила между магнитными полюсами

Сила между двумя магнитными полюсами равна выходной силе магнитных полюсов и соответствует квадрату расстояния между двумя магнитными полюсами. Мы будем использовать это соотношение для определения силы, когда сила полюса удвоена, а расстояние между полюсами удвоено.

(В воздухе или в свободном пространстве между магнитными полюсами)

μ ₀ → проницаемость свободного пространства

m ₁ m ₂ → полюсные силы двух магнитных полюсов.

d→ расстояние между полюсами.

Магнитное поле из-за прямого проводника Несущий ток:

Напряженность магнитного поля на расстоянии d от прямого проводника с током I определяется выражением

Направление магнитного поля определяется по правилу захвата правой руки/большого пальца.

(в среде)

Где &mu = μ ₀ μ _r

μ→ проницаемость среды

μ _r → относительная проницаемость среды

Магнитная индукция в точке в магнитном поле

Сила, действующая на полюс в магнитном поле F = mB

m→ полюсная сила магнитного полюса

Магнитный момент магнита M = 2

l m

​ 2л→ магнитная длина

m→ сила полюса магнита

Пара, действующая на стержневой магнит, помещенный в однородное магнитное поле C = mBsinθ

​ м→ магнитный момент стержневого магнита

B→ Напряженность магнитного поля

θ→ угол между осью магнита и направлением индукции магнитного поля

Магнитная индукция из-за стержневого магнита на осевой линии

Для короткого магнита

B→ магнитная индукция

M→ магнитный момент магнита

d→ расстояние от центра магнита до точки

2l→ магнитная длина

Магнитная индукция на экваториальной линии

M→ магнитный момент магнита

d→ расстояние между центром и точкой.