1 | v=s/t скор. при равном. движ. | 46 | I=q/t сила тока, А | 91.1 | Q= A+∆U кол.тепл., получен. газом | 136 | sinαo= n2/n1 пред. угол полн. отр. |
2 | ρ=m/V плотность, кг/м | 47 | U=A/q напряжение, В | 92 | η=(Q1-Q2)/Q1 КПД тепл. двиг. | 137 | n=c/v показ. прел. v=с/n скор.света в среде |
3 | P=mg вес тела, Н P=m(g±a) | 48 | I=U/R закон Ома | 93 | η =(Т1-Т2)/Т1 КПД тепл. двиг. | 138 | D=1/F оптич. сила, дптр (м!!!) |
4 | F=mg сила тяжести, Н | 49 | R= ρℓ/s сопротивление проводника, Ом | 94 | F=kq1q2/εR2 закон Кулона | 139 | 1/F=1/d+1/f формула линзы (- !!!) |
5 | p=F/S давление, Па | 50 | Q=I2Rt закон Джоуля-Ленца, Дж | 95 | E=F/q напряженность эл. | 140 | Г=f/d=H/h увелич. линзы |
6 | p=ρgh давлен. внутри жидк., Па | 51 | P=IU=I2R=U2/R мощн. тока, Вт | 96 | A=qU работа электр. поля по перемещ зар | 141 | dsinφ =kλ формула дифр. решетки |
7 | F1/F2=S1/S2 гидравл. пресс | 52 | A=IUt=Pt работа тока, Дж (=Q) | 97 | φ=A/q потенциал, В | 142 | Е=hv энергия фотона, Дж |
8 | h1/h2= ρ2/ρ1 сообщ.сосуды | 53 | I=I1=I2 | 98 | φ1-φ2=U=A/q разность потенц. | 143 | m=hv/c2 масса фотона |
9 | FA=gρжVп Архимедова сила (Vвыт.ж.) | 54 | R=R1+R2 Последоват.соединен. | 99 | E=kq/εR2 напряж.точечн. заряда,В/м | 144 | p=mc=hv/c=h/λ имрульс фотона |
10 | A=Fscosα мех. работа, Дж | 55 | U=U1+U2 | 100 | φ=kq/εR потенц точечн. заряда,В | 145 | hv=A+mv2/2 ур. для фотоэффек. |
11 | η=Ап/А КПД 0,8 (80%) | 56 | U=U1=U2 | 101 | Е=U/d связь Е и U, В/м. | 146 | A=hvm работа выхода, Дж |
12 | N=A/t мех. мощность, Вт | 57 | I=I1+I2 Параллельн.соединен. | 102 | W= kq1q2/εR энергия зарядов | 147 | mv2/2=eUз задерж. разность потенц.,В |
13 | N=Fv мех. мощность, Вт | 58 | 1/R=1/R1+1/R2 | 103 | C=q/U ёмкость, Ф | 148 | v=(v1+v2)/(1+ v1* v2/ c2) рел. слож. ск. |
14 | M=Fd момент силы, Нм, М1+М2=М3+М4+… | 59 | Т=t/n период колебаний, с | 104 | W=qU/2=CU2/2= q2/2C энерг. | 149 | ∆m=∆E/c2 измен.массы, (дефект) |
15 | vср=s/t. vср=(vo+v)/2 при равноуск. движ. | 60 | ν=n/t частота колебаний, Гц | 105 | C=εε0S/d ёмкость плоск. конд. | 150 | m= m0/√1-(v/c) 2 масса движ. тела |
16 | vx=vox+axt скор. при равноуск.движ., м/с | 61 | ν =1/T частота, Гц | 106 | С=С1+С2 Параллельн.соединен. | 151 | Rc=1/2πνC емкостное сопротивл |
17 | vy=voy+gyt скор. | 62 | Т=1/ν период, с | 107 | q=q1+q1 | 152 | RL=2πνL индуктивное сопротивл |
18 | sx=voxt + axt2/2 перем.при равноуск.дв., м | 63 | Т=2π√m/k период. кол. груза | 108 | U=U1=U2 | 153 | √1-(v/c) 2 релятив. корень |
19 | hy=voyt+gyt2/2 перемещение по высоте | 64 | Т=2π√ℓ/g период. кол. маятн. | 109 | 1/С=1/С1+1/С2 Послед. | ||
20 | s=(v2-v02)/2a путь при равноус.движ., м | 65 | v=νλ скорость волны | 110 | q=q1=q2 | ||
21 | aц= v2/R= ω2R центростр. ускор. | 66 | ω =2πν циклич. частота (за 2πс) | 111 | U=U1+U2 | Это может пригодиться: | |
22 | aц=4π2R/T2=4π2Rn2 центростр. ускор | 67 | x=Acosωt=Acos2πνt координ.колебл. тела | 112 | I=E/(R+r) зак Ома полн. цепи | 155 | P=m(g±a) вес ускор вверх, вниз. |
23 | Fцс=mv2/R сила, сооб. | 68 | v=Aωsinωt=A2πνsinωt | 113 | Iкз=E/r | 156 | При R=r P максимальна |
24 | φ=ωt=2πνt угол поворота | 69 | H=gt2/2 выс падения из сост.покоя | 114 | Ei=Aст/q ЭДС | 157 | P*=IE мощн. тока во всей цепи |
25 | F=ma R=ma 2-й закон Ньютона, Н | 70 | vx=v0cosα гориз. сост . скор. | 115 | U=E – Ir напряжение | 158 | η=R/(R+r) кпд эл. цепи |
26 | Fтр=μN сила трения | 71 | vy=v0sinα вертик. сост. скор. | 116 | P=IE-I2r мощн. | 159 | η=U/E кпд эл. цепи |
27 | F упр=-kx сила упругости, Н | 72 | tmax=vosinα/g время подъёма до максим. выс. | 117 | m=kIt масса при электролизе | 160 | η=Р/P* кпд эл.цепи |
28 | F=Gm1m2/R2 зак. всем. тягот. | 73 | S=v0хt= (v0cosα)t дальность полёта | 118 | i=I/S плотность тока, А/м2 | 161 | mgsinα «скатывающая» сила |
29 | g= GM/R2 ускорение своб.пад. | 74 | S=vo2sin2α/g дальн. полёта | 119 | W=LI2/2 эн. магн. поля (тока), Дж | 162 | mgcosα сила реакц. |
30 | gh=GM/(R+h)2 ускор. своб. пад. на h | 75 | H= vo2sin2α/2g макс. выс. подъёма | 120 | Ф=ВScos α магн. поток | 163 | mg-Fsinα на гор. или mgcosα-Fsinα на нак.пл. |
31 | v=√gR 1 косм скор h=0 | 76 | p=1/3monv2 давл. газа, Па | 121 | Ф=LI ∆Ф=L∆I | 164 | sinα против.кат./гипотен. sin300=0,5(кальк) |
32 | v=√GM/(R+h) 1 косм скор h0 | 77 | mo=μ/NAмасса молекулы | 122 | B=Fm/Iℓ индукция | 165 | cosα прил.кат. |
33 | v2(R+h)=g0R2 соотношение | 78 | p=nkT давл. газа, Па | 123 | Ei=-∆Ф/∆t (Ei=-S∆B/∆t) закон эл. магн. инд. | 166 | tgα прот.кат./прил.кат. |
34 | p=mv импульс, кг·м/с (→!!!) | 79 | n=N/V концентр. молек.,1/м3 | 124 | Ei=-(∆Ф/∆t )n зак. эл. маг. инд. для катуш.,В | 167 | S= πR2 площадь круга |
35 | m1v1+m2v2=m1u1+m2u2 зак.сохр. имп. (→!!!) | 80 | p=(2/3)nĒ давл. газа, Па | 125 | Еsi=L∆I/∆t ЭДС самоинд. | 168 | C=2πR длина окружности |
36 | Ft=mv-mv0=m∆v=∆ p импульс силы (→!!!) | 81 | E=(3/2)kT кин. энерг. мол., Дж | 126 | Fa=IBℓsinα сила Ампера (лев рука) | 169 | 1м3=1000 л=1000 дм3=1 000 000см3 |
37 | E=mv2/2 кинетич. энерг., Дж | 82 | T=t+273 абсол. темп., К | 127 | Fл=qBvsinα сила Лоренца (лев рука +) | 170 | 54 км/ч=54/3,6=15 м/с |
38 | E=mgh потенц. энергия, Дж | 83 | ν =m/μ= N/NA колич. вещества, моль | 128 | Е= Bvℓsinα эдс в движ. проводн. | 171 | I=q/∆t и I=S∆B/∆tr (тогда q/∆t= S∆B/∆tr) |
39 | E=kx2/2 потенц. | 84 | v=√3kT/m0 скор. молек. | 129 | e=BSωsinωt=Emsinωt эдс во вращ рамке в мп | 172 | Работа газа в осях (pV) равна площади фиг. |
40 | σ=F/s=Eε механич. напряжение, Па | 85 | PV=mRT/M=νRT ур. Менд-Клайп. | 130 | qBR=mv вращ.зар.част.в МП | 173 | 2см=2·10-2м, 2см2=2·10-4м2, 2см3=2·10-6м3 |
41 | ε=∆ℓ/ℓ0 относительное удлинение | 86 | p1V1/T1 = p2V2/T2 ур-е сост-я идеальн. газа | 131 | T=2πR/v=2πm/qB период вращ.зар.част.в мп | 174 | v =x’= – xmωsinωt a= v’= xmω2cosωt |
42 | Q=mc∆t кол. | 87 | U=(3/2) mRT/M вн.эн.одноат.ид.г. | 132 | T=2π√LC периодсвоб. кол. в КК | 175 | Eim=BSωn максим. эдс инд. во вращ. рамке |
43 | Q=mλ кол. тепл. ПЛАВЛ. ОТВЕРД. | 88 | U=(3/2)pV внутр.энерг.одноат.ид.газа | 133 | E=mc2 взаимосв массы и энерг.,Дж | 176 | Fоткл=mgtgα (нить, электр.сила …) |
44 | Q=mL кол. тепл. ПАРООБР. КОНД. | 89 | A=p∆V=mR∆T/M работа газа при р=const | 134 | α=β закон отр. света (\ п / в одной плоск.) | 177 | sinα≈tgα при малых α |
45 | Q=mq кол. тепл. СГОРАНИЕ | 90 | A=Q1-Q2 работа двигателя | 135 | sinα/sinγ=n2/n1 зак прел. | 178 | Прав буравчика: определ направл лин инд |
91 | ∆U=Q+A изменен. внутр. энергии | 179 | d=√2а в квадрате |
Контрольная работа по физике Кинематика 9 класс
Контрольная работа по физике Кинематика Законы взаимодействия и движения тел 9 класс с ответами. Работа состоит из 4 вариантов в каждом варианте по 9 заданий.
1 вариант
1. Исследуется перемещение слона и мухи. Модель материальной точки может использоваться для описания движения
1) только слона
2) только мухи
3) и слона, и мухи в разных исследованиях
4) ни слона, ни мухи, поскольку это живые существа
2. Вертолёт Ми-8 достигает скорости 250 км/ч. Какое время он затратит на перелёт между двумя населёнными пунктами, расположенными на расстоянии 100 км?
1) 0,25 с
2) 0,4 с
3) 2,5 с
4) 1440 с
3. На рисунках представлены графики зависимости координаты от времени для четырёх тел, движущихся вдоль оси ОХ. Какое из тел движется с наибольшей по модулю скоростью?
На рисунках представлены графики зависимости координаты от времени для четырёх тел, движущихся вдоль оси ОХ. Какое из тел движется с наибольшей по модулю скоростью?
4. Велосипедист съезжает с горки, двигаясь прямолинейно и равноускоренно. За время спуска скорость велосипедиста увеличилась на 10 м/с. Ускорение велосипедиста 0,5 м/с2. Сколько времени длится спуск?
1) 0,05 с
2) 2 с
3) 5 с
4) 20 с
5. Лыжник съехал с горки за 6 с, двигаясь с постоянным ускорением 0,5 м/с2. Определите длину горки, если известно, что в начале спуска скорость лыжника была равна 18 км/ч.
1) 39 м
2) 108 м
3) 117 м
4) 300 м
6. Моторная лодка движется по течению реки со скоростью 5 м/с относительно берега, а в стоячей воде — со скоростью 3 м/с. Чему равна скорость течения реки?
1) 1 м/с
2) 1,5 м/с
3) 2 м/с
4) 3,5 м/с
7. Установите соответствие между физическими величинами и формулами, по которым эти величины определяются.
Физические величины
А) Ускорение
Б) Скорость при равномерном прямолинейном движении
В) Проекция перемещения при равноускоренном прямолинейном движении
Формулы
8. На пути 60 м скорость тела уменьшилась в 3 раза за 20 с. Определите скорость тела в конце пути, считая ускорение постоянным.
9. Из населённых пунктов А и В, расположенных вдоль шоссе на расстоянии 3 км друг от друга, в одном направлении одновременно начали движение велосипедист и пешеход. Велосипедист движется из пункта А со скоростью 15 км/ч, а пешеход со скоростью 5 км/ч. Определите, на каком расстоянии от пункта А велосипедист догонит пешехода.
2 вариант
1. Два тела, брошенные с поверхности земли вертикально вверх, достигли высот 10 м и 20 м и упали на землю. Пути, пройденные этими телами, отличаются на
1) 5 м
2) 20 м
3) 10м
4) 30 м
2. За 6 минут равномерного движения мотоциклист проехал 3,6 км. Скорость мотоциклиста равна
Скорость мотоциклиста равна
1) 0,6 м/с
2) 10 м/с
3) 15 м/с
4) 600 м/с
3. На рисунках представлены графики зависимости проекции перемещения от времени для четырёх тел. Какое из тел движется с наибольшей по модулю скоростью?
4. Во время подъёма в гору скорость велосипедиста, двигающегося прямолинейно и равноускоренно, изменилась за 8 с от 18 км/ч до 10,8 км/ч. При этом ускорение велосипедиста было равно
1) -0,25 м/с2
2) 0,25 м/с2
3) -0,9 м/с2
4) 0,9 м/с2
5. Аварийное торможение автомобиля происходило в течение 4 с. Определите, каким был тормозной путь, если начальная скорость автомобиля 90 км/ч.
1) 22,5 м
2) 45 м
3) 50 м
4) 360 м
6. Пловец плывёт по течению реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с.
1) 0,5 м/с
2) 0,1 м/с
3) 0,5 м/с
4) 0,7 м/с
7. Установите соответствие между физическими величинами и их единицами измерения в СИ.
Физические величины
А) скорость
В) время
Единицы измерения СИ
1) мин
2) км/ч
3) м/с
4) с
5) м/с2
8. Поезд начинает равноускоренное движение из состояния покоя и проходит за четвёртую секунду 7 м. Какой путь пройдёт тело за первые 10 с?
9. Катер, переправляясь через реку шириной 800 м, двигался перпендикулярно течению реки со скоростью 4 м/с в системе отсчёта, связанной с водой. На сколько будет снесён катер течением, если скорость течения реки 1,5 м/с?
3 вариант
1. Решаются две задачи:
А: рассчитывается маневр стыковки двух космических кораблей;
Б: рассчитываются периоды обращения космических кораблей вокруг Земли.
В каком случае космические корабли можно рассматривать как материальные точки?
1) Только А
2) Только Б
3) И А, и Б
4) Ни А, ни Б
2. Средняя скорость поезда метрополитена 40 м/ с. Время движения между двумя станциями 4 минуты. Определите, на каком расстоянии находятся эти станции.
Средняя скорость поезда метрополитена 40 м/ с. Время движения между двумя станциями 4 минуты. Определите, на каком расстоянии находятся эти станции.
1) 160 м
2) 1000 м
3) 1600 м
4) 9600 м
3. На рисунках представлены графики зависимости проекции скорости от времени для четырёх тел, движущихся вдоль оси ОХ. Какое из тел движется с постоянной скоростью?
4. Ускорение велосипедиста на одном из спусков трассы равно 1,2 м/с2 На этом спуске его скорость увеличилась на 18 м/с. Велосипедист спускается с горки за
1) 0,07 с
2) 7,5 с
3) 15 с
4) 21,6 с
5. Какое расстояние пройдёт автомобиль до полной остановки, если шофёр резко тормозит при скорости 72 км/ч, а от начала торможения до остановки проходит 6 с?
1) 36 м
2) 60 м
3) 216 м
4) 432 м
6. Катер движется по течению реки со скоростью 11 м/с относительно берега, а в стоячей воде — со скоростью 8 м/с. Чему равна скорость течения реки?
Чему равна скорость течения реки?
1) 1 м/с
2) 1,5 м/с
3) 3 м/с
4) 13 м/с
7. Установите соответствие между физическими величинами и формулами, по которым эти величины определяются.
Физические величины
А) Проекция ускорения
Б) Проекция перемещения при равномерном прямолинейном движении
В) Проекция скорости при равноускоренном прямолинейном движении
Формулы
8. Скорость материальной точки на пути 60 м увеличилась в 5 раз за 10 с. Определить ускорение, считая его постоянным.
9. Товарный поезд едет со скоростью 36 км/ч. Спустя 30 минут с той же станции по тому же направлению выходит экспресс со скоростью 144 км/ч. На каком расстоянии от станции экспресс догонит товарный поезд?
4 вариант
1. Два тела, брошенные с поверхности земли вертикально вверх, достигли высот 10 м и 20 м и упали на землю. Перемещения этих тел соответственно равны
1) 10 м, 20 м
2) 20 м, 40 м
3) Ом, Ом
4) Ом, 20 м
2. Велосипедист, двигаясь равномерно по шоссе, проехал 1800 м за 3 минуты. Скорость велосипедиста равна
Велосипедист, двигаясь равномерно по шоссе, проехал 1800 м за 3 минуты. Скорость велосипедиста равна
1) 12 км/ч
2) 24 км/ч
3) 36 км/ч
4) 60 км/ч
3. На рисунках представлены графики зависимости модуля ускорения от времени для разных видов движения. Какой график соответствует равномерному движению?
4. Санки съехали с одной горки и въехали на другую. Во время подъёма на горку скорость санок, двигавшихся прямолинейно и равноускоренно, за 4 с изменилась от 12 м/с до 2 м/с, при этом модуль ускорения был равен
1) -2,5 м/с2
2) 2,5 м/с2
3) -3,5 м/с2
4) 3,5 м/с2
5. При равноускоренном прямолинейном движении скорость катера увеличилась за 10 с от 5 м/с до 9 м/с. Какой путь пройден катером за это время?
1) 50 м
2) 70 м
3) 80 м
4) 90 м
6. Пловец плывёт против течения реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с.
1) 0,1 м/с
2) 0,2 м/с
3) 0,5 м/с
4) 0,7 м/с
7. Установите соответствие между физическими величинами и их единицами измерения в СИ.
Физические величины
А) перемещение
Б) скорость
В) время
Единицы измерения СИ
1) мин
2) км/ч
3) м/с
4) с
5) м
8. Тело, двигаясь равноускоренно, в течение пятой секунды от начала движения прошло путь 45 м. Какой путь оно пройдёт за 8 с от начала движения?
9. Пловец пересекает реку шириной 240 м. Скорость течения реки 1,2 м/с. Скорость пловца относительно воды 1,5 м/с и направлена перпендикулярно к вектору течения. На сколько метров пловец будет снесён течением к тому моменту, когда он достигнет противоположного берега?
Ответы на контрольную работу по физике Кинематика
1 вариант
1-3, 2-4, 3-4, 4-4, 5-1, 6-3, 7-425, 8-1,5 м/с, 9-4,5 км
2 вариант
1-2, 2-2, 3-3, 4-1, 5-3, 6-4, 7-354, 8-100 м, 9-300 м
3 вариант
1-2, 2-4, 3-1, 4-3, 5-2, 6-3, 7-431, 8-0,8 м/с2, 9-24 км
4 вариант
1-3, 2-3, 3-4, 4-2, 5-2, 6-1, 7-534, 8-320 м, 9-192 м
PDF-версия
Контрольная работа Кинематика(134 Кб, pdf)
|
Каталог Поиск книг Электронные приложения Авторизация Подписка на рассылку Стихи о нас Богатство Трудности эти уже превратились в смыслы. Тивикова С.К., зав. каф. начального образования НИРО Обратная связь Отправить сообщение с сайта Партнёры |
Введение Презентация «Информатика 9 класс. Введение» Презентация «Информатика 9 класс. Введение» (Open Document Format) Плакат «Техника безопасности»Ссылки на ресурсы ЕК ЦОР
Глава 1. Моделирование и формализация 1.1. Моделирование как метод познания Презентация «Моделирование как метод познания» Презентация «Моделирование как метод познания» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР:
Ссылки на ресурсы ФЦИОР:
Ресурсы сети Интернет: Планета Земля § 1.2. Знаковые модели Презентация «Знаковые модели» Презентация «Знаковые модели» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР
Ссылки на ресурсы ФЦИОР:
§ 1.3. Графические информационные модели Презентация «Графические модели» Презентация «Графические модели» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР
§ 1.4. Табличные информационные модели Презентация «Табличные информационные модели» Презентация «Табличные информационные модели» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР
§ 1.5. База данных как модель предметной области Презентация «База данных как модель предметной области» Презентация «База данных как модель предметной области» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР
§ 1.6. Система управления базами данных Презентация «Система управления базами данных» Презентация «Система управления базами данных» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР:
Интерактивный тест «Моделирование и формализация» Тест 1 Глава 2. Алгоритмизация и программирование § 2.1. Решение задач на компьютере Презентация «Программирование как этап решения задачи на компьютере» Презентация «Программирование как этап решения задачи на компьютере» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР
§ 2.2. Одномерные массивы целых чисел Презентация «Одномерные массивы целых чисел» Презентация «Одномерные массивы целых чисел» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР
Ссылки на ресурсы ФЦИОР:
Ссылки на свободно распространяемое программное обеспечение:
§ 2.3. Конструирование алгоритмов Презентация «Конструирование алгоритмов» Презентация «Конструирование алгоритмов» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР:
Ссылки на свободно распространяемое программное обеспечение:
§ 2. Презентация «Запись вспомогательных алгоритмов на языке Паскаль» Презентация «Запись вспомогательных алгоритмов на языке Паскаль» (Open Document Format) Интерактивные тесты
Ссылки на свободно распространяемое программное обеспечение:
§ 2.5. Алгоритмы управления Презентация «Алгоритмы управления» Презентация «Алгоритмы управления» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР:
Интерактивный тест «Алгоритмизация и программирование» Тест 2 Глава 3. § 3.1. Электронные таблицы Презентация «Электронные таблицы» Презентация «Электронные таблицы» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР:
§ 3.2. Организация вычислений в электронных таблицах Презентация «Организация вычислений в электронных таблицах» Презентация «Организация вычислений в электронных таблицах» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР:
§ 3. Презентация «Средства анализа и визуализации данных» Презентация «Средства анализа и визуализации данных» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР:
Ссылки на ресурсы ФЦИОР:
Тест 3 Глава 4. § 4.1. Локальные и глобальные компьютерные сети Презентация «Локальные и глобальные компьютерные сети» Презентация «Локальные и глобальные компьютерные сети» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР:
Ссылки на ресурсы ФЦИОР:
§ 4. Презентация «Всемирная компьютерная сеть Интернет» Презентация «Всемирная компьютерная сеть Интернет» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР:
§ 4.3. Информационные ресурсы и сервисы Интернета Презентация «Информационные ресурсы и сервисы Интернета» Презентация «Информационные ресурсы и сервисы Интернета» (Open Document Format) Интерактивные тесты
Ссылки на ресурсы ЕК ЦОР:
§ 4.4. Создание Web-сайта Презентация «Создание Web-сайта» Презентация «Создание Web-сайта» (Open Document Format) Интерактивные тесты
Интерактивный тест «Коммуникационные технологии» Тест 4 Ссылки на ресурсы ЕК ЦОР:
|
Формула расстояния Класс 9 – Решенные примеры, PDF для скачивания
Учащиеся часто путаются с формулой расстояния и с формулой расстояния и скорости. Важно понимать, что в координатной геометрии «формула расстояния» используется для расчета расстояния между любыми двумя точками, в то время как расстояние и скорость относятся к другой теме скорости, расстояния и времени. Эта статья содержит список формул расстояния для класса 9, а также несколько простых советов по их запоминанию.
Список формул для определения расстояния, класс 9
Ниже приведен краткий список формул, связанных с формулой для определения расстояния.
- Расстояние между координатой P(x 1 , y 1 ) и координатой Q(x 2 , y 2 ) рассчитывается по формуле расстояния: d = √[(x 1 – 90 х 1 ) 2 + (у 2 – у 1 ) 2 ]
- Расстояние точки P(x, y) от начала координат равно √(x 2 + у 2 )
- Середину отрезка, соединяющего точки P(x 1 , y 1 ) и Q(x 2 , y 2 ), можно найти по формуле [(x 1 + x 2 ) / 2 , (у 1 + у 2 ) / 2]
Применение формулы расстояния класса 9
Формула расстояния класса 9 имеет свои приложения в алгебре и геометрии, как показано ниже:
- Формула расстояния получена из теоремы Пифагора и очень полезна при оценке расстояний и поэтому служит интегралом частью навигационной стратегии. Например, мы можем использовать формулу расстояния, чтобы узнать расстояние между источником и пунктом назначения и даже найти кратчайший возможный маршрут.

- Формула расстояния оказывается очень полезной в самой координатной геометрии. Например, если известны координаты четырехугольника, мы можем использовать формулу расстояния, чтобы выяснить, является ли четырехугольник квадратом или нет. Если бы все стороны были одинаковой длины, то это был бы квадрат.
Формула расстояния Класс 9 Примеры
Пример 1: Найдите расстояние между следующими точками A(2,4) и B(-4,4)
Решение: Расстояние между заданными точками (d) = √[(x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 ]. Здесь х 1 = 2, х 2 = -4; Y 1 = 4 и Y 2 = 4. Заменить значения в формуле,
= √ [(-4 -2) 2 + (4 -4) 2 ]
= √ [(-6) 2 + (0) 2 ] = √ [(36)]
= 6 единиц
Пример 2: Найдите среднюю точку сегмента линии, соединяющих точки P (4, 4) и Q (6 , 8).
Решение: Середину отрезка можно вычислить по формуле Середина = [(x 1 + x 2 ) / 2 , (y 1 + y 2 ) / 2] . Здесь х 1 = 4, х 2 = 6, y 1 = 4 и y 2 = 8. Подставляя значения в формулу, Midpoint = [(x 1 + x 2 )/2 , (y 1 + y 2 )/2]
Середина = [(4 + 6)/2, (4 + 8)/2] = [10/2; 12/2] = (5,6)
Следовательно, координаты середины равны (5,6).
Советы по запоминанию формулы расстояния Класс 9
Следующие советы могут помочь учащимся запомнить формулу расстояния:
- Студенты должны искать разъяснения у своих учителей или друзей даже в самых незначительных сомнениях. Они не должны бояться высказывать свои сомнения, так как это приведет лишь к дополнительной путанице в будущем, когда дело дойдет до понимания сложных тем. Устранение любых неопределенностей на этом этапе помогло бы понять основную логику формулы, облегчив ее запоминание.

- Студенты должны стремиться решить как можно больше задач на основе формул. Это позволяет учащимся ознакомиться с различными сценариями, в которых одна и та же формула может применяться несколькими способами, что позволяет им быстро вспоминать их при необходимости.
- В нынешний технологический век учащиеся используют гаджеты, такие как мобильные телефоны и ноутбуки, поэтому они могут сохранять эти формулы в качестве обоев. Это приведет к тому, что каждый раз, когда они используют свое устройство, они будут смотреть на обои с формулой, что даст быстрый пересмотр.
Учащиеся могут скачать лист Math Formulas Class 9 для печати ниже.
Часто задаваемые вопросы о формулах расстояния для класса 9
Какие важные формулы расстояния для класса 9?
Важные формулы расстояний для класса 9 перечислены ниже:
- Расстояние между координатой P(x 1 , y 1 ) и координатой Q(x 2 , y 2 ) рассчитывается с использованием формула расстояния: d = √[(x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 ]
- Расстояние точки P(x, y) от начала координат равно √(x 2 + y 2 )
- Середину отрезка, соединяющего точки P(x 1 , y 1 ) и Q(x 2 , y 2 ), можно найти по формуле [(x 1 + x 2 ) / 2 , (у 1 + у 2 ) / 2]
Каковы основные формулы формулы расстояния класса 9?
Основные формулы класса 9 формулы расстояния, перечисленные в этой статье, составляют основу многих понятий алгебры и тригонометрии. Следовательно, важно, чтобы учащиеся сосредоточились на том, чтобы хорошо их понять. Примеры и практические советы, обобщенные в этой статье, помогут учащимся тщательно пересмотреть свои формулы без какого-либо стресса.
Следовательно, важно, чтобы учащиеся сосредоточились на том, чтобы хорошо их понять. Примеры и практические советы, обобщенные в этой статье, помогут учащимся тщательно пересмотреть свои формулы без какого-либо стресса.
Какие важные формулы охватывают формулу расстояния класса 9?
Важными формулами, покрывающими класс формулы расстояния 9, которые также перечислены в этой статье, являются следующие.
- Расстояние между координатой P(x 1 , y 1 ) и координатой Q(x 2 , y 2 ) рассчитывается по формуле расстояния: d = √[(x 1 – 90 х 1 ) 2 + (у 2 – у 1 ) 2 ]
- Расстояние точки P(x, y) от начала координат равно √(x 2 + y 2 )
- Середину отрезка, соединяющего точки P(x 1 , y 1 ) и Q(x 2 , y 2 ), можно найти по формуле [(x 1 + x 2 ) / 2 , (у 1 + у 2 ) / 2]
Эти формулы помогут учащимся научиться находить расстояние между двумя точками и расстояние от точки до линии, а также средние точки.
Сколько формул в формуле расстояния класса 9?
Существуют три основные формулы расстояний, которые при хорошем изучении упростят для учащихся понятие координатной геометрии. Эти формулы дают подробное представление о том, как двумерная координатная геометрия представляет собой смесь алгебры и геометрии. Акцент делается на алгебраическом представлении линии, причем наклон является наиболее важным фактором.
Как я могу запомнить Формулу расстояния Класс 9?
Для запоминания формулы расстояния 9 класс учащиеся могут воспользоваться следующими советами:
- Тщательно изучите теорию, представленную в главе, и запишите все сомнения, чтобы с помощью учителей или друзей развеять их. Если основы будут ясны, не возникнет трудностей с пониманием формул.
- После того, как теоретическая часть будет понятна, учащиеся должны попытаться выполнить все решенные примеры, а затем перейти к упражнениям. Это поможет дать хорошую практику использования формул в различных контекстах.

- Студенты также могут воспользоваться своими мобильными телефонами и ноутбуками в процессе обучения. Изображения формул можно установить в качестве обоев на этих устройствах, чтобы вы могли видеть их в течение дня.
Скачать БЕСПЛАТНЫЕ учебные материалы
Математические формулы 9 класс
Движение по прямой линии 11 класс Примечания Физика Глава 3
• Введение
Движение – одна из важных тем в физике. Все во Вселенной движется. Это может быть лишь небольшое движение и очень-очень медленное, но движение происходит. Даже если вам кажется, что вы стоите на месте, Земля движется вокруг Солнца, а Солнце движется вокруг нашей галактики.
«Об объекте говорят, что он движется, если его положение изменяется во времени».
Понятие движения есть живое, и тело, которое может двигаться относительно одной системы отсчета, может покоиться относительно другой.
В физике есть две области, изучающие движение объекта.
(i) Кинематика: описывает движение объектов, не рассматривая причину движения.
(ii) Динамика: она связывает движение объектов с силами, которые их вызывают.
• Точечный объект
Если длина, охватываемая объектами, очень велика по сравнению с размером объектов, объекты считаются точечными.
• Системы отсчета
Движение частицы всегда описывается относительно системы отсчета. Система отсчета создается путем взятия произвольной точки за начало координат и представления системы координат, которая будет прикреплена к ней. Эта система координат, выбранная для данной задачи, является для нее системой отсчета. Обычно мы выбираем систему координат, привязанную к земле, в качестве системы отсчета для большинства задач.
• Общая длина пути (расстояние)
Для движущейся частицы общая длина фактического пути, пройденного между начальным и конечным положениями частицы, известна как «общая длина пути» или пройденное ею расстояние.
• Типы движения
Чтобы полностью описать движение объекта, нам нужно указать его положение. Для этого нам нужно знать координаты позиции. В некоторых случаях требуются три координаты положения, в то время как в некоторых случаях требуются две или одна координата положения.
На основании этого движение можно классифицировать как:
(i) Одномерное движение. Говорят, что частица, движущаяся по прямой или траектории, совершает одномерное движение. Например, движение поезда по прямой линии, свободно падающее тело под действием силы тяжести и т. д.
(ii) Двумерное движение. Говорят, что частица, движущаяся в плоскости, совершает двумерное движение. Например, движение снаряда, выпущенного из ружья, монеты из картонной доски и т. д.
(iii) Трехмерное движение. Говорят, что частица, движущаяся в пространстве, совершает трехмерное движение. Например, движение воздушного змея в небе, движение самолета и т. д.
• Смещение
Смещение частицы в заданное время определяется как изменение положения частицы в определенном направлении в течение этого времени. Он задается вектором, проведенным из его начального положения в конечное положение.
Он задается вектором, проведенным из его начального положения в конечное положение.
• Факторы, отличающие смещение от расстояния
—> Смещение имеет направление. Расстояние не имеет направления.
—> Величина смещения может быть как положительной, так и отрицательной.
—> Расстояние всегда положительное. Она никогда не уменьшается со временем.
—> Расстояние ≥ | Смещение |
• Равномерная скорость и равномерная скорость
Равномерная скорость. Говорят, что объект движется с постоянной скоростью, если он преодолевает равные расстояния за равные промежутки времени, какими бы малыми ни были эти промежутки времени.
Равномерная скорость. Говорят, что объект движется с постоянной скоростью, если он совершает равные перемещения за равные промежутки времени, какими бы малыми ни были эти промежутки времени.
• Переменная скорость и переменная скорость
Переменная скорость. Говорят, что объект движется с переменной скоростью, если он проходит неравные расстояния за равные промежутки времени, какими бы малыми ни были эти промежутки времени.
Говорят, что объект движется с переменной скоростью, если он проходит неравные расстояния за равные промежутки времени, какими бы малыми ни были эти промежутки времени.
Переменная скорость. Говорят, что объект движется с переменной скоростью, если он совершает неравные перемещения за равные промежутки времени, какими бы малыми ни были эти промежутки времени.
• Средняя скорость и средняя скорость
Средняя скорость. Это отношение общей длины пройденного пути к соответствующему интервалу времени.
Или
Средняя скорость объекта больше или равна величине средней скорости за данный интервал времени.
• Мгновенная скорость и мгновенная скорость
Мгновенная скорость. Скорость объекта в момент времени называется мгновенной скоростью.
Или
«Мгновенная скорость является пределом средней скорости, поскольку временной интервал становится бесконечно малым».
Мгновенная скорость
Мгновенная скорость частицы — это скорость в любой момент времени или в любой точке ее пути.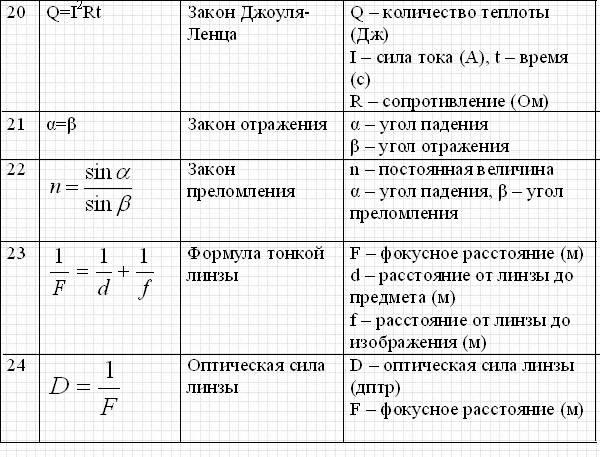
или
«Мгновенная скорость или просто скорость определяется как предел средней скорости, когда временной интервал Δt становится бесконечно малым».
• Ускорение
Скорость изменения скорости называется ускорением.
• Равномерное ускорение
Если объект подвергается одинаковым изменениям скорости за равные промежутки времени, это называется равномерным ускорением.
• Среднее и мгновенное ускорение
Среднее ускорение. Это изменение скорости, деленное на интервал времени, в течение которого происходит изменение.
Мгновенное ускорение. Он определяется как предел среднего ускорения, когда временной интервал Δt стремится к нулю.
• Кинематические графики
Графики «перемещение-время» и «скорость-время» частицы часто используются для визуального представления движения частицы. «Форма» графиков зависит от начальных «координат» и «характера» ускорения частицы (рис. )
)
Всегда справедливы следующие общие результаты
(i) Наклон графика смещения-времени в любой момент времени дает скорость частицы в этот момент.
(ii) Наклон графика зависимости скорости от времени в любой момент дает величину ускорения частицы в этот момент.
(iii) Площадь, ограниченная графиком скорость-время, осью времени и двумя координатами в моменты времени от t 1 до t 2 , дает расстояние, пройденное частицей за интервал времени от т 1 до т 2 .
• Уравнения движения для равноускоренного движения
Для равноускоренного движения можно вывести несколько простых уравнений, которые связывают перемещение (x), затраченное время (f), начальную скорость (u), конечную скорость (v) и ускорение (a) . Следующее уравнение дает связь между конечной и начальной скоростями v и u объекта, движущегося с равномерным ускорением a: v = u + at
• Предположим, что тело брошено вертикально вверх из точки A со скоростью u.
В некоторых задачах направление вниз удобно считать положительным, в этом случае все измерения в направлении вниз считаются положительными, т.е. ускорение будет +g. Но иногда нам может понадобиться принять вверх как положительное, и в этом случае ускорение будет -g.
• Относительная скорость
Относительная скорость объекта A относительно другого объекта B — это скорость, с которой объект A меняет свое положение относительно объекта B.
—> Относительная скорость двух объектов, движущихся в одинаковое направление есть разность скоростей тел.
—> Относительная скорость двух объектов, движущихся в противоположном направлении, равна сумме скоростей объектов.
• ВАЖНЫЕ ТАБЛИЦЫ
Примечания по физике для класса 11
Решения NCERT для класса 9, научная глава 10
- Решения НЦЭРТ
- Класс 9
- Наука
- гравитация
Наука NCERT 9 класс, глава 10, Гравитация , как следует из названия, рассказывает о гравитации и универсальном законе из гравитации . Движение объекта под действием гравитационной силы Земли объясняется в главе Гравитация . Основное обсуждение главы начинается с объяснения концепции гравитации на примере движения Луны вокруг Земли. Здесь термин центростремительная сила определена. После этого определяется универсальный закон гравитации вместе с его математическим выводом и соответствующими примерами.
Движение объекта под действием гравитационной силы Земли объясняется в главе Гравитация . Основное обсуждение главы начинается с объяснения концепции гравитации на примере движения Луны вокруг Земли. Здесь термин центростремительная сила определена. После этого определяется универсальный закон гравитации вместе с его математическим выводом и соответствующими примерами.
Дополнительная информация о Ньютон ‘ s обратный квадрат закон и его вклад включены в главу Гравитация . Впоследствии обсуждается важность всемирного закона тяготения в реальной жизни. Концепция свободное падение и ускорение под действием силы тяжести объясняется с помощью упражнений и примеров. Расчет значения «g» также упоминается вместе с его единицей СИ. После этого объясняются темы масса и инерция с последующим обсуждением тяги и давления .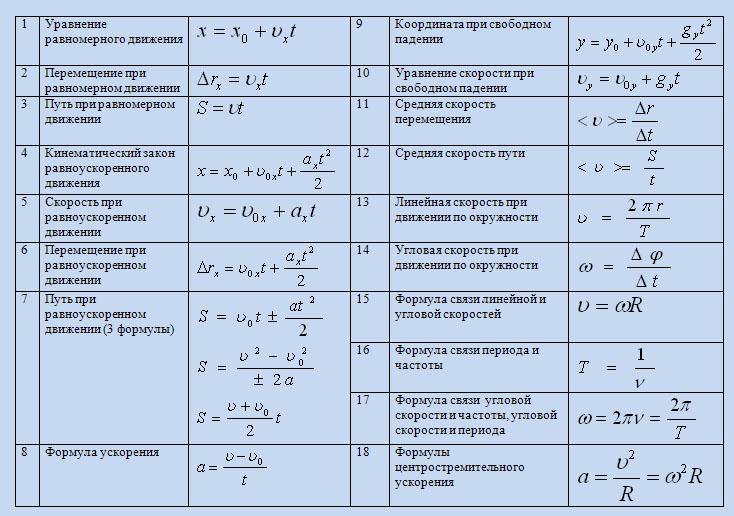
Формула для давления дана вместе с примерами. В более поздних разделах главы Гравитация концепция плавучесть полностью покрыта. Ближе к концу проливается свет на принцип Архимеда и понятие относительной плотности.
Глава Гравитация рассматривается в следующих разделах:
- Гравитация
- Свободное падение
- Масса
- Вес
- Тяга и давление
- Принцип Архимеда
- Относительная плотность
Страница № 134:
Вопрос 1:
Сформулируйте универсальный закон всемирного тяготения
Ответ:
Универсальный закон всемирного тяготения гласит, что каждый объект во Вселенной притягивает любой другой объект с силой, называемой гравитационной силой. Сила, действующая между двумя телами, прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между их центрами.
Для двух объектов массой м 1 и м 2 и расстояние между ними r , сила ( F ) притяжения, действующая между ними, определяется законом всемирного тяготения как:
по:
Видео Решение для гравитации (Страница: 134 , Q.No.: 1)
NCERT Решение для класса 9 науки – гравитация 134 , Вопрос 1
Номер страницы 134:
0 2 Вопрос 2:4 Вопрос 2: Напишите формулу, чтобы найти величину силы притяжения между Землей и объектом на поверхности земли.
Ответ:
Пусть M E будет массой Земли, а m будет массой объекта на ее поверхности. Если R радиус Земли, то согласно закону всемирного тяготения сила тяжести ( F ), действующая между Землей и объектом, определяется соотношением:
Видео Решение для гравитации (Страница: 134, Q.No.: 2)
NCERT Решение для класса 9 науки – гравитация 134, вопрос 2
Страница № 136:
Вопрос 1:
Что вы подразумеваете под свободным падением?
Ответ:
Гравитация Земли притягивает все объекты к своему центру. Когда объект сбрасывается с высоты, он падает к поверхности Земли под действием гравитационной силы. Движение тела называется свободным падением.
Когда объект сбрасывается с высоты, он падает к поверхности Земли под действием гравитационной силы. Движение тела называется свободным падением.
Видео Решение для гравитации (Страница: 136 , Q.No.: 1)
Решение NCERT для класса 9 по науке – гравитация 136 , Вопрос 1
Страница № 136:
Вопрос 2:
Что вы подразумеваете под ускорением под действием силы тяжести?
Ответ:
Когда объект падает на землю с высоты, его скорость изменяется при падении. Эта изменяющаяся скорость вызывает ускорение объекта. Это ускорение известно как ускорение свободного падения ( g ). Его значение равно 9,8 м/с 2 .
Видео Решение для гравитации (Страница: 136 , Q.No.: 2)
NCERT Решение для 9 класса науки – гравитация 136 , Вопрос 2
Страница № 138:
Вопрос 1:
В чем разница между массой объекта и его весом?
Ответ:
С. | Масса | Масса |
И. | Масса – это количество вещества, содержащегося в теле. | Вес – это сила тяжести, действующая на тело. |
II. | Это мера инерции тела. | Это мера силы тяжести. |
III . | Масса является постоянной величиной. | Вес не является постоянной величиной. В разных местах по разному. |
IV . | Он имеет только величину. | Он имеет не только направление, но и величину. |
В . | Единицей СИ является килограмм (кг). | Его единица СИ такая же, как единица силы СИ, т. |
Видео Решение для гравитации (Страница: 138 , Q.No.: 1)
NCERT Решение для класса 9 науки – гравитация 138 , Вопрос 1
Страница № 138:
4 Вопрос 29: 900 вес объекта на луне
-й его вес на земле?Ответ:
Пусть M E будет массой Земли и м быть объектом на поверхности Земли. Пусть R E будет радиусом Земли. Согласно закону всемирного тяготения, вес W E объекта на поверхности Земли равен,
Пусть и будет массой и радиусом Луны. Тогда, согласно закону всемирного тяготения, вес W M объекта на поверхности Луны равен:
Следовательно, вес объекта на Луне равен его весу на Земле.
Видео Решение для гравитации (Страница: 138 , Q.No.: 2)
NCERT Решение для класса 9 науки – гравитация 138 , Вопрос 2
Страница № 141:
Вопрос 1:
9 тяжело удерживать школьную сумку с ремешком из тонкой и прочной бечевки?Ответ:
Трудно удерживать школьную сумку с тонким ремешком, так как нагрузка на плечи довольно велика. Это связано с тем, что давление обратно пропорционально площади поверхности, на которую действует сила. Чем меньше площадь поверхности; тем больше будет давление на поверхность. В случае тонкой ленты площадь контактной поверхности очень мала. Следовательно, давление, оказываемое на плечо, очень велико.
Это связано с тем, что давление обратно пропорционально площади поверхности, на которую действует сила. Чем меньше площадь поверхности; тем больше будет давление на поверхность. В случае тонкой ленты площадь контактной поверхности очень мала. Следовательно, давление, оказываемое на плечо, очень велико.
Видео Решение для гравитации (Страница: 141 , Q.No.: 1)
NCERT Решение для класса 9 науки – гравитация 141 , Вопрос 1
Страница № 141:
Вопрос 2:
9 имеется в виду плавучесть?Ответ:
Подъемная сила, с которой жидкость действует на погруженный в нее предмет, называется выталкивающей силой. Когда вы пытаетесь погрузить предмет в воду, вы можете почувствовать направленную вверх силу, действующую на предмет, которая увеличивается по мере того, как вы погружаете предмет глубже в воду.
Видео Решение для гравитации (Страница: 141 , Q.No.: 2)
NCERT Решение для класса 9 науки – гравитация 141 , Вопрос 2
Страница № 141:
Вопрос 3:
9 предмет плавает или тонет при размещении на поверхности воды?Ответ:
Если плотность предмета больше плотности жидкости, то он тонет в жидкости. Это связано с тем, что выталкивающая сила, действующая на объект, меньше силы тяжести. С другой стороны, если плотность предмета меньше плотности жидкости, то он плавает на поверхности жидкости. Это связано с тем, что выталкивающая сила, действующая на объект, больше силы тяжести.
Это связано с тем, что выталкивающая сила, действующая на объект, меньше силы тяжести. С другой стороны, если плотность предмета меньше плотности жидкости, то он плавает на поверхности жидкости. Это связано с тем, что выталкивающая сила, действующая на объект, больше силы тяжести.
Видео Решение для гравитации (Страница: 141 , Q.No.: 3)
NCERT Решение для класса 9 науки – гравитация 141 , Вопрос 3
Страница № 142:
Вопрос 1:
Масса на весах должна быть 42 кг. Ваша масса больше или меньше 42 кг?Ответ:
Когда вы взвешиваете свое тело, на него действует направленная вверх сила. Эта направленная вверх сила является выталкивающей силой. В результате тело слегка приподнимается, в результате чего показания весов меньше фактического значения.
Видеорешение для гравитации (Страница: 142 , Q.No.: 1)
NCERT Решение для 9 класса науки – гравитация 142 , Вопрос 1
Страница № 142:
Вопрос 2:
У вас есть сумка хлопка и железный брусок, каждый из которых показывает массу 100 кг при измерении на весах. На самом деле один тяжелее другого. Можете ли вы сказать, какой из них тяжелее и почему?
На самом деле один тяжелее другого. Можете ли вы сказать, какой из них тяжелее и почему?
Ответ:
Мешок с хлопком тяжелее железного прута. Это потому, что площадь поверхности хлопкового мешка больше, чем у железного стержня. Следовательно, на мешок действует большая выталкивающая сила, чем на железный стержень. Это делает хлопковый мешок тяжелее, чем его фактическая стоимость. По этой причине железный брусок и мешок с хлопком показывают на весах одинаковую массу, но на самом деле масса хлопкового мешка больше массы железного бруска.
Фактический вес = Измеренный вес + Выталкивающая сила
Видеорешение для гравитации (Страница: 142 , Q.No.: 2)
NCERT Решение для класса 9 – гравитация 142 , Вопрос 2
Страница № 143:
Вопрос 1:
Как изменится сила притяжения между двумя объектами, если расстояние между ними уменьшить вдвое?
Ответ:
Согласно универсальному закону всемирного тяготения гравитационная сила ( F ) действующая между двумя объектами обратно пропорциональна квадрату расстояния ( r) между ними, т. е.
е.
Следовательно, если расстояние уменьшить вдвое, то сила гравитации станет в четыре раза больше прежнего значения.
Видеорешение для гравитации (Страница: 143 , Q.No.: 1)
Решение NCERT для класса 9наука – гравитация 143 , Вопрос 1
Страница № 143:
Вопрос 2:
Гравитационная сила действует на все объекты пропорционально их массам. Почему же тогда тяжелый предмет не падает быстрее легкого?
Ответ:
Все предметы падают на землю с постоянным ускорением, называемым ускорением свободного падения (при отсутствии сопротивления воздуха). Она постоянна и не зависит от массы объекта. Следовательно, тяжелые предметы падают не быстрее, чем легкие.
Видео Решение для гравитации (Страница: 143 , Q.No.: 2)
NCERT Решение для класса 9 науки – гравитация 143 , Вопрос 2
Страница № 143:
Вопрос 3:
сила тяжести между Землей и телом массой 1 кг на ее поверхности? (Масса Земли 6 × 10 24 кг, радиус Земли 6,4 × 10 6 м).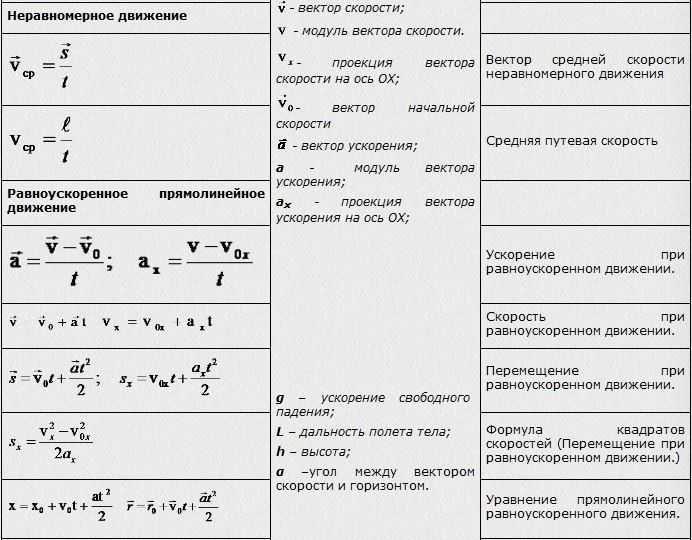
Ответ:
Согласно закону всемирного тяготения сила тяжести действует на объект массой м определяется как:
Где,
Масса Земли, M = 6 × 10 24 кг
Масса объекта, м 900 903 гравитационная постоянная,
= 1 0 6,7 × 10 −11 Н·м 2 кг −2
Поскольку объект находится на поверхности Земли, r = радиус Земли ( R ) 9053 r 3
4 90 = 6,4 × 10 6 мГравитационная сила,
Видео Решение для гравитации (Страница: 143 , Q.No.: 3)
NCERT Решение для класса 9 науки – гравитация 143 , Вопрос 3
Страница № 143 Вопрос 9 4:
9 4:
Земля и Луна притягиваются друг к другу силой гравитации. Притягивает ли Земля Луну с большей или меньшей силой или такой же, как сила, с которой Луна притягивает Землю? Почему?
Ответ:
Согласно закону всемирного тяготения два тела притягиваются друг к другу с одинаковой силой, но в противоположных направлениях. Земля притягивает Луну с такой же силой, с какой Луна притягивает Землю.
Земля притягивает Луну с такой же силой, с какой Луна притягивает Землю.
Видео Решение для гравитации (Страница: 143 , Q.No.: 4)
NCERT Решение для класса 9 науки – гравитация 143 , Вопрос 4
Страница № 143:
Вопрос 5:
2 притягивает землю, почему земля не движется к луне?Ответ:
Земля и Луна испытывают равные гравитационные силы друг от друга. Однако масса Земли намного больше массы Луны. Следовательно, он ускоряется со скоростью меньшей, чем скорость ускорения Луны по отношению к Земле. По этой причине Земля не движется к Луне.
Видеорешение для гравитации (Страница: 143 , Q.No.: 5)
NCERT Решение для класса 9 – гравитация 143 , вопрос 5
Страница № 144:
Вопрос 6:
Что произойдет с силой между двумя телами, если
(i) масса одного тела удвоится?
(ii) расстояние между объектами удваивается и утраивается?
(iii) массы обоих объектов удвоились?
Ответ:
(и) | Двойной | (ii) | Одна четвертая и одна девятая | (iii) | четыре раза |
Согласно закону всемирного тяготения сила притяжения между двумя объектами определяется выражением:
(i) F прямо пропорциональна массам объектов. Если массу одного объекта удвоить, то и гравитационная сила удвоится.
Если массу одного объекта удвоить, то и гравитационная сила удвоится.
(ii) F обратно пропорциональна квадрату расстояний между объектами. Если расстояние удвоится, то сила тяжести станет одной четвертой от своего первоначального значения.
Точно так же, если расстояние утроить, то гравитационная сила станет одной девятой от своего первоначального значения.
(iii) F прямо пропорциональна произведению масс объектов. Если массы обоих объектов удвоить, то гравитационная сила станет в четыре раза больше первоначальной величины.
Видеорешение для гравитации (Страница: 144 , Q.No.: 6)
Решение NCERT для класса 9 по науке – гравитация 144 , вопрос 6
Страница № 144:
Вопрос 7:
Каково значение универсального закона тяготения?
Ответ:
Универсальный закон всемирного тяготения доказывает, что каждый объект во Вселенной притягивает любой другой объект.
Видео Решение для гравитации (Страница: 144 , Q.
 No.: 7)
No.: 7)NCERT Решение для класса 9 науки – гравитация 144 , Вопрос 7
Страница № 144:
Вопрос 8:
2 ускорение свободного падения?Ответ:
Когда объекты падают на Землю только под действием гравитационной силы, говорят, что они находятся в свободном падении. Ускорение свободного падения равно 9,8 м·с −2 и является постоянным для всех тел (независимо от их массы).
Видео Решение для гравитации (Страница: 144 , Q.No.: 8)
NCERT Решение для класса 9 наука – гравитация 144 , Вопрос 8
Страница № 144:
Вопрос 9:
29 назовите гравитационную силу между Землей и объектом?Ответ:
Гравитационная сила между Землей и объектом известна как вес объекта.
Видео Решение для гравитации (Страница: 144 , Q.No.: 9)
NCERT Решение для класса 9 науки – гравитация 144 , вопрос 9 золота на полюсах по указанию одного из его друзей. Он передает то же самое, когда встречает его на экваторе. Согласится ли друг с весом купленного золота? Если нет, то почему? [ Подсказка : Значение г больше на полюсах, чем на экваторе].
Согласится ли друг с весом купленного золота? Если нет, то почему? [ Подсказка : Значение г больше на полюсах, чем на экваторе].
Ответ:
Вес тела на Земле дается:
W = M G
, где,
M = Месса тела
G = ACCELACT гравитация
Величина г больше на полюсах, чем на экваторе. Поэтому золото на экваторе весит меньше, чем на полюсах. Следовательно, друг Амита не согласится с весом купленного золота.
Видео Решение для гравитации (Страница: 144 , Q.No.: 10)
NCERT Решение для класса 9 наука – гравитация 144 , Вопрос 10
Страница № 144:
Вопрос 11: 904 лист бумаги падает медленнее, чем скомканный в комок?
Ответ:
Когда лист бумаги скомкан в шар, то его плотность увеличивается. Следовательно, сопротивление его движению в воздухе уменьшается, и он падает быстрее, чем лист бумаги.
Видео Решение для гравитации (Страница: 144 , Q.
 No.: 11)
No.: 11)NCERT Решение для класса 9 наука – гравитация 144 , Вопрос 11 Поверхность Луны так же сильна, как сила гравитации на Земле. Каков вес в ньютонах объекта массой 10 кг на Луне и на Земле?
Ответ:
Вес объекта на Луне Вес объекта на Земле
Также,
Вес = Масса × Ускорение
Ускорение свободного падения, g = 9,8 м/с 2
Следовательно, вес 10-килограммового объекта на Земле = 10 × 9,8 = 98 Н
И , вес того же объекта на Луне
Видео Решение для гравитации (Страница: 144 , Q.No.: 12)
NCERT Решение для 9 класса науки – гравитация 144 , Вопрос 12
Страница № 144:
Вопрос 13:
Мяч брошен вертикально вверх со скоростью 49РС. Вычислите
(i) максимальную высоту, на которую он поднимается.
(ii) общее время, необходимое для возвращения на поверхность земли.
Answer:
(i) 122.5 m (ii) 10 s
According to the equation of motion under gravity:
v 2 − u 2 = 2 g s
Где
u = начальная скорость мяча
v = конечная скорость мяча
s = высота, достигнутая мячом
g = ускорение свободного падения
На максимальной высоте конечная скорость мяча равна нулю, т. е. v = 0
е. v = 0
u = 49 м/с
При движении вверх g = − 9,8 м с −2
Пусть ч — максимальная высота, достигнутая мячом.
Отсюда
Пусть t – время, за которое мяч достигнет высоты 122,5 м, тогда по уравнению движения:
v = u + g t
Получаем,
Но,
Время подъема = Время спуска 5 +
3 90 = 10 s
Видео Решение для гравитации (Страница: 144 , Q.No.: 13)
NCERT Решение для 9 класса науки – гравитация 144 , Вопрос 13
Страница № 144:
420 Вопрос 42:280 Камень брошен с вершины башни высотой 19.6 м. Вычислите его конечную скорость непосредственно перед касанием земли.Ответ:
Согласно уравнению движения в рамках гравитации:
V 2 – U 2 = 2 G S
, где
3. камень = 0
v = конечная скорость камня
с = высота камня = 19,6 м
г = ускорение свободного падения = 9. 8 м с −2
8 м с −2
∴ V 2 – 0 2 = 2 × 9,8 × 19,6
V 2 = 2 × 9.8 × 19.6 = 19.623923 2 2 2 2 2 2 2 2 2 2 2 2 ). v = 19,6 м с − 1
Следовательно, скорость камня непосредственно перед касанием земли составляет 19,6 м с −1 .
Видеорешение для гравитации (Страница: 144 , Q.No.: 14)
NCERT Решение для класса 9 – гравитация 144 , Вопрос 14
Страница № 144:
Вопрос 15:
Камень брошен вертикально вверх с начальной скоростью 40 м/с. Приняв g = 10 м/с 2 , найдите максимальную высоту, на которую поднялся камень. Чему равно чистое перемещение и общее расстояние, пройденное камнем?
Ответ:
Согласно уравнению движения под действием силы тяжести:
v 2 − u 2 = 2 г с
3 Где0002 u = Начальная скорость камня = 40 м/с
v = Конечная скорость камня = 0
с = Высота камня
g = Ускорение свободного падения = −10 м с −2
Пусть h будет максимальной высотой, достигнутой камнем.
Следовательно,
Следовательно, общее расстояние, пройденное камнем во время его движения вверх и вниз = 80 + 80 = 160 м
Чистое перемещение камня во время его движения вверх и вниз
= 80 + (−80) = 0
Видео Решение для гравитации (Страница: 144 , Q.No.: 15)
NCERT Решение для класса 9 наука – гравитация 144 , Вопрос 15
Страница № 144:
Вопрос 16:
Рассчитайте силу притяжения между Землей и Солнцем, учитывая, что масса Земли = 6 × 10 24 кг и Солнца = 2 × 10 30 кг. Среднее расстояние между ними составляет 1,5 × 10 11 м.
Ответ:
Согласно закону всемирного тяготения сила притяжения между Землей и Солнцем определяется как:
Где,
M Солнце = Масса Солнца = 2 × 10 30 кг
M Земля = Масса Земли = 6 × 10 24 кг
R = Среднее расстояние между Землей и Солнцем = 1,5 × 10 11 3 м гравитационное константа = 6,7 × 10 −11 нм 2 кг −2 Решение NCert для науки класса 9 – Гравитация 144, Вопрос 16 Камень падает с вершины башни высотой 100 м, и в то же время другой камень падает вертикально вверх с земли со скоростью 25 м/с. Рассчитайте, когда и где два камня встретятся. Пусть два камня встретятся через время t . (i) Для камня, упавшего с башни: Начальная скорость, u = 0 Пусть перемещение камня за время t с вершины башни равно с. Ускорение свободного падения, g = 9,8 м с −2 Из уравнения движения, (ii) Для камня, брошенного вверх: Начальная скорость, u = 25 м с −1 Пусть перемещение камня от земли за время t равно с ‘. Ускорение свободного падения, g = −9,8 м с −2 Уравнение движения, Суммарное перемещение обоих камней в точке встречи равно высоте башни 100 м. За 4 с падающий камень преодолел расстояние, определяемое уравнением (1) как Следовательно, камни встретятся через 4 с на высоте (100 − 80) = 20 м от земли Решение NCERT для 9 класса наука – гравитация 144 , Вопрос 17 Вертикально подброшенный мяч возвращается к бросающему через 6 с. Найдите (а) скорость, с которой оно было подброшено вверх, (б) максимальную высоту, на которую оно поднялось, и (в) его положение через 4 с. (а) 29,4 м/с (б) 44,1 м (в) 39,2 м над землей (а) Время подъема равно времени спуска. В общей сложности мяч поднимается и опускается за 6 с. Следовательно, для достижения максимальной высоты потребовалось 3 с. Конечная скорость мяча на максимальной высоте, v = 0 Ускорение свободного падения g = −9,8 м с 0 = u + (−9,8 × 3) u = 9,8 × 3 = 29,4 мс − 1 Следовательно, мяч был брошен вверх со скоростью 4 м с 29.0022 −1 Видео -решение для гравитации (стр.
 : 144, Q.NO.: 16)
: 144, Q.NO.: 16)88. Страница № 144:
Вопрос 17:
Ответ:

Видео Решение для гравитации (Страница: 144, Q.№: 17)
Страница № 144:
Вопрос 18:
Ответ:

(b) Пусть максимальная высота, на которую поднимается мяч, равна h .
Начальная скорость при движении вверх, u = 29,4 м с −1
Конечная скорость, v = 0
Ускорение свободного падения, g = −9,8 м с2 −3 900 движения,
(в) Мяч достигает максимальной высоты через 3 с. Достигнув этой высоты, он начнет падать вниз.
В этом случае
Начальная скорость, u = 0
Положение мяча через 4 с после броска определяется расстоянием, пройденным им при движении вниз за 4 с − 3 с = 1 с.
Уравнение движения даст,
Общая высота = 44,1 м
Это означает, что мяч находится на высоте 39,2 м (44,1 м − 4,9 м) над землей через 4 секунды.
Видеорешение для гравитации (Страница: 144, Q.No.: 18)
Решение NCERT для класса 9наука – гравитация 144 , Вопрос 18
Страница № 145:
Вопрос 19:
В каком направлении действует выталкивающая сила на предмет, погруженный в жидкость?
Ответ:
На предмет, погруженный в жидкость, действует выталкивающая сила, направленная вверх.
Видео Решение для гравитации (Страница: 145 , Q.No.: 19)
NCERT Решение для класса 9 наука – гравитация 145 , Вопрос 19
Страница № 145:
Вопрос 20:
Почему пластиковый блок, выпущенный под воду, всплывает на поверхность воды?
Ответ:
На тело, погруженное в воду, действуют две силы. Одна из них — гравитационная сила, которая тянет объект вниз, а другая — выталкивающая сила, толкающая объект вверх. Если восходящая выталкивающая сила больше, чем направленная вниз гравитационная сила, то объект поднимается на поверхность воды, как только он высвобождается в воде. По этой причине выброшенный под воду блок пластика всплывает на поверхность воды.
По этой причине выброшенный под воду блок пластика всплывает на поверхность воды.
Видео Решение для гравитации (Страница: 145 , Q.No.: 20)
NCERT Решение для класса 9 наука – гравитация 145 , Вопрос 20
Страница № 145:
Том 21: 904 50 г вещества составляет 20 см
3 . Если плотность воды равна 1 г·см −3 , всплывет или утонет вещество?Ответ:
Если плотность объекта больше плотности жидкости, то он тонет в жидкости. С другой стороны, если плотность объекта меньше плотности жидкости, то он плавает на поверхности жидкости.
Здесь плотность вещества =
Плотность вещества больше плотности воды (1 г см −3 ). Следовательно, вещество будет тонуть в воде.
Видео Решение для гравитации (Страница: 145 , Q.No.: 21)
NCERT Решение для 9 класса науки – гравитация 145 , Вопрос 21 запечатанный пакет 500 г составляет 350 см 3 . Будет ли пакет всплывать или тонуть в воде, если плотность воды равна 1 г см 9?0022 −3 ? Какова будет масса воды, вытесненной этим пакетом?
Ответ:
Плотность запечатанного пакета 500 г
Плотность вещества больше плотности воды ().

 , В
, В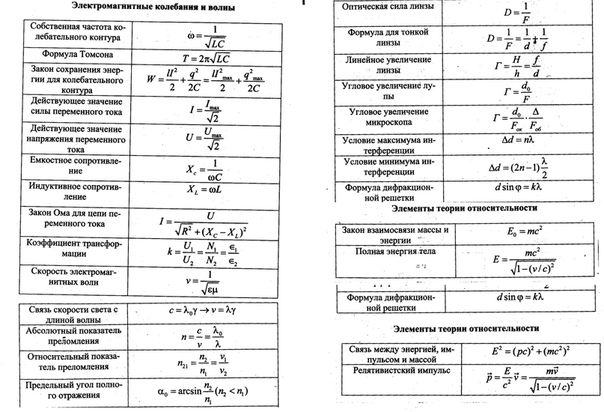
 конденс.
конденс. при движ. по вертик, м/с
при движ. по вертик, м/с -t/T закон радиоактивн распада
-t/T закон радиоактивн распада центростр.уск.
центростр.уск. тока, Вт
тока, Вт на накл.пл. (след.строч.)
на накл.пл. (след.строч.) /гипот.
/гипот. , В
, В энергия, Дж
энергия, Дж тепл. НАГР. ОХЛ, Дж
тепл. НАГР. ОХЛ, Дж света (\ п / в одн.пл.)
света (\ п / в одн.пл.) Л. и др. 5-9 кл.)
Л. и др. 5-9 кл.)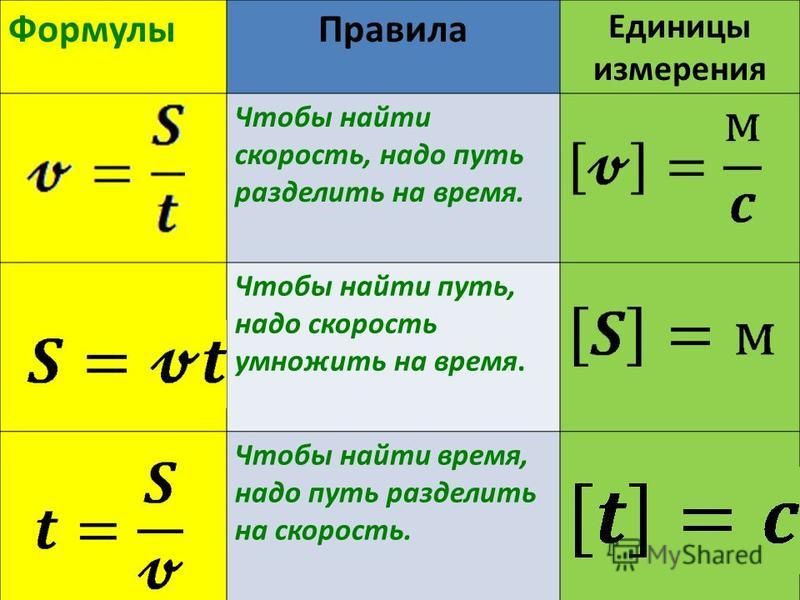 Л.
Л.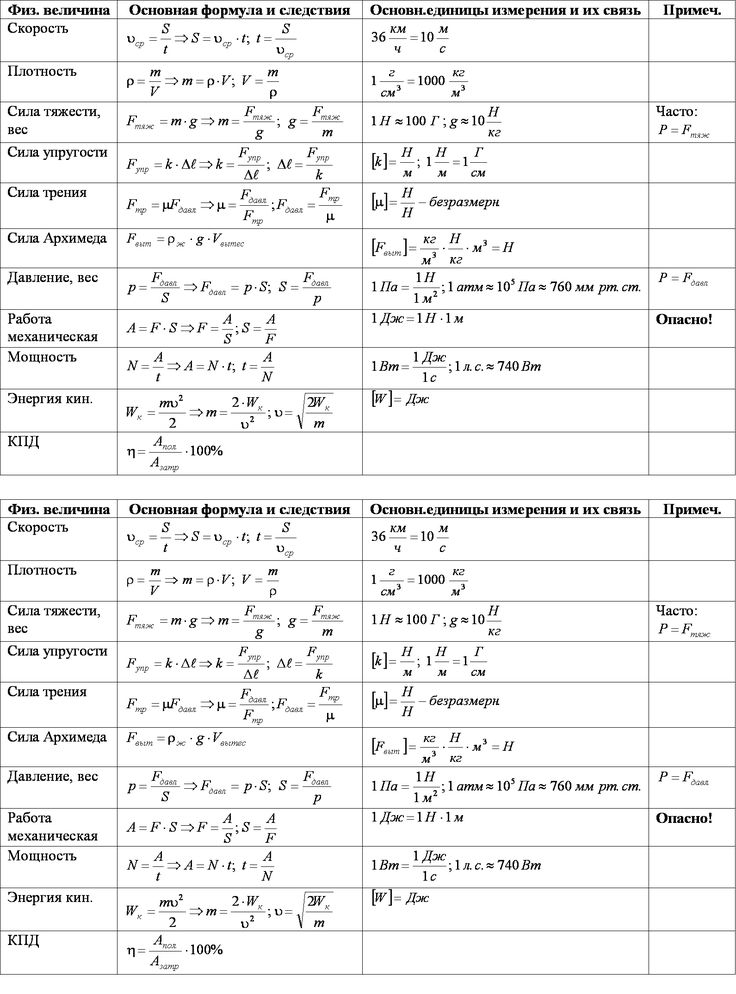
 Вариант 1
Вариант 1
 Вариант 1
Вариант 1 Вариант 1
Вариант 1 Практическая работа
Практическая работа 4. Запись вспомогательных алгоритмов на языке Паскаль
4. Запись вспомогательных алгоритмов на языке Паскаль Обработка числовой информации в электронных таблицах
Обработка числовой информации в электронных таблицах Запись формул» (119384)
Запись формул» (119384) 3. Средства анализа и визуализации данных
3. Средства анализа и визуализации данных Коммуникационные технологии
Коммуникационные технологии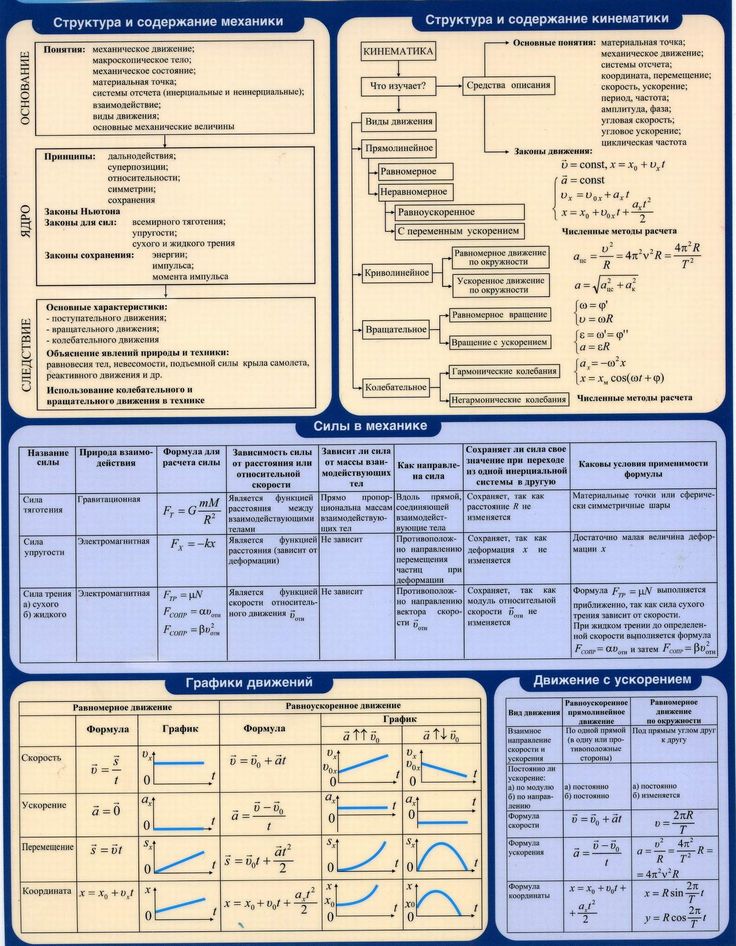 2. Всемирная компьютерная сеть Интернет
2. Всемирная компьютерная сеть Интернет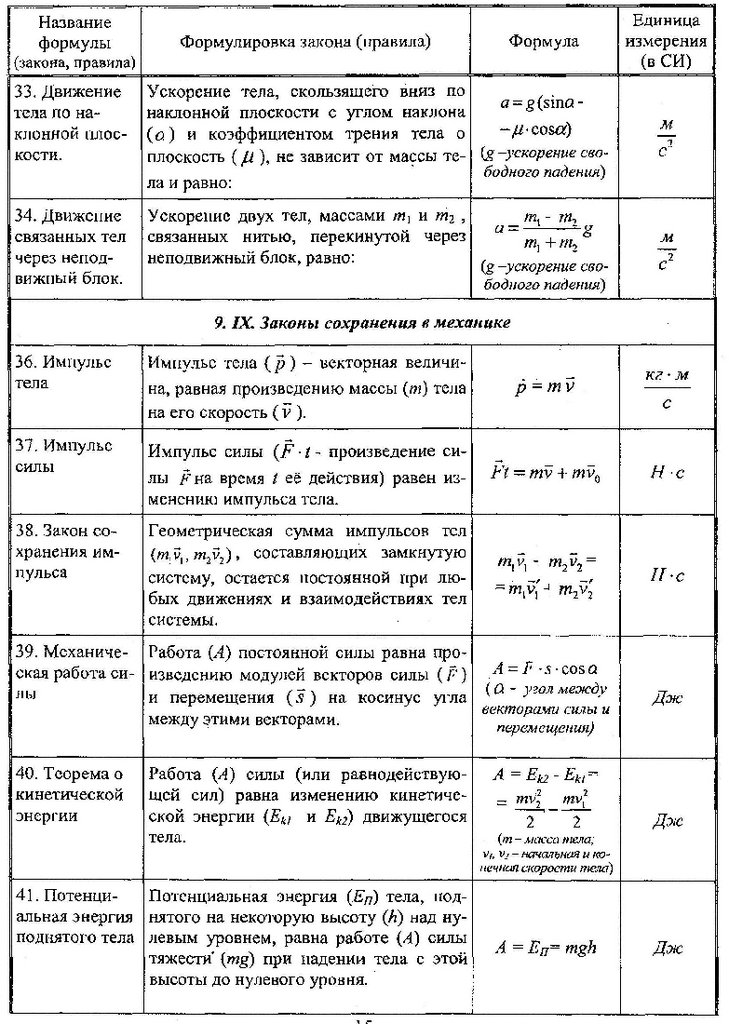
 № .
№ . е. Ньютон (Н).
е. Ньютон (Н).