Формулы кинематика и динамика: Механика - Основные формулы - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Кинематика. Динамика. Законы сохранения

ГОУ ВПО «Воронежский государственный

технический университет»

Кафедра общей физики технологического профиля

363-2008

методические указания

к решению задач

по дисциплине «Общая физика»

для студентов физико-технического факультета

очной формы обучения

Воронеж 2008

Составители: канд.физ.-мат.наук А.Г. Москаленко,

канд. техн. наук М.Н. Гаршина,

канд. физ.-мат. наук Е.П. Татьянина,

канд. физ.мат. наук И.В. Борисова

УДК 531 (07)

Кинематика. Динамика. Законы сохранения: методические указания к решению задач по дисциплине «Общая физика» для студентов физико-технического факультета очной формы обучения /ГОУ ВПО «Воронежский государственный технический университет»; сост.

А.Г. Москаленко, М.Н. Гаршина, Е.П. Татьянина, И.В. Борисова. Воронеж, 2008. 51 с.

В методических указаниях кратко изложен теоретический материал, представлены классификация и методы решения задач, рассмотрены примеры решения типовых задач, соответствующих программе общего курса физики. По каждой теме имеются задачи для самостоятельного решения и варианты контрольных заданий.

Методические указания предназначены для студентов физико-технического факультета.

Табл. 4. Ил. 24. Библиогр.: 6 назв.

Рецензент канд. физ.-мат. наук, доц. Н.В. Матовых

Ответственный за выпуск зав. кафедрой,

профессор В.С. Железный

Печатается по решению редакционно-издательского совета Воронежского государственного технического университета

ГОУВПО «Воронежский государственный

технический университет», 2008

Кинематика.

Динамика. Законы сохранения

методические указания

к решению задач

по дисциплине «Общая физика»

для студентов физико-технического факультета

очной формы обучения

Составители:

Москаленко Александр Георгиевич

Гаршина Мария Николаевна

Татьянина Елена Павловна

Борисова Ирина Владимировна

В авторской редакции

Компьютерный набор Е.П. Татьяниной

Подписано в печать 18.11.2008.

Формат 60х84/16. Бумага для множительных аппаратов.

Усл. печ. л. 3,3 Уч.-изд. л. 3,1. Тираж 100 экз. «С»

Заказ №

ГОУВПО «Воронежский государственный

технический университет»

394026 Воронеж, Московский просп., 14

1. Кинематика

1.

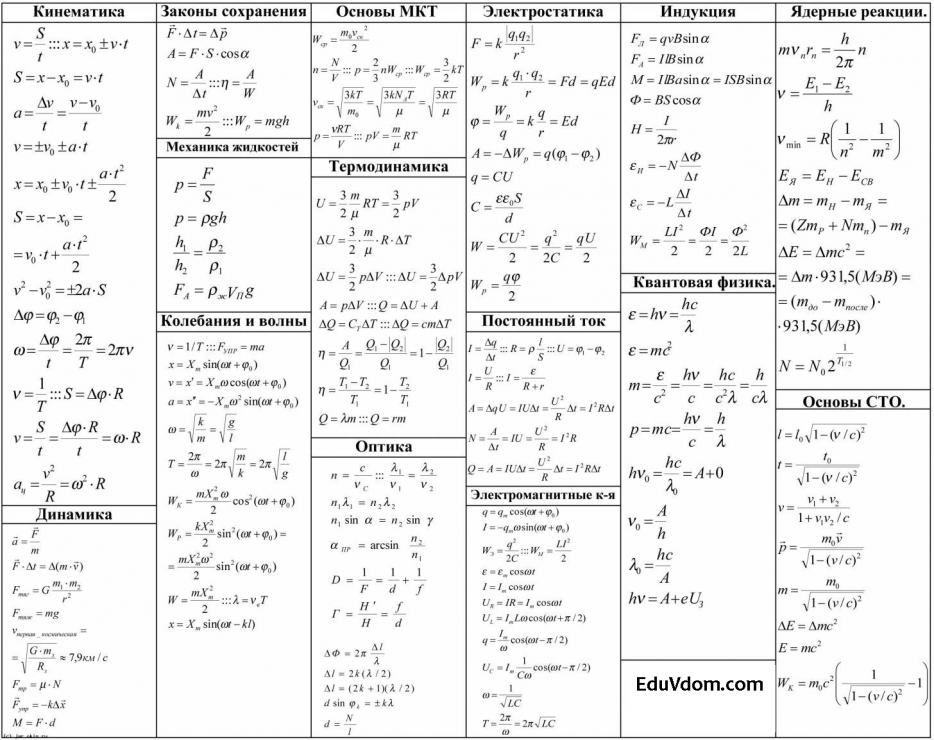1. Основные формулы

1. Кинематическое уравнение движения материальной точки в скалярной и векторной формах:

, , ,

где х, у, z – координаты точки; – радиус-вектор.

2. Скорость движения материальной точки. Вектор средней скорости

где – вектор перемещения.

Вектор скорости в данный момент времени

Модуль вектора скорости

; ,

где S – путь, пройденный точкой.

3. Ускорение движения материальной точки. Вектор среднего ускорения

Вектор ускорения в данный момент времени

, или .

Модуль вектора ускорения

4. Нормальные и тангенциальные составляющие ускорения

, ,

где R – радиус кривизны траектории в данной точке.

Модуль ускорения: .

5. Путь, пройденный материальной точкой: .

6. Угловая скорость вращательного движения твердого тела.

Средняя угловая скорость ,

где – угловой путь при вращательном движении.

Угловая скорость в данный момент времени: .

7. Угловое ускорение твердого тела: .

8. Связь между линейными и угловыми величинами при вращении твердого тела:

, , ,

где R –расстояние от оси вращения.

9. Формулы равнопеременного движения

Поступательное движение

Вращательное движение

Методические указания к решению задач, страница 3

Физика \ Физика

Ответ

: скорость шарика равна и направлена вертикально вниз; координата равна 8,5 м; перемещение направлено вверх и равно 7,2 м.

1.2. Равноускоренное движение на плоскости

Условие равноускоренного движения () не требует, чтобы движение происходило вдоль прямой линии. Если при движении тела в прост-ранстве его ускорение (вектор) остается неизменным, то такое движение будет равноускоренным, следовательно, для его описания справедливы все формулы кинематики, полученные для равноускоренного движения. В качестве примера равноускоренного, но не прямолинейного движения, рассмотрим движение тела, брошенного под углом к горизонту.

Задача 2. С края вертикального утеса, возвышающегося над поверхностью моря на 55 м, под углом 60° к горизонту брошен небольшой камень со скоростью . Пренебрегая сопротивлением воздуха, найти, на каком расстоянии от основания утеса камень упадет в воду, и какую скорость при этом он будет иметь.

Дано:

h = 55 м

α = 60º

v₀ = 15 м/с

s_x, v

– ?

Решение.

Если пренебречь сопротивлением воздуха, то движение тел вблизи поверхности Земли происходит с постоянным ускорением (), направленным вертикально вниз. Воспользуемся формулами кинематики равноускоренного движения:

;

но в отличие от предыдущего примера проекции векторов возьмем на две координатные оси, поскольку движение камня происходит не по прямой, а в плоскости. Выберем начало координат в точке бросания камня, ось Ox направим горизонтально от утеса в сторону моря, а ось

Oy – вертикально вниз. (Из рис. 2 видно, что при таком выборе системы координат проекции всех векторов, входящих в формулы и , кроме , будут положительны.) Возьмем проекции и получим:

Из рис. 2 видно, что проекция вектора перемещения на ось Oy равна высоте утеса h, а на ось Ox – расстоянию от основания утеса до точки падения камня в воду, которое требуется найти.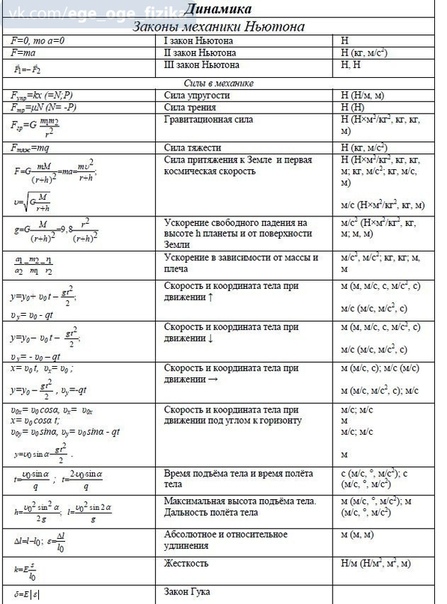 Определим это расстояние, решая сов-местно систему уравнений . Из второго уравнения системы , решая квадратное уравнение и выбирая положительный корень, выразим время:

Подставляя выражение в первое уравнение системы , получим:

;

Теперь найдем скорость, с которой камень упал в воду. Проекции ско-рости определяются системой , а модуль рассчитывается по формуле:

Подставим в формулу время из выражения и, раскрывая скобки и проведя алгебраические преобразования, получим:

;

Этот же результат можно получить иначе. Используя правила векторной алгебры, из выражений и получим:

Расписывая скалярное произведение в правой части равенства , получим формулу:

, поскольку произведение есть проекция перемещения на вертикальную ось. Такой же результат можно получить, расписав скалярное произведение еще одним известным способом и подставив проекции векторов и на координатные оси (см. начало решения задачи):

Ответ: камень упадет в воду на расстоянии 37 м от утеса со скоростью 36 .

1.3. Движение по окружности с постоянной по модулю скоростью

Движение тела по окружности с постоянной по модулю скоростью не является равноускоренным движением, несмотря на то, что модуль ускорения

остается неизменным, так как вектор ускорения постоянно поворачивается. Ускорение, с которым при этом движется тело, называется центростремительным, или нормальным, так как оно направлено к центру окружности и перпендикулярно вектору скорости.

Задача 3. Модель самолета движется с постоянной скоростью по окружности радиусом 6,3 м и пролетает третью часть окружности за 1,2 с. Найти изменение ускорения модели за это время.

Скачать файл

Выбери свой ВУЗ

АлтГТУ 419
АлтГУ 113
АмПГУ 296
АГТУ 267
БИТТУ 794
БГТУ «Военмех» 1191
БГМУ 172
БГТУ 603
БГУ 155
БГУИР 391
БелГУТ 4908
БГЭУ 963
БНТУ 1070
БТЭУ ПК 689
БрГУ 179
ВНТУ 120
ВГУЭС 426
ВлГУ 645
ВМедА 611
ВолгГТУ 235
ВНУ им. Даля 166
ВЗФЭИ 245
ВятГСХА 101
ВятГГУ 139
ВятГУ 559
ГГДСК 171
ГомГМК 501
ГГМУ 1966
ГГТУ им. Сухого 4467
ГГУ им. Скорины 1590
ГМА им. Макарова 299
ДГПУ 159
ДальГАУ 279
ДВГГУ 134
ДВГМУ 408
ДВГТУ 936
ДВГУПС 305
ДВФУ 949
ДонГТУ 498
ДИТМ МНТУ 109
ИвГМА 488
ИГХТУ 131
ИжГТУ 145
КемГППК 171
КемГУ 508
КГМТУ 270
КировАТ 147
КГКСЭП 407
КГТА им. Дегтярева 174
КнАГТУ 2910
КрасГАУ 345
КрасГМУ 629
КГПУ им. Астафьева 133
КГТУ (СФУ) 567
КГТЭИ (СФУ) 112
КПК №2 177
КубГТУ 138
КубГУ 109
КузГПА 182
КузГТУ 789
МГТУ им. Носова 369
МГЭУ им. Сахарова 232
МГЭК 249
МГПУ 165
МАИ 144
МАДИ 151
МГИУ 1179
МГОУ 121
МГСУ 331
МГУ 273
МГУКИ 101
МГУПИ 225
МГУПС (МИИТ) 637
МГУТУ 122
МТУСИ 179
ХАИ 656
ТПУ 455
НИУ МЭИ 640
НМСУ «Горный» 1701
ХПИ 1534
НТУУ «КПИ» 213
НУК им. Макарова 543
НВ 1001
НГАВТ 362
НГАУ 411
НГАСУ 817
НГМУ 665
НГПУ 214
НГТУ 4610
НГУ 1993
НГУЭУ 499
НИИ 201
ОмГТУ 302
ОмГУПС 230
СПбПК №4 115
ПГУПС 2489
ПГПУ им. Короленко 296
ПНТУ им. Кондратюка 120
РАНХиГС 190
РОАТ МИИТ 608
РТА 245
РГГМУ 117
РГПУ им. Герцена 123
РГППУ 142
РГСУ 162
«МАТИ» — РГТУ 121
РГУНиГ 260
РЭУ им. Плеханова 123
РГАТУ им. Соловьёва 219
РязГМУ 125
РГРТУ 666
СамГТУ 131
СПбГАСУ 315
ИНЖЭКОН 328
СПбГИПСР 136
СПбГЛТУ им. Кирова 227
СПбГМТУ 143
СПбГПМУ 146
СПбГПУ 1599
СПбГТИ (ТУ) 293
СПбГТУРП 236
СПбГУ 578
ГУАП 524
СПбГУНиПТ 291
СПбГУПТД 438
СПбГУСЭ 226
СПбГУТ 194
СПГУТД 151
СПбГУЭФ 145
СПбГЭТУ «ЛЭТИ» 379
ПИМаш 247
НИУ ИТМО 531
СГТУ им. Гагарина 114
СахГУ 278
СЗТУ 484
СибАГС 249
СибГАУ 462
СибГИУ 1654
СибГТУ 946
СГУПС 1473
СибГУТИ 2083
СибУПК 377
СФУ 2424
СНАУ 567
СумГУ 768
ТРТУ 149
ТОГУ 551
ТГЭУ 325
ТГУ (Томск) 276
ТГПУ 181
ТулГУ 553
УкрГАЖТ 234
УлГТУ 536
УИПКПРО 123
УрГПУ 195
УГТУ-УПИ 758
УГНТУ 570
УГТУ 134
ХГАЭП 138
ХГАФК 110
ХНАГХ 407
ХНУВД 512
ХНУ им. Каразина 305
ХНУРЭ 325
ХНЭУ 495
ЦПУ 157
ЧитГУ 220
ЮУрГУ 309

Полный список ВУЗов

Что такое кинематика, обратная кинематика, 4 уравнения кинематики

Кинематические формулы представляют собой набор уравнений, описывающих движение объекта под действием постоянного ускорения. Эти уравнения можно использовать для решения задач, связанных с положением, скоростью и ускорением, и они основаны на фундаментальных принципах движения и законах физики .

Что такое кинематические формулы:

Четыре формулы кинематики:

v = v₀ + at
х = х₀ + v₀t + (1/2)at²
v² = v₀² + 2a(x – x₀)
х = (v + v₀)/2t

Где: –

Эти уравнения полезны для решения задач, связанных с движением объектов под действием постоянного ускорения, таких как падение объектов, движение снарядов и ускорение под действием силы тяжести. Их можно использовать для поиска неизвестных переменных, таких как положение, скорость и ускорение, при заданных значениях других переменных.

v — конечная скорость объекта.
v₀ — начальная скорость объекта.
а — ускорение объекта.
t — истекшее время.
x — смещение объекта.
x₀ — исходное положение объекта.

v = v₀ + at:

Это уравнение описывает изменение скорости тела под действием постоянного ускорения. Он связывает начальную и конечную скорости объекта с его ускорением и прошедшим временем.

x = x₀ + v₀t + (1/2)at²:

Это уравнение описывает перемещение объекта под действием постоянного ускорения. Он связывает начальное положение, скорость и ускорение объекта с его перемещением и прошедшим временем.

v² = v₀² + 2a(x – x₀):

Это уравнение связывает начальную и конечную скорости объекта с его ускорением и перемещением. Его можно использовать для определения конечной скорости объекта по его начальной скорости, ускорению и смещению.

x = (v + v₀)/2t:

Это уравнение описывает среднюю скорость объекта за заданный интервал времени. Он связывает начальную и конечную скорости объекта с его перемещением и прошедшим временем.

Обратная кинематика

Обратная кинематика относится к процессу нахождения углов сочленения, необходимых для достижения манипулятором определенного положения. Это противоположно прямой кинематике, которая включает в себя определение конечного положения манипулятора с учетом углов его сочленения.

Чтобы решить задачу обратной кинематики, вам нужно знать геометрию манипулятора и положение, которое вы хотите, чтобы он достиг. Существует несколько методов решения инверсной кинематики, включая аналитические методы, численные методы и методы, основанные на машинном обучении.

Одним из распространенных методов решения инверсной кинематики является метод Якоби, который включает в себя нахождение производной положения рабочего органа по отношению к углам сустава, а затем вычисление углов сустава, которые приведут к желаемому положению рабочего органа.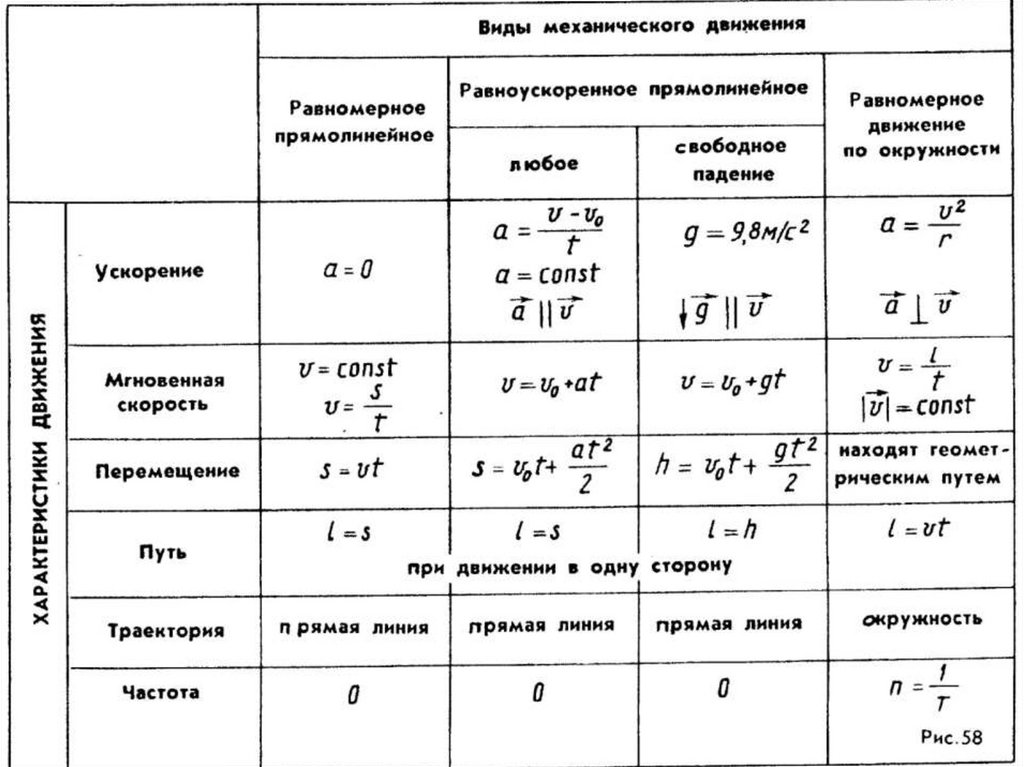

Обратная кинематика является важной проблемой в робототехнике, так как она позволяет роботам двигать конечностями и манипуляторами таким образом, чтобы выполнить желаемую задачу.

Уравнения вращательной кинематики

Вращательная кинематика — это изучение вращательного движения, которое относится к движению объекта вокруг оси вращения. Уравнения кинематики вращения описывают связь между угловым положением, скоростью и ускорением тела, а также силами и моментами, действующими на тело.

Уравнения кинематики вращения:

θ = θ₀ + ω₀t + (1/2)αt²
ω = ω₀ + αt
α = (ω – ω₀)/t
Iα = τ

Где: –

Эти уравнения можно использовать для решения задач, связанных с вращательным движением объекта.

θ — угловое положение объекта
θ₀ — начальное угловое положение объекта
ω — угловая скорость объекта
ω₀ — начальная угловая скорость объекта
α – угловое ускорение объекта
t – истекшее время
I – момент инерции объекта
τ — крутящий момент, приложенный к объекту

Как выбрать и использовать кинематическую формулу?

Чтобы выбрать и использовать кинематическую формулу, необходимо знать переменные, описывающие движение объекта, такие как его положение, скорость и ускорение. Также необходимо знать взаимосвязь между этими переменными, которая описывается кинематическими уравнениями.

-: Вот несколько шагов, которые вы можете выполнить, чтобы выбрать и использовать кинематическую формулу: –

Определите известные и неизвестные переменные. Составьте список переменных, которые приведены в задаче, и отдельный список переменных, которые вам нужно найти.

Определить тип движения. Объект совершает линейное или вращательное движение? Ускорение постоянно или меняется?

Выберите соответствующее уравнение кинематики. В зависимости от типа движения и известных и неизвестных переменных вы можете выбрать подходящее уравнение кинематики для использования.

Подставить известные значения в уравнение кинематики. Подставьте в уравнение значения известных переменных, используя правильные единицы измерения.

Найдите неизвестную переменную. Используйте алгебраические операции, чтобы найти неизвестную переменную.

Проверьте свой ответ. Убедитесь, что единицы ответа соответствуют задаче, и убедитесь, что решение имеет смысл в контексте задачи

Скорость, ускорение и сопротивление воздуха

Скорость — это мера того, насколько быстро движется объект, и определяется как скорость изменения положения объекта. Ускорение — это мера того, насколько быстро изменяется скорость объекта, и оно определяется как скорость изменения скорости объекта.

Сопротивление воздуха — это сила, действующая на объект, движущийся в воздухе, и она вызывается столкновением объекта с молекулами воздуха. Сопротивление воздуха пропорционально скорости объекта и действует в направлении, противоположном движению объекта.

Уравнения, описывающие движение объекта под действием постоянного ускорения и сопротивления воздуха:

v = v₀ + at – (b/m)v² x = x₀ + v₀t + (1/ 2)at² – (b/6m)v₀t³ – (b/24m)at²t

Где:

Эти уравнения можно использовать для решения задач о движении объекта под действием постоянного ускорения и сопротивления воздуха.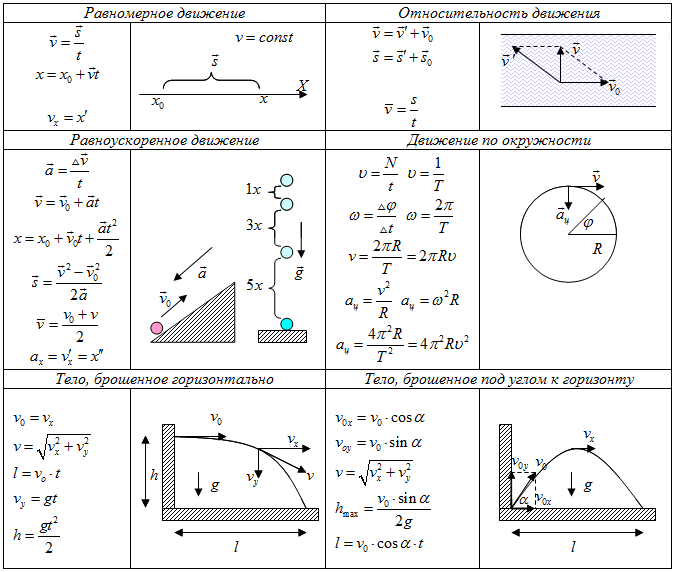

v – скорость объекта
v₀ начальная скорость объекта
а – ускорение объекта
t – истекшее время
x – позиция объекта
x₀ — начальная позиция объекта
b – коэффициент сопротивления воздуха
м – масса объекта

Как вывести уравнения кинематики

Уравнения кинематики можно вывести из фундаментальных принципов движения и законов физики. Вот как вывести основные уравнения кинематики:

Первое кинематическое уравнение , v = v₀ + at можно получить, применяя принцип линейного количества движения к объекту, движущемуся с постоянным ускорением. Линейный импульс определяется как произведение массы и скорости объекта.
Второе кинематическое уравнение, x = x₀ + v₀t + (1/2)at² , может быть получено путем интегрирования первого кинематического уравнения по времени. Это уравнение описывает перемещение объекта под действием постоянного ускорения.
Третье кинематическое уравнение, v² = v₀² + 2a(x – x₀) , может быть получено путем применения принципа сохранения энергии к объекту, движущемуся с постоянным ускорением. Это уравнение связывает начальную и конечную скорости объекта с его ускорением и перемещением.
Четвертое кинематическое уравнение, x = (v + v₀)/2t , может быть получено путем преобразования второго кинематического уравнения. Это уравнение описывает среднюю скорость объекта за заданный интервал времени.

Эти приведенные выше уравнения могут быть использованы для решения задач, связанных с движением объекта под действием постоянного ускорения.

Что смущает в кинематических формулах?

Одним из возможных источников путаницы с кинематическими формулами является запоминание того, какие переменные известны, а какие неизвестны. Кинематические формулы включают в себя несколько переменных, включая положение, скорость, ускорение и время, и их легко перепутать при постановке и решении задачи.

Другим потенциальным источником путаницы является определение подходящей кинематической формулы для решения данной задачи. Существует четыре кинематических формулы, каждая из которых применима к определенному типу задач. Важно выбрать правильную формулу на основе известных и неизвестных переменных, а также типа задействованного движения.

Наконец, отслеживание единиц измерения при использовании кинематических формул может привести к путанице. Важно убедиться, что единицы измерения переменных одинаковы во всей задаче и что единицы измерения ответа верны.

Если у вас возникли трудности с пониманием кинематических формул, может быть полезно поработать над некоторыми практическими задачами, чтобы лучше понять, как они используются. Вы также можете обратиться за помощью к репетитору или учителю, если вы все еще боретесь.

Что такое радиальное ускорение?.

Радиальное ускорение — это ускорение объекта по направлению к центру кругового пути или от него. Это составляющая полного ускорения объекта, движущегося по круговой траектории, и она вызвана изменением направления скорости объекта.

Радиальное ускорение может быть положительным или отрицательным, в зависимости от направления ускорения. Если радиальное ускорение положительное, объект ускоряется по направлению к центру кругового пути. Если радиальное ускорение отрицательное, объект ускоряется от центра круговой траектории.

Величина радиального ускорения определяется уравнением: a_r = v²/r, где v — скорость объекта, а r — радиус кругового пути. Это уравнение можно использовать для нахождения радиального ускорения объекта, движущегося по круговой траектории.

Определение кинетической энергии

Кинетическая энергия — это энергия, которой обладает объект вследствие его движения. Это скалярная величина, и она определяется как работа, проделанная для ускорения объекта из состояния покоя до его текущей скорости.

Кинетическая энергия объекта определяется уравнением:

KE = (1/2)mv²

Где:-

KE — кинетическая энергия объекта
м – масса объекта
v – скорость объекта

Единицей кинетической энергии является джоуль (Дж). Кинетическая энергия — это мера способности объекта совершать работу за счет его движения. Это связано с принципом работы-энергии, который гласит, что работа, совершаемая над объектом, равна изменению кинетической энергии объекта.

Когда максимальная кинетическая энергия?

Кинетическая энергия объекта максимальна, когда скорость объекта максимальна. Это происходит, когда объект движется с максимальной скоростью и достиг своей конечной скорости.

Например, если вы уроните шар для боулинга с высоты, его кинетическая энергия увеличится при падении из-за ускорения свободного падения. Кинетическая энергия мяча будет максимальной, когда он достигнет своей конечной скорости, т. е. точки, в которой сила сопротивления воздуха, действующая на мяч, равна силе тяжести. В этот момент мяч больше не будет ускоряться, и его скорость останется постоянной.

Кинетическая энергия объекта также может быть увеличена путем приложения к объекту силы, заставляющей его ускоряться. Например, если вы толкаете сани в гору, кинетическая энергия саней будет увеличиваться по мере того, как они набирают скорость. Кинетическая энергия саней будет максимальной, когда они достигнут вершины холма и начнут скатываться вниз.

Решенные примеры кинематических уравнений

Пример 1:

Мяч брошен вверх с начальной скоростью 20 м/с. Достигает максимальной высоты 50 метров. Чему равно ускорение мяча под действием силы тяжести?

Ответ:

Чтобы решить эту задачу, мы можем использовать второе уравнение кинематики: x = x₀ + v₀t + (1/2)at²

В этом уравнении x – конечное положение мяча (50 метров), x₀ — начальное положение мяча (0 метров, так как мяч стартует с земли), v₀ — начальная скорость мяча (20 м/с), t — прошедшее время. Пытаемся найти ускорение, а.

Мы можем найти ускорение, изменив уравнение для решения a: a = 2(x – x₀ – v₀t)/t²

Подставив известные значения, мы получим: a = 2(50 – 0 – 20t) /t²

Чтобы найти прошедшее время, мы можем использовать первое уравнение кинематики: v = v₀ + at

Поскольку мяч достигает максимальной высоты в начале своей траектории, его скорость в этой точке равна 0 м/с.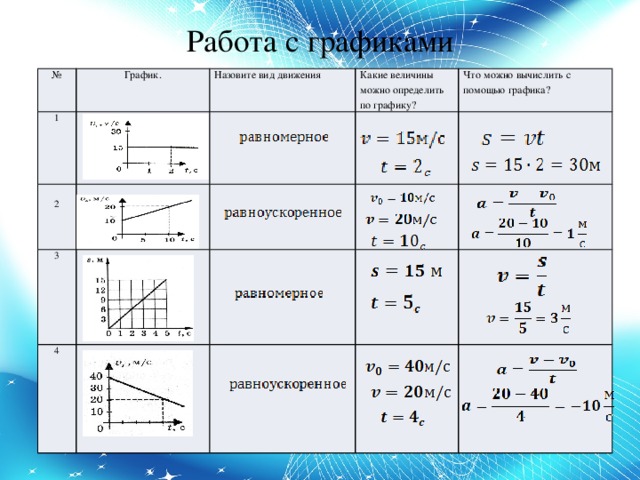 Подставляя это значение в уравнение, получаем: 0 = 20 + a(t)

Решая t, получаем: t = -20/a

Подставляя это значение в уравнение для ускорения, получаем: a = 2(50 – 0 – 20(-20/a))/((-20/a)²) = -10 м/с²

Это ускорение мяча под действием силы тяжести. Знак минус указывает на то, что ускорение направлено в сторону, противоположную первоначальному движению мяча.

Пример 2:

Автомобиль движется по шоссе с постоянной скоростью 60 миль в час. Водитель внезапно ударил по тормозам, в результате чего машина остановилась на расстоянии 200 футов. Каково было ускорение автомобиля?

Ответ:

Для решения этой задачи мы можем использовать второе уравнение кинематики: x = x₀ + v₀t + (1/2)at² 200 футов), x₀ — начальное положение автомобиля (0 футов, так как автомобиль трогается с места), v₀ — начальная скорость автомобиля (60 миль в час), t — прошедшее время. Пытаемся найти ускорение, а.

Мы можем найти ускорение, изменив уравнение для решения a: a = 2(x – x₀ – v₀t)/t²

Подставляя известные значения, получаем: a = 2(200 – 0 – 60t)/t²

Прошедшее время можно найти, разделив пройденное расстояние на начальную скорость: t = 200/60 = 3,33 секунды

Подставляя это значение в уравнение для ускорения, получаем: a = 2(200 – 0 – 60(3,33))/(3,33)² = -11,11 фут/с²

Это ускорение автомобиля в момент остановка. Знак минус указывает на то, что ускорение направлено в сторону, противоположную первоначальному движению автомобиля.

Это всего лишь один пример того, как можно использовать кинематические формулы для решения задачи о движении объекта под действием постоянного ускорения.

Часто задаваемые вопросы – Часто задаваемые вопросы

Вот некоторые часто задаваемые вопросы о кинематических уравнениях:

Что такое кинематические уравнения?

Кинематические уравнения представляют собой набор уравнений, описывающих движение объекта под действием постоянного ускорения. Четыре кинематических уравнения: v = v₀ + at, x = x₀ + v₀t + (1/2)at², v² = v₀² + 2a(x – x₀) и x = (v + v₀)/2t.

Как выбрать правильное уравнение кинематики?

Чтобы выбрать правильное уравнение кинематики, вам необходимо знать переменные, описывающие движение объекта, такие как его положение, скорость и ускорение. Также необходимо знать взаимосвязь между этими переменными, которая описывается кинематическими уравнениями. Определите известные и неизвестные переменные, определите тип вовлеченного движения, а затем выберите соответствующее кинематическое уравнение на основе этих факторов.

Как вы используете кинематические уравнения для решения задач?

Чтобы использовать кинематические уравнения для решения задач, выполните следующие действия: (1) Определите известные и неизвестные переменные, (2) определите подходящее кинематическое уравнение для использования, (3) подставьте известные значения в уравнение, (4 ) найдите неизвестную переменную и (5) проверьте свой ответ, чтобы убедиться, что он разумен.

Каковы некоторые распространенные источники ошибок при использовании кинематических уравнений?

Некоторые распространенные источники ошибок при использовании кинематических уравнений включают смешение известных и неизвестных переменных, выбор неправильного кинематического уравнения, ошибки с единицами измерения и неправильную интерпретацию задачи. Чтобы избежать этих ошибок, важно внимательно прочитать задачу и убедиться, что вы понимаете, о чем спрашивается, а также перепроверить свою работу, чтобы убедиться, что вы правильно поставили и решили задачу.

В чем разница между кинематикой и динамикой?

Кинематика — это изучение движения и отношений между положением, скоростью и ускорением без учета сил, вызывающих движение. Динамика изучает движение и отношения между силами и движением, которое они производят.

В чем разница между линейной и вращательной кинематикой?

Линейная кинематика изучает движение по прямой линии, а вращательная кинематика изучает вращательное движение вокруг оси вращения.

В чем разница между равномерным и неравномерным движением?

Равномерное движение – это прямолинейное движение с постоянной скоростью. Неравномерное движение – это движение с изменяющейся скоростью или направлением.

Как вы используете кинематические уравнения для решения задач, связанных с сопротивлением воздуха?

Для решения задач, связанных с сопротивлением воздуха, можно использовать кинематические уравнения, учитывающие силу сопротивления воздуха, действующую на объект.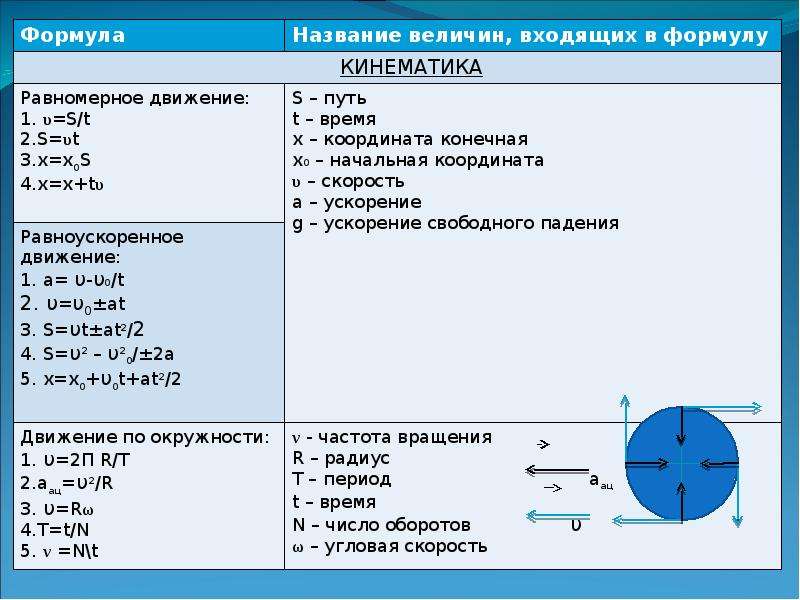 Эти уравнения таковы: v = v₀ + at – (b/m)v² и x = x₀ + v₀t + (1/2)at² – (b/6m)v₀t³ – (b/24m)at²t, где b – коэффициент сопротивление воздуха, а m – масса объекта.

Как вы используете кинематические уравнения для решения задач, связанных с круговым движением?

Для решения задач, связанных с круговым движением, можно использовать уравнения кинематики вращения, которые описывают взаимосвязь между угловым положением, скоростью и ускорением объекта, а также силами и моментами, действующими на объект.

2 Уравнения динамики, кинематика, диаграммы скорости и ускорения

2.1 Вывод формулы вращения
2.2 Разные советы
2.3 Формулы
2.4 Диаграммы скорости и ускорения
2.5 Скорость и ускорение твердого тела 2D
2.6 Скорость и ускорение твердого тела 3D
2.7 Прецессия пробуксовки колес
2.8 Ссылки
2.9 Разное. предметы

2.

1 Вывод формулы вращения

Эта формула очень важна. Теперь подробно покажу его происхождение. Это как выразить векторы во вращающихся кадрах.

Рассмотрим эту схему

Рисунок 2.1: Вращающиеся рамки

В приведенном выше примере малая ось \(x,y\) представляет собой рамку, прикрепленную к некоторому телу, которое вращается вокруг этой оси. с угловой скоростью \(\omega\) (измеряемой, конечно, инерциальной системой отсчета). Все выведенные ниже законы на основе следующего правила\begin {equation} \left . \frac {d}{dt}r\right \vert _{absolute}=\left . \frac {d}{dt}r\right \vert _ {относительный}+\omega \times r \tag {1} \end {уравнение}

Давайте посмотрим, как применить это правило. Выразим вектор положения частицы \(r_{p}\). Мы можем увидеть сложением нормальных векторов, что вектор положения частицы равен \begin {equation} r_{p}=r_{o}+r \tag {2} \end {equation}

Обратите внимание, что ничего особенного здесь не требуется, так как мы еще не рассматривали скорость изменения с помощью время. Сложность (т.е. использование правила (1)) появляется только тогда, когда мы хотим посмотреть на скорости и ускорения. Это когда нам нужно использовать вышеуказанное правило (1). Теперь найдем скорость частица. Сверху\[ \dot {r}_{p}=\dot {r}_{o}+\dot {r} \]

Каждый раз, когда мы берем деривативы, мы останавливаемся и смотрим. Для любого вектора, исходящего из движущегося кадра, мы должны применить к нему правило (1). Это все. В приведенном выше примере только \(r\) нужно применить к нему правило (1), поскольку это единственная векторная мера из движущейся системы отсчета. Замена \(\dot {r}_{p}\) на \(V_{p}\) и \(\dot {r}_{o}\) на \(V_{o}\), что означает скорость \(P\) и \(o\), Следовательно, приведенное выше становится \[ V_{p}=V_{o}+\dot {r} \]

и теперь мы применяем правило (1) для расширения \(\dot {r}\)\begin {equation} V_{p}=V_{o}+\left ( V_{rel}+\omega \times r\ справа ) \tag {3} \end {уравнение}

, где \(V_{rel}\) просто \(\left . \frac {d}{dt}r\right \vert _{relative}\,\)

Приведенное выше окончательное выражение для скорости частицы \(V_{p}\) с использованием ее скорости, измеренной движущуюся рамку, чтобы завершить выражение.

Итак, выше сказано, что абсолютная скорость частицы равна абсолютной скорость основания движущейся системы отсчета + что-то еще и это что-то еще было \(\left ( V_{rel}+\omega \times r\right ) \)

Теперь найдем абсолютное ускорение \(P\). Взятие производных по времени от (3) дает \begin {equation} \dot {V}_{p}=\dot {V}_{o}+\left ( \dot {V}_{rel}+\dot {\ омега }\times r+\omega \times \dot {r}\right ) \tag {4} \end {уравнение}

Как мы сказали выше, каждый раз, когда мы берем производные по времени, мы останавливаемся и ищем векторы, которые на основе подвижной системы отсчета и применить к ним правило (1). В приведенном выше примере \(\dot {V}_{rel}\) и \(\dot {r}\) подходят. Применить правило (1) to \(\dot {V}_{rel}\) дает\begin {equation} \dot {V}_{rel}=a_{rel}+\omega \times V_{rel} \tag {5 } \end {уравнение}

где \(a_{rel}\) просто означает ускорение относительно движущейся системы координат. И применяя правило (1) к \(\dot {r}\) дает\begin {уравнение} \dot {r}=V_{rel}+\omega \times r \tag {6} \end {уравнение}

Замена (5) и (6) на (4) дает \begin {align} a_{p} & =a_{o}+\left ( a_{rel}+\omega \times V_{rel}+\dot {\ omega } \ times r + \ omega \ times \ left ( V_ {rel} + \ omega \ times r \ right ) \ right ) \ nonumber \\ & = a_ {o} + a_ {rel} + \ left ( \ омега \times V_{rel}\right ) +\left ( \dot {\omega }\times r\right ) +\left ( \omega \times V_{rel}\right ) +\left ( \omega \times \ влево ( \omega \times r\right ) \right ) \nonumber \\ & =a_{o}+a_{rel}+2\left ( \omega \times V_{rel}\right ) +\left ( \dot {\ omega } \ times r \ right ) + \ left ( \ omega \ times \ left ( \ omega \ times r \ right ) \ right ) \ tag {7} \ end {align}

Уравнение (7) говорит, что абсолютное ускорение \(a_{p}\) \(P\) равно сумме ускорений основания \(a_{o}\) движущаяся система плюс относительное ускорение \(a_{rel}\) частицы относительно движущейся системы плюс \(2\влево (\omega \times V_{rel}\right) +\влево (\dot {\omega}\times r\right) +\влево (\omega \times \left (\omega \times r\ верно-верно ) \)

Следовательно, использование уравнений (3) и (7) дает нам нужные выражения для скорости и ускорение.

2.2 Разные советы

При нахождении обобщенной силы для пользователя методом Лагранжа (т. самый трудный шаг), используя метод виртуальной работы, если сила (или виртуальная работа сила) ДОБАВЛЯЕТ энергию системе, затем делает знак силы положительным иначе знак отрицательный.
Знак силы демпфирования всегда отрицательный.
Внешние силы, такие как приложенные линейные силы, приложенный крутящий момент, как правило, положительны.
Сила трения отрицательна (в общем случае), так как трение забирает энергию у системы, например демпфирование.

2.3 Формулы

Рисунок 2.2: Формулы 1 Рисунок 2.3: Формулы 2

2.4 Диаграммы скорости и ускорения

2.4.1 Пружинный маятник
2.4.2 маятник с каплей, движущейся в прорези
2.4.3 пружинный маятник с блоком, перемещающимся в прорези
2.4.4 двойной маятник

2.4.1 Пружинный маятник

Рисунок 2.4: Пружинный маятник

2.4.

2 маятник с каплей, движущейся в прорези Рисунок 2.5: маятник с каплей

2.4.3 пружинный маятник с блоком, перемещающимся в пазу

Рисунок 2.6: Пружинный маятник с блоком, движущимся в пазу

2.4.4 двойной маятник

Рисунок 2.7: двойной маятник

2.5 Скорость и ускорение твердого тела 2D

Рисунок 2.8: Скорость и ускорение твердого тела 2D

Нахождение линейного ускорения центра масс твердого тела при чистом вращении с использованием неподвижного тела координаты.

В указанном выше \(U\) скорость центра масс в направлении оси \(x\), где эта ось фиксируется на самом теле. Точно так же \(V\) есть скорость центра масс в направлении оси \(у\), где ось \(у\) связана с самим телом.

Просто помните, что все эти скорости (т.е. \(U\),\(V\)) и ускорения (\(a_{x}\), \(a_{y}\)) все еще измеряются наблюдатель в инерциальной системе отсчета. Только направления компонент скорости центр масс расположен вдоль оси, закрепленной на корпусе. Только направление. Но реальная скорость измерения по-прежнему выполняются стационарным наблюдателем. Поскольку ясно, что если наблюдатель сидел на самом теле, то и скорости будут измерять нулевыми в том дело.

2.6 Скорость и ускорение твердого тела 3D

  2.6.1 Использование обозначений динамики автомобиля
  2.6.2 3D без использования обозначений динамики автомобиля
  2.6.3 Условия ускорения вследствие вращения и ускорения

2.6.1 Использование обозначений динамики автомобиля

Рисунок 2.9: Обозначения динамики автомобиля

2.6.2 3D без использования обозначений динамики автомобиля

   2.6.2.1 Вывод для \(F=ma\) в 3D
   2.6.2.2 Вывод для \(\tau =I\omega \) в 3D
   2.6.2.3 Вывод для \(\tau =I\omega \) в 3D с использованием главных осей

Рисунок 2.10: 3D без использования обозначений динамики автомобиля

2.6.2.1 Вывод для \(F=ma\) в 3D

\begin {align*} \boldsymbol {F} & =\frac {d}{dt}\boldsymbol {p}\\ & =\frac {d}{dt}\left ( m\boldsymbol {v}\right ) \\ & \boldsymbol {=}m\frac {d}{dt}\boldsymbol {v}\\ & =m\left [ \begin {pmatrix} a_{x}\\ a_{y}\\ a_{ z}\end {pmatrix} +\begin {pmatrix} \omega _{x}\\ \omega _{y}\\ \omega _{z}\end {pmatrix} \otimes \begin {pmatrix} v_{x }\\ v_{y}\\ v_{z}\end {pmatrix} \right ] \\ & =m\left [ \begin {pmatrix} a_{x}\\ a_{y}\\ a_{z} \end {pmatrix} +\det \begin {vmatrix} \boldsymbol {i} & \boldsymbol {j} & \boldsymbol {k}\\ \omega _{x} & \omega _{y} & \omega _{ z}\\ v_{x} & v_{y} & v_{z}\end {vmatrix} \right ] \\ & =m\left [ \begin {pmatrix} a_{x}\\ a_{y}\ \ a_{z}\end {pmatrix} +\begin {pmatrix} \omega _{y}v_{z}-\omega _{z}v_{y}\\ -\left ( \omega _{x}v_ {z}-\omega _{z}v_{x}\right ) \\ \omega _{x}v_{y}-\omega _{y}v_{x}\end {pmatrix} \right ] \\ & =m\begin {pmatrix} a_{x}+\omega _{y}v_{z}-\omega _{z}v_{y}\\ a_{y}-\omega _{x}v_{z }+\omega _{z}v_{x}\\ a_{z}+\omega _{x}v_{y}-\omega _{y}v_{x}\end {p матрица} \end {выравнивание*}

2.

6.2.2 Вывод для \(\tau=I\omega\) в 3D

Пусть \(A=I\omega \), затем по правилу\begin {align*} \boldsymbol {\tau} & =\left ( \frac {d}{dt}\boldsymbol {A}\right ) \\ & =\left ( \frac {d}{dt}\boldsymbol {A}\right ) _{\text {разрешено}}+\boldsymbol {\omega \times A} \end {align*}

Тогда \(\tau =I\omega \) можно найти для общего случая\begin {align*} \boldsymbol {\tau } & =\frac {d}{dt}\left [ \overset {\boldsymbol {A}}{\overbrace {\begin {pmatrix} I_{xx} & I_{xy} & I_{xz}\\ I_{yx} & I_{yy} & I_{yz}\\ I_{zx} & I_{yz} & I_{zz}\end {pmatrix}\begin {pmatrix} \omega _{x}\\ \omega _{y}\\ \omega _{z}\end {pmatrix} }}\right ] +\begin {pmatrix} \omega _ {x}\\ \omega _ {y}\\ \omega _ {z}\end {pmatrix} \times \overset {\boldsymbol {A}}{\overbrace {\ begin {pmatrix} I_{xx} & I_{xy} & I_{xz}\\ I_{yx} & I_{yy} & I_{yz}\\ I_{zx} & I_{yz} & I_{zz} \end {pmatrix}\begin {pmatrix} \omega _{x}\\ \omega _{y}\\ \omega _{z}\end {pmatrix} }}\\ & =\begin {pmatrix} I_{ xx} & I_{xy} & I_{xz}\\ I_{yx} & I_{yy} & I_{yz}\\ I_{zx} & I_{yz} & I_{zz}\end {pmatrix}\ begin {pmatrix} \alpha _{x}\\ \alpha _{y}\\ \alpha _{z}\end {pmatrix} +\begin {pmatrix} \omega _{x}\\ \omega _{y }\\ \omega _{z}\end {pmatrix} \times \begin {pmatrix} I_{xx}\omega _{x}+I_{xy}\omega _{y}+I_{xz}\omega _ {г}\\ I_{yx}\omega _{x}+I_{yy}\omega _{y}+I_{yz}\omega _{z}\\ I_{zx}\omega _{x}+I_{yz}\ omega _{y}+I_{zz}\omega _{z}\end {pmatrix} \\ & =\begin {pmatrix} I_{xx} & I_{xy} & I_{xz}\\ I_{yx} & I_{yy} & I_{yz}\\ I_{zx} & I_{yz} & I_{zz}\end {pmatrix}\begin {pmatrix} \alpha _{x}\\ \alpha _{y} \\ \alpha _{z}\end {pmatrix} +\det \begin {vmatrix} \boldsymbol {i} & \boldsymbol {j} & \boldsymbol {k}\\ \omega _{x} & \omega _ {y} & \omega _{z}\\ \left ( I_{xx}\omega _{x}+I_{xy}\omega _{y}+I_{xz}\omega _{z}\right ) & \left ( I_{yx}\omega _{x}+I_{yy}\omega _{y}+I_{yz}\omega _{z}\right ) & \left ( I_{zx}\omega _ {x}+I_{yz}\omega _{y}+I_{zz}\omega _{z}\right ) \end {vmatrix} \\ & =\begin {pmatrix} I_{xx} & I_{xy } & I_{xz}\\ I_{yx} & I_{yy} & I_{yz}\\ I_{zx} & I_{yz} & I_{zz}\end {pmatrix}\begin {pmatrix} \alpha _{x}\\ \alpha _{y}\\ \alpha _{z}\end {pmatrix} +\begin {pmatrix} \omega _{y}\left ( I_{zx}\omega _{x} +I_{yz}\omega _{y}+I_{zz}\omega _{z}\right ) -\omega _{z}\left ( I_{yx}\omega _{x}+I_{yy} \ омега _ {у} + я _{yz}\omega _{z}\right ) \\ \omega _{x}\left ( I_{zx}\omega _{x}+I_{yz}\omega _{y}+I_{zz} \omega _{z}\right ) -\omega _{z}\left ( I_{xx}\omega _{x}+I_{xy}\omega _{y}+I_{xz}\omega _{z }\right ) \\ \omega _{x}\left ( I_{yx}\omega _{x}+I_{yy}\omega _{y}+I_{yz}\omega _{z}\right ) -\omega _{y}\left ( I_{xx}\omega _{x}+I_{xy}\omega _{y}+I_{xz}\omega _{z}\right ) \end {pmatrix} \конец {выравнивание*}

2.

6.2.3 Вывод для \(\tau=I\omega\) в 3D с использованием главных осей

Приведенный выше вывод упрощается, так как мы будем использовать главные оси. В этом случае все пересекаются произведения моментов инерции равны нулю.\[ I=\begin {pmatrix} I_{xx} & 0 & 0\\ 0 & I_{yy} & 0\\ 0 & 0 & I_{zz}\end {pmatrix} \ ]

Отсюда\begin {align*} \boldsymbol {\tau} & =\frac {d}{dt}\left [\overset {\boldsymbol {A}}{\overbrace {\begin {pmatrix} I_{xx} & 0 & 0\\ 0 & I_{yy} & 0\\ 0 & 0 & I_{zz}\end {pmatrix}\begin {pmatrix} \omega _{x}\\ \omega _{y}\\ \omega _{z}\end {pmatrix} }}\right ] +\begin {pmatrix} \omega _{x}\\ \omega _{y}\\ \omega _{z}\end {pmatrix} \ раз \ overset {\ boldsymbol {A}} {\ overbrace {\ begin {pmatrix} I_ {xx} & 0 & 0 \\ 0 & I_ {yy} & 0 \\ 0 & 0 & I_ {zz} \ end { pmatrix}\begin {pmatrix} \omega _{x}\\ \omega _{y}\\ \omega _{z}\end {pmatrix} }}\\ & =\begin {pmatrix} I_{xx} & 0 & 0\\ 0 & I_{yy} & 0\\ 0 & 0 & I_{zz}\end {pmatrix}\begin {pmatrix} \alpha _{x}\\ \alpha _{y}\\ \ alpha _{z}\end {pmatrix} +\begin {pmatrix} \omega _{x}\\ \omega _{y}\\ \omega _{z}\end {pmatrix} \times \begin {pmatrix} I_{xx}\omega _{x}\\ I_{yy}\omega _{y}\\ I_{zz}\omega _{z}\end {pmatrix} \\ & =\begin {pmatrix} I_{ xx}\alpha _{x}\\ I_{yy}\alpha _{y}\\ I_{zz}\alpha _{z}\end {pmatrix} +\det \begin {vmatrix} \boldsymb ol {i} & \boldsymbol {j} & \boldsymbol {k}\\ \omega _{x} & \omega _{y} & \omega _{z}\\ I_{xx}\omega _{x} & I_{yy}\omega _{y} & I_{zz}\omega _{z}\end {vmatrix} \\ & =\begin {pmatrix} I_{xx}\alpha _{x}\\ I_{ yy}\alpha _{y}\\ I_{zz}\alpha _{z}\end {pmatrix} +\begin {pmatrix} \omega _{y}\left ( I_{zz}\omega _{z} \right ) -\omega _{z}\left ( I_{yy}\omega _{y}\right ) \\ -\omega _{x}\left ( I_{zz}\omega _{z}\right ) +\omega _{z}\left ( I_{xx}\omega _{x}\right ) \\ \omega _{x}\left ( I_{yy}\omega _{y}\right ) -\ omega _{y}\left ( I_{xx}\omega _{x}\right ) \end {pmatrix} \\ & =\begin {pmatrix} I_{xx}\alpha _{x}\\ I_{yy }\alpha _{y}\\ I_{zz}\alpha _{z}\end {pmatrix} +\begin {pmatrix} \omega _{y}\omega _{z}\left ( I_{zz}- I_{yy}\right ) \\ \omega _{x}\omega _{z}\left ( I_{xx}-I_{zz}\right ) \\ \omega _{x}\omega _{y} \left ( I_{yy}-I_{xx}\right ) \end {pmatrix} \end {align*}

Итак, мы видим, насколько проще стало при использовании главных осей. Сравните приведенное выше с \[\begin {pmatrix} I_{xx} & I_{xy} & I_{xz}\\ I_{yx} & I_{yy} & I_{yz}\\ I_{zx} & I_{ yz} & I_{zz}\end {pmatrix}\begin {pmatrix} \alpha _{x}\\ \alpha _{y}\\ \alpha _{z}\end {pmatrix} +\begin {pmatrix} \omega _{y}\left ( I_{zx}\omega _{x}+I_{yz}\omega _{y}+I_{zz}\omega _{z}\right ) -\omega _{z }\left ( I_{yx}\omega _{x}+I_{yy}\omega _{y}+I_{yz}\omega _{z}\right ) \\ \omega _{x}\left ( I_{zx}\omega _{x}+I_{yz}\omega _{y}+I_{zz}\omega _{z}\right ) -\omega _{z}\left ( I_{xx}\ omega _{x}+I_{xy}\omega _{y}+I_{xz}\omega _{z}\right ) \\ \omega _{x}\left ( I_{yx}\omega _{x }+I_{yy}\omega _{y}+I_{yz}\omega _{z}\right ) -\omega _{y}\left ( I_{xx}\omega _{x}+I_{xy }\omega _{y}+I_{xz}\omega _{z}\right ) \end {pmatrix} \] Итак, всегда используйте главные оси для фиксированной системы координат тела!

2.6.3 Условия ускорения за счет вращения и ускорения

Рисунок 2.11: Условия ускорения из-за вращения 1. Рисунок 2.12: Условия ускорения из-за вращения 2.