Главная
Формулы кинематика механика: Механика – Основные формулы

Формулы кинематика механика: Механика – Основные формулы

Шпоры по физике – механика, кинематика

Шпаргалка

  • формат docx
  • размер 180.08 КБ
  • добавлен 11 марта 2011 г.

Ответы на 35 вопросов по физике :
– траектория, длина пути, вектор перемещения
– угловая скорость, угловое ускорение
– первый закон Ньютона
– второй закон Ньютона
– третий закон Ньютона
– импульс. Закон сохранения импульса
– момент инерции
– теорема Штейнера
– момент силы. Уравнение динамики вращ. движ. твёрдого тела
– момент импульса
– кинетическая энергия
– работа
– потенциальная энергия
– пружинный маятник
и многое другое.

Похожие разделы

  1. Академическая и специальная литература
  2. Автоматизация
  3. Мехатроника
  1. Академическая и специальная литература
  2. Военные дисциплины
  3. Баллистика и динамика выстрела
  1. Академическая и специальная литература
  2. Математика
  3. История математики
  1. Академическая и специальная литература
  2. Механика
  1. Академическая и специальная литература
  2. Транспорт
  3. Судостроение
  4. Теория корабля, ТУС, устройство и живучесть судов
  1. Академическая и специальная литература
  2. Физика
  3. Астрономия и астрофизика

Смотрите также

  • формат doc
  • размер 447. 18 КБ
  • добавлен 19 декабря 2010 г.

Билеты по физике на 07-08 уч. год в осеннем семестре (УГАТУ). Разобраны 82 билета и почти все задачи. Очень хорошая шпора! Динамика, кинематика, механика, статикаrn

  • формат pdf
  • размер 61.36 КБ
  • добавлен 18 декабря 2008 г.

Основные формулы на одном листе (от кинематики и динамики до квантовой физики). Кинематика. Динамика. Законы сохранения энергии. Механика жидкостей. Основы МКТ. Термодинамика. Колебания и волны. Электростатика. Постоянный ток. Индукция. Электромагнитые колебания. Оптика. Ядерные реакции. Квантовая физика. Основы специальной теории относительности.

  • формат doc
  • размер 162.61 КБ
  • добавлен 02 марта 2009 г.

Кинематика. динамика поступательного движения. механика твердого тела. Элементы специальной теории относительности. Механические колебания и волны. Молекулярно-кинетическая теория идеальных газов. Основы термодинамики 8. Реальные газы, жидкости и твердые тела.

  • формат doc
  • размер 39.79 КБ
  • добавлен 01 декабря 2008 г.

Механика: кинематика, динамика, законы сохранения, статика. хорошие шпоры и удобно распечатывать.

Шпаргалка

  • формат doc
  • размер 114.08 КБ
  • добавлен 23 июня 2009 г.

На одном листе собраны все формулы по школьному курсу физики.

Приводится список физических констант. Механика. Кинематика. Кинематика точки. Кинематика твёрдого тела. Динамика. Законы механики Ньютона. Статика. Законы сохранения в механике. Закон сохранения импульса. Закон сохранения энергии. Колебания и волны. Механические колебания. Электромагнитные колебания. Механические волны. Электромагнитные волны. Молекулярная физика. Тепловые явления. Ос…

  • формат jpg, htm
  • размер 17.33 МБ
  • добавлен 22 октября 2009 г.

Шпоры по Физике. Буквы, используемые для обозначения величин Методика решения задач по физике Векторы Основные положения, законы и формулы Механика Кинематика Динамика Статика Простые механизмы Жидкости и газы Молекулярная физика Термодинамика Электростатика Электричество Магнитное поле Колебания и волны Оптика Элементы теории относительности Квантовая физика Атомная и ядерная физика Приложения Шкала электромагнитных волн. ..

  • формат doc
  • размер 284.6 КБ
  • добавлен 24 февраля 2009 г.

Шпоры содержат ВСЕ формулы по предмету: Электричество Колебания и волны Квантовая физика Молекулярная физика Механика,Площади Пружина. Кинематика. Магнитное поле Электричество и магнетизм.Механика жидкостей и газов.Оптика Закон преломления, Справочные таблицы по физике, Термодинамика,Электростатика,Законы Ньютона Динамика,Статика и гидростатика,Законы сохранения,Электроемкость,Молекулярная физика,Геометрическая оптика,Волновые и корпускул-е свойс…

  • формат doc, txt
  • размер 167.38 КБ
  • добавлен 12 сентября 2010 г.

Кинематика. Динамика. Сила тяжести. Движение под углом к горизонту Криволинейное движение. Механика жидкостей и газов. Закон Менделеева – Клаперона. Объемное расширение твердых тел. Молекулярно-кинетическая теория. Магнитное поле. Квантовая физика.

  • формат doc
  • размер 75.98 КБ
  • добавлен 08 января 2009 г.

Шпаргалка по физике для студентов УГАТУ 1 семестр, Кинематика, динамика поступательного движения, механика твёрдого тела, элементы специальной теории относительности, механические колебания и волны, и. т. д.

  • формат doc
  • размер 360.5 КБ
  • добавлен 21 декабря 2009 г.

Шпоры по физике в виде основных формул, Механика, Кинематика, Электростатика, Магнетизм, МКТ и др.

Формулы по механике за 10 класс :: inbiogena

 

 

 

 

 

 

 

 

 

 

 

 

Механика – основные формулы для решения задач.

Механика Основные формулы.1. Кинематика.1.1 Скорость тела. 10 класс. Основные формулы. Кинематика. Механическая работа. Вложение. Размер. Формулы по механике.1.39 мб. Рабочая учебная программа спецкурса по ФИЗИКЕ «Практикум решения физических задач по механике» 10 класс. Шпаргалка с формулами по физике для ЕГЭ. И не только может понадобиться 7, 8, 9, 10 и 11 классам. Для начала картинка, которую можно распечатать в компактном виде. Механика. § 10. Закон сложения скоростей.§ 11. Собственное время.§ 12. Равноускоренное движение. Главная Справочник физических величин Формулы по физике. Формулы по физике 10 класс. Механическое напряжение Механическое напряжение σ — это отношение модуля силы упругости F к площади поперечного сечения S тела. Основные формулы школьного курса механики. Скачать формулы по механике в виде файла jpg. Формула. Учащийся 10-11 классов. Студент педагогического ВУЗа. Основные формулы для 10-11 классов. Фундаментальные константы. Система единиц. Механика. Кл. Отношение заряда к массе.
Eme. Сборник «Формулы по физике» представляет собой краткий справочник по основным формулам курса физики, предназначенный для учащихся лицея-интерната естественных наук. Лицей-интернат естественных наук 2011 г.2. Механика. 10 класс. Основные формулы. Кинематика. Движение материальной точки в Отношение изменения скорости ΔV = V2 – V1к промежутку времени Δt за. Обозначение, Измеряется в, Описание. S, м, пройденный путь. V, мс, скорость. T, с, время. X, м, координата. A, мс2, ускорение.Ω, с-1, угловая скорость. Механика – основные формулы для решения задач. S — длина участка пути, t — промежуток времени, за который пройден участок пути s. Основные формулы механики, молекулярной физики, электродинамики. Материал для Вас подготовил Бабнищев Никита Александрович. Спасибо! Таблица содержит основные формулы по механике: модуль вектора скорости, ускорение мгновенное, модуль вектора ускорения, угловая скорость и. Основные формулы школьного курса механики Формула квадратов скоростей Перемещение при равноускоренном.
Учащийся 10-11 классов. Формулы по физике с объяснениями – Кинематика: путь, время, скорость, равномерное движение, равномерно ускоренное движение: ускорение,. Все основные формулы по физике за 7-11 класс для ГИА и ЕГЭ Формулы по разделамтемам: МЕХАНИКА – Кинематика. 6 июля 2015 г., 10:18. Формулы по физике для ЕГЭ и 7-11 класса и не только может понадобиться 7, 8, 9, 10 и 11 классам. Механика. Спасибо огромное за помощь. Физика,10,11 класс, ЕГЭ, ГИА Физика. Кинематика формулы задач по физике, подготовка к ЭГЕ и ГИА, механика термодинамика и др. 10 класс. Материалы к зачету по теме Основные законы механики. 1. При вычислениях по этой формуле знаки входящих в нее величин курс перпендикулярно течению реки, достигла противоположного берега за 140 с. Формулировки физических законов и правил из курса 10 класса общеобразовательной школы. Формулы по физике 10 класс. Формулировки физических законов и правил из курса 9 класса общеобразовательной школы. Формулы по физике 9 класс. Которое совершает тело за единицу времени t. 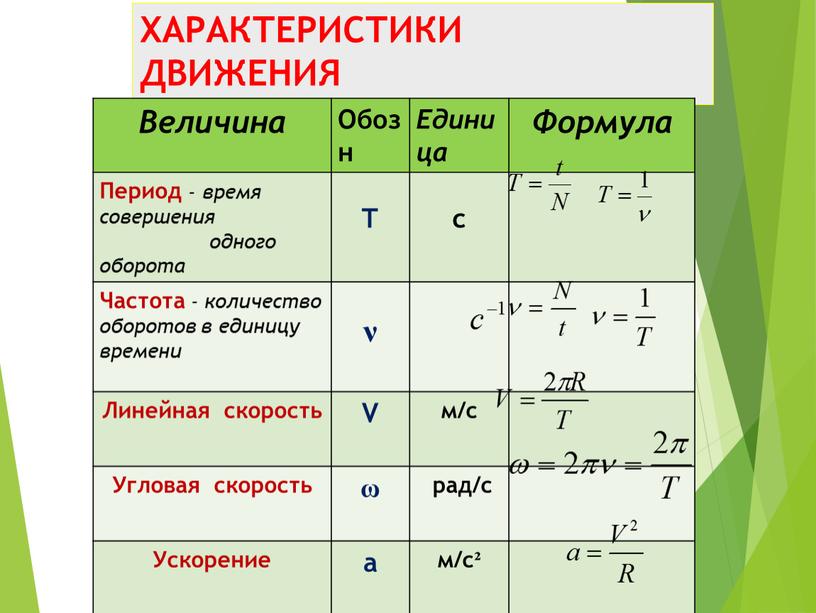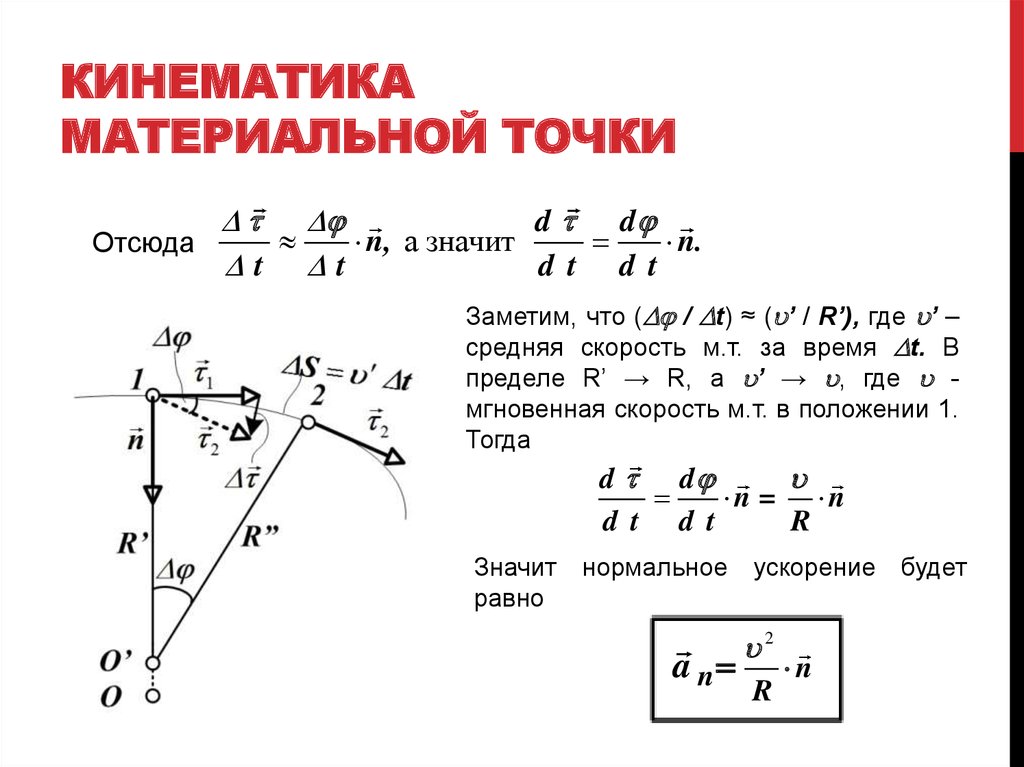{-11}. Законы сохранения в механике. Механика, кинематика. Движение по окружности закон всемирного тяготения закон Гука сила трения сила и импульс закон сохранения импульса Кинематика. Основные формулы кинематики. Онлайн-курсы. Подготовка к ЕГЭ, ГИА для школьников 5 – 11 классов. И не только механики. Физика. Механика 10 класс. Профильный уровень. Учебник для общеобразовательных учреждений.11-е издание, стереотипное. Москва. Дрофа 2009. Все формулы по физике за 9 класс находятся тут! Если же тебе не хватило данных формул за 9 класс, то воспользуйтесь Формулы по механике. Собрание формул за 8 класс формул по физике. Хочешь чтоб появилась тут еще тебе нужная формула за 8 класс, пиши в Формулы по механике. Бесплатные уроки, тесты и тренажёры по физике за 10 класс по школьной программе. Используйте Законы сохранения в механике. Механическая.

 

Вместе с формулы по механике за 10 класс часто ищут

 

Все формулы механики 10 класс.

Физика 10 класс формулы механика.

Основные формулы механики 10 класс.

Механика формулы 1 курс.

Формулы динамики.

Формулы по физике 10 класс с пояснениями.

Механика формулы 9 класс.

Все формулы по физике за 10 класс

 

Читайте также:

 

Гдзпо геометрии рабочая тетрадь

 

Гдзпо геометрии рабочая тетрадь

 

Гдзпо геометрии рабочая тетрадь

 

Кинематические уравнения – Расчеты физики

Соглашение

Рабочий лист рабочих энергии и электроэнергии

Кинематические уравнения движения в физике представляют собой набор уравнений, описывающих движение объектов с точки зрения положения, скорости, ускорения и времени. Эти уравнения выводятся из трех основных кинематических уравнений:

Как вывести уравнения кинематикиУравнения кинематики

Первое уравнение

v = u + at

Второе уравнение

s = ut + (1/2)at 9 0027 2

Третье уравнение

v 2 = u 2 + 2as

Четвертое уравнение

s = [(u + v) / 2 ] x t

Где:

    9 0049 v – конечная скорость
  • u – начальная скорость
  • а это ускорение
  • с – водоизмещение
  • т это время
Первое кинематическое уравнение v = u + at
Второе кинематическое уравнение s = ut + (1/2)at 2 900 28
Третье кинематическое уравнение v 2 = u 2 + 2as
Три (3) уравнения в табличной форме

Приведенные выше уравнения справедливы только для движения с постоянным ускорением. Следовательно, ускорение остается постоянным на протяжении всего движения. Для неравномерно ускоренного движения уравнения движения более сложны.

Объяснение кинематических уравнений

Если вы когда-либо занимались спортом, ездили на машине или просто шли по улице, вы чувствовали движение. Но задумывались ли вы когда-нибудь об основных принципах движения? Кинематика — раздел физики, изучающий движение. С другой стороны, уравнения кинематики — это математические формулы, которые мы используем для описания и прогнозирования поведения движущихся объектов .

На самом базовом уровне кинематика — это изучение движения без учета вызывающих его сил. Кроме того, мы также называем уравнения кинематики уравнения движения . Это математические формулы, описывающие взаимосвязь между положением, скоростью и ускорением объекта во времени. Следовательно, эти уравнения имеют фундаментальное значение для понимания и предсказания поведения движущихся объектов.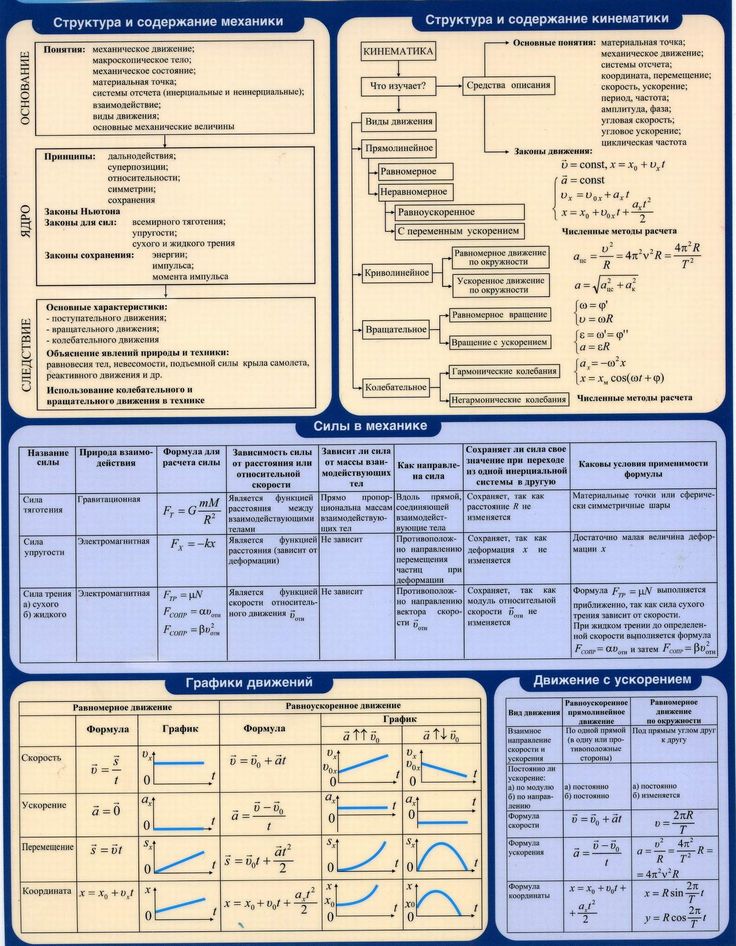 В этой статье мы рассмотрим основы уравнений кинематики, как они работают и почему они важны.

Перемещение, скорость и ускорение

Чтобы понять уравнения кинематики, важно сначала понять понятия перемещения, скорости и ускорения. Смещение — это изменение положения объекта от его начального местоположения до его конечного местоположения. Скорость — это скорость, с которой объект меняет свое положение. Ускорение — скорость, с которой объект изменяет свою скорость.

Как вывести уравнения кинематики

Вывод уравнений кинематики основан на следующих предположениях:

  • Объект движется прямолинейно.
  • Ускорение постоянное.
  • Скорость и ускорение имеют одинаковое направление.

Используя эти предположения, мы можем вывести кинематические уравнения.

Вывод первого уравнения движения

Мы можем вывести первое уравнение, используя определение ускорения, которое представляет собой скорость изменения скорости во времени. Следовательно, теперь мы можем написать:

Ускорение, a = изменение скорости (v – u) / время (t)

Что станет

a = (v – u) / t [Помните, что ускорение, а = изменение скорости/времени]

После преобразования приведенного выше уравнения и превращения v в субъект формулы мы получим:

v = u + at [Это первое уравнение движения]

Вывод второго уравнения движения

Чтобы получить второе уравнение, применим определение перемещения. Поскольку мы знаем, что смещение — это изменение положения объекта. Точно так же мы можем определить смещение как меру разницы между двумя точками в определенном направлении. Следовательно, приведенное выше утверждение приведет нас к уравнению ниже

Поскольку средняя скорость v a = (u + v) / 2

Следовательно, пройденное расстояние будет равно

с = [(u + v) / 2] t [Поскольку v = s/t, что показывает что s = vt]

Мы можем подставить v = u + at в приведенное выше уравнение, чтобы получить

s = [(u + v) / 2] t = [(u + u + at) / 2] t

Таким образом,

Мы будем иметь s = [(2u + at)/2]t = ut + (1/2)at 2

Следовательно, наше второе уравнение движения будет

s = ut + (1/2)at 2

Вывод третьего уравнения движения

Третье уравнение выводится с использованием первых двух уравнений и исключения времени.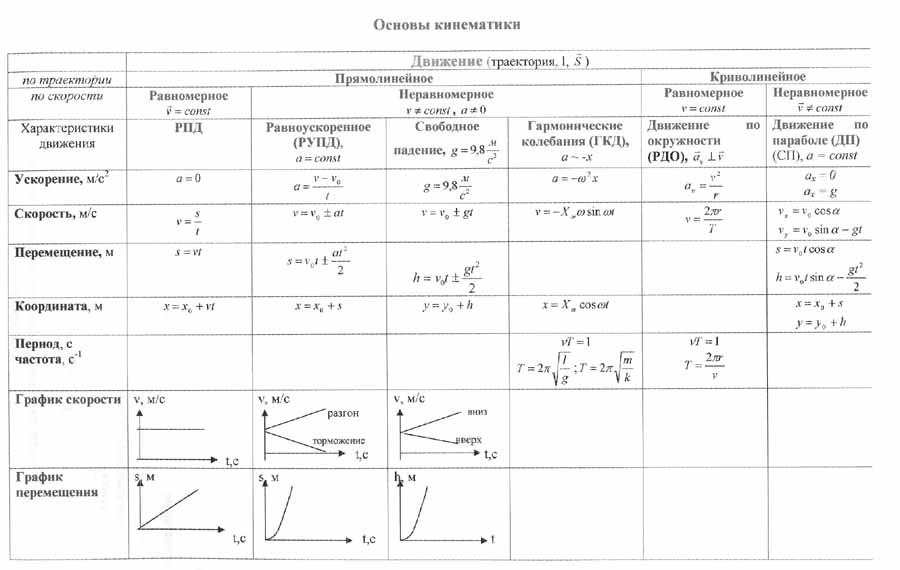 Мы можем написать:

v = u + at

Поскольку s = ut + (1/2)at 2

Следовательно,

Возводя в квадрат обе стороны v = u + at , мы получим

v 2 = (и + ат)(и + ат) = и 2 + 2иат + а 2 t 2

Следовательно,

v 2 = u 2 + 2a[ut + (1/2)at 2 ]

и ut + (1/2)at 2 равно s

Таким образом, наше третье уравнение движения будет иметь вид 1

Уравнения кинематики используются в различных областях, включая физику, технику, и робототехника. Вот некоторые из приложений кинематических уравнений:

  • Расчет траектории снаряда: Уравнения кинематики можно использовать для расчета пути снаряда, такого как пушечное ядро ​​или ракета, под действием силы тяжести.
  • Проектирование американских горок: уравнения кинематики можно использовать для проектирования американских горок путем вычисления

Решенные задачи с использованием кинематических уравнений

Вот несколько решенных задач, которые помогут вам понять, как применять кинематические уравнения (уравнения движения):

Задача 1

Автобус, движущийся со скоростью 60 км/ч, равномерно ускоряется со скоростью 5 м/с 2 . Определить его скорость через 2 мин.

Ответ

Окончательный ответ на этот вопрос: 617 м/с или 2221 км/ч км/ч = (60 х 1000) / 60 x 60 = 16,6 м/с = 17 м/с

Ускорение, a = 5 м/с 2

Время, t = 2 мин = 2 x 60 = 120 секунд

Неизвестно

Конечная скорость, v = ?

Формула

Применим первое уравнение движения v = u + at

Решение

Подставим наши данные в формулу

v = u + at = 17 + (5 х 120 ) = 617 м/с

Мы можем преобразовать приведенный выше ответ в км/ч как

v = (617 / 1000) x 60 x 60 = 2221,2 км/ч = 2221 км/ч

Задача 2

A автомобиль равномерно ускоряется со скоростью 10 м/с 2 с начальной скорости 36 км/ч в течение 30 секунд. Найдите расстояние, пройденное за это время.

Ответ

Окончательный ответ на этот вопрос: 4,8 км

Объяснение

Данные

Начальная скорость, u = 36 км/ч = 10 м/с 9 0003

Ускорение, а = 10 м/с 2

Время, t = 30 секунд

Неизвестно

Пройденное расстояние, с = ?

Формула

Воспользуемся вторым уравнением кинематики, которое гласит:

s = ut + (1/2)at 2

27 2
= 10 x 30 + 0,5 x 10 x 30 2 = 300 + 4500 = 4800 м

Мы можем преобразовать приведенный выше ответ (4800 метров) в км, сказав

с = 4800 / 1000 = 4,8 км

Задача 3

Тело, движущееся с начальной скоростью 30 м/с, равномерно ускоряется со скоростью 10 м/с 2 , пока не достигнет скорости 50 м/с.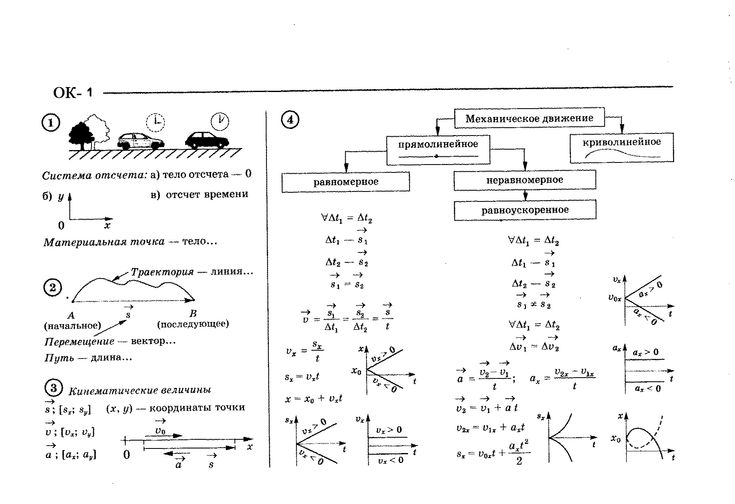 Какое расстояние пройдено за этот период?

Ответ

Окончательный ответ на этот вопрос 80 метров

Объяснение

Данные

Начальная скорость, u = 30 м/с

900 02 Ускорение, а = 10 м/с 2

Конечная скорость, v = 50 м/с

Неизвестно

Пройденное расстояние, с = ?

Формула

Из третьего кинематического уравнения

v 2 = u 2 + 2as

и затем подчинив s формуле, получить уравнение

s = (v 2 – u 90 027 2 ) / 2а

Воспользуемся приведенным выше уравнением, чтобы найти пройденное расстояние. 7 2 – 30 2 ) / 2 x 10

Отсюда следует, что

с = 1600 / 20 = 80 м

Часто задаваемые вопросы (FAQ)

Что такое уравнение кинематики?

Уравнения кинематики представляют собой набор уравнений, описывающих движение объектов с точки зрения их положения, скорости и ускорения.

Какие три уравнения кинематики?
Три кинематических уравнения:

1) v = u + at

2) s = ut + (1/2)at 2

3) v 2 = u 2 + 2as

Как решать кинематические уравнения?
Чтобы решить кинематические уравнения, вам необходимо определить, какие уравнения использовать, подставить известные значения и найти неизвестные значения с помощью алгебры.

Какая кинематическая формула для расстояния?
Кинематическая формула для расстояния: s = ut + (1/2)at 2 , где s — расстояние, u — начальная скорость, t — время, a — ускорение.

Какое кинематическое уравнение для скорости?
Кинематическое уравнение для скорости имеет вид v = u + at, где v — конечная скорость, u — начальная скорость, a — ускорение, t — время.

Какая кинематическая формула ускорения?
Кинематическая формула ускорения: a = (v – u)/t, где a – ускорение, v – конечная скорость, vi – начальная скорость, t – время.

В чем разница между кинематикой и динамикой?
Кинематика изучает движение без учета сил, вызывающих движение, а динамика изучает движение с учетом сил, вызывающих движение.

Для чего используется кинематика?
Кинематика используется во многих областях, включая физику, инженерию и робототехнику, для описания и анализа движения объектов и систем.

Проверьте свои знания

Вопрос: Какое кинематическое уравнение для времени?
Ответ: Специального кинематического уравнения для времени не существует. Время обычно задается в кинематических уравнениях как известное значение, которое используется для решения других переменных, таких как расстояние, скорость или ускорение.

Вы также можете прочитать:

Тело движется по окружности

Объект массой 150 Н движется со скоростью 4,5 м/с Основные понятия

Автомобиль трогается с места и разгоняется

Практические задачи второго закона Ньютона

Гепард присел на 20 м к востоку

Линейное расширение: определение и расчеты

Тело, движущееся со скоростью 20 м/с, равномерно замедляется со скоростью 5 м/с2

Ньютон’ s Законы движения

Ссылка

наука

MathsNet: M1 – Кинематика – Использование формул

ID страницы: 1403

M1 | Кинематика | Постоянное ускорение | «Использование формул»

Потренируйтесь выбирать и применять правильную формулу суват. 92+2as
s=\frac{1}{2}(u+v)t

Кинематика — это раздел механики, описывающий движение объектов без учета масс или сил, вызывающих движение. Напротив, динамика связана с силами и взаимодействиями, которые производят движение или влияют на него.
Кинематика изучает изменение положения объекта во времени. Положение измеряется относительно набора координат. Скорость – это скорость изменения положения. Ускорение – это скорость изменения скорости. Скорость и ускорение — две основные величины, описывающие изменение положения.

Программное обеспечение/апплеты, используемые на этой странице

На этой странице используется jsMath
Вы можете улучшить отображение математики, загрузив специальные шрифты TeX из jsMath. Тем временем мы сделаем все, что в наших силах, со шрифтами, которые у вас есть, но это может быть некрасиво, и некоторые уравнения могут отображаться неправильно.

Глоссарий

ускорение

скорость изменения скорости во времени. Это векторная величина с величиной и направлением.

динамика

Изучение движения объекта или системы объектов.

кинематика

Изучение движения объекта или системы объектов без учета действия масс или сил.

скорость изменения

производная; измерение того, как функция изменяется при изменении ее входных данных.

suvat

Аббревиатура, используемая в механике для формул с постоянным ускорением, где s — смещение, u — начальная скорость, v — конечная скорость, a — ускорение и t — время.

объединение

Объединение двух множеств A и B – это множество, содержащее все элементы A и B.

скорость

скорость изменения смещения. Это векторная величина с величиной и направлением.

Полный глоссарий

Этот вопрос появляется в следующих учебных планах:

90 633 Тема
Учебный план Модуль Раздел Год экзамена
AQA A-Level (Великобритания — до 2017 г. ) M1 Кинематика Постоянное ускорение –
AQA AS Maths 2017 Механика Кинематика с и единицы Формулы постоянного ускорения –
AQA AS/A2 Maths 2017 Механика Кинематика и единицы измерения Формулы постоянного ускорения –
CCEA A-Level (NI) M1 Кинематика Постоянное ускорение –
CIE A-Level (Великобритания) M1 Кинематика Постоянное ускорение –
Edexcel A-Level (Великобритания — до 2017 г.) M1 Кинематика Постоянное ускорение –
Edexcel AS Maths 2017 Механика Движение с постоянным ускорением Формулы постоянного ускорения 900 64 –
Edexcel AS/A2 Maths 2017 Механика Движение с постоянным ускорением Формулы постоянного ускорения –
OCR Уровень A (Великобритания — до 2017 г.

Оставить комментарий