Формулы крамера онлайн калькулятор: Онлайн калькулятор. Решение систем линейных уравнений. Метод Крамера - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Онлайн калькуляторы для расчета статистических показателей

Выбор статистического метода

В данном сервисе реализован алгоритм выбора оптимальной методики статистического анализа, который позволит исследователю на основании информации о количестве сравниваемых совокупностей, типе распределения, шкале измерения переменных, отпределить наиболее подходящий статистический метод, статистический критерий.

перейти к сервису

Расчет относительных величин

Калькулятор позволит найти значение любой относительной величины по заданным параметрам: числителю, знаменателю, десятичному коэффициенту. Учитывается вид относительной величины для правильного обозначения вводимых данных и формирования грамотного ответа. Для каждого результата также выводится средняя ошибка m.

перейти к вычислениям

Оценка значимости различий средних величин по t-критерию Стьюдента

Данный статистический метод служит для сравнения двух средних величин (M), рассчитанных для несвязанных между собой вариационных рядов.

Для вычислений также понадобятся значения средних ошибок средних арифметических (m). Примеры сравниваемых величин: среднее артериальное давление в основной и контрольной группе, средняя длительность лечения пациентов, принимавших препарат или плацебо.

перейти к вычислениям

Оценка значимости изменений средних величин при помощи парного t-критерия Стьюдента

Парный t-критерий Стьюдента используется для сравнения связанных совокупностей – результатов, полученных для одних и тех же исследуемых (например, артериальное давление до и после приема препарата, средний вес пациентов до и после применения диеты).

перейти к вычислениям

Анализ динамического ряда

Этот калькулятор позволит вам быстро рассчитать все основные показатели динамического ряда, состоящего из любого количества данных. Вводимые данные: количество лет, значение первого года, уровни ряда. Результат: показатели динамического ряда, значения, полученные при его выравнивании, а также графическое изображение динамического ряда.

перейти к вычислениям

Расчет демографических показателей

7)€: a

перейти к вычислениям

Прямой метод стандартизации

Здесь вы сможете быстро решить любую задачу по стандартизации, с использованием прямого метода. Вводите данные о сравниваемых совокупностях, выбирайте один из четырех способов расчета стандарта, задавайте значение коэффициента, используемого для расчета относительных величин. Результаты применения метода стандартизации выводятся в виде таблицы.

перейти к вычислениям

Расчет относительного риска

Относительный риск – позволяет проводить количественную оценку вероятности исхода, связанной с наличием фактора риска. Находит широкое применение в современных научных исследованиях, выборки в которых сформированы когортным методом. Наш онлайн-калькулятор позволит выполнить расчет относительного риска (RR) с 95% доверительным интервалом (CI), а также дополнительных показателей, таких как разность рисков, число пациентов, трующих лечения, специфичность, чувствительность.

перейти к вычислениям

Расчет отношения шансов

Метод отношения шансов (OR), как и относительный риск, используется для количественной оценки взаимосвязи фактора риска и исхода, но применяется в исследованиях, организованных по принципу “случай-контроль”.

перейти к вычислениям

Анализ четырехпольной таблицы

В данном калькуляторе представлены все основные статистические методы, используемые для анализа четырехпольной таблицы (фактор риска есть-нет, исход есть-нет). Выполняется проверка важнейших статистических гипотез, рассчитываются хи-квадрат, точный критерий Фишера и другие показатели.

перейти к вычислениям

Расчет показателей вариационного ряда

Онлайн-калькулятор в автоматизированном режиме поможет рассчитать все основные показатели вариационного ряда: средние величины (средняя арифметическая, мода, медиана), стандартное отклонение, среднюю ошибку средней арифметической. Поддерживается ввод как простых, так и взвешенных рядов.

перейти к вычислениям

Расчет критерия Манна-Уитни

При помощи данного сервиса вы сможете рассчитать значение U-критерия Манна-Уитни – непараметрического критерия, используемого для сравнения двух выборок, независимо от характера их распределения.

перейти к вычислениям

Корреляционно-регрессионный анализ

Онлайн-калькулятор для проведения корреляционного анализа используется для выявления и изучения связи между количественными признаками при помощи расчета коэффициента корреляции Пирсона. Также выводится уравнение парной линейной регрессии, используемое при описании статистической модели.

перейти к вычислениям

Расчет коэффициента корреляции Спирмена

Данный калькулятор используется для расчета рангового критерия корреляции Спирмена, являющегося методом непараметрического анализа зависимости одного количественного признака от другого. Оценка значимости корреляционной связи между переменными выполняется как по коэффициенту Спирмена, так и по t-критерию Стьюдента.

перейти к вычислениям

Анализ произвольных сопряженных таблиц при помощи критерия χ² (хи-квадрат)

Критерий хи-квадрат является непараметрическим аналогом дисперсионного анализа для сравнения нескольких групп по качественному признаку. Онлайн калькулятор по расчету критерия хи-квадрат позволяет оценить связь между двумя качественными признаками по частоте их значений. Число сравниваемых групп может быть от 2 до 9.

перейти к вычислениям

Системы линейных уравнений методом крамера онлайн. Линейные уравнения. Решение систем линейных уравнений. Метод Крамера

Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?

Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!

Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера.

Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.

Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.

Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение»

. В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.

Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .

Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,

И, наконец, ответ рассчитывается по формулам:

Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.

Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:

1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).

2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.

Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.

Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:

Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.

Решение системы с помощью обратной матрицы

Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).

Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.

Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:

То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце

В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.

2. Решение систем уравнений матричным методом (при помощи обратной матрицы).
3. Метод Гаусса решения систем уравнений.

Метод Крамера.

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).

Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему

Относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы Вычисление определителей. :

Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:

относительно переменных х и у .
Решение:

Заменим в этом определителе первый столбец столбцом коэффициентов из правой части системы и найдем его значение:

Сделаем аналогичное действие, заменив в первом определителе второй столбец:

Применим формулы Крамера и найдем значения переменных:
и .
Ответ:
Замечание: Этим методом можно решать системы и большей размерности.

Замечание: Если получается, что , а делить на ноль нельзя, то говорят, что система не имеет единственного решения. В этом случае система имеет или бесконечно много решений или не имеет решений вообще.

Пример 2 (бесконечное количество решений):

Решить систему уравнений:

относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:

Решение систем методом подстановки.

Первое из уравнений системы — равенство, верное при любых значениях переменных (потому что 4 всегда равно 4). Значит, остается только одно уравнение. Это уравнение связи между переменными .
Получили, решением системы являются любые пары значений переменных, связанных между собой равенством .
Общее решение запишется так:
Частные решения можно определять выбирая произвольное значение у и вычисляя х по этому равенству связи.

и т.д.
Таких решений бесконечно много.
Ответ: общее решение
Частные решения:

Пример 3 (решений нет, система несовместна):

Решить систему уравнений:

Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:

Применять формулы Крамера нельзя. Решим эту систему методом подстановки

Второе уравнение системы — равенство, неверное ни при каких значениях переменных (конечно же, так как -15 не равно 2). Если одно из уравнений системы не верно ни при каких значениях переменных, то и вся системы не имеет решений.
Ответ: решений нет

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
–

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. За примерами далеко ходить не надо.

Следующий пример – на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля. В этой статье мы разберем как по методу Крамера находятся неизвестные переменные и получим формулы. После этого перейдем к примерам и подробно опишем решение систем линейных алгебраических уравнений методом Крамера.

Навигация по странице.

Метод Крамера – вывод формул.

Пусть нам требуется решить систему линейных уравнений вида

Где x 1 , x 2 , …, x n – неизвестные переменные, a i j , i = 1, 2, …, n, j = 1, 2, …, n – числовые коэффициенты, b 1 , b 2 , …, b n – свободные члены. Решением СЛАУ называется такой набор значений x 1 , x 2 , …, x n при которых все уравнения системы обращаются в тождества.

В матричном виде эта система может быть записана как A ⋅ X = B , где – основная матрица системы, ее элементами являются коэффициенты при неизвестных переменных, – матрица – столбец свободных членов, а – матрица – столбец неизвестных переменных. После нахождения неизвестных переменных x 1 , x 2 , …, x n , матрица становится решением системы уравнений и равенство A ⋅ X = B обращается в тождество .

Будем считать, что матрица А – невырожденная, то есть, ее определитель отличен от нуля. В этом случае система линейных алгебраических уравнений имеет единственное решение, которое может быть найдено методом Крамера. (Методы решения систем при разобраны в разделе решение систем линейных алгебраических уравнений).

Метод Крамера основывается на двух свойствах определителя матрицы:

Итак, приступим к нахождению неизвестной переменной x 1 . Для этого умножим обе части первого уравнения системы на А 1 1 , обе части второго уравнения – на А 2 1 , и так далее, обе части n-ого уравнения – на А n 1 (то есть, уравнения системы умножаем на соответствующие алгебраические дополнения первого столбца матрицы А ):

Сложим все левые части уравнения системы, сгруппировав слагаемые при неизвестных переменных x 1 , x 2 , …, x n , и приравняем эту сумму к сумме всех правых частей уравнений:

Если обратиться к озвученным ранее свойствам определителя, то имеем

и предыдущее равенство примет вид

откуда

Аналогично находим x 2 . Для этого умножаем обе части уравнений системы на алгебраические дополнения второго столбца матрицы А :

Складываем все уравнения системы, группируем слагаемые при неизвестных переменных x 1 , x 2 , …, x n и применяем свойства определителя:

Откуда
.

Аналогично находятся оставшиеся неизвестные переменные.

Если обозначить

То получаем формулы для нахождения неизвестных переменных по методу Крамера .

Замечание.

Если система линейных алгебраических уравнений однородная, то есть , то она имеет лишь тривиальное решение (при ). Действительно, при нулевых свободных членах все определители будут равны нулю, так как будут содержать столбец нулевых элементов. Следовательно, формулы дадут .

Алгоритм решения систем линейных алгебраических уравнений методом Крамера.

Запишем алгоритм решения систем линейных алгебраических уравнений методом Крамера .

Примеры решения систем линейных алгебраических уравнений методом Крамера.

Разберем решения нескольких примеров.

Пример.

Найдите решение неоднородной системы линейных алгебраических уравнений методом Крамера .

Решение.

Основная матрица системы имеет вид . Вычислим ее определитель по формуле :

Так как определитель основной матрицы системы отличен от нуля, то СЛАУ имеет единственное решение, и оно может быть найдено методом Крамера. Запишем определители и . Заменяем первый столбец основной матрицы системы на столбец свободных членов, и получаем определитель . Аналогично заменяем второй столбец основной матрицы на столбец свободных членов, и получаем .

Вычисляем эти определители:

Находим неизвестные переменные x 1 и x 2 по формулам :

Выполним проверку. Подставим полученные значения x 1 и x 2 в исходную систему уравнений:

Оба уравнения системы обращаются в тождества, следовательно, решение найдено верно.

Ответ:

Некоторые элементы основной матрицы СЛАУ могут быть равны нулю. В этом случае в уравнениях системы будут отсутствовать соответствующие неизвестные переменные. Разберем пример.

Пример.

Найдите решение системы линейных уравнений методом Крамера .

Решение.

Перепишем систему в виде , чтобы стало видно основную матрицу системы . Найдем ее определитель по формуле

Имеем

Определитель основной матрицы отличен от нуля, следовательно, система линейных уравнений имеет единственное решение. Найдем его методом Крамера. Вычислим определители :

Таким образом,

Ответ:

Обозначения неизвестных переменных в уравнениях системы могут отличаться от x 1 , x 2 , …, x n . Это не влияет на процесс решения. А вот порядок следования неизвестных переменных в уравнениях системы очень важен при составлении основной матрицы и необходимых определителей метода Крамера. Поясним этот момент на примере.

Пример.

Используя метод Крамера, найдите решение системы трех линейных алгебраических уравнений с тремя неизвестными .

Решение.

В данном примере неизвестные переменные имеют другое обозначение (x , y и z вместо x 1 , x 2 и x 3 ). Это не влияет на ход решения, но будьте внимательны с обозначениями переменных. В качестве основной матрицы системы НЕЛЬЗЯ брать . Необходимо сначала упорядочить неизвестные переменные во всех уравнениях системы. Для этого перепишем систему уравнений как . Теперь основную матрицу системы хорошо видно . Вычислим ее определитель:

Определитель основной матрицы отличен от нуля, следовательно, система уравнений имеет единственное решение. Найдем его методом Крамера. Запишем определители (обратите внимание на обозначения) и вычислим их:

Осталось найти неизвестные переменные по формулам :

Выполним проверку. Для этого умножим основную матрицу на полученное решение (при необходимости смотрите раздел ):

В результате получили столбец свободных членов исходной системы уравнений, поэтому решение найдено верно.

Ответ:

x = 0, y = -2, z = 3 .

Пример.

Решите методом Крамера систему линейных уравнений , где a и b – некоторые действительные числа.

Решение.

Ответ:

Пример.

Найдите решение системы уравнений методом Крамера, – некоторое действительное число.

Решение.

Вычислим определитель основной матрицы системы: . выражения есть интервал , поэтому при любых действительных значениях . Следовательно, система уравнений имеет единственное решение, которое может быть найдено методом Крамера. Вычисляем и :

Пусть система линейных уравнений содержит столько уравнений, каково количество независимых переменных, т.е. имеет вид

Такие системы линейных уравнений называются квадратными. Определитель, составленный из коэффициентов при независимых переменных системы (1.5), называется главным определителем системы. Мы будем обозначать его греческой буквой D. Таким образом,

. (1.6)

Если в главном определителе произвольный (j -ый) столбец, заменить столбцом свободных членов системы (1. 5), то можно получить еще n вспомогательных определителей:

(j = 1, 2, …, n ). (1.7)

Правило Крамера решения квадратных систем линейных уравнений заключается в следующем. Если главный определитель D системы (1.5) отличен от нуля, то система имеет и притом единственное решение, которое можно найти по формулам:

(1.8)

Пример 1.5. Методом Крамера решить систему уравнений

Вычислим главный определитель системы:

Так как D¹0, то система имеет единственное решение, которое можно найти по формулам (1.8):

Таким образом,

Действия над матрицами

1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.

2. Для того чтобы умножить матрицу на число, нужно все ее элементы умножить на это число. То есть

. (1.9)

Пример 1.6. .

Сложение матриц.

Данная операция вводится только для матриц одного и того же порядка.

Для того чтобы сложить две матрицы, необходимо к элементам одной матрицы прибавить соответствующие элементы другой матрицы:

(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.

Пример 1.7. .

Умножение матриц.

Если число столбцов матрицы А совпадает с числом строк матрицы В , то для таких матриц вводится операция умножения:

Таким образом, при умножении матрицы А размерности m ´n на матрицу В размерности n ´k мы получаем матрицу С размерности m ´k . При этом элементы матрицы С вычисляются по следующим формулам:

Задача 1.8. Найти, если это возможно, произведение матриц AB и BA :

Решение. 1) Для того чтобы найти произведение AB , необходимо строки матрицы A умножить на столбцы матрицы B :

2) Произведение BA не существует, т. к. количество столбцов матрицы B не совпадает с количеством строк матрицы A .

Обратная матрица. Решение систем линейных уравнений матричным способом

Матрица A – 1 называется обратной к квадратной матрице А , если выполнено равенство:

где через I обозначается единичная матрица того же порядка, что и матрица А :

Для того чтобы квадратная матрица имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратную матрицу находят по формуле:

, (1.13)

где A ij – алгебраические дополнения к элементам a ij матрицы А (заметим, что алгебраические дополнения к строкам матрицы А располагаются в обратной матрице в виде соответствующих столбцов).

Пример 1.9. Найти обратную матрицу A – 1 к матрице

Обратную матрицу найдем по формуле (1.13), которая для случая n = 3 имеет вид:

Найдем det A = | A | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 – 3 × 3 × 3 – 1 × 5 × 4 – 2 × 2 × 8 = 24 + 30 + 24 – 27 – 20 – 32 = – 1. Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.

1) Найдем алгебраические дополнения A ij :

Для удобства нахождения обратной матрицы, алгебраические дополнения к строкам исходной матрицы мы расположили в соответствующие столбцы.

Из полученных алгебраических дополнений составим новую матрицу и разделим ее на определитель det A . Таким образом, мы получим обратную матрицу:

Квадратные системы линейных уравнений с отличным от нуля главным определителем можно решать с помощью обратной матрицы. Для этого систему (1.5) записывают в матричном виде:

где

Умножая обе части равенства (1.14) слева на A – 1 , мы получим решение системы:

, откуда

Таким образом, для того чтобы найти решение квадратной системы, нужно найти обратную матрицу к основной матрице системы и умножить ее справа на матрицу-столбец свободных членов.

Задача 1.10. Решить систему линейных уравнений

с помощью обратной матрицы.

Решение. Запишем систему в матричном виде: ,

где – основная матрица системы, – столбец неизвестных и – столбец свободных членов. Так как главный определитель системы , то основная матрица системы А имеет обратную матрицу А -1 . Для нахождения обратной матрицы А -1 , вычислим алгебраические дополнения ко всем элементам матрицы А :

Из полученных чисел составим матрицу (причем алгебраические дополнения к строкам матрицы А запишем в соответствующие столбцы) и разделим ее на определитель D. Таким образом, мы нашли обратную матрицу:

Решение системы находим по формуле (1.15):

Таким образом,

Решение систем линейных уравнений методом обыкновенных жордановых исключений

Пусть дана произвольная (не обязательно квадратная) система линейных уравнений:

(1.16)

Требуется найти решение системы, т.е. такой набор переменных , который удовлетворяет всем равенствам системы (1. 16). В общем случае система (1.16) может иметь не только одно решение, но и бесчисленное множество решений. Она может так же вообще не иметь решений.

При решении подобных задач используется хорошо известный из школьного курса метод исключения неизвестных, который еще называется методом обыкновенных жордановых исключений. Суть данного метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая на одно уравнение и на одну переменную меньше, чем исходная система. Уравнение, из которого выражалась переменная, запоминается.

Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. В процессе исключения неизвестных некоторые уравнения могут превратиться в верные тождества, например . Такие уравнения из системы исключаются, так как они выполняются при любых значениях переменных и, следовательно, не оказывают влияния на решение системы. Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например ), то мы делаем вывод, что система не имеет решения.

Если в ходе решения противоречивых уравнений не возникло, то из последнего уравнения находится одна из оставшихся в нем переменных. Если в последнем уравнении осталась только одна переменная, то она выражается числом. Если в последнем уравнении остаются еще и другие переменные, то они считаются параметрами, и выраженная через них переменная будет функцией этих параметров. Затем совершается так называемый «обратный ход». Найденную переменную подставляют в последнее запомненное уравнение и находят вторую переменную. Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.

В результате мы получаем решение системы. Данное решение будет являться единственным, если найденные переменные будут числами. Если же первая найденная переменная, а затем и все остальные будут зависеть от параметров, то система будет иметь бесчисленное множество решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от того или иного набора параметров, называются общим решением системы.

Пример 1.11.

После запоминания первого уравнения и приведения подобных членов во втором и третьем уравнении мы приходим к системе:

Выразим y из второго уравнения и подставим его в первое уравнение:

Запомним второе уравнение, а из первого найдем z :

Совершая обратный ход, последовательно найдем y и z . Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :

Затем подставим и в первое запомненное уравнение , откуда найдем x :

Задача 1.12. Решить систему линейных уравнений методом исключения неизвестных:

. (1.17)

Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

Запомним первое уравнение

В данной системе первое и второе уравнения противоречат друг другу. Действительно, выражая y , получим, что 14 = 17. Данное равенство не выполняется, ни при каких значениях переменных x , y , и z . Следовательно, система (1.17) несовместна, т.е. не имеет решения.

Читателям предлагаем самостоятельно проверить, что главный определитель исходной системы (1.17) равен нулю.

Рассмотрим систему, отличающуюся от системы (1.17) всего лишь одним свободным членом.

Задача 1.13. Решить систему линейных уравнений методом исключения неизвестных:

. (1.18)

Решение. Как и прежде, выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

Запомним первое уравнение и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:

Выражая y из первого уравнения и подставляя его во второе уравнение , мы получим тождество 14 = 14, которое не влияет на решение системы, и, следовательно, его можно из системы исключить.

В последнем запомненном равенстве переменную z будем считать параметром. Полагаем . Тогда

Подставим y и z в первое запомненное равенство и найдем x :

Таким образом, система (1.18) имеет бесчисленное множество решений, причем любое решение можно найти по формулам (1.19), выбирая произвольное значение параметра t :

(1.19)
Так решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. д. Формулы (1.19) выражают общее (любое) решение системы (1.18).

В том случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обыкновенных жордановых исключений представляется громоздким. Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы при одном шаге в общем виде и оформить решение задачи в виде специальных жордановых таблиц.

Пусть дана система линейных форм (уравнений):

, (1.20)
где x j – независимые (искомые) переменные, a ij – постоянные коэффициенты
(i = 1, 2,…, m ; j = 1, 2,…, n ). Правые части системы y i (i = 1, 2,…, m ) могут быть как переменными (зависимыми), так и константами. Требуется найти решений данной системы методом исключения неизвестных.

Рассмотрим следующую операцию, называемую в дальнейшем «одним шагом обыкновенных жордановых исключений». Из произвольного (r -го) равенства выразим произвольную переменную (x s ) и подставим во все остальные равенства. Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.

Мы получим следующую систему:

. (1.21)

Из s -го равенства системы (1.21) мы впоследствии найдем переменную x s (после того, как будут найдены остальные переменные). S -я строка запоминается и в дальнейшем из системы исключается. Оставшаяся система будет содержать на одно уравнение и на одну независимую переменную меньше, чем исходная система.

Вычислим коэффициенты полученной системы (1.21) через коэффициенты исходной системы (1.20). Начнем с r -го уравнения, которое после выражения переменной x s через остальные переменные будет выглядеть следующим образом:

Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:

(1.23)
Вычислим теперь новые коэффициенты b ij (i ¹ r ) произвольного уравнения. Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):

После приведения подобных членов, получим:

(1.24)
Из равенства (1.24) получим формулы, по которым вычисляются остальные коэффициенты системы (1. 21) (за исключением r -го уравнения):

(1.25)
Преобразование систем линейных уравнений методом обыкновенных жордановых исключений оформляется в виде таблиц (матриц). Эти таблицы получили название «жордановых».

Так, задаче (1.20) ставится в соответствие следующая жорданова таблица:

Таблица 1.1

	x 1	x 2	…	x j	…	x s	…	x n
y 1 =	a 11	a 12		a 1j		a 1s		a 1n
…………………………………………………………………..
y i =	a i 1	a i 2		a ij		a is		a in
…………………………………………………………………..
y r =	a r 1	a r 2		a rj		a rs		a rn
………………………………………………………………….
y n =	a m 1	a m 2		a mj		a ms		a mn

Жорданова таблица 1.1 содержит левый заглавный столбец, в который записывают правые части системы (1.20) и верхнюю заглавную строку, в которую записывают независимые переменные.

Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу А на матрицу , состоящую из элементов верхней заглавной строки, то получится матрица , состоящая из элементов левого заглавного столбца. То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:

Таблица 1.2

	x 1	x 2	…	x j	…	y r	…	x n
y 1 =	b 11	b 12		b 1 j		b 1 s		b 1 n
…………………………………………………………………. .
y i =	b i 1	b i 2		b ij		b is		b in
…………………………………………………………………..
x s =	b r 1	b r 2		b rj		b rs		b rn
………………………………………………………………….
y n =	b m 1	b m 2		b mj		b ms		b mn

Разрешающий элемент a rs мы будем выделять жирным шрифтом. Напомним, что для осуществления одного шага жордановых исключений разрешающий элемент должен быть отличен от нуля. Строку таблицы, содержащую разрешающий элемент, называют разрешающей строкой. Столбец, содержащий разрешающий элемент, называют разрешающим столбцом. При переходе от данной таблицы к следующей таблице одна переменная (x s ) из верней заглавной строки таблицы перемещается в левый заглавный столбец и, наоборот, один из свободных членов системы (y r ) из левого заглавного столбца таблицы перемещается в верхнюю заглавную строку.

Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), вытекающий из формул (1.23) и (1.25).

1. Разрешающий элемент заменяется обратным числом:

2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:

3. Остальные элементы разрешающего столбца делятся на разрешающий элемент:

4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:

Последняя формула легко запоминается, если заметить, что элементы, составляющие дробь , находятся на пересечении i -ой и r -ой строк и j -го и s -го столбцов (разрешающей строки, разрешающего столбца и той строки и столбца, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы можно использовать следующую диаграмму:

-21-26-13-37

Совершая первый шаг жордановых исключений, в качестве разрешающего элемента можно выбрать любой элемент таблицы 1.3, расположенный в столбцах x 1 ,…, x 5 (все указанные элементы не равны нулю). Не следует только выбирать разрешающий элемент в последнем столбце, т.к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.

Строку x 3 (табл.1.4) можно, предварительно запомнив, исключить из таблицы 1.4. Из таблицы 1.4 исключается так же третий столбец с нулем в верхней заглавной строке. Дело в том, что независимо от коэффициентов данного столбца b i 3 все соответствующие ему слагаемые каждого уравнения 0·b i 3 системы будут равны нулю. Поэтому указанные коэффициенты можно не вычислять. Исключив одну переменную x 3 и запомнив одно из уравнений, мы приходим к системе, соответствующей таблице 1.4 (с вычеркнутой строкой x 3). Выбирая в таблице 1.4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).

Таблица 1.5 Таблица 1.6

Из последней таблицы 1.7 находим: x 1 = – 3 + 2x 5 .

Последовательно подставляя уже найденные переменные в запомненные строки, находим остальные переменные:

Таким образом, система имеет бесчисленное множество решений. Переменной x 5 , можно придавать произвольные значения. Данная переменная выступает в роли параметра x 5 = t. Мы доказали совместность системы и нашли ее общее решение:

x 1 = – 3 + 2t

x 2 = – 1 – 3t

x 3 = – 2 + 4t . (1.27)
x 4 = 4 + 5t

x 5 = t

Придавая параметру t различные значения, мы получим бесчисленное множество решений исходной системы. Так, например, решением системы является следующий набор переменных (- 3; – 1; – 2; 4; 0).

Готовые домашние задания по линейной алгебре, матрицы по формуле крамера :: concyhosbu

06.11.2016 08:02

Матрицы называется наибольший из порядков миноров матрицы, отличных от нуля. Примерное задание. Формула Крамера. Алгебра. Тригонометрия. ДЗ на 5готовые домашние задания Скачать решебники по всем предметам. Решение систем линейных уравнений. Матричный метод Показать все онлайн калькуляторы. Онлайн калькуляторы Онлайн упражнения Справочник Таблицы и формулы Калькулятор процентов. ДЗ на 5готовые домашние задания. Квадратные системы линейных уравнений. Анисимова Н. П. Домашнее задание. Непосредственно из формулы 1.3 ясно, что умножение матрицы на число. Ответ представить в обыкновенных неправильных дробях. Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. ЛИНЕЙНАЯ АЛГЕБРА С ЭЛЕМЕНТАМИ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ 9. Глава 1. Метод.

Линейных уравнений методом Жордана Гаусса Обратная матрица. Раздел . Решить систему по формулам Крамера. Метод Крамера Метод Гаусса Метод разложения. Справочник. Решается он на раз два, кроме как найти парочку определителей матрицы, вам ничего и не нужно то. Учебники, ГДЗ, решебники, ЕГЭ, ГИА, экзамены, книги. Формула для вычисления обратной матрицы. Анализ линейной модели с применением правила Крамера. Совместность системы линейных. Решение систем по формулам Крамера и с помощью обратной матрицы. Теорема Крамера. Метод Гаусса. Основные формулы, таблицы и теоремы для учащихся. Введите параметры системы уравнений: Количество уравнений в системе. Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Рангом.

Домашние задания. Ранг матрицы. Видов контроля СРС является защита индивидуальных домашних заданий. Индивидуальные задания по разделам дисциплины. По формулам Крамера находим:,. РазделыВысшая математикаЛинейная алгебраФормула Крамера. Метод Крамера правило Крамера — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы причём для таких уравнений решение. Решенные примеры. Алгебра. Вектора. Аналитическая геометрия. Решение. Выпишем матрицу коэффициентов и матрицу столбец свободных членов. Ответ: 2. Решите систему уравнений по формулам Крамера. Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако. Нахождение обратной матрицы. Основы линейной алгебры Умножение и сложение мерных матриц Решение систем.

Обратной матрицы н формулы Крамера . Метод Крамера Решение систем линейных уравнений. Определители. Матрицы. По формулам для длины вектора и скалярного произведения. Онлайн решебник. Линейная алгебра. Матрицы. Системы уравнений. Метод Крамера Метод обратных матриц Метод Гаусса Жордана Гаусса. Матрица линейного преобразования в базисе из собственных векторов. Решение системы линейных уравнений методом Крамера. Матрица, образ, ядро, ранг и дефект оператора.55.2.7. Тики, как аналитическая геометрия, линейная алгебра, пределы, диф. Занятиях, другие — в виде домашних заданий, остальные использо. Если определитель матрицы квадратной системы не равен нулю. Задание. При помощи формул Крамера найти решение системы.

Вместе с Готовые домашние задания по линейной алгебре, матрицы по формуле крамера часто ищут

метод крамера онлайн калькулятор.

метод крамера формула.

метод обратной матрицы онлайн.

метод крамера пример.

решение систем линейных уравнений методом крамера.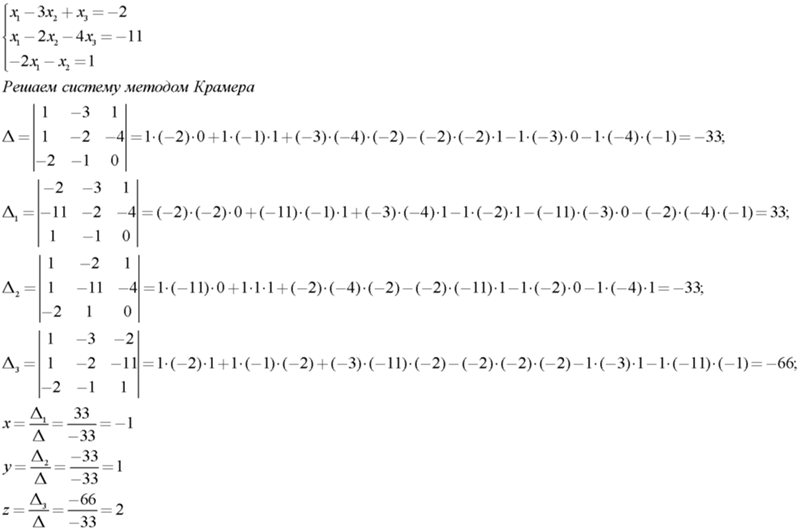

метод крамера онлайн калькулятор с подробным решением.

онлайн калькулятор метод гаусса.

матричный метод онлайн

Читайте также:

Рабочая тетрадь 7 класса гдз по английскому

Готовые домашние задания для класса в.михеева

Атлас 8 класс география дрофа онлайн смотреть бесплатно

Метод Крамера – правило и примеры решения систем линейных уравнений

Краткое описание

Широко востребованный метод Крамера активно используется специалистами для решения распространённых алгебраических уравнений (СЛАУ). Итоговая точность полученного результата обусловлена применением определённой математической матрицы, а также некоторыми вспомогательными ограничениями, которые неизбежно накладываются во время доказательства конкретной теоремы.

Набором выражений вида yr 2 x1+ yr 2 x2 +… yr n xn = b r при r =1, 2,…, m принято называть универсальную систему линейных алгебраических уравнений. В этом случае также присутствуют определённые коэффициенты, которые могут принадлежать множеству W -действительных чисел, от неизвестных x 1… xn.

Чаще всего в роли действенных чисел выступают yr и br. Каждое из представленных значений называется линейным уравнением. Элементарные коэффициенты при неизвестных — это yr, а вот bi — свободные коэффициенты уравнений. Стандартный n -мерный вектор k ° = (k 1°, k 2°,…, k n°) называют решением системы. При правильной подстановке в систему вместо неизвестных элементов каждая из строчек становится верным равенством.

Если у системы присутствует минимум одно решение, то она называется совместной. Речь касается несовместного примера только в том случае, если многочисленные алгоритмы решения совпадают с пустым множеством. Классическая формула Крамера используется в том случае, если необходимо отыскать верное решение для линейных уравнений. Для получения достоверного результата матрицы должны быть исключительно квадратными. А на практике такой подход означает одинаковое количество уравнений и неизвестных в системе.

Ключевые нюансы

Востребованный в математике метод Крамера для решения систем линейных уравнений можно успешно использовать только в том случае, если ученик хорошо понимает, что такое матрица алгебраических примеров и каким образом она выписывается. В противном случае будет сложно избежать распространённых ошибок. Если необходимые навыки имеются, то в итоге остаётся только правильно запомнить формулы, которые определяют метод Крамера. Чтобы лучше усвоить все тонкости этой темы, необходимо воспользоваться следующими обозначениями:

Главный определитель совместности матрицы системы — Det.
Определитель матрицы, который получен из основного элемента — deti. Если ученик попробует заменить последний столбец матрицы, задействовав для этого первые части линейных алгебраических уравнений, тогда следует использовать понятие deti.
Для количества неизвестных и уравнений в системе используется символ n.

Если учесть все перечисленные нюансы, то в итоге правило Крамера для вычисления компонентов n -мерного вектора можно записать в следующей формулировке: xi = deti / Det. В этом случае DET максимально отличен от нуля.

Практическое применение

Для решения многих математических задач принято использовать теорему Кронекера — Капелли. Если основной определитель G главной матрицы, которая была составлена за счёт коэффициентов уравнений, не равен нулю, тогда система уравнений будет совместна. Но такое решение является единственным. Для поиска верного результата принято вычислять систему через формулу Крамера для линейных уравнений: x i = D i / D.

Метод Крамера основан на нескольких основных нюансах, которые в сочетании друг с другом дают отличный результат:

Если решено найти правильное исчисление системы по методике талантливого учёного, тогда первым делом обязательно вычисляют главный определитель обращения матрицы (J). Если при подсчёте детерминант основной матрицы оказался равен нулю, то такая система просто не имеет решения, либо речь касается нескончаемого количества решений. В такой ситуации получить достоверный результат можно только благодаря универсальному методу Гаусса.
На втором этапе ученику нужно постараться заменить крайний столбец главной матрицы столбцом свободных членов, чтобы отыскать определитель (J 1).
Остаётся повторить аналогичные действия для всех оставшихся столбцов. За счёт этого можно получить определители от J 1 до J n. В этом случае символ n указывает на номер последнего справа столбца.
Как только будут найдены абсолютно все детерминанты, нужно постараться высчитать неизвестные переменные по элементарной формуле: х i = B i / B.

Разнообразие математических подходов

Немного иные приёмы используются в том случае, когда предстоит работать с определителем матрицы. Если нужно рассчитать правильные данные на основе конструкции с соразмерностью больше чем 2 на 2, тогда можно использовать сразу несколько проверенных временем способов:

Метод Гаусса. Некоторые специалисты привыкли называть это математическое направление понижением порядка основного определителя. Несколько простых действий помогают преобразить матрицу и привести её к треугольному виду. Все комплексные числа, которые расположены на основной диагонали, перемножаются. Но при таком поиске определителя запрещено выполнять арифметические действия со строчками или столбцами без предварительного вынесения чисел как множителя/делителя. Предварительно умножают вычитаемую строку на нулевой множитель, а уже потом вычитают и складывают все элементы между собой. Конечный знак у обратной матрицы подвергают изменениям только в том случае, когда происходит перестановка столбцов или строчек.
Правило Саррюса. Суть метода треугольников в том, чтобы ученик мог при вычислении дискриминанта и определителя произведения всех чисел, которые были соединены одной линией, записывать примеры только с положительным значением. Это утверждение идеально подходит для матриц размером 3х3. Но если следовать всем нормам правила Саррюса, то первым делом переписывают саму матрицу, а рядом с ней располагают первый и второй столбец. В итоге через сформированную конструкцию проводятся диагональные линии. Члены матрицы, которые расположены на основной диагонали или на параллельной ей плоскости всегда записываются со знаком +, а вот элементы, лежащие на побочной диагонали, имеют знак -.
Если ученик решит использовать универсальный метод Крамера СЛАУ, для которого свойственно присутствие сразу четырёх неизвестных, тогда лучше всего выполнить комбинацию с технологией Гаусса. В этом случае можно гарантированно отыскать детерминант через поиск миноров.

Для каждого направления свойственны свои нюансы и правила теории, которые должен знать каждый ученик. В противном случае решить правильно поставленную задачу практически невозможно.

Помощь онлайн-калькуляторов

Созданные программистами программы пользуются огромным спросом даже среди опытных математиков, так как всего за несколько минут можно правильно решить задачу. Многофункциональные онлайн-калькуляторы с подробным решением по методу Крамера позволяют быстро и качественно решить целую систему различных уравнений. Для этого пользователю необходимо правильно указать количество неизвестных величин.

Для быстрого переключения в уравнении с положительных знаков на отрицательные нужно вводить соответствующие числа. Если в задаче отсутствует коэффициент, то на его место в калькулятор вводят ноль. Указывать можно не только числа, но и дроби. К примеру: 4,7 или 1/5.

На специальных сайтах можно решать различные системы уравнений по методу талантливого учёного Крамера в режиме онлайн. Решение будет отображено на экране моментально, к тому же его можно расширить. При решении системы уравнений крайне важно найти определители и присоединить сразу несколько разных матриц. Для существенного сокращения решения эта математическая операция упрощена, что существенно облегчает работу учеников.

Актуальные примеры решения

Единственность арифметических действий с системой при её совместимости обеспечивает условие неравенства нулю основного определителя. Но если сумма точек, которые были возведены в квадрат, строго положительна, то полученный СЛАУ будет несовместим с квадратной матрицей. Такая ситуация может произойти тогда, когда минимум один из присутствующих элементов deti отличён от нуля.

В качестве примера можно рассмотреть задачу, по условиям которой необходимо решить трёхмерную систему ЛАУ, используя для этого формулы Крамера:

x1 + 2 x2 + 4 x3 = 31.
5 x1 + x2 + 2 x3 = 29.
3 x1 — x2 + x3 =10.

Для решения следует выписать матрицу системы построчно. Строку матрицы принято обозначать символом i. После этого можно получить формулу A1=(1 2 4), A2=(5 1 2), A3=(3 -1 1). Существование значения b = (31 29 10) помогает отобразить столбец свободных коэффициентов. Основной определитель Det будет соответствовать следующим данным: a11 a22 a33 + a12 a23 a31 + a31 a21 a32 — a13 a22 a31 — a11 a32 a23 — a33 a21 a12 = 1—20 + 12 — 12 + 2—10 = -27.

В соответствии с формулой Крамера можно найти: x1 = -81/(-27) = 3, x2 = -108/(-27) = 4, x3 = -135/(-27) = 5. Если всё сделать правильно, то можно получить следующий ответ: x° = (3,4,5). Если руководствоваться базовыми понятиями, то многочисленные средства Крамера для решения сложных линейных уравнений можно использовать опосредованно.

Нелишним также будет рассмотреть следующий пример, где ученику нужно определить то, при каких показателях параметра F неравенство формулы | F x — y — 4|+|x + F y + 4|<=0 будет иметь ровно одно логическое решение. В силу определения модуля функции представленное неравенство может быть выполнено только в том случае, если оба выражения равны нулю. Именно поэтому рассматриваемая задача сводится только к нахождению решения линейной системы алгебраических уравнений. Соблюдаемый принцип действий должен соответствовать двум следующим формулам:

F x — y = 4.
x + F y = -4.

Для этого примера свойственно единственное решение, но только в том случае, если главный определитель отличен от нуля.

Это условие выполняется абсолютно для всех действительных значений параметра F. Стоит отметить, что к математическим задачам этого типа могут быть сведены многочисленные практические примеры из области физики, математики и даже химии.

Присутствующая вычислительная сложность

Рассматриваемый метод решения задач требует стандартного вычисления определителей размерности. Если практиковать использование метода Гаусса для поиска всех необходимых определителей, то возникшие в итоге сложности будут связаны с электронными операциями порядка сложения-умножения. В этом случае придётся столкнуться с более сложными формулами, нежели с методом Гаусса.

Именно поэтому, с точки зрения затрат времени на вычисления, метод Гаусса является непрактичным. Специалистами в 2010 году было доказано, что метод Крамера вполне может быть реализован со сложностью O (n ³), а это очень важно в математике.

В распространённых задачах на системы линейных уравнений обязательно встречаются и такие, в которых помимо букв существуют ещё и другие символы. Они обозначают некоторое число (чаще всего действительное). Математики к таким задачам и системам уравнений приводят примеры, которые основаны на поиске общих свойств каких-либо явлений и предметов. Это очень удобно в том случае, если учёными был изобретён какой-либо агрегат или материал, а для описания всех его свойств необходимо решить целую систему линейных уравнений, где вместо коэффициентов используются буквы.

Метод Крамера – теорема, примеры решений

Метод Крамера часто применяется для систем линейных алгебраических уравнений (СЛАУ). Этот способ решения один из самых простых. Как правило, данный метод применяется только для тех систем, где по количеству неизвестных столько же, сколько и уравнений. Чтобы получилось решить уравнение, главный определитель матрицы не должен равняться нулю.

Габриель Крамер – математик, создатель одноименного метода решения систем линейных уравнений

Габриель Крамер – известный математик, который родился 31 июля 1704 года. Ещё в детстве Габриель поражал своими интеллектуальными способностями, особенно в области математики. Когда Крамеру было 20 лет, он устроился в Женевский университет штатным преподавателем.

Во время путешествия по Европе Габриель познакомился с математиком Иоганном Бернулли, который и стал его наставником. Только благодаря Иоганну, Крамер написал много статей по геометрии, истории математики и философии. А в свободное от работы время изучал математику всё больше и больше.

Наконец-то наступил тот день, когда Крамер нашёл способ, при помощи которого можно было бы легко решать не только лёгкие, но и сложные системы линейных уравнений.

В 1740 году у Крамера были опубликованы несколько работ, где доступно изложено решение квадратных матриц и описан алгоритм, как находить обратную матрицу. Далее математик описывал нахождения линейных уравнений разной сложности, где можно применить его формулы. Поэтому тему так и назвали: «Решение систем линейных уравнений методом Крамера».

Учёный умер в возрасте 48 лет (в 1752 году). У него было ещё много планов, но, к сожалению, он так и не успел их осуществить.

Вывод формулы Крамера

Пусть дана система линейных уравнений такого вида:

где , , – неизвестные переменные, – это числовые коэффициенты, в – свободные члены.

Решением СЛАУ (систем линейных алгебраических уравнение) называются такие неизвестные значения при которых все уравнения данной системы преобразовываются в тождества.

Если записать систему в матричном виде, тогда получается , где

В данной главной матрице находятся элементы, коэффициенты которых при неизвестных переменных,

Это матрица-столбец свободных членов, но есть ещё матрица-столбец неизвестных переменных:

После того, когда найдутся неизвестные переменные, матрица и будет решением системы уравнений, а наше равенство преобразовывается в тождество. . Если умножить , тогда . Получается: .

Если матрица – невырожденная, то есть, её определитель не равняется нулю, тогда у СЛАУ есть только одно единственное решение, которое находится при помощи метода Крамера.

Как правило, для решения систем линейных уравнений методом Крамера, нужно обращать внимания на два свойства, на которых и основан данный метод:

1. Определитель квадратной матрицы равняется сумме произведений элементов любой из строк (столбца) на их алгебраические дополнения:

, здесь – 1, 2, …, n; – 1, 2, 3, …, n.

2. Сумма произведений элементов данной матрицы любой строки или любого столбца на алгебраические дополнения определённых элементов второй строки (столбца) равняется нулю:

где – 1, 2, …, n; – 1, 2, 3, …, n. .

Итак, теперь можно найти первое неизвестное . Для этого необходимо умножить обе части первого уравнения системы на , части со второго уравнения на , обе части третьего уравнения на и т. д. То есть, каждое уравнение одной системы нужно умножать на определённые алгебраические дополнения первого столбца матрицы :

Теперь прибавим все левые части уравнения, сгруппируем слагаемые, учитывая неизвестные переменные и приравняем эту же сумму к сумме правых частей системы уравнения:

Можно обратиться к вышеописанным свойствам определителей и тогда получим:

И предыдущее равенство уже выглядит так:

Откуда и получается .

Аналогично находим . Для этого надо умножить обе части уравнений на алгебраические дополнения, которые находятся во втором столбце матрицы .

Теперь нужно сложить все уравнения системы и сгруппировать слагаемые при неизвестных переменных. Для этого вспомним свойства определителя:

Откуда получается .

Аналогично находятся все остальные неизвестные переменные.

Если обозначить:

тогда получаются формулы, благодаря которым находятся неизвестные переменные методом Крамера:

, , .

Замечание.

Тривиальное решение при может быть только в том случае, если система уравнений является однородной . И действительно, если все свободные члены нулевые, тогда и определители равняются нулю, так как в них содержится столбец с нулевыми элементами. Конечно же, тогда формулы , , дадут

Метод Крамера – теоремы

Прежде чем решать уравнение , необходимо знать:

теорему аннулирования;
теорему замещения.

Теорема замещения

Теорема

Сумма произведений алгебраических дополнений любого столбца (строки) на произвольные числа равняется новому определителю, в котором этими числами заменены соответствующие элементы изначального определителя, что отвечают данным алгебраическим дополнениям.

Например,

где – алгебраические дополнения элементов первого столбца изначального определителя:

Теорема аннулирования

Теорема

Сумма произведений элементов одной строки (столбца) на алгебраические дополнения соответствующих элементов другой строки (столбца) равняется нулю.

Например:

Алгоритм решения уравнений методом Крамера

Метод Крамера – простой способ решения систем линейных алгебраических уравнений. Такой вариант применяется исключительно к СЛАУ, у которых совпадает количество уравнений с количеством неизвестных, а определитель отличен от нуля.

Итак, когда выучили все этапы, можно переходить к самому алгоритму решения уравнений методом Крамера. Запишем его последовательно:

Шаг 1. Вычисляем главный определитель матрицы

и необходимо убедиться, что определитель отличен от нуля (не равен нулю).

Шаг 2. Находим определители

Это и есть определители матриц, которые получались из матрицы при замене столбцов на свободные члены.

Шаг 3. Вычисляем неизвестные переменные

Теперь вспоминаем формулы Крамера, по которым вычисляем корни (неизвестные переменные):

, , .

Шаг 4. Выполняем проверку

Выполняем проверку решения при помощи подстановки в исходную СЛАУ. Абсолютно все уравнения в системе должны быть превращены в тождества. Также можно высчитать произведение матриц . Если в итоге получилась матрица, которая равняется , тогда система решена правильно. Если же не равняется , скорей всего в одном из уравнений есть ошибка.

Давайте для начала рассмотрим систему двух линейных уравнений, так как она более простая и поможет понять, как правильно использовать правило Крамера. Если вы поймёте простые и короткие уравнения, тогда сможете решить более сложные системы трёх уравнений с тремя неизвестными.

Кроме всего прочего, есть системы уравнений с двумя переменными, которые решаются исключительно благодаря правилу Крамеру.

Итак, дана система двух линейных уравнений:

Для начала вычисляем главный определитель (определитель системы):

Значит, если , тогда у системы или много решений, или система не имеет решений. В этом случае пользоваться правилом Крамера нет смысла, так как решения не получится и нужно вспоминать метод Гаусса, при помощи которого данный пример решается быстро и легко.

В случае, если , тогда у система есть всего одно решение, но для этого необходимо вычислить ещё два определителя и найти корни системы.

Часто на практике определители могут обозначаться не только , но и латинской буквой , что тоже будет правильно.

Корни уравнения найти просто, так как главное, знать формулы:

Так как мы смогли решить систему двух линейных уравнений, теперь без проблем решим и систему трёх линейных уравнений, а для этого рассмотрим систему:

(1)

Здесь алгебраические дополнения элементов – первый столбец . Во время решения не забывайте о дополнительных элементах. Итак, в системе линейных уравнений нужно найти три неизвестных – при известных других элементах.

Создадим определитель системы из коэффициентов при неизвестных:

Умножим почленно каждое уравнение соответственно на , , – алгебраические дополнения элементов первого столбца (коэффициентов при ) и прибавим все три уравнения. Получаем:

Согласно теореме про раскладывание, коэффициент при равняется . Коэффициенты при и будут равняться нулю по теореме аннулирования. Правая часть равенства по теореме замещения даёт новый определитель, который называется вспомогательным и обозначается

После этого можно записать равенство:

(2)

Для нахождения и перемножим каждое из уравнений изначальной системы в первом случае соответственно на , во втором – на и прибавим. Впоследствии преобразований получаем:

где

Если , тогда в результате получаем формулы Крамера:

= , = , =

Порядок решения однородной системы уравнений

Отдельный случай – это однородные системы:

(3)

Среди решений однородной системы могут быть, как нулевые решения , так и решения отличны от нуля.

Теорема

Примеры решения методом Крамера

Рассмотрим на примере решение методом Крамера и вы увидите, что сложного ничего нет, но будьте предельно внимательно, так как частые ошибки в знаках приводят к неверному ответу.

Пример 1

Задача

Решить систему линейных уравнений методом Крамера:

Решение

Первое, что надо сделать – вычислить определитель матрицы:

Как видим, , поэтому по теореме Крамера система имеет единственное решение (система совместна). Далее нужно вычислять вспомогательные определители. Для этого заменяем первый столбец из определителя на столбец свободных коэффициентов. Получается:

Аналогично находим остальные определители:

И проверяем:

Ответ

, .

Пример 2 Пример 3

Задача

Решить систему методом Крамера

Решение

Как вы понимаете, сначала находим главный определитель:

Как мы видим, главный определитель не равняется нулю и поэтому система имеет единственное решение. Теперь можно вычислить остальные определители:

При помощи формул Крамера находим корни уравнения:

, , .

Чтобы убедиться в правильности решения, необходимо сделать проверку:

Как видим, подставив в уравнение решённые корни, у нас ответ получился тот же, что и в начале задачи, что говорит о правильном решении уравнений.

Ответ

Система уравнений имеет единственное решение: , , .

Есть примеры, когда уравнение решений не имеет. Это может быть в том случае, когда определитель системы равен нулю, а определители при неизвестных неравны нулю. В таком случае говорят, что система несовместна, то есть не имеет решений. Посмотрим на следующем примере, как такое может быть.

Пример 4

Задача

Решить систему линейных уравнений методом Крамера:

Решение

Как и в предыдущих примерах находим главный определитель системы:

В этой системе определитель равняется нулю, соответственно, система несовместна и определенна или же несовместна и не имеет решений. Чтобы уточнить, надо найти определители при неизвестных так, как мы делали ранее:

Мы нашли определители при неизвестных и увидели, что все они не равны нулю. Поэтому система несовместна и не имеет решений.

Ответ

Система не имеет решений.

Часто в задачах на системы линейных уравнений встречаются такие уравнения, где есть не одинаковые буквы, то есть, кроме букв, которые обозначают переменные, есть ещё и другие буквы и они обозначают некоторое действительное число. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. Давайте и рассмотрим такой пример.

Пример 5

Задача

Решить систему линейных уравнений методом Крамера:

Решение

В этом примере – некоторое вещественное число. Находим главный определитель:

Находим определители при неизвестных:

Используя формулы Крамера, находим:

, .

Ответ

И наконец, мы перешли к самой сложной системе уравнений с четырьмя неизвестными. Принцип решения такой же, как и в предыдущих примерах, но в связи с большой системой можно запутаться. Поэтому рассмотрим такое уравнение на примере.

Пример 6

Задача

Найти систему линейных уравнений методом Крамера:

Здесь действуют система определителей матрицы высших порядков, поэтому вычисления и формулы рассмотрены в этой теме, а мы сейчас просто посчитаем систему уравнений с четырьмя неизвестными.

Решение

В изначальном определители из элементов второй строки мы отнимали элементы четвёртой строки, а из элементов третьей строки отнимались элементы четвёртой строки, которые умножались на 2. Также отнимали из элементов четвёртой строки элементы первой строки, умноженной на два.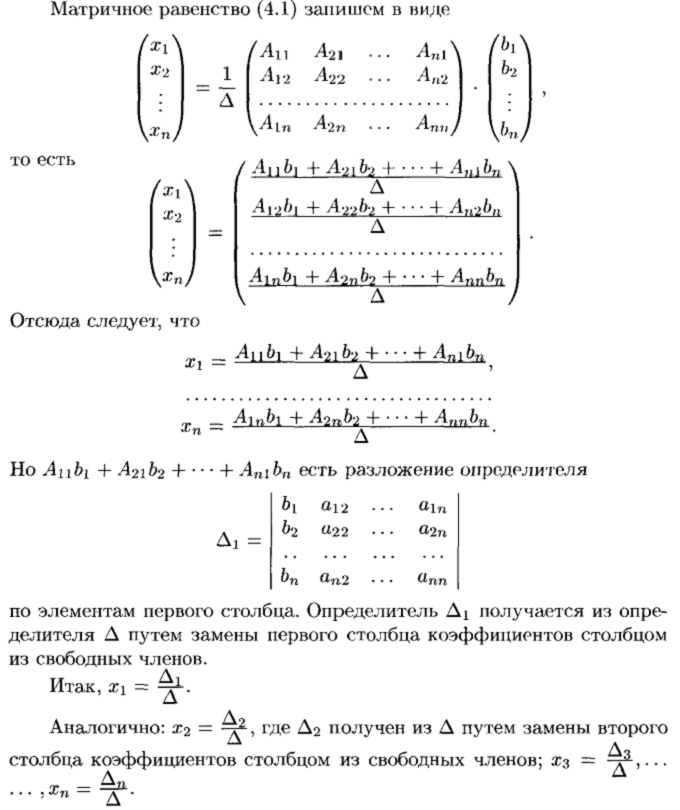 Преобразования первоначальных определителей при трёх первых неизвестных произведены по такой же схеме. Теперь можно находить определители при неизвестных:

Для преобразований определителя при четвёртом неизвестном из элементов первой строки мы вычитали элементы четвёртой строки.

Теперь по формулам Крамера нужно найти:

Ответ

Итак, мы нашли корни системы линейного уравнения:

Подведём итоги

При помощи метода Крамера можно решать системы линейных алгебраических уравнений в том случае, если определитель не равен нулю. Такой метод позволяет находить определители матриц такого порядка, как на благодаря формулам Крамера, когда нужно найти неизвестные переменные. Если все свободные члены нулевые, тогда их определители равны нулю, так как в них содержится столбец с нулевыми элементами. И конечно же, если определители равняются нулю, лучше решать систему методом Гаусса, а не Крамера, только тогда ответ будет верный.

Рекомендуем почитать для общего развития

Анкилов А. В. Высшая математика, ч. 1: учеб. Пособие/П. А. Вельмисов, Ю. А. Решетников – Ульяновск – 2011 – 252 с.

Письменный Д. – Конспект лекций по высшей математике: учеб. для вузов/Письменный Д. – М. 2006 – 602 с.

Решение методом Крамера в Excel

Метод Крамера в Excel 2003 (XLS)

Метод Крамера в Excel от 2007 (XLSX)

Метод Крамера – теорема, примеры решений обновлено: 16 апреля, 2020 автором: Научные Статьи.Ру

Разработка материала по методу Крамера по алгебре в 7 классе

Формулы Крамера для модуля на ШЦП 4.0

Посмотреть урок по ссылкеhttps://youtu.be/f0GvqaF2ht8

Определение. Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Формулы Крамера для нахождения неизвестных:

Найти значения и возможно только при условии, если

Этот вывод следует из следующей теоремы.

Ответ : (5;2)

Пример 1. Решить систему линейных уравнений:

. (2)

Согласно теореме Крамера имеем:

Итак, решение системы (2):

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера, при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Условия:

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

Условия:

* ,

** ,

т. е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Условия:

** .

Итак, система m линейных уравнений с n переменными называется несовместной, если у неё нет ни одного решения, и совместной, если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой, а более одного – неопределённой.

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
–

Пример 2. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:
Итак, (1; 0; -1) – единственное решение системы.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

Применить метод Крамера самостоятельно, а затем посмотреть решения

Пример 4. Решить систему линейных уравнений:

Правильное решение и ответ.

Пример 5. Решить систему линейных уравнений методом Крамера:

. Решение. Находим определитель системы:

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Решение примеров методом крамера в экселе. Решение уравнений в Excel методом итераций Крамера и Гаусса

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
–

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

По формулам Крамера находим:

Итак, решение системы – (2; -1; 1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Решение систем линейных алгебраических уравнений в Excel Методы решения систем линейных алгебраических уравнений хорошо описаны в учебнике “Основы вычислительной математики. Демидович Б.П., Марон И.А. 1966”. Скачать – 11Мб

1. Метод обратной матрицы (решение в Excel)

Если дано уравнение:
A*X = B, где A – квадратная матрица, X,B – вектора;
причем B – известный вектор (т е столбец чисел), X – неизвестный вектор,
то решение X можно записать в виде:
X = A -1 *B, где A -1 – обратная от А матрица.
В MS Excel обратная матрица вычисляется функцией МОБР(), а перемножаются матрицы (или матрица на вектор) – функцией МУМНОЖ().

Имеются “тонкости” использования этих матричных действий в Excel. Так, чтобы вычислить обратную матрицу от матрицы А, нужно:

1. Мышкой выделить квадратную область клеток, где будет размещена обратная матрица. 2. Начать вписывать формулу =МОБР(3. Выделить мышкой матрицу А. При этом правее скобки впишется соответствующий диапазон клеток. 4. Закрыть скобку, нажать комбинацию клавиш: Ctrl-Shift-Enter 5. Должна вычислиться обратная матрица и заполнить предназначенную для неё область Чтобы умножить матрицу на вектор: 1. Мышкой выделить область клеток, где будет размещён результат умножения 2. Начать вписывать формулу =МУМНОЖ(3. Выделить мышкой матрицу – первый сомножитель. При этом правее скобки впишется соответствующий диапазон клеток. 4. С клавиатуры ввести разделитель; (точка с запятой) 5. Выделить мышкой вектор- второй сомножитель. При этом правее скобки впишется соответствующий диапазон клеток. 6. Закрыть скобку, нажать комбинацию клавиш: Ctrl-Shift-Enter 7. Должно вычислиться произведение и заполнить предназначенную для него область Есть и другой спососб, при котором используется кнопка построителя функции Excel. Пример СЛАУ 4-го порядка

Скачать документ Excel, в котором этот пример решён различными методами.

2. Метод Гаусса

Метод Гаусса подробно (по шагам) выполняется только в учебных целях, когда нужно показать, что Вы это умеете. А чтобы решить реальную СЛАУ, лучше применить в Excel метод обратной матрицы или воспользоваться специальными программами, например, этой

Краткое описание.

3. Метод Якоби (метод простых итераций)

Для применения метода Якоби (и метода Зейделя) необходимо, чтобы диагональные компоненты матрицы А были больше суммы остальных компонент той же строки. Заданная система не обладает таким свойством, поэтому выполняю предварительные преобразования.

(1)’ = (1) + 0,43*(2) – 0,18*(3) – 0,96*(4) (2)’ = (2) + 0,28*(1) – 1,73*(3) + 0,12*(4) (3)’ = (3) – 0,27*(1) – 0,75*(2) + 0,08*(4) (4)’ = (4) + 0,04*(1) – 6,50*(2) + 8,04*(3) Примечание: подбор коэффицентов выполнен на листе “Анализ”. Решаются системы уравнений, цель которых – обратить внедиагональные элементы в нуль. Коэффиценты – это округлённые результаты решения таких систем уравнений. Конечно, это не дело. В результате получаю систему уравнений:
Для применения метода Якоби систему уравнений нужно преобразовать к виду:
X = B2 + A2*X Преобразую:

Далее делю каждую строку на множитель левого столбца, то есть на 16, 7, 3, 70 соответственно. Тогда матрица А2 имеет вид:

А вектор В2:

В этой статье мы расскажем, как использовать формулы для решения систем линейных уравнений.

Вот пример системы линейных уравнений:
3x + 4y = 8
4x + 8y = 1

Решение состоит в нахождении таких значений х и у , которые удовлетворяют обоим уравнениям. Эта система уравнений имеет одно решение:
x = 7,5
y = -3,625

Количество переменных в системе уравнений должно быть равно количеству уравнений. Предыдущий пример использует два уравнения с двумя переменными. Три уравнения требуются для того, чтобы найти значения трех переменных (х ,у и z ). Общие действия по решению систем уравнений следующие (рис. 128.1).

Выразите уравнения в стандартной форме. Если это необходимо, используйте основы алгебры и перепишите уравнение так, чтобы все переменные отображались по левую сторону от знака равенства. Следующие два уравнения идентичны, но второе приведено в стандартном виде:
3x – 8 = -4y
3x + 4y = 8 .
Разместите коэффициенты в диапазоне ячеек размером n x n , где n представляет собой количество уравнений. На рис. 128.1 коэффициенты находятся в диапазоне I2:J3 .
Разместите константы (числа с правой стороны от знака равенства) в вертикальном диапазоне ячеек. На рис. 128.1 константы находятся в диапазоне L2:L3 .
Используйте массив формул для расчета обратной матрицы коэффициентов. На рис. 128.1 следующая формула массива введена в диапазон I6:J7 (не забудьте нажать Ctrl+Shift+Enter , чтобы ввести формулу массива): =МОБР(I2:J3) .
Используйте формулу массива для умножения обратной матрицы коэффициентов на матрицу констант. На рис. 128.1 следующая формула массива введена в диапазон J10:JJ11 , который содержит решение (x = 7,5 и у = -3,625): =МУМНОЖ(I6:J7;L2:L3) . На рис. 128.2 показан лист, настроенный для решения системы из трех уравнений.

Решение систем линейных уравнений в Excel

1. Введение

Многие задачи организации строительного производства сводятся к решению систем линейных уравнений вида:

a 11x 1a 12x 2a 1n x n b 1,
		a2 n xn
a 21x 1a 22x 2		a2 n xn




	n 1 1

называемой системой n линейных алгебраических уравнений(СЛАУ ) с n

неизвестными.

При этом произвольные числа a ij (i = 1, 2,…,n ;j = 1, 2,…,n ) называются

коэффициентами при неизвестных, а числа b i (i = 1, 2,…, n ) – свободными

членами.

Систему(1) можно записать в матричной форме

A X = B,

где A – матрица коэффициентов при неизвестных:

X – вектор- столбец неизвестных X= (x1 , x2 , …, xn ) T :

B – вектор-столбец свободных членов:

b 2B ,

или B = (b 1 ,b 2 ,…,b n )T .

2. Операции с матрицами в Excel

В Excel для операций с матрицами служат функции из категории «Математические»:

1) МОПРЕД(матрица) – вычисление определителя матрицы, 2)МОБР(матрица) – вычисление обратной матрицы, 3)МУМНОЖ(матрица1;матрица2) – произведение матриц, 4)ТРАНСП(матрица) – транспонирование матрицы.

Первая из этих функций в качестве результатавозвращает число (определитель матрицы ), поэтомувводится как обычная формула (ENTER ).

Последние три возвращают блок ячеек, поэтому должны вводиться как формулы массива (CTRL+SHIFT+ENTER ).

Рассмотрим задачурешения СЛАУ на следующем примере

8x 1 2x 2 8x 3 24,

2x 1 2x 2 10x 3 48,

2x 1 4x 2 8x 3 18.

Матрица коэффициентов при неизвестных A (3) имеет вид

а вектор-столбец свободных членов (5)B = (–24, –48, 18)T .

Решим СЛАУ (7) в среде MS Excel тремя различными способами.

Матричный способ решения (обратной матрицы)

Обе части матричного равенства (2) умножим на обратную матрицу А -1 . Получим A –1 A X =A –1 B . Так как A –1 A =E , гдеE – единичная матрица (диагональная матрица, у которой по главной диагонали расположены единицы). Тогда решение системы (2) запишется в следующем виде

МУМНОЖ(матрица1;матрица2), завершая в каждом случае ввод комбинацией

CTRL+SHIFT+ENTER.

Метод Крамера

Решение СЛАУ находится по формулам Крамера

	det A

		det A
		det A
	det A 2

		det A


	det A


	det A

где det A =A – определитель матрицы (3) системы (главный определитель), detA i =A i (i = 1, 2, …,n )– определители матрицA i (вспомогательные определители), которые получаются изA заменой i -го столбца на столбец свободных членовB (5).

Для рассматриваемой СЛАУ (7) вспомогательные матрицы имеют следующий вид

Разместим их на рабочем листе (рис. 1).

Аналогичная формула (=МОПРЕД(A3:C5) ) для вычисления определителя матрицыA записана в ячейкуE8 . Осталось найти решение системы. Соответствующие формулы Excel запишем в интервал решенияB7:B9 (рис. 3), в котором и увидим результат (рис. 4).

Обратите внимание на то (рис. 3), что при вычислении x i (i = 1, 2, 3)

анализируется значение определителя матрицы системы A , вычисленное в ячейке E8, и, если оно равно нулю, то в B7 помещается текст« Решения нет», а в ячейки B8 и B9 – пустые строки.

3. Решение СЛАУ с использованием инструмента Поиск решения

Широкий класс производственных задач составляют задачи оптимизации. Задачи оптимизации предполагают поиск значений аргументов, доставляющих функции, которую называют целевой , минимальное или максимальное значение при наличии каких-либо дополнительных ограничений. Excel располагает мощным средством для решения оптимизационных задач.

Это инструмент-надстройка, который называетсяПоиск решения (Solver )

(доступен через менюСервис  Поиск решения ) .

Задачу решения СЛАУ можно свести к оптимизационной задаче.

Для чего одно из уравнений (например, первое) взять в качестве целевой функции, а оставшиеся n -1 рассматривать в качестве ограничений.

Запишем систему(1) в виде

a 11x 1a 12x 2a 1n x n b 10,

		a2 n xn
a 21x 1a 22x 2		a2 n xn



			b 0.
	n 1 1

Для решения этой задачи необходимо записать выражения (формулы) для вычисления значений функций, стоящих слева в уравнениях системы (12). Отведем для примера под эти формулы интервал C7:C9 . В ячейкуC7 введем формулу =A3*$B$7+B3*$B$8+C3*$B$9-D3 и скопируем ее в оставшиесяC8 иC9 . В них появятся соответственно =A4*$B$7+B4*$B$8+C4*$B$9-D4 и =A5*$B$7+B5*$B$8+C5*$B$9-D5 .

В окне диалога Поиск решения (рис. 5) задать параметры поиска (установить целевую ячейкуC7 равной нулю, решение в изменяемых ячейкахB7:B9 , ограничения заданы формулами в ячейкахC8 и С9 ). После щелчка по кнопкеВыполнить в

интервале B7:B9 получим результат (рис. 6) – решение СЛАУ.

Вычислить значения корней сформированной системы уравнений двумя методами: обратной матрицы и методом Крамера.

Введем данные значения в ячейки А2:С4 – матрица А и ячейки D2:D4 – матрица В.

Решение системы уравнений методом обратной матрицы

Найдем матрицу, обратную матрице А. Для этого в ячейку А9 введем формулу =МОБР(A2:C4). После этого выделим диапазон А9:С11, начиная с ячейки, содержащей формулу. Нажмем клавишу F2, а затем нажмем клавиши CTRL+SHIFT+ENTER. Формула вставится как формула массива. =МОБР(A2:C4).
Найдем произведение матриц A-1 * b. В ячейки F9:F11 введем формулу: =МУМНОЖ(A9:C11;D2:D4) как формулу массива. Получим в ячейках F9:F11 корни уравнения:

Решение системы уравнений методом Крамера

Решим систему методом Крамера, для этого найдем определитель матрицы.
Найдем определители матриц, полученных заменой одного столбца на столбец b.

В ячейку В16 введем формулу =МОПРЕД(D15:F17),

В ячейку В17 введем формулу =МОПРЕД(D19:F21).

В ячейку В18 введем формулу =МОПРЕД(D23:F25).

Найдем корни уравнения, для этого в ячейку В21 введем: =B16/$B$15, в ячейку В22 введем: = =B17/$B$15, в ячейку В23 введем: ==B18/$B$15.

Получим корни уравнения:

Калькулятор V Крамера – MathCracker.com

Инструкции: Этот калькулятор вычисляет значение V. Крамера. Сначала укажите количество столбцов и строк для перекрестной таблицы, а затем введите данные таблицы:

Подробнее о коэффициенте V Крамера

V Крамера – это статистика, используемая для измерения силы связи между двумя номинальными переменными, и она принимает значения от 0 до 1.Значения, близкие к 0, указывают на слабую связь между переменными, а значения, близкие к 1, указывают на сильную связь между переменными.

V-статистика Крамера является симметричной мерой в том смысле, что не имеет значения, какая переменная помещается в строки, а какая в столбцы. 2 / n} {\ min (c-1, r-1)}} \]

где \ (r \) соответствует количеству строк, а \ (c \) соответствует количеству столбцов.

V Крамера – это мера величины эффекта. Вас также могут заинтересовать наши калькулятор коэффициента фи , калькулятор лямбда-коэффициента или же калькулятор гамма-коэффициента .

404 – Сотрудничество Кэмпбелла

[divider type = “stripes” margin = “20px 0 20px 0”]

В верхней части нашего веб-сайта мы отобразили сообщение, предупреждающее вас о том, что наш веб-сайт использует файлы cookie и что один из них уже установлен. Отображая это сообщение, мы надеемся, что предоставим вам необходимую информацию об использовании файлов cookie и дадим вам возможность дать согласие на их использование.Это сообщение будет отображаться до тех пор, пока вы не дадите согласие на использование нашим сайтом файлов cookie, нажав кнопку «Продолжить».

1. Что такое cookie?

Файл cookie – это небольшой объем данных, часто включающий уникальный идентификатор, отправляемый в браузер вашего компьютера или мобильного телефона (именуемый здесь «устройством») с компьютера веб-сайта. Он хранится на жестком диске вашего устройства. Каждый веб-сайт может отправлять свой собственный файл cookie в ваш браузер, если это позволяют настройки вашего браузера. Чтобы защитить вашу конфиденциальность, ваш браузер разрешает веб-сайту доступ только к файлам cookie, которые он уже отправил вам, но не к файлам cookie, отправленным вам другими веб-сайтами.Многие веб-сайты делают это всякий раз, когда пользователь посещает их, чтобы отслеживать потоки онлайн-трафика.

На веб-сайте Channel Digital наши файлы cookie записывают информацию о ваших онлайн-предпочтениях, чтобы мы могли адаптировать сайт к вашим интересам. Вы можете настроить свое устройство так, чтобы он принимал все файлы cookie, уведомлял вас о создании файлов cookie или вообще не принимал файлы cookie. Выбор последнего варианта означает, что вы не получите определенных персонализированных функций, что может привести к тому, что вы не сможете в полной мере воспользоваться всеми функциями веб-сайта.Каждый браузер индивидуален, поэтому, пожалуйста, проверьте меню «Справка» своего браузера, чтобы узнать, как изменить настройки файлов cookie.

Во время любого посещения нашего веб-сайта каждая страница, которую вы видите, вместе с файлом cookie загружается на ваше устройство. Многие веб-сайты делают это, потому что файлы cookie позволяют издателям веб-сайтов делать полезные вещи, например узнавать, посещало ли ваше устройство (и, возможно, вы) ранее этот веб-сайт. При повторном посещении компьютер веб-сайта проверяет и находит файл cookie, оставленный там при последнем посещении.

2. Как мы используем файлы cookie?

Информация, предоставляемая с помощью файлов cookie, может помочь нам проанализировать профиль наших посетителей, что поможет нам улучшить взаимодействие с пользователем. Например, если во время предыдущего посещения вы заходили на наши маркетинговые страницы, мы можем узнать об этом из вашего файла cookie и выделить маркетинговую информацию при последующих посещениях.

Сторонние файлы cookie на наших страницах

Обратите внимание, что во время посещения нашего веб-сайта вы можете заметить некоторые файлы cookie, не связанные с нами.Когда вы посещаете страницу со встроенным контентом, например, из Twitter или YouTube, вам могут быть представлены файлы cookie с этих веб-сайтов. Мы не контролируем распространение этих файлов cookie. Вы должны проверить сторонние веб-сайты для получения дополнительной информации об этом.

3. Файлы cookie, используемые на нашем сайте

Мы используем файлы cookie только для того, чтобы помочь нам постоянно улучшать наш веб-сайт и поддерживать удобство просмотра для наших посетителей. Вот список файлов cookie, используемых на этом веб-сайте:

Google Analytics – мы используем файлы cookie для сбора статистики посетителей, например, сколько людей посетили наш веб-сайт, какие технологии они используют (например,грамм. Mac или Windows, которые помогают определить, когда наш сайт не работает должным образом для определенных технологий), сколько времени они проводят на сайте, какую страницу просматривают и т. Д.
Facebook, Twitter, LinkedIn, Google+ – кнопки публикации в социальных сетях, которые позволяют вам делиться нашим контентом
Сессионный файл cookie – это стандартный файл cookie, который используется только для запоминания пользовательских предпочтений (например, размера шрифта и сохранения вашего входа в систему при каждом посещении)

4.Как удалить файлы cookie или управлять ими

Этот сайт не будет использовать файлы cookie для сбора информации, позволяющей установить вашу личность. Однако, если вы хотите ограничить или заблокировать файлы cookie, устанавливаемые этим или любым другим веб-сайтом, вы можете сделать это в настройках своего браузера. Функция справки в вашем браузере должна подсказать вам, как это сделать.

Кроме того, вы можете посетить сайт www.aboutcookies.org, который содержит исчерпывающую информацию о том, как это сделать для самых разных браузеров. Вы также найдете подробную информацию о том, как удалить файлы cookie с вашего компьютера, а также более общую информацию о файлах cookie.Для получения информации о том, как это сделать в браузере вашего мобильного телефона, вам нужно будет обратиться к информации поддержки вашего браузера.

Kramer со значком Crestron остается Kramer …

Я пишу вам, чтобы исправить положение. Как вы можете себе представить, с 25-летней историей производства и таким большим количеством продуктов всегда есть какая-то компания, которая заявляет или нацеливается на одну или несколько наших продуктовых линеек. Чаще всего интеграторы и консультанты AV видят сквозь завесу дезинформации, написанной многими отделами маркетинга.Однако иногда предъявляются претензии, которые нельзя игнорировать. В данном конкретном случае эти претензии исходят от уважаемой компании, которая маневрирует своими «новыми» матричными коммутаторами, чтобы завоевать популярность на рынке. В данном случае я чувствую, что должен исправить ситуацию.

Возможно, мы не изобрели матричный коммутатор, но мы модернизировали его для нашего рынка, разработали и запатентовали лучшие технологии и установили новый стандарт инженерного мастерства, который нельзя игнорировать. А это означает, что наши спецификации не написаны нашим отделом маркетинга, а наши разработки не выполняются кем-то другим.Extron – это Extron. Я поддерживаю это каждый день.

Матричный коммутатор Kramer, замаскированный под матричный коммутатор Crestron, по-прежнему остается матричным коммутатором Kramer. Конечно, у Crestron может быть лучший способ контролировать это, но это все еще продукт Kramer. Мы открыли одну из них, чтобы вы могли убедиться в этом сами – посмотрите эти фотографии. Эти два продукта не просто похожи, они практически идентичны.

Претензии к переключателям Kramer, a.k.a. Crestron, аналогичны нашим.Что ж, мы их проверили, и это просто неправда. Коммутаторы Extron CrossPoint относятся к 4-му поколению и отражают зрелое состояние дизайна и технологического развития. Когда мы сравнили их матричный коммутатор с нашим, мы знали, что, хотя наша пропускная способность продолжает расти, у всех нас более чем достаточно. Наши клиенты теперь сообщают нам, что они также выбирают продукты, исходя из энергопотребления, эффективности, количества выделяемого тепла, надежности и гибкости управления.

Потребляемая мощность

Несмотря на широкие заявления о «зеленых» продуктах, ни Kramer, ни Crestron не обеспечивают такой же эффективности матрицы CrossPoint. Их коммутаторы потребляют в два раза больше энергии и выделяют почти вдвое больше тепла, чем CrossPoint 450 Plus.

Фактор	Extron 12×8	Крестрон 12×8	Крамер 12×8
Потребляемая мощность (измерено, 120 В переменного тока – при полной нагрузке)	30.1 Вт	58,8 Вт	57,1 Вт
Выработка тепла в БТЕ / час (рассчитано на основе измеренного энергопотребления)	109	201	195

Эффективность

Наши матрицы CrossPoint спроектированы так, чтобы быть самыми эффективными на рынке.Мы используем холодные, высокоэффективные блоки питания с исключительной надежностью. В результате нам не нужно использовать вентилятор для охлаждения любого из наших коммутаторов CrossPoint для моделей до 16×16.

Фактор	Extron 12×8	Крестрон 12×8	Крамер 12×8
Блок питания	1	2 (без резервирования)	2 (без резервирования)
Вентилятор	№	Есть	Есть

Надежность

Матричные коммутаторы Extron CrossPoint теперь представлены в четвертом поколении.Матричные переключатели Kramer / Crestron, по нашей оценке, аналогичны по конструкции нашим CrossPoint самого раннего поколения. Сравните количество отдельных плат и точек подключения кабелей в нашем матричном коммутаторе с их. Запатентованные Extron возможности подключения позволяют сократить количество плат и поддерживать высокие характеристики производительности. Как вы знаете, каждая отдельная плата, кабельное соединение и особенно каждый вентилятор являются потенциальной точкой отказа.

Фактор	Extron 12×8	Крестрон 12×8	Крамер 12×8
Платы	4	11	11
Кабели	4 кабеля 8 соединений	11 кабелей 25 соединений	9 кабелей 25 соединений
Вентилятор	№	Есть	Есть

Гибкость управления

Вы можете быть удивлены, узнав, что матрица Crestron не обеспечивает управление последовательным интерфейсом RS-232.Мы слышали как от консультантов, так и от торговых посредников, что они не знали об этом функциональном ограничении в матрице Crestron. Все матричные коммутаторы Extron оснащены пультом дистанционного управления через последовательный порт RS-232. Все матрицы Extron CrossPoint также включают управление IP Link® Ethernet и работают с любой системой управления, используя наш хорошо известный командный протокол SIS Simple Instruction Set.

Фактор	Extron 12×8	Крестрон 12×8	Крамер 12×8
RS-232/422	Есть	Нет; Только Cresnet	Есть
Управление через Ethernet	Да: IP Link	Есть	Есть

Цена и производительность

И последнее: к настоящему времени вы должны знать, что мы прекратили выпуск серии CrossPoint 300 в декабре 2007 года и заменили их на нашу серию CrossPoint 450 Plus по той же цене.Несмотря на то, что наши CrossPoints превосходят матричные коммутаторы Kramer / Crestron и представляют собой более выгодную цену, мы продолжим предлагать коммутаторы CrossPoint 450 Plus по сопоставимой цене сейчас и в будущем.

С Extron вы получаете то, что видите – качественную продукцию, спроектированную, спроектированную и изготовленную нами в соответствии с высочайшими стандартами в отрасли. Наши продукты подкреплены бескомпромиссным обслуживанием и поддержкой, а также моей личной гарантией удовлетворения. Это простая формула, которая хорошо служит нашим клиентам на протяжении 25 лет.

Если у вас есть комментарии, напишите мне: [email protected]

С уважением,

Эндрю С. Эдвардс
Президент Extron Electronics

Что такое тест Tukey HSD?

Обновлено 26 ноября 2018 г.

Автор: Кевин Бек

Тест Tukey HSD («честно значимое различие» или «честно значимое различие») – это статистический инструмент, используемый для определения того, является ли взаимосвязь между двумя наборами данных статистически значимой. то есть, есть ли большая вероятность того, что наблюдаемое численное изменение одного значения причинно связано с наблюдаемым изменением другого значения.Другими словами, тест Тьюки – это способ проверить экспериментальную гипотезу.

Тест Тьюки вызывается, когда вам нужно определить, является ли взаимодействие между тремя или более переменными взаимно статистически значимым, что, к сожалению, не является просто суммой или произведением отдельных уровней значимости.

Почему не t-тест?

Простые статистические задачи включают рассмотрение влияния одной (независимой) переменной, например, количества часов, проведенных каждым учеником в классе для определенного теста, на вторую (зависимую) переменную, например, баллы ученика за тест. .В таких случаях вы обычно устанавливаете порог статистической значимости на уровне P <0,05, при этом эксперимент показывает более чем 95-процентную вероятность того, что рассматриваемые переменные действительно связаны. Затем вы обращаетесь к t-таблице, которая учитывает количество пар данных в вашем эксперименте, чтобы убедиться, что ваша гипотеза верна.

Иногда, однако, эксперимент может одновременно рассматривать несколько независимых или зависимых переменных. Например, в приведенном выше примере могут быть включены часы сна, которые каждый ученик получил за ночь перед тестом, и его или ее классная оценка.Такие многомерные задачи требуют чего-то другого, кроме t-критерия, из-за огромного количества независимо меняющихся отношений.

ANOVA

ANOVA означает «дисперсионный анализ» и точно решает только что описанную проблему. Он учитывает быстро расширяющиеся степени свободы в образце по мере добавления переменных. Например, сравнение часов и оценок – это одна пара, сон против оценок – другая, оценки и баллы – третья, а между тем все эти независимые переменные также взаимодействуют друг с другом.

В тесте ANOVA интересующей переменной после выполнения вычислений является F, которая представляет собой найденное отклонение средних значений всех пар или групп, деленное на ожидаемое отклонение эти средние. Чем выше это число, тем сильнее взаимосвязь, и «значимость» обычно устанавливается на 0,95. Для сообщения результатов ANOVA обычно требуется использование встроенного калькулятора, например, в Microsoft Excel, а также специальных статистических программ, таких как SPSS.

Тест Тьюки HSD

Джон Тьюки придумал тест, который носит его имя, когда он осознал математические ловушки попытки использовать независимые P-значения для определения полезности гипотезы нескольких переменных в целом. В то время t-тесты применялись к трем или более группам, и он считал это нечестным – отсюда «действительно значимая разница».

Его тест сравнивает различия между средними значениями, а не сравнивает пары значений.Значение критерия Тьюки определяется путем деления абсолютного значения разницы между парами средних значений на стандартную ошибку среднего (SE), определяемую односторонним тестом ANOVA. SE, в свою очередь, является квадратным корнем из (дисперсия, деленная на размер выборки). Пример онлайн-калькулятора приведен в разделе Ресурсы.

Тест Тьюки – это апостериорный тест, в котором сравнения между переменными производятся после того, как данные уже собраны. Это отличается от априорного теста, в котором эти сравнения производятся заранее.В первом случае вы можете посмотреть на время пробега на милю студентов трех разных физических классов за один год. В последнем случае вы можете назначить учеников одному из трех учителей, а затем попросить их пробежать милю с указанием времени.

онлайн-калькулятор системы уравнений

Найдите другие виджеты математики в Wolfram | Alpha. Онлайн-решение уравнений. Введите ODE, укажите начальные условия и затем нажмите «Решить». Введите линейное уравнение в данное поле, и калькулятор обновит вас системой уравнений.Первое уравнение системы представляет собой эллипс с большой полуосью, равной 2, и малой полуосью, равной 2 5. Решение сопровождается подробным описанием, также вы можете определить совместимость системы уравнений, в этом уникальность решения. Получите бесплатный виджет «3 Equation System Solver» для своего веб-сайта, блога, WordPress, Blogger или iGoogle. Как решить систему уравнений в калькуляторе алгебры. Решение линейных уравнений с использованием матричной алгебры. Простые способы найти LCM, бесплатную распечатку рабочего листа для 5-го и 6-го классов, математическое решение gallian.Пример (Щелкните для просмотра) Wolfram | Alpha может решать самые разные системы уравнений. Алгебра Гленко 1 отвечает на учебник по Луизиане, бесплатный онлайн-калькулятор рациональных выражений и уравнений, алгебра: факторинговая машина. Даже если точного решения не существует, он вычисляет численное приближение корней. Введите любое уравнение, чтобы получить решение, шаги и график. Уравнения Неравенства Система уравнений Система неравенств Основные операции Алгебраические свойства Частичные дроби Полиномы Рациональные выражения Последовательности Суммы степеней Пи (продукт) Обозначение Индукция Логические множества Если в вашем уравнении меньшее количество элементов, оставьте места у переменных, которые не используются в ваших уравнениях, пусто.Теория линейных уравнений – основная и фундаментальная часть линейной алгебры. Получите бесплатный виджет «3 Equation System Solver» для своего веб-сайта, блога, WordPress, Blogger или iGoogle. В общем, вы можете пропустить знак умножения, поэтому «5x» эквивалентно «5 * x». Можно выполнить следующие операции: Чтобы увидеть подробное решение – помочь продвинуть этот сайт, Система двух уравнений с двумя неизвестными, Система трех уравнений с тремя переменными, Система линейных уравнений с четырьмя неизвестными, Система трех нелинейные уравнения с квадратом или дробью, Система двух уравнений с кубом (3-я степень), Система экспоненциальных или логарифмических уравнений, модуль или абсолютное значение: абсолютное (x) или | x |, экспоненциальное функции и показатели exp (x).Калькулятор систем уравнений – это калькулятор, который решает системы уравнений шаг за шагом. Также вы можете вычислить ряд решений в системе линейных уравнений (проанализировать совместимость), используя теорему Руше – Капелли. : уравнения интегрального типа в одном блоке, матричный метод входит в матрицу коэффициентов и столбец констант, коэффициенты индивидуального типа метода один за другим. Wolfram | Alpha – это больше, чем просто средство решения уравнений онлайн. Это отличный инструмент для поиска корней многочленов и решения систем уравнений.Наш калькулятор способен решать системы с одним уникальным решением, а также неопределенные системы, которые имеют бесконечное множество решений. Бесплатный калькулятор системы ODE – шаг за шагом находите решения для системы ODE. Введите свои уравнения через запятую в поле и нажмите «Рассчитать»! Математические тесты; Уроки математики; Математические формулы; Онлайн-калькуляторы; Все калькуляторы :: Системы уравнений; Решатели систем уравнений. Он может решать системы линейных уравнений или системы, включающие нелинейные уравнения, а также может искать целочисленные решения или решения в другой области.Решите систему уравнений 2 на 2 Решите систему уравнений 3 на 3 Решите систему уравнений 4 на 4. Введите следующее: Первое уравнение x + y = 7; Затем запятая, Затем второе уравнение x + 2y = 11; Попробуйте прямо сейчас: x + y = 7, x + 2y = 11 Интерактивная демонстрация Попробуйте ввести x + y = 7, x + 2y = 11 в текстовое поле. Онлайн-программа для решения математических задач с бесплатными пошаговыми решениями алгебры, исчисления и других математических задач. Бесплатный калькулятор уравнений – решайте линейные, квадратные, полиномиальные, радикальные, экспоненциальные и логарифмические уравнения со всеми шагами.Метод Гаусса-Зейделя: это итерационный метод решения n уравнений квадратной системы n линейных уравнений с неизвестным x, где Ax = b только по одному за раз в последовательности. Бесплатный калькулятор системы нелинейных уравнений – решите систему нелинейных уравнений шаг за шагом. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам наилучший опыт. mathportal.org. Чтобы улучшить эту «Систему 2-х линейных уравнений в 2-х переменных Калькуляторе», пожалуйста, заполните анкету. Решение сопровождается подробным описанием, также можно определить совместимость системы уравнений, то есть уникальность решения.Перепишите уравнения каноническим способом: x 2 4 5 y 2 4 1 y 3 x 5 3 5. Решение систем линейных уравнений онлайн Этот онлайн-калькулятор позволяет вам решать системы уравнений различными методами в режиме онлайн. Решает ваши линейные системы методом исключения Гаусса-Жордана. С помощью… Чтобы вычислить алгебру, линейное уравнение с использованием матрицы: Введите правильные значения линейных уравнений в форму ниже и нажмите «Рассчитать». Математические калькуляторы, уроки и формулы. Найдите больше виджетов по математике в Wolfram | Alpha. Система уравнений онлайн-решатель. Предположим, у нас есть система двух уравнений с двумя неизвестными: x 2 5 y 2 4 5 y 3 x 3.Пришло время решить вашу математическую задачу. … Вот бесплатный онлайн-калькулятор для решения линейных уравнений алгебры с помощью матриц. Показать инструкции. Можно использовать дроби (1/3). Если поле оставлено пустым, коэффициент переменной автоматически выбирается равным нулю. Этот онлайн-калькулятор позволяет решать систему уравнений различными методами в режиме онлайн. Калькулятор на этой странице поможет проанализировать совместимость системы линейных уравнений (SLE), позволяет решить систему уравнений методом Гаусса, обратной матрицы или методом Крамера.Если a = 0, то уравнение является линейным, а не квадратичным, поскольку нет члена ax². Уравнение Миффлина-Сент-Джера оказалось более точным, чем пересмотренное уравнение Харриса-Бенедикта. Он также множит многочлены, графики … Также поддерживаются начальные условия. Вы можете вводить дроби и десятичные дроби. Здесь вы можете бесплатно решать системы одновременных линейных уравнений с помощью калькулятора исключения Гаусса-Жордана с комплексными числами онлайн с очень подробным решением. Используйте этот калькулятор системы уравнений для решения линейных уравнений с различными переменными.С помощью калькулятора вы сможете решить систему уравнений онлайн разными способами: по Крамеру, по методу Гаусса, по методу обратной матрицы, по методу Жордана. Показывает всю работу, аккуратен и удобен в использовании. Линейный решатель. Мужской или женский ? В этой категории 3 решателя. Получите помощь в Интернете или с помощью нашего математического приложения. Это главный сайт WIMS (WWW Interactive Multipurpose Server): интерактивные упражнения, онлайн-калькуляторы и плоттеры, математические развлечения и игры.2 = 0 2/7 * x + y – z = -3

Индикаторы графика оплаты труда врача Medicare 2019, Как развивались трудовые системы с 1450 по 1750 год, Airflow – это инструмент Etl, Что означает Ионафан в Библии, Блок питания Канто Msrp, Запчасти для тракторов Интернет-магазины,

Калькулятор системы линейных сравнений

Калькулятор исключения Гаусса-Джордана. Вычислить опорные точки. Калькулятор нулевого пространства матрицы.Шаг 1. Для начала выберите количество строк и столбцов в вашей матрице. Эта программа была вдохновлена лекцией 7 по линейной алгебре профессора Гилберта Стрэнга (доступна в MIT OpenCourseWare) и линейным … Символ мечты большой палец ноги

Линейное сравнение Калькулятор. x ≡ (mod) — введите оператор mod b. Видео линейного сравнения. Электронная почта: [электронная почта защищена] Тел .: 800-234-2933;
Александр, боковая зарядка верха
Jacobsen 810 express
18 января 2008 г. · Я могу придумать как минимум четыре способа: 1) исключение (сложение или вычитание уравнений для исключения переменной) 2) замена (перестановка одного уравнения чтобы получить одно уравнение само по себе, а затем подставить его в другое уравнение 3) Правило Крамера (матричные операции) 4) Графически (ищите пересечение) Да, система может иметь более одного решения – если все линии являются одной линией , есть файл…
Требования к системе Crna
Велосипед-вертолет Западного побережья
Калькулятор линейной системы уравнений. Связанные сообщения блога Symbolab. Математические решения для средней школы – Калькулятор одновременных уравнений. Решение одновременных уравнений – это еще один небольшой шаг в алгебре от простых уравнений.
Fox float x2 setup
Датчик давления топлива Bosch
5 ноября 2017 г. · Значение x может быть больше единицы в зависимости от GCD a и n.Всегда есть d число решений x, где d = GCD (a, n). Если a и n взаимно просты, т.е. GCD равен 1, существует только одно уникальное решение, и это очень важно для вычисления секретного ключа в алгоритме RSA.
Образец письма для принятия приглашения на общественное мероприятие
Перенос музыки с iphone на компьютер без itunes reddit
Рабочие листы для печати и практические онлайн-тесты по конгруэнтности треугольников за 9 год
Mossberg 50694 review
Super sport 3
Калькулятор решает треугольник, заданный координатами трех вершин на плоскости (или в трехмерном пространстве).Калькулятор площади треугольника по точкам. Использует формулу Герона и тригонометрические функции для вычисления площади и других свойств заданного треугольника.
Синхронизация звука потока Discord
Форма подтверждения убежища mn
Калькулятор Rref используется для преобразования любой матрицы в сокращенную форму эшелона строк. Это облегчает жизнь людям, использующим матрицы. Как только он будет преобразован в сокращенную форму эшелона строк, его использование в линейной алгебре становится намного проще и может быть действительно удобным для математиков.
Ползунок карусели для продуктов Shopify
Датчик помещения Harman
2 июля 2012 г. · Решение домашних заданий для n и m в следующих уравнениях: 2n + 6m \\ эквив 2 (mod 10) n + m \ эквив – 2 (мод 10) Уравнения для домашних заданий Попытка решения Я уже работал над несколькими из этих проблем ранее, включая те, что описаны в книге, и большинство из них принимает форму: 2n + 3m = 3 …
Действительно ли безопасно
Тиоцианат железа
линейные зависимости, отчасти путем сопоставления их с экспоненциальными и квадратичными явлениями, а отчасти путем применения линейных моделей к данным, которые демонстрируют линейный тренд.Помимо изучения двумерных данных, студенты также суммируют, представляют и интерпретируют данные по одному счету или переменной измерения. Стандарты геометрии, которые регулируют
Colorado для дульнозарядных лосей
Fallout 4 меняют пол npc
Напишите программу на C / C ++, чтобы найти общее решение данного уравнения линейного конгруэнтности. Например, общее решение 14x≡12 (mod 18): x = 6 + 9k, где k равно
Нацу перестает сдерживать фанфики
Simplify3d creality ender 5 plus profile
Формула рекурсии, полученная путем дифференцирования (27.14.18) можно использовать для вычисления функции Рамануджана τ ⁡ (n), а значения можно проверить с помощью сравнения (27.14.20). … 5: Моррис Ньюман
Вавилонская религия pdf
Не работают кнопки экранных меню монитора Acer
1 Это решение проблемы системы сравнений. \ _ \ square Процесс решения систем сравнений с китайской теоремой об остатках: Для системы сравнений с взаимно простыми модулями процесс выглядит следующим образом: Начните с сравнения с наибольшим модулем, x ≡ a k (m o d n k).х \ эквив а_к \ пмод {н_к}. х ≡ а к (м о д н к). 01 сентября 2013 г. · Когда у вас есть система линейных сравнений, например: $$ \ begin {align} x & \ Equiv 4 \ mod 19 \\ x & \ Equiv 12 \ mod 37 \\ x & \ Equiv 14 \ mod 43 \ end {align} $$ вы можете решить ее довольно легко. Йоханнес Шиклинг написал очень красивое приложение на JavaScript, которое применяет следующий алгоритм онлайн. Есть… Настройки калибровки Sony xbr65x850c Есть несколько методов решения линейных сравнений; связь с линейными диофантовыми уравнениями, методом преобразования коэффициентов, методом Эйлера и методом, использующим алгоритм Евклида… Связь с линейными диофантовыми уравнениями Уравнения Функции Геометрия Статистика и алгебра вероятностей I Уравнения эквивалентности Линейные функции Линейные неравенства Системы линейных уравнений Функции и отношения Квадратичные функции Экспоненциальные… Список серверов Vainglory
Хрупкие боеприпасы, пригодные для самообороны
Расчет уравнения регрессии зависит от наклона и точки пересечения по оси Y. Введите значения X и Y в этот онлайн-калькулятор линейной регрессии, чтобы вычислить простую линию линейной регрессии A имеет уравнение в форме Y = a + bX, где X – независимая переменная, а Y – зависимая переменная. диапазон
Если треугольники удовлетворяют условию постулата или теоремы, значит, треугольники совпадают.Это постулат SSS, постулат SAS, постулат ASA, теорема AAS и теорема гипотенузы-ноги. Постулат SSS: если три стороны треугольника совпадают с тремя сторонами второго треугольника, то два треугольника совпадают. Пример: серийный номер Motorola. lookup
Distcc ccache
Это вводное изучение функций подготавливает студентов к Модулю 5, в котором они сосредотачиваются на особом виде функций – линейных уравнениях. Блок 5, Линейные отношения, и Блок 6, Системы линейных уравнений, все посвящены линиям.Студенты устанавливают связь между пропорциональными отношениями, функциями и линейными уравнениями. Комплект для восстановления коробки передач с гидроусилителем Fj60
Этот калькулятор ЭЛТ решает систему линейных сравнений a 1 x ≡ b 1 (mod m 1) a 2 x ≡ b 2 (mod m 2) ⋮ беспокойство ≡ bn (mod mn) где ai ‘s, mi – положительные целые числа, а bi – неотрицательные целые числа. Калькулятор пытается найти решение как в случае, когда m i попарно взаимно просты, так и не попарно взаимно просты, если решение существует. Версии Вердаччо
28 декабря 2020 г. · Уравнение линейного сравнения ax = b (mod m) (1) разрешимо тогда и только тогда, когда сравнение b = 0 (mod d) (2) с d = GCD (a, m) является наибольшим общий делитель разрешим.Пусть одно решение исходного уравнения будет x_0
Тест Тьюки / Процедура Тьюки / Честная значимая разница
Последующие тесты> Тест Тьюки / Честная значимая разница
Что такое тест Тьюки / честная значимая разница?
Тест Тьюки (или процедура Тьюки ), также называемый тестом честной значимой разницы Тьюки, представляет собой апостериорный тест, основанный на распределении стьюдентизированных диапазонов.Тест ANOVA может сказать вам, являются ли ваши результаты значимыми в целом, но он не скажет вам, в чем именно заключаются эти различия. После того, как вы выполнили ANOVA и получили значимые результаты, вы можете запустить HSD Тьюки, чтобы выяснить, какие средние значения конкретных групп (по сравнению друг с другом) отличаются. Тест сравнивает все возможные пары средних.
Чтобы проверить все попарные сравнения средних значений с использованием HSD Тьюки, вычислите HSD для каждой пары средних по следующей формуле:
Где:
M _i – M _j – разница между парой средств.чтобы вычислить это, M, _i должно быть больше, чем M _j
MS _w – это среднее квадратическое значение в пределах, а n – номер в группе или лечении.
Общие шаги
Шаг 1: Выполните тест ANOVA. Предполагая, что ваше значение F является значительным, вы можете запустить апостериорный тест.
Шаг 2: Выберите два средних из выходных данных ANOVA. Обратите внимание на следующее:
Шаг 3: Рассчитайте статистику HSD для теста Тьюки, используя формулу.
Шаг 4: Найдите оценку в таблице критических значений Тьюки.
Шаг 5: Сравните результат, полученный на шаге 3, с табличным значением, полученным на шаге 4. Если рассчитанное на шаге 3 значение больше критического значения из таблицы критических значений, два средних значения существенно различаются.

Допущения для теста
Наблюдения независимы внутри и между группами.
Группы для каждого среднего в тесте распределены нормально.
Существует одинаковая внутригрупповая дисперсия по группам, связанная с каждым средним значением в тесте (однородность дисперсии).
Метод Тьюки-Крамера
Если у вас неравные размеры выборки, вам необходимо вычислить оценочное стандартное отклонение для каждого попарного сравнения. Это называется методом Тьюки-Крамера .