Формулы Квантовой физики
Тепловое излучение
R = ς*T4 – Энергетическая светимость по закону Стефана-Больцмана
ς = 5.67*10-8
w = t*S*R – Мощность Sшара = 4*π*r2
b = λ*T
b = 2.9*10-3
; для АЧТ aизл = 1
Условие максимума:
Фотоны
Eф = |
| – Энергия фотона |
|
h = 6.63*10-34 Дж/с с = 3*108 м/с
pф = |
|
|
| – Импульс фотона |
|
| ||||
|
|
|
| |||||||
<Eк> = |
|
| – Средняя кинетическая энергия поступательного движения одной молекулы | |||||||
| ||||||||||
k = 1. |
|
| ||||||||
E = m*c2 – Энергия покоя электрона |
|
| ||||||||
Ep = |
|
|
|
| – Энергия нерелятивистского протона. |
|
| |||
|
|
|
|
|
| |||||
n = |
|
| – Количество фотонов в импульсе, где w0 = |
| – энергия одного фотона. | |||||
|
| |||||||||
Фотоэффект
Eф = A + Eэл – Уравнение Эйнштейна для фотоэффекта.
A = h*νк= – Работа выхода, где λк – красная граница фотоэффекта.
Eэл = |
| = |
| = e*Uз – Энергия вылетающего элемента. |
|
|
m = 9.10938188 × 10-31кг – Масса электрона. e = 1.60217646 × 10-19 Кл – Заряд электрона
Uз – Задерживающая разность потенциалов. 1эВ = 1.6*10-19Дж => 1Дж = 1/(1.6*10-19) эВ
Эффект Комптона
pф = – Импульс падающего фотона.
=– Импульс рассеянного фотона.
Формула Комптона: Δλ = – λ = *(1-cosθ),
где = 2.43*10-12м, θ – угол рассеивания.
при θ = 180®.
E0 = me*c2 = 0.511 МэВ – Энергия покоя электрона.
Энергетические спектры атомов и теория Бора.
ω = R * ( ) – Обобщенная формула Бальмера,
где R = 2.07*1016 c-1 – постоянная Ридберга, а n0 < n.
̅ |
| = |
|
|
|
| см-1. | |
|
|
| ||||||
̅= ̅ * ( |
|
|
|
| ) | |||
|
|
| ||||||
где ̅ = |
| 1.1*107 м-1 – постоянная Ридберга, а n0 < n. |
|
ħ = = 1.054*10-34 Дж/с – постоянная Дирака
ħ*ω = E2- E1 – Правило частот Бора
M = r*m*V = n* ħ – Момент импульса электрона, где n = 1, 2, 3, … – квантовые числа.
– согласно второму закону Ньютона,
где r – радиус окружности, по которой двигается электрон вокруг ядра, Ze – заряд ядра.
Eк = |
|
|
|
|
|
|
|
|
| – Кинетическая энергия электрона. | |||||||||||||
|
|
|
|
| |||||||||||||||||||
E = Eк + U = |
|
|
|
|
|
|
|
|
|
| – Полная энергия | ||||||||||||
|
|
|
|
|
|
|
|
|
| ||||||||||||||
rn = |
|
|
|
|
|
|
|
|
| – радиус n-ой стационарной орбиты. | |||||||||||||
|
|
|
|
|
|
|
|
| |||||||||||||||
r1 = |
|
|
|
| = 0. | ||||||||||||||||||
|
|
|
| ||||||||||||||||||||
En = |
|
|
|
|
|
|
|
|
| – Энергия электрона на n-ой стационарной орбите | |||||||||||||
|
|
|
|
|
|
|
|
| |||||||||||||||
ω = |
|
|
|
|
|
|
|
|
|
| = |
|
|
|
|
| – частота фотона | ||||||
|
|
|
|
|
|
|
|
|
|
| |||||||||||||
Eф = Ei + – Закон сохранения энергии,
где Ei =
Гипотеза де-Бройля.
λ = |
| = |
|
| = |
|
|
|
|
|
|
|
| – длина волны частицы, | |
|
|
| √ |
|
|
|
| √ |
| ||||||
|
|
|
|
|
|
|
|
| |||||||
где E = |
|
|
|
|
|
|
| = e*U, а U – разность потенциалов, | |||||||
|
|
|
|
|
|
| |||||||||
q – ее заряд, для электрона q = e = 1.
Vвер =√
λc = – Длина комптоновской волны.
λБ = |
|
|
|
| – Длина волны де-Бройля. | |
√ |
|
|
| |||
|
|
| ||||
|
|
|
|
| ||
<Vкв> = √ |
|
| – Средняя квадратичная скорость. | |||
|
| |||||
pp = – релятивистский импульс.
√
m0 = 3.34*10-27кг – Масса молекулы водорода.
Eк = m*c2*( |
|
|
| ) – Релятивистская кинетическая энергия. |
|
|
| ||
√ |
| |||
|
|
| ||
|
| |||
Соотношения неопределенностей.
p* x ≈ ħ – Соотношение неопределенностей импульса и координаты. p = m* V – Неопределенность импульса.
x = r – Неопределенность координаты.
E* t ≈ ħ – Соотношение неопределенностей энергии и времени.
E = |
| *Δλ | ||
| ||||
Применение уравнения Шредингера. | ||||
En = |
|
|
| – энергия n-ого возбужденного состояния для частицы в потенциальной яме. |
|
|
| ||
P =
EF =
EF =
P(x) = ∫ | | | |
|
|
| – Плотность вероятности нахождения частицы | ||||||||||
Ψ(x) = √ |
|
|
|
|
|
|
| – для частицы в одномерной прямоугольной потенциальной яме с бесконечно | |||||||
|
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
| |||||||||
высокими стенками в n-ом энергетическом состоянии. | |||||||||||||||
Pmax = | | | | | = |
|
|
|
|
| = 2*sin |
| * cos |
| = 0 | ||
|
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
| |||||||
Ψ(r) = c* – Собственная функция, описывающая основное состояние электрона в атоме водорода,
где a = 0.53*10-9 м – Первый Боровский радиус.
Pmax = | | | | |
| |
|
|
| ||
Eпот = |
| – Потенциальная энергия в случае гармонического осциллографа, | ||
| ||||
где A = ; k = m*ω2
Квантовые числа.
L =ħ*√ |
| – орбитальный момент импульса | ||
|
|
|
| |
Ml = MБ*√ |
| – магнитный момент элемента | ||
N = 2*n2 – Принцип Паули (сколько различных состояний могут иметь электроны с значением главного квантового числа n)
Квантовая статистика и полупроводники.
*(100%) – Вероятность того, что электрон имеет энергию E
– Энергия Ферми, когда дана максимальная скорость.
– Энергия Ферми, где n – концентрация свободных электронов.
<E> = *EF – Средняя кинетическая энергия свободных электронов.
E = – Ширина запрещенной зоны, где λк – длинноволновый край полосы поглощения излучения.
N = ∫
N = ∫
|
| √ |
|
|
|
|
|
|
|
|
|
| |
где f(E) = |
|
|
|
| √ ; E1 ≤ E ≤ E2 |
|
| ||||||
|
|
|
|
|
|
| |||||||
R = R0 * |
|
|
| ; ς = ς0 * |
| ; ρ = ρ0 * |
| , | |||||
|
|
|
|
| |||||||||
где R – сопротивление, ς – удельная проводимость, ρ – удельное сопротивление.
Свойства атомных ядер.
m = (A – Z)*mn + Z*mp + Z* me – масса атома, где Z – нижний индекс, A – верхний. r = 1.3 * 10-15 * √ – Радиус ядра.
ρ = – плотность ядерного вещества.
Nнук = A.
Q = Z * e – электрический заряд в атомном ядре.
|
|
|
| – Альфа-распад. | |
|
|
|
|
| – Бета-распад. |
Радиоактивность и ядерные превращения. | |||||
N1 = N0* |
| – Основной закон радиоактивного распада (количество ядер, не распавшихся за | |||
время t), где λ = |
| , а T – период полураспада. | |||
| |||||
N = N0*(1 – |
| ) – Количество ядер, которые распадутся за время t. | |||
aуд = a0* |
| – Активность радиоактивного изотопа. | |||
N0 = |
| , |
|
|
|
|
|
|
| ||
где NA = 6,022*1023 моль−1, M – молярная масса.
Основные формулы и методические рекомендации по решению задач на квантовую механику
Данная тема посвящена посвятим тому, что вспомним некоторые важные определения, понятия и формулы, относящиеся к квантовой механике, а также дадим общие рекомендации по решению задач на данную тему.
И так, как же возникло учение о квантах? Из курса
электродинамики известно, что теоретические исследования Джеймса Клерка
Максвелла показали, что свет есть электромагнитные волны определенного
диапазона, что позже подтвердил Генрих Герц в своих опытах.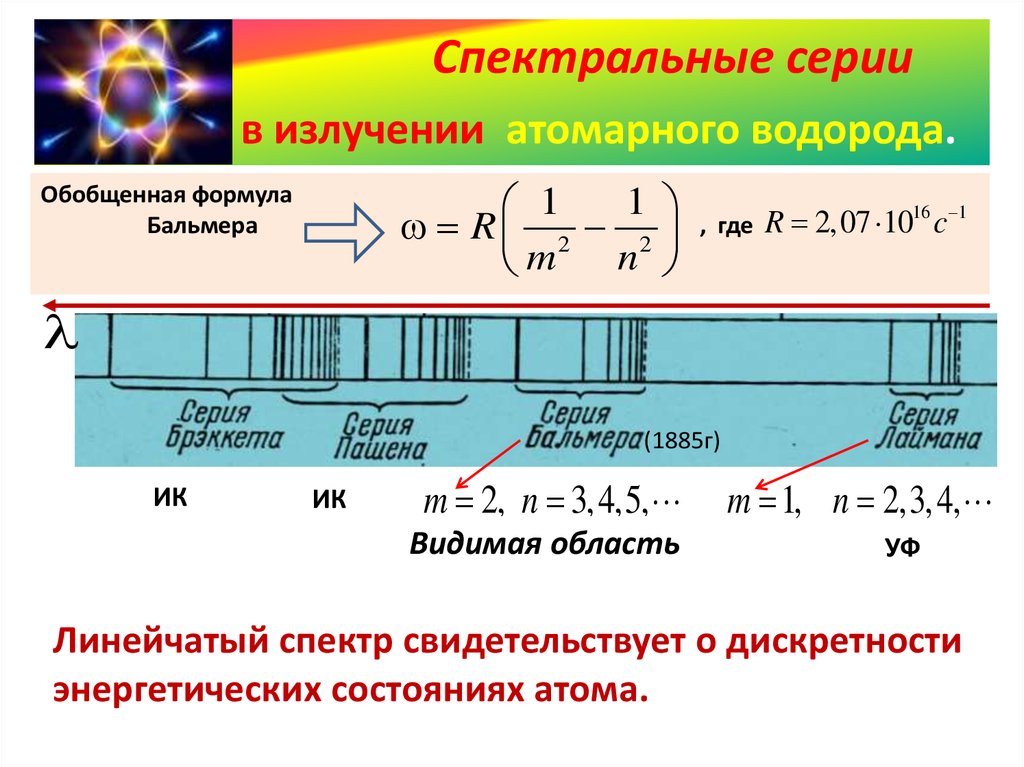 Электромагнитная теория смогла объяснить многие наблюдаемые явления, в том
числе, давление, интерференцию и дифракцию света. Но такое явление, как
дисперсия, теория Максвелла объяснить не смогла. Это было сделано голландским
ученым Хендриком Лоренцем, создавшим электронную теорию взаимодействия света с
веществом.
Электромагнитная теория смогла объяснить многие наблюдаемые явления, в том
числе, давление, интерференцию и дифракцию света. Но такое явление, как
дисперсия, теория Максвелла объяснить не смогла. Это было сделано голландским
ученым Хендриком Лоренцем, создавшим электронную теорию взаимодействия света с
веществом.
Но и дополненная теория Максвелла нуждалась в уточнениях. Ведь такие явления, как, например, распределение мощности излучения в спектре абсолютно черного тела или возникновение линейчатых спектров и законы фотоэффекта, она объяснить не могла.
Нова теория была выдвинута в одна тысяча девятисотом году Максом Планком. Согласно его гипотезе, электроны атомов излучают свет не непрерывно, а отдельными порциями — квантами. При этом энергия кванта пропорциональна частоте колебаний электрона в веществе.
Квантовые представления о свете, введенные в науку Планком,
развил далее Альберт Эйнштейн. Он пришел к выводу о том, что свет
не только излучается, но и распространяется в пространстве, и поглощается
веществом в виде квантов.
Он пришел к выводу о том, что свет
не только излучается, но и распространяется в пространстве, и поглощается
веществом в виде квантов.
Вот таким вот образом и возникло учение о квантах и, собственно, квантовая физика, которая смогла объяснить ряд явлений, наблюдаемых при взаимодействии света с веществом.
В 1887 году Генрих Герц открыл явление внешнего фотоэффекта, которое было изучено русским ученым Александром Григорьевичем Столетовым.
Внешний фотоэффект возникает при взаимодействии вещества с поглощаемым электромагнитным излучением, при этом происходит вырывание электронов с поверхности вещества.
Проводя свои эксперименты, Столетов установил следующий закономерности фотоэффекта:
1) При отсутствии напряжения между электродами фототок отличен от нуля, что можно объяснить наличием у фотоэлектронов при вылете кинетической энергии.
2) При некотором значении напряжения между электродами сила
фототока перестает зависеть от напряжения, то есть достигает насыщения.
3) Если поменять местами полярности катода и анода, то в электростатическом поле между электродами фотоэлектроны будут тормозится и, при некотором значении этого отрицательного напряжения, фототок полностью прекратится.
На основании этих экспериментальных данных были сформулированы законы фотоэффекта.
Первый закон фотоэффекта звучит следующим образом: сила фототока насыщения пропорциональна общему числу фотоэлектронов, покидающих поверхность металла за единицу времени.
Второй закон формулируется так: при увеличении частоты падающего света максимальная кинетическая энергия линейно возрастает. При этом кинетическая энергия не зависит от интенсивности падающего света.
Третий закон говорит о том, что красная граница
фотоэффекта зависит только от рода вещества катода. Напомним, что красная
граница — это минимальная частота (или максимальная длина волны), при
которой еще возможен фотоэффект.
А четвертый закон утверждает, что фотоэффект практически безинерционен, так как с момента облучения металла светом, до вылета электрона проходит время порядка миллиардной доли секунды.
В 1905 году для объяснения экспериментальных законов фотоэффекта Эйнштейн использовал квантовые представления о свете, введенные Планком, и применил их к поглощению света веществом.
И так фотон, обладающей энергией hν, падая на поверхность металла, поглощается электроном поверхностного слоя металла. И если энергия фотона равна или превышает работу выхода, то электрон вылетает из металла. При этом часть энергии фотона тратится на совершение работы выхода, а остальная часть переходит в кинетическую энергию фотоэлектрона.
Таким образом, было установлено, что свету присущи и
корпускулярные свойства. В настоящее время принято считать, что свет
обладает двойственной корпускулярно-волновой природой. Двойственность
свойств света находит свое выражение в формулах, которые вы сейчас видите на
экране. В них корпускулярные характеристики фотона (энергия, масса и импульс)
связаны с волновой характеристикой — частотой.
Двойственность
свойств света находит свое выражение в формулах, которые вы сейчас видите на
экране. В них корпускулярные характеристики фотона (энергия, масса и импульс)
связаны с волновой характеристикой — частотой.
В 1927 году Нильс Бор сформулировал принцип дополнительности. Звучит он следующим образом: для полного понимания природы света необходимо учитывать, как волновые, так и корпускулярные свойства света: они взаимно дополняют друг друга. Однако следует помнить, что для объяснения какого-либо эксперимента следует использовать либо волновые, либо корпускулярные представления о природе света, но не те и другие одновременно.
Теперь немного поговорим о физике атома и атомного ядра.
Bзвестно, что атомы представляют
собой очень прочные системы, несоизмеримо более устойчивые, чем составленные из
атомов молекулы. Поэтому до конца 19 века атомы
считались простейшими неделимыми частицами вещества. Однако последующее
развитие науки опровергло эту точку зрения. Было установлено, что атомы
представляют собой достаточно сложные образования. Одним из таких фактов стали опыты
Резерфорда по рассеиванию альфа-частиц.
Однако последующее
развитие науки опровергло эту точку зрения. Было установлено, что атомы
представляют собой достаточно сложные образования. Одним из таких фактов стали опыты
Резерфорда по рассеиванию альфа-частиц.
На основании проделанных опытов Резерфорд предложил ядерную (или планетарную) модель атома. Согласно модели, в центре атома находится положительно заряженное ядро, в котором сосредоточена почти вся масса атома. А вокруг неподвижного ядра по замкнутым орбитам вращаются электроны, число которых совпадает с порядковым номером элемента в таблице Менделеева.
Однако некоторое время и эта модель считалась не состоятельной, так как согласно расчетам, в этой модели атом должен быть неустойчивым. Противоречия возникли из-за того, что к электронам в атомах применяли законы классической физики, а в микромире действуют свои законы.
Первым, кто признал невозможность применения классических
законов физики к атомам, был датский ученый Нильс Бор, который в 1913
году ввел элементы квантовой теории в модель атома Резерфорда и создал
неклассическую теорию атома. В основе этой теории лежит три постулата.
В основе этой теории лежит три постулата.
Первый постулат (его еще называют постулатом стационарных состояний), говорит о том, что существуют особые, стационарные состояния атома, находясь в которых, атом не излучает энергию, при этом, электроны в атоме движутся с ускорением.
Второй постулат Бора еще называют правилом частот. Согласно ему, атом, при переходе из одного стационарного состояния в другое, излучает или поглощает квант энергии.
В третьем постулате (правило квантования орбит) говорится о том, что в стационарном состоянии атома электрон, движущийся по круговой орбите, должен иметь квантованные (дискретные) значения момента импульса.
Исходя из этих постулатов и используя планетарную модель
строения атома, Бор разработал количественную теорию атома водорода.
Данная модель была крупным шагом в развитии атомной физики и явилась важным
этапом в создании квантовой механики. С ее помощью удалось объяснить основные
закономерности в спектрах атомов водорода и водородоподобных систем и вычислить
частоты спектральных линий.
С ее помощью удалось объяснить основные
закономерности в спектрах атомов водорода и водородоподобных систем и вычислить
частоты спектральных линий.
Оставалось, однако, неясным, от чего зависит интенсивность излучений тех или иных частот. Остался без ответа и вопрос, почему совершаются те или иные переходы. И, самое главное, с помощью модели атома Бора невозможно было описать атом гелия — один из простейших атомов, непосредственно следующий за водородом.
Поэтому в 1925 — 1927 годах на смену модели атома Бора пришла квантовая механика, которая явилась строгой непротиворечивой теорией и имела свой собственный математический аппарат.
Сведём в таблицу основные формулы на световые кванты, действие света.
|
Формула |
Описание формулы |
|
Энергия
фотона, где h = 6,63 ∙ 10−34
Дж ∙ с — постоянная Планка, v — частота, c = 3 ∙ 108
м/с — скорость света в вакууме, λ — длина волны. |
|
|
Импульс фотона. |
|
|
Уравнение Эйнштейна для внешнего фотоэффекта, где Авых — работа выхода электрона, m — масса электрона, υmax — максимальная скорость фотоэлектрона. |
|
|
Максимальная кинетическая энергия фотоэлектрона, где е — заряд электрона, Uз — задерживающее напряжение. |
|
|
Красная граница фотоэффекта. |
|
|
Световое давление, где I — интенсивность света, ρ — коэффициент отражения света. |
Теперь сведём в таблицу основные формулы физики атома.
|
Формула |
Описание формулы |
|
Энергия электрона, находящегося на стационарной орбите в атоме водорода, где е — заряд электрона, ε0 — электрическая постоянная, r — радиус боровской орбиты электрона. |
|
|
Энергия, излученная или поглощенная атомом водорода, где W1 и W2 — энергии атома в соответствующих стационарных состояниях. |
|
|
Обобщенная формула Бальмера, где R — постоянная Ридберга, n — номер орбиты, на которую переходит электрон, k — номер орбиты, с которой переходит электрон. |
|
|
Условие
квантования стационарных орбит, где m — масса
электрона, υn
—скорость электрона на n-ой орбите, rn— радиус n-ой орбиты. |
|
|
Радиус n-ой стационарной орбиты электрона в атоме водорода. |
Сведём в таблицу основные формулы для элементов квантовой механики.
|
Формулы |
Описание формулы |
|
Формула де Бройля, где λБ — длина волны де Бройля, h — постоянная Планка, m — масса частицы, υ — скорость частицы. |
|
|
Соотношение неопределенностей Гейзенберга, где Δх — неопределенность координаты, Δрх— неопределенность проекции импульса, ћ = h/2π. |
|
|
Соотношение неопределенностей, где ΔW — неопределенность значения энергии системы, Δt — неопределенность промежутка времени пребывания системы в данном состоянии |
Методические рекомендации по решению задач по квантовой
физике.
1) Необходимо всегда помнить о взаимосвязи между волновыми и квантовыми характеристиками частиц.
2) Помните, что взаимодействие фотонов с веществом подчиняется законам сохранения импульса и энергии (законы фотоэффекта следуют из закона сохранения энергии, а формула для расчета светового давления является следствием из закона сохранения импульса).
3) Следует помнить и основные положения ядерной модели атома с точки зрения классической электродинамики для расчета характеристик движения электрона в атоме.
4) Необходимо учитывать то, что, согласно положениям квантовой физики, радиус орбиты электрона, энергия атома, энергия излученного или поглощенного кванта могут иметь только определенные дискретные значения.
Квантовая механика | Физика для идиотов
Содержание
|
Вначале был непрерывный поток, а затем появился Макс Планк и предложил квантование. Квантование в основном просто означает, что вместо того, чтобы быть непрерывными, такие вещи, как электромагнитное излучение, могут существовать только в виде кратных определенных значений. Это немного похоже на тюбик умников. Вся трубка представляет собой луч света. Внутри него умники. Вы можете разделить трубку, чтобы в ней было меньше умников, или вы можете взять другую трубку и иметь умников, но у вас должно быть целое количество умников, потому что их нельзя разделить (если кто-нибудь напишет мне по электронной почте предлагаю раздавить/раздавить/расколоть умника, я выследю их и заставлю заплатить!).
Планк пришел к такому выводу, работая над «Ультрафиолетовой катастрофой». Согласно классическому электромагнетизму, количество способов, которыми электромагнитная волна может колебаться в трехмерной полости на единицу частоты, пропорционально квадрату частоты. Это означает, что мощность, которую вы получите на единицу частоты, должна соответствовать закону Рэлея-Джинса, что означает, что мощность будет пропорциональна квадрату частоты. Таким образом, если вы поднимаете частоту все выше и выше, мощность будет неограниченной. Планк сказал, что электромагнитная энергия не соответствует классическому описанию. Он сказал, что она может излучаться только дискретными порциями энергии, пропорциональной частоте
Это означает, что мощность, которую вы получите на единицу частоты, должна соответствовать закону Рэлея-Джинса, что означает, что мощность будет пропорциональна квадрату частоты. Таким образом, если вы поднимаете частоту все выше и выше, мощность будет неограниченной. Планк сказал, что электромагнитная энергия не соответствует классическому описанию. Он сказал, что она может излучаться только дискретными порциями энергии, пропорциональной частоте
или иногда пишется как
, где (произносится как «h bar») равно h/(2). Эти уравнения означают, что излучение в конечном итоге стремится к нулю на бесконечных частотах, а общая мощность конечна. Планк назвал эти пакеты энергии «квантами». Значение h равно Дж·с, а значение равно Дж·с.
Квантовое поведение отличается от классического, потому что h не равно 0
Если достаточно долго освещать металлическую поверхность, поверхность нагреется. Это должно означать, что свет передает энергию металлу, поэтому теоретически возможно, что если вы освещаете поверхность достаточно долго, будет передано достаточно энергии, чтобы освободить электрон с орбиты. Даже при слабом свете вы должны быть в состоянии достаточно долго ждать накопления энергии и испускания электрона. Итак, физики попытались провести эксперимент. Это с треском провалилось. Для некоторых металлов специфический свет будет вызывать эмиссию электронов, для других металлов тот же самый источник света не будет, независимо от того, как долго он остается. И было обнаружено, что электроны вышли с более высокими энергиями в зависимости от цвета света, а не интенсивности.
Даже при слабом свете вы должны быть в состоянии достаточно долго ждать накопления энергии и испускания электрона. Итак, физики попытались провести эксперимент. Это с треском провалилось. Для некоторых металлов специфический свет будет вызывать эмиссию электронов, для других металлов тот же самый источник света не будет, независимо от того, как долго он остается. И было обнаружено, что электроны вышли с более высокими энергиями в зависимости от цвета света, а не интенсивности.
Проблема фотоэлектрического эффекта была решена в 1905 году Эйнштейном, за что он получил Нобелевскую премию в 1921 году. Эйнштейн применил планковскую теорию квантования к свету и сказал, что свет — это не непрерывный поток энергии, а скорее нагрузки. маленьких пакетов определенной энергии, которая зависела от его длины волны. Это объясняет, почему независимо от того, как долго вы оставите свет на поверхности, излучение не будет происходить, если у отдельных фотонов не будет достаточно энергии. Это также объясняет, почему разные цвета дают испускаемым электронам разные значения энергии. Было показано, что энергия связана с длиной волны уравнением Планка. Эйнштейн также показал, что энергия испущенных электронов будет равна
Было показано, что энергия связана с длиной волны уравнением Планка. Эйнштейн также показал, что энергия испущенных электронов будет равна
, где Φ — энергия, необходимая для того, чтобы вывести электрон из металла сразу за пределы поверхности, и называется «работой выхода».
Начнем со стандартного уравнения для волны.
(1)
означает, что вид этой волны зависит от положения () и времени (). Описание представлено в виде комплексных чисел и может быть отображено с помощью диаграммы Аргана (дополнительную информацию см. здесь). Эта волна является решением волнового уравнения, и мы хотим увидеть, можно ли использовать волновое уравнение для описания волн материи. Волновое уравнение
(2)
Это уравнение говорит о том, что если вы частично продифференцируете свою волну, , относительно дважды, оно будет равно частному дифференциалу вашей волны относительно дважды, умноженному на константу, которая в этом случай.
Итак, теперь нам нужно посмотреть, будет ли это работать, поэтому сначала мы берем нашу волну (1) и дважды дифференцируем ее относительно (если вы не знаете, как это сделать, см. здесь помощь). Таким образом, дифференцируя дважды дает.
здесь помощь). Таким образом, дифференцируя дважды дает.
Возможно, вам интересно, почему я изменил исходное уравнение при дифференцировании. Изначально у нас было и теперь есть. Это просто математический трюк, который вы можете проделать с экспоненциальными степенями, и я лично думаю, что это упрощает дифференцирование. Теперь мы дважды продифференцируем волну по времени, чтобы получить
. Теперь мы можем подставить эти два результата в уравнение (2), чтобы получить
Для удобства знаки минус, s и квадраты сокращаются, что дает нам
(3)
Теперь, если мы возьмем 2 базовые квантовые формулы из первого раздела
(4)
(5)
и попытаемся подставить в них (3), мы получим задачу
11
1
Однако по делу. Для нерелятивистской материи соотношение между энергией и импульсом подчиняется следующему закону
(6)
Итак, похоже, у нас есть проблема. Волновое уравнение (2) не работает для материи. Один из способов заставить это работать — сказать, что вместо того, что если бы мы попытались сделать так, чтобы это было? Для этого нам понадобилось бы волновое уравнение, дважды продифференцированное с и только один раз с . Также, если мы заменим константу, мы сможем облегчить себе жизнь. Итак, давайте попробуем
Один из способов заставить это работать — сказать, что вместо того, что если бы мы попытались сделать так, чтобы это было? Для этого нам понадобилось бы волновое уравнение, дважды продифференцированное с и только один раз с . Также, если мы заменим константу, мы сможем облегчить себе жизнь. Итак, давайте попробуем
в качестве нашего нового волнового уравнения. Теперь мы изменились на, так как это уравнение будет работать и является общим символом, используемым для квантово-механических волн, уравнение для такое же, как и для . Итак, если мы теперь проведем дифференцирование
, которое, когда мы вернемся к нашему новому волновому уравнению, даст нам
Это соотношение между и мы искали. Итак, теперь мы можем переставить и подставить в уравнения (4), чтобы получить
Теперь мы можем выбрать нашу константу как
, так что мы получим
Что правильно!! Пока все хорошо, наше новое волновое уравнение для материи дает нам правильную энергию.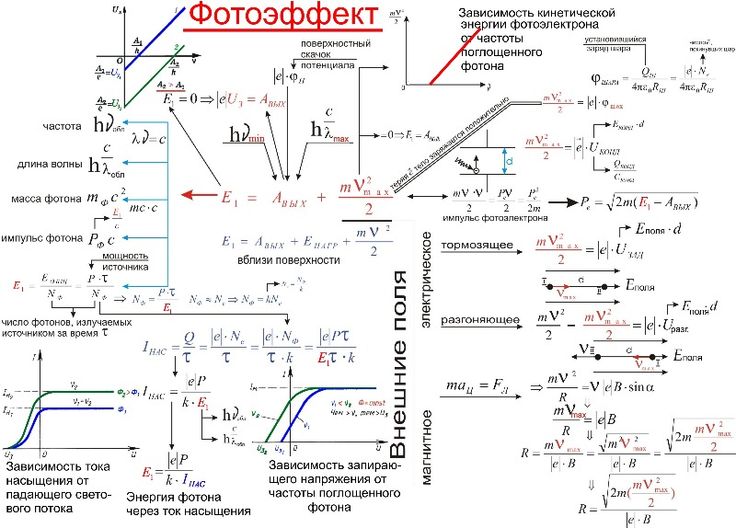 Итак, давайте вернем константу в
Итак, давайте вернем константу в
А теперь еще раз перестроим ее, чтобы получить более красивую форму:
Мы почти у цели. Уравнение почти готово. Однако, когда мы решим его для энергии частицы, мы получим
но иногда частица может получать энергию из своего окружения, например, если она находится в потенциале, поэтому мы должны сделать одну небольшую корректировку, чтобы учесть все возможные энергии частиц
Что означает наше волновое уравнение становится
Это называется Одномерное уравнение Шредингера, зависящее от времени
т внезапно изменить форму после стольких секунд. Если это так (а в большинстве случаев это так), то мы можем использовать метод разделения переменных в уравнении Шредингера.
Первое, что мы делаем, это предположим, что можно разделить на две функции, одну, которая зависит только от , а другую, которая зависит только от , например, так с , так что вы получите
Теперь вы делите на , вы избавляетесь от того, что слева, так как этот дифференциал не зависит от , и если вы делите на , вы избавляетесь от справа, как от этого дифференцирования не зависит от . Таким образом, вы получаете
Таким образом, вы получаете
Теперь, скажем, изменилось, это будет означать, что левая часть уравнения теперь будет иметь другое значение, однако, поскольку оно не зависит от правой части уравнения, оно не изменится. Это вызовет ошибку. Две стороны уравнения раньше были равны, теперь одна сторона изменилась, и они по-прежнему должны быть равны. Чтобы обойти эту проблему, вы устанавливаете обе стороны равными константе, в этом случае мы будем называть это . Итак, теперь у нас есть два отдельных уравнения,
(7)
(8)
Мы уже говорили, что нас интересуют только случаи, когда время не влияет на потенциал, поэтому мы можем игнорировать уравнение (7) и просто использовать уравнение (8), которое является нашим Одномерное независимое от времени уравнение Шрёдингера . В случае свободной частицы решение не зависящего от времени уравнения (8) принимает вид
, где
Это означает, что волновая функция имеет вид
Форма аналогична уравнению (1), при условии, что константа представляет собой полную энергию системы, что хорошо. Это означает, что при условии, что мы знаем энергию системы, мы можем найти решение волнового уравнения. Кроме того, при условии, что энергия остается постоянной, не влияет на , поэтому то же самое, что и , поэтому мы можем написать
Это означает, что при условии, что мы знаем энергию системы, мы можем найти решение волнового уравнения. Кроме того, при условии, что энергия остается постоянной, не влияет на , поэтому то же самое, что и , поэтому мы можем написать
Формула для пи появляется в квантовой механике
Два ученых были удивлены, обнаружив, что пи скрывается в квантовой механическая формула для энергетических состояний атома водорода.
«Мы не просто нашли пи», — говорит Тамар Фридманн, приглашенный доцент математики и научный сотрудник физики высоких энергий в Рочестерском университете и соавтор статьи, опубликованной в журнале Journal of Mathematical Physics . .
«Мы нашли классическую формулу Уоллиса семнадцатого века для числа пи, что сделало нас первыми, кто вывел ее из физики в целом и квантовой механики в частности».
Формула Уоллиса — разработана британским математиком Джоном Уоллисом в его книге Arithmetica Infinitorum — определяет число пи как произведение бесконечной последовательности отношений, состоящих из целых чисел. По мнению Фридмана, открытие формулы Уоллиса для пи в квантовомеханической формуле для энергетических состояний атома водорода подчеркивает вездесущность числа пи в математике и естественных науках.
По мнению Фридмана, открытие формулы Уоллиса для пи в квантовомеханической формуле для энергетических состояний атома водорода подчеркивает вездесущность числа пи в математике и естественных науках.
«Значение числа пи приобрело мифический статус отчасти потому, что его невозможно записать со 100-процентной точностью, — говорит Фридманн. , лучше всего представленный в виде формулы».
«Это прекрасная связь между числом пи и квантовой механикой…»
Фридман не собирался искать ни число пи, ни формулу Уоллиса. Открытие началось с курса квантовой механики, который читал Карл Хаген, профессор физики Рочестерского университета.
В то время как квантовые расчеты, разработанные датским физиком Нильсом Бором в начале двадцатого века, дают точные значения энергетических состояний водорода, Хаген хотел, чтобы его ученики использовали альтернативный метод, называемый вариационным принципом, для аппроксимации значения основного состояния. атома водорода.
Как и формула Уоллиса, вариационный принцип восходит к семнадцатому веку, одним из первых его проявлений был принцип наименьшего времени математика Пьера де Ферма, современника Уоллиса. Хаген также начал думать о том, можно ли применить этот метод к состояниям, отличным от основного. Хаген привлек Фридманн, чтобы воспользоваться ее способностью работать как в физике, так и в математике.
Хотя применение вариационного принципа для расчета основного состояния атома водорода является относительно простой задачей, его применимость к возбужденному состоянию далеко не очевидна. Это связано с тем, что вариационный принцип обычно не может применяться при наличии более низких энергетических уровней. Однако Фридман и Хаген смогли обойти это, разделив проблему на серию из l задач, каждая из которых была сосредоточена на самом низком уровне энергии для данного квантового числа орбитального углового момента, l.
Затем они могли рассчитать значения для различных энергетических состояний и сравнить их со значениями, полученными Бором почти столетие назад. Это позволило им определить, как отношение значений Бора к значениям, полученным с помощью «подправленного» вариационного принципа, менялось по мере того, как учитывались все более высокие уровни энергии.
Это позволило им определить, как отношение значений Бора к значениям, полученным с помощью «подправленного» вариационного принципа, менялось по мере того, как учитывались все более высокие уровни энергии.
И они были удивлены, увидев, что соотношение дает — фактически — формулу Уоллиса для числа пи.
В частности, вычисления Фридмана и Хагена привели к выражению, включающему специальные математические функции, называемые гамма-функциями, что приводит к формуле
, который можно свести к классической формуле Уоллиса.
«Что меня удивило, так это то, что формула возникла таким естественным образом в расчетах, без кругов, участвующих в определении энергетических состояний», — говорит Хаген, соавтор статьи. «И я рад, что не подумал об этом до приезда Тамары в Рочестер, потому что это бы никуда не делось, и мы бы не сделали этого открытия».
Математик Моше Маховер из Королевского колледжа Лондона называет находку «хитрым волшебством».
«Это вычисление числа «пи» — сюрприз для знакомого, очень похожий на фокус фокусника», — говорит Маховер.

 38*10-23 Дж/К
38*10-23 Дж/К



 Ширина ямы .
Ширина ямы .


 1 Независимость от времени
1 Независимость от времени