Формулы магнитное поле: Ошибка: 404 Материал не найден - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Электромагнитное поле | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Тема:

Электромагнетизм

Электромагнитное поле связано с источниками (зарядами) и обладает определенной структурой. Его структура и связь с источниками описываются уравнениями поля (уравнениями Максвелла).

На частицу с зарядом q и скоростью v в пустоте в присутствии внешнего (создаваемого другими частицами) электромагнитного поля действует сила

F̅ = qE̅ + qv̅ × B̅. [1]

Вектор E̅ называется напряженностью электрического поля в точке нахождения частицы, вектор B̅ — индукцией магнитного поля в той же точке. Эти векторы в разных точках пространства, вообще говоря, различны и могут меняться во времени. Таким образом, мы имеем дело с двумя векторными функциями координат и времени:

E̅ = E̅ (r̅,

t), B̅ = B̅ (r̅, t).

Задание этих функций полностью определяет электромагнитное поле.

На фотографии видны силовые линии мощного электрического поля около металлического шарика, под которым установлен ионизатор

Из формулы [1] следует, что напряженность электрического поля определяет силу, действующую на заряженную частицу, не зависящую от состояния движения частицы. Сила, действующая на частицу со стороны магнитного поля, определяется векторным произведением скорости и индукции поля, направлена перпендикулярно плоскости, в которой лежат векторы скорости и индукции, и зависит от величины скорости. Неподвижный заряд не «чувствует» магнитного поля. Материал с сайта http://worldofschool.ru

Силовые линии поля

Электромагнитное поле обнаруживается (и измеряется) по силе, действующей на заряженную частицу. Оно полностью описывается двумя векторными функциями —

напряженностью электрического поля и индукцией магнитного. Векторные поля, представляющие электромагнитное поле, должны обладать специальной структурой. Математически эта структура определяется уравнениями, которым должны удовлетворять векторные поля, обладающие свойствами реального электромагнитного поля. Эти уравнения называются уравнениями поля.

Наглядно поле изображается с помощью силовых линий, представляющих собой множество кривых, проведенных таким образом, что в каждой точке кривой вектор E̅ в этой точке касателен к кривой. Это силовые линии электрического поля. Аналогично проводятся

силовые линии магнитного поля.

На этой странице материал по темам:

Решебник
Конспект “электромагнитное поле”
Все физические формулы по теме электромагнитное поле
Электромагнитное поле конспект лекция
Электромагнитное поле краткий конспект

Формулы для решения задач по физике

№ п/п	Наименование параметра	Формула	Обозначения
4. 1	Закон Био-Савара-Лапласа Модуль вектора Модуль вектора		― магнитная индукция поля, создаваемого элементом проводника с током; μ ― магнитная проницаемость среды, μ₀ = 4π∙10⁻⁷ Гн/м ― магнитная постоянная, ― вектор, равный по модулю длине dl проводника и совпадающий по направлению с током; I ― сила тока в проводнике, ― расстояние до проводника α ― угол между векторами и ― напряженность магнитного поля, создаваемого элементом проводника с током
4.2	Индукция магнитного поля, создаваемого бесконечно длинным прямым проводником с током Напряженность магнитного поля	вывод формул	μ ― магнитная проницаемость среды, μ₀ = 4π∙10⁻⁷ Гн/м ― магнитная постоянная, I ― сила тока в проводнике, a ― расстояние до проводника
4. 3	Индукция магнитного поля в центре кругового проводника с током Напряженность магнитного поля		μ ― магнитная проницаемость среды, μ₀ = 4π∙10⁻⁷ Гн/м ― магнитная постоянная, I ― сила тока в проводнике, R ― радиус проводника
4.4	Индукция магнитного поля на оси кругового проводника с током Напряженность магнитного поля	вывод формул	μ ― магнитная проницаемость среды, μ₀ = 4π∙10⁻⁷ Гн/м ― магнитная постоянная, I ― сила тока в проводнике, R ― радиус проводника, a ― расстояние до плоскости проводника
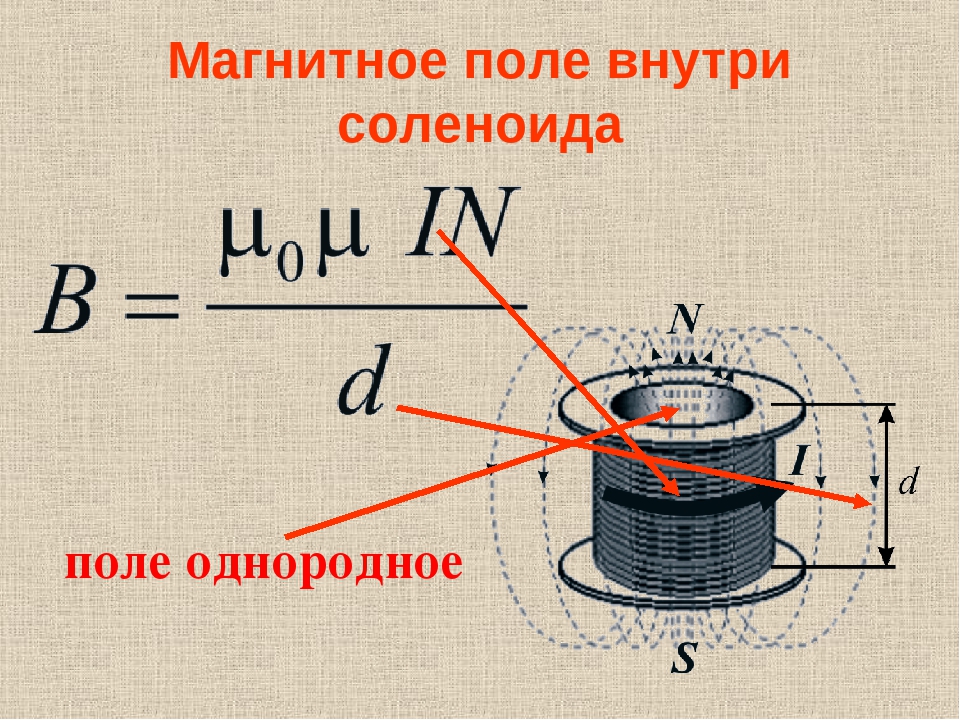
4.5	Индукция магнитного поля внутри длинного соленоида		μ ― магнитная проницаемость среды, μ₀ = 4π∙10⁻⁷ Гн/м ― магнитная постоянная, I ― сила тока в проводнике, N ― количество витков, l ― длина соленоида
4.6	Магнитная индукция поля, создаваемая отрезком проводника	вывод формулы	μ ― магнитная проницаемость среды, μ₀ = 4π∙10⁻⁷ Гн/м ― магнитная постоянная, a ― расстояние до оси проводника, α₁ и α₂ ― углы между направлением тока и направлением на точку, в которой создано магнитное поле, вершинами которых являются соответственно начало и конец прямого участка проводника
4. 7	Связь между напряженностью H и индукцией B магнитного поля		μ ― магнитная проницаемость среды, μ₀ = 4π∙10⁻⁷ Гн/м ― магнитная постоянная
4.8	Связь между электрической и магнитной напряженностями волны		Е₀ ― амплитуда электрической напряженности, H₀ ― амплитуда магнитной напряженности
4.9	Фазовая скорость волны v равна		с ― скорость света в вакууме; ε ― диэлектрическая проницаемость; μ ― магнитная проницаемость
4.10	Индуктивность катушки равна		μ₀ = 4π∙10⁻⁷ Гн/м ― магнитная постоянная; N ― количество витков; N = l/d, d ― диаметр проводника катушки; l ― длина катушки; V ― объем катушки; S ― площадь витка катушки
4.11	Средняя объемная плотность энергии		μ₀ = 4π∙10⁻⁷ Гн/м ― магнитная постоянная; μ ― магнитная проницаемость среды; для вакуума μ = 1; Н ― действующее значение напряженности магнитного поля
4. 12	Средняя объемная плотность энергии		ε₀ = 8,85∙10⁻¹² Ф/м ― электрическая постоянная, ε ― диэлектрическая проницаемость среды, E ― действующее значение напряженности электрического поля
4.13	Сила , действующая на заряд Q, движущийся со скоростью в магнитном поле с индукцией (сила Лоренца)	или	α ― угол, образованный вектором скорости движения частицы и вектором индукции магнитного поля
4.14	Cила Ампера (сила, действующая на проводник с током в магнитном поле)		I ― сила тока, l ― длина проводника, В ― индукция магнитного поля, α ― угол между векторами
4.15	Количество заряда, протекающее в контуре	вывод формулы	ΔΨ ― изменение потокосцепления контура; R ― сопротивление контура; N ― количество витков в контуре; ΔФ ― изменение магнитного потока, пронизывающего контур; S ― площадь витка; ΔB ― изменение магнитной индукции
4. 16	Циклическая частота колебаний в контуре		L ― индуктивность контура; C ― емкость контура
4.17	Мгновенное значение I силы тока в цепи, обладающей активным сопротивлением R и индуктивностью L, после размыкания цепи		I₀ ― значение силы тока в цепи при t = 0; t ― время, прошедшее с момента размыкания цепи
4.18	Мгновенное значение I силы тока в цепи, обладающей активным сопротивлением R и индуктивностью L, после замыкания цепи		ε ― э.д.с. источника тока; t ― время, прошедшее с момента замыкания цепи
4.19	Основной закон электромагнитной индукции		ε_i ― электродвижущая сила индукции; N ― число витков контура; Ψ ― потокосцепление
4.20	Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока I:		L ― индуктивность контура или катушки
4.21	Работа по перемещению проводника или по повороту контура в магнитном поле		I ― сила тока в проводнике, контуре; dФ ― пересекаемый проводником магнитный поток либо изменение магнитного потока через замкнутый контур
4. 22	Вращающий момент, действующий на контур с током, помещенный в магнитное поле Значение вращающего момента	При α=π/2 имеем При α=0 или α=π имеем	― индукция магнитного поля; _m ― магнитный момент контура, _m = IS, где I ― ток, протекающий по контуру, S ― площадь контура; α ― угол между векторами _m и

Магнитное поле в веществе. Часть 1

Всем доброго времени суток. В прошлой статье я рассказывал о основной характеристике магнитного поля – магнитной индукции, однако приведённые расчётные формулы соответствуют магнитному полю в вакууме. Что в практической деятельности встречается довольно редко. Когда проводники с током находятся в какой–либо среде, даже в воздухе, магнитное поле, которое они создают, претерпевает некоторые, а иногда и существенные изменения. Какие изменения происходят с магнитным полем, и от чего это зависит, я расскажу в данной статье.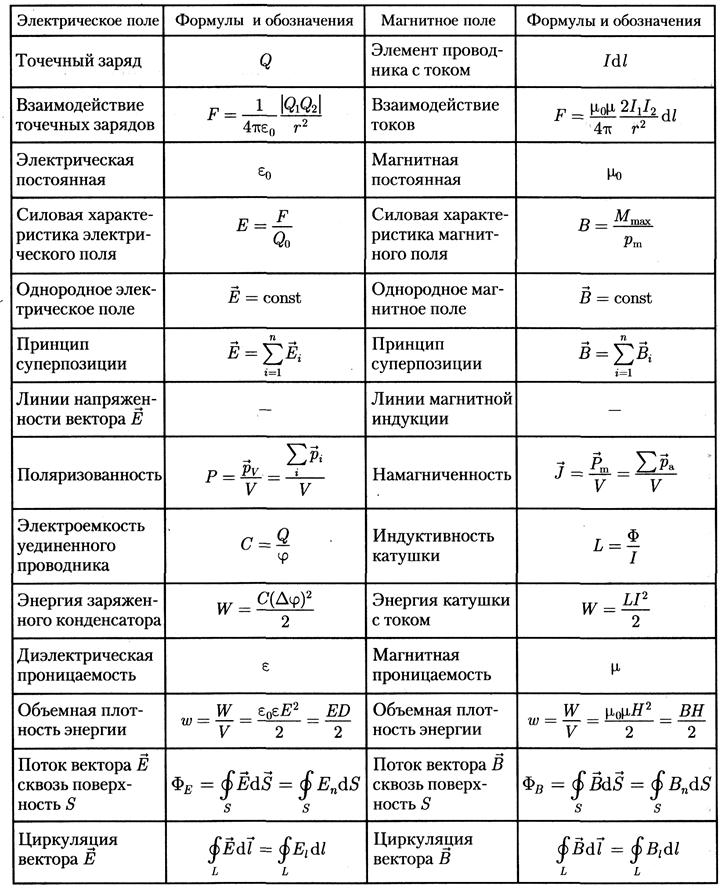

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Как связана индукция и напряженность магнитного поля?

Магнетиком называется вещество, которое под действием магнитного поля способно намагничиваться (или как говорят физики приобретать магнитный момент). Магнетиками являются практически все вещества. Намагничивание веществ объясняется тем, что в веществах присутствуют свои собственные микроскопические магнитные поля, которые создаются вращением электронов по своим орбитам. Когда внешнее магнитное поле отсутствует, то микроскопические поля расположены произвольным образом, а под воздействием внешнего магнитного поля соответствующим образом ориентируются.

Для характеристики намагничивания различных веществ используют так называемый вектор намагничивания J.

Таким образом, под действием внешнего магнитного поля с магнитной индукцией В₀, магнетик намагничивается и создает свое магнитное поле с магнитной индукцией В’. В итоге общая индукция В будет состоять из двух слагаемых

Тут возникает проблема вычисления магнитной индукции намагниченного вещества В’, для решения которой необходимо считать электронные микротоки всего вещества, что практически нереально.

Альтернативой данного решения есть ввод вспомогательных параметров, а именно напряженность магнитного поля

Н и магнитная восприимчивость χ. Напряженность связывает магнитную индукцию В и намагничивание вещества J следующим выражением

где В – магнитная индукция,

μ₀ – магнитная постоянная, μ₀ = 4π*10^-7 Гн/м.

В то же время вектор намагничивания J связан с напряженность магнитного поля В параметром, характеризующим магнитные свойства вещества и называемым магнитной восприимчивостью χ

где J – вектор намагничивания вещества,

μ_r – относительная магнитная проницаемость вещества.

Однако наиболее часто для характеристики магнитных свойств веществ используют относительную магнитную проницаемость μ_r.

Таким образом, связь между напряженностью и магнитной индукцией будет иметь следующий вид

где μ₀ – магнитная постоянная, μ₀ = 4π*10^-7 Гн/м,

μ_r – относительная магнитная проницаемость вещества.

Так как намагничивание вакуума равна нулю (J = 0), то напряженность магнитного поля в вакууме будет равна

Отсюда можно вывести выражения напряженности для магнитного поля, создаваемого прямым проводом с током:

где I – ток протекающий по проводнику,

b – расстояние от центра провода до точки, в которой считается напряженность магнитного поля.

Как видно из данного выражения единицей измерения напряженности является ампер на метр (А/м) или эрстед (Э)

Таким образом, магнитная индукция В и напряженность Н являются основными характеристиками магнитного поля, а магнитная проницаемость μ_r – магнитной характеристикой вещества.

Намагничивание ферромагнетиков

В зависимости от магнитных свойств, то есть способности намагничиваться под действием внешнего магнитного поля, все вещества делятся на несколько классов. Которые характеризуются разной величиной относительной магнитной проницаемости μ_r и магнитной восприимчивости χ. Большинство веществ являются диамагнетиками (χ = -10^-8 … -10^-7 и μ_r < 1) и парамагнетиками (χ = 10^-7 … 10^-6 и μ_r > 1), несколько реже встречаются ферромагнетики (χ = 10³ … 10⁵ и μ_r >> 1). Кроме данных классов магнетиков существует ещё несколько классов магнетиков: антиферромагнетики, ферримагнетики и другие, однако их свойства проявляются только при определённых условиях.

Особый интерес в радиоэлектронике ферромагнитные вещества. Основным отличием данного класса веществ является нелинейная зависимость намагничивания, в отличие от пара- и диамагнетиков, имеющих линейную зависимость намагничивания J от напряженности Н магнитного поля.

Зависимость намагничивания J ферромагнетика от напряженности Н магнитного поля.

На данном графике показана

основная кривая намагничивания ферромагнетика. Изначально намагниченность J, в отсутствие магнитного поля (Н = 0), равна нулю. По мере возрастания напряженности намагничивание ферромагнетика проходит довольно интенсивно, вследствие того что его магнитная восприимчивость и проницаемость очень велика. Однако по достижении напряженности магнитного поля порядка H ≈ 100 А/м увеличение намагниченности прекращается, так как достигается точка насыщения J_НАС. Данное явление называется магнитным насыщением. В данном режиме магнитная проницаемость ферромагнетиков сильно падает и при дальнейшем увеличении напряженности магнитного поля стремится к единице.

Гистерезис ферромагнетиков

Еще одной особенностью ферромагнетиков является наличие петли гистерезиса, которая является основополагающим свойством ферромагнетиков.

Петля гистерезиса ферромагнетика.

Для понимания процесса намагничивания ферромагнетика изобразим зависимость индукции В от напряженности Н магнитного поля, где красным цветом выделим основную кривую намагничивания. Данная зависимость довольно неопределенна, так как зависит от предыдущего намагничивания ферромагнетика.

Возьмём образец ферромагнитного вещества, которое не подвергалось намагничиванию (точка 0) и поместим его в магнитное поле, напряженность Н которого начнем увеличивать, то есть зависимость будет соответствовать кривой 0 – 1, пока не будет достигнуто магнитное насыщение (точка 1). Дальнейшее увеличение напряженности не имеет смысла, потому как намагниченность J практически не увеличивается, а магнитная индукция увеличивается пропорционально напряженности Н. Если же начинать уменьшать напряженность, то зависимость В(Н) будет соответствовать кривой 1 – 2 – 3, при этом когда напряженность магнитного поля упадёт до нуля (точка 2), то магнитная индукция не упадёт до нуля, а будет равна некоторому значению B_r, которое называется остаточной индукцией, а намагничивание будет иметь значение J_r, называемое остаточным намагничиванием.

Для того чтобы снять остаточное намагничивание и уменьшить остаточную индукцию B_r до нуля, необходимо создать магнитное поле, противоположное полю, вызвавшему намагничивание, причем напряженность размагничивающего поля должна составлять Н_с, называемая коэрцитивной силой. При дальнейшем росте напряженности магнитного поля, которое противоположно первоначальному полю, происходит насыщение ферромагнетика (точка 4).

Таким образом, при действии на ферромагнетик переменного магнитного поля зависимость индукции от напряженности будет соответствовать кривой 1 – 2 – 3 – 4 – 5 – 6 – 1, которая называется петлёй гистерезиса. Таких петель для ферромагнетика может быть множество (пунктирные кривые), называемые частными циклами. Однако, если при максимальных значениях напряженности магнитного поля происходит насыщение, то получается максимальная петля гистерезиса (сплошная кривая).

Так как магнитная проницаемость μ_r ферромагнетиков имеет довольно сложную зависимость от напряженности магнитного поля, поэтому нормируются два параметра магнитной проницаемости:

μ_н – начальная магнитная проницаемость соответствует напряженности Н = 0;

μ_max – максимальная магнитная проницаемость достигается в магнитном поле при приближении магнитного насыщения.

Таким образом, у ферромагнетиков величины B_r, Н_с и μ_н (μ_max) являются основными характеристиками, влияющими на выбор вещества в конкретном случае.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Электродинамическое взаимодействие, образованное токами электрического смещения поля

Электромагнитная индукция. Магнитное поле. Формула. Электрическое поле. Ток смещения. Заряд.

ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ

«Всякое возмущение в пространстве распространяется со скоростью не выше скорости света. В частности, электрическое поле при смещении точечного заряда не просто переместится вместе с зарядом, как в случае бесконечно большой скорости распространения поля, а меняется более сложным образом. Возникают эффекты, связанные с запаздыванием появления поля на больших расстояниях от заряда, которые могут быть описаны введением индукции магнитного поля.»
Основы физики. Л.А.Грибов, Н.И.Прокофьев. 1995. С.300.

Магнитное поле (поток) можно рассматривать как релятивистский эффект (эффект движения), связанный с запаздыванием распространения электрического смещения поля. Согласно формуле преобразования полей B = μ₀[vD], магнитная индукция возникает при движении электрического потока. Магнитную энергию можно трактовать как кинетическую энергию движущихся электрических потоков W_м = M_эv² sin²a, где M_э – масса электрического потока, v – скорость движения, a – угол между направлением движения и вектором D.

« B = [vE]/c² »
Электромагнетизм. И.Е.Иродов. 1991. С.135.
«В результате магнитное поле можно рассматривать как неизбежный релятивистский результат движения электрических зарядов (тока) и нестационарности создаваемого ими электрического поля (тока смещения).»
Физическая энциклопедия. ЭЛЕКТРОДИНАМИКА.

Магнитное поле возникает как результат движения электрических зарядов (потоков), но еще недостаточно рассмотрен сам механизм его возникновения. Постараюсь проанализировать и описать электродинамические процессы, протекающие при движении электрических зарядов.

Возмущения поля не распространяются мгновенно, для возникновения возмущения требуется определенное время. При движении заряда возмущение поля, возникая в том месте, куда переместился заряд, и одновременно исчезая в том месте, откуда он переместился, образует в пространстве токи электрического смещения, которые имеют обратное направление. Примеры расчетов обратных токов смещения приведены в учебниках.

«Пример. Точечный заряд q движется равномерно и прямолинейно с нерелятивистской скоростью v. Найти вектор плотности тока смещения в точке P, находящейся на расстоянии r от заряда на прямой, перпендикулярной его траектории и проходящей через заряд. Решение: j_см = -qv/4πr³.»
Электромагнетизм. И.Е.Иродов. 2000. С.302.

Отсюда, за пределами радиуса r от движущегося точечного заряда течет обратный ток смещения:

I_см = -qv/2r.

Получается, если заряд в 1 Кл движется со скоростью 2 м/с, то за пределами радиуса в 1 м течет обратный ток смещения силой в 1 А, плотность же обратного тока смещения на расстоянии 1 м равна 0.16 А/м². Т.е., если движется заряженный шар радиусом в 1 м, с зарядом в 1 Кл и со скоростью 2 м/с, то полный обратный ток смещения, который он создает, равен 1 А. Отсюда следует, что ток смещения не влияет на величину магнитной индукции, так как независимо от величины тока смещения (размера шара) магнитная индукция вокруг шара всегда равна B = μ₀q[vr]/4πr³. То, что ток электрического смещения не создает магнитную индукцию, входит в противоречие с постулатом, утверждающим, что ток смещения создает такое же магнитное поле, как и ток проводимости. Причина возникновения такого противоречия в том, что на ток смещения, без экспериментальной проверки, были перенесены магнитные свойства тока проводимости. Т.е. был упущен тот факт, что магнитное поле, согласно электродинамике, представляет движущийся электрический поток B = μ₀[vD], а не ток, так как в формуле D – это плотность электрического потока. Соответственно, для определения магнитной индукции необходимо рассматривать не то, как течет ток проводимости или смещения, а как движется электрический поток. Данная формула, представляя закон магнитной индукции, лежит в основе всех остальных формул. Например, вместе с движущимся зарядом движется его электрический поток. Зная плотность связанного с зарядом движущегося электрического потока D = qr/4πr³, можно, согласно B = μ₀[vD], вычислить плотность магнитного потока вокруг заряда B = μ₀q[vr]/4πr³. Аналогичным образом, зная, что с каждым движущимся зарядом связан движущийся электрический поток, выводятся и другие формулы для расчета магнитной индукции. Например, плотность движущегося электрического потока вокруг прямого бесконечного провода с током D = P/2πr = q/2πrL, где P – плотность движущихся зарядов в проводе (P = q/L), r – расстояние от провода. Согласно B = μ₀[vD], получим B = μ₀qv/2πrL = μ₀I/2πr, где I – сила тока (I = Pv = qv/L). Все это относится как к току проводимости, так и к току смещения, т.е. сначала надо рассмотреть движение электрических потоков, а потом, согласно B = μ₀[vD], определить магнитную индукцию.

«… поле B точечного заряда q, движущегося с постоянной нерелятивистской скоростью v. … B = μ₀q[vr]/4πr³ …»
Электромагнетизм. И.Е.Иродов. 2000. С.155.
«… магнитная индукция поля прямого тока B = μ₀I/2πr.»
Курс физики. Т.И.Трофимова. 1998. С.208.

Знак минус в формуле I_см = -qv/2r означает, что ток смещения течет в обратном направлении. При этом ток смещения возникает независимо от того, движется ли заряд самостоятельно или, например, по проводнику, где ток смещения распространяется в пространстве за пределами проводника и, если рядом находится другой проводник, то в нем обратный ток смещения будет переходить в ток проводимости. Т.е. ток смещения будет замыкаться током проводимости – это явление называется электромагнитной индукцией.

«Для магнитного поля, так же как для электрического, справедлив принцип суперпозиции; …»
Справочник по физике. Б.М.Яворский, А.А.Детлаф. 1996. С.236.
«… ток смещения по своей сути – это изменяющееся со временем электрическое поле.»
Курс физики. Т.И.Трофимова. 1998. С.250.

Для тока смещения, как и для поля, действует принцип суперпозиции (для любого тока действует принцип суперпозиции), т.е., если движутся несколько зарядов, то их обратные токи смещения складываются в пространстве согласно принципу суперпозиции. Например, плотность обратного постоянного тока смещения вокруг тонкого прямого провода бесконечной длины:

j_см = -I/2πr²,

где r – расстояние от оси провода, I - постоянный ток в проводе. Т.е. не только вокруг движущегося заряда, но и вокруг проводника с током течет обратный ток смещения.

«… каждый заряд возбуждает поле, совершенно не зависящее от наличия других зарядов.»
Общий курс физики. Электричество. Д.В.Сивухин. 1996. Т.3. Ч.2. С.204.

Независимо от того движется заряд самостоятельно или, например, в проводнике, всегда в окружающем пространстве вместе с ним движется электрический поток. Там, где происходит движение электрических потоков, всегда течет ток смещения, даже если не изменяется электрическое поле (электрическая напряженность). Например, если движется заряд, то вокруг него возникает электрический ток смещения, когда же по проводнику движется множество зарядов, представляя постоянный ток проводимости, то электрическое поле в пространстве не изменяется, но суперпозиция токов смещения от всех движущихся зарядов представляет постоянный ток смещения, который течет в обратном направлении.

«Ток смещения входит в Максвелла уравнения на равных правах с током, обусловленным движением зарядов.»
Физический энциклопедический словарь. ЭЛЕКТРИЧЕСКИЙ ТОК.
«Ток смещения, в отличие от тока проводимости, не сопровождается выделением теплоты.»
Справочник по физике. Б.М.Яворский, А.А.Детлаф. 1996. С.290.

Электрический ток смещения поля течет без сопротивления, а раз нет сопротивления, то нет и напряженности (закон Ома). Электрическая напряженность поля возникает только при изменении тока смещения как вихревое электрическое поле. Например, возникновение вихревого электрического поля при включении и выключении электромагнита говорит о том, что ток смещения поля при включении возрастает, а при выключении уменьшается. В период, когда магнитное поле не изменяется, плотность тока смещения также не изменяется и, соответственно, нет вихревого электрического поля, поэтому постоянное магнитное поле не действует на покоящиеся электрические заряды.

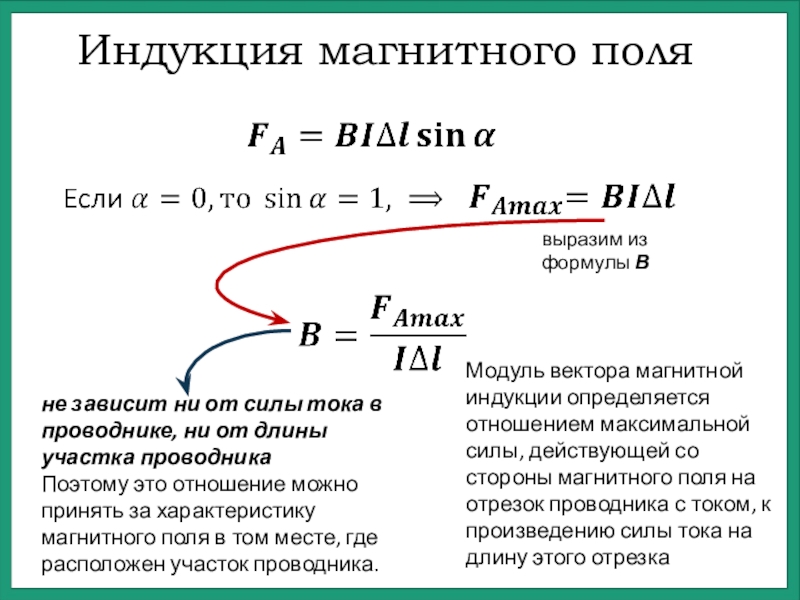
Линиями тока смещения поля можно наглядно представить электродинамику полевых процессов, так как любые изменения поля всегда связаны с токами смещения. В книгах по электродинамике хотя и говорится, что при движении зарядов в окружающем пространстве текут токи смещения, но, к сожалению, ни одного рисунка, наглядно изображающего этот процесс, так и не удалось найти.

Рассмотрим токи смещения, возникающие при движении электрических зарядов.

На рисунке знаком (+) обозначена область, куда переместился положительный заряд и где возникает возмущение (электрическое смещение поля), т.е. распространяется положительное электрическое возмущение поля. Знаком (-) обозначена область, где раньше был заряд и где исчезает возмущение, т.е. распространяется отрицательное возмущение. Линиями изображен обратный ток смещения поля, стрелками – направление тока. Надо заметить, что ток смещения “стекает” в (-)-область, хотя возмущение распространяется из (-)-области (аналогия с током проводимости, где отрицательно заряженные электроны движутся в одну сторону, но принято считать, что ток течет в обратном направлении). Распространение возмущения из (+)-области совпадает с направлением тока смещения. Когда движутся несколько зарядов, надо отдельно рассматривать каждый движущийся заряд, а потом суммировать все токи смещения, которые их сопровождают, на основе принципа суперпозиции. При движении цепочки зарядов поперечные токи смещения, имеющие встречное направление, взаимонейтрализуются и образуется постоянный обратный ток смещения.

Ток проводимости представляет движение зарядов, поэтому в окружающем пространстве возникает обратный ток смещения. Когда ток течет по витку, то в окружающем пространстве возникает круговой ток смещения, имеющий обратное направление. При изменении тока смещения образуется вихревое электрическое поле. Если рядом с витком тока расположить, например, сверхпроводящий контур, то в нем за счет обратного тока электрического смещения синхронно, но в обратном направлении возникает индукционный ток. Ток смещения как бы замыкается через сверхпроводящий проводник.

«… вихревое поле без каких бы то ни было добавочных сил может вызвать непрерывное течение электричества по замкнутым проводам. Это течение и наблюдается в виде индукционных токов.»
Общий курс физики. Электричество. Д.В.Сивухин. 1996. Т.3. Ч.1. С.252.

Также самоиндукция связана с обратными токами смещения, с запаздыванием распространения возмущений. При остановке зарядов обратные токи смещения, еще некоторое время продолжая течь (как возмущения поля), воздействуют на заряды.

«Максвелл приписал току смещения лишь одно – способность создавать в окружающем пространстве магнитное поле. »
Курс физики. Т.И.Трофимова. 1998. С.250.

Точнее, ток смещения сам представляет магнитное поле. Магнитная сила притяжения возникает между двумя проводниками с током, когда обратные токи смещения полевой среды текут в одном направлении, – токи стремятся слиться. Отталкивание же возникает, когда обратные токи смещения полевой среды текут навстречу друг другу, – токи стремятся разойтись. Таким образом, магнитная сила – это обычная гидродинамическая сила, возникающая между текущими потоками среды. Например, если два диска вращаются в одном направлении, то между ними возникает сила притяжения. Если же они вращаются в противоположных направлениях, то, наоборот, возникает сила отталкивания. Это происходит потому, что своим вращением диски увлекают воздух, потоки которого создают гидродинамическую силу притяжения или отталкивания. На покоящийся заряд магнитное поле не действует, так как вокруг него не текут токи электрического смещения поля. На практике же не рассматривают распространяющиеся смещения поля, представляющие движущиеся электрические потоки, а пользуются линиями магнитной индукции, рассматривая взаимодействие с ними электрических токов. Линии магнитной индукции не являются силовыми линиями (линиями действия силы), например, направление вектора магнитной силы, возникающей между параллельными проводниками с постоянным током, не совпадает с направлением линий магнитной индукции. Т.е. индукционные линии магнитных полей силовыми не являются, так как не показывают направление силы, действующей на элементарный ток. Также в данном примере видно, что магнитное поле не является вихревым, так как у вихревых полей работа сил при движении по замкнутой линии может быть отлична от нуля, что является признаком вихревого поля. Вихревые поля могут возбуждать вихревые электрические токи. Таким образом, постоянное магнитное поле является соленоидальным, но не вихревым.

«Прямая, вдоль которой направлена сила, называется линией действия силы. »
Физическая энциклопедия. СИЛА.
«Работа сил вихревого электрического поля при движении электрического заряда по замкнутой линии может быть отлична от нуля.»
Физика. О.Ф.Кабардин. 1991. С.189.

Работа сил вихревого электрического поля или вихревого магнитного поля при движении электрического заряда или магнита по замкнутой линии может быть отлична от нуля. Например, в электромагнитных волнах электрические и магнитные потоки являются вихревыми.

«… магнитное же поле – соленоидальное.»
Электромагнетизм. И.Е.Иродов. 2000. С.170.
«… ускоритель, использующий вихревое магнитное поле.»
Физическая энциклопедия. БЕТАТРОН.

Магнитное поле, хотя соленоидально, но не всегда является вихревым. Надо заметить, что некоторые авторы книг по электродинамике путают соленоидальные поля с вихревыми, индукционные линии с силовыми. У электрического поля, действительно, индукционные линии совпадают с силовыми, но это никак не относится к магнитному полю, где индукционные линии не всегда совпадают с силовыми линиями действия поля.

Также по линиям магнитной индукции, например, невозможно определить направление силы, действующей на покоящийся электрический заряд в момент включения электромагнита в случае, когда магнит и заряд находятся в покое, т.е. по линиям магнитной индукции невозможно определить направление силы, действующей на покоящийся заряд в переменном магнитном поле. Представляя магнитное поле линиями токов смещения, таких проблем не возникает. По силе, действующей на покоящийся электрический заряд в момент включения электромагнита, можно определить направление тока смещения в конкретной точке магнитного поля. Изменение любого электрического тока всегда связано с электрической напряженностью.

«Магнитное поле, непостоянное во времени, оказывает силовое действие на покоящиеся электрические заряды и приводит их в движение; …»
Физический энциклопедический словарь. МАГНИТНОЕ ПОЛЕ.

Данное правило не дает ответа на главный вопрос: куда действует сила? И по сути оно является неверным, так как не учитываются токи смещения (магнитное поле вообще не действует на покоящиеся заряды). Правильной же является такая формулировка: переменное магнитное поле представляет переменный ток электрического смещения, который проявляется как вихревое электрическое поле и оказывает силовое действие на покоящиеся электрические заряды. Например, если покоящийся заряд находится в центре соленоида, то при включении или выключении тока в соленоиде на заряд не действует сила, несмотря на то, что изменяется поток магнитной индукции, так как в центре соленоида ток смещения отсутствует и, соответственно, отсутствует вихревое электрическое поле. Достаточно взглянуть на примеры в учебниках, из которых видно, что ток смещения в центре соленоида отсутствует.

«Пример. Найти плотность тока смещения как функцию расстояния r от оси соленоида.»
Электромагнетизм. И.Е.Иродов. 2000. С.303.

Таким образом, фундаментальное правило имеет исключение: в центре соленоида переменное магнитное поле не оказывает силового действия на покоящиеся электрические заряды и не приводит их в движение. Ось соленоида – это “мертвая” линия магнитного поля, вокруг которой текут электрические токи смещения. Такая “мертвая” линия имеется у любого магнита.

Для примера рассмотрим эксперимент, где электромагнитная индукция возникает “без магнитного поля”. В центральной точке между двумя электромагнитами, где магнитное поле, согласно принципу суперпозиции полей, равно нулю, установлен пробный электрический заряд.

[N] (+) [S]

[N] и [S] – полюса двух электромагнитов, (+) - пробный положительный электрический заряд.

Если электромагниты выключать по отдельности, то на заряд будет действовать сила, направленная вверх.

«Электромагнитная индукция – возникновение электрического поля, электрического тока или электрической поляризации при изменении во времени магнитного поля или при движении материальных сред в магнитном поле. »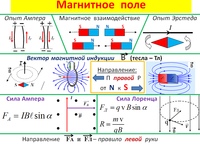
Физическая энциклопедия. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ.
«… изменяющееся во времени магнитное поле порождает электрическое поле …»
Курс физики. Т.И.Трофимова. 1998. С.248.

При одновременном выключении электромагнитов на заряд также будет действовать сила, направленная вверх, хотя магнитное поле в точке, где находится заряд, всегда будет оставаться равным нулю. Т.е. в точке, где находится заряд, магнитное поле не изменяется и всегда равно нулю, но тогда почему на заряд действует сила? Парадокс с электромагнитной индукцией можно объяснить присутствием токов смещения, которые текут в одном направлении и складываются согласно принципу суперпозиции. Обнаружить токи смещения можно по силе действующей на заряд в момент включения или выключения электромагнита. Данный пример показывает, что переменный ток смещения, действует на покоящийся электрический заряд даже в тех точках поля, где нет магнитной индукции. Т.е. фундаментальное утверждение, что изменяющееся во времени магнитное поле порождает электрическое, не всегда соответствует действительности, так как вихревое электрическое поле может возникать даже в тех точках, где нет магнитной индукции. В приведенном примере электромагниты можно заменить на постоянные магниты, которые раздвигаются симметрично относительно покоящегося заряда. Также можно привести и другие примеры, например, возникновение индукционного тока внутри трубки, по которой течет переменный ток, хотя магнитная индукция внутри трубки отсутствует. Т.е., рассматривая переменные магнитные поля, необходимо учитывать не только магнитную индукцию, но и токи смещения. В пространстве, где нет изменения плотности тока смещения, – нет магнитной индукции, например, внутри трубки, по которой течет ток. За пределами же трубки плотность тока смещения изменяется, что представляет магнитную индукцию.

«Если провод имеет вид трубки, то снаружи индукция B определяется формулой (6. 18), а внутри – магнитное поле отсутствует.»
Электромагнетизм. И.Е.Иродов. 2000. С.165.

Если сделать виток из трубки, а внутри трубки расположить виток провода, то в проводе будет возникать индукционный ток. Магнитное поле внутри провода, имеющего вид трубки, отсутствует, но индукционный ток возникает, т.е. изменяющийся ток смещения проявляется как вихревое электрическое поле. Плотность обратного постоянного тока смещения внутри прямого провода бесконечной длины, имеющего вид трубки:

j_см = -I/2πr²,

где r – радиус провода, I – постоянный ток в проводе. Если нет изменения плотности тока смещения, то на движущийся заряд не будет действовать сила Лоренца. Изменение плотности тока смещения представляет магнитную индукцию. Также величина магнитной индукции зависит и от других факторов, в том числе и от кривизны, по которой течет ток смещения.

В пространстве вокруг магнита (в магнитном поле) непрерывно текут токи электрического смещения, которые можно обнаружить, например, как вихревые электрические поля при включении и выключении электромагнита.

Во многих случаях магнитное поле удобнее представлять линиями электрического тока смещения или как движущиеся электрические потоки, тем самым из-за наглядности уменьшается вероятность технических ошибок. Например, в учебной литературе направление линий магнитной индукции между обкладками конденсатора изображено неправильно – в обратную сторону, т.е. получается такой разворот рамок с током (стрелки указывают направление тока).

Курс физики. Т.И.Трофимова. 1998. С.250.

На самом деле у магнитного поля между обкладками конденсатора линии магнитной индукции направлены в обратную сторону. Например, вихревые токи будут иметь обратное направление, так как токи смещения между обкладками конденсатора “прямые”, а не “обратные”. Всем, кто пытался измерить магнитное поле, создаваемое токами смещения (не токами поляризации) в конденсаторе, удавалось обнаружить только магнитное поле, образованное токами проводимости в обкладках конденсатора. В этом случае разворот рамок с током будет выглядеть так.

Направление магнитной индукции между обкладками конденсатора можно просто определить согласно B = μ₀[vD], сформулировав правило возникновения магнитной индукции: если ладонь левой руки расположить так, чтобы четыре пальца указывали направление движения электрического потока, а вектор D входил в ладонь, тогда отставленный большой палец укажет направление вектора B. Т.е., чтобы определить направление линий магнитной индукции, достаточно рассмотреть движение электрических потоков, связанных с зарядами, которые движутся в обкладках конденсатора. Также понять, как развернется рамка с током между обкладками конденсатора, можно по правилу: если токи имеют одинаковое направление, то возникает сила притяжения. Еще направление магнитного поля вокруг обкладок конденсатора можно определить по правилу буравчика, если рассмотреть движение зарядов по обкладкам.

На рисуне наглядно показано, как реально направлено магнитное поле между обкладками и как неправильно рисуют в учебниках. Также это можно экспериментально проверить: берутся две катушки с проводом, одна кладется между обкладками конденсатора, другая рядом с проводом, идущим к конденсатору. Подается переменный ток на конденсатор. На двухлучевом осциллографе будет видно, что ток, возникающий в катушках, сдвинут по фазе на 180 градусов. Направление линий магнитной индукции между обкладками конденсатора имеет принципиальное значение для электродинамики, так как это экспериментально доказывает, что сами токи смещения (исключая токи поляризации) представляют магнитное поле.

«Возбуждение магнитного поля токами поляризации правомерно, так как токи поляризации по своей природе не отличаются от токов проводимости. Однако то, что и другая часть плотности тока смещения (ε₀dE/dt), не связанная с движением зарядов, а обусловленная только изменением электрического поля во времени, также возбуждает магнитное поле, является принципиально новым утверждением Максвелла. Даже в вакууме всякое изменение во времени электрического поля приводит к возникновению в окружающем пространстве магнитного поля.»
Курс физики. Т.И.Трофимова. 1998. С.250.

Ток смещения (не поляризации) представляет изменяющееся электрическое поле (dD/dt) и на него не распространяется правило буравчика, которое действует только для тока проводимости, где подразумевается движение зарядов, а не индукции D. Для тока смещения же, как изменяющегося электрического поля, магнитную индукцию надо определять согласно B = μ₀[vD] (правило левой руки для магнитной индукции). Когда между обкладках конденсатора изменяется электрическое поле, то это означает, что по обкладкам текут заряды и с ними движется индукция D, представляющая ток смещения (dD/dt). Поэтому, хотя изменяющееся (движущееся) электрическое поле в конденсаторе и представляет ток смещения, но магнитное поле одновременно также связано и с током проводимости, который течет по обкладкам конденсатора. Т.е. индукция D, создающая ток смещения j_см = dD/dt, принадлежит зарядам в конденсаторе и, соответственно, магнитное поле также связано с током в обкладках конденсатора. Только в электромагнитной волне, где нет тока проводимости и электрическая индукция D не принадлежит зарядам, магнитное поле и его энергия связаны только с током смещения. Сама же величине тока смещения – это условность (нет движения заряженных частиц) и она никогда не используется при вычислении магнитной индукции, так как ток смещения поля – это изменяющееся электрическое поле, а для полей в электродинамике: B = μ₀[vD]. Например, когда по антенне течет ток проводимости, то точно такой же величины, но в обратном направлении течет ток смещения (ток всегда замкнут).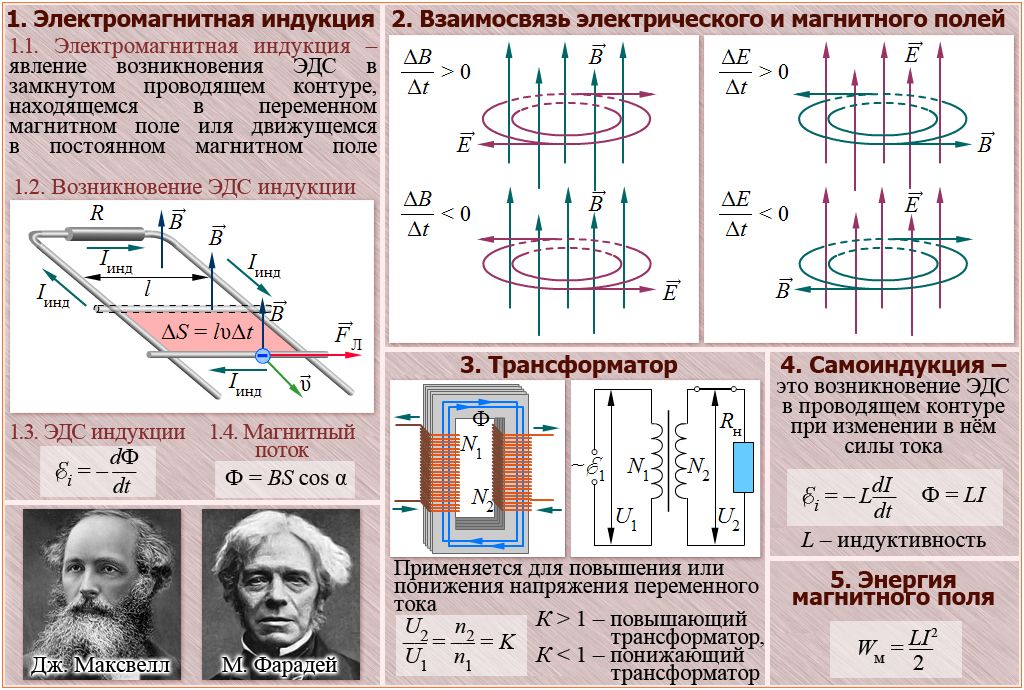 При этом магнитную индукцию можно вычислить либо по величине тока проводимости в антенне, либо по движению потоков электрической индукции B = μ₀[vD], связанных с перемещением зарядов в антенне, но не по величине обратного тока смещения поля. То же самое и между обкладками конденсатора – для определения магнитной индукции надо использовать B = μ₀[vD], применяя правило левой руки.

Для наглядности рассмотрим направление тока, возникающее в незамкнутых рамках, когда по обкладкам конденсатора течет ток.

Видно, что ток за обкладками и между ними имеет противоположное направление, соответственно, так же как и магнитное поле.

Демонстрация студентам магнитного поля между обкладками конденсатора.

Несмотря на то, что сегодня даже студенты могут в кабинете физики на демонстрационном приборе экспериментально проверить направление магнитного поля между обкладками конденсатора, в учебной литературе продолжают приводить рисунки, где магнитная индукция изображена неправильно – в обратную сторону. Т.е. ошибочно применяют для тока смещения поля правило буравчика, как бы забывая, что, согласно электродинамике, “ток смещения по своей сути – это изменяющееся со временем электрическое поле”, а не движение зарядов. Правило буравчика, как и правило левой руки – только для движущихся зарядов, так как ток смещения (не поляризации) не отклоняется в магнитном поле, как, например, катодные лучи, и на него не действует сила Лоренца (Ампера). Неужели авторы рисунков не знают, что между обкладками конденсатора нет реального тока, а есть только изменяющееся электрическое поле, которое условно называют током смещения электрического поля. Магнитное поле в этом случае определяется по движению электрического потока B = μ₀[vD].

Рассмотрим еще один пример. Возьмем два цилиндра, один из которых имеет электрический заряд, а другой представляет собой постоянный магнит из непроводящего материала. Если закрепить их на одной оси, проходящей через центр цилиндров, как изображено на рисунке, и начать вращать (синхронно и в одном направлении), то в зависимости от направления вращения цилиндры будут либо притягиваться, либо отталкиваться, так как заряженный цилиндр будет своим вращением создавать круговой электрический ток и, соответственно, магнитное поле.

Нарушение симметрии между правым и левым вращением в электромагнитном поле (полевом пространстве) позволяет построить электромагнитный датчик, измеряющий направление и скорость вращения. Вращательное движение магнита, в отличие от прямолинейного движения, не создает вихревого электрического поля, т.е. между вращающимися цилиндрами возникает только сила Лоренца, по которой можно определить направление и скорость вращения. При одновременном прямолинейном движении возникающая сила Лоренца между магнитом и зарядом уравновешивается вихревым электрическим полем, которое создает движущийся магнит, образуя в пространстве изменяющееся магнитное поле (изменяющийся магнитный поток). При вращательном же движении цилиндрического магнита с осью вращения, проходящей через полюса, вихревое электрическое поле не возникает, так как магнитное поле в пространстве не изменяется. На этом принципе могут действовать различные конструкции автономных электромагнитных датчиков вращения относительно полевого пространства, для которых не нужны внешние ориентиры, например, такие датчики могут быть использованы в космосе. Если вместо магнита установить компас, где стрелку сделать не острой, а круглой, чтобы исключить центробежную силу, возникающую при вращении, то, в зависимости от направления вращения, магнитная стрелка будет поворачиваться либо в одну, либо в другую сторону. На этом примере видно, что электромагнитный датчик вращения отличается от центробежного тем, что можно определить направление вращения. Это является нарушением симметрии между правым и левым вращением при электромагнитных взаимодействиях (на макроуровне).

«Поэтому есть основание считать, что либо пространство не обладает симметрией между правым и левым, либо эта симметрия нарушается в определенных типах взаимодействий …»
Четность. http://bse.sci-lib.com/article122181.html

Переменное магнитное поле всегда связано с переменным током смещения, который проявляется в виде вихревого электрического поля, поэтому:

«… переменные электрические и магнитные поля не могут существовать друг без друга …»
Энциклопедия элементарной физики. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ.
«Вихревая составляющая электрического поля возникает при изменении во времени магнитного поля: …»
Физическая энциклопедия. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ.

Вихревое электрическое поле – это вихревой поток электрического смещения поля, что представляет переменный ток смещения. Постоянное магнитное поле – это постоянный ток смещения, не представляющий вихревое электрическое поле, поэтому оно не действует на покоящиеся электрические заряды. Постоянный ток смещения, так же как и сверхпроводящий ток, не создает электрической напряженности поля.

Хотя приведенное описание процессов не является достаточно полным и безупречным, оно дает представление о механизме электромагнитной индукции. С другой стороны, более привычно представлять электродинамические взаимодействия через дополнительную характеристику – индукцию магнитного поля, отсюда название – электромагнитные взаимодействия, хотя реально в природе существует только электрическое поле, а магнитное поле образовано движущимися электрическими потоками и связанными с ними токами смещения поля.

«Таким образом, появление магнитного поля токов есть чисто релятивистский эффект и никакой новой физической субстанции (например, в виде магнитных зарядов) появляться не должно, что и подтверждается экспериментально.»
Основы физики. Л.А.Грибов, Н.И.Прокофьев. 1995. С.299.

Так как магнитное взаимодействие представляет электродинамический процесс, для магнитного поля больше подходит термин “электродинамический эффект”.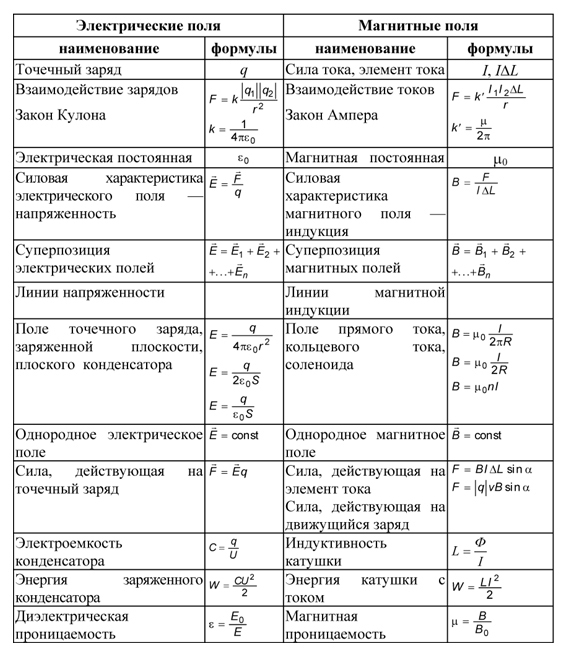 Но несмотря на это, чтобы не возникала путаница, в тексте сохранена привычная терминология, т.е. используется термин “релятивистский” эффект, а не “электродинамический”.

Надо заметить, иногда возникновение магнитного поля пытаются объяснить тем, что при движении зарядов напряженность электрического поля в направлении, перпендикулярном движению, возрастает по отношению к покоящимся зарядам.

«… при движении плоскости создаваемое ею электрическое поле в направлении, перпендикулярном движению, должно возрасти.»
Основы физики. Л.А.Грибов, Н.И.Прокофьев. 1995. С.301.

Приводя такие интерпретации, всегда как бы забывают рассмотреть симметричное движение разноименных зарядов. Например, две разноименно заряженные плоскости одновременно движутся в противоположных направлениях, при этом все равно возникает магнитное поле, т.е., если перпендикулярно плоскостям движется заряд, то на него будет действовать сила Лоренца. Таким образом, нельзя объяснить возникновение магнитного поля как возрастание электрической напряженности поля движущихся зарядов. Поэтому для магнитного поля правильнее вернуться к старой терминологии - “электродинамическое взаимодействие” или “электродинамический эффект”.

«Явление взаимодействия электрических токов Ампер называл электродинамическим взаимодействием.»
Физика. О.Ф.Кабардин. 1991. С.177.

Продолжение …

Левитация графитовой фольги и карандашного грифеля 0,5 мм над магнитами!

Случайно обнаружил, что обычная графитовая фольга, из которой делают прокладки для герметизации, прекрасно левитирует над магнитами (как сверхпроводник). Связался с производителями фольги, они вообще не знали ни про какую левитацию. Показал им видео, они были удивлены. Дали лист графитовой фольги для экспериментов по магнитной антигравитации.

Левитрон (летающий волчок). Китайская игрушка.

Волчок, который, вращаясь, висит в воздухе за счет магнитных сил.

Сила магнитного поля в токе: формула и применение

Магнитные поля и ток

Компас будет вести себя странно, возможно, как компас Колумба, если он находится в присутствии токоведущего провода. Электрический ток – это передача электрической энергии через проводник, обычно металлический. Если этот провод находится в магнитном поле, на провод действует сила. На диаграммах X используются для обозначения магнитного поля, указывающего на экран, а точки используются для обозначения магнитного поля, указывающего за пределы экрана.

Провод проводит ток (I) вправо. Слева: крестики обозначают магнитное поле, направленное на экран перпендикулярно проводу. Справа: точки представляют собой магнитное поле, направленное за пределы экрана перпендикулярно проводу.

Единственный способ воздействия на провод силы – это если провод НЕ параллелен магнитному полю. Сила, действующая на провод с током в магнитном поле, максимальна, когда провод расположен на перпендикулярно магнитному полю.Величину силы можно определить по уравнению:

Где:

n – количество жгутов в проводе.
I – ток через провод в амперах (А).
L – длина провода в магнитном поле в метрах (м)
B – сила (величина) магнитного поля в теслах (Тл).
θ – угол, который жгут образует с магнитным полем в градусах.

В пучке медных проводов n будет числом витков провода.

Мы будем иметь дело только с θ, углом провода, равным 0o или 90o. Синус 0o равен 0 (это означает, что ток параллелен магнитному полю), а синус 90o равен 1 (что означает, что ток перпендикулярен магнитному полю).

Поскольку сила – это вектор, мы должны включить направление силы. Правило говорит нам, в каком направлении действует сила.Возьмите правую руку и большим и указательным пальцами сделайте букву L в обратном направлении. Ваша ладонь должна быть обращена от вас. Теперь вытяните средний палец так, чтобы он был перпендикулярен указательному и большому пальцам.

Расположение правой руки для линейки правой руки

Ваш указательный палец указывает в направлении потока положительных носителей заряда (тока), средний палец указывает в направлении магнитного поля, а большой палец указывает в направлении силы.Если носители заряда отрицательны, сила будет действовать в направлении, противоположном направлению большого пальца.

Если ваш указательный палец указывает вправо, средний палец указывает на экран, а большой палец указывает вверх, это означает, что сила на проводе будет увеличиваться.

Сила на проводе вверх

Приложения

Это интересное явление, но чем оно может быть полезно? Что ж, ток, протекающий через магнитное поле под прямым углом, заставит его вращаться, что важно для двигателей.Электродвигатели вращают лопасти вентилятора, заставляют сверла вращать сверла и даже используются в автомобилях для поворота колес!

Еще одно применение явления силы, действующей на провод с током в магнитном поле, – это масс-спектрометр. Масс-спектрометр – это устройство, которое разделяет заряженные частицы (ионы) в материале в зависимости от их массы. Это помогает идентифицировать вещество, будь то вода, химический остаток взрывчатого вещества или любое другое вещество.

Краткое содержание урока

Электрический ток – это поток заряда через проводник, который может быть проводом. Если провод, по которому проходит ток, находится в магнитном поле, он может испытывать силу, если он находится под любым углом к магнитному полю, кроме параллельного ему. Магнитная сила максимальна при 90o. Следующее уравнение может определить величину силы, действующей на токоведущий провод в магнитном поле:

n – количество жгутов в проводе.
I – ток через провод в амперах (А).
L – длина провода в магнитном поле в метрах (м)
B – сила (величина) магнитного поля в теслах (Тл).
θ – угол, который жгут образует с магнитным полем в градусах.

Направление силы на провод или пучок проводов определяется правилом правой руки , где большой палец указывает направление силы, указательный палец указывает направление потока положительных носителей заряда (тока), а средний палец указывает в направлении магнитного поля.На диаграммах X используются для обозначения магнитного поля, указывающего на экран, а точки используются для отображения магнитного поля за пределами экрана.

Применения этого явления – электродвигатели и масс-спектрометры , которые разделяют вещества на ионы по массе. Это помогает идентифицировать вещество.

магнитных терминов, используемых в магнитных цепях. Определение и формулы

Магнит и магнетизм Важные термины, определения и формулы

Магнитное поле или магнитная индукция (B)

Магнит или электромагнит создает магнитное поле.Поле, в котором магнит притягивает или отталкивает магнитные материалы, такие как железо, сталь и т. Д., Может быть определено как сила, действующая на движущийся заряд,

F = q x v x B

Где

F = сила,
V = скорость частиц,
B = величина поля.

Полезно знать:

Это векторная величина, а единицей измерения магнитного поля в системе СИ является Тесла, где 1 Тесла = (Ньютон x секунда) / (кулон x метр) 10000 Гаусс.Формула для магнитного поля в СИ: B = µ _○ (H + M), а в CGS – B = H + 4π M.

Провод постоянного тока или постоянного магнита создает магнитостатическое (стационарное) поле, величина и направление которого остаются неизменными. При переменном токе или пульсирующем постоянном токе проводник создает переменное магнитное поле, которое непрерывно меняет свое направление и величину.

Также читают

Напряженность магнитного поля (H)

Величина намагничивающей силы (какая сила должна намагничивать магнитные материалы, такие как железо, сталь и т. Д.) Называется силой магнитного поля, которая обозначается (H).Он обратно пропорционален длине провода и прямо пропорционален току, проходящему по нему. В системе СИ единица измерения напряженности магнитного поля – Ампер / метр (А / м), это векторная величина, а формула СИ для силы магнитного поля составляет

H = NI / 1c

Где 1c = магнитный путь в метрах.

Магнитный поток (Φ)

Простыми словами, Магнитное поле x площадь, перпендикулярная магнитному полю (B), называется Магнитным потоком, который обозначается Φ или Φ _м или Φ _B.Или это количество магнитного поля или магнитных силовых линий, проходящих через поверхность, такую как проводящая область, пространство, воздух и т. Д. Единица измерения магнитного потока в системе СИ – Вб (Вебер). Формула для нахождения магнитного потока в системе СИ:

Φ = BAc

Где

Ac = площадь в м ²

И единица CGS и формула для магнитного потока – это Максвелл (М) и Φ = BAc Ac = площадь в см ² соответственно.

Намагничивание (M)

Состояние намагничиваемого материала или процесс намагничивания магнитных материалов.Это плотность дипольных моментов постоянного магнита или электромагнита в магнитных материалах. Или магнитный момент (м) на единицу объема (v) магнитным полем называется намагниченностью. Единица намагничивания в системе СИ – ампер / метр (А / м), также это векторная величина. Формула СИ для намагничивания:

M = м / В

Где,

м = Полный магнитный момент
А V = объем в м ³.

Единица CGS и формула намагничивания: Emu / cm ³ и M = m / V соответственно, где m = общий магнитный момент, V = объем в см ³ и EMU = электромагнитные единицы.Это также может быть определено как M = (N / V) x m → M = nm ……. (N / V) = п. Где «m» – это магнитный момент, а «n» – это плотность магнитных моментов.

Магнитная проницаемость вакуума (µ _○)

Забавно, Perm = Разрешение и способность – это особенность или умение что-то делать. Т.е. проницаемость (µ) – это способность материала, при помощи которого он легко намагничивается?

Магнитная проницаемость вакуума

Это величина сопротивления магнитному полю при формировании в вакууме.

Единица измерения проницаемости в системе СИ – (Г · м ⁻¹) или Ньютон на квадратный ампер (Н · А ⁻²). Единица СИ и формулы магнитной проницаемости вакуума: Ньютон / Ампер ² и µ _○ = 4πx10 ^-7 ≈ 1,2566370614 Гн · м ^-1 соответственно. Единица магнитной проницаемости вакуума СГС 1.

Полезно знать: Противоположностью магнитной проницаемости является магнитная относительность.

Полезно знать: известное магнитное соотношение: B = µH, где µ – проницаемость, которая является скалярной величиной, B – магнитное поле, а H – сила намагничивания или напряженность магнитного поля.

Индуктивность (л)

Индуктивность – это свойство проводника, катушки или провода, которое препятствует изменению тока, протекающего через них. Изменение тока, протекающего по проводнику, создает напряжение, называемое обратной ЭДС или электродвижущей силой.

Даже Изменение тока, протекающего через проводник или катушку, вызывает в нем напряжение, которое называется самоиндуцированной ЭДС, а в любых соседних катушках или проводниках это называется взаимной индуктивностью. В системе СИ единица индуктивности (л) – это Генри «Н», а формула –

L = µ _○ µ N ² Ac / 1c

Где

N = Обороты
Ac = Площадь в м ²
1c = магнитный путь в метрах

Единица CGS и формула индуктивности – Генри «H» (Джозеф Генри) и L = 0.4π мкН ² Ac / 1c x10 ^-8 соответственно

где;

L = индуктивность
N = Обороты
Ac = Площадь в см ²
1c = магнитный путь в см.

Полезно знать : 1 H = 1 Вт / А (Один Генри = 1 Вебер на Ампер)

Формула самоиндукции

L = µ _○ (N ² xA) / л

Где:

L = в Генри
μ _ο = проницаемость свободного пространства (4. π.10 ^-7)
N = Количество витков
A = Площадь внутреннего ядра (π.r ²) в м ²
l = длина катушки в метрах

Формула взаимной индуктивности

M = μ _ο μ _r N ₁ N ₂ A / l

Где:

µ _o = проницаемость свободного пространства (4.π.10 ^-7)
µ _r = относительная проницаемость сердечника из мягкого железа
N = количество витков катушки
A = в поперечном сечении, м ²
l = длина бухт в метрах

Похожие сообщения:

Напряжение или E.М.Ф. (В)

Разница электрических потенциалов между двумя точками называется напряжением. Или работа, совершаемая на единицу заряда в статическом электрическом поле по перемещению заряда между двумя точками, поэтому уравнение принимает вид

V = W / q или E / q.

Где;

В = Напряжение
E = энергия в джоулях
q = Заряд в кулонах

Или электрическая потенциальная энергия на единицу заряда называется напряжением.

По закону Ома, напряжение = V = I x R, где I = ток в амперах, а R = сопротивление в омах (Ом)

Единицей измерения напряжения в системе СИ является вольт (В) или джоуль на кулон.Где 1V = 1 Джоуль / 1 Кулон

Формула напряжения в системе СИ:

V = -N dΦ / dt

Где;

N = количество витков катушки
dΦ = скорость изменения потока
t = время

Полезно знать: Другие связанные слова, используемые для напряжений и ЭДС: Разница электрических потенциалов , Электрическое напряжение , Электрическое давление, разность потенциалов, Pd, ЭДС, электродвижущая сила , и это скалярная величина и это вид электрической энергии.

В следующей таблице показаны все вышеперечисленные основные термины, используемые в магнитных цепях с единицами измерения и формулами SI и CGS.

витков витков

Кол-во	Обозначение	Блок СИ	Уравнение SI	Единица CGS	Уравнение CGS	Коэффициент преобразования
Магнитное поле	B	Тесла (Т)	B = µ _○ (H + M)	Гаусс (G)	B = H + 4π M	1T = 10 ⁴ G
Напряженность магнитного поля	H	Ампер / метр (А / м)	H = NI / 1c 1c = магнитный путь в м	Эрстед Oe	H = 0.4πNI / 1c 1c = магнитный путь в см	1А / м = 4πx10 ^-3 э
Магнитный поток	Φ	Вебер (Wb)	Φ = BAc Ac = площадь в м ²	Максвелл М	Φ = BAc Ac = площадь в см ²	1Wb = 10 ⁸ M
Намагничивание	M	Ампер / метр (А / м)	M = м / В м = Полный магнитный момент, V = объем в м ³	Emu / cm ³ Где EMU = Электромагнитные блоки	M = м / В м = Полный магнитный момент, V = объем в см ³	1А / м = 10-³ emu / cm ³
Магнитная проницаемость вакуума	µ _○	Ньютон / Ампер ²	µ _○ = 4πx10 ^-7 ≈ 1. 2566370614 H · м ⁻¹	1	–	4πx10 ^-7
Индуктивность	л	Генри	L = µ _○ мкН ² Ac / 1c N = витков Ac = Площадь, м ² 1c = магнитный путь в м	Генри	L = 0,4π мкН ² Ac / 1c x10 ^-8 N = витков Ac = Площадь в см ² 1c = магнитный путь в см	1
Напряжение или ЭДС	В	Вольт	В = – NdΦ / dt N =	Вольт	В = -10 ^-8 xNxdΦ / dt N =	1

Ниже приводится таблица в формате изображения для справки.

Похожие сообщения:

Расчет плотности магнитного потока (формула)

Плотность магнитного потока также называется «полем B» или «магнитной индукцией». Поле B наших супермагнитов можно рассчитать на оси север-юг, используя приведенные здесь формулы. Кроме того, мы также предоставляем вам таблицы (Excel / OpenOffice), которые вы можете использовать для автоматического расчета плотности магнитного потока. Напротив, вычисление B-полей всего пространства намного сложнее и требует использования компьютерных программ.

Плотность магнитного потока магнита также называется «полем B» или «магнитной индукцией». Он измеряется в теслах (единица СИ) или гауссах (10 000 гаусс = 1 тесла).

Постоянный магнит создает поле B в своем сердечнике и во внешнем окружении. Направленную напряженность поля B можно отнести к каждой точке внутри и за пределами магнита. Если вы поместите маленькую стрелку компаса в поле B магнита, она сориентируется в направлении поля. Воздействующая сила пропорциональна напряженности поля B.

Не существует простых формул для расчета плотности магнитного потока различных магнитных форм. Для этого были разработаны компьютерные программы (см. 2}} \ bigg) \ right] \ end {align} \)

B _r : остаточное поле, не зависящее от геометрии магнита (см. Физические данные магнита)

z : расстояние от полюсной поверхности на оси симметрии

L : длина блок

W : Ширина блока

D : Толщина (или высота) блока

Единицу длины можно выбрать произвольно, если она одинакова для всех длин .2}} \ right) \ end {align} \)

B _r : поле остаточной силы, не зависящее от геометрии магнита (см. Физические данные магнита)

z : расстояние от лицевой стороны полюса по оси симметрии

D : толщина (или высота) цилиндра

R : Полудиаметр (радиус) цилиндра

Единицу длины можно выбрать произвольно, если она одинакова для всех длин.2}} \ right) \ right] \ end {align} \)

B _r : остаточное поле, не зависящее от геометрии магнита (см.

Физические данные магнита)

z : расстояние от лицевой стороны полюса на оси симметрии

D : толщина (или высота) кольца

R _a : Внешний радиус кольца

R _i : Внутренний радиус кольца

Единицы измерения длины могут быть выбраны произвольно, сколь угодно долго так как он одинаков для любой длины.3} \ end {align} \)

B _r : остаточное поле, не зависящее от геометрии магнита (см. Физические данные магнита)

z : расстояние от края сферы на оси симметрии

R : полудиаметр (радиус) сферы

Единицу длины можно выбрать произвольно, если она одинакова для всех длин.

Таблица с формулами для расчета плотности потока

Вышеупомянутые формулы для плотности потока также можно удобно рассчитать в виде таблицы.Введите данные магнита в желтые поля, и плотность потока будет рассчитана автоматически.

Доступны следующие версии:

Источник вышеуказанных формул: Статья на сайте researchgate.net

Расчет полей B всего пространства

Для расчета полей B, помимо осей симметрии или полей различной магнитной формы, существуют очень сложные и часто очень дорогие компьютерные программы , который может вычислять поля B и многое другое.

Бесплатным программным обеспечением, предназначенным только для вращательно-симметричных магнитов, является FEMM. (“Магнетизм методом конечных элементов”).

Как и другие инструменты, FEMM рассчитывает и отображает только половину магнита, поскольку поля B симметричны. Вы должны представить себе вторую половину, отраженную слева.

Поле

B полумагнита (дискового магнита), проиллюстрировано с помощью FEMM

Закон

Ампера – Физика колледжа: OpenStax

Сводка

Вычислить ток, создающий магнитное поле.
Используйте правило правой руки 2, чтобы определить направление тока или направление контуров магнитного поля.

Какой ток нужен для создания значительного магнитного поля, возможно, такого же сильного, как поле Земли? Геодезисты скажут вам, что воздушные линии электропередач создают магнитные поля, которые мешают показаниям их компаса. Действительно, когда Эрстед в 1820 году обнаружил, что ток в проводе воздействует на стрелку компаса, он не имел дела с очень большими токами.Как форма проводов, по которым проходит ток, влияет на форму создаваемого магнитного поля? Ранее мы отмечали, что токовая петля создает магнитное поле, подобное магнитному полю, но как насчет прямого провода или тороида (бублика)? Как направление создаваемого током поля связано с направлением тока? Ответы на эти вопросы исследуются в этом разделе вместе с кратким обсуждением закона, регулирующего поля, создаваемые токами.

Магнитные поля имеют направление и величину.Как отмечалось ранее, один из способов исследовать направление магнитного поля – это использовать компасы, как показано для длинного прямого токоведущего провода на рисунке 1. Датчики Холла могут определять величину поля. Поле вокруг длинной прямой проволоки находится в виде кольцевых петель. Правило правой руки 2 (RHR-2) возникло в результате этого исследования и справедливо для любого текущего сегмента – указывает большим пальцем в направлении тока, а пальцы сгибаются в направлении петель магнитного поля , созданных Это.

Рис. 1. (a) Компасы, помещенные рядом с длинным прямым токоведущим проводом, показывают, что силовые линии образуют круговые петли с центром на проводе. (b) Правило 2 для правой руки гласит, что если большой палец правой руки указывает в направлении тока, пальцы сгибаются в направлении поля. Это правило согласуется с полем, отображаемым для длинного прямого провода, и действительно для любого текущего сегмента.

Напряженность (величина) магнитного поля , создаваемая длинным прямым проводом с током , экспериментально определена равной

[латекс] \ boldsymbol {B =} [/ latex] [латекс] \ boldsymbol {\ frac {\ mu _0I} {2 \ pi r}} [/ latex] [латекс] \ textbf {(длинный прямой провод)} , [/ латекс]

где [латекс] \ boldsymbol {I} [/ latex] – это ток, [latex] \ boldsymbol {r} [/ latex] – кратчайшее расстояние до провода, а константа [латекс] \ boldsymbol {\ mu _0 = 4 \ pi \ times 10 ^ {- 7} \; \ textbf {T} \ cdot \ textbf {m / A}} [/ latex] – проницаемость свободного пространства . ([latex] \ boldsymbol {\ mu _0} [/ latex] – одна из основных констант в природе. Позже мы увидим, что [latex] \ boldsymbol {\ mu _0} [/ latex] связано со скоростью свет.) Так как провод очень длинный, величина поля зависит только от расстояния от провода [латекс] \ boldsymbol {r} [/ latex], а не от положения вдоль провода.

Пример 1: Расчет тока, создающего магнитное поле

Найдите ток в длинном прямом проводе, который создаст магнитное поле, вдвое превышающее земное, на расстоянии 5.{-7} \; \ textbf {T} \ cdot \ textbf {m / A}}} \\ [1em] & \ boldsymbol {25 \; \ textbf {A}} \ end {array} [/ latex]

Обсуждение

Таким образом, умеренно большой ток создает значительное магнитное поле на расстоянии 5,0 см от длинного прямого провода. Обратите внимание, что ответ состоит только из двух цифр, поскольку поле Земли в этом примере указано только из двух цифр.

Магнитное поле длинного прямого провода имеет большее значение, чем вы можете сначала подумать. Каждый сегмент тока создает магнитное поле, подобное тому, которое имеет длинный прямой провод, а полное поле тока любой формы является векторной суммой полей, создаваемых каждым сегментом. Формальное определение направления и величины поля, создаваемого каждым сегментом, называется законом Био-Савара . Интегральное исчисление необходимо для суммирования поля для тока произвольной формы. Это приводит к более полному закону, который называется законом Ампера , который связывает магнитное поле и ток в общем виде.Закон Ампера, в свою очередь, является частью уравнений Максвелла , которые дают полную теорию всех электромагнитных явлений. Рассмотрение того, как уравнения Максвелла кажутся разным наблюдателям, привело к современной теории относительности и к осознанию того, что электрические и магнитные поля являются разными проявлениями одного и того же. Большая часть этого выходит за рамки этого текста как на математическом уровне, требующем вычислений, так и на объеме места, которое может быть отведено под него. Но для заинтересованного студента, и особенно для тех, кто продолжает заниматься физикой, инженерией или подобными занятиями, дальнейшее углубление в эти вопросы откроет описания природы, как элегантные, так и глубокие.В этом тексте мы будем иметь в виду общие особенности, такие как RHR-2 и правила для линий магнитного поля, перечисленные в главе 22.3 Магнитные поля и линии магнитного поля, концентрируясь при этом на полях, создаваемых в определенных важных ситуациях.

Установление связей: относительность

Слушая все, что мы делаем об Эйнштейне, у нас иногда складывается впечатление, что он из ничего изобрел теорию относительности. Напротив, одной из мотиваций Эйнштейна было решить трудности, связанные с пониманием того, как разные наблюдатели видят магнитные и электрические поля.

Магнитное поле около токоведущей петли показано на рисунке 2. Как направление, так и величина магнитного поля, создаваемого токоведущей петлей, являются сложными. RHR-2 можно использовать для определения направления поля около петли, но для получения более подробной информации необходимы картографирование с помощью компасов и правила для силовых линий, приведенные в главе 22.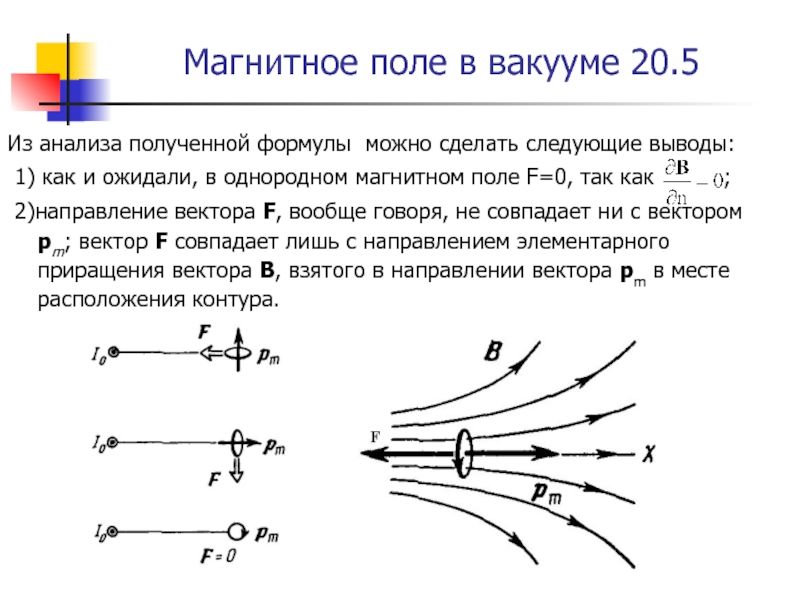 3 Магнитные поля и магнитные силовые линии. Существует простая формула для напряженности магнитного поля в центре круговой петли.Это

[латекс] \ boldsymbol {B =} [/ latex] [латекс] \ boldsymbol {\ frac {\ mu _0I} {2R}} [/ latex] [latex] \ textbf {(в центре петли)} [/ латекс]

где [латекс] \ boldsymbol {R} [/ latex] – радиус петли. Это уравнение очень похоже на уравнение для прямого провода, но действительно только в центре круговой петли провода. Сходство уравнений указывает на то, что аналогичная напряженность поля может быть получена в центре петли. Один из способов увеличить поле – использовать петли [latex] \ boldsymbol {N} [/ latex] ; тогда поле [латекс] \ boldsymbol {B = N \ mu _0I / (2R)} [/ latex].Обратите внимание, что чем больше петля, тем меньше поле в ее центре, потому что ток дальше.

Рис. 2. (a) RHR-2 показывает направление магнитного поля внутри и снаружи токоведущей петли. (б) Более подробное картографирование с помощью компасов или зонда Холла завершает картину.

Поле похоже на поле стержневого магнита.

Соленоид представляет собой длинную катушку провода (с большим количеством витков или петель, в отличие от плоской петли). Из-за своей формы поле внутри соленоида может быть как очень однородным, так и очень сильным.Поле сразу за катушками почти равно нулю. На рисунке 3 показано, как поле выглядит и как его направление задает RHR-2.

Рис. 3. (a) Из-за своей формы поле внутри соленоида длиной l удивительно однородно по величине и направлению, на что указывают прямые и равномерно разнесенные силовые линии. Поле вне катушек почти равно нулю. (b) Этот разрез показывает магнитное поле, создаваемое током в соленоиде.

Магнитное поле внутри соленоида с током очень однородно по направлению и величине.Только ближе к концам он начинает ослабевать и менять направление. Поле снаружи имеет те же сложности, что и плоские петли и стержневые магниты, но напряженность магнитного поля внутри соленоида просто равна

[латекс] \ boldsymbol {B = \ mu _0nI \; (\ textbf {внутри соленоида})}, [/ latex]

где [латекс] \ boldsymbol {n} [/ latex] – количество петель на единицу длины соленоида ([латекс] \ boldsymbol {n = N / l} [/ latex], с [latex] \ boldsymbol { N} [/ latex] – количество петель, а [latex] \ boldsymbol {l} [/ latex] – длина). Обратите внимание, что [latex] \ boldsymbol {B} [/ latex] – это напряженность поля в любом месте однородной области интерьера, а не только в центре. Как следует из примера 2, с соленоидами возможны большие однородные поля, распределенные по большому объему.

Пример 2: Расчет напряженности поля внутри соленоида

Что такое поле внутри соленоида длиной 2,00 м, имеющего 2000 петель и пропускающего ток 1600 А?

Стратегия

Чтобы найти напряженность поля внутри соленоида, мы используем [latex] \ boldsymbol {B = \ mu _0nI} [/ latex].{-1}) \; (1600 \; \ textbf {A})} \\ [1em] & \ boldsymbol {2.01 \; \ textbf {T}}. \ end {array} [/ latex]

Обсуждение

Это большая напряженность поля, которая может быть установлена над соленоидом большого диаметра, например, при использовании в медицине магнитно-резонансной томографии (МРТ). Однако очень большой ток указывает на то, что поля такой силы нелегко получить. Такой большой ток через 1000 петель, сжатых до метра, приведет к значительному нагреву. Более высокие токи могут быть достигнуты с помощью сверхпроводящих проводов, хотя это дорого. Существует верхний предел тока, поскольку сверхпроводящее состояние нарушается очень сильными магнитными полями.

Есть интересные варианты плоской катушки и соленоида. Например, тороидальная катушка, используемая для удержания реактивных частиц в токамаках, очень похожа на соленоид, изогнутый в круг. Поле внутри тороида очень сильное, но круглое. Заряженные частицы движутся по кругу, следуя силовым линиям, и сталкиваются друг с другом, возможно, вызывая синтез.Но заряженные частицы не пересекают силовые линии и не покидают тороид. Целый ряд форм катушек используется для создания всевозможных форм магнитного поля. Добавление ферромагнитных материалов создает большую напряженность поля и может существенно повлиять на форму поля. Ферромагнитные материалы имеют тенденцию улавливать магнитные поля (силовые линии изгибаются в ферромагнитный материал, оставляя более слабые поля за его пределами) и используются в качестве экранов для устройств, на которые неблагоприятно влияют магнитные поля, в том числе магнитное поле Земли.

Исследования PhET: Генератор

Генерируйте электричество с помощью стержневого магнита! Откройте для себя физику, лежащую в основе этого явления, исследуя магниты и узнайте, как их можно использовать, чтобы зажечь лампочку.

Рисунок 4. Генератор

Сила магнитного поля, создаваемого током в длинном прямом проводе, равна

[латекс] \ boldsymbol {B =} [/ latex] [латекс] \ boldsymbol {\ frac {\ mu _0I} {2 \ pi r}} [/ latex] [latex] \ textbf {(длинный прямой провод) }, [/ латекс]

Направление магнитного поля, создаваемого длинным прямым проводом, определяется правилом правой руки 2 (RHR-2): Направьте большой палец правой руки в направлении тока, а пальцы согнуты в направлении петли магнитного поля , созданные им.
Магнитное поле, создаваемое током, идущим по любому пути, является суммой (или интегралом) полей, создаваемых сегментами вдоль пути (величина и направление, как для прямого провода), что приводит к общей взаимосвязи между током и полем, известной как закон Ампера. .
Напряженность магнитного поля в центре круговой петли равна

[латекс] \ boldsymbol {B =} [/ latex] [латекс] \ boldsymbol {\ frac {\ mu _0I} {2R}} [/ latex] [латекс] \ textbf {(в центре петли)} [ / латекс]

где [latex] \ boldsymbol {R} [/ latex] – радиус петли.Это уравнение превращается в [латекс] \ boldsymbol {B = \ mu _0nI / (2R)} [/ latex] для плоской катушки с петлями [латекс] \ boldsymbol {N} [/ latex]. RHR-2 дает направление поля вокруг петли. Длинная катушка называется соленоидом.
Напряженность магнитного поля внутри соленоида

[латекс] \ boldsymbol {B = \ mu _0nI \; (\ textbf {внутри соленоида})}, [/ latex]

где [latex] \ boldsymbol {n} [/ latex] – количество петель на единицу длины соленоида. Поле внутри очень однородно по величине и направлению.

Концептуальные вопросы

1: Сделайте рисунок и используйте RHR-2, чтобы найти направление магнитного поля токовой петли в двигателе (например, в главе 22. 8, рис. 1). Затем покажите, что направление крутящего момента на петле такое же, как и при отталкивании одинаковых полюсов и притяжении разных полюсов.

Глоссарий

линейка правая 2 (RHR-2): правило для определения направления магнитного поля, создаваемого токоведущим проводом: направьте большой палец правой руки в направлении тока, а пальцы согнуты в направлении петель магнитного поля

Напряженность (величина) магнитного поля, создаваемого длинным прямым проводом с током: определяется как [латекс] \ boldsymbol {B = \ frac {\ mu _0I} {2 \ pi r}} [/ latex], где [latex] \ boldsymbol {I} [/ latex] – текущий, [латекс] \ boldsymbol {r} [/ latex] – кратчайшее расстояние до провода, а [latex] \ boldsymbol {\ mu _0} [/ latex] – проницаемость свободного пространства

проницаемость свободного пространства: – мера способности материала, в данном случае свободного пространства, поддерживать магнитное поле; константа [латекс] \ boldsymbol {\ mu _0 = 4 \ pi \ times 10 ^ {- 7} \; \ textbf {T} \ cdot \; \ textbf {m / A}} [/ latex]

Напряженность магнитного поля в центре круговой петли: определяется как [латекс] \ boldsymbol {B = \ frac {\ mu _0I} {2R}} [/ latex], где [латекс] \ boldsymbol {R} [/ latex] – радиус петли

соленоид: тонкая проволока, намотанная на катушку, которая создает магнитное поле, когда через нее пропускается электрический ток

Напряженность магнитного поля внутри соленоида: определяется как [латекс] \ boldsymbol {B = \ mu _0nI} [/ latex], где nn – количество петель на единицу длины соленоида ([латекс] \ boldsymbol {n = N / l} [/ latex], где [latex] \ boldsymbol {N} [/ latex] – количество петель, а [latex] \ boldsymbol {l} [/ latex] – длина)

Закон Био-Савара: физический закон, который описывает магнитное поле, создаваемое электрическим током, с помощью специального уравнения

Закон Ампера: физический закон, который гласит, что магнитное поле вокруг электрического тока пропорционально току; каждый сегмент тока создает магнитное поле, подобное тому, которое имеет длинный прямой провод, а полное поле тока любой формы представляет собой векторную сумму полей, создаваемых каждым сегментом

Уравнения Максвелла: набор из четырех уравнений, описывающих электромагнитные явления

Руководство по проектированию магнитных цепей

| Технические примечания | Магниты

Руководство по проектированию магнитной цепи

1.

Основные формулы расчета

1-1. Полный магнитный поток Φ и магнитная проницаемость P

Основная формула расчета для магнитных цепей аналогична закону Ома; а именно, когда полный магнитный поток обозначен через Φ, магнитодвижущая сила F и магнитное сопротивление R, соотношение между этими тремя элементами выражается следующей формулой:

Однако при расчете магнитной цепи вместо магнитного сопротивления R обычно используется проницаемость P, которая обратно пропорциональна магнитному сопротивлению R.Следовательно, приведенную выше формулу можно заменить следующей формулой:

Когда длина магнитного пути обозначена L, площадь поперечного сечения магнитного пути A и проницаемость магнитного пути μ, проницаемость P выражается следующей формулой:

Эта формула показывает, что чем короче длина магнитного пути L и чем больше площадь поперечного сечения A и магнитная проницаемость μ, тем больше проницаемость P (т. е. тем меньше магнитное сопротивление).

Кроме того, проницаемость Pt для всей магнитной цепи выражается суммой проницаемости зазора Pg, которая определяется как величина, обратная магнитному сопротивлению в зазоре, а проницаемость рассеяния Pf определяется как величина, обратная магнитному сопротивлению, вызванному магнитный поток рассеяния (Pt = Pg + Pf).

Чтобы определить поток рассеяния для каждого пространства магнитного пути, общая проницаемость Pt выражается как сумма проницаемости зазора Pg и проницаемости рассеяния каждого пространства магнитного пути (Pf ₁ + Pf ₂ + Pf ₃ +……. Pf _n).

1-2. Коэффициент потерь магнитодвижущей силы f

Коэффициент потери магнитодвижущей силы f определяется как отношение общей магнитодвижущей силы F магнитопровод к зазору магнитодвижущей силы Fg.

Полная магнитодвижущая сила F магнитной цепи определяется используемым магнитом, а ее значение является произведением напряженности магнитного поля в рабочая точка магнита Hd и длина магнита Lm.
Кроме того, магнитодвижущая сила зазора Fg является произведением плотности магнитного потока зазора Bg и длины зазора Lg; поэтому формулу (5) можно разложить до следующей формулы:

1-3. Коэффициент утечки σ

Коэффициент утечки выражается отношением полного магнитного потока Φt, генерируемого от магнита в магнитной цепи, к магнитному потоку зазора, сходящемуся в зазоре Φg.

Общий магнитный поток Φt, генерируемый магнитом, определяется как произведение плотности магнитного потока в рабочей точке Bd и поперечного сечения магнита. площадь сечения Am, а магнитный поток, сходящийся в зазоре Φg, задается как произведение плотности магнитного потока Bg зазора и площади поперечного сечения зазора Ag; поэтому формулу (7) можно разложить до следующей формулы:

Кроме того, из формулы (2): Φ = FP, формула (7) также может быть выражена следующей формулой:

Поскольку коэффициент потерь магнитодвижущей силы f обычно становится значением, близким к 1, формула (9) станет следующей формулой путем замены формулы (5) и формулы (4):

Эту формулу можно также выразить в следующей форме, разделив Pf на каждое пространство магнитного пути утечки:

1-4.

Коэффициент проницаемости Pc

Коэффициент проницаемости Pc используется для выражения рабочей точки магнита на кривой B-H. Это значение определяется как отношение плотности магнитного потока Bd и напряженности магнитного поля Hd на рабочая точка и выражается следующей формулой (см. рисунок выше):

1-4-а. Коэффициент магнитной проницаемости магнита, встроенного в магнитную цепь

Коэффициент магнитной проницаемости магнита, включенного в магнитную цепь, можно определить, получив Hd и Bd из формулы (6) и формулы (8) и подставив их в формулу (11).

И заменив это на

, может быть получена следующая формула:

1-4-б. Коэффициент магнитной проницаемости монотельного магнита

На коэффициент магнитной проницаемости одиночного магнита в значительной степени влияет форма магнита, и поэтому очень трудно получить точное значение путем расчета.
Следовательно, из приведенного ниже рисунка с использованием столбчатого магнита в качестве образца (график, показывающий соотношение между отношением размеров и коэффициентом проницаемости), получается приблизительная оценка.

Формула приближения будет следующей:

1-5. Методы расчета длины Lm, площади поперечного сечения Am и объема Vm

Длина Lm и площадь поперечного сечения Am, необходимые для магнита, составляют

Задавая Hd, Bd, Bg, Ag, Lg, f и σ в эту формулу, можно получить необходимые Lm и Am.
А необходимый Vm –

, что указывает на то, что необходимый объем магнита обратно пропорционален произведению энергии в рабочей точке.

1-6. Метод определения коэффициента утечки σ и коэффициента потерь магнитодвижущей силы f

1-6-а. Методики экспериментального получения σ и f

■ Метод с использованием поисковой катушки

1. Оберните поисковую катушку вокруг магнита и измерьте магнитный поток в зазоре.
2. Рассчитайте Bd из полного потока Φg / площади поперечного сечения Am магнита.
3. Получите Hd из кривой B-H (кривая размагничивания).
4. Измерьте Bg, Ag, Lg, Am и Lm.
5. Вычислите f и σ по формуле (6) и формуле (8).

■ Метод без поисковой катушки

1. Примите значение f (обычно от 1,0 до 1,2).
2. Измерьте Lm, Bg и Lg.
3. Вычислите Hd по формуле (12) на предыдущей странице.
4. Получите Bd из кривой B-H (кривая размагничивания).
5. Измерьте Am и Ag и рассчитайте σ по формуле (8).

1-6-б. Метод получения σ расчетным путем

Получите Pg и Pf ₁ через Pf _n по формуле (10),

и вычислим σ.

Ссылочный пример

Пример расчета магнитной проницаемости основных компонентов (Pg, P ₁, P ₂ P ₃ и P ₄) пространства магнитного пути утечки показан ниже.

1) Проницаемость области зазора на рисунке

2) Проницаемость полуцилиндрического магнитного тракта утечки

3) Проницаемость полуцилиндрического (полого) магнитного тракта утечки

4) Проницаемость четверти сферического магнитного тракта утечки

5) Магнитная проницаемость полого четверти сферического магнитного тракта утечки

Комбинируя проницаемость с 1) по 5) выше, можно получить приблизительную оценку σ в пространстве магнитного пути утечки (μ ₀: проницаемость вакуума).

2. Формула для расчета плотности магнитного потока B (X) на центральной линии магнита

Когда кривая BH прямая или рабочая точка Bd расположена выше точки перегиба, распределение магнитного поля вне магнита можно рассматривать так же, как магнитное поле, создаваемое током замкнутой цепи на внешней периферии. поверхность пространства длиной X, имеющего такую же проницаемость и форму поперечного сечения, как у магнита.
Формулы расчета для получения этого B (X) для трех типичных форм будут показаны ниже. Эти формулы эффективны в качестве приближенных формул для ферритовых магнитов или неодимовых магнитов.

2-1. Магнит цилиндрической формы

2-2. Магнит квадратно-столбчатый

2-3. Трубчатый магнит

2-4. Когда магнитное тело помещается за магнитным полюсом

Заменить 2L членом L формул 2-1, 2-2 и 2-3.

2-5. Когда магниты одинаковой формы противостоят друг другу на расстоянии 2X

B (X) в центре зазора станет вдвое больше, чем B (X), полученное с использованием формул 2-1, 2-2 и 2-3.
B (X) в точке P внутри промежутка будет суммой B (XP), в которой XP подставляется в член X предыдущей формулы, и B (X + P), в котором X + P вставляется в член X предыдущей формулы.

2-6. Когда магнитное тело расположено за магнитным полюсом в той же конфигурации, что и в предыдущем разделе

Заменить 2L членом L формул 2-1, 2-2 и 2-3.B (X) в центре зазора и точку P внутри зазора можно получить с помощью тех же процедур, что и 2-5.

3. Расчет эффективного магнитного потока магнитопровода для двигателей

В магнитных цепях для двигателей условия магнитной цепи сильно различаются в зависимости от элементов, включая количество пазов ротора, форму пазов и т. Д. и толщину стенки корпуса. Поэтому в этом разделе будут показаны только формулы, отражающие основные понятия.

1) Площадь поперечного сечения магнита Am

2) Соотношение эквивалентных размеров магнита ℓ / d

3) Коэффициент проницаемости одиночного магнита Pi

4) Коэффициент магнитной проницаемости одинарного магнита, включая ярмо PL

5) Коэффициент Куртера K _c

6) Эффективный коэффициент проницаемости P _u

7) Магнитный поток утечки σ

8) Магнитный поток полюсов (или Эффективный магнитный поток) Φg

О насыщении магнитной цепи
Приведенный выше метод расчета Φg не учитывает во внимание насыщение магнитной цепи.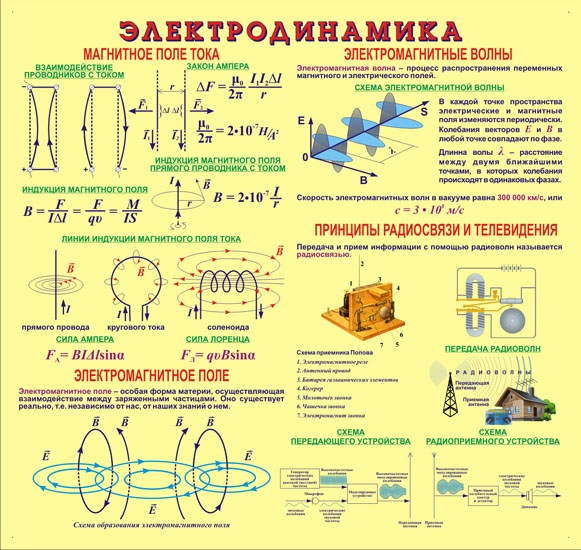 Однако в реальных магнитных цепях насыщение может происходить в области корпуса или ротора. Другими словами, когда сравниваются Φg, полученные вышеуказанным способом вычисления, и Φg в фактическом двигателе, а g в фактическом двигателе меньше расчетного значения, возможно, что магнитная цепь насыщена.

Таблица преобразования единиц SI / CGS

Умножив характеристическое значение в единицах СИ на коэффициент преобразования в левой части ▶, можно получить значение в единицах СГС.
Точно так же, умножив характеристическое значение в единицах CGS на коэффициент преобразования в правой части, можно получить значение в единицах SI.

Единица СИ ▶					◀ Единица СКУ
Магнитный терм	Условное обозначение	Название агрегата	Обозначение единицы	Передаточное число ▶	◀ Передаточное число	Обозначение единицы	Название агрегата
Магнитный поток	Φ	Вебер	Вт	10 ⁸ ▶	◀ 10 ^-8	Mx	Максвелл
Плотность магнитного потока	B	тесла	т	10 ⁴ ▶	◀ 10 ^-4	G	Гаусс
Магнитное поле	H	Ампер / м	А / м	4π × 10 ^-3 ▶	◀ 10 ³ / 4π	Oe	Эрстед
Намагничивание	M	Ампер / м	А / м	10 ^-3 ▶	◀ 10 ³	G	Гаусс
Магнитная поляризация	Дж	тесла	т	10 ⁴ / 4π ▶	◀ 4π × 10 ^-4	G	Гаусс
Магнитодвижущая сила	Fm	Ампер	A	4π × 10 ^-1 ▶	◀ 10 / 4π	Ги	Гилберт
Сила магнитного притяжения	F	Ньютон	N	10 ⁵ ▶	◀ 10 ^-5	дин	Dyne
Проницаемость	мкм	Генри / м	Г / м	10 ⁷ / 4π ▶	◀ 4π × 10 ^-7	Безразмерный
Проницаемость вакуума	мкм ₀	4π × 10 ^-7 Генри / м	Г / м			Безразмерный	1
Магнитное сопротивление	Rm	1 / Генри	H ^-1	4π × 10 ^-9 ▶	◀ 10 ⁹ / 4π	Ги / Мкс	Гилберт / Максвелл
Проницаемость	-P	Генри	H	10 ⁹ / 4π ▶	◀ 4π × 10 ^-9	Mx / Gi	Максвелл / Гилберт
Продукт магнитной энергии	BH	Джоуль / м ³	Дж / м ³	4π × 10 ▶	◀ 10 ^-1 / 4π	G · Oe	Гаусс · Эрстед
Продукт магнитной энергии	BH	Джоуль / м ³	Дж / м ³	10 ▶	10 ^-1	эрг / см ³	эрг / см ³

Магнитное действие электрического тока – заметки, книги, формулы, уравнения

Магнетизм был известен со времен древних греков, но он всегда был немного загадочным. Вы можете увидеть электричество в вспышке молнии, но когда стрелка компаса указывает на магнитный север, вы не можете увидеть никакой силы, заставляющей его вращаться. Вы, должно быть, изучили электростатические силы и поля, которые вызываются электрическими зарядами в состоянии покоя, и эти электрические поля могут перемещать другие свободные заряды, например, создавая ток в цепи. В этой главе мы увидим, что когда электрический заряд движется, он генерирует другие силы и поля. Эти дополнительные силы и поля называются магнетизмом.

Магниты обычно встречаются в повседневных предметах, таких как игрушки, вешалки, лифты, дверные звонки и компьютерные устройства. Эксперименты с этими магнитами показали, что все магниты имеют два полюса: один обозначен как Север (N), а другой – как Южный (S). Магнитные полюса отталкиваются, если они похожи (оба N или оба S), и притягиваются, если они противоположны (один N и другой S), а оба полюса магнита притягивают немагнитные куски железа. Здесь важно отметить, что нельзя изолировать отдельный магнитный полюс.Каждый кусок магнита, независимо от его размера, который содержит северный полюс, должен также содержать южный полюс.

В эксперименте датский физик Ганс Кристиан Эрстед заметил, что ток в прямом проводе вызывает отклонение находящейся поблизости стрелки магнитного компаса. При дальнейших экспериментах было замечено, что игла расположена по касательной к воображаемой окружности, в центре которой находится прямая проволока, а плоскость перпендикулярна проволоке.Было замечено, что когда в проводе течет ток, игла отклоняется, а при изменении направления тока на обратное направление иглы также меняется. Увеличение прогиба наблюдается при увеличении силы тока или приближении иглы к проволоке. Если мы посыпаем проволоку железными опилками, они образуют концентрические круги с проволокой. Эрстед пришел к выводу, что движущиеся заряды или токи создают магнитное поле в окружающем пространстве.

Подготовка к работе в сети для JEE Main / NEET

Crack JEE 2021 с программой онлайн-подготовки JEE / NEET

Начинай сейчас

Примечания к магнитным эффектам тока и магнетизма

Теперь мы обсудим каждую из важных тем вместе с обзором главы, за которым следуют важные формулы главы, которые помогут вам в численном решении связанных с магнитными эффектами тока и магнетизма.

Темы магнитных эффектов тока и магнетизма

Закон Био-Савара и его применение
Закон Ампера и его приложения
Магнитная сила, действующая на движущийся заряд в однородных магнитных полях и электрических полях
Циклотрон
Сила, действующая на проводник с током в однородном магнитном поле
Сила между двумя параллельными проводниками с током
Крутящий момент, испытываемый токоведущей петлей в однородном магнитном поле
Гальванометр с подвижной катушкой
Токовая петля, действующая как магнитный диполь, и ее магнитный дипольный момент
Пара-, диа- и ферромагнитные вещества
Магнитная восприимчивость и проницаемость
Электромагниты и постоянные магниты

Обзор магнитных эффектов тока и магнетизма

В этой главе вы изучите, как магнитное поле оказывает силы на движущиеся заряженные частицы, такие как электроны, протоны и токоведущие провода. Вы также узнаете, как токи создают магнитные поля и как частицы могут быть ускорены до очень высоких энергий в циклотроне. Вы изучите, как гальванометр определяет токи и напряжения. Вы также узнаете о соглашении, согласно которому ток или поле (электрическое или магнитное), выходящие из плоскости бумаги, изображаются точкой (?), А ток или поле, идущие в плоскость бумаги, изображаются изображается крестом (⊗). Вы также узнаете, что направление тока определяется с помощью правила для большого пальца правой руки.

Вы изучите представление магнитных полей в виде силовых линий, что очень полезно для визуализации силы и направления магнитного поля. И каждая из этих строк образует замкнутый цикл. Силовые линии выходят из северного полюса (N), огибают южный полюс (S) и проходят через стержневой магнит обратно к северному полюсу.

Мы обсудим, как магнитные поля создаются произвольным распределением электрического тока, используя закон Био-Савара. Затем мы посмотрим, как токоведущие провода создают магнитные поля, и выведем силы, которые возникают между двумя токоведущими проводами из-за этих магнитных полей. Мы также изучаем крутящие моменты, создаваемые магнитными полями токовых петель, а затем обобщаем эти результаты до важного закона электромагнетизма, называемого законом Ампера. Мы рассмотрим некоторые устройства, которые создают магнитные поля из токов в геометрии, основанной на петлях, известных как соленоиды и тороиды. Наконец, мы рассмотрим, как материалы ведут себя в магнитных полях, и классифицируем материалы на основе их реакции на магнитные поля.

Формулы для магнитных эффектов тока и магнетизма

1. Магнитное поле от элемента тока:

2. Магнитное поле в векторной форме =:

3. Закон Ампера = =

4. Магнитное поле внутри твердого цилиндра =

5. Магнитное поле из-за круглой катушки в центре:

6. Магнитное поле внутри толстой части полого цилиндра:

7. Магнитное поле на оси от круглого токоведущего провода:

8.Магнитное поле в бесконечном листе, несущем ток:, где плотность тока

9. Магнитное поле в соленоиде конечной длины:

10. Магнитное поле в тороиде:

11. Сила, действующая на заряженную частицу в магнитном поле:

12. Радиус заряженной частицы:

13. Период времени заряженной частицы:

14. Частота заряженной частицы:

15. Сила Лоренца:

Как подготовиться к магнитным воздействиям тока и магнетизма

Во-первых, вы должны хорошо владеть концепциями магнитных эффектов тока и магнетизма, а также знать, как правильно применять их во время вступительного экзамена или при решении вопросов.
Пожалуйста, попытайтесь понять каждую концепцию из этой главы с помощью теории, вопросов с решениями и видеолекций по каждой важной концепции. Для каждой концепции практики достаточно задач, чтобы иметь полное представление о концепции.
Решите все вопросы дома с должной концентрацией и постарайтесь провести все расчеты самостоятельно, не видя заранее решения. Очень ясно поймите происхождение каждой формулы, потому что, если вы не помните формулы, вы можете легко вывести их, но постарайтесь запомнить все формулы из этой главы, потому что на определенные вопросы вы получите ответ, непосредственно применяя эти формулы.
Ознакомьтесь со всеми законами из этой главы и их применением. При правильном изучении вы легко сможете решать вопросы из этой главы.

Наконечники для магнитных эффектов тока и магнетизма

Составьте план подготовки к этой главе и придерживайтесь расписания.
Сначала изучите концепцию, а затем приступайте к решению вопроса. Не задавайте вопросы напрямую, не зная концепции.
Ответьте на вопрос прошлого года из этой главы.
Задавайте как можно больше вопросов.

Поскольку, как сказал Аристотель,

Мы то, что делаем постоянно. Таким образом, совершенство – это не действие, а привычка.

Книги по магнитным эффектам тока и магнетизму

Для магнитных эффектов тока и магнетизма достаточно концепций глав в NCERT, но вам придется практиковать множество вопросов, включая вопросы предыдущего года, и вы можете следовать другим стандартным книгам, доступным для подготовки к конкурсным экзаменам, таким как Concepts of Physics (H.К. Верма) и «Понимание физики» Д. К. Панди (Arihant Publications).

Примечания по физике для инженерных и медицинских экзаменов

Уравнения Максвелла

Уравнения Максвелла
следующий: Электромагнитные волны Up: электромагнитных волн Предыдущий: Электромагнитные волны Во второй половине XIX века шотландский физик Джеймс Клерк Максвелл продемонстрировал, что все ранее установленные экспериментальные факты относительно электрических и магнитных поля можно суммировать всего в четыре уравнения.Настоящее время, эти уравнения обычно известны как уравнения Максвелла .

Первое уравнение – это просто уравнение Гаусса. закон (см. раздел 4). Этот Уравнение описывает, как электрические заряды генерируют электрические поля. Закон Гаусса гласит, что:

Электрический поток через любую замкнутую поверхность равен полному заряд, заключенный на поверхности, деленный на.

Математически это можно записать как

(305)

где – замкнутая поверхность, охватывающая заряд.Вышесказанное выражение также может быть написано

(306)

где – объем, ограниченный поверхностью, а это плотность заряда : т.е. , электрический заряд на единицу объема.

Второе уравнение – магнитный эквивалент закона Гаусса. (см. раздел 8.10). Это уравнение описывает, как отсутствие магнитные монополи заставляют силовые линии магнитного поля образовывать замкнутые контуры. Закон Гаусса для магнитных полей гласит, что:

Магнитный поток через любую замкнутую поверхность равен нулю.

Математически это можно записать как

(307)

где – замкнутая поверхность.

Третье уравнение – это закон Фарадея (см. Раздел 9.3). Это уравнение описывает как изменяющиеся магнитные поля создают электрические поля. Закон Фарадея говорится, что:

Линейный интеграл электрического поля вокруг любого замкнутого контура равна минус скорости изменения магнитного потока во времени через петлю.

Математически это можно записать как

(308)

где – поверхность, прикрепленная к петле.

Четвертое и последнее уравнение – это круговой закон Ампера (см.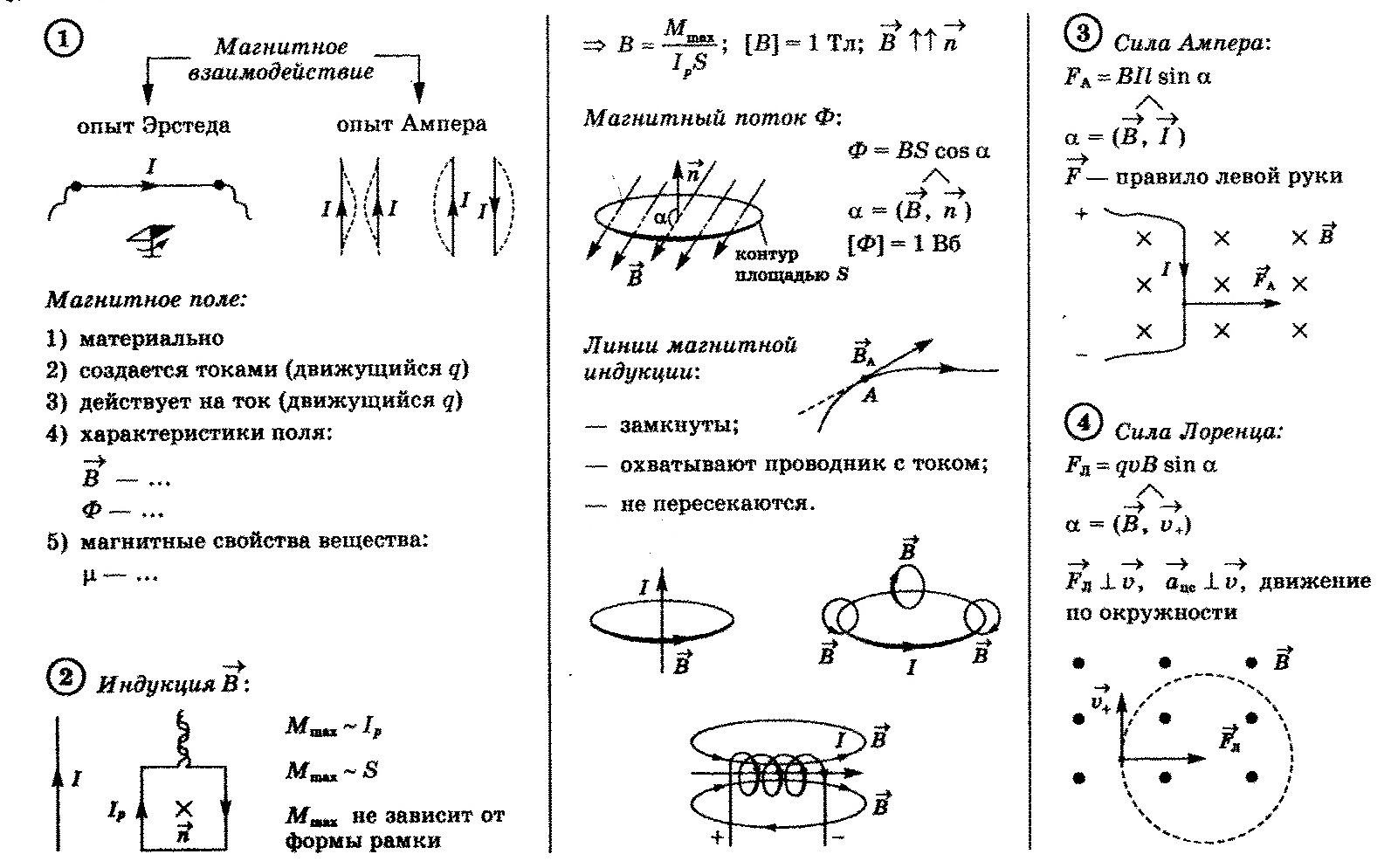 Раздел 8.7). Это уравнение описывает, как электрические токи создают магнитные поля. Закон Ампера гласит, что:

Линейный интеграл магнитного поля вокруг любого замкнутого контура равен равный умножению на алгебраическую сумму токов, которые проходят через петлю .

Математически это можно записать как

(309)

где – чистый ток, протекающий через контур. Это уравнение также может быть написано

(310)

где – поверхность, прикрепленная к петле, а – плотность тока : т.е. , электрический ток на единицу площади.

Когда Максвелл впервые написал Ур. (306), (307), (308), и (310) он был в основном пытаюсь резюмировать все что было известно в то время об электрических и магнитных полях в математической форме. Однако чем больше Максвелл смотрел на свою уравнения, тем больше он убеждался, что они неполны. В конце концов, он предложил добавить новый термин, названный смещением . current , в правую часть его четвертого уравнения. На самом деле Максвелл умел чтобы показать, что (306), (307), (308), и (310) являются математически несовместимыми , если только член тока смещения добавлен к формуле.(310). К несчастью, Максвелла демонстрация этого факта требует некоторых продвинутых математических методы, которые выходят далеко за рамки этого курса. В следующих, мы дадим очень упрощенную версию его вывода пропущенный срок.

**Рисунок 52:** *Цепь, содержащая зарядный конденсатор.*

Рассмотрим схему состоящий из параллельного пластинчатого конденсатора емкости, включенного последовательно с сопротивление и устойчивая ЭДС, как показано на рис. 52. Позвольте быть площадью обкладки конденсатора, и пусть будет их разделение. Предположим, что переключатель закрыт при. Ток, протекающий по цепи начинается с начального значения и постепенно спадает до нуля от времени RC цепи (см. раздел 10.5). Одновременно заряд на положительные обкладки конденсатора начинается с нуля, а постепенно увеличивается до конечного значения. Поскольку заряд меняется, меняется и потенциал разница между обкладками конденсатора, т.к.

Электрическое поле в области между пластинами примерно однородное, направленный перпендикулярно пластинам (идущий от положительно заряженной пластины к отрицательно заряженной пластине) и имеет величину.Следует тот

(311)

Через промежуток времени заряд на положительном пластина конденсатора увеличивается на величину , где соответствующее увеличение напряженности электрического поля между пластинами.

Обратите внимание, что оба и являются не зависящими от времени величинами. Следует тот

(312)

Теперь численно равно мгновенный ток, протекающий по цепи (так как все заряд, протекающий по цепи, должен накапливаться на пластинах конденсатор).Также, для конденсатора с параллельными пластинами. Следовательно, мы можем написать

(313)

Поскольку электрическое поле перпендикулярно области, мы также можем написать

(314)

Уравнение (314) связывает мгновенный ток, протекающий вокруг цепи к скорости изменения электрического поля между обкладки конденсатора. Согласно формуле.(310) ток, протекающий вокруг цепь генерирует магнитное поле. Это поле вращается вокруг токоведущие провода соединение различных компонентов схемы. Однако, поскольку нет фактического тока, протекающего между пластины конденсатора, магнитное поле в этой области не создается, согласно формуле. (310). Максвелл продемонстрировал, что по причинам математической непротиворечивости на самом деле должно быть магнитное поле, генерируемое в область между пластинами конденсатора.Кроме того, это магнитное поле должно быть таким же, как и то, которое будет сгенерирован, если ток ( т.е. , тот же ток, что и обтекает остальную часть цепи) протекла между пластинами. Конечно, нет никакого фактического тока, протекающего между тарелки. Однако есть изменяющееся электрическое поле. Максвелл утверждал, что изменяющееся электрическое поле составляет эффективный ток (, т.е. , он генерирует магнитное поле точно так же, как и настоящий ток).По историческим причинам (которые нас пока не особо интересуют) Максвелл назвал этот тип тока током смещения . 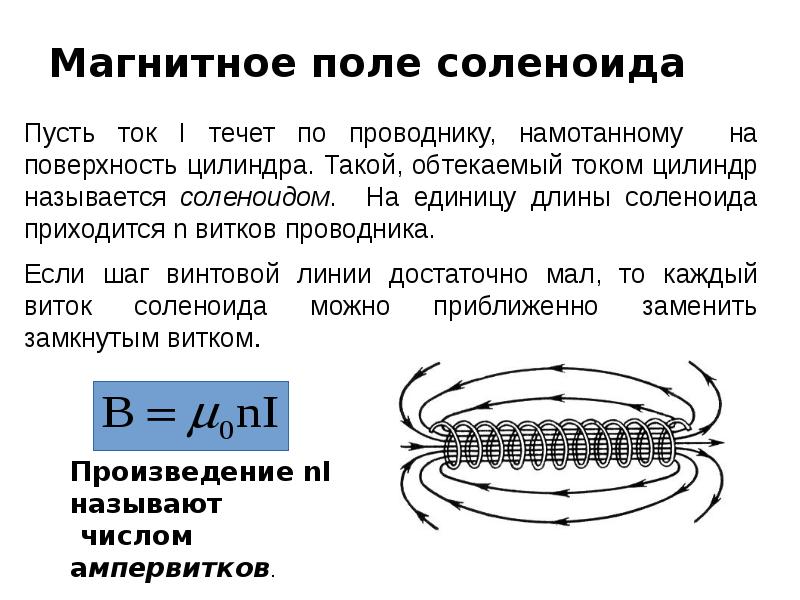Поскольку смещение ток, протекающий между пластинами конденсатора, должен быть равен ток, протекающий по остальной части цепи, следует из уравнения. (314) тот

(315)

Уравнение (315) было получено для частного случая изменения электрического поле генерируется в регионе между пластинами заряжающего конденсатора с параллельными пластинами.Тем не менее это уравнение оказывается вполне общим. Обратите внимание, что равен электрическому потоку между пластинами конденсатор. Таким образом, наиболее общее выражение для тока смещения проход через какой-то замкнутый цикл

(316)

где – электрический поток через петлю.

Согласно аргументу Максвелла, ток смещения столь же эффективен при генерации магнитное поле как реальный ток. Таким образом, нам нужно изменить по закону контура, учитывающему токи смещения. Измененный закон, известный как закон Ампера-Максвелла , написан

Линейный интеграл электрического поля вокруг любого замкнутого контура равен равный умноженной на алгебраическую сумму фактических токов и которые проходят через контур плюс умноженный на ток смещения проходя через петля.

Математически это можно записать как

(317)

где – петля, через которую проходит электрический ток и смещение текущий проход.Это уравнение также можно записать

(318)

где – поверхность, прикрепленная к петле.

Электромагнитное поле | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Электромагнетизм

Решебник

Конспект “электромагнитное поле”

Все физические формулы по теме электромагнитное поле

Электромагнитное поле конспект лекция

Электромагнитное поле краткий конспект

Формулы для решения задач по физике

Магнитное поле в веществе. Часть 1

Как связана индукция и напряженность магнитного поля?

Намагничивание ферромагнетиков

Гистерезис ферромагнетиков

Электродинамическое взаимодействие, образованное токами электрического смещения поля

Сила магнитного поля в токе: формула и применение

Магнитные поля и ток

Приложения

Краткое содержание урока

магнитных терминов, используемых в магнитных цепях. Определение и формулы

Магнит и магнетизм Важные термины, определения и формулы

Расчет плотности магнитного потока (формула)

Таблица с формулами для расчета плотности потока

Расчет полей B всего пространства

Ампера – Физика колледжа: OpenStax

Сводка

Пример 1: Расчет тока, создающего магнитное поле

Установление связей: относительность

Пример 2: Расчет напряженности поля внутри соленоида

Исследования PhET: Генератор

Концептуальные вопросы

Глоссарий

| Технические примечания | Магниты

Руководство по проектированию магнитной цепи

1.

1-1. Полный магнитный поток Φ и магнитная проницаемость P

1-2. Коэффициент потерь магнитодвижущей силы f

1-3. Коэффициент утечки σ

1-4.

1-4-а. Коэффициент магнитной проницаемости магнита, встроенного в магнитную цепь

1-4-б. Коэффициент магнитной проницаемости монотельного магнита

1-5. Методы расчета длины Lm, площади поперечного сечения Am и объема Vm

1-6. Метод определения коэффициента утечки σ и коэффициента потерь магнитодвижущей силы f

1-6-а. Методики экспериментального получения σ и f

1-6-б. Метод получения σ расчетным путем

2. Формула для расчета плотности магнитного потока B (X) на центральной линии магнита

2-1. Магнит цилиндрической формы

2-2. Магнит квадратно-столбчатый

2-3. Трубчатый магнит

2-4. Когда магнитное тело помещается за магнитным полюсом

2-5. Когда магниты одинаковой формы противостоят друг другу на расстоянии 2X

2-6. Когда магнитное тело расположено за магнитным полюсом в той же конфигурации, что и в предыдущем разделе

3. Расчет эффективного магнитного потока магнитопровода для двигателей

Таблица преобразования единиц SI / CGS

Магнитное действие электрического тока – заметки, книги, формулы, уравнения

Уравнения Максвелла

Оставить комментарий Отменить ответ