Магнитное поле | Формулы по физике
Магнитная сила между параллельными проводниками
Найти
Известно, что:
Fμμ0I1I2lπr =
Вычислить ‘F’Магнитная сила между параллельными проводниками
Найти
Известно, что:
FμI1I2lr =
Вычислить ‘F’Магнитная постоянная
Найти
Известно, что:
μ0π =
Вычислить ‘μ0’Напряжённость магнитного поля
Известно, что:
HIl =
Вычислить ‘H’Индукция магнитного поля
Найти
Известно, что:
Bμ0μH =
Вычислить ‘B’Максимальный момент магнитного поля
Найти
Известно, что:
M_максBIS =
Магнитная индукция
Найти
Известно, что:
MISBa =
Вычислить ‘M’Момент однородного магнитного поля
Найти
Известно, что:
p_mIS =
Вычислить ‘p_m’Магнитное поле прямолинейного проводника конечной длины с током
Известно, что:
Bμμ0Ia1a2πr =
Вычислить ‘B’Индукция магнитного поля, созданного бесконечно длинным прямым проводником с током
Найти
Известно, что:
Bμμ0Iπr =
Вычислить ‘B’Магнитная индукция поля в центре кругового тока (витка)
Найти
Известно, что:
Bμμ0IR =
Вычислить ‘B’Напряжённость магнитного поля: бесконечной прямой провод
Найти
Известно, что:
HIπr =
Вычислить ‘H’Напряжённость магнитного поля в центре витка
Найти
Известно, что:
Магнитная индукция соленоида
Найти
Известно, что:
Bμμ0NIl =
Вычислить ‘B’Напряжённость магнитного поля соленоида
Найти
Известно, что:
HNIl =
Вычислить ‘H’Магнитный поток и угол
Известно, что:
ΦBSa =
Вычислить ‘Φ’Магнитный поток
Найти
Известно, что:
ΦBS =
Вычислить ‘Φ’Сила Ампера
Найти
Известно, что:
FIlBa =
Вычислить ‘F’Найти
Известно, что:
BF_максIl =
Вычислить ‘B’Сила Лоренца
Найти
Известно, что:
FqvBa =
Вычислить ‘F’Сила Лоренца и сила Ампера
Найти
F_LF_AN =
Вычислить ‘F_L’Сила электромагнитного поля
Найти
Известно, что:
FqEvBa =
Вычислить ‘F’Радиуса движения заряженной частицы в магнитном поле
Найти
Известно, что:
rmvqB =
Период вращения заряженной частицы в магнитном поле
Найти
Известно, что:
TπmqB =
Вычислить ‘T’Магнитное поле в физике – формулы и определения с примерами решения задач
Содержание:
- Магнитное поле
- Магнитный момент
- Сила Ампера
- Сила, действующая на движущийся заряд
- Магнитное поле, создаваемое постоянными магнитами
- Напряженность магнитного поля
- Взаимодействия токов и магнитов
- Эквивалентность токов и магнитов
- Вихревой характер магнитного поля
- Закон электромагнитной индукции и сила Лоренца
- Измерения магнитного поля методом индукционного толчка
- Ограниченные тела в магнитном поле
- Связь между магнитной проницаемостью и восприимчивостью
- Искажение магнитного поля при внесении в него магнетика
- Магнитный гистерезис
Магнитное поле – особая форма материи, существующая вокруг движущихся электрических зарядов – токов. Источниками магнитного поля являются постоянные магниты, проводники с током.
Источниками магнитного поля являются постоянные магниты, проводники с током.
На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.
Магнитное поле можно назвать особым видом материи, посредством которой осуществляется взаимодействие между движущимися заряженными частицами или телами, обладающими магнитным моментом. В специальной теории относительности магнитные поля являются необходимым следствием существования электрических полей.
Магнитный моментМагнитные поля действуют на токи, движущиеся заряженные тела или частицы, на намагниченные тела. Можно осуществить множество различных приборов и с их помощью судить о свойствах магнитного поля. Наиболее целесообразно характеризовать свойства магнитного поля, изучая его механические действия на контур тока.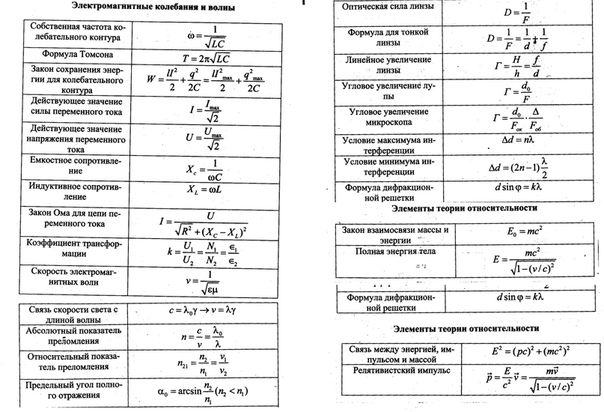 Вполне возможно осуществление проволочного контура весьма малой площади. Такой прибор позволит промерить магнитное поле достаточно детально. Таким образом, «пробный» контур тока играет в теории магнитного поля ту же роль, что «пробный» заряд в теории электрического поля.
Вполне возможно осуществление проволочного контура весьма малой площади. Такой прибор позволит промерить магнитное поле достаточно детально. Таким образом, «пробный» контур тока играет в теории магнитного поля ту же роль, что «пробный» заряд в теории электрического поля.
Производя опыты с подобным прибором, мы придем к следующим основным фактам. В каждой точке поля свободно вращающийся контур займет определенное положение равновесия. При этом положение устойчивого равновесия определяется не только расположением в пространстве оси контура, но также и тем, как располагается в пространстве определенная сторона контура, скажем, та, смотря на которую мы видим ток идущим против часовой стрелки. Назовем эту сторону положительной, или северной; условимся проводить нормаль к контуру так, чтобы она образовывала правовинтовую систему с направлением тока. Смотря против нормали, мы будем видеть положительную (северную) сторону контура.
Сравнивая поведение контура тока с поведением магнитных стрелок, можно обнаружить, что нормаль контура, находящегося в устойчивом равновесии, смотрит туда же, куда и магнитная стрелка.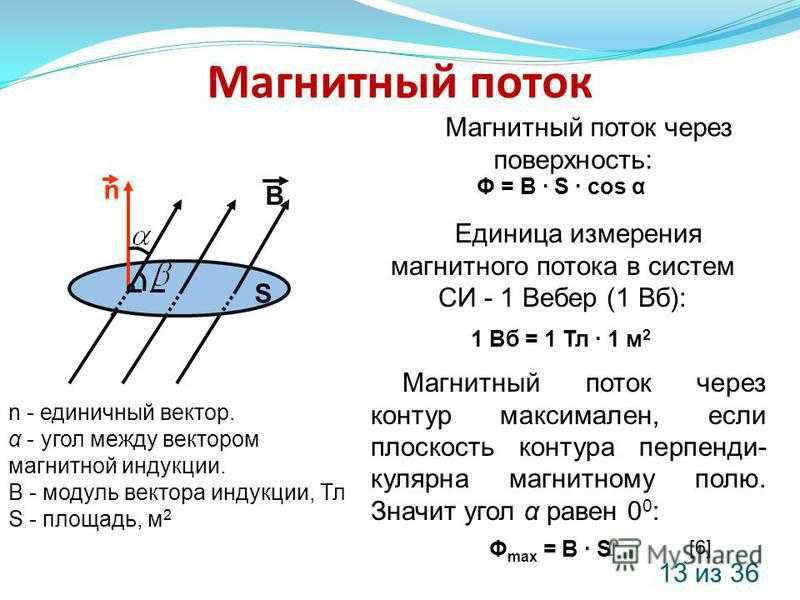 Таким образом, называя направлением магнитного поля то направление, куда смотрит нормаль свободного пробного контура, мы не разойдемся с элементарным определением.
Таким образом, называя направлением магнитного поля то направление, куда смотрит нормаль свободного пробного контура, мы не разойдемся с элементарным определением.
Отклоняя пробный контур от положения равновесия, мы обнаружим действие на него момента сил (рис. 105). При этом отклонение контура от равновесия однозначно описывается отклонением нормали контура от направления поля — синус угла и вращающий момент сил N оказываются пропорциональными:При том же угле а вращательный момент пропорционален произведению площади контура S на силу протекающего тока Уменьшение площади в какое-то число раз приводит к такому же изменению вращающего момента, что и уменьшение силы тока в такое же количество раз.
Из сказанного следует, что магнитное поведение контура зависит от расположения нормали контура и от величины произведения Эти данные можно объединить в одну векторную величину, называемую магнитным моментом кольцевого тока. В электротехнике, где используется система СИ, принято называть магнитным моментом вектор — единичная нормаль). В системе СГС, чаще используемой физиками, в эту формулу вводят коэффициент пропорциональности 1 /с: — скорость распространения электромагнитных волн в вакууме). Введение числового коэффициента, да еще вдобавок размерного, может показаться ненужным усложнением. Однако другие формулы при этом упрощаются; оценить это упрощение читатель сумеет значительно позднее.
В системе СГС, чаще используемой физиками, в эту формулу вводят коэффициент пропорциональности 1 /с: — скорость распространения электромагнитных волн в вакууме). Введение числового коэффициента, да еще вдобавок размерного, может показаться ненужным усложнением. Однако другие формулы при этом упрощаются; оценить это упрощение читатель сумеет значительно позднее.
Результаты опытов с пробным контуром могут быть записаны в виде: где В — коэффициент пропорциональности. Для разных полей или для разных точек пространства одного поля величина В будет иметь разные значения. По смыслу написанной формулы В равно максимальному вращательному моменту, действующему на единичный пробный контур Этот коэффициент В, характеризующий магнитное поле, носит название магнитной индукции. Векторная величина, имеющая направление магнитного поля и численно равная В, носит название вектора магнитной индукции.
Если вращательный момент описывать вектором, направленным вдоль оси вращения (в соответствии с правилами правовинтовой системы), то формула для него может быть записана в виде так называемого векторного произведения векторов, а именно:
Если параллельно это значит, что любой контур тока стремится установиться в магнитном поле таким образом, чтобы его магнитный момент совпал с направлением поля. На тело действует максимальный магнитный момент в том случае, если магнитный момент образует угол 90° с направлением поля. Для контура это соответствует положению плоскости витка проволоки вдоль силовых линий.
На тело действует максимальный магнитный момент в том случае, если магнитный момент образует угол 90° с направлением поля. Для контура это соответствует положению плоскости витка проволоки вдоль силовых линий.
Определив магнитное поле с помощью контура тока, у которого магнитный момент подсчитывается из измерений силы тока и площади, мы можем, наоборот, воспользоваться формулой для определения магнитных моментов таких систем, для которых нельзя измерить ток. Более того, мы переносим понятие магнитного момента и на такие системы, где понятие кольцевого электрического тока теряет смысл. Именно таким образом поступает физик, когда он говорит о магнитном моменте электрона, ядерной частицы. Магнитный момент магнитной стрелки также является нерасчленяемым понятием. Впрочем, к магнитному моменту постоянного магнита мы еще вернемся на стр. 442, обсудив некоторые специфические влияния среды. Как бы то ни было, магнитный момент системы, находящейся в вакууме, всегда может быть определен по приведенной формуле вращательного момента.
Поворот от положения равновесия тела, обладающего магнитным моментом, требует затраты работы. При повороте на малый угол работа вращения может быть представлена в виде
Отклонение тела от положения равновесия связано с накоплением потенциальной энергии Написанное произведение есть скалярное произведение двух векторов; следовательно,
В положении равновесия потенциальная энергия минимальна и равна , при повороте магнитного момента на 90° потенциальная энергия возрастает до нуля, и, наконец, когда магнитный момент устанавливается антипараллельно полю (положение неустойчивого равновесия), потенциальная энергия максимальна и равна
Примеры. 1. Магнитный момент ядра атома водорода (ядерный магнетон) СГС. Магнитный момент электрона (магнетон Бора)
2. Электрический ток в 1 А, текущий по витку с площадью создает магнитный момент
3. В абсолютной системе единиц магнитная индукция измеряется в гауссах (Гс), в системе СИ В измеряется в теслах (Т) и имеет размерность Для магнитного поля Земли
4.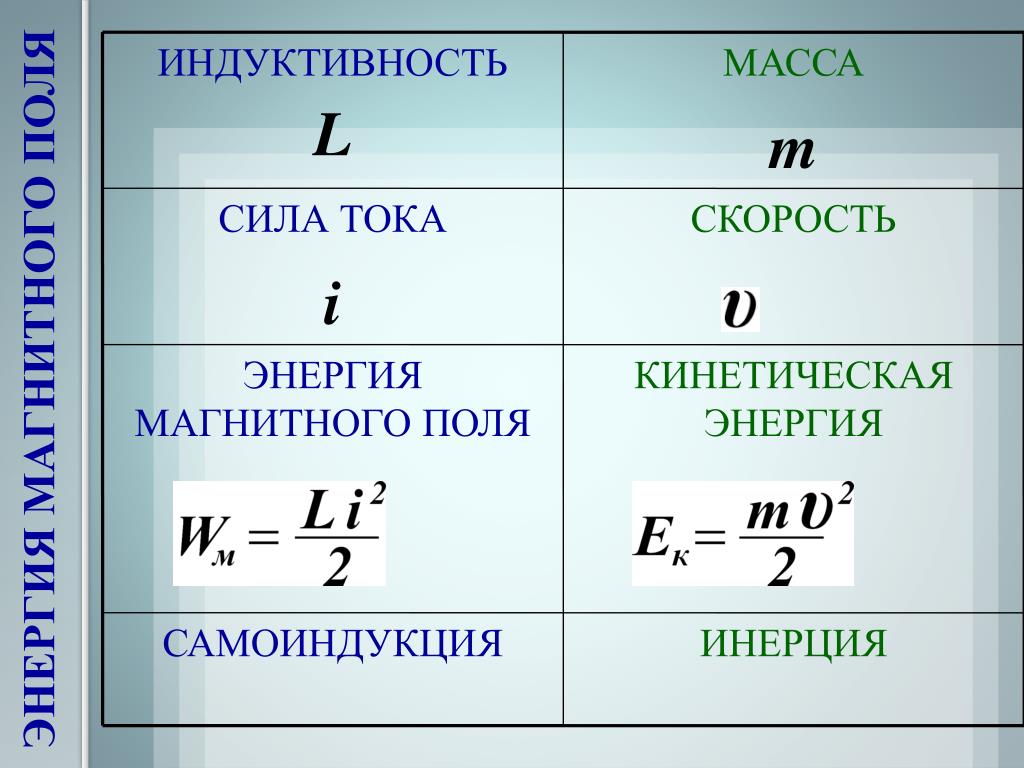 В воздушном зазоре мощной электрической машины магнитная индукция достигает нескольких тысяч гауссов. Академик П. Л. Капица получал импульсные магнитные поля с
В воздушном зазоре мощной электрической машины магнитная индукция достигает нескольких тысяч гауссов. Академик П. Л. Капица получал импульсные магнитные поля с
Наличие вращательного момента, действующего на контур тока, является несомненно результатом действия сил на каждый участок проводника, по которому текут заряды. Закон силы, действующей на элемент тока, можно установить опытным путем. Для этого необходимо выделить участок провода, например, с помощью ртутных контактов. Тогда этот участок может перемещяться под действием
силы. Если это смещение уравновесить натяжением пружины, то магнитная сила может быть измерена (рис. 106).
Закон силы, действующей на элемент тока малой длины, был впервые установлен Ампером и имеет вид
Векторная запись напоминает нам известное правило левой руки. Сила, действующая на элемент длины провода, всегда образует прямой угол с плоскостью, проходящей через ток и вектор магнитной индукции в этом месте. Чтобы выяснить направление силы, надо посмотреть, с какой стороны вращение вектора к вектору представится идущим против часовой стрелки по кратчайшему пути. Эта сторона будет положительной в правовинтовой системе и вектор силы будет «смотреть» на наблюдателя. Сила имеет максимальное значение тогда, когда элемент тока образует прямой угол с вектором поля. Сила обращается в нуль для элемента провода, лежащего вдоль силовой линии.
Чтобы выяснить направление силы, надо посмотреть, с какой стороны вращение вектора к вектору представится идущим против часовой стрелки по кратчайшему пути. Эта сторона будет положительной в правовинтовой системе и вектор силы будет «смотреть» на наблюдателя. Сила имеет максимальное значение тогда, когда элемент тока образует прямой угол с вектором поля. Сила обращается в нуль для элемента провода, лежащего вдоль силовой линии.
Выше записаны формулы в системе СГС. В системе СИ коэффициент 1 /с отсутствует и формула силы Ампера имеет вид
Чтобы определить величину силы, действующей на кусок провода конечной длины, написанное выражение силы надо проинтегрировать:
Только в простейшем случае прямолинейного куска провода длиной находящегося в однородном магнитном поле В, закон Ампера можно применить непосредственно в форме
Представляется совершенно естественной связь между законом Ампера и выражением для вращательного момента, выведенным в
предыдущем параграфе. Мы проведем рассмотрение лишь для простейшего случая прямоугольной рамки, расположенной в однородном магнитном поле параллельно силовым линиям (рис. 107). Две стороны рамки перпендикулярны к силовым линиям, две другие лежат вдоль силовых линий. Следовательно, все силы, действующие на элементы провода, можно свести к двум, показанным на рис. 107. Эти силы равны друг другу и по закону Ампера могут быть записаны в виде Тот же рисунок показывает, что силы Ампера приводят к моменту сил есть площадь рамки, следовательно, что совпадает с формулой для момента сил, выведенной в предыдущем параграфе. Предоставляем читателю сделать это доказательство более общим.
Мы проведем рассмотрение лишь для простейшего случая прямоугольной рамки, расположенной в однородном магнитном поле параллельно силовым линиям (рис. 107). Две стороны рамки перпендикулярны к силовым линиям, две другие лежат вдоль силовых линий. Следовательно, все силы, действующие на элементы провода, можно свести к двум, показанным на рис. 107. Эти силы равны друг другу и по закону Ампера могут быть записаны в виде Тот же рисунок показывает, что силы Ампера приводят к моменту сил есть площадь рамки, следовательно, что совпадает с формулой для момента сил, выведенной в предыдущем параграфе. Предоставляем читателю сделать это доказательство более общим.
Пример. На проводник длиной 3 м с током 50 А в поле 3000 Гс=0,3 Т действует сила При диаметре ротора ~1 м на виток действует вращающий момент Эти величины по порядку соответствуют параметрам крупной электрической машины. В электроизмерительном при боре на проводник длиной 2 см в поле 100 Гс при токе 0,01 А действует сила При диаметре рамки ~1 см на виток действует вращающий момент
Сила, действующая на движущийся зарядМы можем пойти еще дальше и сделать попытку рассмотрения магнитных сил, действующих на токи, как сил, приложенных к элементарным частицам электричества.
Электрический ток есть не что иное, как поток электрических частиц. Если заряд каждой частицы есть е, направленная скорость частицы й концентрация частиц (т. е. их число в единице объема) есть то выражение для силы тока можно представить в виде Действительно, через сечение проводапройдут все частицы, которые занимали объем т. е. протечет количество
электричества (рис. 108). Подставляя это выражение в закон Ампера, получим
Но есть число частиц в рассматриваемом объеме проводника; значит, на одну частицу действует сила
Эту силу называют иногда лоренцевой силой, в честь выдающегося физика Лоренца, много сделавшего для развития теории электронов.
Написанное выражение силы (мы его будем писать только в системе СГС, с коэффициентом 1/с) позволяет сразу же ответить на крайне интересный вопрос о характере движения электрической частицы (электрона, протона и т. д.) в магнитном поле. Сила, действующая на движущийся заряд, направлена перпендикулярно к силовым линиям и к вектору скорости частицы. Если частица движется вдоль силовых линий, то сила на нее не действует. Напротив, сила максимальна, если движение происходит в плоскости, перпендикулярной к силовым линиям. В этом последнем случае
Если частица движется вдоль силовых линий, то сила на нее не действует. Напротив, сила максимальна, если движение происходит в плоскости, перпендикулярной к силовым линиям. В этом последнем случае
Если поле однородно, то электрическая частица, движущаяся перпендикулярно к полю, будет описывать окружность, поскольку движение под действием постоянной силы, направленной под прямым углом к движению, не может быть иным, согласно основному закону механики. Мы вернемся к движению частицы в магнитном поле на стр. 407.
Пример. Электрона в катодной лампе, ускоряемые разностью потенциалов 70 В, приобретают скорость При вхождении под прямым углом в магнитное поле 500 Гс каждый электрон испытывает отклоняющую силу Лоренца Под действием этой силы электрон начнет двигаться по круговой орбите такого радиуса
Магнитное поле, создаваемое постоянными магнитамиКаждый постоянный магнит имеет два полюса *): из северного линии выходят, в южный входят. Мысленно построим поверхность, охватывающую северный полюс магнита. Мы можем найти полное число линий, пронизывающих эту поверхность. Это число по аналогии с соответствующей электрической величиной мы будем называть магнитным потоком и обозначать буквой Ф. Поток через элементарную площадку, перпендикулярную к силовым линиям, равен через произвольную площадку — угол, образованный нормалью к площадке с силовыми линиями;
Мы можем найти полное число линий, пронизывающих эту поверхность. Это число по аналогии с соответствующей электрической величиной мы будем называть магнитным потоком и обозначать буквой Ф. Поток через элементарную площадку, перпендикулярную к силовым линиям, равен через произвольную площадку — угол, образованный нормалью к площадке с силовыми линиями;
через поверхность ,и наконец, через замкнутую поверхность
Поток выходящий из северного полюса магнита и входящий в южный, является основной характеристикой магнита. Чем сильнее магнит, тем больше Это несколько оправдывает название «количество магнетизма» (имеющее только историческое значение) для величины, пропорциональной потоку, а именно, равной Иногда называют (еще более неудачно) магнитной массой. В электротехнике пользуются магнитной массой
Если полюсы магнита имеют небольшой размер (магнитная спица), то силовые линии вблизи таких полюсов расходятся радиально.
При помощи закона Гаусса — Остроградского
мы обосновали формулу для электрической индукции уединенного заряда,Очевидно, что «уединенный» магнитный полюс должен дать магнитную индукцию, удовлетворяющую аналогичному равенству:
Разумеется, никаких «уединенных» магнитных полюсов не существует. Написанная формула имеет смысл лишь в случае длинного магнита с точечным полюсом и при этом не слишком далеко от полюса. Подобный подход к магнитному полю постоянного магнита имеет все же полное право на существование. Это хорошо видно при составлении выражения для поля стержневого магнита, рассматриваемого как магнитный диполь с двумя полюсами находящимися на расстоянии друг от друга. На рис. 109 показано поле стержневого магнита и идеальное поле, рассчитанное по формуле
Написанная формула имеет смысл лишь в случае длинного магнита с точечным полюсом и при этом не слишком далеко от полюса. Подобный подход к магнитному полю постоянного магнита имеет все же полное право на существование. Это хорошо видно при составлении выражения для поля стержневого магнита, рассматриваемого как магнитный диполь с двумя полюсами находящимися на расстоянии друг от друга. На рис. 109 показано поле стержневого магнита и идеальное поле, рассчитанное по формуле
где—расстояния от полюсов до рассматриваемой точки. Совпадение картин вполне удовлетворительное.
Хорошие результаты получаются при расчетах полей на больших расстояниях от магнита. Действительно, если расстояния велики по сравнению с длиной магнита (плечом магнитного диполя), то рассмотрение полюсов как точек вполне оправдано. Расчеты ничуть не отличаются от соответствующих подсчетов электрических взаимодействий. Сравним, например, значения магнитной индукции, создаваемой стержневым магнитом на большом расстоянии от него вдоль оси магнита и перпендикулярно к его оси. В первом случае имеем
В первом случае имеем
где носит название магнитного момента постоянного магнита. Во втором случае (рис. 110)
Итак, поле вдоль оси в два раза сильнее. В системе СИ две последние формулы будут иметь вид соответственно
Пример. Вычислим магнитную индукцию, создаваемую стержневым магнитом длиной на расстоянии от магнита вдоль оси. Площадь поперечного сечения магнита индукция в магните 500 Гс.
Магнитный поток в магните (он же выходящий из полюса) максвелл (Мкс). Тогда на полюсе магнита сосредоточена «магнитная масса» СГС. Магнитный момент магнита
Искомая магнитная индукция
Напряженность магнитного поляРассмотрим взаимодействие уединенного магнитного полюса и элемента тока (рис. 111). Магнитный полюс создает поле В в месте нахождения электрического тока. Следовательно, по закону Ампера на элемент тока будет действовать сила
Мы можем вместо величины магнитной индукции поставить ее выражение для точечного полюса. Учитывая, что поле направлено по радиусу, мы получим для силы взаимодействия следующие выражения:
Учитывая, что поле направлено по радиусу, мы получим для силы взаимодействия следующие выражения:
Вполне естественно принять, что сила, с которой элемент тока действует на магнитный полюс, представится той же формулой с обращением направления силы. Это допущение Рис. 111. нельзя проверить непосредственно на опыте,
так как мы нё можем осуществить ни уединенного полюса, ни отдельно взятого элемента постоянного тока. Однако мы можем проверить правильность высказанного положения, интегрируя силы взаимодействия для опытных случаев. Теория действительно совпадает с опытом.
Итак, сила действия элемента тока на магнитный полюс может быть представлена в видеили в системе СИ, без коэффициента и с заменой на
Мы не ставим знака минус в этой формуле, так как полагаем обращенным радиус-вектор. За направление всегда принимают направление от источника поля до точки наблюдения. Поэтому, когда речь шла о силе, действующей на ток, предполагалось направленным от полюса к элементу тока. Теперь же, когда речь идет, о силе, действующей со стороны тока на полюс, радиус-вектор предполагается направленным от элемента тока к полюсу.
Теперь же, когда речь идет, о силе, действующей со стороны тока на полюс, радиус-вектор предполагается направленным от элемента тока к полюсу.
Сила, действующая на единичный магнитный полюс, носит название напряженности магнитного поля:
Нашим рассуждением доказано, что напряженность магнитного поля, создаваемого элементом тока, выражается формулой
В системе СИ формула, определяющая напряженность магнитного поля, создаваемого током, будет иметь вид
Итак, существуют две характеристики магнитного поля: вектор индукции, измеряемый действием магнитного поля на токи, и вектор напряженности, который может быть получен в эксперименте измерением воздействия поля на магниты.
Практически измерения напряженности удобнее сводить к измерению вращательного момента, действующего на магнитную стрелку (рис. 112). Такая стрелка, помещенная в однородное поле, будет подвергаться действию пары сил; величина силы равна а плечо равноОтсюда для вращательного момента получим выражение
или в векторной форме — магнитный момент стрелки, что весьма напоминает формулу момента сил, действующих на контур тока.
Вопрос о связи между напряженностью магнитного поля и магнитной индукцией должен быть решен опытом. Оказывается, что во всех случаях,.за исключением анизотропных тел, векторы напряженности и индукции параллельны друг другу. Это значит, что магнитная стрелка и ось пробного контура всегда установятся параллельно. Далее, во всех случаях, за исключением ферромагнитных веществ, между имеется простая линейная зависимость: — универсальная постоянная, так называемая магнитная проницаемость вакуума, а — коэффициент, характеризующий среду,— относительная магнитная проницаемость среды.
В системе СГС полагают Это приводит к одинаковой размерности магнитной индукции и напряженности. Эта одинаковость достигнута, однако, не даром, а ценой введения размерного коэффициента 1/с в законе Ампера. В системе СИ магнитная проницаемость вакуума равна
Взаимодействия токов и магнитовЗаконы, рассмотренные в предыдущих параграфах, позволяют в принципе рассчитать взаимодействие любых магнитных систем. Мы располагаем формулами сил и моментов сил, действующих на приборы со стороны магнитного поля любого происхождения:
Мы располагаем формулами сил и моментов сил, действующих на приборы со стороны магнитного поля любого происхождения:
Формулы, связывающие поля с их источниками:
Подставляя любую нижнюю формулу в любую из верхнего ряда и используя связь мы получим формулы магнитных, электромагнитных, магнитоэлектрических и электродинамических взаимодействий. Каждый тип взаимодействия проиллюстрируем одним примером.
Магнитное взаимодействие, т. е. действие магнита на магнит. Два полюса на расстоянии г взаимодействуют по закону Кулона, т. е.
Сила взаимодействия обратно пропорциональна магнитной проницаемости.
Электромагнитное действие, т. е. действие тока на магнит. Магнитная стрелка испытывает вращательный момент со стороны элемента тока. Для простоты принятот. е. магнитная стрелка расположена поперек силовых линий.
Взаимодействие не зависит от магнитной проницаемости, т. е. от свойств среды.
Магнитоэлектрическое действие, т. е. действие магнита наток.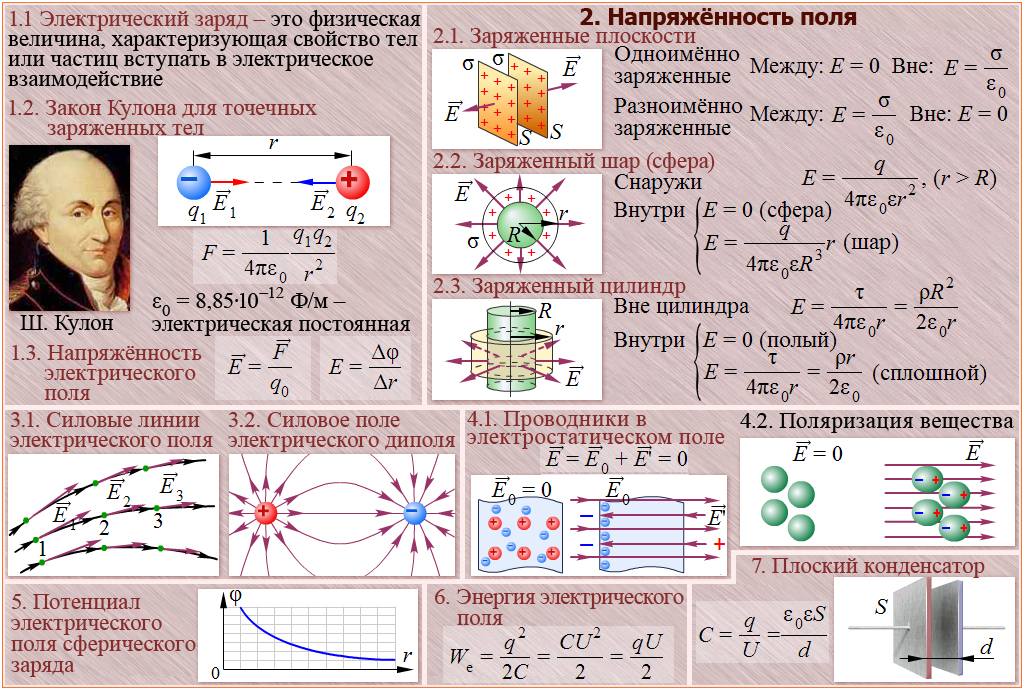 Контур тока расположен на продолжении оси стержневого магнита на расстоянии от него (рис. 113). Контур испытывает вращательный момент
Контур тока расположен на продолжении оси стержневого магнита на расстоянии от него (рис. 113). Контур испытывает вращательный момент
Взаимодействие не зависит от магнитной проницаемости.
Пример. Контур площадью обтекаемый током взаимодействует на расстоянии 100 см со стержневым магнитом, магнитный момент которого На контур будет действовать вращающий момент
Электродинамическое действие, т. е. действие тока на ток. Два параллельных тока притягиваются с силой
Взаимодействие прямо пропорционально магнитной проницаемости.
Таким же точно образом можно составить формулы для любых взаимодействий магнитных систем.
Пример: Электродинамическое взаимодействие надо серьезным образом учитывать при прокладке токопроводящих шин. В случае короткого замыкания шины и поддерживающие их изоляторы должны оказаться достаточно прочными, чтобы выдержать большие электродинамические нагрузки. Пусть по параллельным шинам, отстоящим на расстоянии текут токиНа единицу длины одной из шин действует сила — напряженность магнитного поля, создаваемого прямолинейным током, текущим по другой шине (см. стр. 250). Имеемт. е. на каждый метр шины действует сила — Этот же результат можно было получить интегрированием последней формулы для
стр. 250). Имеемт. е. на каждый метр шины действует сила — Этот же результат можно было получить интегрированием последней формулы для
Мы обращали внимание на сходство между выражениями для вращательных моментов, действующих на магнитную стрелку и контур тока. Действительно, поведение этих двух систем во внешнем поле чрезвычайно похоже. Если характеризовать каждую из систем стрелкой ее магнитного момента, то сходство будет еще более полным. Каждая система стремится расположиться в магнитном поле так, чтобы ее магнитный момент совпал с силовыми линиями поля. Если магнитный момент отклонен от положения устойчивого равновесия, то на систему действует вращательный момент — для магнитной стрелки и — для контура тока. Соответственно потенциальные энергии этих двух систем представятся формулами
Так как то становится очевидным различие между
формулами: они переходят одна в другую введением в формулы магнитной проницаемости. Отсюда следует, что в отношении механического воздействия магнитная стрелка с моментом М эквивалентна контуру тока с моментом
Отсюда следует, что в отношении механического воздействия магнитная стрелка с моментом М эквивалентна контуру тока с моментом
Однако сходство этих двух систем еще не кончается на сказанном. Мы покажем сейчас, что магнитная стрелка и контур тока обладают собственными полями, совпадающими с точностью до постоянного множителя. Такое сходство имеет место на расстояниях, существенно больших размера системы. Докажем это для точки пространства, лежащей на линии магнитного момента на расстоянии от центра системы. Поле магнита для такой точки было уже вычислено, оно равно Остается найти поле кругового тока на его оси.
На рис. 114 произведено построение векторов напряженности, создаваемых двумя элементами длины окружности, пересекающими чертеж. Векторы напряженности направлены перпендикулярно к соответствующему элементу тока и к радиусу-вектору, т. е. лежат в плоскости чертежа. В какую именно сторону смотрит вектор напряженности, следует определить либо при помощи правила векторного произведения, либо при помощи правила буравчика (что в общем одно и то же).
Элементарное поле равно в рассматриваемом случае так как элемент тока и радиус-вектор образуют прямой угол. Сложим изображенные на рисунке два вектора. Для поля, созданного двумя «противоположными» элементами, получим
смысл обозначений ясен из чертежа. Такую же величину поля даст любая пара «противоположных» элементов. Поэтому полное поле мы получим, заменив в последнем выражении длину элемента на длину половины окружности . Напряженность поля кругового тока на его оси на расстоянии от тока *) представится формулой
Но есть момент кругового тока. Следовательно, а магнитная индукция
Этим доказано, что магнитный диполь и контур тока эквивалентны не только в отношении действующих на них сил, но и в отношении создаваемых ими полей. Эквивалентность имеет и здесь тот же характер. Чтобы заменить магнитную стрелку с моментом М, нужно взять контур тока с моментом
В вакууме и для системы и принцип эквивалентности еще проще: магнитная стрелка с моментом М эквивалентна контуру тока с таким же магнитным моментом.
Примеры. 1. Вернемся к примеру на стр. 242. Рассчитаем магнитную индукцию того же магнита в системе СИ:
в полном соответствии с результатом на стр. 242.
2. Контур с током имеющий площадь создает на расстоянии см вдоль оси, перпендикулярной к его плоскости, магнитное поле с напряженностью
Вихревой характер магнитного поляИсследование хода магнитных линий показывает принципиальное различие между электрическим и магнитным полем. Электрические линии имеют начало и конец, не существует замкнутых линий у постоянного электрического поля. Напротив, опыт показывает, что силовые линии магнитного поля (т. е. векторные линии магнитной индукции) всегда замкнуты, не существуют линии, имеющие начало и конец.
По причинам, обсуждавшимся выше, силы и поля сил, в которых работа по замкнутому пути равна нулю, получили название потенциальных. Векторные поля, характеризующиеся замкнутыми силовыми линиями, носят название вихревых. Магнитное поле является вихревым.
Если провести в магнитном поле замкнутую поверхность, то магнитный поток через такую поверхность будет всегда равен нулю. Иначе говоря, число линий, входящих в эту поверхность, будет равно числу линий, выходящих из нее. Уравнение и является математическим выражением того факта, что у магнитных силовых линий нет начала и конца.
Связь магнитных линий с создающими поле токами состоит в том, что магнитные линии всегда охватывают токи. Поэтому интегралы, взятые вдоль силовой линии от индукции или напряженности,должны быть отличны от нуля. Целесообразнее
рассматривать второй интеграл, так как его величина должна быть пропорциональна силе электрического тока, охватываемого силовой линией; ведь согласно основной формуле напряженности между и силой тока имеет место прямая пропорциональность.
По аналогии с электростатикой называют магнитным напряжением. Если интеграл берется вдоль силовой линии, то
Магнитное напряжение вдоль замкнутой линии должно быть пропорционально току, около которого эта линия обворачивается:
где — коэффициент пропорциональности.
Силовая линия может охватывать не один ток, а несколько. Для создаваемого поля существенна алгебраическая сумма токов, и уравнение имеет вид
Более глубокий теоретический анализ, на котором мы здесь не можем останавливаться, показывает, что написанное уравнение подвергается еще двум обобщениям. Во-первых, магнитное напряжение можно взять не только вдоль силовой линии, но и вдоль произвольного контура; во-вторых, коэффициент пропорциональности в уравнении является константой, зависящей лишь от свойств среды и одинаковой для любых геометрических условий. Таким образом, магнитное напряжение, взятое для любой замкнутой кривой линии, одинаково, если только эта кривая охватывает токи определенной силы. Безразлична форма кривой, размеры кривой; кривая может охватывать один ток или десяток токов; эти токи могут быть прямыми, круговыми,— все это безразлично, магнитное напряжение будет одним и тем же, если только алгебраическая сумма токов, пронизывающих кривую, будет иметь одинаковое значение.
Так как коэффициент пропорциональности в формуле магнитного напряжения есть величина универсальная, то мы можем найти если сумеем вычислить магнитное напряжение для любой системы, поле которой нам известно.
Мы познакомились с общим выражением для напряженности магнитного поля элементарного тока. Вычисление магнитного напряжения с помощью формулы напряженности
представляет математические трудности. Кроме того, нам известна формула напряженности магнитного поля на оси кругового тока, Вычисление магнитного напряжения вдоль оси кругового тока не представит особых затруднений. Нас не должно смущать, что интегрирование происходит вдоль прямой линии, в то время как нас интересует магнитное напряжение вдоль замкнутой кривой. Дело в том, что прямая, идущая от отрицательной бесконечности в положительную, является замкнутой кривой — она замыкается в бесконечности. Выражение для магнитного напряжения взятого вдоль такой замкнутой кривой, т. е. вдоль оси кругового тока от отрицательной бесконечности до положительной бесконечности, можно записать в виде
где — радиус, — расстояние, откладываемое по оси контура. Интеграл легко берется, если перейти к новой переменной по формулеи оказывается равным Подставляяи приравнивая значение магнитного напряжения величине получим
Интеграл легко берется, если перейти к новой переменной по формулеи оказывается равным Подставляяи приравнивая значение магнитного напряжения величине получим
Закон магнитного напряжения имеет вид
Закон магнитного напряжения может оказать существенные услуги в подсчете магнитных полей ряда систем. В его применении нам должны помочь соображения симметрии, и в этом отношении рассуждения, к которым мы сейчас переходим, очень похожи на соответствующие задачи, которые решались в электростатике с помощью закона Гаусса — Остроградского.
Рассмотрим, прежде всего, бесконечный прямолинейный ток. Из соображений симметрии очевидно, что силовая линия может иметь лишь форму окружности, центр которой совладает с осью провода. Также несомненно, что во всех точках окружности числовое значение напряженности одно и то же. Применяя к такой силовой
линии закон магнитного напряжения, получим: При
этом есть не что иное как длина силовой линии. Если рассматриваются точки, расположенные на расстоянии от оси провода, то и, таким образом, для магнитного поля бесконечного прямолинейного тока в пространстве вне провода мы получим:
Найдем теперь напряженность магнитного поля внутри провода. Обозначим радиус провода через а и допустим, что ток распределен вдоль сечения провода вполне равномерно. Силовые линии внутри провода также должны иметь вид окружностей. Рассмотрим такую линию радиуса Через нее протекает доля тока и, следовательно, закон магнитного напряжения даст
Обозначим радиус провода через а и допустим, что ток распределен вдоль сечения провода вполне равномерно. Силовые линии внутри провода также должны иметь вид окружностей. Рассмотрим такую линию радиуса Через нее протекает доля тока и, следовательно, закон магнитного напряжения даст
или в системе СИ
Мы видим, что напряженность магнитного поля на оси провода равна нулю, далее она возрастает, становится максимальной на поверхности провода, а затем убывает обратно пропорционально расстоянию (рис. 115).
Если поле определяется в такой точке, для которой расстояние много меньше ее расстояния до конца провода, то формула может быть применена для провода конечных размеров.
Пример. Подсчитаем, какова напряженность магнитного поля на расстоянии 5 см от оси прямолинейного тока силой 20 А.
В системе
Другой важный пример использования закона магнитного напряжения — это вычисление поля соленоида.
Положим, что на окружность длиной равномерно навиты витки соленоида. Поле внутри кругового соленоида должно быть однородным, и все силовые линии должны быть окружностями, концентрическими с Такая система для вопросов теории магнитного поля играет ту же роль, что бесконечный плоский конденсатор в теории электрического поля. Каждая силовая линия охватывает все витков, и поэтому магнитное напряжение, взятое вдоль силовой линии длиной будет равно
Поле внутри кругового соленоида должно быть однородным, и все силовые линии должны быть окружностями, концентрическими с Такая система для вопросов теории магнитного поля играет ту же роль, что бесконечный плоский конденсатор в теории электрического поля. Каждая силовая линия охватывает все витков, и поэтому магнитное напряжение, взятое вдоль силовой линии длиной будет равно
Так как
Напряженность магнитного поля катушки определяется ее «ампер-витками», т. е. произведением силы тока на число витков на единицу длины соленоида. Последняя формула — одно из оправданий электротехнической системы записи уравнений поля. Соленоид является одним из основных элементов электротехнических устройств, поэтому упрощение формулы для вычисления напряженности его магнитного поля очень полезно для практики.
Формулу можно применять и для открытого соленоида, однако лишь для тех внутренних точек, которые находятся достаточно далеко от краев.
Пример. Напряженность магнитного поля в центре узкого и длинного соленоида
В системе СГС тот же расчет примет вид
Как известно, явление электромагнитной индукции, открытое великим английским физиком Фарадеем, состоит в том, что в замкнутом проводнике возникает электрический ток, если только изменяется значение магнитного потока, проходящего через замкнутый провод. При этом э. д. с. индукции оказывается пропорциональной скорости изменения магнитного потока, т. е. производной по времени
При этом э. д. с. индукции оказывается пропорциональной скорости изменения магнитного потока, т. е. производной по времени
Покажем, что закон электромагнитной индукции тесно связан с существованием лоренцовой силы. Если электромагнитная индукция возникает при перемещении провода в магнитном поле, то закон индукции является прямым следствием выражения для силы Лоренца.
Чтобы не загромождать изложения чисто математическими трудностями, проведем упрощенное доказательство, а именно, допустим, что э. д. с. индукции возникает в прямоугольном контуре, расположенном перпендикулярно к силовым линиям однородного магнитного поля. Изменение потока вызывается поступательным перемещением одной из сторон прямоугольника длиной так, как показано на рис. 116. В перемещающемся проводнике находятся свободные заряды, поэтому при движении проводника со скоростью V эти заряды подвергнутся действию силы Лоренца (Ввиду того, что углы между направлением скорости, магнитным полем и направлением проводника равны 90°, мы опустили векторные символы в формуле силы, а синус угла при этом равен единице. ) Сила Лоренца направлена перпендикулярно к плоскости, проходящей через направление скорости перемещения зарядов (вместе с проводом) и магнитные линии, т. е. вдоль провода. Таким образом, заряды придут в движение вдоль провода, создастся индукционный ток.
) Сила Лоренца направлена перпендикулярно к плоскости, проходящей через направление скорости перемещения зарядов (вместе с проводом) и магнитные линии, т. е. вдоль провода. Таким образом, заряды придут в движение вдоль провода, создастся индукционный ток.
Электродвижущей силой называется работа перемещения единицы заряда вдоль замкнутого контура. Сила, действующая на единицу заряда, равна работа этой силы вдоль движущегося провода равна но на остальных участках контура работа не производится. Поэтому последнее выражение и есть искомое выражение для э. д. с. индукции.
Оно имеет вид
Пусть за время провод передвинулся на расстояние Площадь контура возросла при этом на величину а магнитный поток — на величину Так как э.д.с индукции может быть представлена и в такой форме: Но это выражение
— в системе СГС и в системе СИ — и есть закон электромагнитной индукции Фарадея.
Этим показано, что электромагнитная индукция и отклонение движущихся электрических зарядов во внешнем поле представляют собой проявления одних и тех же законов природы. Мы еще раз вернемся к этому интересному вопросу в следующей главе. Сейчас нам нужно было лишь напомнить смысл и содержание закона электромагнитной индукции.
Мы еще раз вернемся к этому интересному вопросу в следующей главе. Сейчас нам нужно было лишь напомнить смысл и содержание закона электромагнитной индукции.
Используя явление электромагнитной индукции, можно разработать весьма совершенные методы измерения магнитного поля. Допустим, что имеется необходимость определить значение магнитного поля в каком-либо месте пространства. Изготовляется плоская катушка малого размера (или берется один проволочный виток) и помещается в магнитное поле в положение, перпендикулярное к силовым линиям. К катушке (витку) идут провода от клемм баллистического гальванометра. Если теперь быстрым движением повернуть плоскость катушки на 90° так, чтобы ее плоскость совпала с силовыми линиями, то за время поворота по катушке пробежит електрический индукционный ток. Этот кратковременный ток, быстро достигающий максимума, а затем спадающий к нулю, носит название индукционного толчка (рис. 117). За время толчка по проводу пройдет определенное количество электричества, которое с большой точностью может быть измерено баллистическим гальванометром—прибором, позволяющим из-за инертности своей поворотной рамки интегрировать электрический ток за время толчка.
117). За время толчка по проводу пройдет определенное количество электричества, которое с большой точностью может быть измерено баллистическим гальванометром—прибором, позволяющим из-за инертности своей поворотной рамки интегрировать электрический ток за время толчка.
Если сопротивление катушки число витков то сила протекающего по катушке индукционного тока запишется в виде
Количество электричества, протекшее через провод за время индукционного толчка, будет равно
где— значение потока, проходящего через катушку в первом положении, а — во втором.
Если Ф1 или Ф2 равно нулю (магнитные линии не проходят через катушку в начальном или конечном положении), то проведенное измерение дает значение магнитной индукции. Остается лишь разделить величину магнитного потока на площадь сечения S катушки: B=QRI(nS).
Разумеется, возможны и другие варианты измерения. Скажем, вместо того чтобы поворачивать катушку, можно включать или выключать поле. Можно также, если надо увеличить эффект, поворачивать катушку не на 90, а на 180°, это удвоит эффект. Для этой же цели прибегают не к включению или выключению поля, а изменяют знак поля на обратный.
Для этой же цели прибегают не к включению или выключению поля, а изменяют знак поля на обратный.
Так как измерительная катушка может быть сделана очень маленькой, вплоть до квадратного миллиметра, то измерения этим способом могут помочь в точном зондировании магнитного поля в небольших объемах.
Этот же самый метод применяется для измерения магнитного напряжения. Для этой цели изготовляется измерительный пояс (его называют поясом Роговского) — длинная катушка, надетая на гибкий ремень. Поясу может быть придана любая форма, и два конца его могут быть подведены к любым двум точкам пространства. Концы пояса могут быть также при желании приведены в соприкосновение. Покажем, что такой измерительный пояс, соединенный с баллистическим гальванометром, будет давать при выключении поля величину, пропорциональную магнитному напряжению вдоль того пути, по которому он уложен.
Баллистический гальванометр измерит величину магнитного потока, проходящего через все витки катушки. Пусть — плотность намотки, т. е. число витков, приходящееся на единицу длины измерительного пояса. Тогда на малом отрезке пояса уложится витков, и магнитный поток, проходящий через эти витков, будет равен
е. число витков, приходящееся на единицу длины измерительного пояса. Тогда на малом отрезке пояса уложится витков, и магнитный поток, проходящий через эти витков, будет равен
Если среда однородна и все витки имеют одинаковую площадь, то
и суммарный магнитный поток, пронизывающий весь измерительный пояс, будет
Переходя к пределу при получим
Так как измерения проводятся в среде, для которой мало отличается от есть константа прибора. Отбросы баллистического гальванометра при измерениях с помощью пояса будут в точности пропорциональны магнитному напряжению между точками, где находятся концы пояса.
Этим прибором легко продемонстрировать закономерности, обсуждавшиеся в § 104. Обводя катушку вокруг одного и того же тока, мы увидим, что при любой конфигурации напряжение будет одним и тем же; мы также легко проверим, что магнитное напряжение вдоль контура, не охватывающего тока, равно нулю. Обводя катушку около одного тока несколько раз, мы убедимся в возрастании магнитного напряжения в соответствующее число раз, и т. д.
д.
Необходимо подчеркнуть особенное значение измерений магнитного поля методом индукционного толчка для тех случаев, когда нас интересует магнитное поле внутри твердого тела. Кроме обсуждаемого метода, можно прибегнуть лишь к вырезыванию в твердом теле щелей. Обычно это невозможный путь.
Остановимся на самой распространенной задаче — измерении магнитной проницаемости железных тел. Наиболее точные результаты могут быть получены, если исследуемое вещество изготовляется в виде тороида. На это кольцо наматываются две обмотки, одна из которых присоединена к источнику тока, а другая — к баллистическому гальванометру. Если ток включен, то через кольцо проходит магнитный поток Переключая направление первичного тока на обратное, мы вызовем во второй катушке индукционный ток. Протекшее по гальванометру количество электричества будет связано с магнитной индукцией внутри кольца уже обсуждавшимся выше соотношением
где — сечение тороида (предполагается, что витки плотно прилегают к кольцу), — число витков и сопротивление вторичной обмотки. Что же касается напряженности магнитного поля, то ее мы можем определить по формуле, справедливой для кругового
Что же касается напряженности магнитного поля, то ее мы можем определить по формуле, справедливой для кругового
соленоида:Частное от деления даст значение магнитной проницаемости материала кольца.
Ограниченные тела в магнитном полеВ той или иной степени все тела обладают магнитными свойствами. Магнитные свойства скажутся, во-первых, в том, что тела будут испытывать силы и моменты сил со стороны магнитного поля; во-вторых, магнитное поле исказится, если поместить в него тело. Как указывалось выше, магнитные свойства вещества характеризуются коэффициентом — магнитной проницаемостью вещества. По значениям тела могут быть отчетливо разбиты натри класса веществ: ферромагнетики, к которым относятся железо, никель и кобальт, обладающие положительными значениями относительной магнитной проницаемости, много большими единицы; парамагнетики — тела с проницаемостью, несколько большей единицы, и диамаг-нетики, у которых магнитная проницаемость чуть меньше единицы. Типичные цифры приведены в таблице.
Типичные цифры приведены в таблице.
Искажение магнитного поля, происходящее при внесении в него диамагнитных и парамагнитных тел, совершенно незначительно. Напротив, магнитное поле искажается весьма существенно, если в пространство будут внесены ферромагнитные тела.
Что же касается силовых действий магнитного поля, то они без особого труда обнаруживаются и для пара- и диамагнитных тел. Не приходится и говорить о значительных силах, которые испытываются со стороны магнитного поля железными телами; эти силы превосходно знакомы каждому.
Остановимся сначала на изучении магнитных сил. Каждое тело, не обладавшее магнитными свойствами, становится магнитным, будучи внесенным в поле. Этот процесс есть намагничивание тела, проявляющееся в приобретении телом магнитного момента. Как нам известно, система, обладающая магнитным моментом, может обнаружить себя двояко. В однородном поле такое тело поворачивается так, чтобы направление момента совпало с внешним полем. В неоднородном поле тело будет, кроме того, испытывать силу, действующую так, что тело придет в движение вдоль силовых линий.
Вращательный момент может быть без труда обнаружен у ферромагнитных тел. По формуле можно найти магнитный момент тела. Однако большей частью нас интересует не тело случайной формы, а вещество. Поэтому по возможности пересчитывают измеренную величину на магнитный момент единицы объема. Век-гор, направленный вдоль магнитного момента и численно равный величине магнитного момента, приходящегося па единицу объема, называют вектором намагничения Разумеется, перерасчет от магнитного момента тела к вектору намагничения не вызывает труд-костей лишь в том случае, если мы уверены в том, что намагничение образца однородно. Это имеет место тогда, когда образец обладает формой эллипсоида или вырожденного эллипсоида, т. е. цилиндра, пластинки, шара (ср. стр. 233). С такими телами и проводят подобные эксперименты.
Определение вектора намагничения измерением вращательного момента легко проводится для ферромагнитных тел. Для парамагнитных и диамагнитных тел вращательные моменты очень малы и измерять их трудно. В этих случаях предпочитают измерение силы, действующей на тело, находящееся в неоднородном поле.
В этих случаях предпочитают измерение силы, действующей на тело, находящееся в неоднородном поле.
Рассмотрим элемент объема магнетика, находящегося в неоднородном поле. Для простоты положим, что поле меняется вдоль одной оси и градиент поля равен Каждый элемент объема магнетика будет вести себя, как магнитный диполь; поэтому потенциальная энергия единицы объема может быть записана в виде Если его момент установился вдоль поля, то сила, действующая на единицу объема магнетика, будет равна производной потенциальной энергии по координате, т. е.
Таким образом, зная градиент поля и измеряя силу, можно найти величину магнитного момента единицы объема исследуемого тела. Практически это осуществляется в различных установках. Простейшими из них являются так называемые магнитные весы. В одной из чашек аналитических микровесов делается отверстие, через которое пропускается пить. На конец нити подвешивается образец н помещается между полюсами магнита. Образец уравновешивается сначала при невключенном магните, а затем при наложении поля. Разность показаний весов дает значение силы
Разность показаний весов дает значение силы
Весы должны быть достаточно точными, что видно из следующего примера. Кусок висмута (наиболее сильное диамагнитное вещество),помещенный в магнитное поле, напряженность которого имеет намагничение При неоднородности магнитного поля на каждый кубический сантиметр висмута будет действовать сила лишь в 1 дин, т. е.
Опыт показывает, что для дна- и парамагнитных тел между вектором намагничения и напряженностью магнитного поля имеется простая зависимость
где носит название магнитной восприимчивости. Для диамагнитных тел отрицательно, для парамагнитных — положительно. Значения были приведены в таблице на стр. 256. При положительных значениях х вектор намагничения параллелен вектору напряженности поля, при отрицательных значениях т. е. для диамагнитных тел, направления векторов намагничения и напряженности магнитного поля противоположны.
Эта разница в знаке делает весьма непохожим поведение тел обоих классов в тождественных условиях. Это иллюстрируется рис. 118. Различия действительно разительны. Парамагнитное тело втягивается в область сильного поля, диамагнитное тело выталкивается. В однородном поле парамагнитная стрелка стремится расположить свою ось вдоль силовых линий, диамагнитная — поперек (ср. аналогичный пример с диэлектриком, стр. 231).
Это иллюстрируется рис. 118. Различия действительно разительны. Парамагнитное тело втягивается в область сильного поля, диамагнитное тело выталкивается. В однородном поле парамагнитная стрелка стремится расположить свою ось вдоль силовых линий, диамагнитная — поперек (ср. аналогичный пример с диэлектриком, стр. 231).
Определение магнитной восприимчивости измерением силы в неоднородном поле можно производить для твердых тел как в виде монокристаллов, так и в виде порошков. Без всякого труда метод приложим и к жидкостям. В этом случае можно поставить опыт так, чтобы измеряемой величиной явилось повышение или понижение уровня жидкости, втягиваемой или выталкиваемой из пространства между полюсами магнита.
Связь между магнитной проницаемостью и восприимчивостьюОбе эти величины могут быть измерены непосредственно: магнитная проницаемость определяется измерением индукции и напряженности с дальнейшим вычислением по формуле а восприимчивость — по силовым действиям на магнетик, как описано только что.
Вернемся к опыту по определению магнитной проницаемости тела, выполненного в виде тороида. Первичная катушка, которой обернут тороид, создает поле с напряженностью не зависящей от вещества тороида; без тороида напряженность поля представится той же формулой. Иное дело — магнитный поток. Мы убеждаемся опытным путем, что значение В зависит от магнитной проницаемости. Если сердечник катушки сделан из железа, то В возрастает в сотни и тысячи раз. Это увеличение магнитного потока мы связываем с явлением намагничивания.
Обратим прежде всего внимание на то обстоятельство, что в отсутствие железа магнитная индукция кругового соленоидаимеет смысл магнитного момента в единице объема.
Магнитный момент витка катушки равняется (будем вести рассуждения применительно к системе СИ). Полный магнитный момент системы будет равен а магнитный момент токов в единице объема есть не что иное как напряженность поля. Магнитный момент эквивалентных диполей будет в раз больше (ср. § 103). Следовательно, магнитная индукция однородного магнитного поля, создаваемого витками кругового соленоида при отсутствии сердечника,может быть представлена как магнитный момент эквивалентных диполей, приходящихся на единицу объема.
Полный магнитный момент системы будет равен а магнитный момент токов в единице объема есть не что иное как напряженность поля. Магнитный момент эквивалентных диполей будет в раз больше (ср. § 103). Следовательно, магнитная индукция однородного магнитного поля, создаваемого витками кругового соленоида при отсутствии сердечника,может быть представлена как магнитный момент эквивалентных диполей, приходящихся на единицу объема.
С полным основанием мы можем полагать, что магнитная индукция сохранит свой смысл, если, не нарушая однородности поля, равномерно заполнить пространство катушки дополнительным числом магнитных диполей. Если на единицу объема от дополнительных диполей приходится магнитный момент то магнитная индукция возрастет на эту величину и станет равной
Такое возрастание В и происходит, когда соленоид заполняется веществом. Так как и, следовательно, магнитная восприимчивость и проницаемость связаны равенством
Аналогичное рассуждение применительно к системе СГС приведет к формулам с другими коэффициентами. Магнитный момент токов (и диполей) в единице объема равен
Магнитный момент токов (и диполей) в единице объема равен
Поэтому при наличии среды
Полагая получимследовательно,
Пример. Проведем расчет примера на стр. 258 в системе СИ. Для висмута
кусок висмута находится в магнитном поле
обладающем неоднородностью
Намагничение висмута будет Тогда на единицу объема будет действовать сила
Ясно, что что совпадает с результатом предыдущего примера.
что совпадает с результатом предыдущего примера.
Вопрос об искажении магнитного поля имеет практическое значение только при внесении в поле железных тел. В значительной части нам придется повторить рассуждения, аналогичные приведенным на стр. 232 для диэлектриков.
На границе двух сред, обладающих разными магнитными про-ницаемостями, векторы магнитного поля (как индукция, так и напряженность) преломляются. Чтобы найти законы этого преломления, рассмотрим, прежде всего, магнитное напряжение, взятое вдоль малого контура A BCD, тесно прилегающего к поверхности раздела так, как это показано на рис. 119. Так как через этот контур токи не протекают, то магнитное напряжение равно нулю. Разложим вектор напряженности магнитного поля с обеих сторон границы на
119. Так как через этот контур токи не протекают, то магнитное напряжение равно нулю. Разложим вектор напряженности магнитного поля с обеих сторон границы на
нормальную и тангенциальную составляющие. Из рисунка ясно, что обращение в нуль магнитного напряжения может иметь место лишь в том случае, если тангенциальные составляющие будут равны друг другу:
Другое условие на границе двух сред мы найдем рассмотрением магнитного потока, проходящего через прилегающий к поверхности раздела небольшой цилиндр (на рисунке не показан). Так как у магнитных линий источников нет, то число силовых линий, входящих в верхнее основание цилиндра, должно равняться числу линий, выходящих через нижнее основание. Боковая поверхность бесконечно мала и поток через нее равен нулю. Разложим вектор магнитной индукции с обеих сторон границы на две составляющие: нормальную и тангенциальную. Очевидно, равенство потоков через основания может иметь место в том случае, если нормальные составляющие вектора индукции не изменятся при переходе через границу:
Из этих двух правил мы находим закон преломления силовых линий. Из рисунка ясно, что
Из рисунка ясно, что
При переходе из воздуха в железо магнитные линии отклоняются от перпендикуляра чрезвычайно значительно и поэтому сильно сгущаются. Именно поэтому железное тело, обладающее магнитной проницаемостью в сотни и тысячи раз больше «вбирает» в себя силовые линии. На этом явлении основана магнитная защита. В пространство, огражденное железом, магнитный поток не пройдет: подавляющая часть магнитных линий будет идти внутрь железа (рис. 120).
В совершенной аналогии с диэлектриками решается задача о характере искажений, вносимых в магнитное поле телом определенной формы. Если тело имеет форму эллипсоида, цилиндра или пластинки, то поле внутри такого тела, как показывают теоретические
расчеты, будет однородным, если поле было однородным и до внесения в него железного тела. Между внешним однородным полем (тем, которое было) И полем внутри железного тела (которое стало) существует соотношение, полностью аналогичное обсужденному в § 96. Напряженность поля, образовавшегося в железном теле, становится меньше той, которая была ранее, на величину, пропорциональную намагничению:
Чтобы фактор размагничения был безразмерным, намагничение поделено на магнитную проницаемость вакуума. Продолжая и далее пользоваться соотношениями системы СИ и подставляя
Продолжая и далее пользоваться соотношениями системы СИ и подставляя
получим следующую связь между внешним и внутренним полем
В системе СГС
и связь между внешним и внутренним полем будет иметь вид
Коэффициент размагничения имеет те же значения, что и в случае диэлектриков: для пластины и т. д.
Магнитный гистерезисГоворя о магнитной проницаемости железных уел, мы могли создать ложное впечатление, что магнитные свойства ферромагнетиков отличаются от магнитных свойств парамагнитных тел только величиной магнитной проницаемости. Это совсем не так. Принципиальное отличие ферромагнетиков от других тел заключается в отсутствии линейной и, более того, однозначной зависимости магнитного состояния тела от напряженности магнитного поля. Поэтому понятие магнитной проницаемости для ферромагнетиков носит весьма условный характер. Правильное представление о магнитных свойствах железа можно получить, рассматривая кривую зависимости намагничения от напряженности или магнитной индукции от напряженности поля. Обе эти кривые довольно близки друг К другу.
Обе эти кривые довольно близки друг К другу.
Будем измерять намагничение железного тела в функции напряженности. Сначала намагничение будет расти медленно, затем быстро и, наконец, наступит магнитное насыщение. Такого типа кривые намагничения, впервые построенные А. Г. Столетовым, типичны для всех ферромагнитных тел (рис. 121). Повторяем, что кривые намагничения и магнитной индукции весьма похожи. Ход кривой намагничения дает магнитную восприимчивость, ход кривой индукции дает магнитную проницаемость. Из приведенной кривой видно, что магнитная проницаемость (восприимчивость) изменяется по кривой с максимумом. При малых полях магнитная проницаемость мала, затем она возрастает до максимума, потом падает и по достижении насыщения остается неизменной. Большей частью, когда приводят значения магнитной проницаемости, не оговаривая внешних условий, имеют в виду максимальную магнитную проницаемость.
Однако описанным не исчерпывается своеобразие поведения ферромагнетиков. Положим, что железо доведено до состояния магнитного насыщения, и начнем уменьшать напряженность магнитного поля. Оказывается, что индукция будет убывать теперь по другой кривой, лежащей выше кривой начального намагничения. Напряженность поля может быть доведена до нуля, но намагничение не будет снято. Соответствующие значения намагничения и индукции называют остаточными. Чтобы снять остаточное намагничение, необходимо переменить направление поля. Если иметь в виду опыт, о котором говорилось на стр. 255, то это значит, что нужно изменить
Положим, что железо доведено до состояния магнитного насыщения, и начнем уменьшать напряженность магнитного поля. Оказывается, что индукция будет убывать теперь по другой кривой, лежащей выше кривой начального намагничения. Напряженность поля может быть доведена до нуля, но намагничение не будет снято. Соответствующие значения намагничения и индукции называют остаточными. Чтобы снять остаточное намагничение, необходимо переменить направление поля. Если иметь в виду опыт, о котором говорилось на стр. 255, то это значит, что нужно изменить
направление тока в первичной катушке, обмотанной около железного тела, на обратное. Размагничивание произойдет тогда, когда напряженность поля достигнет некоторой величины называемой коэрцитивной (задерживающей) силой. При дальнейшем увеличении тока тело начнет намагничиваться в обратном направлении, т. е. там, где был южный полюс, возникнет северный. Магнитный поток будет расти до той же степени насыщения, что и в начальном процессе. Достигнув отрицательного максимума индукции, можно повести процесс в обратную сторону и получить изображенную на рис. 122 петлю гистерезиса.
Достигнув отрицательного максимума индукции, можно повести процесс в обратную сторону и получить изображенную на рис. 122 петлю гистерезиса.
Из этого рисунка следует, что напряженность поля, в которое помещено железо, не определяет еще ни магнитной индукции, ни, следовательно, магнитной проницаемости. Для абсциссы например, возможны три значения индукции: первое имеет место при начальном намагничивании, второе — в процессе размагничивания и третье — по прохождении почти всей петли при повторном намагничивании. Значение магнитной индукции и магнитной проницаемости зависит от предыдущей «исторйи» образца. Отсюда и название «петля гистерезиса».
Обычно рисуют петлю, построенную при условии, что ферромагнитное тело доводится до магнитного насыщения. В то же время ясно, что можно осуществить с куском железа любые петли гистерезиса меньшего размера, как бы вписанные в основную петлю. Для этого надо начать размагничивание, не доходя до насыщения. Тогда каждому значению соответствует сколь угодно большое число значений В.
Отсюда следует способ приведения ферромагнитного тела в состояние, при котором одновременно равны нулю и индукция, и напряженность. Такое приведение магнитного тела в «нулевую точку» осуществляют серией последовательных перемагничиваний, начиная каждый следующий цикл при меньшем значении напряженности, чем предыдущий.
Магнитное состояние железа нельзя характеризовать только значением проницаемости или только величиной напряженности или индукции. Нужно знать две величины, скажем, индукцию и напряженность, которые определят магнитное состояние железа точкой внутри основной гистерезисной петли.
Характер петли гистерезиса сильно зависит от материала. Магнитно-мягкими называют гела, у которых коэрцитивная сила мала (а значит, мала и площадь петли). К мягким материалам относятся чистое железо, кремнистая сталь, сплав железа с никелем (среди них выделяется пермаллой — 78% никеля). Углеродистые и иные стали принадлежат к магнитно-твердым материалам; их используют для изготовления постоянных магнитов.
Опыт показывает, что при перемагничивании ферромагнетик нагревается. Это очень существенно для электротехники, так как при помещении железа в переменное магнитное поле точка графика изображающая магнитное состояние железа, непрерывно обегает петлю гистерезиса. Пробег по петле сопровождается выделением тепла, которое связывается теорией магнитного поля с площадью петли. Разумеется, чем меньше максимальная индукция, тем меньше площадь петли. Поэтому можно попытаться подыскать эмпирические формулы,” связывающие выделяющееся тепло с максимальной индукцией. В электротехнике имеет распространение, например, формула такого вида:
где — коэффициент, значения которого приводятся в таблицах.
Пример. Для хорошего трансформаторного железа потери будут
Это значит, что при перемагничппании железа переменным током частоты мощность потерь в железе составит на каждый кубический сантиметр объема железа.
Услуги по физике:
- Заказать физику
- Заказать контрольную работу по физике
- Помощь по физике
Лекции по физике:
- Физические величины и их измерение
- Основные законы механики
- Прямолинейное равномерное движение
- Прямолинейное равнопеременное движение
- Сила
- Масса
- Взаимодействия тел
- Механическая энергия
- Импульс
- Вращение твердого тела
- Криволинейное движение тел
- Колебания
- Колебания и волны
- Механические колебания и волны
- Бегущая волна
- Стоячие волны
- Акустика
- Звук
- Звук и ультразвук
- Движение жидкости и газа
- Молекулярно-кинетическая теория
- Молекулярно-кинетическая теория строения вещества
- Молекулярно – кинетическая теория газообразного состояния вещества
- Теплота и работа
- Температура и теплота
- Термодинамические процессы
- Идеальный газ
- Уравнение состояния идеального газа
- Изменение внутренней энергии
- Переход вещества из жидкого состояния в газообразное и обратно
- Кипение, свойства паров, критическое состояние вещества
- Водяной пар в атмосфере
- Плавление и кристаллизация
- Тепловое расширение тел
- Энтропия
- Процессы перехода из одного агрегатного состояния в другое
- Тепловое расширение твердых и жидких тел
- Свойства газов
- Свойства жидкостей
- Свойства твёрдых тел
- Изменение агрегатного состояния вещества
- Тепловые двигатели
- Электрическое поле
- Постоянный ток
- Переменный ток
- Электромагнитное поле
- Электромагнитное излучение
- Электрический заряд (Закон Кулона)
- Электрический ток в металлах
- Электрический ток в электролитах
- Электрический ток в газах и в вакууме
- Электрический ток в полупроводниках
- Электромагнитная индукция
- Работа, мощность и тепловое действие электрического тока
- Термоэлектрические явления
- Распространение электромагнитных волн
- Интерференционные явления
- Рассеяние
- Дифракция рентгеновских лучей на кристалле
- Двойное лучепреломление
- Магнитное поле и электромагнитная индукция
- Электромагнитные колебания и волны
- Природа света
- Распространение света
- Отражение и преломление света
- Оптические приборы и зрение
- Волновые свойства света
- Действия света
- Линзы и получение изображений с помощью линз
- Оптические приборы и глаз
- Фотометрия
- Излучение и спектры
- Квантовые свойства излучения
- Специальная теория относительности в физике
- Теория относительности
- Квантовая теория и природа поля
- Строение и свойства вещества
- Физика атомного ядра
- Строение атома
Магнитное поле в физике – виды, формулы и определение с примерами
Содержание:
Магнитное поле:
До сих пор мы изучали явления, связанные с взаимодействием электрических зарядов и электрического поля. Электрическое взаимодействие является составляющей электромагнитных взаимодействий, к которым относится и магнитное взаимодействие. Люди издавна знали, что некоторые руды притягивают железные предметы. Это явление назвали магнетизмом, а куски магнитных руд — природными магнитами. Богатые залежи магнитного железняка есть в Днепропетровской и Запорожской областях. Благодаря магнитному железняку люди впервые ознакомились с магнитными свойствами тел.
Электрическое взаимодействие является составляющей электромагнитных взаимодействий, к которым относится и магнитное взаимодействие. Люди издавна знали, что некоторые руды притягивают железные предметы. Это явление назвали магнетизмом, а куски магнитных руд — природными магнитами. Богатые залежи магнитного железняка есть в Днепропетровской и Запорожской областях. Благодаря магнитному железняку люди впервые ознакомились с магнитными свойствами тел.
Магнит (по-гречески — камень из Магнессии, города, вблизи которого были открыты залежи магнитного железняка) — это тело, обладающее магнитными свойствами. Со временем научились изготовлять искусственные постоянные магниты разнообразной формы и размеров в зависимости от их назначения. Постоянными их называют потому, что они неограниченно долго сохраняют свои магнитные свойства в отличие от электромагнитов, которые можно включать и выключать.
В технике и в лабораторной практике часто используют полосовые (прямые) и подковообразные магниты (рис. 134).
Опыт 1 На столе находятся предметы, изготовленные из разных веществ. Приблизим к ним магнит. Циркуль, гвозди, иглы, стальная пластина притягиваются к магниту (рис. 135), а резинка, монета, спички, алюминиевая фольга, колпачки от ручек остались лежать на столе.
Предметы, содержащие железо, сталь, никель, чугун или их сплавы, притягиваются магнитом. Эти вещества относят к классу ферромагнетиков (от лат. феррум — железо). Бумагу, стекло, пластмассу, медь магнит не притягивает.
Магниты могут притягивать предметы через лист картона или стекло (рис. 136).
Опыт 2 На столе лежат гвозди. Разместим на них магниты. Наибольше гвоздей притягивается у концов магнитов (рис. 137).
Рис. 139 |
Места магнита, где магнитное действие наибольшее, называют полюсами магнита.
Чем дальше от полюсов расположен участок магнита, тем слабее его магнитное действие, тем меньше гвоздей к нему притягивается, а в средней части их совсем нет.
Участок магнита, где не проявляется его магнитное действие, называют средней линией магнита.
Опыт 3. Подвесим на нити магнит, чтобы он был в горизонтальном положении и свободно поворачивался. Если рядом нет предметов, изготовленных из ферромагнетиков, которые сильно взаимодействуют с магнитами, то магнит всегда будет занимать одно и то же положение в направлении север-юг (рис. 138).
Это связано с тем, что Земля имеет два магнитных полюса. На этом основано действие компаса.
Полюс магнита, направленный на север, называется северным (N, от англ. North), а на юг — южным (S, от англ. South).
Демонстрационные и лабораторные магниты, а также магнитные стрелки, как правило, окрашивают традиционно в два цвета: со стороны северного полюса (N) — в синий, со стороны южного (S) — в красный. Граница окрашивания совпадает со средней линией. А может ли магнит иметь один полюс?
Граница окрашивания совпадает со средней линией. А может ли магнит иметь один полюс?
Опыт 4. Разрезаем магнит на две части, отделяя южный полюс от северного. Получили два магнита — с обоими полюсами каждый (рис. 139). Это объясняется тем, что каждый магнит состоит из большого количества малых магнитов, всегда с двумя полюсами (рис. 140).
Рис. 140
Каждый магнит обязательно имеет два полюса: северный и южный.
В технике используют сложные магниты с чётным числом чередующихся полюсов (N — S — N — S). Например, магнит велосипедного генератора имеет 8 полюсов (4 северных и 4 южных) (рис. 141).
Рис. 141
Ориентирование кусков природных и постоянных магнитов в направлении с севера на юг подтверждает, что наша планета обладает магнитными свойствами. Веками многие учёные, мореплаватели и путешественники изучали магнитные свойства Земли в разных географических пунктах.
Странствуя, люди собрали обширные сведения о направлении стрелки компаса в разных местах земной суши и Мирового океана.
В 1595 г. английский физик У. Гильберт изготовил из природного магнита (рис. 142) шар и пришёл к выводу, что у него есть два полюса, а магнитная стрелка вблизи шара устанавливается в направлении от северного полюса к южному. Тогда У. Гильберт предположил, что Земля является большим магнитом (рис. 143). Последующие исследования подтвердили это предположение.
Рис. 142 | Рис. 143 |
Вокруг Земли существует магнитное поле, которое условно изображают магнитными линиями. В каждой точке магнитного поля магнитная стрелка устанавливается вдоль магнитной линии.
На этом явлении основано использование компаса. Каждый компас состоит из магнитной стрелки, свободно вращающейся на оси (рис. 144), и шкалы, на которой нанесены деления и основные стороны света. Стрелка компаса окрашена в сине-красный цвет либо на ней нанесена метка (синий конец и метка указывают северное направление).
Рис. 144
Пользоваться компасом первыми начали китайцы более 4 тысячелетий тому назад. На рисунке 145 вы видите такой компас, а на рисунке 146 — современный компас, его используют на судах. На рисунке 143 схематично изображены магнитные линии поля Земли.
Рис. 145 | Рис. 146 |
Как видим, возле Северного географического поляка размещается Южный магнитный полюс, в котором линии сходятся, а возле Южного географического полюса — Северный магнитный полюс, из которого линии расходятся. Согласно исследованиям намагниченности горных пород магнитные полюса, как и магнитное поле Земли, с течением времени перемещаются, причём это перемещение очень сложное.
Магнитные полюса Земли не совпадают с географическими полюсами.
В связи с этим направление магнитной стрелки не совпадает с направлением географического меридиана. Поэтому магнитная стрелка компаса лишь приблизительно показывает направление на север.
Поэтому магнитная стрелка компаса лишь приблизительно показывает направление на север.
Если активность Солнца возрастает, то с его поверхности в космическое пространство выбрасываются потоки заряженных частиц. Магнитное поле, образующее эти подвижные частицы, изменяет магнитное поле Земли и является причиной магнитных бурь. Во время магнитной бури нарушается радиосвязь, у людей может ухудшаться самочувствие, на Севере наблюдаются полярные сияния и т. д.
Земной магнетизм ещё полностью не изучен, поэтому исследованию магнитного поля Земли уделяется большое внимание во время полётов искусственных спутников и космических кораблей. Установлено, что земное магнитное поле надёжно защищает поверхность нашей планеты от космического излучения, действие которого на живые организмы часто является разрушительным.
Взаимодействие магнитовОпыт 1. Подносим к полюсам магнита магнитную стрелку. Северный полюс стрелки отталкивается от северного полюса магнита и притягивается к южному. Южный полюс стрелки отталкивается от южного полюса и притягивается к северному (рис. 147).
Южный полюс стрелки отталкивается от южного полюса и притягивается к северному (рис. 147).
Опыт 2. Поднесём два магнита сначала их Северными, а потом — южными полюсами. Магниты взаимодействуют между собой, при этом их разноимённые полюса притягиваются, а одноимённые — отталкиваются.
Разместим магнит на карандашах (рис. 148). К магниту приблизим южный (северный) полюс второго магнита. Видим, что и теперь магниты взаимодействуют между собой — притягиваются или отталкиваются.
Рис. 147 | Рис. 148 |
Разноимённые магнитные полюса двух магнитов притягиваются, одноимённые — отталкиваются.
Магниты взаимодействуют между собой, поскольку вокруг любого магнита существует магнитное поле. C одной стороны, магнитное поле одного магнита действует на второй магнит; с другой — магнитное поле второго магнита действует на первый.
Магнитное поле вокруг магнита можно обнаружить разными способами. Один из них состоит в использовании железных опилок (метод спектров).
Опыт 3 Накроем подковообразный магнит стеклом. На стекло насыпем тонкий слой железных опилок и легонько постучим по стеклу. Под действием магнитного поля магнита железные опилки размещаются рядом с магнитом не в беспорядке, а в виде замкнутых линий, которые называют линиями магнитного поля, или магнитными линиями (рис. 149, а).
Линии магнитного поля (магнитные линии) магнита — это воображаемые замкнутые линии, которые выходят из северного полюса магнита и входят в южный, замыкаясь внутри магнита (рис. 149, б).
Направление, которое показывает северный полюс магнитной стрелки в каждой точке поля, принято за направление магнитной линии в этой точке. В данной точке магнитного поля магнитная стрелка имеет единственное направление, это означает, что магнитные линии не пересекаются.
Рис.  149 149 | Рис. 150 |
Рисунок 150 даёт представление о магнитном поле разных магнитов: а — распределение железных опилок в магнитном поле двух магнитов, направленных один к другому одноимёнными полюсами, б — двух магнитов, направленных соответственно разноимёнными полюсами.
Ещё в 1269 г. П. Перегрин написал книгу «Письма о магнитах». В ней были описаны почти все известные в то время свойства магнитов. II. Перегрин установил следующее: если потереть стальную спицу природным магнитом, то она становится магнитом, то есть намагничивается (рис. 151). Такие тела также называют магнитами.
Рис. 151
Каждый из вас может изготовить магнит дома. Для этого возьмите длинный железный гвоздь, молоток или отвёртку и положите их вдоль направления, которое показывает компас, то есть вдоль линии север-юг. А через несколько недель эти предметы начнут проявлять магнитные свойства — притягивать железные гвозди или винтики (рис. 152).
Рис. 152
152
Магнитными свойствами через определённое время будет обладать и лезвие бритвы, если его положить на магнит (рис. 153).
Рис. 153
Железные или стальные тела также становятся магнитами, если их поместить в катушку изолированного провода, по которому проходит электрический ток. Что при этом происходит, рассмотрим позднее.
Долгое время электрические и магнитные явления рассматривали как независимые. Связь между ними установил в 1820 г. датский физик Г. К. Эрстед. В ходе опыта он заметил, что магнитная стрелка, размещённая под проводником (рис. 154, а), при замыкании цепи поворачивается и размещается почти перпендикулярно к проводнику (рис. 154, б). Если электрическую цепь разомкнуть, то стрелка принимает прежнее положение.
Рис. 154
Действие электрического тока на магнитную стрелку означает, что между электрическими и магнитными явлениями существует определённая связь.
В опыте Эрстеда впервые было выявлено магнитное поле тока.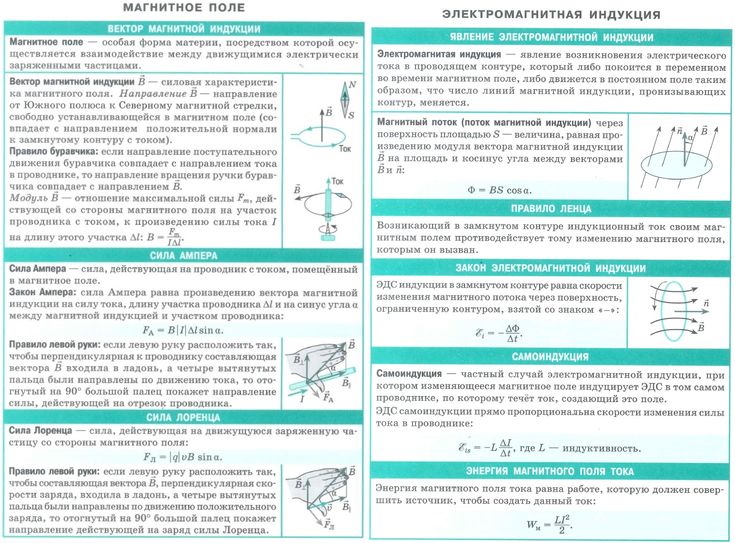 Действительно, если проводник с электрическим током действует на магнитную стрелку, то вокруг этого проводника существует магнитное поле.
Действительно, если проводник с электрическим током действует на магнитную стрелку, то вокруг этого проводника существует магнитное поле.
Вокруг любого проводника с током существует магнитное поле.
Электрический ток — это направленное движение заряженных частиц, следовательно, вокруг движущейся заряженной частицы существуют одновременно магнитное и электрическое поля. А вокруг неподвижных зарядов — только электрическое поле.
Для исследования магнитного поля тока воспользуемся методом спектров, который мы применяли для обнаружения магнитного поля постоянных магнитов.
Опыт 1 Через отверстие в горизонтально размещённом картоне пропускаем вертикальный проводник с током (рис. 155). Картон посыпаем металлическими опилками и замыкаем цепь. В результате видим, что опилки образовали вокруг проводника концентрические окружности.
Рис. 155
Если опилки заменить магнитными стрелками, то они размещаются так, как показано на рисунке 156, а. Здесь изображён вид сверху на картон с цепочками опилок. Кружок в центре — поперечное сечение проводника с током. В нём крестиком обозначен ток в направлении за картон (как хвостовое оперение летящей от нас стрелы). Точкой в кружке обозначен ток в направлении из-за картона (как наконечник летящей на нас стрелы).
Здесь изображён вид сверху на картон с цепочками опилок. Кружок в центре — поперечное сечение проводника с током. В нём крестиком обозначен ток в направлении за картон (как хвостовое оперение летящей от нас стрелы). Точкой в кружке обозначен ток в направлении из-за картона (как наконечник летящей на нас стрелы).
Из опыта следует, что свойства магнитного поля тока такие же, как у магнитного поля постоянного магнита. Поэтому повторим выводы о графическом изображении магнитного поля. При этом помним, что его источником могут быть и постоянный магнит, и электрический ток.
Воображаемые линии, вдоль которых в магнитном поле размещаются продольные оси маленьких магнитных стрелок, называют линиями магнитного поля (магнитными линиями).
Направление, которое показывает северный полюс магнитной стрелки в каждой точке поля, принято за направление линии магнитного поля. В магнитном поле железные или стальные опилки показывают форму магнитных линий этого поля.
Линии магнитного поля тока — это замкнутые линии, окружающиепроводник с током.
Выполним предыдущий опыт, изменив ток в проводнике на противоположное направление. Оказывается, что все магнитные стрелки поворачиваются на 180° (рис. 156, б). Направление линий магнитного поля тока связано с направлением тока в проводнике, на практике его можно установить по правилу буравчика (рис. 156, в).
Если направление поступательного движения буравчика совпадает с направлением тока, то направление вращения ручки буравчика — с направлением магнитных линий.
Рис. 156
Опыт 2. Длинный прямой изолированный провод намотаем на деревянную или пластмассовую катушку. Присоединим её к источнику тока. В катушке проходит электрический ток, а к её концам притягиваются железные предметы, например винт (рис. 157).
Рис. 157
Опыт 3. Подвесим катушку с током на длинных тонких и гибких проводниках. Если рядом нет магнитных материалов или других магнитных полей, то катушка размещается в пространстве так же, как магнитная стрелка компаса: одна сторона катушки поворачивается на север, другая — на юг (рис. 158).
158).
Рис. 158
Катушка с током имеет два магнитных полюса: северный N и южный S.
Опыт 4 На пластинку из оргстекла (рис. 159) кладём железные опилки, по катушке пропускаем электрический ток. Опилки ориентируются в определённом порядке. Линии магнитного поля катушки с током также являются замкнутыми кривыми. То есть вне катушки они направлены от северного полюса катушки к южному (рис. 160, а). Магнитное поле катушки с током подобно магнитному полю штабового магнита (рис. 160, б).
Рис. 159 |
|
На рисунке 158, б показано, как отталкиваются постоянный магнит и катушка с током, поскольку они размещены одноимёнными полюсами один к другому.
Причину, почему тела имеют магнитные свойства, впервые установил французский учёный А. Ампер. Под впечатлением от наблюдений магнитной стрелки, которая поворачивается вблизи проводника с током в опытах Эрстеда, он предположил, что магнетизм Земли вызывают токи, протекающие внутри земного шара. Следовательно, магнитные свойства тела можно объяснить токами, циркулирующими внутри данного тела.
Следовательно, магнитные свойства тела можно объяснить токами, циркулирующими внутри данного тела.
Далее А. Ампер делает обобщение: магнитные свойства любого тела определяются замкнутыми электрическими токами внутри него. Этот решительный шаг от возможности объяснения магнитных свойств тел токами к категорическому утверждению, что магнитные взаимодействия —
это взаимодействия токов, — безусловное доказательство научной смелости А. Ампера.
Гипотеза Ампера
Согласно гипотезе Ампера внутри молекул и атомов циркулируют элементарные электрические токи. Мы уже знаем, что эти токи образуются вследствие движения электронов в атомах, то есть каждый атом обладает магнитными свойствами. Если атомы внутри тела ориентированы хаотически вследствие теплового движения, то действия внутриатомных токов взаимно компенсируются, и магнитных свойств тело не проявляет (рис. 161, α). В намагниченном состоянии элементарные токи в теле ориентированы таким образом, что их действия суммируются (рис. 161, б).
161, б).
Рис. 161
Гипотеза Ампера объясняет, почему магнитная стрелка и рамка с током в магнитном поле ведут себя одинаково. Стрелку (постоянный магнит) можно рассматривать как большую и сложную совокупность небольших рамок с током, ориентированных одинаково.
В ферромагнетиках (вещества, в состав которых входят Fe, Со, Ni и др.) элементарные магнитики-атомы образуют участки спонтанной (произвольной) намагниченности с линейными размерами 0,0010,01 мм, которые называют доменами. В доменах размещается множество одинаково ориентированных атомов, поэтому намагниченность домена максимальна. В ненамагниченном ферромагнетике соседние домены расположены таким образом, что их намагниченности взаимно компенсируются (рис. 162, а). Если образец такого ферромагнетика поместить в магнитное поле постоянного магнита или внутри катушки с током, то под влиянием внешнего магнитного поля атомы в разных доменах преимущественно начинают ориентироваться так, что направление их магнитного поля совмещается с направлением внешнего (рис. 162, б). При этом магнитное поле внутри образца может увеличиться тысячекратно (рис. 162, в). Говорят, что образец намагнитился, при определённых условиях это состояние намагниченности сохраняется и после исчезновения внешнего поля, то есть образец становится постоянным магнитом.
162, б). При этом магнитное поле внутри образца может увеличиться тысячекратно (рис. 162, в). Говорят, что образец намагнитился, при определённых условиях это состояние намагниченности сохраняется и после исчезновения внешнего поля, то есть образец становится постоянным магнитом.
Если его нагревать, то при определённой температуре (для железа 769 °C) домены разрушаются, и намагниченность утрачивается. Температуру, при которой ферромагнетик теряет намагниченность, называют температурой, или точкой Кюри, в честь выдающегося французского физика П. Кюри, открывшего и исследовавшего это явление.
Рис. 162
Открытие Г. К. Эрстеда ознаменовало собой начало ряда исследований по электромагнетизму. В 1820 г. А. Ампер и Д. Араго исследовали магнитное поле катушки. В 1825 г. У. Стерджей, заметил, что магнитное поле катушки значительно усиливается, если в середину её вставить стальной сердечник. Так он получил простейший электромагнит.
В 1828 г. Дж. Генри использовал многослойную обмотку из изолированного провода и получил более мощный электромагнит.
Электромагнит — это коллективное изобретение, прошедшее ряд этапов, где каждый был невозможен без предыдущего.
Электромагнит состоит из следующих деталей (рис. 168): стального сердечника 1, катушки (обмотки) 2 и якоря 3, который притягивается к сердечнику. Выясним, от чего зависит сила, с которой магнитное поле катушки электромагнита действует на его якорь.
Рис. 168
Опыт 1. Замыкаем цепь из электромагнита и реостата; с помощью реостата будем изменять силу тока в катушках. При определённой силе тока электромагнит удерживает определённый груз (рис. 169, а), а если увеличить силу тока в два раза, то электромагнит может удержать груз приблизительно в два раза тяжелее (рис. 169, б).
Рис. 169
Чем больший ток проходит в катушке электромагнита, тем с большей силой притягивается к нему якорь.
Опыт 2 Повторим опыт 1 при начальной силе тока, когда электромагнит удерживал меньший груз, но используем катушку такой же конструкции, содержащую в два раза больше витков. Убедимся, что в этом случае электромагнит способен удерживать такой же большой груз, как в опыте 1, когда в два раза увеличили ток (рис. 169, б).
Чем больше витков в катушке электромагнита, тем с большей I силой притягивается к нему якорь.
Итак, «грузоподъёмность» электромагнита зависит от «ампер-витков» его обмотки, то есть от произведения силы тока в катушке на количество витков в ней.
Электромагниты широко применяют в технике, быту, медицине и т. д. благодаря своим особенностям: быстро размагничиваются при выключении тока; в зависимости от назначения их изготовляют разных размеров; при работе электромагнита можно регулировать его магнитное действие, изменяя силу тока в обмотке.
Электромагниты имеются в каждом автомобиле, телефоне, телевизоре, самолёте, космическом корабле, теплоходе и т. д. Электромагнитный подъёмный кран применяют при погрузке или разгрузке металлолома (рис. 170). Такой кран удобен тем, что груз не требует никаких креплений. Машинист крана размещает электромагнит, например, возле металлолома, включает ток в обмотке и подбирает лом.
д. Электромагнитный подъёмный кран применяют при погрузке или разгрузке металлолома (рис. 170). Такой кран удобен тем, что груз не требует никаких креплений. Машинист крана размещает электромагнит, например, возле металлолома, включает ток в обмотке и подбирает лом.
Рис. 170
После выключения тока металлолом просто отпадает от сердечника. А электромагнит заводского крана, который используют, например, для перенесения бобин листовой стали, имеет 4 обмотки и может поднять бобину диаметром 2 м и массой 28 т (рис. 171).
Рис. 171
На рисунке 172 в разрезе показан магнитный сепаратор для очистки зерна от семян сорняков. В зерно подмешивают сильно измельчённые железные опилки, которые не прилипают к зерну, а только к семенам сорняков. При вращении барабана с электромагнитом внутри происходит распределение зерна и семян сорняков с металлическими опилками.
Рис. 172
Если в глаз попадают тела, на которые действует магнит, то в больнице для их удаления наряду с постоянными магнитами используют электромагниты. Изменяя силу тока в обмотке, регулируют интенсивность магнитного поля и удаляют постороннее тело с глубины до 2,5 мм.
Изменяя силу тока в обмотке, регулируют интенсивность магнитного поля и удаляют постороннее тело с глубины до 2,5 мм.
Два проводника, по которым протекает электрический ток, взаимодействуют между собой с определённой силой, так как на каждый проводник с током действует магнитное поле тока другого проводника.
Магнитное поле действует с определённой силой на любой проводник с током, размещённый в этом поле. Такую силу называют силой Ампера в честь А. М. Ампера, который исследовал и определил зависимость значения и направления этой силы от условий эксперимента.
Опыт 1. Подвесим на подсоединённых к источнику тока гибких проводниках отрезок толстого медного провода АВ. Разместим его горизонтально между полюсами подковообразного магнита (рис. 174, α). В этом случае проводник AjB размещается в магнитном поле, которое образует вокруг себя магнит. Если замкнуть электрическую цепь, то проводник AB начнёт перемещаться, втягиваясь внутрь магнита (рис. 174, б).
174, б).
Если изменить направление электрического тока, то проводник AB будет выталкиваться из магнита (рис. 174, в). Проводник AB также выталкивается, если поменять местами полюса магнита. Направление движения проводника в магнитном поле определяется направлением силы Ампера, действующей на него, и зависит от направления тока в проводнике и размещения относительно полюсов магнита.
Направление силы Ампера, действующей на проводник с током, удобно определять с помощью правила левой руки (рис. 174, в).
Рис. 174
Если ладонь левой руки разместить так, чтобы четыре выпрямленных пальца указывали направление тока в проводнике, а линии магнитного поля входили в ладонь, то отогнутый под прямым углом большой палец укажет направление силы Ампера, действующей на проводник с током.
На практике большое значение имеет вращательное движение проводника с током в магнитном поле как механическое действие электрического тока. На рисунке 175 изображён прибор, с помощью которого можно осуществлять такое движение. В этом приборе лёгкая прямоугольная рамка ABDC посажена на вертикальную ось. На рамку намотано несколько десятков витков провода с изоляцией. Концы катушки соединены с металлическими полукольцами коллектора 2. Один конец провода присоединён к одному полукольцу, а второй — к другому.
В этом приборе лёгкая прямоугольная рамка ABDC посажена на вертикальную ось. На рамку намотано несколько десятков витков провода с изоляцией. Концы катушки соединены с металлическими полукольцами коллектора 2. Один конец провода присоединён к одному полукольцу, а второй — к другому.
Рис. 175 | Рис. 176 |
К каждому полукольцу прижимается металлическая пластина-щётка 1. Щётки необходимы для подведения тока от источника тока к рамке. Одна щётка всегда соединена с положительным полюсом источника, а другая — с отрицательным.
Так как в частях рамки AC и BD ток имеет противоположные направления, то они перемещаются в противоположные стороны, и рамка поворачивается. Присоединённые к её концам полукольца повернутся вместе с ней, и каждое прижмётся к другой щётке, поэтому ток в рамке изменит направление нс противоположное. Поскольку после поворота рамки на 180° одновременно поменялись на противоположные относительно неё и направление магнитного поля, и направление тока, то направления сил Ампера, действующих на части AC и BD рамки не изменяются, а рамка продолжит вращаться в одном направлении. Если бы коллектор 2 не переключал автоматически направление тока в рамке на противоположное, то она останавливалась бы после каждого полуоборота. Вращение катушки с током в магнитном поле используют в конструкции электрического двигателя и электроизмерительных приборов.
Если бы коллектор 2 не переключал автоматически направление тока в рамке на противоположное, то она останавливалась бы после каждого полуоборота. Вращение катушки с током в магнитном поле используют в конструкции электрического двигателя и электроизмерительных приборов.
Без электрических двигателей невозможно представить жизнь современного человека. Вот далеко не полный перечень известных вам устройств, механизмов и машин, в которых используются электрические двигатели: автомобиль, самолёт, трактор, трамвай, троллейбус, лифт и т. д.
Существует множество конструкций разных электродвигателей, но мы будем изучать устройство и принцип действия широко распространённого коллекторного электродвигателя. Он состоит из следующих основных узлов (рис. 176).
- Статор 1 (англ, stator, от латинского слова sto — стою) является постоянным магнитом с наконечниками S и N, или электромагнитом. Он составляет одно целое с корпусом электродвигателя. Статор коллекторного двигателя часто называют индуктором.
 Эта часть двигателя служит для возбуждения магнитного поля.
Эта часть двигателя служит для возбуждения магнитного поля. - Ротор 2 (от латинского слова roto — вращаюсь), или якорь двигателя — собранный из листов специальной стали сердечник определённой формы, на который наматывают изолированный провод — обмотку.
- Концы обмотки припаяны к медным пластинам коллектора, закреплённым на хорошо изолированном барабане на оси ротора.
- Две угольные щётки специальными пружинами плотно прижимаются к коллекторным пластинам. К щёткам от источника тока подаётся напряжение для питания электродвигателя.
Принцип работы рассмотрим на примере простого двигателя (рис. 177). К щёткам 1 и 2 подаётся необходимое для работы электродвигателя напряжение. При взаимодействии тока, проходящего по обмотке, с магнитным полем статора 6 ротор 5 поворачивается таким образом, что рамка оказывается в вертикальном положении, и тока в ней нет, так как щётки касаются не пластин коллектора 3 и 4, а изоляции между ними. Однако благодаря инерции ротор проходит это положение, и щётки снова касаются коллекторных пластин. Каждые пол-оборота коллектор переключает полярность напряжения, поэтому направление тока в обмотке всегда соответствует вращению ротора в одну сторону.
Каждые пол-оборота коллектор переключает полярность напряжения, поэтому направление тока в обмотке всегда соответствует вращению ротора в одну сторону.
При одинаковой мощности размеры электродвигателей меньше, чем у тепловых двигателей. Они не выделяют газов, дыма и пара. Можно изготовить электрический двигатель любой мощности и установить в любом месте. Например, двигатель (рис. 178) имеет мощность 890 кВт, работает при напряжении 1 400 В, и в нём проходит ток 635 А.
Рис. 177 | Рис. 178 |
Один из первых в мире электрических двигателей, пригодных для практического применения, изобрёл российский учёный Б. Якоби.
Электроизмерительные приборыГромкоговоритель предназначен для преобразования электрической энергии в энергию звуковых колебаний. В электродинамическом громкоговорителе используют действие магнитного поля постоянного магнита на переменный ток в подвижной катушке.
Внешний вид и схема устройства громкоговорителя приведены на рисунке 179. Звуковая катушка 1 установлена в зазоре кольцевого магнита 2. C катушкой жёстко соединён бумажный конус — диффузор 4, который по периметру укреплён на упругих подвесках 3.
По катушке проходит переменный электрический ток с частотой звукового сигнала микрофона или радиоприёмника, проигрывателя, магнитофона. Под действием силы Ампера катушка колеблется вдоль своей оси в такт изменениям силы тока. Эти колебания передаются диффузору, и его поверхность излучает звуковые волны.
Рис. 179
Громкоговорители высокого качества передают без значительных искажений звуковые колебания от 40 до 15 000 Гц. Но такие устройства очень сложные. Поэтому используют систему из нескольких громкоговорителей, при этом каждый из них передаёт звук в определённом небольшом интервале частот. Недостаток всех громкоговорителей — малый КПД. Они излучают лишь 1—35 % всей направленной к ним энергии.
В технике широко используют стрелочные измерители электрических величин, основанью на магнитном действии тока. Существуют несколько систем электроизмерителей магнитного действия: в приборах электромагнитной системы стрелка-указатель связана с ферромагнитным сердечником, который втягивается в катушку, где протекает измеряемый ток; в приборах магнитоэлектрической системы указатель связан с лёгкой рамкой с измеряемым током, которая поворачивается в поле магнита на угол, пропорциональный значению этого тока.
Существуют несколько систем электроизмерителей магнитного действия: в приборах электромагнитной системы стрелка-указатель связана с ферромагнитным сердечником, который втягивается в катушку, где протекает измеряемый ток; в приборах магнитоэлектрической системы указатель связан с лёгкой рамкой с измеряемым током, которая поворачивается в поле магнита на угол, пропорциональный значению этого тока.
Рассмотрим подробнее устройство и действие наиболее распространённых приборов магнитоэлектрической системы (рис. 180).
Рис. 180
Они состоят из подковообразного магнита 1, возле полюсов которого размещаются наконечники 6, между которыми на двух полуосях вращается лёгкая алюминиевая рамка 3. На рамку наматывают тонкий изолированный проводник.
Для усиления магнитного поля в пространстве между полюсами размещают неподвижный железный цилиндр 2. К передней полуоси рамки прикрепляют лёгкую алюминиевую стрелку 4. Концы проводника на рамке припаивают к двум пружинам 5, по которым подаётся ток к обмотке рамки.
При прохождении тока по обмотке рамки она поворачивается. Чем большая сила тока проходит через рамку, тем на больший угол поворачивается стрелка. Если электрическую цепь разомкнуть, то пружины под действием сил упругости, возникающих при повороте рамки, возвращают стрелку в нулевое положение шкалы 7.
C помощью приборов магнитоэлектрической системы можно измерять такие электрические величины, как силу тока, напряжение.
Пример №1
В произведении французского физика Д. Ф. Араго «Гром и молния» приводится много случаев перемагничивания компасной стрелки, намагничивания стальных предметов под действием молнии. Как объяснить эти явления?
Ответ: молния — это искровой разряд. Вокруг неё возникает сильное магнитное поле, которое действует на стальные предметы, намагничивая и перемагничивая их.
Пример №2
Объясните результаты опыта (рис. 181).
Ответ: если цепь не замкнута, то все магнитные стрелки размещаются в направлении север-юг. Если цепь замкнуть, то катушка становится магнитом, и магнитные стрелки взаимодействуют с ней.
Если цепь замкнуть, то катушка становится магнитом, и магнитные стрелки взаимодействуют с ней.
Рис. 181
Пример №3
Рамка с током размещена между полюсами подковообразного магнита, при этом её плоскость перпендикулярна линиям магнитного поля. Будет ли поворачиваться рамка?
Ответ: нет, поскольку в этом случае у рамки отсутствует вращательный момент.
- Заказать решение задач по физике
Вы уже знаете свойства электрического поля неподвижных электрических зарядов и магнитного поля постоянных магнитов и постоянных электрических токов в неподвижных проводниках. После открытия в 1820 г. Эрстедом явления возникновения магнитного поля вокруг проводника с током начались исследования явлений в электрических и магнитных полях, изменяющихся с течением времени.
Если электрический ток создаёт магнитное поле, то можно предположить существование обратного явления: возникновение электрического тока в проводнике, помещённом в магнитное поле. Многочисленные попытки обнаружить это явление не принесли ожидаемых результатов. В неподвижных замкнутых проводниках, помещённых в наиболее мощные на то время магнитные поля, электрический ток не возникал.
Многочисленные попытки обнаружить это явление не принесли ожидаемых результатов. В неподвижных замкнутых проводниках, помещённых в наиболее мощные на то время магнитные поля, электрический ток не возникал.
В 1831 г. М. Фарадей экспериментально открыл новое явление электромагнитной индукции, ставшее основой современной электротехники и радиотехники. Его нельзя было предсказать на основе известных в то время сведений о магнитных полях и электрических токах. Выяснилось, что электрический ток все-таки возникает в неподвижном замкнутом проводнике, помещённом в магнитное поле, но лишь при изменении этого магнитного поля.
Опыты Фарадея, которые привели к открытию явления электромагнитной индукции, достаточно просты, их легко провести в условиях школы.
Опыт 1. Присоединим к гальванометру гибкий проводник и поместим его между полюсами магнита (рис. 195). Если проводник и магнит неподвижны, то тока в проводнике нет. При перемещении проводника гальванометр сразу же фиксирует в нём наличие тока. Если при перемещении проводника в одном направлении стрелка гальванометра отклоняется, например, вправо, то при движении в обратном направлении она будет отклоняться влево, то есть направление тока в проводнике изменяется. Ток в проводнике возникает и в случае перемещения магнита относительно проводника.
Если при перемещении проводника в одном направлении стрелка гальванометра отклоняется, например, вправо, то при движении в обратном направлении она будет отклоняться влево, то есть направление тока в проводнике изменяется. Ток в проводнике возникает и в случае перемещения магнита относительно проводника.
Рис. 195
Опыт 2. Присоединим к гальванометру катушку. Если в эту катушку вводить или выводить магнит (рис. 196), то гальванометр показывает возникновение электрического тока в цепи. Если магнит неподвижен — тока нет.
Рис. 196
Опыт 3 Закрепим полосовой магнит в штативе и наденем катушку, присоединив её к гальванометру, на магнит (рис. 197). В катушке снова возникает электрический ток. Этот ток протекает только при движении катушки относительно магнита и изменяет свое направление при изменении направления движения катушки.
Рис. 197
Опыт 4. Замкнём катушку 2 через гальванометр и вставим в неё катушку 1, которую можно присоединить к источнику тока (рис. 198). В момент замыкания цепи катушки 1 стрелка гальванометра отклоняется, то есть при изменении (возникновении) магнитного поля катушки 1 по катушке 2 протекает электрический ток. Но после установления в катушке 1 тока магнитное поле перестаёт изменяться, ток в катушке 2 исчезает — стрелка гальванометра устанавливается на нуле.
198). В момент замыкания цепи катушки 1 стрелка гальванометра отклоняется, то есть при изменении (возникновении) магнитного поля катушки 1 по катушке 2 протекает электрический ток. Но после установления в катушке 1 тока магнитное поле перестаёт изменяться, ток в катушке 2 исчезает — стрелка гальванометра устанавливается на нуле.
Рис. 198
Разомкнём цепь катушки. При исчезновении в ней тока, а вместе с ним и его магнитного поля стрелка гальванометра отклоняется в противоположную сторону. Это означает, что в катушке 2 возникает электрический ток, направление которого обратно тому, который проходил при замыкании катушки 1. В этих опытах при замыкании цепи катушки 1 возникает магнитное поле, а при размыкании — исчезает. В результате изменений магнитного поля в катушке возникает переменный ток, который называют индукционным.
В цепь катушки 1 можно включить реостат для изменения силы тока в цепи. Итак, при увеличении силы тока в цепи катушки 1 в катушке 2 возникает индукционный ток одного направления, при уменьшении — противоположного направления. В результате изменения силы тока в катушке 1 изменяется также магнитное поле тока, при этом в катушке 2 возникает индукционный ток.
В результате изменения силы тока в катушке 1 изменяется также магнитное поле тока, при этом в катушке 2 возникает индукционный ток.
Явление возникновения в замкнутом проводнике переменного электрического тока при пересечении этим проводником линий магнитного поля называют электромагнитной индукцией. Ток, возникающий при этом, называется индукционным.
Из данных примеров следует, что индукционный электрический ток возникает при изменении в пространстве или во времени интенсивности магнитного поля, линии которого окружают проводник замкнутого контура. Изучая свойства электромагнитов, мы узнали, что интенсивность магнитного поля катушки с током можно изменять, регулируя в ней силу тока. Видим, что такие изменения можно выполнить разными способами.
Магнитное поле изображают с помощью магнитных линий. Оказалось, что в местах поля, где его интенсивность меньше, линии проходят реже, а где больше — размещаются гуще. Это видно на рисунках 143,149,150,160, где изображены магнитные поля Земли, постоянных магнитов и катушки с током. Поля с переменными плотностью и направлением линий называют неоднородными. Если плотность и направление линий постоянны, то есть магнитные линии параллельны, а расстояния между соседними линиями одинаковы, то такое поле называют однородным. К однородным приближаются магнитные поля внутри длинной катушки с током (см. рис. 160, а) или между широкими полюсами постоянных магнитов.
Поля с переменными плотностью и направлением линий называют неоднородными. Если плотность и направление линий постоянны, то есть магнитные линии параллельны, а расстояния между соседними линиями одинаковы, то такое поле называют однородным. К однородным приближаются магнитные поля внутри длинной катушки с током (см. рис. 160, а) или между широкими полюсами постоянных магнитов.
В замкнутом проводящем контуре индукционный ток возникает только при изменении плотности магнитных линий, пронизывающих этот контур. Индукционный ток тем больше, чем больше скорость изменения магнитного поля. Проводник, перемещаясь, обязательно должен пересекать магнитные линии. Если проводник контура движется вдоль магнитных линий или катушка перемещается поступательно в однородном магнитном поле, то индукционный ток не возникает.
Индукционный ток в проводнике может иметь разные направления. Опыты показывают, что направление индукционного тока в проводнике, движущемся в магнитном поле, зависит от направления линий магнитного поля и направления движения проводника. На практике направление индукционного тока в подвижном проводнике определяют по правилу правой руки (рис. 199).
На практике направление индукционного тока в подвижном проводнике определяют по правилу правой руки (рис. 199).
Рис. 199
Если ладонь правой руки разместить так, чтобы в неё входили линии магнитного поля, а отведённый под прямым углом большой палец указывал направление движения проводника, то вытянутые четыре пальца руки укажут направление индукционного тока в проводнике.
Пример №4
Если разместить проволочный прямоугольник в плоскости магнитного меридиана и перемещать его в этой плоскости, то будет ли в нём возникать индукционный ток?
Ответ: нет, поскольку стороны прямоугольника не пересекают магнитных линий магнитного поля Земля.
Историческая справка:
Фарадей Майкл (22.09.1791-25.08.1867) — английский физик, член Лондонского королевского общества. Родился в предместье Лондона в семье кузнеца. Из-за бедности не получил систематического образования. Слушая воскресные лекции Г. Деви, попросил взять его на работу в Королевский институт, в котором работал с 1813 г., в 1825 г. возглавил лабораторию в этом институте, с 1827 г. — профессор кафедры химии.
Деви, попросил взять его на работу в Королевский институт, в котором работал с 1813 г., в 1825 г. возглавил лабораторию в этом институте, с 1827 г. — профессор кафедры химии.
Майкл Фарадей
Выполнил фундаментальные исследования по электромагнетизму. Поставил перед собой задачу «преобразовать магнетизм в электричество» и получить электрический ток из магнитного поля. В 1831 г. открыл явление электромагнитной индукции, то есть получил индукционный ток во вторичной обмотке при замыкании и размыкании тока в первичной обмотке. М. Фарадей детально исследовал явления электромагнитной индукции и самоиндукции, высказал предположение, что электрические и магнитные действия не передаются от тела к телу непосредственно, а переносятся в диэлектрической среде, размещённой между ними.
В 1833—1834 гг. установил законы электролиза и ввёл основную терминологию этого явления. Ввёл понятия электрического и магнитного поля, а также электрических и магнитных силовых линий. После исследований М. Фарадея материю начали рассматривать не только в форме вещества, но и в форме поля. В 1843 г экспериментально доказал закон сохранения электрического заряда. Сделал открытия в области магнетизма (1845) и действия магнитного поля на свет (1846).
Фарадея материю начали рассматривать не только в форме вещества, но и в форме поля. В 1843 г экспериментально доказал закон сохранения электрического заряда. Сделал открытия в области магнетизма (1845) и действия магнитного поля на свет (1846).
Вы приобрели начальные знания о постоянном магнитном поле и появлении магнитного поля вокруг проводника с током. В частности, вы получили общие сведения о магнитном поле прямого проводника с током и катушки с током, об электромагнитах и их применении. Однако вы еще не знакомы с математическими выражениями по определению их величин. В данной главе вы познакомитесь, с такими величинами, как магнитная индукция и магнитный поток, индукция магнитного поля прямого тока, индукция магнитного поля катушки с током, сила, действующая на частицу, движущуюся в магнитном поле.
Магнитное поле и величины, характеризующие магнитное полеВ природе существуют природные соединения металлов, которые обладают свойством притягивать к себе некоторые другие тела. Это означает, что они создают вокруг себя поле. Такое поле принято называть магнитным полем. Тела, длительное время сохраняющие свою намагниченность, называются постоянным магнитом, или магнитом.
Это означает, что они создают вокруг себя поле. Такое поле принято называть магнитным полем. Тела, длительное время сохраняющие свою намагниченность, называются постоянным магнитом, или магнитом.
Возьмем магнит прямоугольной формы и приблизим его к мелким частицам железа. Мы увидим, что они прилипают только к двум концам магнита. Те места магнита, где обнаруживается наибольшее магнитное действие, называются полюсами постоянного магнита. Постоянный магнит имеет два магнитных полюса: северный (N) и южный (S) (рис. 1.1).
Из рис. 1.2 видно, что если две магнитные стрелки приблизить друг к другу, то магниты притягиваются разноименными полюсами и отталкиваются одноименными. Это означает, что между намагниченными телами существует сила взаимного действия. Действующие силы характеризуются через силовые линии магнитного поля.
Силовые линии магнитного поля увидеть невозможно. Однако с помощью следующего опыта мы сможем получить представление о расположении (направлении) магнитных силовых линий. Для этого картонную бумагу равномерно покроем железными опилками и положим ее на поверхность плоского магнитного стрежня. Если несколько раз осторожно встряхнуть картонную бумагу, то железные опилки примут вид, как показано на рис. 1.3 а. На рисунке видно, что опилки на картоне собираются плотнее у концов магнита, а между полюсами их меньше.
Для этого картонную бумагу равномерно покроем железными опилками и положим ее на поверхность плоского магнитного стрежня. Если несколько раз осторожно встряхнуть картонную бумагу, то железные опилки примут вид, как показано на рис. 1.3 а. На рисунке видно, что опилки на картоне собираются плотнее у концов магнита, а между полюсами их меньше.
Картина распределения железных опилок на рис. 1.3 а показывает положение силовых линий, связывающих магнитные полюсы. Силовыми линиями магнитного поля принято считать замкнутые кривые, которые выходят из северного полюса, а входят в южный полюс магнита (рис. 1.3 б). Поля с замкнутыми силовыми линиями называются вихревыми полями. Значит, магнитное поле является вихревым полем. Этим свойством силовые линии магнитного поля отличаются от силовых линий электрического поля.
Физическая величина, характеризующая величину силовых линий определенной точки магнитного поля, называется индукцией магнитного поля. Индукция магнитного поля является векторной величиной и обозначается буквой
Индукция магнитного поля является векторной величиной и обозначается буквой
Единицей измерения индукции магнитного поля в системе СИ в честь сербского физика Никола Тесла принято называть тесла (Тл)
Магнитный потокДля описания величины магнитных силовых линий, пересекающих какие-либо поверхности, введено понятие «поток магнитного поля». Потоком магнитной индукции, пересекающим площадь S, называется произведение вектора магнитной индукции на площадь поверхности. Магнитный поток является скалярной величиной и обозначается буквой Ф. Магнитный поток выражается как:
Если индукционные линии магнитного поля создают с поверхностью определенный угол (рис. 1.4), то поток магнитной индукции, проходящий через поверхность, будет зависеть от этого угла, т.е.:
Здесь а – угол между вектором и нормалью к поверхности.
В системе СИ единицу магнитного потока назвали в честь немецкого физика Д. Вебера -вебер (Вб). Из уравнения (1-2):Магнитное поле, проходящее сквозь перпендикулярно расположенную площадь 1 к линиям индукции магнитного поля, равной 1 Тл, составляет 1 Вб.
Пример №5
Силовые линии однородного магнитного поля с индукцией 20 мТ падают под углом 60° на прямоугольную рамку длиной 4 см и шириной 3 см. Определите магнитный поток, проходящий сквозь рамку?
Рис. 1.4.
Дано:
Найти: Ф = ?
Формула:
Решение: Ответ:
Вращательный момент однородного магнитного поля, действующий на рамку с токомТо, что магнитное поле создается не только постоянными магнитами, но и вокруг проводников с токами, показал на своих опытах Эрстед. Теперь мы рассмотрим взаимное действие магнитного поля проводника с током и постоянным магнитным полем.
Если в магнитное поле внести контур или магнитную стрелку, то можно наблюдать, как они поворачиваются (рис. 1.5). Когда меняется направление тока в контуре, контур поворачивается в противоположную сторону.
Давайте определим причину вращения рамки с током, расположенную в магнитном поле. Рамка длиной расположена вертикально в магнитном поле, и через стороны АВ и CD течет ток I. Тогда значение силы Ампера, действующей со стороны магнитного поля на участок рамки, составляет:
Тогда значение силы Ампера, действующей со стороны магнитного поля на участок рамки, составляет:
здесь:
Направление этой силы определяется по правилу левой руки. Модули сил, действующих на участки АВ и CD, являются равными и направлены в противоположные стороны, т.е. на рамку с током со стороны магнитного поля действует пара сил. Под воздействием этой пары сил рамка с током поворачивается.
Эта пара сил относительно оси вращения создает вращательный момент.
Момент силы:
Здесь, a – угол между нормалью, проведенной на поверхность контура и вектора магнитной индукции, плечо сил частей рамки равно
Тогда полный вращательный момент:
Подставляя формулу силы Ампера в выражение (1-5), запишем выражение вращательного момента:
Если учесть, что, выражение (1-6) примет вид:
Значит, момент силы (М), действующей на контур с током, внесенный в магнитное поле, прямо пропорционален силе тока , протекающего через контур, площади контура (S) и синусу угла между направлением магнитной индукции и нормалью, проведенной на поверхность контура
Если,
Согласно этому уравнению индукцию магнитного поле можно выразить:
Принцип действия многих электрических приборов основан на взаимодействии проводника с током с постоянным магнитом. На рис. 1.6 приводится строение одного из таких измерительных приборов. Между полюсами (1) сильного магнита закреплен железный сердечник . Сверху надета проволочная рамка (2). В катушку ток подается через металлические пружины (3), которые держат рамку. Эти пружины, в случае когда не подается ток в катушку, удерживают стрелку (4) в положении, равном нулю. При подключении прибора в электрическую цепь через катушку проходит ток и рамка поворачивается под воздействием магнитного поля. В это время пружины начинают сжиматься. Рамка продолжает поворачиваться до тех пор, пока не сравняются сила упругости пружины и сила Ампера.
На рис. 1.6 приводится строение одного из таких измерительных приборов. Между полюсами (1) сильного магнита закреплен железный сердечник . Сверху надета проволочная рамка (2). В катушку ток подается через металлические пружины (3), которые держат рамку. Эти пружины, в случае когда не подается ток в катушку, удерживают стрелку (4) в положении, равном нулю. При подключении прибора в электрическую цепь через катушку проходит ток и рамка поворачивается под воздействием магнитного поля. В это время пружины начинают сжиматься. Рамка продолжает поворачиваться до тех пор, пока не сравняются сила упругости пружины и сила Ампера.
Когда прибор последовательно подсоединен к электрической цепи, из-за равнозначности силы тока, протекающего через цепь и катушку прибора, угол поворота стрелки будет прямо пропорционален силе тока. В этом случае прибор используется в качестве амперметра.
На рисунке 1.6 б приводится общий вид двигателя постоянного тока. Его принцип работы основан на вращении рамки с током в постоянном магнитном поле.
Пример №6
Проволочная рамка с сечением 20 и имеющая 100 витков размещена в магнитном поле. Когда через рамку проходит ток силой 2 А, в ней появляется максимальный вращательный момент, равный 0,5 . Определите индукцию магнитного поля.
Дано:
Найти:
Формула:
Решение:
Ответ:
Магнитное поле прямого тока, кругового тока и катушки с токомДля наблюдения силовых линий магнитного поля, образующихся вокруг проводника с током, берем картонную бумагу, просверливаем в середине отверстие и пропускаем через нее прямой проводник. На поверхности картонной бумаги рассыпаем железные опилки. Когда проводник подсоединен к источнику тока, картон слегка подергивается. Под воздействием магнитного поля тока железные опилки ведут себя как магнитные стрелки и располагаются по линиям магнитной индукции (рис. 1.7 а.).
Силовые линии магнитного поля прямого тока состоят из окружностей с центрами на оси проводника. Эти окружности перпендикулярны оси проводника (рис. 1.7 б). Направление силовых линий магнитного поля определяется правилом правого винта: если поступательное движение винта совпадает с направлением тока, тогда направление вращения рукоятки винта показывает направление линии магнитной индукции.
Эти окружности перпендикулярны оси проводника (рис. 1.7 б). Направление силовых линий магнитного поля определяется правилом правого винта: если поступательное движение винта совпадает с направлением тока, тогда направление вращения рукоятки винта показывает направление линии магнитной индукции.
Вектор индукции магнитного поля направлен по касательной к силовым линиям. В частном случае направление индукции магнитного поля в точке на расстоянии d от проводника с током приводится на рисунке 1.8 а.
В большинстве случаев магнитное поле создается не одним проводником, а системой проводников с током (рис. 1.8 б). Тогда индукция результирующего поля в определенных точках пространства будет равной векторной сумме индукции магнитного поля, созданного в данной точке каждым проводником с током, т.е.:
Это называется принципом суперпозиции для магнитного поля.
Французские ученые Ж. Био, Ф. Савар и П. Лаплас вывели общий закон, позволяющий вычислять индукцию магнитного поля, создаваемого вокруг проводника с током произвольной формы. Согласно этому закону индукцию магнитного поля, озданного произвольным элементом проводника с током в точке А вокруг проводника, можно определить по следующей формуле:
Согласно этому закону индукцию магнитного поля, озданного произвольным элементом проводника с током в точке А вокруг проводника, можно определить по следующей формуле:
а – угол между вектором, проведенным от элемента в точку А и элементом фис. 1.9). – расстояние от элемента прямого тока до точки А.
Индукция магнитного поля, создаваемая в точке А на расстоянии от прямого тока бесконечной длины, по закону Био-Савара-Лапласа, определяется с помощью следующего выражения:
Значит, индукция магнитного поля, создаваемого в произвольной точке прямого проводника с током бесконечной длины, прямо пропорциональна
силе тока, проходящего через проводник, и обратно пропорциональна кратчайшему расстоянию между проводником и точкой, для которой вычисляется индукция.
Индукция магнитного поля в центре кругового токаПусть постоянный ток течет по кругу с радиусом R (рис. 1.10). По закону Био-Савара-Лапласа индукция магнитного поля, созданного в центре кругового тока, равна векторной сумме индукции, создаваемой элементами проводника длиной в центре круга:
1.10). По закону Био-Савара-Лапласа индукция магнитного поля, созданного в центре кругового тока, равна векторной сумме индукции, создаваемой элементами проводника длиной в центре круга:
здесь:-коэффициент, магнитная постоянная вакуума, его величина равна . Значит, индукция магнитного поля, создаваемого в
центре кругового тока, прямо пропорциональна силе тока, протекающего по проводнику, и обратно пропорциональна радиусу круга.
В частном случае индукцию магнитного поля в центре катушки с током, имеющей количество витков п (рис. 1.11), можно определить следующим выражением:
Значит, индукция магнитного поля, создаваемого внутри катушки с током, прямо пропорциональна силе тока, протекающего через катушку, и количеству витков и обратно пропорциональна радиусу катушки.
Пример №7
По проводнику бесконечной длины протекает ток силой 250 мА. Вычислите индукцию магнитного поля в точке, находящейся на расстоянии 4 см от него.
Дано:
Найти:
Формула:
Решение:
Работа, выполненная при перемещении проводника с током в магнитном полеРассмотрим случай, когда два параллельных плоских металлических провода а и б расположены на расстоянии друг от друга, а сверху установлен легкий металлический проводник с (рис. 1.12). Система проводников расположена в однородном магнитном поле с магнитной индукцией . На рисунке 1.12 знак означает, что вектор магнитной индукции направлен перпендикулярно поверхности рисунка. Когда проводники а и б подключаются к источнику тока, через проводник с протекает ток. Здесь на проводник с током длиной со стороны магнитного поля действует сила Ампера Зная, что угол между направлением тока и направлением индукции магнитного поля равен 90°, направление силы определяется по правилу левой руки.
1.12). Система проводников расположена в однородном магнитном поле с магнитной индукцией . На рисунке 1.12 знак означает, что вектор магнитной индукции направлен перпендикулярно поверхности рисунка. Когда проводники а и б подключаются к источнику тока, через проводник с протекает ток. Здесь на проводник с током длиной со стороны магнитного поля действует сила Ампера Зная, что угол между направлением тока и направлением индукции магнитного поля равен 90°, направление силы определяется по правилу левой руки.
Эта сила, перемещая проводник с на расстояния d, выполняет работу, равную
В этом выражении произведение – это площадь, вычерченная проводником в ходе движения, т.е. . Если магнитный поток, пересекающий проводник в ходе движения, равен , то мы имеем выражение:
Следует отметить, что эта работа выполняется не магнитным полем, а за счет энергии источника тока, питающего электрическую цепь.
Значит, работа, выполненная силой Ампера при перемещении проводника с током в магнитном поле, равна произведению силы тока, протекающего по проводнику, и изменению магнитного потока.
Работа, выполняемая при перемещении проводника с током в магнитном поле, широко используется в практике: на различных видах транспортных средств, в бытовой технике и электронике. Примером этого также могут служить часто используемые на сегодняшний день электронные замки.
Пример №8
По проводнику длиной 30 см протекает ток силой 2 А. Проводник расположен под углом 30° к индукционным линиям однородного магнитного поля с индукцией 1,5 Тл. Какая работа выполняется при перемещении проводника на 4 см в направлении силы Ампера?
Дано:
Найти:
Формула:
Решение:
Сила взаимодействия проводников с током
Между проводниками с током существует сила взаимного действия, как и у электрических зарядов. Чтобы наблюдать это явление на практике, возьмем два эластичных проводника, закрепим их вертикально к опоре.
Если верхние части проводников соединить проволокой, то через них в противоположных направлениях потечет ток (рис. 1. 13 а). В результате проводники будут отталкиваться друг от друга и расстояние между ними увеличится. Если обеспечить течение тока в одном направлении, тогда проводники будут притягиваться друг к другу (рис. 1.13 б).
13 а). В результате проводники будут отталкиваться друг от друга и расстояние между ними увеличится. Если обеспечить течение тока в одном направлении, тогда проводники будут притягиваться друг к другу (рис. 1.13 б).
Используя закона Ампера, определим направление и количественное значение силы взаимодействия, создаваемой между параллельно расположенными в вакууме бесконечными проводниками с током.
Пусть по проводникам, расположенным параллельно, на расстоянии d друг от друга в одном направлении протекают токи (рис. 1.14).
Линии вектора индукции магнитного поля токов протекающих по проводникам, состоят из концентричных кругов. Если ток протекает снизу вверх, тогда на точках, лежащих на втором проводнике, вектор (по закону винта) будет направлен от нас в сторону поверхности, и они расположатся взаимно перпендикулярно. Сила действия со стороны магнитного поля первого тока на второй ток, по закону Ампера, по величине равна:
здесь:-длина части второго проводника, расположенного в магнитном поле. Если в эту формулу подставить выражение магнитной индукции
Если в эту формулу подставить выражение магнитной индукции
прямого тока то
Значит, сила взаимодействия на единицу длины двух параллельных бесконечных проводников с током прямо пропорциональна произведению силы тока, протекающего по ним, и обратно пропорциональна расстоянию между ними.
На основе данного явления в международной системе единиц принята единица силы тока – ампер (А).
Ампер – равен силе постоянного тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади сечения, расположенным в вакууме на расстоянии 1 м друг от друга, вызвал бы на каждом метре длины проводника силу взаимодействия, равную
Пример №9
Найдите силу взаимодействия, приходящуюся на каждый метр длины провода линии электропередачи постоянного электрического тока двух проводников с расстоянием между ними 1,6 м. Принять силу тока, протекающего по проводникам, равную 40 А.
Дано:
Найти:
Формула:
Решение:
Движение заряженных частиц в однородном магнитном поле.
 Сила Лоренца
Сила ЛоренцаСилу Ампера, действующую со стороны магнитного поля на проводник с током, расположенный в магнитном поле, можно рассматривать как сумму действующих сил на каждом участке этого проводника. Если количество всех заряженных частиц, движущихся в проводнике с током длиной равно N, то сила, действующая на одну частицу, движущуюся в магнитном поле, равна:
Сила тока, протекающего по проводнику, равна
Если выражение (1-17) вставить в выражение (1-16), получаем выражение силы, действующей на одну частицу:
здесь: е-заряд электрона; -скорость упорядоченного движения частицы; -концентрация зарядов; S-поперечное сечение проводника.
Сила, действующая со стороны магнитного поля на заряженную частицу, движущуюся в магнитном поле, называется силой Лоренца. Она описывается следующим образом: Сила действующая на заряженную частицу, движущуюся в однородном магнитном поле, равна произведению заряда частицы q, ее скорости движения вектора индукции магнитного поляи синуса угла между вектором индукции магнитного поля и вектором скорости.
Направление силы Лоренца определяется по правилу левой руки (рис.1.15). Если расположить левую ладонь так, чтобы вытянутые пальцы совпадали с направлением положительных зарядов, а силовые линии магнитного поля входили в ладонь, то отогнутый на 90° большой палец укажет направление силы Лоренца.
Сила Лоренца, действующая на протон, влетающий в магнитное поле, согласно правилу левой руки, будет направлена в правую сторону (рис.1.16). При определении движения электрона (отрицательного заряда) в поле,четыре пальца расположим в положении, противоположном направлению тока. Тогда действующая на электрон сила Лоренца будет направлена в левую сторону (рис. 1.16).
Теперь рассмотрим влияние силы Лоренца на движение заряженных частиц. Пусть частица влетает в однородное магнитное поле перпендикулярно силовым линиям (рис. 1.17). Тогда угол между направлением скорости частицы и линией индукции равен 90° и сила Лоренца, действующая на частицу, будет максимальной. Из-за того, что сила Лоренца направлена перпендикулярно направлению движения частиц в магнитном поле, она выполняет функцию центростремительной силы. В результате меняется направление движения заряженной частицы, и ее траектория движения искривляется.Численное значение центробежной силы, которая появляется при движении по окружности, равняется силе Лоренца, т.е.:
Из-за того, что сила Лоренца направлена перпендикулярно направлению движения частиц в магнитном поле, она выполняет функцию центростремительной силы. В результате меняется направление движения заряженной частицы, и ее траектория движения искривляется.Численное значение центробежной силы, которая появляется при движении по окружности, равняется силе Лоренца, т.е.:
Так как сила Лоренца не выполняет работу, скорость движения частицы не меняется. Значит, частица продолжает равномерное движение по окружности.
Траектория движения заряженной частицы в магнитном поле представляет окружность, и ее радиус можно определить из следующего выражения:
Значит, радиус кривизны траектории частицы прямо пропорционален произведению ее массы и скорости и обратно пропорционален произведению ее заряда и индукции магнитного поля.
Теперь определим время, необходимое для одного полного оборота, т.е. период вращения. Для этого разделим путь, пройденный частицей за один оборот (длина окружности на скорость частицы:
Используя выражение (1-21), выражение (1-22) запишем в следующем виде:
Согласно этой формуле период вращения частицы не зависит от ее скорости, а зависит от значений массы и заряда частицы и индукции магнитного поля.
Прибор, разделяющий движущиеся в магнитном и электрическом полях заряженные частицы на составляющие части по массе, называется масс-спектрометром. Масс-спектрометры применяются для определения изотопов химических элементов и химического анализа вещества.
Пример №10
Электрон, влетая перпендикулярно к индукционным линиям поля с индукцией 12 мТ, продолжил движение по окружности радиусом 4 см. Найдите, с какой скоростью электрон влетел в поле.
Дано:
Найти:
Формула:
Решение:
Самые важные понятия, правила и законыМагнитные силовые линии: Магнитные силовые линии представляют собой замкнутые линии, выходящие из северного полюса и входящие в южный полюс.
Поток магнитной индукции: Потоком магнитной индукции Ф, проходящим через площадь называется произведение вектора В магнитной индукции на эту площадь
Единица магнитного потока: Магнитное поле с индукцией, равной 1 Тл, проходящее через площадь расположенную перпендикулярно к линиям индукции магнитного поля, составляет
Формула Био-Савара-Лапласа: Определяет магнитную индукцию, созданную в точке А вокруг проводника с током, произвольным элементом проводника
Принцип суперпозиции магнитного поля: Индукция результирующего поля в определенных точках пространства будет равна векторной сумме индукции магнитного поля, созданного в данной точке каждым проводником с током.
Индукция магнитного поля прямого тока – прямо пропорциональна силе тока, протекающего по проводнику, и обратно пропорциональна расстоянию между точкой, для которой определяется индукция, и проводником.
Индукция магнитного поля в центре кругового тока:-прямо пропорциональна силе тока, протекающего по проводнику, и обратно пропорциональна радиусу окружности.
Вращательный момент рамки с током: – прямо пропорционален силе тока, проходящего по контуру, площади контура и синусу угла между направлением вектора индукции и нормалью проведенной на поверхности контура.
Работа, выполненная в магнитном поле: – работа, выполненная при перемещении проводника в магнитном поле, равна произведению силы тока, протекающего по проводнику, на изменение магнитного потока при движении проводника.
Взаимодействие проводников с током: При течении тока по параллельным проводникам в противоположном направлении проводники отталкиваются друг от друга. В случае течения тока в одном направлении проводники притягиваются друг к другу.
Сила взаимодействия двух параллельных проводников с током: -сила взаимодействия единицы длины параллельного проводника с током прямо пропорциональна произведению силы тока, протекающего по ним, и обратно пропорциональна расстоянию между ними.
Описание ампера – единицы измерения силы тока: Ампер равен силе постоянного тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины, расположенным в вакууме на расстоянии 1 м друг от друга, вызвал бы на каждом метре длины проводника силу взаимодействия, равную
Сила Лоренца: Сила, действующая со стороны магнитного поля на заряженную частицу, движущуюся в магнитном поле
Правило левой руки: Если расположить левую ладонь так, чтобы вытянутые пальцы совпадали с направлением движения положительных зарядов, а силовые линии магнитного поля входили в ладонь, то отогнутый на 90° большой палец укажет направление силы Лоренца.
Радиус кривизны частицы, влетевшей перпендикулярно силовым линиям магнитного поля: -радиус кривизны траектории частицы пря-qB мо пропорционален произведению массы и скорости частицы и обратно пропорционален произведению ее заряда и индукции магнитного поля.
Период вращения частицы, влетевшей перпендикулярно линиям магнитного поля : – период вращения частицы не зависит от ее скорости, а зависит от значений массы и заряда частицы и индукции магнитного поля.
Энергия магнитного поляСила тока в контуре (а значит, и связанное с ним магнитное ноле) достигает своего постоянного значения не мгновенно, а в течение конечного промежутка времени после замыкания цепи. При этом в цепи возникает ЭДС самоиндукции, препятствующая нарастанию силы тока. Следовательно, источник тока при замыкании цепи совершает работу против ЭДС самоиндукции. Работа, затраченная источником на создание тока в контуре (без учета тепловых потерь), и определяет, в конечном счете, энергию магнитного поля, запасаемую контуром с током. Рассматриваемая работа равна взятому со знаком «минус» произведению средней ЭДС самоиндукции и заряда прошедшего по цепи. Знак «минус» появляется потому, что источник тока совершает работу, равную по модулю, но противоположную по знаку работе вихревого электрического поля при замыкании цепи.
Подчеркнем, что при нарастании тока ЭДС самоиндукции изменяется с течением времени, поэтому для вычисления работы рассмотрим малые промежутки времени, в течение которых будем считать неизменной.
Для малого промежутка времени можем записать:
Поскольку ЭДС самоиндукции
а прошедший за малый промежуток времени заряд то получаем
Величина соответствует площади закрашенного прямоугольника (рис. 175).
Тогда всю работу можно вычислить, складывая площади подобных прямоугольников под графиком зависимости В результате при уменьшении интервала разбиений получится площадь прямоугольного треугольника ОВС:
Следовательно, энергию магнитного поля контура с током можно определить по формулам (с учетом Ф = LI):
Энергию магнитного поля, заключенную в единице объема пространства, занятого полем, называют объемной плотностью энергии магнитного поля
Если магнитное поле создано внутри соленоида длиной l и площадью поперечного сечения S, содержащего N витков, то с учетом выражений для индуктивности соленоида и модуля вектора индукции магнитного поля внутри соленоида получаем
Здесь — магнитная проницаемость вещества внутри соленоида.
Так как SI = V, то для вычисления плотности энергии магнитного поля получим выражение
| № п/п | Наименование параметра | Формула | Обозначения |
|---|---|---|---|
| 4.1 | Закон Био-Савара-Лапласа Модуль вектора Модуль вектора | ― магнитная индукция поля, создаваемого элементом проводника с током; μ ― магнитная проницаемость среды, μ0 = 4π∙10−7 Гн/м ― магнитная постоянная, ― вектор, равный по модулю длине dl проводника и совпадающий по направлению с током; I ― сила тока в проводнике, ― расстояние до проводника α ― угол между векторами и ― напряженность магнитного поля, создаваемого элементом проводника с током | |
| 4.2 | Индукция магнитного поля, создаваемого бесконечно длинным прямым проводником с током Напряженность магнитного поля |
| μ ― магнитная проницаемость среды, μ0 = 4π∙10−7 Гн/м ― магнитная постоянная, I ― сила тока в проводнике, a ― расстояние до проводника |
4. 3 3 | Индукция магнитного поля в центре кругового проводника с током Напряженность магнитного поля | μ ― магнитная проницаемость среды, μ0 = 4π∙10−7 Гн/м ― магнитная постоянная, I ― сила тока в проводнике, R ― радиус проводника | |
| 4.4 | Индукция магнитного поля на оси кругового проводника с током Напряженность магнитного поля | вывод формул | μ ― магнитная проницаемость среды, μ0 = 4π∙10−7 Гн/м ― магнитная постоянная, I ― сила тока в проводнике, R ― радиус проводника, a ― расстояние до плоскости проводника |
| 4.5 | Индукция магнитного поля внутри длинного соленоида | μ ― магнитная проницаемость среды, μ0 = 4π∙10−7 Гн/м ― магнитная постоянная, I ― сила тока в проводнике, N ― количество витков, l ― длина соленоида | |
| 4.6 | Магнитная индукция поля, создаваемая отрезком проводника | вывод формулы | μ ― магнитная проницаемость среды, μ0 = 4π∙10−7 Гн/м ― магнитная постоянная, a ― расстояние до оси проводника, α1 и α2 ― углы между направлением тока и направлением на точку, в которой создано магнитное поле, вершинами которых являются соответственно начало и конец прямого участка проводника |
4. 7 7 | Связь между напряженностью H и индукцией B магнитного поля | μ ― магнитная проницаемость среды, μ0 = 4π∙10−7 Гн/м ― магнитная постоянная | |
| 4.8 | Связь между электрической и магнитной напряженностями волны | Е0 ― амплитуда электрической напряженности, H0 ― амплитуда магнитной напряженности | |
| 4.9 | Фазовая скорость волны v равна | с ― скорость света в вакууме; ε ― диэлектрическая проницаемость; μ ― магнитная проницаемость | |
| 4.10 | Индуктивность катушки равна | μ0 = 4π∙10−7 Гн/м ― магнитная постоянная; N ― количество витков; N = l/d, d ― диаметр проводника катушки; l ― длина катушки; V ― объем катушки; S ― площадь витка катушки | |
| 4.11 | Средняя объемная плотность энергии | μ0 = 4π∙10−7 Гн/м ― магнитная постоянная; μ ― магнитная проницаемость среды; для вакуума μ = 1; Н ― действующее значение напряженности магнитного поля | |
4. 12 12 | Средняя объемная плотность энергии | ε0 = 8,85∙10−12 Ф/м ― электрическая постоянная, ε ― диэлектрическая проницаемость среды, E ― действующее значение напряженности электрического поля | |
| 4.13 | Сила , действующая на заряд Q, движущийся со скоростью в магнитном поле с индукцией (сила Лоренца) | или | α ― угол, образованный вектором скорости движения частицы и вектором индукции магнитного поля |
| 4.14 | Cила Ампера (сила, действующая на проводник с током в магнитном поле) | I ― сила тока, l ― длина проводника, В ― индукция магнитного поля, α ― угол между векторами | |
| 4.15 | Количество заряда, протекающее в контуре | вывод формулы | ΔΨ ― изменение потокосцепления контура; R ― сопротивление контура; N ― количество витков в контуре; ΔФ ― изменение магнитного потока, пронизывающего контур; S ― площадь витка; ΔB ― изменение магнитной индукции |
4. 16 16 | Циклическая частота колебаний в контуре | L ― индуктивность контура; C ― емкость контура | |
| 4.17 | Мгновенное значение I силы тока в цепи, обладающей активным сопротивлением R и индуктивностью L, после размыкания цепи | I0 ― значение силы тока в цепи при t = 0; t ― время, прошедшее с момента размыкания цепи | |
| 4.18 | Мгновенное значение I силы тока в цепи, обладающей активным сопротивлением R и индуктивностью L, после замыкания цепи | ε ― э.д.с. источника тока; t ― время, прошедшее с момента замыкания цепи | |
| 4.19 | Основной закон электромагнитной индукции | εi ― электродвижущая сила индукции; N ― число витков контура; Ψ ― потокосцепление | |
| 4.20 | Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока I: | L ― индуктивность контура или катушки | |
| 4.21 | Работа по перемещению проводника или по повороту контура в магнитном поле | I ― сила тока в проводнике, контуре; dФ ― пересекаемый проводником магнитный поток либо изменение магнитного потока через замкнутый контур | |
4. 22 22 | Вращающий момент, действующий на контур с током, помещенный в магнитное поле Значение вращающего момента | При α=π/2 имеем При α=0 или α=π имеем | ― индукция магнитного поля; m ― магнитный момент контура, m = IS, где I ― ток, протекающий по контуру, S ― площадь контура; α ― угол между векторами m и |
3. Магнитное поле в вакууме и веществе Основные формулы:
Закон Био-Савара-Лапласа: ,
где о=410-7Гн/м.
Магнитная индукция в центре кругового тока: .
Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током:
Магнитная индукция поля,
создаваемого отрезком проводника:
Связь магнитной индукции с напряженностью магнитного поля:
Магнитная индукция поля, создаваемого соленоидом в средней его части (или тороида на его оси):
Принцип суперпозиции магнитных полей:
Закон Ампера:
Сила взаимодействия двух прямых бесконечно длинных параллельных проводников с токами:
Магнитный
момент контура с током: Pm=I . S .
S .
Механический момент, действующий на контур с током, помещенный в однородное магнитное поле: M = pm.B sin
Сила, действующая на заряд, движущийся в магнитном поле (сила Лоренца): F = q V B sin
Закон полного тока:
Магнитный поток через плоский контур: Ф = B S cos .
Потокосцепление, то есть полный магнитный поток, сцепленный со всеми витками соленоида или тороида: .
Магнитный поток сквозь тороид, сердечник которого составлен из двух частей, изготовленных из веществ с различными магнитными проницаемостями:
Задача 18. Бесконечно длинный тонкий проводник с током I = 50А имеет изгиб (плоскую петлю) радиусом R = 10см. Определить в точке О магнитную индукцию В поля, создаваемого этим током.
Дано: I = 50А R = 10см | Решение. | |
В— ? | ||
Магнитная индукция в точке О согласно принципа суперпозиции равна где— магнитные индукции поля в точкеО, создаваемые током, текущим соответственно на первом, втором и третьем участках проводника.
Векторы в соответствии с правилом буравчика направлены перпендикулярно плоскости чертежа в одну сторону (к нам), то есть геометрическое суммирование можно заменить алгебраическимВ = В1 + В2 +В3 .
Магнитная индукция В2 в точке О создается половиной кругового проводника с током, поэтому
Таким образом,
Ответ: B=8,05·10-4 Тл.
Задача
19. По двум
бесконечно длинным прямым параллельным
проводам текут токи I1 = 20 А и I2 = 30 А в одном
направлении. Расстояние d между проводами равно 10 см. Вычислить
напряженность магнитного поля H в точке, удаленной от обоих проводов на
одинаковое расстояние r = 10
см.
Вычислить
напряженность магнитного поля H в точке, удаленной от обоих проводов на
одинаковое расстояние r = 10
см.
Дано: I1 = 20 А I 2 = 30 А d = 10см r = 10 см | Решение. | |
H — ? | ||
Напряженность магнитного поля в точке А согласно принципа суперпозиции равна .Результирующая напряженность по модулю и направлению является диагональю параллелограмма, построенного на векторах
, где =60о.
Отсюда .
Ответ: H=69,2 А/м.
Задача
20. Провод в
виде тонкого полукольца радиусом R = 10 см находится в однородном магнитном
поле (В = 50 мТл). По проводу течет ток I=10
А. Найти силу
,
действующую на провод, если плоскость
полукольца перпендикулярна линиям
магнитной индукции, а проводящие провода
находятся вне поля.
По проводу течет ток I=10
А. Найти силу
,
действующую на провод, если плоскость
полукольца перпендикулярна линиям
магнитной индукции, а проводящие провода
находятся вне поля.
Дано: R = 10 см В = 50 мТл = =50 . 10—3 Тл I = 10 А. | Решение. |
F — ? |
Выделим на проводе малый элемент dℓ с током I. На этот элемент тока действует сила Ампера. Направление этой силы определяется по правилу векторного произведения или по правилу левой руки.
Ввиду симметрии провода координатные оси удобно выбрать, как показано на рисунке.
Сила
,
действующая на весь провод, равна.
Из соображений симметрии.
Тогда.
Так как вектор перпендикулярен вектору,
тоdF=JBdℓ.
Из рисунка видно, что
Проинтегрировав последнее выражение в пределах от —π/2 до π/2, имеем
Сила сонаправлена с единичным вектором.
F = 2 I B R = 1 H .
Ответ: F = 1 H .
Задача 21. Электрон в атоме водорода движется вокруг ядра по круговой орбите некоторого радиуса. Найти отношение магнитного момента Рm эквивалентного кругового тока к моменту импульса L орбитального движения электрона. Заряд электрона и его массу считать известными.
Дано: m = 9,1 . 10—31 кг e = 1,6 . 10—19 Кл | Решение. | |
Рm /L — ? | ||
Эквивалентный
круговой ток обусловлен движением
электрона по круговой орбите с периодом T.
,
где V – скорость движения электрона по круговой орбите.
Магнитный момент кругового тока равен
.
Момент импульса электрона определяется по формуле L=mVr. Отсюда .
Ответ: .
Задача 22. Электрон движется в однородном магнитном поле с индукцией В=9 мТл по винтовой линии, радиус которой равен 1см и шаг h=7,8 см. Определить период Т обращения электрона и его скорость V.
Дано: В = 9 мТл R= 1 см h =7,8 см =7,8 . 10-2м m = 9,1 . 10—31 кг e = 1,6 . 10—19 Кл Т— ? V— ? | Решение. |
Электрон в магнитном поле движется по винтовой линии под действием силы Лоренца. Вектор скорости V составляет угол c направлением вектора магнитной индукции . Электрон движется по окружности радиусаR в плоскости, перпендикулярной линиям индукции со скоростью Vy=Vsinα; одновременно он движется и вдоль поля со скоростью .
Уравнение движения электрона по окружности имеет вид . Отсюда.
Шаг винтовой линии h равен пути, пройденному электроном вдоль поля за время, равное периоду обращения электрона Т по окружности h=VxT=Vcosα·T, где . Таким образом, и угол равен .
Подставив значение sin в формулу для скорости , получаем
V.7 м/с.
Период обращения электрона Т = 3,97 . 10—9 с.
Ответ: V. 7 м/с, Т = 3,97 . 10—9 с.
7 м/с, Т = 3,97 . 10—9 с.
Задача 23. Линии напряженности однородного электрического поля и линии индукции однородного магнитного поля взаимно перпендикулярны. Напряженность электрического поля 1 кВ/м, а индукция магнитного поля 1 мТл. Какими должны быть направление и модуль скорости электрона, чтобы его движение было прямолинейным?
Дано: Е = 1кВ/м =103 В/м В = 1 мТл 10—3 Тл | Решение. | |
V— ? | ||
На электрон действуют две силы:
сила Лоренца , направленная перпендикулярно скоростии вектору магнитной индукции;
кулоновская сила , совпадающая по направлению с вектором напряженности электрического поля.

По первому закону Ньютона не будет испытывать отклонения при своем движении, если илиeE – eVB=0. Отсюда .
Ответ: V=106 м/с.
Задача 24. Сколько витков имеет катушка, индуктивность которой L=1мГн, если при токе I = 1A магнитный поток сквозь катушку Ф=2мкВб ?
Дано: L= 1мГн I = 1A Ф = 2мкВб | Решение. Магнитный поток сквозь катушку равен Отсюда число витков |
N— ? |
Ответ: N = 500.
Задача
25. Железное
кольцо диаметром D=11,4
см имеет обмотку из N=200
витков, по которой течет ток I1=15
A.
Какой ток I2 должен проходить через обмотку, чтобы
индукция в сердечнике осталась прежней,
если в кольце сделать зазор шириной b=1
мм? Найти магнитную проницаемость
материала сердечника при этих условиях.
Дано: D = 11,4 см N = 200 I 1 = 15 A b = 1 мм B = const | Решение. Напряженность магнитного поля по средней линии кольца без воздушного зазора равна – длина средней линии кольца. | |
I 2 — ? | Пользуясь графиком зависимости индукции B от | |
напряженности H магнитного поля для железа, который находится в конце любого задачника по физике, определим индукцию магнитного поля в кольце. В = 1,8 Тл.
Пренебрегая
рассеянием магнитного потока, можно
принять, что индукция поля в воздушном
зазоре равна индукции в железе.
По закону полного тока H1ℓ+Hob=I2N, где – напряженность поля в зазоре. Отсюда токI2 равен .
Пользуясь выражением для магнитного поля сквозь тороид, сердечник которой составлен из двух частей, запишем формулу для магнитной индукции в виде
. Отсюда магнитная проницаемость железа равна .
Ответ: I2=21,8 А, μ≈180.
Задача 26. Проводник с активной длиной 15 см движется со скоростью 10 м/с перпендикулярно линиям индукции однородного магнитного поля с индукцией 2 Тл. Какая сила тока возникает в проводнике, если его замкнуть накоротко? Сопротивление цепи 0,5 Ом.
Дано: l = 15 см V10 м/с B = 2 Тл R = 0,5 Ом. | Решение. | |
I— ? | ||
При движении проводника в магнитном поле в нем индуцируется ЭДС индукции, равная , где ∆Ф=B·∆S, ∆S – площадь, которую описывает проводник при своем движении. ∆S=ℓV∆t. Отсюда . Сила тока, возникающая в проводнике.
Ответ: I=6 А.
Задача 27. В однородном магнитном поле с индукцией 0,35 Тл равномерно с частотой 480 мин—1 вращается рамка, содержащая 500 витков площадью 50 см2 . Ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции. Определить максимальную ЭДС индукции, возникшую в рамке.
Дано: B = 0,35 Тл 480 мин—1 N = 500 витков S = 50 см2 = =
5 . | Решение. ЭДС индукции, возникающая в рамке, равна где Ф = N B S cos t — магнитный поток, сцепленный с рамкой. |
in— ? | — циклическая частота. |
Ответ: εmax=44 В.
Задача 28. Рамка, имеющая форму квадрата, помещена в однородное магнитное поле индукции 0,1 Тл. Перпендикуляр к плоскости рамки составляет с направлением магнитного поля угол 60о. Определить длину стороны рамки, если известно, что среднее значение ЭДС индукции, возникающей в рамке при выключении тока в течение 0,03 с, равно 10 мВ.
Дано: B1 = 0,1 Тл B2 = 0 in =10 мВ =0,032 c | Решение. | |
—? | ||
ЭДС индукции, возникающая в рамке, равна
где Ф = B . S cos — изменение магнитного потока за время Δt,
B = B2 — B1 = – B1, S=2 .
. Отсюда .
Ответ: α=4·10-2 м.
Задача 29. Имеется катушка длиной ℓ=20 см и диаметром D=2 см. Обмотка катушки состоит из N=200 витков медной проволоки, площадь поперечного сечения которой S=1 мм2. Катушка включена в цепь с некоторой ЭДС. При помощи переключателя ЭДС выключается, и катушка замыкается накоротко. Через какое время t после выключения ЭДС ток в цепи уменьшится в 2 раза?
Дано: =20 см =0,2 м D=2 см = 0,02 м N=200 витков S=1 мм2 = 10—6 м2 1,7. Io / I = 2 | Решение. Вследствие явления самоиндукции при выключении ЭДС ток в цепи спадает по закону , где – сопротивление катушки, | |
t— ? | – индуктивность катушки, | |
площадь поперечного сечения катушки,
длина катушки.
, .
Отсюда .
Ответ: t=2,5·10-4с.
Задача
30. Уравнение
изменения со временем разности
потенциалов на обкладках конденсатора
в колебательном контуре имеет вид U=
50 cos104t . Емкость конденсатора С=0,1мкФ.
Найти период Т колебаний, индуктивность контура L,
закон изменения со временем тока I в цепи и
длину волны соответствующую
этому контуру.
Дано: U= 50 cos 104t С=0,1мкФ | Решение. Из уравнения U = 50 cos104t следует, что Uo=50, 104 рад/с. | |
T — ? L — ? — ? I = I ( t ) — ? | . Отсюда . , , где V=3·108 м/с – скорость электромагнитных волн, | |
λ=6·104 м.
Закон изменения тока I от времени имеет вид ,
где Io=qoω=UoCω. Отсюда закон изменения тока в
рассматриваемом контуре имеет вид:
Отсюда закон изменения тока в
рассматриваемом контуре имеет вид:
Ответ: L=0,01 Гн, T= 2·10-4 с, λ=6·104 м,
I=-157·10-3sin104πt А.
Задача 31. Колебательный контур состоит из катушки с индуктивностью L=1,2мГн и конденсатора переменной емкости от С1=12.10—12Ф до С2=80.10—12 Ф. Определить диапазон длин электромагнитных волн, которые могут вызвать резонанс в этом контуре. Активное сопротивление контура принять равным нулю.
Дано: L= 1,2 мГн С1 = 12.10—12Ф С2 = 80.10—12 Ф v = 3 . 108 м/с | Решение. Длина электромагнитной волны, которая может вызвать резонанс в контуре, равна V.Т, где V — скорость электромагнитной волны, |
1- ?, 2— ? | —период колебаний. |
Следовательно,
Ответ: λ1=226 м, λ2=585 м.
Задача 32. В колебательном контуре с индуктивностью 0,4 Гн и емкостью 20 мкФ максимальное значение силы тока равно 0,1мА. Каким будет напряжение на конденсаторе в момент, когда энергия электрического и магнитного полей будут равны? Колебания считать незатухающими.
Дано: L= 0,4 Гн С= 10 мФ=10—5Ф Imax= 0,1мА =10—4 А Wэ = Wм | Решение. Энергия колебательного контура в любой момент времени равна сумме энергий электрического и магнитного полей. . . | |
U— ? | Согласно закона сохранения энергии | |
. WЭ=WМ. . Отсюда.
Ответ: U=0,02 В.
Список литературы
Савельев И.В. Курс общей физики. Кн.2. – М.: Наука, 1999.
Трофимова Т.И. Курс физики. – М.: Высшая школа, 1998.
Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высшая школа, 1998.
Волькенштейн В.С. Сборник задач по общему курсу физики. – СПб.: СпецЛит, 2001.
Чертов А.Г., Воробьев А.А. Задачник по физике. – М.: Интеграл-пресс, 1997.
Составители: СТРОКИНА Венера Рамазановна
ШАТОХИН Сергей Алексеевич
ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим занятиям
по курсу общей физики
Редактор Соколова
О. А.
А.
Подписано в печать 23.04.2003 Формат 60 х 84 1/16.
Бумага оберточная. Печать плоская. Гарнитура Times New Roman Cyr.
Усл. печ. л. 2,5. Усл.-кр.-отт. 2,4. Уч-изд.л. 2,4.
Тираж 350 экз. Заказ № .
Уфимский государственный авиационный технический университет
Редакционно-издательский комплекс УГАТУ
450000, Уфа-центр, ул. К.Маркса, 12
0
определение, основные формулы, правило левой и правой руки
Часто бывает, что задачу не удается решить из-за того, что под рукой нет нужной формулы. Выводить формулу с самого начала – дело не самое быстрое, а у нас на счету каждая минута.
Ниже мы собрали вместе основные формулы по теме «Электричество и Магнетизм». Теперь, решая задачи, вы сможете пользоваться этим материалом как справочником, чтобы не терять время на поиски нужной информации.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Магнетизм: определение
Магнетизм – это взаимодействие движущихся электрических зарядов, происходящее посредством магнитного поля.
Поле – особая форма материи. В рамках стандартной модели существует электрическое, магнитное, электромагнитные поля, поле ядерных сил, гравитационное поле и поле Хиггса. Возможно, есть и другие гипотетические поля, о которых мы пока что можем только догадываться или не догадываться вовсе. Сегодня нас интересует магнитное поле.
Магнитная индукция
Так же, как заряженные тела создают вокруг себя электрическое поле, движущиеся заряженные тела порождают магнитное поле. Магнитное поле не только создается движущимися зарядами (электрическим током), но еще и действует на них. По сути магнитное поле можно обнаружить только по действию на движущиеся заряды. А действует оно на них с силой, называемой силой Ампера, о которой речь пойдет позже.
Изображение магнитного поля при помощи силовых линийПрежде чем мы начнем приводить конкретные формулы, нужно рассказать про магнитную индукцию.
Магнитная индукция – это силовая векторная характеристика магнитного поля.
Она обозначается буквой B и измеряется в Тесла (Тл). По аналогии с напряженностью для электрического поля Е магнитная индукция показывает, с какой силой магнитное поле действует на заряд.
Кстати, вы найдете много интересных фактов на эту тему в нашей статье про теорию магнитного поля и интересные факты о магнитном поле Земли.
Как определять направление вектора магнитной индукции? Здесь нас интересует практическая сторона вопроса. Самый частый случай в задачах – это магнитное поле, создаваемое проводником с током, который может быть либо прямым, либо в форме окружности или витка.
Для определения направления вектора магнитной индукции существует правило правой руки. Приготовьтесь задействовать абстрактное и пространственное мышление!
Если взять проводник в правую руку так, что большой палец будет указывать на направление тока, то загнутые вокруг проводника пальцы покажут направление силовых линий магнитного поля вокруг проводника. Вектор магнитной индукции в каждой точке будет направлен по касательной к силовым линиям.
Вектор магнитной индукции в каждой точке будет направлен по касательной к силовым линиям.
Сила Ампера
Представим, что есть магнитное поле с индукцией B. Если мы поместим в него проводник длиной l, по которому течет ток силой I, то поле будет действовать на проводник с силой:
Это и есть сила Ампера. Угол альфа – угол между направлением вектора магнитной индукции и направлением тока в проводнике.
Направление силы Ампера определяется по правилу левой руки: если расположить левую руку так, чтобы в ладонь входили линии магнитной индукции, а вытянутые пальцы указывали бы направление тока, отставленный большой палец укажет направление силы Ампера.
Сила Лоренца
Мы выяснили, что поле действует на проводник с током. Но если это так, то изначально оно действует отдельно на каждый движущийся заряд. Сила, с которой магнитное поле действует на движущийся в нем электрический заряд, называется силой Лоренца. Здесь важно отметить слово «движущийся», так на неподвижные заряды магнитное поле не действует.
Здесь важно отметить слово «движущийся», так на неподвижные заряды магнитное поле не действует.
Итак, частица с зарядом q движется в магнитном поле с индукцией В со скоростью v, а альфа – это угол между вектором скорости частицы и вектором магнитной индукции. Тогда сила, которая действует на частицу:
Как определить направление силы Лоренца? По правилу левой руки. Если вектор индукции входит в ладонь, а пальцы указывают на направление скорости, то отогнутый большой палец покажет направление силы Лоренца. Отметим, что так направление определяется для положительно заряженных частиц. Для отрицательных зарядов полученное направление нужно поменять на противоположное.
Если частица массы m влетает в поле перпендикулярно линиям индукции, то она будет двигаться по окружности, а сила Лоренца будет играть роль центростремительной силы. Радиус окружности и период обращения частицы в однородном магнитном поле можно найти по формулам:
Радиус окружности и период обращения частицы в однородном магнитном поле можно найти по формулам:
Взаимодействие токов
Рассмотрим два случая. Первый – ток течет по прямому проводу. Второй – по круговому витку. Как мы знаем, ток создает магнитное поле.
В первом случае магнитная индукция провода с током I на расстоянии R от него считается по формуле:
Мю – магнитная проницаемость вещества, мю с индексом ноль – магнитная постоянная.
Во втором случае магнитная индукция в центре кругового витка с током равна:
Также при решении задач может пригодиться формула для магнитного поля внутри соленоида. Соленоид – это катушка, то есть множество круговых витков с током.
Пусть их количество – N, а длина самого соленоилда – l. Тогда поле внутри соленоида вычисляется по формуле:
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Магнитный поток и ЭДС
Если магнитная индукция – векторная характеристика магнитного поля, то магнитный поток – скалярная величина, которая также является одной из самых важных характеристик поля. Представим, что у нас есть какая-то рамка или контур, имеющий определенную площадь. Магнитный поток показывает, какое количество силовых линий проходит через единицу площади, то есть характеризует интенсивность поля. Измеряется в Веберах (Вб) и обозначается Ф.
Представим, что у нас есть какая-то рамка или контур, имеющий определенную площадь. Магнитный поток показывает, какое количество силовых линий проходит через единицу площади, то есть характеризует интенсивность поля. Измеряется в Веберах (Вб) и обозначается Ф.
S – площадь контура, альфа – угол между нормалью (перпендикуляром) к плоскости контура и вектором В.
При изменении магнитного потока через контур в контуре индуцируется ЭДС, равная скорости изменения магнитного потока через контур. Кстати, подробнее о том, что такое электродвижущая сила, вы можете почитать в еще одной нашей статье.
По сути формула выше – это формула для закона электромагнитной индукции Фарадея. Напоминаем, что скорость изменения какой-либо величины есть не что иное, как ее производная по времени.
Для магнитного потока и ЭДС индукции также справедливо обратное. Изменение тока в контуре приводит к изменению магнитного поля и, соответственно, к изменению магнитного потока. При этом возникает ЭДС самоиндукции, которая препятствует изменению тока в контуре. Магнитный поток, который пронизывает контур с током, называется собственным магнитным потоком, пропорционален силе тока в контуре и вычисляется по формуле:
Изменение тока в контуре приводит к изменению магнитного поля и, соответственно, к изменению магнитного потока. При этом возникает ЭДС самоиндукции, которая препятствует изменению тока в контуре. Магнитный поток, который пронизывает контур с током, называется собственным магнитным потоком, пропорционален силе тока в контуре и вычисляется по формуле:
L – коэффициент пропорциональности, называемый индуктивностью, который измеряется в Генри (Гн). На индуктивность влияют форма контура и свойства среды. Для катушки с длиной l и с числом витков N индуктивность рассчитывается по формуле:
Формула для ЭДС самоиндукции:
Энергия магнитного поля
Электроэнергия, ядерная энергия, кинетическая энергия. Магнитная энергия – одна из форм энергии. В физических задачах чаще всего нужно рассчитывать энергию магнитного поля катушки. Магнитная энергия катушки с током I и индуктивностью L равна:
Объемная плотность энергии поля:
Конечно, это не все основные формулы раздела физики «электричество и магнетизм», однако они часто могут помочь при решении стандартных задач и расчетах. Если же вам попалась задача со звездочкой, и вы никак не можете подобрать к ней ключ, упростите себе жизнь и обратитесь за решением в сервис студенческой помощи.
Если же вам попалась задача со звездочкой, и вы никак не можете подобрать к ней ключ, упростите себе жизнь и обратитесь за решением в сервис студенческой помощи.
12.4 Магнитное поле токовой петли – University Physics Volume 2
Глава 12. Источники магнитных полей
Цели обучения
К концу этого раздела вы сможете:
- Объяснять, как закон Био-Савара используется для определения магнитного поля, вызванного током в проволочной петле в точке вдоль линии перпендикулярно плоскости петли.
- Определить магнитное поле дуги тока.
Круговая петля на рис. 12.11 имеет радиус R , по ней течет ток I , и она лежит в плоскости xz . Чему равно магнитное поле, обусловленное током в произвольной точке P по оси петли?
Рисунок 12.11 Определение магнитного поля в точке P вдоль оси проволочного контура с током. Мы можем использовать закон Био-Савара, чтобы найти магнитное поле, вызванное током. Сначала мы рассмотрим произвольные сегменты на противоположных сторонах петли, чтобы качественно показать векторными результатами, что чистое направление магнитного поля находится вдоль центральной оси петли. Отсюда мы можем использовать закон Био-Савара, чтобы получить выражение для магнитного поля.
Сначала мы рассмотрим произвольные сегменты на противоположных сторонах петли, чтобы качественно показать векторными результатами, что чистое направление магнитного поля находится вдоль центральной оси петли. Отсюда мы можем использовать закон Био-Савара, чтобы получить выражение для магнитного поля.
Пусть P будет расстоянием y от центра петли. Согласно правилу правой руки, магнитное поле [латекс]d\stackrel{\to }{\textbf{B}}[/latex] на уровне P , создаваемое элементом тока [латекс]I\фантом{\правило {0.2em}{0ex}}d\stackrel{\to }{\textbf{l}},[/latex] направлен под углом [latex]\theta[/latex] над осью y , как показано . Поскольку [latex]d\stackrel{\to }{\textbf{l}}[/latex] параллелен вдоль оси x , а [latex]\hat{\textbf{r}}[/latex] находится в 9{\prime}[/latex], перпендикулярные оси y , поэтому сокращаются, и при расчете чистого магнитного поля необходимо учитывать только компоненты вдоль оси y . Компоненты, перпендикулярные оси петли, попарно равны нулю. {3}}.[/латекс] 9{3}}.[/латекс]
{3}}.[/латекс] 9{3}}.[/латекс]
Расчет магнитного поля из-за круговой токовой петли в точках вне оси требует довольно сложной математики, поэтому мы просто посмотрим на результаты. Линии магнитного поля имеют форму, показанную на рис. 12.12. Обратите внимание, что одна линия поля следует за осью петли. Это линия поля, которую мы только что нашли. Кроме того, в непосредственной близости от провода линии поля почти круглые, как линии длинного прямого провода.
Рисунок 12.12 Эскиз силовых линий магнитного поля круглой петли с током.Пример
Магнитное поле между двумя контурами
Два контура провода пропускают один и тот же ток 10 мА, но текут в противоположных направлениях, как показано на Рис. 12.13. Одна петля имеет радиус [латекс]R=50\phantom{\rule{0.2em}{0ex}}\text{см}[/латекс], а другая петля имеет радиус [латекс]2R= 100\phantom{\rule{0.2em}{0ex}}\text{см}.[/latex] Расстояние от первого контура до точки, где измеряется магнитное поле, равно 0,25 м, а расстояние от этой точки до вторая петля 0,75 м. Какова величина чистого магнитного поля в точке 9?0017 Р ?
Какова величина чистого магнитного поля в точке 9?0017 Р ?
Стратегия
Магнитное поле в точке P было определено по уравнению 12.15. Поскольку токи текут в противоположных направлениях, чистое магнитное поле представляет собой разницу между двумя полями, создаваемыми катушками. Затем, используя заданные в задаче величины, рассчитывается суммарное магнитное поле. 9{\text{−9}}\text{T}\phantom{\rule{0.2em}{0ex}}\text{вправо}.\hfill \end{массив}[/latex]
Значение
Катушки Гельмгольца обычно имеют петли одинакового радиуса с током, текущим в одном направлении, чтобы иметь сильное однородное поле в средней точке между петлями. Аналогичное применение распределения магнитного поля, создаваемого катушками Гельмгольца, можно найти в магнитной бутылке, которая может временно улавливать заряженные частицы. См. Магнитные силы и поля для обсуждения этого.
См. Магнитные силы и поля для обсуждения этого.
Проверьте свое понимание
Используя пример 12.5, на какое расстояние вам придется переместить первую катушку, чтобы иметь нулевое измеряемое магнитное поле в точке P ?
Show Solution0,608 метра
Резюме
- Напряженность магнитного поля в центре круглой петли определяется выражением [латекс]B=\frac{{\mu }_{0}I}{2R}\phantom{\rule{0.2em}{ 0ex}}\text{(в центре петли)},[/latex] где R — радиус петли. РХР-2 дает направление поля вокруг петли.
Концептуальные вопросы
Является ли магнитное поле токовой петли однородным?
Что происходит с длиной подвешенной пружины, когда через нее проходит ток?
Показать решениеДлина пружины уменьшается, так как каждая катушка имеет магнитное поле, создаваемое северным полюсом, рядом с южным полюсом следующей катушки.
По двум концентрическим круглым проводам разного диаметра текут токи в одном направлении. Опишите силу, действующую на внутреннюю проволоку. 9{\text{−5}}\text{T}[/латекс]
Опишите силу, действующую на внутреннюю проволоку. 9{\text{−5}}\text{T}[/латекс]
По круговой петле радиусом R течет ток I . На каком расстоянии вдоль оси петли магнитное поле составляет половину своего значения в центре петли?
Две плоские круглые катушки, каждая с радиусом R и намотанные на N витков, установлены вдоль одной оси так, чтобы они были параллельны на расстоянии d друг от друга. Каково магнитное поле в середине общей оси, если ток 9{3\текст{/}2}}[/латекс]
Для катушек в предыдущей задаче, каково магнитное поле в центре каждой катушки?
Лицензии и атрибуты Магнитное поле токовой петли. Автор: : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/university-physics-volume-2/pages/12-4-magnet-field-of-current-loop. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно на https://openstax. org/books/university-physics-volume-2/pages/1-introduction
org/books/university-physics-volume-2/pages/1-introduction
Закон Ампера – College Physics: OpenStax
Глава 22 Магнетизм
Резюме
- Рассчитайте ток, создающий магнитное поле.
- Используйте правило правой руки 2, чтобы определить направление тока или направление контуров магнитного поля.
Какой ток необходим для создания значительного магнитного поля, возможно, такого же сильного, как поле Земли? Геодезисты скажут вам, что воздушные линии электропередач создают магнитные поля, которые мешают показаниям их компаса. Действительно, когда в 1820 году Эрстед обнаружил, что ток в проводе влияет на стрелку компаса, он не имел дело с чрезвычайно большими токами. Как форма проводов, по которым течет ток, влияет на форму создаваемого магнитного поля? Ранее мы отмечали, что токовая петля создает магнитное поле, подобное магнитному стержню, но как насчет прямого провода или тороида (бублика)? Как направление создаваемого током поля связано с направлением тока? Ответы на эти вопросы исследуются в этом разделе вместе с кратким обсуждением закона, управляющего полями, создаваемыми токами.
Магнитные поля имеют как направление, так и величину. Как отмечалось ранее, одним из способов определения направления магнитного поля является использование компаса, как показано для длинного прямого провода с током на рисунке 1. Датчики Холла могут определять величину поля. Обнаружено, что поле вокруг длинного прямого провода представляет собой кольцевые петли. Из этого исследования вытекает правило правой руки 2 (RHR-2), которое справедливо для любого сегмента тока: направьте большой палец в направлении тока, а остальные пальцы согните в направлении петель магнитного поля , созданный им.
Рис. 1. (a) Компасы, расположенные рядом с длинным прямым проводом с током, показывают, что силовые линии образуют круглые петли с центром на проводе. (b) Правило правой руки 2 гласит, что если большой палец правой руки указывает в направлении течения, остальные пальцы сгибаются в направлении поля. Это правило согласуется с полем, отображаемым для длинного прямого провода, и справедливо для любого текущего сегмента.
Напряженность магнитного поля (величина), создаваемая длинным прямым проводом с током 9{-7} \;\textbf{T} \cdot \textbf{m/A}}[/latex] – проницаемость свободного пространства. ([латекс]\boldsymbol{\mu _0}[/латекс] является одной из основных констант в природе. Позже мы увидим, что [латекс]\жирныйсимвол{\му _0}[/латекс] связан со скоростью свет.) Поскольку провод очень длинный, величина поля зависит только от расстояния от провода [латекс]\boldsymbol{r}[/латекс], а не от положения вдоль провода.
Пример 1: расчет тока, создающего магнитное поле
9{-7} \; \textbf{T} \cdot \textbf{m/A}}} \\[1em] & \boldsymbol{25 \;\textbf{A}} \end{array}[/latex]Обсуждение
Таким образом, умеренно большой ток создает значительное магнитное поле на расстоянии 5,0 см от длинного прямого провода. Обратите внимание, что ответ указан только с двумя цифрами, поскольку в этом примере поле Земли указано только с двумя цифрами.
Магнитное поле длинного прямого провода имеет больше значений, чем вы можете предположить на первый взгляд. Каждый отрезок тока создает магнитное поле, подобное магнитному полю длинного прямого провода, а полное поле тока любой формы представляет собой векторную сумму полей, создаваемых каждым отрезком. Формальная формулировка направления и величины поля, создаваемого каждым сегментом, называется законом Био-Савара . Интегральное исчисление необходимо для суммирования поля для тока произвольной формы. Это приводит к более полному закону, называемому законом Ампера , который связывает магнитное поле и ток в общем виде. Закон Ампера, в свою очередь, является частью Уравнения Максвелла , которые дают полную теорию всех электромагнитных явлений. Рассмотрение того, как уравнения Максвелла кажутся разным наблюдателям, привело к современной теории относительности и осознанию того, что электрические и магнитные поля — это разные проявления одного и того же явления. Большая часть этого выходит за рамки этого текста как на математическом уровне, требующем исчисления, так и на том количестве места, которое может быть уделено этому.
Каждый отрезок тока создает магнитное поле, подобное магнитному полю длинного прямого провода, а полное поле тока любой формы представляет собой векторную сумму полей, создаваемых каждым отрезком. Формальная формулировка направления и величины поля, создаваемого каждым сегментом, называется законом Био-Савара . Интегральное исчисление необходимо для суммирования поля для тока произвольной формы. Это приводит к более полному закону, называемому законом Ампера , который связывает магнитное поле и ток в общем виде. Закон Ампера, в свою очередь, является частью Уравнения Максвелла , которые дают полную теорию всех электромагнитных явлений. Рассмотрение того, как уравнения Максвелла кажутся разным наблюдателям, привело к современной теории относительности и осознанию того, что электрические и магнитные поля — это разные проявления одного и того же явления. Большая часть этого выходит за рамки этого текста как на математическом уровне, требующем исчисления, так и на том количестве места, которое может быть уделено этому. Но для заинтересованных студентов, и особенно для тех, кто продолжает заниматься физикой, инженерией или подобными занятиями, дальнейшее углубление в эти вопросы откроет описания природы, которые элегантны и глубоки. В этом тексте мы будем помнить об общих особенностях, таких как RHR-2 и правила для линий магнитного поля, перечисленные в Главе 22.3 Магнитные поля и силовые линии магнитного поля, концентрируясь на полях, создаваемых в некоторых важных ситуациях.
Но для заинтересованных студентов, и особенно для тех, кто продолжает заниматься физикой, инженерией или подобными занятиями, дальнейшее углубление в эти вопросы откроет описания природы, которые элегантны и глубоки. В этом тексте мы будем помнить об общих особенностях, таких как RHR-2 и правила для линий магнитного поля, перечисленные в Главе 22.3 Магнитные поля и силовые линии магнитного поля, концентрируясь на полях, создаваемых в некоторых важных ситуациях.
Установление связей: теория относительности
Слушая все, что мы делаем об Эйнштейне, иногда создается впечатление, что он изобрел теорию относительности из ничего. Напротив, одним из мотивов Эйнштейна было решить трудности, связанные с пониманием того, как разные наблюдатели видят магнитные и электрические поля.
Магнитное поле вблизи проволочной петли с током показано на рисунке 2. Как направление, так и величина магнитного поля, создаваемого петлей с током, являются сложными. RHR-2 можно использовать для определения направления поля вблизи контура, но для получения более подробной информации необходимо картографирование с помощью компаса и правил относительно силовых линий, приведенных в главе 22. 3 «Магнитные поля и силовые линии магнитного поля». Есть простая формула для напряженность магнитного поля в центре круглой петли. Это
3 «Магнитные поля и силовые линии магнитного поля». Есть простая формула для напряженность магнитного поля в центре круглой петли. Это
[латекс]\boldsymbol{B =}[/латекс] [латекс]\boldsymbol{\frac{\mu _0I}{2R}}[/латекс] [латекс]\textbf{(в центре петли)}[/ латекс]
, где [латекс]\boldsymbol{R}[/латекс] — радиус петли. Это уравнение очень похоже на уравнение для прямого провода, но оно справедливо только для в центре круглой петли из провода. Сходство уравнений указывает на то, что аналогичная напряженность поля может быть получена в центре контура. Один из способов получить большее поле — это [латекс]\boldsymbol{N}[/латекс] петель; тогда поле равно [латекс]\boldsymbol{B = N \mu _0I/(2R)}[/латекс]. Обратите внимание, что чем больше петля, тем меньше поле в ее центре, поскольку ток проходит дальше.
Рис. 2. (a) RHR-2 показывает направление магнитного поля внутри и снаружи контура с током. (b) Более детальное картографирование с помощью компаса или зонда Холла дополняет картину. Поле похоже на поле стержневого магнита.
Поле похоже на поле стержневого магнита.Соленоид представляет собой длинную катушку провода (с множеством витков или петель, в отличие от плоской петли). Из-за своей формы поле внутри соленоида может быть очень однородным, а также очень сильным. Поле сразу за катушками почти равно нулю. На рис. 3 показано, как выглядит поле и как его направление задается RHR-2.
Рис. 3. (a) Из-за своей формы поле внутри соленоида длиной l удивительно однородно по величине и направлению, на что указывают прямые и равномерно расположенные силовые линии. Поле вне катушек почти равно нулю. (b) На этом разрезе показано магнитное поле, создаваемое током в соленоиде.Магнитное поле внутри соленоида с током очень однородно по направлению и величине. Лишь ближе к концам он начинает ослабевать и менять направление. Поле снаружи имеет такую же сложность, как и плоские петли и стержневые магниты, но напряженность магнитного поля внутри соленоида просто
[латекс]\boldsymbol{B = \mu _0nI \; (\textbf{внутри соленоида})},[/latex]
, где [латекс]\boldsymbol{n}[/латекс] — количество петель на единицу длины соленоида ([латекс]\жирныйсимвол{n = N/l}[/латекс], где [латекс]\жирныйсимвол{ N}[/latex] — количество петель, а [latex]\boldsymbol{l}[/latex] — длина). {-1}}.[/latex] 9{-1}) \; (1600 \;\textbf{A})} \\[1em] & \boldsymbol{2.01 \;\textbf{T}}. \end{array}[/latex]
{-1}}.[/latex] 9{-1}) \; (1600 \;\textbf{A})} \\[1em] & \boldsymbol{2.01 \;\textbf{T}}. \end{array}[/latex]
Обсуждение
Это большая напряженность поля, которая может быть установлена на соленоиде большого диаметра, например, при медицинском использовании магнитно-резонансной томографии (МРТ). Однако очень большой ток указывает на то, что поля такой силы получить нелегко. Такой большой ток через 1000 витков, втиснутых в длину метра, произвел бы значительный нагрев. Более высокие токи могут быть достигнуты с помощью сверхпроводящих проводов, хотя это дорого. Существует верхний предел тока, поскольку сверхпроводящее состояние нарушается очень большими магнитными полями.
Есть интересные варианты плоской катушки и соленоида. Например, тороидальная катушка, используемая для удержания реактивных частиц в токамаках, очень похожа на соленоид, согнутый в окружность. Поле внутри тороида очень сильное, но круглое. Заряженные частицы движутся по кругу, следуя линиям поля, и сталкиваются друг с другом, возможно, вызывая синтез. Но заряженные частицы не пересекают силовые линии и не покидают тороид. Целый ряд форм катушек используется для создания всевозможных форм магнитного поля. Добавление ферромагнитных материалов увеличивает напряженность поля и может существенно повлиять на форму поля. Ферромагнитные материалы имеют тенденцию улавливать магнитные поля (силовые линии изгибаются в ферромагнитный материал, оставляя более слабые поля вне его) и используются в качестве экранов для устройств, на которые неблагоприятно влияют магнитные поля, в том числе магнитное поле Земли.
Но заряженные частицы не пересекают силовые линии и не покидают тороид. Целый ряд форм катушек используется для создания всевозможных форм магнитного поля. Добавление ферромагнитных материалов увеличивает напряженность поля и может существенно повлиять на форму поля. Ферромагнитные материалы имеют тенденцию улавливать магнитные поля (силовые линии изгибаются в ферромагнитный материал, оставляя более слабые поля вне его) и используются в качестве экранов для устройств, на которые неблагоприятно влияют магнитные поля, в том числе магнитное поле Земли.
PhET Исследования: Генератор
Генерировать электричество с помощью стержневого магнита! Откройте для себя физику этого явления, исследуя магниты и то, как вы можете использовать их, чтобы зажечь лампочку.
Рис. 4. Генератор- Сила магнитного поля, создаваемого током в длинном прямом проводе, определяется как
[латекс]\boldsymbol{B=}[/латекс] [латекс]\boldsymbol{\frac{\mu _0I}{2 \pi r}}[/латекс] [латекс]\textbf{(длинная прямая проволока) },[/латекс]
- Направление магнитного поля, создаваемого длинным прямым проводом, определяется правилом правой руки 2 (RHR-2): Направьте большой палец правой руки в направлении тока, а остальные пальцы согните в направлении созданные им петли магнитного поля .

- Магнитное поле, создаваемое током, следующим по любому пути, является суммой (или интегралом) полей, создаваемых сегментами вдоль пути (величина и направление, как для прямого провода), что приводит к общей зависимости между током и полем, известной как закон Ампера. .
- Напряженность магнитного поля в центре круглой петли определяется как
[латекс]\boldsymbol{B =}[/латекс] [латекс]\boldsymbol{\frac{\mu _0I}{2R}}[/латекс] [латекс]\textbf{(в центре петли)}[ /латекс]
- где [латекс]\жирныйсимвол{R}[/латекс] — радиус петли. Это уравнение принимает вид [латекс]\boldsymbol{B = \mu _0nI/(2R)}[/латекс] для плоской катушки из [латекса]\boldsymbol{N}[/латекс] петель. РХР-2 дает направление поля вокруг петли. Длинная катушка называется соленоидом.
- Напряженность магнитного поля внутри соленоида равна
[латекс]\boldsymbol{B = \mu _0nI \; (\textbf{внутри соленоида})},[/latex]
- где [латекс]\boldsymbol{n}[/латекс] — количество петель на единицу длины соленоида.
 {-7} \;\textbf{T} \cdot \;\textbf{m/A}}[/latex]
{-7} \;\textbf{T} \cdot \;\textbf{m/A}}[/latex]- напряженность магнитного поля в центре круглой петли
- определяется как [латекс]\boldsymbol{B = \frac{\mu _0I}{2R}}[/latex], где [латекс]\boldsymbol{R}[/latex] — радиус петли
- соленоид
- тонкая проволока, намотанная в катушку, которая создает магнитное поле при пропускании через нее электрического тока
- напряженность магнитного поля внутри соленоида
- определяется как [латекс]\boldsymbol{B = \mu _0nI}[/латекс], где nn — количество петель на единицу длины соленоида ([латекс]\boldsymbol{n = N/l}[/латекс], где [latex]\boldsymbol{N}[/latex] — количество петель, а [latex]\boldsymbol{l}[/latex] — длина)
- Закон Био-Савара
- физический закон, описывающий магнитное поле, создаваемое электрическим током, с помощью специального уравнения
- Закон Ампера
- физический закон, утверждающий, что магнитное поле вокруг электрического тока пропорционально току; каждый отрезок тока создает магнитное поле, подобное магнитному полю длинного прямого провода, а полное поле тока любой формы представляет собой векторную сумму полей, создаваемых каждым отрезком
- Уравнения Максвелла
- набор из четырех уравнений, описывающих электромагнитные явления
Магнитная сила и магнитное поле: определение, формула и примеры
Магнитная сила – это сила притяжения или отталкивания, возникающая в результате движения электрически заряженных частиц.
 Магниты притягиваются или отталкиваются друг от друга из-за этой силы. Компас, мотор, магниты , удерживающие дверцу холодильника, железнодорожные пути и современные американские горки — все это примеры магнитной силы. Магнитное поле создается всеми движущимися зарядами, и заряды , которые проходят через его области, ощущают силу. В зависимости от того, является ли сила притягивающей или отталкивающей, она может быть положительной или отрицательной. Сила магнетизма определяется зарядом объекта, скоростью и магнитным полем 90 026.
Магниты притягиваются или отталкиваются друг от друга из-за этой силы. Компас, мотор, магниты , удерживающие дверцу холодильника, железнодорожные пути и современные американские горки — все это примеры магнитной силы. Магнитное поле создается всеми движущимися зарядами, и заряды , которые проходят через его области, ощущают силу. В зависимости от того, является ли сила притягивающей или отталкивающей, она может быть положительной или отрицательной. Сила магнетизма определяется зарядом объекта, скоростью и магнитным полем 90 026. Подробнее: Магнитное поле из -за тока элемента
Таблица содержимого
- .0026 Fleming’s Right Hand Rule
- Magnetic Field
- Magnetic Field Sue to Current Carrying Conductor
- Things to Remember
- Previous Year’s Questions
- Sample Questions
Ключевые выводы: Магнитное поле, Магнитная сила, Правило правой руки Флеминга, Проводник с током, Заряд
Сила, приложенная к движущемуся заряду
[Щелкните здесь, чтобы просмотреть примеры вопросов]
На заряд действует сила, когда он проходит через магнитное поле под углом.
 Эта сила определяется уравнением:
Эта сила определяется уравнением:F = qvB sinθ
где
q — заряд
B — магнитное поле
v — скорость
θ — угол между магнитным полем направления скоростей.
Сила действует на движение заряда q, движущегося со скоростью v в Магнетизм поле, и эта сила равна:
- Перпендикулярно обоим v и B.
- Перпендикулярно sinθ (где θ — угол между v и B).
- Пропорционально заряду q.
- Proportional to the velocity v.
Magnetic Force
Read More: Important Formula in Electricity
Fleming’s Right Hand Rule
[Click Here for Previous Year’s Questions]
- Правило правой руки можно использовать для определения траектории силы (F).
- Относится к устройствам, которые производят ток, двигаясь в магнитном поле.
- Поместите указательный палец вдоль направления движения заряда v.

- Между v и B отведите средний палец от указательного.
- Сохраняйте перпендикулярное положение между большим пальцем и плоскостью, образованной указательным и средним пальцами.
- Если заряд q положительный, ваш большой палец будет указывать в направлении действия силы (F).
Правило правой руки Флеминга
Читать Дальнейшему: NCERT Solutions Глава 4 Движущиеся заряды и магнетизм
Магнитное поле
[Нажмите здесь на выборку. сила, окружающая магнит. Это термин, который описывает, как магнитная сила распределяется вокруг магнитного объекта. Когда электрический заряд/ток движется вблизи магнита, формируются или генерируются магнитные поля. Магнитное поле возникает, когда субатомная частица с отрицательным зарядом, такая как электроны, путешествует. Атомы магнитных объектов, а также электрические проводники и провода могут генерировать эти поля.
Подробнее: Магнитный спектр
Представление магнитного поля
Магнитное поле можно представить различными способами.
 Его можно математически интерпретировать как векторное поле, которое можно изобразить в виде различных наборов на сетке. Использование линий поля — еще один вариант. Линии используются для связи набора векторов. Линии магнитного поля здесь никогда не пересекаются и никогда не останавливаются.
Его можно математически интерпретировать как векторное поле, которое можно изобразить в виде различных наборов на сетке. Использование линий поля — еще один вариант. Линии используются для связи набора векторов. Линии магнитного поля здесь никогда не пересекаются и никогда не останавливаются.Магнитное поле
Измерение и единица измерения магнитного поля
Магнитное поле измеряется путем определения его интенсивности и направления. Сила магнитного поля изменяется от небольшой и слабой до очень сильной и высокой. Когда мы смотрим на магнитное поле Земли, мы видим, что оно небольшое, но сильное. Несмотря на это, термин магнитное поле относится к двум различным, но связанным полям, обычно обозначаемым буквами H и B. H означает напряженность магнитного поля и измеряется в амперах на метр (единица СИ). B, с другой стороны, означает плотность магнитного потока и измеряется в теслах.
Читайте также:
Магнитное поле иск к проводнику с током
[Нажмите здесь, чтобы просмотреть вопросы предыдущего года]
Когда электрический заряд перемещается, формируется магнитное поле.
 Рассмотрим провод, который подключен к батарее и через который ток вынужден течь. Магнитное поле возрастает относительно тока, протекающего по проводнику. Магнитное поле уменьшается с расстоянием по мере удаления от провода. Закон Ампера описывает это явление. Магнитное поле на расстоянии r от длинного проводника с током I по закону задается уравнением
Рассмотрим провод, который подключен к батарее и через который ток вынужден течь. Магнитное поле возрастает относительно тока, протекающего по проводнику. Магнитное поле уменьшается с расстоянием по мере удаления от провода. Закон Ампера описывает это явление. Магнитное поле на расстоянии r от длинного проводника с током I по закону задается уравнениемB=μ 0 I 2 πr
Где μ 0 — специальная константа, определяемая как проницаемость свободного пространства в уравнении. μ 0 =4π×10 −7 Т⋅м/А
Магнитные поля могут концентрироваться материалами с более высокой магнитной проницаемостью. Поскольку это векторная величина, магнитное поле имеет направление. Правило правой руки Флеминга можно использовать для расчета традиционного тока, протекающего по прямому кабелю. Чтобы применить этот закон, представьте, что вы обхватываете провод правой рукой и указываете большим пальцем направление тока.
 Направление магнитного поля, охватывающего провод, указывается кончиками пальцев.
Направление магнитного поля, охватывающего провод, указывается кончиками пальцев.Что следует помнить
- Магнитная сила — это сила притяжения или отталкивания, возникающая в результате движения электрически заряженных частиц.
- Правило правой руки Флеминга можно использовать для определения траектории магнитной силы (F).
- Магнитное поле — невидимое поле силы притяжения, окружающее магнит.
- При движении электрического заряда образуется магнитное поле.
- Магнитное поле, создаваемое проводником с током, определяется уравнением B=µ0I2πr.
Подробнее:
Вопросы прошлых лет
- Электрон в движении связан с… [KCET 1996]
- По двум параллельным проводам течет электрический ток в одном направлении. Провода… [ KCET 1996]
- Сопротивление идеального амперметра равно…[ KCET 1996]
- Если через катушку пропустить ток 0,1 А, какая пара действует?.
 . .[CBSE Класс 12]
. .[CBSE Класс 12] - Ускорение падающего магнита равно..[NEET]
- Стержневой магнит эквивалентен …………[KCET 2004]
- Металлическое кольцо удерживается горизонтально и стержневой магнит падает через….[NEET]
- Суммарный заряд, индуцируемый в проводящей петле при ее перемещении в магнитном поле, зависит от…[NEET 1992]
- Если заряженная частица входит перпендикулярно в однородном магнитном поле, то…[JIPMER 2016]
- Кто изобрел циклотрон?
- Когда заряженная частица, движущаяся со скоростью, равна….
- Угол падения на месте….
- Соответствующий магнитный момент определяется выражением….
- Однородное электрическое поле и однородное магнитное поле создаются…
- Закон Ампера можно вывести из….
 .
. - Если магнитный диполь с моментом М расположен в направлении …
- Если восприимчивость диам, пара и ферромагнитных материалов составляет ….
- Материалы, подходящие для постоянных магнитов, какими из следующих свойств должны обладать?
- При какой температуре ферромагнитные вещества становятся парамагнитными?
- сила магнитного поля в его центре равна…
Примеры вопросов
Вопросы. Как рассчитать магнитную силу заряженных частиц массой 50 Кл, движущихся со скоростью 3 м/с в магнитном поле силой 1 Тл? Его поле имеет то же направление, что и путь второй частицы. (2 балла)
Ответ. q=50C, v=3м/с и B=1T – заданные параметры.
Поскольку разность путей второй частицы совпадает с направлением ее поля, θ=0°
F= q v B sin θ = 50x3x1x sin θ =0 – это формула величины силы.

Вопросы. Что является источником магнитного поля Земли? (2 балла)
Ответ. Магнитное поле Земли создается глубоко внутри ее ядра. Движение жидкого железа в центре Земли создает электрический ток, который вызывает формирование магнитных полей. Заряженные металлы, проходящие через эти поля, генерируют свои электрические токи, продолжая петлю. Геодинамо — это название этой самоподдерживающейся петли. Отдельные магнитные поля выровнены в одном направлении из-за спирального движения, создаваемого силой Кориолиса. Комбинированное воздействие магнитных полей создает массивное магнитное поле, охватывающее всю Землю.
Вопрос. Дайте определение напряженности магнитного поля. (2 балла)
Ответ. Интенсивность магнитного поля (MFI) или напряженность магнитного поля (MFS) представляет собой отношение MMF, необходимое для создания определенной плотности потока (B) в материале на единицу длины этого материала.

Вопросы. Какое значение имеют силовые линии магнитного поля? (3 балла)
Отв. Линии магнитного потока важны по ряду причин:
Линии магнитного поля — это линии в магнитном поле, тангенс которых определяет направление поля в любой заданной точке, а плотность определяет величину поля.
Они указывают путь магнитного поля.
Количество силовых линий магнитного поля определяет силу магнитного поля. Поскольку линии длиннее на полюсах, магнитное поле там сильнее.
Сила магнитного поля пропорциональна количеству силовых линий магнитного поля в данной области.
Вопросы. Что такое электромагнитные волны и как они работают? (2 балла)
Ответ. Электромагнитные волны — это волны, которые распространяются в результате одновременных периодических изменений напряженности электрического и магнитного полей.
Вопрос. Правда ли, что в космосе есть магнитные поля? (2 балла)
Ответ.
 Магнитные поля действительно существуют в космосе. Основываясь на измерениях большого количества пульсаров и поляризации их радиосигналов, спиральные рукава Млечного Пути, по-видимому, имеют какое-то очень крупномасштабное скоординированное магнитное поле. В межзвездных пылевых облаках были обнаружены магнитные поля. Поля усиливаются по мере того, как падают облака.
Магнитные поля действительно существуют в космосе. Основываясь на измерениях большого количества пульсаров и поляризации их радиосигналов, спиральные рукава Млечного Пути, по-видимому, имеют какое-то очень крупномасштабное скоординированное магнитное поле. В межзвездных пылевых облаках были обнаружены магнитные поля. Поля усиливаются по мере того, как падают облака.Вопросы. Определить плотность магнитного потока. (2 балла)
Ответ. Сумма магнитных потоков в области, измеренной перпендикулярно пути магнитного потока, известна как плотность магнитного потока. Обозначается буквой B и выражается в единицах Тесла.
Выписка:
5.3 Напряженность магнитного поля: Сила, действующая на движущийся заряд в магнитном поле
Цели обучения Правило правой руки 1
Цели обучения
К концу этого раздела вы сможете делать следующее:
- Описать влияние магнитных полей на движущиеся заряды
- Используйте правило правой руки 1 для определения скорости заряда, направления магнитного поля и направления магнитной силы, действующей на движущийся заряд
- Расчет магнитной силы на движущийся заряд
Информация, представленная в этом разделе, поддерживает следующие цели обучения и научные практики AP®:
- 2.
 D.1.1 Учащийся может применять математические процедуры для выражения силы, действующей на движущийся заряженный объект магнитным полем. (СП 2.2)
D.1.1 Учащийся может применять математические процедуры для выражения силы, действующей на движущийся заряженный объект магнитным полем. (СП 2.2) - 3.C.3.1 Учащийся может использовать правила правой руки для анализа ситуации, включающей проводник с током и движущийся электрически заряженный объект, чтобы определить направление магнитной силы, действующей на заряженный объект из-за магнитное поле, создаваемое проводником с током. (Ст.1.4)
Каков механизм, с помощью которого один магнит воздействует на другой? Ответ связан с тем фактом, что весь магнетизм вызван током, потоком заряда. Магнитные поля воздействуют на движущиеся заряды , и поэтому они воздействуют на другие магниты, все из которых имеют движущиеся заряды.
Правило правой руки 1
Магнитная сила, действующая на движущийся заряд, является одной из самых фундаментальных известных.
 Магнитная сила так же важна, как электростатическая или кулоновская сила. И все же магнитная сила более сложна как по количеству воздействующих на нее факторов, так и по своему направлению, чем относительно простая кулоновская сила. Величина магнитной силы FF размером 12{F} {} на заряд qq размером 12{q} {}, движущийся со скоростью vv размером 12{v} {} в магнитном поле напряженностью BB размером 12{B} { } задается
Магнитная сила так же важна, как электростатическая или кулоновская сила. И все же магнитная сила более сложна как по количеству воздействующих на нее факторов, так и по своему направлению, чем относительно простая кулоновская сила. Величина магнитной силы FF размером 12{F} {} на заряд qq размером 12{q} {}, движущийся со скоростью vv размером 12{v} {} в магнитном поле напряженностью BB размером 12{B} { } задается5.1 F=qvBsinθ,F=qvBsinθ, размер 12{F= ital “qvB””sin”θ} {}
, где θθ размер 12{θ} {} — угол между направлениями vv и B.B. размер 12{B} {} Эту силу часто называют силой Лоренца. Фактически так мы определяем напряженность магнитного поля В—В—размер 12{В} {} через силу, действующую на заряженную частицу, движущуюся в магнитном поле. Единица СИ для напряженности магнитного поля BB размера 12{B} {} называется тесла (Т) в честь эксцентричного, но блестящего изобретателя Николы Теслы (1856–1819 гг.).43). Чтобы определить, как тесла соотносится с другими единицами СИ, мы решаем F=qvBsinθF=qvBsinθ size 12{F= ital “qvB””sin”θ} {} для B.
 B.size 12{B} {}
B.size 12{B} {}5.2 B=FqvsinθB=Fqvsinθ размер 12{B= {{F} над {ital “qv””sin”θ} } } {}
Поскольку размер sinθsinθ 12{θ} {} безразмерен, тесла составляет
5,3 1 T=1 NC⋅м/с=1 NA⋅м.1 T=1 NC⋅м/с=1 NA⋅м. size 12{“1 T”= {{“1 N”} над {C cdot “м/с”} } = {{1″ N”} над {A cdot m} } } {}
Обратите внимание, что C/s = A.
Еще одна меньшая единица, называемая гауссом (G), где 1G=10−4T, 1G=10−4T, размер 12{1`G=”10″ rSup { размер 8{ – 4} } `T} { } иногда используется. Самые сильные постоянные магниты имеют поля около 2 Тл; сверхпроводящие электромагниты могут достигать 10 Тл и более. Магнитное поле Земли на ее поверхности составляет всего около 5×10-5 Тл, 5×10-5 Тл, размер 12{5 умножить на “10” rSup { размер 8{ – 5} } `T} {} или 0,5 G.
Направление магнитной силы FF размера 12{F} {} перпендикулярно плоскости, образованной vv размером 12{v} {} и B, B, как определено правилом правой руки 1 (или RHR- 1), что показано на рис. 5.
 9. RHR-1 утверждает, что для определения направления магнитной силы на положительный движущийся заряд вы указываете большим пальцем правой руки в направлении v, v, пальцами в направлении B, B и перпендикуляром к ладонь указывает в сторону Ф.Ф. Один из способов запомнить это состоит в том, что существует одна скорость, и поэтому ее представляет большой палец. Есть много линий поля, поэтому пальцы представляют их. Сила направлена в том направлении, куда вы бы толкнули ладонью. Сила, действующая на отрицательный заряд, направлена прямо противоположно силе на положительном заряде.
9. RHR-1 утверждает, что для определения направления магнитной силы на положительный движущийся заряд вы указываете большим пальцем правой руки в направлении v, v, пальцами в направлении B, B и перпендикуляром к ладонь указывает в сторону Ф.Ф. Один из способов запомнить это состоит в том, что существует одна скорость, и поэтому ее представляет большой палец. Есть много линий поля, поэтому пальцы представляют их. Сила направлена в том направлении, куда вы бы толкнули ладонью. Сила, действующая на отрицательный заряд, направлена прямо противоположно силе на положительном заряде.Рис. 5.9 Магнитные поля воздействуют на движущиеся заряды. Эта сила является одной из самых основных известных. Направление магнитной силы на движущийся заряд перпендикулярно плоскости, образованной vv и BB размером 12{B} {}, и следует правилу правой руки 1 (RHR-1), как показано. Величина силы пропорциональна q,q,size 12{q} {}v,v,size 12{v} {}B,B,size 12{B} {} и синусу угла между vv size 12{v} {} и B.
 B.size 12{B} {}
B.size 12{B} {}Создание соединений: заряды и магниты
На статические заряды не действует магнитная сила. Однако на движущиеся заряды действует магнитная сила. Когда заряды неподвижны, их электрические поля не действуют на магниты. Но когда заряды движутся, они создают магнитные поля, которые воздействуют на другие магниты. При относительном движении возникает связь между электрическим и магнитным полями — одно влияет на другое.
Пример 5.1 Расчет магнитной силы: магнитное поле Земли на заряженном стеклянном стержне
За исключением компаса, вы редко видите или лично испытываете силы, связанные с небольшим магнитным полем Земли. Чтобы проиллюстрировать это, предположим, что в физической лаборатории вы натираете стеклянную палочку шелком, помещая на нее положительный заряд в 20 нКл. Вычислите силу, действующую на стержень со стороны магнитного поля Земли, если вы бросите его с горизонтальной скоростью 10 м/с строго на запад в месте, где поле Земли направлено строго на север параллельно земле.
 (Направление силы определяется правилом правой руки 1 (RHR-1), как показано на рис. 5.10.)
(Направление силы определяется правилом правой руки 1 (RHR-1), как показано на рис. 5.10.)Рис. 5.10. Положительно заряженный объект, движущийся строго на запад в области, где магнитное поле Земли направлено строго на север, подвергается воздействию силы, направленной прямо вниз, как показано на рисунке. Отрицательный заряд, движущийся в том же направлении, испытает силу прямо вверх.
Стратегия
Нам известны заряд, его скорость, напряженность и направление магнитного поля. Таким образом, мы можем использовать уравнение F=qvBsinθF=qvBsinθ size 12{F= ital “qvB””sin”θ} {}, чтобы найти силу.
Решение
Магнитная сила равна
5,4 F=qvbsinθ.F=qvbsinθ. size 12{F= ital “qvb””sin”θ} {}
Мы видим, что sinθ=1,sinθ=1,size 12{“sin”θ=1} {}, так как угол между скоростью и направлением поля 90º.90º.size 12{“90” rSup { size 8{ circ } } } {} Ввод других заданных величин дает
5,5 F=20×10–9C10 м/с5×10–5T=1 ×10–11C⋅м/sNC⋅м/с=1×10–11N.
 F=20×10–9C10 м/с5×10–5T=1×10–11C⋅м/sNC⋅м/с=1× 10–11N.alignl { стек { размер 12 {F = слева (“20” умножить на “10” rSup { размер 8 { – 9} } `C вправо ) влево (“10″`”м/с” вправо ) влево (5 раз “10” rSup { размер 8{- 5} } `T вправо )} {} # “”=1 раз “10 ” rSup { размер 8{ – “11”} } ` влево (C cdot “м/с” вправо) влево ( { {N} над {C cdot “м/с”} } вправо )=1 раз “10” rSup {размер 8{-“11”} } `N “.” {} } } {}
F=20×10–9C10 м/с5×10–5T=1×10–11C⋅м/sNC⋅м/с=1× 10–11N.alignl { стек { размер 12 {F = слева (“20” умножить на “10” rSup { размер 8 { – 9} } `C вправо ) влево (“10″`”м/с” вправо ) влево (5 раз “10” rSup { размер 8{- 5} } `T вправо )} {} # “”=1 раз “10 ” rSup { размер 8{ – “11”} } ` влево (C cdot “м/с” вправо) влево ( { {N} над {C cdot “м/с”} } вправо )=1 раз “10” rSup {размер 8{-“11”} } `N “.” {} } } {}Обсуждение
Этой силой можно пренебречь на любом макроскопическом объекте, что согласуется с опытом. Он рассчитывается только с одной цифрой, потому что поле Земли меняется в зависимости от местоположения и дается только с одной цифрой. Однако магнитное поле Земли оказывает очень важное воздействие, особенно на субмикроскопические частицы. Некоторые из них исследуются в книге «Сила движущегося заряда в магнитном поле: примеры и приложения».
- Печать
- Поделиться
Подробные пояснения и проблемы — Lambda Geeks
Как найти магнитное поле из электрического поля — обширная область исследований, и эта тема является потенциальной темой для многих исследователей.
 Двигаясь дальше, мы увидим пояснение к теме.
Двигаясь дальше, мы увидим пояснение к теме.Электричество и магнетизм предлагает множество тем для обсуждения, где мы узнаем больше об электричестве и магнетизме. Электричество и магнетизм — две разные сущности, происходящие от электромагнитной силы.
Электричество в основном представляет собой движение зарядов, которые создают магнитные силовые линии . Магнитные силовые линии вызовут движение зарядов в среде, которая будет производить электричество.
Электричество и магнетизм идут рука об руку, то есть движущиеся заряды создают электричество и магниты, которые вращаются, будут индуцировать электричество . Таким образом, будет создано другое, способствующее этому, будет присутствие электромагнитной силы в системе.
Используя детализацию, мы можем понять, как найти магнитное поле из электрического поля. Есть эксперименты, которые объясняют создание магнитного поля с помощью электрического поля. Мы увидим детализацию в этой статье как таковую.
Как определить направление магнитного поля по электрическому полю?
Несколько экспериментов помогут понять, как найти магнитное поле из электрического поля. Одним из таких экспериментов является проводник с током.
Рассмотрим провод, по которому течет ток, будет сформирована концентрическая окружность, которую мы называем электрическими силовыми линиями, поскольку заряды кажутся движением по проводу и создают электричество.
При проведении электричества в пространстве мгновенно создается магнитное поле. Таким образом, магнитные силовые линии располагаются таким образом, что никогда не встречаются друг с другом.
Доступны простые способы определения направления магнитного поля по электрическому полю. Используя правило большого пальца правой руки , мы легко найдем направление магнитной силовой линии. Большой палец указывает направление тока в системе, а палец, обернутый вокруг, показывает направление магнитного поля.

Таким образом, направление магнитного поля от электрического поля легко найти из приведенных правил. Эксперимент с проводником с током объясняет направление электрического тока и направление магнитного поля.
«Магнитное поле» Изображение предоставлено Wikimedia Commons Как преобразовать электрическое поле в магнитное поле?Чтобы объяснить преобразование электрического поля в магнитное, нам нужно использовать пример с решением задачи.
Мы начали тему с того, как найти магнитное поле из электрического поля, и теперь нам нужно знать, как преобразовать электрическое поле в магнитное поле. Поэтому мы будем использовать пример проблемы, чтобы понять это лучше.
Во-первых, нам нужно знать, что магнитное поле в основном создается изменяющимся электрическим полем. Когда электрическое поле постоянно меняется, то в действии возникает магнитное поле. И это мы увидим на проблемном примере.
Задача 1:
Говорят, что ток в проводе равен 5А. Этот провод, по которому течет электрический ток, был подключен к параллельной пластине квадратной формы, каждая сторона которой имеет размеры 3 см. Теперь вычислите скорость, с которой меняется электрическое поле.
Решение:Сначала нам нужно использовать формулу для решения этой задачи, и формула будет выглядеть так:
dQ/dt = ε пример задачи результат 6,3 x 10 14 В/мс . Это числовая часть задачи, так что теперь переход к теоретической части будет похож на то, когда ток создается в проводящем проводе, он автоматически будет иметь электрические линии с силой вокруг провода концентрическими кругами. Силовые линии будут создавать электрическое поле в системе. При изменении электрического поля возникает магнитное поле.
В следующем примере задачи мы увидим, как найти магнитное поле из электрического поля.
Задача 2:
Найти магнитное поле из электрического поля, из проводника с током и дать ему нужную формулу, чтобы рассчитать, когда значения заданы.
Решение:В основном формула для электромагнитной силы, содержащей электричество и магнетизм, задается как
F = q (E + v × B) . Здесь f представляет силу, q представляет заряд, E представляет электрическое поле, B представляет магнитное поле, а v представляет скорость.
Переписывая формулу, мы получаем B = F/ q (E+v) , эта формула лучше всего отвечает на вопрос, как найти магнитное поле из электрического поля как электрического поля и электромагнитной силы вместе со скоростью.
Часто задаваемые вопросы Как заряд в электрическом поле создает магнитное поле?Уравнение Максвелла — лучший ответ на этот вопрос. Используя одно из уравнений, мы увидим, как электрическое поле создает магнитное поле.

Ампер Закон цепи, объясните, как найти магнитное поле из электрического поля. Производство магнитного поля обусловлено постоянным изменением электрического поля. Смещение тока и смещения изменит электрическое поле, что приведет к возникновению магнитного поля.
«Уравнение Максвелла» Изображение предоставлено Wikimedia Commons Почему ток создает магнитное поле?Движущийся заряд будет производить электричество, а это электричество, в свою очередь, будет производить электрические силовые линии.
Когда электрические заряды движутся, они производят электричество, когда электрические силовые линии продолжают изменяться, кажется, что меняется электрическое поле. Изменение электрического поля мгновенно создаст магнитное поле.
Действительно ли существует магнитное поле?Да, магнитное поле существует; в этом мире мы знаем, что магнитное поле существует специально в космосе.

В основном физика объясняет, что магнитное поле создается с помощью электрического поля. Когда электрическое поле создается из-за движущихся зарядов, появляются электрические силовые линии, а затем изменяющееся электрическое поле создает магнитное поле. Таким образом, мы знаем, что магнитное поле присутствует. Магнитное поле, в свою очередь, создаст электрическое поле, и это происходит, когда движение зарядов индуцируется магнитным полем.
Размеры магнитного поля – формула, уравнение и вывод
Физическая величина – это любая величина, которую можно измерить с помощью устройства в единицах измерения. Весь список физических величин можно разделить на два типа, а именно: фундаментальные физические величины и производные физические величины.
Последующие разделы этой страницы дают краткое описание основной идеи физических величин и размерной формулы для магнитного поля. На странице также представлены различные единицы измерения.

Размерная формула магнитного поля = M1 T2 I -1
Физические величины . В физике есть семь основных физических величин. Это масса, время, длина, электрический ток, температура, сила света и количество вещества. Эти семь величин называются измерениями физического мира. Вместо использования имен их первые буквы используются для обозначения основных величин. Три механические величины: масса, длина и время представлены как M, L и T. Для обозначения размеров эти символы заключены в пару квадратных скобок.
Важно отметить, что размерность физической величины и размерность их единицы совпадают. Это только природа единицы, представленной как [M], [L] и [T], а не ее величина. Каждая производная физическая величина представляется в терминах ее фундаментальных физических величин с соответствующей степенью. Степени, в которые следует возвести основную физическую величину, чтобы получить производную величину, называются размерностями производной величины.

Подробнее о размерной формуле и размерном уравнении
Формула измерения представляет собой сложное выражение, которое описывает, какие фундаментальные величины участвуют и как они участвуют в моделировании производной физической величины. Физическая величина и ее размерности приравниваются в уравнении, называемом уравнением размерности. Другими словами, размерные уравнения — это уравнения, которые представляют размерности любой физической величины через ее фундаментальные величины.
Магнитное поле
Область вокруг магнита, на которую действует сила этого магнита, называется магнитным полем. Магнитные поля могут создаваться движущимися электрическими зарядами. Магнитное поле проникает сквозь пространство и действует как движущая сила для перемещения электрических зарядов и магнитных диполей.
В случае стержневого магнита линии магнитного поля сильнее на полюсах и слабее в середине стержневого магнита.

