Магнитное поле в физике – виды, формулы и определение с примерами
Содержание:
Магнитное поле:
До сих пор мы изучали явления, связанные с взаимодействием электрических зарядов и электрического поля. Электрическое взаимодействие является составляющей электромагнитных взаимодействий, к которым относится и магнитное взаимодействие. Люди издавна знали, что некоторые руды притягивают железные предметы. Это явление назвали магнетизмом, а куски магнитных руд — природными магнитами. Богатые залежи магнитного железняка есть в Днепропетровской и Запорожской областях. Благодаря магнитному железняку люди впервые ознакомились с магнитными свойствами тел.
Магнит (по-гречески — камень из Магнессии, города, вблизи которого были открыты залежи магнитного железняка) — это тело, обладающее магнитными свойствами. Со временем научились изготовлять искусственные постоянные магниты разнообразной формы и размеров в зависимости от их назначения.
В технике и в лабораторной практике часто используют полосовые (прямые) и подковообразные магниты (рис. 134).
Опыт 1 На столе находятся предметы, изготовленные из разных веществ. Приблизим к ним магнит. Циркуль, гвозди, иглы, стальная пластина притягиваются к магниту (рис. 135), а резинка, монета, спички, алюминиевая фольга, колпачки от ручек остались лежать на столе.
Предметы, содержащие железо, сталь, никель, чугун или их сплавы, притягиваются магнитом. Эти вещества относят к классу ферромагнетиков (от лат. феррум — железо). Бумагу, стекло, пластмассу, медь магнит не притягивает.
Магниты могут притягивать предметы через лист картона или стекло (рис. 136).
Опыт 2 На столе лежат гвозди. Разместим на них магниты. Наибольше гвоздей притягивается у концов магнитов (рис. 137).
137).
Места магнита, где магнитное действие наибольшее, называют полюсами магнита.
Чем дальше от полюсов расположен участок магнита, тем слабее его магнитное действие, тем меньше гвоздей к нему притягивается, а в средней части их совсем нет.
Участок магнита, где не проявляется его магнитное действие, называют средней линией магнита.
Опыт 3. Подвесим на нити магнит, чтобы он был в горизонтальном положении и свободно поворачивался. Если рядом нет предметов, изготовленных из ферромагнетиков, которые сильно взаимодействуют с магнитами, то магнит всегда будет занимать одно и то же положение в направлении север-юг (рис. 138).
Это связано с тем, что Земля имеет два магнитных полюса. На этом основано действие компаса.
Полюс магнита, направленный на север, называется северным (N, от англ. North), а на юг —
Демонстрационные и лабораторные магниты, а также магнитные стрелки, как правило, окрашивают традиционно в два цвета: со стороны северного полюса (N) — в синий, со стороны южного (S) — в красный. Граница окрашивания совпадает со средней линией. А может ли магнит иметь один полюс?
Граница окрашивания совпадает со средней линией. А может ли магнит иметь один полюс?
Опыт 4. Разрезаем магнит на две части, отделяя южный полюс от северного. Получили два магнита — с обоими полюсами каждый (рис. 139). Это объясняется тем, что каждый магнит состоит из большого количества малых магнитов, всегда с двумя полюсами (рис. 140).
Рис. 140
Каждый магнит обязательно имеет два полюса: северный и южный.
В технике используют сложные магниты с чётным числом чередующихся полюсов (N — S — N — S). Например, магнит велосипедного генератора имеет 8 полюсов (4 северных и 4 южных) (рис. 141).
Рис. 141
Ориентирование кусков природных и постоянных магнитов в направлении с севера на юг подтверждает, что наша планета обладает магнитными свойствами. Веками многие учёные, мореплаватели и путешественники изучали магнитные свойства Земли в разных географических пунктах.
Странствуя, люди собрали обширные сведения о направлении стрелки компаса в разных местах земной суши и Мирового океана.
В 1595 г. английский физик У. Гильберт изготовил из природного магнита (рис. 142) шар и пришёл к выводу, что у него есть два полюса, а магнитная стрелка вблизи шара устанавливается в направлении от северного полюса к южному. Тогда У. Гильберт предположил, что Земля является большим магнитом (рис. 143). Последующие исследования подтвердили это предположение.
Рис. 142 | Рис. 143 |
Вокруг Земли существует магнитное поле, которое условно изображают магнитными линиями. В каждой точке магнитного поля магнитная стрелка устанавливается вдоль магнитной линии.
На этом явлении основано использование компаса. Каждый компас состоит из магнитной стрелки, свободно вращающейся на оси (рис. 144), и шкалы, на которой нанесены деления и основные стороны света. Стрелка компаса окрашена в сине-красный цвет либо на ней нанесена метка (синий конец и метка указывают северное направление).
Рис. 144
Пользоваться компасом первыми начали китайцы более 4 тысячелетий тому назад. На рисунке 145 вы видите такой компас, а на рисунке 146 — современный компас, его используют на судах. На рисунке 143 схематично изображены магнитные линии поля Земли.
Рис. 145 | Рис. 146 |
Как видим, возле Северного географического поляка размещается Южный магнитный полюс, в котором линии сходятся, а возле Южного географического полюса — Северный магнитный полюс, из которого линии расходятся. Согласно исследованиям намагниченности горных пород магнитные полюса, как и магнитное поле Земли, с течением времени перемещаются, причём это перемещение очень сложное.
Магнитные полюса Земли не совпадают с географическими полюсами.
В связи с этим направление магнитной стрелки не совпадает с направлением географического меридиана. Поэтому магнитная стрелка компаса лишь приблизительно показывает направление на север.
Поэтому магнитная стрелка компаса лишь приблизительно показывает направление на север.
Если активность Солнца возрастает, то с его поверхности в космическое пространство выбрасываются потоки заряженных частиц. Магнитное поле, образующее эти подвижные частицы, изменяет магнитное поле Земли и является причиной магнитных бурь. Во время магнитной бури нарушается радиосвязь, у людей может ухудшаться самочувствие, на Севере наблюдаются полярные сияния и т. д.
Земной магнетизм ещё полностью не изучен, поэтому исследованию магнитного поля Земли уделяется большое внимание во время полётов искусственных спутников и космических кораблей. Установлено, что земное магнитное поле надёжно защищает поверхность нашей планеты от космического излучения, действие которого на живые организмы часто является разрушительным.
Взаимодействие магнитовОпыт 1. Подносим к полюсам магнита магнитную стрелку. Северный полюс стрелки отталкивается от северного полюса магнита и притягивается к южному. Южный полюс стрелки отталкивается от южного полюса и притягивается к северному (рис. 147).
Южный полюс стрелки отталкивается от южного полюса и притягивается к северному (рис. 147).
Опыт 2. Поднесём два магнита сначала их Северными, а потом — южными полюсами. Магниты взаимодействуют между собой, при этом их разноимённые полюса притягиваются, а одноимённые — отталкиваются.
Разместим магнит на карандашах (рис. 148). К магниту приблизим южный (северный) полюс второго магнита. Видим, что и теперь магниты взаимодействуют между собой — притягиваются или отталкиваются.
Рис. 147 | Рис. 148 |
Разноимённые магнитные полюса двух магнитов притягиваются, одноимённые — отталкиваются.
Магниты взаимодействуют между собой, поскольку вокруг любого магнита существует магнитное поле. C одной стороны, магнитное поле одного магнита действует на второй магнит; с другой — магнитное поле второго магнита действует на первый.
Магнитное поле вокруг магнита можно обнаружить разными способами. Один из них состоит в использовании железных опилок (метод спектров).
Опыт 3 Накроем подковообразный магнит стеклом. На стекло насыпем тонкий слой железных опилок и легонько постучим по стеклу. Под действием магнитного поля магнита железные опилки размещаются рядом с магнитом не в беспорядке, а в виде замкнутых линий, которые называют линиями магнитного поля, или магнитными линиями (рис. 149, а).
Линии магнитного поля (магнитные линии) магнита — это воображаемые замкнутые линии, которые выходят из северного полюса магнита и входят в южный, замыкаясь внутри магнита (рис. 149, б).
Направление, которое показывает северный полюс магнитной стрелки в каждой точке поля, принято за направление магнитной линии в этой точке. В данной точке магнитного поля магнитная стрелка имеет единственное направление, это означает, что магнитные линии не пересекаются.
Рис.  149 149 | Рис. 150 |
Рисунок 150 даёт представление о магнитном поле разных магнитов: а — распределение железных опилок в магнитном поле двух магнитов, направленных один к другому одноимёнными полюсами, б — двух магнитов, направленных соответственно разноимёнными полюсами.
Ещё в 1269 г. П. Перегрин написал книгу «Письма о магнитах». В ней были описаны почти все известные в то время свойства магнитов. II. Перегрин установил следующее: если потереть стальную спицу природным магнитом, то она становится магнитом, то есть намагничивается (рис. 151). Такие тела также называют магнитами.
Рис. 151
Каждый из вас может изготовить магнит дома. Для этого возьмите длинный железный гвоздь, молоток или отвёртку и положите их вдоль направления, которое показывает компас, то есть вдоль линии север-юг. А через несколько недель эти предметы начнут проявлять магнитные свойства — притягивать железные гвозди или винтики (рис. 152).
Рис. 152
152
Магнитными свойствами через определённое время будет обладать и лезвие бритвы, если его положить на магнит (рис. 153).
Рис. 153
Железные или стальные тела также становятся магнитами, если их поместить в катушку изолированного провода, по которому проходит электрический ток. Что при этом происходит, рассмотрим позднее.
Долгое время электрические и магнитные явления рассматривали как независимые. Связь между ними установил в 1820 г. датский физик Г. К. Эрстед. В ходе опыта он заметил, что магнитная стрелка, размещённая под проводником (рис. 154, а), при замыкании цепи поворачивается и размещается почти перпендикулярно к проводнику (рис. 154, б). Если электрическую цепь разомкнуть, то стрелка принимает прежнее положение.
Рис. 154
Действие электрического тока на магнитную стрелку означает, что между электрическими и магнитными явлениями существует определённая связь.
В опыте Эрстеда впервые было выявлено магнитное поле тока. Действительно, если проводник с электрическим током действует на магнитную стрелку, то вокруг этого проводника существует магнитное поле.
Вокруг любого проводника с током существует магнитное поле.
Электрический ток — это направленное движение заряженных частиц, следовательно, вокруг движущейся заряженной частицы существуют одновременно магнитное и электрическое поля. А вокруг неподвижных зарядов — только электрическое поле.
Для исследования магнитного поля тока воспользуемся методом спектров, который мы применяли для обнаружения магнитного поля постоянных магнитов.
Опыт 1 Через отверстие в горизонтально размещённом картоне пропускаем вертикальный проводник с током (рис. 155). Картон посыпаем металлическими опилками и замыкаем цепь. В результате видим, что опилки образовали вокруг проводника концентрические окружности.
Рис. 155
Если опилки заменить магнитными стрелками, то они размещаются так, как показано на рисунке 156, а. Здесь изображён вид сверху на картон с цепочками опилок. Кружок в центре — поперечное сечение проводника с током. В нём крестиком обозначен ток в направлении за картон (как хвостовое оперение летящей от нас стрелы). Точкой в кружке обозначен ток в направлении из-за картона (как наконечник летящей на нас стрелы).
Здесь изображён вид сверху на картон с цепочками опилок. Кружок в центре — поперечное сечение проводника с током. В нём крестиком обозначен ток в направлении за картон (как хвостовое оперение летящей от нас стрелы). Точкой в кружке обозначен ток в направлении из-за картона (как наконечник летящей на нас стрелы).
Из опыта следует, что свойства магнитного поля тока такие же, как у магнитного поля постоянного магнита. Поэтому повторим выводы о графическом изображении магнитного поля. При этом помним, что его источником могут быть и постоянный магнит, и электрический ток.
Воображаемые линии, вдоль которых в магнитном поле размещаются продольные оси маленьких магнитных стрелок, называют линиями магнитного поля (магнитными линиями).
Направление, которое показывает северный полюс магнитной стрелки в каждой точке поля, принято за направление линии магнитного поля. В магнитном поле железные или стальные опилки показывают форму магнитных линий этого поля.
Линии магнитного поля тока — это замкнутые линии, окружающиепроводник с током.
Выполним предыдущий опыт, изменив ток в проводнике на противоположное направление. Оказывается, что все магнитные стрелки поворачиваются на 180° (рис. 156, б). Направление линий магнитного поля тока связано с направлением тока в проводнике, на практике его можно установить по правилу буравчика (рис. 156, в).
Если направление поступательного движения буравчика совпадает с направлением тока, то направление вращения ручки буравчика — с направлением магнитных линий.
Рис. 156
Опыт 2. Длинный прямой изолированный провод намотаем на деревянную или пластмассовую катушку. Присоединим её к источнику тока. В катушке проходит электрический ток, а к её концам притягиваются железные предметы, например винт (рис. 157).
Рис. 157
Опыт 3. Подвесим катушку с током на длинных тонких и гибких проводниках. Если рядом нет магнитных материалов или других магнитных полей, то катушка размещается в пространстве так же, как магнитная стрелка компаса: одна сторона катушки поворачивается на север, другая — на юг (рис. 158).
158).
Рис. 158
Катушка с током имеет два магнитных полюса: северный N и южный S.
Опыт 4 На пластинку из оргстекла (рис. 159) кладём железные опилки, по катушке пропускаем электрический ток. Опилки ориентируются в определённом порядке. Линии магнитного поля катушки с током также являются замкнутыми кривыми. То есть вне катушки они направлены от северного полюса катушки к южному (рис. 160, а). Магнитное поле катушки с током подобно магнитному полю штабового магнита (рис. 160, б).
Рис. 159 |
|
На рисунке 158, б показано, как отталкиваются постоянный магнит и катушка с током, поскольку они размещены одноимёнными полюсами один к другому.
Причину, почему тела имеют магнитные свойства, впервые установил французский учёный А. Ампер. Под впечатлением от наблюдений магнитной стрелки, которая поворачивается вблизи проводника с током в опытах Эрстеда, он предположил, что магнетизм Земли вызывают токи, протекающие внутри земного шара. Следовательно, магнитные свойства тела можно объяснить токами, циркулирующими внутри данного тела.
Следовательно, магнитные свойства тела можно объяснить токами, циркулирующими внутри данного тела.
Далее А. Ампер делает обобщение: магнитные свойства любого тела определяются замкнутыми электрическими токами внутри него. Этот решительный шаг от возможности объяснения магнитных свойств тел токами к категорическому утверждению, что магнитные взаимодействия —
это взаимодействия токов, — безусловное доказательство научной смелости А. Ампера.
Гипотеза Ампера
Согласно гипотезе Ампера внутри молекул и атомов циркулируют элементарные электрические токи. Мы уже знаем, что эти токи образуются вследствие движения электронов в атомах, то есть каждый атом обладает магнитными свойствами. Если атомы внутри тела ориентированы хаотически вследствие теплового движения, то действия внутриатомных токов взаимно компенсируются, и магнитных свойств тело не проявляет (рис. 161, α). В намагниченном состоянии элементарные токи в теле ориентированы таким образом, что их действия суммируются (рис. 161, б).
161, б).
Рис. 161
Гипотеза Ампера объясняет, почему магнитная стрелка и рамка с током в магнитном поле ведут себя одинаково. Стрелку (постоянный магнит) можно рассматривать как большую и сложную совокупность небольших рамок с током, ориентированных одинаково.
В ферромагнетиках (вещества, в состав которых входят Fe, Со, Ni и др.) элементарные магнитики-атомы образуют участки спонтанной (произвольной) намагниченности с линейными размерами 0,0010,01 мм, которые называют доменами. В доменах размещается множество одинаково ориентированных атомов, поэтому намагниченность домена максимальна. В ненамагниченном ферромагнетике соседние домены расположены таким образом, что их намагниченности взаимно компенсируются (рис. 162, а). Если образец такого ферромагнетика поместить в магнитное поле постоянного магнита или внутри катушки с током, то под влиянием внешнего магнитного поля атомы в разных доменах преимущественно начинают ориентироваться так, что направление их магнитного поля совмещается с направлением внешнего (рис. 162, б). При этом магнитное поле внутри образца может увеличиться тысячекратно (рис. 162, в). Говорят, что образец намагнитился, при определённых условиях это состояние намагниченности сохраняется и после исчезновения внешнего поля, то есть образец становится постоянным магнитом.
162, б). При этом магнитное поле внутри образца может увеличиться тысячекратно (рис. 162, в). Говорят, что образец намагнитился, при определённых условиях это состояние намагниченности сохраняется и после исчезновения внешнего поля, то есть образец становится постоянным магнитом.
Если его нагревать, то при определённой температуре (для железа 769 °C) домены разрушаются, и намагниченность утрачивается. Температуру, при которой ферромагнетик теряет намагниченность, называют температурой, или точкой Кюри, в честь выдающегося французского физика П. Кюри, открывшего и исследовавшего это явление.
Рис. 162
Открытие Г. К. Эрстеда ознаменовало собой начало ряда исследований по электромагнетизму. В 1820 г. А. Ампер и Д. Араго исследовали магнитное поле катушки. В 1825 г. У. Стерджей, заметил, что магнитное поле катушки значительно усиливается, если в середину её вставить стальной сердечник. Так он получил простейший электромагнит.
В 1828 г. Дж. Генри использовал многослойную обмотку из изолированного провода и получил более мощный электромагнит.
Электромагнит — это коллективное изобретение, прошедшее ряд этапов, где каждый был невозможен без предыдущего.
Электромагнит состоит из следующих деталей (рис. 168): стального сердечника 1, катушки (обмотки) 2 и якоря 3, который притягивается к сердечнику. Выясним, от чего зависит сила, с которой магнитное поле катушки электромагнита действует на его якорь.
Рис. 168
Опыт 1. Замыкаем цепь из электромагнита и реостата; с помощью реостата будем изменять силу тока в катушках. При определённой силе тока электромагнит удерживает определённый груз (рис. 169, а), а если увеличить силу тока в два раза, то электромагнит может удержать груз приблизительно в два раза тяжелее (рис. 169, б).
Рис. 169
Чем больший ток проходит в катушке электромагнита, тем с большей силой притягивается к нему якорь.
Опыт 2 Повторим опыт 1 при начальной силе тока, когда электромагнит удерживал меньший груз, но используем катушку такой же конструкции, содержащую в два раза больше витков. Убедимся, что в этом случае электромагнит способен удерживать такой же большой груз, как в опыте 1, когда в два раза увеличили ток (рис. 169, б).
Чем больше витков в катушке электромагнита, тем с большей I силой притягивается к нему якорь.
Итак, «грузоподъёмность» электромагнита зависит от «ампер-витков» его обмотки, то есть от произведения силы тока в катушке на количество витков в ней.
Электромагниты широко применяют в технике, быту, медицине и т. д. благодаря своим особенностям: быстро размагничиваются при выключении тока; в зависимости от назначения их изготовляют разных размеров; при работе электромагнита можно регулировать его магнитное действие, изменяя силу тока в обмотке.
Электромагниты имеются в каждом автомобиле, телефоне, телевизоре, самолёте, космическом корабле, теплоходе и т. д. Электромагнитный подъёмный кран применяют при погрузке или разгрузке металлолома (рис. 170). Такой кран удобен тем, что груз не требует никаких креплений. Машинист крана размещает электромагнит, например, возле металлолома, включает ток в обмотке и подбирает лом.
д. Электромагнитный подъёмный кран применяют при погрузке или разгрузке металлолома (рис. 170). Такой кран удобен тем, что груз не требует никаких креплений. Машинист крана размещает электромагнит, например, возле металлолома, включает ток в обмотке и подбирает лом.
Рис. 170
После выключения тока металлолом просто отпадает от сердечника. А электромагнит заводского крана, который используют, например, для перенесения бобин листовой стали, имеет 4 обмотки и может поднять бобину диаметром 2 м и массой 28 т (рис. 171).
Рис. 171
На рисунке 172 в разрезе показан магнитный сепаратор для очистки зерна от семян сорняков. В зерно подмешивают сильно измельчённые железные опилки, которые не прилипают к зерну, а только к семенам сорняков. При вращении барабана с электромагнитом внутри происходит распределение зерна и семян сорняков с металлическими опилками.
Рис. 172
Если в глаз попадают тела, на которые действует магнит, то в больнице для их удаления наряду с постоянными магнитами используют электромагниты. Изменяя силу тока в обмотке, регулируют интенсивность магнитного поля и удаляют постороннее тело с глубины до 2,5 мм.
Изменяя силу тока в обмотке, регулируют интенсивность магнитного поля и удаляют постороннее тело с глубины до 2,5 мм.
Два проводника, по которым протекает электрический ток, взаимодействуют между собой с определённой силой, так как на каждый проводник с током действует магнитное поле тока другого проводника.
Магнитное поле действует с определённой силой на любой проводник с током, размещённый в этом поле. Такую силу называют силой Ампера в честь А. М. Ампера, который исследовал и определил зависимость значения и направления этой силы от условий эксперимента.
Опыт 1. Подвесим на подсоединённых к источнику тока гибких проводниках отрезок толстого медного провода АВ. Разместим его горизонтально между полюсами подковообразного магнита (рис. 174, α). В этом случае проводник AjB размещается в магнитном поле, которое образует вокруг себя магнит. Если замкнуть электрическую цепь, то проводник AB начнёт перемещаться, втягиваясь внутрь магнита (рис. 174, б).
174, б).
Если изменить направление электрического тока, то проводник AB будет выталкиваться из магнита (рис. 174, в). Проводник AB также выталкивается, если поменять местами полюса магнита. Направление движения проводника в магнитном поле определяется направлением силы Ампера, действующей на него, и зависит от направления тока в проводнике и размещения относительно полюсов магнита.
Направление силы Ампера, действующей на проводник с током, удобно определять с помощью правила левой руки (рис. 174, в).
Рис. 174
Если ладонь левой руки разместить так, чтобы четыре выпрямленных пальца указывали направление тока в проводнике, а линии магнитного поля входили в ладонь, то отогнутый под прямым углом большой палец укажет направление силы Ампера, действующей на проводник с током.
На практике большое значение имеет вращательное движение проводника с током в магнитном поле как механическое действие электрического тока. На рисунке 175 изображён прибор, с помощью которого можно осуществлять такое движение. В этом приборе лёгкая прямоугольная рамка ABDC посажена на вертикальную ось. На рамку намотано несколько десятков витков провода с изоляцией. Концы катушки соединены с металлическими полукольцами коллектора 2. Один конец провода присоединён к одному полукольцу, а второй — к другому.
В этом приборе лёгкая прямоугольная рамка ABDC посажена на вертикальную ось. На рамку намотано несколько десятков витков провода с изоляцией. Концы катушки соединены с металлическими полукольцами коллектора 2. Один конец провода присоединён к одному полукольцу, а второй — к другому.
Рис. 175 | Рис. 176 |
К каждому полукольцу прижимается металлическая пластина-щётка 1. Щётки необходимы для подведения тока от источника тока к рамке. Одна щётка всегда соединена с положительным полюсом источника, а другая — с отрицательным.
Так как в частях рамки AC и BD ток имеет противоположные направления, то они перемещаются в противоположные стороны, и рамка поворачивается. Присоединённые к её концам полукольца повернутся вместе с ней, и каждое прижмётся к другой щётке, поэтому ток в рамке изменит направление нс противоположное. Поскольку после поворота рамки на 180° одновременно поменялись на противоположные относительно неё и направление магнитного поля, и направление тока, то направления сил Ампера, действующих на части AC и BD рамки не изменяются, а рамка продолжит вращаться в одном направлении. Если бы коллектор 2 не переключал автоматически направление тока в рамке на противоположное, то она останавливалась бы после каждого полуоборота. Вращение катушки с током в магнитном поле используют в конструкции электрического двигателя и электроизмерительных приборов.
Если бы коллектор 2 не переключал автоматически направление тока в рамке на противоположное, то она останавливалась бы после каждого полуоборота. Вращение катушки с током в магнитном поле используют в конструкции электрического двигателя и электроизмерительных приборов.
Без электрических двигателей невозможно представить жизнь современного человека. Вот далеко не полный перечень известных вам устройств, механизмов и машин, в которых используются электрические двигатели: автомобиль, самолёт, трактор, трамвай, троллейбус, лифт и т. д.
Существует множество конструкций разных электродвигателей, но мы будем изучать устройство и принцип действия широко распространённого коллекторного электродвигателя. Он состоит из следующих основных узлов (рис. 176).
- Статор 1 (англ, stator, от латинского слова sto — стою) является постоянным магнитом с наконечниками S и N, или электромагнитом. Он составляет одно целое с корпусом электродвигателя. Статор коллекторного двигателя часто называют индуктором.
 Эта часть двигателя служит для возбуждения магнитного поля.
Эта часть двигателя служит для возбуждения магнитного поля. - Ротор 2 (от латинского слова roto — вращаюсь), или якорь двигателя — собранный из листов специальной стали сердечник определённой формы, на который наматывают изолированный провод — обмотку.
- Концы обмотки припаяны к медным пластинам коллектора, закреплённым на хорошо изолированном барабане на оси ротора.
- Две угольные щётки специальными пружинами плотно прижимаются к коллекторным пластинам. К щёткам от источника тока подаётся напряжение для питания электродвигателя.
Принцип работы рассмотрим на примере простого двигателя (рис. 177). К щёткам 1 и 2 подаётся необходимое для работы электродвигателя напряжение. При взаимодействии тока, проходящего по обмотке, с магнитным полем статора 6 ротор 5 поворачивается таким образом, что рамка оказывается в вертикальном положении, и тока в ней нет, так как щётки касаются не пластин коллектора 3 и 4, а изоляции между ними. Однако благодаря инерции ротор проходит это положение, и щётки снова касаются коллекторных пластин. Каждые пол-оборота коллектор переключает полярность напряжения, поэтому направление тока в обмотке всегда соответствует вращению ротора в одну сторону.
Каждые пол-оборота коллектор переключает полярность напряжения, поэтому направление тока в обмотке всегда соответствует вращению ротора в одну сторону.
При одинаковой мощности размеры электродвигателей меньше, чем у тепловых двигателей. Они не выделяют газов, дыма и пара. Можно изготовить электрический двигатель любой мощности и установить в любом месте. Например, двигатель (рис. 178) имеет мощность 890 кВт, работает при напряжении 1 400 В, и в нём проходит ток 635 А.
Рис. 177 | Рис. 178 |
Один из первых в мире электрических двигателей, пригодных для практического применения, изобрёл российский учёный Б. Якоби.
Электроизмерительные приборыГромкоговоритель предназначен для преобразования электрической энергии в энергию звуковых колебаний. В электродинамическом громкоговорителе используют действие магнитного поля постоянного магнита на переменный ток в подвижной катушке.
Внешний вид и схема устройства громкоговорителя приведены на рисунке 179. Звуковая катушка 1 установлена в зазоре кольцевого магнита 2. C катушкой жёстко соединён бумажный конус — диффузор 4, который по периметру укреплён на упругих подвесках 3.
По катушке проходит переменный электрический ток с частотой звукового сигнала микрофона или радиоприёмника, проигрывателя, магнитофона. Под действием силы Ампера катушка колеблется вдоль своей оси в такт изменениям силы тока. Эти колебания передаются диффузору, и его поверхность излучает звуковые волны.
Рис. 179
Громкоговорители высокого качества передают без значительных искажений звуковые колебания от 40 до 15 000 Гц. Но такие устройства очень сложные. Поэтому используют систему из нескольких громкоговорителей, при этом каждый из них передаёт звук в определённом небольшом интервале частот. Недостаток всех громкоговорителей — малый КПД. Они излучают лишь 1—35 % всей направленной к ним энергии.
В технике широко используют стрелочные измерители электрических величин, основанью на магнитном действии тока. Существуют несколько систем электроизмерителей магнитного действия: в приборах электромагнитной системы стрелка-указатель связана с ферромагнитным сердечником, который втягивается в катушку, где протекает измеряемый ток; в приборах магнитоэлектрической системы указатель связан с лёгкой рамкой с измеряемым током, которая поворачивается в поле магнита на угол, пропорциональный значению этого тока.
Существуют несколько систем электроизмерителей магнитного действия: в приборах электромагнитной системы стрелка-указатель связана с ферромагнитным сердечником, который втягивается в катушку, где протекает измеряемый ток; в приборах магнитоэлектрической системы указатель связан с лёгкой рамкой с измеряемым током, которая поворачивается в поле магнита на угол, пропорциональный значению этого тока.
Рассмотрим подробнее устройство и действие наиболее распространённых приборов магнитоэлектрической системы (рис. 180).
Рис. 180
Они состоят из подковообразного магнита 1, возле полюсов которого размещаются наконечники 6, между которыми на двух полуосях вращается лёгкая алюминиевая рамка 3. На рамку наматывают тонкий изолированный проводник.
Для усиления магнитного поля в пространстве между полюсами размещают неподвижный железный цилиндр 2. К передней полуоси рамки прикрепляют лёгкую алюминиевую стрелку 4. Концы проводника на рамке припаивают к двум пружинам 5, по которым подаётся ток к обмотке рамки.
При прохождении тока по обмотке рамки она поворачивается. Чем большая сила тока проходит через рамку, тем на больший угол поворачивается стрелка. Если электрическую цепь разомкнуть, то пружины под действием сил упругости, возникающих при повороте рамки, возвращают стрелку в нулевое положение шкалы 7.
C помощью приборов магнитоэлектрической системы можно измерять такие электрические величины, как силу тока, напряжение.
Пример №1
В произведении французского физика Д. Ф. Араго «Гром и молния» приводится много случаев перемагничивания компасной стрелки, намагничивания стальных предметов под действием молнии. Как объяснить эти явления?
Ответ: молния — это искровой разряд. Вокруг неё возникает сильное магнитное поле, которое действует на стальные предметы, намагничивая и перемагничивая их.
Пример №2
Объясните результаты опыта (рис. 181).
Ответ: если цепь не замкнута, то все магнитные стрелки размещаются в направлении север-юг. Если цепь замкнуть, то катушка становится магнитом, и магнитные стрелки взаимодействуют с ней.
Если цепь замкнуть, то катушка становится магнитом, и магнитные стрелки взаимодействуют с ней.
Рис. 181
Пример №3
Рамка с током размещена между полюсами подковообразного магнита, при этом её плоскость перпендикулярна линиям магнитного поля. Будет ли поворачиваться рамка?
Ответ: нет, поскольку в этом случае у рамки отсутствует вращательный момент.
Вы уже знаете свойства электрического поля неподвижных электрических зарядов и магнитного поля постоянных магнитов и постоянных электрических токов в неподвижных проводниках. После открытия в 1820 г. Эрстедом явления возникновения магнитного поля вокруг проводника с током начались исследования явлений в электрических и магнитных полях, изменяющихся с течением времени.
Если электрический ток создаёт магнитное поле, то можно предположить существование обратного явления: возникновение электрического тока в проводнике, помещённом в магнитное поле. Многочисленные попытки обнаружить это явление не принесли ожидаемых результатов. В неподвижных замкнутых проводниках, помещённых в наиболее мощные на то время магнитные поля, электрический ток не возникал.
Многочисленные попытки обнаружить это явление не принесли ожидаемых результатов. В неподвижных замкнутых проводниках, помещённых в наиболее мощные на то время магнитные поля, электрический ток не возникал.
В 1831 г. М. Фарадей экспериментально открыл новое явление электромагнитной индукции, ставшее основой современной электротехники и радиотехники. Его нельзя было предсказать на основе известных в то время сведений о магнитных полях и электрических токах. Выяснилось, что электрический ток все-таки возникает в неподвижном замкнутом проводнике, помещённом в магнитное поле, но лишь при изменении этого магнитного поля.
Опыты Фарадея, которые привели к открытию явления электромагнитной индукции, достаточно просты, их легко провести в условиях школы.
Опыт 1. Присоединим к гальванометру гибкий проводник и поместим его между полюсами магнита (рис. 195). Если проводник и магнит неподвижны, то тока в проводнике нет. При перемещении проводника гальванометр сразу же фиксирует в нём наличие тока. Если при перемещении проводника в одном направлении стрелка гальванометра отклоняется, например, вправо, то при движении в обратном направлении она будет отклоняться влево, то есть направление тока в проводнике изменяется. Ток в проводнике возникает и в случае перемещения магнита относительно проводника.
Если при перемещении проводника в одном направлении стрелка гальванометра отклоняется, например, вправо, то при движении в обратном направлении она будет отклоняться влево, то есть направление тока в проводнике изменяется. Ток в проводнике возникает и в случае перемещения магнита относительно проводника.
Рис. 195
Опыт 2. Присоединим к гальванометру катушку. Если в эту катушку вводить или выводить магнит (рис. 196), то гальванометр показывает возникновение электрического тока в цепи. Если магнит неподвижен — тока нет.
Рис. 196
Опыт 3 Закрепим полосовой магнит в штативе и наденем катушку, присоединив её к гальванометру, на магнит (рис. 197). В катушке снова возникает электрический ток. Этот ток протекает только при движении катушки относительно магнита и изменяет свое направление при изменении направления движения катушки.
Рис. 197
Опыт 4. Замкнём катушку 2 через гальванометр и вставим в неё катушку 1, которую можно присоединить к источнику тока (рис. 198). В момент замыкания цепи катушки 1 стрелка гальванометра отклоняется, то есть при изменении (возникновении) магнитного поля катушки 1 по катушке 2 протекает электрический ток. Но после установления в катушке 1 тока магнитное поле перестаёт изменяться, ток в катушке 2 исчезает — стрелка гальванометра устанавливается на нуле.
198). В момент замыкания цепи катушки 1 стрелка гальванометра отклоняется, то есть при изменении (возникновении) магнитного поля катушки 1 по катушке 2 протекает электрический ток. Но после установления в катушке 1 тока магнитное поле перестаёт изменяться, ток в катушке 2 исчезает — стрелка гальванометра устанавливается на нуле.
Рис. 198
Разомкнём цепь катушки. При исчезновении в ней тока, а вместе с ним и его магнитного поля стрелка гальванометра отклоняется в противоположную сторону. Это означает, что в катушке 2 возникает электрический ток, направление которого обратно тому, который проходил при замыкании катушки 1. В этих опытах при замыкании цепи катушки 1 возникает магнитное поле, а при размыкании — исчезает. В результате изменений магнитного поля в катушке возникает переменный ток, который называют индукционным.
В цепь катушки 1 можно включить реостат для изменения силы тока в цепи. Итак, при увеличении силы тока в цепи катушки 1 в катушке 2 возникает индукционный ток одного направления, при уменьшении — противоположного направления. В результате изменения силы тока в катушке 1 изменяется также магнитное поле тока, при этом в катушке 2 возникает индукционный ток.
В результате изменения силы тока в катушке 1 изменяется также магнитное поле тока, при этом в катушке 2 возникает индукционный ток.
Явление возникновения в замкнутом проводнике переменного электрического тока при пересечении этим проводником линий магнитного поля называют электромагнитной индукцией. Ток, возникающий при этом, называется индукционным.
Из данных примеров следует, что индукционный электрический ток возникает при изменении в пространстве или во времени интенсивности магнитного поля, линии которого окружают проводник замкнутого контура. Изучая свойства электромагнитов, мы узнали, что интенсивность магнитного поля катушки с током можно изменять, регулируя в ней силу тока. Видим, что такие изменения можно выполнить разными способами.
Магнитное поле изображают с помощью магнитных линий. Оказалось, что в местах поля, где его интенсивность меньше, линии проходят реже, а где больше — размещаются гуще. Это видно на рисунках 143,149,150,160, где изображены магнитные поля Земли, постоянных магнитов и катушки с током.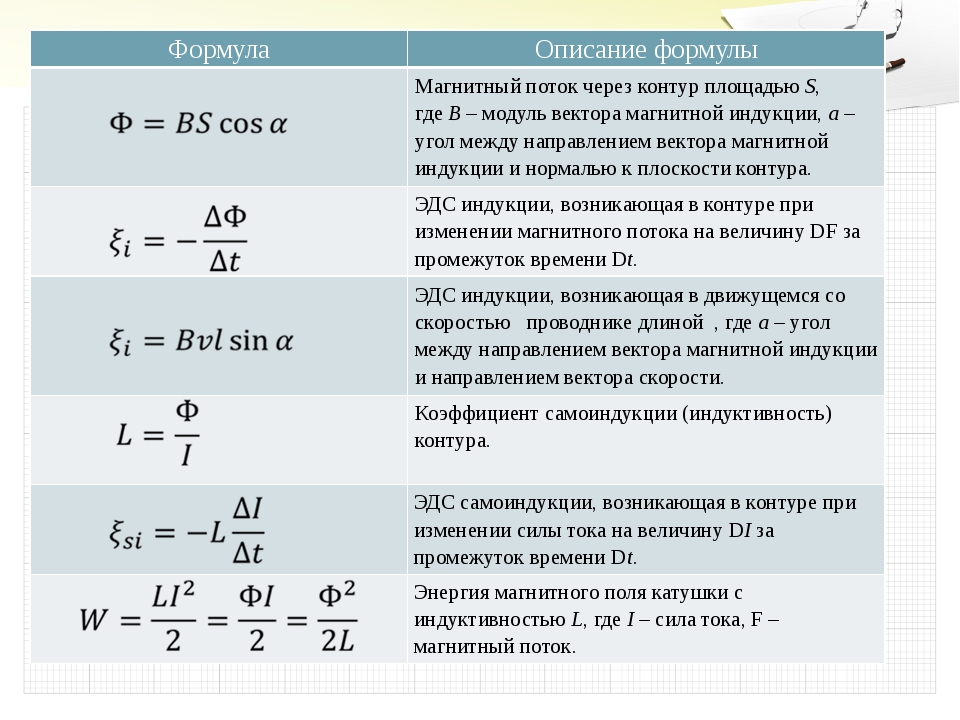 Поля с переменными плотностью и направлением линий называют неоднородными. Если плотность и направление линий постоянны, то есть магнитные линии параллельны, а расстояния между соседними линиями одинаковы, то такое поле называют однородным. К однородным приближаются магнитные поля внутри длинной катушки с током (см. рис. 160, а) или между широкими полюсами постоянных магнитов.
Поля с переменными плотностью и направлением линий называют неоднородными. Если плотность и направление линий постоянны, то есть магнитные линии параллельны, а расстояния между соседними линиями одинаковы, то такое поле называют однородным. К однородным приближаются магнитные поля внутри длинной катушки с током (см. рис. 160, а) или между широкими полюсами постоянных магнитов.
В замкнутом проводящем контуре индукционный ток возникает только при изменении плотности магнитных линий, пронизывающих этот контур. Индукционный ток тем больше, чем больше скорость изменения магнитного поля. Проводник, перемещаясь, обязательно должен пересекать магнитные линии. Если проводник контура движется вдоль магнитных линий или катушка перемещается поступательно в однородном магнитном поле, то индукционный ток не возникает.
Индукционный ток в проводнике может иметь разные направления. Опыты показывают, что направление индукционного тока в проводнике, движущемся в магнитном поле, зависит от направления линий магнитного поля и направления движения проводника. На практике направление индукционного тока в подвижном проводнике определяют по правилу правой руки (рис. 199).
На практике направление индукционного тока в подвижном проводнике определяют по правилу правой руки (рис. 199).
Рис. 199
Если ладонь правой руки разместить так, чтобы в неё входили линии магнитного поля, а отведённый под прямым углом большой палец указывал направление движения проводника, то вытянутые четыре пальца руки укажут направление индукционного тока в проводнике.
Пример №4
Если разместить проволочный прямоугольник в плоскости магнитного меридиана и перемещать его в этой плоскости, то будет ли в нём возникать индукционный ток?
Ответ: нет, поскольку стороны прямоугольника не пересекают магнитных линий магнитного поля Земля.
Историческая справка:
Фарадей Майкл (22.09.1791-25.08.1867) — английский физик, член Лондонского королевского общества. Родился в предместье Лондона в семье кузнеца. Из-за бедности не получил систематического образования. Слушая воскресные лекции Г. Деви, попросил взять его на работу в Королевский институт, в котором работал с 1813 г., в 1825 г. возглавил лабораторию в этом институте, с 1827 г. — профессор кафедры химии.
Деви, попросил взять его на работу в Королевский институт, в котором работал с 1813 г., в 1825 г. возглавил лабораторию в этом институте, с 1827 г. — профессор кафедры химии.
Майкл Фарадей
Выполнил фундаментальные исследования по электромагнетизму. Поставил перед собой задачу «преобразовать магнетизм в электричество» и получить электрический ток из магнитного поля. В 1831 г. открыл явление электромагнитной индукции, то есть получил индукционный ток во вторичной обмотке при замыкании и размыкании тока в первичной обмотке. М. Фарадей детально исследовал явления электромагнитной индукции и самоиндукции, высказал предположение, что электрические и магнитные действия не передаются от тела к телу непосредственно, а переносятся в диэлектрической среде, размещённой между ними.
В 1833—1834 гг. установил законы электролиза и ввёл основную терминологию этого явления. Ввёл понятия электрического и магнитного поля, а также электрических и магнитных силовых линий. После исследований М. Фарадея материю начали рассматривать не только в форме вещества, но и в форме поля. В 1843 г экспериментально доказал закон сохранения электрического заряда. Сделал открытия в области магнетизма (1845) и действия магнитного поля на свет (1846).
Фарадея материю начали рассматривать не только в форме вещества, но и в форме поля. В 1843 г экспериментально доказал закон сохранения электрического заряда. Сделал открытия в области магнетизма (1845) и действия магнитного поля на свет (1846).
Вы приобрели начальные знания о постоянном магнитном поле и появлении магнитного поля вокруг проводника с током. В частности, вы получили общие сведения о магнитном поле прямого проводника с током и катушки с током, об электромагнитах и их применении. Однако вы еще не знакомы с математическими выражениями по определению их величин. В данной главе вы познакомитесь, с такими величинами, как магнитная индукция и магнитный поток, индукция магнитного поля прямого тока, индукция магнитного поля катушки с током, сила, действующая на частицу, движущуюся в магнитном поле.
Магнитное поле и величины, характеризующие магнитное полеВ природе существуют природные соединения металлов, которые обладают свойством притягивать к себе некоторые другие тела. Это означает, что они создают вокруг себя поле. Такое поле принято называть магнитным полем. Тела, длительное время сохраняющие свою намагниченность, называются постоянным магнитом, или магнитом.
Это означает, что они создают вокруг себя поле. Такое поле принято называть магнитным полем. Тела, длительное время сохраняющие свою намагниченность, называются постоянным магнитом, или магнитом.
Возьмем магнит прямоугольной формы и приблизим его к мелким частицам железа. Мы увидим, что они прилипают только к двум концам магнита. Те места магнита, где обнаруживается наибольшее магнитное действие, называются полюсами постоянного магнита. Постоянный магнит имеет два магнитных полюса: северный (N) и южный (S) (рис. 1.1).
Из рис. 1.2 видно, что если две магнитные стрелки приблизить друг к другу, то магниты притягиваются разноименными полюсами и отталкиваются одноименными. Это означает, что между намагниченными телами существует сила взаимного действия. Действующие силы характеризуются через силовые линии магнитного поля.
Силовые линии магнитного поля увидеть невозможно. Однако с помощью следующего опыта мы сможем получить представление о расположении (направлении) магнитных силовых линий. Для этого картонную бумагу равномерно покроем железными опилками и положим ее на поверхность плоского магнитного стрежня. Если несколько раз осторожно встряхнуть картонную бумагу, то железные опилки примут вид, как показано на рис. 1.3 а. На рисунке видно, что опилки на картоне собираются плотнее у концов магнита, а между полюсами их меньше.
Для этого картонную бумагу равномерно покроем железными опилками и положим ее на поверхность плоского магнитного стрежня. Если несколько раз осторожно встряхнуть картонную бумагу, то железные опилки примут вид, как показано на рис. 1.3 а. На рисунке видно, что опилки на картоне собираются плотнее у концов магнита, а между полюсами их меньше.
Картина распределения железных опилок на рис. 1.3 а показывает положение силовых линий, связывающих магнитные полюсы. Силовыми линиями магнитного поля принято считать замкнутые кривые, которые выходят из северного полюса, а входят в южный полюс магнита (рис. 1.3 б). Поля с замкнутыми силовыми линиями называются вихревыми полями. Значит, магнитное поле является вихревым полем. Этим свойством силовые линии магнитного поля отличаются от силовых линий электрического поля.
Физическая величина, характеризующая величину силовых линий определенной точки магнитного поля, называется индукцией магнитного поля. Индукция магнитного поля является векторной величиной и обозначается буквой
Индукция магнитного поля является векторной величиной и обозначается буквой
Единицей измерения индукции магнитного поля в системе СИ в честь сербского физика Никола Тесла принято называть тесла (Тл)
Магнитный потокДля описания величины магнитных силовых линий, пересекающих какие-либо поверхности, введено понятие «поток магнитного поля». Потоком магнитной индукции, пересекающим площадь S, называется произведение вектора магнитной индукции на площадь поверхности. Магнитный поток является скалярной величиной и обозначается буквой Ф. Магнитный поток выражается как:
Если индукционные линии магнитного поля создают с поверхностью определенный угол (рис. 1.4), то поток магнитной индукции, проходящий через поверхность, будет зависеть от этого угла, т.е.:
Здесь а – угол между вектором и нормалью к поверхности.
В системе СИ единицу магнитного потока назвали в честь немецкого физика Д. Вебера -вебер (Вб). Из уравнения (1-2):Магнитное поле, проходящее сквозь перпендикулярно расположенную площадь 1 к линиям индукции магнитного поля, равной 1 Тл, составляет 1 Вб.
Пример №5
Силовые линии однородного магнитного поля с индукцией 20 мТ падают под углом 60° на прямоугольную рамку длиной 4 см и шириной 3 см. Определите магнитный поток, проходящий сквозь рамку?
Рис. 1.4.
Дано:
Найти: Ф = ?
Формула:
Решение: Ответ:
Вращательный момент однородного магнитного поля, действующий на рамку с токомТо, что магнитное поле создается не только постоянными магнитами, но и вокруг проводников с токами, показал на своих опытах Эрстед. Теперь мы рассмотрим взаимное действие магнитного поля проводника с током и постоянным магнитным полем.
Если в магнитное поле внести контур или магнитную стрелку, то можно наблюдать, как они поворачиваются (рис. 1.5). Когда меняется направление тока в контуре, контур поворачивается в противоположную сторону.
Давайте определим причину вращения рамки с током, расположенную в магнитном поле. Рамка длиной расположена вертикально в магнитном поле, и через стороны АВ и CD течет ток I. Тогда значение силы Ампера, действующей со стороны магнитного поля на участок рамки, составляет:
Тогда значение силы Ампера, действующей со стороны магнитного поля на участок рамки, составляет:
здесь:
Направление этой силы определяется по правилу левой руки. Модули сил, действующих на участки АВ и CD, являются равными и направлены в противоположные стороны, т.е. на рамку с током со стороны магнитного поля действует пара сил. Под воздействием этой пары сил рамка с током поворачивается.
Эта пара сил относительно оси вращения создает вращательный момент.
Момент силы:
Здесь, a – угол между нормалью, проведенной на поверхность контура и вектора магнитной индукции, плечо сил частей рамки равно
Тогда полный вращательный момент:
Подставляя формулу силы Ампера в выражение (1-5), запишем выражение вращательного момента:
Если учесть, что, выражение (1-6) примет вид:
Значит, момент силы (М), действующей на контур с током, внесенный в магнитное поле, прямо пропорционален силе тока , протекающего через контур, площади контура (S) и синусу угла между направлением магнитной индукции и нормалью, проведенной на поверхность контура
Если,
Согласно этому уравнению индукцию магнитного поле можно выразить:
Принцип действия многих электрических приборов основан на взаимодействии проводника с током с постоянным магнитом. На рис. 1.6 приводится строение одного из таких измерительных приборов. Между полюсами (1) сильного магнита закреплен железный сердечник . Сверху надета проволочная рамка (2). В катушку ток подается через металлические пружины (3), которые держат рамку. Эти пружины, в случае когда не подается ток в катушку, удерживают стрелку (4) в положении, равном нулю. При подключении прибора в электрическую цепь через катушку проходит ток и рамка поворачивается под воздействием магнитного поля. В это время пружины начинают сжиматься. Рамка продолжает поворачиваться до тех пор, пока не сравняются сила упругости пружины и сила Ампера.
На рис. 1.6 приводится строение одного из таких измерительных приборов. Между полюсами (1) сильного магнита закреплен железный сердечник . Сверху надета проволочная рамка (2). В катушку ток подается через металлические пружины (3), которые держат рамку. Эти пружины, в случае когда не подается ток в катушку, удерживают стрелку (4) в положении, равном нулю. При подключении прибора в электрическую цепь через катушку проходит ток и рамка поворачивается под воздействием магнитного поля. В это время пружины начинают сжиматься. Рамка продолжает поворачиваться до тех пор, пока не сравняются сила упругости пружины и сила Ампера.
Когда прибор последовательно подсоединен к электрической цепи, из-за равнозначности силы тока, протекающего через цепь и катушку прибора, угол поворота стрелки будет прямо пропорционален силе тока. В этом случае прибор используется в качестве амперметра.
На рисунке 1.6 б приводится общий вид двигателя постоянного тока. Его принцип работы основан на вращении рамки с током в постоянном магнитном поле.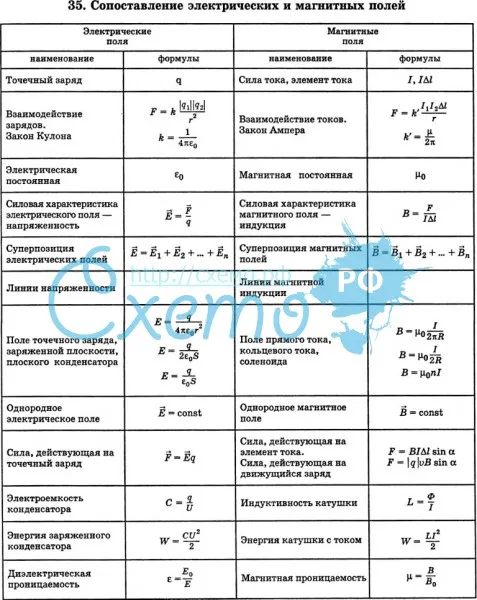
Пример №6
Проволочная рамка с сечением 20 и имеющая 100 витков размещена в магнитном поле. Когда через рамку проходит ток силой 2 А, в ней появляется максимальный вращательный момент, равный 0,5 . Определите индукцию магнитного поля.
Дано:
Найти:
Формула:
Решение:
Ответ:
Магнитное поле прямого тока, кругового тока и катушки с токомДля наблюдения силовых линий магнитного поля, образующихся вокруг проводника с током, берем картонную бумагу, просверливаем в середине отверстие и пропускаем через нее прямой проводник. На поверхности картонной бумаги рассыпаем железные опилки. Когда проводник подсоединен к источнику тока, картон слегка подергивается. Под воздействием магнитного поля тока железные опилки ведут себя как магнитные стрелки и располагаются по линиям магнитной индукции (рис. 1.7 а.).
Силовые линии магнитного поля прямого тока состоят из окружностей с центрами на оси проводника. Эти окружности перпендикулярны оси проводника (рис. 1.7 б). Направление силовых линий магнитного поля определяется правилом правого винта: если поступательное движение винта совпадает с направлением тока, тогда направление вращения рукоятки винта показывает направление линии магнитной индукции.
Эти окружности перпендикулярны оси проводника (рис. 1.7 б). Направление силовых линий магнитного поля определяется правилом правого винта: если поступательное движение винта совпадает с направлением тока, тогда направление вращения рукоятки винта показывает направление линии магнитной индукции.
Вектор индукции магнитного поля направлен по касательной к силовым линиям. В частном случае направление индукции магнитного поля в точке на расстоянии d от проводника с током приводится на рисунке 1.8 а.
В большинстве случаев магнитное поле создается не одним проводником, а системой проводников с током (рис. 1.8 б). Тогда индукция результирующего поля в определенных точках пространства будет равной векторной сумме индукции магнитного поля, созданного в данной точке каждым проводником с током, т.е.:
Это называется принципом суперпозиции для магнитного поля.
Французские ученые Ж. Био, Ф. Савар и П. Лаплас вывели общий закон, позволяющий вычислять индукцию магнитного поля, создаваемого вокруг проводника с током произвольной формы. Согласно этому закону индукцию магнитного поля, озданного произвольным элементом проводника с током в точке А вокруг проводника, можно определить по следующей формуле:
Согласно этому закону индукцию магнитного поля, озданного произвольным элементом проводника с током в точке А вокруг проводника, можно определить по следующей формуле:
а – угол между вектором, проведенным от элемента в точку А и элементом фис. 1.9). – расстояние от элемента прямого тока до точки А.
Индукция магнитного поля, создаваемая в точке А на расстоянии от прямого тока бесконечной длины, по закону Био-Савара-Лапласа, определяется с помощью следующего выражения:
Значит, индукция магнитного поля, создаваемого в произвольной точке прямого проводника с током бесконечной длины, прямо пропорциональна
силе тока, проходящего через проводник, и обратно пропорциональна кратчайшему расстоянию между проводником и точкой, для которой вычисляется индукция.
Индукция магнитного поля в центре кругового токаПусть постоянный ток течет по кругу с радиусом R (рис. 1.10). По закону Био-Савара-Лапласа индукция магнитного поля, созданного в центре кругового тока, равна векторной сумме индукции, создаваемой элементами проводника длиной в центре круга:
1.10). По закону Био-Савара-Лапласа индукция магнитного поля, созданного в центре кругового тока, равна векторной сумме индукции, создаваемой элементами проводника длиной в центре круга:
здесь:-коэффициент, магнитная постоянная вакуума, его величина равна . Значит, индукция магнитного поля, создаваемого в
центре кругового тока, прямо пропорциональна силе тока, протекающего по проводнику, и обратно пропорциональна радиусу круга.
В частном случае индукцию магнитного поля в центре катушки с током, имеющей количество витков п (рис. 1.11), можно определить следующим выражением:
Значит, индукция магнитного поля, создаваемого внутри катушки с током, прямо пропорциональна силе тока, протекающего через катушку, и количеству витков и обратно пропорциональна радиусу катушки.
Пример №7
По проводнику бесконечной длины протекает ток силой 250 мА. Вычислите индукцию магнитного поля в точке, находящейся на расстоянии 4 см от него.
Дано:
Найти:
Формула:
Решение:
Работа, выполненная при перемещении проводника с током в магнитном полеРассмотрим случай, когда два параллельных плоских металлических провода а и б расположены на расстоянии друг от друга, а сверху установлен легкий металлический проводник с (рис. 1.12). Система проводников расположена в однородном магнитном поле с магнитной индукцией . На рисунке 1.12 знак означает, что вектор магнитной индукции направлен перпендикулярно поверхности рисунка. Когда проводники а и б подключаются к источнику тока, через проводник с протекает ток. Здесь на проводник с током длиной со стороны магнитного поля действует сила Ампера Зная, что угол между направлением тока и направлением индукции магнитного поля равен 90°, направление силы определяется по правилу левой руки.
Эта сила, перемещая проводник с на расстояния d, выполняет работу, равную
В этом выражении произведение – это площадь, вычерченная проводником в ходе движения, т. е. . Если магнитный поток, пересекающий проводник в ходе движения, равен , то мы имеем выражение:
е. . Если магнитный поток, пересекающий проводник в ходе движения, равен , то мы имеем выражение:
Следует отметить, что эта работа выполняется не магнитным полем, а за счет энергии источника тока, питающего электрическую цепь.
Значит, работа, выполненная силой Ампера при перемещении проводника с током в магнитном поле, равна произведению силы тока, протекающего по проводнику, и изменению магнитного потока.
Работа, выполняемая при перемещении проводника с током в магнитном поле, широко используется в практике: на различных видах транспортных средств, в бытовой технике и электронике. Примером этого также могут служить часто используемые на сегодняшний день электронные замки.
Пример №8
По проводнику длиной 30 см протекает ток силой 2 А. Проводник расположен под углом 30° к индукционным линиям однородного магнитного поля с индукцией 1,5 Тл. Какая работа выполняется при перемещении проводника на 4 см в направлении силы Ампера?
Дано:
Найти:
Формула:
Решение:
Сила взаимодействия проводников с током
Между проводниками с током существует сила взаимного действия, как и у электрических зарядов. Чтобы наблюдать это явление на практике, возьмем два эластичных проводника, закрепим их вертикально к опоре.
Чтобы наблюдать это явление на практике, возьмем два эластичных проводника, закрепим их вертикально к опоре.
Если верхние части проводников соединить проволокой, то через них в противоположных направлениях потечет ток (рис. 1.13 а). В результате проводники будут отталкиваться друг от друга и расстояние между ними увеличится. Если обеспечить течение тока в одном направлении, тогда проводники будут притягиваться друг к другу (рис. 1.13 б).
Используя закона Ампера, определим направление и количественное значение силы взаимодействия, создаваемой между параллельно расположенными в вакууме бесконечными проводниками с током.
Пусть по проводникам, расположенным параллельно, на расстоянии d друг от друга в одном направлении протекают токи (рис. 1.14).
Линии вектора индукции магнитного поля токов протекающих по проводникам, состоят из концентричных кругов. Если ток протекает снизу вверх, тогда на точках, лежащих на втором проводнике, вектор (по закону винта) будет направлен от нас в сторону поверхности, и они расположатся взаимно перпендикулярно. Сила действия со стороны магнитного поля первого тока на второй ток, по закону Ампера, по величине равна:
Сила действия со стороны магнитного поля первого тока на второй ток, по закону Ампера, по величине равна:
здесь:-длина части второго проводника, расположенного в магнитном поле. Если в эту формулу подставить выражение магнитной индукции
прямого тока то
Значит, сила взаимодействия на единицу длины двух параллельных бесконечных проводников с током прямо пропорциональна произведению силы тока, протекающего по ним, и обратно пропорциональна расстоянию между ними.
На основе данного явления в международной системе единиц принята единица силы тока – ампер (А).
Ампер – равен силе постоянного тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади сечения, расположенным в вакууме на расстоянии 1 м друг от друга, вызвал бы на каждом метре длины проводника силу взаимодействия, равную
Пример №9
Найдите силу взаимодействия, приходящуюся на каждый метр длины провода линии электропередачи постоянного электрического тока двух проводников с расстоянием между ними 1,6 м. Принять силу тока, протекающего по проводникам, равную 40 А.
Принять силу тока, протекающего по проводникам, равную 40 А.
Дано:
Найти:
Формула:
Решение:
Движение заряженных частиц в однородном магнитном поле. Сила Лоренца
Силу Ампера, действующую со стороны магнитного поля на проводник с током, расположенный в магнитном поле, можно рассматривать как сумму действующих сил на каждом участке этого проводника. Если количество всех заряженных частиц, движущихся в проводнике с током длиной равно N, то сила, действующая на одну частицу, движущуюся в магнитном поле, равна:
Сила тока, протекающего по проводнику, равна
Если выражение (1-17) вставить в выражение (1-16), получаем выражение силы, действующей на одну частицу:
здесь: е-заряд электрона; -скорость упорядоченного движения частицы; -концентрация зарядов; S-поперечное сечение проводника.
Сила, действующая со стороны магнитного поля на заряженную частицу, движущуюся в магнитном поле, называется силой Лоренца. Она описывается следующим образом: Сила действующая на заряженную частицу, движущуюся в однородном магнитном поле, равна произведению заряда частицы q, ее скорости движения вектора индукции магнитного поляи синуса угла между вектором индукции магнитного поля и вектором скорости.
Она описывается следующим образом: Сила действующая на заряженную частицу, движущуюся в однородном магнитном поле, равна произведению заряда частицы q, ее скорости движения вектора индукции магнитного поляи синуса угла между вектором индукции магнитного поля и вектором скорости.
Направление силы Лоренца определяется по правилу левой руки (рис.1.15). Если расположить левую ладонь так, чтобы вытянутые пальцы совпадали с направлением положительных зарядов, а силовые линии магнитного поля входили в ладонь, то отогнутый на 90° большой палец укажет направление силы Лоренца.
Сила Лоренца, действующая на протон, влетающий в магнитное поле, согласно правилу левой руки, будет направлена в правую сторону (рис.1.16). При определении движения электрона (отрицательного заряда) в поле,четыре пальца расположим в положении, противоположном направлению тока. Тогда действующая на электрон сила Лоренца будет направлена в левую сторону (рис. 1.16).
Теперь рассмотрим влияние силы Лоренца на движение заряженных частиц. Пусть частица влетает в однородное магнитное поле перпендикулярно силовым линиям (рис. 1.17). Тогда угол между направлением скорости частицы и линией индукции равен 90° и сила Лоренца, действующая на частицу, будет максимальной. Из-за того, что сила Лоренца направлена перпендикулярно направлению движения частиц в магнитном поле, она выполняет функцию центростремительной силы. В результате меняется направление движения заряженной частицы, и ее траектория движения искривляется.Численное значение центробежной силы, которая появляется при движении по окружности, равняется силе Лоренца, т.е.:
Пусть частица влетает в однородное магнитное поле перпендикулярно силовым линиям (рис. 1.17). Тогда угол между направлением скорости частицы и линией индукции равен 90° и сила Лоренца, действующая на частицу, будет максимальной. Из-за того, что сила Лоренца направлена перпендикулярно направлению движения частиц в магнитном поле, она выполняет функцию центростремительной силы. В результате меняется направление движения заряженной частицы, и ее траектория движения искривляется.Численное значение центробежной силы, которая появляется при движении по окружности, равняется силе Лоренца, т.е.:
Так как сила Лоренца не выполняет работу, скорость движения частицы не меняется. Значит, частица продолжает равномерное движение по окружности.
Траектория движения заряженной частицы в магнитном поле представляет окружность, и ее радиус можно определить из следующего выражения:
Значит, радиус кривизны траектории частицы прямо пропорционален произведению ее массы и скорости и обратно пропорционален произведению ее заряда и индукции магнитного поля.
Теперь определим время, необходимое для одного полного оборота, т.е. период вращения. Для этого разделим путь, пройденный частицей за один оборот (длина окружности на скорость частицы:
Используя выражение (1-21), выражение (1-22) запишем в следующем виде:
Согласно этой формуле период вращения частицы не зависит от ее скорости, а зависит от значений массы и заряда частицы и индукции магнитного поля.
Прибор, разделяющий движущиеся в магнитном и электрическом полях заряженные частицы на составляющие части по массе, называется масс-спектрометром. Масс-спектрометры применяются для определения изотопов химических элементов и химического анализа вещества.
Пример №10
Электрон, влетая перпендикулярно к индукционным линиям поля с индукцией 12 мТ, продолжил движение по окружности радиусом 4 см. Найдите, с какой скоростью электрон влетел в поле.
Дано:
Найти:
Формула:
Решение:
Самые важные понятия, правила и законыМагнитные силовые линии: Магнитные силовые линии представляют собой замкнутые линии, выходящие из северного полюса и входящие в южный полюс.
Поток магнитной индукции: Потоком магнитной индукции Ф, проходящим через площадь называется произведение вектора В магнитной индукции на эту площадь
Единица магнитного потока: Магнитное поле с индукцией, равной 1 Тл, проходящее через площадь расположенную перпендикулярно к линиям индукции магнитного поля, составляет
Формула Био-Савара-Лапласа: Определяет магнитную индукцию, созданную в точке А вокруг проводника с током, произвольным элементом проводника
Принцип суперпозиции магнитного поля: Индукция результирующего поля в определенных точках пространства будет равна векторной сумме индукции магнитного поля, созданного в данной точке каждым проводником с током.
Индукция магнитного поля прямого тока – прямо пропорциональна силе тока, протекающего по проводнику, и обратно пропорциональна расстоянию между точкой, для которой определяется индукция, и проводником.
Индукция магнитного поля в центре кругового тока:-прямо пропорциональна силе тока, протекающего по проводнику, и обратно пропорциональна радиусу окружности.
Вращательный момент рамки с током: – прямо пропорционален силе тока, проходящего по контуру, площади контура и синусу угла между направлением вектора индукции и нормалью проведенной на поверхности контура.
Работа, выполненная в магнитном поле: – работа, выполненная при перемещении проводника в магнитном поле, равна произведению силы тока, протекающего по проводнику, на изменение магнитного потока при движении проводника.
Взаимодействие проводников с током: При течении тока по параллельным проводникам в противоположном направлении проводники отталкиваются друг от друга. В случае течения тока в одном направлении проводники притягиваются друг к другу.
Сила взаимодействия двух параллельных проводников с током: -сила взаимодействия единицы длины параллельного проводника с током прямо пропорциональна произведению силы тока, протекающего по ним, и обратно пропорциональна расстоянию между ними.
Описание ампера – единицы измерения силы тока: Ампер равен силе постоянного тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины, расположенным в вакууме на расстоянии 1 м друг от друга, вызвал бы на каждом метре длины проводника силу взаимодействия, равную
Сила Лоренца: Сила, действующая со стороны магнитного поля на заряженную частицу, движущуюся в магнитном поле
Правило левой руки: Если расположить левую ладонь так, чтобы вытянутые пальцы совпадали с направлением движения положительных зарядов, а силовые линии магнитного поля входили в ладонь, то отогнутый на 90° большой палец укажет направление силы Лоренца.
Радиус кривизны частицы, влетевшей перпендикулярно силовым линиям магнитного поля: -радиус кривизны траектории частицы пря-qB мо пропорционален произведению массы и скорости частицы и обратно пропорционален произведению ее заряда и индукции магнитного поля.
Период вращения частицы, влетевшей перпендикулярно линиям магнитного поля : – период вращения частицы не зависит от ее скорости, а зависит от значений массы и заряда частицы и индукции магнитного поля.
Энергия магнитного поляСила тока в контуре (а значит, и связанное с ним магнитное ноле) достигает своего постоянного значения не мгновенно, а в течение конечного промежутка времени после замыкания цепи. При этом в цепи возникает ЭДС самоиндукции, препятствующая нарастанию силы тока. Следовательно, источник тока при замыкании цепи совершает работу против ЭДС самоиндукции. Работа, затраченная источником на создание тока в контуре (без учета тепловых потерь), и определяет, в конечном счете, энергию магнитного поля, запасаемую контуром с током. Рассматриваемая работа равна взятому со знаком «минус» произведению средней ЭДС самоиндукции и заряда прошедшего по цепи. Знак «минус» появляется потому, что источник тока совершает работу, равную по модулю, но противоположную по знаку работе вихревого электрического поля при замыкании цепи.
Рассматриваемая работа равна взятому со знаком «минус» произведению средней ЭДС самоиндукции и заряда прошедшего по цепи. Знак «минус» появляется потому, что источник тока совершает работу, равную по модулю, но противоположную по знаку работе вихревого электрического поля при замыкании цепи.
Подчеркнем, что при нарастании тока ЭДС самоиндукции изменяется с течением времени, поэтому для вычисления работы рассмотрим малые промежутки времени, в течение которых будем считать неизменной.
Для малого промежутка времени можем записать:
Поскольку ЭДС самоиндукции
а прошедший за малый промежуток времени заряд то получаем
Величина соответствует площади закрашенного прямоугольника (рис. 175).
Тогда всю работу можно вычислить, складывая площади подобных прямоугольников под графиком зависимости В результате при уменьшении интервала разбиений получится площадь прямоугольного треугольника ОВС:
Следовательно, энергию магнитного поля контура с током можно определить по формулам (с учетом Ф = LI):
Энергию магнитного поля, заключенную в единице объема пространства, занятого полем, называют объемной плотностью энергии магнитного поля
Если магнитное поле создано внутри соленоида длиной l и площадью поперечного сечения S, содержащего N витков, то с учетом выражений для индуктивности соленоида и модуля вектора индукции магнитного поля внутри соленоида получаем
Здесь — магнитная проницаемость вещества внутри соленоида.
Так как SI = V, то для вычисления плотности энергии магнитного поля получим выражение
Физика_II_семестр
%PDF-1.4 % 1 0 obj /Author /Creator (pdfFactory Pro www.pdffactory.com) /Producer (pdfFactory Pro 4.80 \(Windows 7 Professional x86 Russian\)) /CreationDate (D:20160206124143+03’00’) >> endobj 2 0 obj >stream 1B
Физика 9 кл.
 Индукция магнитного поля
Индукция магнитного поляФизика 9 кл. Индукция магнитного поля
- Подробности
- Просмотров: 183
1. Как называется и каким символом обозначается векторная величина, которая служит количественной характеристикой магнитного поля?
Магнитное поле может действовать с определенной силой на помещенный в него проводник с током.
Магнитное поле характеризуется векторной физической величиной, которая обозначается символом и называется индукцией магнитного поля (или магнитной индукцией).
2. По какой формуле определяется модуль вектора магнитной индукции однородного магнитного поля?
Модуль вектора магнитной индукции В равен отношению модуля силы F, с которой магнитное поле действует на расположенный перпендикулярно магнитным линиям проводник с током, к силе тока I в проводнике и его длине I.
Формула для определения индукции однородного магнитного поля:
Отношение модуля силы F к длине проводника L и силе тока I есть величина постоянная.
Она не зависит ни от длины проводника, ни от силы тока в нём.
Отношение F/IL зависит только от магнитного поля.
3. Что принимается за единицу магнитной индукции? Как называется эта единица?
В СИ единицей магнитной индукции является 1Тесла (1 Тл) в честь югославского электротехника Николы Тесла.
4. Что называется линиями магнитной индукции?
Линиями магнитной индукции называются линии, касательные к которым в каждой точке поля совпадают с направлением вектора магнитной индукции
До сих пор для графического изображения магнитных полей мы пользовались линиями, которые условно называли магнитными линиями или линиями магнитного поля.
Более точное название магнитных линий – это линии магнитной индукции (или линии индукции магнитного поля).
Например:
Вектор магнитной индукции прямого проводника с током направлен по касательной в каждой точке поля.
5. В каком случае магнитное поле называется однородным, а в каком – неоднородным?
Основные признаки однородного и неоднородного магнитных полей:
Во всех точках однородного магнитного поля вектор магнитной индукции одинаков по модулю и по направлению
В разных точках неоднородного магнитного поля вектор магнитной индукции может быть различным как по модулю, так и по направлению
6. Как зависит сила, действующая в данной точке магнитного поля на магнитную стрелку или движущийся заряд, от магнитной индукции в этой точке?
Чем больше магнитная индукция в данной точке поля, тем с большей силой будет действовать поле в этой точке на магнитную стрелку или движущийся электрический заряд.
Следующая страница – смотреть
Назад в “Оглавление” – смотреть
12.S: Источники магнитных полей (сводка)
Ключевые термины
| Закон Ампера | физический закон, который гласит, что линейный интеграл магнитного поля вокруг электрического тока пропорционален току |
| Закон Био-Савара | уравнение, определяющее магнитное поле в точке, создаваемое токоведущим проводом |
| диамагнитные материалы | их магнитные диполи ориентированы противоположно приложенному магнитному полю; при снятии поля материал не намагничивается |
| ферромагнитные материалы | содержат группы диполей, называемых доменами, которые выравниваются по приложенному магнитному полю; когда это поле убирают, материал все еще намагничивается |
| гистерезис | свойство ферромагнетиков, которое наблюдается, когда магнитное поле материала исследуется по сравнению с приложенным магнитным полем; петля создается в результате перемещения приложенного поля вперед и назад |
| магнитные домены | групп магнитных диполей, которые выровнены в одном направлении и квантово-механически связаны между собой |
| магнитная восприимчивость | отношение магнитного поля в материале к приложенному в то время полю; положительные восприимчивости могут быть парамагнитными или ферромагнитными (выровненными по полю), а отрицательные восприимчивости – диамагнитными (выровненными противоположно полю) |
| парамагнитные материалы | их магнитные диполи частично выравниваются в том же направлении, что и приложенное магнитное поле; когда это поле убирается, материал не намагничивается |
| проницаемость свободного пространства | \ (\ displaystyle μ_0 \), мера способности материала, в данном случае свободного пространства, поддерживать магнитное поле. 2} \) 2} \) |
| Магнитное поле из-за длинного прямого провода | \ (\ Displaystyle B = \ гидроразрыва {μ_0I} {2πR} \) |
| Сила между двумя параллельными токами | \ (\ Displaystyle \ frac {F} {l} = \ frac {μ_0I_1I_2} {2πr} \) |
| Магнитное поле токовой петли | \ (\ Displaystyle B = \ frac {μ_0I} {2R} \) (в центре цикла) |
| Закон Ампера | \ (\ Displaystyle ∮ \ vec {B} ⋅d \ vec {l} = μ_0I \) |
| Напряженность магнитного поля внутри соленоида | \ (\ Displaystyle В = μ_0nI \) |
| Напряженность магнитного поля внутри тороида | \ (\ Displaystyle B = \ гидроразрыва {μ_oNI} {2πr} \) |
| Магнитная проницаемость | \ (\ Displaystyle μ = (1 + χ) μ_0 \) |
| Магнитное поле соленоида, заполненного парамагнитным материалом | \ (\ Displaystyle В = мкни \) |
Сводка
12.
 {- 7} T⋅m / s \) – проницаемость свободного пространства.
{- 7} T⋅m / s \) – проницаемость свободного пространства.12.4 Магнитная сила между двумя параллельными токами
- Сила между двумя параллельными токами \ (\ displaystyle I_1 \) и \ (\ displaystyle I_2 \), разделенными расстоянием r, имеет величину на единицу длины, определяемую выражением \ (\ displaystyle \ frac {F} {l} = \ frac {μ_0I_1I_2} {2πr} \).
- Сила притягивающая, если токи в одном направлении, и отталкивающая, если они в противоположных направлениях.
12.5 Магнитное поле токовой петли
- Напряженность магнитного поля в центре круговой петли определяется выражением \ (\ displaystyle B = \ frac {μ_0I} {2R} \) (в центре петли), , где R – радиус петли.
 . RHR-2 дает направление поля вокруг петли.
. RHR-2 дает направление поля вокруг петли.
12.6 Закон Ампера
- Магнитное поле, создаваемое током, идущим по любому пути, является суммой (или интегралом) полей из-за сегментов вдоль пути (величина и направление, как для прямого провода), в результате чего возникает общая взаимосвязь между током и полем, известная как поле Ампера. закон.
- Закон Ампера можно использовать для определения магнитного поля по тонкой или толстой проволоке с помощью геометрически удобного пути интегрирования. Результаты соответствуют закону Био-Савара.
12.7 Соленоиды и тороиды
- Напряженность магнитного поля внутри соленоида
\ (\ Displaystyle B = μ_0nI \) (внутри соленоида)
, где n – количество витков на единицу длины соленоида. Поле внутри очень однородно по величине и направлению.
- Напряженность магнитного поля внутри тороида
\ (\ displaystyle B = \ frac {μ_oNI} {2πr} \) (внутри тороида)
где N – количество витков. Поле внутри тороида неоднородно и изменяется с расстоянием как 1 / r.
Поле внутри тороида неоднородно и изменяется с расстоянием как 1 / r.
12,8 Магнетизм в веществе
- Материалы классифицируются как парамагнитные, диамагнитные или ферромагнитные, в зависимости от того, как они ведут себя в приложенном магнитном поле.
- Парамагнитные материалы имеют частичное выравнивание своих магнитных диполей с приложенным магнитным полем.Это положительная магнитная восприимчивость. Остается только поверхностный ток, создающий магнитное поле, подобное соленоиду.
- Диамагнитные материалы имеют наведенные диполи, противоположные приложенному магнитному полю. Это отрицательная магнитная восприимчивость.
- Ферромагнетики имеют группы диполей, называемых доменами, которые выравниваются по приложенному магнитному полю. Однако, когда поле снимается, ферромагнитный материал остается намагниченным, в отличие от парамагнитных материалов.Это намагничивание материала в зависимости от эффекта приложенного поля называется гистерезисом.

Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Размеры магнитного поля – формулы, уравнения и производные
Физическая величина – это любая величина, которую можно измерить с помощью устройства в единицах измерения.Весь список физических величин можно в общих чертах разделить на два типа, а именно: фундаментальные физические величины и производные физические величины.
В следующих разделах этой страницы дается краткое описание основной идеи физических величин и размерной формулы для магнитного поля. На странице также представлены различные единицы измерения.
Размерная формула магнитного поля = M1 T2 I -1 |
Физические величины
Все физические величины можно в целом разделить на два типа, а именно: основные или базовые физические величины и производные физические величины. .В физике есть семь фундаментальных физических величин. Это масса, время, длина, электрический ток, температура, сила света и количество вещества. Эти семь величин называются измерениями физического мира. Вместо названий используются их первые буквы для обозначения базовых величин. Три механические величины: масса, длина и время представлены как M, L и T. Для обозначения размеров эти символы используются в квадратных скобках.
.В физике есть семь фундаментальных физических величин. Это масса, время, длина, электрический ток, температура, сила света и количество вещества. Эти семь величин называются измерениями физического мира. Вместо названий используются их первые буквы для обозначения базовых величин. Три механические величины: масса, длина и время представлены как M, L и T. Для обозначения размеров эти символы используются в квадратных скобках.
Важно отметить, что размеры физической величины и размеры их единицы совпадают. Это только характер единицы, представленной как [M], [L] и [T], а не ее величина. Каждая производная физическая величина представлена в терминах своих основных физических величин с соответствующей степенью. Степени, до которых необходимо возвести фундаментальную физическую величину для получения производной величины, называются размерностями производной величины.
Подробнее о размерной формуле и размерном уравнении
Размерная формула – это сложное выражение, которое описывает, какие фундаментальные величины задействованы и как они участвуют в моделировании производной физической величины. Физическая величина и ее размеры уравниваются в уравнении, называемом уравнением размерностей. Другими словами, размерные уравнения – это уравнения, которые представляют размерность любой физической величины в терминах ее фундаментальных величин.
Физическая величина и ее размеры уравниваются в уравнении, называемом уравнением размерностей. Другими словами, размерные уравнения – это уравнения, которые представляют размерность любой физической величины в терминах ее фундаментальных величин.
Магнитное поле
Область вокруг магнита, на которую действует сила этого магнита, называется Магнитным полем. Магнитные поля могут создаваться перемещением электрических зарядов. Магнитное поле проникает сквозь пространство и действует как движущая сила для перемещения электрических зарядов и магнитных диполей.
В случае стержневого магнита силовые линии магнитного поля сильнее на полюсах и слабее в середине стержневого магнита. Сила магнитного поля на обоих полюсах одинакова. Магнитное поле – это производная физическая величина. Размерная формула магнитного поля равна [M] 1 [T] -2 [I] -1.
Размерная формула магнитного поля
Размерная формула магнитного поля может быть определена как представление единиц магнитного поля в терминах фундаментальных физических величин с соответствующей мощностью. Размерная формула Магнитного поля задается как [M] 1 [T] -2 [I] -1. В этой формуле «M» представляет собой массу, «T» представляет время, а «I» представляет собой ток.
Размерная формула Магнитного поля задается как [M] 1 [T] -2 [I] -1. В этой формуле «M» представляет собой массу, «T» представляет время, а «I» представляет собой ток.
Вывод размерной формулы магнитного поля
Сила Лоренца задается уравнением
Сила = заряд x магнитное поле (B) x скорость
Вышеприведенное уравнение можно переписать, чтобы найти магнитное поле, как:
Магнитное поле = Сила x [Заряд x Скорость] -1 → (1)
Мы знаем, что скорость может быть записана в терминах расстояния и времени как:
Скорость = Расстояние x [Время] -1
Формула размерностей скорости составляет [L T-1] → (2)
Основная формула для электрического заряда:
Заряд = Электрический ток x время
Размерная формула для электрического заряда: [I1 T1] → (3)
Сила Лоренца задается вторым законом движения Ньютона как:
Сила Лоренца = Масса x Ускорение → (4)
Но ускорение – это скорость изменения скорости и определяется как:
Ускорение = Скорость x [Время] – 1 → (5)
Подставляя (5) в (4) получаем
сила Лоренца = Масса x Скорость x [Время] -1
Формула размеров для силы Лоренца, таким образом, записывается как [ML T-2] → (6)
Подставляя измерения скорости, электрический заряд и сила Лоренца из (2), (3) и (6) в формуле для Магнитного поля, представленного как (1), мы получаем,
Следовательно, B = [ML T-2] {[I1 T1] [ L T-1]} – 1
B = [M1 L0 T-2 I-1]
Следовательно, магнитное поле может быть представлено размерно как [M1 T2 I-1].
Расчет движения в магнитных полях: формула и практика
Центростремительная сила
Центростремительная сила – это общий термин для любой силы, действующей по линии радиуса кругового движения. В случае магнитных полей и электронов единственной центростремительной силой является магнитная сила. Масса электрона настолько мала, что мы не будем обращать внимания на любые гравитационные воздействия на него. Чтобы понять, как центростремительная сила влияет на электрон, взгляните на диаграммы, которые показывают одно и то же явление под разными углами.
Используйте диаграммы в качестве справки при вычислении приведенных ниже уравнений. B – направление магнитного поля, v – скорость электрона, когда он ударяется о поле, θ – угол между B и v, а Fc – направление силы, действующей на электрон.
B – направление магнитного поля, v – скорость электрона, когда он ударяется о поле, θ – угол между B и v, а Fc – направление силы, действующей на электрон.
Уравнения
Уравнение для центростремительной силы, где Fc – центростремительная сила, m – масса, v – скорость, и R – радиус, составляет
Уравнение магнитной силы, действующей на движущуюся заряженную частицу, где B – напряженность магнитного поля, а q – заряд, составляет
Обратите внимание, что это уравнение перекрестного произведения.Это означает, что сила перпендикулярна скорости частицы. Упростив уравнение, чтобы получить величину силы, мы получим следующее уравнение, в котором θ – это угол между направлением магнитного поля и скоростью частицы:
Подстановка уравнения магнитной силы в уравнение центростремительной силы приводит к
, который мы можем упростить, разделив обе стороны на v . Это приводит к окончательному уравнению для любой заряженной частицы, движущейся в магнитном поле.
Это приводит к окончательному уравнению для любой заряженной частицы, движущейся в магнитном поле.
И последнее, что мы должны сделать. Поскольку уравнение магнитной силы представляет собой перекрестное произведение, нам нужно использовать правило правой руки, чтобы указать, каким образом сила действует на заряженную частицу. Это поможет определить ориентацию кругового пути, по которому движется заряженная частица.
Чтобы использовать правило правой руки, сделайте обратную букву «L» указательным и большим пальцем правой руки, а затем выставьте средний палец перпендикулярно указательным пальцам и большим пальцам.
- Указательный палец указывает в направлении скорости заряженной частицы (v).
- Средний палец указывает в направлении магнитного поля (B).

- Большой палец указывает в направлении силы, действующей на движущуюся положительно заряженную частицу. Для отрицательного заряда просто измените направление силы на противоположное.
При обозначении магнитного поля на экране мы можем использовать стрелку для большинства направлений, но иногда нам нужны специальные обозначения. Для магнитных полей, указывающих за пределы экрана, мы используем •. Для магнитных полей, направленных на экран, мы используем ⊗.
Теперь у нас есть все инструменты, необходимые для решения некоторых задач, связанных с движением электронов в магнитном поле.
Пример 1
Подсказка: Определите радиус пути, по которому электрон проходит через магнитное поле, показанное на схеме 1.
Решение: Прежде чем мы перейдем к математике, давайте проанализируем диаграмму. Магнитное поле направлено за пределы экрана. Электрон движется вверх со скоростью, перпендикулярной (90 °) магнитному полю. Используя правило правой руки, мы видим, что большой палец указывает вправо, что соответствует положительному заряду. Электроны заряжены отрицательно, поэтому сила действует влево.
Электрон движется вверх со скоростью, перпендикулярной (90 °) магнитному полю. Используя правило правой руки, мы видим, что большой палец указывает вправо, что соответствует положительному заряду. Электроны заряжены отрицательно, поэтому сила действует влево.
Уравнение, которое мы вывели ранее:
и синус 90 ° равен 1, поэтому мы можем упростить уравнение, дав нам
Решая для R , получаем
Масса электрона 9.11 х 10-31 кг. Мы собираемся игнорировать отрицательный знак заряда, потому что он нужен только для определения направления силы на заряженную частицу. Чтобы получить наш ответ, все, что нам нужно сделать, это подставить значения, что даст нам
Лучше проверить, сводится ли эта комбинация единиц к метрам. Тесла – это ньютон на ампер-метр. Подставляя эти единицы в наше окончательное уравнение и упрощая, мы получаем
Тесла – это ньютон на ампер-метр. Подставляя эти единицы в наше окончательное уравнение и упрощая, мы получаем
Теперь мы можем заменить ньютон в кгм / с2, а на ампер – C / с и упростить, что дает
Похоже, мы в порядке с выводом нашего уравнения.Давайте рассмотрим еще один пример проблемы.
Пример 2
Подсказка: Определите скорость электрона, движущегося по экрану в магнитном поле, направленном вправо. Радиус круга – 1 мм.
Решение: Скорость перпендикулярна магнитному полю, поэтому sinθ нам не нужен. Решая уравнение для v и вставляя информацию, мы получаем
Пример 3
Подсказка: Электрон движется со скоростью 1000 м / с, под углом θ = 15 ° к магнитному полю, направленному на экран. Какова величина магнитного поля и какова ориентация кругового пути?
Какова величина магнитного поля и какова ориентация кругового пути?
Решение: поскольку электрон не движется перпендикулярно магнитному полю, мы должны использовать sinθ в уравнении. Начиная с общего уравнения и заканчивая величиной магнитного поля, получаем
Чтобы получить направление круговой траектории, мы используем правило правой руки.Поскольку скорость находится под углом к полю, мы рисуем компонент скорости перпендикулярно полю, как показано синей стрелкой.
Наведите указательный палец правой руки вверх, а средний палец – на экран. Большой палец указывает влево, но это направление силы положительного заряда. Это означает, что сила, действующая на электрон, находится справа от его положения на диаграмме. Следовательно, круговой путь находится в плоскости экрана, а электрон движется по кругу по часовой стрелке.
Следовательно, круговой путь находится в плоскости экрана, а электрон движется по кругу по часовой стрелке.
Резюме урока
Центростремительные силы – это силы, которые действуют вдоль линии радиуса для объекта, движущегося по круговой траектории.
Уравнение кругового движения заряженных частиц в магнитном поле:
, а правило правой руки определяет направление силы, действующей на заряженную частицу.Это помогает указать ориентацию кругового пути. Если заряд отрицательный, сила, действующая на него, противоположна направлению положения большого пальца правой руки.
12.4 Магнитное поле токовой петли – Университетская физика, том 2
Цели обучения
К концу этого раздела вы сможете:
- Объясните, как закон Био-Савара используется для определения магнитного поля, создаваемого током в проволочной петле в точке вдоль линии, перпендикулярной плоскости петли.

- Определите магнитное поле электрической дуги.
Круговая петля на рисунке 12.11 имеет радиус R , по ней проходит ток I и лежит в плоскости xz . Какое магнитное поле возникает из-за тока в произвольной точке P вдоль оси контура?
Рисунок 12.11 Определение магнитного поля в точке P вдоль оси токоведущей петли провода.Мы можем использовать закон Био-Савара, чтобы найти магнитное поле, создаваемое током.Сначала мы рассмотрим произвольные сегменты на противоположных сторонах петли, чтобы качественно показать с помощью векторных результатов, что чистое направление магнитного поля проходит вдоль центральной оси петли. Отсюда мы можем использовать закон Био-Савара, чтобы получить выражение для магнитного поля.
Пусть P будет расстоянием y от центра петли. Согласно правилу правой руки, магнитное поле [latex] d \ stackrel {\ to} {\ textbf {B}} [/ latex] на P , создаваемое текущим элементом [latex] I \ phantom {\ rule {0. 2em} {0ex}} d \ stackrel {\ to} {\ textbf {l}}, [/ latex] направлено под углом [latex] \ theta [/ latex] над осью y , как показано. Поскольку [latex] d \ stackrel {\ to} {\ textbf {l}} [/ latex] параллелен оси x , а [latex] \ hat {\ textbf {r}} [/ latex] находится в плоскости yz , два вектора перпендикулярны, поэтому мы имеем
2em} {0ex}} d \ stackrel {\ to} {\ textbf {l}}, [/ latex] направлено под углом [latex] \ theta [/ latex] над осью y , как показано. Поскольку [latex] d \ stackrel {\ to} {\ textbf {l}} [/ latex] параллелен оси x , а [latex] \ hat {\ textbf {r}} [/ latex] находится в плоскости yz , два вектора перпендикулярны, поэтому мы имеем
[латекс] дБ = \ frac {{\ mu} _ {0}} {4 \ pi} \ phantom {\ rule {0.2em} {0ex}} \ frac {I \ phantom {\ rule {0.2em} { 0ex}} dl \ phantom {\ rule {0.2em} {0ex}} \ mathrm {sin} \ phantom {\ rule {0.{\ prime} [/ latex], перпендикулярный оси y , поэтому сокращается, и при вычислении чистого магнитного поля необходимо учитывать только компоненты вдоль оси y . Компоненты, перпендикулярные оси контура, попарно суммируются до нуля. Отсюда в точке P :
[латекс] \ stackrel {\ to} {\ textbf {B}} = \ hat {\ textbf {j}} \ underset {\ text {loop}} {\ int} дБ \ phantom {\ rule {0.2em} {0ex}} \ mathrm {cos} \ phantom {\ rule {0. {3}}.{3}}. [/ Латекс]
{3}}.{3}}. [/ Латекс]
Расчет магнитного поля из-за круговой токовой петли в точках вне оси требует довольно сложной математики, поэтому мы просто посмотрим на результаты. Линии магнитного поля имеют форму, показанную на рисунке 12.12. Обратите внимание, что одна линия поля следует за осью цикла. Это та линия поля, которую мы только что нашли. Кроме того, очень близко к проводу силовые линии почти круглые, как линии длинного прямого провода.
Рисунок 12.12 Эскиз силовых линий магнитного поля круговой токовой петли.Пример
Магнитное поле между двумя контурами
Две проволочные петли пропускают одинаковый ток 10 мА, но текут в противоположных направлениях, как показано на рисунке 12.13. Измеренный радиус одной петли составляет [латекс] R = 50 \ phantom {\ rule {0.2em} {0ex}} \ text {cm} [/ latex], а радиус другой петли составляет [латекс] 2R = 100 \ phantom {\ rule {0.2em} {0ex}} \ text {cm}. [/ Latex] Расстояние от первой петли до точки измерения магнитного поля составляет 0,25 м, а расстояние от этой точки до второй цикл – 0.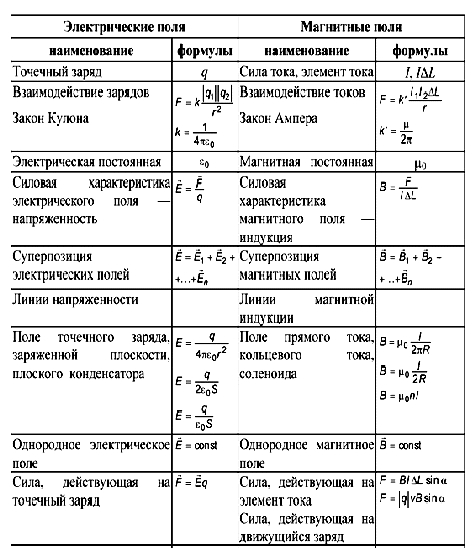 75 м. Какова величина чистого магнитного поля в точке P ?
75 м. Какова величина чистого магнитного поля в точке P ?
Стратегия
Магнитное поле в точке P было определено в уравнении 12.15. Поскольку токи протекают в противоположных направлениях, чистое магнитное поле представляет собой разницу между двумя полями, создаваемыми катушками.{\ text {−9}} \ text {T} \ phantom {\ rule {0.2em} {0ex}} \ text {справа}. \ hfill \ end {array} [/ latex]
Значение
Катушки Гельмгольца обычно имеют петли с одинаковым радиусом, при этом ток течет в одном направлении, чтобы иметь сильное однородное поле в средней точке между петлями. Аналогичное применение распределения магнитного поля, создаваемого катушками Гельмгольца, можно найти в магнитной бутылке, которая может временно улавливать заряженные частицы. См. Обсуждение этого в разделе «Магнитные силы и поля».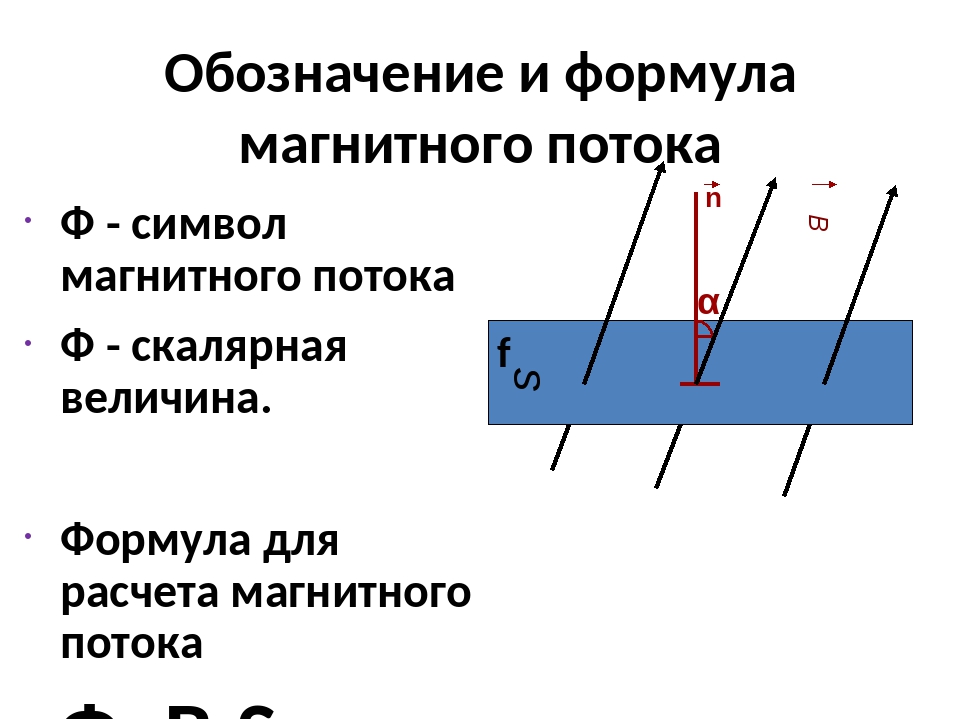
Проверьте свое понимание
Используя пример 12.5, на какое расстояние вам нужно переместить первую катушку, чтобы получить нулевое измеряемое магнитное поле в точке P ?
Показать решениеСводка
- Напряженность магнитного поля в центре круговой петли определяется выражением [латекс] B = \ frac {{\ mu} _ {0} I} {2R} \ phantom {\ rule {0.2em} {0ex}} \ text {(в центре петли)}, [/ latex] где R – радиус петли. RHR-2 дает направление поля вокруг петли.
Концептуальные вопросы
Магнитное поле токовой петли однородно?
Что происходит с длиной подвешенной пружины, когда через нее проходит ток?
Показать решениеДлина пружины уменьшается, поскольку каждая катушка имеет магнитное поле, создаваемое северным полюсом, рядом с южным полюсом следующей катушки.
Два концентрических круглых провода разного диаметра переносят ток в одном направлении. {3 \ text {/} 2}} [/ latex]
{3 \ text {/} 2}} [/ latex]
Какое магнитное поле для катушек в предыдущей задаче находится в центре каждой из катушек?
Лицензии и авторские праваМагнитное поле токовой петли. Автор : OpenStax College. Расположен по адресу : https://openstax.org/books/university-physics-volume-2/pages/12-4-mintage-field-of-a-current-loop. Лицензия : CC BY: Attribution . Условия лицензии : Загрузите бесплатно с https://openstax.org/books/university-physics-volume-2/pages/1-introduction
Энергия в магнитном поле – Университетская физика, том 2
Цели обучения
К концу этого раздела вы сможете:
- Объясните, как можно накапливать энергию в магнитном поле
- Выведите уравнение для энергии, запасенной в коаксиальном кабеле, с учетом плотности магнитной энергии
Энергия конденсатора хранится в электрическом поле между его пластинами. Точно так же индуктор может накапливать энергию, но в своем магнитном поле. Эту энергию можно найти, интегрировав плотность магнитной энергии,
Точно так же индуктор может накапливать энергию, но в своем магнитном поле. Эту энергию можно найти, интегрировав плотность магнитной энергии,
над соответствующей громкостью. Чтобы понять, откуда взялась эта формула, давайте рассмотрим длинный цилиндрический соленоид из предыдущего раздела. Снова используя приближение бесконечного соленоида, мы можем предположить, что магнитное поле по существу постоянное и задается везде внутри соленоида. Таким образом, энергия, запасенная в соленоиде, или плотность магнитной энергии, умноженная на объем, эквивалентна
При замене (Рисунок) это становится
Хотя это уравнение выведено для частного случая, это уравнение дает энергию, запасенную в магнитном поле любого индуктора .Мы можем убедиться в этом, рассмотрев произвольную катушку индуктивности, через которую проходит изменяющийся ток. В любой момент величина наведенной ЭДС такова, что мощность, потребляемая катушкой индуктивности, равна
Полная энергия, запасенная в магнитном поле, когда ток увеличивается от 0 до I в интервале времени от 0 до t может быть определена путем интегрирования этого выражения:
Самоиндуктивность коаксиального кабеля (рисунок) показывает две длинные концентрические цилиндрические оболочки радиусов и. Как обсуждалось в разделе «Емкость по емкости», эта конфигурация является упрощенным представлением коаксиального кабеля.Емкость на единицу длины кабеля уже рассчитана. Теперь (а) определите магнитную энергию, запасенную на единицу длины коаксиального кабеля, и (б) используйте этот результат, чтобы найти самоиндуктивность на единицу длины кабеля.
Как обсуждалось в разделе «Емкость по емкости», эта конфигурация является упрощенным представлением коаксиального кабеля.Емкость на единицу длины кабеля уже рассчитана. Теперь (а) определите магнитную энергию, запасенную на единицу длины коаксиального кабеля, и (б) используйте этот результат, чтобы найти самоиндуктивность на единицу длины кабеля.
(a) Коаксиальный кабель здесь представлен двумя полыми концентрическими цилиндрическими проводниками, по которым электрический ток течет в противоположных направлениях. (b) Магнитное поле между проводниками можно найти, применив закон Ампера к пунктирной траектории.(c) Цилиндрическая оболочка используется для определения магнитной энергии, запасенной на длине l кабеля.
Стратегия Магнитное поле внутри и снаружи коаксиального кабеля определяется законом Ампера. Основываясь на этом магнитном поле, мы можем использовать (рисунок) для расчета плотности энергии магнитного поля. Магнитная энергия рассчитывается как интеграл плотности магнитной энергии, умноженный на дифференциальный объем по цилиндрической оболочке. После того, как интегрирование выполнено, у нас есть закрытое решение для части (а).На основании этого результата и (рисунок) определяется самоиндукция на единицу длины.
После того, как интегрирование выполнено, у нас есть закрытое решение для части (а).На основании этого результата и (рисунок) определяется самоиндукция на единицу длины.
Решение
- Мы определяем магнитное поле между проводниками, применяя закон Ампера к пунктирной круговой траектории, показанной на (Рисунок) (b). Из-за цилиндрической симметрии постоянно вдоль пути, а
Это дает нам
В области за пределами кабеля аналогичное применение закона Ампера показывает, что, поскольку чистый ток не пересекает область, ограниченную круговой траекторией, этот аргумент также справедлив, когда это происходит в области внутри внутреннего цилиндра.Таким образом, вся магнитная энергия кабеля сохраняется между двумя проводниками. Поскольку плотность энергии магнитного поля составляет
энергия, запасенная в цилиндрической оболочке с внутренним радиусом r , внешним радиусом и длиной l (см. Часть (c) рисунка) составляет
Часть (c) рисунка) составляет
Таким образом, полная энергия магнитного поля на длине l кабеля составляет
, а энергия на единицу длины равна. - Из (Рисунок),
, где L – самоиндукция длины l коаксиального кабеля.Приравнивая предыдущие два уравнения, находим, что самоиндукция на единицу длины кабеля составляет
Значение Индуктивность на единицу длины зависит только от внутреннего и внешнего радиусов, как видно из результата. Чтобы увеличить индуктивность, мы могли либо увеличить внешний радиус, либо уменьшить внутренний радиус. В пределе, когда два радиуса становятся равными, индуктивность стремится к нулю. В этом пределе нет коаксиального кабеля. Кроме того, магнитная энергия на единицу длины из части (а) пропорциональна квадрату тока.
Проверьте свое понимание Сколько энергии сохраняется в катушке индуктивности (рисунок) после того, как ток достигает максимального значения?
Сводка
- Энергия, запасенная в катушке индуктивности U , составляет
- Собственная индуктивность на единицу длины коаксиального кабеля составляет
Концептуальные вопросы
Покажите, что имеет единицы энергии.
Проблемы
В данный момент ток 0.20 А протекает через катушку с проволокой, энергия, запасенная в ее магнитном поле, равна. Какова собственная индуктивность катушки?
Предположим, что прямоугольный тороид имеет 2000 обмоток и самоиндукцию 0,040 Н. Если, то какой ток течет через прямоугольный тороид, когда энергия в его магнитном поле равна
Соленоид A плотно намотан, в то время как соленоид B имеет обмотки, которые равномерно разнесены с зазором, равным диаметру провода.В остальном соленоиды идентичны. Определите соотношение энергий, накопленных на единицу длины этих соленоидов, когда через каждый из них протекает одинаковый ток.
Катушка индуктивности 10 Гн проводит ток 20 А. Сколько льда может быть растоплено за счет энергии, накопленной в магнитном поле индуктора? ( Подсказка : используйте значение льда.)
Катушка с самоиндуктивностью 3,0 Гн и сопротивлением 1⁄2 Гц проводит постоянный ток 2,0 А.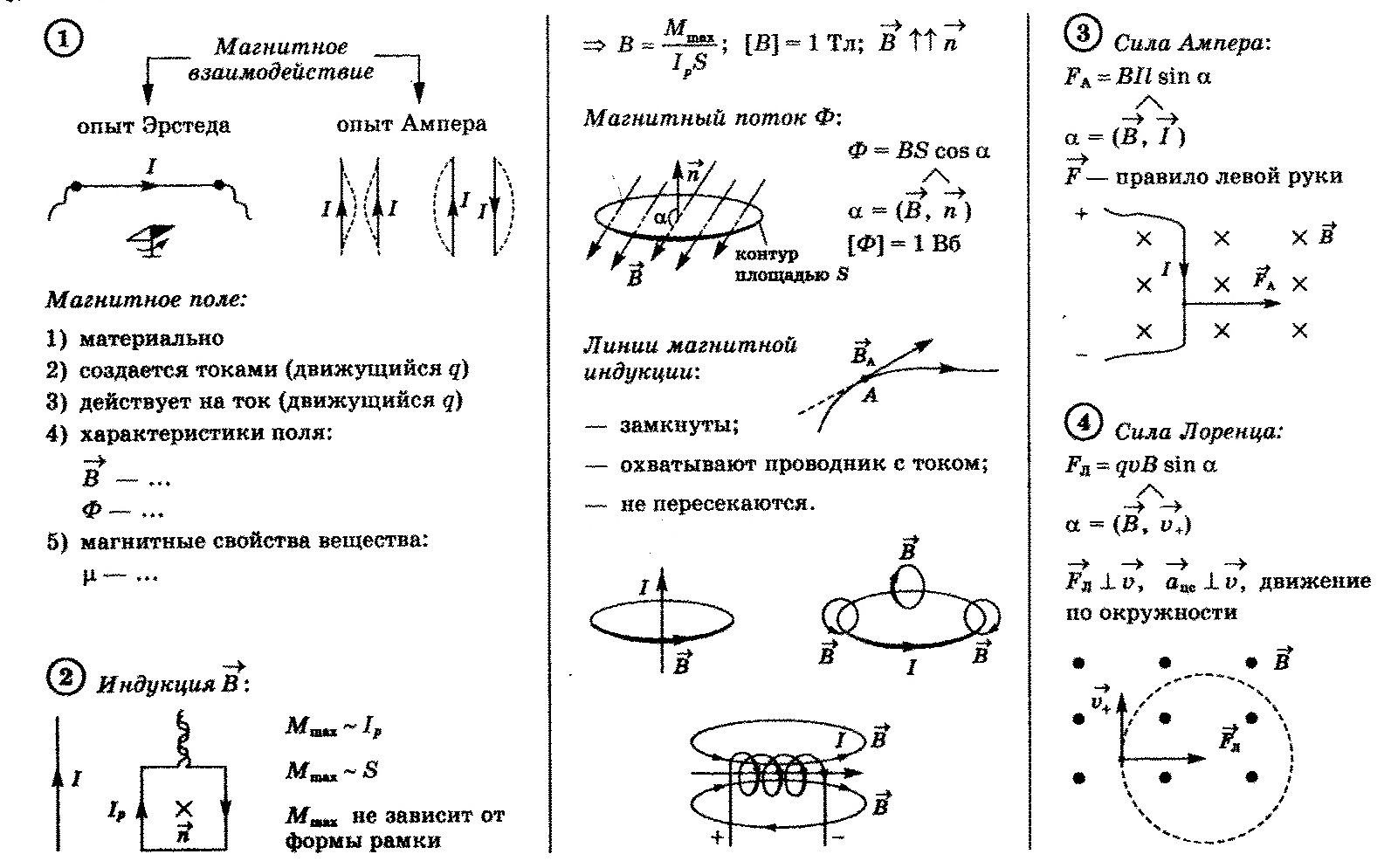 (a) Какая энергия хранится в магнитном поле катушки? (б) Какая энергия в секунду рассеивается на сопротивлении катушки?
(a) Какая энергия хранится в магнитном поле катушки? (б) Какая энергия в секунду рассеивается на сопротивлении катушки?
А ток 1.2 А протекает по коаксиальному кабелю, внешний радиус которого в пять раз превышает его внутренний радиус. Какая энергия магнитного поля хранится в кабеле длиной 3,0 м?
Глоссарий
- Плотность магнитной энергии
- энергия, запасенная на единицу объема в магнитном поле
Электромагнетизм – магнитные поля | Shmoop
Magnetic Fields
Теперь пора окунуться в другой, но похожий мир магнетизма. Мы уже немного узнали о магнитных полях, магнитах, полярности, силе Лоренца с заряженными частицами, движущимися в магнитном поле, электромагнитном излучении и электромагнитном спектре 4 .Чего не хватает?
До сих пор в этом модуле мы изучали стационарные заряды, которые имеют постоянные электрические поля, что известно как электростатический . Магнитостатика , с другой стороны, имеет дело с постоянными токами, которые создают постоянные магнитные поля, а также с ферромагнитными материалами, которые создают постоянные магнитные поля. Однако мы уже достаточно говорили о них раньше, поэтому обратим внимание на магнитные поля, создаваемые токами электричества.
Магнитостатика , с другой стороны, имеет дело с постоянными токами, которые создают постоянные магнитные поля, а также с ферромагнитными материалами, которые создают постоянные магнитные поля. Однако мы уже достаточно говорили о них раньше, поэтому обратим внимание на магнитные поля, создаваемые токами электричества.
Сцена устроена с проводами, идущими туда и сюда, с магнитными полями, бегущими по кругу вокруг них….
Закон Био-Савара
Мы только что узнали об использовании исчисления для нахождения электрического поля непрерывного распределения заряда путем суммирования всех вкладов от каждого заряда по отдельности. Неужто в мире магнетизма есть аналог? Как мы соотносим величину магнитного поля B с током I , который его производит?
Мы находим направление по правилу правой руки: большой палец указывает в направлении тока, а пальцы охватывают воображаемый провод, указывая направление магнитного поля вокруг провода.
Двум французским ученым, Жану Батисту Био и Феликсу Савару, удалось решить проблему величины магнитного поля, вероятно, с помощью бутылки бордо и вонючего сыра. На следующей диаграмме у нас есть вклад магнитного поля, указывающий на страницы в точке P , а также ток и длина на плоскости страницы. Этот вклад поля перпендикулярен как элементу тока I Δ d , так и векторному расстоянию r между точкой P и I Δ d .
На следующей диаграмме у нас есть вклад магнитного поля, указывающий на страницы в точке P , а также ток и длина на плоскости страницы. Этот вклад поля перпендикулярен как элементу тока I Δ d , так и векторному расстоянию r между точкой P и I Δ d .
Нахождение B тогда превращается в вычислительную задачу – ура, – в которой расстояние r постоянно меняется. Давайте сделаем паузу, чтобы отпраздновать пропуск математики.
Уравнение Био-Савара используется для любой геометрической конфигурации и, как мы видели с электрическими полями, для получения различных уравнений для этих различных геометрических конфигураций. Ниже приведены результаты некоторых из этих конфигураций от Biot-Savart.
Магнитное поле вокруг одиночного провода с током
Особенно полезным уравнением магнитного поля, которое необходимо знать, является магнитное поле на расстоянии a от длинного прямого провода с током I , как показано на диаграмме выше.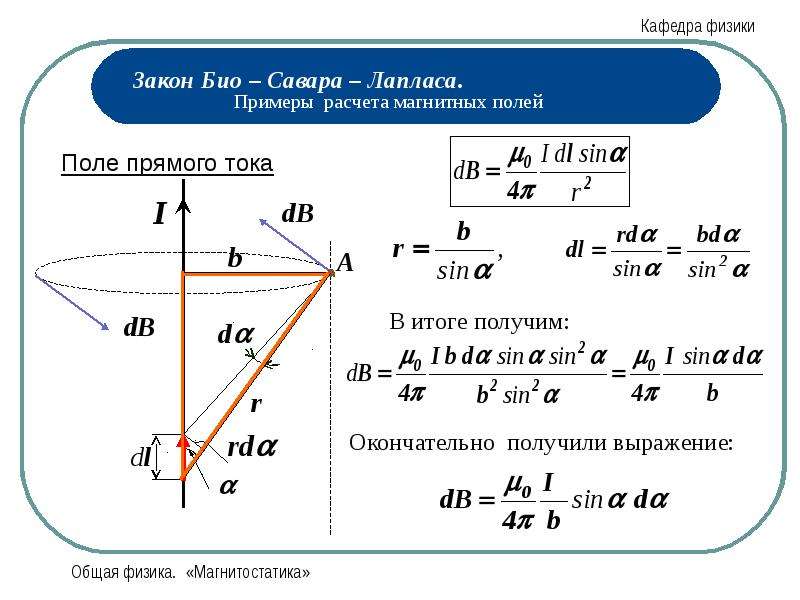 от .Здесь µ o называется проницаемостью свободного пространства и равна.
от .Здесь µ o называется проницаемостью свободного пространства и равна.
Что ж, кто знает … может, это всплывет во время вечеринки по пустякам.
Магнитное поле Два бесконечных провода
Есть три случая для двух параллельных проводов с током, но не с картой. Точки на изображении представляют собой провод, идущий из страницы, а крестики на изображении представляют провод, ведущий на страницы. Таким образом, мы сможем увидеть линии магнитного поля вокруг них.Если два тока движутся в одном направлении, магнитная сила между ними притягивается. К сожалению, не для пары проводов, идущих в противоположных направлениях. Они не хотят находиться рядом друг с другом.
Это может быть хороший научный эксперимент для тех, у кого поблизости есть схемное оборудование.
В любом случае отдельные поля каждого провода рассчитываются по тому же уравнению, как указано выше,. Тогда сила, приходящаяся на единицу длины проволоки, определяется как. Это потому, что F = qvB эквивалентно F = ILB .Скорость за время меняется от скорости к течению, оставляя расстояние само собой.
Это потому, что F = qvB эквивалентно F = ILB .Скорость за время меняется от скорости к течению, оставляя расстояние само собой.
Направление силы требует старого правила правой руки, когда мы проводим указательный палец в текущем направлении, сгибаем другие пальцы в направлении магнитного поля, а затем выставляем большой палец вверх в направлении силы. Все они перпендикулярны друг другу. Попробуйте: используйте три показанных выше случая, чтобы отработать правило правой руки.
Магнитное поле в середине токовой петли
В кольце магнитное поле направлено внутрь или наружу, в зависимости от направления, в котором ток течет в петле.Если токовая петля находится в плоскости этой страницы и движется против часовой стрелки, то магнитное поле в центре петли выходит за пределы страницы. Используйте правило правой руки, описанное ранее, чтобы найти это в любой точке (и в каждой точке) цикла. Его величина рассчитывается по формуле, где r – радиус петли.
Магнитное поле в соленоиде
Так же, как электрическое поле, магнитное поле имеет силовые линии. Мы их уже рисовали. И так же, как есть электрический поток, есть магнитный поток .Это двойное уравнение: или для поля, перпендикулярного нормали к площади поперечного сечения, Φ B = BA . Сделаем шаг назад. Мы утверждали это с помощью закона Гаусса. Если заключенный заряд является диполем или другим чистым нейтральным объектом, то Q enc = 0 и электрический поток Φ E также равен нулю. Аналогично, если бы существовал единственный магнитный «заряд», этот заключенный заряд был бы пропорционален общему магнитному потоку.
Но подождите секунду. Магнитного монополя не существует. Они бывают парами с северным и южным полюсами – даже у сломанного магнита есть северный и южный полюсы. Линии магнитного поля должны образовывать непрерывные петли. Следовательно, уравнение сводится к Φ B = BA = 0 для любой закрытой поверхности , независимо от того, существуют ли токи, создающие магнитные поля.
Присутствие любого магнитного поля гарантирует, что в любой замкнутой области будет входить сколько угодно линий и что магнитный поток равен нулю.Хорошо знать. По мелочи.
Закон Ампера
Мы не лгали, когда говорили, что все станет легче. Оказывается, эквивалент закона Гаусса существует и для непрерывных токов, гарантируя, что магнитный поток остается нулевым по всей площади. Слава Богу.
Закон Ампера позволяет нам приравнять магнитное поле к току, благодаря исчислению, которое мы можем пропустить. Сначала человек, использующий математический анализ, находит линию постоянного магнитного поля, такую как круг вокруг прямого провода, на которой складывается петля расстояния.Затем, сложив все биты длины вокруг петли общей длины, которую мы назовем d , мы свяжем приложенный ток с магнитным полем. В самом общем виде закон Ампера равен Bd = μ 0 I enc , и его можно применять для проводников любой формы.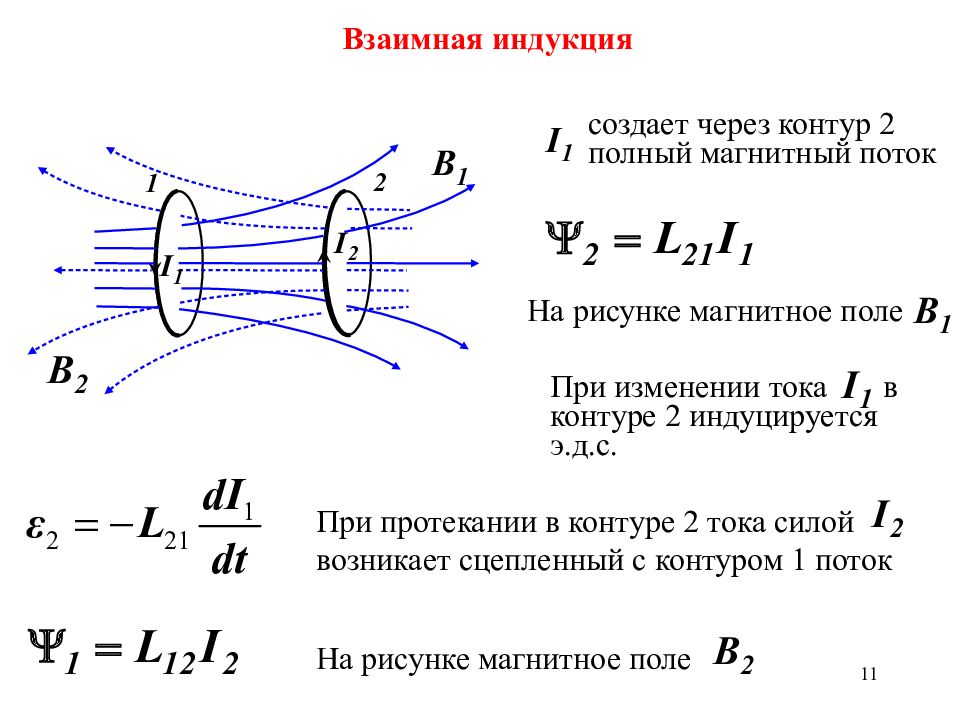
Для окружности вокруг одного прямого проводника с током I путь d равен окружности 2π r , поэтому Bd = μ 0 I enc становится B (2π r ) = μ 0 I , что ведет нас прямо к полю, которое мы обнаружили с помощью Bio-Savart,.
Если мы выберем другую форму, например токовую петлю или соленоид, мы снова придем к тому же выводу, что и Био-Савар. Как и в случае с электрическим полем и электрическим потоком, у нас есть два метода нахождения соответствующих полей. Резервный.
Например, закон Ампера, примененный к соленоиду длиной L , гласит, что BL = μ 0 NI . Тогда, поскольку, B = μ 0 nI . Что мы тебе сказали? Закон Био-Савара и Ампера приводят к одним и тем же уравнениям.
Гораздо сложнее узнать, что проще использовать, но, поскольку мы не несем ответственности за вычисления в этом курсе, мы не принимаем решения. Мы выигрываем.
Мы выигрываем.
Распространенные ошибки
Опять же, как и в случае с электрическими полями, убедитесь, что описанная ситуация соответствует выбранному уравнению. Так много параллелей. А потом опять столько перпендикуляров. Помните, что правило правой руки работает только с правой рукой.
Помните, что движущийся точечный заряд НЕ создает постоянного магнитного поля.Нам необходимо рассмотреть распределения тока, чтобы применить законы магнитостатики.
Brain Snack
Слово магнетизм происходит от древнегреческого города под названием Magnesia , где люди впервые начали находить магнитные камни.
Как магнитное поле просто электрическое поле с применением теории относительности?
Категория: Физика Опубликовано: 18 февраля 2016 г.
Изображение в свободном доступе, источник: Кристофер С.Бэрд
Это заблуждение. Магнитное поле – это не просто электрическое поле с примененной теорией относительности, то есть электрическое поле, рассматриваемое из неправильной системы отсчета. На самом деле, магнитное поле – это фундаментальное поле, которое может существовать в определенной системе отсчета, не нуждаясь в помощи электрического поля. В более общем плане, как электрические, так и магнитные поля являются частью одной фундаментальной единой сущности: электромагнитного поля.
На самом деле, магнитное поле – это фундаментальное поле, которое может существовать в определенной системе отсчета, не нуждаясь в помощи электрического поля. В более общем плане, как электрические, так и магнитные поля являются частью одной фундаментальной единой сущности: электромагнитного поля.
Электрические и магнитные поля подчиняются ряду физических законов, называемых уравнениями Максвелла.Специальная теория относительности Эйнштейна описывает, как пространство и время изменяются в зависимости от выбора инерциальной системы отсчета. Оказывается, специальная теория относительности автоматически содержится в уравнениях Максвелла. Фактически, Эйнштейн открыл специальную теорию относительности, внимательно изучив и поняв уравнения Максвелла. Следовательно, используя уравнения Максвелла в релятивистской форме, мы можем выяснить, как математически преобразовать электрические и магнитные поля из одной системы отсчета в другую.Другими словами, если я измеряю и отображаю электрические и магнитные поля в комнате, когда я неподвижно стою на земле, то, применяя преобразования релятивистской системы координат к этим выражениям поля, я знаю, как поля будут выглядеть для наблюдателя, который мчится по комнате на роликовых коньках. Экспериментально установлено, что эти электромагнитные уравнения преобразования релятивистской системы координат верны.
Экспериментально установлено, что эти электромагнитные уравнения преобразования релятивистской системы координат верны.
Если вы начнете в системе отсчета, которая имеет только электрическое поле и не имеет магнитного поля, то, когда вы сделаете релятивистское преобразование в новую систему отсчета, вы обнаружите, что присутствует и электрическое поле, и магнитное поле, как показано в этот новый кадр.Этот факт, по-видимому, подразумевает, что магнитное поле – это всего лишь электрическое поле, если смотреть из неправильной системы отсчета. Другими словами, этот факт, кажется, подразумевает, что магнитное поле на самом деле является не фундаментальной релятивистской версией электрического поля. Однако более пристальное изучение полей показывает, что этот вывод неверен.
Прежде всего, специальная теория относительности учит нас, что все инерциальные системы отсчета одинаково достоверны и одинаково фундаментальны. Если два шарика катятся друг мимо друга, то с точки зрения красного шарика красный шарик неподвижен, а синий шарик движется. С точки зрения синего шарика синий шарик неподвижен, а красный шарик движется. Обе точки зрения одинаково верны и одинаково фундаментальны. Тот факт, что два шарика видят ситуацию по-разному, не означает, что существует парадокс, что физика нарушена или что одна точка зрения в конечном итоге более верна, чем другая. Это просто означает, что ситуация измеряется в двух разных системах отсчета. Во Вселенной нет «неправильных» систем отсчета или менее фундаментальных систем отсчета.Следовательно, магнитное поле не может быть только электрическим полем, если смотреть из неправильной системы отсчета, потому что нет неправильных систем отсчета. Поскольку существует инерциальная система отсчета, в которой магнитное поле существует без электрического поля, и поскольку каждая инерциальная система отсчета является реальной и фундаментальной, это означает, что магнитное поле реально, является фундаментальным и не обязательно вызвано электрическим поле.
С точки зрения синего шарика синий шарик неподвижен, а красный шарик движется. Обе точки зрения одинаково верны и одинаково фундаментальны. Тот факт, что два шарика видят ситуацию по-разному, не означает, что существует парадокс, что физика нарушена или что одна точка зрения в конечном итоге более верна, чем другая. Это просто означает, что ситуация измеряется в двух разных системах отсчета. Во Вселенной нет «неправильных» систем отсчета или менее фундаментальных систем отсчета.Следовательно, магнитное поле не может быть только электрическим полем, если смотреть из неправильной системы отсчета, потому что нет неправильных систем отсчета. Поскольку существует инерциальная система отсчета, в которой магнитное поле существует без электрического поля, и поскольку каждая инерциальная система отсчета является реальной и фундаментальной, это означает, что магнитное поле реально, является фундаментальным и не обязательно вызвано электрическим поле.
Во-вторых, используя уравнения преобразования электромагнитной релятивистской системы координат, вы можете показать, что невозможно начать с чисто электрического поля (магнитное поле отсутствует) и преобразовать в систему отсчета, в которой есть чисто магнитное поле (электрическое поле отсутствует). ).Это означает, что если бы магнитное поле было только электрическим полем, если смотреть из неправильной системы отсчета, то чисто магнитные поля не существовали бы. Однако чисто магнитные поля все же существуют. Следовательно, магнитные поля – это больше, чем просто релятивистские электрические поля.
).Это означает, что если бы магнитное поле было только электрическим полем, если смотреть из неправильной системы отсчета, то чисто магнитные поля не существовали бы. Однако чисто магнитные поля все же существуют. Следовательно, магнитные поля – это больше, чем просто релятивистские электрические поля.
Правильное утверждение состоит в том, что электрические поля и магнитные поля являются фундаментальными, оба реальны, и оба являются частью одной единой сущности: электромагнитного поля. В зависимости от того, в какой системе отсчета вы находитесь, конкретное электромагнитное поле будет выглядеть более электрическим и менее магнитным или более магнитным и менее электрическим.Однако это не меняет того факта, что они оба являются фундаментальными и являются частью одного и того же единого целого. Чисто электрическое поле, если смотреть в одной инерциальной системе отсчета, является частично электрическим и частично магнитным во всех других системах отсчета. Точно так же чисто магнитное поле, если смотреть в одной инерциальной системе отсчета, является частично электрическим, а частично магнитным во всех других системах отсчета. Магнитное поле – это не просто релятивистская версия электрического поля, а электрическое поле – это не просто релятивистская версия магнитного поля.Скорее, единое электромагнитное поле является внутренне непротиворечивым релятивистским.
Магнитное поле – это не просто релятивистская версия электрического поля, а электрическое поле – это не просто релятивистская версия магнитного поля.Скорее, единое электромагнитное поле является внутренне непротиворечивым релятивистским.
Обратите внимание, что ради обсуждения я проигнорировал квантовые эффекты. Наиболее точным описанием электромагнитных полей в настоящее время являются не исходные уравнения Максвелла, а квантовая форма уравнений Максвелла, которая называется квантовой электродинамикой. Однако, поскольку квантовая электродинамика просто расширяет уравнения Максвелла, а не заменяет их, все концепции в этой статье остаются в силе.
Также обратите внимание, что я много использовал слово «инерционный» в этой статье. Это означает, что мы рассматриваем только системы отсчета, которые имеют плоское пространство-время, то есть системы отсчета, которые не ускоряются и не имеют большого количества гравитации. Чтобы описать неинерциальные системы отсчета, вы должны использовать общую теорию относительности Эйнштейна, которая сложнее специальной теории относительности.

 Эта часть двигателя служит для возбуждения магнитного поля.
Эта часть двигателя служит для возбуждения магнитного поля. . RHR-2 дает направление поля вокруг петли.
. RHR-2 дает направление поля вокруг петли.


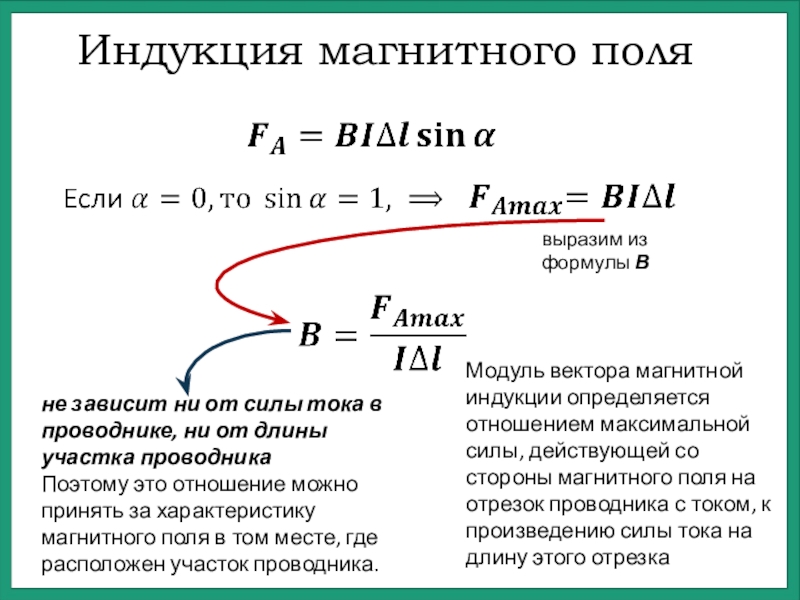 Часть (c) рисунка) составляет
Часть (c) рисунка) составляет