1. Вывод формул для моментов инерции простейших фигур (прямоугольник, треугольник, круг)
Прямоугольное сечение.
Прямоугольное сечение имеет две оси симметрии, а главные центральные оси Сx и Cy проходят через середины параллельных сторон.
Главный центральный момент инерции относительно оси x
Элементарную площадку dA в этом случае можно представить в виде полоски во всю ширину сечения и толщиной dy, значит dA=b*dy. Подставим под знак интеграла значение dA и проинтегрировав по всей площади, т.е. в пределах изменения ординаты y от –h/2 до +h/2, получим
Окончательно
Аналогично получим формулу главного центрального момента инерции прямоугольника относительно оси y:
Круглое сечение
Для круга главные центральные моменты инерции относительно осей x и y равны между собой.
Поэтому из равенства
Треугольник
2.
 Изменение моментов инерции при переходе от центральных осей к параллельным:
Изменение моментов инерции при переходе от центральных осей к параллельным:Jy1=Jy + b2А;
момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями. Jy1x1=Jyx + abF; (“a” и “b” подставляют в формулу с учетом их знака).
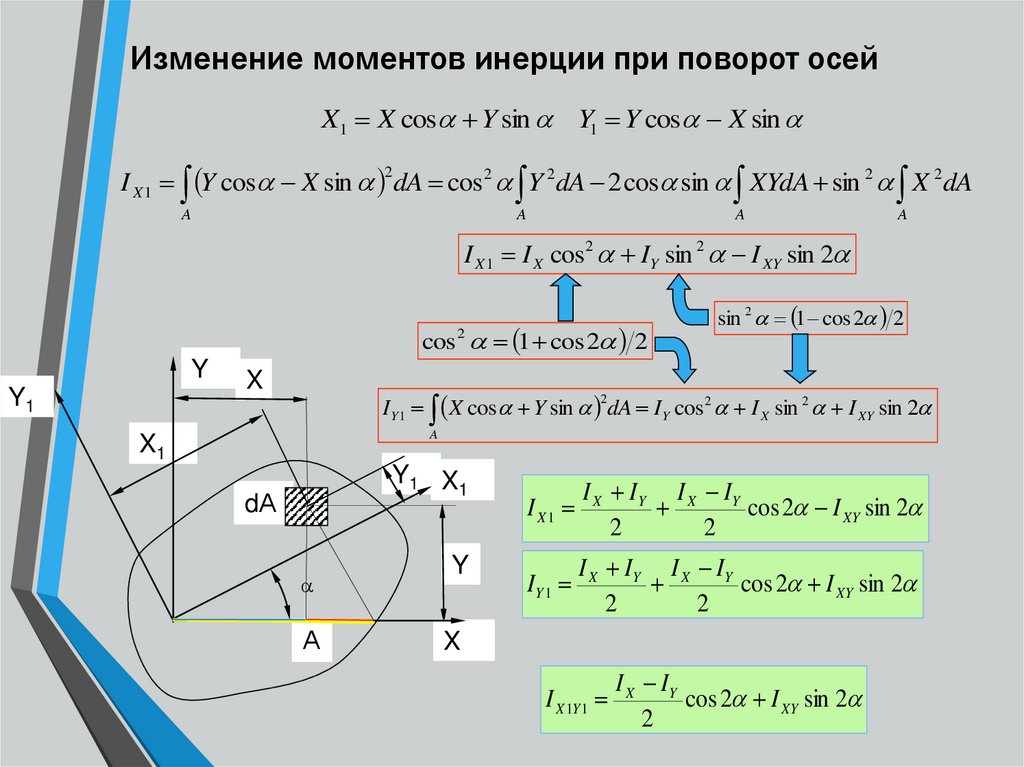
3.Изменение моментов инерции при повороте осей
Jx1=Jxcos2 + Jysin2 — Jxysin2; Jy1=Jycos2 + Jxsin2 + Jxysin2;
J
Угол
>0,
если переход от старой системы координат
к новой происходит против час.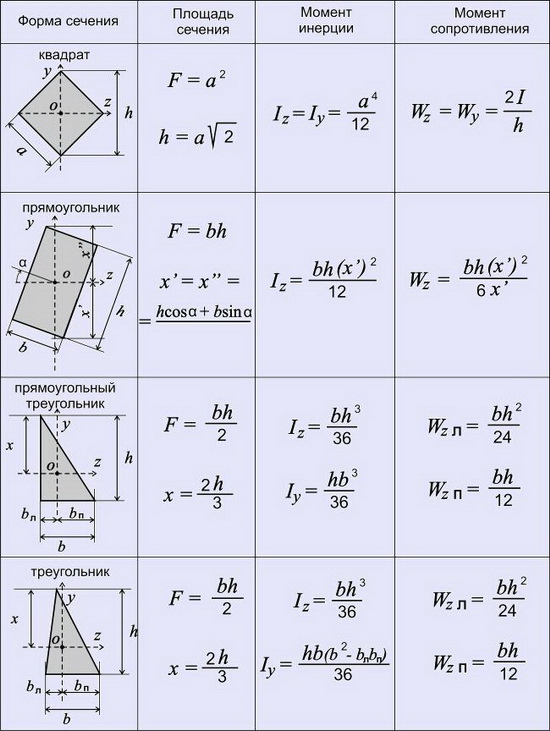 стр. Jy1 + Jx1=
Jy + Jx
стр. Jy1 + Jx1=
Jy + Jx
Экстремальные (максимальное и минимальное) значения моментов инерции называются главными моментами инерции. Оси, относительно которых осевые моменты инерции имеют экстремальные значения, называются главными осями инерции. Главные оси инерции взаимно перпендикулярны. Центробежные моменты инерции относительно главных осей = 0, т.е. главные оси инерции — оси, относительно которых центробежный момент инерции = 0. Если одна из осей совпадает или обе совпадают с осью симметрии, то они главные. Угол, определяющий положение главных осей: , если
0>0 оси поворачиваются против час.стр. Ось максимума всегда составляет меньший угол с той из осей, относительно которой момент инерции имеет большее значение. Главные оси, проходящие через центр тяжести, называются главными центральными осями инерции. Моменты инерции относительно этих осей:
Jmax + Jmin=
Jx + Jy.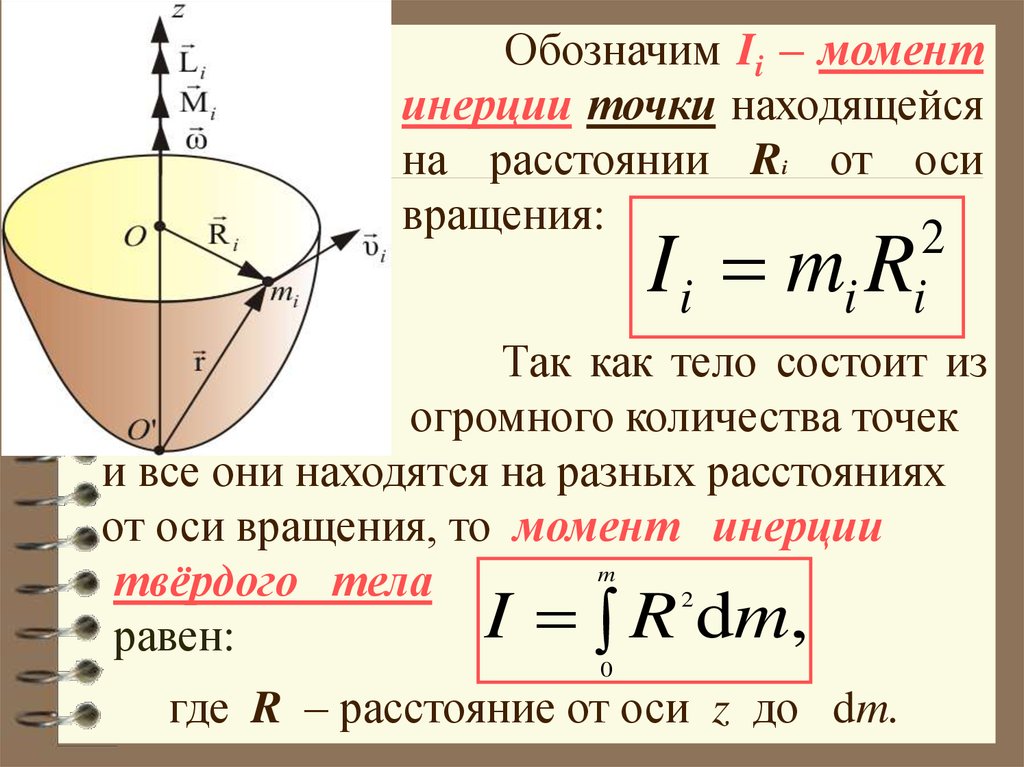
Jx1=Jmaxcos2 + Jminsin2; Jy1=Jmaxcos2 + Jminsin2; Jx1y1=(Jmax — Jmin)sin2;
4.Классификация элементов конструкций
Стержнем наз. Геом тела у которых один из размеров много больше других.
Пластины или оболочки – это геом тела у которых один из размеров << других
Массивные тела– все размеры одного порядка
5.Основные допущения о свойствах материала
Однородные – в люб. точке материалы имеют одинак. физико-химич. св-ва;
Сплошная среда – кристаллич. строение и микроскопич. дефекты не учитываются;
Изотропны
– механич. св-ва не зависят от направления
нагружения;
св-ва не зависят от направления
нагружения;
Идеальная упругость – полностью восстанавливают форму и размеры после снятия нагрузки.
6.Типы опор
а) Шарнирно – неподвижная (двухсвязная) опора: Воспринимает как вертикальные, так и горизонтальные усилия (усилия под углом).
б) Шарнирно – подвижная опора – воспринимает только вертикальные нагрузки. Реакция опоры всегда направлена вдоль опорного стержня, перпендикулярно опорной поверхности
в) Жесткая заделка (трехсвязная)
Реакции в опорах определяют из условия равновесия (уравнение статики).
7.Классификация нагрузок
По месту действия
Поверхностные и объемные
а) сосредоточенная сила
б) распределенная сила
прямоугольная Rq= qa
треугольная Rq= ½ qa
в) сосредоточенный момент
изгибающий
скручивающий
г) распределенный момент
Rmz= mz a –равнодейств распр мом
По времени действия
Постоянные и временные
По характеру действия
Статические и динамические
По характеру возникновения
Активная(известны) и реактивная (неизвестны)
8. Основные
принципы изучаемого курса
Основные
принципы изучаемого курса
При расчете сложного сопротивления используется принцип независимости действия сил. Сложный вид нагружения представляется как система простых видов нагружения действующих независимо друг от друга. Решение при сложном сопротивлении получается в результате сложения решений полученных при простых видах нагружения.
принцип Сен-Венана
на достаточном удалении от места приложения нагрузки характер её воздействия не зависит от способа её приложения, а зависит от величины равнодействующей.
9.Внутренние усилия. Метод сечений (Метод РОЗУ)
Nz=∑z (pi) нормальная с
Qx=∑x (pi) поперечная с
Qy=∑y (pi)
Mz=∑mz (pi) крутящий момент
Mx=∑mx (pi) изгибающий
My=∑my (pi)
Разрезаем мысл тело плоск
Отбрасываем одну из г внутр усил
Заменяем внутр усилиями
Уравновешив внутр ус внеш нагр
10. Правило
знаков внутренних усилий
Правило
знаков внутренних усилий
Правило знаков поперечных сил при изгибе:
Крутящий момент
Против ЧС при взгляде со стороны сеч то +
Правило знаков изгибающих моментов:
Правило проверки правильности построения эпюр нагружения:
В сечениях балки, где приложены внешние сосредоточенные нагрузки на эпюре д.б. скачёк на величину этой нагрузки.
11.Эпюры внутренних усилий
ПРИ РАСТЯЖЕНИИ-СЖАТИИ
ПРИ КРУЧЕНИИ
при прямом изгибе
12.Дифференциальные зависимости при изгибе
; ;
13.Следствия из дифференциальных зависимостей
Если на участке нет распр нагр (q=0) то поперечная сила на этом участке имеет пост вел.
 , а эпюры изгиб мом
меняются по лин закону
, а эпюры изгиб мом
меняются по лин законуНа уч на котором присутст распр нагр пост интенсивн. Поперечная сила меняется по лин зак , а эпюры по закону квадр параболы. Причем эпюра мх всегда напр навстречу распр нагрузке. Где Qy равно 0 эпюра мх имеет экстремум. Если Qy равно 0 на всем участке, то мх постоян величину
4. На участке где Qy>0 эпюра мх возрастает слева направо
5. В том сеч. где приложена сосред сила эпюра Qy имеет скачок на вел этой силы. В сеч где сосред момент эпюра мх имеет скачок на величену этого момента
Вывод формулы момента инерции кольца : Чулан (Ф)
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
| Nikolay_90 |
| ||
17/12/07 |
| ||
| |||
| photon |
| |||||||||
23/12/05 |
| |||||||||
| ||||||||||
| Eiktyrnir |
| ||
30/11/07 |
| ||
| |||
| peregoudov |
| ||
10/03/07 |
| ||
| |||
| Eiktyrnir |
| ||
30/11/07 |
| ||
| |||
| Zai |
| |||
11/04/07 |
| |||
| ||||
| Eiktyrnir |
| ||
30/11/07 |
| ||
| |||
| peregoudov |
| ||
10/03/07 |
| ||
| |||
| Zai |
| |||
11/04/07 |
| |||
| ||||
| Eiktyrnir |
| ||
30/11/07 |
| ||
| |||
| peregoudov |
| ||
10/03/07 |
| ||
| |||
| Eiktyrnir |
| ||
30/11/07 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 12 ] |
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Калькулятор момента инерции
Создано Bogna Szyk
Отзыв Стивена Вудинга
Последнее обновление: 11 февраля 2023 г.
- Что такое момент инерции площади?
- Формулы момента инерции
- Как рассчитать момент инерции относительно любой оси?
- Пример: момент инерции прямоугольника
- Различные применения момента инерции
- Часто задаваемые вопросы
Если у вас возникли проблемы с определением второй момент площади любой распространенной формы (например, круг или шестиугольник), этот калькулятор момента инерции здесь, чтобы помочь вам. Вы также найдете здесь формулы момента инерции — прочитайте описание ниже, чтобы убедиться, что вы используете их правильно! Мы объясним, как работают эти формулы, чтобы вам больше никогда не приходилось задаваться вопросом, как вычислить момент инерции прямоугольника.
Каков момент инерции площади?
момент инерции площади (также называемый вторым моментом площади или вторым моментом инерции ) является геометрическим свойством любой площади.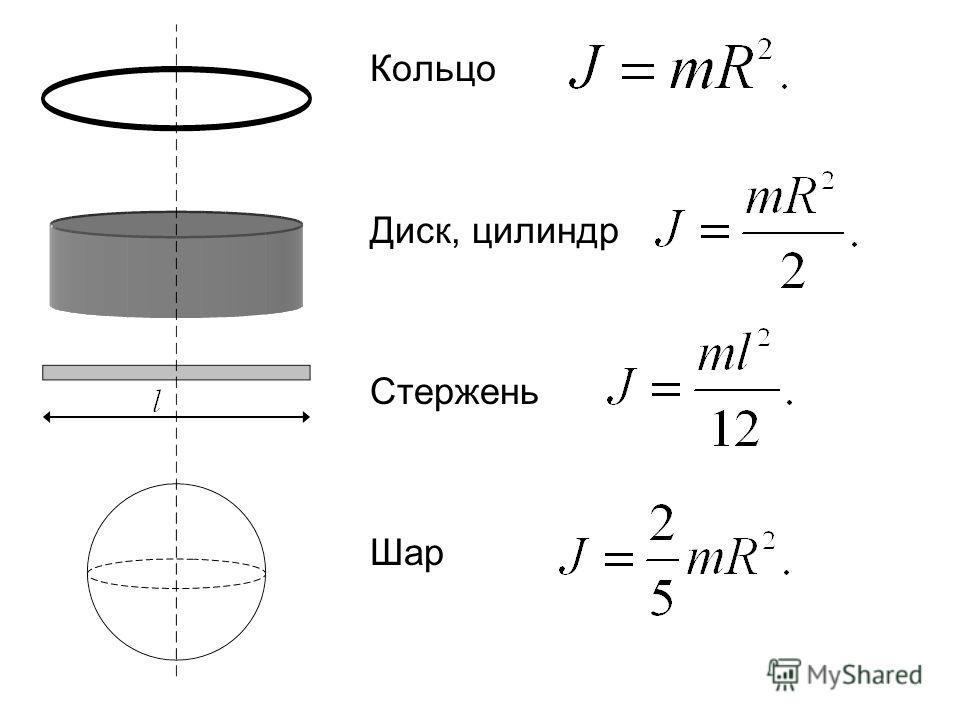 Он описывает, как площадь распределяется вокруг произвольной оси. Единицами момента инерции площади являются метры в четвертой степени (м⁴).
Он описывает, как площадь распределяется вокруг произвольной оси. Единицами момента инерции площади являются метры в четвертой степени (м⁴).
Мы можем различать момент инерции относительно горизонтальной оси x (обозначается Ix ) и момент инерции относительно вертикальной оси y (обозначается Iy ). Обычно мы принимаем, что «ширина» любой фигуры — это длина стороны по оси абсцисс, а высота — по оси у.
🙋 Хотите вместо этого узнать о моменте инерции массы , который мы можем выразить в килограммах на квадратные метры (кг·м²) или фунтах на квадратный фут (фунт·фут²)? Тогда вам нужно проверить наш калькулятор момента инерции.
Формулы момента инерции
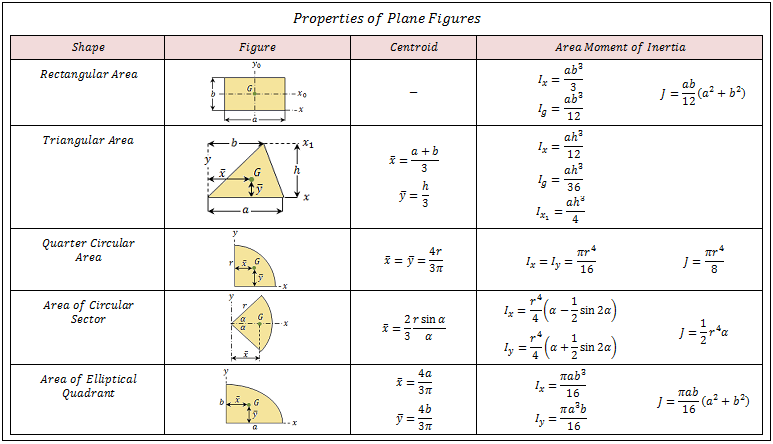
Как правило, для нахождения второго момента площади произвольной формы требуется интегрирование. Однако вы можете использовать следующие уравнения для наиболее распространенных форм. Помните, что эти формулы справедливы, только если начало системы координат совпадает с центроидом области. Другими словами, если и ось x, и ось y пересекают центр тяжести анализируемой формы, то эти уравнения выполняются.
Другими словами, если и ось x, и ось y пересекают центр тяжести анализируемой формы, то эти уравнения выполняются.
Треугольник:
Ix = ширина × высота³ / 36
Iy = (высота × ширина³ – высота × a × ширина² + ширина × высота × a²) / 36 ,
, где a — смещение верхней вершины
Прямоугольник:
Ix = ширина × высота³ / 12
Iy = высота × ширина³ / 12
Круг:
Ix = Iy = π/4 × радиус⁴
Полукруг
Ix = [π/8 – 8/(9*π)] × радиус⁴
Iy = = π/8 × радиус⁴
Эллипс:
Ix = π/4 × radius_x × radius_y³
Iy = π/4 × radius_y × radius_x³
Правильный шестигранник:
Ix = Iy = 5 × √(3)/16 × длина стороны⁴
Как рассчитать момент инерции относительно любой оси?
Чтобы найти второй момент площади, когда начало системы координат не совпадает с центром тяжести, используйте теорему о параллельных осях . Момент площади относительно оси, параллельной оси x, лежащей на расстоянии a от нее, определяется по формуле Ix + Aa² , где:
Момент площади относительно оси, параллельной оси x, лежащей на расстоянии a от нее, определяется по формуле Ix + Aa² , где:
- Ix — момент инерции относительно оси x;
- A — площадь; и
- a — расстояние между двумя параллельными осями.
Чтобы найти площадь круга (а также другие его свойства), воспользуйтесь калькулятором длины окружности.
Пример: момент инерции прямоугольника
Предположим, прямоугольник шириной 12 см и высотой 8 см. Его центроид лежит в начале системы координат. Тогда:
Ix = 12 × 8³ / 12 = 512 см⁴
Iy = 8 × 12³ / 12 = 1152 см⁴
Различные применения момента инерции Мы можем использовать понятие момента инерции
900 проанализировать поперечное сечение материалов, которые мы используем в строительстве, чтобы определить их прочность.
Если вы хотите узнать, как мы можем использовать момент инерции поперечного сечения балки, вы можете воспользоваться нашим калькулятором прогиба балки или калькулятором пролета деревянной балки.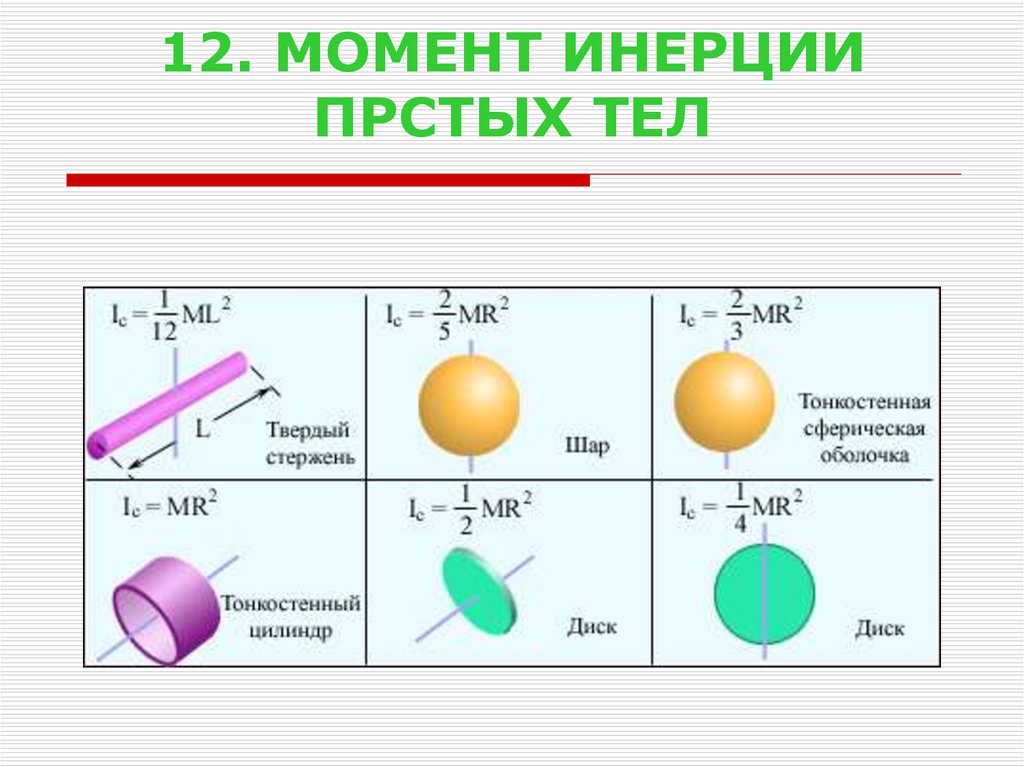 У нас также есть наш калькулятор лаг пола, если он вас интересует.
У нас также есть наш калькулятор лаг пола, если он вас интересует.
Часто задаваемые вопросы
Как рассчитать площадь момента инерции составной формы?
Момент инерции площади равен добавке , что означает, что момент площади для сложной формы равен сумме момента инерции площади всех ее составляющих. Если есть «дыра», вы просто вычитаете момент инерции ее площади (вместо того, чтобы прибавлять).
Чему равен момент инерции площади круга радиусом 4?
Ответ: 201.06 . Чтобы прийти к этому результату, вам нужно запомнить формулу площади момента инерции для круга: r⁴ × π / 4 , где r — радиус вашего круга.
Как рассчитать площадь момента инерции кольца?
Для определения площади момента инерции кольца:
Определите внешний и внутренний радиусы кольца. Обозначим их R и r соответственно.
Вычислите момент инерции площади круга с радиусом R .
 Напомним, формула радиус⁴ × π / 4 .
Напомним, формула радиус⁴ × π / 4 .Вычислите момент инерции площади круга с радиусом r .
Вычтите результат шага 3 из результата шага 2.
Вот оно! Мы использовали аддитивность момента инерции площади.
Bogna Szyk
Ширина (b)
Высота (a)
Ознакомьтесь с 23 похожими калькуляторами 2D-геометрии 📏
ПлощадьПлощадь прямоугольникаПлощадь полумесяца… Еще 20
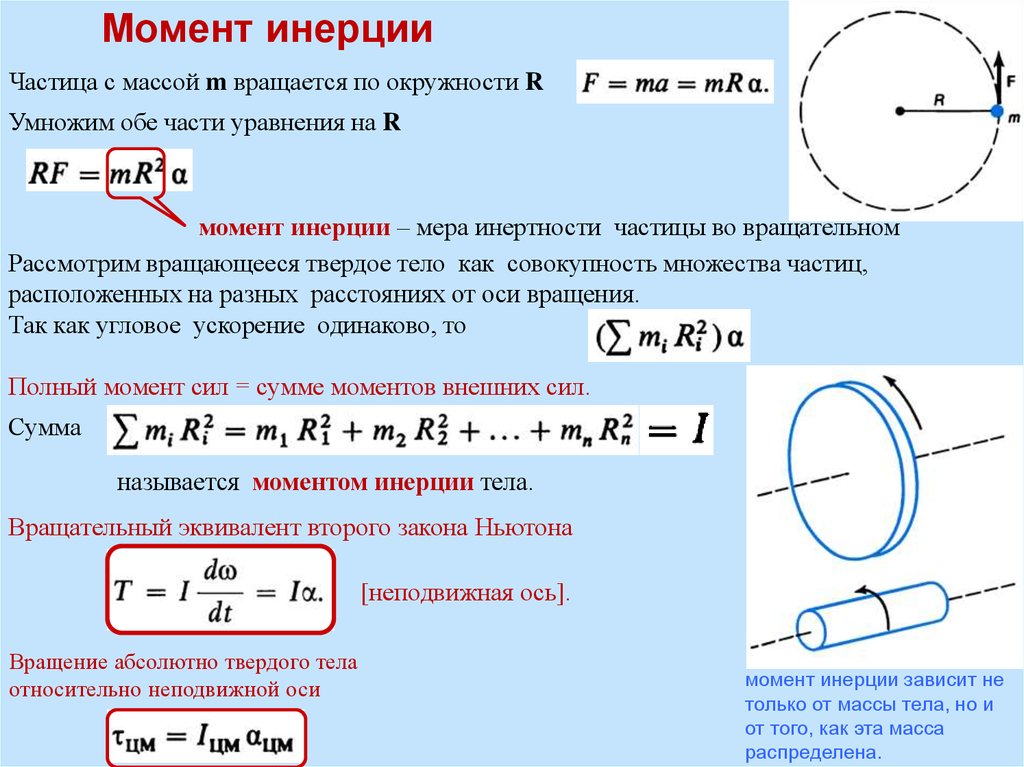
Момент инерции различных объектов
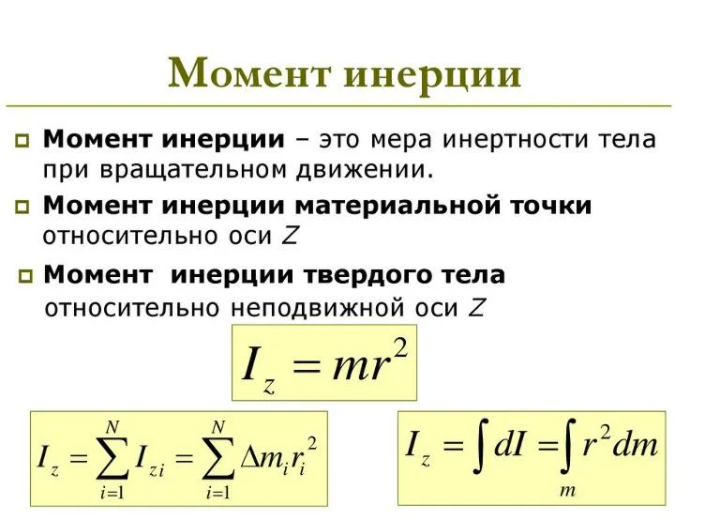
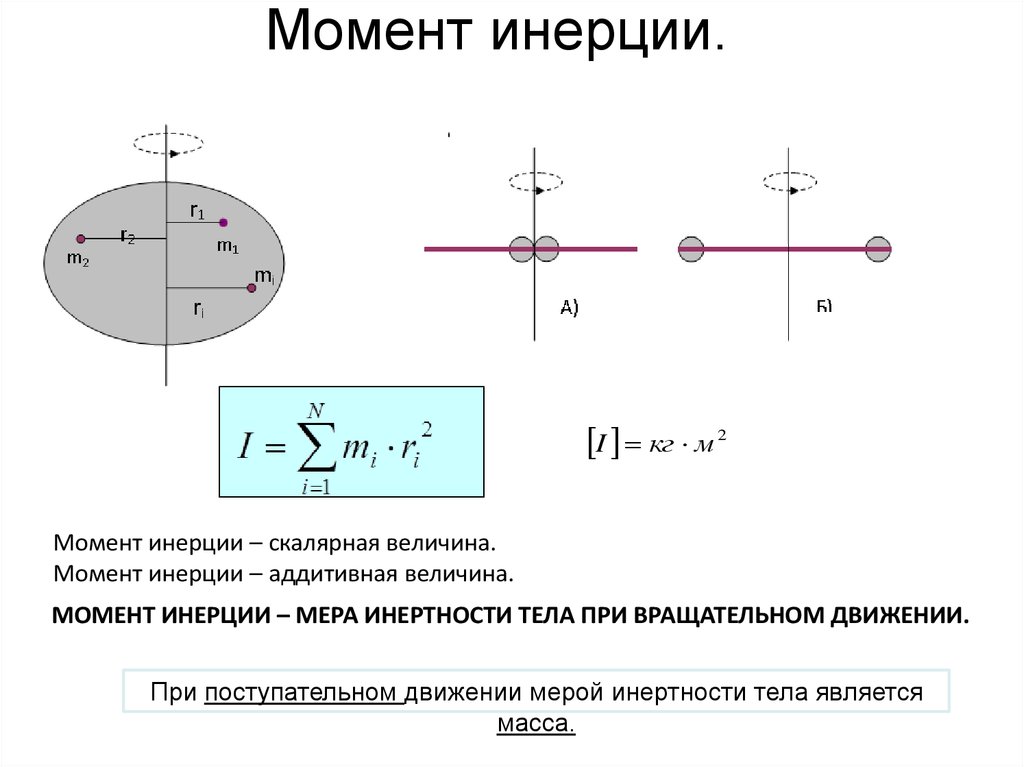
Инерция вращения тела измеряется в моментах инерции относительно определенной фиксированной оси вращения. Он вычисляет крутящий момент, необходимый для достижения желаемого углового ускорения. Точно так же масса определяет силу, необходимую для достижения желаемого ускорения. Иными словами, момент инерции описывает, насколько сложно повернуть предмет вдоль заданной оси. Помните, что выбранная вами ось имеет решающее значение; конечное значение момента инерции может сильно зависеть.
Помните, что выбранная вами ось имеет решающее значение; конечное значение момента инерции может сильно зависеть.
Физическая размерность момента инерции равна массе * длине². Килограмм-метр в квадрате кг * м² является единицей СИ для момента инерции, в то время как имперские или американские единицы представляют собой фунт-фут-секунду в квадрате lbf . футов . с 2 . Вы можете производить расчеты в любой из этих единиц, используя момент массы калькулятора инерции.
Применение момента инерцииВ дополнение к формулам для расчета момента инерции важность , давайте поговорим о приложениях:
- Момент инерции массы — это измерение сопротивления объекта изменению вращения.
- Момент инерции площади геометрической формы — это свойство, которое помогает в расчете напряжений, изгиба и прогиба в балках.
- Полярный момент инерции необходим для расчета касательного напряжения, вызванного скручиванием или крутящим моментом.
- В уравнении потери устойчивости Эйлера слово «I» имеет большое значение при расчете критической нагрузки. Критическая осевая нагрузка, Pcr, определяется как Pcr = π 2EI/L2 где E=модуль упругости I=момент инерции L=длина колонны
- рассчитать напряжение изгиба балки. Момент инерции обратно пропорционален деформациям изгиба. Момент инерции пропорционален моменту сопротивления изгибу.
9Формула 0253 для расчета момента инерции имеет решающее значение в теории балок. Уравнение момента инерции меняется в зависимости от поперечного сечения объекта. Стоит отметить, что момент инерции всегда положителен. В этом разделе мы найдем формулу момента инерции для нескольких популярных геометрических сечений.
· Для квадратного сечения:Для квадрата момент инерции равен Ix=Iy= a4/12, где a=длина стороны.
·
Уравнение для момента инерции круглого поперечного сечения: I= π d4/64, где d=диаметр окружности, представляет собой момент инерции круглого поперечного сечения.
Момент площади трубы рассчитывается аналогично I= π (D4-d4)/64, где D=наружный диаметр трубы и d=внутренний диаметр трубы.
·
Единицы момента инерцииЕдиница измерения момента инерции в системе СИ — кг.м2, а единица FPS — фунт-сила·фут·с2.
·
Полярный момент инерцииПолярный момент инерции определяется как ось, перпендикулярная рассматриваемой области. Он определяет сопротивление балки кручению или скручиванию. Полярный момент инерции круглой области (J) равен J = π d4/32.
Модуль сеченияОтношение момента инерции (I) к расстоянию (y) крайней нити от нейтральной оси в сечении называется модулем сечения. Модуль сопротивления сечения обозначается буквой «Z» и математически выражается как
Z=I/y
Модуль упругости измеряется в м3 в системе СИ и дюймах3 в системе США.
Теорема о параллельных осях Когда момент инерции определен относительно центра масс объекта, его легко пересчитать для всех параллельных осей вращения, не прибегая к формальному определению.

 12.2007, 23:52
12.2007, 23:52  12.2007, 00:33
12.2007, 00:33  12.2007, 20:53
12.2007, 20:53  Теперь запишем элементарный момент инерции этого кусочка – Успешно интегрируем и получаем и поскольку и аналогично , а еще и то и получается восьмерочка, т.е. как на формуле
Теперь запишем элементарный момент инерции этого кусочка – Успешно интегрируем и получаем и поскольку и аналогично , а еще и то и получается восьмерочка, т.е. как на формуле 12.2007, 23:35
12.2007, 23:35 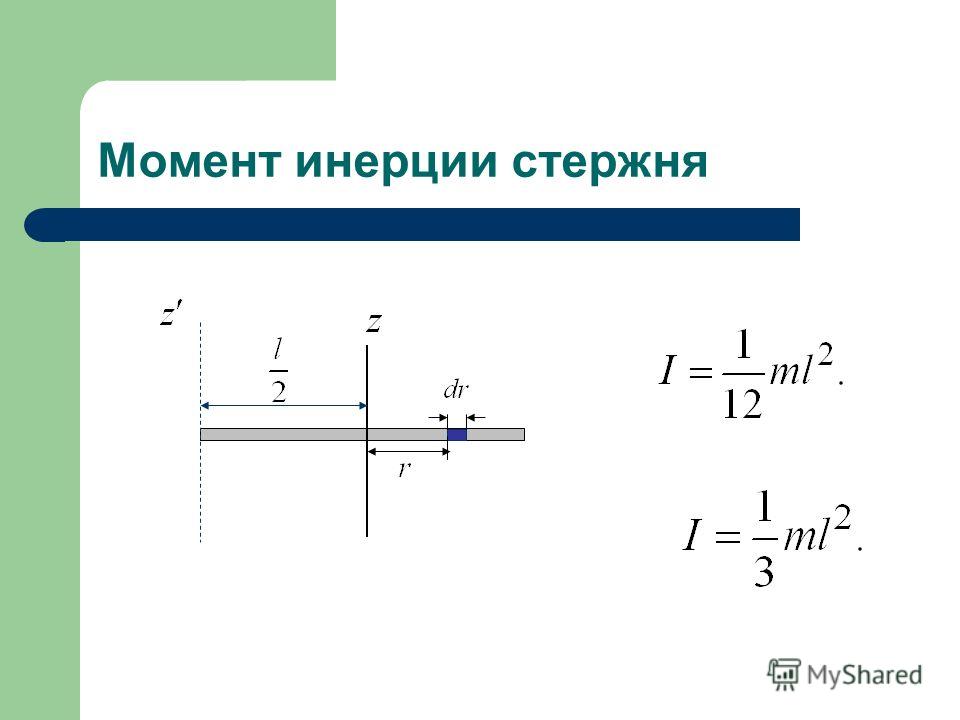 Воспользовавшись аддитивностью массы и момента инерции, можно записать
Воспользовавшись аддитивностью массы и момента инерции, можно записать 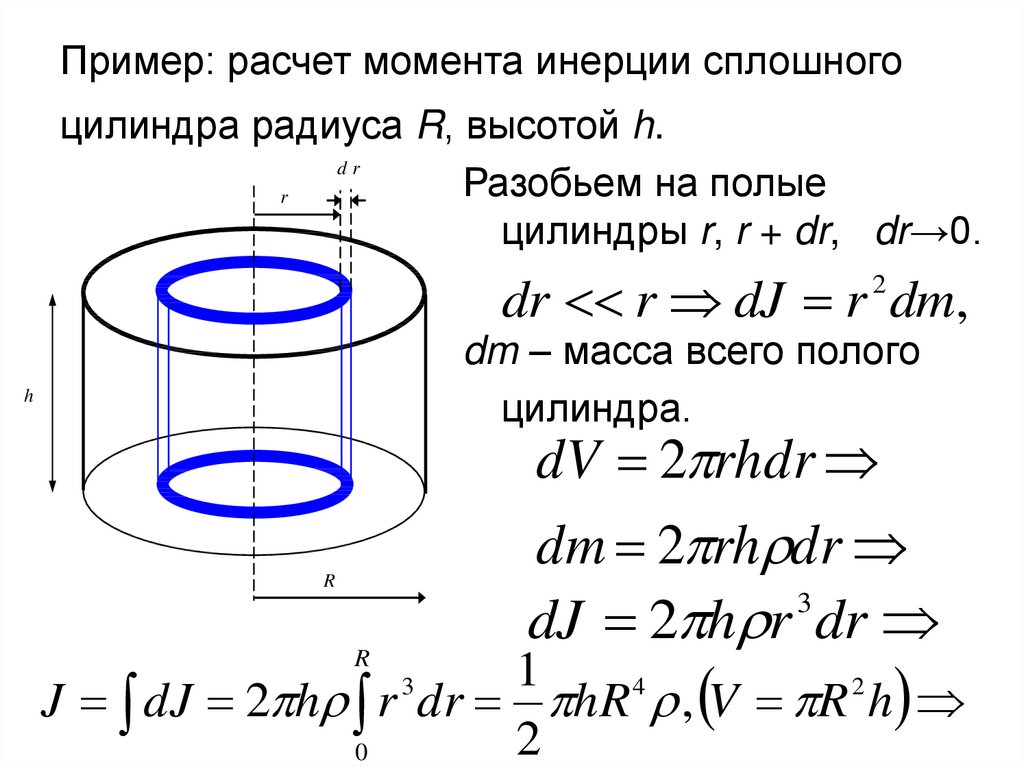

 Так это неважно – в полярных или декартовых (дело выбора системы координат) – ответ должен быть один и тот же. А почему автор сообщения о том, что я не прав – молчит? Мои сомнения ушли после вашего (Zai) сообщения. Спасибо вам.
Так это неважно – в полярных или декартовых (дело выбора системы координат) – ответ должен быть один и тот же. А почему автор сообщения о том, что я не прав – молчит? Мои сомнения ушли после вашего (Zai) сообщения. Спасибо вам.
 12.2007, 19:29
12.2007, 19:29  12.2007, 16:22
12.2007, 16:22 

 Теперь все ясно. Увы потерянные годы практики…
Теперь все ясно. Увы потерянные годы практики…