Формулы момента инерции: Кафедра физики Физико-механический институт СПбПУ

Вывод рабочей формулы для экспериментального определения момента инерции.

Рис. 4.1

При экспериментальном определении момента инерции используется маятник Обербека, который представляет собой крестовину с четырьмя закрепленными на ней на одинаковых расстояниях от оси одинаковыми грузами. На ось крестовины насажен двухступенчатый шкив, на который намотана нить с подвешенным к ней грузом. При движении груза вниз шкив начинает вращаться. Для вывода рабочей формулы рассмотрим упрощенную схему установки, выделив систему связанных движущихся тел: поступательно движущийся груз и вращающийся шкив (рис. 4.1). Поступательное движение груза описывается уравнением:

mg – T = ma (4.1)

Вращательный момент шкива создает сила натяжения нити Т₁, которая по третьему закону Ньютона равна силе Т. Этот момент М = ТR. Тогда уравнение вращательного движения шкива:

ТR=Iε (4.2)

Если отсутствует проскальзывание нити, то тангенциальное ускорение элементов нити, вращающихся вместе со шкивом, равно линейному ускорению груза:

а_τ = а = εR (4.3)

Решая систему уравнений (4.1), (4.2) и (4.3), получим для момента инерции выражение: .

Линейное ускорение груза можно вычислить по измеренным высоте падения груза и времени его падения: h=at²/2.

Таким образом, получена рабочая формула для экспериментального определения момента инерции:

(4.4)

Вывод формулы для теоретического вычисления момента инерции.

Момент инерции является аддитивной величиной, то есть момент инерции системы тел равен сумме моментов инерции всех тел, входящих в систему.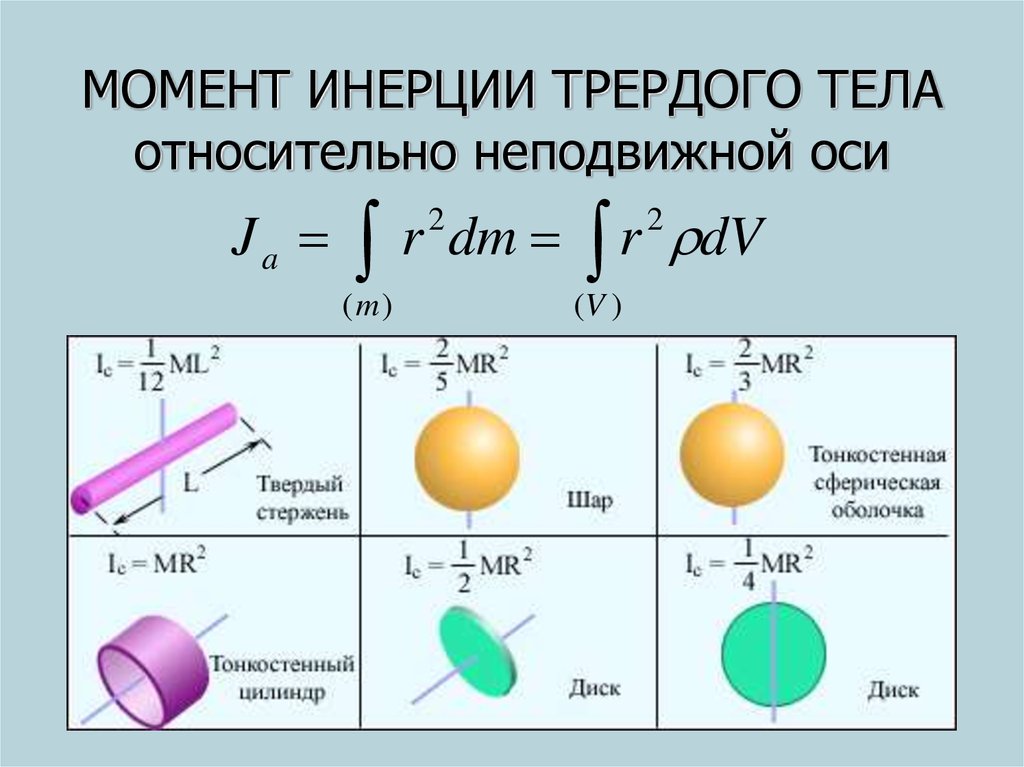 Маятник Обербека состоит из шкива (включая ось и втулку крестовины), четырех стержней крестовины и грузов, укрепленных на крестовине. Момент инерции шкива указан на установке. Момент инерции стержня относительно оси, проходящей через его конец, равен m₂l_c²/3, где m₂ − масса стержня без груза,

l_c − длина стержня крестовины − указаны на установке. Грузы, укрепленные на крестовине, приближенно можно считать за точечные массы. Тогда момент инерции каждого груза равен m₁l², где m₁ − масса одного груза (указана на установке), l − расстояние от оси вращения до центра масс груза (измеряется при выполнении работы).

Теоретический момент инерции после суммирования вычисляется по формуле:

I = I₀ + 4m₁l² + 4m₂l_c²/3 (4.

5)

Описание экспериментальной установки

Рис. 4.2

Внешний вид установки представлен на рис.4.2. Регулировочные винты 1 обеспечивают горизонтальную установку основания 2, к которому крепится вертикальная колонка 3, на которой нанесена миллиметровая шкала. К этой колонке прикреплены неподвижный кронштейн 4 и верхний подвижный 5, с помощью которого можно регулировать длину пути груза h. Через диск 6 перекинута нить 7, один конец которой прикреплен к шкиву 8, а на втором конце закреплены грузы 9. Кронштейн 11 снабжен резиновым амортизатором для ограничения движения грузов. Включение прибора производится нажатием клавиши «сеть» 12, обнуление миллисекундомера производится клавишей «сброс» 13, клавиша «пуск» 14 включает миллисекундомер. Время падения груза высвечивается на индикаторе 15.

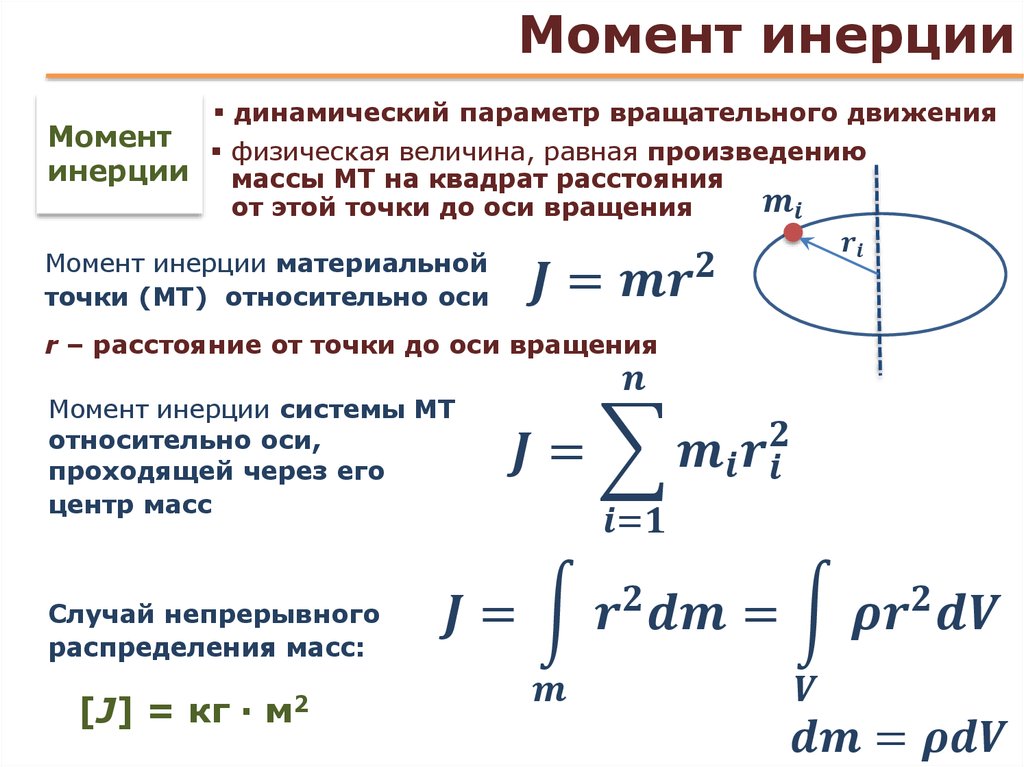
Момент инерции тела и материальной точки. Формулы для цилиндра и стержня. Физический смысл величины

В школьном курсе физики большое внимание уделяется описанию кинематики и динамики поступательного движения тел в трехмерном пространстве. Но вращательное движение играет не менее важную роль в технике и природе. В данной статье рассмотрим, что понимают под моментом инерции тела при его вращении вокруг оси.

Динамика вращения

Прежде чем давать определение момента инерции тела, расскажем, для чего нужна эта величина и в каких уравнениях она появляется. В первую очередь, это главное уравнение динамики вращения – формула моментов. Записывается она так:

M = I*α.

Здесь M, α и I – это момент силы, ускорение угловое и инерции момент, соответственно. По сути, это уравнение можно назвать вторым ньютоновским законом для вращательного движения. Несложно догадаться, что величина I здесь играет ту же самую роль, что инерционная масса в случае поступательного движения.

Помимо приведенного уравнения, существует еще одна важная формула, которая применяется часто для решения задач на вращение тел – это закон сохранения момента импульса. Его, как правило, записывают в следующей удобной для практики форме:

I*ω = const.

Как видим, здесь инерции момент тоже является ключевой величиной, ω – это скорость угловая.

Момент инерции твердого тела

Теперь пришло время дать определение величине I. Сначала рассмотрим его для материальной точки. Ее моментом инерции называется произведение массы на квадрат расстояния до оси вращения. Если массу обозначить буквой m, а дистанцию до оси от точки буквой r, то формула для I запишется так:

I = m*r².

Как видно, I выражается в кг*м². Равенство для точки можно использовать для определения момента инерции тела относительно оси. В этом случае применяют следующее интегральное выражение:

I = ∫_m(r²*dm).

Эта формула применяется для вычисления величин I абсолютно любых систем с разными геометрическими формами. Последнее равенство также используют при решении практических задач в следующем виде:

I = ∫_V(ρ*r²*dV).

Где ρ – плотность вещества. Ниже в статье покажем, как использовать интегральное равенство для решения конкретных задач.

Величина I для цилиндра

Каждый школьник представляет себе фигуру “цилиндр”. По правде говоря, они бывают самыми разными (эллиптическими, гиперболическими, наклонными). Здесь рассмотрим самый простой случай. Это круговой прямой цилиндр, который ограничен цилиндрической поверхностью и двумя одинаковыми кругами. Ось вращения фигуры проходит через ее центр масс и через центры обоих оснований. Вычислим относительно нее инерции момент тела.

Запишем исходную формулу:

I = ∫_V(ρ*r²*dV).

Чтобы ее применить, представим себе цилиндр в виде тонко нарезанных круглых одинаковых слоев. Обозначим их толщину dl, радиус фигуры равен R, а высота – L. Теперь каждый тонкий слой объемом pi*R²*dl разрежем на бесконечное множество колец, толщина каждого из которых равна dr. После выполнения всех описанных мысленных геометрических операций можно записать формулу для элементарного объема dV, то есть для объема одного кольца:

dV = 2*pi*r*dr*dl.

В результате этого представления исходное выражение для I преобразуется в формулу с двойным интегралом:

I = ∫_L∫_R(ρ*r²*2*pi*r*dr*dl) = 2*pi*ρ*L*R⁴/4 = M*R²/2.

Где буквой M обозначена масса всего цилиндра.

Таким образом, мы получили конечное выражение для инерции момента цилиндра. Как видно, он определяется только радиусом фигуры и ее массой и не зависит от длины (высоты). Последнее означает, что аналогичную формулу можно применять для определения величины I для диска любой толщины.

Величина I для стержня

Теперь применим формулу для определения момента инерции тонкого стержня. Принципиальным моментом здесь является тот факт, что его толщина должна быть намного меньше длины L. Массу стержня обозначим буквой M. Момент инерции рассчитаем для положения оси, которая проходит через центр масс тела и перпендикулярна ему.

Начнем расчет все с той же формулы, что и в случае с цилиндром:

I = ∫_V(ρ*r²*dV).

Мысленно разрежем весь стержень на тонкие слои. Обозначим площадь сечения каждого из них S, а его толщину – dl. Тогда получаем формулу для dV:

dV = S*dl.

Теперь можно вычислить инерции момент тела:

I = ∫_-L/2^+L/2(ρ*S*l²*dl).

Заметим, что каждый слой находится от оси вращения на расстоянии l, поэтому мы заменили букву r. Кроме того, обращаем внимание на пределы интегрирования, которые имеют такое значение потому, что ось проходит точно через середину стержня. В итоге получаем:

I = ∫_-L/2^+L/2(ρ*S*l²*dl) = ρ*S*l³/3|_-L/2^+L/2 = M*L²/12.

С помощью аналогичных рассуждений и вычислений можно показать, что если ось вращения проходит через какой-либо конец стержня, то его момент инерции будет в четыре раза больше, то есть:

I = M*L²/3.

Физический смысл величины

Выше мы уже сказали несколько слов о том, что означает момент инерции тела с физической точки зрения. Здесь остановимся несколько подробнее на этом вопросе.

Если внимательно посмотреть на формулу для I, то можно увидеть, что эта величина зависит не только от самой массы тела, но и от ее распределения, то есть от формы тела, а также от его положения относительно оси вращения.

Ярким примером являются обычная швабра или просто стержень. Каждый человек хоть раз в жизни раскручивал швабру вокруг оси, проходящей вдоль ее ручки или перпендикулярно ей. В первом случае легкого движения ладоней достаточно, чтобы придать угловое ускорение швабре, во втором же – приходится прилагать некоторую силу рук, чтобы раскрутить ее. Объяснить этот факт просто. В первом случае момент инерции практически равен нулю, во втором – он имеет некоторую конечную величину.

Формулы момента инерции для различных форм

Расчет момента инерции для различных форм и поперечных сечений, вероятно, единственная вещь в проектировании конструкций, которую мы используем во время учебы, а также в дальнейшей карьере.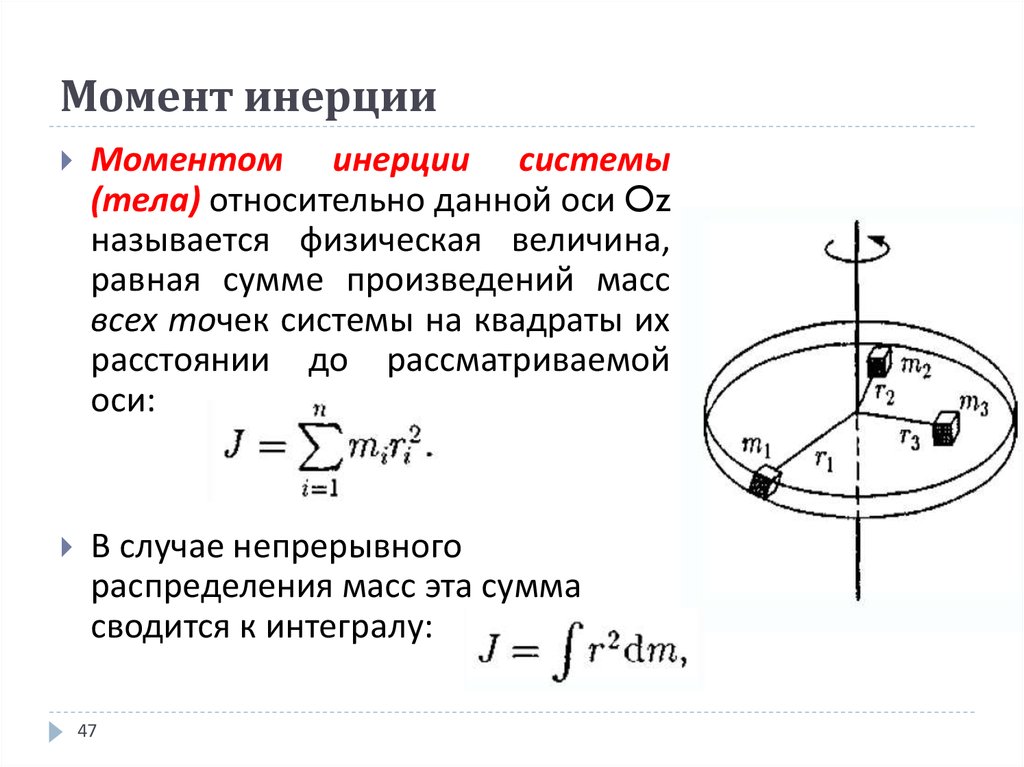 3}{12}$ 94$

Если вы новичок в проектировании конструкций, ознакомьтесь с нашими учебными пособиями по проектированию, в которых вы узнаете, как использовать момент инерции для проектирования таких структурных элементов, как

• Расчет деревянных балок крыши
• Расчет устойчивости деревянных колонн
• Конструкция изгиба ригельной балки

Вы пропустили какие-либо формулы момента инерции для любой формы или поперечного сечения, которые мы забыли в этой статье? Дайте нам знать в комментариях✍️

Уравнения и определения для массы, плоскости и поляры

Вы здесь: Домашняя страница / Часто задаваемые вопросы + основы / Моменты инерции: Определения и уравнения

6 апреля 2018 г. Даниэль Коллинз Оставить комментарий

Термин «момент инерции» часто используется в общем, но в зависимости от контекста и применения он может относиться к одному из трех различных моментов инерции: массы, плоскости , или полярный.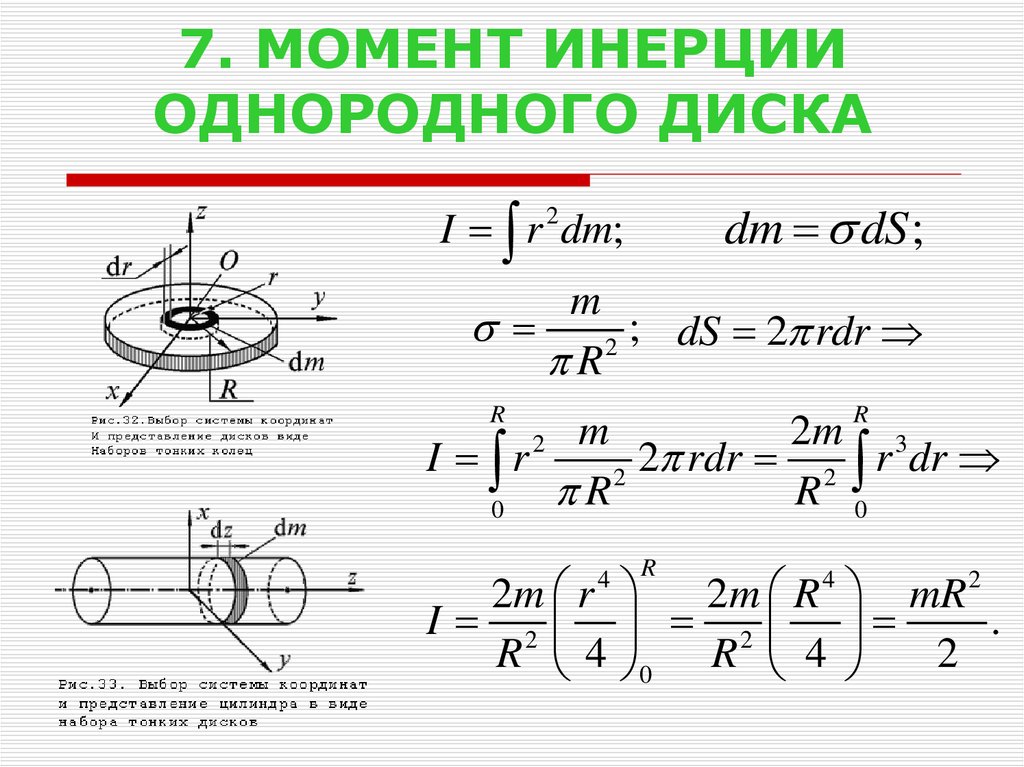

Чтобы знать, какой из них необходим для данного расчета или анализа, важно понимать различия между ними и то, как каждый из них связан с поведением объекта.

---

Формула момента инерции массы

Момент инерции массы описывает способность объекта сопротивляться угловому ускорению, которое зависит от того, как масса объекта распределена относительно оси вращения (т. е. от формы объекта). Массовый момент инерции обычно обозначается буквой «I», хотя буква «J» обычно используется в инженерных справочниках, таких как характеристики инерции двигателя или редуктора. Его единицы массы-расстояния в квадрате: кгм ² или фунт-фут ² . (Обратите внимание, что иногда также используется slug-ft ² .)

Изображение предоставлено: блестящий.org

Во многих приложениях объект моделируется как точечная масса, а момент инерции массы — это просто масса, умноженная на радиус (расстояние до оси вращения) в квадрате.

Изображение предоставлено: блестящий.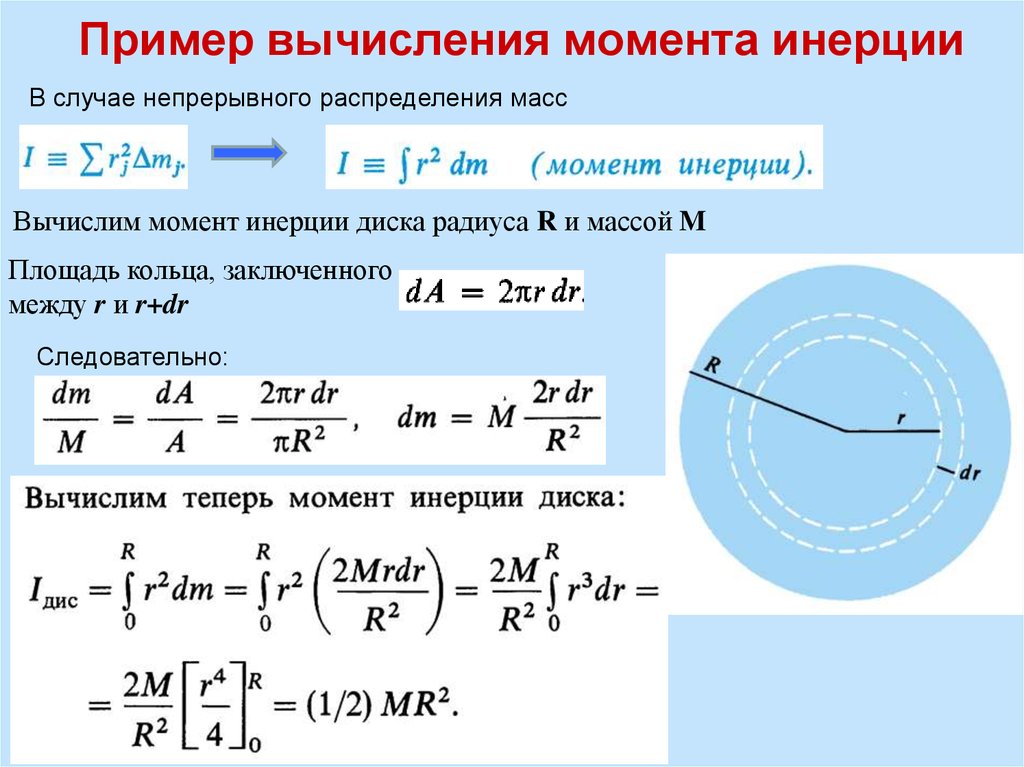 org

Момент инерции массы важен для определения размера двигателя, где коэффициент инерции — отношение инерции нагрузки к инерции двигателя — играет важную роль в определении того, насколько хорошо двигатель может управлять ускорение и торможение груза.

Формулы плоского и полярного моментов инерции

Плоский и полярный моменты инерции подпадают под классификацию «второго момента площади». Плоский момент инерции описывает, как площадь распределяется относительно базовой оси (обычно центроидальной или центральной оси). Это важно, поскольку определяет сопротивление области изгибу.

Уравнение для плоского момента инерции принимает второй интеграл расстояния до базовой плоскости, умноженный на дифференциальный элемент площади. Результат выражается в единицах длины в четвертой степени: м

4 или ⁴ .

Изображение предоставлено: arizona.edu

Полярный момент инерции аналогичен плоскому моменту инерции, но применим к цилиндрическому объекту и описывает его сопротивление кручению (скручиванию из-за приложенного крутящего момента).