Равноускоренное движение: формулы, примеры
Равноускоренное движение
Равноускоренное движение – это движение, при котором вектор ускорения не меняется по модулю и направлению. Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение – частный случай равноускоренного движения с ускорением, равным нулю.
Рассмотрим случай свободного падения (тело брошено под уголом к горизонту) более подробно. Такое движение можно представить в виде суммы движений относительно вертикальной и горизонтальной осей.
В любой точке траектории на тело действует ускорение свободного падения g→, которое не меняется по величине и всегда направлено в одну сторону.
Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y – равноускоренное и прямолинейное. Будем рассматривать проекции векторов скорости и ускорения на оси.
Формулы для равноускоренного движения
Формула для скорости при равноускоренном движении:
v=v0+at.
Здесь v0 – начальная скорость тела, a=const – ускорение.
Покажем на графике, что при равноускоренном движении зависимость v(t) имеет вид прямой линии.
Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC.
a=v-v0t=BCAC
Чем больше угол β, тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.
Для первого графика: v0=-2 мс; a=0,5 мс2.
Для второго графика: v0=3 мс; a=-13 мс2.
Нужна помощь преподавателя?
По данному графику можно также вычислить перемещение тела за время t. Как это сделать?
Выделим на графике малый отрезок времени ∆t. Будем считать, что он настолько мал, что движение за время ∆t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆t.
Тогда, перемещение ∆s за время ∆t будет равно ∆s=v∆t.
Разобьем все время t на бесконечно малые промежутки ∆t. Перемещение s за время t равно площади трапеции ODEF.
s=OD+EF2OF=v0+v2t=2v0+(v-v0)2t.
Мы знаем, что v-v0=at, поэтому окончательная формула для перемещения тела примет вид:
s=v0t+at22
Для того, чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение. Изменение координаты в зависимости от времени выражает закон равноускоренного движения.
Закон равноускоренного движения
Закон равноускоренного движенияЕще одна распространенная задача кинематики, которая возникает при анализе равноускоренного движения – нахождение координаты при заданных значениях начальной и конечной скоростей и ускорения.
Исключая из записанных выше уравнений t и решая их, получаем:
s=v2-v022a.
По известным начальной скорости, ускорению и перемещению можно найти конечную скорость тела:
v=v02+2as.
При v0=0 s=v22a и v=2as
Важно!Величины v, v0, a, y0, s, входящие в выражения, являются алгебраическими величинами. В зависимости от характера движения и направления координатных осей в условиях конкретной задачи они могут принимать как положительные, так и отрицательные значения.
Равномерное движение по окружности. Скорость, ускорение
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: движение по окружности с постоянной по модулю скоростью, центростремительное ускорение.
Равномерное движение по окружности – это достаточно простой пример движения с вектором ускорения, зависящим от времени.
Пусть точка вращается по окружности радиуса . Скорость точки постоянна по модулю и равна . Скорость называется линейной скоростью точки.
Период обращения – это время одного полного оборота. Для периода имеем очевидную формулу:
. (1)
Частота обращения – это величина, обратная периоду:
.
Частота показывает, сколько полных оборотов точка совершает за секунду. Измеряется частота в об/с (обороты в секунду).
Пусть, например, . Это означает, что за время точка совершает один полный
оборот. Частота при этом получается равна: об/с; за секунду точка совершает 10 полных оборотов.
Угловая скорость.
Рассмотрим равномерное вращение точки в декартовой системе координат. Поместим начало координат в центре окружности (рис. 1).
| Рис. 1. Равномерное движение по окружности |
Пусть – начальное положение точки; иными словами, при точка имела координаты . Пусть за время точка повернулась на угол и заняла положение .
Отношение угла поворота ко времени называется угловой скоростью вращения точки:
. (2)
Угол , как правило, измеряется в радианах, поэтому угловая скорость измеряется в рад/с. За время, равное периоду вращения, точка поворачивается на угол . Поэтому
. (3)
Сопоставляя формулы (1) и (3), получаем связь линейной и угловой скоростей:
. (4)
Закон движения.
Найдём теперь зависимость координат вращающейся точки от времени. Видим из рис. 1, что
.
Но из формулы (2) имеем: . Следовательно,
. (5)
Формулы (5) являются решением основной задачи механики для равномерного движения точки по окружности.
Центростремительное ускорение.
Теперь нас интересует ускорение вращающейся точки. Его можно найти, дважды продифференцировав соотношения (5):
С учётом формул (5) имеем:
(6)
Полученные формулы (6) можно записать в виде одного векторного равенства:
(7)
где – радиус-вектор вращающейся точки.
Мы видим, что вектор ускорения направлен противоположно радиус-вектору, т. е. к центру окружности (см. рис. 1). Поэтому ускорение точки, равномерно движущейся по окружности, называется
Кроме того, из формулы (7) мы получаем выражение для модуля центростремительного ускорения:
(8)
Выразим угловую скорость из (4)
и подставим в (8). Получим ещё одну формулу для центростремительного ускорения:
.
Урок 3. равноускоренное движение материальной точки – Физика – 10 класс
Урок Конспект Дополнительные материалыУскорение
Какая из приведённых ниже формул является общей формулой для расчёта ускорения?
Подсказка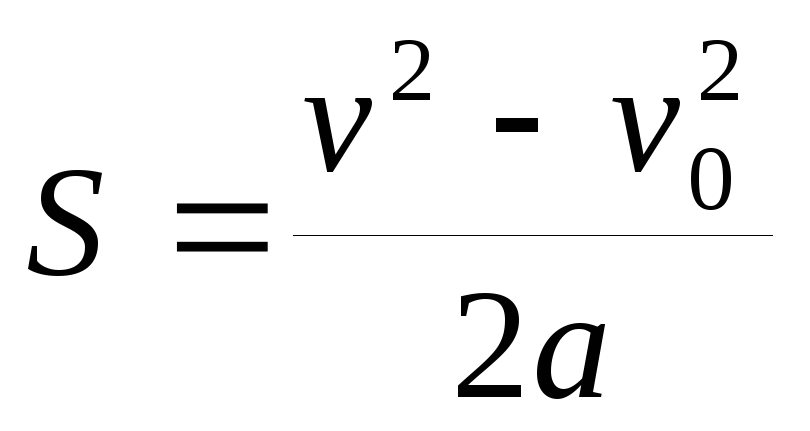
Равноускоренное движение
Заполните пропуски в тексте, выбрав правильные варианты ответа из выпадающего меню.
ПодсказкаДвижение, при котором
скорость
перемещение
криволинейным
равноускоренным
равномерным тела за равные промежутки времени меняется одинаково, называется
перемещение
скорость
криволинейным
равномерным
равноускоренным .
Ускорение
Заполните пропуск в тексте. Для этого решите задачу и наберите пропущенное число на клавиатуре компьютера. Ответ дайте с точностью до десятых.
ПодсказкаВспомните определение ускорения.
Равноускоренное движение
Заполните таблицу.
2$
Физические термины
Решите кроссворд.
Подсказка Вспомните материал конспекта.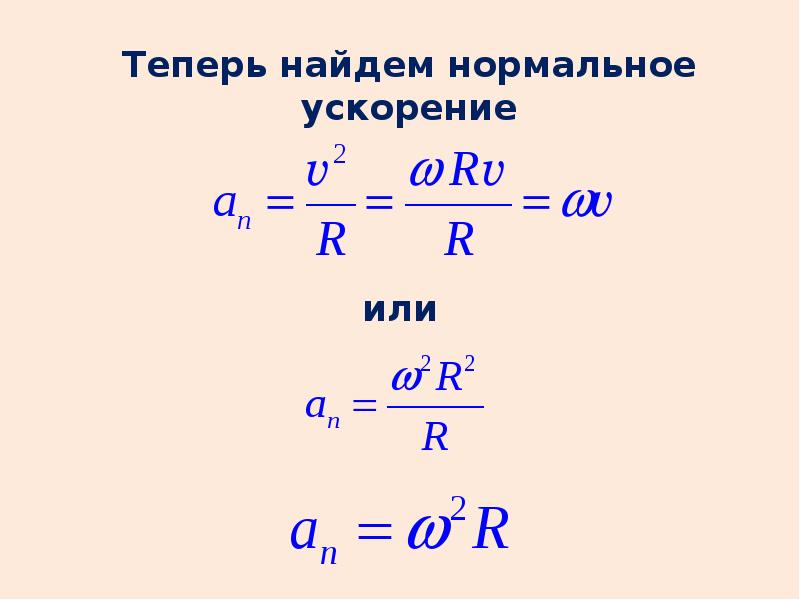
Физические термины
Выделите мышкой 4 слова, которые относятся к теме урока.
1. Итальянский учёный, установивший законы падения.
2. Единица измерения перемещения в СИ.
3. Физическая величина, характеризующая быстроту изменения скорости тела.
4. Единица измерения времени в СИ.
Задачи на нахождение скорости и высоты падения
Решите задачи, чтобы разгадать кроссворд.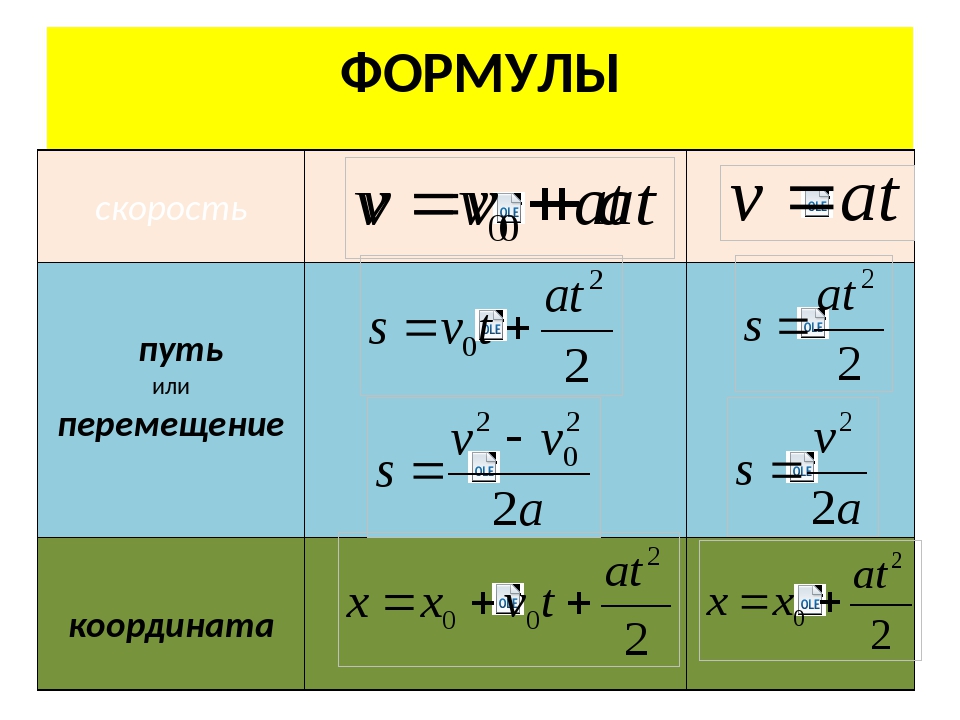
Ответы дайте целыми числами.
Повторите конспект урока.
Торможение
Решите задачи, чтобы увидеть рисунок. Ответы дайте целыми числами.
Подсказка Вспомните формулы перемещения при прямолинейном равноускоренном движении.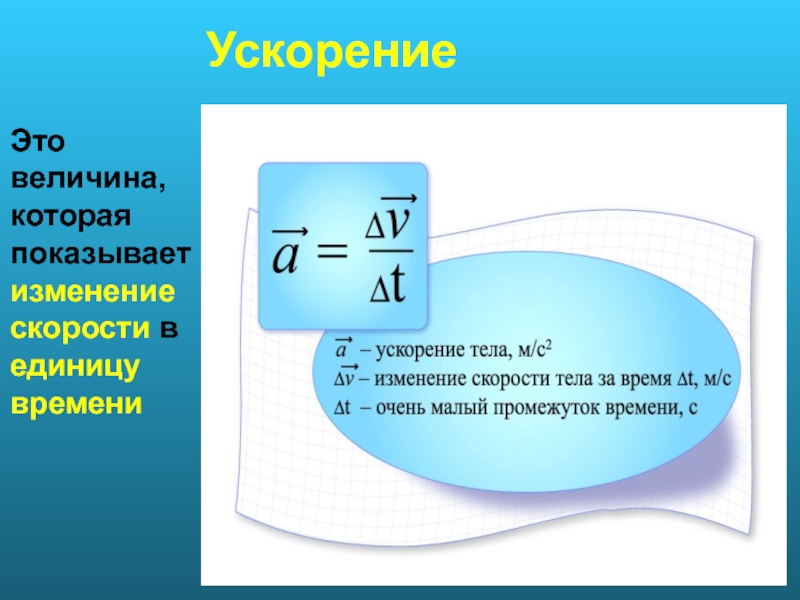
Время разгона
Заполните пропуск в тексте. Для этого наберите пропущенное число на клавиатуре компьютера. Ответ дайте целым числом.
ПодсказкаВспомните формулу ускорения.
Нахождение промежутка времен
Решите задачу и выберите один вариант ответа.
2$. За какой промежуток времени скорость велосипедиста при спуске увеличится на 18 м/с?
Примените формулу ускорения.
Ускорение и скорость
Какое(-ие) утверждение(-я) верно(-ы)? Подчеркните правильный вариант ответа.
А: Если направление вектора ускорения совпадает с направлением вектора начальной скорости, то модуль скорости увеличивается.
Б: Если направление вектора ускорения противоположно направлению вектора начальной скорости, то модуль скорости уменьшается.
1. только А
2. только Б
3. и А, и Б
4. ни А, ни Б
Единицы измерения ускорения
В каких единицах измеряется ускорение в СИ? Выделите цветом все неправильные варианты.
ПодсказкаЕдиницы измерения ускорения.
1) км/ч
2) м/с
3) $км/ч^2$
4) $м/с^2$
Физические термины
Выделите мышкой 4 слова, которые относятся к теме урока.
- Раздел механики, изучающий способы описания движений и связь между величинами, характеризующими движение.
- Физическая величина, характеризующая быстроту изменения скорости.
- Древнегреческий учёный, согласно теории которого чем, тяжелее тело, тем больше его ускорение.
- Физическая величина, единица измерения которой в СИ – 1 м/с.
Средняя скорость
Заполните пропуск в тексте. Для этого наберите пропущенное число на клавиатуре компьютера. Ответ дайте с точностью до сотых.
Вспомните формулу средней скорости.
Море, горы, аэропорт: производственная практика студентов-строителей НГАСУ (Сибстрин) на крупнейшей стройке юга России Благодаря стратегическому партнеру университета – ЗАО «ЛОММЕТА» – студенты работают не на обычном объекте, а на крупнейшей стройке России – возведении нового терминала аэропорта «Геленджик» в Краснодарском крае. Современный аэровокзальный комплекс, строительство которого будет завершено в декабре этого года, значительно улучшит транспортную инфраструктуру курортной зоны юга страны.
В Геленджик приехали 23 студента 3-5 курсов бакалавриата по профилю «Промышленное и гражданское строительство» и специалитета «Строительство уникальных зданий и сооружений». ЗАО «ЛОММЕТА» оплатило студентам стоимость проезда в Геленджик и обратно, проживание и питание, а также выплачивает заработную плату. Непосредственно производственная практика проходит с 24 июня по 28 июля, однако у желающих есть возможность остаться работать на объекте и после ее окончания. |
Профессия дорожник всегда будет востребована! Строительная специальность НГАСУ (Сибстрин) «Автомобильные дороги» Старейший вуз города – Новосибирский государственный архитектурно-строительный университет (Сибстрин) – вот уже более 90 лет занимает лидирующие позиции в обучении студентов по направлению «Строительство».
С 2017 года в нашем вузе началась подготовка специалистов по профилю «Автомобильные дороги»
На сегодняшний день это одно из самых актуальных направлений строительства. Национальный проект «Безопасные и качественные автомобильные дороги» предполагает приоритетное развитие транспортной инфраструктуры страны за счет средств федерального бюджета. Поэтому специалисты – строители автомобильных дорог – будут востребованы во всех регионах страны.
Объектами профессиональной деятельности выпускника являются: изыскания, проектирование, строительство и эксплуатация автомобильных дорог, включая земляное полотно, дорожные одежды, водопропускные сооружения, инженерные транспортные сооружения. |
Важное направление подготовки «Природообустройство и водопользование»: много бюджетных мест Новосибирский государственный архитектурно-строительный университет (Сибстрин) ждет абитуриентов на направление подготовки «Природообустройство и водопользование», профиль «Комплексное использование и охрана водных ресурсов». В 2021 году на данное направление выделено 30 бюджетных мест.
Деятельность выпускников НГАСУ (Сибстрин) по данному профилю направлена на повышение эффективности использования водных и земельных ресурсов, устойчивости и экологической безопасности, а именно:
создание водохозяйственных систем комплексного назначение, охрана и восстановление водных объектов;
охрана земель различного назначения, рекультивация земель, нарушенных или загрязненных в процессе природопользования;
природоохранное обустройство территорий с целью защиты от воздействия природных стихий;
водоснабжение сельских поселений, отвод и очистка сточных вод, обводнение территорий. |
Обучение в НГАСУ (Сибстрин) по актуальному направлению «Жилищное хозяйство и коммунальная инфраструктура»! В 2020 года НГАСУ (Сибстрин) прошел государственную аккредитационную экспертизу и получил аккредитацию (а значит, и право выдавать дипломы государственного образца) по направлениям: 38. 03.10 Жилищное хозяйство и коммунальная инфраструктура (бакалавриат), профиль «Управление жилищным фондом и многоквартирными домами».
38.04.10 Жилищное хозяйство и коммунальная инфраструктура (магистратура), профиль «Управление жилищным фондом и многоквартирными домами».
Подготовка кадров для сферы ЖКХ чрезвычайно актуальна. Особое внимание уделяется подготовке управленческих кадров, компетентных не только в технических вопросах, связанных с функционированием объектов отрасли, но и обладающими управленческими компетенциями: приёмами и методами принятия управленческих решений, способностью к формированию эффективной структуры управления, коммуникативными навыками и организаторскими способностями, проектным мышлением.
После окончан |
Формулы равномерного и равноускоренного движения
Равномерное движение
Формула скорости движения при равномерном движении:
v=const
a=0
v — скорость, м/с
s — перемещение, м
t — время, с
Формула перемещения при равномерном движении:
Координата вычисляются через кинематическое уравнение равномерного прямолинейного движения по формуле:
График — Равномерного прямолинейного движения
Равноускоренное движение
Формула скорости при равноускоренном движении:
a=const
v0 — начальная скорость, м/с
a — ускорение, м/с2
Формула для нахождения перемещения при равноускоренном движении:
или
Уравнение равноускоренного движения в проекции на оси координат:
Формула для определения ускорения при равноускоренном прямолинейном движении:
v0 — начальная скорость, м/с
v — мгновенная скорость, м/с
Формула для определения средней скорости движения:
График — Равноускоренное движение при a>0
Равнозамедленное движение
Формула скорости при равнозамедленном движении:
Формула перемещения при равнозамедленном движении:
График — Равнозамедленное движение при a<0
Свободное падение
Постоянная величина скорости свободного падения тела равна g=9,8 м/с2
Формула для вычисления скорости при свободном падении тела:
Формула для вычисления перемещения при свободном падении тела:
Формула координаты при свободном падении тела:
Формула высоты с которой тело свободно падает:
Формула для определения скорости тела в конце свободного падения:
Время свободного падения тела равно:
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.
9 / 5. Количество оценок: 8
Оценок пока нет. Поставьте оценку первым.
Центрифугирование: как определить ускорение (число g) в зависимости от скорости вращения и диаметра ротора
Центрифугирование – способ разделения неоднородных, дисперсных жидких систем на фракции по плотности под действием центробежных сил. Центрифугирование осуществляют в центрифугах, принцип работы которых основан на создании центробежной силы, увеличивающей скорость разделения компонентов смеси по сравнению со скоростью их разделения только под влиянием силы тяжести. Разделение веществ с помощью центрифугирования основано на разном поведении частиц в центробежном поле. В центробежном поле частицы, имеющие разную плотность, форму или размеры, осаждаются с разной скоростью.
Скорость осаждения, или седиментации, зависит от центробежного ускорения (g), прямо пропорционального угловой скорости ротора (w, рад/с) и расстоянию между частицей и осью вращения (r, см): g = v2x r.
Поскольку один оборот ротора составляет 2π радиан, то угловую скорость можно записать так: v = p x n/60, где n – скорость в оборотах в минуту, π – константа, выражающая отношение длины окружности к длине её диаметра. Угловая скорость – характеристика скорости вращения тела, измеряется обычно в радианах в секунду, полный оборот (360°) составляет 2π радиан.
Центробежное ускорение тогда будет равно: g =p2x r x n2/900.
Центробежное ускорение обычно выражается в единицах g (ускорение свободного падения, равное 980 м/с2) и называется относительным центробежным ускорением (ОЦУ), т.
е. ОЦУ=g/980 или ОЦУ = 1,11 x 10-5 x r x n2 .
Относительное ускорение центрифуги (rcf) задается, как кратное от ускорения свободного падения (g). Оно является безразмерной величиной и служит для сравнения производительности разделения и осаждения. Относительное ускорение центрифуги (rcf) зависит от частоты вращения и радиуса центрифугирования.
Существует номограмма, выражающая зависимость относительного ускорения центрифуги (rcf) от скорости вращения ротора (n) и радиуса (r) – среднего радиуса вращения столбика жидкости в центрифужной пробирке (т.е. расстояния от оси вращения до середины столбика жидкости). Радиус измеряется (см) от оси вращения ротора до середины столбика жидкости в пробирке, когда держатель находится в положении центрифугирования.
Номограмма для определения относительного ускорения центрифуги (rcf) в зависимости от скорости вращения и диаметра ротора
r – радиус ротора, см
n – скорость вращения ротора, оборотов в минуту
rcf (relative centrifuge force) – относительное ускорение центрифуги
Радиус центрифугирования rmax– это расстояние от оси вращения ротора до дна гнезда ротора.
Для определения ускорения с помощью линейки совмещаем значения радиуса и числа оборотов на и на шкале rcf определяем его величину.
Пример: на шкале А отмечаем значение rрадиуса для ротора – 7,2 см, на шкале С отмечаем значение скорости ротора –14,000 об/мин, соединяем эти две точки. Точка пересечения образованного отрезка со шкалой В показывает значение ускорения для данного ротора. В данном случае ускорение равно 15’000.
Кинематика. Формулы
Кинематика. Формулы| Номер | Название формулы | Запись формулы | Примечание |
| (1) | Закон равноускоренного криволинейного движения | vS0 — модуль начальной скорости; aS — ускорение | |
| (2) | Скорость равномерного прямолинейного движения | ||
| (3) | Скорость | ||
| (4) | Ускорение | ||
| (5) | Касательное ускорение | dv = dl/dt, т. е. путевая скорость вдоль рассматриваемой траектории | |
| (6) | Нормальное ускорение | ||
| (7) | Скорость свободного падения тела | ||
| (8) | Время тела при свободном падении | ||
| (9) | Время при равномерном движении по окружности | ||
| (10) | Скорость равномерного движения по окружности | ||
| (11) | Угловая (мгновенная) скорость равномерного движения по окружности | Единица измерения угловой скорости — радианы в секунду | |
| (12) | Скорость равноускоренного движения по окружности | ||
| (13) | Угловая (мгновенная) скорость равноускоренного движения по окружности |
— версия для печати
- Определение
- Кинематикой называется раздел физики, занимающийся исследованием законов движения идеальных тел
- Пояснение
- Под чертой вверху буквы подразумевается знак вектора.
| Если у вас есть мысли или идеи по поводу данной таблицы или, например, вы считаете, что полезно было бы создать определенную вспомогательную памятку, то мы обязательно рассмотрим ваше предложение, которое можно изложить по ссылке (где вы также можете поделиться с нами любыми мыслями по поводу сайта scolaire.ru). Мы готовы устранить любые неудобства, связанные с использованием данной таблицы, или ей подобных, которые можно найти в разделе «Физика». |
© Школяр. Лингвистика (при поддержке «Ветвистого древа») 2009—2016
3 формулы, которые вам нужны
“Ого, вы действительно прошли с нуля до шестидесяти!”
Вы когда-нибудь слышали, чтобы кто-нибудь использовал идиому «от нуля до шестидесяти», как я в приведенном выше примере? Когда кто-то говорит, что что-то пошло с нуля до шестидесяти, на самом деле они говорят, что все ускорилось очень быстро. Ускорение – это величина, на которую скорость чего-либо изменяется за заданный период времени.
В этой статье мы поговорим об ускорении: что это такое и как его рассчитать.Пристегнитесь!
Что такое ускорение?
Ускорение – это скорость изменения скорости за заданный период времени. Для расчета ускорения необходимо иметь как скорость, так и время.
Многие путают ускорение со скоростью (или скоростью). Прежде всего, скорость – это просто скорость с направлением, поэтому они часто используются как синонимы, даже если они имеют небольшие различия. Ускорение – это скорость изменения скорости, означающая, что что-то становится быстрее или медленнее.
Что такое формула ускорения?
Для расчета ускорения можно использовать уравнение ускорения. Вот наиболее распространенная формула ускорения:
$$ a = {Δv} / {Δt} $$
где $ Δv $ – изменение скорости, а $ Δt $ – изменение во времени.
Вы также можете записать уравнение ускорения следующим образом:
$$ a = {v (f) – v (i)} / {t (f) – t (i)} $$
В этом уравнении ускорения $ v (f) $ – это конечная скорость, а – начальная скорость $ v (i) $.
$ T (f) $ – это последнее время, а $ t (i) $ – начальное время.
Еще о некоторых вещах, о которых следует помнить при использовании уравнения ускорения:
- Вам нужно вычесть начальную скорость из конечной скорости. Если вы перевернете их, вы получите неверное направление вашего ускорения.
- Если у вас нет времени начала, вы можете использовать «0».
- Если конечная скорость меньше начальной скорости, ускорение будет отрицательным, что означает, что объект замедлился.
Теперь давайте разберем уравнение ускорения пошагово на реальном примере.
Как рассчитать ускорение: пошаговая разбивка
Теперь мы разберем формулу ускорения шаг за шагом на реальном примере.
Гоночный автомобиль разгоняется с 15 до 35 м / с за 3 секунды. Какое у него среднее ускорение?
Сначала напишите уравнение ускорения.
$$ a = {v (f) – v (i)} / {t (f) – t (i)} $$
Затем определите свои переменные.
2 $$
Давайте попробуем другой пример.
Велосипедист, движущийся со скоростью 23,2 м / с, полностью останавливается за 1,5 $ с $. Что было ее замедлением?
Сначала напишите уравнение ускорения.
$$ a = (v (f) – v (i)) ÷ (t (f) – t (i)) $$
Затем определите свои переменные.
a = то, что мы решаем для
$$ V (f) = 0 м / с $$
$$ V (i) = 23,2 м / с $$
$$ T (f) = 1,4 с $$
$$ T (i) = 0 с $$
Теперь подставьте переменные в уравнение и решите:
$$ A = {{(0 – 23.2} $$
2 Другие общие формулы ускорения
Не знаете, как рассчитать ускорение по другой формуле? Есть несколько других распространенных формул ускорения.
Формула углового ускорения
Угловое ускорение – это скорость, с которой угловое ускорение вращающегося объекта изменяется во времени.
Вот уравнение углового ускорения:
$$ a = {\ change \ in \ angular \ velocity} / {\ change \ in \ time} $$
Формула центростремительного ускорения
Центростремительное ускорение – это скорость движения объекта внутрь к центру круга.
2} / r $$
$ a (c) $ = ускорение, центростремительное
$ v $ = скорость
$ r $ = радиус
Основные выводы
Ускорение – это скорость изменения скорости за заданный период времени.
Вы вычисляете ускорение, разделив изменение скорости на изменение во времени.
Что дальше?
Ищете другие научные объяснения? Мы разбиваем электрическую энергию и как определить различных типов облаков с помощью наших экспертных руководств.
Работаете над исследовательской работой, но не знаете, с чего начать? Тогда ознакомьтесь с нашим руководством, где мы собрали множество высококачественных тем для исследований, которые вы можете использовать бесплатно.
Нужна помощь с уроком английского языка – в частности, с определением литературных приемов в текстах, которые вы читаете? Тогда вы обязательно захотите взглянуть на наше исчерпывающее объяснение самых важных литературных устройств и того, как они используются.
Калькулятор ускорения | Определение | Формула
Калькулятор ускорения – это инструмент, который поможет вам узнать , насколько быстро изменяется скорость объекта .Он работает тремя разными способами, в зависимости от:
- разница между скоростями в два разных момента времени,
- расстояние, пройденное при разгоне,
- масса ускоряющегося объекта и сила, действующая на него.
Если вы спрашиваете себя, что такое ускорение, какова формула ускорения или каковы единицы ускорения, продолжайте читать, и вы узнаете, как найти ускорение. Ускорение строго связано с движением объекта, и каждый движущийся объект обладает определенной энергией.Если вам нужно это оценить, посетите другие наши калькуляторы, где вы можете найти формулу кинетической энергии и ее угловую версию – формулу кинетической энергии вращения.
Чтобы все было понятно, мы также подготовили несколько примеров ускорения, которые распространены в физике.
Вы можете найти там:
- центростремительное ускорение и тангенциальное ускорение,
- угловое ускорение,
- ускорение свободного падения,
- ускоритель частиц.
Ускорение всегда происходит всякий раз, когда на объект действует ненулевая чистая сила.Вы можете почувствовать это в лифте, когда вы станете немного тяжелее (ускорение) или легче (замедление), или когда вы едете по крутому склону на санях по снегу. Более того, из общей теории относительности мы знаем, что вся Вселенная не только расширяется, но даже ускоряется! Это означает, что расстояние между двумя точками постоянно становится все больше и больше, но мы не можем чувствовать это каждый день, потому что каждый масштаб в мире тоже расширяется.
Что такое ускорение? – определение ускорения
Ускорение – это скорость изменения скорости объекта; другими словами, насколько быстро меняется скорость. Согласно второму закону Ньютона, ускорение прямо пропорционально сумме всех сил, действующих на объект, и обратно пропорционально его массе.
Это все здравый смысл – если несколько разных сил толкают объект, вам нужно выяснить, к чему они складываются (они могут действовать в разных направлениях), а затем разделить результирующую чистую силу на массу вашего объекта.
Это определение ускорения гласит, что ускорение и сила, по сути, одно и то же. При изменении силы изменяется и ускорение, но величина его изменения зависит от массы объекта. Это неверно в ситуации, когда масса также изменяется, например, при ракетной тяге, когда сгоревшее топливо выходит из сопла ракеты. Если вы когда-нибудь задумывались, какова физика космических путешествий, взгляните на это уравнение ракеты Циолковского.
Мы можем измерить ускорение объекта напрямую с помощью акселерометра .Если повесить объект на акселерометр, он покажет ненулевое значение. Это почему? Ну, это из-за гравитационных сил, которые действуют на каждую частицу, имеющую массу. А где чистая сила, там и ускорение. Таким образом, акселерометр в состоянии покоя измеряет ускорение свободного падения, которое на поверхности Земли составляет около 31,17405 фут / с² (9,80665 м / с²) .
Другими словами, это ускорение свободного падения, которое любой объект получает при свободном падении в вакууме.
Кстати о пылесосах, вы когда-нибудь смотрели «Звездные войны» или другой фильм, действие которого происходит в космосе? Эпические сражения космических кораблей, звуки бластеров, двигателей и взрывов.Что ж, это ложь. Космос – это вакуум, и в нем нельзя услышать звук (для распространения звуковых волн требуется материя). Эти битвы должны быть беззвучными! В космосе никто не услышит твой крик. Чтобы проверить скорость звука в воздухе или воде, воспользуйтесь нашим калькулятором скорости звука. Учитывается даже температура!
Как найти ускорение? – счетчик ускорения
Калькулятор ускорения на этом сайте учитывает только ситуацию, в которой объект имеет равномерное (постоянное) ускорение.В этом случае уравнение ускорения по определению представляет собой отношение изменения скорости за конкретное время. Однако здесь вы можете узнать, как найти ускорение еще двумя способами.
Давайте посмотрим, как пользоваться нашим калькулятором (уравнения ускорения вы можете найти в разделе после):
- В зависимости от того, какие данные у вас есть, вы можете рассчитать ускорение тремя разными способами. Во-первых, выберите соответствующее окно (# 1, # 2 или # 3),
- [если вы выберете # 1] – Введите начальную
v_iи конечнуюv_fскорости объекта и сколько времениΔtпотребовалось для изменения скорости. - [при выборе # 2] – Введите начальную скорость
v_i, пройденное расстояниеΔdи времяΔt, пройденное во время ускорения. Здесь вам не нужно знать конечную скорость. - [при выборе # 3] – введите массу
мобъекта и чистую силуF, действующую на этот объект. Это совершенно другой набор переменных, который возникает из второго закона движения Ньютона (другое определение ускорения). - Считайте результирующее ускорение из последнего поля. Вы также можете выполнить вычисления другим способом, если знаете, что такое ускорение, например, чтобы оценить расстояние
Δd. Просто укажите остальные параметры в этом окне.
Знание того, что такое ускорение, необходимо для анализа движения объектов. Например, вы можете определить изменение импульса за определенный период времени с помощью этой формулы для импульса. Это одна из физических величин, которые мы используем в нашем калькуляторе автокатастроф, где мы объясняем и визуализируем важность ремней безопасности с помощью чисел и определяем, с какой скоростью вы можете погибнуть в автокатастрофе.Повышение скорости и содержание алкоголя в крови – главные причины автомобильных аварий. Пожалуйста, водите осторожно!
Формула ускорения – три уравнения ускорения
В 17 веке сэр Исаак Ньютон , один из самых влиятельных ученых всех времен, опубликовал свою знаменитую книгу Principia .
В нем он сформулировал закон всемирного тяготения, который гласит, что любые два объекта с массой будут притягивать друг друга с силой, экспоненциально зависящей от расстояния между этими объектами (в частности, она обратно пропорциональна квадрату расстояния).Чем тяжелее объекты, тем больше сила тяжести. Это объясняет, например, почему планеты вращаются вокруг очень плотного Солнца.
В Principia Ньютон также включает три закона движения, которые являются центральными для понимания физики нашего мира. Калькулятор ускорения основан на трех различных уравнениях ускорения, третье из которых получено из работы Ньютона:
-
а = (v_f - v_i) / Δt, -
a = 2 * (Δd - v_i * Δt) / Δt², -
a = Ф / м,
где:
-
a– ускорение, -
v_iиv_f– соответственно начальная и конечная скорости, -
Δt– время разгона, -
Δd– расстояние, пройденное при ускорении, -
F– чистая сила, действующая на объект, который ускоряется, -
м– масса этого объекта.
Теперь вы знаете, как рассчитать ускорение! В следующем абзаце мы обсудим единицы ускорения (СИ и британские). Вы уже видели наши калькуляторы конвертации? Они могут сэкономить вам много времени при работе с различными юнитами. В случае расстояния вас может заинтересовать конвертер длины, который включает в себя таблицу преобразования длины. Если вы хотите переключаться между разными единицами массы, вот наш конвертер веса. Оба калькулятора позволяют быстро выполнять вычисления с любым набором единиц измерения.Попробуйте!
Блоки ускорения
Если вы уже умеете рассчитывать ускорение, давайте сосредоточимся на единицах ускорения. Вы можете вывести их из приведенных выше уравнений. Все, что вам нужно знать, это то, что скорость выражается в футах в секунду (британская / американская система) или в метрах в секунду (система СИ), а время – в секундах. Следовательно, если вы разделите скорость на время (как мы делаем в первой формуле ускорения), вы получите единицу ускорения фут / с² или м / с² в зависимости от того, какую систему вы используете.
В качестве альтернативы можно использовать третье уравнение. В этом случае вам нужно разделить силу (фунты в США и ньютоны в СИ) на массу (фунты в США и килограммы в СИ), получив фунтов / фунт или Н / кг . Они оба представляют одно и то же, поскольку фунт составляет фунтов на квадратный дюйм = фунт * фут / с² , а ньютон составляет Н = кг * м / с² . Если вы замените его и уменьшите единицы, вы получите (фунт * фут / с²) / фунт = фут / с² или (кг * м / с²) / кг = м / с² .
Существует также третий вариант, который фактически широко используется.Вы можете выразить ускорение с помощью стандартного ускорения , обусловленного силой тяжести у поверхности Земли, которое определяется как g = 31,17405 фут / с² = 9,80665 м / с² . Например, если вы говорите, что лифт движется вверх с ускорением 0,2 g , это означает, что он ускоряется примерно со скоростью 6,2 фут / с² или 2 м / с² (т.
Е. 0,2 * g ) . Мы округлили приведенные выше выражения до двух значащих цифр с помощью правил значащих цифр, которые вы можете найти в нашей математической категории.
Примеры разгона
Центростремительное ускорение и тангенциальное ускорение
Ускорение – это обычно вектор, поэтому его всегда можно разложить на составляющие. Обычно у нас есть две части, перпендикулярные друг другу: центростремительная и тангенциальная . Центростремительное ускорение изменяет направление скорости и, следовательно, форму следа, но не влияет на значение скорости. С другой стороны, тангенциальное ускорение всегда перпендикулярно траектории движения.Он изменяет только значение скорости , но не ее направление.
В круговом движении (крайний левый рисунок ниже), когда объект движется по окружности круга, присутствует только центростремительный компонент. Объект будет поддерживать постоянную скорость; подумайте о Земле, которая имеет центростремительное ускорение из-за силы тяжести Солнца (на самом деле ее скорость немного меняется в течение года – см.
калькулятор орбитальной скорости и калькулятор орбитального периода для получения дополнительной информации).
Когда присутствуют оба компонента, траектория объекта выглядит как на правом изображении. Что будет, если есть только тангенциальное ускорение? Затем происходит линейное движение. Это похоже на нажатие педали газа в автомобиле на прямом участке автострады. А если вы водитель, наш счетчик бензина может вас заинтересовать; оценивает стоимость проезда на автомобиле. Вы указываете экономию топлива, расстояние и цену на бензин, и вы быстро получаете стоимость поездки. Есть даже возможность разделить его на несколько человек, ведь вместе путешествовать весело и полезно! Группа разговорчивых друзей в вашей машине будет: e.g., не дать вам заснуть.
Угловое ускорение
Угловое ускорение играет важную роль в описании вращательного движения. Однако не путайте это с ранее упомянутыми центростремительными или тангенциальными ускорениями. Эта физическая величина соответствует скорости изменения угловой скорости.
Другими словами, он сообщает вам, насколько быстро ускоряется вращение объекта – объект вращается все быстрее и быстрее (или все медленнее и медленнее, если угловое ускорение меньше нуля).
Знаете ли вы, что мы можем найти аналогию между этим и законом динамики Ньютона во вращательном движении? Согласно его второму закону, если вы можете переключить ускорение на угловое ускорение, силу на крутящий момент и массу на момент инерции, вы получите уравнение углового ускорения. Вы могли заметить, что некоторые физические законы, подобные этому, универсальны, что делает их действительно важными для физики.
Ускорение свободного падения
Мы несколько раз упоминали ускорение свободного падения.Он возникает из-за гравитационной силы, которая существует между каждыми двумя объектами, имеющими массу (обратите внимание, что уравнение гравитации не зависит от объема объекта – здесь важна только масса). Сначала это может показаться странным, но согласно третьему закону движения Ньютона вы действуете на Землю с той же силой, что и Земля на вас .
Однако масса Земли намного больше, чем масса человека (в ~ 10 ² раз больше), поэтому наше воздействие на Землю практически равно нулю. Это аналогично всем бактериям (в ~ 10¹⁸ раз легче человека), живущим на вашей руке; вы их даже не заметите! С другой стороны, мы чувствуем влияние нашей планеты, и это ускорение силы тяжести.
Стандартная сила тяжести по определению составляет 31,17405 фут / с² (9,80665 м / с²), поэтому, если человек весит 220 фунтов (около 100 кг), на него действует сила тяжести около 7000 фунтов на квадратный дюйм (1000 Н). Давайте введем это значение в окно №3 нашего калькулятора вместе с массой Земли (1,317 × 10²⁵ фунта или 5,972 × 10²⁴ кг в экспоненциальном представлении). Что такое расчетное ускорение? Это настолько мало , что наш калькулятор считает, что это ноль . Мы ничего не значим по сравнению с планетой!
Ускоритель частиц
Поговорив об огромных объектах в космосе, перейдем к микроскопическому миру частиц.
Хотя мы не можем видеть их глазами, мы использовали частицы высоких энергий, такие как электроны и протоны, и регулярно используем их в ускорителях частиц; распространены в физике, химии и медицине. Мы используем их для уничтожения раковых клеток, сохраняя при этом окружающую здоровую ткань, или исследуем структуру материала в атомном масштабе. В последнее время рак – одна из болезней достатка, которая, вероятно, является следствием роста благосостояния в обществе. Даже неправильное питание может увеличить риск рака! С помощью этого ежедневного калькулятора протеина вы можете проверить, сколько протеина вам нужно в день, и, если вы также хотите улучшить свою физическую форму, наш макро-калькулятор здесь, чтобы помочь вам.
Вы, наверное, знаете о Большом адронном коллайдере (ЦЕРН), самом мощном ускорителе элементарных частиц в мире. Это позволяет нам сделать шаг вперед, чтобы понять, как устроена Вселенная, и разработать технологии, которые могут найти множество важных приложений в будущем.
Однако, чтобы достичь таких высоких энергий, мы должны разогнать частицы до скоростей, близких к скорости света. Вкратце, мы можем сделать это с помощью магнитных или электрических полей. Чтобы увидеть, насколько быстро частицы ускоряются по сравнению со стандартной силой тяжести, посмотрите наше ускорение в калькуляторе электрического поля, где мы объяснили, как рассчитать ускорение заряженных частиц.
Мир микроскопических частиц управляется статистической физикой, которая уделяет особое внимание концепции вероятности. У нас есть много калькуляторов, связанных с этой темой. Взгляните на калькулятор вероятностей, чтобы узнать, как найти вероятность, или попробуйте калькулятор перестановок, чтобы определить количество способов, которыми вы можете упорядочить определенное количество элементов. Физики используют перестановку для предсказания теоретических свойств материала, которые затем можно наблюдать в повседневной жизни. Например, вы можете узнать, какова средняя скорость частиц газа.
FAQ
Ускорение – это вектор?
Да , ускорение является вектором, так как имеет как величину, так и направление . Величина – это то, насколько быстро объект ускоряется, а направление – это то, происходит ли ускорение в направлении движения объекта или против него. Это соответственно ускорение и замедление.
Как масса влияет на ускорение?
Если сила, с которой объект толкает, остается прежней, ускорение будет уменьшаться по мере увеличения массы .Это потому, что F / m = a, поэтому по мере увеличения массы фракция становится все меньше и меньше.
Может ли ускорение быть отрицательным?
Да , ускорение может быть отрицательным, , которое известно как замедление . Два объекта с равным, но противоположным ускорением будут ускоряться на одинаковую величину, только в двух противоположных направлениях.
Как найти среднее ускорение?
- Рассчитайте изменение скорости для заданного вами времени.
- Рассчитайте изменение во времени за рассматриваемый период.
- Разделите изменение скорости на изменение во времени.
- Результат – среднее ускорение за этот период.
Как узнать величину ускорения?
- Преобразуйте величину силы в Ньютоны.
- Измените Масса объекта на килограммы.
- Умножьте оба значения на вместе, чтобы найти ускорение в м / с 2 .
В чем разница между ускорением и скоростью?
Скорость – это скорость, с которой объект движется в определенном направлении, а ускорение – это то, как скорость этого объекта изменяется со временем. Оба имеют величину и направление, но их единицы – м / с и м / с 2 соответственно.
Как найти угловое ускорение?
- Используйте уравнения углового ускорения:
a = Δv / Δt. - Найдите начальную и конечную угловую скорость в радианах / с.
- Вычтите начальную угловую скорость из конечной угловой скорости, чтобы получить изменение угловой скорости .
- Найдите начальное и конечное время для рассматриваемого периода.
- Вычтите начальное время из последнего, чтобы получить изменение во времени .
- Разделите изменение угловой скорости на изменение во времени, чтобы получить угловое ускорение в радианах / с. 2 .
3.4 Движение с постоянным ускорением – University Physics Volume 1
Учебные цели
К концу этого раздела вы сможете:
- Определите, какие уравнения движения следует использовать для решения неизвестных.
- Используйте соответствующие уравнения движения для решения задачи преследования двух тел.
Можно предположить, что чем больше ускорение, скажем, у автомобиля, удаляющегося от знака «Стоп», тем больше смещение автомобиля за данный момент времени.Но мы не разработали конкретное уравнение, которое связывает ускорение и смещение. В этом разделе мы рассмотрим некоторые удобные уравнения кинематических отношений, начиная с определений смещения, скорости и ускорения. Сначала мы исследуем движение одного объекта, называемого движением одного тела. Затем мы исследуем движение двух объектов, называемое задачами преследования двух тел.
Обозначение
Во-первых, сделаем несколько упрощений в обозначениях. Принятие начального времени равным нулю, как если бы время измерялось секундомером, является большим упрощением.Поскольку прошедшее время равно Δt = tf − t0Δt = tf − t0, взятие t0 = 0t0 = 0 означает, что Δt = tfΔt = tf, последнее время на секундомере. Когда начальное время принимается равным нулю, мы используем индекс 0 для обозначения начальных значений положения и скорости. То есть x0x0 – это начальная позиция , а v0v0 – начальная скорость . Мы не ставим индексы на окончательные значения. То есть t – это конечный момент времени , x – конечная позиция , а v – конечная скорость . Это дает более простое выражение для затраченного времени: Δt = tΔt = t.Это также упрощает выражение для смещения x , которое теперь равно Δx = x − x0Δx = x − x0. Кроме того, это упрощает выражение для изменения скорости, которое теперь равно Δv = v − v0Δv = v − v0. Подводя итог, используя упрощенные обозначения, с начальным временем, принятым равным нулю,
Δt = tΔx = x − x0Δv = v − v0, Δt = tΔx = x − x0Δv = v − v0,, где нижний индекс 0 обозначает начальное значение, а отсутствие нижнего индекса означает конечное значение в любом рассматриваемом движении.
Теперь мы делаем важное предположение, что ускорение постоянно .Это предположение позволяет нам избегать использования расчетов для определения мгновенного ускорения. Поскольку ускорение постоянно, среднее и мгновенное ускорения равны, то есть
a– = a = постоянная. a– = a = постоянная.Таким образом, мы можем использовать символ a для ускорения в любое время. Предположение, что ускорение является постоянным, не серьезно ограничивает ситуации, которые мы можем изучить, и не ухудшает точность нашего лечения. Во-первых, ускорение равно постоянным в большом количестве ситуаций.Кроме того, во многих других ситуациях мы можем точно описать движение, приняв постоянное ускорение, равное среднему ускорению для этого движения. Наконец, для движения, во время которого ускорение резко меняется, например, когда автомобиль разгоняется до максимальной скорости, а затем тормозит до остановки, движение можно рассматривать в отдельных частях, каждая из которых имеет собственное постоянное ускорение.
Смещение и положение от скорости
Чтобы получить наши первые два уравнения, мы начнем с определения средней скорости:
Замена упрощенных обозначений для ΔxΔx и ΔtΔt дает
v– = x − x0t.v– = x − x0t.Решение относительно x дает нам
x = x0 + v – t, x = x0 + v – t,3,10
, где средняя скорость
v– = v0 + v2.v– = v0 + v2.3,11
Уравнение v– = v0 + v2v– = v0 + v2 отражает тот факт, что при постоянном ускорении v – v– представляет собой просто среднее значение начальной и конечной скоростей. Рисунок 3.18 графически иллюстрирует эту концепцию. В части (а) рисунка ускорение является постоянным, а скорость увеличивается с постоянной скоростью. Средняя скорость в течение 1-часового интервала от 40 км / ч до 80 км / ч составляет 60 км / ч:
v– = v0 + v2 = 40 км / ч + 80 км / ч3 = 60 км / ч.v– = v0 + v2 = 40 км / ч + 80 км / ч3 = 60 км / ч.В части (b) ускорение не является постоянным. В течение 1-часового интервала скорость ближе к 80 км / ч, чем к 40 км / ч. Таким образом, средняя скорость больше, чем в части (а).
Рисунок 3.18 (a) График зависимости скорости от времени с постоянным ускорением, показывающий начальную и конечную скорости v0andvv0andv. Средняя скорость равна 12 (v0 + v) = 60 км / ч22 (v0 + v) = 60 км / ч. (б) График зависимости скорости от времени с изменением ускорения со временем. Средняя скорость не равна 12 (v0 + v) 12 (v0 + v), но превышает 60 км / ч.Решение для окончательной скорости по ускорению и времени
Мы можем вывести еще одно полезное уравнение, манипулируя определением ускорения:
Подстановка упрощенных обозначений для ΔvΔv и ΔtΔt дает
а = v − v0t (константа). a = v − v0t (константа).Решение для v дает
v = v0 + at (constanta). v = v0 + at (constanta).3,12
Пример 3,7
Расчет конечной скорости
Самолет приземляется с начальной скоростью 70.0 м / с, а затем ускоряется против движения со скоростью 1,50 м / с 2 за 40,0 с. Какова его конечная скорость?Стратегия
Сначала мы идентифицируем известные: v0 = 70 м / с, a = -1,50 м / с2, t = 40sv0 = 70 м / с, a = -1,50 м / с2, t = 40 с.Во-вторых, мы идентифицируем неизвестное; в данном случае это конечная скорость vfvf.
Наконец, мы определяем, какое уравнение использовать. Для этого мы выясняем, какое кинематическое уравнение дает неизвестное в терминах известных. Мы рассчитываем окончательную скорость, используя уравнение 3.12, v = v0 + atv = v0 + at.
Решение
Подставьте известные значения и решите: v = v0 + при = 70,0 м / с + (- 1,50 м / с2) (40,0 с) = 10,0 м / с v = v0 + при = 70,0 м / с + (- 1,50 м / с2) (40,0 с) = 10,0 м / с.Рисунок 3.19 представляет собой эскиз, показывающий векторы ускорения и скорости.
Рис. 3.19. Самолет приземляется с начальной скоростью 70,0 м / с и замедляется до конечной скорости 10,0 м / с, прежде чем направиться к терминалу. Обратите внимание, что ускорение отрицательное, потому что его направление противоположно его скорости, которая положительна.
Значение
Конечная скорость намного меньше начальной скорости, требуемой при замедлении, но все же положительная (см. Рисунок). В реактивных двигателях обратная тяга может поддерживаться достаточно долго, чтобы остановить самолет и начать движение назад, на что указывает отрицательная конечная скорость, но в данном случае это не так.Помимо полезности при решении задач, уравнение v = v0 + atv = v0 + at дает нам представление о взаимосвязях между скоростью, ускорением и временем.Мы видим, например, что
- Конечная скорость зависит от того, насколько велико ускорение и как долго оно длится
- Если ускорение равно нулю, то конечная скорость равна начальной скорости ( v = v 0 ), как и ожидалось (другими словами, скорость постоянна)
- Если a отрицательно, то конечная скорость меньше начальной скорости
Все эти наблюдения соответствуют нашей интуиции. Обратите внимание, что всегда полезно исследовать основные уравнения в свете нашей интуиции и опыта, чтобы убедиться, что они действительно точно описывают природу.
Решение для конечного положения с постоянным ускорением
Мы можем объединить предыдущие уравнения, чтобы найти третье уравнение, которое позволяет нам вычислить окончательное положение объекта, испытывающего постоянное ускорение. Начнем с
Добавление v0v0 к каждой стороне этого уравнения и деление на 2 дает
v0 + v2 = v0 + 12at. v0 + v2 = v0 + 12at.Поскольку v0 + v2 = v – v0 + v2 = v– для постоянного ускорения, имеем
v– = v0 + 12at.v– = v0 + 12at.Теперь мы подставляем это выражение для v – v– в уравнение для смещения, x = x0 + v – tx = x0 + v – t, что дает
х = х0 + v0t + 12at2 (константа).х = х0 + v0t + 12at2 (константа).3,13
Пример 3.8
Расчет смещения ускоряющегося объекта
Драгстеры могут развивать среднее ускорение 26,0 м / с 2 . Предположим, драгстер ускоряется из состояния покоя с этой скоростью в течение 5,56 с. Рис. 3.20. Как далеко он пролетит за это время?Рис. 3.20. Пилот Top Fuel в армии США Тони «Сержант» Шумахер начинает гонку с контролируемого выгорания. (Источник: подполковник Уильям Термонд. Фото любезно предоставлено США.Армия.)
Стратегия
Сначала нарисуем набросок Рис. 3.21. Нас просят найти смещение, которое составляет x , если мы возьмем x0x0 равным нулю. (Думайте о x0x0 как о стартовой линии гонки. Она может быть где угодно, но мы называем ее нулевой и измеряем все остальные позиции относительно нее.) Мы можем использовать уравнение x = x0 + v0t + 12at2x = x0 + v0t + 12at2 когда мы идентифицируем v0v0, aa и t из постановки задачи.Рис. 3.21. Эскиз разгоняющегося драгстера.
Решение
Во-первых, нам нужно определить известные.Запуск из состояния покоя означает, что v0 = 0v0 = 0, a задается как 26,0 м / с 2 и t задается как 5,56 с.Во-вторых, мы подставляем известные значения в уравнение, чтобы найти неизвестное:
x = x0 + v0t + 12at2.x = x0 + v0t + 12at2.Поскольку начальное положение и скорость равны нулю, это уравнение упрощается до
Подстановка идентифицированных значений на и t дает
x = 12 (26,0 м / с2) (5,56 с) 2 = 402 м. x = 12 (26,0 м / с2) (5,56 с) 2 = 402 м.Значение
Если мы переведем 402 м в мили, мы обнаружим, что пройденное расстояние очень близко к четверти мили, стандартному расстоянию для дрэг-рейсинга. Итак, наш ответ разумный. Это впечатляющий водоизмещение всего за 5,56 с, но первоклассные драгстеры могут преодолеть четверть мили даже за меньшее время. Если бы драгстеру была присвоена начальная скорость, это добавило бы еще один член в уравнение расстояния. Если в уравнении использовать те же ускорение и время, пройденное расстояние будет намного больше.Что еще мы можем узнать, исследуя уравнение x = x0 + v0t + 12at2? X = x0 + v0t + 12at2? Мы видим следующие отношения:
- Смещение зависит от квадрата истекшего времени, когда ускорение не равно нулю. В примере 3.8 драгстер преодолевает только четверть общего расстояния за первую половину прошедшего времени.
- Если ускорение равно нулю, то начальная скорость равна средней скорости (v0 = v -) (v0 = v–), и x = x0 + v0t + 12at2becomesx = x0 + v0t.x = x0 + v0t + 12at2becomesx = x0 + v0t.
Решение окончательной скорости по расстоянию и ускорению
Четвертое полезное уравнение может быть получено путем другой алгебраической обработки предыдущих уравнений. Если мы решим v = v0 + atv = v0 + at для t , мы получим
Подставляя это и v– = v0 + v2v– = v0 + v2 в x = x0 + v – tx = x0 + v – t, получаем
v2 = v02 + 2a (x − x0) (constanta). v2 = v02 + 2a (x − x0) (constanta).3,14
Пример 3.9
Расчет конечной скорости
Рассчитайте конечную скорость драгстера в Примере 3.8 без использования информации о времени.Стратегия
Уравнение v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) идеально подходит для этой задачи, поскольку оно связывает скорости, ускорение и смещение и не требует информации о времени.Решение
Сначала мы идентифицируем известные значения. Мы знаем, что v 0 = 0, поскольку драгстер запускается из состояния покоя. Мы также знаем, что x – x 0 = 402 м (это был ответ в примере 3.8). Среднее ускорение было равно , а = 26.0 м / с 2 .Во-вторых, мы подставляем известные в уравнение v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) и решаем относительно v :
v2 = 0 + 2 (26,0 м / с2) (402 м). v2 = 0 + 2 (26,0 м / с2) (402 м).Таким образом,
v2 = 2,09 × 104 м2 / с2 v = 2,09 × 104 м2 / с2 = 145 м / с. v2 = 2,09 × 104 м2 / с2v = 2,09 × 104 м2 / с2 = 145 м / с.Значение
Скорость 145 м / с составляет около 522 км / ч или около 324 миль / ч, но даже эта головокружительная скорость не достигает рекорда для четверти мили. Также обратите внимание, что квадратный корень имеет два значения; мы взяли положительное значение, чтобы указать скорость в том же направлении, что и ускорение.Изучение уравнения v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) может дать дополнительное понимание общих соотношений между физическими величинами:
- Конечная скорость зависит от величины ускорения и расстояния, на котором оно действует.
- При фиксированном ускорении автомобиль, который едет вдвое быстрее, не просто останавливается на удвоенном расстоянии. Чтобы остановиться, нужно гораздо дальше. (Вот почему у нас есть зоны с пониженной скоростью возле школ.)
Объединение уравнений
В следующих примерах мы продолжаем исследовать одномерное движение, но в ситуациях, требующих немного большего количества алгебраических манипуляций.Примеры также дают представление о методах решения проблем. Следующее примечание предназначено для облегчения поиска необходимых уравнений. Имейте в виду, что эти уравнения не являются независимыми. Во многих ситуациях у нас есть два неизвестных, и нам нужно два уравнения из набора для решения для неизвестных. Для решения данной ситуации нам нужно столько уравнений, сколько неизвестных.
Сводка кинематических уравнений (константа
a ) х = х0 + v0t + 12at2x = x0 + v0t + 12at2 v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0)Прежде чем мы перейдем к примерам, давайте более внимательно рассмотрим некоторые уравнения, чтобы увидеть поведение ускорения при экстремальных значениях.Переставляя уравнение 3.12, получаем
Из этого мы видим, что в течение конечного времени, если разница между начальной и конечной скоростями мала, ускорение невелико, приближаясь к нулю в том пределе, когда начальная и конечная скорости равны. Напротив, в пределе t → 0t → 0 при конечной разности начальной и конечной скоростей ускорение становится бесконечным.
Аналогичным образом, переставляя уравнение 3.14, мы можем выразить ускорение в терминах скоростей и смещения:
а = v2-v022 (х-х0).а = v2-v022 (х-х0).Таким образом, при конечной разнице между начальной и конечной скоростями ускорение становится бесконечным, в пределе смещение приближается к нулю. Ускорение приближается к нулю в пределе, разница в начальной и конечной скоростях приближается к нулю для конечного смещения.
Пример 3.10
Как далеко уезжает машина?
На сухом бетоне автомобиль может ускоряться противоположно движению со скоростью 7,00 м / с 2 , тогда как на мокром бетоне он может ускоряться противоположно движению со скоростью всего 5 м / с.00 м / с 2 . Найдите расстояния, необходимые для остановки автомобиля, движущегося со скоростью 30,0 м / с (около 110 км / ч) по (а) сухому бетону и (б) мокрому бетону. (c) Повторите оба вычисления и найдите смещение от точки, где водитель видит, что светофор становится красным, принимая во внимание время его реакции 0,500 с, чтобы он нажал ногу на тормоз.Стратегия
Для начала нам нужно нарисовать набросок Рис. 3.22. Чтобы определить, какие уравнения лучше всего использовать, нам нужно перечислить все известные значения и точно определить, что нам нужно решить.Рис. 3.22. Пример эскиза для визуализации ускорения, противоположного движению и тормозному пути автомобиля.
Решение
- Во-первых, нам нужно определить известные и то, что мы хотим решить. Мы знаем, что v 0 = 30,0 м / с, v = 0 и a = −7,00 м / с 2 ( a отрицательно, потому что оно находится в направлении, противоположном скорости) . Возьмем x 0 равным нулю. Ищем смещение ΔxΔx, или x – x 0 .
Во-вторых, мы определяем уравнение, которое поможет нам решить проблему. Лучшее уравнение для использования – v2 = v02 + 2a (x − x0). v2 = v02 + 2a (x − x0). Это уравнение лучше всего, потому что оно включает только одно неизвестное, x . Нам известны значения всех других переменных в этом уравнении. (Другие уравнения позволили бы нам решить для x , но они требуют, чтобы мы знали время остановки, t , которое мы не знаем. Мы могли бы их использовать, но это потребовало бы дополнительных вычислений.)
В-третьих, мы изменим уравнение, чтобы найти x : x − x0 = v2 − v022ax − x0 = v2 − v022a и подставляем известные значения: х − 0 = 02− (30.0 м / с) 22 (-7,00 м / с2). X-0 = 02- (30,0 м / с) 22 (-7,00 м / с2). Таким образом, x = 64,3 м на сухом бетоне. x = 64,3 м на сухом бетоне. - Эта часть может быть решена точно так же, как (а). Единственное отличие состоит в том, что ускорение составляет −5,00 м / с 2 . Результат xwet = 90,0 м по мокрому бетону. xwet = 90,0 м по мокрому бетону.
- Когда водитель реагирует, тормозной путь такой же, как в (a) и (b) для сухого и влажного бетона. Итак, чтобы ответить на этот вопрос, нам нужно вычислить, как далеко проехал автомобиль за время реакции, а затем добавить это время ко времени остановки.Разумно предположить, что скорость остается постоянной в течение времени реакции водителя.
Для этого мы, опять же, определяем известные и то, что мы хотим решить. Мы знаем, что v– = 30,0 м / sv– = 30,0 м / с, treaction = 0,500streaction = 0,500s и areaction = 0areaction = 0. Примем x0-реакцию x0-реакцию равной нулю. Ищем xreactionxreaction.
Во-вторых, как и раньше, мы определяем лучшее уравнение для использования. В этом случае x = x0 + v – tx = x0 + v – t работает хорошо, потому что единственное неизвестное значение – x , что мы и хотим найти.
В-третьих, мы подставляем известные для решения уравнения: x = 0 + (30,0 м / с) (0,500 с) = 15,0 м. x = 0 + (30,0 м / с) (0,500 с) = 15,0 м. Это означает, что автомобиль проезжает 15,0 м, в то время как водитель реагирует, в результате чего общее смещение в двух случаях с сухим и мокрым бетоном на 15,0 м больше, чем если бы он реагировал мгновенно.
Наконец, мы добавляем смещение во время реакции к смещению при торможении (рис. 3.23), xbraking + xreaction = xtotal, xbraking + xreaction = xtotal, и найдите (a) равным 64,3 м + 15,0 м = 79.3 м в сухом виде и (b) должно составлять 90,0 м + 15,0 м = 105 м во влажном состоянии.
Рис. 3.23. Расстояние, необходимое для остановки автомобиля, сильно различается в зависимости от дорожных условий и времени реакции водителя. Здесь показаны значения тормозного пути для сухого и мокрого покрытия, рассчитанные в этом примере для автомобиля, движущегося со скоростью 30,0 м / с. Также показано общее расстояние, пройденное от точки, когда водитель впервые видит, что свет загорается красным, при условии, что время реакции составляет 0,500 с.
Значение
Смещения, обнаруженные в этом примере, кажутся разумными для остановки быстро движущегося автомобиля.Остановка автомобиля на мокром асфальте должна длиться дольше, чем на сухом. Интересно, что время реакции значительно увеличивает смещения, но более важен общий подход к решению проблем. Мы идентифицируем известные и определяемые величины, а затем находим соответствующее уравнение. Если существует более одного неизвестного, нам нужно столько независимых уравнений, сколько неизвестных необходимо решить. Часто есть несколько способов решить проблему. Фактически, различные части этого примера могут быть решены другими методами, но представленные здесь решения являются самыми короткими.Пример 3.11
Расчет времени
Предположим, автомобиль въезжает в движение по автостраде на съезде длиной 200 м. Если его начальная скорость равна 10,0 м / с, а он ускоряется со скоростью 2,00 м / с 2 , сколько времени потребуется автомобилю, чтобы преодолеть 200 м по рампе? (Такая информация может быть полезна транспортному инженеру.)Стратегия
Сначала мы рисуем набросок Рис. 3.24. Нам предлагается решить за время т . Как и раньше, мы идентифицируем известные величины, чтобы выбрать удобную физическую связь (то есть уравнение с одной неизвестной, t .)Рис. 3.24. Эскиз автомобиля, ускоряющегося на съезде с автострады.
Решение
Опять же, мы идентифицируем то, что нам известно, и то, что мы хотим решить. Мы знаем, что x0 = 0, x0 = 0,v0 = 10 м / с, a = 2,00 м / с2v0 = 10 м / с, a = 2,00 м / с2 и x = 200 м.
Нам нужно решить для т . Уравнение x = x0 + v0t + 12at2x = x0 + v0t + 12at2 работает лучше всего, потому что единственной неизвестной в уравнении является переменная t , которую нам нужно решить. Из этого понимания мы видим, что когда мы вводим известные значения в уравнение, мы получаем квадратное уравнение.
Нам нужно изменить уравнение, чтобы найти t , затем подставив известные значения в уравнение:
200 м = 0 м + (10,0 м / с) t + 12 (2,00 м / с2) t2. 200 м = 0 м + (10,0 м / с) t + 12 (2,00 м / с2) t2.Затем мы упрощаем уравнение. Единицы измерения отменяются, потому что они есть в каждом члене. Мы можем получить единицы секунд для отмены, взяв t = t s, где t – величина времени, а s – единица измерения. Остается
Затем мы используем формулу корней квадратного уравнения, чтобы найти t ,
t2 + 10t − 200 = 0t = −b ± b2−4ac2a, t2 + 10t − 200 = 0t = −b ± b2−4ac2a,, что дает два решения: t = 10.0 и t = −20,0. Отрицательное значение времени неразумно, так как это будет означать, что событие произошло за 20 секунд до начала движения. Мы можем отказаться от этого решения. Таким образом,
Значение
Всякий раз, когда уравнение содержит неизвестный квадрат, есть два решения. В некоторых проблемах имеют смысл оба решения; в других случаях разумно только одно решение. Ответ 10,0 с кажется разумным для типичной автострады на съезде.Проверьте свое понимание 3.5
Ракета ускоряется со скоростью 20 м / с 2 во время пуска.Сколько времени нужно, чтобы ракета достигла скорости 400 м / с?
Пример 3.12
Ускорение космического корабля
Космический корабль покинул орбиту Земли и направляется к Луне. Разгоняется со скоростью 20 м / с 2 за 2 мин и преодолевает расстояние в 1000 км. Каковы начальная и конечная скорости космического корабля?Стратегия
Нас просят найти начальную и конечную скорости космического корабля. Глядя на кинематические уравнения, мы видим, что одно уравнение не дает ответа.Мы должны использовать одно кинематическое уравнение для решения одной из скоростей и подставить его в другое кинематическое уравнение, чтобы получить вторую скорость. Таким образом, мы решаем два кинематических уравнения одновременно.Решение
Сначала мы решаем для v0v0, используя x = x0 + v0t + 12at2: x = x0 + v0t + 12at2: x − x0 = v0t + 12at2x − x0 = v0t + 12at21.0 × 106m = v0 (120.0s) +12 (20,0 м / с2) (120,0 с) 21,0 × 106 м = v0 (120,0 с) +12 (20,0 м / с2) (120,0 с) 2v0 = 7133,3 м / с. V0 = 7133,3 м / с.Затем мы подставляем v0v0 в v = v0 + atv = v0 + at, чтобы найти окончательную скорость:
v = v0 + at = 7133.3 м / с + (20,0 м / с2) (120,0 с) = 9533,3 м / с. V = v0 + at = 7133,3 м / с + (20,0 м / с2) (120,0 с) = 9533,3 м / с.Значение
Есть шесть переменных смещения, времени, скорости и ускорения, которые описывают движение в одном измерении. Начальные условия данной задачи могут быть множеством комбинаций этих переменных. Из-за такого разнообразия решения могут быть не такими простыми, как простая подстановка в одно из уравнений. Этот пример показывает, что решения кинематики могут потребовать решения двух одновременных кинематических уравнений.Освоив основы кинематики, мы можем перейти ко многим другим интересным примерам и приложениям. В процессе разработки кинематики мы также увидели общий подход к решению проблем, который дает как правильные ответы, так и понимание физических взаимоотношений. Следующий уровень сложности в наших задачах кинематики включает движение двух взаимосвязанных тел, называемых задачами преследования двух тел .
Задачи преследования двух тел
До этого момента мы рассматривали примеры движения с участием одного тела.Даже для задачи с двумя автомобилями и тормозным путем на мокрой и сухой дороге мы разделили эту задачу на две отдельные задачи, чтобы найти ответы. В задаче преследования двух тел движения объектов связаны, то есть искомое неизвестное зависит от движения обоих объектов. Чтобы решить эти проблемы, мы пишем уравнения движения для каждого объекта, а затем решаем их одновременно, чтобы найти неизвестное. Это показано на Рисунке 3.25.
Рис. 3.25 Сценарий преследования с двумя телами, в котором автомобиль 2 имеет постоянную скорость, а автомобиль 1 идет сзади с постоянным ускорением.Автомобиль 1 догонит автомобиль 2 позже.
Время и расстояние, необходимое для того, чтобы автомобиль 1 догнал автомобиль 2, зависит от начального расстояния, на которое автомобиль 1 находится от автомобиля 2, а также от скорости обоих автомобилей и ускорения автомобиля 1. Кинематические уравнения, описывающие движение обоих автомобилей, должны быть решил найти эти неизвестные.
Рассмотрим следующий пример.
Пример 3.13
Гепард ловит газель
Гепард прячется за кустом. Гепард замечает пробегающую мимо газель со скоростью 10 м / с.В тот момент, когда газель проходит мимо гепарда, гепард из состояния покоя ускоряется со скоростью 4 м / с 2 , чтобы поймать газель. а) Сколько времени нужно гепарду, чтобы поймать газель? б) Что такое смещение газели и гепарда?Стратегия
Мы используем систему уравнений для постоянного ускорения, чтобы решить эту проблему. Поскольку есть два движущихся объекта, у нас есть отдельные уравнения движения, описывающие каждое животное. Но то, что связывает уравнения, – это общий параметр, который имеет одинаковое значение для каждого животного.Если мы внимательно посмотрим на проблему, становится ясно, что общим параметром для каждого животного является их положение x , позднее t . Поскольку оба они начинаются с x0 = 0x0 = 0, их смещения будут такими же в более позднее время t , когда гепард догонит газель. Если мы выберем уравнение движения, которое решает смещение для каждого животного, мы можем затем установить уравнения, равные друг другу, и решить для неизвестного, то есть времени.Решение
- Уравнение для газели: Газель имеет постоянную скорость, которая является ее средней скоростью, поскольку она не ускоряется.Поэтому мы используем уравнение 3.10 с x0 = 0x0 = 0: x = x0 + v – t = v – t. x = x0 + v – t = v – t. Уравнение для гепарда: гепард ускоряется из состояния покоя, поэтому мы используем уравнение 3.13 с x0 = 0x0 = 0 и v0 = 0v0 = 0: x = x0 + v0t + 12at2 = 12at2.x = x0 + v0t + 12at2 = 12at2. Теперь у нас есть уравнение движения для каждого животного с общим параметром, который можно исключить, чтобы найти решение. В этом случае мы решаем для t : x = v – t = 12at2t = 2v – a.x = v – t = 12at2t = 2v – a. Газель имеет постоянную скорость 10 м / с, что составляет ее среднюю скорость.Ускорение гепарда составляет 4 м / с 2 . Оценив t , время, за которое гепард достигнет газели, имеем t = 2v – a = 2 (10 м / с) 4m / s2 = 5s.t = 2v – a = 2 (10 м / с) 4m / s2 = 5s.
- Чтобы получить смещение, мы используем уравнение движения гепарда или газели, поскольку оба они должны дать одинаковый ответ.
Смещение гепарда: x = 12at2 = 12 (4 м / с2) (5) 2 = 50 м. x = 12at2 = 12 (4 м / с2) (5) 2 = 50 м. Водоизмещение газели: x = v – t = 10 м / с (5) = 50 м. x = v – t = 10 м / с (5) = 50 м.Мы видим, что оба смещения равны, как и ожидалось.
Значение
Важно анализировать движение каждого объекта и использовать соответствующие кинематические уравнения для описания отдельного движения. Также важно иметь хорошую визуальную перспективу задачи преследования двух тел, чтобы увидеть общий параметр, который связывает движение обоих объектов.Проверьте свое понимание 3.6
Велосипед имеет постоянную скорость 10 м / с. Человек начинает с отдыха и начинает бежать, чтобы догнать велосипед через 30 секунд, когда велосипед находится в том же положении, что и человек.Какое ускорение у человека?
Формула ускорения (уравнение) в физике: как использовать
Формула ускорения – одно из основных уравнений физики, которое вы обязательно должны изучить и применить на практике. В конце концов, ускорение – один из строительных блоков физики.
«Говорят, что движение равномерно ускоряется, если, начиная с состояния покоя, оно приобретает в течение равных интервалов времени одинаковую скорость». – Галилео Галилей, Две новые науки , 1638
Общая формула для среднего ускорения может быть выражена как:
- ускорение = ( v Final – v Initial ) / ( t Final – t Initial )
Где v обозначает скорость, а t обозначает время.В алгебраической записи формулу можно представить как:
Ускорение можно определить как скорость изменения скорости во времени. Ускорение – одно из самых основных понятий в современной физике, лежащее в основе практически каждой физической теории, связанной с движением объектов.
Единица измерения ускорения в системе СИ – метры в секунду в секунду (м / с 2 ). Несомненно, всем знакомо ощущение ускорения, когда вы нажимаете на педаль газа и вас толкают обратно на сиденье.Фактически, почти каждый наблюдаемый эффект движения возникает из-за ускорения из-за влияния сил. Ускорение, как и скорость, является векторной величиной, что означает, что оно имеет как величину, так и направление. Строго говоря, нет такого понятия, как «замедление», есть только ускорение в обратном направлении.
Ускорение – один из важнейших параметров движения. Параметры смещения ( d ), скорости ( v ) , и ускорения ( a ) имеют тесную математическую взаимосвязь.Информация об одном из параметров может использоваться для определения неизвестной информации о других параметрах. В общем, существует 4 основных уравнения, которые связывают эти 3 параметра друг с другом и со временем:
- d = v i t + (1/2) at 2
- v f = v i + at
- v f = v i +2 ad
- d = (( v + v f ) / 2) t
Эти 4 уравнения могут использоваться для прогнозирования неизвестной информации о движении объекта на основе известной информации о движении объекта.Итак, если кто-то знает ускорение объекта, пройденное расстояние и его начальную скорость, можно определить конечную скорость объекта. Точно так же, если кто-то знает начальную скорость, ускорение и истекшее время объекта, они могут определить, какое расстояние он преодолел. Давайте рассмотрим несколько простых примеров, чтобы проиллюстрировать использование этих формул.
«Ускорение конечно, в соответствии с некоторыми законами физики». – Терри Райли
Использование формул ускорения
(1)
Допустим, вы находитесь на парусной лодке, в частности, на 16-футовом Hobie Cat.Первоначально вы путешествуете со скоростью 3 м / с. Вы ловите сильный порыв ветра и через 7 секунд летите со скоростью 10 м / с. Какое у вас было среднее ускорение?
Подставляя наши значения в нашу формулу для среднего ускорения, мы получаем a = (10−3) / 7 = 7/7 = 1 м / с 2 . Среднее ускорение лодки составляло один метр в секунду в секунду. Другой способ прочитать это значение – сказать: за каждую секунду ваша скорость увеличивается на один метр в секунду.
(2)
Самолет, начинающий движение из состояния покоя, начинает ускоряться со скоростью 3 м / с 2 вниз по взлетно-посадочной полосе и, наконец, отрывается от земли 32 секунды спустя. Как далеко самолет пролетел над землей перед взлетом?
В этом вопросе нам даются три части информации: начальная скорость самолета (0 м / с), ускорение самолета (3 м / с 2 ) и продолжительность движения (32 секунды). Подставляя эти значения в первое из 4 приведенных выше уравнений:
дает нам:
- d = (0) (32) + (.5) (3) (32) 2 = 1536 метров.
То есть самолет пролетел всего 1536 метров перед взлетом.
«Сила тяжести и ускорение эквивалентны». – Альберт Эйнштейн
(3)
Перо падает на поверхность Луны с высоты 8 метров. Ускорение свободного падения на Луне составляет 1,5 м / с 2 . Сколько времени нужно, чтобы перо коснулось земли?
В этом случае нам задана начальная скорость (0 м / с), ускорение (1.5 м / с 2 ) и общее пройденное расстояние (8 м). Подставляя эти значения в первое уравнение
, получаем:
- 8 = (0) t + (0,5) (1,5) t 2
- 8 = (0,5) (1,5) t 2
- 8 = 0,75 т 2
- 10,66 = т 2
- 3,26 = т
Таким образом, для попадания пера потребуется 3,26 секунды поверхность луны.
(4)
В состоянии покоя ракетный корабль ускоряется со скоростью 15 м / с 2 на расстояние 650 м. Какова конечная скорость ракетного корабля?
В этом случае нам известна начальная скорость (0 м / с), пройденное расстояние (650 м) и скорость ускорения (15 м / с 2 ). Подставляя эти значения в третье уравнение:
дает нам:
- v f = 0 + 2 (15) (650)
- v f = (30) (650)
- v f = 19 500 м / с
Конечная скорость корабля-ракеты 19 500 м / с.
Мгновенное ускорение
До сих пор мы рассматривали только случаи, когда у нас либо среднее ускорение, либо ускорение равномерное. Однако просто указание среднего ускорения объекта может упустить важную информацию о движении этого объекта. Наличие только среднего ускорения за определенный период не может сказать вам, изменилось ли ускорение объекта за этот промежуток времени. Может, он начал очень медленно ускоряться, потом его ускорение со временем увеличивалось.Что мы можем сделать, так это разделить эту продолжительность на более мелкие сегменты и вычислить среднее ускорение для этих сегментов, что даст нам больше информации об объекте. Скажем, у нас есть некоторое расстояние от A до E. Мы можем разделить это расстояние на 4 сегмента AB, BC, CD и DE и вычислить среднее ускорение для каждого из этих интервалов.
Теперь представьте, что мы продолжаем делить это расстояние на более мелкие интервалы и вычислять среднее ускорение за эти интервалы до бесконечности .В конце концов, мы достигли бы точки, в которой у нас есть ускорение объекта в одной математической точке. Это также известно как его мгновенное ускорение – ускорение объекта в определенный момент времени. Мгновенное ускорение объекта можно рассматривать как среднее ускорение этого объекта за бесконечно малый интервал времени. Концепция мгновенного ускорения, возможно, является самой важной концепцией в физике и составляет основу практически всей ньютоновской физики.Можно определить мгновенное ускорение объекта, используя инструменты вычисления, чтобы найти вторую производную функции смещения объекта или первую производную функции скорости объекта.
Формула мгновенного ускорения в предельных обозначениях.Сводка
В сумме ускорение можно определить как скорость изменения скорости относительно времени, а формулу, выражающую среднюю скорость объекта, можно записать как:
Остальные 4 уравнения:
- d = v i t + (1/2) при 2
- v f = v i + при
- v f v i +2 ad
- d = (( v i + v f ) / 2) t
также являются важным уравнением, включающим ускорение, и может использоваться для вывода неизвестных фактов о движении объекта из известных фактов.
Была ли эта статья полезной?
😊 ☹️ Приятно слышать! Хотите больше научных тенденций? Подпишитесь на нашу рассылку новостей науки! Нам очень жаль это слышать! Мы любим отзывы 🙂 и хотим, чтобы вы внесли свой вклад в то, как сделать Science Trends еще лучше.4.2 Вектор ускорения | Университетская физика, том 1,
Цели обучения
К концу этого раздела вы сможете:
- Рассчитайте вектор ускорения с учетом функции скорости в единичном векторе.
- Опишите движение частицы с постоянным ускорением в трех измерениях.
- Используйте одномерные уравнения движения вдоль перпендикулярных осей, чтобы решить задачу в двух или трех измерениях с постоянным ускорением.
- Выразите ускорение в единичном векторе.
Мгновенное ускорение
Помимо получения векторов смещения и скорости движущегося объекта, мы часто хотим знать его ускорение вектор в любой момент времени на его траектории.Этот вектор ускорения представляет собой мгновенное ускорение, и его можно получить из производной по времени функции скорости, как мы видели в предыдущей главе. Единственная разница в двух или трех измерениях состоит в том, что теперь это векторные величины. Взяв производную по времени [latex] \ overset {\ to} {v} (t), [/ latex], находим
[латекс] \ overset {\ to} {a} (t) = \ underset {t \ to 0} {\ text {lim}} \ frac {\ overset {\ to} {v} (t + \ text {Δ } t) – \ overset {\ to} {v} (t)} {\ text {Δ} t} = \ frac {d \ overset {\ to} {v} (t)} {dt}.{2}) \ hat {i} + 5t \ hat {j} + 5t \ text {} \ hat {k} \ text {m}. [/ latex] (а) Какая скорость? б) Что такое ускорение? (c) Опишите движение от t = 0 с.
Стратегия
Мы можем получить некоторое представление о проблеме, посмотрев на функцию положения. Оно линейно по y и z , поэтому мы знаем, что ускорение в этих направлениях равно нулю, когда мы берем вторую производную. Также обратите внимание, что положение в направлении x равно нулю для t = 0 с и t = 10 с.{2}. [/ latex] Вектор ускорения постоянен в отрицательном направлении оси x.
(в)
Покажи ответ Траекторию движения частицы можно увидеть на (Рисунок).Давайте сначала посмотрим в направлениях y и z. Положение частицы постоянно увеличивается в зависимости от времени с постоянной скоростью в этих направлениях. Однако в направлении x частица следует по положительному положительному x до тех пор, пока t = 5 с, когда она меняет направление на противоположное. Мы знаем это, глядя на функцию скорости, которая в этот момент становится равной нулю, а затем становится отрицательной.Мы также знаем это, потому что ускорение отрицательное и постоянное, то есть частица замедляется или ускоряется в отрицательном направлении. Положение частицы достигает 25 м, после чего она меняет направление и начинает ускоряться в отрицательном направлении оси x. Положение достигает нуля при t = 10 с.
Рисунок 4.9 Частица начинается в точке (x, y, z) = (0, 0, 0) с вектором положения [latex] \ overset {\ to} {r} = 0. [/ latex] Показана проекция траектории на плоскость xy.Значения y и z линейно увеличиваются как функция времени, тогда как x имеет точку поворота в t = 5 с и 25 м, когда он меняет направление. {2}, [/ latex] где a, b, и c – константы.Что можно сказать о функциональном виде функции скорости?
Показать решениеВектор ускорения постоянный и не меняется со временем. Если a, b и c не равны нулю, то функция скорости должна быть линейной во времени. У нас есть [латекс] \ overset {\ to} {v} (t) = \ int \ overset {\ to} {a} dt = \ int (a \ hat {i} + b \ hat {j} + c \ hat {k}) dt = (a \ hat {i} + b \ hat {j} + c \ hat {k}) t \, \ text {m / s}, [/ latex], поскольку взятие производной функция скорости производит [латекс] \ overset {\ to} {a} (t).[/ latex] Если любой из компонентов ускорения равен нулю, то этот компонент скорости будет постоянным.
Постоянное ускорение
Многомерное движение с постоянным ускорением можно рассматривать так же, как показано в предыдущей главе для одномерного движения. Ранее мы показали, что трехмерное движение эквивалентно трем одномерным движениям, каждое по оси, перпендикулярной другим. {2} +2 {a} _ {y} (y- {y} _ {0}).[/латекс]
Здесь индекс 0 обозначает начальное положение или скорость. (Рисунок) на (Рисунок) можно заменить на (Рисунок) и (Рисунок) без компонента z , чтобы получить вектор положения и вектор скорости как функцию времени в двух измерениях:
[латекс] \ overset {\ to} {r} (t) = x (t) \ hat {i} + y (t) \ hat {j} \, \ text {и} \, \ overset {\ to } {v} (t) = {v} _ {x} (t) \ hat {i} + {v} _ {y} (t) \ hat {j}. [/ латекс]
Следующий пример иллюстрирует практическое использование кинематических уравнений в двух измерениях.{2} [/ latex] вниз по склону [латекс] 15 \ text {°} [/ latex] при t = 0. С началом системы координат в передней части ложи, ее начальное положение и скорость
[латекс] \ overset {\ to} {r} (0) = (75,0 \ hat {i} -50,0 \ hat {j}) \, \ text {m} [/ latex]
и
[латекс] \ overset {\ to} {v} (0) = (4.1 \ hat {i} -1.1 \ hat {j}) \, \ text {m / s}. [/ латекс]
(a) Каковы составляющие x- и y положения и скорости лыжника как функции времени? (b) Каковы ее положение и скорость при t = 10.{2} [/ latex] по склону [латекс] 15 \ text {°}. [/ latex] Начало системы координат находится на лыжной базе.
Стратегия
Поскольку мы оцениваем компоненты уравнений движения в направлениях x и y , нам нужно найти компоненты ускорения и поместить их в кинематические уравнения. Компоненты ускорения находятся в системе координат на (Рисунок). Затем, вставив компоненты начального положения и скорости в уравнения движения, мы можем найти ее положение и скорость в более позднее время t .{2}) (10.0 \, \ text {s}) = – 6.5 \, \ text {m / s}. [/ latex] Положение и скорость при t = 10,0 с, наконец,
[латекс] \ overset {\ to} {r} (10.0 \, \ text {s}) = (216.0 \ hat {i} -88.0 \ hat {j}) \, \ text {m} [/ latex] [латекс] \ overset {\ to} {v} (10.0 \, \ text {s}) = (24.1 \ hat {i} -6.5 \ hat {j}) \ text {m / s}. [/ latex] Величина скорости лыжника на 10,0 с составляет 25 м / с, что составляет 60 миль / ч.
Значение
Полезно знать, что, учитывая начальные условия положения, скорости и ускорения объекта, мы можем найти положение, скорость и ускорение в любое более позднее время.
С (Рисунок) – (Рисунок) мы завершили набор выражений для положения, скорости и ускорения объекта, движущегося в двух или трех измерениях. Если траектории объектов выглядят как «красные стрелки» на начальном рисунке главы, то выражения для положения, скорости и ускорения могут быть довольно сложными. В следующих разделах мы исследуем два частных случая движения в двух и трех измерениях, рассматривая движение снаряда и круговое движение.
Резюме
- В двух и трех измерениях вектор ускорения может иметь произвольное направление и не обязательно указывать вдоль заданного компонента скорости.
- Мгновенное ускорение вызывается изменением скорости за очень короткий (бесконечно малый) период времени. Мгновенное ускорение – это вектор в двух или трех измерениях. Он находится путем взятия производной функции скорости по времени.
- В трех измерениях ускорение [latex] \ overset {\ to} {a} (t) [/ latex] может быть записано как векторная сумма одномерных ускорений [latex] {a} _ {x} (t ), {a} _ {y} (t), \ text {and} \, {a} _ {z} (t) [/ latex] вдоль линий x- , y – и z- осей.
- Кинематические уравнения для постоянного ускорения могут быть записаны как векторная сумма уравнений постоянного ускорения в направлениях x , y и z .
Концептуальные вопросы
Если функция положения частицы является линейной функцией времени, что можно сказать о ее ускорении?
Если объект имеет постоянную составляющую скорости x и внезапно испытывает ускорение в направлении x , изменится ли составляющая x- его скорости?
Показать решениеНет, движения в перпендикулярных направлениях независимы.{2} \ hat {i}. [/ latex] Сильный ветер толкает лодку, придавая ей дополнительную скорость [latex] 2.0 \, \ text {м / с} \ hat {i} +1.0 \, \ text {m / s} \ hat { j}. [/ latex] (a) Какова скорость лодки при t = 10 с? (b) Каково положение лодки на отметке t = 10 с? Нарисуйте эскиз траектории и положения лодки на отметке t = 10 с, показывая оси x- и y .
Положение частицы для t > 0 определяется выражением [latex] \ overset {\ to} {r} (t) = (3.{2} [/ латекс],
г. [латекс] \ overset {\ to} {v} (2.0s) = (12.0 \ hat {i} -84.0 \ hat {j} +1.25 \ hat {k}) \ text {m / s} [/ latex] ,
г. [латекс] \ overset {\ to} {v} (1.0 \, \ text {s}) = 6.0 \ hat {i} -21.0 \ hat {j} +10.0 \ hat {k} \ text {m / s} , \, | \ overset {\ to} {v} (1.0 \, \ text {s}) | = 24.0 \, \ text {m / s} [/ latex]
[латекс] \ overset {\ to} {v} (3.0 \, \ text {s}) = 18.0 \ hat {i} -189.0 \ hat {j} +0,37 \ hat {k} \ text {м / с }, [/ latex] [latex] | \ overset {\ to} {v} (3.0 \, \ text {s}) | = 199.0 \, \ text {m / s} [/ latex],
e. [латекс] \ overset {\ to} {r} (t) = (3.{-2} \ hat {k}) \ text {cm} [/ latex]
[латекс] \ begin {array} {cc} \ hfill {\ overset {\ to} {v}} _ {\ text {avg}} & = 9.0 \ hat {i} -49.0 \ hat {j} -6.3 \ hat {k} \ text {m / s} \ hfill \ end {array} [/ latex]
Ускорение частицы – постоянная величина. При t = 0 скорость частицы равна [latex] (10 \ hat {i} +20 \ hat {j}) \ text {m / s}. [/ latex] При t = 4 с скорость [латекс] 10 \ hat {j} \ text {м / с}. [/ latex] а) Каково ускорение частицы? б) Как положение и скорость меняются со временем? Предположим, что частица изначально находится в начале координат.
У частицы есть функция положения [latex] \ overset {\ to} {r} (t) = \ text {cos} (1.0t) \ hat {i} + \ text {sin} (1.0t) \ hat { j} + t \ hat {k}, [/ latex], где аргументы функций косинуса и синуса выражены в радианах. а) Что такое вектор скорости? б) Что такое вектор ускорения?
Показать решениеа. [латекс] \ overset {\ to} {v} (t) = \ text {−sin} (1.0t) \ hat {i} + \ text {cos} (1.0t) \ hat {j} + \ hat { k} [/ латекс], б. [латекс] \ overset {\ to} {a} (t) = \ text {−cos} (1.0t) \ hat {i} – \ text {sin} (1.0t) \ hat {j} [/ latex]
Реактивный самолет Lockheed Martin F-35 II Lighting взлетает с авианосца с длиной взлетно-посадочной полосы 90 м и скоростью взлета 70 м / с в конце взлетно-посадочной полосы.{2} [/ latex] на [latex] 30 \ text {°} [/ latex] по отношению к горизонтали. (а) Каково начальное ускорение F-35 на палубе авианосца, чтобы он поднялся в воздух? (b) Запишите положение и скорость F-35 в единичном векторе от точки, когда он покидает палубу авианосца. (c) На какой высоте находится истребитель через 5,0 с после выхода из палубы авианосца? (г) Каковы его скорость и скорость в это время? д) Как далеко он прошел по горизонтали?
Глоссарий
- вектор ускорения
- мгновенное ускорение, полученное путем взятия производной функции скорости по времени в обозначении единичного вектора
с примерами и решенными задачами
Что такое ускорение?
Когда неподвижный автомобиль внезапно трогается с места, нас толкает назад, а при торможении нас толкает вперед, к нашему сиденью, или когда наша машина резко поворачивает направо, нас толкает влево.Мы сталкиваемся с такими ситуациями, потому что наша машина ускоряется.
Просто при изменении скорости будет ускорение. Давайте разберемся с концепцией ускорения на наглядных примерах.
Предположим, у меня есть машина, движущаяся с постоянной скоростью 90 км / ч по прямой. Я вижу вертолет, летящий примерно со скоростью 20 000 км / ч. Если бы я спросил вас, что в этих двух случаях, где вы найдете ускорение? Ваш ответ наверняка будет отрицательным, потому что оба движутся в постоянном темпе, поэтому никакого ускорения в обоих случаях.
Теперь, если я спрошу вас, что ускорение равно высокой скорости. Что вы ответите? Вы можете сказать «да», но это точно не так. Хотите знать почему? Потому что ускорение – это скорость изменения скорости. Теперь давайте разберемся, что такое формула ускорения.
Общая формула ускорения
Мы уже знаем, что скорость – это скорость с направлением; следовательно, это векторная величина. Ускорение ‘a’ определяется как:
a = изменение скорости / затраченное время
Эта формула утверждает, что скорость изменения скорости является ускорением, или если скорость объекта изменяется от своего начального значения ‘u’ до конечного значения ‘v’, тогда выражение может быть просто записано как:
a = (v – u) / t
Формула ускорения в физике
В физике ускорение описывается как скорость изменения скорости объект, независимо от того, ускоряется он или замедляется.Если он ускоряется, ускорение считается положительным, а если он замедляется, ускорение – отрицательным. Это вызвано чистой неуравновешенной силой, действующей на объект в соответствии со вторым законом Ньютона. Ускорение – это векторная величина, поскольку она описывает скорость изменения скорости во времени, которая является векторной величиной. Ускорение обозначается а. Его единица СИ – м / с2, размеры – M0L1T – 2.
Если v0, vt и t представляют собой начальную скорость, конечную скорость и время, необходимое для изменения скорости, то ускорение определяется по формуле:
\ [\ vec a = \ frac {{{{\ vec v } _t} – {{\ vec v} _0}}} {t} \]
В одномерном движении мы можем использовать; \ [a = \ frac {{{v_t} – {v_0}}} {t} \]
Формула ускорения
Если \ [\ vec r \] представляет вектор смещения, а \ [\ vec v = \ frac {{ d \ vec r}} {{dt}} \] представляет скорость, тогда;
Ускорение: \ [\ vec a = \ frac {{d \ vec v}} {{dt}} = \ frac {{{d ^ 2} \ vec r}} {{d {t ^ 2}}} \]
При одномерном движении, где x – смещение, а \ [v = \ frac {{dx}} {{dt}} \] – скорость, тогда;
\ [a = \ frac {{dv}} {{dt}} = \ frac {{{d ^ 2} x}} {{d {t ^ 2}}} \]
Пример 1:
Автомобиль трогается с места и развивает скорость 54 км / ч за 3 секунды.2} \]
Тогда; скорость \ [v = \ frac {{dx}} {{dt}} = -2 + 6t \]
Ускорение: \ [a = \ frac {{dv}} {{dt}} = 6 \, \] = 6 м / с².
(Мы видим, что ускорение здесь постоянное. Следовательно, при t = 3 с его значение также равно 6 м / с².
Решенные вопросы по формуле ускорения:
Вопрос 1: Каким будет ускорение автомобиля Если он замедляется с 90 км / ч до остановки за 10 секунд?
Ответ: Здесь u = 90 км / ч = 90 x 5/18 = 25 м / с, потому что первоначально он двигался со скоростью 90 км / ч, а затем достиг нуля.
Конечная скорость ‘v’ = 0 км / ч и t = 10 секунд
Теперь применим формулу здесь:
a = (0-25) / 10 = (-) 2,5 мс²
Вопрос 2: Девушка начинает ее движение по прямой со скоростью 30 м / с, ее скорость изменяется с постоянной скоростью. Если она останавливается через 60 секунд, какое у нее ускорение?
Ответ: Здесь начальная скорость девушки составляла 30 м / с и останавливается, поэтому ее конечная скорость станет 0 м / с. {{t_2}} {\ left | {v \ left (t \ right)} \ right | dt}.2}}} {2}. \]
Решенные проблемы
Щелкните или коснитесь проблемы, чтобы увидеть решение.
Пример 1
Скорость объекта задается уравнением \ (v \ left (t \ right) = \ sqrt {4 + t}, \), где скорость \ (v \) измеряется в \ (\ large {\ frac { \ text {m}} {\ text {s}}} \ normalsize, \) время \ (t \) измеряется в секундах. Найдите расстояние, пройденное объектом за первые \ (5 \, \ text {sec}. \)Пример 2
Частица движется по прямой в положительном направлении оси \ (x – \) со скоростью, заданной уравнением \ (v = 2 \ sqrt {x} \, \ left ({\ large {\ frac {\ text {m}} {\ text {s}}} \ normalsize} \ right).\) Предполагая, что \ (x \ left ({t = 0} \ right) = 0, \) найдите время \ (t \), которое требуется частице, чтобы покрыть первый \ (100 \, \ text {m} \) пути.Пример 3
Начиная с момента времени \ (t = 0, \) объект движется по прямой со скоростью \ (v \ left (t \ right) = 6 – 2t. 2}}}} \ normalsize} \ right).\) Найдите расстояние, пройденное частицей за \ (3 \ text {rd} \) секунду.Пример 5
Объект движется по прямой с ускорением, равным \ [a \ left (t \ right) = 1 + \ cos \ left ({\ pi t} \ right). \] Предполагая, что начальная скорость в точке \ (t = 0 \) равна нулю, найдите общее расстояние, пройденное за первую секунду.Пример 6
Частица начинает движение из состояния покоя с постоянным ускорением. За \ (1 \ text {st} \) секунду он покрывает \ ({d_1} \) метров.2}}}} \ normalsize} \ right) \) на \ ({T_1} = 5 \) секунд. Затем он равномерно замедляется на \ ({T_2} = 10 \) секунд и останавливается. Какое расстояние проходит частица?Пример 10
Мяч, брошенный вертикально, проходит вдвое большее расстояние за \ (1 \ text {st} \) секунду, чем за \ (2 \ text {nd} \) секунду. Какая максимальная высота достигается мячом?Пример 1.
Скорость объекта задается уравнением \ (v \ left (t \ right) = \ sqrt {4 + t}, \), где скорость \ (v \) измеряется в \ (\ large {\ frac { \ text {m}} {\ text {s}}} \ normalsize, \) время \ (t \) измеряется в секундах.3}} – 8} \ right]} = {\ frac {2} {3} \ cdot 19} = {\ frac {{38}} {3} \ приблизительно 12,7 \, \ text {m}} \]Пример 2.
Частица движется по прямой в положительном направлении оси \ (x – \) со скоростью, заданной уравнением \ (v = 2 \ sqrt {x} \, \ left ({\ large {\ frac {\ text {m}} {\ text {s}}} \ normalsize} \ right). \) Предполагая, что \ (x \ left ({t = 0} \ right) = 0, \) найдите время \ (t \) частица покрывает первые \ (100 \, \ text {m} \) пути.Решение.
Уравнение движения частицы имеет вид
\ [v = \ frac {{dx}} {{dt}} = 2 \ sqrt x.\]
У нас есть простое дифференциальное уравнение, описывающее положение частицы как функцию времени. Разделив переменные и интегрировав обе стороны, получим:
\ [{\ frac {{dx}} {{\ sqrt x}} = 2dt,} \; \; \ Rightarrow {\ int {\ frac {{dx}} {{\ sqrt x}}} = 2 \ int {dt},} \; \; \ Rightarrow {2 \ sqrt x = 2t + C,} \; \; \ Rightarrow {\ sqrt x = t + C.} \]
Из начального условия \ (x \ left ({t = 0} \ right) = 0 \) следует, что \ (C = 0. 2}}}} \ normalsize} \ right ) \).2}}}} \ normalsize} \ right) \) на \ ({T_1} = 5 \) секунд. Затем он равномерно замедляется на \ ({T_2} = 10 \) секунд и останавливается. Какое расстояние проходит частица?
Решение.
Определить скорость \ ({v_1} \) в момент \ (t = {T_1}: \)
\ [{{v_1} = {a_1} t = {a_1} {T_1}} = {5 \ cdot 5} = {25 \, \ left ({\ frac {\ text {m}} {\ text {s }}} \ right)} \]
На втором этапе скорость частицы изменяется согласно уравнению
\ [v = {v_1} + {a_2} t, \]
где \ (0 \ le t \ le {T_2}.2}}} {2}} = {125 \, \ text {m}} \]
Следовательно, полное расстояние, пройденное частицей, равно
\ [{d = {d_1} + {d_2}} = {62,5 + 125} = {187,5 \, \ text {m}} \]
Пример 10.
Мяч, брошенный вертикально, проходит вдвое большее расстояние за \ (1 \ text {st} \) секунду, чем за \ (2 \ text {nd} \) секунду. Какая максимальная высота достигается мячом?Решение.
Предположим, что мяч подброшен вверх с начальной скоростью \ ({v_0} \).