Из формулы ускорения, можно выразить и определить конечную скорость движения.
\[V=V_{n}+\alpha \Delta t\]
Однако, следует учесть следующее: что при вычислении по данной формуле, обязательно условие: ускорение, должно иметь постоянное значение.
Виды и характеристики ускорения:
В физике, также существует термин, как среднее ускорение.
Среднее ускорение — это изменение величины скорости к промежутку времени, при котором произошло данное изменение.
Данный вид ускорения, определяется по формуле, схожей с определением равноускоренного ускорения.
\[\bar{\alpha}=\frac{\bar{V}_{1}-\bar{V}_{0}}{t}=\frac{\Delta \bar{V}}{t}\]
Ускорение может быть выражено, также отрицательном знаком. Это происходит, если начальная скорость имеет значение большее, чем конечная, Таким образом происходит процесс замедления.
F — сила тяжести, Н;
M — масса первого тела (часто планеты), кг;
m — масса второго тела, кг;
R — расстояние между телами, м;
G — гравитационная постоянная;
G = 6,67 × 10-11м3·кг-1·с-2.
Принцип вычисления ускорения при движении по окружности
При движении не прямолинейной поверхности, величина его будет изменяться.
Даже при условии, что модуль скорости остается величиной неизменной. В таких случаях ускорение вычисляется по следующему принципу:
- разность начальной и конечной скоростей;
- применение правил векторной математики;
- учитывается изменение направления.
Для определения результата ускорения при, таких условиях. Нужно применить и знать два определения.
- Тангенциальное ускорение. Обозначается буквой αt, направление движения по касательной к траектории направления. Тангенциальное значение может быть равно нулю в случае, если движение по заданной окружности, является равномерным.
 {2}}}\]
{2}}}\]Рассмотрим и закрепим данную тему на примере решения задачи.
Необходимо найти и определить значение ускорение тела, при его движении за 20 секунд от 10 до 100 км/час.
В начальной точке, тело движется со следующей скоростью:
\[V_{0}=\frac{10000}{3600}=2.77_{\text {м/сек }}\]
Определяем скорость в конце движения:
\[V_{K}=\frac{10000}{3600}=27.77_{\text {м/сек }}\]
Полученные значения, подставляем в формулу и вычисляем значение ускорения:
\[\alpha=\frac{V_{1}-V_{0}}{t}\]
\[\alpha=\frac{27,77-2,77}{20}=1,25 \mathrm{м} / \text { сек. }\]
Ответ: ускорение равняется 1,25 м/сек.
Вывод:
Как видно из решенного примера, тема ускорения не является слишком сложной. Однако, как и любой технической науке, никогда нельзя расслабляться. Нужно быть внимательным и сосредоточенным. На этом и построена вся система изучения физики и других технических предметов.
Все формулы ускорения. Виды ускорения
Когда в физике изучают механическое движение, то внимание обращают на две главные величины – это скорость и ускорение.
 Знание их зависимости от времени позволяет определить координату тела в пространстве в любой момент. В данной статье приведем все формулы ускорения для разных его видов.
Знание их зависимости от времени позволяет определить координату тела в пространстве в любой момент. В данной статье приведем все формулы ускорения для разных его видов.Общее понятие
Ускорение – это физическая величина. Она определяет, насколько быстро изменяется скорость. Как найти ускорение? Формула приведена ниже:
a = dv/dt
То есть величина a – это производная скорости по времени. Данное выражение позволяет рассчитать так называемое полное мгновенное ускорение, то есть характеризует величину в данный конкретный момент времени.
На практике чаще всего бывает важно знать не мгновенное, а некоторое среднее ускорение, с которым тело двигалось в течение определенного времени. Рассчитать его можно по такой формуле:
a = (v2-v1)/(t2-t1).
Здесь v2 и v1 – мгновенные скорости в моменты времени t2 и t1 соответственно.

Криволинейное движение
Ускорение определяет величину изменения скорости. У последней варьируется не один параметр. Она может меняться как по направлению, так и по величине. Если тело движется по прямой линии, то вектор скорости сохраняет свое направление. Для такого перемещения полное ускорение определяется исключительно изменением модуля скорости. Его называют касательным или тангенциальным.
Если же тело перемещается по произвольной криволинейной траектории, то вектор скорости обязательно изменяется. Этот факт приводит к появлению нормальной компоненты ускорения. Рассмотрим подробнее. Раскрывая тему всех формул ускорения, приведем выражение для вычисления нормального ускорения:
an = v2/r
Это равенство позволяет сделать два важных вывода:
- Во-первых, нормальная компонента зависит от модуля скорости, а не от его изменения, как тангенциальная составляющая.
- Во-вторых, она обратно пропорциональна радиусу кривизны траектории r.
 Когда тело вращается равномерно по окружности, существует только нормальная компонента.
Когда тело вращается равномерно по окружности, существует только нормальная компонента.
Чтобы определить модуль полного ускорения, следует воспользоваться такой формулой:
a = √(an2+at2)
Вектор a определяется как сумма векторов an и at, первый из них направлен перпендикулярно траектории к центру ее кривизны, а второй – по касательной к траектории в сторону изменения модуля скорости.
Свободное падение
Так называют вертикальное движение тела в гравитационном поле планеты, осуществляемое под действием силы тяжести. Как правило, соответствующее ускорение обозначают буквой g. Например, для Земли оно составляет 9,81 м/с2. Приведем все формулы для ускорения g:
g = G*M/R2;
g = F/m;
g = 2*h/t2
Первое из приведенных выражений позволяет определить ускорение g, если известны масса планеты M и ее радиус R.
 G – это гравитационная постоянная. Эта формула следует из закона Всемирного тяготения Ньютона.
G – это гравитационная постоянная. Эта формула следует из закона Всемирного тяготения Ньютона.Второе выражение – это всем известное уравнение для силы тяжести F, которая действует на тело массой m.
Наконец, третья формула определяет ускорение через высоту падения h и время падения t тела без начальной скорости. Это выражение является одним из основных в кинематике прямолинейного движения.
Угловое ускорение
Этот вид также нельзя оставить без внимания. Приводя все формулы ускорения, стоит отметить, что угловую величину удобно использовать, когда система вращается вокруг некоторой оси. Она определяет быстроту изменения угловой скорости и выражается в радианах в квадратную секунду. Для определения этого вида ускорения применяют следующие формулы:
α = dω/dt = d2θ/dt2;
α = M/I
Первое равенство показывает, что для определения углового ускорения α следует найти производную от угловой скорости ω по времени либо вторую производную по времени от угла поворота θ.

Вторая строчка – это выражение, которое следует из уравнения моментов. Здесь M – момент силы, которая раскручивает систему, I – момент инерции, который играет роль массы тела во время линейного движения.
Ускорение (комплексное) — Frega Physics
Ускорение — это скорость изменения скорости . Так ускорение может быть достигнуто за счет ускорения или замедления изменения скорость), изменение направления или их комбинация. Даже “замедление” называется ускорением, потому что происходит изменение скорости. Объект может иметь положительное ускорение, ускоряясь в положительном направлении или замедляясь в отрицательном направлении. Объект может иметь отрицательное ускорение за счет ускорения в отрицательном направлении или замедление в положительную сторону.
Это векторная величина так как скорость является векторной величиной, то направление учитывается учетная запись.
 На этом уровне физики мы имеем дело только с постоянными или
среднее ускорение, поэтому все уравнения ускорения предполагают, что мы
найти среднее ускорение или что ускорение остается
постоянный. Есть 4-5 постоянных ускорений уравнений:
На этом уровне физики мы имеем дело только с постоянными или
среднее ускорение, поэтому все уравнения ускорения предполагают, что мы
найти среднее ускорение или что ускорение остается
постоянный. Есть 4-5 постоянных ускорений уравнений:Constant Acceleration Equations
Δx = ½ (v + v 0 ) t a = Δv / t = (v – v 0 ) / t … v = v 0 + at*
(*приведенные выше два уравнения представляют собой одно и то же уравнение, только переставленное)Δx = 2 0 в 2 = v 0 2 + 2 a Δx Каждое уравнение постоянного ускорения содержит 4 из 5 переменных (v, v 0 ), без последней Δ переменная.

Символ переменной
Имя переменной
Единица СИ
9 00007 Другие единицы СИ0027 специфики
V Окончательная скорость метров в секунду (M/S)
MPH, KM/H, Ft/S)
MPH, K, H/S)
MPH, K, H/S) MPH, H, Ft/S) MPH, H, Ft/S) MPH, H, Ft/S) MPH. конечная скорость этой части задачи. Поскольку это вектор, берется направление в учетную запись. Будьте осторожны со своими негативами и позитивами. v 0 начальная скорость метров в секунду (м/с)
миль/ч, км/ч, фут/с Начальная скорость — это начальная скорость этой части задачи.  Поскольку это вектор, берется направление
в учетную запись. Будьте осторожны со своими негативами и позитивами.
Поскольку это вектор, берется направление
в учетную запись. Будьте осторожны со своими негативами и позитивами.ускорение (постоянное, среднее, равномерное) метров в секунду в квадрате (м/с 2 ) 9005ч/ч/ч/ч 90с/км км/ч0027Ускорение – это скорость, при которой скорость изменения; это изменение скорости в единицу времени. На этом уровне считать ускорение равномерным или постоянным. Поскольку это вектор, берется направление в учетную запись. Будьте осторожны со своими негативами и позитивами. Положительный ускорение может означать ускорение, движение вперед или замедление, двигаться назад. Отрицательное ускорение может означать замедление, двигаться вперед или ускоряться, двигаться назад. t или Δt секунда (с)
мин, час, день, нед Время может быть общим временем или временем для этой части задачи.  Поскольку это скалярная величина, она никогда не может быть отрицательной.
Поскольку это скалярная величина, она никогда не может быть отрицательной. Δx смещение; изменение положения метр (м)
мили, км, см, дюймы, футы, ярды Перемещение это изменение положения объекта. это длина и направление прямой линии от начала до конца. Поскольку это вектор, берется направление в учетную запись. Будьте осторожны со своими негативами и позитивами. Положительный смещение будет означать движение вверх, вперед или вправо. отрицательный смещение будет означать движение вниз, назад или влево. Вы определяете, какое из этих уравнений вы будете использовать, перечисляя заданные и неизвестные из задачи. Составление этого списка — самый важный шаг в решении любой физической задачи, поскольку это попытка определить, какое уравнение будет использоваться для решения задачи. Ниже приведены несколько примеров, связанных с уравнениями постоянного ускорения.

Маршрутный автобус замедляется до остановки со средним ускорением -1,8 м/с 2 . За какое время скорость автобуса снизится с 9,0 м/с до 0,0 м/с?- Прежде чем делать что-либо еще, сначала прочитайте всю задачу!
- Нарисуйте рисунок.
- Перечислите свои переменные.
- Неизвестно
- t = ?
- Givens
- a = -1.8 m/s 2
- v 0 = 9.0 m/s
- v = 0.0 m/s
- Константы
- Н/Д
- Преобразование переменных в единицы СИ.
- Н/Д
- Выберите уравнение, которое соответствует вашему переменные.
- v = v 0 + at*
- *a = (v – v 0 ) / t также допустимо использовать, так как оба используют одни и те же переменные
- 9024 неизвестная переменная в уравнении.

- t = (v – v 0 ) / a
- Подставьте данные переменные в уравнение.
- t = (0,0 – 9,0) / -1,8
- Решить.
- t = 5 секунд
- Прежде чем делать что-либо еще, сначала прочитайте всю задачу!
- Нарисуй рисунок.
- Перечислите свои переменные.
- Неизвестно
- ∆x = ?
- Givens
- A = +31 м/с 2
- V 0 = 0,023330
- V 0 = 0,023330
- V 0 = 0,023330
- .

- Константы
- Н/Д
- Преобразование переменных в единицы СИ.
- Н/Д
- Выберите уравнение, которое соответствует вашему переменные.
- v 2 = v 0 2 + 2aΔx
- Изолировать для неизвестной переменной в уравнении.
- Δx = (v 2 – v 0 2 ) / 2a
- в уравнение подставить данные переменные.
- Δx = (62 2 – 0 2 ) / (2*31)
- Решить.
- Δx = 62 м
- Прежде чем делать что-либо еще, сначала прочитайте всю задачу!
- Нарисуйте рисунок.

- Перечислите свои переменные.
- Неизвестно
- Δx = ?
- Givens
- v 0 = 0.0 m/s
- t = 3.0 s
- Constants
- a = -10 m/ s 2 *
- * = Ускорение силы тяжести на Земле равно -90,81 м/с 2 . Хотя -9,81 м/с 2 является более точным числом, но -10 более полезно для быстрой оценки. Если иное не указано мной, я приму использование любой константы.
- Преобразование переменных в единицы СИ.
- Н/Д
- Выберите уравнение, которое соответствует вашему переменные.
- Δx = v 0 t + ½(при 2 )
- Изолировать неизвестную переменную в уравнении.

Пример 2:
Самолет взлетает с палубы авианосца. Струя из состояния покоя катапультируется с постоянным ускорением +31 м/с 2 по прямой и достигает скорости +62 м/с. Найдите перемещение струи.строительство. Через 3,00 с свободного падения каково смещение камня?

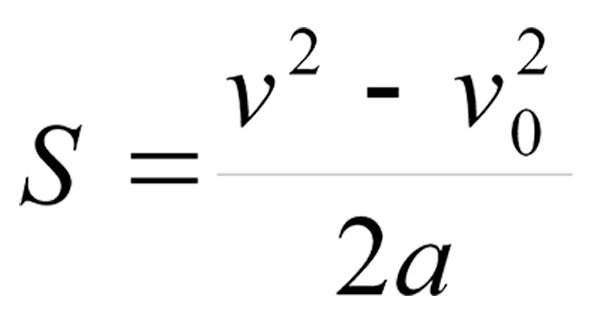 {2}}}\]
{2}}}\] Знание их зависимости от времени позволяет определить координату тела в пространстве в любой момент. В данной статье приведем все формулы ускорения для разных его видов.
Знание их зависимости от времени позволяет определить координату тела в пространстве в любой момент. В данной статье приведем все формулы ускорения для разных его видов.
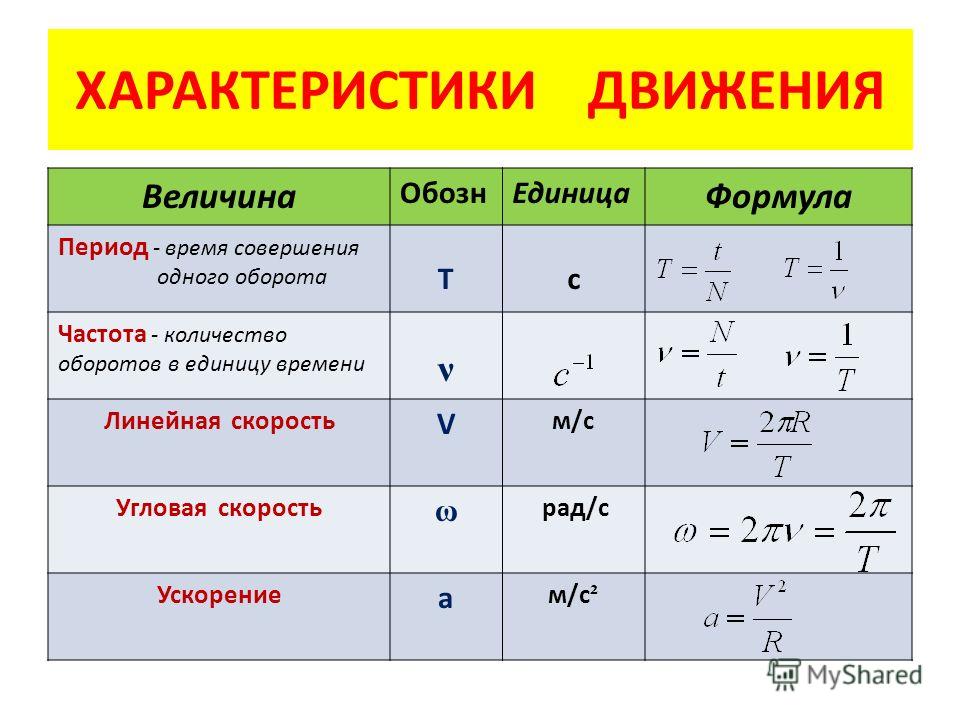 Когда тело вращается равномерно по окружности, существует только нормальная компонента.
Когда тело вращается равномерно по окружности, существует только нормальная компонента. G – это гравитационная постоянная. Эта формула следует из закона Всемирного тяготения Ньютона.
G – это гравитационная постоянная. Эта формула следует из закона Всемирного тяготения Ньютона.
 На этом уровне физики мы имеем дело только с постоянными или
среднее ускорение, поэтому все уравнения ускорения предполагают, что мы
найти среднее ускорение или что ускорение остается
постоянный. Есть 4-5 постоянных ускорений уравнений:
На этом уровне физики мы имеем дело только с постоянными или
среднее ускорение, поэтому все уравнения ускорения предполагают, что мы
найти среднее ускорение или что ускорение остается
постоянный. Есть 4-5 постоянных ускорений уравнений:
 Поскольку это вектор, берется направление
в учетную запись. Будьте осторожны со своими негативами и позитивами.
Поскольку это вектор, берется направление
в учетную запись. Будьте осторожны со своими негативами и позитивами. Поскольку это скалярная величина, она никогда не может быть отрицательной.
Поскольку это скалярная величина, она никогда не может быть отрицательной. 



