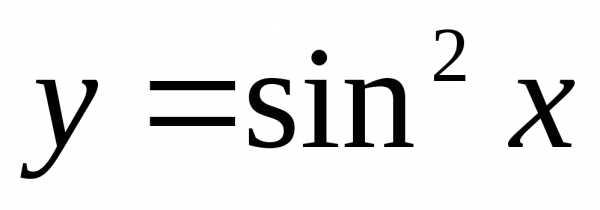Правила и формулы нахождения производных. Производная сложной функции.
Основные правила дифференцирования:
Производная постоянной равна нулю, т.е. .
Производная аргумента равна единице, т.е.
 .
.Производная алгебраической суммы конечного числа дифференцируемых функций равна алгебраической сумме производных этих функций, т.е. .
Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т.е. .
Следствие 1. Постоянный множитель можно выносить за знак производной: .
Производная частного двух дифференцируемых функций может быть найдена по формуле
 (при условии,
что
(при условии,
что  ).
).Производная сложной функции. Пусть задана сложная функция .
Теорема. Если 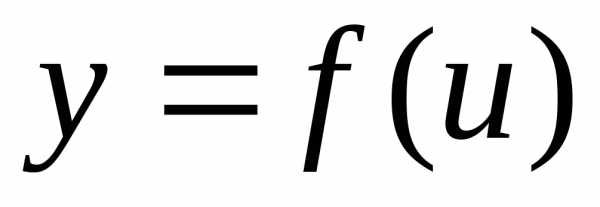
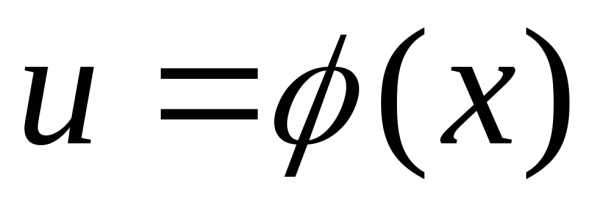
дифференцируемые функции от своих
аргументов, то производная сложной
функции существует и равна производной
данной функции по промежуточному
аргументу и умноженной на производную
промежуточного аргумента по независимой
переменной
дифференцируемые функции от своих
аргументов, то производная сложной
функции существует и равна производной
данной функции по промежуточному
аргументу и умноженной на производную
промежуточного аргумента по независимой
переменной  ,
т.е..
,
т.е..Производные основных элементарных функций (таблица производных):
Производная логарифмической функции.
А) 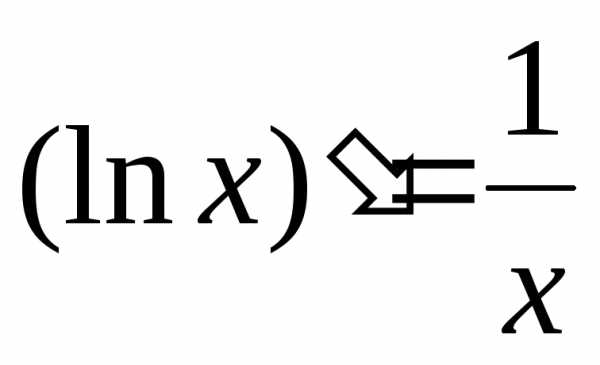 и
и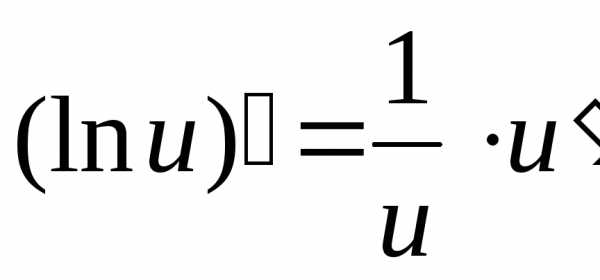

некоторая функция зависящая от
некоторая функция зависящая от 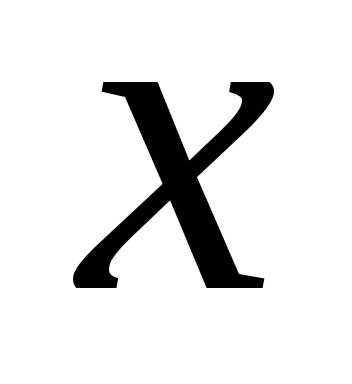 .
. Б) 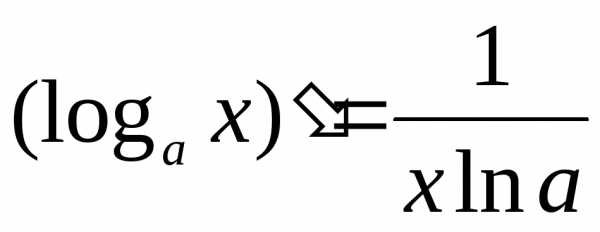 и.
и.
Производная показательной функции.
А) 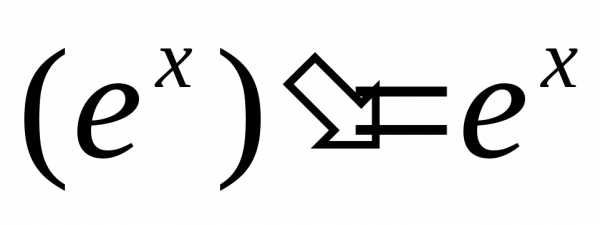 и.
и.
Б) и.
Производная степенной функции.
и .
.
Производная тригонометрических функций.
и ;
и ;
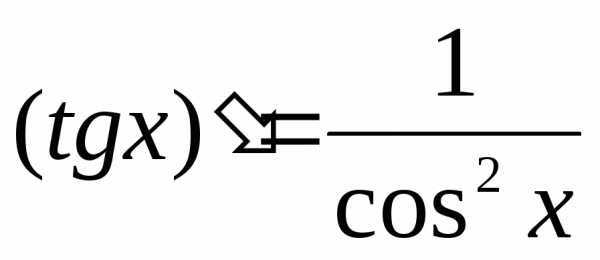 и
и 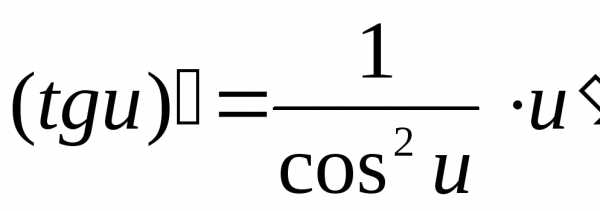 ;
;
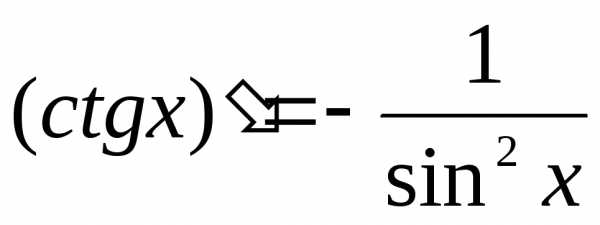 и
.
и
.
Производная обратных тригонометрических функций.
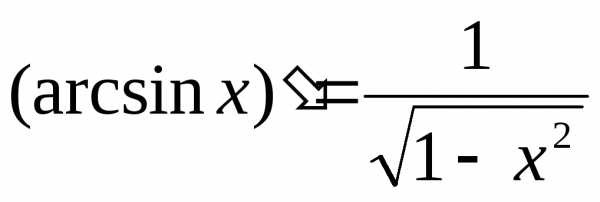
и ;
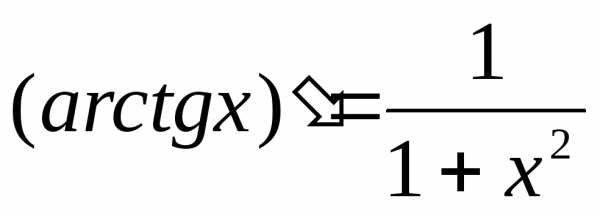 и ;
и ;
и .
Пример. Найти производные следующих функций:
Производные высших порядков.
Производной
второго порядка или второй
производной функции 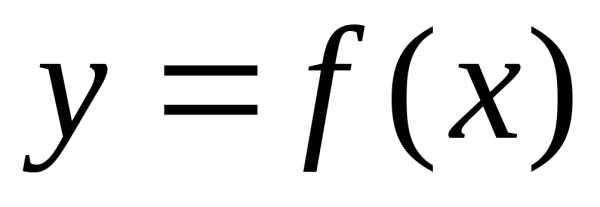 называется производная от ее первой
производной, т.е.
называется производная от ее первой
производной, т.е.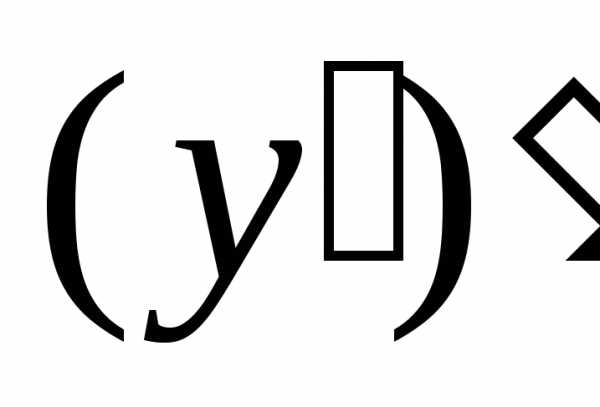 ,
и обозначается
,
и обозначается или
или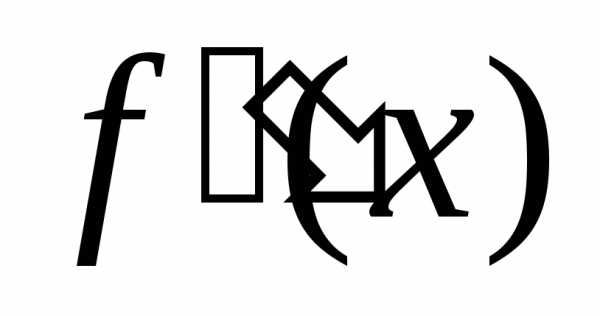
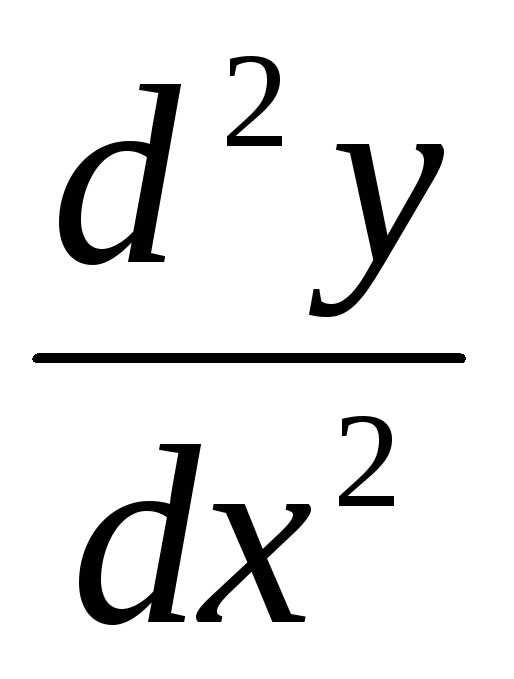 .
. Аналогично
определяются и обозначаются: производная
3-го порядка 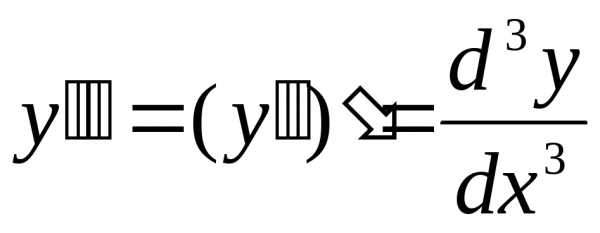 ;
производная 4-го порядка
;
производная 4-го порядка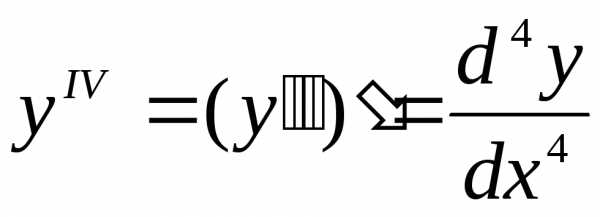 ;
………… производная
;
………… производная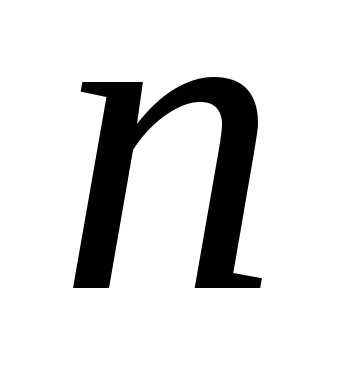 -го
порядка.
-го
порядка.
Пример. Найти производную 2-го и 3-го порядка:
А) | 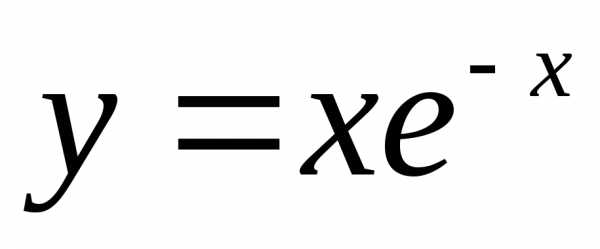 |
Понятие дифференциала и его геометрический смысл.
Пусть функция 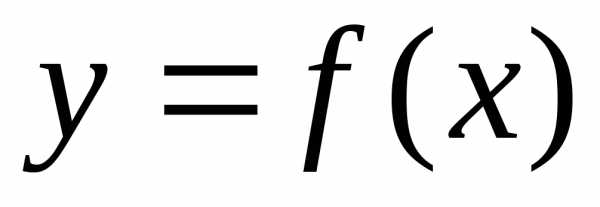 определена на промежутке
определена на промежутке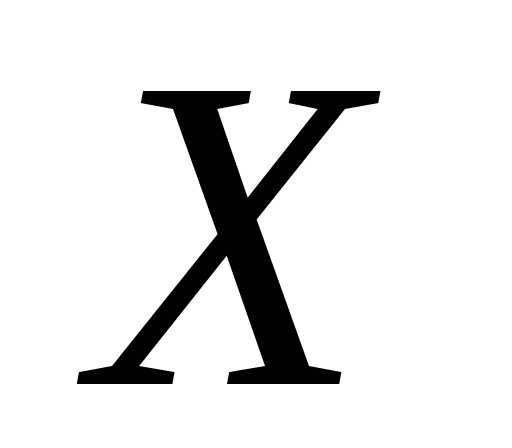 и дифференцируема в окрестности точки
и дифференцируема в окрестности точки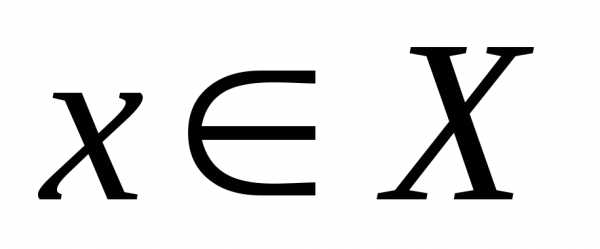 ,тогда
,тогда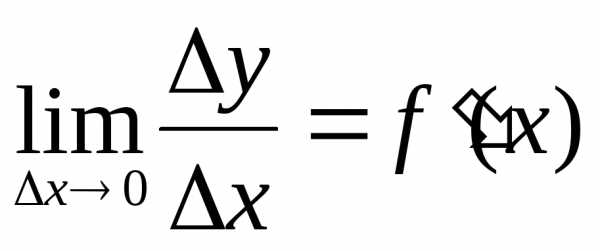 или по теореме о связи бесконечно малых
с пределами функций имеем,
где
или по теореме о связи бесконечно малых
с пределами функций имеем,
где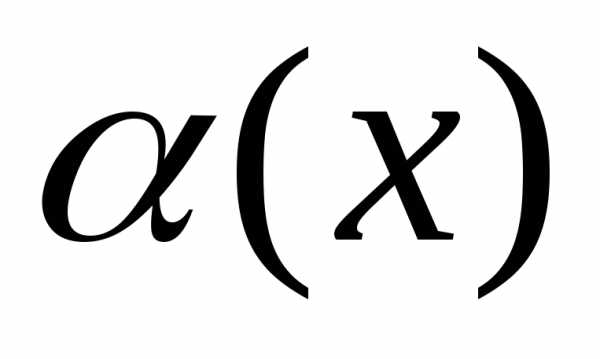
бесконечно малая величина при
.
Отсюда:.
Таким образом, приращение функции
бесконечно малая величина при
.
Отсюда:.
Таким образом, приращение функции

линейного относительно
линейного относительно 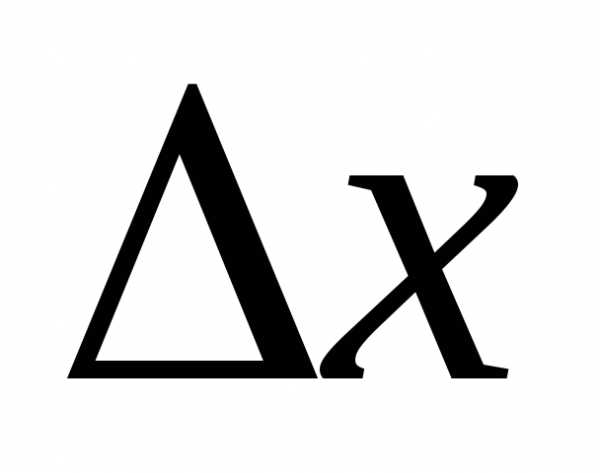 ,
т.к.;
2.
,
т.к.;
2.
нелинейного относительно
нелинейного относительно  ,
т.к..
,
т.к.. Дифференциалом
функции называется главная, линейная относительно 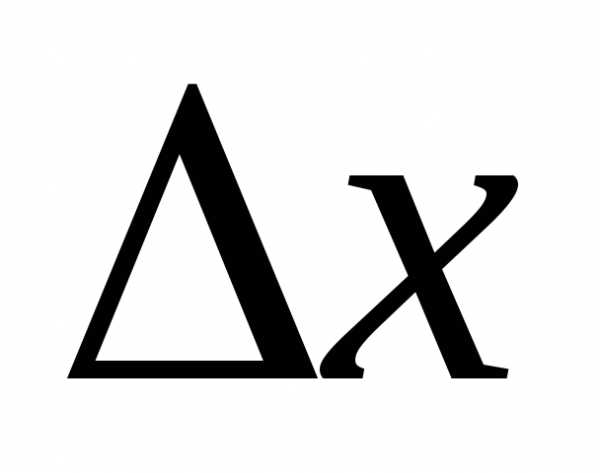 часть приращения функции, равная
произведению производной на приращение
независимой переменной:.
часть приращения функции, равная
произведению производной на приращение
независимой переменной:.
Пример. Найти приращение функции
при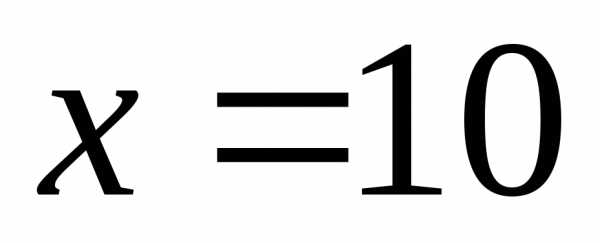 и
и
Пример. Найти дифференциал функции 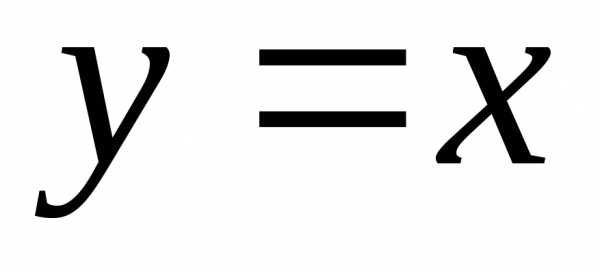 .
.
Дифференциал
независимой переменной 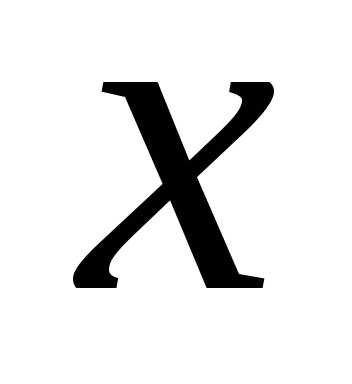 равен приращению этой переменной:.
равен приращению этой переменной:.
Тогда формулу для
дифференциала функции можно записать
в виде:
.
Откуда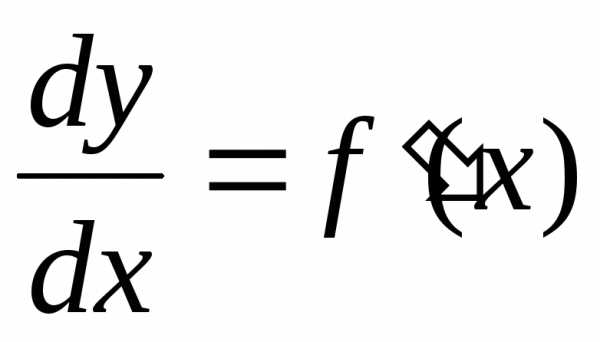
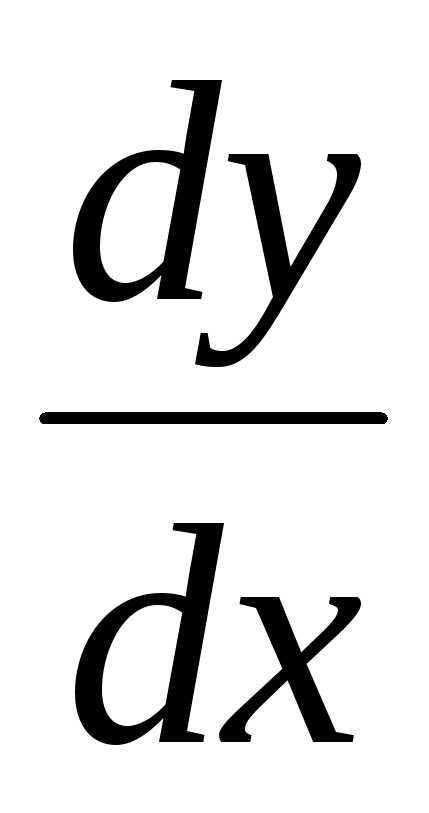 можно рассматривать не только как
символическое обозначение производной,
но и как обычную дробь с числителем
можно рассматривать не только как
символическое обозначение производной,
но и как обычную дробь с числителем и знаменателем
и знаменателем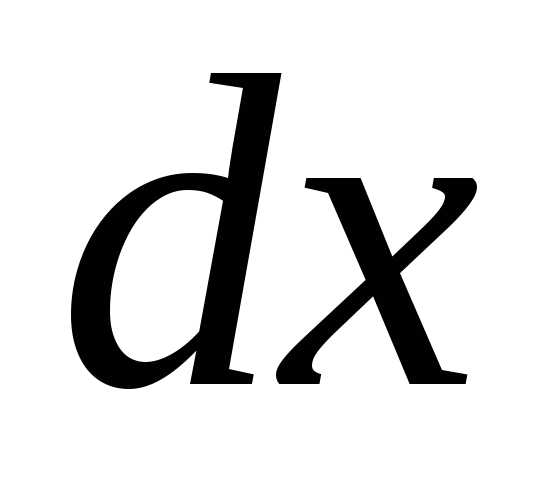 .
. Геометрический
смысл. На
графике функции 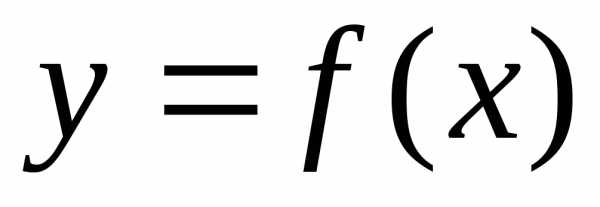 (рис.
5.) возьмем
произвольную точку
(рис.
5.) возьмем
произвольную точку 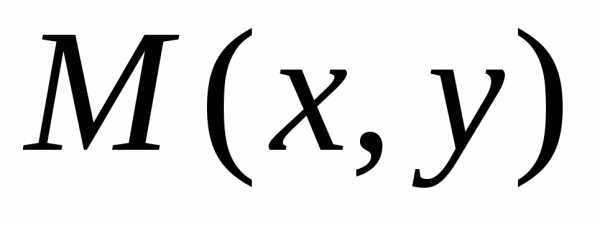 .
Дадим аргументу
.
Дадим аргументу
 ,
тогда функция получает приращение.
В точке
,
тогда функция получает приращение.
В точке проведем касательную, образующую угол
проведем касательную, образующую угол с осью
с осью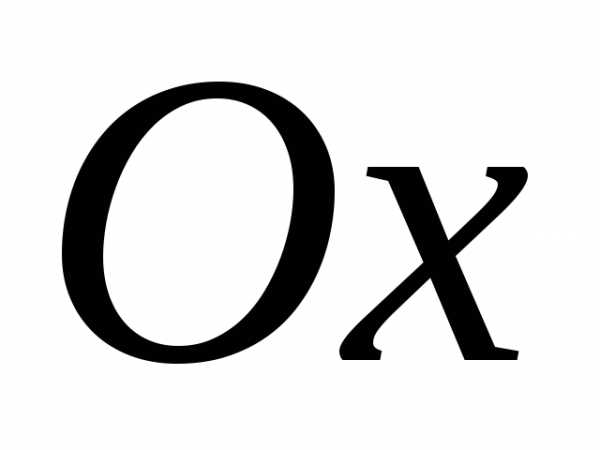 .
Из
.
Из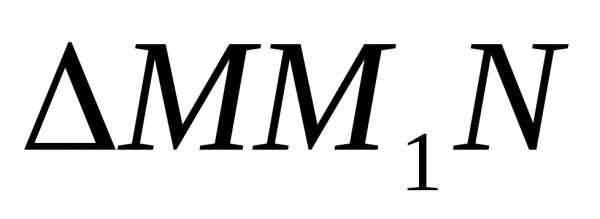 видно,
что.
Из
видно,
что.
Из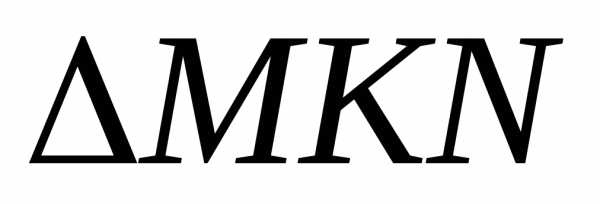 имеем:.
Таким образом,и соответствует формуле.
имеем:.
Таким образом,и соответствует формуле. 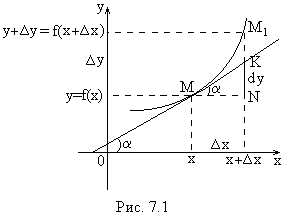
Следовательно, с
геометрической точки зрения дифференциал
функции есть приращение ординаты
касательной, проведенной к графику
функции 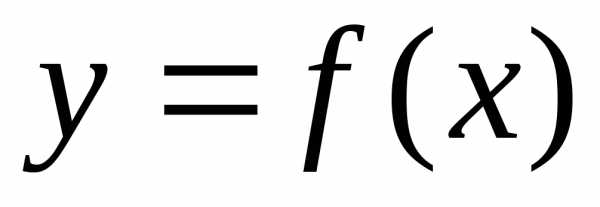 в данной точке, когда
в данной точке, когда получает приращение
получает приращение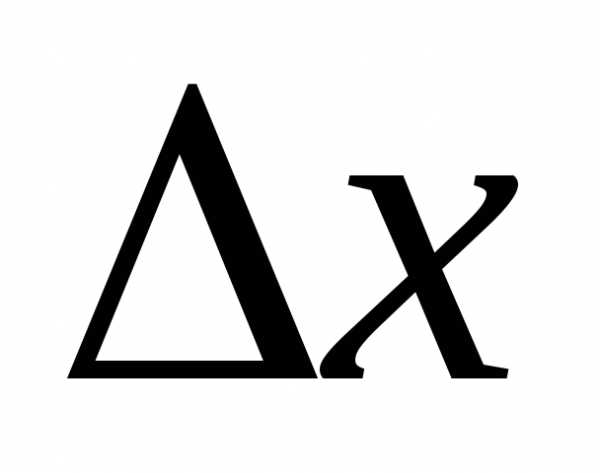 .
.
Свойства дифференциала аналогичны свойствам производной:
Формула дифференциала
не изменится, если вместо функции от
независимой переменной 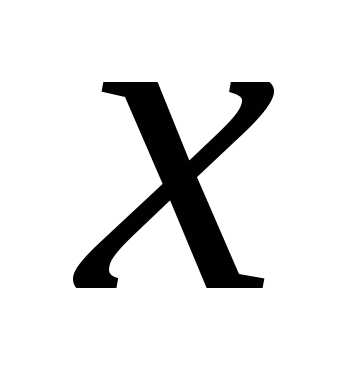 рассматривать функцию от зависимой
переменной
рассматривать функцию от зависимой
переменной
Приближенные
вычисления с помощью дифференциала. Согласно
формулы
,
т.е.,
при достаточно малых значениях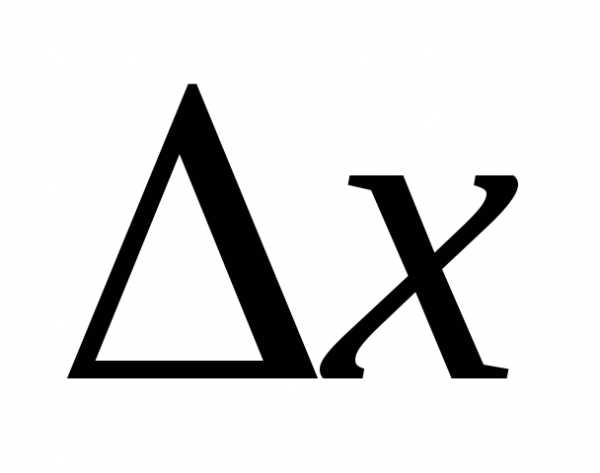 приращение функции
приращение функции приблизительно равно ее дифференциалу
приблизительно равно ее дифференциалу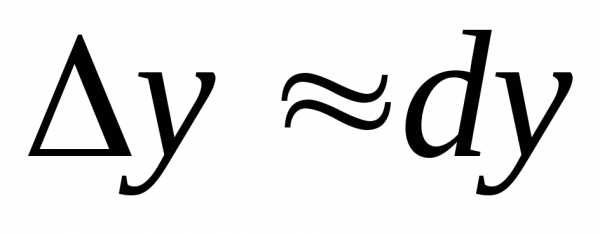 ,.
Эту формулу часто используется в
приближенных вычислениях.
,.
Эту формулу часто используется в
приближенных вычислениях.
Пример. Вычислить  .
.
studfiles.net
Формулы производных
Что такое производная функция – это основное математическое понятие, находится на одном уровне с интегралами, при анализе. Данная функция в определенной точке дает характеристику скорости изменений функции в данной точке.
Такие понятия как дифференцирование и интегрирование, первое расшифровывается как действие поиска производной, второе наоборот, восстанавливает функцию отталкиваясь от данной производной.
Вычислениям производной отводится важная часть в дифференциальных расчетах.
Для наглядного примера, изобразим производную на координатной плоскости.
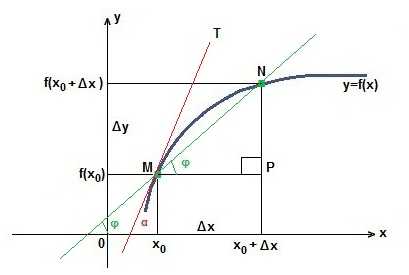
в функции у=f(х) фиксируем точки М в которой (х0; f(X0)) и N f (x0+?x) к каждой абсциссе есть приращение в виде ?x. Приращением называется процесс когда изменяется абсцисса, тогда меняется и ордината. Обозначается как ?у.
Найдем тангенс угла в треугольнике MPN используя для этого точки М и N.
tg? = NP/MP = ?у/?x.
При ?x идущем к 0. Пересекающая МN все ближе к касательной МТ и угол ? будет ?. Следовательно, tg ? максимальное значение для tg ?.
tg ? = lim от ?x-0 tg ? = lim от ?x-0 ?у/?x
Таблица производныхЕсли проговаривать формулировку каждой формулы производных. Таблица будет проще запоминаться.
1) Производная от постоянного значения равняется 0.
2) Х со штрихом равняется единице.
3) Если есть постоянный множитель, просто выносим ео за производную.
4) Чтобы найти производную степень, нужно показатель данной степени умножить на степень с таким же основанием, у которого показатель на 1 меньше.
5) Поиск корня равен одному, деленному 2 этих корня.
6) Производная одного, деленного на Х равняется одному разделенному на Х возведенный в квадрат, со знаком минус.
7) П синус равняется косинусу
8) П косинус равняется синусу со знаком минус.
9) П тангенс равняется одному, деленному на косинус в квадрате.
10) П котангенс равняется одному со знаком минус, деленная на синус в квадрате.
В дифференцировании также существуют правила, которые тоже проще выучить проговаривая их в слух.
1) Очень просто, п. слагаемых равняется их сумме.
2) Производная в умножении равняется умножению первого значения на второе, прибавляя к себе умножение второго значения на первое.
3) Производная в делении равняется умножению первого значения на второе, отнимая от себя умножение второго значения на первое. Дробь деления на второе значение в квадрате.
4) Формулировка является частным случаем третьей формулы.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
Формулы производной | Формулы с примерами
ФормулыПриращение аргумента
Приращение функции
Производная функции ?(x) в точке x0
Касательная к графику
Геометрический смысл производной
Уравнение касательной к графику ? (x)
Физический смысл производной
Правила дифференцирования

Таблица производных
Достаточное условие монотонности функции ? (x)
Экстремумы функции ? (x)
Необходимое условие экстремума ? (x)
Достаточное условие экстремума непрерывной в точке x0 функции ? (x)

formula-xyz.ru

 .
.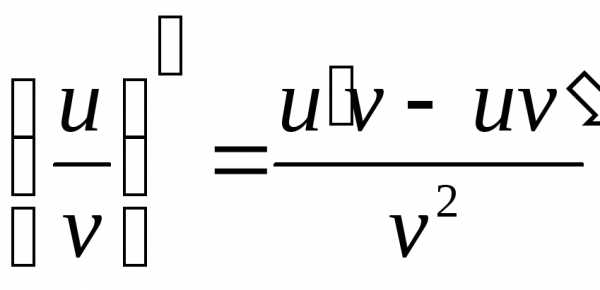 (при условии,
что
(при условии,
что 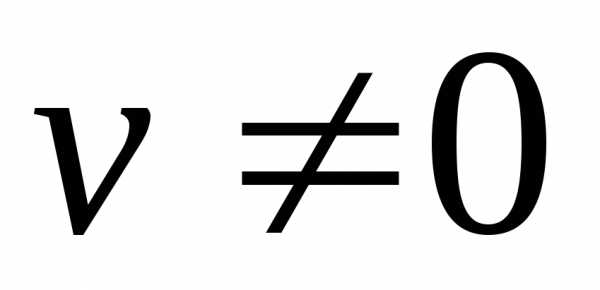 ).
).