Формулы неопределенный интеграл: Формулы и уравнения неопределенных интегралов

{\prime}=x+0=f(x)$

Больше примеров решений Решение интегралов онлайн

Таким образом, если функция $y=f(x)$ имеет первообразную, то она имеет бесконечное множество первообразных.

Теорема

(Об общем виде первообразной для функции)

Если функции $F(x)$ и $\Phi(x)$ – две любые первообразные функции $y=f(x)$, то их разность равна некоторой постоянной, то есть

$$\Phi(x)-F(x)=C=\text { const }$$

Последнюю теорему можно сформулировать иначе: каждая функция, которая является первообразной для функции $f(x)$, может быть представлена в виде $F(x)+C$.

Неопределенный интеграл

Определение

Совокупность всех первообразных функции $y=f(x)$, определенных на заданном промежутке, называется неопределенным интегралом от функции $y=f(x)$ и обозначается символом $\int f(x) d x$. То есть

$\int f(x) d x=F(x)+C$

Знак $\int$ называется интегралом, $f(x) d x$ – подынтегральным выражением

, $f(x)$ – подынтегральной функцией, а $x$ – переменной интегрирования.

Операция нахождения первообразной или неопределенного интеграла от функции $f(x)$ называется интегрированием функции $f(x)$. Интегрирование представляет собой операцию, обратную дифференцированию.

Геометрическая интерпретация неопределенного интеграла

Неопределенный интеграл представляет собой семейство параллельно расположенных кривых $F(x)+C$, где каждому конкретному числовому значению постоянной $C$ соответствует определенная кривая из указанного семейства.

График каждой кривой из семейства называется интегральной кривой.

Теорема

Каждая непрерывная на промежутке $(a ; b)$ функция, имеет на этом интервале первообразную.

Читать дальше: свойства неопределенного интеграла.

Неопределенный интеграл.

Понятие неопределенного интеграла. Дифференцирование – это действие, с помощью которого по данной функции находится ее производная или диф­ференциал. Например, если F(x) = x¹⁰, то F‘ (х) = 10х⁹, dF(х) = 10х⁹ dх.

Интегрирование – это действие, обратное дифференцированию. С помощью интегрирования по данной производной или дифференциалу функции находится сама функция. Например, если

F‘ х = 7x⁶ , то F(х) = х⁷ , так как (х⁷)’ = 7х⁶ .

Дифференцируемая функция F(x), x ]a b[ называется первообразной для функции f(х) на интервале ]a; b[, если F‘(x) = f(x) для каждого

х] а; b [.

Так, для функции f{x) = 1/cos²х первообразной служит функция F(х) = tg х, поскольку (tg x)’= = 1/cos² x.

Совокупность всех первообразных функций f(x) на интервале ]а;b[ на­зывают неопределенным интегралом от функции f(x) на этом интервале и пишут f(x) dx = F(x) + С.

Здесь f(x)dx –подынтегральное выражение; f(x )- подынтегральная функция; х – переменная интегрирования; С – произвольная постоянная.

Например, 5x’dx = х⁵ + С, так как (x⁵ + С)’ = 5х¹.

Приведем основные свойства неопределенного интеграла.

1. Дифференциал неопределенного интеграла равен подынтегральному выражению:

d f(x

)dx = f(x)dx.

2. Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной, т. е.

dF(x) =F(x + C.

3. Постоянный множитель можно выносить за знак неопределенного интеграла:

∫ af(x) dx = a ∫ f(x)dx.

4. Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме неопределенных интегралов от каждой функции:

∫ (f₁ (х) ± f₂ (x)) dx = ∫ f₁ (х) dx ± ∫ f₂ (x) dx.

Основные формулы интегрирования (табличные интегралы).

1.	∫ dx = x + C	7.
2.	∫ xndx = + С (п ≠ – 1)	8.
3.	∫ x-1dx =	9.
4.		10.
5.		11.
6.

Если интеграл затруднительно привести к табличному с помощью элемен­тарных преобразований, то в этом случае пользуются методом подстановки.

Пример 1.

Найти

Решение. Произведем подстановку 2 – Зх² = t; тогда –6xdx = dt, xdx = -(1/6) dt. Далее, получаем

Пример 2. Найти

_{Решение. Сначала положим 2 + cosx = t; тогда 10dx = dt, откуда dx = (1/10) dt.}

_{Далее получаем}

Вопросы и упражнения для самопроверки:

1. Какое действие называется интегрированием?

2. Какая функция называется первообразной для функции f(х)?

3. Дайте определение неопределенного интеграла.

4. Перечислите основные свойства неопределенного интеграла.

5. Каким действием можно проверить интегрирование?

6. Напишите основные формулы интегрирования (табличные интегралы).

7. Найдите интегралы: a) б)

Определенный интеграл.

По данной теме сначала изучите §7-10 (1, 2), 11 (1, 2) гл. 3, §12, 14 (1 – 3) гл. 4 [3] или § 1 – 14 гл. 8 [4]. Затем ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия. Ответьте на вопросы и выполните упражнения для самопроверки. Решите следующие задачи: [3] гл. 3 §10 №3.5-3.8, 3.12, гл. 4 §12 № 4.1, §14 №4.3 – 4.29 или [4], гл. 8 №1-5, 8-13, 17-21, 23-27, 42-49, 50-55, 60-63.

Из контрольной работы выполните четвертое задание своего варианта.

Понятие определенного интеграла. Непосредственное вычисление определенного интеграла производится по

формуле Ньютона—Лейбница;

где a – нижний предел, b – верхний предел, F(x) – какая-нибудь первообразная функции f(x).

Из этой формулы виден порядок вычисления определенного интеграла:

1. Находят одну из первообразных F(x) данной функции;

2. Находят значения F(x) при x = a и x = b;

3. Вычисляют разность F(b) – F(a).

Пример 1. Вычислить интеграл

Решение. Воспользуемся определением степени с дробным и отрицательным показателем и вычислим определенный интеграл:

Приведем основные свойства определенного интеграла.

1. Перестановка пределов интеграла знак интеграла меняется на противоположный:

2. Отрезок интегрирования можно разбивать на части:

3. Постоянный множитель можно выносить за знак интеграла:

4. Интеграл от суммы функций равен сумме интегралов от всех слагаемых:

Пример 2. Вычислить интеграл

Решение.

1. Произведем подстановку x³ + 2 = t; тогда 3x³dx = dt, x²dx =

2. Определим пределы интегрирования для переменной t. При x = 1 получаем t_н = 1³+2 = 3, при x = 2 получаем t_в = 2³ + 2 = 10.

3. Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим:

Пример 3. Вычислить интеграл

Решение.

1. Положим cos x = t; тогда –sin xdx = dt и sin xdx = –dt;

2. Определим пределы интегрирования для переменной t: t_H = cos 0 = t_H = cos (π/2) = 0.

3. Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим:

[PDF] Две формулы для численного неопределенного интегрирования

• title={Две формулы для неопределенного числового интегрирования}, автор={Сеймур Хабер}, журнал={Математика вычислений}, год = {1993}, объем={60}, страницы = {279-296} }
  • С. Хабер
  • Опубликовано в 1993 г.
  • Математика
  • Математика вычислений

  Выведены две формулы для аппроксимации неопределенного интеграла на конечном интервале. Ошибка аппроксимации равномерно равна 0(c-cv’), где m – количество вычислений подынтегральной функции. Подынтегральная функция должна быть аналитической внутри интервала интегрирования, но может быть сингулярной на концах. Некоторые примерные расчеты показывают, что фактическая скорость сходимости соответствует полученной границе ошибки.

  Просмотр через Publisher

  ams.org

  Численное бесконечное интегрирование методом двойного экспоненциального sinc

  • Кенитиро Танака, М. Сугихара, К. Мурота

  • Математика

    Матем. вычисл.

  • 2005

  Численный метод аппроксимации неопределенного интеграла методом двойного экспоненциального синка с N вычислениями подынтегральных функций для достаточно широкого класса подынтегральных выражений, в том числе имеющих концевые особенности.

  Двойные экспоненциальные формулы для численного неопределенного интегрирования

  • М. Мухаммед, М. Мори

  • Математика

  • 2003

  Оценки ошибок с явными констант для квадратуреции SINC и непрекращающейся интеграции SINC в течение бесконечных интервалов

  • 2020202020202020202020202 вычисл.

  • 2013

  Для проверенного автоматического интегрирования недавно были даны более явные вычислимые границы ошибки на конечном интервале, а в остальных случаях даны полубесконечные и бесконечные интервалы.

  Оценки погрешности с явными константами для правила танга и формулы ДУ для неопределенных интегралов

  • Томоаки Окаяма, Такаясу Мацуо, М. Сугихара

  • Математика

    JSIAM Lett.

  • 2010

  Правило танга и формула двойной экспоненты (DE) известны как эффективные квадратурные правила для определенных интегралов на конечном интервале (a, b). В этой заметке мы рассматриваем численный метод для…

  Численное неопределенное интегрирование функций с особенностями

  • Aeyoung Park Jang, S. Haber

  • Математика, информатика

    Math. вычисл.

  • 2001

  На основании теоремы Ганелиуса выведена неопределенная квадратурная формула для H p функций при p > 1 на интервале (-1,1), которая предполагает, что формула имеет наилучшую возможную значение этой константы.

  Оценки ошибок с явными константами для аппроксимации Sinc, квадратур Sinc и неопределенного интегрирования Sinc

  • Томоаки Окаяма, Такаясу Мацуо, М. Сугихара

  • Математика, информатика

    Numerische Mathematik

  • 2013

  Эта статья раскрывает все константы в той же форме, что и вычисление, в той же форме, что и вычисление теоремы: приближаемая функция аналитична в подходящей области.

  Оценки ошибок с явными константами для аппроксимации Sinc, квадратур Sinc и неопределенного интегрирования Sinc

  • Томоаки Окаяма, Такаясу Мацуо, М. Сугихара

  • Математика, информатика

    Numerische Mathematik

  • 2013

  Эта статья раскрывает все константы в той же форме, что и вычисление, в той же форме, что и вычисление теоремы: приближаемая функция аналитична в подходящей области.

  SINC БЕСКОНЕЧНАЯ ИНТЕГРАЦИЯ И ПРОБЛЕМЫ НАЧАЛЬНЫХ ЗНАЧЕНИЙ

  • Ф. Стенгер, Б. Киз, М. О’Рейли, К. Паркер

  • Математика

  • 1992

  Неопределенный интеграл Sinc обсуждался несколькими авторами: Kear-fott (1983), Haber (1991) и Stenger (1981). Следующая презентация суммирует некоторые результаты в…

  Сравнение производительности четырех методов Sinc для численного неопределенного интегрирования

  Цели/задачи: Сравнить производительность четырех методов Sinc для численной аппроксимации неопределенных интегралов с алгебраическим или логарифмическим окончанием. -точечные особенности. Методология:…

  Численное решение дифференциальных уравнений интеграции, основанных на двойной экспоненциальной трансформации в методе SINC-Collocation

  • M. A. Araghi, G. K. Gelian

  • Matematics

  • 2012

  В этой статье мы рассмотрим Double Expronations (DE). решать интегро-дифференциальные уравнения методом коллокаций Синка. Численные примеры иллюстрируют обоснованность и применимость…

  ПОКАЗАНЫ 1-9 ИЗ 9 ССЫЛОК

  Синк-аппроксимация неопределенного интеграла

  • Кирфот Р. Б.

  • Математика

  • 1983

  Описан метод вычисления fo’ f(t), 0 dt, t) может иметь сингулярности при t = 0 и t = 1. Метод зависит от аппроксимационных свойств кардинала Уиттекера, или sinc функций

• 1981

В этой статье обобщаются известные на сегодняшний день результаты использования синусоидальных функций, составленных из других функций, в качестве основы для аппроксимаций в численном анализе. В этой статье описаны методы…

Оптимальные квадратуры в H(sub)p-пространствах

• К. Сикорский, Ф. Стенгер

• Математика, информатика

  ACM Trans. Мат. ПО

• 1984

Описано семейство квадратурных оптимальных формул для приближения интеграла ∫ ω −1 ([−1,1]) f(z)dz, или кажущееся в классе Харди Hp(D ),1

Методы автоматических вычислений для специальных функций

• И. Стегун, Р. Цукер

• Информатика

• 1970

Часть I настоящей статьи посвящена функциям ошибки, вероятности и связанным с ними функциям.

Справочник по математическим функциям с формулами, графиками и математическими таблицами (серия № 55 Национального бюро стандартов по прикладной математике)

• М. Абрамовиц, И. Стегун, Дэвид М. Миллер

• Математика

• 1964

Справочник по математическим функциям, предназначенный для обеспечения научных исследований исчерпывающим и самодостаточным обзором математических функций, возникающих в физических и… интеграция в H(sub)p

Эта работа поддерживается исследовательским контрактом армии США DAAG-29-77-G-0139, Департаментом компьютерных наук Колумбийского университета, Нью-Йорк, штат Нью-Йорк 10027, и Университетом Олд-Доминион, Норфолк, Вирджиния. 23508.

Автоматические методы расчета для специальных функций. Часть 3. Синус, косинус, экспоненциальные интегралы и родственные функции

• И. Стегун, Р. Цукер

• Информатика

• 1976

В то время как точность во всей основной области определения сохраняется В связи с этим авторы стремились к методам, которые также обеспечивают эффективность, переносимость и простоту программирования и модификации.

Правило Таня для численного интегрирования 92$. Определен оптимальный выбор параметров и показано, что норма функционала ошибки равна…

Кардинальная функция Уиттекера в ретроспективе*

• Дж. Макнейми, Ф. Стенгер, Э. Уитни

• Математика

• 197111

В этой статье раскрываются свойства кардинальной функции Уиттакера и иллюстрируется использование этой функции в качестве математического инструмента. Кардинальная функция выводится с использованием теоремы Пэли-Винера. В…

Unit-4:Integration – исследование BCA

Список интегральных формул
Список интегральных формул: (n+1))+С; n≠1
∫ sin x dx = – cos x + C
∫ cos x dx = sin x + C
∫ sec2 dx = tan x + C
∫ csc2 dx = -cot x + C
∫ sec x (tan x ) dx = sec x + C
∫ csc x ( cot x) dx = – csc x + C
∫ (1/x) dx = ln |x| + C
∫ ex dx = ex+ C
∫ ax dx = (ax/ln a) + C ; a>0, a≠1
Эти интегральные формулы так же важны, как и формулы дифференцирования.

Некоторые другие важные формулы интегрирования:

Вывод формулы интегрирования по частям

Если u(x) и v(x) любые две дифференцируемые функции одной переменной y. Тогда по правилу дифференцирования произведения получаем;

u’ — производная от u, а v’ — производная от v.

Чтобы найти значение ∫vu′dx, нам нужно найти первообразную v’, присутствующую в исходном интеграле ∫uv′dx.

Примечание:

• Интегрирование по частям неприменимо для таких функций, как ∫ √x sin x dx.
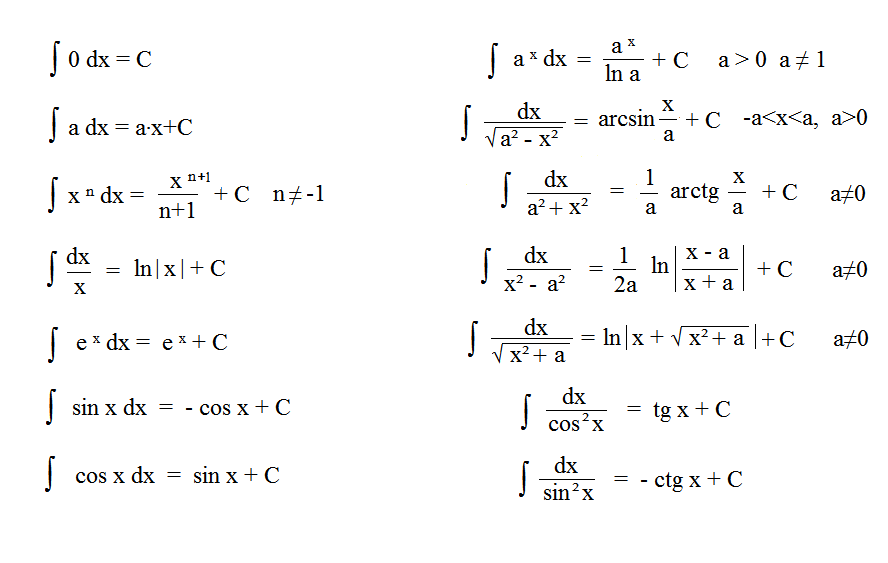
• Мы не добавляем никаких констант при нахождении интеграла второй функции.
• Обычно, если какая-либо функция является степенью x или полиномом от x, то мы берем ее в качестве первой функции. Однако в тех случаях, когда другая функция является обратной тригонометрической функцией или логарифмической функцией, мы берем их в качестве первой функции.

Ilate Правило

При интегрировании по частям мы научились, когда нам дано произведение двух функций, тогда мы применяем требуемую формулу. Интеграл двух функций берется, рассматривая левый член как первую функцию, а второй член как вторую функцию. Этот метод называется  Правило Илате.  

Предположим, нам нужно проинтегрировать x e ^x , тогда мы рассматриваем x как первую функцию и e ^x  как вторую функцию. Таким образом, в основном первая функция выбирается таким образом, чтобы производную функции можно было легко проинтегрировать. Обычно порядок предпочтения этого правила основан на некоторых функциях, таких как обратная, алгебраическая, логарифмическая, тригонометрическая, показательная.

Основная теорема исчисления

 Основная теорема исчисления (FTC) показывает, что дифференцирование и интегрирование являются обратными процессами.

Итак, вторая часть основной теоремы гласит, что если мы возьмем функцию F, сначала продифференцируем ее, а затем проинтегрируем результат, мы вернемся к исходной функции, но в виде F(b)−F(a) .

Таким образом, две части основной теоремы исчисления говорят, что дифференцирование и интегрирование являются обратными процессами.

Определенный интеграл как предел суммы.

Свойства определенного интеграла

Существуют некоторые свойства определенного интеграла, которые могут помочь легко решать основанные на нем задачи.

• ∫ _A ^B F (x) DX = ∫ _A ^B F (T) D (T)
• ∫ _A ^B 5. x ^B 5553555. – x ^B 555355. ^A F (x) DX
• ∫ _A ^A F (X) DX = 0
• ∫ _A ^B F (x) DX = ∫ A F F (x) DX = ∫ _A B F (x) DX = ∫ _A B F (x) DX = ∫ _A B F (x). ) dx + ∫ _c ^b f(x) dx
• ∫ _a ^b f(x) dx = ∫ _a ^{b 9 (x)d} 0011 ∫ ₀ ^a f(x) dx = f(a – x) dx

неопределенное интегральное среднее?

Ответ : Неопределенный интеграл относится к функции, которая получает первообразную другой функции. Мы визуально представляем его как интегральный символ, функцию, а после этого dx в конце.

Формулы для неопределенных интегралов

Теперь, когда мы уже позаботились о концепции интегрирования, давайте кратко рассмотрим некоторые из основных формул неопределенных интегралов –

Метод подстановки

В соответствии с методом подстановки заданный интеграл ∫ f(x) dx можно преобразовать в другую форму, заменив независимую переменную x на t. Это делается путем замены x = g (t).

Рассмотрим I = ∫ f(x) dx
Теперь подставим x = g(t) так, чтобы dx/dt = g’(t) или dx = g’(t)dt.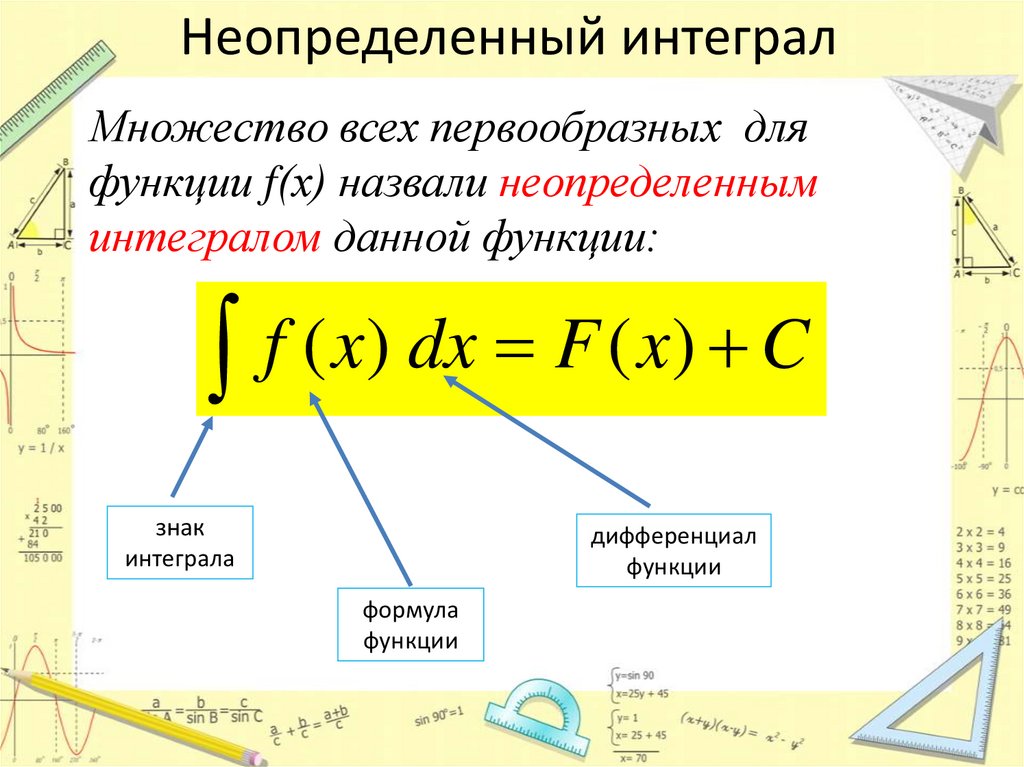
Следовательно, I = ∫ f(x) dx = ∫ f[g(t)] g'(t)dt

Здесь важно отметить, что здесь следует сделать замену функции, производная которой также входит в подынтегральную функцию как показано в следующих примерах.

Интегрирование различных форм с помощью дробей

Допустим, мы хотим вычислить ∫ [P(x)/Q(x)] dx, где P(x)/Q(x) — правильная рациональная дробь. В таких случаях можно записать подынтегральное выражение в виде суммы более простых рациональных функций, используя разложение на неполные дроби. После этого интеграция может быть выполнена легко. На следующем рисунке показаны некоторые простые дроби, которые могут быть связаны с различными рациональными функциями:

Обратите внимание, что A, B и C являются действительными числами, и их значения должны быть определены соответствующим образом.

Примечание. Уравнение (1) верно для всех допустимых значений x. Некоторые авторы используют символ «≡», чтобы указать, что утверждение является тождеством, и используют символ «=», чтобы указать, что утверждение является уравнением, то есть указать, что утверждение верно только для определенных значений x.

Определение.
Для x  положительных значений мы определяем Гамма-функцию  через

В общем случае этот интеграл нелегко вычислить, поэтому сначала мы рассмотрим Гамма-функцию в двух важных моментах. Начнем с x  = 1:

Теперь посмотрим на значение x  = 1/2:

Последний интеграл нельзя вычислить с помощью первообразной . Однако этот конкретный определенный интеграл очень важен (например, в вероятности), поэтому люди в конце концов нашли способ найти его значение.

Чтобы найти значение Гамма-функции в других точках, мы выводим интересное тождество, используя интегрирование по частям:

Предел оценивается с помощью правила Лопиталя несколько раз. Мы видим, что для x  положительно, мы имеем

Если мы применим это к положительному целому числу  n , мы получим

Таким образом, мы видим, что гамма-функция является обобщением факториальной функции.