Формулы основные по кинематике: Какие существуют кинематические формулы? (статья)

Письменный зачет по теме “Кинематика” | Методическая разработка по физике (9, 10 класс) на тему:

Опубликовано 03.04.2018 – 0:58 – Стручкова Лариса Владимировна

Данная работа содержит обобщающее повторение учебного материала по теме “Кинематика”. Проверяются основные понятия, буквенное обозначение кинематических величин и их единицы измерения, основные формулы кинематики. Также предложено задание на применение имеющихся знаний по кинематике: определить перемещение по графику скорости или по уравнению координаты записать уравнение скорости. Зачетная работа представлена в 6 вариантах. Работу можно предложить учащимся 9 класса и учащимся 10 класса (базовый уровень).

Скачать:

Предварительный просмотр:

Класс_____________

Ф.И.__________________________________

Письменный зачет по теме «Кинематика»

1. Записать название физического понятия:

• изменение координаты тела – _____________________________________________________
• линия, вдоль которой движется тело, – _____________________________________________
• быстрота изменения скорости – ___________________________________________________

2. Записать буквенное обозначение физической величины:

• вектор начальной скорости – _______, проекция ускорения – ______, координата – __________

3. Записать единицу измерения:

• для времени – ______,  для  скорости -________, для координаты – _________

4. Записать формулу:

• уравнение перемещения – __________________________________________________________

• уравнение координаты – ___________________________________________________________

• для расчета ускорения – ___________________________________________________________

5. Определить перемещение за время t =10с.    

Класс_____________

Ф.И.__________________________________

Письменный зачет по теме «Кинематика»

1. Записать название физического понятия:

• быстрота изменения координаты тела – ______________________________________________
• изменение положения тела в пространстве относительно других тел – ____________________
• определяет положение тела в пространстве – __________________________________________

2. Записать буквенное обозначение физической величины:

• вектор перемещения – _______, проекция скорости – ______, модуль ускорения – __________

3. Записать единицу измерения:

• для перемещения – ______,  для скорости – ________, для ускорения – _________

4. Записать формулу:

• для расчета ускорения – ___________________________________________________________

• для расчета перемещения без времени t – ____________________________________________

• уравнение скорости – _____________________________________________________________

5. По уравнению координаты записать уравнение скорости:

x = 25t + 3t2

Класс_____________

Ф. И.__________________________________

Письменный зачет по теме «Кинематика»

2. Записать название физического понятия:

• быстрота изменения скорости – _____________________________________________________
• тело, размерами которого можно пренебречь, – ________________________________________
• величина, определяющая положение тела в пространстве, – _____________________________

2. Записать буквенное обозначение физической величины:

• проекция скорости – _______, модуль ускорения – ______, начальная координата – __________

3. Записать единицу измерения:

• для перемещения – ______,  для ускорения – ________, для скорости – _________

4. Записать формулу:

• для расчета перемещения без времени t – _____________________________________________

• для расчета ускорения – ___________________________________________________________

• уравнение координаты – ___________________________________________________________

5. Определить перемещение за время t =10с.    

Класс_____________

Ф.И.__________________________________

Письменный зачет по теме «Кинематика»

3. Записать название физического понятия:

• быстрота изменения координаты тела – ______________________________________________
• изменение положения тела в пространстве относительно других тел – ____________________
• изменение координаты тела – ______________________________________________________

2. Записать буквенное обозначение физической величины:

1. проекция перемещения – _______, модуль скорости – ______, вектор ускорения – __________

3. Записать единицу измерения:

• для координаты – ______,  для скорости – ________, для ускорения – _________

4. Записать формулу:

• уравнение перемещения – _________________________________________________________

• для расчета мгновенной скорости – __________________________________________________

• для расчета ускорения – ___________________________________________________________

5. По уравнению координаты записать уравнение скорости:

x = 100 + 15t – 2t2

Класс_____________

Ф. И.__________________________________

Письменный зачет по теме «Кинематика»

4. Записать название физического понятия:

• быстрота изменения координаты тела – ______________________________________________
• тело, размерами которого можно пренебречь, – ________________________________________
• величина, определяющая положение тела в пространстве, – _____________________________

2. Записать буквенное обозначение физической величины:

• модуль скорости – _______, вектор ускорения – ______, начальная координата – __________

3. Записать единицу измерения:

• для перемещения – ______,  для ускорения – ________, для скорости – _________

4. Записать формулу:

• для расчета перемещения без времени t – _____________________________________________

• для расчета ускорения – ___________________________________________________________

• уравнение координаты – ___________________________________________________________

5. Определить перемещение за время t =15с.    

Класс_____________

Ф.И.__________________________________

Письменный зачет по теме «Кинематика»

5. Записать название физического понятия:

• быстрота изменения скорости – _____________________________________________________
• линия, вдоль которой движется тело, – _____________________________________________
• изменение координаты тела – ______________________________________________________

2. Записать буквенное обозначение физической величины:

• модуль перемещения – _______, проекщия скорости – ______, вектор ускорения – __________

3. Записать единицу измерения:

• для координаты – ______,  для скорости – ________, для ускорения – _________

4. Записать формулу:

• для расчета ускорения – ___________________________________________________________

• уравнение перемещения – _________________________________________________________

• для расчета мгновенной скорости – __________________________________________________

5. По уравнению координаты записать уравнение скорости:

x = 10 – 5t – t2

По теме: методические разработки, презентации и конспекты

ИЗ ИСТОРИИ ПИСЬМЕННОСТИ КОНСПЕКТ ВНЕКЛАССНОГО ЗАНЯТИЯ ПО РУССКОМУ ЯЗЫКУ ИЗ ИСТОРИИ ПИСЬМЕННОСТИ Цель занятия: познакомить учащихся с истоками возникновения славянской письменности.

КОНСПЕКТ ВНЕКЛАССНОГО ЗАНЯТИЯ ПО РУССКОМУ ЯЗЫКУИЗ ИСТОРИИ ПИСЬМЕННОСТИЦель занятия:  познакомить учащихся с истоками возникновения славянской письменности. Наше внеклассное мероприятие по русском…

Выявление недостатков устной и письменной речи у учащихся начальных классов. Рекомендации учителям начальных классов по работе с детьми, имеющими недостатки устной и письменной речи.

В данном материале в доступной форме описываются рекомендации учителя-логопеда учителям начальных классов по выявлению обучающихся с недостатками устной и письменной речи и своевременной помощи данной…

Славянская письменность. Презентация к 1150-летию славянской письменности.

Материал посвящен 1150-летию славянской письменностии был представлен для участия в муниципальном конкурсе презентаций обучающихся 7-8 классов, посвященном этому юбилею. В нем рассматривается вопросы …

Письменный зачет по геометрии за 1 полугодие (8 класс)

Задачи из базы ОГЭ…

Материалы для проведения устно-письменного зачета по геометрии (8 класс, УМК: Атанасян Л.

С. и др., 2016-2017 учебный год). Тема: «Четырехугольники»

В течение многих лет работы я использую форму устно-письменного зачета как средство индивидуального контроля качества усвоения учебного материала. Зачет проводится в течение 2 уроков, в ходе которого …

Методическая разработка письменного зачета по литературе (8 класс)

Методическая разработка письменного зачета по литературе (8 класс)по рассказу И.С.Тургенева “Ася”Учащимся 8 класса предлагается письменно ответить на ряд вопросов по содержанию рассказа. За …

Письменный зачет по геометрии по теме “Параллельные прямые”

Для проведения зачета разработано 2 варианта. Каждый вариант разбит на 3 блока:I. Заполнить пропуски, чтобы получились верные утверждения.II.Установить, истинны или ложны следующие утверждения.III.Реш…

Поделиться:

 

Основные уравнения кинематики — Грег Скул

Уравнения, управляющие движением снаряда

Как описать движение пушечного ядра? В более общем смысле, как мы описываем движение любого объекта, движущегося вблизи поверхности Земли? Поиск ответов на эти вопросы был борьбой, длившейся почти 2500 лет, которая началась еще с Аристотеля. Только когда Ньютон и Либнез изобрели исчисление, у нас появилась математика, необходимая для описания движения снаряда. Всякий раз, когда какой-либо объект приближается к поверхности Земли, вся планета Земля оказывает «притяжение» на этот объект в направлении вниз к земле. Это «притяжение» всегда имело одинаковую силу и всегда было направлено вниз. На вопрос, почему Земля постоянно притягивает объекты, впервые ответил Ньютон, когда открыл универсальный закон всемирного тяготения. Этот закон гласит, что среди всех триллионов галактик, которые мы видим (и, возможно, больше, если там будет больше вещества), вся эта материя или «вещество» обладает свойством, называемым массой, и притягивается к каждой из них. другой. Для Ньютона, должно быть, было удивительным осознание того, что пылинка в его комнате притягивает к себе другую пылинку по ту сторону Вселенной — да и все остальное во Вселенной.

Из повседневного опыта мы знаем, что когда мы «тянем» что-то, это «тянет», в общем, приводит к движению этого предмета. Мы также знаем из общего опыта, что должна существовать какая-то связь между силой притяжения и тем, насколько сильно изменяется движение объектов. Если я очень слабо потяну стул, он может немного сдвинуться; но если я потяну тот же самый стул изо всех сил, он может полететь через всю комнату. Мы также знаем из повседневного опыта, что то, насколько тяжело или массивно что-либо, также должно быть связано с изменением его движения по инерции. Например, если я потяну за небольшой камешек, я могу довольно легко изменить его движение по инерции; но если я попытаюсь потянуть Эмпайр Стейт Билдинг, он вообще не сдвинется с места.

Все эти величины связаны друг с другом математически в соответствии со вторым законом Ньютона, который гласит, что «притяжение» или «толчок» \(\vec{F}\) равно массивности объекта (т.е. представленный \(m\)) умноженный на его мгновенное ускорение: \(\vec{F}=m\vec{a}\). Из закона всемирного тяготения Ньютона и второго закона мы можем заключить, что: Земля оказывает «притяжение» на объект, и это «притяжение» в направлении вниз приводит к ускорению объекта на величину \(\vec{a}\) в направлении вниз, что означает, что скорость объекта должна изменяться в направлении вниз.

Я попытался дать некое дружеское введение в закон всемирного тяготения Ньютона и второй закон, которые вместе описывают, почему объект падает. Эти законы также говорят нам, что сила \(\vec{F}_g\), с которой Земля притягивает объекты, всегда будет направлена ​​вниз, к земле. Это означает, что ускорение объектов по направлению к земле (которое мы назовем \(\vec{g}\)) также всегда будет направлено вниз и будет иметь одинаковую постоянную величину.

Хорошо иметь хоть какое-то представление о том, что дальнейшие результаты, которые мы получим с помощью алгебры и исчисления, по существу исходят из законов Ньютона. Поскольку, как я уже говорил в предыдущем уроке, кинематика сводится к описанию движения объекта без учета того, что вызвало это движение (которой была сила \(\vec{F}_g\)), мы не будем вдаваться в подробности. любые дополнительные сведения о том, почему объект движется так, как он это делает. Оставим это для уроков динамики и механики.

Постоянное нисходящее ускорение любого произвольного объекта с любой произвольной траекторией вблизи поверхности Земли определяется выражением

$$\frac{d\vec{v}}{dt}=\vec{g}=9. 8\frac{m} {s}(-\hat{j}).\tag{1}$$

Ускорение \(\vec{g}(t)\) (его можно записать как функцию времени, хотя оно и является константой ) является своего рода «\(f'(x)\)-подобной функцией». Как я говорил в своих уроках по исчислению с одной переменной, исчисление связано с математическими инструментами, которые нужно использовать, чтобы переходить туда и обратно между \(f(x)\) и \(\frac{df}{dx}\) когда \(\frac{df}{dx}\) не является константой. Мы используем интегралы для перехода от \(\frac{df}{dx}\) к \(f(x)\) и производные для перехода от \(f(x)\) к \(\frac{df}{dx }\). К сожалению, когда \(f'(x)\) продолжает меняться, нам приходится использовать эти два математических инструмента, чтобы получить площадь или наклон.

Наша цель — найти движение \(\vec{R}(t)\) объекта. Если вы заметили это из предыдущего урока, вы получите подсказку о том, как мы можем определить \(\vec{R}(t)\) по заданному \(\vec{g}(t)\): обратите внимание, что \ (\vec{R}(t)\) и \(\vec{v}(t)\) подобны \(f(x)\) и \(f'(x)\), и что \(\ vec{v}(t)\) и \(\vec{g}(t)\) подобны \(g(x)\) и \(g'(x)\).

В моих уроках по исчислению с одной переменной я объясняю, как перейти от некоторой функции \(h'(x)\) к функции \(h(x)\), вы должны найти площадь под \(h ‘(Икс)\). Когда \(h'(x)\) является константой, найти площадь довольно просто. В уравнении (1) функция \(\frac{d\vec{v}}{dt}\) является константой (мы подробно объясним почему, когда будем рассматривать динамику), а площадь под этой функцией равна \ (gΔt+C\). Мы также можем взять интеграл с обеих сторон уравнения (1) и использовать правила интегрального исчисления (хотя на этом шаге нет необходимости получать

$$\int{\frac{d\vec{v}(t)}{dt}}dt=\int{\vec{g}(t)}dt$$

$$\vec{v} (t)=\vec{g}(t)t+c.\tag{2}$$

Чтобы найти константу \(C\), мы можем просто установить \(t=0\), что даст нам \ (С=\vec{v}(0)\). Таким образом, \(C\) равно начальной скорости \(\vec{v}(0)\), которую мы представим как \(\vec{v}_0\). Если мы подставим \(c\) в уравнение (2), мы получим

$$\vec{v}(t)=\vec{v}_0+\vec{g}(t)t.\tag{ 3}$$

Остался последний шаг: перейти от \(\vec{v}=\frac{d\vec{R}}{dt}\) к \(\vec{R}( т)\). В отличие от случая, когда мы перешли от \(\vec{a}=\frac{d\vec{v}}{dt}\) к \(\vec{v}\), на этот раз производные функции продолжают изменяться и не являются постоянный. Это означает, что на этот раз нам действительно нужно взять интеграл, чтобы получить площадь и найти \(\vec{R}(t)\). Взяв интеграл от обеих частей уравнения (3), получим 92.\tag{6}$$

Уравнения (6) являются основными уравнениями кинематики, которые мы используем для описания объектов, движущихся вблизи поверхности Земли под действием земного притяжения, поэтому они используются в задачах о движении снарядов. Используя интегральное исчисление и законы Ньютона, мы смогли вывести уравнения движения для всех земных объектов, что отсылает нас к некоторым величайшим мыслителям за последние 2500 лет.

Уравнения кинематики, управляющие движением снаряда (или вы могли бы также назвать его земным движением), — одно из первых великих обобщений в истории физики. Одно из основных направлений работы Грега Школы будет заключаться в рассмотрении множества приложений каждого из великих обобщений в физике.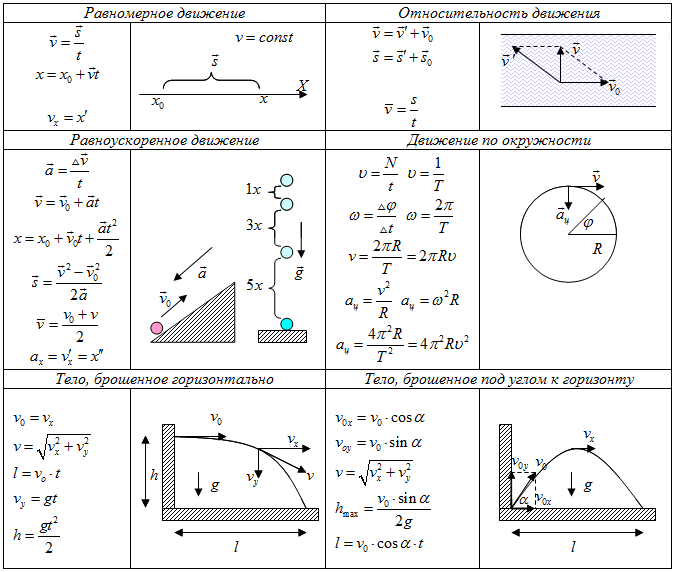 По педагогическим соображениям мы всегда будем начинать с простых приложений, а также с нескольких сложных, чтобы понять, как они используются на практике. Но мы также всегда будем стремиться к возвышенному и глубокому: мы также уделим значительное внимание некоторым наиболее важным приложениям, некоторые из которых значительно изменили качество нашей жизни и наш взгляд на вселенную. 92.\tag{8}$$

Есть два других уравнения, которые обычно используются в кинематике, над выводом которых мы сейчас поработаем. Первый довольно простой. Мы знаем, что если объект движется с постоянной скоростью (где \(\vec{a}=0\)), то его движение можно описать уравнением \( Δ R=vt\). Теперь средняя скорость объекта определяется как \(\bar{v} ≡\frac{v_0+v}{2}\). Но обратите внимание, что поскольку \(v\) является константой, отсюда следует, что скорость \(v_0\) (в какой-то момент \(t_0\)) должна быть такой же, как скорость \(v\) (в какой-то момент \ (т\)). Таким образом,

$$\bar{v}=\frac{v_0+v}{2} = \frac{v+v}{2}= \frac{2v}{2}=v. $$

Другими словами , мы можем подставить \(\frac{v_0+v}{2}\) вместо \(v\) в уравнение \( Δ R=vt\), чтобы получить

$$ΔR=(\frac{v_0+v }{2})t.\tag{9}$$

Уравнение (9) является третьим уравнением в стандартных уравнениях кинематики. Чтобы вывести четвёртое уравнение кинематики, нам просто придётся проделать много алгебраических операций и сделать много замен. Выполнив некоторые алгебраические вычисления с обеих сторон уравнения (9), мы находим, что время определяется как 92+2aΔR.\tag{12}$$

Уравнения (12) являются стандартными уравнениями кинематики. Какое уравнение используется, зависит от начальных условий задачи, которую мы обсудим на следующем уроке, где мы поговорим о практическом применении уравнений (12).

Дополнительная литература

1. «Что такое кинематические формулы?» khanacademy.org . Академия Хана. Веб. 08/2017.

Примечания

1. Мы не будем включать уравнение \(\frac{d\vec{v}}{dt}=\vec{a}(t)\), так как это уравнение не входит в четыре стандартных уравнения кинематики.

Уравнения кинематики – ФИЗИЧЕСКИЕ РАСЧЕТЫ

Содержание

Что такое уравнения кинематики в физике?

Уравнения кинематики в физике представляют собой набор уравнений, описывающих движение объектов с точки зрения положения, скорости, ускорения и времени. Эти уравнения получены из трех основных уравнений кинематики:

Как получить уравнения кинематики уравнения кинематики

Первое уравнение

v = u + at

Second equation

s = ut + (1/2)at ²

Third equation

v ² = u ² + 2as

Fourth Equation

s = [ (u + v) / 2 ] x t

Где:

• v — конечная скорость
• u — начальная скорость
• а это ускорение
• с – водоизмещение
• т это время

Первое кинематическое уравнение	V = U + при
Второе кинематическое уравнение	S = UT + (1/2) в 2
ТРЕТКА ТРЕТКА KINEM
ТРЕТКА TTER THIT + 2as

Три (3) уравнения в табличной форме

Приведенные выше уравнения справедливы только для движения с постоянным ускорением. Следовательно, ускорение остается постоянным на протяжении всего движения. Для неравномерно ускоренного движения уравнения движения более сложны.

Объяснение уравнений кинематики

Если вы когда-либо занимались спортом, ездили на машине или просто шли по улице, вы испытывали движение. Но задумывались ли вы когда-нибудь об основных принципах движения? Кинематика — раздел физики, изучающий движение. С другой стороны, уравнения кинематики — это математические формулы, которые мы используем для описания и предсказания поведения движущихся объектов .

На самом базовом уровне кинематика — это изучение движения без учета вызывающих его сил. Кроме того, мы также называем уравнения кинематики уравнения движения . Это математические формулы, описывающие взаимосвязь между положением, скоростью и ускорением объекта во времени. Следовательно, эти уравнения имеют фундаментальное значение для понимания и предсказания поведения движущихся объектов. В этой статье мы рассмотрим основы уравнений кинематики, как они работают и почему они важны.

Перемещение, скорость и ускорение

Чтобы понять уравнения кинематики, важно сначала понять понятия перемещения, скорости и ускорения. Смещение — это изменение положения объекта от его начального местоположения до его конечного местоположения. Скорость — это скорость, с которой объект меняет свое положение. Ускорение — скорость, с которой объект изменяет свою скорость.

Как вывести уравнения кинематики

Вывод уравнений кинематики основан на следующих предположениях:

• Объект движется по прямой.
• Ускорение постоянное.
• Скорость и ускорение имеют одинаковое направление.

Используя эти предположения, мы можем вывести кинематические уравнения.

Получение первого уравнения движения

Мы можем вывести первое уравнение, используя определение ускорения, которое представляет собой скорость изменения скорости во времени.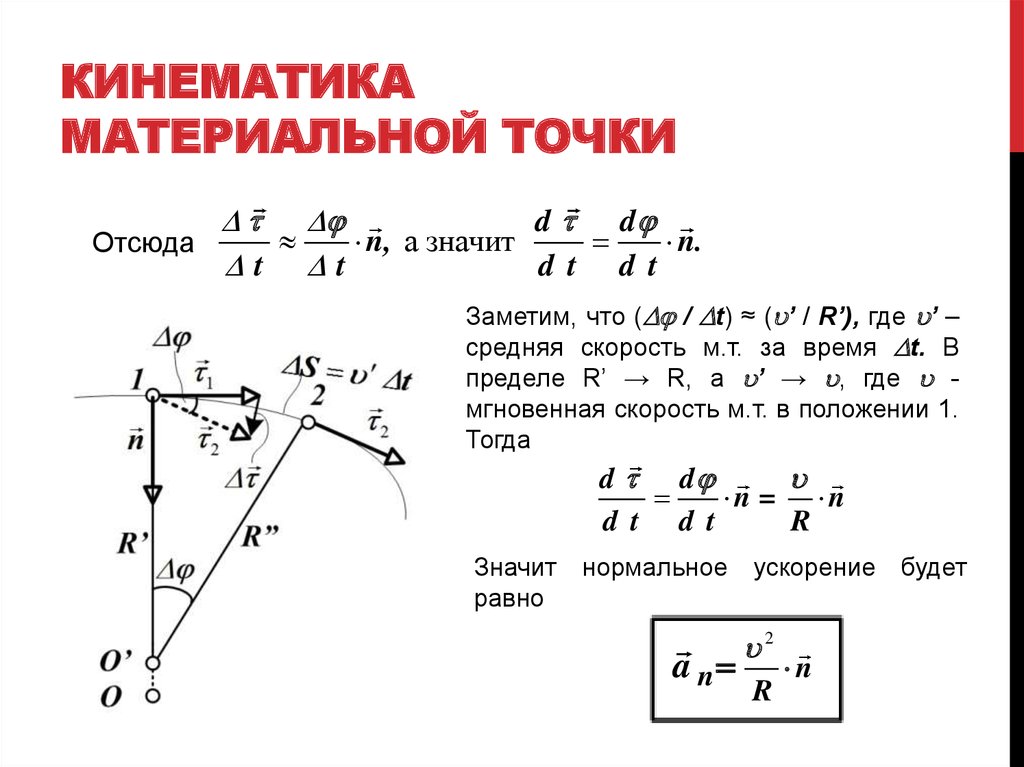 Следовательно, теперь мы можем написать:

Ускорение, a = изменение скорости (v – u) / время (t)

Что станет

a = (v – u) / t [Помните, что ускорение, а = изменение скорости/времени]

После преобразования приведенного выше уравнения и превращения v в субъект формулы мы получим:

v = u + at [Это первое уравнение движения]

Вывод второго уравнения движения

Чтобы получить второе уравнение, применим определение перемещения. Поскольку мы знаем, что смещение — это изменение положения объекта. Точно так же мы можем определить смещение как меру разницы между двумя точками в определенном направлении. Следовательно, приведенное выше утверждение приведет нас к уравнению ниже

Поскольку средняя скорость v _a = (u + v) / 2

Следовательно, пройденное расстояние станет равным

с = [(u + v) / 2] t [Поскольку v = s/t, что показывает что s = vt]

Мы можем подставить v = u + at в приведенное выше уравнение, чтобы получить

s = [(u + v) / 2] t = [(u + u + at) / 2] t

Таким образом,

Мы будем иметь s = [(2u + at)/2]t = ut + (1/2)at ²

Следовательно, наше второе уравнение движения будет

s = ut + (1/2)at ²

Вывод третьего уравнения движения

Третье уравнение выводится с использованием первых двух уравнений и исключения времени. Мы можем написать:

v = u + at

Так как s = ut + (1/2)at ²

Следовательно,

Возводя в квадрат обе стороны v = u + at , мы получим

v ² = (и + ат)(и + ат) = и ² + 2иат + а ² t ²

Следовательно,

v ² = u ² + 2a[ut + (1/2)at ² ]

и ut + (1/2)at 4 9014 s

Таким образом, наше третье уравнение движения будет иметь вид

v ² = u ² + 2as

. и робототехника. Вот некоторые из приложений кинематических уравнений:

• Расчет траектории снаряда. Уравнения кинематики можно использовать для расчета пути снаряда, такого как пушечное ядро ​​или ракета, под действием силы тяжести.
• Проектирование американских горок: уравнения кинематики можно использовать для проектирования американских горок путем вычислений

Решенные задачи с использованием уравнений кинематики

Преобразование процентов в дроби

Включите JavaScript

Преобразование процентов в дроби

Вот несколько решенных задач, которые помогут вам понять, как применять кинематические уравнения (уравнения движения):

Задача 1

Автобус, движущийся со скоростью 60 км/ч, равномерно ускоряется со скоростью 5 м/с ² . Определить его скорость через 2 мин.

Ответ

Окончательный ответ на этот вопрос: 617 м/с или 2221 км/ч. 60 х 60 = 16,6 м/с = 17 м/с

Ускорение, a = 5 м/с ²

Время, t = 2 мин = 2 x 60 = 120 секунд

Неизвестно

Конечная скорость, v = ?

Формула

Применим первое уравнение движения v = u + at

Решение

Подставим наши данные в формулу ) = 617 м/с

Мы можем преобразовать приведенный выше ответ в км/ч как

v = (617/1000) x 60 x 60 = 2221,2 км/ч = 2221 км/ч

Задача 2

Автомобиль равномерно ускоряется со скоростью 10 м/с ² с начальной скорости 36 км/ч в течение 30 секунд. Найдите расстояние, пройденное за это время.

Ответ

Окончательный ответ на этот вопрос 4,8 км

Объяснение

Данные

Начальная скорость, u = 36 км/ч = 10 м/с ускорение, а

5 ²

Время, t = 30 секунд

Неизвестно

Пройденное расстояние, с = ?

Формула

Воспользуемся вторым кинематическим уравнением, которое гласит:

s = ut + (1/2)at ²

)at

² = 10 x 30 + 0,5 x 10 x 30 ² = 300 + 4500 = 4800 м

Мы можем преобразовать приведенный выше ответ (4800 метров) в км, сказав

/

0 0 с = 1 = 4,8 км

Задача 3

Тело, движущееся с начальной скоростью 30 м/с, равномерно ускоряется со скоростью 10 м/с ² , пока не достигнет скорости 50 м/с. Какое расстояние пройдено за этот период?

Ответ

Окончательный ответ на этот вопрос составляет 80 метров

Объяснение

Данные

Начальная скорость, U = 30 м/с

Ука Конечная скорость, v = 50 м/с

Неизвестно

Пройденное расстояние, с = ?

Формула

Из третьего кинематического уравнения

V ² = U ² + 2AS

, а затем сделайте S -субъект формулы для получения уравнения

S = (V ² 44444444 гг. ² ) / 2a

Мы будем использовать приведенное выше уравнение, чтобы найти пройденное расстояние

Решение

Подставив наши данные в формулу, мы получим

с = (v ² – U ² ) / 2A = (50 ² – 30 ² ) / 2 x 10

, что подразумевает, что

S = 1600/20 = 80 M

. Задача на зачастие (вопросы.

Часто задаваемые вопросы)

Что такое уравнение кинематики?

Уравнения кинематики представляют собой набор уравнений, описывающих движение объектов с точки зрения их положения, скорости и ускорения.

Какие три уравнения кинематики?
Три кинематических уравнения:

1) v = u + at

2) s = ut + (1/2)at ²

3) v ² = u ^{2 30} + 2 как 90 решить 90 кинематические уравнения?
Чтобы решить кинематические уравнения, вам нужно определить, какие уравнения использовать, подставить известные значения и найти неизвестные значения с помощью алгебры.

Какова кинематическая формула расстояния?
Кинематическая формула для расстояния: s = ut + (1/2) при ² , где s — расстояние, u — начальная скорость, t — время, a — ускорение.

Какое кинематическое уравнение для скорости?
Кинематическое уравнение для скорости имеет вид v = u + at, где v — конечная скорость, u — начальная скорость, a — ускорение, t — время.