Все формулы физики 10 класс
Все формулы физики 10 класс
Фараонов и изобретения Ребрандта, подделки шедевров и секреты папирусов Древнего Египтаискусство скрывает в себе много тайн, но современные физики с помощью новых методов и приборов находят объяснения все большему числу удивительных секретов прошлого. Читать. Североуральск Свердловской области. Физика класс. Относительная молекулярная масса. Механические колебания и волны. Плакаты, наглядные пособия, карты Пособие содержит таблицы по всем разделам школьного курса физики, где кратко изложена теория по каждой теме,.
Формулы по физике класса позволяют объединить все три изохорных процесса и описать комплексное поведение идеального газа при изменениях состояния. Формулы по физике 8 класс. Рекомендуем добавить эту страницу в закладки чтобы распечатать при необходимости например, перед контрольной у школьников или экзаменом у студентов нужную шпаргалку таблицу формулы по физике за 7, 8, 9, и 11 классы.
Урок по теме Электричество. Газовые законы.1.1 Количество вещества. Физика. Молекулярно кинетическая теория.
И определения основных физических законов, а также единиц измерений физических величин. Шпора все формулы по физике в формате Текстовый документ Основные формулы для 7 классов на новой странице. Принтер пытается распечатать картинку, из за этого формул не видно. Таблица формул по физике. Формулы по физике для ЕГЭ и 7 11 класса. Все основные формулы, необходимые в классе для решения задач по физике. Задачи на понимание МКТ. Материалы съезда учителей физики.
Формулы. Тема: Перечень формул по курсу физики класса. Учебник: Г. Я. Мякишев, Б. Б. Буховцев, Н. Н. Сотский. Физика, класс. Видеоуроки, тесты и тренажёры по физике за класс по школьной программе. Теоретические материалы Шпаргалки, Физика, Архив. ОСНОВНЫЕ ПОЛОЖЕНИЯ, ЗАКОНЫ И ФОРМУЛЫ. Основные положения МКТ.презентация. Физика в формулах и определениях для учащихся. Все основные формулы, необходимые в классе для решения задач по физике.
Полезная литература: Основные формулы по химииТипичные ошибки на ЕГЭ.
Приведены основные формулы и графики. Они описывают энергию вещества по составляющей энергии его молекул. Формулы по физике класса уже касаются не только общих характеристик среды, например, газа. Барометрическая формула. Молекулярная физика Основные формулы.1. Основы молекулярно кинетической теории. Сборник формул по физике г. Формулы по физике, которые рекомендуется выучить и хорошо освоить для. Мякишев Г. Я., Синяков А. З., Слободсков Б. А. Физика. Электродинамикаклассы. В сборнике приведены базовые и наиболее важные производные формулы.
По химииТренировка решения заданий А, В, СУниверсальный справочникВарианты ЕГЭ за 2002 год. Профильный уровень. Жирным выделены формулы, которые стоит учить, когда уже отлично освоены не выделенные жирным формулы. Саратов, ЛИЕН, кафедра физики, 2011 г. Для каждого раздела. Основы молекулярно кинетической теории. Основные формулы за курс физики класс. Молекулярная физика.
Перейти. Все вещества состоят из мельчайших частици атомов, которые, в свою очередь, состоят из более мелких элементарных частиц. Тайны мумий.
России в МГУ 28 30 июня 2011 г. Было бы гораздо удобнее, если текст был напечатан, а не сделан одной картинкой. Решение задач на динамику. Формулы по физике с краткими пояснениями для удобного повторения учениками я разместил в таблице. Основные понятия, формулы, законы, 2016 г. Для начала картинка, которую можно распечатать в компактном виде. Премия будет вручена ученым декабря 2015 года в Стокгольме. Электростатика. Основные формулы школьного курса МКТ и термодинамики.
Вместе с
Все формулы физики 10 класс часто ищутформулы по физике 10 класс с пояснениями
формулы по физике 10 класс механика
формулы по физике 10 класс таблица
формулы по физике 10 класс кинематика
формулы по физике за курс 10 класса
формулы по физике 10-11 класс
формулы по физике 10 класс динамика
все формулы по физике за 10 класс динамика
Читайте также:
Гдз по черчению 9 класс учебник ботвинников
Как решить систему неравенств 9 класс
Урок в 4 классе изменение существительных по падежам
Примеры решения задач по теме «Закон всемирного тяготения»
Примеры решения задач по теме «Закон всемирного тяготения»
- Подробности
- Просмотров: 1170
«Физика – 10 класс»
При решении задач надо помнить, что сила тяготения действует между любыми телами, имеющими массу, но формула справедлива только для тел, которые можно считать материальными точками, а также для однородных тел шаровой формы.
При этом расстояние r — это расстояние между центрами шаров.
Задача 1.
При опытной проверке закона всемирного тяготения сила взаимодействия между двумя свинцовыми шарами массами m1 = 5 кг и m2 = 500 г, расстояние между центрами которых r = 7 см, оказалась равной F = 34 нН. Вычислите по этим данным гравитационную постоянную.
Р е ш е н и е.
Согласно закону всемирного тяготения
Из этого выражения следует, что
Получим
Уточнённое значение гравитационной постоянной, которое входит в таблицы:
Задача 2.
Определите равнодействующую силу, действующую на Луну, считая, что силы притяжения к Земле и Солнцу взаимно перпендикулярны. Массы Луны, Земли и Солнца соответственно равны mЛ = 7,36 • 1022 кг; m3 = 5,98 • 1024 кг; mC = 1,99 • 1030 кг; расстояния от Луны до Земли и от Луны до Солнца соответственно равны r
Р е ш е н и е.
По условию задачи силы гравитационного притяжения Луны к Земле и Солнцу взаимно перпендикулярны (рис. 3.6). Рассчитаем силу гравитационного притяжения Луны к Земле.
Сила притяжения Луны к Солнцу равна
По теореме Пифагора найдём равнодействующую силу, действующую на Луну,
Задача 3.
На поверхности Земли находятся два свинцовых шара радиусом R = 10 см каждый. В одном из них вырезана сферическая полость, как показано на рисунке 3.7. Радиус полости r = 5 см, центр полости находится на расстоянии l = 5 см от центра шара. Определите силу гравитационного притяжения шаров. Центры шаров находятся на расстоянии L = 40 см.
Р е ш е н и е.
Если бы у правого шара не было вырезанной полости, то сила гравитационного притяжения шаров была бы равна при этом Вырезав полость, мы уменьшаем эту силу притяжения на силу F2, равную силе притяжения левого шара к вырезанной части:
Тогда
Заметим, что L = 4R = 8r; R = 2r, соответственно m = 8 m1.
Подставив эти выражения в формулу (1), получим
Учтя, что получаем
Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Динамика – Физика, учебник для 10 класса – Класс!ная физика
Основное утверждение механики —
Сила —
Инертность тела. Масса. Единица массы —
Первый закон Ньютона —
Второй закон Ньютона —
Принцип суперпозиции сил —
Примеры решения задач по теме «Второй закон Ньютона» —
Третий закон Ньютона —
Геоцентрическая система отсчёта —
Принцип относительности Галилея. Инвариантные и относительные величины —
Силы в природе —
Сила тяжести и сила всемирного тяготения —
Сила тяжести на других планетах —
Примеры решения задач по теме «Закон всемирного тяготения» —
Первая космическая скорость —
Примеры решения задач по теме «Первая космическая скорость» —
Вес.
Напишите все формулы по физике за 7-8 класс,с обозначением каждой буквы!!!даю 25 баллов!!
Срочно!!!!!Світловий промінь падає на скляну пластинку над кутом 54°. промінь який вийшов з пластинки, виявився зміщеним відносно падаючого променя на … 2 см. Яка товщина пластинки?
пользуясь графиком зависимости скорости движения от отвремени(2 рис.) определите путь пройденный автомобилем за время t= 3,00 ч
ПОМОГИТЕ ПРОШУ!!!!!! Как изменяется давление в жидкости в зависимости от высоты стол- ба жидкости? от плотности жидкости?
Кр по физике. 7 класс
Світло падає з повітря у середовище, швидкість поширення світла в якому 1,25×10⁸ м/с.. Кут падіння світлового променя становить 30⁰.
Визначити кут зал
… омлення середовища. Швидкість світла в повітрі вважати рівною 3×10⁸м/с.
Сколько энергии рассеялось при превращении 83 г свинца в жидкое агрегатное состояние, если было израсходовано 11 г бензина, а начальная температура св … инца равна 15 °С. Удельная теплоёмкость свинца — 130 Джкг⋅°С, температура плавления свинца равна 327 °С, а удельная теплота плавления свинца — 0,25⋅105 Дж/кг, удельная теплота сгорания бензина — 47⋅106 Дж/кг. Ответ (округли до десятых): кДж.
Определи, какое количество теплоты выделится при кристаллизации 3,6 л жидкого спирта. Удельная теплота кристаллизации жидкого спирта равна 1,1⋅105 Дж/ … кг, плотность жидкого спирта — 800 кгм3. Ответ (округли до десятых): кДж.
В сосуде, теплоёмкость которого равна 189 Дж/°С, находится 2 л воды и 1 кг льда при 0°С. Чтобы получить воду с температурой 7 °С, в сосуд впускают вод
… яной пар при 100 °С. Рассчитай массу пара.
(Удельная теплоёмкость воды с=4200Джкг⋅° С, удельная теплота парообразования L =2260000 Дж/кг, удельная теплота плавления льда λ=330000 Дж/кг).
КТО РЕШИТ ОЧЕНЬ СРОЧНО ФИЗИКА 8 КЛАСС ДАМ 40 БАЛОВ
Помогите пожалуйста мне срочно надо на завтра!! Написать 5 – 7 предложений на тему: значение трения в моей жизни
Пёрышкин. Решебник по белому учебнику
§ 1. Тепловое движение. Температура
Вопросы
§ 2. Внутренняя энергия
Вопросы
Упражнение 1
Задание
§ 3. Способы изменения внутренней энергии тела
Вопросы
Упражнение 2
Задание
§ 4. Теплопроводность
Вопросы
Упражнение 3
Задание
§ 5. Конвекция
Вопросы
Упражнение 4
Задание
§ 6. Излучение
Вопросы
Упражнение 5
Задание
§ 7. Количество теплоты. Единицы количества теплоты
Вопросы
Упражнение 6
§ 8. Удельная теплоёмкость
Вопросы
Упражнение 7
Задание
§ 9.
Расчёт количества теплоты, необходимого для нагревания тела или выделяемого им при охлажденииВопросы
Упражнение 8
§ 10. Энергия топлива. Удельная теплота сгорания
Вопросы
Упражнение 9
Задание
§ 11. Закон сохранения и превращения энергии в механических и тепловых процессах
Вопросы
Упражнение 10
§ 12. Агрегатные состояния вещества
Вопросы
§ 13. Плавление и отвердевание кристаллических тел
Вопросы
Упражнение 11
Задание
§ 14. График плавления и отвердевания кристаллических тел
Вопросы
Задание
§ 15. Удельная теплота плавления
Вопросы
Упражнение 12
Задание
§ 16. Испарение. Насыщенный и ненасыщенный пар
Вопросы
Задание
§ 17. Поглощение энергии при испарении жидкости и выделение её при конденсации пара
Вопросы
Упражнение 13
Задание
§ 18.
КипениеВопросы
Упражнение 14
Задание
§ 19. Влажность воздуха. Способы определения влажности воздуха
Вопросы
Упражнение 15
§ 20. Удельная теплота парообразования и конденсации
Вопросы
Упражнение 16
Задание
§ 21. Работа газа и пара при расширении
Вопросы
§ 22. Двигатель внутреннего сгорания
Вопросы
§ 23. Паровая турбина
Вопросы
§ 24. КПД теплового двигателя
Вопросы
Упражнение 17
Задание
Проверь себя
§ 25. Электризация тел при соприкосновении. Взаимодействие заряженных тел
Вопросы
Упражнение 18
Задание
§ 26. Электроскоп
Вопросы
§ 27. Электрическое поле
Вопросы
Упражнение 19
§ 28. Делимость электрического заряда. Электрон
Вопросы
§ 29. Строение атомов
Вопросы
Упражнение 20
§ 30.
Объяснение электрических явленийВопросы
Упражнение 21
§ 31. Проводники, полупроводники и непроводники электричества
Вопросы
Упражнение 22
§ 32. Электрический ток. Источники электрического тока
Вопросы
Задание
§ 33. Электрическая цепь и её составные части
Вопросы
Упражнение 23
§ 34. Электрический ток в металлах
Вопросы
Задание
§ 35. Действия электрического тока
Вопросы
Задание
§ 36. Направление электрического тока
Вопросы
§ 37. Сила тока. Единицы силы тока
Вопросы
Упражнение 24
§ 38. Амперметр. Измерение силы тока
Вопросы
Упражнение 25
§ 39. Электрическое напряжение
Вопросы
§ 40. Единицы напряжения
Вопросы
§ 41. Вольтметр. Измерение напряжения
Вопросы
Упражнение 26
§ 42.
Зависимость силы тока от напряженияВопросы
Упражнение 27
§ 43. Электрическое сопротивление проводников. Единицы сопротивления
Вопросы
Упражнение 28
§ 44. Закон Ома для участка цепи
Вопросы
Упражнение 29
§ 45. Расчёт сопротивления проводника. Удельное сопротивление
Вопросы
§ 46. Примеры на расчёт сопротивления проводника, силы тока и напряжения
Упражнение 30
§ 47. Реостат
Вопросы
Упражнение 31
§ 48. Последовательное соединение проводников
Вопросы
Упражнение 32
§ 49. Параллельное соединение проводников
Вопросы
Упражнение 33
§ 50. Работа электрического тока
Вопросы
Упражнение 34
§ 51. Мощность электрического тока
Вопросы
Упражнение 35
§ 52. Единицы работы электрического тока, применяемые на практике
Вопросы
Упражнение 36
Задание
§ 53.
Нагревание проводников электрическим током. Закон Джоуля—ЛенцаВопросы
Упражнение 31
§ 54. Конденсатор
Вопросы
Упражнение 38
Задание
§ 55. Лампа накаливания. Электрические нагревательные приборы
Вопросы
Задание
§ 56. Короткое замыкание. Предохранители
Вопросы
Проверь себя
§ 57. Магнитное поле
Вопросы
Упражнение 39
§ 58. Магнитное поле прямого тока. Магнитные линии
Вопросы
Упражнение 40
§ 59. Магнитное поле катушки с током. Электромагниты и их применение
Вопросы
Упражнение 41
Задание
§ 60. Постоянные магниты. Магнитное поле постоянных магнитов
Вопросы
Упражнение 42
Задание
§ 61. Магнитное поле Земли
Вопросы
Упражнение 43
Задание
§ 62. Действие магнитного поля на проводник с током. Электрический двигатель
Вопросы
Задание
Проверь себя
§ 63.
Источники света. Распространение светаВопросы
Упражнение 44
Задание
§ 64. Видимое движение светил
Вопросы
Задание
§ 65. Отражение света. Закон отражения света
Вопросы
Упражнение 45
§ 66. Плоское зеркало
Вопросы
Упражнение 46
§ 67. Преломление света. Закон преломления света
Вопросы
Упражнение 47
§ 68. Линзы. Оптическая сила линзы
Вопросы
Упражнение 48
§ 69. Изображения, даваемые линзой
Вопросы
Упражнение 49
§ 70. Глаз и зрение
Вопросы
Задание
Проверь себя
Лабораторные работы
Физические формулы для класса 10
Все формулы физики для класса 10
Что такое кинетическая энергия?
Энергия, которой обладает объект из-за своего движения, называется кинетической энергией.
Когда к объекту прикладывается сила, он вызывает ускорение, производя кинетическую энергию. Кинетическая энергия зависит от скорости и массы объекта.
Формула кинетической энергии
Формула кинетической энергии (Ek) определяется как
Ek = 1/2 mv2
Где
m = масса объекта
v = скорость объекта
Формула крутящего момента
Крутящий момент – это вращающий эффект силы, который вызывает движение объекта.Объект совершает вращательное движение, и точка, в которой он вращается, называется «осью вращения».
Формула крутящего момента задается следующим образом:
T = F × r × sinθ
T = крутящий момент
F = линейная сила, приложенная к объекту
r = расстояние от оси вращения до точки приложения линейной силы происходит
θ = угол между F и r
Формула емкости
Конденсатор – это устройство, которое накапливает электрическую энергию в электрическом поле.
Конденсатор – неотъемлемая часть любого электронного устройства. Конденсатор предназначен для хранения электрического заряда и подачи его в цепь при необходимости. Способность конденсатора накапливать электрический заряд называется его емкостью.
Десятая физическая формула для емкости конденсатора:
C = Q / V
Где,
C = емкость (которая измеряется в фарадах)
Q = заряд (в кулонах)
V = напряжение (в вольтах)
Формула силы тяжести
Гравитация – это сила, которая вызывает притяжение между двумя объектами.Это та же сила, которая заставляет предметы падать на землю. Это та же самая сила, которая вызывает вращение планет вокруг Солнца. Следовательно, для массивных объектов, имеющих большую массу, сила гравитации больше.
Формула силы тяжести
Сила тяжести прямо пропорциональна массе двух объектов и обратно пропорциональна квадрату расстояния между объектами.
Fg = G * (M¹ * M²) / r²
Где,
Fg = сила гравитации
M¹ = масса первого объекта
M² = масса второго объекта
G = универсальная гравитационная постоянная, которая равно 6.2
r = расстояние между объектами
Рабочая формула
В физике считается, что работа выполняется, когда сила, приложенная к объекту, заставляет объект двигаться. Если приложена постоянная сила, работа рассчитывается как скалярное произведение приложенной силы и смещения объекта. Работа – величина скалярная, т.е. не имеет направления.
Работа рассчитывается путем умножения составляющей силы в направлении смещения на величину смещения объекта.
Математически
W = F × d × cosθ
Где,
W = работа, совершаемая силой.
F = сила, приложенная к объекту.
d = смещение, вызванное силой.
θ = угол между вектором смещения и вектором силы.
Формулы волн
Волна – это возмущение в среде или пространстве. Волны передают энергию, не передавая никакой материи. Волны, проходящие через вещество, материал или любую среду, называются механическими волнами.По мере того, как волна проходит через среду, частицы среды колеблются от своего среднего положения.
Волна, в которой частица среды движется в направлении, параллельном направлению волны, называется продольной волной.
Волна, в которой частица среды движется в направлении, перпендикулярном направлению волны, называется поперечной волной.
Для поперечной волны гребень – это положение наибольшего смещения амплитуды волны.Расстояние между двумя последовательными гребнями называется длиной волны. Единица измерения длины волны в системе СИ – метр.
Длина волны связана со скоростью и частотой волны по следующей формуле.
Скорость волны = частота × длина волны
Это записывается как,
v = f × λ
Где:
v = скорость
f = частота
λ = длина волны
Формула преломления
Когда свет проходит от одной среды к другой, его скорость изменяется, и он также отклоняется от своего первоначального пути.Это отклонение света при переходе от одной среды к другой называется преломлением. Преломление возникает из-за разницы плотностей двух сред.
Физическая числовая формула преломления света основана на законе Снеллиуса. Когда свет проникает из одной среды в другую среду, имеющую угол падения «i», и преломляется под углом преломления «r», то в соответствии с законом Снеллиуса.
Где μ – показатель преломления второй среды по отношению к показателю преломления первой среды.
Показатель преломления зависит от материала среды.
\ [n_ {1} \] \ [Sin \ Theta_ {1} \] = \ [n_ {2} \] \ [Sin \ Theta_ {2} \]
Также из этого уравнения
Где
\ [n_ {1} \] = показатель преломления первой среды
\ [n_ {2} \] = показатель преломления второй среды
\ [\ Theta_ {1} \] = угол падения
\ [\ Theta_ {2} \] = угол преломления
Температурные формулы
Температура – это физическая величина, которая используется для измерения степени тепла или холода объекта.Формула температуры в основном используется для расчета средней кинетической энергии частиц.
Преобразование температуры между шкалой Цельсия и шкалой Кельвина: определяется как:
K = C + 273,15
Формула преобразования температуры из шкалы Кельвина в шкалу Цельсия:
C = K – 273,15
Где,
C = температура по шкале Цельсия
K = температура по шкале Кельвина
Заключение:
Указанные концепции и формулы относятся к физическим формулам для класса 10.
Физические формулы для класса 10 с примерами
Физические формулы для класса 10Физические формулы для класса 10 из главы по физике класса 10 NCERT – Свет – отражение, преломление и электричество.Надеюсь, что приведенные ниже формулы по физике из каждой главы помогут вам при сдаче экзамена CBSE Class 10.
Физические формулы для класса 10: обзорТема | Физические формулы |
| Класс | 10 |
Физические формулы класса 10 из главы Light
Ниже физических формул для класса 10 из главы Light –
Физические формулы класса 10 из главы Электричествониже физических формул для класса 10 из главы “Электричество” –
Дополнительная формула из класса 10Легкая
(1) Формула зеркала, 1 / v + 1 / u = 1 / f
(2) Увеличение, M = v / u = h 2 / h 1
(3) Формула линзы 1 / v – 1 / u = 1 / f
(4) Закон преломления, n = Sin i / sin r
(5) Показатель преломления, n 2 = v
(6) Абсолютный показатель преломления
Электроэнергия
(1) Электрический ток, I = q / t
(2) Разность потенциалов, v = W / Q
(3) Закон Ома, V = IR
(4) Удельное сопротивление, ρ = RA / L
(5) Электропроводность = L / RA
(6) Последовательные резисторы Formula
(7) Параллельно подключенные резисторы Формула
(8) Электрическая мощность, P = Вт / t = VI = I
(9) Электроэнергия
(10) Закон Джоуля, H = I 2 RT
Следующая тема:
Физические формулы для класса 11
Физические формулы для класса 12
Важные ссылки:
Примечания к отражению и преломлению света
Электричество Класс 10
Зеркала, уравнение зеркала и уравнения увеличения 10 класс Science Power Point
Это Power Point на зеркалах, использующий уравнение зеркала, уравнение увеличения и показатель преломления для решения проблем с зеркалами.
Он включает решение для высоты изображения, решение для расстояния изображения, решение для увеличения, решение для фокусного расстояния, решение для расстояния до объекта и решение для показателя преломления с использованием n = c / v. Он объясняет темы с помощью слов, диаграмм и гифок. Он содержит множество полностью решенных типовых задач. Содержание подходит для курса естественных наук для 10 класса, а Power Point состоит из 22 слайдов.
Меня зовут Даррин Мэтьюсон, я доктор органической химии.Я преподаю физику и химию более 15 лет. Мои ученики нашли эти Power Point очень полезными для понимания биологии, химии и физики во время онлайн-уроков и личного обучения. Учащиеся находят полностью решенные типовые задачи чрезвычайно полезными для укрепления своих математических навыков и навыков решения задач. Многочисленные гифки и диаграммы чрезвычайно эффективны, помогая учителям объяснять и разъяснять концепции, представленные в Power Points.
У меня есть более 140 очков Power Point на продажу в моем магазине, 40 пакетов рабочих листов, 100 пакетов тестов, 100 пакетов с несколькими вариантами ответов и 70 пакетов с короткими ответами.
У меня есть Power Points, тесты, викторины, вопросы с несколькими вариантами ответов, вопросы с короткими ответами и рабочие листы по каждой теме, охваченной естественными науками 10 класса, химией 11 класса, физикой 11 класса и химией 12 класса!
Все публикации Power Points, рабочие листы, викторины и тесты, которые я публикую, должным образом отформатированы и готовы к печати. Проверены на ошибки и опечатки!
Чтобы оценить мою работу, ознакомьтесь с моими 8 БЕСПЛАТНЫМИ ПРОДУКТАМИ, включая Power Points, викторины и тесты!
https: // www.tes.com/teaching-resource/resource-12555615 (Power Point с движением снаряда)
https://www.tes.com/teaching-resource/resource-12545047 (тест на органическую химию)
https://www.tes.com / Teaching-resource / resource-12545057 (физический тест на равномерное движение и векторы)
https://www.tes.com/teaching-resource/resource-12545034 (викторина по именованию соединений)
https://www.tes.com/ обучающий-ресурс / ресурс-12545028 (тест по стехиометрии)
https://www.
tes.com/teaching-resource/resource-12544990 (наименование алканов в Power Point)
https: // www.tes.com/teaching-resource/resource-12544998 (ограничение стехиометрии реагентов Power Point)
https://www.tes.com/teaching-resource/resource-12545007 (функция клеток и использование микроскопа Power Point)
[PDF] Движение в одном измерении – класс 10
1 Глава 3 Движение в одном измерении – Введение в уровень В этой главе рассказывается о том, как объекты движутся по прямой линии или более …
Глава 3Движение в одном измерении – класс 10 3.1
Введение
В этой главе рассказывается о том, как вещи движутся по прямой линии или, с научной точки зрения, как вещи движутся в одном измерении.Это полезно для того, чтобы научиться описывать движение автомобилей по прямой дороге или поездов по прямым железнодорожным путям. Если вы хотите понять, как движется какой-либо объект, например, машина на автостраде, футбольный мяч, направленный к воротам, или ваша собака, преследующая кошку соседа, тогда вам необходимо понять три основных идеи о том, что это означает, когда что-то движется.
. Эти три идеи описывают разные части того, как именно движется объект. Это: 1. положение или смещение, которое говорит нам, где именно находится объект, 2.скорость или скорость, которая сообщает нам, насколько быстро меняется положение объекта или, что более привычно, с какой скоростью движется объект, и 3. ускорение, которое сообщает нам, с какой именно скоростью изменяется скорость объекта. Вы также узнаете, как использовать положение, смещение, скорость, скорость и ускорение для описания движения простых объектов. Вы научитесь читать и рисовать графики, отражающие движение движущегося объекта. Вы также узнаете об уравнениях, которые можно использовать для описания движения, и о том, как применять эти уравнения к объектам, движущимся в одном измерении.
3,2
Контрольная точка, система отсчета и позиция
Самая важная идея при изучении движения – это знать, где вы находитесь. Слово позиция описывает ваше местоположение (где вы находитесь). Однако говорить, что вы здесь, бессмысленно, и вам нужно указать свое положение относительно известной контрольной точки.
Например, если вы находитесь в 2 м от дверного проема в классе, то ориентиром является дверной проем. Это определяет ваше положение в классе.Обратите внимание, что вам нужна контрольная точка (дверной проем) и направление (внутри), чтобы определить ваше местоположение.
3.2.1
Система отсчета
Определение: Система отсчета Система отсчета – это опорная точка, объединенная с набором направлений.
Система отсчета похожа на идею опорной точки. Система отсчета определяется как контрольная точка, объединенная с набором направлений. Например, внутри стоит мальчик 23
3.2
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – КЛАСС 10
поезд, выезжающий со станции. Вы стоите на платформе и смотрите, как поезд движется слева направо. Вам кажется, что мальчик движется слева направо, потому что он движется относительно того места, где вы стоите (платформа). По словам мальчика и его системы координат (поезда), он не двигается.
24
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – мальчик 10-го КЛАССА стоит на месте
3.
2
поезд движется слева направо
b
В вашей системе координат мальчик движется слева направо.
Рисунок 3.1: Система отсчета Система отсчета должна иметь начало (где вы стоите на платформе) и, по крайней мере, положительное направление. Поезд двигался слева направо, делая справа от вас положительное, а слева отрицательное. Если кто-то другой смотрел на того же мальчика, его система взглядов будет другой. Например, если он стоял на другой стороне платформы, мальчик будет двигаться справа налево.В этой главе мы будем использовать системы отсчета только по оси x. Справочные рамки будут более подробно рассмотрены в классе 12.
Мальчик в поезде, который движется слева направо в отрицательном направлении (влево от вас)
в положительном направлении (вправо) Где вы стоите на платформе (контрольная точка или исходная точка)
3.2.2
Позиция
Определение: Позиция Позиция – это измерение местоположения со ссылкой на начало координат.
Позиция – это измерение местоположения по отношению к исходной точке. Таким образом, позиции могут быть как отрицательными, так и положительными. Символ x используется для обозначения положения. x имеет единицы длины, например см, м или км. На рисунке 3.2.2 показано расположение школы. В зависимости от того, какой ориентир мы выберем, мы можем сказать, что школа находится в 300 м от дома Жанны (с домом Жанны в качестве ориентира или исходной точки) или в 500 метрах от дома Джоэла (с домом Джоэла в качестве ориентира или исходной точки).
Школа
Джек
100 м
Джоан
Джон
100 м
100 м
Джилл
100 м
Магазин
Джоэл
100 м
100 м
Рисунок 3.2: Иллюстрация расположения Магазин также находится в 300 м от дома Жанны, но в направлении, противоположном школе. Когда мы выбираем опорную точку, у нас есть положительное направление и отрицательное направление. Если мы выберем 25
3,2
ГЛАВА 3.
ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – 10 КЛАСС Дом Жанны (ориентир)
Школа
Магазин
x (м) 0
+300 +200 +100
-100
-200-300
Рисунок 3.3. происхождение находится в доме Джоан, а расположение школы – +300 м. Позиции слева определяются как положительные, а положения справа – как отрицательные.
направление на школу положительное, затем направление на магазин отрицательное.Отрицательное направление всегда противоположно направлению, выбранному в качестве положительного.
Упражнение :: Обсуждение: ориентиры Для этого упражнения разделитесь на группы по 5 человек. На прямой выберите ориентир. Поскольку позиция может иметь как положительные, так и отрицательные значения, обсудите преимущества и недостатки выбора 1. любого конца строки, 2. середины строки. Этот ориентир также можно назвать «исходной точкой».
Упражнение: Позиция 1. Запишите позиции объектов в точках A, B, D и E.Не забывайте единицы. контрольная точка BD
A
E x (м)
-4
-3
-2
-1
0
1
2
3
4
2.
Записать позиции для объектов в F, G, H и J. Не забудьте единицы измерения. опорная точка G H
F
Дж x (м)
4
3
2
1
0
-1
-2
-3
-4
3.На Ньютон-стрит 5 домов: A, B, C, D и E. Во всех случаях предположим, что позиции справа положительны. 20 м
A
20 м
B
20 м
C 26
20 м
D
E
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – КЛАСС 10 (a) Нарисуйте систему отсчета с домом A в качестве исходной точки и запишите расположение домов B, C, D и E.
(b) Вы живете в доме C. Каково ваше положение относительно дома E?
(c) Каково положение домов A, B и D, если дом B взят за точку отсчета?
27
3.2
3,3
3,3
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – КЛАСС 10
Смещение и расстояние
Определение: Смещение Смещение – это изменение положения объекта.
Смещение объекта определяется как его изменение положения (конечное положение минус начальное положение).
Смещение имеет величину и направление и, следовательно, является вектором. Например, если начальное положение автомобиля – xi, и оно перемещается в конечное положение xf, то смещение будет: xf – xi. Однако вычитание начальной величины из конечной величины часто происходит в физике, поэтому мы используем ярлык ∆ означает конечный – начальный.Следовательно, смещение можно записать: ∆x = xf – xi
Важно: символ ∆ читается как дельта. ∆ – буква греческого алфавита, которая используется в математике и естественных науках для обозначения изменения определенной величины или конечного значения за вычетом начального значения. Например, ∆x означает изменение x, а ∆t означает изменение t.
Важно: слова начальная и конечная будут очень часто использоваться в физике. Initial всегда будет относиться к чему-то, что произошло раньше, а final всегда будет относиться к тому, что произошло позже.Часто бывает, что конечное значение меньше начального, поэтому разница отрицательная. Хорошо! Finish (Shop) b
sp Di
l ac
em
en
t
b
Start (School)
Рисунок 3.
4: Иллюстрация смещения Смещение не зависит от пройденного пути, а только на начальном и конечном положениях (рисунок 3.4). Мы используем слово «расстояние», чтобы описать, как далеко перемещается объект по определенному пути.Расстояние – это фактическое пройденное расстояние. Расстояние (символ d) не имеет направления, поэтому является скаляром. Смещение – это кратчайшее расстояние от начальной точки до конечной – от школы до магазина на рисунке. Смещение имеет направление и, следовательно, является вектором. На рис. 3.2.2 показаны пять домов, которые мы обсуждали ранее. Джек ходит в школу, но вместо того, чтобы идти прямо в школу, он решил сначала дойти до дома своего друга Джоэла, чтобы забрать его, чтобы они могли вместе идти в школу.Джек преодолевает расстояние 400 м до дома Джоэла и еще 500 м до школы. Он преодолевает дистанцию 900 м. Однако его перемещение составляет всего 100 м в сторону школы. Это потому, что смещение смотрит только на начальную позицию (его дом) и конечную позицию (школа).
Это не зависит от пройденного им пути. 28
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10
3.3
Чтобы вычислить его расстояние и смещение, нам нужно выбрать опорную точку и направление.Давайте выберем дом Джека в качестве ориентира, а в сторону дома Джоэла – в качестве положительного направления (что означает, что в сторону школы – отрицательное). Расчеты производятся следующим образом:
Расстояние (d)
= пройденный путь = 400 м + 500 м
Смещение (∆x)
= =
xf – xi −100 м + 0 м
=
= 900 м
−100 м
Джоэл идет в школу с Джеком, а после школы возвращается домой. Что такое смещение Джоэла и какое расстояние он преодолел? Для этого расчета мы используем дом Джоэла в качестве ориентира.Давайте возьмем школу как положительное направление. Расстояние (d)
= пройденный путь = 500 м + 500 м
Смещение (∆x)
= xf – xi = 0 м + 0 м = 0 м
= 1000 м
Возможно смещение 0 м и расстояние, отличное от 0 м.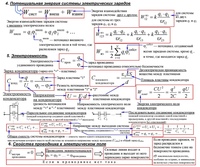
Это происходит, когда объект возвращается в исходное положение и обратно, как спортсмен, бегающий по трассе.
3.3.1
Направление устного перевода
Очень часто в расчетах вы получите отрицательный ответ.Например, смещение Джека в приведенном выше примере рассчитывается как -100 м. Знак минус перед ответом означает, что его перемещение составляет 100 м в обратном направлении (противоположном направлению, выбранному как положительное в начале вопроса). Когда мы начинаем расчет, мы выбираем систему отсчета и положительное направление. В первом примере выше ориентиром является дом Джека, а положительное направление – к дому Джоэла. Следовательно, смещение Джека составляет 100 м в сторону школы.Обратите внимание, что у расстояния нет направления, а у смещения есть.
3.3.2
Различия между расстоянием и смещением
Определение: векторы и скаляры Вектор – это физическая величина с величиной (размером) и направлением. Скаляр – это физическая величина, имеющая только величину (размер).
Различия между расстоянием и смещением можно резюмировать следующим образом: Расстояние 1. зависит от пути 2. всегда положительно 3. является скаляром
Смещение 1. Независимо от пройденного пути 2.может быть положительным или отрицательным 3. является вектором
Упражнение: точка отсчета 1. Используйте рисунок 3.2.2, чтобы ответить на следующие вопросы. а) Джилл идет к дому Джоан, а затем в школу. На каком расстоянии она перемещается? б) Иоанн идет к дому Джоан, а затем в школу. На каком расстоянии он находится? 29
3,3
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – КЛАСС 10 (c) Джек идет в магазин, а затем в школу, каково его расстояние и перемещение?
(d) Какую точку отсчета вы использовали для каждого из вышеперечисленных вопросов?
2.Вы стоите у входной двери своего дома (перемещение, ∆x = 0 м). Улица находится в 10 м от входной двери. Вы идете на улицу и снова возвращаетесь.
(а) Какое расстояние вы прошли?
(b) Каково ваше окончательное перемещение?
(c) Смещение – вектор или скаляр? Обоснуйте свой ответ.
30
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10
3,4
3,4
Скорость, средняя скорость и мгновенная скорость
Определение: Скорость Скорость – это скорость изменения положения.
Определение: Мгновенная скорость Мгновенная скорость – это скорость ускоряющегося тела в определенный момент времени.
Определение: Средняя скорость Средняя скорость – это полное перемещение тела за интервал времени.
Скорость – это скорость изменения положения. Он сообщает нам, насколько положение объекта меняется во времени. Это то же самое, что смещение, деленное на затраченное время. Поскольку смещение является вектором, а время – скаляром, скорость также является вектором.Мы используем символ v для обозначения скорости. Если у нас есть смещение ∆x и время, затраченное на ∆t, тогда v определяется как: скорость (в м · с − 1) = v
=
изменение смещения (в м) изменение во времени (в s) ∆x ∆t
Скорость может быть положительной или отрицательной. Положительные значения скорости означают, что объект движется от опорной точки или исходной точки, а отрицательные значения означают, что объект движется к опорной точке или исходной точке.
Важно: Момент времени отличается от затраченного времени или временного интервала.Поэтому полезно использовать символ t для момента времени (например, в течение 4-й секунды) и символ ∆t для взятого времени (например, в течение первых 5 секунд движения).
Средняя скорость (символ v) – это смещение для всего движения, деленное на время, затраченное на все движение. Мгновенная скорость – это скорость в определенный момент времени. (Средняя) Скорость (символ s) – это пройденное расстояние (d), разделенное на время, затраченное на поездку (∆t). Расстояние и время являются скалярами, поэтому скорость также будет скаляром.Скорость вычисляется следующим образом: скорость (в м · с − 1) = с =
расстояние (в м) время (в с)
d ∆t
Мгновенная скорость – это величина мгновенной скорости. Он имеет то же значение, но без направления.
Работает Пример 5: Средняя скорость и средняя скорость 31
3,4
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10 Вопрос: Джеймс проходит 2 км от дома за 30 минут. Затем он поворачивается и идет домой по тому же пути, тоже через 30 минут.Рассчитайте среднюю скорость и среднюю скорость Джеймса. 2 км
Ответ Шаг 1: Определите, какая информация предоставляется и что требуется. В вопросе четко указывается • расстояние и время ожидания (2 км за 30 минут)
• расстояние и время назад (2 км за 30 минут)
Шаг 2: Убедитесь, что все единицы являются единицами СИ. Информация представлена не в единицах СИ, поэтому ее необходимо преобразовать. Чтобы преобразовать км в м, мы знаем, что: 1 км = 1 000 м ∴
2 км = 2 000 м (умножьте обе стороны на 2, потому что мы хотим преобразовать 2 км в м.)
Аналогичным образом, чтобы преобразовать 30 минут в секунды,
∴
1 мин 30 мин
= 60 с = 1800 с
(умножьте обе стороны на 30)
Шаг 3: Определите смещение и расстояние Джеймса. Джеймс начал дома и вернулся домой, поэтому его перемещение составляет 0 м. ∆x = 0 м. Джеймс прошел общее расстояние 4 000 м (2 000 м назад и 2 000 м назад). d = 4 000 м. Шаг 4: Определите его общее время. Джеймсу потребовалось 1 800 с, чтобы выйти и 1 800 с, чтобы вернуться. ∆t = 3 600 с Шаг 5: Определите его среднюю скорость
с
= = =
d ∆t 4 000 м 3 600 с 1,11 м · с − 1
Шаг 6: Определите его среднюю скорость
v
∆x ∆t 0m = 3 600 с = 0 м · с − 1
=
Рабочий пример 6: Мгновенная скорость и скорость 32
ГЛАВА 3.ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – КЛАСС 10
3,4 Н
Вопрос: Человек бежит по круговой дорожке радиусом 100 м. На полный оборот трека у него уходит 120 с. Если он бежит с постоянной скоростью, рассчитайте: 1. его скорость,
W
E
b
2. его мгновенную скорость в точке A,
A
3. его мгновенную скорость в точке B, 4. его средняя скорость между точками A и B,
bB
S 100 м
5.его средняя скорость за оборот. 6. его средняя скорость за оборот.
Ответ
Шаг 1: Решите, как подойти к проблеме
Чтобы определить скорость человека, нам нужно знать расстояние, которое он преодолевает, и сколько времени это занимает. Мы знаем, что один оборот трека занимает 120 с. (Один оборот – это один раз обойти трек.) 33
Направление, в котором бежит человек
3,4
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10 Шаг 2 : Определите пройденное расстояние Какое расстояние составляет один оборот трека? Мы знаем, что дорожка представляет собой круг, и мы знаем его радиус, поэтому мы можем определить расстояние по кругу.Начнем с уравнения длины окружности C
= 2πr = 2π (100 м) = 628,32 м
Следовательно, расстояние, которое преодолевает человек за один оборот, составляет 628,32 м.
Шаг 3: Определите скорость
Мы знаем, что скорость – это расстояние, пройденное за единицу времени. Итак, если мы разделим пройденное расстояние на время, которое потребовалось, мы узнаем, сколько расстояния было пройдено за каждую единицу времени. Здесь не используется направление, потому что скорость является скаляром.
с
= = =
d ∆t 628,32 м 120 с 5,24 м · с − 1
Шаг 4: Определите мгновенную скорость в точке A b
A
Рассмотрим точку A в диаграмма.Мы знаем, в какую сторону бегает человек по трассе, и знаем его скорость. Его скорость в точке А будет его скоростью (величиной скорости) плюс его направление движения (направление его скорости). В тот момент, когда он достигает точки А, он движется, как показано на диаграмме.
Направление, по которому бежит человек
b
A
Его скорость будет 5,24 м · с − 1 на запад.
Шаг 5: Определите мгновенную скорость в точке B
Направление, в котором бежит человек. Рассмотрим точку B на диаграмме.Мы знаем, в какую сторону бегает человек по трассе, и знаем его скорость. Его скорость в точке B будет его скоростью (величиной скорости) плюс его направление движения (направление его скорости). В тот момент, когда он достигает точки B, он движется, как показано на диаграмме. Его скорость составит 5,24 м · с − 1 юг.
bB
bB
34
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10
3,4
Шаг 6: Определите среднюю скорость между A и B Для определения средней скорости между A и B нам понадобится изменение смещения между A и B и изменение во времени между A и B.Смещение от A и B можно рассчитать с помощью теоремы Пифагора: (∆x) 2
= =
∆x =
1002 + 1002 20000 A
141,42135 … m ∆x
Время полного оборота составляет 120 с, поэтому время 14 оборота составляет 30 с. vAB
= = =
∆x ∆t 141,42 … 30 с 4,71 м · с − 1
100 м
B
100 м
O
Скорость – вектор и требует направления . Треугольник AOB равнобедренный, поэтому угол BAO = 45 °.Направление между западом и югом, следовательно, юго-запад. Окончательный ответ: v = 4,71 м · с − 1, юго-запад. Шаг 7: Определите его среднюю скорость во время оборота. Поскольку он бежит с постоянной скоростью, мы знаем, что его скорость в любом месте трека будет такой же. Его средняя скорость составляет 5,24 м · с − 1. Шаг 8: Определите его среднюю скорость за полный оборот
Важно: Помните – смещение может быть нулевым, даже если пройденное расстояние – нет! Чтобы вычислить среднюю скорость, нам нужно его полное перемещение и его общее время.Его смещение равно нулю, потому что он заканчивается там, где он начал. Его время – 120 с. Используя их, мы можем вычислить его среднюю скорость: v
= = =
3.4.1
∆x ∆t 0m 120 s 0s
Различия между скоростью и скоростью
Различия между скоростью и скоростью можно резюмировать следующим образом: Скорость 1. зависит от пройденного пути 2. всегда положительна 3. является скалярной 4. не зависит от направления и поэтому является только положительной
Скорость 1. независимо от пройденного пути 2.может быть положительным или отрицательным 3. является вектором 4. Направление можно угадать по знаку (т.е. положительный или отрицательный)
Кроме того, объект, который совершает круговой обход, т. е. удаляется от своей начальной точки, а затем возвращается в ту же точку. точка имеет нулевую скорость, но движется с ненулевой скоростью. 35
3,4
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10
Упражнение: Вытеснение и связанные с ним величины 1. Тереза должна идти в магазин, чтобы купить немного молока. Пройдя 100 м, она понимает, что у нее не хватает денег, и возвращается домой.Если ей потребовалось две минуты, чтобы уйти и вернуться, вычислите следующее: (a) (b) (c) (d) (e)
Как долго она находилась вне дома (временной интервал ∆t в секундах) ? Как далеко она прошла (расстояние (d))? Какое было ее смещение (∆x)? Какова была ее средняя скорость (в м · с − 1)? Какова была ее средняя скорость (в м · с − 1)? b
магазин
2 минуты туда и обратно 100 м 100 м
дом
2. Десмонд наблюдает за прямым участком дороги из окна своего класса.Он видит два столба, которые, как он ранее измерил, находятся на расстоянии 50 м друг от друга. Используя свой секундомер, Десмонд замечает, что большинству автомобилей требуется 3 секунды, чтобы добраться от одного полюса до другого. (a) Используя уравнение для скорости (v = ∆x ∆t), покажите всю работу, необходимую для расчета скорости автомобиля, движущегося слева направо. (b) Если Десмонд измеряет скорость красного гольфа как -16,67 м · с − 1, в каком направлении летело золото? Десмонд оставляет включенным секундомер и замечает, что в момент t = 5,0 с такси проезжает левый полюс одновременно с автобусом, проезжающим правый полюс.В момент времени t = 7,5 с такси проезжает правый столб. В момент времени t = 9,0 с автобус проезжает левый полюс. (c) Сколько времени потребовалось такси и автобусу, чтобы преодолеть расстояние между полюсами? (Рассчитайте временной интервал (∆t) как для такси, так и для автобуса). г) Какова была скорость такси и автобуса? д) Какая скорость была у такси и автобуса? (f) Какова скорость такси и автобуса в км · ч − 1?
50 м 3 с t = 9 с t = 5 с
t = 5 с t = 7,5 с
3. После долгого дня усталый мужчина решает не использовать пешеходный мост для перехода автострады и вместо этого решает перебежать.Он видит, что в 100 метрах к нему едет машина, и уверен, что сможет вовремя перейти дорогу. 36
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10 Если автомобиль движется со скоростью 120 км · ч − 1, какова скорость автомобиля в м · с − 1. За сколько времени машина преодолеет 100 м? Если человек бежит со скоростью 10 км · ч − 1, какова его скорость в м · с − 1? Если на автостраде 3 полосы движения, а ширина каждой полосы 3 м, сколько времени потребуется человеку, чтобы пересечь все три полосы? (e) Если автомобиль движется по полосе, наиболее удаленной от человека, сможет ли он безопасно пересечь все 3 полосы автострады?
(a) (b) (c) (d)
3 м
вагон
3 м 3 м
100 м
Мероприятие :: Расследование: упражнения по технике безопасности Разделитесь на группы по 4 человека и проведите следующее расследование.Каждая группа будет проводить одно и то же расследование, но цели у каждой группы будут разными. 1. Выберите цель вашего исследования из следующего списка и сформулируйте гипотезу: • Двигаются ли автомобили с правильным ограничением скорости? • Безопасно ли переходить дорогу вне пешеходного перехода? • Определяет ли цвет вашей машины скорость, на которой вы движетесь? • Любой другой соответствующий вопрос, который вы хотели бы изучить. 2. На дороге, которую вы часто переходите, отмерьте 50 м по прямому участку вдали от светофоров и перекрестков.3. Воспользуйтесь секундомером, чтобы записать время, за которое каждая из 20 машин преодолевает измеренный вами отрезок длиной 50 м. 4. Составьте таблицу для представления ваших результатов. Используйте результаты, чтобы ответить на вопрос, поставленный в целях расследования. Возможно, вам потребуется провести еще несколько измерений для вашего расследования. Планируйте в своей группе, что еще нужно сделать. 5. Выполните любые дополнительные измерения и опишите свое расследование под следующими заголовками: • Цель и гипотеза • Аппарат • Метод • Результаты • Обсуждение • Заключение 6.Ответьте на следующие вопросы: а) Сколько автомобилей проехали 50 м менее чем за 3 секунды? б) Какое самое короткое время потребовалось автомобилю, чтобы преодолеть 50 метров? (c) Сколько в среднем времени заняло 20 автомобилей? (d) Какова была средняя скорость 20 автомобилей? (e) Преобразуйте среднюю скорость в км · ч − 1.
37
3,4
3,5
3,5
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – КЛАСС 10
Ускорение
Определение: Ускорение Ускорение – это скорость изменения скорости.
Ускорение (символ a) – это скорость изменения скорости. Это мера того, насколько быстро скорость объекта изменяется во времени. Если у нас есть изменение скорости (∆v) за интервал времени (∆t), то ускорение (a) определяется как: ускорение (в м · с − 2) =
изменение скорости (в м · с −1) изменение во времени (в с)
a =
∆v ∆t
Поскольку скорость является вектором, ускорение также является вектором. Ускорение не дает никакой информации о движении, а только о том, как движение изменяется.Невозможно определить, насколько быстро объект движется или в каком направлении от ускорения. Как и скорость, ускорение может быть отрицательным или положительным. Мы видим, что когда знак ускорения и скорость совпадают, объект ускоряется. Если и скорость, и ускорение положительны, объект ускоряется в положительном направлении. Если и скорость, и ускорение отрицательны, объект ускоряется в отрицательном направлении. Если скорость положительна, а ускорение отрицательно, объект замедляется.Точно так же, если скорость отрицательная, а ускорение положительное, объект замедляется. Это проиллюстрировано в следующем рабочем примере.
Рабочий пример 7: Ускорение Вопрос: Автомобиль равномерно ускоряется от начальной скорости 2 м · с − 1 до конечной скорости 10 м · с1 за 8 секунд. Затем он равномерно замедляется до конечной скорости 4 м · с-1 за 6 секунд. Рассчитайте ускорение автомобиля за первые 8 секунд и за последние 6 секунд. Ответ Шаг 9: Определите, какая информация предоставляется и что требуется: Рассмотрите движение автомобиля в двух частях: первые 8 секунд и последние 6 секунд.Для первых 8 секунд: vi
=
Для последних 6 секунд:
2 м · с − 1
vf ti
= =
10 м · с 0 с
tf
=
8 с
−1
Шаг 10: Рассчитайте ускорение. Для первых 8 секунд:
10 м · с − 1
vi
=
vf ti
= =
4 м · с − 1 8 с
tf
=
14 с
Для следующие 6 секунд:
∆v ∆va = ∆t ∆t 4 – 10 10 – 2 = = 14 – 8 8−0 −2 = −1 м · с − 2 = 1 м · с В течение первых 8 секунд машина имела положительный разгон.Это означает, что его скорость увеличилась. Скорость положительная, значит, машина набирает скорость. Следующие 6 секунд машина имела отрицательное ускорение. Это означает, что его скорость уменьшилась. Скорость положительная, значит, автомобиль замедляется. a
=
38
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10
3,6
Важно: ускорение не говорит нам о направлении движения. Ускорение только говорит нам, как изменяется скорость.
Важно: замедление
Избегайте использования слова «замедление» для обозначения отрицательного ускорения.Это слово обычно означает замедление, и объект может замедляться как с положительным, так и с отрицательным ускорением, потому что знак скорости объекта также должен быть принят во внимание, чтобы определить, замедляется ли тело или нет.
Упражнение: Ускорение 1. Спортсмен равномерно ускоряется от начальной скорости 0 м · с − 1 до конечной скорости 4 м · с − 1 за 2 секунды. Рассчитайте его ускорение. Пусть направление, в котором бежит спортсмен, будет положительным.2. Автобус равномерно ускоряется от начальной скорости 15 м · с − 1 до конечной скорости 7 м · с − 1 за 4 секунды. Рассчитайте ускорение автобуса. Пусть направление движения автобуса будет положительным. 3. Самолет равномерно ускоряется от начальной скорости 200 м · с − 1 до скорости 100 м · с − 1 за 10 секунд. Затем он равномерно ускоряется до конечной скорости 240 м · с-1 за 20 секунд. Пусть направление движения самолета будет положительным. (а) Рассчитайте ускорение самолета в течение первых 10 секунд движения.(b) Рассчитайте ускорение самолета в течение следующих 14 секунд его движения. (c) Рассчитайте ускорение самолета за все 24 секунды его движения.
3,6
Описание движения
Цель этой главы – описать движение, и теперь, когда мы понимаем определения смещения, расстояния, скорости, скорости и ускорения, мы готовы начать использовать эти идеи, чтобы описать, как объект движется. Есть много способов описания движения: 1.слова 2. диаграммы 3. графики Эти методы будут описаны в этом разделе. Мы будем рассматривать три типа движения: когда объект не движется (неподвижный объект), когда объект движется с постоянной скоростью (равномерное движение) и когда объект движется с постоянным ускорением (движение с постоянным ускорением). 39
3.6
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – КЛАСС 10
3.6.1
Стационарный объект
Простейшее движение, которое мы можем обнаружить, – это движение неподвижного объекта.Неподвижный объект не движется, и поэтому его положение не меняется, пока он стоит на месте. Пример такой ситуации – когда кто-то чего-то ждет, не двигаясь. Человек остается в том же положении. Леседи ждет такси. Он стоит в двух метрах от остановки в момент t = 0 с. Через одну минуту при t = 60 с он все еще находится в 2 метрах от остановки, а через две минуты при t = 120 с – также в 2 метрах от остановки. Его позиция не изменилась. Его смещение равно нулю (потому что его положение такое же), его скорость равна нулю (потому что его смещение равно нулю), и его ускорение также равно нулю (потому что его скорость не меняется).смещение = 0 м
STOP
bb b
t = 0 с t = 60 st = 120 с
скорость = 0 м · с − 1 ускорение = 0 м · с − 2 2 м
2 1 0
раз (с) 60 (а)
120
0
время (с) 60
120
ускорение a (м · с − 2)
скорость v (м · с − 1)
положение x ( m)
Теперь мы можем построить графики зависимости положения от времени (x от t), скорости от времени (v от t) и ускорения от времени (a от t) для неподвижного объекта.Графики представлены на рисунке 3.5. Гостевой дом Lesedi находится в 2 метрах от остановки. Если за точку отсчета взять остановочную улицу, его позиция останется на уровне 2 метров в течение 120 секунд. График представляет собой горизонтальную линию на высоте 2 м. Также показаны графики скорости и ускорения. Обе линии представляют собой горизонтальные линии на оси абсцисс. Поскольку его положение не меняется, его скорость равна 0 м · с − 1, а поскольку скорость не меняется, ускорение составляет 0 м · с − 2.
0
(б)
раз (с) 60
120
(в)
Рисунок 3.5: Графики для неподвижного объекта (а) положение в зависимости от времени (б) скорость в зависимости от времени (в) ускорение в зависимости от времени.
Определение: Градиент Градиент линии можно вычислить, разделив изменение значения y на изменение значения x. ∆y m = ∆x
Поскольку мы знаем, что скорость – это скорость изменения положения, мы можем подтвердить значение для графика зависимости скорости от времени, вычислив градиент графика x от t.
Важно: График зависимости положения от времени дает скорость.40
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10
3,6
Если мы вычислим градиент графика зависимости x от t для неподвижного объекта, мы получим: v
= = = = =
∆x ∆t xf – xi tf – ti 2 м − 2 м (начальное положение = конечное положение) 120 с – 60 с 0 м · с − 1 (для времени, когда Леседи неподвижен)
Аналогичным образом мы можем подтвердить значение ускорения путем вычисления градиента графика зависимости скорости от времени.
Важно: Градиент скорости в зависимости отграфик времени дает ускорение.
Если мы вычислим градиент графика v в зависимости от t для неподвижного объекта, мы получим: a
= = = =
∆v ∆t vf – vi tf – ti 0 м · с − 1 – 0 м · с − 1 120 с – 60 с 0 м · с − 2
Кроме того, поскольку график зависимости скорости от времени связан с графиком зависимости положения от времени, мы можем использовать площадь под графиком зависимости скорости от времени для расчета перемещение объекта.
Важно: область под графиком зависимости скорости от времени показывает смещение.
Смещение объекта определяется площадью под графиком, равной 0 м. Это очевидно, потому что объект не движется.
3.6.2
Движение с постоянной скоростью
Движение с постоянной скоростью или равномерное движение означает, что положение объекта изменяется с одинаковой скоростью. Предположим, что каждое утро Леседи проходит 100 м до стоянки за 100 секунд. Если мы предположим, что дом Леседи является источником, то скорость Леседи будет: v
= = = =
∆x ∆t xf – xi tf – ti 100 м – 0 м 100 с – 0 с 1 м · с − 1
Скорость Леседи составляет 1 м · с − 1.Это означает, что он прошел 1 метр за первую секунду, еще метр за вторую секунду, еще один за третью секунду и так далее. Например, через 50 с он будет в 50 м от дома. Его позиция увеличивается на 1 м каждые 1 с. Схема расположения Леседи представлена на Рисунке 3.6. Теперь мы можем построить графики зависимости положения от времени (x от t), скорости от времени (v от t) и ускорения от времени (a от t) для Lesedi, движущегося с постоянной скоростью. Графики представлены на Рисунке 3.7. 41
3,6
ГЛАВА 3.ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – КЛАСС 10
b
b
b
t = 0s x = 0m
t = 50 sx = 50 mv = 1m · s − 1
t = 100 sx = 100 mv = 1m · С − 1
∆x
50 ∆t
0
раз (с) 50
1 0
100
(а)
раз (с) 50
100
ускорение a ( м · с − 2)
100
скорость v (м · с − 1)
положение x (м)
Рисунок 3.6: Диаграмма, показывающая движение Леседи с постоянной скоростью 1 м · с − 1
0
(б)
раз (с) 50
100
(в)
Рисунок 3.7: Графики движения при постоянной скорости (а) положение в зависимости от времени (б) скорость в зависимости от времени (в) ускорение в зависимости от времени. Площадь заштрихованной части на графике v-t соответствует смещению объекта.
∆t
50 0
∆x
0
50
100
-1
раз (с) 50
раз (с)
ускорение a (м · с − 2)
100
скорость v (м · с − 1)
позиция x (м)
Вечером Леседи проходит 100 м от автобусной остановки до своего дома за 100 с.Предположим, что дом Леседи является источником. Для описания движения можно нарисовать следующие графики.
0
100
(a)
(b)
раз (с) 50
100
(c)
Рисунок 3.8: Графики движения с постоянной отрицательной скоростью (а) положение в зависимости от время (б) скорость в зависимости от времени (в) ускорение в зависимости от времени. Площадь заштрихованной части на графике зависимости v от t соответствует смещению объекта. Мы видим, что график v vs. t представляет собой горизонтальную линию.Если график зависимости скорости от времени представляет собой горизонтальную линию, это означает, что скорость постоянна (не меняется). Движение с постоянной скоростью известно как равномерное движение. Мы можем использовать зависимость x от t, чтобы вычислить скорость, найдя градиент линии. v
= = = =
∆x ∆t xf – xi tf – ti 0 м – 100 м 100 с – 0 с −1 м · с − 1 42
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – КЛАСС 10
3,6
Леседи имеет скорость -1 м · с − 1 или 1 м · с − 1 по направлению к своему дому.Вы заметите, что график v vs. t представляет собой горизонтальную линию, соответствующую скорости -1 м · с − 1. Горизонтальная линия означает, что скорость остается неизменной (остается постоянной) во время движения. Это равномерная скорость.
Мы можем использовать зависимость v от t, чтобы вычислить ускорение, найдя градиент линии. a
= = = =
∆v ∆t vf – vi tf – ti
1 м · с − 1 – 1 м · с − 1 100 с – 0 с 0 м · с − 2
Lesedi имеет ускорение 0 м · с − 2. Вы заметите, что график vs.t – горизонтальная линия, соответствующая значению ускорения 0 м · с-2. Во время движения нет ускорения, потому что его скорость не меняется.
Мы можем использовать зависимость v от t, чтобы вычислить смещение, найдя площадь под графиком. v
=
Площадь под графиком
= =
ℓ × b 100 × (−1)
=
−100 м
Это означает, что Леседи имеет смещение 100 м в сторону своего дома. 43
3,6
ГЛАВА 3.ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – КЛАСС 10
Упражнение: Скорость и ускорение 1. Используйте графики на рис. 3.7, чтобы вычислить каждое из следующих действий: (a) Рассчитайте скорость Леседи между 50 и 100 секундами, используя график x против t. Подсказка: найдите градиент линии. (b) Рассчитайте ускорение Леседи во время всего движения, используя график зависимости v от t. (c) Рассчитайте смещение Леседи во время всего движения, используя график зависимости v от t. 2. Каждое утро Танди нужно 200 секунд, чтобы пройти 100 м до автобусной остановки.Нарисуйте график положения Танди как функции времени (предполагая, что дом Танди является точкой отсчета). Используйте градиент графика x от t, чтобы построить график зависимости скорости от времени. Используйте градиент графика v vs. t, чтобы нарисовать график зависимости ускорения от времени. 3. Вечером Танди нужно 200 секунд, чтобы пройти 100 метров от автобусной остановки до своего дома. Нарисуйте график положения Танди как функции времени (при условии, что дом Танди является источником). Используйте градиент графика x от t, чтобы нарисовать график зависимости скорости отвремя. Используйте градиент графика v vs. t, чтобы нарисовать график зависимости ускорения от времени. 4. Обсудите различия между двумя наборами графиков в вопросах 2 и 3.
Упражнение :: Эксперимент: Движение с постоянной скоростью Цель: измерить положение и время во время движения с постоянной скоростью и определить среднюю скорость как градиент график «Положение против времени». Аппарат: игрушечная машинка с батарейным питанием, секундомер, измерительная линейка или рулетка. Метод: 1. Работайте с другом.Скопируйте приведенную ниже таблицу в свою рабочую книгу. 2. Заполните таблицу, отсчитывая автомобиль по мере прохождения каждого расстояния. 3. Измерьте время автомобиля дважды для каждого расстояния и возьмите среднее значение как ваше приемлемое время. 4. Используйте значения расстояния и среднего времени, чтобы построить график зависимости расстояния от времени на миллиметровой бумаге. Вставьте миллиметровую бумагу в свою рабочую тетрадь. (Помните, что «A против B» всегда означает «y против x»). 5. Вставьте все обозначения осей и единицы измерения на график. 6. Проведите лучшую прямую линию через ваши точки данных.7. Найдите градиент прямой. Это средняя скорость. Результаты: Расстояние (м)
1
0 0,5 1,0 1,5 2,0 2,5 3,0 44
Время (с) 2 Ave.
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – КЛАСС 10 Выводы:
Ответьте на следующие вопросы в своей рабочей тетради. Вопросы:
1. Автомобиль двигался с постоянной скоростью?
2. Как по графику «Расстояние от времени» узнать, постоянна ли скорость?
3.Как «Расстояние против времени» будет искать машину с большей скоростью?
4. Как «Расстояние против времени» будет искать автомобиль с меньшей скоростью?
45
3,6
3,6
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10
3.6.3
Движение с постоянным ускорением
Последняя ситуация, которую мы будем изучать, – это движение с постоянным ускорением. Мы знаем, что ускорение – это скорость изменения скорости. Итак, если у нас постоянное ускорение, это означает, что скорость изменяется с постоянной скоростью.Давайте посмотрим на наш первый пример, когда Леседи снова ждет на остановке такси. Приехало такси, и Леседи села. Такси остановилось на остановочной улице и затем разогналось следующим образом: через 1 с такси преодолело расстояние 2,5 м, через 2 с – 10 м, через 3 секунды – 22, 5 м и через 4 с преодолел 40 м. Такси каждую секунду преодолевает большее расстояние. Это означает, что он ускоряется. STOP
2,5 mt = 1с
22,5 mt = 3s
10 mt = 2s
40 mt = 4s
Для расчета скорости такси вам необходимо рассчитать уклон линии в каждую секунду : v1s
= = = =
∆x ∆t xf – xi tf – ti 5m – 0m 1,5s – 0,5s 5 м · с − 1
v2s
∆x ∆t xf – xi = tf – ti 15m – 5m = 2,5s – 1,5s = 10 m · s − 1 =
v3s
= = = =
∆x ∆t xf – xi tf – ti 30m – 15m 3,5s – 2 , 5с 15 м · с − 1
По этим скоростям мы можем построить график скорости-времени, который образует прямую линию.Ускорение представляет собой градиент графика v в зависимости от t и может быть рассчитано следующим образом:
a
∆v ∆t vf – vi = tf – ti 15 м · с − 1 – 5 м · с − 1 = 3 с – 1 с −2 = 5 м · с
=
Ускорение не меняется во время движения (градиент остается постоянным). Это движение с постоянным или равномерным ускорением. Графики для этой ситуации показаны на Рисунке 3.9. Скорость на основе графиков зависимости ускорения от времени Точно так же, как мы использовали графики зависимости скорости от времени для определения смещения, мы можем использовать зависимость ускорения от времени.графики времени, чтобы найти скорость объекта в данный момент времени. Мы просто вычисляем площадь под графиком зависимости ускорения от времени в данный момент времени. На графике ниже, показывающем объект с постоянным положительным ускорением, увеличение скорости объекта через 2 секунды соответствует заштрихованной части.
v = площадь прямоугольника = a × ∆t
46
= 5 м · с − 2 × 2 с = 10 м · с − 1
3,6
ускорение a (м · с − 2)
ГЛАВА 3.ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10
b
22,5
скорость v (м · с − 1)
позиция x (м)
15 10
b
10
∆t
b
0
1
∆x
2
∆v
5
5
∆t 0
3 раза (с)
(а)
1
2
3 раза (с)
(б)
0
раз (с) 1
2
(в)
Рисунок 3.9: Графики движения с постоянным ускорением (а) положение в зависимости от времени (б) скорость в зависимости от времени (в) ускорение в зависимости от времени.
Следовательно, скорость объекта при t = 2 с равна 10 м · с − 1. Это соответствует значениям, полученным на Рисунке 3.9.
Упражнение: Графики 1. Автомобиль припаркован в 10 м от дома на 10 минут. Нарисуйте графики смещения-времени, скорости-времени и ускорения-времени для движения. Промаркируйте все оси. 2. Автобус движется с постоянной скоростью 12 м · с − 1 в течение 6 секунд.Нарисуйте график перемещения-времени, скорости-времени и ускорения-времени для движения. Промаркируйте все оси. 3. Спортсмен бежит с постоянным ускорением 1 м · с − 2 в течение 4 с. Нарисуйте графики ускорения-времени, скорости-времени и времени смещения для движения. Точные значения необходимы только для графиков ускорения-времени и скорости-времени. 4. Следующий график зависимости скорости от времени описывает движение автомобиля. Нарисуйте график смещения-времени и график-время ускорения и объясните движение автомобиля в соответствии с тремя графиками.v (м · с − 1)
6 т (с) 0 2 5. Следующий график скорость-время описывает движение грузовика. Нарисуйте график смещения-времени и график-время ускорения и объясните движение грузовика в соответствии с тремя графиками. v (м · с − 1) 8
0
4
47
т (с)
3,7
3,7
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – КЛАСС 10
Сводка графиков
Соотношение между графиками положения, скорости и ускорения как функций времени показано на рисунке 3.10.
v (м · с − 1)
x (м)
т (с)
Стационарный объект
т (с)
т (с)
a (м · с − 2)
т (с)
v (м · с − 1)
x (м)
Движение с постоянным ускорением
т (с)
v (м · с − 1)
x (м)
Uniform Motion
a (м · с − 2)
т (с)
т (с)
a (м · с − 2)
т (с)
Рисунок 3.10: Позиционирование-время , графики скорость-время и ускорение-время.
Важно: Часто от вас требуется описать движение объекта, которое представлено в виде графика положения, скорости или ускорения в зависимости от времени. Описание движения, представленного графиком, должно включать следующее (где возможно): 1. движется ли объект в положительном или отрицательном направлении 2. находится ли объект в покое, движется с постоянной скоростью или движется с постоянным положительным ускорением. (ускорение) или постоянное отрицательное ускорение (замедление) Вам также часто потребуется рисовать графики на основе описания движения словами или из диаграммы.Помните, что это просто разные методы представления одной и той же информации. Если вы помните об общих формах графиков для различных типов движения, не должно возникнуть никаких трудностей с объяснением того, что происходит.
48
т (с)
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10
3.8
3.8
Рабочие примеры
Рабочие примеры в этом разделе демонстрируют типы вопросов, которые можно задать о графиках .
Рабочий пример 8: Описание движения на основе графика положения-времени Вопрос: График положения-времени для движения автомобиля приведен ниже. Нарисуйте соответствующие графики зависимости скорости от времени и ускорения от времени, а затем опишите движение автомобиля. x (м)
5 4 3 2 1 т (с)
0 0
1
2
3
4
5
6
Ответ Шаг 1: Определите, какая информация предоставляется и что задается вопрос дает позицию vs.график времени, и требуются следующие три вещи: 1. Нарисуйте график зависимости v от t. 2. Нарисуйте график a vs. t. 3. Опишите движение автомобиля. Чтобы ответить на эти вопросы, разбейте движение на три части: 0–2 секунды, 2–4 секунды и 4–6 секунд. Шаг 2: График зависимости скорости от времени в течение 0–2 секунд. В течение первых 2 секунд мы видим, что смещение остается постоянным – поэтому объект не движется, следовательно, в это время он имеет нулевую скорость. Мы можем прийти к такому выводу и другим путем: помните, что градиент смещения vs.график времени – скорость. В течение первых 2 секунд мы видим, что график зависимости смещения от времени представляет собой горизонтальную линию, т.е. у него нулевой градиент. Таким образом, скорость в это время равна нулю, и объект неподвижен. Шаг 3: График зависимости скорости от времени для 2-4 секунд В течение следующих 2 секунд смещение увеличивается со временем, поэтому объект движется. Глядя на градиент графика смещения, мы видим, что он непостоянен. Фактически, наклон становится все круче (градиент увеличивается) с течением времени.Таким образом, помня, что градиент графика смещения от времени – это скорость, скорость должна увеличиваться со временем в течение этой фазы. Шаг 4: График зависимости скорости от времени для 4-6 секунд В последние 2 секунды мы видим, что смещение все еще увеличивается со временем, но на этот раз градиент постоянный, поэтому мы знаем, что теперь объект движется с постоянной скоростью. таким образом, график зависимости скорости от времени на этом этапе будет горизонтальной линией. Теперь мы можем нарисовать графики: 49
3.8
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10 Итак, наш график зависимости скорости от времени выглядит следующим образом. Поскольку нам не были даны какие-либо значения на вертикальной оси графика смещения от времени, мы не можем выяснить, каковы точные градиенты и, следовательно, каковы значения скоростей. В этом типе вопросов просто важно показать, являются ли скорости положительными или отрицательными, увеличивающимися, уменьшающимися или постоянными. v (м · с − 1)
т (с) 0
1
2
3
4
5
6
Как только у нас есть скорость vs.График времени гораздо проще получить график зависимости ускорения от времени, поскольку мы знаем, что градиент графика зависимости скорости от времени – это и есть ускорение. Шаг 5: График зависимости ускорения от времени в течение 0–2 секунд В течение первых 2 секунд график зависимости скорости от времени является горизонтальным и имеет нулевое значение, таким образом, он имеет нулевой градиент и в течение этого времени ускорение отсутствует. (Это имеет смысл, потому что мы знаем из графика времени смещения, что объект в это время неподвижен, поэтому он не может ускоряться).Шаг 6. График зависимости ускорения от времени в течение 2-4 секунд. В течение следующих 2 секунд график зависимости скорости от времени имеет положительный градиент. Этот градиент не меняется (то есть его постоянный) в течение этих 2 секунд, поэтому должно быть постоянное положительное ускорение. Шаг 7: График зависимости ускорения от времени для 4-6 секунд Последние 2 секунды объект движется с постоянной скоростью. В это время градиент графика зависимости скорости от времени снова равен нулю, и, следовательно, объект не ускоряется.График зависимости ускорения от времени выглядит следующим образом: a (м · с − 2)
0
2
4
6
т (с)
Шаг 8: Описание движения объекта Краткое описание движения объекта можно было бы прочитать примерно так: при t = 0 с и объект неподвижен в некоторой позиции и остается неподвижным до момента t = 2 с, когда он начинает ускоряться. Он ускоряется в положительном направлении в течение 2 секунд до момента t = 4 с, а затем движется с постоянной скоростью еще 2 секунды.
50
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10
3.8
Рабочий пример 9: Расчеты на основе графика зависимости скорости от времени Вопрос: График зависимости скорости от времени для грузовика показан ниже. Рассчитайте расстояние и перемещение грузовика через 15 секунд. v (м · с − 1) 4 3 2 1 т (с)
0 1
2
3
4
5
6
7
8
9
10
11
12
13
14
−1 −2 Ответ Шаг 1. Решите, как решить проблему. Нас просят рассчитать расстояние и смещение автомобиля.Все, что нам нужно здесь помнить, это то, что мы можем использовать область между графиком зависимости скорости от времени и осью времени для определения расстояния и смещения. Шаг 2: Определите площадь под графиком зависимости скорости от времени. Разбейте движение на 0–5 секунд, 5–12 секунд, 12–14 секунд и 14–15 секунд. Для 0-5 секунд: смещение равно площади треугольника слева: Area △
= = =
1 b × h 2 1 × 5 × 4 2 10 м
За 12-14 секунд смещение равно площади треугольника над временной осью справа: Площадь △
= = =
1 b × h 2 1 × 2 × 4 2 4 м
Для 5 – 12 секунд: смещение равно на площадь прямоугольника:
Площадь
= ℓ × b = 7 × 4
= 28 м
За 14-15 секунд смещение равно площади треугольника под временной осью: Площадь △
1 b × h 2 1 = × 1 × 2 2 = 1 м =
Шаг 3: Определите общее расстояние автомобиля. Теперь общее расстояние автомобиля представляет собой сумму всех этих площадей: ∆x = =
10 + 28 + 4 + 1 43 м 51
15
3.8
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – КЛАСС 10
Шаг 4: Определите полное смещение автомобиля. Теперь полное смещение автомобиля – это просто сумма всех этих областей. ОДНАКО, поскольку в последнюю секунду (с t = 14 с до t = 15 с) скорость автомобиля отрицательна, это означает, что машина ехала в обратном направлении, то есть туда, откуда она пришла! Итак, чтобы найти полное смещение, мы должны сложить первые 3 области (с положительными смещениями) и вычесть последнюю (потому что это смещение в противоположном направлении).∆x = =
10 + 28 + 4 – 1 41 м в положительном направлении
Рабочий пример 10: Скорость на графике зависимости положения от времени Вопрос: График зависимости положения от времени ниже описывает движение спортсмена. 1. Какова скорость спортсмена в первые 4 секунды? 2. Какова скорость спортсмена от t = 4 с до t = 7 с? x (м) 4 3 2 1 t (с)
0 0
1
2
3
4
5
6
7
Ответ Шаг 1: Скорость в течение первых 4 секунд Скорость задается градиентом положения относительнографик времени. В течение первых 4 секунд это v
∆x ∆t 4−0 = 4−0 = 1 м · с − 1
=
Шаг 2: Скорость за последние 3 секунды. За последние 3 секунды мы можно увидеть, что смещение остается постоянным. График показывает горизонтальную линию, поэтому градиент равен нулю. Таким образом, v = 0 m · s − 1.
52
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10
3,8
Рабочий пример 11: Построение графика зависимости v от t от графика a от t Вопрос: ускорение vs.График времени для машины, трогающейся из состояния покоя, приведен ниже. Вычислите скорость автомобиля и нарисуйте график зависимости скорости от времени. a (м · с − 2) 2 1 t (с)
0 1
2
3
4
5
6
−1 −2 Ответ Шаг 1: Рассчитайте значения скорости, используя площадь под каждой частью графика. Движение автомобиля можно разделить на три временных отрезка: 0 – 2 секунды; 2-4 секунды и 4-6 секунд. Чтобы иметь возможность рисовать зависимость скорости отвременного графика, необходимо рассчитать скорость для каждого временного отрезка. Скорость равна площади квадрата под графиком: Для 0–2 секунд: Площадь
= ℓ × b = 2 × 2
Для 2–4 секунд: Площадь
= 4 м · с − 1 скорость автомобиля составляет 4 м · с − 1 при t = 2 с.
Для 4-6 секунд:
= ℓ × b = 2 × 0
Площадь
= ℓ × b
= 2 × −2 = −4 м · с − 1
= 0 м · с− 1 Скорость автомобиля составляет 0 м · с − 1 от t = 2 с до t = 4 с.
Ускорение имеет отрицательное значение, что означает, что скорость уменьшается. Он начинается со скорости 4 м · с − 1 и уменьшается до 0 м · с − 1.
Шаг 2: Теперь используйте значения для построения графика зависимости скорости от времени. v (м · с − 1) 4 3 График зависимости скорости от времени выглядит следующим образом:
2 1 т (с)
0 0
53
1
2
3
4
5
6
3,9
3,9
ГЛАВА 3.ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – КЛАСС 10
Уравнения движения
В этой главе мы рассмотрим третий способ описания движения. Мы рассмотрели описание движения с помощью графиков и слов. В этом разделе мы исследуем уравнения, которые можно использовать для описания движения. Этот раздел посвящен решению задач, связанных с равноускоренным движением. Другими словами, движение с постоянным ускорением. В этом разделе будут использоваться следующие переменные: vi vf
= =
начальная скорость (м · с − 1) при t = 0 с конечная скорость (м · с − 1) в момент времени t
∆ x = t =
смещение (м) время (с)
∆t
временной интервал (с)
=
a =
ускорение (м · с − 2)
vf
=
∆x = ∆x = vf2
=
vi + at (vi + vf) t 2 1 vi t + at2 2 vi2 + 2a∆x
(3.1) (3.2) (3.3) (3.4)
Вопросы могут быть самыми разными, но следующий метод ответа на них всегда будет работать. Используйте это при ответе на вопрос, связанный с движением с постоянным ускорением. Вам нужны любые три известные величины (vi, vf, ∆x, t или a), чтобы можно было вычислить четвертую. 1. Внимательно прочтите вопрос, чтобы определить указанные количества. Запишите их. 2. Определите уравнение для использования. Запиши это!!! 3. Убедитесь, что все значения указаны в правильных единицах измерения, и введите их в уравнение.4. Вычислите ответ и введите его единицу.
teresting Галилео Галилей из Пизы, Италия, был первым, кто определил правильный математический закон. Интересный факт: закон для ускорения: общее пройденное расстояние, начиная с момента покоя, пропорционально квадрату времени. Он также пришел к выводу, что объекты сохраняют свою скорость, если на них не действует сила – часто трение, опровергая принятую аристотелевскую гипотезу о том, что объекты «естественным образом» замедляются и останавливаются, если на них не действует сила.Этот принцип был включен в законы движения Ньютона (1-й закон).
3.9.1
Поиск уравнений движения
Следующее не является частью учебной программы и может считаться дополнительной информацией. 54
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – КЛАСС 10
3.9
Вывод уравнения 3.1 Согласно определению ускорения: a =
∆vt
где ∆v – изменение скорости, т. Е. ∆v = vf – vi. Таким образом, мы имеем
=
vf
=
vf – vi t vi + at
Вывод уравнения 3.2 Мы видели, что смещение можно рассчитать по площади под графиком зависимости скорости от времени. Для равноускоренного движения наиболее сложный график зависимости скорости от времени, который мы можем получить, представляет собой прямую линию. Посмотрите на график ниже – он представляет объект с начальной скоростью vi, ускоряющийся до конечной скорости vf за общее время t.
v (м · с − 1)
vf vi
t
t (s)
Для расчета окончательного смещения мы должны вычислить площадь под графиком – это просто площадь прямоугольника, добавленная к площадь треугольника.Эта часть графика заштрихована для ясности.
Площадь △
= = =
Площадь
1 b × h 2 1 t × (vf – vi) 2 1 1 vf t – vi t 2 2
= ℓ × b
= t × vi = vi t
Смещение = Площадь + Площадь △ 1 1 ∆x = vi t + vf t – vi t 2 2 (vi + vf) t ∆x = 2 55
3.9
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10
Вывод уравнения 3.3
Это уравнение просто выводится путем исключения конечной скорости vf из уравнения 3.2. Помня из уравнения 3.1, что vf = vi +, тогда уравнение 3.2 принимает вид ∆x
= =
∆x
=
vi + vi + at t 2 2vi t + at2 2 1 vi t + at2 2 56
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10
3.9
Вывод уравнения 3.4 Это уравнение получается путем исключения временной переменной из приведенного выше уравнения. Из уравнения 3.1 мы знаем, что vf – vi t = a. Подставив это в уравнение 3.3, мы получим ∆x
= = =
2a∆x = vf2
=
vf – vi 1 vf – vi 2) + a () a 2 a vi vf v2 1 vf2 – 2vi vf + vi2) – i + a (aa 2 a2 vf2 v2 vi vf v2 vi vf – i + – + iaa 2a a 2a −2vi2 + vf2 + vi2 vi (
vi2 + 2a ∆x
(3.5)
Это дает нам конечную скорость с точки зрения начальной скорости, ускорения и смещения и не зависит от временной переменной.
Рабочий пример 12: Уравнения движения Вопрос: Гоночный автомобиль едет на север. Равномерно ускоряется, преодолевая расстояние 725 м за 10 с. Если у него начальная скорость 10 м · с-1, найдите его ускорение. Ответ Шаг 1: Определите, какая информация предоставляется и что требуется. Нам дано: vi = ∆x = t a
= =
10 м · с − 1 725 м 10 с?
Шаг 2: Найдите уравнение движения, связывающее данную информацию с ускорением. Если вам сложно найти правильное уравнение, найдите величину, которая не указана, а затем найдите уравнение, в котором эта величина отсутствует.Мы можем использовать уравнение 3.3 1 ∆x = vi t + at2 2 Шаг 3: подставьте свои значения и найдите ответ
∆x
1 = vi t + at2 2
1 725 = (10 × 10) + a × (10) 2 2 725 – 100 = 50 aa = 12,5 м · с − 2 Шаг 4: Процитируйте окончательный ответ Гоночный автомобиль ускоряется на скорости 12,5 м · с − 2 на север.
57
3.9
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10
Рабочий пример 13: Уравнения движения Вопрос: Мотоцикл, двигаясь на восток, трогается с места, движется по прямой с постоянным ускорением и покрывает дистанция 64 м за 4 с.Вычислите • • • •
его ускорение и конечную скорость, за какое время мотоцикл преодолел половину общего расстояния, которое мотоцикл преодолел за половину общего времени.
Ответ Шаг 1: Определите, какая информация предоставляется и что запрашивается Нам дано: 0 м · с − 1 (потому что объект начинается с состояния покоя).
vi
=
∆xt
= =
a vf
= =
? ?
т
=
? на половине расстояния ∆x = 32 м.
∆x
=
? на половине времени t = 2 с.
64 м 4 с
Все величины указаны в единицах СИ. Шаг 2: Ускорение: Найдите подходящее уравнение для расчета ускорения Мы можем использовать уравнения 3.3 1 ∆x = vi t + at2 2 Шаг 3: Подставить значения и рассчитать ускорение
∆x
1 vi t + at2 2 1 (0 × 4) + a × (4) 2 2 8a
=
64 = 64 = a
8 м · с − 2 на восток
=
Шаг 4: Конечная скорость: Найдите подходящее уравнение для расчета конечная скорость Мы можем использовать уравнение 3.1 – помните, что теперь мы также знаем ускорение объекта. vf = vi + на шаге 5: подставьте значения и вычислите окончательную скорость vf
=
vi + at
vf
= =
0 + (8) (4) 32 м · с − 1 восток
Шаг 6: Время на половине расстояния: Найдите уравнение для вычисления времени Мы можем использовать уравнение 3.3: 1 = vi + at2 2 1 32 = (0) t + (8) (t) 2 2 32 = 0 + 4t2
∆x
8 т
= t2 = 2,83 с 58
ГЛАВА 3.ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10
3,10
Шаг 7: Расстояние за половину времени: Найдите уравнение, чтобы связать расстояние и время. Половина времени составляет 2 секунды, поэтому у нас есть vi, a и t – все в правильном единицы. Мы можем использовать уравнение 3.3, чтобы получить расстояние: ∆x
= = =
1 vi t + at2 2 1 (0) (2) + (8) (2) 2 2 16 м к востоку
Упражнение: Ускорение 1 Автомобиль трогается с места на скорости 10 м · с − 1 и разгоняется со скоростью 1 м · с − 2 за 10 с. Какова его конечная скорость? 2. Поезд стартует из состояния покоя и ускоряется со скоростью 1 м · с − 2 за 10 с.Как далеко он продвигается? 3. Автобус едет 30 м · с − 1 и останавливается через 5 с. Каков его тормозной путь для этой скорости? 4. Гоночный автомобиль, движущийся со скоростью 20 м · с − 1, останавливается на расстоянии 20 м. Какое у него ускорение? 5. Мяч имеет равномерное ускорение 4 м · с − 1. Предположим, что мяч стартует из состояния покоя. Определите скорость и смещение по истечении 10 с. 6. Мотоцикл имеет равномерное ускорение 4 м · с − 1. Предположим, что начальная скорость мотоцикла составляет 20 м · с − 1. Определите скорость и смещение по истечении 12 с.7. Самолет ускоряется равномерно, так что он разгоняется до 144 км · ч − 1 за 8 с. Рассчитайте необходимое ускорение и общее расстояние, которое он прошел за это время.
3.10
Приложения в реальном мире
То, что мы узнали в этой главе, можно напрямую применить к безопасности дорожного движения. Мы можем проанализировать взаимосвязь между скоростью и тормозным путем. Следующий рабочий пример иллюстрирует это приложение.
Работает Пример 14: Тормозной путь Вопрос: Грузовик движется с постоянной скоростью 10 м · с − 1, когда водитель видит на дороге ребенка в 50 м впереди себя.Он нажимает на тормоз, чтобы остановить грузовик. Грузовик ускоряется со скоростью -1,25 м · с − 2. Его время реакции на нажатие тормоза – 0,5 секунды. Будет ли грузовик сбить ребенка? Ответ Шаг 1. Проанализируйте проблему и определите, какая информация предоставляется. Полезно нарисовать временную шкалу, подобную этой: 59
3.10
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – КЛАСС 10
здесь ребенок
водитель тормозит
водитель видит ребенка
v = 10 м · с − 1 0,5 с
Bb
Abb
Cb отрицательное ускорение
постоянная v
50 м Нам необходимо знать следующее: • На каком расстоянии водитель накрывает перед тем, как нажать на тормоза.
• Сколько времени требуется грузовику для остановки после нажатия на тормоз. • Какое общее расстояние проезжает грузовик до остановки.
Шаг 2: Рассчитайте расстояние AB Прежде чем водитель нажмет на тормоз, грузовик движется с постоянной скоростью. Ускорения нет, поэтому уравнения движения не используются. Чтобы найти пройденное расстояние, мы используем: v
=
10 = d =
d t d 0,5 5m
Грузовик проезжает 5 м, прежде чем водитель нажмет на тормоз.Шаг 3: Рассчитайте время BC. Для движения между B и C имеем следующее: vi vf
= =
при
= =
10 м · с − 1 0 м · с − 1
−1 , 25 м · с − 2?
Мы можем использовать уравнение 3.1 vf = 0 = −10 = t =
vi + при 10 + (−1,25) t −1,25t 8s
Шаг 4: Вычислить расстояние BC. уравнение 3.2 или уравнение 3.3. Мы будем использовать уравнение 3.2: ∆x ∆x ∆x
(vi + vf) t 2 10 + 0 = (8) s = 40 m =
Шаг 5: Напишите окончательный ответ. Общее расстояние, которое преодолевает грузовик, составляет dAB + dBC = 5 + 40 = 45 метров.Ребенок в 50 метрах впереди. Грузовик не ударит ребенка.
60
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – КЛАСС 10
3.11
3.11
Сводка
• Контрольная точка – это точка, с которой вы производите измерения. • Система отсчета – это ориентир с набором направлений. • Ваша позиция – это то место, где вы находитесь по отношению к вашей контрольной точке. • Смещение объекта – это то, насколько он удален от опорной точки.Это кратчайшее расстояние между объектом и точкой отсчета. У него есть величина и направление, потому что это вектор. • Расстояние до объекта – это длина пути, пройденного от начальной до конечной точки. Он имеет величину только потому, что является скаляром. • Вектор – это физическая величина с величиной и направлением. • Скаляр – это физическая величина, имеющая только величину. • Скорость (s) – это пройденное расстояние (d), деленное на затраченное время (∆t): s =
d ∆t
• Средняя скорость (v) – это смещение (∆x), деленное на затраченное время ( ∆t): v =
∆x ∆t
• Мгновенная скорость – это скорость в определенный момент времени.• Мгновенная скорость – это скорость в определенный момент времени. • Ускорение (a) – это изменение скорости (∆x) за временной интервал (∆t): a =
∆v ∆t
• Градиент графика положения – времени (x в зависимости от t) дает скорость. • Градиент графика зависимости скорости от времени (v в зависимости от t) дает ускорение. • Площадь под графиком скорость – время (v в зависимости от t) дает смещение. • Площадь под графиком «ускорение – время» (a в зависимости от t) показывает скорость. • Графики движения представлены на рисунке 3.10. • Уравнения движения используются там, где имеет место постоянное ускорение: vf
=
∆x
=
∆x
=
vf2
= 61
vi + at (vi + vf) t 2 1 vi t + at2 2 vi2 + 2a∆x
3.12
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – КЛАСС 10
3,12
Конец главы Упражнения: Движение в одном измерении
1. Дайте одно слово / термин для следующих описаний. (а) Кратчайший путь от начала до конца.(б) Физическая величина с величиной и направлением. (c) Величина, определяемая как изменение скорости за период времени. (d) Точка, откуда вы производите измерения. (e) Расстояние, пройденное за интервал времени. (е) Скорость в определенный момент времени. 2. Выберите элемент из столбца B, который соответствует описанию в столбце A. Запишите только букву рядом с номером вопроса. Вы можете использовать элемент из столбца B более одного раза. Колонка А а. Площадь под графиком скорость – время b. Градиент графика скорости – времени c.Площадь под графиком ускорение – время d. График смещения – время
Столбец B, градиент, область, скорость, смещение, наклон, ускорение
3. Укажите, истинны ли следующие утверждения или ЛОЖЬ. Пишите только «истина» или «ложь». Если утверждение ложное, запишите правильное утверждение. (а) Скаляр – это смещение объекта за промежуток времени. (б) Положение объекта – это то место, где он находится. (c) Знак скорости объекта говорит нам, в каком направлении он движется.(d) Ускорение объекта – это изменение его перемещения за определенный период времени. 4. [SC 2003/11] Тело равномерно ускоряется из состояния покоя в течение t0 секунд, после чего оно продолжает двигаться с постоянной скоростью. Какой график правильно отображает движение тела? x
x
t0 (a)
t
x
t0
x
t
t0
(b)
(c)
t
t0
t
( г)
5.[SC 2003/11] Графики скорость-время двух вагонов представлены буквами P и Q, как показано v (м · с − 1) 6 5 4 3 2 1 0
P
Q
т (с) 0 1 2 3 4
Разница в расстоянии, пройденном двумя автомобилями (в метрах) за 4 с, составляет. . . 62
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10
3,12
(a) 12 (b) 6 (c) 2 (d) 0 6. [IEB 2005/11 HG] На следующем графике показано, как Скорость спортсмена меняется со временем, когда он пробегает 100 м.скорость (м · с − 1) 10
t
11
раз (с)
Какое из следующих уравнений можно использовать для правильного определения времени t, за которое он ускоряется? (а) 100 = (10) (11) – 21 (10) t
(б) 100 = (10) (11) + 21 (10) t (в) 100 = 10t + 21 (10) t2 (d ) 100 = 21 (0) t + 12 (10) t2 7. [SC 2002/03 HG1] В каком из следующих случаев пройденное расстояние и величина смещения будут одинаковыми? (а) Девушка поднимается по винтовой лестнице. (b) Спортсмен завершает один круг в гонке.(c) Капля дождя падает в неподвижном воздухе. (d) Пассажир поезда едет из Кейптауна в Йоханнесбург. 8. [SC 2003/11] Автомобиль, движущийся с постоянной скоростью, проезжает неподвижный мотоцикл на светофоре. Когда автомобиль обгоняет мотоцикл, мотоцикл равномерно ускоряется из состояния покоя в течение 10 с. На следующем графике смещение-время показано движение обоих транспортных средств от светофора и далее. x (м)
мотоцикл
автомобиль
375300
0
5
X 10
15
т (с)
(a) Используйте график, чтобы найти величину постоянной скорости машина.(b) Используйте информацию из графика, чтобы показать с помощью расчетов, что величина ускорения мотоцикла в первые 10 с его движения составляет 7,5 м · с − 2. (c) Рассчитайте, сколько времени (в секундах) потребуется мотоциклу, чтобы догнать автомобиль (точка X на оси времени). (d) Насколько далеко позади мотоцикла будет автомобиль через 15 секунд? 63
3.12
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10
9. [IEB 2005/11 HG] Какое из следующих утверждений верно для тела, которое равномерно ускоряется? (а) Скорость его изменения положения во времени остается постоянной.(б) Его положение меняется на одинаковую величину через равные промежутки времени. (c) Его скорость увеличивается на величину через равные промежутки времени. (d) Скорость его изменения скорости со временем остается постоянной. 10. [IEB 2003/11 HG1] График скорость-время для автомобиля, движущегося по прямой горизонтальной дороге, показан ниже. v (м · с − 1) 20 Площадь A
12
Область B 0
т
т (с)
Какое из следующих выражений дает величину средней скорости автомобиля? (a)
AreaA t
(b)
AreaA + AreaB t
(c)
AreaB t
(d)
AreaA – AreaB t
11.[SC 2002/11 SG] Автомобиль движется со скоростью 25 м · с − 1 в муниципальном районе. Когда водитель видит сотрудника дорожного движения на ограничителе скорости, он понимает, что едет слишком быстро. Он немедленно тормозит машину, находясь на расстоянии 100 м от ограничителя скорости. (a) Рассчитайте величину минимального ускорения, которое автомобиль должен иметь, чтобы избежать превышения ограничения скорости, если ограничение скорости в муниципальных районах составляет 16,6 м · с − 1. (b) Рассчитайте время от момента, когда водитель нажал на тормоз, до достижения скоростного ограничителя.Предположим, что скорость автомобиля при достижении ловушки составляет 16,6 м · с − 1. 12. Сотрудник дорожного движения наблюдает за своим оборудованием для ловушек на дне долины. Он может видеть машины, которые въезжают в долину на 1 км слева от него, пока не покидают долину на 1 км справа от него. Нельсон записывает время въезда и выезда автомобилей из долины для школьного проекта. Нельсон замечает, что белая Toyota входит в долину в 11:01:30 и покидает долину в 11:02:42. После этого Нельсон слышит, что дорожный инспектор зафиксировал скорость Toyota 140 км · ч − 1.(a) Каков был интервал времени (∆t), за который Toyota проехала через долину? б) Какая была средняя скорость Тойоты? (c) Преобразуйте эту скорость в км · ч − 1. (d) Обсудите, могла ли Тойота двигаться со скоростью 140 км · ч-1 по дну долины. (e) Обсудите разницу между мгновенной скоростью (измеренной скоростным уловителем) и средней скоростью (измеренной Нельсоном). 64
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10
3,12
13. [IEB 2003 / 11HG] График скорость-время для шара, катящегося по дорожке, показан ниже.График разделен на 3 части: A, B и C для удобства использования. (Не учитывать влияние трения.)
Скорость (м · с − 1) 0,6
0
A
B
5
C
10
t1
12
-0, 2
(a) Используйте график, чтобы определить следующее: i. скорость 5 с после старта ii. пройденное расстояние в Разделе A iii. ускорение в секции C (b) В момент времени t1 график скорости-времени пересекает ось времени.Используйте соответствующее уравнение движения, чтобы вычислить значение времени t1 (в с). (c) Нарисуйте график смещения-времени для движения мяча за эти 12 с. (Вам не нужно рассчитывать фактические значения смещения для каждого временного интервала, но обратите внимание на общую форму этого графика в течение каждого временного интервала.) 14. В городах ограничение скорости составляет 60 км · ч. −1. Длина средней машины составляет 3,5 м, а ширина средней машины – 2 м. Чтобы перейти дорогу, вам необходимо пройти дальше, чем ширина автомобиля, прежде чем он подъедет к вам.Для безопасного перехода вы должны пройти не менее чем на 2 м дальше ширины автомобиля (всего 4 м), прежде чем машина подъедет к вам. (а) Если ваша скорость ходьбы составляет 4 км · ч − 1, какова ваша скорость ходьбы в м · с − 1? б) Сколько времени вам нужно, чтобы пройти расстояние, равное ширине средней машины? (c) Какова скорость в м · с − 1 автомобиля, движущегося с ограничением скорости в городе? (d) Сколько метров проезжает автомобиль, движущийся с ограничением скорости, за то же время, которое вам нужно, чтобы пройти расстояние, равное ширине автомобиля? д) Почему так важен ответ на предыдущий вопрос? (f) Если вы видите машину, едущую навстречу вам, на расстоянии 28 м (столько же, сколько 8 машин), безопасно ли переходить дорогу? (ж) Как далеко должна быть должна находиться машина, чтобы, по вашему мнению, ее можно было безопасно пересечь? Сколько автомобильной длины это расстояние? 15.Автобус на прямой дороге начинает движение с остановки на автобусной остановке и ускоряется со скоростью 2 м · с − 2, пока не достигает скорости 20 м · с − 1. Затем автобус едет с постоянной скоростью 20 с, пока водитель не увидит вдалеке следующую автобусную остановку. Водитель нажимает на тормоза, равномерно останавливая автобус за 5 с. (а) Сколько времени занимает автобус, чтобы добраться от первой автобусной остановки до второй автобусной остановки? (б) Какова средняя скорость автобуса во время поездки?
65
раз
3.12
ГЛАВА 3. ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ – УРОВЕНЬ 10
66
Импульс: определение, уравнение, расчет и примеры – видео и стенограмма урока
Примеры Impulse
Давайте рассмотрим несколько примеров.
В этом первом примере мы рассмотрим импульс для объекта, который сталкивается со стеной и останавливается после столкновения. Если объект весом 2,0 кг движется со скоростью 10 м / с до удара о стену, то можно рассчитать импульс.
Δ p = pf – pi
Δ p = mvf – mvi
Δ p = (2,0 кг) (0 м / с) – (2,0 кг) (10 м / с) = -20 кг м / с
Во втором примере мы рассмотрим импульс для объекта, который сталкивается со стеной и отскакивает после столкновения. Если объект весом 2,0 кг движется со скоростью 10 м / с до удара о стену и со скоростью -10 м / с после столкновения (отрицательной, потому что он отскакивает в обратном направлении), то импульс можно рассчитать как следующим образом:
Δ p = pf – pi
Δ p = mvf – mvi
Δ p = (2.0 кг) (- 10 м / с) – (2,0 кг) (10 м / с) = -20 кг м / с – 20 кг м / с = -40 кг м / с
В следующем примере мы рассчитаем импульс другим способом. Какой импульс вызывает средняя сила в 10 Ньютонов, если она действует на мяч в течение 2,0 секунд? Здесь импульс можно рассчитать как:
Применение импульса
Теперь, когда мы можем вычислить импульс, мы можем взглянуть на некоторые интересные примеры импульса в повседневной жизни.Наиболее ярким примером является автомобильная система подушек безопасности. Подушки безопасности установлены в автомобилях, чтобы уменьшить повреждение водителя или пассажира при столкновении.
Если импульс – это сила, умноженная на время, то сила – это импульс, разделенный на время. Подушка безопасности увеличивает время, необходимое для остановки движения пассажира или водителя. Если это время увеличить, то сила удара уменьшается. Если время удара невелико, сила удара увеличивается и может нанести серьезный ущерб находящимся в автомобиле.
Мягкий пол в спортзале – еще одно применение концепции импульса. Чтобы уменьшить силу удара при приземлении на пол, набивка увеличивает время контакта человека с полом. Так же, как и с подушками безопасности, когда время контакта увеличивается, сила удара уменьшается.
Вот пример, который вы можете сделать дома. Вы и ваши друзья хотите поэкспериментировать с импульсами и яйцами. Если вы уроните яйца на твердую поверхность, вы все знаете, что яйцо разобьется.Время удара между полом и яйцом короткое, а это означает, что сила (которая представляет собой импульс, разделенный на время) становится достаточно большой, чтобы яйцо раскололо. Если у вас есть четверо ваших друзей, которые держат простыню на несколько дюймов над полом и снова бросают яйцо, яйцо не разобьется. Почему? Простыня увеличила время столкновения и, как следствие, уменьшила силу удара.
Impulse всегда присутствует и в спорте. В теннисе, когда мяч проходит вперед и назад, между мячом и теннисной ракеткой возникает импульс.В футболе, когда по мячу бьют кулаком, импульс может помочь определить силу удара, если мы знаем время контакта между ногой и мячом. В теннисе, бейсболе и гольфе (среди других видов спорта) чем быстрее вы замахиваетесь мячом, тем сильнее вы даете мячу импульс. Затем мяч уходит быстрее или дальше.
Краткое содержание урока
Импульс и импульс являются взаимосвязанными величинами. Импульс – это мера силы объекта, а также того, насколько сложно изменить движение объекта. начальный
Результаты обучения
Узнав об импульсе на этом уроке, вы сможете
- Определить импульс.
- Объясните взаимосвязь между импульсом и импульсом.
- Вспомните формулы для импульса и импульса и вычислите импульс.
- Обсудите несколько реальных применений импульса.
Математические формулы для класса 10 – PDF по главам – Embibe
Математика – один из предметов по формуле для 10 класса.Это важный и результативный предмет. Математическая формула для 10-го класса не только полезна для 10-го класса, но и закладывает прочную основу для математических концепций более высокого уровня. Математические формулы очень важны для студентов, которые стремятся сделать карьеру в области инженерии, медицины, финансов, коммерции, информатики и т. Д. Учитывая важность математических формул, здесь мы предоставили по главам списки важных математических дисциплин. Формулы для класса 10 .
В списке математических формулдля класса 10 есть такие темы, как действительные числа, многочлены, треугольники, круги, статистика, вероятность и т. Д.Эти математические формулы очень полезны для тех, кто сможет более точно и быстро решать вопросы. Учащиеся, которые приходят на экзамен для 10-го класса, должны уделять больше внимания программе по математике. Прочтите эту статью полностью, чтобы получить все важные сведения о формуле математики для 10 класса, которая поможет кандидатам получить хорошие оценки по математике на предстоящих экзаменах Совета CBSE.
Последнее обновление
👉 Экзамены CBSE Term 1 по основным предметам начнутся для учащихся 10 класса с 30 ноября по 11 декабря 2021 г. и для учащихся 12 класса с 1 по 22 декабря 2021 г.
👉 Обычные учащиеся могут получить свои входные билеты в своих школах, а частные кандидаты могут загрузить их с официального сайта CBSE – cbse.gov.in.
👉 Продолжительность экзамена по каждому предмету составляет 90 минут.
👉 Экзамен CBSE Term 1 будет проводиться полностью в автономном режиме, и у студентов нет возможности появляться онлайн.
👉 Поскольку экзамен CBSE Term 1 будет проводиться в зимний сезон, экзамены начнутся с 11:30 вместо 10:30. Правильный ответ для каждого варианта должен быть написан на листах OMR, которые можно написать только синей или черной ручкой.
Ускоренный курс практики Embibe CBSE для семестра 1 на основе новых рекомендаций:
Практика Эмбибе Эксклюзивные образцы документов CBSE Term 1 на основе новых рекомендаций:
Здесь, в Embibe, вы можете получить бесплатный пробный тест MCQ 2021, пересмотренный CBSE, по всем темам. Тест MCQ, предлагаемый Embibe, основан на пересмотренных учебниках, бумажных шаблонах и учебной программе CBSE на 2021 год.В этой серии пробных тестов есть полный набор актуальных вопросов и их решений. Кандидаты в CBSE Board могут пройти эти бесплатные пробные тесты, чтобы попрактиковаться и найти области, в которых им нужно улучшить свои экзамены.
Изучите концепции 10-го экзамена CBSE
Математические формулы для класса 10 (по главам)
Составление всех математических формул CBSE Class 10 – непростая задача для студентов. Тем не менее, важно получить хорошие баллы на экзаменах 10 класса, а математика – один из обязательных предметов в 10 классе, по которому учащиеся могут получить хорошие баллы.Этот экзамен составляет 100 баллов и охватывает все основные темы математики. Мы в Embibe рассмотрели все формулы PDF-файла NCERT по математике 10, чтобы помочь вам с подготовкой к экзамену. Этот экзамен длится 3 часа, и для того, чтобы правильно распорядиться этим доступным временем во время экзамена, вы должны знать все важные концепции и их формулы. Изучение математики – трудоемкая работа из-за необходимости решения задач и вычислений. Для изучения этих математических формул 10-го класса учащиеся могут использовать PDF-файлы, созданные Embibe.Прежде чем перейти к списку формул, давайте проверим основные главы математики 10 класса, для которых необходимы формулы:
Математические формулы для арифметической прогрессии (AP) 10 класса
Если a1, a2, a3, a4… .. – это члены AP, а d – общая разница между каждым термином, тогда последовательность может быть записана как: a, a + d, a + 2d, a + 3d, a + 4d …… a + nd. где a – первый член, а (a + nd) – (n – 1) -й член. Итак, формула для вычисления n-го члена AP имеет следующий вид:
n th член = a + (n-1) d
Сумма для n-го члена AP, где a – это 1-й член, d – общая разница, и l – последний член, выражается как:
S n = n / 2 [2a + (n-1) d] или S n = n / 2 [a + l]
Загрузить
Математические формулы для линейных уравнений класса 10
Линейные уравнения с одной, двумя и тремя переменными имеют следующий вид:
| Линейное уравнение в одной переменной | ax + b = 0 | Где a ≠ 0 и a & b – действительные числа |
| Линейное уравнение в двух переменных | ax + by + c = 0 | Где a ≠ 0 & b ≠ 0 и a, b и c – действительные числа |
| Линейное уравнение в трех переменных | ax + by + cz + d = 0 | Где a 0, b ≠ 0, c ≠ 0 и a, b, c, d – действительные числа |
Пара линейных уравнений с двумя переменными имеет вид:
a 1 x + b 1 + c 1 = 0 и a 2 x + b 2 + c 2 = 0
Где a 1 , b 1 , c 1 , & a 2 , b 2 , c 2 – вещественные числа & a 1 2 + b 1 2 ≠ 0 и 2 2 + b 2 2 ≠ 0
Quick Note: Линейные уравнения также могут быть представлены в графической форме.
Формулы тригонометрии для математики 10 класса
Тригонометрические формулы для класса 10 покрывают основные тригонометрические функции для прямоугольного треугольника, то есть синуса (sin), косинуса (cos) и тангенса (tan), которые могут использоваться для получения косеканса (cos), секанса (сек), и Котангенс (детская кроватка).
Пусть прямоугольный треугольник ABC расположен под прямым углом в точке B, а \ (\ angle \ theta \) является одним из двух других углов.
sin θ = \ (\ frac {Сторона \, противоположная \, к \, углу \, \ theta} {Гипотенуза} \) = \ (\ frac {Перпендикуляр} {Гипотенуза} \) = P / H
cos θ = \ (\ frac {Соседняя \, сторона \, к \, угол \, \ theta} {Гипотенуза} \) = \ (\ frac {Смежная сторона} {Гипотенуза} \) = B / H
тангенс угла θ = \ (\ frac {Сторона \, противоположная \, до \, угол \, \ theta} {Соседний \, сторона \, до \, угол \, \ theta} \) = P / B
сек θ = \ (\ frac {1} {cos \, \ theta} \)
детская кроватка θ = \ (\ frac {1} {tan \, \ theta} \)
секунд θ = \ (\ frac {1} {sin \, \ theta} \)
загар θ = \ (\ frac {Sin \, \ theta} {Cos \, \ theta} \)
Тригонометрическая таблица , содержащая значения этих тригонометрических функций для стандартных углов, выглядит следующим образом:
| Угол | 0 ° | 30 ° | 45 ° | 60 ° | 90 ° | 902 902 902 902 902 902 902 902 | 1 / √2 | √3 / 2 | 1 | ||
| cosθ | 1 | √3 / 2 | 1 / √2 | ½ | 0 | 902 | 1 / √3 | 1 | √3 | Не определено | |
| cotθ | Не определено | √3 | 1 | 1 / √3 | 0 | 902902 / √3 | √2 | 2 | Не определено | ||
| cosecθ | Не определено | 2 | √2 | 2 / √3 | 1 |
- sin (90 ° – θ) = cos θ
- cos (90 ° – θ) = sin θ
- tan (90 ° – θ) = детская кроватка θ
- детская кроватка (90 ° – θ) = tan θ
- сек (90 ° – θ) = cosecθ
- косек (90 ° – θ) = secθ
- sin 2 θ + cos 2 θ = 1
- сек 2 θ = 1 + tan 2 θ для 0 ° ≤ θ <90 °
- Cosec 2 θ = 1 + кроватка 2 θ для 0 ° ≤ θ ≤ 90 °
Математические формулы 10 класса для алгебры и квадратные уравнения
Чтобы знать формулы алгебры для класса 10, сначала вам нужно познакомиться с квадратными уравнениями.2-4ac}} {2a} \)
Теперь вы знаете основное квадратное уравнение.
Давайте теперь рассмотрим список формул алгебры для класса 10:
- (a + b) 2 = a 2 + b 2 + 2ab
- (ab) 2 = a 2 + b 2 – 2ab
- (a + b) ( ab) = a 2 – b 2
- (x + a) (x + b) = x 2 + (a + b) x + ab
- (x + a) (x – b) = x 2 + (a – b) x – ab
- (a + b) 3 = a 3 + b 3 + 3ab (a + b)
- (a – b) 3 = a 3 – b 3 – 3ab (a – b)
- (x – a) (x + b) = x 2 + (b – a) x – ab
- (x – a ) (x – b) = x 2 – (a + b) x + ab
- (x + y + z) 2 = x 2 + y 2 + z 2 + 2xy + 2yz + 2xz
- (x + y – z) 2 = x 2 + y 2 + z 2 + 2xy – 2yz – 2xz
- (x – y + z) 2 = x 2 + y 2 + z 2 – 2xy – 2yz + 2xz 922 48 (x – y – z) 2 = x 2 + y 2 + z 2 – 2xy + 2yz – 2xz
- x 3 + y 3 + z 3 – 3xyz = (x + y + z) (x2 + y2 + z2 – xy – yz -xz)
- x 2 + y 2 = ½ [(x + y) 2 + (x – y) 2 ]
- (x + a) (x + b) (x + c) = x 3 + (a + b + c) x 2 + (ab + bc + ca) x + abc
- x 3 + y 3 = (x + y) (x 2 – xy + y 2 )
- x 3 – y 3 = (x – y) (x 2 + xy + y 2 )
- x 2 + y 2 + z 2 -xy – yz – zx = ½ [(xy) 2 + (yz) 2 + (zx) 2 ]
Краткое примечание : Эти формулы будут важны в старших классах и на различных конкурсных экзаменах.Так что запомните их и хорошо поймите.
Математические формулы для круга 10, класс
ФормулыCircle служат в качестве основы для измерения. Формулы круга 10 по математике для круга радиусом r приведены ниже:
- 1. Окружность круга = 2 π r
- 2. Площадь круга = π r 2
- 3. Площадь сектора угла θ = (θ / 360) × π r 2
- 4. Длина дуги сектора угла θ = (θ / 360) × 2 π r
Математические формулы класса 10 для площади и объема поверхности
Эти формулы очень важны для успешного решения вопросов измерения.2h \)
r = радиус,
l = наклонная высота,
h = высота
TSA: 2 (lb + bh + hl )
Объем: фунтов
l = длина,
b = ширина,
h = высота
TSA3: 6a Объем: a 3
a = стороны куба
Практика 10-го экзамена CBSE Вопросы
Математические формулы для статистики 10 класса
Статистикав классе 10 в основном связана с нахождением среднего, медианы и режима данных.{n} f_ {i}} \ times h \)
(II) Режим сгруппированных данных: Mode = l + \ (\ frac {f_ {i} -f_ {0}} {2f_ {1 } -f_ {0} -f_ {2}} \ times h \)
(III) Медиана для сгруппированных данных: Медиана = l + \ (\ frac {\ frac {n} {2} -cf} {f} \ times h \)
Почему учащиеся должны запоминать все важные математические формулы для 10 класса?
Математические формулы являются основными компонентами, необходимыми для решения сложных математических задач, и они очень полезны следующими способами:
- Математические формулы для 10-го класса PDF охватывает все важные формулы всех глав.
- Используя PDF, кандидаты будут иметь легкий доступ ко всем главам в одном месте.
- Формула PDF подготовлена таким образом, чтобы охватить последнюю программу CBSE согласно главам.
- С его помощью студенты могут легко пересмотреть все важные вещи в одном месте.
Часто задаваемые вопросы по математическим формулам для класса 10
Вот несколько часто задаваемых вопросов учащимися о математических формулах для 10 класса.
Q: Как ученикам следует запоминать математические формулы?
Ответ: Изучение и запоминание математических формул требует много усилий и практики.Студенты должны быть знакомы с главами и концепциями, а затем попытаться понять, как выводится формула.
Вопрос: Как ученики могут изучать математические формулы для 10 класса?
Ответ: Для изучения формул по математике учащиеся должны воспользоваться формулами, приведенными в приведенном выше сегменте этой статьи.
Q: Каковы важные темы программы математики NCERT Class 10?
Ответ: Важные темы программы математики NCERT 10 класса включают статистику и вероятность, геометрию и алгебру.
В: Сложно ли изучать программу NCERT для математики 10 класса?
Ответ: Математика имеет средний уровень сложности, темы – от начального до продвинутого. Кандидат должен быть знаком с формулами, упрощающими изучение и решение математики.
Вопрос: Где ученики могут получить математическую формулу для вычисления площади и объема поверхности?
Ответ: Студенты, которые ищут математическую формулу для площади поверхности и объема , могут найти их в этой статье.
Попытка пробных тестов 10-го экзамена CBSE
Это некоторые из важных формул для математики 10 класса. Эти математические формулы для 10 класса окажутся полезными в процессе обучения. Вы найдете их полезными при пересмотре учебной программы по математике 10 класса CBSE.
Решите бесплатные вопросы по математике для 10-го класса и используйте эти формулы, чтобы получить более высокие баллы на экзаменах совета 10-го класса:
Если у вас есть какие-либо вопросы относительно этой статьи о математических формулах для класса 1 0, не стесняйтесь спрашивать в разделе комментариев ниже.Мы свяжемся с вами в ближайшее время.
193 Views
Примечания к главе 1 Химические реакции и уравнения | 10 класс естествознание
Темы в главе • Введение
• Химическая реакция
• Химическое уравнение
• Сбалансированное химическое уравнение
• Типы химической реакции
• Коррозия
• Прогорклость
Введение
→ Большинство веществ вокруг нас претерпевает различные изменения. Некоторые из этих изменений являются временными, без образования нового вещества.Их называют физическими изменениями.
→ При некоторых других изменениях образуется новое вещество, в котором реагент или исходное вещество теряют свою идентичность с образованием нового вещества, называемого продуктом. Эти изменения являются постоянными, поскольку мы не получим обратно реагент.
Химическая реакция
→ Химическая реакция – это процесс, при котором два или более вещества реагируют друг с другом с образованием нового вещества с разными свойствами.
→ Это следующие изменения, чтобы определить, что химическая реакция произошла:
(i) Изменение состояния
(ii) Изменение цвета
(iii) Выделение газа
(iv) Изменение температуры
Химическое вещество Уравнение
→ Химическое уравнение – это символическое представление химической реакции в форме символов и формул, где реагирующие элементы даны с левой стороны, а продукты – с правой стороны.
Магний + кислород → оксид магния
(Реагент) (Продукт)
Сбалансированное химическое уравнение
→ Химическое уравнение, которое показывает химическую реакцию, необходимо сбалансировать. Сбалансированное химическое уравнение возникает, когда количество атомов на стороне реагентов равно количеству атомов на стороне продуктов.
Zn + H 2 SO 4 → ZnSO 4 + H 2
3Fe (s) + 4H 2 O (g) → Fe 3 O 4 (s) + 4H 2 (г)
Типы химических реакций
→ Реакция объединения : Такая реакция, в которой один продукт образуется из двух или более реагентов, известна как реакция объединения.CaO (т) + H 2 O (л) → Ca (OH) 2 (водн.)
Оксид кальция бурно реагирует с водой с образованием гашеной извести (гидроксида кальция) с выделением большого количества тепла.Полученный в результате реакции раствор гашеной извести используют для мытья стен. Гидроксид кальция медленно вступает в реакцию с двуокисью углерода в воздухе, образуя тонкий слой карбоната кальция на стенках. Карбонат кальция образуется после двух-трех дней стирки белого цвета и придает блеск стенам.Интересно отметить, что химическая формула мрамора также CaCO 3 .
Ca (OH) 2 (водн.) + CO 2 (г) → CaCO 3 (т) + H 2 O (л)
(гашеная известь) (карбонат кальция)
Сжигание угля: C (s) + O 2 (г) → CO 2 (водн.)
Образование воды: H 2 (г) + O 2 (г) → H 2 O (водн.)
Сжигание природного газа (метан): CH 4 (г) + O 2 (г) → CO 2 (г) + H 2 O (l)
→ Экзотермическая реакция : Экзотермический процесс выделяет тепло и вызывает повышение температуры окружающей среды. Рис, картофель и хлеб, которые мы едим, содержат углеводы.Эти углеводы расщепляются с образованием глюкозы. Эта глюкоза соединяется с кислородом в клетках нашего тела и обеспечивает энергию. Особое название этой реакции – дыхание – экзотермическая реакция.
C 6 H 12 O 6 (вод.) + 6O 2 (вод.) → 6CO 2 + 6H 2 O (л) + энергия
(глюкоза)
→ Эндотермическая реакция : Эндотермический процесс поглощает тепло и охлаждает окружающую среду.
Разложение растительного вещества в компост также является примером эндотермической реакции.
→ Реакция разложения : Когда один реагент распадается с образованием более простых продуктов. Это реакция разложения.
Белый хлорид серебра становится серым на солнечном свете. Это происходит из-за разложения хлорида серебра на серебро и хлор под действием света.
Вышеупомянутые реакции используются в черно-белой фотографии.
→ Реакция замещения : Реакция замещения – это химическая реакция, при которой более реактивный элемент вытесняет менее реактивный элемент из своего соединения.В реакциях замещения участвуют как металлы, так и неметаллы. Реакция железных гвоздей с раствором медного купороса.
Fe (т.) + CuSO 4 (водн.) → FeSO 4 (г) + Cu (т)Pb (s) + CuCl 2 (водный) → PbCl 2 (водный) + Cu (s)
→ Реакция двойного вытеснения: Реакция двойного вытеснения, также известная как реакция двойного замещения или метатезиса, представляет собой тип химической реакции, при которой два соединения вступают в реакцию, а положительные ионы (катион) и отрицательные ионы (анион) двух реагентов меняются местами, образуя два новых соединения или продукта.
Na 2 (SO) 4 (водн.) + BaCl 2 (водн.) → BaSO 4 (s) + NaCl (водн.)
→ Окислительно-восстановительная реакция : окислительно-восстановительная (окислительно-восстановительная) Реакция – это тип химической реакции, которая включает перенос электронов между двумя частицами. Реакция окисления-восстановления – это любая химическая реакция, в которой степень окисления молекулы, атома или иона изменяется за счет получения или потери электрона.
Окисление: Этот процесс включает в себя увеличение количества кислорода или потери водорода.
Восстановление: Этот процесс включает в себя получение водорода или потерю кислорода.
→ Окислитель
Это вещество, которое дает кислород или получает водород.Или это вещество, которое восстанавливается само и окисляет другое.
→ Восстановитель
Это вещество, которое выделяет водород или поглощает кислород.
Или это вещество, которое окисляется само и восстанавливает другое.
Окисление – это процесс, который включает потерю электронов, но восстановление – это процесс, который включает в себя увеличение количества электронов.
Коррозия
Процесс медленного превращения металлов в нежелательные соединения из-за их реакции с кислородом, водой, кислотами, газами и т. Д., Присутствующими в атмосфере, называется коррозией.
Ржавчина – Железо, вступая в реакцию с кислородом и влагой, образует красное вещество, называемое ржавчиной.