Обозначения физических величин, система СИ – Физика – Теория, тесты, формулы и задачи
Обозначения физических величин и другие сведения о системе СИ приводятся здесь в качестве справочного материала, так как они требуются при решении многих задач по физике. И хотя на большинстве экзаменов, в том числе и на ЦТ или ЕГЭ, все физические величины указываются вместе со своими единицами измерения, тем не менее очень важно всегда точно знать и хорошо уметь переводить любые единицы измерения любых физических величин в систему СИ, так как в большинстве задач корректно рассчитать ответ можно только выполняя расчеты именно в системе СИ.
Изучать обозначения физических величин и систему СИ онлайн:
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте.
 Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач. - Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике.
 Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка.
Формулы и буквенные обозначения по физике. Основные физические величины, их буквенные обозначения в физике. Производные физические величины
В математике повсеместно используются символы для упрощения и сокращения текста. Ниже приведён список наиболее часто встречающихся математических обозначений, соответствующие команды в TeXе, объяснения и примеры использования. Кроме указанных… … Википедия
Список используемых в математике специфических символов можно увидеть в статье Таблица математических символов Математические обозначения («язык математики») сложная графическая система обозначений, служащая для изложения абстрактных… … Википедия
Список знаковых систем (систем обозначений и т.п.), используемых человеческой цивилизацией, за исключением письменностей, для которых имеется отдельный список. Содержание 1 Критерии включения в список 2 Математика … Википедия
Содержание 1 Критерии включения в список 2 Математика … Википедия
Поль Адриен Морис Дирак Paul Adrien Maurice Dirac Дата рождения: 8& … Википедия
Дирак, Поль Адриен Морис Поль Адриен Морис Дирак Paul Adrien Maurice Dirac Дата рождения: 8 августа 1902(… Википедия
Готфрид Вильгельм Лейбниц Gottfried Wilhelm Leibniz … Википедия
У этого термина существуют и другие значения, см. Мезон (значения). Мезон (от др. греч. μέσος средний) бозон сильного взаимодействия. В Стандартной модели, мезоны это составные (не элементарные) частицы, состоящие из чётного… … Википедия
Ядерная физика … Википедия
Альтернативными теориями гравитации принято называть теории гравитации, существующие как альтернативы общей теории относительности (ОТО) или существенно (количественно или принципиально) модифицирующие ее. К альтернативным теориям гравитации… … Википедия
Альтернативными теориями гравитации принято называть теории гравитации, существующие как альтернативы общей теории относительности или существенно (количественно или принципиально) модифицирующие ее.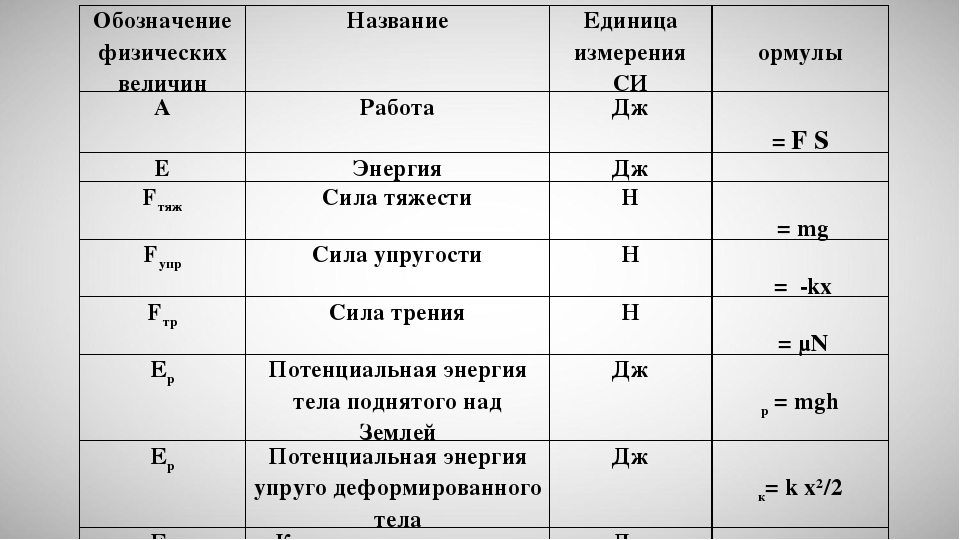
Ни для кого не секрет, что существуют специальные обозначения для величин в любой науке. Буквенные обозначения в физике доказывают, что данная наука не является исключением в плане идентификации величин при помощи особых символов. Основных величин, а также их производных, достаточно много, каждая из которых имеет свой символ. Итак, буквенные обозначения в физике подробно рассматриваются в данной статье.
Физика и основные физические величины
Михаил Васильевич Ломоносов ввел в русский язык слово физика посредством издания учебника в переводе с немецкого – первого в России учебника по физике.
Итак, физика представляет собой раздел естествознания, посвященный изучению общих законов природы, а также материи, ее движение и структуре. Основных физических величин не так много, как может показаться на первый взгляд – их всего 7:
- длина,
- масса,
- время,
- сила тока,
- температура,
- количество вещества,
- сила света.
Конечно, у них есть свои буквенные обозначения в физике. Например, для массы выбран символ m, а для температуры – Т. Также у всех величин есть своя единица измерения: у силы света – кандела (кд), а у количества вещества единицей измерения является моль.
Производные физические величины
Производных физических величин значительно больше, чем основных. Их насчитывается 26, причем часто некоторые из них приписывают к основным.
Итак, площадь является производной от длины, объем – также от длины, скорость – от времени, длины, а ускорение, в свою очередь, характеризует быстроту изменения скорости. Импульс выражается через массу и скорость, сила – произведение массы и ускорения, механическая работа зависит от силы и длины, энергия пропорциональна массе. Мощность, давление, плотность, поверхностная плотность, линейная плотность, количество теплоты, напряжение, электрическое сопротивление, магнитный поток, момент инерции, момент импульса, момент силы – все они зависят от массы. Частота, угловая скорость, угловое ускорение обратно пропорциональны времени, а электрический заряд имеет прямую зависимость от времени. Угол и телесный угол являются производными величинами из длины.
Импульс выражается через массу и скорость, сила – произведение массы и ускорения, механическая работа зависит от силы и длины, энергия пропорциональна массе. Мощность, давление, плотность, поверхностная плотность, линейная плотность, количество теплоты, напряжение, электрическое сопротивление, магнитный поток, момент инерции, момент импульса, момент силы – все они зависят от массы. Частота, угловая скорость, угловое ускорение обратно пропорциональны времени, а электрический заряд имеет прямую зависимость от времени. Угол и телесный угол являются производными величинами из длины.
Какой буквой обозначается напряжение в физике? Напряжение, которое является скалярной величиной, обозначается буквой U. Для скорости обозначение имеет вид буквы v, для механической работы – А, а для энергии – Е. Электрический заряд принято обозначать буквой q, а магнитный поток – Ф.
СИ: общие сведения
Международная система единиц (СИ) представляет собой систему физических единиц, которая основана на Международной системе величин, включая наименования и обозначения физических величин. Она принята Генеральной конференцией по мерам и весам. Именно эта система регламентирует буквенные обозначения в физике, а также их размерность и единицы измерения. Для обозначения используются буквы латинского алфавита, в отдельных случаях – греческого. Также возможно в качестве обозначения использование специальных символов.
Она принята Генеральной конференцией по мерам и весам. Именно эта система регламентирует буквенные обозначения в физике, а также их размерность и единицы измерения. Для обозначения используются буквы латинского алфавита, в отдельных случаях – греческого. Также возможно в качестве обозначения использование специальных символов.
Заключение
Итак, в любой научной дисциплине есть особые обозначения для различного рода величин. Естественно, физика не является исключением. Буквенных обозначений достаточно много: сила, площадь, масса, ускорение, напряжение и т. д. Они имеют свои обозначения. Существует специальная система, которая называется Международная система единиц. Считается, что основные единицы не могут быть математически выведены из других. Производные же величины получают при помощи умножения и деления из основных.
Изучение физики в школе длится несколько лет. При этом ученики сталкиваются с проблемой, что одни и те же буквы обозначают совершенно разные величины. Чаще всего этот факт касается латинских букв. Как же тогда решать задачи?
Чаще всего этот факт касается латинских букв. Как же тогда решать задачи?
Пугаться такого повтора не стоит. Ученые постарались ввести их в обозначение так, чтобы одинаковые буквы не встретились в одной формуле. Чаще всего ученики сталкиваются с латинской n. Она может быть строчной или прописной. Поэтому логично возникает вопрос о том, что такое n в физике, то есть в определенной встретившейся ученику формуле.
Что обозначает прописная буква N в физике?
Чаще всего в школьном курсе она встречается при изучении механики. Ведь там она может быть сразу в дух значениях – мощность и сила нормальной реакции опоры. Естественно, что эти понятия не пересекаются, ведь используются в разных разделах механики и измеряются в разных единицах. Поэтому всегда нужно точно определить, что такое n в физике.
Мощность — это скорость изменения энергии системы. Это скалярная величина, то есть просто число. Единицей ее измерения служит ватт (Вт).
Сила нормальной реакции опоры — сила, которая оказывает действие на тело со стороны опоры или подвеса. Кроме числового значения, она имеет направление, то есть это векторная величина. Причем она всегда перпендикулярна поверхности, на которую производится внешнее воздействие. Единицей измерения этой N является ньютон (Н).
Кроме числового значения, она имеет направление, то есть это векторная величина. Причем она всегда перпендикулярна поверхности, на которую производится внешнее воздействие. Единицей измерения этой N является ньютон (Н).
Что такое N в физике, помимо уже указанных величин? Это может быть:
постоянная Авогадро;
увеличение оптического прибора;
концентрация вещества;
число Дебая;
полная мощность излучения.
Что может обозначать строчная буква n в физике?
Список наименований, которые могут за ней скрываться, достаточно обширен. Обозначение n в физике используется для таких понятий:
показатель преломления, причем он может быть абсолютным или относительным;
нейтрон — нейтральная элементарная частица с массой незначительно большей, чем у протона;
частота вращения (используется для замены греческой буквы «ню», так как она очень похожа на латинскую «вэ») — число повторения оборотов за единицу времени, измеряется в герцах (Гц).
Что означает n в физике, кроме уже указанных величин? Оказывается, за ней скрываются основное квантовое число (квантовая физика), концентрация и постоянная Лошмидта (молекулярная физика). Кстати, при вычислении концентрации вещества требуется знать величину, которая также записывается латинской «эн». О ней будет идти речь ниже.
Какая физическая величина может быть обозначена n и N?
Ее название происходит от латинского слова numerus, в переводе оно звучит как «число», «количество». Поэтому ответ на вопрос о том, что значит n в физике, достаточно прост. Это количество любых предметов, тел, частиц — всего, о чем идет речь в определенной задаче.
Причем «количество» — одна из немногих физических величин, которые не имеют единицы измерения. Это просто число, без наименования. Например, если в задаче идет речь о 10 частицах, то n будет равно просто 10. Но если получается так, что строчная «эн» уже занята, то использовать приходится прописную букву.
Формулы, в которых фигурирует прописная N
Первая из них определяет мощность, которая равна отношению работы ко времени:
В молекулярной физике имеется такое понятие, как химическое количество вещества. Обозначается греческой буквой «ню». Чтобы его сосчитать, следует разделить количество частиц на число Авогадро :
Обозначается греческой буквой «ню». Чтобы его сосчитать, следует разделить количество частиц на число Авогадро :
Кстати, последняя величина тоже обозначается столь популярной буквой N. Только у нее всегда присутствует нижний индекс — А.
Чтобы определить электрический заряд, потребуется формула:
Еще одна формула с N в физике – частота колебаний. Чтобы ее сосчитать, нужно их число разделить на время:
Появляется буква «эн» в формуле для периода обращения:
Формулы, в которых встречается строчная n
В школьном курсе физики эта буква чаще всего ассоциируется с показателем преломления вещества. Поэтому важным оказывается знание формул с ее применением.
Так, для абсолютного показателя преломления формула записывается следующим образом:
Здесь с — скорость света в вакууме, v — его скорость в преломляющей среде.
Формула для относительного показателя преломления несколько сложнее:
n 21 = v 1: v 2 = n 2: n 1 ,
где n 1 и n 2 — абсолютные показатели преломления первой и второй среды, v 1 и v 2 — скорости световой волны в указанных веществах.
Как найти n в физике? В этом нам поможет формула, в которой требуется знать углы падения и преломления луча, то есть n 21 = sin α: sin γ.
Чему равно n в физике, если это показатель преломления?
Обычно в таблицах приводятся значения для абсолютных показателей преломления различных веществ. Не стоит забывать, что эта величина зависит не только от свойств среды, но и от длины волны. Табличные значения показателя преломления даются для оптического диапазона.
Итак, стало ясно, что такое n в физике. Чтобы не осталось каких-либо вопросов, стоит рассмотреть некоторые примеры.
Задача на мощность
№1. Во время пахоты трактор тянет плуг равномерно. При этом он прилагает силу 10 кН. При таком движении в течение 10 минут он преодолевает 1,2 км. Требуется определить развиваемую им мощность.
Перевод единиц в СИ. Начать можно с силы, 10 Н равны 10000 Н. Потом расстояние: 1,2 × 1000 = 1200 м. Осталось время — 10 × 60 = 600 с.
Выбор формул. Как уже было сказано выше, N = А: t. Но в задаче нет значения для работы. Для ее вычисления пригодится еще одна формула: А = F × S. Окончательный вид формулы для мощности выглядит так: N = (F × S) : t.
Как уже было сказано выше, N = А: t. Но в задаче нет значения для работы. Для ее вычисления пригодится еще одна формула: А = F × S. Окончательный вид формулы для мощности выглядит так: N = (F × S) : t.
Решение. Вычислим сначала работу, а потом – мощность. Тогда в первом действии получится 10 000 × 1 200 = 12 000 000 Дж. Второе действие дает 12 000 000: 600 = 20 000 Вт.
Ответ. Мощность трактора равна 20 000 Вт.
Задачи на показатель преломления
№2. Абсолютный показатель преломления у стекла равен 1,5. Скорость распространения света в стекле меньше, чем в вакууме. Требуется определить, во сколько раз.
В СИ переводить данные не требуется.
При выборе формул остановиться нужно на этой: n = с: v.
Решение. Из указанной формулы видно, что v = с: n. Это значит, что скорость распространения света в стекле равна скорости света в вакууме, деленному на показатель преломления. То есть она уменьшается в полтора раза.
Ответ. Скорость распространения света в стекле меньше, чем в вакууме, в 1,5 раза.
№3. Имеются две прозрачные среды. Скорость света в первой из них равна 225 000 км/с, во второй — на 25 000 км/с меньше. Луч света идет из первой среды во вторую. Угол падения α равен 30º. Вычислить значение угла преломления.
Нужно ли переводить в СИ? Скорости даны во внесистемных единицах. Однако при подстановке в формулы они сократятся. Поэтому переводить скорости в м/с не нужно.
Выбор формул, необходимых для решения задачи. Потребуется использовать закон преломления света: n 21 = sin α: sin γ. А также: n = с: v.
Решение. В первой формуле n 21 — это отношение двух показателей преломления рассматриваемых веществ, то есть n 2 и n 1 . Если записать вторую указанную формулу для предложенных сред, то получатся такие: n 1 = с: v 1 и n 2 =с: v 2 . Если составить отношение двух последних выражений, получится, что n 21 = v 1: v 2 . Подставив его в формулу закона преломления, можно вывести такое выражение для синуса угла преломления: sin γ = sin α × (v 2: v 1).
Подставляем в формулу значения указанных скоростей и синуса 30º (равен 0,5), получается, что синус угла преломления равен 0,44. По таблице Брадиса получается, что угол γ равен 26º.
Ответ. Значение угла преломления — 26º.
Задачи на период обращения
№4. Лопасти ветряной мельницы вращаются с периодом, равным 5 секундам. Вычислите число оборотов этих лопастей за 1 час.
Переводить в единицы СИ нужно только время 1 час. Оно будет равно 3 600 секундам.
Подбор формул . Период вращения и число оборотов связаны формулой Т = t: N.
Решение. Из указанной формулы число оборотов определяется отношением времени к периоду. Таким образом, N = 3600: 5 = 720.
Ответ. Число оборотов лопастей мельницы равно 720.
№5. Винт самолета вращается с частотой 25 Гц. Какое время потребуется винту, чтобы совершить 3 000 оборотов?
Все данные приведены с СИ, поэтому переводить ничего не нужно.
Необходимая формула : частота ν = N: t. Из нее необходимо только вывести формулу для неизвестного времени. Оно является делителем, поэтому его полагается находить делением N на ν.
Из нее необходимо только вывести формулу для неизвестного времени. Оно является делителем, поэтому его полагается находить делением N на ν.
Решение. В результате деления 3 000 на 25 получается число 120. Оно будет измеряться в секундах.
Ответ. Винт самолета совершает 3000 оборотов за 120 с.
Подведем итоги
Когда ученику в задаче по физике встречается формула, содержащая n или N, ему нужно разобраться с двумя моментами. Первый — из какого раздела физики приведено равенство. Это может быть ясно из заголовка в учебнике, справочнике или слов учителя. Потом следует определиться с тем, что скрывается за многоликой «эн». Причем в этом помогает наименование единиц измерения, если, конечно, приведено ее значение. Также допускается еще один вариант: внимательно посмотрите на остальные буквы в формуле. Возможно, они окажутся знакомыми и дадут подсказку в решаемом вопросе.
Шпаргалка с формулами по физике для ЕГЭ
и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
Для начала картинка, которую можно распечатать в компактном виде.
Механика
- Давление Р=F/S
- Плотность ρ=m/V
- Давление на глубине жидкости P=ρ∙g∙h
- Сила тяжести Fт=mg
- 5. Архимедова сила Fa=ρ ж ∙g∙Vт
- Уравнение движения при равноускоренном движении
X=X 0 +υ 0 ∙t+(a∙t 2)/2 S=(υ 2 –υ 0 2) /2а S=(υ +υ 0) ∙t /2
- Уравнение скорости при равноускоренном движении υ =υ 0 +a∙t
- Ускорение a=(υ –υ 0)/t
- Скорость при движении по окружности υ =2πR/Т
- Центростремительное ускорение a=υ 2 /R
- Связь периода с частотой ν=1/T=ω/2π
- II закон Ньютона F=ma
- Закон Гука Fy=-kx
- Закон Всемирного тяготения F=G∙M∙m/R 2
- Вес тела, движущегося с ускорением а Р=m(g+a)
- Вес тела, движущегося с ускорением а↓ Р=m(g-a)
- Сила трения Fтр=µN
- Импульс тела p=mυ
- Импульс силы Ft=∆p
- Момент силы M=F∙ℓ
- Потенциальная энергия тела, поднятого над землей Eп=mgh
- Потенциальная энергия упруго деформированного тела Eп=kx 2 /2
- Кинетическая энергия тела Ek=mυ 2 /2
- Работа A=F∙S∙cosα
- Мощность N=A/t=F∙υ
- Коэффициент полезного действия η=Aп/Аз
- Период колебаний математического маятника T=2π√ℓ/g
- Период колебаний пружинного маятника T=2 π √m/k
- Уравнение гармонических колебаний Х=Хmax∙cos ωt
- Связь длины волны, ее скорости и периода λ= υ Т
Молекулярная физика и термодинамика
- Количество вещества ν=N/ Na
- Молярная масса М=m/ν
- Cр.
 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT - Основное уравнение МКТ P=nkT=1/3nm 0 υ 2
- Закон Гей – Люссака (изобарный процесс) V/T =const
- Закон Шарля (изохорный процесс) P/T =const
- Относительная влажность φ=P/P 0 ∙100%
- Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
- Работа газа A=P∙ΔV
- Закон Бойля – Мариотта (изотермический процесс) PV=const
- Количество теплоты при нагревании Q=Cm(T 2 -T 1)
- Количество теплоты при плавлении Q=λm
- Количество теплоты при парообразовании Q=Lm
- Количество теплоты при сгорании топлива Q=qm
- Уравнение состояния идеального газа PV=m/M∙RT
- Первый закон термодинамики ΔU=A+Q
- КПД тепловых двигателей η= (Q 1 – Q 2)/ Q 1
- КПД идеал. двигателей (цикл Карно) η= (Т 1 – Т 2)/ Т 1
Электростатика и электродинамика – формулы по физике
- Закон Кулона F=k∙q 1 ∙q 2 /R 2
- Напряженность электрического поля E=F/q
- Напряженность эл.
 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 - Поверхностная плотность зарядов σ = q/S
- Напряженность эл. поля бесконечной плоскости E=2πkσ
- Диэлектрическая проницаемость ε=E 0 /E
- Потенциальная энергия взаимод. зарядов W= k∙q 1 q 2 /R
- Потенциал φ=W/q
- Потенциал точечного заряда φ=k∙q/R
- Напряжение U=A/q
- Для однородного электрического поля U=E∙d
- Электроемкость C=q/U
- Электроемкость плоского конденсатора C=S∙ε ∙ε 0 /d
- Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
- Сила тока I=q/t
- Сопротивление проводника R=ρ∙ℓ/S
- Закон Ома для участка цепи I=U/R
- Законы послед. соединения I 1 =I 2 =I, U 1 +U 2 =U, R 1 +R 2 =R
- Законы паралл. соед. U 1 =U 2 =U, I 1 +I 2 =I, 1/R 1 +1/R 2 =1/R
- Мощность электрического тока P=I∙U
- Закон Джоуля-Ленца Q=I 2 Rt
- Закон Ома для полной цепи I=ε/(R+r)
- Ток короткого замыкания (R=0) I=ε/r
- Вектор магнитной индукции B=Fmax/ℓ∙I
- Сила Ампера Fa=IBℓsin α
- Сила Лоренца Fл=Bqυsin α
- Магнитный поток Ф=BSсos α Ф=LI
- Закон электромагнитной индукции Ei=ΔФ/Δt
- ЭДС индукции в движ проводнике Ei=Вℓυ sinα
- ЭДС самоиндукции Esi=-L∙ΔI/Δt
- Энергия магнитного поля катушки Wм=LI 2 /2
- Период колебаний кол.
 контура T=2π ∙√LC
контура T=2π ∙√LC - Индуктивное сопротивление X L =ωL=2πLν
- Емкостное сопротивление Xc=1/ωC
- Действующее значение силы тока Iд=Imax/√2,
- Действующее значение напряжения Uд=Umax/√2
- Полное сопротивление Z=√(Xc-X L) 2 +R 2
Оптика
- Закон преломления света n 21 =n 2 /n 1 = υ 1 / υ 2
- Показатель преломления n 21 =sin α/sin γ
- Формула тонкой линзы 1/F=1/d + 1/f
- Оптическая сила линзы D=1/F
- max интерференции: Δd=kλ,
- min интерференции: Δd=(2k+1)λ/2
- Диф.решетка d∙sin φ=k λ
Квантовая физика
- Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=U з е
- Красная граница фотоэффекта ν к = Aвых/h
- Импульс фотона P=mc=h/ λ=Е/с
Физика атомного ядра
- Закон радиоактивного распада N=N 0 ∙2 – t / T
- Энергия связи атомных ядер
Рекомендуем также
Формула мощности в физике
Содержание:
Определение и формулы мощности
Определение
Мощностью некоторой силы является скалярная физическая величина, которая характеризует скорость произведения работы данной силой. Мощность часто обозначают буквами: N, P.
Мощность часто обозначают буквами: N, P.
В том случае, если за равные малые промежутки времени выполняется разная работа, то мощность является переменной во времени. Тогда вводят мгновенное значение мощности:
$$P=\lim _{\Delta t \rightarrow 0} \frac{\delta A}{\Delta t}=\frac{d A}{d t}$$где $\delta A$ – элементарная работа, которую выполняет сила, $\Delta t$ – отрезок времени в течение, которого данная работа была выполнена. Если мгновенная мощность не является постоянной величиной, то выражение (1) определяет среднюю мощностьза время $\Delta t$.
Мощность силы можно определить как скалярное произведение силы на скорость, с которой движется точка приложения рассматриваемой силы:
$$P=\bar{F} \bar{v}=F_{\tau} v$$где $F_{\tau}$ – проекция силы $\bar{F}$ на направление вектора скорости ( $\bar{v}$).
При поступательном движении некоторого тела, имеющего массу m под воздействием силы $\bar{F}$ мощность можно вычислить, применяя формулу:
$$P=m v \dot{v}(4)$$В общем случае произвольного перемещения твердого тела суммарная мощность есть алгебраическая сумма мощностей всех сил, которые действуют на тело:
$$P=\sum_{i=1}^{k} \bar{F}_{i} \cdot \bar{v}_{i}(5)$$где $\bar{v}_{i}$ – скорость перемещения точки, к которой приложена сила
$\bar{F}_{i}$.
В случае поступательного движения твердого тела со скоростью $\bar{v}$ мощность можно определить при помощи формулы:
$$P=\overline{F v}(6)$$где $\bar{F}$ – главный вектор внешних сил.
Если твердое тело совершает вращение вокруг точки О или вокруг неподвижной оси, которая проходит через точку О, то формулой для счет мощности можно считать выражение:
$$P=\bar{M} \bar{\omega}(7)$$где $\bar{M}$ – главный момент внешних сил по отношению к точке О, $\bar{omega}$ – мгновенная угловая скорость вращения тела.
Единицы измерения мощности
Основной единицей измерения мощности силы в системе СИ является: [P]=вт (ватт)
В СГС: [P]=эрг/с.
1 вт=107 эрг/( с).
Примеры решения задач
Пример
Задание. Какова мощность (P(t)), развиваемая силой, если она действует на тело, которое имеет массу m и под воздействием приложенной силы движется поступательно. Сила описывается законом: $F(t)=2 t \cdot \bar{i}+3 t^{2} \bar{j}$
Решение. {5}\right)$
{5}\right)$
Слишком сложно?
Формула мощности не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Какова мгновенная мощность силы тяжести на высоте h/2. если камень массы m падает с высоты h. Сопротивление воздуха не учитывать.
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для мгновенной мощности вида:
$$P=\bar{F} \cdot \bar{v}(2.1)$$Сила, действующая на тело – сила тяжести. Она направлена по оси Y, выражение для ее проекции на ось Y запишем как:
$$F=m g(2.2)$$В начальный момент времени тело имело скорость равную нулю, тогда скорость тела в проекции на ось Y можно вычислить, используя выражение:
$$v=v_{0}+g t=g t(2.3)$$где v0=0.
Найдем момент времени, в который тело окажется на половине высоты (y=h/2), применим уравнение, которое описывает равноускоренное движение (из начальных условий y0=0, v0=0):
$$y=y_{0}+v_{0} t+\frac{g t^{2}}{2}=\frac{g t^{2}}{2}=\frac{h}{2} \rightarrow t=\sqrt{\frac{h}{g}}(2.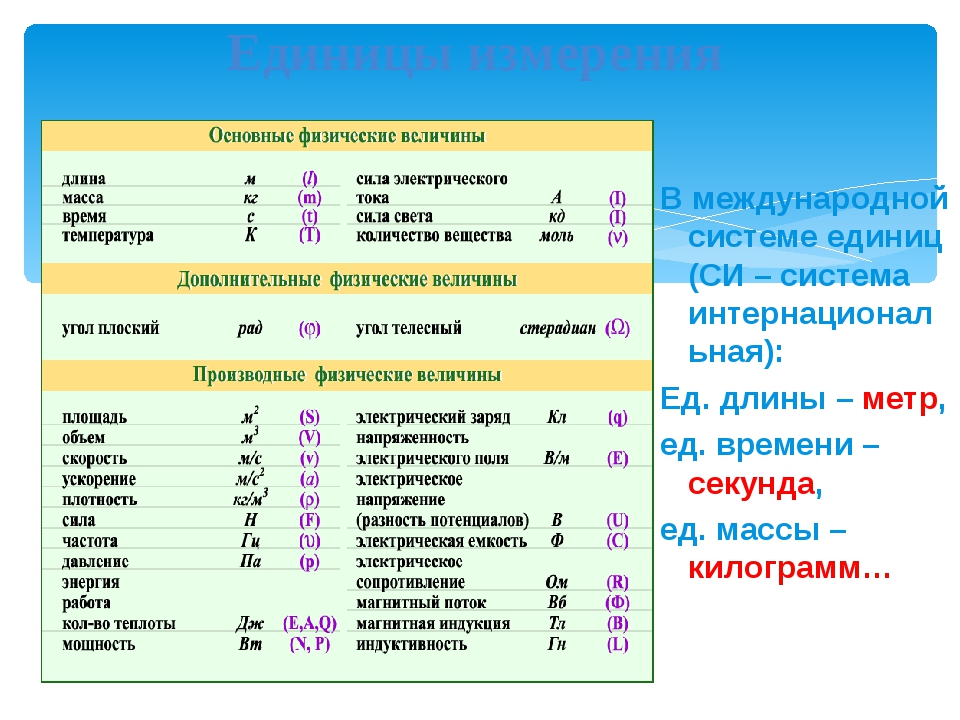 {3} h}$
{3} h}$Читать дальше: Формула плотности вещества.
Построение чертежей – дело непростое, но без него в современном мире никак. Ведь чтобы изготовить даже самый обычный предмет (крошечный болт или гайку, полку для книг, дизайн нового платья и подобное), изначально нужно провести соответствующие вычисления и нарисовать чертеж будущего изделия. Однако часто составляет его один человек, а занимается изготовлением чего-либо по этой схеме другой. Чтобы не возникло путаницы в понимании изображенного предмета и его параметров, во всем мире приняты условные обозначения длины, ширины, высоты и других величин, применяемых при проектировании. Каковы они? Давайте узнаем. ВеличиныПлощадь, высота и другие обозначения подобного характера являются не только физическими, но и математическими величинами. Единое их буквенное обозначение (используемое всеми странами) было уставлено в середине ХХ века Международной системой единиц (СИ) и применяется по сей день. Именно по этой причине все подобные параметры обозначаются латинскими, а не кириллическими буквами или арабской вязью. Чтобы не создавать отдельных трудностей, при разработке стандартов конструкторской документации в большинстве современных стран решено было использовать практически те же условные обозначения, что применяются в физике или геометрии. Любой выпускник школы помнит, что в зависимости от того, двухмерная или трехмерная фигура (изделие) изображена на чертеже, она обладает набором основных параметров. Если присутствуют два измерения – это ширина и длина, если их три – добавляется еще и высота. Итак, для начала давайте выясним, как правильно длину, ширину, высоту обозначать на чертежах. ШиринаКак было сказано выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта, при условии что его замеры производятся в поперечном направлении. Вероятно, здесь дело в том, что данный параметр наиболее широкое применение изначально имел в геометрии. В этой науке, описывая фигуры, часто длину, ширину, высоту обозначают буквами «а», «b», «с». Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы). Большинство полагает, что это было сделано, дабы не путать ширину (обозначение буквой «B»/«b») с весом. Дело в том, что последний иногда именуется как «W» (сокращение от английского названия weight), хотя допустимо использование и других литер («G» и «Р»). ДлинаКак уже было указано, в математике длина, высота, ширина – это три пространственных измерения. При этом, если ширина является линейным размером в поперечном направлении, то длина – в продольном. Рассматривая ее как величину физики можно понять, что под этим словом подразумевается численная характеристика протяжности линий. В английском языке этот термин именуется length. Именно из-за этого данная величина обозначается заглавной или строчной начальной литерой этого слова – «L». Как и ширина, длина измеряется в метрах или их кратных (дольных) единицах. ВысотаНаличие этой величины указывает на то, что приходится иметь дело с более сложным – трехмерным пространством. На английском она пишется как “height”. Поэтому, согласно международным нормам, ее обозначают латинской литерой «Н»/«h». Помимо высоты, в чертежах иногда эта буква выступает и как глубины обозначение. Высота, ширина и длина – все все эти параметры измеряются в метрах и их кратных и дольных единицах (километры, сантиметры, миллиметры и т. п.). Радиус и диаметрПомимо рассмотренных параметров, при составлении чертежей приходится иметь дело и с иными. Например, при работе с окружностями возникает необходимость в определении их радиуса. Так именуется отрезок, который соединяет две точки. Первая из них является центром. Вторая находится непосредственно на самой окружности. На латыни это слово выглядит как “radius”. Отсюда и строчная или заглавная «R»/«r». Чертя окружности, помимо радиуса часто приходится сталкиваться с близким к нему явлением – диаметром. Численно диаметр равен двум радиусам. По-английски это слово пишется так: “diameter”. Отсюда и сокращение – большая или маленькая латинская буква «D»/«d». Часто диаметр на чертежах обозначают при помощи перечеркнутого круга – «Ø». Хотя это распространенное сокращение, стоит иметь в виду, что ГОСТ предусматривает использование только латинской «D»/«d». ТолщинаБольшинство из нас помнят школьные уроки математики. Ещё тогда учителя рассказывали, что, латинской литерой «s» принято обозначать такую величину, как площадь. Однако, согласно общепринятым нормам, на чертежах таким способом записывается совсем другой параметр – толщина. Почему так? Известно, что в случае с высотой, шириной, длиной, обозначение буквами можно было объяснить их написанием или традицией. Вот только толщина по-английски выглядит как “thickness”, а в латинском варианте – “crassities”. Периметр и площадьВ отличие от всех перечисленных выше величин, слово «периметр» пришло не из латыни или английского, а из греческого языка. Оно образовано от “περιμετρέο” («измерять окружность»). И сегодня этот термин сохранил свое значение (общая длина границ фигуры). Впоследствии слово попало в английский язык (“perimeter”) и закрепилось в системе СИ в виде сокращения буквой «Р». Площадь – это величина, показывающая количественную характеристику геометрической фигуры, обладающей двумя измерениями (длиной и шириной). В отличие от всего перечисленного ранее, она измеряется в квадратных метрах (а также в дольных и кратных их единицах). Что касается буквенного обозначения площади, то в разных сферах оно отличается. Например, в математике это знакомая всем с детства латинская литера «S». Некоторые по незнанию думают, что это связано с английским написанием слова “square”. Однако в нем математическая площадь – это “area”, а “square” – это площадь в архитектурном понимании. Кстати, стоит вспомнить, что “square” – название геометрической фигуры “квадрат”. Так что стоит быть внимательным при изучении чертежей на английском языке. Из-за перевода “area” в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» (“fortis”). Другие распространенные сокращенияОбозначения высоты, ширины, длины, толщины, радиуса, диаметра являются наиболее употребляемыми при составлении чертежей. Однако есть и другие величины, которые тоже часто присутствуют в них. Например, строчное «t». В физике это означает «температуру», однако согласно ГОСТу Единой системы конструкторской документации, данная литера – это шаг (винтовых пружин, и подобного). Заглавная и строчная буква «A»/«a» (согласно все тем же нормам) в чертежах применяется, чтобы обозначать не площадь, а межцентровое и межосевое расстояние. Помимо различных величин, в чертежах часто приходится обозначать углы разного размера. Для этого принято использовать строчные литеры греческого алфавита. Наиболее применяемые – «α», «β», «γ» и «δ». Однако допустимо использовать и другие. Какой стандарт определяет буквенное обозначение длины, ширины, высоты, площади и других величин?Как уже было сказано выше, чтобы не было недопонимания при прочтении чертежа, представителями разных народов приняты общие стандарты буквенного обозначения. Иными словами, если вы сомневаетесь в интерпретации того или иного сокращения, загляните в ГОСТы. Таким образом вы узнаете, как правильно обозначается высота, ширины, длина, диаметр, радиус и так далее. Ни для кого не секрет, что существуют специальные обозначения для величин в любой науке. Физика и основные физические величиныБлагодаря Аристотелю начало употребляться слово физика, так как именно он впервые употребил этот термин, который в ту пору считался синонимом термина философия. Это связано с общностью объекта изучения – законы Вселенной, конкретнее – то, как она функционирует. Как известно, в XVI-XVII веках произошла первая научная революция, именно благодаря ей физика была выделена в самостоятельную науку. Михаил Васильевич Ломоносов ввел в русский язык слово физика посредством издания учебника в переводе с немецкого – первого в России учебника по физике. Итак, физика представляет собой раздел естествознания, посвященный изучению общих законов природы, а также материи, ее движение и структуре.
Конечно, у них есть свои буквенные обозначения в физике. Например, для массы выбран символ m, а для температуры – Т. Также у всех величин есть своя единица измерения: у силы света – кандела (кд), а у количества вещества единицей измерения является моль. Производные физические величиныПроизводных физических величин значительно больше, чем основных. Их насчитывается 26, причем часто некоторые из них приписывают к основным. Итак, площадь является производной от длины, объем – также от длины, скорость – от времени, длины, а ускорение, в свою очередь, характеризует быстроту изменения скорости. Импульс выражается через массу и скорость, сила – произведение массы и ускорения, механическая работа зависит от силы и длины, энергия пропорциональна массе. Какой буквой обозначается напряжение в физике? Напряжение, которое является скалярной величиной, обозначается буквой U. Для скорости обозначение имеет вид буквы v, для механической работы – А, а для энергии – Е. Электрический заряд принято обозначать буквой q, а магнитный поток – Ф. СИ: общие сведенияМеждународная система единиц (СИ) представляет собой систему физических единиц, которая основана на Международной системе величин, включая наименования и обозначения физических величин. Она принята Генеральной конференцией по мерам и весам. Именно эта система регламентирует буквенные обозначения в физике, а также их размерность и единицы измерения. ЗаключениеИтак, в любой научной дисциплине есть особые обозначения для различного рода величин. Естественно, физика не является исключением. Буквенных обозначений достаточно много: сила, площадь, масса, ускорение, напряжение и т. д. Они имеют свои обозначения. Существует специальная система, которая называется Международная система единиц. Считается, что основные единицы не могут быть математически выведены из других. Производные же величины получают при помощи умножения и деления из основных. В математике повсеместно используются символы для упрощения и сокращения текста. Ниже приведён список наиболее часто встречающихся математических обозначений, соответствующие команды в TeXе, объяснения и примеры использования. Кроме указанных… … Википедия Список используемых в математике специфических символов можно увидеть в статье Таблица математических символов Математические обозначения («язык математики») сложная графическая система обозначений, служащая для изложения абстрактных… … Википедия Список знаковых систем (систем обозначений и т. Поль Адриен Морис Дирак Paul Adrien Maurice Dirac Дата рождения: 8& … Википедия Дирак, Поль Адриен Морис Поль Адриен Морис Дирак Paul Adrien Maurice Dirac Дата рождения: 8 августа 1902(… Википедия Готфрид Вильгельм Лейбниц Gottfried Wilhelm Leibniz … Википедия У этого термина существуют и другие значения, см. Мезон (значения). Мезон (от др. греч. μέσος средний) бозон сильного взаимодействия. В Стандартной модели, мезоны это составные (не элементарные) частицы, состоящие из чётного… … Википедия Ядерная физика … Википедия Альтернативными теориями гравитации принято называть теории гравитации, существующие как альтернативы общей теории относительности (ОТО) или существенно (количественно или принципиально) модифицирующие ее. К альтернативным теориям гравитации… … Википедия Альтернативными теориями гравитации принято называть теории гравитации, существующие как альтернативы общей теории относительности или существенно (количественно или принципиально) модифицирующие ее. Времена, когда ток обнаруживался с помощью личных ощущений ученых, пропускавших его через себя, давно миновали. Теперь для этого применяют специальные приборы, называемые амперметрами. Амперметр – это прибор, служащий для измерения силы тока. Что понимают под силой тока? Обратимся к рисунку 21, б. На нем выделено поперечное сечение проводника, через которое проходят заряженные частицы при наличии в проводнике электрического тока. В металлическом проводнике этими частицами являются свободные электроны. В процессе своего движения вдоль проводника электроны переносят некоторый заряд. Чем больше электронов и чем быстрее они движутся, тем больший заряд будет ими перенесен за одно и то же время. Силой тока называется физическая величина, показывающая, какой заряд проходит через поперечное сечение проводника за 1 с. Пусть, например, за время t = 2 с через поперечное сечение проводника носители тока переносят заряд q = 4 Кл. I – сила тока. Итак, чтобы найти силу тока I, надо электрический заряд q, прошедший через поперечное сечение проводника за время t, разделить на это время: Единица силы тока называется ампером (А) в честь французского ученого А. М. Ампера (1775-1836). В основу определения этой единицы положено магнитное действие тока, и мы на нем останавливаться не будем.Если сила тока I известна, то можно найти заряд q, проходящий через сечение проводника за время t. Для этого надо силу тока умножить на время: Полученное выражение позволяет определить единицу электрического заряда – кулон (Кл): 1 Кл = 1 А · 1 с = 1 А·с. 1 Кл – это заряд, который проходит за 1 с через поперечное сечение проводника при силе тока 1 А. Помимо ампера на практике часто применяются и другие (кратные и дольные) единицы силы тока, например миллиампер (мА) и микроампер (мкА): 1 мА = 0,001 А, 1 мкА = 0,000001 А. Как уже говорилось, измеряют силу тока с помощью амперметров (а также милли- и микроамперметров). Демонстрационный гальванометр, о котором упоминалось выше, представляет собой обычный микроамперметр. Существуют разные конструкции амперметров. Амперметр, предназначенный для демонстрационных опытов в школе, изображен на рисунке 28. На этом же рисунке приведено его условное обозначение (кружок с латинской буквой «А» внутри).При включении в цепь амперметр, как и всякий другой измерительный прибор, не должен оказывать заметного влияния на измеряемую величину. Поэтому амперметр устроен так, что при его включении сила тока в цепи почти не изменяется. В зависимости от назначения в технике используют амперметры с разной ценой деления. По шкале амперметра видно, на какую наибольшую силу тока он рассчитан. Включать его в цепь с большей силой тока нельзя, так как прибор может испортиться. Для включения амперметра в цепь ее размыкают и свободные концы проводов присоединяют к клеммам (зажимам) прибора. 1) амперметр включают последовательно с тем элементом цепи, в котором измеряют силу тока; 2) клемму амперметра со знаком «+» следует соединять с тем проводом, который идет от положительного полюса источника тока, а клемму со знаком «–» – с тем проводом, который идет от отрицательного полюса источника тока. При включении амперметра в цепь не имеет значения, с какой стороны (слева или справа) от исследуемого элемента его подключать. В этом можно убедиться на опыте (рис. 29). Как видим, при измерении силы тока, проходящего через лампу, оба амперметра (и тот, что слева, и тот, что справа) показывают одно и то же значение. 1. Что такое сила тока? Какой буквой она обозначается? 2. По какой формуле находится сила тока? 3. Как называется единица силы тока? Как она обозначается? 4. Как называется прибор для измерения силы тока? Как он обозначается на схемах? 5. Какими правилами следует руководствоваться при включении амперметра в цепь? 6. phscs.ru Основные физические величины, их буквенные обозначения в физике.Ни для кого не секрет, что существуют специальные обозначения для величин в любой науке. Буквенные обозначения в физике доказывают, что данная наука не является исключением в плане идентификации величин при помощи особых символов. Основных величин, а также их производных, достаточно много, каждая из которых имеет свой символ. Итак, буквенные обозначения в физике подробно рассматриваются в данной статье. Физика и основные физические величиныБлагодаря Аристотелю начало употребляться слово физика, так как именно он впервые употребил этот термин, который в ту пору считался синонимом термина философия. Это связано с общностью объекта изучения – законы Вселенной, конкретнее – то, как она функционирует. Как известно, в XVI-XVII веках произошла первая научная революция, именно благодаря ей физика была выделена в самостоятельную науку. Михаил Васильевич Ломоносов ввел в русский язык слово физика посредством издания учебника в переводе с немецкого – первого в России учебника по физике. Итак, физика представляет собой раздел естествознания, посвященный изучению общих законов природы, а также материи, ее движение и структуре. Основных физических величин не так много, как может показаться на первый взгляд – их всего 7:
Конечно, у них есть свои буквенные обозначения в физике. Например, для массы выбран символ m, а для температуры – Т. Также у всех величин есть своя единица измерения: у силы света – кандела (кд), а у количества вещества единицей измерения является моль. Производные физические величиныПроизводных физических величин значительно больше, чем основных. Их насчитывается 26, причем часто некоторые из них приписывают к основным. Итак, площадь является производной от длины, объем – также от длины, скорость – от времени, длины, а ускорение, в свою очередь, характеризует быстроту изменения скорости. Импульс выражается через массу и скорость, сила – произведение массы и ускорения, механическая работа зависит от силы и длины, энергия пропорциональна массе. Мощность, давление, плотность, поверхностная плотность, линейная плотность, количество теплоты, напряжение, электрическое сопротивление, магнитный поток, момент инерции, момент импульса, момент силы – все они зависят от массы. Частота, угловая скорость, угловое ускорение обратно пропорциональны времени, а электрический заряд имеет прямую зависимость от времени. Угол и телесный угол являются производными величинами из длины. Какой буквой обозначается напряжение в физике? Напряжение, которое является скалярной величиной, обозначается буквой U. Для скорости обозначение имеет вид буквы v, для механической работы – А, а для энергии – Е. Электрический заряд принято обозначать буквой q, а магнитный поток – Ф. СИ: общие сведенияМеждународная система единиц (СИ) представляет собой систему физических единиц, которая основана на Международной системе величин, включая наименования и обозначения физических величин. Она принята Генеральной конференцией по мерам и весам. Именно эта система регламентирует буквенные обозначения в физике, а также их размерность и единицы измерения. Для обозначения используются буквы латинского алфавита, в отдельных случаях – греческого. Также возможно в качестве обозначения использование специальных символов. ЗаключениеИтак, в любой научной дисциплине есть особые обозначения для различного рода величин. Естественно, физика не является исключением. Буквенных обозначений достаточно много: сила, площадь, масса, ускорение, напряжение и т. д. Они имеют свои обозначения. Существует специальная система, которая называется Международная система единиц. Считается, что основные единицы не могут быть математически выведены из других. Производные же величины получают при помощи умножения и деления из основных. fb.ru
dik.academic.ru
tutata. Физические величины электрического токаЗдравствуйте, уважаемые читатели нашего сайта! Мы продолжаем цикл статей, посвященных начинающим электрикам. Сегодня мы вкратце рассмотрим физические величины электрического тока, виды соединений и закон Ома. Для начала давайте вспомним, какие существуют виды тока: Переменный ток (буквенное обозначение AC) – вырабатывается благодаря магнитному эффекту. Это тот самый ток, который мы с вами имеем в наших жилищах. Он не имеет никаких полюсов, потому что меняет их много раз за секунду. Это явление (смену полярностей) называют частотой, ее выражают в герцах (Гц). В данный момент у нас в сети используется переменный ток в 50 Гц (то есть перемена направления происходит 50 раз в секунду). Два провода, которые входят в жилище, называются фазным и нулевым, поскольку здесь нет полюсов. Постоянный ток (буквенное обозначение DC) – это тот ток, который получают химическим способом (например батарейки, аккумуляторы). Основные физические величины:
Виды соединений потребителейПроводники при включении в цепь можно соединять друг с другом различными способами:
Последовательным называется соединение, при котором конец предыдущего проводника соединяется с началом следующего. Параллельным называется соединение, при котором все начала проводников соединяются в одной точке, а концы в другой. Смешанное соединение проводников представляет собой совокупность последовательных и параллельных соединений. Все рассказанное нами в данной статье базируется на основном законе электротехники – законе Ома, который гласит, что сила тока в проводнике прямо пропорциональна приложенному напряжению на его концах и обратно пропорциональна сопротивлению проводника. В виде формулы данный закон выражается так: fazaa.ru Шпаргалка с формулами по физике для ЕГЭ и не только (может понадобиться 7, 8, 9, 10 и 11 классам). Для начала картинка, которую можно распечатать в компактном виде. Механика
X=X 0 +υ 0 ∙t+(a∙t 2)/2 S=(υ 2 –υ 0 2) /2а S=(υ +υ 0) ∙t /2
Молекулярная физика и термодинамика
Электростатика и электродинамика – формулы по физике
Оптика
Квантовая физика
Физика атомного ядра
| |||
6/2(2+1)= Как решается этот проклятый пример: denis_demakhin — LiveJournal
Уже давно я увлечен этим примером:Делал по нему опросы
И сейчас попробую обосновать мою новую точку зрения, которая теперь выглядит так:
Дело в том, что между алгеброй и арифметикой есть разница в порядке действий:
Теперь понятно, почему инженерный калькулятор показывает ответ: 1.
Он не сломался. Он алгебраический.
Алгебраический калькулятор считает по правилам алгебры.
Осталось понять, алгебраический это пример или арифметический. От этого будет зависеть ответ.
Букв в примере нет, однако, в нем есть пропущенный знак умножения перед скобкой:
Случаи возможного пропуска знака умножения:
- Между буквенными множителями;
- Между числовым и буквенным множителем;
- Между множителем и скобкой;
- Между выражениями в скобках.
И получается, что если выражение (2+1) заменить на икс, то написание 6/2Х читается как “шесть, разделить на два икса”.
Тогда ответ: 1.
Но почему тогда самая умная штука на Земле – Гугл-поисковик считает, что ответ 9?
Потому что и Гугл и смартфон считают по арифметическим правилам.
Но вот тут есть тонкий момент. Арифметические правила должны, по-правильному то, действовать при указании знака умножения. Так, как я написал здесь:
Тут уже нет оснований применять правила алгебры, в которых пропущенный знак умножения считается неразрывным. И ответ получается: 9.
Вывод:
Всё зависит от того, алгебра это или арифметика.
Еще интересные штуки:
Задачи, ломающие мозг (с ответами, спрятанными под спойлер)
Тренировка ума развивальщика предприятий
Подписывайся, мыслитель!
22 секрета сериала «Теория Большого взрыва», от которых даже у Шелдона глаз задергается
«Теория Большого взрыва» стала самым длинным ситкомом в истории американского телевидения, а также получила 46 номинаций на престижную премию «Эмми» и завоевала любовь миллионов зрителей во всем мире. Илон Маск, Билл Гейтс, Стивен Хокинг, Стэн Ли и многие другие знаменитости с радостью приняли участие в съемках этого популярного сериала.
Мы в AdMe.ru внимательно посмотрели 279 серий ситкома, чтобы раскрыть все секреты легендарного телевизионного шоу.
1. Настоящая фамилия Пенни
Пенни — единственная героиня в сериале, чью фамилию никто точно не знает, но фанаты догадались, что ее могут звать Джонсон.
Ведь еще до замужества с Леонардом она сыграла «шуточную» свадьбу с Заком Джонсоном в Лас-Вегасе, но в одной из серий призналась, что не восприняла этот поступок всерьез.
2. Замена главной героини
Изначально вместо Кейли Куоко, которая сыграла Пенни, на главную женскую роль в сериале пригласили канадскую актрису Аманду Уолш, а вместо Раджа и Говарда должна была быть девушка-ученый Гилда в исполнении американо-израильской актрисы Ирис Бар. Но пилотный выпуск был отклонен каналом CBS, и тогда продюсеры решили переписать сценарий, ввести дополнительных героев и найти новые актерские лица.
3. Две мамы девушки Шелдона
На роль миссис Фаулер изначально пригласили актрису Энни О’Доннелл, которая снялась в нескольких сезонах. Однако вскоре продюсеры решили отдать роль мамы Эми более известной актрисе Кэти Бэйтс.
Однако вскоре продюсеры решили отдать роль мамы Эми более известной актрисе Кэти Бэйтс.
4. Один актер на две роли
А иногда продюсеры еще сильнее запутывали фанатов сериала с выборами актеров на те или иные эпизодические роли. Так, Ланс Барбер был замечен сначала в роли одноклассника Леонарда в пятом сезоне сериала, но во время съемок спин-оффа «Детство Шелдона» тот же самый актер сыграл роль папы маленького Купера.
5. Как выглядит мама Говарда Воловица
Зрители постоянно слышали лишь голос мамы Говарда, но никогда не замечали ее. Хотя в нескольких сценах внимательные фанаты смогли ее увидеть. Например, на заднем плане в этом эпизоде виден был ее силуэт.
А здесь уже можно хорошо рассмотреть фотографии из молодости Деборы Мелвины Воловиц и представить, как она могла бы выглядеть. К сожалению, создатели сериала вынуждены были попрощаться с этим персонажем в 8-м сезоне, так как актрисы Кэрол Энн Сьюзи, которая озвучивала мать Говарда, не стало в ноябре 2014 года.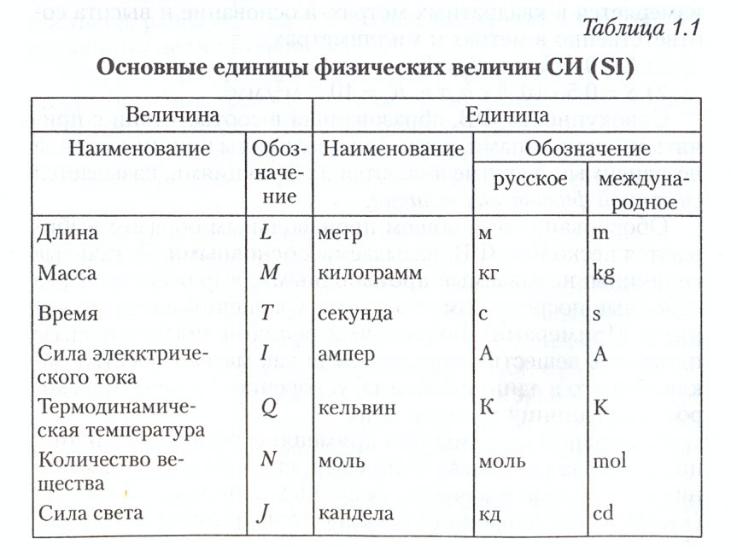
6. Что не так с голосом у Бернадетт
Дотошные зрители обратили внимание на необычную трансформацию голоса Бернадетт Ростенковски. Во время первой встречи с Говардом ее голос абсолютно нормальный, но уже после длительного знакомства с Воловицом голос Бернадетт вдруг становится неестественно высоким.
7. Фотографии съемочной группы на холодильнике
Если внимательно посмотреть на холодильник Пенни, то можно увидеть фотографии, на которых она радостно обнимает каких-то незнакомых всем зрителям персонажей. На самом деле это все настоящие фото актрисы Кейли Куоко с членами съемочной команды «Теории Большого взрыва».
8. Загадка с флагом квартиры главных героев
Многие фанаты сериала помнят, что у квартиры, в которой живут Шелдон и Леонард, есть свой собственный флаг, но мало кто замечал, что голубое полотно со львом есть и на холодильнике.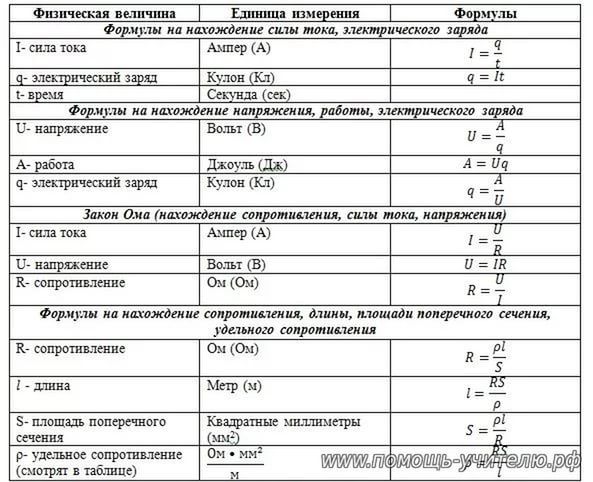 Оно висит там не просто так, а является важным символом. В сценах, где между героями возникают ссора и недопонимание, флаг всегда будет перевернут.
Оно висит там не просто так, а является важным символом. В сценах, где между героями возникают ссора и недопонимание, флаг всегда будет перевернут.
9. Неувязка в сценарии о болезни Шелдона
В первом сезоне мы узнаем, что у Шелдона астма, поэтому в квартире нельзя держать домашних животных. Но после нескольких серий заболевание таинственным образом исчезает, но появляется уже у Леонарда, который везде носит с собой ингалятор.
10. Ошибка в заставке и саундтреке к сериалу
Одну маленькую опечатку можно увидеть во всех сериях сериала, так как она присутствует в самом начале. Видимо, кто-то, кто набирал текст для заставки, вместо буквы «в» случайно поставил 9. А еще одна досадная ошибка нашлась в тексте саундтрека к сериалу, где вместо 14 млрд лет назад поется про 14 млн лет.
11. Неправильные формулы
В сериале много научных фактов, которые требуют тщательной проверки, поэтому создатели ситкома пригласили ученого Дэвида Зальцберга, который проверял все формулы, поправлял реплики актеров, чтобы все выглядело максимально достоверно. Но одно уравнение на доске все-таки оказалось неправильным, и это не случайность. Это была отсылка к фильму об Индиане Джонсе, где точно такое же уравнение было на доске в одном из эпизодов.
Но одно уравнение на доске все-таки оказалось неправильным, и это не случайность. Это была отсылка к фильму об Индиане Джонсе, где точно такое же уравнение было на доске в одном из эпизодов.
12. Докторская степень есть только у одной актрисы
Единственная актриса сериала, которая действительно имела отношение к науке, — это Маим Бялик, сыгравшая Эми Фару Фаулер. В 2008 году она получила степень доктора наук по нейробиологии, защитив диссертацию о синдроме Прадера — Вилли.
13. Фамилии главных героев настоящие
Немногие зрители догадались, что главные герои сериала Шелдон и Леонард были названы в честь нобелевских лауреатов по физике Леона Купера и Роберта Хофштадтера.
14. Непростой номер квартиры Эми
Все цифры в сериале не являются случайными. Так, номер квартиры девушки Шелдона — это на самом деле отсылка к первым знакам числа пи: 3,14.
15. Послание на футболке
Еще одна важная цифра в сериале — это 73. Именно в 73-м эпизоде сериала Шелдон делится своими мыслями, почему он считает это число своим самым любимым: «73 — это 21-е простое число. Его зеркальное отражение, 37, является 12-м, чье отражение 21 является результатом умножения, не упадите, 7 и 3… В двоичной системе 73 — это еще и 1001001, что справа налево читается как 1001001». Кроме того, актер Джим Парсонс, который блестяще исполнил роль Шелдона, родился в 1973 году.
Именно в 73-м эпизоде сериала Шелдон делится своими мыслями, почему он считает это число своим самым любимым: «73 — это 21-е простое число. Его зеркальное отражение, 37, является 12-м, чье отражение 21 является результатом умножения, не упадите, 7 и 3… В двоичной системе 73 — это еще и 1001001, что справа налево читается как 1001001». Кроме того, актер Джим Парсонс, который блестяще исполнил роль Шелдона, родился в 1973 году.
16. Что за «бугагашенька!»
«Базинга!» (или «бугагашенька!») — это фирменное восклицание Шелдона, которое стало настолько популярным, что в его честь даже назвали новый вид пчел в Бразилии. А само слово было придумано сценаристами и буквально означает «я тебя подловил!». Однако внимательные зрители могли заметить, что слово «базинга» появляется и в спин-оффе сериала, «Детство Шелдона». Так на самом деле назывался магазин комиксов, в который любил ходить маленький Купер.
17. Боязнь женщин была у коллеги продюсера сериала
Боязнь разговаривать с девушками у Раджеша появилась не случайно. Исполнительного продюсера сериала, Билла Прэди, на создание образа застенчивого парня вдохновил его бывший коллега, который не мог преодолеть страх общения с женщинами.
Исполнительного продюсера сериала, Билла Прэди, на создание образа застенчивого парня вдохновил его бывший коллега, который не мог преодолеть страх общения с женщинами.
18. Реальные страхи, с которыми столкнулись актеры
В эпизоде 2016 года «Загрязнение джакузи» Кевину Зусману пришлось побороть свою гидрофобию и задержать дыхание на несколько секунд под водой. Позже актер, сыгравший владельца магазина комиксов Стюарта, признался, что это был один из самых ужасных съемочных дней в его кинокарьере.
19. Сломанная нога и рука у героинь сериала
В 2010 году Кейли Куоко упала с лошади, сильно повредила ногу и не могла ходить, поэтому сценаристам пришлось переписать несколько эпизодов с участием актрисы, чтобы ее гипс не попадал в кадр. Несколько серий мы видим Пенни исключительно за столом или барной стойкой.
Через два года Майим Бялик попала в автомобильную аварию и получила травму левой руки, поэтому в некоторых сериях актрисе приходилось скрывать ссадины с помощью перчаток и одежды с длинным рукавом.
20. Фирменный стиль главных героев
Все главные мужские персонажи сериала имеют свой неповторимый стиль в одежде. Шелдон предпочитает носить яркие футболки поверх лонгсливов. Леонард практически все время одет в худи и куртку. Радж носит рубашки с пуловером и куртки. А страстью Говарда являются узкие джинсы и водолазки с рубашками. Только у Пенни нет единого стиля в одежде на каждый день, она всегда экспериментирует с образами и прическами.
У модного парня Говарда в гардеробе лишь пара ремней, но зато сотни необычных и ярких пряжек. Однако есть еще одна маленькая деталь, которая всегда присутствует на одежде Воловица. Это значок с инопланетянином.
21. Особый дизайн комнаты Говарда Воловица
То, что этот герой сериала страдает от недостатка женского внимания, ярко показывает и его комната. Если приглядеться, то можно заметить, что здесь все постеры и фигурки из комиксов и фильмов — это популярные женские персонажи.
22. Главный символ сериала
Фанаты сериала знают, что знаменитый лифт был сломан в результате неудачного эксперимента Леонарда с ракетным топливом, которое взорвалось в шахте лифта. В финальных сериях зрителям дают понять, что именно об этом взрыве и поется в саундтреке сериала, после которого и началась крепкая дружба главных героев. Поэтому сломанный лифт — это не просто декорация, а один из главных символов ситкома, который напоминает, как подружились главные герои и, как порой тяжело бывает гикам найти точки соприкосновения с внешним миром.
В финальных сериях зрителям дают понять, что именно об этом взрыве и поется в саундтреке сериала, после которого и началась крепкая дружба главных героев. Поэтому сломанный лифт — это не просто декорация, а один из главных символов ситкома, который напоминает, как подружились главные герои и, как порой тяжело бывает гикам найти точки соприкосновения с внешним миром.
Продюсеры и сценаристы сериала официально не подтверждают наличие у главного героя каких-либо расстройств психики. А вы верите в то, что у Шелдона мог быть синдром Аспергера?
🏫 Формула успеха в физике: больше букв, меньше чисел.
Одна из худших привычек, которые студент может развить на первом курсе физики.
состоит в том, чтобы заполнить свой рабочий лист строкой за строкой чисел. Я считаю такой подход большой ошибкой; это может
работать над простыми задачами, которые видны в первые несколько недель или месяцев физики, но когда вопросы
начинают усложняться, это больше не будет работать. Хуже того, это ненадежно и приводит к ошибкам, которые почти
невозможно обнаружить.За эти годы я обучал многих студентов-физиков, и первая корректировка, которую я сделал,
с каждым – убедить его в простом принципе: должна быть только одна математическая строка с реальными
числа в решении любой физической задачи. Остальное должно быть алгеброй. Такой подход помогает минимизировать
ошибок, подготовить студентов к решению более сложных проблем и позволить людям понять физику
любая проблема вместо того, чтобы просто потеряться в математике.
Хуже того, это ненадежно и приводит к ошибкам, которые почти
невозможно обнаружить.За эти годы я обучал многих студентов-физиков, и первая корректировка, которую я сделал,
с каждым – убедить его в простом принципе: должна быть только одна математическая строка с реальными
числа в решении любой физической задачи. Остальное должно быть алгеброй. Такой подход помогает минимизировать
ошибок, подготовить студентов к решению более сложных проблем и позволить людям понять физику
любая проблема вместо того, чтобы просто потеряться в математике.
Рассмотрим следующую задачу:
Мяч весом 1 кг катится со скоростью 5 метров в секунду от края крыши высотой 10 метров. Как быстро это идет
когда он падает на землю? Это проблема, с которой вы можете столкнуться в первую неделю
вводный курс физики. Логика довольно проста: как далеко мяч перемещается по горизонтали в
сколько времени нужно, чтобы упасть на землю? Как только они поймут, как рассматривать эту проблему в двух частях,
большинство студентов найдут два необходимых уравнения из списка и подставят числа, указанные в
проблема, отдельно. Во-первых, они найдут количество секунд, в течение которых мяч упадет на землю.
подставляя заданные числа в уравнение h = ½ * a * t 2 и решая для t = 1,43 секунды.
(h – высота крыши, a – ускорение свободного падения, t – время.) Затем они будут
возьмите это число и подставьте его в другое уравнение для горизонтального движения, v = x / t, и решите относительно x =
7,14 метра.
Во-первых, они найдут количество секунд, в течение которых мяч упадет на землю.
подставляя заданные числа в уравнение h = ½ * a * t 2 и решая для t = 1,43 секунды.
(h – высота крыши, a – ускорение свободного падения, t – время.) Затем они будут
возьмите это число и подставьте его в другое уравнение для горизонтального движения, v = x / t, и решите относительно x =
7,14 метра.
Итак, у нас есть ответ: мяч приземлится 7.14 метров со стороны здания. Но у нас нет возможности смысла этого ответа, нет возможности проверить, правильно ли мы составили систему уравнений. представляет нашу физическую интуицию. Последняя часть об интуиции является ключевой. Это самая большая причина почему студенты, которые используют слишком много чисел при решении задач, чувствуют себя потерянными при решении задач по физике.
Вместо использования чисел по ходу дела я предлагаю алгебраически решить первое уравнение для времени:
t = √ (h / [½ * a]). Затем мы можем решить второе уравнение для горизонтального расстояния: x = v * t. Вдоль
Таким образом, мы можем логически исследовать эти уравнения, чтобы увидеть, согласуются ли они с нашей физической интуицией. За
Например, мы знаем, что если крыша становится выше (h увеличивается), то мяч будет падать дольше.
(т.е. он должен увеличиться). В первом из двух преобразованных уравнений h стоит в верхней части дроби
внутри квадратного корня, поэтому мы знаем, что с увеличением h будет увеличиваться t.Хорошо, это соответствует нашему
интуиция. Точно так же во втором уравнении мы можем видеть, что либо время (t), когда мяч падает
или горизонтальная скорость (v) увеличивается, расстояние от стороны здания (x) должно увеличиваться
слишком. Это также согласуется с тем, что мы знаем, наблюдая за движением объектов в реальном мире.
Затем мы можем решить второе уравнение для горизонтального расстояния: x = v * t. Вдоль
Таким образом, мы можем логически исследовать эти уравнения, чтобы увидеть, согласуются ли они с нашей физической интуицией. За
Например, мы знаем, что если крыша становится выше (h увеличивается), то мяч будет падать дольше.
(т.е. он должен увеличиться). В первом из двух преобразованных уравнений h стоит в верхней части дроби
внутри квадратного корня, поэтому мы знаем, что с увеличением h будет увеличиваться t.Хорошо, это соответствует нашему
интуиция. Точно так же во втором уравнении мы можем видеть, что либо время (t), когда мяч падает
или горизонтальная скорость (v) увеличивается, расстояние от стороны здания (x) должно увеличиваться
слишком. Это также согласуется с тем, что мы знаем, наблюдая за движением объектов в реальном мире.
Итак, теперь мы можем объединить два уравнения, подключив первое преобразованное уравнение ко второму, используя t:
х = v * √ (h / [½ * a]). Теперь мы можем проанализировать это уравнение аналогичным образом, убедившись, что оно соответствует нашему
интуиция: с увеличением высоты x увеличивается. По мере того, как сила тяжести становится сильнее (а увеличивается), x уменьшается. Оба
из этих результатов имеют смысл.
Теперь мы можем проанализировать это уравнение аналогичным образом, убедившись, что оно соответствует нашему
интуиция: с увеличением высоты x увеличивается. По мере того, как сила тяжести становится сильнее (а увеличивается), x уменьшается. Оба
из этих результатов имеют смысл.
Теперь мы готовы использовать нашу единственную математическую строку с числами . Мы вставляем значения, которые знаем из настройте задачу (h = 10 м, a = -9,8 м / с 2 ) и решите: x = 7,14 метра.
Вы могли подумать, что эти два метода очень похожи, и были бы правы.Это достаточно легко решить проблема новичка в любом случае. Но есть две причины, по которым использование алгебраического метода делает кто-то более сильный студент-физик:
- Чем чаще вы используете числа для вычислений, тем больше возможностей избежать
ошибка. Это особенно верно, когда вопросы пытаются обмануть вас, вводя разные единицы.
 Мы
не имеют возможности проверить, что промежуточные результаты (например,г. количество секунд, t = 1,43, мы
найдены с помощью первого метода) верны, поэтому мы можем пойти по неправильному пути. Эта проблема
становится намного хуже, поскольку проблемы усложняются.
Мы
не имеют возможности проверить, что промежуточные результаты (например,г. количество секунд, t = 1,43, мы
найдены с помощью первого метода) верны, поэтому мы можем пойти по неправильному пути. Эта проблема
становится намного хуже, поскольку проблемы усложняются. - Как только мы получим окончательный ответ, x = 7,14 м, невозможно будет проверить, отражает ли этот результат нашу
физическая интуиция. По окончании решения проблемы первым способом нет возможности
знать, как изменение высоты крыши повлияет на расстояние, на которое пролетит мяч.Но когда мы ждем
чтобы вставить цифры до конца, мы можем убедиться, что увеличение высоты крыши увеличивает
расстояние, которое проходит мяч. Когда проблемы усложняются, очень важно всегда проверять, что
ваши уравнения отражают физику, которую мы понимаем интуитивно.

Когда я начинаю работать со студентами, первое, что я всегда делаю, это проверяю, как они используют числа и алгебраические переменные.Внесение этого небольшого изменения в начале вашей карьеры физика будет стоить огромных денег. дивиденды в будущем. Больше букв, меньше цифр: вот формула успеха в физике.
Дополнительные ресурсы:
Оксбридж Физикс
Интервью
Физика
в университете
Физика:
Fun Learning
Journal of Computational Physics – Journal
Journal of Computational Physics имеет зеркальный журнал с открытым доступом Journal of Computational Physics: X , который имеет те же цели и объем, редакционную коллегию и процесс рецензирования.Чтобы отправить в журнал Journal of Computational Physics: X , посетите https://www. editorialmanager.com/JCPX/default.aspx.
editorialmanager.com/JCPX/default.aspx.
The Journal of Computational Physics фокусируется на вычислительных аспектах физических проблем . JCP поощряет оригинальные научные вклады в расширенное математическое и численное моделирование , отражающее комбинацию концепций, методов и принципов, которые часто имеют междисциплинарный характер и охватывают несколько областей физики, механики, прикладной математики, статистики, прикладной геометрии, информатики , химия и другие научные дисциплины: редакторы журнала стремятся выделить методы, которые пересекают дисциплинарные границы.
The Journal of Computational Physics также публикует коротких заметок объемом 4 страницы или меньше (включая рисунки, таблицы и ссылки, но исключая титульные страницы). Письма в редакцию, комментирующие статьи, уже опубликованные в этом журнале, также будут рассмотрены. Резюме не должно быть ни в заметках, ни в письмах. Обзорные статьи , содержащие обзор конкретных областей, особенно приветствуются. Полнотекстовые статьи имеют рекомендуемый объем – 35 страниц .Чтобы оценить ограничение на количество страниц, воспользуйтесь нашим шаблоном.
Резюме не должно быть ни в заметках, ни в письмах. Обзорные статьи , содержащие обзор конкретных областей, особенно приветствуются. Полнотекстовые статьи имеют рекомендуемый объем – 35 страниц .Чтобы оценить ограничение на количество страниц, воспользуйтесь нашим шаблоном.
Опубликованные статьи конференции приветствуются при условии, что представленная рукопись является значительным улучшением статьи конференции с существенными дополнениями.
Воспроизводимость , то есть способность воспроизводить результаты, полученные другими, является основным принципом научного метода. По мере того, как влияние и открытие знаний, обеспечиваемых вычислительной наукой и инженерией, продолжает расти, крайне важно, чтобы воспроизводимость стала естественной частью этой деятельности.Журнал настоятельно рекомендует авторам сделать доступным все программное обеспечение или данные , которые позволят воспроизвести опубликованные результаты, и приложить все усилия, чтобы включить в рукописи достаточную информацию для этого. Это должно включать не только информацию, используемую для настройки, но также подробности о постобработке для восстановления опубликованных результатов.
Это должно включать не только информацию, используемую для настройки, но также подробности о постобработке для восстановления опубликованных результатов.
Вы можете ссылаться на данные, размещенные в репозитории, или загружать их в Mendeley Data. Мы также рекомендуем авторам отправлять элементы исследования, описывающие их данные, в Data in Brief, а программное обеспечение – в Software X.
Преимущества для авторов
Мы также предоставляем множество преимуществ для авторов, такие как бесплатные PDF-файлы, либеральная политика в отношении авторских прав, специальные скидки на публикации Elsevier и многое другое. Щелкните здесь, чтобы получить дополнительную информацию о наших услугах для авторов.
Информацию о подаче статей см. В нашем Руководстве для авторов.
Если вам потребуется дополнительная информация или помощь, посетите наш Центр поддержки
Modern Physics Letters B | ScienceGate
В этой работе значения критических сил связи решеток Изинга, которые меняют свою решетчатую структуру (или не автодуальную) при децимационных преобразованиях, таких как сотовая, треугольная и объемноцентрированная кубическая решетки Изинга, получены с помощью модифицированный подход ренормгруппы реального пространства (RSRG).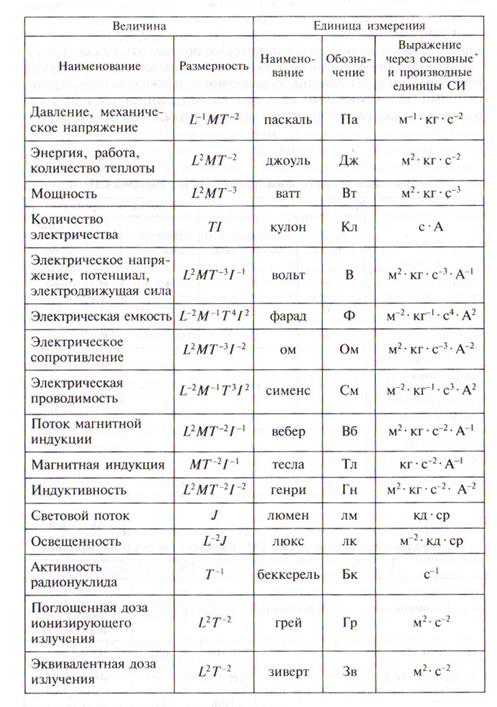 Эта модификация необходима для получения правильного соотношения между силами связи исходной и прореженной решеток. Действительно, мы легко достигли правильного перенормированного соотношения силы связи для сотовой и треугольной решеток, поскольку децимационное преобразование сотовой решетки дает треугольную решетку или наоборот. Здесь проблема наличия физически неразрешимых взаимодействий между степенями свободы в перенормированном гамильтониане, которое в конечном итоге приводит к неизбежным приближениям в трактовке, за исключением одномерной цепочки Изинга, была решена с помощью надлежащего приближения.В особенности для трехмерных решеток Изинга, физически неразрешимые взаимодействия, появляющиеся в перенормированном гамильтониане, делают математическое рассмотрение слишком громоздким. В результате недостаточно исследований, посвященных трехмерным решеткам Изинга с использованием теории РГ. Наше приближение основано на использовании простого отношения [Формула: см. Текст], которое, конечно, является очень важным приближением первого порядка, если [Формула: см.
Эта модификация необходима для получения правильного соотношения между силами связи исходной и прореженной решеток. Действительно, мы легко достигли правильного перенормированного соотношения силы связи для сотовой и треугольной решеток, поскольку децимационное преобразование сотовой решетки дает треугольную решетку или наоборот. Здесь проблема наличия физически неразрешимых взаимодействий между степенями свободы в перенормированном гамильтониане, которое в конечном итоге приводит к неизбежным приближениям в трактовке, за исключением одномерной цепочки Изинга, была решена с помощью надлежащего приближения.В особенности для трехмерных решеток Изинга, физически неразрешимые взаимодействия, появляющиеся в перенормированном гамильтониане, делают математическое рассмотрение слишком громоздким. В результате недостаточно исследований, посвященных трехмерным решеткам Изинга с использованием теории РГ. Наше приближение основано на использовании простого отношения [Формула: см. Текст], которое, конечно, является очень важным приближением первого порядка, если [Формула: см. Текст]. С помощью этого приближения процесс децимационного преобразования производит только парные взаимодействия в перенормированном гамильтониане вместо четырех спинов, шести спинов или даже восьми спиновых взаимодействий, которые возникают естественным образом, если все члены сохраняются в перенормированных гамильтонианах решеток Изинга в 2D и выше.Без этого приближения невозможно применить аналитическую РГ-обработку даже к простой кубической решетке, не говоря уже о применении ее к объемно-центрированной кубической решетке. Используя этот модифицированный подход RG, значения критической силы сцепления сотовой, треугольной и объемно центрированной кубической решетки Изинга получают аналитически как [Формула: см. Текст], [Формула: см. Текст] и [Формула: см. Текст] соответственно . По-видимому, эти оценки действительно близки к результатам, полученным в результате громоздких точных обработок, а именно [Формула: см. Текст], [Формула: см. Текст] и [Формула: см. Текст] для сотовой, треугольной и объемно-центрированной кубической решетки.
Текст]. С помощью этого приближения процесс децимационного преобразования производит только парные взаимодействия в перенормированном гамильтониане вместо четырех спинов, шести спинов или даже восьми спиновых взаимодействий, которые возникают естественным образом, если все члены сохраняются в перенормированных гамильтонианах решеток Изинга в 2D и выше.Без этого приближения невозможно применить аналитическую РГ-обработку даже к простой кубической решетке, не говоря уже о применении ее к объемно-центрированной кубической решетке. Используя этот модифицированный подход RG, значения критической силы сцепления сотовой, треугольной и объемно центрированной кубической решетки Изинга получают аналитически как [Формула: см. Текст], [Формула: см. Текст] и [Формула: см. Текст] соответственно . По-видимому, эти оценки действительно близки к результатам, полученным в результате громоздких точных обработок, а именно [Формула: см. Текст], [Формула: см. Текст] и [Формула: см. Текст] для сотовой, треугольной и объемно-центрированной кубической решетки.
% PDF-1.4
%
129 0 obj>
эндобдж
xref
129 91
0000000016 00000 н.
0000002676 00000 н.
0000002935 00000 н.
0000002961 00000 н.
0000003013 00000 н.
0000003047 00000 н.
0000003673 00000 н.
0000003834 00000 п.
0000003966 00000 н.
0000004087 00000 н.
0000004209 00000 н.
0000004332 00000 н.
0000004454 00000 п.
0000004577 00000 н.
0000004700 00000 н.
0000004823 00000 н.
0000004980 00000 н.
0000005102 00000 п.
0000005225 00000 н.
0000005349 00000 п.
0000005473 00000 н.
0000005597 00000 п.
0000005721 00000 н.
0000005845 00000 н.
0000005969 00000 н.
0000006093 00000 п.
0000006216 00000 н.
0000006340 00000 н.
0000006514 00000 н.
0000006593 00000 н.
0000006671 00000 н.
0000006750 00000 н.
0000006828 00000 н.
0000006906 00000 н.
0000006983 00000 н.
0000007061 00000 п.
0000007138 00000 п.
0000007216 00000 н.
0000007293 00000 п.
0000007370 00000 п.
0000007446 00000 н.
0000007525 00000 н.
0000008298 00000 н.
0000009314 00000 п. 0000009786 00000 н.
0000010146 00000 п.
0000010536 00000 п.
0000011868 00000 п.
0000012212 00000 п.
0000012585 00000 п.
0000012824 00000 п.
0000012901 00000 п.
0000013472 00000 п.
0000013643 00000 п.
0000013945 00000 п.
0000014948 00000 п.
0000015109 00000 п.
0000015986 00000 п.
0000016328 00000 п.
0000016746 00000 п.
0000016974 00000 п.
0000020468 00000 п.
0000021379 00000 п.
0000022093 00000 п.
0000022240 00000 п.
0000022760 00000 п.
0000022993 00000 п.
0000023080 00000 п.
0000023862 00000 п.
0000024729 00000 п.
0000025548 00000 п.
0000026305 00000 п.
0000026940 00000 п.
0000029968 00000 н.
0000034756 00000 п.
0000042373 00000 п.
0000059534 00000 п.
0000078836 00000 п.
0000079858 00000 п.
0000080289 00000 п.
0000080503 00000 п.
0000080789 00000 п.
0000080854 00000 п.
0000080910 00000 п.
0000081058 00000 п.
0000081154 00000 п.
0000081248 00000 п.
0000081361 00000 п.
0000081468 00000 п.
0000081594 00000 п.
0000002116 00000 п.
трейлер
] >>
startxref
0
%% EOF
219 0 obj> поток
xb“`f`tg`g`eb @
0000009786 00000 н.
0000010146 00000 п.
0000010536 00000 п.
0000011868 00000 п.
0000012212 00000 п.
0000012585 00000 п.
0000012824 00000 п.
0000012901 00000 п.
0000013472 00000 п.
0000013643 00000 п.
0000013945 00000 п.
0000014948 00000 п.
0000015109 00000 п.
0000015986 00000 п.
0000016328 00000 п.
0000016746 00000 п.
0000016974 00000 п.
0000020468 00000 п.
0000021379 00000 п.
0000022093 00000 п.
0000022240 00000 п.
0000022760 00000 п.
0000022993 00000 п.
0000023080 00000 п.
0000023862 00000 п.
0000024729 00000 п.
0000025548 00000 п.
0000026305 00000 п.
0000026940 00000 п.
0000029968 00000 н.
0000034756 00000 п.
0000042373 00000 п.
0000059534 00000 п.
0000078836 00000 п.
0000079858 00000 п.
0000080289 00000 п.
0000080503 00000 п.
0000080789 00000 п.
0000080854 00000 п.
0000080910 00000 п.
0000081058 00000 п.
0000081154 00000 п.
0000081248 00000 п.
0000081361 00000 п.
0000081468 00000 п.
0000081594 00000 п.
0000002116 00000 п.
трейлер
] >>
startxref
0
%% EOF
219 0 obj> поток
xb“`f`tg`g`eb @
Инструмент для переупаковки: преобразование физических уравнений в математические (и обратно)
Когда вам задают запутанное уравнение, у вас может возникнуть соблазн попытаться упростить его, введя числа. Не делай этого! Когда вы вводите конкретные числа, вы теряете понимание того, как различные параметры влияют на ваш результат. Гораздо лучший способ – «поместить параметры в коробку» и изменить физическое уравнение так, чтобы оно выглядело как математическое. Вы можете вернуть его обратно, когда закончите с математикой, ничего не потеряв.
Не делай этого! Когда вы вводите конкретные числа, вы теряете понимание того, как различные параметры влияют на ваш результат. Гораздо лучший способ – «поместить параметры в коробку» и изменить физическое уравнение так, чтобы оно выглядело как математическое. Вы можете вернуть его обратно, когда закончите с математикой, ничего не потеряв.
Наши уравнения в физике часто выглядят беспорядочно по сравнению с тем, что вы привыкли видеть на уроках математики. Это потому, что уравнения в математике сосредоточены на математических отношениях, может быть только небольшое количество символов, обозначающих переменные в задаче, а все остальное – числа.
Уравнения в физике обычно имеют много символов. Часто это параметры, показывающие, как уравнение зависит от множества измерений в физической ситуации.
Кроме того, в математике они любят использовать буквы в конце алфавита для переменных (x, y, z) и буквы в начале алфавита для параметров (a, b, c). Мы не можем избежать этого в физике. У нас так много символов, что нам нужно использовать символы, которые напоминают нам о том, что символ представляет собой физически.Но когда у нас есть уравнение, мы можем временно преобразовать его в математическую форму, решить как математическую задачу, а затем снова изменить его, чтобы интерпретировать результат в физике.
У нас так много символов, что нам нужно использовать символы, которые напоминают нам о том, что символ представляет собой физически.Но когда у нас есть уравнение, мы можем временно преобразовать его в математическую форму, решить как математическую задачу, а затем снова изменить его, чтобы интерпретировать результат в физике.
Пример
Вот пример. Обратите внимание, что вам не нужно изучать физику задачи, чтобы ее решить!
Для очень маленьких объектов в жидкости преобладает вязкая сила сопротивления, $ F_ {visc} = 6 \ pi \ mu Rv $, где $ \ mu $ – вязкость жидкости, $ R $ – радиус (размер ) объекта, а $ v $ – его скорость в жидкости.2 $, преобладает, где $ C $ – безразмерная константа, $ \ rho $ – плотность жидкости, $ R $ – радиус (размер) объекта, а $ v $ – его скорость в жидкости.
Если мы смоделируем силу сопротивления на объекте промежуточного размера, ощущая обе эти силы, существует ли когда-нибудь скорость, при которой величина этих двух сил одинакова?
Эти силы имеют очень сложные формы. 2) = 6 \ pi \ mu / C \ rho R $$
2) = 6 \ pi \ mu / C \ rho R $$
Мы не только ответили на вопрос решительным «да», но и выяснили, с какой скоростью это происходит.Мы перешли от физики к математике и обратно. Конечно, чтобы оценить, имеет ли этот ответ какой-либо биологический смысл, мы должны рассмотреть, действительно ли этот организм может достичь такой скорости!
Этот трюк «изменить вид проблемы» действительно может помочь вам распутать уравнения, содержащие кучу незнакомых символов. Сделайте его стандартным элементом вашего пояса для инструментов!
Джо Редиш 11.07.17
Математических выражений – оборотная сторона, онлайн-редактор LaTeX
ВозможностиLaTeX для набора математических данных делают его отличным выбором для написания технических документов.п \] \ конец {документ}
Открыть этот пример на обороте
Как видите, способ отображения уравнений зависит от разделителя, в данном случае \ [... \] и \ (..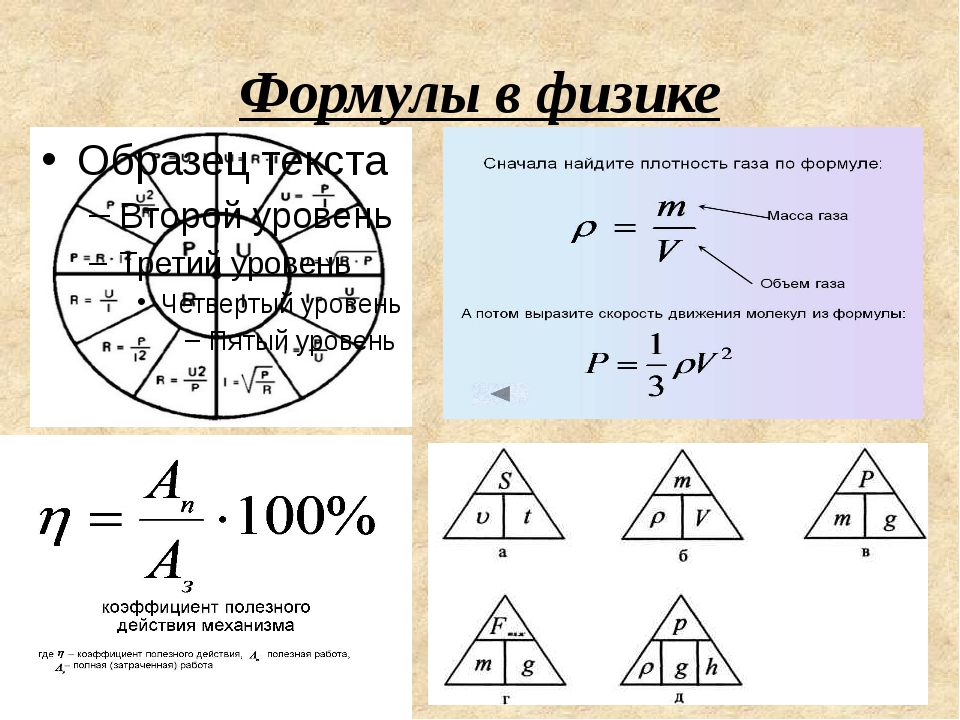 .. \)
.. \)
LaTeX допускает два режима записи математических выражений: встроенный математический режим и дисплей математический режим:
- встроенный математический режим используется для записи формул, которые являются частью абзаца
- дисплей математический режим используется для записи выражений, которые не являются частью абзаца и поэтому помещаются в отдельные строки
Встроенный математический режим
Вы можете использовать любой из этих «разделителей» для набора математических формул в встроенном режиме:
-
\ (.2 \ end {math}, открытый в 1905 году Альбертом Эйнштейном. \ end {quote} \ конец {документ}Открыть этот пример на обороте
Отображение математического режима
Используйте одну из этих конструкций для набора математических вычислений в режиме отображения:
-
\ [... \] -
\ begin {displaymath} . 2 + 1} \) внутри текста.2 + 1}
\ end {уравнение *} \ конец {документ}
2 + 1} \) внутри текста.2 + 1}
\ end {уравнение *} \ конец {документ} Открыть этот пример на обороте
Ниже представлена таблица с некоторыми общими математическими символами. Для более полного списка см. Список греческих букв и математических символов:
Различные классы математических символов характеризуются разным форматированием (например, переменные выделены курсивом, а операторы - нет) и разным интервалом.
Математический режим в LaTeX очень гибкий и мощный, с его помощью можно сделать гораздо больше:
Пионеры квантовой механики | по истории физики | Dec, 2021
Альберт Эйнштейн и фотоэлектрические явления
В 1905 году Альберт Эйнштейн (26 лет) постулировал, что полная энергия светового луча квантуется в лет. He объяснил фотоэлектрический эффект, постулировав, что свет или, в более общем смысле, все электромагнитное излучение можно разделить на конечное число «квантов энергии» , которые являются локализованными точками в пространстве.
Фотоэлектрический эффект. Входящие слева фотоны ударяются о металлическую пластину (внизу) и выбрасывают электроны, которые изображены летящими справа. Изображение: Wikipedia Эти квантов энергии позже стали называть фотонами - термин, введенный Гилбертом Льюисом в 1926 году. Идея о том, что каждый фотон должен состоять из энергии в терминах квантов, была замечательным достижением; он эффективно решил проблему получения излучения черного тела бесконечной энергии, которая возникла бы в теории, если бы свет можно было объяснить только в терминах волн.
Эти квантов энергии позже стали называть фотонами - термин, введенный Гилбертом Льюисом в 1926 году. Идея о том, что каждый фотон должен состоять из энергии в терминах квантов, была замечательным достижением; он эффективно решил проблему получения излучения черного тела бесконечной энергии, которая возникла бы в теории, если бы свет можно было объяснить только в терминах волн.Эйнштейн получил Нобелевскую премию по физике 1921 года за открытие фотоэлектрических явлений.
Эрнест Резерфорд и эксперимент по рассеянию альфа-частиц
Новозеландец Эрнест Резерфорд выполнил свою самую известную работу после получения Нобелевской премии в 1908 году. Вместе с Хансом Гейгером и Эрнестом Марсденом в 1909 году он провел эксперимент Гейгера – Марсдена , который продемонстрировал ядерную природу атомов, отклоняя альфа-частицы, проходящие через тонкую золотую фольгу.
Эрнест Резерфорд Резерфорд был вдохновлен на то, чтобы попросить Гейгера и Марсдена в этом эксперименте найти альфа-частицы с очень большими углами отклонения, которых не ожидали в то время ни в одной теории материи. Такие отклонения, хотя и редкие, были обнаружены и оказались гладкой, но высокой функцией угла отклонения.
Резерфорд был вдохновлен на то, чтобы попросить Гейгера и Марсдена в этом эксперименте найти альфа-частицы с очень большими углами отклонения, которых не ожидали в то время ни в одной теории материи. Такие отклонения, хотя и редкие, были обнаружены и оказались гладкой, но высокой функцией угла отклонения.Именно интерпретация этих данных Резерфордом привела его к формулированию модели атома Резерфорда в 1911 году. Он пришел к выводу, что весь положительный заряд и большая часть массы атома должны быть сосредоточены в очень маленькое пространство внутри атома, которое он назвал ядром.Ядро - это крошечное плотное центральное ядро атома, состоящее из протонов и нейтронов.
Результаты
Атомная модель Резерфорда стала известна как ядерная модель . В ядерном атоме протоны и нейтроны, составляющие почти всю массу атома, расположены в ядре в центре атома. Электроны распределены вокруг ядра и занимают большую часть объема атома.
 Стоит подчеркнуть, насколько маленькое ядро по сравнению с остальной частью атома.Если бы мы могли взорвать атом до размеров большого профессионального футбольного стадиона, ядро было бы размером с шарик.
Стоит подчеркнуть, насколько маленькое ядро по сравнению с остальной частью атома.Если бы мы могли взорвать атом до размеров большого профессионального футбольного стадиона, ядро было бы размером с шарик.Нильс Бор и постулаты атомной модели Бора
Модель атома Бора была предложена Нильсом Бором в 1915 году. Она возникла с модификацией модели атома Резерфорда. Его теория оказалась удивительно успешной в объяснении цвета, излучаемого водородом, светящимся в газоразрядной трубке, и вызвала огромный интерес к развитию и расширению старой квантовой теории.Чтобы преодолеть проблемы атома Резерфорда, в 1913 году Нильс Бор выдвинул три постулата, которые суммируют большую часть его модели:
- Согласно теории Бора, электроны вращаются по определенным круговым орбитам вокруг ядра, и эти орбиты обозначены буквами K , L, M, N или числами 1, 2, 3, 4 и так далее.
- Пока электроны вращаются по определенной орбите, они не могут ни набирать, ни терять энергию.
 Такие орбиты называются стационарными орбитами или стационарными состояниями.
Такие орбиты называются стационарными орбитами или стационарными состояниями. - Когда электрон прыгает с более высокой орбиты на более низкую орбиту, он выделяет энергию в форме излучения, а когда электрон прыгает с более низкой орбиты на более высокую орбиту, он поглощает энергию в форме излучения.
- Угловой момент электрона является целым кратным h / 2π
mvr = nh / 2π
Наименьшее значение n равно 1; это дает наименьший возможный радиус орбиты 0,0529 нм, известный как радиус Бора. Когда электрон оказывается на этой нижней орбите, он не может приблизиться к протону.Исходя из квантового правила углового момента, которое, как признает Бор, ранее было дано Николсоном в его статье 1912 года, Бор смог вычислить энергии разрешенных орбит атома водорода и других водородоподобных атомов и ионов. Эти орбиты связаны с определенными энергиями и также называются энергетическими оболочками или энергетическими уровнями. На этих орбитах ускорение электрона не приводит к потере излучения и энергии.
 Модель атома Бора основана на квантовой теории излучения Планка.
Модель атома Бора основана на квантовой теории излучения Планка.5. Это объясняет стабильность атома, а также линейчатый спектр атома водорода.
Фраза «квантовая физика» впервые была использована в книге Джонстона «Вселенная Планка в свете современной физики » (1931 г.).
Луи де Бройль и дуальность волна-частица
В 1924 году Луи-Виктор де Бройль сформулировал гипотезу де Бройля, утверждая, что вся материя имеет волнообразную природу, он связал длину волны и импульс:
λ = h / p
Это обобщение приведенного выше уравнения Эйнштейна, поскольку импульс фотона задается как p = E / c , а длина волны (в вакууме) - как λ = c / f , где c - скорость света в вакууме.
Луи де БройляФормула Де Бройля была подтверждена тремя годами позже для электронов при наблюдении дифракции электронов в двух независимых экспериментах.
 В Университете Абердина Джордж Пэджет Томсон пропустил пучок электронов через тонкую металлическую пленку и наблюдал предсказанные интерференционные картины. В Bell Labs Клинтон Джозеф Дэвиссон и Лестер Халберт Гермер направили электронный луч через кристаллическую решетку в своем эксперименте, широко известном как эксперимент Дэвиссона-Гермера .
В Университете Абердина Джордж Пэджет Томсон пропустил пучок электронов через тонкую металлическую пленку и наблюдал предсказанные интерференционные картины. В Bell Labs Клинтон Джозеф Дэвиссон и Лестер Халберт Гермер направили электронный луч через кристаллическую решетку в своем эксперименте, широко известном как эксперимент Дэвиссона-Гермера .Де Бройль был удостоен Нобелевской премии по физике в 1929 году за свою гипотезу. Томсон и Дэвиссон разделили Нобелевскую премию по физике в 1937 году за свои экспериментальные работы.
Вернер Гейзенберг и принцип неопределенности
23 февраля 1927 года физик Вернер Гейзенберг изложил свой новый принцип в 14-страничном письме к Вольфгангу Паули. В марте он отправил свою статью в печать. Нильс Бор указал на некоторые ошибки, но согласился с тем, что сам принцип верен, и статья была опубликована.Статья называлась «О перцептивном содержании квантовой теоретической кинематики и механики». Более знакомая форма уравнения появилась несколько лет спустя, когда он уточнил свои мысли в последующих лекциях и статьях.
Неопределенность положения и импульса
Новый принцип имел глубокие последствия. Вскоре этот принцип стал частью основы копенгагенской интерпретации QM, и на прошедшей конференции Solvay Гейзенберг и Макс Борн объявили квантовую революцию завершенной.
Принцип неопределенности Гейзенберга гласит: чем точнее мы знаем положение частицы, тем менее точно мы можем узнать ее импульс.И положение, и импульс частицы нельзя определить точно в данный момент времени.Математически принцип неопределенности Гейзенберга представляет собой нижнюю границу произведения неопределенностей пары сопряженных переменных. Наиболее известное выражение принимает положение и импульс как сопряженные переменные:
Еще одно соотношение неопределенности, на которое часто ссылаются при обсуждении квантовой механики, - это принцип неопределенности энергия-время.Заманчиво интерпретировать это уравнение как утверждение, что система может колебаться по энергии на произвольно большую величину в течение достаточно короткого времени. Этот принцип лежит в основе многих вещей, которые мы наблюдаем, но не можем объяснить с помощью классической физики. Возьмем, к примеру, атомы, где отрицательно заряженные электроны вращаются вокруг положительно заряженного ядра. Согласно классической логике, мы можем ожидать, что два противоположных заряда притянутся друг к другу, в результате чего все схлопнется в шар частиц.
Этот принцип лежит в основе многих вещей, которые мы наблюдаем, но не можем объяснить с помощью классической физики. Возьмем, к примеру, атомы, где отрицательно заряженные электроны вращаются вокруг положительно заряженного ядра. Согласно классической логике, мы можем ожидать, что два противоположных заряда притянутся друг к другу, в результате чего все схлопнется в шар частиц.Принцип неопределенности объясняет, почему этого не происходит: если электрон подойдет слишком близко к ядру, то его положение в пространстве будет точно известно, и, следовательно, ошибка измерения его положения будет незначительной.
Это означает, что ошибка измерения его импульса (и, следовательно, его скорости) будет огромной. В этом случае электрон мог бы двигаться достаточно быстро, чтобы вообще вылететь из атома. Идея Гейзенберга также может объяснить тип ядерного излучения, называемый альфа-распадом.Возможно, самым странным результатом принципа неопределенности является то, что он объясняет отсутствие частиц в вакууме.
Матричная формулировка квантовой механики
Матричная механика - это формулировка квантовой механики, созданная Вернером Гейзенбергом, Максом Борном и Паскуалем Джорданом в 1925 году. Это была первая концептуально автономная и логически последовательная формулировка квантовой механики. Его учет квантовых скачков вытеснил электронные орбиты в модели Бора.
Он чрезвычайно математичен, и даже для опытных математиков с ним было трудно работать.Хотя теперь мы знаем, что он полон и последователен, это стало ясно гораздо позже. Гейзенберг держал Вольфганга Паули в курсе его успехов.
Уравнение Шредингера и формализм волновой функции квантовой механики
Уравнение Шредингера - это уравнение, управляющее временной эволюцией волновой функции отдельной нерелятивистской частицы. Грубая аналогия заключается в том, что уравнение Шредингера делает для квантово-механической частицы то же, что Второй закон Ньютона делает для классической частицы.Мы можем решить уравнение Шредингера, чтобы определить, как частица эволюционирует во времени, точно так же, как мы используем Второй закон Ньютона для определения будущего положения и импульса классической частицы.
Уравнение Шредингера
Хотя Второй закон Ньютона точно определяет количественно изменение импульса, в квантовой механике требуется другой подход, поскольку частицы не имеют точных положений и импульсов. Вместо этого, когда мы измеряем положение частицы, результат по своей природе неопределенен. Существует вероятностное распределение возможных результатов измерения.То же самое верно, если мы измеряем импульс частицы. Отсюда ясно, что мы не можем описать состояние квантово-механической частицы, используя набор из шести действительных чисел, как это делается в классической механике. Чтобы полностью указать состояние квантово-механической частицы, мы используем волновую функцию. Волновая функция - это функция, которая присваивает комплексное число каждой точке пространства. Таким образом, хотя для описания классической частицы достаточно всего шести чисел, для описания квантово-механической частицы необходимо бесконечное количество чисел.
Дирак, Гейзенберг и ШредингерРичард Фейнман и формулировка амплитуды квантовой механики
Также известна как метод суммирования историй , или метод многих путей, или формулировка интеграла по путям или метод Минимум действие , и он был разработан Ричардом Фейнманом в 1941 году, когда он был аспирантом (23 года) в Принстоне.
 Фейнман, по его собственным словам, во время своей Нобелевской лекции заявил:
Фейнман, по его собственным словам, во время своей Нобелевской лекции заявил:Я был на пивной вечеринке в таверне Нассау в Принстоне.Был джентльмен, только что прибывший из Европы (Герберт Йеле), который подошел и сел рядом со мной. Европейцы гораздо серьезнее, чем мы в Америке, потому что они думают, что хорошее место для обсуждения интеллектуальных вопросов - это пивная вечеринка. Итак, он сел рядом со мной и спросил: «Что ты делаешь?» И так далее, а я сказал: «Я пью пиво». Затем я понял, что он хочет знать, чем я занимаюсь, и сказал ему, что борюсь с этой проблемой, и я просто повернулся к нему и сказал: «Послушайте, вы знаете какой-нибудь способ заниматься квантовой механикой, начиная с действия - где интеграл действия входит в квантовую механику? » «Нет, - сказал он, - но у Дирака есть работа, в которой лагранжиан, по крайней мере, входит в квантовую механику.Я тебе завтра покажу.
На следующий день мы пошли в Библиотеку Принстона (у них есть маленькие комнаты сбоку, чтобы обсудить вещи), и он показал мне эту бумагу.

-

 Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.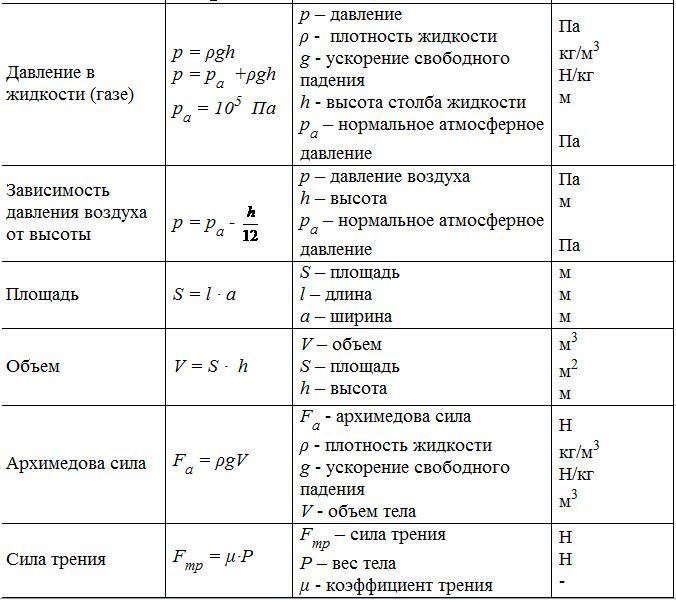 Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным. кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT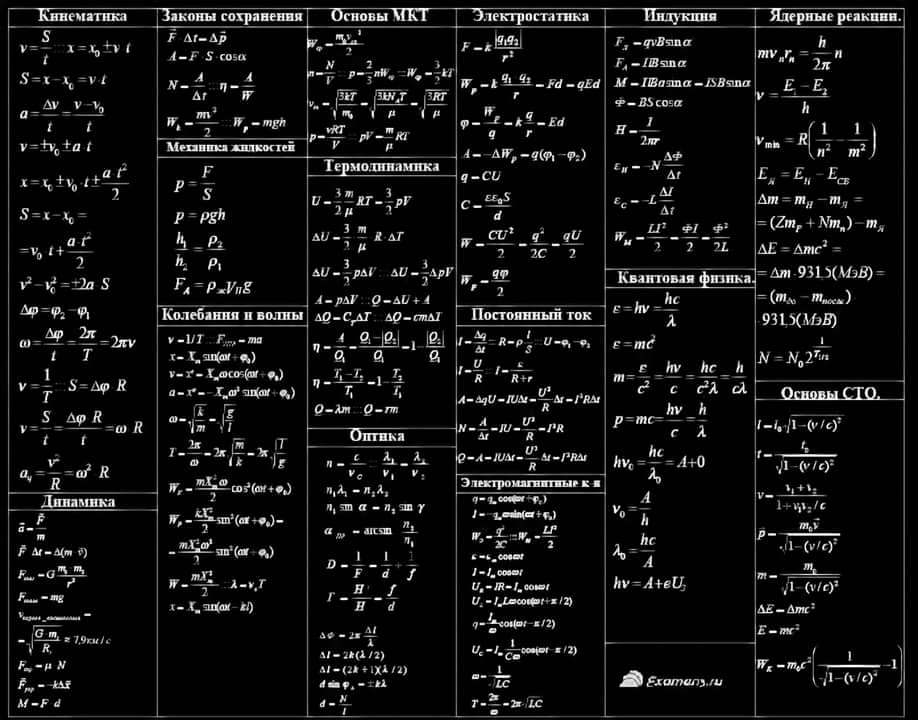 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2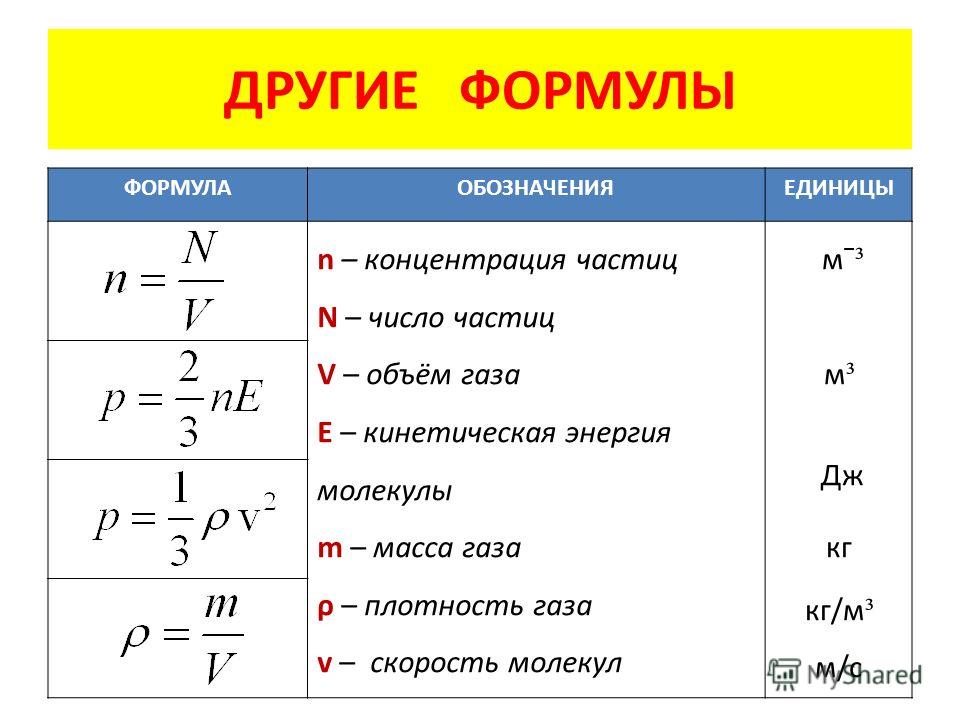 контура T=2π ∙√LC
контура T=2π ∙√LC
 Так чем знаменита ширина? Обозначение буквой «В» она имеет. Об этом известно во всём мире. Причем, согласно ГОСТу, допустимо применение как заглавной, так и строчной латинских литер. Часто возникает вопрос о том, почему именно такая буква выбрана. Ведь обычно сокращение производится по первой греческого или английского названия величины. При этом ширина на английском будет выглядеть как “width”.
Так чем знаменита ширина? Обозначение буквой «В» она имеет. Об этом известно во всём мире. Причем, согласно ГОСТу, допустимо применение как заглавной, так и строчной латинских литер. Часто возникает вопрос о том, почему именно такая буква выбрана. Ведь обычно сокращение производится по первой греческого или английского названия величины. При этом ширина на английском будет выглядеть как “width”. Согласно международным нормам системы СИ, измеряется ширина в метрах или кратных (дольных) их единицах. Стоит отметить, что в геометрии иногда также допустимо использовать «w» для обозначения ширины, однако в физике и остальных точных науках такое обозначение, как правило, не применяется.
Согласно международным нормам системы СИ, измеряется ширина в метрах или кратных (дольных) их единицах. Стоит отметить, что в геометрии иногда также допустимо использовать «w» для обозначения ширины, однако в физике и остальных точных науках такое обозначение, как правило, не применяется. В отличие от длины и ширины, высота численно характеризует размер объекта в вертикальном направлении.
В отличие от длины и ширины, высота численно характеризует размер объекта в вертикальном направлении. Он также является отрезком, соединяющим две точки на окружности. При этом он обязательно проходит через центр.
Он также является отрезком, соединяющим две точки на окружности. При этом он обязательно проходит через центр. Также непонятно, почему, в отличие от других величин, толщину можно обозначать только строчной литерой. Обозначение «s» также применяется при описании толщины страниц, стенок, ребер и так далее.
Также непонятно, почему, в отличие от других величин, толщину можно обозначать только строчной литерой. Обозначение «s» также применяется при описании толщины страниц, стенок, ребер и так далее. Почему так – нет информации.
Почему так – нет информации. При этом она не используется, когда речь идет о зубчатых зацеплениях и резьбе.
При этом она не используется, когда речь идет о зубчатых зацеплениях и резьбе.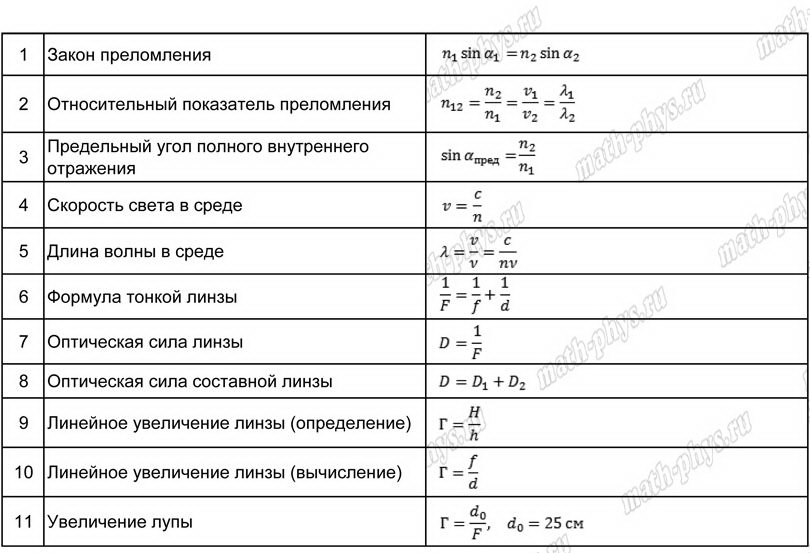 Буквенные обозначения в физике доказывают, что данная наука не является исключением в плане идентификации величин при помощи особых символов. Основных величин, а также их производных, достаточно много, каждая из которых имеет свой символ. Итак, буквенные обозначения в физике подробно рассматриваются в данной статье.
Буквенные обозначения в физике доказывают, что данная наука не является исключением в плане идентификации величин при помощи особых символов. Основных величин, а также их производных, достаточно много, каждая из которых имеет свой символ. Итак, буквенные обозначения в физике подробно рассматриваются в данной статье. Основных физических величин не так много, как может показаться на первый взгляд – их всего 7:
Основных физических величин не так много, как может показаться на первый взгляд – их всего 7: Мощность, давление, плотность, поверхностная плотность, линейная плотность, количество теплоты, напряжение, электрическое сопротивление, магнитный поток, момент инерции, момент импульса, момент силы – все они зависят от массы. Частота, угловая скорость, угловое ускорение обратно пропорциональны времени, а электрический заряд имеет прямую зависимость от времени. Угол и телесный угол являются производными величинами из длины.
Мощность, давление, плотность, поверхностная плотность, линейная плотность, количество теплоты, напряжение, электрическое сопротивление, магнитный поток, момент инерции, момент импульса, момент силы – все они зависят от массы. Частота, угловая скорость, угловое ускорение обратно пропорциональны времени, а электрический заряд имеет прямую зависимость от времени. Угол и телесный угол являются производными величинами из длины. Для обозначения используются буквы латинского алфавита, в отдельных случаях – греческого. Также возможно в качестве обозначения использование специальных символов.
Для обозначения используются буквы латинского алфавита, в отдельных случаях – греческого. Также возможно в качестве обозначения использование специальных символов. п.), используемых человеческой цивилизацией, за исключением письменностей, для которых имеется отдельный список. Содержание 1 Критерии включения в список 2 Математика … Википедия
п.), используемых человеческой цивилизацией, за исключением письменностей, для которых имеется отдельный список. Содержание 1 Критерии включения в список 2 Математика … Википедия К альтернативным теориям гравитации часто… … Википедия
К альтернативным теориям гравитации часто… … Википедия Заряд, переносимый ими за 1 с, будет в 2 раза меньше. Разделив 4 Кл на 2 с, получим 2 Кл/с. Это и есть сила тока. Обозначается она буквой I:
Заряд, переносимый ими за 1 с, будет в 2 раза меньше. Разделив 4 Кл на 2 с, получим 2 Кл/с. Это и есть сила тока. Обозначается она буквой I:
 При этом необходимо соблюдать следующие правила:
При этом необходимо соблюдать следующие правила: По какой формуле находится электрический заряд, проходящий через поперечное сечение проводника, если известны сила тока и время его прохождения?
По какой формуле находится электрический заряд, проходящий через поперечное сечение проводника, если известны сила тока и время его прохождения?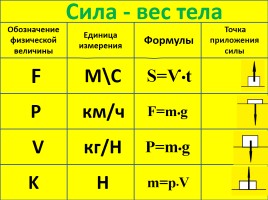

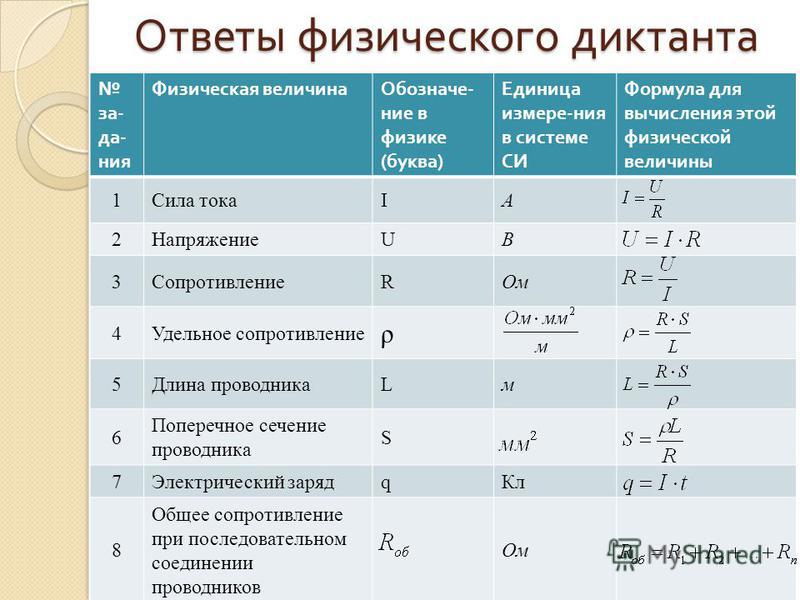

 Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные – заглавными буквами.
Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные – заглавными буквами. baryon number), удельная газовая постоянная, вириальний коэффициент, функция Бриллюэна (англ. Brillion function), ширина интерференционной полосы (нем. Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулы
baryon number), удельная газовая постоянная, вириальний коэффициент, функция Бриллюэна (англ. Brillion function), ширина интерференционной полосы (нем. Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулы electric displacement field), коэффициент диффузии (англ. diffusion coefficient), оптическая сила (англ. dioptric power), коэффициент прохождения, тензор квадрупольного электрического момента, угловая дисперсия спектрального прибора, линейная дисперсия спектрального прибора, коэффициент прозрачности потенциального барьера, де-плюс мезон (англ. Dmeson), де-ноль мезон (англ. Dmeson), диаметр (лат. diametros, др.-греч. διάμετρος)
electric displacement field), коэффициент диффузии (англ. diffusion coefficient), оптическая сила (англ. dioptric power), коэффициент прохождения, тензор квадрупольного электрического момента, угловая дисперсия спектрального прибора, линейная дисперсия спектрального прибора, коэффициент прозрачности потенциального барьера, де-плюс мезон (англ. Dmeson), де-ноль мезон (англ. Dmeson), диаметр (лат. diametros, др.-греч. διάμετρος) electron), элементарный электрический заряд (англ. elementaty electric charge), константа электромагнитного взаимодействия
electron), элементарный электрический заряд (англ. elementaty electric charge), константа электромагнитного взаимодействия gravitational acceleration), глюон (англ. gluon), фактор Ланде, фактор вырождения, весовая концентрация, гравитон (англ. graviton), константа Калибровочные взаимодействия
gravitational acceleration), глюон (англ. gluon), фактор Ланде, фактор вырождения, весовая концентрация, гравитон (англ. graviton), константа Калибровочные взаимодействия kaons), термодинамическая константа равновесия, коэффициент электронной теплопроводности металлов, модуль всестороннего сжатия, механический импульс, постоянная Джозефсона
kaons), термодинамическая константа равновесия, коэффициент электронной теплопроводности металлов, модуль всестороннего сжатия, механический импульс, постоянная Джозефсона massa), магнитное квантовое число (англ. magnetic quantum number), магнитный момент (англ. magnetic moment), эффективная масса, дефект массы, масса Планка
massa), магнитное квантовое число (англ. magnetic quantum number), магнитный момент (англ. magnetic moment), эффективная масса, дефект массы, масса Планка quantity of electricity), количество теплоты (англ. quantity of heat), обобщенная сила, энергия излучения, световая энергия, добротность (англ. quality factor), нулевой инвариант Аббе, квадрупольный электрический момент (англ. quadrupole moment), энергия ядерной реакции
quantity of electricity), количество теплоты (англ. quantity of heat), обобщенная сила, энергия излучения, световая энергия, добротность (англ. quality factor), нулевой инвариант Аббе, квадрупольный электрический момент (англ. quadrupole moment), энергия ядерной реакции spin), спиновое квантовое число (англ. spin quantum number), странность (англ. strangeness), главная функция Гамильтона, матрица рассеяния (англ. scattering matrix), оператор эволюции, вектор Пойнтинга
spin), спиновое квантовое число (англ. spin quantum number), странность (англ. strangeness), главная функция Гамильтона, матрица рассеяния (англ. scattering matrix), оператор эволюции, вектор Пойнтинга volume), напряжение (англ. voltage), потенциальная энергия, видность полосы интерференции, постоянная Верде (англ. Verdet constant)
volume), напряжение (англ. voltage), потенциальная энергия, видность полосы интерференции, постоянная Верде (англ. Verdet constant) Так, постоянная величина в формуле обозначается часто как const. Дифференциал обозначается малой буквой d перед названием величины, например dx.
Так, постоянная величина в формуле обозначается часто как const. Дифференциал обозначается малой буквой d перед названием величины, например dx. ), оператор Лапласа, дисперсия, флуктуация, степень линейной поляризации, квантовый дефект
), оператор Лапласа, дисперсия, флуктуация, степень линейной поляризации, квантовый дефект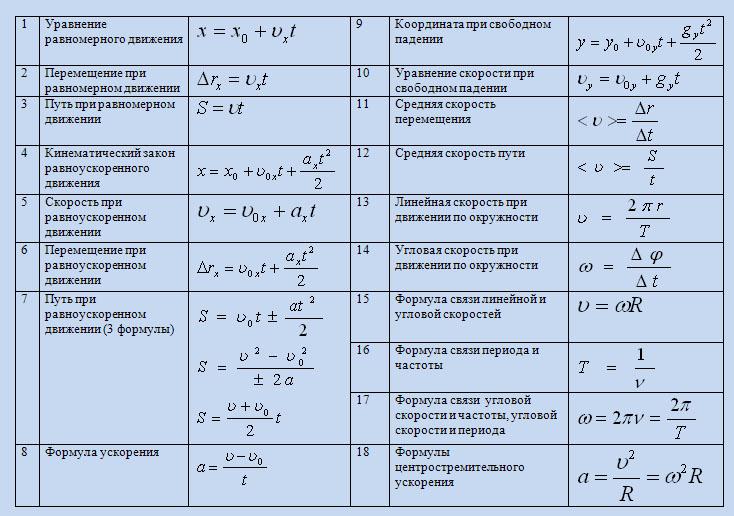 14159…, пи-связь, пи-плюс мезон, пи-ноль мезон
14159…, пи-связь, пи-плюс мезон, пи-ноль мезон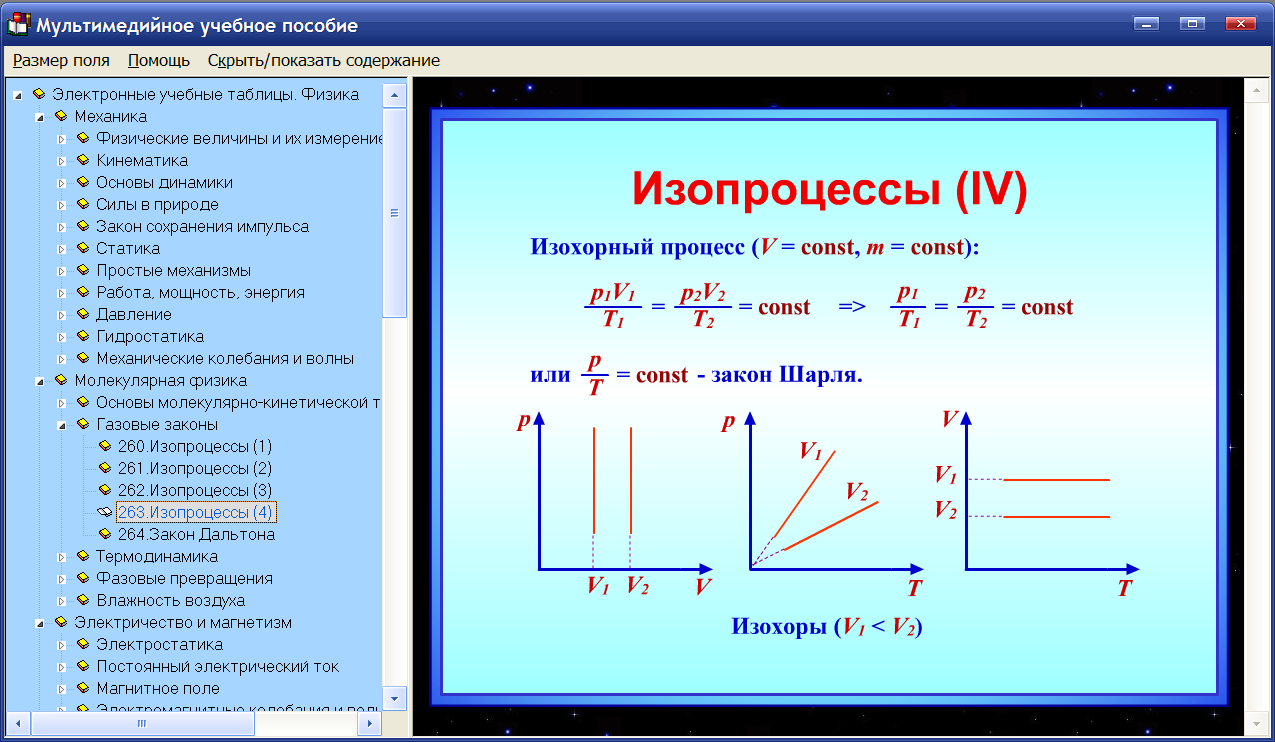 Одним примером использования кириллической буквы в современной международной научной литературе есть обозначения инварианта Лагранжа буквой Ж. Гребень Дирака иногда обозначают буквой Ш, так как график функции визуально схож с формой буквы.
Одним примером использования кириллической буквы в современной международной научной литературе есть обозначения инварианта Лагранжа буквой Ж. Гребень Дирака иногда обозначают буквой Ш, так как график функции визуально схож с формой буквы.
 ru
ru Он поляризован и течет в определенном направлении.
Он поляризован и течет в определенном направлении.

 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 контура T=2π ∙√LC
контура T=2π ∙√LC Мы
не имеют возможности проверить, что промежуточные результаты (например,г. количество секунд, t = 1,43, мы
найдены с помощью первого метода) верны, поэтому мы можем пойти по неправильному пути. Эта проблема
становится намного хуже, поскольку проблемы усложняются.
Мы
не имеют возможности проверить, что промежуточные результаты (например,г. количество секунд, t = 1,43, мы
найдены с помощью первого метода) верны, поэтому мы можем пойти по неправильному пути. Эта проблема
становится намного хуже, поскольку проблемы усложняются.
 2 + 1} \) внутри текста.2 + 1}
\ end {уравнение *} \ конец {документ}
2 + 1} \) внутри текста.2 + 1}
\ end {уравнение *} \ конец {документ}  Эти квантов энергии позже стали называть фотонами - термин, введенный Гилбертом Льюисом в 1926 году. Идея о том, что каждый фотон должен состоять из энергии в терминах квантов, была замечательным достижением; он эффективно решил проблему получения излучения черного тела бесконечной энергии, которая возникла бы в теории, если бы свет можно было объяснить только в терминах волн.
Эти квантов энергии позже стали называть фотонами - термин, введенный Гилбертом Льюисом в 1926 году. Идея о том, что каждый фотон должен состоять из энергии в терминах квантов, была замечательным достижением; он эффективно решил проблему получения излучения черного тела бесконечной энергии, которая возникла бы в теории, если бы свет можно было объяснить только в терминах волн.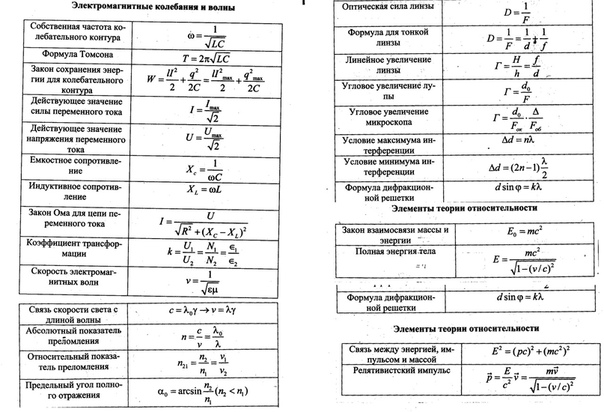 Резерфорд был вдохновлен на то, чтобы попросить Гейгера и Марсдена в этом эксперименте найти альфа-частицы с очень большими углами отклонения, которых не ожидали в то время ни в одной теории материи. Такие отклонения, хотя и редкие, были обнаружены и оказались гладкой, но высокой функцией угла отклонения.
Резерфорд был вдохновлен на то, чтобы попросить Гейгера и Марсдена в этом эксперименте найти альфа-частицы с очень большими углами отклонения, которых не ожидали в то время ни в одной теории материи. Такие отклонения, хотя и редкие, были обнаружены и оказались гладкой, но высокой функцией угла отклонения. Стоит подчеркнуть, насколько маленькое ядро по сравнению с остальной частью атома.Если бы мы могли взорвать атом до размеров большого профессионального футбольного стадиона, ядро было бы размером с шарик.
Стоит подчеркнуть, насколько маленькое ядро по сравнению с остальной частью атома.Если бы мы могли взорвать атом до размеров большого профессионального футбольного стадиона, ядро было бы размером с шарик. Такие орбиты называются стационарными орбитами или стационарными состояниями.
Такие орбиты называются стационарными орбитами или стационарными состояниями. Модель атома Бора основана на квантовой теории излучения Планка.
Модель атома Бора основана на квантовой теории излучения Планка. В Университете Абердина Джордж Пэджет Томсон пропустил пучок электронов через тонкую металлическую пленку и наблюдал предсказанные интерференционные картины. В Bell Labs Клинтон Джозеф Дэвиссон и Лестер Халберт Гермер направили электронный луч через кристаллическую решетку в своем эксперименте, широко известном как эксперимент Дэвиссона-Гермера .
В Университете Абердина Джордж Пэджет Томсон пропустил пучок электронов через тонкую металлическую пленку и наблюдал предсказанные интерференционные картины. В Bell Labs Клинтон Джозеф Дэвиссон и Лестер Халберт Гермер направили электронный луч через кристаллическую решетку в своем эксперименте, широко известном как эксперимент Дэвиссона-Гермера .
 Этот принцип лежит в основе многих вещей, которые мы наблюдаем, но не можем объяснить с помощью классической физики. Возьмем, к примеру, атомы, где отрицательно заряженные электроны вращаются вокруг положительно заряженного ядра. Согласно классической логике, мы можем ожидать, что два противоположных заряда притянутся друг к другу, в результате чего все схлопнется в шар частиц.
Этот принцип лежит в основе многих вещей, которые мы наблюдаем, но не можем объяснить с помощью классической физики. Возьмем, к примеру, атомы, где отрицательно заряженные электроны вращаются вокруг положительно заряженного ядра. Согласно классической логике, мы можем ожидать, что два противоположных заряда притянутся друг к другу, в результате чего все схлопнется в шар частиц.

 Фейнман, по его собственным словам, во время своей Нобелевской лекции заявил:
Фейнман, по его собственным словам, во время своей Нобелевской лекции заявил: