Формулы по физике кинематика все формулы: Какие существуют кинематические формулы? (статья)

Тест на все формулы для огэ по физике. кинематика по физике для ОГЭ

Первичное тестирование для определения вашего уровня знаний — бесплатно.

Советуем пройти тестирование за весь класс по физике, чтобы узнать пробелы в знаниях по всем темам и получить индивидуальный план обучения.

Вопросов в тесте: 21

Среднее время прохождения: ~10:00

Как работает платформа Skills4u

Платформа определит, насколько хорошо сформирован навык. Если тема усвоена плохо, предложит «прокачать» ее до 100%.

Не забудьте, что для формирования стойкого навыка нужно выполнить 5 коротких повторений по несколько минут в течение ближайших 4 дней.

Платформа пришлет своевременное напоминание.

Содержание каждого из последующих вопросов будет подстраиваться под ваши индивидуальные особенности с учетом уже выполненных заданий.

Почему нужно пройти общее тестирование по физике за класс, а не по отдельной теме «Все формулы для ОГЭ по физике. Кинематика»

Пройдя тестирование за класс вы получите ПОЛНУЮ КАРТИНУ ЗНАНИЙ ПО ВСЕМ ТЕМАМ.

Такой подход позволит глубинно проанализировать знания, вывести успеваемость и понимание предмета на качественно новый уровень.

Пройдя тестирование по одной теме вы получите РЕЗУЛЬТАТ ЗНАНИЙ ТОЛЬКО ЭТОЙ ТЕМЫ, которая, возможно, плохо изучена. Такой метод не является комплексным и дает лишь точечное понимание знаний по предмету.

Зарегистрироваться и пройти тестирование

Как растут результаты учеников
после занятий на тренажерах Skills4u

Занятия
на Skills4u

Занятия
с учебником

Успеваемость

Мотивация

Внимательность

Скорость

Самостоятельность

Запоминание

Первичный Тест «Все формулы для ОГЭ по физике. Кинематика» по физике для ОГЭ онлайн и бесплатно предоставляется всем желающим.

Советуем пройти тестирование за весь класс по физике, чтобы узнать пробелы в знаниях по всем темам и получить индивидуальный план обучения.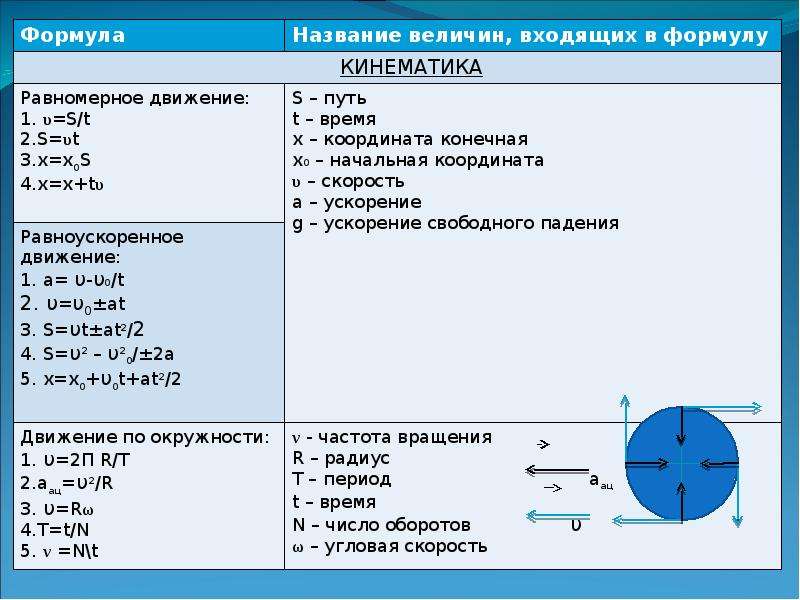

После регистрации вы получите 7 дней бесплатного доступа, чтобы увидеть первые результаты занятий и оценить эффективность тренажеров.

Зарегистрироваться и пройти тестирование

А для комплексного результата пройдите общее тестирование за

класс! Узнайте пробелы в знаниях по всем темам

Ученик

Занимайся 20 минут в день и прокачай знания по школьной программе за месяц!

Родитель

Наслаждайтесь прогрессом вашего ребенка в школе и на платформе

Учитель/
репетитор

Задавайте и проверяйте домашние задания прямо на платформе

Зарегистрироваться и пройти тестирование

59041

---

учеников уже занимаются с нами

Все формулы по физике для подготовки к ЦТ 🙂

Item Categories

choose an option . .

• 01 Кинематика
• 02 Динамика
• 03 Законы сохранения
• 04 гидростатика
• 05 МКТ
• 06 Термодинамика
• 07 Электростатика
• 08 Электрический ток
• 09 Магнитное поле и ЭМИ
• 10_01 Мех. колебания
• 10_02 ЭМ колебания
• 10_03 Мех. волны
• 11 Оптика
• 12 Квантовая и ядерная физика
• 13 Математика

ФИЛЬТР важности

choose an option ..

• 100 главных формул
• II уровень
• III уровень
• Формулы быстрого доступа

Your selections:

Проекция перемещения через координаты

Уравнение координаты при равномерном движении

Средняя скорость

Средняя скорость перемещения

Уравнение координаты при равноПеременном движении

Проекция перемещения при равнопеременном движении

Проекция скорости при равнопеременном движении

Уравнение квадратов скоростей

Частота вращения

Линейная скорость при “равномерном” движении по окружности

Угловая скорость вращения

Связь линейной и угловой скорости

Центростремительное ускорение

Закон сложения скоростей

Горизонтальный бросок.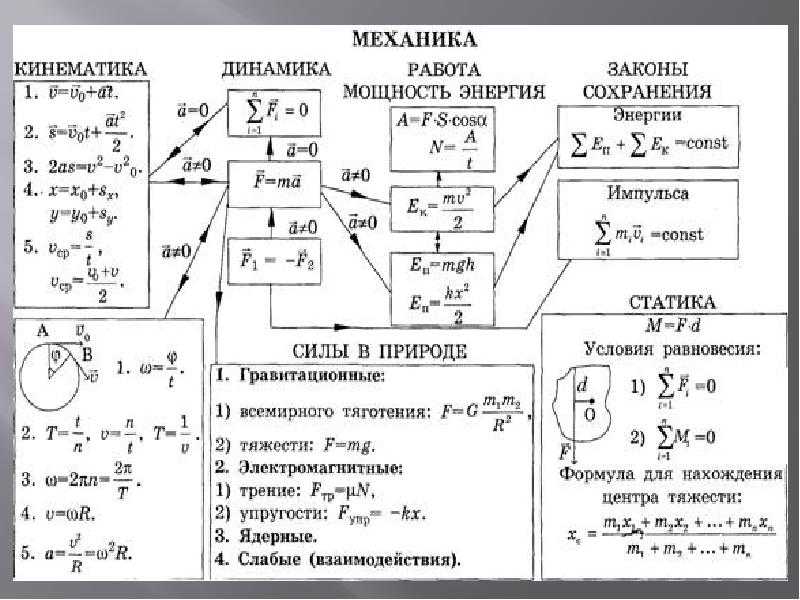 Проекции вектора скорости на оси OX и OY

Горизонтальный бросок. Скорость тела.

Горизонтальный бросок. Время падения.

Горизонтальный бросок. Дальность полета.

Горизонтальный бросок. Направление вектора скорости в произвольный момент времени.

Равнодействующая сила

Второй закон Ньютона

Третий закон Ньютона

Закон Гука

Сила трения скольжения

Максимальное значение силы трения покоя

Промежуточное значение силы трения покоя

Закон всемирного тяготения

Скорость спутника и первая космическая скорость

Сила тяжести и ускорение свободного падения

Импульс тела и системы тел

Импульс силы

Закон сохранения импульса

Работа силы F

Средняя мощность силы F

Коэффициент Полезного Действия

Кинетическая энергия тела

Теорема о изменении кинетической энергии

Потенциальная энергия Силы упругости

Потенциальная энергия силы тяжести

Работа потенциальной силы

Закон сохранения механической энергии

Закон сохранения механической энергии для незамкнутых систем

Высота при движении по окружности

Давление силы F

Гидростатическое давление

Закон Паскаля. Общее давление.

Соотношение для пресса

Условие не сжимаемости жидкости

Условие равновесия жидкости в сообщающихся сосудах

Средняя плотность тела

Сила Архимеда

Количество вещества через массу

Количество вещества через число частиц

Масса одной молекулы

Концентрация частиц газа

Связь плотности и концентрации частиц газа

Средняя квадратичная скорость молекул газа

Основное уравнение МКТ

Средняя квадратичная скорость, определение через давление

Давление газа через его плотность среднюю квадратичную скорость

Связь давления газа его концентрации и средней кинетической энергии молекул газа

Связь температурных шкал

Средняя кинетическая энергия одной частицы газа

Средняя квадратичная скорость, определение через температуру

Связь давления газа его концентрации и температуры

Уравнение Менделева-Клайперона

Абсолютная влажность

Относительная влажность

Изменение внутренней энергии идеального одноатомного газа

Работа газа при постоянном давлении (изобарный процесс)

Первый закон термодинамики

Количество теплоты при нагревании

Количество теплоты для плавления / кристаллизации

Количество теплоты для парообразования / конденсации

Уравнение теплового баланса

КПД теплового двигателя

КПД идеального теплового двигателя

Закон сохранения заряда

Закон Кулона для точечных зарядов

Диэлектрическая проницаемость среды

Напряженность электрического поля через пробный заряд

Напряженность электрического поля заряженной металлической сферы

Напряженность электрического поля создаваемого точечным зарядом.

Напряженность создаваемая бесконечной заряженной плоскостью

Принцип суперпозиции электрических полей

Потенциал точечного заряда

Потенциал электрического поля заряженной металлической сферы

Напряженность однородного электрического поля

Работа электрического поля

Работа ЭП по перемещению заряда в однородном электрическом поле

Емкость конденсатора

Емкость конденсатора через геометрические параметры

Энергия конденсатора

Сила тока

Сопротивление проводника

ЭДС источника тока

Закон ома для участка цепи

Закон Ома для полной цепи

Параллельное соединение проводников

Последовательное соединение проводников

Работа электрического тока. Закон Джоуля-Ленца.

Напряжение на клеммах источника тока

Мощность эл. тока на участке цепи

Мощность источника тока (полная мощность)

КПД источника тока

Сила Ампера

Сила Лоренца

Принцип суперпозиции магнитных полей

Правило левой руки

Правило буравчика или правило правой руки (направление линий магнитной индукции проводника с током)

Магнитный поток

Закон электромагнитной индукции

ЭДС самоиндукции

Энергия магнитного поля соленоида с током

Циклическая частота

Фаза колебания

Уравнение гармонических колебаний. Закон изменения координаты.

Уравнение скорости для процесса гармонических колебаний

Уравнение ускорения для процесса гармонических колебаний

Амплитуда скорости (максимальная скорость) в процессе ГК

Амплитуда ускорения (максимальное ускорение ) в процессе ГК

Период колебаний математического маятника

Период колебаний пружинного маятника

Закон сохранения энергии для гармонических колебаний

Связь скорости волны с частотой и длинной волны

Фаза колеблющейся точки среды плоской волны

Условие максимумов/минимумов через разность фаз

Уравнение плоской волны

Формула Томпсона (период колебаний в электро-магнитном контуре)

Закон изменения заряда в ЭлектроМагнитном контуре

Закон изменения напряжения в ЭлектроМагнитном контуре

Закон изменения тока в ЭлектроМагнитном контуре

Амплитудное значение тока в ЭлектроМагнитном контуре

Полная энергия в ЭлектроМагнитном контуре. Закон сохранения энергии для ЭМК.

Закон отражения

Закон преломления света

Критический угол полного внутреннего отражения

Угол поворота луча призмой

Абсолютный показатель преломления

Условия максимума и минимума интерференции

Уравнение максимумов для дифракционной решетки

Оптическая сила линзы

Формула тонкой линзы

Линейное увеличение линзы

Энергия кванта электромагнитного излучения

Связь энергии кванта с энергиями орбит атома (второй постулат Бора)

Энергия n – го уровня атома водорода

Связь энергии и массы (формула Эйнштейна)

Уравнение фотоэффекта

Красная граница фотоэффекта

Задерживающее напряжение

Масса фотона через частоту

Импульс фотона через частоту

Массовое число ядра

Энергия связи ядра

Закон радиоактивного распада (закон полураспада)

Теорема Пифагора

Теорема косинусов

Косинус угла

Синус угла

Тангенс угла

Длинна окружности

Площадь круга

Площадь треугольника

Объем сферы

Средняя скорость пути для участков с одинаковым временем.

Средняя скорость пути для участков с одинаковым расстоянием.

Средняя скорость пути в случае ускоренного (замедленного) движения.

Ускорение тел на блоке

Ускорение тела на наклонной плоскости

Процент погруженной части тела

Плотность газа

Скорость заряженной частицы после прохождения ускоряющей разности потенциалов

Равенство плеч процессов

Максимальная полезная мощность источника тока

Соотношение сопротивлений внешних участков цепи для случая одинаковой полезной мощности

Сопротивление при параллельном соединении двух проводников

Радиус окружности, при движении заряженной частицы в магнитном поле

Заряд протекающий по контуру при изменении магнитного потока

ЭДС индукции в поступательно движущемся проводнике

———————————————————————————-
В школьном курсе физике более двухсот формул!  Но ведь многие из них легко ( часто в одно два действия) выводятся друг из друга,  да и  ВСЕ они так уж ли важны и актуальны для успешной сдачи экзамена? Вероятно нет 😉 .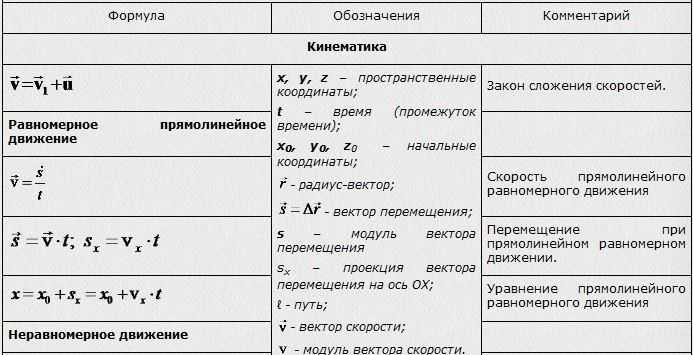
На этой страничке я собрал для вас ВСЕ основные формулы школьного курса физики ≈160 . 

Все формулы прошли отбор в соответствии с программой по физике для поступающих в ВУЗы в 2020 году.

К каждой формуле есть пояснение,  для многих есть ссылка на развернутое объяснение и примеры и, на десерт, – 100 главных формул можно скачать в удобной компактной форме.

КАК ПОЛЬЗОВАТЬСЯ СПРАВОЧНИКОМ

Главная особенность справочника формул – это ДВА ФИЛЬТРА (две группы кнопок серого цвета).

Первый фильтр называется “ТЕМЫ” , кликая по кнопке с названием темы вы можете быстро отобрать формулы соответсвующей темы. Фильтр работает по принципу исключения т.е. выбирая какую-либо одну тему , вы исключаете другие.

Второй фильтр называется “ВАЖНОСТЬ” , он содержит три кнопки :

– “100 главных формул”. Как следует из названия он позволяет отобрать 100 наиболее важных формул (топ 100 главных формул школьного курса физики).

– “Доп. формулы” – это формулы второго уровня важности, большинство из них выводятся и первой группы, а те что не выводятся более или менее второстепенны.

– “третий уровень” – это формулы частные случаи, работающие для узкого круга задач (например формула отклонения луча призмой) , либо формулы появление на ЦТ которых маловероятно.

Фильтр важности работает по принципу дополнения т.е. нажав кнопку “100 главных формул” – отфильтруются 100 основных формул, затем нажав кнопку “Доп. формулы” к предыдущим формулам добавятся формулы второго уровня важности и т.д.

ЦВЕТОВОЙ КОД

Возможно вы уже заметили, что многие формулы раскрашены разными цветами. ЭТО НЕ ДЛЯ КРАСОТЫ (хотя и для нее то же), это способ показать, что с чем соотносится. Например, если в формуле вы видите букву F синего цвета и на рисунке вектор (стрелку) синего цвета, значить эта F характеризует этот вектор. Впрочем смотрите сами, я надеюсь разберетесь 😉

К КАЖДОЙ ФОРМУЛЕ ЕСТЬ ПОЯСНЕНИЕ, что бы его увидеть КЛИКНИТЕ ПО ФОРМУЛЕ !

Для пользователе мобильных устройств.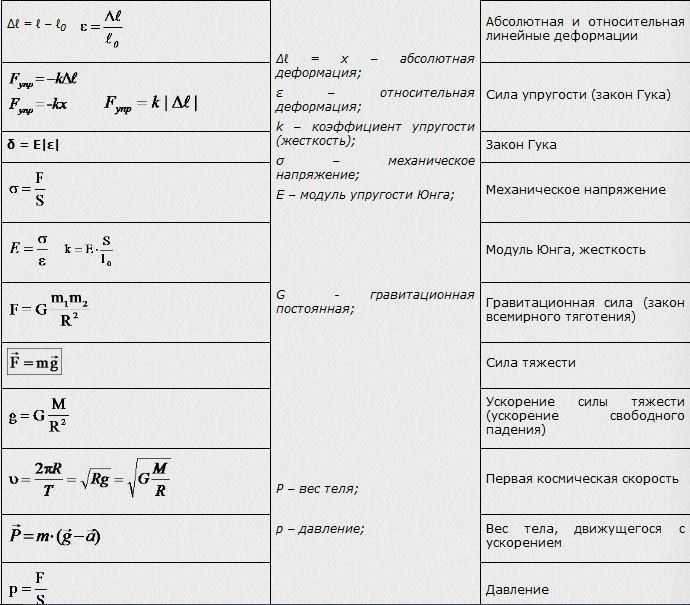 Что бы увидеть описание нужен ДВОЙНОЙ ТАП по экрану (двойное касание к экрану) для большинства формул есть поясняющий рисунок, для многих формул (пока в рамках механики) есть ссылка на развернутое объяснение, примеры или конспект. Так же многие формулы я снабдил информацией о том, на что следует обратить внимание, при работе с этой формулой.

В конце списка формул присутствует форма обратной связи, если вы считаете что какой-то формулы не хватает, или хотите предложить как можно улучшить справочник – пишите!
Ну и не забывайте делится этой информацией в соцсетях (значки справа вверху экрана).

СМОТРИТЕ ТАК ЖЕ

Список ВСЕХ формул по физике для самопроверки и подготовки к ЦТ 2020

Здесь вы можете оставить ваше сообщение или отзыв.

Уравнения кинематики: когда и как использовать каждую формулу (с производными)

Уравнения кинематики описывают движение объекта, испытывающего постоянное ускорение. Эти уравнения связывают переменные времени, положения, скорости и ускорения движущегося объекта, позволяя решать любую из этих переменных, если другие известны. 2+2a(x_f – x_i)

Примечания к кинематическим уравнениям

• Эти уравнения работают только с постоянным ускорением (которое может быть равно нулю в случае постоянной скорости).
• В зависимости от того, какой источник вы читаете, окончательные величины могут не иметь нижнего индекса f и/или могут быть представлены в функциональном обозначении как x(t) – читать « x как функция времени» или « x в момент времени t » — и v(t) . Обратите внимание, что х (т) НЕ означает x , умноженное на t !

• Иногда количество x _f – x _i записывается как

  Δx , что означает «изменение x », или даже просто как

  6 d, что означает смещение. Все эквивалентны.

  Положение, скорость и ускорение являются векторными величинами, то есть с ними связано направление. В одном измерении направление обычно обозначается знаками — положительные величины указывают положительное направление, а отрицательные величины — отрицательное. Нижние индексы: “0” может использоваться для начального положения и скорости вместо i . Этот «0» означает «при t = 0», а x ₀ и v ₀ обычно произносятся как «x-ноль» и «v-ноль». * Только одно из уравнений не включает время. Когда вы записываете данные и определяете, какое уравнение использовать, это является ключевым моментом!

Особый случай: свободное падение

Движение в свободном падении — это движение объекта, ускоряющегося только за счет силы тяжести в отсутствие сопротивления воздуха. Применяются те же кинематические уравнения; однако известно значение ускорения у поверхности Земли. Величина этого ускорения часто представляется как г , где г = 9,8 м/с ² . Направление этого ускорения – вниз, к поверхности Земли. (Обратите внимание, что в некоторых источниках г может быть аппроксимировано 10 м/с ² , а в других может использоваться значение с точностью более двух знаков после запятой. )

Стратегия решения задач кинематики в одном измерении:

Нарисуйте схему ситуации и выберите подходящую систему координат. (Напомним, что x , v и и являются векторными величинами, поэтому, задав четкое положительное направление, будет легче отслеживать знаки.)

Напишите список известных величин. (Остерегайтесь, что иногда известное неочевидно. Ищите такие фразы, как «начинается с состояния покоя», что означает, что v _i = 0, или «ударяется о землю», что означает, что x _f = 0, и т. д.)

Определите, какое количество нужно найти в соответствии с вопросом. Какое неизвестное вы будете решать?

Выберите подходящее уравнение кинематики. Это будет уравнение, которое содержит вашу неизвестную величину вместе с известными величинами.

Решите уравнение для неизвестной величины, затем подставьте известные значения и вычислите окончательный ответ. (Будьте осторожны с единицами измерения! Иногда вам нужно преобразовать единицы перед вычислениями.)

Примеры одномерной кинематики

Пример 1: В рекламе утверждается, что спортивный автомобиль может разгоняться от 0 до 60 миль в час за 2,7 секунды. Чему равно ускорение этого автомобиля в м/с ² ? Какое расстояние он проходит за эти 2,7 секунды?

Решение:

(Вставьте изображение 2)

Известные и неизвестные величины:

v_i=0\text{ миль/ч}\\ v_f=60\text{ миль/ч}\\ t=2.7\text{ s} \\ x_i=0\\ a=\text{?}\\ x_f=\text{?}

Первая часть вопроса требует решения для неизвестного ускорения. Здесь мы можем использовать уравнение № 1:

v_f=v_i+at\implis a =\frac {(v_f-v_i)} t

Прежде чем мы подставим числа, нам нужно преобразовать 60 миль в час в м/с: 92+2(-9,8)(0-1,5)}=\pm\sqrt{254,4}\приблизительно\pm16\text{ м/с}

Здесь есть два решения. Который правильный? Из нашей диаграммы видно, что конечная скорость должна быть отрицательной. Таким образом, ответ:

v_f=\underline{\bold{-16}\text{ м/с}}

Чтобы найти время, мы можем использовать либо уравнение №1, либо уравнение №2. Поскольку с уравнением №1 работать проще, мы будем использовать его:

v_f=v_i+at\implies t=\frac {(v_f-v_i)} {a}=\frac {(-16-15)} {-9,8}\приблизительно \подчеркивание{\жирный{3,2}\текст{s}}

Обратите внимание, что ответ на первую часть этого вопроса не был 0 м/с. Хотя верно то, что после приземления мяч будет иметь нулевую скорость, этот вопрос требует узнать, как быстро он движется в эту долю секунды перед ударом. Как только мяч касается земли, наши кинематические уравнения больше не применяются, поскольку ускорение не будет постоянным.

Кинематические уравнения движения снаряда (два измерения)

Снаряд — это объект, движущийся в двух измерениях под действием силы тяжести Земли. Его траектория представляет собой параболу, потому что единственное ускорение связано с гравитацией. Кинематические уравнения движения снаряда имеют несколько иной вид, чем кинематические уравнения, перечисленные выше. Мы используем тот факт, что компоненты движения, перпендикулярные друг другу, такие как горизонтальные 9Направление 0005 x и вертикальное направление y – независимы.

Стратегия решения задач по кинематике движения снаряда Задачи:

Нарисуйте схему ситуации. Как и в случае с одномерным движением, полезно набросать сценарий и указать систему координат. Вместо того, чтобы использовать метки x , v и a для положения, скорости и ускорения, нам нужен способ маркировки движения в каждом измерении отдельно.

Для горизонтального направления чаще всего используется x для положения и v _x для x-компонента скорости (обратите внимание, что ускорение равно 0 в этом направлении, поэтому нам не нужна переменная для it. ) В направлении y чаще всего используется y для положения и v _y для y-составляющей скорости. Ускорение можно обозначить как a _y , или мы можем использовать тот факт, что мы знаем, что ускорение свободного падения равно g в отрицательном направлении Y, и просто используйте его вместо этого.

Напишите список известных и неизвестных величин, разделив задачу на две части: вертикальное и горизонтальное движение. Используйте тригонометрию, чтобы найти x- и y-компоненты любых векторных величин, которые не лежат вдоль оси. Может быть полезно перечислить это в двух столбцах:

(вставьте таблицу 1)

Примечание: если скорость дана как величина вместе с углом, Ѳ , над горизонталью, тогда используйте векторное разложение, 92-2g(y_f – y_i)

Обратите внимание, что ускорение в направлении y равно -g, если предположить, что вверх положительно. Распространенным заблуждением является то, что g = -9,8 м/с ² , но это неверно; g само по себе является просто величиной ускорения: g = 9,8 м/с ² , поэтому нам нужно указать, что ускорение отрицательно.

Найдите одно неизвестное в одном из этих измерений, а затем подставьте то, что является общим для обоих направлений. Хотя движение в двух измерениях независимо, оно происходит в одном и том же масштабе времени, поэтому временная переменная одинакова в обоих измерениях. (Время, необходимое мячу для совершения вертикального движения, равно времени, которое требуется для его горизонтального движения.)

Примеры кинематики движения снаряда

Пример 1: Снаряд пущен горизонтально со скалы высотой 20 м с начальной скоростью 50 м/с. Сколько времени нужно, чтобы удариться о землю? На каком расстоянии от основания скалы он приземлится?

(вставьте изображение 4)

Известные и неизвестные количества:

(вставьте таблицу 2)

Мы можем найти время, необходимое для удара о землю, используя второе уравнение вертикального движения:

92\implies t=\sqrt{\frac{(2\times 20)} g}=\underline{\bold{2. 02}\text{s}}

Затем, чтобы найти, где он приземляется, x _f , мы можем использовать уравнение горизонтального движения:

x_f=x_i+v_xt=50\times2.02=\underline{\bold{101}\text{s}}

Пример 2: Мяч запущен на 100 м/с от уровня земли под углом 30 градусов к горизонту. Где он приземляется? Когда его скорость наименьшая? Каково его местонахождение в это время?

(вставьте изображение 5)

Известные и неизвестные величины:

Сначала нам нужно разбить вектор скорости на составляющие:

v_x=v_i\cos(\theta)=100\cos(30)\приблизительно 86,6 \text{ м/с}\\ v_{yi}=v_i\sin(\theta)=100\sin(30)=50 \text{ м/с}

Тогда наша таблица величин будет следующей:

(вставьте таблицу 3)

Сначала нам нужно найти время полета мяча. Мы можем сделать это со вторым вертикальным уравнением_. Обратите внимание, что мы используем симметрию параболы, чтобы определить, что окончательная _y скорость отрицательна от начальной:

Затем мы определяем, как далеко он продвинется в направлении x за это время:

x_f=x_i+v_xt=86,6\times 10,2\приблизительно\underline{\bold{883} \text m}

Используя симметрию параболического пути, мы можем определить, что скорость наименьшая при 5,1 с , когда снаряд находится на пике своего движения и вертикальная составляющая скорости равна 0. x- а y-компоненты его движения в это время равны:

92\приблизительно \underline{\bold{128}\text{ m}}

Вывод кинематических уравнений

Уравнение №1: Если ускорение постоянно, то:

a=\frac{(v_f-v_i) }{t}

Решая скорость, мы имеем:

v_f=v_i+at

Уравнение № 2: Среднюю скорость можно записать двумя способами:

v_{avg}=\frac{( x_f-x_i)}{t}=\frac{(v_f+v_i)}{2}

Если мы заменим _v _f _ на выражение из уравнения № 1, мы получим: 92+2a(x_f – x_i)

Уравнение кинематики в квадрате скорости Обзор

Уравнение кинематики в квадрате скорости

Уравнение кинематики в квадрате скорости используется для объектов, которые движутся в одном измерении с постоянным ускорением. Примером может служить транспортное средство, которое движется по прямой дороге с заданным ускорением. Мы можем использовать уравнение для определения скорости после того, как он ускорился на определенном расстоянии. Обратите внимание, что в этом уравнении нет времени. Это полезно, когда время не указано непосредственно в информации, описывающей ситуацию. Два других уравнения кинематики могут быть объединены для получения этого уравнения.

Переменные в уравнении кинематики в квадрате скорости

Это уравнение связывает начальную скорость, конечную скорость, ускорение, а также начальное и конечное положения объекта, который движется с постоянным ускорением.

v _x представляет конечную скорость объекта.

v _{x 0} представляет начальную скорость объекта.

a _x представляет ускорение объекта.

x представляет конечное положение объекта.

x ₀ представляет начальное положение объекта.

Единицы в этом уравнении

Вы можете использовать это уравнение со многими различными комбинациями переменных. Обычно мы используем следующую комбинацию.

v _{x имеет единицы измерения м/с.}

v _{x 0} также имеет единицы измерения м/с.

a _x имеет единицы измерения м/с².

x имеет единицы измерения метры.

x ₀ также имеет единицы измерения метры.

Если вы используете другие группы переменных, убедитесь, что они непротиворечивы. В частности, убедитесь, что единицы времени в единицах измерения ускорения и расстояния совпадают. Например, если ускорение указано в м/с², убедитесь, что расстояния указаны в м.

Также убедитесь, что единицы измерения расстояния совпадают. Вы можете использовать MPH для единиц скорости и MPH/s для ускорения. Обе эти единицы имеют мили как часть единиц измерения расстояния.

Убедитесь, что все единицы измерения указаны в метрических или британских единицах измерения. Например, не смешивайте миль в час и км без преобразования в общий набор.