Тренажёр формул по физике (ЕГЭ)
Пользоваться тренажёром предельно просто. Открой нужный раздел физики в списке разделов ниже. Ты увидишь описания формул из этого раздела.
Напиши эти формулы на листочке. Затем кликни на надпись “Кликни и проверь себя” и выясни, какие из формул ты еще плохо знаешь.
Подучи и повтори всё сначала.Успехов в изучении формул по физике, да и вообще физики!
МеханикаКинематика
- Напиши формулы
- Кликни и проверь себя
Динамика
- Напиши формулы
- Кликни и проверь себя
Статика
- Напиши формулы
- Кликни и проверь себя
Гидростатика
- Напиши формулы
- Кликни и проверь себя
Законы сохранения энергии и импульса
- Напиши формулы
- Кликни и проверь себя
Механические колебания и волны
- Напиши формулы
- Кликни и проверь себя
Молекулярно-кинетическая теория
- Напиши формулы
- Кликни и проверь себя
Термодинамика
- Напиши формулы
- Кликни и проверь себя
Электростатика
- Напиши формулы
- Кликни и проверь себя
Постоянный электрический ток
- Напиши формулы
- Кликни и проверь себя
Магнитное поле
- Напиши формулы
- Кликни и проверь себя
Электромагнитные колебания и волны
- Напиши формулы
- Кликни и проверь себя
Переменный ток
- Напиши формулы
- Кликни и проверь себя
Геометрическая оптика
- Напиши формулы
- Кликни и проверь себя
Волновая оптика
- Напиши формулы
- Кликни и проверь себя
Основы специальной теории относительности
- Напиши формулы
- Кликни и проверь себя
Корпускулярно-волновой дуализм
- Напиши формулы
- Кликни и проверь себя
Физика атома и атомного ядра
- Напиши формулы
- Кликни и проверь себя
- Назад
- Вперед
əyləncəli FİZİKA kurikulumu: Механика.
Формулы по физикеКинематика
| Обозначение | Измеряется в | Описание |
|---|---|---|
| S | м | пройденный путь |
| v | м/с | скорость |
| t | с | время |
| x | м | координата |
| a | м/с2 | ускорение |
| ω | с-1 | угловая скорость |
| T | с | период |
| ν | Гц | частота |
| ε | с-2 | угловое ускорение |
| R | м | радиус |
Скорость и ускорение:
Равномерное движение: ν = const
Равнопеременное движение:
Криволинейное движение:
Вращательное движение:
Динамика и статика
| Обозначение | Измеряется в | Описание |
|---|---|---|
| F | Н | сила |
| P | кг*м/с | импульс |
| a | м/с2 | ускорение |
| m | кг | масса |
| v | м/с | скорость |
| p | Н | вес тела |
| g | м/с2 | ускорение свободного падения |
| E | Дж | энергия |
| A | Дж | работа |
| N | Вт | мощность |
| t | с | время |
| I | кг*м2 | момент инерции |
| L | кг*м2/с | момент импульса |
| M | Н*м | момент силы |
| ω | с-1 | угловая скорость |
Первый закон Ньютона:
При ∑ F = 0 => v = const
Второй закон Ньютона:
Третий закон Ньютона:
Основной закон динамики для неинерциальных систем отчета.
ma=ma0+Fинерц ,где а- ускорение в неинерциальной а0– в инерциальной системе отчета.
Скорость центра масс:
Закон всемирного тяготения:
Вес тела:
Сила трения:
Закон Гука:
Закон Гука: σ = Eε, где Е- модуль Юнга.
Динамика и статика вращательного движения:
| система | ось | I |
| точка по окружности | ось симметрии | mR2 |
| стержень | через середину | 1/12 mR2 |
| стержень | через конец | 1/3 mR2 |
| шар | через центр шара | 2/5 mR2 |
| сфера | через центр сферы | 2/3 mR2 |
| кольцо или тонкостенный цилиндр | ось симметрии | mR2 |
| диск сплошной цилиндр | ось симметрии | 1/2 mR2 |
Условие равновесия тел ∑ M = 0
Закон сохранения импульса:
Потенциальная и кинетическая энергия.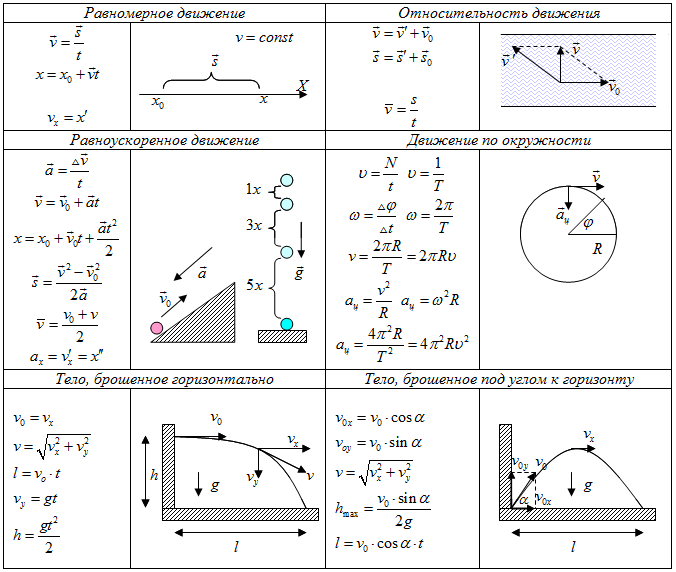
Мощность:
Закон сохранения энергии:
Использование Spring Equations — AP Physics C: Mechanics
Все ресурсы AP Physics C: Mechanics
2 диагностических теста 92 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая
AP Physics C: Mechanics Help » Экзамен по механике » Движение ” Гармоничное движение » Использование уравнений пружины
К пружине прикреплена масса с постоянной силой . Масса опирается на поверхность без трения и совершает горизонтальные колебания с амплитудой колебаний . Какова максимальная скорость этой массы с точки зрения , и ?
Возможные ответы:
Правильный ответ:
Пояснение:
Соответствующие уравнения:
Напишите выражения для начальной кинетической и потенциальной энергий, если перед освобождением пружина сначала растягивается до максимальной амплитуды.
Напишите выражения для конечной кинетической и потенциальной энергии, когда пружина пересекает точку равновесия.
Используйте закон сохранения энергии, чтобы приравнять начальную и конечную суммы энергии.
Решите уравнение для выделения.
Сообщить об ошибке
Шарик прикреплен к пружине на горизонтальной плоскости без трения. Если жесткость пружины равна , а масса шарика равна трем килограммам, с какой угловой частотой система будет колебаться?
Возможные ответы:
Правильный ответ:
Объяснение:
Единицами угловой частоты являются радианы в секунду.
Нам нужно вывести уравнение для угловой частоты, используя закон сохранения энергии.
Преобразуйте, чтобы найти скорость:
Скорость также является произведением угловой частоты и расстояния колебания:
Используйте это уравнение для получения уравнения для угловой частоты:
Наконец, используя данные массы и жесткости пружины, решите:
Сообщить об ошибке
Мяч массой 1 кг прикреплен к невесомой пружине на горизонтальной плоскости без трения.
Если в положении равновесия мяч движется со скоростью , сколько полной энергии находится в системе?
Возможные ответы:
Правильный ответ:
Пояснение:
В положении равновесия пружина не передает никакой потенциальной энергии. Он не растягивается и не сжимается.
Вся энергия в системе представляет собой кинетическую энергию, полученную из заданной скорости:
Сообщить об ошибке
Мяч массой 500 г прикреплен к невесомой пружине на горизонтальной плоскости без трения. Если в положении равновесия шарик движется со скоростью , а постоянная пружины равна , каково максимальное смещение шарика из положения равновесия?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы решить этот вопрос, нам понадобится закон сохранения энергии.
Без смещения мяч имеет скорость и нулевое смещение. При его максимальном смещении скорость будет равна нулю, и вся энергия будет преобразована в потенциальную энергию пружины.
Используйте наши значения для решения:
Сообщить об ошибке
Банджи-джампинг работает на мосту на высоте 200 м над землей. Они используют банджи-шнуры длиной 100 м в ненатянутом состоянии; эти эластичные шнуры имеют жесткость пружины . Какой может быть масса их крупнейшего клиента, прежде чем удар о землю станет проблемой?
Возможные ответы:
Правильный ответ:
Пояснение:
Когда масса находится в свободном падении, ее потенциальная энергия увеличивается. В этом случае всей этой энергии должен противодействовать эластичный шнур, который мы можем рассматривать как пружину , чтобы человек остановился.
Это означает, что мы можем положить эти два уравнения равными друг другу:
Затем мы можем изменить это уравнение, чтобы найти массу, при которой эластичный шнур может быть растянут до земли:
Подставляя известные значения, мы можем найти:
900 05
Сообщить об ошибке
85-килограммовый каскадер стоит на подпружиненной платформе во время съемок фильма. Жесткость пружины платформы равна . Насколько сильно должна сжаться платформа, чтобы каскадер взлетел на высоту 7,0 м?
Возможные ответы:
Правильный ответ:
Пояснение:
Вся энергия, накопленная сжатой пружиной, должна превратиться в гравитационную потенциальную энергию, чтобы каскадер смог остановиться на высоте 7,0 м в воздухе. Гравитационная потенциальная энергия моделируется уравнением , а энергия в пружинной системе моделируется уравнением .
Таким образом, мы можем приравнять эти уравнения друг к другу:
Затем мы преобразуем полученное уравнение для сжатого расстояния, которое :
Подставив данные значения, мы можем решить для :
Сообщить об ошибке
Пружина с пружиной константа прикреплена к масса 3,0 кг. Затем массу смещают на 5 см и отпускают. Сколько времени потребуется, чтобы масса переместилась в точку, которая находится на расстоянии 3,0 см от точки равновесия пружины во время ее первого колебания?
Возможные ответы:
Правильный ответ:
Объяснение:
Начнем с , где это точка, в которую перемещается масса, это максимальное перемещение, и это время, необходимое для преодоления расстояния.
Преобразование этого уравнения для дает
Здесь это потому, что точка, которую мы ищем, находится по другую сторону от точки равновесия.
Сообщить об ошибке
Груз массой 10 кг прикреплен к вертикальной пружине, свисающей с потолка. Постоянная пружины равна . Насколько сильно гравитация растянет пружину?
Возможные ответы:
Правильный ответ:
Объяснение:
Мы сравниваем силу из закона Гука с силой гравитации и находим перемещение:
Преобразовывая это уравнение, чтобы решить для , мы получаем
Подставляя данные значения, мы получаем
9000 5
Решая для , получаем
Сообщить об ошибке
К пружине, прикрепленной к стене, прикреплен груз массой 3 кг. Массу оттягивают на 10 см от точки равновесия пружины и отпускают. Если пружина имеет константу , какой максимальной скорости достигнет масса?
Возможные ответы:
Правильный ответ:
Объяснение:
Когда пружина максимально сжата, ее потенциальная энергия максимальна, а кинетическая энергия равна 0.
Когда масса находится в точке равновесия пружины, вся потенциальная энергия преобразуется в кинетическую энергию, поэтому кинетическая энергия равна максимальна (и равна максимальной потенциальной энергии), а потенциальная энергия равна 0. Мы приравниваем эти два уравнения друг к другу и находим скорость.
Сообщить об ошибке
Все углы в этой задаче выражены в радианах.
Объект колеблется горизонтально, и его отклонение от равновесия можно найти с помощью уравнения:
, где в секундах. Какова скорость объекта при ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти уравнение для скорости, мы берем первую производную функции положения. Не забывайте цепное правило для внутренней части косинуса!
Сообщить об ошибке
← Назад 1 2 Далее →
Уведомление об авторских правах
Все ресурсы AP Physics C: Mechanics Resources
2 диагностических теста 92 практических теста Вопрос дня Карточки Учитесь по концепции
ньютоновская механика – Что означает неопределенная формула в физике?
спросил
Изменено 7 лет, 6 месяцев назад
Просмотрено 4к раз
$\begingroup$
Я пытаюсь понять, как неопределенные формулы в математике связаны с физикой.
Возьмем следующую формулу для конечной скорости.
$$V_\text{terminal} = \sqrt{ mg \over{c \rho A}} $$
Предположим, что плотность воздуха равна 0; $ \rho = 0 $ (вакуум)
Логика подсказывает мне, что частица будет продолжать ускоряться и никогда не достигнет предельной скорости, но в математике эта формула не определена.
Очевидно, это один из многих примеров того, что может произойти в физических задачах, но что на самом деле означает undefined с точки зрения физики? Надеюсь, я ясно объясняю себя.
- ньютоновская механика
- ньютоновская гравитация
- снаряд
- сопротивление
- сингулярности
$\endgroup$
2
$\begingroup$
Да, частица будет продолжать ускоряться и никогда не достигнет конечной скорости. Но это не то, что говорит вам это уравнение.
Это уравнение говорит вам, какова конечная скорость при заданных параметрах функции. В вакууме конечной скорости нет. Это не ноль, это не бесконечность. Конечной скорости буквально не существует, и это именно то, что говорит вам уравнение.
$\endgroup$
8
$\begingroup$
Как и в математике, вы получаете физический смысл через предел: он не “не определен”, он “уходит в бесконечность”, когда $\rho$ стремится к 0 сверху. (это единственный способ в физическом мире, поэтому он там хорошо определен).
$\endgroup$
7
$\begingroup$
Проблема здесь в том, что существование конечной скорости зависит от предположения, что частица движется через жидкость. Поскольку реальные жидкости имеют только положительную ненулевую плотность, простая подстановка 0 нарушает это предположение.
Можно сказать, что классический предел конечной скорости при приближении жидкости к вакууму (т. е. при приближении плотности к 0) равен бесконечности, но этот предел не является действительным числом, поэтому частица в вакууме не имеет предельная скорость. (Как указано в комментариях, если принять во внимание относительность, этот предел становится равным c , скорость света в вакууме. Включение относительности в формулу сделало бы ее излишне сложной для практических целей.)
$\endgroup$
2
$\begingroup$
Очевидно, это один из многих примеров того, что может произойти в задачах по физике, но что на самом деле означает undefined с точки зрения физики? Надеюсь, я ясно объясняю себя.
Математические формулы, используемые для моделирования физических наблюдаемых величин, действительны в определенных системах, где они соответствуют наблюдениям и успешно предсказывают новые наблюдения.
Неопределенный или бесконечность означает, что математическая модель не работает и необходимо найти новую физическую модель/теорию. В вашем примере модель не работает для плотности 0, и либо для вакуума требуется новая формула, либо цель (конечная скорость) не имеет смысла в вакууме.
Изучение существования конечной скорости в вакууме приводит к специальной теории относительности. Частица в вакууме никогда не сможет достичь скорости света, и это совершенно новая модель поведения частиц, проверенная бесчисленное количество раз.
Элементарные частицы — это точечные частицы, бесконечность электрического потенциала 1/r при r=0 классически рассеивается развитием квантовой механики, совершенно новой основы, лежащей в основе всей природы.
Итак, неопределенная математика указывает на необходимость новых теорий/моделей.
$\endgroup$
1
$\begingroup$
Ваш вопрос действительно очень ясен, хороший пример, и затрагивает суть физики – способность определять, предсказывать мир с помощью математических моделей.
Но вы должны убедиться, что ваши модели верны и полны.
Фабрис и Роберт правы – скорость будет стремиться к бесконечности без ограничений. И есть ключ к тому, что происходит, как интерпретация физики — ограничений . Уравнение, которое вы цитируете, является стационарным решением – скорость небольшой массы, ускоряющейся по направлению к большему телу с ускорением свободного падения g, с площадью проекции, $A$, и в атмосфере с плотностью $\rho$.
Удалите атмосферу, и, как вы говорите, больше не будет силы сопротивления, поэтому начальная динамическая модель, из которой вы вывели эту формулу устойчивого состояния, равна 9.0007 разные . Но когда вы позволяете $\rho$ обнулиться, это (почти) дает вам правильный ответ. Я говорю почти потому, что уравнение, которое вы приводите, не является полным без дополнительного уравнения: того, которое ограничивает путь притягивающих тел к точке их столкновения — жесткий предел. Вещи не могут падать вечно — в конце концов они падают на землю.
Это реальная и полная физика вопроса.
Предупреждение: «Вещи не могут падать вечно». Это может быть не так для черной дыры. Время и пространство настолько искривлены, что, если верить часам вне черной дыры, объекту может потребоваться «вечность», чтобы достичь сингулярности. Но эта физика требует дополнительной математики для моделирования поведения.
$\endgroup$
$\begingroup$
По сути это означает “вопрос бессмысленный, так что не спрашивайте”.
Например, в данном конкретном случае мы пытаемся найти конечную скорость. Конечная скорость — это скорость, при которой ускорение силы тяжести и сопротивление ветра уравновешивают друг друга. Если нет атмосферы, обеспечивающей сопротивление ветру, то по определению такой скорости никогда не может быть, и поэтому невозможно определить, какой будет конечная скорость в такой ситуации.
$\endgroup$
2
$\begingroup$
Уравнение, которое вы дали, представляет собой приближение для ситуации, когда $\rho$ не равно нулю и гравитация постоянна , и представляет предел скорости, к которой может приблизиться объект (обратите внимание – это значение никогда не будет быть достигнутым, просто приблизиться).
Также можно рассчитать, сколько времени потребуется, чтобы добраться туда (опять же, исходя из предположения о постоянной плотности и силе тяжести). В уравнениях есть “характерное время” $\tau= \frac{v_t}{g}$ – иными словами, понятие “предельная скорость” даже не начинает иметь никакого смысла, пока не наступит время, равное нескольким $\тау$ прошло.
Несколько вещей, на которые следует обратить внимание:
гравитация непостоянна: и если вы вычислите скорость, достигаемую объектом при свободном падении из «бесконечности», и примите, что все трение из-за атмосферного сопротивления равно нулю, объект достигнет скорости всего около 11 км/с — это вся потенциальная энергия, перешедшая в кинетическую.
при наличии сопротивления объекту придется падать в течение времени, равного нескольким $\tau$, чтобы хотя бы приблизиться к конечной скорости (чтобы ускорение замедлилось).
при экстремальных скоростях релятивистские эффекты начнут играть роль
Ни одна из этих вещей не рассматривается в вашей простой трактовке уравнения конечной скорости.