Путь и перемещение – чем отличается, формулы
4.2
Средняя оценка: 4.2
Всего получено оценок: 122.
4.2
Средняя оценка: 4.2
Всего получено оценок: 122.
Важнейшими понятиями кинематики являются понятия пути и перемещения. Рассмотрим их подробнее, а также узнаем, чем отличается путь от перемещения.
Траектория пути
Кинематика изучает движение тел безотносительно причин этого движения. Главной задачей кинематики является математическое описание положения тела в принятой системе отсчета и изменение этого положения со временем.
Положение тела в системе отсчета задается одной или несколькими координатами (в зависимости от числа измерений) и временем.
Рис. 1. Координаты тела в пространстве.Если тело движется, то в разные моменты времени координаты тела будут различны. Умножая скорость тела на время движения, можно найти длину пройденного пути:
$$s=vt$$
Однако, даже зная точку, где находилось тело в нулевой момент времени, мы далеко не всегда можем определить, в какой точке тело будет находиться в другой произвольный момент времени.
Дело в том, что с помощью приведенной формулы можно найти длину пройденного пути. А сам путь при этом может иметь любую, сколь угодно сложную форму. Линия, вдоль которой перемещается тело, вовсе необязательно будет прямой, она может быть и окружностью, и ломанной, и более сложной фигурой, состоящих из многих частей.
Линия, вдоль которой двигалось тело на рассматриваемом участке времени, называется траекторией пути или просто траекторией.
Перемещение
Чтобы всегда знать, в какой точке находится тело в заданный момент времени, необходимо знать не длину пройденного пути, а другую кинематическую характеристику – перемещение.
Перемещение – это вектор, соединяющий начальное положение тела с его конечным положением.
Зная начальную точку в нулевой момент времени и перемещение за некоторое время, можно всегда найти координату тела в конце пути.
Рис. 2. Путь и перемещение.Сходство и различие.
Путь и перемещение – это не одно и то же. Если движение происходит на плоскости или в пространстве и криволинейно, то длина траектории всегда будет больше модуля перемещения.
Происходит этот потому, что вектор является прямой, то есть, кратчайшим расстоянием между двумя точками. Криволинейная траектория же прямой не является.
Более того, перемещение может быть равно нулю, несмотря на то, что путь будет иметь большую длину. Например, планеты, двигаясь по окружностям, проходят за каждый оборот большой путь, однако, перемещение при этом никогда не превышает диаметра орбиты, и может быть равно нулю, если планета делает полный оборот.
Рис. 3. Орбиты планет.Однако, и перемещение и траектория пути служат одной и той же цели – описанию движения. Обе этих величины измеряются в единицах длины, к обоим могут быть применены формулы движения.
Но, если траектория описывает весь путь, пройденный телом, то перемещение акцентирует внимание на разнице положения тела между первым и последним моментами движения. Поэтому большинство формул в кинематике, в которые входит время, работают именно с перемещением.
Единственный случай, когда путь и перемещение равны – это случай прямолинейного движения, при условии, что скорость движения не меняла знак.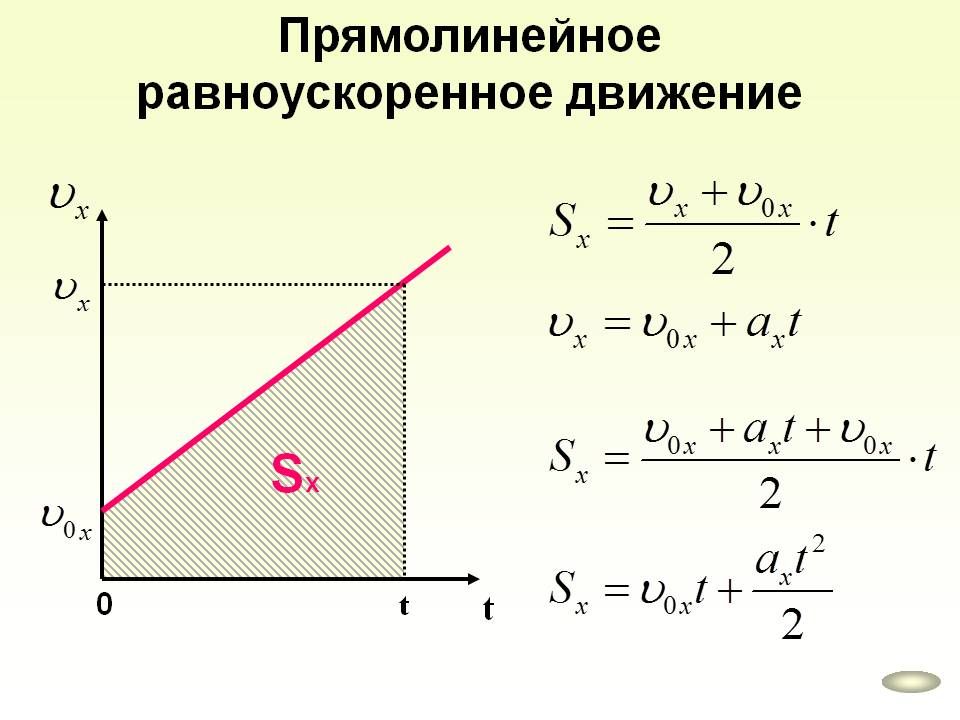
Что мы узнали?
Траектория пути – это линия, вдоль которой перемещалось тело во время своего движения. Перемещение – это вектор, направленный из точки начала движения в точку конца движения. Длина пути всегда равна или больше, чем длина перемещения.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.2
Средняя оценка: 4.2
Всего получено оценок: 122.
А какая ваша оценка?
виды и формулы, примеры механического перемещения тел, решение задачи
Физика
12.11.21
13 мин.
Движение различных объектов окружает человека с самого рождения. Перемещение автомобиля по асфальтированной дороге, полет самолета, бег атлета на спортивных соревнованиях, вращение планеты Земля вокруг своей звезды — это лишь малая доля примеров изменения пространственного положения объектов.
Для решения задач по физике нужно знать, что такое равномерное движение.
Оглавление:
- Пространственная система координат
- Понятие механического движения
- Физические величины
- Виды перемещения в пространстве
- Равномерное изменение положения
- Пример решения задачи
Пространственная система координат
Состояние Вселенной в общем случае можно представить в виде функции, зависящей от четырех координат. Три координаты описывают положение тела в пространстве, четвертая — это время, которое характеризует последовательность событий. Пространственные координаты в большинстве задач по физике и геометрии удобно представлять в виде прямоугольной декартовой системы. Эта система является совокупностью трех пересекающихся под углом 90 градусов осей, на каждой из которых выбран единичный вектор.
Положение любой точки в декартовой системе координат можно математически представить в виде суммы целых длин единичных векторов для каждой из трех осей.
Благодаря этой системе можно легко описывать изменение положения тел в пространстве.
Благодаря этой системе можно легко описывать изменение положения тел в пространстве.Понятие механического движения
Любое изменение пространственных координат тела во времени принято называть механическим движением. Школьников слово «механический» может вводить в заблуждение, поскольку оно связано с каким-либо механизмом. Для некоторых из них перемещение автомобиля или мотоциклиста — это движение механическое, а бег животного или полет птицы уже не вписывается в эту категорию.
При рассмотрении типа изменения пространственных координат физика сосредотачивает свое внимание на законах этого изменения, а также на силах, которые его вызвали. При этом она не исследует природу объекта, поэтому любое движение считается механическим.
Физические величины
Путь, время, скорость и ускорение — это 4 главные величины, которые характеризуют пространственное изменение координат объектов.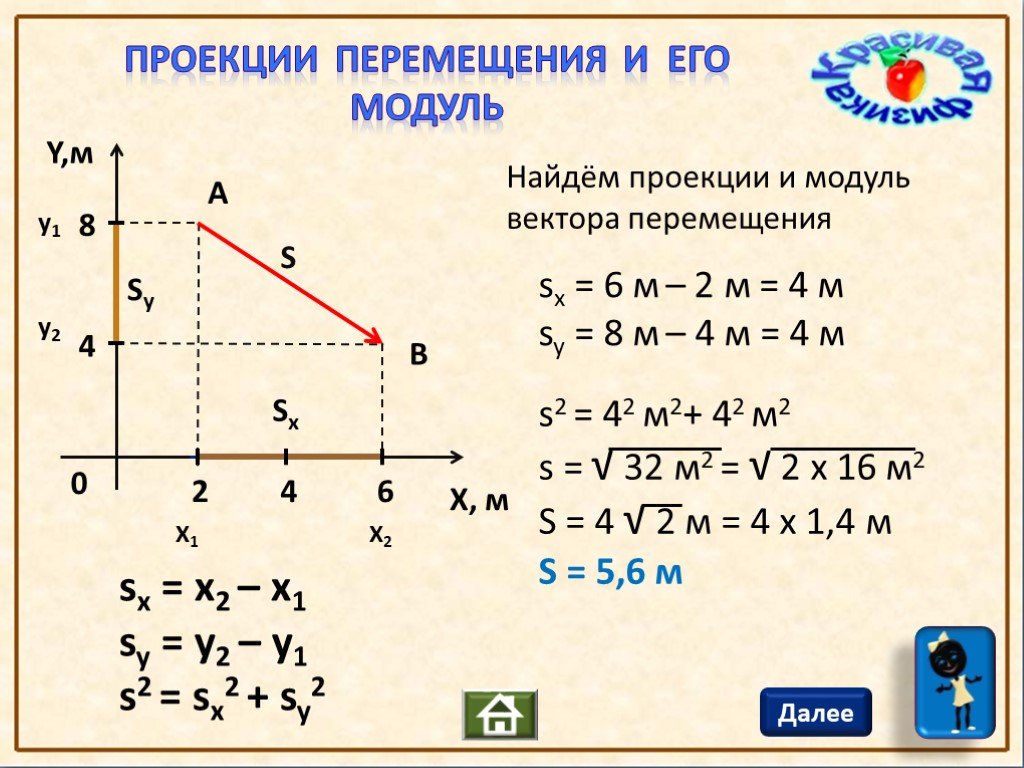
- векторная;
- скалярная.
Путь и время — это скаляры, для их определения достаточно знать начальное и конечное состояние тела. Например, объект, перед тем как начать движение, имел координату x0, в момент завершения своего перемещения его координата стала равной x1. Численное значение пройденного пути S в этом случае определяется просто:
S = x1 — x0.
Скорость и ускорение — характеристики векторные. Это означает, что для их полного определения недостаточно знать только начальное и конечное положение тела. Обе величины определяют характер самого движения.
По определению, скорость v — это быстрота изменения координат объекта в пространстве, ускорение a — это быстрота изменения самой скорости. Величина v для всякого типа перемещения тел направлена всегда вдоль траектории (воображаемая линия, вдоль которой объект движется). Ускорение a совершенно не связано ни с величиной v, ни с траекторией.
Направление вектора a однозначно определяется результирующей суммой сил, действующих на изучаемое тело в движении.
Виды перемещения в пространстве
Примеры механического движения можно встретить в живом и неживом мире, в технике, в микромасштабе и в масштабах галактики. Несмотря на огромное разнообразие, физика выделяет всего 2 группы видов перемещения тел:
- равномерное;
- неравномерное.
В первую группу входят все явления, перемещение тел для которых происходит без изменения абсолютного значения скорости на протяжении всего пути. Соответственно, вторая группа описывает виды движения, в процессе которых скорость, так или иначе изменяется по модулю.
Во время равномерного перемещения объектов в пространстве ускорение не всегда равно нулю. В процессе неравномерного движения величина a всегда отлична от нуля. Примером, относящимся к первой группе, является перемещение автомобиля с заданной скоростью по дороге.
Равномерное изменение положения
Этот тип перемещения в пространстве рассматривают в начальных классах школ, поскольку он наиболее простой в изучении и понимании смысла физических формул. Тем не менее часто школьники отождествляют равномерное и прямолинейное перемещение, что неправильно.
По прямой линии
Самолет, летящий в облаках с постоянной скоростью по воображаемой прямой линии, в первом приближении можно полагать хорошим примером равномерного прямолинейного движения. Для физического описания подобных перемещений используют 2 скалярные величины — пройденный путь S и время t, и одну векторную характеристику — скорость v. Формула равномерного движения по прямой имеет следующий вид:
S = v*t.
Левая и правая часть выражения имеет размерность длины, которая в международной системе СИ выражается в метрах (м).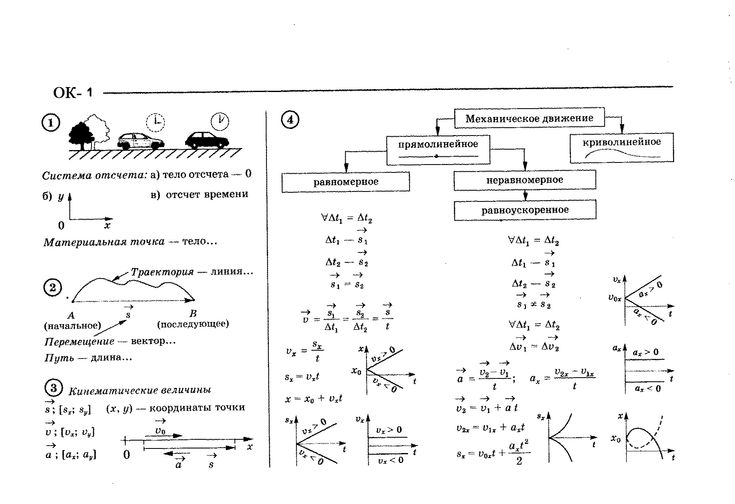
Часто S также выражают в миллиметрах, сантиметрах или километрах. Поскольку t имеется размерность времени (секунды, минуты, часы), величина v выражается в единицах длины по отношению к единицам времени, то есть в метрах в секунду (м/с), километрах в час (км/ч) и т. д.
Формулу пути S можно легко переписать, чтобы определить скорость равномерного движения v или время t:
v = S/t; t = S/v.
Кривая траектория
Планета Земля вращается вокруг Солнца в космическом пространстве. Является ли ее движение равномерным? Да. Является ли оно прямолинейным? Нет. Если бы наблюдатель мог со стороны посмотреть на движение Земли, то увидел бы, что она перемещается по окружности с огромной скоростью (приблизительно 30 км/с). В каждый момент времени вектор скорости планеты изменяется за счет действия гравитационного притяжения Солнца, однако абсолютная величина скорости не испытывает каких-либо изменений. По этой причине продолжительность года на Земле является постоянной величиной.
Движение тел по кривым траекториям, в процессе которого ускорение изменяет только направление скорости, а не ее величину, в физике принято называть равномерным криволинейным перемещением. Чаще всего рассматривают круговое движение, для которого вводят важную характеристику — центростремительное ускорение ac. Эта величина всегда направлена к центру окружности, а ее модуль вычисляется по следующей формуле:
ac = v 2 /r.
Здесь r — радиус круговой траектории, v 2 — квадрат скорости.
Угловые характеристики и период
Равномерное движение по окружности удобно описывать не линейными, а угловыми физическими величинами, то есть угловой скоростью w и углом перемещения Q. Величина w измеряется в радианах в секунду (рад/с), Q — в радианах. Поскольку полная окружность представляет собой 2*pi радиан (pi = 3,14 — число пи), угловые характеристики через их линейные аналоги можно рассчитать по следующим формулам:
w = v/r; Q = S/r.
Еще одна важная величина, которую необходимо знать для полного описания равномерного движения по окружности — период T. Он представляет собой время, которое затрачивает тело для совершения полного оборота по замкнутой траектории. Вычисляется период следующим образом:
T = 2*pi/w.
Период обращения Земли вокруг своей звезды равен продолжительности года, то есть 365 дней и 6 часов. Для удобства времяисчисления каждый четвертый год на планете на 1 день длиннее предыдущих трех.
Пример решения задачи
Мотоциклисту необходимо попасть из пункта A в пункт C, совершая при этом остановку в пункте B на 1 час. Известно, что между пунктами A и B мотоциклист двигался с некоторой постоянной средней скоростью v1. Между пунктами B и C его движение также было равномерным, но уже со скоростью v2, которая на 20% была больше, чем v1. Какое расстояние преодолел мотоциклист, если известно, что затраченное на переезд время составило 5 часов, скорость v1 была равна 50 км/ч, и расстояние между B и С он преодолел в 1,5 раза быстрее, чем путь между A и B.
Пусть на переезды между пунктами A-B и B-C мотоциклист затратил время t1 и t2, соответственно. Справедливо следующее выражение:
t1 + 1 + t2 = 5.
Здесь 1 час в левой части равенства отражает время отдыха в пункте B. Чтобы найти t1 и t2, следует обратиться к условию задачи. Известно, что величина t2 в 1,5 раза меньше, чем t1:
t1 = 1,5*t2.
Из двух записанных выражений следует, что t1 = 2,4 часа, t2 = 1,6 часа.
Прохождение пути определяется как сумма дистанций между AB и BC. Длина траектории S, то есть расстояние между A и C, рассчитывается по формуле для равномерного движения:
S = v1*t1 + v2*t2.
Согласно условию v1 = 50 км/ч, и v2 = 1,2*v1, значит, v2 = 60 км/ч. Все определенные величины, подставленные в формулу для S, приводят к следующему результату:
S = 50*2,4 + 60*1,6 = 216 км.
Траектория движения мотоциклиста между пунктами A и C необязательно должна быть прямолинейной. Для нахождения пройденного расстояния S важно, чтобы на каждом отрезке пути он двигался с некоторой постоянной по модулю скоростью.
Использование уравнений движения — физика для старших классов
Все ресурсы по физике для старших классов
6 диагностических тестов 233 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Справка по физике для старших классов » Движение и механика » Линейное движение » Использование уравнений движения
Растение в горшке падает с подоконника с высоты 3 метра над землей. Через какое время растение упадет на землю?
Возможные ответы:
Правильный ответ:
Объяснение:
Используя приведенное выше уравнение и данные значения, мы можем найти время.
Сначала нам нужно найти изменение расстояния.
Установка перемещается на несколько метров вниз. Теперь мы можем подставить заданные значения из вопроса, чтобы решить на время.
Сообщить об ошибке
Вальтер бросает диск с высоты 1,5 метра над землей чисто горизонтальным движением. Сколько времени пройдет, прежде чем диск упадет на землю?
Возможные ответы:
Правильный ответ:
Объяснение:
Горизонтальное движение не повлияет на время нахождения диска в воздухе. Время будет определяться скоростью падения диска: ускорением свободного падения.
Мы можем найти время, используя приведенное ниже уравнение и значения, указанные в вопросе.
Сообщить о ошибке
Лесли бросает мяч из окна на 10 метров над землей, так что первоначальная у непрочнения-Zero.
Какова будет конечная скорость мяча непосредственно перед тем, как он упадет на землю?
Возможные ответы:
Правильный ответ:
Пояснение:
Нам известны начальная скорость, ускорение, а также начальное и конечное расстояния.
Используя приведенное ниже уравнение и данные значения, мы можем найти конечную скорость.
Сообщить об ошибке
Ящик скользит по полу, пока не остановится из исходного положения.
Какова начальная скорость ящика?
Возможные ответы:
Правильный ответ:
Пояснение:
Задача дает нам расстояние, конечную скорость и изменение во времени.
Мы можем использовать эти значения в приведенном ниже уравнении для определения начальной скорости.
Подставьте полученные значения и решите.
Разделите обе части на .
Умножить обе части на .
Сообщить об ошибке
Ящик скользит по полу, прежде чем остановиться из исходного положения.
Каково чистое ускорение ящика?
Возможные ответы:
Правильный ответ:
Объяснение:
Все уравнения, касающиеся ускорения, требуют начальной скорости. Нам нужно будет найти начальную скорость, используя заданные переменные. Задача дает нам расстояние, конечную скорость и изменение во времени. Мы можем использовать эти значения в приведенном ниже уравнении для определения начальной скорости.
Подставьте полученные значения и решите.
Мы можем использовать уравнение линейного движения, чтобы найти ускорение, используя только что найденную скорость. Теперь у нас есть расстояние, время и начальная скорость.
Подставьте данные значения, чтобы найти ускорение.
Сообщить об ошибке
Мяч начинает катиться в . Он ускоряется с постоянной скоростью за . Какова конечная скорость?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы найти конечную скорость, помните, что соотношение между скоростью, ускорением и временем равно .
Используя заданные значения начальной скорости, ускорения и времени, мы можем найти конечную скорость.
Сообщить об ошибке
Книга, начиная с покоя, падает со стола.
Какова его скорость после движения?
Возможные ответы:
Правильный ответ:
Объяснение:
Мы можем решить этот вопрос, используя уравнение для ускорения через скорость:
Мы знаем нашу начальную скорость (нулевую, так как мы начинаем с состояния покоя), время и ускорение свободного падения. Используйте эти значения, чтобы изолировать переменную для конечной скорости.
Обратите внимание, что конечная скорость отрицательна, так как книга движется вниз.
Сообщить об ошибке
Автомобиль, движущийся по шоссе, движется с начальной скоростью до того, как начинает ускоряться. Если он ускоряется за , какова конечная скорость автомобиля?
Возможные ответы:
Правильный ответ:
Объяснение:
Используйте кинематическое уравнение:
Нам известны начальная скорость, прошедшее время и ускорение.
Используя эти значения, мы можем определить конечную скорость.
Сообщить об ошибке
Частица движется на север от начального положения. После перемещения из начального положения частица начинает ускоряться на север в течение . Каково конечное расстояние между частицей и начальным положением?
Возможные ответы:
Правильный ответ:
Объяснение:
Используйте кинематическое уравнение:
Движение частицы можно разбить на две части: начальное расстояние и расстояние, пройденное при ускорении. Начальное расстояние задано.
Расстояние при ускорении можно найти с помощью кинематической формулы и заданных значений начальной скорости, ускорения и времени.
Сложите два расстояния вместе.
Конвертируйте окончательный ответ в километры.
Сообщить об ошибке
Кикер, играющий в американский футбол, забивает мяч с игры из-за стойки ворот. Мяч находился в воздухе и приземлился за стойкой ворот.
Учитывая эту информацию, какова была общая начальная скорость и угол, под которым был нанесен удар по мячу?
Возможные ответы:
Правильный ответ:
Объяснение:
Хотя этот вопрос состоит из нескольких шагов, если разобрать его, мы увидим, что это проблема, связанная с кинематикой в двух измерениях.
Сначала запишите то, что мы знаем:
Расстояние до стойки ворот:
Расстояние до стойки ворот:
Что мы хотим знать:
Для начала,
вычислить каждую из компонент вектора скорости. Мы можем начать с горизонтальной составляющей. Мы знаем, что скорость равна расстоянию, деленному на время, и что горизонтальная скорость не изменится, потому что в горизонтальном направлении нет ускорения.
Нам нужно найти общее расстояние, которое проходит мяч, чтобы решить.
Нам нужно найти общее расстояние , которое проходит мяч, чтобы решить.
Используйте это расстояние и заданное время, чтобы найти горизонтальную скорость.
Теперь найдем начальную вертикальную скорость,. Поскольку мы предполагаем, что на мяч не влияет ничего, кроме гравитации, мы можем сказать, что мяч тратит половину времени на достижение пика своей траектории, где вертикальная скорость на мгновение становится равной нулю. Имея эту информацию, мы можем найти начальную вертикальную скорость:
Мы используем только половину заданного времени, потому что мы берем только время от момента удара по мячу до момента, когда он достигает вершины своей траектории (что составляет половину его полета). Как мы сказали выше, скорость будет равна нулю в верхней части траектории. Мы используем отрицательное значение ускорения свободного падения, потому что гравитация направлена вниз, что в данном случае является отрицательным направлением.
Используйте данные значения для определения начальной вертикальной скорости.
Теперь, когда у нас есть обе составляющие направления начальной скорости, мы можем использовать теорему Пифагора для определения общей начальной скорости.
Теперь, чтобы найти угол, воспользуемся тригонометрией. В треугольнике, образованном максимальной высотой мяча, землей и траекторией, тангенс угла будет равен вертикальному катету треугольника, деленному на горизонтальный катет треугольника.
Отчет о ошибке
← Предыдущий 1 2 Далее →
Уведомление об авторских правах
233 практических теста Вопрос дня Карточки Learn by Concept
ЗАМЕТКИ ПО ФИЗИКЕ ОНЛАЙН: УРАВНЕНИЯ ДВИЖЕНИЯ
УРАВНЕНИЯ ДВИЖЕНИЯ
Уравнения движения – это формулы, которые используются при решении задач, связанных с движением.
Есть для уравнений движения. Четыре уравнения движения:
- V = u + at
- В² = U² + 2 как
- S или h = ut + ½at²
- S = ((v+u)t)/2
Определение переменных:
U — начальная скорость объекта. Измеряется в метрах в секунду (м/с).
В — конечная скорость объекта. Измеряется в метрах в секунду (м/с).
А — ускорение объекта. Измеряется в метрах на секунду в квадрате (м/с кв.)
S — расстояние, пройденное объектом. Измеряется в метрах, (м)
T – время, за которое объект проходит заданное расстояние. Измеряется в секундах (с).
ВЫВОД УРАВНЕНИЙ ДВИЖЕНИЯ
Давайте посмотрим, как выводятся четыре уравнения.
ВЫВОД УРАВНЕНИЯ 1
Уравнение 1 получено из формулы ускорения. Вывод следующий:
Из формулы ускорения
Ускорение = изменение скорости/времени
Ускорение a = (конечная скорость v – начальная скорость u) / время t
Используя их символы, формула примет вид:
A = (v-u) / t
Умножьте крест и сделайте v предметом формулы.
A*t = v-u
V = u + at что является уравнением 1.
ВЫВОД УРАВНЕНИЯ 2
Чтобы получить уравнение 2, мы воспользуемся формулой для средней скорости и подставим v = u + at в формулу средняя скорость следующим образом:
Средняя скорость Vaverage = (v+u)/2
В этот момент вы заменяете v.
Следовательно,
Vaverage = (v+u)/2
Vaverage = (u+at+u)/2
Vaverage = (2u+at)/2 ….. уравнение 1
На этом этапе вы вводите скобку:
Vaverage = u+½at
Кроме того, формула для средней скорости:
Vaverage = расстояние с / время t два уравнения следующим образом:
уравнение 1 = уравнение 2
Среднее значение уравнения 1 = Среднее значение уравнения 2
u+½at = s/t
Вы делаете s подлежащим путем перекрестного умножения t.
(u+½at)t = s
ut+½at*t = s
ut+½at² = s
s = ut+½at² … уравнение 2
ВЫВОД УРАВНЕНИЯ 3 1.
Следовательно,
v² = (u+at)²
v² = (u+at)*(u+at)
v² = u²+2uat+a²t²
v² = u²+2uat+(at)²
При этом точка, вы факторизуете 2a из 2uat+(at)².
Следовательно, вы получите
v² = u²+2a(ut+½(at)² …….*
В этот момент вы должны вспомнить, что
s = ut+½at²
вам нужно будет заменить s на ut+½at² в уравнении *
, следовательно,
v² = u²+2a(ut+½(at)² …… .*
v² = u²+2as, что дает уравнение 3.
ВЫВОД УРАВНЕНИЯ 4
Уравнение 4 получается приравниванием двух формул средней скорости
Две формулы для средней скорости:
Vaverage = s/t
Vaverage = (v+u)/2
Следовательно,
Vсреднее = Vсреднее
s/t = (v+u)/2
вы делаете s предметом формулы:
s = (v+u)t / 2 , что дает уравнение 4.
ПРИМЕНЕНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ
Применение уравнений движения означает использование уравнений движения для решения задач, связанных с движением . Это я покажу и объясню, используя примеры работы, как показано ниже.
Примеры работы:
Объект, брошенный вертикально вверх с начальной скоростью 30 м/с, имеет замедление 10 м/с sqr. Вычислите его скорость через 2 с и время достижения максимальной высоты.
(g = 10 м/с кв.)
Решение:
Данные, указанные в вопросе:
Начальная скорость u = 30 м/с; время t = 2 с; скорость в момент времени 2s = ?; замедление = 10 м/с sqr (замедление = отрицательное ускорение).
Формула для расчета:
Вы должны знать, что формула, которую вы используете для расчета, определяется данными, которые вы дали в вопросе. Другими словами, формула, содержащая данные, указанные в вопросе, является правильной формулой для расчета.
Скорость через 2 с.
Формула:
В = и + ат.
Замена:
В = 30+(-10)*2
В = 30 – 20
В = 10 м/с
Время, необходимое для достижения максимальной высоты.
Чтобы вычислить время, необходимое для достижения максимальной высоты, вы должны помнить, что на максимальной высоте конечная скорость v = 0 м/с.
Формула:
V = u + at.
Замена:
0 = 30 + (-10)*t
0 = 30 – 10t
Соберите одинаковые термины и сделайте t предметом формулы.
10t = 30
T = 30/10
Время достижения максимальной высоты = 3 с
Автомобиль равномерно ускоряется со скоростью 1 м/с в течение 12 с со скоростью 5 м/с.
Рассчитайте пройденное расстояние. (g = 10 м/с кв.)
Решение:
Пройденное расстояние:
Данные, данные в вопросе:
A = 1 м/с кв.; и = 5 м/с; т = 12 с; g = 10 м/с кв. ; с = ?
Примечание:
Вы используете формулу, содержащую данные, указанные в вопросе, и те, которые вам предстоит вычислить.
Формула:
s = ut+½at²
замена:
s = 5*12+½*1*(12)²
с = 60+1*144
с = 60+145.; s = 204 м
Камень брошен вертикально вверх с земли со скоростью 20 м/с.
(g = 10 м/с кв.). рассчитать:
Максимально достигнутая высота.
Время достижения максимальной высоты;
Время снова достичь земли;
Скорость достигла половины пути.
Решения:
Напомним, что на максимальной высоте v = 0 м/с
Данные, приведенные в вопросе:
U = 20 м/с; v = 0 м/с; g = 10 м/с кв.
Максимально достигнутая высота:
Формула:
v² = u²+2as
замена:
0² = 20²+2*(-10)*s
0 = 400+(-20s)
0 = 400 – 20s
Соберите одинаковые термины и сделайте s предметом формула.
20с = 400
С = 400/20;
Максимальная достигнутая высота = 20м.
ii. время достижения максимальной высоты:
формула:
с = ut+½at²
подстановка:
20 = 20*t+½*(-10)*t²
20 = 20t – 5t²
Вы переставляете квадратное уравнение и находите t по любой удобной для вас формуле.
Таким образом,
0 = 20t – 5t² – 20
0 = -5t² + 20t – 20
Теперь вы можете разложить на множители или использовать общую формулу, чтобы найти t.
Используя общую формулу:
T = (- b ± √(b² – 4ac)) / 2a
Где,
A = – 5; б = 20; c -20
Замена:
T = (- 20 ± √(20² – 4*(-5)*(-20)) / 2*(- 5)
T = (-20 ± √(20² – 4*( -5)*(-20)) / -10
T = (-20 ± √(400 – 400)) / -10
T = (- 20 ± √0) / -10
T = -20/(- 10)
Время достижения максимальной высоты = 2 с
iii время повторного достижения земли:
: Время достижения земли равно времени, необходимому для достижения максимальной высоты.
Следовательно,
Время достижения земли = 2 * время, необходимое для достижения максимальной высоты.