Формулы по молекулярной физике: Молекулярная физика в формулах - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Молекулярная физика в 📙 формулах

1. Базовые формулы молекулярной физики
2. Формулы, описывающие процессы в молекулярной физике

Задачей молекулярной физики является исследование физических свойств тел, основанное на длительном наблюдении состояний их кристаллических решеток. Данный раздел физики ориентируется на методологию статической механики, кинетики и термодинамики.

Областью изучения молекулярной физики являются поведение и взаимодействие мельчайших частиц физического тела – атомов, молекул, ионов.

То есть данный раздел физики исследует свойства тел, исходя из характеристик отдельных молекул. Считается, что все взаимные действия и движения происходят на микроуровне, и при этом все изменения, которые можно наблюдать невооруженным взглядом, являются последствием данных микропроцессов.

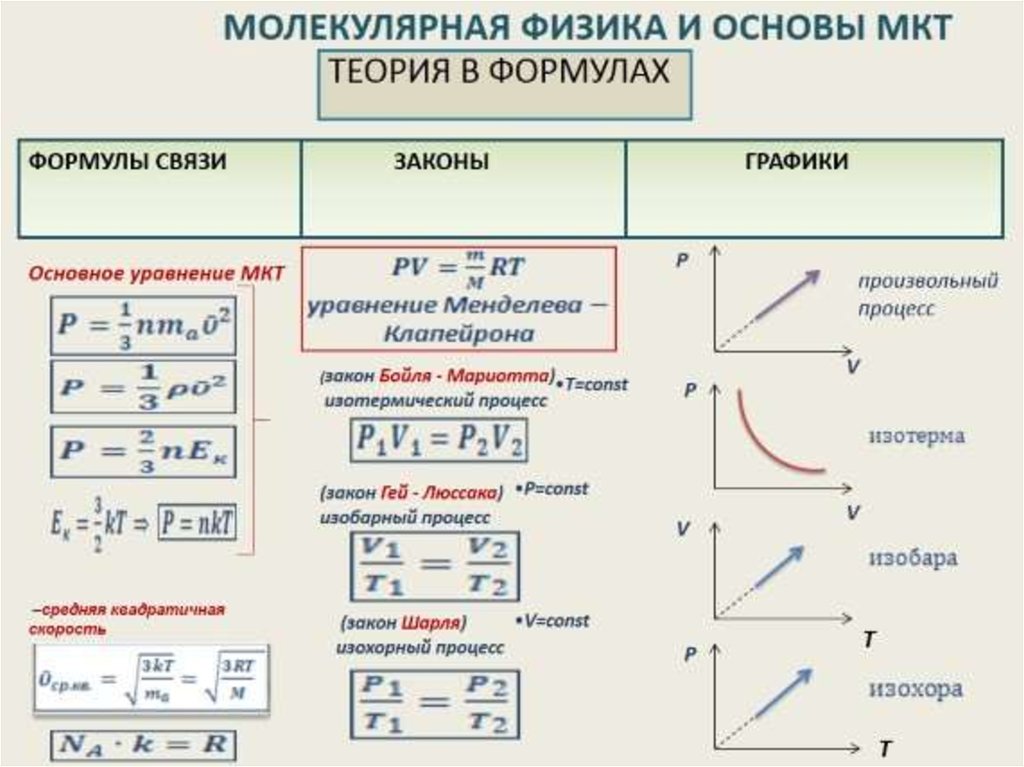
Основными формулами молекулярной физики устанавливаются взаимосвязи разных характеристик системы, при этом пользуются уравнением Клапейрона, законами Бойля-Мариотта, Шарля и Гей-Люссака.

Уравнение Клапейрона имеет следующий вид:

\(pV=nRT\),

где \(p\) – давление;
\(V\) – объем, который занимает газ;
\(n\) – количество вещества, моль;
\(R\) – универсальная газовая постоянная;
\(T\) – температура.

Путем простых преобразований из данной формулы выводятся следующие законы:

Бойля-Мариотта для изотермического процесса:

\(pV=const.\)

Гей-Люссака для изобарического процесса:

\({V\over T}=const.\)

Шарля для изохорического процесса:

\({p\over T}=const.\)

Все физические величины и явления имеют свои особенные обозначения и их описывают свои формулы, отображающие взаимосвязь различных параметров. Различные явления пересекаются в своем проявлении, поэтому в разных формулах встречаются одни и те же величины, выраженные различными способами.

Например, количество вещества зависит от его массы и числа молекул в этой массе. Причиной этого является различие в количестве молекул в одной и той же массе для разных веществ. В процессах, что происходят на микроуровне, принимают участие атомы, они являются непосредственными участниками различных взаимных действий.

Количество вещества определяется по следующей формуле:

\(m={N\over N_A}\) ,

где \(m\) – масса;
\( N\) – число молекул;
\(N_A\) – число Авогадро.

Молекулы являются сложными системами и обладают многоступенчатой структурой. Для упрощенного понимания представим газ, находящийся в закрытом сосуде, частичками которого есть упругие однородные шарики, которые не взаимодействуют между собой. Такой газ принято считать идеальным, формула для его расчета имеет следующий вид:

\(P=nkT\),

где \(n\) – концентрация молекул;
\(T\) – абсолютная температура.

Количество частичек (молекул) \(N\) в этой массе можно рассчитать таким образом:

\(N=mN_A\).

Один моль всегда содержит одинаковое число минимальных частиц, которое равно числу Авогадро. То есть, если мы знаем массу моля, то поделив ее на число Авогадро, мы получим массу системной единицы:

\(m={M\over N_A}\) ,

где \(M\) – молярная масса.

Необходимо помнить, что данная формула используется лишь для молекул неорганической химии. Если рассматривать молекулы органических веществ, то они намного больше в размерах и весе.

Молярная масса показывает массу одного моля вещества. Так как один моль вещества вмещает одинаковое число частичек вещества, формула для расчета молярной массы будет иметь вид:

\(M=kM_r\),

где \(k\) – коэффициент пропорциональности;
\(M_r\) – атомная масса вещества.

Молярную массу вещества можно выразить из закона Менделеева-Клапейрона, который имеет следующий вид:

\(pV={mRT\over M}\),

отсюда молярная масса запишется как:

\(M={mRT\over pV}\).

Формулы статической физики и термодинамики

Для статической физики, как раздела молекулярной физики, справедливы такие формулы:

\(Q=mc(t_2-t_1) \\ Q=A+(U_2-U_1)\\ H=TdS+Vdp. \\\)

\(H\) – это энтальпия.

\(V={dG\over dpS}\),

где \(G\) – энергия Гиббса или термодинамический потенциал;

\(S\) – энтропия, которую ввел ученый Клаузиус.

С помощью формул термодинамики и молекулярной физики становится возможным рассчитывать все процессы, происходящие в твердых веществах и газах. Данные расчеты являются немаловажными при исследованиях и на практике, так как позволяют решать различные задачи.

«Сборник основных формул по молекулярной физике и термодинамике» Мартинсон Л. К. – описание книги | Крат.спр.студ.

«Сборник основных формул по молекулярной физике и термодинамике» Мартинсон Л. К. – описание книги | Крат.спр.студ. | Издательство АСТ

Сборник основных формул по молекулярной физике и термодинамике

Мартинсон Л. К.

Прослушать отрывок

Перейти
в читальню

Серия: Крат. спр.студ.

Foreign rights >>

Аннотация

В справочнике приведены все основные формулы вузовского курса молекулярной физики и термодинамики.
Пособие предназначено для студентов и преподавателей технических вузов.

Случайная новинка

Отзывы читателей

Характеристики

Автор:

Мартинсон Л. К.

Редакция:

Образовательные проекты

Серия:

Крат.спр.студ.

ISBN:

978-5-17-042380-4

Ниша:

ЕСТЕСТВЕННЫЕ НАУКИ

Вес (кг):

0.054

Переплет:

Мягкий

Страниц:

160

Ширина (мм):

103

Высота (мм):

132

Дата последнего тиража:

29.06.2007 г.

ББК:

22.3я73

УДК:

53(075.8)(035)

Знак информационной продукции:

Смотрите также

Вы просматривали

Мы в социальных сетях

Мы в соцсетях

Пожалуйста, выберите рубрику

На новинки книги

Введите вашу почту*

@izdatelstvoast

Новости, новинки,
подборки и рекомендации

Введите вашу почту* Введите текст жалобы*

Спасибо за обращение!

Ваша жалоба будет рассмотрена в самое ближайшее время.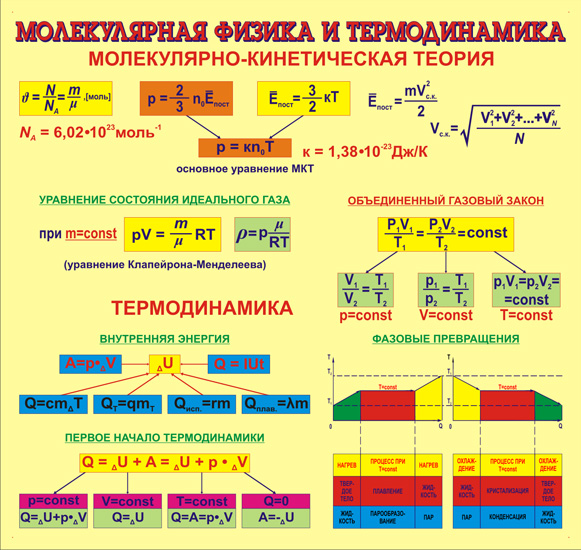

Введите вашу почту* Как к Вам обращаться* Введите пароль*

Спасибо за регистрацию!

На указанный E-mail придёт запрос на подтверждение регистрации.

моделей молекул показывают неожиданную физику | Рис Новости | Новости и связи со СМИ

ХЬЮСТОН — (15 марта 2022 г.) — Небольшие сферы, подвешенные в жидкости, движутся достаточно подобно молекулам, поэтому физику одного можно использовать для имитации физики другого.

Вот почему открытие некоторых необычных физических свойств коллоидов — частиц, диспергированных в растворе, например, в молоке, — может заинтересовать исследователей, изучающих биологические взаимодействия.

Диполярные коллоидные частицы выводятся из равновесия вращающимся магнитным полем. Эксперимент Университета Райса демонстрирует, как газы, представленные дисперсными частицами, и жидкости, представленные конденсированным кластером, могут сосуществовать как пар и жидкость, что соответствует уравнению Кельвина для молекулярных систем. Видео любезно предоставлено лабораторией Biswal

Химик и биомолекулярный инженер Сибани Лиза Бисвал и научный сотрудник Кедар Джоши из инженерной школы Джорджа Р. Брауна Университета Райса обнаружили, что коллоид — в данном случае суспензия парамагнитных частиц микронного размера – сталкивается с магнитным полем, он по-прежнему стремится искать состояние с наименьшей энергией, как это делают газообразные и жидкие системы.

«Это все равно, что пытаться надуть пузырь странной формы, — сказал Бисвал. «Всегда возвращается к сфере».

Их открытие, подробно описанное в Proceedings of the National Academy of Sciences, не противоречит уравнению Кельвина, описывающему термодинамические взаимодействия между жидкостями и газами. Но это немного растягивает уравнение.

«Уравнение Кельвина взято из классической термодинамики и говорит нам, как жидкая и газовая фазы находятся в равновесии друг с другом», — сказал Бисваль. «Кедар любит приводить в пример капли воды: как они остаются определенного размера, даже когда вокруг них находятся вода и пар».

Сибани Лиза Бисвал и Кедар Джоши. Фото Джеффа Фитлоу

«Эти коллоидные группы похожи на капли», — сказал Джоши. «Они стараются оставаться круглыми, а не принимать произвольную форму. Мы думали, что эти уравнения должны объяснить не только одно или два, но и каждое свойство наших коллоидов».

Исследование расширяет предыдущую работу лаборатории, чтобы охарактеризовать, как частицы взаимодействуют в растворах, самая последняя демонстрирует, как суперпарамагнитные коллоиды взаимодействуют друг с другом в быстро вращающемся магнитном поле.

«Это относится к тому, как мы думаем о газах и жидкостях, но по-другому», — сказал Бисваль. «Кедар решил применить формулу к нашей системе, в которой мы можем видеть частицы, мы можем их считать и фактически отслеживать их через их «газовую» и конденсированную фазы».

Результаты были неожиданными, писали они, потому что уравнение Кельвина не предназначено для применения к системам, выведенным из равновесия. В экспериментах Райса частицы представляли собой молекулы жидкости, когда они слипались, и молекулы газа, когда они были рассредоточены, причем оба свойства контролировались вращающимся магнитным полем, заменяющим температурную переменную уравнения.

Исследователи вывели коллоид из равновесия, вращая его полем. Несмотря на это, они обнаружили, что уравнение по-прежнему верно для взаимодействий, которые они наблюдали, когда частицы сближались или разлетались в зависимости от силы поля.

«Частицы следовали за вращающимся полем; они выглядят как маленькие миниатюрные мешалки», — сказал Бисваль. «Но если мы увеличили частоту, мы обнаружили, что она создает изотропное притягивающее взаимодействие между частицами».

Постдокторант Райс Кедар Джоши готовит эксперимент в лаборатории Бисвала, чтобы увидеть, как магнитные поля повлияют на коллоид магнитных частиц.

Фото Джеффа Фитлоу

Сила этого быстро вращающегося магнитного поля стала регулятором, который повышал и понижал «температуру» и контролировал, конденсируются ли частицы в жидкость или рассеиваются, как газ. «Система ведет себя так, как будто на нее влияет температура», — сказал Джоши, который недавно покинул Райс, чтобы поступить на факультет Индийского технологического института в Гоа. «Мы стремились показать, что он будет повторять то, что делают классические фазы с точки зрения давления пара, вязкости и поверхностного натяжения».

Бисвал сказал, что исследование также имеет значение для таких устройств, как контрольные дисплеи, в которых используются жидкие кристаллы. «Новая статья посвящена идее сосуществования (между жидкой и газовой фазами)», — сказала она. «Возможность увидеть, как магнитные поля можно использовать для управления тем, как эти системы могут достигать сосуществующих фаз, важна для разработки материалов, которые можно реконфигурировать или обладать желаемыми свойствами».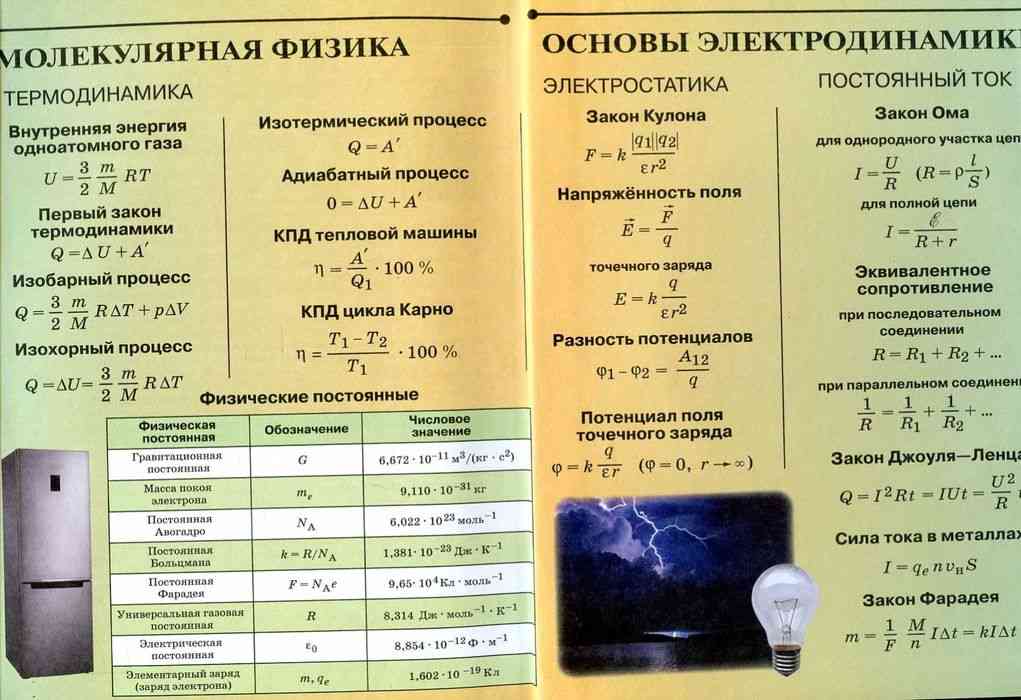

Национальный научный фонд (17055703) поддержал исследование. Бисвал – профессор химического машиностроения Уильяма М. Маккарделла, профессор химической и биомолекулярной инженерии, а также материаловедения и наноинженерии, а также заместитель декана по развитию факультета.

Рецензируемая статья

Распространение уравнения Кельвина на диполярные коллоиды: https://www.pnas.org/doi/full/10.1073/pnas.2117971119

загрузок изображений

https://news-network.rice.edu/news/files/2022/02/0228_KELVIN-1-web.jpg

Сибани Лиза Бисвал и Кедар Джоши. (Источник: Джефф Фитлоу/Университет Райса)

https://news-network.rice.edu/news/files/2022/02/0228_KELVIN-2-web.jpg

Постдокторант Университета Райса Кедар Джоши готовит эксперимент в лаборатории Biswal, чтобы увидеть, как магнитные поля будут влиять на коллоид магнитных частиц. Джоши и его наставник, инженер-химик и биомолекулярный инженер Сибани Лиза Бисвал, недавно обнаружили необычные свойства намагниченных коллоидов, которые подчиняются уравнению Кельвина, моделирующему термодинамику. (Источник: Джефф Фитлоу/Университет Райса)

Сопутствующие материалы

Следите за Rice News и связями со СМИ через Twitter @RiceUNews.

Вращающиеся нити намекают на динамику складывания: news2.rice.edu/2017/10/16/spinning-strands-hint-at-folding-dynamics-2/

Быстро вращающиеся сферы раскрывают секреты наносистем: news2.rice.edu/2018/02/07/fast-spinning-spheres-show-nanoscale-systems-secrets-2/

Biswal Lab: ruf.rice.edu/~biswalab/Biswal_Research_Group/Welcome.html

Кафедра химической и биомолекулярной инженерии: chbe.rice.edu

Инженерная школа Джорджа Р. Брауна: engineering.rice.edu

О рисе

Университет Райса, расположенный в кампусе площадью 300 акров в Хьюстоне, постоянно входит в число 20 лучших университетов страны по версии US News & World Report. Райс имеет очень уважаемые школы архитектуры, бизнеса, непрерывного обучения, инженерии, гуманитарных наук, музыки, естественных и социальных наук, а также является домом для Института государственной политики Бейкера. С 4 052 студентами и 3 484 аспирантами соотношение студентов бакалавриата и преподавателей в Райс составляет чуть менее 6 к 1. Его система колледжей-интернатов создает сплоченные сообщества и дружбу на всю жизнь, что является лишь одной из причин, по которой Райс занимает первое место по количеству взаимодействий между расами и классами и первое место по качеству жизни по версии Princeton Review. Райс также оценивается как лучший среди частных университетов по версии Kiplinger’s Personal Finance.

Колебательные энергии некоторых двухатомных молекул для модифицированного и деформированного потенциала

1. Hu XT, Liu JY, Jia CS. Состояние 3 ³ Σ ⁺ _g молекулы Cs2. вычисл. Теор. хим. 2013;1019:137. [Google Scholar]

2. Лино да Силва М., Герра В., Лоурейро Х., Са П.А. Колебательные распределения в N2 с улучшенным расчетом энергетических уровней методом RKR. хим. физ. 2008; 348:187. [Академия Google]

3. Egrifes H, Demirhan D, Buyukkılıc F. Точные решения уравнения Шредингера для деформированной гиперболической потенциальной ямы и деформированного четырехпараметрического потенциала экспоненциального типа. физ. лат. А. 2000; 275:229. [Google Scholar]

4. Horchani R, Al-Kindi N, Jelassi H. Ro-вибрационные энергии молекул цезия с осциллятором Tietz-Hua. Мол. физ. 2020 г.: 10.1080/00268976.2020.1812746. [CrossRef] [Google Scholar]

5. Whang T, Cheng C-P. Наблюдение за L разобщение в 5 ¹ Δ _g ридберговском состоянии Na2. Дж. Хим. физ. 2005;123:224303. [PubMed] [Google Scholar]

6. Фараут М., Бассалат А., Ихдаир С.М. Точные квантованные собственные значения импульса и собственные состояния модели общего потенциала. Дж. Заявл. Мат. физ. 2020;8:1434. [Google Scholar]

7. Фараут М., Бассалат А., Ихдаир С.М. Точные импульсные состояния Фейнберга-Городецкого улучшенного деформированного потенциала экспоненциального типа. Дж. Заявл. Мат. физ. 2020;8:1496. [Академия Google]

8. Цзя К-С, Дяо Ю-Ф, Лю С-Дж, Ван П-К, Лю Д-Ю, Чжан Г-Д. Эквивалентность модели потенциала Вея и модели потенциала Титца для двухатомных молекул. Дж. Хим. физ. 2012;137:014101. [PubMed] [Google Scholar]

9. Liu J-Y, Hu X-T, Jia C-S. Молекулярные энергии улучшенной модели потенциальной энергии Розена-Морса. Можно. Дж. Хим. 2014;92:40. [Google Scholar]

10. Сун X-Q, Ван C-W, Цзя C-S. Термодинамические свойства димера натрия. хим. физ. лат. 2017;673:50. [Академия Google]

11. Хамзави М., Раджаби А.А., Тилве К.Э. Вращательно-колебательный спектр двухатомных молекул с вращающимся осциллятором Титца-Хуа. Междунар. Дж. Квант. хим. 2012;112:2701. [Google Scholar]

12. Falaye BJ, Oyewumi KJ, Ikhdair SM, Hamzavi M. Методы собственных решений, их приложения и информационная энтропия Фишера двухатомной молекулярной модели Титца-Вея. физ. Скр. 2014;89:115204. [Google Scholar]

13. Onyeaju MC, Onate CA. Колебательная энтропия и меры сложности в модифицированном потенциале Пёшля-Теллера плюс потенциал Вудса-Саксона. Система с несколькими телами. 2020;61:21. [Академия Google]

14. Okorie US, Ibekwe EE, Onyeaju MC, Ikot AN. Решения уравнений Дирака и Шрёдингера со сдвинутым потенциалом Титца-Вея. Евро. физ. Дж. Плюс. 2018;133:433. [Google Scholar]

15. Onate CA, Adebiyi LS, Bankole DT. Собственные решения и теоретические величины нерелятивистского волнового уравнения. Дж. Теор. вычисл. хим. 2020;19:2050007. [Google Scholar]

16. Никифоров АФ, Уваров ВБ. Специальные функции математической физики. Биркхойзер; 1988. [Google Академия]

17. Тезкан С., Север Р. Общий подход к точному решению уравнения Шредингера. Междунар. Дж. Теор. физ. 2009; 48:337. [Google Scholar]

18. Байрак О., Бозтосун И. Решения в связанном состоянии потенциала Хультена с использованием метода асимптотической итерации. физ. Скр. 2007;76:92. [Google Scholar]

19. Виттен Э. Динамическое нарушение суперсимметрии. Нукл. физ. Б. 1981; 188:513. [Google Scholar]

20. Купер Ф., Кхаре А. , Сукхатме У. Суперсимметрия и квантовая механика. физ. Представитель 1995;251:267. [Google Scholar]

21. Донг С-Х. Метод факторизации в квантовой механике. Спрингер; 2007. [Google Scholar]

22. Ma Z-Q, Xu B-W. Квантовая коррекция в правилах точного квантования. Еврофиз. лат. 2005;69:685. [Google Scholar]

23. Qiang W-C, Dong S-H. Правильное правило квантования. ЭПЛ. 2010;89:10003. [Google Scholar]

24. Икот А.Н., Окорие США, Рамфо Г.Дж., Амади П.О. Приближенные аналитические решения уравнения Клейна-Гордона с обобщенным потенциалом Морзе. Междунар. Дж. Термофиз. 2021;42:10. [Академия Google]

25. Икот А.Н., Окорие У.С., Амади П.О., Эдет К.О., Рамфо Г.Дж., Север Р. Метод функционального анализа Никифорова–Уварова (NUFA): новый подход к решению потенциала экспоненциального типа. Несколько систем для тела. 2021;62:1. [Google Scholar]

26. Dong S-H, Gu XY. Произвольные решения уравнения Шрёдингера с молекулярным потенциалом Денга-Фана в l-состоянии. Дж. Физ. конф. сер. 2008;96:012109. [Google Scholar]

27. Zhang LH, Li XP, Jia C-S. Приближенные решения уравнения Шредингера с обобщенной моделью потенциала Морзе, включающей центробежный член. Междунар. Дж. Квант. хим. 2011;111:1870. [Академия Google]

28. Онате К.А., Икот А.Н., Онеаджу М.С., Эбомвони О., Идиоди ДЖОА. Влияние энергии диссоциации на энтропии Шеннона и Руньи. Кербела Интерн. Дж. Мод. науч. 2018;4:134–142. [Google Scholar]

29. Наджафизаде С.А., Хассанабади Х., Зарринкамар С. Нерелятивистская информационная энтропия Шеннона для потенциала Кратцера. Подбородок. физ. Б. 2016; 25:040301. [Google Scholar]

30. Гафурян М., Хассанабади Х. Информационная энтропия Шеннона для трехмерной задачи Клейна-Гордона с потенциалом Пошла-Теллера. J. Корейская физ. соц. 2016;68:1267. [Академия Google]

31. Боумали А., Лабиди М. Энтропия Шеннона и информация Фишера одномерного осциллятора Клейна-Гордона с энергозависимым потенциалом. Мод. физ. лат. А. 2018; 33:1850033. [Google Scholar]

32. Идиоди Джоа, Онате, Калифорния. Энтропия, информация Фишера и дисперсия с потенциалом Фроста-Мусулина. общ. Теор. физ. 2016;66:269. [Google Scholar]

33. Okorie US, Ikot AN, Chukwuocha EO, Rampho GJ. Термодинамические свойства улучшенного деформированного потенциала экспоненциального типа (ИДЭП) для некоторых двухатомных молекул. Результаты Физ. 2020;17:103078. [Академия Google]

34. Хордад Р., Ганбари А. Теоретическое предсказание термодинамических функций TiC: кольцеобразный потенциал Морзе. Низкая темп. физ. 2020;199:1198. [Google Scholar]

35. Wang J, Jia CS, Li CJ, Peng XL, Zhang LH, Liu JY. Термодинамические свойства углекислого газа. АСУ Омега. 2019;4:19193. [Бесплатная статья PMC] [PubMed] [Google Scholar]

36. Onate CA, Ojonubah JO. Релятивистские и нерелятивистские решения обобщенных потенциалов Пешля-Теллера и гиперболических потенциалов с некоторыми термодинамическими свойствами. Междунар. Дж. Мод. физ. Э. 2015; 24:1550020. [Академия Google]

37. Яхья В.А., Оевуми К.Дж. Термодинамические свойства и приближенные решения ℓ-состояния потенциала типа Пёшля-Теллера. Дж. Асс. араб. ун-т Базовое приложение науч. 2016;21:53. [Google Scholar]

38. Oyewumi KJ, Falaye BJ, Onate CA, Oluwadare OJ, Yahya WA. Термодинамические свойства и приближенные решения уравнения Шрёдингера со сдвинутой моделью потенциала Денга-Фана. Мол. физ. 2014;112:127. [Google Scholar]

39. Mesa ADS, Quesne C, Smirnov YF. Обобщенный потенциал Морзе: симметрия и сателлитные потенциалы. Дж. Физ. Математика. Теор. 1998;31:321. [Google Scholar]

40. Rong Z, Kjaergaard HG, Sage ML. Сравнение потенциалов Морзе и Денга-Фана для связей X-H в малых молекулах. Мол. физ. 2003;101:2285. [Google Scholar]

41. Gordillo-Vazquez FJ, Kunc JA. Сравнение схем датчиков температуры на основе флуоресценции: теоретический анализ и экспериментальная проверка. Дж. Заявл. физ. 1998;84:4649. [Google Scholar]

42. Chackerian C, Tipping RH. Колебательно-вращательные и вращательные интенсивности для изотопов СО. Дж. Мол. Спектроск. 1983;99:431. [Google Scholar]

43. Manai I, Horchani R, Lignier H, Pillet P, Comparat D. Вибрационное охлаждение молекул с помощью оптической накачки. физ. Преподобный Летт. 2012;109:183001. [PubMed] [Google Scholar]

44. Вито М., Хотиа А., Аллегрини М., Булуфа Н., Дулье О., Компарат Д., Пиллет П. Оптическая накачка и колебательное охлаждение молекул. Наука. 2008; 321:232. [PubMed] [Google Scholar]

45. Vala J, Dulieu O, Masnou-Seeuws F, Pillet P, Kosloff R. Когерентный контроль образования молекул холода посредством фотоассоциации с использованием импульсного лазерного поля. физ. Ред. А. 2000; 63:013412. [Академия Google]

46. Fioretti A, Sofikitis D, Horchani R, Li X, Pichler M, Weber S, Allegrini M, Chatel B, Comparat D, Pillet P. Холодные молекулы цезия: от формирования до охлаждения. Дж. Мод. Опц. 2009;56:2089. [Google Scholar]

47. Ватасеску М. Подготовка изолированных колебательных волновых пакетов со светоиндуцированными молекулярными потенциалами с помощью чирпированных лазерных импульсов. Нукл. Инструм. Методы Б. 2012;279:8. [Google Scholar]

48. Белой К., Борщевский А., Фламбаум В.В., Швердтфегер П. Влияние вариации α на предполагаемый эксперимент по обнаружению вариаций me/mp в двухатомных молекулах. физ. Ред. А. 2011; 84:042117. [Академия Google]

49. Li D, Xie F, Li L. Наблюдение состояния Cs ₂ (3 ³ Σ ⁺ _g ) с помощью двойного инфракрасно-инфракрасного резонанса. хим. физ. лат. 2008; 458:267. [Google Scholar]

50. Ли Д., Се Ф., Ли Л., Магнье С., Совков В.Б., Иванов В.С. 3 ³ Σ ⁺ _g и 3Σ ⁺ _u состояния Cs ₂ : Наблюдение и расчет. хим. физ. лат. 2007; 441:39. [Академия Google]

51. Онатэ К.А., Идиоди ДЖОА. Информация Фишера и мера сложности модели обобщенного потенциала Морса. коммун. Теор. физ. 2016;66:275. [Google Scholar]

52. Jia C-S, Liu J-Y, Wang P-Q, Lin X. Приближенные аналитические решения уравнения Дирака с гиперболическим потенциалом при наличии спиновой и псевдоспиновой симметрии. Междунар. Дж. Теор. физ. 2009;48:2633. [Google Scholar]

53. Икот А.Н., Окори Ю.С., Рамфо Г.Дж., Амади П.О., Эдет К.О., Акпан И.О., Абдулла Х.И., Хорчани Р. Уравнение Клейна-Гордона и нерелятивистские термодинамические свойства с улучшенным экранированным потенциалом Кратцера. J. Низкотемпературный. физ. 2021 г.: 10.1007/S10909-020-02544-ш. [CrossRef] [Google Scholar]

54. Dong S-H, Lozada-Cassou M, Yu J, Jiménez-Angeles F, Rivera AL. Скрытые симметрии и термодинамические свойства гармонического осциллятора плюс потенциал обратного квадрата. Междунар. Дж. Квант. хим. 2007; 107:366. [Google Scholar]

55. Эшги М., Мехрабан Х., Ихдаир С.М. Приблизительные энергии и тепловые свойства заряженной частицы с массой, зависящей от положения, во внешних магнитных полях.