Динамика и статика.
Фундаментальные константы.
Название константы. | Обозн. | Значение. | Измерение |
Гравитационная постоянная. | G | 6,672*10-11 | Н*м2/кг2 |
Ускорение свободного падения | G | 9,8065 | м/с2 |
Атмосферное давление | p0 | 101325 | Па |
Постоянная Авогадро | Na | 6,022045*1023 | Моль-1 |
Объем 1моль идеального газа | V0 | 22,41383 | м3/моль |
Газовая постоянная | R | 8,31441 | |
Постоянная Больцмана | K | 1,380662*10 | Дж/К |
Скорость света в вакууме | C | 2,99792458*108 | м/с |
Магнитная постоянная | 0 | 4*10-7= 1,25663706*10-6 | Гн/м |
Электрическая постоянная | 0 | 8,8541878*10-12 | Ф/м |
Масса покоя электрона | me | 9,109534*10-31 | кг |
Масса покоя протона | mp | 1,6726485*10-27 | кг |
Масса покоя нейтрона | mn | 1,6749543*10-27 | кг |
Элементарный заряд | E | 1,6021892*10-19 | Кл |
Отношение заряда к массе | e/me | 1,7588047*1011 | Кл/кг |
Постоянная Фарадея | F | 9,648456*104 | Кл/моль |
Постоянная Планка | H | 6,626176*10-34 1,054887*10-34 | Дж*с Дж*с |
Радиус 1 боровской орбиты | a0 | 0,52917706*10-10 | м |
Энергия покоя электрона | mec2 | 0. | МэВ |
Энергия покоя протона | 938.2796 | МэВ | |
.Энергия покоя нейтрона | mnc2 | 939.5731 | МэВ |
Система единиц.
Приставки Си.
пристав. | поряд. | пристав. | поряд. | пристав. | порядок | Пристав. | порядок | ||||
экса | Э | 18 | мега | М | 6 | деци | д | -1 | Нано | н | -9 |
пета | П | 15 | кило | к | 3 | санти | с | -2 | пико | п | -12 |
Т | 12 | гекто | г | 2 | милли | м | -3 | фемто | ф | -15 | |
гига | Г | 9 | дека | да | 1 | мк | -6 | атто | а | -18 |
Механика.
Кинематика.
Обозн. | Изм. | Смысл |
S | м | пройденный путь |
v | м/с | скорость |
t | с | время |
x | м | координата |
a | м/с2 | ускорение |
| с-1 | угловая скорость |
T | с | период |
Гц | частота | |
| с-2 | угловое ускорение |
R | м | радиус |
Скорость
и ускорение.
, ,
Равномерное движение:
, ;
Равнопеременное движение: a=const,
, ;
, ;
v=v0+at , ;;
Криволинейное движение.
,
Вращательное движение.
, , ; ;
, ; , ;
, , , ;
Обозн. | Изм. | Смысл |
F | Н | сила |
P | кг*м/с | импульс |
a | м/с2 | ускорение |
m | кг | масса |
v | м/с | скорость |
p | Н | вес тела |
g | м/с2 | ускорение свободного падения |
E | Дж | энергия |
A | Дж | работа |
N | Вт | мощность |
t | с | время |
I | кг*м2 | момент инерции |
L | кг*м2/с | момент импульса |
M | Н*м | момент силы |
| с-1 | угловая скорость |
Первый закон Ньютона:
Второй
закон Ньютона.
,, приm=const
Третий закон Ньютона.
Основной закон динамики для неинерциальных систем отчета.
ma=ma0+Fинерц ,где а- ускорение в неинерциальной а0– в инерциальной системе отчета.
Скорость центра масс ;
Закон всемирного тяготения.
,
– ускорение свободного падения на планете.
– первая космическая скорость.
Вес тела.
P = mg – вес тела в покое.
P = m(g+a) – опора движется с ускорением вверх.
P = m(g-a) – опора движется с ускорением вниз.
P = m(g-v2/r) – движение по выпуклой траектории.
P = m(g+v2/r) – движение по вогнутой траектории.
Сила трения.
,
Закон Гука.
Fупр= – kx, – сила упругости деформированной пружины.
– механическое напряжение
– относител-ное продольное удлинение (сжатие)
– относит-ное поперечное удлинение (сжатие)
,
где -
коэффициент Пуассона.
Закон Гука:,
где Е- модуль Юнга.
, кинетическая энергия упругорастянутого (сжатого) стержня. (V- объем тела)
Динамика и статика вращательного движения.
– момент импульса
; – момент силы
L=const – закон сохранения момента импульса.
M=Fl, где l- плечо
I=I0+mb2 – теорема Штейнера
система | ось | I |
точка по окружности | ось симметрии | mR2 |
стержень | через середину | 1/12 mR2 |
стержень | через конец | 1/3 mR2 |
шар | через центр шара | 2/5 mR2 |
сфера | через центр сферы | 2/3 mR2 |
кольцо или тонкостенный цилиндр | ось симметрии | mR2 |
диск сплошной цилиндр | ось симметрии | 1/2 mR2 |
Условие равновесия тел
Законы
сохранения.
Закон сохранения импульса.
P=mv; – импульс тела. Ft=P
Потенциальная и кинетическая энергия. Мощность.
– работа силы F
A=E
– мощность
– кинетическая энергия
– кинетическая энергия вращательного движения.
Ep=mgh – потенциальная энергия поднятого
над землей тела.
– потенциальная энергия пружины
Закон сохранения энергии.
Eк1+Eр1=Eк2+Eр2
Решаем задания по статике
Статикой называется раздел механики, изучающий равновесие механических систем при воздействии сил и моментов. В статье разберем законы статики, приведем основные формулы.
Условия равновесия
Статика в физике рассматривает абсолютно твердые тела — тела с постоянным расстоянием между любыми двумя точками. В природе они невозможны, однако для упрощения статика сводится к изучению исключительно данных объектов.
Статика изучает равновесие тела, то есть состояние механической системы, сохраняющей неподвижность относительно выбранной системы отсчета.
Первое условие равновесия: твердое тело приобретает состояние покоя, состояние равномерного прямолинейного движения, если геометрическая сумма сил, приложенных к объекту, равна нулю. Рассмотрим рисунок. На объект действуют F1, F2, F3, их можно разложить на дополнительные равнодействующие силы. Условие равновесия следующее:
F1 + F12 + F13 + F2 + F21 + F23 + F3 + F31 + F32 = 0
F1 + F2 + F3 = 0
Второе условие равновесия: тело приобретает состояние покоя, состояние равномерного прямолинейного движения, когда сумма моментов сил, влияющих на тело по выбранной оси, равна нулю. Момент — модуль силы, умноженный на плечо. Плечом называют наиболее короткое расстояние, проведенное от оси вращения до линии действия.
Например, рисунок отражает момент F1, равный F1 • OC, момент F2, равный F2 • OB. Момент обозначается буквой M, закон записывается M1 + M2 + M3 +… = 0.
Последний закон статики: объект, обладающий площадью опоры, сохраняет покой, когда линия действия силы тяжести проходит через площадь опоры. Левый рисунок отражает данную ситуацию, тело приобрело состояние покоя. На правом наблюдается расстояние между линией опоры и линией действия силы тяжести — объект приходит во вращение.
Задача
Решим задачу на статику из ЕГЭ по физике.
Условие. Груз, подвешенный на треугольном кронштейне АВС, весит 40 кг. АВ = 0,5 м, угол между АВ и ВС равен 45°. Чему равен момент силы тяжести, проходящий через точку В?
Решение. Помним, момент — показатель, равный произведению модуля на плечо. Внимательно изучим рисунок.
Сила тяжести направлена вниз. Плечо — расстояние от точки до линии действия.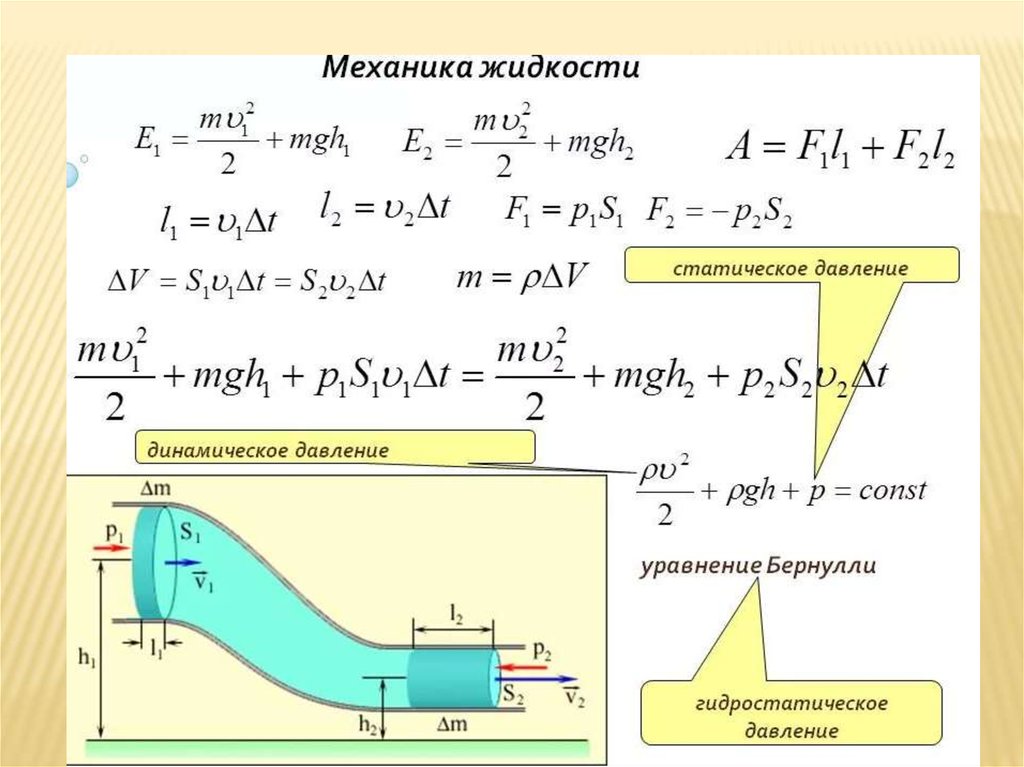
Получается, им является сторона АС. Поскольку по рисунку один угол прямой, а другой равен 45°, понимаем: треугольник равнобедренный, АС = АВ.
Модуль определяем, используя формулу F = mg = 40 • 10 = 400 Н. Далее ищем момент: M = F • AC = 400 • 0,5 = 200 Н.
Ответ: 200 Н.
Разобрали тему «Статика» по физике, примеры решения задач. Дополнительно выполнять задания можно на курсах «Уникум» Российского университета дружбы народов. Их преимущества:
- возможность посещать онлайн-вебинары;
- доступ к учебному порталу Unikum с полезными материалами, тестами;
- скидка на первый год обучения поступающим на коммерческое отделение.
Содержание данной статьи носит ознакомительный характер. Для подготовки к сдаче ЕГЭ пользуйтесь дополнительными источниками информации!
Полное руководство по базовой формуле статистики
Большинству учащихся трудно изучать статистику. Но вот несколько основных статистических формул, которые могут помочь учащимся начать работу со статистикой.
Но прежде мы изучим эти формулы. Начнем со знакомства со статистикой.
Статистика — это один из разделов математики, который используется для изучения анализа данных. Методы статистики создаются для изучения больших данных и их свойств.
Статистические формулы используются несколькими компаниями для расчета отчетов людей или сотрудников. В следующих параграфах мы обсудим несколько статистических формул, которые используются для разных целей.
Прежде чем перейти к основным формулам статистики; давайте проверим, можете ли вы проанализировать, какое утверждение является статистическим, а какое нестатистическим.
Q1 . В зоопарке совиные обезьяны обычно весят больше, чем паукообразные?
| (A) Статистический | (B) Нестатистический |
Q2 . В колледжах Нью-Йорка тренерам по футболу обычно платят больше, чем тренерам по теннису?
| (A) Статистический | (B) Нестатистический |
Q3.
Сколько зубов у Алана во рту?»
| (A) Статистический | (B) Нестатистический |
Q4. Сколько дней в июле месяце?
| (A) Статистический | (B) Нестатистический |
Q5. Какова общая площадь ушей жирафа? Q6. А вообще какой средний рост у жирафов?
| (A) Статистический | (B) Нестатистический |
Q7. Есть ли у Дева докторская степень? степень?
| (A) Statistical | (B) Not statistical |
Answers:–
- Statistical
- Statistical
- Not statistical
- Не статистически
- Статистические
- Статистические
- Нестатистические
После того, как вы проверили свои статистические знания, теперь вы можете перейти к проверке основных формул статистики.
Это поможет вам решить статистические задачи.
Содержание
Статистика — это наука об анализе, представлении, сборе, интерпретации, организации, анализе и представлении больших данных. Его можно определить как функцию заданных данных. Вот почему статистика сочетается с классификацией, представлением, сбором и упорядочиванием числовой информации. Это также облегчает интерпретацию нескольких результатов и прогнозирование различных возможностей для будущих приложений. С помощью статистики можно найти несколько показателей центральных данных и отклонений разнородных значений от основных значений.
Что такое формулы элементарной статистики?Для всех статистических вычислений базовая концепция и формулы среднего, моды, стандартного отклонения, медианы и дисперсии являются ступеньками. Таким образом, мы представили все подробности по основной формуле статистики:
где
x = данные наблюдений
x (бар) = среднее значение
n = общее количество наблюдений
Теоретически, это сумма компонентов набора, деленная на общее количество компонентов.
Вы можете легко понять всю концепцию вычисления среднего значения. Таким образом, формула среднего:
Среднее значение = (сумма всех данных элементов) / общее количество. элементов
Способность среднего используется для отображения всего набора данных с одним значением.
МедианаЭто центральное значение всего набора данных. Но если множество имеет нечетное число значений, то центральное значение множества можно рассматривать как медиану. С другой стороны, если конкретный набор содержит даже нет. наборов, то два центральных значения можно использовать для вычисления медианы.
Медиану можно использовать для разделения набора данных на две разные части. Чтобы вычислить медиану, вы должны расположить компоненты набора в порядке возрастания; только тогда вы можете найти медиану данных.
Медиана = (n+1)/2 ; , где n — нечетное число
Или
Медиана = [(n/2) член + ((n/2) + 1)] /2 ; , где n — четное число
Это формула базовой статистики для расчета медианы заданных данных.
Это значение часто используется в одном наборе данных. Или мы можем сказать, что мода — это сводка набора данных с одними данными.
Режим = Часто используемые данные в заданном наборе
ДисперсияИспользуется для расчета отклонения набора данных по его среднему значению. Следовательно, это должно быть положительное значение, и оно также используется для измерения значения стандартного отклонения, которое считается основным понятием статистических значений.
Где дисперсия; х = заданные предметы; х бар = среднее значение; и n = общее количество элементов
Стандартное отклонениеЭто квадратный корень из дисперсии данной информации.
S =
Где S = стандартное отклонение и квадратный корень из дисперсии.
Некоторые примеры основных статистических формулНиже приведены некоторые примеры основных статистических формул, которые вам следует знать:
Среднее значение: Найдите среднее значение данных 1,2,3,4,5.
Среднее значение = (сумма всех данных элементов) / общее количество.
Следовательно, среднее = (1+2+3+4+5)/5
15/5 =3
Следовательно, среднее = 3
Найдите медиану данных 10,20,30,40,50.
Затем можно рассчитать медиану, записав набор данных в порядке возрастания, т.е.
10,20,30,40,50
Следовательно, 30 — это медиана, так как это центральное значение набора данных.
Или Медиана = (n+1)/2 ;
Где n=5, поэтому (5+1)/2 = 3, что означает, что 3-й член является медианой набора данных.
Если n четное числоНайдите медиану данных 4,10,15,2.
Затем можно рассчитать медиану, записав набор данных в порядке возрастания, т. е.
2,4,10,15
0011 Медиана = [(n/2) срок + ((n/2) + 1)] /2 ; , следовательно,
[(4/2) + (4/2)+1)]/2 = 2,5
Это означает, что 2-й и 3-й члены будут использоваться для медианы, т.
е.
(4+10)/2 = 7 , Медиана 7 .
Поскольку 3 повторяется 4 раза; поэтому мода данных равна 3.
[100+25+36+9+144]/5 = 62,8
Дисперсия равна 62,8.
Стандартное отклонениеВ приведенном выше примере мы рассчитали дисперсию данных. Теперь, используя значение дисперсии, мы можем вычислить стандартное отклонение.
S = √ (дисперсия)
S = √ (62,8)
= 7,92
Следовательно, стандартное отклонение равно 7,92.
Ниже мы упомянули некоторые важные формулы статистики. Студенты могут использовать любой из них в соответствии со своими потребностями.
| Термины статистики | Базовая формула статистики |
| Процентиль | Преобразуйте исходную формулу с помощью стандартной формулы z. Затем используйте Z-таблицу для ее решения. Здесь x — исходное значение, среднее значение генеральной совокупности, а σ — стандартное отклонение. |
| Погрешность среднего значения выборки | Здесь Z * — стандартное нормальное значение, σ — стандартное отклонение, а n — размер выборки. |
| Размер выборки | Здесь Z * — стандартное нормальное значение, σ — стандартное отклонение, а MOE — предел погрешности. |
| Тестовая статистика для среднего | Здесь — это среднее значение выборки, σ — стандартное отклонение, а среднее значение n выборки. |
| Корреляция | Здесь s x — стандартное отклонение всех значений x и sy — стандартное отклонение всех значений x . |
| Линия регрессии. | |
| Доля объединенной выборки | p = (p1 * n1 + p2 * n2) / (n1 + n2) Здесь n1 и n2 — размер выборки 1 и выборки 2, а p1 и p2 – доля выборки, взятая из совокупностей 1 и 2 соответственно. 92 Здесь σ1 и σ2 — стандартные отклонения данной совокупности 1 и 2, с 1 и с 2 — стандартное отклонение совокупности 1 и 2 соответственно. |
| Одновыборочный t-тест для среднего . | |
| Двухвыборочный t-критерий для средних значений | t = [(x1 – x2) – d] / SE Здесь x1 и x2 — среднее значение выборки 1 и 2, SE — стандартная ошибка, d — предполагаемая разница между средними значениями генеральной совокупности. |
| Статистика теста хи-квадрат | Χ2 = Σ [ (Oi – Ei)2 / Ei ] уровень категориальной переменной. |
| Среднее отрицательного биномиального распределения | μ = r / P Здесь r — количество успешных попыток, μ — среднее число испытаний, а P — вероятность успеха. |
| Стандартное нормальное распределение | Z = ( x – µ) / σ Здесь µ – это среднее значение – µ) / σ здесь µ x , , , , , , , , , , , , . переменная, а σ – стандартное отклонение X. |
| Критерий согласия хи-квадрат | DF = k – 1 Здесь DF — степень свободы, а K — уровни категориальной переменной. |
В этом блоге есть актуальная информация о основных формулах статистики, которые могут помочь вам понять основную концепцию статистики. Поскольку статистика имеет разные термины, такие как среднее значение, медиана, мода, дисперсия и стандартное отклонение, вы можете использовать вышеупомянутый пример для решения проблемы этих статистических терминов.
Даже в этом случае, если у вас возникнут трудности с выполнением статистических заданий; то вы можете получить лучшую справку по назначению статистики прямо сейчас. Тем не менее, у нас есть команда экспертов, которые могут мгновенно помочь вам с вашими запросами, и мы доступны для вас 24 * 7 и доставляем данные без плагиата до истечения срока вместе с отчетом о плагиате.
Q1.
Как рассчитать базовую статистику? Вот некоторые из основных формул статистики:
1. Стандартное отклонение населения = σ = sqrt [Σ (Xi – μ )2 / N ]
2. Среднее значение населения = μ = (Σ Xi ) / N.
3. Дисперсия доли населения = σP2 = PQ / n .
4. Дисперсия населения = σ2 = Σ ( Xi – μ )2 / N.
5. Стандартизированная оценка = Z = (X – μ) / σ
Q2.
Типы статистики по математике ?Статистика в основном подразделяется на два типа:
1. Описательная статистика
2. Логическая статистика
Формулы статистики – GeeksforGeeks
Статистика — это раздел математики, который занимается анализом числовых данных. Он представляет данные в организованном порядке. Статистика – это изучение сбора данных, их анализ, интерпретация и представление данных в хорошо организованной форме. Это позволяет нам интерпретировать различные результаты из имеющихся данных и прогнозировать множество возможностей. Теория статистики определяет функцию выборки, где функция полностью не зависит от распределения выборки. Статистика помогает находить различные меры центральных тенденций и отклонения различных наблюдений от центра. Давайте обсудим формулы статистики, которые находят меры центральных тенденций и отклонений.
Статистические формулы
Статистические формулы включают среднее значение, медиану, моду, а также стандартное отклонение. Среднее указывает среднее значение данных, медиана указывает середину центрального значения данных, медиана указывает наиболее часто встречающееся значение в данных. Давайте узнаем об этих терминах и их формулах более подробно.
Среднее
Среднее является одним из показателей центральной тенденции. Он находит среднее значение для заданных данных/наблюдений. Среднее арифметическое определяется как сумма всех чисел в данных, деленная на общее количество чисел. Формула для нахождения среднего дается,
Среднее арифметическое () = ∑x/n
Где ∑x — сумма всех наблюдений.
n представляет общее количество всех чисел/наблюдений.
Медиана
Медиана также является одним из показателей центральной тенденции. Это дает среднее значение в заданных упорядоченных данных. Формула для нахождения медианы задается следующим образом:
Медиана = [(n + 1)/2] th term
Где n — общее количество чисел/наблюдений.
Приведенная выше формула применима, только если n нечетно.
Если n четное, то медиана рассчитывается по формуле : Приведенные выше формулы можно применять только при упорядоченных данных. Поэтому перед вычислением медианы данные должны быть упорядочены либо по возрастанию, либо по убыванию.
Режим
Режим определяет наиболее повторяющийся элемент в данных. Он указывает значение, которое встречается чаще всего.
Дисперсия
Дисперсия измеряет отклонение заданных данных от среднего значения. Это ожидание квадрата отклонения случайной величины от ее среднего значения по выборке. Дисперсия равна квадрату стандартного отклонения. Формула для расчета дисперсии задается следующим образом:
Дисперсия (σ 2 ) =
Где x — данные наблюдений,
— среднее значение заданных данных,
n — общее количество наблюдений.
Стандартное отклонение
Стандартное отклонение измеряет степень вариации/дисперсии набора значений. Дисперсия говорит о том, сколько данных распределено. Более низкое стандартное отклонение указывает на то, что данные близки к центру. Чем выше значение стандартного отклонения, тем больше разброс данных.
Стандартное отклонение (σ) =
Стандартное отклонение = √{Дисперсия}
Примеры задач
Вопрос 1. Найдите среднее значение для данных0014
Решение:
Данные,
10, 20, 60, 40, 25, 35
n = 6
Арифметическое среднее () = ∑x/n
= (10 + 20 + 60 + 40 + 25 + 35)/6
= 190/6
= 31,66
Среднее значение для заданных данных равно 31,66
, 40, 25, 35
Решение:
Данные не упорядочены.
Таким образом, чтобы рассчитать медианное значение, данные должны быть упорядочены.
Здесь данные упорядочены по возрастанию.
10, 20, 25, 35, 40, 60
n = 6
n четно, формула медианы
Медиана = [(n/2) th член + [(n/2) + 1] -й срок ]/2
= [(6/2) -й срок + [(6/2) + 1] -й срок]/2
= (3 -й срок + 4 -й срок)/2
= (25 + 35)/2
= 30
Медиана для приведенных данных равна 30.
Вопрос 3: Найдите медиану для заданных данных 10, 20, 60, 40, 25, 35, 50
Решение:
Данные неупорядочены. Таким образом, чтобы рассчитать медианное значение, данные должны быть упорядочены.
Здесь данные упорядочены по возрастанию.
10, 20, 25, 35, 40, 50, 60
n = 7
n нечетное, формула медианы
[(7 + 1)/2] -й терм= 4 -й терм
= 35
Медиана для заданных данных равна 35.