Глава 1. Путь, перемещение, скорость. Движение с постоянной скоростью. Относительность движения
В рамках этой темы необходимо знать ряд простых определений, понимать логику определения скорости и закона сложения скоростей.
Перемещением тела называется вектор, связывающий начальное и конечное положение тела, а пройденным путем — длина траектории. Поэтому величина(или модуль) перемещения — это расстояние от конечной до начальной точки по прямой, а путь — расстояние траектории тела. В задаче 1.1.1 пройденный телом за четверть периода путь — длина четверти окружности , перемещение — (см. рисунок), правильный ответ — 3.
Скорость тела определяется как отношение перемещения тела ко времени , затраченному на это перемещение
(1.1) |
Для прямолинейного движения в одном направлении для величины вектора скорости получаем из (1.
(1.2) |
где — путь, пройденный за время . Если определение (1.1) приводит к одной и той же величине для любого интервала времени , то скорость тела есть величина постоянная, а такое движение называется равномерным (задача 1.1.2 — ответ 4). В этом случае согласно (1.1) и (1.2) перемещение и пройденный путь линейно зависят от времени и . По этой причине линейно зависят от времени и координаты тела в любой системе координат. Поэтому графиком зависимости координат тела от времени для равномерного движения является прямая (задача 1.1.3 — ответ 1). Как следует из (1.1), (1.2), наклон этой прямой определяется скоростью: чем больше скорость, тем «круче» наклонен график зависимости координаты тела от времени к оси времени. Поэтому в
В задаче 1.1.5 нужно по графику зависимости координаты тела от времени найти его скорость. Это можно сделать так. Перемещение тела внутри каждого из интервалов времени — 0–1, 1–2 и 2–3 с — разность координат тела вначале и в конце этого интервала. Поэтому из графика находим
Таким образом, скорость тела равна 2 м/с внутри интервала времени 1–2 с (ответ 2).
Задача 1.1.6 посвящена размерности скорости. Из определения заключаем, что размерность скорости есть
И, следовательно, размерностью скорости могут быть
(или любые другие отношения единиц расстояний и времени). Для пересчета скорости из одних единиц в другие нужно выразить расстояние и время в требуемых единицах. Например, в задаче 1.1.6 имеем
(правильный ответ —
При движении с постоянной скоростью определения (1.
1) или (1.2) могут быть применены к любым этапам движения. Например, в задаче 1.1.7 можно из данных о движении жука вдоль периметра прямоугольника найти его скорость (=14/7=2 см/с), а затем использовать ее для описания движения жука вдоль диагонали (длина которой составляет 5 см): 1=5/2=2,5 с (правильный ответ 2).
Аналогичные соотношения используются в задаче 1.1.8. Рассматривая движение автомобиля на одной трети пути, получаем , где — расстояние между городами. А на оставшихся двух третях (с учетом трехкратного увеличения скорости)
В задаче 1.1.9 следует использовать следующее свойство графика зависимости проекции скорости тела на некоторую ось от времени: площадь под этим графиком есть проекция перемещения тела на рассматриваемую ось. Причем площадь под участками графика, лежащими выше оси времени, нужно считать положительной, ниже оси времени — отрицательной.
Если же все площадь под всеми участками графика считать положительной, площадь под графиком скорости дает пройденный телом путь. Находя площадь под данным в условии графиком, получаем
(ответ — 4).
Важным физическим законом, знание которого часто проверяется на едином государственном экзамене по физике, является закон сложения скоростей. Этот закон утверждает, что скорости одного и того же тела по отношению к разным системам отсчета связаны соотношением
(1.3) |
Здесь и — скорости тела относительно первой и второй системы отсчета, — скорость второй системы отсчета относительно первой. Закон сложения скоростей является векторным. Это означает, три вектора , и образуют треугольник векторного сложения, и соотношение между величинами скоростей , и — такое же, как и между длинами сторон треугольника. Углы этого треугольника равны углам между направлениями скоростей , и .
Примеры треугольников сложения скоростей приведены на рисунке, причем на среднем и правом рисунке приведены примеры «треугольников» скоростей в случаях, когда скорость тела в системе 2 и скорость системы 2 относительно системы 1 направлены одинаково (средний рисунок) и противоположно (правый рисунок). Из этих рисунков следует, что скалярное соотношение, аналогичное (1.3) для величин скоростей , справедливо только, если векторы и направлены одинаково (средний рисунок). Если же векторы и направлены противоположно, для значений скоростей справедливо соотношение (или наоборот , если — правый рисунок. Из этих рассуждений ясно, что поскольку в
Поэтому , направлен вектор на север — правильный ответ В задаче 1.2.2 эти идеи применяются к движению лодки по и против течения. Из закона сложения скоростей заключаем, что при движении лодки по течению ее скорость относительно земли равна , при движении против течения — ( — скорость лодки в стоячей воде, — скорость течения). Отсюда находим, что при движении лодки по течению, ее скорость относительно земли 15 км/ч, а при движении против течения — 5 км/ч. Поэтому время движения между городами и по течению втрое больше времени движения лодки между этими городами против течения (ответ — 2).
Все следующие задачи этой главы являются более сложными, поскольку в них рассматривается движение не одного, а двух тел, а закон сложения скоростей используется в случаях, когда векторы скоростей не направлены вдоль одной прямой. В
Поэтому при выходе из точки тела встретятся в такой точке , что длины дуг отличаются в три раза. Следовательно, угол — прямой, и длина отрезка равна . (ответ 4).Если два тела, начав движение одновременно, движутся навстречу друг другу (задача 1.2.4), то время встречи тел можно найти следующим образом. Так как тела двигались до встречи одинаковое время, они прошли расстояния и , сумма которых равна первоначальному расстоянию между телами . Поэтому (ответ
Сокращая в этой формуле величину , получаем
или ч (правильный ответ — 1).
В задаче 1.2.6 начальное и конечное положения вагона и человека показаны на правой и левой частях рисунка.
Отсюда заключаем, что разность перемещений вагона и человека равна длине вагона . Поэтому время, через которое провожающий окажется около конца вагона, определяется из соотношения . Из этой формулы находится время, а затем и расстояние, пройденное провожающим (ответ 1). Отметим, что ответы 3 и 4 могли быть отброшены сразу, поскольку не описывают случай одинаковых скоростей. Действительно, при одинаковых скоростях вагон никогда не обгонит провожающего, и расстояние, пройденное при «обгоне» провожающим, должно обратиться в бесконечность. Другими словами, ответ должен содержать нуль в знаменателе при .
Задача 1.2.7 посвящена вычислению средней скорости движения на некотором пути, которая определяется как отношение этого пути к затраченному времени. Если расстояние между городами и равно , то полное время движения между городами складывается из времен, затраченных на первую и вторую половины пути
Отсюда находим км/ч (правильный ответ — 3).
В задачах 1.2.8–1.2.9 закон сложения скоростей рассматривается в ситуациях, когда векторы , и направлены не вдоль одной прямой. В этом случае необходимо использовать закон сложения скоростей в векторной форме (1.3). Когда человек в поезде идет перпендикулярно направлению его движения (задача 1.2.8), треугольник сложения скоростей (1.3) имеет вид, показанный на рисунке.
Здесь — вектор скорости поезда относительно земли, — вектор скорости человека относительно поезда, который по условию направлен перпендикулярно вектору . Поэтому согласно закону сложения скоростей вектор скорости человека относительно земли представляет собой гипотенузу прямоугольного треугольника, катетами которого являются векторы и (см. рисунок). Следовательно, величину скорости человека относительно земли можно найти по теореме Пифагора (ответ 3).
Задачи 1.2.9. и 1.2.10 удобнее решать, переходя из той системы отсчета, в которой задача поставлена (в системе отсчета, связанной с землей) в некоторую другую систему, в которой рассматриваемое явление является более простым.
При переправе через реку (задача 1.2.9) скорость лодки относительно земли зависит от траектории — на траекториях, направленных под острыми углами к течению, скорость лодки больше, чем на траекториях, на которых угол между скоростью лодки и скоростью течения — тупой. Поэтому время переправы по самой короткой траектории (перпендикулярной берегам) не является минимальным. Траекторию с минимальным временем переправы легко найти в системе отсчета, связанной с водой. В этой системе отсчета вода покоится, и, следовательно, минимальное время переправы достигается на такой траектории, на которой вектор скорости лодки относительно воды перпендикулярен берегам реки. Поэтому вектор скорости лодки относительно земли на этой траектории наклонен под углом к течению (см. рисунок). Под таким углом к берегу и расположена траектория, на переправу по которой лодка затрачивает минимальное время (правильный ответ — 1).
В задаче 1.2.10 рассматривается движение трех тел. В системе отсчета, связанной с землей ответ неочевиден.
Быстрый катер дольше уплывет от лодки, но будет двигаться быстрее и при обратном движении, медленный — наоборот. Однако если перейти в систему отсчета, связанную с водой, решение очень несложно. В этой системе отсчета плот покоится, каждый катер при движении от плота и к плоту движется с одинаковой скоростью. Поэтому каждый катер вернется к плоту через то же самое время после разворота, в течение которого он двигался от плота. Следовательно, катера вернутся одновременно (ответ 3).
Путь при неравномерном движении – материалы для подготовки к ЕГЭ по Физике
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Сейчас мы будем рассматривать неравномерное движение – то есть движение, при котором абсолютная величина скорости меняется со временем. Оказывается, существует простая геометрическая интерпретация пути, пройденного телом при произвольном движении.
Начнём с равномерного движения. Пусть скорость тела постоянна и равна . Возьмём два момента времени: начальный момент и конечный момент . Длительность рассматриваемого промежутка времени равна .
Очевидно, что за промежуток времени тело проходит путь:
(1)
Давайте построим график зависимости скорости от времени. В данном случае это будет прямая, параллельная оси абсцисс (рис. 1).
| Рис. 1. Путь при равномерном движении |
Нетрудно видеть, что пройденный путь равен площади прямоугольника, расположенного под графиком скорости. В самом деле, первый множитель в формуле (1) есть вертикальная сторона этого прямоугольника, а второй множитель – его горизонтальная сторона.
Теперь нам предстоит обобщить эту геометрическую интерпретацию на случай неравномерного движения.
Пусть скорость тела зависит от времени, и на рассматриваемом промежутке график скорости выглядит, например, так (рис.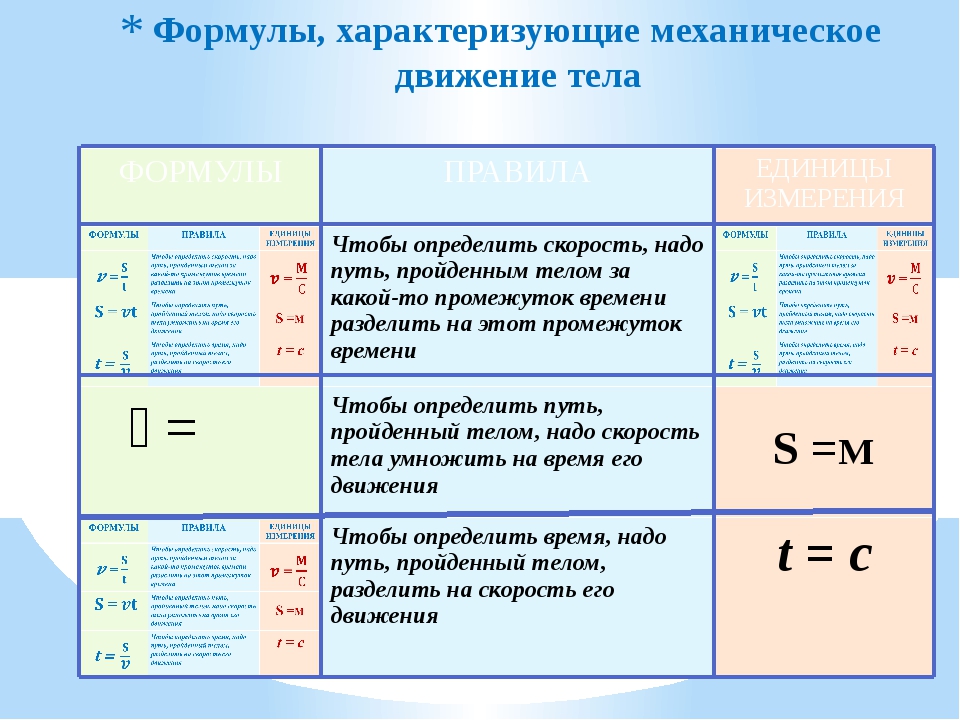
2):
| Рис. 2. Неравномерное движение |
Дальше мы рассуждаем следующим образом.
1. Разобьём наш промежуток времени на небольшие отрезки величиной .
2. Предположим, что на каждом таком отрезке тело движется с постоянной скоростью . То есть, плавное изменение скорости заменим ступенчатой аппроксимацией*: в течение каждого небольшого отрезка времени тело движется равномерно, а затем скорость тела мгновенно и cкачком меняется.
На рис. 3 показаны две ступенчатые аппроксимации. Ширина ступенек на правом рисунке вдвое меньше, чем на левом.
| Рис. 3. Ступенчатая аппроксимация |
Путь, пройденный за время равномерного движения – это площадь прямоугольника, расположенного под ступенькой.
Поэтому путь, пройденный за всё время такого “ступенчатого” движения – это сумма площадей всех прямоугольников на графике.
3. Теперь устремляем к нулю. Ясно, что в пределе наша ступенчатая аппроксимация перейдёт в исходный график скорости на рис. 2. Сумма площадей прямоугольников перейдёт в площадь под графиком скорости; следовательно, эта площадь и есть путь, пройденный телом за время от до . (рис. 4
| Рис. 4. Путь при неравномерном движении |
В итоге мы приходим к нужному нам обобщению геометрической интерпретации пути, полученной выше для случая равномерного движения.
| Аппроксимация – это приближённая замена достаточно сложного объекта более простой моделью, которую удобнее изучать. |
Геометрическая интерпретация пути.
Путь, пройденный телом при любом движении, равен площади под графиком скорости на заданном промежутке времени.
Посмотрим, как работает эта геометрическая интерпретация в важном частном случае равноускоренного движения.
Задача. Тело, имеющее скорость в начальный момент , разгоняется с постоянным ускорением . Найти путь, пройденный телом к моменту времени .
Решение. Зависимость скорости от времени в данном случае имеет вид:
(2)
График скорости – прямая, изображённая на рис. 5. Искомый путь есть площадь трапеции, расположенной под графиком скорости.
| Рис. 5. Путь при равноускоренном движении |
Меньшее основание трапеции равно . Большее основание равно . Высота трапеции равна . Поскольку площадь трапеции есть произведение полусуммы оснований на высоту, имеем:
Эту формулу можно переписать в более привычном виде:
Она, разумеется, вам хорошо известна из темы “Равноускоренное движение”.
Задача. График скорости тела является полуокружностью диаметра (рис. 6). Максимальная скорость тела равна . Найти путь, пройденный телом за время .
Решение. Как вы знаете, площадь круга радиуса равна . Но в данной задаче необходимо учесть, что радиусы полуокружности имеют разные размерности: горизонтальный радиус есть время , а вертикальный радиус есть скорость .
Поэтому пройденный путь, вычисляемый как площадь полукруга, равен половине произведения на горизонтальный радиус и на вертикальный радиус:
| Рис. 6. К задаче |
Путь при равноускоренном движении | Физика
Зная среднюю скорость и время движения, можно найти пройденный путь:
Подставляя в эту формулу выражение (3.3), мы найдем путь, пройденный при равноускоренном движении из состояния покоя:
Если же мы подставим в формулу (4.
1) выражение (3.4), то получим путь, пройденный при торможении:
В последние две формулы входят скорости v0 и v. Их можно найти по формулам (3.1) и (3.2). Подставляя выражение (3.1) в формулу (4.2), а выражение (3.2) — в формулу (4.3), получим
Полученная формула справедлива как для равноускоренного движения из состояния покоя, так и для движения с уменьшающейся скоростью, когда тело в конце пути останавливается. В обоих этих случаях пройденный путь пропорционален квадрату времени движения (а не просто времени, как это было в случае равномерного движения). Первым, кто установил эту закономерность, был Г. Галилей.
В таблице 2 даны основные формулы, описывающие равноускоренное прямолинейное движении.
Своей книги, в которой излагалась теория равноускоренного движения (наряду со многими другими его открытиями), Галилею увидеть не довелось. Когда она была издана, 74-летний ученый был уже слепым. Галилей очень тяжело переживал потерю зрения. «Вы можете себе представить, писал он,— как я горюю, когда я сознаю, что это небо, этот мир и Вселенная, которые моими наблюдениями и ясными доказательствами расширены в сто и в тысячу раз по сравнению с тем, какими их считали люди науки во все минувшие столетия, теперь для меня так уменьшились и сократились».
За пять лет до этого Галилей был подвергнут суду инквизиции. Его взгляды на устройство мира (а он придерживался системы Коперника, в которой центральное место занимало Солнце, а не Земля) уже давно не нравились служителям церкви. Еще в 1614 г. доминиканский священник Каччини объявил Галилея еретиком, а математику — изобретением дьявола. А в 1616 г. инквизиция официально заявила, что «учение, приписываемое Копернику, что Земля движется вокруг Солнца, Солнце же стоит в центре Вселенной, не двигаясь с востока на запад, противно Священному писанию, а потому его не можно ни защищать, ни принимать за истину». Книга Коперника с изложением его системы мира была запрещена, а Галилея предупредили, что если «он не успокоится, то его подвергнут заключению в тюрьму».
Но Галилей «не успокоился». «В мире нет большей ненависти,— писал ученый,— чем у невежества к знанию». И в 1632 г. выходит его знаменитая книга «Диалог о двух главнейших системах мира — птолемеевой и коперниковой», в которой он привел многочисленные аргументы в пользу системы Коперника.
Однако продать удалось всего лишь 500 экземпляров этого сочинения, так как уже через несколько месяцев по распоряжению Папы Римского издатель книги получил приказ приостановить продажу этого труда.
Осенью того же года Галилей получает предписание инквизиции явиться в Рим, и через некоторое время больного 69-летнего ученого на носилках доставляют в столицу. Здесь, в тюрьме инквизиции, Галилея заставляют отречься от своих взглядов на устройство мира, и 22 июня 1633 г. в римском монастыре Минервы Галилей зачитывает и подписывает заранее приготовленный текст отречения:
«Я, Галилео Галилей, сын покойного Винченцо Галилея из Флоренции, 70 лет от роду, доставленный лично на суд и коленоприклоненный перед Вашими Преосвященствами, высокопреподобными господами кардиналами, генеральными инквизиторами против ереси во всем христианском мире, имея перед собой священное Евангелие и возлагая на него руки, клянусь, что я всегда верил, верую ныне и с Божией помощью буду веровать впредь во все то, что святая католическая и апостольская римская церковь признает, определяет и проповедует».
Согласно решению суда, книга Галилея была запрещена, а сам он был приговорен к тюремному заключению на неопределенный срок. Однако Папа Римский помиловал Галилея и заменил заключение в тюрьме изгнанием. Галилей переезжает в Арчетри и здесь, находясь под домашним арестом, пишет книгу «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к Механике и Местному движению». В 1636 г. рукопись книги была переправлена в Голландию, где и была издана в 1638 г. Этой книгой Галилей подводил итог своим многолетним физическим исследованиям.
В том же году Галилей полностью ослеп. Рассказывая о постигшем великого ученого несчастье, Вивиани (ученик Галилея) писал: «Случились у него тяжкие истечения из глаз, так что спустя несколько месяцев совсем остался он без глаз — да, говорю я, без своих глаз, которые за краткое время увидели в этом мире более, чем все человеческие глаза за все ушедшие столетия смогли увидеть и наблюсти».
Посетивший Галилея флорентийский инквизитор в своем письме в Рим сообщил, что нашел его в очень тяжелом состоянии.
На основании этого письма Папа Римский разрешил Галилею вернуться в родной дом во Флоренции. Здесь ему сразу же вручили предписание: «Под страхом пожизненного заключения в истинную тюрьму и отлучения от церкви не выходить в город и ни с кем, кто бы это ни был, не говорить о проклятом мнении насчет двоякого движения Земли».
У себя дома Галилей пробыл недолго. Через несколько месяцев ему снова было приказано приехать в Арчетри. Жить ему оставалось около четырех лет. 8 января 1642 г. в четыре часа ночи Галилей умер.
1. Чем отличается равноускоренное движение от равномерного? 2. Чем отличается формула пути при равноускоренном движении от формулы пути при равномерном движении? 3. Что вы знаете о жизни и творчестве Г. Галилея? В каком году он родился?
формулы скорости,перемещения , ускорения при всех видах движения
Помогите с тестом по физике!!1.Вимірюючи потужність струму в споживачі, мивизначаємо його:а)номінальну потужністьб)фактичну потужністьв) час2.Прилад д
… ля вимірювання потужності електричного струму є:а) вольтметрб) амперметрв) ватметр3.
За незмінної сили струму в провіднику кількість теплоти, яка виділяється в ньому під час проходження струму…а) обернено пропорційна опору провідникаб)прямо пропорційна опору провідникав) дорівнює опору провидника4.Що являє собою електричний струм уметалах?а)рух електронів дорівнюватиме об)хаотичний рух вільних електронівв) направлений рух вільних електронів5.Чи залежить опір металів від температури?а) залежитьб) не залежитьв) у різних випадках порізному6.Принцип дії автоматичного запобіжника?а)розмикає електричне колоб) замикає електричне колов) збільшує силу струму7.Праска увімкнута у мережу,якщо опірнагрівального елемента праски становить 30 Ом,а сила струму в ньому дорівнює 6А. Скількитеплоти виділиться за 7 хвилин?а)3566)256в) 453,68.Два провідника опорами 20 і 80 Ом увімкнутів мережу, що має напругу 100В. Яка кількістьтеплоти виділиться за 5с у сумі двох провідників„якщо вони з’єднані паралельно?а)1246)3124в) 6509.Обчисліть роботу, яку виконує єлектричнийструм за 10хв роботи єлектродвигуна дитячоїіграшки, як4,8що напруга на двигуні становить20В, а сила струму в обмотці двигуна- 0,4А.
а) 4,86)6,2в) 5,810. Два провідника опорами 100 і 250 Омувімкнено до мережі,напруга в якій дорівнює100В. Визначте,яку роботу виконує електричнийструм у кожному провіднику за 1 хв,якщопровідники з’єднані послідовно?а) 490,12246) 85,652в)1000,490
Быстреее Срочно При помощи лебёдки поднимают груз массой 2 т на высоту 7 м. Вычисли работу, которую надо произвести для этого подъёма, если коэффициен … т полезного действия лебёдки равен 80 %. Принять g=9.8Нкг. Ответ (округли до целого числа): A≈ кДж.
Решите задачу пж. Заранее огромное спасибо. Найдите изменения кинетической энергии поезда массой 800т при увеличении его скорости от 36км/ч до 54км/ч … . Оформление дано-решение
Лабораторна робота номер 11
Помогите пожалуйста На лабораторной работе Яна определял объем медного кубика. Для этого ей выдали 24 одинаковых медных кубика и мерный цилиндр. Для п
… роведения опыта Яна налила в цилиндр воду до уровня 32мл, а затем стала кидать туда кубики, отмечая уровень воды и соответствующее количество кубиков.
3 точно. Ответ округди до сотых
срочно нужны ответы на это задания к вечеруДАЮ 40 БАЛЛОВ
Постройте дальнейший ход лучей в собирающей линзе
У ванні з мідним купоросом за 20 хв виділилося 1,98 г міді. Визначте,яка потужність витрачається на нагрівання електроліту. Опірелектроліту у ванні 0, … 8 Ом.
3 резистора соединены последовательно. У 1 сопротивления есть 2 значения: сопротивление 10 Ом и напряжение 20 вольт. На 2 резисторах напряжение 40 вол … ьт, но общее напряжение 300в. Найдите все сопротивления и общие сопротивления
. Ниже 12 картинок. Заполните таблицу НОМЕРАМИ КАРТИНОК Тело обладает кинетической энергией, но не обладает потенциальной (ТОЛЬКО 1 ВИД ЭНЕРГИИ) Тело … обладает потенциальной энергией, но не обладает кинетической (ТОЛЬКО 1 ВИД ЭНЕРГИИ) Тело обладает и кинетической и потенциалной энергиями (2 ВИДА ЭНЕРГИИ) Тело НЕ обладает ни кинетической не потенциальной энергиями (НЕТ МЕХАНИЧЕСКОЙ ЭНЕРГИИ) А В С Д 1 2 3 45 6 7 89 10 11 12
Как найти длину пути в физике
В физике следует различать траекторию, путь и перемещение.
Определение 1
Траектория – форма линии, описываемая телом. Ее длина представляет собой путь и является скалярной величиной. Перемещением же называется вектор, соединяющий точки начала и конца пути, и направленный от начала к концу.
Длина пути измеряется в системе СИ в метрах, в СГС (сантиметр, грамм, секунда) – в сантиметрах. Применяются и другие единицы измерения длины, в том числе внесистемные (дюйм, фут, ярд, миля и т.д.).
При движении без ускорения путь равен произведению скорости на расстояние:
$S = v \cdot (t_2 – t_1) = v \cdot \Delta t$,
где $v_0$ – скорость тела, $t_2$ — момент времени окончания движения, $t_1$ — момент времени начала движения, $\Delta t$ – время движения. График зависимости пути от времени на координатной плоскости в случае такого, называемого равномерным, движения является прямой линией.
Замечание 1
Поскольку скорость – векторная величина, равномерным можно считать только движение по прямой, т.
2}{2} + 10 \cdot 20 = 600 м$.
Ответ: длина пути составила 600 метров.
Расчет пути и времени движения
Зная скорость равномерного движения тела, можно узнать путь, пройденный им за определенное время. Пусть, например, поезд равномерно движется со скоростью 20 м/с. Это значит, что за каждую секунду он проходит путь 20 м. Тогда за 5 с поезд пройдет путь в 5 раз больший, чем за 1 с, т. е. 20 м/с * 5 с = 100 м, а за 10 с – в 10 раз больший, т. е. 20 м/с * 10 с =200 м и т. д.
Чтобы определить путь, пройденный при равномерном движении, надо скорость тела умножить на время его движения:
s = vt
Зная путь и скорость равномерного движения тела, можно определить время этого движения.
Определим, за какое время пешеход, скорость движения которого 1,5 м/с, пройдет путь, равный 3 км, т. е. 3000 м.
Из формулы s=vt следует, что:
t = s/v
Подставляя в эту формулу числовое значение пути и скорости, мы найдем время: t = 3000 м/ 1,5 м/с = 2000 с.
Среднюю скорость неравномерного движения вычисляют, предполагая, что движение является равномерным. Поэтому если нужно по средней скорости вычислить путь, то можно воспользоваться правилом, установленным для равномерного движения. Таким образом, путь, пройденный телом при неравномерном движении, равен произведению средней скорости на время движения, т. е.
s = vсрt.
Время, необходимое для прохождения какого-нибудь пути при неравномерном движении, равно частному от деления этого пути на среднюю скорость.
Вопросы. 1. Как определяют путь, пройденный телом при равномерном движении, если известны скорость и время движения? Как по пути и скорости определить время равномерного движения? 2. Ответьте на такие же вопросы для случая неравномерного движения.
Упражнение. 1. Найдите в таблице 1 скорости пешехода, конькобежца, поезда и определите (устно) пути, пройденные этими телами за 10 с.
2. Самолет летит со средней скоростью 750 км/ч. Какой путь он пройдет за 6 ч полета? 3. Какое время понадобится поезду и самолету для прохождения пути 4000 м? (Скорости этих тел указаны в таблице 1.) 4. На рисунке 29 изображен график пути равномерного движения. На этом графике Os — ось пройденных путей; Ot — ось времени. Определите по этому графику путь, пройденный за 10 ч, и скорость движения. 5. На рисунке 30 изображены графики путей двух равномерных движений I и II. По графикам определите, скорость какого из этих движений больше. Ответ обоснуйте. 6. На рисунке 31 дан график скорости равномерного движения тела. Чему равна скорость движения тела? Определите путь, пройденный телом за 5 с.
Механика. Формулы по физике – Физика для всех
Кинематика
| Обозначение | Измеряется в | Описание |
|---|---|---|
| S | м | пройденный путь |
| v | м/с | скорость |
| t | с | время |
| x | м | координата |
| a | м/с2 | ускорение |
| ω | с-1 | угловая скорость |
| T | с | период |
| ν | Гц | частота |
| ε | с-2 | угловое ускорение |
| R | м | радиус |
Скорость и ускорение:
Равномерное движение: ν = const
Равнопеременное движение:
Криволинейное движение:
Вращательное движение:
Динамика и статика
| Обозначение | Измеряется в | Описание |
|---|---|---|
| F | Н | сила |
| P | кг*м/с | импульс |
| a | м/с2 | ускорение |
| m | кг | масса |
| v | м/с | скорость |
| p | Н | вес тела |
| g | м/с2 | ускорение свободного падения |
| E | Дж | энергия |
| A | Дж | работа |
| N | Вт | мощность |
| t | с | время |
| I | кг*м2 | момент инерции |
| L | кг*м2/с | момент импульса |
| M | Н*м | момент силы |
| ω | с-1 | угловая скорость |
Первый закон Ньютона:
При ∑ F = 0 => v = const
Второй закон Ньютона:
Третий закон Ньютона:
Основной закон динамики для неинерциальных систем отчета.
ma=ma0+Fинерц ,где а- ускорение в неинерциальной а0– в инерциальной системе отчета.
Скорость центра масс:
Закон всемирного тяготения:
Вес тела:
Сила трения:
Закон Гука:
Закон Гука: σ = Eε, где Е- модуль Юнга.
Динамика и статика вращательного движения:
| система | ось | I |
| точка по окружности | ось симметрии | mR2 |
| стержень | через середину | 1/12 mR2 |
| стержень | через конец | 1/3 mR2 |
| шар | через центр шара | 2/5 mR2 |
| сфера | через центр сферы | 2/3 mR2 |
| кольцо или тонкостенный цилиндр | ось симметрии | mR2 |
| диск сплошной цилиндр | ось симметрии | 1/2 mR2 |
Условие равновесия тел ∑ M = 0
Закон сохранения импульса:
Потенциальная и кинетическая энергия.
Мощность:
Закон сохранения энергии:
Калькулятор траектории – Движение снаряда
Используйте этот калькулятор траектории для определения траектории полета снаряда. Введите три значения: скорость, угол и начальную высоту, и вы сразу же найдете формулу траектории и ее форму. Продолжайте читать, если хотите проверить определение траектории, а также простой пример расчетов.
Определение траектории
Траектория, также называемая траекторией полета, – это путь, по которому движущийся объект находится под действием силы тяжести .Обычно этот термин используется, когда мы говорим о снарядах или спутниках (где регулярно повторяющаяся траектория называется орбитой). Если объект брошен на короткие расстояния, парабола является хорошим приближением формы траектории.
Некоторые примеры движения снаряда:
- Хоккейная шайба, мяч для бейсбола или гольфа в полете ⚾
- пуля, выпущенная из оружия 🔫
- Струя воды из фонтана ⛲
- Предмет, брошенный со стола / самолета / здания / моста ✈️
Формула траектории
Теперь, когда вы знаете определение траектории, давайте проверим, как выглядит формула траектории.
- Начнем с уравнений движения:
-
x = Vx * t -
y = h + Vy * t - g * t² / 2
- Поскольку мы знаем, что три вектора –
V₀,VxиVy– образуют прямоугольный треугольник, мы можем записать, что:
- Горизонтальная составляющая скорости
VxравнаV₀ * cos (α). - Вертикальная составляющая скорости
Vy = V₀ * sin (α).
- Затем объединяем уравнения движения и составляющие скорости в одну формулу:
-
x = Vx * t=>t = x / Vx -
y = h + Vy * t - g * t² / 2 = h + x * Vy / Vx - g * (x / Vx) ² / 2 -
y = h + x * (V₀ * sin (α)) / (V₀ * cos (α)) - g * (x / V₀ * cos (α)) ² / 2
И, как мы знаем, синус по косинусу – это определение тангенса.
Итак, окончательная формула траектории может быть выражена как:
-
y = h + x * tan (α) - g * x² / 2 * V₀² * cos² (α)
Если вас интересуют различные аспекты движения снаряда, воспользуйтесь другими нашими специальными инструментами для расчета:
Калькулятор траектории: как использовать
Давайте посмотрим, как движется вода из фонтана:
- Введите скорость . Предположим, что это 5 футов / с.
- Введите угол . Например, 60 °.
- Выберите начальную высоту . Выберем 5 дюймов.
- Вот, пожалуйста! Калькулятор траектории отображает формулу и траекторию полета!
Важнейшая вещь, на которую следует обратить внимание, – это возможная разница в масштабировании осей, поэтому угол может не выглядеть на графике должным образом. Помните, что во всех расчетах не учитывается сопротивление воздуха.
Формула траектории
Снаряд – это объект, которому задана начальная скорость, и на который действует сила тяжести.
Путь, по которому следует объект, называется его траекторией. Траектория имеет горизонтальную (x) и вертикальную (y) компоненты положения. Если снаряд запускается с начальной скоростью v 0 под углом θ к горизонтальной плоскости, то его вертикальное положение можно определить из его горизонтального положения по следующей формуле. Единицы измерения горизонтального и вертикального положения – метры ( м ).
y = вертикальное положение ( м )
x = горизонтальное положение ( м )
v 0 = начальная скорость (комбинированные компоненты, м / с )
g = ускорение свободного падения (9.80 м / с 2 )
θ = угол начальной скорости относительно горизонтальной плоскости (радианы или градусы)
Вопросы по формуле траектории:
1) Бейсболист ударяет по мячу, отбрасывая его от биты со скоростью 45,0 м / с и под углом 66,4 ° относительно поля.
В направлении движения мяча конец поля находится на расстоянии 140,0 м . Какова высота мяча, когда он достигает конца поля?
Ответ: Высота мяча – это его вертикальное положение.Горизонтальное положение, представляющее интерес в этом вопросе, – это конец поля, x = 140,0 м . Вертикальное положение y должно быть решено. В вопросе представлены угол θ и начальная скорость v 0 . Формулу траектории можно использовать для решения относительно y :
Вертикальное положение мяча в конце поля ( x = 140.0 м ) есть.
2) Водный лыжник устроил трюк, в котором он планирует перепрыгнуть горящее препятствие. Огонь будет на расстоянии 4,00 м от пандуса на м и на 1,00 м на м выше высоты пандуса. Если аппарель наклонена под углом 36,9 ° по отношению к воде, и он планирует взлететь с аппарели со скоростью 9,00 м / с , сможет ли он перепрыгнуть через пламя?
Ответ: Представляющим интерес горизонтальным положением является положение горящего препятствия относительно рампы.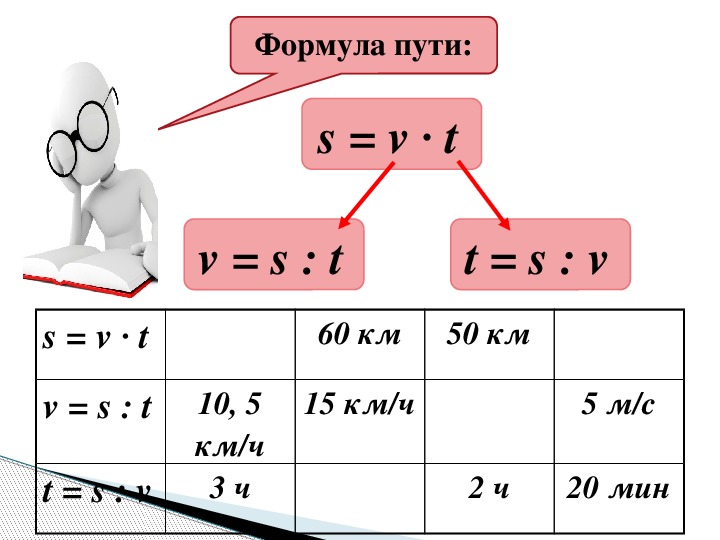
Это означает, что положение x равно x = 4,00 м . Вертикальное положение y должно быть решено. В вопросе представлены угол θ и начальная скорость v 0 . Формулу траектории можно использовать для решения относительно y :
Вертикальное положение лыжника при горизонтальном положении х = 4.00 м будет. Это больше, чем высота горящего препятствия 1,00 м , поэтому водный лыжник сможет его перепрыгнуть.
Веб-сайт класса физики
Круговое движение и гравитация: обзор набора задач
Этот набор из 27 задач нацелен на вашу способность комбинировать законы Ньютона и уравнения кругового движения и гравитации для анализа движения объектов, движущихся по кругу, включая орбитальные спутники.Проблемы варьируются по сложности от очень простых и простых до очень сложных и сложных.
Более сложные задачи обозначены цветом , синие проблемы .
Характеристики движения объектов, движущихся по кругам.
Объекты, движущиеся по кругу, имеют скорость, равную пройденному за время пути расстоянию. Расстояние вокруг круга эквивалентно длине окружности и рассчитывается как 2 • pi • R, где R – радиус.Время одного оборота по окружности называется периодом и обозначается символом T. Таким образом, средняя скорость объекта, движущегося по кругу, определяется выражением 2 • pi • R / T. Часто в постановке задачи указывается частота вращения в оборотах в минуту или в оборотах в секунду. Каждый оборот по окружности эквивалентен длине окружности. Таким образом, умножение частоты вращения на длину окружности позволяет определить среднюю скорость объекта.
Ускорение объектов, движущихся по кругу, основано в первую очередь на изменении направления. Фактическая скорость ускорения зависит от скорости изменения направления и напрямую связана со скоростью и обратно пропорциональна радиусу поворота.
В итоге ускорение определяется выражением v 2 / R, где v – скорость, а R – радиус окружности.
Уравнения для средней скорости (v) и среднего ускорения (a) приведены ниже.
v = d / t = 2 • pi • R / T = частота • 2 • pi • R
а = v 2 / R
Направленные величины для объектов, движущихся по кругам
Успешный математический анализ объектов, движущихся по кругу, во многом зависит от концептуального понимания направления векторов ускорения и результирующей силы. Движение по круговой траектории требует чистой силы, направленной к центру круга.В каждой точке пути результирующая сила должна быть направлена внутрь. Хотя может существовать отдельная сила, направленная наружу, должна существовать внутренняя сила, которая подавляет ее по величине и удовлетворяет требованию для внутренней чистой силы. Поскольку чистая сила и ускорение всегда в одном и том же направлении, ускорение объектов, движущихся по кругу, также должно быть направлено внутрь.
Диаграммы свободного тела и второй закон Ньютона
Часто силовой анализ должен проводиться для объекта, движущегося по кругу.Целью анализа является определение величины отдельной силы, действующей на объект, или использование значений отдельных сил для определения ускорения. Как и любая задача анализа сил, эти задачи должны начинаться с построения диаграммы свободного тела, показывающей тип и направление всех сил, действующих на объект. Из диаграммы F net = m • можно записать уравнение. При написании уравнения помните, что сетка F представляет собой векторную сумму всех индивидуальных сил.Лучше всего это записывать, складывая все силы, действующие в направлении ускорения (внутрь), и вычитая те, которые ему противостоят. Два примера показаны на рисунке ниже.
Закон всемирного тяготения Ньютона
Спутники, движущиеся по орбите, – это просто снаряды – объекты, на которые действует только сила тяжести.
Сила, управляющая их движением, – это сила гравитационного притяжения к объекту, который находится в центре их орбиты.Планеты вращаются вокруг Солнца в результате гравитационной силы притяжения к Солнцу. Естественные луны вращаются вокруг планет в результате гравитационной силы притяжения к планете. Гравитация – это сила, которая действует на больших расстояниях таким образом, что любые два объекта с массой будут притягиваться. Ньютон был первым, кто предложил теорию, чтобы описать это универсальное массовое притяжение и выразить его математически. Закон, известный как закон всемирного тяготения, гласит, что сила гравитационного притяжения прямо пропорциональна произведению масс и обратно пропорциональна квадрату расстояния между их центрами.В форме уравнения:
F grav = G • m 1 • m 2 / d 2
где m 1 и m 2 – массы притягивающих объектов (в кг), а d – расстояние разделения, измеренное от центра объекта до центра объекта (в метрах), а G – константа пропорциональности (иногда называемая всемирная гравитационная постоянная).
Значение G составляет 6,673 x 10 -11 Н • м 2 / кг 2 .
Ускорение свободного падения
Поскольку на орбитальные спутники действует исключительно сила тяжести, их ускорение является ускорением силы тяжести (g). На земной поверхности это значение составило 9,8 м / с 2 . Для местоположений, отличных от поверхности Земли, необходимо уравнение, которое выражает g через соответствующие переменные. Ускорение свободного падения зависит от массы объекта, который находится в центре орбиты (M central ), и расстояния разделения от этого объекта (d).Уравнение, связывающее эти две переменные с ускорением свободного падения, получено из закона всемирного тяготения Ньютона. Уравнение
g = G • M центральный / d 2
где G составляет 6,673 x 10 -11 Н • м 2 / кг 2 .
Орбитальная скорость
Скорость, необходимая для того, чтобы спутник оставался на орбите вокруг центрального тела (планеты, солнца, другой звезды и т.
Д.).) зависит от радиуса орбиты и массы центрального тела. Уравнение, выражающее взаимосвязь между этими переменными, получается путем объединения определений ускорения кругового движения с законом всемирного тяготения Ньютона. Уравнение
v = SQRT (G • M центральный / R)
где M central – масса центрального тела, вокруг которого вращается спутник, R – радиус орбиты, а G – 6,673 x 10 -11 Н • м 2 / кг 2 .
Орбитальный период
Для общего движения объекта по кругу период связан с радиусом круга и скоростью объекта уравнением v = 2 • pi • R / T. В случае орбитального спутника это уравнение для скорости можно приравнять к уравнению для орбитальной скорости, полученной из всемирного тяготения, чтобы получить новое уравнение для орбитального периода. Результат вывода:
T 2 / R 3 = 4 • pi 2 / (G • M центральный )
где M central – масса центрального тела, вокруг которого вращается спутник, R – радиус орбиты, а G – 6.
673 x 10 -11 Н • м 2 / кг 2 . Выраженное таким образом уравнение показывает, что отношение квадрата периода к радиусу в кубе для любого спутника, вращающегося вокруг центрального тела, одинаково независимо от природы спутника или радиуса его орбиты. Это соотношение зависит только от массы объекта, который втягивает орбитальный спутник внутрь. Этот принцип согласуется с третьим законом движения планет Кеплера.
Резюме математических формул
Одна из трудностей, с которыми может столкнуться учащийся в этом наборе задач, – это путаница относительно того, какую формулу использовать.В таблице ниже представлено полезное резюме формул, относящихся к круговому движению и движению спутника. В таблице многие формулы получены из других уравнений. Таким образом, часто будет несколько способов определения неизвестной величины. Подходя к этим проблемам, рекомендуется практиковать обычные привычки эффективного решателя проблем; определить известные и неизвестные величины в виде символов физических формул, разработать стратегию использования известных для решения неизвестного, а затем, наконец, выполнить необходимые алгебраические шаги и замены, необходимые для решения.
| Для расчета … | … используйте уравнение (а): |
|---|---|
| Скорость (v) | v = 2 • pi • R / T v = SQRT (G • M центральный / R) только для спутников |
| Разгон (а) | a = v 2 / R или a = F net / m a = g = G • M центральный / d 2 только для сателлитов |
| Чистая сила (F net ) | F net = m • a или F net = m • v 2 / R F net = F grav = G • m sat • M центральный / d 2 только для спутников |
| Период (Т) | T = 2 • pi • R / v T 2 = 4 • pi 2 / (G • M центральный ) • R 3 только для спутников |
Привычки эффективно решать проблемы
Эффективный решатель проблем по привычке подходит к физической проблеме таким образом, который отражает набор дисциплинированных привычек.
Хотя не все эффективные специалисты по решению проблем используют один и тот же подход, все они имеют общие привычки. Эти привычки кратко описаны здесь. Эффективное решение проблем …
- … внимательно читает задачу и создает мысленную картину физической ситуации. При необходимости они набрасывают простую схему физической ситуации, чтобы помочь визуализировать ее.
- … определяет известные и неизвестные величины в организованном порядке, часто записывая их на диаграмме.Они приравнивают заданные значения к символам, используемым для представления соответствующей величины (например, m = 61,7 кг, v = 18,5 м / с, R = 30,9 м, F norm = ???).
- … строит стратегию решения неизвестной величины; стратегия, как правило, сосредоточена вокруг использования физических уравнений и во многом зависит от понимания физических принципов.
- … определяет подходящую (ые) формулу (ы) для использования, часто записывая их. При необходимости они выполняют необходимое преобразование количеств в правильные единицы.
- … выполняет подстановки и алгебраические манипуляции, чтобы найти неизвестную величину.
Подробнее …
Дополнительная литература / Учебные пособия:
Следующие страницы из учебного пособия по физике могут быть полезны для понимания концепций и математики, связанных с этими проблемами.
Набор задач кругового движения и гравитации
Просмотреть набор задач
Решения с аудиогидом для кругового движения и гравитации
Просмотрите аудиогид решения проблемы:1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27
Как рассчитывать траектории | Sciencing
Обновлено 28 декабря 2020 г.
Кевин Бек
Движение снаряда относится к движению частицы, которой передается начальная скорость, но впоследствии на нее не действуют никакие силы, кроме силы тяжести.
Сюда входят задачи, в которых частица отбрасывается под углом от 0 до 90 градусов к горизонтали, причем горизонталь обычно является землей. Для удобства предполагается, что эти снаряды движутся в плоскости ( x, y ), причем x представляют горизонтальное смещение, а y вертикальное смещение.
Путь, пройденный снарядом, называется его траекторией . (Обратите внимание, что общее звено между «снарядом» и «траекторией» – это слог «-дъект», латинское слово, означающее «бросок».«Катапультировать кого-то означает буквально выбросить его.) Точка происхождения снаряда в задачах, в которых вам нужно вычислить траекторию, обычно принимается равной (0, 0) для простоты, если не указано иное.
Траектория полета снаряд представляет собой параболу (или, по крайней мере, отслеживает часть параболы), если частица запускается таким образом, что имеет ненулевую горизонтальную составляющую движения и отсутствует сопротивление воздуха, которое могло бы воздействовать на частицу.
Кинематика Уравнения
Переменными, представляющими интерес в движении частицы, являются ее координаты положения x и y , ее скорость v и ее ускорение a , все в соотношении к заданному истекшему времени t с момента начала проблемы (когда частица запущена или выпущена).Обратите внимание, что отсутствие массы (m) означает, что гравитация на Земле действует независимо от этой величины.
Отметим также, что эти уравнения игнорируют роль сопротивления воздуха, которое создает силу сопротивления, противодействующую движению в реальных земных условиях. Этот фактор вводится на курсах механики более высокого уровня.
Переменные с нижним индексом «0» относятся к значению этой величины в момент времени t = 0 и являются константами; часто это значение равно 0 благодаря выбранной системе координат, и уравнение становится намного проще.2-2g (y-y_0)
Примеры движения снаряда
Ключом к решению задач, включающих расчет траектории, является знание того, что горизонтальная (x) и вертикальная (y) компоненты движения могут быть проанализированы отдельно , как показано выше, и их соответствующие вклады в общее движение аккуратно суммированы в конце задачи.
Проблемы с движением снаряда считаются проблемами свободного падения, потому что независимо от того, как все выглядит сразу после времени t = 0, единственной силой, действующей на движущийся объект, является гравитация.
- Имейте в виду, что, поскольку сила тяжести направлена вниз, а это считается отрицательным направлением оси y, значение ускорения в этих уравнениях и задачах равно -g.
Расчет траектории
1. Самые быстрые питчеры в бейсболе могут бросать мяч со скоростью чуть более 100 миль в час или 45 м / с. Если мяч брошен вертикально вверх с этой скоростью, насколько высоко он поднимется и сколько времени потребуется, чтобы вернуться в точку, в которой он был выпущен?
Здесь v y0 = 45 м / с, – g = –9.8 м / с, а интересующие нас величины – это максимальная высота, или y, и полное время возвращения на Землю.
2 – (2) (9.8) (y – 0) = 2,025 – 19,6y \ подразумевает y = 103,3 \ text {m}
Уравнение v y = v 0y – gt показывает, что время t, которое на это требуется, равно ( 45 / 9,8) = 4,6 секунды. Чтобы получить общее время, прибавьте это значение ко времени, которое требуется, чтобы мяч свободно упал в исходную точку. Это определяется как y = y 0 + v 0y t – (1/2) gt 2 , где теперь, поскольку мяч все еще находится в данный момент прежде чем он начнет резко падать, v 0y = 0.2 \ подразумевает t = 4,59 \ text {s}
Таким образом, общее время составляет 4,59 + 4,59 = 9,18 секунды. Возможно, удивительный результат, когда каждый «этап» путешествия, вверх и вниз, занимал одно и то же время, подчеркивает тот факт, что гравитация является единственной силой, действующей здесь.
2. Уравнение дальности: Когда снаряд запускается со скоростью v 0 и углом θ от горизонтали, он имеет начальную горизонтальную и вертикальную составляющие скорости v 0x = v 0 (cos θ) и v 0y = v 0 (sin θ).
2 \ sin {2 \ theta}} {g}
(Последний шаг следует из тригонометрического тождества 2 sinθ ⋅ cosθ = sin 2θ.2} {g}
% PDF-1.6
%
196 0 объект
>
эндобдж
xref
196 88
0000000016 00000 н.
0000002463 00000 н.
0000002576 00000 н.
0000003307 00000 н.
0000003494 00000 н.
0000004086 00000 н.
0000004662 00000 н.
0000005132 00000 н.
0000008710 00000 н.
0000008822 00000 н.
0000009414 00000 н.
0000010053 00000 п.
0000010682 00000 п.
0000010866 00000 п.
0000011401 00000 п.
0000011935 00000 п.
0000012378 00000 п.
0000012790 00000 п.
0000013302 00000 п.
0000013634 00000 п.
0000013721 00000 п.
0000013852 00000 п.
0000014176 00000 п.
0000014649 00000 п.
0000014763 00000 п.
0000015268 00000 п.
0000015865 00000 п.
0000016355 00000 п.
0000017955 00000 п.
0000018285 00000 п.
0000018596 00000 п.
0000018952 00000 п.
0000020272 00000 п.
0000020556 00000 п.
0000020877 00000 п.
0000021657 00000 п.
0000021986 00000 п.
0000022980 00000 п.
0000023269 00000 п.
0000024587 00000 п.
0000025115 00000 п.
0000025464 00000 п.
0000025862 00000 п.
0000026203 00000 п.
0000026636 00000 п.
0000027181 00000 п.
0000027527 00000 п.
0000028883 00000 п.
0000029065 00000 н.
0000030478 00000 п.
0000030592 00000 п.
0000030756 00000 п.
0000030973 00000 п.
0000031315 00000 п.
0000031473 00000 п.
0000031840 00000 п.
0000032286 00000 п.
0000036189 00000 п.
0000037997 00000 п.
0000038729 00000 п.
0000039093 00000 п.
0000039581 00000 п.
0000040832 00000 п.
0000042283 00000 п.
0000043757 00000 п.
0000049972 00000 н.
0000057291 00000 п.
0000061943 00000 п.
0000066030 00000 п.
0000069993 00000 н.
0000072788 00000 п.
0000077171 00000 п.
0000077438 00000 п.
0000077872 00000 н.
0000077901 00000 п.
0000078301 00000 п.
0000078398 00000 п.
0000078544 00000 п.
0000078828 00000 п.
0000079128 00000 п.
0000079249 00000 п.
0000079395 00000 п.
0000081371 00000 п.
0000081730 00000 п.
0000082136 00000 п.
0000082249 00000 п.
\ circ $, либо под углом $ \ theta $.
В первом случае его путь приводит к круговой траектории, а во втором случае образуется спиральная траектория.
Теперь мы хотим ответить на этот вопрос: почему заряженные частицы движутся по спирали?
Как только заряженная частица входит в магнитное поле $ B $ под некоторым углом $ \ theta $, ее скорость можно разложить на параллельную и вертикальную составляющие относительно вектора магнитного поля $ B $, которые равны $ v _ {\ parallel} = v \, \ cos \ theta $ и $ v _ {\ bot} = v \, \ sin \ theta $.{\ circ} = q \, v _ {\ bot} \, B $, что заставляет заряженную частицу равномерно двигаться по круговой траектории.
Эти два вышеуказанных движения, равномерное движение, параллельное полю $ B $ и равномерное круговое движение, перпендикулярное полю $ B $, создают реальный путь заряженной частицы в однородном магнитном поле $ B $, которое похоже на пружину и называется спиральной или винтовой.
Характеристики винтовой траектории:
Каждая спиральная траектория имеет три различных характеристики: радиус, период времени и шаг.{2}} R \\ \\ \ Rightarrow R & = \ frac {m \, v _ {\ bot}} {q \, B} \\ \\ & = \ frac {mv \, \ sin \ theta} {qB } \ end {align *} Где $ m $ – масса заряженной частицы.
Период времени: Время, необходимое для совершения одного оборота, получается путем определения средней скорости как \ begin {align *} v & = \ frac {\ Delta x} {\ Delta t} \\ \\ v _ {\ bot} & = \ frac {2 \ pi \, R} {T} \\ \\ \ Rightarrow T & = \ frac {2 \ pi \, R} {v _ {\ bot}} \\ \\ & = \ frac {2 \ pi} {q \, B} \, m \ end {align *}, где выше мы использовали предыдущую формулу для $ R $ и $ v _ {\ bot} = v \, \ sin \ theta $.Этот период также называется циклотронным периодом, а его частота является обратной величине периода по формуле \ [f = \ frac 1T = \ frac {q \, B} {2 \ pi \, m} \]
Шаг спирали: расстояние, пройденное параллельно магнитному полю $ B $ за один оборот, называется шагом спиральной траектории и получается как \ begin {align *} p & = v _ {\ parallel} \, T \\ & = (v \, \ cos \ theta) \, \ left (\ frac {2 \ pi \, m} {q \, B} \ right) \ end {align *} Таким образом, формула для шага спираль – $ p = \ frac {2 \ pi \, mv \, \ cos \ theta} {q \, B} $.
{\ circ} $ создается круговое движение.
Последнее обновление: 02.09.2020
Криволинейное движение
Общее криволинейное движениеКриволинейное движение определяется как движение, которое происходит, когда частица движется по криволинейной траектории.Изогнутый путь может быть двухмерным (на плоскости) или трехмерным. Этот тип движения более сложен, чем прямолинейное (прямолинейное) движение.
Трехмерное криволинейное движение описывает наиболее общий случай движения частицы.
Чтобы найти скорость и ускорение частицы, испытывающей криволинейное движение, нужно только знать положение частицы как функцию времени.
Допустим, нам дано положение частицы P в трехмерных декартовых координатах ( x , y , z ) относительно времени, где
Скорость частицы P определяется выражением
Ускорение частицы P определяется выражением
Как видите, если мы знаем положение частицы как функцию времени, это довольно простое упражнение для определения скорости и ускорения.
Вы просто берете первую производную, чтобы найти скорость, и вторую производную, чтобы найти ускорение.
Величина скорости частицы P определяется выражением
Величина ускорения частицы P определяется выражением
Обратите внимание, что направление скорости частицы P всегда касается кривой (т. Е. Пройденного пути, обозначенного синей кривой на рисунке выше). Но направление ускорения обычно , а не касательно кривой.
Однако касательная к кривой составляющая ускорения равна производной по времени от величины скорости частицы P (вдоль кривой). Другими словами, если v t – величина скорости частицы (касательная к кривой), компонент ускорения касательной к кривой частицы ( a t ) просто
Кроме того, нормальная к кривой составляющая ускорения ( a n ) определяется выражением
, где R – радиус кривизны кривой в данной точке кривой ( x p , y p , z p ).
На рисунке ниже показаны компоненты ускорения a t и a n в заданной точке кривой ( x p , y p , z p ).
Для конкретного случая, когда путь синей кривой задается как y = f (x) (двумерное движение), радиус кривизны R определяется как
где | x | означает «абсолютное значение» x .Например, | -2,5 | = 2,5 и | 3,1 | = 3,1.
Однако обычно нет необходимости знать радиус кривизны R вдоль кривой. Но, тем не менее, информативно понимать это на основе его отношения к нормальному ускорению ( a n ).
Криволинейное движение в полярных координатах
Иногда удобно выразить плоское (двумерное) движение частицы в терминах полярных координат ( R , θ ), чтобы мы могли явно определить скорость и ускорение частицы в радиальном направлении. ( R, – направление) и круговое ( θ, – направление).
Для этого типа движения частица может двигаться только в радиальном направлении R для заданного угла θ .
Для частицы P , определенной в полярных координатах (как показано ниже), мы можем вывести общее уравнение для ее радиальной скорости ( v r ), радиального ускорения ( a r ), окружной скорости ( v c ) и окружное ускорение ( a c ).
Обратите внимание, что окружное направление перпендикулярно радиальному направлению.
Положение частицы P дано относительно времени, где
Чтобы найти скорость, возьмите первую производную от x (t) и y (t) по времени:
Чтобы найти ускорение, возьмите вторую производную от x (t) и y (t) по времени:
Без ограничения общности мы можем оценить скорости и ускорения под углом θ = 0, зная, что (под этим углом) радиальная скорость и радиальное ускорение находятся в направлении x , а окружная скорость и окружное ускорение находится в направлении y .
Установив θ = 0, мы имеем:
Уравнения (1), (2), (3) и (4) полностью описывают криволинейное движение частицы P в полярных координатах.
Член dθ / dt называется угловой скоростью. Единицы измерения рад / с. Один рад (радиан) = 57,296 градуса.
Член d 2 θ / dt 2 называется угловым ускорением. Имеет единицы рад / с 2 .
Поскольку v r и v c перпендикулярны друг другу, величина скорости частицы P определяется как
Поскольку a r и a c перпендикулярны друг другу, величина ускорения частицы P определяется как
Пример задачи для криволинейного движения
Щелевое звено вращается вокруг неподвижной оси O с угловой скоростью против часовой стрелки 3 рад / с и угловым ускорением по часовой стрелке 2 рад / с 2 .
Движение звена заставляет шток скользить по изогнутому каналу, как показано. Радиус канала как функция θ определяется как R = 0,7 θ (при R в метрах и θ в радианах). Определите компоненты скорости и ускорения стержня при θ = 45 °
Решение
Угол θ = 45 ° равен π /4 радиан. В уравнениях угловая скорость против часовой стрелки положительна, а угловое ускорение по часовой стрелке отрицательно (так как оно «замедляет» скорость вращения звена).
Радиальная скорость стержня определяется уравнением (1):
(Радиальная скорость в направлении увеличения R ).
Окружная скорость стержня определяется уравнением (3):
(окружная скорость в направлении увеличения θ ).
Радиальное ускорение стержня определяется уравнением (2):
(Радиальное ускорение в сторону уменьшения R ).
Окружное ускорение стержня определяется уравнением (4):
(Окружное ускорение в направлении увеличения θ ).