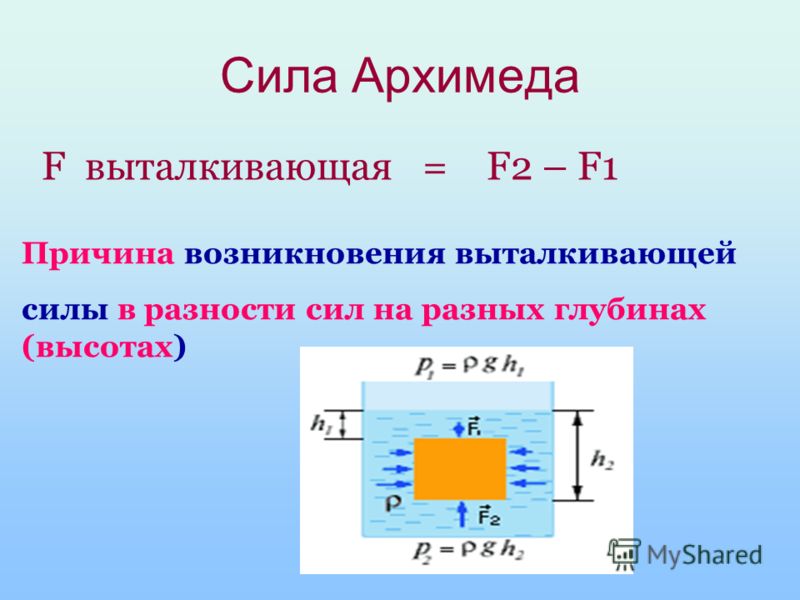
определение и формула. Какое значение имеет закон Архимеда
Проделаем простой эксперимент: возьмем слабо надутый резиновый мяч и «притопим» его в воде. Если глубина погружения будет даже 1-2 метра, то нетрудно видеть, что его объем уменьшится, т.е. со всех сторон мяч обжала некая сила. Обычно говорят, что здесь «виновато» гидростатическое давление – физический аналог силы, действующей в неподвижных жидкостях на погруженное тело. Гидростатические силы действуют на тело со всех сторон, а их результирующая, известная как архимедова сила, еще называется выталкивающей, что соответствует ее направлению действия на погруженное в жидкость тело.
Архимед открыл свой закон чисто экспериментально, а его теоретическое обоснование ждало еще почти 2000 лет до того, как Паскаль открыл для неподвижной жидкости. Согласно этому закону давление передается через жидкость по всем направлениям независимо от площади, на которую оно действует, на все плоскости, ограничивающие жидкость, а его величина P пропорциональна поверхности S и направлена по нормали к ней.
Допустим, что в сосуд с водой погружено тело в форме куба с ребром L на глубину H – расстояние от поверхности воды до верхней грани. При этом нижняя грань находится на глубине H+L. Вектор силы F1, действующей на верхнюю грань, направлен вниз и F1 = r * g * H * S, где r – плотность жидкости, g – ускорение
Вектор силы F2, действующей на нижнюю плоскость, направлен вверх, а ее величина определяется выражением F2 = r * g * (H+L) * S .
Векторы сил, действующих на боковые поверхности, взаимно уравновешиваются, поэтому в дальнейшем из рассмотрения исключаются. Архимедова сила F2 > F1 и направлена снизу вверх, и приложена к нижней грани куба. Определим ее величину F:
F = F2 – F1 = r * g * (H+L) * S – r * g * H * S = r * g * L * S
Заметим, что L * S – это объем куба V, а т. к. r * g = p представляет собой вес единицы жидкости, то формула архимедовой силы определяет вес объема жидкости, равный объему куба, т. е. это как раз и есть вес вытесненной телом жидкости. Интересно, что говорить о возможно только для среды, где присутствует сила тяжести – в условиях невесомости закон не работает. Окончательно формула закона Архимеда имеет следующий вид:
е. это как раз и есть вес вытесненной телом жидкости. Интересно, что говорить о возможно только для среды, где присутствует сила тяжести – в условиях невесомости закон не работает. Окончательно формула закона Архимеда имеет следующий вид:
F = p * V, где p – удельный вес жидкости.
Архимедова сила может служить основанием для анализа плавучести тел. Условием для анализа служит соотношение веса погруженного тела Рт и веса жидкости Рж с объемом, равным объему погруженной в жидкость части тела. Если Рт = Рж, то тело плавает в жидкости, а если Рт > Рж, то тело тонет. В противном случае тело всплывает, пока выталкивающая сила не сравняется с весом вытолкнутой утопленной частью тела воды.
Закон Архимеда и его использование имеют длинную историю в технике, начиная с классического примера применения во всех известных плавсредствах и до воздушных шаров и дирижаблей. Здесь сыграло роль то, что газ относится к такому состоянию вещества, которое вполне моделирует жидкость. При этом, в воздушной среде на любые предметы действует архимедова сила, сродни такой же, как в жидкости.
Закон Архимеда – закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.
История вопроса
«Эврика!» («Нашел!») – именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу.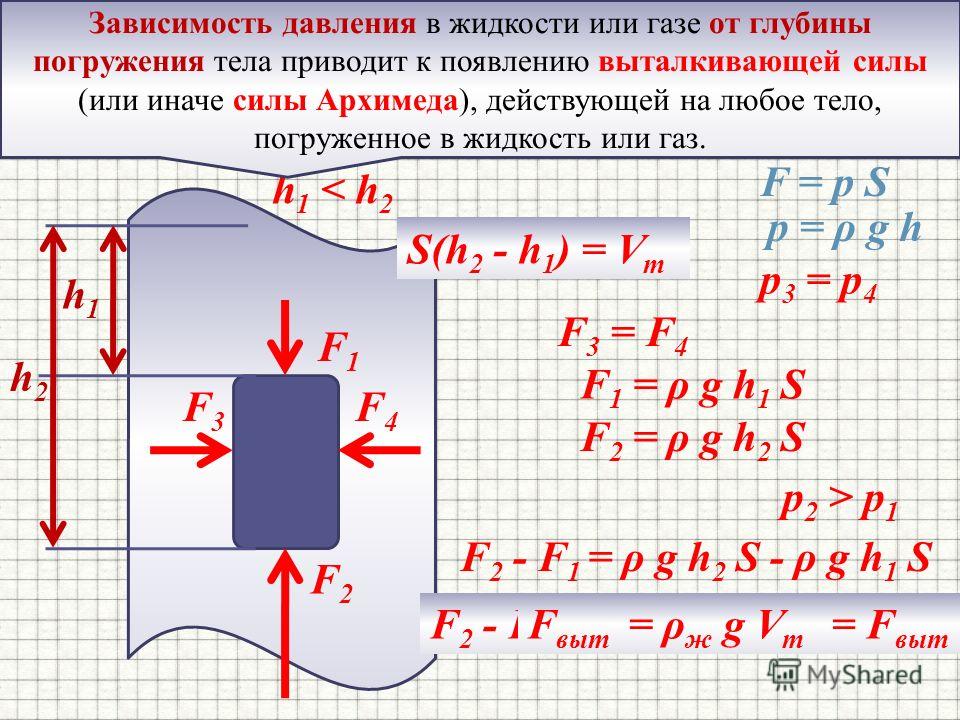 Взвесить корону Архимеду труда не составило, но этого было мало – нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото. Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Взвесить корону Архимеду труда не составило, но этого было мало – нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото. Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Однако, что правда – то правда: именно Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Закон Архимеда и молекулярно-кинетическая теория
В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Таково объяснение выталкивающей силы на молекулярном уровне.
Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.
Формулировка и пояснения
Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается поднять на суше.
Существование гидростатического давления приводит к тому, что на любое тело, находящееся в жидкости или газе, действует выталкивающая сила. Впервые значение этой силы в жидкостях определил на опыте Архимед. Закон Архимеда формулируется так:
Формула
Сила Архимеда, действующая на погруженное в жидкость тело, может быть рассчитана по формуле: F А = ρ ж gV пт,
где ρж – плотность жидкости,
g – ускорение свободного падения,
Vпт – объем погруженной в жидкость части тела.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести Fт и архимедовой силы FA, которые действуют на это тело. Возможны следующие три случая:
1) Fт > FA – тело тонет;
2) Fт = FA – тело плавает в жидкости или газе;
3) Fт
Цели урока: убедиться в существовании выталкивающей силы, осознать причины её возникновения и вывести правила для её вычисления, содействовать формированию мировоззренческой идеи познаваемости явлений и свойств окружающего мира.
Задачи урока: Работать над формированием умений анализировать свойства и явления на основе знаний, выделять главную причину, влияющую на результат. Развивать коммуникативные умения. На этапе выдвижения гипотез развивать устную речь. Проверить уровень самостоятельности мышления школьника по применению учащимися знаний в различных ситуациях.
Архимед – выдающийся ученый Древней
Греции, родился в 287 году до н. э. в портовом и
судостроительном г. Сиракузы на острове Сицилия.
Архимед получил блестящее образование у своего
отца, астронома и математика Фидия, родственника
сиракузского тирана Гиерона,
покровительствовавшего Архимеду. В юности
провёл несколько лет в крупнейшем культурном
центре в Александрии, где у него сложились
дружеские отношения с астрономом Кононом и
географом-математиком Эратосфеном. Это
послужило толчком к развитию его выдающихся
способностей. В Сицилию вернулся уже зрелым
ученым. Он прославился многочисленными научными
трудами главным образом в области физики и
геометрии.
э. в портовом и
судостроительном г. Сиракузы на острове Сицилия.
Архимед получил блестящее образование у своего
отца, астронома и математика Фидия, родственника
сиракузского тирана Гиерона,
покровительствовавшего Архимеду. В юности
провёл несколько лет в крупнейшем культурном
центре в Александрии, где у него сложились
дружеские отношения с астрономом Кононом и
географом-математиком Эратосфеном. Это
послужило толчком к развитию его выдающихся
способностей. В Сицилию вернулся уже зрелым
ученым. Он прославился многочисленными научными
трудами главным образом в области физики и
геометрии.
Последние годы жизни Архимед был в
Сиракузах, осажденных римским флотом и войском.
Шла 2-я Пуническая война. И великий ученый, не
жалея сил, организовывает инженерную оборону
родного города. Он построил множество
удивительных боевых машин, топивших вражеские
корабли, разносивших их в щепы, уничтожавших
солдат. Однако слишком маленьким было войско
защитников города по сравнению с огромным
римским войском.
Гений Архимеда вызывал восхищение у римлян и римский полководец Марцелл приказал сохранить ему жизнь. Но солдат, не знавший в лицо Архимеда, убил его.
Одним из важнейших его открытий стал закон, впоследствии названный законом Архимеда. Существует предание, что идея этого закона посетила Архимеда, когда он принимал ванну, с возгласом “Эврика!” он выскочил из ванны и нагим побежал записывать пришедшую к нему научную истину. Суть этой истины и предстоит выяснить, нужно убедиться в существовании выталкивающей силы, осознать причины её возникновения и вывести правила для её вычисления.
Давление в жидкости или газе зависит от глубины погружения тела и приводит к появлению выталкивающей силы, действующей на тело и направленной вертикально вверх.
Если тело опустить в жидкость или газ, то под
действием выталкивающей силы оно будет
всплывать из более глубоких слоев в менее
глубокие. Выведем формулу для определения силы
Архимеда для прямоугольного параллелепипеда.
Давление жидкости на верхнюю грань равно
где: h2 – высота столба жидкости над верхней гранью.
Сила давления на верхнюю грань равна
F1= р1*S = ж*g*h2*S,
Где: S – площадь верхней грани.
Давление жидкости на нижнюю грань равно
где: h3 – высота столба жидкости над нижней гранью.
Сила давления на нижнюю грань равна
F2= p2*S = ж*g*h3*S,
Где: S – площадь нижней грани куба.
Поскольку h3 > h2, то р2 > р1 и F2 > F1.
Разность между силами F2 и F1 равна:
F2 – F1 = ж*g*h3*S – ж*g*h2*S = ж*g*S* (h3 – h2).
Так как h3 – h2 = V – объему тела или части тела, погруженной в жидкость или газ, то F2 – F1 = ж*g*S*H = g* ж*V
Произведение плотности на объем есть масса жидкости или газа. Следовательно, разность сил равна весу вытесненной телом жидкости:
F2 – F1= mж*g = Pж = Fвыт.
Выталкивающая сила есть сила Архимеда, определяющая закон Архимеда
Равнодействующая сил, действующих на боковые
грани равна нулю, поэтому в расчетах не
участвует.
Таким образом, на тело, погруженное в жидкость или газ, действует выталкивающая сила равная весу вытесненной им жидкости или газа.
Закон Архимеда, впервые был упомянут Архимедом в трактате “О плавающих телах”. Архимед писал: “тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела”.
Рассмотрим, как зависит сила Архимеда и зависит ли от веса тела, объема тела, плотности тела и плотности жидкости.
Исходя из формулы силы Архимеда, она зависит от
плотности жидкости, в которую погружено тело, и
от объёма этого тела. Но она не зависит, например,
от плотности вещества тела, погружаемого в
жидкость, так как эта величина не входит в
полученную формулу.
Определим теперь вес тела, погружённого в
жидкость (или газ). Так как две силы, действующие
на тело в этом случае, направлены в
противоположные стороны (сила тяжести вниз, а
архимедова сила вверх), то вес тела в жидкости
будет меньше веса тела в вакууме на архимедову
силу:
P А = m т g – m ж g = g (m т – m ж)
Таким образам, если тело погружено в жидкость
(или газ), то оно теряет в своём весе столько,
сколько весит вытесненная им жидкость (или газ).
Следовательно:
Сила Архимеда зависит от плотности жидкости и объема тела или его погруженной части и не зависит от плотности тела, его веса и объема жидкости.
Определение силы Архимеда лабораторным методом.
Оборудование: стакан с чистой водой, стакан с соленой водой, цилиндр, динамометр.
Ход работы:
- определяем вес тела в воздухе;
- определяем вес тела в жидкости;
- находим разницу между весом тела в воздухе и весом тела в жидкости.
4. Результаты измерений:
Сделать вывод как зависит сила Архимеда от плотности жидкости.
Выталкивающая сила действует на тела любых геометрических форм. В технике наиболее распространены тела цилиндрической и сферической форм, тела с развитой поверхностью, полые тела в форме шара, прямоугольного параллелепипеда, цилиндра.
Гравитационная сила приложена к центру масс погруженного в жидкость тела и направлена перпендикулярно к поверхности жидкости.
Подъемная сила действует на тело со стороны
жидкости, направлена по вертикали вверх,
приложена к центру тяжести вытесненного объема
жидкости.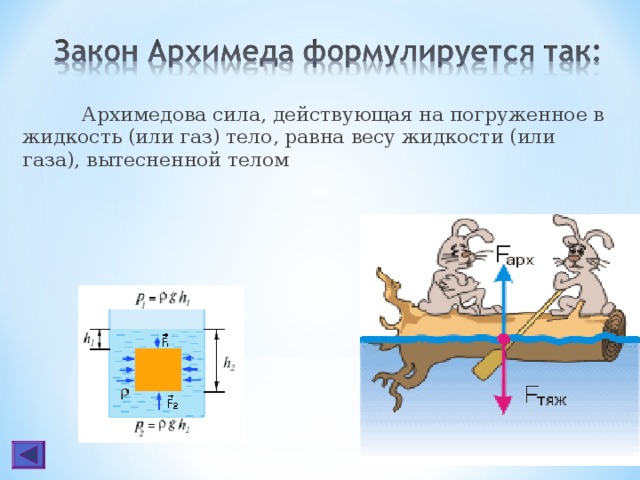 Тело движется в направлении,
перпендикулярном к поверхности жидкости.
Тело движется в направлении,
перпендикулярном к поверхности жидкости.
Выясним условия плавания тел, которые основываются на законе Архимеда.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести F т и силы Архимеда F A , которые действуют на это тело. Возможны следующие три случая:
- F т > F A – тело тонет;
- F т = F A – тело плавает в жидкости или газе;
- F т
Другая формулировка (где P t – плотность тела, P s – плотность среды, в которую оно погружено):
- P t > P s – тело тонет;
- P t = P s – тело плавает в жидкости или газе;
- P t
Плотность организмов живущих в воде почти не отличается от плотности воды, поэтому прочные скелеты им не нужны! Рыбы регулируют глубину погружения, меняя среднюю плотность своего тела. Для этого им необходимо лишь изменить объем плавательного пузыря, сокращая или расслабляя мышцы.
Если тело лежит на дне в жидкости или газе, то
сила Архимеда равна нулю.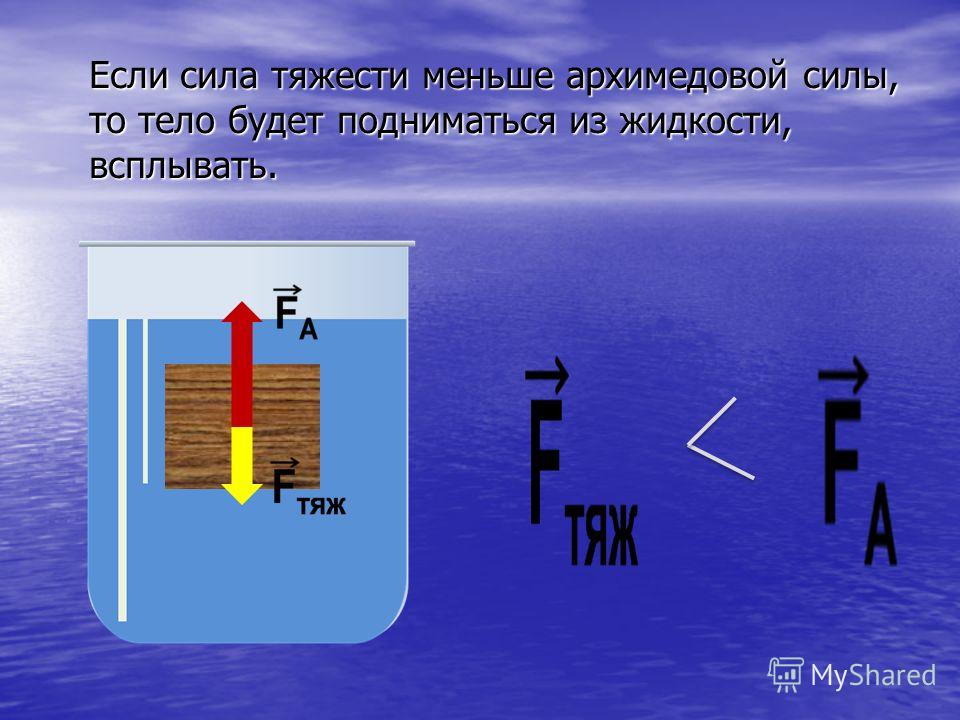
Закон Архимеда используется в судостроении и воздухоплавании.
Схема плавающего тела:
Линия действия силы тяжести тела G проходит через центр тяжести K (центр водоизмещения) вытесненного объема жидкости. В нормальном положении плавающего тела центр тяжести тела Т и центр водоизмещения K размещены по одной вертикали, называемой осью плаванья.
При качке центр водоизмещения К перемещается в точку К1, и сила тяжести тела и Архимедова сила FА образуют пару сил, которая стремится либо вернуть тело в исходное положение, либо увеличить крен.
В первом случае плавающее тело обладает статической устойчивостью, во втором случае устойчивость отсутствует. Устойчивость тела зависит от взаимного расположения центра тяжести тела Т и метацентра М (точки пересечения линии действия архимедовой силы при крене с осью плавания).
В 1783 году братья МОНГОЛЬФЬЕ изготовили
огромный бумажный шар, под которым поместили
чашку с горящим спиртом. Шар наполнился горячим
воздухом и начал подниматься, достигнув высоты
2000 метров.
Закон Архимеда – закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.
История вопроса
«Эврика!» («Нашел!») – именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало – нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото. Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Однако, что правда – то правда: именно Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Закон Архимеда и молекулярно-кинетическая теория
В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.
Формулировка и пояснения
Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается поднять на суше. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.
Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается поднять на суше. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.
Существование гидростатического давления приводит к тому, что на любое тело, находящееся в жидкости или газе, действует выталкивающая сила. Впервые значение этой силы в жидкостях определил на опыте Архимед. Закон Архимеда формулируется так: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу того количества жидкости или газа, которое вытеснено погруженной частью тела.
Формула
Сила Архимеда, действующая на погруженное в жидкость тело, может быть рассчитана по формуле: F А = ρ ж gV пт,
где ρж – плотность жидкости,
g – ускорение свободного падения,
Vпт – объем погруженной в жидкость части тела.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести Fт и архимедовой силы FA, которые действуют на это тело. Возможны следующие три случая:
1) Fт > FA – тело тонет;
2) Fт = FA – тело плавает в жидкости или газе;
3) Fт
Часто научные открытия становятся следствием простой случайности. Но только люди с подготовленным умом могут оценить важность простого совпадения и сделать из него далеко идущие выводы. Именно благодаря цепи случайных событий в физике появился закон Архимеда, объясняющий поведение тел в воде.
Предание
В Сиракузах об Архимеде слагали легенды. Однажды правитель этого славного города усомнился в честности своего ювелира. В короне, изготовленной для правителя, должно было содержаться определенное количество золота. Проверить этот факт поручили Архимеду.
Однажды правитель этого славного города усомнился в честности своего ювелира. В короне, изготовленной для правителя, должно было содержаться определенное количество золота. Проверить этот факт поручили Архимеду.
Архимед установил, что в воздухе и в воде тела имеют разный вес, причем разность прямо пропорциональна плотности измеряемого тела. Измерив вес короны в воздухе и в воде, и проведя аналогичный опыт с целым куском золота, Архимед доказал, что в изготовленной короне существовала примесь более легкого металла.
По преданию, Архимед сделал это открытие в ванне, наблюдая за выплеснувшейся водой. Что стало дальше с нечестным ювелиром, история умалчивает, но умозаключение сиракузского ученого легло в основу одного из важнейших законов физики, который известен нам, как закон Архимеда.
Формулировка
Результаты своих опытов Архимед изложил в труде «О плавающих телах», который, к сожалению, дошел до наших дней лишь в виде отрывков. Современная физика закон Архимеда описывает, как совокупную силу, действующую на тело, погруженное в жидкость. Выталкивающая сила тела в жидкости направлена вверх; ее абсолютная величина равна весу вытесненной жидкости.
Выталкивающая сила тела в жидкости направлена вверх; ее абсолютная величина равна весу вытесненной жидкости.
Действие жидкостей и газов на погруженное тело
Любой предмет, погруженный в жидкость, испытывает на себе силы давления. В каждой точке поверхности тела данные силы направлены перпендикулярно поверхности тела. Если бы эти они были одинаковы, тело испытывало бы только сжатие. Но силы давления увеличиваются пропорционально глубине, поэтому нижняя поверхность тела испытывает больше сжатие, чем верхняя. Можно рассмотреть и сложить все силы, действующие на тело в воде. Итоговый вектор их направления будет устремлен вверх, происходит выталкивание тела из жидкости. Величину этих сил определяет закон Архимеда. Плавание тел всецело основывается на этом законе и на различных следствиях из него. Архимедовы силы действуют и в газах. Именно благодаря этим силам выталкивания в небе летают дирижабли и воздушные шары: благодаря воздухоизмещению они становятся легче воздуха.
Физическая формула
Наглядно силу Архимеда можно продемонстрировать простым взвешиванием. Взвешивая учебную гирю в вакууме, в воздухе и в воде можно видеть, что вес ее существенно меняется. В вакууме вес гири один, в воздухе – чуть ниже, а в воде – еще ниже.
Взвешивая учебную гирю в вакууме, в воздухе и в воде можно видеть, что вес ее существенно меняется. В вакууме вес гири один, в воздухе – чуть ниже, а в воде – еще ниже.
Если принять вес тела в вакууме за Р о, то его вес в воздушной среде может быть описан такой формулой: Р в =Р о – F а;
здесь Р о – вес в вакууме;
Как видно из рисунка, любые действия со взвешиванием в воде значительно облегчают тело, поэтому в таких случаях сила Архимеда обязательно должна учитываться.
Для воздуха эта разность ничтожна, поэтому обычно вес тела, погруженного в воздушную среду, описывается стандартной формулой.
Плотность среды и сила Архимеда
Анализируя простейшие опыты с весом тела в различных средах, можно прийти к выводу, что вес тела в различных средах зависит от массы объекта и плотности среды погружения. Причем чем плотнее среда, тем больше сила Архимеда. Закон Архимеда увязал эту зависимость и плотность жидкости или газа отражается в его итоговой формуле. Что же еще влияет на данную силу? Другими словами, от каких характеристик зависит закон Архимеда?
Что же еще влияет на данную силу? Другими словами, от каких характеристик зависит закон Архимеда?
Формула
Архимедову силу и силы, которые на нее влияют, можно определить при помощи простых логических умозаключений. Предположим, что тело определенного объема, погруженное в жидкость, состоит из тоже же самой жидкости, в которую оно погружено. Это предположение не противоречит никаким другим предпосылкам. Ведь силы, действующие на тело, никоим образом не зависят от плотности этого тела. В этом случае тело, скорее всего, будет находиться в равновесии, а сила выталкивания будет компенсироваться силой тяжести.
Таким образом, равновесие тела в воде будет описываться так.
Но сила тяжести, из условия, равна весу жидкости, которую она вытесняет: масса жидкости равна произведению плотности на объём. Подставляя известные величины, можно узнать вес тела в жидкости. Этот параметр описывается в виде ρV * g.
Подставляя известные значения, получаем:
Это и есть закон Архимеда.
Формула, выведенная нами, описывает плотность, как плотность исследуемого тела. Но в начальных условиях было указано, что плотность тела идентична плотности окружающей его жидкости. Таким образом, в данную формулу можно смело подставлять значение плотности жидкости. Визуальное наблюдение, согласно которому в более плотной среде сила выталкивания больше, получило теоретическое обоснование.
Применение закона Архимеда
Первые опыты, демонстрирующие закон Архимеда, известны еще со школьной скамьи. Металлическая пластинка тонет в воде, но, сложенная в виде коробочки, может не только удерживаться на плаву, но и нести на себе определенный груз. Это правило – важнейший вывод из правила Архимеда, оно определяет возможность построения речных и морских судов с учетом их максимальной вместимости (водоизмещения). Ведь плотность морской и пресной воды различна и суда, и подводные лодки должны учитывать перепады этого параметра при вхождении в устья рек. Неправильный расчет может привести к катастрофе – судно сядет на мель, и для его подъема потребуются значительные усилия.
Закон Архимеда необходим и подводникам. Дело в том, что плотность морской воды меняет свое значение в зависимости от глубины погружения. Правильный расчет плотности позволит подводникам правильно рассчитать давление воздуха внутри скафандра, что повлияет на маневренность водолаза и обеспечит его безопасное погружение и всплытие. Закон Архимеда должен учитываться также и при глубоководном бурении, огромные буровые вышки теряют до 50% своего веса, что делает их транспортировку и эксплуатацию менее затратным мероприятием.
Как найти выталкивающую силу формула в воде. Формула силы выталкивания
Казалось бы, нет ничего проще, чем закон Архимеда. Но когда-то сам Архимед здорово поломал голову над его открытием. Как это было?
С открытием основного закона гидростатики связана интересная история.
Интересные факты и легенды из жизни и смерти Архимеда
Помимо такого гигантского прорыва, как открытие собственно закона Архимеда, ученый имеет еще целый список заслуг и достижений. Вообще, он был гением, трудившимся в областях механики, астрономии, математики. Им написаны такие труды, как трактат «о плавающих телах», «о шаре и цилиндре», «о спиралях», «о коноидах и сфероидах» и даже «о песчинках». В последнем труде была предпринята попытка измерить количество песчинок, необходимых для того, чтобы заполнить Вселенную.
Вообще, он был гением, трудившимся в областях механики, астрономии, математики. Им написаны такие труды, как трактат «о плавающих телах», «о шаре и цилиндре», «о спиралях», «о коноидах и сфероидах» и даже «о песчинках». В последнем труде была предпринята попытка измерить количество песчинок, необходимых для того, чтобы заполнить Вселенную.
Роль Архимеда в осаде Сиракуз
В 212 году до нашей эры Сиракузы были осаждены римлянами. 75-летний Архимед сконструировал мощные катапульты и легкие метательные машины ближнего действия, а также так называемые “когти Архимеда”. С их помощью можно было буквально переворачивать вражеские корабли. Столкнувшись со столь мощным и технологичным сопротивлением, римляне не смогли взять город штурмом и вынуждены были начать осаду. По другой легенде Архимед при помощи зеркал сумел поджечь римский флот, фокусируя солнечные лучи на кораблях. Правдивость данной легенды представляется сомнительной, т.к. ни у одного из историков того времени упоминаний об этом нет.
Смерть Архимеда
Согласно многим свидетельствам, Архимед был убит римлянами, когда те все-таки взяли Сиракузы. Вот одна из возможных версий гибели великого инженера.
На крыльце своего дома ученый размышлял над схемами, которые чертил рукой прямо на песке. Проходящий мимо солдат наступил на рисунок, а Архимед, погруженный в раздумья, закричал: «Прочь от моих чертежей». В ответ на это спешивший куда-то солдат просто пронзил старика мечом.
Ну а теперь о наболевшем: о законе и силе Архимеда…
Как был открыт закон Архимеда и происхождение знаменитой “Эврика!”
Античность. Третий век до нашей эры. Сицилия, на которой еще и подавно нет мафии, но есть древние греки.
Изобретатель, инженер и ученый-теоретик из Сиракуз (греческая колония на Сицилии) Архимед служил у царя Гиерона второго. Однажды ювелиры изготовили для царя золотую корону. Царь, как человек подозрительный, вызвал ученого к себе и поручил узнать, не содержит ли корона примесей серебра. Тут нужно сказать, что в то далекое время никто не решал подобных вопросов и случай был беспрецедентным.
Архимед долго размышлял, ничего не придумал и однажды решил сходить в баню. Там, садясь в тазик с водой, ученый и нашел решение вопроса. Архимед обратил внимание на совершенно очевидную вещь: тело, погружаясь в воду, вытесняет объем воды, равный собственному объему тела.
Именно тогда, даже не потрудившийся одеться, Архимед выскочил из бани и кричал свое знаменитое «эврика», что означает «нашел». Явившись к царю, Архимед попросил выдать ему слитки серебра и золота, равные по массе короне. Измеряя и сравнивая объем воды, вытесняемой короной и слитками, Архимед обнаружил, что корона изготовлена не из чистого золота, а имеет примеси серебра. Это и есть история открытия закона Архимеда.
Суть закона Архимеда
Если Вы спрашиваете себя, как понять закон Архимеда, мы ответим. Просто сесть, подумать, и понимание придет. Собственно, этот закон гласит:
На тело, погруженное в газ или жидкость действует выталкивающая сила, равная весу жидкости (газа) в объеме погруженной части тела.
Эта сила называется силой Архимеда.
Как видим, сила Архимеда действует не только на тела, погруженные в воду, но и на тела в атмосфере. Сила, которая заставляет воздушный шар подниматься вверх – та же сила Архимеда. Высчитывается Архимедова сила по формуле:
Здесь первый член – плотность жидкости (газа), второй – ускорение свободного падения, третий – объем тела. Если сила тяжести равна силе Архимеда, тело плавает, если больше – тонет, а если меньше – всплывает до тех пор, пока не начнет плавать.
В данной статье мы рассмотрели закон Архимеда для чайников. Если Вы хотите узнать, как как решать задачи, где есть закон Архимеда, обращайтесь к нашим специалистам . Лучшие авторы с удовольствием поделятся знаниями и разложат решение самой сложной задачи «по полочкам».
Почему мы можем лежать на поверхности моря, не опускаясь на дно? Почему плавают на поверхности воды тяжелые корабли?
Наверное, существует какая-то сила, которая выталкивает людей и кораблики, то есть, все тела из воды и позволяет плавать на поверхности.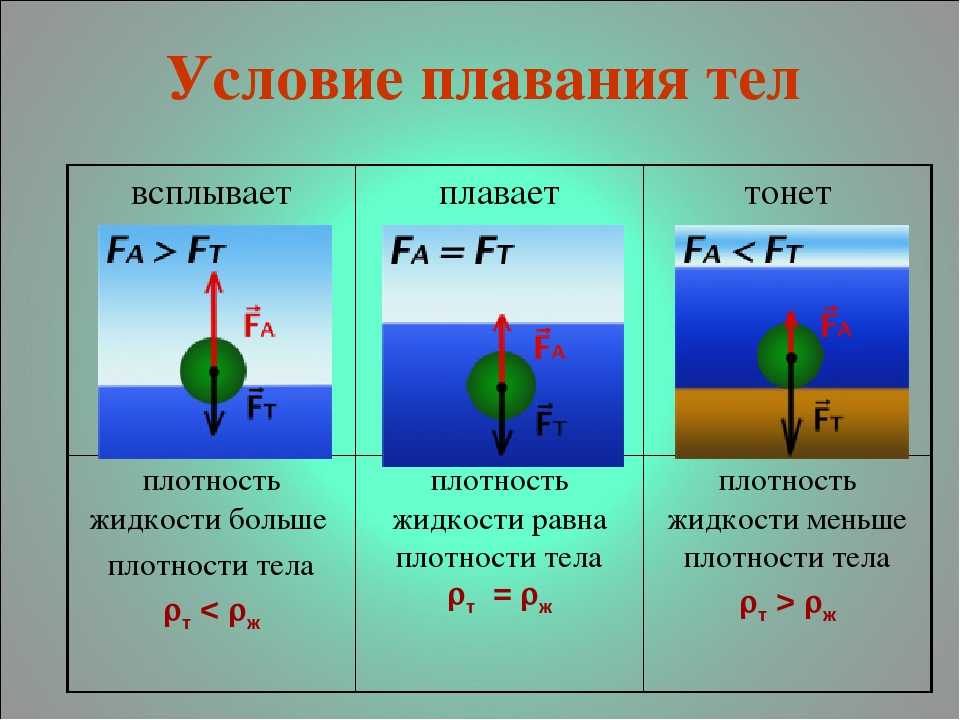
Зависимость давления в жидкости или газе от глубины погружения тела приводит к появлению выталкивающей силы,или иначе силы Архимеда, действующей на любое тело, погруженное в жидкость или газ. Рассмотрим силу Архимеда подробнее на примере.
Все мы пускали кораблики по лужам. А какой кораблик без капитана? Что мы наблюдали? Кораблик под весом капитана погружается глубже. А если мы мы размещали на нашем кораблике пять или восемь капитанов? Наш кораблик опускался на дно.
Что же мы можем извлечь полезного из данного опыта? Когда увеличивался вес кораблика, то мы видели, что кораблик ниже опускался в воду. То есть, вес тела увеличивал давление на воду, а выталкивающая сила оставалась прежней.
Когда же вес тела превысил величину выталкивающей силы, то кораблик под действием этой силы опустился на дно. То есть, существует выталкивающая сила, одинаковая для конкретного тела, но разная для различных тел.
Выталкивающая сила, она же сила Архимеда, действующая на тело, погружённое в жидкость, равна весу жидкости, вытесненной этим телом.
Кирпич, как всем известно, пойдет на дно в любом случае, а вот деревянная дверь не только будет плавать на поверхности, но и может еще удержать пару пассажиров. Сила эта и называется архимедовой силой и выражается формулой:
Fвыт = g*m ж = g* ρ ж * V ж = P ж,
где m ж – это масса жидкости,
а P ж – вес вытесненной телом жидкости.
А так как масса у нас равна: m ж = ρ ж * V ж, то из формулы архимедовой силы мы видим, что она не зависит от плотности погруженного тела, а только от объема и плотности вытесненной телом жидкости.
Архимедова сила – это векторная величина. Причина существования выталкивающей силы – разница в давлении на верхнюю и нижнюю часть тела.Указанное на рисунке давление P 2 > P 1 из-за большей глубины. Для возникновения силы Архимеда достаточно того, чтобы тело было погружено в жидкость хотя бы частично.
Так, если тело плывёт по поверхности жидкости, значит выталкивающая сила, действующая на погружённую в жидкость часть этого тела равна силе тяжести всего тела. Если плотность тела больше плотности жидкости, то тело тонет, если меньше – то всплывает.
Если плотность тела больше плотности жидкости, то тело тонет, если меньше – то всплывает.
Тело же, погруженное в жидкость, теряет в своем весе ровно столько, сколько весит вытесненная им вода. Поэтому, естественно предположить, что если вес тела меньше веса воды такого же объема, то оно будет плавать на поверхности, а если больше – то утонет.
Если же вес тела и воды будет равен, то тело может замечательно плавать в толще воды, как и поступают все водные обитатели. Плотность оганизмов, живущих в воде почти не отличается от плотности воды, поэтому прочные скелеты им не нужны!
Рыбы регулируют глубину погружения, меняя среднюю плотность своего тела. Для этого им необходимо лишь изменить объем плавательного пузыря, сокращая или расслабляя мышцы.
У берегов Египта, водится удивительная рыба фагак. Приближение опасности заставляет фагака быстро заглатывать воду. При этом в пищеводе рыбы происходит бурное разложение продуктов питания с выделением значительного количества газов. Газы заполняют не только действующую полость пищевода, но и имеющийся при ней слепой вырост. В результате тело фагака сильно раздувается, и, в соответствии с законом Архимеда, он быстро всплывает на поверхность водоема. Здесь он плавает, повиснув вверх брюхом, пока выделившиеся в его организме газы не улетучатся. После этого сила тяжести опускает его на дно водоема, где он укрывается среди придонных водорослей.
Газы заполняют не только действующую полость пищевода, но и имеющийся при ней слепой вырост. В результате тело фагака сильно раздувается, и, в соответствии с законом Архимеда, он быстро всплывает на поверхность водоема. Здесь он плавает, повиснув вверх брюхом, пока выделившиеся в его организме газы не улетучатся. После этого сила тяжести опускает его на дно водоема, где он укрывается среди придонных водорослей.
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Введение
Актуальность: Если внимательно присмотреться к окружающему миру, то можно открыть для себя множество событий, происходящих вокруг. Издревле человека окружает вода. Когда мы плаваем в ней, то наше тело выталкивает на поверхность какие-то силы. Я давно задаю себе вопрос: «Почему тела плавают или тонут? Вода выталкивает предметы?»
Моя исследовательская работа направлена на то, чтобы углубить полученные на уроке знания об архимедовой силе. Ответы на интересующие меня вопросы, используя жизненный опыт, наблюдения за окружающей действительностью, провести собственные эксперименты и объяснить их результаты, которые позволят расширить знания по данной теме. Все науки связаны между собой. А общий объект изучения всех наук – это человек «плюс» природа. Я уверен, что исследование действия архимедовой силы сегодня является актуальным.
Ответы на интересующие меня вопросы, используя жизненный опыт, наблюдения за окружающей действительностью, провести собственные эксперименты и объяснить их результаты, которые позволят расширить знания по данной теме. Все науки связаны между собой. А общий объект изучения всех наук – это человек «плюс» природа. Я уверен, что исследование действия архимедовой силы сегодня является актуальным.
Гипотеза: Я предполагаю, что в домашних условиях можно рассчитать величину выталкивающей силы действующей на погруженное в жидкость тело и определить зависит ли она от свойств жидкости, объема и формы тела.
Объект исследования: Выталкивающая сила в жидкостях.
Задачи:
Изучить историю открытия архимедовой силы;
Изучить учебную литературу по вопросу действия архимедовой силы;
Выработать навыки проведения самостоятельного эксперимента;
Доказать, что значение выталкивающей силы зависит от плотности жидкости.
Методы исследования:
Исследовательские;
Расчетные;
Информационного поиска;
Наблюдений
1. Открытие силы Архимеда
Открытие силы Архимеда
Существует знаменитая легенда о том, как Архимед бежал по улице и кричал «Эврика!» Это как раз повествует об открытии им того, что выталкивающая сила воды равна по модулю весу вытесненной им воды, объем которой равен объему погруженного в нее тела. Это открытие названо законом Архимеда.
В III веке до нашей эры жил Гиерон – царь древнегреческого города Сиракузы и захотел он сделать себе новую корону из чистого золота. Отмерил его строго сколько нужно, и дал ювелиру заказ. Через месяц мастер вернул золото в виде короны и весила она столько, сколько и масса данного золота. Но ведь всякое бывает и мастер мог схитрить, добавив серебро или того хуже – медь, ведь на глаз не отличишь, а масса такая, какая и должна быть. А царю узнать охота: честно ль сделана работа? И тогда, попросил он ученого Архимеда, проверить из чистого ли золота сделал мастер ему корону. Как известно, масса тела равна произведению плотности вещества, из которого сделано тело, на его объем: . Если у разных тел одинаковая масса, но они сделаны из разных веществ, то значит, у них будет разный объем. Если бы мастер вернул царю не ювелирно сделанную корону, объем которой определить невозможно из-за ее сложности, а такой же по форме кусок металла, который дал ему царь, то сразу было бы ясно, подмешал он туда другого металла или нет. И вот принимая ванну, Архимед обратил внимание, что вода из нее выливается. Он заподозрил, что выливается она именно в том объеме, какой объем занимают его части тела, погруженные в воду. И Архимеда осенило, что объем короны можно определить по объему вытесненной ей воды. Ну а коли можно измерить объем короны, то его можно сравнить с объемом куска золота, равного по массе. Архимед погрузил в воду корону и измерил, как увеличился объем воды. Также он погрузил в воду кусок золота, у которого масса была такая же, как у короны. И тут он измерил, как увеличился объем воды. Объемы вытесненной в двух случаях воды оказались разными. Тем самым мастер был изобличен в обмане, а наука обогатилась замечательным открытием.
Если у разных тел одинаковая масса, но они сделаны из разных веществ, то значит, у них будет разный объем. Если бы мастер вернул царю не ювелирно сделанную корону, объем которой определить невозможно из-за ее сложности, а такой же по форме кусок металла, который дал ему царь, то сразу было бы ясно, подмешал он туда другого металла или нет. И вот принимая ванну, Архимед обратил внимание, что вода из нее выливается. Он заподозрил, что выливается она именно в том объеме, какой объем занимают его части тела, погруженные в воду. И Архимеда осенило, что объем короны можно определить по объему вытесненной ей воды. Ну а коли можно измерить объем короны, то его можно сравнить с объемом куска золота, равного по массе. Архимед погрузил в воду корону и измерил, как увеличился объем воды. Также он погрузил в воду кусок золота, у которого масса была такая же, как у короны. И тут он измерил, как увеличился объем воды. Объемы вытесненной в двух случаях воды оказались разными. Тем самым мастер был изобличен в обмане, а наука обогатилась замечательным открытием.
Из истории известно, что задача о золотой короне побудила Архимеда заняться вопросом о плавании тел. Опыты, проведенные Архимедом, были описаны в сочинении «О плавающих телах», которое дошло до нас. Седьмое предложение (теорема) этого сочинения сформулировано Архимедом следующим образом: тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела.
Интересно, что сила Архимеда равна нулю, когда погруженное в жидкость тело плотно, всем основанием прижато ко дну.
Открытие основного закона гидростатики – крупнейшее завоевание античной науки.
2. Формулировка и пояснения закона Архимеда
Закон Архимеда описывает действие жидкостей и газов на погруженное в них тело, и является одним из главных законов гидростатики и статики газов.
Закон Архимеда формулируется следующим образом: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу жидкости (или газа) в объёме погруженной части тела – эта сила называется силой Архимеда :
,
где – плотность жидкости (газа), – ускорение свободного падения, – объём погружённой части тела (или часть объёма тела, находящаяся ниже поверхности).
Следовательно, архимедова сила зависит только от плотности жидкости, в которую погружено тело, и от объема этого тела. Но она не зависит, например, от плотности вещества тела, погруженного в жидкость, так как эта величина не входит в полученную формулу.
Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.
3. Определение силы Архимеда
Силу, с которой тело, находящееся в жидкости, выталкивается ею, можно определить на опыте используя данный прибор:
Небольшое ведерко и тело цилиндрической формы подвешиваем на пружине, закрепленной в штативе. Растяжение пружины отмечаем стрелкой на штативе, показывая вес тела в воздухе. Приподняв тело, под него подставляем стакан с отливной трубкой, наполненный жидкостью до уровня отливной трубки. После чего тело погружают целиком в жидкость. При этом часть жидкости, объём которой равен объёму тела, выливается из отливного сосуда в стакан.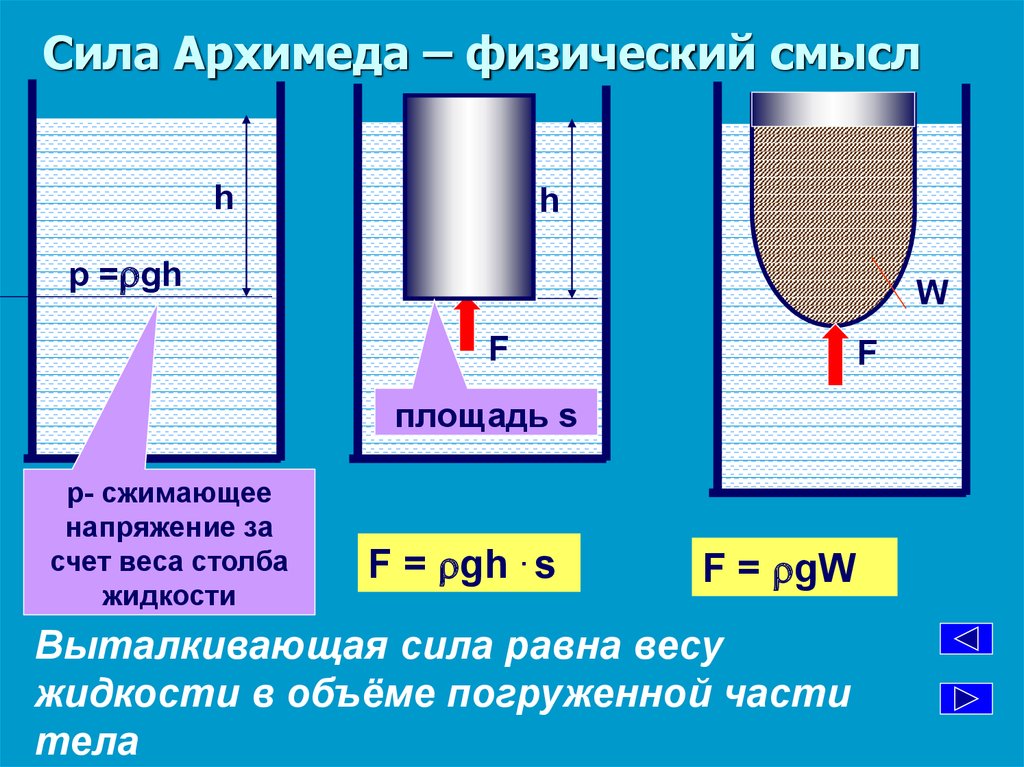 Указатель пружины поднимается вверх, пружина сокращается, показывая уменьшение веса тела в жидкости. В данном случае на тело, наряду с силой тяжести, действует еще и сила, выталкивающая его из жидкости. Если в ведёрко налить жидкость из стакана (т.е. ту, которую вытеснило тело), то указатель пружины возвратится к своему начальному положению.
Указатель пружины поднимается вверх, пружина сокращается, показывая уменьшение веса тела в жидкости. В данном случае на тело, наряду с силой тяжести, действует еще и сила, выталкивающая его из жидкости. Если в ведёрко налить жидкость из стакана (т.е. ту, которую вытеснило тело), то указатель пружины возвратится к своему начальному положению.
На основании этого опыта можно заключить, что сила, выталкивающая тело, целиком погруженное в жидкость, равна весу жидкости в объёме этого тела. Зависимость давления в жидкости (газе) от глубины погружения тела приводит к появлению выталкивающей силы (силы Архимеда), действующей на любое тело, погруженное в жидкость или газ. Тело при погружении двигается вниз под действием силы тяжести. Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.
Данный опыт подтверждает, что архимедова сила равна весу жидкости в объёме тела.
4. Условие плавания тел
На тело, находящееся внутри жидкости, действуют две силы: сила тяжести, направленная вертикально вниз, и архимедова сила, направленная вертикально вверх. Рассмотрим, что будет происходить с телом под действием этих сил, если вначале оно было неподвижно.
Рассмотрим, что будет происходить с телом под действием этих сил, если вначале оно было неподвижно.
При этом возможны три случая:
1) Если сила тяжести больше архимедовой силы, то тело опускается вниз, то есть тонет:
, то тело тонет;
2) Если модуль силы тяжести равен модулю архимедовой силы, то тело может находиться в равновесии внутри жидкости на любой глубине:
, то тело плавает;
3) Если архимедова сила больше силы тяжести, то тело будет поднимается из жидкости – всплывать:
, то тело плавает.
Если всплывающее тело частично выступает над поверхностью жидкости, то объем погруженной части плавающего тела такой, что вес вытесненной жидкости равен весу плавающего тела.
Архимедова сила больше силы тяжести, если плотность жидкости больше плотности погруженного в жидкость тела, если
1) =— тело плавает в жидкости или газе,2) >— тело тонет,3)
Именно эти принципы соотношения силы тяжести и силы Архимеда применяются в судоходостронии. Однако на воде держатся громадные речные и морские суда, изготовленные из стали, плотность которой почти в 8 раз больше плотности воды. Объясняется это тем, что из стали делают лишь сравнительно тонкий корпус судна, а большая часть его объема занята воздухом. Среднее значение плотности судна при этом оказывается значительно меньше плотности воды; поэтому оно не только не тонет, но и может принимать для перевозки большое количество грузов. Суда, плавающие по рекам, озерам, морям и океанам, построены из разных материалов с различной плотностью. Корпус судов обычно делают из стальных листов. Все внутренние крепления, придающие судам прочность, также изготавливают из металлов. Для постройки судов используют разные материалы, имеющие по сравнению с водой как большую, так и меньшую плотность. Вес воды, вытесненной подводной частью судна, равен весу судна с грузом в воздухе или силе тяжести, действующей на судно с грузом.
Однако на воде держатся громадные речные и морские суда, изготовленные из стали, плотность которой почти в 8 раз больше плотности воды. Объясняется это тем, что из стали делают лишь сравнительно тонкий корпус судна, а большая часть его объема занята воздухом. Среднее значение плотности судна при этом оказывается значительно меньше плотности воды; поэтому оно не только не тонет, но и может принимать для перевозки большое количество грузов. Суда, плавающие по рекам, озерам, морям и океанам, построены из разных материалов с различной плотностью. Корпус судов обычно делают из стальных листов. Все внутренние крепления, придающие судам прочность, также изготавливают из металлов. Для постройки судов используют разные материалы, имеющие по сравнению с водой как большую, так и меньшую плотность. Вес воды, вытесненной подводной частью судна, равен весу судна с грузом в воздухе или силе тяжести, действующей на судно с грузом.
Для воздухоплавания вначале использовали воздушные шары, которые раньше наполняли нагретым воздухом, сейчас – водородом или гелием. Для того чтобы шар поднялся в воздух, необходимо, чтобы архимедова сила (выталкивающая), действующая на шар, была больше силы тяжести.
Для того чтобы шар поднялся в воздух, необходимо, чтобы архимедова сила (выталкивающая), действующая на шар, была больше силы тяжести.
5. Проведение эксперимента
Исследовать поведение сырого яйца в жидкостях разного рода.
Задача: доказать, что значение выталкивающей силы зависит от плотности жидкости.
Я взял одно сырое яйцо и жидкости разного рода (приложение 1):
Вода чистая;
Вода, насыщенная солью;
Подсолнечное масло.
Сначала я опустил сырое яйцо в чистую воду – яйцо утонуло – «пошло ко дну» (приложение 2). Потом в стакан с чистой водой я добавил столовую ложку поваренной соли, в результате яйцо плавает (приложение 3). И наконец, я опустил яйцо в стакан с подсолнечным маслом – яйцо опустилось на дно (приложение 4).
Вывод: в первом случае плотность яйца больше плотности воды и поэтому яйцо утонуло. Во втором случае плотность солёной воды больше плотности яйца, поэтому яйцо плавает в жидкости. В третьем случае плотность яйца также больше плотности подсолнечного масла, поэтому яйцо утонуло. Следовательно, чем больше плотность жидкости, тем сила тяжести меньше.
Следовательно, чем больше плотность жидкости, тем сила тяжести меньше.
2. Действие Архимедовой силы на тело человека в воде.
Определить на опыте плотность тела человека, сравнить ее с плотностью пресной и морской воды и сделать вывод о принципиальной возможности человека плавать;
Вычислить вес человека в воздухе, архимедову силу, действующую на человека в воде.
Для начала с помощью весов я измерил массу своего тела. Затем измерил объем тела (без объема головы). Для этого я налил в ванну воды столько, чтобы при погружении в воду я был полностью в воде (за исключением головы). Далее с помощью сантиметровой ленты отметил от верхнего края ванны расстояние до уровня воды ℓ 1 , а затем – при погружении в воду ℓ 2 . После этого с помощью предварительно проградуированной трехлитровой банки стал наливать в ванну воду от уровня ℓ 1 до уровня ℓ 2 – так я измерил объем вытесненной мной воды (приложение 5). Плотность я рассчитал с помощью формулы:
Сила тяжести, действующая на тело в воздухе, была рассчитана по формуле: , где – ускорение свободного падения ≈ 10 . Значение выталкивающей силы было рассчитано с помощью формулы описанной в пункте 2.
Значение выталкивающей силы было рассчитано с помощью формулы описанной в пункте 2.
Вывод:Тело человекаплотнее пресной воды, а, значит, оно в ней тонет. Человеку легче плавать в море, чем в реке, так как плотность морской воды больше, а следовательно больше значение выталкивающей силы.
Заключение
В процессе работы над этой темой мы узнали для себя много нового и интересного. Круг наших познаний увеличился не только в области действия силы Архимеда, но и применении ее в жизни. Перед началом работы мы имели о ней далеко неподробное представление. При проведении опытов мы подтвердили экспериментально справедливость закона Архимеда и выяснили, что выталкивающая силазависит от объема тела и плотности жидкости, чем больше плотность жидкости, тем архимедова сила больше. Результирующая сила, которая определяет поведение тела в жидкости, зависит от массы, объёма тела и плотности жидкости.
Помимо проделанных экспериментов, была изучена дополнительная литература об открытии силы Архимеда, о плавании тел, воздухоплавании.
Каждый из Вас может сделать удивительные открытия, и для этого не нужно обладать ни особенными знаниями, ни мощным оборудованием. Нужно лишь немного внимательней посмотреть на окружающий нас мир, быть чуть более независимым в своих суждениях, и открытия не заставят себя ждать. Нежелание большинства людей познавать окружающий мир оставляет большой простор любознательным в самых неожиданных местах.
Список литературы
1.Большая книга экспериментов для школьников – М.: Росмэн, 2009. – 264 с.
2. Википедия: https://ru.wikipedia.org/wiki/Закон_Архимеда.
3. Перельман Я.И. Занимательная физика. – книга 1. – Екатеринбург.: Тезис, 1994.
4. Перельман Я.И. Занимательная физика. – книга 2.- Екатеринбург.: Тезис, 1994.
5. Перышкин А.В. Физика: 7 класс: учебник для общеобразовательных учреждений / А.В. Перышкин. – 16-е изд., стереотип. – М.: Дрофа, 2013. – 192 с.: ил.
Приложение 1
Приложение 2
Приложение 3
Приложение 4
Один из первых физических законов, изучаемых учениками средней школы. Хотя бы примерно этот закон помнит любой взрослый человек, как бы далек он ни был от физики. Но иногда полезно вернуться к точным определениям и формулировкам – и разобраться в деталях этого закона, которые могли позабыться.
Хотя бы примерно этот закон помнит любой взрослый человек, как бы далек он ни был от физики. Но иногда полезно вернуться к точным определениям и формулировкам – и разобраться в деталях этого закона, которые могли позабыться.
О чем говорит закон Архимеда?
Существует легенда, что свой знаменитый закон древнегреческий ученый открыл, принимая ванну. Погрузившись в емкость, наполненную водой до краев, Архимед обратил внимание, что вода при этом выплеснулась наружу – и испытал озарение, мгновенно сформулировав суть открытия.
Скорее всего, в реальности дело обстояло иначе, и открытию предшествовали долгие наблюдения. Но это не столь важно, потому что в любом случае Архимеду удалось открыть следующую закономерность:
- погружаясь в любую жидкость, тела и объекты испытывают на себе сразу несколько разнонаправленных, но направленных перпендикулярно по отношению к их поверхности сил;
- итоговый вектор этих сил направлен вверх, поэтому любой объект или тело, оказавшись в жидкости в состоянии покоя, испытывает на себе выталкивание;
- при этом сила выталкивания в точности равна коэффициенту, который получится, если умножить на ускорение свободного падения произведение объема предмета и плотности жидкости.

Итак, Архимед установил, что тело, погружённое в жидкость, вытесняет такой объём жидкости, который равен объёму самого тела. Если в жидкость погружается только часть тела, то оно вытеснит жидкость, объём которой будет равен объёму только той части, которая погружается.
Та же самая закономерность действует и для газов – только здесь объем тела необходимо соотносить с плотностью газа.
Можно сформулировать физический закон и немного проще – сила, которая выталкивает из жидкости или газа некий предмет, в точности равна весу жидкости или газа, вытесненных этим предметом при погружении.
Закон записывается в виде следующей формулы:
Какое значение имеет закон Архимеда?
Закономерность, открытая древнегреческим ученым, проста и совершенно очевидна. Но при этом ее значение для повседневной жизни невозможно переоценить.
Именно благодаря познаниям о выталкивании тел жидкостями и газами мы можем строить речные и морские суда, а также дирижабли и воздушные шары для воздухоплавания. Тяжелые металлические корабли не тонут благодаря тому, что их конструкция учитывает закон Архимеда и многочисленные следствия из него – они построены так, что могут удерживаться на поверхности воды, а не идут ко дну. По аналогичному принципу действуют воздухоплавательные средства – они используют выталкивающие способности воздуха, в процессе полета становясь как бы легче него.
Тяжелые металлические корабли не тонут благодаря тому, что их конструкция учитывает закон Архимеда и многочисленные следствия из него – они построены так, что могут удерживаться на поверхности воды, а не идут ко дну. По аналогичному принципу действуют воздухоплавательные средства – они используют выталкивающие способности воздуха, в процессе полета становясь как бы легче него.
Наблюдения и опыты показывают, что на тела, помещенные в жидкость и газ оказывается давление. Давление жидкости и газа на одной высоте одинаково во всех направлениях. С изменением высоты происходит изменение давления. По этой причине возникает выталкивающая сила, которую называют архимедовой силой. Узнаем чему равна архимедова сила в жидкости и газе.
Чему равно давление в газах и жидкостях
Напомним определение давления. Давлением p называют физическую величину, равную отношению силы F , направленной перпендикулярно поверхности с площадью S :
$p={F\over S}$ (1)
Французский исследователь Блез Паскаль открыл закон, названный в последствии его именем, который звучит так: жидкости и газы передают производимое на них давление во все стороны одинаково.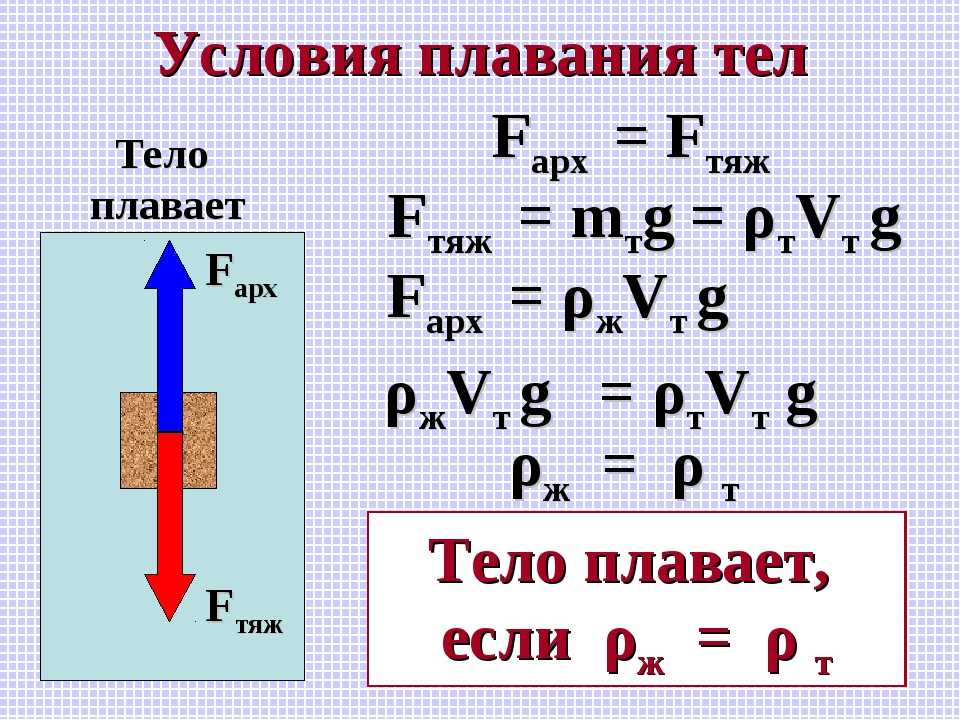
На основании закона Паскаля и формулы (1) можно вычислить давление столба жидкости:
$p={F\over S}={m*g\over S}$ (2)
где: m — масса жидкости, g = 9,8 Н/кг — ускорение свободного падения.
Тогда, если выразить массу жидкости через плотность ρ и объем V , получим:
$p={ρ*V*g\over S}$ (3)
Выразив объем V через площадь S и высоту h , получим окончательную формулу для давления:
$p={ρ*g*h}$ (4)
В физике всегда необходимо знать в чем измеряется физическая величина. В честь Паскаля назван не только закон, но и единица измерения давления. Так как сила измеряется в ньютонах, а площадь в метрах квадратных, то:
$$={ \over }$$
Часто используются кратные единицы давления: килопаскаль (кПа) и мегапаскаль (МПа).
Закон Архимеда
Тяжелый предмет, который мы с огромным трудом отрываем от земли, удается довольно легко поднять, когда он находится в воде. Если взять пустую пластиковую бутылку с закрытой пробкой, погрузить ее полностью в воду и отпустить, то бутылка всплывет. Почему это происходит?
Почему это происходит?
Для объяснения этих явлений достаточно взглянуть на последнюю формулу (4). Зависимость давления p в жидкости или газе от глубины h (высоты), приводит к появлению выталкивающей силы, действующей на любое тело, погруженное в жидкость или газ. Эта сила называется архимедовой силой.
Рис. 1. Портрет, изображение Архимеда
Древнегреческий математик, инженер и физик Архимед (287-212 г.г. до н.э.) не только обнаружил это явление, но смог найти ему объяснение и вывел формулу для расчета выталкивающей силы. Кроме закона Архимеда он открыл знаменитое правило рычага, первым вывел математические формулы для вычисления площадей и объемов сложных геометрических поверхностей, открыл первый планетарий, изобрел много полезных приспособлений.
Рис. 2. Действие выталкивающей силы на тело, погруженное в воду
Рисунок, на котором изображен прямоугольный параллелепипед (высотой h и площадью основания S ), помещенный в жидкость, поможет ответить на вопрос: как найти архимедову силу. Силы давления на боковые грани уравновешивают друг друга, а силы F 2 и F 1 отличаются, поскольку согласно формулы (4) давление на верхнюю и нижнюю грани будут разными из-за того, что h 2 > h 1 :
Силы давления на боковые грани уравновешивают друг друга, а силы F 2 и F 1 отличаются, поскольку согласно формулы (4) давление на верхнюю и нижнюю грани будут разными из-за того, что h 2 > h 1 :
Получим формулу для результирующей силы F A , равную разности F 2 и F 1 :
$F_А=F_2−F_1=p_2*S−p_1*S=ρ*g*h_2*S−ρ*g*h_1*S=$
$ρ*g*S*{(h_2− h_1)}=ρ*g*S*h$ (5)
где: $S*h=V$ — объем, а $ρ*V=m$ — масса жидкости, которую вытеснило тело. Тогда, поскольку m * g — это вес вытесненной жидкости, то получаем окончательную формулу архимедовой силы F A :
$F_A =m*g=ρ*V*g$ (6)
Полученная формула позволяет сформулировать закон Архимеда:
Сила, выталкивающая погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом.
Погружение, равновесие, всплытие
Теперь становится понятно почему в воде мы запросто поднимаем тяжелые камни: нам “помогает” архимедова сила, т. к. она направлена противоположно силе тяжести. По этой же причине вес тела при взвешивании в жидкости будет всегда меньше веса, измеренного в воздухе.
к. она направлена противоположно силе тяжести. По этой же причине вес тела при взвешивании в жидкости будет всегда меньше веса, измеренного в воздухе.
Из формулы (6) следует, что величина архимедовой силы зависит прямо пропорционально от плотности жидкости ρ и от объема погруженного тела V . Плотность вещества, из которого изготовлено тело, может быть любой — на величину выталкивающей силы она не влияет. В зависимости от соотношения архимедовой силы F A и силы тяжести F g возможно три положения тела в жидкости:
- Если FA > Fg, то тело будет выталкиваться наверх — “всплывать”;
- Если FA
- Если FA = Fg, то тело может находиться в жидкости на любой глубине в состоянии равновесия.
Закон Архимеда положен в основу ареометра — прибора для измерения плотности жидкости. Ареометр представляет собой стеклянную, герметичную колбу, утяжеленную с нижнего конца грузиком. Верхняя часть выполнена в виде длинного отростка, на котором нанесена измерительная шкала. При помещении в жидкость ареометр погружается на большую или меньшую глубину в зависимости от плотности жидкости. Чем больше плотность жидкости, тем меньше погружается ареометр. Показания на шкале указывают на плотность данной жидкости, когда ареометр занимает равновесное положение.
При помещении в жидкость ареометр погружается на большую или меньшую глубину в зависимости от плотности жидкости. Чем больше плотность жидкости, тем меньше погружается ареометр. Показания на шкале указывают на плотность данной жидкости, когда ареометр занимает равновесное положение.
Рис. 3. Ареометр
Что мы узнали?
Итак, мы узнали, почему возникает архимедова сила в газах и жидкостях, и от каких величин зависит ее значение. На тело, погруженное в жидкость (или газ) действует выталкивающая сила. Сила, выталкивающая погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом. Для более подробного доклада об архимедовой силе можно подготовить интересные примеры с разными жидкостями, отличными от воды, например с керосином или ртутью. Тема этой статьи тесно связана с особенностями плавания и воздухоплавания тел, которые мы рассмотрим в следующих главах курса физики за 7 класс.
Тест по теме
Оценка доклада
Средняя оценка: 4. 4
. Всего получено оценок: 118.
4
. Всего получено оценок: 118.
Формула вытесненной воды. Чему равна выталкивающая сила? Условие плавания тел
Инструкция
Архимедова сила возникает из-за разности давлений воды на уровне верхнего и нижнего срезов тела. На верхнюю часть давит столб воды высотой h2 с силой, равной весу этого . На нижнюю часть действует сила, равная весу столба высотой h3. Эта высота определяется сложением h2 и высотой самого тела. Согласно закону Паскаля, давление в жидкости или газе распределяется равномерно во все стороны. В том числе и вверх.
Очевидно, что сила, действующая вверх, превышает силу, действующую вниз. Но, следует учесть, что принимается во внимание только воздействие столба жидкости. От собственного веса тела выталкивающая сила не зависит. Ни материал, из которого сделано тело, ни его иные качества, кроме размеров при вычислениях не используются. Расчет архимедовой силы базируется только на плотности жидкости и геометрических размерах погруженной части.
Существует два способа, архимедову силу, действующую на тело, погруженное в жидкость. Первый состоит в измерении объема тела и вычислении веса жидкости, занимающей аналогичный объем. Для этого необходимо, чтобы тело обладало правильной геометрической формой, то есть, было кубом, параллелепипедом, шаром, полусферой, конусом. Объем твердого тела более сложной формы рассчитать очень трудно, поэтому для определения силы Архимеда в этом случае существует более практичный способ № 2. Но о нем несколько позже.
Первый состоит в измерении объема тела и вычислении веса жидкости, занимающей аналогичный объем. Для этого необходимо, чтобы тело обладало правильной геометрической формой, то есть, было кубом, параллелепипедом, шаром, полусферой, конусом. Объем твердого тела более сложной формы рассчитать очень трудно, поэтому для определения силы Архимеда в этом случае существует более практичный способ № 2. Но о нем несколько позже.
Определив объем погружаемого тела, умножаем его на плотность жидкости и находим величину выталкивающей силы, действующей на это тело в однородной среде заданной плотности и на ускорение свободного падения g (9,8 м/с2). Формула для определения силы Архимеда выглядит так:
F=ρgV
ρ – удельная плотность жидкости;
g – ускорение свободного падения;
V – объем вытесненной жидкости.
Как и любая сила, она измеряется в Ньютонах (Н).
Второй способ базируется на измерении объема вытесненной жидкости. Он наиболее соответствует тому опыту, который и привел Архимеда к открытию своего закона. Этот способ очень удобен и при вычислении архимедовой силы при частичном погружении тела. Для получения необходимых данных исследуемое тело подвешивают на нитке и медленно опускают в жидкость.
Этот способ очень удобен и при вычислении архимедовой силы при частичном погружении тела. Для получения необходимых данных исследуемое тело подвешивают на нитке и медленно опускают в жидкость.
Достаточно замерить уровень жидкости в сосуде до погружения тела и после, умножить разницу уровней на площадь поверхности и найти объем вытесненной жидкости. Как и в первом случае, умножаем этот объем на плотность жидкости и g. Полученная величина и является силой Архимеда. Чтобы единицей измерения силы стал Ньютон, следует объем измерять в м3, а плотность – в кг/м3.
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Введение
Актуальность: Если внимательно присмотреться к окружающему миру, то можно открыть для себя множество событий, происходящих вокруг. Издревле человека окружает вода. Когда мы плаваем в ней, то наше тело выталкивает на поверхность какие-то силы. Я давно задаю себе вопрос: «Почему тела плавают или тонут? Вода выталкивает предметы?»
Моя исследовательская работа направлена на то, чтобы углубить полученные на уроке знания об архимедовой силе. Ответы на интересующие меня вопросы, используя жизненный опыт, наблюдения за окружающей действительностью, провести собственные эксперименты и объяснить их результаты, которые позволят расширить знания по данной теме. Все науки связаны между собой. А общий объект изучения всех наук – это человек «плюс» природа. Я уверен, что исследование действия архимедовой силы сегодня является актуальным.
Ответы на интересующие меня вопросы, используя жизненный опыт, наблюдения за окружающей действительностью, провести собственные эксперименты и объяснить их результаты, которые позволят расширить знания по данной теме. Все науки связаны между собой. А общий объект изучения всех наук – это человек «плюс» природа. Я уверен, что исследование действия архимедовой силы сегодня является актуальным.
Гипотеза: Я предполагаю, что в домашних условиях можно рассчитать величину выталкивающей силы действующей на погруженное в жидкость тело и определить зависит ли она от свойств жидкости, объема и формы тела.
Объект исследования: Выталкивающая сила в жидкостях.
Задачи:
Изучить историю открытия архимедовой силы;
Изучить учебную литературу по вопросу действия архимедовой силы;
Выработать навыки проведения самостоятельного эксперимента;
Доказать, что значение выталкивающей силы зависит от плотности жидкости.
Методы исследования:
Исследовательские;
Расчетные;
Информационного поиска;
Наблюдений
1. Открытие силы Архимеда
Открытие силы Архимеда
Существует знаменитая легенда о том, как Архимед бежал по улице и кричал «Эврика!» Это как раз повествует об открытии им того, что выталкивающая сила воды равна по модулю весу вытесненной им воды, объем которой равен объему погруженного в нее тела. Это открытие названо законом Архимеда.
В III веке до нашей эры жил Гиерон – царь древнегреческого города Сиракузы и захотел он сделать себе новую корону из чистого золота. Отмерил его строго сколько нужно, и дал ювелиру заказ. Через месяц мастер вернул золото в виде короны и весила она столько, сколько и масса данного золота. Но ведь всякое бывает и мастер мог схитрить, добавив серебро или того хуже – медь, ведь на глаз не отличишь, а масса такая, какая и должна быть. А царю узнать охота: честно ль сделана работа? И тогда, попросил он ученого Архимеда, проверить из чистого ли золота сделал мастер ему корону. Как известно, масса тела равна произведению плотности вещества, из которого сделано тело, на его объем: . Если у разных тел одинаковая масса, но они сделаны из разных веществ, то значит, у них будет разный объем. Если бы мастер вернул царю не ювелирно сделанную корону, объем которой определить невозможно из-за ее сложности, а такой же по форме кусок металла, который дал ему царь, то сразу было бы ясно, подмешал он туда другого металла или нет. И вот принимая ванну, Архимед обратил внимание, что вода из нее выливается. Он заподозрил, что выливается она именно в том объеме, какой объем занимают его части тела, погруженные в воду. И Архимеда осенило, что объем короны можно определить по объему вытесненной ей воды. Ну а коли можно измерить объем короны, то его можно сравнить с объемом куска золота, равного по массе. Архимед погрузил в воду корону и измерил, как увеличился объем воды. Также он погрузил в воду кусок золота, у которого масса была такая же, как у короны. И тут он измерил, как увеличился объем воды. Объемы вытесненной в двух случаях воды оказались разными. Тем самым мастер был изобличен в обмане, а наука обогатилась замечательным открытием.
Если у разных тел одинаковая масса, но они сделаны из разных веществ, то значит, у них будет разный объем. Если бы мастер вернул царю не ювелирно сделанную корону, объем которой определить невозможно из-за ее сложности, а такой же по форме кусок металла, который дал ему царь, то сразу было бы ясно, подмешал он туда другого металла или нет. И вот принимая ванну, Архимед обратил внимание, что вода из нее выливается. Он заподозрил, что выливается она именно в том объеме, какой объем занимают его части тела, погруженные в воду. И Архимеда осенило, что объем короны можно определить по объему вытесненной ей воды. Ну а коли можно измерить объем короны, то его можно сравнить с объемом куска золота, равного по массе. Архимед погрузил в воду корону и измерил, как увеличился объем воды. Также он погрузил в воду кусок золота, у которого масса была такая же, как у короны. И тут он измерил, как увеличился объем воды. Объемы вытесненной в двух случаях воды оказались разными. Тем самым мастер был изобличен в обмане, а наука обогатилась замечательным открытием.
Из истории известно, что задача о золотой короне побудила Архимеда заняться вопросом о плавании тел. Опыты, проведенные Архимедом, были описаны в сочинении «О плавающих телах», которое дошло до нас. Седьмое предложение (теорема) этого сочинения сформулировано Архимедом следующим образом: тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела.
Интересно, что сила Архимеда равна нулю, когда погруженное в жидкость тело плотно, всем основанием прижато ко дну.
Открытие основного закона гидростатики – крупнейшее завоевание античной науки.
2. Формулировка и пояснения закона Архимеда
Закон Архимеда описывает действие жидкостей и газов на погруженное в них тело, и является одним из главных законов гидростатики и статики газов.
Закон Архимеда формулируется следующим образом: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу жидкости (или газа) в объёме погруженной части тела – эта сила называется силой Архимеда :
,
где – плотность жидкости (газа), – ускорение свободного падения, – объём погружённой части тела (или часть объёма тела, находящаяся ниже поверхности).
Следовательно, архимедова сила зависит только от плотности жидкости, в которую погружено тело, и от объема этого тела. Но она не зависит, например, от плотности вещества тела, погруженного в жидкость, так как эта величина не входит в полученную формулу.
Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.
3. Определение силы Архимеда
Силу, с которой тело, находящееся в жидкости, выталкивается ею, можно определить на опыте используя данный прибор:
Небольшое ведерко и тело цилиндрической формы подвешиваем на пружине, закрепленной в штативе. Растяжение пружины отмечаем стрелкой на штативе, показывая вес тела в воздухе. Приподняв тело, под него подставляем стакан с отливной трубкой, наполненный жидкостью до уровня отливной трубки. После чего тело погружают целиком в жидкость. При этом часть жидкости, объём которой равен объёму тела, выливается из отливного сосуда в стакан. Указатель пружины поднимается вверх, пружина сокращается, показывая уменьшение веса тела в жидкости. В данном случае на тело, наряду с силой тяжести, действует еще и сила, выталкивающая его из жидкости. Если в ведёрко налить жидкость из стакана (т.е. ту, которую вытеснило тело), то указатель пружины возвратится к своему начальному положению.
Указатель пружины поднимается вверх, пружина сокращается, показывая уменьшение веса тела в жидкости. В данном случае на тело, наряду с силой тяжести, действует еще и сила, выталкивающая его из жидкости. Если в ведёрко налить жидкость из стакана (т.е. ту, которую вытеснило тело), то указатель пружины возвратится к своему начальному положению.
На основании этого опыта можно заключить, что сила, выталкивающая тело, целиком погруженное в жидкость, равна весу жидкости в объёме этого тела. Зависимость давления в жидкости (газе) от глубины погружения тела приводит к появлению выталкивающей силы (силы Архимеда), действующей на любое тело, погруженное в жидкость или газ. Тело при погружении двигается вниз под действием силы тяжести. Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.
Данный опыт подтверждает, что архимедова сила равна весу жидкости в объёме тела.
4. Условие плавания тел
На тело, находящееся внутри жидкости, действуют две силы: сила тяжести, направленная вертикально вниз, и архимедова сила, направленная вертикально вверх. Рассмотрим, что будет происходить с телом под действием этих сил, если вначале оно было неподвижно.
Рассмотрим, что будет происходить с телом под действием этих сил, если вначале оно было неподвижно.
При этом возможны три случая:
1) Если сила тяжести больше архимедовой силы, то тело опускается вниз, то есть тонет:
, то тело тонет;
2) Если модуль силы тяжести равен модулю архимедовой силы, то тело может находиться в равновесии внутри жидкости на любой глубине:
, то тело плавает;
3) Если архимедова сила больше силы тяжести, то тело будет поднимается из жидкости – всплывать:
, то тело плавает.
Если всплывающее тело частично выступает над поверхностью жидкости, то объем погруженной части плавающего тела такой, что вес вытесненной жидкости равен весу плавающего тела.
Архимедова сила больше силы тяжести, если плотность жидкости больше плотности погруженного в жидкость тела, если
1) =— тело плавает в жидкости или газе,2) >— тело тонет,3)
Именно эти принципы соотношения силы тяжести и силы Архимеда применяются в судоходостронии. Однако на воде держатся громадные речные и морские суда, изготовленные из стали, плотность которой почти в 8 раз больше плотности воды. Объясняется это тем, что из стали делают лишь сравнительно тонкий корпус судна, а большая часть его объема занята воздухом. Среднее значение плотности судна при этом оказывается значительно меньше плотности воды; поэтому оно не только не тонет, но и может принимать для перевозки большое количество грузов. Суда, плавающие по рекам, озерам, морям и океанам, построены из разных материалов с различной плотностью. Корпус судов обычно делают из стальных листов. Все внутренние крепления, придающие судам прочность, также изготавливают из металлов. Для постройки судов используют разные материалы, имеющие по сравнению с водой как большую, так и меньшую плотность. Вес воды, вытесненной подводной частью судна, равен весу судна с грузом в воздухе или силе тяжести, действующей на судно с грузом.
Однако на воде держатся громадные речные и морские суда, изготовленные из стали, плотность которой почти в 8 раз больше плотности воды. Объясняется это тем, что из стали делают лишь сравнительно тонкий корпус судна, а большая часть его объема занята воздухом. Среднее значение плотности судна при этом оказывается значительно меньше плотности воды; поэтому оно не только не тонет, но и может принимать для перевозки большое количество грузов. Суда, плавающие по рекам, озерам, морям и океанам, построены из разных материалов с различной плотностью. Корпус судов обычно делают из стальных листов. Все внутренние крепления, придающие судам прочность, также изготавливают из металлов. Для постройки судов используют разные материалы, имеющие по сравнению с водой как большую, так и меньшую плотность. Вес воды, вытесненной подводной частью судна, равен весу судна с грузом в воздухе или силе тяжести, действующей на судно с грузом.
Для воздухоплавания вначале использовали воздушные шары, которые раньше наполняли нагретым воздухом, сейчас – водородом или гелием. Для того чтобы шар поднялся в воздух, необходимо, чтобы архимедова сила (выталкивающая), действующая на шар, была больше силы тяжести.
Для того чтобы шар поднялся в воздух, необходимо, чтобы архимедова сила (выталкивающая), действующая на шар, была больше силы тяжести.
5. Проведение эксперимента
Исследовать поведение сырого яйца в жидкостях разного рода.
Задача: доказать, что значение выталкивающей силы зависит от плотности жидкости.
Я взял одно сырое яйцо и жидкости разного рода (приложение 1):
Вода чистая;
Вода, насыщенная солью;
Подсолнечное масло.
Сначала я опустил сырое яйцо в чистую воду – яйцо утонуло – «пошло ко дну» (приложение 2). Потом в стакан с чистой водой я добавил столовую ложку поваренной соли, в результате яйцо плавает (приложение 3). И наконец, я опустил яйцо в стакан с подсолнечным маслом – яйцо опустилось на дно (приложение 4).
Вывод: в первом случае плотность яйца больше плотности воды и поэтому яйцо утонуло. Во втором случае плотность солёной воды больше плотности яйца, поэтому яйцо плавает в жидкости. В третьем случае плотность яйца также больше плотности подсолнечного масла, поэтому яйцо утонуло. Следовательно, чем больше плотность жидкости, тем сила тяжести меньше.
Следовательно, чем больше плотность жидкости, тем сила тяжести меньше.
2. Действие Архимедовой силы на тело человека в воде.
Определить на опыте плотность тела человека, сравнить ее с плотностью пресной и морской воды и сделать вывод о принципиальной возможности человека плавать;
Вычислить вес человека в воздухе, архимедову силу, действующую на человека в воде.
Для начала с помощью весов я измерил массу своего тела. Затем измерил объем тела (без объема головы). Для этого я налил в ванну воды столько, чтобы при погружении в воду я был полностью в воде (за исключением головы). Далее с помощью сантиметровой ленты отметил от верхнего края ванны расстояние до уровня воды ℓ 1 , а затем – при погружении в воду ℓ 2 . После этого с помощью предварительно проградуированной трехлитровой банки стал наливать в ванну воду от уровня ℓ 1 до уровня ℓ 2 – так я измерил объем вытесненной мной воды (приложение 5). Плотность я рассчитал с помощью формулы:
Сила тяжести, действующая на тело в воздухе, была рассчитана по формуле: , где – ускорение свободного падения ≈ 10 .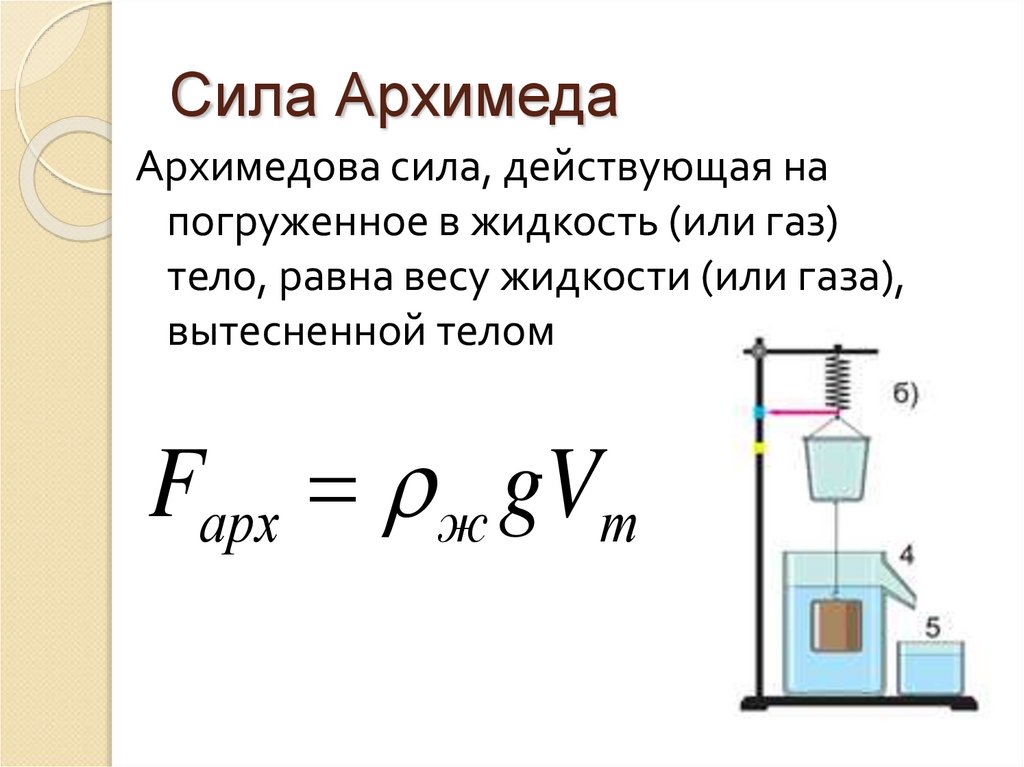 Значение выталкивающей силы было рассчитано с помощью формулы описанной в пункте 2.
Значение выталкивающей силы было рассчитано с помощью формулы описанной в пункте 2.
Вывод:Тело человекаплотнее пресной воды, а, значит, оно в ней тонет. Человеку легче плавать в море, чем в реке, так как плотность морской воды больше, а следовательно больше значение выталкивающей силы.
Заключение
В процессе работы над этой темой мы узнали для себя много нового и интересного. Круг наших познаний увеличился не только в области действия силы Архимеда, но и применении ее в жизни. Перед началом работы мы имели о ней далеко неподробное представление. При проведении опытов мы подтвердили экспериментально справедливость закона Архимеда и выяснили, что выталкивающая силазависит от объема тела и плотности жидкости, чем больше плотность жидкости, тем архимедова сила больше. Результирующая сила, которая определяет поведение тела в жидкости, зависит от массы, объёма тела и плотности жидкости.
Помимо проделанных экспериментов, была изучена дополнительная литература об открытии силы Архимеда, о плавании тел, воздухоплавании.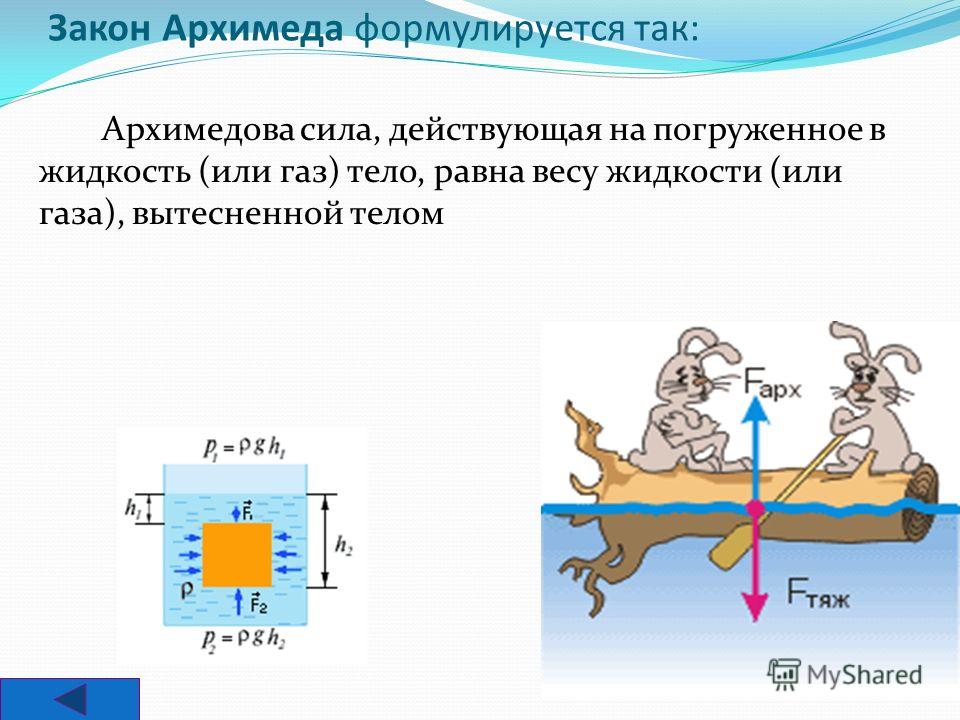
Каждый из Вас может сделать удивительные открытия, и для этого не нужно обладать ни особенными знаниями, ни мощным оборудованием. Нужно лишь немного внимательней посмотреть на окружающий нас мир, быть чуть более независимым в своих суждениях, и открытия не заставят себя ждать. Нежелание большинства людей познавать окружающий мир оставляет большой простор любознательным в самых неожиданных местах.
Список литературы
1.Большая книга экспериментов для школьников – М.: Росмэн, 2009. – 264 с.
2. Википедия: https://ru.wikipedia.org/wiki/Закон_Архимеда.
3. Перельман Я.И. Занимательная физика. – книга 1. – Екатеринбург.: Тезис, 1994.
4. Перельман Я.И. Занимательная физика. – книга 2.- Екатеринбург.: Тезис, 1994.
5. Перышкин А.В. Физика: 7 класс: учебник для общеобразовательных учреждений / А.В. Перышкин. – 16-е изд., стереотип. – М.: Дрофа, 2013. – 192 с.: ил.
Приложение 1
Приложение 2
Приложение 3
Приложение 4
Закон Архимеда – закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.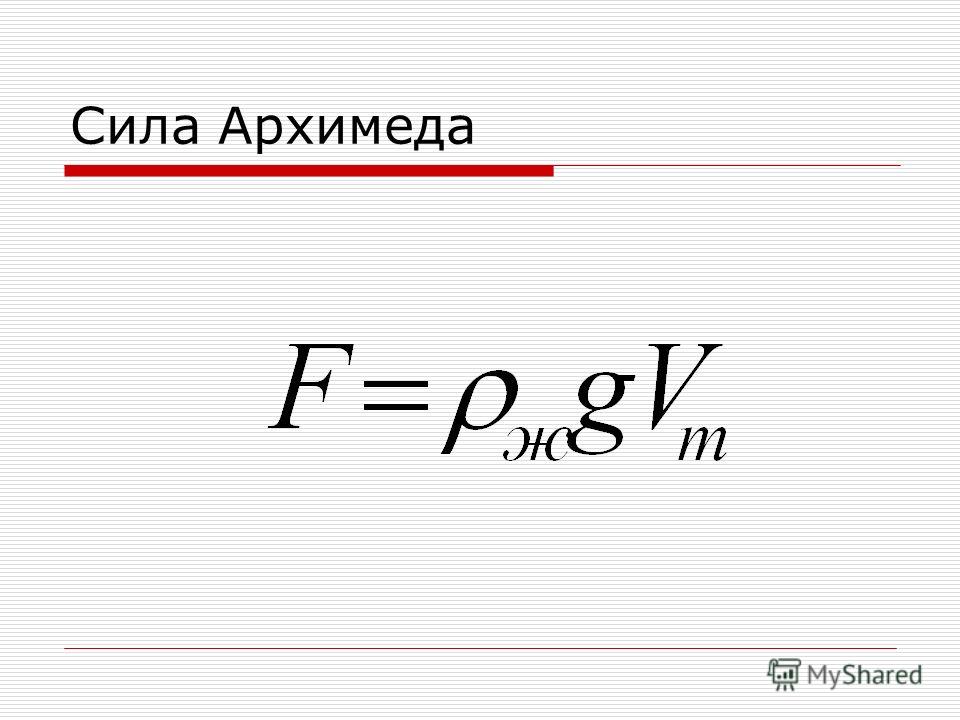
История вопроса
«Эврика!» («Нашел!») – именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало – нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото. Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Однако, что правда – то правда: именно Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Закон Архимеда и молекулярно-кинетическая теория
В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.
Формулировка и пояснения
Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается поднять на суше. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.
Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается поднять на суше. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.
Существование гидростатического давления приводит к тому, что на любое тело, находящееся в жидкости или газе, действует выталкивающая сила. Впервые значение этой силы в жидкостях определил на опыте Архимед. Закон Архимеда формулируется так: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу того количества жидкости или газа, которое вытеснено погруженной частью тела.
Формула
Сила Архимеда, действующая на погруженное в жидкость тело, может быть рассчитана по формуле: F А = ρ ж gV пт,
где ρж – плотность жидкости,
g – ускорение свободного падения,
Vпт – объем погруженной в жидкость части тела.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести Fт и архимедовой силы FA, которые действуют на это тело. Возможны следующие три случая:
1) Fт > FA – тело тонет;
2) Fт = FA – тело плавает в жидкости или газе;
3) Fт
Плавучесть – это выталкивающая сила, действующая на тело, погруженное в жидкость (или газ), и направленная противоположно силе тяжести. В общих случаях выталкивающая сила может быть вычислена по формуле: F b = V s × D × g, где F b – выталкивающая сила; V s – объем части тела, погруженной в жидкость; D – плотность жидкости, в которую погружают тело; g – сила тяжести.
Шаги
Вычисление по формуле
Найдите объем части тела, погруженной в жидкость (погруженный объем). Выталкивающая сила прямо пропорциональна объему части тела, погруженной в жидкость. Другими словами, чем больше погружается тело, тем больше выталкивающая сила. Это означает, что даже на тонущие тела действует выталкивающая сила. Погруженный объем должен измеряться в м 3 .
- У тел, которые полностью погружены в жидкость, погруженный объем равен объему тела. У тел, плавающих в жидкости, погруженный объем равен объему части тела, скрытой под поверхностью жидкости.
- В качестве примера рассмотрим шар, плавающий в воде. Если диаметр шара равен 1 м, а поверхность воды доходит до середины шара (то есть он погружен в воду наполовину), то погруженный объем шара равен его объему, деленному на 2. Объем шара вычисляется по формуле V = (4/3)π(радиус) 3 = (4/3)π(0,5) 3 = 0,524 м 3 . Погруженный объем: 0,524/2 = 0,262 м 3 .
Найдите плотность жидкости (в кг/м 3), в которую погружается тело.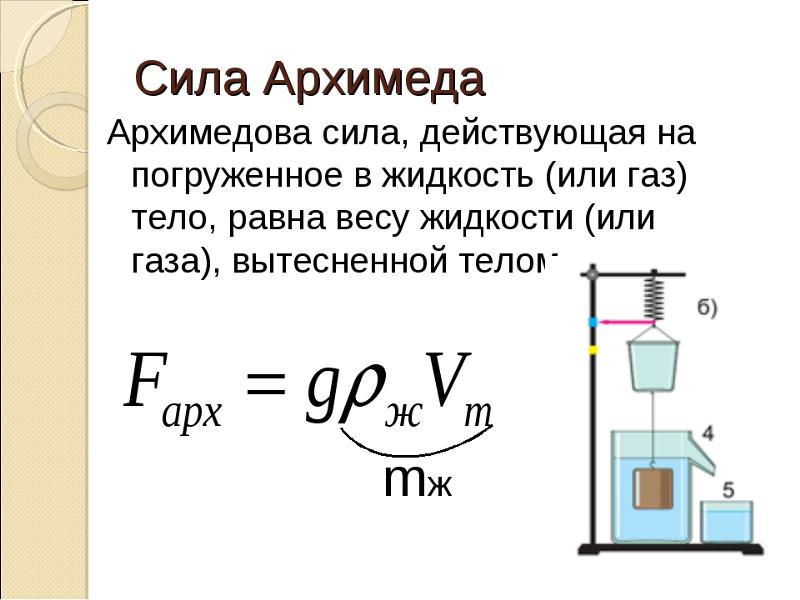 Плотность – это отношение массы тела к занимаемому этим телом объему. Если у двух тел одинаковый объем, то масса тела с большей плотностью будет больше. Как правило, чем больше плотность жидкости, в которую погружается тело, тем больше выталкивающая сила. Плотность жидкости можно найти в интернете или в различных справочниках.
Плотность – это отношение массы тела к занимаемому этим телом объему. Если у двух тел одинаковый объем, то масса тела с большей плотностью будет больше. Как правило, чем больше плотность жидкости, в которую погружается тело, тем больше выталкивающая сила. Плотность жидкости можно найти в интернете или в различных справочниках.
- В нашем примере шар плавает в воде. Плотность воды приблизительно равна 1000 кг/м 3 .
- Плотности многих других жидкостей можно найти .
Найдите силу тяжести (или любую другую силу, действующую на тело вертикально вниз). Не важно, плавает ли тело или тонет, на него всегда действует сила тяжести. В естественных условиях сила тяжести (а точнее сила тяжести, действующая на тело массой 1 кг) приблизительно равна 9,81 Н/кг. Тем не менее, если на тело действуют и другие силы, например, центробежная сила, такие силы необходимо учесть и вычислить результирующую силу, направленную вертикально вниз.
- В нашем примере мы имеем дело с обычной стационарной системой, поэтому на шар действует только сила тяжести, равная 9,81 Н/кг.

- Однако если шар плавает в емкости с водой, которая вращается вокруг некоторой точки, то на шар будет действовать центробежная сила, которая не позволяет шару и воде выплескиваться наружу и которую необходимо учесть в расчетах.
Если у вас есть значения погруженного объема тела (в м 3), плотность жидкости (в кг/м 3) и сила тяжести (или любая другая сила, направленная вертикально вниз), то вы можете вычислить выталкивающую силу. Для этого просто перемножьте указанные выше значения, и вы найдете выталкивающую силу (в Н).
- В нашем примере: F b = V s × D × g. F b = 0,262 м 3 × 1000 кг/м 3 × 9,81 Н/кг = 2570 Н.
Выясните, будет ли тело плавать или тонуть. По приведенной выше формуле можно вычислить выталкивающую силу. Но, выполнив дополнительные расчеты, вы можете определить, будет ли тело плавать или тонуть. Для этого найдите выталкивающую силу для всего тела (то есть в вычислениях используйте весь объем тела, а не погруженный объем), а затем найдите силу тяжести по формуле G = (масса тела)*(9,81 м/с 2). Если выталкивающая сила больше силы тяжести, то тело будет плавать; если же сила тяжести больше выталкивающей силы, то тело будет тонуть. Если силы равны, то тело обладает «нейтральной плавучестью».
Если выталкивающая сила больше силы тяжести, то тело будет плавать; если же сила тяжести больше выталкивающей силы, то тело будет тонуть. Если силы равны, то тело обладает «нейтральной плавучестью».
- Например, рассмотрим 20 килограммовое бревно (цилиндрической формы) с диаметром 0,75 м и высотой 1,25 м, погруженное в воду.
- Найдите объем бревна (в нашем примере объем цилиндра) по формуле V = π(радиус) 2 (высота) = π(0,375) 2 (1,25) = 0,55 м 3 .
- Далее вычислите выталкивающую силу: F b = 0,55 м 3 × 1000 кг/м 3 × 9,81 Н/кг = 5395,5 Н.
- Теперь найдите силу тяжести: G = (20 кг)(9,81 м/с 2) = 196,2 Н. Это значение намного меньше значения выталкивающей силы, поэтому бревно будет плавать.
Используйте описанные выше вычисления для тела, погруженного в газ. Помните, что тела могут плавать не только в жидкостях, но и в газах, которые вполне могут выталкивать некоторые тела, несмотря на очень небольшую плотность газов (вспомните про шар, наполненный гелием; плотность гелия меньше плотности воздуха, поэтому шар с гелием летает (плавает) в воздухе).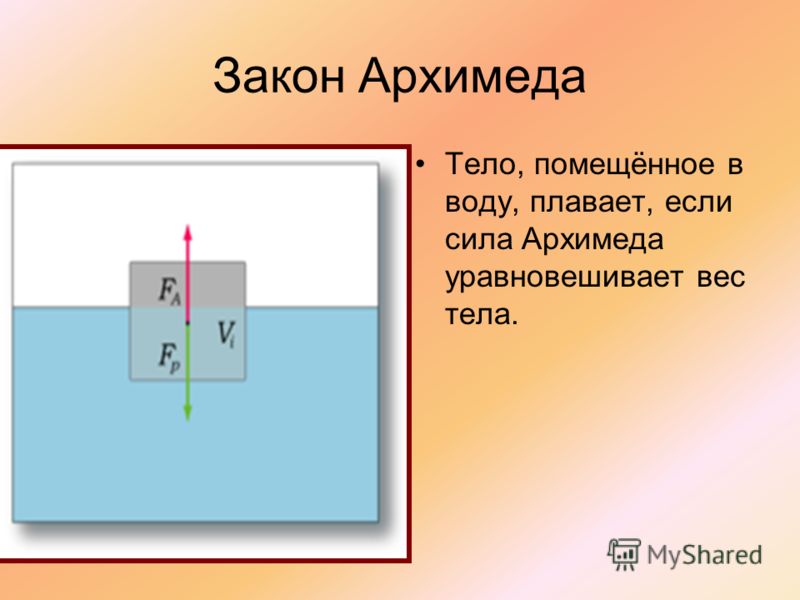
Постановка эксперимента
Поместите небольшую чашку в ведро. В этом простом эксперименте мы покажем, что на тело, погруженное в жидкость, действует выталкивающая сила, так как тело выталкивает объем жидкости, равный погруженному объему тела. Мы также продемонстрируем, как найти выталкивающую силу при помощи эксперимента. Для начала поместите небольшую чашку в ведро (или кастрюлю).
Наполните чашку водой (до краев). Будьте осторожны! Если вода из чашки вылилась в ведро, вылейте воду и начните заново.
- Для эксперимента предположим, что плотность воды равна 1000 кг/м 3 (только если вы не используете соленую воду или другую жидкость).
- Для наполнения чашки до краев используйте пипетку.
Возьмите небольшой предмет, который поместится в чашке и не будет поврежден водой. Найдите массу этого тела (в килограммах; для этого взвесьте тело на весах и конвертируйте значение в граммах в килограммы).
 Затем медленно опустите предмет в чашку с водой (то есть погрузите тело в воду, но при этом не погружайте пальцы). Вы увидите, что некоторое количество воды вылилось из чашки в ведро.
Затем медленно опустите предмет в чашку с водой (то есть погрузите тело в воду, но при этом не погружайте пальцы). Вы увидите, что некоторое количество воды вылилось из чашки в ведро.- В этом эксперименте мы опустим в чашку с водой игрушечный автомобиль массой 0,05 кг. Объем этого автомобиля нам не нужен, чтобы вычислить выталкивающую силу.
При погружении тела в воду оно выталкивает некоторый объем воды (иначе тело не погрузилось бы в воду). Когда тело выталкивает воду (то есть тело действует на воду), на тело начинает действовать выталкивающая сила (то есть вода действует на тело). Вылейте воду из ведра в мерный стакан. Объем воды в мерном стакане должен быть равен объему погруженного тела.
- Другими словами, если тело плавает, то объем вытесненной жидкости равен погруженному объему тела. Если тело утонуло, то объем вытесненной жидкости равен объему всего тела.
Вычислите массу вытесненной воды по известным значениям объема этой воды и плотности воды.
 Значение объема воды, показанного шкалой мерного стакана, конвертируйте в м 3 (вы можете сделать это ), а затем умножьте объем вытесненной воды на плотность воды (1000 кг/м 3).
Значение объема воды, показанного шкалой мерного стакана, конвертируйте в м 3 (вы можете сделать это ), а затем умножьте объем вытесненной воды на плотность воды (1000 кг/м 3).- В нашем примере игрушечный автомобиль утонул, вытеснив около двух столовых ложек воды (0,00003 м 3). Вычислим массу вытесненной воды: 1000 кг/м 3 × 0,00003 м 3 = 0,03 кг.
Сравните массу вытесненной воды с массой погруженного тела. Если масса погруженного тела больше массы вытесненной воды, то тело утонет. Если масса вытесненной воды больше массы тела, то оно плавает. Поэтому для того, чтобы тело плавало, оно должно вытеснять количество воды с массой, превышающей массу самого тела.
- Таким образом, тела, имеющие небольшую массу, но большой объем, обладают наилучшей плавучестью. Эти два параметра характерны для полых тел. Вспомните лодку – она обладает превосходной плавучестью, потому что она полая и вытесняет много воды при небольшой массе самой лодки. Если бы лодка не была полой, она бы вообще не плавала (а тонула).

- В нашем примере масса автомобиля (0,05 кг) больше массы вытесненной воды (0,03 кг). Поэтому автомобиль и утонул.
- Таким образом, тела, имеющие небольшую массу, но большой объем, обладают наилучшей плавучестью. Эти два параметра характерны для полых тел. Вспомните лодку – она обладает превосходной плавучестью, потому что она полая и вытесняет много воды при небольшой массе самой лодки. Если бы лодка не была полой, она бы вообще не плавала (а тонула).
На поверхность тела, которое находится в жидкости или газе действуют силы давления. Известно, что давление увеличивается с увеличением глубины погружения. Значит, что силы давления, которые действуют на нижнюю часть тела и направлены вверх больше по модулю, чем силы, которые действуют на верхнюю часть тела и направлены вниз.
Определение и формула силы выталкивания
Определение
Равнодействующую сил давления на тело, которое погружено в жидкость или газ называют выталкивающей силой . Выталкивающая сила может быть больше, чем сила тяжести, которая действует на тело. Силы выталкивания появляются и в том случае,если тело находится в жидкости или газе частично.
Если тело, находящееся в жидкости оставить в покое, то оно тонет, находится в равновесии или всплывает на поверхность.
Это зависит от соотношения силы тяжести и выталкивающей силы (F A),действующих на тело. В первом случае (тело тонет)
mg>F A . Если mg=F A , то тело находится в равновесии. При mg
В первом случае (тело тонет)
mg>F A . Если mg=F A , то тело находится в равновесии. При mg
На тело, погруженное в жидкость или газ, действует сила выталкивания (сила Архимеда F A), равная весу вытесненной им жидкости или газа. В математическом виде данный закон выглядит как:
где – плотность жидкости (газа), в которую погружено тело, g=9,8 м/с 2 – ускорение свободного падения, V – объем тела (его части), которое находится в жидкости (газе). Сила Архимеда приложена к центру тяжести объема части тела, которая находится в жидкости (газе).
Закон Архимеда можно применять для вычисления плотности однородного тела неправильной формы. При этом тело взвешивают два раза: один раз в воздухе, второй раз, погрузив тело в жидкость, плотность которой известна.
Основной единицей измерения силы Архимеда, как и любой силы в системе СИ является: =Н
В СГС: F A ]=дин
1Н= (кг м)/с 2
Примеры решения задач
Пример
Задание. Какова сила выталкивания, которая действует на куб, погруженный в систему жидкостей. Сосуд наполнен водой, поверх воды налит керосин. Граница раздела жидкостей проходит посередине грани куба. Плотность воды считайте равной
1 =10 3 кг/м 3 ,
плотность керосина равна 2 =0,81 10 3
кг/м 3 . Сторона куба равна a=0,1 м.
Сосуд наполнен водой, поверх воды налит керосин. Граница раздела жидкостей проходит посередине грани куба. Плотность воды считайте равной
1 =10 3 кг/м 3 ,
плотность керосина равна 2 =0,81 10 3
кг/м 3 . Сторона куба равна a=0,1 м.
Решение. Сделаем рисунок.
Сила выталкивания, которая действует со стороны воды, на половину куба равна:
Сила выталкивания, которая действует со стороны керосина, на половину куба равна:
Обе силы направлены вверх. Приложены они к разным точкам (центрам масс объемов тел, погруженных в соответствующие жидкости), при суммировании векторы можно перенести в одну точку параллельно самим себе. Получим, результирующая сила выталкивания равна:
Подставим компоненты силы (1.2), (1.3) в выражение (1.1), имеем:
Проведем вычисления:
Ответ. Ответ: F A =8,8 Н
Пример
Задание. Какова плотность камня, если его вес в воздухе 3,2 Н, а вес в воде 1,8 Н.
Решение. Вес камня в воздухе:
где – плотность камня, V – объем камня.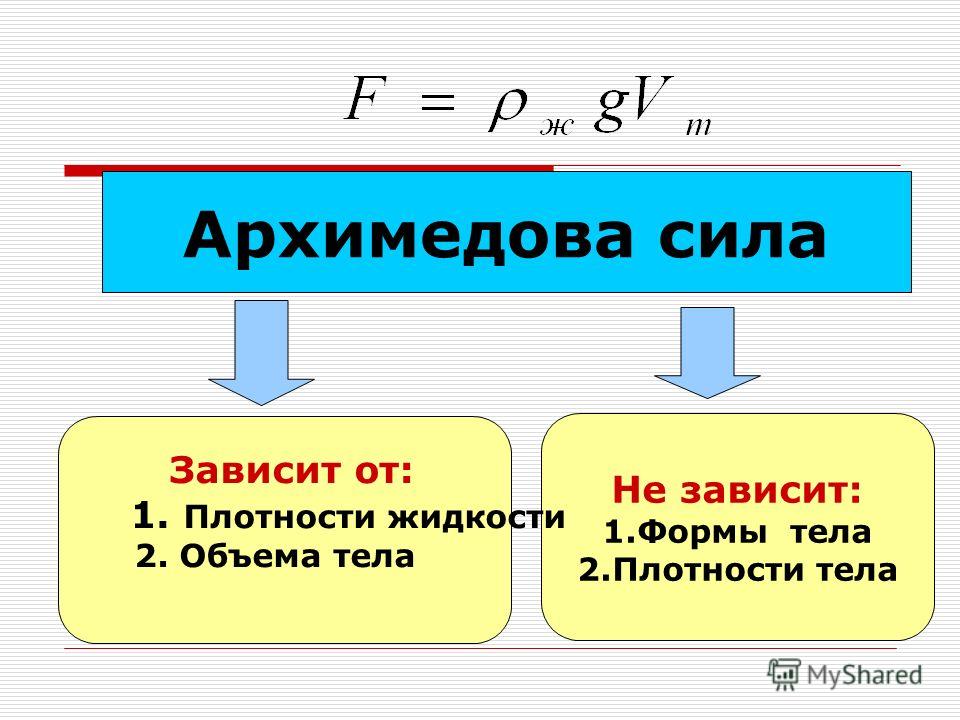 Взвешивая камень в воде, получаем вес камня в жидкости, равный.
Взвешивая камень в воде, получаем вес камня в жидкости, равный.
Принцип Архимеда | безграничная физика |
Плавучесть и принцип Архимеда
Выталкивающую силу, действующую на объект, можно рассчитать по закону Архимеда.
Цели обучения
Вычислите направление выталкивающей силы
Ключевые выводы
Ключевые моменты
- Выталкивающая сила создается давлением жидкости, в которую погружен объект.
- Выталкивающая сила всегда направлена вверх, потому что давление жидкости увеличивается с глубиной.
- Вы можете рассчитать выталкивающую силу либо напрямую, вычислив силу, действующую на каждую из поверхностей объекта, либо косвенно, найдя вес вытесненной жидкости.
Ключевые термины
- выталкивающая сила : Восходящая сила, создаваемая жидкостью и противодействующая весу погруженного объекта.
- Закон Архимеда : Выталкивающая сила, действующая на тело, погруженное в жидкость, равна весу жидкости, вытесненной телом.

Когда вы встаете после купания в теплой ванне, ваши руки могут казаться странно тяжелыми. Этот эффект связан с потерей плавучей поддержки воды. Что создает эту выталкивающую силу? Почему одни вещи плавают, а другие нет? Получают ли объекты, которые тонут, какую-либо поддержку от жидкости? Ваше тело поддерживается атмосферой или это касается только гелиевых шаров?
Выталкивающая сила: причина и расчет
Мы находим ответы на поставленные выше вопросы в том факте, что в любой данной жидкости давление увеличивается с глубиной. Когда объект погружен в жидкость, направленная вверх сила на нижнюю часть объекта больше, чем направленная вниз сила на верхнюю часть объекта. Результатом является чистая восходящая сила (выталкивающая сила) на любой объект в любой жидкости. Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса объекта, то он утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует в жидкости, независимо от того, плавает ли объект, тонет или остается подвешенным.
Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует в жидкости, независимо от того, плавает ли объект, тонет или остается подвешенным.
Выталкивающая сила является результатом давления, оказываемого жидкостью. Жидкость давит на погруженный объект со всех сторон, но по мере увеличения давления с глубиной давление на нижнюю поверхность объекта сильнее, чем на верхнюю (как видно на рис. ).
Вы можете рассчитать выталкивающую силу, действующую на объект, суммируя силы, действующие на все стороны объекта. Например, рассмотрим объект, показанный на рис.2}}g≈9,81с2м
— ускорение свободного падения. Величина силы на верхней поверхности:
F1=P1A=h2ρgA\text{F}_1 = \text{P}_1 \text{A} = \text{h}_1 \rho \text{g} \text{A}F1=P1A=h2ρgA
.
Эта сила направлена вниз. Аналогично сила на нижней поверхности:
F2=P2A=h3ρgA\text{F}_2 = \text{P}_2 \text{A} = \text{h}_2 \rho \text{g} \ text{A}F2=P2A=h3ρgA
и указывает вверх. Поскольку он цилиндрический, результирующая сила на сторонах объекта равна нулю – силы на разных частях поверхности противодействуют друг другу и точно компенсируются. Таким образом, чистая направленная вверх сила, действующая на цилиндр со стороны жидкости, равна:
Поскольку он цилиндрический, результирующая сила на сторонах объекта равна нулю – силы на разных частях поверхности противодействуют друг другу и точно компенсируются. Таким образом, чистая направленная вверх сила, действующая на цилиндр со стороны жидкости, равна:
FB=F2−F1=ρgA(h3−h2)\text{F}_\text{B} = \text{F}_2 – \text{F}_1 = \rho \text{g} \text{ A} (\text{h}_2 – \text{h}_1)FB=F2−F1=ρgA(h3−h2)
Закон Архимеда
Хотя расчет выталкивающей силы таким способом всегда возможен, часто это бывает очень сложно. Более простой метод следует из принципа Архимеда, который гласит, что выталкивающая сила, действующая на тело, погруженное в жидкость, равна весу жидкости, вытесняемой телом. Другими словами, для расчета выталкивающей силы на объект мы предполагаем, что погруженная часть объекта состоит из воды, а затем вычисляем вес этой воды (как показано на рис. ).
Закон Архимеда : Выталкивающая сила корабля (а) равна весу воды, вытесненной кораблем, что показано заштрихованной областью на (б).
Принцип можно выразить формулой:
FB=wfl\text{F}_\text{B} = \text{w}_\mathrm{\text{fl}}FB=wfl
Рассуждение Принцип Архимеда заключается в том, что выталкивающая сила объекта зависит от давления, оказываемого жидкостью на его погруженную поверхность. Представьте, что мы заменяем погруженную часть объекта жидкостью, в которой он содержится, как в (б). Выталкивающая сила на это количество жидкости должна быть такой же, как и на исходный объект (корабль). Однако мы также знаем, что выталкивающая сила жидкости должна быть равна ее весу, так как сама по себе жидкость не тонет. Следовательно, выталкивающая сила исходного объекта равна весу «вытесненной жидкости» (в данном случае воды внутри заштрихованной области (б)).
Принцип Архимеда действителен для любой жидкости — не только для жидкостей (таких как вода), но и для газов (таких как воздух). Мы рассмотрим это подробнее, когда будем обсуждать применение принципа в последующих разделах.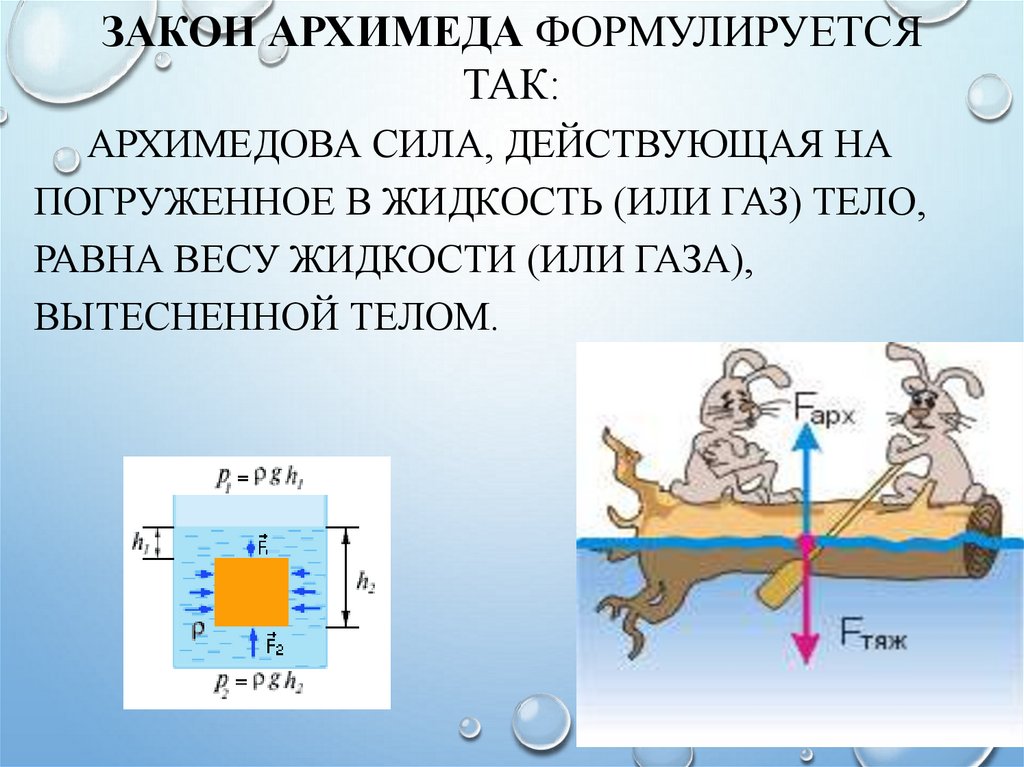
Принцип Архимеда – Простой пример : Мы используем принцип Архимеда, чтобы определить количество пингвинов, которое может выдержать ледоход.
Полное погружение
Выталкивающая сила на полностью погруженном в воду предмете объемом
FB=Vρg\text{F}_\text{B} = \text{V} \rho \text{g}FB=Vρg
.
Цели обучения
Определите факторы, определяющие силу плавучести на полностью погруженном объекте
Ключевые выводы
Ключевые моменты
- Если объект полностью погружен, объем вытесненной жидкости равен объему объекта.
- Выталкивающую силу воздушных шаров, дирижаблей и других объектов можно рассчитать, если предположить, что они полностью погружены в воздух.
- Выталкивающая сила не зависит от формы предмета, а только от его объема.

Ключевые термины
- Закон Архимеда : Выталкивающая сила, действующая на тело, погруженное в жидкость, равна весу жидкости, вытесненной телом.
Принцип Архимеда проще всего понять и применить к полностью погруженным объектам. В этом разделе мы обсудим несколько соответствующих примеров. В общем случае выталкивающая сила на полностью погруженный объект определяется по формуле:
FB=Vρg,\text{F}_\text{B} = \text{V} \rho \text{g},FB=Vρg,
где
V\text{V}V
— объем объекта,
ρ\rhoρ
— плотность жидкости,
g\text{g}g
— ускорение свободного падения. Это непосредственно следует из принципа Архимеда и того факта, что объект полностью погружен в воду (поэтому объем вытесненной жидкости равен объему объекта).
Цилиндр
В предыдущем разделе мы рассчитали выталкивающую силу на цилиндре (показанном на рисунке), учитывая силу, действующую на каждую из сторон цилиндра. Теперь мы вычислим эту силу, используя закон Архимеда. Выталкивающая сила на цилиндре равна весу вытесненной жидкости. Этот вес равен массе вытесненной жидкости, умноженной на ускорение свободного падения:
Теперь мы вычислим эту силу, используя закон Архимеда. Выталкивающая сила на цилиндре равна весу вытесненной жидкости. Этот вес равен массе вытесненной жидкости, умноженной на ускорение свободного падения:
Выталкивающая сила : Жидкость давит на погруженный объект со всех сторон. Однако, поскольку давление увеличивается с глубиной, восходящее давление на нижнюю поверхность (F2) больше, чем направленное вниз давление на верхнюю поверхность (F1). Следовательно, чистая выталкивающая сила всегда направлена вверх.
FB=wfl=mflg\text{F}_\text{B} = \text{w}_\mathrm{\text{fl}} = \text{m}_\mathrm{\text{fl}} \text{g}FB=wfl=mflg
Масса вытесненной жидкости равна ее объему, умноженному на ее плотность:
mfl=Vflρ\text{m}_\mathrm{\text{fl }} = \text{V}_\mathrm{\text{fl}}\rhomfl=Vflρ
.
Однако ( и это ключевая точка ), цилиндр полностью погружен в воду, поэтому объем вытесненной жидкости равен объему цилиндра (см. ), и:
), и:
Закон Архимеда : Объем вытесненной жидкости (b) равен объему исходного цилиндра (a).
mfl=Vflρ=Vcylinderρ\text{m}_\mathrm{\text{fl}} = \text{V}_\mathrm{\text{fl}} \rho = \text{V}_\mathrm{ \text{цилиндр}}\rhomfl=Vflρ=Vцилиндрρ
.
Объем цилиндра равен площади его основания, умноженной на его высоту, или в нашем случае:
Vcylinder=A(h3−h2)\text{V}_\mathrm{\text{цилиндр}} = \ text{A}(\text{h}_2 – \text{h}_1)Vцилиндр=A(h3−h2)
.
Следовательно, выталкивающая сила, действующая на цилиндр, равна: fl}} \text{g} = \text{V}_\mathrm{\text{цилиндр}} \rho \text{g} = (\text{h}_1 – \text{h}_2)\rho \ text{g} \text{A}FB=mflg=Vцилиндрρg=(h2−h3)ρgA
.
Это тот же результат, полученный в предыдущем разделе при рассмотрении силы, вызванной давлением, оказываемым жидкостью.
Гелиевый дирижабль
Рассмотрим USS Macon, наполненный гелием дирижабль (показан на ). Его конверт («воздушный шар») содержал 184 059.5 кубометров гелия. Если не учитывать небольшой объем гондолы, какова была выталкивающая сила этого дирижабля? Если бы дирижабль весил 108 000 кг, сколько груза он мог бы нести? Предположим, что плотность воздуха равна 1,225 кг на кубический метр. Выталкивающая сила дирижабля обусловлена воздухом, в который он погружен. Хотя мы не знаем точную форму дирижабля, мы знаем его объем и плотность воздуха, и, таким образом, мы можем рассчитать выталкивающую силу:
Его конверт («воздушный шар») содержал 184 059.5 кубометров гелия. Если не учитывать небольшой объем гондолы, какова была выталкивающая сила этого дирижабля? Если бы дирижабль весил 108 000 кг, сколько груза он мог бы нести? Предположим, что плотность воздуха равна 1,225 кг на кубический метр. Выталкивающая сила дирижабля обусловлена воздухом, в который он погружен. Хотя мы не знаем точную форму дирижабля, мы знаем его объем и плотность воздуха, и, таким образом, мы можем рассчитать выталкивающую силу:
Гелиевый дирижабль : USS Macon,5\,\mathrm{\text{кг}} = 120\,\mathrm{\text{тонн}}mcargo=gFcargo=1,2×105 кг=120 тонн
.
Плавающие
Если выталкивающая сила больше веса предмета, предмет поднимается на поверхность и всплывает. Если выталкивающая сила меньше веса тела, то оно тонет. Если выталкивающая сила равна весу объекта, объект может оставаться подвешенным на своей текущей глубине. Выталкивающая сила всегда присутствует, независимо от того, плавает ли объект, тонет или подвешен в жидкости.
Выталкивающая сила всегда присутствует, независимо от того, плавает ли объект, тонет или подвешен в жидкости.
Цели обучения
Выразите взаимосвязь между силой плавучести и весом плавучего объекта жидкости, вытесняемой телом.
Почему одни предметы плавают, а другие нет? Если положить металлическую монету в стакан с водой, она утонет. Но большинство кораблей построено из металла, и они плавают. Так как же это возможно?
Состояние флотации
Объект будет плавать, если выталкивающая сила, действующая на него со стороны жидкости, уравновешивает его вес, т. е. если
FB=mg\text{F}_\text{B} = \text{mg}FB=mg
.
Но закон Архимеда утверждает, что выталкивающая сила равна весу вытесненной жидкости. Так, для плавающего на жидкости объекта вес вытесненной жидкости равен весу объекта. Таким образом, только в частном случае плавания выталкивающая сила, действующая на объект, равна его весу. Рассмотрим однотонный блок твердого железа. Поскольку железо почти в восемь раз плотнее воды, оно вытесняет только 1/8 тонны воды при погружении, чего недостаточно, чтобы удерживать его на плаву. Предположим, что тот же самый железный блок превращается в чашу. Он по-прежнему весит одну тонну, но когда его опускают в воду, он вытесняет больший объем воды, чем когда он был блоком. Чем глубже погружена железная чаша, тем больше воды она вытесняет и тем больше действующая на нее выталкивающая сила. Когда выталкивающая сила равна одной тонне, он больше не будет тонуть.
Рассмотрим однотонный блок твердого железа. Поскольку железо почти в восемь раз плотнее воды, оно вытесняет только 1/8 тонны воды при погружении, чего недостаточно, чтобы удерживать его на плаву. Предположим, что тот же самый железный блок превращается в чашу. Он по-прежнему весит одну тонну, но когда его опускают в воду, он вытесняет больший объем воды, чем когда он был блоком. Чем глубже погружена железная чаша, тем больше воды она вытесняет и тем больше действующая на нее выталкивающая сила. Когда выталкивающая сила равна одной тонне, он больше не будет тонуть.
Когда любая лодка вытесняет вес воды, равный ее собственному весу, она всплывает. Это часто называют «принципом плавучести», когда плавающий объект вытесняет вес жидкости, равный его собственному весу. Каждый корабль, подводная лодка и дирижабль должны быть спроектированы так, чтобы вытеснять вес жидкости, равный их собственному весу. Корабль водоизмещением 10 000 тонн должен быть построен достаточно широко, чтобы вытеснить 10 000 тонн воды, прежде чем он слишком глубоко погрузится в воду. То же верно и для судов в воздухе (поскольку воздух — это жидкость): дирижабль весом 100 тонн вытесняет не менее 100 тонн воздуха; если больше смещается, то поднимается; если он смещается меньше, он падает. Если дирижабль смещает точно свой вес, он зависает на постоянной высоте.
То же верно и для судов в воздухе (поскольку воздух — это жидкость): дирижабль весом 100 тонн вытесняет не менее 100 тонн воздуха; если больше смещается, то поднимается; если он смещается меньше, он падает. Если дирижабль смещает точно свой вес, он зависает на постоянной высоте.
Плавучесть и плотность
Плотность играет решающую роль в принципе Архимеда. Средняя плотность объекта — это то, что в конечном итоге определяет, плавает ли он. Если его средняя плотность меньше плотности окружающей жидкости, он будет плавать. Это связано с тем, что жидкость, имеющая более высокую плотность, содержит большую массу и, следовательно, больший вес в том же объеме. Таким образом, выталкивающая сила, равная весу вытесненной жидкости, больше веса объекта. Точно так же объект, более плотный, чем жидкость, утонет. Степень погружения плавучего объекта зависит от того, как плотность объекта связана с плотностью жидкости. Например, незагруженный корабль имеет меньшую плотность, и меньшая его часть находится под водой по сравнению с тем же кораблем, загруженным грузом. Мы можем получить количественное выражение для фракции, погруженной в воду, учитывая плотность. Погруженная доля представляет собой отношение погруженного объема к объему объекта, или
Мы можем получить количественное выражение для фракции, погруженной в воду, учитывая плотность. Погруженная доля представляет собой отношение погруженного объема к объему объекта, или
Плотность и погружение : Ненагруженное судно (а) плавает выше в воде, чем загруженное судно (б).
дробь погруженный = VsubVobj = VflVobj \ mathrm {\ text {фракция} \, \ text {погруженный}} = \ frac {\ text {V} _ \ mathrm {\ text {sub}}} {\ text {V} _ \ mathrm {\ text {obj}}} = \ frac {\ text {V} _ \ mathrm {\ text {fl}}} {\ text {V} _ \ mathrm {\ text {obj}}} fractionsubmerged = VobjVsub=VobjVfl
Погруженный объем равен объему вытесненной жидкости, который мы называем
Vfl\text{V}_\mathrm{\text{fl}}Vfl
. Теперь мы можем получить связь между плотностями, подставив в выражение
ρ=mV\rho = \text{m} \text{V}ρ=mV
. Это дает
фракций погруженных = mfl / ρflmobj / ρˉobj \ mathrm {\ text {фракция} \, \ text {погруженный}} = \ frac {\ text {m} _ \ mathrm {\ text {fl}} / \ rho_ \ mathrm {\ text {fl}}} {\ text {m} _ \ mathrm {\ text {obj}} / \ bar {\ rho} _ \ mathrm {\ text {obj}}}fractionsubmerged = mobj/ρˉ objmfl/ρfl
где
ρˉobj\bar{\rho}_\mathrm{\text{obj}}ρˉobj
— средняя плотность объекта,
ρfl\rho_\mathrm{\text{fl}}ρfl
— плотность жидкости. Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они сокращаются в уравнении, в результате чего
Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они сокращаются в уравнении, в результате чего
дробь погружается=ρˉobjρfl\mathrm{\text{фракция}\,\текст{погружается}} = \frac {\bar{\rho}_\mathrm{\text{obj}}}{\rho_\mathrm{\text{fl}}}fractionsubmerged=ρflρˉobj
.
Об этом выражении следует помнить пару вещей:
- Обратите внимание, что здесь указана средняя плотность объекта. Это может быть намного меньше, чем плотность материала, из которого сделан объект. Например, стальной корабль на самом деле в основном заполнен воздухом (подумайте о коридорах, грузовых отсеках и т. д.), поэтому его средняя плотность находится между плотностью воздуха и стали. Точнее, средняя плотность определяется как общая масса объекта, деленная на его общий объем:
ρˉ=m/V\bar{\rho} = \text{m}/\text{V}ρˉ= т/с
. - Эта формула имеет смысл, только если плотность объекта меньше плотности жидкости. В противном случае доля погруженных становится больше единицы — признак того, что объект вовсе не плавает, а тонет!
Лицензии и ссылки
Контент под лицензией CC, совместно используемый ранее
- Курирование и доработка.
 Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензионный контент CC, конкретное указание авторства
- OpenStax College, College Physics. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://openstax.org/books/college-physics/pages/11-7-archimedes-principle. Лицензия : CC BY: Атрибуция
- Принцип Архимеда. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- выталкивающая сила. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Принцип Архимеда — простой пример. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Безграничный.
 Предоставлено : Amazon Web Services. Лицензия : Общественное достояние: неизвестно Авторские права
Предоставлено : Amazon Web Services. Лицензия : Общественное достояние: неизвестно Авторские права - OpenStax College, College Physics. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Принцип Архимеда. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Принцип Архимеда. Простой пример. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Без ограничений. Предоставлено : Amazon Web Services. Лицензия : Общественное достояние: неизвестно Авторское право
- USS Macon F9C. Предоставлено : Wikimedia. Лицензия : Общественное достояние: неизвестно Авторские права
- OpenStax College, College Physics.
 3 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://openstax.org/books/college-physics/pages/11-7-archimedes-principle. Лицензия : CC BY: Атрибуция
3 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://openstax.org/books/college-physics/pages/11-7-archimedes-principle. Лицензия : CC BY: Атрибуция - Колледж OpenStax, Колледж физики. 3 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Атрибуция
- Принцип Архимеда. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Принцип Архимеда. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Принцип Архимеда — простой пример.
 Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube - Без ограничений. Предоставлено : Amazon Web Services. Лицензия : Общественное достояние: неизвестно Авторское право
- USS Macon F9C. Предоставлено : Wikimedia. Лицензия : Общественное достояние: неизвестно Авторские права
- OpenStax College, College Physics. 3 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://openstax.org/books/college-physics/pages/11-7-archimedes-principle. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 3 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 3 ноября 2012 г.
 Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
Узнайте о формулах с выводом
0
Сохранить
Скачать публикацию в формате PDFВы когда-нибудь задумывались, почему монета тонет в воде, а корабль нет? На это можно ответить по закону Архимеда. Архимед предположил, что «Когда тело частично или полностью погружено в покоящуюся жидкость, оно испытывает направленную вверх силу, равную весу вытесненной жидкости».
В этой статье давайте разберемся с принципом Архимеда. Перед этим давайте узнаем о жидкости.
Жидкость : Вещества, обладающие способностью течь, определяются как жидкости. Примеры: нефть, вода, газы и т. д.
Для простоты предположим, что жидкостью является вода. Теперь рассмотрим стакан, наполненный водой (жидкостью). Когда тело погружается в воду, оно должно создавать пространство между молекулами воды. Это пространство равно объему погруженного тела. Следовательно, такой же объем воды вытесняется (выпадает из стакана).
Это пространство равно объему погруженного тела. Следовательно, такой же объем воды вытесняется (выпадает из стакана).
Согласно закону Архимеда, на тело действует направленная вверх сила, равная весу вытесненной воды. Эта сила известна как «плавучесть» или «выброс», которая направлена нормально к земле в направлении вверх. Поскольку эта сила действует в направлении, противоположном гравитационному притяжению, вес тела, погруженного в воду, оказывается меньше его веса в воздухе. Вес объекта при погружении в воду, также называемый кажущимся весом, рассчитывается как:
вес объекта в воде = вес объекта в воздухе (вакуум) – вес вытесненной воды внутри жидкости на глубине d от поверхности жидкости, как показано на рисунке ниже-
Поскольку твердое тело погружено в жидкость, на каждую сторону куба действует сила из-за давления внутри жидкость. Пусть P t и P b по давлению сверху и давлению снизу куба соответственно. Пусть F t и F b будут силами, действующими на верхнюю и нижнюю части куба соответственно.
Мы знаем, что
F T = P T L 2 (сила = давление • Площадь поверхности)
F B =P b l 2
Силы, действующие на остальные стороны куба, уравновешивают друг друга, поскольку они равны, противоположны и направлены.
Let F n be the net force acting on the cube then
F n = F b -F t
=P b l 2 -P t l 2
=(P b -P T ) L 2 -(1)
Сейчас
P T = ⍴ DG (давление = плотность • Глубина • Аккурация из -за гравитации)
40. плотность жидкости
Аналогично,
P B = ⍴ ( D + L) G
= ⍴ DG + ⍴ LG
заменить в (1),
F 3334340 nembilituttututututtututututtututututtutututtutututtutututtutututtutututtutututtutututtututututtutututut LG – ⍴ DG ) L 2
F N = ⍴ GL 3
, где L 3
, где L 3
. объем вытесненной воды
объем вытесненной воды
Следовательно,
F n = M w г (Масса = Объем•плотность)
Где M w — масса вытесненной воды.
Следовательно, результирующая сила, действующая на куб из-за давления жидкости, также известная как плавучесть, рассчитывается как
F b = ⍴ гВ
Плотность жидкости
В: Объем вытесненной жидкости
г: Ускорение свободного падения
Расчет кажущегося веса с использованием формулы принципа АрхимедаДля полностью погруженного объекта массой M o пусть M w будет массой вытесненной жидкости, тогда кажущийся вес объекта рассчитывается как
Кажущийся вес = вес объекта в воздухе (вакууме) – вес вытесненной жидкости0003
- Объем вытесненной жидкости равен объему погруженного объекта.
- Кажущееся уменьшение веса погруженного объекта равно весу вытесненной жидкости.

- Выталкивающая сила (или выталкивающая сила) пропорциональна плотности жидкости и не зависит от плотности объекта.
Итак, все дело в законе Архимеда. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Часто задаваемые вопросыQ.1 Как был открыт закон Архимеда?
Ответ 1
За открытием закона Архимеда стоит интересная история. Архимед провел большую часть своей жизни в Сиракузах. Легенды гласят, что король Сиракуз, король Гиерон II, подозревал, что заказанная им золотая корона подделана каким-то другим металлом того же цвета, что и золото. Он поручил Архимеду определить, сделана корона из чистого золота или нет. В то время было трудно определить чистоту золота, однако было известно, что золото является самым плотным материалом, известным в то время.
Легенды также гласят, что когда Архимед вошел в ванну, он увидел, что из воды выпало равное количество воды. Это вдохновило его связать это с плотностью, и с дальнейшими подтверждающими экспериментами он пришел к тому, что мы знаем как принцип Архимеда. После открытия принципа и того, как его можно применять для определения плотности, он выбежал на улицу с криком «Эврика!» «Эврика!» (в переводе с греческого означает «Я нашел!»).
Это вдохновило его связать это с плотностью, и с дальнейшими подтверждающими экспериментами он пришел к тому, что мы знаем как принцип Архимеда. После открытия принципа и того, как его можно применять для определения плотности, он выбежал на улицу с криком «Эврика!» «Эврика!» (в переводе с греческого означает «Я нашел!»).
Q.2 Почему важен принцип Архимеда?
Ответ 2
Поскольку принцип Архимеда помогает понять, почему объект тонет или плавает, он помогает в проектировании кораблей и создании конструкций современных машин и транспортных средств, которые передвигаются по воде или под водой.
Q.3 Почему некоторые объекты плавают, а некоторые нет, даже если они сделаны из одного и того же материала?
Ответ 3
Теперь вернемся к вопросу, поднятому в начале статьи. Если объект тонет в воде, это означает, что гравитационное притяжение больше выталкивающей силы, т. е.
е.
M O G > M W G
или M O > M W
OR V⍴ 33434> V 4> V 4> V 34> V 34> V 34 3434 34343434 3434343434343434343434334334 3.
или ⍴ o > ⍴ w
Следовательно, тонет ли объект, если его плотность больше плотности жидкости.
Теперь, даже если монета и корабль сделаны из одного и того же материала, форма и дизайн будут влиять на плотность объекта. Следовательно, следует учитывать плотность объектов, а не плотность используемого материала.
Q.4 Выполняется ли принцип Архимеда в случае газов?
Ответ 4
Да, закон Архимеда применим ко всем жидкостям, и газы также относятся к категории жидкостей. Газы также обладают выталкивающей силой, но она мала по величине.
В.5 В каких случаях принцип Архимеда не работает?
Ответ 5
Эксперименты показали исключение из принципа Архимеда, известное как нижний (или боковой) случай. Когда сторона объекта касается дна (или стороны) контейнера с жидкостью, он погружается в него. Кроме того, жидкость не просачивается вдоль этой стороны. В этом случае полная сила, действующая на объект, оказывается отличной от рассчитанной по закону Архимеда.
Когда сторона объекта касается дна (или стороны) контейнера с жидкостью, он погружается в него. Кроме того, жидкость не просачивается вдоль этой стороны. В этом случае полная сила, действующая на объект, оказывается отличной от рассчитанной по закону Архимеда.
| Закон сохранения импульса – формула, определение, вывод и приложения |
| Что такое скорость дрейфа? Знайте его определение, формулу и связанные понятия |
| Эксперимент с метровым мостом – определение, принцип, компоненты со схемой |
| Квантование заряда – понимание концепции электрического заряда |
| Принцип потенциометра – Изучите определение, применение, структуру и работу |
11.7 Принцип Архимеда – Колледж физики
Резюме
- Определение выталкивающей силы.
- Государственный закон Архимеда.

- Поймите, почему объекты плавают или тонут.
- Поймите взаимосвязь между плотностью и принципом Архимеда.
Когда вы встаете после принятия теплой ванны, ваши руки кажутся странно тяжелыми. Это потому, что у вас больше нет плавучей поддержки воды. Откуда берется эта выталкивающая сила? Почему одни вещи плавают, а другие нет? Получают ли объекты, которые тонут, какую-либо поддержку от жидкости? Ваше тело поддерживается атмосферой или это касается только гелиевых шаров? (См. рис. 1.)
Рис. 1. (a) Даже объекты, которые тонут, как этот якорь, частично поддерживаются водой при погружении. (b) Подводные лодки имеют регулируемую плотность (балластные цистерны), так что они могут плавать или тонуть по желанию. (Фото: Allied Navy) (c) Наполненные гелием воздушные шары тянут вверх свои нити, демонстрируя плавучесть воздуха. (кредит: Crystl) Ответы на все эти и многие другие вопросы основаны на том факте, что давление в жидкости увеличивается с глубиной. Это означает, что восходящая сила на нижней части объекта в жидкости больше, чем направленная вниз сила на верхней части объекта. Есть сетка наверху, или выталкивающая сила на любой предмет в любой жидкости. (См. рис. 2.) Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в жидкости.
Это означает, что восходящая сила на нижней части объекта в жидкости больше, чем направленная вниз сила на верхней части объекта. Есть сетка наверху, или выталкивающая сила на любой предмет в любой жидкости. (См. рис. 2.) Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в жидкости.
ВЫПУТНАЯ СИЛА
Выталкивающая сила – это результирующая восходящая сила, действующая на любой объект в любой жидкости.
Рисунок 2. Давление из-за веса жидкости увеличивается с глубиной, так как P=hρg . Это давление и связанная с ним восходящая сила на дне цилиндра больше, чем направленная вниз сила на верхней части цилиндра. Их отличие – выталкивающая сила F B .
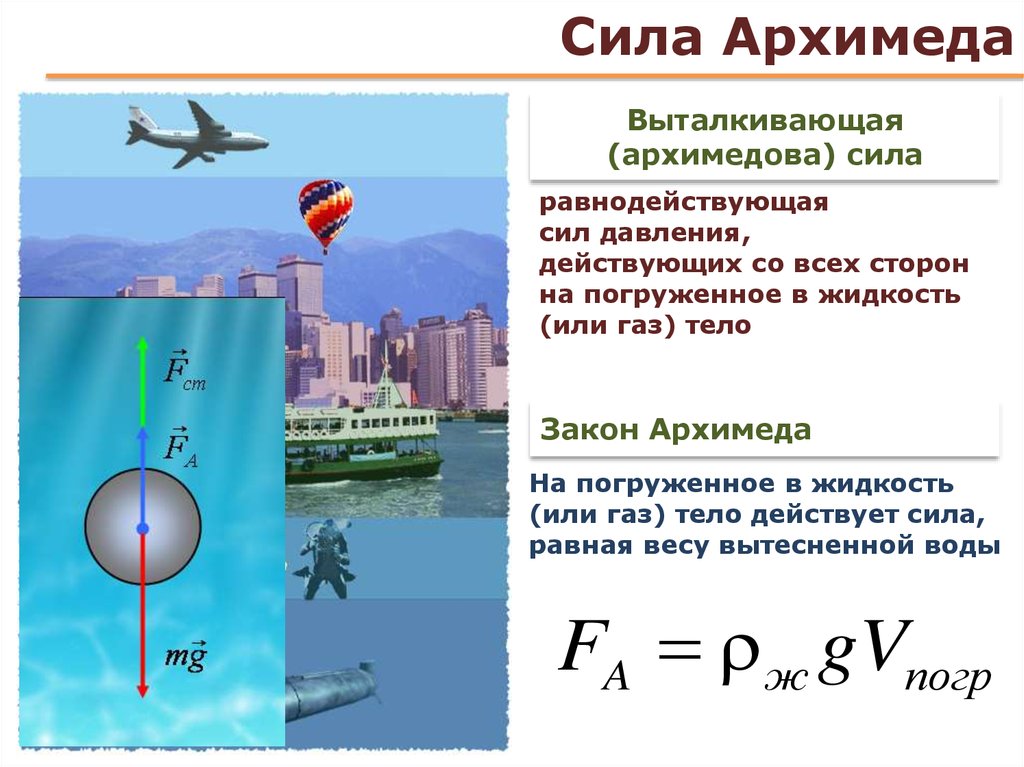 (Горизонтальные силы компенсируются.)
(Горизонтальные силы компенсируются.)Насколько велика эта выталкивающая сила? Чтобы ответить на этот вопрос, подумайте о том, что происходит, когда погруженный объект вынимают из жидкости, как показано на рис. 3.9.0005 Рис. 3. (a) На объект, погруженный в жидкость, действует выталкивающая сила F B . Если F B больше веса объекта, объект поднимется. Если F B меньше веса объекта, объект утонет. (b) Если объект удаляется, он заменяется жидкостью, имеющей вес w fl . Поскольку этот вес поддерживается окружающей жидкостью, выталкивающая сила должна равняться весу вытесненной жидкости. то есть F B = w fl , утверждение закона Архимеда.
Пространство, которое он занимает, заполнено жидкостью, имеющей вес [латекс]\boldsymbol{w _{\textbf{fl}}}. [/latex]Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна быть равна[латексу] ]\boldsymbol{w_{\textbf{fl}}},[/latex]вес жидкости, вытесненной объектом. Это дань уважения гению греческого математика и изобретателя Архимеда (ок. 287–212 до н. э.), который сформулировал этот принцип задолго до того, как понятия силы были прочно установлены. Говоря словами, принцип Архимеда выглядит следующим образом: выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда равен
[/latex]Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна быть равна[латексу] ]\boldsymbol{w_{\textbf{fl}}},[/latex]вес жидкости, вытесненной объектом. Это дань уважения гению греческого математика и изобретателя Архимеда (ок. 287–212 до н. э.), который сформулировал этот принцип задолго до того, как понятия силы были прочно установлены. Говоря словами, принцип Архимеда выглядит следующим образом: выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда равен
[латекс]\boldsymbol{F_{\textbf{B}}=w_{\textbf{fl}}},[/латекс]
, где [латекс]\boldsymbol{F_{\textbf{B}}}[/latex]является выталкивающей силой, а[латекс]\boldsymbol{w_{\textbf{fl}}}[/latex]является весом жидкость, вытесненная объектом. Принцип Архимеда действителен в целом для любого объекта в любой жидкости, полностью или частично погруженного в воду.
ПРИНЦИП АРХИМЕДА
В соответствии с этим принципом выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда равен
В форме уравнения принцип Архимеда равен
[латекс]\boldsymbol{F_{\textbf{B}}=w_{\textbf{fl}}},[/latex]
, где[латекс]\boldsymbol{F_{\textbf{B}}}[ /latex] – выталкивающая сила, а [latex]\boldsymbol{w _{\textbf{fl}}}[/latex] – вес жидкости, вытесненной объектом.
Humm … Высокотехнологичные купальники для тела были представлены в 2008 году в рамках подготовки к Олимпийским играм в Пекине. Одна проблема (и международное правило) заключалась в том, что эти костюмы не должны давать никакого преимущества в плавучести. Как вы думаете, можно ли проверить это правило?
ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ: ИССЛЕДОВАНИЕ НА ДОМУ
Плотность алюминиевой фольги в 2,7 раза больше плотности воды. Возьмите кусок фольги, скатайте его в шар и бросьте в воду. Он тонет? Почему или почему нет? Можете ли вы заставить его утонуть?
Бросьте кусок глины в воду. Он утонет. Затем слепите кусок глины в форме лодки, и она будет плавать. Из-за своей формы лодка вытесняет больше воды, чем глыба, и испытывает большую выталкивающую силу. То же самое и со стальными кораблями. 93}[/latex]воды?
То же самое и со стальными кораблями. 93}[/latex]воды?
Стратегия для (a)
Чтобы найти выталкивающую силу, мы должны найти вес вытесненной воды. Мы можем сделать это, используя плотности воды и стали, приведенные в таблице 1. Заметим, что, поскольку сталь полностью погружена в воду, ее объем и объем воды одинаковы. Зная объем воды, мы можем найти ее массу и вес.
Решение для (a)
Сначала мы используем определение плотности [латекс]\boldsymbol{\rho=\frac{m}{V}}[/латекс], чтобы найти объем стали, а затем мы замените значения массы и плотности. Это дает 97\textbf{ N}},[/latex]что намного больше, чем выталкивающая сила, поэтому сталь останется погруженной. Обратите внимание, что выталкивающая сила округляется до двух цифр, потому что плотность стали выражается только двумя цифрами.
Стратегия для (b)
Здесь нам дан максимальный объем воды, который может вытеснить стальная лодка. Выталкивающая сила равна весу этого объема воды.
Решение для (b)
Масса вытесненной воды определяется по ее отношению к плотности и объему, оба из которых известны. то есть 98\textbf{ N.}} \end{array}[/latex]
Обсуждение
Максимальная выталкивающая сила в десять раз превышает вес стали, а это означает, что корабль может нести груз, в девять раз превышающий его собственный вес, без тонет.
ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ: ИССЛЕДОВАНИЕ НА ДОМУ
Кусок бытовой алюминиевой фольги толщиной 0,016 мм. Возьмите кусок фольги размером 10 на 15 см. а) Какова масса этого куска фольги? (b) Если фольгу сложить так, чтобы получились четыре стороны, и добавить к этой «лодке» скрепки или шайбы, то какая форма лодки позволит вместить больше всего «груза» при погружении в воду? Проверьте свой прогноз.
Плотность играет решающую роль в законе Архимеда. Средняя плотность объекта — это то, что в конечном итоге определяет, плавает ли он. Если его средняя плотность меньше плотности окружающей жидкости, он будет плавать. Это связано с тем, что жидкость, имеющая более высокую плотность, содержит большую массу и, следовательно, больший вес в том же объеме. Таким образом, выталкивающая сила, равная весу вытесненной жидкости, больше веса объекта. Точно так же объект, более плотный, чем жидкость, утонет.
Это связано с тем, что жидкость, имеющая более высокую плотность, содержит большую массу и, следовательно, больший вес в том же объеме. Таким образом, выталкивающая сила, равная весу вытесненной жидкости, больше веса объекта. Точно так же объект, более плотный, чем жидкость, утонет.
Степень погружения плавучего объекта зависит от того, как плотность объекта связана с плотностью жидкости. На рисунке 4, например, незагруженный корабль имеет меньшую плотность и меньше погружено в воду по сравнению с тем же загруженным кораблем. Мы можем получить количественное выражение для фракции, погруженной в воду, учитывая плотность. Погруженная доля представляет собой отношение погруженного объема к объему объекта, или
[латекс]\boldsymbol{\textbf{фракция погружена}\:=}[/латекс][латекс]\boldsymbol{\frac{V _{\textbf{sub}}}{V _{\textbf{obj}}}} [/latex][latex]\boldsymbol{=}[/latex][latex]\boldsymbol{\frac{V _{\textbf{fl}}}{V _{\textbf{obj}}}}.[/latex]
Погруженный объем равен объему вытесненной жидкости, который мы называем [латекс]\boldsymbol{V_{\textbf{fl}}}. [/latex]Теперь мы можем получить соотношение между плотностями, подставив [латекс]\жирныйсимвол {\rho=\frac{m}{V}}[/latex]в выражение. Это дает
[/latex]Теперь мы можем получить соотношение между плотностями, подставив [латекс]\жирныйсимвол {\rho=\frac{m}{V}}[/latex]в выражение. Это дает
[латекс]\boldsymbol{\frac{V _{\textbf{fl}}}{V_{\textbf{obj}}}}[/latex][латекс]\boldsymbol{=}[/latex][латекс]\ жирный символ {\ гидроразрыва {m _ {\ textbf {fl}}/\ rho _ {\ textbf {fl}}} {m _ {\ textbf {obj}}/\ bar {\ rho} _ {\ textbf {obj}}}} ,[/латекс]
, где [латекс]\boldsymbol{\bar{\rho}_{\textbf{obj}}}[/latex] — средняя плотность объекта, а [латекс]\boldsymbol{\rho _{\textbf{fl}} }[/latex] — плотность жидкости. Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, в результате чего остается
[латекс]\boldsymbol{\textbf{фракция погружена}\:=}[/латекс][латекс]\boldsymbol{\frac{\bar{\rho}_{\textbf{obj}}}{\rho_{\ textbf{fl}}}}.[/latex]
Рисунок 4. Незагруженное судно (а) плавает выше в воде, чем загруженное судно (б). Мы используем это последнее соотношение для измерения плотности. Это делается путем измерения доли погруженного плавучего объекта, например, с помощью ареометра. Полезно определить отношение плотности объекта к жидкости (обычно воде) как удельный вес :
Это делается путем измерения доли погруженного плавучего объекта, например, с помощью ареометра. Полезно определить отношение плотности объекта к жидкости (обычно воде) как удельный вес :
[латекс]\boldsymbol{\textbf{удельный вес}\:=}[/латекс][латекс]\boldsymbol{\frac{\bar{\rho}}{\rho _{\textbf{w}}}}, [/латекс]
, где[латекс]\boldsymbol{\bar{\rho}}[/латекс]является средней плотностью объекта или вещества, а[латекс]\boldsymbol{\rho _{\textbf{w}}}[/латекс]является плотность воды при 4,00°С. Удельный вес безразмерен, независимо от того, какие единицы измерения используются для [латекс]\жирныйсимвол{\ро}.[/латекс]Если объект плавает, его удельный вес меньше единицы. Если он тонет, его удельный вес больше единицы. Более того, доля плавучего объекта, находящегося под водой, равна его удельному весу. Если удельный вес объекта точно равен 1, то он останется в жидкости во взвешенном состоянии, не тонет и не плавает. Аквалангисты пытаются получить это состояние, чтобы они могли парить в воде. Мы измеряем удельный вес жидкостей, таких как аккумуляторная кислота, радиаторная жидкость и моча, как показатель их состояния. Одно из устройств для измерения удельного веса показано на рис. 5.9.0005
Мы измеряем удельный вес жидкостей, таких как аккумуляторная кислота, радиаторная жидкость и моча, как показатель их состояния. Одно из устройств для измерения удельного веса показано на рис. 5.9.0005
УДЕЛЬНЫЙ ВЕС
Удельный вес — это отношение плотности объекта к жидкости (обычно воде).
Рисунок 5. Этот ареометр плавает в жидкости с удельным весом 0,87. Стеклянный ареометр наполнен воздухом и утяжелен свинцом на дне. Он лучше всего всплывает в самых плотных жидкостях и был откалиброван и промаркирован таким образом, чтобы по нему можно было напрямую считывать удельный вес.
Пример 2: расчет средней плотности: плавающая женщина
Предположим, что женщина весом 60,0 кг плавает в пресной воде, и [латекс]\жирныйсимвол{97,0\%}[/латекс] ее объема находится под водой, когда ее легкие наполнены воздухом. Какая у нее средняя плотность?
Стратегия
Мы можем найти плотность тела женщины, решив уравнение {\rho}_{\textbf{obj}}}{\rho_{\textbf{fl}}}}[/latex]
для плотности объекта.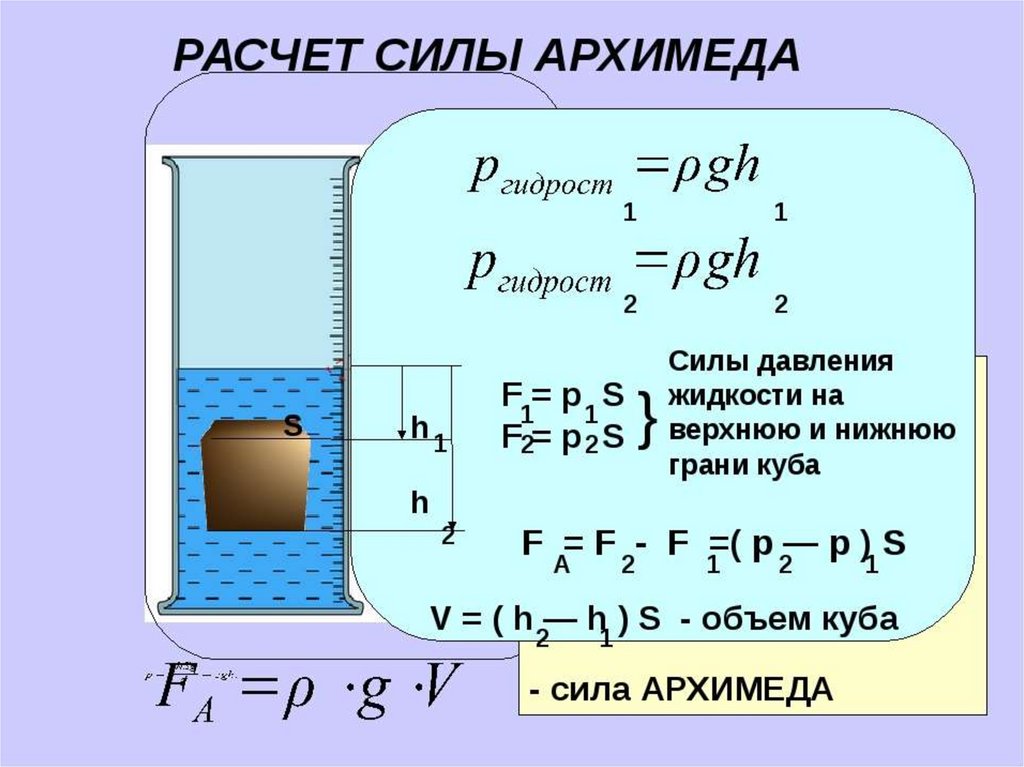 3}}[/латекс][латекс ])[/латекс][латекс]\boldsymbol{=\:93}}.[/latex]
3}}[/латекс][латекс ])[/латекс][латекс]\boldsymbol{=\:93}}.[/latex]
Обсуждение
Ее плотность меньше плотности жидкости. Мы ожидаем этого, потому что она плавает. Плотность тела — один из показателей процентного содержания жира в организме человека, представляющий интерес для медицинской диагностики и спортивных тренировок. (См. рис. 6.)
Рисунок 6. Субъект в «резервуаре для жира», где его взвешивают, когда он полностью погружен в воду, что является частью определения плотности тела. Субъект должен полностью опорожнить легкие и удерживать металлический груз, чтобы утонуть. Делаются поправки на остаточный воздух в его легких (измеряемый отдельно) и вес металла. Его скорректированный вес в погруженном состоянии, его вес в воздухе и щипковые тесты стратегических жировых областей используются для расчета его процентного содержания жира в организме.
Существует много очевидных примеров объектов или веществ с более низкой плотностью, плавающих в жидкостях с более высокой плотностью: масло на воде, воздушный шар, кусочек пробки в вине, айсберг и горячий воск в «лавовой лампе». назвать несколько. Менее очевидные примеры включают лаву, поднимающуюся из вулкана, и горные хребты, плавающие на более плотной коре и мантии под ними. Даже кажущаяся твердой Земля обладает жидкими характеристиками.
назвать несколько. Менее очевидные примеры включают лаву, поднимающуюся из вулкана, и горные хребты, плавающие на более плотной коре и мантии под ними. Даже кажущаяся твердой Земля обладает жидкими характеристиками.
Один из наиболее распространенных методов определения плотности показан на рис. 7.
Рис. 7. (а) Монета взвешивается в воздухе. (b) Определяется кажущийся вес монеты, когда она полностью погружена в жидкость известной плотности. Эти два измерения используются для расчета плотности монеты.Предмет, в данном случае монета, взвешивается в воздухе, а затем снова взвешивается при погружении в жидкость. Плотность монеты, показатель ее подлинности, можно рассчитать, если известна плотность жидкости. Этот же метод можно использовать и для определения плотности жидкости, если известна плотность монеты. Все эти расчеты основаны на законе Архимеда.
Принцип Архимеда гласит, что выталкивающая сила, действующая на объект, равна весу вытесненной жидкости. Это, в свою очередь, означает, что объект кажется весящим меньше в погруженном состоянии; мы называем это измерение кажущимся весом объекта . Объект испытывает кажущуюся потерю веса , равную весу вытесненной жидкости. В качестве альтернативы, на весах, измеряющих массу, объект испытывает кажущуюся потерю массы , равную массе вытесненной жидкости. это
Это, в свою очередь, означает, что объект кажется весящим меньше в погруженном состоянии; мы называем это измерение кажущимся весом объекта . Объект испытывает кажущуюся потерю веса , равную весу вытесненной жидкости. В качестве альтернативы, на весах, измеряющих массу, объект испытывает кажущуюся потерю массы , равную массе вытесненной жидкости. это
[латекс]\boldsymbol{\textbf{очевидная потеря веса}=\textbf{вес вытесненной жидкости}}[/латекс]
или
[латекс]\boldsymbol{\textbf{кажущаяся потеря массы}=\textbf{масса вытесненной жидкости.}}[/латекс]
Следующий пример иллюстрирует использование этой техники.
Пример 3. Расчет плотности: является ли монета подлинной?
Масса древнегреческой монеты определена на воздухе как 8,630 г. Когда монета погружена в воду, как показано на рисунке 7, ее кажущаяся масса составляет 7800 г. Вычислите его плотность, учитывая, что плотность воды составляет[латекс]\boldsymbol{1,000\textbf{ г/см}^3}[/латекс]и что эффекты, вызванные проволокой, подвешивающей монету, незначительны. 3}.[/latex]Это также объем монеты, так как она полностью погружена в воду. Теперь мы можем найти плотность монеты, используя определение плотности: 93}.[/latex]
3}.[/latex]Это также объем монеты, так как она полностью погружена в воду. Теперь мы можем найти плотность монеты, используя определение плотности: 93}.[/latex]
Обсуждение
Из таблицы 1 видно, что эта плотность очень близка к плотности чистого серебра, подходящего для этого типа древних монет. Большинство современных подделок не являются чистым серебром.
Это возвращает нас к принципу Архимеда и тому, как он возник. Как гласит история, царь Сиракуз поручил Архимеду определить, поставляет ли королевский коронщик корону из чистого золота. Чистоту золота трудно определить по цвету (оно может быть разбавлено другими металлами и все равно выглядеть таким же желтым, как чистое золото), а другие аналитические методы еще не были придуманы. Однако даже древние люди понимали, что плотность золота больше, чем у любого другого известного тогда вещества. Архимед якобы мучился над своей задачей и однажды получил вдохновение в общественных банях, размышляя о поддержке, которую вода оказала его телу. Он придумал свой ныне знаменитый принцип, увидел, как применять его для определения плотности, и голышом побежал по улицам Сиракуз с криком «Эврика!» (по-гречески «я нашел»). Подобное поведение время от времени можно наблюдать и у современных физиков!
Он придумал свой ныне знаменитый принцип, увидел, как применять его для определения плотности, и голышом побежал по улицам Сиракуз с криком «Эврика!» (по-гречески «я нашел»). Подобное поведение время от времени можно наблюдать и у современных физиков!
ИССЛЕДОВАНИЯ PHET: ПЛАВУЧОСТЬ
Когда объекты всплывут и когда они утонут? Узнайте, как плавучесть работает с блоками. Стрелки показывают приложенные силы, и вы можете изменять свойства блоков и жидкости.
Рис. 8. Плавучесть- Выталкивающая сила — это результирующая восходящая сила, действующая на любой объект в любой жидкости. Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в жидкости. 93}?[/latex]
2: Иногда бревна плавают вертикально в озере, потому что один конец стал заболоченным и более плотным, чем другой.
 Какова средняя плотность бревна одинакового диаметра, которое [латекс]\boldsymbol{20,0\%}[/латекс]длины плавает над водой?
Какова средняя плотность бревна одинакового диаметра, которое [латекс]\boldsymbol{20,0\%}[/латекс]длины плавает над водой?3: Найдите плотность жидкости, в которой плавает ареометр с плотностью[латекс]\boldsymbol{0,750\textbf{ г/мл}}[/латекс]с [латексом]\boldsymbol{92,0\% }[/latex] его объема погружено.
93}?[/latex]5: В костях птиц есть воздушные карманы, чтобы уменьшить их вес — это также дает им среднюю плотность, значительно меньшую, чем у костей других животных. Предположим, орнитолог взвешивает птичью кость в воздухе и в воде и обнаруживает, что ее масса равна[latex]\boldsymbol{45.0\textbf{g}}[/latex], а видимая масса в погруженном состоянии равна[latex]\boldsymbol{3.60\textbf {g}}[/latex](кость водонепроницаема). а) Какая масса воды вытесняется? б) Каков объем кости? в) Какова его средняя плотность?
6: Камень массой 540 г в воздухе имеет кажущуюся массу 342 г при погружении в воду. а) Какая масса воды вытесняется? б) Каков объем камня? в) Какова его средняя плотность? Соответствует ли это стоимости гранита?
7: Принцип Архимеда можно использовать для расчета плотности как жидкости, так и твердого тела.
 Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? (b) Каков объем железа, используя его плотность, как указано в таблице 1 (c) Рассчитайте плотность жидкости и определите ее.
Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? (b) Каков объем железа, используя его плотность, как указано в таблице 1 (c) Рассчитайте плотность жидкости и определите ее.8: При иммерсионном измерении плотности женщины установлено, что ее масса в воздухе составляет 62,0 кг, а кажущаяся масса 0,0850 кг при полном погружении с пустыми легкими. а) Какую массу воды она вытесняет? б) Каков ее объем? (c) Рассчитайте ее плотность. (d) Если объем ее легких составляет 1,75 л, может ли она плавать, не топчась на месте, с легкими, наполненными воздухом?
9: Некоторые рыбы имеют плотность чуть меньше плотности воды и должны прилагать усилия (плавать), чтобы оставаться под водой. Какую силу должен приложить морской окунь массой 85,0 кг, чтобы оставаться погруженным в соленую воду, если плотность его тела составляет[latex]\boldsymbol{1015\textbf{ кг/м}^3}?[/latex]
10: (a) Рассчитайте выталкивающую силу 2-литрового гелиевого баллона.
 (b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова результирующая вертикальная сила, действующая на воздушный шар, если его отпустить? Можно пренебречь объемом резины.
(b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова результирующая вертикальная сила, действующая на воздушный шар, если его отпустить? Можно пренебречь объемом резины.11: (a) Какова плотность женщины, плавающей в пресной воде с [латексом]\boldsymbol{4,00\%}[/латекс] ее объема над поверхностью? Это можно измерить, поместив ее в резервуар с отметками на боку, чтобы измерить, сколько воды она вытесняет, когда плавает и удерживается под водой (кратковременно). б) Сколько процентов ее объема находится над поверхностью, когда она плавает в морской воде? 93}[/latex](за исключением воздуха в легких). а) Вычислите его объем. б) Найдите выталкивающую силу воздуха, действующую на него. в) Каково отношение выталкивающей силы к его весу?
13: Простой компас можно сделать, поместив небольшой стержневой магнит на плавающую в воде пробку. а) Какая часть простой пробки окажется под водой, когда она будет плавать в воде? б) Если пробка массой 10,0 г поместить на нее магнит массой 20,0 г, какая часть пробки окажется под водой? в) Будут ли стержневой магнит и пробка плавать в этиловом спирте?
14: Какая часть веса железного якоря будет поддерживаться выталкивающей силой при погружении в соленую воду?
15: Известны случаи, когда подлые мошенники выдавали позолоченные вольфрамовые слитки за чистое золото и продавали их жадным по ценам намного ниже стоимости золота, но заслуженно намного выше стоимости вольфрама.
 С какой точностью вы должны быть в состоянии измерить массу такого слитка в воде и вне воды, чтобы сказать, что это почти чистый вольфрам, а не чистое золото?
С какой точностью вы должны быть в состоянии измерить массу такого слитка в воде и вне воды, чтобы сказать, что это почти чистый вольфрам, а не чистое золото?16: Двуспальный надувной матрас для кемпинга имеет размеры 100 см на 200 см на 15 см в надутом состоянии. Вес матраса 2 кг. Насколько тяжелый человек может выдержать надувной матрас, если его поместить в пресную воду?
17: По рисунку 3 докажите, что выталкивающая сила, действующая на цилиндр, равна весу вытесненной жидкости (принцип Архимеда). Вы можете предположить, что выталкивающая сила равна[латекс]\boldsymbol{F_2-F_1}[/latex]и что концы цилиндра имеют одинаковую площадь[латекс]\boldsymbol{A}.[/latex]Обратите внимание, что объем цилиндр (и вытесняемая им жидкость) равен [латекс]\boldsymbol{(h_2-h_1)A}.[/latex]
18: (a) Мужчина массой 75,0 кг плавает в пресной воде, [latex]\boldsymbol{3,00\%}[/latex] его объема над водой, когда его легкие пусты, и[latex]\boldsymbol{ 5,00\%}[/latex] его объема над водой, когда его легкие полны.



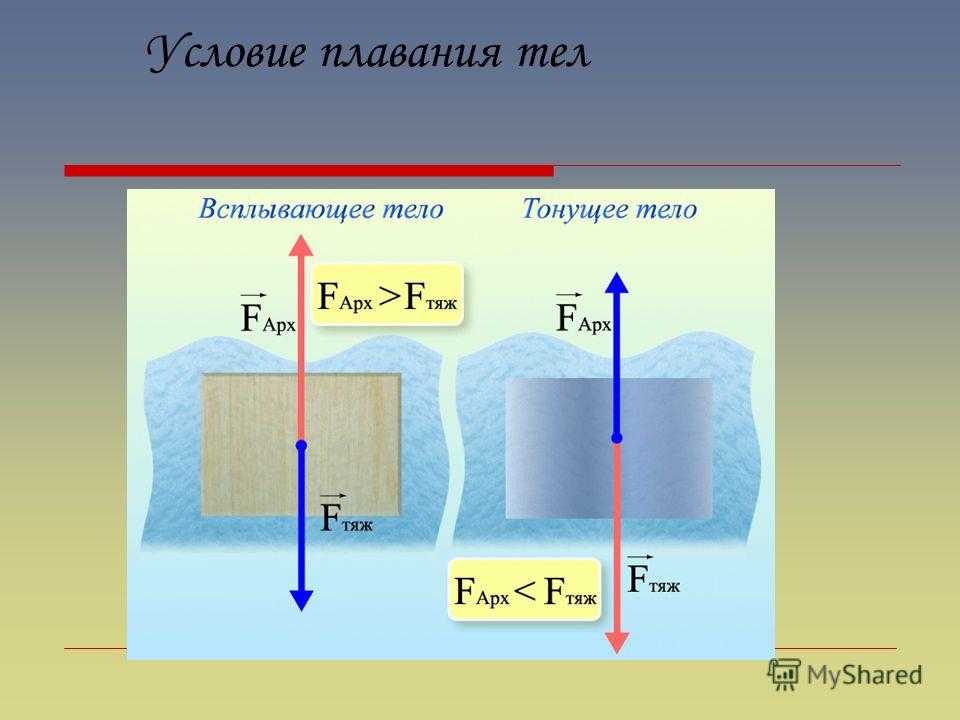 Эта сила называется силой Архимеда.
Эта сила называется силой Архимеда.

 Затем медленно опустите предмет в чашку с водой (то есть погрузите тело в воду, но при этом не погружайте пальцы). Вы увидите, что некоторое количество воды вылилось из чашки в ведро.
Затем медленно опустите предмет в чашку с водой (то есть погрузите тело в воду, но при этом не погружайте пальцы). Вы увидите, что некоторое количество воды вылилось из чашки в ведро.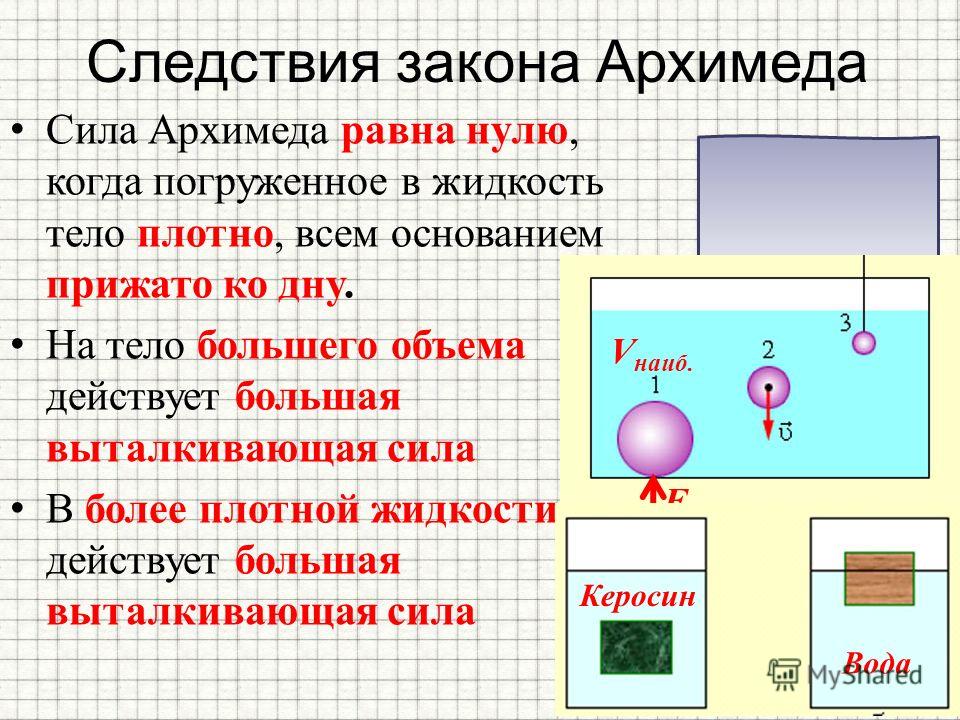 Значение объема воды, показанного шкалой мерного стакана, конвертируйте в м 3 (вы можете сделать это ), а затем умножьте объем вытесненной воды на плотность воды (1000 кг/м 3).
Значение объема воды, показанного шкалой мерного стакана, конвертируйте в м 3 (вы можете сделать это ), а затем умножьте объем вытесненной воды на плотность воды (1000 кг/м 3).


 Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike  Предоставлено : Amazon Web Services. Лицензия : Общественное достояние: неизвестно Авторские права
Предоставлено : Amazon Web Services. Лицензия : Общественное достояние: неизвестно Авторские права 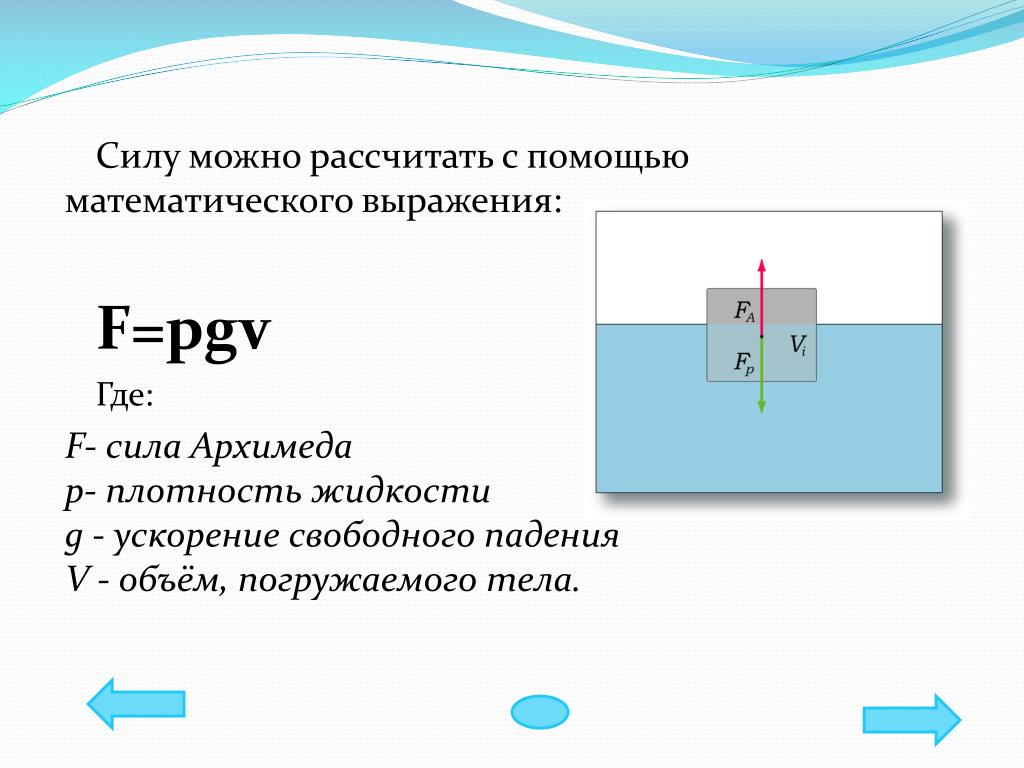 3 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://openstax.org/books/college-physics/pages/11-7-archimedes-principle. Лицензия : CC BY: Атрибуция
3 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://openstax.org/books/college-physics/pages/11-7-archimedes-principle. Лицензия : CC BY: Атрибуция 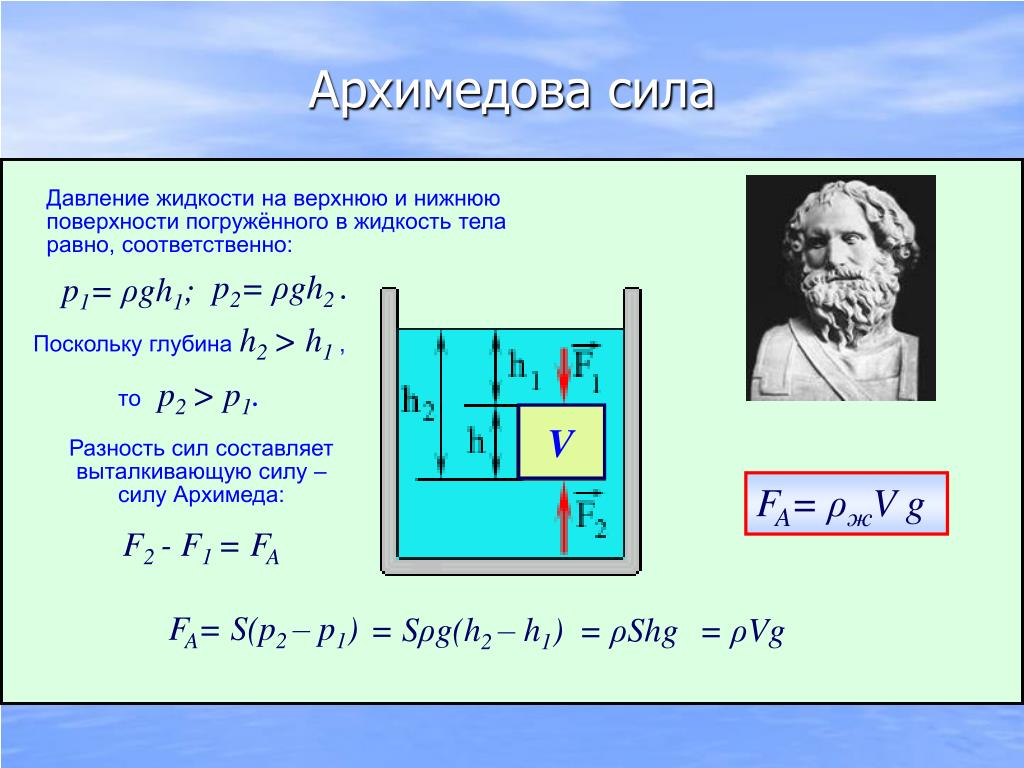 Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube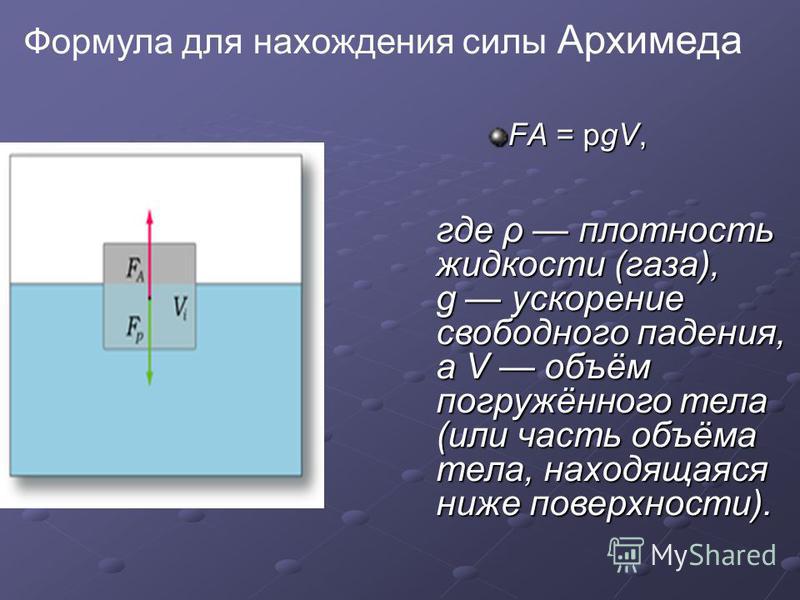 Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution 

 Какова средняя плотность бревна одинакового диаметра, которое [латекс]\boldsymbol{20,0\%}[/латекс]длины плавает над водой?
Какова средняя плотность бревна одинакового диаметра, которое [латекс]\boldsymbol{20,0\%}[/латекс]длины плавает над водой? Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? (b) Каков объем железа, используя его плотность, как указано в таблице 1 (c) Рассчитайте плотность жидкости и определите ее.
Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? (b) Каков объем железа, используя его плотность, как указано в таблице 1 (c) Рассчитайте плотность жидкости и определите ее. (b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова результирующая вертикальная сила, действующая на воздушный шар, если его отпустить? Можно пренебречь объемом резины.
(b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова результирующая вертикальная сила, действующая на воздушный шар, если его отпустить? Можно пренебречь объемом резины. С какой точностью вы должны быть в состоянии измерить массу такого слитка в воде и вне воды, чтобы сказать, что это почти чистый вольфрам, а не чистое золото?
С какой точностью вы должны быть в состоянии измерить массу такого слитка в воде и вне воды, чтобы сказать, что это почти чистый вольфрам, а не чистое золото?