Формулы скорости ускорения перемещения: 1. Формула скорости для равноускоренного движения. 2. Формула расчета перемещения от времени. 3. Формула расчета…

Равноускоренное движение-Теория.Скорость в физике

На главную Теория Задачи Учёные Интересные статьи Шкала скоростей Мгновенная скорость неравномерного движения При уменьшении величины интервала t = t2 – t1 вектор r = s все точнее совпадает с вектором касательной в точке, отвечающей моменту времени t1 . Таким образом, вектор v(t) в каждой точке траектории (т.е. в каждый момент времени) направлен по касательной к траектории в этой точке. Ускорение неравномерного движения Направление вектора ускорения совпадает с направлением вектора изменения скорости за малый промежуток времени. Когда тело движется с переменной скоростью по криволинейной траектории, то направление ускорения по отношению к направлению скорости зависит от того, как меняется скорость: а) скорость возрастает, вектор ускорения образует острый угол с вектором скорости; б) скорость не меняется по величине, ускорение перпендикулярно скорости; в) скорость убывает, вектор ускорения образует тупой угол с вектором скорости. В любом случае вектор ускорения при движении по криволинейной траектории всегда имеет отличную от нуля проекцию, направленную в сторону искривления траектории. Размерность ускорения: [a] = м/с2. Пусть тело движется по прямой с переменной скоростью v(t). Перемещение тела геометрически есть площадь под кривой v(t) между двумя фиксированными точками во времени. Аналитически это перемещение определяется как Если вектор ускорения а постоянен по величине и направлению, то движение называется прямолинейным равноускоренным движением. Если принять направление скорости тела за направление движения и выбрать ось х в эту же сторону, то основные формулы, определяющие равноускоренное движение, примут вид: a = const, v = v0 + at, s = v 0t + at2/2, x = x0 + v0t + at2/2. Знак ускорения определяет характер движения: а > 0 – равноускоренное; a < 0 – равнозамедленное. Если исключить время t из уравнений для скорости v и перемещения s прямолинейного равноускоренного движения, то получается формула, связывающая перемещение, скорость и ускорение (эта формула, конечно, верна при любом знаке a): v2 = v20 + 2as. Уравнения равноускоренного прямолинейного движения в векторной форме: Важным случаем равноускоренного движения является свободное падение в поле тяжести Земли с постоянным ускорением g = 9,8 м/с2. Для описания такого движения удобно выбрать систему координат с осью y, направленной вертикально вверх. Тогда вектор ускорения g = -gj направлен вертикально вниз. Основные формулы принимают вид: ay = – g, vy(t) = vy0 – gt, y(t) = y0 + vy0t – gt2/2. Эти формулы в равной степени справедливы как для случая падения тела с некоторой высоты, так и для случая бросания тела вверх с некоторой начальной скоростью. Пусть y0 = 0, vy0 = v0 (тело брошено вертикально вверх с нулевой высоты в момент времени t = 0). В момент достижения максимальной высоты vy = 0. Этому соответствует момент времени, определяемый из уравнения: 0 = vy0 – gt*. Итак, время движения брошенного вверх тела до достижения максимальной высоты (время подъема) t* = v0/g. Максимальная высота равна Движение тела, брошенного под углом к горизонту Задачи на эту тему

3. Равномерное прямолинейное движение.

Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).

Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.

Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела.

То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости:

v_cp = v

Скорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка t:

V(вектор) = s(вектор) / t

Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.

Перемещение при равномерном прямолинейном движении определяется формулой:

s(вектор) = V(вектор)  • t

Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна:

v_x = v, то есть v > 0

Проекция перемещения на ось ОХ равна:

s = vt = x – x₀

где x₀ – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)

Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:

х = x₀ + vt

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:

х = x₀ – vt

Равномерное прямолинейное движение – это частный случай неравномерного движения.

Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.

Равнопеременное движение

 – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.

Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).

Равнопеременное движение может быть равноускоренным или равнозамедленным.

Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.

Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется.

t

Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:

a(вектор) = v(вектор)’ = s(вектор)”

Учитывая, что ₀ – скорость тела в начальный момент времени (начальная скорость), – скорость тела в данный момент времени (конечная скорость), t – промежуток времени, в течение которого произошло изменение скорости,формула ускорения будет следующей:

a(вектор) = v(вектор)-v0(вектор)/t

Отсюда формула скорости равнопеременного движения в любой момент времени:

v(вектор) = v₀(вектор) + a(вектор)t

Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:

v_x = v_0x ± a_xt

Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.

Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).

  Рис. 1.15. Зависимость ускорения тела от времени.

Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).

  Рис. 1.16. Зависимость скорости тела от времени.

График зависимости скорости от времени (рис. 1.16) показывает, что

При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).

Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:

0a = v₀

bc = v

Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:

В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).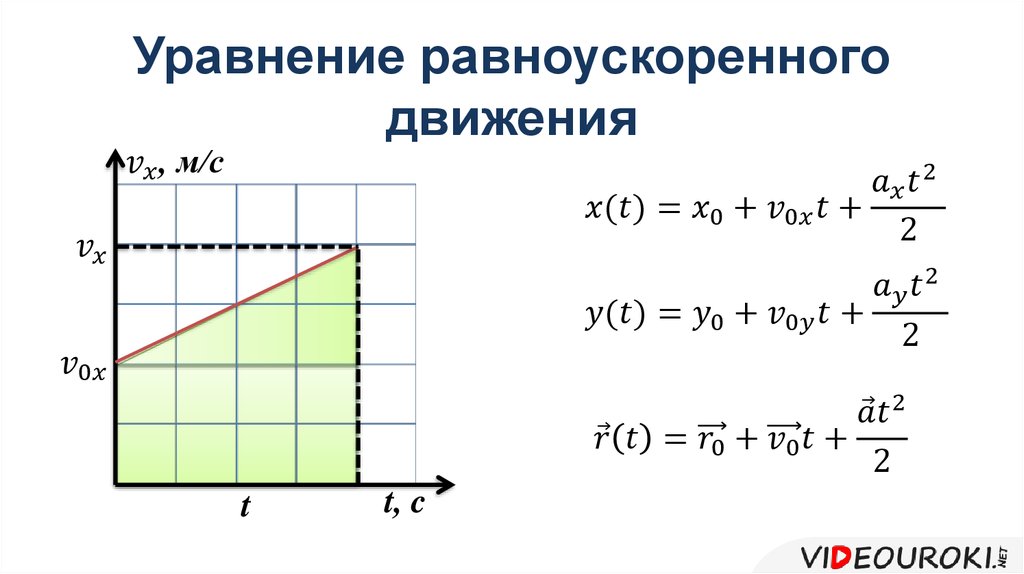

Общая формула для определения проекции перемещения:

График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.

  Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.

  Рис. 1.18. Зависимость перемещения тела от времени.

Скорость тела в данный момент времени t₁ равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:

Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:

Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:

Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:

Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат.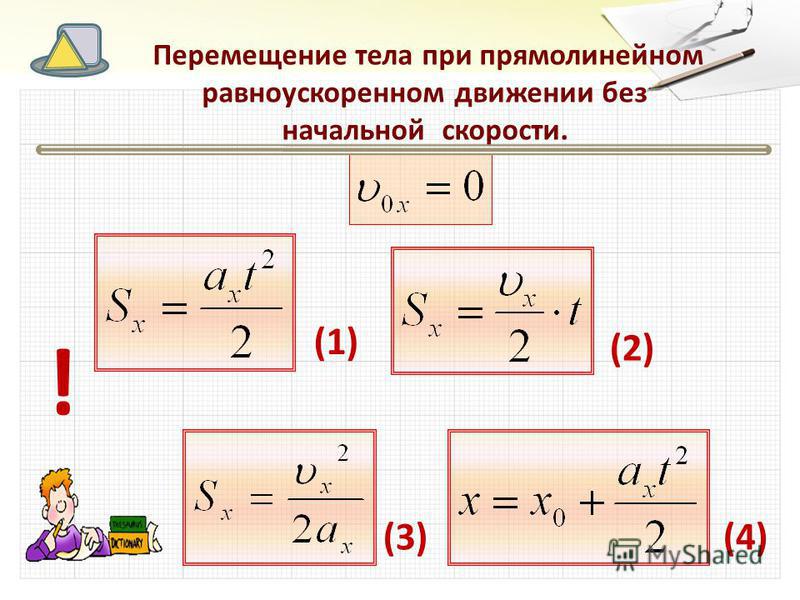 При а_x < 0 и х₀ = 0 ветви параболы направлены вниз (рис. 1.18).

фактов об ускорении для детей | Интересные факты о детях

Пожалуйста, напишите или поделитесь этой статьей!

• Электронная почта
• ФБ

Ускорение — это вектор и скорость, с которой объект изменяет свою скорость. Разгон идет не быстро. Если человек движется быстро, но не меняет скорости, он не ускоряется.

Человек или объект должны двигаться иногда быстро, иногда быстрее, а иногда медленнее.

Например, если водитель едет по шоссе с разной скоростью, мы можем рассчитать ускорение.

Однако, если водитель включает круиз-контроль на скорости 60 миль в час, автомобиль больше не ускоряется, пока включен круиз-контроль.

Ускорение в зависимости от скорости

Поскольку ускорение рассчитывается с использованием скорости (которая учитывает как скорость, так и направление объекта), оно должно включать скорость и направление, а также скорость изменения скорости.

Пока объект меняет свою скорость, он имеет ускорение. Но если объект меняет свою скорость с одной и той же скоростью каждую секунду, это называется постоянным ускорением.

Свободно падающий объект падает под действием гравитации. Это странное явление, что свободно падающий объект имеет ускорение.

Он не падает с одинаковой скоростью на всем протяжении падения. Он на самом деле ускоряется и постоянно ускоряется на протяжении пройденного при падении расстояния.

Все объекты падают с одинаковой скоростью, независимо от размера или веса объекта.

Свободно падающий объект проходит определенное расстояние за одну секунду. Фактическое расстояние не имеет значения; это может быть любое расстояние, измеренное в футах, дюймах, метрах, милях или чем-то еще. Расстояние, которое он преодолевает за 2 секунды, равно 2 в квадрате = 4.

Другими словами, в 4 раза больше расстояния, которое он проходит за 1 секунду; расстояние, которое он проходит за 6 секунд, равно 6 в квадрате = 36. Другими словами, в 36 раз больше расстояния, которое он преодолел за 1 секунду.

Ускорение выражается в единицах скорости ÷ время. Примерами являются метры в секунду в секунду (м/с/с), или мили в час в секунду (ми/ч/с), или километры в час в секунду (к/ч/с).

Ускорение является вектором

Поскольку ускорение является вектором, оно имеет направление. Направление зависит от того, ускоряется или замедляется объект и движется ли объект в положительном или отрицательном направлении.

Если объект замедляется, но продолжает двигаться в том же направлении, что и скорость, ему присваивается отрицательный знак (-). Если объект ускоряется и движется в том же направлении, что и скорость, ему присваивается положительный знак (+).

Другими словами, если объект имеет положительное направление, он имеет положительную скорость, и мы можем сказать, что он ускоряется и имеет положительное ускорение.

Если объект имеет отрицательное направление, он имеет отрицательную скорость, и мы можем сказать, что он замедляется, а ускорение направлено в сторону, противоположную скорости. Но он все еще имеет положительное ускорение.

Вопросы:

1. Что такое ускорение?
2. Какие 3 вещи должны быть у ускорения?
3. Что такое постоянное ускорение?
4. От чего зависит направление ускорения?
5. Что такое свободно падающий объект?

Ответы:

1. Ускорение — это скорость, с которой объект изменяет свою скорость.
2. Ускорение должно иметь скорость и направление и скорость изменения скорости.
3. Постоянное ускорение — это когда объект меняет свою скорость с одинаковой скоростью каждую секунду.
4. Направление ускорения зависит от того, ускоряется или замедляется объект.
5. Свободно падающий объект падает под действием силы тяжести.

Физика

Как сделать резиновое яйцо — попробуй этот веселый и простой эксперимент!

Скорость падающего объекта: расчет с примерами и формулами

Содержание :

1. Что такое скорость?
2. Функция скорости
3. Нахождение скорости с помощью вычислений
4. Средняя скорость
5. Скорость падающего объекта:
   • Используя уравнение v = g*t
   • Использование функции положения
   • Другие полезные уравнения
6. Скорость (расчет)
7. Движение снаряда

См. также : Мгновенная скорость

Посмотрите три примера в видео или прочитайте ниже:

Скорость падающего объекта

Посмотрите это видео на YouTube.

Видео не видно? Кликните сюда.

Какова скорость падающего объекта? При повседневном использовании скорость часто используется взаимозаменяемо с скорость . Однако в исчислении между ними есть существенная разница. В математике скорость относится к тому, как быстро движется объект. Скорость , однако, определяется как скорость, с которой движется объект (т. е. как быстро), так и его направление . В исчислении это первая производная функции положения.

Поскольку исчисление — это математическое исследование скорости изменения, а скорость — это мера изменения положения объекта по отношению ко времени, они часто соприкасаются. Нахождение скорости основных функций может быть выполнено без использования исчисления.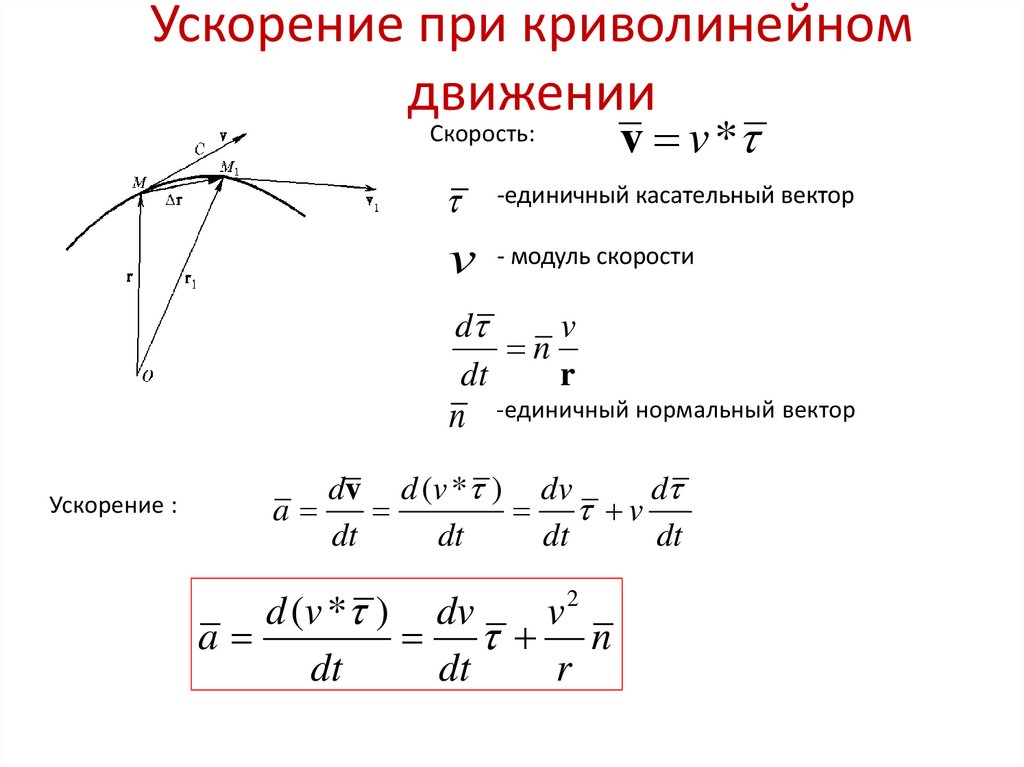 Однако, когда график функции искривлен, изменение не является постоянным, и становится необходимым выполнение вычислительных операций.

Вернуться к началу

Это дает вам скорость изменения положения объекта относительно системы отсчета (например, начала координат или начальной точки) и является функцией времени. Он сообщает скорость объекта и направление (например, 70 км/ч на юг). Обычно его обозначают как v(t). Например, v(t) = 2x ² + 9.

Обратите внимание, что это отличается от уравнения скорости , которое вы, вероятно, встречали в алгебре. 9Уравнение 0139 v = S/T дает вам среднюю скорость объекта, учитывая расстояние и время. Функция позволяет найти мгновенное изменение , а также среднее изменение. Он также должен соответствовать требованиям, предъявляемым к функциям.

Знак

Знак функции указывает направление движения объекта.

• Положительный : v(t) > 0 = движение вправо по числовой прямой (т.е. в положительном направлении).
• Отрицательный : v(t) < 0 = движение влево по числовой прямой (т.е. в отрицательном направлении).

Если объект движется прямолинейно (т.е. с прямолинейным движением), вы можете использовать знак, чтобы сказать вам, ускоряется ли объект или замедляется:

• Замедление : скорость и ускорение имеют противоположные знаки (например, +-).
• Ускорение : они имеют одинаковый знак (например, + +).

Посмотрите видео с примером использования функции для определения общего пройденного расстояния.

Рабочий объем и общий пройденный путь

Посмотрите это видео на YouTube.

Вернуться к началу

Как найти функцию скорости

Вы можете использовать дифференцирование и интегрирование, чтобы найти функцию. На следующем рисунке показана взаимосвязь между первыми несколькими производными и интегралами по отношению к функции скорости:
То, как вы находите функцию, зависит от того, с какой функции вы начинаете.

Производная функции положения дает вам скорость движущегося объекта, предполагая, что объект а/ движется по прямой и b/ сопротивление воздуха равно нулю. Более формально мы говорим, что скорость объекта — это скорость изменения положения объекта во времени.

В качестве примера предположим, что вам дали функцию положения. Вы можете продифференцировать его (т.е. взять первую производную), чтобы получить функцию скорости. Пример того, как это сделать, см. в разделе Скорость падающего объекта.

С другой стороны, если у вас есть функция рывка, вы захотите работать в обратном направлении. Другими словами, вам нужно интегрировать функцию. Как вы это сделаете, зависит от того, какой тип функции у вас есть. См.: Интегральные правила.

Решение проблемы падающего предмета зависит от того, какую информацию вы получили. Например, если вам дано время (обычно в секундах), то скорость любого падающего объекта можно найти с помощью уравнения v = g * t, где g — ускорение свободного падения. Однако, если вам дана функция положения (например, для высоты), вам потребуется немного вычислений, чтобы получить ответ.

Если вам дана функция положения (для расстояния, пройденного объектом), вы можете взять производную и получить функцию. Если вам дана формула ускорения тела, вы можете найти интеграл и снова прийти к решению.

1. Функция заданного положения (перемещения)

Пример вопроса: Найдите функцию скорости для следующей функции положения: x(t) = 4t ² + 4t + 4

Шаг 1: Чтобы получить от смещения к скорости вы возьмете производная смещения по времени. Сначала составим уравнение, чтобы подготовиться к нахождению производной:
x(t) = 4t ² + 4t + 4
dx/dt = d/dt 4t ² + 4t + 4 = v(t)

Шаг 2: Найдите производную.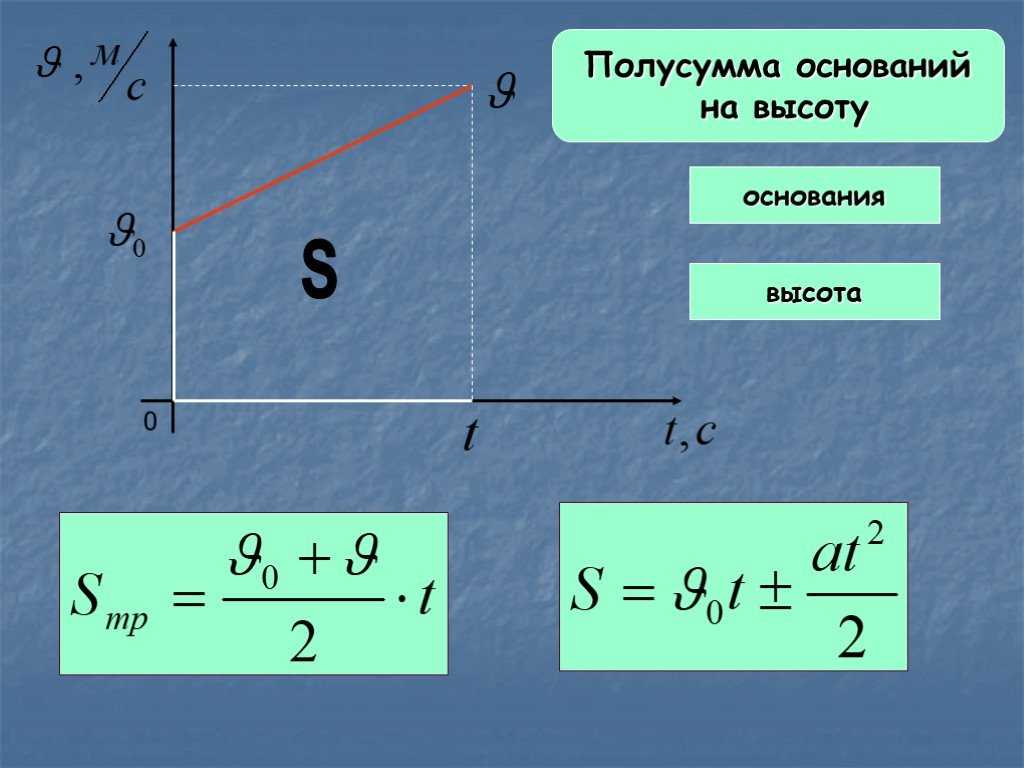 Здесь вы можете использовать правило мощности и правило для производных констант.
d/dt 4t ² + 4t + 4 = 8t + 4
v(t) = 8t + 4
Вот и все!
Совет: скорость не является постоянной во времени, поэтому t появляется. Если бы она была постоянной, в ней не было бы переменной, а ускорение также было бы равно 0.

2. Найдите функцию скорости при заданном ускорении.

Пример вопроса: Найдите функцию скорости из следующей функции ускорения:
a(t) = 10t + 5
Шаг 1: Подготовьте уравнение для выполнения интегрирования:
a(t) = 10t + 5
v (t) = ∫ a(t) dt = ∫ 10t + 5 dt
Шаг 2: Выполните интегрирование на a(t). Интеграция — это несколько продвинутый метод исчисления, поэтому обязательно ознакомьтесь со статьями, подробно описывающими его (см. Интегралы), если вы не знакомы с ним.
∫ a(t) dt = ∫ 10t + 5 dt = 5t ² + 5t + c = v(t)

Примечание: c — константа интегрирования, которую невозможно определить без дополнительной информации. Если вам задано начальное значение, вы можете найти константу, установив время равным 0. Используя приведенное выше, например:
v (0) = 5 (0 ² ) + 5 (0) + c = c = v (0)

Вернуться к началу

Средняя скорость определяется как отношение между пройденным расстоянием и временем, затрачиваемым на преодоление этого расстояния. Формула для нахождения средней скорости:

v _av = x _f – x _i / t _f – t _i

Где:

• v 909024 средняя скорость,
• x _f — конечное положение объекта,
• x _i – начальная позиция объекта,
• т _ф последний раз,
• t _i — начальное время.

Пример:

Автомобиль стартует с позиции x = 16 футов. Через 8 секунд автомобиль находится в 134 футах к востоку от своего начального положения. Какова средняя скорость автомобиля?

Шаг первый: Найдите разницу между начальным и конечным положениями автомобиля.
Автомобиль проехал от 16 футов до 134 футов (134 – 16 = 118). Автомобиль проехал на восток в общей сложности 118 футов.

Шаг второй: Подсчитайте количество прошедшего времени, , если это не указано явно. Мы знаем, что машина ехала 8 секунд. Никаких дополнительных расчетов здесь не требуется.

Шаг третий: Подставьте значения в формулу и решите .

V _av = 118 футов / 8 с = 14,75 фут/с на восток

Средняя скорость, с которой двигалась машина, составляла 14,75 фута в секунду в восточном направлении.

Вернуться к началу

На падающий объект действует сила тяжести: -9,81 м/с ² (32 фута/с ² ). Гравитация ускоряет падающий объект, увеличивая его скорость на 9,81 м/с ² (или на 32 фута/с ² ) за каждую секунду свободного падения.

Чтобы найти скорость конкретного падающего объекта, просто умножьте силу тяжести (g) на время (t). Формула:
v = g * t
v = -9,81 м/с ² *t

Пример #1 : Объект падает в течение 1,2 секунды. Какова его скорость?

• v = -9,81 м/с ² *t
• v = -9,81 м/с ² *1,2 с
• v = 11,77200 м/с

Исчисление очень полезно для определения скорости падающего объекта, если все, что у вас есть, это функция положения, например, высота объекта. Во-первых, продифференцируйте функцию положения, чтобы получить функцию скорости. Тогда используйте , что функция , чтобы найти ответ.

Пример #2: Функция положения

Функция v(t) является производной функции положения. Если вам дано уравнение положения, такое как h(t) или s(t), вам нужно продифференцировать эту функцию, чтобы найти скорость падающего объекта.

Пример задачи: Разочаровавшись в своем классе по математике, вы прикрепляете к нему ракету и запускаете ее из окна общежития. Высота книги в футах над автомобилем через t секунд определяется функцией h(t) = 200 – 16t ² . Книга оставит вмятину на вашей машине, если она будет двигаться со скоростью более 100 футов в секунду.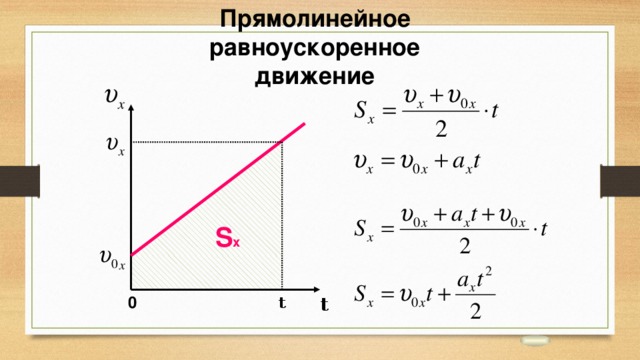 Будет ли ваша машина помята?
Подсказка: Данное уравнение , а не для скорости падающего объекта. Это позиционная функция.

Шаг 1: Дифференцируйте функцию положения, h(t) = 200 – 16t ² , чтобы получить функцию (вам нужно знать скорость, чтобы ответить на вопрос).

• 200 — константа, поэтому она исчезает.
• 16t ² можно дифференцировать по степенному правилу.

Дифференцированная функция 2(16)t ^2-1 = -32t.

Шаг 2: Решите функцию положения для нуля (другими словами, когда высота равна нулю), чтобы узнать, когда книга ударит по машине.
Установка h(t) = 0 дает:

• 0 = 200 – 16t ²
• т = 14,14213…

Шаг 3: Вставьте свой ответ из шага 2 в функцию из шага 1:

• v(14.14213) = -32(14.14213)
• v(14,14213) = -452,54816

Скорость составляет -452,54816 футов в секунду, когда книга ударяется о машину. Это более 100 метров в секунду. Да будет вмятина!
Вот и все!

Совет : знак минус указывает на уменьшение высоты.

Вернуться к началу

Если вам известна высота/расстояние, на которое упал объект (d), то используйте это уравнение, чтобы найти время (t):

Если вам известна высота/расстояние, на которое упал объект (d), то используйте это уравнение, чтобы найти мгновенную скорость объекта:

Если вам известна высота/расстояние, на которое упал объект ( г), затем используйте это уравнение, чтобы найти среднюю скорость объекта:

Вернуться к началу

На повседневном языке «скорость» говорит вам, как быстро объект перемещается между двумя местами.

Формула следующая:

S = D/T

• S = Скорость
• D = Расстояние
• Т = Время

S, D и T могут иметь разные единицы измерения. Например:

• S = мили в час (миль в час) или километры в час.
• D = мили, миллиметры или футы.
• T = большие интервалы, такие как световые годы, или меньшие, такие как наносекунды.

Иногда «скорость» и «скорость» используются для обозначения одного и того же. Однако между ними есть очень важные различия при использовании в исчислении (или физике).

Скорость получает более точное определение при использовании в вычислениях. Он определяется как абсолютное значение скорости:

S = │v(t)│

Где:

• t = время

Скорость — это скалярная величина, представленная величиной (т. е. величиной) и не имеющая направления — в отличие от скорости, которая представляет собой вектор с величиной и направлением . Скорость измеряет скорость движения независимо от направления и измеряется расстоянием в единицу времени. Поскольку вы берете абсолютные значения, они всегда положительны.

Пример: вычисление скорости с использованием производных

На самом деле мы не вычисляем «скорость» в математических вычислениях, поэтому, если вам задают вопрос вроде «как быстро движется объект», на самом деле этот вопрос касается вас. скорость объекта.

Когда вам задана функция положения, вы можете найти скорость с помощью первой производной функции положения:
s′(t) = v(t)

Пример вопроса: На основе функции s(t ) = т ³ + 4t футов за время (t), найти S при t = 4,24 секунды.

Шаг 1. Возьмите производную функции s(t) = t ³ + 4t:

• s′(t) = v(t)
• v(t) = 3t ² + 4

Шаг 2: Подставьте заданное время (в этом примере t = 4,24 секунды) в функцию, найденную на шаге 1:

• v(4,24) = 3(4,24) ² + 4
• v(4,24) = 3(17,9776) + 4
• v(4,24) = 53,93 + 4
• v(4,24) = 57,93

Шаг 3. Найдите абсолютное значение:

• S = │v(4,24)│ = 4,24 секунды = 57,93 фута/сек

Объект движется со скоростью 57,93 фута в секунду за 4,24 секунды.

Вернуться к началу

Снарядное движение — это движение объекта, на который действует не сила, а гравитационное поле. Этот тип объекта называется снарядом .

Посмотрите это видео, чтобы получить отличный обзор того, что такое движение снаряда (с НФЛ и Лестером Холтом):

Движение снаряда и параболы [Наука о футболе НФЛ]

Посмотрите это видео на YouTube.

Движение снаряда без начальной скорости

В простейших задачах о движении снаряда нет начальной скорости. Объект просто падает так, что магнитное поле Земли притягивает его к земле со скоростью 9,81 м/с ² . Все это ускорение происходит в вертикальном направлении (то есть к поверхности Земли). Гравитация не имеет горизонтальной составляющей, поэтому (в отличие от футбольного мяча на видео выше) в этом типе ускорения нет горизонтальной составляющей: объект просто падает прямо вниз.

Например, если вы высунете руку из окна небоскреба и уроните яблоко, его скорость будет равна 0 в тот момент, когда вы откроете руку (t ₀ ). В момент t = 1 секунда яблоко будет двигаться со скоростью 9,81 м/с ² . Через k секунд он будет двигаться вниз со скоростью 9,81 м/с ² k , если предположить, что он еще не коснулся земли и предположить (для простоты), что мы можем игнорировать сопротивление.

Движение снаряда с начальной скоростью

Во многих случаях снаряд начинает полет с начальной скоростью. Мы определили снаряд как объект, на который в настоящее время не действует никакая сила, кроме гравитационного поля. Однако важно понимать, что в прошлом на него могли воздействовать другие силы. Ваша рука, например, могла оказывать давление на мяч, когда вы его бросали.

Предположим, вы стоите у окна своего дома на высоте 150 метров над землей и бросаете мяч под углом 20 градусов над горизонтом с начальной скоростью 8,40 м/с.

В момент, когда мяч покидает вашу руку, в момент времени t ₀ он движется со скоростью 8,40 м/с, и с этого момента на него действует только сила тяжести, которая придает ему ускорение 9,81 м/с ² . Мяч начинает подниматься вверх, но через секунду уже начинает двигаться вниз. Вы не можете добавлять или вычитать эти ставки напрямую; это векторные величины, что означает, что мы должны обращать внимание на направление и добавлять и вычитать только то, что совпадает.

Допустим, вы стоите в начале простой декартовой системы координат x y. Когда вы бросаете этот мяч под углом 20 градусов, его скорость будет состоять из двух частей. Назовите их v _0x и v _0y . Нарисуйте треугольник и, используя свои навыки геометрии, найдите v _0x и v _0y .

• v _0x = v _0x cos (20) = 8,40 cos(20) = 7,893 м/с и
• v _0y = v _0y sin (20) = 8,40 sin 20 = 2,873.

Поскольку мы делаем вид, что эффект сопротивления пренебрежимо мал, на наш мяч не действует никакая сила по горизонтали: a _x = 0. v _0x = v _x = 7,893 м/с в каждой точке, пока мяч не упадет на землю.

Это вертикальная скорость, на которую будет действовать сила тяжести. При t ₀ это было 2,873, в направлении + или вверх, и сила тяжести заставляет его ускоряться со скоростью 9,81 м/с ² в направлении – или вниз. Через одну минуту его вертикальная скорость составит 2,873 – 9,81 = -6,937, или около 6,9 м/с в направлении вниз.

Параметрические уравнения могут моделировать движение снаряда.

Ссылки

Аллен, Ретт. Движение снаряда. Введение в лабораторию физики. Получено с https://www2.southeast.edu/Academics/Faculty/rallain/plab193/page1/page31/page31.html 26 января 2019 г.
Даффи, Эндрю. Пример движения снаряда. Получено с http://physics.bu.edu/~duffy/semester1/c3_projectile.