Что такое статика в физике и что она изучает? Основные формулы / Справочник :: Бингоскул
Что такое статика в физике и что она изучает? Основные формулыдобавить в закладки удалить из закладок
Содержание:
Физика изучает законы природы. С получением всё большего количества знаний о мироздании учёные пытались структурировать их – физические законы группировались. В итоге появились десятки разделов: механика, электричество, магнетизм, волновые процессы, ядерная физика и т. д. Каждый состоит из десятков подразделов, с одним из которых познакомимся: что такое статика в физике, что изучает. Рассмотрим её основные законы и формулы.
Что изучает статика
Известно, что тело под воздействием внешних или внутренних сил совершает работу, испытывает ускорение, покоившиеся тела двигаются. Встречаются случаи, когда тела, на которые действуют несколько сил, остаются неподвижными. Так, если на объект в состоянии покоя оказывается давление парой равных по значению (модулю), но противоположных по направлению сил, он остаётся в состоянии покоя – не двигается относительно системы отсчёта. Это идеальный случай. В иных, реальных, ситуациях внешнее давление на тела значительно сложнее. Изучением таких случаев занимается отдельный раздел науки о законах природы.
Это идеальный случай. В иных, реальных, ситуациях внешнее давление на тела значительно сложнее. Изучением таких случаев занимается отдельный раздел науки о законах природы.
Статика – это раздел в физике, определяющий условия нахождения тел, сооружений (здания, мосты) и прочего, что изучает и использует человек, в равновесии. Направление также даёт ответы на ряд вопросов, касающихся перемещения тел. Для примера: груз подвешен на не растягивающейся верёвке, перекинутой через блок. Пользуясь открытыми века назад законами статики, определяется сила T, которую необходимо приложить к другому концу шнурка, чтобы система осталась в равновесии. По модулю она будет равной притяжению (P). При этом учитываются силы или коэффициент трения, растяжения верёвки.
Статика даёт намного больше, чем условия равновесия. Позволяет узнать, что нужно сделать, чтобы ввести систему в такое состояние или вывести из него. Для перемещения груза вверх следует приложить усилие, превышающее P, для опускания – уменьшить ниже силы притяжения. Статика даёт понимание направления движения тел при нарушении равновесия определённым образом.
Статика даёт понимание направления движения тел при нарушении равновесия определённым образом.
Изначально статика была разделом механики, отвечающим и на вопросы перемещения тел. Например, когда возникала необходимость использования простых механизмов – рычагов, блоков – для изменения положения массивных предметов, то есть нарушения их равновесия. Различают следующие виды равновесий:
- Устойчивое – при мизерном отклонении равновесия тело возвращается в начальное положение.
- Безразличное – при малом отклонении тело не теряет равновесия.
- Неустойчивое – при отклонении от состояния равновесия возникает воздействие, повышающее отклонение.
Статика имела огромное значение для инженеров и архитекторов древности. Увы, она не позволяет узнать, насколько быстро будет передвигаться груз на нитке, переброшенной через блок. Вопрос производительности подняли с появлением сложных механизмов, развитием тепловых двигателей.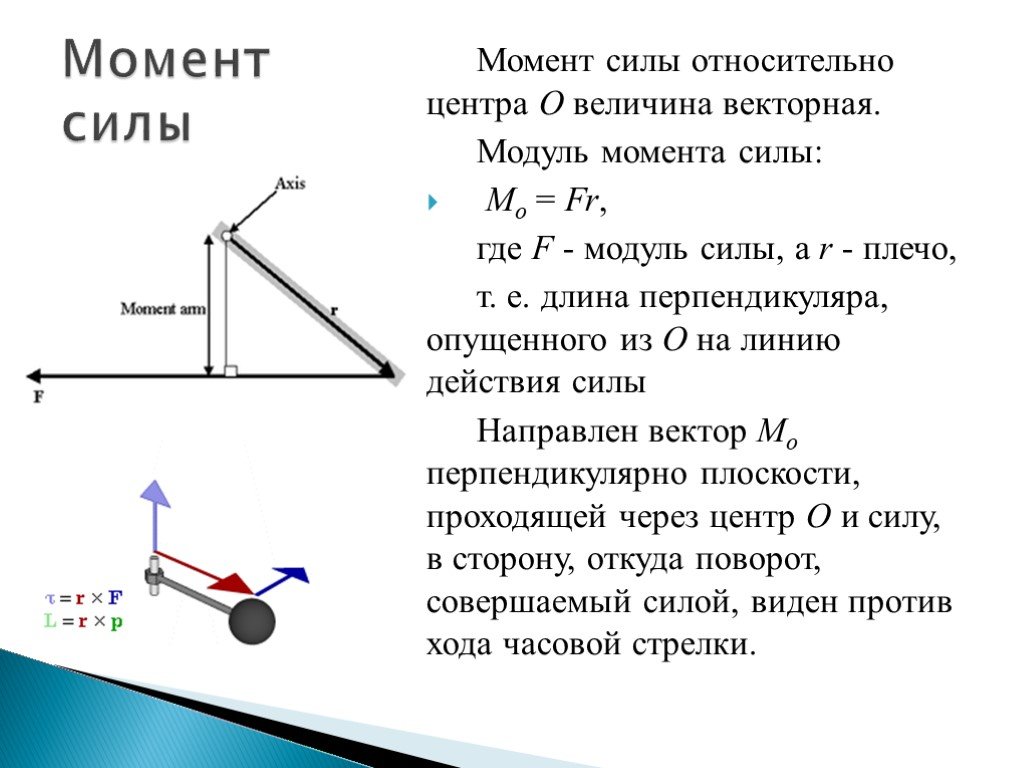
Формулы статики в физике
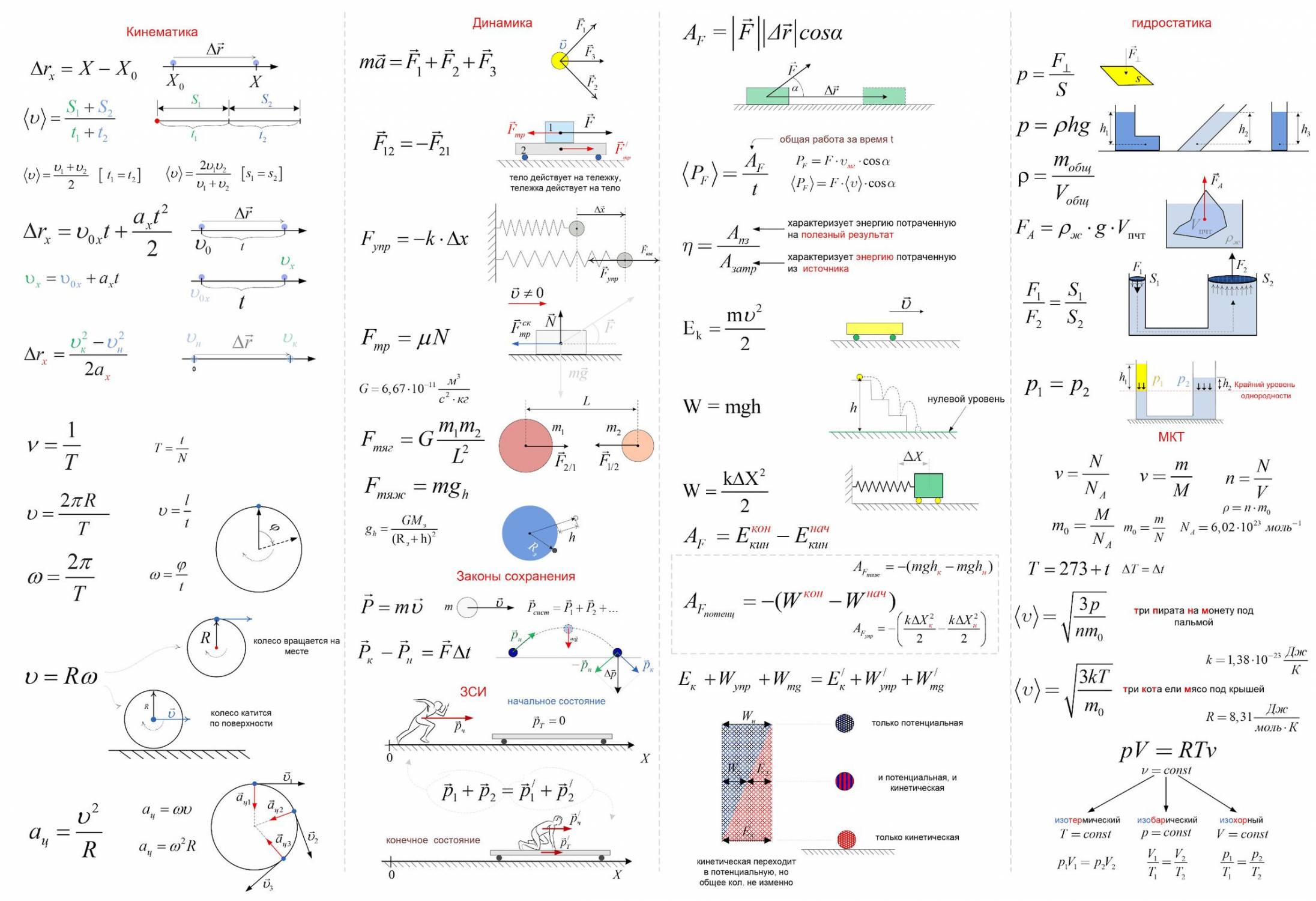
Для проведения расчётов, проектирования и решения задач достаточно знать основные формулы статики.
Сила трения:
Fтр= μN, здесь:
- μ – коэффициент трения – указывает на отношение между трением и силой, прижимающей тело к опоре;
- N – сила реакции нитки, опоры.
Момент силы:
M = Fd или M = Fl, здесь:
- F – модуль действующей на тело силы;
- d или l – длина плеча.
Вращающий по часовой стрелке момент силы считается положительным, против – отрицательным.
Векторная сумма действующих на тело сил равняется нулю: F=0.
Момент инерции:
J = mr2, здесь:
- m – масса тела;
- r – радиус.
Давление, оказываемое телом на опору: нитку, поверхность:
p = F : S,
- F – сила;
- S – площадь контакта.
Правило рычага:
- F1 : F2 = d1: d2, здесь:
- F1, F2 – приложенные к плечам рычага силы;
- d1, d2 – длина плеч.

В отдельный подраздел выносится гидростатика – изучает поведение неподвижной жидкости.
Поделитесь в социальных сетях:
1 ноября 2021, 16:31
Физика
Could not load xLike class!
Статика. условия равновесия. Виды равновесия.
Основные ссылки
CSS adjustments for Marinelli theme
Объединение учителей Санкт-Петербурга
Форма поиска
Поиск
Вы здесь
Главная » Статика. условия равновесия. Виды равновесия.
| СТАТИКА. УСЛОВИЯ РАВНОВЕСИЯ ТЕЛ. | |
Статика – раздел механики, в котором рассматривается равновесие тел. Равновесие тел – состояние механической системы, в которой тела остаются неподвижными по отношению к выбранной системе отсчета. | |
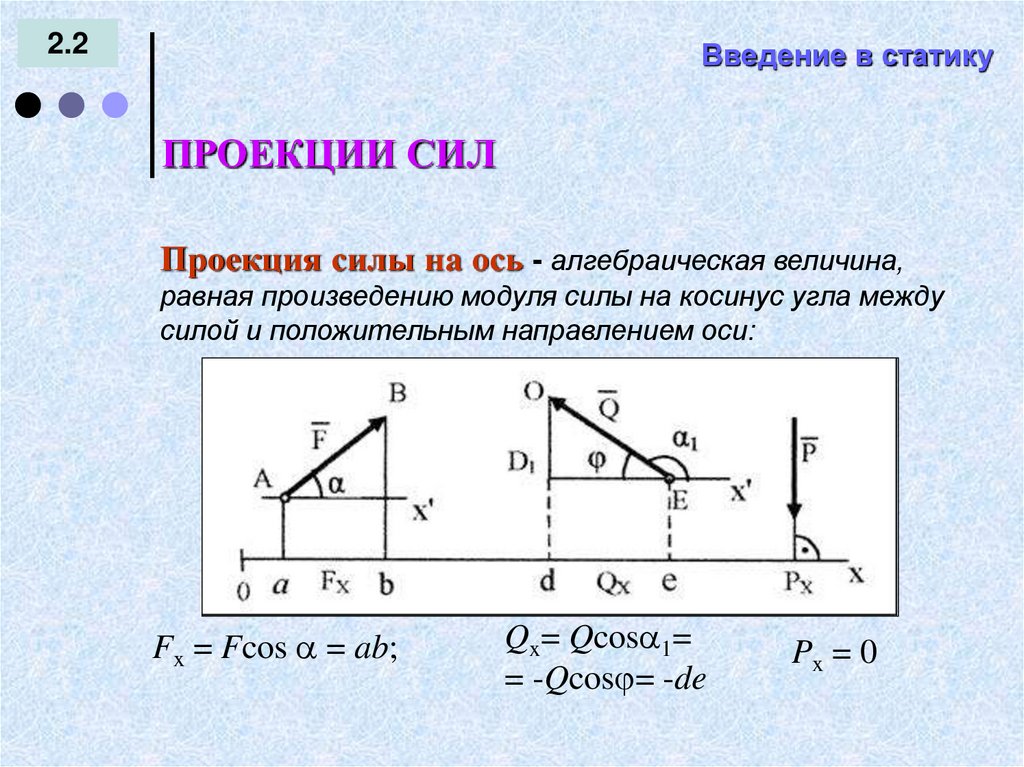
Равновесие тел при отсутствии вращения (линии действия сил пересекаются в одной точке): Векторная сумма всех сил, действующих на тело, равна нулю(алгебраическая сумма проекций всех сил на любую ось равна нулю). | |
Момент силы – равен произведению силы на плечо: Плечо силы – расстояние от оси вращения до линии действия силы. (обозначают буквами ℓ или d). Момент силы, вращающий тело против часовой стрелки, считают положительным, по часовой стрелке – отрицательным. | |
Центр масс – точка, через которую должна проходить линия действия силы, чтобы под действием этой силы тело двигалось поступательно. Центр тяжести – точка приложения силы тяжести, действующей на тело. В однородном поле тяготения центр тяжести и центр масс совпадают. | |
Рычаг (Архимед). Разновидности рычага: блок, ворот. Условие равновесия рычага: отношение сил обратно пропорционально отношению плеч этих сил. “Золотое правило механики”: выигрывая в силепроигрываешь в расстоянии. | |
Равновесие тел при отсутствии вращения (линии действия сил не пересекаются в одной точке): 1. Векторная сумма всех сил, действующих на тело, равна нулю; 2. Алгебраическая сумма моментов всех сил, действующих на тело, относительно любой точки равна нулю. | |
Т.е. | |
ПАРА СИЛ: Момент пары: Пару нельзя уравновесить одной силой (равной величины)! Примеры: завинчивание гайки гаечным ключом, вращение рамки с током в магнитном поле и т.д. | |
Виды равновесия: Устойчивое: При малом отклонении тела от положения равновесия возникает сила, стремящаяся возвратить тело в исходное состояние. | |
Безразличное: При малом отклонении тело остается в равновесии. | |
Неустойчивое: При малом отклонении тела из положения равновесия возникают силы, стремящиеся увеличить это отклонение. | |
В положении устойчивого равновесия тело обладает минимальной потенциальной энергией. При выведении тела из этого положения его потенциальная энергия увеличивается. Если работу над телом совершает только сила тяжести, то в положении устойчивого равновесия центр тяжести тела находится на наименьшей высоте. Все тела стремятся к минимуму потенциальной энергии. (Потенциальная яма). |
|
Равновесие тел на опоре: линия действия силы тяжести проходит через площадь опоры (Пизанская башня). Чем ниже центр тяжести, тем более устойчиво равновесие. |
|
Теги:
конспект
Статика для чат-шпаргалки на чайники
BY: James H. Allen III и III и
Allen III и III и
Обновлен: 02-02-2022
Из книги: Статика для Dummies
Статиса Dummies
. Купить книгу на Amazon
Как и в любой области физики, решение задач статики требует, чтобы вы помнили всевозможные расчеты, диаграммы и формулы. Таким образом, ключом к успеху в статике является сохранение диаграмм сдвига и моментов прямо из диаграмм свободного тела и знание различий между расчетами моментов, центроидов, векторов и давлений.Контрольный список для решения задач статики
Решение задач статики может быть сложным; каждая проблема требует списка элементов для учета и уравнений для создания и решения. С легкостью решайте проблемы статики с помощью этого контрольного списка:
Нарисуйте схему всей системы в свободном теле.

В дополнение к размерам и углам вы должны включить четыре основные категории элементов в правильно построенную диаграмму свободного тела:
Прикладываемые внешние нагрузки
Открытые внутренние нагрузки
Опорные реакции
Собственный вес
Напишите уравнения равновесия, чтобы вычислить как можно больше неизвестных опорных реакций.
Чтобы найти внутренние силы, определите тип конструкции и напишите уравнения равновесия.
После того, как вы определили тип структуры, вы знаете, какую технику использовать для написания уравнений равновесия:
Фермы/осевые элементы: Элементы нагружаются только внутренними осевыми силами. Для решения можно использовать метод стыков или метод сечений.
Балки (изгибаемые элементы): Элементы нагружены внутренними осевыми силами, поперечными силами и моментами. Чтобы решить эту проблему, разрежьте элемент в нужном месте, нарисуйте новую диаграмму свободного тела разреза и напишите уравнения равновесия.

Рамы/машины: Элементы нагружены внутренними осевыми силами, поперечными силами и моментами. Чтобы решить эту проблему, используйте подход «взорвать все на части», чтобы разбить структуру на более мелкие части. Ищите внутренние шарниры как общие места, чтобы разделить вашу конструкцию, и нарисуйте диаграммы свободного тела, чтобы решить силы соединительных штифтов.
Вантовые конструкции: Стержни изготовлены из тросов с осевой нагрузкой. Определите тип нагрузки кабеля (сосредоточенная, параболическая/равномерная или цепная). Рассчитайте натяжение троса в месте известного максимального провисания (или наоборот).
Поверхности, погруженные в воду: Элементы подвергаются давлению жидкости. Чтобы решить, нарисуйте диаграмму свободного тела диаграммы гидростатического давления, которая равна нулю на поверхности жидкости и линейно увеличивается с глубиной. Учитывайте вес жидкости на объектах с невертикальными гранями.
Вычисление давлений на подводных поверхностях
При решении задач на подводные поверхности в статике помните, что на все подводные поверхности действует жидкость, вызывающая давление. Вы должны вычислить два давления: результирующее гидростатическое давление и собственный вес жидкости.
Вы должны вычислить два давления: результирующее гидростатическое давление и собственный вес жидкости.
Результирующая гидростатического давления:
Собственный вес жидкости: Собственный вес жидкости:
, действующий вниз в центроиде (геометрический центр) области жидкости.
Расчет области или центра нагрузки: центроиды
Центроид или центр области геометрической области является геометрическим центром формы объекта. Вычисления центроида очень распространены в статике, независимо от того, вычисляете ли вы местоположение равнодействующей распределенной нагрузки или определяете центр масс объекта. Чтобы вычислить центр области области (или распределенную нагрузку), вы можете вычислить
Для дискретных областей: Дискретные области можно разбивать на простые фигуры, такие как треугольники, прямоугольники, круги и т.
 д.
д.Для дискретных фигур может быть полезно создать простую таблицу, подобную следующей для каждой координаты. Вы можете создать столько строк, сколько вам нужно, для любого количества регионов.
| х я | А и | x i А i | |
| Район 1 | x-расстояние для региона 1 | Район Района 1 | Продукт x i и A i |
| Всего | ——————- | Сумма всех A i строк | Сумма всех x я А я строки |
Для непрерывных регионов: Непрерывные регионы обычно определяются более сложными границами, поэтому вы должны задать их с помощью математических уравнений, подобных следующему:
Разработка диаграмм сдвига и моментов
Диаграммы сдвига и моментов — это статический инструмент, который инженеры создают для определения внутренних поперечных сил и моментов во всех точках внутри объекта.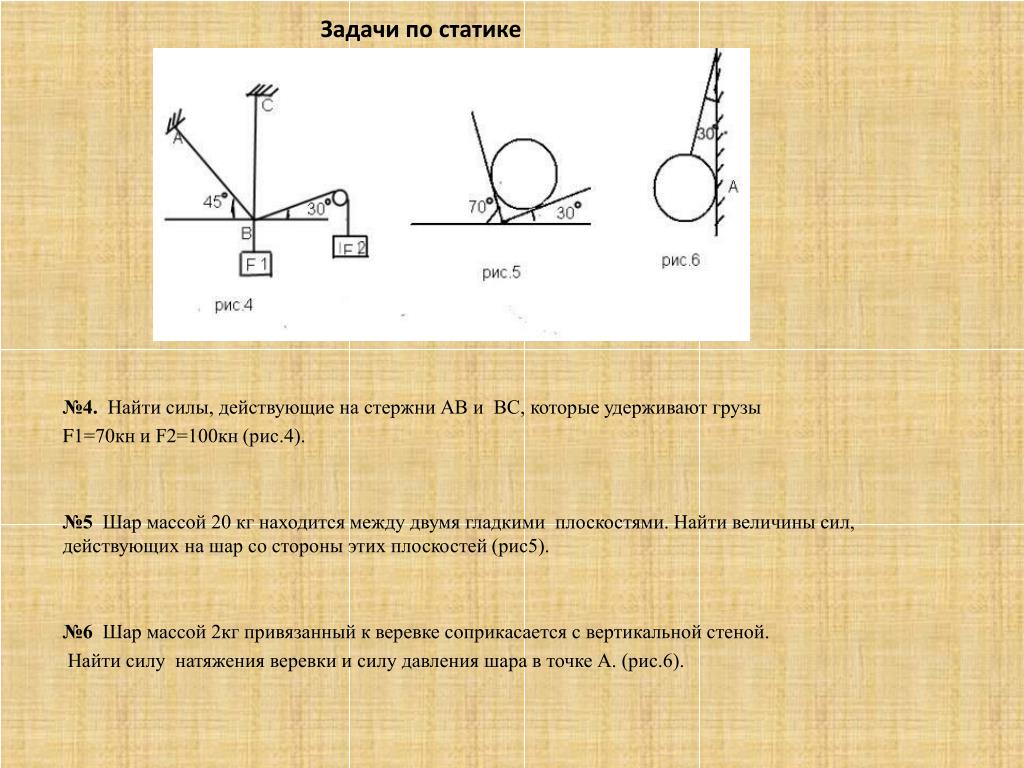 Начните с определения критических точек, а затем зарисуйте диаграмму сдвига.
Начните с определения критических точек, а затем зарисуйте диаграмму сдвига.
Расположение критических точек:
Запуск и остановка конструкции (крайние концы)
Сосредоточенные силы
Сосредоточенные моменты
Пуск и останов распределенных нагрузок
Внутренние петли
Места поддержки
Точки нулевого сдвига (V = 0) — только для моментных диаграмм.
Важные особенности, которые следует помнить при рисовании диаграммы:
Сосредоточенные силы вызывают мгновенный скачок сдвига.
Концентрированные моменты вызывают мгновенный скачок момента.
Порядок увеличивается от нагрузки к сдвигу к моменту (то есть диаграмма нагрузки 1-го порядка, сдвиг 2-го порядка, момент 3-го порядка).
Наклон диаграммы моментов равен величине сдвига.

Если площадь нагрузки положительна, изменение сдвига положительно. Если площадь сдвига положительна, изменение момента положительно.
Декартовы векторные формулы для решения задач статики
Во многих задачах статики необходимо уметь быстро и эффективно создавать векторы в декартовой плоскости. К счастью, вы можете легко создавать декартовы вектора с помощью удобных векторных формул из этого списка:
Векторы силы и векторы расстояния — самые основные векторы, с которыми вы имеете дело.
Как рассчитать момент силы
В статике м oments – эффекты (силы), вызывающие вращение. При вычислении равновесия вы должны быть в состоянии рассчитать момент для каждой силы на вашей диаграмме свободного тела. Чтобы определить момент силы, вы используете один из двух различных расчетов, как показано в следующем списке.
Скалярный расчет (для двух измерений): Для расчета момента относительно точки О в скалярных расчетах, нужна величина силы и перпендикулярное расстояние от точки О до линии действия Силы F.
Вычисление вектора (для двух или трех измерений): Для вычисления вектора момента относительно точки О в векторных вычислениях необходимо определить Силу F в декартовой векторной форме и вектор положения от точки О до линии действия Силы Ф.
Об этой статье
Эта статья взята из книги:
- Статика для чайников,
Об авторе книги:
Джеймс Х. Аллен III, PE, PhD, зарегистрированный профессиональный инженер, который преподает курсы в области статики, механика, проектирование конструкций и проектирование стали.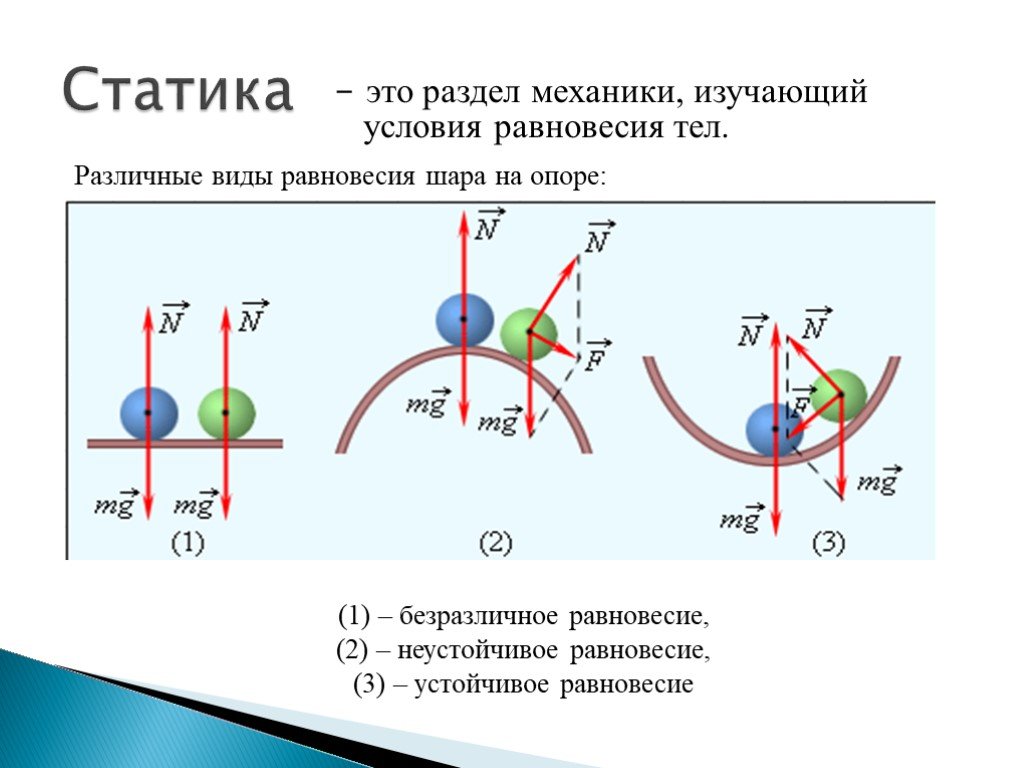
Эту статью можно найти в категории:
- Торговля, техника и инженерная карьера,
Формулы статистики
На этой веб-странице перечислены формулы статистики, используемые в Stat Trek учебники. Каждая формула ссылается на веб-сайт страница, которая объясняет, как использовать формулу.
Параметры
- Среднее значение населения = μ = ( Σ X i ) / N
- Стандартное отклонение населения = σ = sqrt [ Σ ( X i – мк) 2 /Н]
- Дисперсия населения = σ 2 = Σ ( X i – мк) 2 / N
- Дисперсия доли населения = σ P 2 = PQ / n
- Стандартизированная оценка = Z = (X – μ) / σ
- Коэффициент корреляции населения = ρ = [ 1 / N ] * Σ { [ (X i – μ X ) / σ x ] * [ (Y i – μ Y ) / σ y ] }
Статистика
Если не указано иное, в этих формулах предполагается
простая случайная выборка.
- Среднее значение выборки = х = ( Σ х и ) / №
- Стандартное отклонение выборки = s = sqrt [ Σ ( x i – х) 2 / (п – 1)]
- Выборочная дисперсия = с 2 = Σ ( х i – х) 2 / (н – 1)
- Дисперсия доли выборки = с р 2 = pq / (n – 1)
- Доля объединенной выборки = р = (р 1 * п 1 + п 2 * п 2 ) / (№ 1 + № 2 )
- Стандартное отклонение объединенной выборки = с р = sqrt [ (n 1 – 1) * s 1 2 + (n 2 – 1) * с 2 2 ] / (n 1 + n 2 – 2) ]
- Коэффициент корреляции выборки = г = [ 1 / (п – 1) ] * Σ { [ (x и – х) / с x ] * [ (у я – у) / с г ] }
Корреляция
- Корреляция Пирсона продукт-момент = r = Σ (xy) / sqrt [ ( Σ x 2 ) * ( Σ y 2 ) ]
- Линейная корреляция (выборочные данные) = r = [ 1 / (n – 1) ] * Σ { [ (x i – x) / s x ] * [ (y i – y) / s y ] }
- Линейная корреляция (данные населения) = ρ = [ 1 / N ] * Σ { [ (X i – μ X ) / σ x ] * [ (Y i – μ Y ) / σ y ] 4 } 9000
Простая линейная регрессия
- Простая линия линейной регрессии: ŷ = b 0 + b 1 x
- Коэффициент регрессии = б 1 = Σ [ (х i – х) (у я – у) ] / Σ [ (х и – х) 2 ]
- Пересечение наклона регрессии = б 0 = у – б 1 * х
- Коэффициент регрессии = б 1 = г * (с у / с х )
- Стандартная ошибка наклона регрессии = с б 1 = sqrt [ Σ(y i – ŷ i ) 2 / (п – 2) ] / sqrt [ Σ(x и – х) 2 ]
Подсчет
- п факториал:
н! = п * (п-1) * (п – 2) * .
 . . * 3 * 2 * 1. По соглашению,
0! = 1.
. . * 3 * 2 * 1. По соглашению,
0! = 1. - Перестановки n вещей, взятых r за раз: n P r = n! / (н – р)!
- Комбинации из n вещей, взятых r за один раз: № С р = н! / г!(п – г)! = n P r / r!
Вероятность
- Правило добавления: Р (А ∪ В) = Р(А) + Р(В) – Р(А ∩ В)
- Правило умножения: Р (А ∩ В) = П(А) П(В|А)
- Правило вычитания: P(A’) = 1 – P(A)
Случайные величины
В следующих формулах X и Y — случайные величины, а a и b являются константами.
- Ожидаемое значение X = E (X) = μ x = Σ [ x i * P (x i ) ]
- Дисперсия X = Var(X) = σ 2 = Σ [ х i – E(x) ] 2 * P(x i ) = Σ [ x i – μ x ] 2 * P(x i )
- Нормальная случайная величина = z-оценка = z = (X – μ)/σ
- Статистика хи-квадрат = Χ 2 = [ ( n – 1 ) * с 2 ] / σ 2
- f статистика = ж = [ с 1 2 /σ 1 2 ] / [ с 2 2 /σ 2 2 ]
- Ожидаемое значение суммы случайных величин = Е(Х + У) = Е(Х) + Е(У)
- Ожидаемое значение разницы между случайными величинами = Е(Х – У) = Е(Х) – Е(У)
- Дисперсия суммы независимых случайных величин = Вар(Х + Y) = Вар(Х) + Вар(Y)
- Дисперсия разности между независимыми случайными величинами = Вар(Х – Y) = Вар(Х) + Вар(Y)
Распределение проб
- Среднее выборочное распределение среднего = μ х = №
- Среднее выборочное распределение доли = мк р = р
- Стандартное отклонение пропорции = σ р = sqrt[P * (1 – P)/n] = sqrt(PQ/n)
- Стандартное отклонение среднего = σ x = σ/sqrt(n)
- Стандартное отклонение разности выборочных средних = σ d = sqrt[ (σ 1 2 / № 1 ) + (σ 2 2 / п 2 ) ]
- Стандартное отклонение разницы пропорций выборки = σ d = sqrt{ [P 1 (1 – P 1 ) / п 1 ] + [P 2 (1 – P 2 ) / № 2 ] }
Стандартная ошибка
- Стандартная ошибка пропорции = SE р = с р = sqrt[p * (1 – p)/n] = sqrt(pq/n)
- Стандартная ошибка разности пропорций = SE p = с р = sqrt{ p * ( 1 – p ) * [ (1/n 1 ) + (1/n 2 ) ] }
- Стандартная ошибка среднего = SE x = с х = с/кв (n)
- Стандартная ошибка разности выборочных средних = ЮВ д = с д = sqrt[ (s 1 2 / п 1 ) + (с 2 2 / № 2 ) ]
- Стандартная ошибка разности парных выборочных средних = SE д = с д = { квт [ (Σ(д и – д) 2 / (n – 1) ] } / sqrt(n)
- Стандартная ошибка объединенной выборки = с объединено = sqrt [ (n 1 – 1) * s 1 2 + (n 2 – 1) * с 2 2 ] / (n 1 + n 2 – 2) ]
- Стандартная ошибка разности пропорций выборки = с д = sqrt{ [p 1 (1 – p 1 ) / п 1 ] + [п 2 (1 – п 2 ) / п 2 ] }
Дискретные распределения вероятностей
- Биномиальная формула: P(X = x) = б( х ; п, Р ) = n C x * P x * (1 – P) n – x = n C x * P x * Q n – x
- Среднее биномиальное распределение = μ x = n * P
- Дисперсия биномиального распределения = σ х 2 = н * Р * ( 1 – Р )
- Отрицательная биномиальная формула: P(X = x) = b*( x ; r, P ) = x-1 C r-1 * Р р * (1 – Р) х – р
- Среднее отрицательного биномиального распределения = μ x = rQ / P
- Дисперсия отрицательного биномиального распределения = о х 2 = р * Q/P 2
- Геометрическая формула: P(X = x) = g( x ; P ) = P * Q x – 1
- Среднее геометрическое распределение = мк х = Q / P
- Дисперсия геометрического распределения = σ x 2 = В/П 2
- Гипергеометрическая формула: P(X = x) = h( x ; N , N , k ) = [ k C x ] [ N-k C n-x ] / [ Н С Н ]
- Среднее значение гипергеометрического распределения = мк х = n * к / N
- Дисперсия гипергеометрического распределения = σ x 2 = п * к * ( Н – к ) * ( Н – п ) / [ № 2 * (Н-1)]
- Формула Пуассона: P( x; µ ) = (e -µ ) (µ x ) / x!
- Среднее значение распределения Пуассона = мк х = мк
- Дисперсия распределения Пуассона = σ x 2 = μ
- Полиномиальная формула: P = [ n! / ( п 1 !
* п 2 ! * .
 .. п к ! )]
* ( стр 1 п 1 * p 2 n 2 * . . .
* p k n k )
.. п к ! )]
* ( стр 1 п 1 * p 2 n 2 * . . .
* p k n k )
Линейные преобразования
Для следующих формул предположим, что Y является линейное преобразование случайной величины X, определяемой уравнением: Y = aX + b.
- Среднее линейного преобразования = E(Y) = У = аХ + б.
- Дисперсия линейного преобразования = Var(Y) = а 2 * Вар(Х).
- Стандартизированная оценка = z = (x – μ x ) / σ x .
- t статистика = t = (x – μ x ) / [s/sqrt(n)].
Оценка
- Доверительный интервал: Выборочная статистика + Критическое значение * Стандартная ошибка статистики
- Погрешность = (Критическое значение) * (Стандартное отклонение статистики)
- Погрешность = (Критическое значение) * (Стандартная ошибка статистики)
Проверка гипотез
- Стандартизированная тестовая статистика = (Статистика – Параметр) / (Стандартное отклонение статистики)
- Одновыборочный z-тест для пропорций: z-оценка = z = (p – P 0 ) / sqrt(p * q/n)
- Двухвыборочный z-тест для пропорций: z-оценка = z = z = [(p 1 – p 2 ) – d ] / SE
- Одновыборочный t-критерий для средних: t статистика = t = (x – μ) / SE
- Двухвыборочный t-критерий для средних: t статистика = t = [ (x 1 – х 2 ) – д ] / SE
- Стьюдентный критерий с согласованной выборкой для средних значений: t статистика = t = [ (x 1 – х 2 ) – Д ] / ЮВ = (д – Д) / SE
- Статистика критерия хи-квадрат = Χ 2 = Σ[ (Наблюдается – Ожидается) 2 / Ожидается ]
Степени свободы
Правильная формула для степеней свободы (DF) зависит от ситуации
(характер тестовой статистики, количество образцов,
исходные предположения и др. ).
).
- Одновыборочный t-критерий: ДФ = п – 1
- Двухвыборочный t-критерий: ДФ = (s 1 2 /n 1 + с 2 2 /n 2 ) 2 / { [ (с 1 2 / п 1 ) 2 / (n 1 – 1) ] + [ (с 2 2 / п 2 ) 2 / (n 2 – 1) ] }
- Двухвыборочный t-критерий, объединенная стандартная ошибка: ДФ = п 1 + п 2 – 2
- Простая линейная регрессия, тестовый наклон: ДФ = n – 2
- Хи-квадрат критерия согласия: ДФ = к – 1
- Критерий хи-квадрат на однородность: ДФ = (г – 1) * (с – 1)
- Тест хи-квадрат на независимость: ДФ = (г – 1) * (с – 1)
Размер выборки
Ниже первые две формулы находят наименьшие размеры выборки.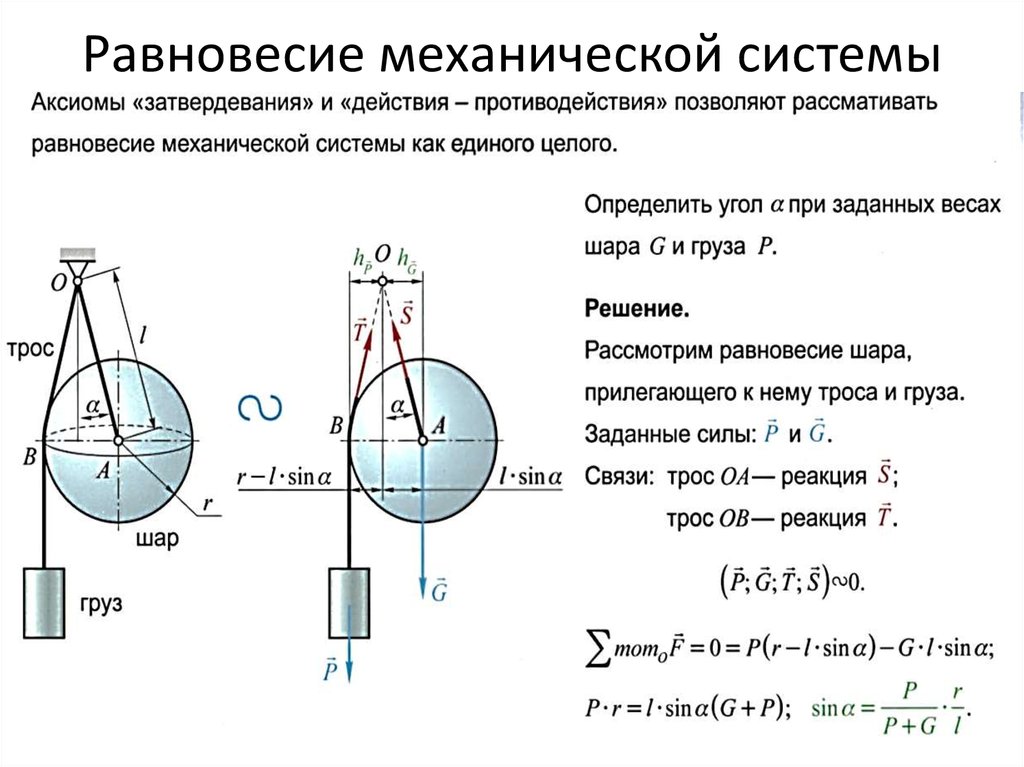


 или
или 


 д.
д.
 . . * 3 * 2 * 1. По соглашению,
0! = 1.
. . * 3 * 2 * 1. По соглашению,
0! = 1. .. п к ! )]
* ( стр 1 п 1 * p 2 n 2 * . . .
* p k n k )
.. п к ! )]
* ( стр 1 п 1 * p 2 n 2 * . . .
* p k n k )