Основные формулы термодинамики 📙 – Физика
- Термодинамическая формула идеального газа
- Первое начало термодинамики. Формулы для изопроцессов
- Уравнение теплоёмкости и основное уравнение коэффициента полезного действия в термодинамике
- Формула состояния и её функции
В термодинамике осуществляется изучение всеобщих законов и материальных явлений изменения внутренней энергии. В то же время принято, каждый физический объект обладает тепловой энергией U, зависящей от температурных показателей данного объекта. До рассмотрения ключевых термодинамических уравнений требуется определить формулировку термодинамики.
Термодинамика является широким раздел физики, который изучает более всеобщие характеристики макроскопических структур, а также методы передачи и изменения энергии в данных структурах. Термодинамика описывает процессы, которые происходят в системах и их состояния.
Данная наука основывается на всеобщих и распространённых фактах, полученные путём экспериментальных методов.
- Температурные показатели.
- Давление.
- Мольный объём.
- Показатели плотности.
- Концентрация.
- Энергия.
Отдельно к молекулам эти свойства не имеют никакого отношения, а выражаются в развёрнутом описании структуры, по её существу. Большое количество реализованных результатов, основанных на законах термодинамики, возможно наблюдать в области электрической энергетики и теплотехники. Это подтверждает восприятие фазовых переходов, химических явлений и процессов переноса. В определённой степени термодинамические законы взаимодействуют с законами квантовой динамики.
Работа газа в термодинамике определяется следующей формулой:
\(A` = p (V2 – V1) = pΔV\)
Работа внешних сил приравнивается работе газа с противоположным знаком:
\(A = – A`\)
Определение 2.
Идеальный газ является теоретической моделью, которая широко применяется для описания характеристик и поведения фактических газов при ограниченных показателях давления и температурных параметров.
В данной модели, полагается, что создающие газ частицы не воздействуют один на одного, т.е. их величины являются пренебрежительно малыми, по данной причине, в объеме, который занят идеальным газом, не присутствует ударение элементов. Элементы идеального газа испытывают ударения исключительно со стенками ёмкости.
Молекулы такой модели считаются физическими точками, а ударения элементов являются полностью упругими. В термодинамических задачах фактические газы периодически принимают идеальные. Таким образом, намного проще создавать уравнения, и нет необходимости иметь дело с большим числом различных значений в формулах.
Молекулы идеального газа осуществляют перемещения, и осталось определить с какой скоростью и массой, они это осуществляют. Для этого требуется применить формулу состояния идеального газа Клапейрона-Менделеева: \(PV = {m\over M}RT,\)
где m – масса исследуемого газа.
M– его первоначальная молекулярная масса.
R – универсальная константа, которая равна 8,3144598 Дж/(моль*кг).
Массу идеального газа возможно рассчитать, как умножение объёма и плотности \(m = pV.\)
Присутствует определённая взаимосвязь меж средней кинетической энергией \(E\) и давлением газа. Данная связь именуется в физике главной формулой молекулярно-кинетической теории. Описывается данная формула следующим образом \(p = {2\over 3}nE,\)
где \(n\) – концентрация перемещающихся молекул относительно всеобщего объёма.
\(E\) – коэффициент средней кинетической энергии.
Уравнение состояния идеального газа выглядит следующим образом: \(F (P, V, T) = 0\). Соотношение, которое даёт взаимосвязь между параметрами какого-либо объекта, именуется уравнением состояния данного объекта.
Рисунок 1. Закон Бойля-Мариотта.
Первый термодинамический закон говорит: число внутренней теплоты, которое передано газу, идет исключительно на преобразование всеобщей энергии газа U, а также на осуществление газом работы \(A\).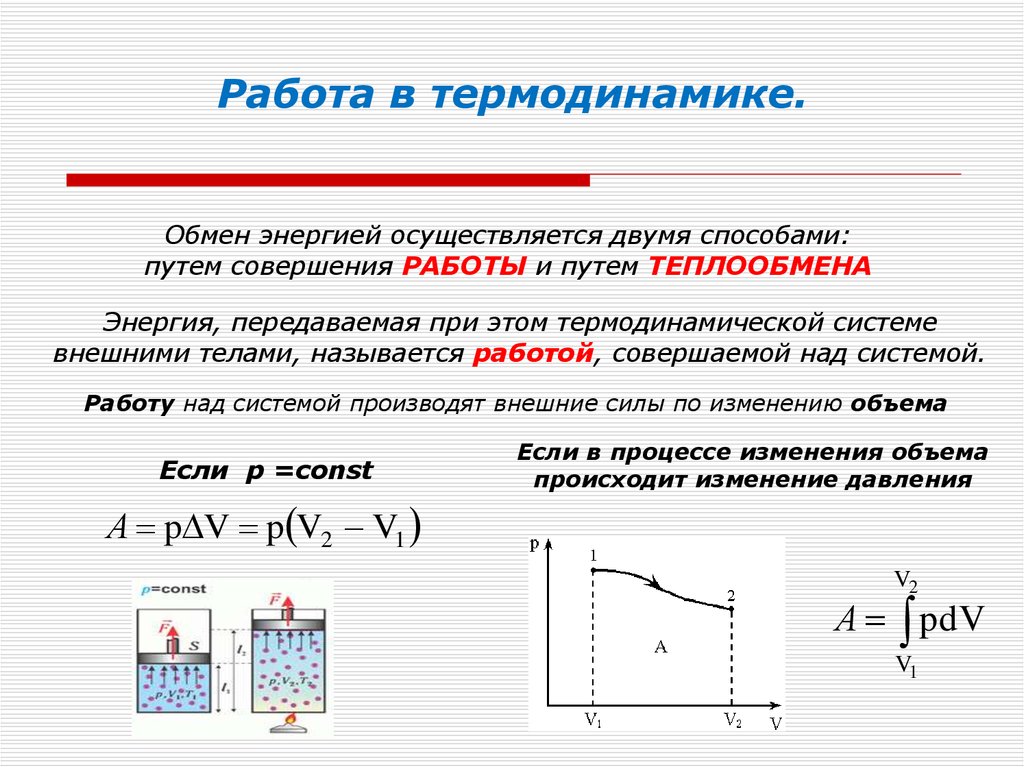
В этой ситуации требуется рассмотрение таких явлений, которые происходят при одном постоянном показателе. Первый закон термодинамики в изотермическом случае, протекающем при константе температурного показателя, использует закон Бойля-Мариотта. По итогу изотермического процесса давление газа обратно пропорционально его первоначальному объему: \(Q = A.\)
Изохорный процесс рассматривается при величине объёма равном постоянной составляющей. Для данного процесса применяется закон Шарля, в согласовании с которым, давление прямо пропорционально всеобщему температурному показателю. В изохорном явлении всё подведённое к газу тепло идёт на преобразование внутреннего энергетического потенциала, и в математической форме выглядит следующим образом: \(Q=ΔA.\)
Изобарное явление осуществляется при величине давления равной постоянной составляющей. Закон Гей-Люссака полагает, что при постоянном давлении идеального газа, его изначальный объем прямо пропорционален результирующему температурному показателю. При изобарном явлении тепло идёт на осуществление работы газом и на преобразование внутренней энергии, и в математической форме выглядит следующим образом: \(Q = ΔU + pΔV.\)
Закон Гей-Люссака полагает, что при постоянном давлении идеального газа, его изначальный объем прямо пропорционален результирующему температурному показателю. При изобарном явлении тепло идёт на осуществление работы газом и на преобразование внутренней энергии, и в математической форме выглядит следующим образом: \(Q = ΔU + pΔV.\)
Количество теплоты – это часть внутреннего энергетического потенциала, которую объект получает либо, теряет при тепловой передаче.
Рисунок 2. Количество теплоты.
Замечание 1
Удельная тепловая ёмкость в структуре термодинамики постоянно приравнивается числу теплоты, выделяемом для нагрева 1 кг существующего вещества на 1°С.
Формула тепловой ёмкости в математической форме выглядит следующим образом: \(c = {Q \over mΔt}\)). Кроме вышеуказанного показателя, присутствует и молярная тепловая ёмкость, работающая при стабильном объёме и давлении. Её функционирование просматривается в следующем уравнении: \(Cv = {i \over 2} R\), где \(i\) – число степеней свободы молекул газа.
Тепловая оборудование, в самом примитивном случае, слагается из холодильной, нагревательной и рабочей части физического объекта. Нагревательная часть оборудования первоначально передаёт тепло материальному объекту и осуществляет определённую работу, и после чего со временем осуществляется охлаждение холодильной частью оборудования. Далее, всё осуществляется повторно вкруговую. Классическим образом теплового оборудования является двигатель внутреннего сгорания. Расчёт коэффициента полезного действия теплового оборудования производится согласно уравнению:
\(n = {Qh-Qx\over Qh}\)
Во время исследования термодинамических основ и формул необходимо воспринять, что сегодня присутствует две методики представления материальных явлений, которые происходят в макроскопических физических объектах:
- Статистическая методика.
- Термодинамическая методика.
Термодинамические методики и её уравнения предоставляют возможность обнаружить, развернуть и осуществить описание сущности опытных обоснований в виде закона Менделеева-Клапейрона.
Рисунок 3. Термодинамические формулы состояния.
При изучении макроскопических состояний используются функции состояния, предполагающие параметры, которые демонстрируют определенные равновесные состояния термодинамики. Данные параметры не зависят от предыстории системы и методики ее перехода в абсолютное состояние. Ключевыми функциями состояния при правильном термодинамическом строении считаются:
- Температурные показатели.
- Внутренняя энергия.
- Энтропия.
- Потенциалы термодинамики.
Но термодинамические функции состояния не считаются в полной мере свободными. Для однородной структуры каждый принцип термодинамики имеет возможность быть определён, как уравнение двух отдельных переменных. Данные функциональные взаимные связи именуются формулами всеобщего состояния. Сегодня различаются следующие типы формул:
Данные функциональные взаимные связи именуются формулами всеобщего состояния. Сегодня различаются следующие типы формул:
- Термические формулы состояния. Данные формулы определяют взаимосвязь меж давлением, объемом и температурными показателями.
- Калорические формулы состояния. Данные формулы выражают внутреннюю энергию, как функцию от объема и температурных показателей.
- Канонические формулы состояния. Данные формулы записываются в роли термодинамического потенциала в определённых переменных.
Сведения о формулах состояния являются довольно существенными для практического применения всеобщих принципов термодинамики. Для любой определённой термодинамической системы данные формулы устанавливаются из экспериментальных данных либо методами статистической механики, и в границах термодинамики они являются заданными при первоначальном определении системы.
Основные формулы термодинамики Условные обозначения
Обозначение | Название величины | Размерность / Значение | Формула |
Абсолютная температура | K | ||
[4] | Давление | Па | |
Объём | м³ | ||
Средняя энергия молекулы | Дж | ||
Средняя кинетическая энергия молекулы | Дж | ||
Масса | кг | ||
[5] | Молярная масса | кг/моль | |
Постоянная Авогадро | 6. | ||
Постоянная Больцмана | 1.3806505(24)·10−23 Дж/К | ||
Газовая постоянная | 8.314472(15) Дж/(К·моль) | ||
Число степеней свободы молекулы | – | ||
Количество вещества в -й компоненте -компонентной смеси | моль | ||
вектор с координатами | моль | ||
Химический потенциал -й компоненты -компонентной смеси | Дж/моль | ||
Внутренняя энергия | Дж | ||
Энтропия | Дж/К | ||
Энтальпия | Дж | ||
[6] | Изохорно-изотермический потенциал (свободная энергия Гельмгольца) | Дж | |
Изобарно-изотермический потенциал (свободная энергия Гиббса, свободная энтальпия) | Дж | ||
Работа, совершённая газом | Дж | ||
Тепло, переданное газу | Дж | ||
Молярная теплоёмкость газа при постоянном давлении | Дж/(К·моль) | ||
Молярная теплоёмкость газа при постоянном объёме | Дж/(К·моль) | ||
Удельная теплоёмкость | Дж/(К·кг) | ||
Показатель адиабаты | – |
Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона) | |
Изменение внутренней энергии газа | |
Работа газа | |
Средняя энергия молекулы газа | |
Средняя кинетическая энергия молекулы газа: | |
Внутренняя энергия газа | |
Теплоёмкость газа при постоянном объёме | |
Теплоёмкость газа при постоянном давлении |
Выражение основных величин через термодинамические потенциалы
Все
термодинамические потенциалы имеют
свои канонические наборы переменных и
используются для анализа процессов при
соответствующих условиях. Так, для
изотермических изохорических процессов
()
удобно использовать ,
для изотермических изобарических
() — ,
а для изолированных систем () — .
Так, для
изотермических изохорических процессов
()
удобно использовать ,
для изотермических изобарических
() — ,
а для изолированных систем () — .
Термодинамический потенциал (энтропия)— независимые переменные;
;
;
;
;
;
.
Термодинамический потенциал (свободная энергия Гельмгольца) — независимые переменные;
;
;
;
;
;
.
Термодинамический потенциал (энергия Гиббса) — независимые переменные;
;
;
;
;
;
.

Термодинамический потенциал (внутренняя энергия)— независимые переменные;
;
;
;
;
;
.
Фундаментальное уравнение Гиббса, экстенсивность и уравнение Гиббса — Дюгема
Выражение для полного дифференциала внутренней энергии называется фундаментальным уравнением Гиббса или просто уравнением Гиббса:
Значимость этого
уравнения (и его более общих вариантов)
состоит в том, что оно представляет
собой тот фундамент, на котором базируется
весь математический аппарат современной
феноменологической термодинамики, как
равновесной, так и неравновесной. По
большому счёту, рассмотренные выше
законы (начала) термодинамики нужны
были именно для обоснования этого
соотношения. Всю аксиоматику равновесной
термодинамики можно свести к постулированию
самого этого уравнения и свойств входящих
в него термодинамических переменных.
Всю аксиоматику равновесной
термодинамики можно свести к постулированию
самого этого уравнения и свойств входящих
в него термодинамических переменных.
С использованием других термодинамических потенциалов уравнение Гиббса можно переписать в следующих эквивалентных формах:
Среди термодинамических величин выделяют экстенсивные (внутренняя энергия, энтропия, объём и др.) и интенсивные (давление, температура и др.) величины. Величина называется экстенсивной, если ее значение для системы, сложенной из нескольких частей, равно сумме значений этой величины для каждой части. Предположением об экстенсивности термодинамических величин, однако, можно пользоваться, если рассматриваемые системы достаточно большие и можно пренебречь различными краевыми эффектами при соединении нескольких систем, например, энергией поверхностного натяжения. Пусть U (экстенсивная величина) является однородной функцией первого порядка от своих экстенсивных аргументов (математическое выражение аксиомы экстенсивности): для любого
Для любой дифференцируемой однородной функции первого порядка выполняется теорема Эйлера:
Для энергии теорема Эйлера имеет вид:
Отсюда легко следует уравнение Гиббса — Дюгема:
Это
уравнение показывает, что между
интенсивными переменными существует
одна связь, являющаяся следствием
предположения об аддитивности свойств
системы. В частности, непосредственным
следствием соотношений Гиббса-Дюгема является
выражение для термодинамического
потенциала Гиббса через химические
потенциалы компонент
смеси:
В частности, непосредственным
следствием соотношений Гиббса-Дюгема является
выражение для термодинамического
потенциала Гиббса через химические
потенциалы компонент
смеси:
Первый закон термодинамики – формула, определение, применение
4.6
Средняя оценка: 4.6
Всего получено оценок: 198.
4.6
Средняя оценка: 4.6
Всего получено оценок: 198.
Важнейшим законом, на котором основываются термодинамические расчеты для самых различных случаев, является Первый Закон термодинамики (иногда говорится Первое Начало термодинамики). Рассмотрим этот закон подробнее.
Энергия и ее сохранение
Энергия – это общая физическая мера взаимодействий и движений в Природе. Понятие энергии было использовано еще Аристотелем для обозначения механической работы. Позже оно было математически формализовано Г. Лейбницем (он, фактически описал кинетическую энергию), а впервые использовано в современном смысле Т. Юнгом.
Одно из важнейших свойств энергии – ее сохранение в замкнутой системе. Энергия не может возникать и исчезать. Все процессы в Природе лишь перераспределяют энергию между различными телами и видами.
Однако, доказать это свойство удалось далеко не сразу. Если рассмотреть примеры различных механических процессов с потерей энергии в результате трения, то все выглядит так, как будто механическая энергия исчезает. То, что при трении происходит нагрев, было известно давно, однако, то, что тепло является энергией, которая при трении перешла из кинетической во внутреннюю, впервые отмечено лишь в конце XVIIв Г. Лейбницем.
Современный вид закон сохранения энергии принял в работах Р. Майера.
Рис. 1. Р. Майер.Позже он был расширен Дж. Джоулем, а окончательную строгую формулировку получил в трудах Г. Гельмгольца.
Полное теоретическое обоснование закона было получено лишь в 1918 г Э. Нёттер. Было доказано, что закон сохранения энергии – это следствие симметрии времени (равноправности всех моментов времени в замкнутой инерциальной системе).
Первый Закон термодинамики
Закон сохранения энергии, распространенный на тепловые явления, стал называться Первым Законом (иногда говорится Первым Началом) термодинамики.
Если в механике рассматривается энергия движения тел, то термодинамика рассматривает их внутреннюю энергию, а также ее изменение за счет совершения работы либо за счет теплообмена. Вся энергия, полученная телом за счет этих двух способов, пойдет на увеличение внутренней энергии. То есть, суть Первого Закона термодинамики будет сформулирована следующим образом.
Изменение внутренней энергии системы равно сумме работы внешних сил над системой и количества теплоты, переданной системе.
Математически формула первого закона термодинамики имеет вид:
$$ΔU=A+Q,$$
где:
- $ΔU$ – изменение внутренней энергии системы;
- $A$ – работа внешних сил над системой;
- $Q$ – количество теплоты, переданное системе.
Из представленной формулы Первого Закона термодинамики следует, что, после того, как системе были подведены тепло и работа, говорить о том, что тело «содержит» это количество теплоты или работы нельзя. Подводимая к телу теплота или совершаемая работа влияет только на изменение внутренней энергии. Определение же общего количества внутренней энергии тела может быть получено в рамках не термодинамики, а молекулярно-кинетической теории. Характеристикой общей внутренней энергии тела является температура.
Подводимая к телу теплота или совершаемая работа влияет только на изменение внутренней энергии. Определение же общего количества внутренней энергии тела может быть получено в рамках не термодинамики, а молекулярно-кинетической теории. Характеристикой общей внутренней энергии тела является температура.
Также из данной формулы можно получить закон сохранения внутренней энергии. В самом деле, для изолированной системы работа внешних сил и количество теплоты равно нулю ( $A = 0$ и $Q = 0$). А значит, $ΔU = U_2 – U_1 = 0$ или $U_2 = U_1$, то есть:
$$U=const, при A=0,Q=0$$
Внутренняя энергия изолированной системы постоянна.
Вечный Двигатель и Первый Закон термодинамики
Устройство, совершающее работу без затрат энергии, называется Вечным Двигателем первого рода. Применение такого устройства сулит пользователю огромную выгоду. Многие изобретатели прошлого пытались построить такую машину, но всегда терпели неудачу.
Рис. 3. Примеры Вечного Двигателя первого рода.
Причина кроется в нарушении таким Вечным Двигателем Первого Закона термодинамики.
Если система не получает тепло, то полезная работа (то есть, работа, которую совершает система над внешними объектами) может быть совершена только за счет уменьшения внутренней энергии:
$$А_{полезн}=-ΔU$$
А значит, рано или поздно запасы внутренней энергии будут израсходованы, и двигатель не сможет совершать полезную работу. Смысл же Вечного Двигателя в постоянном совершении работы.
Что мы узнали?
Первый Закон термодинамики гласит, что изменение внутренней энергии системы равно сумме работы внешних сил и количества теплоты, переданной системе. Этот закон является следствием закона сохранения энергии, который, в свою очередь, является следствием симметрии времени. Первый Закон термодинамики обосновывает невозможность существования Вечного Двигателя первого рода.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Виктор Лисицкий
8/10
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 198.
А какая ваша оценка?
основные понятия, формулы и определения с примерами
Содержание:
Термодинамические системы и макропараметры состояния вещества:
Термодинамический подход основывается на понятии термодинамической системы, которая представляет собой любое макроскопическое тело или совокупность таких тел. Состояние термодинамической системы определяется ее внутренними параметрами, например состоянием движения микрочастиц, из которых состоит тело. Тепловое состояние тела, которое характеризуется температурой, тесно связано со скоростью движения атомов и молекул – чем больше скорость их движения, тем выше температура тела.
Температура тела зависит от скорости движения атомов и молекул, из которых оно состоит, – чем больше скорость, тем выше температура.
Внутреннее состояние тела очень сложно определить через параметры движения микрочастиц, потому что их очень много. Поэтому, чтоб упростить описание состояния термодинамической системы, его связывают с физическими величинами, которые характеризуют тело в целом, независимо от его молекулярного строения. К таким величинам принадлежат, в частности, масса, объем, плотность, давление, температура и т. п.
Их называют макропараметрами системы. Фактически они являются усредненными значениями данных физических величин на протяжении длительного времени.
Температура – один из основных макропараметров термодинамической системы, характеризующий состояние ее теплового или термодинамического равновесия. Сущность данного понятия объясняется течением тепловых явлений и процессов.
Например, из собственного опыта нам известно, что более нагретые тела отдают теплоту менее нагретым, вследствие чего со временем их температуры станут одинаковыми. Если, к примеру, кусочек льда бросить в стакан с теплой водой (рис. 5.1), то лед будет таять, а вода в стакане охлаждаться, отдавая определенное количество теплоты тающему льду. Кроме того, стакан с водой и лед пребывают в состоянии теплообмена с окружающей средой. Поэтому со временем температуры всех этих тел станут одинаковыми.
Если, к примеру, кусочек льда бросить в стакан с теплой водой (рис. 5.1), то лед будет таять, а вода в стакане охлаждаться, отдавая определенное количество теплоты тающему льду. Кроме того, стакан с водой и лед пребывают в состоянии теплообмена с окружающей средой. Поэтому со временем температуры всех этих тел станут одинаковыми.
Тела с более высокой температурой отдают тепловую энергию телам с более низкой температурой; теплообмен происходит до тех пор, пока их температуры не станут одинаковыми.
Следовательно, со временем вследствие теплообмена в термодинамических системах наступает состояние термодинамического равновесия, когда температуры всех тел становятся одинаковыми и теплообмен между ними прекращается. Значение температуры характеризует вполне определенное состояние теплового равновесия термодинамической системы, в котором она пребывает в данный момент. Он может быть изменен в результате термодинамического процесса.
Если, например, на поршень в цилиндре с газом положить груз (рис. 5.2), то объем газа будет изменяться до тех пор, пока давление не сравняется с внешним давлением. Т. е. термодинамическая система «цилиндр – газ» перейдет в иное состояние, характеризующееся новыми значениями макропараметров – давлением объемом температурой плотностью Такой переход термодинамической системы из одного состояния в другое, в результате которого параметры системы изменяются, называется термодинамическим процессом.
5.2), то объем газа будет изменяться до тех пор, пока давление не сравняется с внешним давлением. Т. е. термодинамическая система «цилиндр – газ» перейдет в иное состояние, характеризующееся новыми значениями макропараметров – давлением объемом температурой плотностью Такой переход термодинамической системы из одного состояния в другое, в результате которого параметры системы изменяются, называется термодинамическим процессом.
Термодинамика рассматривает в основном состояния термодинамического равновесия и процессы, которые происходят достаточно медленно, и поэтому каждое новое их состояние можно считать равновесным. В состоянии термодинамического равновесия между макропараметрами системы существуют определенные функциональные зависимости, отображаемые уравнениями состояния термодинамической системы.
Карта основ термодинамики:
Термодинамическая системаРаздел физики, изучающий тепловые явления в макроскопических системах, называется термодинамикой. В основе термодинамики лежат термодинамические законы, опирающиеся на большое количество экспериментальных фактов. Эти законы отвечают на вопрос “как?”, например, как изменяется состояние тела (твердого тела, жидкости или газа) при нагревании (или охлаждении), в каком направлении и как передается тепло, как изменяется температура газа при его расширении и другие. Объектами исследования термодинамики являются термодинамические системы.
В основе термодинамики лежат термодинамические законы, опирающиеся на большое количество экспериментальных фактов. Эти законы отвечают на вопрос “как?”, например, как изменяется состояние тела (твердого тела, жидкости или газа) при нагревании (или охлаждении), в каком направлении и как передается тепло, как изменяется температура газа при его расширении и другие. Объектами исследования термодинамики являются термодинамические системы.
Любое макроскопическое тело или система макроскопических тел называется термодинамической системой. Состояние термодинамической системы характеризуется макроскопическими или термодинамическими параметрами (масса, плотность, объем, давление, температура).
Внутренняя энергияВеличины, определяющие состояние термодинамической системы в данный момент времени, то есть соответствующие этому состоянию макроскопические параметры, называются функциями состояния. Основной среди этих величин является внутренняя энергия.
Внутренняя энергия – это сумма кинетических энергий различных видов, движения частиц системы и потенциальных энергий взаимодействия этих частиц (см.: таблица 7.1).
Внутренняя энергия термодинамической системы является функцией температуры и объема, определяющих состояние системы:
Внутренняя энергия одноатомного идеального газаГаз, молекулы которого состоят из одного атома, называют одноатомным газом. Внутренняя энергия одноатомного газа равна сумме кинетических энергий поступательного движения частиц и потенциальных энергий их взаимодействия:
Однако внутренняя энергия идеального газа данной массы равна сумме средних кинетических энергий хаотического движения частиц:
Средняя кинетическая энергия одной частицы одноатомного идеального газа определяется выражением следовательно, внутренняя энергия такого газа зависит только от температуры:
Это выражение является формулой закона Джоуля:
Внутренняя энергия идеального газа зависит от ее массы, рода (молярной массы) и температуры. Даже если давление и объем газа изменятся, при постоянной температуре его внутренняя энергия не изменится.
Даже если давление и объем газа изменятся, при постоянной температуре его внутренняя энергия не изменится.
Сопоставив формулу (7.1) с выражением Менделеева-Клапейрона, получим:
Способы изменения внутренней энергииДля изменения внутренней энергии термодинамической системы необходимо изменить или среднюю кинетическую энергию теплового движения молекул системы, или потенциальную энергию их взаимодействия, или же изменить обе энергии одновременно. Из многочисленных опытов было определено, что существует два способа изменения внутренней энергии: теплопередача и совершение работы.
Изменение внутренней энергии системы происходит двумя способами: передачей количества теплоты и совершением работы
Если внутренняя энергия изменяется только в результате теплообмена, то изменение внутренней энергии равно полученному (или отданному) системой количеству теплоты. Например, при нагревании и охлаждении тела изменение его внутренней энергии определяется так:
Изменение внутренней энергии в процессе плавления твердого тела или кристаллизации жидкости происходит за счет изменения потенциальной энергии взаимодействия молекул тела. Изменение внутренней энергии при этих процессах численно равно теплоте плавления (кристаллизации):
Изменение внутренней энергии при этих процессах численно равно теплоте плавления (кристаллизации):
Где – удельная теплота плавления.
Изменение внутренней энергии тела в процессе парообразования и конденсации также равно затраченному во время этого процесса количеству теплоты:
Где — удельная теплота парообразования.
Изменение внутренней энергии одноатомного идеального газа определяется изменением его температуры:
Где и – соответственно, значения внутренней энергии одноатомного газа в начальном и конечном состояниях.
Внимание. Изменение внутренней энергии термодинамической системы зависит не от вида процесса, а от его начального и конечного состояния.
Работа в термодинамикеЕсли изменение внутренней энергии происходит только в результате совершения механической работы, то это изменение равно или работе внешних сил над системой или работе системы против внешних сил
Работа в термодинамике — это одна из мер изменения внутренней энергии термодинамической системы.
Предположим, что в толстостенном цилиндре находится газ, сжимаемый поршнем. При сжатии поршень передает часть своей кинетической энергии молекулам газа, в результате чего увеличивается внутренняя энергия газа и повышается его температура — внешние силы совершают работу над газом. При расширении, наоборот, молекулы газа, передавая часть своей кинетической энергии поршню, уменьшают свою скорость и газ охлаждается – он совершает работу над внешними силами (b).
Таким образом, работа, совершенная газом над внешними силами, в результате расширении газа данной массы при постоянном давлении равна:
или
Работа же, совершенная внешними силами над газом равна :
Где — сила, с которой газ действует на поршень, — смещение поршня, — давление газа, — площадь поперечного сечения цилиндра, — изменение объема газа. Совершенная работа численно равна площади фигуры, образованная графиком в системе координат при расширении газа (т. е. при увеличении объема газа) или при сжатии же газа (т.е. при уменьшении объема газа) или (с).
е. при увеличении объема газа) или при сжатии же газа (т.е. при уменьшении объема газа) или (с).
Если в процессе совершения работы газ через некоторое время возвращается в первоначальное состояние, то такой процесс называется замкнутым или циклическим процессом.
Если стрелки, показывающие направление циклического процесса, совпадают с направлением вращения часовых стрелок, то работа газа положительна, а работа внешних сил отрицательна (d). Если же стрелки, определяющие направление процесса, направлены против вращения часовых стрелок, то работа газа отрицательна, а работа внешних сил положительна.
Что такое термодинамическая системаПолную энергию физической системы можно представить как алгебраическую сумму её механической энергии и внутренних энергий тел, образующих систему. Убыль механической энергии системы в ряде случаев происходит при самопроизвольном переходе её части во внутреннюю энергию тел системы. Так, например, режущие инструменты заметно нагреваются при заточке. При скольжении конькобежца под коньками тает лёд, что обеспечивает хорошее скольжение. В этих примерах тела при трении нагреваются, и интенсивность теплового движения их молекул возрастает, что приводит к увеличению внутренней энергии тел. Как же определить внутреннюю энергию термодинамической системы? И что понимают под термодинамической системой?
Так, например, режущие инструменты заметно нагреваются при заточке. При скольжении конькобежца под коньками тает лёд, что обеспечивает хорошее скольжение. В этих примерах тела при трении нагреваются, и интенсивность теплового движения их молекул возрастает, что приводит к увеличению внутренней энергии тел. Как же определить внутреннюю энергию термодинамической системы? И что понимают под термодинамической системой?
В термодинамике физические тела и их модели называют термодинамическими системами. Для их описания используют параметры системы, такие, как давление, объём, температура (макропараметры), а не физические характеристики молекул (микропараметры). Макропараметры можно непосредственно измерить, используя приборы, или выразить через другие величины, которые можно измерить на опыте. Мы рассмотрим простейшие термодинамические системы, состояние которых определяют, используя только давление, объём и температуру.
Тела, образующие термодинамическую систему, могут обмениваться с окружающей средой энергией, а также веществом. Если этого не происходит, то термодинамическую систему называют замкнутой или изолированной.
Если этого не происходит, то термодинамическую систему называют замкнутой или изолированной.
Рассматривая полную энергию макроскопического тела, необходимо учитывать не только его механическую энергию (кинетическую и потенциальную), но также и энергию, заключённую внутри самого тела, — внутреннюю энергию.
Внутренняя энергия макроскопического тела — алгебраическая сумма кинетической энергии теплового движения всех частиц, образующих тело, и потенциальной энергии их взаимодействия.
Внутренняя энергия любой термодинамической системы состоит из внутренних энергий тел, входящих в данную систему, и является одной из основных физических величин, используемых в термодинамике.
В термодинамике представляет интерес не само значение внутренней энергии системы, а её изменение. Поэтому обычно принимают во внимание только те составляющие внутренней энергии, которые изменяются в рассматриваемых процессах.
Рассмотрим переход некоторой массы идеального газа из состояния 1, в котором его внутренняя энергия в состояние 3, в котором его внутренняя энергия (рис. 62). Смену состояний можно осуществить или при изохорном нагревании, а затем при изобарном расширении (процесс ), пли при изобарном расширении, а затем при изохорном нагревании (процесс ). Однако приращение* внутренней энергии газа в обоих случаях одинаково:
62). Смену состояний можно осуществить или при изохорном нагревании, а затем при изобарном расширении (процесс ), пли при изобарном расширении, а затем при изохорном нагревании (процесс ). Однако приращение* внутренней энергии газа в обоих случаях одинаково:
Внутренняя энергия зависит от конкретного состояния системы. Это означает, что изменение внутренней энергии при переходе термодинамической системы из одного состояния в другое зависит только от значений параметров этих состояний и не зависит от процесса перехода.
- * — приращение физической величины, т. е. разность между её конечным и начальным значениями;
- — убыль величины, т. е. разность между её начальным и конечным значениями.
Определим внутреннюю энергию идеального одноатомного газа, т. е. газа, образованного атомами. Например, одноатомными газами являются инертные газы — гелий, неон, аргон и др.
Из определения понятия «идеальный газ» следует, что его внутренняя энергия является суммой кинетических энергий хаотического движения всех атомов (или молекул) (потенциальная энергия взаимодействия между частицами отсутствует). Следовательно, внутренняя энергия идеального одноатомного газа равна произведению средней кинетической энергии теплового движения частиц на их число N, т. е. Поскольку
где — масса газа, а то
С учётом того, что произведение постоянной Больцмана и постоянной Авогадро — универсальная газовая постоянная, получим:
или
Из формулы (11.1) следует, что внутренняя энергия данной массы идеального одноатомного газа пропорциональна его абсолютной температуре. Она не зависит от других макроскопических параметров состояния — давления и объёма. Следовательно, изменение внутренней энергии данной массы одноатомного идеального газа происходит только при изменении его температуры:
При определении внутренней энергии реальных газов, жидкостей и твёрдых тел необходимо учитывать потенциальную энергию взаимодействия частиц, которая зависит от расстояния между ними. Поэтому в общем случае внутренняя энергия макроскопических тел зависит не только от абсолютной температуры, но и от объёма.
Поэтому в общем случае внутренняя энергия макроскопических тел зависит не только от абсолютной температуры, но и от объёма.
Изменить внутреннюю энергию термодинамической системы можно двумя способами: используя теплообмен и совершая работу. Процесс теплообмена и совершение работы характеризуют соответственно физическими величинами — количеством теплоты Q и работой А, которые являются мерами изменения внутренней энергии системы.
Пример решения задачи №1При изобарном охлаждении внутренняя энергия идеального одноатомного газа изменилась на Определите давление газа, если его объём изменился на
Решение. Приращение внутренней энергии некоторого количества идеального одноатомного газа
Используя уравнение Клапейрона—Менделеева, можно осуществить замену:
Решая совместно уравнения (1) и (2), получим:
Ответ:
Внутренняя энергия телаЛюбое макроскопическое тело обладает энергией, что обусловлено его микросостоянием. Эта энергия называется внутренней (обозначается U). Она равна энергии всех микрочастиц вещества, из которых состоит данное тело. Например, внутренняя энергия идеального газа состоит из кинетической энергии всех его молекул, без учета их потенциальной энергии, поскольку взаимодействием молекул в модели идеального газа пренебрегают.
Эта энергия называется внутренней (обозначается U). Она равна энергии всех микрочастиц вещества, из которых состоит данное тело. Например, внутренняя энергия идеального газа состоит из кинетической энергии всех его молекул, без учета их потенциальной энергии, поскольку взаимодействием молекул в модели идеального газа пренебрегают.
Модель идеального газа предусматривает, что молекулы пребывают на расстоянии нескольких диаметров друг от друга. Поэтому энергия их взаимодействия намного меньше энергии их движения, следовательно, ею можно пренебречь.
В реальных газах, а также в жидкостях и твердых телах внутреннюю энергию необходимо учитывать, потому что она соизмерима с кинетической энергией и существенно влияет на их свойства. В таком случае их внутренняя энергия состоит из кинетической энергии теплового движения микрочастиц и потенциальной энергии их взаимодействия.
Для того чтобы изменить внутреннюю энергию тела, следует фактически изменить или кинетическую энергию теплового движения микрочастиц, или потенциальную энергию их взаимодействия, или и ту и другую вместе. Многовековой опыт человечества убеждает нас в том, что это можно сделать двумя способами – либо в процессе теплообмена, либо в ходе выполнения работы. В первом случае это произойдет вследствие передачи определенного количества теплоты Q; во втором – в результате выполнения работы А.
Многовековой опыт человечества убеждает нас в том, что это можно сделать двумя способами – либо в процессе теплообмена, либо в ходе выполнения работы. В первом случае это произойдет вследствие передачи определенного количества теплоты Q; во втором – в результате выполнения работы А.
Изменение внутренней энергии тела может произойти за счет теплообмена или в результате выполнения работы:
Следовательно, передача количества теплоты и выполнение работы являются факторами, благодаря которым можно изменить внутреннюю энергию тела:
В случае, когда происходит лишь теплообмен, полученное или отданное телом количество теплоты полностью идет на изменение его внутренней энергии, в частности кинетической энергии его атомов и молекул: Во время нагревания или охлаждения тела она равна:
В процессе плавления или кристаллизации твердых тел внутренняя энергия изменяется за счет потенциальной энергии взаимодействия микрочастиц, потому что происходит структурная перестройка вещества. В данном случае изменение внутренней энергии равно теплоте плавления (кристаллизации) тела:
В данном случае изменение внутренней энергии равно теплоте плавления (кристаллизации) тела:
где – удельная теплота плавления (кристаллизации) твердого тела.
Если изменение внутренней энергии тела происходит вследствие теплообмена, то или или
Испарение жидкости или конденсация пара также ведет к изменению внутренней энергии, которая равна в таком случае теплоте парообразования:
где r – удельная теплота парообразования (конденсации) жидкости.
Изменение внутренней энергии тела вследствие выполнения механической работы (без теплообмена) равно значению работы:
Следовательно, с точки зрения молекулярной физики внутренняя энергия тела является суммой кинетической энергии теплового движения атомов, молекул и других частиц, из которых оно состоит, и потенциальной энергии их взаимодействия. Это энергия термодинамической системы, которая зависит от ее внутреннего состояния. Поэтому вычисляют изменение внутренней энергии которое происходит в результате теплообмена или выполнения работы, а не само ее значение U.
Вычисление выполненной работы в термодинамике связывают с макропараметрами системы. Рассмотрим газ, находящийся в цилиндре под поршнем площадью S (рис. 5.3).
Пусть на газ действует поршень, вызывая его сжатие. Под действием силы F поршень опускается на высоту выполняя работу (направление действия силы имеет то же направление, что и перемещение, поэтому cos – 1). Если перемещение поршня будет незначительным, то давление газа практически не изменится (р = const). Учитывая, что согласно третьему закону Ньютона сила F по модулю равна силе давления газа – это изменение объема газа, получим:
Поскольку следовательно, то работа внешних сил над газом будет равна:
Если под действием силы давления F’ газ расширяется (рис. 5.4), т. е. он сам выполняет работу то ее значение также равно Выполненная газом работа в данном случае будет положительной, поскольку
Во время незначительных изменений объема и при постоянном давлении формулы (1) и (2) справедливы не только для газов, но и иных термодинамических систем. Поскольку изменение объема при постоянном давлении сопровождается изменением температуры тела, то можно сделать вывод, что выполнение работы в термодинамике вызывает изменение состояния тела, ведь при этом изменяются его температура Т и объем V.
Поскольку изменение объема при постоянном давлении сопровождается изменением температуры тела, то можно сделать вывод, что выполнение работы в термодинамике вызывает изменение состояния тела, ведь при этом изменяются его температура Т и объем V.
Тот факт, что внутреннюю энергию тела можно изменить двумя способами – в результате выполнения работы или за счет теплопередачи, вынуждал ученых искать соотношение между соответствующими величинами. Вначале в 1842 г. немецкий естествоиспытатель Р. Майер теоретически установил, а затем в 1843 г. английский ученый Дж. Джоуль экспериментально измерил эквивалентность значений количества теплоты и работы. В соответствии с полученными результатами ученые сделали обобщения, которые касались сохранения энергии в природе: энергия в природе не возникает из ничего и не пропадает бесследно; она лишь переходит из одного вида в другой.
Позже этот фундаментальный закон природы приобрел логическую форму первого закона термодинамики: переход термодинамической системы из одного состояния в другое характеризуется изменением ее внутренней энергии, равной сумме работы внешних сил и количества теплоты, переданной системе:
В каком бы состоянии не было тело, оно обладает определенной внутренней энергией. Однако нельзя утверждать, что оно содержит определенное количество теплоты либо запас выполненной работы. Независимо от того, каким из этих способов произведено изменение состояния тела, его состояние однозначно определяется внутренней энергией. Например, газ может быть нагрет за счет передачи ему некоторого количества теплоты либо в результате выполнения внешними силами над ним работы (сжатие газа). Однако невозможно однозначно указать, благодаря какому из этих процессов – выполнению работы или теплопередаче – произошло нагревание газа.
Однако нельзя утверждать, что оно содержит определенное количество теплоты либо запас выполненной работы. Независимо от того, каким из этих способов произведено изменение состояния тела, его состояние однозначно определяется внутренней энергией. Например, газ может быть нагрет за счет передачи ему некоторого количества теплоты либо в результате выполнения внешними силами над ним работы (сжатие газа). Однако невозможно однозначно указать, благодаря какому из этих процессов – выполнению работы или теплопередаче – произошло нагревание газа.
Если система сама выполняет работу (А = -А’), то первый закон термодинамики приобретает другой вид:
т. е. передача термодинамической системе определенного количества теплоты вызывает изменение ее внутренней энергии или выполнение работы, либо то и другое одновременно.
Еще в 1775 г. Французская академия наук приняла решение не рассматривать проекты вечных двигателей.
Последняя формулировка первого закона термодинамики важна с точки зрения отрицания возможности создания вечного двигателя: нельзя создать машину, которая бы неограниченно выполняла работу, не получая энергию извне. Ведь, если количество теплоты Q = 0, то А’ = т. е. работа выполняется за счет уменьшения внутренней энергии, которая не безгранична по размеру.
Ведь, если количество теплоты Q = 0, то А’ = т. е. работа выполняется за счет уменьшения внутренней энергии, которая не безгранична по размеру.
Человечество научилось использовать тепловую энергию, создав тепловые машины и двигатели. В основу их действия положена идея, что выполнение механической работы может осуществляться за счет теплоты, получаемой от какого-либо нагревателя и частично отдаваемой холодильнику.
Принцип действия тепловой машины можно представить схематически (рис. 5.5). Нагреватель передает рабочему телу определенное количество теплоты часть которой идет на выполнение работы А’. Рабочим телом в тепловых машинах
может быть газ или пар, выполняющие работу вследствие своего расширения при нагревании. В паровых турбинах это происходит благодаря паровым котлам, в двигателях внутреннего сгорания – в результате сгорания топливной смеси, в реактивных двигателях – за счет большой теплоотдачи топлива во время быстрого его сгорания.
Выполняя работу, рабочее тело отдает определенную часть количества теплоты охладителю (специальному устройству или окружающей среде), вследствие чего его температура снижается до значения Оно не может использовать всю предоставленную тепловую энергию, поскольку часть ее рассеивается в окружающей среде из-за выбросов отработанного пара или выхлопных газов.
Согласно закону сохранения энергии значение выполненной работы По определению коэффициент полезного действия равен:
Следовательно, коэффициент полезного действия тепловой машины всегда меньше 1 (часто его представляют в процентах). К примеру, у двигателей внутреннего сгорания он равен приблизительно 44 %, у паровых турбин – до 40 %.
Коэффициент полезного действия равен отношению величины выполненной работы к затраченной при этом энергии:
Холодильник также является тепловой машиной. Принцип его действия основан на обратимости цикла тепловой машины. Холодильная машина работает как тепловой насос: она отбирает тепловую энергию у менее нагретого тела и передает ее более нагретому (рис. 5.6). Это не противоречит законам термодинамики, поскольку охлаждение происходит за счет выполнения работы.
5.6). Это не противоречит законам термодинамики, поскольку охлаждение происходит за счет выполнения работы.
Для того чтобы привести в действие холодильную машину, необходимо над рабочим телом выполнить работу. В таком случае нагревателю будет передаваться количество теплоты, превышающее по значению то, которое отбирается у охладителя: Следовательно, температура охладителя будет еще больше снижаться, а температура нагревателя при этом будет повышаться.
Эффективность работы холодильной машины характеризуется отношением количества теплоты отобранного у тела, к выполненной при этом работе А: Данный коэффициент может быть больше 1. Он зависит от разницы температур нагревателя и охладителя
Основные определения и формулыВ основу термодинамического подхода положено описание термодинамической системы при помощи легко измеримых макропараметров – температуры (Т), давления (р), объема (V), массы (m) и др.
Внутренняя энергия тела равна энергии всех микрочастиц вещества, из которых оно состоит. Ее можно изменить за счет теплообмена или в результате выполнения работы. Количество теплоты, переданное телу (либо отобранное у него), определяется в зависимости от теплового процесса, который при этом осуществляется:
Ее можно изменить за счет теплообмена или в результате выполнения работы. Количество теплоты, переданное телу (либо отобранное у него), определяется в зависимости от теплового процесса, который при этом осуществляется:
при нагревании (охлаждении )
при плавлении (кристаллизации )
при парообразовании (конденсации)
Работа газа при постоянном давлении (р = const) равна: и изменяет знак на противоположный при выполнении работы внешними силами над газом:
Первый закон термодинамики устанавливает, что количество теплоты, переданное термодинамической системе, вызывает изменение ее внутренней энергии или выполнение работы, либо и той другое одновременно:
Он отражает сущность фундаментального закона сохранения энергии, которым отрицается возможность создания вечного двигателя: нельзя создать машину, которая неограниченно выполняла бы работу, не получая энергию извне.
Законы термодинамики получили широкое практическое применение, в частности, в технике, при конструировании тепловых машин. Все тепловые машины (двигатели внутреннего сгорания, реактивные двигатели, паровые и газовые турбины, холодильные машины и пр.) построены по принципу выполнения механической работы за счет внутренней энергии. Их КПД всегда меньше 1 и равен:
Основы термодинамикиВ 9 классе вы узнали, что полная энергия физической системы представляет собой сумму её механической энергии и внутренних энергий тел, образующих систему. Причём изменение механической энергии в ряде случаев происходит в результате перехода её части во внутреннюю энергию тел системы. Режущие инструменты заметно нагреваются при заточке их на точильном камне. При скольжении конькобежца по льду под коньками тает лёд, что обеспечивает хорошее скольжение. В этих примерах тела при трении нагреваются, и интенсивность хаотического движения молекул возрастает, что приводит к увеличению внутренней энергии тел. Как же определить внутреннюю энергию термодинамической системы? И что понимают под термодинамической системой?
Как же определить внутреннюю энергию термодинамической системы? И что понимают под термодинамической системой?
Выводы термодинамики основаны на фундаментальных законах, называемых началами термодинамики. Эти законы установлены в результате обобщения многочисленных экспериментальных фактов. Опираясь на них, термодинамика позволяет делать определённые выводы о свойствах исследуемых систем, которые подтверждаются экспериментально. Физические тела и их модели в термодинамике называют термодинамическими системами. Термодинамическую систему характеризуют набором параметров, определяющих её состояние. В отличие от молекулярно-кинетической теории в термодинамике не рассматривают микроскопическое строение тел и для их описания используют не физические характеристики молекул (микропараметры), а параметры системы (макропараметры), такие как давление, объём, температура.
Замкнутая, или же изолированная, термодинамическая система стремится к равновесию, когда все её макропараметры не изменяются с течением времени. Иначе говоря, для каждой изолированной термодинамической системы существует состояние термодинамического равновесия, в которое она переходит самопроизвольно.
Иначе говоря, для каждой изолированной термодинамической системы существует состояние термодинамического равновесия, в которое она переходит самопроизвольно.
Это утверждение называют нулевым началом термодинамики.
Говоря о полной энергии макроскопического тела, необходимо всегда учитывать не только его механическую энергию (кинетическую и потенциальную), но также кинетическую энергию теплового движения его частиц и потенциальную энергию их взаимодействия. В термодинамике под внутренней энергией тела понимают полную энергию, относящуюся к самим частицам, образующим тело. Это кинетическая энергия теплового движения молекул, кинетическая энергия движения атомов внутри молекул, потенциальная энергия взаимодействия между молекулами, энергия электронных оболочек атомов и внутриядерная энергия.
Внутренняя энергия любой термодинамической системы состоит из внутренних энергий тел, входящих в данную систему.
В термодинамике главную роль играет не сама внутренняя энергия, а её изменение, которое происходит при переходе системы из одного состояния в другое. Под приращением (изменением) внутренней энергии понимают разность внутренних энергий в конечном и начальном состояниях:
Под приращением (изменением) внутренней энергии понимают разность внутренних энергий в конечном и начальном состояниях:
Например, переход некоторой массы идеального газа из состояния / в состояние 3 (рис. 49) можно осуществить или в ходе процесса (при изохорном нагревании, а затем при изобарном расширении), или в ходе процесса (при изобарном расширении, а затем при изохорном нагревании). Однако приращение (изменение) внутренней энергии газа и в одном и в другом случае будет одинаковым:
Внутренняя энергия является функцией состояния системы. Это означает, что изменение внутренней энергии при переходе термодинамической системы из одного состояния в другое зависит только лишь от значений параметров этих состояний, а не от процесса перехода.
Внутренняя энергия идеального одноатомного газа:
Определим внутреннюю энергию идеального одноатомного газа, т. е. газа, состоящего из отдельных атомов. Например, к одноатомным газам относят инертные газы — гелий, неон, аргон и др.
Из определения понятия «идеальный газ» следует, что его внутренняя энергия является суммой кинетических энергий хаотического движения всех молекул или атомов (взаимодействие между частицами отсутствует). Следовательно, внутренняя энергия идеального одноатомного газа равна произведению средней кинетической энергии теплового движения частиц на их число N,
т. е. . Поскольку , где m — масса газа, а , то
С учётом того, что получим:
(9.1)
или
Как видно из формулы (9.1), внутренняя энергия данной массы идеального одноатомного газа пропорциональна абсолютной температуре газа. Она не зависит от других макроскопических параметров состояния — давления и объёма. Следовательно, изменение внутренней энергии данной массы идеального одноатомного газа происходит только при изменении его температуры:
При определении внутренней энергии реальных газов, жидкостей и твёрдых тел необходимо учитывать потенциальную энергию взаимодействия частиц, которая зависит от расстояния между ними. Поэтому в общем случае внутренняя энергия макроскопических тел зависит не только от абсолютной температуры, но и от объёма.
Поэтому в общем случае внутренняя энергия макроскопических тел зависит не только от абсолютной температуры, но и от объёма.
При изучении физики в 8 классе вы узнали, что изменить состояние термодинамической системы можно двумя способами: используя теплопередачу и совершая работу. Процесс теплопередачи и совершение работы характеризуют соответственно физическими величинами — количеством теплоты Q и работой А, которые являются мерами изменения внутренней энергии системы.
- Физические тела и их модели в термодинамике называют термодинамическими системами. Термодинамическую систему характеризуют набором макронараметров, определяющих её состояние.
- Состояние изолированной термодинамической системы, когда все её макропараметры не изменяются с течением времени, называют равновесным.
- Под внутренней энергией термодинамической системы понимают сумму кинетической энергии всех частиц системы и потенциальной энергии их взаимодействия.
- Изменение внутренней энергии тела при переходе из одного состояния в другое зависит только лишь от значений параметров этих состояний, а не от процесса перехода.

- Внутренняя энергия данной массы идеального одноатомного газа зависит только от температуры:
На рисунке 51 в координатах (р, V) изображён процесс перехода идеального одноатомного газа определённой массы из состояния 1 в состояние 2. Определите приращение внутренней энергии газа, если давление газа в конечном состоянии = 1,5 МПа, а его объём в начальном состоянии = 2,0 л.
Решение.
Приращение внутренней энергии идеального одноатомного газа Найти массу m газа, его молярную массу M и
изменение температуры не представляется возможным. Однако, используя уравнение Клапейрона—Менделеева, для состояний 1 и 2 можно определить значение выражения . Из рисунка 51 видно, что в состоянии 1 давление газа а его объём а в состоянии 2 — Тогда уравнение Клапейрона—Менделеева для состояний 1и 2 примет вид:
Вычтем из уравнения (2) уравнение (1): и получим, что . Тогда
Ответ:
Термодинамика: основные формулы и законы.
 первый закон термодинамики, кпд
первый закон термодинамики, кпдТермодинамика. Законы и формулы
Термодина́мика (греч. θέρμη — «тепло», δύναμις — «сила») — раздел физики, изучающий соотношения и превращения теплоты и других форм энергии. В отдельные дисциплины выделились химическая термодинамика, изучающая физико-химические превращения, связанные с выделением или поглощением тепла, а также теплотехника.
В термодинамике имеют дело не с отдельными молекулами, а с макроскопическими телами, состоящими из огромного числа частиц. Эти тела называютсятермодинамическими системами. В термодинамике тепловые явления описываются макроскопическими величинами — давление, температура, объём, …, которые не применимы к отдельным молекулам и атомам.
В теоретической физике наряду с феноменологической термодинамикой, изучающей феноменологию тепловых процессов, выделяют термодинамику статистическую, которая была создана для механического обоснования термодинамики и была одним из первых разделов статистической физики.
Термодинамика может быть применена в широком круге вопросов в области науки и техники, таких, как двигатели, фазовые переходы, химические реакции, явления переноса, и даже чёрные дыры.
Обратите внимание
Термодинамика имеет важное значение для других областей физики и химии, химической технологии, аэрокосмической техники, машиностроения, клеточной биологии, биомедицинской инженерии, материаловедения, и полезно в таких других областях, как экономика.
Термодинамика исторически возникла как эмпирическая наука об основных способах преобразования внутренней энергии тел для совершения механической работы. Однако в процессе своего развития термодинамика проникла во все разделы физики, где возможно ввести понятие «температура» и позволила теоретически предсказать многие явления задолго до появления строгой теории этих явлени
Традиционно считается, что термодинамика основывается на четырёх законах (началах), которые сформулированы на основе экспериментальных данных и поэтому могут быть приняты как постулаты.
* 0-й закон — нулевое начало термодинамики: Постулирует существование термодинамического равновесия и вводит понятие абсолютной температуры.
Термодинамическое равновесие. Для каждой изолированной термодинамической системы существует состояние термодинамического равновесия, которого она при фиксированных внешних условиях с течением времени самопроизвольно достигает. Если две изолированные системы и приведены в контакт друг с другом, то после достижения термодинамического равновесия полной системой системы и находятся в состоянии теплового (термического) равновесия друг с другом. При этом каждая из систем и в отдельности также находится в состоянии термодинамического равновесия. Это равновесие не нарушится, если устранить контакт между системами, а затем восстановить его. Следовательно, если установление контакта между двумя системами и , которые до этого были изолированными, не приводит ни к каким изменениям, то эти системы находятся в тепловом равновесии друг с другом. Закон транзитивности теплового равновесия. Если системы и находятся в тепловом равновесии и системы и находятся в тепловом равновесии, то системы и также находятся в тепловом равновесии между собой. На основании этого закона делается вывод о существовании абсолютной температуры как термодинамического параметра, обладающего свойствами эмпирической температуры, но не зависящего от способа её измерения. Равенство температур есть условие теплового равновесия систем (или частей одной и той же системы).
Закон транзитивности теплового равновесия. Если системы и находятся в тепловом равновесии и системы и находятся в тепловом равновесии, то системы и также находятся в тепловом равновесии между собой. На основании этого закона делается вывод о существовании абсолютной температуры как термодинамического параметра, обладающего свойствами эмпирической температуры, но не зависящего от способа её измерения. Равенство температур есть условие теплового равновесия систем (или частей одной и той же системы).
* 1-й закон — первое начало термодинамики: Представляет собой формулировку обобщённого закона сохранения энергии для термодинамических процессов. В наиболее простой форме его можно записать как
,где есть полный дифференциал внутренней энергии системы, а и есть элементарное количество теплоты, переданное системе, и элементарная работа, совершенная системой соответственно. Нужно учитывать, что и нельзя считать дифференциалами в обычном смысле этого понятия, поскольку эти величины существенно зависят от типа процесса, в результате которого состояние системы изменилось. В литературе можно встретить и другие варианты приведённого выше соотношения, отличающиеся от него знаками ( или ) перед и . Отличия вызваны тем, что конкретный вид этого уравнения зависит от соглашений, называемых «правилами знаков для работы и теплоты». Выше использовано «теплотехническое правило знаков для работы» (положительной считают работу, совершаемую системой, когда она отдаёт энергию, а отрицательной — работу, совершаемую над системой, когда она получает энергию) и «термодинамическое правило знаков для теплоты» (положительной считают теплоту, получаемую системой, а отрицательной — теплоту, отдаваемую системой). В «термодинамическом правиле знаков для работы» положительной считают работу, совершаемую над системой, а отрицательной — работу, совершаемую системой. Наконец, в «термохимическом правиле знаков для теплоты» положительной считают теплоту, отдаваемую системой, а отрицательной — теплоту, получаемую системой. Мнемоническое правило: в термодинамической системе знаков имеет тот же знак, что и энергия, передаваемая системе в виде работы или теплоты; в остальных случаях знак противоположен знаку передаваемой энергии.
В литературе можно встретить и другие варианты приведённого выше соотношения, отличающиеся от него знаками ( или ) перед и . Отличия вызваны тем, что конкретный вид этого уравнения зависит от соглашений, называемых «правилами знаков для работы и теплоты». Выше использовано «теплотехническое правило знаков для работы» (положительной считают работу, совершаемую системой, когда она отдаёт энергию, а отрицательной — работу, совершаемую над системой, когда она получает энергию) и «термодинамическое правило знаков для теплоты» (положительной считают теплоту, получаемую системой, а отрицательной — теплоту, отдаваемую системой). В «термодинамическом правиле знаков для работы» положительной считают работу, совершаемую над системой, а отрицательной — работу, совершаемую системой. Наконец, в «термохимическом правиле знаков для теплоты» положительной считают теплоту, отдаваемую системой, а отрицательной — теплоту, получаемую системой. Мнемоническое правило: в термодинамической системе знаков имеет тот же знак, что и энергия, передаваемая системе в виде работы или теплоты; в остальных случаях знак противоположен знаку передаваемой энергии. Стандарта, предписывающего использовать конкретный набор правил знаков, не существует, так что уместно рассматривать только степень распространённости того или иного правила в научной и учебной литературе. По этому поводу однозначно можно говорить лишь о том, что в современной литературе предпочитают использовать термодинамическое, а не термохимическое правило знаков для теплоты.
Стандарта, предписывающего использовать конкретный набор правил знаков, не существует, так что уместно рассматривать только степень распространённости того или иного правила в научной и учебной литературе. По этому поводу однозначно можно говорить лишь о том, что в современной литературе предпочитают использовать термодинамическое, а не термохимическое правило знаков для теплоты.
Иногда в рассматриваемое выражение для первого начала наряду с работой и теплотой включают ещё и работу переноса массы (химическую работу), выделяя её из общего выражения для работы в отдельное слагаемое.
* 2-й закон — второе начало термодинамики: Второй закон термодинамики исключает возможность создания вечного двигателя второго рода. Имеется несколько различных, но в то же время эквивалентных формулировок этого закона.
1 — Постулат Клаузиуса. Процесс, при котором не происходит других изменений, кроме передачи теплоты от горячего тела к холодному, является необратимым, то есть теплота не может перейти от холодного тела к горячему без каких-либо других изменений в системе.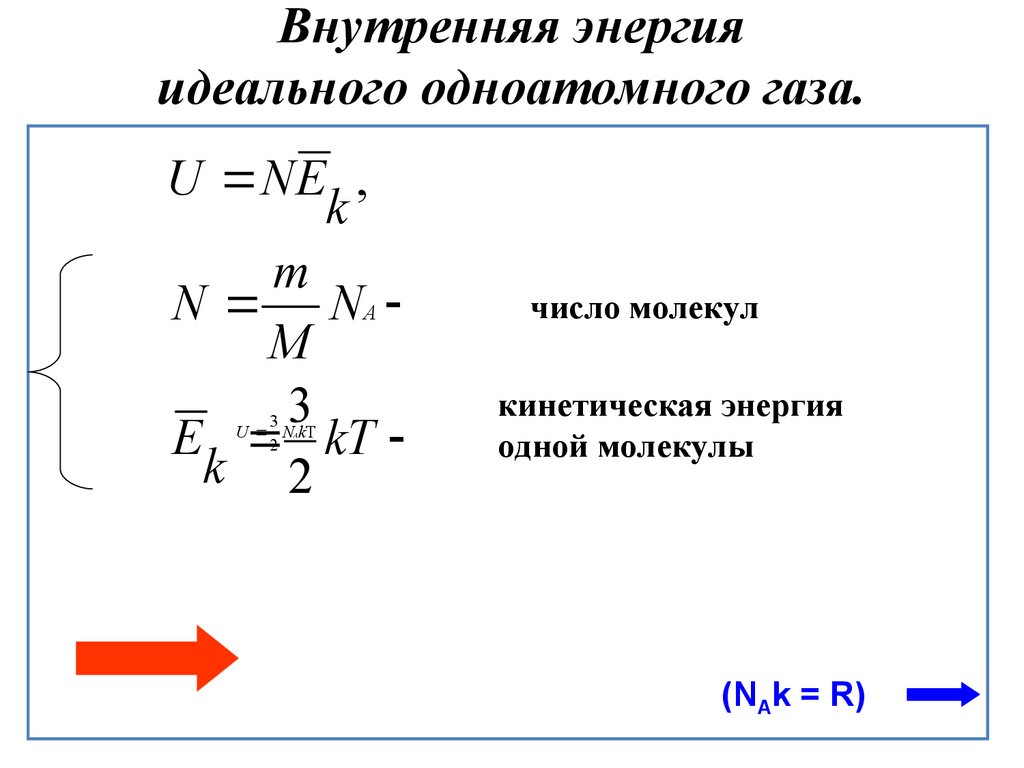 Это явление называют рассеиванием или диссипацией энергии.
Это явление называют рассеиванием или диссипацией энергии.
Приведем второе начало термодинамики в ещё одной формулировке Рудольфа Юлиуса Клаузиуса (1865): для любой квазиравновесной термодинамической системы существует однозначная функция термодинамического состояния , называемая энтропией, такая, что ее полный дифференциал .
[3]
2 — Постулат Кельвина.
Процесс, при котором работа переходит в теплоту без каких-либо других изменений в системе, является необратимым, то есть невозможно превратить в работу всю теплоту, взятую от источника с однородной температурой, не проводя других изменений в системе.
* 3-й закон — третье начало термодинамики: Теорема Нернста: энтропия любой равновесной системы при абсолютном нуле температуры всегда равна нулю (традиционная формулировка).
Здесь важно различать аксиомы, отражающие законы природы, и имеющие исторические корни соглашения, необходимые для построения шкалы измерения соответствующей термодинамической величины.
Так, аксиомами являются утверждения, что и энтропия, и температура есть односторонне ограниченные величины, и что своих граничных значений обе величины достигают одновременно. Согласно стандартным соглашениям принято, что и энтропия, и температура ограничены снизу, т. е.
не могут быть меньше некоторых предельных значений. Из этого логично вытекают следующие соглашения, согласно которым наименьшее значение энтропии принято равным нулю, а наименьшее (нулевое) значение температуры служит реперной точкой для построения термодинамической шкалы температур.
Все термодинамические потенциалы имеют свои канонические наборы переменных и используются для анализа процессов при соответствующих условиях.
Так, для изотермических изохорических процессов () удобно использовать , для изотермических изобарических () — , а для изолированных систем () — .
- — независимые переменные;
- ;
- ;
- ;
- ;
- ;
- .
- — независимые переменные;
- ;
- ;
- ;
- ;
- ;
- .
- — независимые переменные;
- ;
- ;
- ;
- ;
- ;
- .
- — независимые переменные;
- ;
- ;
- ;
- ;
- ;
- .
Выражение для полного дифференциала внутренней энергии называется фундаментальным уравнением Гиббса или просто уравнением Гиббса:
Значимость этого уравнения (и его более общих вариантов) состоит в том, что оно представляет собой тот фундамент, на котором базируется весь математический аппарат современной феноменологической термодинамики, как равновесной, так и неравновесной.
По большому счёту, рассмотренные выше законы (начала) термодинамики нужны были именно для обоснования этого соотношения.
Всю аксиоматику равновесной термодинамики можно свести к постулированию самого этого уравнения и свойств входящих в него термодинамических переменных.
Важно
С использованием других термодинамических потенциалов уравнение Гиббса можно переписать в следующих эквивалентных формах:
Среди термодинамических величин выделяют экстенсивные (внутренняя энергия, энтропия, объём и др.) и интенсивные (давление, температура и др.) величины. Величина называется экстенсивной, если ее значение для системы, сложенной из нескольких частей, равно сумме значений этой величины для каждой части.
Предположением об экстенсивности термодинамических величин, однако, можно пользоваться, если рассматриваемые системы достаточно большие и можно пренебречь различными краевыми эффектами при соединении нескольких систем, например, энергией поверхностного натяжения.
Пусть U (экстенсивная величина) является однородной функцией первого порядка от своих экстенсивных аргументов (математическое выражение аксиомы экстенсивности): для любого Для любой дифференцируемой однородной функции первого порядка выполняется теорема Эйлера:Для энергии теорема Эйлера имеет вид:
Отсюда легко следует уравнение Гиббса — Дюгема:
Это уравнение показывает, что между интенсивными переменными существует одна связь, являющаяся следствием предположения об аддитивности свойств системы. В частности, непосредственным следствием соотношений Гиббса-Дюгема является выражение для термодинамического потенциала Гиббса через химические потенциалы компонент смеси:Приведённые выше формулировки аксиом термодинамики и соотношения для термодинамических потенциалов имеют место для простых моделей (сред) — для идеальных газов. Для более сложных моделей сред — упругих твердых сред, вязкоупругих сред, пластических сред, вязких жидкостей, сред с электромагнитными свойствами и других, законы термодинамики имеют более сложную формулировку, а термодинамические потенциалы формулируются в обобщенном виде с использованием тензоров[7][8][9][10]. В физике сплошных сред (физике континуума) термодинамика рассматривается как её составная часть, вводящая в рассмотрение переменные, характеризующие тепловые (термические) и химические свойства среды, и их связь с другими физическими величинами, а аксиомы термодинамики включаются в общую систему аксиом.
В физике сплошных сред (физике континуума) термодинамика рассматривается как её составная часть, вводящая в рассмотрение переменные, характеризующие тепловые (термические) и химические свойства среды, и их связь с другими физическими величинами, а аксиомы термодинамики включаются в общую систему аксиом.
Источник: http://tytphysiki.blogspot.com/p/blog-page_7.html
Первый закон термодинамики
ПодробностиКатегория: ТермодинамикаОпубликовано 21.12.2014 19:26Просмотров: 10543
Первое начало термодинамики, или первый закон термодинамики, называют законом сохранения энергии для термодинамической системы.
Из истории
Юлиус Роберт фон Майер
Впервые этот закон был сформулирован немецким врачом и естествоиспытателем Юлиусом Робертом фон Майером. В качестве судового врача в 1840 г. он прибыл на остров Ява. Во время лечения больных ему приходилось делать кровопускание.
он прибыл на остров Ява. Во время лечения больных ему приходилось делать кровопускание.
И вот тут Майер обратил внимание на то, что венозная кровь у жителей тропиков светлее, чем у европейцев. Она была почти такой же ярко-красной, как и артериальная кровь.
Читайте также: Мобильные приложения для изучения иностранных языков. как выучить язык быстро и бесплатно
Учёный нашёл объяснение этому факту, предположив, что причина кроется в разнице температур между теплом собственного организма человека и теплом окружающей среды. В тропиках высокая температура, и организму требуется вырабатывать меньше теплоты. Следовательно, он сжигает меньше кислорода.
Совет
Его в крови остаётся больше, и кровь переходит из артерий в вены, оставаясь практически такого же цвета. А в холодном климате организм нуждается в большем количестве тепла. И чем больше кислорода потребляет организм для этой цели, тем заметнее разница в цвете артериальной и венозной крови.
Теплоту организм получает, сжигая кислород, то есть, совершая работу. Работа превращается в теплоту. Обоснование первого закона термодинамики Майер опубликовал в 1842 г. в своей работе «Замечания о силах неживой природы». Более того, учёный нашёл и соотношение между количеством работы и количеством теплоты, полученной в результате этой работы.
Это же соотношение, независимо от Майера, экспериментально установил английский физик Джеймс Прескотт Джоуль. Результаты оказались такими же, как и у Майера. В разных экспериментах одно и то же количество работы превращалось в одно и то же количество тепла, и наоборот.
В изолированной физической системе энергия никуда не исчезает. Она лишь переходит из одной формы в другую. Так утверждает общий закон сохранения энергии. Он справедлив и для изолированной термодинамической системы. Запас энергии в такой системе также остаётся постоянным. Работа превращается в теплоту, а теплота – в работу.
В результате различных процессов, происходящих в термодинамической системе, начальное и конечное состояния системы отличаются.
Так как внутренняя энергия системы U зависит только от её состояния – давления, объёма и температуры (U = U(P, V, T) ), то изменение энергии ∆U определяется начальным и конечным состоянием системы и не зависит от того, каким образом она перешла из одного состояния в другое.
∆U = U2 –U1.
Внутреннюю энергию термодинамической системы можно изменить, сообщив ей некоторое количество теплоты или совершив над ней работу. Математически связь между количеством теплоты, полученной термодинамической системой, изменением её внутренней энергии и работой, совершённой за счёт этой теплоты математически выглядит так:
∆U = Q – A, или Q = ∆U + A,
где ∆U – изменение внутренней энергии системы при сообщении ей теплоты;
Q – количество теплоты, полученное системой при теплопередаче;
A – работа, совершённая системой против внешних сил.
Это и есть математическое выражение первого закона термодинамики.
Теплота, которую получила термодинамическая система, расходуется на изменение её внутренней энергии и работу, совершённую над внешними телами.
При переходе из начального состояния в конечное термодинамическая система может получать теплоту различными способами. В технической термодинамике положительной считают теплоту, получаемую системой, а отрицательной – теплоту, которую система отдаёт. Общее количество теплоты Q – это алгебраическая сумма всех количеств теплоты, получаемых или отдаваемых системой.
В отличие от теплоты работа, совершённая системой, не является её характеристикой. Она зависит от пути перехода системы из начального состояния в конечное. Поэтому работа характеризует сам процесс перехода.
Частные случаи первого закона термодинамики
Первый закон термодинамики удобно рассматривать на примере изопроцессов для газа.
При изохорном процессе работа не совершается, так как объём газа остаётся постоянным (V = const). Поэтому Q = ∆U.
Поэтому Q = ∆U.
Изотермический процесс в системе происходит при постоянной температуре (T = const). Следовательно, вся теплота, полученная системой, расходуется на совершение работы. Так как ∆U=0, то Q = A.
Изобарный процесс происходит при постоянном давлении (P = const).Теплота, сообщаемая системе, идёт и на изменение внутренней энергии, и на совершение работы.
Q = ∆U + A
Обратите внимание
Работа, которую газ совершает при расширении или сжатии, равна A = P·∆V.
Отсюда Q = ∆U + P·∆V.
При адиабатическом процессе нет обмена теплотой с внешней средой. Q = 0, А = -∆U. Это означает, что работа совершается за счёт уменьшения внутренней энергии системы.
Термодинамический цикл
Если термодинамическая система, независимо от того, какие превращения (нагревания, охлаждения, сжатия, расширения, химические превращения и др.) в ней не происходили бы, в конечном счёте возвращается в своё первоначальное состояние, то термодинамический процесс, в результате которого это происходит, называется термодинамическим циклом.
Пример термодинамического цикла – круговорот воды в природе.
Под воздействием солнечных лучей быстро нагревается вода в лужах, образовавшихся после дождя. Растёт её температура, и вода начинает испаряться, при этом увеличиваясь в объёме. Пар поднимается вверх.
Там он остывает, и его объём снова уменьшается. Конденсируясь, пар превращается в облако. Капли дождя падают на землю и снова образуют лужи. Цикл завершается. После этого процесс повторяется снова.
Цикл завершается. После этого процесс повторяется снова.
В результате термодинамического цикла в системе всё остаётся по-прежнему, хотя в процессе цикла совершалась работа и выделялась или поглощалась теплота.
Все параметры системы, несмотря на процессы, происходящие в ней, возвращаются в исходное состояние. В этом случае изменения внутренней энергии не происходит.
Следовательно, работа, совершённая системой по замкнутому циклу, равна количеству теплоты.
A = Q, или Q – A = 0,
В замкнутом цикле любая произведённая работа преобразуется в теплоту.
На основе замкнутых циклов построена работа тепловых машин.
Тепловые двигатели
Принцип преобразования внутренней энергии системы в механическую лежит в основе тепловых двигателей. Такой двигатель представляет собой тепловую машину, превращающую тепло в механическую энергию.
Основные части таких двигателей – нагреватель, рабочее тело и охладитель. Очень часто рабочим телом в тепловом двигателе служит газ. Получая теплоту от нагревателя, он расширяется и совершает работу.
Чтобы работа такого двигателя не прекращалась, параметры рабочего тела, в нашем случае газа, после совершения работы возвращаются в первоначальное состояние (газ охлаждается в холодильнике).
Далее процесс повторяется сначала. Реальные тепловые машины (двигатели внутреннего сгорания, паровые машины и др.
) работают циклически, повторяя теплопередачу и превращение теплоты в работу. Рабочим телом могут быть пары бензина, водяные пары, воздух, уголь, нефть и др.
Важно
Вещество с более высокой температурой находится в резервуаре, который называется нагревателем, а с более низкой – в резервуаре, называемом холодильником.
Для любой тепловой машины очень важна такая величина, как коэффициент полезного действия (КПД). Это отношение количества работы, совершённой двигателем, к количеству теплоты, полученной от нагревателя.
Это отношение количества работы, совершённой двигателем, к количеству теплоты, полученной от нагревателя.
А = QH– QХ,
где QH– количество теплоты, отданное нагревателем рабочему телу;
QХ – количество теплоты, которое рабочее тело отдаёт охладителю.
Так как часть теплоты теряется при передаче, то КПД двигателя всегда меньше единицы.
Наибольший КПД возможен в двигателе Карно.
Вечный двигатель первого рода
Создание двигателя, который мог бы совершать рабóту, превышающую затраченную на её производство энергию, с древних времён было мечтой многих изобретателей.
Вечным двигателем первого рода называют устройство, которое может бесконечно совершать работу, не затрачивая на это энергии. Но согласно первому закону термодинамики термодинамическая система может совершать работу за счёт теплоты, получаемой извне и убыли своей внутренней энергии.
A = Q– ∆U
Если к системе не подводить теплоту, то работу можно совершить только за счёт внутренней энергии. Но в таком случае через некоторое время запас этой энергии иссякнет. Это означает, что нельзя создать такую машину, которая смогла бы работать без подведения энергии извне. Таким образом, вечный двигатель невозможен. Эта также одна из формулировок первого закона термодинамики.
Но в таком случае через некоторое время запас этой энергии иссякнет. Это означает, что нельзя создать такую машину, которая смогла бы работать без подведения энергии извне. Таким образом, вечный двигатель невозможен. Эта также одна из формулировок первого закона термодинамики.
Источник: http://ency.info/materiya-i-dvigenie/termoinamika/372-pervyj-zakon-termodinamiki
Первый закон термодинамики
На рис. 3.9.1 условно изображены энергетические потоки между выделенной термодинамической системой и окружающими телами. Величина Q > 0, если тепловой поток направлен в сторону термодинамической системы. Величина A > 0, если система совершает положительную работу над окружающими телами.
| Рисунок 3.9.1.Обмен энергией между термодинамической системой и окружающими телами в результате теплообмена и совершаемой работы |
Если система обменивается теплом с окружающими телами и совершает работу (положительную или отрицательную), то изменяется состояние системы, т. е. изменяются ее макроскопические параметры (температура, давление, объем).
е. изменяются ее макроскопические параметры (температура, давление, объем).
Так как внутренняя энергия U однозначно определяется макроскопическими параметрами, характеризующими состояние системы, то отсюда следует, что процессы теплообмена и совершения работы сопровождаются изменением ΔU внутренней энергии системы.
Первый закон термодинамики является обобщением закона сохранения и превращения энергии для термодинамической системы. Он формулируется следующим образом:
Изменение ΔU внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q, переданной системе, и работой A, совершенной системой над внешними телами.
Соотношение, выражающее первый закон термодинамики, часто записывают в другой форме:
Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами.
Первый закон термодинамики является обобщением опытных фактов. Согласно этому закону, энергия не может быть создана или уничтожена; она передается от одной системы к другой и превращается из одной формы в другую.
Согласно этому закону, энергия не может быть создана или уничтожена; она передается от одной системы к другой и превращается из одной формы в другую.
Важным следствием первого закона термодинамики является утверждение о невозможности создания машины, способной совершать полезную работу без потребления энергии извне и без каких-либо изменений внутри самой машины.
Такая гипотетическая машина получила название вечного двигателя (perpetuum mobile) первого рода. Многочисленные попытки создать такую машину неизменно заканчивались провалом.
Любая машина может совершать положительную работу A над внешними телами только за счет получения некоторого количества теплоты Q от окружающих тел или уменьшения ΔU своей внутренней энергии.
Применим первый закон термодинамики к изопроцессам в газах.
1. В изохорном процессе (V = const) газ работы не совершает, A = 0. Следовательно,
| Q = ΔU = U (T2) – U (T1). |
Здесь U (T1) и U (T2) – внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит только от температуры (закон Джоуля).
Читайте также: Что такое электричество: что такое переменный ток, как используется в природе, откуда берется
При изохорном нагревании тепло поглощается газом (Q > 0), и его внутренняя энергия увеличивается.
При охлаждении тепло отдается внешним телам (Q 0 – тепло поглощается газом, и газ совершает положительную работу. При изобарном сжатии Q
Источник: http://www.its-physics.org/pervyy-zakon-termodinamiki
Первый закон термодинамики и его применение в физике
Содержание:
- Определение первого закона термодинамики
- Формула первого закона термодинамики
- Процессы первого закона термодинамики
- Первый закон термодинамики для изохорного процесса
- Первый закон термодинамики для изобарного процесса
- Применение первого закона термодинамики
- Первый закон термодинамики, видео
- Энергия ни откуда не появляется и ни куда не пропадает, она лишь переходит из одного вида в другой (закон сохранения энергии).

- Количество теплоты, полученной системой, идет на совершение ее работы против внешних сил и изменение внутренней энергии.
- Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданной системе, и не зависит от способа, которым осуществляется этот переход.
- Изменение внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты, переданной системе, и работой, совершенной системой над внешними силами.
- Внутренняя энергия тела это сумма кинетических энергий беспорядочного движения всех молекул тела и потенциальных энергий взаимодействия всех молекул тела и потенциальных энергий взаимодействия всех молекул друг с другом:
- Внутренняя энергия одноатомного идеального газа прямо пропорциональна его абсолютной температуре:
- Работа внешней силы изменяющей объем газа на
- Работа, совершаемая газом при изобарном расширении:
- Теплообмен (теплопередача) это процесс передачи энергии от одного тела к другому без совершения работы
- Количество теплоты Q это количественная мера изменения внутренней энергии при теплообмене.
 Если система (тело) получает энергию, то ΔQ системы > 0, если отдает энергию, то ΔQ системы < 0
Если система (тело) получает энергию, то ΔQ системы > 0, если отдает энергию, то ΔQ системы < 0 - Адиабатный (адиабатический процесс) это процесс, протекающий в теплоизолированной системе (которая не поличает тепло извне и не отдает его): ΔQ=0
- Теплоемкость это отношение количества теплоты, которое необходимо для изменения температуры тела на ΔT к разности температур:
- Удельная теплоемкость это количество теплоты, которое получает или отдает 1 кг вещества при изменении его температуры на 1°К:
- Испарение (парообразование) это процесс, при котором молекулы жидкости высвобождаются из жидкости и становятся молекулами газа.

- Кипение это испарение, происходящее как с поверхности жидкости, так и внутри самой жидкости.
- Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил A и количества теплоты, переданного системе Q:
- Количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами:
- Изотермический
- T=const
- Q=A’
- Изобарный
- p=const
- Q=ΔU=A’
- В адиабатной системе сумма количеств теплоты, полученных и отданных телами равен нулю:
- Второй закон термодинамики. Формулировка Р. Клаузиуса: Невозможен процесс, при котором теплота переходила бы самостоятельно от тел более холодных к телам более нагретым.

- Тепловой двигатель – устройство, превращающее внутреннюю энергию топлива в механическую.
- Коэффициент полезного действия теплового двигателя (КПД):
- Машина Карно: идеальная тепловая машина с идеальным газом в качестве рабочего тела.
- КПД машины Карно:
- Теорема Карно: КПД всякой тепловой машины не может превосходить КПД идеальной машины с теми же температурами нагревателя и холодильника.
Простая формулировка первого закона термодинамики может звучать примерно так: изменение внутренней энергии той или иной системы возможно исключительно при внешнем воздействии. То есть другими словами, чтобы в системе произошли какие-то изменения необходимо приложить определенные усилия извне.
То есть другими словами, чтобы в системе произошли какие-то изменения необходимо приложить определенные усилия извне.
В народной мудрости своеобразным выражением первого закона термодинамики могут служить пословицы – «под лежачий камень вода не течет», «без труда не вытащишь рыбку из пруда» и прочая.
То есть на примере пословицы про рыбку и труд, можно представить, что рыбка и есть наша условно закрытая система, в ней не произойдет никаких изменений (рыбка сама себя не вытащит из пруда) без нашего внешнего воздействия и участия (труда).
Совет
Интересный факт: именно первый закон термодинамики устанавливает, почему потерпели неудачу все многочисленные попытки ученых, исследователей, изобретателей изобрести «вечный двигатель», ведь его существование является абсолютно невозможным согласно этому самому закону, почему, смотрите абзац выше.
В начале нашей статьи было максимального простое определение первого закона термодинамики, в действительности в академической науке существует целых четыре формулировки сути данного закона:
Формулу первого закона термодинамики можно записать таким образом:
Q = ΔU + A
Количество теплоты Q, передаваемое системе равно суме изменения ее внутренней энергии ΔU и работы A.
Также первый закон термодинамики имеет свои нюансы в зависимости от проходящих термодинамических процессов, которые могут быть изохронными и изобарными, и ниже мы детально опишем о каждом из них.
Изохорным процессом в термодинамике называют процесс, происходящий при постоянном объеме. То есть, если будь-то в газе или жидкости нагреть вещество в сосуде, произойдет изохорный процесс, так как объем вещества останется неизменным. Это условие имеет влияние и на первый закон термодинамики, проходящий при изохорном процессе.
В изохорном процессе объем V является константой, следовательно, газ работы не совершает A = 0
Из этого выходит следующая формула:
Q = ΔU = U (T2) – U (T1).
Здесь U (T1) и U (T2) – внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит только от температуры (закон Джоуля). При изохорном нагревании тепло поглощается газом (Q > 0), и его внутренняя энергия увеличивается. При охлаждении тепло отдается внешним телам (Q < 0).
Аналогично изобарным процессом называется термодинамический процесс, происходящий в системе при постоянном давлении и массе газа. Следовательно, в изобарном процессе (p = const) работа, совершаемая газом, выражается следующим уравнением первого закона термодинамики:
Следовательно, в изобарном процессе (p = const) работа, совершаемая газом, выражается следующим уравнением первого закона термодинамики:
A = p (V2 – V1) = p ΔV.
Изобарный первый закон термодинамики дает:
Q = U (T2) – U (T1) + p (V2 – V1) = ΔU + p ΔV. При изобарном расширении Q > 0 – тепло поглощается газом, и газ совершает положительную работу. При изобарном сжатии Q < 0 – тепло отдается внешним телам. В этом случае A < 0. Температура газа при изобарном сжатии уменьшается, T2 < T1; внутренняя энергия убывает, ΔU < 0.
Первый закон термодинамике имеет практическое применение к различным процессам в физике, например, позволяет вычислить идеальные параметры газа при разнообразных тепловых и механических процессах.
Помимо сугубо практичного применение можно этому закону найти применение и философское ведь что ни говорите, но первый закон термодинамики является выражением одного из самых общих законов природы – закона сохранения энергии.
Еще Еклезиаст писал, что ничто ни откуда не появляется и никуда не уходит, все пребывает вечно, постоянно трансформируясь, в этом и кроется вся суть первого закона термодинамики.
И в завершение нашей статьи вашему вниманию образовательное видео о первом законе термодинамике и внутренней энергии.
Эта статья доступна на английском — First Law of Thermodynamics.
Источник: http://www.poznavayka.org/fizika/pervyiy-zakon-termodinamiki-i-ego-primenenie-v-fizike/
Термодинамика. Внутренняя энергия. Работа. Количество теплоты. Тепловые явления. Первый закон термодинамики. Применение первого закона термодинамики к различным процессам. Уравнение теплового балланса. Второй закон термодинамики. Тепловые двигатели
| Раздел недели: | ||||||||||||||||||||||||||
главная страница / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа. / / Термодинамика. Внутренняя энергия. Работа. Количество теплоты. Тепловые явления. Первый закон термодинамики. Применение первого закона термодинамики к различным процессам. Уравнение теплового балланса. Второй закон термодинамики. Тепловые двигатели Шпаргалки. Школа. / / Термодинамика. Внутренняя энергия. Работа. Количество теплоты. Тепловые явления. Первый закон термодинамики. Применение первого закона термодинамики к различным процессам. Уравнение теплового балланса. Второй закон термодинамики. Тепловые двигатели
Поиск в инженерном справочнике DPVA. | ||||||||||||||||||||||||||
| Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | ||||||||||||||||||||||||||
| Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. |
Источник: https://www.dpva.ru/Guide/GuidePhysics/PhysicsForKids/Thermodinamics/
Первый закон термодинамики
Здравствуйте! Первый закон термодинамики раскрывает связь между тепловой энергией и механической. Он устанавливает, что теплота может превращаться в работу, а работа в теплоту.
Первый закон термодинамики представляет собой балансовое уравнение изменения энергии в термодинамической системе:
Читайте также: 10 фактов о солнечной системе: масса планет, водяные вулканы, алмазные дожди и др.
u1-u2 = q + l + a, (1)
где u1- u2 — изменение удельной внутренней энергии тела; q — удельная теплота, которой обменивается тело с окружающей средой; l — удельная работа, связанная с изменением объема; а — работа немеханического характера.
Примером работы немеханического характера является работа, связанная с переносом электрического заряда, если система является диэлектриком, с мерой химического сродства при химическом взаимодействии веществ.
Если в системе не совершается работа немеханического характера, то уравнение первого закона термодинамики принимает вид
u1-u2 = q + l. (2)
(2)
Таким образом, первый закон термодинамики является частным случаем закона сохранения и превращения энергии.
Если рабочее тело получает от окружающей среды q теплоты и совершает при этом l работы, то разность между подведенной теплотой и работой выразит изменение удельной внутренней энергии тела:
u2 — u1 = q — l. (3)
или
q = u2 – u1 + l. (4)
Обратите внимание
Это уравнение является математическим выражением первого закона термодинамики: вся подведенная к рабочему телу теплота идет на изменение его внутренней энергии и на совершение работы.
Уравнение (4) можно также представить в виде:
q = Cv*(T2-T1) + p*(u2-u1).
Теплоту, подведенную к телу, принято считать положительной; теплоту, отведенную от тела, — отрицательной. Положительное изменение внутренней энергии тела характеризуется ее увеличением, отрицательное — уменьшением.
Положительное изменение внутренней энергии тела характеризуется ее увеличением, отрицательное — уменьшением.
Количественным критерием различных форм движения материи (тепловой, механической, химической и так далее) служит энергия.
Таким образом, первый закон термодинамики является частным случаем закона сохранения энергии, если брать термодинамические процессы.
В основе закона сохранения и превращения энергии постулат о том, что количество энергии сохраняется при различных превращениях одной формы движения в другую.
Общий принцип сохранения в природе был сформулирован значительно раньше, а сохраняемость энергии при переходе из одной формы в другую была сформулирована после накопления большого экспериментального объема информации о взаимопревращении энергии. Первый закон термодинамики определяет невозможность создания вечного двигателя первого рода, то есть двигателя, работающего и не заимствующего при этом энергию извне.
Если система может обмениваться с окружающей средой теплотой и работой, то подводимая к системе теплота Q затрачивается на изменение ее внутренней энергии ∆U и на совершение работы L против внешних сил:
Q = ∆U + L .
Исп. литература: 1) Теплотехника и теплотехническое оборудование предприятий промышленности строительных материалов и изделий, Н.М. Никифорова, под ред. Н.В. Тресковой, Москва, «Высшая школа», 1981. 2) Теплотехника, Бондарев В.А., Процкий А.Е., Гринкевич Р.Н. Минск, изд. 2-е,”Вышейшая школа”, 1976.
Источник: http://teplosniks.ru/texnicheskaya-termodinamika/pervyj-zakon-termodinamiki.html
Законы термодинамики и их описание :
Законы термодинамики называют также ее началами. На самом деле начало термодинамики представляет собой не что иное, как совокупность тех или иных постулатов, которые лежат в основе соответствующего раздела молекулярной физики.
Данные положения устанавливали в течение научных исследований. В то же время они были доказаны экспериментальным путем.
Почему же законы термодинамики принимают за постулаты? Все дело в том, что таким образом термодинамику можно строить аксиоматическим путем.
Основные законы термодинамики
Немного о структуризации. Законы термодинамики разделяются на четыре группы, каждая из которых имеет определенный смысл. Итак, что могут поведать нам начала термодинамики?
Первое и второе
Первое начало расскажет о том, как применяется закон сохранения энергии по отношению к той или иной термодинамической системе.
Второе начало выдвигает некоторые ограничения, которые применяются к направлениям термодинамических процессов. Более конкретно, они запрещают самопроизвольную передачу тепла, совершаемую от менее нагретого к более нагретому телу.
Есть у второго закона термодинамики и альтернативное название: закон возрастания энтропии.
Третье и четвертое
Третий закон описывает поведение энтропии вблизи абсолютного температурного нуля. Есть еще одно начало, последнее. Оно носит название “нулевой закон термодинамики”. Смысл его заключается в том, что любая замкнутая система придет к состоянию термодинамического равновесия и из него выйти уже самостоятельно не сможет. При этом ее начальное состояние может быть любым.
Зачем нужны начала термодинамики?
Законы термодинамики были изучены для того, чтобы описывать макроскопические параметры тех или иных систем. При этом конкретные предложения, имеющие связь с микроскопическим устройством, не выдвигаются.
Этот вопрос изучается отдельно, но уже другим ответвлением науки – статистической физикой. Законы термодинамики независимы друг от друга.
Что это может означать? Это нужно понимать так, что ни одно начало термодинамики из другого вывести невозможно.
Первое начало термодинамики
Как известно, термодинамическая система характеризуется несколькими параметрами, в числе которых есть и внутренняя энергия (обозначается буквой U). Последняя формируется из кинетической энергии, которую имеют все частицы.
Это может быть энергия поступательного, а также колебательного и вращательного движения. На этом моменте вспомним о том, что энергия может быть не только кинетической, но и потенциальной. Так вот, в случае идеальных газов потенциальной энергией пренебрегают.
Именно поэтому внутренняя энергия U будет складываться исключительно из кинетической энергии движения молекул и зависеть от температуры.
Важно
Эта величина – внутренняя энергия – называется иными словами функцией состояния, поскольку она определяется состоянием термодинамической системы. В нашем случае она определяется температурой газа. Следует отметить, что внутренняя энергия не зависит от того, каким был переход в состояние.
В нашем случае она определяется температурой газа. Следует отметить, что внутренняя энергия не зависит от того, каким был переход в состояние.
Допустим, что термодинамическая система совершает круговой процесс (цикл, как его называют в молекулярной физике). Иными словами, система, выйдя из начального состояния, подвергается определенным процессам, но в результате возвращается в первичное состояние.
Тогда нетрудно догадаться, что изменение внутренней энергии будет равно 0.
Как изменяется внутренняя энергия?
Изменить внутреннюю энергию идеального газа можно двумя способами. Первый вариант – совершить работу. Второй – сообщить системе то или иное количество теплоты. Логично, что второй способ подразумевает не только сообщение теплоты, но и ее отнятие.
Формулировка первого начала термодинамики
Их (формулировок) может быть несколько, так как все любят говорить по-разному. Но на самом деле суть остается той же.
Но на самом деле суть остается той же.
Она сводится к тому, что количество теплоты, которое было подведено к термодинамической системе, расходуется на совершение идеальным газом механической работы и изменение внутренней энергии.
Если говорить о формуле или математической записи первого начала термодинамики, то она выглядит следующим образом: dQ = dU + dA.
– Все величины, которые входят в состав формулы, могут иметь разные знаки. Ничто не запрещает им быть отрицательными. Допустим, что к системе подводится количество теплоты Q. Тогда газ будет нагреваться.
Возрастает температура, а значит, увеличивается и внутренняя энергия газа. То есть и Q, и U будут иметь положительные значения. Но если внутренняя энергия газа увеличивается, он начинает вести себя активнее, расширяться.
Следовательно, работа также будет положительной. Можно сказать, что работу совершает сама система, газ.
– В случае если у системы забирают определенное количество теплоты, внутренняя энергия уменьшается, а газ сжимается. В таком случае можно говорить уже о том, что работу совершают над системой, а не она сама.
Предположим опять, что некоторая термодинамическая система совершает цикл. В таком случае (как уже было сказано ранее) изменение внутренней энергии будет равно 0.
Значит, работа, совершаемая газом или над ним, будет численно равна подведенной или отведенной к системе теплоте.
– Математическую запись этого следствия называют еще одной формулировкой первого начала термодинамики. Примерно она звучит следующим образом: “В природе невозможно существование двигателя первого рода, то есть, двигателя, который совершал бы работу, превосходящую полученную извне теплоту”.
Второе начало термодинамики
Нетрудно догадаться, что термодинамическое равновесие характерно для системы, в которой макроскопические величины остаются неизменными во времени. Это, конечно же, давление, объем и температура газа.
Это, конечно же, давление, объем и температура газа.
Их неизменность может быть построена на нескольких условиях: на отсутствии теплопроводности, химических реакций, диффузии и других процессов. Если под действием внешних факторов система была выведена из термодинамического равновесия, она к нему со временем вернется.
Но если эти факторы будут отсутствовать. Причем произойдет это самопроизвольно.
Мы пойдем немного другим путем, отличным от того, что рекомендуют многие учебники. Для начала ознакомимся со вторым началом термодинамики, а уже потом разберемся, что за величины в него входят, и что они обозначают.
Совет
Итак, в замкнутой системе при наличии любых протекающих в ней процессов энтропия не убывает. Записывается второе начало термодинамики следующим образом: dS >(=) 0.
Здесь знак > будет связан с необратимым процессом, а знак = – с обратимым.
Что же называется в термодинамике обратимым процессом? А это такой процесс, при котором система возвращается (спустя череду каких-то процессов) к своему первоначальному состоянию. Причем в этом случае ни в системе, ни в окружающей среде никаких изменений не остается.
Иными словами, обратимый процесс – это такой процесс, для которого возможно возвращение в начальное состояние через промежуточные состояния, идентичные прямому процессу. В молекулярной физике таких процессов очень мало. Например, переход количества теплоты от более нагретого тела к менее нагретому будет необратимым.
Аналогично и в случае диффузии двух веществ, а также распространения газа на весь объем.
Энтропия
Энтропия, имеющая место во втором законе термодинамики, равна изменению количества теплоты, деленному на температуру. Формула: dS = dQ/T. Она имеет определенные свойства.
Источник: https://www. syl.ru/article/206000/mod_zakonyi-termodinamiki-i-ih-opisanie
syl.ru/article/206000/mod_zakonyi-termodinamiki-i-ih-opisanie
Работа в термодинамике | ЕГЭ по физике
Работа в термодинамике
В термодинамике, в отличие от механики, рассматривается не движение тела как целого, а лишь относительное изменение частей термодинамической системы, в результате которого меняется ее объем.
Рассмотрим работу газа при изобарическом расширении.
Вычислим работу, совершаемую газом при его действии на поршень с силой ${F’}↖{→}$, равной по величине и противоположной по направлению силе ${F’}↖{→}$, действующей на газ со стороны поршня: ${F’}↖{→}=-{F’}↖{→}$ (согласно третьему закону Ньютона), $F’=pS$, где $p$ — давление газа, а $S$ — площадь поверхности поршня. Если перемещение поршня $∆h$ в результате расширения мало, то давление газа можно считать постоянным и работа газа равна:
$A’=F’∆h=pS∆h=p∆V$
Если газ расширяется, он совершает положительную работу, та к как перемещение поршня совпадает по направлению с силой ${F’}↖{→}$.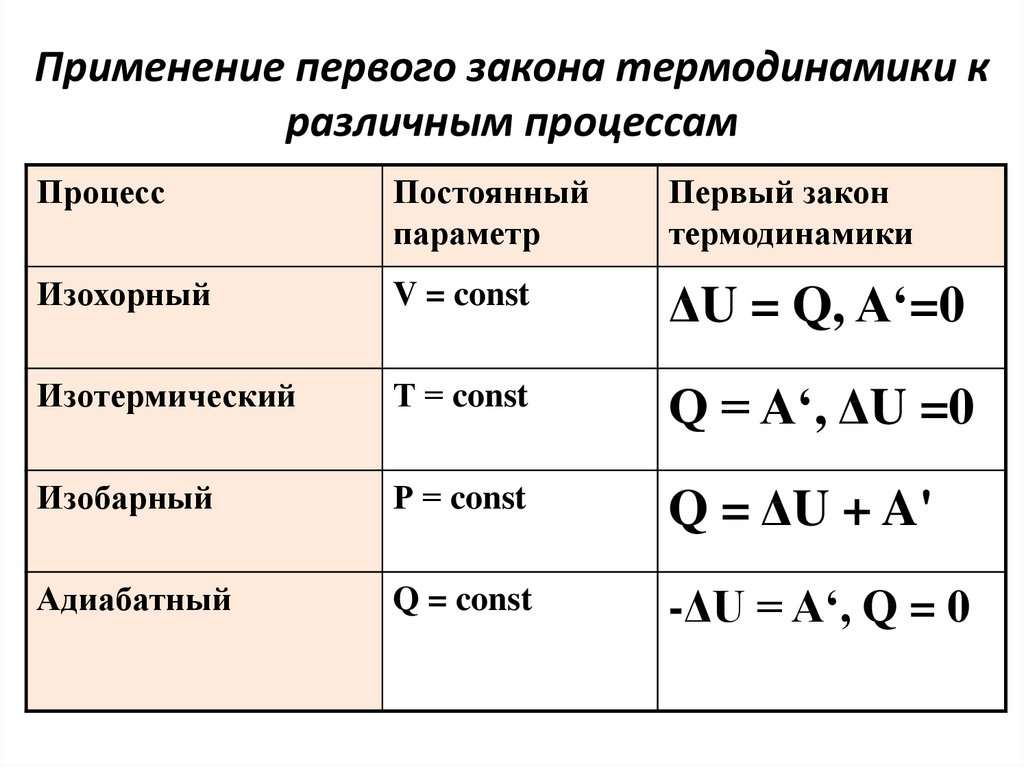 Если газ сжимается, то работа газа отрицательна, поскольку перемещение поршня противоположно силе ${F’}↖{→}$. В формуле $A’=F’∆h=pS∆h=p∆V$ появится знак «минус»: $∆V
Если газ сжимается, то работа газа отрицательна, поскольку перемещение поршня противоположно силе ${F’}↖{→}$. В формуле $A’=F’∆h=pS∆h=p∆V$ появится знак «минус»: $∆V
Работа внешних сил $А$, наоборот, положительна при сжатии газа и отрицательна при расширении:
$A=-A’=-p∆V$
Совершая над газом положительную работу, внешние тела передают ему часть своей энергии. При расширении газа внешние тела отбирают у газа часть его энергии — работа внешних сил отрицательна.
На графике зависимости давления от объема $р(V)$ работа определяется как площадь, ограниченная кривой $р(V)$, осью $V$ и отрезками $ab$ и $cd$, равными давлениям $р_1$ в начальном ($V_1$) и $р_2$ в конечном ($V_2$) состояниях, как для изобарного, так и для изотермического процессов.
Первый закон термодинамики
Первое начало (первый закон) термодинамики — это закон сохранения и превращения энергии для термодинамической системы.
Согласно первому началу термодинамики, работа может совершаться только за счет теплоты или какой-либо другой формы энергии. Следовательно, работу и количество теплоты измеряют в одних единицах — джоулях (как и энергию).
Следовательно, работу и количество теплоты измеряют в одних единицах — джоулях (как и энергию).
Первое начало термодинамики было сформулировано немецким ученым Ю. Л. Майером в 1842 г. и подтверждено экспериментально английским ученым Дж. Джоулем в 1843 г.
Первый закон термодинамики формулируется так:
Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:
$∆U=A+Q$
где $∆U$ — изменение внутренней энергии, $А$ — работа внешних сил, $Q$ — количество теплоты, переданной системе.
Из $∆U=A+Q$ следует закон сохранения внутренней энергии. Если систему изолировать от внешних воздействий, $A=0$ и $Q=0$,а следовательно, $∆U=0$.
При любых процессах, происходящих в изолированной системе, ее внутренняя энергия остается постоянной.
Если работу совершает система, а не внешние силы, то уравнение ($∆U=A+Q$) записывается в виде:
$Q=∆U+A’$
где $А’$ — работа, совершаемая системой ($А’=-А$).
Количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами.
Первое начало термодинамики может быть сформулировано как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника, т. е. только за счет внутренней энергии.
Действительно, если к телу не поступает теплота ($Q=0$), то работа $А’$, согласно уравнению $Q=∆U+A’$, совершается только за счет убыли внутренней энергии $A’=-∆U$. После того, как запас энергии окажется исчерпанным, двигатель перестает работать.
Следует помнить, что как работа, так и количество теплоты являются характеристиками процесса изменения внутренней энергии, поэтому нельзя говорить, что в системе содержится определенное количество теплоты или работы. Система в любом состоянии обладает лишь определенной внутренней энергией.
Применение первого закона термодинамики к различным процессам
Рассмотрим применение первого закона термодинамики к различным термодинамическим процессам.
Изохорный процесс. Зависимость $р(Т)$ на термодинамической диаграмме изображается изохорой.
Изохорный (изохорический) процесс — термодинмический процесс, происходящий в системе при постоянном объеме.
Изохорный процесс можно осуществить в газах и жидкостях, заключенных в сосуд с постоянным объемом.
При изохорном процессе объем газа не меняется ($∆V=0$), и, согласно первому началу термодинамики $Q=∆U+A’$,
$∆U=Q$
т. е. изменение внутренней энергии равно количеству переданного тепла, т. к. работа ($A=p∆V=0$) газом не совершается.
Если газ нагревается, то $Q > 0$ и $∆U > 0$, его внутренняя энергия увеличивается. При охлаждении газа $Q
Изотермический процесс графически изображается изотермой.
Изотермический процесс — это термодинамический процесс, происходящий в системе при постоянной температуре.
Поскольку при изотермическом процессе внутренняя энергия газа не меняется ($T=const$), то все переданное газу количество теплоты идет на совершение работы:
$Q=A’$
При получении газом теплоты ($Q > 0$) он совершает положительную работу ($А’ > 0$). Если газ отдает тепло окружающей среде, $Q
Если газ отдает тепло окружающей среде, $Q
Изобарный процесс на термодинамической диаграмме изображается изобарой.
Изобарный (изобарический) процесс — термодинамический процесс, происходящий в системе с постоянным давлением $p$.
Примером изобарного процесса является расширение газа в цилиндре со свободно ходящим нагруженным поршнем.
При изобарном процессе согласно формуле $Q=∆U+A’$ передаваемое газу количество теплоты идет на изменение его внутренней энергии $∆U$ и на совершение им работы $A’$ при постоянном давлении:
$Q=∆U+A’$
Работа идеального газа определяется по графику зависимости $p(V)$ для изобарного процесса ($A’=p∆V$).
Для идеального газа при изобарном процессе объем пропорционален температуре, в реальных газах часть теплоты расходуется на изменение средней энергии взаимодействия частиц.
Адиабатический процесс
Адиабатический процесс (адиабатный процесс) — это термодинамический процесс, происходящий в системе без теплообмена с окружающей средой ($Q=0$).
Адиабатическая изоляция системы приближенно достигается в сосудах Дьюара, в так называемых адиабатных оболочках. На адиабатически изолированную систему не оказывает влияния изменение температуры окружающих тел. Ее внутренняя энергия и может меняться только за счет работы, совершаемой внешними телами над системой, или самой системой.
Согласно первому началу термодинамики ($∆U=A+Q$), в адиабатной системе
$∆U=A$
где $А$ — работа внешних сил.
При адиабатном расширении газа $А
Следовательно,
$∆U={i}/{2}·{m}/{M}R∆T
что означает уменьшение температуры при адиабатном расширении. Оно приводит к тому, что давление газа уменьшается более резко, чем при изотермическом процессе.
На рисунке адиабата $1—2$, проходящая между двумя изотермами, наглядно иллюстрирует сказанное. Площадь под адиабатой численно равна работе, совершаемой газом при его адиабатическом расширении от объема $V_1$ до $V_2$.
Адиабатное сжатие приводит к повышению температуры газа, т. к. в результате упругих соударений молекул газа с поршнем их средняя кинетическая энергия возрастает, в отличие от расширения, когда она уменьшается (в первом случае скорости молекул газа увеличиваются, во втором — уменьшаются).
к. в результате упругих соударений молекул газа с поршнем их средняя кинетическая энергия возрастает, в отличие от расширения, когда она уменьшается (в первом случае скорости молекул газа увеличиваются, во втором — уменьшаются).
Резкое нагревание воздуха при адиабатическом сжатии используется в двигателях Дизеля.
Принцип действия тепловых двигателей
Тепловой двигатель — это устройство, преобразующее внутреннюю энергию топлива в механическую энергию.
Согласно второму началу термодинамики, тепловой двигатель может непрерывно совершать периодически повторяющуюся механическую работу за счет охлаждения окружающих тел, если он не только получает теплоту от более горячего тела (нагревателя), но при этом отдает теплоту менее нагретому телу (холодильнику). Следовательно, на совершение работы идет не все количество теплоты, полученное от нагревателя, а только часть ее.
Таким образом, основными элементами любого теплового двигателя являются:
- рабочее тело (газ или пар), совершающее работу;
- нагреватель, сообщающий энергию рабочему телу;
- холодильник, поглощающий часть энергии от рабочего тела.

Коэффициент полезного действия теплового двигателя
Согласно закону сохранения энергии, работа, совершаемая двигателем, равна:
$A’=|Q_1|-|Q_2|$
где $Q_1$ — количество теплоты, полученное от нагревателя, $Q_2$ — количество теплоты, отданное холодильнику.
Коэффициентом полезного действия (КПД) теплового двигателя называется отношение работы $А’$, совершаемой двигателем, к количеству теплоты, полученному от нагревателя:
$η={A’}/{|Q_1|}={|Q_1|-|Q_2|}/{|Q_1|}=1-{|Q_2|}/{|Q_1|}$
Так как у всех двигателей некоторое количество теплоты передается холодильнику, то $η
КПД теплового двигателя пропорционален разности температур нагревателя и холодильника. При $T_1 – T_2=0$ двигатель не может работать.
Цикл Карно
Цикл Карно — это круговой обратимый процесс, состоящий из двух изотермических и двух адиабатических процессов.
Впервые этот процесс был рассмотрен французским инженером и ученым Н. Л. С. Карно в 1824 г. в книге «Размышления о движущей силе огня и о машинах, способных развивать эту силу».
С. Карно в 1824 г. в книге «Размышления о движущей силе огня и о машинах, способных развивать эту силу».
Целью исследований Карно было выяснение причин несовершенства тепловых машин того времени (они имели КПД $< 5%$)и поиски путей их усовершенствования.
Выбор двух изотермических и двух адиабатических процессов был обусловлен тем, что работа газа при изотермическом расширении совершается за счет внутренней энергии нагревателя, а при адиабатном процессе — за счет внутренней энергии расширяющегося газа. В этом цикле исключен контакт тел с разной температурой, следовательно, исключена теплопередача без совершения работы.
Цикл Карно — самый эффективный из всех возможных. Его КПД максимален.
На рисунке изображены термодинамические процессы цикла. В процессе изотермического расширения ($1-2$) при температуре $Т_1$ работа совершается за счет изменения внутренней энергии нагревателя, т. е. за счет подведения к газу количества теплоты $Q_1$:
$A_{12}=Q_1.$ Охлаждение газа перед сжатием ($3-4$) происходит при адиабатном расширении ($2-3$). Изменение внутренней энергии $∆U_{23}$ при адиабатном процессе ($Q=0$) полностью преобразуется в механическую работу:
Изменение внутренней энергии $∆U_{23}$ при адиабатном процессе ($Q=0$) полностью преобразуется в механическую работу:
$A_{23}=-∆U_{23}$
Температура газа в результате адиабатического расширения ($2-3$) понижается до температуры холодильника $Т_2
$A_{34}=Q_2,$
Цикл завершается процессом адиабатического сжатия ($4—1$), при котором газ нагревается до температуры $Т_1$.
Максимальное значение КПД тепловых двигателей, работающих на идеальном газе, по циклу Карно:
$η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$
Суть формулы $η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$ выражена в доказанной С. Карно теореме о том, что КПД любого теплового двигателя не может превышать КПД цикла Карно, осуществляемого при той же температуре нагревателя и холодильника.
термодинамика | Законы, определения и уравнения
- Ключевые люди:
- Макс Планк Джеймс Клерк Максвелл Гилберт Н. Льюис Дж. Уиллард Гиббс Илья Пригожин
- Похожие темы:
- нагревать энергия законы термодинамики Транспортное уравнение Больцмана классическая термодинамика
Просмотреть весь связанный контент →
Популярные вопросы
Что такое термодинамика?
Термодинамика изучает отношения между теплом, работой, температурой и энергией. Законы термодинамики описывают, как изменяется энергия в системе и может ли система выполнять полезную работу над окружающей средой.
Законы термодинамики описывают, как изменяется энергия в системе и может ли система выполнять полезную работу над окружающей средой.
Является ли термодинамика физикой?
Да, термодинамика — это раздел физики, изучающий изменение энергии в системе. Ключевое понимание термодинамики заключается в том, что тепло — это форма энергии, соответствующая механической работе (то есть действующая на объект сила на расстоянии).
Сводка
Прочтите краткий обзор этой темы
термодинамика , наука о взаимосвязи между теплом, работой, температурой и энергией. В широком смысле термодинамика имеет дело с переносом энергии из одного места в другое и из одной формы в другую. Ключевое понятие состоит в том, что теплота — это форма энергии, соответствующая определенному количеству механической работы.
Тепло не было официально признано формой энергии примерно до 179 г.8, когда граф Румфорд (сэр Бенджамин Томпсон), британский военный инженер, заметил, что при сверлении пушечных стволов может выделяться неограниченное количество тепла и что количество выделяемого тепла пропорционально работе, выполняемой при повороте тупого сверлильного инструмента. . Наблюдение Румфордом пропорциональности между произведенным теплом и выполненной работой лежит в основе термодинамики. Другим пионером был французский военный инженер Сади Карно, который в 1824 г. ввел понятие теплового цикла и принцип обратимости. высокотемпературный теплообмен как его движущая сила. Позже в том же столетии эти идеи были развиты Рудольфом Клаузиусом, немецким математиком и физиком, в первый и второй законы термодинамики соответственно.
. Наблюдение Румфордом пропорциональности между произведенным теплом и выполненной работой лежит в основе термодинамики. Другим пионером был французский военный инженер Сади Карно, который в 1824 г. ввел понятие теплового цикла и принцип обратимости. высокотемпературный теплообмен как его движущая сила. Позже в том же столетии эти идеи были развиты Рудольфом Клаузиусом, немецким математиком и физиком, в первый и второй законы термодинамики соответственно.
Наиболее важные законы термодинамики:
Нулевой закон термодинамики. Когда две системы находятся в тепловом равновесии с третьей системой, первые две системы находятся в тепловом равновесии друг с другом. Это свойство делает целесообразным использование термометров в качестве «третьей системы» и для определения температурной шкалы.
Первый закон термодинамики или закон сохранения энергии. Изменение внутренней энергии системы равно разнице между теплом, переданным системе из окружающей среды, и работой, совершенной системой над окружающей средой.

Второй закон термодинамики. Теплота не перетекает самопроизвольно из более холодной области в более горячую, или, что то же самое, теплота при данной температуре не может быть полностью преобразована в работу. Следовательно, энтропия замкнутой системы, или тепловая энергия на единицу температуры, со временем увеличивается до некоторого максимального значения. Таким образом, все закрытые системы стремятся к равновесному состоянию, в котором энтропия максимальна и нет энергии для выполнения полезной работы.
Третий закон термодинамики. Энтропия идеального кристалла элемента в его наиболее стабильной форме стремится к нулю, когда температура приближается к абсолютному нулю. Это позволяет установить абсолютную шкалу энтропии, которая со статистической точки зрения определяет степень случайности или беспорядка в системе.
Хотя термодинамика быстро развивалась в 19 веке в связи с необходимостью оптимизации характеристик паровых двигателей, широкая общность законов термодинамики делает их применимыми ко всем физическим и биологическим системам. В частности, законы термодинамики дают полное описание всех изменений энергетического состояния любой системы и ее способности совершать полезную работу над своим окружением.
В частности, законы термодинамики дают полное описание всех изменений энергетического состояния любой системы и ее способности совершать полезную работу над своим окружением.
Викторина “Британника”
Наука: правда или вымысел?
Вас увлекает физика? Устали от геологии? С помощью этих вопросов отделите научный факт от вымысла.
Эта статья посвящена классической термодинамике, которая не включает рассмотрение отдельных атомов или молекул. Такие проблемы находятся в центре внимания раздела термодинамики, известного как статистическая термодинамика или статистическая механика, которая выражает макроскопические термодинамические свойства с точки зрения поведения отдельных частиц и их взаимодействий. Он уходит своими корнями во вторую половину XIX в.ХХ века, когда стали общепринятыми атомарная и молекулярная теории материи.
Фундаментальные концепции
Термодинамические состояния
Применение термодинамических принципов начинается с определения системы, которая в некотором смысле отличается от своего окружения. Например, системой может быть образец газа внутри цилиндра с подвижным поршнем, целая паровая машина, марафонец, планета Земля, нейтронная звезда, черная дыра или даже вся Вселенная. В общем, системы могут свободно обмениваться теплом, работой и другими формами энергии со своим окружением.
Например, системой может быть образец газа внутри цилиндра с подвижным поршнем, целая паровая машина, марафонец, планета Земля, нейтронная звезда, черная дыра или даже вся Вселенная. В общем, системы могут свободно обмениваться теплом, работой и другими формами энергии со своим окружением.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Состояние системы в любой момент времени называется ее термодинамическим состоянием. Для газа в цилиндре с подвижным поршнем состояние системы определяется по температуре, давлению и объему газа. Эти свойства являются характеристическими параметрами, которые имеют определенные значения в каждом состоянии и не зависят от того, каким образом система пришла в это состояние. Другими словами, любое изменение значения свойства зависит только от начального и конечного состояний системы, а не от пути, пройденного системой из одного состояния в другое. Такие свойства называются функциями состояния. Напротив, работа, совершаемая при движении поршня и расширении газа, и тепло, поглощаемое газом из окружающей среды, зависят от подробного способа, которым происходит расширение.
Напротив, работа, совершаемая при движении поршня и расширении газа, и тепло, поглощаемое газом из окружающей среды, зависят от подробного способа, которым происходит расширение.
Поведение сложной термодинамической системы, такой как атмосфера Земли, можно понять, если сначала применить принципы состояний и свойств к ее составным частям — в данном случае к воде, водяному пару и различным газам, составляющим атмосферу. Изолируя образцы материала, состояния и свойства которых можно контролировать и манипулировать ими, можно изучать свойства и их взаимосвязи по мере изменения системы от состояния к состоянию.
Топ 10 формул термодинамики – fxSolver
Термодинамика! Удивительное поле со многими важными уравнениями. Специально для вас мы собрали топ-10 этих формул!
1. Теплопроводность – скорость теплового потока
В физике теплопроводность — это свойство материала проводить тепло. Он оценивается в первую очередь с точки зрения закона Фурье для теплопроводности. Теплопередача происходит с большей скоростью через материалы с высокой теплопроводностью, чем через материалы с низкой теплопроводностью. Соответственно, материалы с высокой теплопроводностью широко используются в радиаторах, а материалы с низкой теплопроводностью используются в качестве теплоизоляции.
Теплопередача происходит с большей скоростью через материалы с высокой теплопроводностью, чем через материалы с низкой теплопроводностью. Соответственно, материалы с высокой теплопроводностью широко используются в радиаторах, а материалы с низкой теплопроводностью используются в качестве теплоизоляции.
2. Явное тепло
Явное тепло — это теплообмен тела или термодинамической системы, который изменяет температуру и некоторые макроскопические переменные тела, но оставляет неизменными некоторые другие макроскопические переменные, такие как объем или давление. Этот термин используется в отличие от скрытой теплоты, которая количество скрытого теплообмена, т. е. без изменения температуры. Например, во время фазового перехода, такого как таяние льда, температура системы, содержащей лед и жидкость, остается постоянной до тех пор, пока весь лед не растает.
3. Скрытая течка
Термины латентный и чувственный коррелятивны. Это означает, что они определяются как пара, в зависимости от того, какие другие макроскопические переменные остаются постоянными в течение процесса.
Скрытая теплота – это энергия, выделяемая или поглощаемая телом или термодинамической системой в ходе процесса с постоянной температурой. Типичным примером является изменение состояния вещества, означающее фазовый переход, такой как таяние льда или кипение воды. Удельная скрытая теплота (L) выражает количество энергии в виде тепла (Q), необходимое для полного фазового перехода единицы массы (m), обычно 1 кг, вещества в качестве интенсивного свойства. Интенсивные свойства являются характеристиками материала и не зависят от размера или протяженности образца.
4. Тепловой КПД тепловой машины
Тепловые двигатели преобразуют тепловую энергию или теплоту в механическую энергию или работу. Они не могут выполнить эту задачу идеально, поэтому часть подводимой тепловой энергии не преобразуется в работу, а рассеивается в виде отработанного тепла в окружающую среду. Тепловой КПД тепловой машины – это процент тепловой энергии, которая преобразуется в работу.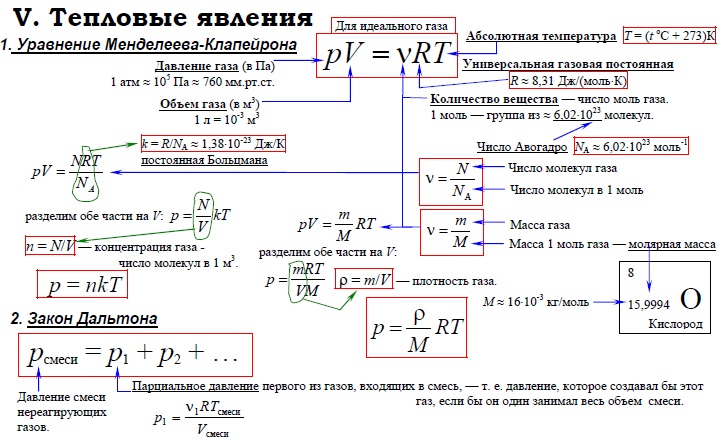
5. Тепловая энергия идеального газа
Тепловая энергия — это термин, который иногда используется для обозначения внутренней энергии, присутствующей в системе в состоянии термодинамического равновесия в силу ее температуры. Средняя поступательная кинетическая энергия, которой обладают свободные частицы в системе свободных частиц, находящихся в термодинамическом равновесии (измеряемая в системе отсчета центра масс этой системы), также может называться тепловой энергией, приходящейся на одну частицу. Идеальный газ — это газ частиц, рассматриваемых как точечные объекты идеальной сферической симметрии, которые взаимодействуют только за счет упругих столкновений и заполняют такой объем, что их длина свободного пробега между столкновениями намного больше их диаметра. Полная тепловая энергия газа, состоящего из N атомов, определяется как сумма кинетических энергий частиц без учета потерь в сосуд или окружающую среду
6. Энтальпия
Энтальпия — это определенный термодинамический потенциал, который состоит из внутренней энергии системы (U) плюс произведение давления (p) и объема (V) системы. Он включает в себя внутреннюю энергию, которая представляет собой энергию, необходимую для создания системы, и количество энергии, необходимое для того, чтобы освободить для нее место путем смещения окружающей среды и создания ее объема и давления. Это также изменение учитывает энергию, передаваемую окружающей среде при постоянном давлении за счет расширения или нагревания.
Он включает в себя внутреннюю энергию, которая представляет собой энергию, необходимую для создания системы, и количество энергии, необходимое для того, чтобы освободить для нее место путем смещения окружающей среды и создания ее объема и давления. Это также изменение учитывает энергию, передаваемую окружающей среде при постоянном давлении за счет расширения или нагревания.
7. Закон Гей-Люссака (закон давления-температуры)
Давление газа фиксированной массы и фиксированного объема прямо пропорционально абсолютной температуре газа. Если температура газа увеличивается, то увеличивается и его давление, если масса и объем газа остаются постоянными.
Этот закон справедлив, потому что температура является мерой средней кинетической энергии вещества; по мере увеличения кинетической энергии газа его частицы быстрее сталкиваются со стенками сосуда, тем самым оказывая повышенное давление.
8. Первый закон Джоуля
Джоулев нагрев — это процесс, при котором при прохождении электрического тока через проводник выделяется тепло. Оно зависит от сопротивления проводника, силы тока и времени. Хотя, это не зависит от направления тока. Джоулев нагрев вызывается взаимодействиями между движущимися частицами, образующими ток (обычно, но не всегда, электронами) и атомарными ионами, составляющими тело проводника. Заряженные частицы в электрической цепи ускоряются электрическим полем, но теряют часть своей кинетической энергии каждый раз, когда сталкиваются с ионом. Увеличение кинетической или колебательной энергии ионов проявляется в виде нагревания и повышения температуры проводника.
Оно зависит от сопротивления проводника, силы тока и времени. Хотя, это не зависит от направления тока. Джоулев нагрев вызывается взаимодействиями между движущимися частицами, образующими ток (обычно, но не всегда, электронами) и атомарными ионами, составляющими тело проводника. Заряженные частицы в электрической цепи ускоряются электрическим полем, но теряют часть своей кинетической энергии каждый раз, когда сталкиваются с ионом. Увеличение кинетической или колебательной энергии ионов проявляется в виде нагревания и повышения температуры проводника.
9. Формула энтропии Больцмана
Уравнение Больцмана — это вероятностное уравнение, связывающее энтропию S идеального газа с величиной W, которая представляет собой число микросостояний, соответствующих данному макросостоянию.
Короче говоря, формула Больцмана показывает связь между энтропией и числом способов расположения атомов или молекул в термодинамической системе.
10. Уравнение состояния Ван-дер-Ваальса
Уравнение Ван-дер-Ваальса можно рассматривать как закон идеального газа, «улучшенный» по двум независимым причинам: молекулы рассматриваются как частицы с объемом, а не как материальные точки, и хотя молекулы идеального газа не взаимодействуют, мы рассматриваем молекулы, притягивающие другие внутри расстояние в несколько радиусов молекул.
Вы можете попытаться найти все, что хотите, просто нажав кнопку «Обзор формул» в левом верхнем углу экрана.
Если вам нужна помощь, вы найдете ее в нашем видео fxSolver.
Также не забывайте подписываться на нас или взаимодействовать с нами на наших страницах в социальных сетях . Вы найдете ссылки ниже.
Формулы первого закона термодинамики
Увеличение внутренней энергии замкнутой системы равно количеству теплоты, переданной системе, за вычетом совершенной ею работы.
Формула:
∆E int = Q – W
Это первый закон термодинамики. это принцип сохранения энергии, означающий, что энергия не может ни создаваться, ни уничтожаться , а скорее преобразовываться в различные формы по мере изучения жидкости в контрольном объеме.
Это самый важный закон для анализа большинства систем, который определяет количество тепловой энергии преобразуется в другие формы энергии.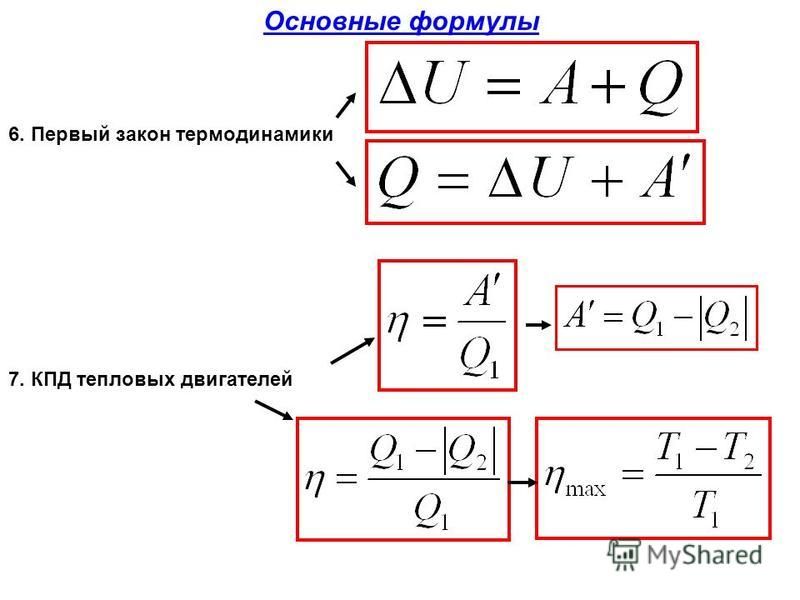 Отсюда следует, что вечные двигатели первого рода невозможны.
Отсюда следует, что вечные двигатели первого рода невозможны.
Дифференциальная форма:
Дифференциальная форма:
dE int = dQ – dW
Внутренняя энергия E int увеличивается как энергия системы и имеет тенденцию к уменьшению, поскольку энергия системы если энергия теряется в виде работы W, совершаемой системой.
Первый закон энтальпии dH = dQ + Vdp
Энтальпия определяется как сумма внутренней энергии E плюс произведение давления p и объема V. Во многих термодинамических анализах появляется сумма внутренней энергии U и произведения давления p и объема V. Поэтому удобно дать этой комбинации название энтальпия и отдельный символ H.
H = U + pV
из энтальпия показывает нам, почему инженеры используют энтальпию в термодинамических циклах (например, цикл Брайтона или цикл Ренкина ).
Классическая форма закона представляет собой следующее уравнение:
dU = dQ – dW
В этом уравнении dW равно dW = pdV 90 39 как граница 6 0 39 и известна как работа границы 6 0 39.
Граничная работа – pdV Работа
Граничная работа возникает потому, что масса вещества, содержащегося в пределах границы системы, заставляет силу, произведение давления на площадь поверхности, воздействовать на граничную поверхность и заставлять ее двигаться. Граничная работа (или pΔV Работа ) происходит, когда объем В системы изменяется . Он используется для расчета работы смещения поршня в закрытой системе . Вот что происходит, когда пар или газ, содержащийся в поршне-цилиндровом устройстве, расширяется против поршня и заставляет поршень двигаться.
Поскольку H = U + pV , следовательно, dH = dU + pdV + Vdp и подставляем dU = dH – pdV – Vdp в классическую форму закона:
dH – pdV – Vdp = dQ – pdV
от 10 энтальпий.
DH = DQ + VDP
или
DH = TDS + VDP
. В этом уравнении термин VDP 6. Настоящая работа, Вдп , используется для открытых проточных систем , таких как турбина или насос , в которых имеется «dp» , т. е. изменение давления. В контрольной громкости изменений нет. Как видно, эта форма закона упрощает описание передачи энергии . При постоянном давлении изменение энтальпии равно энергии переданной из окружающей среды при нагревании:
Изобарический процесс (Vdp = 0):
DH = DQ → Q = H 2 – H 1
At Constant Encropy , I. E.E.E. I. I. I. I. I. I. I. I. I. I. I. I. I. I. I. I.E. I. I. I.E.E. I. I.E. I.E., I.E., I.E., I.E.E., I.E.E., I.E. work done on or by the system:
E.E.E. I. I. I. I. I. I. I. I. I. I. I. I. I. I. I. I.E. I. I. I.E.E. I. I.E. I.E., I.E., I.E., I.E.E., I.E.E., I.E. work done on or by the system:
Isentropic process (dQ = 0):
dH = Vdp → W = H 2 – H 1
Это очевидно и будет очень полезно при анализе обоих термодинамических циклов, используемых в энергетике, т. е. в циклах Брайтона и Ренкина.
pΔV Работа
pΔV Работа равна площади под кривой процесса, нанесенной на диаграмму давление-объем.Пример:
Рассмотрим поршень без трения, который используется для обеспечения постоянного давления 500 кПа в цилиндре, содержащем пар (перегретый пар) объемом 2 м 3 в 500 К .
Рассчитайте конечную температуру, если 3000 кДж из тепла добавить.
Решение:
Используя таблицы паров, мы знаем, что удельная энтальпия такого пара (500 кПа; 500 К) составляет около 2912 кДж/кг . Так как при этих условиях пар имеет плотность 2,2 кг/м 3 , то мы знаем, что в поршне находится около 4,4 кг пара при энтальпии 2912 кДж/кг x 4,4 кг = 12812 кДж .
When we use simply Q = H 2 − H 1 , then the resulting enthalpy of steam will be:
H 2 = H 1 + Q = 15812 кДж
Из паровых столов такой перегретый пар (15812/4,4 = 3593 кДж/кг) будет иметь температуру 828 К (555°С) . Так как при этой энтальпии пар имеет плотность 1,31 кг/м 3 , очевидно, что он расширился примерно на 2,2/1,31 = 1,67 (+67%). Следовательно, результирующий объем равен 2 м 3 x 1,67 = 3,34 м 3 и ∆V = 3,34 м 3 – 2 м 3 = 1,34 м 3 .
P∆V Часть энтальпии, т.е. –
Каталожные номера:
Ядерная и реакторная физика:
- Дж. Р. Ламарш, Введение в теорию ядерных реакторов, 2-е изд., Addison-Wesley, Reading, MA (1983).
- Дж. Р. Ламарш, А. Дж. Баратта, Введение в ядерную технику, 3-е изд., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
- WM Stacey, Физика ядерных реакторов, John Wiley & Sons, 2001, ISBN: 0-471-39127-1.
- Гласстоун, Сезонске. Разработка ядерных реакторов: разработка реакторных систем, Springer; 4-й выпуск, 1994, ISBN: 978-0412985317
- W.S.C. Уильямс. Ядерная физика и физика элементарных частиц. Кларендон Пресс; 1 издание, 1991 г., ISBN: 978-0198520467
- Кеннет С. Крейн. Введение в ядерную физику, 3-е издание, Wiley, 1987, ISBN: 978-0471805533
- Г. Р. Кипин. Физика ядерной кинетики. Паб Эддисон-Уэсли. Ко; 1-е издание, 1965 г.

- Роберт Рид Берн, Введение в работу ядерных реакторов, 1988 г.
- Министерство энергетики, ядерной физики и теории реакторов США. Справочник по основам Министерства энергетики, том 1 и 2, 19 января.93.
Advanced Reactor Physics:
- KO Ott, WA Bezella, Introductory Nuclear Reactor Static, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033.
- К. О. Отт, Р. Дж. Нойхольд, Введение в динамику ядерных реакторов, Американское ядерное общество, 1985, ISBN: 0-894-48029-4.
- Д. Л. Хетрик, Динамика ядерных реакторов, Американское ядерное общество, 1993, ISBN: 0-894-48453-2.
- Э. Э. Льюис, В. Ф. Миллер, Вычислительные методы переноса нейтронов, Американское ядерное общество, 1993, ISBN: 0-894-48452-4.
См. выше:
Первый закон
сообщите об этом объявлении
Вывод термодинамических уравнений
Вывод термодинамических уравненийОтношение химического потенциала к концентрации
Из-за простоты системы это легче всего рассмотреть. для случая идеального газа, претерпевающего изменение состояния при постоянной температуре.
В этом случае состояние системы может быть определено переменными состояния
P, V и T, которые определяют содержание энергии и могут использоваться для описания
работа, выполняемая системой или системой.
для случая идеального газа, претерпевающего изменение состояния при постоянной температуре.
В этом случае состояние системы может быть определено переменными состояния
P, V и T, которые определяют содержание энергии и могут использоваться для описания
работа, выполняемая системой или системой.Для идеального газа, подвергающегося обратимому изменению при постоянной температуре, когда не проводятся химические работы,
dG = VdP ————- (1)
При переходе из состояния 1 со свободной энергией G 1 в состояние 2 с свободная энергия G 2 , по обратимому пути, изменение свободной энергии (G 2 -G 1 ) является суммой по пути или интегралом все значения dG на пути, если процесс обратим.
Так как P связан с V посредством:
PV = нРТ
, где n — количество газа в молях, а R — газовая постоянная. Из правила интегрирования:
Теперь мы определим наше начальное состояние как стандартное состояние, в котором газ
находился под давлением 1 атм. затем
затем
G 2 = G o + nRT ln P 2 —————————————— (4)
где G o – свободная энергия газа в стандартном состоянии.
В смеси идеальных газов парциальное давление каждого газа равно давление, которое имел бы газ, если бы он один занимал объем. Таким образом, парциальное давление эквивалентно концентрации газа. Для газов A, B, C, D частичная свободная энергия каждого газа (G # А , Г # Б , Г # К , Г # Д ) связано с парциальным давлением газа уравнением 4:
G # A = G #o A + n A RT ln P A , G # B = G #o B + n B RT ln P B и т.д.
Рассмотрим теперь идеальный газ, находящийся в равновесии с газом в растворе.
Концентрация газа в растворе (при условии идеального раствора) будет
пропорциональна давлению газа, так что эквивалентный набор
должны существовать уравнения, связывающие парциальную свободную энергию газа в растворе
его концентрации, X.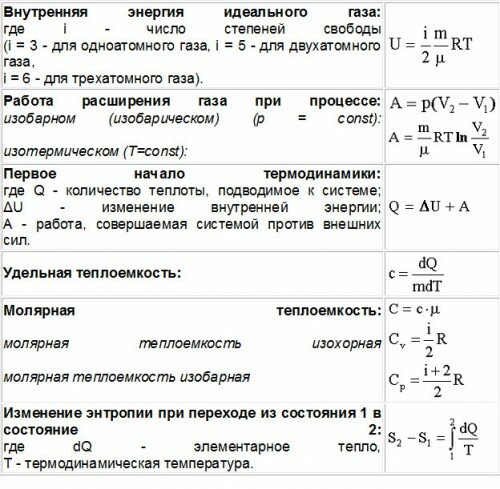
Частичная свободная энергия на моль компонента – это его химический потенциал, поэтому мы можем написать:
G A #soln = n A µ A , G B #soln = n B µ B и т. д.
и, разделив на n A , n B и т.д.
G A #soln = µ A = µ o A + РТ пер Х А ,
п А
G B #soln = µ B = µ o B + RT ln X B и т. д. ——–(5)
n B
где X A , X B и т.д. газы в растворе.
Обратите внимание, что разделив G # на n, мы изменили единицы измерения
от свободной энергии (измеряемой в джоулях, Дж или калориях) до свободной энергии на
моль (Дж.моль -1 , или кал.моль -1 ). Это более полезно
параметр для сравнения энергетических условий для различных химических процессов,
потому что нам не нужно беспокоиться о размере системы при сравнении
рабочий потенциал, доступный от различных реакций.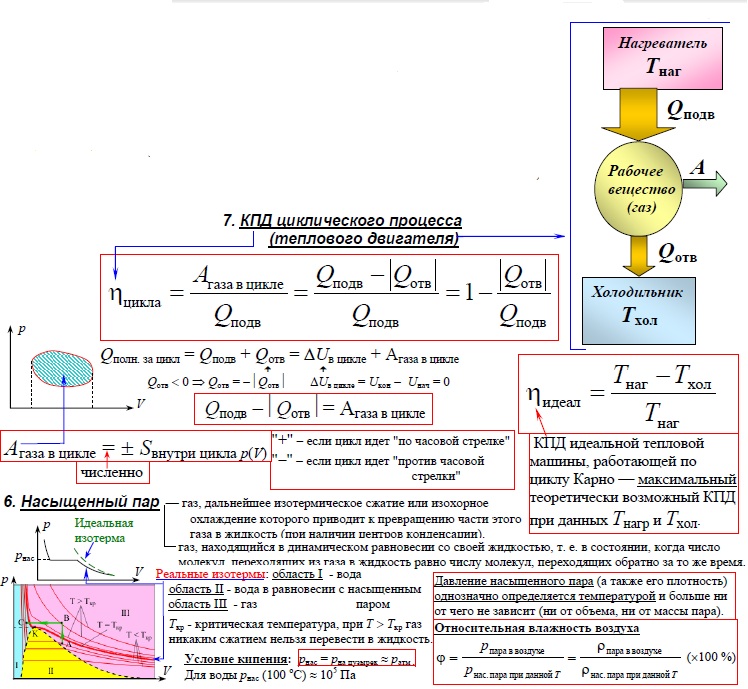
Для неидеальных растворов связь между концентрацией и давлением газа, находящегося в равновесии с раствором, зависит от взаимодействия между молекул в растворе. Это приводит к отклонению от постоянной пропорциональность между давлением и концентрацией, так что уравнения 5 точно не применять. Это отклонение компенсируется рассмотрением деятельности ( A , a B и т. д.) вместо концентраций. Активность связана с концентрацией коэффициентом активности (g), чтобы
а = гХ
Тогда
µ A = µ o A + RT ln a A ——– (6)
= µ o A + RT ln X A г A
В разбавленном растворе коэффициент активности приближается к единице, так что
поведение молекул приближается к идеальному, а активность приближается к
к концентрациям. Как мы увидим ниже, при рассмотрении изменения энергии
в реакциях члены активности встречаются в соотношениях, а коэффициенты активности
склонны отменять. (Обратите внимание, что в уравнении 6 член значения единицы, соответствующий
активности в стандартном состоянии, по соглашению исключен из
логарифмический член.)
(Обратите внимание, что в уравнении 6 член значения единицы, соответствующий
активности в стандартном состоянии, по соглашению исключен из
логарифмический член.)
Изменение свободной энергии для химической реакции
Рассмотрим гипотетическую простую химическую реакцию.А + В <===> С + Г
В равновесии реагенты и продукты имеют активности [A], [B], [С], [Г], так что
К = [С].[Д]
[А].[Б]
Предположим, что реакция находится в равновесии применение работы в новом равновесии с действиями [A’], [B’], [C’], [D’]. Изменение частичной свободной энергии на моль (химический потенциал) для каждого реагент, так как реакция обратимо возвращается к истинному равновесию дан кем-то:
мк А = мк’ А – µ A = µ o A + RT ln [A’] – µ o A – RT ln [A] = RT ln [A’]/[A]
мк В = мк’ В – µ B = µ o B + RT ln [B’] – µ o B – RT ln [B] = RT ln [B’]/[B]
мк С = мк’ С – µ C = µ o C + RT ln [C’] –
№ или С – RT пер. [C] = RT пер. [C’]/[C]
[C] = RT пер. [C’]/[C]
µ D = µ’ D – µ D = µ o D + RT ln [D’] – µ o D – RT ln [D] = RT ln [D’]/[D]
Тогда, приняв условность, что изменения концентраций продукты положительные
Предположим, что активность реагентов вдали от истинным равновесием были равновесия стандартных состояний [A o ], [B o ], [C o ], [D o ]. По определению они имеют значение 1, так что второй член справа уравнения 7 становится равным нулю. Затем изменение свободной энергии при переходе реакции из стандартного состояния обратно в равновесие (G o ) есть данный
G o = -RT ln K ——- (7а)
и
Для рассмотрения реакций, в которых стехиометрические коэффициенты не эквимолярны, мы просто расширяем соотношения уравнений 7 и 8 к более общему случаю.
аА + ЬВ <===> сС + dD
и
Уравнение 9 в целом применимо ко всем химическим реакциям, и мы
использовать его при описании биохимических процессов. Обратите внимание, что G’
имеет единицы Дж.моль -1 ,- это коэффициент интенсивности, и должен быть
умноженное на n, количество молей реагента, претерпевающего изменение
в состоянии, представленном реакцией, чтобы получить изменение свободной энергии.
Обратите внимание, что G’
имеет единицы Дж.моль -1 ,- это коэффициент интенсивности, и должен быть
умноженное на n, количество молей реагента, претерпевающего изменение
в состоянии, представленном реакцией, чтобы получить изменение свободной энергии.
Г = п Г’
Г’, Г или , и G o ‘ больше удобные параметры для сравнения свободных энергий, доступных из химических реакции, потому что они нормированы, чтобы избежать необходимости учитывать от размера системы.
Термодинамические процессы
Термодинамические процессыЧасто система, из которой мы хотят извлечь теплоту, чтобы сделать работу, является газом. Когда газ расширяется, как какую работу он производит над своим окружением?
Рассмотрим идеальный газ в цилиндре с подвижным поршнем.
газ занимает объем V, температура T, давление
P. Предположим, что поршень имеет площадь поперечного сечения A. Предположим, что
газ расширяется на небольшую величину, а поршень выдвигается на небольшую
количество Δу. Газ действует на поршень с силой F = PA и
поэтому на поршень действует работа ΔW = FΔy.
Газ действует на поршень с силой F = PA и
поэтому на поршень действует работа ΔW = FΔy.
ΔW = FΔy = PAΔy = PΔV
ΔV — изменение объема газа. ΔV положителен, потому что газ расширяется. (Если газ сжимается, то ΔV равно отрицательный и над газом совершается работа.)
Если объем газа изменится с V 1 на V 2 ,
то полная работа, совершаемая газом, зависит от того, как именно изменяется давление во время
процесс расширения.
Вт = ∑ Дж П Дж ΔV j . Мы суммируем
работа, совершаемая при большом количестве малых изменений объема.
Если давление и объем известны на каждом шаг процесса расширения, то работу можно представить в виде площадь под кривой на PV-диаграмме.
- Адиабатический процесс — это процесс, во время
входит или выходит из системы.
Тогда имеем ΔU = -ΔW, т. е. ΔW равно изменение физического свойства системы.
Физическое свойство системы зависит только на состояние системы (P, V, T), а не на то, как система был приведен в это состояние.
На практике существует два различных способа предотвращения передача тепла.
(a) Обеспечьте очень хорошую теплоизоляцию системы.
(b) Завершить процесс за очень короткий промежуток времени, так что нет времени для заметной теплопередачи. Процесс сгорания в автомобильном двигателе по существу адиабатический по этой причине. - Изобарический процесс — это процесс, происходящий при постоянном давлении.
Тогда мы имеем W = P(V 2 – V 1 ).
Если давление идеального газа поддерживается постоянным, то температура должна увеличиваться по мере расширения газа. (PV/T = константа.) В процессе расширения необходимо добавлять тепло.
Определим энтальпию H системы как уравнение H = U + PV.
Энтальпия — это физическое свойство системы. зависит только от состояния системы (внутренняя энергия, давление, объем), а не от того, как оно достигло этого государство. Энтальпия имеет размерность энергии и единицу СИ энтальпия – джоуль.
Для изобарического процесса запишем ΔU = ΔQ — ΔW = ΔQ — P(V 2 — V 1 ), или, переставляя члены, ΔH = ΔQ.
Это выражение, часто употребляемое в химии, можно рассматривать как изобарическую форму первого закона.
ΔH = ΔQ справедливо только для изобарических процессов. Химические реакции (в том числе биологические) часто протекают при постоянное давление, и тогда ΔQ равно изменению физического свойства системы. - Ан изоволюметрический или изометрический процесс протекает при постоянном объеме.
Затем W = 0 и ΔU = ΔQ.
Все тепло, добавляемое в систему, уходит в увеличивает его внутреннюю энергию. - Изотермический процесс происходит при постоянной температуре.
Поскольку внутренняя энергия газа зависит только от его температуры, ΔU = 0 для изотермического процесса.
Для изотермического расширения идеального газа имеем W = nRT ln(V 2 /V 1 ).
W положителен, если V 2 > V 1 . Поскольку ΔU = 0 тепло, переданное газу, равно ΔQ = W.
Проблема:
Решение:
- Обоснование:
Процесс изобарный. Для изобарического процесса W = P(V 2 – V 1 ). - Детали расчета:
W = P(V 2 – V 1 ) = P(2V 1 – V 1 ) = PV 1 = 151500 Па*4 м 3 = 606000 Дж.
(Работа — это площадь под кривой на диаграмме PV. ΔV положительно, потому что газ расширяется, поэтому работа W, совершаемая газом, равна положительный.)
Проблема:
Г в баллоне находится при давлении 1,5 атм и объеме 4 м 3 . Какую работу совершит газ, если его сжать при постоянном давлении до 1/4 первоначального объема?
Решение:
- Обоснование:
Процесс изобарный. Для изобарического процесса W = P(V 2 – V 1 ).
- Детали расчета:
Вт = P(0,25 В 1 – В 1 ) = -0,75 PV 1 = -454500 Дж.
(Работа — это площадь под кривой на диаграмме PV. ΔV — это отрицательно, так как газ сжат, и поэтому работа W, совершаемая газ отрицательный.)
Проблема:
Газ в баллоне находится при давлении 1,5 атм и объеме 4 м 3 . Какую чистую работу совершит газ, если он совершит следующий цикл?
(i) Газ расширяется при постоянном давлении 1,5 атм до объема
4 м 3 .
(ii) При постоянном объеме 4 м 3 давление снижается
до 1 атм.
(iii) Газ сжимают при постоянном давлении 1 атм до
объем 4 м 3 .
(iv) При постоянном объеме 4 м 3 давление равно
увеличилось до 1,5 атм.
Решение:
- Обоснование:
Процессы (i) и (iii) являются изобарными. W = PΔV.
Процессы (i) и (iii) изометричны. Вт = 0, - Детали расчета:
(i) W = PΔV = 151500 Па*4 м 3 = 606000 Дж.
(ii) W = 0, поскольку ΔV = 0. (без смещения <--> без работы).
(iii) W = PΔV = -101000 Па*4 м 3 = -404000 Дж.
(iv) W = 0.
Чистая работа, совершаемая газом: W чистая = 606000 Дж – 404000 Дж = 202000 Дж.
Чистая работа, совершаемая газом за один цикл процесса, возвращающего газа до его начального состояния – это площадь внутри замкнутого контура в PV диаграмма. Если петлю пройти по часовой стрелке, сеть работа положительная. Если петля проходится против часовой стрелки направление чистой работы отрицательно.
- При расширении газ совершает положительную работу. Он упирается в стену контейнер и стенка контейнера перемещаются наружу. Имеем ∆W = F*∆r = (F/A)*A*∆r = P *∆V. Здесь А — площадь стенки контейнера. который сместился, а ∆r — насколько он сместился наружу.
- Когда объем газа уменьшается, газ совершает отрицательную работу. ∆W =
-P*∆V. Газ по-прежнему выталкивается наружу, к стене, но стена движется.
 внутрь.
внутрь. - Когда объем не меняется, газ не работает, независимо от значение давления.
- Итак, когда у вас есть диаграмма P-V (вертикальная ось P, горизонтальная ось V)
показывая замкнутый цикл, вы можете разбить цикл на маленькие шаги, которые
либо увеличьте, либо уменьшите громкость, либо не изменяйте ее.
Любое положительное ∆V (в сторону большего V) означает, что газ совершает положительную работу P*∆V, и любое отрицательное ∆V (в сторону меньшего V) означает, что газ совершает отрицательную работу -P*∆V. - Сложив все это, вы обнаружите, что работа, выполненная газом, равна площади внутри петли на диаграмме PV. Работа положительна, если давление больше при расширении, чем при сжатии, а работа отрицательное (работа совершается над газом), если давление меньше во время расширение, чем при сжатии.
Проблема:
Рассчитайте чистую выходную мощность тепловой машины по пути ABCDA в рисунок справа.
Решение:
- Обоснование:
Путь представляет собой замкнутый контур на диаграмме PV.
Чистая проделанная работа — это площадь внутри замкнутого контура на диаграмме PV. - Детали расчета:
Вт = (1,5 * 3)*(10 6 Н/м 2 )(10 -3 м 3 ) = 4,5*10 3 Дж,
с использованием площади = средняя высота * ширина.
или
область внутри цикла = площадь центрального прямоугольника + площадь верхнего треугольника – площадь нижнего треугольника
= (1*3 + 0,6*3/2 – 0,4*3/2)*(10 6 Н/м 2 )(10 -3 м 3 ) = 4,5*10 3 Дж.
Проблема:
Газ сжимают при постоянном давлении 0,8 атм из 9 литров в 2 литра.
(1 литр = 10 -3 м 3 ) При этом из газа уходит 400 Дж тепловой энергии.
а) Какую работу совершает газ?
(б) Как изменится его внутренняя энергия?
Решение:
- Обоснование:
Для изобарического процесса W = P(V 2 – V 1 ).
Энергосбережение: ΔU = ΔQ – ΔW. - Детали расчета:
(a) W = P(V 2 – V 1 ) = -80800 Па*7*10 -3 м 3 = -565,6 Дж. (На газе совершается работа.)
(б) ΔU = -400 Дж + 565,6 Дж = 165,6 Дж.
Проблема:
Один моль идеального газа совершает над окружающей средой работу 3000 Дж.
изотермически расширяется до конечного давления 1 атм и объема 25 л.
Определить
(а) начальный объем и
(б) температура
газ.
Решение:
Велосипед Эргометр — это устройство, которое
напоминает велосипед и используется для измерения количества работы, выполненной человеком
крутя педали, чтобы вращать большой маховик, обычно переднее колесо
стационарный велосипед, против силы трения. Проделанная работа по преодолению
сила трения преобразуется в тепловую энергию, которая вызывает температуру
маховика и других компонентов, контактирующих с системой, увеличиться. Нейлоновый ремень, натянутый и намотанный на колесо, может обеспечить
сила трения. Натяжение можно измерить калиброванной пружиной.
работа W, совершаемая человеком на эргометре, является произведением силы,
натяжение F ремня, умноженное на расстояние, на котором действует эта сила.
сила касается обода колеса. Таким образом, расстояние в 2π раз
радиус маховика r, умноженный на число оборотов N, совершаемых маховиком.
рулевое колесо. Имеем W = NF2πr. Для эргометра имеем из первого закона
термодинамика ΔU = ΔQ – ΔW. ΔW положителен, если система работает на своем
окружающей среды и является отрицательным, если в системе выполняется работа. Здесь ΔW
отрицательно, так как человек работает на эргометре. ΔW = -W. ΔQ – это
тепло, поступающее в систему или отводимое из нее. Имеем ∆U – ∆Q = NF2πr. Если мы
теплоотдачей системы в окружающую среду пренебречь и положить ΔQ = 0, тогда
увеличение тепловой энергии системы равно ΔU = NF2πr. Температура
маховика поэтому увеличивается на ΔT = ΔU/mc, где m — масса
маховика, c – его удельная теплоемкость.
Нейлоновый ремень, натянутый и намотанный на колесо, может обеспечить
сила трения. Натяжение можно измерить калиброванной пружиной.
работа W, совершаемая человеком на эргометре, является произведением силы,
натяжение F ремня, умноженное на расстояние, на котором действует эта сила.
сила касается обода колеса. Таким образом, расстояние в 2π раз
радиус маховика r, умноженный на число оборотов N, совершаемых маховиком.
рулевое колесо. Имеем W = NF2πr. Для эргометра имеем из первого закона
термодинамика ΔU = ΔQ – ΔW. ΔW положителен, если система работает на своем
окружающей среды и является отрицательным, если в системе выполняется работа. Здесь ΔW
отрицательно, так как человек работает на эргометре. ΔW = -W. ΔQ – это
тепло, поступающее в систему или отводимое из нее. Имеем ∆U – ∆Q = NF2πr. Если мы
теплоотдачей системы в окружающую среду пренебречь и положить ΔQ = 0, тогда
увеличение тепловой энергии системы равно ΔU = NF2πr. Температура
маховика поэтому увеличивается на ΔT = ΔU/mc, где m — масса
маховика, c – его удельная теплоемкость.
Эргометр преобразует полезную работу в тепловую энергию. По анализу воздуха
выдыхаемый человеком, крутящим педали эргометра, скорость, с которой тело использует
можно измерить химическую энергию. Зная, сколько химической энергии в организме
использует в покое и сколько он использует при вращении педалей, эффективность тела в
можно определить превращение химической энергии в полезную работу.
Модуль 10: Вопрос 1
Внутренняя энергия идеального газа не меняется. изотермический процесс, так как внутренняя энергия зависит только от температуры. Поэтому правильно ли говорить, что изотермический процесс — это то же самое, что и адиабатический процесс для идеального газа? Поясните свой ответ.
Обсудите это со своими однокурсниками на дискуссионном форуме!
Все, что вам нужно знать — Shemmassian Academic Consulting
Изучите основные понятия MCAT о термодинамике, а также практические вопросы и ответы (ПРИМЕЧАНИЕ. Это руководство является частью нашей серии Physics MCAT . )
Это руководство является частью нашей серии Physics MCAT . )
9
. и HEAT HEAT 555.). удельная теплоемкость b) Теплота превращения C) Теплопередача D) Термическое расширение Часть 3: Четыре закона термодинамики A) Закон термодинамики 9132 A). Зерт a) Зерт a). c) Второй закон термодинамики d) Третий закон термодинамики Часть 4. Термодинамические функции, системы и процессы A) Типы функций B) Типы систем C) Типы процессов Часть 5: Условия высокого уровня и уравнения . Часть 7: Практические задачи по термодинамике и ответы Часть 1: Введение в термодинамику
Часть 7: Практические задачи по термодинамике и ответы Часть 1: Введение в термодинамику Термодинамика — важная тема, которую вы, вероятно, изучали в химии (или физической химии) в студенческие годы. Хотя это не очень продуктивный предмет MCAT, он может служить важной основой для других тем, которые вам нужно знать для экзамена.
По мере изучения этого руководства по термодинамике мы выделили несколько важных терминов жирным шрифтом, и мы рекомендуем вам создавать свои собственные определения и примеры по мере того, как вы перемещаетесь по этому ресурсу, чтобы они имели наибольший смысл для вас ! В конце этого руководства есть практический отрывок по термодинамике в стиле MCAT и отдельные вопросы, которые проверят ваши знания в области термодинамики и покажут вам, как AAMC любит задавать вопросы.
Начнем!
Часть 2: Тепло Когда мы говорим о динамике термо , многие понятия связаны с важным словом: тепло. Важно отметить, что тепло — это , а не , то же самое, что и температура. Давайте посмотрим на определения каждого слова:
Важно отметить, что тепло — это , а не , то же самое, что и температура. Давайте посмотрим на определения каждого слова:
Тепло : передача энергии на основе разницы температур между двумя объектами
Температура : мера средней энергии из-за движения частиц в объекте ( т. е. у холодного объекта есть медленно движущиеся частицы, а у горячего объекта есть быстро движущиеся частицы)
Рисунок: Тепловая зависимость от температуры
Теперь, когда мы определили тепло, давайте углубимся в некоторые его свойства.
а) Теплоемкость и удельная теплоемкость Теплоемкость – это количество тепла, необходимое для повышения температуры объекта на определенную единицу температуры. Например, предположим, что наш «объект» — это стул, и мы хотим повысить температуру на 5 °C. Теплоемкость скажет нам, сколько тепла нам нужно, чтобы это произошло.
Единицами СИ для теплоемкости являются джоули (Дж) / кельвины (К), и это имеет смысл, если мы вспомним, что джоули — это единицы энергии, а кельвины — единицы измерения температуры.
Удельная теплоемкость очень похожа на теплоемкость, но определяет количество нашего «объекта» и насколько мы хотим повысить температуру этого объекта. Мы определяем удельную теплоемкость как количество тепла, необходимое для нагревания одного грамма объекта на один градус Кельвина (или Цельсия). Если мы вернемся к примеру со стулом, то теперь нас не волнует весь стул или повышение температуры на 5 °C. Вместо этого мы хотим знать, сколько тепла нам нужно, чтобы поднять один грамм стула на 1 °K.
b) Теплота превращения Теплота превращения — еще один важный термодинамический термин. Чтобы понять теплоту трансформации, давайте рассмотрим пример. Лед — это твердая форма воды, и процесс превращения льда в воду требует тепла. Точно так же процесс преобразования воды в водяной пар (газообразная форма воды) требует тепла. Эти переходы называются фазовыми переходами , и их часто представляют в виде диаграммы фазовых переходов :
Эти переходы называются фазовыми переходами , и их часто представляют в виде диаграммы фазовых переходов :
Рисунок: Диаграмма фазового перехода
На диаграмме фазового перехода показана зависимость температуры от энергии. По мере увеличения энергии температура увеличивается, и мы наблюдаем переход от твердых тел к жидкостям и к газам. Однако на графике вы заметите плоские точки, в которых увеличение энергии не приводит к повышению температуры.
Эти плоские точки и есть фазовые изменения, о которых мы говорили выше. Во время фазового перехода температура не меняет , и мы можем описать точки следующим уравнением:
$$q=m\раз L$$ $$\mbox{где }q\mbox{ = количество теплоты, получаемое или отдаваемое веществом,}$$ $$m \mbox{ = масса вещества,}$$ $$L \mbox{ = скрытая теплота или } \textbf{теплота превращения} \mbox{ вещества}$$
Теплота превращения — это внутреннее свойство вещества, которое определяет энергию, необходимую для создания фазового перехода. Теплота плавления — постоянная теплоты превращения твердого тела в жидкое, а — теплота парообразования — постоянная теплоты превращения из жидкости в газ.
Теплота плавления — постоянная теплоты превращения твердого тела в жидкое, а — теплота парообразования — постоянная теплоты превращения из жидкости в газ.
Поскольку это свойства, присущие веществу, они будут меняться в зависимости от того, на какое вещество мы смотрим. Например, вода и алюминий имеют разную теплоту превращения, и эта информация будет предоставлена вам в отрывке, если она понадобится вам на экзамене.
в) ТеплопередачаМы говорили о нескольких различных свойствах тепла, а теперь поговорим о том, как именно тепло передается от одного объекта к другому. Теплопередача может происходить тремя способами:
1. Теплопроводность : прямая передача тепла через контакт и без движения объектов
2. Конвекция : передача тепла посредством движения жидкости или газ над другим объектом
3. Излучение : непрямой перенос тепла посредством электромагнитных волн, вызывающий , а не требуют, чтобы два объекта соприкасались
Рисунок: Различные формы теплопередачи. На этих диаграммах система a изначально горячая, а система b изначально холодная (не имеет тепла).
На этих диаграммах система a изначально горячая, а система b изначально холодная (не имеет тепла).
Давным-давно исследователи сделали интересное наблюдение: изменение температуры твердых тел может изменить их длину. Твердые объекты имеют тенденцию увеличиваться в длину при нагревании, и чтобы проиллюстрировать это на примере, давайте посмотрим на железные дороги. Из-за теплового расширения железные дороги должны иметь «пространство для маневра», чтобы железные дороги не изгибались и не перегибались, когда солнце выходит.
Формула теплового расширения:
$$\Delta L = \alpha \times L \times \Delta T$$ $$\mbox{где }\Delta L \mbox{ = изменение длины,}$$ $$\alpha \mbox{ = коэффициент линейного расширения,}$$ $$L \mbox{ = длина,}$$ $$\Delta T\mbox{ = изменение температуры}$$
Из уравнения видно, что увеличение температуры вызывает увеличение длины, а снижение температуры вызывает уменьшение длины.
Коэффициент линейного расширения — константа, присущая конкретному материалу. В результате вам не нужно запоминать это значение, и оно будет дано вам в день теста. То же уравнение можно использовать для объемного расширения, но длину «L» заменить на объем «V», а коэффициент линейного расширения заменить на коэффициент объемного расширения .
Часть 3: Четыре закона термодинамики а) Нулевой закон термодинамикиНулевой закон термодинамики утверждает, что когда два объекта находятся в тепловом равновесии с третьим объектом, исходные два объекта находятся в тепловом равновесии друг с другом. Давайте посмотрим, что это означает на простой диаграмме:
Рис. Нулевой закон термодинамики
При тепловом равновесии температуры объектов будут одинаковыми, и не будет чистого теплообмена между тремя объектами.
Первый закон термодинамики лучше всего представлен следующим уравнением:
$$\Дельта U = Q-W$$ $$\mbox{где }\Delta U \mbox{ = изменение внутренней энергии системы,}$$ $$Q \mbox{ = количество тепла, добавленное в систему,}$$ $$W \mbox{ = работа, проделанная системой}$$
∆U пропорционально температуре объекта, поэтому увеличение ∆U означает, что температура объекта увеличивается. Если Q положителен, тепло поступает в систему. Если W положительно, система совершает работу над окружающей средой.
Если ∆U отрицательное, температура объекта снижается. Если Q отрицательно, тепло уходит из системы. Если W отрицательно, то окружение совершает работу над системой.
c) Второй закон термодинамики Второй закон термодинамики утверждает, что общая энтропия изолированной системы (мы дадим определение этому термину в следующем разделе) не может уменьшаться со временем. Прежде чем мы рассмотрим пример, давайте подумаем об энтропии. Энтропия утверждает, что энергия со временем распределяется, и мы можем думать об энтропии как о движении к неупорядоченному состоянию. Чем больше энтропия, тем больше неупорядоченность энергии.
Прежде чем мы рассмотрим пример, давайте подумаем об энтропии. Энтропия утверждает, что энергия со временем распределяется, и мы можем думать об энтропии как о движении к неупорядоченному состоянию. Чем больше энтропия, тем больше неупорядоченность энергии.
Давайте теперь рассмотрим пример. Представьте себе пляж как нашу изолированную систему. Если на пляже есть замок из песка, это состояние высокой или низкой энтропии? Замок из песка находится в состоянии с низкой энтропией , потому что песок находится в высокоупорядоченном состоянии.
Если бы мы просидели на пляже сто лет, возник бы спонтанно замок из песка? Возможно нет. Согласно нашему второму закону термодинамики, песок, вероятно, стал бы еще более рассредоточенным и не образовал бы упорядоченный замок из песка с низкой энтропией.
Рис. Второй закон термодинамики
Энтропия может быть описана следующим уравнением:
$$\Delta S = \frac{Q_{rev}}{T} $$ $$\mbox{где }\Delta S \mbox{ = изменение энтропии,}$$ $$Q_{об} \mbox{ = теплота, вводимая или теряемая в обратимом процессе,}$$ $$T \mbox{ = температура}$$
Мы можем видеть, что по мере увеличения тепла в системе увеличивается энтропия.
Энтропия также может быть описана вторым эквивалентным уравнением: 9J/_K$$ $$ln(W) \mbox{ = натуральный логарифм W}$$
В этом контексте W представляет не работу, а общее количество возможных микросостояний , которые система может адаптировать. Микросостояние относится к любой комбинации всех возможных ориентаций частиц в системе. Таким образом, поскольку количество микросостояний зависит от количества частиц в системе, энтропия системы имеет тенденцию к увеличению по мере добавления новых частиц.
Постоянная Больцмана, представленная цифрой k или k B — фундаментальная константа, используемая в нескольких термодинамических уравнениях. Хотя вам может не понадобиться запоминать точное количество этой константы, полезно понимать, что это определенная константа.
d) Третий закон термодинамики Третий закон термодинамики утверждает, что энтропия чистого кристаллического вещества при абсолютном нуле равна нулю. Если вы что-то уберете из этого закона, просто помните, что понижение температуры системы обычно уменьшают энтропию, поскольку молекулы менее способны двигаться.
Если вы что-то уберете из этого закона, просто помните, что понижение температуры системы обычно уменьшают энтропию, поскольку молекулы менее способны двигаться.
Термодинамические функции обычно описываются как функции состояния или пути.
Функции состояния — это свойства, которые не зависят от пути достижения значения и зависят только от текущего состояния системы. Примерами функций состояния являются масса, давление, температура, объем, свободная энергия Гиббса, энтальпия, энтропия и другие.
Функции пути зависят от пути достижения определенного значения. Примеры функций пути включают теплоту и работу.
b) Типы системСуществует три типа систем, с которыми вы можете столкнуться на MCAT: открытые, закрытые или изолированные.
Открытые системы могут обмениваться веществом и энергией с окружающей средой. Закрытые системы могут обмениваться с окружающей средой энергией, но не веществом. Изолированные системы не могут обмениваться ни энергией, ни веществом с окружающей средой.
Закрытые системы могут обмениваться с окружающей средой энергией, но не веществом. Изолированные системы не могут обмениваться ни энергией, ни веществом с окружающей средой.
Рис. Открытые, закрытые и изолированные системы
c) Типы процессовВ последнем разделе мы рассмотрим четыре термодинамических процесса, с которыми вы должны быть знакомы: изотермический, адиабатический, изоволюметрический и изобарический. В каждом из этих процессов (кроме одного) член первого закона термодинамики (помните: ∆U = Q – W) остается постоянным.
Изотермические процессы имеют постоянную температуру, и как мы обсуждали ранее, и поэтому ∆U = 0. В адиабатических процессах теплообмен не происходит и Q = 0. В изоволюметрических процессах объем не может измениться, работа не может быть совершена, и поэтому W = 0. Наконец, в изобарных процессах давление постоянно, но это не влияет на наше уравнение ∆U = Q – W.
Наконец, в изобарных процессах давление постоянно, но это не влияет на наше уравнение ∆U = Q – W.
Наиболее распространенным способом изображения этих процессов является диаграмма P-V , в котором давление отложено по оси ординат, а объем — по оси абсцисс. Для любой диаграммы P-V выполненная работа представляет собой площадь под кривой для процесса без обратной связи или площадь внутри петли для процесса с обратной связью.
Рисунок: Кривая давление-объем
Различные значения теплоемкости могут использоваться в различных контекстах в зависимости от того, допускается ли изменение давления или объема окружающей среды с течением времени. В общем случае удельная теплоемкость процесса, протекающего при постоянном давлении, обычно выше, чем удельная теплоемкость процесса, протекающего при постоянном объеме. Эти два значения обычно представлены c p (теплоемкость при постоянном давлении) и c v (теплоемкость при постоянном объеме).
Об авторе
получил высший балл MCAT (528) и многолетний опыт профессионального репетиторства, помогающий нашим ученикам максимизировать результаты тестов.
Часть 5: Термины и уравнения высокой доходностиПлавка : передача энергии на основе разницы температур между двумя объектами
Температура : мера средней энергии, обусловленная движением частиц в объекте
Теплоемкость: количество тепла, необходимое для повышения температуры тела. объекта на определенную единицу температуры
Удельная теплоемкость: количество тепла, необходимое для нагревания одного грамма объекта на один градус Кельвина (или Цельсия)
Фазовые превращения : переход между различными фазами вещества, например как из твердого в жидкое или из жидкого в газообразное
Диаграмма фазового перехода : диаграмма зависимости температуры от энергии для конкретной молекулы, которая показывает ее фазовые переходы
Теплота превращения : внутреннее свойство вещества, которое определяет энергию, необходимую для создания фазового перехода
Теплота плавления: константа теплоты превращения твердого тела в жидкое
Теплота парообразования : константа теплоты превращения жидкого состояния в газообразное
Теплопередача: передача тепла от одного объекта к другому посредством теплопроводности, конвекции или излучения теплоты за счет движения жидкости или газа над другим объектом
Излучение : косвенная передача тепла посредством электромагнитных волн, которая , а не требует, чтобы два объекта находились в контакте
Коэффициент линейного расширения : константа, присущая конкретному материалу, которая определяет, насколько он восприимчив к линейному расширению при повышении температуры
Коэффициент объемного расширения: константа, присущая конкретному материалу, которая определяет, насколько он восприимчив к объемному расширению при повышении температуры
Нулевой закон термодинамики : когда два объекта находятся в тепловом равновесии с третьим объектом, исходные два объекта находятся в тепловом равновесии друг с другом
Первый закон термодинамики : ∆U = Q – W
Второй закон термодинамики : полная энтропия изолированной системы не может уменьшаться со временем
Третий закон термодинамики: энтропия чистого кристалла вещество при абсолютном нуле равно нулю
Функции состояния : свойства, которые не имеют зависят от пути достижения значения и зависят только от текущего состояния системы
Функции пути : зависят от пути достижения определенного значения
Открытые системы: обмениваются веществом и энергией с окружающей средой
Закрытые системы : обмениваются с окружающей средой энергией, но не материей
Изолированные системы: не обмениваются ни энергией, ни веществом с окружающей средой
Изотермические процессы : постоянная температура и, следовательно, ∆U = 0
Адиабатические процессы : теплообмена нет и Q = 0
Изоволюметрические процессы: объем не может измениться, работа не может быть выполнена, поэтому W = 0
Изобарические процессы : давление постоянно
P-V диаграмма: а диаграмма, на которой давление отложено по оси ординат, а объем отложен по оси абсцисс, а проделанная работа представляет собой площадь под кривой для процесса без обратной связи или площадь внутри контура для процесса с обратной связью
Нагрев при изменении фазы: $$ q = m \times L$$ Тепловое расширение: $$\Delta L = \alpha \times L \times \Delta T$$ Объемное расширение: $$\Delta V = \beta \times V \times \Delta T$$ Первый закон термодинамики: $$\Delta U = Q- W $$ Энтропия: $$\Delta S= \frac{Q_{rev}}{T} $$
Часть 6: Практический отрывок по термодинамике (Примечание: информация в этом отрывке была создана с единственной целью представить отрывок в стиле MCAT и не должна толковаться как правдивая на самом деле. )
)
Исследователи изучают тепловое равновесие между клеточной цитоплазмой и различными органеллами на панели раковых стволовых клеток. Исследователи предполагают, что аберрации в этом тепловом равновесии могут вызывать злокачественные фенотипы, приводя к усилению регуляции белков клеточного стресса.
Исследователи разрабатывают эксперимент, в котором средние температуры трех органелл (митохондрий, аппарата Гольджи и шероховатого эндоплазматического ретикулума) измеряют и сравнивают со средними температурами цитоплазмы в раковых стволовых клетках и здоровых клетках человека. Для точного и точного получения этих значений используется микротермометр, и для каждого отдельного показания температура измеряется каждую секунду в течение шестидесяти секунд. Затем отдельные показания для каждой органеллы усредняются вместе, чтобы определить окончательное значение. Все различия были определены как статистически значимые.
Результаты этого эксперимента представлены в таблице 1:
| Средняя температура | Здоровые клетки | Раковые стволовые клетки |
|---|---|---|
После измерения температуры исследователи хотят проверить влияние измененных температур на объемы органелл, чтобы увидеть, может ли это частично объяснить фенотипические различия между раковыми стволовыми клетками и здоровыми клетками. Коэффициенты объемного расширения митохондрий, аппарата Гольджи и шероховатого эндоплазматического ретикулума составляют: 1,1 х 10 -3 К -1 , 1,4 х 10 -2 К -1 и 1,9 х 10 -3 К -1 . Исследователи предполагают, что различия в размерах могут привести к апоптозу.
Коэффициенты объемного расширения митохондрий, аппарата Гольджи и шероховатого эндоплазматического ретикулума составляют: 1,1 х 10 -3 К -1 , 1,4 х 10 -2 К -1 и 1,9 х 10 -3 К -1 . Исследователи предполагают, что различия в размерах могут привести к апоптозу.
В заключительном эксперименте исследователи измеряют давление и объем митохондрий в течение двух часов синтеза АТФ. Митохондрии поддерживаются при постоянной температуре на протяжении всего процесса.
Вопрос 1: Учитывая характеристику цитоплазмы как жидкости, какой тип теплообмена происходит между цитоплазмой и органеллами?
A) Конвекция
B) Радиация
C) Проводимость
D) Изоляция
Вопрос 2: Исследователи обнаруживают, что для постоянного повышения температуры и того же начального объема, который из следующих органалелов имеет наибольшее увеличение объема?
A) Митохондрии
B) Шероховатый эндоплазматический ретикулум
C) Цитоплазма
D) Аппарат Гольджи
Вопрос 3: Какой тип системы представляет собой нормальную сердечную клетку живого человека?
A) Закрытый
B) Открытый
C) Изолированный
D) Адиабатический
Вопрос о термодинамическом эксперименте какого типа?
A) Адиабатический
B) Изотермический
C) Изоволюметрический
D) Изобарическая
Вопрос 5: Исследователи строят замкнутую кривую зависимости давления от объема по результатам последнего эксперимента. Что из следующего лучше всего представляет площадь внутри кривой?
Что из следующего лучше всего представляет площадь внутри кривой?
A) Работа
B) Power
C) Энтропия
D) Энтальпия
Ответ Ключ для Термодинамики Практический отрывок1. Выбор ответа A является правильным. Конвекция — это тип теплопередачи, возникающий при движении жидкости или газа над другим объектом. В этом случае цитоплазма представляет собой жидкость, которая движется по органеллам, тем самым напрямую передавая тепло путем конвекции (верный вариант А). Излучение не является прямым и передается через электромагнитные волны. Поскольку цитоплазма и органеллы соприкасаются, излучение не является типом переноса тепла в этом случае (вариант B неверен). Проводимость — вид теплопередачи, возникающий при соприкосновении двух твердых тел, но цитоплазма которых жидкая (вариант В неверный). Изоляция не является одним из трех видов теплопередачи (выбор D неверен).
2. Вариант ответа D правильный. Уравнение объемного расширения имеет вид ∆V = β * V * ∆T, где V — объем, β — коэффициент объемного расширения, а T — температура. Здесь мы видим, что коэффициент объемного расширения и изменение объема прямо пропорциональны. Таким образом, при постоянном повышении температуры и начальном объеме ∆V зависит от β, и большее β приведет к большему увеличению. Аппарат Гольджи имеет наибольший коэффициент объемного расширения по пассажу (верный вариант D, неправильные варианты A, B и C).
Уравнение объемного расширения имеет вид ∆V = β * V * ∆T, где V — объем, β — коэффициент объемного расширения, а T — температура. Здесь мы видим, что коэффициент объемного расширения и изменение объема прямо пропорциональны. Таким образом, при постоянном повышении температуры и начальном объеме ∆V зависит от β, и большее β приведет к большему увеличению. Аппарат Гольджи имеет наибольший коэффициент объемного расширения по пассажу (верный вариант D, неправильные варианты A, B и C).
3. Вариант ответа B правильный. Все клетки могут обмениваться веществом и энергией с окружающей средой, что делает их примерами открытой системы (выбор B правильный, варианты A, C и D неверны).
4. Вариант ответа B правильный. Последний эксперимент описан в последнем абзаце отрывка, и в отрывке говорится, что температура поддерживается постоянной. В изотермических процессах температура поддерживается постоянной (выбор B правильный, варианты A, C и D неверны).
5. Вариант ответа A правильный. Площадь внутри замкнутого процесса на кривой давление-объем равна выполненной работе (выбор A правильный, варианты B, C и D неверны).
Часть 7: Практические задачи по термодинамике и ответыВопрос 1: Что из следующего лучше всего описывает второй закон термодинамики?
A) Объекты в движении имеют тенденцию оставаться в движении
B) Энергия не может быть создана или уничтожена
C) Энтропия увеличивается со временем
D) Энтропия идеального кристалла при абсолютном нуле равна нулю
Вопрос 2: Актиновую нить можно смоделировать как линейный стержень. Исследователи определили коэффициент линейного расширения для актина как 1,8 x 10 -1 K -1 . Как увеличится длина актиновой нити длиной 10 мм, если температура клетки повысится на 2 градуса Кельвина?
A) 1,05 мм
B) 21,9мм
C) 3,60 мм
D) 36,0 мм
Вопрос 3: Два твердых тела с разными начальными температурами соприкасаются друг с другом и достигают теплового равновесия. Процесс, который производит эту форму теплопередачи:
Процесс, который производит эту форму теплопередачи:
A) Кондукция
B) Конвекция
C) Излучение
D) Производство
Вопрос 4: Какая из следующих функций не является 9004?
A) Теплота
B) Объем
C) Свободная энергия Гиббса
D) Энтальпия
A больше, чем средняя кинетическая энергия частиц в объекте B. Какое из следующих свойств больше в объекте A?
A) Объем
B) Температура
C) Энтальпия
D) Свободная энергия Гиббса
Ключ к ответу на практическое занятие по термодинамике 1. Вариант ответа C правильный. Второй закон термодинамики обсуждает энтропию и утверждает, что энтропия увеличивается со временем, если только не действуют ограничительные силы (верный вариант C). Вариант А — первый закон Ньютона. Вариант B описывает закон сохранения энергии. Вариант D описывает третий закон термодинамики.
Вариант D описывает третий закон термодинамики.
2. Вариант ответа C правильный. Формула линейного расширения: ∆L = α * L * ∆T, поэтому все, что нам нужно сделать, это подставить числа и найти ∆L, то есть увеличение длины. Так как на экзамене у вас не будет калькулятора, мы можем применить несколько простых трюков. Во-первых, посмотрите на варианты ответов. Поскольку все варианты ответов даны в миллиметрах, , вам не нужно беспокоиться об экспоненциальном представлении в этой задаче. Итак, мы упростили наш расчет до ∆L = 0,18 * 10 * 2. Все, что нам нужно сделать, это приблизительно определить приблизительные значащие цифры, которые появятся в нашем ответе. 10 * 2 равно 20, и мы знаем, что 20 * 0,18 немного меньше, чем 4 при 3,6 (вариант C правильный, варианты A, B и D неверны).
3. Вариант ответа A правильный. Теплопроводность возникает, когда два твердых тела соприкасаются друг с другом и передают тепло (верный вариант А).

 0221415(10)·1023 моль-1
0221415(10)·1023 моль-1


 Если система (тело) получает энергию, то ΔQ системы > 0, если отдает энергию, то ΔQ системы < 0
Если система (тело) получает энергию, то ΔQ системы > 0, если отдает энергию, то ΔQ системы < 0
 При охлаждении – внутренняя энергия уменьшается за счет передачи тепла окружающей среде.
При охлаждении – внутренняя энергия уменьшается за счет передачи тепла окружающей среде.

 Введите свой запрос:
Введите свой запрос:


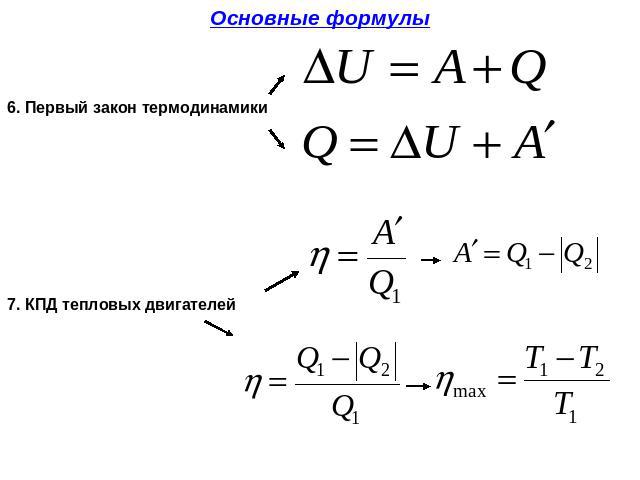

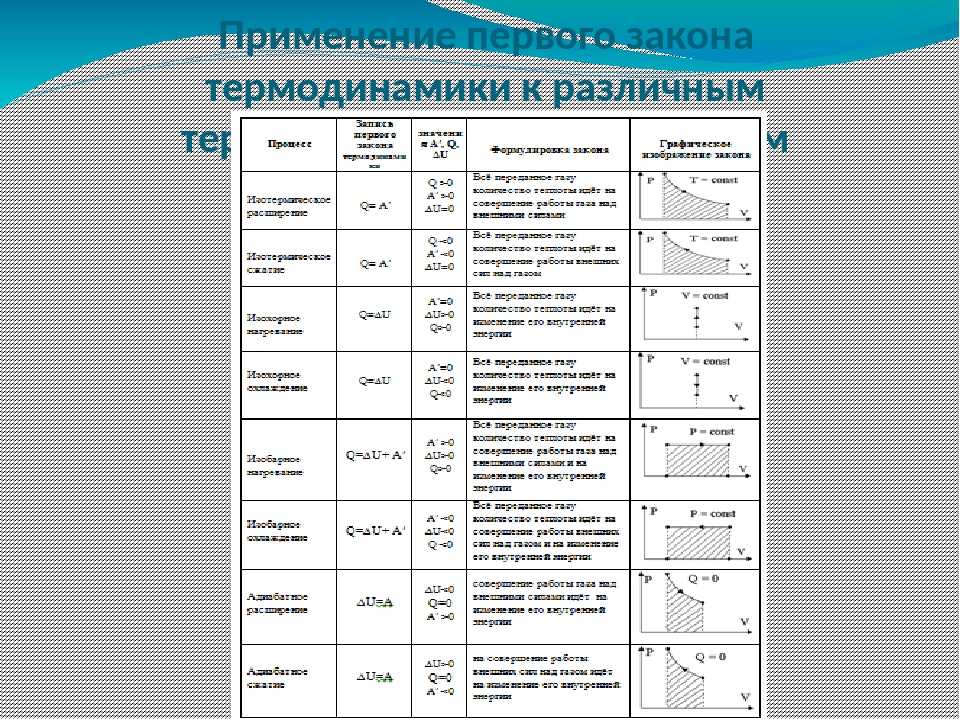
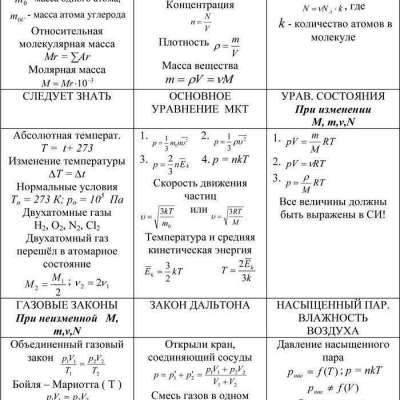

 внутрь.
внутрь.