просто и понятно о его применении в физике
ОпределениеОпределение
Простая формулировка первого закона термодинамики может звучать примерно так: изменение внутренней энергии той или иной системы возможно исключительно при внешнем воздействии. То есть другими словами, чтобы в системе произошли какие-то изменения необходимо приложить определенные усилия извне. В народной мудрости своеобразным выражением первого закона термодинамики могут служить пословицы – «под лежачий камень вода не течет», «без труда не вытащишь рыбку из пруда» и прочая. То есть на примере пословицы про рыбку и труд, можно представить, что рыбка и есть наша условно закрытая система, в ней не произойдет никаких изменений (рыбка сама себя не вытащит из пруда) без нашего внешнего воздействия и участия (труда).
Интересный факт: именно первый закон термодинамики устанавливает, почему потерпели неудачу все многочисленные попытки ученых, исследователей, изобретателей изобрести «вечный двигатель», ведь его существование является абсолютно невозможным согласно этому самому закону, почему, смотрите абзац выше.
В начале нашей статьи было максимального простое определение первого закона термодинамики, в действительности в академической науке существует целых четыре формулировки сути данного закона:
- Энергия ни откуда не появляется и ни куда не пропадает, она лишь переходит из одного вида в другой (закон сохранения энергии).
- Количество теплоты, полученной системой, идет на совершение ее работы против внешних сил и изменение внутренней энергии.
- Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданной системе, и не зависит от способа, которым осуществляется этот переход.
- Изменение внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты, переданной системе, и работой, совершенной системой над внешними силами.
Формула
Формулу первого закона термодинамики можно записать таким образом:
Q = ΔU + A
Количество теплоты Q, передаваемое системе равно суме изменения ее внутренней энергии ΔU и работы A.
Процессы
Также первый закон термодинамики имеет свои нюансы в зависимости от проходящих термодинамических процессов, которые могут быть изохронными и изобарными, и ниже мы детально опишем о каждом из них.
Закон для для изохорного процесса
Изохорным процессом в термодинамике называют процесс, происходящий при постоянном объеме. То есть, если будь-то в газе или жидкости нагреть вещество в сосуде, произойдет изохорный процесс, так как объем вещества останется неизменным. Это условие имеет влияние и на первый закон термодинамики, проходящий при изохорном процессе.
В изохорном процессе объем V является константой, следовательно, газ работы не совершает A = 0
Из этого выходит следующая формула:
Q = ΔU = U (T2) – U (T1).
Здесь U (T1) и U (T2) – внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит только от температуры (закон Джоуля). При изохорном нагревании тепло поглощается газом (Q > 0), и его внутренняя энергия увеличивается. При охлаждении тепло отдается внешним телам (Q < 0).
При охлаждении тепло отдается внешним телам (Q < 0).
Закон для для изобарного процесса
Аналогично изобарным процессом называется термодинамический процесс, происходящий в системе при постоянном давлении и массе газа. Следовательно, в изобарном процессе (p = const) работа, совершаемая газом, выражается следующим уравнением первого закона термодинамики:
A = p (V2 – V1) = p ΔV.
Изобарный первый закон термодинамики дает:
Q = U (T2) – U (T1) + p (V2 – V1) = ΔU + p ΔV. При изобарном расширении Q > 0 – тепло поглощается газом, и газ совершает положительную работу. При изобарном сжатии Q < 0 – тепло отдается внешним телам. В этом случае A < 0. Температура газа при изобарном сжатии уменьшается, T2 < T1; внутренняя энергия убывает, ΔU < 0.
Практическое применение
Первый закон термодинамике имеет практическое применение к различным процессам в физике, например, позволяет вычислить идеальные параметры газа при разнообразных тепловых и механических процессах.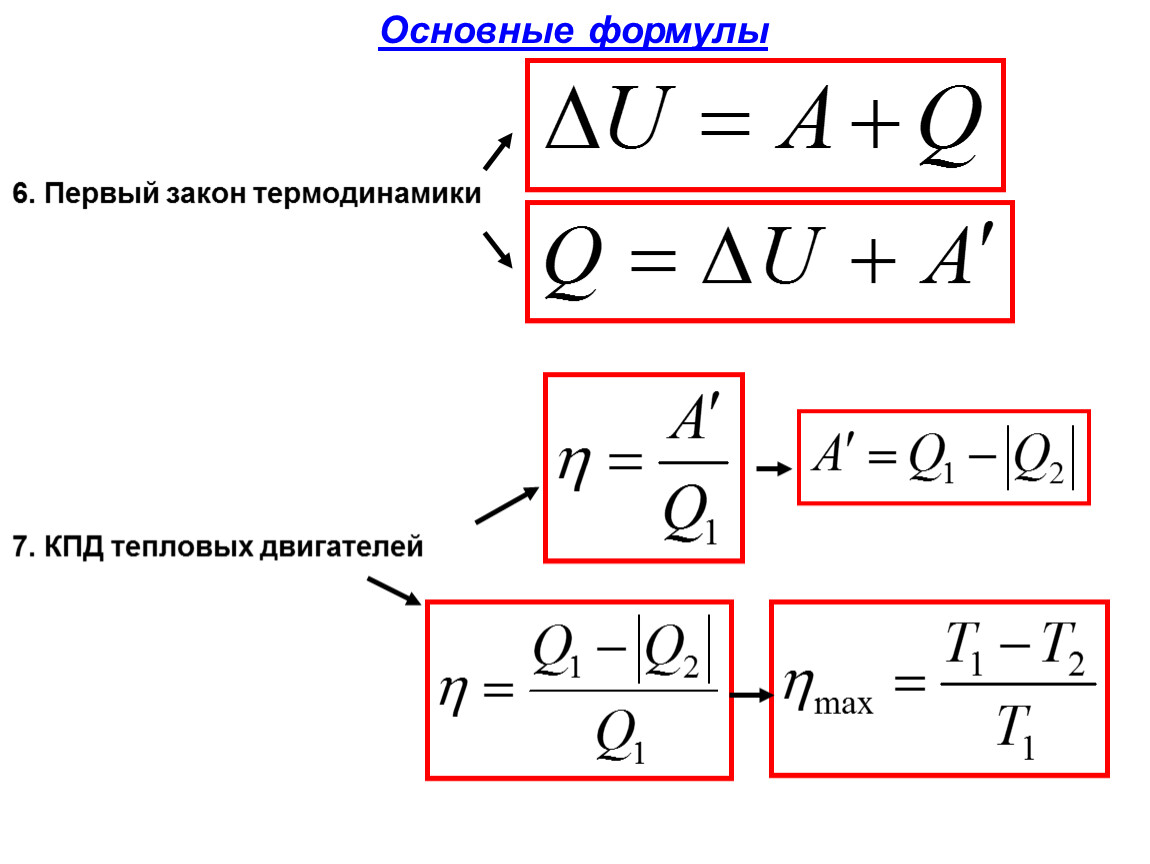
Видео
И в завершение нашей статьи вашему вниманию образовательное видео о первом законе термодинамике и внутренней энергии.
Автор: Павел Чайка, главный редактор журнала Познавайка
При написании статьи старался сделать ее максимально интересной, полезной и качественной. Буду благодарен за любую обратную связь и конструктивную критику в виде комментариев к статье. Также Ваше пожелание/вопрос/предложение можете написать на мою почту pavelchaika1983@gmail. com или в Фейсбук, с уважением автор.
com или в Фейсбук, с уважением автор.
Эта статья доступна на английском – First Law of Thermodynamics.
| Обозначение | Название величины | Размерность / Значение | Формула |
|---|---|---|---|
| Абсолютная температура | K | ||
| [4] | Давление | Па | |
| Объём | м³ | ||
| Средняя энергия молекулы | Дж | ||
| Средняя кинетическая энергия молекулы | Дж | ||
| Масса | кг | ||
| [5] | Молярная масса | кг/моль | |
| Постоянная Авогадро | 6. 0221415(10)·1023 моль-1 0221415(10)·1023 моль-1 | ||
| Постоянная Больцмана | 1.3806505(24)·10−23 Дж/К | ||
| Газовая постоянная | 8.314472(15) Дж/(К·моль) | ||
| Число степеней свободы молекулы | – | ||
| Количество вещества в -й компоненте -компонентной смеси | моль | ||
| вектор с координатами | моль | ||
| Химический потенциал -й компоненты -компонентной смеси | Дж/моль | ||
| Внутренняя энергия | Дж | ||
| Энтропия | Дж/К | ||
| Энтальпия | Дж | ||
[6] | Изохорно-изотермический потенциал (свободная энергия Гельмгольца) | Дж | |
| Изобарно-изотермический потенциал (свободная энергия Гиббса, свободная энтальпия) | Дж | ||
| Работа, совершённая газом | Дж | ||
| Тепло, переданное газу | Дж | ||
| Молярная теплоёмкость газа при постоянном давлении | Дж/(К·моль) | ||
| Молярная теплоёмкость газа при постоянном объёме | Дж/(К·моль) | ||
| Удельная теплоёмкость | Дж/(К·кг) | ||
| Показатель адиабаты | – |
К.
 А. ПУТИЛОВ – ТЕРМОДИНАМИКА. К.А. ПУТИЛОВ – ТЕРМОДИНАМИКА.
А. ПУТИЛОВ – ТЕРМОДИНАМИКА. К.А. ПУТИЛОВ – ТЕРМОДИНАМИКА.
Предисловие. От редактора
Введение. Термодинамика. Термодинамика и статистика. Методы изложения термодинамики
Глава 1. Предварительные сведения
1.1. Предмет термодинамики
1.2. Понятия «тело» и «фаза» в термодинамике
1.3. Простейшие параметры: масса, объем, давление
1.4. Работа расширения
1.5. Тепловое равновесие и температура
1.6. Термодинамика идеальных газов
1.7. Уравнение Ван-дер-Ваальса
1.8. Уравнения Дитеричи, Бертело, Камерлинг-Оннеса
Глава 2. Первое начало термодинамики. Теплота и работа
2.1. Дискуссии о первом начале
Дискуссии о первом начале
2.2. Шесть формулировок первого начала
2.3. Различные трактовки понятия тепла
2.4. Историческая справка
2.5. Статистическая интерпретация тепла
2.6. Теплота и работа
2.7. Классификация видов энергии
2.8. Внутренняя энергия
Глава 3. Второе начало термодинамики
Второе начало
3.1. Понятие о компенсации и шесть простейших формулировок второго начала
3.2. Цикл Карно
3.3.Рассуждение Клаузиуса о двух сопряженных машинах Карно
3.4. Коэффициент полезного действия любого обратимого цикла
3.5. Энтропия как сумма приведенных теплот. Аналитические формулировки второго начала
3.6. О проблеме термодинамических неравенств
3.7. Обратимые и необратимые процессы
3. 8. Равновесные и неравновесные процессы
8. Равновесные и неравновесные процессы
3.10. Уравнение и неравенство Клаузиуса
3.11. Теорема о возрастании энтропии
3.12. Два признака необратимости процесса
3.13. Второе начало в трактовке Клаузиуса
3.14. Второе начало в трактовке Больцмана
3.15. Принцип положительной работы
Логическое развитие второго начала. Теоремы о существовании энтропии и абсолютной температуры
3.16. О термодинамической аксиоматике
3.17. Теорема о существовании энтропии
3.18. Связанная энергия и абсолютная температура
3.19. Теорема об элементе тепла
Логическое развитие второго начала. Принципы, определяющие направление самопроизвольных процессов.
3.20. Квазистатические процессы
3. 21. Термодинамическая неравновесность лабильных состояний
21. Термодинамическая неравновесность лабильных состояний
3.22. Максимальная работа как условие равновесности процесса
3.23. Принцип максимальной работы и принцип положительной работы в формулировках Вертело и Нернста
3.24. Принцип максимальной работы и принцип положительной работы для термостатных процессов
3.25. Квазиравновесные процессы
3.26. Принцип максимальной и принцип положительной работы для адиабатных процессов
Глава 4. Термодинамические величины и соотношения между ними
4.1. Некоторые частные производные от
4.2. Уравнение Клапейрона — Клаузиуса, уравнение Томсона и простейшие формулы для равновесия фаз
4.3. Уравнение для элемента теплоты и формулы для теплоемкрстей и адиабатных производных
4. 4. Вспомогательные таблицы термодинамических формул
4. Вспомогательные таблицы термодинамических формул
4.5. Некоторые формулы для вторых производных
4.6. Классификация термодинамических величин
4.7. Обобщенное уравнение Клапейрона — Клаузиуса и закон взаимности
Глава 5. Статистические методы в термодинамике
Статистический смысл второго начала
5.1. Термодинамическая вероятность состояния
5.2. Смысл больцмановской формулировки второго начала
5.3. Флуктуации
5.4. Определение термодинамической вероятности по методам Больцмана, Бозе — Эйнштейна и Ферми — Дирака
5.5. Метод Гиббса
5.6. Опровержение ложной концепции тепловой смерти мира
Статистический метод вычисления энтропии и других термодинамических величин. Квантовая теория твердых тел.
5.7. Вывод формулы для энтропии
5. 8. Вывод е-теоремы Больцмана
8. Вывод е-теоремы Больцмана
5.9. Сумма состояний и формулы, выражающие энтропию и свободную энергию через сумму состояний
5.10. Обобщение основных формул на случай вырождения
5.11. Сумма состояний по энергетическим уровням системы
5.12. Эйнштейнова теория твердых тел
5.13. Дебаевская теория твердых тел
5.14. Обсуждение дебаевской теории твердых тел
Квантовая и квазиклассическая теория газов
5.15. Расчленение энергии и энтропии газов на составляющие
5.16. Составляющие энергии и энтропии, зависящие от поступательного движения молекул
5.17. Методы экспериментального исследования энергетических уровней вращения молекул, колебания ядер и электронного состояния молекул
5.18. Энергетические уровни вращения молекул и колебания ядер
5. 19. Вычисление составляющих энергии и энтропии, зависящих
от вращения молекул и колебания атомных ядер
19. Вычисление составляющих энергии и энтропии, зависящих
от вращения молекул и колебания атомных ядер
5.20. Составляющие энергии и энтропии, зависящие от электронного состояния молекул
5.21. Квазиклассическая теория газов
5.22. Квазиклассические формулы энтропии газов и химические постоянные
5.22. (Продолжение) Функции Энштейна и Дебая
Глава 6. Тепловой закон Нернста и эмпирическое вычисление энтропии и свободной энергии
6.1. Физический смысл закона Нернста
6.2. Вычисление энтропии на основе закона Нернста и некоторые следствия закона Нернста
6.3. Вычисление полного термодинамического потенциала (и свободной энергии) на основе закона Нернста
6.4. Формула Нернста для давления насыщенного пара
6. 5. Эмпирическое вычисление энтропийных и химических
констант и физический смысл этих величин
5. Эмпирическое вычисление энтропийных и химических
констант и физический смысл этих величин
6.6. Принцип термодинамической допустимости и связь эмпирического и теоретического способов вычисления химических постоянных
Глава 7. Теория термодинамических потенциалов
Термодинамические потенциалы
7.1. Основы теории
7.2. Физический смысл термодинамического потенциала
7.3. Гиббсовские критерии равновесия
7.4. Выводы закона термодинамического равновесия из принципа максимальной работы
7.5. О понятии самопроизвольности процесса
7.6. Вывод общей формулы термодинамических потенциалов
7.7. Анализ общей формулы, определяющей термодинамические потенциалы. Четыре потенциала Гиббса
7.8. Полные термодинамические потенциалы активированных систем
7. 9. Примеры термодинамических потенциалов пассивных
систем
9. Примеры термодинамических потенциалов пассивных
систем
7.10. Закон обратимого процесса и метод вычисления максимальной работы
Парциальные величины и химические потенциалы
7.11. Некоторые замечания, касающиеся обоснования теории термодинамических потенциалов в книге Ван Лаара
7.12. Парциальные величины
7.13. К проблеме аддитивности в термодинамике
7.14. Обоснованней анализ основного уравнения химической термодинамики
7.15. Фазовое равновесие
7.16. Мольные и удельные химические потенциалы
7.17. Фундаментальные уравнения теории термодинамических потенциалов
7.18. Мольнодолевые химические потенциалы
7.19. О замене масс компонентов объемными концентрациями
7.20. Уравнения Гиббса — Гельмгольца и Клапейрона — Клаузиуса
7. 21. Фазовые равновесия и уравнение Гиббса
— Дюгема
21. Фазовые равновесия и уравнение Гиббса
— Дюгема
7.22. Законы смещения обратимых процессов. Уточненная формулировка неравенств («принципа») Ле Шателье — Брауна
7.23. Химический потенциал идеального газа. Обобщение формул для смеси газов, для идеальных растворов и для реальных веществ. Теоремы Гиббса об аддитивности и об энтропии смешения
Глава 8. Метод подобия в термодинамике
8.1. О связи теории соответственных состояний с некоторыми уравнениями состояния реальных газов
8.2. О проверке законов соответственных состояний
8.3. Дальнейшая проверка теории и попытки ее усовершенствования
8.4. Последующее развитие теории соответственных состояний
8.5. Заключение из сделанного обзора
8. 6. Условия термодинамического подобия
6. Условия термодинамического подобия
8.7. О подобии в дебаевской области
Глава 9. Термодинамика химических реакций
9.1. О возможных формах изложения. Принятые термины и обозначения
9.2. Формула Кирхгофа и некоторые эмпирические соотношения для тепло-емкостей
9.3. Изотермическая теплота и изотермическая работа реакции
9.4. Зависимость химического сродства от температуры
9.5. Формула Кирхгофа для изотермической теплоты
9.6. О равновесном осуществлении реакций
9.7. Ящик Вант-Гоффа и уравнение изотермы реакции
9.8. Закон действующих масс и константа равновесия
9.9. Обобщенная форма закона действующих масс
9.10. Уравнения Вант-Гоффа для изобары и изохоры реакций и адиабаты реакций
9. 11. Гетерогенные реакции
11. Гетерогенные реакции
9.12. Вычисление константы равновесия и полноты реакций
9.13. О применении точных статистических и приближенных практических методов расчета
Глава 10. Летучесть и активность
10.1. Летучесть
10.2. Методы вычисления летучести
10.3. Летучесть и термодинамические соотношения, аналогичные е-теореме Больцмана
10.4. Активность
10.5. Методы вычисления активности
10.6. Коэффициенты активности для разных шкал концентраций
10.7. Коэффициенты активности ионов
10.8. Вычисление коэффициентов активности ионов по формулам теории электролитов
Литература
На главную страницу | Теоретическая физика
Используются технологии uCozТермодинамика газа формулы.
 Законы термодинамики и их описание. Идеальный тепловой двигаель. Цикл Карно
Законы термодинамики и их описание. Идеальный тепловой двигаель. Цикл КарноТермодинамика (греч. θέρμη – «тепло», δύναμις – «сила») – раздел физики, изучающий наиболее общие свойства макроскопических систем и способы передачи и превращения энергии в таких системах.
В термодинамике изучаются состояния и процессы, для описания которых можно ввести понятие температуры. Термодинамика (Т.) – это феноменологическая наука, опирающаяся на обобщения опытных фактов. Процессы, происходящие в термодинамических системах, описываются макроскопическими величинами (температура, давление, концентрации компонентов), которые вводятся для описания систем, состоящих из большого числа частиц, и не применимы к отдельным молекулам и атомам, в отличие, например, от величин, вводимых в механике или электродинамике.
Современная феноменологическая термодинамика является строгой теорией, развиваемой на основе нескольких постулатов. Однако связь этих постулатов со свойствами и законами взаимодействия частиц, из которых построены термодинамические системы, даётся статистической физикой. Статистическая физика позволяет выяснить также и границы применимости термодинамики.
Статистическая физика позволяет выяснить также и границы применимости термодинамики.
Законы термодинамики носят общий характер и не зависят от конкретных деталей строения вещества на атомарном уровне. Поэтому термодинамика успешно применяется в широком круге вопросов науки и техники, таких как энергетика, теплотехника, фазовые переходы, химические реакции, явления переноса и даже чёрные дыры. Термодинамика имеет важное значение для самых разных областей физики и химии, химической технологии, аэрокосмической техники, машиностроения, клеточной биологии, биомедицинской инженерии, материаловедения и находит своё применение даже в таких областях, как экономика.
Важные годы в истории термодинамики
- Зарождение термодинамики как науки связано с именем Г. Галилея (G. Galilei), корый ввёл понятие температуры и сконструировал первый прибор, реагирующий на изменения температуры окружающей среды (1597).
- Вскоре Г. Д. Фаренгейт (G. D. Fahrenheit, 1714), Р. Реомюр (R.
 Reaumur, 1730} и А. Цельсий (A. Celsius, 1742) создали температурные шкалы в соответствии с этим принципом.
Reaumur, 1730} и А. Цельсий (A. Celsius, 1742) создали температурные шкалы в соответствии с этим принципом. - Дж.Блэк (J. Black) в 1757 году уже ввёл понятия скрытой теплоты плавления и теплоемкости (1770). А Вильке (J. Wilcke, 1772) ввёл определение калории как количества тепла, необходимого для нагревания 1 г воды на 1 °С.
- Лавуазье (A. Lavoisier) и Лаплас (P. Laplace) в 1780 сконструировали калориметр (см. Калориметрия) и впервые экспериментально определили уд. теплоёмкости ряда веществ.
- В 1824 С. Карно (N. L, S. Carnot) опубликовал работу, посвящённую исследованию принципов работы тепловых двигателей.
- Б. Клапейрон (В. Clapeyron) ввёл графическое представление термодинамических процессов и развил метод бесконечно малых циклов (1834).
- Г. Хельмгольц (G. Helmholtz) отметил универсальный характер закона сохранения энергии (1847). Впоследствии Р. Клаузиус (R. Clausius) и У. Томсон (Кельвин; W. Thomson) систематически развили теоретический аппарат термодинамики, в основу которого положены первое начало термодинамики и второе начало термодинамики.

- Развитие 2-го начала привело Клаузиуса к определению энтропии (1854) и формулировке закона возрастания энтропии (1865).
- Начиная с работ Дж. У. Гиббса (J. W. Gibbs, 1873), предложившего метод термодинамических потенциалов, развивается теория термодинамического равновесия.
- Во 2-й пол. 19 в. проводились исследования реальных газов. Особую роль сыграли эксперименты Т. Эндрюса (Т. Andrews), который впервые обнаружил критическую точку системы жидкость-пар (1861), её существование предсказал Д. И. Менделеев (1860).
- К концу 19 в. были достигнуты большие успехи в получении низких температур, в результате чего были ожижены О2, N2 и Н2.
- В 1902 Гиббс опубликовал работу, в которой все основные термодинамические соотношения были получены в рамках статистической физики.
- Связь между кинетич. свойствами тела и его термодинамич. характеристиками была установлена Л. Онсагером (L. Onsager, 1931).
- В 20 в. интенсивно исследовали термодинамику твёрдых тел, а также квантовых жидкостей и жидких кристаллов, в которых имеют место многообразные фазовые переходы.

- Л. Д. Ландау (1935-37) развил общую теорию фазовых переходов, основанную на концепции спонтанного нарушения симметрии.
Разделы термодинамики
Современную феноменологическую термодинамику принято делить на равновесную (или классическую) термодинамику, изучающую равновесные термодинамические системы и процессы в таких системах, и неравновесную термодинамику, изучающую неравновесные процессы в системах, в которых отклонение от термодинамического равновесия относительно невелико и ещё допускает термодинамическое описание.
Равновесная (или классическая) термодинамика
В равновесной термодинамике вводятся такие переменные, как внутренняя энергия, температура, энтропия, химический потенциал. Все они носят название термодинамических параметров (величин). Классическая термодинамика изучает связи термодинамических параметров между собой и с физическими величинами, вводимыми в рассмотрение в других разделах физики, например, с гравитационным или электромагнитным полем, действующим на систему.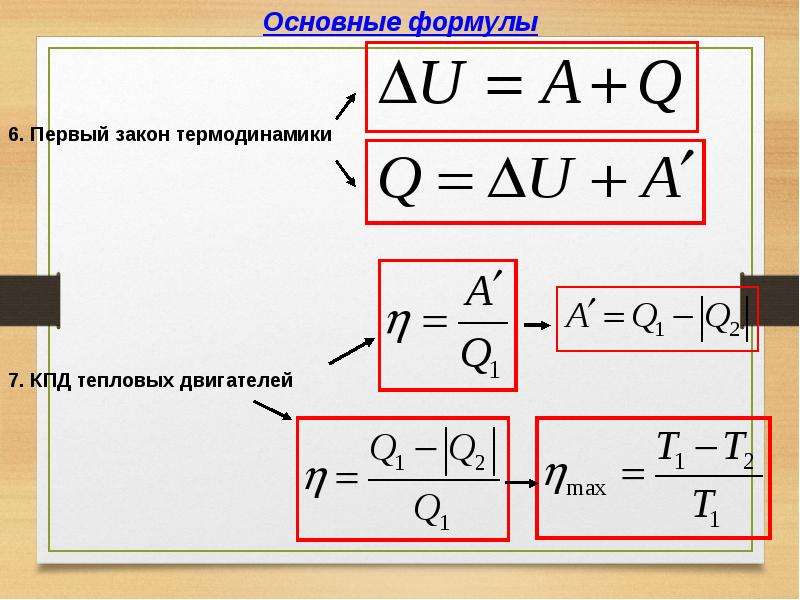 Химические реакции и фазовые переходы также входят в предмет изучения классической термодинамики. Однако изучение термодинамических систем, в которых существенную роль играют химические превращения, составляет предмет химической термодинамики, а техническими приложениями занимается теплотехника.
Химические реакции и фазовые переходы также входят в предмет изучения классической термодинамики. Однако изучение термодинамических систем, в которых существенную роль играют химические превращения, составляет предмет химической термодинамики, а техническими приложениями занимается теплотехника.
Классическая термодинамика включает в себя следующие разделы:
- начала термодинамики (иногда также называемые законами или аксиомами)
- уравнения состояния и свойства простых термодинамических систем (идеальный газ, реальный газ, диэлектрики и магнетики и т. д.)
- равновесные процессы с простыми системами, термодинамические циклы
- неравновесные процессы и закон неубывания энтропии
- термодинамические фазы и фазовые переходы
Кроме этого, современная термодинамика включает также следующие направления:
- строгая математическая формулировка термодинамики на основе выпуклого анализа
- неэкстенсивная термодинамика
В системах, не находящихся в состоянии термодинамического равновесия, например, в движущемся газе, может применяться приближение локального равновесия, в котором считается, что соотношения равновесной термодинамики выполняются локально в каждой точке системы.
Неравновесная термодинамика
В неравновесной термодинамике переменные рассматриваются как локальные не только в пространстве, но и во времени, то есть в её формулы время может входить в явном виде. Отметим, что посвящённая вопросам теплопроводности классическая работа Фурье «Аналитическая теория тепла» (1822) опередила не только появление неравновесной термодинамики, но и работу Карно «Размышления о движущей силе огня и о машинах, способных развивать эту силу» (1824), которую принято считать точкой отсчёта в истории классической термодинамики.
Основные понятия термодинамики
Термодинамическая система – тело или группа тел, находящихся во взаимодействии, мысленно или реально обособленные от окружающей среды.
Гомогенная система – система, внутри которой нет поверхностей, разделяющих отличающиеся по свойствам части системы (фазы).
Гетерогенная система – система, внутри которой присутствуют поверхности, разделяющие отличающиеся по свойствам части системы.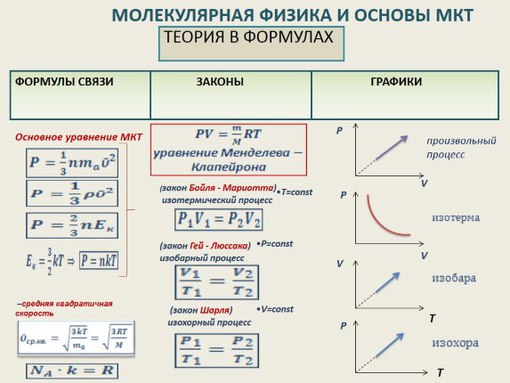
Фаза – совокупность гомогенных частей гетерогенной системы, одинаковых по физическим и химическим свойствам, отделённая от других частей системы видимыми поверхностями раздела.
Изолированная система – система, которая не обменивается с окружающей средой ни веществом, ни энергией.
Закрытая система – система, которая обменивается с окружающей средой энергией, но не обменивается веществом.
Открытая система – система, которая обменивается с окружающей средой и веществом, и энергией.
Совокупность всех физических и химических свойств системы характеризует её термодинамическое состояние . Все величины, характеризующие какое-либо макроскопическое свойство рассматриваемой системы – параметры состояния . Опытным путем установлено, что для однозначной характеристики данной системы необходимо использовать некоторое число параметров, называемых независимыми ; все остальные параметры рассматриваются как функции независимых параметров. В качестве независимых параметров состояния обычно выбирают параметры, поддающиеся непосредственному измерению, например температуру, давление, концентрацию и т.д. Всякое изменение термодинамического состояния системы (изменения хотя бы одного параметра состояния) есть термодинамический процесс .
В качестве независимых параметров состояния обычно выбирают параметры, поддающиеся непосредственному измерению, например температуру, давление, концентрацию и т.д. Всякое изменение термодинамического состояния системы (изменения хотя бы одного параметра состояния) есть термодинамический процесс .
Обратимый процесс – процесс, допускающий возможность возвращения системы в исходное состояние без того, чтобы в окружающей среде остались какие-либо изменения.
Равновесный процесс – процесс, при котором система проходит через непрерывный ряд равновесных состояний.
Энергия – мера способности системы совершать работу; общая качественная мера движения и взаимодействия материи. Энергия является неотъемлемым свойством материи. Различают потенциальную энергию, обусловленную положением тела в поле некоторых сил, и кинетическую энергию, обусловленную изменением положения тела в пространстве.
Внутренняя энергия системы – сумма кинетической и потенциальной энергии всех частиц, составляющих систему. Можно также определить внутреннюю энергию системы как её полную энергию за вычетом кинетической и потенциальной энергии системы как целого.
Можно также определить внутреннюю энергию системы как её полную энергию за вычетом кинетической и потенциальной энергии системы как целого.
Формы перехода энергии
Формы перехода энергии от одной системы к другой могут быть разбиты на две группы.
- В первую группу входит только одна форма перехода движения путем хаотических столкновений молекул двух соприкасающихся тел, т.е. путём теплопроводности (и одновременно путём излучения). Мерой передаваемого таким способом движения является теплота. Теплота есть форма передачи энергии путём неупорядоченного движения молекул.
- Во вторую группу включаются различные формы перехода движения, общей чертой которых является перемещение масс, охватывающих очень большие числа молекул (т.е. макроскопических масс), под действием каких-либо сил. Таковы поднятие тел в поле тяготения, переход некоторого количества электричества от большего электростатического потенциала к меньшему, расширение газа, находящегося под давлением и др.
 Общей мерой передаваемого такими способами движения является работа – форма передачи энергии путём упорядоченного движения частиц.
Общей мерой передаваемого такими способами движения является работа – форма передачи энергии путём упорядоченного движения частиц.
Теплота и работа характеризуют качественно и количественно две различные формы передачи движения от данной части материального мира к другой. Теплота и работа не могут содержаться в теле. Теплота и работа возникают только тогда, когда возникает процесс, и характеризуют только процесс. В статических условиях теплота и работа не существуют. Различие между теплотой и работой, принимаемое термодинамикой как исходное положение, и противопоставление теплоты работе имеет смысл только для тел, состоящих из множества молекул, т.к. для одной молекулы или для совокупности немногих молекул понятия теплоты и работы теряют смысл. Поэтому термодинамика рассматривает лишь тела, состоящие из большого числа молекул, т.е. так называемые макроскопические системы.
Три начала термодинамики
Начала термодинамики – совокупность постулатов, лежащих в основе термодинамики. Эти положения были установлены в результате научных исследований и были доказаны экспериментально. В качестве постулатов они принимаются для того, чтобы термодинамику можно было построить аксиоматически.
Эти положения были установлены в результате научных исследований и были доказаны экспериментально. В качестве постулатов они принимаются для того, чтобы термодинамику можно было построить аксиоматически.
Необходимость начал термодинамики связана с тем, что термодинамика описывает макроскопические параметры систем без конкретных предположений относительно их микроскопического устройства. Вопросами внутреннего устройства занимается статистическая физика.
Начала термодинамики независимы, то есть ни одно из них не может быть выведено из других начал. Аналогами трех законов Ньютона в механике, являются три начала в термодинамике, которые связывают понятия «тепло» и «работа»:
- Нулевое начало термодинамики говорит о термодинамическом равновесии.
- Первое начало термодинамики – о сохранении энергии.
- Второе начало термодинамики – о тепловых потоках.
- Третье начало термодинамики – о недостижимости абсолютного нуля.
Общее (нулевое) начало термодинамики
Общее (нулевое) начало термодинамики гласит, что два тела находятся в состоянии теплового равновесия, если они могут передавать друг другу теплоту, но этого не происходит.
Нетрудно догадаться, что два тела не передают друг другу теплоту в том случае, если их температуры равны. Например, если измерить температуру человеческого тела при помощи термометра (в конце измерения температура человека и температура градусника будут равны), а затем, этим же термометром измерить температуру воды в ванной, и при этом окажется, что обе температуры совпадают (наблюдается тепловое равновесие человека с термометром и термометра с водой), можно говорить о том, что человек находится в тепловом равновесии с водой в ванной.
Из сказанного выше, можно сформулировать нулевое начало термодинамики следующим образом: два тела, находящиеся в тепловом равновесии с третьим, также находятся в тепловом равновесии между собой.
С физической точки зрения нулевое начало термодинамики устанавливает точку отсчета, поскольку, между двумя телами, которые имеют одинаковую температуру, тепловой поток отсутствует. Другими словами, можно сказать, что температура есть не что иное, как индикатор теплового равновесия.
Первое начало термодинамики
Первое начало термодинамики есть закон сохранения тепловой энергии, утверждающий, что энергия никуда не девается бесследно.
Система может либо поглощать, либо выделять тепловую энергию Q, при этом система выполняет над окружающими телами работу W (или окружающие тела выполняют работу над системой), при этом внутренняя энергия системы, которая имела начальное значение Uнач, будет равна Uкон:
Uкон-Uнач = ΔU = Q-W
Тепловая энергия, работа и внутренняя энергия определяют общую энергию системы, которая является постоянной величиной. Если системе передать (забрать) некое кол-во тепловой энергии Q, при отсутствии работы кол-во внутренней энергии системы U, увеличится (уменьшится) на Q.
Второе начало термодинамики
Второе начало термодинамик гласит, что тепловая энергия может переходить только в одном направлении – от тела с более высокой температурой, к телу, с более низкой температурой, но не наоборот.
Третье начало термодинамики
Третье начало термодинамики гласит, что любой процесс, состоящий из конечного числа этапов, не позволит достичь температуры абсолютного нуля (хотя к нему можно существенно приблизиться).
Что такое термодинамика? Это раздел физики, который занимается изучением свойств макроскопических систем. При этом под изучение также попадают способы превращения энергии и методы ее передачи. Термодинамика – это который изучает процессы, происходящие в системах, и их состояния. О том, что еще попадает в список изучаемых ей вещей, мы сегодня и поговорим.
Определение
На картинке ниже можно увидеть пример термограммы, полученной при изучении кувшина с горячей водой.
Термодинамика – это наука, которая опирается на обобщенные факты, полученные опытным путем. Происходящие в термодинамических системах процессы описываются при помощи использования макроскопических величин. В их список входят такие параметры, как концентрация, давление, температура и тому подобные. Понятное дело, что к отдельным молекулам они неприменимы, а сводятся к описанию системы в общем ее виде (в отличие от тех величин, которые используются в электродинамике, например).
Термодинамика – это раздел физики, который также имеет и свои законы. Они, подобно остальным, носят общий характер. Конкретные детали строения того или иного выбранного нами вещества не окажут значительного влияния на характер законов. Именно поэтому говорят, что данный раздел физики является одним из наиболее применимых (или, вернее сказать, успешно применимых) в науке и технике.
Они, подобно остальным, носят общий характер. Конкретные детали строения того или иного выбранного нами вещества не окажут значительного влияния на характер законов. Именно поэтому говорят, что данный раздел физики является одним из наиболее применимых (или, вернее сказать, успешно применимых) в науке и технике.
Применение
Перечислять примеры можно очень долго. Например, много решений, основанных на термодинамических законах, можно встретить в области тепловой техники или электроэнергетики. Что и говорить об описании и понимании химических реакций, явлений переноса. В некотором роде термодинамика “сотрудничает” с квантовой динамикой. Сфера их соприкосновения – это описание явления черных дыр.
Законы
Картинка выше демонстрирует суть одного из термодинамических процессов – конвекции. Теплые слои вещества поднимаются наверх, холодные – опускаются вниз.
Альтернативное название законов, которое, кстати, употребляется не в пример чаще, это начала термодинамики. На сегодняшний день их известно три (плюс одно “нулевое“, или “общее”). Но перед тем как говорить о том, что предполагает каждый из законов, попытаемся ответить на вопрос о том, что такое начала термодинамики.
На сегодняшний день их известно три (плюс одно “нулевое“, или “общее”). Но перед тем как говорить о том, что предполагает каждый из законов, попытаемся ответить на вопрос о том, что такое начала термодинамики.
Они представляют собой совокупность определенных постулатов, которые ложатся в основу понимания происходящих в макросистемах процессов. Положения начал термодинамики устанавливались эмпирическим путем по мере проведения целых серий опытов и научных исследований. Таким образом, существуют определенные доказательства, позволяющие нам взять постулаты на вооружение без единого сомнения в их точности.
Некоторые люди задаются вопросом о том, зачем термодинамике нужны эти самые законы. Ну, можно сказать, что необходимость их использования обусловлена тем, что в данном разделе физики макроскопические параметры описываются в общем виде, без какого-либо намека на рассмотрения их микроскопической природы или особенностей того же плана. Это сфера не термодинамики, а уже статистической физики, если говорить конкретнее. Еще одной важной вещью является тот факт, что начала термодинамики не зависят друг от друга. То есть одно из второго вывести не получится.
Еще одной важной вещью является тот факт, что начала термодинамики не зависят друг от друга. То есть одно из второго вывести не получится.
Применение
Применение термодинамики, как было сказано ранее, идет по многим направлениям. За основу берется, кстати, одно из ее начал, которое иначе интерпретируется в форме закона сохранения энергии. Термодинамические решения и постулаты успешно внедряются в такие отрасли, как энергетическая промышленность, биомедицина, химия. Вот в биологической энергетике повсеместно используется закон сохранения энергии и закон вероятности и направленности термодинамического процесса. Наряду с этим, там используются три наиболее распространенных понятия, на которых базируется вся работа и ее описание. Это термодинамическая система, процесс и фаза процесса.
Процессы
Процессы в термодинамике имеют разную степень сложности. Их насчитывается семь штук. Вообще, под процессом в таком случае следует понимать не что иное, как изменение макроскопического состояния, в которое система была приведена ранее. Следует понимать, что разница между условным начальным состоянием и конечным результатом может быть ничтожной.
Следует понимать, что разница между условным начальным состоянием и конечным результатом может быть ничтожной.
Если разница бесконечно мала, то произошедший процесс мы вполне можем назвать элементарным. Если мы будем обсуждать процессы, то придется прибегнуть к упоминанию дополнительных терминов. Один из них – это “рабочее тело”. Рабочим телом называется система, в которой происходит один тепловой процесс или несколько.
Условно процессы подразделяются на неравновесные и равновесные. В случае с последним все состояния, через которые предстоит пройти термодинамической системе, являются, соответственно, неравновесными. Зачастую изменение состояний идет в таких случаях быстрыми темпами. А вот равновесные процессы близки к квазистатическим. В них изменения проходят на порядок медленнее.
Тепловые процессы, происходящие в термодинамических системах, могут быть как обратимыми, так и необратимыми. Для того чтобы понять суть, разобьем в своем представлении последовательность действий на определенные промежутки.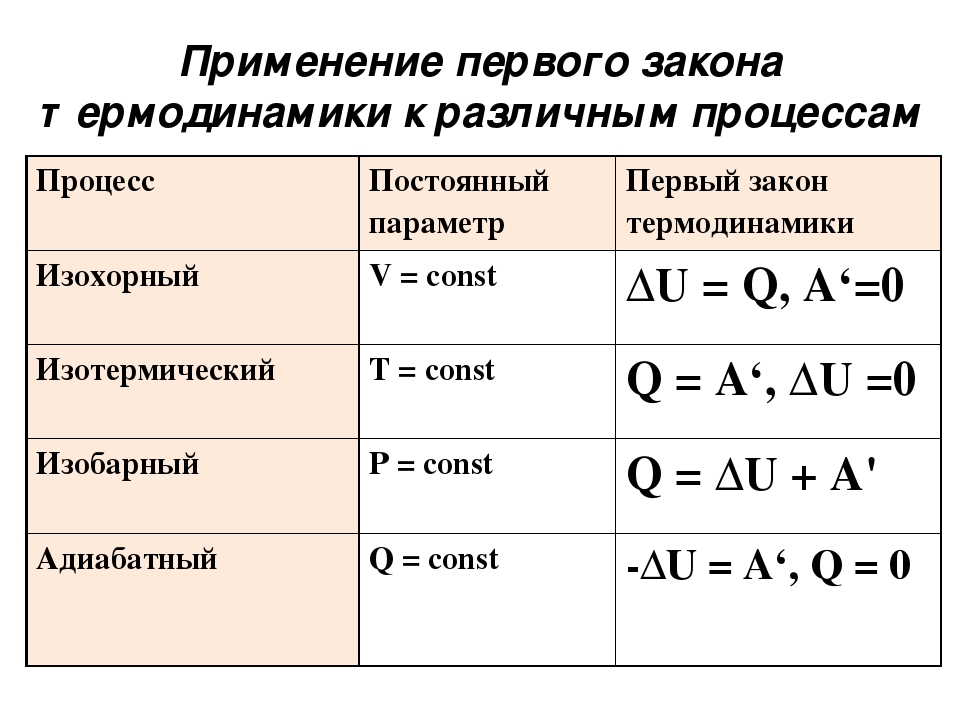 Если мы можем сделать тот же процесс в обратном направлении с теми же “промежуточными станциями”, то его можно назвать обратимым. В противном случае сделать это не получится.
Если мы можем сделать тот же процесс в обратном направлении с теми же “промежуточными станциями”, то его можно назвать обратимым. В противном случае сделать это не получится.
Основные формулы термодинамики и молекулярной физики, которые вам пригодятся.
Еще один отличный день для практических занятий по физике. Сегодня мы соберем вместе формулы, которые чаще всего используются при решении задач в термодинамике и молекулярной физике.
Итак, поехали. Попытаемся изложить законы и формулы термодинамики кратко.
Идеальный газ
Идеальный газ – это идеализация, как и материальная точка. Молекулы такого газа являются материальными точками, а соударения молекул – абсолютно упругие. Взаимодействием же молекул на расстоянии пренебрегаем. В задачах по термодинамике реальные газы часто принимаются за идеальные. Так гораздо легче жить, и не нужно иметь дела с массой новых членов в уравнениях.
Итак, что происходит с молекулами идеального газа? Да, они движутся! И резонно спросить, с какой скоростью? Конечно, помимо скорости молекул нас интересует еще и общее состояние нашего газа. Какое давление P он оказывает на стенки сосуда, какой объем V занимает, какая у него температура T.
Какое давление P он оказывает на стенки сосуда, какой объем V занимает, какая у него температура T.
Для того, чтобы узнать все это, есть уравнение состояния идеального газа, или уравнение Клапейрона-Менделеева
Здесь m – масса газа, M – его молекулярная масса (находим по таблице Менделеева), R – универсальная газовая постоянная, равная 8,3144598(48) Дж/(моль*кг).
Универсальная газовая потоянная может быть выражена через другие константы (постоянная Больцмана и число Авогадро )
Масс у , в свою очередь, можно вычислить, как произведение плотности и объема .
Основное уравнение молекулярно-кинетической теории (МКТ)
Как мы уже говорили, молекулы газа движутся, причем, чем выше температура – тем быстрее. Существует связь между давлением газа и средней кинетической энергией E его частиц. Эта связь называется основным уравнением молекулярно-кинетической теории и имеет вид:
Здесь n – концентрация молекул (отношение их количества к объему), E – средняя кинетическая энергия. Найти их, а также среднюю квадратичную скорость молекул можно, соответственно, по формулам:
Найти их, а также среднюю квадратичную скорость молекул можно, соответственно, по формулам:
Подставим энергию в первое уравнение, и получим еще один вид основного уравнения МКТ
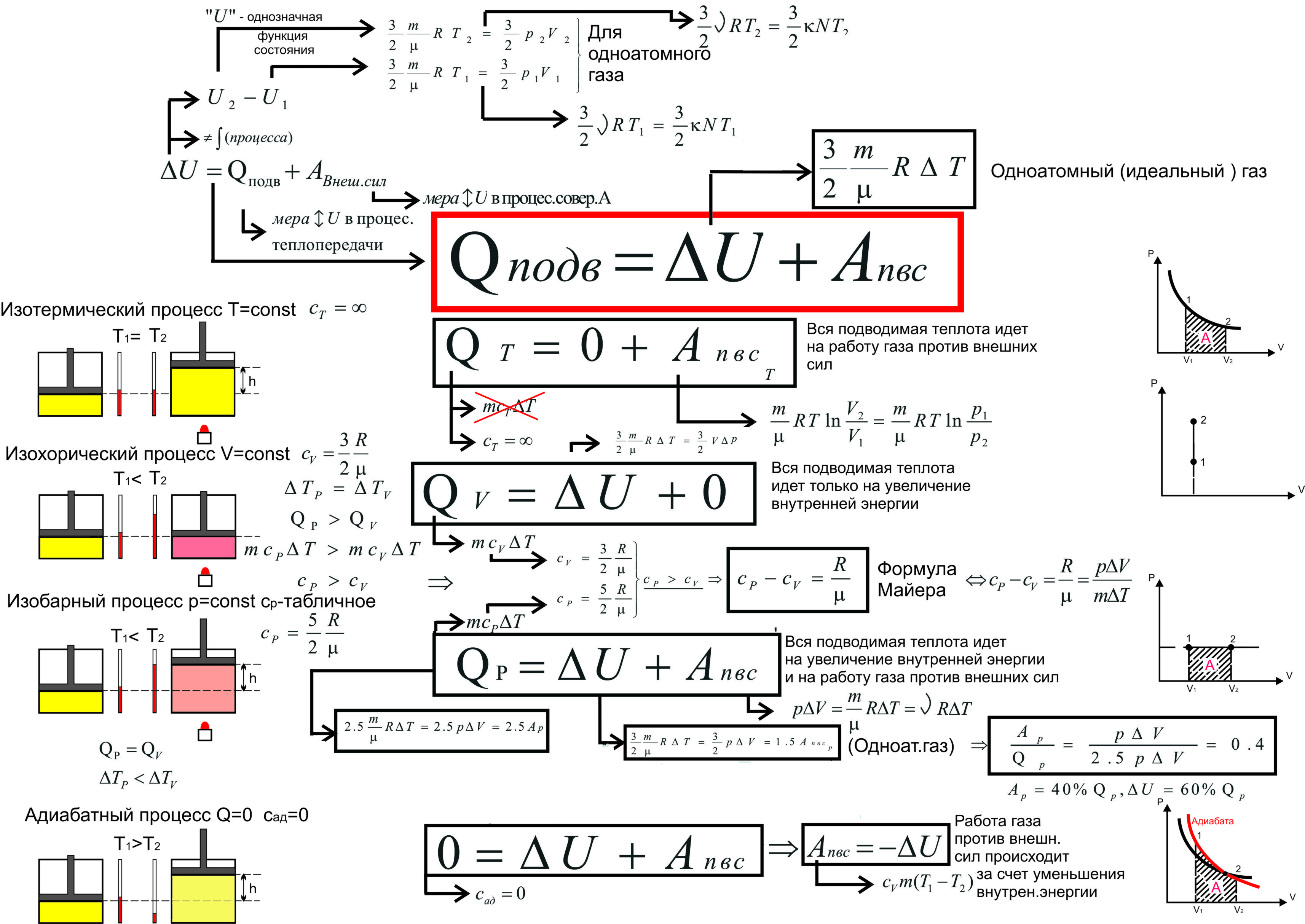
Первое начало термодинамики. Формулы для изопроцессов
Напомним Вам, что первый закон термодинамики гласит: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа U и на совершение газом работы A. Формула первого закона термодинамики записывается так:
Как известно, с газом что-то происходит, мы можем сжать его, можем нагреть. В данном случае нас интересуют такие процессы, которые протекают при одном постоянном параметре. Рассмотрим, как выглядит первое начало термодинамики в каждом из них.
Кстати! Для всех наших читателей сейчас действует скидка 10% на .
Изотермический процесс протекает при постоянной температуре. Тут работает закон Бойля-Мариотта: в изотермическом процессе давление газа обратно пропорционально его объёму. В изотермическом процессе:
В изотермическом процессе:
протекает при поcтоянном объеме. Для этого процесса характерен закон Шарля: При постоянном объеме давление прямо пропорционально температуре. В изохорном процессе все тепло, подведенное к газу, идет на изменение его внутренней энергии.
идет при постоянном давлении. Закон Гей-Люссака гласит, что при постоянном давлении газа его объём прямо пропорционален температуре. При изобарном процессе тепло идет как на изменение внутренней энергии, так и на совершение газом работы.
. Адиабатный процесс – это такой процесс, который проходит без теплообмена с окружающей средой. Это значит, что формула первого закона термодинамики для адиабатного процесса выглядит так:
Внутренняя энергия одноатомного и двухатомного идеального газа
Теплоемкость
Удельная теплоемкость равна количеству теплоты, которое необходимо для нагревания одного килограмма вещества на один градус Цельсия.
Помимо удельной теплоемкости, есть молярная теплоемкость (количество теплоты, необходимое для нагревания одного моля вещества на один градус) при постоянном объеме, и молярная теплоемкость при постоянном давлении. В формулах ниже, i – число степеней свободы молекул газа. Для одноатомного газа i=3, для двухатомного – 5.
Тепловые машины. Формула КПД в термодинамике
Тепловая машина , в простейшем случае, состоит из нагревателя, холодильника и рабочего тела. Нагреватель сообщает тепло рабочему телу, оно совершает работу, затем охлаждается холодильником, и все повторяется вно вь. Типичным примером тепловой машины является двигатель внутреннего сгорания.
Коэффициент полезного действия тепловой машины вычисляется по формуле
Вот мы и собрали основные формулы термодинамики, которые пригодятся в решении задач. Конечно, это не все все формулы из темы термодинамика, но их знание действительно может сослужить хорошую службу. А если возникнут вопросы – помните о студенческом сервисе , специалисты которого готовы в любой момент прийти на выручку.
А если возникнут вопросы – помните о студенческом сервисе , специалисты которого готовы в любой момент прийти на выручку.
Термодинамика – раздел физики, изучающий тела, находящиеся в состоянии термодинамического равновесия и явления, сопровождающие переходы между этими состояниями.
Термодинамическое равновесие – состояние тел (или частей тела), при котором остаются постоянными все величины, характеризующие эти тела (или части тела): объёмы, давления, расположение масс и др.
Температура – единственная физическая величина, всегда одинаковая у всех тел (или частей тела), находящихся в состоянии термодинамического равновесия.
Термометр – прибор для измерения температуры. Единица температуры – 1 кельвин (1 К). Также используется 1 °С, равный 1 К.
Теплообмен – переход внутренней энергии одного тела во внутреннюю энергию другого тела без совершения механической работы.
Количество теплоты – физическая величина, показывающая энергию, полученную (отданную) телом при теплообмене.
Калориметр – прибор для измерения количества теплоты. Единица количества теплоты – 1 джоуль (1 Дж).
Удельная теплоемкость вещества – физическая величина, показывающая количество теплоты, необходимое для изменения температуры 1 кг этого вещества на 1 °С. Единица удельной теплоёмкости – 1 Дж/(кг·°С).
Количество теплоты, полученное (отданное) телом при теплообмене, пропорционально массе тела и изменению его температуры. Коэффициент пропорциональности – удельная теплоёмкость вещества.
Превращение твёрдого тела в жидкость называют плавлением . Обратное явление называют отвердеванием . Если при этом получается кристаллическое тело, то отвердевание называют кристаллизацией .
Температура
Температурой плавления называют температуру, при которой нагреваемое кристаллическое тело тело начинает плавиться, и при этом одновременно существуют твёрдое и жидкое состояния его вещества.
Температурой кристаллизации называют температуру, при которой охлаждаемая жидкость начинает кристаллизоваться, и при этом одновременно существуют её твёрдое и жидкое состояния.
Как правило, температура кристаллизации вещества равна температуре его плавления . Температура плавления/кристаллизации вещества зависит от внешнего давления и других факторов.
Удельная теплота плавления – физическая величина, показывающая количество теплоты, необходимое для плавления или выделяющееся при кристаллизации 1 кг вещества, находящегося при температуре плавления/кристаллизации. Единица удельной теплоты плавления – 1 Дж/кг.
Количество теплоты, поглощаемое (выделяющееся) при плавлении (кристаллизации), пропорционально массе расплавившегося (кристаллизовавшегося) вещества. Коэффициент пропорциональности – удельная теплота плавления вещества.
Видами парообразования являются: испарение – парообразование, происходящее с поверхности жидкости; кипение – парообразование, происходящее по всему объёму жидкости вследствие возникновения и всплытия на поверхность пузырей пара; сублимация – парообразование, происходящее с поверхности твёрдого тела.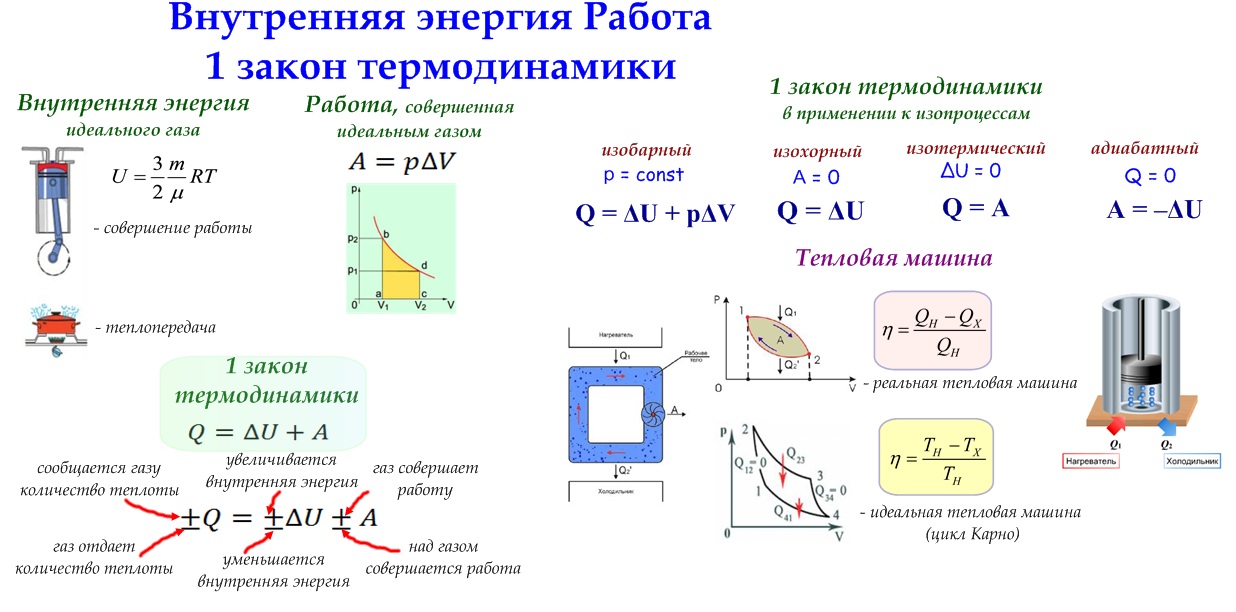
Температурой кипения называют температуру, при которой наблюдается кипение вещества (интенсивное парообразование по всему объёму этого вещества). Температура кипения зависит от внешнего давления и других факторов.
Удельная теплота парообразования – физическая величина, показывающая количество теплоты, необходимое для превращения в пар 1 кг вещества (как правило, при температуре кипения). Единица удельной теплоты парообразования – 1 Дж/кг.
Количество теплоты, поглощённое кипящей (или испаряющейся при постоянной температуре) жидкостью, прямо пропорционально массе образовавшегося пара. Коэффициент пропорциональности – удельная теплота парообразования вещества.
При охлаждении/кристаллизации/конденсации выделяется точно такое же количество теплоты, которое было затрачено для нагревания/плавления/парообразования вещества (если температуры и давления при прямом и обратном процессах соответствуют друг другу). Утверждение будет верным и наоборот.
Законы термодинамика
Первый закон термодинамики устанавливает равенство между изменением внутренней энергии тела и суммой полученной телом теплоты и совершённой над ним работы.
Тепловой двигатель – периодически действующее устройство, служащее для превращения внутренней энергии рабочего тела (как правило, газа или пара) в механическую энергию.
Количество теплоты, выделяющееся при полном сгорании вещества (топлива), прямо пропорционально массе сгоревшего вещества (топлива) . Коэффициент пропорциональности – удельная теплота сгорания топлива.
Известно три способа теплопередачи
(теплообмена) – теплопроводность, конвекция и излучение. При теплопроводности теплота проникает через вещество без его перемещения (в случае отсутствия вещества теплопроводность является нулевой). При конвекции теплота перемещается неравномерно нагретым движущимся веществом (в условиях, когда возможно возникновение архимедовой силы). При излучении теплота передаётся через пространство или вещество в виде электромагнитных волн (для излучения наличие вещества не является обязательным, в отличие от первых двух способов теплопередачи).
При излучении теплота передаётся через пространство или вещество в виде электромагнитных волн (для излучения наличие вещества не является обязательным, в отличие от первых двух способов теплопередачи).
Второй закон термодинамики гласит, что теплообмен самостоятельно протекает только в таком направлении, что температура менее нагретого тела возрастает, а более нагретого – уменьшается.
Дополнительные материалы по теме:Содержание статьи
ТЕРМОДИНАМИКА, раздел прикладной физики или теоретической теплотехники, в котором исследуется превращение движения в теплоту и наоборот. В термодинамике рассматриваются не только вопросы распространения теплоты, но и физические и химические изменения, связанные с поглощением теплоты веществом, а также, наоборот, выделение теплоты в ходе физических и химических превращений.
Термодинамика находит широкое применение в физической химии и химической физике при анализе физических и химических процессов, в современной физиологии и биологии, в двигателестроении, теплотехнике, авиационной и ракетно-космической технике. Первоначально в термодинамике много внимания уделялось обратимым процессам и равновесным состояниям, так что более подходящим для нее казалось название «термостатика», но благодаря С.Аррениусу (1859–1927) и Г.Эйрингу (1901–1981) получило весьма основательную разработку ее применение к анализу скоростей химических реакций (химической кинетике). В настоящее время главной проблемой в термодинамике является ее применение к необратимым процессам, и уже достигнуты большие успехи в построении теории, по широте охвата сравнимой с термодинамикой обратимых процессов.
Первоначально в термодинамике много внимания уделялось обратимым процессам и равновесным состояниям, так что более подходящим для нее казалось название «термостатика», но благодаря С.Аррениусу (1859–1927) и Г.Эйрингу (1901–1981) получило весьма основательную разработку ее применение к анализу скоростей химических реакций (химической кинетике). В настоящее время главной проблемой в термодинамике является ее применение к необратимым процессам, и уже достигнуты большие успехи в построении теории, по широте охвата сравнимой с термодинамикой обратимых процессов.
ЭНЕРГИЯ
Для той физической величины, которую мы теперь называем энергией, долгое время употреблялся термин «живая сила», введенный И.Ньютоном (1643–1727). Но поскольку «живую силу» можно было спутать с обычной силой, последнюю приходилось для ясности называть «мертвой силой», что нельзя признать удачным. Специальный термин «энергия» был введен в 1807 Т.Юнгом (1773–1829).
Одним из видов энергии является работа, которая совершается, когда тело движется, преодолевая действие некой силы.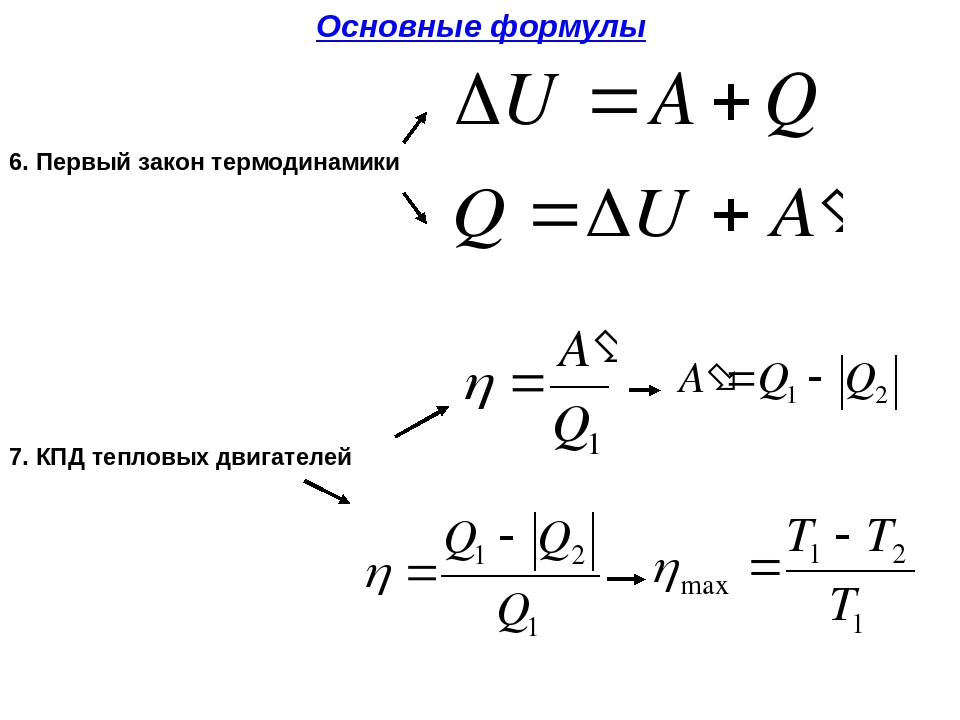 Примером может служить подача насосом воды в водонапорную башню. О воде в башне говорят, что она имеет потенциальную энергию. Благодаря гравитационному притяжению Земли существует возможность обратного преобразования этой энергии в кинетическую, т.е. в энергию движения воды, текущей по трубам. Когда вода в трубе в конце концов останавливается из-за внутреннего трения, или вязкости, эта энергия оказывается превратившейся в теплоту, т.е. тепловую энергию, которая рассеивается в окружающей среде.
Примером может служить подача насосом воды в водонапорную башню. О воде в башне говорят, что она имеет потенциальную энергию. Благодаря гравитационному притяжению Земли существует возможность обратного преобразования этой энергии в кинетическую, т.е. в энергию движения воды, текущей по трубам. Когда вода в трубе в конце концов останавливается из-за внутреннего трения, или вязкости, эта энергия оказывается превратившейся в теплоту, т.е. тепловую энергию, которая рассеивается в окружающей среде.
Еще в 1620 Ф.Бэкон высказал предположение, что теплота есть просто другая форма движения, но лишь в 1789 это с несомненностью установил Б.Томпсон (Румфорд), наблюдая за выделением теплоты при рассверливании ствола пушки. Дополнительным подтверждением явились опыты Х.Дэви 1799.
Эти опыты и наблюдения говорили о том, что тепловая и механическая энергия – одно и то же и что, вероятно, можно найти экспериментально механический эквивалент теплоты, т.е. количество работы в механических единицах, эквивалентное данному количеству теплоты в тепловых единицах.
Механический эквивалент теплоты.
Заметив, что температура воды в медицинской колбе повышается, если ее несколько минут встряхивать, Ю.Майер в 1842 вычислил механический эквивалент теплоты по разности удельных теплоемкостей воздуха при постоянном давлении и постоянном объеме. В ту пору точные значения этих удельных теплоемкостей еще не были известны, а потому его результат был не совсем верным, хотя и правильным по порядку величины. В 1845 Дж.Джоуль точно измерил количество теплоты, получаемое при преобразовании механической работы в тепловую энергию, и уточнил результат Майера.
Работа.
Если некое вещество находится под ограничивающим воздействием внешней силы, например атмосферного давления P , то при изменении его объема V , скажем расширении, вследствие движения против действующей силы совершается работа. Полную совершаемую работу можно найти как площадь зависимости силы от соответствующего размера, как показано на рис. 1, где площадью участка, выделенного ретушью, представлена работа, совершаемая газом при расширении от V 1 до V 2 . Такой способ ее определения необходим, поскольку давление может меняться. При малом изменении объема давление намного не изменится, так что малое количество совершаемой работы будет равно:
Такой способ ее определения необходим, поскольку давление может меняться. При малом изменении объема давление намного не изменится, так что малое количество совершаемой работы будет равно:
Следовательно, полная совершаемая работа
При быстром сжатии газа некоторая часть работы, совершаемой над ним, может заметно повысить его температуру. Если газ находится в теплоизолированном сосуде (или сжимается столь быстро, что не успевает хотя бы частично отдать свою теплоту), такое изменение объема называется адиабатическим. Если же газ не теплоизолирован, то происходит теплоотдача, и газ сохраняет температуру окружающей среды. Такое изменение объема называется изотермическим.
«Полезность» энергии.
Полное преобразование работы в теплоту вполне возможно, но обратный процесс преобразования всей теплоты в эквивалентную ей работу невозможен. К такому выводу еще в 1824 пришел путем теоретических рассуждений французский физик Н.Карно (1796–1832). Рассматривая полный цикл обратимых изменений рабочего тела в тепловой машине, в конце которого это тело возвращается в исходное состояние, он показал, что максимальный КПД преобразования теплоты в работу зависит не от природы рабочего тела, а только от максимальной температуры, при которой подводится теплота, и от минимальной температуры, при которой она отводится. Полное преобразование теплоты в работу было бы возможно лишь в том случае, если бы минимальная температура была равна абсолютному нулю, при которой рабочее тело не имело бы никакой тепловой энергии.
Полное преобразование теплоты в работу было бы возможно лишь в том случае, если бы минимальная температура была равна абсолютному нулю, при которой рабочее тело не имело бы никакой тепловой энергии.
На существование абсолютного нуля указывает закон расширения газов. Поскольку при охлаждении от 0 до – 1° C газы сжимаются на 1/273, можно представить себе некий «идеальный» газ, который не конденсируется, как реальные газы, но с понижением температуры продолжает сжиматься, пока его объем не уменьшится до нуля при – 273° C. Это было бы абсолютным нулем температуры для тепловой машины, рабочим телом которой является идеальный газ. Проведя гораздо более сложные рассуждения, У.Томсон (Кельвин) (1824–1907) доказал, что это действительно абсолютный нуль температуры, и ввел названную его именем «термодинамическую» шкалу температуры T (шкалу Кельвина), в соответствии с которой T = 273,16 + t ° C.
Первое начало термодинамики.
Мерой полезной работы, совершенной машиной, является разность площадей (рис. 3,а и б ), показанная на рис. 3,в . Нетрудно сообразить, что при заданном изменении объема эту разность площадей можно увеличить либо повысив T 1 , либо понизив T 2 . Если же температура T 1 фиксирована (а это значит, что фиксировано полное количество подводимой теплоты), то работу, производимую машиной, можно увеличить, только понизив T 2 . С особой наглядностью это показывает «диаграмма Молье» (график зависимости температура – энтропия), представленная на рис. 3,г . Здесь тоже полезная работа пропорциональна выделенной площади; подводимая теплота определяется площадью T 1 D S , а часть ее, соответствующая площади прямоугольника T 2 D S , «бесполезна» в смысле совершения работы. Таким образом, какова бы ни была температура T 1 , отличная от абсолютного нуля, какая-то часть подводимой теплоты не может быть превращена в работу.
3,а и б ), показанная на рис. 3,в . Нетрудно сообразить, что при заданном изменении объема эту разность площадей можно увеличить либо повысив T 1 , либо понизив T 2 . Если же температура T 1 фиксирована (а это значит, что фиксировано полное количество подводимой теплоты), то работу, производимую машиной, можно увеличить, только понизив T 2 . С особой наглядностью это показывает «диаграмма Молье» (график зависимости температура – энтропия), представленная на рис. 3,г . Здесь тоже полезная работа пропорциональна выделенной площади; подводимая теплота определяется площадью T 1 D S , а часть ее, соответствующая площади прямоугольника T 2 D S , «бесполезна» в смысле совершения работы. Таким образом, какова бы ни была температура T 1 , отличная от абсолютного нуля, какая-то часть подводимой теплоты не может быть превращена в работу.
На изложенных соображениях основан вывод формулы Карно, которая дает максимально возможный КПД идеальной тепловой машины, работающей при заданной разности температур нагревателя и холодильника:
Реальная машина не может работать с таким КПД, поскольку в ней неизбежны трение и утечки тепла. Для паровой машины, работающей, например, при температуре котла 130°
C (403 К) и температуре конденсатора 30°
C (303 К), термодинамический КПД равен 100/403, т.е. меньше 25%.
Для паровой машины, работающей, например, при температуре котла 130°
C (403 К) и температуре конденсатора 30°
C (303 К), термодинамический КПД равен 100/403, т.е. меньше 25%.
Цикл холодильной машины.
Поскольку рабочее тело в цикле Карно возвращается в исходное состояние, можно представить себе обращенную тепловую машину. Если в прямом цикле передача тепла от нагревателя к холодильнику используется для получения работы, то в обращенном за счет совершения механической работы теплота передается от холодильника нагревателю, так что холодильник становится еще холоднее, а нагреватель – еще горячее. Таков цикл холодильной машины (используемый, например, в холодильниках и кондиционерах): работа, совершаемая электродвигателем домашнего холодильника, идет на то, чтобы внутри холодильника было холодно за счет нагревания окружающего воздуха.
Другие циклы тепловой машины.
В реальных тепловых машинах циклы с изотермическими процессами не находят применения, поскольку такие процессы требуют много времени. Предпочтение отдается адиабатическим процессам, ибо они ближе к реальности в быстро работающих машинах. Простейший из таких циклов – цикл Отто (рис. 4,а ), названный по имени немецкого изобретателя и инженера Н.Отто (1832–1891). В этом цикле подводимая теплота повышает давление газа при постоянном объеме, а затем газ адиабатически расширяется с совершением полезной работы. После того как достигнут заданный объем, теплота отводится, а часть работы затрачивается на адиабатическое сжатие газа, после чего цикл может повториться. КПД определяется степенью сжатия r :
Предпочтение отдается адиабатическим процессам, ибо они ближе к реальности в быстро работающих машинах. Простейший из таких циклов – цикл Отто (рис. 4,а ), названный по имени немецкого изобретателя и инженера Н.Отто (1832–1891). В этом цикле подводимая теплота повышает давление газа при постоянном объеме, а затем газ адиабатически расширяется с совершением полезной работы. После того как достигнут заданный объем, теплота отводится, а часть работы затрачивается на адиабатическое сжатие газа, после чего цикл может повториться. КПД определяется степенью сжатия r :
где g – отношение удельных теплоемкостей газа при постоянном давлении и при постоянном объеме. Чем больше r , тем больше КПД.
Цикл Дизеля (рис. 4,б ) назван по имени немецкого изобретателя Р.Дизеля (1858–1913). В этом цикле теплота тоже отдается при постоянном объеме после адиабатического расширения, но подводится (после адиабатического сжатия) при постоянном давлении. В дизельном двигателе тепло не подводится от внешнего источника, а вырабатывается внутри при сгорании топлива, самовоспламеняющегося при сильном сжатии. Высокотемпературные газы не охлаждаются, а совершают работу и выводятся наружу с заменой холодной смесью топлива с воздухом. Теоретический цикл почти полностью воспроизводится, если не считать влияния механических факторов и других неизбежных тепловых потерь.
Высокотемпературные газы не охлаждаются, а совершают работу и выводятся наружу с заменой холодной смесью топлива с воздухом. Теоретический цикл почти полностью воспроизводится, если не считать влияния механических факторов и других неизбежных тепловых потерь.
В менее известном цикле Аткинсона (рис. 4,г ) последовательность ветвей обратна последовательности в цикле Дизеля. Только в цикле Джоуля (рис. 4,в ) теплота и отдается и подводится при постоянном давлении, но этот цикл обычно не используется для преобразования теплоты в работу; он применяется в обращенной (холодильной) машине.
Графики зависимости давление – объем типа представленных на рис. 3 и 4 называются индикаторными диаграммами. Ими пользуются инженеры для расчета КПД двигателей. Для примера на рис. 5 представлена индикаторная диаграмма четырехтактного бензинового двигателя. За тактом сжатия CD , начинающимся в точке C , следуют сгорание топлива на вертикальной ветви DE и рабочий такт EF . В точке F открывается выпускной клапан, так что давление понижается до атмосферного давления P A , и отработанные газы выбрасываются из цилиндра двигателя соответственно горизонтальной ветви AB . На участке B ў C в цилиндр впускается новая горючая смесь, и цикл заканчивается. В реальном двигателе сгорание не происходит мгновенно. Если зажигание производится в точке D , то пламя распространяется по цилиндру, когда объем уже начал увеличиваться, и поэтому максимальное теоретическое давление не достигается. Значительная часть площади, пропорциональной совершаемой работе, теряется, что показано штриховой линией DG . Если же зажигание производится с опережением, например в точке H , то теряется лишь малая часть полезной площади, как показано штриховой линией HI . Это объясняется тем, что при нарастании давления объем все еще продолжает уменьшаться.
В точке F открывается выпускной клапан, так что давление понижается до атмосферного давления P A , и отработанные газы выбрасываются из цилиндра двигателя соответственно горизонтальной ветви AB . На участке B ў C в цилиндр впускается новая горючая смесь, и цикл заканчивается. В реальном двигателе сгорание не происходит мгновенно. Если зажигание производится в точке D , то пламя распространяется по цилиндру, когда объем уже начал увеличиваться, и поэтому максимальное теоретическое давление не достигается. Значительная часть площади, пропорциональной совершаемой работе, теряется, что показано штриховой линией DG . Если же зажигание производится с опережением, например в точке H , то теряется лишь малая часть полезной площади, как показано штриховой линией HI . Это объясняется тем, что при нарастании давления объем все еще продолжает уменьшаться.
ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ
Внутренняя энергия.
Когда к системе подводится некоторое количество теплоты d
Q , за счет этой теплоты, как было показано ранее на примере цикла Карно, может быть совершена лишь определенная работа d
W , так что часть полученной тепловой энергии система теряет. Эти две величины, вообще говоря, неодинаковы, и, следовательно, система либо теряет, либо приобретает энергию, равную их разности. Предположим, что эта разность энергий остается в системе в виде т.н. внутренней энергии E . Тогда последняя увеличится от E до (E + dE ), причем
Эти две величины, вообще говоря, неодинаковы, и, следовательно, система либо теряет, либо приобретает энергию, равную их разности. Предположим, что эта разность энергий остается в системе в виде т.н. внутренней энергии E . Тогда последняя увеличится от E до (E + dE ), причем
где d Q и d W – бесконечно малые приращения.
Вообще говоря, приращения d
Q и d
W не являются независимыми (почему они и обозначены здесь символом d в отличие от приращения dE ). Так, поглощение теплоты обычно сопровождается изменением объема и, следовательно, совершением работы против внешнего давления. И наоборот, если допускается расширение, то оно обычно сопровождается поглощением теплоты, отбираемой у окружающей среды. Никакие ограничения, налагаемые реально на систему, не могут полностью исключить такого взаимодействия, но мысленно можно представить себе идеальную теплоизоляцию (d
Q = 0) или строго выполняющееся условие постоянного объема (d
W = 0), так же как в теоретической механике вводятся понятия идеально гладких и идеально твердых тел. Только в идеальных условиях, когда d
Q и d
W независимы друг от друга, приращение d
Q или d
W можно рассматривать как полный дифференциал, тогда как их разность dE всегда является таковой.
Только в идеальных условиях, когда d
Q и d
W независимы друг от друга, приращение d
Q или d
W можно рассматривать как полный дифференциал, тогда как их разность dE всегда является таковой.
Энтропия.
Тепловая энергия d Q ў , которая не может быть преобразована в работу, пропорциональна нижней температуре T , так что можно записать d Q ў = TdS , где dS – приращение энтропии S системы. Как и E , величина S является характеристикой самой системы, а потому мы обозначаем ее приращение буквой d , а не d .
Обозначив через d W работу, которую можно получить за счет теплоты d Q , можно написать
Если рабочее тело в результате некоего термодинамического процесса не возвращается в исходное состояние, то значительная часть энергии оказывается бесполезной с точки зрения совершения работы, и внутренняя энергия увеличивается на соответствующую разность dE . Увеличение внутренней энергии может проявиться в изменении физического состояния рабочего тела, например в переходе из твердого в жидкое состояние (плавлении) или из жидкого в газообразное (испарении). Такая тепловая энергия называется теплотой плавления и теплотой парообразования соответственно. Повышение внутренней энергии может быть связано также с химическими изменениями (диссоциацией, разрывом связей) и даже с делением ядер.
Увеличение внутренней энергии может проявиться в изменении физического состояния рабочего тела, например в переходе из твердого в жидкое состояние (плавлении) или из жидкого в газообразное (испарении). Такая тепловая энергия называется теплотой плавления и теплотой парообразования соответственно. Повышение внутренней энергии может быть связано также с химическими изменениями (диссоциацией, разрывом связей) и даже с делением ядер.
Энтальпия.
Если изменения энергии системы происходят при постоянном давлении, то, как оказывается, функция
позволяет придать более простую и изящную форму уравнениям, описывающим различные процессы. Дело в том, что при небольшом изменении состояния системы в силу равенств (1) и (2) можно записать
Следовательно, если процесс протекает при постоянном давлении (dP = 0), то выполняется равенство
dH = d Q ,
т.е. подведенное количество теплоты может быть представлено в виде полного дифференциала некой величины, характеризующей внутреннее состояние системы. Эта величина называется энтальпией. Ранее она называлась тепловой функцией или теплосодержанием системы.
Эта величина называется энтальпией. Ранее она называлась тепловой функцией или теплосодержанием системы.
Свободная энергия.
В изотермических условиях (dT = 0) более, чем H , удобна другая термодинамическая функция:
Такие же выкладки, как и в случае энтальпии, дают dF = d W . Ранее величина F называлась свободной энергией Гельмгольца, поскольку именно Гельмгольц первым указал на ее значение, но сейчас ее называют просто свободной энергией.
Потенциал Гиббса.
В тех случаях, когда изменяться могут и температура и давление, используется более общая функция
Эту функцию иногда называют полным термодинамическим потенциалом или полезной энергией, но сейчас ее принято называть потенциалом Гиббса или гиббсовой энергией и обозначать символом G по имени Дж.Гиббса (1839–1903). Как будет показано ниже, представленные термодинамические функции позволяют определить условия, необходимые для равновесия.
В случае повышения давления на малую величину dP в системе, поддерживаемой при постоянной температуре (dT = 0), потенциал Гиббса увеличится на величину dG , а скорость его увеличения, или «чувствительность» потенциала Гиббса G к изменениям давления, дается термодинамическим выражением для объема системы
где символ частной производной указывает на то, что изменение происходит при постоянных значениях всех других параметров (в данном случае температуры T ).
Точно так же чувствительность потенциала Гиббса к изменениям температуры (при постоянном давлении) есть мера энтропии системы:
и это равенство можно рассматривать как еще одно определение энтропии.
Соотношения между термодинамическими функциями.
Величины E , H , F и G имеют размерность энергии, и любые три из них могут быть выражены через четвертую. Если d W = PdV , то, пользуясь равенствами (7) и (8), можно H , F и E выразить через G :
Если считать функцией только G , то из независимых переменных достаточно будет рассматривать лишь P и T , что почти всегда оказывается наиболее удобным. Если же в качестве единственной функции выбрать E , то самыми удобными с математической точки зрения будут независимые переменные V и T или V и S , но последняя из них, очевидно, не очень удобна для прямых измерений.
Теплоемкость.

Изменение энтропии dS вещества можно вычислить по количеству теплоты, необходимому для повышения его температуры на один градус, т.е. по измеренной теплоемкости C . Но теплоемкость зависит от того, может ли вещество расширяться при постоянном давлении P , так как тогда за счет теплоты должна совершаться работа, связанная с расширением. Поэтому теплоемкость при постоянном давлении C P больше теплоемкости при постоянном объеме C V . Эти величины даются равенствами
Разность теплоемкостей C P и C V выражается в тепловых единицах, а избыточная энергия, необходимая для совершения работы при расширении против сил давления, может быть выражена в механических единицах [см . формулу (2) и рис. 1]. Именно так Майер и вычислил механический эквивалент теплоты.
Вычисление энтропии.
Если давление P постоянно, то, поскольку H = E + PV , с учетом равенства (3) можно написать
Следовательно, построив график зависимости отношения C P /T от T (или, что с математической точки зрения то же самое, график зависимости C P от ln T ), можно найти приращение энтропии D S как площадь кривой на графике (рис. 6):
6):
Неупорядоченность и энтропия.
Австрийский физик Л.Больцман показал, опираясь на статистическую механику, что энтропия есть мера неупорядоченности, а именно:
где S – энтропия N молей вещества, а R – постоянная из общего уравнения для газов
которое представляет собой математическую запись отдельных законов, открытых Р.Бойлем (1627–1691) и Э.Мариоттом (1620–1684) и объединенных Ж.Гей-Люссаком (1778–1850) с законом, установленным Ж.Шарлем (1746–1823). Универсальная газовая постоянная R для всех газов равна 8,3144 Дж/мольЧ К.
Величина F
– это число способов, которыми энергия может быть распределена среди молекул при данной температуре, отнесенное к соответствующему числу способов при абсолютном нуле температуры. Если температура выше абсолютного нуля, то система стремится перейти в состояние, в котором величина Ф больше, так как в этом случае будет меньше энергия, приходящаяся на каждую молекулу, а это более вероятная ситуация, нежели распределение, при котором вся энергия приходится на небольшое число молекул.
Таким образом, энтропия вещества, находящегося в данном состоянии, есть относительная вероятность этого состояния, взятая в логарифмическом масштабе и умноженная на NR , для того чтобы она выражалась в термодинамических единицах.
Идеальный кристалл со строго упорядоченным расположением всех атомов – очень маловероятная структура, которая может поддерживаться лишь при наличии больших межатомных сил или, иначе говоря, при низком уровне его внутренней энергии. При нагревании кристалла тепловое движение нарушает эту упорядоченность. При определенной температуре (точке плавления), когда тепловая энергия становится больше энергии межатомного взаимодействия, твердая кристаллическая решетка разрушается и вещество переходит в менее упорядоченное жидкое состояние. Свободная энергия, которой характеризуется равновесное состояние [формула (5)], определяется соотношением между упорядочивающим действием внутренней энергии и разупорядочивающим действием повышенной температуры, причем энтропия служит количественной мерой действия температуры.
Равновесие.
Таким образом, условием равновесия при постоянной внутренней энергии является максимум энтропии S . Возможны некоторые флуктуации, кратковременно выводящие систему из этого состояния, но в среднем за любое достаточно длительное время выполняется равенство
Поскольку величины F и G являются функциями энтропии S , взятой со знаком «минус», данное условие означает, что равновесие возможно только тогда, когда либо величина F , либо величина G имеет минимум. Таким образом, при любом мыслимом изменении dX условия равновесия таковы:
Это соотношение было выведено путем анализа теплового цикла, предложенного французским инженером Б.Клапейроном (1799–1864) в 1834. Оно показывает, что теплоту парообразования необязательно определять калориметрическими методами; ее можно вычислить по расширению, происходящему при испарении, если известна скорость повышения давления насыщенного пара жидкости при повышении температуры, когда поддерживается постоянным объем системы. Это типичное уравнение термодинамики, устанавливающее соотношение между казалось бы не связанными друг с другом переменными.
Это типичное уравнение термодинамики, устанавливающее соотношение между казалось бы не связанными друг с другом переменными.
Путем аналогичных рассуждений Р.Клаузиус (1822–1888) вывел выражение для разности теплоемкостей C s твердой и C l жидкой фаз:
которое, впрочем, проще вывести из соотношения (15).
Поскольку он рассматривал уравнение Клапейрона и внес, по его словам, «небольшие изменения» в ход рассуждений, за соотношением (30) укрепилось название уравнения Клаузиуса – Клапейрона.
Рассуждая в какой-то мере аналогично, можно, пользуясь первым из соотношений Максвелла, вывести формулу, показывающую влияние давления на температуру плавления твердого вещества, теплоизолированного так, что его энтропия постоянна:
Здесь L – теплота плавления, T – температура плавления при данном давлении P , а (V l – v s ) – изменение объема твердого вещества при плавлении. В случае льда при плавлении происходит сжатие, и формула (32) показывает, что с повышением давления температура плавления понижается. Опытные данные согласуются с результатами вычислений. Большинство других твердых веществ при плавлении расширяется, и, следовательно, их температуры плавления повышаются с повышением давления.
Опытные данные согласуются с результатами вычислений. Большинство других твердых веществ при плавлении расширяется, и, следовательно, их температуры плавления повышаются с повышением давления.
Влияние давления.
Другие эффекты, связанные с изотермическим изменением давления, описываются формулами
Эффект Джоуля – Томсона.
Если газ находится в теплоизолированном сосуде и над ним не совершается работа (H = const), то изменение его температуры, обусловленное изменением давления, дается формулой
Для идеального газа a T = 1, и поэтому его температура не должна изменяться. Следовательно, по изменению температуры, измеренному, например, при расширении газа в вакуум, можно оценивать степень отклонения реального газа от идеального. Такой эффект действительно наблюдается, и по имени ученых, открывших его, называется эффектом Джоуля – Томсона.
Влияние температуры.
Точно так же выводятся формулы, описывающие влияние температуры при постоянном давлении:
Например, в диапазоне от абсолютного нуля до некоторой предельной температуры, для каждого вещества своей, теплоемкость всех веществ при постоянном объеме пропорциональна кубу температуры (по шкале Кельвина):
Это выражение вывел на основе квантовой теории П. Дебай (1884–1966). Оно позволяет простым интегрированием вычислять полную энтропию при температурах, близких к 0 К:
Дебай (1884–1966). Оно позволяет простым интегрированием вычислять полную энтропию при температурах, близких к 0 К:
Уравнения состояния.
Благодаря своей простой форме газовый закон [формула (18)] позволяет делать важные выводы о свойствах идеального газа. Но при адиабатическом сжатии идеальный газ нагревается. В этом случае изотермический закон PV = NRT не выполняется, и его необходимо заменить уравнением
где g – отношение удельных теплоемкостей при постоянном давлении и при постоянном объеме, т. е. g = C P /C V . Это уравнение вывел французский математик С.Пуассон (1781–1840).
В рабочих цилиндрах тепловых машин (паровых машин, бензиновых, газовых и дизельных двигателей) скорость сжатия велика, но процесс не является полностью адиабатическим и называется политропным. При решении большинства проектно-конструкторских задач в таких случаях принимается уравнение вида
где n – постоянная величина, меньшая чем g , и ее превышение над единицей зависит от быстроты сжатия. Кроме того, поведение реальных газов отклоняется от уравнений (18), (47) и (48), и для них используются т.н. уравнения состояния.
Кроме того, поведение реальных газов отклоняется от уравнений (18), (47) и (48), и для них используются т.н. уравнения состояния.
Примером таких уравнений может служить
где a и b – константы, зависящие от природы газа. Это уравнение вывел Я.Ван-дер-Ваальс (1837–1923). Было предложено немало и других уравнений; некоторые из них справедливы только для одного газа.
Литература:
Бэр Г. Техническая термодинамика . М., 1973
Базаров И.П. Термодинамика . М., 1983
Вукалович М.П., Новиков И.И. Термодинамика . М., 1984
Квасников И.А. Введение в теорию квазистатических процессов . М., 1986
Произошла ошибка при установке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.
Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.

Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт
не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к
остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Формулы первого закона термодинамики
Граничная работа – pdV Работа
Граничная работа возникает из-за того, что масса вещества, содержащегося внутри границы системы, вызывает силу, умноженную на давление, умноженное на площадь поверхности, на граничную поверхность и это двигаться. Граничная работа (или pΔV Работа ) возникает, когда объем V системы изменяется на . Он используется для расчета работы поршня в замкнутой системе .Вот что происходит, когда пар или газ, содержащийся в поршневом цилиндре, расширяется относительно поршня и заставляет поршень двигаться. Так как H = U + pV , следовательно, dH = dU + pdV + Vdp и подставляем dU = dH – pdV – Vdp в классическую форму закона:dH – pdV – Vdp = dQ – pdV
Получаем закон в терминах энтальпии:
dH = dQ + Vdp
или
dH = TdS + Vdp
В этом уравнении член Vdp представляет собой процесс потока . Эта работа, Vdp , используется для систем с открытым потоком , таких как турбина или насос , в которых есть «dp» , то есть изменение давления. Изменений в контрольной громкости нет. Как видно, эта форма закона упрощает описание передачи энергии. При постоянном давлении изменение энтальпии равно энергии , переданной из окружающей среды при нагревании:
Эта работа, Vdp , используется для систем с открытым потоком , таких как турбина или насос , в которых есть «dp» , то есть изменение давления. Изменений в контрольной громкости нет. Как видно, эта форма закона упрощает описание передачи энергии. При постоянном давлении изменение энтальпии равно энергии , переданной из окружающей среды при нагревании:
Изобарический процесс (Vdp = 0):
dH = dQ → Q = H 2 – H 1
При постоянной энтропии , т.е.е., в изэнтропическом процессе изменение энтальпии равняется работе потока , выполняемой системой или системой:
Изэнтропический процесс (dQ = 0):
dH = Vdp → W = H 2 – H 1
Это очевидно и будет очень полезно при анализе обоих термодинамических циклов, используемых в энергетике, т. Е. Циклов Брайтона и Ренкина.
Е. Циклов Брайтона и Ренкина.
Термодинамическая связь – обзор
4.2.1 Термодинамические потенциалы
Мы начнем с краткого изложения основных термодинамических соотношений, действующих для общей системы с однородными свойствами. Позже мы сконцентрируем это описание на магнитном корпусе.
Первый закон термодинамики. Этот закон выражает закон сохранения энергии и утверждает, что при общем преобразовании, когда работа δL выполняется в системе и тепло δQ поглощается ею,
(4,27) dU = δL + δQ
, где U , внутренняя энергия , – функция состояния.Мы предполагаем, что работа δL может быть выражена через две соответствующие сопряженные рабочие переменные, H и X , согласно выражению
(4.28) δL = HdX
X – переменная состояния, описывает некоторое свойство системы, а H характеризует внешнее воздействие, оказываемое на систему.
Второй закон термодинамики. Этот закон вводит вторую функцию состояния, энтропию S, , которая при любом обратимом или необратимом преобразовании всегда удовлетворяет неравенству
Этот закон вводит вторую функцию состояния, энтропию S, , которая при любом обратимом или необратимом преобразовании всегда удовлетворяет неравенству
(4.29) dS≥δQT
Знак равенства применяется к обратимым преобразованиям. В этом случае
(4,30) δQ = TdS
Между формулой (4.28) и уравнение. (4.30). T и S являются сопряженными переменными по отношению к тепловой энергии так же, как H и X являются сопряженными переменными по отношению к энергии, исходящей от внешней работы. T и H – интенсивные переменные , тогда как S и X – экстенсивные переменные.
Термодинамические потенциалы. Термодинамические превращения могут происходить при различных ограничениях, таких как постоянная температура, постоянная энтропия и так далее. Ограничение в целом будет касаться как аспектов внешней работы, так и аспектов тепловой энергии и будет соответствовать фиксированию одной переменной в каждом из наборов ( T , S ) и ( H , X ).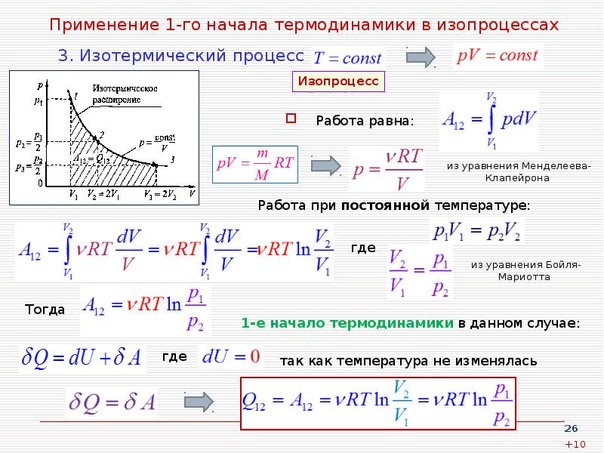 Учитывая ограничение, можно ввести соответствующий термодинамический потенциал , , то есть функцию состояния, контролирующую, как будет развиваться преобразование.Существует четыре возможных варианта ограничивающих переменных, поэтому можно определить четыре термодинамических потенциала. Это внутренняя энергия U ( X, S ), энтальпия E ( H, S ), свободная энергия F ( X, T ) и функция Гиббса G ( H, Т ). Каждый из них обладает тем свойством, что он никогда не увеличивается ни при каком преобразовании, если его аргументы остаются фиксированными. Термодинамическое равновесие достигается, когда соответствующий термодинамический потенциал достигает своего глобального минимума.Нас, в частности, интересуют свойства потенциалов превращений при постоянной температуре.
Учитывая ограничение, можно ввести соответствующий термодинамический потенциал , , то есть функцию состояния, контролирующую, как будет развиваться преобразование.Существует четыре возможных варианта ограничивающих переменных, поэтому можно определить четыре термодинамических потенциала. Это внутренняя энергия U ( X, S ), энтальпия E ( H, S ), свободная энергия F ( X, T ) и функция Гиббса G ( H, Т ). Каждый из них обладает тем свойством, что он никогда не увеличивается ни при каком преобразовании, если его аргументы остаются фиксированными. Термодинамическое равновесие достигается, когда соответствующий термодинамический потенциал достигает своего глобального минимума.Нас, в частности, интересуют свойства потенциалов превращений при постоянной температуре.
Свободная энергия F ( X, T ). Эта функция также называется функцией Гельмгольца или свободной энергии Гельмгольца. Он определяется как
Он определяется как
(4,31) F = U-TS
Уравнение (4.27) через уравнение. (4.29) показывают, что
(4.32) dF≤HdX − SdT
Таким образом, неравенство dF ≤ 0 выполняется при любом преобразовании при постоянных X и T .С другой стороны, в типичном обратимом преобразовании, то есть преобразовании, при котором система проходит через последовательность состояний термодинамического равновесия, знак равенства сохраняется в уравнении (1). (4.32) и находим
(4.33) ∂F∂XT = H∂F∂TX = −S
Функция Гиббса G ( H, T ). Эта функция также называется свободной энергии Гиббса или просто термодинамическим потенциалом . Он определяется как
(4,34) G = U − TS − HX = F − HX
Из уравнения. (4.27) через формулу. (4.29) получаем
(4.35) dG≤ − XdH − SdT
Таким образом, dG ≤ 0 при постоянных H и T . В состоянии равновесия
(4. 36) ∂G∂HT = −X∂G∂TH = −S
36) ∂G∂HT = −X∂G∂TH = −S
Самопроизвольное преобразование может иметь место только тогда, когда система изначально не находится в равновесии. Неравновесное состояние описывается другими внутренними переменными в дополнение к ограниченным переменным, которые могут быть пространственно-зависимыми и эволюционировать во времени, пока не достигнут значения, для которого термодинамический потенциал достигает своего глобального минимального значения.Когда система находится в равновесии, любое спонтанное колебание свойств системы обязательно приводит к неотрицательному изменению потенциала. Например, любое спонтанное колебание δX или δS при постоянных H и T должно быть таким, чтобы δG ≥ 0. Это требование стабильности приводит к полезным неравенствам. В частности, можно показать, что в состоянии равновесия
(4.37) ∂X∂HT≥0
. (4.33) относительно X и уравнения.(4.36) относительно H и используя уравнение. (4.37), можно также найти, что в состоянии равновесия
(4.37), можно также найти, что в состоянии равновесия
(4.38) ∂2F∂X2T≥0∂2G∂h3T≤0
, что показывает, что F всегда является выпуклой функцией от X и G . вогнутая функция H .
Термодинамические процессы – типы и уравнения
Определение термодинамической системы
Термодинамическая система – это определенное пространство или макроскопическая область во Вселенной, состояние которой может быть выражено в терминах давления, температуры и объема, и в которой один или происходит более одного термодинамического процесса.Все, что находится вне этой термодинамической системы, представляет собой окружение и отделено от системы границей. Окружение, система и граница вместе составляют вселенную. Типы систем в термодинамике следующие:
Открытая система: Она позволяет энергии, а также массе течь в нее и выходить из нее.
Закрытая система: Она позволяет передавать только энергию (работу и тепло) через ее границу.

Изолированная система: Ни масса, ни энергия не могут взаимодействовать с ней.
(изображение будет добавлено в ближайшее время)
(изображение будет добавлено в ближайшее время) (изображение будет добавлено в ближайшее время) (изображение будет добавлено в ближайшее время)
Типы термодинамических процессов
Состояние данной термодинамической системы может выражаться различными параметрами, такими как давление (P), температура (T), объем (V) и внутренняя энергия (U). Если любые два параметра фиксированы, скажем, давление (P) и объем (V) фиксированной массы газа, то температура (T) газа будет автоматически фиксирована в соответствии с уравнением PV = RT.Невозможно изменить T без изменения P и V.
Состояние системы может быть изменено различными процессами. В термодинамике к типам процессов относятся:
Изобарический процесс, в котором давление (P) поддерживается постоянным (ΔP = 0).

Изохорный процесс, в котором объем (V) поддерживается постоянным (ΔV = 0).
Изотермический процесс, в котором температура (T) поддерживается постоянной (ΔT = 0).
Адиабатический процесс, в котором теплопередача равна нулю (Q = 0).
Замечания по термодинамическому процессу обсуждались позже.
Работа в термодинамических процессах
Когда объем (V) системы изменяется, говорят, что произошла работа давления и объема. Термодинамический процесс, происходящий в замкнутой системе таким образом, что скорость изменения объема достаточно медленная, чтобы давление (P) оставалось постоянным и однородным во всей системе, является квазистатическим процессом. В этом случае работа (W) представлена как:
δW = PdV, где δW – бесконечно малое приращение работы системы, а dV – бесконечно малое приращение объема.
Кроме того, W = ∫ PdV, где W – работа, которую выполняет система в течение всего обратимого процесса.
Изобарический процесс
Поскольку давление (P) в этом процессе постоянно, объем системы изменяется. Сделанная работа (W) может быть рассчитана как W = P (Vfinal – Vinitial).
Если ΔV положительное (расширение), проделанная работа положительна. При отрицательном ΔV (сжатие) проделанная работа отрицательная.
Изохорный процесс
Объем остается постоянным в изохорическом процессе.Следовательно, система не выполняет никакой работы (поскольку ΔV = 0, PΔV или W также равны нулю). Такой процесс, при котором нет изменения объема, может быть достигнут путем помещения термодинамической системы в закрытый контейнер, который не сжимается и не расширяется. Таким образом, из первого закона термодинамики (Q = ΔU + W) изменение внутренней энергии становится равным теплопередаче (ΔU = Q) для изохорного процесса.
Изотермический процесс
(Изображение будет добавлено в ближайшее время)
Температура системы остается постоянной при изотермическом процессе.Мы знаем,
W = ∫ PdV
Из закона о газах,
PV = nRT
P = nRT / V. Использование значения P в уравнении работы:
W = nRT VB ∫VA (dV / V)
W = nRT ln (VB / VA)
Если VB выше VA, выполненная работа будет положительной, иначе отрицательный.
Поскольку внутренняя энергия зависит от температуры, ΔU = 0, поскольку температура постоянна, и, таким образом, из первого закона термодинамики (Q = ΔU + W) мы получим Q = W.
Адиабатический процесс
Нет теплообмен с системой происходит адиабатически (Q = 0).Его математическое представление:
PVƔ = K (константа).
Также W = ∫ PdV. Подставляя значение P в уравнение работы:
W = K Vf ∫Vi (dV / VƔ)
W = K [(Vf1-Ɣ – Vi1-Ɣ) / 1-Ɣ]
Поскольку Q = 0 для адиабатический процесс, из первого закона термодинамики (Q = ΔU + W), мы получим ΔU = -W. Таким образом, внутренняя энергия будет увеличиваться, если проделанная работа отрицательная, и наоборот.
Таким образом, внутренняя энергия будет увеличиваться, если проделанная работа отрицательная, и наоборот.
Типы термодинамических процессов: формулы, примеры, уравнения
Термодинамический процесс зависит от таких факторов, как температура (T), давление (P), объем (V) и теплообмен в системе (ΔQ).В зависимости от изменения этих физических свойств термодинамические процессы делятся на разные типы. У этих типов есть определенные отношения, управляющие ими. В этой статье мы собираемся изучить различные типы термодинамических процессов.
Проверьте все законы термодинамики на примерах.
Циклический процесс
Если система называется обратимой, то есть для процесса, если система возвращается в исходное состояние после выполнения некоторой работы, то процесс называется циклическим.
Для циклического процесса ΔU = 0.
Теперь согласно Первому закону термодинамики ΔQ = ΔW + ΔU, поэтому, если ΔU = 0.
∴ ΔQ = ΔW
Изобарический процесс
- Для термодинамики процесс, если давление в системе остается постоянным, то этот процесс называется изобарическим процессом.

- Таким образом, если давление постоянное, чистая работа, выполняемая системой, может быть представлена как
W = PΔV = P (V2 – V1)
- Это означает, что тепло, подаваемое в систему, частично расходуется в изменение его объема и частично в изменении температуры.
Узнайте, как здесь применяется термодинамика.
Изохорный процесс
- Для термодинамического процесса, если объем остается постоянным для системы, процесс известен как изохорный процесс
- Для этого процесса согласно первому закону термодинамики ΔQ = ΔW + ΔU, поэтому, если объем остается постоянным, это означает, что ΔV = 0, следовательно, ΔW = 0.
∴ ΔQ = ΔU
- Следовательно, в этом процессе подводимое тепло будет использоваться для увеличения его внутренней энергии
Изотермический процесс
- Согласно Согласно закону Бойля для фиксированной массы газа при постоянной температуре объем обратно пропорционален давлению.
 {V_2} PdV = 2.3026nRTlog_ {10} {V_2 \ over {V_1}} \)
{V_2} PdV = 2.3026nRTlog_ {10} {V_2 \ over {V_1}} \)- Аналогично, работа, выполняемая в изотермическом процессе от давления p1 и p2, составляет
W = 2,3026nRTlog_ {10} {P_2 \ over {P_1}} [ / latex]
Изучите проводник в магнитном поле здесь.
Адиабатический процесс
- Адиабатический процесс – это термодинамический процесс, в котором отсутствует теплообмен между системой и окружающей средой, то есть тепло остается постоянным,
, т.е. ΔQ = 0
- Для адиабатический процесс, мы следуем закону Пуассона, т.{\ gamma-1}}} = константа \)
- Теперь согласно первому закону термодинамики ΔQ = ΔW + ΔU, значит, если ΔQ = 0.
- Это означает, что для адиабатического процесса система выполняет Работу (ΔW ) на основе внутренней энергии, поскольку ΔW = – ΔU из приведенного выше уравнения
- Для адиабатического процесса работа, выполняемая системой, задается как
\ (W = {P_1V_1-P_2V_2 \ over {\ гамма-1}} = {nR (T_1-T_2) \ over {\ gamma-1}} \\\)
\ (\ gamma = {c_p \ over c_v} \)
- Здесь R – газовая постоянная, n – молярная масса, а Cp и Cv – удельная теплоемкость при постоянном давлении и объеме.
 адиабатические процессы идеального газа
адиабатические процессы идеального газаПонять эффект Доплера с решенными примерами.
Обратимый и необратимый процесс:
Обратимый процесс – это процесс, который выполняется таким образом, что на заключительном этапе процесса и система, и окружающая среда возвращаются в исходное состояние без каких-либо изменений. На самом деле обратимого процесса нет.
- Если начальная и конечная стадии обратимого процесса представлены цифрами 1 и 2. В таком процессе система будет переходить от 1 к 2 с очень медленной скоростью.
- Это потому, что обратимый процесс не должен оставлять после себя следов или реликвий.Обратимый процесс выполняется бесконечно медленно с бесконечно малым градиентом, так что каждое состояние, пройденное между 1 и 2, является равновесием.
- Такой процесс также носит квазистатический характер. Следовательно, его также называют обратимым квазистатическим процессом.
- Эти процессы гипотетичны и асимптотичны.
- Все самопроизвольные процессы необратимы.

Итак, это все о типах термодинамических процессов. Надеюсь, это помогло вам изучить концепции.Если вы с нетерпением ждете такой же практики, то были бы рады узнать, что мы предлагаем бесплатные пробные тесты в нашем приложении Testbook. Скачайте бесплатно прямо сейчас!
Часто задаваемые вопросы о типах термодинамических процессов
Q.1 Что такое циклический процесс?
Ans.1 Если система называется обратимой, то есть для процесса, если система возвращается в исходное состояние после выполнения некоторой работы, то процесс называется циклическим.
В.2 Что такое изобарический процесс?
Ans.2 Для термодинамического процесса, если давление в системе остается постоянным, этот процесс называется изобарическим процессом.
Q.3 Что такое изохарический процесс?
Ans.3 Для термодинамического процесса, если объем остается постоянным для системы, процесс известен как изохорный процесс.

Q.4 Что такое изотермический процесс?
Отв.4 Для термодинамического процесса, если температура остается постоянной для системы, процесс известен как изотермический процесс
Q.5 Что такое адиабатический процесс?
Ans.5 Адиабатический процесс – это термодинамический процесс, в котором нет обмена теплом между системой и окружающей средой, то есть тепло остается постоянным.
Создайте бесплатную учетную запись, чтобы продолжить чтение
Получите мгновенные оповещения о вакансиях бесплатно!
Получите ежедневную капсулу GK и текущие новости и PDF-файлы
Получите более 100 бесплатных пробных тестов и викторин
Подпишитесь бесплатно Уже есть аккаунт? Войти
Next Post
Термодинамические процессы и уравнения
Термодинамические процессы и уравнения!
Процесс – это изменение состояния газа в результате потока энергии.
 Во время этого потока происходят изменения в свойствах вещества, таких как давление, объем, температура, а также в количествах энергии, таких как внутренняя энергия, тепло и работа.
Во время этого потока происходят изменения в свойствах вещества, таких как давление, объем, температура, а также в количествах энергии, таких как внутренняя энергия, тепло и работа.Пять важных процессов, обычно рассматриваемых в инженерии, следующие: 1. Процесс с постоянным объемом или изохорный процесс 2. Процесс с постоянным давлением или изобарический процесс 3. Процесс с постоянной температурой или изотермический процесс 4. Адиабатический процесс или изоэнтропический процесс 5. Политропный процесс 6 Гиперболическое расширение 7.Бесплатное расширение 8. Дросселирование.
Графическое представление этих процессов, которые показывают одновременные значения давления и объема, называются кривыми, и серии этих кривых построены таким образом, что они образуют диаграмму, известную как диаграмма P-V.
В нашем дальнейшем обсуждении суффикс 1 указывает состояние газа в начале процесса, а суффикс 2 указывает состояние газа в конце процесса. Обозначим массу газа m.Таким образом, P 1 , V 1 и будут давлением, объемом и температурой определенного количества газа в начале процесса и будут давлением, объемом и температурой того же количества газа в конце.
 процесса.
процесса.Если это процесс расширения, то отношение V 2 / V 1 известно как отношение расширения. Если процесс сжатия, то отношение V 1 / V 2 известно как степень сжатия.Обычно степень расширения или сжатия обозначается буквой «r».
1. Процесс постоянного объема:(a) Изображение на диаграмме P-V и T-:
2. Процесс с постоянным давлением:3.
Изотермический процесс:Изотермический процесс – это процесс, при котором температура рабочего тела остается неизменной.В этом процессе температура остается постоянной во время процесса. Этот процесс следует закону Бойля.
(a) Изображение на диаграмме P-V и T-(рис. 2-16):
Поскольку во время этого процесса температура остается постоянной, по закону Бойля
PV = постоянный.
Это приводит нас к тому, что кривая, показывающая соотношение между P и V на диаграмме P-V (рис.
 2-16), представляет собой прямоугольную гиперболу. Диаграмма будет прямоугольной.
2-16), представляет собой прямоугольную гиперболу. Диаграмма будет прямоугольной.Изотермический процесс на диаграмме температурной энтропии представлен горизонтальной линией ab, как показано на рис. 2-16. Заштрихованная область под линией ab представляет общее добавленное тепло.
4.
Изэнтропический процесс:В этом процессе газ не получает и не отдает тепло. Мы можем представить себе, что газ содержится в баллоне из идеального непроводящего материала. Затем газ можно расширять или сжимать, но нельзя ни отдавать тепло, ни отводить от него тепло.
Студенты очень часто неправильно понимают значение изэнтропического (адиабатического) расширения или сжатия. Во время расширения температура падает, и происходит потеря внутренней энергии, но тепло из системы не теряется. На рис. 2-17 показан полностью изолированный цилиндр и поршневой механизм теплового двигателя без трения.
В изоэнтропическом процессе газ не теряет тепла в окружающую среду и является полностью изолированной системой за счет использования идеальных изоляционных материалов.
 Если в механизме присутствует трение, то такой процесс называется адиабатическим процессом, а изэнтропический процесс – адиабатическим процессом без трения.
Если в механизме присутствует трение, то такой процесс называется адиабатическим процессом, а изэнтропический процесс – адиабатическим процессом без трения.(a) Закон изэнтропического процесса:
По первому закону термодинамики применительно к непроточным процессам,
поставленного тепла = изменение внутренней энергии + проделанная работа.
Рассмотрим единицу массы газа.
Пусть dQ обозначает небольшое количество тепла, поглощаемое единицей массы идеального газа, а dT и dv представляют собой результирующие небольшие приращения температуры и объема соответственно; затем, согласно первому закону термодинамики,
Таким образом, мы получаем уравнение, которому следует газ, когда он расширяется или сжимается изоэнтропически.
(b) Представительство на P-V и T-ɸ Диаграмма:
Изэнтропический процесс на диаграмме P-V представлен, как показано на рис. 2-18. Диаграмма T-показывает, что энтропия остается постоянной.

(e) Изменение внутренней энергии:
Как обычно получаем
изменение внутренней энергии = U 2 – U 1 = m x C v (T 2 – T 1 ).
Другой способ определения изменения внутренней энергии очень распространен в изоэнтропических режимах.
По первому закону термодинамики применительно к непроточным процессам,
поставленного тепла = изменение внутренней энергии + проделанная работа; но подводимого тепла ноль.
∴ Изменение внутренней энергии = – работа сделана.
Таким образом, мы получаем важное соотношение в изоэнтропическом процессе. Это соотношение можно сформулировать так: «Изменение внутренней энергии численно равно проделанной работе».Когда работа выполняется газом, он теряет внутреннюю энергию и приобретает внутреннюю энергию, когда работа выполняется с газом.
(f) Передаваемое тепло:
Во время изоэнтропической операции передаваемое тепло равно нулю.

Δ Q = 0.
(г) Изменение энтальпии:
Изменение энтальпии = H 2 – H 1 = m x C p (T 2 – T 1 ).
(ч) Изменение энтропии:
Изменение энтропии равно 0, потому что dQ = 0.
dɸ = ɸ 2 – ɸ 1 = 0.
Что касается изэнтропического процесса без трения, добавляемое или отводимое тепло будет равно нулю, изменение энтропии также будет нулевым. Отсюда получаем ɸ 1 = ɸ 2 ; другими словами, мы говорим, что во время изэнтропического процесса без трения энтропия остается постоянной, и ее представление на диаграмме энтропии температуры будет вертикальной прямой линией ab, как показано на рис. 2-18.
Изэнтропический процесс без трения называется изэнтропическим процессом, поскольку энтропия остается постоянной.Из рис. 2-18 видно, что под вертикальной линией, представляющей изоэнтропическую операцию, нет области.
5. Политропный процесс:
Многие процессы, которые происходят на практике, можно приблизительно описать уравнением вида PV n = константа, где n – константа. Такой процесс называется политропным.
(a) Связь для политропных процессов:
Каждый из четырех процессов, которые были рассмотрены ранее
, является частным случаем политропного процесса.Основное различие в уравнениях изоэнтропического и политропного процессов состоит в том, что если мы заменим γ на n в соотношениях изоэнтропического действия, мы получим соотношение для политропных процессов.Когда эти значения нанесены на диаграмму P-V, как показано на рис. 2-19 видно, что они образуют семейство кривых.
6. Гиперболическое расширение:Когда газ расширяется или сжимается таким образом, что произведение давления и объема остается постоянным в течение всего расширения или сжатия, расширение известно как гиперболическое расширение, потому что такой процесс на диаграмме P-V даст прямоугольную гиперболу.
 Следовательно, гиперболическое расширение – это расширение, которое следует закону, давление × объем – константа.
Следовательно, гиперболическое расширение – это расширение, которое следует закону, давление × объем – константа.∴ PV = постоянный.
Для идеальных газов эта операция аналогична изотермической операции. На рис. 2-22 показана PV диаграмма для гиперболического расширения.
7. Бесплатное расширение:Когда жидкость внезапно расширяется в вакуумную камеру через отверстие больших размеров, происходит свободное расширение газа.Во время этой операции не подавалось и не отбрасывалось тепло, и не производились никакие внешние работы. Помещая эти нулевые значения в Первый закон термодинамики применительно к непроточному процессу, ΔQ = ΔU + ΔW, мы получаем ΔU = 0, то есть U 1 = U 2 .
Таким образом, внутренние энергии до и после свободного расширения равны. На Рис. 2-23 показано свободное расширение.
8. Процесс дросселирования:
Процесс дросселирования: Процесс дросселирования – это процесс расширения, при котором давление уменьшается после расширения, а скорость незначительна.Дросселирующее расширение происходит, когда газ или пар расширяются через отверстие малых размеров, такое как горловина или слегка приоткрытый клапан.
В процессе дросселирования расширяющаяся жидкость проталкивается через отверстие под действием своего давления, но отверстие настолько узкое, что сопротивление трения между жидкостью и стенкой снижает скорость жидкости до незначительной величины; в результате жидкость выходит с небольшим количеством кинетической энергии.
Из-за трения кинетическая энергия снова появляется в виде тепла, и газ нагревается до своей начальной температуры.Во время процесса дросселирования тепло не подается и не отбрасывается, никакие внешние работы не выполняются, а в случае идеального газа нет изменений температуры.
Когда жидкость расширяется через дроссельный клапан или суженное отверстие, энтальпия до дроссельного клапана равна энтальпии после дросселирования.
 Однако это не означает, что процесс дросселирования является процессом с постоянной энтальпией. Здесь определяются свойства до и после процесса. На рис. 2-24 показан процесс дросселирования.
Однако это не означает, что процесс дросселирования является процессом с постоянной энтальпией. Здесь определяются свойства до и после процесса. На рис. 2-24 показан процесс дросселирования.H 1 = H 2 .
В этом процессе энтальпия остается постоянной. Энтальпия при условии 1 равна энтальпии при условии 2.
Теория цикла Ренкина – уравнения и расчеты
Тепловой КПД цикла Ренкина
В целом тепловой КПД η th любой тепловой машины определяется как отношение работа, которую он выполняет, W , с тепловложением при высокой температуре Q H .
Тепловой КПД , η th , представляет собой долю тепла , Q H , преобразованного в рабочий .
 Так как энергия сохраняется в соответствии с первым законом термодинамики и энергия не может быть полностью преобразована для работы, подвод тепла, Q H , должен равняться проделанной работе, Вт, плюс тепло, которое должно рассеиваться в виде отработанного тепла . Q C в окружающую среду.Следовательно, мы можем переписать формулу теплового КПД как:
Так как энергия сохраняется в соответствии с первым законом термодинамики и энергия не может быть полностью преобразована для работы, подвод тепла, Q H , должен равняться проделанной работе, Вт, плюс тепло, которое должно рассеиваться в виде отработанного тепла . Q C в окружающую среду.Следовательно, мы можем переписать формулу теплового КПД как:Это очень полезная формула, но мы выражаем тепловой КПД, используя первый закон, через энтальпию. Цикл Ранкина – Ц-диаграмма
Обычно большинство атомных электростанций работают с многоступенчатыми конденсационными паровыми турбинами . В этих турбинах ступень высокого давления получает пар (этот пар является почти насыщенным паром – x = 0,995 – точка C на рисунке; 6 МПа ; 275.6 ° C) из парогенератора и отводит его в сепаратор-подогреватель влаги (точка D). Чтобы избежать повреждения лопаток паровой турбины некачественным паром, необходимо повторно нагреть пар.
 Подогреватель нагревает пар (точка D), а затем пар направляется в ступень низкого давления паровой турбины, где он расширяется (точка E – F). Затем отработанный пар конденсируется в конденсаторе. Он находится под давлением значительно ниже атмосферного (абсолютное давление 0,008 МПа, ) и находится в частично конденсированном состоянии (точка F), как правило, с качеством около 90%.
Подогреватель нагревает пар (точка D), а затем пар направляется в ступень низкого давления паровой турбины, где он расширяется (точка E – F). Затем отработанный пар конденсируется в конденсаторе. Он находится под давлением значительно ниже атмосферного (абсолютное давление 0,008 МПа, ) и находится в частично конденсированном состоянии (точка F), как правило, с качеством около 90%.В этом случае парогенераторы, паровые турбины, конденсаторы и насосы питательной воды составляют тепловую машину с ограничениями по эффективности, налагаемыми вторым законом термодинамики . В идеальном случае (отсутствие трения, обратимые процессы, идеальная конструкция) этот тепловой двигатель имел бы КПД Карно
= 1 – T холодный / T горячий = 1 – 315/549 = 42,6%
где температура горячего резервуара 275,6 ° С (548,7К), температура холодного резервуара 41.5 ° С (314,7 К). Но АЭС – это настоящая тепловая машина , в которой термодинамические процессы почему-то необратимы.
 Они не делаются бесконечно медленно. В реальных устройствах (турбины, насосы и компрессоры) механическое трение и тепловые потери вызывают дополнительные потери эффективности.
Они не делаются бесконечно медленно. В реальных устройствах (турбины, насосы и компрессоры) механическое трение и тепловые потери вызывают дополнительные потери эффективности.Для расчета термического КПД простейшего цикла Ренкина (без повторного нагрева) инженеры используют первый закон термодинамики в терминах энтальпии , а не в терминах внутренней энергии.
Первый закон в терминах энтальпии:
dH = dQ + Vdp
В этом уравнении член Vdp представляет собой процесс потока . Эта работа, Vdp , используется для систем с открытым потоком , таких как турбина или насос , в которых есть «dp», то есть изменение давления. Изменений в контрольной громкости нет. Как видно, эта форма закона упрощает описание передачи энергии.
 При постоянном давлении изменение энтальпии равно энергии , переданной из окружающей среды при нагревании:
При постоянном давлении изменение энтальпии равно энергии , переданной из окружающей среды при нагревании:Изобарический процесс (Vdp = 0):
dH = dQ → Q = H 2 – H 1
При постоянной энтропии , т. Е. В изоэнтропическом процессе, изменение энтальпии равняется работе процесса потока , выполненной системой или ею:
Изэнтропический процесс (dQ = 0):
dH = Vdp → W = H 2 – H 1
Это очевидно и будет очень полезно при анализе обоих используемых термодинамических циклов. в энергетике, т.э., в циклах Брайтона и Ренкина.
Энтальпия может быть преобразована в интенсивную или конкретную переменную путем деления на массу.
 Инженеры используют удельную энтальпию в термодинамическом анализе больше, чем саму энтальпию. Он указан в таблицах пара вместе с удельным объемом и удельной внутренней энергией. Тепловой КПД такого простого цикла Ренкина с точки зрения удельных энтальпий будет:
Инженеры используют удельную энтальпию в термодинамическом анализе больше, чем саму энтальпию. Он указан в таблицах пара вместе с удельным объемом и удельной внутренней энергией. Тепловой КПД такого простого цикла Ренкина с точки зрения удельных энтальпий будет:Это очень простое уравнение, и для определения теплового КПД вы можете использовать данные из таблиц пара .Такаиши, Тацуо; Нумата, Акира; Накано, Рёдзи; Сакагути, Кацухико (март 2008 г.). «Подход к высокоэффективным дизельным и газовым двигателям» (PDF). Технический обзор Mitsubishi Heavy Industries. 45 (1). Проверено 4 февраля 2011.
На современных атомных электростанциях общий тепловой КПД составляет около 1/3 (33%), поэтому для выработки 1000 МВт или электроэнергии требуется 3000 МВт тепл. тепловой энергии от реакции деления. Причина кроется в относительно низкой температуре пара ( 6 МПа, ; 275.


 Reaumur, 1730} и А. Цельсий (A. Celsius, 1742) создали температурные шкалы в соответствии с этим принципом.
Reaumur, 1730} и А. Цельсий (A. Celsius, 1742) создали температурные шкалы в соответствии с этим принципом.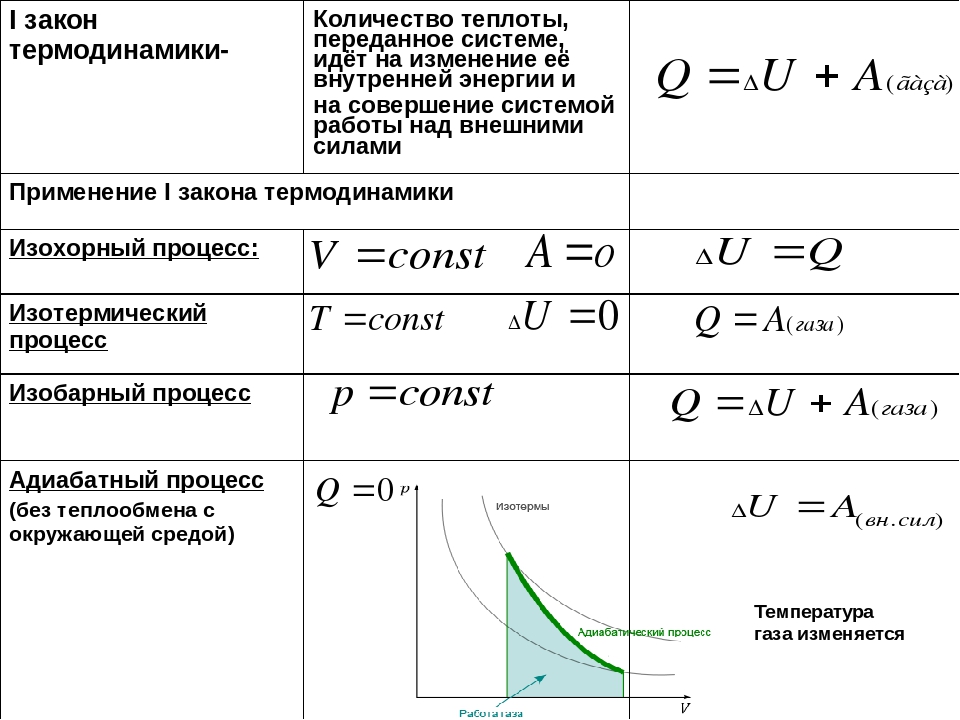

 Общей мерой передаваемого такими способами движения является работа – форма передачи энергии путём упорядоченного движения частиц.
Общей мерой передаваемого такими способами движения является работа – форма передачи энергии путём упорядоченного движения частиц.



 {V_2} PdV = 2.3026nRTlog_ {10} {V_2 \ over {V_1}} \)
{V_2} PdV = 2.3026nRTlog_ {10} {V_2 \ over {V_1}} \) адиабатические процессы идеального газа
адиабатические процессы идеального газа

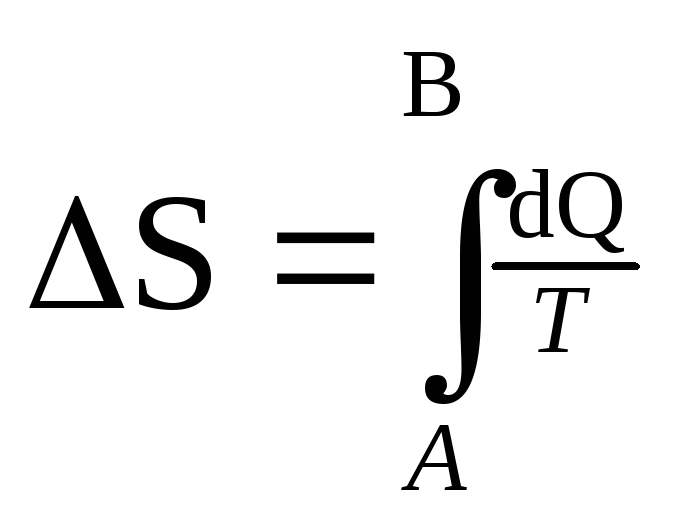 Во время этого потока происходят изменения в свойствах вещества, таких как давление, объем, температура, а также в количествах энергии, таких как внутренняя энергия, тепло и работа.
Во время этого потока происходят изменения в свойствах вещества, таких как давление, объем, температура, а также в количествах энергии, таких как внутренняя энергия, тепло и работа. процесса.
процесса. 2-16), представляет собой прямоугольную гиперболу. Диаграмма будет прямоугольной.
2-16), представляет собой прямоугольную гиперболу. Диаграмма будет прямоугольной. Если в механизме присутствует трение, то такой процесс называется адиабатическим процессом, а изэнтропический процесс – адиабатическим процессом без трения.
Если в механизме присутствует трение, то такой процесс называется адиабатическим процессом, а изэнтропический процесс – адиабатическим процессом без трения.


 Следовательно, гиперболическое расширение – это расширение, которое следует закону, давление × объем – константа.
Следовательно, гиперболическое расширение – это расширение, которое следует закону, давление × объем – константа. Процесс дросселирования:
Процесс дросселирования:  Однако это не означает, что процесс дросселирования является процессом с постоянной энтальпией. Здесь определяются свойства до и после процесса. На рис. 2-24 показан процесс дросселирования.
Однако это не означает, что процесс дросселирования является процессом с постоянной энтальпией. Здесь определяются свойства до и после процесса. На рис. 2-24 показан процесс дросселирования. Так как энергия сохраняется в соответствии с первым законом термодинамики и энергия не может быть полностью преобразована для работы, подвод тепла, Q H , должен равняться проделанной работе, Вт, плюс тепло, которое должно рассеиваться в виде отработанного тепла . Q C в окружающую среду.Следовательно, мы можем переписать формулу теплового КПД как:
Так как энергия сохраняется в соответствии с первым законом термодинамики и энергия не может быть полностью преобразована для работы, подвод тепла, Q H , должен равняться проделанной работе, Вт, плюс тепло, которое должно рассеиваться в виде отработанного тепла . Q C в окружающую среду.Следовательно, мы можем переписать формулу теплового КПД как: Подогреватель нагревает пар (точка D), а затем пар направляется в ступень низкого давления паровой турбины, где он расширяется (точка E – F). Затем отработанный пар конденсируется в конденсаторе. Он находится под давлением значительно ниже атмосферного (абсолютное давление 0,008 МПа, ) и находится в частично конденсированном состоянии (точка F), как правило, с качеством около 90%.
Подогреватель нагревает пар (точка D), а затем пар направляется в ступень низкого давления паровой турбины, где он расширяется (точка E – F). Затем отработанный пар конденсируется в конденсаторе. Он находится под давлением значительно ниже атмосферного (абсолютное давление 0,008 МПа, ) и находится в частично конденсированном состоянии (точка F), как правило, с качеством около 90%.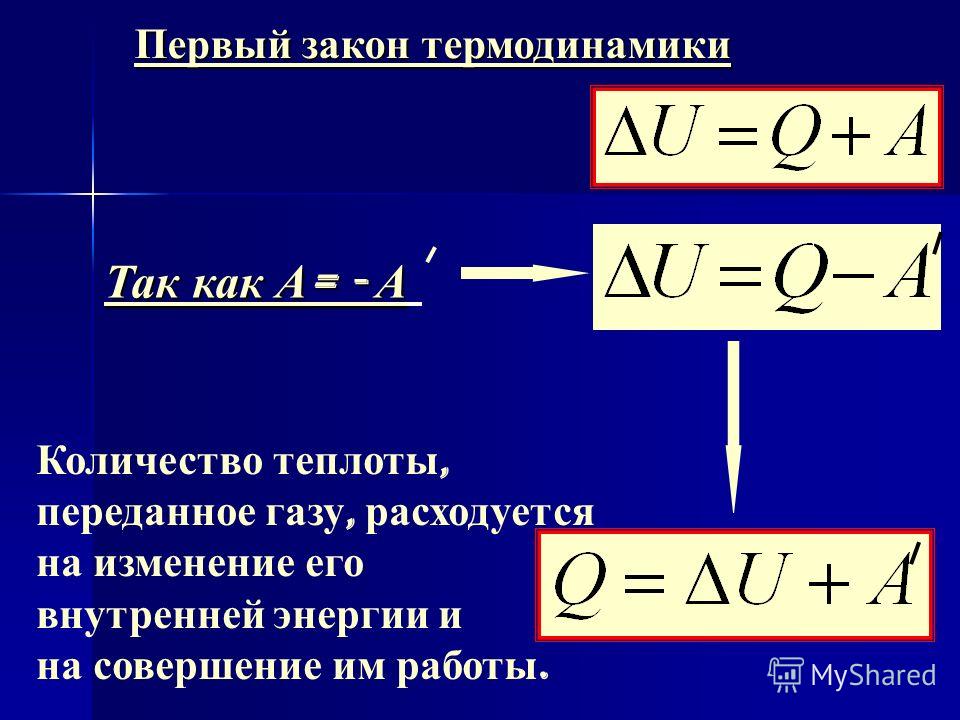 Они не делаются бесконечно медленно. В реальных устройствах (турбины, насосы и компрессоры) механическое трение и тепловые потери вызывают дополнительные потери эффективности.
Они не делаются бесконечно медленно. В реальных устройствах (турбины, насосы и компрессоры) механическое трение и тепловые потери вызывают дополнительные потери эффективности. При постоянном давлении изменение энтальпии равно энергии , переданной из окружающей среды при нагревании:
При постоянном давлении изменение энтальпии равно энергии , переданной из окружающей среды при нагревании: Инженеры используют удельную энтальпию в термодинамическом анализе больше, чем саму энтальпию. Он указан в таблицах пара вместе с удельным объемом и удельной внутренней энергией. Тепловой КПД такого простого цикла Ренкина с точки зрения удельных энтальпий будет:
Инженеры используют удельную энтальпию в термодинамическом анализе больше, чем саму энтальпию. Он указан в таблицах пара вместе с удельным объемом и удельной внутренней энергией. Тепловой КПД такого простого цикла Ренкина с точки зрения удельных энтальпий будет: