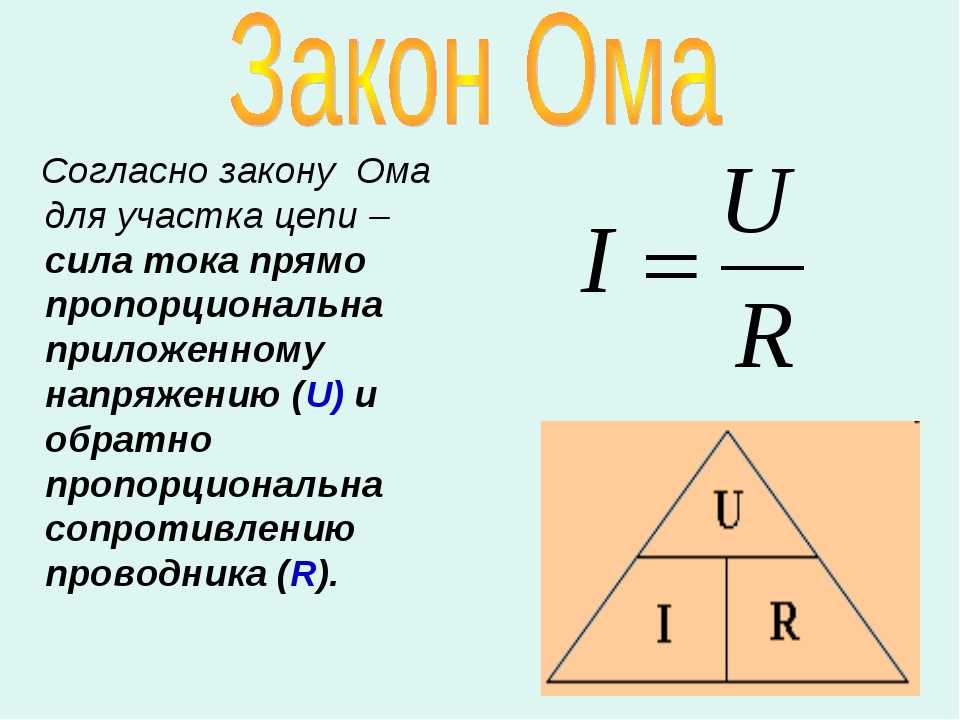
основные понятия, нахождение через силу тока и сопротивление
При проектировании схем различных устройств радиолюбителю необходимо производить точные расчеты c помощью измерительных приборов и формул. В электротехнике используются формулы для вычислений величин электричества (формулы напряжения, сопротивления, силы тока и так далее).
- Общие сведения об электрическом токе
- Физический смысл
- Пагубное влияние на человека
- Единицы измерения
- Цепи переменного и постоянного тока
- Переменное однофазное напряжение
- Рекомендации по выбору прибора
Общие сведения об электрическом токе
Электрическим током является процесс движения заряженных частиц (свободных электронов), имеющий вектор направленности. Частицы перемещаются под действием напряженности электрического поля, имеющей векторное направление. Это поле совершает работу по перемещению этих частиц. Влияют на работу электрического поля сила тока, напряжение и сопротивление.
Физический смысл
Под физическим смыслом понимается работа тока на участке, соотносящаяся с величиной заряда. Положительный заряд перемещается из одной точки, обладающей одним потенциалом, в другую, причем потенциал в этой точке отличается от предыдущего. В результате этого и возникает разность потенциалов, именуемая напряжением или ЭДС (электродвижущей силой).
Для полного понимания этого физического процесса и выяснения физического смысла напряжения необходимо провести аналогию с трубой. Допустим, труба наполнена водой и к ней прикручен кран для слива воды. Эта труба также оборудована краном для заливания воды с помощью мощного насоса.
Для демонстрации аналогии нужно открыть кран полностью, вода начнет выливаться и можно сделать вывод о незначительном давлении. Во втором случае спускной кран открыт не полностью и происходит набор воды при помощи насоса. В трубе создается давление и напор усиливается. Насос, создающий давление, и является в этом примере напряженностью электрического поля.
Насос, создающий давление, и является в этом примере напряженностью электрического поля.
Электричество, если его не контролировать и не знать о пагубном влиянии на организм человека, способно создать множество проблем начиная от сгорания приборов и пожаров, и заканчивая угрозой жизни и здоровью человека. Техника безопасности очень важна в любой сфере.
Пагубное влияние на человека
Электричество очень опасно и является причиной несчастных случаев. Радиолюбители подвержены риску поражения электрическим током довольно часто. Некоторые радиолюбители пробуют наличие напряжения пальцами и пренебрегают техникой безопасности. Большинство из них считает опасным для жизни напряжение от 500 В, а 110 и 220 — не наносящими вреда здоровью. Удары от маломощных источников тока (маломощный силовой трансформатор, конденсатор), по их мнению, являются неопасными.
Согласно технике безопасности при работах с электричеством, они ошибаются, но есть и другая сторона этого вопроса: организм каждого человека индивидуален, обладает разными параметрами.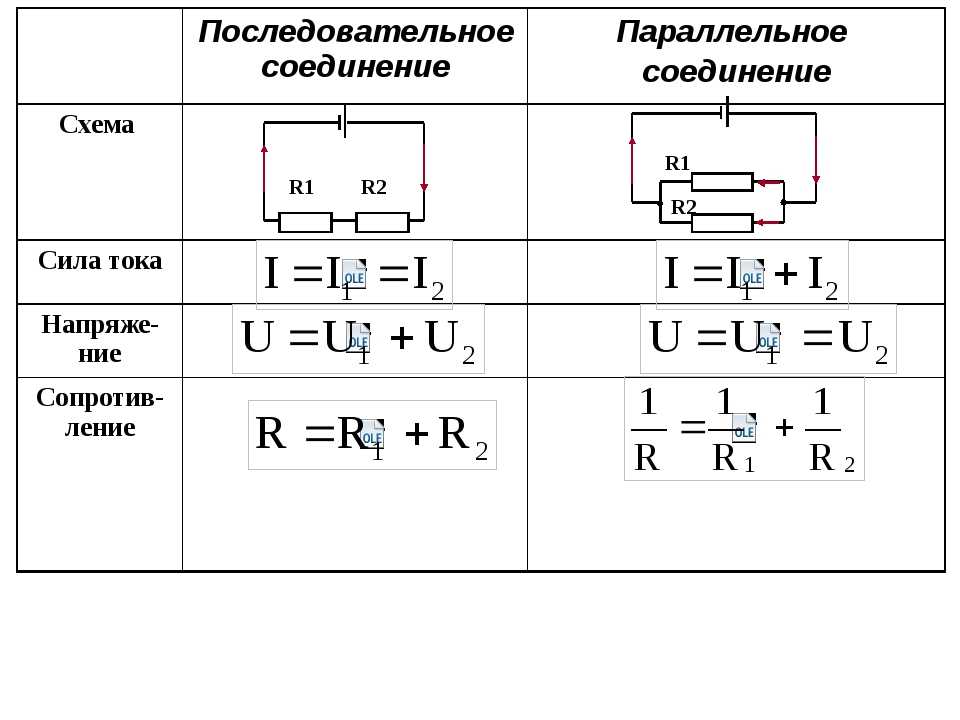 Из этого утверждения следует, что смертельные характеристики электричества (напряжение и ток) индивидуальны для каждого человека. Одних может ударить 36 В, а других не пробивает и 220 В.
Из этого утверждения следует, что смертельные характеристики электричества (напряжение и ток) индивидуальны для каждого человека. Одних может ударить 36 В, а других не пробивает и 220 В.
Действие электричества на организм человека зависит от нескольких факторов: силы и частоты, времени и пути прохождения через организм, сопротивления организма или участка тела, по которому протекает ток.
Исследованиями ученых установлено, что величина смертельного тока, поражающего сердце, составляет более 100 мА. Токи от 50 мА до 100 мА вызывают потерю сознания при кратковременном касании к поверхности, которая проводит ток. Токи до 50 мА могут стать причиной травм, например, падения с лестницы, выпускания из рук токоведущего проводника и т. д.
Влияние на фактор поражения еще оказывает и сопротивление тела человека. Сопротивление для каждого индивида определить сложно и диапазон его составляет от 30 кОм до 200 кОм.
Формула расчета напряжения, опасного для жизни, предполагая, что Rч = 2кОм и I = 60 мА, выглядит так: U = I * R = 0,06 * 2000 = 120 В. В этой ситуации опасным напряжением можно считать 120 В и выше.
Частота тока является еще одной опасной характеристикой, обладающей поражающим действием. При увеличении частоты опасность уменьшается прямо пропорционально. Ток оказывает и тепловое действие, поэтому считать высокочастотные токи безопасными нельзя.
Травмы, происходящие из-за электричества, называются электротравмами. Каждая из них несет в себе меньшую или большую опасность. Наиболее опасными являются травмы, полученные от электрической дуги, которая обладает высокой температурой от 5 тыс. до 12 тыс. градусов по Цельсию. Виды электрических травм:
до 12 тыс. градусов по Цельсию. Виды электрических травм:
- Электрические ожоги происходят при тепловом воздействии на ткани организма человека, по которым течет ток.
- Обожженные участки на коже возникают при прямом контакте ее с токоведущей частью проводника. Пораженный участок приобретает серый или бледно-серый цвет.
- Металлизация кожи — пропитывание кожи частицами металла при коротком замыкании или сварке.
- Механические повреждения — самопроизвольная судорога мышц, приводящая к падению. При падении происходят переломы, ушибы вывихи суставов и т. д.
- Электроофтальмия — воспаление слизистой оболочки глаз при воздействии излучения электрической дуги.
Существует еще один вид поражения — электрический удар. Этот вид поражения можно условно разделить на 5 групп: без потери сознания; с потерей сознания, связанной с нарушением сердечной деятельности или без нее; клиническая смерть и электрический шок.
Единицы измерения
Работа электрического поля по перемещению заряда измеряется в Дж (Джоуль), заряд в Кл (кулон). Вот, как обозначается напряжение или его единица измерения: отношение этих величин (работа по перемещению в Дж к электрическому заряду в Кл) и является разностью потенциалов, измеряется в вольтах (В) и обозначается U. Разность потенциалов бывает:
- Переменной (амплитуда и полярность изменяются с течением времени, в зависимости от характерной частоты).
- Постоянной (имеет постоянное значение амплитуды и полярность есть величина постоянная).
А также у единиц измерения есть приставки, например, кВ (Киловольт = 1000В) и МВ (мегавольт = 1000000В). Существуют о совсем низкие значения, например, мВ (милливольт = 0,001В).
Цепи переменного и постоянного тока
В цепях постоянного и переменного тока U обладает различными свойствами и производит иные влияния на проводники. Для постоянного напряжения существуют законы по вычислению его характеристик, но для переменного способы вычисления показателей заметно отличаются. Разберем более подробно все различия и сходства.
Для постоянного напряжения существуют законы по вычислению его характеристик, но для переменного способы вычисления показателей заметно отличаются. Разберем более подробно все различия и сходства.
Расчет и анализ цепей выполняется при помощи закона Ома: сила тока полной цепи прямо пропорциональна напряжению и обратно пропорциональна сумме сопротивлений цепи и источника питания.
Следствие из закона при условии пренебрежения внутренним сопротивлением источника электричества: сила тока участка цепи прямо пропорциональна ЭДС и обратно пропорциональна сопротивлению этого участка.
Запись закона Ома, из которого следует формула напряжения, тока и сопротивления: I = U / (Rц + Rвн), где I — сила тока, U — ЭДС, Rц — сопротивление цепи, Rвн — внутреннее сопротивление источника питания.
Формула силы тока через сопротивление и напряжение: I = U / Rц.
Формула напряжения электрического тока: U = I * Rц.
Для расчета мощности необходимо U умножить на I: P = U * I = U * U / R, где P — мощность.
Переменное однофазное напряжение
В цепях для переменного тока происходят совершенно другие явления и процессы, для них справедливы другие законы. Различают такие основные виды:
- Мгновенное (разность потенциалов в конкретный промежуток времени: u = u (t)).
- Амплитудное значение (максимальное значение мгновенного U в момент времени: u (t) = Uм * sin (wt + f), где w — угловая частота, t — конкретный момент времени и f — угол начальной фазы напряжения).
- Среднее значение (для синусоиды равно нулю).
- Среднеквадратичное — Uq (U за весь период колебаний и для синусоиды имеет вид: Uq = 0,707 * Uм).
- Средневыпрямленное — Uv (среднее значение модуля U: Um примерно равно 0,9 * Uq).
В цепях 3-фазного тока различают 2 вида напряжений: линейное (фаза-фаза) и фазное (фаза-ноль). При соединении в цепь «треугольником» фазное и линейное U равны. В случае соединения «звездой» — фазное в 1,732050808 раз меньше линейного.
Рекомендации по выбору прибора
Для расчетов необходимо измерять значения величин электричества. Существуют специальные приборы, которые помогают произвести точные расчеты. Для измерения разности потенциалов применяют вольтметр.
Вольтметр (вольт — единица измерения ЭДС, метр — измеряю) — прибор для измерения ЭДС в цепи, подключаемый параллельно участку, на котором необходимо провести замер.
Для конкретного случая необходимо применять тот или иной прибор. Для более точных расчетов приобретаются приборы с высоким классом точности. Классификация вольтметров:
- Принцип действия: электромеханические (стрелочные) и электронные.
- Назначение: постоянного и переменного тока, импульсные, селективные и универсальные.
- Конструктивное исполнение: щитовые, переносные и стационарные.
Аналоговый электромеханический вольтметр имеет большие погрешности измерений в высокоомных цепях, но отлично зарекомендовал себя в низкоомных цепях и возможностью модернизации (увеличение значений измерения U за счет добавочного резистора).
Выпрямительный вольтметр обладает более высоким классом точности. Состоит из самого измерительного прибора (обладает чувствительностью к постоянному току) и выпрямительного устройства. Они получили не очень широкое распространение из-за высоких погрешностей, и применяются в качестве сигнальных приборов (примерное значение U).
Цифровые вольтметры применяются в комбинированных приборах-мультиметрах. Поступающее напряжение на клеммы (измерительные щупы) прибора преобразовывается в сигнал при помощи аналого-цифрового преобразователя (АЦП). Происходит отображение на цифровом табло. Этот вид приборов получил широкое применение благодаря высокой точности и универсальности.
Импульсный вольтметр необходимо применять при измерении амплитуд импульсных сигналов и одиночных импульсов.
Основным применением фазочувствительных вольтметров является измерение квадратурных составляющих комплексного напряжения (наличие мнимой и действительной частей) первичной гармоники.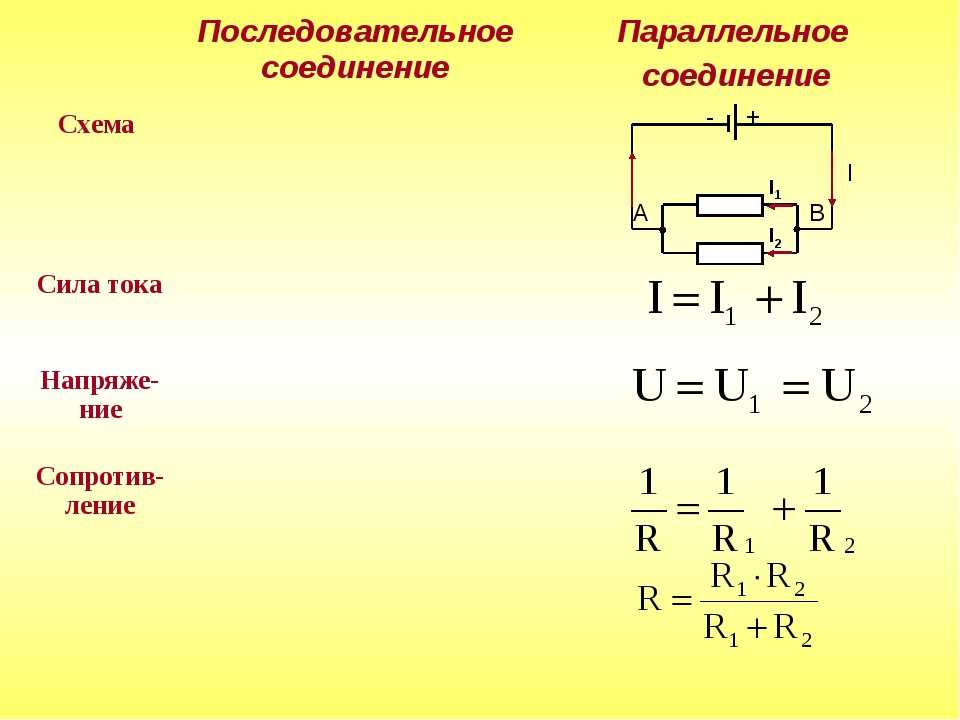 Они, как правило, снабжены 2-мя индикаторами для выявления мнимой и действительной частей. Они получили широкое применение в измерении АФХ (амплитудно-фазовая характеристика) для подбора деталей и настройки усилителей.
Они, как правило, снабжены 2-мя индикаторами для выявления мнимой и действительной частей. Они получили широкое применение в измерении АФХ (амплитудно-фазовая характеристика) для подбора деталей и настройки усилителей.
Для измерения номинала постоянного напряжения используются вольтметры подгруппы В2 (вольтметры для постоянного напряжения), а также В7 (универсальные).
Для определения переменного напряжения необходимо использовать устройства из подгруппы В3 или универсального типа (В7). Однако часто в этих вольтметрах применяются специальные преобразователи из переменного напряжения в постоянное.
В3 и В7 рассчитаны только для определения среднеквадратического гармонического напряжения. В этих электроизмерительных приборах возможно применение детекторов (преобразователей): пикового, выпрямительного и квадратичного. Оптимальным вариантом является вольтметр на квадратичном детекторе, при этом измеряемое значение выдается напрямую без всяких преобразований. Измерительные приборы на пиковых и выпрямительных детекторах пересчитывают значения, тем самым уменьшая точность измерений. Для измерения периодического негармонического напряжения выбирают вольтметр на квадратичном детекторе.
Для измерения периодического негармонического напряжения выбирают вольтметр на квадратичном детекторе.
Таким образом, расчет напряжения играет важную роль в электротехнике. Расчеты для переменных и постоянных цепей электрического тока существенно отличаются, в результате чего необходимо определить сначала тип тока, а затем производить расчеты. Но также необходимо соблюдать технику безопасности при работах с электричеством. Ведь ее основные положения основаны на горьком опыте человечества.
Ток, напряжение, сопротивление. Закон Ома.
Продолжаем публикацию материалов новой рубрики “Основы электроники“, и в сегодняшней статье речь пойдет о фундаментальных понятиях, без которых не проходит обсуждение ни одного электронного устройства или схемы. Как вы уже догадались, я имею ввиду ток, напряжение и сопротивление. Кроме того, мы не обойдем стороной закон Ома (как же иначе), который определяет взаимосвязь этих величин, но не буду забегать вперед, давайте двигаться постепенно, и начнем с понятия напряжения.
Напряжение.
По определению напряжение – это энергия (или работа), которая затрачивается на перемещение единичного положительного заряда из точки с низким потенциалом в точку с высоким потенциалом (т. е. первая точка имеет более отрицательный потенциал по сравнению со второй). Из курса физики мы помним, что потенциал электростатического поля – это скалярная величина, равная отношению потенциальной энергии заряда в поле к величине этого заряда. Давайте рассмотрим небольшой пример:
В пространстве действует постоянное электрическое поле, напряженность которого равна E. Рассмотрим две точки, расположенные на расстоянии d друг от друга. Так вот напряжение между двумя точками представляет из себя ни что иное, как разность потенциалов в этих точках:
U = \phi_1\medspace-\medspace \phi_2
В то же время не забываем про связь напряженности электростатического поля и разности потенциалов между двумя точками:
\phi_1\medspace-\medspace \phi_2 = Ed
И в итоге получаем формулу, связывающую напряжение и напряженность:
U = Ed
В электронике, при рассмотрении различных схем, напряжение все-таки принято считать как разность потенциалов между точками. Соответственно, становится понятно, что напряжение в цепи – это понятие, связанное с двумя точками цепи. То есть говорить, к примеру, “напряжение в резисторе” – не совсем корректно. А если говорят о напряжении в какой-то точке, то подразумевают разность потенциалов между этой точкой и “землей”. Вот так плавно мы вышли к еще одному повсеместно используемому понятию, а именно к понятию “земля”. Так вот “землей” в электрических цепях чаще всего принято считать точку нулевого потенциала (то есть потенциал этой точки равен 0).
Соответственно, становится понятно, что напряжение в цепи – это понятие, связанное с двумя точками цепи. То есть говорить, к примеру, “напряжение в резисторе” – не совсем корректно. А если говорят о напряжении в какой-то точке, то подразумевают разность потенциалов между этой точкой и “землей”. Вот так плавно мы вышли к еще одному повсеместно используемому понятию, а именно к понятию “земля”. Так вот “землей” в электрических цепях чаще всего принято считать точку нулевого потенциала (то есть потенциал этой точки равен 0).
Еще пару слов скажем о единицах, которые помогают охарактеризовать величину напряжения. Единицей измерения является Вольт (В). Классическое количественное определение величины в 1 Вольт звучит так: для перемещения заряда величиной 1 Кулон между точками, имеющими разность потенциалов 1 Вольт, необходимо совершить работу, равную 1 Джоулю. С этим вроде бы все понятно и можно двигаться дальше.
А на очереди у нас еще одно основополагающее понятие, а именно – ток.
Ток, сила тока в цепи.
Проанализируем, что будет происходить если под действие электрического поля попадут заряженные частицы, например, электроны. Рассмотрим проводник, к которому приложено определенное напряжение:
Из направления напряженности электрического поля (E) мы можем сделать вывод о том, что \phi_1 > \phi_2 (вектор напряженности всегда направлен в сторону уменьшения потенциала). На каждый электрон начинает действовать сила:
F = Ee
где e − это заряд электрона.
И поскольку электрон является отрицательно заряженной частицей, то вектор силы будет направлен в сторону противоположную направлению вектора напряженности поля. Таким образом, под действием силы частицы наряду с хаотичным движением приобретают и направленное (вектор скорости V на рисунке). В результате и возникает электрический ток.
В итоге получаем, что ток – это упорядоченное движение заряженных частиц под воздействием электрического поля.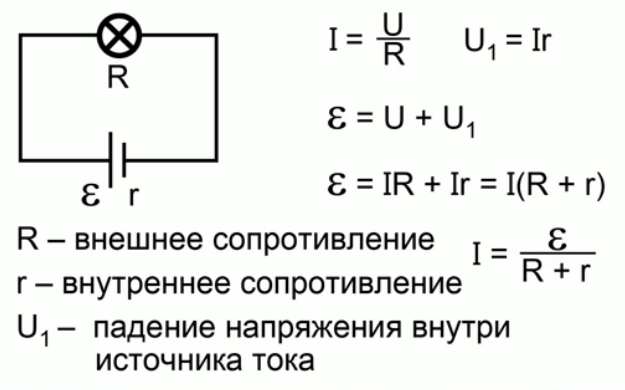
Важным нюансом является то, что принято считать, что ток протекает от точки с более положительным потенциалом к точке с более отрицательным потенциалом, несмотря на то, что электрон перемещается в противоположном направлении.
Носителями заряда могут выступать не только электроны. Например, в электролитах и ионизированных газах протекание тока в первую очередь связано с перемещением ионов, которые являются положительно заряженными частицами. Соответственно, направление вектора силы, действующей на них (а заодно и вектора скорости) будет совпадать с направлением вектора E. И в этом случае противоречия не возникнет, ведь ток будет протекать именно в том направлении, в котором движутся частицы.
Для того, чтобы оценить ток в цепи, существует такая величина как сила тока. Итак, сила тока (I) – это величина, которая характеризует скорость перемещения электрического заряда в точке. Единицей измерения силы тока является Ампер. Сила тока в проводнике равна 1 Амперу, если за 1 секунду через поперечное сечение проводника проходит заряд 1 Кулон.
Мы уже рассмотрели понятия силы тока и напряжения, теперь разберемся, каким образом эти величины могут бы связаны. И для этого нам предстоит понять, что же из себя представляет сопротивление проводника.
Сопротивление проводника/цепи.
Термин “сопротивление” уже фактически говорит сам за себя ) Итак, сопротивление – физическая величина, характеризующая свойства проводника препятствовать (сопротивляться) прохождению электрического тока.
Рассмотрим медный проводник длиной l с площадью поперечного сечения, равной S:
Сопротивление проводника зависит от нескольких факторов:
- удельного сопротивления проводника \rho
- длины проводника l
- площади поперечного сечения проводника S
Удельное сопротивление – это табличная величина. Формула, с помощью которой можно вычислить сопротивление данного проводника выглядит следующим образом:
R = \rho\medspace \frac{l}{S}Для нашего случая \rho будет равно 0,0175 (Ом * кв. мм / м) – удельное сопротивление меди. Пусть длина проводника составляет 0.5 м, а площадь поперечного сечения равна 0.2 кв. мм. Тогда:
мм / м) – удельное сопротивление меди. Пусть длина проводника составляет 0.5 м, а площадь поперечного сечения равна 0.2 кв. мм. Тогда:
R =0,0175 \cdot \frac{0.5}{0.2} = 0.04375\medspace ОмИ, как вы уже поняли из примера, единицей измерения сопротивления является Ом. Рассмотрим взаимосвязь напряжения, силы тока и сопротивления цепи.
Закон Ома.
И тут на помощь нам приходит основополагающий закон – закон Ома:
Сила тока в цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению рассматриваемого участка цепи.
Рассмотрим простейшую электрическую цепь:
Как следует из закона Ома напряжение и сила тока этой в цепи связаны следующим образом:
I = \frac{U}{R}Пусть напряжение составляет 10 В, а сопротивление цепи равно 200 Ом. Тогда сила тока в цепи вычисляется следующим образом:
I = \frac{10}{200} = 0.05 = 50\medspaceмАКак видите, все довольно несложно и абсолютно логично.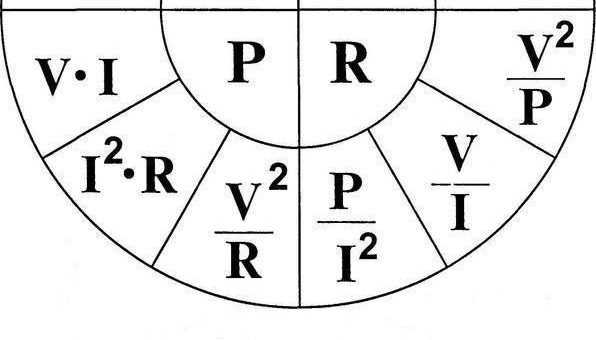 Пожалуй на этом мы и закончим сегодняшнюю статью, спасибо за внимание и до скорых встреч 🤝
Пожалуй на этом мы и закончим сегодняшнюю статью, спасибо за внимание и до скорых встреч 🤝
Электрическое сопротивление источника силы тока формула в Омах
ГЛАВНАЯ » МАТЕРИАЛЫ » Ток, сопротивление, Ом — что объединяет эти слова?
16 ноября, 2016 МАТЕРИАЛЫ 1 комментарий
Каждый человек знает, что по проводам течет электрический ток, за счет чего горит свет или работает прибор, потребляющий электрическую энергию. Это настолько прочно вошло в обычную жизнь, что никто не задумывается о физической составляющей данного явления. Человек, чья профессиональная деятельность не связана с физикой, слышал про электрическое сопротивление, силу тока или мощность последний раз в разрезе школьного курса физики.
Физика очень сложная наука, которая базируется не только на формулах и вычислениях, но в большей степени на понятиях. Особенно ярко это проявляется в разделе «электричество», которое само по себе не является материальной субстанцией, его не возможно «пощупать» или увидеть, но при этом оно занимает важную нишу в человеческой жизни.
Что есть сила сопротивления? Что такое электрическая цепь? Почему ток обладает силой? Для человека, который давно окончил школу, вопросов больше, чем ответов и немногие обладают хотя бы общим представлением, что на самом деле происходит под изоляцией электрического провода.
Какие процессы протекают в проводниках при прохождении через них тока?
Если некое тело, обладающее способностью проводить электрический ток, поместить таким образом, что с одной стороны будет находиться положительный полюс, а с другой отрицательный, то по нему начинает проходить электрический ток. Ток представляет собой в очень упрощенном виде движение отрицательных электронов, имеющее направленность. При этом частицы, имеющие отрицательный заряд, притягиваются к положительному полюсу. Именно за счет этого принято различать полярность электрической цепи, что легко заметить при подключении элементов питания, которые устанавливаются с учетом плюса и минуса.
При движении электроны встречают на своем пути атомы вещества, которым передается часть энергии в результате столкновения, что приводит к нагреву тела, пропускающее ток. При этом при столкновении происходит подтормаживание электронов. Появляющееся электрическое поле имеет способность заново ускорять замедленные электроны, которые снова начинают свое движение к положительному полюсу. Весь этот процесс будет бесконечным, пока тело подключено к источнику электрического поля. Именно движущиеся электроны испытывают на себе сопротивление поля, при этом существует прямая связь между количеством препятствий на пути заряженных частиц и значением данной величины. Сопротивление тока в цепи увеличивается при увеличении количества столкновении электронов.
При этом при столкновении происходит подтормаживание электронов. Появляющееся электрическое поле имеет способность заново ускорять замедленные электроны, которые снова начинают свое движение к положительному полюсу. Весь этот процесс будет бесконечным, пока тело подключено к источнику электрического поля. Именно движущиеся электроны испытывают на себе сопротивление поля, при этом существует прямая связь между количеством препятствий на пути заряженных частиц и значением данной величины. Сопротивление тока в цепи увеличивается при увеличении количества столкновении электронов.
Сопротивление цепи — что это?
Существует два вида определения сопротивления. Первое базируется на законе Ома. Согласно данному определению сопротивление цепи есть численная величина, определяемая как результат деления значения напряжения, создаваемого в проводнике на силу тока, который протекает через него. Формула сопротивления в данном случае будет иметь вид:
R=U:I, где
R — сопротивление;
U — напряжение;
I — сила тока.
Второе определение формулы сопротивления базируется на физических особенностях токопроводящего материала. Сопротивление источника есть также числовая величина, указывающая на способность тела превращать электрическую энергию в тепловую. Формула сопротивления в Омах для второго случая выглядит следующим образом:
R=(p*l)/S, где
R — сопротивление;
p — удельное сопротивление;
l — длина проводника;
S — площадь сечения.
При этом оба определения являются правильными и имеют право быть, но преимущественно в школьном курсе изучают лишь первый постулат. Единицы, определяющие сопротивление — Ом, названы так по имени ученого, который открыл сам факт существования данного явления и описал его природу.
Закон Ома или что есть сила в Омах
Одним очень важным открытием для понимания физической сущности электричества является открытый Омом закон, который выводит зависимость силы тока от напряжения. В основе закона лежит простой эксперимент. Представим, что существует простейшая цепь, которая состоит из обычной лампочки и амперметра. При добавлении в цепь большого гальванического элемента можно наблюдать, что нить накаливания лампы не нагревается и в сети практически отсутствует ток. Но если имеющийся гальванический элемент заменить свежим аккумулятором или элементом питания, то лампочка моментально загорается и ток в сети увеличивается. Замерив ток на обоих концах сети можно заметить, что при включении в сеть элемента питания напряжение значительно возрастает.
Представим, что существует простейшая цепь, которая состоит из обычной лампочки и амперметра. При добавлении в цепь большого гальванического элемента можно наблюдать, что нить накаливания лампы не нагревается и в сети практически отсутствует ток. Но если имеющийся гальванический элемент заменить свежим аккумулятором или элементом питания, то лампочка моментально загорается и ток в сети увеличивается. Замерив ток на обоих концах сети можно заметить, что при включении в сеть элемента питания напряжение значительно возрастает.
Закон Ома для участка цепи
Из проведенного опыта вытекает сформулированный Омом закон, который гласит, что сила тока в проводящем электрический ток теле увеличивается при увеличении напряжения, подаваемого к концам цепи или проводника. При этом сила тока находится в прямо пропорциональной зависимости от напряжения и обратно пропорциональной связи с сопротивлением. Закон Ома — это зависимая связь, в которой принимают участие сила тока, сопротивление и напряжение.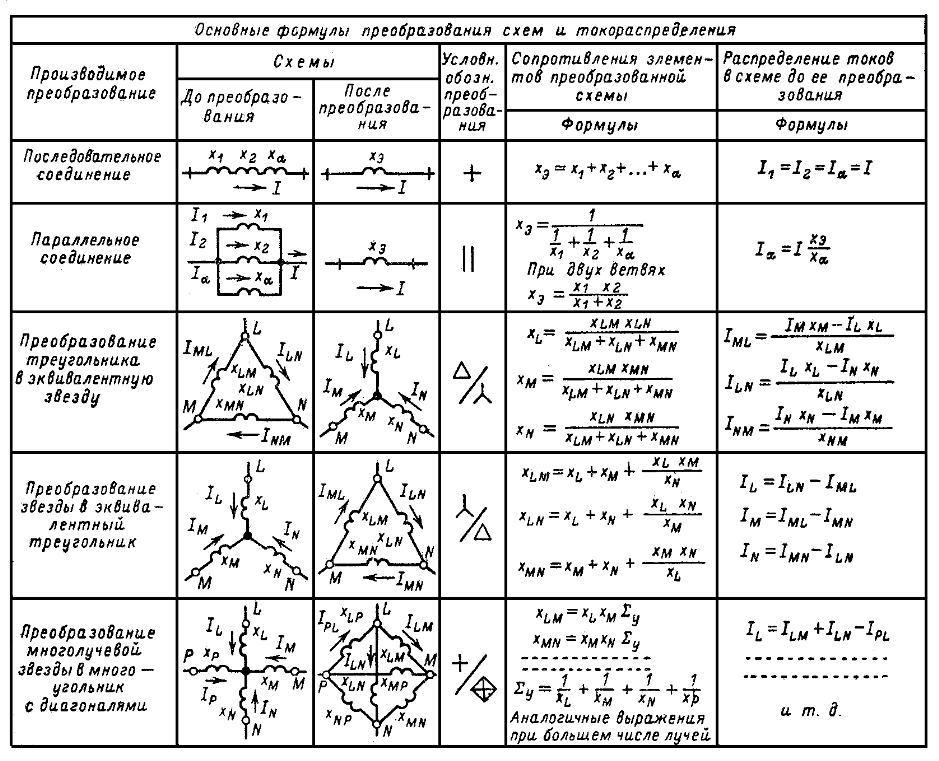
Виды сопротивлений
Физика выделяет несколько видов электрического сопротивления:
- Удельное. Под удельным сопротивлением понимается способность металла или иного тела противостоять прохождению электрического тела. Высокая величина удельного сопротивления будет означать, что данный материал является плохим проводником;
- Сопротивление провода. В данном случае формула сопротивления в Омах будет включать в себя диаметр сечения провода, удельное сопротивление конкретного металла и длину провода;
- Поверхностное сопротивление. Этот вид применяется для расчета удельного сопротивления тонких материалов, в частности пленок. В случае поверхностного сопротивления диаметр сечения в формуле представлен в виде габаритных размеров (толщина, длина, ширина).
Электрическое сопротивление является важным понятием, сделавшее возможным создание резистора, главная задача которого является осуществление контроля и ограничения действия электрического тока. Применение резисторов сводится к препятствованию возрастанию напряжения, поскольку эта деталь способна рассеивать тепло.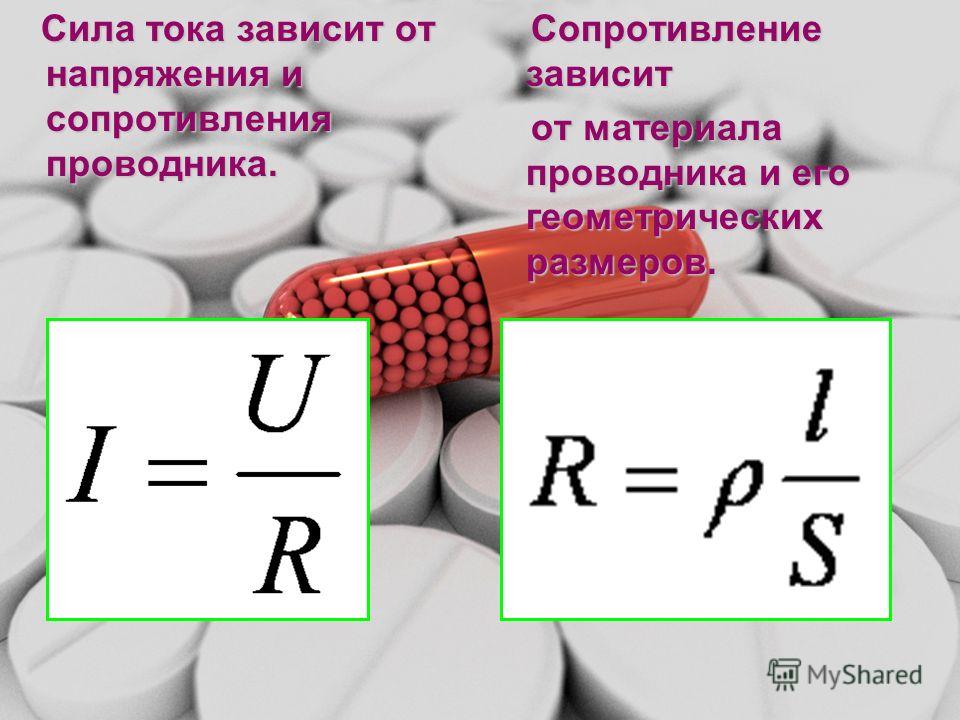 Также резистор, который является неотъемлемой частью любой современной платы и схемы, применяется для разделения напряжения, понижая данную характеристику.
Также резистор, который является неотъемлемой частью любой современной платы и схемы, применяется для разделения напряжения, понижая данную характеристику.
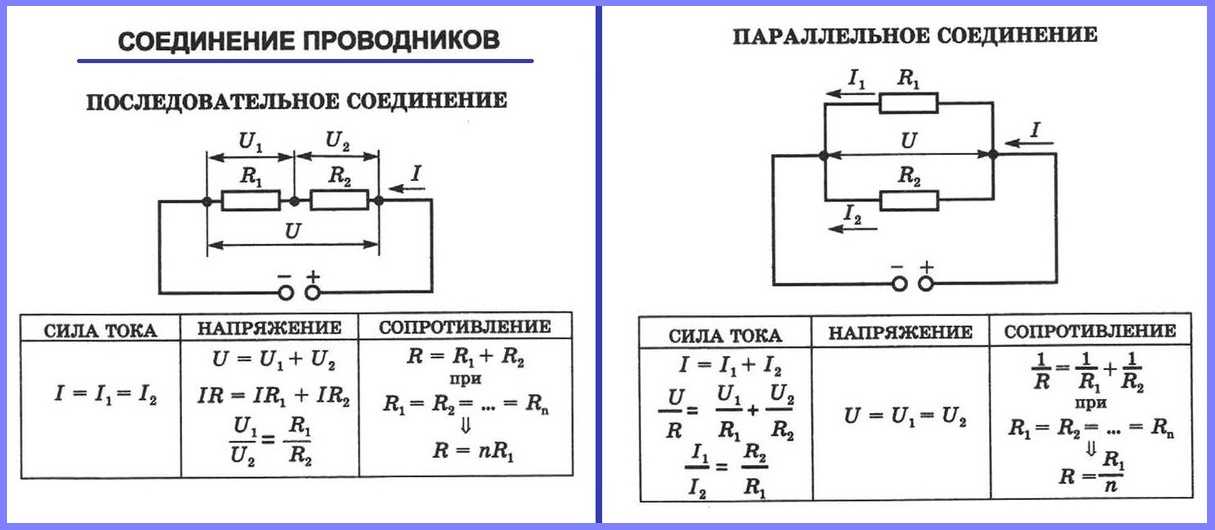
Сила тока при последовательном соединении
В электрических цепях используются различные типы соединений. Основными являются последовательные, параллельные и смешанные схемы подключений. В первом случае используется несколько сопротивлений, соединенных в единую цепочку друг за другом. То есть, начало одного резистора соединяется с концом второго, а начало второго – с концом третьего и так далее, до любого количества сопротивлений. Сила тока при последовательном соединении будет одинаковой во всех точках и на всех участках. Для определения и сравнения других параметров электрической цепи, следует рассматривать и остальные виды соединений, обладающие собственными свойствами и характеристиками.
Последовательное и параллельное соединение сопротивлений
Любая нагрузка обладает сопротивлением, препятствующим свободному течению электрического тока.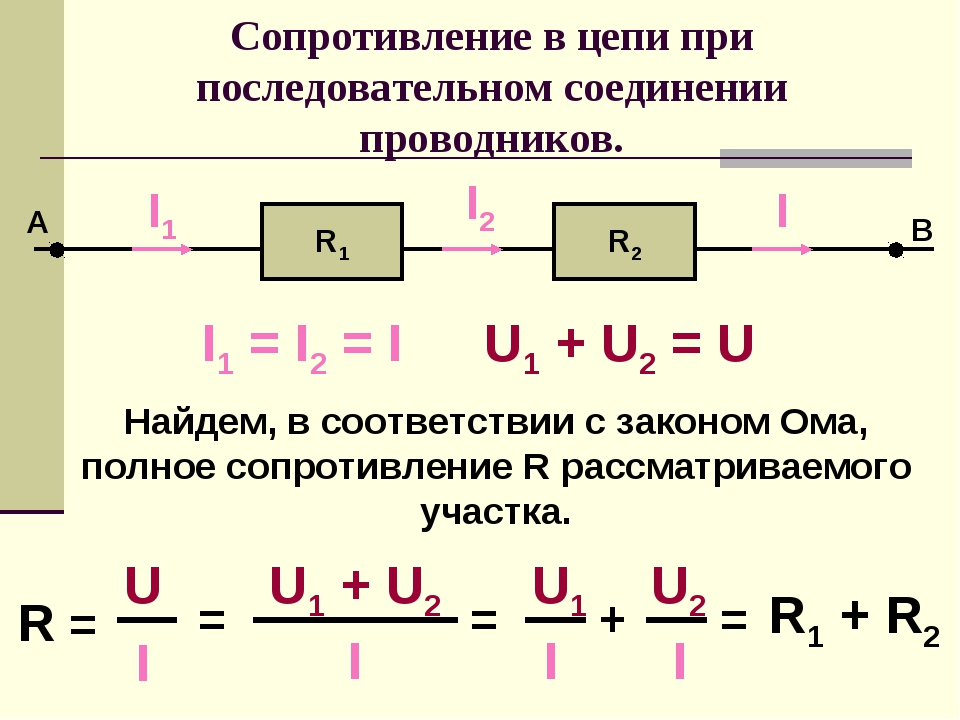 Его путь проходит от источника тока, через проводники к нагрузке. Для нормального прохождения тока, проводник должен обладать хорошей проводимостью и легко отдавать электроны. Это положение пригодится далее при рассмотрении вопроса, что такое последовательное соединение.
Его путь проходит от источника тока, через проводники к нагрузке. Для нормального прохождения тока, проводник должен обладать хорошей проводимостью и легко отдавать электроны. Это положение пригодится далее при рассмотрении вопроса, что такое последовательное соединение.
В большинстве электрических цепей применяются медные проводники. Каждая цепь содержит приемники энергии – нагрузки, обладающие различными сопротивлениями. Параметры соединения лучше всего рассматривать на примере внешней цепи источника тока, состоящей из трех резисторов R1, R2, R3. Последовательное соединение предполагает поочередное включение этих элементов в замкнутую цепь. То есть начало R1 соединяется с концом R2, а начало R2 – с концом R3 и так далее. В такой цепочке может быть любое количество резисторов. Эти символы используют в расчетах последовательные и параллельные соединения.
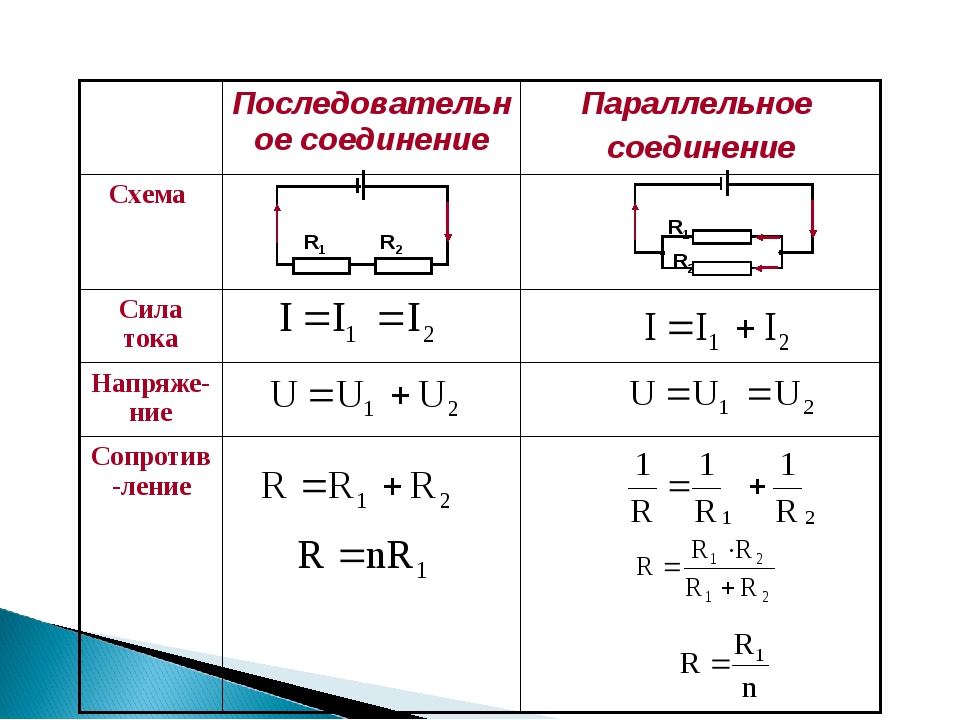
Сила тока на всех участках будет одинаковой: I = I1 = I2 = I3, а общее сопротивление цепи составит сумму сопротивлений всех нагрузок: R = R1 + R2 + R3. Остается лишь определить, каким будет напряжение при последовательном соединении. В соответствии с законом Ома, напряжение представляет собой силу тока и сопротивления: U = IR. Отсюда следует, что напряжение на источнике тока будет равно сумме напряжений на каждой нагрузке, поскольку ток везде одинаковый: U = U1 + U2 + U3.
Остается лишь определить, каким будет напряжение при последовательном соединении. В соответствии с законом Ома, напряжение представляет собой силу тока и сопротивления: U = IR. Отсюда следует, что напряжение на источнике тока будет равно сумме напряжений на каждой нагрузке, поскольку ток везде одинаковый: U = U1 + U2 + U3.
При постоянном значении напряжения, ток при последовательном соединении будет находиться в зависимости от сопротивления цепи. Поэтому при изменении сопротивления хотя-бы на одной из нагрузок, произойдет изменение сопротивления во всей цепи. Кроме того, изменятся ток и напряжение на каждой нагрузке. Основным недостатком последовательного соединения считается прекращение работы всех элементов цепи, при выходе из строя даже одного из них.
Совершенно другие характеристики тока, напряжения и сопротивления получаются при использовании параллельного соединения. В этом случае начала и концы нагрузок соединяются в двух общих точках. Происходит своеобразное разветвление тока, что приводит к снижению общего сопротивления и росту общей проводимости электрической цепи.
Для того чтобы отобразить эти свойства, вновь понадобится закон Ома. В данном случае сила тока при параллельном соединении и его формула будет выглядеть так: I = U/R. Таким образом, при параллельном соединении n-го количества одинаковых резисторов, общее сопротивление цепи будет в n раз меньше любого из них: Rобщ = R/n. Это указывает на обратно пропорциональное распределение токов в нагрузках по отношению к сопротивлениям этих нагрузок. То есть, при увеличении параллельно включенных сопротивлений, сила тока в них будет пропорционально уменьшаться. В виде формул все характеристики отображаются следующим образом: сила тока – I = I1 + I2 + I3, напряжение – U = U1 = U2 = U3, сопротивление – 1/R = 1/R1 + 1/R2 + 1/R3.
При неизменном значении напряжения между элементами, токи в этих резисторах не имеют зависимости друг от друга. Если один или несколько резисторов будут выключены из цепи, это никак не повлияет на работу других устройств, остающихся включенными. Данный фактор является основным преимуществом параллельного соединения электроприборов.
В схемах обычно не используется только последовательное соединение и параллельное соединение сопротивлений, они применяются в комбинированном виде, известном как смешанное соединение. Для вычисления характеристик таких цепей применяются формулы обоих вариантов. Все расчеты разбиваются на несколько этапов, когда вначале определяются параметры отдельных участков, после чего они складываются и получается общий результат.
Законы последовательного и параллельного соединения проводников
Основным законом, применяемым при расчетах различных видов соединений, является закон Ома. Его основным положением является наличие на участке цепи силы тока, прямо пропорциональной напряжению и обратно пропорциональной сопротивлению на данном участке. В виде формулы этот закон выглядит так: I = U/R. Он служит основой для проведения расчетов электрических цепей, соединяемых последовательно или параллельно. Порядок вычислений и зависимость всех параметров от закона Ома наглядно показаны на рисунке. Отсюда выводится и формула последовательного соединения.
Отсюда выводится и формула последовательного соединения.
Более сложные вычисления с участием других величин требуют применения правила Кирхгофа. Его основное положение заключается в том, что несколько последовательно соединенных источников тока, будут обладать электродвижущей силой (ЭДС), составляющей алгебраическую сумму ЭДС каждого из них. Общее сопротивление этих батарей будет состоять из суммы сопротивлений каждой батареи. Если выполняется параллельное подключение n-го количества источников с равными ЭДС и внутренними сопротивлениями, то общая сумма ЭДС будет равно ЭДС на любом из источников. Значение внутреннего сопротивления составит rв = r/n. Эти положения актуальны не только для источников тока, но и для проводников, в том числе и формулы параллельное соединение проводников.
В том случае, когда ЭДС источников будет иметь разное значение, для расчетов силы тока на различных участках цепи применяются дополнительные правила Кирхгофа.
Расчет напряжения тока с помощью формулы: сопротивления через силу тока и напряжение
g84jsm9tB4S
В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением.
Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником.
Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.
Пример 1 Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r= 0,5 Ом.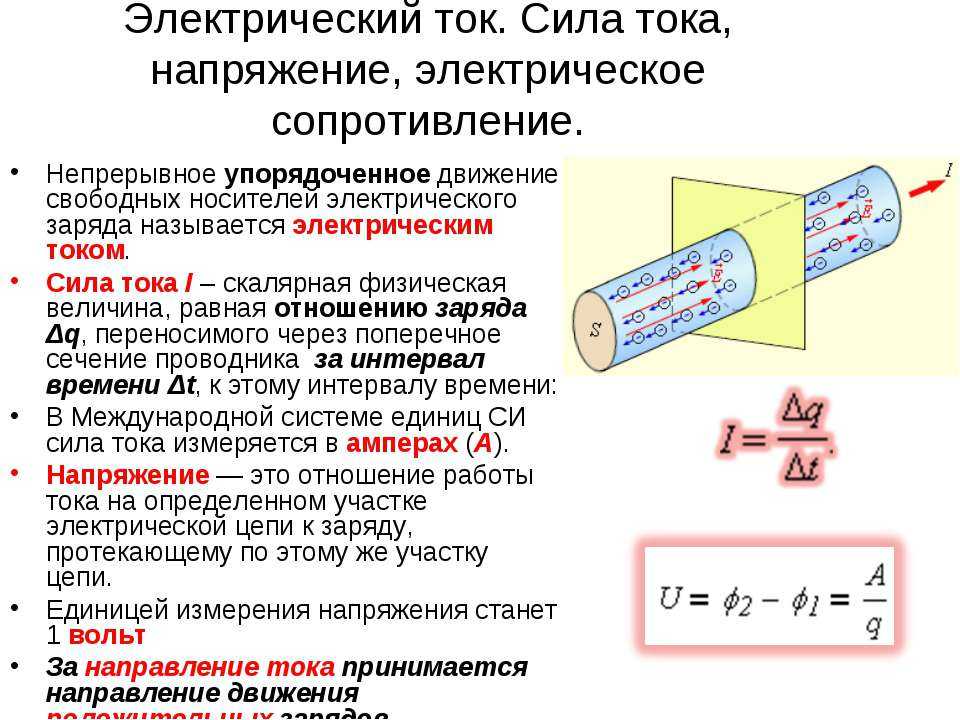 Сопротивления резисторов R1 = 20 и R2 = 32 Ом. Определить ток в цепи и напряжения на резисторах.
Сопротивления резисторов R1 = 20 и R2 = 32 Ом. Определить ток в цепи и напряжения на резисторах.
Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи.
Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем.
Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей.
В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками.
Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.
Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.
Общий ток цепи, содержащей два соединенных параллельно резистора R1=70 Ом и R2=90 Ом, равен 500 мА. Определить токи в каждом из резисторов.
Два последовательно соединенных резистора ничто иное, как делитель тока. Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов.
В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.
Если у вас возникли затруднения, прочтите статью законы Кирхгофа.
Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала рассчитать сопротивление цепи
- А затем напряжение
- Зная напряжения, найдем токи, протекающие через резисторы
- Как видите, токи получились теми же.

В электрической цепи, изображенной на схеме R1=50 Ом, R2=180 Ом, R3=220 Ом.
Найти мощность, выделяемую на резисторе R1, ток через резистор R2, напряжение на резисторе R3, если известно, что напряжение на зажимах цепи 100 В.
Чтобы рассчитать мощность постоянного тока, выделяемую на резисторе R1, необходимо определить ток I1, который является общим для всей цепи. Зная напряжение на зажимах и эквивалентное сопротивление цепи, можно его найти.
Интернет магазин паровой утюг
- Эквивалентное сопротивление и ток в цепи
- Отсюда мощность, выделяемая на R 1
- Ток I2 определим с помощью формулы делителя тока, учитывая, что ток I1 для этого делителя является общим
- Так как, напряжение при параллельном соединении резисторов одинаковое, найдем U3, как напряжение на резисторе R2
- Таким образом производится расчет простых цепей постоянного тока.

- Резистор тока выполняет сразу несколько очень важных задач: служит ограничителем электрического тока в цепи, создает падение напряжения на отдельных ее участках и разделяет пульсирующий ток.
Помимо номинального сопротивления, одним из наиболее важных параметров резистора является рассеиваемая мощность. Она зависима от напряжения и тока. Мощность – это то тепло, которое выделяется на резисторе, когда под воздействием протекающего тока он нагревается. При пропуске тока, превышающего заданное значение мощности, резистор может сгореть.
Мощность постоянного тока может быть рассчитана по простой формуле P(Вт) = U(В) * I(А),
Чтобы избежать сгорания резистора тока, необходимо учитывать его мощность. Соответственно, если схема указывает на замену резистора с мощностью 0,5 Ватт – 0,5 Ватт в данном случае – минимум.
Мощность резистора может зависеть от его размеров. Как правило, чем меньше резистор — тем меньше мощность его рассеивания. Стандартный ряд мощностей резисторов тока состоит из значений:
Стандартный ряд мощностей резисторов тока состоит из значений:
Рассмотрим на примере: номинальное сопротивление нашего резистора тока – 100 Ом. Через него течет ток 0,1 Ампер. Чтобы узнать мощность, на которую рассчитан наш резистор тока, необходимо воспользоваться следующей формулой: P(Вт) = I2(А) * R(Ом),
- P(Вт) – мощность,
- R(Ом) – сопротивление цепи (в данном случае резистора),
- I(А) – ток, протекающий через резистор.
Внимание! При расчётах следует соблюдать размерность. Например, 1 кА= 1000 А . Это же касается и других величин.
Итак, рассчитаем мощность для нашего резистора тока: P(Вт) = 0,12(А) *100 (Ом)= 1(Вт)
Получилось, что минимальная мощность нашего резистора составляет 1 Ватт. Однако в схему следует установить резистор с мощностью в 1,5 – 2 раза выше рассчитанной. Соответственно идеальным для нас будет резистор тока мощностью 2 Вт.
Бывает, что ток, протекающий через резистор неизвестен.
Для расчёта мощности в таком случае предусмотрена специальная формула:
Соединение цепи может быть последовательным и параллельным. Однако никакого труда не составляет рассчитать мощность резистора тока как в параллельной, так и в последовательной цепи. Следует учитывать лишь то, что в последовательно цепи через резисторы течет один ток.
Например, нам необходимо произвести замену резистора тока сопротивлением 100 Ом. Ток, протекающий через него – 0,1 Ампер. Соответственно, его мощность – 1 Ватт.
Следует рассчитать мощность двух соединенных последовательно резисторов для его замены. Согласно формуле расчёта мощности, мощность рассеивания резистора на 20 Ом – 0,2 Вт, мощность резистора на 80 Ом – 0,8 Вт.
Стандартный ряд мощностей поможет выбрать резисторы тока:
Как починить москитную сетку ручки
R1 – 20 Ом (0.5 Вт)
R2 – 80 Ом (1 Вт)
Из всего вышесказанного можно сделать вывод, что разное сопротивление резисторов гарантирует их разную выделяемую мощность, так как она распределяется между резисторами разных номиналов.
Если не учитывать это обстоятельство, то можно столкнуться с большим количеством трудностей. Если один из резисторов выбран неправильно – второй работает в тяжелом температурном режиме.
Также присутствует угроза возгорания резистора из-за несоблюдения правил мощности.
Для того, чтобы сэкономить время и не рассчитывать мощность каждого отдельного резистора тока нужно запомнить одно простое правило: мощность заменяемого резистора должна быть равна мощности каждого резистора, составляющего параллельную или последовательную цепь. То есть при замене резистора мощностью 0,5 Вт надо следить за тем, чтобы каждый из резисторов для замены имел мощность не менее 0,5 Вт.
При параллельном соединение резисторов важно помнить, что чем меньше сопротивление резистора, тем больший ток через него протекает, а значит на нем будет рассеяна большая мощность.
В упрощенном понимании электрическая цепь представляет собой совокупность элементов, реализующих определенные задачи при взаимодействии с электрическим током. При этом каждая из деталей выполняет свои функции при строго определенных параметрах. Они могут значительно отличаться от входящих значений. Одним из самых распространенных элементов электрической схемы является резистор.
При этом каждая из деталей выполняет свои функции при строго определенных параметрах. Они могут значительно отличаться от входящих значений. Одним из самых распространенных элементов электрической схемы является резистор.
Резистор выступает своеобразным ограничителем силы тока. По своей сути этот элемент является дополнительным сопротивлением, которое измеряется в омах. Собственно, зная это значение можно определить силу тока в резисторе, а также напряжение в цепи после него.
Определение силы тока на резисторе при разных типах соединения
Самым простым способом определить силу тока в резисторе можно воспользовавшись мультиметром. Измерение проводятся в разрыве цепи после резистора. На тестере выставляется максимальный диапазон величин, а щупы прибора подсоединяются к месту разъединения проводника. На дисплее мультиметра будут отображены результаты измерения силы тока в резисторе.
Но данный вариант не всегда возможен. Под рукой может не оказаться тестера или технически невозможно разорвать цепь чтобы измерить силу тока на резисторе. В такой ситуации на помощь придет известный из школьной физики закон Ома, который выглядит следующим образом:
В такой ситуации на помощь придет известный из школьной физики закон Ома, который выглядит следующим образом:
- I = U/R, где у нас I – сила тока, U – напряжение, R – сопротивление.
- В системе СИ эти величины измеряются в амперах (А), вольтах (В), омах (Ом) соответственно.
- Подставляя необходимые значения в формулу можно определить сопротивление, напряжение и силу тока на резисторе или любом участке, или элементе электрической цепи.
Последовательное соединение резисторов
Рассмотрим электрическую цепь, в которой три резистора расположены последовательно, т.е. друг за другом. Общее их сопротивление (R) будет рано сумме сопротивлений отдельного резистора (r).
Как починить сломанную ножку стула
Для наглядности примера, в качестве резисторов рассмотрим обычные 40 Вт лампы накаливании. В данном случае вольфрамовая нить обладает своим сопротивлением и ее вполне можно считать резистором. Также введем понятие мощности нагрузки или резистора (P), которая измеряется в ватах (Вт).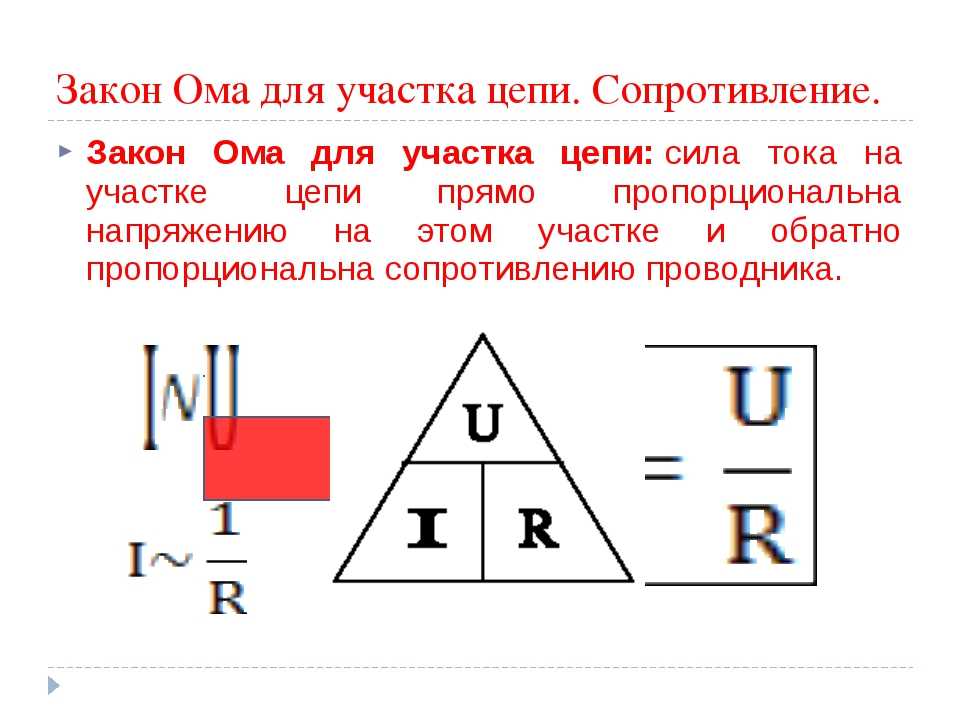
Она имеет прямолинейную зависимость от силы тока и напряжения и вычисляется по формуле: P=I х U. С помощью несложных вычислений мы можем найти силу тока на резисторе, в качестве которого выступает лампочка.
Сила тока (I) = Мощность лампы (Р) / Напряжение (U) = 40 Вт / 220 В = 0,1818 А.
Для последовательного соединения элементов в электрической цепи справедливо правило, что силы тока протекающие через все проводники одинакова. Таким образом сила тока в резисторе r2 или r3 также будет 0,1818 А.
Но в нашем варианте с лампочками будет отмечена одна особенность – яркость свечения уменьшится. Это происходит из-за того, что резистор выступает в качестве делителя напряжения. Этот нюанс часто используют для продления срока службы не ответственных устройств.
Например, впаяв сопротивление перед лампочкой можно продлить срок ее службы, но при этом придется смерится с недостатком освещенности.
Параллельное соединение резисторов
При параллельном расположении резисторов в сети, они имеют общую точку контакта на входе и на выходе. В этом случае общее напряжение будет соответствовать значению напряжения на каждом отрезке, а вот ток будет суммироваться (I об= I1 + I2 +I3). Это соотношение имеет большое значение для практического применения и получило название – закон разветвленной цепи.
В этом случае общее напряжение будет соответствовать значению напряжения на каждом отрезке, а вот ток будет суммироваться (I об= I1 + I2 +I3). Это соотношение имеет большое значение для практического применения и получило название – закон разветвленной цепи.
Несмотря на то, что общий ток в цепочке резисторов, соединенных параллельно на выходе равен сумме токов в самостоятельной ветке, для конкретного участка он может отличаться. Это обусловлено тем же законом Ома, при условии разности сопротивлений.
Чтобы узнать силу тока на каждом резисторе в соответствующей ветке, необходимо знать их сопротивление. При параллельном соединении, напряжение на обособленном участке, является постоянной величиной.
Соответственно сила тока отельного резистора легко вычисляется по закону Ома для участка цепи.
Смешанное соединение резисторов в цепи
В чистом виде параллельные и последовательные цепи в электротехнике встречаются крайне редко. Как правило, присутствует их совместная комбинация.
Для того чтобы найти силу тока в каждом резисторе при смешанном соединении, необходимо цепь разбить на участки. Таким образом при расположении элементов друг после друга, т.н.
«каскадом», применяются правила и формулы для последовательного соединения.
Результаты измерения силы тока в резисторе. Различные типы резисторов.
Необходимо отметить, что для упрощения расчетов параллельно расположенные резисторы можно группировать. При вычислении силы тока на определенном участке, они принимаются за самостоятельный элемент. Соответственно в этом случае формулы используются как для расчета параметров при параллельном соединении.
Источник: https://pechi-sibiri.ru/kak-najti-silu-toka-na-kazhdom-rezistore/
Закон Ома
Закон Ома, основанный на опытах, представляет собой в электротехнике основной закон, который устанавливает связь силы электрического тока с сопротивлением и напряжением.
Появление смартфонов, гаджетов, бытовых приборов и прочей электротехники коренным образом изменило облик современного человека. Приложены огромные усилия, направленные на исследование физических закономерностей для улучшения старой и создания новой техники. Одной из таких зависимостей является закон Ома.
Приложены огромные усилия, направленные на исследование физических закономерностей для улучшения старой и создания новой техники. Одной из таких зависимостей является закон Ома.
Георг Симон Ом
- Закон Ома – полученный экспериментальным путём (эмпирический) закон, который устанавливает связь силы тока в проводнике с напряжением на концах проводника и его сопротивлением, был открыт в 1826 году немецким физиком-экспериментатором Георгом Омом.
- Строгая формулировка закона Ома может быть записана так: сила тока в проводнике прямо пропорциональна напряжению на его концах (разности потенциалов) и обратно пропорциональна сопротивлению этого проводника.
- Формула закона Ома записывается в следующем виде:
- где
- I – сила тока в проводнике, единица измерения силы тока — ампер [А];
- U – электрическое напряжение (разность потенциалов), единица измерения напряжения- вольт [В];
- R – электрическое сопротивление проводника, единица измерения электрического сопротивления — ом [Ом].
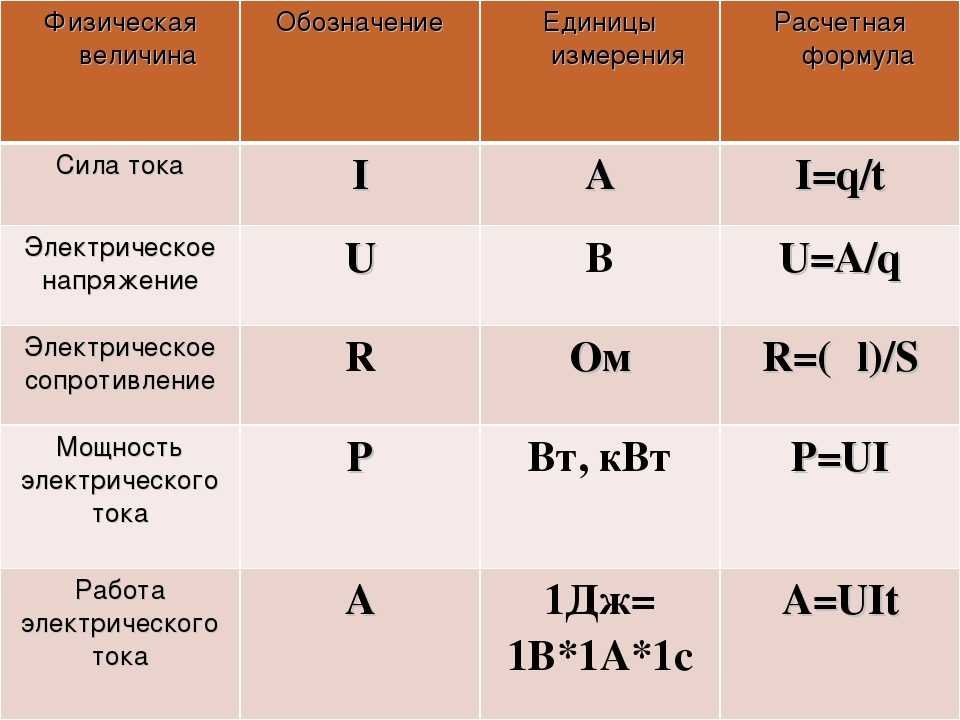
Согласно закону Ома, увеличение напряжения, например, в два раза при фиксированном сопротивлении проводника, приведёт к увеличению силы тока также в два раза
И напротив, уменьшение тока в два раза при фиксированном напряжении будет означать, что сопротивление увеличилось в два раза.
Рассмотрим простейший случай применения закона Ома. Пусть дан некоторый проводник сопротивлением 3 Ом под напряжением 12 В. Тогда, по определению закона Ома, по данному проводнику течет ток равный:
Существует мнемоническое правило для запоминания этого закона, которое можно назвать треугольник Ома. Изобразим все три характеристики (напряжение, сила тока и сопротивление) в виде треугольника. В вершине которого находится напряжение, в нижней левой части – сила тока, а в правой – сопротивление.
Правило работы такое: закрываем пальцем величину в треугольнике, которую нужно найти, тогда две оставшиеся дадут верную формулу для поиска закрытой.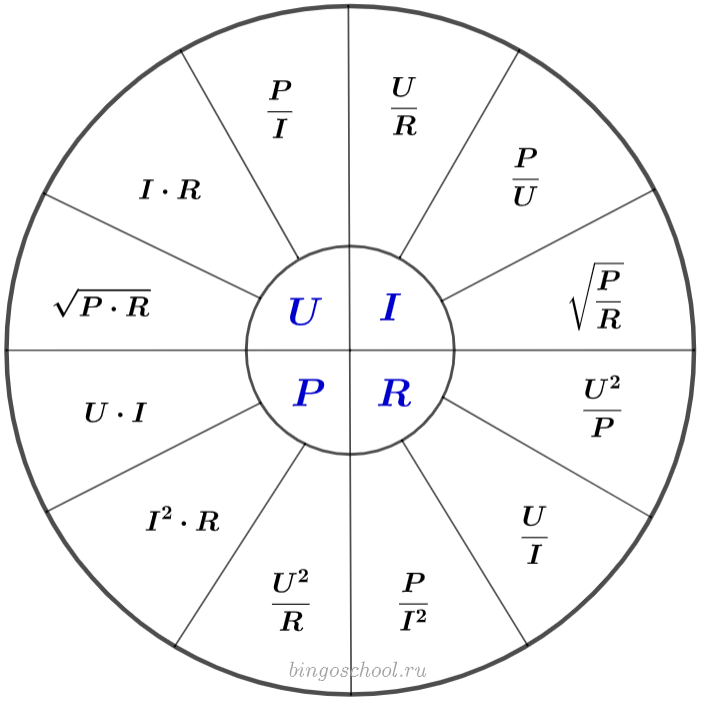
Где и когда можно применять закон Ома?
Нужна помощь в написании работы?
Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).
Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.
Значение Закона Ома
Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении.
Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.
Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления.
Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.
Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:
Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.
Источник: https://zakon-oma.ru/
Закон ома
Электроника сейчас получила большое распространение, у всех дома много радиоприёмников, телефонов, компьютеров, планшетов, телевизоров фонариков и т.д. Это всё радиоэлектроника, поэтому некоторые люди заинтересовываются этим хобби, но не знают с чего начать. Наша цель рассказать в данном материале всё о Законе Ома.
Обозначения напряжения, тока, сопротивления
Всё же многие радиолюбители начинают с закона Ома. В закон Ома входят три единицы: напряжение, ток, сопротивление.
- Напряжение измеряется в вольтах (В) и обозначается U.

- Сопротивление измеряется в Омах (Ом) и обозначается R.
- Ток в Амперах (А) и обозначается I.
Расчёт напряжения, тока и сопротивления
Закон Ома предназначен для того, чтобы найти неизвестную третью, если известны первая и вторая. С этого по подробней, чтобы облегчить закон Ома, будем пользоваться треугольником Ома. Вот этот треугольник:
Давайте разберёмся с напряжением, чтобы найти напряжение, используя треугольник Ома, надо закрыть рукой напряжение — U, остались только I-ток и R-сопротивление, передними стоит вертикальная черта, вертикальная это черта снизу вверх, это вертикальная линия обозначает умножение, значит, чтобы найти напряжение надо ток умножить на сопротивление.
Вот такая формула получилась: U=I*R, где U-напряжение, I-ток, R-сопротивление.
Теперь давайте попробуем найти ток, прикроем рукой I, теперь перед напряжением и сопротивление стоит горизонтальная черта, горизонтальная, это та черта, которая идёт слева направо. Горизонтальная черта означает деление. Значит, чтобы найти ток, надо напряжение разделить на сопротивление.
Горизонтальная черта означает деление. Значит, чтобы найти ток, надо напряжение разделить на сопротивление.
Формула получилась следующая: I= UR, где I-ток, U-напряжение, R-сопротивление.
Найдём сопротивление, закроем рукой R, то получим опять горизонтальную черту перед напряжением и током, значит нужно делить.
Формула получилась для расчёта сопротивления: R=UI, где R-сопротивление, U-напряжение, I-ток. Итак, мы научились пользовать треугольником Ома и узнали о Законе Ома. Теперь, пожалуй, поучимся на примерах.
Примеры расчётов закона Ома
Давайте, найдём напряжение, если ток равен 0,9 Ампер, а сопротивление 100 Ом, пользуясь треугольником, прикрываем напряжение рукой, смотрим, вертикальная черта, значит умножить. Опять пользуемся той формулой, только подставляем числа, U = 0,9 А * 100 Ом, считаем, получиться 90, значит U = 90 вольт.
Теперь рассчитываем сопротивление, берём те же единицы, только убираем сопротивление, получиться вот такая формула: R = 90 В 0,9 А, получим 100 Ом.
Чтобы рассчитать ток, опять же убираем ток, получаем эту формулу I = 90 В 100 Ом, получаем 0,9 Ампер.
Итак, на этом всё, кстати, закон Ома действует там, где нет катушек индуктивности и конденсаторов, не забивайте голову конденсаторами и катушками индуктивности, просто, запомните, что закон Ома действует, там, где нет катушек индуктивности и конденсаторов. Надеюсь, моя статья была полезной, всем удачи, с вами был Дмитрий Цывцын.
Справочники радиодеталей
|
|
|
Источник: https://elwo.ru/publ/spravochniki/zakon_oma/2-1-0-898
10 формул
Доброго дня уважаемые радиолюбители!
Приветствую вас на сайте “Радиолюбитель“
Формулы составляют скелет науки об электронике.
Вместо того, чтобы сваливать на стол целую кучу радиоэлементов, а потом переподключать их между собой, пытаясь выяснить, что же появится на свет в результате, опытные специалисты сразу строят новые схемы на основе известных математических и физических законов. Именно формулы помогают определять конкретные значения номиналов электронных компонентов и рабочих параметров схем.
Точно так же эффективно использовать формулы для модернизации уже готовых схем.
К примеру, для того, чтобы выбрать правильный резистор в схеме с лампочкой, можно применить базовый закон Ома для постоянного тока (о нем можно будет прочесть в разделе “Соотношения закона Ома” сразу после нашего лирического вступления). Лампочку можно заставить, таким образом, светить более ярко или, наоборот — притушить.
В этой главе будут приведены многие основные формулы физики, с которыми рано или поздно приходится сталкиваться в процессе работы в электронике. Некоторые из них известны уже столетия, но мы до сих пор продолжаем ими успешно пользоваться, как будут пользоваться и наши внуки.
Закон Ома представляет собой взаимное соотношение между напряжением, током, сопротивлением и мощностью. Все выводимые формулы для расчета каждой из указанных величин представлены в таблице:
| Искомая величина | Формула |
| Напряжение, В | U=I*R |
| Ток, А | I=U/R |
| Сопротивление, Ом | R=U/I |
| Мощность, Вт | P=U*I |
- В этой таблице используются следующие общепринятые обозначения физических величин:
- U — напряжение (В),
- I — ток (А),
- Р — мощность (Вт),
- R — сопротивление (Ом),
Потренируемся на следующем примере: пусть нужно найти мощность схемы. Известно, что напряжение на ее выводах составляет 100 В, а ток— 10 А. Тогда мощность согласно закону Ома будет равна 100 х 10 = 1000 Вт.
Полученное значение можно использовать для расчета, скажем, номинала предохранителя, который нужно ввести в устройство, или, к примеру, для оценки счета за электричество, который вам лично принесет электрик из ЖЭК в конце месяца.
А вот другой пример: пусть нужно узнать номинал резистора в цепи с лампочкой, если известно, какой ток мы хотим пропускать через эту цепь. По закону Ома ток равен:
I = U / R
Схема, состоящая из лампочки, резистора и источника питания (батареи) показана на рисунке. Используя приведенную формулу, вычислить искомое сопротивление сможет даже школьник.
Что же в этой формуле есть что? Рассмотрим переменные подробнее.
> U пит (иногда также обозначается как V или Е): напряжение питания. Вследствие того, что при прохождении тока через лампочку на ней падает какое-то напряжение, величину этого падения (обычно рабочее напряжение лампочки, в нашем случае 3,5 В) нужно вычесть из напряжения источника питания. К примеру, если Uпит = 12 В, то U = 8,5 В при условии, что на лампочке падает 3,5 В.
К примеру, если Uпит = 12 В, то U = 8,5 В при условии, что на лампочке падает 3,5 В.
> I: ток (измеряется в амперах), который планируется пропустить через лампочку. В нашем случае – 50 мА. Так как в формуле ток указывается в амперах, то 50 миллиампер составляет лишь малую его часть: 0,050 А.
- > R: искомое сопротивление токоограничивающего резистора, в омах.
- В продолжение, можно проставить в формулу расчета сопротивления реальные цифры вместо U, I и R:
- R = U/I = 8,5 В / 0,050 А= 170 Ом
Рассчитать сопротивление одного резистора в простой цепи достаточно просто. Однако с добавлением в нее других резисторов, параллельно или последовательно, общее сопротивление цепи также изменяется. Суммарное сопротивление нескольких соединенных последовательно резисторов равно сумме отдельных сопротивлений каждого из них. Для параллельного же соединения все немного сложнее.
Почему нужно обращать внимание на способ соединения компонентов между собой? На то есть сразу несколько причин.
> Сопротивления резисторов составляют только некоторый фиксированный ряд номиналов. В некоторых схемах значение сопротивления должно быть рассчитано точно, но, поскольку резистор именно такого номинала может и не существовать вообще, то приходится соединять несколько элементов последовательно или параллельно.
> Резисторы — не единственные компоненты, которые имеют сопротивление. К примеру, витки обмотки электромотора также обладают некоторым сопротивлением току. Во многих практических задачах приходится рассчитывать суммарное сопротивление всей цепи.
Расчет сопротивления последовательных резисторов- Формула для вычисления суммарного сопротивления резисторов, соединенных между собой последовательно, проста до неприличия. Нужно просто сложить все сопротивления:
- Rобщ = Rl + R2 + R3 + … (столько раз, сколько есть элементов)
- В данном случае величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов или других компонентов цепи, а Rобщ — результирующая величина.
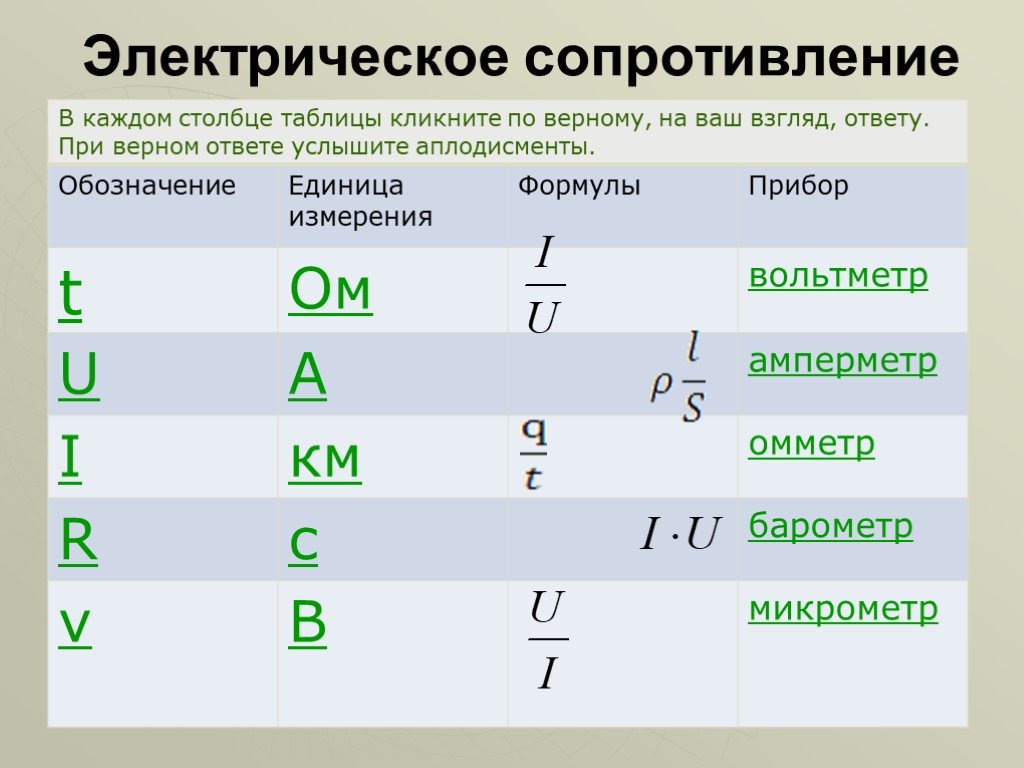
- Так, к примеру, если имеется цепь из двух соединенных последовательно резисторов с номиналами 1,2 и 2,2 кОм, то суммарное сопротивление этого участка схемы будет равно 3,4 кОм.
- Все немного усложняется, если требуется вычислить сопротивление цепи, состоящей из параллельных резисторов.
Формула приобретает вид:
- R общ = R1 * R2 / (R1 + R2)
- где R1 и R2 — сопротивления отдельных резисторов или других элементов цепи, а Rобщ -результирующая величина.
Так, если взять те же самые резисторы с номиналами 1,2 и 2,2 кОм, но соединенные параллельно, получим
- 776,47 = 2640000 / 3400
- Для расчета результирующего сопротивления электрической цепи из трех и более резисторов используется следующая формула:
- Здесь снова величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов, a Rобщ — суммарная величина.
Формулы, приведенные выше, справедливы и для расчета емкостей, только с точностью до наоборот. Так же, как и для резисторов, их можно расширить для любого количества компонентов в цепи.
Расчет емкости параллельных конденсаторов- Если нужно вычислить емкость цепи, состоящей из параллельных конденсаторов, необходимо просто сложить их номиналы:
- Собщ = CI + С2 + СЗ + …
- В этой формуле CI, С2 и СЗ — емкости отдельных конденсаторов, а Собщ суммирующая величина.
- Для вычисления общей емкости пары связанных последовательно конденсаторов применяется следующая формула:
- Собщ = С1 * С2 /( С1+С2)
- где С1 и С2 — значения емкости каждого из конденсаторов, а Собщ — общая емкость цепи
В схеме имеются конденсаторы? Много? Ничего страшного: даже если все они связаны последовательно, всегда можно найти результирующую емкость этой цепи:
И здесь опять величины C1, С2, СЗ и так далее — емкости отдельных конденсаторов, а Собщ. — суммарная величина.
— суммарная величина.
Так зачем же вязать последовательно сразу несколько конденсаторов, когда могло хватить одного? Одним из логических объяснений этому факту служит необходимость получения конкретного номинала емкости цепи, аналога которому в стандартном ряду номиналов не существует. Иногда приходится идти и по более тернистому пути, особенно в чувствительных схемах, как, например, радиоприемники.
Расчёт энергетических уравненийНаиболее широко на практике применяют такую единицу измерения энергии, как киловатт-часы или, если это касается электроники, ватт-часы. Рассчитать затраченную схемой энергию можно, зная длительность времени, на протяжении которого устройство включено. Формула для расчета такова:
ватт-часы = Р х Т
В этой формуле литера Р обозначает мощность потребления, выраженную в ваттах, а Т — время работы в часах. В физике принято выражать количество затраченной энергии в ватт-секундах, или Джоулях. Для расчета энергии в этих единицах ватт-часы делят на 3600.
В электронных схемах часто используются RC-цепочки для обеспечения временных задержек или удлинения импульсных сигналов. Самые простые цепочки состоят всего лишь из резистора и конденсатора (отсюда и происхождение термина RC-цепочка).
Принцип работы RC-цепочки состоит в том, что заряженный конденсатор разряжается через резистор не мгновенно, а на протяжении некоторого интервала времени. Чем больше сопротивление резистора и/или конденсатора, тем дольше будет разряжаться емкость. Разработчики схем очень часто применяют RC-цепочки для создания простых таймеров и осцилляторов или изменения формы сигналов.
Каким же образом можно рассчитать постоянную времени RC-цепочки? Поскольку эта схема состоит из резистора и конденсатора, в уравнении используются значения сопротивления и емкости. Типичные конденсаторы имеют емкость порядка микрофарад и даже меньше, а системными единицами являются фарады, поэтому формула оперирует дробными числами.
T = RC
В этом уравнении литера Т служит для обозначения времени в секундах, R — сопротивления в омах, и С — емкости в фарадах.
Пусть, к примеру, имеется резистор 2000 Ом, подключенный к конденсатору 0,1 мкФ. Постоянная времени этой цепочки будет равна 0,002 с, или 2 мс.
Для того чтобы на первых порах облегчить вам перевод сверхмалых единиц емкостей в фарады, мы составили таблицу:
| Значение емкости конденсатора, мкФ | Емкость конденсатора для расчета |
| 10 | 0,000 01 |
| 1 | 0,000 001 |
| 0,1 | 0,000 000 1 |
| 0,01 | 0,000 000 01 |
Частота сигнала является величиной, обратно пропорциональной его длине волны, как будет видно из формул чуть ниже. Эти формулы особенно полезны при работе с радиоэлектроникой, к примеру, для оценки длины куска провода, который планируется использовать в качестве антенны. Во всех следующих формулах длина волны выражается в метрах, а частота — в килогерцах.
Во всех следующих формулах длина волны выражается в метрах, а частота — в килогерцах.
Предположим, вы хотите изучать электронику для того, чтобы, собрав свой собственный приемопередатчик, поболтать с такими же энтузиастами из другой части света по аматорской радиосети.
Частоты радиоволн и их длина стоят в формулах бок о бок. В радиолюбительских сетях часто можно услышать высказывания о том, что оператор работает на такой-то и такой длине волны.
Вот как рассчитать частоту радиосигнала, зная длину волны:
Частота = 300000 / длина волны
Длина волны в данной формуле выражается в миллиметрах, а не в футах, аршинах или попугаях. Частота же дана в мегагерцах.
Расчет длины волны сигнала- Ту же самую формулу можно использовать и для вычисления длины волны радиосигнала, если известна его частота:
- Длина волны = 300000 / Частота
- Результат будет выражен в миллиметрах, а частота сигнала указывается в мегагерцах.
Приведем пример расчета. Пусть радиолюбитель общается со своим другом на частоте 50 МГц (50 миллионов периодов в секунду). Подставив эти цифры в приведенную выше формулу, получим:
6000 миллиметров = 300000 / 50 МГц
Однако чаще пользуются системными единицами длины — метрами, поэтому для завершения расчета нам остается перевести длину волны в более понятную величину. Так как в 1 метре 1000 миллиметров, то в результате получим 6 м. Оказывается, радиолюбитель настроил свою радиостанцию на длину волны 6 метров. Прикольно!
Источник: http://radio-stv.ru/nachinayushhim-radiolyubitelyam/10-formul
Как рассчитать мощность, силу тока и напряжение: взаимосвязи величин
Установка автоматических выключателей, выбор сечения провода, подбор нового электроприбора для домашних целей – все это требует знания и умения манипулировать основными характеристиками электрического тока. Напряжение, сила тока, мощность неразрывно связаны между собой, изменение одного оказывает влияние на остальные величины. Эту взаимосвязь, а также определение разных характеристик рассмотрим в этой статье.
Эту взаимосвязь, а также определение разных характеристик рассмотрим в этой статье.
- Как узнать ток, зная мощность и напряжение?
- Как узнать напряжение, зная силу тока?
- Как рассчитать мощность, зная силу тока и напряжения?
- Как определить потребляемую мощность цепи, имея тестер, который мерит сопротивление?
- Формула расчета сечения провода и как определяется сечение провода
Как узнать ток, зная мощность и напряжение?
В металлах, из которых сделаны провода, находятся свободные электроны, участвующие в работе. На клеммах источника тока создается сила, заставляющая заряды перемещаться по проводнику. Эта сила называется электродвижущей (э. д. с.). В постоянных цепях электроны выходят из источника с одной клеммы и «втягиваются» другой. При движении электронов совершается какая-то работа, зависящая от напряжения и тока. Связь силы тока с мощностью и напряжением видна в формуле:
P = UI,
где P – мощность, Вт; U – напряжение, В; I – ток, А.
Что такое ток? Для наглядности возьмем несколько рек, вода в которых течет с одинаковой скоростью. Однако русло у всех разное: одни реки широкие, другие узкие, какие-то глубокие или мелкие. Понятно, что объем воды, проходящий через контрольную точку, у всех будет разным. Выходит, что чем глубже или шире река, тем большее воды проходит по ней.
То же самое относится к электронам – чем больше их проходит через точку на проводнике, тем больший ток мы имеем. В отличие от рек, которые в половодье могут разливаться, избыток носителей заряда не может выходить за пределы провода. Как рассчитать пропускную способность кабеля рассмотрим в последнем подзаголовке.
Сравним зависимость силы тока от мощности и напряжения. Для этого воспользуемся приведенной выше формулой.
Внимание! Эта формула предназначена для постоянного тока. Отличие от переменного напряжения будет рассмотрено в следующем подзаголовке.
Сначала все значения следует привести к единой системе. Если мощность выражена в киловаттах или милливаттах, их нужно перевести в ватты. В одном киловатте 1 000 ватт. В одном ватте содержится 1 000 милливатт. То же самое относится и к напряжению. Если переделать формулу в такой вид: I = , то можно рассчитать ток. Например, есть утюг мощностью 1,2 кВт, как узнать ток?
Вольтметром измеряем напряжение в розетке, если прибора нет, можно считать его равным 220 В. Киловатты утюга переводим в ватты, получаем 1 200 ватт. Эти значения вставляем в формулу:
Как узнать напряжение, зная силу тока?
Снова поговорим о постоянном напряжении. Напряжение – это сила, действующая на заряженные частицы, заставляющая их двигаться. Вернемся к реке. Даже если она будет широкой и глубокой, но вода в ней не будет двигаться, она не сможет совершать какую-то работу. Движение воды происходит из-за перепада уровней поверхности земли. Чем больше разница между уровнями дна на каком-то участке, тем быстрее будет поток, и тем большую работу может совершать вода.
Чем больше разница между уровнями дна на каком-то участке, тем быстрее будет поток, и тем большую работу может совершать вода.
Напряжение в каком-то смысле можно сравнить с таким перепадом: чем выше напряжение при одном и том же токе, тем большей мощностью обладает энергия, проходящая по проводнику. При постоянном напряжении электроны движутся всегда в одном направлении, но существуют более сложные схемы изменения напряжения или тока:
- переменный;
- периодический;
- синусоидальный;
- квазистационарный;
- высокочастотный;
- пульсирующий;
- однонаправленный.
Эти разновидности часто сопутствуют друг другу. Так в домашней сети применяются сразу три разновидности: переменный, периодический, синусоидальный. Переменное напряжение указывает на противоположные знаки напряжения в течение одного периода. Происходит это следующим образом: напряжение от ноля поднимается до максимального положительного значения, затем опускается до ноля и опускается до максимального отрицательного значения. Поскольку такие изменения происходят за равный промежуток времени, их называют периодическими. Плавные переходы носят синусоидальный вид, что соответствует названию такого тока.
Поскольку такие изменения происходят за равный промежуток времени, их называют периодическими. Плавные переходы носят синусоидальный вид, что соответствует названию такого тока.
Переменное напряжение может быть:
- однофазным;
- двухфазным;
- трехфазным.
В первом случае есть фазный и нулевой провод. При подключении нагрузки электроны движутся то в одном направлении, то в другом. Чтобы определить соотношение напряжения и мощности в переменном токе используют среднеквадратическое значение. Оно определяется по нагреванию нагрузки одного и того же номинала. Сначала пропускают постоянный ток одного напряжения в течение определенного времени и замеряют температуру нагрева испытуемого тела. Затем опытным путем подбирают такое переменное напряжение, при котором за то же время происходит такое же нагревание.
Для однофазного переменного тока оно будет меньше в от амплитудного значения. То есть в сети вольтметр показывает 220 В среднеквадратическое значение, а амплитудное будет составлять 311 В.
То есть в сети вольтметр показывает 220 В среднеквадратическое значение, а амплитудное будет составлять 311 В.
Пояснение! На переменное напряжение сильное влияние оказывает емкость и индуктивность, снижая полезную мощность, но в этой статье мы подробно это не будем разбирать.
Двухфазный ток может быть либо сдвинутым, как, например, взятые две фазы у трехфазной сети, либо противоположным. В последнем случае фазы работают таким образом, что максимальное положительное значение одной фазы, соответствует максимальному отрицательному значению другой.
Для создания вращающегося магнитного поля применяют трехфазную сеть. Обычно к ней подключают электродвигатели. Если обмотки соединены по схеме треугольника, то суммарная мощность каждой фазы будет равна линейной. При подключении по схеме звезда суммарная мощность будет в больше линейной. Схема подключения электродвигателя указана на его шильдике (табличке).
Определение напряжения при известном токе и мощности, осуществляется по той же формуле. Если определяется трехфазное напряжение, то следует учитывать схему подключения нагрузки и добавлять или нет коэффициент .
Если определяется трехфазное напряжение, то следует учитывать схему подключения нагрузки и добавлять или нет коэффициент .
Как рассчитать мощность, зная силу тока и напряжения?
Разобравшись с током и напряжением, уже будет легче посчитать мощность, используя все ту же формулу. Однако для переменного тока различают несколько мощностей:
- мгновенная;
- активная;
- реактивная;
- полная.
Мгновенная мощность рассчитывается в момент измерения и может сильно отличаться от полной мощности. Активной называют полезную мощность, которая определяется по формуле:
Косинус фи в синусоидальном токе является коэффициентом мощности, выражается в процентах от 0 до 100 или цифрах от 0 до 1. Показывает сдвиг фаз между током и напряжением. Для трехфазной сети общая активная мощность складывается из отдельных фазных мощностей.
Реактивная мощность учитывает расход энергии на реактивную нагрузку (индуктивность, конденсатор, обмотка электродвигателя), которая снова возвращается к источнику. Для этого используется формула:
Полная мощность состоит из активной и реактивной, причем реактивная может иметь отрицательный или положительный знак.
Как определить потребляемую мощность цепи, имея тестер, который мерит сопротивление?
Кроме перечисленных формул, есть еще и другие, например, такие:
С их помощью можно узнать мощность, не имея данных о напряжении или токе. Стоит отметить, что сопротивление измеряется в Омах.
Осторожно! При измерении сопротивления цепи в ней не должно быть электричества.
Если сопротивление известно, тогда можно узнать, как рассчитать нагрузку по току. Для этого
где R – сопротивление нагрузки, P – мощность нагрузки, I – ток нагрузки. Однако нагрузки, содержащие емкость или индуктивность, таким способом нельзя рассчитать.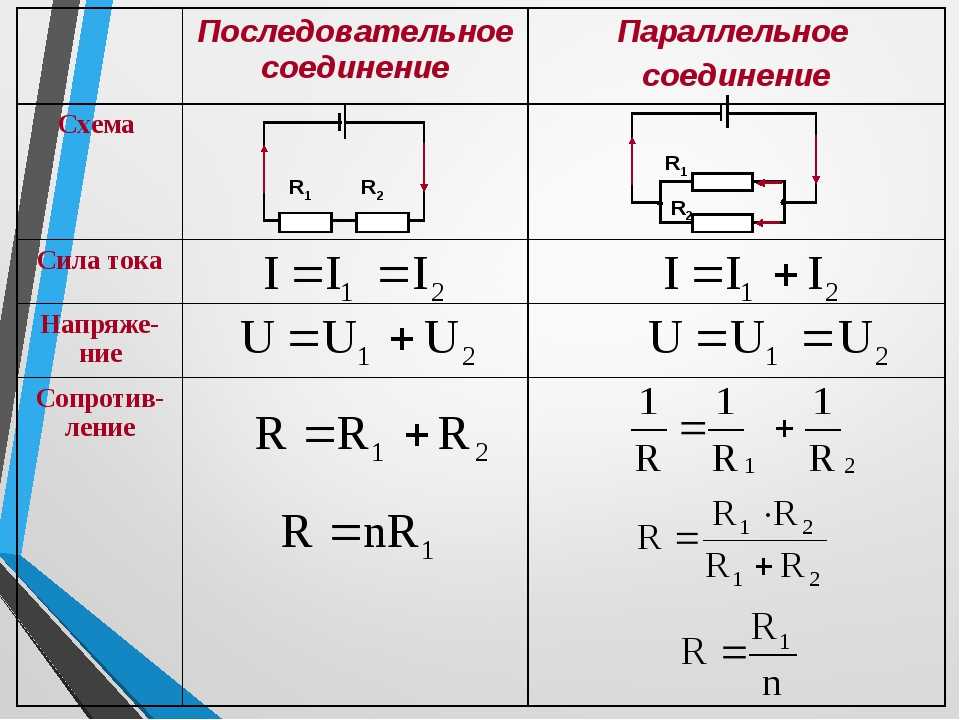 Также не получится узнать мощность лампы накаливания, измерив сопротивление ее нити, потому что вольфрам при нагревании увеличивает свое сопротивление.
Также не получится узнать мощность лампы накаливания, измерив сопротивление ее нити, потому что вольфрам при нагревании увеличивает свое сопротивление.
Формула расчета сечения провода и как определяется сечение провода
Раньше уже говорилось, что чрезмерный ток недопустим для проводов. Это связано с их перегревом. Поэтому каждый проводник способен пропускать через себя ограниченный ток. Почему провода греются? Любой материал в нормальных условиях имеет собственное сопротивление. Проходящий через него ток производит работу по нагреву металла. Этот нагрев допускается до определенной температуры, после чего начинается его плавление.
Рекомендуем прочитать: Принцип работы регулятора напряжения
Существуют специальные таблицы, помогающие подобрать сечение провода в зависимости от рабочего тока. Сечение – это площадь проволоки в разрезе. Как правило, такой разрез имеет вид круга. Чтобы найти сечение, необходимо найти площадь этого круга. Можно воспользоваться формулой:
Можно воспользоваться формулой:
где S – площадь круга или сечение в мм2; П – постоянное число равное 3,14159265; r – радиус круга. Для определения радиуса диаметр делят на два, затем подставляют в формулу.
Интересно! Многожильный и одножильный провод с одинаковым диаметром способны пропускать разную силу тока.
Мощность, напряжение, сила тока – это основные величины, зависящие друг от друга. Используя одну из приведенных формул, можно найти необходимую величину.
Понравилась статья? Расскажите друзьям:
Оцените статью, для нас это очень важно:
Проголосовавших: 5 чел.
Средний рейтинг: 5 из 5.
Закон Ома и взаимосвязь V-I-R
В физике есть определенные формулы, настолько мощные и всеобъемлющие, что они достигли уровня общеизвестности. Студент-физик столько раз записывал такие формулы, что запоминал их, даже не пытаясь. Конечно, для профессионалов в этой области такие формулы настолько важны, что они запечатлеваются в их сознании. В области современной физики есть E = m • c 2 . В области ньютоновской механики есть F нетто = м • а. В области волновой механики есть v = f • λ. А в области тока электричества есть ΔV = I • R.
Студент-физик столько раз записывал такие формулы, что запоминал их, даже не пытаясь. Конечно, для профессионалов в этой области такие формулы настолько важны, что они запечатлеваются в их сознании. В области современной физики есть E = m • c 2 . В области ньютоновской механики есть F нетто = м • а. В области волновой механики есть v = f • λ. А в области тока электричества есть ΔV = I • R.
Преобладающее уравнение, которое пронизывает изучение электрических цепей, это уравнение двух точках цепи ( ΔV ) эквивалентно произведению тока между этими двумя точками ( I ) и общего сопротивления всех электрических устройств между этими двумя точками ( Р ). В оставшейся части этого раздела «Класс физики» это уравнение станет наиболее распространенным уравнением, которое мы видим. Это уравнение, часто называемое уравнением закона Ома , является мощным предсказателем взаимосвязи между разностью потенциалов, током и сопротивлением.
Закон Ома как показатель силы тока и сопротивление известно. Тем не менее, хотя это уравнение служит мощным рецептом решения проблем, оно представляет собой гораздо больше. Это уравнение указывает две переменные, которые могут повлиять на величину тока в цепи. Сила тока в цепи прямо пропорциональна разности электрических потенциалов на ее концах и обратно пропорциональна общему сопротивлению внешней цепи. Чем больше напряжение батареи (т. е. разность электрических потенциалов), тем больше ток. И чем больше сопротивление, тем меньше ток. Заряд течет с наибольшей скоростью, когда напряжение батареи увеличивается, а сопротивление уменьшается. В самом деле, двукратное увеличение напряжения батареи приведет к двукратному увеличению тока (если все остальные факторы остаются равными). А увеличение сопротивления нагрузки в два раза приведет к уменьшению тока в два раза до половины его первоначального значения.
В таблице ниже эта взаимосвязь иллюстрируется как качественно, так и количественно для нескольких цепей с различными напряжениями и сопротивлениями аккумуляторов.
Сопротивление | ||||
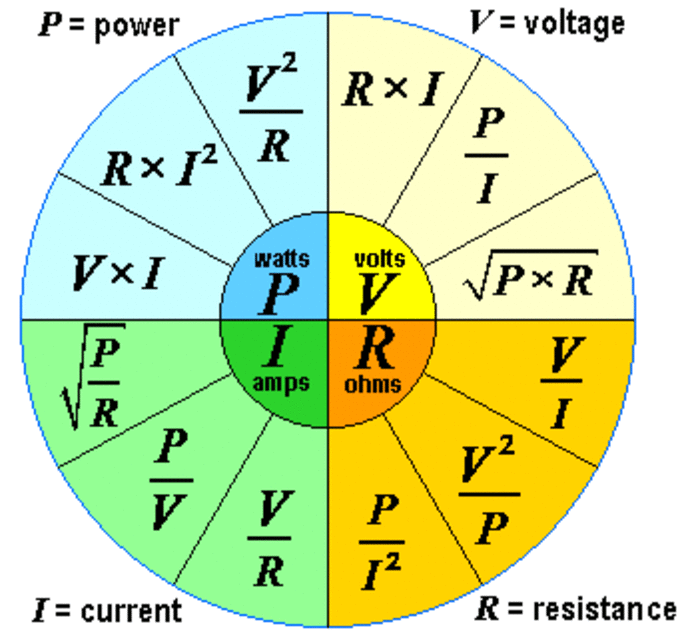 | ||||
Строки 1, 2 и 3 показывают, что удвоение и утроение напряжения батареи приводит к удвоению и утроению тока в цепи. Сравнение строк 1 и 4 или строк 2 и 5 показывает, что удвоение общего сопротивления позволяет вдвое уменьшить ток в цепи.
Сравнение строк 1 и 4 или строк 2 и 5 показывает, что удвоение общего сопротивления позволяет вдвое уменьшить ток в цепи.
Поскольку на ток в цепи влияет сопротивление, резисторы часто используются в цепях электроприборов, чтобы влиять на величину тока, присутствующего в его различных компонентах. Увеличивая или уменьшая величину сопротивления в конкретной ветви цепи, производитель может увеличивать или уменьшать величину тока в этой ветви . Кухонные приборы, такие как электрические смесители и регуляторы освещенности, работают, изменяя ток на нагрузке путем увеличения или уменьшения сопротивления цепи. Нажатие различных кнопок на электрическом миксере может изменить режим с смешивания на взбивание, уменьшив сопротивление и позволив большему току присутствовать в миксере. Точно так же поворот диска на диммерном переключателе может увеличить сопротивление его встроенного резистора и, таким образом, уменьшить ток.
На приведенной ниже схеме изображена пара цепей, содержащих источник напряжения (батарейный блок), резистор (лампочка) и амперметр (для измерения силы тока). В какой цепи лампочка имеет наибольшее сопротивление? Нажмите кнопку «Просмотреть ответ», чтобы убедиться, что вы правы.
В какой цепи лампочка имеет наибольшее сопротивление? Нажмите кнопку «Просмотреть ответ», чтобы убедиться, что вы правы.
Уравнение закона Ома часто изучается в физических лабораториях с использованием резистора, аккумуляторной батареи, амперметра и вольтметра. Амперметр — это прибор, используемый для измерения силы тока в заданном месте. Вольтметр — это устройство, оснащенное щупами, которые можно прикоснуться к двум точкам цепи, чтобы определить разность электрических потенциалов в этих точках. Изменяя количество элементов в аккумуляторной батарее, можно изменять разность электрических потенциалов во внешней цепи. Вольтметр можно использовать для определения этой разности потенциалов, а амперметр можно использовать для определения тока, связанного с этим ΔV. Батарея может быть добавлена к блоку батарей, и процесс может быть повторен несколько раз, чтобы получить набор данных I-ΔV. График зависимости I от ΔV даст линию с наклоном, эквивалентным обратной величине сопротивления резистора.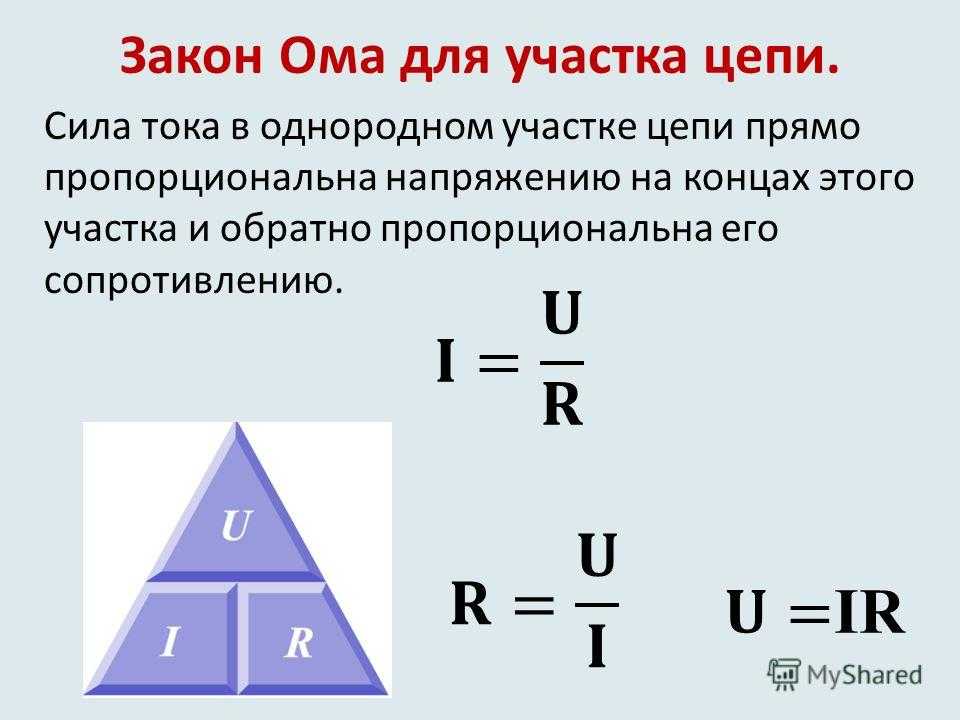 Это можно сравнить с заявленным производителем значением, чтобы определить точность лабораторных данных и достоверность уравнения закона Ома.
Это можно сравнить с заявленным производителем значением, чтобы определить точность лабораторных данных и достоверность уравнения закона Ома.
Величины, символы, уравнения и единицы!
Склонность обращать внимание на единицы измерения — неотъемлемая черта любого хорошего студента-физика. Многие трудности, связанные с решением задач, могут быть связаны с неспособностью уделить внимание единицам. По мере того, как все больше и больше электрических величин и соответствующих им метрических единиц вводятся в этом разделе учебника «Класс физики», становится все более важным организовать информацию в вашей голове. В таблице ниже перечислены некоторые количества, которые были введены до сих пор. Символ, уравнение и соответствующие метрические единицы также перечислены для каждой величины. Было бы разумно часто обращаться к этому списку или даже сделать свою собственную копию и дополнять ее по мере продвижения модуля. Некоторые учащиеся считают полезным сделать пятую колонку, в которой указано определение каждой величины.
(он же напряжение) | ΔV = I • R | |||
I = ΔV/R | или В/Ом | |||
(больше будет) | ||||
R = ΔV / I | ||||
ΔPE = P • t | Вт • с |
(Обратите внимание, что символ единицы измерения C представляет единицу измерения Кулоны.)
В следующем разделе урока 3 мы еще раз рассмотрим количественную мощность. Новое уравнение для мощности будет введено путем объединения двух (или более) уравнений из приведенной выше таблицы.
Мы хотели бы предложить …
Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного конструктора цепей постоянного тока. Вы можете найти его в разделе Physics Interactives на нашем сайте. Конструктор цепей постоянного тока предоставляет учащимся набор для создания виртуальных схем. Легко перетащите источник напряжения, резисторы и провода на рабочую область. Соедините их, и у вас есть схема. Добавьте амперметр для измерения тока и используйте датчики напряжения для определения падения напряжения. Это так просто. И не нужно беспокоиться о поражении электрическим током (если, конечно, вы не читаете это в ванной).
Это так просто. И не нужно беспокоиться о поражении электрическим током (если, конечно, вы не читаете это в ванной).
Посетите: DC Circuit Builder
1. Что из следующего приведет к уменьшению тока в электрической цепи? Выберите все подходящие.
а. уменьшить напряжение
б. уменьшить сопротивление
в. увеличить напряжение
д. увеличить сопротивление
2. Некоторая электрическая цепь содержит батарею с тремя ячейками, провода и лампочку. Что из нижеперечисленного заставит лампочку светить менее ярко? Выберите все подходящие.
а. увеличить напряжение батареи (добавить еще одну ячейку)
б. уменьшить напряжение батареи (удалить элемент)
в. уменьшить сопротивление цепи
д.
увеличить сопротивление цепи
3. Вас, вероятно, предупредили о необходимости избегать контакта с электроприборами или даже электрическими розетками мокрыми руками. Такой контакт более опасен, когда ваши руки мокрые (а не сухие), потому что мокрые руки вызывают ____.
а. напряжение цепи должно быть выше
б. напряжение цепи должно быть ниже
в. ваше сопротивление будет выше
д. ваше сопротивление должно быть ниже
эл. ток через вас будет ниже
4. Если сопротивление цепи увеличить втрое, то ток в цепи будет ____.
а. одна треть от
б. в три раза больше
с. без изменений
д. … бред какой то! Не было бы никакой возможности сделать такой прогноз.
5. Если напряжение в цепи увеличить в четыре раза, то ток в цепи будет ____.
Если напряжение в цепи увеличить в четыре раза, то ток в цепи будет ____.
а. одна четвертая часть
б. в четыре раза больше
в. без изменений
д. … бред какой то! Не было бы никакой возможности сделать такой прогноз.
6. Цепь соединена с источником питания, резистором и амперметром (для измерения силы тока). Амперметр показывает ток 24 мА (миллиампер). Определить новый ток, если напряжение источника питания было…
а. … увеличилось в 2 раза, а сопротивление осталось постоянным.
б. … увеличилось в 3 раза, а сопротивление осталось постоянным.
в. … уменьшилось в 2 раза, а сопротивление осталось постоянным.
д. … оставался постоянным, а сопротивление увеличивалось в 2 раза.
эл. … оставался постоянным, а сопротивление увеличивалось в 4 раза.
ф. … оставался постоянным, а сопротивление уменьшалось в 2 раза.
г. … увеличилось в 2 раза, а сопротивление увеличилось в 2 раза.
час. … увеличилось в 3 раза, а сопротивление уменьшилось в 2 раза.
я. … уменьшилось в 2 раза, а сопротивление увеличилось в 2 раза.
7. Используйте уравнение закона Ома, чтобы дать численные ответы на следующие вопросы:
а. Электрическое устройство с сопротивлением 3,0 Ом пропустит через себя ток силой 4,0 А, если на устройство будет воздействовать падение напряжения ________ Вольт.
б. Когда на электрический нагреватель подается напряжение 120 В, через нагреватель потечет ток силой 10,0 ампер, если сопротивление составляет ________ Ом.
в. Фонарик, который питается от 3 Вольт и использует лампочку с сопротивлением 60 Ом, будет иметь силу тока ________ Ампер.
8. Используйте уравнение закона Ома, чтобы определить недостающие значения в следующих цепях.
9. См. вопрос 8 выше. В цепях схем А и Б каким способом регулировали ток в цепях? А в цепях схем С и Г каким методом регулировали ток в цепях?
Следующий раздел:
Перейти к следующему уроку:
Формула, график и 3 простых примера
Уровень 2 (без высшей математики)Уровень 2 требует школьной математики. Подходит для школьников.
Обновлено Александром Фуфаевым
Содержание- 1-я составляющая: Напряжение
- 2-я составляющая: Электрический проводник
- 3-я составляющая: Электрический ток
- Вот график Ома научитесь определять закон Ома на вольтамперной диаграмме.
- Закон Ома как формула Здесь вы узнаете о знаменитой формуле URI, о том, как легко ее запомнить и как она получается.
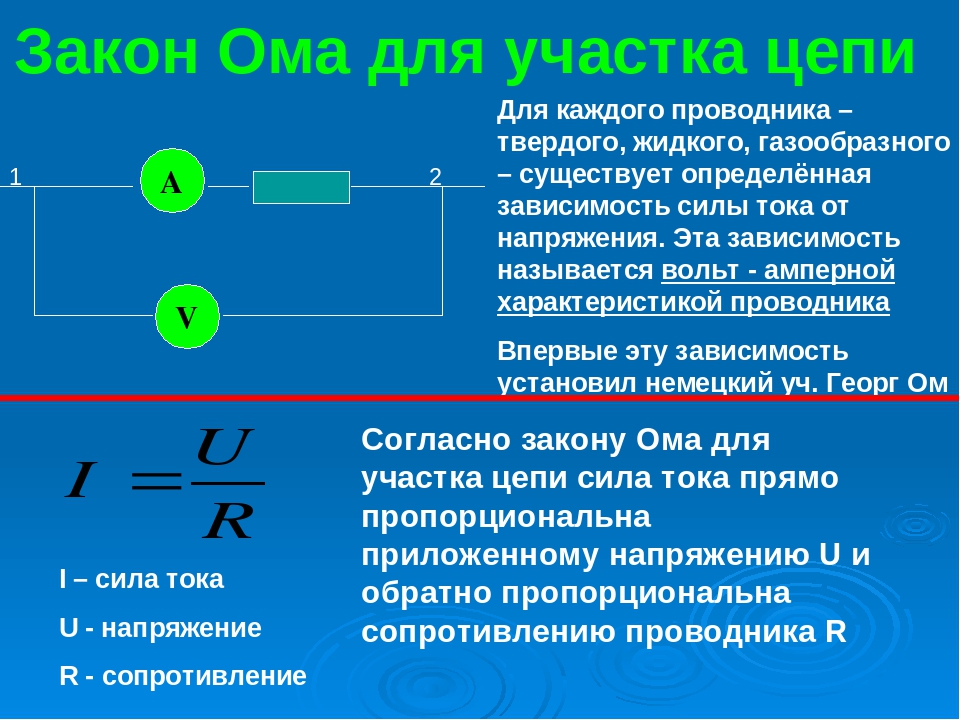
- Электрическое сопротивление Здесь вы узнаете, что такое единица электрического сопротивления и какое отношение она имеет к проводникам.
- 3 Примеры применения формулы URI Здесь на трех примерах вы узнаете, как рассчитать напряжение, ток или сопротивление, когда заданы две другие величины.
Видео — Закон Ома: 2 простых способа понять и применить его к цепям
Воспроизвести видео: Keynote (Google I/O ’18)
Скачать видео РазблокироватьЗакон Ома, названный в честь немецкого физика Георга Симона Ома, описывает, как электрический ток \(I\) и напряжение \(U\ ) относятся к.
Итак, если вы хотите понять и построить электрические цепи, без закона Ома далеко не уедешь. Так что стоит понять этот закон. Тем более, что это самый простой физический закон, который вы можете себе представить.
На предыдущих уроках вы узнали, что физически означают электрический ток и напряжение.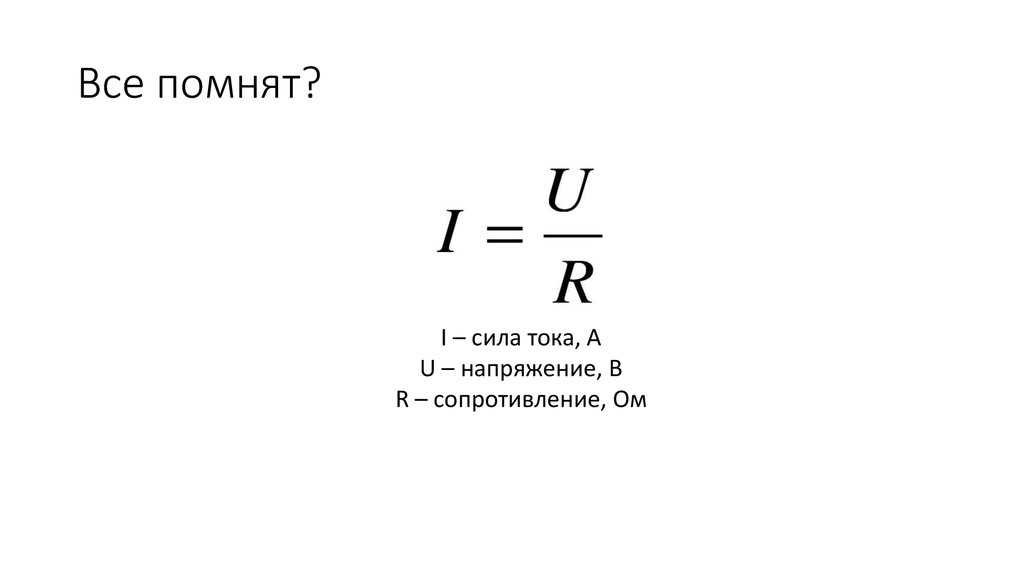 Вот краткий обзор!
Вот краткий обзор!
1-й ингредиент: Напряжение
Напряжение между отрицательным и положительным полюсами.Если разделить положительные и отрицательные электрические заряды и поместить их в две коробки, связка отрицательных зарядов образует отрицательный полюс , а связка положительных зарядов образует положительный полюс .
Напряжение создается между отрицательным и положительным полюсами. Напряжение обозначается буквой \(U\) и изображается, например, так. Напряжение показывает, сколько кинетической энергии получит положительный заряд, если он переместится от положительного полюса к отрицательному. Напряжение измеряется в вольтах, сокращенно \(\text{V}\). Предположим, что между полюсами имеется напряжение \( 10 \, \text{V} \).
2-й ингредиент: электрический проводник
Мы мало что можем сделать с одним только напряжением. Далее нам понадобится электропроводник . Это может быть, например, медный или алюминиевый провод. Этот проводник нам нужен для соединения двух полюсов друг с другом. Конечно, имеет значение, используем ли мы для соединения медь или алюминий, потому что разные материалы проводят заряды по-разному. Но об этом позже.
Это может быть, например, медный или алюминиевый провод. Этот проводник нам нужен для соединения двух полюсов друг с другом. Конечно, имеет значение, используем ли мы для соединения медь или алюминий, потому что разные материалы проводят заряды по-разному. Но об этом позже.
3-й ингредиент: Электрический ток
После соединения двух полюсов по проводнику протекает электрический ток \(I\).Поскольку два полюса теперь соединены током, положительные заряды могут перемещаться к отрицательному полюсу вдоль проводника. В конечном итоге их притягивают отрицательные заряды. Таким образом, по этому проводнику протекает электрического тока \(I\). Отрицательные заряды, конечно же, также будут перемещаться к положительному полюсу. Однако мы закрепили их в коробке, чтобы они не могли двигаться, чтобы не усложнять наш мысленный эксперимент.
Результирующий электрический ток \(I\) измеряется в амперах (или коротких амперах), обозначаемых буквой \(\text{A}\). Предположим, что по проводнику протекает ток \( 1 \, \text{A}\).
Предположим, что по проводнику протекает ток \( 1 \, \text{A}\).
Со временем количество положительных зарядов на положительном полюсе будет уменьшаться, поскольку заряды все время движутся к отрицательному полюсу. Таким образом, напряжение и ток также будут уменьшаться со временем, поскольку разделяется меньше зарядов. Чтобы предотвратить это, мы будем постоянно поставлять заряды для поддержания разделения зарядов. Это пополнение зарядов является целью источник напряжения .
С источником напряжения мы гарантируем, что напряжение и ток остаются постоянными и не снижаются.
Закон Ома в виде графика
Напряжение между полюсами установлено равным \( 10 \, \text{V}\) и течет ток \( 1 \, \text{A}\). Теперь давайте изменим напряжение и посмотрим, как это повлияет на электрический ток. Мы можем изменить напряжение, изменив количество разделенных зарядов.
Если мы увеличим напряжение с \( 10 \, \text{В}\) до \( 20 \, \text{В}\), то ток возрастет с \( 1 \, \text{A }\) в \( 2 \, \text{A}\).
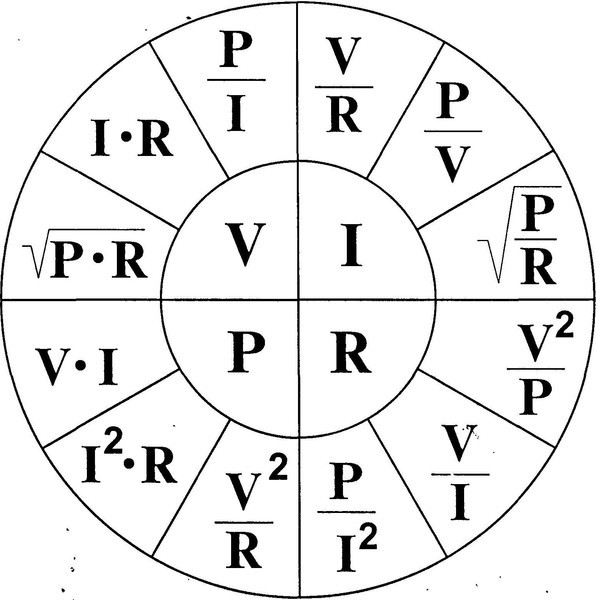 У нас есть удвоил напряжение \(U\) и, таким образом, ток \(I\) также удвоил .
У нас есть удвоил напряжение \(U\) и, таким образом, ток \(I\) также удвоил .Если мы увеличим напряжение с \( 20 \, \text{В}\) до \( 60 \, \text{В}\), то ток возрастет с \( 2 \, \text{A }\) в \( 6 \, \text{A}\). У нас утроило напряжение \(U\) и, таким образом, ток \(I\) также увеличил втрое .
Если уменьшить напряжение с \( 60 \, \text{В}\) до \( 40 \, \text{В}\), то ток уменьшится с \( 6 \, \text{А }\) в \( 4 \, \text{A}\). Мы уменьшили напряжение \(U\) в раз \(\frac{2}{3}\) и, таким образом, ток \(I\) также уменьшился в раз \(\frac{2}{3}\).
Независимо от того, во сколько раз мы изменим напряжение, во столько же раз изменится и ток.
Напряжение \(U\) и \(I\) нанесены на график. Прямая линия получается, когда точки соединяются. Мы можем проиллюстрировать измеренные значения на диаграмме. По оси \(y\), то есть по вертикальной оси, откладываем напряжение. А по оси \(x\), то есть по горизонтальной оси, откладываем ток. Этот график называется график напряжение-ток , потому что он иллюстрирует взаимосвязь между напряжением и током.
А по оси \(x\), то есть по горизонтальной оси, откладываем ток. Этот график называется график напряжение-ток , потому что он иллюстрирует взаимосвязь между напряжением и током.
Если мы теперь соединим измеренные точки данных друг с другом, мы получим прямую линию . Всякий раз, когда на графике выходит прямая линия, мы говорим, что нанесенные на график величины связаны линейно друг с другом. Итак, мы нашли закон, согласно которому напряжение и ток связаны линейно. А это и есть утверждение закона Ома!
Что визуально выражает закон Ома?Закон Ома гласит, что если изобразить напряжение \(U\) как функцию тока \(I\), мы получим прямую линию.
Что, если мы нанесем наши измерения напряжения и тока и получим такой график, как на иллюстрации (4)?
Омические проводники имеют прямую линию напряжение-ток. Этот проводник, соединяющий полюса и по которому течет ток, соответствует закону Ома? Нет! Потому что это не прямая линия. Проводник удовлетворяет закону Ома только в том случае, если график напряжения-силы представляет собой прямую линию. Электрический ток по таким проводникам, дающим прямую линию, называется 9.0011 омические проводники
Проводник удовлетворяет закону Ома только в том случае, если график напряжения-силы представляет собой прямую линию. Электрический ток по таким проводникам, дающим прямую линию, называется 9.0011 омические проводники
Прямая вольтамперная линия представлена наклоном . Обозначим наклон как электрическое сопротивление и сократим буквой \(R\):
Сопротивление есть наклон прямой линии
Якорь формулы $$ \begin{align} \text{Steigung der Geraden = Widerstand } R \end{align} $$
Таким образом, мы можем сказать:
крутая прямая имеет большой уклон и, таким образом, представляет собой большое электрическое сопротивление .

Неглубокая прямая линия имеет небольшой наклон и, таким образом, представляет малое электрическое сопротивление .
Какое влияние оказывает наклон прямой линии на напряжение и ток?
Неглубокая прямая линия, то есть небольшое сопротивление, означает: Если вы увеличите напряжение \(U\) лишь немного, то ток \(I\) увеличится очень сильно.
С другой стороны, крутая прямая, то есть большое сопротивление, означает: Если немного увеличить напряжение \(U\), то ток \(I\) также увеличится очень незначительно .
Закон Ома в виде формулы
Как теперь мы можем объединить три величины: напряжение \(U\), ток \(I\) и сопротивление \(R\) в одной формуле? Давайте на языке физики, то есть математики, переведем эту прямую в формулу.
Из математики известно, что прямая, проходящая через начало системы координат, описывается уравнением прямой:
Уравнение прямой
Якорь формулы $$ \begin{align} y ~=~ м \, х \end{align} $$
Здесь \(m\) – наклон прямой. В нашем случае наклон сопротивления равен \(R\). Итак, давайте заменим \(m\) на \(R\): \( y = R \, x \). \(y\) находится на оси \(y\) и представляет собой напряжение \(U\). Таким образом, мы заменяем \(y\) на \(U\): \(U = R\,x\). \(x\) находится на оси \(x\) и в нашем случае представляет текущий \(I\). Заменим \(x\) на \(I\). И у нас есть прямая линия на диаграмме, переведенная в формулу. Итак, закон Ома в виде формулы:
Закон Ома в виде формулы
Якорь формулы $$ \begin{align} U ~=~ R \, I \end{align} $$
Правило памяти Вы знаете, как запомнить формулу 2
навсегда? Просто запомните слово ‘\(URI\)’! Просто добавьте знак равенства между \(U\) и \(R\), и вы получите закон Ома!
Электрическое сопротивление
Единицу сопротивления можно узнать из формулы закона Ома. Вам нужно только решить формулу сопротивления \(R\). Перенесите \(I\) на другую сторону и вы получите:
Вам нужно только решить формулу сопротивления \(R\). Перенесите \(I\) на другую сторону и вы получите:
Формула: Сопротивление по закону Ома
Анкер формулы $$ \begin{align} R ~=~ \frac{U}{I} \end{align} $$
Напряжение имеет единицу измерения Вольт и сила тока имеет единицу Ампер. Следовательно, сопротивление должно иметь единицу измерения Вольт на Ампер :
Единица измерения сопротивления: Вольт на Ампер
Якорь формулы $$ \begin{align} [R] &~=~ \frac{\text{Вольт}} {\text{Ампер}} \\\\
&~=~ \frac{\mathrm{V}}{\mathrm{A}} \end{align} $$
Мы обозначаем Вольт на Ампер кратко единицей измерения Ом :
Ом как единицу сопротивления
Якорь формулы end{align} $$
Кстати, этот символ \(\Omega\) является греческой буквой “Омега”. Значение этого электрического сопротивления \(R\) зависит от проводника, используемого для соединения положительного и отрицательного полюсов.
Значение этого электрического сопротивления \(R\) зависит от проводника, используемого для соединения положительного и отрицательного полюсов.
Проводник из меди имеет меньшее сопротивление \(R\), чем проводник из алюминия. Для медного проводника мы ожидаем более пологую прямую линию, чем для алюминиевого проводника.
Проводник из алюминия имеет меньшее сопротивление \(R\), чем проводник из железа. Таким образом, железный проводник имеет более крутую прямую, чем алюминиевый проводник.
3 Примеры применения формулы URI
Давайте рассмотрим несколько конкретных примеров применения формулы закона Ома.
Пример: Рассчитать неизвестное сопротивлениеНапряжение между полюсами равно \(U ~=~ 10 \, \text{V}\), а ток, протекающий по проводнику, равен \(I ~=~ 1 \, \text{A }\). Чему равно сопротивление проводника?
Решаем закон Ома для сопротивления \(R\):
Формула URI переставлена для R
Якорь формулы $$ \begin{align} R ~=~ \frac{U}{I} \end{ align} $$
Затем вставляем заданные значения:
Пример расчета сопротивления
Якорь формулы $$ \begin{align} R &~=~ \frac{10 \, \mathrm{V}}{1 \, \mathrm{A}} \\\\
&~=~ 10 \, \mathrm{\Omega} \end{align} $$
Ток, текущий через проводник, равен \(I = 2 \, \text{A} \), а сопротивление проводника равно \(R = 100 \, \Omega \). Чему равно напряжение между концами проводника, то есть между двумя полюсами?
Чему равно напряжение между концами проводника, то есть между двумя полюсами?
Здесь мы можем напрямую использовать формулу URI:
Формула URI
Якорь формулы $$ \begin{align} U ~=~ R\, I \end{align} $$
Вставить заданные значения:
Расчет напряжения по закону Ома
Анкерная формула $$ \begin{align} U &~=~ 100 \, \Omega ~\cdot~ 2 \, \mathrm{A} \\\\
&~=~ 200 \, \mathrm{V} \end{align} $$
Напряжение между концами проводника равно \(U ~=~ 6 \, \text{V}\), а сопротивление проводника \(R ~=~ 2 \, \Omega \). Чему равен электрический ток через проводник?
Чтобы определить ток \(I\), мы решаем \(U ~=~ R\,I\) для тока, перенося сопротивление \(R\) на другую сторону. Тогда мы получаем:
Формула URI изменена для текущей
Якорь формулы $$ \begin{align} I ~=~ \frac{U}{R} \end{align} $$
Вставьте заданные значения:
Расчет силы тока по закону Ома
Привязка к формуле $$ \begin{align} I &~=~ \frac{6 \, \mathrm{V}}{2 \, \mathrm{\Omega} } \\\ \
&~=~ 3 \, \mathrm{A} \end{align} $$
Вот и все! Вы узнали, что проводник подчиняется закону Ома, если на диаграмме напряжение-ток получается прямая линия.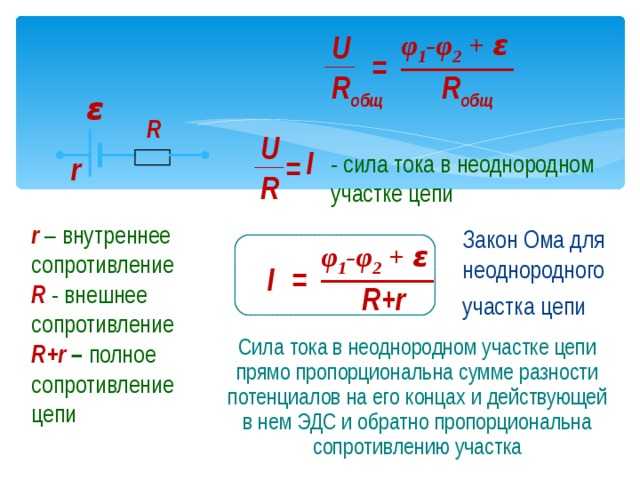 Кроме того, закон Ома описывается формулой \( U ~=~ R\,I \). Где сопротивление \(R\) представляет собой наклон прямой линии.
Кроме того, закон Ома описывается формулой \( U ~=~ R\,I \). Где сопротивление \(R\) представляет собой наклон прямой линии.
На следующем уроке вы научитесь применять закон Ома к простым электрическим цепям.
Калькуляторы и формулы закона Ома
Прежде чем щелкнуть в каждом калькуляторе закона Ома для ответа, введите числа в уравнение, которое вы хотите использовать. для расчета тока, мощности, сопротивления или напряжения. *Обновлено 8 января 2011 г., чтобы принять/изменить запятые на точки для тех, кто использует запятые в качестве десятичных разделителей.
Калькуляторы закона Ома
• Текущие (I) калькуляторы
• Калькулятор мощности (P)
• Калькулятор сопротивления (R)
• Калькуляторы напряжения (E)
Ваш блокировщик рекламы препятствует правильному отображению этой страницы.
Текущие калькуляторы
|
Калькуляторы мощности
|
Калькулятор сопротивления
|
Вычислители напряжения
| 3 | 3
|
Основы мобильной электроники:
• Диоды
• Глоссарий терминов и определений
• Закон Ома
• Рекомендуемые книги и DVD
• Рекомендуемые сечения проводов
• Реле
• Резисторы
• Инструменты и оборудование
Подпишитесь на the12volt. com
com
Понедельник, 19 сентября 2022 г.
• Copyright © 1999-2022 the12volt.com, Все права защищены.
• Политика конфиденциальности и использование файлов cookie
Отказ от ответственности: *Вся информация на этом сайте (the12volt.com) предоставляется «как есть» без каких-либо явных или подразумеваемых гарантий, включая, помимо прочего, пригодность для конкретного использования. Любой пользователь принимает на себя весь риск в отношении точности и использования этой информации. Пожалуйста проверьте все цвета проводов и схемы, прежде чем применять какую-либо информацию.
Сопротивление и удельное сопротивление
Сопротивление и удельное сопротивление
Независимо от того, подчиняется ли материал закону Ома, его сопротивление можно описать с помощью объемного удельного сопротивления. Удельное сопротивление и, следовательно, сопротивление зависят от температуры. В значительных диапазонах температур эту температурную зависимость можно предсказать по температурному коэффициенту сопротивления.
| Индекс Цепи постоянного тока | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


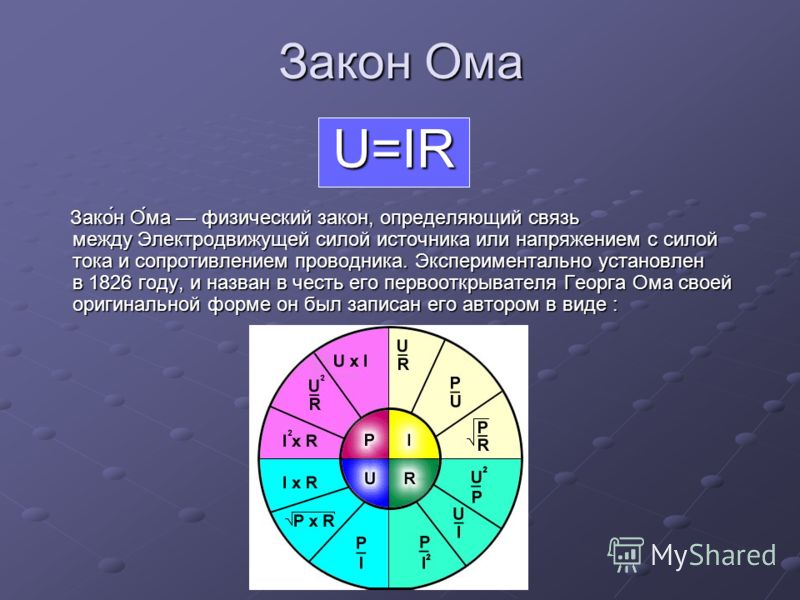

 Хотя приведенное выше определение включает в себя постоянный ток и напряжение, то же самое определение справедливо и для применения резисторов на переменном токе.
Хотя приведенное выше определение включает в себя постоянный ток и напряжение, то же самое определение справедливо и для применения резисторов на переменном токе. Экспериментально зависимость от этих свойств является прямой для широкого диапазона условий, и сопротивление провода может быть выражено как
Экспериментально зависимость от этих свойств является прямой для широкого диапазона условий, и сопротивление провода может быть выражено как
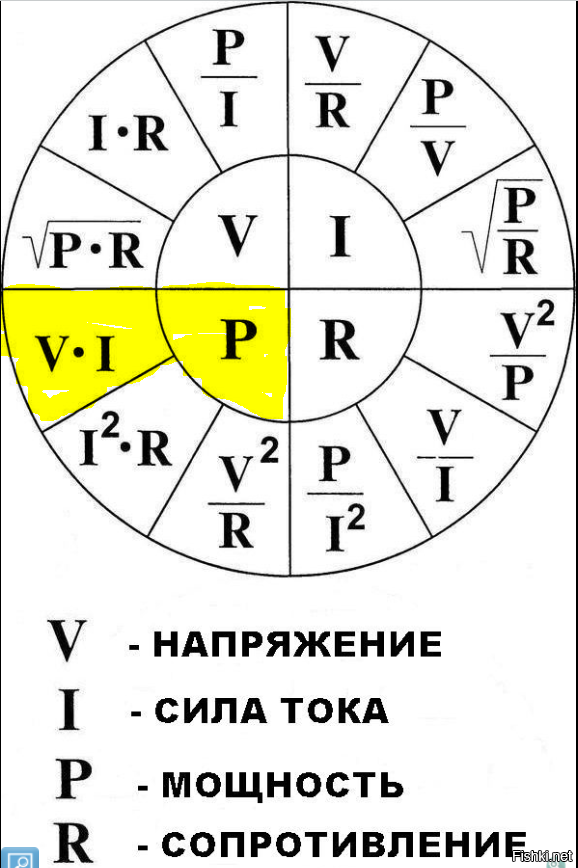 Экспериментально зависимость от этих свойств является прямой для широкого диапазона условий, и сопротивление провода может быть выражено как 9Ом-метры
Экспериментально зависимость от этих свойств является прямой для широкого диапазона условий, и сопротивление провода может быть выражено как 9Ом-метры  0013
0013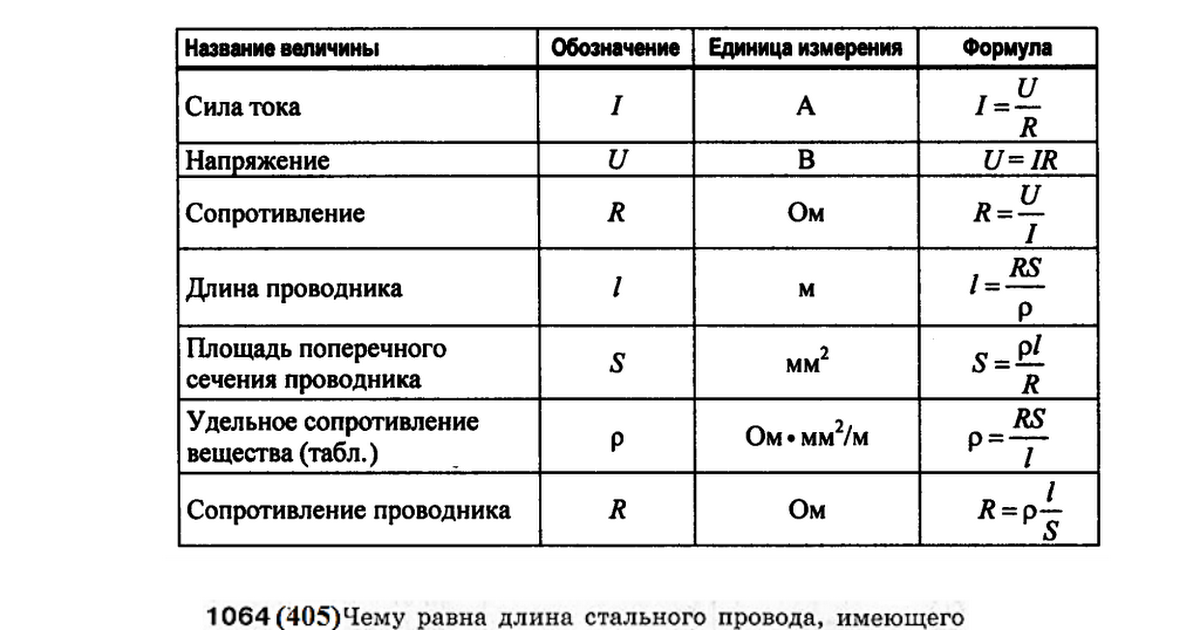 Хотя оно зависит от температуры, его можно использовать при заданной температуре для расчета сопротивления провода заданной геометрии.
Хотя оно зависит от температуры, его можно использовать при заданной температуре для расчета сопротивления провода заданной геометрии.

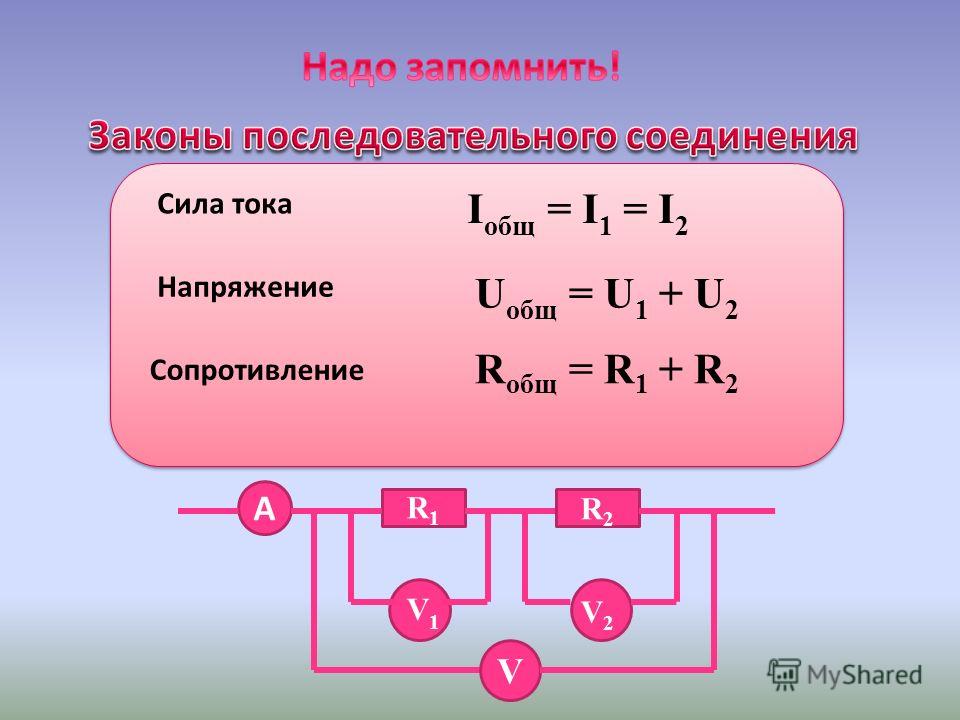 Если у вас есть усилитель, выдающий 100 Вт в нагрузку, и вы измеряете 2,5 А в нагрузке, напряжение на нагрузке можно рассчитать как E = P/I = 100 Вт/2,5 А = 40 В.
Если у вас есть усилитель, выдающий 100 Вт в нагрузку, и вы измеряете 2,5 А в нагрузке, напряжение на нагрузке можно рассчитать как E = P/I = 100 Вт/2,5 А = 40 В.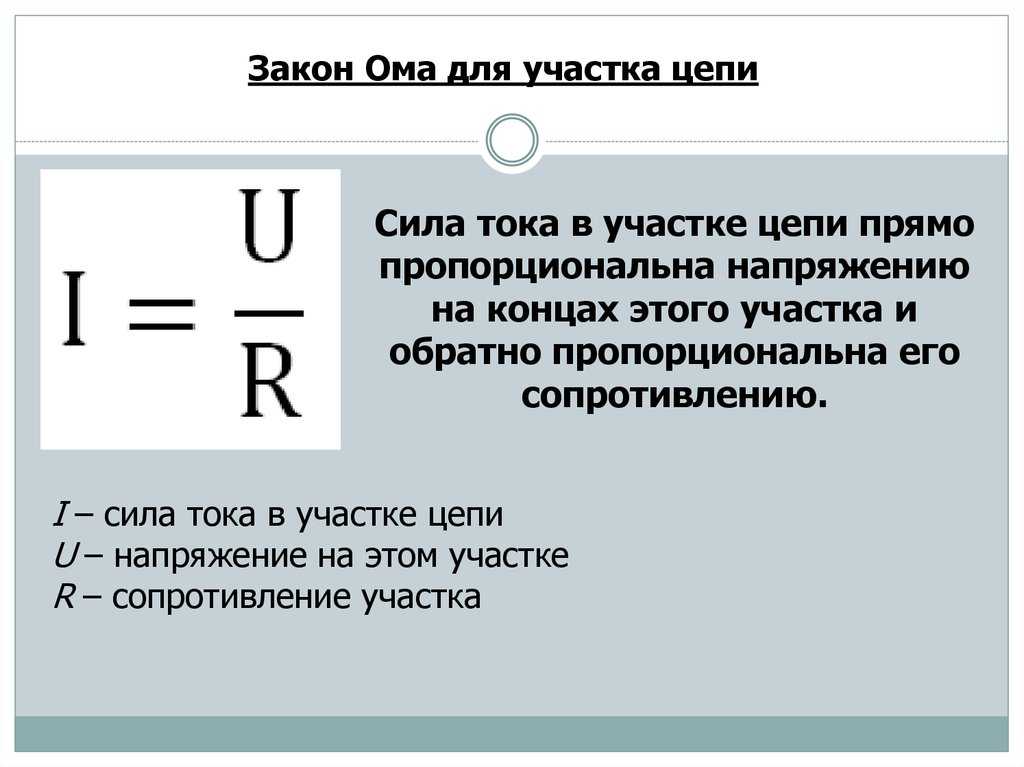 Какой номинальной мощности должен быть резистор 10 Ом, если он используется в качестве развязывающего фильтра в источнике питания и через него будет протекать общий ток 10 мА? Ответ можно найти, используя уравнение (1): P = I 2 R = (10 мА) 2 * 10K = 1 Вт.
Какой номинальной мощности должен быть резистор 10 Ом, если он используется в качестве развязывающего фильтра в источнике питания и через него будет протекать общий ток 10 мА? Ответ можно найти, используя уравнение (1): P = I 2 R = (10 мА) 2 * 10K = 1 Вт. Для нагрузки 16 Ом I = sqrt(P/R) = sqrt(100/16) = 2,5 А. Для нагрузки 8 Ом I = sqrt(100/8) = 3,54 А. Для нагрузки 4 Ом I = sqrt(100/4) = 5А.
Для нагрузки 16 Ом I = sqrt(P/R) = sqrt(100/16) = 2,5 А. Для нагрузки 8 Ом I = sqrt(100/8) = 3,54 А. Для нагрузки 4 Ом I = sqrt(100/4) = 5А.  Запрещается воспроизводить в любой форме без письменного разрешения Aiken Amplification.
Запрещается воспроизводить в любой форме без письменного разрешения Aiken Amplification. Закон Ома,
простая схема исследования и вычисления V= IR
Закон Ома,
простая схема исследования и вычисления V= IR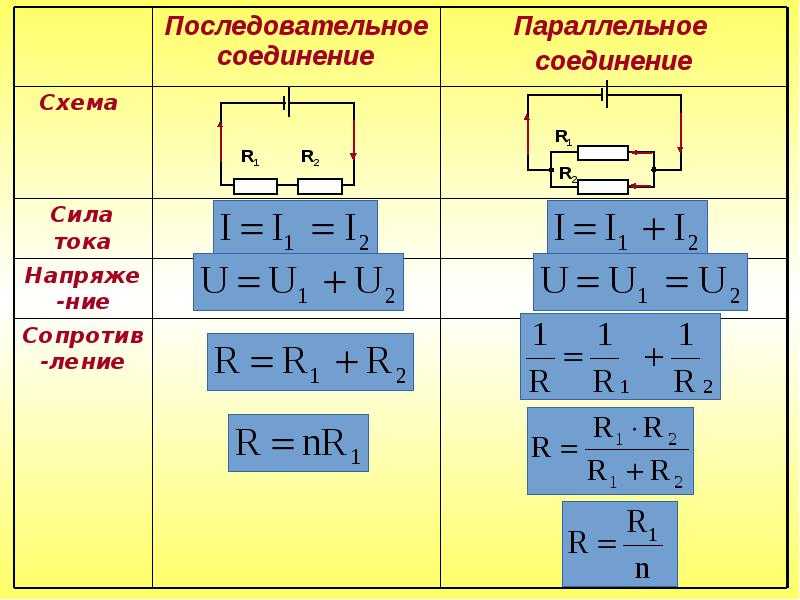 д. в альбомной ориентации
д. в альбомной ориентации

 графики, а также как получить сопротивление графическим методом – см. указатель
вверху страницы.
графики, а также как получить сопротивление графическим методом – см. указатель
вверху страницы.