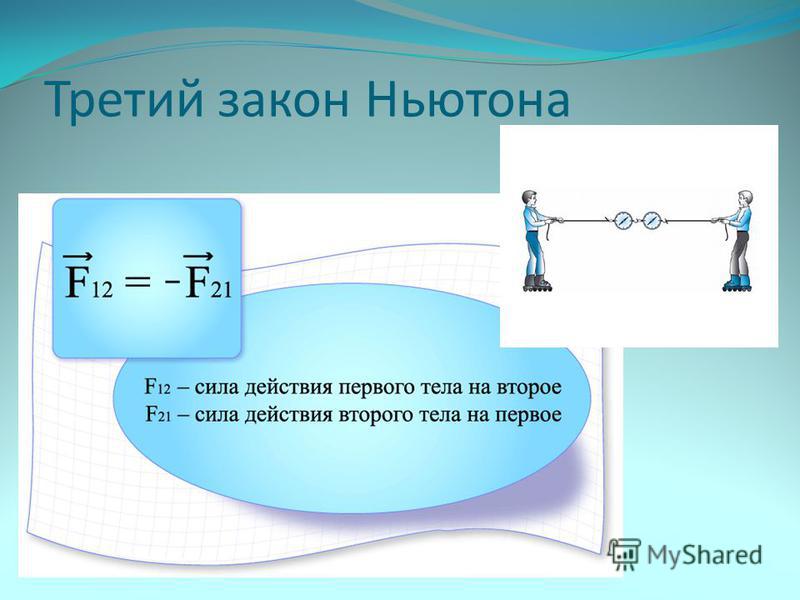
Третий закон Ньютона просто и понятно: определение и формула
Наши прошлые статьи о первом и втором законах открытых великим английским физиком Исааком Ньютоном были бы не полными, если б мы не написали о последнем третьем законе Ньютона, описывающем взаимодействие тел. В чем его суть, какая его формула, об этом читайте далее.
Третий закон Ньютона говорит нам, о том, что на всякое действие найдется свое противодействие. Академическое определение звучит так: «Два тела воздействуют друг на друга с силами, противоположными по направлению, но равными по модулю».
Как видите, это, по сути, закон действия и противодействия.
Исходя из вышесказанного, формулу для третьего закона Ньютона можно написать так:
Где F1 и F2 – разные силы, действующие на одно и то же тело. Как мы видим, силы равные за модулем (или силы равные за силой, простите за тавтологию), но при этом с разным направлением, уравновешивают друг друга.
Попробуем проиллюстрировать третий закон Ньютона на примере практической задачи.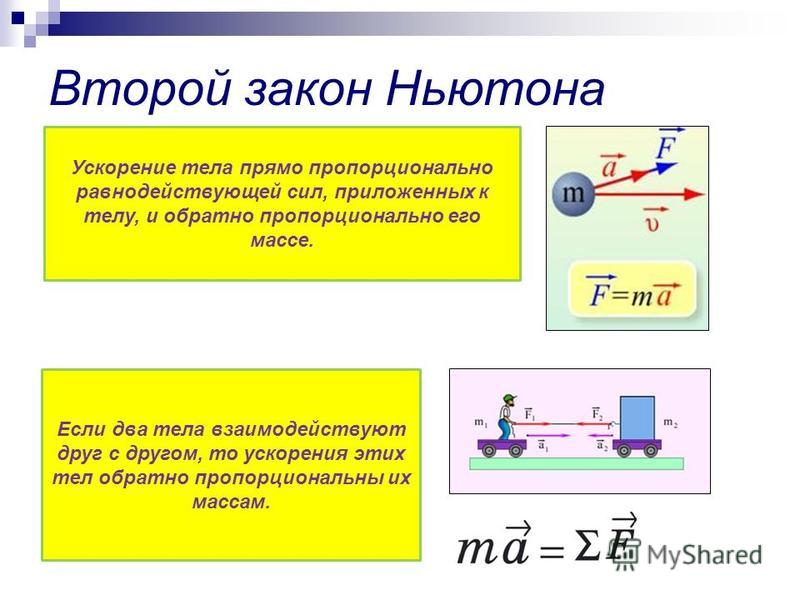
Представим, некий десантник спускается на парашюте. Спускается он с постоянной скоростью, обусловленной силой земной гравитации, какая при этом будет сила сопротивления воздуха, притом, что масса десантника 100 кг.
Согласно второму закону Ньютона сила гравитации равна ускорению свободного падения, умноженному на массу десантника. Но согласно третьему закону Ньютона помимо силы тяжести на десантника еще действует уравновешивающая сила сопротивления воздуха, позволяющая ему совершить плавное приземление. Третий закон нам говорит, что сила сопротивления воздуха равна силе гравитации. Итак, получаем следующее:
И в завершении образовательное видео по теме нашей статьи.
Автор: Павел Чайка, главный редактор журнала Познавайка
При написании статьи старался сделать ее максимально интересной, полезной и качественной. Буду благодарен за любую обратную связь и конструктивную критику в виде комментариев к статье. Также Ваше пожелание/вопрос/предложение можете написать на мою почту pavelchaika1983@gmail. com или в Фейсбук, с уважением автор.
com или в Фейсбук, с уважением автор.
Закон всемирного тяготения — формула, определение, формулировка
Гравитационное взаимодействие
Земля — это большой магнит. Причем на самом деле магнит, с настоящим магнитным полем. Но сейчас речь пойдет о другом явлении, которое притягивает к Земле тела — от прыгающего с дерева котика до летящего мимо астероида. Называется это явление гравитацией.Земля — это большой магнит. Причем на самом деле магнит, с настоящим магнитным полем. Но сейчас речь пойдет о другом явлении, которое притягивает к Земле тела — от прыгающего с дерева котика до летящего мимо астероида. Называется это явление гравитацией.
Возьмем два тела — одно с большой массой, другое с маленькой. Натянем гигантское полотно ткани и положим на него тело с большей массой. После чего положим туда тело с массой поменьше. Мы будем наблюдать примерно такую картину:
Маленькое тело начнет притягиваться к тому, что больше, — это и есть гравитация.
Гравитационное взаимодействие универсально. Оно справедливо для всех видов материи. Гравитация проявляется только в притяжении — отталкивание тел гравитация не предусматривает.
Из всех фундаментальных взаимодействий гравитационное — самое слабое. Хотя гравитация действует между всеми элементарными частицами, она настолько слаба, что ее принято не учитывать. Все дело в том, что гравитационное взаимодействие зависит от массы объекта, а у частиц она крайне мала. Эту зависимость впервые сформулировал Исаак Ньютон.
Закон всемирного тяготения
В 1682 году Исаак Ньютон открыл закон всемирного тяготения. Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.
Формула силы тяготения согласно этому закону выглядит так:
Закон всемирного тяготения F = G * (Mm/R2) F — сила тяготения [Н] M — масса первого тела (часто планеты) [кг] R — расстояние между телами [м] G — гравитационная постоянная G = 6,67 × 10-11м3·кг-1·с-2 |
Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.
Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.
Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.
Если мы возьмем два шара, то для них можно использовать этот закон вне зависимости от расстояния между ними. За расстояние R между телами в этом случае принимается расстояние между центрами шаров.
Приливы и отливы существуют благодаря закону всемирного тяготения. В этом видео я рассказываю, что общего у приливов и прыщей.
@keepalmagainПриливы и отливы #физика #огэ #егэ #математика #школа #онлайншкола
♬ оригинальный звук – 43 43
Задачка раз
Две планеты с одинаковыми массами обращаются по круговым орбитам вокруг звезды. У первой из них радиус орбиты вдвое больше, чем у второй. Каково отношение сил притяжения первой и второй планеты к звезде?
У первой из них радиус орбиты вдвое больше, чем у второй. Каково отношение сил притяжения первой и второй планеты к звезде?
Решение
По закону всемирного тяготения сила притяжения планеты к звезде обратно пропорциональна квадрату радиуса орбиты. Таким образом, в силу равенства масс отношение сил притяжения к звезде первой и второй планет обратно пропорционально отношению квадратов радиусов орбит:
По условию, у первой планеты радиус орбиты вдвое больше, чем у второй, то есть R1=2R2.
Это значит, что:
Ответ: отношение сил притяжения первой и второй планет к звезде равно 0,25.
Задачка два
У поверхности Луны на космонавта действует сила тяготения 144 Н. Какая сила тяготения действует со стороны Луны на того же космонавта в космическом корабле, движущемся по круговой орбите вокруг Луны на расстоянии трех лунных радиусов от ее центра?
Решение
По закону всемирного тяготения сила притяжения космонавта со стороны Луны обратно пропорциональна квадрату расстояния между ним и центром Луны.
144 : 9 = 16 Н
Ответ: на расстоянии трех лунных радиусов от центра сила притяжения космонавта будет равна 16 Н.
Правильно говорить не «на тело действует сила тяготения», а «Земля притягивает тело с силой тяготения».
Ускорение свободного падения
Сила тяжести — сила, с которой Земля притягивает все тела.
Сила тяжести F = mg F — сила тяжести [Н] m — масса тела [кг] g — ускорение свободного падения [м/с2] На планете Земля g = 9,8 м/с2, но подробнее об этом чуть позже. |
На первый взгляд сила тяжести очень похожа на вес тела. Действительно, в состоянии покоя на поверхности Земли формулы силы тяжести и веса идентичны. Вес тела в состоянии покоя численно равен массе тела, умноженной на ускорение свободного падения, разница состоит лишь в точке приложения силы.
Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.
Также важно понимать, что сила тяжести зависит исключительно от массы и планеты, на которой тело находится. А вес зависит еще и от ускорения, с которым движется тело или опора.
Например, в лифте вес зависит от того, куда и с каким ускорением двигаются его пассажиры. А силе тяжести все равно, куда и что движется — она не зависит от внешних факторов.
На второй взгляд сила тяжести очень похожа на силу тяготения. В обоих случаях мы имеем дело с притяжением — значит, можем сказать, что это одно и то же. Практически.
Мы можем сказать, что это одно и то же, если речь идет о Земле и каком-то предмете, который к этой планете притягивается. Тогда мы можем даже приравнять эти силы и выразить формулу для ускорения свободного падения:
F = mg
F = G * (Mm/R2)
Приравниваем правые части:
mg = G * (Mm/R2)
Делим на массу левую и правую части:
g = G * (M/R2)
Это и будет формула ускорения свободного падения. Ускорение свободного падения для каждой планеты уникально.
Закон всемирного тяготения g = G * (M/R2) g — ускорение свободного падения [м/с2] M — масса планеты [кг] R — расстояние между телами [м] G — гравитационная постоянная G = 6,67 × 10-11м3·кг-1·с-2 |
Ускорение свободного падения характеризует то, как быстро увеличивается скорость тела при свободном падении.
Свободное падение — это ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести.
Но разве это не зависит еще и от массы предмета?
Нет, не зависит. На самом деле все тела падают одинаково вне зависимости от массы. Если мы возьмем перо и мяч, то перо, конечно, будет падать медленнее, но не из-за ускорения свободного падения. Просто из-за небольшой массы пера сопротивление воздуха оказывает на него большее воздействие, чем на мяч. А вот если бы мы поместили перо и мяч в вакуум, они бы упали одновременно.
Третий закон Ньютона
Третий закон Ньютона обобщает огромное количество опытов, которые показывают, что силы — результат взаимодействия тел.
Он звучит так: тела действуют друг на друга с силами, равными по модулю и противоположными по направлению.
Если попроще — сила действия равна силе противодействия.
Если вам вдруг придется объяснять физику во дворе, то можно сказать и так: на каждую силу найдется другая сила. 🙈
Третий закон Ньютона F1 — сила, с которой первое тело действует на второе [Н] F2 — сила, с которой второе тело действует на первое [Н] |
Так вот, для силы тяготения третий закон Ньютона тоже справедлив. С какой силой Земля притягивает тело, с той же силой тело притягивает Землю.
Задачка для практики
Земля притягивает к себе подброшенный мяч с силой 5 Н. С какой силой этот мяч притягивает к себе Землю?
Решение
Согласно третьему закону Ньютона, сила, с которой Земля притягивает мяч, равна силе, с которой мяч притягивает Землю.
Ответ: мяч притягивает Землю с силой 5 Н.
Поначалу это кажется странным, потому что мы ассоциируем силу с перемещением: мол, если сила такая же, то на то же расстояние подвинется Земля. Формально это так, но у мяча масса намного меньше, чем у Земли. И Земля смещается на такое крошечное расстояние, притягиваясь к мячу, что мы его не видим, в отличие от падения мяча.
Если каждый брошенный мяч смещает Землю на какое-то расстояние, пусть даже крошечное, возникает вопрос — как она еще не слетела с орбиты из-за всех этих смещений. Но тут как в перетягивании каната: если его будут тянуть две равные по силе команды, канат никуда не сдвинется. Так же и с нашей планетой.
Знаменитые законы Ньютона
4 января – это особая дата в научном обществе, ведь именно в этот день появился на свет Исаак Ньютон. О том, как его законы действуют в “Артеке”, читайте в статье медиаотряда д/л “Янтарный”
4 января весь мир отмечает День Ньютона.
Не слышали о таком празднике? Сейчас мы вам расскажем!
Кто такой Исаак Ньютон? Это выдающийся английский ученый, разработавший и открывший ряд важнейших для мировой науки законов и теорий в физике, математике и астрономии. Многие из его открытий входят в школьную программу для старших классов.
Самый знаменитый закон Ньютона — это закон всемирного тяготения: Два любых тела притягиваются друг к другу с силой, прямо пропорциональной массе каждого из них и обратно пропорциональной квадрату расстояния между ними.
Каждую смену артековцы обязательно притягиваются к вкусной анимации.
Второй закон Ньютона: Ускорение тела прямо пропорционально равнодействующей всех сил, приложенных к телу, и обратно пропорционально его массе.
Приходя к Дереву Желаний, каждый артековец хочет, чтобы его мечта сбылась намного скорее.
Третий закон Ньютона гласит: Взаимодействия двух тел друг на друга равны между собой и направлены в противоположные стороны.
Интересный факты:
– Хотя многоцветный спектр радуги непрерывен, по традиции в нём выделяют семь цветов. Считается, что первым выбрал число семь Исаак Ньютон. Причём первоначально, он различал только пять цветов – красный, жёлтый, зелёный, голубой и фиолетовый, о чём и написал в своей книге ”Оптика”.
– Благодаря Ньютону сократилось создание фальшивых монет, так как он сообразил по бокам делать линии, которые предотвращали срезание металла.
– На первом логотипе Apple был изображён Исаак, который сидел под яблоней.
Авторы: медиаотряд д/л «Янтарный», 15 смена 2019 года
Третий закон Ньютона | Физика
В своем первом законе Ньютон описал состояние тела, не подверженного действию других тел. В этом случае тело либо сохраняет свое состояние покоя, либо движется равномерно и прямолинейно (относительно инерциальной системы отсчета).
Во втором законе Ньютона речь идет о прямо противоположной ситуации. Теперь на данное тело действуют внешние тела, причем их количество может быть произвольным. Под действием окружающих тел рассматриваемое тело начинает двигаться с ускорением, причем произведение массы данного тела на его ускорение оказывается равным действующей силе.
Теперь на данное тело действуют внешние тела, причем их количество может быть произвольным. Под действием окружающих тел рассматриваемое тело начинает двигаться с ускорением, причем произведение массы данного тела на его ускорение оказывается равным действующей силе.
Сформулировав эти два закона, Ньютон обратился к анализу ситуации, когда во взаимодействии участвуют только два тела. Допустим, имеются два тела А и В, которые притягивают друг друга с некоторыми силами F и F’. Может ли одна из этих сил быть больше другой? Размышление над этой проблемой привело Ньютона к выводу, что такого быть не может: силы взаимодействия двух тел всегда равны друг другу. Каким образом Ньютон пришел к этому заключению? Вот как он рассуждал:
«Относительно притяжения дело может быть изложено вкратце следующим образом: между двумя взаимопритягивающимися телами надо вообразить помещенным какое-либо препятствие, мешающее их сближению. Если бы одно из тел А притягивалось телом В сильнее, нежели тело В притягивается телом А, то препятствие испытывало бы со стороны тела А большее давление, нежели со стороны тела В, и, следовательно, не осталось бы равновесия. Преобладающее давление вызвало бы движение системы, состоящей из этих двух тел и препятствия в сторону тела В, ив свободном пространстве эта система, двигаясь ускоренно, ушла бы в бесконечность. Такое заключение нелепо и противоречит первому закону… Отсюда следует, что оба тела давят на препятствие с равными силами, а значит, и притягиваются взаимно с таковыми же».
Преобладающее давление вызвало бы движение системы, состоящей из этих двух тел и препятствия в сторону тела В, ив свободном пространстве эта система, двигаясь ускоренно, ушла бы в бесконечность. Такое заключение нелепо и противоречит первому закону… Отсюда следует, что оба тела давят на препятствие с равными силами, а значит, и притягиваются взаимно с таковыми же».
Опыты подтверждают вывод Ньютона. Если, например, взять две тележки и на одной из них закрепить магнит, а на другой — кусок железа, а затем соединить их с динамометрами, то мы увидим, что показания этих приборов совпадут (рис. 13). Это означает, что сила, с которой магнит притягивает к себе железо, равна по величине силе, с которой железо притягивает к себе магнит. Эти силы имеют равные числовые значения, но противоположные направления: сила притяжения к магниту направлена влево, а сила притяжения к железу — вправо.
Итак,
Силы, с которыми взаимодействуют любые два тела, всегда равны по величине и противоположны по направлению.
Это утверждение является третьим законом Ньютона. Третий закон Ньютона обосновывает введение самого термина «взаимодействие»: если одно тело действует на другое, то второе также действует на первое. Другими словами, не может быть такого, чтобы одно тело на другое действовало, а второе на первое — нет. Как писал сам Ньютон, «действию всегда есть равное и противоположное противодействие»; в частности, «если кто нажимает пальцем на камень, то и палец его также нажимается камнем. Если лошадь тащит камень, привязанный к канату, то и обратно (если можно так выразиться) она с равным усилием оттягивается к камню».
Из третьего закона Ньютона следует, что вес тела, т. е. сила, с которой тело давит на свою опору (или растягивает подвес), совпадает по величине с силой, действующей со стороны опоры на данное тело_ Сила, с которой опора давит на находящееся на ней тело, называется силой реакции опоры. Обозначив силу реакции опоры через N, мы можем записать:
P = N. (9.1)
(9.1)
Соответствующая ситуация изображена на рисунке 14.
Полученная формула является более общей, чем P=mg, так как она остается справедливой и в том случае, когда тело вместе с опорой совершает ускоренное движение.
Закономерность, выражаемую формулой (9.1), можно проверить на опыте. Возьмем два демонстрационных динамометра с круглым циферблатом и поставим их друг на друга (рис. 15). Мы увидим, что верхний прибор покажет точно такую же силу, что и нижний.
Следует помнить, что силы взаимодействия, о которых говорится в третьем законе Ньютона, не могут быть приложены к одному и тому же телу: это есть силы, с которыми тела действуют друг на друга (рис. 16).
Когда Ньютона спросили, каким путем он пришел к своим открытиям, Ньютон ответил: «Всегда думал о них. Предмет исследования постоянно передо мной, и я жду, пока первые пробивающиеся лучи рассвета постепенно не осветят его сильным и ярким светом».
О том, какой титанический труд стоял на самом деле за этим «ожиданием рассвета», рассказал впоследствии его секретарь Гэмфри: «Он (Ньютон) постоянно был занят работой. .. Он не позволял себе никакого отдыха и передышки, не ездил верхом, не гулял, не играл в кегли, не занимался спортом; он считал потерянным всякий час, не посвященный занятиям. Редко уходил он из своей комнаты, за исключением только тех случаев, когда ему надо было читать лекции как люкасовскому профессору. Лекции мало кто посещал и еще меньше того понимал. Часто приходилось читать перед пустыми стенами… Занятиями он увлекался настолько, что часто забывал обедать. Нередко, заходя в его комнату, я находил обед нетронутым на столе, и только после моего напоминания он стоя что-нибудь съедал… Раньше двух-трех часов он редко ложился спать, а в некоторых случаях засыпал только в пять, шесть часов утра. Спал он всегда четыре или пять часов, особенно осенью и весной. Судя по его озабоченности и постоянной работе, думаю, что он стремился перейти черту человеческой силы и искусства».
.. Он не позволял себе никакого отдыха и передышки, не ездил верхом, не гулял, не играл в кегли, не занимался спортом; он считал потерянным всякий час, не посвященный занятиям. Редко уходил он из своей комнаты, за исключением только тех случаев, когда ему надо было читать лекции как люкасовскому профессору. Лекции мало кто посещал и еще меньше того понимал. Часто приходилось читать перед пустыми стенами… Занятиями он увлекался настолько, что часто забывал обедать. Нередко, заходя в его комнату, я находил обед нетронутым на столе, и только после моего напоминания он стоя что-нибудь съедал… Раньше двух-трех часов он редко ложился спать, а в некоторых случаях засыпал только в пять, шесть часов утра. Спал он всегда четыре или пять часов, особенно осенью и весной. Судя по его озабоченности и постоянной работе, думаю, что он стремился перейти черту человеческой силы и искусства».
Отдавая дань трудам своих великих предшественников, Ньютон говорил, что если он и «видел дальше, чем другие, то лишь потому, что стоял на плечах гигантов». А незадолго до смерти он написал: «Не знаю, каким представляет себе меня мир, но самому себе я кажусь просто ребенком, который играет на морском берегу и забавляется, отыскивая лучше обкатанные камешки или более красивые, чем обычно, ракушки, в то время как великий океан истины лежит передо мной совершенно неразгаданный».
А незадолго до смерти он написал: «Не знаю, каким представляет себе меня мир, но самому себе я кажусь просто ребенком, который играет на морском берегу и забавляется, отыскивая лучше обкатанные камешки или более красивые, чем обычно, ракушки, в то время как великий океан истины лежит передо мной совершенно неразгаданный».
На статуе, воздвигнутой Ньютону в Кембридже, помещена надпись: «Разумом он превосходил род человеческий». Слава Ньютона была настолько велика, что известный математик Лопиталь еще при жизни Ньютона удивлялся тому, что этот великий человек мог есть, пить и спать, как прочие люди. А в Вестминстерском аббатстве, где похоронен Ньютон, на памятнике ему можно прочитать такие слова: «Пусть смертные радуются, что существовало такое украшение рода человеческого».
Влияние взглядов Ньютона на дальнейшее развитие физики огромно. «Ньютон, — писал академик С. И. Вавилов, — заставил физику мыслить по-своему, «классически», как мы выражаемся теперь. На языке Ньютона мы думали и говорили, и только теперь делаются попытки изобрести новый язык. Вот почему можно утверждать, что на всей физике лежал индивидуальный отпечаток его мысли; без Ньютона наука развивалась бы иначе».
1. Сформулируйте третий закон Ньютона. 2. Предположим, что муха, летящая навстречу автомобилю, ударилась о его лобовое стекло. Автомобиль или муха действовали с большей силой в момент столкновения? 3. Известно, что Земля притягивает к себе все находящиеся вблизи нее тела. Притягивают ли эти тела Землю? 4. Что сильнее притягивает: яблоко Землю или Земля яблоко? 5. С какой силой численно совпадает вес тела согласно третьему закону Ньютона?
13-г. Третий закон Ньютона
§ 13-г. Третий закон Ньютона
Первый закон Ньютона говорит, что в инерциальных системах отсчёта у тела нет ускорения, если на него не действуют другие тела. Второй закон Ньютона развивает сказанное: он говорит о том, какое именно ускорение появляется у тела, если на него начнёт действовать другое тело или другие тела. Третий закон Ньютона говорит нам о том, какова будет сила, действующая на второе из взаимодействующих тел:
Итак, взаимодействующие тела действуют друг на друга с силами, векторы которых равны по модулю и противоположны по направлению – гласит третий закон Ньютона.
Рассмотрим опыт, иллюстрирующий этот закон (см. рисунок). Два круглых динамометра закреплены друг над другом в штативе. К верхнему динамометру подвешен шар, а на подставке нижнего динамометра стоит сосуд с водой. Заметим показания динамометров. Теперь удлиним нить так, чтобы шар погрузился в воду, не касаясь дна. Тогда верхний динамометр покажет уменьшение силы действия шара на нить, а нижний – увеличение силы давления сосуда с водой на подставку. Показания динамометров изменились на равные значения – как и предсказывает третий закон Ньютона.
То есть сила действия воды на шар по модулю равна силе действия шара на воду, но противоположна ей по направлению. Как же шар, не касаясь дна, увеличивает силу давления на подставку? Обратите внимание: уровень воды повысился, и, согласно формуле p=rgh (см. § 4-б), возросло давление на дно сосуда. Значит, возросла и сила давления.
Как видите, третий закон Ньютона справедлив как для твёрдых, так и для жидких тел. Он также справедлив для тех сил, которые возникают между телами, не касающимися друг друга. Это, например, магниты или массивные космические тела, взаимодействующие силами тяготения.
Третий закон Ньютона имеет следствие: силы взаимодействия тел всегда возникают и исчезают парами. То есть нельзя подействовать на тело так, чтобы не вызвать появление «ответной» силы. Например, если тянуть тело нитью, мы создадим «ответную» силу, с которой тело тянет за нить.
Задача. Определите вес гири массой 1 кг, которую поднимают вверх на нити, двигая её с ускорением 2 м/с2. Сделайте чертёж.
Решение. На гирю действуют два тела: нить и Земля, то есть действуют две силы: сила упругости, направленная вверх, и сила тяжести, направленная вниз. Поскольку гиря движется вверх с ускорением, значит, сила упругости больше силы тяжести, что мы и показали в левой части чертежа. Поскольку нас просят найти вес гири, мы это показали в правой части чертежа. Напомним: вес гири – это сила, с которой она действует на подвес (см. § 3-г). По третьему закону Ньютона вектор веса гири равен взятому с противоположным знаком вектору силы упругости.
Запишем второй закон Ньютона и заменим вектор силы упругости на взятый с отрицательным знаком вектор веса:
Спроектируем последнее уравнение на ось Y:
Wy = mgy – may
Wy = –mg – ma
Подставим значения и проведём вычисления:
Wy = –1 кг · 10 м/с2 – 1 кг · 2 м/с2 = – 10 Н – 2 Н = –12 Н
Ответ: вес гири будет составлять 12 Н, оставаясь направленным вниз.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Больше интересного в телеграм @calcsboxШКОЛЬНАЯ ФИЗИКА: ТРЕТИЙ ЗАКОН НЬЮТОНА
1 Кычкин И.С. 1 Сивцев В.И. 11 ФГАОУ ВПО «Северо-Восточный федеральный университет им. М.К. Аммосова»
В статье рассматриваются случаи нарушения третьего закона Ньютона. Показывается, что более общим является закон изменения импульса. Статья будет полезна учителям общеобразовательных школ и преподавателям высших учебных заведений.
физика в школе
третий закон Ньютона
сила Лоренца
закон изменения импульса
преобразования Лоренца
1. Пурышева Н.С., Важеевская Н.Е., Исаев Д.А. Физика 10 класс. – М.: Дрофа, 2013. – 272 с.
2. Перышкин А.В., Гутник Е.М., Физика 9. – М.: Дрофа, 2014. – 320 с.
3. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика 10. – М.: Просвещение, 2014. – 416 с.
4. Кычкин И.С. Механика: Учеб. пособие для вузов. – Якутск: Изд. ЯГУ, 2003. – 357 с.
Третий закон Ньютона в его собственной формулировке гласит, что [1-3] действию всегда есть равное и противоположное противодействие – взаимные действия двух тел друг на друга равны и направлены в противоположные стороны.
Сегодня формулировка этого закона несколько иная, но эквивалентная: силы, с которыми два тела действуют друг на друга, одинаковы по модулю, но направлены противоположно:
12= –21, (1)
где 12 (21) – сила, действующая на первое (второе) тело, со стороны второго (первого) тела. Мы знаем, что тела могут взаимодействовать друг с другом непосредственно при соприкосновении или на расстоянии через поля.
Но можно показать, что и взаимодействие при соприкосновении является частным случаем взаимодействия через поля (полевого взаимодействия). Взаимодействие на расстоянии осуществляется гравитационными, электромагнитными и другими (в мире элементарных частиц) полями. Например, какое-то тело создает вокруг себя какое-то поле (гравитационное, электрическое, магнитное и т.д.), которое воздействует на другое тело, находящееся на расстоянии, с какой-то силой. И наоборот. Взаимодействие при соприкосновении тел также проявляется из-за полевого взаимодействия – взаимодействия через молекулярные поля. Молекула, находящаяся близко от поверхности тела, создает свое поле, которое проявляется на очень небольшом расстоянии (порядка м), и поэтому взаимодействие «пограничных» молекул двух тел проявляется на расстоянии порядка м, что и происходит практически при соприкосновении тел.
Есть случай, когда третий закон Ньютона в виде формулы (1) нарушается [4]. Рассмотрим (см. рис. 1) две частицы с зарядами и , движущиеся в непараллельных направлениях со скоростями и . Для определенности рисунка заряды положительные (от этого выводы не меняются).
Подвижный заряд создает вокруг себя не только электрическое, но и магнитное поле. Силы взаимодействия за счет электрического поля (кулоновские силы) равны по величине, направлены противоположно по линии, соединяющей частицы (это силы и ), т.е. они подчиняются третьему закону Ньютона. Но силы и , возникающие за счет того, что подвижные заряды (т.е. токи) создают магнитные поля и , направления которых определяются правилом правого буравчика и показаны на рисунке символами ( направлена к нам) и ⊕ ( направлена от нас), не направлены вдоль линии, соединяющей частицы. Это силы Лоренца, определяемые по формулам
Рис. 1
Их направления (опять!) определяются правилом правого буравчика (вспомните определение векторного произведения), и они показаны на рисунке. Из рисунка видно, что силы взаимодействия и подвижных зарядов не подчиняются третьему закону Ньютона:
(2)
Но (см. определение сил Лоренца) отношение силы Лоренца к кулоновской силе имеет величину порядка :
т.е. в случае нерелятивистских скоростей
отклонением от третьего закона Ньютона можно пренебречь.
Да, в виде (1) третий закон Ньютона в электродинамике нарушается. Если воспользоваться законом изменения импульса
, (3)
то неравенство (2) принимает вид:
==>
==>
, (4)
где – импульс первой (второй) частицы. Получили неожиданный (на первый взгляд) результат – полный импульс изолированной системы из 2-х электрически заряженных частиц не сохраняется! Но дело в том, что эти частицы электрически заряженные и создают вокруг себя электромагнитные поля, которые также обладают импульсом, плотность которого определяется формулой
. (5)
Поэтому полный импульс рассмотренной системы сохраняется:
, (6)
т.е., закон сохранения импульса не нарушается.
Здесь
– (7)
импульс электромагнитного поля, создаваемого этими зарядами.
Мы видим, что третий закон Ньютона сводится к закону сохранения импульса и, поэтому, хотя в электродинамике этот закон в виде (1) нарушается, но в виде закона сохранения импульса выполняется.
Приведем еще один пример, который был бы полезен учителям физики. Имеем в виду мысленный опыт академика, лауреата Нобелевской премии П. Капицы. Пусть за двумя одноименными положительными зарядами е наблюдают Коля и Вася, находящиеся в системах отсчета К и К’, причем относительно системы отсчета К заряды покоятся, а система отсчета К’ движется вниз со скоростью v, т.е., заряды e движутся относительно К’ (относительно Васи) вверх со скоростью v (см. рис. 2).
Рис. 2
Коля скажет, что заряды отталкиваются по закону Кулона:
, (8)
а Вася скажет, что заряды образуют параллельные токи, которые притягиваются друг к другу, поэтому их сила взаимодействия уменьшится на величину силы их притяжения:
(9)
и, на первый взгляд, оба правы. Легко оценить отношение этих сил:
, (10)
которое не равно единице, т.е., получается, что сила взаимодействия зарядов зависит от того, где мы находимся, чего не должно быть. Получается парадокс. В чем дело?
Дело в том, что это релятивистский эффект (множитель ( всегда говорит о наличии релятивистского эффекта), поэтому при переходе с одной системы отсчета (например, К) в другую (например, К’) необходимо воспользоваться преобразованиями Лоренца для и , тогда никаких парадоксов не получается – сила взаимодействия между зарядами не зависит от того, где мы находимся.
Заключение
В статье постарались обратить внимание преподавателей физики (в школах, вузах) на некоторые моменты в третьем законе Ньютона, на которые в школьных учебниках по физике (и не только в школьных) не уделяется достаточного внимания, хотя преподаватели (учителя) должны все это «держать в уме» в процессе преподавания физики или даже постараться объяснить (в школах с углубленным изучением физики).
Библиографическая ссылка
Кычкин И.С., Сивцев В.И. ШКОЛЬНАЯ ФИЗИКА: ТРЕТИЙ ЗАКОН НЬЮТОНА // Международный журнал экспериментального образования. – 2016. – № 3-2. – С. 191-193;URL: https://expeducation.ru/ru/article/view?id=9698 (дата обращения: 10.08.2021).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
особенности формулы Ампера и третий закон Ньютона – тема научной статьи по электротехнике, электронной технике, информационным технологиям читайте бесплатно текст научно-исследовательской работы в электронной библиотеке КиберЛенинка
УДК 537
Ш
Малыгин В.М.
Силы магнитного взаимодействия проводников с токами: особенности формулы Ампера и третий закон Ньютона
(Wk
Малыгин Вячеслав Михайлович, кандидат технических наук, начальник лаборатории отдела метрологии и измерительной техники НИИ электромеханики (ОАО НИИЭМ, г. Истра, Московская область)
ORCID ID https://orcid.org/0000-0002-6095-5568
E-mail: [email protected]; [email protected]
Показано, что утверждение Ампера о том, что элементы тока, расположенные на одной прямой, взаимно отталкиваются, связано с тем, что полученная им формула для определения силового взаимодействия элементов проводников уединенной электрической цепи включает в себя внешнюю магнитную и внутреннюю механическую, а по существу электрическую на уровне микрополей в проводнике, составляющие.
Ключевые слова: магнитное поле; сила Ампера; электрическая цепь; постоянный ток.
Введение
У истоков современной электродинамики лежат работы ученых XIX в., среди которых можно выделить Ампера, Фарадея и Максвелла, причем в работе Ампера (которого Максвелл называл «Ньютоном электричества») результаты проведенных им экспериментов сопровождаются далеко идущими теоретическими обобщениями, являющимися первой попыткой подхода к созданию теории электричества. «Электродинамика» Ампера1 представляет собой анализ фактов, размышления и удачные догадки ученого, стоявшего на передовых рубежах науки своего времени, относительно только создававшейся теории электричества. Научное наследие таких крупных ученых до сих пор представляет интерес, причем не только их достижения, включенные в учебники физики, но и путь к ним с успехами и заблуждениями, знание которых могут быть полезны следующим поколениям, начинающим изучение физики.
Силы, действующие на токи в магнитных полях, называют в современных курсах физики силами Ампера2, и закон Ампера, позволяющий определить силы взаимодействия проводников при протекании по ним электрического тока, в настоящее время широко применяется на практике при расчетах электромагнитных моментов электрических машин (электромеханических преобразователей энергии). Которые были предложены в период с тридцатых годов девятнадцатого века (когда М. Фарадей открыл явление электромагнитной индукции) и до восьмидесятых лет девятнадцатого века (когда Н. Тесла предложил использовать в машинах вращающееся в современном понимании магнитное поле). И в дальнейшем машины эти не претерпели принципиальных изменений, как и мощные силовые трансформаторы3, где закон Ампера тоже используется при расчетах на прочность и устойчивость обмоток.
1 Ампер А.-М. Электродинамика. М.: Изд-во АН СССР, 1954.
2 Сивухин Д.В.Общий курс физики. Том 3. Электричество. М.:ФИЗМАТЛИТ, 2006. С. 212.
3 Иванов-Смоленский А.В. Электрические машины. М.: Энергия, 1980. С. 21, 367.
Однако и теперь, судя по научно технической литературе и некоторым журнальным публикациям (примеры приведем ниже), остаются не понятыми некоторые особенности и физический смысл формулы, предложенной самим Ампером для определения силы взаимодействия двух элементов постоянного тока в электрической цепи. Поэтому выясним более детально, что же сделал Ампер и как он получил свою формулу.
Формула Ампера
На основании результатов опытов, подробно описанных и позволивших установить общий вид формулы и значения входящих в нее постоянных коэффициентов, Ампер предложил формулу1 для определения силы взаимодействия двух элементов линейных проводников с постоянным электрическим током в них в виде
dF= k(I1I2ds1ds2/r2)(cos s -(3/2) cos 91 cos 02), (1)
где k – коэффициент, определяемый принятой системой единиц, I1 и I2 – токи в элементах проводника, ds1 и ds2 – длины элементов проводника (элементов тока), r – длина прямой, соединяющей середины элементов проводника, s – угол между двумя элементами тока, 91 и 92 – углы между элементами тока и прямой r. В (1) длины прямолинейных отрезков (элементов проводников с токами) ds1 и ds2 должны быть много меньше длины отрезка r (расстояния между ds1 и ds2 ).
В настоящее время выражение (1) представляют в векторной форме, и его можно, вынеся за скобки 1/r212, чтобы приблизить к форме записи Ампера, написать в виде2
dF12 = k( I1l2/r212)[(3/r512)( ds1 r12))( ds2 Гп) – (2/ru)( ds1ds2)] r 12 (2)
Из курсов математики известно, что скалярное произведение векторов равно произведению численных значений векторов на косинус угла между ними, например, ds1r12 = ds1r12 cos 91. Исходя из этого, можно перейти от (2) к (1), изменение знаков с плюс на минус условно и связано с тем, считать положительным притяжение параллельных проводников с токами одного направления или их отталкивание. Кроме того, в выражении (1) имеется сомножитель 1/2, чего нет в (2), к чему мы вернемся позже. А пока попробуем разобраться с физических позиций с тем, что же сделал Ампер.), к чему мы вернемся позже. А пока попробуем разобраться с физических позиций с тем, что же сделал Ампер.
Обсуждение экспериментов Ампера
Эксперименты Ампера им подробно описаны, они доступны для повторения и никогда их результаты не оспаривались, а формулы, полученные в результате обобщения многочисленных достоверных экспериментальных фактов, «имеют главным образом то преимущество, что они остаются независимыми как от гипотез, которыми могли пользоваться авторы при отыскании этих формул, так и от гипотез, которые впоследствии могут прийти им на смену»2.
Ампер придерживался точки зрения, что силы взаимодействия элементов проводника с током направлены в пространстве так, что совпадают с прямой, соединяющей середины элементов тока, и при этом выполняется третий закон Ньютона. В «Основах теории электричества» И. Тамма сказано, что использованный Ампером математический прием разложения конечных токов на совокупность токов элементарных в известном отношении соответствует современным физическим
4
представлениям .
Что касается третьего закона Ньютона, то известно, что силы взаимодействия двух замкнутых токов удовлетворяют принципу равенства действия и противодействия, что проверено экспериментально. То же имеет место и в случае переменного электромагнитного поля, но для выполнения третьего закона Ньютона в этом случае должно обобщить понятие импульса так, чтобы обеспечить справедливость этого принципа (который должен выполняться во всех электромагнитных явлениях)5.
Но как конкретно показать равенство действия и противодействия при взаимодействии элементов проводников с постоянным током в одной электрической цепи – этот вопрос оставлен открытым, и мы постараемся в нем разобраться. При этом рассмотрим проблему шире с учетом того, что это область электромеханики, где нужно учитывать как магнитные силы, так и силы механические.
1 Ампер А.-М. Указ. соч. С. 37, 425.
2 Тамм И.Е. Основы теории электричества. М.: ФИЗМАТЛИТ, 2003.С. 206.
3 Ампер А.-М. Указ. соч. С. 12.
4 Тамм И.Е. Указ. соч. С. 202.
5 Там же. С. 205.
Покажем, что действующая на элемент проводника с током сила (в работе самого Ампера), – это суммарная сила (сумма векторов) внешней (магнитной) и внутренней (механической) сил. Сделаем это на примере электрической цепи с линейными проводниками в виде сторон прямоугольника, изображенной на рис. 1.
Рис. 1. Электрическая цепь постоянного тока I, с источником электродвижущей силы и, где F это результирующие силы, приложенные к противоположным сторонам В и D цепи (контура) и уравновешивающие друг друга. Подобные силы, приложенные к сторонам С и Е, условно не показаны.
Цепь жесткая и проводники не могут деформироваться под действием приложенных к ним сил со стороны магнитного поля (или со стороны других элементов проводников с током на расстоянии, как считалось во времена Ампера, когда не было введено понятие поля). Впрочем, при постоянных токах введение понятия магнитного поля дает правильную физическую картину явления, но на результаты расчетов не влияет1. Жесткость цепи может быть обеспечена также и за счет налагаемых связей из диэлектрика, практически исключающих изгиб и движение проводников.
Равновесие механической системы цепи рис. 1 не нарушится, если разделить пополам приложенные к сторонам Б и В прямоугольника силы (равнодействующие распределенным магнитным силам) и перенести к углам, как показано на рис. Там же. С. 528.
! Лойцянский Л.Г., Лурье А.И. Курс теоретической механики. Т. 1: Статика и кинематика. М.: Наука, 1982. С. 15, 103.
нитная (действующая со стороны магнитного поля, создаваемого всеми другими элементами цепи). А вот с продольной относительно элемента проводника силой ситуация сложнее. Наибольшие споры и недоумение вызывает до сих пор1 утверждение Ампера о том, что элементы тока, расположенные на одной прямой, взаимно отталкиваются. Максвелл о работе Ампера писал, что «метод Ампера, однако, хотя и изложен в индуктивной форме, не позволяет нам проследить процесс образования и развития идей, которыми он руководствовался»2.
Работе Ампера уделил внимание и А. Пуанкаре, который отметил, что опытов, которые относились бы к взаимодействию двух незамкнутых токов, не существует, и поэтому Ампер, сам того не замечая, прибег к гипотезам, которые приводят к противоречиям, так как исчезает единство магнитной силы в разных ситуациях. Сравнивая работы Ампера, Гельмгольца и Максвелла Пуанкаре показал поучительность истории развития теории электричества и важность ее знания, так как она помогает понять, какие ловушки встречает ученый на своем пути и как он может надеяться их избежать3.
Но если мы учтем внутренние для проводника электрической цепи механические силы (электрические силы в атомной решетке проводника), то ситуация с объяснением экспериментов Ампера проясняется. Обратимся к экспериментальной установке Ампера, изображенной у него на рис. 8, а у нас схема этого эксперимента представлена на рис. 4.
На такой установке можно измерить силу F, действующую на сторону D и изображенную также на рис. 1. Но в отличие от ситуации на рис.1 здесь растягивающие силы в проводниках С и Е отсутствуют, из-за наличия скользящих контактов механическая целостность проводников С и Е нарушена (а электрический ток не прерывается)., растягивающие стороны С и Е на рис. 1, не меняют значений по длине этих сторон, но зависят от геометрии цепи и значений тока. Первопричиной появления этих механических сил являются магнитные силы, приложенные к сторонам В и D, то есть магнитное взаимодействие движущихся внутри проводника электрических зарядов, в том числе удаленных от того элемента проводника, действие сил на который мы определяем. И именно к получению зависимости результирующей силы сГРА взаимодействия элементов проводников цепи с током от значений тока и геометрии цепи стремился Ампер. При этом с учетом недостаточного развития науки об электричестве в то время он «избегал упоминать о тех представлениях, которые могли у меня сложиться в отношении причины и природы сил»4.
Теперь же с использованием понятия магнитного поля и имеющихся знаний о природе электрического тока и внутреннем строении вещества, изложенных в курсах физики, об этом можно судить более определенно. На элемент проводника ds, рассмотренный Ампером, действует поперечная магнитная сила аГм, создающая касательные напряжения в плоскости поперечного сечения проводника, и растягивающие этот элемент перпендикулярные плоскости поперечного сечения проводника механические силы аГэм , создающие напряжения растяжения в проводнике. А так как рассматривалась статика, то эти силы уравновешиваются суммарными в плоскостях сечений касательными и нормальными напряжениями в материале проводника, что в целом и обеспечивает выполнение третьего закона Ньютона.
Внутренние силы изучает механика, где физические свойства тел в модели сплошной среды (проводники электрической цепи) задаются феноменологическими закономерностями (в твердых
1 Демирчян К.С., Жохова М.П. Электродинамика проводников с токами по Максвеллу // Электричество. 2005. № 7. С . 4151; Николаев Г.В. Современная электродинамика и причины ее парадоксальности. Томск.: Твердыня, 2003. 149 с.
2 Максвелл Дж.К. Избранные сочинения по теории электромагнитного поля. М.: Гостехтеориздат, 1952. С. 382.
3 Пуанкаре А. О науке. М.: Наука, 1983. С. 138.
4 Ампер А.-М. Указ. соч. С. 10.
2 I
2
Рис. 4. Упрощенная схема эксперимента Ампера, условные обозначения те же, что и на предыдущих рисунках.
телах это закон Гука)1 и есть понятие напряжения (механического) в точке среды. Внутренняя механическая сила (растягивающая проводник) – это, по существу, усредненная электрическая сила (с учетом действующих между атомами микрополей2 по длине проводника). На элемент ds действуют как магнитная (поперечная) составляющая, так и механическая (продольная со стороны соседних элементов проводника) составляющая силы Ампера. Внешние же механические силы к проводникам цепи не приложены. И мы убеждаемся на рассмотренном примере в единстве физики, где границы между ее разделами является весьма условными.
Использование при расчетах формулы Ампера
Большее, чем формула (1), распространение3 получило еще одно выражение для определения силы взаимодействия двух элементов проводников с током, которое представим в виде, удобном для сравнения с (1) и (2)
dFi2 = k( Wr2i2)( ds2*( dsi X r el2)), (3)
где косым крестом обозначено векторное произведение, а r e12 – это единичный вектор, совпадающий по направлению с вектором ri2.
Но у Ампера это не самостоятельная формула для расчета значения dF, а одна из двух составляющих в (1), «зачаток известного закона Ампера», как сказано в послесловии к его работе. Явно это не просматривается в (1) из-за того, что для более компактной записи окончательной формулы Ампер произвел тригонометрические преобразования, введя в (1) cos е. При сравнении формул (2) и (3) с формулой (1) надо еще учесть, что Ампер использовал сферическую тригонометрию, а не векторную алгебру.
Выражение (3) – это магнитная составляющая силы Ампера dF&. Силы оГм направлены перпендикулярно каждому отрезку ds1 и ds2, направления их и значения не совпадают, как видно на рис. 2. Результаты расчета значения силы dF взаимодействия элементов ds1 и ds2 проводников цепи с током по формулам (1) и (3) не должны совпадать, что и подтвердили В.В. Кузьмин и В.С. Шпа-тенко4 на примере контура квадратной конфигурации (но не объяснили причин этого, а представили как ошибку Ампера, что свидетельствует о затруднениях с пониманием его работы).
А объяснение заключается в том, что сумма (у нас сумма двух векторов) не может быть равна одному из слагаемых, если только при некоторых условиях второе слагаемое не принимает нулевого значения. Что имеет место в частном случае, а именно при вычислении результирующей силы, действующей на элемент ds2 второй электрической цепи со стороны всех элементов замкнутого тока I1 первой электрической цепи, когда использование формул (1) и (3) приводит к одинаковому результату. И, естественно, не нужно проводить лишние вычисления, используя (1), а сразу обратиться к (3).
Математическое доказательство этого приведено в «Основах теории электричества» Тамма5, проще же можно дать объяснение с физических позиций, заключающееся в следующем. Механические силы с№эм в первой замкнутой целостной цепи являются внутренними для проводников этой цепи, в статике они взаимно уравновешиваются и не действуют на элемент ds2 второй цепи. На него со стороны всех элементов замкнутого тока I1 действует только внешняя результирующая составляющая магнитных сил (со стороны магнитного поля).
1-, 6
В настоящее время с введением понятия магнитного поля силу, с которой действует магнитное поле на элемент линейного проводника с током, помещенный в это поле, определяют по формуле7
dF = I(ds x B), (4)
где B – вектор магнитной индукции в точке (в макроскопическом понимании) пространства, в которой находится элемент проводника, ds – вектор, совпадающий по направлению с током и характеризующий элемент длины линейного проводника (или его обозначают в виде dl). И это подход, признающий реальное существование полей, а выражение (4) называют законом Ампера в честь его вклада в развитие теории электромагнетизма.
1 Лойцянский Л.Г., Лурье А.И. Указ. соч. С. 103.
2 Сивухин Д.В. Общий курс физики. Том 1. Механика. М.:ФИЗМАТЛИТ, 2005. С. 94.
3 Демирчян К.С., Жохова М.П. Указ. соч.; Тамм И.Е. Указ. соч.
4 Кузьмин В.В., Шпатенко В.С. К выбору вариантов закона Ампера для расчета пондеромоторных сил в токоведущих контурах. //Электротехника. 2013. № 7. С. 41-44.
5 Тамм И.Е. Указ. соч. С. 568.
6 Там же. С. 199.
7 Иродов И.Е. Электромагнетизм. Основные законы. – М.: БИНОМ. Лаборатория знаний, 2007. С.160.
Однако если нужно проводить расчеты элементов проводников цепи на механическую прочность, то придется считаться и с наличием рассмотренных выше продольных механических сил в элементах проводников. Для чего, интегрируя выражение (4) по длине проводника цепи (а при необходимости по его объемным элементам), следует найти силы, действующие на участки цепи, которые показаны на рис. 1, и далее воспользоваться методами теоретической механики и сопротивления материалов для определения механических напряжений. Например, в экспериментах с получением магнитных полей с напряженностью до 40 Тесла катушки индуктивности иногда разлетались на куски, взрывались1 под действием сил Ампера, что было эквивалентно действию гидростатического давления внутри соленоида в несколько тысяч атмосфер (наглядная и полезная при изучении отдельных случаев электродинамики аналогия). А если проводники цепи рис. 1 гибкие (без связей), то цепь примет форму окружности. X г e), (5)
где г – расстояние от элемента проводника с током до точки определения вектора магнитной индукции, г e – единичный вектор, проведенный от ds к точке, в которой рассчитывают магнитную индукцию. Выражение (5) названо законом Био-Савара (окончательную форму ему придал математик Лаплас) в честь этих ученых, также стоявших у истоков развития теории электромагнетизма. А интегрируя (5) по всем элементам тока, получим значение вектора B
B = (Ц0 /4п) | (I/ Г2)С X Г e) в выражении (4) и затем перейдем к (3).
Заключение
Изучая работу Ампера, можно выяснить, что в экспериментах он имел дело с точки зрения классической теоретической механики со статикой (в проводниках и окружающем их пространстве, в диэлектрике), а с точки зрения теории электричества с частным случаем макроскопической электродинамики. Когда динамические электромагнитные процессы локализованы в пространстве, занятом проводниками с током в них, а в остальном пространстве вне проводников электрического поля нет2 из-за почти идеального баланса положительных и отрицательных зарядов в проводнике. Зато вне проводников имеется не меняющееся во времени магнитное поле, это магнитостатика. Ампер был в шаге от открытия явления электромагнитной индукции (если бы не исключал при экспериментах движение проводников друг относительно друга), которая вскоре была обнаружена Фарадеем. Однако Ампер высказал смелое для того времени предположение, что магнитное поле создают не магнитные заряды, а электрические токи, в том числе молекулярные3, что затем подтвердилось. Так мы считаем и сейчас, не заходя в область квантовой механики с элементарными частицами и их спином, где в физике проходит граница наших сегодняшних знаний.
В завершение заметим, что эксперименты Ампера явились истоком некоторых последующих практических достижений электромеханики. Схема на рис. 4 по существу представляет собой до предела упрощенную схему модели известного из курсов физики и электрических машин электродвигателя постоянного тока с последовательным возбуждением, развернутая на плоскости, где роль заторможенного якоря выполняет проводник D, и это также схема простейшего заторможенного рельсотронного линейного двигателя (ускорителя или пушки). Принцип его действия вполне объясним с использованием закона Ампера и электродинамики Максвелла, так как при движении стороны D относительно В из-за увеличения магнитного потока в контуре возникнет электродвижущая сила, направленная встречно источнику электропитания цепи и.
Интерес к почти забытым рельсотронам возник после сообщений в прессе об исследованиях возможности применения их для нужд военно-морского флота США4; подобные исследования ведутся
1 Капица П.Л. Эксперимент. Теория. Практика/ М.: Наука, 1987. С. 80.
2 Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Вып. 5. Электричество и магнетизм. Пер. с англ. -М.: Едиториал УРСС, 2004. С. 26.
3 Сивухин Д.В. .Общий курс физики. Т. 3: Электричество. М.:ФИЗМАТЛИТ, 2006. С. 234.
4 См., напр.: Office of Naval Research. “Electromagnetic Railgun Program.” Official Website of US Offie of Naval Research. ONR, US Department of the Navy, n.d. Web. <http://www.onr.navy.mil/Science-Technology/Departments/Code-35/All-Programs/air-warfare-352/Electromagnetic-Railgun.aspx>; Рельсотрон ВМФ США стал самым мощным оружием планеты [Электронный ресурс] // SOFTMIXER.COM. Сетевой журнал. 2010. Январь. Режим доступа: http://www.softmixer.com/2011/0l/blog-
и в России1. Однако заметим, что для достижения удовлетворительных характеристик подобных устройств надо будет еще решить много сложных научно технических проблем.
Выводы
Формула, полученная Ампером для определения сил, возникающих в неподвижных проводниках электрической цепи постоянного тока вследствие магнитного взаимодействия элементов их токов, включает в себя сумму двух сил. Это внешняя для элемента проводника магнитная перпендикулярная к нему сила и внутренняя для проводника механическая, а по существу – дополнительная электрическая на уровне микрополей между атомами проводника цепи продольная сила.
ЛИТЕРАТУРА
1. Алимов Т. В России впервые испытали пушку-«рельсотрон» [Электронный ресурс] // RG.RU Русское оружие. Интер-
нет-портал «Российской газеты». 2016. 12 июля. Режим доступа: https://rg.ru/2016/07/12/v-rossii-vpervye-ispytali-pushku-relsotron.html.
2. Ампер А.-М. Электродинамика. М.: Изд-во АН СССР, 1954. 492 с.
3. В России испытан рельсотрон собственного производства [Электронный ресурс] // Взгляд. Деловая газета. 2016. 12
июля. Режим доступа: http://www.vz.ru/news/2016/7/12/821036.html.
4. Демирчян К.С., Жохова М.П. Электродинамика проводников с токами по Максвеллу // Электричество. 2005. № 7.
С. 41-51.
5. Иванов-Смоленский А.В. Электрические машины. М.: Энергия, 1980. 928 с.
6. Иродов И.Е. Электромагнетизм. Основные законы. М.: БИНОМ. Лаборатория знаний, 2007. 319 с.
7. Капица П.Л. Эксперимент. Теория. Практика. М.: Наука, 1987. 496 с.
8. Кузьмин В.В., Шнатенко В.С. К выбору вариантов закона Ампера для расчета пондеромоторных сил в токоведущих
контурах // Электротехника. 2013. № 7. С. 41-44.
9. Лойцянский Л.Г., Лурье А.И. Курс теоретической механики. Т. 1. Статика и кинематика. М.: Наука, 1982. 352 с.
10. Максвелл Дж.К. Избранные сочинения но теории электромагнитного ноля. М.: Гостехтеориздат, 1952. 688 с.
11. Николаев Г.В. Современная электродинамика и причины ее парадоксальности. Томск.: Твердыня, 2003. 149 с.
12. Пуанкаре А. О науке. Пер. с франц. М.: Наука, 1983. 560 с.
13. Рельсотрон ВМФ США стал самым мощным оружием планеты [Электронный ресурс] // SOFTMIXER.COM. Сетевой
журнал. 2010. Январь. Режим доступа: http://www.softmixer.com/2011/01/blog-post_9330.html.
14. Рельсотрон для эсминца США «Zumwalt»: Фантастическое оружие для фантастического корабля [Электронный ресурс]
// Информационное агентство Newsader. 2016. 15 февр. Режим доступа: http://newsader.com/19071-flot-rassmatrivaet-yelektromagnitnuyu/.
15. Сивухин Д.В. Общий курс физики. Т. 1: Механика. М.:ФИЗМАТЛИТ, 2005. 560 с.
16. Сивухин Д.В. Общий курс физики. Т. 3: Электричество. М.: ФИЗМАТЛИТ, 2006. 656 с.
17. Сычев В. Разгон болванки до сверхзвуковой скорости. Что такое рельсотрон и когда он появится на вооружении [Элек-
тронный ресурс] // Meduza. 2016. 5 июня. Режим доступа: https://meduza.io/feature/2016/06/05/razgon-bolvanki-do-sverhzvukovoy-skorosti.
18. Тамм И.Е. Основы теории электричества. М.ФИЗМАТЛИТ, 2003. 616 с.
19. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции но физике. Вып. 5 Электричество и магнетизм. М.: Едиториал
УРСС, 2004. 304 с.
20. Office of Naval Research. “Electromagnetic Railgun Program.” Official Website of US Offie of Naval Research. ONR, US De-
partment of the Navy, n.d. Web. <http://www.onr.navy.mil/Science-Technology/Departments/Code-35/All-Programs/air-warfare-352/Electromagnetic-Railgun. aspx>.
21. “Russia’s Rail-Gun Passed Its First Tests.” South Front. N.p., 14 Jul. 2016. Web. <https://southfront.org/russias-rail-gun-passed-
its-first-tests/>.
Цитирование по ГОСТ Р 7.0.11—2011:
Малыгин, В. М. Силы магнитного взаимодействия проводников с токами: особенности формулы Ампера и третий закон Ньютона / В.М. Малыгин // Пространство и Время. — 2016. — № 3—4(25—26). — С. 86—92. Стационарный сетевой адрес: 2226-7271provr_st3_4-25_26.2016.34.
post_9330.html; Рельсотрон для эсминца США «Zumwalt»: Фантастическое оружие для фантастического корабля [Электронный ресурс] // Информационное агентство Newsader. 2016. 15 февр. Режим доступа: http://newsader.com/19071-flot-rassmatrivaet-yelektromagnitnuyu/; Сычев В. Разгон болванки до сверхзвуковой скорости. Что такое рельсотрон и когда он появится на вооружении [Электронный ресурс] // Meduza. 2016. 5 июня. Режим доступа: https://meduza.io/feature/2016/06/ 05/razgon-bolvanki-do-sverhzvukovoy-skorosti и др.
1 Алимов Т. В России впервые испытали пушку-«рельсотрон» [Электронный ресурс] // RG.RU Русское оружие. Интернет-портал «Российской газеты». 2016. 12 июля. Режим доступа: https://rg.ru/2016/07/12/v-rossii-vpervye-ispytali-pushku-relsotron.html; В России испытан рельсотрон собственного производства [Электронный ресурс] // Взгляд. Деловая газета. 2016. 12 июля. Режим доступа: http://www.vz.ru/news/2016/7/12/821036.html; “Russia’s Rail-Gun Passed Its First Tests.” South Front. N.p., 14 Jul. 2016. Web. <https://southfront.org/russias-rail-gun-passed-its-first-tests/>.
5.5 Третий закон Ньютона – University Physics Volume 1
5.5 Третий закон Ньютона
Цели обучения
К концу этого раздела вы сможете:
- Третий закон движения Ньютона
- Определение сил действия и противодействия в различных ситуациях
- Применять третий закон Ньютона для определения систем и решения проблем движения
До сих пор мы рассматривали силу как толчок или тягу; однако, если вы подумаете об этом, вы поймете, что никакие толчки или тяги никогда не возникают сами по себе.Когда вы толкаете стену, стена давит на вас. Это подводит нас к третьему закону Ньютона.
Третий закон движения Ньютона
Каждый раз, когда одно тело оказывает силу на второе тело, первое тело испытывает силу, равную по величине и противоположную по направлению силе, которую оно оказывает. Математически, если тело A оказывает силу F → F → на тело B , то B одновременно оказывает силу -F → -F → на A , или в форме векторного уравнения,
F → AB = −F → BA.F → AB = −F → BA.5.10
Третий закон Ньютона представляет собой определенную симметрию в природе: силы всегда возникают парами, и одно тело не может воздействовать на другое, не испытав силы. Мы иногда в общих чертах называем этот закон «действие-противодействие», где приложенная сила – это действие, а сила, испытываемая как следствие, – это противодействие. Третий закон Ньютона имеет практическое применение при анализе происхождения сил и понимании того, какие силы являются внешними по отношению к системе.
Мы можем легко увидеть в действии третий закон Ньютона, посмотрев на то, как люди передвигаются. Представьте себе пловца, отталкивающегося от края бассейна (рис. 5.16). Она отталкивается ногами о стену бассейна и ускоряется в направлении, противоположном ее толчку. Стена оказала на пловца равную и противоположную силу. Вы можете подумать, что две равные и противоположные силы уравновешиваются, но они не действуют , потому что действуют на разные системы . В этом случае есть две системы, которые мы могли бы исследовать: пловец и стенка.Если мы выберем пловца в качестве интересующей системы, как показано на рисунке, тогда стена на ногах является внешней силой для этой системы и влияет на ее движение. Пловец движется в направлении этой силы. Напротив, сила Ffeet на стене Ffeet на стене действует на стену, а не на нашу интересующую систему. Таким образом, Ffeet on wallFfeet on wall не влияет напрямую на движение системы и не отменяет Fwall на ногах. Пловец толкает в направлении, противоположном тому, в котором она хочет двигаться.Таким образом, реакция на ее толчок идет в желаемом направлении. В диаграмме свободного тела, такой как показанная на рис. 5.16, мы никогда не включаем обе силы пары действие-противодействие; в этом случае мы используем только Fwall на ногах, Fwall на ногах, а не Ffeet на стене, Ffeet на стене.
Фигура 5,16 Когда пловец воздействует на стену, она ускоряется в противоположном направлении; Другими словами, чистая внешняя сила действует на нее в направлении, противоположном Ffeet на стене. Ffeet на стене.Это противодействие возникает потому, что в соответствии с третьим законом Ньютона стена оказывает на пловца силу Fwall на ступни, стену на ступни ног, равную по величине, но в направлении, противоположном тому, которое она оказывает на нее. Линия вокруг пловца указывает на интересующую его систему. Таким образом, диаграмма свободного тела показывает только Fwall на ступнях, Fwall на ступнях, w (сила тяжести) и BF , которая является выталкивающей силой воды, поддерживающей вес пловца. Вертикальные силы w и BF уравновешиваются, поскольку нет вертикального ускорения.Легко найти другие примеры третьего закона Ньютона:
- Когда профессор ходит перед доской, он прикладывает силу назад к полу. Пол оказывает на профессора противодействующую силу, которая заставляет его ускоряться.
- Автомобиль ускоряется вперед, потому что земля толкает ведущие колеса вперед, в ответ на движение ведущих колес по земле. Вы можете увидеть свидетельство того, что колеса отталкиваются назад, когда шины вращаются на гравийной дороге и отбрасывают камни назад.
- Ракеты движутся вперед, выбрасывая газ назад с большой скоростью. Это означает, что ракета оказывает большое обратное усилие на газ в камере сгорания ракеты; следовательно, газ оказывает на ракету большую реактивную силу. Эта сила реакции, которая толкает тело вперед в ответ на обратную силу, называется толчком. Распространенное заблуждение, что ракеты двигаются сами по себе, толкаясь о землю или воздух позади них. На самом деле они лучше работают в вакууме, где им легче выводить выхлопные газы.
- Вертолеты создают подъемную силу, выталкивая воздух вниз, тем самым испытывая восходящую силу реакции.
- Птицы и самолеты также летают, воздействуя на воздух силой в направлении, противоположном той силы, которая им нужна. Например, крылья птицы заставляют воздух двигаться вниз и назад, чтобы подняться и двигаться вперед.
- Осьминог движется в воде, выбрасывая воду через воронку из своего тела, подобно водному мотоциклу.
- Когда человек тянет вниз по вертикальной веревке, веревка тянет человека вверх (Рисунок 5.17).
Фигура 5,17 Когда альпинист тянет веревку вниз, веревка тянет вверх альпиниста. (кредит слева: модификация работы Кристиана Бортеса)
У третьего закона Ньютона есть две важные особенности. Во-первых, прилагаемые силы (действие и противодействие) всегда равны по величине, но противоположны по направлению. Во-вторых, эти силы действуют на разные тела или системы: сила A, действует на B, , а сила B, действует на A, .Другими словами, две силы – это разные силы, которые не действуют на одно и то же тело. Таким образом, они не отменяют друг друга.
Для ситуации, показанной на рисунке 5.6, третий закон указывает, что, поскольку стул толкает мальчика вверх с силой C →, C →, он толкает стул вниз с силой -C →. − C →. Точно так же он толкает вниз с силами −F → −F → и −T → −T → на пол и стол, соответственно. Наконец, поскольку Земля тянет мальчика вниз с силой w →, w →, он тянет вверх на Земле с силой −w → −w →.Если бы этот студент в отчаянии сердито ударил по столу, он быстро усвоил бы болезненный урок (которого можно избежать, изучая законы Ньютона), что стол наносит столь же сильный удар.
Человек, идущий или бегущий, инстинктивно применяет третий закон Ньютона. Например, бегун на рис. 5.18 толкает назад землю так, что это толкает его вперед.
Фигура 5,18 Бегун подчиняется третьему закону Ньютона. (а) Бегун прилагает силу к земле.(b) Сила реакции земли на бегуна толкает его вперед. (кредит “бегун”: модификация работы “Greenwich Photography” / Flickr)
Пример 5.9
Силы на стационарном объекте
Пакет на рис. 5.19 стоит на весах. Силы на упаковке: S →, S →, что связано с масштабом, и −w →, −w →, которое связано с гравитационным полем Земли. Силы реакции, которые оказывает пакет, равны −S → −S → по шкале и w → w → на Земле. Поскольку упаковка не ускоряется, применение второго закона дает S → −w → = ma → = 0 →, S → −w → = ma → = 0 →,т.
Таким образом, показания весов показывают величину веса упаковки.Однако весы не измеряют вес упаковки; он измеряет силу −S → −S → на своей поверхности. Если система ускоряется, S → S → и −w → −w → не будут равны, как объясняется в разделе «Применение законов Ньютона».
Фигура 5,19 (а) Силы на упаковке, расположенные на шкале, вместе с их силами реакции. Сила w → w → – это вес упаковки (сила земного притяжения), а S → S → – сила весов на упаковке. (b) Изоляция системы «пакет-масштаб» и системы «пакет-Земля» делает ясными пары действия и реакции.Пример 5.10
Начало работы: выбор правильной системы
Профессор физики толкает тележку с демонстрационным оборудованием в лекционный зал (рис. 5.20). Ее масса 65,0 кг, масса тележки 12,0 кг, масса оборудования 7,0 кг. Вычислите ускорение, возникающее при приложении профессором к полу обратной силы 150 Н. Все силы, препятствующие движению, такие как трение колес тележки и сопротивление воздуха, составляют в сумме 24,0 Н. Фигура 5.20 Профессор толкает тележку со своим демонстрационным оборудованием. Длины стрелок пропорциональны величине сил (за исключением f →, f →, потому что они слишком малы для масштабирования). Система 1 подходит для этого примера, потому что она запрашивает ускорение всей группы объектов. Только F → floorF → floor и f → f → – внешние силы, действующие на Систему 1 вдоль линии движения. Все остальные силы либо отменяют, либо действуют во внешнем мире. Система 2 выбрана для следующего примера, так что F → profF → prof является внешней силой и входит во второй закон Ньютона.Диаграммы свободного тела, которые служат основой второго закона Ньютона, меняются в зависимости от выбранной системы.Стратегия
Поскольку они ускоряются как единое целое, мы определяем систему как профессора, тележку и оборудование. Это Система 1 на рисунке 5.20. Профессор отталкивается назад с силой FfootFfoot, равной 150 Н. Согласно третьему закону Ньютона, пол оказывает прямую противодействующую силу FfloorFfloor, равную 150 Н для Системы 1. Поскольку все движения горизонтальны, мы можем предположить, что в вертикальном направлении нет результирующей силы. направление.Следовательно, задача одномерная по горизонтали. Как уже отмечалось, трение f противодействует движению и, таким образом, находится в противоположном направлении от Ffloor.Floor. Мы не включаем силы FprofFprof или FcartFcart, потому что это внутренние силы, и мы не включаем FfootFfoot, потому что он действует на пол, а не на систему. Никаких других значительных сил, действующих на Систему 1. Если чистая внешняя сила может быть найдена из всей этой информации, мы можем использовать второй закон Ньютона, чтобы найти требуемое ускорение.См. Диаграмму свободного тела на рисунке.Решение
Второй закон Ньютона дается формулойЧистая внешняя сила в Системе 1 выводится из рисунка 5.20 и предыдущего обсуждения как
. Fnet = Ffloor − f = 150N − 24.0N = 126N. Fnet = Ffloor − f = 150N − 24.0N = 126N.Масса Системы 1
m = (65,0 + 12,0 + 7,0) кг = 84 кг. m = (65,0 + 12,0 + 7,0) кг = 84 кг.Эти значения FnetFnet и м дают ускорение
a = Fnetm = 126N84kg = 1,5 м / с2. a = Fnetm = 126N84kg = 1,5 м / с2.Значение
Ни одна из сил между компонентами Системы 1, например между руками профессора и тележкой, не влияет на чистую внешнюю силу, потому что они являются внутренними по отношению к Системе 1. Другой способ взглянуть на это состоит в том, что силы между компонентами системы отменяются, потому что они равны по величине и противоположны по направлению. Например, сила, прилагаемая профессором к тележке, приводит к равной и противоположной силе, действующей на профессора. В этом случае обе силы действуют на одну и ту же систему и, следовательно, отменяются.Таким образом, внутренние силы (между компонентами системы) отменяются. Выбор Системы 1 имел решающее значение для решения этой проблемы.Пример 5.11
Усилие на тележке: выбор новой системы
Вычислите силу, которую профессор оказывает на тележку, показанную на рис. 5.20, при необходимости используя данные из предыдущего примера.Стратегия
Если мы определим интересующую систему как тележку плюс оборудование (Система 2 на рис. 5.20), то чистая внешняя сила в Системе 2 – это сила, которую профессор оказывает на тележку за вычетом трения.Сила, которую она оказывает на тележку, FprofFprof, является внешней силой, действующей на Систему 2. FprofFprof был внутренним по отношению к Системе 1, но внешним по отношению к Системе 2 и, таким образом, входит во второй закон Ньютона для этой системы.Решение
Второй закон Ньютона можно использовать для нахождения Fprof.Fprof. Начнем сВеличина чистой внешней силы в Системе 2 составляет
. Fnet = Fprof-f.Fnet = Fprof-f.Решаем для FprofFprof, желаемое количество:
Fprof = Fnet + f.Fprof = Fnet + f.Дано значение f , поэтому мы должны рассчитать чистый Fnet.Fnet. Это можно сделать, потому что известны и ускорение, и масса Системы 2. Используя второй закон Ньютона, мы видим, что
, где масса Системы 2 составляет 19,0 кг (m = 12,0 кг + 7,0 кгм = 12,0 кг + 7,0 кг), а ее ускорение в предыдущем примере было равно a = 1,5 м / с2a = 1,5 м / с2. Таким образом,
Fnet = ma = (19,0 кг) (1,5 м / с2) = 29 N. Fnet = ma = (19,0 кг) (1,5 м / с2) = 29 N.Теперь мы можем найти желаемую силу:
Fprof = Fnet + f = 29N + 24.0N = 53N. Fprof = Fnet + f = 29N + 24.0N = 53N.Значение
Эта сила значительно меньше, чем сила в 150 Н, которую профессор приложил к полу.Не вся сила 150 Н передается на тележку; кое-что ускоряет профессора. Выбор системы – важный аналитический шаг как в решении проблем, так и в глубоком понимании физики ситуации (что не обязательно одно и то же).Проверьте свое понимание 5,7
Два блока находятся в покое и контактируют на поверхности без трения, как показано ниже, с m1 = 2,0 кг, m1 = 2,0 кг, m2 = 6,0 кг, m2 = 6,0 кг и приложенной силой 24 Н. (a) Найдите ускорение системы блоков.(б) Предположим, что блоки позже разделятся. Какая сила даст второму блоку массой 6,0 кг такое же ускорение, как и система блоков?
5.5 Третий закон Ньютона – Университетская физика, том 1
Цели обучения
К концу раздела вы сможете:
- Третий закон движения Ньютона
- Определение сил действия и противодействия в различных ситуациях
- Применять третий закон Ньютона для определения систем и решения проблем движения
До сих пор мы рассматривали силу как толчок или тягу; однако, если вы подумаете об этом, вы поймете, что никакие толчки или тяги никогда не возникают сами по себе.Когда вы толкаете стену, стена давит на вас. Это подводит нас к третьему закону Ньютона .
Третий закон движения Ньютона
Каждый раз, когда одно тело оказывает силу на второе тело, первое тело испытывает силу, равную по величине и противоположную по направлению силе, которую оно оказывает. Математически, если тело A прикладывает силу [латекс] \ mathbf {\ overset {\ to} {F}} [/ latex] к телу B , то B одновременно прикладывает силу [латекс] \ text {-} \ mathbf {\ overset {\ to} {F}} [/ latex] на A , или в форме векторного уравнения
[латекс] {\ mathbf {\ overset {\ to} {F}}} _ {\ text {AB}} = \ text {-} {\ mathbf {\ overset {\ to} {F}}} _ { \ text {BA}}.[/ латекс]
Третий закон Ньютона представляет собой определенную симметрию в природе: силы всегда возникают парами, и одно тело не может воздействовать на другое, не испытав силы. Мы иногда в общих чертах называем этот закон «действие-противодействие», где приложенная сила – это действие, а сила, испытываемая как следствие, – это противодействие. Третий закон Ньютона имеет практическое применение при анализе происхождения сил и понимании того, какие силы являются внешними по отношению к системе.
Мы можем легко увидеть в действии третий закон Ньютона, посмотрев на то, как люди передвигаются.Представьте себе пловца, отталкивающегося от края бассейна (рисунок). Она отталкивается ногами о стену бассейна и ускоряется в направлении, противоположном ее толчку. Стена оказала на пловца равную и противоположную силу. Вы можете подумать, что две равные и противоположные силы уравновешиваются, но это не , потому что они действуют на разные системы . В этом случае есть две системы, которые мы могли бы исследовать: пловец и стенка. Если мы выберем пловца в качестве интересующей нас системы, как на рисунке, тогда [латекс] {F} _ {\ text {wall on feet}} [/ latex] является внешней силой в этой системе и влияет на ее движение.Пловец движется в направлении этой силы. Напротив, сила [латекс] {F} _ {\ text {feet on wall}} [/ latex] действует на стену, а не на интересующую нас систему. Таким образом, [латекс] {F} _ {\ text {ноги на стене}} [/ латекс] не влияет напрямую на движение системы и не отменяет [латекс] {F} _ {\ text {стена на ногах} }. [/ latex] Пловчиха толкает в направлении, противоположном тому, в котором она хочет двигаться. Таким образом, реакция на ее толчок идет в желаемом направлении. В диаграмме свободного тела, такой как показанная на рисунке, мы никогда не включаем обе силы пары действие-противодействие; в этом случае мы используем только [латекс] {F} _ {\ text {стена на ногах}} [/ латекс], а не [латекс] {F} _ {\ text {ноги на стене}} [/ латекс].
Рис. 5.16 Когда пловец воздействует на стену, она ускоряется в противоположном направлении; другими словами, чистая внешняя сила, действующая на нее, направлена в направлении, противоположном [латексу] {F} _ {\ text {feet on wall}}. [/ latex] Это противостояние возникает потому, что в соответствии с третьим законом Ньютона, стена оказывает на пловца силу [латекс] {F} _ {\ text {wall on feet}} [/ latex], равную по величине, но в направлении, противоположном тому, которое она оказывает на нее. Линия вокруг пловца указывает на интересующую его систему.Таким образом, диаграмма свободного тела показывает только [латекс] {F} _ {\ text {wall on feet}}, [/ latex] w (гравитационная сила) и BF, которая является выталкивающей силой воды, поддерживающей вес пловца. Вертикальные силы w и BF компенсируются, потому что нет вертикального ускорения.Легко найти другие примеры третьего закона Ньютона:
- Когда профессор ходит перед доской, он прикладывает силу назад к полу. Пол оказывает на профессора противодействующую силу, которая заставляет его ускоряться.
- Автомобиль ускоряется вперед, потому что земля толкает ведущие колеса вперед, в ответ на движение ведущих колес по земле. Вы можете увидеть свидетельство того, что колеса отталкиваются назад, когда шины вращаются на гравийной дороге и отбрасывают камни назад.
- Ракеты движутся вперед, выбрасывая газ назад с большой скоростью. Это означает, что ракета оказывает большое обратное усилие на газ в камере сгорания ракеты; следовательно, газ оказывает на ракету большую реактивную силу.Эта сила реакции, которая толкает тело вперед в ответ на силу, направленную назад, называется толчком , толчком . Распространенное заблуждение, что ракеты двигаются сами по себе, толкаясь о землю или воздух позади них. На самом деле они лучше работают в вакууме, где им легче выводить выхлопные газы.
- Вертолеты создают подъемную силу, выталкивая воздух вниз, тем самым испытывая восходящую силу реакции.
- Птицы и самолеты также летают, воздействуя на воздух силой в направлении, противоположном той силы, которая им нужна.Например, крылья птицы заставляют воздух двигаться вниз и назад, чтобы подняться и двигаться вперед.
- Осьминог движется в воде, выбрасывая воду через воронку из своего тела, подобно водному мотоциклу.
- Когда человек тянет вниз по вертикальной веревке, веревка тянет человека вверх (рисунок).
У третьего закона Ньютона есть две важные особенности.Во-первых, прилагаемые силы (действие и противодействие) всегда равны по величине, но противоположны по направлению. Во-вторых, эти силы действуют на разные тела или системы: сила A, действует на B , а сила B действует на A . Другими словами, две силы – это разные силы, которые не действуют на одно и то же тело. Таким образом, они не отменяют друг друга.
Для ситуации, показанной на рисунке, третий закон указывает, что, поскольку стул толкает мальчика вверх с силой [latex] \ mathbf {\ overset {\ to} {C}}, [/ latex] он толкает вниз. стул с силой [латекс] \ text {-} \ mathbf {\ overset {\ to} {C}}.[/ latex] Точно так же он толкает вниз силами [latex] \ text {-} \ mathbf {\ overset {\ to} {F}} [/ latex] и [latex] \ text {-} \ mathbf {\ overset {\ to} {T}} [/ latex] на полу и на столе соответственно. Наконец, поскольку Земля тянет мальчика вниз с силой [latex] \ mathbf {\ overset {\ to} {w}}, [/ latex] он тянет вверх на Землю с силой [latex] \ text {-} \ mathbf { \ overset {\ to} {w}} [/ латекс]. Если бы этот студент в отчаянии сердито ударил по столу, он быстро усвоил бы болезненный урок (которого можно избежать, изучая законы Ньютона), что стол наносит столь же сильный удар.
Человек, идущий или бегущий, инстинктивно применяет третий закон Ньютона. Например, бегун на рисунке толкает землю назад, так что это толкает его вперед.
Рис. 5.18 Бегун подчиняется третьему закону Ньютона. (а) Бегун прилагает силу к земле. (b) Сила реакции земли на бегуна толкает его вперед.Пример
Силы на стационарном объекте
Пакет на рисунке стоит на весах.Силы, действующие на упаковку, следующие: [latex] \ mathbf {\ overset {\ to} {S}}, [/ latex], что связано с масштабом, и [latex] \ text {-} \ mathbf {\ overset {\ to} {w}}, [/ latex], который возникает из-за гравитационного поля Земли. Силы реакции, которые оказывает упаковка, следующие: [latex] \ text {-} \ mathbf {\ overset {\ to} {S}} [/ latex] на шкале и [latex] \ mathbf {\ overset {\ to} { w}} [/ latex] на Земле. Поскольку пакет не ускоряется, применение второго закона дает
[латекс] \ mathbf {\ overset {\ to} {S}} – \ mathbf {\ overset {\ to} {w}} = m \ mathbf {\ overset {\ to} {a}} = \ mathbf { \ overset {\ to} {0}}, [/ latex]
т.
[латекс] \ mathbf {\ overset {\ to} {S}} = \ mathbf {\ overset {\ to} {w}}.[/ латекс]
Таким образом, показания весов показывают величину веса упаковки. Однако весы не измеряют вес упаковки; он измеряет силу [латекс] \ text {-} \ mathbf {\ overset {\ to} {S}} [/ latex] на его поверхности. Если система ускоряется, [latex] \ mathbf {\ overset {\ to} {S}} [/ latex] и [latex] \ text {-} \ mathbf {\ overset {\ to} {w}} [/ латекс] не будет равным, как объясняется в «Применении законов Ньютона».
Рис. 5.19 (a) Силы, действующие на упаковку, лежащую на весах, вместе с их силами реакции.Сила [латекс] \ mathbf {\ overset {\ to} {w}} [/ latex] – это вес упаковки (сила гравитации Земли) и [латекс] \ mathbf {\ overset {\ to} { S}} [/ latex] – это сила весов на упаковке. (b) Изоляция системы «пакет-масштаб» и системы «пакет-Земля» делает ясными пары действия и реакции.Пример
Начало работы: выбор правильной системы
Профессор физики толкает тележку с демонстрационным оборудованием в лекционный зал (рисунок).Ее масса 65,0 кг, масса тележки 12,0 кг, масса оборудования 7,0 кг. Вычислите ускорение, возникающее при приложении профессором к полу обратной силы 150 Н. Все силы, противодействующие движению, такие как трение колес тележки и сопротивление воздуха, составляют 24,0 Н.
Рисунок 5.20 Профессор толкает тележку со своим демонстрационным оборудованием. Длины стрелок пропорциональны величине сил (кроме [latex] \ mathbf {\ overset {\ to} {f}} \ text {,} [/ latex], потому что они слишком малы, чтобы их можно было нарисовать в масштабе. ).Система 1 подходит для этого примера, потому что она запрашивает ускорение всей группы объектов. Только [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {\ text {floor}} [/ latex] и [латекс] \ mathbf {\ overset {\ to} {f}} [/ латекс] – это внешние силы, действующие на Систему 1 вдоль линии движения. Все остальные силы либо отменяют, либо действуют во внешнем мире. Система 2 выбрана для следующего примера, так что [latex] {\ mathbf {\ overset {\ to} {F}}} _ {\ text {prof}} [/ latex] является внешней силой и входит во второй закон Ньютона .Диаграммы свободного тела, которые служат основой второго закона Ньютона, меняются в зависимости от выбранной системы.Стратегия
Поскольку они ускоряются как единое целое, мы определяем систему как профессора, тележку и оборудование. Это Система 1 на рисунке. Профессор толкает назад с силой [латекс] {F} _ {\ text {foot}} [/ latex] в 150 Н. Согласно третьему закону Ньютона, пол создает силу реакции вперед [латекс] {F} _ { \ text {floor}} [/ latex] 150 Н в Системе 1. Поскольку все движения горизонтальны, мы можем предположить, что в вертикальном направлении нет результирующей силы.Следовательно, задача одномерная по горизонтали. Как уже отмечалось, трение f препятствует движению и, таким образом, имеет направление, противоположное [латексу] {F} _ {\ text {floor}}. [/ Latex] Мы не включаем силы [латекс] {F} _ {\ text {prof}} [/ latex] или [latex] {F} _ {\ text {cart}} [/ latex], потому что это внутренние силы, и мы не включаем [латекс] {F} _ {\ text {foot}} [/ latex], потому что он действует на пол, а не на систему. Никаких других значительных сил, действующих на Систему 1. Если чистая внешняя сила может быть найдена из всей этой информации, мы можем использовать второй закон Ньютона, чтобы найти требуемое ускорение.См. Диаграмму свободного тела на рисунке.
Решение
Второй закон Ньютона дает
[латекс] a = \ frac {{F} _ {\ text {net}}} {m}. [/ Latex]
Чистая внешняя сила в Системе 1 выводится из рисунка и предыдущего обсуждения как
.[латекс] {F} _ {\ text {net}} = {F} _ {\ text {floor}} – f = 150 \, \ text {N} -24.0 \, \ text {N} = 126 \ , \ text {N} \ text {.} [/ latex]
Масса Системы 1
[латекс] m = (65,0 + 12,0 + 7,0) \, \ text {кг} = 84 \, \ text {кг} \ text {.{2}. [/ Латекс]
Значение
Ни одно из сил между компонентами Системы 1, например, между руками профессора и тележкой, не влияет на чистую внешнюю силу, потому что они являются внутренними по отношению к Системе 1. Другой способ взглянуть на это состоит в том, что силы между компонентами системы отменяются. потому что они равны по величине и противоположны по направлению. Например, сила, прилагаемая профессором к тележке, приводит к равной и противоположной силе, действующей на профессора. В этом случае обе силы действуют на одну и ту же систему и, следовательно, отменяются.Таким образом, внутренние силы (между компонентами системы) отменяются. Выбор Системы 1 имел решающее значение для решения этой проблемы.
Пример
Усилие на тележке: выбор новой системы
Рассчитайте усилие, которое профессор оказывает на тележку на рисунке, используя данные из предыдущего примера, если это необходимо.
Стратегия
Если мы определим интересующую систему как тележку плюс оборудование (Система 2 на рисунке), то чистая внешняя сила в Системе 2 – это сила, которую профессор оказывает на тележку за вычетом трения.Сила, которую она оказывает на тележку, [латекс] {F} _ {\ text {prof}} [/ latex], является внешней силой, действующей на Систему 2. [latex] {F} _ {\ text {prof}} [/ latex] был внутренним по отношению к Системе 1, но он был внешним по отношению к Системе 2 и, таким образом, входит во второй закон Ньютона для этой системы.
Решение
Второй закон Ньютона можно использовать, чтобы найти [латекс] {F} _ {\ text {prof}}. [/ Latex] Начнем с
[латекс] a = \ frac {{F} _ {\ text {net}}} {m}. [/ Latex]
Величина чистой внешней силы в Системе 2 составляет
.[латекс] {F} _ {\ text {net}} = {F} _ {\ text {prof}} – ф.[/ латекс]
Решаем за [латекс] {F} _ {\ text {prof}} [/ latex], желаемое количество:
[латекс] {F} _ {\ text {prof}} = {F} _ {\ text {net}} + f. [/ Latex]
Дано значение f , поэтому мы должны вычислить net [latex] {F} _ {\ text {net}}. [/ Latex] Это можно сделать, потому что и ускорение, и масса Системы 2 известны . Используя второй закон Ньютона, мы видим, что
[латекс] {F} _ {\ text {net}} = ma, [/ latex]
, где масса Системы 2 составляет 19,0 кг ([латекс] m = 12.{2}) = 29 \, \ text {N} \ text {.} [/ Latex]
Теперь мы можем найти желаемую силу:
[латекс] {F} _ {\ text {prof}} = {F} _ {\ text {net}} + f = 29 \, \ text {N} +24.0 \, \ text {N} = 53 \ , \ text {N} \ text {.} [/ latex]
Значение
Эта сила значительно меньше, чем сила в 150 Н, которую профессор приложил к полу назад. Не вся сила 150 Н передается на тележку; кое-что ускоряет профессора. Выбор системы – важный аналитический шаг как в решении проблем, так и в глубоком понимании физики ситуации (что не обязательно одно и то же).
Проверьте свое понимание
Два блока находятся в покое и контактируют на поверхности без трения, как показано ниже, с [latex] {m} _ {1} = 2.0 \, \ text {kg}, [/ latex] [latex] {m} _ { 2} = 6.0 \, \ text {kg}, [/ latex] и приложенная сила 24 Н. (a) Найдите ускорение системы блоков. (б) Предположим, что блоки позже разделятся. Какая сила даст второму блоку массой 6,0 кг такое же ускорение, как и система блоков?
Показать решениеa. [латекс] 3.{2} [/ латекс]; б. 18 N
Сводка
- Третий закон движения Ньютона представляет собой основную симметрию в природе, с испытываемой силой, равной по величине и противоположной по направлению действующей силе.
- Две равные и противоположные силы не отменяются, потому что они действуют на разные системы.
- Пары действие-реакция включают пловца, отталкивающего стену, вертолеты, создающие подъемную силу, выталкивая воздух вниз, и осьминога, толкающего себя вперед, выбрасывая воду из своего тела.Ракеты, самолеты и автомобили толкаются вперед за счет силы реакции тяги.
- Выбор системы – важный аналитический шаг в понимании физики проблемы и ее решении.
Концептуальные вопросы
Определите силы действия и противодействия в следующих ситуациях: (а) Земля притягивает Луну, (б) мальчик бьет футбольный мяч, (в) ракета ускоряется вверх, (г) машина ускоряется вперед, (д) высоко прыгун прыгает, и (е) из ружья выпускается пуля.
Показать решениеa. действие: Земля притягивает Луну, реакция: Луна притягивает Землю; б. действие: ступня прикладывает силу к мячу, реакция: мяч прикладывает силу к ступне; c. действие: ракета толкает газ, реакция: газ толкает ракету обратно; d. действие: автомобильные шины толкают назад по дороге, реакция: дорога толкает вперед шины; е. действие: парашютист толкает перемычку вниз, реакция: земля толкает перемычку; f. Действие: пистолет толкает пулю вперед, реакция: пуля толкает пистолет назад.
Предположим, вы держите в руке чашку кофе.Определите все силы на чашке и реакцию на каждую силу.
(a) Почему обычная винтовка дает отдачу (отдачу назад) при выстреле? (b) Ствол безоткатного ружья открыт с обоих концов. Опишите, как действует третий закон Ньютона при увольнении. (c) Можете ли вы безопасно стоять рядом с одним из них, когда из него стреляют?
Показать решениеa. Винтовка (снаряд, поддерживаемый винтовкой) прикладывает силу, чтобы выбить пулю; реакция на эту силу – это сила, которую пуля оказывает на винтовку (снаряд) в противоположном направлении.{2} [/ латекс]. (а) Какова сила трения между ногами проигравшего игрока и травой? (b) Какую силу прилагает выигравший игрок к земле, чтобы двигаться вперед, если его масса плюс снаряжение составляет 110,0 кг?
Книга по истории лежит на столе по физике, как показано ниже; также показана диаграмма свободного тела. Книги по истории и физике весят 14 Н и 18 Н соответственно. Обозначьте каждую силу, действующую на каждую книгу, с помощью двойного индекса (например, сила контакта книги истории, прижатой к книге физики, может быть описана как [латекс] {\ mathbf {\ overset {\ to} {F}}} _ { \ text {HP}} [/ latex]) и определите значение каждой из этих сил, объясняя используемый процесс.
Показать решениеПоскольку вес книги истории – это сила, прилагаемая Землей к книге истории, мы представляем ее как [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {\ text {EH} } = – 14 \ mathbf {\ hat {j}} \, \ text {N} \ text {.} [/ Latex] Помимо этого, книга истории взаимодействует только с книгой физики. Поскольку ускорение учебника истории равно нулю, чистая сила, действующая на него, равна нулю по второму закону Ньютона: [latex] {\ mathbf {\ overset {\ to} {F}}} _ {\ text {PH}} + { \ mathbf {\ overset {\ to} {F}}} _ {\ text {EH}} = \ mathbf {\ overset {\ to} {0}}, [/ latex] где [latex] {\ mathbf {\ overset {\ to} {F}}} _ {\ text {PH}} [/ latex] – сила, прилагаемая книгой по физике к книге по истории.Таким образом, [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {\ text {PH}} = \ text {-} {\ mathbf {\ overset {\ to} {F}}} _ {\ text {EH}} = \ text {-} (- 14 \ mathbf {\ hat {j}}) \, \ text {N} = 14 \ mathbf {\ hat {j}} \, \ text {N } \ text {.} [/ latex] Мы обнаруживаем, что книга по физике оказывает на книгу по истории восходящую силу величиной 14 Н. На книгу по физике действуют три силы: [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {\ text {EP}} [/ latex] из-за Земли, [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {\ text {HP}} [/ latex] из-за книги по истории и [latex] {\ mathbf {\ overset {\ to} {F}}} _ {\ text {DP}} [/ latex] из-за рабочего стола.Поскольку книга по физике весит 18 Н, [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {\ text {EP}} = – 18 \ mathbf {\ hat {j}} \, \ text {N} \ text {.} [/ Latex] Из третьего закона Ньютона [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {\ text {HP}} = \ text {-} { \ mathbf {\ overset {\ to} {F}}} _ {\ text {PH}}, [/ latex] так [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {\ text {HP}} = – 14 \ mathbf {\ hat {j}} \, \ text {N} \ text {.} [/ Latex] Второй закон Ньютона, примененный к книге по физике, дает [латекс] \ sum \ mathbf {\ overset {\ to} {F}} = \ mathbf {\ overset {\ to} {0}}, [/ latex] или [latex] {\ mathbf {\ overset {\ to} {F}}} _ {\ текст {DP}} + {\ mathbf {\ overset {\ to} {F}}} _ {\ text {EP}} + {\ mathbf {\ overset {\ to} {F}}} _ {\ text { HP}} = \ mathbf {\ overset {\ to} {0}}, [/ latex] так [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {\ text {DP}} = \ text {-} (- 18 \ mathbf {\ hat {j}}) – (- 14 \ mathbf {\ hat {j}}) = 32 \ mathbf {\ hat {j}} \, \ text {N} \текст{.{2} [/ латекс]. Найдите величину ускорения автомобиля.
Глоссарий
- Третий закон движения Ньютона
- всякий раз, когда одно тело прикладывает силу ко второму телу, первое тело испытывает силу, равную по величине и противоположную по направлению силе, которую оно прикладывает.
- тяга
- сила реакции, толкающая тело вперед в ответ на обратную силу
Практика применения третьего закона Ньютона – Видео и стенограмма урока
Примеры
Например, допустим, автомобиль весом 50 кг движется с постоянной скоростью 50 м / с.Он врезается в стену с силой в 5000 Ньютонов. В результате столкновения автомобиль полностью останавливается, но стена не движется. Какую силу стена приложила к машине?
В этой задаче объект движется, ударяется о другой объект и полностью останавливается. Мы могли бы использовать все три закона силы Ньютона, чтобы решить эту проблему для множества неизвестных переменных. Однако эта проблема требует только силы, которую стена прилагает к машине.
Мы можем использовать третий закон Ньютона, чтобы решить эту проблему.Хотя может показаться, что стена прикладывала к машине больше силы, чем машина к стене, поскольку стена не двигалась, мы знаем, что согласно Третьему закону Ньютона на каждое действие существует равная и противоположная реакция. Итак, поскольку машина доставила 5000 Ньютонов на стену, стена также доставила 5000 Ньютонов на машину.
Во втором примере задачи есть два блока. Большой блок имеет массу M1 10 кг, а меньший блок имеет массу M2 5 кг.Какова сила натяжения T1 струны, удерживающей объект массой 10 кг, и сила натяжения T2 струны, удерживающая блок 5 кг? Если не учитывать трение, каково ускорение двух блоков?
Во-первых, нам нужно определить, какой из законов силы Ньютона мы будем использовать для этой задачи. Нам говорят, что блоки ускоряются, поэтому мы сразу понимаем, что нам нужно будет использовать Второй закон Ньютона, Сила = масса * ускорение. Кроме того, с помощью Третьего закона Ньютона мы знаем, что на каждое действие существует равное и противоположное противодействие.Следовательно, сила натяжения T1 тетивы, натягивающая блок 10 кг, равна силе натяжения T2 тетивы, удерживающей блок 5 кг. Наконец, мы знаем, что каждый блок ощущает силу тяжести, направленную вниз. Эту силу тяжести можно рассчитать как:
Сила тяжести = Масса объекта * сила тяжести, в которой сила тяжести составляет 9,8 Н / кг
Это изображение дает нам лучшее представление о силах, действующих на блоки.
Подставляя известные нам переменные и используя Второй и третий законы Ньютона, мы получаем T1 = T2 = T. Осталось два уравнения.
Для массы 10 кг:
мг – T = мА
10 г – T = 10 a
и для массы 5 кг:
T – mg = ma
T – 5 g = 5 a
Поскольку у нас есть два уравнения и два неизвестных, мы можем решить для T в одном уравнении и подставить его в другое уравнение и решите для ускорения блоков.Это дает нам уравнение:
5 г – 5 a = 10 a
5 (9,8 Н / кг) = 15 a
49 = 15 a
a = 3,27 м / с2
Теперь все, что нам нужно сделать, это подставить вычисленное ускорение в одно из двух уравнений, чтобы получить силу натяжения струны. Подставив 3,27 м / с2 в первое уравнение, мы получим ответ силы натяжения струны T = 65.3 ньютона.
Краткое содержание урока
Третий закон Ньютона гласит: «На каждое действие (в природе) существует равная и противоположная реакция». Третий закон Ньютона – причина того, что птицы могут летать, а рыбы – плавать. Даже если размеры двух объектов сильно различаются, они оба оказывают одинаковое количество силы друг на друга. Используя третий закон Ньютона и другие законы силы, мы можем найти другие неизвестные силы или другие неизвестные переменные, такие как ускорение объекта.
Законы движения, столкновения и т. Д. Ньютона
Импульс – это термин, используемый в физике для описания количества движения движущегося тела, измеряемого как произведение его массы и скорости.
СВЯЗАННЫЕ: 9+ ЛУЧШИХ КАНАЛОВ YOUTUBE ДЛЯ ЛЮБИТЕЛЕЙ ФИЗИКИ
Движущиеся объекты обладают импульсом. Это тенденция объекта продолжать движение в одном и том же направлении, если на него не действует внешняя сила. Импульс – это произведение массы тела и его скорости. Поскольку он имеет как величину, так и направление, импульс является векторной величиной.
Это означает, что импульс имеет как величину, так и направление. Уравнение для Momentum приведено ниже.
В этом уравнении:
p – импульс
м – масса
v – скорость
Однако импульс зависит не только от массы и скорости объекта.Поскольку скорость – это скорость в определенном направлении, импульс объекта также зависит от направления движения. Это означает, что импульс объекта может измениться, если объект ускоряется или замедляется; или если он меняет направление.
Это означает, что мы можем думать об импульсе двумя способами, основываясь на движении объекта.
1. Линейный импульс
Линейный импульс – это импульс тела, движущегося по прямой линии. Когда мы пишем общее уравнение количества движения (см. Выше), мы используем уравнение количества движения.
2. Угловой момент
Угловой момент – это импульс тела, движущегося под углом. В этом случае масса тела такая же, но мы заменяем скорость угловой скоростью.
Это приводит к изменению уравнения. Угловой момент также создается, когда объект вращается вокруг своей оси. Например, волчок обладает угловым моментом, когда вращается вокруг собственной оси, даже если он не двигается с места.
Уравнение для углового момента выглядит следующим образом:
В этом уравнении:
L – угловой момент
м – масса
v – скорость
r – радиус
У нас уже есть обсуждали, что импульс зависит от массы и скорости.Если любое из этих двух значений равно нулю, то импульс также равен нулю.
Но есть исключение – свет. У света нет массы, но он имеет импульс. Мы не видим, как предметы падают, когда на них падает свет, потому что импульс света очень мал, но его можно измерить. Фактически, для фотонов (самых маленьких частиц света) энергия E и импульс p связаны уравнением:
Где:
E – энергия
P – импульс
c – скорость света
Импульс света настолько мал, что мы не замечаем этого в повседневной жизни.Но он достаточно большой, чтобы его можно было измерить и даже использовать. Например, устройства для лазерного охлаждения используют импульс света от a для замедления атомов в образце, тем самым охлаждая его. В оптических ловушках импульс света используется для улавливания и манипулирования небольшими объектами.
Итак, как момент инерции, сопротивление вращающегося тела угловому моменту, связан с импульсом? Это то же самое, что и импульс, или это что-то совсем другое?
Инерция – это сопротивление объекта изменению движения.Согласно первому закону Ньютона, тело будет оставаться в состоянии покоя или равномерного движения по прямой, если на него не действует внешняя сила. Инерция – это скалярная величина, что означает, что она имеет только величину, а не направление.
Момент инерции выражает способность тела сопротивляться угловому ускорению, которое представляет собой сумму произведений массы каждой частицы в теле на квадрат расстояния до оси вращения.
Импульс играет важную роль в формировании второго и третьего законов движения Ньютона.
Второй закон Ньютона гласит, что ускорение объекта, создаваемое чистой силой, прямо пропорционально величине чистой силы в том же направлении, что и результирующая сила, и обратно пропорционально массе объекта.
Другими словами, скорость изменения количества движения в объекте прямо пропорциональна приложенной силе, а изменение количества движения будет происходить в направлении приложенной силы.
Третий закон Ньютона гласит, что для силы, прикладываемой объектом A к объекту B, объект B оказывает равную по величине силу, но противоположную по направлению.Эта идея была использована Ньютоном для вывода закона сохранения количества движения. Это часто выражается так: на каждое действие есть равное и противоположное противодействие.
Закон сохранения импульса гласит, что если два объекта сталкиваются друг с другом, объединенный импульс объектов до столкновения будет равен объединенному импульсу двух объектов после столкновения.
Другими словами, импульс изолированной системы всегда остается неизменным. Суммарный импульс остается неизменным, потому что импульс, потерянный объектом A, будет получен объектом B.
Вы можете быть удивлены, когда мы скажем, что импульс, потерянный объектом A, будет получен объектом B. Мы не видим этого в реальной жизни!
Это потому, что существует два типа коллизий.
Упругое столкновение: Упругое столкновение – это тип столкновения, при котором два объекта сталкиваются и происходит передача энергии от одного объекта к другому, но без чистой потери кинетической энергии. Например, два одинаковых шара летят навстречу друг другу с одинаковой скоростью.Они сталкиваются, отскакивая друг от друга без потери скорости. Это столкновение – идеальный случай, поскольку энергия не теряется.
Совершенно упругое столкновение невозможно в повседневной жизни, так как действуют другие силы, которые вызывают потерю энергии из-за трения, тепла и т. Д. В механике есть несколько примеров столкновений, при которых потеря энергии очень мала, и могут считаться эластичными, даже если они не совсем эластичны.
Неупругое столкновение: При неупругом столкновении часть кинетической энергии изменяется на другую форму энергии, такую как тепло или звук.Вместо того, чтобы отскочить назад, объект имеет тенденцию слипаться. Импульс сохраняется при неупругих столкновениях.
Столкновения, которые мы наблюдаем в повседневной жизни, находятся между упругими и неупругими столкновениями.
Импульс – важный фактор в физике, потому что он описывает взаимосвязь между скоростью, массой и направлением.
Импульс описывает силу, необходимую для остановки объектов и удержания их в движении. Например, в нем объясняется, что вам нужно приложить больше силы, чтобы остановить объект с большим импульсом, по сравнению с объектом с меньшим импульсом.Следовательно, импульс является важным фактором, который следует учитывать при проектировании систем для остановки движущегося объекта.
На первый взгляд маленький объект может проявлять большую силу, если у него достаточно импульса. Один из лучших примеров этого явления – пуля. Импульс также можно использовать для прогнозирования конечного направления и скорости движения объектов после столкновения.
СВЯЗАННЫЕ С: 9 ОБЪЕКТОВ, ИЗОБРЕТЕННЫХ ДЛЯ ЗАЩИТЫ ФИЗИКИ
Формула и приложения – StudiousGuy
Сэр Исаак Ньютон, родился в 1643 году, всемирно известный английский физик и ученый.Его вклад был огромен в области физики. В 1687 году Ньютон опубликовал « Philosophiæ Naturalis Principia Mathematica», , в котором он предложил три закона движения. Эти три революционных физических закона закладывают фундамент «классической механики». Он представил логическое объяснение идей Галилея и Аристотеля, которые в прошлом были только теориями. Чтобы сформулировать законы движения, сэр Исаак Ньютон рассматривал массивные тела как математические точки.Эти математические точки не имели размера или вращения, что позволяло ему игнорировать дополнительные факторы, такие как трение, сопротивление воздуха и температуру, среди прочего, и принимать во внимание только массу, длину и время объекта. Однако три физических закона нельзя применить к массивным и деформируемым объектам; тем не менее, во многих таких случаях они действительно дают точные приближения.
Давайте подробно обсудим «Три закона Ньютона».
Первый закон НьютонаПервый закон движения гласит, что каждое тело продолжает находиться в состоянии покоя или равномерного движения по прямой линии, если его не вынуждает некоторая внешняя сила изменить это состояние.
- Тело, которое находится в состоянии покоя, продолжает находиться в этом состоянии. Чтобы заставить его двигаться, к нему должна быть приложена внешняя сила.
- Движущееся тело продолжает двигаться по прямой. Однако это утверждение может показаться немного противоречащим нашему повседневному опыту, когда мы видим, как мяч, катящийся по неровной поверхности, внезапно останавливается. Что происходит, так это то, что внешняя сила, действующая на катящийся шар, имеет противоположное направление, то есть трение, и, следовательно, замедляет его.
- Требуется сила, чтобы изменить исходное состояние, а также движение объекта.
Первый закон Ньютона также известен как «Закон инерции». Инерция – это врожденная способность тела, благодаря которой оно имеет тенденцию сохранять свое первоначальное состояние и противодействует любым изменениям в этом состоянии. Математически инерция тела прямо пропорциональна его массе; следовательно, более тяжелым телам требуется больше силы / усилий для изменения состояния.
Математическое представление:
Применение первого закона движения Ньютона:
- На игральную карту, накрывающую стакан, кладется монета.При резком рывке карта отлетает, и монета падает в стакан. Это происходит потому, что монета все еще находится в покое из-за инерции покоя.
- Пыль с ковра удаляют, подвешивая ковер и ударяя по нему палкой. Когда ковер бьют, он движется вперед и назад. Частицы пыли в ковре остаются в покое из-за инерции покоя и, следовательно, падают.
- Сидящие в автобусе пассажиры испытывают внезапный рывок при трогании с места.Это происходит из-за инерции покоя, которая действует на верхнюю часть тела пассажиров; заставляя их отступать, когда автобус ускоряется.
- При выстреле пули в оконном стекле делается чистая дыра; тогда как оконное стекло разбивается на мелкие кусочки при ударе камня. Камень с меньшей скоростью остается в контакте со стеклянным окном в течение более длительного периода времени; в то время как частицы оконного стекла около отверстия не могут участвовать в быстром движении пули и, следовательно, остаются нетронутыми.Поэтому на оконном стекле вырезается отверстие.
- Спортсмен обычно пробегает некоторую дистанцию перед прыжком в длину. Он делает это, чтобы преодолеть инерцию покоя и получить импульс; следовательно, имея большую скорость во время прыжка.
- При выталкивании кетчупа со дна бутылки она переворачивается вверх дном и быстро толкается. Толчок помогает кетчупу внизу достичь инерции движения. Теперь, когда напор резко прекращается, кетчуп, который все еще находится в движении, выходит из бутылки.
Второй закон движения гласит, что ускорение движущегося тела зависит от массы объекта, а также от силы, действующей на объект; F = ma, где,
F = сила,
м = масса и
a = ускорение.
- Внешние силы – это силы, которые действуют на тело и существуют вне / вне системы этого тела.
- Только внешние силы ответственны за любое изменение состояния тела.
- Приложенная сила прямо пропорциональна массе тела и ускорению.
Математическое представление:
Применение второго закона движения Ньютона:
- Для толкания автомобиля требуется гораздо большая сила по сравнению с силой, необходимой для толкания футбольного мяча.
- Один человек чрезвычайно сложно поднять ящик весом 6 фунтов, в то время как один и тот же ящик могут легко поднять несколько человек.Так как чем больше будет людей, тем больше будет сила, и, следовательно, ящик можно будет поднять с меньшими трудностями.
- Руки полевого игрока отведены назад, когда он ловит мяч для крикета, летящий с высокой скоростью. Небольшая задержка снижает импульс мяча. Второй закон гласит, что скорость изменения количества движения прямо пропорциональна силе, приложенной в этом направлении. В случае, если мяч останавливается быстро, импульс внезапно уменьшается до нуля. Поскольку скорость изменения импульса высока, игрок может травмировать руки.Когда игрок отводит руки назад, дается больше времени для изменения скорости импульса до нуля.
- Рассмотрим игру в перетягивание каната, две команды тянут канаты в противоположном направлении. Однако движение веревки будет результатом действующей на нее силы. Чистая сила, в свою очередь, определяется разницей в силе, применяемой двумя командами. Та команда, которая будет сильнее тянуть или прилагать больше усилий, победит.
Факты:
- Так как масса тела m всегда скалярна, сила и ускорение всегда положительны.
- Второй закон Ньютона также называют «действительным законом», потому что два других закона можно объяснить с помощью второго закона.
- В системе СИ единица измерения силы – Ньютон (Н). Сила 1Н объясняется как; сила 1Н, действующая на тело массой 1 кг и создающая ускорение 1 м / с 2 .
Третий закон движения гласит, что для каждого действия существует равное и противоположное противодействие.
- Сила всегда существует попарно. Единая и изолированная сила не может существовать.
- Если два объекта взаимодействуют, сила F 12 , приложенная к объекту 1 объектом 2 (называемая действием), равна по величине, но противоположна по направлению силе F 21 , приложенной к объекту 2 со стороны объект 1 (называемый реакцией).
- Хотя действие-противодействие равны и противоположны, они никогда не отменяют друг друга.
Математическое представление:
Применение третьего закона движения Ньютона:
- Это горизонтальный компонент реакции, создаваемый землей, который позволяет нам ходить, двигаться вперед и бегать.
- Газы, выбрасываемые вниз из-за сгорания топлива в ракете, вызывают восходящую реакцию, которая вызывает движение ракеты вверх.
- Действие ротационной оросительной машины основано на третьем законе движения. Вода, выходящая из форсунки, оказывает в обратном направлении равную и противоположную силу. Это заставляет разбрызгиватель вращаться в противоположном направлении, и, следовательно, вода разбрасывается во всех направлениях.
- Когда человек прыгает с лодки на берег, лодка движется назад.
- Пожарный должен крепко держать трубу, чтобы она не ускользнула назад; поскольку вода, вытекающая из трубы, толкает ее назад.
Законы движения, предложенные Ньютоном, действительны только для:
- Инерционные кадры или неускоренные кадры.
- Твердые тела без деформации.
- нерелятивистские тела; тела движутся со скоростью, меньшей скорости света.
- Тела размером больше атомного.
Законы Ньютона представлены в мультимедийном руководстве: Глава 5 Physclips. Эта страница дает более глубокую и обширную информацию. В частности, он обращается к философской основе и ограничениям законов Ньютона.Законы Ньютона записаны по-разному
Первый закон Ньютона : Каждое тело остается в своем состоянии покоя или равномерного движения по прямой линии, если только оно не вынуждено изменить это состояние под действием приложенных к нему сил.
Второй закон Ньютона : Изменение движения всегда пропорционально приложенной движущей силе; и производится в направлении правой линии, в которой действует эта сила.
Третий закон Ньютона : Каждому действию всегда противопоставляется равное и противоположное противодействие: или взаимные действия двух тел друг на друга всегда равны и направлены на противоположные части.
Первый и второй закон Ньютона вместе: F = m a , где установка F = 0 дает первый закон. Как мы уже говорили, силы приходят парами, которые в сумме равны нулю. Например, сила, которую я прикладываю к своему стулу, равна силе, которую он оказывает на меня, или сила тяготения, которую Земля оказывает на Луну, равна силе, оказываемой Луной на Землю. Или вообще для тел 1 и 2 и при любом взаимодействии между ними Третий закон Ньютона : F 1,2 = – F 2,1 , или F 1,2 + F 2,1 = 0. Можно спросить, что имеется в виду под ускорением для тела конечных размеров. В данном случае a – это ускорение его центра масс. Мы занимаемся этим в одном из модулей центра масс на Physclips. Мы также имеем дело с более общей версией законов Ньютона в модулях импульса и энергии. Применяются ли законы Ньютона? Инерционные и неинерциальные фреймы
В изображенной здесь ситуации, если пренебречь сопротивлением воздуха, оба наблюдателя согласятся, что мяч в полете не подвергается действию горизонтальных сил.На анимации слева Зои, наблюдатель на карусели, видит, как мяч ускоряется в горизонтальном направлении, что нарушает F = m a . Напротив, Джаспер, наблюдатель на земле, не видит горизонтального ускорения мяча. Он видит, что карусель и метатель мяча ускоряются за счет своего кругового движения. Итак, Джаспер считает, что законы Ньютона подчиняются (с превосходным приближением), и объясняет наблюдение Зои как результат ускорения системы отсчета Зои. Итак, каковы системы отсчета, для которых справедливы законы Ньютона? Такие кадры называются инерциальными. Кадры (например, системы Зои), в которых законы Ньютона не выполняются, называются неинерциальными системами отсчета. Есть ли способ, помимо проведения ньютоновских экспериментов, определить, инерционна ли система отсчета или нет? На самом деле есть: смотришь на далекие звезды. Но это поднимает тему относительности и работ Галилея, Ньютона, Маха и Эйнштейна. Чтобы продолжить эти идеи, перейдите по ссылке: Работают ли законы Ньютона для различных инерциальных систем отсчета?
Эта анимация также взята с нашего сайта по теории относительности, где относительное движение обсуждается более подробно. Однако вкратце приведем здесь важный результат на примере движения мяча. Предположим, поезд движется со скоростью v , измеренной человеком, покоящимся на станции.Давайте дадим этому наблюдателю показанные координаты x, y. Относительно этой системы координат (в состоянии покоя относительно станции) пусть положение шара будет r . Что касается точки покоя относительно поезда (начало координат x ‘, y’), пусть положение мяча будет r ‘. Обратите внимание, что мы используем тире для обозначения измерений относительно поезда (например, x ‘, y’, r ‘). Пусть исходная точка, зафиксированная в поезде, имеет положение p , как измерено от станции в кадре x, y. Теперь в кадре станции скорость любой точки, зафиксированной в поезде, равна v . Интегрируя по времени, его положение r дается выражением где r 0 , постоянная интегрирования, является его положением при t = 0. (Для уточнения см. вводные страницы по исчислению и векторам.) В частности, мы можем написать для зависящего от времени положения начала отсчета системы отсчета на поезде, измеренного от станции.Теперь давайте рассмотрим положение мяча r , измеренное в раме станции, и положение r ‘, измеренное в раме поезда. Производная от r по времени – это скорость в этой системе отсчета, которую мы назовем u (помня, что мы уже использовали v для скорости поезда). И производная по времени от u равна a , ускорение в этом кадре.Теперь давайте свяжем измерения r и r ‘и их производные, помня, что r ‘ измеряется относительно рамки x ‘, y’. Мы предположили, что по отношению к станции поезд не ускоряется, поэтому производная по времени v равна нулю. Это дает нам важный результат Другими словами, два наблюдателя получат одинаковое значение ускорения мяча.Итак, если станция представляет собой инерциальную раму, то a = F / м, где m – масса шара, а F – полная сила, действующая на него. Если два наблюдателя согласны в отношении сил и согласны в отношении массы, то они будут иметь одинаковые значения F и m, и мы показали, что оба имеют одинаковое значение ускорения: a = a ‘.Таким образом, система отсчета, движущаяся с постоянной скоростью относительно инерциальной системы, также является инерциальной системой . Мы сознательно не упомянули еще одно предположение, сделанное выше, и оно связано с взятием производных по времени. Мы молчаливо предположили, что часы в двух кадрах измеряют одно и то же время. Если вы не заметили этого предположения, вы попали в хорошую компанию – во времена Ньютона и Эйнштейна оно было практически незамеченным. Однако это одно из предположений, которое необходимо учитывать при изучении теории относительности.Что мы и делаем на сайте по теории относительности.
Что такоеF ?Понятие силы – полезный способ количественной оценки того, как объект механически взаимодействует с окружающей средой, и наоборот , и оно введено по этой причине.Если две большие массы находятся близко друг к другу и далеко друг от друга, мы видим, что они ускоряются по направлению друг к другу. Следовательно, мы определяем гравитационную силу и определяем ее количественно. Аналогичные наблюдения сделаны и в отношении других сил. Как мы видели выше, по определению (чистая) сила – это то, что заставляет массу ускоряться. Итак, как это определить количественно? Мы можем измерить размер и направление сил, используя F = m a . Мы также можем сравнить две силы, «уравновешивая их», установив F 1 + F 2 = 0: общая сила равна нулю, поэтому ускорение отсутствует (в инерциальной системе отсчета).Например, когда мы взвешиваем объект на весах, мы часто регулируем магнитную силу до тех пор, пока она не станет равной и противоположной весу объекта. (На практике также часто бывают рычаги.) Такие измерения очень убедительно и прагматично рассказывают нам все, что мы знаем о силах. Из наблюдений мы знаем, как объект взаимодействует с окружающей средой. Может ускоряться или нет. Иногда мы можем ощущать силы: мы можем почти напрямую ощущать силы контакта с нашими ногами или с задницей на стульях.Однако в большинстве случаев мы не ощущаем и не наблюдаем силы напрямую. Силы появляются в наших моделях, т.е. в наших объяснениях. Обычно они несколько удалены от прямого наблюдения. Поскольку силы часто немного отстранены от наблюдения, их описание с философской точки зрения можно назвать несколько произвольным. На этой картинке (со страницы фона, посвященной электричеству и магнетизму, мы объясняем наблюдение в терминах электрического взаимодействия, но само это объяснение зависит от моделей гравитации и натяжения струн. Иногда силы моделируются как действие на расстоянии, а иногда через поля (два логически почти эквивалентны). Как мы показываем в модуле об энергии, можно создавать модели, использующие распределения потенциальной энергии и, таким образом, полностью избегать использования сил. Опять же, в большинстве случаев эти разные модели логически почти эквивалентны. (В прошлом, однако, философы могли рассматривать эти картины как совершенно разные: картина ньютоновской силы выглядит как причина и следствие, а картина гамильтоновой энергии больше похожа на цель.) В очень мелком масштабе силы часто анализируются как обмен виртуальными частицами. Как правило, силы менее полезны в качестве модели в очень маленьком масштабе, отчасти потому, что положение, скорость и ускорение плохо определяются в этом масштабе. Подробнее см. Принцип неопределенности. Чторавно м?
Гравитационная масса , м г , с другой стороны, может быть определена как м г = W / г , где W – это вес объекта, а г – местное гравитационное поле. Знаменитые эксперименты Галилея, версия Дэвида Скотта, показанная ниже, а также некоторые гораздо более сложные и точные эксперименты с тех пор демонстрируют, что m g и m i пропорциональны, и поэтому могут быть установлены равными путем выбора единиц. Однако нет никаких философских причин, по которым Аристотель был неправ, а Галилей прав: как и везде в науке, только эксперимент и наблюдение говорят нам об этом. С философской точки зрения, m g и m i могли быть разными *.То, что пропорциональность не случайна, – это принцип Маха. То, что эти два понятия неотличимы – принцип эквивалентности – является отправной точкой для общей теории относительности Эйнштейна, которая является теорией гравитации Эйнштейна. * Космические зонды Pioneer 10 и 11 теперь находятся дальше от Солнца, чем Нептун. Аномалия Pioneer – это крошечная разница между кажущимся ускорением этих космических зондов на более поздних стадиях их траекторий и ускорением, рассчитанным на основе гравитационных эффектов планет, приливных эффектов, давления света на них и некоторых других небольших эффектов.Некоторые исследователи считают, что это различие связано с ошибками вычислений, другие полагают, что здесь задействованы новые физические принципы. Некоторые предполагают, что для объяснения разницы может потребоваться неньютоновская механика. Да, но что такое м на самом деле?
Многие физики подозревают, что еще не открытое поле, поле Хиггса, играет роль в определении массы некоторых фундаментальных частиц. Взаимодействие частиц с полем Хиггса в некоторых случаях может определять их массы. С полем Хиггса связана частица, бозон Хиггса, который может быть создан только с помощью энергий, которые находятся вне досягаемости ядерных экспериментов, проводимых на сегодняшний день.Большой адронный коллайдер в Европейском центре ядерных исследований (ЦЕРН) был частично построен для создания бозонов Хиггса и измерения некоторых их свойств. Мы можем узнать больше о массе, когда и если будет открыт «Хиггс». Однако даже без учета Хиггса мы можем кое-что сказать о происхождении массы. Если эта теория окажется верной, то она объяснит массу электрона, но лишь небольшую часть массы нейтрона и протона (которые в несколько тысяч раз массивнее электрона).Фактически, большая часть массы нейтронов и протонов (и, следовательно, большая часть массы обычных объектов), вероятно, связана с эффектом, который, хотя и является экзотическим, гораздо лучше изучен, чем поле Хиггса. Многие физики подозревают, что обычная масса m равна E / c 2 . Сказать, что это всего лишь перестановка знаменитого уравнения Эйнштейна E = mc 2 . Масса и энергия либо взаимопреобразуемы (через очень большой коэффициент преобразования c 2 ), либо, по мнению некоторых теоретиков, одно и то же.Квантовая хромодинамика (КХД) анализирует, как «обычные» ядерные частицы, такие как нейтроны и протоны, состоят из кварков, которые взаимодействуют через хромоэлектрическое поле, переносимое глюонами. (Здесь есть ограниченная аналогия с квантовой электродинамикой, которая анализирует, как протоны и электроны взаимодействуют через электрическое поле, переносимое фотонами.) Согласно КХД, почти вся масса нейтронов, протонов и большинства ядерных частиц обусловлена энергией различных распределений кварков и антикварков, которые из-за квантовой неопределенности никогда не могут полностью компенсировать цветовой заряд друг друга.(См. E = mc 2 , Энергия в механике Ньютона и в теории относительности и принцип неопределенности для получения дополнительной информации). Как именно это работает, неизвестно. Энергии зависят от того, как удерживаются кварки и глюоны, и сама КХД не дает масштаба для удержания – в настоящее время это вводится эмпирически. Возможно, этот масштаб также связан с взаимодействием поля Хиггса. Некоторые подозревают, что это может иметь какое-то отношение к темной материи. Это может быть решено довольно скоро.Тем не менее, весьма вероятно, что большая часть вашей массы – это фактически энергия, запасенная в нейтронах и протонах в различных конфигурациях их кварков и глюонов. Конечно, это не говорит нам, что такое энергия. В Physclips есть модуль по энергии, но там мы связываем его с силами, поэтому, хотя я думаю, что модуль действительно многое говорит об энергии, вы могли бы справедливо обвинить меня в круговой аргументации, если бы я утверждал, что это решило вопрос. Кроме того, КХД не сообщает нам массу электрона, а также не учитывает практически всю массу нейтронов и протонов.Некоторые читатели могут здесь помочь: если вы платите налоги в Европе, значит, вы помогаете финансировать Большой адронный коллайдер и, таким образом, поиск бозона Хиггса. Тем не менее, мы можем отложить физику элементарных частиц и сказать, что масса (и, по крайней мере, до некоторой степени, ее другое «я», энергия) определяется вторым законом Ньютона в одной из его форм. Следовательно, я настойчиво пытаюсь показать, что F = ma действительно может определять массу и силу, а также является проверяемым законом. И если вас это не удовлетворяет, стоит отметить, что в физике всегда будут оставаться отправные точки, точно так же, как есть постулаты или аксиомы как отправные точки в математике, так же как есть постулаты или аксиомы как отправные точки в математике. * Итак, как создать бозон Хиггса? LHC будет ускорять два пучка протонов или ядер свинца в противоположных направлениях в накопительных кольцах длиной 27 км. На скоростях около 99,99999% c они столкнутся. Большая часть их кинетической энергии будет преобразована в пары частица-античастица. Можно надеяться, что в том числе иногда и неуловимый (и массивный) Хиггс. Это большой проект. Например, LHC нужно 100 тонн жидкого гелия только для охлаждения магнитов. Что делать, если m меняется?
Что же тогда, если масса меняется? В этом случае мы используем более обобщенную версию первого и второго законов Ньютона, используя определение импульса p = m v . Затем запишем первый и второй законы Ньютона так: который, конечно, возвращается к знакомому F = m a для постоянной массы.Мы обсуждаем это в модуле по импульсу. В очень во многих случаях второй член пренебрежимо мал. Однако имейте в виду, что в некоторых случаях вам может понадобиться приведенное выше уравнение. третий закон Ньютона
Силы всегда приходят парами, и сумма пары равна нулю. Вы часто будете видеть этот закон, записанный как «На каждое действие есть равная и противоположная реакция». Проблема с этим утверждением в том, что оно приводит к некоторой путанице: «действие» и «противодействие» предполагают, что одна из сил приходит первой, а другая – позже. Однако в большинстве случаев силы полностью симметричны. Я прижимаюсь к стене, это означает, что существует электростатическое отталкивание между электронами в моей руке и электронами в стене. В моих электронах нет ничего особенного, что делает их силу действием, а силу стены – реакцией: между электронами существует полностью симметричное электрическое отталкивание. Все три закона в одном уравнении
(И, как частный случай, если никакие внешние силы не действуют на систему, то ее полный импульс сохраняется.) Этот более общий закон, насколько нам известно, полностью верен. Есть даже странный аргумент, который подсказывает, почему это должно быть правдой: см. Третий закон Ньютона и антропный принцип.Однако точно так же, как F = m , не применяется, если m не является постоянным, мы должны указать, что третий закон Ньютона не применяется, если некоторые эффекты не учитываются. Например, если мы рассматриваем магнитное взаимодействие между двумя движущимися зарядами, в общем случае силы не складываются до нуля. В таких случаях необходимо учитывать релятивистские эффекты и импульс излучения, вызванный ускоряющими зарядами. Заключение
Эти предостережения сделаны, однако, мы отмечаем, что в макроскопическом масштабе и в широком диапазоне практических энергий и сил законы Ньютона работают очень хорошо и являются основой значительной части физики и инженерии.И, если вы собираетесь работать в масштабе очень малых или очень высоких энергий, вам просто нужно будет изучить некоторую квантовую механику и некоторую теорию относительности – что тоже будет весело! В конце главы, посвященной механике, есть раздел, в котором мы приводим количественные данные о пределах ньютоновской механики. Демонстрация законов Ньютона с помощью пружины и шара для боулингаВ клипах ниже используется пружина для ускорения шара для боулинга. Ты можешь определить, прикладывает ли пружина силу, независимо от того, растянута она или нет, как на этих фотографиях.Используйте кнопку пошагового кадра на клипах. Пример: Circe и круговое движение
См. Также Законы Ньютона: дополнительная информация |
Законы Ньютона
Законы движения Ньютона – Первый законПервый закон Ньютона гласит, что если никакая чистая внешняя сила не действует на тело в состоянии покоя, это тело будет продолжать оставаться в покое. Если чистая внешняя сила не действует на тело, движущееся по прямой с постоянной скоростью, это тело будет продолжать двигаться по прямой с постоянной скоростью.
Законы движения Ньютона – второй закон
Второй закон Ньютона гласит, что когда на частицу действует сила, эта сила равна массе, умноженной на ускорение.
Где:
F – сила, действующая на частицу
м – масса частицы
a – ускорение частицы в направлении силы относительно инерциальной системы отсчета.
Мы также можем записать второй из законов Ньютона для системы частиц:
Где:
ΣF – векторная сумма внешних сил, действующих на систему частиц.Эту сумму иногда называют чистой внешней силой.
м – полная масса системы частиц
a G – это ускорение центра масс системы частиц относительно инерциальной системы отсчета. Это ускорение происходит в направлении чистой внешней силы
Обратите внимание, что нет никаких ограничений в способе соединения частиц. В результате вышеприведенное уравнение также будет справедливо для твердого тела, деформируемого тела, жидкости или газовой системы.
Для доказательства приведенного выше уравнения см. Второй закон Ньютона.
Законы движения Ньютона – третий закон
Третий закон Ньютона гласит, что для каждого действия существует равное и противоположное противодействие. Это означает, что, когда два тела находятся в контакте, реакции между этими телами равны по величине и противоположны по направлению. На рисунке ниже показан пример контакта двух тел.
Если бы мы изолировали каждое тело, реакции, действующие на них, будут равными и противоположными.На рисунке ниже показан общий пример реакций, действующих на каждое тело.
, где F 1 – результирующая вертикальная сила, F 2 – результирующая горизонтальная сила, а M – результирующий момент (крутящий момент) на контактной поверхности.
Результирующая вертикальная сила, действующая на каждое тело, представляет собой сумму всех сил, действующих в вертикальном направлении вдоль контактной поверхности.
Результирующая горизонтальная сила, действующая на каждое тело, представляет собой сумму всех сил, действующих в горизонтальном направлении вдоль контактной поверхности.
Результирующий момент (крутящий момент), действующий на каждое тело, представляет собой сумму всех крутящих моментов вдоль контактной поверхности. Крутящие моменты вызываются равными силами, действующими в противоположных направлениях. Например, на рисунке ниже показаны равные силы F c , действующие в противоположных направлениях (на каждый из корпусов) и разделенные перпендикулярным расстоянием R друг от друга.
Отсюда момент (крутящий момент) рассчитывается как:
Момент M вызывает чистое вращение тела.Он не входит в баланс сил во втором законе Ньютона ( F = ma ), поскольку силы F c взаимно компенсируются. Вместо этого он включается в баланс моментов при применении уравнений моментов (см. Динамика твердого тела).
В общем, при решении реальных физических задач каждая контактная поверхность (или точка контакта) между одним телом и другим телом может быть заменена одной равнодействующей силой F (которая может быть разделена на ее компоненты; такие как горизонтальная и вертикальный, как показано выше), и момент М .И эта сила и момент будут равны по величине и противоположны по направлению на каждом из тел.
Обратите внимание, что в некоторых случаях на контактную поверхность будет действовать только результирующая сила F или результирующий момент M . Однако может быть неочевидно, какой именно. Поэтому вместо этого нужно вычислить это (решая уравнения динамики).
Например, смазанный шаровой шарнир не может сопротивляться скручиванию, поэтому у него нет момента M .Но он будет сопротивляться толканию и вытягиванию, поэтому он будет иметь результирующую силу F , действующую на контактную поверхность (между шаром и гнездом). С другой стороны, на некоторых контактных поверхностях действует только результирующий момент M (чистое скручивание). Примером этого может служить ручка отвертки.
Основным преимуществом замены контактной поверхности (или точки контакта) с единственной равнодействующей силой F и единым равнодействующим моментом M является математическое удобство.Это позволяет решать уравнения динамики настолько просто, насколько это возможно.