Механическое движение — определение, формулы, примеры
Механическое движение
Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.
Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.
«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:
- тело отсчета
- система координат
- часы
В совокупности эти три параметра образуют систему отсчета.
В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют  Это любое движение с постоянной скоростью.
Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
- Время — в международной системе единиц СИ измеряется в секундах [с].
- Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].
Векторные величины (определяются значением и направлением)
- Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
- Путь — вектор, проведенный из начальной точки пути в конечную [м].
Чтобы сразу практиковаться, приходите в современную школу для подростков Skysmart. Ученики занимаются на интерактивной платформе по индивидуальной программе, отслеживает прогресс в личном кабинете и чувствуют себя увереннее на школьных контрольных.
Ученики занимаются на интерактивной платформе по индивидуальной программе, отслеживает прогресс в личном кабинете и чувствуют себя увереннее на школьных контрольных.
Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю. |

Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость → → → |
Средняя путевая скорость V ср.путевая = S/t V ср.путевая — средняя путевая скорость [м/с] |
В чем разница между перемещением и путем?
Перемещение — это вектор, проведенный из начальной точки в конечную, а путь — это длина траектории.
Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = S/t
Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уравнение движения
Основной задачей механики является определение положения тела в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения x(t) = x0 + vxt x(t) — искомая координата [м] |
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:
Уравнение движения при движении против оси x(t) = x0 – vxt x(t) — искомая координата [м] |
Графики
Изменение любой величины можно описать графически.
В видео ниже разбираемся, как строить графики кинематических величин и зачем они нужны.
Прямолинейное равноускоренное движение
Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».
Итак, прямолинейное движение — это движение с ускорением по прямой линии. 2, а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).
2, а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).
Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с2. В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с2.
И кому же верить?
Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 , в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8 м/с2.
Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.
Помните о том, что свободное падение — это не всегда движение по вертикали. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.
Примеров механического движения в жизни — масса.
Приходите на бесплатный вводный урок и начните заниматься физикой в удовольствие уже завтра!
Все формулы ускорения. Виды ускорения
Когда в физике изучают механическое движение, то внимание обращают на две главные величины – это скорость и ускорение. Знание их зависимости от времени позволяет определить координату тела в пространстве в любой момент. В данной статье приведем все формулы ускорения для разных его видов.
Общее понятие
Ускорение – это физическая величина. Она определяет, насколько быстро изменяется скорость. Как найти ускорение? Формула приведена ниже:
a = dv/dt
То есть величина a – это производная скорости по времени. Данное выражение позволяет рассчитать так называемое полное мгновенное ускорение, то есть характеризует величину в данный конкретный момент времени.
На практике чаще всего бывает важно знать не мгновенное, а некоторое среднее ускорение, с которым тело двигалось в течение определенного времени. Рассчитать его можно по такой формуле:
a = (v2-v1)/(t2-t1).
Здесь v2 и v1 – мгновенные скорости в моменты времени t2 и t1 соответственно.
Криволинейное движение
Ускорение определяет величину изменения скорости. У последней варьируется не один параметр. Она может меняться как по направлению, так и по величине. Если тело движется по прямой линии, то вектор скорости сохраняет свое направление. Для такого перемещения полное ускорение определяется исключительно изменением модуля скорости. Его называют касательным или тангенциальным.
Если же тело перемещается по произвольной криволинейной траектории, то вектор скорости обязательно изменяется. Этот факт приводит к появлению нормальной компоненты ускорения. Рассмотрим подробнее. Раскрывая тему всех формул ускорения, приведем выражение для вычисления нормального ускорения:
Рассмотрим подробнее. Раскрывая тему всех формул ускорения, приведем выражение для вычисления нормального ускорения:
an = v2/r
Это равенство позволяет сделать два важных вывода:
- Во-первых, нормальная компонента зависит от модуля скорости, а не от его изменения, как тангенциальная составляющая.
- Во-вторых, она обратно пропорциональна радиусу кривизны траектории r. Когда тело вращается равномерно по окружности, существует только нормальная компонента.
Чтобы определить модуль полного ускорения, следует воспользоваться такой формулой:
a = √(an2+at2)
Вектор a определяется как сумма векторов an и at, первый из них направлен перпендикулярно траектории к центру ее кривизны, а второй – по касательной к траектории в сторону изменения модуля скорости.
Свободное падение
Так называют вертикальное движение тела в гравитационном поле планеты, осуществляемое под действием силы тяжести. Как правило, соответствующее ускорение обозначают буквой g. Например, для Земли оно составляет 9,81 м/с2. Приведем все формулы для ускорения g:
Как правило, соответствующее ускорение обозначают буквой g. Например, для Земли оно составляет 9,81 м/с2. Приведем все формулы для ускорения g:
g = G*M/R2;
g = F/m;
g = 2*h/t2
Первое из приведенных выражений позволяет определить ускорение g, если известны масса планеты M и ее радиус R. G – это гравитационная постоянная. Эта формула следует из закона Всемирного тяготения Ньютона.
Второе выражение – это всем известное уравнение для силы тяжести F, которая действует на тело массой m.
Наконец, третья формула определяет ускорение через высоту падения h и время падения t тела без начальной скорости. Это выражение является одним из основных в кинематике прямолинейного движения.
Угловое ускорение
Этот вид также нельзя оставить без внимания. Приводя все формулы ускорения, стоит отметить, что угловую величину удобно использовать, когда система вращается вокруг некоторой оси. Она определяет быстроту изменения угловой скорости и выражается в радианах в квадратную секунду. Для определения этого вида ускорения применяют следующие формулы:
Для определения этого вида ускорения применяют следующие формулы:
α = dω/dt = d2θ/dt2;
α = M/I
Первое равенство показывает, что для определения углового ускорения α следует найти производную от угловой скорости ω по времени либо вторую производную по времени от угла поворота θ.
Вторая строчка – это выражение, которое следует из уравнения моментов. Здесь M – момент силы, которая раскручивает систему, I – момент инерции, который играет роль массы тела во время линейного движения.
Формулы равномерного и равноускоренного движения
Равномерное движение
Формула скорости движения при равномерном движении:
v=const
a=0
v — скорость, м/с
s — перемещение, м
t — время, с
Формула перемещения при равномерном движении:
Координата вычисляются через кинематическое уравнение равномерного прямолинейного движения по формуле:
График — Равномерного прямолинейного движения
Равноускоренное движение
Формула скорости при равноускоренном движении:
a=const
v0 — начальная скорость, м/с
a — ускорение, м/с2
Формула для нахождения перемещения при равноускоренном движении:
или
Уравнение равноускоренного движения в проекции на оси координат:
Формула для определения ускорения при равноускоренном прямолинейном движении:
v0 — начальная скорость, м/с
v — мгновенная скорость, м/с
Формула для определения средней скорости движения:
График — Равноускоренное движение при a>0
Равнозамедленное движение
Формула скорости при равнозамедленном движении:
Формула перемещения при равнозамедленном движении:
График — Равнозамедленное движение при a<0
Свободное падение
Постоянная величина скорости свободного падения тела равна g=9,8 м/с2
Формула для вычисления скорости при свободном падении тела:
Формула для вычисления перемещения при свободном падении тела:
Формула координаты при свободном падении тела:
Формула высоты с которой тело свободно падает:
Формула для определения скорости тела в конце свободного падения:
Время свободного падения тела равно:
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4. 8 / 5. Количество оценок: 6
8 / 5. Количество оценок: 6
Оценок пока нет. Поставьте оценку первым.
Расчет с постоянным ускорением – Nexus Wiki
Если у нас есть постоянное ускорение – скорость либо увеличивается, либо уменьшается с одинаковой скоростью – тогда мы можем выяснить много полезного. В этом разделе мы предположим, что движемся по линии. Мы могли бы путешествовать вперед и назад, но мы не будем рассматривать изменения угла нашего движения. Поэтому мы отбросим $ \ hat {i} $ или $ \ hat {j} $, которые выбирают, по какой линии мы движемся, и работаем только с одной координатой.Для удобства мы назовем его $ x $.
Скорость
Если ускорение постоянное, значит, скорость изменяется с постоянной скоростью. Тогда наше уравнение, определяющее ускорение, равно
.$$ a_0 = \ frac {\ Delta v} {\ Delta t} $$
или
$$ a_0 = \ frac {v_2 – v_1} {\ Delta t} $$
, где $ v_1 $ – наша скорость в начале временного интервала (начальная скорость), а $ v_2 $ – наша скорость в конце временного интервала (конечная скорость).
Если мы решим окончательную скорость, мы получим
$$ v_2 = v_1 + a_0 (t_2 – t_1) $$
Поскольку мы выбрали конкретное время, все в этом уравнении является константой. Но мы можем выбрать один или несколько из них, чтобы снова превратить их в переменную. В частности, давайте назовем $ t_2 $, «$ t $» и будем рассматривать его как независимую переменную. Затем мы можем увидеть, как выглядит скорость как функция времени. «Конечная скорость», поскольку она соответствует скорости в момент времени $ t_2 $, станет зависимой переменной $ v $.
Если вам это кажется немного странным, привыкните к этому. В физике, поскольку мы склонны описывать как общие, так и конкретные ситуации, мы часто позволяем константе «блуждать», становясь переменной. И мы часто фиксируем переменную на определенном значении, чтобы уравнение применялось к конкретной ситуации.
Это дает нам уравнение для $ v $ (которое выполняется между временем t 1 и некоторым более поздним временем t, которое не указано)
$$ v (t) = v_t + a_0 (t – t_1) $$
Если мы построим эту скорость как функцию $ t $, мы получим цифру, которая выглядит как та, что слева на рисунках ниже. Если мы хотим выяснить, какова средняя скорость в этом временном интервале, мы должны найти постоянную линию, чтобы площади под кривой истинной скорости равнялись площади под линией средней скорости (константа). Мы делаем это, настраивая линию средней скорости так, чтобы светло-розовая область (область, которая больше не включена) и светло-голубая область (теперь включена дополнительная область) были равны.
Если мы хотим выяснить, какова средняя скорость в этом временном интервале, мы должны найти постоянную линию, чтобы площади под кривой истинной скорости равнялись площади под линией средней скорости (константа). Мы делаем это, настраивая линию средней скорости так, чтобы светло-розовая область (область, которая больше не включена) и светло-голубая область (теперь включена дополнительная область) были равны.
Совершенно ясно, как если подумать о том, как изменяется скорость, так и глядя на график, что средняя скорость будет на полпути между конечными точками; то есть, если а постоянна, то
$$ \ langle v \ rangle = \ frac {v_1 + v_2} {2} $$
Поскольку мы знаем, что определение средней скорости – это «та скорость, которая, если вы постоянно будете следовать ей, будет производить такое же смещение», мы можем видеть, что если ускорение постоянное:
$$ \ Delta v = a \ Delta t $$
$$ \ Delta x = \ langle v \ rangle \ Delta t $$
$$ \ Delta v = v_2 – v_1 $$
$$ \ langle v \ rangle = \ frac {v_1 + v_2} {2} $$
Каждое из этих 4 уравнений имеет ясный и понятный концептуальный смысл и позволяет вам рассчитывать все, что вам нужно, исходя из того, что вы знаете, когда ускорение является постоянным. Иногда сложнее всего вспомнить, какое уравнение работает для $ \ Delta v $, а какое – для $ \ langle v \ rangle $. Легко сохранить ясность, если помнить о значениях «изменение» и «среднее» и думать о том, какими они были бы, если бы скорость была постоянной.
Иногда сложнее всего вспомнить, какое уравнение работает для $ \ Delta v $, а какое – для $ \ langle v \ rangle $. Легко сохранить ясность, если помнить о значениях «изменение» и «среднее» и думать о том, какими они были бы, если бы скорость была постоянной.
Тренировка: расчет с постоянным ускорением
Джо Редиш 9.10.11
Как использовать скорость, вело
Физика – это предмет, основанный на разных формулах. В основном он содержит понятия скорости, скорости, ускорения и расстояния.Все, что вы видите в своем окружении, работает по формулам физики. Скорость, скорость и ускорение – три основных понятия в физике, и каждый объект работает с этими тремя понятиями. Это основные формулы физики, которые вам следует знать для овладения предметом. Давайте подробно обсудим связь между скоростью, скоростью и ускорением.
СкоростьЗначение
Вы можете подумать, что скорость и скорость – это похожие термины, но на самом деле это не так. Скорость – это мера того, как движется вещь. Вы можете разделить скорость на быструю и медленную. Имеет числовое значение.
Скорость – это мера того, как движется вещь. Вы можете разделить скорость на быструю и медленную. Имеет числовое значение.
Формулу средней скорости мы изучаем со школьных времен.
Это скорость = расстояние / время.
Средняя скоростьСредняя скорость предмета – это расстояние, которое проходит объект, деленное на время, затраченное на прохождение этого расстояния. Это определяется величиной. Далее, средняя скорость – это изменение расстояния во времени.
Способы вычисления средней скоростиПостоянная скорость – важное понятие в этой формуле. Если объект движется с постоянной скоростью, формула для скорости будет следующей:
Скорость = общее расстояние / прошедшее время
В основном объект движется с разными скоростями на определенном расстоянии. Например, скорость автомобиля не остается постоянной на протяжении всего пути. В поездке все меняется. Есть несколько причин, по которым скорость автомобиля меняется во время поездки, например, красный свет, прерыватели скорости и другие препятствия на дороге. Эти препятствия замедляют скорость автомобиля. Тогда формула средней скорости автомобиля будет такой:
Эти препятствия замедляют скорость автомобиля. Тогда формула средней скорости автомобиля будет такой:
Средняя скорость = общее расстояние / прошедшее время
Средняя скорость измеряется в единицах расстояния, таких как мили в час, метры в секунду или футы в секунду. .
Грузовой поезд преодолевает расстояние 160 миль за 4 часа. Вычислите среднюю скорость этого поезда.
Средняя скорость = Общее расстояние / затраченное время
160/4 часа = 40 миль в час
Мальчик проехал 50 миль до дома своей тети за 2 часа.Обратный путь занял 3 часа. Рассчитайте среднюю скорость этой поездки.
Средняя скорость = Общее расстояние / прошедшее время, Скорость = расстояние / время
Скорость (миль / ч) | Время (час) | Расстояние (миль) | 50/1 = 50 | 1 | 50 |
Возврат | 50/2 = 25 |
Средняя скорость = 50 (1) + 25 (2) / 1 + 2 = 50 + 50/3
100/3 = 30. 34 миль / ч
34 миль / ч
Следующее важное понятие – скорость. Это скорость, с которой вещь или объект меняет свое положение. Его можно определить как числовым значением, так и направлением.
Формула средней скорости представляет собой пройденное расстояние, разделенное на скорость + направление движения.
Давайте посмотрим на проблемы скорости.
Человек прошел 6 км всего за 2 часа и 3 км всего за 1 час в том же направлении. Вычислите среднюю скорость человека в пути.
Средняя скорость = расстояние / время = 6 км + 3 км / 2 часа + 1 час = 9 км / 3 часа = 3 км / ч
Человек начинает идти из точки на круговом поле радиусом 1,5 км и через 2 часа вы в той же точке. Рассчитайте среднюю скорость для этого путешествия.
Средняя скорость = расстояние / время = окружность / время = 2 * 1,5 * 3,14 / 2 часа = Pi км / ч = 3,14 км / ч.
Если вы пройдете по круговой области и вернетесь к той же точке, где вы начали ходить, смещение будет нулевым. Тогда и средняя скорость будет равна нулю.
Тогда и средняя скорость будет равна нулю.
Автомобиль едет в восточном направлении на 120 метров за 6 секунд, а затем поворачивает в западном направлении на 60 метров за 2 секунды. Рассчитайте среднюю скорость.
Расстояние = 120 метров + 60 метров = 180 метров
Смещение = 120 метров – 60 метров = 60 метров, на восток
Истекшее время = 6 секунд + 2 секунды = 8 секунд
Средняя скорость = Смещение / прошедшее время = 60 метров / 8 секунд = 7,5 метров / секунду.
УскорениеТретье важное понятие в физике – это ускорение. Ускорение – это измерение изменения скорости конкретного объекта в определенное время. Время обычно составляет 1 секунду. Кроме того, скорость объекта может увеличиваться или уменьшаться в определенное время.
Формула ускоренияИзмеряется в метрах на секунду в квадрате.
Когда объект меняет скорость во времени, это называется постоянным ускорением.Когда объект меняет скорость, уменьшаясь, это называется отрицательным ускорением.
Есть 2 уравнения для ускорения. Первая формула включает силу, массу и ускорение, как показано ниже:
F = ma
Вторая формула как под:
Ускорение = изменение скорости / изменение во времени
Примеры
Рассчитайте ускорение объекта, движущегося с постоянной скоростью.
При равномерной скорости начальная и конечная скорости равны V.Формула следующая:
Среднее ускорение = изменение скорости / изменение во времени.
Итак, ускорение объекта, движущегося с постоянной скоростью, равно нулю.
Скорость автомобиля снижается с 75 км / ч до остановки за 30 секунд. Рассчитайте ускорение автомобиля в м / с2.
Начальная скорость автомобиля составляет 75 км / ч, а конечная скорость равна 0.
Среднее ускорение = 0-75 км / ч / 30 секунд =
Теперь мы должны преобразовать 75 км / ч в м / с, как показано ниже. :
75 * 1000 м / 3600 с = 20.83 м / с
Среднее ускорение = -20,83 м / с / 30 секунд = -0,69 м / с2
Автомобиль с постоянной скоростью 60 км / ч ускоряется за 36 секунд со скоростью 1,5 м / с2. Рассчитайте скорость автомобиля по истечении 36 секунд разгона.
Рассчитайте скорость автомобиля по истечении 36 секунд разгона.
Решение: Начальная скорость автомобиля 60 км / ч.
Среднее ускорение = 1,5 м / с2 = V – 60 км / ч / 36 секунд
Уравнение следующее:
V – 60 км / ч = 1,5 м / с2 * 36 секунд = 54 м / с
ср. теперь необходимо преобразовать 54 м / с в км / ч
54 м / с = 54 м * (1 км / 1000 м) / (1 с * 1 час / 3600 с)
= 54 * 3600/1000 км / ч = 194.4 км / ч
V = 194,4 км / ч + 60 км / ч = 254,4 км / ч.
Интересные факты о скорости, скорости и ускорении, которые вы можете не знать.Первым ученым, измерившим скорость, был Галилей.
Сила тяжести связана с ускорением. Падающий на землю объект имеет увеличивающееся ускорение и низкую скорость. Это из-за земного притяжения.
Скорость света самая высокая во Вселенной.
Ньютон заявил, что кинетическая энергия движущегося объекта линейна и равна квадрату скорости.Скорость предмета изменяется массой предмета.
Если вы находите физику немного сложной, вы можете попробовать эти методы, чтобы научиться эффективно.
Овладение базовыми понятиямиЧтобы стать экспертом в этом предмете, вы должны правильно запомнить все основные формулы физики. Вы должны быть мастером в знании центральных теорий физики. Эти теории упростят вам решение даже математических задач.Центральные теории также широко используются в физическом мире.
Подробнее математикаМатематика напрямую связана с физикой. Есть несколько математических задач, которые вам нужно решить, чтобы в дальнейшем лучше изучать физику. Вы должны получить опыт в уравнении скорости и других формулах. Вы можете изучать математику и физику одновременно для лучшего понимания.
Запомните основные уравнения Физика в основном описывает взаимосвязь между скоростью, скоростью, силой и ускорением.С помощью этих концепций вы можете решить любую простую или сложную проблему физики. Вы должны запомнить формулу средней скорости и формулу скорости для решения задач. Изучение основных уравнений облегчит вам изучение предмета.
Вы должны запомнить формулу средней скорости и формулу скорости для решения задач. Изучение основных уравнений облегчит вам изучение предмета.
Решая задачи физики, важно понимать, как она работает. Вы должны пройти каждый этап проблемы и понять, как она возникает. Здесь вы должны снова хорошо разбираться в основных уравнениях физики.
Знайте важные шаги в каждой проблемеФизика – это все важные шаги, которые должны выполняться при решении проблем. Если вы хотите получить хорошие результаты на экзаменах, вам следует сделать упор на важных этапах в задачах. Следует избегать шагов, которые не являются важными. На экзамене по физике вам следует подробно объяснить каждый этап проблемы.
Рисуй и разбирайся Физику можно легко изучить с помощью графиков и рисунков.Вы можете нарисовать и лучше понять концепции в деталях. На экзаменах вы можете показывать концепции с помощью рисунков. Это принесет вам хорошую оценку в статье.
Большинство студентов с первого взгляда на экзамен считают задачи по физике очень сложными. Но это не так, потому что анализ проблемы – лучший способ решить каждую проблему. Студенты должны тщательно изучить и проанализировать проблемы и найти шаги, на которые легче получить ответ.
КарточкиТак же, как дети, которые изучают алфавиты с помощью карточек, вы также можете изучать физику. Вы можете использовать карточки, чтобы запомнить основные формулы физики и другие концепции. Они также могут выучить основы физики с помощью карточек.
Интересуйтесь предметом большеВы можете найти это скучным, но физика – это предмет, в котором ваше участие имеет большое значение. Вам следует обсудить различные формулы и основные концепции физики со своими учителями и друзьями, что развеет все ваши сомнения.Обсуждение поможет вам лучше понять предмет.
Посмотрите программу курса Перед экзаменом по физике вы должны пройти полную программу предмета. Вы должны взглянуть на все главы предмета и сначала сделать важные заметки и аспекты. Это автоматически сделает вашу работу намного лучше. Затем вы можете переходить к самым сложным разделам предмета.
Вы должны взглянуть на все главы предмета и сначала сделать важные заметки и аспекты. Это автоматически сделает вашу работу намного лучше. Затем вы можете переходить к самым сложным разделам предмета.
После лекции по физике следует пройти по главам, которые изучаются в классе.Вы должны пересмотреть уроки и спросить о сомнениях у учителей или учеников. Вы также можете обсудить формулы и уроки с друзьями после школы.
Больше практикиКак мы уже говорили ранее, физика и математика взаимосвязаны. Так же, как вы каждый день решаете задачи по математике, вы также должны выполнять задачи по физике, чтобы в момент экзаменов у вас не возникало никаких сомнений.
Загрузка приложений Сегодня смартфоны выполняют больше работы, чем другие способы.Вы можете загрузить приложение физики и изучать основные формулы физики через приложения. Студентам понравится больше изучать предмет с помощью приложений. Эксперты также показывают этапы решения физических задач с помощью приложений.
YouTube сделает физику более интересным предметом для вас. Вы также можете воспользоваться онлайн-лекциями, которые читают преподаватели из разных уголков мира. Некоторые из лучших лекторов мира профессионально обучат вас концепциям, принципам и формулам.
Пройдите ускоренные курсыВы можете выбрать ускоренные курсы в любом классе или частном учебном заведении. На этих курсах вы можете углубленно изучить предмет. Они также составляют расписание и своевременно излагают программу. Они проводят тесты и экзамены, чтобы правильно знать предметы.
Кроме того, к другим способам изучения физики относятся эксперименты, подкасты и другие образовательные сайты. Они делают предмет более простым и понятным.
Это основные формулы физики и способы, с помощью которых вы можете легко изучить предмет.Вам следует сначала просмотреть и проанализировать главы, преподаваемые в классе. Затем вы можете воспользоваться всеми новейшими способами и приемами, чтобы изучить концепции, принципы и единицы.
Затем вы можете воспользоваться всеми новейшими способами и приемами, чтобы изучить концепции, принципы и единицы.
Таким образом, физика представляет собой предмет уравнений, задач и математических выражений, которыми можно пользоваться с помощью различных методов.
Формула ускорения (уравнение) в физике: как ею пользоваться
Формула ускорения – одно из основных уравнений физики, которое вы обязательно должны изучить и применить на практике.В конце концов, ускорение – один из строительных блоков физики.
«Говорят, что движение равномерно ускоряется, если, начиная с состояния покоя, оно приобретает в течение равных интервалов времени одинаковую скорость». – Галилео Галилей, Two New Sciences , 1638
Общая формула для среднего ускорения может быть выражена как:
- ускорение = ( v Final – v Initial ) / ( t Final – t Initial )
Где v обозначает скорость, а t обозначает время. В алгебраической записи формулу можно представить как:
В алгебраической записи формулу можно представить как:
Ускорение можно определить как скорость изменения скорости во времени. Ускорение – одно из самых основных понятий в современной физике, лежащее в основе практически каждой физической теории, связанной с движением объектов.
Единица измерения ускорения в системе СИ – метры в секунду в секунду (м / с 2 ). Несомненно, всем знакомо ощущение ускорения, как при нажатии на педаль газа, когда вас толкают обратно на сиденье.Фактически, почти каждый наблюдаемый эффект движения возникает из-за ускорения из-за влияния сил. Ускорение, как и скорость, является векторной величиной, что означает, что оно имеет как величину, так и направление. Строго говоря, нет такого понятия, как «замедление», есть только ускорение в обратном направлении.
Ускорение – один из важнейших параметров движения. Параметры смещения ( d ), скорости ( v ) , и ускорения ( a ) имеют тесную математическую взаимосвязь. Информация об одном из параметров может использоваться для определения неизвестной информации о других параметрах. В общем, существует 4 основных уравнения, которые связывают эти 3 параметра друг с другом и со временем:
Информация об одном из параметров может использоваться для определения неизвестной информации о других параметрах. В общем, существует 4 основных уравнения, которые связывают эти 3 параметра друг с другом и со временем:
- d = v i t + (1/2) at 2
- v f = v i + at
- v f = v i +2 ad
- d = (( v i + v f ) / 2) t
Эти 4 уравнения могут использоваться для прогнозирования неизвестной информации о движении объекта на основе известной информации о движении объекта.Итак, если кто-то знает ускорение объекта, пройденное расстояние и его начальную скорость, можно определить конечную скорость объекта. Точно так же, если кто-то знает начальную скорость, ускорение и затраченное время объекта, они могут определить, какое расстояние он преодолел. Давайте рассмотрим несколько простых примеров, чтобы проиллюстрировать использование этих формул.
Давайте рассмотрим несколько простых примеров, чтобы проиллюстрировать использование этих формул.
«Ускорение конечно, в соответствии с некоторыми законами физики». – Терри Райли
Использование формул ускорения
(1)
Допустим, вы находитесь на парусной лодке, в частности, на 16-футовом Hobie Cat.Первоначально вы путешествуете со скоростью 3 м / с. Вы ловите сильный порыв ветра и через 7 секунд летите со скоростью 10 м / с. Какое у вас было среднее ускорение?
Подставляя наши значения в нашу формулу для среднего ускорения, мы получаем a = (10−3) / 7 = 7/7 = 1 м / с 2 . Среднее ускорение лодки составляло один метр в секунду в секунду. Другой способ прочитать это значение – сказать: за каждую секунду ваша скорость увеличивается на один метр в секунду.
(2)
Самолет, взлетающий из состояния покоя, начинает ускоряться со скоростью 3 м / с 2 по взлетно-посадочной полосе и, наконец, отрывается от земли 32 секунды спустя. Как далеко самолет пролетел над землей перед взлетом?
Как далеко самолет пролетел над землей перед взлетом?
В этом вопросе нам даются три части информации: начальная скорость самолета (0 м / с), ускорение самолета (3 м / с 2 ) и продолжительность движения (32 секунды). Подставляя эти значения в первое из 4 приведенных выше уравнений:
дает нам:
- d = (0) (32) + (.5) (3) (32) 2 = 1536 метров.
То есть самолет пролетел всего 1536 метров перед взлетом.
«Сила тяжести и ускорение эквивалентны». – Альберт Эйнштейн
(3)
Перо падает на поверхность Луны с высоты 8 метров. Ускорение свободного падения на Луне составляет 1,5 м / с 2 . Сколько времени нужно, чтобы перо коснулось земли?
В этом случае нам задана начальная скорость (0 м / с), ускорение (1.5 м / с 2 ) и общее пройденное расстояние (8 м). Подставляя эти значения в первое уравнение
, получаем:
- 8 = (0) t + (0,5) (1,5) t 2
- 8 = (0,5) (1,5) t 2
- 8 = 0,75 т 2
- 10,66 = т 2
- 3,26 = т
Таким образом, на перо потребуется от до 3,26 секунды. поверхность Луны.
поверхность Луны.
(4)
В состоянии покоя ракетный корабль ускоряется со скоростью 15 м / с 2 на расстояние 650 м. Какова конечная скорость ракетного корабля?
В этом случае нам известна начальная скорость (0 м / с), пройденное расстояние (650 м) и скорость ускорения (15 м / с 2 ). Подставляя эти значения в третье уравнение:
дает нам:
- v f = 0 + 2 (15) (650)
- v f = (30) (650)
- v f = 19 500 м / с
Конечная скорость корабля-ракеты 19 500 м / с.
Мгновенное ускорение
До сих пор мы рассматривали только случаи, когда у нас либо среднее ускорение, либо ускорение равномерное. Однако наличие среднего ускорения объекта может упустить важную информацию о движении этого объекта. Наличие только среднего ускорения за определенный период не может сказать вам, изменилось ли ускорение объекта за этот промежуток времени. Может, он начал очень медленно ускоряться, потом его ускорение со временем увеличивалось.Что мы можем сделать, так это разделить эту продолжительность на более мелкие сегменты и вычислить среднее ускорение для этих сегментов, что даст нам больше информации об объекте. Скажем, у нас есть некоторое расстояние от A до E. Мы можем разделить это расстояние на 4 сегмента AB, BC, CD и DE и вычислить среднее ускорение для каждого из этих интервалов.
Может, он начал очень медленно ускоряться, потом его ускорение со временем увеличивалось.Что мы можем сделать, так это разделить эту продолжительность на более мелкие сегменты и вычислить среднее ускорение для этих сегментов, что даст нам больше информации об объекте. Скажем, у нас есть некоторое расстояние от A до E. Мы можем разделить это расстояние на 4 сегмента AB, BC, CD и DE и вычислить среднее ускорение для каждого из этих интервалов.
Теперь представьте, что мы продолжаем делить это расстояние на более мелкие интервалы и вычислять среднее ускорение за эти интервалы от до бесконечности .В конце концов, мы достигли бы точки, в которой у нас есть ускорение объекта в одной математической точке. Это также известно как его мгновенное ускорение – ускорение объекта в определенный момент времени. Мгновенное ускорение объекта можно рассматривать как среднее ускорение этого объекта за бесконечно малый промежуток времени. Концепция мгновенного ускорения, возможно, является самой важной концепцией в физике и составляет основу практически всей ньютоновской физики. Можно определить мгновенное ускорение объекта, используя инструменты вычисления, чтобы найти вторую производную функции смещения объекта или первую производную функции скорости объекта.
Можно определить мгновенное ускорение объекта, используя инструменты вычисления, чтобы найти вторую производную функции смещения объекта или первую производную функции скорости объекта.
Сводка
В сумме ускорение можно определить как скорость изменения скорости относительно времени, а формулу, выражающую среднюю скорость объекта, можно записать как:
Остальные 4 уравнения:
- d = v i t + (1/2) at 2
- v f = v i + at
- v f = v i +2 ad
- d = (( v i + v f ) / 2) t
также является важным уравнением, включающим ускорение, и может использоваться для вывода неизвестных фактов о движении объекта из известных фактов.
Была ли эта статья полезной?
😊 ☹️ Приятно слышать! Хотите больше научных тенденций? Подпишитесь на нашу рассылку новостей науки! Нам очень жаль это слышать! Мы любим отзывы 🙂 и хотим, чтобы вы внесли свой вклад в то, как сделать Science Trends еще лучше. Формула ускоренияс примерами и решенными задачами
Что такое ускорение?
Когда неподвижный автомобиль внезапно трогается с места, нас толкает назад, а при торможении нас толкает вперед, к нашему сиденью, или когда наша машина резко поворачивает направо, нас толкает влево.Мы сталкиваемся с такими ситуациями, потому что наша машина ускоряется.
Просто при изменении скорости будет ускорение. Давайте разберемся с концепцией ускорения на наглядных примерах.
Предположим, у меня есть машина, движущаяся с постоянной скоростью 90 км / ч по прямой. Я вижу вертолет, летящий примерно со скоростью 20 000 км / ч. Если бы я спросил вас, что в этих двух случаях, где вы найдете ускорение? Ваш ответ наверняка будет отрицательным, потому что оба движутся в постоянном темпе, поэтому никакого ускорения в обоих случаях.
Теперь, если я спрошу вас, что ускорение равно высокой скорости. Что вы ответите? Вы можете сказать «да», но это точно не так. Хотите знать почему? Потому что ускорение – это скорость изменения скорости. Теперь давайте разберемся, что такое формула ускорения.
Общая формула ускорения
Мы уже знаем, что скорость – это скорость с направлением; следовательно, это векторная величина. Ускорение ‘a’ задается как:
a = изменение скорости / затраченное время
Эта формула утверждает, что скорость изменения скорости является ускорением, или если скорость объекта изменяется от своего начального значения ‘u’ до конечного значения ‘v’, тогда выражение может быть просто записано как:
a = (v – u) / t
Формула ускорения в физике
В физике ускорение описывается как скорость изменения скорости объект, независимо от того, ускоряется он или замедляется.Если он ускоряется, ускорение считается положительным, а если он замедляется, ускорение – отрицательным. 2}}} \]
2}}} \]
Пример 1:
Автомобиль трогается с места и развивает скорость 54 км / ч за 3 секунды.2} \]
Тогда; скорость \ [v = \ frac {{dx}} {{dt}} = -2 + 6t \]
Ускорение: \ [a = \ frac {{dv}} {{dt}} = 6 \, \] = 6 м / с².
(Мы видим, что ускорение здесь постоянное. Следовательно, при t = 3 с его значение также равно 6 м / с².
Решенные вопросы с использованием формулы ускорения:
Вопрос 1: Каким будет ускорение автомобиля Если он замедляется с 90 км / ч до остановки за 10 секунд?
Ответ: Здесь u = 90 км / ч = 90 x 5/18 = 25 м / с, потому что первоначально он двигался со скоростью 90 км / ч, а затем достиг нуля.
Конечная скорость ‘v’ = 0 км / ч и t = 10 секунд
Теперь, применив формулу здесь:
a = (0-25) / 10 = (-) 2,5 мс²
Вопрос 2: Девушка начинает ее движение по прямой со скоростью 30 м / с, ее скорость изменяется с постоянной скоростью.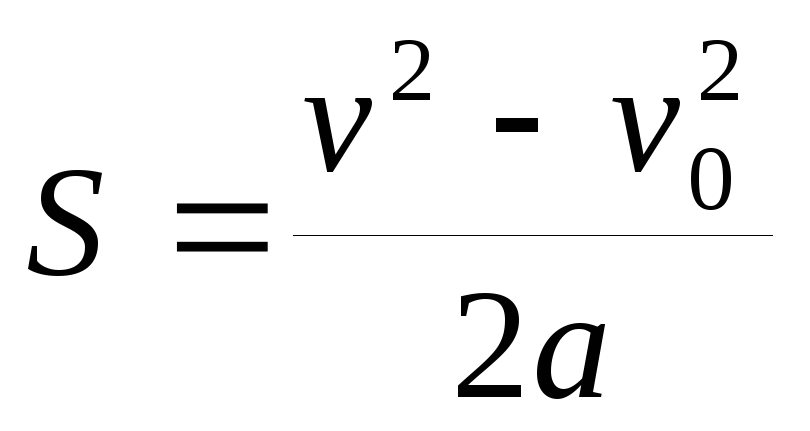 Если она останавливается через 60 с, какое у нее ускорение?
Если она останавливается через 60 с, какое у нее ускорение?
Ответ: Здесь начальная скорость девушки составляла 30 м / с и останавливается, поэтому ее конечная скорость станет 0 м / с. Теперь происходит замедление или замедление, что прямо противоположно ускорению, и его можно определить как:
a = 0 – 30) / 60 = (-) 0.5 мс²
Вопрос 3: Автомобиль движется по круговой колее с постоянной скоростью; будет ли это ускорение?
Ответ: Здесь скорость постоянна; однако направление постоянно меняется, а это значит, что меняется и скорость. В нем указано, что автомобиль будет испытывать ускорение.
Двумерные уравнения кинематики
Двумерные уравнения кинематики3.2. Уравнения кинематики в двух измерениях
|
Чтобы понять, как смещение, скорость и ускорение применяются к двумерному движению, рассмотрим космический корабль, оснащенный двумя двигателями, которые установлены перпендикулярно друг другу. Эти двигатели создают единственные силы, которые испытывает аппарат, и предполагается, что космический аппарат находится в начале координат, когда t 0 = 0 с, так что r 0 = 0 м.В более поздний момент времени t смещение КА составит Dr = r – r 0 = r. Относительно осей x и y смещение r имеет компоненты вектора x и y соответственно.
На рисунке 3.3 работает только двигатель, ориентированный вдоль направления x, и транспортное средство ускоряется в этом направлении. Предполагается, что скорость в направлении y равна нулю, и она остается нулевой, поскольку двигатель y выключен. Движение космического корабля в направлении x описывается пятью кинематическими переменными x, a x , v x , v 0x и t. Здесь символ «x» напоминает нам, что мы имеем дело с компонентами x векторов смещения, скорости и ускорения. (См. Разделы 1.7 и 1.8 для обзора компонентов вектора.) Переменные x, a x , v x и v 0x являются скалярными компонентами (или для краткости «компонентами»). Как обсуждается в разделе 1.7, эти компоненты являются положительными или отрицательными числами (с единицами измерения), в зависимости от того, указывают ли соответствующие компоненты вектора вдоль оси + x или –x. Если космический корабль имеет постоянное ускорение в направлении x, движение точно такое же, как описано в главе 2, и можно использовать уравнения кинематики.Для удобства эти уравнения записаны в левом столбце таблицы 3.1.
Здесь символ «x» напоминает нам, что мы имеем дело с компонентами x векторов смещения, скорости и ускорения. (См. Разделы 1.7 и 1.8 для обзора компонентов вектора.) Переменные x, a x , v x и v 0x являются скалярными компонентами (или для краткости «компонентами»). Как обсуждается в разделе 1.7, эти компоненты являются положительными или отрицательными числами (с единицами измерения), в зависимости от того, указывают ли соответствующие компоненты вектора вдоль оси + x или –x. Если космический корабль имеет постоянное ускорение в направлении x, движение точно такое же, как описано в главе 2, и можно использовать уравнения кинематики.Для удобства эти уравнения записаны в левом столбце таблицы 3.1.
| ||
| Таблица 3.1 Уравнения кинематики для двумерного движения с постоянным ускорением |
Рисунок 3.4 аналогичен рисунку 3.3, за исключением того, что теперь работает только двигатель y, а космический корабль ускоряется в направлении y. Такое движение можно описать с помощью кинематических переменных y, a y , v y , v 0y и t.И если ускорение в направлении y постоянно, эти переменные связаны уравнениями кинематики, как написано в правом столбце Таблицы 3. 1. Как и их аналоги в направлении x, скалярные компоненты y, a y , v y и v 0y могут быть положительными (+) или отрицательными (-) числами (с единицами измерения).
1. Как и их аналоги в направлении x, скалярные компоненты y, a y , v y и v 0y могут быть положительными (+) или отрицательными (-) числами (с единицами измерения).
|
Если оба двигателя космического корабля работают одновременно, результирующее движение происходит частично по оси x и частично по оси y, как показано на рисунке 3.5. Тяга каждого двигателя придает автомобилю соответствующую составляющую ускорения. Двигатель x ускоряет корабль в направлении x и вызывает изменение x-компоненты скорости. Точно так же y-двигатель вызывает изменение y-компоненты скорости. Важно понимать, что x-часть движения происходит точно так же, как если бы y-часть не происходила вообще. Аналогично, y-часть движения происходит точно так же, как если бы x-часть движения не существовала. Другими словами, движения по осям x и y не зависят друг от друга.
Аналогично, y-часть движения происходит точно так же, как если бы x-часть движения не существовала. Другими словами, движения по осям x и y не зависят друг от друга.
|
ОБЗОР КОНЦЕПЦИИ Независимость движений по осям x и y лежит в основе двумерной кинематики. Это позволяет нам рассматривать двумерное движение как два отдельных одномерных движения, одно для направления x, а другое – для направления y. Как показано на диаграмме «Обзор концепций» на рис. 3.6, все, что мы узнали в главе 2 о кинематике в одном измерении, теперь будет применяться отдельно к каждому из двух направлений. Поступая таким образом, мы сможем описать переменные x и y по отдельности, а затем объединить эти описания, чтобы понять двумерную картину. В примере 4 этот подход применяется к движущемуся космическому кораблю.
В примере 4 этот подход применяется к движущемуся космическому кораблю.
|
| Пример 1 Движущийся космический корабль |
| Проверьте свое понимание 2 |
| |
Следующая стратегия рассуждений дает обзор того, как уравнения кинематики применяются для описания движения в двух измерениях, например, в примере 1.
Авторские права © 2000-2003, John Wiley & Sons, Inc. или связанных компаний. Все права защищены. или связанных компаний. Все права защищены. |
Практическое применение формул силы и ускорения – урок физики [видео 2021]
Примеры задач
- Автомобиль весом 250 кг движется с постоянным ускорением 50 м / с2. Рассчитайте силу, необходимую для ускорения. Также найдите новое ускорение автомобиля, если сила, ускоряющая автомобиль, упала до 5000 Ньютонов.
В этом уравнении автомобиль с заданной массой ускоряется. Поэтому мы знаем, что для решения этой проблемы следует использовать Второй закон Ньютона.
Второй закон Ньютона в виде формулы:
F = м * a
Для первой части задачи нам нужно найти силу, которая вызвала ускорение, подставив значения:
F = м * a = 250 * 50
Это дает силу 12500 Ньютонов.Кроме того, в вопросе предлагается решить для нового ускорения автомобиля, если сила упадет до 5000 Н.
Следовательно, используя то же уравнение:
F = м * a
a = F / м
a = 5000/250
Это дает нам новое ускорение 20 м / с2.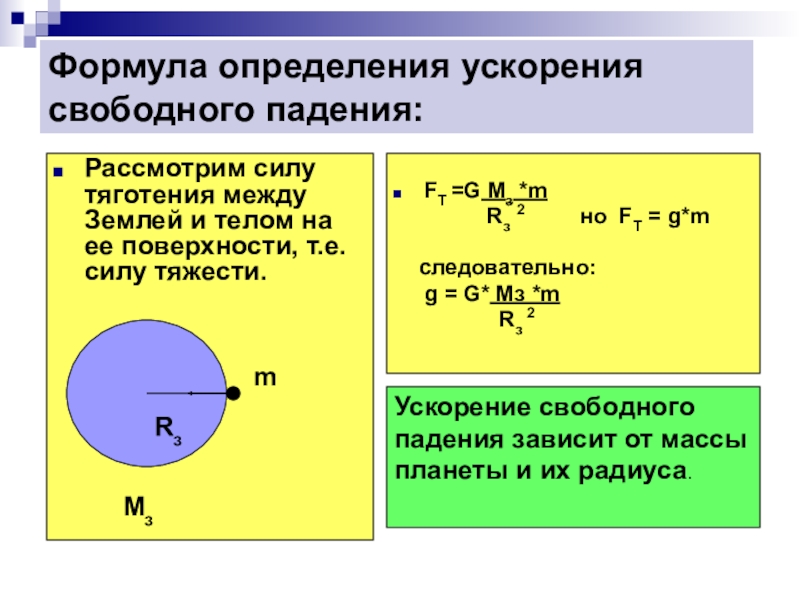
Попробуем еще.
- Мужчина тянет ящик весом 30 кг по полу с помощью веревки под углом 30 ° с приложенной силой F a = 500 Н.Сила, приложенная человеком, заставляет коробку ускоряться по ровной поверхности пола с коэффициентом кинетического трения μ = 0,5. Какое ускорение у коробки?
Чтобы решить эту проблему, нам нужно нарисовать диаграмму свободного тела и проанализировать силы в направлениях x и y . Обратите внимание, что ускорение коробки будет в направлении x ; Поскольку коробка скользит по ровной поверхности пола, мы знаем, что она не движется в направлении x , а только в направлении x .Следовательно, ускорение в направлении y равно 0, и мы знаем, что чистая сила в направлении y также должна быть равна 0.
Давайте начнем наш анализ со диаграммы свободного тела. Из диаграммы свободного тела мы можем использовать синус и косинус, чтобы найти компоненты x и y вектора приложенной силы. Вектор приложенной силы, F A , равен компоненту x , F AX плюс компоненту y , F AY , что равно величине приложенной силы, умноженной на косинус тета в направлении x плюс величина приложенной силы, умноженная на синус теты в направлении y .
Вектор приложенной силы, F A , равен компоненту x , F AX плюс компоненту y , F AY , что равно величине приложенной силы, умноженной на косинус тета в направлении x плюс величина приложенной силы, умноженная на синус теты в направлении y .
Теперь, когда мы устранили несколько неизвестных, давайте проанализируем силы в направлениях x и y , используя Второй закон Ньютона. Сначала давайте решим единственную неизвестную силу в направлении y – нормальную силу.
Чистая сила в направлении y равна нормальной силе плюс y составляющая приложенной силы F AY минус сила тяжести, F g . Скорость в направлении y равна 0; следовательно, мы знаем, что чистая сила в направлении y также равна 0.Решая для нормальной силы, получаем:
F N = F g – F AY
Подставляя неизвестные уравнения для F g и F AY и известные значения массы, силы тяжести и приложенной силы, мы находим, что нормальная сила = 44 Н в положительном направлении y .
Теперь, когда у нас есть нормальная сила, давайте воспользуемся ею, чтобы найти ускорение, проанализировав силы в направлении x .
Чистая сила в направлении x равна составляющей x приложенной силы за вычетом силы трения и равна массе коробки, умноженной на ускорение коробки. Выделяя a x , мы обнаруживаем, что ускорение равно x составляющей приложенной силы за вычетом силы трения по массе коробки. Подставляя известные уравнения для составляющей x приложенной силы и силы трения и известные значения угла theta, приложенной силы, коэффициента трения и массы, мы находим, что ускорение равно 14 м / с2 в положительное направление x .
Давай сделаем еще один.
- Футболист бросает футбольный мяч со скалы высотой 10 метров с горизонтальной скоростью 25 м / с. Как далеко улетает футбол, пока не упадет на землю?
Во-первых, нам нужно определить, какое уравнение следует использовать для решения проблемы. Принимая во внимание, что мы ищем пройденное расстояние, нам нужно использовать наше кинематическое уравнение. Мы также знаем, что это проблема движения снаряда. Используя наши знания о законах силы Ньютона, мы поняли, что, поскольку мяч находится в свободном падении, единственная сила, действующая на мяч, – это сила тяжести.Следовательно, мы знаем, что a x = 0 и a y = 9,8 м / с2.
Принимая во внимание, что мы ищем пройденное расстояние, нам нужно использовать наше кинематическое уравнение. Мы также знаем, что это проблема движения снаряда. Используя наши знания о законах силы Ньютона, мы поняли, что, поскольку мяч находится в свободном падении, единственная сила, действующая на мяч, – это сила тяжести.Следовательно, мы знаем, что a x = 0 и a y = 9,8 м / с2.
Теперь давайте поместим наше кинематическое уравнение в компоненты x и y .
Однако у нас все еще есть слишком много неизвестных, чтобы вычислить расстояние. Если мы решим для времени, представленного t , используя компонент y кинематической формулы, чтобы узнать, сколько времени потребовалось для того, чтобы мяч ударился о землю, то мы можем решить для расстояния, представленного как d .
Это дает время 1,43 секунды. Когда мы подключаем это время к нашему компоненту кинематического уравнения x , получаем:
Это говорит о том, что пройденное расстояние составляет 35,75 метра.
Краткое содержание урока
Второй закон Ньютона гласит, что результирующая сила, действующая на объект, равна массе объекта, умноженной на его ускорение.Мы можем использовать Второй закон Ньютона и кинематические уравнения , которые описывают движение объекта, для решения неизвестных сил и ускорений объектов в реальных задачах и примерах.
Формула среднего ускорения с примерами и проблемами
Это полное руководство, чтобы узнать, как найти ускорение в физике с помощью формулы ускорения.
Итак, если вы хотите извлечь пользу из этого руководства, вам будут полезны полезные советы в этом новом руководстве.
Это руководство включает:
- Определение ускорения
- Формула ускорения
- Примеры из жизни
- Типы
- Подробнее
Давайте нырнем.
Что такое ускорение?
В физике ускорение определяется как скорость изменения скорости тела во времени. Когда скорость тела изменяется, говорят, что оно ускоряется. Ускорения – это векторные величины. Метр в секунду в квадрате (м / с²) – это единица ускорения.Положительное ускорение и отрицательное ускорение – это два типа ускорения.
Что такое формула ускорения?
Ускорение можно найти по следующей формуле и из второго закона движения Ньютона.
Принимая a как ускорение, начальную скорость как Vi, конечную скорость как Vf, а t – временной интервал, единица измерения ускорения в системе СИ – метр в секунду в секунду мс -2
Ускорение относительно силы
С другой стороны, ньютоновская механика устанавливает для тела постоянной массы (m), рассматриваемого инерционным наблюдателем, соотношение пропорциональности по отношению к силе, приложенной к объекту (F), и полученному ускорению (a), что составляет:
F = m. to
to
Это соотношение действует в любой инерциальной системе отсчета и позволяет рассчитать ускорение по следующей формуле:
a = F / m
Эта формула подчиняется второму закону Ньютона.
Примеры ускорения
Некоторые примеры ускорения приведены в списке ниже:
1.- Когда вы нажимаете педаль акселератора в автомобиле, автомобиль движется все быстрее и быстрее. Это изменение скорости и есть ускорение.
2.- Если одна и та же сила используется для толкания грузовика и толкания автомобиля, автомобиль будет иметь большее ускорение, чем грузовик, потому что автомобиль имеет меньшую массу.
3.- Пустую тележку для покупок толкать легче, чем полную, потому что полная корзина для покупок имеет большую массу, чем пустая.
4.- Объект двигался на север со скоростью 10 метров в секунду. Объект ускоряется и теперь движется на север со скоростью 15 метров в секунду. Объект был ускорен.
5.- При движении скейтборда ногой происходит изменение ускорения. Давай быстрее.
Давай быстрее.
Что такое среднее ускорение в физике?
Среднее ускорение тела, указанное в приведенном выше уравнении, равно a за время t.Пусть время t разделено на множество более мелких интервалов времени. Если скорость изменения скорости в течение всех этих интервалов остается постоянной, то и ускорение также остается постоянным. Говорят, что такое тело обладает равномерным ускорением.
Формула среднего ускорения
«Тело имеет равномерное ускорение, если оно имеет равные изменения скорости в равные промежутки времени, какими бы короткими они ни были.”
Типы разгона
Есть два типа ускорения:
- Положительное ускорение
- Отрицательное ускорение
Ускорение тела положительно, если его скорость увеличивается со временем. Направление этого ускорения такое же, как и тело движется без изменения своего направления.
Примеры положительного ускорения
- Когда поезд покидает станцию, его скорость увеличивается с увеличением времени, это пример положительного ускорения.
- Когда мы заводим автомобиль, его скорость увеличивается со временем, это положительное ускорение.
Ускорение тела отрицательное, если скорость тела уменьшается. Направление отрицательного ускорения противоположно направлению, в котором движется тело. Отрицательное ускорение также называется замедлением или замедлением.
Примеры отрицательного ускорения
- Когда поезд достигает станции, его скорость со временем уменьшается, этот тип ускорения называется отрицательным ускорением.
аналогично:
Например, лифт, движущийся вверх (который мы принимаем за направление положительной скорости), может ускоряться вверх с положительным ускорением и двигаться быстрее или ускоряться вниз с отрицательным ускорением и двигаться медленнее.
Когда он движется вниз с отрицательной скоростью, он может ускоряться вниз с отрицательным ускорением и двигаться медленнее. Когда ускорение и скорость имеют положительные знаки, так что скорость (величина скорости) уменьшается, мы называем замедление.
Как рассчитать ускорение свободного падения?
«Ускорение свободно падающих тел называется ускорением свободного падения». Бросьте объект с некоторой высоты и наблюдайте за его движением. Увеличивается ли его скорость, уменьшается или остается постоянной по мере приближения к земле? Галилей был первым ученым, заметившим, что все свободно падающие объекты имеют одинаковое ускорение независимо от их масс.
Примеры расчета ускорения
- Гоночный автомобиль увеличивает скорость с постоянной скоростью 18.5 м / с со скоростью 46,1 м / с за 2,47 секунды. Каким будет его среднее ускорение?
a = dv / dt = (v f – v i ) / (t f – t i ), где v f = 46,1 м / с, v i = 18,5 м / s, t f = 2,47 с, t i = 0 с.
Итак: a = (46,1 – 18,5) / 2,47 = 11,17 м / с 2
- Мотоциклист едет со скоростью 22,4 м / с и понимает, что ошибся маршрутом.Затяните тормоз, и мотоцикл остановится через 2,55 с. Каким будет его замедление?
a = dv / dt = (v f – v i ) / (t f – t i ), где v f = 0 м / с, v i = 22,4 м / с, t f = 2,55 с, t i = 0 с.
Итак: a = (0 – 22,4) / 2,55 = -8,78 м / с 2
- Сила величиной 10 ньютонов равномерно действует на массу 2 кг.Каким будет ускорение толкаемого объекта?
a = F / m, где F = 10 Н, m = 2 кг.
Таким образом:
a = 10/2 = 5 м / с 2
- Кто-то тянет в сторону предмет мебели весом 400 кг с чистой силой 150 ньютонов. Другой человек толкает его в том же направлении с силой 200 ньютонов, но есть ветер, дующий в противоположном направлении с силой 10 ньютонов.
 Какое будет ускорение мебели?
Какое будет ускорение мебели?
Мы знаем, что a = F / m, где результирующая сила будет суммой сил в том же смысле минус сила, которая им противостоит: F = 150 Н (человек 1) + 200 Н (человек 2) – 10 Н ( ветер), что дает 340 Н.Мы также знаем, что m = 400 кг.
Тогда: a = 340 Н / 400 кг = 0,85 м / с 2
- Самолет с дистанционным управлением массой 10 кг летит с ускорением 2 м / с 2 в северном направлении. В этот момент дует восточный ветер силой в 100 Н. Какое будет новое ускорение самолета, сохраняющего свой курс?
Поскольку сила ветра перпендикулярна направлению движения самолета, он не оказывает никакого влияния на его движение.Он продолжит ускоряться на север со скоростью 2 м / с 2 .
- Два мальчика, один слабый и один сильный, играют в перетягивание каната, каждый на одном конце веревки. Первая тяга влево делает это с силой 5 Н, а вторая тянет в противоположном направлении с силой 7 Н.
 Принимая во внимание, что 1 ньютон (Н) равен 1 килограмм-метру / секунда в квадрате. (кг-м / с2), какое ускорение достигнет тело самого слабого ребенка, когда другой тащит его в противоположном направлении?
Принимая во внимание, что 1 ньютон (Н) равен 1 килограмм-метру / секунда в квадрате. (кг-м / с2), какое ускорение достигнет тело самого слабого ребенка, когда другой тащит его в противоположном направлении?
Из F = ma мы знаем, что a = F / m, но мы должны найти чистую силу, которая будет равна 2 Н (7 Н для сильного ребенка и 5 Н для слабого ребенка).
Затем мы должны найти массу, которая для целей расчета должна быть получена из силы, которой противодействует слабый ребенок, а именно: 1 Н = 1 кг · м / с 2 , то есть это количество силы мобилизовать килограмм массы со скоростью один метр в секунду в квадрате.
Следовательно, 5N = 5кг.м / с 2 . Следовательно, m = 5 кг.
И, наконец, мы знаем, что a = 2N (F) / 5 кг (м) = 0,4 м / с 2
- Пожарная машина увеличивает скорость с 0 до 21 м / с на восток, в 3 раза.5 секунд. Какое у него ускорение?
Мы знаем, что: V i = 0 м / с, V f = 21 м / с, t = 3,5 секунды.

 Нет движения в направлении y, и двигатель y выключен.
Нет движения в направлении y, и двигатель y выключен. Затем он снова взлетает и пробегает 62 м на восток за 21 секунду. Во время этого второго пробега его ускорение постоянное. Для всего 39-секундного интервала найдите величину и направление средней скорости лисы (а) и (б) среднего ускорения.Укажите направления относительно юга.
Затем он снова взлетает и пробегает 62 м на восток за 21 секунду. Во время этого второго пробега его ускорение постоянное. Для всего 39-секундного интервала найдите величину и направление средней скорости лисы (а) и (б) среднего ускорения.Укажите направления относительно юга. По прошествии определенного времени t его смещение и скорость равны r и v. Каковы были бы его смещение и скорость в момент времени 2, если предположить, что ускорение останется прежним?
По прошествии определенного времени t его смещение и скорость равны r и v. Каковы были бы его смещение и скорость в момент времени 2, если предположить, что ускорение останется прежним?