Формулы в физике электричество: Ошибка: 404 Категория не найдена - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Все формулы связанные с электрическим током. Основные формулы по физике

В проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда. Такое движение называется электрическим током . За направление электрического тока принято направление движения положительных свободных зарядов, хотя в большинстве случае движутся электроны – отрицательно заряженные частицы.

Количественной мерой электрического тока служит сила тока I – скалярная физическая величина, равная отношению заряда q , переносимого через поперечное сечение проводника за интервал времени t , к этому интервалу времени:

Если ток не постоянный, то для нахождения количества прошедшего через проводник заряда рассчитывают площадь фигуры под графиком зависимости силы тока от времени.

Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным . Сила тока измеряется амперметром, который включается в цепь последовательно.

В Международной системе единиц СИ сила тока измеряется в амперах [А]. 1 А = 1 Кл/с.

Находится как отношение всего заряда ко всему времени (т.е. по тому же принципу, что и средняя скорость или любая другая средняя величина в физике):

Если же ток равномерно меняется с течением времени от значения I 1 до значения I 2 , то можно значение среднего тока можно найти как среднеарифметическое крайних значений:

Плотность тока – сила тока, приходящаяся на единицу поперечного сечения проводника, рассчитывается по формуле:

При прохождении тока по проводнику ток испытывает сопротивление со стороны проводника. Причина сопротивления – взаимодействие зарядов с атомами вещества проводника и между собой. Единица измерения сопротивления 1 Ом.

Сопротивление проводника R определяется по формуле:

где: l – длина проводника, S – площадь его поперечного сечения, ρ – удельное сопротивление материала проводника (будьте внимательны и не перепутайте последнюю величину с плотностью вещества), которое характеризует способность материала проводника противодействовать прохождению тока. То есть это такая же характеристика вещества, как и многие другие: удельная теплоемкость, плотность, температура плавления и т.д. Единица измерения удельного сопротивления 1 Ом·м. Удельное сопротивление вещества – табличная величина.

Сопротивление проводника зависит и от его температуры:

где: R 0 – сопротивление проводника при 0°С, t – температура, выраженная в градусах Цельсия, α – температурный коэффициент сопротивления. Он равен относительному изменению сопротивления, при увеличении температуры на 1°С. Для металлов он всегда больше нуля, для электролитов наоборот, всегда меньше нуля.

Диод в цепи постоянного тока

Диод – это нелинейный элемент цепи, сопротивление которого зависит от направления протекания тока. Обозначается диод следующим образом:

Стрелка в схематическом обозначении диода показывает, в каком направлении он пропускает ток. В этом случае его сопротивление равно нулю, и диод можно заменить просто на проводник с нулевым сопротивлением. Если ток течет через диод в противоположном направлении, то диод обладает бесконечно большим сопротивлением, то есть не пропускает ток совсем, и является разрывом в цепи. Тогда участок цепи с диодом можно просто вычеркнуть, так как ток по нему не идет.

Закон Ома. Последовательное и параллельное соединение проводников

Немецкий физик Г.Ом в 1826 году экспериментально установил, что сила тока I , текущего по однородному металлическому проводнику (то есть проводнику, в котором не действуют сторонние силы) сопротивлением

R , пропорциональна напряжению U на концах проводника:

Величину R принято называть электрическим сопротивлением . Проводник, обладающий электрическим сопротивлением, называется резистором . Это соотношение выражает закон Ома для однородного участка цепи : сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.

Проводники, подчиняющиеся закону Ома, называются линейными .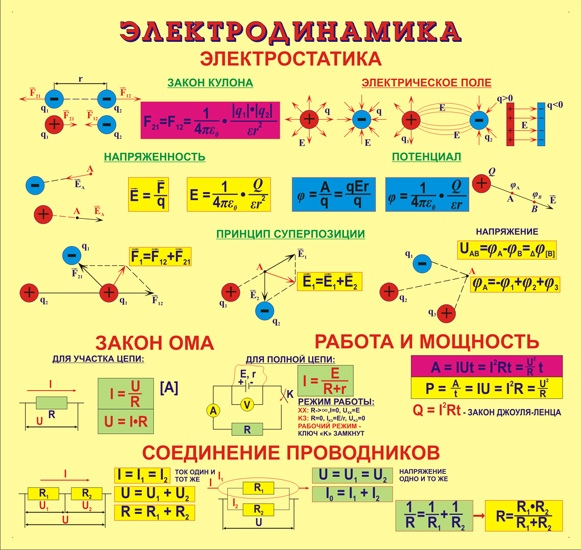 Графическая зависимость силы тока I от напряжения U (такие графики называются вольт-амперными характеристиками, сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при достаточно больших токах наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.

Проводники в электрических цепях можно соединять двумя способами: последовательно и параллельно . У каждого способа есть свои закономерности.

1. Закономерности последовательного соединения:

Формула для общего сопротивления последовательно соединенных резисторов справедлива для любого числа проводников. Если же в цепь последовательно включено

n одинаковых сопротивлений R , то общее сопротивление R 0 находится по формуле:

2. Закономерности параллельного соединения:

Формула для общего сопротивления параллельно соединенных резисторов справедлива для любого числа проводников. Если же в цепь параллельно включено n одинаковых сопротивлений R , то общее сопротивление R 0 находится по формуле:

Электроизмерительные приборы

Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы –

вольтметры и амперметры .

Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением R B . Для того чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен.

Амперметр предназначен для измерения силы тока в цепи.

Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением R A . В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи.

ЭДС. Закон Ома для полной цепи

Для существования постоянного тока необходимо наличие в электрической замкнутой цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками постоянного тока . Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются

сторонними силами .

Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.

При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу. Физическая величина, равная отношению работы

A ст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС) :

Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).

Закон Ома для полной (замкнутой) цепи: сила тока в замкнутой цепи равна электродвижущей силе источника, деленной на общее (внутреннее + внешнее) сопротивление цепи:

Сопротивление r – внутреннее (собственное) сопротивление источника тока (зависит от внутреннего строения источника).

Сопротивление R – сопротивление нагрузки (внешнее сопротивление цепи).

Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника ):

Важно понять и запомнить: ЭДС и внутреннее сопротивление источника тока не меняются, при подключении разных нагрузок.

Если сопротивление нагрузки равно нулю (источник замыкается сам на себя) или много меньше сопротивления источника, то тогда в цепи потечет ток короткого замыкания :

Сила тока короткого замыкания – максимальная сила тока, которую можно получить от данного источника с электродвижущей силой

ε и внутренним сопротивлением r . У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик, и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер).

Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.

Несколько источников ЭДС в цепи

Если в цепи присутствует несколько ЭДС подключенных последовательно , то:

1. При правильном (положительный полюс одного источника присоединяется к отрицательному другого) подключении источников общее ЭДС всех источников и их внутреннее сопротивление может быть найдено по формулам:

Например, такое подключение источников осуществляется в пультах дистанционного управления, фотоаппаратах и других бытовых приборах, работающих от нескольких батареек.

2. При неправильном (источники соединяются одинаковыми полюсами) подключении источников их общее ЭДС и сопротивление рассчитывается по формулам:

В обоих случаях общее сопротивление источников увеличивается.

При параллельном подключении имеет смысл соединять источники только c одинаковой ЭДС, иначе источники будут разряжаться друг на друга. Таким образом суммарное ЭДС будет таким же, как и ЭДС каждого источника, то есть при параллельном соединении мы не получим батарею с большим ЭДС. При этом уменьшается внутреннее сопротивление батареи источников, что позволяет получать большую силу тока и мощность в цепи:

В этом и состоит смысл параллельного соединения источников. В любом случае при решении задач сначала надо найти суммарную ЭДС и полное внутреннее сопротивление получившегося источника, а затем записать закон Ома для полной цепи.

Работа и мощность тока. Закон Джоуля-Ленца

Работа A электрического тока I , протекающего по неподвижному проводнику с сопротивлением R , преобразуется в теплоту Q , выделяющееся на проводнике. Эту работу можно рассчитать по одной из формул (с учетом закона Ома все они следуют друг из друга):

Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж.Джоулем и Э.Ленцем и носит название закона Джоуля–Ленца . Мощность электрического тока равна отношению работы тока A к интервалу времени Δt , за которое эта работа была совершена, поэтому она может быть рассчитана по следующим формулам:

Работа электрического тока в СИ, как обычно, выражается в джоулях (Дж), мощность – в ваттах (Вт).

Энергобаланс замкнутой цепи

Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой ε и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R . В этом случае полезная мощность или мощность, выделяемая во внешней цепи:

Максимально возможная полезная мощность источника достигается, если R = r и равна:

Если при подключении к одному и тому же источнику тока разных сопротивлений R 1 и R 2 на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле:

Мощность потерь или мощность внутри источника тока:

Полная мощность, развиваемая источником тока:

КПД источника тока:

Электролиз

Электролитами принято называть проводящие среды, в которых протекание электрического тока сопровождается переносом вещества. Носителями свободных зарядов в электролитах являются положительно и отрицательно заряженные ионы. К электролитам относятся многие соединения металлов с металлоидами в расплавленном состоянии, а также некоторые твердые вещества. Однако основными представителями электролитов, широко используемыми в технике, являются водные растворы неорганических кислот, солей и оснований.

Прохождение электрического тока через электролит сопровождается выделением вещества на электродах. Это явление получило название электролиза .

Электрический ток в электролитах представляет собой перемещение ионов обоих знаков в противоположных направлениях. Положительные ионы движутся к отрицательному электроду (катоду ), отрицательные ионы – к положительному электроду (аноду ). Ионы обоих знаков появляются в водных растворах солей, кислот и щелочей в результате расщепления части нейтральных молекул. Это явление называется электролитической диссоциацией .

Закон электролиза был экспериментально установлен английским физиком М. Фарадеем в 1833 году. Закон Фарадея определяет количества первичных продуктов, выделяющихся на электродах при электролизе. Итак, масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q , прошедшему через электролит:

Величину k называют электрохимическим эквивалентом . Он может быть рассчитан по формуле:

где: n – валентность вещества, N A – постоянная Авогадро, M – молярная масса вещества, е – элементарный заряд. Иногда также вводят следующее обозначение для постоянной Фарадея:

Электрический ток в газах и в вакууме

Электрический ток в газах

В обычных условиях газы не проводят электрический ток. Это объясняется электрической нейтральностью молекул газов и, следовательно, отсутствием носителей электрических зарядов. Для того чтобы газ стал проводником, от молекул необходимо оторвать один или несколько электронов. Тогда появятся свободные носителя зарядов – электроны и положительные ионы. Этот процесс называется ионизацией газов .

Ионизировать молекулы газа можно внешним воздействием – ионизатором . Ионизаторами может быть: поток света, рентгеновские лучи, поток электронов или α -частиц. Молекулы газа также ионизируются при высокой температуре. Ионизация приводит к возникновению в газах свободных носителей зарядов – электронов, положительных ионов, отрицательных ионов (электрон, объединившийся с нейтральной молекулой).

Если создать в пространстве, занятом ионизированным газом, электрическое поле, то носители электрических зарядов придут в упорядоченное движение – так возникает электрический ток в газах. Если ионизатор перестает действовать, то газ снова становится нейтральным, так как в нем происходит рекомбинация – образование нейтральных атомов ионами и электронами.

Электрический ток в вакууме

Вакуумом называется такая степень разрежения газа, при котором можно пренебречь соударением между его молекулами и считать, что средняя длина свободного пробега превышает линейные размеры сосуда, в котором газ находится.

Электрическим током в вакууме называют проводимость межэлектродного промежутка в состоянии вакуума. Молекул газа при этом столь мало, что процессы их ионизации не могут обеспечить такого числа электронов и ионов, которые необходимы для ионизации. Проводимость межэлектродного промежутка в вакууме может быть обеспечена лишь с помощью заряженных частиц, возникших за счет эмиссионных явлений на электродах.

Как успешно подготовиться к ЦТ по физике и математике?

Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:

Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
Выучить все формулы и законы в физике, и формулы и методы в математике . На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.

Успешное, старательное и ответственное выполнение этих трех пунктов позволит Вам показать на ЦТ отличный результат, максимальный из того на что Вы способны.

Нашли ошибку?

Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно также в социальной сети (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.

Электричество и магнетизм формулы.

Закон Кулона

1. закон Кулона

2 . напряженность электрического поля

3. модуль напряженности поля точечного заряда

4 . принцип суперпозиции

5. -вектор электрического момента диполя – дипольный момент

2. Теорема Гаусса

9. теорема Гаусса

10. теорема Гаусса

11.

12. – дивергенция поля

Потенциал электростатического поля

14. -работа сил электростатического поля по перемещению пробного заряда q в электрическом поле точечного заряда Q

15. – интегральный признак потенциальности электростатического поля

16. – приращение потенциала электростатического поля

17 . – убыль потенциала электростатического поля

18 . – нормировка потенциала (выбор начала отсчета)

19 . – принцип суперпозиции для

20. – квазистатическая работа сил поля при перемещении

по произвольному пути из т. 1 в т.2

21. – локальное соотношение между и

22. – потенциал точечного заряда

23. – потенциал диполя

24. – дифференциальный оператор Гамильтона («набла») в полярной системе координат

25 . – оператор Лапласа или лапласиан

26. – уравнение Лапласа

27. – уравнение Пуассона

4. Энергия в электростатике.

28. – энергия электростатического взаимодействия зарядов друг с другом

29 . – полная электростатическая энергия заряженного тела

30. – объемная плотность энергии (энергия, локализованная в единичном объеме)

31. – энергия взаимодействия точечного диполя с внешним полем

5. Проводники электростатике

32. – поле вблизи поверхности проводника

33. – электроемкость уединенного проводника

34. – емкость плоского конденсатора

35 . – емкость сферического конденсатора, образованного сферическими проводящими поверхностями радиусов а и b

36 . – энергия конденсатора

6. Электростатическое поле в диэлектриках

37. , – диэлектрическая восприимчивость вещества

38. – поляризованность (электрический дипольный момент единицы объема вещества)

39. – связь между напряженностью и поляризованностью

40 . теорема Гаусса для вектора в интегральной форме

41. – теорема Гаусса для вектора в дифференциальной форме

42. – граничные условия для вектора

43. – теорема Гаусса для вектора в диэлектриках

44 . – электрическое смещение

45. – интегральная и локальная теорема Гаусса для вектора

46. – граничные условия для вектора , где – поверхностная плотность сторонних зарядов

47. – связь и для изотропных сред

Постоянный ток

48. – сила тока

49 . – заряд, проходящий через сечение проводника

50. – уравнение непрерывности (закон сохранения заряда)

51. – уравнение непрерывности в дифференциальной форме

52 . – разность потенциалов для проводника, в котором не действуют сторонние силы, отождествляется с падением напряжения

53. – закон Ома

54. – закон Джоуля -Ленца

55. – сопротивление провода из однородного материала одинаковой толщины

56. – закон Ома в дифференциальной форме

57 . – величина, обратная удельному сопротивлению называется удельной электрической проводимостью

58 . – закон Джоуля –Ленца в дифференциальной форме

59. -интегральная форма закона Ома с учетом поля сторонних сил для участка цепи, содержащего ЭДС.

60 . – первый закон Кирхгофа. Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю.

61. -второй закон Кирхгофа. Сумма напряжений вдоль любого замкнутого контура цепи равна алгебраической сумме ЭДС, действующих в этом контуре.

62 . – удельная тепловая мощность тока в неоднородной проводящей среде

Закон Био-Савара

63 . – сила Лоренца

64 . – если в некоторой системе отсчета электромагнитное поле является электрическим

(т.е. ), то в другой системе отсчета , движущейся относительно К со скоростью , компоненты электромагнитного поля отличны от нуля и связаны соотношением 64

65 . – если в некоторой системе отсчета электрически заряженное тело имеет скорость , то электрическая и магнитная компоненты электромагнитного поля, создаваемого его зарядом, связаны в этой системе отсчета соотношением

66 . – если в некоторой системе отсчета электромагнитное поле является магнитным (), то в любой другой системе отсчета, движущейся со скоростью относительно первой, компоненты и электромагнитного поля отличны от нуля и связаны соотношением

67. – индукция магнитного поля движущегося заряда

68 . – магнитная постоянная

2. Теорема Гаусса

7 . – поток поля через произвольную поверхность

8. – принцип аддитивности потоков

9. теорема Гаусса

10. теорема Гаусса

11. – дифференциальный оператор Гамильтона («набла»)в декартовой системе координат

12. – дивергенция поля

13 . локальная (дифференциальная) теорема Гаусса

Формулы электричества и магнетизма. Изучение основ электродинамики традиционно начинается с электрического поля в вакууме. Для вычисления силы взаимодействия между двумя точными зарядами и вычисления напряженности электрического поля, созданного точечным зарядом, нужно уметь применять закон Кулона. Для вычисления напряженностей полей, созданных протяженными зарядами (заряженной нитью, плоскостью и т.д.), применяется теорема Гаусса. Для системы электрических зарядов необходимо применять принцип

При изучении темы “Постоянный ток” необходимо рассмотреть во всех формах законы Ома и Джоуля-Ленца При изучении “Магнетизма” необходимо иметь в виду, что магнитное поле порождается движущимися зарядами и действует на движущиеся заряды. Здесь следует обратить внимание на закон Био-Савара-Лапласа. Особое внимание следует обратить на силу Лоренца и рассмотреть движение заряженной частицы в магнитном поле.

Электрические и магнитные явления связаны особой формой существования материи – электромагнитным полем. Основой теории электромагнитного поля является теория Максвелла.

Таблица основных формул электричества и магнетизма

Физические законы, формулы, переменные

Формулы электричество и магнетизм

Закон Кулона:
где q 1 и q 2 – величины точечных зарядов, ԑ 1 – электрическая постоянная;
ε – диэлектрическая проницаемость изотропной среды (для вакуума ε = 1),
r – расстояние между зарядами.

Напряженность электрического поля:

где Ḟ – сила, действующая на заряд q 0 , находящийся в данной точке поля.

Напряженность поля на расстоянии r от источника поля:

1) точечного заряда

2) бесконечно длинной заряженной нити с линейной плотностью заряда τ:

3) равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда σ:

4) между двумя разноименно заряженными плоскостями

Потенциал электрического поля:

где W – потенциальная энергия заряда q 0 .

Потенциал поля точечного заряда на расстоянии r от заряда:

По принципу суперпозиции полей, напряженность:

Потенциал:

где Ē i и ϕ i – напряженность и потенциал в данной точке поля, создаваемый i-м зарядом.

Работа сил электрического поля по перемещению заряда q из точки с потенциалом ϕ 1 в точку с потенциалом ϕ 2 :

Связь между напряженностью и потенциалом

1) для неоднородного поля:

2) для однородного поля:

Электроемкость уединенного проводника:

Электроемкость конденсатора:

Электроемкость плоского конденсатора:

где S – площадь пластины (одной) конденсатора,

d – расстояние между пластинами.

Энергия заряженного конденсатора:

Сила тока:

Плотность тока:

где S – площадь поперечного сечения проводника.

Сопротивление проводника:

l – длина проводника;

S – площадь поперечного сечения.

Закон Ома

1) для однородного участка цепи:

2) в дифференциальной форме:

3) для участка цепи, содержащего ЭДС:

Где ε – ЭДС источника тока,

R и r – внешнее и внутреннее сопротивления цепи;

4) для замкнутой цепи:

Закон Джоуля-Ленца

1) для однородного участка цепи постоянного тока:
где Q – количество тепла, выделяющееся в проводнике с током,
t – время прохождения тока;

2) для участка цепи с изменяющимся со временем током:

Мощность тока:

Связь магнитной индукции и напряженности магнитного поля:

где B – вектор магнитной индукции,
μ √ магнитная проницаемость изотропной среды, (для вакуума μ = 1),
µ 0 – магнитная постоянная ,
H – напряженность магнитного поля.

Магнитная индукция (индукция магнитного поля):
1) в центре кругового тока
где R – радиус кругового тока,

2) поля бесконечно длинного прямого тока
где r – кратчайшее расстояние до оси проводника;

3) поля, созданного отрезком проводника с током
где ɑ 1 и ɑ 2 – углы между отрезком проводника и линией, соединяющей концы отрезка и точкой поля;
4) поля бесконечно длинного соленоида
где n – число витков на единицу длины соленоида.

Часто бывает, что задачу не удается решить из-за того, что под рукой нет нужной формулы. Выводить формулу с самого начала – дело не самое быстрое, а у нас на счету каждая минута.

Ниже мы собрали вместе основные формулы по теме «Электричество и Магнетизм». Теперь, решая задачи, вы сможете пользоваться этим материалом как справочником, чтобы не терять время на поиски нужной информации.

Магнетизм: определение

Магнетизм – это взаимодействие движущихся электрических зарядов, происходящее посредством магнитного поля.

Поле – особая форма материи. В рамках стандартной модели существует электрическое, магнитное, электромагнитные поля, поле ядерных сил, гравитационное поле и поле Хиггса. Возможно, есть и другие гипотетические поля, о которых мы пока что можем только догадываться или не догадываться вовсе. Сегодня нас интересует магнитное поле.

Магнитная индукция

Так же, как заряженные тела создают вокруг себя электрическое поле, движущиеся заряженные тела порождают магнитное поле. Магнитное поле не только создается движущимися зарядами (электрическим током), но еще и действует на них. По сути магнитное поле можно обнаружить только по действию на движущиеся заряды. А действует оно на них с силой, называемой силой Ампера, о которой речь пойдет позже.

Прежде чем мы начнем приводить конкретные формулы, нужно рассказать про магнитную индукцию.

Магнитная индукция – это силовая векторная характеристика магнитного поля.

Она обозначается буквой B и измеряется в Тесла (Тл ) . По аналогии с напряженностью для электрического поля Е магнитная индукция показывает, с какой силой магнитное поле действует на заряд.

Кстати, вы найдете много интересных фактов на эту тему в нашей статье про .

Как определять направление вектора магнитной индукции? Здесь нас интересует практическая сторона вопроса. Самый частый случай в задачах – это магнитное поле, создаваемое проводником с током, который может быть либо прямым, либо в форме окружности или витка.

Для определения направления вектора магнитной индукции существует правило правой руки . Приготовьтесь задействовать абстрактное и пространственное мышление!

Если взять проводник в правую руку так, что большой палец будет указывать на направление тока, то загнутые вокруг проводника пальцы покажут направление силовых линий магнитного поля вокруг проводника. Вектор магнитной индукции в каждой точке будет направлен по касательной к силовым линиям.

Сила Ампера

Представим, что есть магнитное поле с индукцией B . Если мы поместим в него проводник длиной l , по которому течет ток силой I , то поле будет действовать на проводник с силой:

Это и есть сила Ампера . Угол альфа – угол между направлением вектора магнитной индукции и направлением тока в проводнике.

Направление силы Ампера определяется по правилу левой руки: если расположить левую руку так, чтобы в ладонь входили линии магнитной индукции, а вытянутые пальцы указывали бы направление тока, отставленный большой палец укажет направление силы Ампера.

Сила Лоренца

Мы выяснили, что поле действует на проводник с током. Но если это так, то изначально оно действует отдельно на каждый движущийся заряд. Сила, с которой магнитное поле действует на движущийся в нем электрический заряд, называется силой Лоренца . Здесь важно отметить слово «движущийся» , так на неподвижные заряды магнитное поле не действует.

Итак, частица с зарядом q движется в магнитном поле с индукцией В со скоростью v , а альфа – это угол между вектором скорости частицы и вектором магнитной индукции. Тогда сила, которая действует на частицу:

Как определить направление силы Лоренца? По правилу левой руки. Если вектор индукции входит в ладонь, а пальцы указывают на направление скорости, то отогнутый большой палец покажет направление силы Лоренца. Отметим, что так направление определяется для положительно заряженных частиц. Для отрицательных зарядов полученное направление нужно поменять на противоположное.

Если частица массы m влетает в поле перпендикулярно линиям индукции, то она будет двигаться по окружности, а сила Лоренца будет играть роль центростремительной силы. Радиус окружности и период обращения частицы в однородном магнитном поле можно найти по формулам:

Взаимодействие токов

Рассмотрим два случая. Первый – ток течет по прямому проводу. Второй – по круговому витку. Как мы знаем, ток создает магнитное поле.

В первом случае магнитная индукция провода с током I на расстоянии R от него считается по формуле:

Мю – магнитная проницаемость вещества, мю с индексом ноль – магнитная постоянная.

Во втором случае магнитная индукция в центре кругового витка с током равна:

Также при решении задач может пригодиться формула для магнитного поля внутри соленоида. – это катушка, то есть множество круговых витков с током.

Пусть их количество – N , а длина самого соленоилда – l . Тогда поле внутри соленоида вычисляется по формуле:

Кстати! Для наших читателей сейчас действует скидка 10% на

Магнитный поток и ЭДС

Если магнитная индукция – векторная характеристика магнитного поля, то магнитный поток – скалярная величина, которая также является одной из самых важных характеристик поля. Представим, что у нас есть какая-то рамка или контур, имеющий определенную площадь. Магнитный поток показывает, какое количество силовых линий проходит через единицу площади, то есть характеризует интенсивность поля. Измеряется в Веберах (Вб) и обозначается Ф .

S – площадь контура, альфа – угол между нормалью (перпендикуляром) к плоскости контура и вектором В .

При изменении магнитного потока через контур в контуре индуцируется ЭДС , равная скорости изменения магнитного потока через контур. Кстати, подробнее о том, что такое электродвижущая сила , вы можете почитать в еще одной нашей статье.

По сути формула выше – это формула для закона электромагнитной индукции Фарадея. Напоминаем, что скорость изменения какой-либо величины есть не что иное, как ее производная по времени.

Для магнитного потока и ЭДС индукции также справедливо обратное. Изменение тока в контуре приводит к изменению магнитного поля и, соответственно, к изменению магнитного потока. При этом возникает ЭДС самоиндукции, которая препятствует изменению тока в контуре. Магнитный поток, который пронизывает контур с током, называется собственным магнитным потоком, пропорционален силе тока в контуре и вычисляется по формуле:

L – коэффициент пропорциональности, называемый индуктивностью, который измеряется в Генри (Гн) . На индуктивность влияют форма контура и свойства среды. Для катушки с длиной l и с числом витков N индуктивность рассчитывается по формуле:

Формула для ЭДС самоиндукции:

Энергия магнитного поля

Электроэнергия, ядерная энергия, кинетическая энергия. Магнитная энергия – одна из форм энергии. В физических задачах чаще всего нужно рассчитывать энергию магнитного поля катушки. Магнитная энергия катушки с током I и индуктивностью L равна:

Объемная плотность энергии поля:

Конечно, это не все основные формулы раздела физики « электричество и магнетизм» , однако они часто могут помочь при решении стандартных задач и расчетах. Если же вам попалась задача со звездочкой, и вы никак не можете подобрать к ней ключ, упростите себе жизнь и обратитесь за решением в

Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.

Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика , термодинамика и молекулярная физика , электричество . Их и возьмем!

Основные формулы по физике динамика, кинематика, статика

Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.

Формулы кинематики:

Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.

После динамики самое время рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику

Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!

Основные формулы молекулярной физики и термодинамики

Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.

Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева – все эти милые сердцу формулы собраны ниже.

Кстати! Для всех наших читателей сейчас действует скидка 10% на .

Основные формулы по физике: электричество

Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.

И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.

На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».

Формула силы тока

ОПРЕДЕЛЕНИЕ

Сила тока определяется как отношение количества заряда, прошедшего через какую-то поверхность, ко времени прохождения.

В формуле – сила тока, – количество заряда, – время.

Единица измерения силы тока – А (ампер).

Обычно под поверхностью, через которую прошёл заряд, понимают сечение проводника. В цепях с постоянным током силу тока находят по закону Ома:

Где – напряжение, – сопротивление проводника. Прибор, которой используется для измерения силы тока, называют амперметром.

Примеры решения задач по теме «Сила тока»

ПРИМЕР 1

Задание	Найти силу тока в проводнике, если за 50 сек через него прошёл заряд 43 кКл.
Решение	Напомним, что кКл = Кл. Подставим численные значения в формулу:
Ответ	Сила тока была равна 860 Ампер.

ПРИМЕР 2

Задание

Через сечение проводника за 1 минуту прошёл заряд 10 Кл. Найти сопротивление участка цепи, если напряжение в нём 50 В.

Решение

Найдём силу тока через заряд:

По закону Ома:

Сопоставим формулы:

Подставим числа:

(Ом)

Ответ

Сопротивление цепи равно 300 Ом.

Понравился сайт? Расскажи друзьям!

Мощность в физике — обозначение, формулы и примеры

Определение мощности

Допустим, нам необходимо убрать урожай пшеницы с поля площадью 100 га. Это можно сделать вручную или с помощью комбайна. Очевидно, что пока человек обработает 1 га площади, комбайн успеет сделать намного больше. В данном случае разница между человеком и техникой — именно то, что называют мощностью. Отсюда вытекает первое определение.

Мощность в физике — это количество работы, которая совершается за единицу времени.

Рассмотрим другой пример: между точкой А и точкой Б расстояние 15 км, которое человек проходит за 3 часа, а автомобиль может проехать всего за 10 минут. Понятно, что одно и то же количество работы они сделают за разное время. Что показывает мощность в данном случае? Как быстро или с какой скоростью выполняется некая работа.

В электромеханике данная величина тоже связана со скоростью, а конкретно — с тем, как быстро передается ток по участку цепи. Исходя из этого, мы можем рассмотреть еще одно определение.

Мощность — это скалярная физическая величина, которая характеризует скорость передачи энергии от системы к системе или скорость преобразования, изменения, потребления энергии.

Напомним, что скалярными величинами называются те, значение которых выражается только числом (без вектора направления).

Мощность человека в зависимости от деятельности

Вид деятельности	Мощность, Вт
Неспешная ходьба	60–65
Бег со скоростью 9 км/ч	750
Плавание со скоростью 50 м/мин	850
Игра в футбол	930

Как обозначается мощность: единицы измерения

В таблице выше вы увидели обозначение в ваттах, и читая инструкции к бытовой технике, можно заметить, что среди характеристик прибора обязательно указано количество ватт. Это единица измерения механической мощности, используемая в международной системе СИ. Она обозначается буквой W или Вт.

Измерение мощности в ваттах было принято в честь шотландского ученого Джеймса Уатта — изобретателя паровой машины. Он стал одним из родоначальников английской промышленной революции.

В физике принято следующее обозначение мощности: 1 Вт = 1 Дж / 1с.

Это значит, что за 1 ватт принята мощность, необходимая для совершения работы в 1 джоуль за 1 секунду.

В каких единицах еще измеряется мощность? Ученые-астрофизики измеряют ее в эргах в секунду (эрг/сек), а в автомобилестроении до сих пор можно услышать о лошадиных силах.

Интересно, что автором этой последней единицы измерения стал все тот же шотландец Джеймс Уатт. На одной из пивоварен, где он проводил свои исследования, хозяин накачивал воду для производства с помощью лошадей. И Уатт выяснил, что 1 лошадь за секунду поднимает около 75 кг воды на высоту 1 метр. Вот так и появилось измерение в лошадиных силах. Правда, сегодня такое обозначение мощности в физике считается устаревшим.

Одна лошадиная сила — это мощность, необходимая для поднятия груза в 75 кг за 1 секунду на 1 метр. 🐴

Единицы измерения	Вт
1 ватт	1
1 киловатт	10³
1 мегаватт	10⁶
1 эрг в секунду	10^-7
1 метрическая лошадиная сила	735,5

Все формулы мощности

Зная определения, несложно понять формулы мощности, используемые в разных разделах физики — в механике и электротехнике.

В механике

Механическая мощность (N) равна отношению работы ко времени, за которое она была выполнена.

Основная формула:

N = A / t, где A — работа, t — время ее выполнения.

Если вспомнить, что работой называется произведение модуля силы, модуля перемещения и косинуса угла между ними, мы получим формулу измерения работы.

Если направления модуля приложения силы и модуля перемещения объекта совпадают, угол будет равен 0 градусов, а его косинус равен 1. В таком случае формулу можно упростить:

A = F × S

Используем эту формулу для вычисления мощности:

N = A / t = F × S / t = F × V

В последнем выражении мы исходим из того, что скорость (V) равна отношению перемещения объекта на время, за которое это перемещение произошло.

В электротехнике

В общем случае электрическая мощность (P) говорит о скорости передачи энергии. Она равна произведению напряжения на участке цепи на величину тока, проходящего по этому участку.

P = I × U, где I — напряжение, U — сила тока.

В электротехнике существует несколько видов мощности: активная, реактивная, полная, пиковая и т. д. Но это тема отдельного материала, сейчас же мы потренируемся решать задачи на основе общего понимания этой величины. Посмотрим, как найти мощность, используя вышеуказанные формулы по физике.

Задача 1

Допустим, человек поднимает ведро воды из колодца, прикладывая силу 60 Н. Глубина колодца составляет 10 м, а время, необходимое для поднятия — 30 сек. Какова будет мощность в этом случае?

Решение:

Найдем вначале величину работы, используя тот факт, что мы знаем расстояние перемещения (глубину колодца 10 м) и приложенную силу 60 Н.

A = F × S = 60 Н × 10 м = 600 Дж

Когда известно значение работы и времени, найти мощность несложно:

N = A / t = 600 Дж / 30 сек = 20 Вт

Ответ: человек развивает мощность 20 ватт.

Задача 2

В комнате включена лампа мощностью 100 Вт. Напряжение домашней электросети — 220 В. Какая сила тока пройдет через эту лампу?

Решение:

Мы знаем, что Р = 100 Вт, а U = 220 В.

Поскольку P = I × U, следовательно I = P / U.

I = 100 / 220 = 0,45 А.

Ответ: через лампу пройдет сила тока 0,45 А.

Вопросы для самопроверки

Что характеризует механическая мощность?
Какие существуют единицы измерения мощности в физике?
Какая из единиц измерения считается устаревшей?
Мощность можно назвать скалярной величиной? Что это означает?
Как из формулы нахождения мощности получить работу?
Какой буквой обозначается мощность в механике, а какой — в электротехнике?
Какую работу производит за 30 минут устройство мощностью 600 Вт?
Как узнать напряжение в сети, если мы знаем мощность подключенного к ней прибора и силу тока, проходящую через прибор?
Если в течение 1 часа автомобиль №1 едет со скоростью 60 км/ч, а автомобиль №2 — со скоростью 90 км/ч, одинаковую ли мощность они развивают в это время?
Допустим, автобус отвез пассажиров из города А в город В за 1 час. Если он планирует вернуться в город А пустым по той же трассе и потратить на это 1 час, ему понадобится развить такую же мощность или меньшую?

Таблица по физике физические тела. Основные формулы по физике: электричество

«Компьютерные модели» – Нажмите кнопку “Начальн. А нужен ли компьютер на уроке? Задание N4. Выяснить характер зависимости дальности полета l от величины начальной скорости v0. Подтвердить словесный вывод формулой. Нетрадиционные виды учебной деятельности учащихся. 221 (203). Задания: Выбрать определенное значение начальной скорости v0.

«ЕГЭ по физике 2010» – Документы, определяющие содержание экзаменационной работы. На экзамене в аудиторию не допускаются специалисты по физике. Распределение заданий экзаменационной работы по видам проверяемой деятельности. Часть 3 содержит 6 заданий, для которых необходимо привести развернутый ответ. А25. Распределение заданий по уровню сложности.

«Уроки здоровья» – Массу мы легко найдем, умножим плотность на объем. Слабое звено. Факторы, влияющие на здоровье школьников: ПОЧЕМУ? Медики констатируют существенное ухудшение здоровья детей в нашей стране. Пименение здоровьесберегающих технологий на уроках физики. Здоровье сберегающие технологии на уроках физики. Острый глаз.

«Демонстрация опытов» – Опыт 1: Цель: А потеряв опору, монета упала вниз. Опыт 6: Движение тела по “мертвой петле. Заключение: Через некоторое время переставьте бутылку в кастрюлю с холодной водой. Опыт 4: Монета в бутылке. Конус двойной, катящийся вверх. ОПЫТ 2: Реактивное движение. Вот так можно убедиться в зависимости давления воздуха от окружающей температуры.

«Лабораторные работы по физике» – Виртуальный лабораторный практикум по физике. Исследование явления фотоэффекта. Таблицы измерений. Введение. Презентация. Построение графика. Виртуальная лабораторная установка. Изохорный процесс. Исследование явления интерференции света. Авторы: Р.В. Дронова, А.И. Приходченко. Таблица измерений.

«Лабораторная работа» – Все возможности тестового режима для проверки знаний. Автоматическая проверка знаний при подготовке или после эксперимента. Создание тренингов и зачетов в автоматическом и ручном режиме. Как методическое пособие для учителя по выполнению широкого спектра экспериментов с цифровым датчиками как лабораторный практикум для выполнения работ учащимися как рабочую тетрадь – рабочие бланки учащихся как редактируемую открытую коллекцию ресурсов, для подготовки к урокам и планирования занятий, позволяющую осуществлять экспорт и импорт учебных материалов как удобную оболочку, позволяющую организовать контроль знаний учащихся (тренинги, зачеты, экзамены).

ПЕРИОДИЧЕСКАЯ СИСТЕМА ХИМИЧЕСКИХ ЭЛЕМЕНТОВ Д.И. МЕНДЕЛЕЕВА

Бериллий

Кислород

Алюминий

Марганец

Германий

Стронций

Цирконий

Молибден

Технеций

Палладий

Вольфрам

Резерфордий

Сиборгий

Мейтнерий

Унуннилий

Празеодим

Прометий

Гадолиний

Диспрозий

Протактиний

Нептуний

Плутоний

Америций

Калифорний

Эйнштейний

Менделеевий

Лоуренсий

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ Государственное высшее учебное заведение

«ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

СПРАВОЧНЫЕ МАТЕРИАЛЫ ПО ФИЗИКЕ

Рассмотрено на заседании кафедры физики

Утверждено учебно-издательским советом ДонНТУ Протокол № 1 от 02.03.2010

Справочные материалы по физике / Сост.: Волков А.Ф., Лумпиева Т.П. – Донецк: ДонНТУ. − 2010.− 28 с.

Предлагаемые «Справочные материалы» охватывают все разделы курса физики, предусмотренные программой.

Материалы разбиты на разделы. В первом разделе приведены некоторые сведения по математике. Во втором разделе даны значения основных физических постоянных и сведения о единицах физических величин. Значения постоянных округлены до значений, достаточных для расчетов при решении задач и лабораторных расчетов.

Содержание третьего раздела составляют таблицы физических величин и графики. Приведенные таблицы и графики не претендуют на полноту охвата всех справочных сведений по тому или иному разделу курса физики. Из многочисленных сведений отобраны те, которые используются при решении типовых задач, а также те, которые необходимы при выполнении лабораторных работ физического практикума.

Составители: А.Ф. Волков, доц. Т.П. Лумпиева, ст. преп.


ПРЕДИСЛОВИЕ. . . . . . . .. . . . . . . . . . . . . . . . . . . . . .
ПОЯСНЕНИЯ К ТАБЛИЦАМ. . . . . . . . . . . . . . . . . .
1. НЕКОТОРЫЕ СВЕДЕНИЯ ПО МАТЕМАТИКЕ. .	. . . . . . . . . . . . . . . . . . . . . . . . . . .
2. ОСНОВНЫЕ ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ.
ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН. . . . . . . . .	. . . . . . . . . . . . . . . . . . . . . . . . . .
2.1. Основные физические постоянные. . . . . . . .	. . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2. Греческий и латинский алфавиты. . . . . . . . . .	. . . . . . . . . . . . . . . . . . . . . . . . . .
2.3. Множители и приставки для образования десятичных, кратных и дольных
единиц и их наименований. . . . . . . . . . . . . . .	. . . . . . . . . . . . . . . . . . . . . . . . . .
2.4. Некоторые сведения о единицах физических величин. . . . . . . . . . . . . . . . . . . .
3. ТАБЛИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН. . . . . . . . . .	. . . . . . . . . . . . . . . . . . . . . . . . . .
3.1. Астрономические величины. . . . . . . . . . . . . .	. . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2. Плотность и модуль упругости твердых тел.	. . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3. Тепловые свойства твердых тел. . . . . . . . . . .	. . . . . . . . . . . . . . . . . . . . . . . . . . .
3.4. Свойства жидкостей при 20° C . . . . . . . . . . . .	. . . . . . . . . . . . . . . . . . . . . . . . . . .
3.5. Свойства газов при 20° C . . . . . . . . . . . . . . . . .	. . . . . . . . . . . . . . . . . . . . . . . . . . .
3.6. Скорость звука при 20° C . . . . . . . . . . . . . . . . .	. . . . . . . . . . . . . . . . . . . . . . . . . . .
3.7. Состав сухого атмосферного воздуха. . . . . . .	. . . . . . . . . . . . . . . . . . . . . . . . . .
3.8. Критические параметры и поправки Ван-дер-Ваальса. . . . . . . . . . . . . . . . . . .
3.9. Элементы периодической системы. . . . . . . . .	. . . . . . . . . . . . . . . . . . . . . . . . . .
3.10. Электрические свойства веществ. . . . . . . . .	. . . . . . . . . . . . . . . . . . . . . . . . . . .
3.11. Удельное электрическое сопротивление ρ 0	и температурный коэффициент
сопротивления α некоторых проводников при 0° С. . . . . . . . . . . . . . . . . . . . .
3.12. Связь между магнитной индукцией В поля в ферромагнетике
и напряженностью Н намагничивающего поля. . . . . . . . . . . . . . . . . . . . . . .
3.13. Показатели преломления. . . . . . . . . . . . . . . .	. . . . . . . . . . . . . . . . . . . . . . . . . . .
3.14. Интервалы длин волн и частот и соответствующие им цвета
видимой части спектра. . . . . . . . . . . . . . . .	. . . . . . . . . . . . . . . . . . . . . . . . . . .
3.15. Шкала электромагнитных волн. . . . . . . . . . .	. . . . . . . . . . . . . . . . . . . . . . . . . .
3.16. Длины волн ярких линий в спектре ртутной лампы ПРК-4 . . . . . . . . . . . . . .
3.17. Длины волн некоторых ярких линий в спектре неона. . . . . . . . . . . . . . . . . . .
3.18. Спектральные линии атома водорода в видимой части спектра. . . . . . . . . . .
3.19. Основные физические свойства некоторых	полупровод-
никовых материалов. . . . . . . . . . . . . . . . . .	. . . . . . . . . . . . . . . . . . . . . . . . . . .
3.20. Работа выхода для химически чистых элементов и элементов, покрытых
слоем адсорбата. . . . . . . . . . . . . . . . . . . . . .	. . . . . . . . . . . . . . . . . . . . . . . . . . .
3.21. Зависимость удельной энергия связи от массового числа. . . . . . . . . . . . . . . .
2.22. Зависимость линейного коэффициента ослабления от энергии падающих
фотонов для некоторых материалов. . . . .	. . . . . . . . . . . . . . . . . . . . . . . . . .
3.23. Основные свойства некоторых изотопов. . .	. . . . . . . . . . . . . . . . . . . . . . . . . .

1 слайд

Составитель: Гринякин Станислав Александрович Руководитель: Талалай Ольга Георгиевна, учитель физики Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа №6 с углубленным изучением отдельных предметов» г. Надыма, Тюменская область, Ямало-Ненецкий автономный округ,

2 слайд

Формула Название величин, входящих в формулу КИНЕМАТИКА Равномерное движение: υ=S/t S=υt x=x0S x=x+tυ S – путь t – время х – координата конечная х0 – начальная координата υ – скорость a – ускорение g – ускорение свободного падения Равноускоренное движение: a= υ-υ0/t υ=υ0±at S=υt±at2/2 S=υ2 – υ20/±2a х=х0+υ0t+at2/2 Движение по окружности: υ=2П R/T aац=υ2/R υ=Rω T=t/N ν =N\t ν – частота вращения R – радиус T – период aац t – время N – число оборотов υ ω – угловая скорость

3 слайд

ДИНАМИКА Законы Ньютона: F=ma (II зaкон Ньютона) F1=-F2 (III закон Ньютона) I з.Н. если ∑F = 0, υ = const II з.Н. ∑F = ma III з.Н. F1= – F2 Закон всемирного тяготения: m1 m2 r F=Gm1m2/r2 G – гравитационная постоянная m1 , m2 – массы тел r – расстояние Закон Гука: Fупр= -kx x – удлинение k – жесткость ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ υ = √gR R – радиус вращения, g – ускорение свободного падения Импульс: P=mυ Закон сохранения импульса m1υ1+m2υ2=m1U1+m2U2 P – импульс m – масса υ – скорость m1,m2 – массы υ1 – скорость 1-ого тела до взаимодействия υ2 – скорость 2-ого тела до взаимодействия U1 – скорость 1-ого тела после взаимодействия U2 – скорость 2-ого тела после взаимодействия

4 слайд

РАБОТА И ЭНЕРГИЯ A=FScosα F – сила S – перемещение Угол α – угол между F и S P=A/t P=Fυ P – мощность F – сила υ – скорость КПД=(А полезн./А затрач.)100% Eк = mυ2/2 – кинетическая энергия Eп = mgh – потенциальная энергия Eп = kx2/2 – потенциальная энергия Закон сохранения энергии: Eк1 + Eп1 = Eк2 + Eп2 mυ21/2+mgh2 = mυ22/2+mgh3 mυ21/2+kx21/2 = mυ22/2+kx22/2

5 слайд

Давление(P): p=F/S p=рgh Fa=ржgVпчт Р ж- плотность жидкость S – площадь поверхности F – сила Vпчт – объем погруженной части тела Колебания и волны: T=t/N T=2π√ ℓ/g ω=2πν =υ/ν T=2π √m/k λ = υT = υ/ν ℓ – длина нити T – период Ν – число колебаний m – масса k – жесткость пружины ν – частота МОЛЕКУЛЯРНАЯ ФИЗИКА ν = m/μ = N/Na n = N/V μ = m0Na m = m0N p = ⅓m0nυ2 p = ⅔nE p = nkT p = ⅓рυ2 E = (3/2)kT T = t⁰ + 273 pV = (m/μ)RT p1V1/T1 = p2V2/T2 μ – молярная масса вещества m – масса вещества Na – постоянная Авогадро N – число молекул T – температура в Кельвинах t – температура в Цельсиях V – объем вещества p – давление R – универсальная газовая постоянная n – концентрация вещества υ – среднеквадратичная скорость k – постоянная Больцмана ν – количество вещества E – кинетическая энергия m0 – масса одной молекулы

6 слайд

ТЕРМОДИНАМИКА Q = ∆U + A| ∆U = A + Q Q – кол-во теплоты сообщаемое системе ∆U – изменение внутренней энергии А – работа внешних сил А| – работа газа U=(i/2)(m/μ)RT=(i/2)pV U – внутренняя энергия A=p∆V=(m/μ)R∆T ТЕПЛОВЫЕ ДВИГАТЕЛИ η=Ап/Qн η=(Qн – Qx)/Qн η=(Tн – Tx)/Tн Ап – полезная работа Qн – количество теплоты, полученное от нагревателя Qx – количество теплоты, полученное от холодильника Tн – температура нагревателя Tx – температура холодильника ТЕПЛОВЫЕ ЯВЛЕНИЯ Qнагр = cm(t2 – t1) Qпл = λm Qпар = Lm Qсгор = qm с – удельная теплоемкость вещества λ – удельная теплота плавления L – удельная теплота парообразования q – удельная теплота сгорания ЭЛЕКТРОСТАТИКА F = (k|q1||q2|)/ E r2 E = F/qпр E=(k|q|)/r2 k – коэффициент пропорциональности q1, q2 – заряды тел r – расстояние между телами E – диэлектрическая проницаемость среды

7 слайд

ПОСТОЯННЫЙ ТОК I=U/R I= E /R+r R=рℓ/S A=IUt P=UI Q=I2Rt I – сила тока U – напряжение R – сопротивление A – работа тока P – мощность тока Q – количество теплоты t – время E – ЭДС ℓ – длина проводника р – удельное сопротивление S – площадь сечения ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ПРОВОДНИКОВ ǿ ǿ R0 = R1+R2+… U0 = U1+U2+… I0=I1=I2=… 1. U0=U1=U2 ǿ ǿ 2. 1/R0=1/R1+1/R2+… 3. I0=I1+I2+… СИЛА ЛОРЕНЦА, АМПЕРА Fл=qBℓsinα Fа=υBSIsinα В – магнитная индукция q – электрический заряд ℓ – длина проводника υ – скорость частицы I – сила тока

8 слайд

Сила Определение. Направление. Формула Рисунок 1.Сила тяжести -это сила, с которой Земля притягивает к себе тело. Направлена вниз к центру Земли. Fтяж = mg где: m – масса тела g – ускорение свободного падения mg mg 2.Сила упругости -это сила, возникающая в результате деформации. Направлена противоположно деформации. Fупр=-kx где: k–коэффициент жесткости x – удлинение Fупр Fупр 3.Сила трения -это сила, возникающая в результате движения одного тела по поверхности другого. Направлена в сторону, противоположную движению. Fтр=μN где: μ– коэффициент трения N – сила нормального давления V Fтр 4.Вес тела -это сила, с которой тело действует на горизонтальную опору или вертикальный подвес. Направлен вниз, т.к. возникает в следствии притяжения Земли. P=mg(если тело покоится или движется равномерно и прямолинейно) P=m(g+a) a P=m(g-a) a P P

Составитель: Гринякин Станислав Александрович Руководитель: Талалай Ольга Георгиевна, учитель физики Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа 6 с углубленным изучением отдельных предметов» г. Надыма, Тюменская область, Ямало-Ненецкий автономный округ,

ФормулаНазвание величин, входящих в формулу КИНЕМАТИКА Равномерное движение: 1. υ = S/t 2.S= υ t 3.x=x 0 S 4.x=x+t υ S – путь t – время х – координата конечная х 0 – начальная координата υ – скорость a – ускорение g – ускорение свободного падения Равноускоренное движение: 1. a= υ – υ 0 /t 2. υ = υ 0 ±at 3. S= υ t±at 2 / 2 4. S= υ 2 – υ 2 0 /±2a 5. х=х 0 + υ 0 t+at 2 /2 Движение по окружности: 1. υ =2 П R/T 2.a ац = υ 2 /R 3. υ =R ω 4.T=t/N 5. ν =N\t ν – частота вращения R – радиус T – период a ац t – время N – число оборотов υ ω – угловая скорость

ДИНАМИКА Законы Ньютона: F=ma (II зaкон Ньютона) F 1 =-F 2 (III закон Ньютона) I з.Н. еслиF = 0, υ = const II з.Н. F = ma III з.Н. F 1 = – F 2 Закон всемирного тяготения: m 1 m 2 r F=Gm 1 m 2 /r 2 G – гравитационная постоянная m 1, m 2 – массы тел r – расстояние Закон Гука: F упр = -kx x – удлинение k – жесткость ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ υ =gR R – радиус вращения, g – ускорение свободного падения Импульс: P=m υ Закон сохранения импульса m 1 υ 1 +m 2 υ 2 =m 1 U 1 +m 2 U 2 P – импульс m – масса υ – скорость m 1,m 2 – массы υ 1 – скорость 1-ого тела до взаимодействия υ 2 – скорость 2-ого тела до взаимодействия U 1 – скорость 1-ого тела после взаимодействия U 2 – скорость 2-ого тела после взаимодействия

РАБОТА И ЭНЕРГИЯ A=FScos α F – сила S – перемещение Угол α – угол между F и S P=A/t P=F υ P – мощность F – сила υ – скорость КПД=(А полезн. /А затрач.)100% E к = mυ 2 /2 – кинетическая энергия E п = mgh – потенциальная энергия E п = kx 2 /2 – потенциальная энергия Закон сохранения энергии: E к 1 + E п 1 = E к 2 + E п 2 m υ 2 1 /2+mgh 1 = m υ 2 2 /2+mgh 2 m υ 2 1 /2+kx 2 1 /2 = m υ 2 2 /2+kx 2 2 /2

Давление(P): p=F/S p= р gh F a = р ж gV пчт Р ж – плотность жидкость S – площадь поверхности F – сила V пчт – объем погруженной части тела Колебания и волны: T=t/N T=2 π /g ω =2 πν = υ / ν T=2 π m/k λ = υ T = υ / ν – длина нити T – период Ν – число колебаний m – масса k – жесткость пружины ν – частота МОЛЕКУЛЯРНАЯ ФИЗИКА ν = m/ μ = N/Na n = N/V μ = m 0 N a m = m 0 N p = m 0 n υ 2 p = nE p = nkT p = р υ 2 E = (3/2)kT T = t pV = (m/ μ)RT p 1 V 1 /T 1 = p 2 V 2 /T 2 μ – молярная масса вещества m – масса вещества N a – постоянная Авогадро N – число молекул T – температура в Кельвинах t – температура в Цельсиях V – объем вещества p – давление R – универсальная газовая постоянная n – концентрация вещества υ – среднеквадратичная скорость k – постоянная Больцмана ν – количество вещества E – кинетическая энергия m 0 – масса одной молекулы

ТЕРМОДИНАМИКА Q = U + A | U = A + Q Q – кол-во теплоты сообщаемое системе U – изменение внутренней энергии А – работа внешних сил А | – работа газа U=(i/2)(m/ μ)RT=(i/2)pVU – внутренняя энергия A=pV=(m/ μ)RT ТЕПЛОВЫЕ ДВИГАТЕЛИ η=А п /Q н η=(Q н – Q x)/Q н η=(T н – T x)/T н А п – полезная работа Q н – количество теплоты, полученное от нагревателя Q x – количество теплоты, полученное от холодильника T н – температура нагревателя T x – температура холодильника ТЕПЛОВЫЕ ЯВЛЕНИЯ Q нагр = cm(t2 – t1) Q пл = λm Q пар = Lm Q сгор = qm с – удельная теплоемкость вещества λ – удельная теплота плавления L – удельная теплота парообразования q – удельная теплота сгорания ЭЛЕКТРОСТАТИКА F = (k|q 1 ||q 2 |)/ E r 2 E = F/q пр E=(k|q|)/r 2 k – коэффициент пропорциональности q1, q2 – заряды тел r – расстояние между телами E – диэлектрическая проницаемость среды

ПОСТОЯННЫЙ ТОК I=U/R I= E /R+r R= р/S A=IUt P=UI Q=I 2 Rt I – сила тока U – напряжение R – сопротивление A – работа тока P – мощность тока Q – количество теплоты t – время E – ЭДС – длина проводника р – удельное сопротивление S – площадь сечения ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ПРОВОДНИКОВ ǿ 1.R 0 = R 1 +R 2 +… 2.U 0 = U 1 +U 2 +… 3.I 0 =I 1 =I 2 =… 1. U 0 =U 1 =U 2 ǿ ǿ 2. 1/R 0 =1/R 1 +1/R 2 +… 3. I 0 =I 1 +I 2 +… СИЛА ЛОРЕНЦА, АМПЕРА F л =qBsin α F а = υ BSIsin α В – магнитная индукция q – электрический заряд – длина проводника υ – скорость частицы I – сила тока R1R2 R1

СилаОпределение. Направление.ФормулаРисунок 1.Сила тяжести -это сила, с которой Земля притягивает к себе тело. Направлена вниз к центру Земли. F тяж = mg где: m – масса тела g – ускорение свободного падения mg mg 2.Сила упругости -это сила, возникающая в результате деформации. Направлена противоположно деформации. F упр =-kx где: k–коэффициент жесткости x – удлинение F упр F упр 3.Сила трения -это сила, возникающая в результате движения одного тела по поверхности другого. Направлена в сторону, противоположную движению. F тр = μ N где: μ – коэффициент трения N – сила нормального давления V F тр 4.Вес тела-это сила, с которой тело действует на горизонтальную опору или вертикальный подвес. Направлен вниз, т.к. возникает в следствии притяжения Земли. P=mg(если тело покоится или движется равномерно и прямолинейно) P=m(g+a) a P=m(g-a) a P

P – давление V – объем T – температура p=nkT n=N/V p=nkT=NkT/V=N a kT V \V V=N а V N а k=R p= V N a kT/V= V RT/V => pV= V RT=> V =m/ μ => pV=mRT/ μ – уравнение Менделеева – Клаперона pV= V RT=> V =m/ μ => pV=mRT/ μ – уравнение Менделеева – Клаперона”> pV= V RT=> V =m/ μ => pV=mRT/ μ – уравнение Менделеева – Клаперона”> pV= V RT=> V =m/ μ => pV=mRT/ μ – уравнение Менделеева – Клаперона” title=”p – давление V – объем T – температура p=nkT n=N/V p=nkT=NkT/V=N a kT V \V V=N а V N а k=R p= V N a kT/V= V RT/V => pV= V RT=> V =m/ μ => pV=mRT/ μ – уравнение Менделеева – Клаперона”> title=”p – давление V – объем T – температура p=nkT n=N/V p=nkT=NkT/V=N a kT V \V V=N а V N а k=R p= V N a kT/V= V RT/V => pV= V RT=> V =m/ μ => pV=mRT/ μ – уравнение Менделеева – Клаперона”>

Изопроцесс – процессы, протекающие при неизменном значении одного из параметров называют изопроцессами. 1. ИЗОТЕРМИЧЕСКИЙ Процесс изменения состояния термодинамической системы макроскопических тел при постоянной температуре называют изотермическим процессом. T 2 >T 1 T-const – характеризует множество состояний газа при данной температуре (любая точка изотермы характеризует состояние газа, либо для неё известны p 1 V 1 при определенной температуре). А любая прямая или кривая составляет множество точек, значит множество состояний. T 1 T-const – характеризует множество состояний газа при данной температуре (любая точка изотермы характеризует состояние газа, либо для неё известны p 1 V 1 при определенной температуре). А любая прямая или кривая составляет множество точек, значит множество состояний.”>

P 1 p-const – изобара характеризует множество состояний газа при определенном давлении.” title=”2.изобарный Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным процессом p 2 >p 1 p-const – изобара характеризует множество состояний газа при определенном давлении.”> 11 2.изобарный Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным процессом p 2 >p 1 p-const – изобара характеризует множество состояний газа при определенном давлении. p 1 p-const – изобара характеризует множество состояний газа при определенном давлении.”> p 1 p-const – изобара характеризует множество состояний газа при определенном давлении.”> p 1 p-const – изобара характеризует множество состояний газа при определенном давлении.” title=”2.изобарный Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным процессом p 2 >p 1 p-const – изобара характеризует множество состояний газа при определенном давлении.”> title=”2.изобарный Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным процессом p 2 >p 1 p-const – изобара характеризует множество состояний газа при определенном давлении.”>

Основные формулы по физике динамика, кинематика, статика

Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.

Формулы кинематики:

Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.

После динамики самое время рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику

Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!

Основные формулы молекулярной физики и термодинамики

Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.

Кстати! Для всех наших читателей сейчас действует скидка 10% на .

Основные формулы по физике: электричество

Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.

Потенциал, работа электростатического поля. Потенциальная энергия, разность потенциалов, принцип суперпозиции. Тесты, формулы

Тестирование онлайн

Работа электростатического поля

Рассмотрим ситуацию: заряд q₀ попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q₀ со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.

Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными, а само поле называется потенциальным.

Потенциал

Система “заряд – электростатическое поле” или “заряд – заряд” обладает потенциальной энергией, подобно тому, как система “гравитационное поле – тело” обладает потенциальной энергией.

Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал – это характеристика электростатического поля.

Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.

Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.

В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело – наоборот.

Потенциальная энергия поля – это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.

Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.

Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.

Разность потенциалов

Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов

Эту формулу можно представить в ином виде

Эквипотенциальная поверхность (линия) – поверхность равного потенциала. Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.

Напряжение

Разность потенциалов называют еще электрическим напряжением при условии, что сторонние силы не действуют или их действием можно пренебречь.

Напряжение между двумя точками в однородном электрическом поле, расположенными по одной линии напряженности, равно произведению модуля вектора напряженности поля на расстояние между этими точками.

От величины напряжения зависит ток в цепи и энергия заряженной частицы.

Принцип суперпозиции

Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности

При решении задач возникает много путаницы при определении знака потенциала, разности потенциалов, работы.

На рисунке изображены линии напряженности. В какой точке поля потенциал больше?

Верный ответ – точка 1. Вспомним, что линии напряженности начинаются на положительном заряде, а значит положительный заряд находится слева, следовательно максимальным потенциалом обладает крайняя левая точка.

Если происходит исследование поля, которое создается отрицательным зарядом, то потенциал поля вблизи заряда имеет отрицательное значение, в этом легко убедиться, если в формулу подставить заряд со знаком “минус”. Чем дальше от отрицательного заряда, тем потенциал поля больше.

Если происходит перемещение положительного заряда вдоль линий напряженности, то разность потенциалов и работа являются положительными. Если вдоль линий напряженности происходит перемещение отрицательного заряда, то разность потенциалов имеет знак “+”, работа имеет знак “-“.

Порассуждайте самостоятельно отрицательные или положительные значения будут принимать работа и разность потенциалов, если заряд перемещать в обратном направлении относительно линий напряженности.

Напряжение в клетках сетчатки глаза при попадания в них света около 0,01 В.
Напряжение в телефонных сетях может достигать 60 В.
Электрический угорь способен создавать напряжение до 650 В.

Из определения потенциала следует, что потенциальная энергия электростатического взаимодействия двух зарядов q₁ и q₂, находящихся на расстоянии r друг от друга, численно равна работе, которая совершается при перемещении точечного заряда q₂ из бесконечности в данную точку поля, созданного зарядом q₁

Аналогично Тогда энергия взаимодействия двух точечных зарядов

Энергия взаимодействия n зарядов

Использование уравнений конденсатора – AP Physics C Electricity

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

7.3: Электрический потенциал и разность потенциалов

Цели обучения

К концу этого раздела вы сможете:

Определение электрического потенциала, напряжения и разности потенциалов
Определите электрон-вольт
Вычислить электрический потенциал и разность потенциалов на основе потенциальной энергии и электрического поля
Опишите системы, в которых электрон-вольт является полезной единицей.
Применение энергосбережения в электрических системах

Напомним, что ранее мы определили электрическое поле как величину, не зависящую от тестового заряда в данной системе, что, тем не менее, позволило бы нам вычислить силу, которая возникнет при произвольном тестовом заряде.(При отсутствии другой информации по умолчанию предполагается, что тестовый заряд положительный.) Мы кратко определили поле для гравитации, но гравитация всегда притягивает, тогда как электрическая сила может быть либо притягивающей, либо отталкивающей. Следовательно, хотя потенциальная энергия вполне достаточна в гравитационной системе, удобно определить величину, которая позволяет нам вычислить работу над зарядом независимо от величины заряда. Непосредственный расчет работы может быть затруднен, поскольку \ (W = \ vec {F} \ cdot \ vec {d} \), а направление и величина \ (\ vec {F} \) могут быть сложными для нескольких зарядов, например предметы необычной формы и по произвольным путям.Но мы знаем, что, поскольку \ (\ vec {F} \), работа и, следовательно, \ (\ Delta U \) пропорциональны испытательному заряду \ (q \). Чтобы получить физическую величину, не зависящую от пробного заряда, мы определяем электрический потенциал \ (В \) (или просто потенциал, поскольку понимается электрический) как потенциальную энергию на единицу заряда:

Электрический потенциал

Потенциальная электрическая энергия на единицу заряда составляет

\ [V = \ dfrac {U} {q}. \ label {eq-1} \]

Поскольку U пропорционально q , зависимость от q отменяется.Таким образом, V не зависит от q . Изменение потенциальной энергии \ (\ Delta U \) имеет решающее значение, поэтому нас интересует разность потенциалов или разность потенциалов \ (\ Delta V \) между двумя точками, где

Разница электрических потенциалов

Разность электрических потенциалов между точками A, и B , \ (V_B – V_A \) определяется как изменение потенциальной энергии заряда q , перемещенного от A к B , разделенное по заряду.Единицами разности потенциалов являются джоули на кулон, получившие название вольт (В) в честь Алессандро Вольта.

\ [1 \, V = 1 \, J / C \ label {eq0} \]

Знакомый термин напряжение – это общее название разности электрических потенциалов. Имейте в виду, что всякий раз, когда указывается напряжение, под ним понимается разность потенциалов между двумя точками. Например, каждая батарея имеет две клеммы, а ее напряжение – это разность потенциалов между ними. По сути, точка, которую вы выбираете как ноль вольт, произвольна.Это аналогично тому факту, что гравитационная потенциальная энергия имеет произвольный ноль, например, на уровне моря или, возможно, на полу лекционного зала. Стоит подчеркнуть различие между разностью потенциалов и электрической потенциальной энергией.

Разность потенциалов и электрическая потенциальная энергия

Связь между разностью потенциалов (или напряжением) и электрической потенциальной энергией определяется формулой

\ [\ Delta V = \ dfrac {\ Delta U} {q} \ label {eq1} \]

или

\ [\ Delta U = q \ Delta V.\ label {eq2} \]

Напряжение – это не то же самое, что энергия. Напряжение – это энергия на единицу заряда. Таким образом, аккумулятор мотоцикла и автомобильный аккумулятор могут иметь одинаковое напряжение (точнее, одинаковую разность потенциалов между клеммами аккумулятора), но один хранит гораздо больше энергии, чем другой, потому что \ (\ Delta U = q \ Delta V \) . Автомобильный аккумулятор может заряжать больше, чем аккумулятор мотоцикла, хотя оба аккумулятора – 12 В.

Пример \ (\ PageIndex {1} \): расчет энергии

У вас 12.0-В мотоциклетный аккумулятор, способный переносить заряд 5000 C, и автомобильный аккумулятор на 12 В, способный переносить 60 000 C. Сколько энергии дает каждый? (Предположим, что числовое значение каждого заряда соответствует трем значащим цифрам.)

Стратегия

Сказать, что у нас батарея на 12,0 В, означает, что на ее выводах разность потенциалов составляет 12,0 В. Когда такая батарея перемещает заряд, она пропускает заряд через разность потенциалов 12,0 В, и заряд получает изменение потенциальной энергии, равное \ (\ Delta U = q \ Delta V \).5 \, J. \ nonumber \]

Значение

Напряжение и энергия связаны, но это не одно и то же. Напряжения батарей одинаковы, но энергия, подаваемая каждым из них, совершенно разная. Автомобильный аккумулятор требует запуска гораздо более мощного двигателя, чем мотоцикл. Также обратите внимание, что когда аккумулятор разряжен, часть его энергии используется внутри, а напряжение на его клеммах падает, например, когда фары тускнеют из-за разряда автомобильного аккумулятора. Энергия, подаваемая батареей, по-прежнему рассчитывается, как в этом примере, но не вся энергия доступна для внешнего использования.

Упражнение \ (\ PageIndex {1} \)

Сколько энергии у 1,5-В батареи AAA, которая может нагреться до 100 градусов Цельсия?

Ответ: \ (\ Delta U = q \ Delta V = (100 \, C) (1.5 \, V) = 150 \, J \)

Обратите внимание, что энергии, вычисленные в предыдущем примере, являются абсолютными значениями. Изменение потенциальной энергии для аккумулятора отрицательное, так как он теряет энергию. Эти батареи, как и многие другие электрические системы, действительно перемещают отрицательный заряд – в частности, электроны.Батареи отталкивают электроны от своих отрицательных выводов ( A ) через любую задействованную схему и притягивают их к своим положительным выводам ( B ), как показано на рисунке \ (\ PageIndex {1} \). Изменение потенциала равно \ (\ Delta V = V_B – V_A = +12 \, V \), а заряд q отрицателен, так что \ (\ Delta U = q \ Delta V \) отрицателен, что означает потенциальная энергия батареи уменьшилась, когда q переместилось с A на B .

Рисунок \ (\ PageIndex {1} \): Аккумулятор перемещает отрицательный заряд от отрицательного вывода через фару к положительному выводу. Соответствующие комбинации химикатов в батарее разделяют заряды, так что отрицательный вывод имеет избыток отрицательного заряда, который отталкивается им и притягивается к избыточному положительному заряду на другом выводе. С точки зрения потенциала положительный вывод имеет более высокое напряжение, чем отрицательный. Внутри аккумулятора движутся как положительные, так и отрицательные заряды.

Пример \ (\ PageIndex {2} \): Сколько электронов проходит через фару каждую секунду?

Когда автомобильный аккумулятор на 12,0 В питает одну фару мощностью 30,0 Вт, сколько электронов проходит через нее каждую секунду?

Стратегия

Чтобы узнать количество электронов, мы должны сначала найти заряд, который перемещается за 1,00 с. Перемещаемый заряд связан с напряжением и энергией посредством уравнений \ (\ Delta U = q \ Delta V \). Лампа мощностью 30,0 Вт потребляет 30,0 джоулей в секунду. Поскольку батарея теряет энергию, мы имеем \ (\ Delta U = – 30 \, J \) и, поскольку электроны переходят от отрицательной клеммы к положительной, мы видим, что \ (\ Delta V = +12.0 \, V \).

Решение

Чтобы найти заряд q перемещенного, решаем уравнение \ (\ Delta U = q \ Delta V \):

\ [q = \ dfrac {\ Delta U} {\ Delta V}. \]

Вводя значения для \ (\ Delta U \) и \ (\ Delta V \), получаем

\ [q = \ dfrac {-30.0 \, J} {+ 12.0 \, V} = \ dfrac {-30.0 \, J} {+ 12.0 \, J / C} = -2,50 \, C. \]

Число электронов \ (n_e \) – это общий заряд, деленный на заряд одного электрона. То есть

\ [n_e = \ dfrac {-2.{19} \, электрон. \]

Значение

Это очень большое количество. Неудивительно, что мы обычно не наблюдаем отдельные электроны, так много которых присутствует в обычных системах. Фактически, электричество использовалось в течение многих десятилетий, прежде чем было установлено, что движущиеся заряды во многих обстоятельствах были отрицательными. Положительный заряд, движущийся в направлении, противоположном отрицательному, часто производит идентичные эффекты; это затрудняет определение того, что движется или оба движутся.{19} \, электроны \)

Электрон-вольт

Энергия, приходящаяся на один электрон, очень мала в макроскопических ситуациях, подобных тому, что было в предыдущем примере – крошечная доля джоуля. Но в субмикроскопическом масштабе такая энергия, приходящаяся на частицу (электрон, протон или ион), может иметь большое значение. Например, даже крошечной доли джоуля может быть достаточно, чтобы эти частицы разрушили органические молекулы и повредили живые ткани. Частица может нанести ущерб при прямом столкновении или может создать опасные рентгеновские лучи, которые также могут нанести ущерб.Полезно иметь единицу энергии, относящуюся к субмикроскопическим эффектам.

На рисунке \ (\ PageIndex {2} \) показана ситуация, связанная с определением такой единицы энергии. Электрон ускоряется между двумя заряженными металлическими пластинами, как это могло бы быть в телевизионной лампе или осциллографе старой модели. Электрон приобретает кинетическую энергию, которая позже преобразуется в другую форму – например, в свет в телевизионной трубке. (Обратите внимание, что с точки зрения энергии «спуск» для электрона означает «подъем» для положительного заряда.) Поскольку энергия связана с напряжением соотношением \ (\ Delta U = q \ Delta V \), мы можем рассматривать джоуль как кулон-вольт.

Рисунок \ (\ PageIndex {2} \): Типичная электронная пушка ускоряет электроны, используя разность потенциалов между двумя отдельными металлическими пластинами. По закону сохранения энергии кинетическая энергия должна равняться изменению потенциальной энергии, так что \ (KE = qV \). Энергия электрона в электрон-вольтах численно равна напряжению между пластинами. Например, разность потенциалов 5000 В производит электроны с энергией 5000 эВ.{-19} \, J. \]

Электрону, ускоренному через разность потенциалов 1 В, придается энергия 1 эВ. Отсюда следует, что электрон, ускоренный до 50 В, приобретает 50 эВ. Разность потенциалов 100 000 В (100 кВ) дает электрону энергию 100 000 эВ (100 кэВ) и так далее. Точно так же ион с двойным положительным зарядом, ускоренный до 100 В, получает 200 эВ энергии. Эти простые соотношения между ускоряющим напряжением и зарядами частиц делают электрон-вольт простой и удобной единицей энергии в таких обстоятельствах.

Электрон-вольт обычно используется в субмикроскопических процессах – химические валентные энергии, молекулярные и ядерные энергии связи входят в число величин, часто выражаемых в электрон-вольтах. Например, для разрушения некоторых органических молекул требуется около 5 эВ энергии. Если протон ускоряется из состояния покоя через разность потенциалов 30 кВ, он приобретает энергию 30 кэВ (30 000 эВ) и может разрушить до 6000 таких молекул \ ((30 000 \, эВ \,: \, 5 \, эВ \, на \, молекула = 6000 \, молекул) \).Энергия ядерного распада составляет порядка 1 МэВ (1000000 эВ) на событие и, таким образом, может нанести значительный биологический ущерб.

Сохранение энергии

Полная энергия системы сохраняется, если нет чистого добавления (или вычитания) из-за работы или теплопередачи. Для консервативных сил, таких как электростатическая сила, закон сохранения энергии утверждает, что механическая энергия постоянна.

Механическая энергия – это сумма кинетической энергии и потенциальной энергии системы; то есть \ (K + U = константа \).Потеря U для заряженной частицы становится увеличением ее K . Сохранение энергии выражается в форме уравнения как

\ [K + U = константа \] или \ [K_i + U_i = K_f + U_f \]

, где i и f обозначают начальные и конечные условия. Как мы уже много раз выясняли ранее, учет энергии может дать нам понимание и облегчить решение проблем.

Пример \ (\ PageIndex {3} \): электрическая потенциальная энергия преобразована в кинетическую энергию

Вычислите конечную скорость свободного электрона, ускоренного из состояния покоя через разность потенциалов 100 В.6 \, м / с. \]

Значение

Обратите внимание, что и заряд, и начальное напряжение отрицательны, как показано на рисунке \ (\ PageIndex {2} \). Из обсуждения электрического заряда и электрического поля мы знаем, что электростатические силы, действующие на мелкие частицы, обычно очень велики по сравнению с силой тяжести. Большая конечная скорость подтверждает, что гравитационная сила здесь действительно незначительна. Большая скорость также указывает на то, насколько легко ускорить электроны с помощью малых напряжений из-за их очень малой массы.В электронных пушках обычно используются напряжения, намного превышающие 100 В. Эти более высокие напряжения вызывают настолько большие скорости электронов, что необходимо учитывать эффекты специальной теории относительности, которые будут обсуждаться в другом месте. Вот почему в этом примере мы рассматриваем низкое напряжение (точно).

Упражнение \ (\ PageIndex {3} \)

Как этот пример изменится с позитроном? Позитрон идентичен электрону, за исключением того, что заряд положительный.

Ответ

Он будет двигаться в противоположном направлении, что не повлияет на представленные расчеты.p \ vec {E} \ cdot d \ vec {l}. \]

Из нашего предыдущего обсуждения потенциальной энергии заряда в электрическом поле результат не зависит от выбранного пути, и, следовательно, мы можем выбрать наиболее удобный интегральный путь. 2 } \ hat {r} \).2} dr = \ dfrac {kq} {r} – \ dfrac {kq} {\ infty} = \ dfrac {kq} {r}. \]

Этот результат,

\ [V_r = \ dfrac {kq} {r} \]

– это стандартная форма потенциала точечного заряда. Это будет подробнее рассмотрено в следующем разделе.

Чтобы изучить еще один интересный частный случай, предположим, что однородное электрическое поле \ (\ vec {E} \) создается путем размещения разности потенциалов (или напряжения) \ (\ Delta V \) на двух параллельных металлических пластинах, обозначенных A и B (Рисунок \ (\ PageIndex {3} \)).Изучение этой ситуации покажет нам, какое напряжение необходимо для создания определенной напряженности электрического поля. Это также покажет более фундаментальную взаимосвязь между электрическим потенциалом и электрическим полем.

Рисунок \ (\ PageIndex {3} \): соотношение между V и E для параллельных проводящих пластин равно \ (E = V / d \). (Обратите внимание, что по величине \ (\ Delta V = V_ {AB} \). Для заряда, который перемещается от пластины A при более высоком потенциале к пластине B при более низком потенциале, необходимо включить знак минус следующим образом : \ (- \ Delta V = V_A – V_B = V_ {AB} \).)

С точки зрения физика, \ (\ Delta V \) или \ (\ vec {E} \) можно использовать для описания любого взаимодействия между зарядами. Однако \ (\ Delta V \) является скалярной величиной и не имеет направления, тогда как \ (\ vec {E} \) является векторной величиной, имеющей как величину, так и направление. (Обратите внимание, что величина электрического поля, скалярная величина, представлена как E .) Связь между \ (\ Delta V \) и \ (\ vec {E} \) выявляется путем вычисления работы, выполняемой электрическая сила при перемещении заряда из точки A в точку B .Но, как отмечалось ранее, произвольное распределение заряда требует расчетов. Поэтому мы рассматриваем однородное электрическое поле как интересный частный случай.

Работа, совершаемая электрическим полем на рисунке \ (\ PageIndex {3} \) по перемещению положительного заряда q от A , положительная пластина, более высокий потенциал, к B , отрицательная пластина, более низкий потенциал. , это

\ [W = – \ Delta U = – q \ Delta V. \]

Разница потенциалов между точками A и B составляет

\ [- \ Delta V = – (V_B – V_A) = V_A – V_B = V_ {AB}.\]

Если ввести это в выражение для работы, получаем

\ [W = qV_ {AB}. \]

Работа равна \ (W = \ vec {F} \ cdot \ vec {d} = Fd \, cos \, \ theta \): здесь \ (cos \, \ theta = 1 \), поскольку путь параллелен поле. Таким образом, \ (W = Fd \). Поскольку \ (F = qE \), мы видим, что \ (W = qEd \).

Подстановка этого выражения для работы в предыдущее уравнение дает

\ [qEd = qV_ {AB}. \]

Заряд отменяется, поэтому для напряжения между точками мы получаем A и B .

Только в однородном E-поле: \ [V_ {AB} = Ed \] \ [E = \ dfrac {V_ {AB}} {d} \], где d – это расстояние от A до B , или расстояние между пластинами на рисунке \ (\ PageIndex {3} \). Обратите внимание, что это уравнение подразумевает, что единицы измерения электрического поля – вольт на метр. Мы уже знаем, что единицы измерения электрического поля – ньютоны на кулон; таким образом, верно следующее соотношение между единицами:

\ [1 \, N / C = 1 \, В / м. \]

Кроме того, мы можем продолжить это до интегральной формы.B \ vec {E} \ cdot d \ vec {l}. \]

В качестве демонстрации из этого мы можем вычислить разность потенциалов между двумя точками ( A, и B ), равноудаленными от точечного заряда q в начале координат, как показано на рисунке \ (\ PageIndex {4} \) . 2} \ hat {r} \).6 В / м \). Выше этого значения поле создает достаточную ионизацию в воздухе, чтобы сделать воздух проводником. Это допускает разряд или искру, которые уменьшают поле. Каково же максимальное напряжение между двумя параллельными проводящими пластинами, разделенными 2,5 см сухого воздуха?

Стратегия

Дано максимальное электрическое поле E между пластинами и расстояние d между ними. Мы можем использовать уравнение \ (V_ {AB} = Ed \) для вычисления максимального напряжения.4 \, V \] или \ [V_ {AB} = 75 \, kV. \]

(Ответ состоит только из двух цифр, поскольку максимальная напряженность поля является приблизительной.)

Значение

Одним из следствий этого результата является то, что требуется около 75 кВ, чтобы совершить скачок искры через зазор размером 2,5 см (1 дюйм), или 150 кВ для искры 5 см. Это ограничивает напряжения, которые могут существовать между проводниками, возможно, на линии электропередачи. Меньшее напряжение может вызвать искру, если на поверхности есть шипы, поскольку острые точки имеют большую напряженность поля, чем гладкие поверхности.Влажный воздух разрушается при более низкой напряженности поля, а это означает, что меньшее напряжение заставит искру проскочить через влажный воздух. Наибольшие напряжения могут создаваться статическим электричеством в засушливые дни (рис. \ (\ PageIndex {5} \)).

Рисунок \ (\ PageIndex {5} \): Искровая камера используется для отслеживания траекторий частиц высоких энергий. Ионизация, создаваемая частицами при прохождении через газ между пластинами, позволяет искре прыгнуть. Искры расположены перпендикулярно пластинам, следуя силовым линиям электрического поля между ними.Разность потенциалов между соседними пластинами недостаточно высока, чтобы вызвать искры без ионизации, производимой частицами из экспериментов на ускорителях (или космическими лучами). Эта форма детектора сейчас устарела и больше не используется, кроме как в демонстрационных целях. (кредит b: модификация работы Джека Коллинза)

Пример \ (\ PageIndex {1B} \): Поле и сила внутри электронной пушки

Электронная пушка (рисунок \ (\ PageIndex {2} \)) имеет параллельные пластины, разделенные расстоянием 4,00 см, и дает 25 электронов.0 кэВ энергии. а) Какова напряженность электрического поля между пластинами? б) Какую силу это поле окажет на кусок пластика с зарядом \ (0,500- \ мкКл), который проходит между пластинами?

Стратегия

Поскольку напряжение и расстояние между пластинами указаны, напряженность электрического поля может быть вычислена непосредственно из выражения \ (E = \ frac {V_ {AB}} {d} \). Как только мы узнаем напряженность электрического поля, мы можем найти силу, действующую на заряд, используя \ (\ vec {F} = q \ vec {E} \).Поскольку электрическое поле имеет только одно направление, мы можем записать это уравнение в терминах величин, \ (F = qE \).

Решение

а. Выражение для величины электрического поля между двумя однородными металлическими пластинами равно

\ [E = \ dfrac {V_ {AB}} {d}. \] Поскольку электрон является однозарядным и ему дается энергия 25,0 кэВ, разность потенциалов должна составлять 25,0 кВ. Вводя это значение для \ (V_ {AB} \) и расстояния между плитами 0,0400 м, получаем \ [E = \ frac {25.5 В / м) = 0,313 \, Н. \]

Значение Обратите внимание, что единицы измерения – ньютоны, поскольку \ (1 \, V / m = 1 \, N / C \). Поскольку электрическое поле между пластинами однородно, сила, действующая на заряд, одинакова независимо от того, где находится заряд между пластинами.

Пример \ (\ PageIndex {4C} \): расчет потенциала точечного заряда

Учитывая точечный заряд \ (q = + 2,0-n C \) в начале координат, вычислите разность потенциалов между точкой \ (P_1 \) на расстоянии \ (a = 4,0 \, см \) от q и \ (P_2 \) расстояние \ (b = 12.2} \ hat {r} \ cdot r \ hat {\ varphi} d \ varphi \), но \ (\ hat {r} \ cdot \ hat {\ varphi} = 0 \) и, следовательно, \ (\ Delta V = 0 \). Складывая две части вместе, получаем 300 В.

Значение

Мы продемонстрировали использование интегральной формы разности потенциалов для получения численного результата. Обратите внимание, что в этой конкретной системе мы могли бы также использовать формулу для потенциала из-за точечного заряда в двух точках и просто взять разницу.

Упражнение \ (\ PageIndex {4} \)

Из приведенных примеров, как энергия удара молнии зависит от высоты облаков над землей? Считайте систему облако-земля двумя параллельными пластинами.

Ответ: При фиксированной максимальной напряженности электрического поля потенциал, при котором происходит удар, увеличивается с увеличением высоты над землей. Следовательно, каждый электрон будет переносить больше энергии. Определение влияния на общее количество электронов – дело будущего.

Прежде чем описывать проблемы, связанные с электростатикой, мы предлагаем стратегию решения проблем, которой следует придерживаться для этой темы.

Стратегия решения проблем: электростатика

Изучите ситуацию, чтобы определить, присутствует ли статическое электричество; это может касаться отдельных стационарных зарядов, сил между ними и создаваемых ими электрических полей.
Определите интересующую систему. Это включает в себя указание количества, местоположения и типов взимаемых сборов.
Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен. Определите, следует ли рассматривать кулоновскую силу напрямую – если да, может быть полезно нарисовать диаграмму свободного тела, используя силовые линии электрического поля.
Составьте список того, что дано или может быть выведено из проблемы, как указано (указать известные).Например, важно отличать кулоновскую силу F от электрического поля E .
Решите соответствующее уравнение для количества, которое необходимо определить (неизвестное), или нарисуйте линии поля, как требуется.
Изучите ответ, чтобы увидеть, разумен ли он: имеет ли он смысл? Правильны ли единицы и разумны ли числа?

Авторы и авторство

Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами.Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

Формулы электричества: введение, типы и объяснение

Введение в электричество

Физическое явление с наличием и потоком электрического заряда называется электричеством. Чтобы понять, как образуется электричество, это происходит, когда электроны неплотно упакованы ядром, они легко перемещаются внутри тела.Известно, что они являются отрицательно заряженными частицами, поэтому, когда они производят несколько зарядов, это движение называется электрическим током или электричеством.

Различные типы, вызывающие электричество

Электрический заряд – это свойство субатомных частиц, которое определяет их электромагнитную связь.

Электрический ток – Типичный поток заряженных электрических частиц, измеряемый в амперах. ).Это заставляет электрическое поле создавать силу на другие заряды, находящиеся поблизости. Когда заряды движутся, они создают магнитное поле.

Электрический потенциал – показывает калибр электрического поля для работы с электрическим зарядом, который измеряется в вольтах.

Прежде чем перейти к формулам электричества, ниже приводится глоссарий терминологии и определений, связанных с электричеством.

Разница потенциалов – когда есть необходимость переместить электрический заряд между двумя выбранными точками, то работа, выполняемая таким образом, называется разницей потенциалов.Проще говоря, это определяется как работа, проделанная для перемещения одного заряда из одной точки в другую.

I.e V (единица измерения разности потенциалов S.I) = W (от одной точки к другой).

Таким образом, мы можем определить, что 1 вольт или 1 В = 1 Дж (Джоуль) или 1 кулон.

Итак, разность потенциалов называется 1 вольт, когда 1 Дж работы выполняется путем перемещения заряда из одной точки в другую. Вольтметр – это оборудование, которое используется для измерения его величины. Кроме того, соединение является параллельным из-за его высокого удельного сопротивления, а разность потенциалов остается постоянной.

Мощность – определяется как скорость выполнения работы, другими словами, это работа, выполненная в единицу времени. Стандартная единица мощности – ватт (Вт), что означает джоули в секунду.

Заряд – для определения электрического заряда это свойство материи, которое заставляет ее испытывать силу, когда она находится в электромагнитном поле. Он состоит из двух зарядов, положительных и отрицательных, где одинаковые заряды отталкиваются, а разные – притягиваются.

Работа или энергия – Работа в физике определяется как мера передачи энергии, которая происходит, когда объект перемещается из-за внешней силы в направлении смещения

Сопротивление – это свойство проводника где он сдерживает прохождение тока через него.Резистор – это часть цепи, которая препятствует прохождению тока. Для обеспечения переменного сопротивления используется устройство под названием реостат.

Электрический ток – это количество заряда, проходящего через определенную область в единицу времени. Электрический ток – это непрерывное движение отрицательно заряженных частиц, называемых электронами. Они перемещаются от отрицательной клеммы к положительной клемме аккумулятора.

Удельное сопротивление – это электрическое сопротивление проводника единичного поперечного сечения и единичной длины.Сопротивление прямо пропорционально протяженности проводника и обратно пропорционально площади поперечного сечения проводника.

Электродвижущая сила – электродвижущая сила относится к электрическому потенциалу, который возникает в результате электрохимического воздействия или изменения магнитного поля. Единица S.I для электродвижущей силы – джоуль на кулон.

Закон Ома – это соотношение, которое существует между разностью потенциалов, приложенной к концам проводника, и током, протекающим через проводник.Проще говоря, если физическое состояние проводника остается неизменным, тогда ток, протекающий через проводник, всегда прямо пропорционален разности потенциалов на двух концах проводника.

Проводники – Вещества, через которые легко протекают электрические заряды, называются проводниками. Известно, что в проводниках больше свободных электронов, неплотно упакованных ядрами своих атомов.

Изоляторы. Вещества, через которые с трудом проходят электрические заряды, называются изоляторами.Изоляторы не имеют свободных электронов и плотно упакованы ядрами своих атомов.

Эквивалентное сопротивление – Эквивалентное сопротивление – это суммарное сопротивление, подключенное параллельно или последовательно.

Закон комбинированного сопротивления при параллельном подключении – Закон комбинированного сопротивления при параллельном подключении гласит, что величина, обратная суммарному сопротивлению всех параллельно подключенных резисторов, равна сумме обратных величин всех индивидуальных сопротивлений.

Символы и единицы СИ, представленные в главе Электричество

906 (В)

906 м

на 905 потока зарядов (Q) через проводник называется и определяется выражением

Ток – Заряд / Время или t = Q / t, где S.I единица измерения тока – ампер (А)

1 ампер = 1 кулон / 1 секунда

Примеры вопросов для формулы тока

Электрическая лампа светит ровно 4 часа и получает ток 0,5 А. Определить количество заряда, протекающего через лампу.

Отв. Ток I = 0,5 A

Затраченное время t = 4 часа

t = 4 × 3600 = 14400 с,

Заряд Q = I × t

= 0,5 × 14400

Q = 7200 C

Электрическая лампа светится ровно 8 часов в сутки.Он получает ток 1 А. Определите количество заряда, проходящего через лампу.

Отв. Ток, I = 1 A

Затраченное время, t = 8 часов

Затраченное время = 8 × 3600

Затраченное время = 28800 с,

Теперь, количество заряда,

Q = I × t

Q = 1 × 28800

Q = 28800 C

Разница потенциалов – Разность потенциалов между двумя концами в цепи описывается как работа, выполняемая для перемещения электрического заряда из разных точек в электрической цепи.

Для расчета потенциальной разницы –

Потенциальная разница = выполненная работа / заряд или V = Вт / квартал

Решенные вопросы о потенциальной разнице

Рассчитайте выполненную работу, чтобы нести заряд в 3 К, если разность потенциалов между двумя баллов – 10 В.

Отв. Приведенный заряд = 3C

Разница потенциалов между двумя концами = 10 В

Выполненная работа (Вт) =?

V = W / Q

Итак, W = V x Q

W = 10V x 3C = 30J

5000 Дж работы будет выполнено, чтобы нести сколько заряда между двумя точками, имеющими разность потенциалов 100 V ?

Отв.Принято, что разность потенциалов = 100 В

Выполненная работа (Вт) = 5000 Дж

Заряд (Q) =?

Так как V = W / Q

Q = W / V

Q = 5000 Дж / 100V = 50C

Закон Ома = разность потенциалов в двух точках проводника прямо пропорциональна току, протекающему по цепи где температура постоянна.

Математически это представлено как –

V ∝ I или V = IR, I = VR & R = V / I

Где R – постоянное сопротивление для любого данного металла.

Значение сопротивления зависит от природы и физических размеров конкретного проводника.

Решенные вопросы по закону Ома

В электрической цепи есть батарея на 24 В и резистор на 60 Ом. Какой будет ток в цепи? Сопротивлением соединительного провода можно пренебречь.

Отв. Учитывая это, разность потенциалов (В) = 24 В

И сопротивление = 60 Ом

Ток (I) =?

Поскольку R = V / I, тогда I = V / R

I = V / R

I = 24 В / 60 Ом = 0.4A

Если разность потенциалов между концами электродвигателя составляет 220 В и через него проходит электрический ток силой 5 А, каково будет сопротивление электродвигателя?

Отв. Учитывая, что электрический ток (I) = 5 А

Разность потенциалов (В) = 220 В

Сопротивление (R) =?

Так как R = V / I

Итак, R = 220 В / 5 А = 44 Ом

Закон Кулона = он гласит, что сила притяжения или отталкивания между двумя неподвижными точечными зарядами прямо пропорциональна произведению величины двух зарядов. и обратно пропорциональна квадрату расстояния между ними.

Для ясного понимания

На рисунке изображены два заряда q1 и q2, и эти два заряда разделены расстоянием r. Затем, согласно закону Кулона, сила притяжения или отталкивания между ними равна – F ∝ q1q2 или F ∝ 1 / (r) 2

Следовательно,

F ∝ q1q2 / (r) 2

Или

F = k q1q2 / (r) 2

Где k – коэффициент пропорциональности. Значение k зависит от таких факторов, как природа среды между двумя зарядами.

Электроэнергия – это скорость, с которой энергия потребляется в электрической цепи.

Мощность = Напряжение x Ток

Вывод формулы мощности –

Мы знаем, что потенциальная разница = Выполненная работа / Зарядка

В = Вт / Кв

Кроме того, Вт = В x Q… .. (I )

Сейчас,

Мощность = Выполненная работа / Затраченное время

P = W / T

Положим W = VQ

P = V (Q / T)

Таким образом, P = V x I

Решенные вопросы on Electric Power

Электрический нагреватель имеет разность потенциалов 220 В и сопротивление 70 Ом.Определите величину тока, протекающего через нагреватель.

Отв. Предполагается, что:

Сопротивление R = 70 Ом

Напряжение V = 220 В

Используя формулу тока:

I = V / R

= 220/70

I = 3,1428 A

Электрическая лампа светится ровно 4 часа и выдает ток 0,5 А. Определите количество заряда, проходящего через лампу.

Отв. Ток I = 0,5 A

Затраченное время t = 4 часа

t = 4 × 3600 = 14400 с,

Q = I × t

= 0.5 × 14400

Q = 7200 C

Удельное сопротивление – это протекание тока от одного конца к другому в материале

Рассчитывается как

ρ = RA / l.

Где ρ – удельное сопротивление, R – сопротивление, l – длина материала и A – площадь поперечного сечения.

Некоторые другие важные формулы

Комбинация серий – цепь подключается последовательно, когда через резисторы проходит равная величина тока.В таких схемах напряжение вокруг каждого резистора разное. При последовательном соединении, если обнаруживается, что какой-либо резистор имеет технические проблемы, вся цепь отключается.

Он рассчитывается как: Rtotal = R1 + R2 +… .. + Rn

Параллельная комбинация – Считается, что цепь подключена параллельно, когда напряжение на резисторах одинаковое. В таких цепях ток рассеивается и снова объединяется, когда ветви встречаются в общей точке.

Рассчитывается как: 1 / RTotal = 1 / R1 + 1 / R2 ………..1 / R (n)

для равных сопротивлений

Rs = nR (для последовательного соединения)

Rp = R / n (для параллельного соединения) \

Rs / Rp = n ²

Rs = эффективное Последовательное сопротивление

Rp = Эффективное сопротивление при параллельном подключении

Мощность (P) = Работа (Вт) / Время (T) = Потребляемая энергия / Время

Мощность = Разница потенциалов x Ток x время; W = V x I x t

(W = I ² RT) = (W = V ² т / об)

Мощность = разность потенциалов x ток; P = W x T

Мощность = (ток) 2 x Сопротивление; P = I ² x R

Мощность = (разность потенциалов) 2./Сопротивление ; P = V2 / R

Электроэнергия = Мощность x время; Электрическая энергия = P xt

Вопросы за предыдущий год

Вопрос:

(a) С помощью подходящей принципиальной схемы докажите, что величина, обратная эквивалентному сопротивлению группы параллельно соединенных сопротивлений, равна сумма обратных величин отдельных сопротивлений.

(б) В электрической цепи два резистора по 12? каждый из них подключается параллельно к батарее на 6 В.Найдите ток, потребляемый от батареи. (2019)

Отв.

Видно, что общая величина тока I равна сумме различных токов.

I = I? + I? + I? … (I)

Возьмем Rp как эквивалентное сопротивление комбинации резисторов, сформированных параллельно.

Вопрос:

Лампа электрическая сопротивления 20? а проводник сопротивления 4? подключены к батарее 6 В, как показано на схеме.Вычислите:

(a) общее сопротивление цепи,

(b) ток в цепи,

(г) мощность лампы. (2019)

Отв.

Вопрос:

(а) Как вы с помощью эксперимента сделаете вывод, что один и тот же ток течет через каждую часть цепи, содержащей три последовательно подключенных резистора к батарее?

(b) Рассмотрите данную схему и найдите ток, протекающий в цепи, и разность потенциалов на 15? резистор при замкнутой цепи.(За пределами Дели, 2019 г.)

Отв.

Возьмем R ₁, R ₂, R ₃ в качестве трех резисторов, которые подключены последовательно, а также к батарее, амперметру и ключу, как показано ниже:

Когда ключ закрыт, ток течет по цепи. Затем, получая показания амперметра, когда мы перемещаем положение амперметра между резисторами, мы получим конкретное показание. Когда мы примем во внимание оба показания, мы сможем увидеть, что в обоих случаях показания будут одинаковыми в отношении тока, протекающего через каждую часть цепи.

Имеем, R ₁ = 5? , R ₂ = 10 ?, R ₃ = 15 ?, V = 30V

Сумма сопротивлений R = R ₁ + R ₂ + R ₃ [5 ?, 10 ?, 15? связаны в формате серии]

= 5 + 10 + 15

= 30?

Разность потенциалов может быть обозначена как V = 30V

Нам нужно найти схему, I

Извлекая из закона Ома, получаем,

I = V / R = 30/30 = 1A

Ток, протекающий внутри схема 1А

Разность потенциалов на протяжении 15? резисторы = IR ₃ = 1 * 15 = 15V

Вопрос:

Три резистора R ₁, R ₂ и R ₃ подключены параллельно, и комбинация подключена к батарее, амперметру , вольтметр и ключ.Нарисуйте подходящую принципиальную схему и получите выражение для эквивалентного сопротивления комбинации резисторов.

(b) Рассчитайте эквивалентное сопротивление следующей сети: (За пределами Дели, 2019 г.)

Отв.

Возьмем R ₁, R ₂ и R ₃ как три сопротивления, которые соединены параллельно друг с другом, а R – эквивалентное сопротивление цепи. Комбинация представлена батареей с напряжением вольт на концах.Когда переключатель ключа замкнут, ток I проходит по цепи следующим образом:

Вопрос:

Значения тока (I), протекающего через данный резистор сопротивления (R ), соответствующие значения разности потенциалов (В) на резисторе приведены ниже: [2]

Физическое количество	Символы	Единица СИ
Вольт
Мощность	P	Ватт (Вт)
Заряд	Q		Q
Рабочая энергия	W	Джоуль (Дж)
Сопротивление		R Ом 0	I 90 685	Ампер (A)
Удельное сопротивление	ρ	Ом метр (Ом м)

906

В (вольт)	0,5	1.0	1,5	2,0	2,5	3,0	4,0	5,0
0,2	0,3	0,4	0,5	0,6	0.8	1.0

Отв.

Имеем V = IR

Из графика:

V = 0,5

I = 0,1

0,5 = 0,1 * R

R = 5?

Заключение

Данный товар является частью воздействия токов и имеет всего 13 оценок.
CBSE посоветовал школам не разделять учащихся на разные группы, а позволить им брать те предметы, которые они хотят выбрать.
Студентам рекомендуется регулярно отрабатывать соответствующие вопросы, чтобы успешно сдать выпускной экзамен.
Студенты также могут проверить образцы экзаменов и различные практические задания, предоставленные ncert, на их официальном сайте.

Расчет электрических сил, полей и потенциала – видео и стенограмма урока

Электрическое поле

Электрические заряды также могут создавать электрические поля. Электрическое поле – это то, что исходит от заряженной частицы в окружающее ее пространство.Один заряд генерирует стандартное электрическое поле, в то время как несколько полей заряда объединяются, чтобы создать «чистое» электрическое поле. Электрические поля направлены от положительных зарядов во всех направлениях, и они указывают на отрицательные заряды во всех направлениях.

На диаграмме показано чистое электрическое поле, создаваемое двумя зарядами:

Электрические поля подобны связям между двумя людьми в нашей комнате. Их интересы направлены в одном направлении или они противоположны друг другу? Будет ли новый человек в комнате двигаться к человеку слева или справа в зависимости от их интересов?

Если небольшой пробный заряд поместить в электрическое поле из нашего сценария, он будет двигаться вдоль силовых линий.Если тестовый заряд был положительным, он двигался бы вместе с направлением чистого электрического поля, а если отрицательный, он двигался бы против направления чистого электрического поля.

Рассчитаем чистое электрическое поле на расстоянии 1,5 мм от обоих зарядов, обозначенное X на этой диаграмме:

Уравнение электрического поля:

где:

| E | – величина электрического поля в ньютонах на кулон (Н / Кл)
q – величина заряда в кулонах
k – постоянная Кулона
r – расстояние от заряда в метрах (м)

У нас есть два заряда, поэтому сначала нужно определить электрическое поле, создаваемое ими обоими, а затем выполнить сложение векторов.Мы не будем обращать внимания на знаки зарядов, пока не будет определена величина. Затем мы решим, является ли поле положительным или отрицательным, в зависимости от того, как электрическое поле указывает на X. Начнем с заряда 1 (q1):

(Первый заряд положительный, поэтому мы присвоили ему положительный знак.)

Затем мы вычислим электрическое поле, возникающее из-за заряда 2 (q2):

(Заряд 2 отрицательный, поэтому мы поставили ему знак минус.)

При добавлении векторов мы обязательно добавляем компоненты в одном направлении. Складывая электрические поля, получаем:

Электрический потенциал

Электрический потенциал – это энергия на единицу заряда, также известная как напряжение (В). Напряжение – это «толчок», который перемещает нового человека, вошедшего в нашу комнату, к определенному месту или от него, в зависимости от обвинений между двумя исходными людьми.

Электрические заряды перемещаются из-за разницы в напряжении. Это называется разностью потенциалов, которая показывает, как работают батареи. Мы можем вычислить электрические потенциалы каждого из наших точечных зарядов в средней точке между ними.

Формула напряжения:

В – напряжение в вольтах (В)
k – постоянная Кулона
q – это обвинение
d – расстояние от заряда, q

Чтобы вычислить напряжение в средней точке, мы должны определить напряжения для каждого заряда и просто сложить их, потому что они не являются векторами.Напряжение от q1 в средней точке:

и от q2:

и сетевое напряжение:

Если электрическое поле постоянно, напряжение является произведением электрического поля и расстояния между зарядами.

Итоги урока

Давайте рассмотрим…

Когда присутствует более одного заряда, существует электрическая сила. Сила – это толкание или притяжение объекта, являющееся вектором. Если заряды противоположны по знаку, они притягиваются. Если заряды одного знака, они отталкиваются друг от друга. Это легко представить, если подумать о том, как магнитные полюса реагируют друг на друга. Поскольку сила является вектором, результирующая сила равна векторной сумме всех сил между зарядами.

Электрическое поле также является вектором и исходит от заряженной частицы в окружающее ее пространство. Силовые линии электрического поля движутся от положительных зарядов к отрицательным.Если рядом с исходными зарядами, которые сформировали электрическое поле, есть какие-либо другие заряды, они будут двигаться вдоль силовых линий. Величина электрического поля аналогична уравнению электрической силы, но включает только один заряд вместо двух.

Другой аспект электрического заряда – это электрический потенциал , который представляет собой энергию на единицу заряда; также называется напряжением. Напряжение можно рассчитать для каждого заряда исходя из расстояния до заряда.Также важно отметить, что это не вектор.

Напряжение также является произведением постоянного электрического поля и расстояния между зарядами.

HSC Физический модуль 6 Электромагнетизм

Категория: Физика

Это Часть II серии пересмотров формул, охватывающая Модуль 6 (Электромагнетизм).Щелкните здесь, чтобы просмотреть ссылки на Модуль 5, Модуль 7 и Модуль 8.

Знание, где искать формулу, как ее применять и как ее интерпретировать, необходимо для успешной сдачи экзаменов HSC Physics или пробных экзаменов. Справочный лист является бесценным инструментом, поэтому в этом руководстве по пересмотру мы объясним данные формулы и дадим некоторое представление обо всех формулах и типах вопросов, в которых они применяются. Формулы описаны в тематическом порядке, который не всегда соответствует в том же порядке, в каком они даны в справочном листе.Однако таким образом будет легче понять, как они связаны и применяются, поскольку многие формулы тематически «связаны». Кроме того, здесь не рассматриваются многие формулы 11-го года обучения, которые не имеют отношения к большинству вопросов по HSC Physics.

Электрические поля

Напряжение

Электрический потенциал определяется как количество энергии на единицу заряда заряженной частицы внутри электрического поля из-за ее положения. Его можно рассматривать как эквивалент гравитационной потенциальной энергии.Однако в физике нас больше интересует разность электрических потенциалов между двумя точками, а не $ ΔV $ или просто $ V $. Короче говоря, это также известно как напряжение между двумя точками. $$ V = \ frac {ΔU} {q} $$

Однородные электрические поля

Первая приведенная формула описывает напряженность однородного электрического поля между двумя металлическими пластинами. $$ E = \ frac {V} {d} $$ $ E $ представляет электрическое поле, а $ V $ – напряжение между двумя пластинами. Помните, что напряжение – это разница между двумя параллельными пластинами (в HSC Physics оно всегда должно быть положительным, поскольку мы вычисляем величину $ E $).

Электростатическая сила

Электростатическая сила – это сила, прилагаемая, когда объект или частица с зарядом $ q $ попадает в электрическое поле с напряженностью $ E $: $$ F = qE $$ E $ здесь представляет собой напряженность электрического поля. Почти всегда в HSC Physics это будет использоваться в вопросах с однородным электрическим полем (параллельные силовые линии электрического поля между металлическими пластинами). Направление силы зависит от типа заряда:
• Положительные заряды испытывают силу по отношению к отрицательному напряжению.
• Отрицательные заряды действуют по направлению к положительному напряжению.

Более подробную информацию об электрических полях можно найти здесь.{-3} $
• $ q_1 $ и $ q_2 $ – это две платы соответственно
• $ r $ – расстояние между центрами двух заряженных частиц.

Направление электростатической силы в этом случае зависит от знака двух зарядов:

Работа

В справочном листе есть две формулы для расчета работы, совершаемой заряженной частицей при ее движении в электрическом поле. $$ W = qV $$ $$ W = qEd $$ В первом случае заряженная частица с зарядом $ q $ движется между двумя точками с напряжением $ V $.
Во втором случае заряженная частица с зарядом $ q $ перемещается на расстояние $ d $ внутри однородного электрического поля с напряженностью $ E $.

Здесь следует помнить, что если:
• Положительный заряд движется в том же направлении, что и силовая линия электрического поля, работа выполняется посредством частицы. Это движение спонтанное (происходит само по себе).
• Положительный заряд движется в направлении, противоположном силовой линии электрического поля, работа выполняется на частице . Это движение не является самопроизвольным (для его выполнения требуется внешняя энергия / работа).

Очевидно, что вышеупомянутые правила обратны для отрицательных зарядов.

Магнитные поля

Напряженность магнитного поля (также известная как плотность магнитного потока)

Магнитные поля возникают вокруг движущихся заряженных частиц, проводников с током, постоянных магнитов или электромагнитов. Как и другие поля, они определяются как области пространства, в которых происходят магнитные взаимодействия. Вы можете узнать больше о магнитных полях здесь.

Хотя в основном полезны в 11-м классе, есть две формулы для расчета величины напряженности магнитного поля ($ B $): $$ B = \ frac {μ_0I} {2πr} $$ $$ B = \ frac {μ_0NI} {L} $$ Первая формула используется для расчета напряженности поля на расстоянии $ r $ от прямого токопровода с током $ I $.
Вторая формула используется для расчета напряженности поля внутри соленоида длиной $ L $, имеющего $ N $ витков, по которым проходит ток $ I $.

Направление силовых линий магнитного поля можно определить с помощью правила для правой руки:

Магнитный поток

Магнитный поток представляет собой количество силовых линий магнитного поля, проходящих через область. Обозначение магнитного потока $ Φ $ измеряется в Веберсах (Вб). Это зависит от площади, через которую проходят линии ($ A $), плотности магнитного потока ($ B $) и угла между силовыми линиями и нормалью к плоскости области ($ θ $).$$ Φ = BA \ cos {θ} $$ Мы можем использовать пример с количеством капель дождя (представляющих магнитный магнитный поток), проходящих через круговое кольцо под разными углами, чтобы понять концепцию магнитного потока и угла:

Отсюда следует, что:
• Максимальный магнитный поток через зону возникает, когда плоскость площадки перпендикулярна силовым линиям магнитного поля (θ = 0 °).
• Нулевой магнитный поток через зону возникает, когда плоскость площадки параллельна силовым линиям магнитного поля (θ = 90 °).

Магнитная сила на движущемся заряде

Каждый раз, когда заряженная частица с зарядом $ q $ движется в магнитном поле напряжённостью $ B $ со скоростью $ v $, на нее действует сила, равная: $$ F = qvB \ sinθ $$ Прост в использовании, вам просто нужно быть осторожным, чтобы избежать “ловушки” с углом. Угол $ θ $ здесь – угол между вектором скорости и силовыми линиями магнитного поля.

Вы также должны помнить, что направление силы определяется правилом для правой руки.2} {r} = qvB \ sinθ $$ $$ R = \ frac {mv} {qB \ sinθ} $$

Моторный эффект

Эффект двигателя и его применение в двигателях постоянного и переменного тока описано более подробно здесь.

Магнитная сила, действующая на проводник с током

Сила моторного эффекта – это магнитная сила, приложенная к проводнику с током длиной $ l $, находящемуся в магнитном поле: $$ F = liB \ sinθ $$ Несколько вещей, о которых следует соблюдать осторожность:
• Как и в случае движущихся зарядов, угол $ θ $ – это угол между силовыми линиями магнитного поля ($ B $) и током ($ I $).В большинстве случаев, когда катушка двигателя вращается в магнитном поле, она должна составлять 90 градусов для двух сторон (постоянная) и, следовательно, $ \ sinθ = 1 $. Будьте очень осторожны с вопросами о ловушках, которые дают вам угол, но это не требуется для расчета силы моторного эффекта! Например, вопрос по физике HSC ниже:

Угол 30 ° вообще не должен использоваться в формуле силы моторного эффекта, поскольку угол между $ B $ и $ I $ фактически равен 90 ° (в 3-х измерениях). 30 ° по-прежнему полезно, чтобы найти длину проводника с помощью теоремы Пифагора.Попробуйте и посмотрите, правильно ли вы понимаете!
• Если у вас квадратная или прямоугольная катушка, вы должны применить формулу моторного эффекта для перпендикулярной и параллельной сторон поля отдельно (следовательно, углы будут 90 ° и 0 ° соответственно).
• Направление силы можно найти с помощью правила правой руки: большой палец – это направление тока, пальцы – направление силовых линий, а ладонь – направление силы моторного эффекта.

Магнитная сила на двух параллельных токоведущих проводниках

Эта формула представляет собой конкретное приложение силы воздействия двигателя, когда есть два параллельных проводника длиной $ l $, несущие токи $ I_1 $ и $ I_2 $ и разделенные расстоянием $ r $: $$ \ frac {F} {l} = \ frac {μ_0I} {2π} \ frac {I_1 I_2} {r} $$ Для этой формулы вам нужно помнить:
• Когда токи имеют одинаковое направление, проводники притягиваются.
• Когда токи имеют противоположное направление, проводники отталкиваются. (Вы можете вывести эти правила, применяя правила для ладони и захвата правой руки).
• Вы должны применять эту формулу отдельно для каждого проводника; согласно третьему закону Ньютона, существует пара сил, по одной на каждый проводник с равными величинами и противоположными направлениями.
• Длина провода $ l $ – это всегда длина, на которую перекрываются оба проводника – если один из них длиннее, вы должны пренебречь дополнительной длиной.

Крутящий момент на обмотке двигателя

Эта формула представляет собой конкретное приложение крутящего момента к катушкам двигателя, по которым протекает ток в магнитном поле.$$ τ = nBIA \ sin {θ} $$ Здесь $ A $ представляет площадь катушки двигателя, а $ θ $ – угол между нормалью к плоскости катушки и линиями магнитного поля. На рисунке ниже угол воздействия двигателя для расчета силы по бокам составляет 90 °, поскольку левая и правая стороны перпендикулярны силовым линиям. Нормаль к плоскости катушки под углом и силовые линии также имеют угол 90 °.

Однако имейте в виду, что углы $ θ $ в формуле крутящего момента и формуле силы воздействия двигателя не всегда одинаковы; см. примеры здесь.

Электромагнитная индукция

Более подробную информацию о явлении электромагнитной индукции можно найти здесь. Электромагнитная индукция – одно из основных понятий физики HSC. Он описывает индукцию электродвижущей силы ($ EMF $) в результате ненулевой скорости изменения потока через контур с $ N $ витками: $$ EMF = -N \ frac {ΔΦ} {Δt} $$ Эта формула иногда известна как закон Фарадея / Ленца. Перво-наперво, $ EMF $ звучит как сила (ElectroMotive Force), но на самом деле это напряжение, поэтому оно измеряется в вольтах.Каждый раз, когда происходит изменение количества магнитных линий, проходящих через область (из-за перемещения компонентов относительно друг друга или изменения магнитного поля), отношение $ \ frac {ΔΦ} {Δt} $ не равно нулю. а значит будет и ЭДС. На следующей диаграмме представлен возможный пошаговый подход к рассуждению, которому вы можете следовать, чтобы объяснить большинство ситуаций.

Вы всегда должны пытаться определить изменение магнитного потока на шаге 2 с точки зрения увеличения / уменьшения магнитного потока (силовых линий) через область и их направления.Например, изменение может быть «более сильным потоком, выходящим за пределы страницы». На шаге 7 закон Ленца всегда заставляет поле $ B_2 $ противодействовать этому изменению – в нашем примере это будет «меньший поток, выходящий за пределы страницы», или «более высокий поток, проходящий внутри страницы» (оба утверждения эквивалентны).

Следует отметить, что более точный способ вычисления $ EMF $ – это мгновенная скорость изменения (однако в HSC Physics расчет не используется): $$ EMF = -N \ frac {dΦ} {dt} $$

Трансформаторы

Трансформатор – это электрическое устройство, используемое для изменения переменного напряжения между двумя частями цепи.Он основан на принципе электромагнитной индукции.

Существует несколько конфигураций и типов трансформаторов в зависимости от того, для чего они нужны. В HSC Physics мы почти всегда предполагаем, что трансформатор идеален; это означает, что потери мощности при преобразовании напряжения равны нулю. Формулы трансформатора имеют следующий вид: $$ \ frac {V_p} {V_s} = \ frac {N_p} {N_s} $$ $$ V_pV_s = I_pI_s $$ Приложения в вопросах физики HSC просты: индекс «$ p $» относится к первичной катушке, «$ s $» относится к вторичной катушке, и, очевидно, $ V $, $ I $ и $ N $ представляют напряжение, ток. и количество витков соответственно.

Электрические цепи (11 год физики)

Электрический ток

Иногда вам, возможно, придется ссылаться или рассчитывать ток, исходя из первых принципов. Ток определяется как количество электрического заряда $ q $, протекающего через поперечное сечение за время $ t $, или скорость изменения заряда. $$ I = \ frac {q} {t} $$

Закон Ома

В редких случаях вы можете получить некоторые вопросы на экзаменах по физике HSC с использованием закона Ома. Напомним, что закон Ома показывает падение напряжения $ V $, которое происходит, когда ток $ I $ проходит через резистор с сопротивлением $ R $.