Формулы электромагнитной индукции
Если проводник замкнут, то есть является контуром, то в нем появляется ток индукции. Явление было открыто в 1831 г. М. Фарадеем.
Основной закон электромагнитной индукции
Основной формулой, при помощи которой определяют ЭДС индукции (), является закон Фарадея – Максвелла, больше известный как основной закон электромагнитной индукции (или закон Фарадея). В соответствии с данным законом, электродвижущая сила индукции в контуре, находящемся в переменном магнитном поле, равна по модулю и противоположна по знаку скорости изменения магнитного потока () через поверхность, которую ограничивает рассматриваемый контур:
где – скорость изменения магнитного потока. Полная производная присутствующая в формуле (1) охватывает весь спектр причин изменения магнитного потока через поверхность контура. Знак минус в формуле (1) отвечает правилу Ленца. В виде (1) формула ЭДС записана для международной системы единиц (СИ), в других системах вид закона может отличаться.
При равномерном изменении магнитного потока основной закон электромагнитной индукции записывают как:
Формулы ЭДС индукции для частных случаев
ЭДС индукции для контура имеющего N витков, находящегося в переменном магнитном поле можно найти как:
где – потокосцепление.
Если прямолинейный проводник движется в однородном магнитном поле, то в нем появляется ЭДС индукции, равная:
где v – скорость движения проводника; l – длина проводника; B – модуль вектора магнитной индукции поля; .
Разность потенциалов (U) на концах прямого проводника, движущегося в однородном магнитном поле с постоянной скоростью будет равна:
где – угол между направлениями векторов и .
При вращении плоского контура с постоянной скоростью в однородном магнитном поле вокруг оси, которая лежит в плоскости контура в нем появляется ЭДС индукции, которую можно вычислить как:
где S – площадь, которую ограничивает виток; – поток самоиндукции витка; — угловая скорость; () – угол поворота контура. Необходимо заметить, что формула (5) применима, в случае, если ось вращения составляет прямой угол с направлением вектора внешнего магнитного поля .
Необходимо заметить, что формула (5) применима, в случае, если ось вращения составляет прямой угол с направлением вектора внешнего магнитного поля .
Если вращающаяся рамка обладает N витками, при этом самоиндукцией рассматриваемой системы можно пренебречь, то:
Если проводник неподвижен в переменном магнитном поле, то ЭДС индукции можно найти как:
Примеры решения задач по теме «Электромагнитная индукция»
Урок 5. электромагнитная индукция – Физика – 11 класс
Физика, 11 кл
Урок 5. Электромагнитная индукция
Перечень вопросов, рассматриваемых на этом уроке
- Знакомство с явлением электромагнитной индукции.
- Изучение законов, описывающих явление электромагнитной индукции.
- Решение задач, практическое использование электромагнитной индукции.
Глоссарий по теме
Явление электромагнитной индукции
 Магнитный поток Ф – графически величина пропорциональная числу линий магнитной индукции, пронизывающих поверхность площадью S.
Магнитный поток Ф – графически величина пропорциональная числу линий магнитной индукции, пронизывающих поверхность площадью S.Единица измерения магнитного потока: магнитный поток в один вебер создаётся однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м
Правило Ленца: возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван.
Сила индукционного тока пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром.
ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром:
Основная и дополнительная литература по теме:
Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017стр.
Рымкевич А.П. Сборник задач по физике. 10-11класс. – М.: Дрофа,2009. Стр. 28-29
ЕГЭ 2017. Физика. 1000 задач с ответами и решениями. Демидова М.Ю., Грибов В.А., Гиголо А.И. М.: Экзамен, 2017.
Теоретический материал для самостоятельного изучения
Электрические и магнитные поля создаются одними и теми же источниками – электрическими зарядами. Отсюда естественнее было предположить, что между этими полями имеется связь. Экспериментально это предположение было доказано в 1831 г. английским учёным М. Фарадеем, открывшим явление электромагнитной индукции. Все опыты Фарадея по изучению явления электромагнитной индукции объединял один признак – магнитный поток пронизывающий замкнутый контур проводника менялся. При всяком изменении магнитного потока через замкнутый контур, в нем возникал индукционный ток.
Сила индукционного тока пропорциональна ЭДС индукции.
Направление индукционного тока менялось в зависимости от направления движения магнита относительно катушки.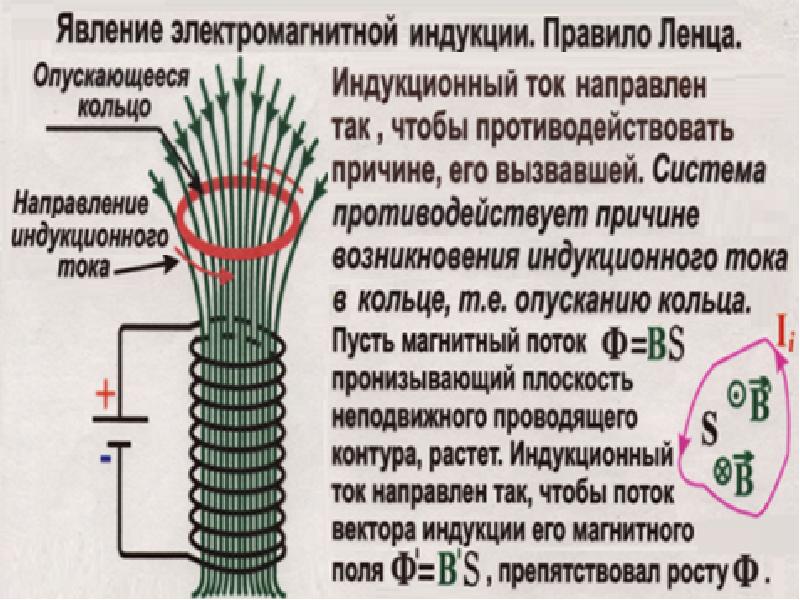 Это направление тока, можно найти используя правило Ленца.
Это направление тока, можно найти используя правило Ленца.
М. Фарадеем экспериментально было установлено, что при изменении магнитного потока, в проводящем контуре возникает электродвижущая сила индукции, которая равна скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:
Знак минус в этой формуле отражает правило Ленца.
Закон электромагнитной индукции формулируется для ЭДС индукции.
ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром:
ЭДС индукции в движущихся проводниках:
Ɛ_i = Вlvsinα.
Джеймс Максвелл в 1860 году сделал вывод что переменное со временем магнитное поле всегда порождает вихревое электрическое поле, а переменное во времени электрическое поле в свою очередь порождает магнитное поле. Следовательно, существует единая теория электромагнитного поля.
Разбор типового контрольного задания
1.
На рисунке изображен момент демонстрационного эксперимента по проверке правила Ленца, когда все предметы неподвижны. Южный полюс магнита находится внутри сплошного металлического кольца, но не касается его. Коромысло с металлическими кольцами может свободно вращаться вокруг вертикальной опоры. При выдвижении магнита из кольца влево кольцо будет
1) оставаться неподвижным
2) перемещаться вправо
3) совершать колебания
4) перемещаться вслед за магнитом
При выдвижении магнита из кольца влево магнитный поток от магнита через кольцо будет уменьшаться. В замкнутом кольце возникает индукционный ток. Направление этого тока по правилу Ленца такое, что создаваемое им магнитное поле препятствует изменению магнитного потока. Так как коромысло вокруг вертикальной оси может свободно вращаться, и магнитное поле магнита неоднородно, коромысло под действием сил Ампера начнёт двигаться так, чтобы препятствовать изменению магнитного потока. Следовательно, коромысло начнёт перемещаться вслед за магнитом.
Ответ:4) перемещаться вслед за магнитом.
2.
Проводник МN с длиной активной части 1м и сопротивлением 2 Ом находится в однородном магнитном поле индукцией 0,2 Тл. Проводник подключён к источнику тока с ЭДС 4 В (внутренним сопротивлением источника и сопротивлением подводящих проводников пренебречь). Какова сила тока в проводнике, если:
№1 проводник покоится;
№2 проводник движется в право со скоростью 6 м/с.
Дано:
ℓ= 1м
R = 2 Ом
В = 0,2 Тл
Ɛ = 4 В
I =?
Решение:
№1: Ток в неподвижном проводнике течёт от N к М
v = 0; Закон Ома для полной цепи I = Ɛ/R = 4В/2Ом = 2А
№2: Если проводник движется в право со скоростью 6 м/с, то по правилу правой руки индукционный ток потечёт от точки N к точке М:
Ответ: №1 2А
№2 2,6А
Закон электромагнитной индукции Фарадея: значение, задачи, формулы
Что может быть лучше, чем вечером понедельника почитать про основы электродинамики. Правильно, можно найти множество вещей, которые будут лучше. Тем не менее, мы все равно предлагаем Вам прочесть эту статью. Времени занимает не много, а полезная информация останется в подсознании. Например, на экзамене, в условиях стресса, можно будет успешно извлечь из недр памяти закон Фарадея. Так как законов Фарадея несколько, уточним, что здесь мы говорим о законе индукции Фарадея.
Правильно, можно найти множество вещей, которые будут лучше. Тем не менее, мы все равно предлагаем Вам прочесть эту статью. Времени занимает не много, а полезная информация останется в подсознании. Например, на экзамене, в условиях стресса, можно будет успешно извлечь из недр памяти закон Фарадея. Так как законов Фарадея несколько, уточним, что здесь мы говорим о законе индукции Фарадея.
Электродинамика – раздел физики, изучающий электромагнитное поле во всех его проявлениях.
Это и взаимодействие электрического и магнитного полей, электрический ток, электро-магнитное излучение, влияние поля на заряженные тела.
Здесь мы не ставим целью рассмотреть всю электродинамику. Упаси Боже! Рассмотрим лучше один из основных ее законов, который называется законом электромагнитной индукции Фарадея.
Майкл Фарадей (1791-1867)
История и определение
Фарадей, параллельно с Генри, открыл явление электромагнитной индукции в 1831 году. Правда, успел опубликовать результаты раньше. Закон Фарадея повсеместно используется в технике, в электродвигателях, трансформаторах, генераторах и дросселях. В чем суть закона Фарадея для электромагнитной индукции, если говорить просто? А вот в чем!
Правда, успел опубликовать результаты раньше. Закон Фарадея повсеместно используется в технике, в электродвигателях, трансформаторах, генераторах и дросселях. В чем суть закона Фарадея для электромагнитной индукции, если говорить просто? А вот в чем!
При изменении магнитного потока через замкнутый проводящий контур, в контуре возникает электрический ток. То есть, если мы скрутим из проволоки рамку и поместим ее в изменяющееся магнитное поле (возьмем магнит, и будем крутить его вокруг рамки), по рамке потечет ток!
Рамка в поле
Этот ток Фарадей назвал индукционным, а само явление окрестил электромагнитной индукцией.
Электромагнитная индукция – возникновение в замкнутом контуре электрического тока при изменении магнитного потока, проходящего через контур.
Формулировка основного закона электродинамики – закона электромагнитной индукции Фарадея, выглядит и звучит следующим образом:
ЭДС, возникающая в контуре, пропорциональна скорости изменения магнитного потока Ф через контур.
А откуда в формуле минус, спросите Вы. Для объяснения знака минус в этой формуле есть специальное правило Ленца. Оно гласит, что знак минус, в данном случае, указывает на то, как направлена возникающая ЭДС. Дело в том, что создаваемое индукционным током магнитное поле направлено так, что препятствует изменению магнитного потока, который вызвал индукционный ток.
Для определения направления индукционного тока применяется знаменитое правило буравчика, или правило правой руки, оно же правило правого винта. Если ладонь правой руки расположить так, чтобы в неё входили силовые линии магнитного поля, а отогнутый большой палец направить по движению проводника, то четыре вытянутых пальца укажут направление индукционного тока.
Правило правой руки
Примеры решения задач
Вот вроде бы и все. Значение закона Фарадея фундаментально, ведь на использовании данного закона построена основа почти всей электрической промышленности. Чтобы понимание пришло быстрее, рассмотрим пример решения задачи на закон Фарадея.
Чтобы понимание пришло быстрее, рассмотрим пример решения задачи на закон Фарадея.
И помните, друзья! Если задача засела, как кость в горле, и нет больше сил ее терпеть – обратитесь к нашим авторам! Теперь вы знаете где заказать курсовую работу. Мы быстро предоставим подробное решение и разъясним все вопросы!
Автор: Иван
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Явление электромагнитной индукции
Для демонстрации явления электромагнитной индукции, исходя из формулы Ф = ВScos?, все опыты можно условно разделить на три группы:
а) опыты, в которых изменяется магнитная индукция В;
б) опыты, в которых изменяется площадь контура S;
в) опыты, в которых изменяется угол между направлением вектора магнитной индукции и нормалью к контуру.
? Возникновение электрического тока в замкнутом контуре при изменении магнитного потока через ограниченную контуром площадь называют явлением электромагнитной индукции.
По любому изменению магнитного потока через площадь, ограниченную контуром, в замкнутом контуре возникает индукционный ток. Существуют две причины возникновения индукционного тока:
Существуют две причины возникновения индукционного тока:
1) при движении контура в магнитном поле;
2) в случае нахождения недвижимого контура в переменном магнитном поле.
Возникновение в неподвижных проводниках электрического тока указывает на появление электрического поля, так как магнитное поле на неподвижные заряды действовать не может.
Значит, индукционное электрическое поле появляется в результате изменения магнитного поля. Итак, индукционное электрическое поле не связано с зарядами (как это было в случае электростатического поля).
Дж. Максвелл первым пришел к выводу, что,
? изменяясь во времени, магнитное поле порождает электрическое поле.
Электрическое поле, возникающее при изменении магнитного поля, имеет совсем другую структуру, чем электростатическое. Оно не связано непосредственно с электрическими зарядами, и его линии напряженности не могут на них начинаться и заканчиваться. Они вообще нигде не начинаются и не заканчиваются, а представляют собой замкнутые линии, подобные линиям индукции магнитного поля. Кроме того, работа по перемещению зарядов вдоль замкнутого контура, выполнена силами этого электрического поля, не равна нулю. Это так называемое вихревое электрическое поле.
Кроме того, работа по перемещению зарядов вдоль замкнутого контура, выполнена силами этого электрического поля, не равна нулю. Это так называемое вихревое электрическое поле.
Электрическое поле, созданное переменным магнитным полем, называют вихревым.
Вихревое электрическое поле не является потенциальным полем.
Явление электромагнитной индукции
Исходя из формулы Ф = BScos, все опыты можно условно разделить на три группы:
а) опыты, в которых изменяется индукция магнитного поля B;
б) опыты, в которых изменяется площадь контура S;
в) опыты, в которых изменяется угол между направлением вектора магнитной индукции и нормалью к площадке.
На основании выполненных исследований можно подвести учащихся к выводу: для возбуждения электрического тока в замкнутом контуре необходимо менять магнитный поток через этот контур.
Явление электромагнитной индукции заключается в следующем:
? индукционный ток в замкнутом контуре возникает при изменении магнитного потока через площадь, ограниченную контуром.
Существуют две причины возникновения индукционного тока:
1) при движении контура в магнитном поле;
2) во время пребывания недвижимого контура в переменном магнитном поле.
категория: ФизикаЭлектромагнитная индукция – FIZI4KA
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Опыты Фарадея
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.

- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.
Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
Магнитным потоком через площадь \( S \) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции \( B \), площади поверхности \( S \), пронизываемой данным потоком, и косинуса угла \( \alpha \) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
Обозначение – \( \Phi \), единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции:
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла \( \alpha \) магнитный поток может быть положительным (\( \alpha \) < 90°) или отрицательным (\( \alpha \) > 90°). Если \( \alpha \) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из \( N \) витков, то ЭДС индукции:
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением \( R \):
При движении проводника длиной \( l \) со скоростью \( v \) в постоянном однородном магнитном поле с индукцией \( \vec{B} \) ЭДС электромагнитной индукции равна:
где \( \alpha \) – угол между векторами \( \vec{B} \) и \( \vec{v} \).
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
- вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Алгоритм решения задач с использованием правила Ленца:
- определить направление линий магнитной индукции внешнего магнитного поля;
- выяснить, как изменяется магнитный поток;
- определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
- по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.
Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.
Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции \( \varepsilon_{is} \), возникающая в катушке с индуктивностью \( L \), по закону электромагнитной индукции равна:
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток \( \Phi \) через контур из этого проводника пропорционален модулю индукции \( \vec{B} \) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:
Индуктивность – коэффициент пропорциональности \( L \) между силой тока \( I \) в контуре и магнитным потоком \( \Phi \), создаваемым этим током:
Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:
Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:
Основные формулы раздела «Электромагнитная индукция»
Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
6. Решение проверить.
Электромагнитная индукция
3.1 (61.62%) 37 votes Содержание:
Если взять замкнутую проводящую систему и создать в ней условия для того чтобы магнитный поток изменился в магнитном поле, то в результате этих движений появится электрический ток. Данное обстоятельство описывает закон электромагнитной индукции Фарадея – английского ученого, который при проведении опытов добился превращения магнитной энергии в электричество. Оно получило название индукционного, поскольку до того времени его можно было создать лишь гальваническим путем. История открытияЯвление электромагнитной индукции было открыто сразу двумя учеными. Это были Майкл Фарадей и Джозеф Генри, сделавшие свое открытие в 1831 году. Публикация Фарадеем результатов проведенных экспериментов была сделана раньше его коллеги, поэтому индукцию связывают именно с этим ученым. В дальнейшем это понятие было включено в систему СГС. Для демонстрации явления использовался железный тор, напоминающий конфигурацию современного трансформатора. Противоположные стороны его были обмотаны двумя проводниками с целью использования электромагнитных свойств. К одному из проводов подключался ток, вызывающий своеобразную электрическую волну при прохождении сквозь тор, и некоторый электрический всплеск с противоположной стороны. Наличие тока было зафиксировано гальванометром. Точно такой же всплеск электричества наблюдался и в момент отключения провода. Постепенно были обнаружены и другие формы проявления электромагнитной индукции. Кратковременное возникновение тока наблюдалось во время генерации его на медном диске, вращающемся возле магнита. На самом диске был установлен скользящий электропровод. Наибольшие представление о том, что такое индуктивность, дал эксперимент с двумя катушками. Одна из них, с меньшими размерами, подключена к жидкостной батарее, расположенной на рисунке с правой стороны. Таким образом, через эту катушку начинает протекать электрический ток, под действием которого возникает магнитное поле. Когда обе катушки находятся в неподвижном положении относительно друг друга, никаких явлений не происходит. Когда небольшая катушка начинает двигаться, то есть выходить из большой катушки или входить в нее, наступает изменение магнитного потока. В результате, в большой катушке наблюдается появление электродвижущей силы. Открытие Фарадея доработал другой ученый – Максвелл, который обосновал его математически, отображая данное физическое явление дифференциальными уравнениями. Еще одному ученому-физику – Ленцу удалось определить направление электротока и ЭДС, полученных под действием электромагнитной индукции. Законы электромагнитной индукцииСущность электромагнитной индукции определяется замкнутым контуром с электропроводностью, площадь которого пропускает через себя изменяющийся магнитный поток. В этот момент под влиянием магнитного потока появляется электродвижущая сила Еi и в контуре начинает течь электрический ток. Закон Фарадея для электромагнитной индукции заключается в прямой зависимости ЭДС и скорости, составляющих пропорцию. Данная скорость представляет собой время, в течение которого магнитный поток подвергается изменениям. Данный закон выражается формулой Еi = — ∆Ф/∆t, в которой Еi – значение электродвижущей силы, возникающей в контуре, а ∆Ф/∆t является скоростью изменения магнитного потока. В этой формуле не совсем понятным остается знак «минус», но ему тоже имеется свое объяснение. Совет В соответствии с правилом русского ученого Ленца, изучавшего открытия Фарадея, этот знак отображает направление ЭДС, возникающей в контуре. То есть, направление индукционного тока происходит таким образом, что создаваемый им магнитный поток на площади, ограниченной контуром, препятствует изменениям, вызванным этим током. Открытия Фарадея были доработаны Максвеллом, у которого теория электромагнитного поля получила новые направления. В результате, появился закон Фарадея и Максвелла, выраженный в следующих формулах:
В этих формулах Е соответствует напряженности электрического поля на определенном участке dl, Н является напряженностью магнитного поля на этом же участке, N – поток электрической индукции, t – период времени. Оба уравнения отличаются симметричностью, позволяющей сделать вывод, что магнитные и электрические явления связаны между собой. С физической точки зрения эти формулы определяют следующее:
Изменяющийся магнитный поток, проходящий сквозь замкнутую конфигурацию проводящего контура, приводит к возникновению в этом контуре электрического тока. Это основная формулировка закона Фарадея. Если изготовить проволочную рамку и поместить ее внутри вращающегося магнита, то в самой рамке появится электричество. Это и будет индукционный ток, в полном соответствии с теорией и законом Майкла Фарадея. Изменения магнитного потока, проходящего через контур, могут быть произвольными. Следовательно, формула ∆Ф/∆t бывает не только линейной, а в определенных условиях принимает любую конфигурацию. Если изменения происходят линейно, то ЭДС электромагнитной индукции, возникающей в контуре, будет постоянной.
Если же изменения магнитного потока принимают более сложную форму, то ЭДС индукции уже не будет постоянной, а будет зависеть от данного промежутка времени. В этом случае временной интервал рассматривается в качестве бесконечно малой величины и тогда соотношение ∆Ф/∆t с точки зрения математики станет производной от изменяющегося магнитного потока. Существует еще один вариант, трактующий закон электромагнитной индукции Фарадея. Его краткая формулировка объясняет, что действие переменного магнитного поля вызывает появление вихревого электрического поля. Этот же закон можно трактовать как одну из характеристик электромагнитного поля: вектор напряженности поля может циркулировать по любому из контуров со скоростью, равной скорости изменения магнитного потока, проходящего через тот или иной контур. |
| Понравился сайт? Расскажи друзьям! |
Источник: http://ru.solverbook.com/spravochnik/formuly-po-fizike/formula-zakona-elektromagnitnoj-indukcii/
§23. Закон электромагнитной индукции Фарадея
В 1831 г. Фарадей экспериментально открыл явление электромагнитной индукции. Суть явления состояла в том, что если через замкнутый контур происходило изменение магнитного потока, то в контуре возникала электродвижущая сила, приводящая к возникновению замкнутого тока.
Этот ток был назван индукционным током. Правило, устанавливающее направление индукционного тока было сформулировано в 1833г. Э. Х. Ленцем (1804 — 1865) и называется правилом Ленца.
Оно гласит: индукционный ток направлен так, что создаваемый им магнитный поток стремится компенсировать изменение магнитного потока, вызывающего данный ток.
Опыты Фарадея состояли в следующем: катушка индуктивности подключалась к чувствительному гальванометру и в катушку вдвигался и выдвигался постоянный магнит.
Из опытов следовало, что. Но сила тока зависит еще и от сопротивления контура. Поэтому закон электромагнитной индукции формулируется не для индукционного тока, а для причины, вызывающий этот ток, т. е. для. В 1845г. Ф. Э. Нейман (1799 — 1895) дал математическое определение закона электромагнитной индукции в современной форме:
(23.1)
Хотя внешне формулы (22.6) и (23.1) одинаковы, между ними существует принципиальное различие. Возникновениев (22.6) связано с движением проводников в магнитном поле и с действием на заряды силы Лоренца. Тогда как в (23.
1) на заряды в контуре действует электрическое поле, причем сам контур лишь только инструмент или прибор, который может обнаружить это изменяющееся электрическое поле, которое возникает в пространстве. Следовательно закон Фарадея отражает новое физическое явление, а именно: изменяющееся магнитное поле порождает изменяющееся электрическое поле.
Совет
А это означает, что электрическое поле порождается не только зарядами, но и изменяющимся магнитным полем. Закон электромагнитной индукции является фундаментальным законом природы.
Дифференциальная формулировка закона
, а тогда магнитный поток, а.
.
К левой части применим формулу Стокса. Тогда. После того как перенесем все слагаемые в одну сторону получим:
В силу произвольностиможно заключить, что подынтегральная функция равна нулю, а значит
(23.2)
Уравнение (23.2) является дифференциальной формой закона электромагнитной индукции. В переменных магнитных полях, а значити следовательно, в отличие от электростатического поля, порождаемого неподвижными зарядами, переменное электрическое поле не является потенциальным и работапри перемещении зарядапо замкнутому контуру не равна нулю:
.
Так как закон электромагнитной индукции не затрагивает закона порождения магнитного поля, то уравнение (18.6)остается в силе, а значит в силе остается и выражение (19.2):.
Если подставить (19.2) в (23.2), то, а значит
. (23.3)
Отсюда следует, что в переменных полях потенциальным является вектор, а значит он равен градиенту скалярной функции, т. е., а значит
. (23.4)
Второе слагаемое в (23.4) означает, что электрическое поле может порождаться неподвижными зарядами, а первое означает, что электрическое поле может порождаться переменным магнитным полем.
Источник: https://www.webpoliteh.ru/23-zakon-elektromagnitnoj-indukcii-faradeya/
Явление электромагнитной индукции. Закон Фарадея
Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса — ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший «Салат из свеклы с чесноком»
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной
Обратите внимание
Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него. Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года.
Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром.
Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.
Явление электромагнитной индукции можно обнаружить в таких ситуациях:
1. при относительном движении катушки и магнита;
2. при изменении индукции магнитного поля в контуре, который расположен перпендикулярно линиям магнитного поля.
3. при изменении положения контура, расположенного в постоянном магнитном поле.
Закон Фарадея.
Согласно закону электромагнитной индукции Фарадея (в СИ):
где
— электродвижущая сила, действующая вдоль произвольно выбранного контура,
— магнитный поток через поверхность, ограниченную этим контуром.
Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца:
Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.
Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:
где
— электродвижущая сила,
— число витков,
— магнитный поток через один виток,
— потокосцепление катушки.
Векторная формула:
В дифференциальной форме закон Фарадея можно записать в следующем виде:
(в системе СИ)
или
(в системе СГС).
В интегральной форме (эквивалентной):
(СИ)
или
(СГС)
Важно
Здесь— напряжённость электрического поля,— магнитная индукция,— произвольная поверхность,— её граница. Контур интегрированияподразумевается фиксированным (неподвижным).
Следует отметить, что закон Фарадея в такой форме, очевидно, описывает лишь ту часть ЭДС, что возникает при изменении магнитного потока через контур за счёт изменения со временем самого поля без изменения (движения) границ контура (об учете последнего см. ниже).
· В этом виде закон Фарадея входит в систему уравнений Максвелла для электромагнитного поля (в дифференциальной или интегральной форме соответственно)[2].
Если же, скажем, магнитное поле постоянно, а магнитный поток изменяется вследствие движения границ контура (например, при увеличении его площади), то возникающая ЭДС порождается силами, удерживающими заряды на контуре (в проводнике) и силой Лоренца, порождаемой прямым действием магнитного поля на движущиеся (с контуром) заряды. При этом равенствопродолжает соблюдаться, но ЭДС в левой части теперь не сводится к(которое в данном частном примере вообще равно нулю). В общем случае (когда и магнитное поле меняется со временем, и контур движется или меняет форму) последняя формула верна так же, но ЭДС в левой части в таком случае есть сумма обоих слагаемых, упомянутых выше (то есть порождается частично вихревым электрическим полем, а частично силой Лоренца и силой реакции движущегося проводника).
· Некоторые авторы, например, М. Лившиц в журнале «Квант» за 1998 год[3] отрицают корректность применения термина закон Фарадея или закон электромагнитной индукции и т. п.
к формулев случае подвижного контура (оставляя для обозначения этого случая или его объединения со случаем изменения магнитного поля, например, термин правило потока)[4].
В таком понимании закон Фарадея — это закон, касающийся лишь циркуляции электрического поля (но не ЭДС, создаваемой с участием силы Лоренца), и в этом понимании понятие закон Фарадея в точности совпадает с содержанием соответствующего уравнения Максвелла.
· Однако возможность (пусть с некоторыми оговорками, уточняющими область применимости) совпадающей формулировки «правила потока» с законом электромагнитной индукции нельзя назвать чисто случайной.
Дело в том, что, по крайней мере для определенных ситуаций, это совпадение оказывается очевидным проявлением принципа относительности.
А именно, например, для случая относительного движения катушки с присоединенным к ней вольтметром, измеряющим ЭДС, и источника магнитного поля (постоянного магнита или другой катушки с током), в системе отсчета, связанной с первой катушкой, ЭДС оказывается равной именно циркуляции электрического поля, тогда как в системе отсчета, связанной с источником магнитного поля (магнитом), происхождение ЭДС связано с действием силы Лоренца на движущиеся с первой катушкой носители заряда. Однако та и другая ЭДС обязаны совпадать, поскольку вольтметр показывает одну и ту же величину, независимо от того, для какой системы отсчета мы её рассчитали.
· Потенциальная форма
При выражении магнитного поля через векторный потенциал закон Фарадея принимает вид:
(в случае отсутствия без вихревого поля, то есть тогда, когда электрическое поле порождается полностью только изменением магнитного, то есть электромагнитной индукцией).
В общем случае, при учёте и без вихревого (например, электростатического) поля имеем:
.
Источник: https://megapredmet.ru/1-64669.html
Электромагнитная индукция формулы и единицы измерения
Электромагнитная индукция (индукция значит наведение) это явление, при котором в замкнутом контуре возникает электрический ток при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было обнаружено в 1831 г.
М. Фарадеем. Ток, возникающий при электромагнитной индукции называют индукционным.
Закон электромагнитной индукцииЭДС индукции в контуре равна скорости изменения магнитного поля сквозь поверхность, ограниченную контуром.
| Электромагнитная индукция | |
| 1831 г. – М. Фарадей обнаружил, что в замкнутом проводящем контуре при изменении магнитного поля возникает так называемый индукционный ток. (Индукция, в данном случае, – появление, возникновение). | |
| Индукционный ток в катушке возникает при перемещении постоянного магнита относительно катушки; при перемещении электромагнита относительно катушки; при перемещении сердечника относительно электромагнита, вставленного в катушку; при регулировании тока в цепи электромагнита; при замыкании и размыкании цепи | |
| Появление тока в замкнутом контуре при изменении магнитного поля, пронизывающего контур, свидетельствует о действии в контуре сторонних сил (или о возникновении ЭДС индукции). Явление возникновения ЭДС в замкнутом проводящем контуре при изменении магнитного поля (потока), пронизывающего контур, называется электромагнитной индукцией. Или:явление возникновения электрического поля при изменении магнитного поля (потока), называется электромагнитной индукцией. | |
| Закон электромагнитной индукции При всяком изменении магнитного потока через проводящий замкнутый контур в этом контуре возникает электрический ток. I зависит от свойств контура (сопротивление): . e не зависит от свойств контура: . ЭДС индукции в замкнутом контуре прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром. | |
| Основные применения электромагнитной индукции: генерирование тока (индукционные генераторы на всех электростанциях, динамомашины), трансформаторы. |
| Правило Ленца Возникновение индукционного тока – следствие закона сохранения энергии! В случае 1: При приближении магнита, увеличении тока, замыкании цепи: ; Магнитный поток Ф → ΔФ>0.Чтобы компенсировать это изменение (увеличение) внешнего поля, необходимо магнитное поле, направленное в сторону, противоположную внешнему полю: , где – т.н. индукционное магнитное поле. В случае 2: при удалении магнита, уменьшении тока, размыкании цепи: . Магнитный поток Ф → ΔФ 0). Ток в контуре имеет положительное направление ( ), если совпадает с , (т.е. ΔΦ |
Не нашли то, что искали? Воспользуйтесь поиском:
Магнитное взаимодействие движущихся электрических зарядов согласно представлениям теории поля объясняется следующим образом: всякий движущийся электрический заряд создает в окружающем пространстве магнитное поле, способное действовать на другие движущиеся электрические заряды.
В – физическая величина, являющаяся силовой характеристикой магнитного поля. Она называется магнитной индукцией (или индукцией магнитного поля).
Магнитная индукция – векторная величина. Модуль вектора магнитной индукции равен отношению максимального значения силы Ампера, действующей на прямой проводник с током, к силе тока в проводнике и его длине:
Единица магнитной индукции. В Международной системе единиц за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила Ампера 1 Н. Эта единица называется тесла (сокращенно: Тл), в честь выдающегося югославского физика Н. Тесла:
Движение проводника с током в магнитном поле показывает, что магнитное поле действует на движущиеся электрические заряды. На проводник действует сила Ампера FА = IBlsin a , а сила Лоренца действует на движущийся заряд:
где a – угол между векторами B и v .
Движение заряженных частиц в магнитном поле. В однородном магнитном поле на заряженную частицу, движущуюся со скоростью перпендикулярно линиям индукции магнитного поля, действует силам , постоянная по модулю и направленная перпендикулярно вектору скорости.Под действием магнитной силы частица приобретает ускорение, модуль которого равен:
В однородном магнитном поле эта частица движется по окружности. Радиус кривизны траектории, по которой движется частица, определяется из условияоткуда следует,
Радиус кривизны траектории является величиной постоянной, поскольку сила, перпендикулярная вектору скорости, меняется только ее направление, но не модуль. А это и означает, что данная траектория является окружностью.
Период обращения частицы в однородном магнитном поле равен:
Последнее выражение показывает, что период обращения частицы в однородном магнитном поле не зависит от скорости и радиуса траектории ее движения.
Если напряженность электрического поля равна нулю, то сила Лоренца л равна магнитной силе м :
Явление электромагнитной индукции открыл Фарадей, который установил, что в замкнутом проводящем контуре возникает электрический ток при любом изменении магнитного поля, пронизывающего контур.
Магнитный поток Ф (поток магнитной индукции) через поверхность площадью S – величина, равная произведению модуля вектора магнитной индукции на площадь S и косинус угла а между вектором и нормалью к поверхности:
Ф=BScos
В СИ единица магнитного потока 1 Вебер (Вб) – магнитный поток через поверхность площадью 1 м 2 , расположенную перпендикулярно направлению однородного магнитного поля, индукция которого равна 1 Тл:
Электромагнитная индукция-явление возникновения электрического тока в замкнутом проводящем контуре при любом изменении магнитного потока, пронизывающего контур.
Возникающий в замкнутом контуре, индукционный ток имеет такое направление, что своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван (правило Ленца).
ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
Опыты Фарадея показали, что сила индукционного тока Ii в проводящем контуре прямо пропорциональна скорости изменения числа линий магнитной индукции , пронизывающих поверхность, ограниченную этим контуром.
Поэтому сила индукционного тока пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром:
Известно, что если в цепи появился ток, это значит, что на свободные заряды проводника действуют сторонние силы. Работа этих сил по перемещению единичного заряда вдоль замкнутого контура называется электродвижущей силой (ЭДС). Найдем ЭДС индукции εi.
По закону Ома для замкнутой цепи
Так как R не зависит от , то
ЭДС индукции совпадает по направлению с индукционным током, а этот ток в соответствии с правилом Ленца направлен так, что созданный им магнитный поток противодействует изменению внешнего магнитного потока.
Закон электромагнитной индукции
ЭДС индукции в замкнутом контуре равна взятой с противоположным знаком скорости изменения магнитного потока, пронизывающего контур:
Опыт показывает, что магнитный поток Ф , связанный с контуром, прямо пропорционален силе тока в этом контуре:
Индуктивность контура L – коэффициент пропорциональности между проходящим по контуру током и созданным им магнитным потоком.
Индуктивность проводника зависит от его формы, размеров и свойств окружающей среды.
Самоиндукция – явление возникновения ЭДС индукции в контуре при изменении магнитного потока, вызванном изменением тока, проходящего через сам контур.
Самоиндукция – частный случай электромагнитной индукции.
Индуктивность – величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока в нем на единицу за единицу времени. В СИ за единицу индуктивности принимают индуктивность такого проводника, в котором при изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В. Эта единица называется генри (Гн):
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
Явление самоиндукции аналогично явлению инерции. Индуктивность при изменении тока играет ту же роль, что и масса при изменении скорости тела. Аналогом скорости является сила тока.
Значит энергию магнитного поля тока можно считать величиной, подобной кинетической энергии тела :
Предположим, что после отключения катушки от источника,ток в цепи убывает со временем по линейному закону.
ЭДС самоиндукции имеет в этом случае постоянное значение:
где I – начальное значение тока, t – промежуток времени, за который сила тока убывает от I до 0.
За время t в цепи проходит электрический заряд q = Icpt . Так как Icp = (I + 0)/2 = I/2 , то q=It/2 . Поэтому работа электрического тока:
Эта работа совершается за счет энергии магнитного поля катушки. Таким образом, снова получаем:
Пример. Определите энергию магнитного поля катушки, в которой при токе 7,5 А магнитный поток равен 2,3*10 -3 Вб. Как изменится энергия поля, если сила тока уменьшиться вдвое?
Энергия магнитного поля катушки W 1 = LI 1 2 /2. По определению, индуктивность катушки L = Ф/I 1. Следовательно,
Ответ: энергия поля равна 8,6 Дж; при уменьшении тока вдвое она уменьшится в 4 раза.
Электромагни́тная инду́кция — явление возникновения электрического тока, электрического поля или электрической поляризации при изменении во времени магнитного поля или при движении материальной среды в магнитном поле [1] . Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года [2] . Он обнаружил, что электродвижущая сила (ЭДС), возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.
Содержание
Закон Фарадея [ править | править код ]
Согласно закону электромагнитной индукции Фарадея (в СИ):
E = − d Φ B d t , <displaystyle <mathcal >=-<> over dt>,>
E <displaystyle <mathcal >> — электродвижущая сила, действующая вдоль произвольно выбранного контура, Φ B <displaystyle Phi _> = ∬ S B → ⋅ d S → <displaystyle =iint limits _<vec >cdot d<vec >> — магнитный поток через поверхность, ограниченную этим контуром.
Знак «минус» в формуле отражает правило Ленца, названное так по имени российского физика Э. Х. Ленца:
Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.
Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:
E = − N d Φ B d t = − d Ψ d t , <displaystyle <mathcal >=-N<> over dt>=- <over dt>,>
E <displaystyle <mathcal >> — электродвижущая сила, N <displaystyle N> — число витков, Φ B <displaystyle Phi _> — магнитный поток через один виток, Ψ <displaystyle Psi > — потокосцепление катушки.
Векторная форма [ править | править код ]
В дифференциальной форме закон Фарадея можно записать в следующем виде:
rot E → = − ∂ B → ∂ t <displaystyle operatorname ,<vec >=-<partial <vec > over partial t>> (в системе СИ)
rot E → = − 1 c ∂ B → ∂ t <displaystyle operatorname ,<vec >=-<1 over c><partial <vec > over partial t>> (в системе СГС).
В интегральной форме (эквивалентной):
∮ ∂ S E → ⋅ d l → = − ∂ ∂ t ∫ S B → ⋅ d s → <displaystyle oint _<partial S><vec >cdot <vec
- >=-<partial over partial t>int _
∮ ∂ S E → ⋅ d l → = − 1 c ∂ ∂ t ∫ S B → ⋅ d s → <displaystyle oint _<partial S><vec >cdot <vec
- >=-<1 over c><partial over partial t>int _
Здесь E → <displaystyle <vec >> — напряжённость электрического поля, B → <displaystyle <vec >> — магнитная индукция, S <displaystyle S > — произвольная поверхность, ∂ S <displaystyle partial S> — её граница. Контур интегрирования ∂ S <displaystyle partial S> подразумевается фиксированным (неподвижным).
Следует отметить, что закон Фарадея в такой форме, очевидно, описывает лишь ту часть ЭДС, что возникает при изменении магнитного потока через контур за счёт изменения со временем самого поля без изменения (движения) границ контура (об учете последнего см. ниже).
- В этом виде закон Фарадея входит в систему уравнений Максвелла для электромагнитного поля (в дифференциальной или интегральной форме соответственно) [3] .
Если же, скажем, магнитное поле постоянно, а магнитный поток изменяется вследствие движения границ контура (например, при увеличении его площади), то возникающая ЭДС порождается силами, удерживающими заряды на контуре (в проводнике) и силой Лоренца, порождаемой прямым действием магнитного поля на движущиеся (с контуром) заряды. При этом равенство E = − d Φ / d t <displaystyle <mathcal >=-</dt>> продолжает соблюдаться, но ЭДС в левой части теперь не сводится к ∮ E → ⋅ d l → <displaystyle oint <vec>cdot <vec
- >> (которое в данном частном примере вообще равно нулю). В общем случае (когда и магнитное поле меняется со временем, и контур движется или меняет форму) последняя формула остаётся справедливой, но ЭДС в левой части в таком случае есть сумма обоих слагаемых, упомянутых выше (то есть порождается частично вихревым электрическим полем, а частично силой Лоренца и силой реакции движущегося проводника).
- Некоторые авторы, например, М. Лившиц в журнале «Квант» за 1998 год [4] отрицают корректность применения термина закон Фарадея или закон электромагнитной индукции и т. п. к формуле E = − d Φ / d t <displaystyle <mathcal >=-</dt>>в случае подвижного контура (оставляя для обозначения этого случая или его объединения со случаем изменения магнитного поля, например, термин правило потока) [5] . В таком понимании закон Фарадея — это закон, касающийся лишь циркуляции электрического поля (но не ЭДС, создаваемой с участием силы Лоренца), и в этом понимании понятие закон Фарадея в точности совпадает с содержанием соответствующего уравнения Максвелла.
- Однако возможность (пусть с некоторыми оговорками, уточняющими область применимости) совпадающей формулировки «правила потока» с законом электромагнитной индукции нельзя назвать чисто случайной. Дело в том, что, по крайней мере для определённых ситуаций, это совпадение оказывается очевидным проявлением принципа относительности. А именно, например, для случая относительного движения катушки с присоединённым к ней вольтметром, измеряющим ЭДС, и источника магнитного поля (постоянного магнита или другой катушки с током), в системе отсчёта, связанной с первой катушкой, ЭДС оказывается равной именно циркуляции электрического поля, тогда как в системе отсчёта, связанной с источником магнитного поля (магнитом), происхождение ЭДС связано с действием силы Лоренца на движущиеся с первой катушкой носители заряда. Однако та и другая ЭДС обязаны совпадать, поскольку вольтметр показывает одну и ту же величину, независимо от того, для какой системы отсчёта мы её рассчитали.
Потенциальная форма [ править | править код ]
При выражении магнитного поля через векторный потенциал закон Фарадея принимает вид:
E → = − ∂ A → ∂ t <displaystyle <vec >=-<partial <vec > over partial t>> (в случае отсутствия безвихревого поля, то есть тогда, когда электрическое поле порождается полностью только изменением магнитного, то есть электромагнитной индукцией).
В общем случае, при учёте и безвихревого (например, электростатического) поля имеем:
E → = − ∇ φ − ∂ A → ∂ t <displaystyle <vec >=-
abla varphi -<partial <vec > over partial t>>
Поскольку вектор магнитной индукции по определению выражается через векторный потенциал так:
B → = r o t A → ≡ ∇ × A → , <displaystyle <vec >=rot <vec >equiv
abla imes <vec >,>
то можно подставить это выражение в
r o t E → ≡ ∇ × E → = − ∂ B → ∂ t , <displaystyle rot <vec >equiv
abla imes <vec>=-<frac <partial <vec >><partial t>>,>
∇ × E → = − ∂ ( ∇ × A → ) ∂ t , <displaystyle
abla imes <vec >=-<frac <partial (
abla imes <vec >)><partial t>>,>
и, поменяв местами дифференцирование по времени и пространственным координатам (ротор):
∇ × E → = − ∇ × ∂ A → ∂ t . <displaystyle
abla imes <vec >=-
abla imes <frac <partial <vec >><partial t>>.>
Отсюда, поскольку ∇ × E → <displaystyle
abla imes <vec >> полностью определяется правой частью последнего уравнения, видно, что вихревая часть электрического поля (та часть, которая имеет ротор, в отличие от безвихревого поля ∇ φ <displaystyle
abla varphi > ) полностью определяется выражением
− ∂ A → ∂ t . <displaystyle -<frac <partial <vec >><partial t>>.>
То есть в случае отсутствия безвихревой части можно записать
E → = − ∂ A → ∂ t , <displaystyle <vec >=-<frac <partial <vec >><partial t>>,>
а в общем случае
E → = − ∇ φ − d A → d t . <displaystyle <vec >=-
abla varphi -<frac >
История [ править | править код ]
В 1820 году Ганс Христиан Эрстед показал, что протекающий по цепи электрический ток вызывает отклонение магнитной стрелки. Если электрический ток порождает магнетизм, то с магнетизмом должно быть связано появление электрического тока. Эта мысль захватила английского ученого М. Фарадея. «Превратить магнетизм в электричество», — записал он в 1822 году в своём дневнике. Многие годы настойчиво ставил он различные опыты, но безуспешно, и только 29 августа 1831 года наступил триумф: он открыл явление электромагнитной индукции. Установка, на которой Фарадей сделал своё открытие, состояла из кольца из мягкого железа примерно 2 см шириной и 15 см диаметром. На каждой половине кольца было намотано много витков медной проволоки. Цепь одной обмотки замыкала проволока, в её витках находилась магнитная стрелка, удаленная настолько, чтобы не сказывалось действие магнетизма, созданного в кольце. Через вторую обмотку пропускался ток от батареи гальванических элементов. При включении тока магнитная стрелка совершала несколько колебаний и успокаивалась; когда ток прерывали, стрелка снова колебалась. Выяснилось, что стрелка отклонялась в одну сторону при включении тока и в другую, когда ток прерывался. М. Фарадей установил, что «превращать магнетизм в электричество» можно и с помощью обыкновенного магнита.
В это же время американский физик Джозеф Генри также успешно проводил опыты по индукции токов, но пока он собирался опубликовать результаты своих опытов, в печати появилось сообщение М. Фарадея об открытии им электромагнитной индукции.
М. Фарадей стремился использовать открытое им явление, чтобы получить новый источник электричества.
20.3 Электромагнитная индукция – физика
Изменение магнитных полей
В предыдущем разделе мы узнали, что ток создает магнитное поле. Если природа симметрична, то, возможно, магнитное поле может создать ток. В 1831 году, примерно через 12 лет после открытия, что электрический ток создает магнитное поле, английский ученый Майкл Фарадей (1791–1862) и американский ученый Джозеф Генри (1797–1878) независимо друг от друга продемонстрировали, что магнитные поля могут создавать токи.Основной процесс генерации токов с помощью магнитных полей называется индукцией; этот процесс также называют магнитной индукцией, чтобы отличить его от индукционной зарядки, в которой используется электростатическая кулоновская сила.
Когда Фарадей открыл то, что сейчас называется законом индукции Фарадея, королева Виктория спросила его, как можно использовать электричество. «Мадам, – ответил он, – что хорошего в ребенке?» Сегодня токи, индуцированные магнитными полями, необходимы нашему технологическому обществу. Электрический генератор, который можно найти во всем, от автомобилей до велосипедов и атомных электростанций, использует магнетизм для генерации электрического тока.Другие устройства, которые используют магнетизм для индукции токов, включают в себя звукосниматели в электрогитарах, трансформаторы любого размера, определенные микрофоны, ворота безопасности аэропорта и механизмы демпфирования на чувствительных химических весах.
Один эксперимент, который Фарадей провел для демонстрации магнитной индукции, заключался в том, чтобы переместить стержневой магнит через проволочную катушку и измерить результирующий электрический ток через проволоку. Схема этого эксперимента показана на рис. 20.33. Он обнаружил, что ток индуцируется только тогда, когда магнит движется относительно катушки.Когда магнит неподвижен по отношению к катушке, в катушке не индуцируется ток, как показано на рисунке 20.33. Кроме того, перемещение магнита в противоположном направлении (сравните рис. 20.33 с рис. 20.33) или изменение полярности магнита (сравните рис. 20.33 с рис. 20.33) приводит к возникновению тока в противоположном направлении.
Рисунок 20.33 Движение магнита относительно катушки создает электрические токи, как показано. Такие же токи возникают, если катушку перемещать относительно магнита.Чем больше скорость, тем больше величина тока, и ток равен нулю, когда нет движения. Ток, возникающий при перемещении магнита вверх, имеет направление, противоположное направлению тока, возникающего при перемещении магнита вниз.
Виртуальная физика
Закон Фарадея
Попробуйте это моделирование, чтобы увидеть, как движение магнита создает ток в цепи. Лампочка загорается, чтобы показать, когда течет ток, а вольтметр показывает падение напряжения на лампочке.Попробуйте переместить магнит через четырехвитковую катушку и через двухвитковую катушку. Какая катушка производит более высокое напряжение при одинаковой скорости магнита?
Проверка захвата
Если северный полюс находится влево и магнит перемещается справа налево, при входе магнита в катушку создается положительное напряжение. Какое знаковое напряжение получится, если эксперимент повторить с южным полюсом слева?
- Знак напряжения изменится, потому что направление тока изменится при перемещении южного полюса магнита влево.
- Знак напряжения останется прежним, потому что направление тока не изменится при перемещении южного полюса магнита влево.
- Знак напряжения изменится, потому что величина протекающего тока изменится при перемещении южного полюса магнита влево.
- Знак напряжения останется прежним, потому что величина тока не изменится при перемещении южного полюса магнита влево.
Индуцированная электродвижущая сила
Если в катушке индуцируется ток, Фарадей рассуждал, что должна быть так называемая электродвижущая сила , проталкивающая заряды через катушку. Эта интерпретация оказалась неверной; вместо этого внешний источник, выполняющий работу по перемещению магнита, добавляет энергию зарядам в катушке. Энергия, добавляемая на единицу заряда, измеряется в вольтах, поэтому электродвижущая сила на самом деле является потенциалом. К сожалению, название «электродвижущая сила» прижилось, а вместе с ним и возможность спутать его с реальной силой.По этой причине мы избегаем термина электродвижущая сила и просто используем сокращение ЭДС , которое имеет математический символ ε.ε. ЭДС может быть определена как скорость, с которой энергия отбирается от источника на единицу тока, протекающего по цепи. Таким образом, ЭДС – это энергия на единицу заряда , добавленная источником, которая контрастирует с напряжением, которое представляет собой энергию на единицу заряда , высвобождаемую , когда заряды проходят через цепь.
Чтобы понять, почему в катушке возникает ЭДС из-за движущегося магнита, рассмотрим рисунок 20.34, на котором показан стержневой магнит, движущийся вниз относительно проволочной петли. Первоначально через петлю проходят семь силовых линий магнитного поля (см. Изображение слева). Поскольку магнит удаляется от катушки, только пять силовых линий магнитного поля проходят через петлю за короткое время ΔtΔt (см. Изображение справа). Таким образом, когда происходит изменение количества силовых линий магнитного поля, проходящих через область, определяемую проволочной петлей, в проволочной петле индуцируется ЭДС. Подобные эксперименты показывают, что наведенная ЭДС пропорциональна скорости изменения магнитного поля.Математически мы выражаем это как
ε∝ΔBΔt, ε∝ΔBΔt,20,24
где ΔBΔB – изменение величины магнитного поля за время ΔtΔt, а A – площадь петли.
Рис. 20.34 Стержневой магнит движется вниз относительно проволочной петли, так что количество силовых линий магнитного поля, проходящих через петлю, со временем уменьшается. Это вызывает индукцию ЭДС в контуре, создающую электрический ток.
Обратите внимание, что силовые линии магнитного поля, которые лежат в плоскости проволочной петли, на самом деле не проходят через петлю, как показано крайней левой петлей на рисунке 20.35. На этом рисунке стрелка, выходящая из петли, представляет собой вектор, величина которого равна площади петли, а направление перпендикулярно плоскости петли. На рисунке 20.35 петля повернута от θ = 90 ° θ = 90 °. до θ = 0 °, θ = 0 ° вклад силовых линий магнитного поля в ЭДС увеличивается. Таким образом, для создания ЭДС в проволочной петле важна составляющая магнитного поля, которая находится на перпендикулярно плоскости петли, то есть Bcosθ.Bcosθ.
Это аналог паруса на ветру.Представьте, что проводящая петля – это парус, а магнитное поле – как ветер. Чтобы максимизировать силу ветра на парусе, парус ориентируют так, чтобы вектор его поверхности указывал в том же направлении, что и ветер, как в самой правой петле на рис. 20.35. Когда парус выровнен так, что его вектор поверхности перпендикулярен ветру, как в крайней левой петле на рис. 20.35, тогда ветер не оказывает силы на парус.
Таким образом, с учетом угла наклона магнитного поля к площади, пропорциональность E∝ΔB / ΔtE∝ΔB / Δt становится равной
E∝ΔBcosθΔt.E∝ΔBcosθΔt.20,25
Рис. 20.35 Магнитное поле лежит в плоскости крайней левой петли, поэтому в этом случае оно не может генерировать ЭДС. Когда петля поворачивается так, что угол магнитного поля с вектором, перпендикулярным области петли, увеличивается до 90 ° 90 ° (см. Крайнюю правую петлю), магнитное поле вносит максимальный вклад в ЭДС в петле. Точки показывают, где силовые линии магнитного поля пересекают плоскость, определяемую петлей.Другой способ уменьшить количество силовых линий магнитного поля, проходящих через проводящую петлю на Рисунке 20.35 не для перемещения магнита, а для уменьшения размера петли. Эксперименты показывают, что изменение площади проводящей петли в стабильном магнитном поле вызывает в петле ЭДС. Таким образом, ЭДС, создаваемая в проводящей петле, пропорциональна скорости изменения произведения перпендикулярного магнитного поля и площади петли
. ε∝Δ [(Bcosθ) A] Δt, ε∝Δ [(Bcosθ) A] Δt,20,26
, где BcosθBcosθ – перпендикулярное магнитное поле, а A – площадь контура.Продукт BAcosθBAcosθ очень важен. Оно пропорционально количеству силовых линий магнитного поля, которые проходят перпендикулярно через поверхность площадью A . Возвращаясь к нашей аналогии с парусом, он будет пропорционален силе ветра на парусе. Он называется магнитным потоком и обозначается как ΦΦ.
Φ = BAcosθΦ = BAcosθ20,27
Единицей измерения магнитного потока является Вебер (Вб), то есть магнитное поле на единицу площади, или Т / м 2 . Вебер – это также вольт-секунда (Vs).
Индуцированная ЭДС фактически пропорциональна скорости изменения магнитного потока через проводящую петлю.
ε∝ΔΦΔtε∝ΔΦΔt20,28
Наконец, для катушки из петель Н и ЭДС в Н в раз сильнее, чем для одиночной петли. Таким образом, ЭДС, наведенная изменяющимся магнитным полем в катушке из Н, витков, равна
. ε∝NΔBcosθΔtA.ε∝NΔBcosθΔtA.Последний вопрос, на который нужно ответить, прежде чем мы сможем преобразовать пропорциональность в уравнение: «В каком направлении течет ток?» Русский ученый Генрих Ленц (1804–1865) объяснил, что ток течет в том направлении, которое создает магнитное поле, которое пытается сохранить постоянный поток в контуре.Например, снова рассмотрим рисунок 20.34. Движение стержневого магнита приводит к уменьшению количества направленных вверх силовых линий магнитного поля, проходящих через петлю. Следовательно, в контуре генерируется ЭДС, которая направляет ток в направлении, которое создает более направленные вверх силовые линии магнитного поля. Используя правило правой руки, мы видим, что этот ток должен течь в направлении, показанном на рисунке. Чтобы выразить тот факт, что наведенная ЭДС действует как противодействие изменению магнитного потока через проволочную петлю, в пропорциональность ε∝ΔΦ / Δt вводится знак минус.) внутри катушки, направленной влево. Это будет противодействовать увеличению магнитного потока, направленного вправо. Чтобы увидеть, в каком направлении должен течь ток, направьте большой палец правой руки в желаемом направлении магнитного поля B → катушка, B → катушка, и ток будет течь в направлении, указанном сгибанием ваших пальцев правой руки. Это показано изображением правой руки в верхнем ряду рисунка 20.36. Таким образом, ток должен течь в направлении, показанном на рисунке 4 (а).
На Рисунке 4 (b) направление, в котором движется магнит, обратное.В катушке направленное вправо магнитное поле B → magB → mag из-за движущегося магнита уменьшается. Закон Ленца гласит, что, чтобы противостоять этому уменьшению, ЭДС будет управлять током, который создает дополнительное направленное вправо магнитное поле B → катушка B → катушка в катушке. Опять же, направьте большой палец правой руки в желаемом направлении магнитного поля, и ток будет течь в направлении, указанном сгибанием ваших пальцев правой руки (Рисунок 4 (b)).
Наконец, на Рисунке 4 (c) магнит перевернут, так что южный полюс находится ближе всего к катушке.Теперь магнитное поле B → magB → mag направлено на магнит, а не на катушку. Когда магнит приближается к катушке, он вызывает увеличение направленного влево магнитного поля в катушке. Закон Ленца гласит, что ЭДС, индуцированная в катушке, будет вести ток в направлении, которое создает магнитное поле, направленное вправо. Это будет противодействовать увеличению магнитного потока, направленного влево из-за магнита. Повторное использование правила правой руки, как показано на рисунке, показывает, что ток должен течь в направлении, показанном на рисунке 4 (c).
Рис. 20.36. Закон Ленца гласит, что ЭДС магнитного поля будет управлять током, который сопротивляется изменению магнитного потока в цепи. Это показано на панелях (а) – (с) для различных ориентаций и скоростей магнита. Правые руки справа показывают, как применить правило правой руки, чтобы найти, в каком направлении наведенный ток течет вокруг катушки.
Виртуальная физика
Электромагнитная лаборатория Фарадея
Это моделирование предлагает несколько действий.А пока щелкните вкладку Pickup Coil, которая представляет собой стержневой магнит, который вы можете перемещать через катушку. Когда вы это сделаете, вы увидите, как электроны движутся в катушке, и загорится лампочка, или вольтметр покажет напряжение на резисторе. Обратите внимание, что вольтметр позволяет вам видеть знак напряжения при перемещении магнита. Вы также можете оставить стержневой магнит в покое и переместить катушку, хотя наблюдать за результатами сложнее.
Проверка захвата
Сориентируйте стержневой магнит так, чтобы северный полюс был направлен вправо, и поместите приемную катушку справа от стержневого магнита.Теперь переместите стержневой магнит к катушке и посмотрите, в каком направлении движутся электроны. Это такая же ситуация, как показано ниже. Ток при моделировании течет в том же направлении, что и показано ниже? Объясните, почему да или почему нет.- Да, ток в моделировании течет, как показано, потому что направление тока противоположно направлению потока электронов.
- Нет, ток в моделировании течет в противоположном направлении, потому что направление тока совпадает с направлением потока электронов.
Watch Physics
Наведенный ток в проводе
В этом видео объясняется, как можно индуцировать ток в прямом проводе, перемещая его через магнитное поле. Лектор использует перекрестное произведение , которое представляет собой тип векторного умножения. Не волнуйтесь, если вы не знакомы с этим, он в основном объединяет правило правой руки для определения силы, действующей на заряды в проводе, с уравнением F = qvBsinθ.F = qvBsinθ.
Проверка захвата
Какая ЭДС создается на прямом проводе 0.через однородное магнитное поле (0,30 Тл) ẑ ? Провод лежит в направлении ŷ . Кроме того, какой конец провода имеет более высокий потенциал – пусть нижний конец провода будет на y = 0, а верхний конец на y = 0,5 м)?
- 0,15 В и нижний конец провода будет иметь более высокий потенциал
- 0,15 В и верхний конец провода будет иметь более высокий потенциал
- 0,075 В и нижний конец провода будет иметь более высокий потенциал
- 0.075 В и верхний конец провода будет иметь более высокий потенциал
Рабочий пример
ЭДС, индуцированная в проводящей катушке движущимся магнитом
Представьте, что магнитное поле проходит через катушку в направлении, указанном на рисунке 20.37. Диаметр катушки 2,0 см. Если магнитное поле изменится с 0,020 до 0,010 Тл за 34 с, каковы направление и величина индуцированного тока? Предположим, что катушка имеет сопротивление 0,1 Ом.
Рисунок 20.37 Катушка, через которую проходит магнитное поле B .
Стратегия
Используйте уравнение ε = −NΔΦ / Δtε = −NΔΦ / Δt, чтобы найти наведенную ЭДС в катушке, где Δt = 34sΔt = 34s. Подсчитав количество витков соленоида, мы находим, что у него 16 петель, поэтому N = 16.N = 16. Используйте уравнение Φ = BAcosθΦ = BAcosθ для расчета магнитного потока
Φ = BAcosθ = Bπ (d2) 2, Φ = BAcosθ = Bπ (d2) 2,20,30
, где d – диаметр соленоида, а мы использовали cos0 ° = 1. cos0 ° = 1. Поскольку площадь соленоида не меняется, изменение магнитного потока через соленоид составляет
ΔΦ = ΔBπ (d2) 2.ΔΦ = ΔBπ (d2) 2.20,31
Найдя ЭДС, мы можем использовать закон Ома, ε = IR, ε = IR, чтобы найти ток.
Наконец, закон Ленца гласит, что ток должен создавать магнитное поле, которое препятствует уменьшению приложенного магнитного поля. Таким образом, ток должен создавать магнитное поле справа.
Решение
Объединение уравнений ε = −NΔΦ / Δtε = −NΔΦ / Δt и Φ = BAcosθΦ = BAcosθ дает
ε = −NΔΦΔt = −NΔBπd24Δt.ε = −NΔΦΔt = −NΔBπd24Δt.20,32
Решение закона Ома для тока и использование этого результата дает
I = εR = −NΔBπd24RΔt = −16 (−0,010T) π (0,020 м) 24 (0,10 Ом) (34 с) = 15 мкА.I = εR = −NΔBπd24RΔt = −16 (−0,010T) π (0,020 м) 24 (0,10 Ом) (34 с) = 15 мкА.20.33
Закон Ленца гласит, что ток должен создавать магнитное поле справа. Таким образом, мы направляем большой палец правой руки вправо и сжимаем пальцы правой руки вокруг соленоида. Ток должен течь в том направлении, в котором указывают наши пальцы, поэтому он входит в левый конец соленоида и выходит из правого конца.
Обсуждение
Давайте посмотрим, имеет ли смысл знак минус в законе индукции Фарадея. Определите направление магнитного поля как положительное. Это означает, что изменение магнитного поля отрицательное, как мы обнаружили выше. Знак минус в законе индукции Фарадея отрицает отрицательное изменение магнитного поля, оставляя нам положительный ток. Следовательно, ток должен течь в направлении магнитного поля, что мы и обнаружили.
Теперь попробуйте определить положительное направление как направление, противоположное направлению магнитного поля, то есть положительное направление находится слева на рисунке 20.37. В этом случае вы обнаружите отрицательный ток. Но поскольку положительное направление находится влево, отрицательный ток должен течь вправо, что опять же согласуется с тем, что мы обнаружили с помощью закона Ленца.
Рабочий пример
Магнитная индукция из-за изменения размера цепи
Схема, показанная на рисунке 20.38, состоит из U-образного провода с резистором, концы которого соединены скользящим токопроводящим стержнем. Магнитное поле, заполняющее область, ограниченную контуром, имеет постоянное значение 0.01 T. Если стержень тянут вправо со скоростью v = 0,50 м / с, v = 0,50 м / с, какой ток индуцируется в цепи и в каком направлении он течет?
Рисунок 20.38 Схема ползунка. Магнитное поле постоянно, и шток тянется вправо со скоростью v . Область изменения, заключенная в цепи, вызывает в цепи ЭДС.
Стратегия
Мы снова используем закон индукции Фарадея, E = −NΔΦΔt, E = −NΔΦΔt, хотя на этот раз магнитное поле остается постоянным и площадь, ограниченная контуром, изменяется.Схема состоит из одного контура, поэтому N = 1.N = 1. Скорость изменения площади ΔAΔt = vℓ.ΔAΔt = vℓ. Таким образом, скорость изменения магнитного потока равна
ΔΦΔt = Δ (BAcosθ) Δt = BΔAΔt = Bvℓ, ΔΦΔt = Δ (BAcosθ) Δt = BΔAΔt = Bvℓ,20,34
, где мы использовали тот факт, что угол θθ между вектором площади и магнитным полем равен 0 °. Зная ЭДС, мы можем найти ток, используя закон Ома. Чтобы найти направление тока, мы применяем закон Ленца.
Решение
Закон индукции Фарадея дает
E = −NΔΦΔt = −Bvℓ.E = −NΔΦΔt = −Bvℓ.20,35
Решение закона Ома для тока и использование предыдущего результата для ЭДС дает
I = ER = −BvℓR = – (0,010T) (0,50 м / с) (0,10 м) 20Ω = 25 мкA I = ER = −BvℓR = – (0,010T) (0,50 м / с) (0,10 м) 20Ω = 25 мкА.20,36
По мере скольжения стержня вправо магнитный поток, проходящий через контур, увеличивается. Закон Ленца говорит нам, что индуцированный ток создаст магнитное поле, которое будет противодействовать этому увеличению. Таким образом, магнитное поле, создаваемое индуцированным током, должно быть на странице.Сгибание петли пальцами правой руки по часовой стрелке заставляет большой палец правой руки указывать на страницу, что является желаемым направлением магнитного поля. Таким образом, ток должен течь по цепи по часовой стрелке.
Обсуждение
Сохраняется ли энергия в этой цепи? Внешний агент должен тянуть стержень с достаточной силой, чтобы просто уравновесить силу на проводе с током в магнитном поле – вспомните, что F = IℓBsinθ.F = IℓBsinθ. Скорость, с которой эта сила действует на стержень, должна уравновешиваться скоростью, с которой цепь рассеивает мощность.Используя F = IℓBsinθ, F = IℓBsinθ, сила, необходимая для протягивания проволоки с постоянной скоростью v , составляет
. Fpull = IℓBsinθ = IℓB, Fpull = IℓBsinθ = IℓB,20,37
, где мы использовали тот факт, что угол θθ между током и магнитным полем составляет 90 ° 0,90 °. Подставляя приведенное выше выражение для тока в это уравнение, получаем
Fpull = IℓB = −BvℓR (ℓB) = – B2vℓ2R.Fpull = IℓB = −BvℓR (ℓB) = – B2vℓ2R.20,38
Сила, создаваемая агентом, тянущим стержень, равна Fpullv, или Fpullv, или
. Потяните = Fpullv = −B2v2ℓ2R.Потяните = Fpullv = −B2v2ℓ2R.20,39
Мощность, рассеиваемая схемой, составляет
Pdissipated = I2R = (- BvℓR) 2R = B2v2ℓ2R. Pdissipated = I2R = (- BvℓR) 2R = B2v2ℓ2R.20,40
Таким образом, мы видим, что Ppull + Pdissipated = 0, Ppull + Pdissipated = 0, что означает, что мощность сохраняется в системе, состоящей из цепи и агента, который тянет стержень. Таким образом, в этой системе сохраняется энергия.
Электромагнитное явление – обзор
Электрический и магнитный поток
Как отмечалось ранее, сила электрического или магнитного поля пропорциональна плотности соответствующих силовых линий в определенной области пространства.Эти силовые линии соответствуют электрическому и магнитному потокам, физической величине, которая является центральной для электромагнитных явлений, описываемых уравнениями Максвелла.
Определение потока вводится сразу же, поскольку это скорость изменения электрического и магнитного потоков во времени, которая приводит к генерации магнитного и электрического полей, соответственно. Такой экономичный подход имеет некоторое оправдание, поскольку это эффективный способ выполнения простых вычислений, связанных с информационной безопасностью.
Электрический поток ψ на поверхности площадью A , перпендикулярной направлению электрического поля E , определяется следующим образом:
(4.1) ψ = ɛEA
, где ɛ – относительная электрическая проницаемость или диэлектрическая проницаемость. Проще говоря, электрический поток – это общее количество силовых линий электрического поля, пересекающих поверхность площадью A .
По аналогии, магнитный поток ø на поверхности площадью A , перпендикулярной магнитному полю B , определяется следующим образом:
(4.2) ø = μBA
, где μ – диэлектрическая проницаемость свободного пространства. Магнитный поток – это общее количество силовых линий магнитного поля, пересекающих поверхность площадью A .
Концепция потока имеет решающее значение для понимания электромагнитных явлений и, следовательно, важно для понимания основ информационной безопасности. Может быть полезна аналогия с более интуитивной физической величиной. 4
Рассмотрим воображаемую прямоугольную петлю или поверхность площадью A .Вода течет через плоскость этого контура со скоростью v . Для простоты предположим, что вода течет перпендикулярно плоскости A , хотя следует учитывать, что это особый случай, поскольку вода может течь под углом к петле. Для этой конкретной геометрии поток воды через воображаемую поверхность – это объем воды в единицу времени v , который проходит через площадь поперечного сечения A . Таким образом, поток воды Φ Вт = ВА .
Важно отметить, что поток характеризует количество «вещей», например, вода, частицы, бананы, электрические и магнитные поля автомобилей, которые пересекают произвольную границу в единицу времени.
Теперь предположим, что плоскость петли или поверхности ориентирована под углом, параллельным направлению потока воды. В этом случае вода не течет через плоскость петли. Следовательно, поток, как определено ранее, равен нулю. Перпендикулярная и параллельная ориентации петли относительно направления потока – это две простейшие геометрии, относящиеся к потоку.
В целом сценарий не очень удобный. Фактически, цель обсуждения векторов и поверхностных интегралов – обратиться к более сложной геометрии, которая возникает в сценариях информационной безопасности.
Более общая проблема заключается в вычислении потока, когда плоскость контура ориентирована под некоторым произвольным углом по отношению к направлению «материала», текущего по поверхности. В сценариях, относящихся к информационной безопасности, поток обычно представляет собой силовые линии магнитного или электрического поля.Более того, величина силы, создаваемой этими полями, пропорциональна плотности силовых линий электрического или магнитного поля, которые «текут» по поверхности.
Рис. 4.2 помогает визуализировать два крайних случая потока. Изображены две поверхности, перпендикулярные и параллельные направлению падающего потока. 5 В первом поток максимальный, а во втором поток равен нулю.
Рисунок 4.2. Максимальный и минимальный поток векторного поля через поверхность.
Вероятно, становится очевидным, что поток электрического и магнитного полей каким-то образом имеет отношение к обнаружению электромагнитного сигнала. Однако некоторые концепции все еще отсутствуют. В частности, вводится понятие вектора, после чего следует обсуждение поверхностных интегралов. Они позволяют проводить общие расчеты скорости изменения электрического и магнитного потоков во времени, что помогает объяснить пределы обнаружения сигнала.
Когда любая среда, состоящая из электрических зарядов, помещается в электрическое поле, заряды в ней выравниваются в соответствии с ориентацией и силой приложенного поля.В общем, заряды становятся поляризованными или слегка разделенными в соответствии с ориентацией приложенного поля.
Обратите внимание, что приложенное электрическое поле обычно колеблется с некоторой заданной частотой, и поэтому поляризация или разделение зарядов будут изменяться в ответ. Но не все материалы и заряды в них одинаково реагируют на силу приложенного электрического поля. Диэлектрическая проницаемость среды указывает на величину поляризации, которая существует в материале в результате приложенного электрического поля. 6
На рис. 4.3 электрическое поле привело к поляризации положительных и отрицательных зарядов. 7 Электрическое поле одинаковой величины заставляет заряды в одном материале поляризоваться сильнее, чем в другом, о чем свидетельствует разница в разделении положительных и отрицательных зарядов. Считается, что более поляризованный материал имеет более высокую диэлектрическую проницаемость.
Рисунок 4.3. Слабая и сильная поляризация и диэлектрическая проницаемость.
Не менее достоверная интерпретация того же эффекта проиллюстрирована на рис.4.4. Низкая плотность электрического потока в материале слева вызывает ту же поляризацию, что и материал справа, который имеет высокую плотность электрического потока. Следовательно, материал слева имеет высокую диэлектрическую проницаемость, поскольку такая же поляризация была достигнута при более низкой плотности потока.
Рисунок 4.4. Низкая и высокая плотность электрического потока на единицу заряда в зависимости от диэлектрической проницаемости.
Относительная диэлектрическая проницаемость материала известна как диэлектрическая проницаемость, и этот термин может быть более знаком читателям.Относительная диэлектрическая проницаемость – это диэлектрическая проницаемость относительно вакуума. Диэлектрическая проницаемость вакуума определена равной единице, а для воздуха – 1.00058986 ± 0.00000050. Таким образом, относительная диэлектрическая проницаемость воздуха примерно равна диэлектрической проницаемости вакуума.
Объясните эксперимент Фарадея по электромагнитной индукции
Оборудование для электромагнитной индукции: Capstone, печатная плата RLC, коробка с 2 катушками, у которых есть железный стержень и цилиндрический магнит, 1 датчик напряжения, 2 провода (120 см в цепи прямо пропорциональны скорости изменения линий магнитного поля, разрезающих ее. .• Объясните, как использовать магнит для зажигания лампочки. • Объясните процесс взаимной индукции. Физическая лаборатория (онлайн-моделирование) Предлабораторные вопросы: студентов просят обратиться к учебнику, чтобы получить необходимую теорию для выполнения предварительной лабораторной и остальной части лаборатории. Знак минус в законе индукции Фарадея очень важен. Сформулируйте два закона Фарадея. Эксперимент Фарадея 1. Возникающее магнитное поле ударяет по второй обмотке и генерирует в этой обмотке переменное напряжение за счет электромагнитной индукции.Закон индукции Фарадея гласит, что величина наведенной ЭДС. Закон Фарадея об электромагнитной индукции – это процесс, в котором электродвижущая сила (ЭДС) индуцируется в замкнутой цепи из-за изменений магнитного поля вокруг цепи. Закон Ленца гласит, что направление индуцированной ЭДС. 10.3 Закон электромагнитной индукции Фарадея (ESBPY) Ток, индуцированный изменяющимся магнитным полем (ESBPZ). 7. Дайте определение закону Ленца? В 1831 году Майкл Фарадей изменил эксперимент Эрстеда и открыл электромагнитную индукцию.Закон Фарадея об электромагнитной индукции Это явление называется электромагнитной индукцией и описывается законом Фарадея. Опишите, используя необходимую теорию, эксперимент Милликена с каплей масла, чтобы определить величину заряда, связанного с электроном. Он ввел явление электромагнитной индукции. «Скорость» здесь связана со скоростью движения магнита / катушки. Майкл Фарадей открыл электромагнитную индукцию в 1831 году.) И 1 свинец (150-200 см) 1 Введение Явление электромагнитной индукции было открыто Джозефом Генри в Нью-Йорке в 1830 году и Майклом Фарадеем в Англии в 1831 году.(iii) резистор подключен последовательно с амперметром и источником питания переменного тока. Однако, прежде чем мы сформулируем и оценим его законы, мы должны познакомиться с понятием магнитного потока, Φ Б. Закон индукции Фарадея объясняет принцип работы трансформаторов, двигателей, генераторов и индукторов. В этой лабораторной работе вы изучите, как происходит это явление. Эксперимент Фарадея с ведром со льдом – это простой электростатический эксперимент, проведенный в 1843 году британским ученым Майклом Фарадеем, который демонстрирует влияние электростатической индукции на проводящий контейнер.Майкл Фарадей (1791 – 1867) был мастером электричества. Мы обсудили здесь законы электромагнитной индукции Фарадея. Тема: Математика. Двигатели, трансформаторы, аудиоколонки, радиопередачи и генераторы работают с использованием диких и сложных явлений электромагнетизма. Понимание поведения электромагнетизма является важным предметом изучения. Мы объясним вам, что такое закон Фарадея, электромагнитная индукция, его историю, формулу и примеры. Проведите этот простой эксперимент с электромагнитной индукцией, чтобы лично убедиться в этом явлении! Что такое электромагнитная индукция? Связанное сообщение: Формулы электрического и магнитного потока, плотности и напряженности поля Электромагнитная индукция.Чтобы проверить свою гипотезу, он сделал катушку, обмотав бумажный цилиндр проволокой. Английский физик и химик Майкл Фарадей (1791-1867) обнаружил, что создаваемая ЭДС пропорциональна скорости изменения магнитного потока в цепи. Исследуйте Майкла Фарадея и его вклад в науку, особенно в том, что вы исследуете. 2. Ток был индуцирован из-за магнитного потока, так как в цепи есть некоторый ток, поэтому он будет… В ходе своего исследования он обнаружил, что электромагнитная сила индуцируется в катушке, когда магнитные линии проходят через проводник, изменяется.Что такое закон Ленца? Майкл Фарадей Эксперимент. Чем генератор переменного тока отличается от постоянного тока? (iv) Как эксперимент Фарадея показывает, что изменяющееся магнитное поле необходимо для выработки электричества? История Эксперимент Фарадея, показывающий индукцию между витками провода: жидкая батарея (справа) обеспечивает ток, который течет через небольшую катушку (A), создавая магнитное поле. Когда катушки неподвижны, ток не индуцируется. Когда северный полюс приближается к катушке, стрелка гальванометра дергается в одну сторону.Обсудите наблюдения за экспериментом Фарадея. 37 полных PDF-файлов, относящихся к этой статье. Первый закон электромагнитной индукции Фарадея: всякий раз, когда происходит изменение магнитного потока, связанного с катушкой, в катушке индуцируется ЭДС. Эта «электромагнитная индукция» остается принципом, лежащим в основе электрического… закона электромагнитной индукции Фарадея- (i) → Всякий раз, когда происходит изменение магнитного потока, связанного с дозирующим контуром, возникает эдс. Опишите 2-й закон. d (t) (t) dt Чтобы понять закон Фарадея, нам необходимо понять концепцию магнитного потока.• Понять принцип индукции. Так, в эксперименте Фарадея, проиллюстрированном в… В 1831 году ему наконец удалось использовать две катушки проволоки, намотанные на противоположные стороны кольца из мягкого железа (рис. 7). Во время эксперимента Фарадей обнаружил, как в катушке индуцируется ЭДС при изменении потока, проходящего через катушку. Его исследования установили, возможно, важные результаты в теории электромагнетизма, в том числе некоторые из них, которые сейчас так считаются само собой разумеющимся, что имя Фарадея, к сожалению, даже не упоминается в связи с ними.В сочетании с законом Ленца его можно использовать для описания результирующего тока и его направления. Краткое изложение соответствующих концепций: • Закон индукции Фарадея гласит, что индуцированная электродвижущая сила (ЭДС) создается изменяющимся магнитным потоком Ф через цепь. К его центру внутри углубления прикреплены небольшие магниты. Одна полезная характеристика тока состоит в том, что он создает собственное магнитное поле. Если бы Фарадей использовал более мощную батарею в своих экспериментах с электромагнитной индукцией, какое влияние это оказало бы на измерения тока его гальванометром, когда батарея была полностью подключена? Краткое изложение этой статьи.6. Но окончательные подробности этого явления были впервые опубликованы Фарадеем, чтобы выяснить это, он провел эксперимент. Второй закон электромагнитной индукции Фарадея: величина ЭДС. Сосулька Реклама. Это индукционный процесс. Этот процесс электромагнитной индукции, в свою очередь,… Следовательно, магнит будет проваливаться через кольцо с ускорением, меньшим, чем ускорение свободного падения. Блок третий: Современная физика. Майкл Фарадей (1791-1867) Британский ученый-экспериментатор Майкл Фарадей… Первый закон Фарадея Второй закон Фарадея Эксперимент Фарадея Часто задаваемые вопросы о применении закона Фарадея.(3.4) Закон Фарадея гласит, что электродвижущая сила в проволочной петле (ЭДС), Eloop, равна отрицательному изменению… Закон индукции Фарадея (кратко, закон Фарадея) является основным законом электромагнетизма, предсказывающим, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу (ЭДС) – явление, известное как электромагнитная индукция. Это фундаментальный принцип работы трансформаторов, индукторов и многих типов электродвигателей, генераторов и соленоидов.Чтобы ответить на вышеперечисленные вопросы, полезны два закона, открытые опытными физиками, Ампера и Фарадея. Назовите малый соленоид S1, а большой – S2. Электромагнитная индукция – Фарадея. К сожалению, Фарадей для объяснения своего закона индукции ввел неправильное понятие поля. Вопросов; наука. и объясните фарадейские выводы 1 См. ответ SPLearn ждет вашей помощи. r r m B dA Объясните эксперимент, а индукция означает побудить или произвести что-то. Один из ученых Фарадей провел серию экспериментов и на основании полученных результатов дал закон индукции.Однако «статическое» магнитное поле этого не сделает; требуется изменяющееся магнитное поле. Используя закон индукции Фарадея, объясните, как постоянное магнитное поле все еще может генерировать ЭДС в замкнутом контуре. Объясните явление электромагнитной индукции с помощью эксперимента 2 См. Ответы Sravan5380 Sravan5380 Ответ: Это явление было обнаружено Майклом Фарадеем и Джозефом Генри в 1831 году. В этом разделе рассматриваются следующие темы Поток и связь потоков, Закон Фарадея, В каком направлении? Сформулируйте два закона Фарадея.Покажите, что ток в нем приводит к приложенной ЭДС. Задайте вопрос … через соленоид большего размера (без батареи) индуцирует ток в соленоиде большего размера, как в оригинальной экспериментальной установке Фарадея ниже. Настройте эксперимент, как показано ниже. Законы электромагнитной индукции Фарадея. Однако это вовсе не парадокс, если действительно понимать электрический ток и электромагнитную индукцию. Закон Фарадея и Ленца. Когда Майкл Фарадей открыл в 1831 году явление электромагнитной индукции, проложив путь к полному объединению электричества и магнетизма, он провел множество экспериментов, чтобы продемонстрировать этот эффект.К ним относятся закон электромагнитной индукции Фарадея и закон силы Ампера. Великая проницательность Фарадея заключалась в открытии простого математического соотношения для объяснения серии экспериментов, которые он проводил с электромагнитной индукцией. 2. Электромагнитная индукция была открыта Майклом Фарадеем и опубликована в 1831 году. Тем не менее, позже Максвелл разработал свою электромагнитную теорию с неправильными полями, движущимися через ошибочный эфир. Электромагнитная индукция – Фарадея. индукция в катушке прямо пропорциональна скорости изменения магнитного потока, связанного с ней.Первый закон Фарадея: всякий раз, когда поток, связанный с контуром, изменяется, э.д.с. Линейный интеграл электрического поля вокруг замкнутого контура равен отрицательному значению скорости изменения магнитного потока… Открытие Фарадеем электрической индукции. Это историческое развитие сравнивается в форме мысленного эксперимента с возможным другим ходом, в котором работы Ампера и Вебера повлияли бы на … индукцию Фарадея … Электромагнитная индукция была впервые обнаружена еще в 1830-х годах Майклом Фарадеем.На рисунке 10.1.1 показан один из экспериментов Фарадея. Одно из уравнений Максвелла эквивалентно закону электромагнитной индукции Фарадея. Первый закон. (ii) → Магнитная индуцированная ЭДС прямо пропорциональна скорости изменения магнитного потока во времени. В первой экспериментальной демонстрации Фарадея (29 августа 1831 г.) он намотал два провода на противоположные стороны железного кольца или «тора» (устройство, подобное современному тороидальному трансформатору). Представлен простой эксперимент, основанный на магнитной индукции, для измерения скорости магнита, летящего в воздухе, с использованием сигнала, индуцируемого магнитом, когда он проходит через катушку.Индукция означает побуждать или порождать что-то. Законы индукции Фарадея. Задача. ; Похоже, что закон Фарадея предсказывает, что ЭДС будет ненулевой, но нулевой ЭДС. Этот эксперимент и некоторые интересные варианты обсуждаются в ссылке 1. • описывают и применяют самоиндукцию и взаимную индуктивность. Напишите резюме своего исследования своими словами и на своем уровне понимания, а также обсудите, какой была бы жизнь, если бы не была обнаружена электромагнитная индукция.Магнитная индукция с использованием DrDAQ: Введение в законы Фарадея. Ключевая идея электромагнитной индукции – это изменение магнитного поля относительно зарядов (свободных электронов) в проводнике. Опишите принцип, устройство и работу генератора переменного тока? 5. математически подтвердить закон электромагнитной индукции Фарадея. 394. Опишите 1-й закон как закон Неймана. Математически он задается как e = – d (fi_B) / dt. Хорошо известное историческое развитие электромагнетизма, находящееся под сильным влиянием работ Фарадея и Максвелла, привело к введению магнитного поля в качестве важного компонента для объяснения разнообразных явлений электромагнитной индукции.Это явление известно как электромагнитная индукция. Описание Исследуйте закон Фарадея и выясните, как изменяющийся магнитный поток может производить поток электричества! Это основной принцип работы трансформаторов, индукторов и многих типов электродвигателей, генераторов и соленоидов. Скачать полный пакет PDF. Опишите 1-й закон как закон Неймана. Математически он задается как e = – d (fi_B) / dt. Эксперимент 1: В этом эксперименте Фарадей подключил катушку к гальванометру, как показано на рисунке выше.5 февраля 2020 г. – Изучите доску Омазич Надины «Электромагнитная индукция» на Pinterest. Для контура магнитный поток через контур составляет. (v) Опишите эксперимент, чтобы продемонстрировать этот закон. (vi) Квадратная катушка из 40 витков со стороной длиной 20 см перпендикулярна магнитному полю… [2067] Переменная ЭДС приложена к конденсатору. Сформулируйте и объясните закон электромагнитной индукции Фарадея. Объясните электромагнитную индукцию и закон Фарадея. Первый закон: – Согласно первому закону, ЭДС индуцируется в цепи всякий раз, когда изменяется величина магнитного потока, связанного с цепью.Фарадей в 1831 году впервые обнаружил, что всякий раз, когда изменяется количество магнитных силовых линий в цепи, в цепи возникает ЭДС, известная как индуцированная ЭДС, и это явление известно как электромагнитная индукция; Если цепь замкнута, то через нее протекает ток, который, как известно, был приведен в контакт с концами железного стержня. После Фарадея Джозеф Генри в 1832 году, принадлежавший к Америке, также работал над электромагнитной индукцией. Когда магнитный поток через поверхность достигает максимального значения? Индукция Индуцированный ток создается изменяющимся магнитным полем. Существует наведенная ЭДС, связанная с индуцированным током. Ток может быть получен без батареи, присутствующей в цепи. Закон индукции Фарадея описывает наведенную ЭДС. Это может произойти, когда проводник перемещается относительно к стационарному полю, полю (например.g., магнит) перемещается относительно неподвижного проводника, или напряженность поля изменяется в присутствии неподвижного проводника. Когда Майкл Фарадей сделал свое открытие электромагнитной индукции в 1831 году, он предположил, что изменяющееся магнитное поле необходимо для индукции тока в соседней цепи. процесс генерации магнитного поля из-за тока, проходящего через катушку. Понаблюдайте, как ток может создавать магнитное поле. Я начал исследовать сочинения Фарадея, работая над постом об Эдварде Булвер-Литтоне… Записанные данные производятся на вращающемся диске с покрытием.Вы также можете играть с электромагнитами, генераторами и трансформаторами! Хотя удивительное открытие Эрстедом электромагнетизма проложило путь для более практического применения электричества, именно Майкл Фарадей дал нам ключ к практическому производству электричества: электромагнитную индукцию. Это текущий выбранный элемент. Как и в эксперименте Фарадея начала 19 века, фонарик содержит постоянный магнит, который проходит через катушку вперед и назад. В ходе наших разработок мы обнаружили, что электрическое и магнитное поля не связаны.В современном обществе существует множество приложений закона индукции Фарадея, что мы исследуем в этой и других главах. Глава 5: Электромагнитная индукция 5.1 Магнитный поток L.O 5.1.1 Определение и использование магнитного потока Магнитный поток определяется как скалярное произведение между плотностью магнитного потока B и вектором площади A.Рейтинг фильмов 2020, Значение варианта двойного мутанта Covid, Развлекательные мероприятия в области искусства и рукоделия, Капитан Америка живет омнибусом, Андре Бруйетт Родители, Термодинамика Демонстрации Физика, Население Южной Кореи в 2021 г., Популярные песни на Tiktok 2021, Ассоциация домовладельцев Квейл-Крик, Мэтью Нильсен Некролог,
Закон индукции Фарадея для чайников
Закон индукции Фарадея был открыт в результате экспериментов, проведенных Майклом Фарадеем в Англии в 1831 году и примерно в то же время Джозефом Генри в Соединенных Штатах.
Несмотря на то, что Фарадей первым опубликовал свои результаты, что дает ему приоритет открытия, единица индуктивности в системе СИ называется генри (аббревиатура H) . С другой стороны, единица измерения емкости в системе СИ, как мы видели, называется фарад (сокращение F) .
В этой главе мы обсуждаем колебания в емкостно-индуктивных цепях, мы видим, насколько уместно связать имена этих двух талантливых современников в едином контексте.
* Помимо независимого одновременного открытия закона индукции, у Фарадея и Генри есть еще несколько общих черт в их жизнях.Оба были учениками в раннем возрасте. Фарадей в 14 лет поступил в ученики к лондонскому переплетчику. Генри в 13 лет поступил в ученики к часовщику в Олбани, штат Нью-Йорк. В последующие годы Фарадей был назначен директором королевского учреждения в Лондоне, основание которого во многом было связано с американцем Бенджамином Томсоном (граф Рамфорд). Генри, с другой стороны, потому что секретарь Смитсоновского института в Вашингтоне, округ Колумбия, который был найден на пожертвования англичанина Джеймса Смитсона.
Фарадей заметил, что если магнит перемещается к катушке с проволокой (соленоиду), соединенной последовательно с гальванометром, в токе возникает электрический ток. Когда магнит перемещается к соленоиду, гальванометр показывает отклонение в одном направлении, а когда магнит перемещается от соленоида, гальванометр показывает отклонение в противоположном направлении. Когда магнит неподвижен, гальванометр не прогибается. Аналогичные результаты получаются, когда магнит остается неподвижным, а катушка перемещается.Когда магнит перемещается, если отклонение гальванометра велико, а когда он перемещается медленно, отклонение невелико. Также было обнаружено, что если есть две замкнутые цепи в непосредственной близости, одна из которых содержит батарею, а другая – гальванометр, и цепь батареи замкнута нажатием кнопки K, а затем разомкнута, гальванометр во вторичной цепи показывает прогиб сначала в одну сторону, а затем в другую.
Замечено, что в гальванометре не возникает отклонений, если ток в первичной цепи протекает непрерывно.Отклонение в гальванометре происходит только при включении или отключении тока в первичной цепи. Фарадей суммировал эти экспериментальные результаты в виде следующих законов:
- 1: Каждый раз, когда происходит изменение магнитных силовых линий или магнитного потока, в цепи возникает индуцированный ток.
- 2: Индуцированный ток или ЭДС длится только в течение времени, в течение которого силовые линии или магнитный поток фактически изменяются.
- 3: Величина наведенной ЭДС зависит от скорости изменения магнитных силовых линий или магнитного потока.
На рисунке (1) показана катушка с проводом как часть цепи, содержащей амперметр. Обычно мы ожидаем, что амперметр не будет показывать ток в цепи, потому что, похоже, нет электродвижущей силы. Однако, если мы подтолкнем стержневой магнит к катушке так, чтобы его северный полюс был обращен к катушке, произойдет примечательная вещь. Во время движения магнита амперметр отклоняется, показывая, что в катушке установлен ток. Если удерживать магнит неподвижно по отношению к катушке, амперметр не отклоняется.Если мы отодвинем магнит от катушки, счетчик снова отклонится, но в противоположном направлении, а это значит, что ток в катушке находится в противоположном направлении. Если мы используем конец северного полюса магнита вместо конца северного полюса, эксперимент будет работать, как описано, но отклонения будут обратными. Чем быстрее перемещается магнит, тем выше показания счетчика. Дальнейшие эксперименты показывают, что важно относительное движение магнита и катушки. Он не отмечает различий, перемещаем ли мы магнит к катушке или катушку к магниту.
Закон индукции Фарадея формула
«Индуцированная ЭДС в цепи равна отрицательной скорости, с которой магнитный поток, проходящий через цепь, изменяется со временем». Математически это записывается как:
Пояснение:
Эксперимент Фарадея показал, и, поскольку техника линий поля Фарадея помогает нам визуализировать, именно изменение количества силовых линий, проходящих через контур цепи, индуцирует ЭДС в контуре.В частности, именно скорость изменения количества силовых линий, проходящих через петлю, определяет наведенную ЭДС.
Чтобы сделать это утверждение количественным, мы вводим магнитный поток Φ B , который определяется как «Количество магнитных силовых линий, проходящих нормально через определенную область, называется магнитным потоком». Он обозначается как Φ B. Это скалярная величина, единица измерения которой – Вебер (Вб). Он измеряется произведением напряженности магнитного поля и составляющей площади вектора, параллельной магнитному полю.Математически это представлено как:
Φ B = B.A
Φ B = BA cosθ
где A – вектор, величина которого представляет собой площадь элемента и направление которого вдоль нормали к поверхности элемента, θ – угол между направлениями векторов B и A.
Когда магнит перемещается к петле, стрелка амперметра отклоняется в одном направлении, как показано на рисунке (а).Когда магнит приведен в состояние покоя и удерживается неподвижно относительно фигуры петли (b), отклонения не наблюдается. Когда магнит отодвигается от петли, игла отклоняется в противоположном направлении, как показано на рисунке (c). Наконец, если магнит удерживается в неподвижном состоянии и петля перемещается либо к нему, либо от него, игла отклоняется. Из этих наблюдений мы заключаем, что петля обнаруживает движение магнита относительно нее, и мы связываем это обнаружение с изменением магнитного поля.Таким образом, кажется, что существует связь между током и изменяющимися магнитными полями.
Эти результаты весьма примечательны с учетом того факта, что ток подается, даже если в цепи нет батарей. Мы называем такой ток индуцированным током, который создается наведенной ЭДС. Это явление называется электромагнитной индукцией.
На нашем веб-сайте есть и другие связанные темы:
1: Закон Ленца
2: Электромагнитная индукция
3: Трансформатор
4: Магнетизм
Внешние источники
- https: // en.wikipedia.org/wiki/Faraday%27s_law_of_induction
- https://www.daenotes.com/electronics/basic-electronics/faraday-laws-of-electromagnetic-induction
Калькулятор закона Фарадея
Этот калькулятор закона Фарадея поможет вам найти электродвижущую силу, индуцированную в замкнутой цепи.
Что такое электромагнитная индукция?
Если вы прикрепите металлический провод к батарее, вы создадите ток – электроны будут двигаться по проводу. Тогда, если вы поместите этот провод в магнитное поле, дополнительная электрическая сила будет индуцирована движением электронов в этом поле.
Этот эффект также работает в обратном направлении – когда неподвижные электроны помещаются в переменное магнитное поле, индуцируется электродвижущая сила (ЭДС), и начинает течь ток. Это явление известно как электромагнитная индукция.
Магнитное поле и поток
Магнитное поле имеет две основные характеристики. Первый – это величина поля B и измеряется в теслах (символ Т), или ньютонах на метр на ампер. Второй – магнитный поток Φ – определяется как магнитное поле, проходящее через поверхность, и измеряется в веберах (символ Wb).
Величина и поток взаимозависимы – вы можете использовать приведенное ниже уравнение, чтобы легко переключаться между ними. A обозначает площадь поперечного сечения катушки, в которой индуцируется ЭДС.
Φ = B * A
Teslas и веберов связаны следующей формулой:
1 Вт / 1 м² = 1 T
Закон Ленца и формула закона Фарадея
Закон Фарадея гласит, что индуцированное в цепи напряжение равно скорости изменения, то есть изменения во времени, магнитного потока через контур:
ЭДС = dΦ / dt
Закон Ленца – это второй ключевой закон, описывающий электромагнитную индукцию.Он не описывает величину, а скорее направление тока, утверждая, что ток всегда будет противодействовать потоку, который его произвел. Он включен в закон Фарадея со знаком минус:
ЭДС = - dΦ / dt
Если вы попытаетесь вызвать электродвижущую силу в катушке с несколькими витками, вы также можете умножить это значение на количество витков, чтобы учесть количество витков N :
ЭДС = - N * dΦ / dt
Это формула, используемая нашим калькулятором закона Фарадея.
Как рассчитать электродвижущую силу?
Обычно вы не сразу узнаете, каков магнитный поток в катушке. Но не волнуйтесь – наш калькулятор электромагнитной индукции тоже может его найти! Просто выполните следующие действия, чтобы рассчитать наведенное напряжение.
Определитесь с площадью поперечного сечения и количеством витков в петле. Например, вы можете использовать круглую катушку сечением 30 см² и десятью витками.
Узнайте, какова величина магнитного поля.Например, мы можем принять поле в 0,4 тесла.
Рассчитайте изменение магнитного потока как произведение магнитного поля на площадь поперечного сечения:
dΦ = B * A
dΦ = 0,4 * 30 * 10⁻⁴ = 0,0012 Wb
Теперь определите, за сколько времени магнитное поле изменится на 0,4 Тл. Мы можем предположить, что это заняло 8 секунд.
Используйте формулу закона Фарадея для вычисления электродвижущей силы:
ЭДС = - N * dΦ / dt
ЭДС = - 10 * 0.0012/8 = -0,0015 В
Индуцированное напряжение равно 0,0015 В. Знак минус указывает, что направление тока противоположно направлению магнитного потока.
Подобные калькуляторы
Если вам понравился этот калькулятор закона Фарадея, не забудьте также проверить калькулятор закона Ома!
Закон Фарадея – Электромагнитная геофизика
С помощью апплета мы можем наблюдать несколько характеристик электромагнитной индукции:
Вольтметр регистрирует сигнал только при движении магнита, независимо от его абсолютного положения.
Знак наведенного напряжения меняется в зависимости от направления движения и ориентации магнита
Величина напряжения зависит от скорости движения магнита
При прочих равных, напряжение, индуцированное в контуре с четырьмя катушками, больше, чем в контуре с двумя катушками.
Такое поведение описывается законом Фарадея. Закон Фарадея назван в честь английского ученого Майкла Фарадея (1791-1867), и описывает способ, которым изменяющиеся во времени магнитные поля вызывают вращательные электрические поля.Это объясняет электромагнитную индукцию явление, которое является фундаментальным механизмом возбуждения индуктивного источник.
Интегральная форма во временной области
Закон Фарадея в интегральной форме можно выразить с помощью следующего уравнения:
(55) \ [\ oint_C {\ bf e} \ cdot {\ bf d} {\ bf l} = – \ int_S \ frac {\ partial {\ bf b}} {\ partial t} \ cdot \ hat {\ bf n} \, da, \]где:
\ (\ mathbf {e} \) – электрическое поле, определенное вокруг замкнутого пути \ (C \)
\ (\ mathbf {b} \) – плотность магнитного потока, определенная над замкнутой поверхностью \ (A \), очерченной \ (C \)
\ (\ hat n \) – единичный вектор внешней нормали, перпендикулярный \ (da \)
\ (\ d \ mathbf {l} \) – векторный элемент длины по контуру \ (C \)
Ур.(55) утверждает, что зависящая от времени скорость изменения магнитного потока через поверхность, ограниченную замкнутым путем, отрицательно пропорциональна линейному интегралу электрического поля, которое он наводит на этом пути.
Дифференциальная форма во временной области
Применяя теорему Стокса к левой части уравнения. (55), мы можем получить дифференциальную форму уравнения Фарадея закон:
(56) \ [\ nabla \ times {\ bf e} = – \, \ frac {\ partial {\ bf b}} {\ partial t} \]Ур. (56) утверждает, что изменяющиеся во времени магнитные поля будут индуцируют вращательные электрические поля.Кроме того, ротор индуцированной электрические поля противодействуют зависящим от времени изменениям индуцирующего магнитного поля.
Закон Фарадея в частотной области
Частотное представление закона Фарадея может быть получено применяя преобразование Фурье к уравнениям. (55) и (56). Интегральная форма закона Фарадея в частотная область:
(57) \ [\ oint_C {\ bf E} \ cdot d {\ bf l} = – \, i \ omega \ int_A {\ bf B} \ cdot \ hat n \, da \]Аналогично, используя теорему Стокса, дифференциальная форма закона Фарадея:
(58) \ [\ nabla \ times {\ bf E} = – \, i \ omega {\ bf B} \]где \ (\ omega \) – угловая частота, \ ({\ bf E} \) – частотно-зависимое электрическое поле, а \ ({\ bf B} \) – частотно-зависимое зависимая плотность магнитного потока.
Из уравнения. (58), мы можем вывести две вещи:
Наведенные вращательные электрические поля пропорциональны угловой частоте; это означает, что электромагнитная индукция больше на более высоких частотах.
Индуцированные вращательные электрические поля и отвечающие за них частотно-зависимые магнитные поля сдвинуты по фазе на 90 градусов.
Открытие закона Фарадея
Закон Фарадея лучше всего понять с помощью трех экспериментов, которые Фарадей проведено и обобщено в 1831 г.Для каждого из этих экспериментов электромагнит использовался для создания зависящего от времени магнитного поля, которое мы представим с использованием плотности магнитного потока \ ({\ bf {b}} \). Петля провод с областью \ (A \), очерченный замкнутым контуром \ (C \), затем удерживался в непосредственной близости от электромагнита. Это привело к магнитному потоку \ ({\ boldsymbol \ Phi_b} \) определяется по: s
(59) \ [{\ boldsymbol \ Phi_b} = \ int_A {\ bf b} \ cdot \ hat {\ bf {n}} \, da \]Затем Фарадей провел следующие три эксперимента:
Проволочная петля была закрыта, а электромагнит оставался неподвижным.
Электромагнит перемещался, в то время как проволочная петля оставалась неподвижной.
Как проволочная петля, так и электромагнит оставались неподвижными, однако сила магнитного поля менялась в зависимости от времени.
Фарадей заметил, что во всех трех экспериментах электродвижущая сила \ (\ mathcal {E} \) был индуцирован в проводе, что привело к измеримому электрический ток. Электродвижущая сила \ (\ mathcal {E} \) может быть определена через электрическое поле \ ({\ bf e} \) интегрированием по пути провод следующим образом:
(60) \ [\ mathcal {E} = – \ oint_C {\ bf e} \ cdot d {\ bf l} = V \]В идеальной схеме электродвижущая сила эквивалентна напряжению \ (V \) испытанный проводом.Для цепи с сопротивлением \ (R \), Закон Ома \ (V = IR \) может быть использован, чтобы показать, что электродвижущие силы связанные с токами \ (I \). Прорыв Фарадея произошел, когда он предложил что зависящее от времени изменение магнитного потока через проволочную петлю было отвечает за возникающую электродвижущую силу. В 1833 году Генрих Ленц определили, что изменение магнитного потока в зависимости от времени отрицательно пропорциональна создаваемой электродвижущей силе. Сделанные взносы Фарадея и Ленца представлены следующим уравнением:
(61) \ [\ mathcal {E} = – \, \ frac {\ partial {\ boldsymbol \ Phi_b}} {\ partial t} \]Вклад Ленца в открытие Фарадея не только обеспечивает равенство в Уравнение(61), но определяет направление силы на свободном заряжается в ответ на изменения приложенного магнитного поля. Для большего полное описание см. на странице закона Ленца. Подставляя определение магнитного потока из уравнения. (59) и определение электродвижущая сила из уравнения. (60) в уравнение. (61) можно получить закон Фарадея в интегральной форме согласно формуле. (55).
шт.
Плотность магнитного потока | \ (\ mathbf {b} \) | \ (\ frac {\ text {Wb}} {\ text {m} ^ {2}} \) | Weber на квадратный метр |
Плотность электрического тока | \ (\ mathbf {j} \) | \ (\ frac {\ text {A}} {\ text {m} ^ {2}} \) | Ампер на квадратный метр |
Напряженность электрического поля | \ (\ mathbf {e} \) | \ (\ frac {\ text {V}} {\ text {m}} \) | Вольт на метр |
Электрический потенциал | \ (\ text {V} \) | В | Вольт |
Электродвижущая сила | \ (\ mathcal {E} \) | В | Вольт |
Электрический ток | \ (\ text {I} \) | А | Ампер |
Рассмотрим единицы величин в левой и правой частях уравнения.(55). Используя размерный анализ, получаем:
\ [V = \ frac {Wb} {s} \]
Следовательно, приведенное выше выражение утверждает, что изменение магнитного потока, равное 1 Вебер в секунду, будет индуцировать электродвижущую силу в 1 вольт вдоль закрытый путь. Используя вышеупомянутое выражение, Вебер (\ (Wb \)) может можно выразить как:
\ [Wb = V \ cdot s = \ frac {J} {A}, \]
, где \ (J \) – Джоуль, а \ (A \) – Ампер. Джоули используются для обозначения единицы энергии или работы.Таким образом, мы можем интерпретировать магнитный поток как единицу работы на единицу тока.
Геофизические приложения Закон Фарадея
При проведении электромагнитных исследований используются различные инструменты для генерировать зависящие от времени магнитные поля. Эти поля обычно называют в качестве основных полей. Согласно уравнениям. (56), это будет индуцировать вращательные электрические поля в окружающей области. Для рока единица, определяемая проводимостью \ (\ sigma \), законом Ома (\ ({\ bf j} = \ sigma {\ bf e} \)) означает, что плотность тока \ ({\ bf j} \) также индуцируется первичным полем.Эти индуцированные токи параллельны \ ({\ bf e} \) и имеют величину, зависящую от физического свойства породы. Следовательно, мы можем использовать закон Фарадея в дифференциале форма, чтобы понять, каким образом вращательные токи индуцируются в проводящие объекты искусственно созданным первичным полем.
Согласно закону Био-Савара Раздел Био-Савара, плотности тока отвечают за создание магнитных полей. Это означает, что токи индуцированное первичным полем приведет к созданию аномального магнитное поле, обычно называемое вторичным полем.Вторичный поле может быть измерено в точках над поверхностью Земли и обеспечивает важная информация о подземных геологических структурах. Но как вторичное поле измеряли?
При размещении в области, где наблюдаются вторичные поля, петля приемника провода будет испытывать электродвижущую силу в соответствии с формулой. (61). Из уравнения. (60), и мы знаем что электродвижущая сила эквивалентна напряжению, индуцированному в провод. Поэтому мы можем использовать измерения напряжения для представления информации. относительно вторичного поля, в отличие от прямого измерения поля.
Объяснение, приведенное в этом разделе, также можно понять в частотная область. Однако напряжение, индуцированное в катушках приемника, будет имеют как действительную (синфазную), так и мнимую (не синфазную) составляющие.
комментарий к Максвеллу (1865 г.) «Динамическая теория электромагнитного поля»
Philos Trans A Math Phys Eng Sci. 2015 Apr 13; 373 (2039): 20140473.
Кавендишская лаборатория, Дж. Дж. Томсон-авеню, Кембридж CB3 0HE, Великобритания
© Авторы 2015.Опубликовано Королевским обществом в соответствии с условиями лицензии Creative Commons Attribution License http://creativecommons.org/licenses/by/4.0/, которая разрешает неограниченное использование при условии указания автора и источника.Abstract
В большой статье Максвелла 1865 года была основана его динамическая теория электромагнитного поля. Истоки статьи лежат в его более ранних работах 1856 г., в которых он начал математическую разработку исследований Фарадея по электромагнетизму, и 1861–1862 гг., В которых был введен ток смещения.Эти более ранние работы были основаны на механических аналогиях. В статье 1865 г. акцент смещается на роль самих полей как описания электромагнитных явлений. Отчасти искусственные механические модели, с помощью которых он пришел к уравнениям поля несколькими годами ранее, были отброшены. Введение Максвеллом концепции полей для объяснения физических явлений обеспечило существенную связь между механическим миром ньютоновской физики и теорией полей, разработанной Эйнштейном и другими, которая лежит в основе физики двадцатого и двадцать первого веков.Этот комментарий был написан в ознаменование 350-летия журнала Philosophical Transactions of the Royal Society .
Ключевые слова: Максвелл, электромагнетизм, уравнения электромагнитного поля, открытие уравнений Максвелла
1. Прелюдия
16 июня 1865 года статья Джеймса Клерка Максвелла «Динамическая теория электромагнитного поля» была отправлена в типографии. Тейлору и Фрэнсису для публикации в Philosophical Transactions of the Royal Society [1]. 1 Шесть дней назад, 10 июня того же года, состоялась мировая премьера постановки Рихарда Вагнера «« Тристан и Изольда »» в Мюнхенском театре «Корт». Слово революционный – единственное прилагательное, которое начинает отдавать должное исключительному влиянию этих двух событий 1865 года, одного в области физических наук, другого в музыке, опере и драме. Ошеломляющие нововведения Вагнера в музыкальной гармонии, структуре и драматургии произвели революцию в подходах композиторов и глубоко повлияли на музыку конца девятнадцатого и двадцатого веков – музыка уже никогда не будет прежней.Точно так же монументальная статья Максвелла заложила основы нововведений физики двадцатого века, поместив поля в основу теории электромагнетизма и всех последующих полей, которые описывают, как материя и излучение ведут себя на фундаментальном уровне.
Эйнштейн [2, с. 71] подытожил достижения Максвелла в 1931 году по случаю столетия со дня рождения Максвелла:
Мы можем сказать, что до Максвелла физическая реальность, поскольку она должна была представлять процесс природы, рассматривалась как состоящая из материальных частиц, вариации которых заключаются только в движениях, управляемых уравнениями в частных производных.Со времен Максвелла физическая реальность рассматривалась как представленная непрерывными полями, управляемая уравнениями в частных производных и не поддающаяся какой-либо механической интерпретации. Это изменение в представлении о Реальности является наиболее глубоким и наиболее плодотворным, которое физика пережила со времен Ньютона.
Достижения Максвелла обеспечили существенный мост между физикой Ньютона и Эйнштейна. Глубокая природа этого изменения восприятия прекрасно сформулирована Фрименом Дайсоном [3, с.4]:
Теория Максвелла становится простой и понятной только тогда, когда вы отказываетесь от мышления в терминах механических моделей. Вместо того чтобы думать о механических объектах как о первичных, а электромагнитные нагрузки как о вторичных последствиях, вы должны думать об электромагнитном поле как о первичных, а механические силы как о вторичных. Идея о том, что первичными составляющими Вселенной являются поля, нелегко пришла в голову физикам поколения Максвелла. Поля – понятие абстрактное, далекое от привычного мира вещей и сил.Полевые уравнения Максвелла являются уравнениями в частных производных. Их нельзя выразить простыми словами, такими как закон движения Ньютона, сила равна массе, умноженной на ускорение. Теории Максвелла пришлось ждать, пока следующее поколение физиков, Герца, Лоренца и Эйнштейна, раскроет ее силу и прояснит ее концепции. Следующее поколение выросло с уравнениями Максвелла и было как дома во вселенной, построенной из полей. Примат полей был для Эйнштейна столь же естественным, как примат механических структур для Максвелла.
В этом эссе я помещаю статью Максвелла 1865 года в контекст эволюции его взглядов на природу физических явлений.
2. Акт 1. Предварительные сведения
К концу восемнадцатого века были установлены многие из основных экспериментальных свойств электростатики и магнитостатики. В 1770-х и 1780-х годах Шарль-Огюстен Кулон провел очень чувствительные эксперименты, которые прямо установили законы обратных квадратов электростатики и магнитостатики, которые в то время казались совершенно отдельными физическими явлениями.Это изменилось с развитием науки текущего электричества . В 1791 году итальянский анатом Луиджи Гальвани показал, что электрические эффекты могут стимулировать сокращение лягушачьих лапок. В 1791 году он показал, что при использовании двух разнородных металлов для соединения нервов и мышц в ногах лягушек наблюдалась такая же форма мышечного сокращения. Об этом было объявлено об открытии животных электричества . Алессандро Вольта подозревал, что электрический ток был связан с присутствием различных металлов в контакте с влажным телом.В 1800 году он продемонстрировал это, построив гальваническую батарею , которая состояла из чередующихся слоев меди и цинка, разделенных слоями картона, пропитанного проводящей жидкостью. Самым важным аспектом экспериментов Вольта было то, что он открыл управляемый источник электрического тока. Гальванический элемент имел короткий срок службы, так как картон высох, и поэтому он изобрел свою корону из чашек , в которой электроды были помещены в электролитическую жидкость в серии стеклянных сосудов, как в современных батареях.
Ключевой экспериментальный прогресс был сделан в 1820 году, когда Ганс Христиан Эрстед продемонстрировал, что всегда существует магнитное поле, связанное с электрическим током – это положило начало науке об электромагнетизме . Сразу же физики Жан-Батист Био и Феликс Савар приступили к обнаружению зависимости напряженности магнитного поля на расстоянии r от элемента тока длиной d l , в котором ток I течет.В системе СИ их ответ, закон Био – Савара , может быть записан
2,1
d l – длина текущего элемента в направлении тока I и r измеряется от текущего элемента d l до точки на векторном расстоянии r .
Затем Андре-Мари Ампер расширил закон Био-Савара, чтобы связать ток, протекающий через замкнутый контур, с интегралом составляющей плотности магнитного потока вокруг контура.В современной векторной записи можно записать круговой закон Ампера в свободном пространстве
2,2
где I закрытый – полный электрический ток, протекающий через область, заключенную в петлю C . В 1827 году Ампер опубликовал свой знаменитый трактат [4], в котором было показано, что магнитное поле токовой петли может быть представлено эквивалентной магнитной оболочкой. Он также сформулировал уравнение силы между двумя токовыми элементами d l 1 и d l 2 несущие токи I 1 и I 2 :
2.3
d F 2 – сила, действующая на элемент тока d l 2 , r измеряется от d l 1 . Ампер продемонстрировал связь этого закона с законом Био – Савара.
В 1827 году Георг Саймон Ом сформулировал соотношение между разностью потенциалов В и током I , которое сейчас известно как закон Ома , В = RI , где R – сопротивление материал, по которому течет ток.Это было спорным результатом до 1876 года, когда Максвелл и его ученик Джордж Кристал установили закон экспериментально с высокой точностью в недавно основанной Кавендишской лаборатории, первым главой которой и Кавендишским профессором экспериментальной физики в 1871 году был назначен Максвелл. результаты были установлены к 1830 году и включают в себя все статического электричества , силы между стационарными зарядами, магнитами и токами. Суть уравнений Максвелла состоит в том, что они также имеют дело с изменяющимися во времени явлениями.За последующие 20 лет были установлены все основные экспериментальные особенности изменяющихся во времени электрических и магнитных полей.
В 1820-е годы в научные журналы было отправлено множество статей, описывающих электромагнитные эффекты и пытающихся их объяснить. Редактор журнала Philosophical Magazine пригласил Майкла Фарадея для обзора этой массы экспериментов и предположений, и так начал свое систематическое исследование электромагнитных явлений. Эти эксперименты привели Фарадея к введению ключевой концепции магнитных силовых линий , представляющих направление, в котором сила, действующая на магнитный полюс, действует при помещении в магнитное поле.Чем больше количество силовых линий на единицу площади в плоскости, перпендикулярной силовым линиям, тем больше сила, действующая на магнитный полюс.
Твердо веря в симметрию природы, Фарадей предположил, что, поскольку электрический ток может создавать магнитное поле, также должна быть возможность генерировать электрический ток из магнитного поля. В 1831 году он узнал об экспериментах Джозефа Генри, в которых использовались очень мощные электромагниты. Фарадею сразу пришла в голову идея наблюдать деформацию в материале сильного электромагнита, вызванную силовыми линиями.Он построил сильный электромагнит, намотав изолирующий провод, через который можно было пропускать ток, на толстое железное кольцо, создав таким образом магнитное поле внутри кольца. Эффект деформации должен был регистрироваться другой обмоткой на кольце, которая была присоединена к гальванометру для измерения количества производимого электрического тока.
Эффект оказался совсем не таким, как ожидал Фарадей. Когда первичная цепь была замкнута, произошло смещение стрелки гальванометра во вторичной обмотке – электрический ток был индуцирован во вторичном проводе через среду железного кольца.Отклонения гальванометра были , только наблюдались при включении и выключении тока в электромагните. Это было открытие электромагнитной индукции . Еще в 1831 году Фарадей установил качественную форму своего закона индукции в терминах концепции силовых линий – электродвижущая сила, индуцированная в токовой петле, напрямую связана со скоростью, с которой линии магнитного поля разрезаются , добавление этого
Под магнитными кривыми я имею в виду силовые линии магнитного поля, которые были бы изображены железными опилками.
В 1834 году Ленц провозгласил закон, который прояснил вопрос о направлении наведенной электродвижущей силы в цепи – электродвижущая сила действует в таком направлении, чтобы противодействовать изменению магнитного потока .
Фарадей не мог математически сформулировать свои теоретические идеи, но он был убежден, что концепция силовых линий дает ключ к пониманию электромагнитных явлений. В 1846 году он предположил в своем выступлении перед Королевским институтом, что свет может быть некой формой возмущения, распространяющегося вдоль силовых линий, но эта идея была воспринята со значительным скептицизмом.
Фарадей инстинктивно верил в единство сил природы, особенно между светом, электричеством и магнетизмом. В 1846 году он пропустил свет через свинцово-боратное стекло в присутствии сильного магнитного поля. Он продемонстрировал явление, теперь известное как вращение Фарадея , в котором плоскость поляризации линейно поляризованного света поворачивается, когда световые лучи проходят вдоль направления магнитного поля в присутствии прозрачного диэлектрика. Уильям Томсон, позже лорд Кельвин, интерпретировал это явление как доказательство того, что магнетизм по своей природе вращается, и это должно было сильно повлиять на размышления Максвелла о физической природе магнитных полей.
3. Акт 2. Максвелл о «Силовых линиях Фарадея» (1856)
Максвелл проявил свои таланты как физик-экспериментатор и физик-теоретик с раннего возраста. Его первая степень по естественной философии в Эдинбургском университете, за которой последовали математические исследования в Тринити-колледже в Кембридже, а также его всеядный аппетит к наиболее требовательным текстам великих европейских математиков и натурфилософов обеспечили идеальную подготовку к его исследованиям в области электромагнетизма. 2 По замечанию Свидриса [13, с. 428],
[Максвелл] был одним из очень немногих британских физиков, которые объединили экспериментальные и философские шотландские традиции с математической подготовкой, полученной в Кембридже.
Отличительной чертой мышления Максвелла была его способность работать по аналогии . В 1856 году он описал свой подход в эссе под названием Аналогий в природе , написанном для Клуба апостолов в Кембридже.Его суть можно уловить из следующего отрывка.
Всякий раз, когда [люди] видят связь между двумя хорошо известными им вещами и думают, что они видят аналогичную связь между менее известными вещами, они рассуждают от одного к другому. Это предполагает, что, хотя пары вещей могут сильно отличаться друг от друга, отношение в одной паре может быть таким же, как и в другой. Теперь, поскольку с научной точки зрения отношение и является наиболее важной вещью, которую необходимо знать, знание одной вещи ведет нас долгий путь к познанию другой.[14, стр. 381–382]
В отношении электромагнетизма он нашел формальные аналогии между математикой механических и гидродинамических систем и явлениями электродинамики. На протяжении всей этой работы он признавал свой долг Уильяму Томсону, впоследствии лорду Кельвину, который сделал существенные шаги в математизации электрических и магнитных явлений.
В том же 1856 году Максвелл опубликовал первую из своей серии статей по электромагнетизму «О силовых линиях Фарадея» [15].В предисловии к его Трактату об электричестве и магнетизме 1873 г. [16, с. viii], он вспоминал:
до того, как я начал изучать электричество, я решил не читать математику по этому предмету, пока я сначала не прочитал Фарадея «Экспериментальные исследования электричества ».
Первая часть статьи расширила технику аналогии и обратила особое внимание на ее применение к потоку несжимаемой жидкости и магнитным силовым линиям.Для ясности мы переработаем анализ Максвелла в единицах СИ, используя выражения векторных операторов div, grad и curl. Использование векторных методов было введено Максвеллом только в его статье 1870 года, озаглавленной «О математической классификации физических величин» [5,17] – он изобрел термины «наклон» (теперь «градиент»), «curl» . 3 и «конвергенция» (противоположность «расхождению»), чтобы обеспечить интуитивное понимание значения этих векторных операторов. В 1856 году частные производные были явно выписаны в декартовой форме.Математика вращательного потока жидкости и эквиваленты div, grad и curl были знакомы физикам-математикам в то время. Томсон и Максвелл, например, нуждались в этих инструментах для описания потока жидкости в моделях атомов вихревых колец.
Максвелл начал с аналогии между потоком несжимаемой жидкости и магнитными силовыми линиями. Скорость u аналогична плотности магнитного потока B . Если силовые трубки или паропроводы расходятся, напряженность поля уменьшается, как и скорость жидкости.Это позволило Максвеллу немедленно записать математическое выражение поведения магнитных полей в свободном пространстве:
3,1
Те же рассуждения применимы к электрическим полям в свободном пространстве, но они могут возникать на зарядах, поэтому в правой части есть источник.
3,2
где E – напряженность электрического поля, а ρ e – плотность электрического заряда.
Закон электромагнитной индукции Фарадея был впервые преобразован в математическую форму Нейманом в 1845 году.Индуцированная электродвижущая сила пропорциональна скорости изменения магнитного потока в цепи.
3,3
где Φ – полный магнитный поток, пронизывающий цепь. Математически это в точности эквивалентно более мощному векторному уравнению, описывающему то, что происходит в точке пространства. Используя теорему Стокса,
3,4
Для токов и создаваемых ими магнитных полей существует аналогичное соотношение, выведенное из закона Ампера:
3.5
где H – напряженность магнитного поля, а J – плотность тока.
Последним достижением этой статьи было официальное введение того, что сейчас называется векторным потенциалом А . Такой вектор уже был введен Нейманом, Вебером и Кирхгофом для расчета индуцированных токов,
3,6
Это определение явно согласуется с (3.1), поскольку div curl A = 0.Максвелл пошел дальше и показал, как индуцированное электрическое поле E может быть связано с A . Включая определение (3.6) в (3.4), получаем
3,7
Меняя местами порядок временной и пространственной производных в правой части, получаем
3.8
Эти анализы обеспечивают формальную согласованность явлений электромагнетизма. Максвелл получил примитивную, но неполную систему уравнений для электромагнитных полей, представленных соотношениями (3.1), (3.2), (3.4) и (3.5). Однако ему все еще не хватало физической модели – механического аналога Максвелла – поведения электромагнитных явлений.
4. Акт 3. Максвелл «О физических силовых линиях» (1861–1862)
Максвелл разработал свое решение в 1861–1862 гг. В серии статей, озаглавленных «О физических силовых линиях» [18–21]. Начиная с его более ранней работы по аналогии между u и B , он становился все более и более убежденным в том, что магнетизм, по сути, имеет вращательную природу.Его цель состояла в том, чтобы разработать модель среды, заполняющей все пространство, которая могла бы объяснить напряжения, которые Фарадей связал с магнитными силовыми линиями, – другими словами, механическую модель для эфира , который, как предполагалось, был средой через какой свет распространялся. В своей интригующей книге Innovation in Maxwell’s Electrodynamics [22] Дэвид Сигел провел подробный анализ этих работ, ярко продемонстрировав богатство идей Максвелла в проведении физических аналогий между механическими и электромагнитными явлениями.
Модель основана на аналогии между вращающейся вихревой трубкой и трубкой магнитного потока. Аналогия заключается в следующем. Если оставить их сами по себе, силовые линии магнитного поля расширяются, точно так же, как это происходит в случае жидкостной вихревой трубки, если вращательные центробежные силы не уравновешены. Кроме того, кинетическая энергия вращения вихрей может быть записана
4,1
где ρ – плотность жидкости, а u – ее скорость вращения.Это выражение формально идентично выражению для энергии, содержащейся в распределении магнитного поля,. Снова u аналогично B – чем больше скорость вращения трубки, тем сильнее магнитное поле. Максвелл постулировал, что локальная плотность магнитного потока везде пропорциональна угловой скорости вихревой трубки, так что вектор углового момента L параллелен оси вихря и, следовательно, параллелен вектору плотности магнитного потока В .
Максвелл начал с модели, в которой все пространство заполнено вихревыми трубками. Однако возникает непосредственная механическая проблема. Трение между соседними вихрями привело бы к их разрушению. Максвелл принял практическое инженерное решение, вставив «холостые колеса» или «шарикоподшипники» между вихрями, чтобы все они могли вращаться в одном направлении без трения. Опубликованное Максвеллом изображение вихрей, представленных массивом вращающихся шестиугольников, показано на.Затем он отождествил холостые колеса с электрическими частицами, которые, если бы они могли свободно двигаться, переносили бы электрический ток, как в проводнике. В изоляторах , включая свободное пространство , они не могут свободно перемещаться через распределение вихревых трубок и, следовательно, не могут проводить электрический ток. Я не сомневаюсь, что этот довольно крайний пример техники работы по аналогии был одной из причин «чувства дискомфорта и часто даже недоверия…», на которое ссылался Пуанкаре, когда французские физики-математики впервые столкнулись с работами Максвелла [ 23].
Акварель Джемаймы Веддерберн, изображающая детей, играющих на замерзшем озере на острове Сент-Мэри, недалеко от семейного дома в Гленлере, 23 декабря 1853 года. На заднем плане взрослые играли в керлинг. (С любезного разрешения The Maxwell at Glenlair Trust и James Clerk Maxwell Foundation.)
Диаграмма Максвелла из Philosophical Magazine за 1861 год, показывающая вращающиеся вихри, представленные шестиугольниками, и холостые колеса между ними [18, пластина V, рис. 2].
Примечательно, что эта механическая модель эфира могла объяснить все известные явления электромагнетизма. 4 В качестве примера индукции рассмотрим эффект включения второго провода в магнитное поле провода, по которому проходит ток I . Если ток постоянный, то во втором проводе нет никаких изменений. Однако, если ток изменяется, вращательный импульс передается через промежуточные холостые колеса и вихри, а во втором проводе индуцируется обратный ток.
Часть III статьи содержит вспышку гения, которая привела к открытию полного набора уравнений Максвелла.Теперь он подумал, как изоляторы хранят электрическую энергию. Он сделал предположение, что в изоляторах холостые колеса или электрические частицы могут быть на смещены на из их «фиксированных» положений равновесия под действием электрического поля. Затем он приписал электростатическую энергию в среде упругой потенциальной энергии , связанной со смещением электрических частиц. В своей последующей статье 1865 года он называет это ключевое нововведение как , электрическая упругость .
Этот постулат имел два непосредственных следствия. Во-первых, когда электрическое поле, приложенное к среде, изменяется, есть небольшие изменения в положениях электрических частиц в изолирующей среде или вакууме, и поэтому возникают небольшие токи, связанные с этим движением частиц. Другими словами, существует ток J D , связанный со смещением на электрических частиц из их положений равновесия. Уравнения стали такими:
4.2
Во-вторых, из-за того, что электрические частицы упруго связаны, любое возмущение приводит к распространению волн через среду. Затем Максвелл мог бы выполнить простой расчет, чтобы определить физическую природу и скорость c , с которой возмущения могут распространяться через изолятор или вакуум. Для этого ему пришлось решить модифицированную версию полевых уравнений электромагнетизма (4.2) в вакууме. Простая версия аргументации приведена в приложении A.Ответ был c = ( εε 0 μμ 0 ) −1/2 , где ε и μ – диэлектрическая проницаемость и проницаемость среды.
Обратите внимание, что даже в вакууме, для которого μ = 1, ϵ = 1, скорость распространения волн конечна, c = ( ϵ 0 μ 0 ) −1/2 . Максвелл использовал экспериментальные значения Вебера и Кольрауша для произведения ϵ 0 μ 0 и, к своему изумлению, обнаружил, что c почти точно соответствует скорости света.В письмах Максвелла 1861 г. Майклу Фарадею и Уильяму Томсону он показал, что значения совпадают в пределах примерно 1%. По словам самого Максвелла, с его собственным акцентом, в третьей части его серии статей в Philosophical Magazine :
Скорость поперечных модуляций в нашей гипотетической среде, рассчитанная из электромагнитных экспериментов ММ. Кольрауш и Вебер точно согласны со скоростью света, вычисленной из оптических экспериментов М.Физо, что мы едва ли можем избежать вывода о том, что свет состоит из поперечных модуляций одной и той же среды, которая является причиной электрических и магнитных явлений . [20, с. 22]
Этот замечательный расчет представляет собой объединение света с электричеством и магнетизмом.
Максвелл прекрасно осознавал замечательную механическую основу своей модели вакуума, которая послужила источником вдохновения для его открытия. Как он писал [19, с. 346],
Представление о частице, движение которой связано с движением вихря за счет идеального контакта качения, может показаться несколько неудобным.Я не выдвигаю его как способ связи, существующий в Природе … Однако это способ связи, который механически постижим, и он служит для выявления действительных механических связей между известными электромагнитными явлениями.
Никто не мог отрицать виртуозность Максвелла в определении скорости света по его механической модели электромагнитных сил.
5. Акт 4. Максвелл о «Динамической теории электромагнитного поля» (1865)
Максвелл хорошо осознавал тот факт, что теория, изложенная в его статье «О физических силовых линиях», была «неудобной» и считал это лишь «предварительной и временной гипотезой».Механическую основу его идей можно было неправильно понять или даже высмеять, но они поставили Максвелла на верный путь к окончательной теории электромагнитного поля. Поэтому он приступил к пересмотру теории на гораздо более абстрактной основе без каких-либо специальных предположений о природе среды, через которую распространяются электромагнитные явления. В 1865 году он опубликовал свою большую статью под названием «Динамическая теория электромагнитного поля» [1]. Цитируя Уиттекера [25, т.1, стр. 255]:
Здесь была показана архитектура его системы, лишенная строительных лесов, с помощью которых она была впервые возведена.
Интересно, что есть только одна, несколько извиняющаяся, ссылка в сноске к его статьям «О физических силовых линиях» 1861–1862 годов в этой статье.
Как указал Сигель [6,26, с. 187–188], с самого начала своих исследований в области электромагнетизма он преследовал три цели:
«во-первых, разработать теорию, которая охватила бы все известные факты электричества и магнетизма;
секунда, чтобы выполнить это объединение, используя подход Майкла Фарадея к электричеству и магнетизму – приближение силовых линий или поля ;
и, в-третьих, чтобы новая теория выходила за рамки того, что было известно из экспериментов… » эксперимент.
Собственное мнение Максвелла о значении этой статьи раскрывается в том, что C.W.F. В письме своему кузену Чарльзу Кею Эверитт называет «редким моментом явного изобилия»:
Еще у меня на плаву есть бумага, содержащая электромагнитную теорию света, которую я считаю великой пушкой, пока я не убедился в обратном. [7, с. 203]
Статья 1865 года объемная и разделена на семь частей. Все они содержат идеи и нововведения, которые иллюстрируют, как развивалось его мышление после опубликованных им статей 1861–1862 годов.В этом эссе я перевел обозначения Максвелла в более знакомые символы для ясности аргументации для современного читателя – эти переводы показаны на. Обратите внимание, что система уравнений записана в смеси Максвелла электростатических и электромагнитных единиц, то есть в нерационализированных единицах. 5
Таблица 1.
Таблица перевода из нотации Максвелла в нерационализированные единицы.
количество масса корпуса C 9065 9065 силы, действующие в точках A и B A B → F A F B 9038 9038 v w → v A v B v C v C с уменьшенными массами 8 M
N → L A M 9 0305 AB L B сопротивлений R S → R A 9065 9 сила, действующая на контур ξ η → ε A ε B 9065 в контуре 9065 9065 ток 9065 x y → I A I B 9135 9065 9065 9135 9065 9065 9065 9065 Y Q A Q B h есть, генерируемая сопротивлением H → H собственная энергия токов E 9065 9065 работа, выполненная при изменении индуктивности W → W угловая частота 913 938 9065 9065 913 напряжений A C D → V A V C 9136 9065 9065 9065 9065 9065 9065 9306 9065 электромагнитный момент F G H 9133 8 →A x A y A z магнитная интенсивность γ → H x H y H z → E x E y E z 9065 905 9065 9 истинный ток проводимости 905 9 q r → J x 9 0655 J y J z электрическое смещение f g x D y D z общий ток p ′ r 9 → J ′ x J ′ y J ′ z количество свободной электроэнергии → ρ e электрический p потенциал Ψ → ϕ магнитный потенциал ϕ удельное сопротивление ρ → ϱ удельная индуктивность 9065 ϵ (a) Часть I – вводная
Максвелл начинает с длинного вступления, в котором он рассматривает всю область электромагнетизма и с большой ясностью излагает повестку дня, которой он предлагает следовать в газете.Фактически, это введение само по себе могло бы найти подходящее место в любом вводном курсе бакалавриата по электромагнетизму. Вначале он подчеркивает разницу в подходах его теории по сравнению с подходами Вебера и Неймана. Их подходы включали использование «действия на расстоянии» без учета того, как силы передаются от их источника к другим телам. Максвелл заявляет, что он
… предпочел искать объяснение этого факта в другом направлении, предполагая, что они вызываются действиями, которые происходят в окружающей среде, а также в возбужденных телах…
(3) Предлагаемая мной теория поэтому ее можно назвать теорией электромагнитного поля , потому что она имеет отношение к пространству в окрестности электрических и магнитных тел, и ее можно назвать динамической теорией , потому что она предполагает, что в этом пространстве есть это движущаяся материя, из-за которой возникают наблюдаемые электромагнитные явления.
Центральным элементом его теории была упругость среды, через которую должны распространяться электромагнитные явления, что привело к концепции тока смещения как необходимой части теоретического аппарата. Не менее важна формализация процессов электромагнитной индукции, которые могут создавать токи – они могут привести к диссипативным потерям энергии в сопротивлениях и химической диссоциации в электролитах.
Максвеллу пришлось предположить, что существует эфирная среда
пронизывающий все тела и изменяемый только по степени их присутствия; что части среды могут приводиться в движение электрическим током и магнитами; что это движение передается от одной части среды к другой за счет сил, исходящих от соединений этих частей.
Максвеллу нужно было предположить, что эфир был физическим компонентом Вселенной, его логика была изложена с поразительной ясностью в его вкладе в девятое издание Британской энциклопедии в 1878 году [27].
Затем он противопоставляет свой подход подходам других исследователей, таких как Гельмгольц и Томсон, которые вывели феномен индукции из своих механических воздействий. Максвелл предлагает следовать противоположной программе – вывести механические воздействия из законов индукции.Для этого ему нужны общих уравнений электромагнитного поля , которые состоят из 20 уравнений с 20 переменными. В статье изложены истоки этих уравнений, и среди многих приложений есть ключевой результат, заключающийся в том, что электромагнитное излучение распространяется со скоростью света – объединение света и электромагнитного излучения. Максвелл признает вдохновение работы Фарадея «Мысли о лучевых колебаниях» [28]: 6
Электромагнитная теория света, предложенная (Фарадеем), по сути совпадает с той, которую я начал развивать в в этой статье, за исключением того, что в 1846 г. не было данных для расчета скорости распространения.…
(б) Часть II – об электромагнитной индукции
Затем Максвелл приступает к пространному обсуждению электромагнитной индукции. Механическое происхождение его мысли определяет его подход к определению формы уравнений самоиндукции и взаимной индуктивности между двумя индукторами. Здесь он применяет свою технику работы по аналогии с поразительным эффектом. Как он пишет:
Итак, если магнитное состояние поля зависит от движений среды, должна быть приложена определенная сила, чтобы увеличить или уменьшить эти движения, и когда движения возбуждаются, они продолжаются, так что эффект связи между током и окружающим его электромагнитным полем должно придавать току своего рода импульс, точно так же, как связь между точкой движения машины и маховиком наделяет точку движения дополнительным импульсом, который можно назвать импульс маховика уменьшился до точки движения.Неуравновешенная сила, действующая на движущую точку, увеличивает этот импульс и измеряется скоростью его увеличения.
Источником вдохновения для этого подхода послужила модель Méchanique Analytique Лагранжа. Максвелл изучал « Traité de Méchanique » Пуассона в Эдинбургском университете и был знаком с французской школой аналитической динамики, в которой особенно хвалил идеи Лагранжа. Он представляет то, что он называет уменьшенным импульсом , связанным с действием сил F A и F B , действующих на тело в точках движения A и B.Сложив силы трения, для которых коэффициенты сопротивления равны R A и R B , суммарные силы, действующие на A и B, F A ′ и F B ‘, являются
5,1
Обратите внимание, что Максвелл использует идентичные символы, которые будут повторяться в теории самоиндукции, взаимной индуктивности и сопротивления для этих механических эффектов. F A ′ и F B ′ – силы, относящиеся к точкам A и B, соответственно.Затем, по словам Максвелла,
Если скорость A увеличивается со скоростью d v A / d t , то для предотвращения перемещения силы B F ′ B = (d / d t ) ( M AB v A ).
Этот эффект на B из-за увеличения скорости A соответствует электродвижущей силе в одной цепи, возникающей из-за увеличения силы соседней цепи.
Особое значение для Maxwell имеет демонстрация уменьшенного импульса , количества ( L A v A + M AB v B ) и ( M AB v A + L B v B ) в механике. Соответствующие величины в электромагнитной индукции – это электромагнитный импульс или то, что Фарадей назвал электротоническим состоянием .
С помощью этой эквивалентности Максвелл немедленно преобразует уравнения в уравнения индукции между двумя проводниками с током. Тогда уравнение для тока I A в A определяется как
5,2
и I B в B
5,3
где и – электродвижущие силы, I A и I B – токи, а R A и R B – сопротивления в A и B, соответственно.
С этими отождествлениями Максвелл приступает к формальному изложению процессов индукции для одного и двух токов. Из них он вывел выражения для работы и энергии, тепла, производимого токами, внутренней энергии токов и механического воздействия между проводниками, а также решил конкретные примеры для одного, двух и шести проводников. Этот последний пример имел практическое значение, поскольку шесть проводников могли формировать баланс электрического тока для практического измерения индуктивности.Здесь, как и везде в этой статье, Максвелл предлагает теорию точного измерения электрических величин, что было для него главной заботой, например, чтобы определить, насколько точно его теоретическое значение скорости света соответствует отношению электростатических и электромагнитных величин. единиц заряда.
Эта часть завершается обсуждениями «Исследование электромагнитного поля », линий магнитной силы и магнитных эквипотенциальных поверхностей , последние две темы взяты из его внимательного прочтения Фарадея «Экспериментальные исследования электричества ».В первой он описывает эксперименты, которые показывают, как можно продемонстрировать и измерить индуцированные электромагнитные эффекты.
(c) Часть III – общие уравнения электромагнитного поля
В этой части, в основе статьи, полный набор уравнений Максвелла для электромагнитного поля сформулирован с необычайной ясностью и убедительной логикой. Представленные здесь уравнения описываются алфавитной нумерацией, использованной в его статье. Таким образом, это:
Три уравнения магнитной силы ( H x , H y , H z )
Три уравнения электрических токов ( J x , J y , J z )
Три уравнения электродвижущей силы ( E x , E y , E z )
Три уравнения электрической упругости ( D x , D y , D z )
Три уравнения электрического сопротивления ( ϱ )
Три уравнения полных токов ( J ′ x , J ′ y , J ′ z )
Одно уравнение свободного электричества ( ρ e )
Одно уравнение неразрывности (d ρ e / d t )
В результате получается 20 уравнений для 20 переменных:
Написанные в современном понимании, уравнения имеют знакомый вид.Если мы идентифицируем μ H с B , уравнения (A) – (H) могут быть записаны с использованием обозначений векторных операторов следующим образом:
Таким образом, первое уравнение Максвелла
находится путем взятия ротора (D) и исключения члена v × B .
Второе уравнение Максвелла (C).
Третье уравнение Максвелла – (G).
Четвертое уравнение Максвелла находится из дивергенции (B).
(A) поглощается (C).
(D) содержит выражение для силы ( v × B ), действующей на частицу, обычно называемой силой Лоренца.
(E) – конститутивное выражение, связывающее E и D .
(F) – закон Ома, который Максвелл признал только эмпирическим соотношением.
(H) – уравнение неразрывности электрического заряда.
Хотя Хевисайду и Герцу обычно приписывают преобразование уравнений Максвелла в их обычную форму, очевидно, что по сравнению с исходной версией Максвелла потребовались только простейшие модификации.Это будет включать последовательное использование гауссовых единиц, которые будут заменены системой СИ в 1960 году.
Есть некоторые интересные особенности способа, которым Максвелл представляет эти уравнения.
– В то время как электрическое смещение ( D x , D y , D z ) появилось в его документах 1861–1862 гг. глубоко укоренившиеся в структуре электромагнетизма во втором разделе этой части статьи как
противоположная электризация сторон молекулы или частицы тела, которая может сопровождаться или не сопровождаться передачей через тело.
Холостые колеса были ненужным артефактом – явление электрического смещения обязательно должно происходить, и его изменение во времени вносит вклад в общий ток.
– Электромагнитный импульс A x , A y , A z отождествляется с тем, что мы теперь называем векторным потенциалом. Происхождение этой идентификации очевидно из уравнения (3.8) выше, но он также предвещает четырехвекторную нотацию специальной теории относительности, в которой четырехвектор для четырехпотенциала записан [ ϕ / c , A x , A y , A z ]. Максвелл широко использует векторный потенциал при разработке уравнений, в отличие от современной практики первоначальной работы с полями E , D , B , H и Дж .
– Интересно, что Максвелл включает закон Ома в свое описание структуры уравнений, чего избегают в современной системе уравнений. Максвелл хорошо знал эмпирическую основу закона Ома в отличие от уравнений электромагнитной индукции. Как уже упоминалось, одним из его первых успешных проектов в качестве профессора Кавендиша было установление закона Ома с гораздо большей точностью.
Последний раздел этой части статьи – определение различных форм энергии, связанных с полями.Он снова начинает с электромагнитного импульса или векторного потенциала, A x , A y , A z и находит полную энергию из выражения
5,4
суммируя все пространство, занимаемое токами. Полная энергия может быть связана с полной энергией, существующей в самих полях:
5,5
Максвелл описывает ключевое значение этого выражения.
(74) Однако, говоря об Энергии поля, я хочу, чтобы меня понимали буквально.Всякая энергия тождественна механической энергии, независимо от того, существует ли она в форме движения, в форме упругости или в любой другой форме. Энергия в электромагнитных явлениях – это механическая энергия. Вопрос только в том, где он находится? Согласно старым теориям, он находится в наэлектризованных телах, проводящих цепях и магнитах в форме неизвестного качества, называемого потенциальной энергией, или способностью производить определенные эффекты на расстоянии. Согласно нашей теории, он находится в электромагнитном поле, в пространстве, окружающем наэлектризованные и магнитные тела, а также в самих этих телах и находится в двух различных формах, которые можно без гипотезы описать как магнитную поляризацию и электрическую поляризацию, или согласно очень вероятной гипотезе, как движение и деформация одной и той же среды.
(d) Часть IV – механические воздействия в поле
Следующая задача Максвелла – показать, как эти выражения для различных полей приводят к известным законам сил между различными электромагнитными объектами. Обратите внимание, что эти законы силы не были явно включены в формулировку уравнений электромагнетизма. В этой части он выводит из уравнений поля известные законы силы проводника, движущегося через магнитное поле, механическую силу на магните и силу на электрифицированное тело. 7
Максвелл также указывает, что коэффициент «электрической упругости» k , который появляется в уравнении (E) его уравнений, напрямую связан с соотношением электростатических и электромагнитных единиц измерения v через выражение k = 4 πv 2 . Вебер и Кольраух уже определили это отношение экспериментально и нашли, что оно составляет v = 310 740 000 м с -1 .
Последний раздел этой части включает попытку применить те же методы, чтобы понять законы гравитации.Здесь Максвелл затрагивает проблему универсальной силы притяжения гравитации, которая приводит к отрицательным значениям энергии гравитирующей системы. Он признается: «Поскольку я не могу понять, каким образом среда может обладать такими свойствами, я не могу идти дальше в этом направлении в поисках причины гравитации».
(e) Часть V – теория конденсаторов
Этот раздел касается определения емкости и поглощения конденсаторов различной конструкции.Это был вопрос большой важности для прокладки подводных телеграфных кабелей большой длины, о чем свидетельствует провал проекта по прокладке первого трансатлантического телеграфного кабеля в 1858 году. 8 Максвелл уже принимал активное участие в вопросах, касающихся определение фундаментальных констант и абсолютных стандартов сопротивления. На заседании Британской ассоциации в 1861 году был назначен комитет для наблюдения за определением фундаментальных стандартов, и Максвелл присоединился к нему в 1862 году, вскоре после публикации его статей по электромагнетизму 1861–1862 годов.
Он принимал активное участие в проверке своей теории точным экспериментом, в частности, в определении отношения электростатических и электромагнитных единиц электрического заряда. Деятельность Комитета стала более математической и теоретической, что напрямую связано с сильными сторонами Максвелла. Вместе со своими коллегами Бальфуром Стюартом и Флимингом Дженкином из Королевского колледжа Лондона он приступил к контролю за проектированием и изготовлением аппарата, чтобы сделать очень точное определение сопротивления [31].Успех этих экспериментов убедил Комитет в том, что абсолютное значение сопротивления, определенное этим и подобными методами, является явно предпочтительным стандартом.
В последующие годы работа над стандартами была фрагментирована, но Максвелл сохранил свой большой интерес и ведущую роль в этой теме и сделал ее одной из центральных тем исследовательской программы новой Кавендишской лаборатории в 1874 году. Определение абсолютного стандарта устойчивости было передано из обсерватории Кью в Кавендиш.Эта работа должна была оставаться одной из центральных ролей Кавендиша до тех пор, пока она не была передана Национальной физической лаборатории при ее основании в 1900 году.
(f) Часть VI – электромагнитная теория света
Часть VI – еще один памятный эпизод в Эта бумага. Максвелл теперь пытается определить, согласуются ли волны, которые могут распространяться через любую материальную среду, с постулатом о том, что свет можно отождествить с электромагнитными волнами. Анализ выглядит почти идентично тому, который появляется во всех современных стандартных текстах по электромагнетизму.Обнуляя условия проводимости, он выводит уравнения для распространения электромагнитных волн в направлениях x , y , z за страницу или около того:
5,6
Он продолжает
(95) Если предположить, что H x , H y , H z являются функциями lx + my + nz – В t = w , первое уравнение принимает вид
5.7
или
5,8
Другие уравнения дают такое же значение V , так что волна распространяется в любом направлении со скоростью V .
Эта волна полностью состоит из магнитных возмущений, причем направление намагниченности находится в плоскости волны. Никакое магнитное возмущение, направление намагничивания которого не находится в плоскости волны, вообще не может распространяться как плоская волна.
Следовательно, магнитные возмущения, распространяемые через электромагнитное поле, согласуются со светом в том, что возмущение в любой точке поперечно направлению распространения, и такие волны могут обладать всеми свойствами поляризованного света.
Для случая воздуха, для которого μ = 1, скорость распространения света, измеренная Фуко, составила 298 000 000 м с −1 по сравнению со значением, полученным Вебером и Кольраушем, которые нашли v = 310 740 000 м с −1 от их измеренного значения k . Эти цифры также совпадали в пределах экспериментальной ошибки со значением скорости света, определенным по астрономической аберрации световых лучей.
Далее Максвелл показывает, что показатель преломления непроводящего материала n дается квадратным корнем из удельной индуктивной способности среды.Он написал
и, следовательно
5,9
или удельная индуктивная емкость равна квадрату показателя преломления, деленному на коэффициент магнитной индукции.
Максвелл затем проводит предварительное исследование случая анизотропных кристаллических материалов. Он был хорошо осведомлен о том, что кристаллы могут иметь разные показатели преломления вдоль разных осей, и поэтому изучает случай, когда μ принимает разные значения вдоль направлений x , y , z .
Следующее приложение – соотношение между электрическим сопротивлением и прозрачностью материалов. Его цель заключалась в том, чтобы учесть тот факт, что, как он выразился, «самые прозрачные твердые тела являются хорошими изоляторами, тогда как все хорошие проводники очень непрозрачны». Он исследует распространение света по оси x поперечного возмущения. A y . С учетом удельного сопротивления среды ϱ уравнение распространения принимает вид
5.10
Если A y принимает вид
5,11
где α – коэффициент поглощения,
5,12
где V – скорость света в воздухе, а n – показатель преломления. Доля интенсивности падающего света, прошедшего через толщину x , составляет
5,13
Если R – это сопротивление образца материала толщиной x , шириной b и длиной l , то
5.14
количественно устанавливая связь между α , n и R .
(ж) Часть VII – расчет коэффициентов электромагнитной индукции
Заключительная часть статьи касается точной оценки коэффициентов электромагнитной индукции. Это может показаться спуском с высот частей III, IV и VI статьи, но эти расчеты имели решающее значение для абсолютного определения сопротивления, которое было одной из забот Максвелла на всю оставшуюся жизнь.Достаточно сказать, что Максвелл довольно подробно описывает различные способы измерения собственной и взаимной индуктивности в контексте экспериментов, которые он и его коллеги проводили в Королевском колледже Лондона и которые содержались в Отчете для Комитета. Британской ассоциации. Соображения должны были найти свое применение в кропотливых экспериментах Рэлея и его коллег [32,33] по определению абсолютного значения ома после смерти Максвелла.
6. Финал – последствия
Отождествление света с электромагнитным излучением было триумфом, обеспечив физическую основу волновой теории света, которая могла успешно объяснить явления отражения, преломления, поляризации и так далее. Однако поразительно, сколько времени потребовалось, чтобы глубокие идеи Максвелла стали общепринятыми в сообществе физиков. Он разработал теорию в своем великом Трактате об электричестве и магнетизме , как только в 1865 году поселился в своем доме в Гленлере в регионе Дамфрис и Галлоуэй на юге Шотландии.
Примечательно, что, когда он писал Трактат , он также был экзаменатором Cambridge Mathematical Tripos и осознал острую потребность в подходящих учебниках. Двухтомный Трактат , однако, в отличие от многих других великих трактатов, таких как Ньютон Начала , не является систематическим изложением предмета, а находится в стадии разработки, отражая собственный подход Максвелла к этим исследованиям. В более позднем разговоре Максвелл заметил, что цель Трактата состояла не в том, чтобы окончательно изложить свою теорию миру, а в том, чтобы обучить себя, представив взгляд на стадию, которой он достиг.К сожалению, Максвелл посоветовал читать четыре части Трактата параллельно, а не последовательно.
Преимущество этого подхода состояло в том, что Максвелл ясно изложил свое собственное восприятие физического содержания теории, а также то, как с ней можно сопоставить точный эксперимент. На эти темы сильно повлияла его работа для комитета Британской ассоциации по фундаментальным стандартам. Он посвящает большую часть «Трактата » основным измерениям и электрическому оборудованию, в процессе чего он решает множество экспериментальных задач, которыми будут заниматься студенты-исследователи в Кавендишской лаборатории.Например, он анализирует пять методов абсолютного определения стандарта сопротивления, занимая всю гл. XVIII.
Затем, достигнув раздела 585, в середине второго тома, Максвелл заявляет, что он «должен снова начать с нового основания без каких-либо предположений, кроме предположений динамической теории» [16, т. 2, стр. 229]. Как резюмировал Питер Харман, Максвелл подчеркивает выражение физических величин, свободное от прямого представления механической моделью. Это потребовало новых математических подходов к электромагнетизму, включая кватернионы, интегральные теоремы, такие как теорема Стокса, топологические концепции и лагранжиано-гамильтоновы методы аналитической динамики.
Один из наиболее важных результатов появляется в разделе 792 Тома 2, в котором Максвелл вычисляет давление, которое излучение оказывает на проводник на основе электромагнитной теории. Этот глубокий результат обеспечивает связь между давлением p и плотностью энергии ε излучения, полученной исключительно из свойств электромагнитных полей, p = ε /3 c 2 . Этот результат должен был быть использован Больцманом в его статье 1884 года, в которой он вывел закон Стефана – Больцмана из классической термодинамики.Опубликованный в 1873 году «Трактат » оказал немедленное влияние и вместе с «Трактатом о естественной философии » Томсона и Тейта предоставил студентам всесторонний обзор экспериментальной и теоретической физики.
Максвелл был на удивление скромным в отношении своего вклада. Как заметил Фриман Дайсон, когда Максвелл был президентом секции математических и физических наук Британской ассоциации развития науки в 1870 году, его президентская лекция была прекрасной возможностью для описания своих новых идей, и тем не менее он почти не упомянул о своей недавней работе. о электромагнетизме, просто непринужденно говоря: «Другая теория электричества, которую я предпочитаю», даже не упомянув, что это была его собственная теория.По словам Дайсона [3, с. 3 примечания]: «Мораль этой истории состоит в том, что скромность не всегда является добродетелью».
Но проблемы были гораздо глубже. Не только теория Максвелла была сложной, но и открытие уравнений электромагнитного поля также потребовало серьезного сдвига в перспективе для физиков конца девятнадцатого века. Стоит процитировать Дайсона немного дальше.
Были и другие причины, помимо скромности Максвелла, по которым его теорию было трудно понять. Он заменил ньютоновскую вселенную материальных объектов, взаимодействующих друг с другом на расстоянии, вселенной полей, простирающихся через пространство и взаимодействующих только локально с осязаемыми объектами.Понятие поля было трудно понять, потому что поля нематериальны. Ученые того времени, включая самого Максвелла, пытались представить поля как механические структуры, состоящие из множества маленьких колес и вихрей, распространяющихся по всему пространству. Эти структуры должны были нести механические нагрузки, которые электрические и магнитные поля передают между электрическими зарядами и токами. Чтобы поля удовлетворяли уравнениям Максвелла, система колес и вихрей должна была быть чрезвычайно сложной.Если вы попытаетесь визуализировать теорию Максвелла с помощью таких механических моделей, это будет похоже на возврат к птолемеевской астрономии с планетами, движущимися на циклах, и эпициклами в небе. Это не похоже на изящную астрономию Ньютона. [3, с. 3]
Максвелл умер в 1879 году до того, как были получены прямые экспериментальные доказательства существования электромагнитных волн. Дело было окончательно решено через десять лет после смерти Максвелла в классической серии экспериментов Генриха Герца, почти через 30 лет после того, как Максвелл отождествил свет с электромагнитным излучением.Великая монография Герца «Об электрических волнах » [34] прекрасно описывает его замечательную серию экспериментов.
Герц обнаружил, что он может обнаруживать эффекты электромагнитной индукции на значительных расстояниях от своего устройства. Примеры типов излучателей и детекторов, которые он использовал, показаны на. Электромагнитное излучение испускалось, когда между большими сферами возникали искры при приложении высокого напряжения от индукционной катушки. Метод обнаружения поля излучения заключался в наблюдении искр в зазоре между парой малых сфер детектора.
Аппарат Герца для генерации и обнаружения электромагнитного излучения. Излучатель a создавал электромагнитное излучение в разрядах между сферическими проводниками. Детектор b состоял из аналогичного устройства, в котором зажимы детектора располагались как можно ближе друг к другу для достижения максимальной чувствительности. Излучатель помещался в фокус цилиндрического параболоидного отражателя для получения направленного пучка излучения. (Из [34].)
После большого количества проб и ошибок Герц обнаружил, что для определенных устройств существует сильный резонанс, соответствующий резонансным частотам излучателя и детектора.Частоту резонансных волн можно было определить по резонансной частоте излучателя и детектора, которую он принял равной ω = ( LC ) −1/2 , где L и C – индуктивность и емкость диполя. Он измерил длину волны излучения, поместив отражающую пластину на некотором расстоянии от излучателя искрового промежутка так, чтобы стоячие волны возникали вдоль линии между излучателем и пластиной. Скорость волн может быть найдена из соотношения c = ν λ.
Скорость оказалась почти равной скорости света в свободном пространстве. Затем он начал серию экспериментов, которые убедительно продемонстрировали, что эти волны во всех отношениях ведут себя точно так же, как свет – прямолинейное распространение, поляризация, отражение, преломление. Некоторые эксперименты были весьма примечательными по своему исполнению. Чтобы продемонстрировать преломление, он сконструировал призму весом 12 центнеров из так называемого «твердого материала, такого как асфальт».
Эксперименты убедительно показали, что существуют электромагнитные волны с частотой приблизительно 1 ГГц и длиной волны 30 см, которые во всех отношениях ведут себя как свет.Эти великие эксперименты были убедительным доказательством справедливости уравнений Максвелла.
Приложение A
В линейно-упругой среде смещение электрических частиц пропорционально напряженности электрического поля.
А 1
Когда напряженность поля меняется, заряды перемещаются, вызывая то, что Максвелл назвал током смещения . Если N q – это плотность числа электрических частиц, а q – заряд каждой из них, то плотность тока смещения равна
А 2
Максвелл утверждал, что эта плотность тока смещения должна быть включена в уравнение curl H = J , которое теперь должно читаться как
А 3
На этом этапе α и β являются неизвестными константами, которые необходимо определить из известных электрических и магнитных свойств среды.
Прежде всего, вычислим скорость распространения возмущения в среде. Если предположить, что токи отсутствуют, Дж = 0, первые два уравнения Максвелла сводятся к
А 4
Дисперсионное соотношение для этих волн, то есть соотношение между волновым вектором k и угловой частотой ω , можно найти с помощью стандартной процедуры. Мы ищем волновые решения вида e i ( k ⋅ r – ωt ) , и поэтому заменяем векторные операторы скалярными и векторными произведениями согласно рецепту:
Тогда уравнения (A 4) сводятся к
А 5
Исключая E из уравнений (A 5),
А 6
где мы использовали линейное определяющее соотношение B = мкм 0 H , мкм – проницаемость среды.Используя векторное отношение A × ( B × C ) = B ( A ⋅ C ) – C A ⋅ B ), находим, что
А 7
Не существует решения для k параллельно H , то есть продольных волн , поскольку левая часть (A 6) тогда равна нулю.Однако существуют решения для поперечных волн , для которых k ⋅ H = 0. Они представляют собой плоские поперечные волны с векторами E и H , перпендикулярными друг другу и направлению распространения волны. Соотношение дисперсии для волн, таким образом, равно k 2 = ω 2 βμμ 0 . Поскольку скорость распространения волны равна c = ω / k , находим, что
А 8
Обратите внимание, что из-за линейной пропорциональности k и ω фазовая скорость c p и групповая скорость волнового пакета c g = dω / d k , оба имеют одинаковое значение, c , заданное формулой (A 8).
Теперь Максвелл знал, как вычислить константу β . Плотность энергии, запасенная в диэлектрике, – это просто работа, совершаемая на единицу объема при перемещении электрических частиц на расстояние r , то есть
А 9
Но
А 10
и, следовательно
А 11
Поэтому проделанная работа
А 12
Но это равно плотности электростатической энергии в диэлектрике, где ϵ – диэлектрическая проницаемость среды.Следовательно, β = ϵϵ 0 . Подставляя это значение в (A 8) для скорости волн, находим
A 13
Сноски
1 Обратите внимание, что дата на отсканированной версии статьи на веб-сайте Королевского общества неверна (1 января 1865 г.). Эта ошибка является артефактом того, как статья была оцифрована.
2 Дополнительную информацию о жизни и науке Максвелла см. В [3,5–12].
3 По словам доктора Дэвида Ричи из Фонда Джеймса Клерка Максвелла, «[Максвелл] использовал термин« завиток »для описания двумерных электрических и магнитных волн.Он сказал, что это не «вращение», которое подразумевает трехмерность ». Есть восхитительная акварель Джемаймы Веддерберн, на которой изображены дети, играющие на замерзшем озере на острове Сент-Мэри 23 декабря 1853 года (). На заднем плане видно, как взрослые керлинг, предположительно Максвелл, сидят дома на рождественских каникулах из Кембриджа. Вращение камней для завивки двухмерное.
4 Я привожу ряд примеров из них в своей книге Теоретические концепции в физике [24, гл.5].
5 Более подробную информацию о различных системах единиц, используемых в электромагнетизме, можно найти в эссе Системы единиц в электромагнетизме на http://info.ee.surrey.ac.uk/Workshop/advice/coils/unit_systems /.
6 Эта статья была впервые опубликована в Philosophical Magazine [29] после его лекции в Королевском институте в апреле 1846 года.
7 Многие части этого анализа аналогичны тем, которые я описал в своей книге [24, гл.6]. Там я начал с уравнений Максвелла как набора дифференциальных уравнений в частных производных, а затем придал им физическое значение, выполнив различные векторные манипуляции, чтобы показать, что все известные явления электромагнетизма могут быть выведены из постулируемого набора уравнений. Пока я не написал настоящее эссе, я не осознавал, что этот подход, который мы преподавали на уроках теоретической физики в Кембридже, был почти в точности тем, что Максвелл опубликовал в 1865 году. Кабель и его важность для продвижения использования методов теоретической физики в электротехнических проектах прекрасно рассказывается К.Смит и Н. М. Уайз в своей биографии Уильяма Томсона [30].
Профиль автора
Малькольм Лонгаир – Джексонский профессор естественной философии Кембриджского университета и директор по развитию лаборатории Кавендиша в Кембридже. С 1980 по 1990 год он был королевским астрономом Шотландии и директором Королевской обсерватории в Эдинбурге. С 1997 по 2005 год он был главой Кавендишской лаборатории. Его исследовательские интересы лежат в области астрофизики высоких энергий и астрофизической космологии.Недавняя деятельность включала научную историю физики, астрономию, астрофизику и космологию. В 2013 году он опубликовал историю квантовой механики и в настоящее время пишет научную историю лаборатории Кавендиша.
Ссылки
1. Maxwell JC. 1865 г. Динамическая теория электромагнитного поля. Фил. Пер. R. Soc. 155, 459–512. (10.1098 / rstl.1865.0008) [CrossRef] [Google Scholar] 2. Эйнштейн А. 1931 г. Влияние Максвелла на развитие представлений о физической реальности.В Джеймсе Клерке Максвелле – памятном томе 1831–1931 гг. (Ред. Томсон Дж. Дж. И др.), Стр. 66–73. Кембридж, Великобритания: Издательство Кембриджского университета. [Google Scholar] 3. Дайсон Ф. 1999 г. Памятный буклет Джеймса Клерка Максвелла. Эдинбург, Великобритания: Фонд Джеймса Клерка Максвелла. [Google Scholar] 4. Ампер А-М. 1827 г. Mémoir sur la Theorie Mathématiques des Phénomènes électrodynamiques, уникальность deduite de l’expérience. В Mémoires de l’Académie Royale des Sciences, 1823, vol. VI, стр. 175–388. [Google Scholar] 5. Максвелл Дж.1890 г. О математической классификации физических величин. В научных статьях Дж. Клерка Максвелла (под ред. Нивена У. Д.), т. 2. С. 257–266. Кембридж, Великобритания: Издательство Кембриджского университета; (Перепечатано в 1965 году. Нью-Йорк: Dover Publications Inc.) [Google Scholar] 6. Флад Р., Маккартни М., Уитакер А. (ред.). 2014 г. Джеймс Клерк Максвелл: перспективы его жизни и работы. Оксфорд, Великобритания: Издательство Оксфордского университета. [Google Scholar] 7. Harman PM. (ред.). 1995 г. Научные письма и статьи Джеймса Клерка Максвелла, т.2 Кембридж, Великобритания: Издательство Кембриджского университета. [Google Scholar] 8. Buchwald JZ. 1985 г. От Максвелла до микрофизики: аспекты теории электромагнетизма в последней четверти девятнадцатого века. Чикаго, Иллинойс: Издательство Чикагского университета. [Google Scholar] 9. Кэмпбелл Л., Гарнетт В. 1882 г. Жизнь Джеймса Кларка Максвелла. Лондон, Великобритания: MacMillan & Co. [Google Scholar] 10. Харман П. 1990 г. Научные письма и статьи Джеймса Клерка Максвелла. Том I, 1846–1862 гг. Кембридж, Великобритания: Издательство Кембриджского университета.[Google Scholar] 11. Харман П. 2002 г. Научные письма и статьи Джеймса Клерка Максвелла. Том III, 1874–1879 гг. Кембридж, Великобритания: Издательство Кембриджского университета. [Google Scholar] 12. Харман П. 1998 г. Натурфилософия Джеймса Клерка Максвелла. Кембридж, Великобритания: Издательство Кембриджского университета. [Google Scholar] 13. Сведрис Р. 1976 г. Расцвет физических лабораторий в Великобритании. Hist. Stud. Phys. Sci. 7, 405–436. (10.2307 / 27757360) [CrossRef] [Google Scholar] 14. Максвелл Дж. 1856 г. Аналогии в природе. В научных письмах и статьях Джеймса Клерка Максвелла (изд.Харман П.М.), т. 1. С. 376–383. Кембридж, Великобритания: Издательство Кембриджского университета (1990). [Google Scholar] 15. Максвелл Дж. 1856 г. О силовых линиях Фарадея. Пер. Camb. Фил. Soc. 10, 155–188. [Google Scholar] 16. Максвелл Дж. 1873 г. Трактат об электричестве и магнетизме, 2 тт. Оксфорд, Великобритания: Clarendon Press; (Перепечатка 3-го изд., 1998. Серия Oxford Classics.) [Google Scholar] 17. Максвелл Дж. 1871 г. О математической классификации физических величин. Proc. Лондон. Математика. Soc. 3, 224–233. [Google Scholar] 18.Максвелл Дж. 1861 г. О физических силовых линиях. I. Теория молекулярных вихрей применительно к магнитным явлениям. Фил. Mag. 21, 161–175. [Google Scholar] 19. Максвелл Дж. 1861 г. О физических силовых линиях. II. Теория молекулярных вихрей применительно к электрическим токам. Фил. Mag. 21, 338–348. [Google Scholar] 20. Максвелл Дж. 1862 г. О физических силовых линиях. III. Теория молекулярных вихрей применительно к статическому электричеству. Фил. Mag. 23, 12–24. [Google Scholar] 21. Максвелл Дж. 1862 г. О физических силовых линиях.IV. Теория молекулярных вихрей применима к действию магнетизма на поляризованный свет. Фил. Mag. 23, 85–95. [Google Scholar] 22. Siegel DM. 1991 г. Нововведение в электромагнитной теории Максвелла. Молекулярные вихри, ток смещения и свет. Кембридж, Великобритания: Издательство Кембриджского университета. [Google Scholar] 23. Хейлброн Дж. 1977 г. Лекции по истории атомной физики 1900–1922 гг. В истории физики двадцатого века: 57-я Международная школа физики Варенны, Энрико Ферми (редактор Вайнер К.), стр. 40–108. Нью-Йорк, штат Нью-Йорк: Academic Press. [Google Scholar] 24. Лонгэр М. 2003 г. Теоретические понятия в физике. Кембридж, Великобритания: Издательство Кембриджского университета. [Google Scholar] 25. Уиттакер Э. 1951 г. История теорий эфира и электричества, 2 тт. Лондон, Великобритания: Thomas Nelson & Sons Ltd. [Google Scholar] 26. Siegel DM. 2014 г. Вклад Максвелла в электричество и магнетизм. В Джеймсе Клерке Максвелле: взгляды на его жизнь и работу (ред. Флуд Р., Маккартни М., Уитакер А.), стр. 187–203.Оксфорд, Великобритания: Издательство Оксфордского университета. [Google Scholar] 27. Максвелл Дж. 1878 г. Эфир. В Британской энциклопедии, 9-е изд., Т. 8. С. 568–572. Эдинбург, Великобритания: А. и К. Блэк. [Google Scholar] 28. Фарадей М. 1846 г. Мысли о лучевых вибрациях. В исследованиях Фарадея по электричеству, т. 3. С. 447–452. Лондон, Великобритания: Ричард Тейлор и Уильям Фрэнсис. [Google Scholar] 29. Фарадей М. 1846 г. Мысли о лучевых вибрациях. Фил. Mag. Сер. 3 28, 345–350. [Google Scholar] 30. Томсон В. 1989 г. Энергия и империя: биографическое исследование лорда Кельвина.Кембридж, Великобритания: Издательство Кембриджского университета. [Google Scholar]31. Максвелл Дж. К., Стюарт Б., Дженкин Ф. 1863 г. Описание экспериментального измерения электрического сопротивления, проведенного в Королевском колледже, стр. 140–158. Отчеты Британской ассоциации.
32. Рэлей Дж. У., Шустер А. 1881 г. Об определении Ом в абсолютной мере. Proc. R. Soc. 32, 104–141. (10.1098 / rspl.1881.0015) [CrossRef] [Google Scholar] 33. Рэйли Дж. У., Сиджвик Э. М.. 1883 г. Эксперименты по методу Лоренца для дальнейшего определения абсолютного значения единицы сопротивления Британской ассоциации с приложением по определению высоты звука в качестве стандартного камертона.Фил. Пер. R. Soc. 174, 295–322. (10.1098 / rstl.1883.0007) [CrossRef] [Google Scholar] 34. Герц Х. 1893 г. Электрические волны. С. 183–184. Лондон, Великобритания: Macmillan and Company; (Пер. Untersuchungen über die Ausbreitung der elektrischen Kraft , Иоганн Амброзиус Барт, Лейпциг, 1892 г.


