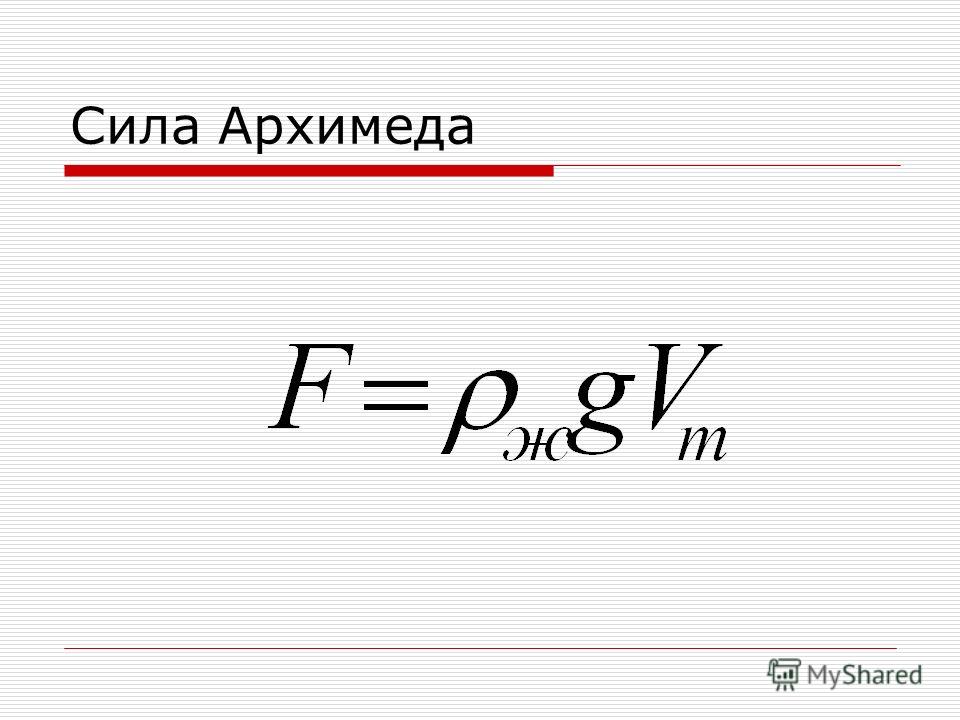Формулы закон архимеда: Закон Архимеда — урок. Физика, 7 класс.

Вывод полного закона Архимеда – Завершение формирования комплекса законов физики

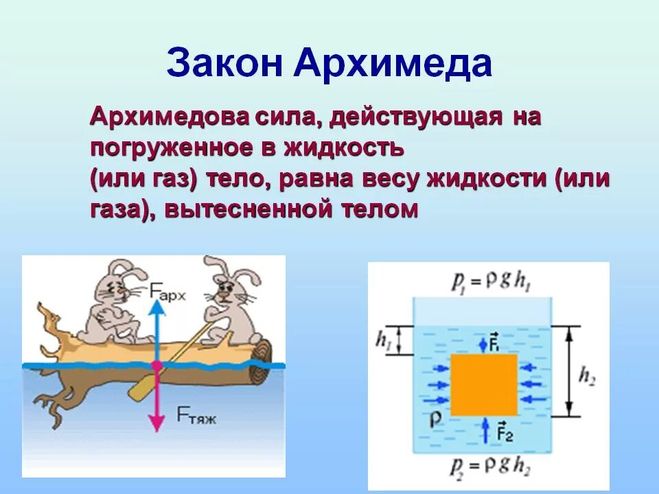
На главную страницу Вывод полного закона Архимеда   Мы живём в мире, где век географических открытий в мире может смениться веком открытий в самом себе.  Для новых открытий в окружающем нас мире не нужно готовить экспедиции в неизведанные страны. Самая неизведанная страна это сам человек. Каждый из Вас может сделать удивительные открытия, и для этого не нужно обладать ни особенными знаниями, ни мощным оборудованием. Нужно лишь немного внимательней посмотреть на окружающий нас мир, быть чуть более независимым в своих суждениях, и открытия не заставят себя ждать.  Любознательность позволит познавать окружающий мир без фундаментальных затрат в самых неожиданных местах. Физика это одна из основных наук, изучающих природу. Но даже первый закон физики – закон Архимеда, за 23 века своего существования до сих пор окончательно не сформулирован. Под этим названием в учебниках физики изучается правило Архимеда для выталкивающей силы.   В этом законе отсутствует как формулировка, так и основное уравнение, без чего физических законов не бывает. Всем известная формулировка: “на всякое тело, погруженное в жидкость, действует выталкивающая сила, направленная вверх и равная весу вытесненной жидкости” является формулировкой правила Архимеда для определения выталкивающей силы. Но нигде не определено, что потом с этой силой делать.   Если мы попытаемся узнать конечный результат – что произойдёт с телом, погруженным в жидкость (решить физическую задачу), то увидим, что нам это определение мало что даёт. Для того чтобы узнать, что произойдёт с телом, нужно ещё знать объём тела, вес этого тела, удельный вес выталкивающей среды. Причём проблема закона Архимеда состоит не в том, что он не правильно описывает архимедову силу, а в том что он не имеет алгоритма, что потом с ней делать. В дополнение к этим проблемам, закон Архимеда для жидкостей и газов в учебниках по физике рассматривается раздельно, что усложняет его понимание. Полный закон Архимеда был опубликован в http://drjukow.narod.ru/. Решение задач в школе по закону Архимеда происходит без единой методики. Показывается буквально на пальцах, что делать с архимедовой силой в одном случае, что в другом. Этот подход значительно усложняет как преподавание этого предмета, так и его усвоение. Не проще ли один раз вывести общее уравнение (формулу) закона Архимеда, включающую  архимедову силу и решать все примеры по закону Архимеда одним способом, по одной формуле?     Для вывода основного уравнения (формулы) закона Архимеда рассмотрим общий случай тела, погруженного в выталкивающую среду.    На это тело действуют три силы:   Первая сила – архимедова сила , равная весу вытесненной среды.           Вторая сила –  вес тела . Но есть ещё третья сила, не очень известная в теории.  Это архимедова сила, не задействованная для плавания – запас плавучести . В судостроении эта величина называется грузоподъёмностью. Если к телу, не полностью погруженному в выталкивающую среду, добавить вес, по величине равный , тело полностью погрузится. В этом случае тело будет уравновешенно в выталкивающей среде, и мы можем написать основное уравнение (формулу) закона Архимеда. Закон Архимеда определяет условие плавания тел (рис.1).      ,                         Где  – максимально возможная архимедова сила (в судостроении называется       водоизмещением ),  – архимедова сила, используемая для плавания (равна весу судна Р).   – запас плавучести (в судостроении называется грузоподъёмностью).                                                                                                    Рис.1. У не полностью погруженного тела  запас плавучести .   Основное уравнение закона Архимеда можно также составить относительно веса погруженного тела , равного и противоположного  архимедовой силе , но смысла это не меняет. Физическое определение полного закона Архимеда можно вывести из его основного уравнения: максимально возможная архимедова сила погруженного тела равна сумме архимедовой силы и запаса плавучести, и равна весу жидкости в объёме тела. Без учёта запаса плавучести  невозможно узнать конечный результат погружения тела в выталкивающую среду. Именно её величина определяет поведение погруженного тела в выталкивающей среде: 1) При   погруженное тело висит неподвижно, или сохраняет направление своего движения (при отсутствии других сил). 2) При , погруженное тело всплывает (при отсутствии других сил). 3) При , погруженное тело тонет (при отсутствии других сил). Строители кораблей на практике давно поняли, что закон Архимеда не полный. Они ввели понятие водоизмещения, имеющего смысл максимально возможной выталкивающей силы ,  грузоподъёмности , и собственного веса корабля , равного архимедовой силе  и противоположно ей направленного. Это показывает, что в судостроении давно пользуются основным уравнением Архимеда. Однако это уравнение выводят каждый раз, исходя из здравого смысла. Это же самое делают и в  школе. Не проще ли один раз вывести уравнение и потом им пользоваться? Полный закон Архимеда ЛИТЕРАТУРА          1. Дрюков В.М. О чём молчат физики. Тула. 2004.   2. Дрюков В.М. Физика. Дополнительные материалы. Тула изд. ООО Аквариус. 2021   3.  http://sciteclibrary.ru/rus/catalog/pages/9433.html

Чему равна выталкивающая сила?

☰

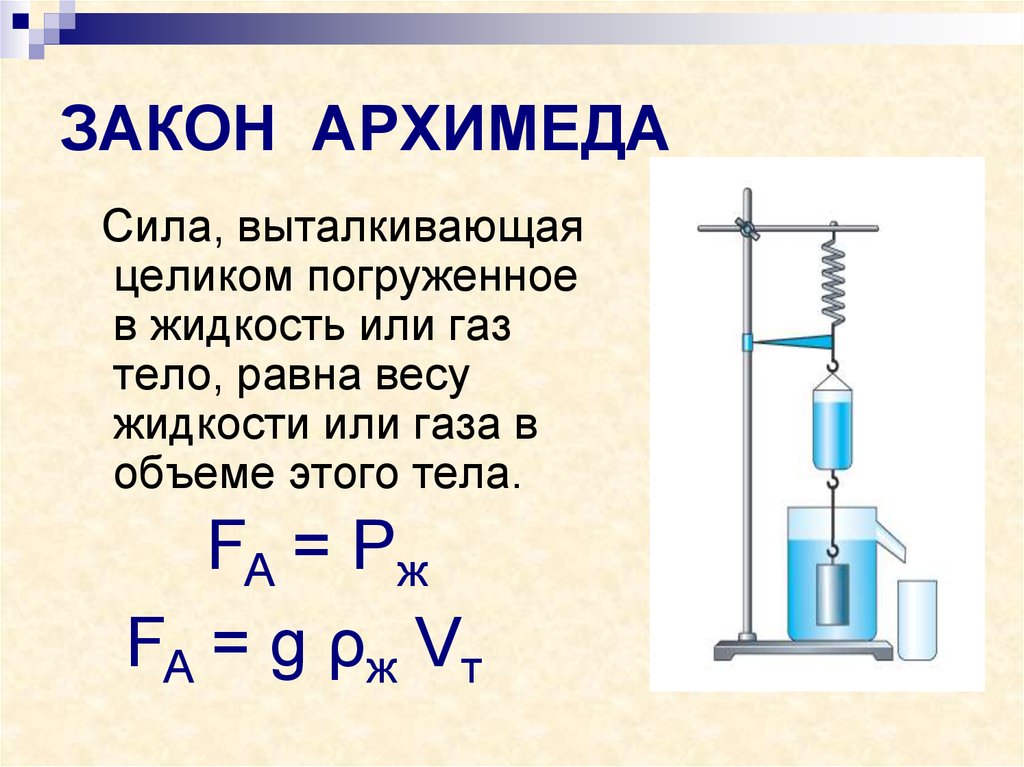
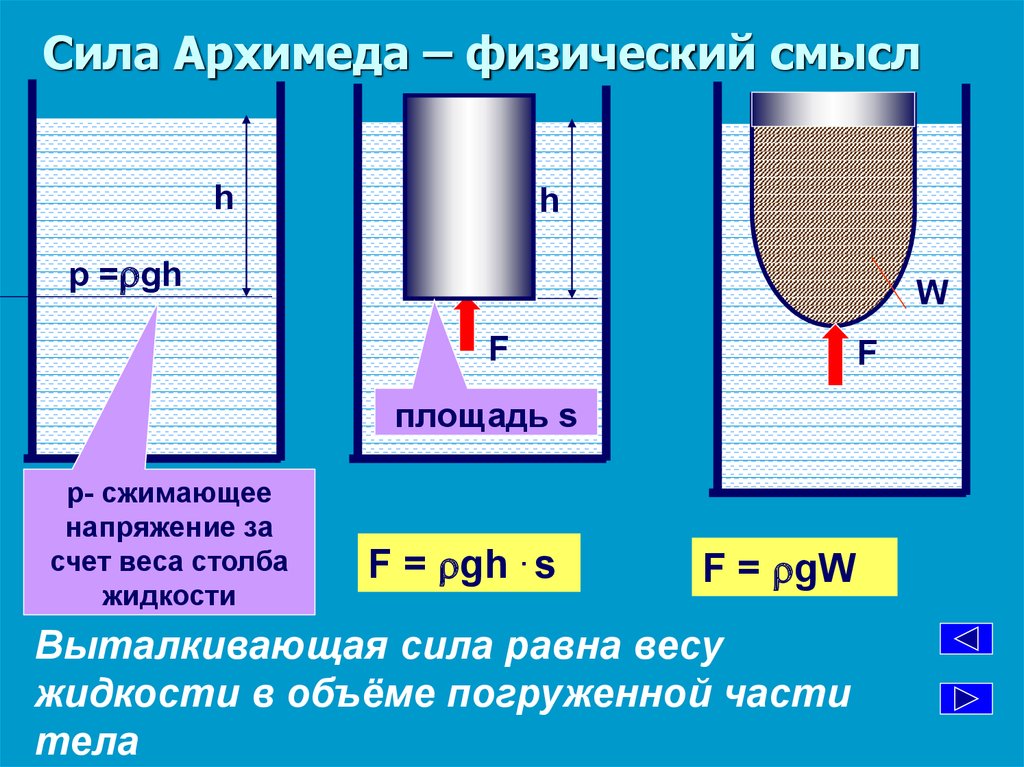
Выталкивающую силу, или силу Архимеда, можно вычислить. Особенно легко это сделать для тела, стороны которого прямоугольники (прямоугольного параллелепипеда). Например, такую форму имеет брусок.

Поскольку боковые силы давления жидкости можно не учитывать, так как они взаимно уничтожаются (их равнодействующая равна нулю), то рассматриваются только силы давления воды, действующие на нижнюю и верхнюю поверхности.

Если тело не полностью погружено в воду, то есть только сила давления воды, действующая снизу. Она единственная, которая создает выталкивающую силу.

Давление жидкости на глубине h определяется формулой:

p = ρgh

Сила давления определяется формулой:

F = pS

Заменив давление во второй формуле на равную ему правую часть из первой формулы, получим:

F = ρghS

Это и есть сила давления жидкости, действующая на поверхность тела на определенной глубине. Если тело плавает на поверхности, то эта сила будет выталкивающей силой (силой Архимеда). h здесь определяется высотой подводной части тела. В таком случае формулу можно записать так: F

A = ρghS. Тем самым подчеркнув, что речь идет о силе Архимеда.

Произведение высоты (h) погруженной в воду части прямоугольного бруска на площадь его основания (S) — это объем (V) погруженной части этого тела. Действительно, чтобы найти объем параллелепипеда надо перемножить его ширину (a), длину (b) и высоту (h).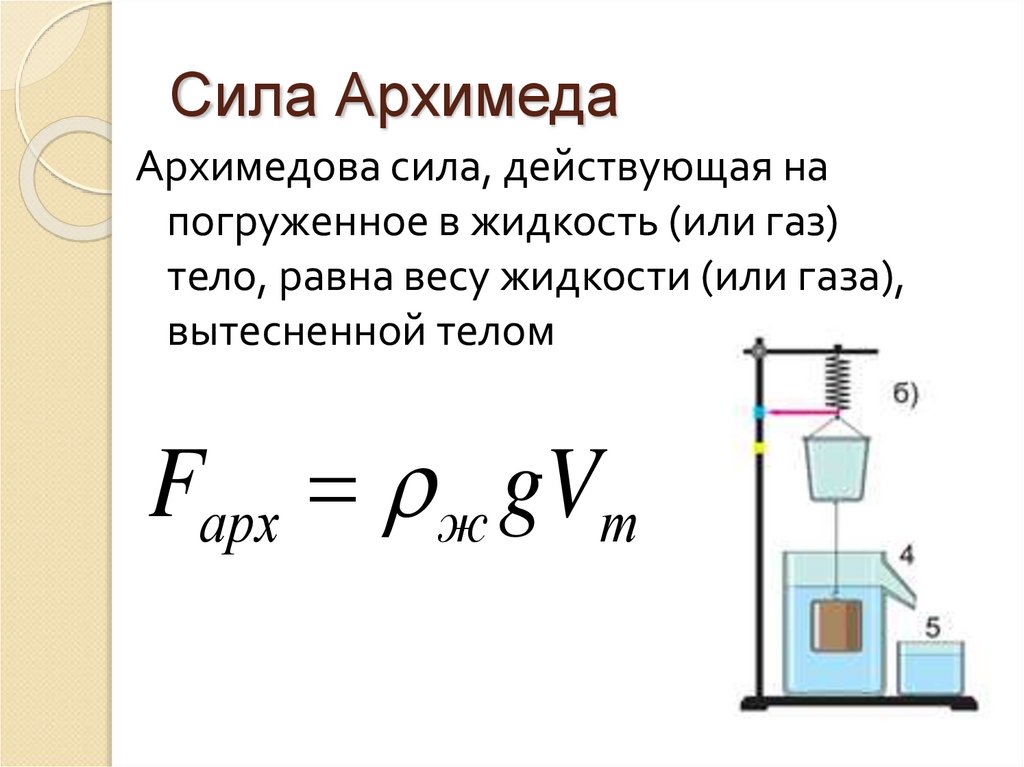 Произведение ширины на длину есть площадь основания (S). Поэтому в формуле мы можем заменить произведение hS на V:

F_A = ρgV

Теперь обратим внимание на то, что ρ – это плотность жидкости, а V — это объем погруженного тела (или части тела). Но ведь тело, погружаясь в жидкость, вытесняет из нее объем жидкости, равный погруженному телу. То есть, если погрузить в воду тело объемом 10 см³, то оно вытеснит 10 см³ воды. Конечно, этот объем воды скорее всего не выскочит из емкости, заменившись объемом тела. Просто уровень воды в емкости поднимется на 10 см³.

Поэтому в формуле F_A = ρgV мы можем иметь в виду не объем погруженного тела, а объем вытесненной телом воды.

Вспомним, что произведение плотности (ρ) на объем (V) — это масса тела (m):

m = ρV

В таком случае формулу, определяющую выталкивающую силу, можно записать так:

F_A = mg

Но ведь произведение массы тела (m) на ускорение свободного падения (g) есть вес (P) этого тела. Тогда получается такое равенство:

F_A = P

Таким образом, сила Архимеда (или выталкивающая сила) равна по модулю (численному значению) весу жидкости в объеме, равном объему погруженного в нее тела (или его погруженной части). Это и есть закон Архимеда

.

Если тело в виде бруска полностью погружено в воду, то выталкивающую силу для него определяет разность между силой давления воды сверху и силой давления снизу. Сверху на тело давит сила, равная

F_верх = ρgh_верхS,

а снизу –

F_низ = ρgh_низS,

Тогда мы можем записать

F_A = ρgh_низS – ρgh_верхS = ρgS(h_низ – h_верх)

h_верх – это расстояние от кромки воды до верхней поверхности тела, а h_низ — это расстояние от кромки воды до нижней поверхности тела. Их разность есть высота тела. Следовательно,

F_A = ρghS, где h — это высота тела.

Получилось то же самое, что и для частично погруженного тела, хотя там h — это высота части тела, находящейся под водой. В том случае уже было доказано, что F_A = P. То же самое выполняется и здесь: выталкивающая сила, действующая на тело, равна по модулю весу вытесненной им жидкости, которая равна по объему погруженному телу.

Обратите внимание, что вес тела и вес жидкости одинаковых объемов чаще всего разный, так как у тела и жидкости чаще всего разные плотности. Поэтому нельзя говорить, что выталкивающая сила равна весу тела. Она равна весу жидкости, объемом равному телу. Причем весу по модулю, так как выталкивающая сила направлена вверх, а вес вниз.

Принципиальный калькулятор Архимеда

С помощью этого калькулятора Архимеда вы можете измерить плотность короны или изучить изменения массы и веса погруженного в жидкость объекта или выталкивающую силу. В любом случае мы вас прикроем!

Когда король Сиракуз Хейрон II не был уверен, сделал ли ювелир ему корону из чистого золота или нет, он попросил Архимеда выяснить это. Принимая ванну, Архимед заметил, что по мере того, как он погружался в воду, уровень воды поднимался, и Эврика! Все, что ему нужно было сделать, это погрузить корону в воду, чтобы получить ее массу в воде, сравнить ее с ее массой в воздухе и с помощью вытесненного объема воды определить плотность короны 👑

Продолжайте читать, чтобы узнать:

• Что такое принцип Архимеда ;
• Принцип Архимеда или уравнение выталкивающей силы ; и
• Закон о плавании .

Давайте погрузимся!

Что такое закон Архимеда? – определение принципа Архимеда

Если вы когда-нибудь плавали на пляже или в бассейне, вы могли заметить, что объекта в воде кажутся легче, чем в воздухе. Вы когда-нибудь задумывались, почему это происходит? Что ж, ответ был найден греческим физиком Архимедом примерно в 246 году до нашей эры и сведен в принцип, названный в его честь.

Закон Архимеда гласит, что когда тело частично или полностью погружено в жидкость, на него действует направленная вверх сила, равная весу вытесненной жидкости. 93)(ρair​=1,275 кг/м3), восходящая сила, связанная с водой, выше, и кажущийся вес объекта будет значительно меньше при погружении в воду по сравнению с воздухом.

Это станет яснее в следующем разделе, где мы введем основную формулу Архимеда или уравнение выталкивающей силы.

Принципиальная формула Архимеда – Выталкивающая сила

Теперь, когда мы увидели, что представляет собой принцип Архимеда, мы можем ввести родственную формулу. Это уравнение для расчета выталкивающей силы или 93)(ρвоздух=1,275 кг/м3). Поскольку выталкивающая сила прямо пропорциональна плотности жидкости, чем выше плотность, тем больше выталкивающая сила.

Обратите внимание: если мы умножим плотность жидкости на объем жидкости, вытесненной объектом, мы получим массу жидкости mfluidm_{\text{fluid}}mfluid​. Таким образом, мы также можем выразить выталкивающую силу как вес вытесненной жидкости F_B = m_{\text{жидкость}}\ g = W_{\text{флюид}}FB​=mfluid​ g=Wfluid​

Вы можете узнать больше о соотношении объема и массы с помощью нашего калькулятора объема и массы .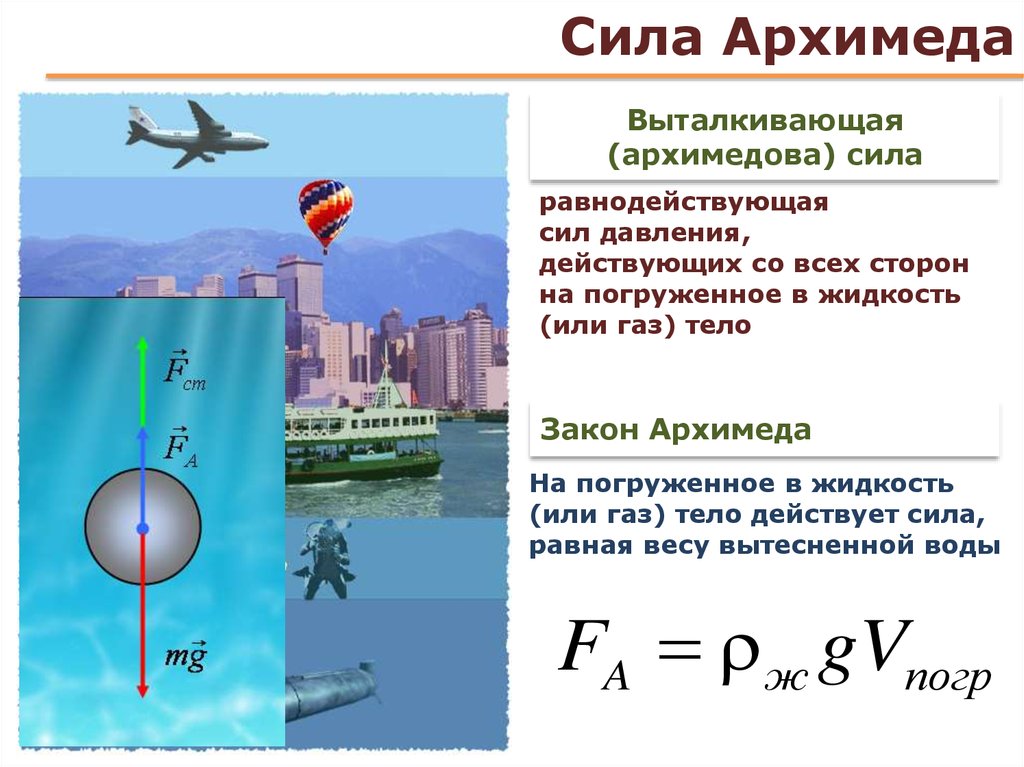 верхний, F1F_1F1​, а другой нижний, F2F_2F2​.

Поскольку давление увеличивается с глубиной, нижняя сила всегда больше, чем верхняя (F2>F1)(F_2 > F_1)(F2​>F1​). Это означает, что результирующая сила между ними всегда будет направленной вверх силой, известной как 9.0003 выталкивающая сила FBF_BFB​:

FB=F2−F1\small F_B = F_2 – F_1FB​=F2​−F1​

Если вы не знаете, почему давление увеличивается с глубиной, воспользуйтесь нашим калькулятором гидростатического давления , чтобы узнать это!

Закон плавучести

Закон плавучести, или принцип плавучести, указывает на то, что любой плавучий объект вытесняет собственный вес жидкости.

Вышеизложенное показывает, что для плавания тела в жидкости выталкивающая сила FBF_BFB​ должно быть больше веса объекта WobjW _{\text{obj}}Wobj​, иначе объект утонет в жидкости.

• If FB>WobjF_B > W_{\text{obj}}FB​>Wobj​ – Объект плавает;
• Если FB=WobjF_B = W_{\text{obj}}FB​=Wobj​ — Объект находится в нейтральном равновесии, то есть остается на месте, не поднимаясь и не опускаясь; и
• Если FB

Вы можете узнать больше о плавучести с нашими калькулятор плавучести!

Как пользоваться калькулятором закона Архимеда

Этот калькулятор принципа Архимеда представляет собой универсальный инструмент, который можно использовать для расчета выталкивающей силы или плотности объекта. Посмотрим, как пользоваться этим инструментом!

Чтобы найти выталкивающую силу

Вот как использовать этот инструмент для определения выталкивающей силы:

1. В разделе Свойства объекта укажите значения для Истинная масса объекта и Плотность объекта .
2. Выберите жидкость из раскрывающегося меню в разделе Свойства жидкости . Для пользовательских жидкостей введите плотность в поле Плотность жидкости .
3. Как только все это будет определено, калькулятор покажет вам результат для Силы плавучести .

Чтобы определить плотность объекта

Чтобы определить плотность неизвестного объекта, выполните следующие действия:

1. Введите Истинную массу объекта и Кажущаяся масса объекта в разделе Свойства объекта .
2. В раскрывающемся меню выберите Тип жидкости  как вода. Поле плотности будет заполнено автоматически.
3. Принципиальный калькулятор Архимеда отобразит  Плотность объекта в разделе Свойства объекта .

🙋 Нажав на Расширенный режим этого инструмента, вы можете найти Объем вытесненной жидкости , указав Площадь поверхности жидкости и Изменение высоты жидкости.

Принцип Архимеда с рабочими примерами – JEE First

В этой статье рассматривается принцип Архимеда и развивается идея с тремя полностью решенными примерами. Читателю предлагается попробовать решить задачи самостоятельно, прежде чем проверять решение.

Рассмотрим контейнер с жидкостью на остальное , как показано на рисунке ниже. Поскольку жидкость находится в состоянии покоя, результирующая сила, действующая на любую часть жидкости, равна нулю. Проведем воображаемую границу вокруг некоторой области жидкости, как показано на рисунке. Этот пакет жидкости имеет вес , где плотность жидкости и объем пакета. Посылка не падает сквозь жидкость под своим весом, потому что жидкость вокруг посылки воздействует на посылку восходящей силой, называемой выталкивающей силой, которая противодействует ее весу. То есть, .

Теперь представьте, что мы каким-то образом заменяем пакет с жидкостью на предмет точно такой же формы и размера, как в контейнере. На окружающую жидкость не влияет то, что находится внутри посылки, а это означает, что она оказывает на нее ту же выталкивающую силу, что и раньше. Это принцип Архимеда :

Выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости.

(1)  

Как насчет веса объекта в контейнере? Есть три возможности, в зависимости от того, как средняя плотность объекта сравнивается со средней плотностью жидкости:0005

1. : Объект тяжелее, чем сгусток жидкости, который он вытесняет. Следовательно, и предмет опускается на дно, так как выталкивающей силы недостаточно, чтобы удержать его.
2. : Выталкивающая сила точно уравновешивает вес объекта, и объект остается полностью погруженным.
3. : В этом случае необходимо вытеснить меньший объем жидкости, чтобы сбалансировать вес объекта, что означает, что объект погружен только частично (то есть он плавает), как показано на рисунке. Затем

(2)  

где — общий объем объекта, а — объем его погруженной части, который также является объемом вытесняемой им жидкости.

На этом мы можем перейти к обсуждению некоторых примеров.

Пример 1: Подвешенный между маслом и водой

(a) Объект с одинаковой плотностью помещен в сосуд, содержащий воду и масло, как показано на рисунке ниже. Объект подвешен между двумя жидкостями так, что три четверти его объема погружены в воду, а остальная часть находится в контакте с маслом. Какова плотность объекта? Используйте и .

Решение: Используя принцип Архимеда, выталкивающая сила равна

(3)  

Поскольку объект не касается дна сосуда, его вес должен быть равен . Это приводит нас к заключению

(4)

(b) В предыдущем обсуждении мы утверждали, что выталкивающая сила представляет собой направленную вверх силу, действующую на объект со стороны жидкости. Итак, вот вопрос: если под объектом нет масла, как оно воздействует на объект в направлении вверх?

Решение: Масло воздействует на объект, воздействуя на воду своим собственным весом. Чтобы увидеть это явно, мы можем рассмотреть происхождение выталкивающей силы с несколько иной точки зрения. Мы знаем, что давление на верхнюю грань объекта равно, а на нижнюю грань равно (см. рисунок ниже). Поскольку объект имеет однородную площадь поперечного сечения на всем протяжении, мы находим результирующую восходящую силу равной

(5)  

Это как раз выталкивающая сила, которую мы нашли в (3). Но теперь мы понимаем, как давление масла проявляется как направленная вверх сила на объект. Если тот же предмет поместить в сосуд только с водой, то часть его объема окажется ниже поверхности воды, тогда как при наличии масла в воду погружен только предмет.

Пример 2: Тающий лед

(a) Кусок льда плавает в сосуде с водой. Через некоторое время лед полностью растает. Уровень воды в сосуде

1. поднимется
2. осень
3. остаются прежними

Решение: Вес льда должен быть таким же, как вес вытесненной жидкости, . Когда лед тает, он превращается в воду с объемом . Другими словами, он заполняет ровно тот объем, который лед вытеснил до того, как растаял. Таким образом, уровень воды остается прежним.

(b) Подобный кубик льда плавает в сосуде, содержащем соли воды. Когда лед полностью растает, уровень воды поднимется ( Подсказка: Соленая вода плотнее чистой воды.)

1. поднимется
2. осень
3. остаются прежними

Решение: Здесь у нас есть . Однако лед тает в объеме. Так как , находим, что означает повышение уровня воды. Вот почему уровень моря повышается из-за таяния полярных ледяных шапок — лед в основном состоит из чистой воды, тогда как океан соленый.

Пример 3: Груз плавучести

(a) Два одинаковых стакана стоят на весах и наполнены водой. В стакан погружена железная сфера, которая также соединена с потолком натянутой нитью, как показано на рисунке. Уровень воды в обоих стаканах одинаков. Если весы измеряют вес и , что из следующего верно?

Решение: Объем воды, вытесненный железной сферой, действует на сферу выталкивающей силой, направленной вверх.