основные формулы по первому и второму законам и их формулировки или определения в физике, задачи на это и их решение
Мы уже говорили об основах классической механики. Настала пора поговорить о них подробнее и затронуть в обсуждении чуть больше, чем просто основу. В этой статье мы подробно разберем основные законы классической механики. Как вы уже догадались, речь пойдет о законах Ньютона.
Основные законы классической механики Исаак Ньютон (1642-1727) собрал и опубликовал в 1687 году. Три знаменитых закона были включены в труд, который назывался «Математические начала натуральной философии».
Законы Ньютона для «чайников»: объяснение 1, 2, 3 закона, пример с формулами
- Был долго этот мир глубокой тьмой окутан
Да будет свет, и тут явился Ньютон. - (Эпиграмма 18-го века)
- Но сатана недолго ждал реванша —
Пришел Эйнштейн, и стало все как раньше. - (Эпиграмма 20-го века)
Что стало, когда пришел Эйнштейн, читайте в отдельном материале про релятивистскую динамику. А мы пока приведем формулировки и примеры решения задач на каждый закон Ньютона.
А мы пока приведем формулировки и примеры решения задач на каждый закон Ньютона.
Первый закон Ньютона
Первый закон Ньютона гласит:
Существуют такие системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно, если на них не действуют никакие силы или действие других сил скомпенсировано.
Проще говоря, суть первого закона Ньютона можно сформулировать так: если мы на абсолютно ровной дороге толкнем тележку и представим, что можно пренебречь силами трения колес и сопротивления воздуха, то она будет катиться с одинаковой скоростью бесконечно долго.
Инерция – это способность тела сохранять скорость как по направлению, так и по величине, при отсутствии воздействий на тело. Первый закон Ньютона еще называют законом инерции.
До Ньютона закон инерции был сформулирован в менее четкой форме Галилео Галилеем. Инерцию ученый называл «неистребимо запечатленным движением». Закон инерции Галилея гласит: при отсутствии внешних сил тело либо покоится, либо движется равномерно.
Огромная заслуга Ньютона в том, что он сумел объединить принцип относительности Галилея, собственные труды и работы других ученых в своих «Математических началах натуральной философии».
Понятно, что таких систем, где тележку толкнули, а она покатилась без действия внешних сил, на самом деле не бывает. На тела всегда действуют силы, причем скомпенсировать действие этих сил полностью практически невозможно.
Например, все на Земле находится в постоянном поле силы тяжести. Когда мы передвигаемся (не важно, ходим пешком, ездим на машине или велосипеде), нам нужно преодолевать множество сил: силу трения качения и силу трения скольжения, силу тяжести, силу Кориолиса.
Второй закон Ньютона
Помните пример про тележку? В этот момент мы приложили к ней силу! Интуитивно понятно, что тележка покатится и вскоре остановится. Это значит, ее скорость изменится.
В реальном мире скорость тела чаще всего изменяется, а не остается постоянной.
Если рояль падает с крыши дома вниз, то он движется равноускоренно под действием постоянного ускорения свободного падения g. Причем любой дугой предмет, выброшенный из окна на нашей планете, будет двигаться с тем же ускорением свободного падения.
Второй закон Ньютона устанавливает связь между массой, ускорением и силой, действующей на тело. Приведем формулировку второго закона Ньютона:
Ускорение тела (материальной точки) в инерциальной системе отсчета прямо пропорционально приложенной к нему силе и обратно пропорционально массе.
Если на тело действует сразу несколько сил, то в данную формулу подставляется равнодействующая всех сил, то есть их векторная сумма.
В такой формулировке второй закон Ньютона применим только для движения со скоростью, много меньшей, чем скорость света.
Существует более универсальная формулировка данного закона, так называемый дифференциальный вид.
В любой бесконечно малый промежуток времени dt сила, действующая на тело, равна производной импульса тела по времени.
Третий закон Ньютона
В чем состоит третий закон Ньютона? Этот закон описывает взаимодействие тел.
3 закон Ньютона говорит нам о том, что на любое действие найдется противодействие. Причем, в прямом смысле:
Два тела воздействуют друг на друга с силами, противоположными по направлению, но равными по модулю.
Формула, выражающая третий закон Ньютона:
Другими словами, третий закон Ньютона — это закон действия и противодействия.
Пример задачи на законы Ньютона
Вот типичная задачка на применение законов Ньютона. В ее решении используются первый и второй законы Ньютона.
Десантник раскрыл парашют и опускается вниз с постоянной скоростью. Какова сила сопротивления воздуха? Масса десантника – 100 килограмм.
Решение:
Движение парашютиста – равномерное и прямолинейное, поэтому, по 
На десантника действуют сила тяжести и сила сопротивления воздуха. Силы направлены в противоположные стороны.
По второму закону Ньютона, сила тяжести равна ускорению свободного падения, умноженному на массу десантника.
Ответ: Сила сопротивления воздуха равна силе тяжести по модулю и противоположна направлена.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
А вот еще одна физическая задачка на понимание действия третьего закона Ньютона.
Комар ударяется о лобовое стекло автомобиля. Сравните силы, действующие на автомобиль и комара.
Решение:
По третьему закону Ньютона, силы, с которыми тела действуют друг на друга, равны по модулю и противоположны по направлению. Сила, с которой комар действует на автомобиль, равна силе, с которой автомобиль действует на комара.
Другое дело, что действие этих сил на тела сильно отличаются вследствие различия масс и ускорений.
Исаак Ньютон: мифы и факты из жизни
На момент публикации своего основного труда Ньютону было 45 лет. За свою долгую жизнь ученый внес огромный вклад в науку, заложив фундамент современной физики и определив ее развитие на годы вперед.
Он занимался не только механикой, но и оптикой, химией и другими науками, неплохо рисовал и писал стихи. Неудивительно, что личность Ньютона окружена множеством легенд.
Ниже приведены некоторые факты и мифы из жизни И. Ньютона. Сразу уточним, что миф – это не достоверная информация. Однако мы допускаем, что мифы и легенды не появляются сами по себе и что-то из перечисленного вполне может оказаться правдой.
Факт. Исаак Ньютон был очень скромным и застенчивым человеком. Он увековечил себя благодаря своим открытиям, однако сам никогда не стремился к славе и даже пытался ее избежать.
Миф. Существует легенда, согласно которой Ньютона осенило, когда на наго в саду упало яблоко. Это было время чумной эпидемии (1665-1667), и ученый был вынужден покинуть Кембридж, где постоянно трудился. Точно неизвестно, действительно ли падение яблока было таким роковым для науки событием, так как первые упоминания об этом появляются только в биографиях ученого уже после его смерти, а данные разных биографов расходятся.
Точно неизвестно, действительно ли падение яблока было таким роковым для науки событием, так как первые упоминания об этом появляются только в биографиях ученого уже после его смерти, а данные разных биографов расходятся.
Факт. Ньютон учился, а потом много работал в Кембридже. По долгу службы ему нужно было несколько часов в неделю вести занятия у студентов. Несмотря на признанные заслуги ученого, занятия Ньютона посещались плохо. Бывало, что на его лекции вообще никто не приходил. Скорее всего, это связано с тем, что ученый был полностью поглощен своими собственными исследованиями.
Миф. В 1689 году Ньютон был избран членом Кембриджского парламента. Согласно легенде, более чем за год заседания в парламенте вечно поглощенный своими мыслями ученый взял слово для выступления всего один раз. Он попросил закрыть окно, так как был сквозняк.
Факт. Неизвестно, как бы сложилась судьба ученого и всей современной науки, если бы он послушался матери и начал заниматься хозяйством на семейной ферме.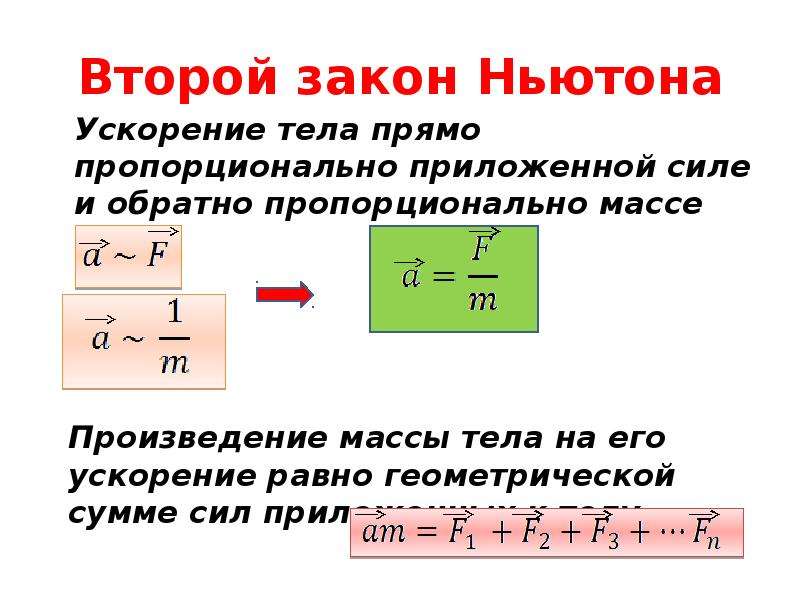
Дорогие друзья, помните — любую задачу можно решить! Если у вас возникли проблемы с решением задачи по физике, посмотрите на основные физические формулы. Возможно, ответ перед глазами, и его нужно просто рассмотреть. Ну а если времени на самостоятельные занятия совершенно нет, специализированный студенческий сервис всегда к вашим услугам!
Источник: https://Zaochnik-com.ru/blog/zakony-nyutona-dlya-chajnikov-obyasnenie-primer/
Первый закон Ньютона — Класс!ная физика
Закон инерции относится к самому простому случаю движения — движению тела, которое не взаимодействует с другими телами, т. е. движению свободного тела.
Ответить на вопрос, как же движутся свободные тела, не обращаясь к опыту, нельзя.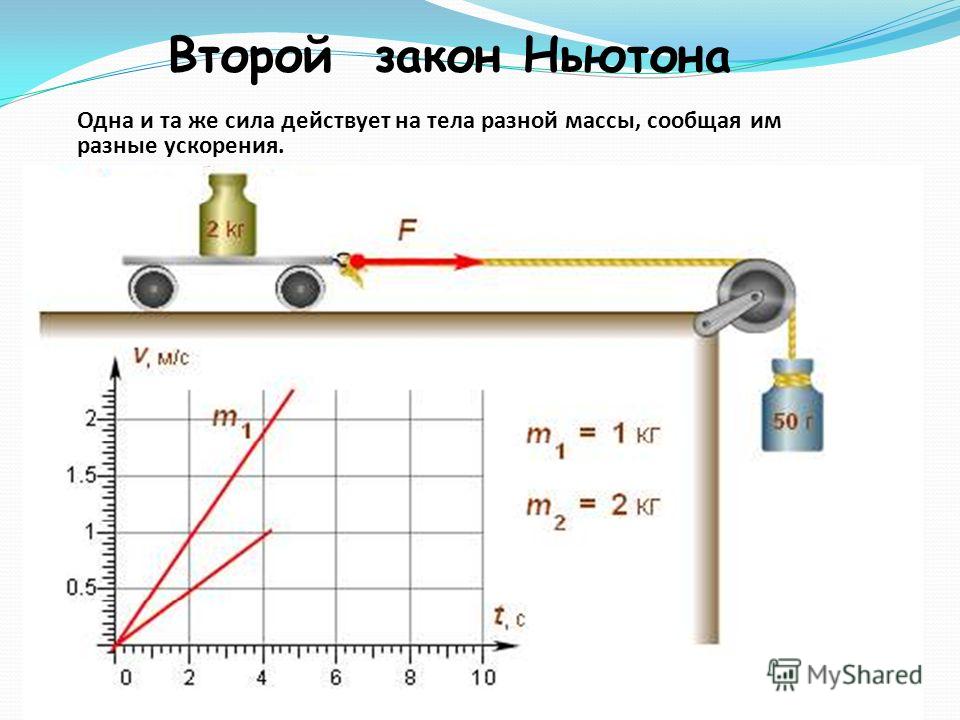 Однако нельзя поставить ни одного опыта, который бы в чистом виде показал, как движется ни с чем не взаимодействующее тело, так как таких тел нет. Как же быть?
Однако нельзя поставить ни одного опыта, который бы в чистом виде показал, как движется ни с чем не взаимодействующее тело, так как таких тел нет. Как же быть?
Имеется лишь один выход. Надо поместить тело в условия, при которых влияние внешних взаимодействий можно делать всё меньшим и меньшим, и наблюдать, к чему это ведёт.
Можно, например, наблюдать за движением гладкого камня на горизонтальной поверхности, после того как ему сообщена некоторая скорость. (Притяжение камня к Земле компенсируется действием поверхности, на которую он опирается; на скорость его движения влияет только трение.)
При этом легко обнаружить, что, чем более гладкой является поверхность, тем медленнее будет уменьшаться скорость камня. На гладком льду камень скользит весьма долго, не меняя заметно скорость.
На основе подобных наблюдений можно сделать вывод: если бы поверхность была идеально гладкой, то при отсутствии сопротивления воздуха (в вакууме) камень совсем не менял бы своей скорости. Именно к такому выводу пришёл впервые Галилей.
Именно к такому выводу пришёл впервые Галилей.
Первый закон Ньютона:
Существуют системы отсчёта, называемые инерциальными, относительно которых тело движется прямолинейно и равномерно, если на него не действуют другие тела.
Первый закон, или закон инерции, как его часто называют, фактически был открыт Галилеем, но строгую формулировку дал и включил его в число основных законов механики Исаак Ньютон.
Этот закон, с одной стороны, содержит определение инерциальной системы отсчёта. С другой стороны, он содержит утверждение (которое с той или иной степенью точности можно проверить на опыте) о том, что инерциальные системы отсчёта существуют в действительности.
Инерциальные и неинерциальные системы отсчёта.
До сих пор систему отсчёта мы связывали с Землёй, т. е. рассматривали движение относительно Земли. В системе отсчёта, связанной с Землёй, ускорение тела определяется только действием на него других тел. Система отсчёта, связанная с Землёй, является инерциальной.
Система отсчёта, связанная с Землёй, является инерциальной.
Из формулировки первого закона следует, что если есть одна инерциальная система отсчёта, то любая другая движущаяся относительно неё прямолинейно и равномерно также является инерциальной.
Однако, помимо инерциальных систем отсчёта, есть и другие, в которых тело имеет ускорение даже в том случае, когда на него другие тела не действуют.
В качестве примера рассмотрим систему отсчёта, связанную с автобусом. При равномерном движении автобуса пассажир может не держаться за поручень, действие со стороны автобуса компенсируется взаимодействием с Землёй. При резком торможении автобуса стоящие в проходе пассажиры падают вперёд, получая ускорение относительно стенок автобуса (рис. 2.6).
Однако это ускорение не вызвано какими-либо новыми воздействиями со стороны Земли или автобуса непосредственно на пассажиров. Относительно Земли пассажиры сохраняют свою постоянную скорость, но автобус начинает двигаться с ускорением, и пассажиры относительно него также движутся с ускорением.
Ускорение появляется вследствие того, что движение их рассматривается относительно тела отсчёта (автобуса), движущегося с ускорением.
Рассмотрим маятник, находящийся на вращающемся диске (рис. 2.7). Нить маятника отклонена от вертикали, хотя сам он неподвижен относительно диска. Натяжение нити не может быть скомпенсировано силой притяжения к Земле. Следовательно, отклонение маятника нельзя объяснить только его взаимодействием с телами.
Рассмотрим ещё один маятник, находящийся в неподвижном вагоне. Нить маятника вертикальна (рис. 2.8, а). Шарик взаимодействует с нитью и Землёй, сила натяжения нити равна силе тяжести. С точки зрения пассажира в вагоне и человека, стоящего на перроне, шарик находится в равновесии вследствие того, что сумма сил, действующих на него, равна нулю.
Как только вагон начинает двигаться с ускорением, нить маятника отклоняется (шарик по инерции стремится сохранить состояние покоя).
С точки зрения человека, стоящего на перроне, ускорение шарика должно быть равно ускорению вагона, так как нить не разрывается и шарик движется вместе с вагоном.
Шарик по-прежнему взаимодействует с теми же телами, сумма сил этого взаимодействия должна быть отлична от нуля и определять ускорение шарика.
С точки зрения пассажира, находящегося в вагоне, шарик неподвижен, следовательно, сумма сил, действующих на шарик, должна быть равна нулю, однако на шарик действуют те же силы — натяжения нити и сила Рис. 2.8 тяжести. Значит, на шарик (рис.2.8, б) должна действовать сила ин, которая определяется тем, что система отсчёта, связанная с вагоном, неинерциальная. Эту силу называют силой инерции (см. рис. 2.8, б).
В неинерциальных системах отсчёта основное положение механики о том, что ускорение тела вызывается действием на него других тел, не выполняется.
Системы отсчёта, в которых не выполняется первый закон Ньютона, называются неинерциальными.
Источник: http://class-fizika.ru/10_a22.html
Физика простыми словами
Взаимодействие тел рассматривает динамика, в основе которой лежат 3 закона, носящих имя прославленного английского физика сэра Исаака Ньютона.
Первый закон Ньютона гласит: тело будет находится в состоянии покоя или прямолинейного равномерного движения пока и поскольку на него не подействуют другие тела. Это как раз то, о чем мы и говорили.
То есть автомобиль не может остановиться без взаимодействия колес с дорогой, с другой стороны, отсутствие этого взаимодействия не позволит неподвижному автомобилю тронутся с места, колеса будут просто напросто пробуксовывать.
Количественно взаимодействие тел в физике определяют силой — векторной физической величиной, которую принято обозначать буквой F и измерять в ньютонах.
Исходя из всего вышесказанного можно заключить, что сила является причиной изменения скорости. Но возможно ли изменение скорости тела без непосредственного действия на него сил? И казалось бы правильный ответ нет, но… Тут нужно вспомнить тот факт, что движение относительно, соответственно, очень важна система отсчета, которую мы выбрали, а что если она начнет двигаться с ускорением?
К примеру, вы решили прокатить понравившуюся девушку на своём мотоцикле, она садится сзади и относительно мотоцикла неподвижна.
Но вот вы по привычке резко трогаетесь и видите в зеркало, как девушка падает сзади на асфальт со словами: «чтоб я еще когда нибудь…!!!!» Или другой пример, опять же с мотоциклом: вы едите по дороге, и вдруг вам под колёса выскакивает собака, вы пытаетесь резко затормозить и, немного перестаравшись с передним тормозом, летите через руль прямиком к этой злосчастной собаке.
В обоих примерах, если брать мотоцикл за тело отсчета, и рассматривать движение относительно его, вы не обнаружите сил, которые действуют на вас или вашу девушку, вызывая изменение скорости.
Поэтому когда говорят о первом законе Ньютона, уточняют, что он справедлив для инерциальных систем отсчета, то есть систем, относительно которых тело сохраняет свою скорость при отсутствии на него воздействий внешних сил, ну или при их взаимной компенсации.
Если же система отсчета движется с ускорением, то она неинерциальная. Понятно? Нет. Идем дальше.
Второй закон Ньютона позволяет нам определить как же изменяется скорость при взаимодействии тел, или, проще говоря, позволяет найти ускорение. Давайте попробуем разобраться и вывести этот закон.
Давайте попробуем разобраться и вывести этот закон.
От чего же зависит ускорение? Если мы пинаем футбольный мяч, то скорость полета мяча напрямую зависит от силы удара — чем сильнее пинаем тем быстрее летит, соответственно, ускорение будет напрямую зависеть от приложенной силы. И с другой стороны, если вместо мяча с той же силой пнуть любимую папину гирю… В общем, ускорение будет обратно пропорционально массе тела.
Чем масса больше, тем труднее изменить скорость тела. Поэтому иногда говорят, что масса является мерой инертности тела, то есть характеризует его способность сохранять скорость постоянной.
Если собрать все вместе можно сформулировать второй закон Ньютона следующим образом: ускорение прямо пропорционально силе приложенной к телу и обратно пропорционально его массе.
Часто этот закон можно встретить в другой интерпретации: сила, действующая на тело, равна произведению его массы и ускорения.
Третий закон Ньютона определяет силы, с которыми тела взаимодействуют друг с другом.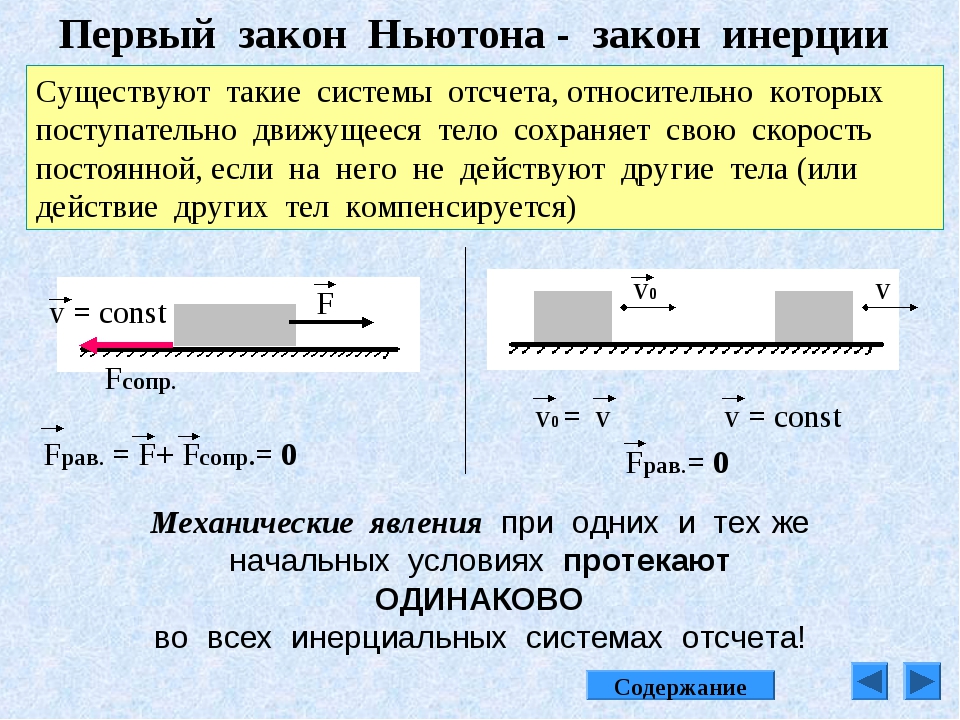 Как вы думаете, зачем боксерам перчатки? Наиболее часто встречаются два варианта ответа. Первый, чтоб не травмировать свои руки, и второй, чтоб излишне не травмировать противника. В принципе, оба ответа верны.
Как вы думаете, зачем боксерам перчатки? Наиболее часто встречаются два варианта ответа. Первый, чтоб не травмировать свои руки, и второй, чтоб излишне не травмировать противника. В принципе, оба ответа верны.
Согласно третьему закону Ньютона, если мы действуем на какое-либо тело с силой F, то это тело будет действовать на нас с той же по модулю силой, но обратной по направлению:
Или как еще говорят, сила действия равна силе противодействия.
Источник: https://physicsline.ru/teoriya/fizika-prostymi-slovami/fizika-prostymi-slovami-dinamika/
Законы ньютона простым языком
Законы Ньютона — это три важнейших закона классической механики, которые позволяют записать уравнения движения для любой механической системы, если известны силы, действующие на составляющие её тела.
Эти законы, естественно, сформулировал сэр Исаак Ньютон в 1687 году в книге «Математические начала натуральной философии».
В ньютоновском изложении механики эти законы являются аксиомами, базирующимися на обобщении экспериментальных результатов, то есть уже не требуют доказательства в настоящее время.
Первый закон Ньютона
Если на тело нет внешних воздействий, то это тело находится в состоянии покоя или равномерного прямолинейного движения по горизонтали относительно Земли.
Смысл Закона заключался в том, что он полностью совпадает с Законом инерции Галилео Галилея! Соответственно, если для этой системы отсчёта выполняется Первый закон Ньютона, то такая система отсчёта и называется инерциальной. А инерция — это и есть свойство тела оставаться в состоянии покоя или равномерного прямолинейного/прямого движения в отсутствие внешних воздействий.
Для примера полетим в далёкий-далёкий космос. Там почти нет никаких воздействий других тел. Вынем из кармана скафандра мячик и оставим его. Он не будет двигаться, то есть останется в состоянии покоя.
А теперь толкнём его, придадим импульс — и мячик плавно полетит в одном, прямом направлении, то есть перейдёт в состояние равномерного прямолинейного движения.
На Земле действует сила тяготения планеты, поэтому данный закон реализуем в нашей природе условно.
Второй закон Ньютона
Ускорение тела прямо пропорционально действующей на тело силе и обратно пропорционально массе этого тела.
Формула Закона: a = F / m, где а — ускорение, m — масса тела, F — сила, действующая на тело.
Смысл Закона в том, что сила, действующая на тело создаёт ускорение этого тела. Следовательно, чем больше масса тела, тем меньшее ускорение оно получит от действия данной (такой же) силы.
Для примера можно взять два человека, спускающихся со склона на лыжах. На каждого из них действует две силы. Тот лыжник, что тяжелее, будет медленнее спускаться при одинаковом пинке каждому из них! ))) Если мы хотим, чтобы оба лыжника спускались с одной скоростью, то более тяжёлого человека надо подтолкнуть сильнее. На сколько сильнее? На сколько он тяжелее — на 10%, 20% или 30%.
Третий Закон Ньютона
Пусть одно тело действует на данное тело с силой F1, тогда данное тело действует на первое тело с силой F2, равной по модулю силе F1 и противоположной по направлению.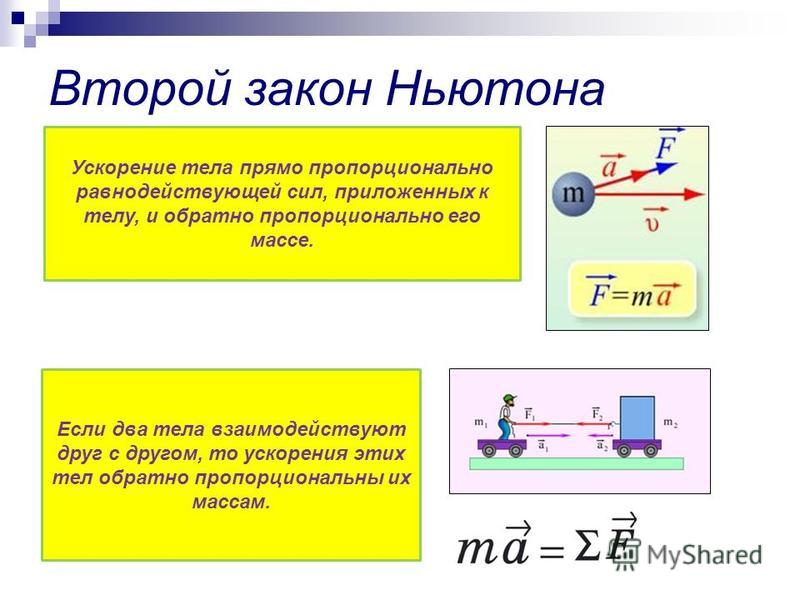
Формула Закона: F1 = -F2
Смысл Закона в том, что каждому действию есть противодействие.
Для примера два бильярдных (пластиковых) шара на столе. Подтолкнём один из них в направлении второго. При столкновении первый шар изменит и скорость, и направление, а второй покатится в направлении, обратном точке удара по нему.
Первый шар изменил направление и скорость при столкновении со вторым шаром из-за того, что то воздействовал на него, то ест произвёл противодействие.
Вот и все сложности! Ничего сложного.
Источник: https://zen.yandex.ru/media/id/5b955f924e008900ad8d15f2/5ba0a6957c147200ab5dc616
первый, второй, третий закон кратко с объяснением, формулами
Мы уже говорили об основах классической механики. Настала пора поговорить о них подробнее и затронуть в обсуждении чуть больше, чем просто основу. В этой статье мы подробно разберем основные законы классической механики. Как вы уже догадались, речь пойдет о законах Ньютона.
Как вы уже догадались, речь пойдет о законах Ньютона.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Основные законы классической механики Исаак Ньютон (1642-1727) собрал и опубликовал в 1687 году. Три знаменитых закона были включены в труд, который назывался «Математические начала натуральной философии».
Был долго этот мир глубокой тьмой окутан
Да будет свет, и тут явился Ньютон.
(Эпиграмма 18-го века)
Но сатана недолго ждал реванша –
Пришел Эйнштейн, и стало все как раньше.
(Эпиграмма 20-го века)
Что стало, когда пришел Эйнштейн, читайте в отдельном материале про релятивистскую динамику. А мы пока приведем формулировки и примеры решения задач на каждый закон Ньютона.
Первый закон Ньютона
Первый закон Ньютона гласит:
Существуют такие системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно, если на них не действуют никакие силы или действие других сил скомпенсировано.
Проще говоря, суть первого закона Ньютона можно сформулировать так: если мы на абсолютно ровной дороге толкнем тележку и представим, что можно пренебречь силами трения колес и сопротивления воздуха, то она будет катиться с одинаковой скоростью бесконечно долго.
Инерция – это способность тела сохранять скорость как по направлению, так и по величине, при отсутствии воздействий на тело. Первый закон Ньютона еще называют законом инерции.
До Ньютона закон инерции был сформулирован в менее четкой форме Галилео Галилеем. Инерцию ученый называл «неистребимо запечатленным движением». Закон инерции Галилея гласит: при отсутствии внешних сил тело либо покоится, либо движется равномерно. Огромная заслуга Ньютона в том, что он сумел объединить принцип относительности Галилея, собственные труды и работы других ученых в своих “Математических началах натуральной философии”.Понятно, что таких систем, где тележку толкнули, а она покатилась без действия внешних сил, на самом деле не бывает. На тела всегда действуют силы, причем скомпенсировать действие этих сил полностью практически невозможно.
На тела всегда действуют силы, причем скомпенсировать действие этих сил полностью практически невозможно.
Например, все на Земле находится в постоянном поле силы тяжести. Когда мы передвигаемся (не важно, ходим пешком, ездим на машине или велосипеде), нам нужно преодолевать множество сил: силу трения качения и силу трения скольжения, силу тяжести, силу Кориолиса.
Второй закон Ньютона
Помните пример про тележку? В этот момент мы приложили к ней силу! Интуитивно понятно, что тележка покатится и вскоре остановится. Это значит, ее скорость изменится.
В реальном мире скорость тела чаще всего изменяется, а не остается постоянной. Другими словами, тело движется с ускорением. Если скорость нарастает или убывает равномерно, то говорят, что движение равноускоренное.
Если рояль падает с крыши дома вниз, то он движется равноускоренно под действием постоянного ускорения свободного падения g. Причем любой дугой предмет, выброшенный из окна на нашей планете, будет двигаться с тем же ускорением свободного падения.
Второй закон Ньютона устанавливает связь между массой, ускорением и силой, действующей на тело. Приведем формулировку второго закона Ньютона:
Ускорение тела (материальной точки) в инерциальной системе отсчета прямо пропорционально приложенной к нему силе и обратно пропорционально массе.
Если на тело действует сразу несколько сил, то в данную формулу подставляется равнодействующая всех сил, то есть их векторная сумма.
В такой формулировке второй закон Ньютона применим только для движения со скоростью, много меньшей, чем скорость света.Существует более универсальная формулировка данного закона, так называемый дифференциальный вид.
В любой бесконечно малый промежуток времени dt сила, действующая на тело, равна производной импульса тела по времени.
Третий закон Ньютона
В чем состоит третий закон Ньютона? Этот закон описывает взаимодействие тел.
3 закон Ньютона говорит нам о том, что на любое действие найдется противодействие. Причем, в прямом смысле:
Причем, в прямом смысле:
Два тела воздействуют друг на друга с силами, противоположными по направлению, но равными по модулю.
Формула, выражающая третий закон Ньютона:
Другими словами, третий закон Ньютона – это закон действия и противодействия.
Пример задачи на законы Ньютона
Вот типичная задачка на применение законов Ньютона. В ее решении используются первый и второй законы Ньютона.
Десантник раскрыл парашют и опускается вниз с постоянной скоростью. Какова сила сопротивления воздуха? Масса десантника – 100 килограмм.
Решение:
Движение парашютиста – равномерное и прямолинейное, поэтому, по первому закону Ньютона, действие сил на него скомпенсировано.
На десантника действуют сила тяжести и сила сопротивления воздуха. Силы направлены в противоположные стороны.
По второму закону Ньютона, сила тяжести равна ускорению свободного падения, умноженному на массу десантника.
Ответ: Сила сопротивления воздуха равна силе тяжести по модулю и противоположна направлена.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
А вот еще одна физическая задачка на понимание действия третьего закона Ньютона.
Комар ударяется о лобовое стекло автомобиля. Сравните силы, действующие на автомобиль и комара.
Решение:
По третьему закону Ньютона, силы, с которыми тела действуют друг на друга, равны по модулю и противоположны по направлению. Сила, с которой комар действует на автомобиль, равна силе, с которой автомобиль действует на комара.
Другое дело, что действие этих сил на тела сильно отличаются вследствие различия масс и ускорений.
Исаак Ньютон: мифы и факты из жизни
На момент публикации своего основного труда Ньютону было 45 лет. За свою долгую жизнь ученый внес огромный вклад в науку, заложив фундамент современной физики и определив ее развитие на годы вперед.
Он занимался не только механикой, но и оптикой, химией и другими науками, неплохо рисовал и писал стихи. Неудивительно, что личность Ньютона окружена множеством легенд.
Ниже приведены некоторые факты и мифы из жизни И. Ньютона. Сразу уточним, что миф – это не достоверная информация. Однако мы допускаем, что мифы и легенды не появляются сами по себе и что-то из перечисленного вполне может оказаться правдой.
- Факт. Исаак Ньютон был очень скромным и застенчивым человеком. Он увековечил себя благодаря своим открытиям, однако сам никогда не стремился к славе и даже пытался ее избежать.
- Миф. Существует легенда, согласно которой Ньютона осенило, когда на наго в саду упало яблоко. Это было время чумной эпидемии (1665-1667), и ученый был вынужден покинуть Кембридж, где постоянно трудился. Точно неизвестно, действительно ли падение яблока было таким роковым для науки событием, так как первые упоминания об этом появляются только в биографиях ученого уже после его смерти, а данные разных биографов расходятся.

- Факт. Ньютон учился, а потом много работал в Кембридже. По долгу службы ему нужно было несколько часов в неделю вести занятия у студентов. Несмотря на признанные заслуги ученого, занятия Ньютона посещались плохо. Бывало, что на его лекции вообще никто не приходил. Скорее всего, это связано с тем, что ученый был полностью поглощен своими собственными исследованиями.
- Миф. В 1689 году Ньютон был избран членом Кембриджского парламента. Согласно легенде, более чем за год заседания в парламенте вечно поглощенный своими мыслями ученый взял слово для выступления всего один раз. Он попросил закрыть окно, так как был сквозняк.
- Факт. Неизвестно, как бы сложилась судьба ученого и всей современной науки, если бы он послушался матери и начал заниматься хозяйством на семейной ферме. Только благодаря уговорам учителей и своего дяди юный Исаак отправился учиться дальше вместо того, чтобы сажать свеклу, разбрасывать по полям навоз и по вечерам выпивать в местных пабах.

Дорогие друзья, помните – любую задачу можно решить! Если у вас возникли проблемы с решением задачи по физике, посмотрите на основные физические формулы. Возможно, ответ перед глазами, и его нужно просто рассмотреть. Ну а если времени на самостоятельные занятия совершенно нет, специализированный студенческий сервис всегда к вашим услугам!
В самом конце предлагаем посмотреть видеоурок на тему “Законы Ньютона”.
формула и определение / Блог / Справочник :: Бингоскул
Кратко о 1 законе Ньютона: формула, определение и формулировка
Помни!!!
- В основе динамики материальной точки лежат три закона Ньютона.
- Первый закон Ньютона – закон инерции
- Под телом подразумевают материальную точку, движение которой рассматривают в инерциальной системе отсчета.
1.
 Формулировка
Формулировка«Существуют такие инерциальные системы отсчёта, относительно которых тело, если на него не действуют другие силы (либо действие других сил компенсируется), находится в покое либо движется равномерно и прямолинейно».
2. Определение
Первый закон Ньютона — всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит её изменить это состояние.
Первый закон Ньютона — закон инерции (Галилей вывел закон инерции)
Закон инерции: Если на тело нет внешних воздействий, то данное тело сохраняет состояние покоя или равномерного прямолинейного движения относительно Земли.
Инерциальная система отсчёта (ИСО) – система, которая либо покоится, либо движется равномерно и прямолинейно относительно какой-то другой инерциальной системы. Т.е. система отсчета, в которой выполняется 1-й закон Ньютона.
- Масса тела – количественная мера его инертности. В СИ она измеряется в килограммах.
- Сила – количественная мера взаимодействия тел. Сила – векторная величина и измеряется в ньютонах (Н). Сила, которая производит на тело такое же действие, как несколько одновременно действующих сил, называется равнодействующей этих сил.
3. Формула
Формулы нет. Формула первого закона Ньютона не существует.
Первый закон Ньютона содержится 2 важных утверждения:
- все тела обладают свойством инерции;
- инерциальные системы отсчета существуют.
Это интересно:
Законы механики Ньютона • Джеймс Трефил, энциклопедия «Двести законов мироздания»
Законы Ньютона — в зависимости от того, под каким углом на них посмотреть, — представляют собой либо конец начала, либо начало конца классической механики. В любом случае это поворотный момент в истории физической науки — блестящая компиляция всех накопленных к тому историческому моменту знаний о движении физических тел в рамках физической теории, которую теперь принято именовать классической механикой. Можно сказать, что с законов движения Ньютона пошел отсчет истории современной физики и вообще естественных наук.
Можно сказать, что с законов движения Ньютона пошел отсчет истории современной физики и вообще естественных наук.
Однако Исаак Ньютон взял названные в его честь законы не из воздуха. Они, фактически, стали кульминацией долгого исторического процесса формулирования принципов классической механики. Мыслители и математики — упомянем лишь Галилея (см. Уравнения равноускоренного движения) — веками пытались вывести формулы для описания законов движения материальных тел — и постоянно спотыкались о то, что лично я сам для себя называю непроговоренными условностями, а именно — обе основополагающие идеи о том, на каких принципах зиждется материальный мир, которые настолько устойчиво вошли в сознание людей, что кажутся неоспоримыми. Например, древним философам даже в голову не приходило, что небесные тела могут двигаться по орбитам, отличающимся от круговых; в лучшем случае возникала идея, что планеты и звезды обращаются вокруг Земли по концентрическим (то есть вложенным друг в друга) сферическим орбитам. Почему? Да потому, что еще со времен античных мыслителей Древней Греции никому не приходило в голову, что планеты могут отклоняться от совершенства, воплощением которой и является строгая геометрическая окружность. Нужно было обладать гением Иоганна Кеплера, чтобы честно взглянуть на эту проблему под другим углом, проанализировать данные реальных наблюдений и вывести из них, что в действительности планеты обращаются вокруг Солнца по эллиптическим траекториям (см. Законы Кеплера).
Почему? Да потому, что еще со времен античных мыслителей Древней Греции никому не приходило в голову, что планеты могут отклоняться от совершенства, воплощением которой и является строгая геометрическая окружность. Нужно было обладать гением Иоганна Кеплера, чтобы честно взглянуть на эту проблему под другим углом, проанализировать данные реальных наблюдений и вывести из них, что в действительности планеты обращаются вокруг Солнца по эллиптическим траекториям (см. Законы Кеплера).
Первый закон Ньютона
Учитывая столь серьезный, исторически сложившийся провал, первый закон Ньютона сформулирован безоговорочно революционным образом. Он утверждает, что если какую-либо материальную частицу или тело попросту не трогать, оно будет продолжать прямолинейно двигаться с неизменной скоростью само по себе. Если тело равномерно двигалось по прямой, оно так и будет двигаться по прямой с неизменной скоростью. Если тело покоилось, оно так и будет покоиться, пока к нему не приложат внешних сил.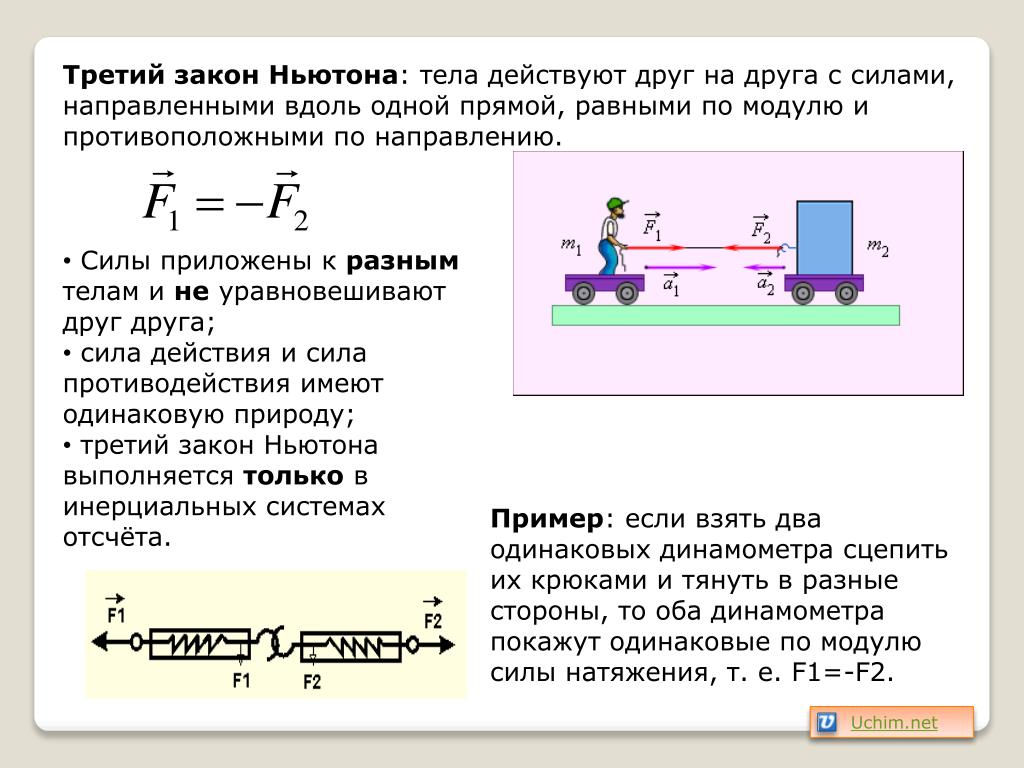 Чтобы просто сдвинуть физическое тело с места, к нему нужно обязательно приложить стороннюю силу. Возьмем самолет: он ни за что не стронется с места, пока не будут запущены двигатели. Казалось бы, наблюдение самоочевидное, однако, стоит нам отвлечься от прямолинейного движения, как оно перестает казаться таковым. При инерционном движении тела по замкнутой циклической траектории его анализ с позиции первого закона Ньютона только и позволяет точно определить его характеристики.
Чтобы просто сдвинуть физическое тело с места, к нему нужно обязательно приложить стороннюю силу. Возьмем самолет: он ни за что не стронется с места, пока не будут запущены двигатели. Казалось бы, наблюдение самоочевидное, однако, стоит нам отвлечься от прямолинейного движения, как оно перестает казаться таковым. При инерционном движении тела по замкнутой циклической траектории его анализ с позиции первого закона Ньютона только и позволяет точно определить его характеристики.
Представьте себе что-то типа легкоатлетического молота — ядро на конце струны, раскручиваемое вами вокруг вашей головы. Ядро в этом случае движется не по прямой, а по окружности — значит, согласно первому закону Ньютона, его что-то удерживает; это «что-то» — и есть центростремительная сила, которую вы прилагаете к ядру, раскручивая его. Реально вы и сами можете ее ощутить — рукоять легкоатлетического молота ощутимо давит вам на ладони. Если же вы разожмете руку и выпустите молот, он — в отсутствие внешних сил — незамедлительно отправится в путь по прямой. Точнее будет сказать, что так молот поведет себя в идеальных условиях (например, в открытом космосе), поскольку под воздействием силы гравитационного притяжения Земли он будет лететь строго по прямой лишь в тот момент, когда вы его отпустили, а в дальнейшем траектория полета будет всё больше отклоняться в направлении земной поверхности. Если же вы попробуете действительно выпустить молот, выяснится, что отпущенный с круговой орбиты молот отправится в путь строго по прямой, являющейся касательной (перпендикулярной к радиусу окружности, по которой его раскручивали) с линейной скоростью, равной скорости его обращения по «орбите».
Точнее будет сказать, что так молот поведет себя в идеальных условиях (например, в открытом космосе), поскольку под воздействием силы гравитационного притяжения Земли он будет лететь строго по прямой лишь в тот момент, когда вы его отпустили, а в дальнейшем траектория полета будет всё больше отклоняться в направлении земной поверхности. Если же вы попробуете действительно выпустить молот, выяснится, что отпущенный с круговой орбиты молот отправится в путь строго по прямой, являющейся касательной (перпендикулярной к радиусу окружности, по которой его раскручивали) с линейной скоростью, равной скорости его обращения по «орбите».
Теперь заменим ядро легкоатлетического молота планетой, молотобойца — Солнцем, а струну — силой гравитационного притяжения: вот вам и ньютоновская модель Солнечной системы.
Такой анализ происходящего при обращении одного тела вокруг другого по круговой орбите на первый взгляд кажется чем-то само собой разумеющимся, но не стоит забывать, что он вобрал в себя целый ряд умозаключений лучших представителей научной мысли предшествующего поколения (достаточно вспомнить Галилео Галилея). Проблема тут в том, что при движении по стационарной круговой орбите небесное (и любое иное) тело выглядит весьма безмятежно и представляется пребывающим в состоянии устойчивого динамического и кинематического равновесия. Однако, если разобраться, сохраняется только модуль (абсолютная величина) линейной скорости такого тела, в то время как ее направление постоянно меняется под воздействием силы гравитационного притяжения. Это и значит, что небесное тело движется равноускоренно. Кстати, сам Ньютон называл ускорение «изменением движения».
Первый закон Ньютона играет и еще одну важную роль с точки зрения нашего естествоиспытательского отношения к природе материального мира. Он подсказывает нам, что любое изменение в характере движения тела свидетельствует о присутствии внешних сил, воздействующих на него. Условно говоря, если мы наблюдаем, как железные опилки, например, подпрыгивают и налипают на магнит, или, доставая из сушилки стиральной машины белье, выясняем, что вещи слиплись и присохли одна к другой, мы можем чувствовать себя спокойно и уверенно: эти эффекты стали следствием действия природных сил (в приведенных примерах это силы магнитного и электростатического притяжения соответственно).
Второй закон Ньютона
Если первый закон Ньютона помогает нам определить, находится ли тело под воздействием внешних сил, то второй закон описывает, что происходит с физическим телом под их воздействием. Чем больше сумма приложенных к телу внешних сил, гласит этот закон, тем большее ускорение приобретает тело. Это раз. Одновременно, чем массивнее тело, к которому приложена равная сумма внешних сил, тем меньшее ускорение оно приобретает. Это два. Интуитивно эти два факта представляются самоочевидными, а в математическом виде они записываются так:
F = ma
где F — сила, m — масса, а — ускорение. Это, наверное, самое полезное и самое широко используемое в прикладных целях из всех физических уравнений. Достаточно знать величину и направление всех сил, действующих в механической системе, и массу материальных тел, из которых она состоит, и можно с исчерпывающей точностью рассчитать ее поведение во времени.
Именно второй закон Ньютона придает всей классической механике ее особую прелесть — начинает казаться, будто весь физический мир устроен, как наиточнейший хронометр, и ничто в нем не ускользнет от взгляда пытливого наблюдателя. Назовите мне пространственные координаты и скорости всех материальных точек во Вселенной, словно говорит нам Ньютон, укажите мне направление и интенсивность всех действующих в ней сил, и я предскажу вам любое ее будущее состояние. И такой взгляд на природу вещей во Вселенной бытовал вплоть до появления квантовой механики.
Третий закон Ньютона
За этот закон, скорее всего, Ньютон и снискал себе почет и уважение со стороны не только естествоиспытателей, но и ученых-гуманитариев и попросту широких масс. Его любят цитировать (по делу и без дела), проводя самые широкие параллели с тем, что мы вынуждены наблюдать в нашей обыденной жизни, и притягивают чуть ли не за уши для обоснования самых спорных положений в ходе дискуссий по любым вопросам, начиная с межличностных и заканчивая международными отношениями и глобальной политикой. Ньютон, однако, вкладывал в свой названный впоследствии третьим закон совершенно конкретный физический смысл и едва ли замышлял его в ином качестве, нежели как точное средство описания природы силовых взаимодействий. Закон этот гласит, что если тело А воздействует с некоей силой на тело В, то тело В также воздействует на тело А с равной по величине и противоположной по направлению силой. Иными словами, стоя на полу, вы воздействуете на пол с силой, пропорциональной массе вашего тела. Согласно третьему закону Ньютона пол в это же время воздействует на вас с абсолютно такой же по величине силой, но направленной не вниз, а строго вверх. Этот закон экспериментально проверить нетрудно: вы постоянно чувствуете, как земля давит на ваши подошвы.
Тут важно понимать и помнить, что речь у Ньютона идет о двух силах совершенно разной природы, причем каждая сила воздействует на «свой» объект. Когда яблоко падает с дерева, это Земля воздействует на яблоко силой своего гравитационного притяжения (вследствие чего яблоко равноускоренно устремляется к поверхности Земли), но при этом и яблоко притягивает к себе Землю с равной силой. А то, что нам кажется, что это именно яблоко падает на Землю, а не наоборот, это уже следствие второго закона Ньютона. Масса яблока по сравнению с массой Земли низка до несопоставимости, поэтому именно его ускорение заметно для глаз наблюдателя. Масса же Земли, по сравнению с массой яблока, огромна, поэтому ее ускорение практически незаметно. (В случае падения яблока центр Земли смещается вверх на расстояние менее радиуса атомного ядра.)
По совокупности же три закона Ньютона дали физикам инструменты, необходимые для начала комплексного наблюдения всех явлений, происходящих в нашей Вселенной. И, невзирая на все колоссальные подвижки в науке, произошедшие со времен Ньютона, чтобы спроектировать новый автомобиль или отправить космический корабль на Юпитер, вы воспользуетесь все теми же тремя законами Ньютона.
См. также:
Второй закон Ньютона
Определение 1Второй закон Ньютона представляет собой основной закон динамики. Данный закон может выполняться только в инерциальных системах отсчета.
Формулируя второй закон, стоит обратить внимание на то, что в динамике вводятся масса тела m и сила F→, а также способы их измерения. Масса является количественной характеристикой инертных свойств тела и показывает реакцию тела на внешнее воздействие. Сила же F→ представляет из себя количественную меру действия одного объекта на другой.
2-ой закон Ньютона, определение и формула
Второй закон Ньютона – фундаментальный закон природы, являющийся обобщением опытных фактов, подразделяющихся на две категории:
- Если на обладающие разной массой тела подействовать одной и той же силой, то приобретаемые телами ускорения окажутся обратно пропорциональны их массам:
a~1m, при F=const.
- Если силами различной величины подействовать на одно тело, то ускорения тела окажутся прямо пропорциональными приложенным силам:
a→~F→, при m=const.
Основной закон динамики был сформулирован Ньютоном путем обобщения данных фактов:
Определение 2Сила, которая оказывает воздействие на тело, эквивалентна произведению массы тела на сообщаемое данной силой ускорение:
F→=ma→.
Приведенное выражение и представляет собой второй закон Ньютона.
С помощью него стало возможным вычисление ускорение тела в случае, если известна его масса m и действующая на него сила F→:
a→=F’m.
Определение 3В Международной системе единиц (СИ) в качестве единицы силы считают такую силу, которая сообщающая телу массой 1 кг ускорение 1 м/с2. Данная единица называется ньютоном (Н). В (СИ) ее принимают за эталон силы.
1 Н=1кг·мс2.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеРавнодействующая сила
В том случае, если на тело одновременно воздействуют несколько сил, как например, F1→, F2→ и F3→, то силой F→ в формуле второго закона Ньютона считается равнодействующая всех сил это величина, выражающаяся в виде формулы:
F→=F1→+F2→+F3→.
Рисунок 1.8.1. Сила F→ – равнодействующая силы тяжести F→Т и силы нормального давления FN→, действующих на лыжницу на гладкой горе. Сила F→ вызывает ускорение лыжника.
В случае же, когда равнодействующая сила F→=0, тело будет пребывать в состоянии покоя или равномерного прямолинейного движения. Выходит, что формально второй закон Ньютона включает в себя в качестве частного случая первый закон Ньютона. Но первый закон Ньютона обладает более глубоким физическим значением. Он обуславливает существование инерциальных систем отсчета.
Рисунок 1.8.1. Модель движения тел на легком блоке.
Урок 7. законы динамики ньютона – Физика – 10 класс
Законы динамики Ньютона
Необходимо запомнить
ВАЖНО!
Масса – одна из основных характеристик материи. Способы измерения массы:
– сравнение с эталоном;
– взвешивание на весах.
В классической механике масса – аддитивная величина; не зависит от рода взаимодействия и скорости движения тела: $m_{сист} = \sum_{i=1}^{n}mi$.{n}Fi$.
Первый закон Ньютона: если на тело не действуют другие тела, то тело движется прямолинейно и равномерно: $\overrightarrow{F} = 0$.
Важно! Если есть ИСО, то любая другая система, движущаяся относительно неё прямолинейно и равномерно, также является инерциальной.
Второй закон Ньютон: ускорение тела прямо пропорционально силе, действующей на него, и обратно пропорционально его массе: $\overrightarrow{a} = \frac{\overrightarrow{F}}{m}$.
Другая запись формулы второго закона Ньютона (основное уравнение динамики): $\overrightarrow{F} = m \overrightarrow{a}$ .
Третий закон Ньютона: тела действуют друг на друга с силами, равными по модулю и противоположными по направлению: $\overrightarrow{F}_{12} = -\overrightarrow{F}_{21}$.
Второй закон Ньютона для системы тел: приращение импульса $\Delta \overrightarrow{P}$ системы тел равно по величине и по направлению импульсу внешних сил, действующих на тело, за то же время: $\Delta \overrightarrow{p} = \overrightarrow{F} \Delta t$.
Границы применимости: справедливы для материальных точек или поступательно движущихся тел; для скоростей много меньше скорости света в вакууме; выполняются в ИСО.
Решение задачи на применение второго закона Ньютона
определение, формула + рассуждения по теме
В первом законе Ньютона говорится о поведении тела, изолированного от воздействия других тел. Второй закон говорит о прямо противоположной ситуации. В нем рассматриваются случаи, когда тело или несколько тел воздействуют на данное.
Оба эти закона описывают поведение одного конкретного тела. Но во взаимодействии всегда участвуют минимум два тела. Что будет происходить с обоими этими телами? Как описать их взаимодействие? Анализом этой ситуации и занялся Ньютон после формулировки своих первых двух законов. Займемся и мы такими же изысканиями.
Взаимодействие двух тел
Мы знаем, что при взаимодействии воздействуют друг на друга оба тела. Не бывает такого, чтобы одно тело толкнуло другое, а второе в ответ никак не отреагировало бы. Такое может происходить среди по-разному воспитанных людей, но никак не в природе.
Мы знаем, что если мы пинаем мяч, то мяч в ответ пинает нас. Другое дело, что мяч имеет намного меньшую массу, чем тело человека, и потому его воздействие практически не ощутимо.
Однако, если вы попробуете пнуть тяжелый железный мяч, то живо ощутите это ответное воздействие. Фактически, мы каждый день по многу раз пинаем очень и очень тяжелый мяч нашу планету. Мы толкаем ее каждым своим шагом, только при этом отлетает не она, а мы. А все потому, что планета в миллионы раз превосходит нас по массе.
Соотношение сил во взаимодействии между телами
Так что из этих рассуждений видно, что при взаимодействии двух тел, не только первое действует на второе с некоторой силой, но и второе в ответ действует на первое также с некоторой силой. Возникает вопрос: а как соотносятся эти силы? Какая из них больше, какая меньше?
Для этого необходимо проделать некоторые измерения. Потребуются два динамометра, но в домашних условиях их вполне могу заменить два безмена. Они измеряют вес, а вес это тоже сила, только выраженная в единицах массы в случае безмена. Поэтому, если у вас есть два безмена, то проделайте следующее.
Один из них оденьте колечком на что-то неподвижное, например, на гвоздь в стене, а второй соедините с первым крючками. И потяните за колечко второго безмена. Проследите за показаниями обоих приборов. Каждый из них покажет силу, с которой на него воздействует другой безмен.
И хотя мы тянем только за один из них, окажется, что показания обоих, как на очной ставке, будут совпадать. Получается, что сила, с которой мы воздействуем вторым безменом на первый, равна силе, с которой первый безмен воздействует на второй.
Третий закон Ньютона: определение и формула
Сила действия равна силе противодействия. В этом и состоит суть третьего закона Ньютона. Определение его таково: силы, с которыми два тела действуют друг на друга, равны по величине и противоположны по направлению. Третий закон Ньютона можно записать в виде формулы:
F_1 = – F_2,
Где F_1 и F_2 силы действия друг на друга соответственно первого и второго тела.
Справедливость третьего закона Ньютона была подтверждена многочисленными экспериментами. Этот закон справедлив как для случая, когда одно тело тянет другое, так и для случая, когда тела отталкиваются. Все тела во Вселенной взаимодействуют друг с другом, подчиняясь этому закону.
Нужна помощь в учебе?
Предыдущая тема: Второй закон Ньютона: формула и определение + маленький опыт
Следующая тема:   Свободное падение тел: суть, ускорение свободного падения, формулы
Веб-сайт класса физики
Законы движения Ньютона: обзор набора задач
Этот набор из 30 задач нацелен на вашу способность различать массу и вес, определять чистую силу по значениям отдельных сил, связывать ускорение с чистой силой и массой, анализировать физические ситуации, чтобы нарисовать диаграмму свободного тела и решить неизвестная величина (ускорение или значение индивидуальной силы) и объединить анализ второго закона Ньютона с кинематикой для определения неизвестной величины (кинематической величины или значения силы).Проблемы варьируются по сложности от очень простых и простых до очень сложных и сложных. Более сложные задачи обозначены цветом , синие задачи .
Масса против веса
Этот набор из 30 задач нацелен на вашу способность различать массу и вес, определять чистую силу по значениям отдельных сил, связывать ускорение с чистой силой и массой, анализировать физические ситуации, чтобы нарисовать диаграмму свободного тела и решить неизвестная величина (ускорение или индивидуальное значение силы), масса – это величина, которая зависит от количества вещества, присутствующего в объекте; обычно выражается в килограммах.Масса материи, которой обладает объект, не зависит от его местоположения во Вселенной. С другой стороны, вес – это сила тяжести, с которой Земля притягивает к себе объект. Поскольку гравитационные силы меняются в зависимости от местоположения, вес объекта на поверхности Земли отличается от его веса на Луне. Вес, как сила, чаще всего выражается в метрических единицах измерения в ньютонах. Каждое место во Вселенной характеризуется постоянной гравитационного поля, представленной символом g (иногда называемое ускорением свободного падения).Вес (или F grav ) и масса ( м ) связаны уравнением:
F грав = m • g
Второй закон движения Ньютона
Второй закон движения Ньютона гласит, что ускорение ( a ), испытываемое объектом, прямо пропорционально чистой силе ( F net ), испытываемой объектом, и обратно пропорционально массе объекта.В форме уравнения можно сказать, что a = F net / m . Чистая сила – это векторная сумма всех индивидуальных значений силы. Если величина и направление отдельных сил известны, то эти силы могут быть добавлены как векторы для определения результирующей силы. Следует обратить внимание на векторную природу силы. Направление важно. Поднимающую силу и прижимающую силу можно добавить, присвоив прижимной силе отрицательное значение, а восходящей силе положительное значение. Аналогичным образом, сила, направленная вправо, и сила, направленная влево, могут быть добавлены путем присвоения левой силе отрицательного значения и правой силы положительного значения.
Уравнение a = F net / m можно использовать как формулу для решения проблем и как руководство к размышлениям. При использовании уравнения в качестве формулы для решения проблемы важно, чтобы числовые значения двух из трех переменных в уравнении были известны, чтобы найти неизвестную величину. При использовании уравнения в качестве руководства к размышлениям необходимо учитывать прямые и обратные отношения между ускорением и чистой силой и массой. Двукратное или трёхкратное увеличение чистой силы вызовет такое же изменение ускорения, удвоение или утроение его значения.Увеличение массы в два или три раза вызовет обратное изменение ускорения, уменьшив его значение в два или три раза.
Диаграммы свободного тела
Диаграммы свободного тела представляют силы, которые действуют на объект в данный момент времени. Отдельные силы, действующие на объект, представлены векторными стрелками. Направление стрелок указывает направление силы, а приблизительная длина стрелки представляет относительную величину силы.Силы обозначены в соответствии с их типом. Схема свободного тела может оказаться полезным подспорьем в процессе решения проблем. Он обеспечивает визуальное представление сил, действующих на объект. Если величины всех отдельных сил известны, диаграмму можно использовать для определения чистой силы. И если ускорение и масса известны, то можно рассчитать чистую силу, и диаграмму можно использовать для определения значения единственной неизвестной силы.
Коэффициент трения
Объект, который движется (или событие, пытающееся двигаться) по поверхности, встречает силу трения.Сила трения возникает из-за того, что две поверхности плотно прижаты друг к другу, вызывая межмолекулярные силы притяжения между молекулами разных поверхностей. Таким образом, трение зависит от природы двух поверхностей и от степени их прижатия друг к другу. Силу трения можно рассчитать по формуле:
F frict = µ • F norm
Символ µ (произносится как «мью») представляет коэффициент трения и будет отличаться для разных поверхностей.
Смешение законов Ньютона и кинематических уравнений
Кинематика относится к описанию движения объекта и фокусируется на вопросах, как далеко?, Как быстро?, Сколько времени? а с каким ускорением? Чтобы помочь ответить на такие вопросы, в модуле «Одномерная кинематика» были представлены четыре кинематических уравнения. Четыре уравнения перечислены ниже.
- d = v o • t + 0.5 • а • т 2
- v f = v o + a • t
- v f 2 = v o 2 + 2 • a • d
- d = (v o + v f ) / 2 • t
где
- d = рабочий объем
- t = время
- a = ускорение
- v o = исходная или начальная скорость
- v f = конечная скорость
Законы Ньютона и кинематика разделяют один из этих общих вопросов: с каким ускорением? Ускорение (a) F net = m • a уравнение – это то же ускорение, что и в кинематических уравнениях.Таким образом, общие задачи включают:
- использование кинематической информации для определения ускорения, а затем использование ускорения в анализе законов Ньютона, или
- использование информации о силе и массе для определения значения ускорения, а затем использование ускорения в кинематическом анализе.
При анализе словесной проблемы физики целесообразно идентифицировать известные величины и систематизировать их либо как кинематические, либо как величины типа F-m-a.
Привычки эффективно решать проблемы
Эффективный решатель проблем по привычке подходит к физической проблеме таким образом, который отражает набор дисциплинированных привычек. Хотя не все эффективные специалисты по решению проблем используют один и тот же подход, все они имеют общие привычки. Эти привычки кратко описаны здесь. Эффективное решение проблем …
- …. внимательно читает задачу и создает мысленную картину физической ситуации. При необходимости они набрасывают простую схему физической ситуации, чтобы помочь визуализировать ее.
- … определяет известные и неизвестные величины в организованном порядке, часто записывая их на диаграмме. Они приравнивают заданные значения к символам, используемым для представления соответствующей величины (например, v o = 0 м / с, a = 2,67 м / с / с, v f = ???).
- …построит стратегию решения неизвестной величины; стратегия, как правило, сосредоточена вокруг использования физических уравнений и во многом зависит от понимания физических принципов.
- … определяет подходящую (ые) формулу (ы) для использования, часто записывая их. При необходимости они выполняют необходимое преобразование количеств в правильные единицы.
- … выполняет подстановки и алгебраические манипуляции, чтобы найти неизвестную величину.
Подробнее …
Дополнительная литература / Учебные пособия:
Следующие страницы из учебного пособия по физике могут быть полезны для понимания концепций и математики, связанных с этими проблемами.
Набор задач о законах движения Ньютона
Просмотреть набор задач
Законы Ньютона о движении Решения с аудиосистемой
Просмотрите решение проблемы с аудиогидом:1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30
Второй закон движения Ньютона
Первый закон движения Ньютона предсказывает поведение объектов, для которых все существующие силы уравновешены.Первый закон – иногда называемый законом инерции – гласит, что если силы, действующие на объект, уравновешены, то ускорение этого объекта будет 0 м / с / с. Объекты в состоянии равновесия (состояние, при котором все силы уравновешены) не будут ускоряться. Согласно Ньютону, объект будет ускоряться только в том случае, если на него действует чистая или неуравновешенная сила. Присутствие неуравновешенной силы ускоряет объект, изменяя его скорость, направление или одновременно скорость и направление.
Второй закон движения Ньютона относится к поведению объектов, для которых все существующие силы не сбалансированы. Второй закон гласит, что ускорение объекта зависит от двух переменных – чистой силы, действующей на объект, и массы объекта. Ускорение объекта напрямую зависит от чистой силы, действующей на объект, и обратно – от массы объекта. По мере увеличения силы, действующей на объект, ускорение объекта увеличивается.По мере увеличения массы объекта ускорение объекта уменьшается.
БОЛЬШОЕ УравнениеВторой закон движения Ньютона можно формально сформулировать следующим образом:
Ускорение объекта, создаваемое чистой силой, прямо пропорционально величине чистой силы в том же направлении, что и чистая сила, и обратно пропорционально массе объекта.
Это словесное утверждение можно выразить в виде уравнения следующим образом:
a = F нетто / мПриведенное выше уравнение часто преобразовывается в более знакомую форму, как показано ниже. Чистая сила равна произведению массы на ускорение.
F net = m • aВо всем этом обсуждении упор был сделан на чистую силу .Ускорение прямо пропорционально чистой силе ; чистая сила равна массе, умноженной на ускорение; ускорение в том же направлении, что и чистая сила ; ускорение создается чистой силой . СЕТЕВАЯ СИЛА. Важно помнить об этом различии. Не используйте в приведенном выше уравнении значение просто «какой-либо старой силы». Это чистая сила, связанная с ускорением. Как обсуждалось в предыдущем уроке, результирующая сила – это векторная сумма всех сил.Если известны все индивидуальные силы, действующие на объект, то можно определить результирующую силу. При необходимости просмотрите этот принцип, вернувшись к практическим вопросам в Уроке 2.
В соответствии с приведенным выше уравнением единица силы равна единице массы, умноженной на единицу ускорения. Подставив стандартные метрические единицы для силы, массы и ускорения в приведенное выше уравнение, можно записать следующую эквивалентность единиц.
1 Ньютон = 1 кг • м / с 2Определение стандартной метрической единицы силы определяется приведенным выше уравнением.Один ньютон определяется как количество силы, необходимое для придания 1 кг массы ускорения в 1 м / с / с.
Ваша очередь практиковаться Сеть F = m • уравнение часто используется при решении алгебраических задач. Приведенную ниже таблицу можно заполнить, подставив в уравнение и решив неизвестную величину. Попробуйте сами, а затем используйте кнопки, чтобы просмотреть ответы.
| Чистая сила (н.) | Масса (кг) | Разгон (м / с / с) | |
| 1. | 10 | 2 | |
| 2. | 20 | 2 | |
| 3. | 20 | 4 | |
| 4. | 2 | 5 | |
| 5. | 10 | 10 |
Числовая информация в таблице выше демонстрирует некоторые важные качественные отношения между силой, массой и ускорением.Сравнивая значения в строках 1 и 2, можно увидеть, что удвоение чистой силы приводит к удвоению ускорения (если масса остается постоянной). Аналогичным образом сравнение значений в строках 2 и 4 показывает, что уменьшение вдвое чистой силы на приводит к уменьшению вдвое ускорения (если масса остается постоянной). Ускорение прямо пропорционально чистой силе.
Кроме того, качественную взаимосвязь между массой и ускорением можно увидеть, сравнив числовые значения в приведенной выше таблице.Из строк 2 и 3 обратите внимание, что удвоение массы приводит к уменьшению вдвое ускорения (если сила остается постоянной). Аналогично, строки 4 и 5 показывают, что уменьшение вдвое массы на приводит к удвоению ускорения (если сила остается постоянной). Ускорение обратно пропорционально массе.
Анализ табличных данных показывает, что такое уравнение, как F net = m * a, может быть руководством к размышлениям о том, как изменение одной величины может повлиять на другую величину.Какое бы изменение ни производилось в чистой силе, такое же изменение произойдет и с ускорением. Удвойте, утроите или учетверите чистую силу, и ускорение будет делать то же самое. С другой стороны, какое бы изменение массы ни производилось, с ускорением будет происходить противоположное или обратное изменение. Удвойте, утроите или учетверите массу, и ускорение составит половину, одну треть или одну четвертую от первоначального значения.
Направление чистой силы и ускорения
Как указано выше, направление результирующей силы совпадает с направлением ускорения.Таким образом, если известно направление ускорения, то известно и направление результирующей силы. Рассмотрим две диаграммы падения масла ниже для ускорения автомобиля. По диаграмме определите направление чистой силы, действующей на автомобиль. Затем нажмите кнопки, чтобы просмотреть ответы. (При необходимости проверьте ускорение предыдущего блока.)
В заключение, второй закон Ньютона дает объяснение поведения объектов, на которых силы не уравновешиваются.Закон гласит, что несбалансированные силы заставляют объекты ускоряться с ускорением, которое прямо пропорционально чистой силе и обратно пропорционально массе.
1. Определите ускорения, возникающие при приложении чистой силы 12 Н к объекту массой 3 кг, а затем к объекту массой 6 кг.
2. К энциклопедии прилагается чистая сила 15 Н, которая заставляет ее ускоряться со скоростью 5 м / с. 2 .Определите массу энциклопедии.
3. Предположим, что салазки ускоряются со скоростью 2 м / с. 2 . Если чистая сила утроится, а масса – вдвое, то каково новое ускорение салазок?
4. Предположим, что салазки ускоряются со скоростью 2 м / с. 2 . Если чистая сила утроится, а масса уменьшится вдвое, то каково новое ускорение салазок?
6.1 Решение проблем с помощью законов Ньютона – Университетская физика, том 1
Сила сопротивления на барже
Два буксира толкают баржу под разными углами (рис. 6.4). Первый буксир прикладывает силу 2,7 × 105 Н2,7 × 105 Н в направлении x , а второй буксир прикладывает силу 3,6 × 105 Н3,6 × 105 Н в направлении y . Масса баржи составляет 5,0 × 106 кг 5,0 × 106 кг, а ее ускорение составляет 7,5 × 10–2 м / с27,5 × 10–2 м / с2 в указанном направлении. Какова сила сопротивления воды барже, сопротивляющейся движению? ( Примечание: Сила сопротивления – это сила трения, создаваемая жидкостями, такими как воздух или вода.Сила сопротивления препятствует движению объекта. Поскольку баржа имеет плоское дно, можно предположить, что сила сопротивления направлена в направлении, противоположном движению баржи.) Рис. 6.4 (a) Вид сверху двух буксиров, толкающих баржу. (b) Схема свободного тела для корабля содержит только силы, действующие в плоскости воды. В нем не учитываются две вертикальные силы – вес баржи и выталкивающая сила поддерживающей ее воды, которые не показаны. Обратите внимание, что F → appF → app – это общая прилагаемая сила буксиров.Стратегия
Направления и величины ускорения и приложенных сил показаны на Рисунке 6.4 (а). Мы определяем общую силу буксиров на барже как F → appF → app так, чтобы F → приложение = F → 1 + F → 2.F → приложение = F → 1 + F → 2.Сопротивление воды F → DF → D направлено в направлении, противоположном направлению движения лодки; эта сила, таким образом, действует против F → app, F → app, как показано на диаграмме свободного тела на рис. 6.4 (b). Здесь представляет интерес система баржа, поскольку на нее действуют силы, а также ее ускорение.Поскольку приложенные силы перпендикулярны, оси x и y находятся в том же направлении, что и F → 1F → 1 и F → 2.F → 2. Проблема быстро становится одномерной в направлении F → appF → app, поскольку трение происходит в направлении, противоположном F → app.F → app. Наша стратегия состоит в том, чтобы найти величину и направление чистой приложенной силы F → appF → app, а затем применить второй закон Ньютона для определения силы сопротивления F → D.F → D.
Решение
Поскольку FxFx и FyFy перпендикулярны, мы можем определить величину и направление F → appF → app напрямую.Во-первых, результирующая величина определяется теоремой Пифагора: Fapp = F12 + F22 = (2.7 × 105N) 2+ (3.6 × 105N) 2 = 4.5 × 105N. Fapp = F12 + F22 = (2.7 × 105N) 2+ (3.6 × 105N) 2 = 4.5 × 105N.Угол равен
θ = tan − 1 (F2F1) = tan − 1 (3,6 × 105N2,7 × 105N) = 53,1 °. θ = tan − 1 (F2F1) = tan − 1 (3,6 × 105N2,7 × 105N) = 53,1 °.Из первого закона Ньютона мы знаем, что это то же направление, что и ускорение. Мы также знаем, что F → DF → D находится в противоположном направлении от F → app, F → app, поскольку он замедляет ускорение. Следовательно, чистая внешняя сила имеет то же направление, что и F → app, F → app, но ее величина немного меньше, чем F → app.F → приложение. Проблема теперь одномерная. Из диаграммы свободного тела видно, что
Fnet = Fapp-FD.Fnet = Fapp-FD.Однако второй закон Ньютона гласит, что
Таким образом,
Fapp-FD = ma.Fapp-FD = ma.Это может быть решено для величины силы сопротивления водного FDFD в терминах известных величин:
FD = Fapp-ma. FD = Fapp-ma.Подстановка известных значений дает
FD = (4,5 × 105 Н) – (5,0 × 106 кг) (7,5 × 10–2 м / с2) = 7,5 × 104 Н. FD = (4,5 × 105 Н) – (5,0 × 106 кг) (7,5 × 10–2 м / с2) = 7,5 × 104 Н.Направление F → DF → D уже определено как направление, противоположное F → app, F → app, или под углом 53 ° 53 ° к югу от запада.
Значение
Числа, использованные в этом примере, приемлемы для баржи среднего размера. Конечно, трудно добиться большего ускорения на буксирах, и желательна небольшая скорость, чтобы баржа не врезалась в доки. Сопротивление относительно невелико для хорошо спроектированного корпуса на низких скоростях, что соответствует ответу на этот пример, где FDFD составляет менее 1/600 веса корабля.Второй закон движения Ньютона: концепция системы
Цели обучения
К концу этого раздела вы сможете:
- Определите чистую силу, внешнюю силу и систему.
- Поймите второй закон движения Ньютона.
- Примените второй закон Ньютона для определения веса объекта.
Второй закон движения Ньютона тесно связан с первым законом движения Ньютона. Он математически устанавливает причинно-следственную связь между силой и изменениями в движении.Второй закон движения Ньютона является более количественным и широко используется для расчета того, что происходит в ситуациях, связанных с действием силы. Прежде чем мы сможем записать второй закон Ньютона в виде простого уравнения, дающего точное соотношение силы, массы и ускорения, нам необходимо отточить некоторые идеи, которые уже упоминались.
Во-первых, что мы подразумеваем под изменением движения? Ответ заключается в том, что изменение движения эквивалентно изменению скорости. Изменение скорости по определению означает наличие ускорения .Первый закон Ньютона гласит, что чистая внешняя сила вызывает изменение движения; таким образом, мы видим, что чистая внешняя сила вызывает ускорение .
Сразу возникает еще один вопрос. Что мы подразумеваем под внешней силой? Интуитивное представление о внешнем является правильным – внешняя сила действует извне из интересующей системы . Например, на рис. 1 (а) интересующая нас система – это вагон плюс ребенок в нем. Две силы, действующие со стороны других детей, – это внешние силы.Между элементами системы действует внутренняя сила. Снова посмотрев на рисунок 1 (а), сила, которую ребенок в повозке прикладывает, чтобы повиснуть на повозке, представляет собой внутреннюю силу между элементами интересующей системы. Согласно первому закону Ньютона, только внешние силы влияют на движение системы. (Внутренние силы фактически отменяются, как мы увидим в следующем разделе.) Вы должны определить границы системы, прежде чем вы сможете определить, какие силы являются внешними . Иногда система очевидна, а иногда определение границ системы более тонкое.Концепция системы является фундаментальной для многих областей физики, как и правильное применение законов Ньютона. Эта концепция будет многократно пересмотрена в нашем путешествии по физике.
Рис. 1. Различные силы, действующие на одну и ту же массу, вызывают разное ускорение. а) двое детей толкают телегу с ребенком в ней. Показаны стрелки, представляющие все внешние силы. Интересующая система – это повозка и ее водитель. Вес w системы и опора земли N также показаны для полноты и, как предполагается, компенсируются.Вектор f представляет трение, действующее на вагон, и действует влево, противодействуя движению вагона. (b) Все внешние силы, действующие на систему, в сумме образуют чистую силу, F net . На диаграмме свободного тела показаны все силы, действующие на интересующую систему. Точка представляет собой центр масс системы. Каждый вектор силы простирается от этой точки. Поскольку справа действуют две силы, мы рисуем векторы коллинеарно.(c) Большая чистая внешняя сила вызывает большее ускорение ( a ‘> a ), когда взрослый толкает ребенка.
Теперь кажется разумным, что ускорение должно быть прямо пропорционально и в том же направлении, что и чистая (полная) внешняя сила, действующая на систему. Это предположение было проверено экспериментально и показано на рисунке 1. В части (а) меньшая сила вызывает меньшее ускорение, чем большая сила, показанная в части (с). Для полноты картины также показаны вертикальные силы; предполагается, что они отменяются, поскольку нет ускорения в вертикальном направлении.Вертикальные силы – это вес w и опора на землю N , а горизонтальная сила f представляет собой силу трения. Они будут обсуждаться более подробно в следующих разделах. На данный момент мы определим трение как силу, которая противодействует движению мимо друг друга соприкасающихся объектов. На рисунке 1 (b) показано, как векторы, представляющие внешние силы, складываются вместе, чтобы получить результирующую силу,
.F net .
Чтобы получить уравнение для второго закона Ньютона, сначала запишем соотношение ускорения и чистой внешней силы как пропорциональность
[латекс] \ text {a} \ propto {\ text {F} _ {net}} \\ [/ latex]
, где символ ∝ означает «пропорционально», а F net – это чистая внешняя сила .(Чистая внешняя сила представляет собой векторную сумму всех внешних сил и может быть определена графически, используя метод “голова к хвосту”, или аналитически, используя компоненты. Методы такие же, как и для сложения других векторов, и рассматриваются в двумерной кинематике.) Эта пропорциональность выражает то, что мы сказали словами: ускорение прямо пропорционально чистой внешней силе . После выбора интересующей системы важно определить внешние силы и игнорировать внутренние.Это огромное упрощение – не учитывать многочисленные внутренние силы, действующие между объектами внутри системы, такие как мышечные силы в теле ребенка, не говоря уже о мириадах сил между атомами в объектах, но, делая это, мы можем легко решить некоторые очень сложные проблемы с минимальной ошибкой благодаря нашему упрощению.
Теперь также кажется разумным, что ускорение должно быть обратно пропорционально массе системы. Другими словами, чем больше масса (инерция), тем меньше ускорение, создаваемое данной силой.И действительно, как показано на рисунке 2, та же самая чистая внешняя сила, приложенная к автомобилю, вызывает гораздо меньшее ускорение, чем при приложении к баскетболу. Пропорциональность записывается как
.[латекс] \ text {a} \ propto {\ frac {1} {m}} \\ [/ latex]
, где м – масса системы. Эксперименты показали, что ускорение прямо обратно пропорционально массе, точно так же, как оно прямо линейно пропорционально чистой внешней силе.
Рис. 2. Одна и та же сила, действующая на системы разной массы, вызывает разное ускорение.(a) Баскетболист толкает баскетбольный мяч, чтобы сделать передачу. (Влияние силы тяжести на мяч игнорируется.) (B) Тот же игрок оказывает идентичную силу на остановившийся внедорожник и производит гораздо меньшее ускорение (даже если трение незначительно). (c) Диаграммы свободного тела идентичны, что позволяет напрямую сравнить две ситуации. По мере того, как вы будете решать больше задач, появится серия паттернов для диаграммы свободного тела.
Было обнаружено, что ускорение объекта зависит только от чистой внешней силы и массы объекта.Объединение двух только что приведенных пропорциональностей дает второй закон движения Ньютона.
Второй закон движения Ньютона
Ускорение системы прямо пропорционально чистой внешней силе, действующей на систему, и в том же направлении, и обратно пропорционально ее массе. В форме уравнения второй закон движения Ньютона равен
.[латекс] {\ text {a}} = \ frac {{{\ text {F}}} _ {\ text {net}}} {m} \\ [/ latex].
Это часто записывается в более знакомой форме
F нетто = м a .
Если рассматривать только величину силы и ускорения, это уравнение просто
F net = ma.
Хотя эти последние два уравнения на самом деле одинаковы, первое дает больше понимания того, что означает второй закон Ньютона. Закон – причинно-следственная связь между тремя величинами, которая не просто основана на их определениях. Справедливость второго закона полностью основана на экспериментальной проверке.
F net = м a используется для определения единиц силы в терминах трех основных единиц массы, длины и времени. Единица силы в системе СИ называется ньютон (сокращенно Н) и представляет собой силу, необходимую для ускорения системы массой 1 кг со скоростью 1 м / с 2 . То есть, поскольку F net = м a ,
1 Н = 1 кг ⋅ м / с 2 .
В то время как почти весь мир использует ньютон в качестве единицы силы, в Соединенных Штатах наиболее известной единицей силы является фунт (фунт), где 1 N = 0.225 фунтов
Вес и сила тяжести
Когда объект падает, он ускоряется к центру Земли. Второй закон Ньютона гласит, что общая сила, действующая на объект, отвечает за его ускорение. Если сопротивление воздуха незначительно, результирующая сила, действующая на падающий объект, – это сила тяжести, обычно называемая его весом Вт. Вес можно обозначить как вектор w, потому что он имеет направление; вниз – это, по определению, направление силы тяжести, и, следовательно, вес – это сила, направленная вниз.Величина веса обозначается как w . Галилей показал, что при отсутствии сопротивления воздуха все объекты падают с одинаковым ускорением g . Используя результат Галилея и второй закон Ньютона, мы можем вывести уравнение для веса.
Рассмотрим объект массой м , падающий на Землю. Он испытывает только направленную вниз силу тяжести, величина которой составляет w . Второй закон Ньютона гласит, что величина чистой внешней силы, действующей на объект, составляет F net = ма .Поскольку объект испытывает только направленную вниз силу тяжести, F net = w . Мы знаем, что ускорение объекта под действием силы тяжести составляет g , или a = g . Подставляя их во второй закон Ньютона, получаем
МассаЭто уравнение для веса – силы тяжести, действующей на массу m:
w = мг
Так как g = 9,80 м / с 2 на Земле, вес 1.0 кг объекта на Земле составляет 9,8 Н, как мы видим:
w = мг = (1,0 кг) (9,80 м / с 2 ) = 9,8 Н.
Напомним, что g может принимать положительное или отрицательное значение в зависимости от положительного направления в системе координат. Обязательно учтите это при решении задач с весом.
Когда чистая внешняя сила, действующая на объект, равна его весу, мы говорим, что он находится в свободном падении . То есть единственная сила, действующая на объект, – это сила тяжести.В реальном мире, когда объекты падают вниз к Земле, они никогда не находятся в состоянии свободного падения, потому что на объект всегда действует некоторая восходящая сила из воздуха.
Ускорение свободного падения g незначительно меняется по поверхности Земли, поэтому вес объекта зависит от местоположения и не является внутренним свойством объекта. Вес резко меняется, если человек покидает поверхность Земли. На Луне, например, ускорение свободного падения всего 1.67 м / с 2 . Таким образом, масса в 1,0 кг имеет вес 9,8 Н на Земле и всего около 1,7 Н на Луне.
Самое широкое определение веса в этом смысле состоит в том, что вес объекта – это сила тяжести, действующая на него со стороны ближайшего большого тела , такого как Земля, Луна, Солнце и так далее. Это наиболее распространенное и полезное определение веса в физике. Однако оно кардинально отличается от определения веса, используемого НАСА и популярными СМИ в отношении космических путешествий и исследований.Когда они говорят о «невесомости» и «микрогравитации», они на самом деле имеют в виду явление, которое мы называем «свободным падением» в физике. Мы будем использовать приведенное выше определение веса и проведем тщательное различие между свободным падением и фактической невесомостью.
Важно знать, что вес и масса – очень разные физические величины, хотя они тесно связаны. Масса – это количество материи (сколько «вещества») и не изменяется в классической физике, тогда как вес – это сила тяжести, которая зависит от силы тяжести.Заманчиво приравнять эти два понятия, поскольку большинство наших примеров имеет место на Земле, где вес объекта лишь немного зависит от его местоположения. Кроме того, в повседневном языке термины масса и масса используются взаимозаменяемо; например, в наших медицинских записях наш «вес» часто указывается в килограммах, но никогда в правильных единицах – ньютонах.
Распространенные заблуждения: масса против весаВ обиходе масса и вес часто используются как синонимы.Однако в науке эти термины существенно отличаются друг от друга. Масса – это мера количества вещества в объекте. Типичной мерой массы является килограмм (или «пуля» в английских единицах измерения). С другой стороны, вес – это мера силы тяжести, действующей на объект. Вес равен массе объекта (м), умноженной на ускорение свободного падения (g). Как и любая другая сила, вес измеряется в ньютонах (или фунтах в английских единицах). Предполагая, что масса объекта остается неизменной, она останется неизменной независимо от его местоположения.Однако, поскольку вес зависит от ускорения свободного падения, вес объекта может измениться на , когда объект входит в область с большей или меньшей силой тяжести. Например, ускорение свободного падения на Луне составляет 1,67 м / с 2 (что намного меньше ускорения свободного падения на Земле, 9,80 м / с 2 ). Если вы измерили свой вес на Земле, а затем измерили свой вес на Луне, вы бы обнаружили, что «весите» намного меньше, хотя и не выглядите худее.Это потому, что сила тяжести на Луне слабее. Фактически, когда люди говорят, что они «худеют», они на самом деле имеют в виду, что они теряют «массу» (что, в свою очередь, заставляет их весить меньше).
Эксперимент на вынос: масса и вес
Что измеряют весы для ванной? Когда вы стоите на весах в ванной, что происходит с весами? Слегка угнетает. Весы содержат пружины, которые сжимаются пропорционально вашему весу – подобно резиновым лентам, расширяющимся при натяжении.Пружины позволяют измерить ваш вес (для объекта, который не ускоряется). Это сила в ньютонах (или фунтах). В большинстве стран результат делится на 9,80, чтобы получить значение в килограммах. Весы измеряют вес, но откалиброваны для предоставления информации о массе. Стоя на весах в ванной, нажмите на соседний стол. Что происходит с чтением? Почему? Будет ли ваша шкала измерять ту же «массу» на Земле, что и на Луне?
Пример 1.Какое ускорение может дать человек, толкая газонокосилку?
Предположим, что чистая внешняя сила (толчок минус трение), действующая на газонокосилку, составляет 51 Н (около 11 фунтов) параллельно земле. Масса косилки 24 кг. Какое у него ускорение?Рис. 3. Сила полезного действия на газонокосилку справа составляет 51 Н. С какой скоростью газонокосилка ускоряется вправо?
СтратегияПоскольку даны F net и m, ускорение можно рассчитать непосредственно из второго закона Ньютона, как указано в F net = m a .{2} \\ [/ латекс].
ОбсуждениеНаправление ускорения совпадает с направлением результирующей силы, параллельной земле. В этом примере нет информации об отдельных внешних силах, действующих на систему, но мы можем кое-что сказать об их относительных величинах. Например, сила, прикладываемая человеком, толкающим косилку, должна быть больше, чем трение, препятствующее движению (поскольку мы знаем, что косилка движется вперед), а вертикальные силы должны нейтрализоваться, если не должно быть ускорения в вертикальном направлении ( косилка движется только горизонтально).Обнаруженное ускорение достаточно мало, чтобы быть приемлемым для человека, толкающего косилку. Такое усилие не будет длиться слишком долго, потому что человек скоро достигнет максимальной скорости.
Пример 2. Какая ракетная тяга разгоняет салазки?
До пилотируемых космических полетов ракетные сани использовались для испытания самолетов, ракетного оборудования и физиологических воздействий на людей на высоких скоростях. Они состояли из платформы, которая была установлена на одной или двух направляющих и приводилась в движение несколькими ракетами.Вычислите величину силы, прилагаемой каждой ракетой, которая называется ее тягой T, для четырехракетной двигательной установки, показанной на рисунке 4. Начальное ускорение салазок составляет 49 м / с2, масса системы – 2100 кг, а сила трения. противодействие движению, как известно, составляет 650 Н.Рис. 4. Салазки испытывают ракетную тягу, которая ускоряет их вправо. Каждая ракета создает одинаковую тягу T. Как и в других ситуациях, когда есть только горизонтальное ускорение, вертикальные силы нейтрализуются.Земля оказывает на систему направленную вверх силу N, равную по величине и противоположную по направлению ее весу w. Система здесь – сани, его ракеты и всадник, поэтому никакие силы между этими объектами не рассматриваются. Стрелка, обозначающая трение (f), нарисована крупнее шкалы.
СтратегияНесмотря на то, что существуют силы, действующие вертикально и горизонтально, мы предполагаем, что вертикальные силы компенсируются, поскольку нет вертикального ускорения. Это оставляет нам только горизонтальные силы и более простую одномерную задачу.Направления указываются знаками плюс или минус, при этом вправо принимается за положительное направление. См. Диаграмму свободного тела на рисунке.
РешениеПоскольку ускорение, масса и сила трения даны, мы начнем со второго закона Ньютона и ищем способы найти тягу двигателей. Поскольку мы определили направление силы и ускорения как действующие «вправо», нам нужно учитывать в расчетах только величины этих величин.Следовательно, мы начинаем с
F net = ma,
, где F net – чистая сила в горизонтальном направлении. Из рисунка 4 видно, что тяга двигателя увеличивается, а трение противодействует тяги. В форме уравнения чистая внешняя сила равна
.Подставляя это во второй закон Ньютона, получаем
Используя небольшую алгебру, мы решаем общую тягу 4 T :
Подстановка известных значений дает
[латекс] 4T = \ text {ma} + f = \ left (\ text {2100 кг} \ right) \ left ({\ text {49 м / с}} ^ {2} \ right) + \ text { 650 Н} \ [/ латекс]
[латекс] 4Т = 1.{4} \ text {N} \\ [/ латекс].
ОбсуждениеЦифры довольно большие, поэтому результат может вас удивить. Подобные эксперименты проводились в начале 1960-х годов для проверки пределов человеческой выносливости и установки, предназначенной для защиты людей при аварийных выбросах реактивных истребителей. Были получены скорости 1000 км / ч с ускорением 45 g. (Напомним, что g, ускорение свободного падения, составляет 9,80 м / с 2 . Когда мы говорим, что ускорение составляет 45 g, это 45 × 9.80 м / с 2 , что составляет примерно 440 м / с 2 .) Хотя живые предметы больше не используются, с помощью ракетных саней была получена сухопутная скорость 10 000 км / ч. В этом примере, как и в предыдущем, интересующая система очевидна. В последующих примерах мы увидим, что выбор интересующей системы имеет решающее значение, и этот выбор не всегда очевиден.
Второй закон движения Ньютона – это больше, чем определение; это соотношение между ускорением, силой и массой.Это может помочь нам делать прогнозы. Каждую из этих физических величин можно определить независимо, поэтому второй закон говорит нам что-то основное и универсальное о природе. В следующем разделе представлен третий и последний закон движения.
Сводка раздела
- Ускорение, a , определяется как изменение скорости, то есть изменение ее величины или направления, или и того, и другого.
- Внешняя сила – это сила, действующая на систему извне, в отличие от внутренних сил, которые действуют между компонентами внутри системы.
- Второй закон движения Ньютона гласит, что ускорение системы прямо пропорционально и в том же направлении, что и чистая внешняя сила, действующая на систему, и обратно пропорционально ее массе.
- В форме уравнения второй закон движения Ньютона выглядит так: [latex] {\ text {a}} = \ frac {{{\ text {F}}} _ {\ text {net}}} {m} \\ [/ латекс].
- Это часто записывается в более привычной форме: F net = m a .
- Вес объекта w определяется как сила тяжести, действующая на объект массой м .Объект испытывает ускорение свободного падения g :
w = м г .
- Если единственная сила, действующая на объект, вызвана гравитацией, объект находится в свободном падении.
- Трение – это сила, которая препятствует движению соприкасающихся объектов друг за другом.
Концептуальные вопросы
1. Какое утверждение верно? (а) Чистая сила вызывает движение. (б) Чистая сила вызывает изменение движения. Объясните свой ответ и приведите пример.
2. Почему мы можем пренебрегать такими силами, как силы, удерживающие тело вместе, когда мы применяем второй закон движения Ньютона?
3. Объясните, как выбор «интересующей системы» влияет на то, какие силы необходимо учитывать при применении второго закона движения Ньютона.
4. Опишите ситуацию, в которой чистая внешняя сила, действующая на систему, не равна нулю, но ее скорость остается постоянной.
5. Система может иметь ненулевую скорость, в то время как чистая внешняя сила, действующая на нее , равна нулю.Опишите такую ситуацию.
6. Камень брошен вверх. Какая чистая внешняя сила действует на скалу, когда она находится на вершине своей траектории?
7. (a) Приведите пример различных чистых внешних сил, действующих на одну и ту же систему, вызывая разные ускорения. (b) Приведите пример одной и той же чистой внешней силы, действующей на системы разной массы, вызывая разные ускорения. (c) Какой закон точно описывает оба эффекта? Сформулируйте это словами и в виде уравнения.
8. Если ускорение системы равно нулю, не действуют ли на нее внешние силы? А как насчет внутренних сил? Объясни свои ответы.
9. Если к объекту приложена постоянная ненулевая сила, что вы можете сказать о скорости и ускорении объекта?
10. Сила тяжести, действующая на баскетбольный мяч на рисунке 2, игнорируется. Если принять во внимание гравитацию и , каково направление чистой внешней силы на баскетбольный мяч – выше горизонтали, ниже горизонтали или все еще горизонтально?
Задачи и упражнения
Вы можете предположить, что данные, взятые с иллюстраций, имеют точность до трех цифр.
1. Спринтер весом 63,0 кг начинает забег с ускорением 4,20 м / с. 2 . Какая чистая внешняя сила действует на него?
2. Если спринтер из предыдущей задачи разгоняется с такой скоростью на 20 м, а затем сохраняет эту скорость до конца 100-метрового рывка, сколько у него времени для забега?
3. Пылесос толкает тележку для белья весом 4,50 кг таким образом, чтобы чистая внешняя сила, действующая на нее, составляла 60,0 Н. Вычислите величину ее ускорения.
4. Поскольку астронавты на орбите явно невесомые, необходим умный метод измерения их массы, чтобы отслеживать прирост или потерю массы для корректировки рациона. Один из способов сделать это – приложить известную силу к космонавту и измерить возникающее ускорение. Предположим, что действует чистая внешняя сила 50,0 Н и измеренное ускорение астронавта составляет 0,893 м / с 2 . (а) Рассчитайте ее массу. (b) При приложении силы к космонавту, аппарат, в котором он движется по орбите, испытывает равную и противоположную силу.Обсудите, как это повлияет на измерение ускорения космонавта. Предложите метод, позволяющий избежать отдачи автомобиля.
5. На рисунке 3 чистая внешняя сила на газонокосилке 24 кг заявлена равной 51 Н. Если сила трения, препятствующая движению, равна 24 Н, то какая сила F (в ньютонах) – это сила, действующая на человека. косилка? Предположим, косилка движется со скоростью 1,5 м / с при снятии усилия F . Как далеко уйдет косилка до остановки?
6.Те же ракетные салазки, изображенные на рисунке 5, замедляются со скоростью 196 м / с 2 . Какая сила необходима, чтобы вызвать это замедление? Предположим, что ракеты выключены. Масса системы 2100 кг.
Рисунок 5.
7. (a) Если салазки ракеты, показанные на рисунке 6, запускаются с горящей только одной ракетой, какова величина ее ускорения? Предположим, что масса системы составляет 2100 кг, тяга T составляет 2,4 × 10 4 Н, а сила трения, препятствующая движению, известна как 650 Н.б) Почему ускорение не в четыре раза меньше, чем у всех горящих ракет?
Рисунок 6.
8. Какое замедление у ракетных саней, если они останавливаются через 1,1 с со скорости 1000 км / ч? (Из-за такого замедления один испытуемый потерял сознание и временно потерял сознание.)
9. Предположим, двое детей толкаются горизонтально, но в противоположных направлениях, на третьего ребенка в повозке. Первый ребенок прикладывает силу 75,0 Н, второй – 90.{2} \\ [/ latex] при скорости 90,0 км / ч. На этой скорости силы сопротивления движению, включая трение и сопротивление воздуха, составляют в сумме 400 Н. (Сопротивление воздуха аналогично трению воздуха. Оно всегда противодействует движению объекта.) Какова величина силы, которую мотоцикл прилагает к движению в обратном направлении. земля, чтобы произвести его ускорение, если масса мотоцикла с водителем составляет 245 кг?
11. Ракетные салазки, показанные на рисунке 8, ускоряются со скоростью 49,0 м / с. 2 . Его пассажирская масса 75.0 кг. (а) Рассчитайте горизонтальную составляющую силы, которую сиденье оказывает на его тело. Сравните это с его весом, используя соотношение. (b) Рассчитайте направление и величину общей силы, которую сиденье оказывает на его тело.
Рисунок 8.
12. Повторите предыдущую задачу для ситуации, когда салазки ракеты замедляются со скоростью 201 м / с. 2 . В этой задаче силы прилагаются к сиденью и удерживающим ремням.
13. Вес космонавта вместе с его скафандром на Луне составляет всего 250 Н.Сколько они весят на Земле? Какая масса на Луне? На земле?
14. Предположим, масса полностью загруженного модуля, в котором космонавты взлетают с Луны, составляет 10 000 кг. Тяга его двигателей составляет 30 000 Н. (а) Рассчитайте величину ускорения при вертикальном взлете с Луны. б) Может ли он взлететь с Земли? Если нет, то почему? Если бы это было возможно, вычислите величину его ускорения.
Глоссарий
- ускорение:
- скорость, с которой скорость объекта изменяется за период времени
- свободное падение:
- ситуация, в которой единственной силой, действующей на объект, является сила тяжести
- трение:
- – сила соприкасающихся объектов друг с другом; Примеры включают шероховатую поверхность и сопротивление воздуха
- чистая внешняя сила:
- векторная сумма всех внешних сил, действующих на объект или систему; заставляет массу ускоряться
- Второй закон движения Ньютона:
- чистая внешняя сила F net на объекте с массой m пропорциональна и в том же направлении, что и ускорение объекта, a , и обратно пропорциональна массе; математически определяется как [latex] \ mathbf {\ text {a}} = \ frac {{\ mathbf {\ text {F}}} _ {\ text {net}}} {m} \\ [/ latex]
- система
- определяется границами наблюдаемого объекта или набора объектов; все силы, возникающие извне системы, считаются внешними силами
- вес
- сила w за счет силы тяжести, действующей на объект массой [латекс] м [/ латекс]; математически определяется как: w = mg , где g – величина и направление ускорения свободного падения
Избранные решения проблем и упражнения
1.265 N
3. 13,3 м / с 2
7. (a) 12 м / с 2 (b) Ускорение не в четверть от того, что было при горящих ракетах, потому что сила трения все еще такая же большая, как при всех горящих ракетах.
9. (a) Система – это ребенок в вагоне плюс вагон.
Рисунок 9
(б)
(c) a = 0,130 м / с 2 в направлении толчка второго ребенка.
(г) a = 0,00 м / с 2
11.(а) 3,68 × 10 3 Н. Эта сила в 5,00 раз превышает его вес. (b) 3750 Н; 11,3º над горизонтом
13. 1,5 × 10 3 Н, 150 кг, 150 кг
Как использовать формулы законов Ньютона – Видео и стенограмма урока
Первый закон Ньютона
Первый закон Ньютона – это закон инерции. Он гласит, что любой объект в состоянии покоя или в движении будет оставаться в покое или в движении, если на него не действует другая сила. Другими словами, скорость объекта остается постоянной, если на него не действует другая сила.В отличие от того, что вы увидите, когда мы перейдем ко второму и третьему законам, с первым законом Ньютона нет конкретной формулы. Однако это не делает его менее важным, чем два других.
Из трех законов этот может быть самым легким для людей, не знакомых с физикой, для повседневной жизни. Например, вы чувствуете действие первого закона Ньютона всякий раз, когда путешествуете в транспортном средстве: автомобиле, автобусе, поезде, самолете и т. Д. закон инерции в действии.Ваше тело было в состоянии покоя, и когда автомобиль начал движение, ваше тело хотело оставаться в покое. Вы чувствуете силу, прилагаемую к вам автомобилем, заставляющую вас двигаться.
На вводном уроке физики вы все время будете работать с первым законом Ньютона. Каждый раз, когда объект меняет скорость, вы знаете, что действует первый закон Ньютона. Хотя вы, возможно, не зацикливаетесь на этом напрямую, первый закон Ньютона будет работать повсеместно на протяжении всего вашего изучения классической механики в физике.
Второй закон Ньютона
В то время как первый закон Ньютона рассматривает, как сила влияет на движение объектов, второй закон углубляется в то, как мы определяем саму силу. Второй закон Ньютона гласит, что ускорение объекта (или a ) прямо пропорционально чистой силе (или F ), действующей на него, и обратно пропорционально его массе (или м ). В отличие от первого закона Ньютона, у этого нет сокращенного названия, но он более известен своей математической формулой, которую вы можете увидеть:
Однако гораздо чаще можно увидеть, что это написано в форме, где оно имеет знак равенства вместо знака пропорциональности, который вы можете увидеть:
Эта формула говорит нам, что сила, действующая на объект, равна массе этого объекта, умноженной на ускорение, вызванное силой.Вы обнаружите, что эта формула постоянно используется во время изучения вводной физики.
Отличным примером действия второго закона Ньютона в нашей жизни является наш вес. Обычно вы можете не думать об этом таким образом, но ваш вес на самом деле является гравитационной силой земли, действующей на вас. Ваш вес равен вашей массе, умноженной на ускорение свободного падения, 9,81 м / с.
Теперь давайте воспользуемся этой информацией, чтобы найти силу гравитации, действующую на человека массой 81 килограмм:
Обратите внимание, что мы дали наш ответ в Ньютонах ( N ).Это стандартная международная единица силы. 1 N равно силе, необходимой для ускорения массы 1 кг со скоростью 1 метр в секунду. Эта формула работает не только для силы тяжести. Если вы знаете ускорение и массу любого объекта, вы можете найти результирующую силу, действующую на него, с помощью второго закона Ньютона.
Третий закон Ньютона
Третий закон Ньютона , вероятно, тот, о котором большинство людей слышало раньше. В нем говорится, что «на каждое действие есть равное и противоположное противодействие.Это означает, что когда один объект создает силу для другого объекта, этот второй объект будет создавать равную силу в обратном направлении на первый объект. Математически мы можем записать это, поскольку сила объекта A на объекте B равна отрицательному значению силы объекта B на объект A:
FAB = -FBA
Определение того, какая сила получает отрицательный знак в проблема произвольная; это просто показывает, что силы действуют в противоположных направлениях.
Эта формула показывает нам, что силы всегда приходят парами.Когда вы ударяете по бейсбольному мячу битой, бита оказывает на мяч силу ( Fbat ), но мяч также воздействует на биту назад ( Fball ).
Этот закон распространяется не только на движущиеся объекты, но и на неподвижные. Когда вы сидите на земле, земля прикладывает к вам силу тяжести ( Fg ) вниз, в то время как земля прикладывает равную нормальную силу ( FN ) вверх. Обычная сила – это то, что не дает вам провалиться в землю.
Краткое содержание урока
Сэр Исаак Ньютон – один из самых известных ученых, когда-либо живших в области физики, и его три закона движения являются одними из выдающихся его многочисленных открытий.
Первый закон Ньютона гласит, что любой объект в состоянии покоя или в движении будет оставаться в покое или в движении, если на него не действует другая сила. Это означает, что объект будет сохранять постоянную скорость, если на него не действует сила. У этого закона нет формулы, связанной с ним, но он будет использоваться постоянно, когда вы работаете с силами.
Второй закон Ньютона гласит, что ускорение объекта (или a ) прямо пропорционально действующей на него чистой силе (или F ) и обратно пропорционально его массе (или м ).Чаще всего это записывается как сила, равная массе, умноженной на ускорение.
F = ma
Наконец, третий закон Ньютона гласит, что «на каждое действие есть равная и противоположная реакция». Итак, если объект A создает силу на объект B ( FAB ), этот закон говорит нам, что объект B должен создать равную силу на объект A ( FBA ) в противоположном направлении.
FAB = -FBA
Это закон, который позволяет нам знать, что силы всегда действуют парами.
законов Ньютона | Законы Ньютона
В этом разделе мы рассмотрим влияние сил на объекты и то, как мы можем заставить их двигаться. Это свяжет воедино то, что вы узнали о движении, и то, что вы узнали о силах.
Первый закон Ньютона (ESBKS)
Сэр Исаак Ньютон был ученым, жившим в Англии (1642-1727) и интересовавшимся движением объектов в различных условиях. Он предположил, что неподвижный объект будет оставаться неподвижным, если на него не действует сила, и что движущийся объект будет продолжать движение, если сила не замедлит его, не ускорит или не изменит направление движения.Исходя из этого, он сформулировал так называемый первый закон движения Ньютона:
- Первый закон движения Ньютона
Объект продолжает находиться в состоянии покоя или равномерного движения (движение с постоянной скоростью), если на него не действует неуравновешенная (чистая или результирующая) сила.
Это свойство объекта продолжать в своем текущем состоянии движения, если на него не действует чистая сила, называется инерцией .
Рассмотрим следующие ситуации:
Фигуристка отталкивается от края катка и катается по льду.Она продолжит движение по льду по прямой, если ее что-то не остановит. Объекты тоже такие. Если мы пнем футбольный мяч по футбольному полю, согласно первому закону Ньютона, футбольный мяч должен двигаться вечно! Однако в реальной жизни этого не происходит. Закон Ньютона неверен? Не совсем. Первый закон Ньютона применим к ситуациям, когда отсутствуют какие-либо внешние силы. Это означает, что трение отсутствует. В случае с фигуристкой трение между коньками и льдом очень мало, и она продолжит движение на довольно большое расстояние.В случае футбольного мяча присутствует сопротивление воздуха (трение между воздухом и мячом) и трение между травой и мячом, что замедляет мяч.
Первый закон Ньютона в действии
Давайте посмотрим на следующие два примера. {- 1} $} \).{-1} $} \) согласно первому закону Ньютона. Если они пристегнуты ремнями безопасности, ремни безопасности остановят их, оказывая на них силу, и тем самым не допустят травм.
Ракеты :
Космический корабль запущен в космос. Сила взрывающихся газов толкает ракету по воздуху в космос. Когда он оказывается в космосе, двигатели выключаются, и он продолжает двигаться с постоянной скоростью. Если астронавты хотят изменить направление полета космического корабля, им нужно запустить двигатель.Затем к ракете будет приложена сила, и она изменит свое направление.
Рабочий пример 8: действие первого закона Ньютона
Почему пассажиров отбрасывает в сторону, когда машина, в которой они едут, заворачивает за угол?
Что происходит до того, как машине исполнится
Перед началом поворота и пассажиры, и автомобиль движутся с одинаковой скоростью. (рисунок А)
Что происходит, когда машина поворачивает
Водитель поворачивает колеса автомобиля, которые затем воздействуют на автомобиль, и автомобиль поворачивается.Эта сила действует на автомобиль, но не на пассажиров, поэтому (согласно первому закону Ньютона) пассажиры продолжают двигаться с той же исходной скоростью. (рисунок B)
Почему пассажиров отбрасывает в сторону?
Если пассажиры пристегнуты ремнями безопасности, они будут прикладывать силу к пассажирам до тех пор, пока их скорость не станет такой же, как у автомобиля (рисунок C). Без ремня безопасности пассажир может удариться о борт автомобиля.
Ты справишься! Позвольте нам помочь вам учиться с умом для достижения ваших целей.Siyavula Practice поможет вам в удобном для вас темпе, когда вы задаете вопросы в Интернете.
Зарегистрируйтесь, чтобы улучшить свои оценки Упражнение 2.4Если пассажир сидит в машине и машина поворачивает вправо, что происходит с пассажиром? Что будет, если машина повернет налево?
Перед началом поворота и пассажир, и автомобиль движутся с одинаковой скоростью.
Когда автомобиль поворачивает вправо, сила действует на автомобиль, но не на пассажиров, поэтому (согласно первому закону Ньютона) пассажир продолжает движение с той же исходной скоростью.(Другими словами, машина поворачивается, а пассажир – нет).
В результате этого пассажира тянет влево, когда машина поворачивает направо.
Если вместо этого автомобиль повернет налево, пассажира потянет направо.
Гелий менее плотен, чем воздух, которым мы дышим. Обсудите, почему воздушный шар с гелием в автомобиле, объезжающем поворот, кажется, нарушает первый закон Ньютона и движется внутрь поворота, а не наружу, как пассажир.
Когда машина заворачивает за угол, весь воздух продолжает двигаться вперед (он действует так же, как и пассажир). Это приводит к увеличению давления воздуха с одной стороны автомобиля (это будет со стороны, противоположной направлению поворота автомобиля). Это небольшое увеличение давления воздуха толкает гелиевый шар на другую сторону автомобиля.
Из-за этого кажется, что воздушный шар с гелием не подчиняется первому закону Ньютона.
Второй закон движения Ньютона (ESBKT)
Согласно первому закону Ньютона, вещи «любят продолжать делать то, что они делают». Другими словами, если объект движется, он имеет тенденцию продолжать движение (по прямой линии и с той же скоростью), а если объект неподвижен, он имеет тенденцию оставаться неподвижным. Так как же объекты начинают двигаться?
Давайте посмотрим на пример коробки \ (\ text {10} \) \ (\ text {kg} \) на грубой таблице. Если мы слегка надавим на коробку, как показано на диаграмме, коробка не сдвинется с места.Допустим, мы приложили силу \ (\ text {100} \) \ (\ text {N} \), но ящик остается неподвижным. В этот момент на коробку действует сила трения \ (\ text {100} \) \ (\ text {N} \), не позволяющая коробку двигаться. Если мы увеличим силу, скажем, до \ (\ text {150} \) \ (\ text {N} \), и ящик почти начнет двигаться, сила трения составит \ (\ text {150} \) \ ( \ text {N} \). Чтобы иметь возможность перемещать коробку, нам нужно толкнуть достаточно сильно, чтобы преодолеть трение, а затем переместить коробку. Поэтому, если мы применим силу \ (\ text {200} \) \ (\ text {N} \), помня, что сила трения из \ (\ text {150} \) \ (\ text {N} \) присутствует, ‘первый’ \ (\ text {150} \) \ (\ text {N} \) будет использоваться для преодоления или ‘ отмените трение, а другой \ (\ text {50} \) \ (\ text {N} \) будет использован для перемещения (ускорения) блока.Чтобы ускорить объект, мы должны иметь равнодействующую силу, действующую на блок.
Итак, что, по вашему мнению, произойдет, если мы будем действовать сильнее, скажем, \ (\ text {300} \) \ (\ text {N} \)? Или, как вы думаете, что произойдет, если масса блока будет больше, скажем, \ (\ text {20} \) \ (\ text {kg} \), или что, если она будет меньше? Давайте исследуем, как на движение объекта влияют масса и сила.
Рекомендуемый эксперимент для формальной оценки второго закона движения Ньютона также включен в эту главу.В этом эксперименте учащиеся исследуют взаимосвязь между силой и ускорением (второй закон Ньютона). Вам понадобятся тележки, разной массы, наклонная плоскость, резинки, линейка для измерений, тикерный ленточный аппарат, тикерный таймер, миллиметровая бумага.
Второй закон движения Ньютона
Цель
Для исследования связи между ускорением объектов и приложением постоянной равнодействующей силы.
Метод
Постоянная сила \ (\ text {20} \) \ (\ text {N} \), действующая под углом \ (\ text {60} \) \ (\ text {°} \) к горизонтали. , применяется к динамической тележке.
Тикерная лента, прикрепленная к тележке, проходит через тикерный таймер с частотой \ (\ text {20} \) \ (\ text {Hz} \), когда тележка движется по поверхности без трения.
Вышеупомянутая процедура повторяется 4 раза, каждый раз с одинаковой силой, но изменяя массу тележки следующим образом:
Случай 1: \ (\ text {6,25} \) \ (\ text {kg} \)
Случай 2: \ (\ text {3,57} \) \ (\ text {kg} \)
Случай 3: \ (\ text {2,27} \) \ (\ text {kg} \)
Случай 4: \ (\ text {1,67} \) \ (\ text {kg} \)
Ниже показаны фрагменты четырех полученных тикерных лент. {- 2} $} \) по оси Y и \ (\ text {1} \) \ (\ text {cm} \) = \ (\ text {1} \) \ (\ text {kg } \) по оси абсцисс.
Используйте график, чтобы определить ускорение тележки, если ее масса равна \ (\ text {5} \) \ (\ text {kg} \).
Запишите заключение эксперимента.
В ходе исследования выше вы заметили, что чем тяжелее тележка, тем медленнее она двигалась при постоянной силе. Ускорение равно обратно пропорционально массе .Математически:
\ (а \ propto \ frac {1} {м} \)В аналогичном исследовании, где масса остается постоянной, но прикладываемая сила меняется, вы обнаружите, что чем больше сила, тем быстрее будет двигаться объект. Таким образом, ускорение тележки составляет прямо пропорционально результирующей силе. Математически:
\ (а \ propto F. \)Переставляя приведенные выше уравнения, мы получаем \ (\ propto \) \ (\ frac {F} {m} \) или \ (F = ma \).
Помните, что сила и ускорение являются векторными величинами.Ускорение происходит в том же направлении, что и прилагаемая сила. Если несколько сил действуют одновременно, нам нужно работать только с результирующей силой или чистой силой.
- Второй закон движения Ньютона
Если на тело действует результирующая сила, это заставляет тело ускоряться в направлении результирующей силы. Ускорение тела будет прямо пропорционально результирующей силе и обратно пропорционально массе тела.Математическое представление: \ [\ vec {F} _ {net} = m \ vec {a} \]
Сила – это векторная величина . Второй закон движения Ньютона следует применять к направлениям \ (y \) и \ (x \) по отдельности. Вы можете использовать результирующие результирующие в направлениях \ (y \) и \ (x \) для вычисления общего результата, как мы видели в предыдущей главе.
Применение второго закона движения Ньютона
Второй закон Ньютона можно применять в самых разных ситуациях.Мы рассмотрим основные типы примеров, которые вам необходимо изучить.
Рабочий пример 9: Второй закон Ньютона: Коробка на поверхности
Коробка \ (\ text {10} \) \ (\ text {kg} \) помещается на стол. К коробке прикладывается горизонтальная сила величиной \ (\ text {32} \) \ (\ text {N} \). Между поверхностью и коробкой присутствует сила трения величины \ (\ text {7} \) \ (\ text {N} \).
Нарисуйте диаграмму сил, показывающую все силы, действующие на коробку.
Рассчитайте ускорение коробки.
Определите горизонтальные силы и начертите диаграмму сил
Мы смотрим только на силы, действующие в горизонтальном направлении (влево-вправо), а не на вертикальные (вверх-вниз) силы. Приложенная сила и сила трения будут включены. Сила тяжести, которая является вертикальной силой, не учитывается.
Рассчитать ускорение коробки
Помните , что мы рассматриваем направления \ (y \) и \ (x \) отдельно. {- 2} $} \ \ text {слева.{-2} $} \) вправо. Одна треть общей силы трения действует на блок \ (\ text {10} \) \ (\ text {kg} \), а две трети – на \ (\ text {15} \) \ (\ text {kg }\) блокировать. Вычислить:
– величина и направление общей имеющейся силы трения.
Величина натяжения каната у т.
Важно: когда у вас есть натяжение веревки в такой задаче, вам нужно знать, что оба конца веревки прикладывают силу с одинаковой величиной , но в противоположном направлении .Мы называем эту силу натяжением, и вам следует внимательно изучить диаграммы сил в этой задаче .
Оцените, что дано
Чтобы упростить задачу, давайте дадим двум ящикам ярлыки, давайте назовем ящик \ (\ text {10} \) \ (\ text {kg} \) номер 2 и \ (\ text {15} \) \ ( \ text {kg} \) ящик № 1.
У нас есть два ящика с указанным общим ускорением. Тот факт, что ящики связаны веревкой, означает, что у них обоих будет одинаковое ускорение.Они оба будут чувствовать одинаковую силу из-за натяжения веревки.
Нам говорят, что трение существует, но нам дают только соотношение между общей силой трения, которую испытывают оба ящика, и долей, которую испытывает каждый из них. Общее трение \ (\ vec {F} _ {fT} \) будет суммой трения о ящик 1, \ (\ vec {F} _ {f1} \), и трения о ящик 2, \ (\ vec {F} _ {f2} \). Нам говорят, что \ (\ vec {F} _ {f1} = \ frac {\ text {2}} {\ text {3}} \ vec {F} _ {fT} \) и \ (\ vec {F } _ {f2} = \ frac {\ text {1}} {\ text {3}} \ vec {F} _ {fT} \).Мы знаем, что блоки ускоряются вправо, и мы знаем, что трение будет в направлении, противоположном направлению движения и параллельно поверхности.
Нарисовать силовые диаграммы
Схема для ящика 1 будет:
Диаграмма для ящика 1 (обозначена синими пунктирными линиями) будет:
Где:
- \ (\ vec {F} _ {g1} \) – сила тяжести на первом ящике.
- \ (\ vec {N} _ {1} \) – нормальная сила, действующая на поверхность первого ящика.
- \ (\ vec {T} \) – сила натяжения в канате
- \ (\ vec {F} _ {application} \) – внешняя сила, прикладываемая к ящику.
- \ (\ vec {F} _ {f1} \) – сила трения о первом ящике.
Диаграмма для ящика 2 (обозначена оранжевыми пунктирными линиями) будет:
Где:
- \ (\ vec {F} _ {g2} \) – сила тяжести на втором ящике.
- \ (\ vec {N} _ {2} \) – нормальная сила, действующая на поверхность второго ящика.
- \ (\ vec {T} \) – сила натяжения в канате
- \ (\ vec {F} _ {f2} \) – сила трения на втором ящике.
Примените второй закон движения Ньютона
Проблема сообщает нам, что ящики ускоряются в направлении \ (x \), что означает, что силы в направлении \ (y \) не приводят к результирующей силе.Мы можем рассматривать разные направления по отдельности, поэтому нам нужно рассматривать только \ (x \) – направление.
Мы работаем с одним измерением и можем выбрать знаковое соглашение, чтобы указать направление векторов. Выберем векторы вправо (или в положительном \ (x \) – направлении) положительными.
Теперь мы можем применить второй закон движения Ньютона к первому ящику, потому что мы знаем ускорение и все силы, действующие на ящик. Используя положительный знак для обозначения силы справа, мы знаем, что \ ({F} _ {res1} = F_ {application} – {F} _ {f1} -T \) \ begin {align *} \ vec {F} _ {res1} & = m_1 \ vec {a} \\ F_ {применено} – {F} _ {f1} -T & = m_1a \\ F_ {применено} – \ frac {\ text {2}} {\ text {3}} {F} _ {fT} -T & = m_1a \\ (500) – \ frac {\ text {2}} {\ text {3}} {F} _ {fT} -T & = (\ text {15}) (2) \\ -T & = (\ text {15}) (2) – (500) + \ frac {\ text {2}} {\ text {3}} {F} _ {fT} \ end {align *}
Теперь примените второй закон движения Ньютона ко второму ящику, потому что мы знаем ускорение и все силы, действующие на ящик.Мы знаем, что \ ({F} _ {res2} = T- {F} _ {f2} \). Обратите внимание, что натяжение происходит в противоположном направлении. \ begin {align *} \ vec {F} _ {res2} & = m_2 \ vec {a} \\ T- {F} _ {f2} & = m_2a \\ T – \ frac {\ text {1}} {\ text {3}} {F} _ {fT} & = m_2a \\ T & = (\ text {10}) (2) + \ frac {\ text {1}} {\ text {3}} {F} _ {fT} \ end {align *}
Решить одновременно
Мы использовали второй закон движения Ньютона, чтобы создать два уравнения с двумя неизвестными, это означает, что мы можем решать одновременно. Мы решили для \ (T \) в приведенных выше уравнениях, но одно имеет отрицательный знак, поэтому, если мы сложим два уравнения, мы вычтем значение натяжения, позволяющее нам решить для \ ({F} _ {fT} \) : \ begin {align *} (T) + (-T) & = ((\ text {10}) (2) + \ frac {\ text {1}} {\ text {3}} {F} _ {fT}) + ((\ текст {15}) (2) – (500) + \ frac {\ text {2}} {\ text {3}} {F} _ {fT}) \\ 0 & = \ text {20} + \ text {30} – \ text {500} + \ frac {\ text {1}} {\ text {3}} {F} _ {fT} + \ frac {\ text {2}} {\ text {3}} {F} _ {fT} \\ 0 & = – \ text {450} + {F} _ {fT} \\ {F} _ {fT} & = \ text {450} \ text {N} \ end {align *}
Мы можем подставить величину \ ({F} _ {fT} \) в уравнение для ящика 2, чтобы определить величину натяжения: \ begin {align *} T & = (\ text {10}) (2) + \ frac {\ text {1}} {\ text {3}} {F} _ {fT} \\ T & = (\ text {10}) (2) + \ frac {\ text {1}} {\ text {3}} (\ text {450}) \\ T & = \ text {20} + \ text {150} \\ Т & = \ текст {170} \ текст {N} \ end {align *}
Цитировать окончательные ответы
Общая сила трения равна \ (\ text {450} \) \ (\ text {N} \) влево.{-2} $} \) вправо. Одна треть общей силы трения действует на блок \ (\ text {10} \) \ (\ text {kg} \), а две трети – на \ (\ text {15} \) \ (\ text {kg }\) блокировать. Вычислить:
– величина и направление общей имеющейся силы трения.
Величина натяжения каната у т.
Важно: когда у вас есть натяжение веревки в такой задаче, вам нужно знать, что оба конца веревки прикладывают силу с одинаковой величиной , но в противоположном направлении .Мы называем эту силу натяжением, и вам следует внимательно изучить диаграммы сил в этой задаче .
Нарисуйте силовую диаграмму
Всегда рисуйте диаграмму сил, хотя вопрос может не задавать этого. Дано ускорение всей системы, поэтому будет построена силовая диаграмма всей системы. Поскольку два ящика рассматриваются как единое целое, диаграмма сил будет выглядеть следующим образом:
Рассчитать силу трения
Чтобы найти силу трения, применим второй закон Ньютона.{-2} $} \)). Выберите положительное направление движения (справа положительное).
\ begin {align *} {F} _ {R} & = ma \\ {F} _ {\ text {application}} + {F} _ {f} & = ma \\ \ text {500} + {F} _ {f} & = \ left (10 + 15 \ right) \ left (2 \ right) \\ {F} _ {f} & = 50- \ text {500} \\ {F} _ {f} & = – \ text {450} N \ end {выровнять *}Сила трения \ (\ text {450} \) \ (\ text {N} \) противоположна направлению движения (влево).
Найдите натяжение троса
Чтобы определить натяжение веревки, нам нужно посмотреть на один из двух ящиков отдельно. Выберем ящик \ (\ text {10} \) \ (\ text {kg} \). Для начала нам нужно нарисовать диаграмму сил:
Рисунок 2.5: Силовая диаграмма ящика \ (\ text {10} \) \ (\ text {kg} \).Сила трения в блоке \ (\ text {10} \) \ (\ text {kg} \) составляет одну треть от общей, поэтому:
\ ({F} _ {f} = \ frac {\ text {1}} {\ text {3}} \ times \ text {450} \)
\ ({F} _ {f} = \ text {150} \ text {N} \)
Если применить второй закон Ньютона:
\ begin {align *} {F} _ {R} & = ma \\ T + {F} _ {f} & = \ left (10 \ right) \ left (2 \ right) \\ T + \ влево (- \ text {150} \ right) & = 20 \\ Т & = \ текст {170} \ текст {N} \ end {выровнять *}Примечание. Если бы мы использовали тот же принцип и применили его к ящику \ (\ text {15} \) \ (\ text {kg} \), наши вычисления были бы следующими:
\ begin {align *} {F} _ {R} & = ma \\ {F} _ {\ text {application}} + T + {F} _ {f} & = \ left (15 \ right) \ left (2 \ right) \\ \ text {500} + T + \ left (- \ text {300} \ right) & = 30 \\ T & = – \ text {170} \ text {N} \ end {выровнять *}Отрицательный ответ здесь означает, что сила направлена в направлении, противоположном движению, другими словами влево, что правильно.Однако в вопросе задается величина силы, и ваш ответ будет указан как \ (\ text {170} \) \ (\ text {N} \).
Рабочий пример 12: Второй закон Ньютона: человек тянет ящик
Мужчина тянет ящик \ (\ text {20} \) \ (\ text {kg} \) веревкой, которая составляет угол \ (\ text {60} \) \ (\ text {°} \ ) с горизонталью. Если он применяет силу величиной \ (\ text {150} \) \ (\ text {N} \) и силу трения величиной \ (\ text {15} \) \ (\ text {N} \), будет присутствует, рассчитать ускорение коробки.
Нарисуйте диаграмму сил или диаграмму свободного тела
Движение горизонтальное, поэтому мы будем рассматривать силы только в горизонтальном направлении. Помните, что вертикальные силы не влияют на горизонтальное движение и наоборот.
Вычислить горизонтальную составляющую приложенной силы
Сначала нам нужно выбрать направление, которое будет положительным направлением в этой проблеме. Выберем положительное \ (x \) – направление (вправо) положительным.
Приложенная сила действует под углом \ (\ text {60} \) \ (\ text {°} \) к горизонтали. Мы можем рассматривать только силы, параллельные движению. Прежде чем мы продолжим, необходимо вычислить горизонтальную составляющую приложенной силы: \ begin {align *} F_x & = F_ {применено} \ cos (\ theta) \\ & = \ text {150} \ cos (\ text {60} \ text {°}) \\ & = \ текст {75} \ текст {N} \ end {align *}
Рассчитать ускорение
Чтобы найти ускорение, применим второй закон Ньютона: \ begin {align *} F_R & = ma \\ F_x + F_f & = (\ text {20}) a \\ (\ text {75}) + (- \ text {15}) & = (\ text {20}) a \\ a & = \ frac {\ text {60}} {\ text {20}} \\ а & = \ текст {3} \ текст {м · s $ ^ {- 2} $} \ end {align *} Ускорение \ (\ text {3} \) \ (\ text {m · s $ ^ {- 2} $} \) вправо.
Рабочий пример 13: Второй закон Ньютона: грузовик и прицеп
Грузовик \ (\ text {2 000} \) \ (\ text {kg} \) тянет прицеп \ (\ text {500} \) \ (\ text {kg} \) с постоянным ускорением. Двигатель грузовика развивает тягу \ (\ text {10 000} \) \ (\ text {N} \). Не обращайте внимания на эффект трения. Вычислите:
разгон грузовика; и
натяжение буксирного устройства T между грузовиком и прицепом, если буксирное устройство составляет угол \ (\ text {25} \) \ (\ text {°} \) с горизонтом.
Нарисуйте силовую диаграмму
Нарисуйте диаграмму сил, показывающую все силы в системе в целом:
Рисунок 2.7: Бесплатные схемы кузова тягача с прицепом.Примените второй закон движения Ньютона
Мы выбираем положительное направление \ (x \) как положительное направление. Нам нужно учитывать только горизонтальные силы.Использование только горизонтальных сил означает, что нам сначала нужно отметить, что натяжение действует под углом к горизонтали, и нам нужно использовать горизонтальную составляющую натяжения в наших расчетах.
Горизонтальный компонент имеет величину \ (T \ cos (\ text {25} \ text {°}) \).
В отсутствие трения единственная сила, которая заставляет систему ускоряться, – это тяга двигателя. Если теперь применить второй закон движения Ньютона к грузовику, мы получим: \ begin {align *} \ vec {F} _ {Rtruck} & = m_ {truck} \ vec {a} \ \ text {(мы используем знаки для указания направления)} \\ {F} _ {двигатель} – T \ cos (\ text {25} \ text {°}) & = (\ text {2 000}) a \\ (\ text {10 000}) – T \ cos (\ text {25} \ text {°}) & = (\ text {2 000}) a \\ a & = \ frac {(\ text {10 000}) – T \ cos (\ text {25} \ text {°})} {(\ text {2 000})} \ end {align *}
Теперь применим тот же принцип к прицепу (помните, что направление натяжения будет противоположным в случае с грузовиком): \ begin {align *} \ vec {F} _ {Rtrailer} & = m_ {трейлер} \ vec {a} \ \ text {(мы используем знаки для указания направления)} \\ T \ cos (\ text {25} \ text {°}) & = (\ text {500}) a \\ a & = \ frac {T \ cos (\ text {25} \ text {°})} {(\ text {500})} \ end {align *}
Теперь у нас есть два уравнения и два неизвестных, поэтому мы можем решать их одновременно.Вычтем второе уравнение из первого, чтобы получить: \ begin {align *} (a) – (a) & = (\ frac {(\ text {10 000}) – T \ cos (\ text {25} \ text {°})} {(\ text {2 000})}) – (\ frac {T \ cos (\ text {25} \ text {°})} {(\ text {500})}) \\ 0 & = (\ frac {(\ text {10 000}) – T \ cos (\ text {25} \ text {°})} {(\ text {2 000})}) – (\ frac {T \ cos (\ text {25} \ text {°})} {(\ text {500})}) \\ & \ text {(умножить на \ text {2 000})} \\ 0 & = (\ text {10 000}) – T \ cos (\ text {25} \ text {°}) – 4T \ cos (\ text {25} \ text {°}) \\ \ text {5} T \ cos (\ text {25} \ text {°}) & = (\ text {10 000}) \\ T & = \ frac {(\ text {10 000})} {\ text {5} \ cos (\ text {25} \ text {°})} \\ T & = \ text {2 206,76} \ text {N} \ end {align *}
Теперь подставьте этот результат во второе уравнение, чтобы найти величину \ (a \) \ begin {align *} a & = \ frac {T \ cos (\ text {25} \ text {°})} {(\ text {500})} \\ & = \ frac {(\ text {2 206,76}) \ cos (\ text {25} \ text {°})} {(\ text {500})} \\ & = \ text {4,00} \ text {m · s $ ^ {- 2} $} \ end {align *}
Объект на наклонной плоскости
В предыдущем разделе мы рассмотрели компоненты силы тяжести, параллельные и перпендикулярные склону для объектов на наклонной плоскости.Когда мы смотрим на задачи на наклонной плоскости, нам необходимо учитывать составляющую силы тяжести, параллельную наклону.
Вспомните изображения книги на столе: когда одна сторона стола поднимается выше, книга начинает скользить. Почему? Книга начинает скользить, потому что составляющая силы тяжести, параллельная поверхности стола, увеличивается с увеличением угла наклона. Это похоже на приложенную силу, и она в конечном итоге становится больше силы трения, и книга ускоряется по столу или наклонной плоскости.
Сила тяжести также будет толкать объект «в» склон. Это составляющая силы, перпендикулярная уклону. В этом направлении нет движения, так как эта сила уравновешивается наклоном, отталкивающим объект. Эта «толкающая сила» является нормальной силой (N), о которой мы уже узнали, и она равна по величине перпендикулярной составляющей гравитационной силы, но противоположна по направлению.
Не используйте сокращение \ (W \) для обозначения веса, поскольку оно используется для сокращения «работы».Лучше использовать силу тяжести \ ({F} _ {g} \) для веса.
Рабочий пример 14: Второй закон Ньютона: прямоугольник на наклонной плоскости
Тело массой \ (M \) покоится на наклонной плоскости из-за трения.
Какой из следующих вариантов является величина силы трения, действующей на тело?
\ (F_g \)
\ (F_g \ cos (θ) \)
\ (F_g \ sin (θ) \)
\ (F_g \ tan (θ) \)
Проанализировать ситуацию
Вопрос просит нас определить величину силы трения.Говорят, что тело покоится на плоскости, что означает, что оно не движется, и поэтому ускорение равно нулю. Мы знаем, что сила трения будет действовать параллельно уклону. Если бы не было трения, коробка соскользнула бы вниз по склону, поэтому трение должно действовать вверх по склону. Мы также знаем, что будет составляющая силы тяжести, перпендикулярная склону и параллельная склону. Диаграмма свободного тела для сил, действующих на блок:
Определить величину силы трения
К этой проблеме можно применить второй закон Ньютона.Мы знаем, что объект не движется, поэтому результирующее ускорение равно нулю. В качестве положительного направления выбираем подъем вверх. Следовательно: \ begin {align *} \ vec {F} _R & = m \ vec {a} \; \ text {указатели направления} \\ F_f – F_g \ sin (\ theta) & = m (0) \\ F_f – F_g \ sin (\ theta) & = m (0) \\ F_f & = F_g \ sin (\ theta) \ end {align *}
Процитируйте свой окончательный ответ
Сила трения имеет ту же величину, что и составляющая силы гравитации, параллельная наклону, \ (F_g \ sin (\ theta) \).
Рабочий пример 15: Второй закон Ньютона: объект на склоне
Сила величиной \ (T = \ text {312} \ text {N} \), направленная вверх по уклону, необходима, чтобы удерживать тело в покое на наклонной плоскости без трения, которая составляет угол \ (\ text {35} \ ) \ (\ text {°} \) с горизонталью. Вычислите величину силы тяжести и нормальной силы, дав свои ответы до трех значащих цифр.
Найдите звездную величину \ (\ vec {F} _g \)
Обычно нас просят найти величину \ (\ vec {T} \), но в этом случае задается \ (\ vec {T} \), и нас просят найти \ (\ vec {F} _g \ ).Мы можем использовать то же уравнение. \ (T \) – это сила, которая уравновешивает компонент \ (\ vec {F} _g \), параллельный плоскости (\ ({F} _ {gx} \)), и, следовательно, имеет ту же величину.
К этой проблеме можно применить второй закон Ньютона. Мы знаем, что объект не движется, поэтому результирующее ускорение равно нулю. В качестве положительного направления выбираем подъем вверх. Следовательно: \ begin {align *} \ vec {F} _R & = m \ vec {a} \; \ text {указатели направления} \\ Т – F_g \ sin (\ theta) & = m (0) \\ F_g & = \ frac {T} {\ sin (\ theta)} \\ & = \ frac {\ text {312}} {\ sin (\ text {35} \ text {°})} \\ & = \ text {543,955} \ text {N} \ end {align *}
Найдите звездную величину \ (\ vec {N} \)
Мы рассматриваем силы, параллельные и перпендикулярные склону отдельно.Блок неподвижен, поэтому ускорение, перпендикулярное уклону, равно нулю. Мы снова можем применить второй закон движения Ньютона. Мы выбираем направление нормальной силы в качестве положительного направления. \ begin {align *} \ vec {F} _R & = m \ vec {a} \; \ text {указатели направления} \\ N – F_g \ cos (\ theta) & = m (0) \\ N & = F_g \ cos (\ theta) \ end {align *}
Мы можем подставить значение \ (F_g \), вычисленное ранее.Мы хотели бы проиллюстрировать, что существует другой подход, который следует принять, чтобы гарантировать получение правильного ответа, даже если вы ошиблись при вычислении \ (F_g \). \ (F_g \ cos (\ theta) \) также можно определить с использованием тригонометрических соотношений. Из предыдущей части вопроса мы знаем, что \ (T = F_g \ sin (\ theta) \). Мы также знаем, что \ begin {align *} \ tan (\ theta) & = \ frac {F_g \ sin (\ theta)} {F_g \ cos (\ theta)} \\ & = \ frac {T} {N} \\ N & = \ frac {T} {\ tan (\ theta)} \\ & = \ frac {\ text {312}} {\ tan (\ text {35} \ text {°})} \\ & = \ текст {445,58} \ текст {N} \ end {align *}
Обратите внимание, что в вопросе требуется, чтобы ответы давались до 3 значащих цифр.Поэтому мы округляем \ (\ vec {N} \) от \ (\ text {445,58} \) \ (\ text {N} \) до \ (\ text {446} \) \ (\ text {N } \) перпендикулярно поверхности вверх и \ (\ vec {T} \) от \ (\ text {543,955} \) \ (\ text {N} \) до \ (\ text {544} \) \ ( \ text {N} \) параллельно плоскости вверх по склону.
Лифты и ракеты
До сих пор мы рассматривали объекты, которые тянут или толкают по поверхности, другими словами, движение, параллельное поверхности, на которой лежит объект. Здесь мы учитывали только силы, параллельные поверхности, но мы также можем поднимать предметы или позволять им падать.Это вертикальное движение, при котором учитываются только вертикальные силы.
Рассмотрим лифт \ (\ text {500} \) \ (\ text {kg} \) без пассажиров, подвешенный на тросе. Назначение троса – тянуть лифт вверх, чтобы он мог добраться до следующего этажа, или опускать лифт, чтобы он мог опускаться на этаж ниже. Мы рассмотрим пять возможных стадий движения лифта и применим наши знания о втором законе движения Ньютона к ситуации. 5 этапов:
- Стационарный лифт, подвешенный над землей.
- Лифт, ускоряющийся вверх.
- Лифт, движущийся с постоянной скоростью.
- Лифт замедляется (замедляется).
- Лифт, ускоряющийся вниз (разрыв троса!).
Мы выбираем восходящее направление в качестве положительного направления для этого обсуждения.
1 этап:
Лифт \ (\ text {500} \) \ (\ text {kg} \) стационарный на втором этаже высотного дома.
Лифт не ускоряется.Трос, действующий на подъемник, должен иметь натяжение \ (\ vec {T} \) и силу тяжести \ (\ vec {F} _g \). Других сил нет, и мы можем нарисовать диаграмму свободного тела:
Применим второй закон Ньютона к вертикальному направлению: \ begin {align *} \ vec {F} _R & = m _ {\ text {lift}} \ vec {a} \ \ text {(мы используем знаки для указания направления)} \\ T – F_g & = m _ {\ text {lift}} (0) \\ T & = F_g \ end {align *}
Силы равны по величине и противоположны по направлению.{-2} $} \).
Если лифт ускоряется, это означает, что в направлении движения действует равнодействующая сила. Это означает, что сила, действующая вверх, теперь больше силы тяжести \ (\ vec {F} _g \) (вниз). Чтобы найти величину \ (\ vec {T} \), приложенного кабелем, мы можем выполнить следующий расчет: (Помните, что мы выбрали восходящее движение как положительное.)
Применим второй закон Ньютона к вертикальному направлению: \ begin {align *} \ vec {F} _R & = m _ {\ text {lift}} \ vec {a} \ \ text {(мы используем знаки для указания направления)} \\ T – F_g & = m _ {\ text {lift}} (\ text {1}) \\ T & = F_g + m _ {\ text {лифт}} (\ text {1}) \ end {align *}
Ответ имеет смысл, поскольку нам нужна большая сила, направленная вверх, чтобы нейтрализовать эффект гравитации, а также иметь положительную результирующую силу.
Этап 3:
Лифт движется с постоянной скоростью.
Когда лифт движется с постоянной скоростью, ускорение равно нулю, \ begin {align *} \ vec {F} _R & = m _ {\ text {lift}} \ vec {a} \ \ text {(мы используем знаки для указания направления)} \\ T – F_g & = m _ {\ text {lift}} (0) \\ T & = F_g \ end {align *}
Силы равны по величине и противоположны по направлению. Распространенная ошибка – думать, что из-за того, что лифт движется, на него действует чистая сила.{-2} $} \). Лифт двигался вверх, поэтому это означает, что он замедляется или ускоряется в направлении, противоположном направлению движения. Это означает, что ускорение идет в отрицательном направлении. \ begin {align *} \ vec {F} _R & = m _ {\ text {lift}} \ vec {a} \ \ text {(мы используем знаки для указания направления)} \\ T – F_g & = m _ {\ text {lift}} (- \ text {2}) \\ T & = F_g – \ text {2} m _ {\ text {lift}} \ end {align *}
Поскольку лифт теперь замедляется, возникает результирующая сила, направленная вниз.Это означает, что сила, действующая вниз, больше силы, действующей вверх.
Это имеет смысл, поскольку нам нужна меньшая сила, направленная вверх, чтобы гарантировать, что результирующая сила направлена вниз. Сила тяжести теперь больше, чем тяга троса вверх, и подъемник замедлится.
Этап 5:
Трос защелкивается.
Когда трос рвется, сила, которая раньше действовала вверх, больше не присутствует. Единственная сила, которая присутствует, – это сила тяжести.Лифт будет свободно падать и его ускорение.
Видимая масса
Ваш вес – это величина гравитационной силы, действующей на ваше тело. Когда вы стоите в стационарном лифте, а затем начинаете ускоряться вверх, вы чувствуете, что прижимаетесь к полу, пока лифт ускоряется. Вы чувствуете, что вы тяжелее, а ваш вес больше. Когда вы находитесь в канцелярском лифте, который начинает ускоряться вниз, вам становится легче на ногах. Вы чувствуете, что ваш вес стал меньше.
Вес измеряется с помощью нормальных сил. Когда лифт ускоряется вверх, вы чувствуете, что на вас действует большая нормальная сила, необходимая для ускорения вверх в дополнение к уравновешиванию силы тяжести.
Когда лифт ускоряется вниз, вы чувствуете, что на вас действует меньшая нормальная сила. Это потому, что для ускорения вниз требуется чистая сила, направленная вниз. Это явление называется кажущимся весом , потому что ваш вес на самом деле не изменился.
Ракеты
Как и в случае с лифтами, ракеты также являются примерами объектов, движущихся в вертикальном направлении. Сила тяжести тянет ракету вниз, а тяга двигателя толкает ракету вверх. Сила, которую оказывает двигатель, должна преодолевать силу тяжести, чтобы ракета могла разогнаться вверх. В приведенном ниже рабочем примере рассматривается применение второго закона Ньютона при запуске ракеты.
Рабочий пример 16: Второй закон Ньютона: ракета
Ракета (массы \ (\ text {5 000} \) \ (\ text {kg} \)) запускается вертикально вверх в небо с ускорением \ (\ text {20} \) \ (\ text {m · s $ ^ {- 2} $} \).{-2} $} \) вверх.
\ (\ vec {F} _g \) = \ (\ text {49 000} \) \ (\ text {N} \) вниз.
Нас просят найти тягу ракетного двигателя \ (\ vec {F} \).
Найдите тягу двигателя
Применим второй закон Ньютона: \ begin {align *} \ vec {F} _R & = m \ vec {a} \ \ text {(с помощью знаков для указания направления)} \\ F – F_g & = (\ text {5 000}) (\ text {20}) \\ F – (\ text {49 000}) & = (\ text {5 000}) (\ text {20}) \\ F & = \ text {149 000} \ text {N} \ end {align *}
Процитируйте свой окончательный ответ
Сила толчка направлена вверх \ (\ text {149 000} \) \ (\ text {N} \).
Рабочий пример 17: Ракеты
Как ракеты ускоряются в космосе?
Внутри ракеты взрывается газ.
Взрывающийся газ воздействует на каждую сторону ракеты. (как показано на рисунке ниже взрывной камеры внутри ракета).
Вследствие симметрии ситуации были приложены все силы. на ракете уравновешиваются силами противоположной стороны, кроме силы напротив открытой стороны.Эта сила на верхней поверхности неуравновешена.
Следовательно, это равнодействующая сила, действующая на ракету, и ее заставляет ракету ускоряться вперед.
Ты справишься! Позвольте нам помочь вам учиться с умом для достижения ваших целей. Siyavula Practice поможет вам в удобном для вас темпе, когда вы задаете вопросы в Интернете.
Зарегистрируйтесь, чтобы улучшить свои оценки Упражнение 2.5Буксир может тянуть судно с силой \ (\ text {100} \) \ (\ text {kN} \).Если два таких буксира тянут на одном судне, они могут создавать любую силу в диапазоне от минимум \ (\ text {0} \) \ (\ text {kN} \) до максимум \ (\ text {200} \ ) \ (\ текст {kN} \). Подробно объясните, как это возможно. Используйте диаграммы, чтобы подтвердить свой результат.
Мы начинаем с двух буксиров, тянущих в противоположных направлениях:
Результирующая сила равна \ (\ text {0} \) \ (\ text {kN} \), поскольку буксиры тянут с равными силами в противоположных направлениях.
Если два буксира тянут в одном направлении, то получим:
Результирующая сила равна \ (\ text {200} \) \ (\ text {kN} \), поскольку буксиры тянут с равными силами в одном направлении.
Чтобы получить силу между этими двумя крайностями, один буксир должен тянуть судно под другим углом по сравнению со вторым буксиром, например:
Обратите внимание, что результирующая сила в этой ситуации меньше, чем \ (\ text {200} \) \ (\ text {kN} \) (Вы можете проверить это, используя любой из методов сложения векторов).{-2} $} \). {2} \\ & = \ текст {562,5} \ текст {м} \ end {выровнять *}
Вычислите составляющую силы \ (\ text {200} \) \ (\ text {N} \), которая ускоряет блок по горизонтали.{-2} $} \), вычислите величину силы трения на блоке.
\ begin {align *} F_ {R} & = ma \\ F_ {x} + F_ {f} & = ma \\ \ text {100} + F_ {f} & = (50) (\ text {1,5}) \\ F_ {f} & = \ text {75} – \ text {100} \\ & = – \ текст {25} \ текст {N} \ end {выровнять *}
Рассчитайте вертикальную силу, прилагаемую блоком к плоскости.
\ begin {align *} F_ {y} & = F \ sin \ theta \\ & = (\ текст {200}) \ sin (60) \\ & = \ текст {173,2} \ текст {N} \ end {выровнять *}
Игрушечная ракета испытывает силу тяжести величиной \ (\ text {4,5} \) \ (\ text {N} \) поддерживается вертикально, помещая ее в бутылку.{-2} $} \).
Принимая восходящее направление как положительное:
\ begin {align *} F_ {R} & = ma \\ F_ {1} + F_ {g} & = ma \\ F_ {1} + – \ text {4,5} & = (\ text {0,5}) (\ text {8}) \\ F_ {1} & = \ text {4} + \ text {4,5} \\ & = \ текст {8,5} \ текст {N} \ end {выровнять *}Постоянная сила величины \ (\ text {70} \) \ (\ text {N} \) применяется вертикально к блоку, как показано. Блок испытывает силу тяжести \ (\ text {49} \) \ (\ text {N} \).{-2} $} \ end {выровнять *}
Движение лифта вверх или вниз? Обоснуйте свой ответ.
Этап 1: Вниз. На шкале меньше силы тяжести, которую он испытывает.
Этап 2: Стационарный. Шкала показывает то же самое, что и сила гравитации, которую он испытывает.
Этап 3: Вверх. Шкала показывает больше, чем гравитационная сила, которую он испытывает.
Запишите величину и направление результирующей силы, действующей на учащегося для каждого из этапов 1, 2 и 3.{-2} $} \). Сила трения \ (\ text {700} \) \ (\ text {N} \) препятствует его движению. Какую силу производит двигатель автомобиля?
\ begin {align *} F_ {R} & = ma \\ F_ {f} + F_ {E} & = ma \\ \ text {700} + F_ {E} & = (\ text {800}) (4) \\ F_ {E} & = \ text {3 200} – \ text {700} \\ & = \ текст {2 500} \ текст {N} \ end {выровнять *}
Два объекта массой \ (\ text {1} \) \ (\ text {kg} \) и \ (\ text {2} \) \ (\ text {kg} \) соответственно помещаются на гладкая поверхность и связана с отрезком веревочки.Горизонтальная сила \ (\ text {6} \) \ (\ text {N} \) применяется с помощью пружинных весов к \ (\ text {1} \) \ (\ text {kg} \ ) объект. Если не учитывать трение, какой будет сила, действующая на массу \ (\ text {2} \) \ (\ text {kg} \), измеренная вторыми пружинными весами?
Сила, действующая на блок \ (\ text {2} \) \ (\ text {kg} \), равна \ (\ text {6} \) \ (\ text {N} \). Поскольку предполагается, что поверхность не имеет трения, приложенная сила к блоку \ (\ text {1} \) \ (\ text {kg} \) равна силе, испытываемой \ (\ text {2} \) \ (\ text {kg} \) блок.
Каково его ускорение на Земле, где он испытывает силу тяжести \ (\ text {1 960} \) \ (\ text {N} \)?
Сила, действующая на ракету, направлена вверх, а сила тяжести – вниз. Принимая вверх как положительное:
\ begin {align *} F_ {R} & = ma \\ F_ {g} + F _ {\ text {rocket}} & = ma \\ – \ text {1 960} + \ text {4 000} & = ma \\ a & = \ frac {\ text {2 040}} {\ text {200}} \\ & = \ text {10,2} \ text {m · s $ ^ {- 2} $} \ end {выровнять *}Какая движущая сила требуется ракетному двигателю для воздействия на заднюю часть ракеты на Земле?
На Земле ракетные двигатели должны преодолевать гравитационную силу и поэтому должны проявлять силу \ (\ text {1 960} \) \ (\ text {N} \) или больше.{-2} $} \ end {выровнять *}
Если автомобиль \ (\ text {1 000} \) \ (\ text {kg} \), какое усилие оказывают тормоза?
\ begin {align *} F & = ma \\ & = (\ text {1 000}) (\ text {10}) \\ & = \ текст {10 000} \ текст {N} \ end {выровнять *}
Блок на наклонной плоскости испытывает силу тяжести \ (\ vec {F} _g \) из \ (\ text {300} \) \ (\ text {N} \) прямо вниз. Если склон наклонен на \ (\ text {67,8} \) \ (\ text {°} \) к горизонтали, какова составляющая силы, создаваемой силой тяжести, перпендикулярной и параллельной склону? Под каким углом будут равны перпендикулярная и параллельная составляющие силы тяжести?
Составляющая, параллельная откосу:
\ begin {align *} F_ {gx} & = F \ sin \ theta \\ & = (\ text {300}) \ sin (\ text {67,8}) \\ & = \ текст {277,76} \ текст {N} \ end {выровнять *}Составляющая, перпендикулярная откосу:
\ begin {align *} F_ {gy} & = F \ cos \ theta \\ & = (\ text {300}) \ cos (\ text {67,8}) \\ & = \ текст {113,35} \ текст {N} \ end {выровнять *}Чтобы два компонента были равны, угол должен быть \ (\ text {45} \) \ (\ text {°} \).(\ (\ sin (45) = \ cos (45) \)).
Блок на наклонной плоскости подвергается действию силы тяжести \ (\ vec {F} _g \) из \ (\ text {287} \) \ (\ text {N} \) прямо вниз. Если составляющая гравитационной силы, параллельная наклону, равна \ (\ vec {F} _ {gx} \) = \ (\ text {123,7} \) \ (\ text {N} \) в отрицательном значении \ (x \) – направление (вниз по склону), какой уклон склона?
\ begin {align *} F_ {gx} & = F \ sin \ theta \\ \ text {123,7} & = (\ text {287}) \ sin \ theta \\ \ sin \ theta & = \ text {0,431} \ ldots \\ \ theta & = \ text {25,53} \ text {°} \ end {выровнять *}
Блок на наклонной плоскости испытывает силу тяжести \ (\ vec {F} _g \) из \ (\ text {98} \) \ (\ text {N} \) прямо вниз.Если наклон наклонен под неизвестным углом к горизонтали, но нам говорят, что соотношение составляющих силы тяжести, перпендикулярной и параллельной наклону, составляет 7: 4. Каков угол наклона к горизонту?
Сначала запишем уравнения для параллельной и перпендикулярной составляющих:
\ begin {align *} F_ {gx} & = F \ sin \ theta \\ & = (98) \ грех \ тета \ end {выровнять *} \ begin {align *} F_ {gy} & = F \ cos \ theta \\ & = (98) \ соз \ тета \ end {выровнять *}Теперь отметим следующее:
\ begin {align *} 7F_ {gx} & = 4F_ {gy} \\ \ поэтому 7 (98) \ sin \ theta & = 4 (98) \ cos \ theta \ end {выровнять *}Теперь нам нужно решить для theta:
\ begin {align *} \ sin \ theta & = \ frac {\ text {392}} {\ text {686}} \ cos \ theta \\ & = \ текст {0,5714} \ cos \ theta \\ \ frac {\ sin \ theta} {\ cos \ theta} & = \ text {0,5714} \\ \ tan \ theta & = \ text {0,5714} \\ \ theta & = \ text {25,53} \ text {°} \ end {выровнять *}Вспомните из тригонометрии, что \ (\ frac {\ sin \ theta} {\ cos \ theta} = \ tan \ theta \).{-2} $} \)). Выберите положительное направление движения (справа положительное).
\ begin {align *} F_ {R} & = ma \\ F _ {\ text {application}} + F_ {f} & = ma \\ \ text {1 500} + {F} _ {f} & = (30 + 50) (2) \\ F_ {f} & = \ text {160} – \ text {1 500} \\ F_ {f} & = – \ text {1 340} \ text {N} \ end {выровнять *}величина натяжения каната у Т.
Отметим, что \ (m_ {1} = \ frac {\ text {5}} {\ text {3}} m_ {2} \), поэтому \ (F_ {f1} = \ frac {\ text {5} } {\ text {3}} F_ {f2} \).
Чтобы определить натяжение веревки, нам нужно посмотреть на один из двух ящиков отдельно. Выберем ящик \ (\ text {30} \) \ (\ text {kg} \).
Сила трения в блоке \ (\ text {30} \) \ (\ text {kg} \) указана выше. Мы можем вычислить \ (F_ {f2} \):
\ begin {align *} F_ {f} & = F_ {f1} + F_ {f2} \\ \ text {1 340} & = F_ {f2} + \ frac {\ text {5}} {\ text {3}} F_ {f2} \\ \ text {1 340} & = \ frac {\ text {8}} {\ text {3}} F_ {f2} \\ F_ {f2} & = \ text {502,5} \ text {N} \ end {выровнять *}Если применить второй закон Ньютона:
\ begin {align *} F_ {R} & = ma \\ Т + F_ {f} & = (30) (2) \\ T + – \ text {502,5} & = 60 \\ Т & = \ текст {562,5} \ текст {N} \ end {выровнять *}– величина и направление общей имеющейся силы трения. {2} & = \ text {63 555,88} \\ F_ {gx1} & = \ text {252,10} \ text {N} \ end {выровнять *}
Теперь мы можем написать выражение для равнодействующей силы на каждом ящике:
\ begin {align *} \ vec {F} _ {R} & = ma \\ F_ {A} – F_ {gx1} – F_ {f} – T & = ma \\ \ text {500} – \ text {420,17} – F_ {f1} – T & = (\ text {50}) (\ text {7}) \\ -T & = \ text {420,17} + F_ {f} \ end {выровнять *} \ begin {align *} \ vec {F} _ {R} & = ma \\ Т – F_ {gx2} – F_ {f} & = ma \\ T – \ text {252,10} – F_ {f} & = (\ text {30}) (\ text {7}) \\ T & = \ text {462,1} + F_ {f} \ end {выровнять *}И одновременно решите для силы трения:
\ begin {align *} -T + T & = \ text {420,17} + F_ {f} + \ text {462,1} + F_ {f} \\ 0 & = \ text {882,27} + 2F_ {f} \\ F_ {f} & = – \ text {441,14} \ text {N} \ end {выровнять *}величина натяжения каната у Т.
Мы можем использовать любое из двух приведенных выше выражений, чтобы найти напряжение. Мы будем использовать выражение для ящика 1:
\ begin {align *} -T & = \ text {420,17} + F_ {f} \\ & = \ text {420,17} + – \ text {441,14} \\ T & = \ text {20,97} \ text {N} \ end {выровнять *}Третий закон движения Ньютона (ESBKV)
Третий закон движения Ньютона касается взаимодействия между парами объектов. Например, если вы держите книгу у стены, вы прилагаете силу к книге (чтобы удержать ее там), а книга оказывает на вас силу (чтобы вы не провалились сквозь книгу).Это может показаться странным, но если бы книга не давила на вас, ваша рука проталкивала бы книгу! Эти две силы (сила руки на книге (\ ({F} _ {1} \)) и сила книги на руке (\ ({F} _ {2} \))) называются пара сил действие-противодействие. Они имеют одинаковую величину, но действуют в противоположных направлениях и действуют на разные объекты (одна сила действует на книгу, а другая – на вашу руку).
В этой ситуации присутствует еще одна пара сил действие-противодействие.Книга толкает стену (сила действия), а стена толкает книгу (реакция). Сила силы книги на стене (\ ({F} _ {3} \)) и силы стены на книгу (\ ({F} _ {4} \)) показаны на диаграмме.
Рисунок 2.8: Пары действие-реакция Ньютона.- Третий закон движения Ньютона
Если тело A воздействует на тело B, то тело B действует на тело A с силой равной величины, но в противоположном направлении.
Эти пары действие-реакция обладают несколькими свойствами:
- То же сила действует на предметы,
- силы имеют ту же величину, но противоположное направление, а
- Силы действуют на разные объекты.
Пары действие-реакция Ньютона можно найти повсюду в жизни, где два объекта взаимодействуют друг с другом. Следующие рабочие примеры иллюстрируют это:
Рабочий пример 18: третий закон Ньютона – ремень безопасности
Динео сидит на пассажирском сиденье автомобиля с пристегнутым ремнем безопасности.Автомобиль внезапно останавливается, и он движется вперед (первый закон Ньютона – он продолжает движение), пока его не остановит ремень безопасности. Нарисуйте помеченную диаграмму сил, идентифицирующую две пары действие-противодействие в этой ситуации.
Нарисуйте силовую диаграмму
Начните с рисования картинки. Вы будете использовать стрелки для обозначения сил, поэтому сделайте изображение достаточно большим, чтобы можно было добавить подробные метки. Картинка должна быть точной, но не художественной! Если нужно, используйте человечков-палочек.
Обозначьте схему
Возьмите по одной паре и тщательно пометьте их. Если на чертеже недостаточно места, то используйте ключ сбоку.
Рабочий пример 19: Третий закон Ньютона: силы в лифте
Тэмми поднимается с первого этажа на пятый этаж отеля на лифте, движущемся с постоянной скоростью. Какое ОДНО из следующих утверждений о величине силы, оказываемой полом лифта на ноги Тэмми, является ИСТИННЫМ? Используйте третий закон Ньютона, чтобы оправдать свой ответ.
Это больше, чем вес Тэмми.
По величине она равна силе, которую ступни Тэмми прикладывают к полу лифта.
То же, что и в стационарном лифте.
Это больше, чем у стационарного лифта.
Проанализировать ситуацию
Это вопрос третьего закона Ньютона, а не второго закона Ньютона. Нам нужно сосредоточиться на парах сил действие-противодействие, а не на движении лифта. На следующей диаграмме показаны пары действие-реакция, которые присутствуют, когда человек стоит на весах в лифте.
Рисунок 2.9: Пары действие-реакция Ньютона в лифте.В этом вопросе говорится о силе пола (лифта) на ступни Тэмми.Эта сила соответствует \ ({F} _ {2} \) на нашей диаграмме. Сила реакции, которая сочетается с этим, равна \ ({F} _ {1} \), то есть сила, которую ноги Тэмми прилагают к полу лифта. Величина этих двух сил одинакова, но действуют в противоположных направлениях.
Выберите правильный ответ
Важно сначала проанализировать вопрос, прежде чем искать ответы. Ответы могут запутать вас, если вы сначала посмотрите на них. Убедитесь, что вы понимаете ситуацию и знаете, о чем спрашивают, прежде чем рассматривать варианты.
Правильный ответ – число \ (\ text {2} \).
Рабочий пример 20: Третий закон Ньютона: книга и стена
Бриджит прижимает книгу к вертикальной стене, как показано на фотографии.
Нарисуйте помеченную диаграмму сил, показывающую все силы, действующие на книгу.
Сформулируйте словами третий закон движения Ньютона.
Назовите пары сил действие-противодействие, действующие в горизонтальной плоскости.
Нарисуйте силовую диаграмму
Силовая диаграмма будет выглядеть так:
Обратите внимание, что мы должны были нарисовать все силы, действующие на книгу, а не пары действие-противодействие. Ни одна из привлеченных сил не является парами действие-противодействие, потому что все они действуют на один и тот же объект (книгу). Когда вы обозначаете силы, будьте как можно более конкретными, включая направление силы и оба вовлеченных объекта, например, не говорите «гравитация» (что является неполным ответом), а скорее говорите «Нисходящая (направленная) сила тяжести Земли ( объект) на книге (объекте) ‘.
Государственный третий закон Ньютона
Если тело A прикладывает силу к телу B, то тело B прикладывает силу, равную по величине, но противоположную по направлению к телу A.
Назовите пары действие-противодействие
Вопрос касается только сил действие-противодействие в горизонтальной плоскости. Следовательно:
Пара 1: Действие: Приложение силы Бриджит к книге; Реакция: Сила книги на девушке.
Пара 2: Действие: Сила книги на стене; Реакция: Сила стены на книгу.
Обратите внимание, что пара третьего закона Ньютона всегда будет включать одну и ту же комбинацию слов, например «книга на стене» и «стена на книге». Объекты «меняются местами» при именовании пар.
Ракета-воздушный шар
Прицел
В этом эксперименте для всего класса вы будете использовать ракету на воздушном шаре, чтобы исследовать третий закон Ньютона. В качестве дорожки будет использоваться леска, а пластиковая соломка, прикрепленная к воздушному шару, поможет прикрепить его к дорожке.
Аппарат
Для этого эксперимента вам понадобятся следующие предметы:
воздушных шара (по одному на каждую команду)
пластиковых трубочки (по одной на каждую команду)
лента (целлофановая или малярная)
леска, длина \ (\ text {10} \) метров
секундомер – опционально (можно использовать сотовый телефон)
рулетка – опция
Метод
Разделитесь на группы не менее пяти человек.
Прикрепите один конец лески к доске скотчем. Попросите одного из товарищей по команде придержать другой конец лески так, чтобы она была натянутой и примерно горизонтальной. Линия должна удерживаться устойчиво, и нельзя перемещать вверх или вниз во время эксперимента.
Пусть один из товарищей по команде надует воздушный шар и удерживает его пальцами. Попросите другого товарища по команде закрепить соломинку вдоль стороны воздушного шара.Проденьте леску через соломинку и удерживайте воздушный шарик за дальний конец лески.
Отпустите ракету и посмотрите, как она движется вперед.
По желанию, ракеты каждой группы могут быть рассчитаны по времени, чтобы определить победителя самой быстрой ракеты.
Назначьте одного товарища по команде для измерения времени события. Воздушный шар следует отпускать, когда хронометрист кричит «Вперед!» Наблюдайте, как ваша ракета движется к доске.
Попросите другого товарища по команде встать рядом с доской и крикнуть «Стой!» когда ракета поражает цель. Если воздушный шарик не добрался до доски, «Стой!» должен вызываться, когда воздушный шар перестает двигаться. Хронометрист должен записывать время полета.
Измерьте точное расстояние, которое прошла ракета. Вычислите среднюю скорость полета воздушного шара.Для этого разделите пройденное расстояние на время, когда воздушный шар находился «в полете». Заполните свои результаты для Испытания 1 в таблице ниже.
Каждая команда должна провести еще две гонки и заполнить разделы в Таблице испытаний 2 и 3. Затем вычислить среднюю скорость для трех испытаний, чтобы определить время участия вашей команды в гонке. {- 1} $} \) )
Пробная 1
Пробная 2
Пробная 3
Средн.
Выводы
Победителем этой гонки становится команда с самой высокой средней скоростью воздушного шара.
При проведении эксперимента следует подумать о,
Что заставило вашу ракету двигаться?
Как это действие демонстрирует третий закон Ньютона?
Нарисуйте картинки, используя помеченные стрелки, чтобы показать силы, действующие на внутреннюю часть воздушного шара до его выпуска и после того, как он был выпущен.
Saturn V (произносится как «Saturn Five») – американская одноразовая ракета, предназначенная для людей и использовавшаяся в программах NASA Apollo и Skylab с 1967 по 1973 год.Многоступенчатая ракета-носитель на жидком топливе NASA запустила 13 ракет Saturn V из Космического центра Кеннеди во Флориде без потери экипажа или полезной нагрузки. Она остается самой высокой, самой тяжелой и самой мощной ракетой, когда-либо доведенной до рабочего состояния, и до сих пор удерживает рекорд по самой тяжелой полезной нагрузке ракеты-носителя.
Упражнение 2.6Муха попадает в лобовое стекло движущегося автомобиля. По сравнению с силой, с которой муха воздействует на лобовое стекло, величина силы, которую ветровое стекло оказывает на лету во время столкновения, составляет:
ноль.
меньше, но не ноль.
больше.
то же.
тоже самое
Какая из следующих пар сил правильно иллюстрирует третий закон Ньютона?
А или В
Силы в равновесии (ESBKW)
В начале этой главы упоминалось, что результирующие силы заставляют объекты ускоряться по прямой.Если объект неподвижен или движется с постоянной скоростью, то либо
на объект не действуют силы, или
силы, действующие на этот объект, точно сбалансированы.
Другими словами, для неподвижных объектов или объектов, движущихся с постоянной скоростью, результирующая сила, действующая на объект, равна нулю.
- Равновесие
У объекта в равновесии сумма действующих на него сил равна нулю.
Законы движения Ньютона | Живая наука
Три закона движения сэра Исаака Ньютона описывают движение массивных тел и их взаимодействие. Хотя сегодня законы Ньютона могут показаться нам очевидными, более трех веков назад они считались революционными.
Ньютон был одним из самых влиятельных ученых всех времен. Его идеи легли в основу современной физики. Он опирался на идеи, выдвинутые из работ предыдущих ученых, включая Галилея и Аристотеля, и смог доказать некоторые идеи, которые в прошлом были только теориями.Он изучал оптику, астрономию и математику – он изобрел исчисление. (Немецкому математику Готфриду Лейбницу также приписывают независимую разработку примерно в то же время.)
Ньютон, пожалуй, наиболее известен своими работами по изучению гравитации и движения планет. По настоянию астронома Эдмона Галлея после признания того, что он потерял свое доказательство эллиптических орбит за несколько лет до этого, Ньютон опубликовал свои законы в 1687 году в своей основополагающей работе «Philosophiæ Naturalis Principia Mathematica» (Математические принципы естественной философии), в которой он формализовал описание того, как массивные тела движутся под действием внешних сил.
Формулируя свои три закона, Ньютон упростил рассмотрение массивных тел, рассматривая их как математические точки без размера и вращения. Это позволило ему игнорировать такие факторы, как трение, сопротивление воздуха, температуру, свойства материала и т. Д., И сосредоточиться на явлениях, которые можно описать исключительно в терминах массы, длины и времени. Следовательно, эти три закона нельзя использовать для точного описания поведения больших твердых или деформируемых объектов; однако во многих случаях они обеспечивают достаточно точные приближения.
Законы Ньютона относятся к движению массивных тел в инерциальной системе отсчета , иногда называемой ньютоновской системой отсчета , хотя сам Ньютон никогда не описывал такую систему отсчета. Инерциальная система отсчета может быть описана как трехмерная система координат, которая либо неподвижна, либо находится в равномерном линейном движении, то есть не ускоряется и не вращается. Он обнаружил, что движение в такой инерциальной системе отсчета можно описать тремя простыми законами.
Первый закон движения гласит: «Покоящееся тело будет оставаться в покое, а тело в движении будет оставаться в движении, если на него не действует внешняя сила». Это просто означает, что вещи не могут запускаться, останавливаться или менять направление сами по себе. Требуется некоторая сила, действующая на них извне, чтобы вызвать такое изменение. Это свойство массивных тел сопротивляться изменениям в их состоянии движения иногда называют инерцией .
Второй закон движения описывает, что происходит с массивным телом, когда на него действует внешняя сила.В нем говорится: «Сила, действующая на объект, равна массе этого объекта, умноженной на его ускорение». Это записывается в математической форме как F = м a , где F – сила, м – масса, а a – ускорение. Жирными буквами обозначено, что сила и ускорение векторных величин, что означает, что они имеют как величину, так и направление. Сила может быть одной силой или векторной суммой более чем одной силы, которая представляет собой результирующую силу после объединения всех сил.
Когда на массивное тело действует постоянная сила, она заставляет его ускоряться, то есть изменять его скорость с постоянной скоростью. В простейшем случае сила, приложенная к неподвижному объекту, заставляет его ускоряться в направлении силы. Однако, если объект уже находится в движении или если эта ситуация рассматривается из движущейся системы отсчета, это тело может казаться ускоряющимся, замедляющимся или меняющим направление в зависимости от направления силы и направлений, в которых объект и системы отсчета движутся относительно друг друга.
Третий закон движения гласит: «На каждое действие есть равное и противоположное противодействие». Этот закон описывает, что происходит с телом, когда оно воздействует на другое тело. Силы всегда возникают парами, поэтому, когда одно тело толкает другое, второе тело с такой же силой отталкивается. Например, когда вы толкаете тележку, тележка толкает вас назад; когда вы тянете за веревку, веревка тянется назад против вас; когда сила тяжести прижимает вас к земле, земля толкает вас вверх по ногам; и когда ракета воспламеняет свое топливо позади себя, расширяющийся выхлопной газ толкает ракету, заставляя ее ускоряться.
Если один объект намного, намного массивнее другого, особенно в случае, когда первый объект привязан к Земле, фактически все ускорение передается второму объекту, и ускорение первого объекта может быть безопасно игнорировать.



