Функция стремится к нулю: Бесконечно большая величина - это... Что такое Бесконечно большая величина? - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Бесконечно большая величина – это… Что такое Бесконечно большая величина?

Бесконечно малая величина — числовая функция или последовательность, которая стремится к нулю.

Бесконечно большая величина — числовая функция или последовательность, которая стремится к бесконечности определённого знака.

Исчисление бесконечно малых и больших

Исчисление бесконечно малых — вычисления, производимые с бесконечно малыми величинами, при которых производный результат рассматривается как бесконечная сумма бесконечно малых. Исчисление бесконечно малых величин является общим понятием для дифференциальных и интегральных исчислений, составляющих основу современной высшей математики. Понятие бесконечно малой величины тесно связано с понятием предела.

Бесконечно малая

Последовательность a_n называется бесконечно малой, если . Например, последовательность чисел — бесконечно малая.

Функция называется бесконечно малой в окрестности точки x₀, если .

Функция называется бесконечно малой на бесконечности, если либо .

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если , то f(x) − a = α(x), .

Бесконечно большая величина

Последовательность a_n называется бесконечно большой, если .

Функция называется бесконечно большой в окрестности точки x₀, если .

Функция называется бесконечно большой на бесконечности, если либо .

Во всех случаях бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция

xsinx не является бесконечно большой при .

Свойства бесконечно малых и бесконечно больших

Сумма конечного числа бесконечно малых — бесконечно малая.
Произведение бесконечно малых — бесконечно малая.
Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.
Если a_n — бесконечно малая последовательность, сохраняющая знак, то — бесконечно большая последовательность.

Сравнение бесконечно малых величин

Как сравнивать бесконечно малые величины?
Отношение бесконечно малых величин образует так называемую неопределённость .

Определения

Допустим, у нас есть бесконечно малые при одном и том же величины α(x) и β(x) (либо, что не суть важно для определения, бесконечно малые последовательности).

Если , то β — бесконечно малая высшего порядка малости, чем α. Обозначают β = o(α).
Если , то β — бесконечно малая низшего порядка малости, чем α. Соответственно α = o(β).

Если (предел конечен и не равен 0), то α и β являются бесконечно малыми величинами одного порядка малости.
Это обозначается как β = O(α) или α = O(β) (в силу симметричности данного отношения).

Если (предел конечен и не равен 0), то бесконечно малая величина β имеет m-й порядок малости относительно бесконечно малой α.

Для вычисления подобных пределов удобно использовать правило Лопиталя.

Примеры сравнения

При величина x⁵ имеет высший порядок малости относительно x³, так как С другой стороны, x³ имеет низший порядок малости относительно x⁵, так как

С использованием О-символики полученные результаты могут быть записаны в следующем виде x⁵ = o(x³).

то есть при функции f(x) = 2x² + 6x и g(x) = x являются бесконечно малыми величинами одного порядка.

В данном случае справедливы записи 2x² + 6x = O(x) и x = O(2x² + 6x).

При бесконечно малая величина 2x³ имеет третий порядок малости относительно x, поскольку бесконечно малая 0,7x² — второй порядок, бесконечно малая — порядок 0,5.

Эквивалентные величины

Определение

Если , то бесконечно малые величины α и β называются эквивалентными ().
Очевидно, что эквивалентные величины являются частным случаем бесконечно малых величин одного порядка малости.

При справедливы следующие соотношения эквивалентности: , , .

Теорема

Предел частного (отношения) двух бесконечно малых величин не изменится, если одну из них (или обе) заменить эквивалентной величиной.

Данная теорема имеет прикладное значение при нахождении пределов (см. пример).

Пример использования

Найти

Заменяя sin2x эквивалентной величиной 2x, получаем

Исторический очерк

Понятие «бесконечно малое» обсуждалось ещё в античные времена в связи с концепцией неделимых атомов, однако в классическую математику не вошло.

Вновь оно возродилось с появлением в XVI веке «метода неделимых» — разбиения исследуемой фигуры на бесконечно малые сечения.

В XVII веке произошла алгебраизация исчисления бесконечно малых. Они стали определяться как числовые величины, которые меньше всякой конечной (ненулевой) величины и всё же не равны нулю. Искусство анализа заключалось в составлении соотношения, содержащего бесконечно малые (дифференциалы), и затем — в его интегрировании.

Математики старой школы подвергли концепцию бесконечно малых резкой критике. Мишель Ролль писал, что новое исчисление есть «набор гениальных ошибок»; Вольтер ядовито заметил, что это исчисление представляет собой искусство вычислять и точно измерять вещи, существование которых не может быть доказано. Даже Гюйгенс признавался, что не понимает смысла дифференциалов высших порядков.

Споры в Парижской Академии наук по вопросам обоснования анализа приобрели настолько скандальный характер, что Академия однажды вообще запретила своим членам высказываться на эту тему (в основном это касалось Ролля и Вариньона).

В 1706 году Ролль публично снял свои возражения, однако дискуссии продолжались.

В 1734 году известный английский философ, епископ Джордж Беркли выпустил нашумевший памфлет, известный под сокращенным названием «Аналист». Полное его название: «Аналист или рассуждение, обращенное к неверующему математику, где исследуется, более ли ясно воспринимаются или более ли очевидно выводятся предмет, принципы и умозаключения современного анализа, чем религиозные таинства и догматы веры».

«Аналист» содержал остроумную и во многом справедливую критику исчисления бесконечно малых. Метод анализа Беркли считал несогласным с логикой и писал, что, «

как бы он ни был полезен, его можно рассматривать только как некую догадку; ловкую сноровку, искусство или скорее ухищрение, но не как метод научного доказательства». Цитируя фразу Ньютона о приращении текущих величин «в самом начале их зарождения или исчезновения», Беркли иронизирует: «это ни конечные величины, ни бесконечно малые, ни даже ничто. Не могли ли бы мы их назвать призраками почивших величин?… И как вообще можно говорить об отношении между вещами, не имеющими величины?.. Тот, кто может переварить вторую или третью флюксию [производную], вторую или третью разность, не должен, как мне кажется, придираться к чему-либо в богословии ».

Невозможно, пишет Беркли, представить себе мгновенную скорость, то есть скорость в данное мгновение и в данной точке, ибо понятие движения включает понятия о (конечных ненулевых) пространстве и времени.

Как же с помощью анализа получаются правильные результаты? Беркли пришел к мысли, что это объясняется наличием в аналитических выводах взаимокомпенсации нескольких ошибок, и проиллюстрировал это на примере параболы. Занятно, что некоторые крупные математики (например, Лагранж) согласились с ним.

Сложилась парадоксальная ситуация, когда строгость и плодотворность в математике мешали одна другой. Несмотря на использование незаконных действий с плохо определёнными понятиями, число прямых ошибок было на удивление малым — выручала интуиция.

И всё же весь XVIII век математический анализ бурно развивался, не имея по существу никакого обоснования. Эффективность его была поразительна и говорила сама за себя, но смысл дифференциала по-прежнему был неясен. Особенно часто путали бесконечно малое приращение функции и его линейную часть.

В течение всего XVIII века предпринимались грандиозные усилия для исправления положения, причём в них участвовали лучшие математики столетия, однако убедительно построить фундамент анализа удалось только Коши в начале XIX века. Он строго определил базовые понятия — предел, сходимость, непрерывность, дифференциал и др., после чего актуальные бесконечно малые исчезли из науки. Некоторые оставшиеся тонкости разъяснил позднее Вейерштрасс.

Как иронию судьбы можно рассматривать появление в середине XX века нестандартного анализа, который доказал, что первоначальная точка зрения — актуальные бесконечно малые — также непротиворечива и могла бы быть положена в основу анализа.

См. также

Wikimedia Foundation. 2010.

Курс по математическому анализу

Вашему вниманию предлагается курс по математическому анализу.

Наверх

1. Предел числовой последовательности.

Последовательность – это функция, заданная на множестве натуральных чисел . Число называется пределом последовательности , если для любого положительного числа , как бы мало оно ни было, существует такой номер, что для всех c номерами справедливо неравенство . Неравенство , эквивалентное неравенству , означает, что для любого существует такой номер , что все c номерами расположены между и . Последовательность, предел которой – конечное число , называется сходящейся, и ее предел обозначают. Если изобразить элементы последовательности на плоскости точками с координатами , то неравенства означают, что все точки с номерами расположены между параллельными оси абсцисс прямыми и .

Бесконечно малая последовательность. Последовательность , предел которой равен нулю , называется бесконечно малой.

Бесконечно большая последовательность. Последовательность называется бесконечно большой, если для любого положительного числа , как бы велико оно ни было, существует такой номер , что для всех с номерамисправедливо неравенство , записываем .

Наверх

2. Методы вычисления пределов последовательностей.

Пусть заданы две последовательности и . Если существуют и , то существуют и пределы суммы и произведения последовательностей, а при и предел частного, причем , , . Для правильного применения этих теорем очень важно существование пределов каждой последовательности.

Неопределенности и их раскрытие.

Если и , то может существовать . В этом случае говорят, что имеем неопределенность типа . Также может существовать , в этом случае имеем неопределенность типа . Если и , то может существовать . В этом случае говорят, что имеем неопределенность типа . Поскольку в перечисленных случаях не применимы теоремы о пределе суммы, произведения и частного, используют другие способы вычисления, которые называют методами раскрытия неопределенностей. Это, как правило, алгебраические преобразования, приводящие выражения к виду, при котором можно пользоваться упомянутыми теоремами.

Наверх

3. Предел функции в точке.

Рассмотрим функцию , определенную в некоторой окрестности точки , , , за исключением, быть может, самой точки . Число называется пределом функции при , стремящемся к , если для любого положительного числа , как бы мало оно ни было, существует такое положительное число , что для всех , удовлетворяющих неравенству , справедливо неравенство . Говорят “предел функции в точке ” и обозначают . Неравенство для всех , эквивалентное неравенствам , , означают, что для любого существует такое , что для график функции расположен на плоскости в прямоугольнике . При вычислениях на компьютере мы имеем дело с дискретными значениями переменных. Поэтому удобнее пользоваться другим, эквивалентным приведенному, определением предела. А именно: , если для любой, сходящейся к последовательности значений аргумента , соответствующая последовательность значений функции сходится к числу . Отсюда следует, в частности, что для любого существует такое , что для любой последовательности , сходящейся к , точки с координатами находятся на плоскости внутри прямоугольника .

Бесконечно большие функции.

Если для любой последовательности значений аргумента соответствующая последовательность значений функции бесконечно большая, то функция называется бесконечно большой в точке . Если бесконечно большая в точке , то для любого положительного числа , как бы велико оно ни было, существует такое число , что для всех , удовлетворяющих неравенству , справедливо неравенство ; обозначают .

Наверх

4. Бесконечно малые функции. Сравнение бесконечно малых функций.

Рассмотрим функцию, определенную в некоторой окрестности точки , , за исключением, быть может, самой точки . Функция называется бесконечно малой при , стремящемся к , если . Если — бесконечно малая в точке , то для любого положительного числа , как бы мало оно ни было, существует такое положительное число , что для всех , удовлетворяющих неравенству , справедливо неравенство . Неравенства для всех , эквивалентные неравенствам , , означают, что для любого существует такое , что для график функции расположен на плоскости в прямоугольнике . Важно, что слова “за исключением, быть может, самой точки ” означают, что нас не интересует сама эта точка. Это можно понять, если рассмотреть функцию. При x, стремящемся к нулю, функция-таки стремится к нулю, независимо от того, какое значение она принимает в точке x=0. Следовательно, предел равен нулю и функция является бесконечно малой.

Сравнение бесконечно малых функций.

Пусть и — две функции, бесконечно малые в точке . Если , то говорят, что более высокого порядка малости, чем и обозначают . Если же , то более высокого порядка малости, чем ; обозначают . Бесконечно малые функции и называются бесконечно малыми одного порядка малости, если , обозначают . И, наконец, если не существует, то бесконечно малые функции и несравнимы.

Эквивалентные бесконечно малые функции.

Если , то бесконечно малые функции и называются эквивалентными, обозначают ~ .

Наверх

5. Методы вычисления пределов функций.

Пусть заданы две функции и . Если существуют и , то существуют и пределы суммы и произведения этих функций, а при и предел частного, причем

Для правильного применения этих теорем очень важно существование пределов каждой функции. Не трудно доказать, что предел постоянной функции равен этой постоянной, то есть . Из приведенных формул следует полезное утверждение:

, то есть постоянный множитель можно выносить за знак предела. Если сделать замену переменной , то вычисление предела при всегда можно свести к вычислению предела при . Из определения непрерывной функции следует, что ее предел совпадает со значением функции в этой точке. Доказывают, что все элементарные функции непрерывны в области определения, поэтому, если функция определена, то вычисление предела сводится к применению указанных теорем и подстановке в выражение для функции.

Неопределенности и их раскрытие.

Существуют случаи, когда не применимы теоремы о пределах суммы, произведения, частного, но предел существует и может быть вычислен. Если и , то может существовать . В этом случае говорят, что имеем неопределенность типа . Также может существовать , в этом случае имеем неопределенность типа . Если и , то может существовать . В этом случае говорят, что имеем неопределенность типа . Если и , то может существовать – неопределенность типа . Рассматривают также неопределенности типа , и т. д. Основным признаком неопределенности является невозможность корректного вычисления функции простой подстановкой в выражение для функции. Полезно запомнить замечательные пределы:

(е = 2.71828… – основание натуральных логарифмов) – неопределенность типа .

– неопределенность типа .

Использование эквивалентных бесконечно малых.

Если мы имеем неопределенность типа , то это означает, что мы вычисляем предел отношения двух бесконечно малых функций. Напомним, что функция называется бесконечно малой, если ее предел в точке равен нулю. Пусть, , , – бесконечно малые функции при , причем эквивалентна , т.е. ~ , ~ (напомним, что две бесконечно малых называются эквивалентными, если предел их отношения равен 1). Тогда, т.е. при вычислении пределов отношений бесконечно малых любую из них можно заменять на эквивалентную.

Правило Лопиталя.

Неопределенности типа или удобно раскрывать с помощью правила Лопиталя. Пусть и две бесконечно малые или бесконечно большие функции при и существует предел отношения их производных при . Тогда . Если в результате применения правила Лопиталя снова получится неопределенность, то его можно применить еще раз.

Формула Тейлора.

Пусть функция имеет в точке производные всех порядков до -го включительно. Тогда для справедлива формула Тейлора:

где называется остаточным членом формулы Тейлора.

Наверх

6. Непрерывность функции в точке, на отрезке.

Рассмотрим функцию , определенную на некотором промежутке . Функция непрерывна в точке , если предел функции в точке равен значению функции в этой точке,.

Свойства функций, непрерывных на отрезке.

Функция, непрерывная в каждой точке промежутка , называется непрерывной на промежутке. Для функции, непрерывной на отрезке , справедливы следующие утверждения.

Функция, непрерывная на отрезке , достигает на нем своих наибольшего и наименьшего значений, т.е. на отрезке существуют точки такие, что

Если функция непрерывна на отрезке и принимает на концах значения разных знаков, то на интервале существует точка , в которой функция обращается в нуль, т.е. . Это утверждение применяют для отделения корней уравнений с непрерывной левой частью — если найден отрезок, на концах которого функция принимает значения разных знаков, то можно утверждать, что на этом отрезке есть хотя бы один корень уравнения.

Если функция непрерывна на отрезке , дифференцируема хотя бы на интервале , то на интервале существует точка , такая, что . Это свойство называют формулой Лагранжа или формулой конечных приращений.

Наверх

7. Классификация точек разрыва

Односторонние пределы функции в точке.

Функция, непрерывная в каждой точке промежутка , называется непрерывной на промежутке. Если функция определена на промежутке , , то при исследовании поведения функции в окрестности точки имеет смысл говорить о пределе функции в точке справа, а при исследовании в окрестности точки – о пределе функции в точке слева. Число называется пределом справа функции при , стремящемся к , если для любого положительного числа , как бы мало оно ни было, существует такое положительное число , что для всех , удовлетворяющих неравенству , справедливо неравенство . Говорят “предел справа функции в точке ” и обозначают . Аналогично говорят “предел слева функции в точке ” и обозначают , если для любого положительного числа , как бы мало оно ни было, существует такое положительное число , что для всех , удовлетворяющих неравенству , справедливо неравенство . Для существования предела функции в точке, необходимо и достаточно, чтобы существовали и совпадали односторонние пределы функции в этой точке. По той же схеме вводится понятие непрерывности слева и непрерывности справа. Функция, определенная на отрезке , , непрерывна справа в точке , если и непрерывна слева в точке , если. Для того чтобы функция была непрерывна в точке необходимо и достаточно, чтобы односторонние пределы функции в точке совпадали со значением функции в этой точке:. Если хотя бы одно из равенств нарушается, говорят о разрыве в точке .

Классификация разрывов.

Если хотя бы одно из равенств нарушается, говорят о разрыве в точке . Если и односторонние пределы конечны, то разрыв в точке называется устранимым. Если и оба односторонние пределы конечны, то говорят о скачке функции в точке . Устранимый разрыв и скачок называются разрывами первого рода. Если один из односторонних пределов бесконечен или не существует, то разрыв называется разрывом второго рода. Так же, как для предела и непрерывности, говорят о разрыве слева и разрыве справа.

Наверх

8. Производная, ее вычисление, геометрический смысл.

Производная функции в точке – Пусть функция определена на промежутке . Точка — произвольная точка из области определения функции, — приращение функции в точке , вызванное приращением независимой переменной . Производной функции по независимой переменной в точке , называется предел отношения приращения функции к приращению при стремлении к нулю, т.е.

— производная функции в точке .

Односторонние производные – Если определена при , то можно определить правую производную функции в точке :

Аналогично, если определена при , определяется левая производная функции в точке :

Функция имеет в точке производную тогда и только тогда, когда в точкесовпадают ее левая и правая производные: .

Секущая графика функции – Пусть — функция, определенная на промежутке .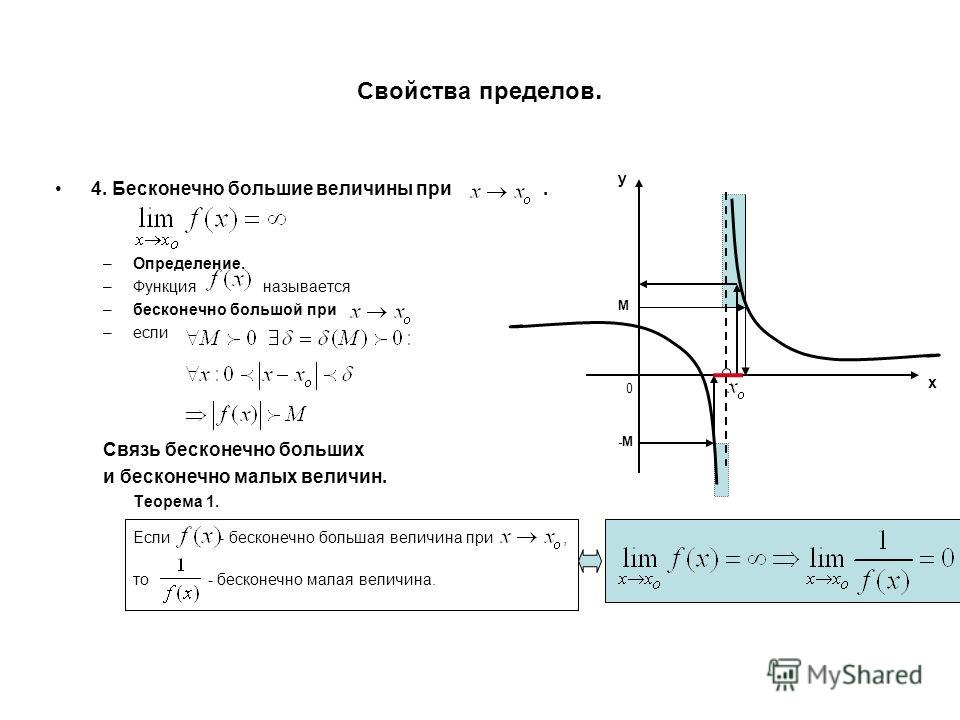 Прямая, проходящая через точки , , , называется секущей графика функции . Угловой коэффициент секущей равен и ее уравнение имеет вид .

Касательная и нормаль к графику функции – Касательной к графику функции в точке называется предельное положение секущей, проходящей через точки , , когда . Угловой коэффициент касательной равен значению производной в точке и ее уравнение имеет вид . Нормалью к графику функции в точке называется прямая , проходящая через эту точку перпендикулярно касательной. Угловой коэффициент нормали равен и ее уравнение имеет вид .

Наверх

9. Производные сложных, обратных функций.

Пусть – функция, дифференцируемая в точке , – функция, дифференцируемая в точке , причем . Тогда – сложная функция независимого переменного , дифференцируема в точке и ее производная в этой точке вычисляется по формуле .

Обычно называют внешней функцией, а – внутренней. При вычислении производной сложной функции сначала дифференцируют внешнюю функцию, не обращая внимания на внутреннюю (ведь она может быть любой), затем умножают на производную конкретной внутренней функции.

Производная обратной функции.

Пусть функция дифференцируема и строго монотонна на . Пусть также в точке производная . Тогда в точке определена дифференцируемая функция , которую называют обратной к , а ее производная вычисляется по формуле .

Наверх

10. Дифференцируемость, дифференциал.

Дифференцируемость функции в точке.

Пусть функция определена в некоторой окрестности точки . Рассмотрим приращение функции в этой точке: . Функция называется дифференцируемой в точке , если ее приращение можно записать в виде , где – приращение независимой переменной, А – постоянная, не зависящая от , – бесконечно малая функция при .

Дифференциал функции.

Дифференциалом функции в точке называется линейная по часть приращения . Дифференциал обозначается , то есть . Рассматривая функцию , нетрудно убедиться, что , если – независимая переменная.

Связь дифференциала и производной.

Воспользуемся определением производной для дифференцируемой функции в точке : .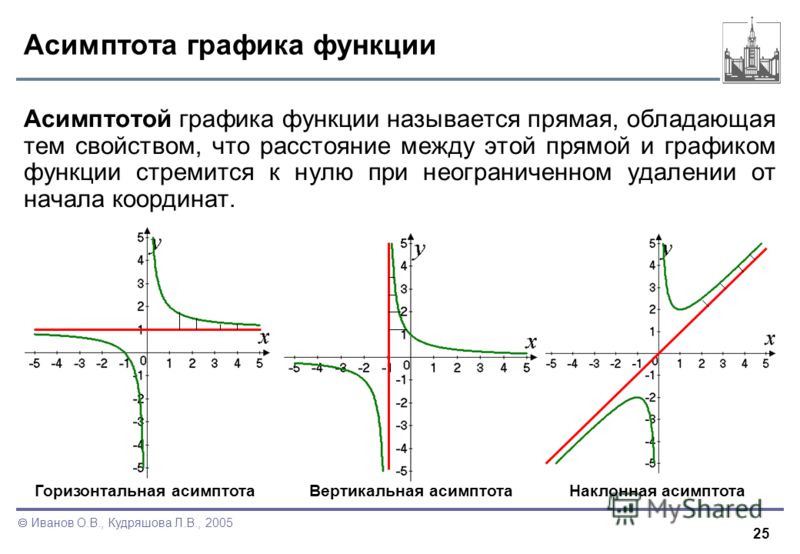 Таким образом, дифференциал функции выражается формулой , то есть для вычисления дифференциала необходимо лишь вычислить производную и умножить ее на . Поэтому часто слова “вычисление производной” и “дифференцирование” считают синонимами. Для того, чтобы функция была дифференцируема в точке, необходимо и достаточно, чтобы в этой точке существовала конечная производная.

Наверх

11. Производные и дифференциалы высших порядков.

Производные высших порядков.

Рассмотрим функцию , определенную на некотором промежутке . Вычислим производную , которая также является функцией на . Производной второго порядка от функции называется производная от ее производной: . Аналогично определяют производную любого порядка: .

Дифференциалы высших порядков.

Рассмотрим дифференциал функции в произвольной точке промежутка : . Здесь – приращение независимой переменной, которое является числом и не зависит от . Сам же дифференциал есть функция от , и можно вычислить дифференциал от этой функции: При этот дифференциал от дифференциала называется дифференциалом второго порядка и вычисляется по формуле Аналогично вычисляется дифференциал любого порядка .

Понятие инвариантности формы дифференциала.

Рассмотрим дифференциал функции в произвольной точке промежутка : . Здесь – приращение независимой переменной, которое является числом и не зависит от . Пусть теперь – функция независимого переменного , определенная на промежутке . Тогда – сложная функция переменного . Вычислим ее дифференциал, используя формулу для производной сложной функции: . Заметим, что и выражение для дифференциала принимает ту же форму , хотя здесь уже функция переменного . Это свойство дифференциала первого порядка называется инвариантностью (т.е. неизменностью) его формы. При вычислении дифференциала второго порядка придется учитывать, что – функция переменного . Поэтому и форма второго (а также и всех следующих) дифференциала неинвариантна.

Наверх

12. Исследование функций и построение графиков.

Рассмотрим функцию , определенную на промежутке (возможно, ) . Характер поведения функции в области определения можно исследовать, опираясь на следующие утверждения.

Если , то график функции пересекает ось абсцисс в точке .

Если , то график функции пересекает ось ординат в точке .

Если в точке функция имеет бесконечный разрыв, то график функции имеет вертикальную асимптоту (Если расстояние от точки кривой до некоторой определенной прямой по мере удаления точки в бесконечность стремится к нулю, то эта прямая называется асимптотой кривой. В случае бесконечного разрыва расстояние от кривой до вертикальной асимптоты стремится к нулю при справа, слева или с обеих сторон).

Если , или , существуют и конечны пределы и , то прямая — асимптота графика функции.

Если , то график функции имеет на левой границе области сходимости вертикальную асимптоту ; аналогично, если , то график функции имеет на правой границе области сходимости вертикальную асимптоту .

Если и существует такое число , что для любого , то исследуемая функция периодична с периодом ; в этом случае достаточно построить график функции на промежутке и доопределить его по периодичности на всю числовую ось.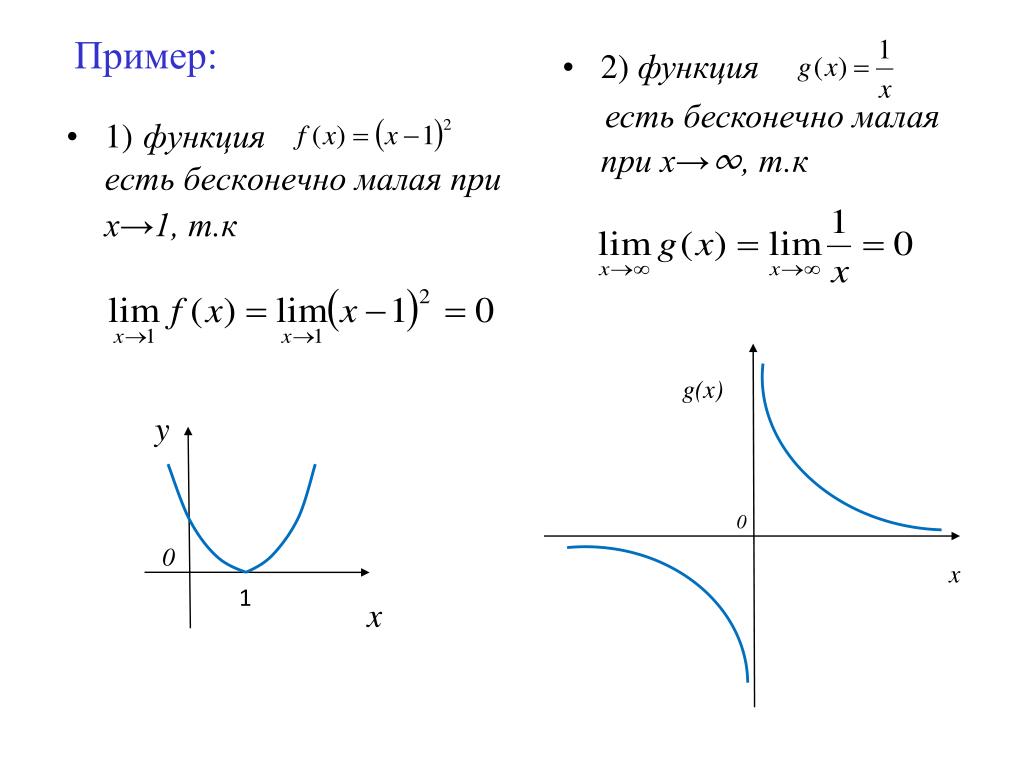

Если , то исследуемая функция четная; этом случае график симметричен относительно оси ординат; достаточно построить график функции на промежутке и отобразить его симметрично относительно оси ординат на .

Если , то исследуемая функция нечетная; этом случае график симметричен относительно начала координат; достаточно построить график функции на промежутке и отобразить его симметрично относительно начала координат на .

Исследование функций с помощью производной.

Если функция дифференцируема на промежутке , за исключением, быть может, конечного числа точек этого промежутка, то можно дополнить изучение поведения функции исследованием на экстремум (точки максимума и точки минимума функции имеют общее название — точки экстремума), используя следующие утверждения.

Для того, чтобы дифференцируемая на функция не убывала (не возрастала) на этом промежутке, необходимо и достаточно, чтобы () на .

Пусть в точке производная или не существует. Если существует окрестность точки , такая, что для из этой окрестности при и при , то функция имеет в точке максимум. Если же при и при , то функция имеет в точке минимум (в этом случае говорят, что “производная меняет знак при переходе через точку ”).

Если непрерывная в точке функция дифференцируема на , при этом на и на , то функция имеет в точке максимум; если же при и при , то функция имеет в точке минимум.

Исследование функций с помощью второй производной.

Если функция дважды дифференцируема на промежутке , за исключением, быть может, конечного числа точек этого промежутка, то исследование поведения функции можно дополнить исследованием выпуклости и вогнутости.

График функции называется выпуклым (выпуклым вниз) на промежутке , если он расположен выше касательной, проведенной в любой точке , . Если же график функции лежит ниже касательной, — то он называется вогнутым (выпуклым вверх).

Если дважды дифференцируемая на промежутке функция имеет на нем положительную вторую производную, то функция выпуклая на . Если же вторая производная отрицательна на промежутке , то функция на нем вогнута.

Если вторая производная равна нулю в точке , а слева и справа от нее имеет значения разных знаков, точка — точка перегиба.

Наверх

13. Кривые на плоскости.

Кривые на плоскости в декартовых координатах.

Кривая на плоскости в прямоугольных (декартовых) координатах — это множество точек, координаты которых связаны соотношениями , , , или ; первые два соотношения задают кривую явно, последнее — неявно. Кривая, заданная уравнением , , называется гладкой, если функция дифференцируема на промежутке . В каждой точкегладкой кривой можно провести касательную , уравнение которой . Уравнение нормали в той же точке имеет вид или . Кривая, заданная неявно уравнением , называется гладкой, если на ней нет особых точек (точка линии называется особой, если в ней одновременно обращаются в нуль обе частные производные функции : ). Уравнения касательной и нормали к такой кривой, проходящих через точку , , имеют соответственно вид и

Кривые, заданные параметрически.

Уравнения , , устанавливающие зависимость декартовых координат точки плоскости от значения параметра , определяют на плоскости кривую, заданную в параметрической форме (говорят еще — заданную параметрически). Поскольку производная функции , заданной параметрически уравнениями , в точке, которая не является особой точкой кривой, вычисляется по формуле , то уравнения касательной и нормали к кривой, проходящих через точку , имеют соответственно вид: .

Кривые в полярных координатах.

Декартовы координаты точки на плоскости связаны с полярными координатамисоотношениями . Многие кривые на плоскости удобно описывать как функции радиуса-вектора и полярного угла — в полярных координатах. Так, уравнение единичной окружности в полярных координатах имеет вид . Уравнение кривой в полярных координатахобычно имеет вид . Угловой коэффициент касательной к графику функции, заданной уравнением , в точке равен , а декартовы координаты точки равны соответственно и .

Наверх

14.

Формула Тейлора.

Остаточный член формулы Тейлора – Пусть функция имеет в точке производные всех порядков до -го включительно. Тогда для справедлива формула Тейлора:

где , называется остаточным членом формулы Тейлора в форме Пеано; — бесконечно малая более высокого порядка малости, чем . Если отбросить остаточный член, то получится приближенная формула Тейлора

правая часть которой называется многочленом Тейлора функции ; его обозначают . Приближенная формула позволяет заменять в различных математических расчетах (аналитических и численных) произвольную функцию ее многочленом Тейлора.

Из формулы Тейлора видно, что чем точка ближе к точке , тем выше точность такой аппроксимации и эта точность растет с ростом степени многочлена. Это означает, в свою очередь, что чем больше производных имеет функция в некоторой окрестности точки , тем выше точность, с которой многочлен Тейлора аппроксимирует функцию в этой окрестности.

Разложение основных элементарных функций – Положив и вычислив соответствующие производные в нуле, получим формулы Тейлора для основных элементарных функций:

Разложение функций с использованием стандартных разложений – Для разложения по формуле Тейлора функции в окрестности произвольной точки необходимо сделать замену переменной , то есть , и воспользоваться одним из приведенных выше разложений основных функций в окрестности точки .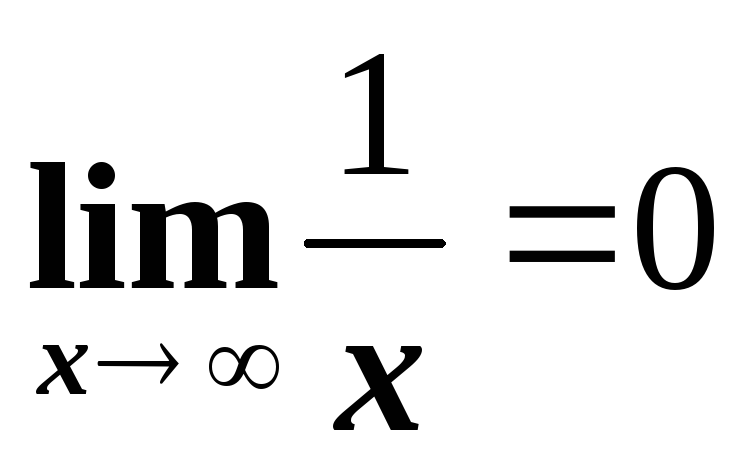

Наверх

15. Неопределенный интеграл, простейшие методы интегрирования.

Первообразная и неопределенный интеграл – Рассмотрим функцию , определенную на промежутке (здесь возможно ). Дифференцируемая на промежутке функция , производная которой в каждой точке равна , называется первообразной функции : . Поскольку , то можно говорить о семействе первообразных — множестве функций вида , . Семейство первообразных функции называется неопределенным интегралом функции и обозначается символом : для всех . Здесь — знак интеграла, — подынтегральное выражение, — подынтегральная функция, — переменная интегрирования, — значение неопределенного интеграла, семейство первообразных функции , . То есть производнаянеопределенного интеграла равна подынтегральной функции. Наоборот, , следовательно, дифференцирование и вычисление неопределенного интеграла, – взаимно обратные операции. Не представляет труда с помощью таблицы производных составить таблицу неопределенных интегралов. Важным свойством неопределенного интеграла является линейность: , здесь – постоянные. Вычисление неопределенного интеграла обычно сводится к преобразованию подынтегрального выражения так, чтобы можно было воспользоваться таблицей интегралов.

Интегрирование заменой переменной – Если — непрерывно дифференцируемая функция, то, полагая , получим формулу интегрирования заменой переменной . Если замена переменной выбрана правильно, то интеграл в правой части должен легко вычисляться. Для некоторых классов функций существуют стандартные замены, сводящие интеграл к табличному.

Интегрирование по частям – Пусть – непрерывно дифференцируемые функции. Тогда справедлива формула интегрирования по частям . Название “по частям” связано с тем, что для записи интеграла в правой части нужно проинтегрировать “часть” подынтегрального выражения в левой части. Метод интегрирования по частям используется для интегралов вида , , , и некоторых других.

Наверх

16.

Интегрирование некоторых классов функций.

Интегрирование рациональных функций – Функция называется рациональной, если она вычисляется с помощью четырех арифметических действий, то есть в общем случае является частным от деления двух многочленов: . Если , рациональная дробь называется правильной. Неопределенный интеграл от рациональной функции всегда можно вычислить. Для этого:

Если , выделяем целую часть рациональной дроби с помощью деления многочлена на многочлен. Правильную рациональную дробь (или правильный остаток от деления) раскладываем на простейшие дроби. Вид разложения определяется корнями многочлена , а именно:

Каждому действительному корню кратности 1 в разложении соответствует член .

Каждому действительному корню кратности в разложении соответствует набор из членов .

Каждой паре комплексно сопряженных корней кратности 1 в разложении соответствует член ( – корни уравнения ).

Каждой паре комплексно сопряженных корней кратности в разложении соответствует набор из членов .

В приведенных выражениях – неопределенные коэффициенты, которые можно найти, приводя разложение обратно к общему знаменателю , приравнивая полученные коэффициенты при степенях к соответствующим коэффициентам и решая систему относительно .

Наконец, полученное разложение интегрируем почленно.

Интегрирование тригонометрических функций – Интегралы вида , где – рациональная функция своих аргументов, вычисляются с помощью универсальной замены переменной . При этом . Однако универсальная замена обычно связана с большими вычислениями, поэтому в некоторых случаях можно ее избежать.

Интегралы вида вычисляются с помощью замены . Интегралы вида вычисляются с помощью замены . Интегралы вида , если , то есть четная рациональная функция своих аргументов вычисляются с помощью замены .

Интегралы вида вычисляются с помощью формул понижения степени .

Интегрирование иррациональных функций – Общий принцип интегрирования иррациональных выражений заключается в замене переменной, позволяющей избавиться от корней в подынтегральном выражении. Для некоторых классов функций эта цель достигается с помощью стандартных замен.

Интегралы вида , где – рациональная функция своих аргументов, вычисляются заменой .

Интегралы вида вычисляются заменой или .

Интегралы вида вычисляются заменой или . Интегралы вида вычисляются заменой или .

Наверх

17. Определенный интеграл. Формула Ньютона-Лейбница.

Определенный интеграл, его геометрический смысл.

Рассмотрим функцию , определенную на промежутке . Разобьем промежуток на произвольных частей точками и обозначим , , . На каждом промежутке возьмем произвольную точку и вычислим в ней значение функции. Выражение называется интегральной суммой функции на .Если при существует и конечен предел последовательности частичных сумм , не зависящий ни от способа разбиения промежутка точками , ни от выбора , то этот предел называют определенным интегралом от функции по промежутку , а саму функцию — интегрируемой на . Обозначают .

Из приведенного определения естественно следует геометрический смысл определенного интеграла: если , то равен площади фигуры, ограниченной графиком функции, осью абсцисс и прямыми .

Формула Ньютона-Лейбница.

Значение определенного интеграла может быть вычислено по формуле Ньютона-Лейбница =, здесь символ означает, что из значения при верхнем пределе b нужно вычесть значение при нижнем пределе a , — первообразная функция для . Таким образом, вычисление определенного интеграла сводится к нахождению первообразной, то есть неопределенного интеграла.

Методы вычисления определенного интеграла.

Если — непрерывно дифференцируемая на отрезке функция, , и , когда изменяется на , то, положив , получим формулу замены переменной в определенном интеграле .

Пусть – непрерывно дифференцируемые функции. Тогда справедлива формула интегрирования по частям . Эта формула применяется для тех же классов функций, что и при вычислении неопределенного интеграла.

Наверх

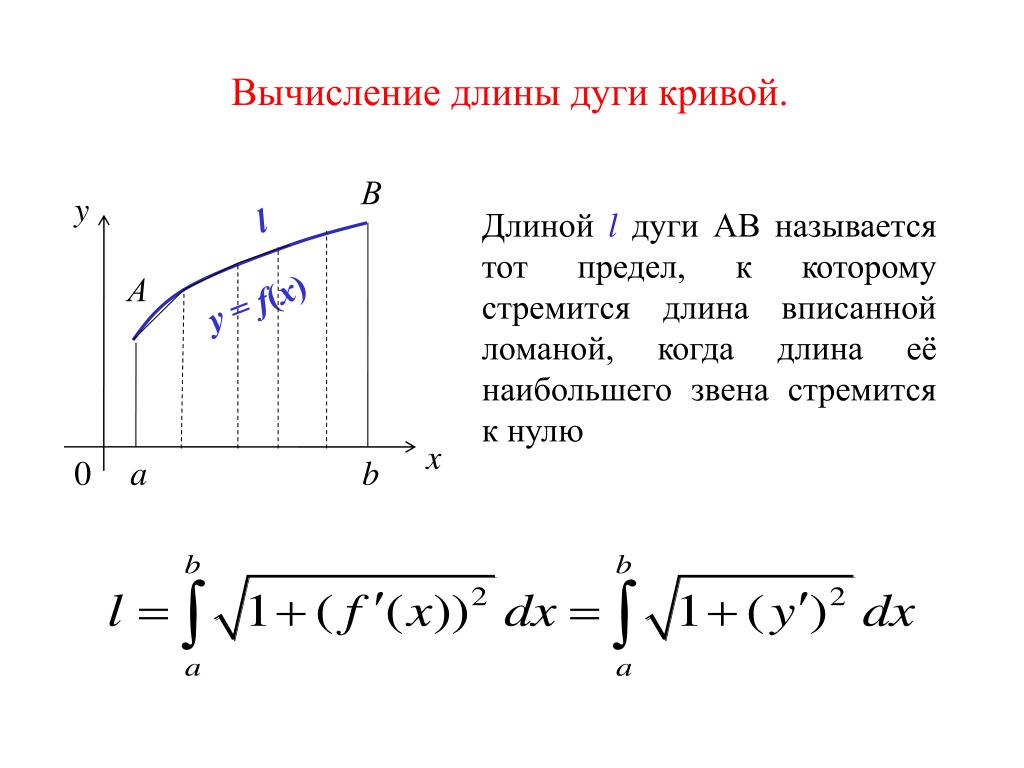
18. Применение определенного интеграла для площадей и длин дуг.

Вычисление площадей и длин дуг кривых в декартовых координатах.

Пусть на плоскости задана область, ограниченная снизу кривой , заданной в декартовых координатах, сверху – кривой , слева – прямой (ее может и не быть, если ), справа – прямой . Исходя из геометрического смысла определенного интеграла, площадь этой области можно вычислить по формуле . Здесь не нужно заботиться, какая из функций и где положительная, а какая отрицательная. Если, например, , то формула сама прибавит нужную площадь. Более сложные области всегда можно разбить так, чтобы выполнялись указанные условия.

Пусть на отрезке уравнением задана плоская кривая. Ее длина вычисляется по формуле

Вычисление площадей и длин дуг при параметрическом задании кривых.

Если область на плоскости снизу ограничена кривой, заданной параметрически, то есть , при этом , а сверху – кривой . Тогда площадь такой плоской фигуры вычисляем по формуле . Эта формула совпадает с формулой вычисления площади в декартовых координатах, если учесть, что .

Пусть кривая на плоскости задана параметрически . Тогда длина этой кривой вычисляется по формуле .

Вычисление площадей и длин дуг кривых в полярных координатах.

Когда кривая, ограничивающая область, задана в полярных координатах , то площадь этой области вычисляем по формуле . Основная трудность в использовании этой формулы заключается в определении пределов интегрирования . Здесь нужно понимать, что кривая определена только, если . Поскольку в формуле присутствует , то она учтет и не существующую площадь, когда . Решив уравнение , найдем пределы интегрирования.

Если кривая, ограничивающая область, задана в полярных координатах , то ее длина вычисляется по формуле . Пределы интегрирования определяются из тех же соображений, что и при вычислении площади.

Наверх

19.

Несобственные интегралы.

Интеграл как функция верхнего предела.

Для функции , интегрируемой для всех , значение интеграла зависит от значения верхнего предела ; можно рассмотреть функцию переменной : каждому значению ставится в соответствие число, равное значению интеграла . Таким образом, можно рассматривать определенный интеграл как функцию верхнего предела: ; функция определена в области интегрируемости подынтегральной функции . Если — первообразная для , то значение можно вычислить по формуле Ньютона—Лейбница: . Функцию можно исследовать, не вычисляя первообразной. Для интегрируемой при функции справедливы следующие утверждения: непрерывна на промежутке , причем ; если при , то монотонно возрастает на промежутке ; если непрерывна при , то дифференцируема на промежутке , причем .

Несобственные интегралы по неограниченному промежутку.

Пусть функция интегрируема для всех и . Если существует предел , то этот предел называют несобственным интегралом по неограниченному промежутку и обозначают его . Если предел конечен, то говорят, что несобственный интеграл сходится и его значение вычисляют по формуле . Аналогично определен интеграл для интегрируемой при функции и интеграл для функции , интегрируемой на . Если рассмотренные пределы бесконечны, то говорят, что соответствующий несобственный интеграл расходится.

Несобственные интегралы от неограниченных функций.

Пусть функция интегрируема на любом отрезке, целиком содержащемся в промежутке, и бесконечно большая в точке . Если существует предел , то этот предел называют несобственным интегралом от неограниченной функции по и обозначают его . Если предел конечен, то говорят, что несобственный интеграл сходится и его значение вычисляют по формуле . Аналогично определен интеграл от интегрируемой на любом конечном отрезке, содержащемся в , бесконечно большой в точке функции . Если пределы бесконечны, то говорят, что соответствующий несобственный интеграл расходится.

Исследование несобственных интегралов на сходимость.

Вычисление несобственных интегралов сводится к вычислению первообразной, использованию формулы Ньютона-Лейбница и вычислению предела. Каждый из этапов сам по себе достаточно сложен, и разумно приступать к ним, если есть уверенность, что интеграл сходится, то есть предел конечен. Поэтому, в конечном счете, самым важным в теории несобственных интегралов является исследование их на сходимость: если интеграл расходится, то его и вычислять не надо. Одним из главных инструментов исследования несобственных интегралов на сходимость являются теоремы сравнения.

Рассмотрим две неотрицательные функции и , определенные при . Пусть для всех , начиная с некоторого числа . Тогда, если сходится интеграл от большей функции , то сходится и интеграл от меньшей, то есть. Если расходится интеграл от меньшей функции ,то расходится и интеграл от большей – .

Если , то несобственные интегралы от этих функций или оба сходятся или оба расходятся.

Аналогичные утверждения, которые называют признаками сравнения, имеют место и для интегралов по конечному промежутку от неограниченных функций.

Наверх

20. Числовые ряды.

Числовой ряд. Рассмотрим произвольную числовую последовательность и формально составим сумму ее членов Это выражение называют числовым рядом, или просто рядом. Члены последовательности называют членами ряда. Конечно, невозможно вычислить сумму бесконечного числа слагаемых, но легко вычислить сумму первых n членов ряда . Эта сумма называется n-ой частичной суммой.

Сходимость числового ряда. Ряд называют сходящимся, если существует и конечен предел последовательности частичных сумм ряда. Сам предел при этом называют суммой ряда и обозначают , . Если предел частичных сумм не существует или бесконечен, то ряд расходится. Разность называется остатком ряда. Очевидно, что для сходящегося ряда . Это означает, что сумму сходящегося ряда можно вычислить с любой точностью, заменяя ее частичной суммой соответствующего порядка. Для расходящегося ряда это не так. Поэтому сходимость или расходимость конкретного ряда является основным вопросом для исследования. Если ряд сходится, то (необходимое условие сходимости ряда). Обратное, вообще говоря, неверно. Члены ряда могут стремиться к нулю, но ряд при этом может расходиться.

Суммирование числовых рядов. Если возможно найти общий член последовательности , то по определению можно найти и сумму ряда, вычисляя предел этой последовательности.

Наверх

21. Сходимость знакоположительных рядов.

Теоремы сравнения.

1. Рассмотрим два числовых ряда с неотрицательными членами и , . Если при всех n, начиная с некоторого номера, , то из сходимости ряда следует сходимость ряда. Наоборот, из расходимости ряда следует расходимость ряда.

2. Если для таких же двух рядов , то оба ряда или сходятся или расходятся одновременно. При использовании теорем сравнения нужно иметь ряд-эталон, с которым сравнивать и про сходимость которого известно заранее. В качестве таких рядов чаще всего берут обобщенный гармонический ряд , который сходится при и расходится при , или геометрический ряд , который сходится при и расходится при .

Признаки сходимости. Признаки сходимости Даламбера. Для ряда с положительными членами , вычислим . Если , то ряд сходится, – расходится. При признак Даламбера ответа не дает: ряд может как сходиться, так и расходиться.

Признак сходимости Коши. Для ряда с неотрицательными членами , вычислим . Если , то ряд сходится, – расходится. При признак Коши ответа не дает: ряд может как сходиться, так и расходиться.

Наверх

22. Сходимость знакопеременных рядов.

Абсолютная и условная сходимость. Если в последовательности бесконечно много положительных и отрицательных членов, то ряд называется знакопеременным. Ряд называется знакочередующимся. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд . Если ряд из модулей расходится, а сам ряд сходится, то его называют условно сходящимся. Исследование знакопеременного ряда начинают с исследования на сходимость ряда из модулей методами для рядов с неотрицательными членами. Если такой ряд сходится, то получен ответ: ряд сходится абсолютно.

Исследование знакочередующихся рядов. Если ряд из модулей расходится, то для знакочередующегося ряда можно применить признак Лейбница: если последовательность стремится к нулю, монотонно убывая, , то ряд сходится, по крайней мере, условно. Для знакочередующегося ряда очень просто оценивается остаток ряда: .

Наверх

23. Функциональные ряды, равномерная сходимость.

Функциональный ряд, его сходимость. Рассмотрим ряд, , членами которого являются функции, определенные на промежутке . При каждом фиксированном имеем числовой ряд, сходимость которого может быть исследована рассмотренными ранее методами. Сумма функционального ряда также является функцией от х: . По определению предела последовательности: если для можно указать номер ( что интересно, для каждого фиксированного – свой номер, т.е. ), такой, что для выполняется неравенство , то это и означает, что функциональный ряд сходится к функции. Множество , для которого это выполняется, называется областью сходимости функционального ряда.

Равномерная сходимость функционального ряда. Пусть , т.е. функциональный ряд сходится. Если для можно указать номер независимо от , такой, что для выполняется неравенство , то говорят, что функциональный ряд сходится равномерно на множестве .

Исследование на равномерную сходимость. Признак Вейерштрасса равномерной сходимости функционального ряда: если существует сходящийся числовой ряд с положительными членами, такой, что для всех , начиная с некоторого номера и всех выполняется неравенство , то функциональный ряд сходится на равномерно. Числовой ряд в этом случае называют мажорантой для функционального ряда.

Наверх

24. Ряд Тейлора.

Степенные ряды. Функциональный ряд , где – числовая последовательность, называется степенным рядом. Степенной ряд сходится на интервале с центром в точке . Число – радиус сходимости степенного ряда может быть вычислено по формулам , или . Степенной ряд сходится равномерно на любом отрезке, целиком лежащем внутри интервала сходимости. Сходимость степенного ряда на границах интервала сходимости необходимо исследовать специально для конкретного ряда.

Разложение функций в ряд Тейлора. При исследовании свойств бесконечно дифференцируемых функций изучают их степенные ряды ряды Тейлора. Пусть функция определена в некоторой окрестности точки и имеет в этой точке производные всех порядков. Ряд

называется рядом Тейлора для функции в точке . При такой ряд называют также рядом Маклорена: . Функция может быть разложена в степенной ряд на интервале , если существует степенной ряд, сходящийся к на этом интервале. Если функция раскладывается в степенной ряд в некоторой окрестности точки , то это ряд Тейлора. Пусть функция бесконечно дифференцируема на интервале и все ее производные ограничены в совокупности на этом интервале, то есть существует число , такое, что для всех и для всех справедливо неравенство . Тогда ряд Тейлора сходится к для всех . Приведем разложения в ряд Тейлора для основных элементарных функций.

Наверх

25. Ряд Фурье.

Ряд Фурье, его сходимость. Пусть функция абсолютно интегрируема на отрезке , то есть существует . Тогда ей можно поставить в соответствие ее тригонометрический ряд Фурье: . Коэффициенты тригонометрического ряда Фурье называют коэффициентами Фурье и вычисляют по формулам Эйлера-Фурье: . Если функция кусочно-гладкая на отрезке , то ее тригонометрический ряд Фурье сходится в каждой точке этого отрезка. При этом, если – сумма ряда Фурье, то для любого . То есть, если непрерывна в точке , то . Если в точке у разрыв первого рода, то ряд Фурье сходится к среднеарифметическому левого и правого пределов функции в точке .

Разложение в ряд Фурье на произвольном отрезке. Для кусочно-гладкой на отрезке функции задача о разложении в ряд Фурье на этом отрезке линейной заменой сводится к задаче о разложении функции на отрезке : , .

Наверх

26. Сходимость ряда Фурье.

Сходимость ряда Фурье, явление Гиббса. Если функция кусочно-гладкая на отрезке , то ее тригонометрический ряд Фурье сходится в каждой точке этого отрезка. При этом, если – сумма ряда Фурье, то для любого . То есть, если непрерывна в точке , то . Если в точке у разрыв первого рода, то ряд Фурье сходится к среднеарифметическому левого и правого пределов функции в точке . В окрестности точек непрерывности функции разность между значением функции в точке и значением частичной суммы ряда в этой точке стремится к нулю при , что полностью соответствует теории, поскольку в этом случае . В окрестности точек разрыва частичные суммы ряда Фурье ведут себя иначе. Эта особенность поведения частичных сумм Фурье в окрестности точек разрыва называется явлением Гиббса. Оно состоит в том, что для некоторых функций в точке ее скачка существуют такие значения , что

Это не противоречит теории, поскольку у Гиббса рассмотрен предел , а в теории v .

Приближение функций, минимальное свойство коэффициентов Фурье. Функция , где – произвольные числа, называется тригонометрическим многочленом. Тригонометрическим многочленом наилучшего приближения n-ой степени для функции на отрезке называется такой многочлен , среднеквадратичное отклонение которого от функции минимально: . Для любой ограниченной интегрируемой на функции частичная сумма ее ряда Фурье является тригонометрическим многочленом наилучшего приближения n-ой степени.

Зависимость скорости сходимости от гладкости функций. Скорость сходимости ряда Фурье функции зависит от ее гладкости (количества непрерывных производных). Если непрерывно дифференцируема r раз на отрезке , то справедливо неравенство , где . Для среднеквадратичного отклонения справедлива оценка , где .

Наверх

27. Функции многих переменных.

Функция двух переменных. Переменная (с областью изменения ) называется функцией независимых переменных в множестве , если каждой паре их значений из по некоторому правилу или закону ставится в соответствие одно определенное значение из множества . Множество v область определения функции, множество v область ее значений. Функциональная зависимость от обозначается так: и т.п. Выберем в пространстве систему координат , изобразим на плоскости множество ; в каждой точке этого множества восстановим перпендикуляр к плоскости и отложим на нем значение . Геометрическое место полученных таким образом точек и является пространственным графиком функции двух переменных.

Линии и поверхности уровня. Линией уровня функции двух переменных называется геометрическое место точек на плоскости , в которых функция принимает одно и то же значение. Линии уровня функции определяются уравнением , где . Изучая линии уровня функции, можно исследовать характер ее изменения, не прибегая к пространственному графику. Поверхностью уровня функции трех переменных называется геометрическое место точек в пространстве, в которых функция принимает одно и то же значение. Уравнение поверхностей уровня имеет вид: . Поскольку график функции трех переменных нам недоступен, поверхности уровня являются единственным средством изучения таких функций.

Локальные экстремумы. Точка называется точкой локального минимума (максимума) функции , определенной в области , если существует окрестность этой точки, такая, что для всех точек этой окрестности, отличных от . Такие экстремумы (максимумы и минимумы) называются нестрогими. Строгие экстремумы имеют место в случае, когда выполнены строгие неравенства.

Наверх

28. Частные производные, градиент.

Частные производные. Пусть – функция двух переменных, определенная в некоторой окрестности точки . Если существует конечный предел , то говорят, что функция имеет в точке частную производную по переменной . Аналогично определяется частная производная по . Обозначают:

Пусть – функция n переменных, определенная в области n-мерного пространства. Частной производной функции по переменной называется предел

Из определения частной производной следует правило: при вычислении производной по одной из переменных все остальные переменные считаем постоянными, учитывая, что производная постоянной равна нулю и постоянную можно выносить за знак производной.

Производная по направлению. Если в n-мерном пространстве задан единичный вектор , то изменение дифференцируемой функции в направлении этого вектора характеризуется производной по направлению: . В частности, для функции трех переменных , – направляющие косинусы вектора .

Градиент. Производная по направлению представляет собой скалярное произведение вектора и вектора с координатами , который называется градиентом функции и обозначается . Поскольку , где – угол между и , то вектор указывает направление скорейшего возрастания функции , а его модуль равен производной по этому направлению.

Полный дифференцал. Для приращения дифференцируемой функции справедливо равенство . Линейная по приращениям аргументов часть приращения функции называется полным дифференциалом функции и обозначается .

Производные и дифференциалы высших порядков. Дифференцируя частную производную как функцию нескольких переменных по одной из переменных, получим производные второго порядка. Например, для функции двух переменных: . Если смешанные производные и непрерывны, то они равны, то есть не зависят от порядка дифференцирования. Аналогично определяются, например, . Если при вычислении полного дифференциала от дифференциала первого порядка учесть, что приращения аргументов есть числа и оставить их неизменными, то получим дифференциал второго порядка. Например, для функции двух переменных: . Здесь учтено равенство смешанных производных второго порядка и принято . При этих допущениях формулу дифференциала любого порядка можно получить из символического выражения: .

Наверх

29. Неявные функции.

Неявная функция одной переменной. Пусть в некоторой области плоскости задана функция , и пусть линия уровня этой функции , определяемая уравнением , является графиком некоторой функции , определяемой уравнением . В этом случае говорят, что функция задана неявно уравнением . Для существования неявной функции требуется выполнение следующих условий: функция и ее частная производная по непрерывны в , . Тогда в некоторой окрестности точки существует единственная непрерывная функция , задаваемая уравнением , так, что в этой окрестности .

Неявная функция многих переменных. Аналогично рассматривают функции многих переменных, заданные неявно. Например, при выполнении соответствующих условий, уравнение задает неявно функцию . Это же уравнение может задавать неявно функцию или .

Производная неявной функции. При вычислении производной неявной функции воспользуемся правилом дифференцирования сложной функции. Продифференцируем уравнение : . Отсюда получим формулу для производной функции , заданной неявно: . Таким же способом нетрудно получить формулы для частных производных функции нескольких переменных, заданной неявно, например, уравнением : , .

Наверх

30. Формула Тейлора для многих переменных.

Формулы Тейлора и Маклорена. Если функция имеет в некоторой окрестности точки непрерывные частные производные до (n+1)-го порядка включительно, то для любой точки из этой окрестности справедлива формула Тейлора n-го порядка: , где ,

и т.д. Формула Тейлора, записанная в окрестности точки (0,0) называется формулой Маклорена. Например, для функции двух переменных при n=2: .

Аппроксимация функции многочленом. Выражение

называется многочленом Тейлора n-го порядка. Поскольку , то в окрестности точки функцию можно приближенно заменить, или, как говорят, аппроксимировать, ее многочленом Тейлора, т.е. . Чем ближе точка к точке , тем выше точность такой аппроксимации; кроме того, точность возрастает с ростом n. Это означает, что, чем больше непрерывных производных имеет функция , тем точнее представляет ее многочлен Тейлора.

Наверх

31. Исследование на экстремум.

Исследование на экстремум функции двух переменных. Обозначим через приращение функции в точке . Если – точка локального минимума функции , то существует окрестность , в которой (обратное неравенство в случае максимума). Из формулы Тейлора первого порядка следует, что приращение дважды непрерывно дифференцируемой функции может сохранять знак, если главная линейная часть приращения функции в точке экстремума (максимума или минимума) равна нулю, т.е. выполнено необходимое условие экстремума: если точка – точка экстремума, то . Такая точка называется стационарной точкой функции. Приращение функции в стационарной точке имеет вид . Обозначим . Справедливо следующее достаточное условие экстремума. Пусть функция дважды непрерывно дифференцируема в окрестности точки и . Если , то в точке функция достигает экстремума. Если при этом , то этот экстремум v минимум, при – максимум. Если же , то в точке экстремума нет. Геометрически достаточное условие означает, что в окрестности экстремума график функции близок к поверхности . Если , то для определения знака приращения необходимо изучить члены формулы Тейлора более высокого порядка.

Наверх

32. Условный экстремум.

Условные экстремумы. Пусть функция определена в некоторой области и в этой области задана кривая уравнением . Условным экстремумом функции двух переменных называют ее экстремум при условии, что точки берутся на заданной кривой. Если из уравнения кривой можно, например, выразить , то задача о нахождении условного экстремума сводится к исследованию на экстремум функции одной переменной .

Метод множителей Лагранжа. Если уравнение не разрешимо ни относительно , ни относительно , то рассматривают функцию Лагранжа. Необходимым условием существования условного экстремума функции при условии является равенство нулю всех частных производных функции Лагранжа: .

Наибольшее и наименьшее значение функции в области. Поскольку функция , непрерывная в ограниченной замкнутой области достигает в ней своего наибольшего и наименьшего значений, задача об их нахождении разделяется на две части: найти экстремумы функции двух переменных внутри области, найти ее условные экстремумы на границе области, при условии, что граница задана уравнением .

Наверх

33. Двойной и тройной интегралы.

Двойной интеграл в декартовых координатах. Пусть ограниченная замкнутая область плоскости с кусочно-гладкой границей и пусть функция определена и ограничена на . Посредством сетки кусочно-гладких кривых разобьем на конечное число элементарных областей с площадями (разбиение ). Пусть – наибольший из диаметров областей , получающийся при разбиении . В каждой из элементарных областей выберем произвольную точку . Число называется интегральной суммой и ставится в соответствие каждому разбиению и каждому выбору точек . Если существует и он не зависит от выбора разбиения и точек , то функция называется интегрируемой по Риману в области , а сам предел называется двойным интегралом от функции по области и обозначается или . Двойной интеграл существует, если непрерывна на . Допустимы точки разрыва первого рода, лежащие на конечном числе гладких кривых в .

Свойства двойного интеграла. Свойства двойного интеграла аналогичны свойствам определенного интеграла:

Линейность:

. Аддитивность:

, если S1 и S2 две области без общих внутренних точек.

Если для каждой точки выполнено неравенство , то .

Если интегрируема на , то функция также интегрируема, причем .

Если и наименьшее и наибольшее значения функции в области, а ее площадь, то .

Теорема о среднем значении: если непрерывна в связной области , то существует, по крайней мере, одна точка такая, что .

Вычисление двойного интеграла.

Если , где – непрерывные на функции, то двойной интеграл может быть вычислен двумя последовательными интегрированиями: . Аналогично, если , то .

Тройной интеграл и его свойства. Пусть – ограниченная замкнутая пространственная область, границей которой является кусочно-гладкая поверхность, и пусть функция определена и ограничена в . Посредством сетки кусочно-гладких поверхностей разобьем на конечное число элементарных областей с объемами (разбиение). Пусть . наибольший из диаметров областей , получающийся при разбиении . В каждой из элементарных областей выберем произвольную точку . Число ставится в соответствие каждому разбиению и каждому выбору точек и называется интегральной суммой. Если существует и он не зависит от выбора разбиения и точек, то функция называется интегрируемой по Риману в области , а сам предел называется тройным интегралом от функции по области и обозначается . Свойства тройных интегралов такие же, как и у двойных интегралов.

Вычисление тройного интеграла в декартовых координатах. Пусть является цилиндрическим телом, проекция которого на плоскость есть область и которое ограничено снизу поверхностью , а сверху v поверхностью , где – непрерывные функции в . Тогда , то есть интегрированием по z тройной интеграл сводится к двойному интегралу по области . Для областей более сложной формы вычисление двойных и тройных интегралов производится разбиением областей на конечное число простых областей с уже рассмотренными свойствами.

Наверх

34. Замена переменных в кратных интегралах.

Замена переменных в двойном интеграле. Пусть функции взаимно однозначно отображают открытое множество, содержащее область плоскости на открытое множество, содержащее область , и пусть является образом . Если и их частные производные непрерывны, а определитель , то . Выражение называется элементом площади в криволинейных координатах, функциональный определитель – якобианом.

Вычисление площади.

Замена переменных в тройном интеграле. Пусть посредством функций производится взаимно однозначное отображение открытого множества, содержащего область пространства на открытое множество, содержащее область пространства и есть образ . Если эти три функции непрерывны вместе со своими первыми частными производными в области и якобиан, то . Выражение называется элементом объема в криволинейных координатах .

Вычисление объема.

Двойной интеграл в полярных координатах. Введем на плоскости полярные координаты. Пусть – область, полученная взаимно однозначным отображением области плоскости , определяемым функциями . Тогда , а двойной интеграл в полярных координатах вычисляется по формуле: .Элемент площади в полярных координатах есть .

Наверх

35. Сферические и цилиндрические координаты.

Тройной интеграл в цилиндрических координатах. Введем в пространстве цилиндрические координаты. Для этого на плоскости используем полярные координаты, а третья координата произвольной точки остается . Учитывая связь полярных координат с декартовыми, получим выражение декартовых координат через цилиндрические: . Тогда и тройной интеграл в цилиндрических координатах вычисляется по формуле: . Элемент объема в цилиндрической системе координат есть .

Тройной интеграл в сферических координатах. Введем в пространстве сферическую систему координат. Для этого рассмотрим произвольную точку в декартовой системе координат. Спроектируем ее на плоскость , получив точку . Положение точки в пространстве будем характеризовать ее расстоянием от начала координат , углом между отрезком и положительной полуосью , углом между отрезком и положительной полуосью . Декартовы координаты точки выражаются через сферические по формулам: . В этом случае . Тогда тройной интеграл в сферических координатах вычисляется по формуле:

Элемент объема в сферической системе координат есть .

Наверх

36. Поверхностный интеграл по площади поверхности.

Площадь гладкой поверхности. Рассмотрим кусок поверхности , заданной уравнением . Пусть выполняется условие , что означает, что в каждой точке поверхности существует нормаль с направляющим вектором . Разобьем поверхность сеткой гладких кривых на элементарные области ( разбиение ). Пусть – наибольший из диаметров элементарных областей. Если независимо от разбиения существует , то он и называется площадью данной поверхности. Пусть однозначно проектируется на плоскость и – эта проекция. Элементу площади области на плоскости соответствует элемент площади поверхности , равный , где – угол между нормалью к поверхности и осью . Поэтому вычисление площади поверхности сводится к вычислению двойного интеграла по проекции поверхности на плоскость. Если поверхность задана уравнением , то и площадь поверхности вычисляется по формуле , здесь – проекция поверхности на плоскость . Если поверхность однозначно проектируется на другие координатные плоскости, то соответственно изменится формула вычисления площади поверхности.

Поверхностный интеграл 1-го рода. Пусть некоторая функция определена и ограничена на гладкой поверхности . Выберем разбиение поверхности и точки на каждой элементарной области и составим интегральную сумму . Если независимо от выбора разбиения и точек существует , то он называется поверхностным интегралом по площади поверхности (1-го рода) от функции и обозначается .

Свойства и вычисление поверхностного интеграла по площади поверхности. Если поверхность задана уравнением и однозначно проектируется на плоскость , то поверхностный интеграл 1-го рода вычисляется по формуле . Нетрудно получить аналогичные формулы, если поверхность однозначно проектируется на другие координатные плоскости. Поскольку вычисление поверхностного интеграла сводится к двойному интегралу, то, естественно, все свойства поверхностного интеграла 1-го рода такие же, как и у двойного.

Наверх

37. Криволинейный интеграл по длине дуги.

Криволинейный интеграл 1-го рода. Пусть – отрезок кусочно-гладкой кривой с началом в точке и концом в точке и – ограниченная функция, определенная в некоторой области, содержащей кривую . Выберем на кривой произвольные точки , разбивая ее на элементарные отрезки (разбиение ), длина каждого . Обозначим . Пусть – произвольная точка на элементарном отрезке . Составим интегральную сумму . Если независимо от разбиения и выбора точек существует , то он называется криволинейным интегралом по длине кривой (1-го рода) и обозначается . Аналогично определяется криволинейный интеграл 1-го рода от функции трех переменных по отрезку пространственной кривой.

Свойства и вычисление криволинейного интеграла по длине дуги. Криволинейный интеграл 1-го рода не зависит от направления движения по кривой , то есть. Это единственное свойство, которое не совпадает с обычными свойствами интегралов, определеямых через предел интегральной суммы. Если – отрезок кусочно-гладкой кривой, заданной параметрически:

, то криволинейный интеграл вычисляется по формуле:

. Если плоская кривая задана в явном виде, то криволинейный интеграл вычисляется по формуле: .

Наверх

38. Скалярное поле.

Скалярное поле. Если каждой точке пространства ставится в соответствие скалярная величина , то возникает скалярное поле (например, поле температуры, поле электрического потенциала). Если введены декартовы координаты, то обозначают также

или . Поле может быть плоским, если , центральным (сферическим), если , цилиндрическим, если .

Поверхности и линии уровня. Свойства скалярных полей можно наглядно изучать с помощью поверхностей уровня. Это поверхности в пространстве, на которых принимает постоянное значение. Их уравнение: . В плоском скалярном поле линиями уровня называют кривые, на которых поле принимает постоянное значение: . В отдельных случаях линии уровня могут вырождаться в точки, а поверхности уровня в точки и кривые.

Производная по направлению и градиент скалярного поля. Пусть – единичный вектор с координатами , – скалярное поле. Производная по направлению характеризует изменение поля в данном направлении и вычисляется по формуле . Производная по направлению представляет собой скалярное произведение вектора и вектора с координатами , который называется градиентом функции и обозначается . Поскольку , где – угол между и , то вектор указывает направление скорейшего возрастания поля , а его модуль равен производной по этому направлению. Так как компоненты градиента являются частными производными, нетрудно получить следующие свойства градиента:

Наверх

39. Векторное поле.

Векторное поле. Если каждой точке пространства ставится в соответствие вектор , то говорят, что задано векторное поле (поле скоростей частиц движущейся жидкости, силовое поле, поле электрической напряженности). В декартовой системе координат векторное поле можно записать в виде: . Скалярные функции однозначно определяют векторное поле. Векторное поле может быть плоским, если , сферическим, когда , , цилиндрическим, когда , .

Векторные линии (линии тока). Для наглядного представления векторных полей используют векторные линии (линии тока). Это кривые, в каждой точке которых вектор является касательным вектором. Через каждую точку проходит одна линия тока. За исключением точек, где поле не определено или , линии тока никогда не пересекаются. В декартовых координатах дифференциальные уравнения линий тока имеют вид:

Наверх

40. Поток векторного поля.

Поток векторного поля. Рассмотрим кусок поверхности , заданной уравнением . Пусть выполняется условие , что означает, что в каждой точке поверхности существует нормаль с направляющим вектором . Выберем одну из сторон поверхности следующим образом: построим на поверхности достаточно малый замкнутый контур, на котором задано направление обхода. Построим вектор нормали в точке поверхности, лежащей внутри контура. Если из конца вектора нормали обход контура кажется происходящим против часовой стрелки, то будем называть сторону поверхности, обращенную к вектору нормали положительной стороной. Таким образом, будем рассматривать ориентированную двухстороннюю поверхность, а односторонние поверхности лист Мебиуса, бутылку Клейна оставим в покое. Потоком векторного поля через ориентированную поверхность называется поверхностный интеграл по площади поверхности (1-го рода) , где – единичный вектор нормали, направленный в положительную сторону. Выбор положительной стороны обычно диктуется физическими условиями задачи.

Непосредственное вычисление потока. Поскольку поток векторного поля определен с помощью поверхностного интеграла, вычисление потока сводится к вычислению такого интеграла от функции , где – компоненты векторного поля, – направляющие косинусы вектора нормали.

Наверх

41. Формула Остроградского.

Поток векторного поля через замкнутую поверхность. Рассмотрим кусочно-гладкую двухстороннюю замкнутую ориентированную поверхность . Поток векторного поля через замкнутую поверхность является важной характеристикой поля и позволяет судить о наличии источников и стоков поля. При непосредственном вычислении потока через замкнутую поверхность приходится разбивать ее на части, однозначно проектируемые на координатные плоскости.

Формула Остроградского. Пусть замкнутая поверхность ограничивает некоторый объем . Тогда в декартовых координатах справедлива формула Остроградского: , где – компоненты векторного поля.

Дивергенция векторного поля. Дивергенцией векторного поля называется . Точка находится внутри замкнутой поверхности , ограничивающей объем , который при вычислении предела стягивается в эту точку. является скалярной величиной и служит мерой источников поля. Если в некоторой области поля , то источников поля в этой области нет. Такое поле называют соленоидальным. Используя формулу Остроградского, нетрудно получить выражение для вычисления дивергенции в декартовых координатах: . Из свойств частных производных следуют свойства дивергенции векторного поля:

Наверх

42. Криволинейный интеграл в векторном поле.

Криволинейный интеграл в векторном поле. Пусть заданы некоторое векторное поле и кривая АВ (А – начальная точка, В – конечная). Криволинейный интеграл в векторном поле есть скаляр, полученный следующим образом:

Разобьем кривую точками А=А0, А1, А2-Аn=В на n частей, приближенно изображаемых векторами (разбиение ).

Обозначим .

На границе или внутри каждой элементарной дуги Аi-1Ai выберем точку, которой соответствует радиус-вектор и составим интегральную сумму .

Если существует и он не зависит от разбиения и выбора точек, то этот предел называется криволинейным интегралом в векторном поле. В декартовой системе координат:, где – компоненты векторного поля.

Если кривая задана в параметрической форме:

, то вычисление криволинейного интеграла сводится к определенному интегралу:

. Используя определение и формулу для вычисления нетрудно получить свойства криволинейного интеграла:

Подчеркнем, что, в отличие от криволинейного интеграла по длине дуги, криволинейный интеграл в векторном поле меняет знак при изменении направления интегрирования.

Если векторное поле, описывающее физическое силовое поле, то криволинейный интеграл выражает работу, которую совершает сила при переносе материальной точки из пункта А в пункт В вдоль кривой АВ.

Циркуляция векторного поля. Важной характеристикой векторного поля является циркуляция векторного поля, которая равна криволинейному интегралу по замкнутой кривой в области поля, или, как говорят, по замкнутому контуру: . Циркуляция векторного поля является скалярной величиной и характеризует вихревые свойства поля. Если в некоторой области поля циркуляция равна нулю, то поле называют безвихревым.

Наверх

43. Формула Стокса.

Формула Стокса. Рассмотрим в пространстве кусок двухсторонней кусочно-гладкой поверхности , край которой образуется кусочно-гладкой кривой . Выберем положительную сторону поверхности (из конца единичного вектора нормали обход границы представляется против часовой стрелки). Для циркуляции векторного поля вдоль контура границы имеет место формула Стокса: , где – компоненты векторного поля, – направляющие косинусы вектора нормали.

Ротор векторного поля. Рассмотрим в пространстве замкнутый контур с выбранным направлением обхода, лежащий в ориентированной плоскости на ее положительной стороне (из конца единичного вектора нормали обход контура представляется против часовой стрелки). Ротором (или вихрем) векторного поля в точке называется вектор, проекция которого на направление вектора нормали есть . Точка лежит на плоскости внутри контура , который стягивается в эту точку при вычислении предела. Поскольку ротор поля определяется через циркуляцию, то он тоже является мерой завихренности поля. Найдем компоненты ротора в декартовой системе координат, воспользовавшись формулой Стокса. Для этого выберем сначала координатную плоскость y0z с нормальным вектором , затем x0z, , затем x0y, . Применяя каждый раз теорему о среднем для интеграла, получим:

Теперь теорема Стокса может быть сформулирована следующим образом: циркуляция векторного поля вдоль контура равна потоку ротора поля через поверхность, натянутую на этот контур. Выражение для ротора поля проще запомнить, если записать его в виде определителя:. Используя свойства частных производных и определителей, получим следующие свойства ротора векторного поля:

Наверх

44. Потенциальное поле.

Потенциальное поле. Если векторное поле , то оно называется потенциальным, а скалярное поле , соответственно, его потенциалом. Самым известным примером такого соответствия является электрическое поле, напряженность которого , где – потенциал электрического поля. Минус в формуле связан с историческим выбором направления вектора напряженности от плюса к минусу, когда уже умели тереть шерсть об янтарь, но не знали, как это описывать математически.

Условие потенциальности поля. Пусть задано скалярное поле , причем данная функция дважды непрерывно дифференцируема. Напомним, что в этом случае смешанные частные производные второго порядка не зависят от порядка дифференцирования. Вычислим .

Нетрудно видеть, что при этих условиях получается тождественный ноль. То есть, если поле потенциальное, то его .

Вычисление потенциала векторного поля. Если мы убедились, что поле является потенциальным, то есть его ротор равен нулю, то представляет интерес вычислить потенциал этого поля. Для этого рассмотрим криволинейный интеграл в данном векторном поле: , где точки А и В – начальная и конечная точки кривой. Поскольку , то скалярное произведение векторов и является полным дифференциалом функции : . Поэтому из свойств криволинейного интеграла следует, что . Смысл полученной формулы состоит в том, что работа поля по перемещению материальной точки из А в В не зависит от пути интегрирования, а только от конечной и начальной точек, точнее, от разности потенциалов в этих точках. Понятие разности потенциалов хорошо известно из физики. Для вычисления потенциала поля в произвольной точке В выберем начальную точку А, от которой начнем отсчет (в физике часто это – бесконечно удаленная точка). Тогда . Поскольку интеграл не зависит от пути интегрирования, то выберем его так, как нам удобно: сначала параллельно оси 0х, потом параллельно 0у, наконец, параллельно 0z. Обозначая , получим:

Здесь – компоненты векторного поля . Поскольку выбор начальной точки произволен, потенциал поля определяется с точностью до произвольной постоянной, которая определяется физическими соображениями.

Бесконечно малые функции

Бесконечно малые функции.

Определение. Функция f(x) называется бесконечно малой при х®а, где а может быть числом или одной из величин ¥, +¥ или -¥, если .

Бесконечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет.

Пример. Функция f(x) = xⁿ является бесконечно малой при х®0 и не является бесконечно малой при х®1, т.к. .

Теорема. Для того, чтобы функция f(x) при х®а имела предел, равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие

f(x) = A + a(x),

где a(х) – бесконечно малая при х ® а (a(х)®0 при х ® а).

Свойства бесконечно малых функций:

1) Сумма фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.

2) Произведение фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.

3) Произведение бесконечно малой функции на функцию, ограниченную вблизи точки х = а является бесконечно малой функцией при х®а.

4) Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть величина бесконечно малая.

Используя понятие бесконечно малых функций, приведем доказательство некоторых теорем о пределах, приведенных выше.

Доказательство теоремы 2. Представим f(x) = A + a(x), g(x) = B + b(x), где

, тогда

f(x) ± g(x) = (A + B) + a(x) + b(x)

A + B = const, a(х) + b(х) – бесконечно малая, значит

Теорема доказана.

Доказательство теоремы 3. Представим f(x) = A + a(x), g(x) = B + b(x), где

, тогда

A×B = const, a(х) и b(х) – бесконечно малые, значит

Теорема доказана.

Бесконечно большие функции и их связь с

бесконечно малыми.

Определение. Предел функции f(x) при х®а, где а- число, равен бесконечности, если для любого числа М>0 существует такое число D>0, что неравенство

ïf(x)ï>M

выполняется при всех х, удовлетворяющих условию

0 < ïx – aï < D

Записывается .

Собственно, если в приведенном выше определении заменить условие ïf(x)ï>M на f(x)>M, то получим:

а если заменить на f(x)<M, то:

Графически приведенные выше случаи можно проиллюстрировать следующим образом:

a x a x a x

Определение. Функция называется бесконечно большой при х®а, где а – чосли или одна из величин ¥, +¥ или -¥, если , где А – число или одна из величин ¥, +¥ или -¥.

Связь бесконечно больших и бесконечно малых функций осуществляется в соответствии со следующей теоремой.

Теорема. Если f(x)®0 при х®а (если х®¥ ) и не обращается в ноль, то

Сравнение бесконечно малых функций.

Пусть a(х), b(х) и g(х) – бесконечно малые функции при х ® а. Будем обозначать эти функции a, b и g соответственно. Эти бесконечно малые функции можно сравнивать по быстроте их убывания, т.е. по быстроте их стремления к нулю.

Например, функция f(x) = x¹⁰ стремится к нулю быстрее, чем функция f(x) = x.2

Функция МАКС

В этой статье описаны синтаксис формулы и использование функции МАКС в Microsoft Excel.

Описание

Возвращает наибольшее значение из набора значений.

Синтаксис

МАКС(число1;[число2];…)

Аргументы функции МАКС описаны ниже.

Число1, число2,… Аргумент “число1” является обязательным, последующие числа необязательные. От 1 до 255 чисел, среди которых требуется найти наибольшее.

Замечания

Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения и текст в массиве или ссылке игнорируются.
Если аргументы не содержат чисел, функция МАКС возвращает значение 0 (ноль).
Аргументы, которые являются значениями ошибки или текстами, не преобразуемыми в числа, приводят в возникновению ошибок.
Если в ссылку в качестве части вычислений необходимо добавить логические значения и текстовые представления, воспользуйтесь функцией МАКСА.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные
10
7
9
27
2
Формула	Описание	Результат
=МАКС(A2:A6)	Наибольшее значение в диапазоне A2:A6.	27
=МАКС(A2:A6; 30)	Наибольшее значение в диапазоне A2:A6 и значение 30.	30

Функция нуля – значение, график, примеры

Есть разные виды функций, которые мы изучаем в математике. Функция – это отношение, которое отображает элементы в домене на элементы в ко-домене, так что каждый элемент в домене отображается только на один элемент в ко-домене. Нулевая функция – это функция, область значений которой состоит из всех действительных чисел, а диапазон состоит из одного элемента, то есть 0. Нулевая функция также является постоянной функцией, поскольку ее значение никогда не изменяется при изменении входных данных.В этой статье мы исследуем свойства нулевой функции и ее природу.

Что такое функция нуля?

Нулевая функция – это постоянная функция, для которой выходное значение всегда равно нулю, независимо от входов. Вход нулевой функции может принимать любое значение из действительных чисел, тогда как выход нулевой функции фиксирован, то есть 0. Поскольку изображение каждого элемента в области равно 0, нулевая функция не является однозначной. -одна функция.

Значение функции нуля

Функция f: R → R, определенная как f (x) = 0, для всех значений x в R, называется нулевой функцией. Диапазон нулевой функции – это одноэлементный набор, то есть {0}. Как и любой другой график постоянной функции, параллельный оси x, график нулевой функции – это сама ось x, поскольку значение координаты y равно 0 на всем графике. Это функция «многие к одному», поскольку все элементы в домене имеют одно и то же изображение, то есть 0.

График нулевой функции

График нулевой функции f (x) = 0 аналогичен графикам других постоянных функций, которые параллельны оси x.Любая функция может рассматриваться как постоянная функция, если она имеет вид y = k, где k – константа, а k – любое действительное число. Он также записывается как f (x) = k. Поскольку диапазон нулевой функции равен нулю, а значение координаты y всегда равно нулю, поэтому график нулевой функции представляет собой саму ось X. Другими словами, мы можем сказать, что график нулевой функции – это горизонтальная ось.

Характеристики нулевой функции

Функции имеют различные характеристики, такие как наклон, область, диапазон, дифференцируемость, предел и непрерывность.Давайте теперь исследуем различные характеристики нулевой функции. Являясь типом постоянной функции, нулевая функция имеет свойства, аналогичные постоянным функциям.

Наклон нулевой функции: Нулевая функция также может быть записана как y = 0x + 0. Сравнивая эту форму с формой пересечения наклона прямой y = mx + b, где m – наклон линии, а b – точка пересечения по оси Y, получаем, что наклон нулевой функции равен 0.
Область и диапазон нулевой функции: Нулевая функция – это линейная функция, диапазон которой содержит только один элемент независимо от количества элементов в домене.Поскольку нулевая функция определена для всех значений x, поэтому область значений – это все действительные числа R, а диапазон нулевой функции равен {0}.
Производная нуля функции: Дифференциация любой постоянной функции нуля. Производная считается наклоном функции в любой заданной точке, и мы уже знаем, что наклон нулевой функции всегда равен 0. Следовательно, производная нулевой функции равна 0.
Предел функции нуля: Согласно свойствам пределов, предел постоянной функции равен той же константе.Следовательно, предел нулевой функции равен 0.
Непрерывность нуля Функция: Постоянные функции являются непрерывными, поскольку они представляют собой горизонтальные линии, которые непрерывно проходят с обеих сторон без каких-либо разрывов. Поскольку нулевая функция является постоянной функцией, поэтому нулевая функция является непрерывной функцией без каких-либо разрывов во всей области.

Нулевая функция четная или нечетная?

Функция f называется четной, если f (-x) = f (x), для всех значений x в области определения f, а функция называется нечетной, если f (-x) = -f (x) , для всех значений x в области определения f.Нулевая функция – единственная функция, которая удовлетворяет обоим этим условиям вместе для всех значений x в области определения f. Следовательно, нулевая функция бывает как четной, так и нечетной. Если f (x) = 0 – нулевая функция, то f (-x) = f (x) = -f (x) = 0, поскольку выход всегда остается прежним.

Важные примечания относительно функции нуля

Выход (диапазон) нулевой функции всегда 0.
Функция нуля может быть как четной, так и нечетной.
График нулевой функции – это ось X, и это непрерывная функция.

Связанные темы с функцией нуля

Часто задаваемые вопросы о функции нуля

Что такое функция нуля в математике?

Функция f: R → R, определенная как f (x) = 0, для всех значений x в R, называется нулевой функцией. Диапазон нулевой функции – это одноэлементный набор, то есть {0}. Нулевая функция – это постоянная функция, для которой выходное значение всегда равно нулю, независимо от входов.

Что такое ненулевое значение?

Функция, выход которой не равен нулю для всех значений входов, называется ненулевой функцией.Ненулевая функция может иметь 0 на выходе для некоторых значений в области, но если она равна нулю для всех элементов в области, то это нулевая функция.

Нулевая функция четна или нечетна?

Нулевая функция – это единственная функция, которая является как четной, так и нечетной, поскольку она удовлетворяет условиям f (-x) = f (x) и f (-x) = -f (x) для всех значений x в области выключенный.

Что является неотъемлемой частью функции нуля?

Интеграл от нулевой функции f (x) = 0 – это произвольная константа C, которая может принимать любое значение действительных чисел.Поскольку производная любой константы равна нулю, следовательно, интеграл от нулевой функции является произвольной константой.

Как найти нули функции?

Нули функции можно вычислить с помощью различных методов, таких как квадратная формула и факторизация полинома.

Бесконечные ограничения

Некоторые функции «взлетают» в положительном или отрицательном направлении (неограниченное увеличение или уменьшение) около определенных значений независимой переменной.Когда это происходит, говорят, что функция имеет бесконечный предел ; значит, вы пишите. Также обратите внимание, что функция имеет вертикальную асимптоту при x = c , если выполняется любой из вышеуказанных пределов.

В общем, дробная функция будет иметь бесконечный предел, если предел знаменателя равен нулю, а предел числителя не равен нулю. Знак бесконечного предела определяется знаком частного числителя и знаменателя при значениях, близких к числу, к которому приближается независимая переменная.

Пример 1: Оценить.

Когда x приближается к 0, числитель всегда положителен, а знаменатель приближается к 0 и всегда положителен; следовательно, функция неограниченно возрастает и. Функция имеет вертикальную асимптоту при x = 0 (см. Рисунок).

Рисунок 1 График y = 1/ x ².

Пример 2: Оценить.

Поскольку x приближается к 2 слева, числитель приближается к 5, а знаменатель приближается к 0 через отрицательные значения; следовательно, функция неограниченно убывает и.Функция имеет вертикальную асимптоту при x = 2.

Пример 3: Оценить.

Перезапись 1/ x ² – 1/ x ³ как эквивалентное дробное выражение ( x – 1) / x ³, числитель приближается к -1, а знаменатель приближается к 0 через положительные значения, когда x приближается к 0 справа; следовательно, функция неограниченно убывает и. Функция имеет вертикальную асимптоту при x = 0.

Предупреждение: не оценивайте пределы по отдельности и вычитайте их, потому что ± ∞ не являются действительными числами. В этом примере

, что бессмысленно.

4.6 Пределы на бесконечности и асимптоты – Объем расчетов 1

Решение

Шаг 1. Функция определяется до тех пор, пока знаменатель не равен нулю. Следовательно, домен – это набор всех действительных чисел, кроме

Шаг 2. Найдите перехватчики. Если тогда 0 – это перехват.Если то, что означает Следовательно, является единственным перехватом.

Шаг 3. Оцените пределы на бесконечности. Поскольку это рациональная функция, разделим числитель и знаменатель на наибольшую степень знаменателя: получаем

Следовательно, имеет горизонтальную асимптоту as и

Шаг 4. Чтобы определить, есть ли вертикальные асимптоты, сначала проверьте, есть ли в знаменателе нули. Мы обнаруживаем, что знаменатель равен нулю, когда для определения того, являются ли линии или вертикальными асимптотами оценки, и глядя на каждый односторонний предел, когда мы видим, что

Кроме того, глядя на каждый односторонний предел, мы обнаруживаем, что

Шаг 5.Вычислить первую производную:

Критические точки возникают в точках, где или не определено. Мы видим, что, когда производная не является неопределенной ни в одной точке в области значений, однако они не находятся в области значений Следовательно, чтобы определить, где увеличивается, а где уменьшается, разделите интервал на четыре меньших интервала: и и выберите контрольную точку. в каждом интервале, чтобы определить знак в каждом из этих интервалов. Значения и являются хорошим выбором для контрольных точек, как показано в следующей таблице.

Из этого анализа мы заключаем, что имеет локальный минимум на уровне, но не имеет локального максимума.

Шаг 6. Вычислить вторую производную:

Чтобы определить интервалы, где вогнутость вверх и где вогнута вниз, нам сначала нужно найти все точки, где или не определено. Поскольку числитель для любого никогда не равен нулю. Кроме того, не является неопределенным ни для одного в области Однако, как обсуждалось ранее, они не входят в область действия Следовательно, чтобы определить вогнутость, мы делим интервал на три меньших интервала и выбираем контрольную точку в каждом из этих интервалов. чтобы оценить знак в каждом из этих интервалов.Значения и являются возможными контрольными точками, как показано в следующей таблице.

Объединив всю эту информацию, мы приходим к графику, показанному ниже. Обратите внимание, что, несмотря на то, что вогнутость изменяется и ни в одном из этих мест нет точек перегиба, так как не является непрерывным в точке

или

деление по нулю и непрерывности.

Деление на ноль и непрерывность.

Понимание математики к Питер Альфельд, Кафедра математики, Университет Юты

Деление на ноль и непрерывность.

Что значит a / b близко к a / c когда b близко к c ? Настоящая проблема вот что a / b зависит от непрерывно от b , если b не равно нулю. Исчисление учителя тратят много времени на определение и объяснение непрерывность и когда-нибудь может произойти ясное и подробное объяснение на этих страницах.Но пока позволь мне просто дайте вам то, что на самом деле составляет определение преемственность. Для меня это имеет смысл, но может показаться чрезмерно загадочен для вас.

Для ненулевого b и любого числа a , a / b непрерывно зависит от b , поскольку для любого положительного числа epsilon мы можем найти положительное число дельта такое что а / б отличается от а / ц не более чем эпсилон , пока b не отличается от c более чем на дельта.

Другими словами, мы можем изменить соотношение произвольно малым, выбирая разницу в знаменатели достаточно малы .

В оставшейся части этой страницы позвольте мне предположить, что вы знаете Исчисление. Рассмотрим соотношение двух функций

ф (х) / г (х)

и предположим, что

f (0) = g (0) = 0.

Тогда предел f (x) / g (x) , поскольку x стремится к ноль может существовать. Причем, если и f , и g дифференцируемы, и предел f ‘(x) / g’ (x) существует, то

lim f (x) / g (x) = lim f ‘(x) / g’ (x)

поскольку x стремится к нулю.

Это известно как Правило Л’Опиталя.

Мелкий шрифт, ваши комментарии, дополнительные ссылки, Питер Альфельд, PA1UM

[18 апреля 1997 г.]

0 Разделено на 0: Решите задачи о предельных значениях в исчислении, часть 1

Если вы, как и многие студенты, изучающие математику, понимаете идею о пределах , но, возможно, у вас могут возникнуть проблемы с решением проблем с предельными значениями в домашней работе, особенно когда вы поначалу найти «0 делится на 0.В этом посте мы покажем вам методы, которые должен знать, , для решения подобных проблем.

I. Идея пределов и замена

(супер просто, когда это работает)

Вам, наверное, уже говорили что-то вроде

$ \ displaystyle {\ lim_ {x \ to a} f (x)} = L $ означает, что по мере приближения x к a ,
функция f приближается к L (даже если она никогда не равна L ).
Вы на правильном пути к пониманию ограничений, если это утверждение имеет для вас смысл, и вы можете взглянуть на рисунок, подобный приведенному ниже, и сразу увидеть, что
$$ \ lim_ {x \ to 2} f (x) = 4 $$
, потому что независимо от того, движемся ли мы к $ x = 2 $ слева или справа, мы приближаемся к высоте $ y = 4 $.

В этом случае предел – это просто значение функции при x = 2: $ \ displaystyle {\ lim_ {x \ to 2} f (x)} = f (2) = 4 $.

А в некоторых домашних заданиях и контрольных вопросах (если ваш учитель чувствует себя хорошо), чтобы найти предел, вы просто подставляете значение x в функцию и находите значение в этом месте.Мы назовем этот подход . Тактика №1: замена .

Пример 1 .
Найдите $ \ displaystyle {\ lim_ {x \ to 2} x + 2} $.

Решение .
Давайте попробуем просто подставить $ x = 2 $ в выражение:
$$ \ lim_ {x \ to 2} x + 2 = 2 + 2 = 4 \ quad \ cmark $$

Это тот же предел, что и показано на графике выше: изображенная на графике функция равна $ f (x) = x + 2 $, и поэтому, когда мы приближаемся к $ x = 2 $ слева или справа, мы приближаемся к фактическому значению функции при $ x = 2 $, что составляет $ y = f (2) = 4 $.

В этом случае простая замена значения x = 2 в функцию работает: вы получаете число ($ f (2) = 4 $), и все готово. Достаточно простой техники «подстановки».
[Конец примера 1.]

Пример 2 .
Найдите $ \ displaystyle {\ lim_ {x \ to \ pi / 2} \ sin x} $.

Решение .
Давайте снова попробуем подстановку и установим $ x = \ dfrac {\ pi} {2} $:
$$ \ lim_ {x \ to \ dfrac {\ pi} {2}} \ sin x = \ sin \ dfrac { \ pi} {2} = 1 \ quad \ cmark $$

На графике показано, что $ y = \ sin x $.По мере приближения к $ x = \ dfrac {\ pi} {2} $ слева или справа вы приближаетесь к высоте y = 1, что является значением функции при $ x = \ dfrac {\ pi} {2} $. Следовательно, предел $ x \ to \ dfrac {\ pi} {2} $ для sin x равен 1.

Опять же, в этом случае подстановка работает: вы вставляете значение $ x = \ dfrac {\ pi} {2} $, и вы получите номер $ \ left (f \ left (\ dfrac {\ pi} {2} \ right) = 1 \ right) $ out. Готово; легкий.
[Конец примера 2]

Пример 3 .2-4} {x-2} = \ frac {4-4} {2-2} = \ frac {0} {0} $$

Ой, ой: $ \ dfrac {0} {0} $.
Это проблема. Давайте ненадолго остановимся на этом примере. . .

Практически во всех домашних заданиях и контрольных вопросах, когда вы пробуете замену, вы получите 0, разделенный на 0. Затем вам понадобится другая тактика, чтобы найти предел.

Морщинка : Нам не понадобилась бы концепция лимита, если бы вы всегда могли просто вставить число и найти там значение функции. Вместо этого правда в том, что когда вы пробуете замену почти со всеми своими домашними заданиями и контрольными вопросами, вы получите $ \ dfrac {0} {0} $, «ноль делится на ноль.Этот результат известен как неопределенный предел , что является причудливым способом сказать «еще не известно». Он говорит вам, что на самом деле ответом может быть что угодно – вы просто еще не знаете, – и поэтому вам нужно еще поработать.

В частности, результат $ \ dfrac {0} {0} $ сигнализирует о том, что для определения предела необходимо использовать другой метод. К счастью, три простых тактики позволят вам решить большинство проблем. Давайте посмотрим на каждого.

II. Когда вы получите 0, разделенное на 0, сначала попробуйте

разложить на множители

Если вы попробуете подстановку и получите $ \ dfrac {0} {0} $, следующим шагом будет попытка . Тактика № 2: Разложите на множитель числитель или знаменатель если возможно.2-4} {x-2}} $ \ (= \) $ \ displaystyle {\ lim_ {x \ to 2} \ frac {(x + 2) (x-2)} {x -2}} $ А, теперь мы можем отменить проблемный термин: \ (= \) $ \ displaystyle {\ lim_ {x \ to 2} \ frac { (x + 2) \ cancel {(x-2)}} {\ cancel {x-2}}} $ \ (= \) $ \ displaystyle {\ lim_ {x \ to 2} \, (x + 2)} $ А теперь простая замена для завершения: \ (= \) $ \ displaystyle {2 + 2 = 4 \ quad \ cmark} $

Обратите внимание, что функция $ \ dfrac {x ^ 2-4} {x-2} $ упростилась до $ x + 2 $, когда мы разложили ее на множители.2-4} {x-2}} = \ lim_ {x \ to 2} (x + 2) = 4 $.
[End Example 3.]

Если вы работаете в классе Calculus, мы гарантируем, что вы столкнетесь с множеством проблем, которые потребуют факторизации функции, чтобы найти предел. В самом деле, на каждом экзамене по математическому анализу, касающемуся ограничений, который мы видели, была по крайней мере одна проблема, когда вы изначально получали $ \ dfrac {0} {0} $ и должны были пересчитать, чтобы получить окончательный ответ. Откройте следующее поле, чтобы увидеть больше примеров.

Откройте, чтобы увидеть больше примеров факторинга для определения лимита.2 -3x + 2} && = \ lim_ {x \ to 1} \ frac {(x + 2) (x-1)} {(x-2) (x-1)} && = \ lim_ {x \ to 1} \ frac {x + 2} {x-2} && = \ frac {1 + 2} {1-2} = -3 \ quad \ cmark
\ end {align *}

[свернуть]

Эти проблемы являются просто, как только вы научитесь их распознавать и учитывать фактор.

Если можете, фактор.

Результат : Если подстановка дает результат в форме $ \ dfrac {0} {0} $, первое, что вы должны попробовать, это факторинг. Если вы можете разложить числитель и / или знаменатель на множители, проблемный член в знаменателе аннулируется.Гарантированно.

III. Тактика № 3: используйте конъюгаты

Если функция имеет квадратный корень и подстановка дает $ \ dfrac {0} {0} $, 0 делится на 0, затем умножьте числитель и знаменатель на
$$ 1 = \ frac {\ text {конъюгат термина (числитель или знаменатель) с корнем}} {\ text {конъюгат термина (числитель или знаменатель) с корнем}} $$
Как и в случае факторинга, этот подход, вероятно, приведет к к возможности отменить срок. Пример 4 иллюстрирует.

Пример 4 .
Найдите $ \ displaystyle {\ lim_ {x \ to 0} \ dfrac {\ sqrt {x + 5} – \ sqrt {5}} {x}} $.
Решение .
Сначала мы пробуем замену:
$$ \ lim_ {x \ to 0} \ frac {\ sqrt {x + 5} – \ sqrt {5}} {x} = \ frac {\ sqrt {0 + 5} – \ sqrt {5}} {0} = \ frac {0} {0} $$
Поскольку ограничение указано в форме $ \ dfrac {0} {0} $, оно не определено – мы еще не знаем, что Это. Нам нужно поработать, чтобы привести его в форму, в которой мы сможем определить предел.

Итак, давайте избавимся от квадратных корней, используя сопряжение, как вы практиковали в алгебре: умножьте числитель и знаменатель на сопряжение числителя, $ \ sqrt {x + 5} + \ sqrt {5} $.
\ begin {align *}
\ lim_ {x \ to 0} \ dfrac {\ sqrt {x + 5} – \ sqrt {5}} {x} & = \ lim_ {x \ to 0} \ dfrac {\ sqrt {x + 5} – \ sqrt {5}} {x} \ cdot \ dfrac {\ sqrt {x + 5} + \ sqrt {5}} {\ sqrt {x + 5} + \ sqrt {5}} \\ \\
& = \ lim_ {x \ to 0} \ dfrac {\ sqrt {x + 5} \ sqrt {x + 5} + \ sqrt {x + 5} \ sqrt {5} – \ sqrt {5 } \ sqrt {x + 5} – \ sqrt {5} \ sqrt {5}} {x [\ sqrt {x + 5} + \ sqrt {5}]} \\ \\
& = \ lim_ {x \ в 0} \ dfrac {(x + 5) – 5} {x [\ sqrt {x + 5} + \ sqrt {5}]} \\ \\
& = \ lim_ {x \ to 0} \ dfrac { x} {x [\ sqrt {x + 5} + \ sqrt {5}]} \\ \\
& = \ lim_ {x \ to 0} \ dfrac {\ cancel {x}} {\ cancel {x} [\ sqrt {x + 5} + \ sqrt {5}]} \\ \\
& = \ lim_ {x \ to 0} \ dfrac {1} {\ sqrt {x + 5} + \ sqrt {5} } \\ \\
& = \ dfrac {1} {\ sqrt {0 + 5} + \ sqrt {5}} = \ dfrac {1} {2 \ sqrt {5}} \ quad \ cmark
\ end { align *}
Функция, с которой мы начали, $ \ dfrac {\ sqrt {x + 5} – \ sqrt {5}} {x} $, и та, которой мы закончили (после умножения на сопряжение), $ \ dfrac {1} {\ sqrt {x + 5} + \ sqrt {5}} $, то же самое, за исключением того, что первая функция не определена при x = 0 (поскольку ее знаменатель равен нулю о там), а второго нет.Мы показали это на расположенных рядом диаграммах ниже. Следовательно, их пределы такие же, как от $ x \ to 0 $, и поэтому $ \ displaystyle {\ lim_ {x \ to 0} \ dfrac {\ sqrt {x + 5} – \ sqrt {5}} {x} = \ lim_ {x \ to 0} \ dfrac {1} {\ sqrt {x + 5} + \ sqrt {5}} = \ dfrac {1} {2 \ sqrt {5}}} $.

[Конец примера 4.]

Как показывает пример 4, если подстановка дает вам $ \ dfrac {0} {0} $ и функция имеет квадратные корни, тактика умножения числителя и знаменателя на сопряжение квадратного корня даст вам новую функцию, в которой работает подстановка.Всегда.

Откройте, чтобы увидеть другой пример с квадратными корнями.

Пример 5 .
Найдите $ \ displaystyle {\ lim_ {x \ to 9} \ dfrac {9-x} {3- \ sqrt {x}}} $.
Решение .
Сначала мы пробуем замену:
$$ \ lim_ {x \ to 9} \ frac {9-x} {3- \ sqrt {x}} = \ frac {9-9} {3- \ sqrt {9}} = \ frac {0} {0} $$
Поскольку лимит имеет форму $ \ dfrac {0} {0} $, он не определен – мы еще не знаем, что это такое. Итак, давайте умножим числитель и знаменатель на сопряжение знаменателя, $ 3 + \ sqrt {x} $:
\ begin {align *}
\ lim_ {x \ to 9} \ frac {9-x} {3- \ sqrt {x}} & = \ lim_ {x \ to 9} \ frac {9-x} {3- \ sqrt {x}} \ cdot \ frac {3+ \ sqrt {x}} {3+ \ sqrt { x}} \\ [8 пикселей] & = \ lim_ {x \ to 9} \ frac {(9-x) \ left (3+ \ sqrt {x} \ right)} {9 +3 \ sqrt {x} -3 \ sqrt {x} -x } \\ [8px] & = \ lim_ {x \ to 9} \ frac {(9-x) \ left (3+ \ sqrt {x} \ right)} {9 -x} \\ [8px] & = \ lim_ {x \ to 9} \ frac {\ cancel {(9-x)} \ left (3+ \ sqrt {x} \ right)} {\ cancel {9-x}} \\ [8px] & = \ lim_ {x \ to 9} 3+ \ sqrt {x} \\ [8px] & = 3+ \ sqrt {9} = 3 + 3 = 6 \ quad \ cmark
\ end {align *}

[свернуть]

Результат: Если у вас есть квадратные корни, умножьте числитель и знаменатель на сопряженная часть квадратного корня.

Мы рассмотрим другие ключевые тактики работы с 0, деленным на 0, в нашем следующем посте «Как решить проблемы с предельными значениями в исчислении – часть 2. Мы представим еще несколько ограничений, которые вы должны просто научиться распознавать.

Конечно вам нужно практиковаться.

Конечно, прочитать наше обсуждение недостаточно. Вместо этого вам нужно попрактиковаться и сделать несколько ошибок для себя, чтобы это стало для вас рутиной, когда вы будете сдавать экзамен. У нас есть множество проблем, которые вы можете попробовать, все с комплексными решениями, которые можно найти в один клик, чтобы вы могли быстро проверить свою работу или выйти из строя, без каких-либо проблем.{\ displaystyle x} $ и $ 1 $ на $ x $, когда $ x $ приближается к $ 0 $, равняется $ 1 $.

Когда предел f (x) не определен?

Привет Николаса,

Существует техническое определение предела функции, которое обычно выражается греческими буквами дельта и эпсилон. Ответ на ваш вопрос заключается в том, что предел не определен, если предел не существует, как описано в этом техническом определении. Однако я думаю, что это не тот ответ, который вы ищете.Что я сделаю, так это приведу вам три примера ситуаций, когда предел не существует.

Пример 1.

f (x) = ¹/_{x ²}

Эта функция существует для всех ненулевых значений x.

f (x) = ¹/_{x ²}

В этом примере предел f (x), когда x приближается к нулю, не существует, поскольку, когда x приближается к нулю, значения функции неограниченно увеличиваются.Значения функции «приближаются к бесконечности», я имею в виду, что они становятся большими и не приближаются к действительному числу.

Пример 2.

f (t) = 0, если t <0
f (t) = 1, если t = 0
f (t) = 1, если t> 0

Это функция, которая представляет ток, протекающий по проводу, соединяющему лампу на вашем столе с настенной розеткой. Здесь переменная t – время.Лампа изначально выключена, и в нулевой момент времени вы включаете лампу, так что в этот момент ток перескакивает с нуля на единицу и остается на этом значении до тех пор, пока вы не выключите лампу.

Здесь снова не существует предела f (t), когда t приближается к нулю. Причина на этот раз в том, что если t приближается к нулю с левой стороны, кажется, что предел должен быть равен нулю, но если t приближается к нулю справа, кажется, что предел должен быть 1. Когда возникает такая ситуация, предел не существует. .

Пример 3.

f (x) = 0, если x <0
f (x) = 0, если x = 0
f (x) = sin (¹/_x), если x> 0

Для x больше нуля эта функция имеет «дикое» поведение. Он колеблется между -1 и 1, и колебания происходят тем быстрее, чем ближе вы приближаетесь к нулю.