Геодезия триангуляция: Триангуляция и коррида. Геодезия и отвага / Хабр

Триангуляция и коррида. Геодезия и отвага / Хабр

Это продолжение истории Экваториальной Градусной экспедиции, в XVIII веке отправившейся к, как следует из названия, экватору, чтобы уточнить форму Земли.

Мы остановились на том, что ученые выполнили первую часть своих измерений: определили базис, но никак не могли продолжить (им не выдавали квадранты и зенитный сектор со складов города Кито). Эта история вылилась в серьезный конфликт, который разрешился только при личном вмешательстве вице-короля Перу. Любопытно, что когда Хорхе Хуан и Лакондамин вернулись в город, проблема рассосалась сама собой. Ульоа вышел из монастыря, его никто не арестовал, а квадранты выдали просто так, без пошлины. 

Так что же с измерением углов в треугольниках? Пока испанцы конфликтовали с президентом Кито, Годен и Буге спорили о том, в каком направлении развивать звено триангуляции: с севера на юг (Буге) или с запада на восток (Годен). Конец спору положили прямые инструкции из Франции: с севера на юг.

Треугольники Экваториальной экспедиции

Почему эта подробность кажется мне примечательной? Я с утешением обнаруживаю, что позиция: “у нас тут – какой-то бардак, в старые добрые времена люди думали головой!” – мифическая. Даже в таком деле, как научная экспедиция (что в 18 веке, что в любом другом) люди всегда найдут, где поконфликтовать. 

Напомню, что ученые планировали измерить длину дуги меридиана в 3 градуса (300+ км). И для этого применяли триангуляцию – популярнейший метод точных геодезических измерений вплоть до конца XX века.

Триангуляция

Идея триангуляции заключается в том, чтобы разместить на местности цепочку стыкующихся треугольников. Если измерены два угла треугольника и одна сторона (базис), то, последовательно решая треугольники, можно отыскать все их элементы (все стороны и все углы). При этом, для достижения наивысшей точности, вершины треугольников следует выбирать на местности с особой тщательностью, чтобы:

• Обеспечить видимость на соседние пункты. То есть, стоя с квадрантом в одной вершине треугольника, надо видеть одновременно две другие вершины. 

• Обеспечить (по возможности) равнобедренные, а лучше, равносторонние треугольники. 

Сигнал триангуляции. Тульская область.

Как вершины треугольников отмечали на местности? Устанавливали сигналы. Современные нам сигналы – это каркасные пирамиды (высотой от 4 до 10 м и выше). Их собирают из железных труб или из стволов деревьев, оснащают лесенкой, площадкой наблюдателя и столиком для инструмента. Вы их можете встретить повсеместно: в городах, в тундре, в лесу, обычно на возвышенностях. У наших героев с сигналами дело обстояло трудно: высокого леса в горах не водилось. Его приходилось тащить на себе (и индейцы-носильщики крутили пальцем у виска от этой очевидной глупости). Для лучшей видимости каркасы сигналов обтягивали белой тканью или обкладывали листьями. Получались такие “вигвамы”. Но сильные ветра сдували одни сигналы, а другие воровали местные жители. Вот поставил ты на одном вулкане свой “вигвам” и пошел за 40 км на другую гору. Смотришь с горы – и не видишь цель. Потому что некий крестьянин приметил, что хорошая палатка оставлена без присмотра. Но не только местные жители доставляли трудности ученым.

Сама природа, казалось, сговорилась против них. В Париже отличной идеей казалось работать на вершинах Анд, где видно предметы издалека, дует свежий ветерок, не жарко. На деле горы обернулись постоянной облачностью. На первом своем сигнале Лакондамин провел целый месяц в ожидании, когда обе цели будут видны. И так и не дождался.

Перемещаться (с оборудованием, палатками, припасами) приходилось по крутым горным склонам, прячась от камнепадов. То, что для индейца хорошо, для француза смерть: европейцы познали прелести высотной болезни. И тем обиднее было, что страдали от нее больше молодые и сильные, а ипохондрик Буге, как ни в чем не бывало, делал свои записи, сидя у инструмента. Вот как описывал Антонио Ульоа быт команды в 1737-1739 годах, пока выполняли работы по триангуляции: 

“От непогоды мы укрывались в хижине. Бури и грозы, бушевашие над Кито, гремели в облаках где-то под нами. И климат сказывался на здоровье: ноги так отекали и становились такими чувствительными, что каждый шаг причинял сильнейшую боль. Руки были обморожены, губы так растрескались, что у говорившего проступала кровь на губах. В этом негостеприимном краю нашей пищей была лишь горсть риса с мясом или птицей, взятыми из Кито. Чтобы сварить их, мы набирали снега в котел и топили его. А тарелки во время трапезы приходилось отогревать над жаровней. Мы поначалу пытались пить горячительные напитки, но в этом холоде они не оказывали никакого согревающего воздействия и мало отличались от воды. Пришлось подарить огненную воду слугам”.

Европейские кюлоты-чулки-сюртуки, сшитые из льна и шерсти, плохо подходили для обитания в диких горах. Довольно быстро ученые начали одеваться на манер местных: в плотные пончо и широкие шляпы. Благодаря этому их часто принимали за слуг и беседовали с ними о них же самих, куда более открыто, чем намеревались. Так, от местных жителей не укрылись странные действия непонятных иностранцев. И, конечно, им было очень интересно, зачем эти люди тут в горах копошатся. Объяснение про форму Земли местное население переиначило и назвало французов “рыцарями твердой точки”. Мол, они ищут центр Земли, за который ту Землю развернуть можно. Другие оказались скептически настроены и в эту сказочку не поверили. Наверняка дело в золоте. Старом золоте Инков, которое спрятано в горах. Кстати, Лакондамин вспоминал об одном отце-иезуите, который, якобы, владел секретом местонахождения клада и предлагал свои услуги. Во славу святой Инквизиции.

Но поговорим, собственно, об измерениях

Квадрант, 2 фута, 2 трубы.

 Работа велась двумя параллельными бригадами. Основным угломерным инструментом были квадранты с двумя 2-футовыми зрительными трубами. Зрительная труба с окуляром свободно вращалась относительно мерной дуги. Трубу можно было установить для вращения в вертикальной или горизонтальной плоскости. Мерная дуга изготавливалась из латуни. Зрительная труба – из железа. Квадранты были оснащены винтовым микрометром. Отсчеты брались с точностью до 1” (согласно журналам).

В процессе наблюдений выполнялись различные поверки квадрантов. Важнейшая из них: поверка нанесения делений на лимб (мерную шкалу). В ходе поверки измерялись одни и те же известные углы на разных участках шкалы. По результатам исследования, в измеренные углы вводились поправки.

Порядок наблюдений: два угла в треугольнике измеряла одна бригада, третий угол им сообщала другая. Таким образом, работа ускорялась, и появлялся внешний промежуточный контроль результатов. Угол измеряли несколько раз и брали среднее его значение. Сначала построили 29 треугольников, однако, когда оказалось, что они не покрывают 3 градуса меридиана, то к северу от Кито построили еще 4 треугольника. Самая короткая линия в треугольнике составила около 12 км (базис). Самая длинная линия – 45 км. После измерения углов, вычислялись невязки в треугольниках (отличие суммы углов в треугольнике от 180 градусов). Невязки опубликованы у Хорхе Хуана, Лакондамина и Буге. В среднем, они колеблются от 0 до 30”.

О качестве наблюдений

Антонио Лафуэнте. автор большой работы, в которой анализируется материал экспедиции: La geometrización de la tierra (1735-1744), выражает сомнения в требовательности участников к своим результатам. Так, к примеру, Лакондамин приводит крайне низкую для тех времен погрешность (расхождение) измеренного угла в 5”, при этом, согласно журналу, работал он в семь раз быстрее, чем Хорхе Хуан, обладавший куда большим опытом. В среднем, измеренные углы в треугольниках расходятся у разных бригад на 20-30”, что тоже удивительно немного, на мой взгляд.

Выборочно приведу сложности, с которыми ученым приходилось сталкиваться на вершинах: 

Карабуро — Северный пункт базиса. Индейские проводники украли палатки.

Памбамарка — Сильные ветра и низкие температуры. Годен упал со склона и был серьезно ранен. Сбежали индейские проводники. Пока искали других, Годен отправился в Кито исследовать цену деления квадрантов.

Ималагуа — Склоны были так круты, что подъем возможен только на четвереньках.

Шангалли — Ветер унес ранее установленный сигнал.

Чусай — Очень низкие температуры приводили к обморожениям. Снова пришлось перейти перевал, чтобы проверить наличие сигналов. Буге упал со склона и получил травму.

Поиск расстояния между северной и южной частью дуги

Конечной целью работы со звеном триангуляции было отыскание расстояния между широтами “верха” и “низа” дуги. Как это происходило:

Все вычисленные длины сторон треугольников должны были быть спроецированы сначала в горизонт (на уровне самого низкого из сигналов), потом на уровень вулкана Карабуро.

1. Измеренные углы треугольников приводили к горизонту, после распределяли невязку (относительно 180 градусов).

2. Находили азимут западной стороны треугольника и длину ее проекции на меридиан (при помощи астрономических наблюдений).

3. Суммировали проекции всех западных сторон на меридиан и находили расстояние вдоль меридиана dX.  

Фиолетовые стрелки показывают проекцию сторон треугольников на меридиан. Они формируют искомую длину дуги меридиана.

Вот вам еще анекдот об особенностях работы в Латинской Америке. Как бы ученые ни пытались нагнать потерянное время, на Пасху приходилось прерываться и возвращаться в Кито. Опыт показывал, что нанятые индейцы все равно разбегутся домой на праздники, а архиепископ Кито, не увидев французов на праздничной мессе, снова натравит на них инквизицию. Но любая, даже самая трудная работа рано или поздно заканчивается. Заняв вместо 8 месяцев почти два года, измерение углов в 33 треугольниках к лету 1739 года все же закончилось. Ученые готовились вкусить заслуженный отдых на южной оконечности измеряемой дуги меридиана: в городе Куэнке.

Про местные нравы

Прежде, чем рассказывать о трагических событиях, которые закончились гибелью экспедиционного врача, есть смысл дать пояснения по поводу нравов местного населения. Хорхе Хуан (испанский офицер и астроном) оставил записки о том, чем и как живут в вице-королевстве Перу.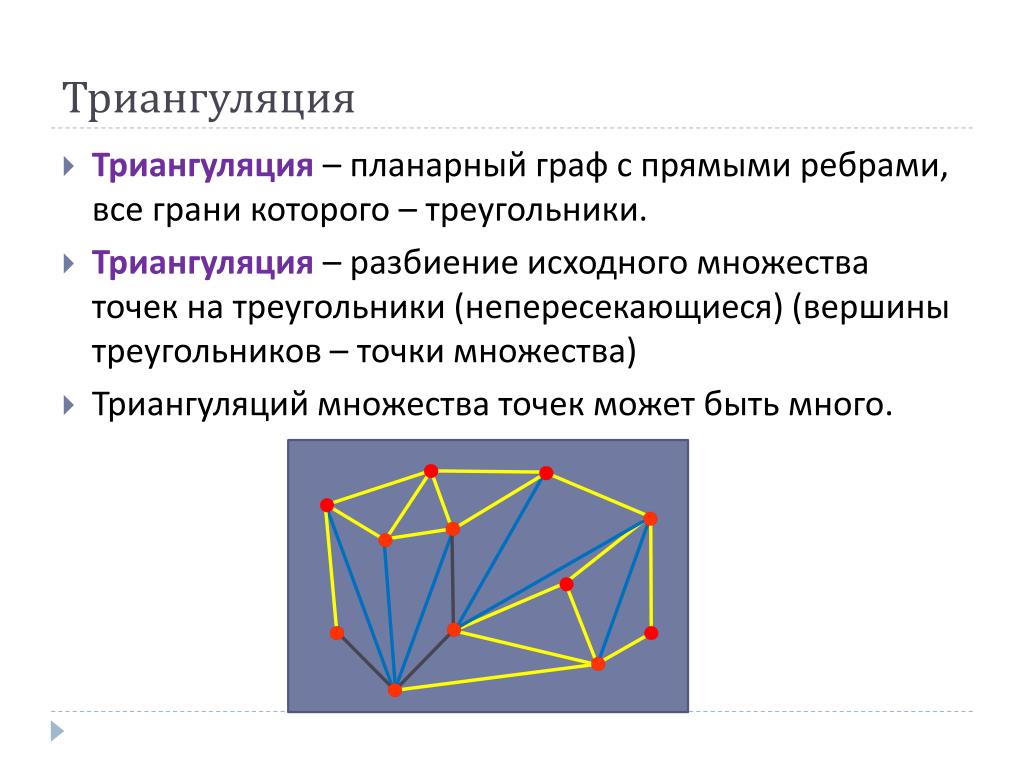 Эти записки я с удовольствием читаю, и все, что написано ниже – вольная цитата оттуда.

Мы уже упоминали, что “чапотонес” – испанцы из Испании назначались на самые важные должности. Однако они редко пускали корни. По завершении службы они отправлялись обратно домой или по новому назначению. Земли и доход с земель принадлежал “креольцам” – испанцам, рожденным в Перу. При этом, если только у них не было влиятельных родственников, особенный карьерный рост для креольцев был невозможен. 

Такое положение вещей вело к равнодушию и демотивации среди молодых людей. Они рано женились, мало учились (ибо зачем?) и ничем особенно не интересовались. Много пили, много ели и много играли. Единственным их развлечением было ходить друг к другу в гости, когда не было жарко (а жарко было всегда). Хорхе Хуан, например, пишет о том, что местные не носят париков и галстуков (слишком жарко), а женщины ходят к мессе в три часа ночи, пока прохладно. Курили все: и мужчины и женщины, причем с самого нежного возраста, приучаемые нянями. Пили тоже все и, преимущественно, огненную воду. Она считалась лучшим лекарством от паразитов, лихорадок, отсутствия аппетита и всех остальных болезней. Причем самые сдержанные начинали в 11 утра (так и называли: “tomar las once”). Люди же более раскованные, первую стопочку опрокидывали, не вставая с постели. Иногда вообще с нее не вставая. Кроме костей и выпивки, развлекались сплетнями и танцами. Тут я дам прямую цитату:

“Из танцев самый любимый – это Фанданго. Он происходит из колоний, и его танцуют на всех религиозных праздниках. От местных этот танец перенимают моряки с галеонов и офицеры Армады, таким образом привозя его в Испанию. Если Фанданго танцуют в знатных домах, он наполнен благопристойностью и гармонией, фигуры в нем исполняются на манер испанских, c известной долей изящества. Так, перемежаясь песнями, танцы длятся до рассвета. Простонародным фанданго предшествует неумеренное употребление вин и огненной воды, танец полон непристойных и скандальных движений, вместо песен танцы перемежаются возлияниями, далее перерастая в потасовку, в которой редко когда нет пострадавших. Ибо, поскольку выпивки много и она доступна, единожды начав пить, народ уже не может остановиться”.

Про трагедию в Куэнке

Отдыхающие после долгих измерений ученые были приглашены на народные гуляния по случаю дня Девы Марии Снежной. Гуляния должны были завершиться боем быков. Его все ждали с нетерпением.

Между тем, экспедиционный хирург Жан Синьержи, в той же Куэнке, излечил от малярии местного жителя. Вообще, пример Синьержи – пример успеха простого человека. Хирургия в те времена считалась не самым почетным занятием: не более почетным, чем ремесло цирюльника. И те и другие рвали зубы да пускали кровь на ярмарках. И экспедиция на экватор стала для молодого хирурга счастливым билетом в будущее. Однажды, после успешной операции на катаракте для одного из благородных горожан Кито (я даже боюсь думать о впечатлениях пациента), доктор Синьержи проснулся известным человеком. Однако последний пациент Синьержи – дон Франсиско Кесада был благодарен, однако беден (или жаден) и, заметив, как благосклонно мсье Жан поглядывает на его единственную дочь Мануэлу, решил разойтись полюбовно.

Дальше начинается латиноамериканский сериал (они, оказывается, были еще в 18 веке). И нам эта история интересна: а) истинно жизненной абсурдностью б) несоразмерным резонансом в обществе. 

Дело в том, что некогда прекрасная Мануэла Кесада (так звали дочь) была обручена с обер-прокурором Куэнки Диего де Леоном, и тот поспешил сорвать цветок ее невинности с молчаливого согласия родителей. Увы после этого прокурор нашел себе другую невесту, кстати, сестру городского главы, а опозоренной девушке обещал выделить щедрое приданое. Да вот все никак не выделяет. Будет очень удобно, если доктор Синьержи направит дону де Леону счет за лечение несостоявшегося тестя: приличия будут соблюдены, и свои люди сочтутся. Доктор так и поступил. Вместо денег в дом к пациенту (что там делал поздним вечером Синьержи, остается для меня загадкой) пришла прокурорская рабыня и при всем честном народе залепила Мануэле пощечину. На словах передала, что теперь иностранный доктор может исцелить и утешить Мануэлу любым приятным ему способом. Синьержи обиделся, поколотил рабыню до полусмерти и отправил с ней вызов на дуэль. В колониальном Перу это было не совсем нормой. Портить чужую собственность – как царапать чужую машину. 

С одной стороны, нет ни подарков, ни писем, которые бы указывали на любовную связь девушки с хирургом. С другой – верховный инквизитор несколько дней спустя призывал арестовать француза за «аморальные действия», ибо они с Мануэлой “среди дня прогуливаясь по площадям и паркам Куэнки, без стыда демонстрируя взаимную симпатию”. Город бурлил от возбуждения и предчувствия скандала.

Через два дня доктор подстерег дона Диего, прокурора, на главной площади, где тот гулял с супругой и друзьями, и потребовал немедленного удовлетворения. Обидчик посмеялся. Тогда Синьержи выстрелил в Диего из пистолета (тот дал осечку) и, обнажив шпагу, бросился на врага… но упал, запутавшись в полах плаща. Дело принимало некрасивый оборот. Вопросы чести частных лиц – это одно, а вот угрожать оружием на улице должностному лицу – совсем другое, очень серьезное дело.

Лакондамин потом по мотивам трагедии напишет книгу с картинками

Всю неделю в Куэнке чествовали Богоматерь Снежную (Ntra Señora de las Nieves). Как празднуют местные жители – мы уже упоминали чуть выше, в воспоминаниях Хорхе Хуана. Главной частью торжества должна была стать воскресная коррида. Ученых (и всех их коллег), само собой, тоже пригласили.И вот, последние минуты перед корридой. Публика ждет и обливается потом. Отца Мануэлы зажимают в угол неравнодушные родственники и ставят на вид , что слишком он любезничает с доктором. Прекрасная Мануэла поднимает крик: папу, мол, убивают. И на помощь бросается Жан Синьержи. Уже порядком причастившийся огненной воды. Как ему ни объясняли, что это просто семейная беседа, доктор обнажил шпагу и пообещал “продырявить всякого, кто к нему приблизится, как бычка”. Потом Синьержи еще и выстрелил (снова с осечкой) в главу городской стражи из пистолета, когда тот пытался его урезонить. Наступила точка невозврата: распорядитель объявил, что коррида отменяется.

Простой перуанский народ не затем, не желая сил, праздновал всю неделю, чтобы из-за наглого иностранца лишиться любимого зрелища. Толпа хлынула на арену. У толпы при себе имелись дубинки, палки и вилы (ножи и шпаги не-белым носить было запрещено). Началась свалка, в которой кому-то пришла светлая идея поколотить вообще всех ученых. Лакондамин и Буге, кинувшиеся было на защиту коллеги, вынуждены были прыгать с трибун и спасаться бегством. Во время бегства, кстати, Буге получил кинжалом в спину и камнем в голову. 

Глава стражи и алькальд пытались закрыть доктора от гнева толпы, но в свалке кто-то пырнул его кинжалом в печень. Доктор, поначалу не заметивший раны, скончался через три дня на руках у друзей.

Когда все закончилось, Шарль Мари Лакондамин (любитель ходить через джунгли и собирать деньги) потребовал у местных властей правосудия и наказания виновных. На следующие два года он ввяжется в тяжбу против влиятельных лиц Куэнки в чужой стране, на чужом языке. Он наживет много врагов и сделает невозможное: глава городской стражи Нейра и прокурор Диего де Леон будут приговорены к заключению.  

Дьявол в деталях 

Когда я читала испанский анализ обвинений в отношении Нейры и Диего де Леона, то удивлялась: как это Лакондамин взял и выиграл суд в отношении главных лиц города? Это в коррумпированной Южной Америке? Чудо? Не совсем. 

Дело в том, что, кроме криков “Убивай французов!”, разъяренная толпа, громя магазинчики на улицах города, кричала “Долой правительство!”. И убийство доктора, а также разбитые витрины можно было окрестить “мятежом”, а значит, устроить разбирательство в отношении организаторов мятежа: Нейры и Диего де Леона. И все “выигрыши” Лакондамина были на самом деле способом “руководящего центра” (Лимы) напомнить Куэнке, кто тут в колонии главный. В итоге, Нейра и Леон были приговорены к длительному заключению. О судьбе Нейры знаем только то, что его не арестовали. Он бежал? Умер? Переехал к родственникам? А вот дону де Леону не повезло: пару лет он провел в тюрьме в Куэнке, откуда потом бежал через открытое окно. По крышам добрался до иезуитского колледжа (привет Эскобару!) и отсиживался там еще пару лет. Через пару лет дело пересмотрели, полностью сняв с него обвинения. Лакондамин, на свое счастье, к этому моменту давно отбыл во Францию – эти заботы его более не трогали.

А нашим ученым от экспедиции останется всего ничего: определить широту севера и юга дуги в городах Кито и Куэнка.

Все статьи этого цикла:

1. О форме Земли: тыква или дыня?

2. Как набрать команду к экватору?

3. Планирование экспедиции.

4. Приборы и инструменты.

5. Дорога на Запад.

6. Базисные измерения и политика.

7. Триангуляция и коррида.

8. О звездном непостоянстве.

9. Нельзя просто так взять и вернуться из экспедиции.

Триангуляция (в геодезии) — Универсальная научно-популярная энциклопедия

Триангуляция (от лат. triangulum — треугольник), один из способов создания сети опорных геодезических пунктов и сама сеть, созданная этим способом; пребывает в построении последовательностей либо сетей примыкающих друг к другу треугольников и в определении положения их вершин в избранной совокупности координат. В каждом треугольнике измеряют все три угла, а одну из его сторон определяют из вычислений путём последовательного ответа прошлых треугольников, начиная от того из них, в котором одна из его сторон взята из измерений.

В случае если сторона треугольника взята из ярких измерений, то она именуется базовой стороной Т. В прошлом вместо базовой стороны конкретно измеряли маленькую линию, именуемую базисом, и от неё путём тригонометрических вычислений через особенную сеть треугольников переходили к стороне треугольника Т. Эту сторону Т. в большинстве случаев именуют выходной стороной, а сеть треугольников, через каковые она вычислена,— базовой сетью. В рядах либо сетях Т. для повышения и контроля их точности измеряют большее число базисов либо базовых сторон, чем это минимально нужно.

Принято вычислять, что способ Т. изобрёл и в первый раз применил В. Снеллиус в 1615—17 при прокладке последовательности треугольников в Нидерландах для градусных измерений. Работы по применению способа Т. для топографических съёмок в дореволюционной России начались на рубеже 18—19 вв. К началу 20 в. способ Т. взял повсеместное распространение.

Т. имеет громадное научное и практическое значение. Она помогает для: размеров Земли и определения фигуры способом градусных измерений; изучения горизонтальных перемещений земной коры; обоснования топографических съёмок в целях и различных масштабах; обоснования разных геодезических работ при изыскании, строительстве и проектировании больших инженерных сооружений, при планировке и постройке городов и т.д.

При построении Т. исходят из принципа перехода от общего к частному, от больших треугольников к более небольшим. Вследствие этого Т. подразделяется на классы, отличающиеся последовательностью и точностью измерений их построения. В малых по территории государствах Т. высшего класса строят в виде целых сетей треугольников. В странах с громадной территорией (СССР, Канада, КНР, др и США.) Т. строят по программе и некоторой схеме.

Наиболее программа построения и стройная схема Т. используется в СССР.

Национальная Т. в СССР делится на 4 класса (рис.). Национальная Т. СССР 1-го класса строится в виде последовательностей треугольников со сторонами 20—25 км, расположенных приблизительно на протяжении меридианов и образующих и параллелей полигоны с периметром 800—1000 км. Углы треугольников в этих последовательностях измеряют точными теодолитами, с погрешностью не более ± 0,7. В местах пересечения последовательностей Т. 1-го класса измеряют базисы при помощи мерных проволок (см.

Базовый прибор), причём погрешность измерения базиса не превышает 1 : 1000000 доли его длины, а выходные стороны базовых сетей определяются с погрешностью около 1 : 300 000. По окончании изобретения точных электрооптических дальномеров стали измерять конкретно базовые стороны с погрешностью не более 1 : 400 000.

Пространства в полигонов Т. 1-го класса покрывают целыми сетями треугольников 2-го класса со сторонами около 10—20 км, причём углы в них измеряют с той же точностью, как и в Т. 1-го класса. В целой сети Т. 2-го класса в полигона 1-го класса измеряется кроме этого базовая сторона с вышеуказанной точностью.

На финишах каждой базовой стороны в Т. 1-го и 2-го классов делают долготы и астрономические определения широты с погрешностью не более ± 0,4, и азимута с погрешностью около ± 0,5. Помимо этого, долготы и астрономические определения широты делают и на промежуточных пунктах последовательностей Т. 1-го класса через каждые приблизительно 100 км, а по некоторым очень выделенным последовательностям и существенно чаще.

На базе сетей и рядов Т. 1-го и 2-го классов определяют пункты Т. 3-го и 4-го классов, причём их густота зависит от масштаба топографической съёмки. К примеру, при масштабе съёмки 1 : 5000 один пункт Т. обязан приходиться на каждые 20—30 км2. В Т. 3-го и 4-го классов погрешности измерения углов не превышают соответственно 1,5 и 2,0.

В практике СССР допускается вместо Т. использовать способ полигонометрии.Наряду с этим ставится условие, дабы при построении опорной геодезической сети тем и др. способом достигалась однообразная точность определения положения пунктов земной поверхности.

Вершины треугольников Т. обозначаются на местности древесными либо железными башнями высотой от 6 до 55 м в зависимости от условий местности (см. Сигнал геодезический). Пункты Т. в целях долгосрочной их сохранности на местности закрепляются закладкой в грунт особенных устройств в виде железных труб либо цементных монолитов с вделанными в них железными марками (см.

Центр геодезический), фиксирующими положение точек, для которых даются координаты в соответствующих каталогах.

Координаты пунктов Т. определяют из математической обработки последовательностей либо сетей Т. Наряду с этим настоящую Почву заменяют некоторым референц-эллипсоидом, на поверхность которого приводят результаты базисных сторон и измерения углов Т. В СССР принят референц-эллипсоид Красовского (см. Красовского эллипсоид).

Построение Т. и её математическая обработка приводят к созданию по всей стране единой совокупности координат, разрешающей ставить топографо-геодезические работы в различных регионах одновременно и независимо друг от друга. Наряду с этим обеспечивается соединение этих работ в создание и одно целое единой общегосударственной топографической карты страны в установленном масштабе.

Лит.: Красовский Ф. Н., Данилов В. В., Управление по высшей геодезии, 2 изд., ч. 1, в. 1—2, М., 1938—39; Инструкция о построении национальной геодезической сети СССР, 2 изд., М., 1966.

Л. А. Изотов.

Читать также:

• Тоталитаризм
• Тьюринга машина
• Туника (у животных)

Геодезия 2015 Видеолекция №9 Геодезические сети

Связанные статьи:

• Геодезия

  Геодезия (греч. geodaisia, от ge — Земля и daio — дроблю, разделяю), наука об определении фигуры, гравитационного поля и размеров Почвы и об измерениях…

• Спутниковая геодезия

  Спутниковая геодезия, раздел геодезии, разглядывающий теории и способы ответа практических и научных задач геодезии по итогам наблюдений ИСЗ и др….

• У Н-П энциклопедия

методов съемки | Межправительственный комитет по геодезии и картографии

Триангуляция

В прошлом было трудно точно измерить очень большие расстояния, но можно было точно измерить углы между точками на расстоянии многих километров, ограничиваясь только возможностью видеть дальние маяк. Это может быть от нескольких километров до 50 километров и более.

Триангуляция — это метод съемки, при котором измеряются углы в треугольнике, образованном тремя контрольными точками съемки. Используя тригонометрию и измеренную длину только одной стороны, рассчитываются другие расстояния в треугольнике. Форма треугольников важна, так как в длинном тонком треугольнике много неточностей, но идеален треугольник с углами основания около 45 градусов.

Каждое из рассчитанных расстояний затем используется как одна сторона в другом треугольнике для расчета расстояний до другой точки, которая, в свою очередь, может стать началом другого треугольника. Это делается так часто, как это необходимо, чтобы сформировать цепочку треугольников, соединяющих исходную точку с центром съемки в нужном месте. Затем углы и расстояния используются с известным начальным положением и сложными формулами для расчета положения (широты и долготы) всех других точек в сети триангуляции.

Хотя используемые расчеты аналогичны тригонометрии, преподаваемой в средней школе, поскольку расстояние между точками съемки обычно большое (обычно около 30 километров), расчеты также учитывают кривизну Земли.

Измеренное расстояние в первом треугольнике известно как «базовая линия» и является единственным измеренным расстоянием; все остальные вычисляются из него и измеренных углов. До 1950-х годов это начальное базовое расстояние нужно было очень тщательно измерять с помощью последовательных стержней, длина которых была точно известна. Это означало, что расстояние будет относительно коротким (может быть, километр или около того) и оно будет находиться на достаточно ровном участке, таком как долина или равнина. Треугольники, отмеренные от него, постепенно увеличивались в размерах и поднимались к вершинам холмов, где можно было легко увидеть отдаленные точки.

Рис. 9. Сеть триангуляции

Углы в треугольниках измеряются с помощью теодолита, который представляет собой инструмент с телескопом, соединенным с двумя вращающимися кругами (один горизонтальный и один вертикальный) для измерения горизонтальных и вертикальных углов. Теодолит хорошего качества, используемый для геодезических съемок, будет иметь градуировку с точностью до 0,1 угловой секунды, а угол, полученный в результате повторных измерений, обычно будет иметь точность около 1 угловой секунды, что эквивалентно примерно 5 см на расстоянии 10 километров.

При триангуляции вертикальные углы не нужны, но их можно использовать для измерения разницы высот между точками.

 

Объяснение жаргона – угловое измерение

Полный круг содержит 360 градусов. Один градус содержит 60 минут, а каждая минута содержит 60 секунд.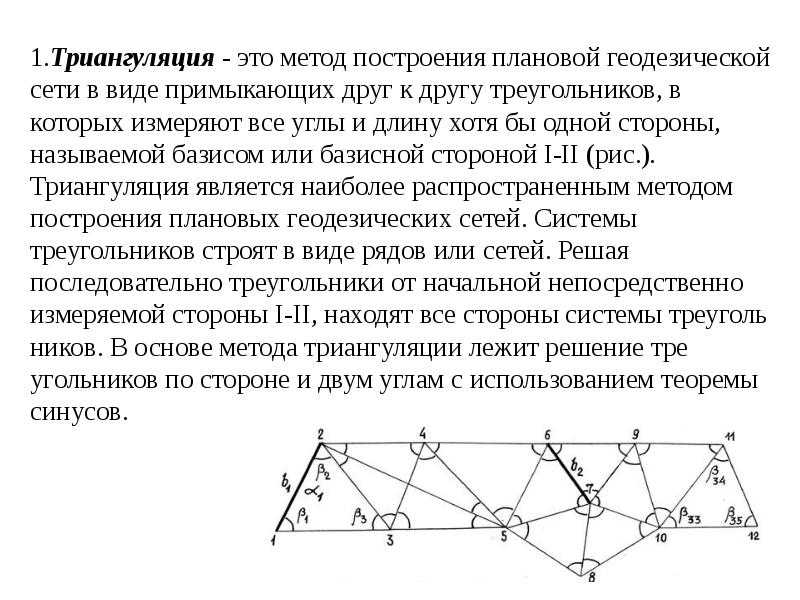 Таким образом, в одном градусе 3600 секунд, а в полном круге 1 296 000 секунд. Эти секунды или минуты часто называют «угловыми секундами» или «угловыми минутами», чтобы отличить их от секунд и минут времени.

Figure 10:  Theodolite SchematicFigure 11:  A Theodolite

 

 

 

 

 

 

 

 

 

 

 

Trilateration

In the 1950s, accurate methods of measuring long distances (обычно от 30 до 50 км). Они использовали известную скорость света (299 792,458 км в секунду) и синхронизированное отражение микроволны или световой волны вдоль измеряемой линии. Известные как электромагнитное измерение расстояния (EDM), двумя первоначальными типами приборов были «теллурометр», в котором использовалась микроволновая печь, и «геодиметр», в котором использовалась световая волна.

Тогда расстояния в треугольнике можно было бы измерять напрямую, а не вычислять их по наблюдаемым углам. При необходимости можно рассчитать углы. Тогда процесс вычисления позиций по цепочке треугольников такой же, как и для триангуляции.

Иногда в некоторых треугольниках измерялись и углы, и расстояния, чтобы проверить наблюдения и повысить точность вычислений.

Рис. 12. Сеть трилатерации Рис. 14. Геодиметр модели 8 Рис. 13. Теллурометр

Ранние инструменты EDM могут измерять на большие расстояния с точностью около 5 частей на миллион (т.е. 5 мм на каждые км или 150 мм на 30 км примерно на миллион (т.е. линия), но более поздние версии были более точными, способными измерять с точностью около 1 части на миллион (1 мм на километр или 30 мм на 30 км линии)

В наши дни также существует множество типов точных и компактных электроэрозионных станков. инструменты, интегрированные с электронным теодолитом и известные как «тахеометр». Эти инструменты также могут измерять с точностью около 1 части на миллион, но, как правило, только для более коротких линий длиной около одного километра.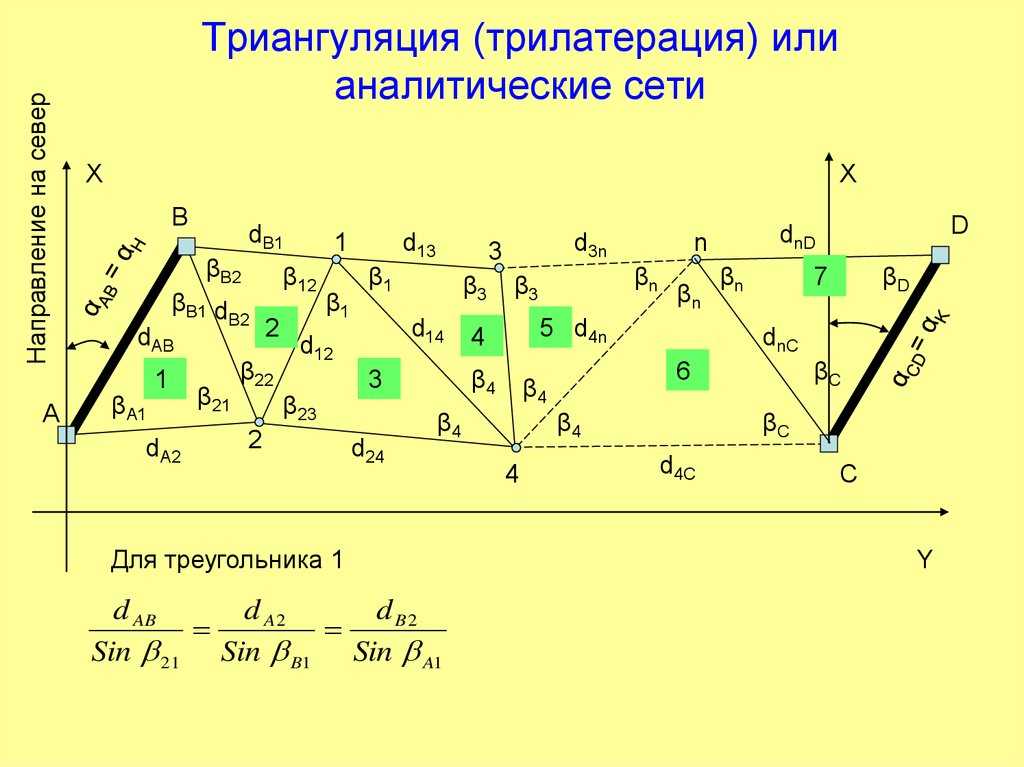

 

Рисунок 15: Теодолит тахеометра

Траверсирование

Триангуляция и трилатерация затруднены, а иногда и невозможны на равнинной местности, где мало холмов. Такая ситуация часто наблюдается в отдаленных районах Австралии.

С помощью EDM эту проблему можно свести к минимуму путем измерения расстояний и углов между последовательными контрольными точками съемки. При известном начальном положении и ориентации (или двух известных начальных положениях) повторение этого процесса через цепочку точек позволяет вычислить положение каждой точки.

Однако в ходе, если допущена ошибка, это может быть неочевидно, поэтому эти ходы обычно возвращаются к исходной точке, образуя петлю, или заканчиваются в другом известном положении. Разница между известным конечным положением и расчетным положением для этой точки является невязкой и указывает на точность измерений и расчетов хода.

Рис. 16. Схема хода

В небольших проектах ход часто используется с тахеометром. Варианты триангуляции и трилатерации также часто используются при небольших съемках, особенно для измерения недоступных точек.

Что такое триангуляционная съемка? Операции, применение и преимущества

🕑 Время чтения: 1 минута

Содержание:

• Что такое триангуляционная съемка?
• Операции в триангуляции
• Применение триангуляции в съемке
• Системы триангуляции
  • Треугольники
  • Четырехугольники
  • Многоугольники

3

3

3 Триангуляция Что такое?

Триангуляционная съемка – это отслеживание и измерение ряда или сети треугольников для определения расстояний и относительных положений точек, разбросанных по площади, путем измерения длины одной стороны каждого треугольника и определения его углов и длины двух других сторон путем наблюдения из этот базовый уровень. Триангуляционная съемка была впервые введена голландцем по имени Снели. Триангуляция предпочтительнее для холмов и волнистых участков, поскольку легко установить станции на разумном расстоянии друг от друга и с возможностью взаимной видимости.

В самолетах и ​​людных местах не подходит, так как нарушается видимость станций. Трудность преодолевается строительством башен, что довольно дорого. Основным недостатком триангуляции является накопление ошибки в длинах и направлениях линий, поскольку и то, и другое для последовательных линий зависит от вычислений для предыдущей линии, что требует контрольных баз. При триангуляции вся исследуемая площадь покрывается каркасом из треугольников. Для треугольника длина первой линии, которая точно измерена, называется базовой линией. Две другие вычисленные стороны используются в качестве новых базовых линий для двух других треугольников, связанных с первым треугольником. Расширяя этот процесс, можно распространить цепочку или сеть треугольников на всю площадь.

Операции по триангуляции Съемка

Полевые работы по триангуляции проводятся в рамках следующих четко определенных операций:

• Разведка
• Подготовка станции
• Базовое измерение
• Измерение углов.

Помимо полевых работ, триангуляция состоит из спецификаций, проектирования станций и сигналов, а также обработки и корректировки наблюдений.

Применение триангуляционной съемки

• Установление точно расположенных контрольных точек для плоских и геодезических съемок больших площадей.
• Установление точно расположенных контрольных точек в связи с аэросъемкой
• Точное расположение инженерных объектов, таких как осевые линии, конечные точки и шахты для длинных туннелей, а также осевые линии и опоры для мостов с большими пролетами.

Системы триангуляции

Система, состоящая из станций триангуляции, соединенных цепочкой треугольников. Полная фигура называется системой триангуляции или фигурой триангуляции. Наиболее распространенными типами фигур, используемых в системе триангуляции, являются
• Треугольники
• Четырехугольники
• Полигоны

Геометрические условия, которым должны удовлетворять приведенные выше фигуры в системе триангуляции:

• Сумма внутренних углов должна быть (2n-4)x90 ^o , где n = количество сторон фигуры
• Если все углы измерены на станции, их сумма должна быть 360 ^o .
• Длина сторон, рассчитанная по более чем одному маршруту, должна совпадать.

Выполнение всех геометрических условий невозможно из-за погрешностей до тех пор, пока не будут проведены полевые измерения.

Треугольники

1. Цепочка треугольников очень быстра и экономична, когда нужно обследовать узкую полосу местности. 2. Углы меньше 30 ^o или больше 120 ^o не допускаются. 3. У хорошо обусловленных треугольников углы не должны быть меньше 30 ^o или больше 120 ^o . Преимуществ треугольников:

• Это просто и быстро
• Экономичный метод

Недостатки:

• Поскольку он используется для съемки длинной узкой полосы, необходимо часто вводить количество базовых линий, чтобы уменьшить накопление ошибок. Следовательно, одна цепочка треугольников никогда не допускается в триангуляции высокого порядка.