Геометрический смысл уравнения бернулли: 2.4. Геометрический и энергетический смысл уравнения д.Бернулли

2.4. Геометрический и энергетический смысл уравнения д.Бернулли

Все члены, входящие в уравнение Д.Бернулли, имеют линейную размерность, поэтому их принято называть высотами. Соответственно общеприняты следующие названия для этих членов:

– геометрическая или геодезическая высота;

– пьезометрическая высота или высота давления;

– скоростная высота или скоростной напор.

Легко усмотреть следующий геометрический смысл уравнения Д.Бернулли, который заключается в том, что при установившемся движении идеальной жидкости сумма трех высот (геометрической, пьезометрической и скоростной) не меняется вдоль данной элементарной струйки. Это положение наглядно иллюстрируется II.01.

Можно трактовать смысл отдельных членов уравнения Бернулли иначе. Выше было показано, что сумма представляет собой удельную энергию жидкости.

В соответствии с этим можно считать, что:

– есть удельная энергия положения;

– есть удельная энергия давления;

– есть удельная кинетическая энергия.

Энергетический смысл уравнения Бернулли заключается в том, что при установившемся движении идеальной жидкости сумма удельных энергий положения, давления и кинетической не меняется вдоль данной элементарной струйки.

Очевидно, двучлен представляет собойудельную потенциальную кинетическую энергию движущейся частицы жидкости. Полная удельная энергия (т.е. потенциальная + кинетическая) называется гидродинамическим напором и обозначается . Таким образом, уравнение Бернулли показывает, что при установившемся движении идеальной жидкости для данной струйки гидродинамический напор есть величина постоянная.

Рис. II.01

На графике линия гидродинамического напора изображается горизонтальной линией.

2.5. Уравнение д.Бернулли для элементарной струйки реальной жидкости. Пьезометрический и гидравлический уклоны

При движении реальной жидкости между соседними струйками возникают силы трения, на преодоление которых затрачивается часть энергии жидкости. Поэтому удельная энергия жидкости в сечении элементарной струйки 2-2 будет мене удельной энергии жидкости в сечении 1-1 на некоторую величину , которую называют потерянной высотой или потерянной удельной энергией, затрачиваемой на преодоление гидравлических сопротивлений. Аналитически это положение запишется таким образом:

(11.14)

Следовательно, при установившемся движении реальной жидкости сумма четырех высот (геометрической, пьезометрической, скоростной и потерянной) или, что то же самое, сумма четырех удельных энергий 9положения, давления, кинетической и потерянной) не изменяется вдоль данной элементарной струйки.

Легко изобразить уравнение Бернулли для рассматриваемого случая графически.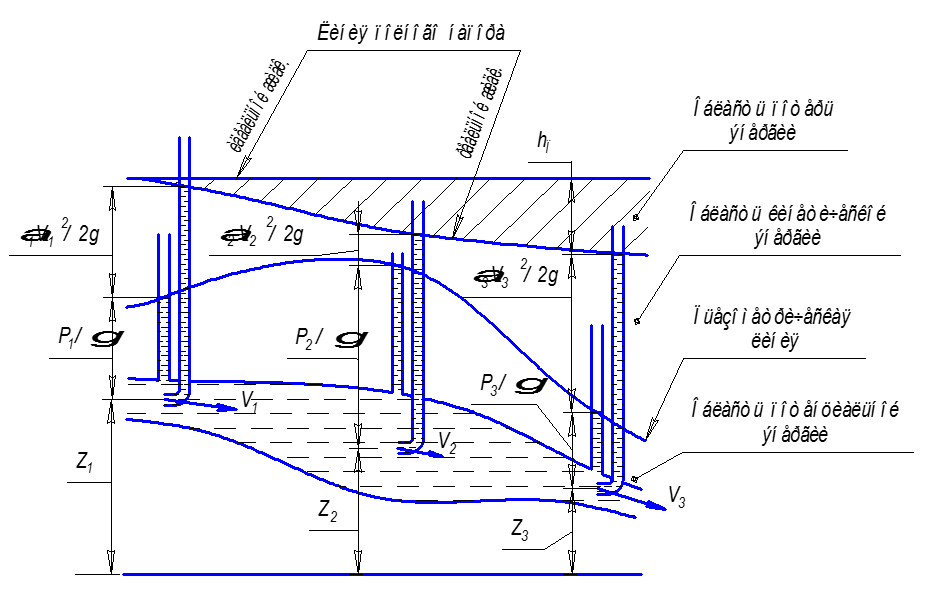

Для этого следует, выбрав произвольную горизонтальную плоскость сравнения, отложить на ней в каждом сечении высоты ;;и. Концы отрезков, соединенные плавной кривой, покажут положение оси струйки. Соединяя концы отрезковплавной кривой, получим так называемую пьезометрическую линию. Отложив в каждом сечении вверх от пьезометрической линии отрезки, равные скоростным напорам, и соединив их концы плавной кривой, получим линию гидродинамического напора или, как ее часто называют, гидравлическую линию (рис.II.02). Отрезки, равные расстояниям по вертикали от гидравлической линии, проходящей над плоскостью сравнения на высоте, равной начальной удельной энергии на гидравлические сопротивления на участке от начального до рассматриваемого сечения.

Рис. II.02

Проделаем теперь следующее построение: разверзнем криволинейную ось струйки s в горизонтальную прямую линию и в каждой ее точке отложим по вертикали значения удельных энергий ;и. Соединяя концы отрезкови , получим изображение пьезометрической и гидравлической линий. Падение пьезометрической линии на единицу длины элементарной струйки назовем пьезометрическим уклоном:

. (11.15)

Соответственно падение гидравлической линии на единицу длины элементарной струйки назовем гидравлическим уклоном

I:

(11.16)

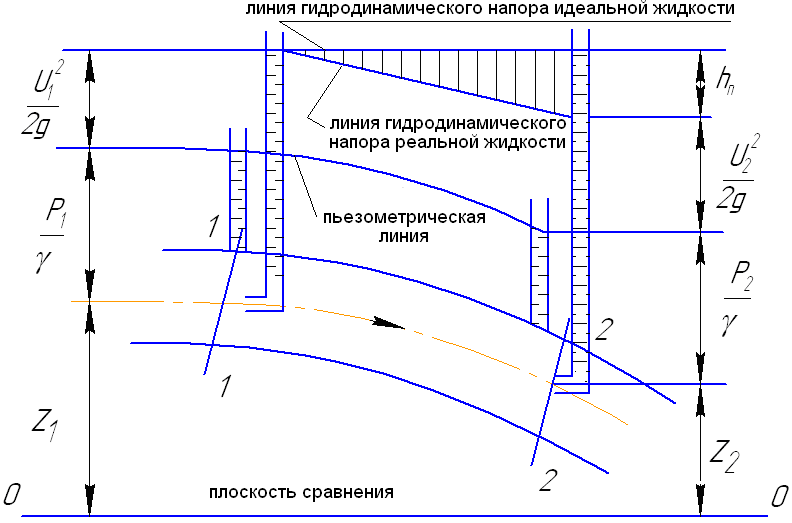
На графике (рис. II.03) пьезометрический уклон представляется тангенсом угла наклона касательной к пьезометрической линии, а гидравлический уклон – тангенсом угла наклона касательной к гидравлической линии. Значение пьезометрического уклона может быть положительным или отрицательным в зависимости от того, увеличивается или уменьшается величина удельной потенциальной энергии вдоль элементарной струйки.

Рис. II.03

Гидравлиеческий уклон есть всегда величина положительная, так как полная удельная энергия движущейся части жидкости постепенно уменьшается по мере ее продвижения вдоль элементарной струйки, затрачиваясь на преодоление сил трения, превращаясь в тепловую энергию и рассеиваясь.

30. Геометрический смысл уравнения Бернулли. Гидравлика

Читайте также

7. Анализ основного уравнения гидростатики

7. Анализ основного уравнения гидростатики Высоту напора принято называть пьезометрической высотой, или напором.Согласно основному уравнению гидростатики,p1+ ?ghA= p2+ ?ghH,где ? – плотность жидкости;g – ускорение свободного падения.p2, как правило, задается p2= pатм, поэтому,

22. Дифференциальные уравнения движения невязкой жидкости

22. Дифференциальные уравнения движения невязкой жидкости Уравнение Эйлера служит одним из фундаментальных в гидравлике, наряду с уравнением Бернулли и некоторыми другими.Изучение гидравлики как таковой практически начинается с уравнения Эйлера, которое служит

24.

 Форма Громеки уравнения движения невязкой жидкости

24. Форма Громеки уравнения движения невязкой жидкости Уравнения Громеки – попросту другая, несколько преобразованная форма записи уравнения Эйлера.Например, для координаты x Чтобы его преобразовать, используют уравнения компонентов угловой скорости для вихревого

25. Уравнение Бернулли

25. Уравнение Бернулли Уравнение Громеки подходит для описания движения жидкости, если компоненты функции движения содержат какуююто вихревую величину. Например, эта вихревая величина содержится в компонентах ?x, ?y,?z угловой скорости w.Условием того, что движение

26. Анализ уравнения Бернулли

26. Анализ уравнения Бернулли это уравнение есть не что иное, как уравнение линии тока при установившемся движении.

Отсюда следуют выводы:1) если движение установившееся, то первая и третья строки в уравнении Бернулли пропорциональны.2) пропорциональны строки 1 и 2,

27. Примеры прикладного применения уравнения Бернулли

27. Примеры прикладного применения уравнения Бернулли Во всех случаях требуется определить математическую формулу потенциальной функции, которая входит в уравнение Бернулли: но эта функция имеет разные формулы в разных ситуациях. Ее вид зависит от того, какие массовые

29. Энергетический смысл уравнения Бернулли

29. Энергетический смысл уравнения Бернулли Пусть теперь имеем установившееся движение жидкости, которая невязкая, несжимаемая.И пусть она находится под воздействием сил тяжести и давления, тогда уравнение Бернулли имеет вид: Теперь требуется идентифицировать каждое

31.

 Уравнения движения вязкой жидкости

31. Уравнения движения вязкой жидкости Для получения уравнения движения вязкой жидкости рассмотрим такой же объем жидкости dV = dxdydz, который принадлежит вязкой жидкости (рис. 1).Грани этого объема обозначим как 1, 2, 3, 4, 5, 6. Рис. 1. Силы, действующие на элементарный объем

33. Уравнение Бернулли для движения вязкой жидкости

33. Уравнение Бернулли для движения вязкой жидкости Элементарная струйка при установившемся движении вязкой жидкостиУравнение для этого случая имеет вид (приводим его без вывода, поскольку его вывод сопряжен с применением некоторых операций, приведение которых

35. Уравнение Бернулли для неустановившегося движения вязкой жидкости

35.

 Уравнение Бернулли для неустановившегося движения вязкой жидкости Для того, чтобы получить уравнение Бернулли, придется определить его для элементарной струйки при неустановившемся движении вязкой жидкости, а затем распространять его на весь потокПрежде всего,

53. Дифференциальные уравнения неустановившегося движения

53. Дифференциальные уравнения неустановившегося движения Для того, чтобы составить уравнение любого вида движения, нужно проецировать все действующие силы на систему и приравнивать их сумму к нулю. Так и поступим.Пусть имеем напорный трубопровод круглого сечения, в

39. Принцип возрастания энтропии и физический смысл второго закона термодинамики

39. Принцип возрастания энтропии и физический смысл второго закона термодинамики Исследуем понятие энтропии как функции состояния: Второй закон термодинамики можно сформу лировать в виде: Величина энтропии представляет собой полный диффереренциал, т. е. является

46. Основные дифференциальные уравнения термодинамики

46. Основные дифференциальные уравнения термодинамики Дифференциальные уравнения в термодинамике используются для исследования реальных газов, при теоретических (и практических) вычислениях.Рассмотрим следующие случаи.1. Независимыми переменными являются параметры p,

13.4. Философский смысл торговли и дарвинизм

13.4. Философский смысл торговли и дарвинизм Принципы рыночной экономики и международной торговли своими философскими корнями восходят к работе Адама Смита «Богатство народов» и к концепциям Давида Рикардо о специализации и конкурентных преимуществах народов. Их теория

Геометрический смысл – уравнение – Большая Энциклопедия Нефти и Газа, статья, страница 2

Геометрический смысл – уравнение

Cтраница 2

Следовательно, геометрический смысл уравнения Бернулли заключается в том, что при установившемся движении идеальной жидкости сумма трех высот ( напоров) – геометрической, пьезометрической и обусловленной скоростным напором – есть величина постоянная вдоль потока.  [17]

Следовательно, геометрический смысл уравнения Бернулли можно сформулировать так: при установившемся движении идеальной жидкости сумма трех высот ( пьезометрической; высоты, соответствующей скоростному напору, и высоты положения) вдоль потока остается неизменной.  [19]

Следовательно, геометрический смысл уравнения Бернулли может быть сформулирован так: при установившемся движении жид – кости сумма четырех высот ( высоты положения, пьезометрической вы-сс ты, высоты, соответствующей скоростному напору, и высоты, со – ornsemcmeyioiui u потерям напора) остается неизменной вдоль потока.  [21]

Если мы вспомним геометрический смысл уравнения ( 9), то увидим: при преобразованиях группы О16 ( действительные, собственные) прямые каждого отдельного слоя таким образом преобразуются друг в друга, что ортогональное пересечение прямых различных слоев сохраняется.  [22]

Все изложенное отражает геометрический смысл уравнения Бернулли.  [23]

Данный вывод поясняет геометрический смысл уравнения Бернулли для элементарной струйки вязкой жидкости. Согласно рис. 80, потеря энергии или потеря напора h m представляет собой разность между высотой горизонтальной линии О – О, проведенной через уровень жидкости в трубке Пито в начальном сечении, и высотой уровня жидкости в трубке Пито в рассматриваемом сечении относительно плоскости сравнения О – О.  [24]

Все изложенное и заключает в себе геометрический смысл уравнения Бернулли.  [25]

Данный вывод является одновременно и пояснением геометрического смысла уравнения Бернулли для элементарной струйки вязкой жидкости.  [26]

Гамильтоновы структуры на группах Ли, биалгебры Ли и геометрический смысл уравнения Янга – Бакстера.  [27]

Гамилътоновы структуры на группах Ли, биалгеб-ры Ли и геометрический смысл уравнений Янга Бакстера.  [28]

В – 3L Вставляя полученные значения коэффициентов в уравнение искомой прямой, получим Ч х – ЗХу О, или 2х – Зу 0, Так как геометрический смысл уравнения не меняется от умножения ( или деления) всех его членов на одно и то же число, то при составлении уравнения прямой, параллельной данной, можно брать коэффициенты при координатах не только пропорциональными, но равными соответствующим коэффициентам данного уравнения.  [29]

Не все уравнения первой степени с двумя неизвестными являются Уравнениями прямых. Например, уравнению 0 – л: 0 – г / 0 соответствует вся плоскость, а уравнение 0 – х – – 0-у не соответствует ничему. Это следует иметь в виду, когда мы говорим о геометрическом смысле уравнений первой степени: из того, что все решения одного уравнения удовлетворяют другому уравнению, отнюдь не следует, что и всякое решение второго уравнения есть в же время решение первого уравнения.  [30]

Страницы:      1    2    3

Уравнение Бернулли – вывод формулы, физический смысл, примеры использования

Исследования учёного

Даниил Бернулли родился в Голландии в 1700 году. В 1725 году он начал работать на кафедре физиологии, где увлёкся основами теоретической физики. Через 25 лет он возглавил кафедру экспериментальной физики, которой и руководил до конца своих дней. Основным его трудом считается создание теории гидродинамической зависимости, известной как Закон Бернулли. Открытие учёного предвосхитило зарождение молекулярно-кинетического учения поведения газов.

Причиной открытия принципа стало изучение действия закона сохранения энергии в различных ситуациях. Бернулли установил, что давление жидкости в замкнутом пространстве зависит от сечения объекта, в котором она находится. Чем меньше сечение трубы, тем ниже будет созданное давление в пропускаемом через неё жидком веществе.

Этот факт был доказан экспериментально и описан математически.

Правило в математической формулировке имеет вид (pv²/ 2) + p * g * h + ρ = const, где:

• p — количество жидкости на единицу объёма;
• v — скорость движения потока;
• h — уровень, на который поднят элемент жидкости;
• ρ — сила, действующая на единицу площади;
• g — ускорение, придаваемое жидкости под действием притяжения Земли.

Чтобы понять физический смысл уравнения Бернулли, нужно рассмотреть трубу переменного сечения, в которой существует точка А и Б. Первая располагается в широкой части, а вторая — в узкой. В соответствии с уравнением непрерывности скорость V1 в части трубы, имеющей большее сечение, будет меньше, чем скорость жидкости V2 в узком сечении. Если в жидкость поместить прибор для измерения давления, он покажет какое-то значение P1 в точке A и P2 в точке Б. При этом там, где скорость движения жидкости медленнее, давление будет больше.

Объясняется это следующим образом: если V1 больше V2, значит, при движении происходит изменение скорости течения. Представив, что в жидкости находится точка, можно утверждать о её движении с ускорением. Это означает, что на неё действуют силы.

Одна из них совпадает с направлением течения, тем самым ускоряя движение. Обусловлена эта сила разностью давления.

Так как движение происходит от точки А к Б, то и давление возле А будет больше, чем около Б. Эта разность давлений и приводит к ускорению.

Условия действия

Закон применим для условия, при котором соблюдается неразрывность струи воздуха или жидкости. В тех участках потока, где скорость течения больше, давление будет меньше и наоборот. Это утверждение и называется теоремой Бернулли. По сути, закон позволяет установить связь между давлением, скоростью, высотой.

Пусть имеется труба переменного сечения с изменяющейся высотой. Внизу она широкая, а затем сужается. По ней течёт жидкость. Площадь сечения можно обозначить как S1 и S2, а давление участков и скорость движения на них P1, P2, V1, V2. Высота внизу будет равняться S1, а вверху S2.

Выделив участок в трубе с жидкостью, можно сказать, что она движется слева направо и через некоторое время полностью сдвинется в область S2. Изменение положения слева будет равно расстоянию дельта L1, а справа — дельта L2.

Течение является:

• ламинарным — находящаяся в трубке жидкость перемешивается слоями без хаотических изменений давления и скорости, турбулентность отсутствует;
• стационарным — распределение скоростей не изменяется с течением времени;
• скоростным — в движении принимает участие такой параметр, как ускорение;
• идеальным с несжимаемой жидкостью.

Последнее обозначает, что нет вязкости. Поэтому на жидкость действует только сила упругости и тяжести, а силы трения нет. Система не является замкнутой, а значит закон сохранения энергии применительно к рассматриваемому участку использовать нельзя. Зато вполне можно применить теорему о кинетической энергии.

Для газов уравнение можно использовать лишь в том случае, если их плотность изменяется незначительно. Но касаемо аэродинамики учитывается и то, что изменение давления воздуха гораздо меньше атмосферного. Поэтому уравнение можно применять в аэродинамических расчётах.

Согласно ему, сумма действующих всех сил на тело (рассматриваемый кусок жидкости) равняется изменению кинетической энергии объекта: ΣAi = ΔEk. На нижний участок действует сила давления, выполняющая положительную работу, а на верхний — отрицательную. Кроме этого, действует и сила тяжести. Так как жидкость поднимается, она имеет тоже отрицательный знак. Сила бокового давления перпендикулярна любой точке в системе, поэтому никакого влияния она не оказывает.

Количественная сторона

Исходя из сил, действующих на тело, изменение кинетической энергии можно описать выражением: ΔEk = Ap1 +Ap2 +Ag. Чтобы найти работу, необходимо силу умножить на пройденное расстояние. Поэтому работа силы давления равна произведению самой силы F на модуль перемещения ΔL и косинусу угла между ними: Ap1 = F1* ΔL *1.

Чтобы найти силу, нужно давление умножить на площадь. Значит: Ap1 = p 1 * S1 * ΔL1 = p1V1. Таким же образом находится работа для второго состояния: Ap2 = F1* ΔL2 *(-1) = – p2 * S2 * ΔL2 = -p2 * V2. Жидкость несжимаемая, следовательно: V1=V2=V.

Работу силы тяжести можно вычислить исходя из того, что рассматриваемый кусок жидкости является относительным, то есть он, хотя и не статический, в любом месте будет подвергаться воздействию одинаковой силы тяжести. Верным будет выражение: Ag = – ΔEp = – (m2 * g * h3 — m1 * g * h2) = m1 * g * h2 — m2 * g * h3. Так как жидкость несжимаемая, её плотность не изменится. Отсюда можно утверждать: Ag = ρ * V * g * h2 — ρ * V * g * h3.

Зная количественные показатели всех трёх работ, можно найти изменение кинетической энергии. Из физики известно, что оно равно разнице конечной и начальной энергии. Течение стационарное, значит, скорость с течением времени не изменится. Следовательно, кинетическая энергия будет определяться разницей появившейся энергии в верхней части и ушедшей из нижней области: ΔEk = (m2 * v2²)/2 — (m1 * v1²) / 2.

Воспользовавшись тем, что масса равняется произведению плотности на объём, формулу можно привести к виду: ΔEk = (ρ * V * v2²)/2 — (ρ * V * v1²) / 2. Теперь найденные выражения для работ нужно подставить в теорему о кинетической энергии. Получится следующее равенство: p1V — p2V + ρ * V * g * h2 — ρ * V * g * h3 = (ρ * V * v2²) / 2 — (ρ * V * v1²) / 2. Разделив левую и правую часть на объём, выражение можно упростить до вида: p1 — p2 + ρ * g * h2 — ρ * g * h3 = (ρ * v2²)/2 — (ρ * v1²) / 2 .

То место, где давление p1, некая точка внутри трубки, пусть будет обозначено цифрой один, а там, где p2, — цифрой два. Всё что относится к единице можно записать в левой части, а к двойке — в правой: ρ1 * g * h2 + (ρ * v1²) / 2 = ρ * g * h3 + (ρ * v2²) / 2. Полученная формула показывает, что при переходе в пределе одной линии скорость, давление и высота изменяются. Поэтому в любой точке будет справедливым выражение: ρ1+ ρ * g * h + (ρ * v1) / 2 = const. Это и есть количественное описание уравнения Бернулли для идеальной жидкости.

Применение в гидравлике

Наиболее типичным примером использования уравнения является решение заданий по нахождению скорости вытекания жидкости из отверстия в широком сосуде. Такой ёмкостью называют систему, в которой диаметр сосуда значительно больше размера отверстия. Необходимо найти скорость вытекающей жидкости U1. Известно, что высота столба жидкости, на который действует сила тяжести g, равна h.

Пусть в жидкости, находящейся сверху, имеется точка один. Через некоторое время она окажется внизу в положении два. На верх жидкости давит атмосферное давление, поэтому p1=pатм. Высота в точке один равна h. Скорость U1 считают равной нулю. Давление p2 в точке два будет также равно атмосферному. Так как жидкость опустится на дно, то высота h3 станет нулевой.

Все эти величины следует подставить в уравнение Бернулли. Получится выражение: pатм + ρ * g * h + 0 = pатм + (ρ * U²) / 2 + 0. Атмосферное давление взаимно уничтожается: ρ * g * h = (ρ * U²) / 2. В левой и правой части стоит плотность, на которую можно сократить. Отсюда получается, что вид жидкости значения не имеет. Это может быть: вода, ртуть, расплавленный металл. Эффект от этого не поменяется. Из формулы можно выразить искомое U2. Оно будет равно: U2 = (2 * g * h)^½.

Интересным фактом является то, что полученный ответ при решении задачи называется формулой Торричелли. Она показывает, что скорость, с которой вытекает жидкость из широкого сосуда, равна скорости тела при свободном падении с той же высоты.

Используя уравнение, можно легко рассчитать давление жидкости на дно и стенки сосуда. В этом случае закон Бернулли является обобщением для формулы гидростатического давления. Пусть имеется сосуд с жидкостью высотой h. Точка, находящаяся наверху, характеризуется давлением p1 = pатм., высотой h2 равной h и скоростью U1. Для точки на дне параметры будут следующие: p2 = p, h3 = 0, U2 = 0. Скорости принимаются равными нулевому значению, так как рассматриваемая жидкость находится в состоянии покоя.

Данные следует подставить в уравнение. В итоге получится равенство: pатм + ρ * g * h + 0 = p + 0 + 0. Из него несложно найти неизвестное: p = pатм + ρ * g * h. Полученный ответ является формулой гидростатического давления и подтверждает закон Паскаля.

Аналогично уравнение Бернулли для потока реальной жидкости используется при расчёте расхода в карбюраторе, пульверизаторе, учёте статического и динамического давления.

Подъёмная сила

Самолёт летает благодаря тому, что набегающий на крыло напор воздуха создаёт подъёмную силу. Её можно рассчитать и оценить с помощью уравнения. Геометрически крыло можно представить в виде плоскости с углом a (угол атаки). На него действует поток воздуха со скоростью U. Частица воздуха ударяет в твёрдую поверхность и отражается от неё. Угол отражения равен углу атаки, а её скорость равняется U’. Нужно рассчитать подъёмную силу. Для этого необходимо выполнить три шага:

• рассмотреть изменение скорости воздуха;
• узнать импульс частиц;
• используя закон Ньютона, определить силу.

В результате получится, что на крыло действует сила, состоящая из двух компонентов: подъёмной силы Fy и аэродинамического сопротивления Fx. Fy = Cy * p * U² * S, а Fx = Cx * p * U² * S. В формулах С является коэффициентом, а S — площадью крыла.

Для расчёта используется уравнение Бернулли. Выглядеть оно будет следующим образом: Pп. к + (ρ * Uп. к) * 2 / 2 + ρ * g * hп. к = Pн. к + (ρ * Uн. к) * 2 / 2 + ρ * g * hн. к, где: п. к — под крылом, а н. к — над крылом. Это уравнение можно упростить, приняв, что давления над и под крылом примерно одинаковые, поэтому плотность будет также одинаковая. Кроме того, высота крыла довольно маленькая. Исходя из этого, формулу можно упростить, и она примет вид: pп. к-pн.к = (ρ * (Uн.к + Uп. к) * (Uн.к — Uп. к)) / 2 = 2 * U1 * U2. Теперь можно найти подъёмную силу. Для этого разность давлений нужно умножить на площадь крыла: Fy = (pп.к-pн. к) * S.

Таким образом, используя метод, можно рассчитать подъёмную силу, обусловленную эффектом Бернулли. Например, пусть дано, что площадь крыла равна 50 м². Скорость потока воздуха над крылом и под ним соответственно равны: U1 = 320 м/с, U2 = 290 м/с. Найти грузоподъёмность. Для решения задания нужно знать дифференциальную плотность воздуха. Это справочная величина, равная 1,29 кг/м3.

Используя уравнение Бернулли, можно записать: pп. к-pн.к = ρ * (U2н.к — U2п. к). Подъёмная сила равна площади крыла, умноженной на разность давления. Подставив одно выражение в другое, получим рабочую формулу: Fy = ρ * (U2н.к — U2п. к) * S / 2. После выполнения расчёта получится ответ 590 кН. То есть грузоподъёмность самолёта составит порядка 59 тонн.

Реальные вычисления для таких задач довольно сложные, поэтому часто используют онлайн-калькуляторы.

Энергетический смысл уравнения Бернулли – Энциклопедия по машиностроению XXL

Пра необходимости подчеркнуть энергетический смысл уравнения Бернулли будем обозначать удельную энергию частицы буквой Е вместо Н  [c.58]

Таким образом, энергетический смысл уравнения Бернулли для установившегося движения невязкой капельной жидкости заключается в том, что удельная энергия, т. е. энергия, присущая каждой единице веса движущейся невязкой жидкости и состоящая из кинетической и потенциальной энергии, остается неизменной.  [c.58]

Энергетический смысл уравнения Бернулли для элементарной струйки при установившемся движении идеальной жидкости заключается в том, что полная удельная энергия вдоль струйки остается неизменной.  [c.279]

Следовательно, энергетический смысл уравнения Бернулли можно выразить так при установившемся движении потока жидкости сумма четырех удельных энергий (энергии положения, давления, кинетической и потерь) остается неизменной вдоль потока.  [c.36]

З.Л. ГЕОМЕТРИЧЕСКИЙ И ЭНЕРГЕТИЧЕСКИЙ СМЫСЛ УРАВНЕНИЯ БЕРНУЛЛИ ДЛЯ СТРУЙКИ НЕВЯЗКОЙ (ИДЕАЛЬНОЙ) ЖИДКОСТИ  [c.76]

ГЕОМЕТРИЧЕСКИЙ И ФИЗИЧЕСКИЙ (ЭНЕРГЕТИЧЕСКИЙ) СМЫСЛ УРАВНЕНИЯ БЕРНУЛЛИ  [c.113]

Ознакомимся с энергетическим смыслом уравнения Бернулли.  [c.86]

Энергетический смысл уравнения Бернулли  [c.62]

Энергетический смысл уравнения Бернулли заключается в том, что при установившемся движении идеальной жидкости сумма удельных энергий не меняется вдоль данной элементарной струйки.  [c.35]

Рассмотрим смысл уравнения Бернулли с точек зрения гидравлической, геометрической и энергетической.  [c.74]

Представленные три формы уравнения Бернулли с энергетической точки зрения характеризуют удельную энергию жидкости, отнесенную соответственно к единице массы, веса и объема. Поэтому в дальнейшем уравнение Бернулли для потока жидкости будем также называть уравнением энергии, подчеркивая тем самым его энергетический смысл.  [c.124]

Дополнительные замечания в отношении энергетического смысла слагаемых, входящих в уравнение Бернулли для целого потока жидкости . В отношении слагаемых этого уравнения (которое, вообще говоря, имеет только некоторое чисто внешнее сходство с интегралом Бернулли , полученным Эйлером) отметим дополнительно следующее  [c.115]

Все члены уравнения Бернулли в формуле (3.3) имеют линейную размерность и в энергетическом смысле представляют собой удельную энергию жид-  [c.50]

Геометрический, физический (энергетический) и механический смысл уравнения Д. Бернулли  [c.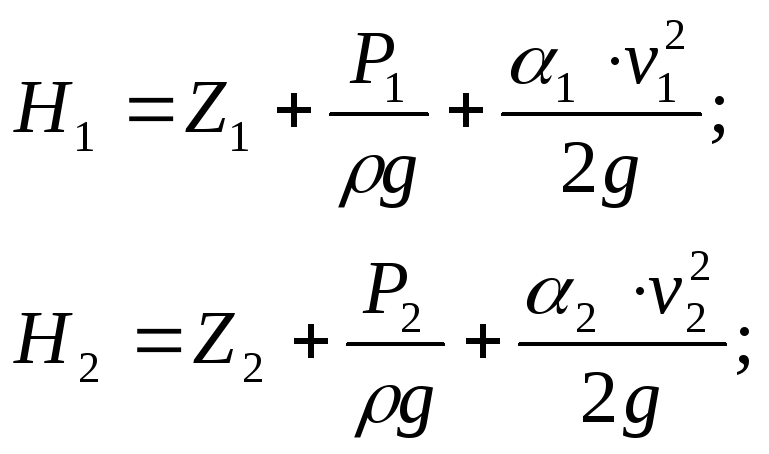 26]

Уравнение Бернулли можно рассматривать и в энергетическом смысле, подобно тому как рассматривалось основное уравнение гидростатики ( 1.2)  [c.89]

Это и есть уравнение Бернулли для элементарной струйки идеального газа. В уравнении все члены имеют тот же энергетический смысл, что и в соответствующем уравнении для капель-  [c.443]

Вывод уравнения Бернулли на основе энергетического баланса делает более понятным физический смысл входящих в него членов. Так, статическое давление р численно равно работе сил давления, совершаемых над еди-  [c.48]

Из чего следует, что каждый член уравнения выражает энергию, отнесенную к единице массы, т.е. удельную энергию. Это позволяет придать уравнению Бернулли энергетический смысл. Первые два члена выражают удельную потенциальную энергию (положения – дг и  [c.70]

Члены этого уравнения имеют тот же энергетический и геометрический смысл, что и члены уравнения Бернулли для элементарной струйки реальной жидкости.  [c.63]

Энергетический смысл уравнения Бернулли. Как следует из самого вывода уравнения (116), оно представляет собой уравнение работы, т. е. энергии. Каждый его член харак-т изует энергию жидкости, отнесенную к единице массы (Дж/кг). При этом размерность каждого члена уравнения  [c.97]

Геометрический и энергетический смысл уравнения Бернулли. Все члены уравнения Бернулли выражаются в единицах длины, по-sioMy каждый из них может называться высотой  [c.32]

Тогда энергетический смысл уравнения Бернулли можно сформулировать следующим образом при установивилемся движении жидкости сумма четырех удельных энергий (энергии положения, энергии гидродинамического давления, кинетической энергии и потерь энергии) остается неизменной вдоль потока.  [c.33]

Выражение (22.15) является уравнением баланса удельных энергий реального потока жидкости с учетом потерь. Все члены этого уравнения имеют тот же геометрический и энергетический смысл, что и уравнение Бернулли для элементарной струйкп идеальной жидкости. Из уравнения (22.15) следует, что удельная энергия ,гр, затраченная на преодоление сил трения на участке /—2, равна изменению полной удельной энергии потока (потенциальной и кинетической) на том же участке.  [c.282]

M=l, поднятой от плоскости 00 на высоту z, т. е. gz — удельная (отнесенная к массе) потенциальная энергия положения. Величина р/р выражает удельную (отнесенную к массе) потенциальную энергию давления. Энергетический смысл первых двух членов уравнения Бернулли таков же, как и в гидростатике gz- -p/p — удельная потенциальная энергия жидкости. Третий член 2/2 представляет собой кинетическую энергию уКид-кости массой М=1 (удельную кинетическую энергию), так как  [c.84]

Сопоставляя основное уравнение гидростатики с уравнением Бернулли (3.54), легко видеть, что первые два слагаемых уравнения Бернулли по написанию и по энергетическому смыслу совпадают с левой частью основного уравнения гидростатики и представляют собой потенциальную энергию положения и давления, отнесенную к е. динице веса жилкосттт. По совокупности потенциальная энергия здесь равна  [c.89]

---

Геометрический и энергетический смысл уравнения Бернулли для струйки

Поскольку все члены уравнений (3.22) и (3.23) имеют размерность длины, они могут быть легко проиллюстрированы гео­метрически.

Изобразим элементарную струйку и выделим в ней два сечения (рис. 3.4).

Ось трубки является линией тока и траекторией при установившемся движении.

Геометрический и энергетический смысл членов z и р/γрассмотрены в гидростатике.

На рис. 3.4 показаны гео­метрические высоты z (геометрические напоры) относительно горизон­тальной плоскости сравнения, след которой обозначен 0 – 0.

В каждой точке линии тока отложим вверх пьезометрические высоты. Соединив концы отрезков, изображающих эти высоты, плав­ной кривой, получим линию, называемую пьезометрической. Одновременно эта линия изображает изменение гидростатического напора z + р/γ.

Третий член уравнения Бернулли имеет размерность длины.

Величину u²/2g называют скоростной высотой или скоростным напо­ром.

Отложим эти отрезки вверх от пьезометрической ли­нии.

Если рассматривать невяз­кую жидкость, то согласно уравнению (3.22) верхние концы отрезков должны находиться на линии е – е, параллельной линии 0 – 0.

Рис. 3.4. Геометрическая и энергети­ческая интерпретация уравнения Бернулли для струйки вязкой жид­кости

Сумма пьезометрического и скоростного напоров представ­ляет собой полный напор, называемый гидродинамическим напором. Различают гидродинамический напор при абсолютном давлении и избыточном (избыточный гидродинамический напор).

Геометрический смысл уравнения Бернулли для струйки невяз­кой жидкости состоит в том, что гидродинамический напор остается постоянным по длине струйки.

Иначе – линия, соединяющая верх­ние концы гидродинамических напоров, расположена в горизонталь­ной плоскости, след которой на рис. 3.4 обозначен е – е.

Кинетичес­кая энергия частицы, имеющей массу т, равна т и²/2. Отнеся её к единице веса, т. е. тg, получим:

Кинематическая энергия частицы жидкости, отнесенная к единице её веса, количественно равная е_к, называется удельной кинетической энергией частицы.

Энергия движущейся частицы жидкости, отнесен­ная к единице её веса и условной горизонтальной плоскости, количест­венно равная е = е_п + е_к, называется удельной энергией частицы, где е_п – удельная потенциальная энергия частицы.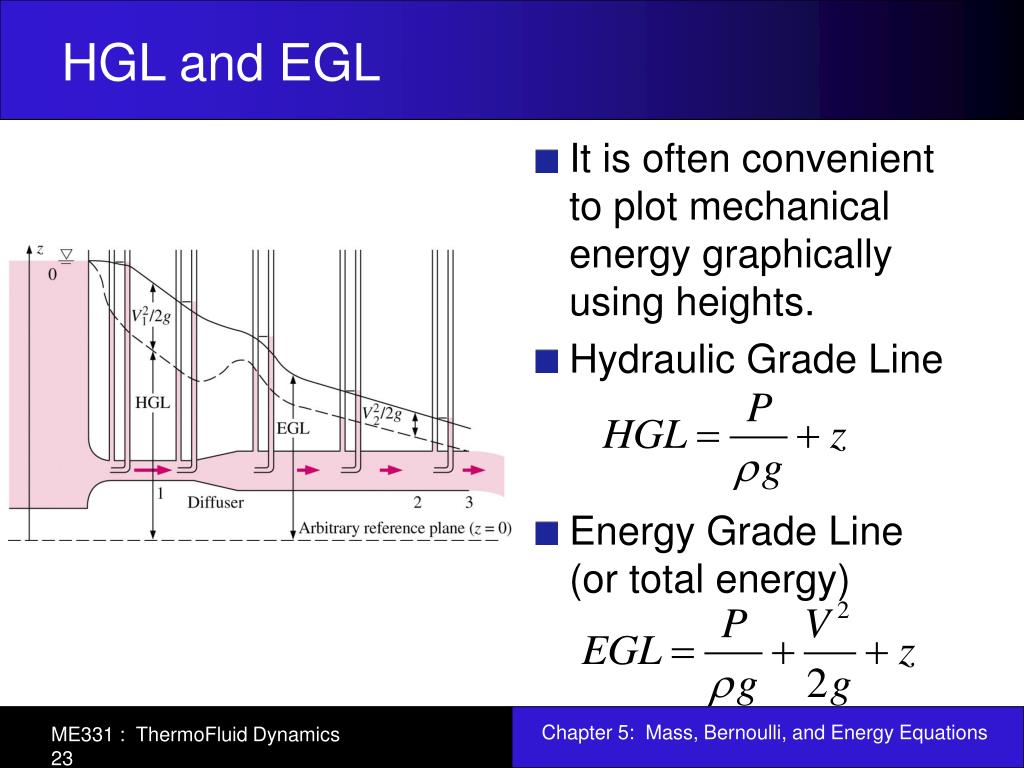

Поскольку удельная энергия выражается в единицах длины, то пол­ная удельная энергия е равна гидродинамическому напору.

Геометри­ческий смысл уравнения Бернулли для струйки вязкой жидкости: сумма геометрической, пьезометрической и ско­ростной высот уменьшается вниз по течению.

Энергетический смысл уравнения Бернулли струйки реальной жидкости определяется не­равенством е₁ > е₂, или согласно уравнению (3.23) е_х – е₂ = h′_ω, т. е. полная удельная энергия струйки вязкой жидкости убывает по длине струйки, затрачиваясь на преодоление сопротивлений.

Линию, характеризующую изменение пьезометрического напора по длине струй­ки, называют пьезометрической линией п — п(см. рис. 3.4).

Если представить себе пьезометры, установленные вдоль струйки, то пьезо­метрическая линия пройдет по горизонтам жидкости в пьезометрах.

Пьезометрическая линия может не только понижаться, но и повышать­ся, если площадь живого сечения струйки увеличивается. Линию, характеризующую изменение гидродинамического напора по длине струйки, называют линией гидродинамического напора, или напорной линией е — е’.

Эта линия может только понижаться.

Чтобы построить напорную линию, необходимо измерить скоростные высоты (напоры).

Напорная линия возвышается над пьезометрической на величину е_к= u²/2g.

На рис. 3.4 показана вертикальной штриховкой эпюра изменения удельной энергии, потерянной на сопротивление движе­нию. В сечении 2она равна h′_ω.

Уравнение Бернулли для элементарной струйки идеальной жидкости

Рассмотрим элементарную струйку идеальной жидкости. Выделим в ней отсек 1-2, ограниченный сечениями 1-1 и 2-2. В сечении 1-1 площадью dS₁(рис.3.4), действует давление p₁, а скорость движения жидкости U₁. В сечении 2-2 – давление p₂, площадь dS₂ , скорость U₂.

Центры тяжести выбранных сечений расположены на высотах Z₁ и Z₂ над плоскостью х₀у. Если бы жидкость, расположенная в трубке тока между сечениями 1-1 и 2-2 былa неподвижна, то можно было бы записать уравнение равновесия жидкости в соответствии с основным уравнением гидростатики:

или умножив все члены на g, получим:

. (3.13)

Уравнение (3.13) описывает закон сохранения потенциальной энергии в условиях покоя жидкости. Действительно, если 1 кг жидкости поднять на высоту Z₁над условной плоскостью сравнения, а под действием давления в этом сечении жидкость в трубке пьезометра сможет подняться еще на высоту , то она обладает суммарной удельной потенциальной энергией единицы массы:

Е¹ _пот=, Дж/кг. (3.14)

При движении жидкость обладает также кинетической энергией. Удельная кинетическая энергия единицы массы жидкости для первого сечения:

, Дж/кг. (3.15)

Присоединяя значение кинетической энергии к суммарной потенциальной энергии жидкости в состоянии покоя получим уравнение, характеризующее равновесие жидкости в условиях движения:

, Дж/кг. (3.16)

А так как действует закон сохранения энергии, то можно записать:

. (3.17)

Уравнение (3.17) устанавливает связь между геометрическим положением, давлением и скоростью жидкости в произвольном сечении. Оно называется уравнением Бернулли для элементарной струйки идеальной жидкости.

Анализируя уравнение можно увидеть, что расширение струйки (увеличение площади живого сечения струйки) приводит к уменьшению скорости струйки, а это уменьшает кинетическую энергию. А так как полная энергия струйки в любом сечении является величиной постоянной, т.е. сумма членов является константой, то увеличивается потенциальная энергия давления жидкости в данном сечении. И наоборот, уменьшение площади живого сечения струйки вызывает увеличение скорости и, следовательно, увеличение кинетической энергии, что приводит к уменьшению энергии потенциальной и соответственному падению давления. Проведем анализ размерности всех членов входящих в уравнение (3.17) помня о том, что силы инерции и силы тяжести были отнесены к единице массы жидкости, то есть члены уравнения, в которых присутствует скорость либо ускорение необходимо помножить на кг/кг:

Мы получили размерность удельной энергии, энергии отнесенной к единице массы жидкости (Дж/кг– это энергия 1 кг жидкости):

Уравнение (3.17) иллюстрирует энергетический смысл уравнения Бернулли – в любом сечении струйка жидкости обладает одной и той же суммарной энергией. Энергия трансформируется переходя из одного вида в другой при изменении условий течения, но сумма потенциальной и кинетической энергии остается постоянной. Рассмотрим еще один вид уравнения Бернулли – вид иллюстрирующий геометрический смысл.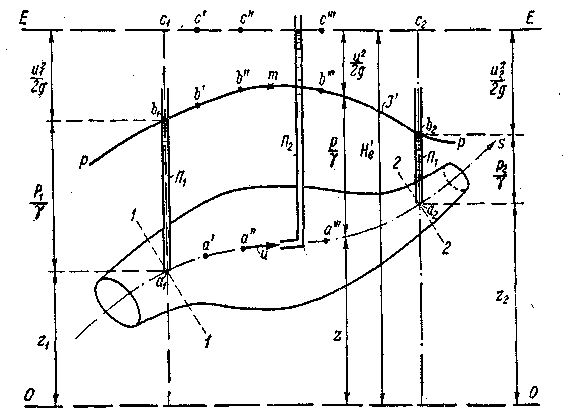 Для этого разделим все члены уравнения (3.17) на g:

. (3.18)

При геометрической интерпретации трактовки уравнения Бернулли все члены уравнения (3.18) могут быть представлены отрезками. Здесь:

z – высота положения выбранного сечения над плоскостью сравнения, м;

— пьезометрическая высота или высота, на которую поднимется жидкость под действием давления в заданной точке, если в эту точку поместить пьезометр, м;

— скоростной напор, м;

— полный гидростатический напор, м;

Н – полный гидродинамический напор, м.

Все члены уравнения (3.18) имеют линейную размерность – м.

14.8: Уравнение Бернулли – Physics LibreTexts

Цели обучения

• Объясните члены уравнения Бернулли
• Объясните, как уравнение Бернулли связано с сохранением энергии
• Опишите, как вывести принцип Бернулли из уравнения Бернулли.
• Выполнение расчетов по принципу Бернулли
• Опишите некоторые применения принципа Бернулли

Как показано на рисунке 14. 7.4, когда жидкость течет в более узкий канал, ее скорость увеличивается. Это означает, что его кинетическая энергия также увеличивается. Повышенная кинетическая энергия возникает из-за чистой работы, проделанной с жидкостью, чтобы протолкнуть ее в канал. Кроме того, если жидкость меняет вертикальное положение, с ней действует сила тяжести.

При сужении канала возникает перепад давления. Эта разница давлений приводит к действию результирующей силы на жидкость, потому что давление, умноженное на площадь, равно силе, и эта чистая сила действительно работает.{2} \ ldotp \]

Произведенная чистая работа увеличивает кинетическую энергию жидкости. В результате в быстро движущейся текучей среде давление падает независимо от того, заключена она в трубку или нет.

Есть много распространенных примеров падения давления в быстро движущихся жидкостях. Например, занавески для душа имеют неприятную привычку выпирать в душевую кабину, когда душ включен. Причина в том, что высокоскоростной поток воды и воздуха создает область более низкого давления внутри душа, тогда как давление на другой стороне остается на уровне стандартного атмосферного давления. Эта разница давлений приводит к возникновению чистой силы, толкающей завесу внутрь. Точно так же, когда автомобиль проезжает мимо грузовика на шоссе, кажется, что эти два автомобиля тянутся навстречу друг другу. Причина та же: высокая скорость воздуха между автомобилем и грузовиком создает область более низкого давления между транспортными средствами, и они сталкиваются друг с другом за счет большего давления снаружи (рисунок \ (\ PageIndex {1} \) ). Этот эффект наблюдался еще в середине 1800-х годов, когда было обнаружено, что поезда, идущие в противоположных направлениях, опасно наклоняются навстречу друг другу.

Рисунок \ (\ PageIndex {1} \): вид сверху автомобиля, проезжающего грузовик по шоссе. Воздух, проходящий между транспортными средствами, проходит по более узкому каналу и должен увеличивать свою скорость (v2 больше, чем v1), в результате чего давление между ними падает (pi меньше po). Более сильное давление снаружи сближает автомобиль и грузовик.

Сохранение энергии и уравнение Бернулли

Применение принципа сохранения энергии к ламинарному потоку без трения приводит к очень полезному соотношению между давлением и скоростью потока в жидкости.Это соотношение называется уравнением Бернулли , в честь Даниэля Бернулли (1700–1782), который опубликовал свои исследования движения жидкости в своей книге Hydrodynamica (1738).

Рассмотрим несжимаемую жидкость, протекающую по трубе различного диаметра и высоты, как показано на рисунке \ (\ PageIndex {2} \). Индексы 1 и 2 на рисунке обозначают два местоположения вдоль трубы и иллюстрируют взаимосвязь между площадями поперечных сечений A, скоростью потока v, высотой от земли y и давлением p в каждой точке.Здесь мы предполагаем, что плотность в двух точках одинакова – поэтому плотность обозначается как \ (\ rho \) без индексов – и, поскольку жидкость несжимаемая, заштрихованные объемы должны быть одинаковыми.

Рисунок \ (\ PageIndex {2} \): геометрия, использованная для вывода уравнения Бернулли.

Мы также предполагаем, что в жидкости нет вязких сил, поэтому энергия любой части жидкости будет сохранена. Чтобы вывести уравнение Бернулли, мы сначала вычисляем работу, которая была проделана с жидкостью:

\ [\ begin {split} dW & = F_ {1} dx_ {1} – F_ {2} dx_ {2} \\ & = p_ {1} A_ {1} dx_ {1} – p_ {2} A_ {2} dx_ {2} \\ & = p_ {1} dV – p_ {2} dV = (p_ {1} – p_ {2}) dV \ ldotp \ end {split} \]

Работа была проделана из-за консервативной силы тяжести и изменения кинетической энергии жидкости. {2} + \ rho gy = constant \ label {14.16} \]

Здесь следует особо отметить тот факт, что в динамической ситуации давления на одной и той же высоте в разных частях жидкости могут быть разными, если они имеют разные скорости потока.

Анализ уравнения Бернулли

Согласно уравнению Бернулли, если мы проследим небольшой объем жидкости по его пути, различные суммы в сумме могут измениться, но общая сумма останется постоянной. Фактически, уравнение Бернулли – это просто удобное утверждение сохранения энергии для несжимаемой жидкости в отсутствие трения.

Общая форма уравнения Бернулли состоит из трех членов, и оно широко применимо. Чтобы лучше понять это, давайте рассмотрим некоторые конкретные ситуации, которые упрощают и иллюстрируют его использование и значение.

Уравнение Бернулли для статических жидкостей

Сначала рассмотрим очень простую ситуацию, когда жидкость статична, то есть \ (v_1 = v_2 = 0 \). Уравнение Бернулли в этом случае –

\ [p_ {1} + \ rho gh_ {1} = p_ {2} + \ rho gh_ {2} \ ldotp \]

Мы можем еще больше упростить уравнение, установив h ₂ = 0.(Любая высота может быть выбрана для нулевой контрольной высоты, как это часто делается для других ситуаций, связанных с гравитационной силой, делая все остальные высоты относительными.) В этом случае мы получаем

\ [p_ {2} = p_ {1} + \ rho gh_ {1} \ ldotp \]

Это уравнение говорит нам, что в статических жидкостях давление увеличивается с глубиной. При переходе от точки 1 к точке 2 в жидкости глубина увеличивается на h ₁ , и, следовательно, p ₂ больше p ₁ на величину \ (\ rho gh_1 \).В простейшем случае p ₁ равно нулю в верхней части жидкости, и мы получаем знакомое соотношение \ (p = \ rho gh \). (Напомним, что p = \ (\ rho gh \) и \ (\ Delta Ug = −mgh \).) Таким образом, уравнение Бернулли подтверждает тот факт, что изменение давления из-за веса жидкости равно \ (\ rho gh \ ). Хотя мы вводим уравнение Бернулли для движения жидкости, оно включает в себя многое из того, что мы изучили для статических жидкостей ранее.

Принцип Бернулли

Предположим, что жидкость движется, но ее глубина постоянна, то есть \ (h_1 = h_2 \).{2} \ ldotp \ label {Бернулли} \]

Ситуации, в которых жидкость течет на постоянной глубине, настолько распространены, что это уравнение часто также называют принципом Бернулли , который представляет собой просто уравнение Бернулли для жидкостей на постоянной глубине. (Заметим еще раз, что это относится к небольшому объему жидкости, когда мы следуем за ней по ее пути.) Принцип Бернулли подтверждает тот факт, что давление падает с увеличением скорости в движущейся жидкости: если v ₂ больше, чем v ₁ дюйм уравнения, тогда p ₂ должно быть меньше p ₁ , чтобы равенство соблюдалось.

Пример 14.6: Расчет давления

В примере 14.5 мы обнаружили, что скорость воды в шланге увеличилась с 1,96 м / с до 25,5 м / с, идя от шланга к соплу. Рассчитайте давление в шланге, учитывая, что абсолютное давление в форсунке составляет 1,01 x 10 ⁵ Н / м ² (атмосферное, как и должно быть) и предполагая ровный поток без трения.

Стратегия

Уровень потока означает постоянную глубину, поэтому применяется принцип Бернулли.{2} \ ldotp \ end {align *} \]

Значение

Это абсолютное давление в шланге больше, чем в форсунке, как и ожидалось, поскольку v больше в форсунке. Давление p ₂ в сопле должно быть атмосферным, так как вода выходит в атмосферу без других изменений условий.

Применение принципа Бернулли

Существует множество устройств и ситуаций, в которых жидкость течет с постоянной высотой, и поэтому их можно проанализировать с помощью принципа Бернулли.

Захват

Люди давно используют принцип Бернулли, используя пониженное давление в высокоскоростных жидкостях для перемещения предметов. При более высоком давлении снаружи высокоскоростная жидкость выталкивает другие жидкости в поток. Этот процесс называется увлечение . Улавливатели использовались с древних времен в качестве насосов для подъема воды на небольшую высоту, что необходимо для осушения болот, полей или других низинных мест. Некоторые другие устройства, использующие концепцию увлечения, показаны на рисунке \ (\ PageIndex {3} \).

Рисунок \ (\ PageIndex {3} \): Устройства захвата используют увеличенную скорость жидкости для создания низкого давления, которое затем увлекает одну жидкость в другую. (а) В горелке Бунзена используется регулируемое газовое сопло, увлекающее воздух для правильного сгорания. (б) В распылителе используется сжимаемая груша для создания струи воздуха, в которую попадают капли духов. Краскораспылители и карбюраторы используют очень похожие методы для перемещения соответствующих жидкостей. (c) Обычный аспиратор использует высокоскоростной поток воды для создания области более низкого давления.Аспираторы могут использоваться в качестве отсасывающих насосов в стоматологических и хирургических ситуациях или для осушения затопленного подвала или создания пониженного давления в сосуде. (г) Дымоход водонагревателя предназначен для увлечения воздуха в трубу, ведущую через потолок.

Измерение скорости

На рисунке \ (\ PageIndex {4} \) показаны два устройства, которые применяют принцип Бернулли для измерения скорости жидкости. Манометр в части (а) подсоединен к двум трубкам, которые достаточно малы, чтобы заметно не мешать потоку.{2} \ ldotp \]

(Напомним, что символ \ (\ propto \) означает «пропорционально.») Решая для v ₂ , мы видим, что

\ [v_ {2} \ propto \ sqrt {h} \ ldotp \]

Часть (b) показывает версию этого устройства, которое обычно используется для измерения различных скоростей жидкости; такие устройства часто используются в качестве указателей воздушной скорости в самолетах.

Рисунок \ (\ PageIndex {4} \): Измерение скорости жидкости на основе принципа Бернулли. (а) Манометр подсоединяется к двум трубкам, которые расположены близко друг к другу и достаточно малы, чтобы не мешать потоку.{2} \). (б) Этот тип устройства для измерения скорости представляет собой трубку Прандтля, также известную как трубка Пито.

Рукав пожарный

Все предыдущие применения уравнения Бернулли включали упрощающие условия, такие как постоянная высота или постоянное давление. Следующий пример представляет собой более общее приложение уравнения Бернулли, в котором изменяются давление, скорость и высота.

Пример 14.7: Расчет давления – сопло пожарного рукава

Пожарные рукава, используемые при крупных строительных пожарах, имеют внутренний диаметр 6.40 см (Рисунок \ (\ PageIndex {5} \)). Предположим, такой шланг пропускает поток 40,0 л / с, начиная с манометрического давления 1,62 x 10 ⁶ Н / м ² . Шланг поднимается по лестнице на 10,0 м к патрубку с внутренним диаметром 3,00 см. Какое давление в насадке?

Рисунок \ (\ PageIndex {5} \): Давление в сопле этого пожарного рукава ниже, чем на уровне земли по двум причинам: вода должна подниматься вверх, чтобы добраться до сопла, и скорость в сопле увеличивается. Несмотря на пониженное давление, вода может оказывать большую силу на все, на что она ударяется, благодаря своей кинетической энергии.{2}) (10,0 \; м) \\ & = 0 \ ldotp \ end {align *} \]

Значение

Это значение составляет манометрическое давление , поскольку начальное давление было задано как манометрическое. Таким образом, давление в форсунке равно атмосферному давлению, как и должно быть, потому что вода выходит в атмосферу без изменения ее условий.

Авторы и авторство

• Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами.Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

Давление

Уравнение Бернулли можно рассматривать как утверждение принципа сохранения энергии, подходящего для текущих жидкостей. Качественное поведение, которое обычно обозначается термином «эффект Бернулли», представляет собой снижение давления жидкости в областях, где скорость потока увеличивается. Такое понижение давления в сужении пути потока может показаться нелогичным, но кажется менее очевидным, если рассматривать давление как плотность энергии.В высокоскоростном потоке через сужение кинетическая энергия должна увеличиваться за счет энергии давления.

Предупреждение о стационарном потоке : Хотя уравнение Бернулли сформулировано в терминах универсально обоснованных идей, таких как сохранение энергии и идеи давления, кинетической энергии и потенциальной энергии, его применение в приведенной выше форме ограничено случаями стационарного потока. . Для потока через трубку такой поток можно визуализировать как ламинарный поток, что все еще является идеализацией, но если поток является ламинарным в хорошем приближении, то кинетическая энергия потока в любой точке жидкости может быть смоделирована и рассчитана.Кинетическая энергия на единицу объема в уравнении – это тот член, который требует строгих ограничений для применения уравнения Бернулли – это в основном предположение, что вся кинетическая энергия жидкости вносит непосредственный вклад в процесс прямого потока жидкости. Это должно сделать очевидным, что наличие турбулентности или любого хаотического движения жидкости потребует некоторой кинетической энергии, которая не способствует продвижению жидкости по трубке.

Следует также сказать, что, хотя сохранение энергии применяется всегда, эта форма анализа этой энергии определенно не описывает, как эта энергия распределяется в переходных условиях.Хорошая визуализация эффекта Бернулли – это поток через сужение, но эта четкая картинка не описывает жидкость, когда вы впервые включаете поток.

Другое приближение, включенное в формулировку приведенного выше уравнения Бернулли, – это пренебрежение потерями от жидкостного трения. Идеализированный ламинарный поток через трубу можно смоделировать с помощью закона Пуазейля, который учитывает потери на вязкость, приводящие к снижению давления по мере продвижения по трубе. Утверждение уравнения Бернулли выше привело бы к ожиданию, что давление вернется к значению P ₁ после сужения, поскольку радиус возвращается к своему исходному значению.Это не так из-за потери некоторой энергии из процесса активного потока на трение в неупорядоченное движение молекул (тепловая энергия). Более точное моделирование можно сделать, объединив уравнение Бернулли с законом Пуазейля. Реальным примером, который может помочь визуализировать процесс, является мониторинг давления потока через суженную трубу.

Расчет Бернулли

Теорема Бернулли – обзор

1.17.5.2.1 Измерение движения жидкости: вода

Для измерения расхода потока в гидравлических лотках используются два общих метода.Измерители Вентури, диафрагмы и сопловые расходомеры – все это линейные устройства, которые используют уравнение Бернулли для связи изменения давления, наблюдаемого в двух местах, имеющих две разные площади поперечного сечения для постоянного расхода (см. Young et al., 2007) . Во втором методе также используется уравнение Бернулли, но используются водосливы различной конфигурации (например, прямоугольные, широкополосные, V-образные; см. Young et al., 2007). Этот последний подход требует свободного перепада в конце канала и над хвостовиком.Исследователи лотков нередко используют водосливы или измерители тока (см. Ниже) для калибровки измерителей перепада давления, разработанных на месте для конкретного применения.

Измерители тока обычно используются для измерения скорости в точке. Эти устройства можно опустить в лоток и удерживать над слоем в течение дискретного периода времени. В гидравлических лотках обычно используются три разных измерителя (Рисунок 5).

Рис. 5. Типичные примеры измерителей тока, используемых в гидравлических лотках (слева направо): механический (измеритель тока Price), электромагнитный (Marsh – McBirney) и акустический доплеровский измеритель скорости (Nortek).

Механические измерители тока полагаются на вращение ковша, колеса или пропеллера, помещенного в движущуюся жидкость (рис. 5), а скорость вращения связана со скоростью потока (Whiting, 2003). Число оборотов в единицу времени можно измерять или контролировать оптически, магнитно или электронно, а основная ось вращения измерителя тока ориентирована параллельно основному направлению потока. Эти зонды действительно одномерные (отрицательные скорости не могут быть зарегистрированы), и они относительно большие по размеру по сравнению с масштабом экспериментальных потоков, что ограничивает их использование для исследований.Фулфорд (2001) обсудил использование и применение механических измерителей тока.

Электромагнитные измерители тока (ECM) используются для сбора одно- и двумерных измерений скорости и турбулентности в гидравлических лотках. Эти измерители (рис. 5, в центре) основаны на законе Фаради, который гласит, что когда электрический проводник (жидкость) движется через магнитное поле (созданное головкой зонда), электромагнитная сила индуцируется под прямым углом к ​​магнитным полям. , воспринимаемое зондом, и эти поля пропорциональны скорости потока жидкости (Lane et al., 1993). Блоки управления двигателем обычно подключаются к системе сбора данных, в которой напряжения от каждого компонента собираются на относительно низких частотах (приблизительно 15 Гц). Эти напряжения могут быть преобразованы в колебания скорости, и могут быть получены как средние по времени, так и параметры турбулентности. ECM, разработанные для лабораторных настроек, имеют относительно малые диаметры головки зонда (например, 13 мм), а магнитные поля, создаваемые зондом, обычно примерно в два раза больше диаметра зонда. ECM чаще используются в полевых исследованиях, чем в гидравлических лотках (см. Lane et al., 1993; Беннетт и Бридж, 1995b).

Последняя группа измерителей тока является акустической и включает акустические доплеровские измерители скорости (ADV) и ультразвуковые доплеровские профилометры скорости (UVDP). ADV используют доплеровский сдвиг частоты акустических сигналов, рассеянных назад мелкими частицами, присутствующими в потоке. Зонд (Рисунок 5, справа) излучает относительно высокочастотный сигнал (10 МГц), и этот сигнал передается в измерительный объем длиной 3–9 мм и шириной 6 мм, расположенный на расстоянии 50–100 мм.Сдвиг этой частоты, наблюдаемый 2–4 приемными преобразователями, пропорционален скорости частиц в этом измерительном объеме (Lane et al., 1998). Используя геометрию и количество приемных преобразователей, а также встроенные возможности обработки в реальном времени устройства и его программного обеспечения, эти обратно рассеянные сигналы преобразуются в колеблющиеся компоненты скорости потока. Данные ADV могут быть записаны с частотой от 25 до 200 Гц, и теперь эти устройства стали стандартными измерителями тока, используемыми в экспериментальных исследованиях в гидравлических лотках, при условии, что должное внимание уделяется постобработке сигнала (Goring and Nikora, 2002) .ADV широко использовались в гидравлических лотках для решения таких вопросов, как турбулентный поток через структурированные гравийные пласты (Lawless and Robert, 2001), макротурбулентный поток через дюны (Venditti and Bennett, 2000), средний и турбулентный поток через растительность (Lopez and Garcia, 2001), течение в изгибах меандра и сложных каналах (Wormleaton et al., 2004; Abad and Garcia, 2009) и размыв, связанный с лопастями, водосливами и отрогами (Kuhnle et al., 2008; Bhuiyan et al., 2009). ). Подобно ADV, UVDP также используют высокочастотный акустический сигнал в качестве источника энергии (до 8 МГц), и они также полагаются на обнаружение частоты доплеровского сдвига обратно рассеянной энергии от частиц в потоке (Best et al., 2001). Однако вместо точечных измерений UDVP могут регистрировать до 128 одномерных скоростей вдоль оси ультразвукового луча, а расстояние между последовательными точками может варьироваться примерно от 1 до 5 мм. Хотя UDVP не так широко используются, как ADV, они использовались для количественной оценки скорости турбулентных потоков в плотных течениях с отложениями (Best et al., 2001; Leeder et al., 2005).

Страница не найдена | MIT

Перейти к содержанию ↓

• Образование
• Исследовательская работа
• Инновации
• Прием + помощь
• Студенческая жизнь
• Новости
• Выпускников
• О Массачусетском технологическом институте
• Подробнее ↓
  • Прием + помощь
  • Студенческая жизнь
  • Новости
  • Выпускников
  • О Массачусетском технологическом институте

Меню ↓ Поиск Меню Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов

Предложения или отзывы?

Уравнение Бернулли – GeeksforGeeks

Когда часто спрашивают, как самолет создает подъемную силу или как работают действительно крутые краскораспылители, наиболее распространенным ответом является принцип Бернулли – кажущийся простым двусмысленным ответом на откровенно многослойный феномен. .Эта концепция жидкостей и их механических свойств может показаться сложной темой для понимания, в основном из-за длинных уравнений вывода и непривлекательных представлений. Однако помните, что понимание идеи является ключевым моментом. Визуализация концепции может творить чудеса с любым человеком, решающим проблемы.

В этой статье мы поможем построить определение и перспективу принципа Бернулли и, следовательно, связанного с ним уравнения (как и все, что когда-либо объяснялось в физике – с помощью уравнений).

Принцип Бернулли

Как показано выше, уравнение Бернулли – это просто математическое выражение, которое помогает связать скорость, давление и высоту жидкости. Это соотношение было построено с учетом того, что энергия сохраняется на протяжении всего движения жидкости. Поэтому мы смотрим на формы энергии, связанные с жидкостью.

1. Энергия, обусловленная давлением жидкости (статическое давление): это просто энергия системы, когда жидкость статична и оказывает давление на стенки контейнера.Фактически это статическое давление.
2. Кинетическая энергия, обусловленная движением жидкости: очевидная энергия, связанная с любой движущейся массой – здесь движение жидкости приводит к существованию этой формы энергии. Другой способ интерпретации – энергия, связанная с динамическим давлением.
3. Гравитационная потенциальная энергия от возвышения: потенциальная энергия – понятие скорее референциальное. Здесь высота жидкости объясняет накопление такой потенциальной энергии.Другими словами, это возникает из-за гидростатического давления.

Следовательно, по определению:

Полная механическая энергия , которая определяется как сумма всех этих энергий (кинетической, гравитационного потенциала и жидкости), должна оставаться постоянной , если не выполняется какая-либо работа с ней. система. Это принцип Бернулли года.

Следовательно, может быть записано следующее выражение:

Наиболее очевидное соотношение, которое может быть установлено с использованием этого выражения, – это своего рода пропорциональность между давлением жидкости и ее скоростью.На любой определенной высоте, которая является постоянной, гравитационная потенциальная энергия также может быть принята как постоянная. В результате мы остаемся со следующим выражением и пониманием.

P + (½) ρv ² = k

∴ P = k – (½) ρv ²

По мере увеличения P уменьшается v.

Ясно, что давление и скорость обратно пропорциональны. Эта идея будет применена в следующих разделах. Обратите внимание, что мы все еще не придерживаемся этого принципа.Нам нужно вывести уравнение, чтобы иметь дело с различными экземплярами одной и той же системы .

Уравнение Бернулли

Поскольку было установлено, что принцип Бернулли является проявлением принципа сохранения энергии, мы продолжим рассмотрение работы, проделанной для перемещения жидкости вдоль линии тока от одной точки к другой. Представим плотность жидкости через ρ.

Потоки жидкости из точки A в точку B

Мы предполагаем, что жидкость в точках A и B поднимается на высоту h ₁ и h ₂ , соответственно.Очевидно, что гравитационная потенциальная энергия на h ₂ больше. Также обратите внимание, что площадь поперечного сечения в точке A составляет A ₁ , а в точке B – A ₂ . Теперь, если нужно выполнить некоторую работу, жидкость должна переместиться на определенное расстояние, что также подразумевает соответствующую скорость.

Если жидкость движется на dx ₁ из точки A и на dx ₂ из точки B, она должна достичь скорости v ₁ и v ₂ , соответственно.Мы разработаем наш вывод вместе со следующим выражением:

dW = d (кинетическая энергия жидкости) + d (гравитационный потенциал жидкости)

или

dW = dK + dU

Работа, проделанная жидкость при перемещении из точки A в точку B как dW = dW ₁ – dW ₂ . Поскольку жидкость перемещается на dx ₁ и dx ₂ , мы перепишем выражение в терминах сил, действующих в точках A и B.

dW = F ₁ .dx ₁ – F ₂ .dx ₂ = P ₁ .A ₁ .dx ₁ – P ₂ .A ₂ .dx ₂

F ₁ и F ₂ – силы, действующие на жидкость в точках A и B, соответственно. Теперь вспомните, что Сила – это давление, испытываемое на единицу площади. Затем выражение для dW может быть изменено. Обратите внимание, что A ₁ dx ₁ = A ₂ dx ₂ = дифференциальный объем (элементарный / малый объем), поскольку любая площадь, умноженная на прилегающую длину, дает объем.Допустим, dV – это дифференциальный объем.

dW = P ₁ .dV – P ₂ .dV = (P ₁ -P ₂ ) .dV

Между тем, выражение для кинетической энергии жидкости можно записать используя массы и скорости жидкости в точках A и B. Мы будем использовать стандартное выражение для кинетической энергии, связанной с движущейся массой, т.е. dK = 0,5 м ₂ v ₂ ² – 0,5 м ₁ v ₁ ²

Напомним, что нам даны плотность жидкости (ρ) и дифференциальные объемы жидкости (dV).Поскольку мы хотели бы работать с меньшим количеством членов, мы можем использовать приведенное выше, чтобы поочередно выразить массы жидкости в точках A и B. Следовательно, мы имеем:

dK = ½ρdV (v ₂ ² – v ₁ ² )

Связанная с этим гравитационная потенциальная энергия довольно проста. Еще раз, мы можем еще больше упростить его, выразив массы в качестве альтернативы, то есть масса равна плотности, умноженной на объем. GPE обозначается dU.

dU = m ₁ gh ₁ – m ₂ gh ₂ = ρdVg (h ₂ – h ₁ ).

Приравнивая две части уравнения (dW = dK + dU), получаем следующее выражение:

(P ₁ – P ₂ ) dV = ½ρdV (v ₂ ² – v ₁ ² ) + ρdVg (h ₂ – h ₁ )

P ₁ – P ₂ = ½ρv ₂ ² – ½ρv ₁ ² + ρgh ₂ – ρgh ₁

Фактически это уравнение Бернулли.

При выводе этого выражения мы сделали несколько предположений, чтобы выявить динамику проблемы. Одно весьма важное предположение – несжимаемость жидкости. Это свойство позволило сделать плотность неизменной в зависимости от давления в разных точках трубы. Как это повлияло на наше уравнение, объясняется ниже.

Уравнение непрерывности

Изменение плотности – даже небольшое, если не такое значительное – в действительности является довольно обычным явлением.Следовательно, никакая жидкость не является идеально несжимаемой. Вы можете сказать, что жидкость гораздо более несжимаема, чем газ, но не несжимаема буквально. При этом это влияет на массу жидкости, учитываемой при расчетах энергии.

Поскольку плотность остается постоянной на всем протяжении, отобранная масса также остается эквивалентной до тех пор, пока объемы также остаются эквивалентными – объемы, использованные в приведенных выше расчетах, были дифференциальными / элементарными, то есть dV, и, следовательно, равными. В результате наши массы сравнялись.Как мы можем лучше это понять?

Другая перспектива: сохранение массы

Рассмотрим диаграмму ниже.

Следующие несколько строк в этой статье будут тесно связаны с идеей сохранения массы – скорость, с которой определенная масса втекает в трубу вначале, должна быть такой же, как скорость, с которой она покидает трубу. Это очень важно.

Скорость поступления массы = Скорость выхода массы

Масса, по сути, равна плотности (ρ), умноженной на объем.Итак, мы можем выразить массы в этих терминах и приравнять различные примеры потока – в начале и в конце. Скорости наверняка будут различаться из-за разного давления. Итак, у нас есть

ρdV ₁ = ρdV ₂

, где V ₁ – это объем в начале (левый край трубы). V ₂ – объем в конце (самая правая заштрихованная область). Не путайте их со скоростями v ₁ и v ₂ . Объемы могут быть визуализированы как цилиндры с точки зрения их площади поперечного сечения и высоты – цилиндры имеют объем, выраженный как площадь поперечного сечения x-высота их тела. Итак, если цилиндры имеют высоту dx ₁ и dx _2,

ρA ₁ dx ₁ = ρA ₂ dx ₂

Поскольку мы имеем дело с «СКОРОСТЬ» массы, мы будем измерять расход через равные промежутки времени Δt. Мы можем выразить смещение через скорость жидкости v ₁ и v ₂ .

ρ.A ₁ .v ₁ .Δt = ρ.A ₂ .v ₂ .Δt

∴ A ₁ v ₁ = A ₂ v ₂

Это уравнение непрерывности. Это полезно при работе с несколькими приложениями принципа Бернулли.

Применение принципа Бернулли

(1) Разрушение кораблей

Ужасающая история прошлого, когда два корабля врезались друг в друга, путешествуя параллельно друг другу, – классический пример действующего принципа Бернулли.

Более высокое давление снаружи лодки приводит к столкновению

Представьте себе две лодки, плывущие параллельно друг другу с равной скоростью. Поскольку средняя часть лодки самая широкая, она действует как воронка или сжатая труба для воды между двумя лодками. Это уменьшение и увеличение площади, через которую проходит вода, приводит к увеличению скорости (принцип Бернулли). Однако, как только скорость увеличивается, давление между лодками уменьшается. В результате, чтобы стабилизировать это более низкое давление, вода снаружи толкается внутрь, заставляя лодки двигаться навстречу друг другу.

(2) Профиль и подъемная сила

Многие связывают причину полета только с принципом Бернулли. Однако другой принцип – эффект Коанды – также играет важную роль, когда дело доходит до создания необходимой подъемной силы для взлета самолета.

Падающий воздух должен проходить над и под аэродинамическим профилем. При этом воздух проходит дополнительное расстояние над крылом. В соответствии с эффектом Коанда воздух движется быстрее по искривленным поверхностям.Таким образом, воздух движется с большей скоростью, чем профиль крыла. Согласно принципу Бернулли, более высокая скорость жидкости приводит к соответствующей области более низкого давления. Между тем давление под аэродинамическим профилем относительно выше. Эта разница в давлении приводит к возникновению восходящей силы – подъемной силы, которая является единственной причиной полета и конструкции крыльев самолета.

(3) Отклонение вращающегося шара от его траектории

Наблюдается, что любой мяч при обычном броске (без вращения) поддается воздействию силы тяжести и очерчивает параболическую траекторию.Однако, когда мяч вращается, он отклоняется от своей траектории и поднимается или опускается в зависимости от направления вращения и относительного воздуха.

Когда мяч вращается и воздух движется к нему, линия потока воздуха увлекается вместе с мячом, что мы видим в верхней половине рисунка выше. Между тем, направление воздуха под мячом противоположно вращению, что приводит к минимальному сопротивлению (линия тока продолжается в обычном режиме). Поскольку воздух над мячом должен проходить большее расстояние вместе с мячом, он должен делать это с большей скоростью.Согласно принципу Бернулли, более высокая скорость связана с более низким давлением. Эта разница в скоростях и, как следствие, создаваемое давление приводит к динамическому подъему, заставляющему мяч подниматься. Этот эффект также известен как эффект Magnus Effect , который является основной темой во всех видах спорта с мячом, поскольку вращение приводит к отклоненному движению (желательному или нежелательному в зависимости от обстоятельств).

Примеры задач

Задача 1. Теперь, когда у нас есть представление о том, как принцип Бернулли используется для объяснения полета, как бы вы объяснили полет, когда самолет летит вверх ногами?

Решение:

Рассмотрим крыловой профиль, за исключением перевернутого вдоль оси x.

Немного сбивает с толку то, что внизу находится область более низкого давления из-за более высокой скорости вдоль линий тока. Кроме того, наверху воздух движется медленнее, а это означает, что самолет по логике может разбиться, если его толкнуть вниз! Но вот умный момент. Самолеты, такие как каскадеры или истребители, часто используют симметричные крылья, которые могут наклоняться для обеспечения подъемной силы. Поскольку они в значительной степени симметричны, скорости вверху и внизу относительно равны. Однако для создания подъемной силы наклон крыльев вверх на небольшой угол помогает удерживать самолет в полете.Этот наклон также иногда называют углом атаки.

Проблема 2: Два цилиндрических резервуара с площадями поперечного сечения A и 2A соответственно хранятся на горизонтальном полу. Первый резервуар заполнен до высоты H, а другой пуст. Если они соединены трубой с незначительным поперечным сечением, имеющей «a» внизу в момент времени t = 0, найдите, сколько времени потребуется, чтобы высоты в двух резервуарах сравнялись.

Решение:

Возьмите цилиндр слева как точку 1, трубу как точку 2 и цилиндр справа как трубу 3.Многие студенты совершают ошибку, напрямую применяя уравнение Бернулли между двумя цилиндрами. Это неверно, поскольку происходит потеря энергии, когда жидкость течет из трубы в цилиндр 3 из-за неупругих столкновений, когда жидкость сталкивается с некоторой массой жидкости в цилиндре 3, когда он заполняется (см. Ниже).

Энергия сохраняется только между цилиндром 1 и трубой. Однако масса сохраняется повсюду! Это означает, что мы можем использовать уравнение неразрывности.Следовательно, мы имеем следующее:

A ₁ v ₁ = av ₂ = A ₂ v ₃ (уравнение непрерывности)

Теперь возьмем разность высот y т.е. h – h ‘= y

Нам нужно, чтобы эта разница равнялась 0, поскольку в какой-то момент высоты будут равны. Скорость или то, как быстро это происходит, можно записать как дифференциал.

dy / dt = – (v ₁ + v ₃ ) …………… v ₁ вниз, а v ₃ вверх)

⇒ dy / dt = -v ₁ (1 + A ₁ / A ₂ ) ……… взяв v ₁ common и записав v ₃ / v ₁ , используя уравнение неразрывности.

Теперь применим уравнение Бернулли между цилиндром 1 и трубой:

P ₁ + (1/2) ρv ₁ ² + ρgh = P2 + (1/2) ρv ₂ ² + ρgh ‘

⇒ ρg (h – h’) = (1/2) ρv ₁ ² ((A ₁ ² / a ² ) – 1) …………… путем перестановки и использования уравнения неразрывности для (v ₂ / v ₁ ).

На предыдущем шаге мы аппроксимируем ((A ₁ ² / a ² ) – 1) до A ₁ / a, поскольку << A ₁ .На следующем шаге мы проинтегрируем дифференциальное уравнение, перенеся dy в одну сторону, а dt – в другую.

Пределы y имеют тенденцию от H к 0, поскольку мы хотим, чтобы разница высот равнялась 0 в конце.

Прошедшее время будет =

Проблема 3: Вода течет по горизонтальной трубе с поперечным сечением 4 м ² со скоростью 5 м / с при давлении 0,3 МПа в точке A. В точке B , площадь поперечного сечения 2 м ² .Какая скорость и воды в точке B? Рассчитайте давление в точке B.

Решение:

Давайте визуализируем представленный нам случай.

Используя уравнение непрерывности, мы можем найти скорость в точке B. A ₁ xv ₁ = A ₂ xv ₂

Следовательно, v ₂ = (A ₁ xv ₁ ) / A ₂

⇒ v ₂ = (4 x 5) / 2 м / с = 10 м / с

Теперь рассчитаем скорость в точке B.Обратите внимание, как увеличилась скорость. Это означает, что давление будет пропорционально уменьшаться – в соответствии с принципом Бернулли. Это поможет нам проверить наш ответ. Используя уравнение Бернулли:

P ₁ + (1/2) ρv ₁ ² + ρgh = P ₂ + (1/2) ρv ₂ ² + ρgh … …… .поскольку высота жидкости такая же.

⇒ 0,3 × 10 ⁶ + 0,5x1000x25 = P ₂ + 0,5x1000x10 ²

⇒ P ₂ = 0.2625 МПа

Задача 4. Вода течет по трубе постоянного радиуса = 10 см со скоростью 4 м / с и давлением 250 кПа. Найдите скорость на выходе и укажите, какой закон сохранения используется в этом расчете. Какое давление в точке B?

Решение:

Если радиус трубы остается постоянным на всем протяжении, площадь поперечного сечения выпускного отверстия останется прежней. Исходя из уравнения неразрывности, A ₁ x v ₁ = A ₂ x v ₂ , поскольку площади одинаковые, скорость воды на выходе составляет 4 м / с. v ₂ = 4 м / с . Уравнение неразрывности основано на принципе сохранения массы.

Используя уравнение Бернулли, замените значения скорости давления и высоты в точке A, а также скорость и высоту в точке B. Примите плотность жидкости равной 1000 кг / м ³ .

⇒ 250 кПа + 0,5x1000x16 + 1000 × 9,8 × 0 = P ₂ + 1000 × 9,8 × 10 + 0,5x1000x16

⇒ P ₂ = 152 кПа

8 9000 Проблема 5: Обратитесь к рисунку ниже и расположите давления в точках A, B , и C в порядке возрастания.Сделайте то же самое для скоростей в точках A, B , и C.

Решение:

Давайте сначала вычислим скорости. Мы знаем, что v _a = 16 м / с . Поскольку площади в точках A и B одинаковы, скорости также останутся прежними. Многих студентов это может сбить с толку, поскольку скорость увеличивается по мере падения. Однако в этом случае давление увеличивается из-за изменения высоты – не забудьте это принять к сведению.Итак, v _b = 16 м / с

Используя уравнение неразрывности, A _b x v _b = A _c x v _c . Следовательно, v _c = (5/7) x 16 м / с = 11,429 м / с .

⇒ v _a = v _b > v _c

Теперь мы можем найти давление в точке B, используя полученные скорости. Из уравнения Бернулли между A и B мы можем найти давление в точке B.

P _a + (1/2) ρv _a ² + ρgh = P _b + (1 / 2) ρv _b ² + ρgh, поскольку скорости в точках A и B одинаковы.

⇒ 300 кПа + 1000 × 9,8 × 16 = P _b + 1000 × 9,8 × 0

⇒ P _b = 156,8 кПа

Используя уравнение Бернулли между точками A и C, получаем следующее:

P _a + (1/2) ρv _a ² + ρgh = P _c + (1/2) ρv _c ² + ρgh ⇒ 300 + 0,5x1000x256 + 1000 × 9,8 × 20 = P _c + 0,5x1000x (11,429) ² + 1000 × 9,8 × 0

⇒ P _c = 258.9 кПа

⇒ P _a

b

c

Вопрос 6. Дом спроектирован так, чтобы выдерживать сильные порывы ветра с максимальной скоростью 80 м / с. Площадь кровли A = 450 м. Какое усилие выдерживают опоры крыши? Возьмем плотность воздуха = 1,029 кг / м ³

Решение:

Предположим, что вокруг крыши есть две точки – одна снаружи, а другая внутри.В большем масштабе расстояние между точками было бы совсем небольшим. См. Рисунок ниже.

По логике вещей, мы не должны чувствовать ветры внутри дома. Таким образом, мы можем предположить внутреннюю скорость или v _a = 0. Поскольку точки довольно близки друг к другу, их можно считать приподнятыми на одной и той же высоте. Наше уравнение Бернулли теперь довольно простое.

⇒ P _A + (1/2) ρv _A ² + ρgh = P _B + (1/2) ρv _B ² + ρgh

Начиная с v _A = 0, ⇒ P _A – P _B = (1/2) ρv _B ²

⇒ ΔP = (1/2) ρv _B ²

⇒ Сила / Площадь крыши = ΔP

⇒ Сила = 0.5ρv _B ² x Площадь

⇒ Сила = 0,5 x 1,029 x 80 ² x 450

Крыша может выдерживать максимальную силу 1,481 x 10 ⁶ Н.

Внимание, читатель! Не прекращайте учиться сейчас. Примите участие в тесте на получение стипендии для курса «Первый шаг к DSA» для учащихся 9–12 классов .

Уравнение Бернулли: формулы, примеры и задачи – видео и стенограмма урока

Уравнение Бернулли

Мы можем аккуратно упаковать концепцию сохранения жидкости в уравнение Бернулли , которое связывает давление, скорость и высоту в любых двух точках в идеальной жидкости.2), h, – высота жидкости над землей, а v – скорость жидкости.

Вы видите, как если одна переменная изменяется в точке 1, то должно измениться что-то еще, чтобы уравнение оставалось равным?

Пример уравнения Бернулли

Возможно, вам все еще трудно понять эту концепцию и связать ее с сохранением энергии, поэтому давайте рассмотрим реальный пример.

Скажем, вода течет по S-образной трубе.2 * (0 м – 2 м)

Проведя вычисления, мы обнаружим, что наше давление во второй точке трубы составляет 92 900 Па.

В этом случае давление снизилось, потому что оно увеличилось. Но также обратите внимание, что в этот момент скорость была больше ( v2 = 10 м / с), что имеет смысл. И, если мы составим наше уравнение так, чтобы оно читалось так, как оно было изначально, обе стороны все равно будут равны. Вы видите, как изменяется одна переменная, а другие изменяются, чтобы приспосабливаться и сохранять отношения внутри жидкости?

При желании вы могли бы исследовать эту взаимосвязь дальше, найдя любую недостающую переменную.Пока вы знаете другие, вы можете перемешать уравнение, чтобы увидеть, как переменные поддерживают баланс не только в уравнении Бернулли, но и в нашей идеальной жидкости.

Резюме урока

Закон сохранения энергии – полезное руководство для понимания сохранения в идеальных жидкостях. Этот закон гласит, что энергия не может быть создана или уничтожена, она только меняет форму или передается между объектами. 2 + ρgh3 .Это уравнение связывает давление, скорость и высоту в любых двух точках идеальной жидкости.

Поскольку это уравнение, обе стороны должны быть равны. Даже если отдельные компоненты давления, скорости и высоты различаются в одной точке трубы, взаимосвязь между ними будет такой же, как взаимосвязь между этими переменными в другой точке. Зная это, мы можем увидеть, как даже когда мы перестраиваем уравнение, чтобы найти пропущенное значение, обе стороны всегда будут одинаковыми, потому что отношения в идеальной жидкости одинаковы для всей жидкости.

Результаты обучения

По завершении этого урока вы должны уметь:

• Понимать концепцию консервации в идеальных жидкостях
• Выражение уравнения Бернулли
• Решите уравнение давления, скорости или высоты жидкости, используя уравнение Бернулли

Уравнение Бернулли – AP Physics 2

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

.