Что такое гироскоп в телефоне и для чего он нужен. Что такое гироскоп и как узнать есть ли он в телефоне
Гироскоп в телефоне впервые появился с выходом iPhone 4. Таким образом, в мобильные устройства снова внедрили дополнительные аппаратные средства. Теперь смартфоны умеют не только определять свое географическое местоположение, ориентацию в пространстве и автоматически разворачивать фотографии для удобного просмотра. Благодаря очередному нововведению устройства также научились фиксировать вращение (например, если пользователь находится на офисном стуле, который может поворачиваться в разные стороны). В результате функциональные возможности смартфонов расширились еще больше.
Что такое гироскоп?
Акселерометр может измерять линейное ускорение относительно системы координат. Это используется для определения ориентации телефона. В результате этого нововведения в свое время появилось множество новых полезных функций. В зависимости от ориентации телефона пользовательский интерфейс (UI) может автоматически поворачиваться в портретном или ландшафтном режиме.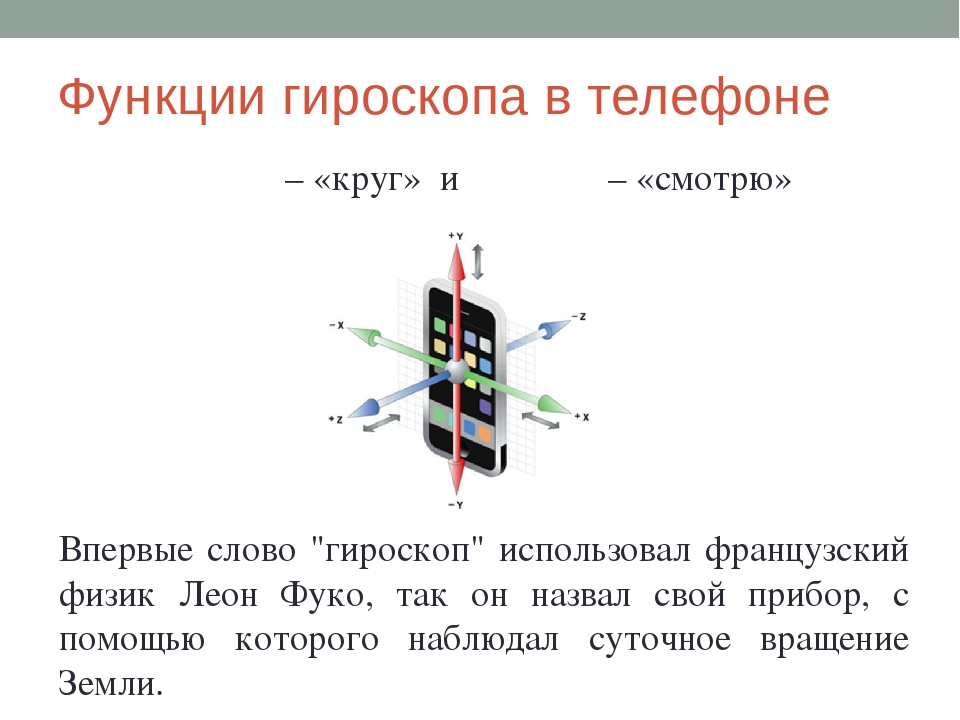 Благодаря этому появились новые возможности для создания мобильных игр.
Благодаря этому появились новые возможности для создания мобильных игр.
В наше время сложно представить себе гоночную игру для смартфона, которая не поддерживает акселерометр. Каждый раз, когда автомобиль нужно было повернуть, приходилось нажимать определенную кнопку на сенсорном экране. Калибровка акселерометра вывела игровой процесс на новый уровень, ведь теперь мы можем выполнять повороты за счет наклонов мобильного устройства. Благодаря этому нововведению было создано множество популярных игр.
Но зачем телефону нужен гироскоп, если уже есть акселерометр? На самом деле акселерометр измеряет только линейное ускорение устройства, тогда как гироскоп определяет его ориентацию. Фактически он может фиксировать свое движение в пространстве, включая вертикальное и горизонтальное вращение.
Тем, кто интересуется, что такое гироскоп в смартфоне, будет интересно узнать о его практическом применении. Чтобы понять принцип действия этого устройства, нужно представить себе игру Counter-Strike, которую перенесли на мобильную платформу. В таких играх мы должны двигаться во всех направлениях. Без поддержки гироскопа нам нужно было бы провести пальцем по сенсорному экрану, чтобы получить возможность двигаться в правильном направлении. В результате через некоторое время пользователь пришел бы к выводу, что управление игрой реализовано неудачно.
В таких играх мы должны двигаться во всех направлениях. Без поддержки гироскопа нам нужно было бы провести пальцем по сенсорному экрану, чтобы получить возможность двигаться в правильном направлении. В результате через некоторое время пользователь пришел бы к выводу, что управление игрой реализовано неудачно.
С внедрением гироскопа игровой процесс стал более приятным. Теперь пользователь может просто передвигать телефон в пространстве для управления игрой. Гироскоп определит ваше движение, и умная система поймет, что вы хотите сделать. Теперь игроку не нужно использовать свои пальцы для управления ходьбой и прицеливанием. Вместо этого появляется возможность сосредоточиться на стрельбе за счет прикосновений к сенсорному экрану.
Для управления подобными играми можно использовать акселерометр и встроенный компас, но в таком случае очень сильно страдает точность и плавность. Благодаря гироскопу появилась возможность сделать управление играми максимально приближенным к игровым консолям и ПК. Что касается аппаратных средств, то в мобильных телефонах используются устройства на основе MEMS (микроэлектромеханических систем). Далее в качестве примеров будут рассмотрены популярные телефоны с гироскопом.
Что касается аппаратных средств, то в мобильных телефонах используются устройства на основе MEMS (микроэлектромеханических систем). Далее в качестве примеров будут рассмотрены популярные телефоны с гироскопом.
Компания Apple впервые представила новое изобретение за счет его внедрения в iPhone 4. Когда эта фирма установила акселерометр на своем телефоне первого поколения, он сразу же приобрел всемирную известность. В результате был установлен новый тренд, и каждый производитель смартфонов стремился внедрить это нововведение на своих устройствах. Затем история повторилась, потому что гироскоп тоже стал объектом зависти среди конкурентов. Пользователи мобильных устройств были в восторге, когда Стив Джобс продемонстрировал возможности iPhone 4. В результате в магазине приложений появилось множество интересных игр с задействованным гироскопом.
Телефон Nexus S – это совместный продукт компаний Google и Samsung. Он стал первым устройством на базе Android, получившим гироскоп. Благодаря добавлению некоторых действительно продвинутых функций, таких как NFC, телефон составил серьезную конкуренцию iPhone 4. Поддержка API-интерфейса гироскопа была добавлена в Android 2.3 Gingerbread, благодаря чему разработчики получили возможность создавать интересные игры и приложения.
Поддержка API-интерфейса гироскопа была добавлена в Android 2.3 Gingerbread, благодаря чему разработчики получили возможность создавать интересные игры и приложения.
Список устройств Андроид, оснащенных этим нововведением, стремительно расширялся, благодаря чему многие пользователи смогли оценить его возможности. Вскоре после Nexus гироскоп установили на телефоне LG Optimus 2X. Кроме того, это устройство прославилось как первый в мире смартфон с двухъядерным процессором (1 GHz NVIDIA Tegra 2 AP20H Dual Core Processor).
Видео обзор: что такое гироскоп на Андроид
Современные смартфоны оснащены огромным количеством функций, за работу которых отвечает ряд датчиков.
Нередко об их назначении владельцы даже не догадываются. К числу таких датчиков относится гироскоп в телефоне: что это такое, не знают даже многие «продвинутые» пользователи, поэтому не лишним будет детально изучить это устройство.
Принцип действия оборудования
Гироскоп представляет собой волчок, вращающийся вокруг оси.
Наличие гиродатчика в смартфоне – это не просто прихоть, такой аппарат открывает перед обладателем гаджета множество дополнительных возможностей:
- прием вызовов простым встряхиванием аппарата,
- стабилизация камеры во время съемок,
- управление приложениями при помощи поворотов устройства,
- ориентация положения головы в виртуальной реальности.

В каких телефонах есть гироскоп?
Воспользоваться перечисленными выше преимуществами могут далеко не все владельцы смартфонов, так как гиродатчики установлены не везде. Самый надежный способ узнать, есть ли гироскоп в телефоне – спросить об этом у продавца-консультанта или прочитать паспорт к изделию. Если говорить о брендах, то впервые гиродатчик был установлен на iPhone 4. Поскольку новинка пришлась покупателям по вкусу, все последующие модели от Apple также получили это оборудование.
Несмотря на популярность этого датчика, многие задают вопрос о том, что такое гироскоп. Попробуем разобраться.
1. Гироскоп в классическом понимании
Рассматриваемое нами устройство, фактически, представляет собой волчок, который вращается вокруг вертикальной оси. Он закреплен в поворачивающейся вокруг другой оси раме. Эта другая ось тоже закреплена в своей раме, поворачивающейся вокруг третьей оси.
Благодаря этому как бы не поворачивался волчок, он всегда будет иметь вертикальное положение в пространстве.
Принцип работы гироскопа можно также увидеть на рисунке №1. Из него, в частности, можно понять, что в классическом устройстве есть вибрирующие грузики. А частота их вибрации равна скорости, умноженной на перемещение.
Благодаря такому явлению, как Кариолисово ускорение, несмотря на поворот тела, оно способно сохранять свое положение относительно плоскости вращения. Разумеется, оно имеет место только во время вращения.
Собственно, на этом простом свойстве вращающихся тел и основывается принцип работы того гироскопа, который есть у большинства из нас в смартфоне.
Разработчики научились делать гироскоп намного проще и меньше. Это позволило им умещать его в небольшую плату, которую можно разместить под корпусом любого современного мобильного девайса.
2. Предназначение датчика в телефоне
В телефоне он нужен для того, чтобы определять положение аппарата в пространстве.
Для пользователя все выглядит предельно просто – Вы поворачиваете смартфон горизонтально или вертикально и положение всех значков на экране меняется.
Во многих случаях повороты экрана можно использовать для выполнения определенных действий, например, для блокировки клавиатуры.
Интересно: Впервые гироскоп использовали в Айфоне 4. С тех пор этот датчик стал обязательным элементом любого мобильного девайса.
Теперь Вы знаете, как работает этот датчик. Стоит разобраться в том, как узнать есть ли он в Вашем гаджете.
3. Как проверить наличие гироскопа
В зависимости от операционной системы для этой цели можно использовать разные программы:
- Sensor Box для Андроид;
- Sensor Kinetics для iOS.
В первой программе нужно нажать иконку «Accelerometer sensor». Во второй делать не нужно ничего.
Существует способ еще проще – если в настройках есть пункт «Поворот экрана» (или что-то подобное), гироскоп есть. Но вышеупомянутые приложения помогают выявить проблемы в работе этого датчика.
Гироскоп в телефоне — что это? Если вы также задаетесь этим вопросом, как и многие пользователи, то эта статья для вас. В ней мы поговорим о том, что такое гироскоп в смартфоне, зачем он нужен, и как узнать есть ли данный прибор на вашем устройстве.
Что такое гироскоп
Современные смартфоны снабжены целым рядом различных датчиков. Практически каждое устройство оснащено регулятором освещения, движения, приближения. Кроме этих приборов большинство современных телефонов имеют на своем борту акселерометр, который способен реагировать на перемещение смартфона в двух- или же трехмерной плоскости. Тем не менее для того, чтобы мобильный девайс мог полноценно ориентироваться в пространстве, в нем должен быть установлен гироскоп.
Гироскоп в телефоне – это микроэлектромеханическая система, которая способна превращать угловые скорости в электрические сигналы. Проще говоря, это прибор, благодаря которому можно определить, на сколько градусов телефон наклонился относительно оси.
Зачем нужен гироскоп
Что такое гироскоп в телефоне разобрались, но для каких целей он используется? Этот прибор имеет целый ряд применений. Чаще всего датчик ориентации используют в игровой индустрии. На просторах Плэй Маркета можно найти кучу приложений, которые основаны на использовании гироскопа. Гонки, шутеры, симуляторы – благодаря датчику ориентации эти игры становятся реалистичнее и интереснее.
Кроме этого, гироскопы получили широкое применение в области GPS-навигации. Благодаря данному прибору карты стали по-настоящему интерактивными. Теперь навигационные приложения отслеживают не только ваше месторасположение, но и поворот тела. К примеру, если вы стоите лицом к лесу, то это обязательно отобразиться на карте. Если же вы измените положение своего тела на 180 градусов, то соответствующие изменения произойдут и в навигационном приложении.
Порой разработчики привязывают к гироскопу определенный функционал. К примеру, в некоторых моделях чтобы ответить на звонок или же перелистнуть страницу электронной книжки достаточно слегка встряхнуть телефон. А в некоторых случаях гироскоп отвечает за активацию функции Bluetooth.
Есть ли гироскоп на телефоне?
Чтобы определить есть ли гироскоп на вашем телефоне достаточно взглянуть на характеристики устройства. Просто вбейте в Гугл название своего смартфона и почитайте его технические параметры. Если же вы не знаете какая у вас модель телефона, то в таком случае есть альтернативный способ. Проверить наличие гироскопа на телефоне можно, воспользовавшись специальными мобильными утилитами. Благо, на просторах Плэй Маркета подобных программ пруд пруди. Рассмотрим же как проверить гироскоп через Gyroscope Test.
Мобильные телефоны с каждым годом становятся сложнее. Чтобы пересчитать количество всех датчиков, встроенных в современные смартфоны, может не хватить пальцев обеих рук. Гироскоп в телефоне – что это за сенсор, как он работает, каково его применение, можно ли отключить этот прибор? Эти вопросы будут рассмотрены для тех, кто хочет хорошо разбираться в своем смартфоне.
Чтобы пересчитать количество всех датчиков, встроенных в современные смартфоны, может не хватить пальцев обеих рук. Гироскоп в телефоне – что это за сенсор, как он работает, каково его применение, можно ли отключить этот прибор? Эти вопросы будут рассмотрены для тех, кто хочет хорошо разбираться в своем смартфоне.
Что такое гироскоп
Юла, она же волчок – известная игрушка. Она при быстром вращении сохраняет устойчивость на одной точке опоры. Это незамысловатое устройство является простейшим примером гироскопа – приспособления, реагирующего на изменения углов ориентации тела, на котором оно установлено, в трех плоскостях. Термин впервые использовал французский физик и математик Жан Фуко.
Гироскопы классифицируют по количеству степеней свободы и по принципу действия (механические и оптические). Вибрационные гиродатчики, подвид механических, широко используются в мобильных устройствах. Применение GPS-навигации отодвинуло на второй план изначальную функцию гироскопов – помощь при ориентации на местности, но эта технология все еще незаменима в современных моделях телефонов.
Отличие от акселерометра
На современных мобильных гаджетах часто установлены оба эти прибора. Ключевое отличие гироскопа от акселерометра и других сенсоров заключается в самом принципе работы данных аппаратов. Первый определяет собственный угол наклона относительно земли, а второй способен измерять линейное ускорение. Преимущество акселерометра – знание ускорения позволяет точно вычислить расстояние, на которое было перемещено устройство.
На практике оба прибора могут как заменять, так и дополнять друг друга. Фактически и тот, и тот лишь регистрируют положение относительно земной поверхности. Как и гироскоп, акселерометр может передавать сведения об ускорении смартфону, на который он установлен.Часто используются оба датчика; они хорошо взаимодействуют. В таблице зафиксированы ключевые особенности приборов.
Принцип работы
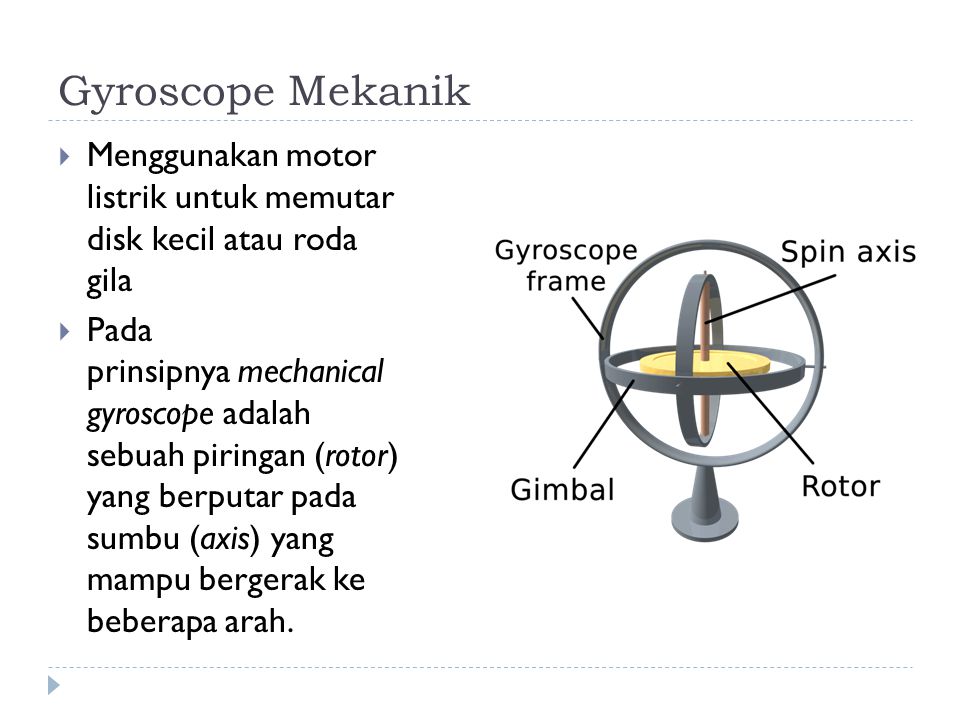
Простыми словами, гироскоп – это волчок, быстро вращающийся вокруг вертикальной оси, закрепленный на раме, которая способна поворачиваться вокруг горизонтальной оси, и закреплена на другой раме, которая поворачивается вокруг третьей оси. Как бы мы ни поворачивали волчок, он всегда имеет возможность все равно находиться в вертикальном положении. Датчики снимают сигнал, как волчок ориентирован относительно рам, а процессор получает информацию и считывает с высокой точностью, как рамы в этом случае должны быть расположены относительно силы тяжести.
Как бы мы ни поворачивали волчок, он всегда имеет возможность все равно находиться в вертикальном положении. Датчики снимают сигнал, как волчок ориентирован относительно рам, а процессор получает информацию и считывает с высокой точностью, как рамы в этом случае должны быть расположены относительно силы тяжести.
Что такое гироскоп в смартфоне
Современные мобильные устройства в большинстве своем оснащены гироскопами. Их еще называют гиродатчиками. Этот элемент смартфона работает на постоянной основе, автономно, не требует калибровки. Этот прибор не нужно включать, но в некоторых телефонах есть функция отключения с целью экономии энергии. Выполнен он в виде микроэлектромеханической схемы, расположенной под корпусом смартфона.
Для чего нужен
Внедрение технологии гиродачиков в мобильные девайсы существенно расширило их функционал и добавило новый способ управления устройствами. Например, простое встряхивание телефона позволит ответить на входящий звонок. Изменение ориентации экрана с помощью наклонов смартфона тоже реализовано благодаря гиродатчикам; этот прибор обеспечивает стабилизацию камеры. В приложении «Калькулятор» простой поворот экрана на 90 градусов открывает дополнительные функции программы.
Изменение ориентации экрана с помощью наклонов смартфона тоже реализовано благодаря гиродатчикам; этот прибор обеспечивает стабилизацию камеры. В приложении «Калькулятор» простой поворот экрана на 90 градусов открывает дополнительные функции программы.
Гиродатчик очень упростил пользование встроенными в смартфон картами. Если человек повернет свой девайс «лицом» к, скажем, конкретной улице, то это отобразится на карте с высокой точностью. Хороший смартфон с гироскопом обеспечивает пару интересных возможностей для мобильного гейминга. Управление виртуальным автомобилем становится невероятно реалистичным, когда для вождения машины используются повороты смартфона. В технологиях виртуальной реальности с помощью гиродатчиков отслеживаются повороты головы.
Как работает гироскопический датчик
В гиродатчике есть две массы, двигающиеся в противоположных направлениях. Когда появляется угловая скорость, на массу действует сила Кориолиса, направленная перпендикулярно их движению. Происходит смещение масс на величину, пропорциональную прикладываемой скорости. Меняется расстояние между подвижными и неподвижными электродами, что приводит к изменению емкости конденсатора и напряжению на его обкладках, а это уже электрический сигнал. Такие электронные сигналы и распознаются гиродатчиком.
Происходит смещение масс на величину, пропорциональную прикладываемой скорости. Меняется расстояние между подвижными и неподвижными электродами, что приводит к изменению емкости конденсатора и напряжению на его обкладках, а это уже электрический сигнал. Такие электронные сигналы и распознаются гиродатчиком.
Как узнать, есть ли гироскоп в смартфоне
Простой способ – ознакомиться с характеристиками девайса на официальном сайте производителя. Если гиродатчик имеется – это обязательно будет указано. Некоторые производители умалчивают о том, есть ли гироскоп на телефоне, не желая тратить на него место. Их можно понять – все сейчас стремятся сделать телефон легче и тоньше. В таких случаях помогут сторонние приложения.
На YouTube есть целый раздел видео, которые можно поворачивать на 360 градусов. Если у вас поддерживается возможность управления таким видео через повороты смартфона, значит работает гироскоп. Еще можно установить приложение AnTuTu Benchmark, которое проводит полную диагностику вашего устройства. Там вы найдете строку о наличии или отсутствии гироскопа.
Там вы найдете строку о наличии или отсутствии гироскопа.
В каких телефонах есть гироскоп
Первым смартфоном, в котором был установлен гиродатчик, является Iphone 4. Покупатели позитивно отнеслись к такому нововведению и с тех пор телефоны с гироскопом начали заполнять рынок. Все последующие версии смартфонов Apple были оборудованы гиродатчиками. Владельцам андроид-устройств в этом плане немного сложнее, благо, о наличии датчика можно спросить у консультанта перед покупкой, или проверить самому. Гироскоп в телефоне – это важный бонус.
Видео
Рекомендуем также
Для чего в смартфоне нужен гироскоп? | Свет
В этой статье поговорим о ещё одном датчике в смартфонах – это гироскоп. Что такое гироскоп и зачем он нужен в наших смартфонах?
Название гироскоп происходит от древнегреческого языка, где γῦρος переводится как «круг» и слово σκοπέω переводится как «смотрю».
Вообще, термин “гироскоп” впервые использовал французский физик Жан Бернар Фуко, ещё в 1852 году в своём докладе о способах экспериментального определения вращения Земли. Поэтому название имеет отношение к кругу (Земли).
Гироскопом называется устройство, которое реагирует на изменение угла какого-либо объекта в пространстве.
Изобрел гироскоп в современном его техническом понимании немецкий астроном и математик в 1817 году. Постепенно гироскоп начал находить практическое применение и в 20 веке стал использоваться в самолётах, ракетах и подводных лодках вместо компаса или совместно с ним.
Для чего гироскоп используется в смартфонах?
- Просмотр видео 360 градусов и использование игр с очками виртуальной реальности. В этом случае когда мы будем поворачивать голову, чтобы осмотреть виртуальное пространство, то как раз таки гироскоп будет помогать правильно отображать картинку.

- Гироскоп также отвечает за корректную работу программы “строительный уровень” в смартфоне, так как определяет точное отклонение горизонтали и углов в пространстве.
- При использовании в электронных картах местности гироскоп помогает определить направление сторон света в пространстве и таким образом на карте мы видим в какую сторону нам двигаться.
- Использование гироскопа в мобильных играх также используется и для управления персонажем или автомобилем, чтобы совершать движения или повороты.
- Поворот экрана смартфона. Тут стоит отметить, что гироскоп работая вместе с акселерометром позволяет более точно выполнять эту функцию, что способствует более точному срабатыванию и наоборот исключает возможности поворота экрана, тогда, когда это совсем не нужно.
Чем гироскоп отличается от акселерометра?
Иногда пользователи путают между собой эти датчики и хотя в некоторых программах они могут работать сообща у них есть свои особенности и это два совершенно разных датчика.
Акселерометр отвечает за ускорение смартфона в пространстве, а гироскоп за изменения углов наклона в пространстве.
Если было полезно, поставьте палец вверх и подпишитесь на канал, спасибо!
Гироскоп в планшете – что это? Гироскоп в телефоне: что это и зачем нужно.
Функциональные возможности современных мобильных телефонов давно вышли за рамки совершения звонков и обмена текстовыми сообщениями SMS. Смартфон сегодня это универсальный гаджет, начиненный всевозможными сенсорами. Имеются во многих моделях и специфические датчики, с помощью которых телефон может определять свое положение в пространстве. Примером таких чувствительных устройств являются гироскоп и акселерометр.
Что такое гироскоп и для чего он нужен, принцип работы
Начнем с того, что гироскоп – это механическое или электромеханическое устройство, способное определять собственный угол наклона относительно земной поверхности. Если сравнивать его с другими подобными устройствами, изобретен он был относительно поздно, а именно в 1817 году.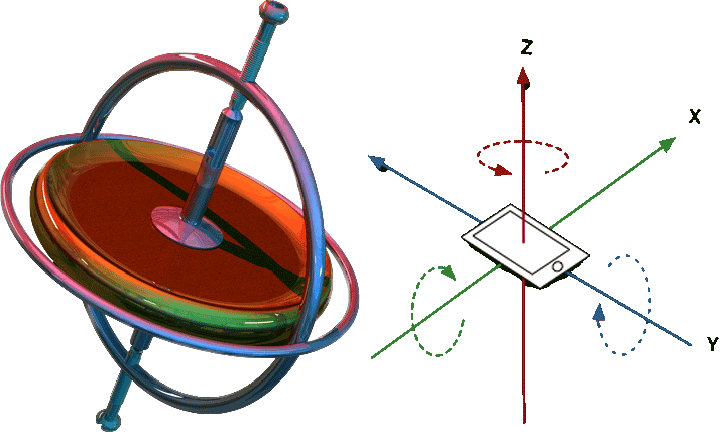 Основной элемент конструкции гироскопа представляет собой вращающийся вокруг вертикальной оси ротор-волчок, причем его ось может изменять положение в пространстве, а скорость вращения волчка значительно превышает скорость поворота оси его вращения. Благодаря этому волчок всегда сохраняет свое положение независимо от действующих на него извне сил, в чём и заключается весь принцип работы гироскопа.
Основной элемент конструкции гироскопа представляет собой вращающийся вокруг вертикальной оси ротор-волчок, причем его ось может изменять положение в пространстве, а скорость вращения волчка значительно превышает скорость поворота оси его вращения. Благодаря этому волчок всегда сохраняет свое положение независимо от действующих на него извне сил, в чём и заключается весь принцип работы гироскопа.
Первоначально это нехитрое устройство использовалось в качестве учебного пособия. Практическое применение ему нашли только спустя 60 лет, когда инженер Обри додумался устанавливать его в торпеды для стабилизации их курса. Сегодня это полезное изобретение, будучи многократно усовершенствованным, широко применяется в самых разных механизмах. Для точного определения положения в пространстве гироскопы используются в морских судах, самолетах, космических аппаратах, ракетах, симуляторах, радиоуправляемых устройствах вроде квадрокоптеров и, конечно же, в смартфонах.
Как устроен гироскоп в смартфоне, отличие гироскопа от акселерометра
Естественно, гироскоп в смартфоне существенно отличается в плане конструкции от классических гироскопов, хотя и служит той же цели.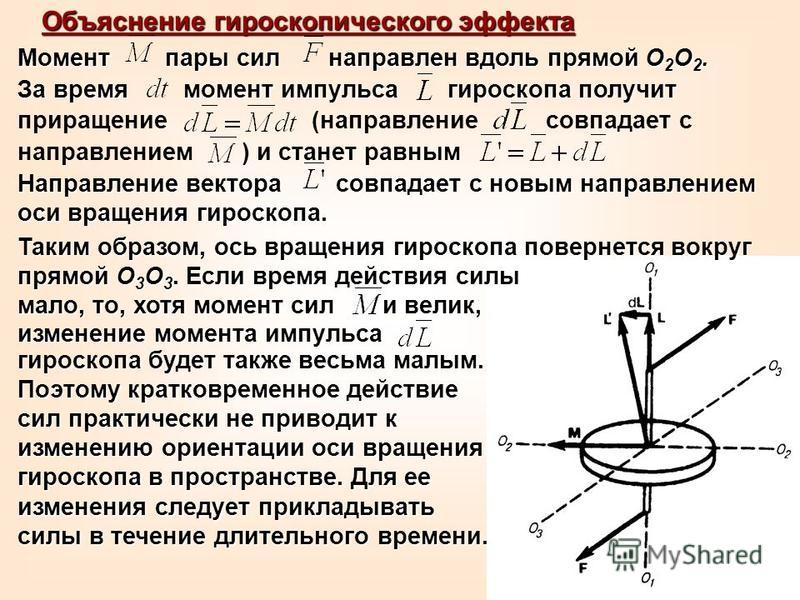 Механическая энергия в нём преобразуется в электрическую, формирующую последовательность битов – бинарный код, лежащий в основе всех компьютерных программных систем. Никаких вращающихся волчков в гироскопах электронных устройств, разумеется, нет, они слишком малы для этого. Вместо них используется подвижные массы вещества, смещение которых вызывает изменение электрической емкости конденсаторов, регистрируемое микропроцессором.
Механическая энергия в нём преобразуется в электрическую, формирующую последовательность битов – бинарный код, лежащий в основе всех компьютерных программных систем. Никаких вращающихся волчков в гироскопах электронных устройств, разумеется, нет, они слишком малы для этого. Вместо них используется подвижные массы вещества, смещение которых вызывает изменение электрической емкости конденсаторов, регистрируемое микропроцессором.
Вместо конденсаторов могут использоваться вырабатывающие ток пьезокристаллы, особенно часто встречающиеся в определяющих положение в пространстве датчиках другого типа – акселерометрах. Конструктивно акселерометры очень похожи на гироскопы, в них также имеется подвижный элемент – специальный грузик, смещение которого при наклоне устройства оказывает воздействие на пьезокристалл. Таким образом, скорость и давление преобразуются в электрический сигнал, обрабатываемый соответствующим образом микропроцессором. Итак, некоторое представление о том, что это такое гироскоп в смартфоне вы, надеемся, получили.
И вот еще пару моментов. И гироскопы, и акселерометры являются инерционными МЭМС-датчиками, отличаясь, однако, принципом получения данных. Если гироскоп определяет только угол наклона по отношению к земной поверхности, то акселерометр может измерять линейное ускорение, то есть перемещение по горизонтали относительно земли. На практике в смартфонах и прочих устройствах нередко устанавливаются оба датчика, которые прекрасно дополняют друг друга. Теперь давайте посмотрим, как узнать есть ли гироскоп в телефоне.
Как проверить наличие гироскопа в телефоне
Мы уже знаем, для чего нужен гироскоп в смартфоне, но как проверить его наличие на том или ином мобильном устройстве. Гироскоп используется всеми приложениями, регистрирующими наклон устройства – навигационными и строительными программами, 3D-играми, средствами просмотра 3D-панорамного контента, поворачивающим экран встроенным ПО и так далее. Но поддержка этих функций еще не означает, что указанный датчик в телефоне есть, ведь выше мы уже отмечали, что отчасти его может заменить акселерометр.
Если вы хотите узнать, интегрирован ли гироскоп в гаджет или нет, зайдите на официальный сайт производителя устройства, найдите там вашу модель и изучите ее технические характеристики. Есть и более быстрый способ получить нужную информацию. Установите на смартфон бесплатное приложение-бенчмарк AnTuTu Bеnchmаrk , в разделе «Мое устройство» оно выводит список всех датчиков, среди которых будут данные и о гироскопе. Если напротив пункта «Гироскоп» вместо его названия указано «Не поддерживается», значит, датчик на устройстве отсутствует.
В качестве альтернативы можно воспользоваться другим приложением – Sеnsor Sеnse. В отличие от AnTuTu Bеnchmаrk, кроме списка датчиков оно еще выводит все их показания. Ставим программу и смотрим, есть ли в списке гироскоп. Если нет, то нет его и на устройстве.
Стоит также обратить внимание еще на один замечательный программный инструмент – AIDA64 , предоставляющий полный набор сведений о конфигурации устройства. Какие сенсоры есть на борту можно просмотреть на вкладке «Датчики». Если в списке будет значиться гироскоп, можно быть уверенным, что в телефоне он установлен.
Если в списке будет значиться гироскоп, можно быть уверенным, что в телефоне он установлен.
Включение/отключение и калибровка гироскопа на Андроиде
Как правило, гироскоп в телефонах является самостоятельным датчиком, с программными настройками никак не связанным. Гироскоп либо есть, и он всегда включен, либо его нет, но тогда и ни о каком включении/отключении датчика не может быть и речи. Правда, пользователи часто спрашивают, как включить гироскоп на Андроиде, но этот вопрос исходит из недопонимания принципа его взаимодействия с программной частью устройства. Можно включить и отключить функции акселерометра, например, автоповорот экрана, но это опять же никак напрямую не связано с гироскопом.
То же самое касается калибровки гироскопа, отрегулировать программно можно лишь акселерометр. Встроенными средствами самой ОС это сделать вряд ли получится, для этих целей нужно использовать специальные утилиты вроде Accelerometer Calibration Free. Тут всё очень просто – мобильное устройство укладывается на ровную поверхность, а когда показывающий равновесие красный шарик окажется ровно в центре «прицела», нажимается кнопка «Calibrate».
В общем, если в сети вам попадется информация на тему как откалибровать гироскоп на Андроид, знайте, что речь идет о настройке акселерометра.
Однажды я наблюдал разговор двух друзей, точнее подруг:
А: О, знаешь, у меня новый смартфон, в нем есть даже встроенный гироскоп
Б: Аа, да, я тоже скачала себе, поставила гироскоп на месяц
А: Эмм, ты точно уверена, что это гироскоп?
Б: Да, гироскоп для всех знаков зодиака.
Чтобы таких диалогов в мире стало чуть меньше, предлагаем узнать, что такое гироскоп и как он работает.
Гироскоп: история, определение
Гироскоп – прибор, имеющий свободную ось вращения и способный реагировать на изменение углов ориентации тела, на котором он установлен. При вращении гироскоп сохраняет свое положение неизменным.
Само слово происходит от греческих gyreuо – вращаться и skopeo – смотреть, наблюдать. Впервые термин гироскоп был введен Жаном Фуко в 1852 году, но изобрели прибор раньше. Это сделал немецкий астроном Иоганн Боненбергер в 1817 году.
Впервые термин гироскоп был введен Жаном Фуко в 1852 году, но изобрели прибор раньше. Это сделал немецкий астроном Иоганн Боненбергер в 1817 году.
Представляют собой вращающиеся с высокой частотой твердые тела. Ось вращения гироскопа может изменять свое направление в пространстве. Свойствами гироскопа обладают вращающиеся артиллерийские снаряды, винты самолетов, роторы турбин.
Простейший пример гироскопа – волчок или хорошо всем известная детская игрушка юла. Тело, вращающееся вокруг определенной оси, которая сохраняет положение в пространстве, если на гироскоп не действуют какие-то внешние силы и моменты этих сил. При этом гироскоп обладает устойчивостью и способен противостоять воздействию внешней силы, что во многом определяется его скоростью вращения.
Например, если мы быстро раскрутим юлу, а потом толкнем ее, она не упадет, а продолжит вращение. А когда скорость волчка упадет до определенного значения, начнется прецессия – явление, когда ось вращения описывает конус, а момент импульса волчка меняет направление в пространстве.
Виды гироскопов
Существует множество видов гироскопов: двух и трехстепенные (разделение по степеням свободы или возможным осям вращения), механические , лазерные и оптические гироскопы (разделение по принципу действия).
Рассмотрим самый распространенный пример – механический роторный гироскоп . По сути это волчок, вращающийся вокруг вертикальной оси, которая поворачивается вокруг горизонтальной оси и в свою очередь закреплена в еще одной раме, поворачивающейся уже вокруг третьей оси. Как бы мы не поворачивали волчок, он всегда будет находится именно в вертикальном положении.
Применение гироскопов
Благодаря своим свойствам гироскопы находят очень широкое применение. Они используются в системах стабилизации космических аппаратов, в системах навигации кораблей и самолетов, в мобильных устройствах и игровых приставках, а также в качестве тренажеров.
Интересует, как такой прибор может поместиться в современный мобильный телефон и зачем он там нужен? Дело в том, что гироскоп помогает определить положение устройства в пространстве и узнать угол отклонения. Конечно, в телефоне нет непосредственно вращающегося волчка, гироскоп представляет собой микроэлектромеханическую систему (МЭМС), содержащую микроэлектронные и микромеханические компоненты.
Конечно, в телефоне нет непосредственно вращающегося волчка, гироскоп представляет собой микроэлектромеханическую систему (МЭМС), содержащую микроэлектронные и микромеханические компоненты.
Как это работает на практике? Представим, что вы играете в любимую игру. Например, гонки. Чтобы повернуть руль виртуального автомобиля не нужно нажимать никаких кнопок, достаточно лишь изменить положение своего гаджета в руках.
Как видим, гироскопы – удивительные приборы, обладающие полезными свойствами. Если вам понадобится решить задачу на расчет движения гироскопа в поле внешних сил, обращайтесь к специалистам студенческого сервиса , которые помогут вам справится с ней быстро и качественно!
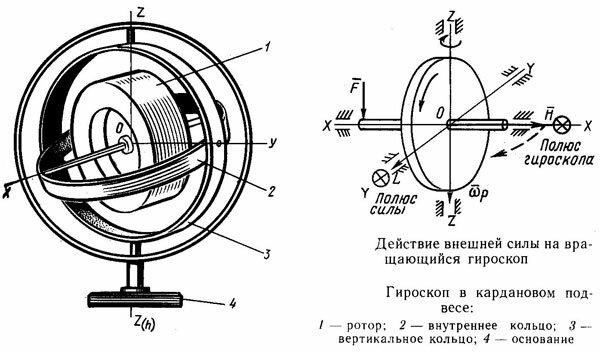
ГИРОСКОП
навигационный прибор, основным элементом которого является быстро вращающийся ротор, закрепленный так, что ось его вращения может поворачиваться. Три степени свободы (оси возможного вращения) ротора гироскопа обеспечиваются двумя рамками карданова подвеса. Если на такое устройство не действуют внешние возмущения, то ось собственного вращения ротора сохраняет постоянное направление в пространстве. Если же на него действует момент внешней силы, стремящийся повернуть ось собственного вращения, то она начинает вращаться не вокруг направления момента, а вокруг оси, перпендикулярной ему (прецессия).
Если же на него действует момент внешней силы, стремящийся повернуть ось собственного вращения, то она начинает вращаться не вокруг направления момента, а вокруг оси, перпендикулярной ему (прецессия).
В хорошо сбалансированном (астатическом) и достаточно быстро вращающемся гироскопе, установленном на высокосовершенных подшипниках с незначительным трением, момент внешних сил практически отсутствует, так что гироскоп долго сохраняет почти неизменной свою ориентацию в пространстве. Поэтому он может указывать угол поворота основания, на котором закреплен. Именно так французский физик Ж. Фуко (1819-1868) впервые наглядно продемонстрировал вращение Земли. Если же поворот оси гироскопа ограничить пружиной, то при соответствующей установке его, скажем, на летательном аппарате, выполняющем разворот, гироскоп будет деформировать пружину, пока не уравновесится момент внешней силы. В этом случае сила сжатия или растяжения пружины пропорциональна угловой скорости движения летательного аппарата. Таков принцип действия авиационного указателя поворота и многих других гироскопических приборов. Поскольку трение в подшипниках очень мало, для поддержания вращения ротора гироскопа не требуется много энергии. Для приведения его во вращение и для поддержания вращения обычно бывает достаточно маломощного электродвигателя или струи сжатого воздуха.
Таков принцип действия авиационного указателя поворота и многих других гироскопических приборов. Поскольку трение в подшипниках очень мало, для поддержания вращения ротора гироскопа не требуется много энергии. Для приведения его во вращение и для поддержания вращения обычно бывает достаточно маломощного электродвигателя или струи сжатого воздуха.
Применение. Гироскоп чаще всего применяется как чувствительный элемент указывающих гироскопических приборов и как датчик угла поворота или угловой скорости для устройств автоматического управления. В некоторых случаях, например в гиростабилизаторах, гироскопы используются как генераторы момента силы или энергии.
См. также МАХОВИК . Основные области применения гироскопов – судоходство, авиация и космонавтика (см. ИНЕРЦИАЛЬНАЯ НАВИГАЦИЯ). Почти каждое морское судно дальнего плавания снабжено гирокомпасом для ручного или автоматического управления судном, некоторые оборудованы гиростабилизаторами. В системах управления огнем корабельной артиллерии много дополнительных гироскопов, обеспечивающих стабильную систему отсчета или измеряющих угловые скорости. Без гироскопов невозможно автоматическое управление торпедами. Самолеты и вертолеты оборудуются гироскопическими приборами, которые дают надежную информацию для систем стабилизации и навигации. К таким приборам относятся авиагоризонт, гировертикаль, гироскопический указатель крена и поворота. Гироскопы могут быть как указывающими приборами, так и датчиками автопилота. На многих самолетах предусматриваются гиростабилизированные магнитные компасы и другое оборудование – навигационные визиры, фотоаппараты с гироскопом, гиросекстанты. В военной авиации гироскопы применяются также в прицелах воздушной стрельбы и бомбометания. Гироскопы разного назначения (навигационные, силовые) выпускаются разных типоразмеров в зависимости от условий работы и требуемой точности. В гироскопических приборах диаметр ротора составляет 4-20 см, причем меньшее значение относится к авиационно-космическим приборам. Диаметры же роторов судовых гиростабилизаторов измеряются метрами.
Без гироскопов невозможно автоматическое управление торпедами. Самолеты и вертолеты оборудуются гироскопическими приборами, которые дают надежную информацию для систем стабилизации и навигации. К таким приборам относятся авиагоризонт, гировертикаль, гироскопический указатель крена и поворота. Гироскопы могут быть как указывающими приборами, так и датчиками автопилота. На многих самолетах предусматриваются гиростабилизированные магнитные компасы и другое оборудование – навигационные визиры, фотоаппараты с гироскопом, гиросекстанты. В военной авиации гироскопы применяются также в прицелах воздушной стрельбы и бомбометания. Гироскопы разного назначения (навигационные, силовые) выпускаются разных типоразмеров в зависимости от условий работы и требуемой точности. В гироскопических приборах диаметр ротора составляет 4-20 см, причем меньшее значение относится к авиационно-космическим приборам. Диаметры же роторов судовых гиростабилизаторов измеряются метрами.
ОСНОВНЫЕ ПОНЯТИЯ
Гироскопический эффект создается той же самой центробежной силой, которая действует на юлу, вращающуюся, например, на столе. В точке опоры юлы о стол возникают сила и момент, под действием которых ось вращения юлы отклоняется от вертикали, а центробежная сила вращающейся массы, препятствуя изменению ориентации плоскости вращения, вынуждает юлу вращаться и вокруг вертикали, сохраняя тем самым заданную ориентацию в пространстве. Таким вращением, называемым прецессией, ротор гироскопа отвечает на приложенный момент силы относительно оси, перпендикулярной оси его собственного вращения. Вклад масс ротора в этот эффект пропорционален квадрату расстояния до оси вращения, поскольку чем больше радиус, тем больше, во-первых, линейное ускорение и, во-вторых, плечо центробежной силы. Влияние массы и ее распределения в роторе характеризуется его “моментом инерции”, т.е. результатом суммирования произведений всех составляющих его масс на квадрат расстояния до оси вращения. Полный же гироскопический эффект вращающегося ротора определяется его “кинетическим моментом”, т.е. произведением угловой скорости (в радианах в секунду) на момент инерции относительно оси собственного вращения ротора.
В точке опоры юлы о стол возникают сила и момент, под действием которых ось вращения юлы отклоняется от вертикали, а центробежная сила вращающейся массы, препятствуя изменению ориентации плоскости вращения, вынуждает юлу вращаться и вокруг вертикали, сохраняя тем самым заданную ориентацию в пространстве. Таким вращением, называемым прецессией, ротор гироскопа отвечает на приложенный момент силы относительно оси, перпендикулярной оси его собственного вращения. Вклад масс ротора в этот эффект пропорционален квадрату расстояния до оси вращения, поскольку чем больше радиус, тем больше, во-первых, линейное ускорение и, во-вторых, плечо центробежной силы. Влияние массы и ее распределения в роторе характеризуется его “моментом инерции”, т.е. результатом суммирования произведений всех составляющих его масс на квадрат расстояния до оси вращения. Полный же гироскопический эффект вращающегося ротора определяется его “кинетическим моментом”, т.е. произведением угловой скорости (в радианах в секунду) на момент инерции относительно оси собственного вращения ротора. Кинетический момент – векторная величина, имеющая не только численное значение, но и направление. На рис. 1 кинетический момент представлен стрелкой (длина которой пропорциональна величине момента), направленной вдоль оси вращения в соответствии с “правилом буравчика”: туда, куда подается буравчик, если его поворачивать в направлении вращения ротора. Прецессия и момент силы тоже характеризуются векторными величинами. Направление вектора угловой скорости прецессии и вектора момента силы связано правилом буравчика с соответствующим направлением вращения.
Кинетический момент – векторная величина, имеющая не только численное значение, но и направление. На рис. 1 кинетический момент представлен стрелкой (длина которой пропорциональна величине момента), направленной вдоль оси вращения в соответствии с “правилом буравчика”: туда, куда подается буравчик, если его поворачивать в направлении вращения ротора. Прецессия и момент силы тоже характеризуются векторными величинами. Направление вектора угловой скорости прецессии и вектора момента силы связано правилом буравчика с соответствующим направлением вращения.
См. также ВЕКТОР .
ГИРОСКОП С ТРЕМЯ СТЕПЕНЯМИ СВОБОДЫ
На рис. 1 дана упрощенная кинематическая схема гироскопа с тремя степенями свободы (тремя осями вращения), причем направления вращения на ней показаны изогнутыми стрелками. Кинетический момент представлен жирной прямой стрелкой, направленной вдоль оси собственного вращения ротора. Момент силы прикладывается нажатием пальца так, что он имеет составляющую, перпендикулярную оси собственного вращения ротора (вторую силу пары создают вертикальные полуоси, закрепленные в оправе, которая связана с основанием). Согласно законам Ньютона, такой момент силы должен создавать кинетический момент, совпадающий с ним по направлению и пропорциональный его величине. Поскольку же кинетический момент (связанный с собственным вращением ротора) фиксирован по величине (заданием постоянной угловой скорости посредством, скажем, электродвигателя), это требование законов Ньютона может быть выполнено только за счет поворота оси вращения (в сторону вектора внешнего момента силы), приводящего к увеличению проекции кинетического момента на эту ось. Этот поворот и есть прецессия, о которой говорилось ранее. Скорость прецессии возрастает с увеличением внешнего момента силы и убывает с увеличением кинетического момента ротора.
Согласно законам Ньютона, такой момент силы должен создавать кинетический момент, совпадающий с ним по направлению и пропорциональный его величине. Поскольку же кинетический момент (связанный с собственным вращением ротора) фиксирован по величине (заданием постоянной угловой скорости посредством, скажем, электродвигателя), это требование законов Ньютона может быть выполнено только за счет поворота оси вращения (в сторону вектора внешнего момента силы), приводящего к увеличению проекции кинетического момента на эту ось. Этот поворот и есть прецессия, о которой говорилось ранее. Скорость прецессии возрастает с увеличением внешнего момента силы и убывает с увеличением кинетического момента ротора.
Гироскопический указатель курса. На рис. 2 показан пример применения трехстепенного гироскопа в авиационном указателе курса (гирополукомпасе). Вращение ротора в шарикоподшипниках создается и поддерживается струей сжатого воздуха, направленной на рифленую поверхность обода. Внутренняя и наружная рамки карданова подвеса обеспечивают полную свободу вращения оси собственного вращения ротора. По шкале азимута, прикрепленной к наружной рамке, можно ввести любое значение азимута, выровняв ось собственного вращения ротора с основанием прибора. Трение в подшипниках столь незначительно, что после того как это значение азимута введено, ось вращения ротора сохраняет заданное положение в пространстве, и, пользуясь стрелкой, скрепленной с основанием, по шкале азимута можно контролировать поворот самолета. Показания поворота не обнаруживают никаких отклонений, если не считать эффектов дрейфа, связанных с несовершенствами механизма, и не требуют связи с внешними (например, наземными) средствами навигации.
По шкале азимута, прикрепленной к наружной рамке, можно ввести любое значение азимута, выровняв ось собственного вращения ротора с основанием прибора. Трение в подшипниках столь незначительно, что после того как это значение азимута введено, ось вращения ротора сохраняет заданное положение в пространстве, и, пользуясь стрелкой, скрепленной с основанием, по шкале азимута можно контролировать поворот самолета. Показания поворота не обнаруживают никаких отклонений, если не считать эффектов дрейфа, связанных с несовершенствами механизма, и не требуют связи с внешними (например, наземными) средствами навигации.
ДВУХСТЕПЕННЫЙ ГИРОСКОП
Во многих гироскопических приборах используется упрощенный, двухстепенный вариант гироскопа, в котором наружная рамка трехстепенного гироскопа устранена, а полуоси внутренней закрепляются непосредственно в стенках корпуса, жестко связанного с движущимся объектом. Если в таком устройстве единственная рамка ничем не ограничена, то момент внешней силы относительно оси, связанной с корпусом и перпендикулярной оси рамки, заставит ось собственного вращения ротора непрерывно прецессировать в сторону от этого первоначального направления.
 Прецессия будет продолжаться до тех пор, пока ось собственного вращения не окажется параллельной направлению момента силы, т.е. в положении, при котором гироскопический эффект отсутствует. На практике такая возможность исключается благодаря тому, что задаются условия, при которых поворот рамки относительно корпуса не выходит за пределы малого угла. Если прецессия ограничивается только инерционной реакцией рамки с ротором, то угол поворота рамки в любой момент времени определяется проинтегрированным ускоряющим моментом. Поскольку момент инерции рамки обычно сравнительно мал, она слишком быстро реагирует на вынужденное вращение. Имеются два способа устранить этот недостаток.
Прецессия будет продолжаться до тех пор, пока ось собственного вращения не окажется параллельной направлению момента силы, т.е. в положении, при котором гироскопический эффект отсутствует. На практике такая возможность исключается благодаря тому, что задаются условия, при которых поворот рамки относительно корпуса не выходит за пределы малого угла. Если прецессия ограничивается только инерционной реакцией рамки с ротором, то угол поворота рамки в любой момент времени определяется проинтегрированным ускоряющим моментом. Поскольку момент инерции рамки обычно сравнительно мал, она слишком быстро реагирует на вынужденное вращение. Имеются два способа устранить этот недостаток.Противодействующая пружина и вязкостный демпфер. Датчик угловой скорости. Прецессию оси вращения ротора в направлении вектора момента силы, направленного вдоль оси, перпендикулярной оси рамки, можно ограничить пружиной и демпфером, воздействующими на ось рамки. Кинематическая схема двухстепенного гироскопа с противодействующей пружиной представлена на рис.
 3. Ось вращающегося ротора закреплена в рамке перпендикулярно оси вращения последней относительно корпуса. Входной осью гироскопа называется направление, связанное с основанием, перпендикулярное оси рамки и оси собственного вращения ротора при недеформированной пружине.
3. Ось вращающегося ротора закреплена в рамке перпендикулярно оси вращения последней относительно корпуса. Входной осью гироскопа называется направление, связанное с основанием, перпендикулярное оси рамки и оси собственного вращения ротора при недеформированной пружине.Момент внешней силы относительно опорной оси вращения ротора, приложенный к основанию в тот момент времени, когда основание не вращается в инерциальном пространстве и, следовательно, ось вращения ротора совпадает со своим опорным направлением, заставляет ось вращения ротора прецессировать в сторону входной оси, так что угол отклонения рамки начинает увеличиваться. Это эквивалентно приложению момента силы к противодействующей пружине, в чем состоит важная функция ротора, который в ответ на возникновение входного момента силы создает момент силы относительно выходной оси (рис. 3). При постоянной входной угловой скорости выходной момент силы гироскопа продолжает деформировать пружину, пока создаваемый ею момент силы, воздействующий на рамку, не заставит ось вращения ротора прецессировать вокруг входной оси.
 Когда скорость такой прецессии, вызванной моментом, создаваемым пружиной, сравняется с входной угловой скоростью, достигается равновесие и угол рамки перестает изменяться. Таким образом, угол отклонения рамки гироскопа (рис. 3), указываемый стрелкой на шкале, позволяет судить о направлении и угловой скорости поворота движущегося объекта. На рис. 4 показаны основные элементы указателя (датчика) угловой скорости, ставшего в настоящее время одним из самых обычных авиакосмических приборов.
Когда скорость такой прецессии, вызванной моментом, создаваемым пружиной, сравняется с входной угловой скоростью, достигается равновесие и угол рамки перестает изменяться. Таким образом, угол отклонения рамки гироскопа (рис. 3), указываемый стрелкой на шкале, позволяет судить о направлении и угловой скорости поворота движущегося объекта. На рис. 4 показаны основные элементы указателя (датчика) угловой скорости, ставшего в настоящее время одним из самых обычных авиакосмических приборов.Вязкостное демпфирование. Для гашения выходного момента силы относительно оси двухстепенного гироузла можно использовать вязкостное демпфирование. Кинематическая схема такого устройства представлена на рис. 5; она отличается от схемы на рис. 4 тем, что здесь нет противодействующей пружины, а вязкостный демпфер увеличен. Когда такое устройство поворачивается с постоянной угловой скоростью вокруг входной оси, выходной момент гироузла заставляет рамку прецессировать вокруг выходной оси.
 За вычетом эффектов инерционной реакции (с инерцией рамки связано в основном лишь некоторое запаздывание отклика) этот момент уравновешивается моментом сил вязкостного сопротивления, создаваемым демпфером. Момент демпфера пропорционален угловой скорости вращения рамки относительно корпуса, так что выходной момент гироузла тоже пропорционален этой угловой скорости. Поскольку этот выходной момент пропорционален входной угловой скорости (при малых выходных углах рамки), выходной угол рамки увеличивается по мере того, как корпус поворачивается вокруг входной оси. Стрелка, движущаяся по шкале (рис. 5), указывает угол поворота рамки. Показания пропорциональны интегралу угловой скорости вращения относительно входной оси в инерциальном пространстве, и поэтому устройство, схема которого представлена на рис. 5, называется интегрирующим двухстепенным гиродатчиком.
За вычетом эффектов инерционной реакции (с инерцией рамки связано в основном лишь некоторое запаздывание отклика) этот момент уравновешивается моментом сил вязкостного сопротивления, создаваемым демпфером. Момент демпфера пропорционален угловой скорости вращения рамки относительно корпуса, так что выходной момент гироузла тоже пропорционален этой угловой скорости. Поскольку этот выходной момент пропорционален входной угловой скорости (при малых выходных углах рамки), выходной угол рамки увеличивается по мере того, как корпус поворачивается вокруг входной оси. Стрелка, движущаяся по шкале (рис. 5), указывает угол поворота рамки. Показания пропорциональны интегралу угловой скорости вращения относительно входной оси в инерциальном пространстве, и поэтому устройство, схема которого представлена на рис. 5, называется интегрирующим двухстепенным гиродатчиком.На рис. 6 изображен интегрирующий гиродатчик, ротор (гиромотор) которого заключен в герметично запаянный стакан, плавающий в демпфирующей жидкости.
 Сигнал угла поворота плавающей рамки относительно корпуса вырабатывается индукционным датчиком угла. Положение поплавкового гироузла в корпусе задает датчик момента в соответствии с поступающими на него электрическими сигналами. Интегрирующие гиродатчики обычно устанавливают на элементах, снабженных сервоприводом и управляемых выходными сигналами гироскопа. При таком расположении выходной сигнал датчика момента можно использовать как команду на поворот объекта в инерциальном пространстве.
Сигнал угла поворота плавающей рамки относительно корпуса вырабатывается индукционным датчиком угла. Положение поплавкового гироузла в корпусе задает датчик момента в соответствии с поступающими на него электрическими сигналами. Интегрирующие гиродатчики обычно устанавливают на элементах, снабженных сервоприводом и управляемых выходными сигналами гироскопа. При таком расположении выходной сигнал датчика момента можно использовать как команду на поворот объекта в инерциальном пространстве.См. также ГИРОКОМПАС .
ЛИТЕРАТУРА
Ригли У., Холлистер У., Денхард У. Теория, проектирование и испытания гироскопов. М., 1972 Бабаева Н.Ф. Гироскопы. Л., 1973 Поплавский М.А. Теория гироскопов. Киев, 1986
Энциклопедия Кольера. – Открытое общество . 2000 .
Современные смартфоны оснащены огромным количеством функций, за работу которых отвечает ряд датчиков.
Нередко об их назначении владельцы даже не догадываются. К числу таких датчиков относится гироскоп в телефоне: что это такое, не знают даже многие «продвинутые» пользователи, поэтому не лишним будет детально изучить это устройство.
Принцип действия оборудования
Гироскоп представляет собой волчок, вращающийся вокруг оси. Благодаря способности демонстрировать устойчивое положение во время движения, он используется для определения положения в пространстве и изменения угловой скорости. Существует несколько разновидностей: они различаются между собой по принципу действия (оптические или механические) и количеству степеней свободы. Если говорить о моделях, которые устанавливаются в смартфоны, то это обычно вибрационные гиродатчики. В этом устройстве есть две массы, которые перемещаются в противоположные стороны. В тот момент, когда появляется угловая скорость, на массу воздействует сила Кориолиса, вектор которой направлен перпендикулярно движению массы. В результате воздействия этой силы происходит смещение, что приводит к изменению расстояния между подвижными и неподвижными электронами и, как следствие, к смене емкости конденсатора. Эти электронные сигналы впоследствии обрабатываются процессором.
Наличие гиродатчика в смартфоне – это не просто прихоть, такой аппарат открывает перед обладателем гаджета множество дополнительных возможностей:
- прием вызовов простым встряхиванием аппарата,
- стабилизация камеры во время съемок,
- управление приложениями при помощи поворотов устройства,
- ориентация положения головы в виртуальной реальности.

В каких телефонах есть гироскоп?
Воспользоваться перечисленными выше преимуществами могут далеко не все владельцы смартфонов, так как гиродатчики установлены не везде. Самый надежный способ узнать, есть ли гироскоп в телефоне – спросить об этом у продавца-консультанта или прочитать паспорт к изделию. Если говорить о брендах, то впервые гиродатчик был установлен на iPhone 4. Поскольку новинка пришлась покупателям по вкусу, все последующие модели от Apple также получили это оборудование.
Современные смартфоны оснащены множеством датчиков, которые не только садят аккумулятор, но и постоянно отслеживают состояние телефона и делают пользование им значительно удобнее. Сегодня мы разберёмся с таким датчиком, как гироскоп в телефоне, что это , зачем он нужен и где пригождается.
Немного истории
Самым примитивным примером гироскопа может стать детский волчок или юла. Именно они наглядно визуализируют принцип действия датчика.
Общественности прибор был впервые представлен немецким учёным в области математики и астрономии И. Боненбергером. Хотя в некоторых научных документах указано, что на самом деле изобретение было сделано тремя годами раньше.
Боненбергером. Хотя в некоторых научных документах указано, что на самом деле изобретение было сделано тремя годами раньше.
Первая компания, которая применила датчик в своём устройстве, Apple. Именно iPhone первыми смогли похвастаться подобным оснащением. Сегодня почти каждый имеет гироскоп. Уточнить его наличие можно в технической документации к устройству. Как правило, в характеристиках устройства в разделе датчиков находится полная информация о наличии приборов. Если по каким-то причинам кажется, что информация недостоверная можно установить дополнительный софт, например, Sensor Box for Android. Программа показывает .
Гироскоп в телефоне, что это?
Фактически это специальный чип, расположенный внутри устройства. Чтобы его увидеть придётся разобрать смартфон, так как он скрыт от глаз пользователей. Он распознает и анализирует положение гаджета в окружающем пространстве и вычисляет углы его размещения.
Помимо смартфонов, подобные датчики успешно зарекомендовали себя и в других сферах деятельности человека: авиация, судоходство, космонавтика. Также можно встретить подобные датчики в некоторых приборах и бытовой технике.
Также можно встретить подобные датчики в некоторых приборах и бытовой технике.
Функции гироскопа в смартфоне
Внедрение технологии позволило реализовать новые возможности для мобильных устройств. Разберёмся что именно берёт на себя гироскоп и какие функции выполняет в современных гаджетах.
Технология помогает ориентироваться на местности с большей точностью. Исходя из описанных функций, гироскоп удобная и нужная в смартфоне вещь.
Есть, конечно, и некоторые нюансы, портящие впечатление от пользования датчиком. Ряд приложений могут потерять часть быстродействия и медленнее реагировать на команды пользователя при включённом гироскопе. Также может наблюдаться ненужный отклик датчика, например, когда владелец смартфона лёжа читает книгу и переворачивается на другой бок. Но это погрешности незначительны и устраняются путём временного отключения датчика.
Многие, отвечая на вопрос,
гироскоп в телефоне, что это
, искренне полагают, будто он и акселерометр – это либо идентичные устройства, либо вовсе разные названия одной технологии. На самом деле оба этих суждения ложны. Эти датчики фиксируют положение смартфона в пространстве, но в разных плоскостях. Акселерометр призван отследить повороты, гироскоп же имеет значительно больше возможностей:
На самом деле оба этих суждения ложны. Эти датчики фиксируют положение смартфона в пространстве, но в разных плоскостях. Акселерометр призван отследить повороты, гироскоп же имеет значительно больше возможностей:
- не только повороты, но и перемещение устройства в пространстве;
- определение сторон света, то есть функции компаса;
- скорость перемещения в пространстве.
То есть гироскоп фиксирует перемещения прибора сразу в трёх плоскостях. Отсюда и большие возможности смартфонов, оснащённых датчиком. А если устройство совмещает оба прибора, то это делает его ещё более функциональным.
Где чаще используется
Итак, мы немного разобрались с вопросом, что такое гироскоп в телефоне . Теперь постараемся наглядно привести примеры его наиболее частого использования.
По статистике, на практике устройство, оснащённое гироскопом, приходится по душе любителям поиграть в мобильные игры. Гироскоп меняет принцип игры в лучшую сторону. Помимо того, что картинка получается более качественной, а сам процесс игры интерактивным и захватывающим. Если раньше для смены положения персонажа приходилось водить пальцами по экрану и нажимать на определённые зоны, то сейчас достаточно повернуть в пространстве сам гаджет, датчик захватит положение и интерпретирует его в игре. В зависимости от угла поворота смартфона сменяется и угол поворота персонажа. В итоге получается почти виртуальная реальность. В шутерах гироскоп очень удобен для прицела. Также датчик активно используется в различных симуляторах.
Если раньше для смены положения персонажа приходилось водить пальцами по экрану и нажимать на определённые зоны, то сейчас достаточно повернуть в пространстве сам гаджет, датчик захватит положение и интерпретирует его в игре. В зависимости от угла поворота смартфона сменяется и угол поворота персонажа. В итоге получается почти виртуальная реальность. В шутерах гироскоп очень удобен для прицела. Также датчик активно используется в различных симуляторах.
Ещё одна категория пользователей, которая не обошла датчик стороной – представители усложнённых профессий, в которых требуется точный расчёт и измерения. Например, автослесарь может определить расположение детали, просто приложив к ней телефон. В строительной отрасли таким же образом отслеживаются несущие конструкции на предмет ровного расположения. При этом информация о градусе наклона выводится прямо на экран смартфона и отличается удивительной точностью.
В качестве вывода, хочется отметить, что гироскоп – очень удобное и практичное изобретение. Благодаря ему мобильные устройства имеют значительно больше доступных возможностей, которые облегчают и упрощают их использование. Телефон, оснащённый датчиком способен выступать в качестве измерительного прибора, навигатора, компаса и т. д. Также позволяет выполнять частичное управление системой, не касаясь экрана, особенно удобно последнее в период зимы, когда не очень хочется снимать варежки, чтобы ответить на звонок или сменить текущую мелодию. Кроме того, производители постоянно сокращают энергозатратность датчика, что позволяет использовать его без заметного расхода заряда аккумулятора.
Благодаря ему мобильные устройства имеют значительно больше доступных возможностей, которые облегчают и упрощают их использование. Телефон, оснащённый датчиком способен выступать в качестве измерительного прибора, навигатора, компаса и т. д. Также позволяет выполнять частичное управление системой, не касаясь экрана, особенно удобно последнее в период зимы, когда не очень хочется снимать варежки, чтобы ответить на звонок или сменить текущую мелодию. Кроме того, производители постоянно сокращают энергозатратность датчика, что позволяет использовать его без заметного расхода заряда аккумулятора.
Вконтакте
Одноклассники
Google+
Гироскоп в телефоне что это?
Многие пользователи, изучая характеристики своего смартфона, часто встречаются с наличием на телефоне такого устройства как «гироскоп». Что это такое, и каковы его функции, пользователи часто не знают и не представляют, довольно часто путая его с акселерометром. В этой статье я постараюсь «пролить свет» на данную проблематику и расскажу, что такое в смартфоне гироскоп, каковы его функции, какая разница между гироскопом и акселерометром, а также как узнать, есть ли на вашем гаджете гироскоп.
В этой статье я постараюсь «пролить свет» на данную проблематику и расскажу, что такое в смартфоне гироскоп, каковы его функции, какая разница между гироскопом и акселерометром, а также как узнать, есть ли на вашем гаджете гироскоп.
Что такое гироскоп
Гироскоп — это специальный датчик в смартфоне, позволяющий определить положение вашего телефона в пространстве. Гироскоп научен реагировать на изменение углов ориентации тела, на которое он установлен, относительно инерциальной системы отчёта.
Ширина такого датчика внутри телефона обычно не превышает 10 миллиметров, а высота – 5 миллиметров.
Прототип устройства с описанными выше функциями был изобретён ещё в далёком 1817 году немцем Иоанном Боненбергом, а сам термин «гироскоп» был введён в лексический оборот значительно позже – в 1852 году.
Важно! Если вы ещё не знаете, что такое OTG и датчик Холла в телефоне и их предназначения, вам следую прочесть материалы по ссылкам.
Функции гироскопа
После того, как мы разобрались с тем, что это за устройство гироскоп, стоит перечислить те функции, которое он выполняет. Основной функцией гироскопа на современных смартфонах и планшетах является автоматический поворот изображения на экране вслед за изменением положения мобильного устройства.
Кроме того его активно задействуют различные игровые программы (в частности гоночные), навигационные приложения, разнообразный служебный софт и так далее. К примеру, переворот смартфона экраном вниз можно заблокировать экран или выключить звук, встряхивание телефона позволит ответить на входящий звонок или запустить блютуз, ну и наличие гироскопа на телефоне позволяет более точно работать с GPS-навигацией и ориентироваться на карте.
Ну а о пользе гироскопа в играх и говорить не приходится. Недавний мировой хит – игра Pokemon Go в полной мере задействовала возможности гироскопа, позволяя игроку ловить покемонов на знакомой местности, а сами покемоны довольно корректно используют особенности окружающего ландшафта, считываемые камерой телефона.
Используется гироскоп и в шлемах виртуальной реальности, фиксируя повороты и наклоны головы игрока, и соответственно подстраивая под это компьютерную картинку.
Разница между гироскопом и акселерометром
В сети довольно часто можно встретить мнения о том, что гироскоп и акселерометр – это одно и то же, что гироскоп – это более точный акселерометр и прочее подобное. На самом деле это два разных датчика, и если акселерометр обычно устанавливается в мобильных устройствах по умолчанию, то гироскоп присутствует в смартфонах и планшетах пользователей далеко не всегда.
Суть различия между этими устройствами лежит в их функциях. Если гиродатчик (гироскоп) определяет положение вашего устройства в пространстве, то акселерометр измеряет ускорение вашего устройства и выдаёт информацию о его перемещении (например, показатель скорости перемещения).
Как включить и отключить гироскоп
При разборе вопроса о том, что значит гироскоп, стоит также упомянуть как включить и отключить гироскоп. Вообще, de facto, данный датчик работает практически всегда, мы лишь может включать и выключать различные функции, в которых он задействован (к примеру, переворот экрана нашего устройства).
К примеру, чтобы задействовать упомянутый переворот экрана, следует перейти в настройки вашего мобильного устройства, в них тапнуть на «Экран», а в настройках экрана задействовать функцию «Автоповорот экрана».
Соответственно, для выключения данной функции нужно её деактивировать таким же способом.
Используйте функцию автоповорота экранаКак узнать, есть ли гироскоп на вашем мобильном
Большинство современных телефонов обладает встроенными датчиками гироскопа. Если же вы, всё же, сомневаетесь в его наличии, достаточно вбить в строку поиска поисковой системы марку и модель вашего устройства, а затем прочитать его полные технические характеристики.
Если же вы, всё же, сомневаетесь в его наличии, достаточно вбить в строку поиска поисковой системы марку и модель вашего устройства, а затем прочитать его полные технические характеристики.
Также можно воспользоваться вспомогательными программами, предоставляющими полную информацию об устройстве. Можно порекомендовать AnTuTu Benchmark или Sensor Sense – они помогут вам определить наличие или отсутствие гироскопа на вашем аппарате.
Заключение
При разборе того, для чего гироскоп на смартфоне следует, прежде всего, указать на активное задействование данного устройства в современных смартфонах и планшетах. Многие мобильные игры не обходятся без показателей гироскопа, он активно применяется в GPS-навигации, да и просто при обычной работе смартфона он может делать взаимодействие с последним более лёгким и удобным. Даже великий Стив Джобс активно «лоббировал» применение гироскопа на презентации четвёртого айфона. И видать не зря.
Автор Дмитрий Опубликовано Обновлено
7 датчиков, которые делают ваш смартфон таким умным
Акселерометр
Акселерометр измеряет ускорение и позволяет смартфону определять характеристики движения и положения в пространстве. Именно этот датчик работает, когда вертикальная ориентация меняется на горизонтальную при повороте устройства. Он же отвечает за подсчёт шагов и измерение скорости движения во всевозможных приложениях-картах. Акселерометр даёт информацию о том, в какую сторону повёрнут смартфон, что становится важной функцией в различных приложениях с дополненной реальностью.
Именно этот датчик работает, когда вертикальная ориентация меняется на горизонтальную при повороте устройства. Он же отвечает за подсчёт шагов и измерение скорости движения во всевозможных приложениях-картах. Акселерометр даёт информацию о том, в какую сторону повёрнут смартфон, что становится важной функцией в различных приложениях с дополненной реальностью.
Этот сенсор сам состоит из маленьких датчиков: микроскопических кристаллических структур, под влиянием сил ускорения переходящих в напряжённое состояние. Напряжение передаётся акселерометру, который интерпретирует его в данные о скорости и направлении движения.
Гироскоп
Этот датчик помогает акселерометру ориентироваться в пространстве. Он, например, позволяет делать на смартфон панорамные фото. В играх с гонками, где управление происходит с помощью перемещения устройства, работает как раз гироскоп. Он чувствителен к поворотам устройства относительно своей оси.
В смартфонах используются микроэлектромеханические системы, а первые подобные приборы, сохраняющие ось при поворотах, появились ещё в начале XIX века.
Магнитометр
Последний в тройке сенсоров для ориентации в пространстве — магнитометр. Он измеряет магнитные поля и, соответственно, может определить, где находится север. Функция компаса в различных приложениях с картами и отдельные программы-компасы работают с помощью магнитометра.
Подобные датчики есть в металлодетекторах, так что можно найти специальные приложения, превращающие смартфон в такой прибор.
Магнитометр действует в тандеме с акселерометром и GPS для определения географического положения и навигации.
GPS
Где бы мы были без технологии GPS (Global Positioning System)? Смартфон соединяется с несколькими спутниками и высчитывает своё положение на основании углов пересечения. Бывает, что спутники недоступны: например, при большой облачности или внутри помещений.
GPS не использует данные мобильной сети, поэтому геолокация работает и вне зоны покрытия сотовой связи: даже если саму карту загрузить не получится, точка геолокации всё равно будет.
При этом функция GPS тратит много заряда аккумулятора, поэтому лучше её отключать вне надобности.
Ещё один способ геолокации, хотя и не очень точный, — это определение расстояния от вышек сотовой связи. Смартфон добавляет к данным GPS другую информацию, например силу мобильного сигнала, для уточнения местоположения.
Барометр
Многие смартфоны, в том числе iPhone, имеют этот сенсор, измеряющий атмосферное давление. Он нужен для регистрации изменения погоды и определения высоты над уровнем моря.
Бесконтактный выключатель
Этот сенсор обычно находится около динамика в верхней части смартфона и состоит из инфракрасного диода и датчика света. Он использует невидимый человеку луч, чтобы определить, находится ли устройство возле уха. Так смартфон «понимает», что во время разговора по телефону нужно отключить дисплей.
Датчик освещённости
Как можно догадаться по названию, этот сенсор измеряет уровень освещённости окружающей среды, что позволяет автоматически настраивать комфортную яркость дисплея.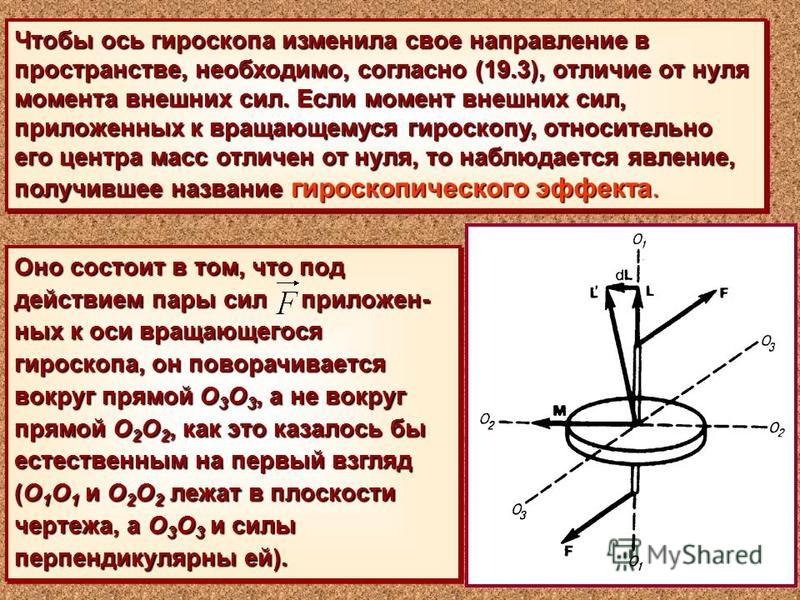
Датчики с каждым новым поколением смартфонов становятся всё более эффективными, маленькими и менее энергозатратными. Поэтому не стоит думать, что, например, функция GPS в устройстве, которому уже несколько лет, будет работать так же хорошо, как в новом. И даже если в информации о новых смартфонах не указывают характеристики всех этих датчиков, будьте уверены, что именно они позволяют вам пользоваться многими впечатляющими функциями современных гаджетов.
Iphone se гироскоп – Ай-Ай-Ай-фон
Эксперты из ChipWorks разобрали и изучили начинку нового смартфона Apple, показанного 21 марта. 4-дюймовый iPhone SE часто называют «6S в теле 5/5S». Как показало вскрытие, в целом, дела обстоят именно так — новинка позаимствовала очень многие внутренности у флагманской модели.
Во-первых, в SE установлен точно такой же 64-разрядный 2-ядерный процессор A9. Мощный «мозг» обеспечивает его даже более высокими вычислительными способностями, чем iPhone 6S. Чип в смартфоне, который достался ChipWorks, изготовила тайваньская компания TSMC, однако в других экземплярах у него может быть другой производитель, например Samsung.
Чип в смартфоне, который достался ChipWorks, изготовила тайваньская компания TSMC, однако в других экземплярах у него может быть другой производитель, например Samsung.
Во-вторых, SE комплектуется оперативной памятью (LPDDR4) объемом 2 гигабайта — аналогичный модуль установлен в «старшую» модель. Судя по маркировке, «оперативка» для SE была изготовлена еще в августе—сентябре прошлого года и, вероятно, могла предназначаться для iPhone 6S. Модуль флеш-памяти емкостью 16 гигабайт, напротив, абсолютно новый. Его произвела Toshiba, узнали в ChipWorks.
Кроме того, iPhone SE оснащается таким же, как 6S, бесконтактным NFC-чип для платежной функции Apple Pay: NXP 66VIO, состоящим из Secure Element 008 и NXP PN549. Не изменила Apple и 6-осевому инерциальному датчику (для акселерометра и гироскопа): в iPhone SE по-прежнему используются сенсоры AISC и MEMS. Аудиоконтроллер (338S1285) и модем Qualcomm (MDM9625M), опять же, аналогичны таковым в iPhone 6S.
Прочую начинку SE переняла у iPhone 5S, увидевшего свет в 2013 году. В частности, у «старичка» новый смартфон взял контроллеры тачскрина Broadcom (BCM5976) и Texas Instruments (343S0645). Впрочем, решение BCM Apple использует где только можно, включая iPod, MacBook Pro, MacBook Ai и iPad Mini.
В частности, у «старичка» новый смартфон взял контроллеры тачскрина Broadcom (BCM5976) и Texas Instruments (343S0645). Впрочем, решение BCM Apple использует где только можно, включая iPod, MacBook Pro, MacBook Ai и iPad Mini.
В ChipWorks выявили у iPhone SE всего один «эксклюзивный» компонент. Им оказалась новая плата с серийным номером 338S00170. Как предположили эксперты, она используется для управления электропитанием.
Источник: ChipWorks
Поделитесь новостью:
Описание услуги
Гироскоп в iPhone SEявляется компонентом, который отвечает за определение смартфоном его ориентации в пространстве. Гироскоп в iPhone SE состоит из вращающегося в трех измерениях ротора. Люди часто путают акселерометр и гироскоп, думая, что это разные названия одного и того же компонента, что в корне не верно. Так чем же отличаются акселерометр от гироскопа в iPhone SE? Акселерометр состоит из небольшого грузика известной массы, который зажат между датчиками давления, который реагирует на изменение положения в пространстве за счет изменения ускорения движения, но не измеряет ориентацию в пространстве. Именно для измерений ориентации в пространстве и предназначен гироскоп. Таким образом, оба компонента предназначены для отслеживания перемещений смартфона в пространстве, но измеряют разные величины: акселерометр — измеряет ускорения, гироскоп — ориентацию. Акселерометр и гироскоп работают в связке, так что неисправность одного компонента приведет к неадекватной работе другого. Основные признаки того, что требуется замена гироскопа в iPhone SE:
Именно для измерений ориентации в пространстве и предназначен гироскоп. Таким образом, оба компонента предназначены для отслеживания перемещений смартфона в пространстве, но измеряют разные величины: акселерометр — измеряет ускорения, гироскоп — ориентацию. Акселерометр и гироскоп работают в связке, так что неисправность одного компонента приведет к неадекватной работе другого. Основные признаки того, что требуется замена гироскопа в iPhone SE:
- при поворотах iPhone SE не меняет ориентацию изображения на дисплее;
- приложения с отслеживанием движений смартфона работают неадекватно;
- обои на заднем фоне экрана сами по себе двигаются из стороны в сторону.
Гироскоп на iPhone SE сломался по одной из следующих причин:
- сильный удар или падение устройства;
- попадание внутрь устройства влаги, грязи или пыли;
- резкий скачок напряжения сети, во время зарядки устройства;
- внутреннее короткое замыкание устройства.

При возникновении любой из вышеописанных проблем, вероятно, понадобится перепайка гироскопа на материнской платеiPhone SE. Данную операцию не рекомендуется делать самому, по причине ее сложности. Замена гироскопа на айфон SE требует наличие специального оборудования, а так же определенных навыков пайки микросхем, которыми обладают специалисты только самого высокого уровня. Самостоятельная попытка заменить данный компонент может привести к окончательной и необратимой поломке всего устройства, без возможности восстановления. Доверьте ремонт гироскопа в айфон СЕ специалистам сервисного центра Multi-labs, и мы выполним ремонт максимально качественно и в короткие сроки.
Почему велосипед под нами не падает? Эффект гироскопа тут ни при чем
- Хью Хант
- Кембриджский университет
Автор фото, Getty
Мы и не подозреваем, насколько напряженно и неустанно наш мозг работает над тем, чтобы мы не упали.
Об очень легком задании британцы говорят, что это “просто, как кататься на велосипеде”. Но как нам удается удерживать этот самый велосипед от падения?
Большинство скажет, что дело в эффекте гироскопа. Но в действительности дело обстоит совсем иначе.
Иными словами, гироскопический эффект объясняется тем, что вращающееся колесо стремится продолжить вращение вокруг своей оси (так остаются на своей оси вращения волчок и даже планета Земля).
Этот эффект заметен мотоциклистам, ведь колеса у мотоциклов большие, массивные и вращаются быстро. Но простой велосипедист с ним не сталкивается – колеса велосипеда намного легче, а на прогулочной скорости они крутятся недостаточно быстро.
Если бы в педальном велосипеде использовался эффект гироскопа, то любому новичку было бы достаточно оттолкнуться ногой – все остальное сделали бы за него законы природы.
Но на самом деле вам придется учиться кататься на велосипеде так же, как вы в свое время учились ходить.
За умение ездить на велосипеде отвечает исключительно ваш мозг.
Представьте себе, что вам нужно проехать по абсолютно прямой линии, нарисованной на совершенно ровной поверхности. Конечно, это же очень просто! А вот и нет.
По узкой прямой линии проехать почти невозможно – точно так же, как даже в трезвом состоянии вам вряд ли удастся пройти по ней, не оступившись. Попробуйте сами.
Проведите еще один маленький эксперимент: попробуйте устоять на одной ноге на цыпочках, используя руки, чтобы удержать равновесие.
Трудно, правда? А теперь попробуйте то же самое, но перепрыгивая с ноги на ногу. Сохранять равновесие станет намного легче.
Автор фото, Tejvan Pettinger
Подпись к фото,Конструкция велосипеда позволяет управлять им без рук, наклоняясь влево или вправо
Именно так вы бегаете. Ваш мозг научился вносить маленькие коррективы при каждом прыжке: например, если вы отклонились вправо, то на следующем шаге сдвинетесь чуть влево.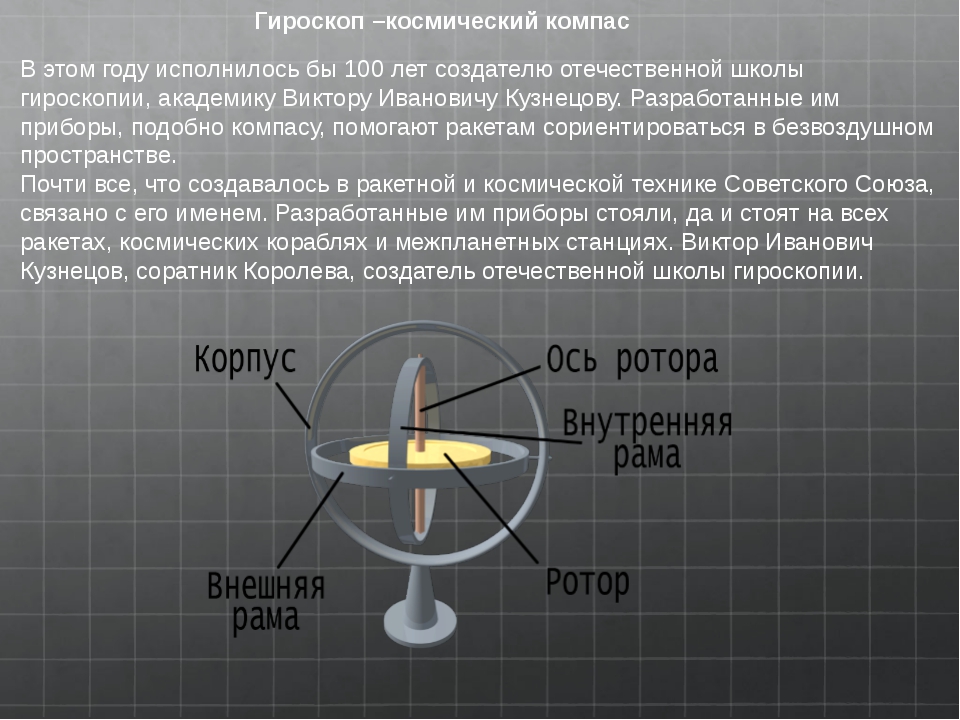
Точно так же происходит езда на велосипеде: с каждым оборотом педалей вы немного меняете направление.
Начиная падать вправо, вы неосознанно поворачиваете руль в ту же сторону, чтобы изменить положение колеса, а затем так же неосознанно возвращаетесь на прежнюю траекторию движения.
Такое “виляние” совершенно нормально. Оно более заметно у новичков (особенно у детей), которые ездят по довольно крутой “синусоиде”, и практически незаметно у опытных велосипедистов.
Тем не менее эти небольшие колебания являются частью процесса и объясняют, почему так сложно пройти (или проехать) по совершенно прямой линии – в этом случае вы лишены возможности совершать те самые необходимые движения из стороны в сторону.
Кроме того, в конструкции велосипеда есть несколько полезных решений, облегчающих езду.
Самое важное из них – наклон рулевой колонки (или так называемого рулевого стакана), благодаря которому переднее колесо касается земли в точке, находящейся сзади от точки проекции рулевой оси на землю.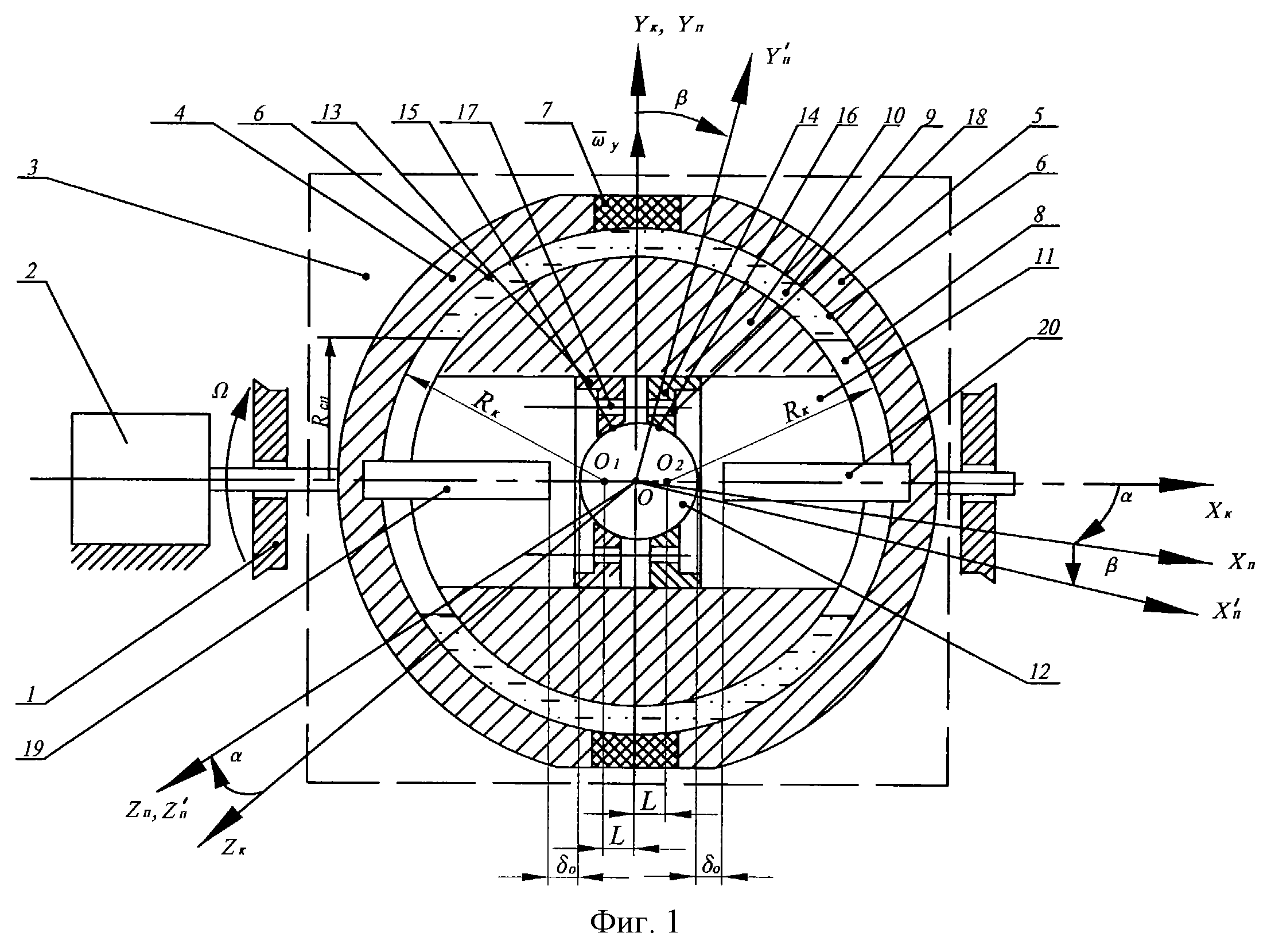 Расстояние между этими точками называется выкатом.
Расстояние между этими точками называется выкатом.
Автор фото, Thinkstock
Подпись к фото,Велосипед сконструирован очень умно, его даже носить удобно
Выкат в значительной степени помогает сохранять равновесие, когда вы едете без рук: если вы, например, наклонитесь вправо, сила, действующая на так называемое пятно контакта с землей, повернет переднее колесо направо.
Это свойство облегчает управление и позволяет рулить без рук, слегка наклоняясь влево или вправо.
Но существуют и велосипеды с вертикальными рулевыми колонками, на которых также можно отлично ездить. На самом деле, сделать велосипед, на котором будет невозможно ездить, весьма сложно, хотя многие и предпринимали такие попытки.
Дело в том, что велосипед не падает только благодаря вам и вашему сознанию, и доказать это просто.
Попробуйте, например, перекрестить руки. Вы не сможете даже тронуться с места, а если сделаете это на ходу, то рискуете сразу же упасть. Если бы велосипед удерживался вертикально с помощью эффекта гироскопа, этого бы не произошло.
Если бы велосипед удерживался вертикально с помощью эффекта гироскопа, этого бы не произошло.
Клоуны и уличные артисты ездят на велосипедах с обратным рулем. На то, чтобы научиться этому, уходят месяцы тренировок: ведь нужно полностью разучиться ездить на обычном велосипеде. Просто поразительно, как работает наш мозг!
А что же с эффектом гироскопа, о котором я упоминал выше? Помогает ли он хоть немного? Нет, если только вы не разгонитесь до очень большой скорости.
Существует известный эксперимент, якобы доказывающий влияние этого эффекта на колесо велосипеда, однако расчеты показывают, что его сила далека от того значения, которое могло бы удержать вас в вертикальном положении во время езды.
Чтобы доказать, что эффект гироскопа не имеет значения, я построил велосипед со вторым передним колесом, вращающимся в противоположном направлении. Эта идея не нова: такое же устройство сделал в 1970 году Дэвид Джонс. Нам обоим пришла в голову одна и та же идея.
Если объяснить вкратце, то вращающееся в обратную сторону колесо уничтожает эффект гироскопа для переднего колеса и доказывает, что на самом деле единственное, что удерживает вас от падения, – это деятельность вашего мозга.
Это еще и забавный эксперимент, проделать который может каждый.
Итак, какой же способ обучения езде на велосипеде является наилучшим? Знаете, мне не нравится, когда дети учатся кататься с тренировочными маленькими колесиками по бокам: каждый раз, касаясь ими земли, они утрачивают навык сохранения равновесия.
Ваш мозг должен научиться корректировать курс, так что снимите тренировочные колесики – и чем больше вы будете вилять, тем лучше.
За умение ездить на велосипеде на самом деле отвечает только ваша голова.
- Оригинал этой статьи на английском языке вы можете прочитать на сайте BBC Future. Полная ее версия первоначально была опубликована на сайте The Conversation и была перепечатана по лицензии Creative Commons.

Гироскопы
Строительство
Следующие требования относятся к механическим гироскопам и не применяются к лазерным кольцевым гироскопам.
[AFM 51-37, 1966, стр. 4-1.]
- Гироскоп представляет собой цилиндрическую массу, установленную для быстрого вращения вокруг оси. Есть три основных компонента: вращающаяся масса или ротор, ось вращения и шарниры, которые используются для установки оси вращения. Ротор должен соответствовать двум основным конструктивным характеристикам: большой вес или плотность для своего размера и высокая скорость вращения.Эти два фактора во многом определяют качество гироскопа.
- Мощность, необходимая для привода ротора и его быстрого вращения, обеспечивается либо всасывающей, либо электрической системой.
- Существует два типа креплений, используемых в пилотажных приборах: универсальное крепление, позволяющее поворачивать и наклонять ось вращения, и узкое крепление, позволяющее только наклонять ось вращения.
 Индикаторы положения и курсоуказатели имеют универсальное крепление. Индикаторы поворота и скольжения используют ограниченное крепление.
Индикаторы положения и курсоуказатели имеют универсальное крепление. Индикаторы поворота и скольжения используют ограниченное крепление.
Кольцевые лазерные гироскопы (RLG)
Рисунок: Кольцевой лазерный гироскоп от King, фигура 8.
- Корпус РЛГ представляет собой цельный стеклянный блок, в котором просверлены три узкие трубки. В каждом углу размещено зеркало, образующее треугольный оптический резонаторный тракт. Трубки заполнены гелий-неоновой смесью при низком давлении. Между катодом и двумя анодами подается высокое напряжение (около 1 кВ), вызывающее разряд (просто дорогая неоновая лампа).Разряд обеспечивает достаточно энергии, чтобы вызвать регенеративное генеративное действие в газе, при этом световые лучи циркулируют по треугольному пути резонатора. Фактически в одном резонаторе находятся два лазера — один с лучом по часовой стрелке (CW), другой против часовой стрелки (CCW). Когда гироскоп находится в состоянии покоя, два луча имеют одинаковую частоту (обычно с длиной волны 633 нанометра).

- Теперь рассмотрим блок, вращающийся по часовой стрелке. Фотон в непрерывном пучке, начиная с нижнего левого зеркала, после одного прохода резонатора обнаруживает, что зеркало сместилось немного дальше.Таким образом, он видит немного увеличенную длину пути. Точно так же фотон в луче CCW находит более короткую длину пути. Разница в длине пути вызывает небольшую разницу в частоте. Сделав одно из зеркал частично передающим, можно извлечь образцы обоих лучей и измерить разность частот. Это точно пропорционально применяемой скорости вращения.
- Осложнение возникает при очень низких скоростях вращения. Зеркала не идеальны и производят незначительное количество обратного рассеяния, которое связывает энергию между двумя лучами.Эта связь энергии между двумя генераторами с очень высокой добротностью может привести к смыканию частот. Чтобы преодолеть это, двигатель дизеринга применяет очень маленькое колебательное вращение (пиковое значение около 1 угловой минуты при частоте около 400 Гц) ко всему блоку.

Итак, вы можете спросить себя, как свет, отражающийся от набора зеркал, дублирует вращающийся гироскоп? Вот как я об этом думаю. . . любые астрофизики, которые могут лучше выразить это на пилотном языке, пожалуйста, нажмите «Связаться с Эдди» ниже и дайте мне знать.. . .
- Луч лазера (усиление света за счет стимулированного излучения) движется со скоростью света и может быть синхронизирован.
- Два луча направляются в противоположных направлениях по времени. Движение платформы приведет к тому, что лучи будут двигаться дальше или короче, что повлияет на прошедшее время.
- Два луча направляются на фотодетектор. Если по этой оси нет движения, два луча синхронизированы. Если есть вращение по этой оси, один луч не совпадает по фазе с другим.Разницу можно измерить, как если бы это было движение оси вращения гироскопа.
Свойства гироскопического действия
[AFM 51-37, 1966, стр. 4-3.] Двумя основными свойствами гироскопа, используемого в пилотажных приборах, являются жесткость в пространстве и прецессия.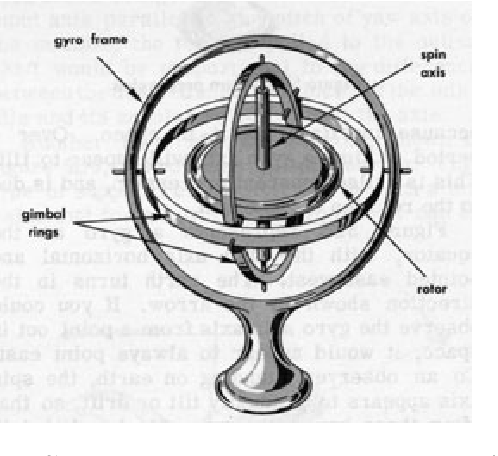
- Жесткость в пространстве . Первый закон движения Ньютона гласит, что тело, находящееся в состоянии покоя, останется в покое или, если оно движется прямолинейно, оно будет продолжать двигаться прямолинейно, если на него не подействуют внешние силы.
- Второй закон Ньютона гласит, что отклонение движущегося тела прямо пропорционально приложенной силе и обратно пропорционально весу и скорости тела.
- Индикаторы положения и индикаторы курса используют гироскопическое свойство жесткости в пространстве.
- Прецессия . Прецессия — это такое свойство гироскопа, которое заставляет ось вращения смещаться в направлении 90° от приложенной силы и в направлении вращения ротора.Двумя типами прецессии, наиболее влияющими на индикаторы положения и курса самолета, являются реальная прецессия и кажущаяся прецессия.
- Настоящая Прецессия. Настоящая прецессия — это отклонение оси вращения, вызванное приложенной извне силой.
 В пилотажных приборах эта сила является результатом перегрузки или ускорения/замедления, вызванного поворотом самолета или изменением скорости. Чтобы вызвать реальную прецессию, сила должна попытаться либо повернуть, либо наклонить ось вращения. Сила, которая пытается повернуть ось вращения, заставит ее наклониться.Сила, которая пытается наклонить ось вращения, заставит ее повернуться.
В пилотажных приборах эта сила является результатом перегрузки или ускорения/замедления, вызванного поворотом самолета или изменением скорости. Чтобы вызвать реальную прецессию, сила должна попытаться либо повернуть, либо наклонить ось вращения. Сила, которая пытается повернуть ось вращения, заставит ее наклониться.Сила, которая пытается наклонить ось вращения, заставит ее повернуться.
- Кажущаяся прецессия. Из-за гироскопического свойства жесткости в пространстве ось вращения универсально установленного гироскопа указывает в фиксированном направлении. Однако Земля вращается, поворачивается под гироскопом, и кажется, что ось вращения наклонена. Например, представьте себе гироскоп на экваторе с осью вращения, горизонтальной относительно земли, как показано [на рисунке]. Земля вращается в направлении стрелки (против часовой стрелки) с угловой скоростью один оборот каждые 24 часа.Наблюдателю на Земле кажется, что ось вращения постепенно наклоняется или дрейфует.
 Через 3 часа ось вращения наклонилась на 45°, а через 6 часов ось вращения наклонилась на 90° в вертикальное положение. По истечении 12 часов ось вращения снова становится горизонтальной, а по истечении 24 часов возвращается в исходное положение.
Через 3 часа ось вращения наклонилась на 45°, а через 6 часов ось вращения наклонилась на 90° в вертикальное положение. По истечении 12 часов ось вращения снова становится горизонтальной, а по истечении 24 часов возвращается в исходное положение. - Это явление создает иллюзию того, что гироскоп перевернулся, конец за концом, и что полный оборот совершается каждые 24 часа. Однако на самом деле гироскоп сохранил свое положение в пространстве, а земля под ним сдвинулась.Движение Земли относительно гироскопа называется кажущейся гироскопической прецессией.
Рисунок: Изменение оси вращения из-за транспортировки гироскопа, из AFM 51-37, 1966 г., рис. 4-5.
- Перемещение гироскопа по земле дает аналогичные результаты. Изменения состоят из наклона, поворота или комбинации того и другого.
- Только вертикальный гироскоп, расположенный на полюсах, или горизонтальный гироскоп с осью, выровненной с севера на юг, расположенный на экваторе, не будут показывать явной прецессии.

Основы инерциальной навигации
Рисунок: Карданная инерционная платформа от King, рисунок 1.
- Акселерометр можно рассматривать как прибор, измеряющий ускорение по одной оси. Интегрируйте вывод один раз, и вы получите скорость. Интегрируйте снова, и у вас есть положение – или, скорее, изменение положения – вдоль оси акселерометра. Если вы знаете направление движения, вы можете определить текущее положение. Инерциальная навигация — это просто форма «счисления».Вам нужно знать начальную точку – инерциальное навигационное устройство/система (ИН) не может найти свое начальное положение на земле (с трудом может найти широту, но не долготу).
- Возьмите три акселерометра с ортогональными осями считывания. Расположите их так, чтобы их оси были выровнены с севера на юг, с востока на запад и по вертикали. Чтобы сохранить эту ориентацию при маневрировании транспортного средства, акселерометры подвешены в наборе из трех шарниров, которые гиростабилизированы для сохранения направления.

- Гироскопы также представляют собой одноосевые устройства типа «интегрирующих» гироскопов, т. е. они дают выходной сигнал, пропорциональный углу, на который они повернуты (относительно своих входных осей). Гироскопы используются в качестве чувствительных элементов в сервоприводах с нулевым поиском, при этом выход каждого гироскопа подключен к серводвигателю, приводящему в движение соответствующий карданный вал, таким образом поддерживая карданный вал в постоянной ориентации в инерциальном пространстве.
- Интегрирующие гироскопы также имеют так называемый «крутящий момент», средство прецессии входной оси со скоростью, пропорциональной входному току. Это является удобным средством устранения любых ошибок дрейфа в гироскопе, а также предоставляет другую функцию, которая будет описана ниже.

- Кардан, как показано, имеет подшипник на каждом конце. У каждого есть двигатель, построенный вокруг одного из подшипников, а на другом конце синхронизатор (электромагнитное устройство измерения угла). Независимо от того, как транспортное средство маневрирует, самый внутренний шарнир сохраняет свою ориентацию в инерциальном пространстве.Таким образом, синхронизатор на самом внутреннем подвесе измеряет азимут (или направление), синхронизатор на среднем подвесе измеряет шаг, а синхронизатор на внешнем подвесе измеряет крен.
- Внутренний карданный подвес можно рассматривать как “стабильную платформу”, на которой установлены гироскопы и акселерометры (хотя на практике он выглядит совсем не как платформа, являясь чудом механической упаковки). Вся конструкция обычно называется «карданной платформой».
Подвес — это механизм, предназначенный для поддержания уровня инструмента. Первоначально он был разработан для удержания компаса корабля в горизонтальном положении с помощью двух концентрических колец с шарнирами под прямым углом.
Границы | Интуитивное объяснение прецессии
1.Введение
Интерпретация раскачивания вращающейся пластины без крутящего момента, подъема волчка, а также прецессии быстрой прялки, подвешенной на конце оси и подвергающейся воздействию гравитационного или электромагнитного момента, вдохновляла самых ярких исследователей во время прошлые века. Хотя математическая трактовка этих явлений известна, их интуитивное понимание не является тривиальным [1–6]. Некоторые основные учебники предоставляют упрощенные экспериментальные конфигурации (например,г., гантели) для более понятного объяснения [7, 8]. Однако ни один из них не раскрывает взаимодействие сил, ответственных за такое контринтуитивное поведение. Такое описание имело бы ключевое значение, поскольку силы, в отличие от законов сохранения, ближе к нашему повседневному опыту. Более глубокое понимание прецессии, вызванной крутящим моментом, было бы особенно важно для изучения ряда ее приложений, таких как гироскоп, электронный спиновой резонанс (ЭПР) [9] и ядерный магнитный резонанс (ЯМР) [10, 11].Более того, математические основы, описывающие движение волчков и равновесную форму идеализированных изогнутых и скрученных стержней, аналогичны. Это сходство называется кинетической аналогией Кирхгофа (см. Дополнительный раздел III).
Хотя математическая трактовка этих явлений известна, их интуитивное понимание не является тривиальным [1–6]. Некоторые основные учебники предоставляют упрощенные экспериментальные конфигурации (например,г., гантели) для более понятного объяснения [7, 8]. Однако ни один из них не раскрывает взаимодействие сил, ответственных за такое контринтуитивное поведение. Такое описание имело бы ключевое значение, поскольку силы, в отличие от законов сохранения, ближе к нашему повседневному опыту. Более глубокое понимание прецессии, вызванной крутящим моментом, было бы особенно важно для изучения ряда ее приложений, таких как гироскоп, электронный спиновой резонанс (ЭПР) [9] и ядерный магнитный резонанс (ЯМР) [10, 11].Более того, математические основы, описывающие движение волчков и равновесную форму идеализированных изогнутых и скрученных стержней, аналогичны. Это сходство называется кинетической аналогией Кирхгофа (см. Дополнительный раздел III).
Здесь мы даем интуитивно понятное и простое объяснение прецессии, вызванной крутящим моментом. После краткого повторения лежащих в основе концепций мы вводим и определяем модель квадратного колеса . Наша модель основана на жесткой трубе квадратной формы с тяжелой жидкостью или цепью внутри, которая может плавно и без сопротивления циркулировать по замкнутому контуру, определяемому жесткой трубкой.Этот поток создает угловой момент, позволяющий сравнить новую конфигурацию с классическими тяжелыми волчками, которые представляют собой симметричные вращающиеся объекты. Что еще более важно, трубка квадратной формы облегчает интуитивное и элементарное количественное определение внешней пары сил (в инерционной, лабораторной системе отсчета) или пары инерционных сил (в двух типах вращающихся систем), которые противодействуют гравитационному моменту и предотвращают сверху от падения.
После краткого повторения лежащих в основе концепций мы вводим и определяем модель квадратного колеса . Наша модель основана на жесткой трубе квадратной формы с тяжелой жидкостью или цепью внутри, которая может плавно и без сопротивления циркулировать по замкнутому контуру, определяемому жесткой трубкой.Этот поток создает угловой момент, позволяющий сравнить новую конфигурацию с классическими тяжелыми волчками, которые представляют собой симметричные вращающиеся объекты. Что еще более важно, трубка квадратной формы облегчает интуитивное и элементарное количественное определение внешней пары сил (в инерционной, лабораторной системе отсчета) или пары инерционных сил (в двух типах вращающихся систем), которые противодействуют гравитационному моменту и предотвращают сверху от падения.
Вращающиеся симметричные волчки представляют собой продолговатые или сплюснутые тела с цилиндрической или дискретной вращательной симметрией, вращающиеся вокруг своей оси симметрии . Ось симметрии совпадает с главной осью, имеющей наименьший или наибольший момент инерции, в то время как два дополнительных главных момента инерции, связанные с перпендикулярными главными осями ( e ⊥ ), имеют одинаковую величину. Одним из характерных явлений, демонстрируемых волчками, является прецессия . Этот термин используется для обозначения нескольких явлений, имеющих различное физическое происхождение. И наоборот, в разных областях науки и техники одно и то же событие может называться прецессией , вихлянием или нутацией [7, 8, 13, 14].
Ось симметрии совпадает с главной осью, имеющей наименьший или наибольший момент инерции, в то время как два дополнительных главных момента инерции, связанные с перпендикулярными главными осями ( e ⊥ ), имеют одинаковую величину. Одним из характерных явлений, демонстрируемых волчками, является прецессия . Этот термин используется для обозначения нескольких явлений, имеющих различное физическое происхождение. И наоборот, в разных областях науки и техники одно и то же событие может называться прецессией , вихлянием или нутацией [7, 8, 13, 14].
Безмоментная прецессия возникает, когда на вершину не действует пара внешних сил; его ось симметрии будет огибать мантию конуса с углом раскрытия ϑ, далее угол нутации , при этом полный угловой момент L системы, определяющий ось конуса, сохраняется [15–19] ( см. дополнительный раздел II.B). В основной физической литературе вращение вокруг прецессионной оси симметрии называется вращением , а вращение вокруг стационарной оси, определяемой угловым моментом, как прецессия . Заметим, что различные точки свободно прецессирующего тела испытывают переменное в пространстве и времени ускорение, поэтому внутри прецессирующих свободных вершин будут возникать механические напряжения. Это явление имеет большое значение в физике планет [20] (см. дополнительный раздел II.D).
Заметим, что различные точки свободно прецессирующего тела испытывают переменное в пространстве и времени ускорение, поэтому внутри прецессирующих свободных вершин будут возникать механические напряжения. Это явление имеет большое значение в физике планет [20] (см. дополнительный раздел II.D).
Прецессия , вызванная крутящим моментом (рис. 1), имеет место, если на волчок действует пара сил (также называемых моментом или крутящим моментом) [7, 22–30]. Волчки с осью, имеющей цилиндрическую или, по крайней мере, дискретную вращательную симметрию третьего порядка, вращающиеся вокруг этой оси и подвергающиеся воздействию крутящего момента, следуют по регулярной траектории (см. Дополнительный раздел II.Е). Здесь плавное изменение угла прецессии оси вращения (и симметрии), то есть прецессии , может сопровождаться нутацией , закономерным «киванием» угла нутации. что асимметричные волчки обычно демонстрируют хаотическое поведение [31].Наличие диссипации может привести к экзотической динамике, такой как инверсия волчка [5, 32]. Мы исследуем только чистую прецессию (установившийся угол нутации) симметричных волчков, подвергающихся воздействию момент («тяжелые» волчки), где диссипацией пренебрегают.
Мы исследуем только чистую прецессию (установившийся угол нутации) симметричных волчков, подвергающихся воздействию момент («тяжелые» волчки), где диссипацией пренебрегают.
Рисунок 1 . (в цвете онлайн) Прецессия тяжелого симметричного волчка. (A) фокусируется на угловых частотах, а (B) — на угловых моментах. Индекс lab указывает ось лабораторной (инерциальной) системы отсчета. Величины, связанные с прецессией, отмечены p , с вращением – s , а связанные с осью симметрии и перпендикулярными ей главными осями – n и ⊥ соответственно. (C) Взаимозависимость ориентации ϑ, прецессии ω p и спина ω s тяжелого волчка, описываемая уравнением (1). Линии представляют кривые постоянного угла нутации (ϑ). Пересечение кривых горизонтальной линией показывает разрешенное значение(я) для угловой частоты прецессии ω p . Заметим, что при ϑ∈{0, π} ω p и ω s нельзя различить [21].
Заметим, что при ϑ∈{0, π} ω p и ω s нельзя различить [21].
1.1. Гироскопическая прецессия Essentials
В зависимости от начальных условий и параметров крутящая (гироскопическая) прецессия может иметь динамику различной сложности. Соответственно, его математическое описание требует инструментов разной степени совершенства [7, 22, 33–35].
В основном подходе классический волчок параметризуется углами Эйлера, а именно углом нутации ϑ, углом прецессии φ и углом вращения ψ (рис. 1А). Не ограничивая общности, можно считать, что волчок подвешен в такой точке вращения, что он может свободно вращаться, а крутящий момент имеет гравитационное происхождение и соответствующая сила действует вдоль вертикальной оси.Случай без нутации, когда ϑ постоянна, легко обрабатывается уравнением Ньютона-Эйлера в лабораторной системе отсчета [36]. Это соотношение утверждает, что крутящий момент Н , действующий на волчок, определяет скорость изменения его полного углового момента L , а именно d L / dt = Н . Ось симметрии волчка будет вращаться вокруг вертикали с равномерной угловой частотой прецессии , ω p = dφ / dt [37, 38], а угловая частота вращения ω с = dψ / dt .
Ось симметрии волчка будет вращаться вокруг вертикали с равномерной угловой частотой прецессии , ω p = dφ / dt [37, 38], а угловая частота вращения ω с = dψ / dt .
Вывод уравнений общего движения симметричного тяжелого волчка можно осуществить несколькими способами. Помимо метода крутящего момента, основанного на уравнениях Ньютона-Эйлера, могут применяться также уравнения Эйлера или инструментарий аналитической механики [29, 30, 39]. В большинстве выводов используется специальное разложение векторов углового момента и угловой частоты. Для случая без нутации это приводит к соотношению, включающему ω p , гравитационный момент mgH , главные моменты инерции I n и I , как ϑ и ω s , а именно
(I⊥-In)ωp2cosϑ-Inωpωs+mgH=0 , ϑ∉{0,π} , (1), где м — масса волчка, H — расстояние центра масс волчка от точки вращения, и моменты инерции также рассчитываются относительно этой точки [7] (см. также дополнительный рисунок 5).
также дополнительный рисунок 5).
Взаимодействие параметров может привести к различному поведению. Квадратичный характер (1) обычно дает два решения в ω p . Рисунок 1C суммирует основные особенности этого уравнения [40]. Отметим, что эта фазовая диаграмма может «пальпироваться» тяжелым волчком, где угловые частоты вращения и прецессии контролируются независимо, а угол нутации может свободно изменяться [41].
Для вытянутого волчка, т.е. I ⊥ > I n , из рис. существуют ниже критического значения ω s (или ω p ).Если существуют два решения, их называют «медленной» и «быстрой» прецессией [23, 25]. При ϑ > π/2 разные знаки двух решений представляют собой прецессии в двух противоположных направлениях. Случай ϑ = π/2 приводит к линейному уравнению с единственным решением.
Приближенное линейное решение может быть получено для диапазона 0 < ϑ < π/2, если предположить, что угловой момент прецессии L p (или, что то же самое, L ⊥ ) дает незначительный вклад к полному угловому моменту L (см. рис. 1В).Точнее, мы пренебрегаем своим вкладом в изменение л , то есть D L ≈ D L L S = Ω S I N N д е п . Это общее приближение выполняется в пределе больших частот спина, когда ω s /ω p ≫ 1, что позволяет пренебречь первым слагаемым слева в (1) и дает единственное решение «медленной прецессии». Ω P = MGH / L S S = MGH / I N Ω S .
рис. 1В).Точнее, мы пренебрегаем своим вкладом в изменение л , то есть D L ≈ D L L S = Ω S I N N д е п . Это общее приближение выполняется в пределе больших частот спина, когда ω s /ω p ≫ 1, что позволяет пренебречь первым слагаемым слева в (1) и дает единственное решение «медленной прецессии». Ω P = MGH / L S S = MGH / I N Ω S .
В общем случае также будет происходить нутация, т. е. периодическое изменение угла нутации ϑ. Хотя ньютоновские методы также могут объяснить нутацию [7], это явление можно менее утомительно рассматривать, возвращаясь к инструментарию аналитической механики [24, 30, 39, 42], что в конечном итоге приводит к уравнениям с эллиптическими функциями [43].
1.2. Попытки интуитивных объяснений до сих пор
Прецессирующие тяжелые волчки демонстрируют несколько динамических особенностей, которые на первый взгляд могут показаться парадоксальными (см. Дополнительный раздел II.Ф). Было предпринято несколько попыток интуитивного объяснения прецессии, вызванной крутящим моментом. Однако ни одна из них не дает простого и легко поддающегося количественному измерению объяснения «таинственного» крутящего момента, противодействующего внешнему. Основная цель нашей статьи состоит в том, чтобы представить почти тривиальную и интуитивную модель чистой, вызванной крутящим моментом прецессии, основанной на силах вместо законов сохранения.
Первые попытки интерпретировать прецессию, вызванную крутящим моментом, представлены в фундаментальной книге Клейна и Зоммерфельда [44].Они ввели понятие «сопротивление девиации» (также называемое девиационным моментом), то есть момента, противодействующего внешнему (гравитационному), и определили его связь с центробежной и кориолисовой силами [44–46]. Фейнман предложил объяснение заметив, что траектории, полученные при проецировании траекторий точки волчка на горизонтальную плоскость, заметаемую осью симметрии, криволинейны, что требует наличия пар радиальных сил [47], но идея имеет не был определен количественно (для аналитического и числового подхода см. Дополнительный раздел I.А).
Фейнман предложил объяснение заметив, что траектории, полученные при проецировании траекторий точки волчка на горизонтальную плоскость, заметаемую осью симметрии, криволинейны, что требует наличия пар радиальных сил [47], но идея имеет не был определен количественно (для аналитического и числового подхода см. Дополнительный раздел I.А).
Для простого случая, а именно четырех одинаковых масс на перекладине, Баркер вычислил изменение ориентации их скоростей в результате совместного вращения и прецессии и определил общий крутящий момент, требуемый соответствующими ускорениями [48, 49]. Снайдер рассчитал, используя силы Кориолиса, распределение крутящего момента и общий крутящий момент, необходимый для прецессии вращающегося кольца [50]. Усубаматов вывел распределение центробежных сил и их суммарного крутящего момента, противодействующего силе тяжести, для вращающегося и прецессирующего диска [51].
Широко используемые основные учебники также изо всех сил пытаются предложить некоторые интуитивно понятные подходы. Например, Морин [7] и Клеппнер и Коленкоу [8] анализируют влияние импульсов, приложенных к гантели или к волчку в свободном падении. Однако все перечисленные выше попытки либо опираются на довольно трудоемкие расчеты, либо не улавливают некоторых важных аспектов прецессии. Таким образом, потребность в интуитивной и простой для количественной оценки модели, учитывающей наиболее важный аспект прецессии, еще не удовлетворена.
Например, Морин [7] и Клеппнер и Коленкоу [8] анализируют влияние импульсов, приложенных к гантели или к волчку в свободном падении. Однако все перечисленные выше попытки либо опираются на довольно трудоемкие расчеты, либо не улавливают некоторых важных аспектов прецессии. Таким образом, потребность в интуитивной и простой для количественной оценки модели, учитывающей наиболее важный аспект прецессии, еще не удовлетворена.
2. Модель квадратного колеса
2.1. Схема модели
Динамическое равновесие вращающегося и прецессирующего волчка будет обсуждаться путем определения действующих на него сил и моментов, а не рассмотрения уравнения Ньютона-Эйлера. Выполнение количественных исследований было бы проще, если бы можно было рассматривать очень специальные формы вершины. Жесткость классического топа ограничивает выбор правильной геометрии. Заменим, однако, прялку ( рис. 2А ) течением идеальной и несжимаемой жидкости с линиями тока, строго параллельными замкнутой и жесткой трубе, или идеально гибкой цепью без трения, бегущей по неподвижной и замкнутая траектория ( Фигуры 2B,C ).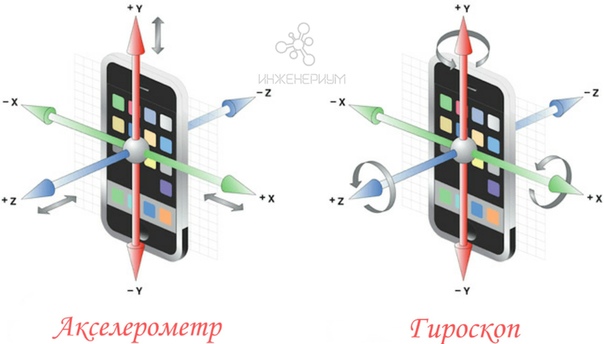 Таким образом, мы можем генерировать те же угловые моменты, что и с колесом, в то время как поток или цепная петля могут быть изменены таким образом, что это значительно упрощает вычисления 90–102 (см. Дополнительный раздел I.B). Динамика классического волчка и предлагаемого нами квадратного расположения колес однозначно определяется действующим на них крутящим моментом и вектором их углового момента. Следовательно, системы можно считать динамически эквивалентными, если крутящие моменты и угловые моменты для двух систем одинаковы.Угловой момент имеет две составляющие, связанные с двумя типами движения: вращение вокруг оси симметрии и вращение вокруг фиксированной вертикальной оси. Отметим, что форма предлагаемой системы, определяющая траекторию идеальной цепи или жидкости, также фиксирована. Однако для некруглого обруча, в отличие от вращательно-симметричных твердых тел, расстояния между осью симметрии и элементами массы, движущимися по замкнутой траектории, не являются постоянными. Таким образом, приведенная выше гибридная модель сочетает в себе жесткую опору и идеально гибкий компонент, создающий угловой момент, жидкость или цепь.
Таким образом, мы можем генерировать те же угловые моменты, что и с колесом, в то время как поток или цепная петля могут быть изменены таким образом, что это значительно упрощает вычисления 90–102 (см. Дополнительный раздел I.B). Динамика классического волчка и предлагаемого нами квадратного расположения колес однозначно определяется действующим на них крутящим моментом и вектором их углового момента. Следовательно, системы можно считать динамически эквивалентными, если крутящие моменты и угловые моменты для двух систем одинаковы.Угловой момент имеет две составляющие, связанные с двумя типами движения: вращение вокруг оси симметрии и вращение вокруг фиксированной вертикальной оси. Отметим, что форма предлагаемой системы, определяющая траекторию идеальной цепи или жидкости, также фиксирована. Однако для некруглого обруча, в отличие от вращательно-симметричных твердых тел, расстояния между осью симметрии и элементами массы, движущимися по замкнутой траектории, не являются постоянными. Таким образом, приведенная выше гибридная модель сочетает в себе жесткую опору и идеально гибкий компонент, создающий угловой момент, жидкость или цепь.
Рисунок 2 . (в цвете онлайн) Простые модели тяжелого верха. v представляют скорости потока относительно центра масс. (а) спиннинг колесо с угловым моментом LS = MR2ωs, где V = rω S (b) квадратное колесо с угловым моментом L S = MVH = генерируемое течением тяжелой идеальной жидкости или идеально гибкой цепью без трения, движущейся по прямоугольному кольцу.Эта модель позволяет проводить прямое аналитическое рассмотрение проблемы в инерциальной и прецессирующей системах отсчета. (C) Модель тяжелого волчка с изогнутым квадратным колесом, обеспечивающая круговые траектории движения цепи или частиц жидкости в верхнем и нижнем сегментах обруча. Этот подход позволяет просто интуитивно понять прецессию в инерциальной и объемной (связанной с жидкостью/цепью) системе отсчета.
Эта модель была введена в 1945 г.![]() Рудом [52], но была забыта физическим сообществом и позже была вновь открыта [53].До этого инерционные свойства жидкостей, циркулирующих в трубах различной формы, исследовались только в технологических целях, а именно для измерения скорости течения жидкости [54, 55].
Рудом [52], но была забыта физическим сообществом и позже была вновь открыта [53].До этого инерционные свойства жидкостей, циркулирующих в трубах различной формы, исследовались только в технологических целях, а именно для измерения скорости течения жидкости [54, 55].
Рассмотрим колесо радиусом r , масса которого м целиком сосредоточена в тонком обруче (рис. 2А). При вращении с угловой частотой ω с (без вращения вокруг вертикального вала) колесо имеет угловой момент вращения Ls=r2mωsen, где e n — единичный вектор вдоль оси колеса (рис. 1А).Очевидно, что угловой момент не изменился бы, если бы колесо не вращалось, но тяжелый обруч был заменен безмассовой трубкой, содержащей идеальную жидкость или цепь без трения, текущую с m (см. дополнительный раздел IA). Более того, круглая трубка может быть преобразована в квадратную (рис. 2В).
Если обруч с циркулирующей жидкостью или цепью будет вращаться вокруг вертикали (например, прецессировать), то полный момент импульса приобретет составляющую L p вдоль оси z , поэтому его полный угловой момент равен L = L с + L p .
Эта форма позволяет просто описать силы, действующие на нее во время прецессии, и последующие расчеты также станут технически менее сложными. Легко показать, что квадратное колесо с длиной стороны 2 ч , содержащее идеальную жидкость или цепь массой м и скоростью потока v , имеет угловой момент L с = mvh относительно его центра [56].
Некоторые аспекты модели можно еще больше упростить, если мы рассмотрим квадратное колесо, изогнутое таким образом, что его верхний и нижний сегменты образуют дуги радиусом H (рис. 2C).Например, в случае прецессирующего (вращающегося вокруг вертикальной оси) плоского квадратного колеса элементы цепи/жидкости будут двигаться по сложным циклоидальным орбитам. Такие орбиты могут даже привести к центростремительным силам, направленным наружу (см. Дополнительный рисунок 1). Для прецессирующего изогнутого квадратного колеса с радиусом кривизны, равным длине оси H , для элементов вращающейся массы в горизонтальных кольцевых сегментах разрешены только круговые орбиты, и поэтому центростремительная сила всегда будет направлена внутрь. Угловой момент можно рассчитать для различных форм с помощью теоремы Стокса (см. Дополнительный раздел I.C).
Угловой момент можно рассчитать для различных форм с помощью теоремы Стокса (см. Дополнительный раздел I.C).
Интерпретация сил, присутствующих в системе, зависит от выбора системы отсчета. Будет рассмотрен сравнительный анализ сил и моментов в лабораторных (инерционных), а также в двух видах вращающихся (неинерционных) систем отсчета, где играют роль разные реальные и инерционные силы. В этой статье мы ограничимся случаем без нутации и ϑ = π/2.Таким образом, угол нутации постоянен, угол закрутки не имеет значения для модели квадратного колеса (движение цепи или элементов жидкости характеризуется их скоростью), и только угол прецессии играет роль динамической переменной. Чтобы представить простые аналитические расчеты или интуитивные объяснения в различных системах отсчета, мы также будем использовать модели плоского и изогнутого квадратного колеса. В то время как аналитические расчеты облегчаются плоской геометрией, в рамках качественного, основанного на интуиции подхода роль и действие сил легче понять в модели изогнутого квадратного колеса (см. 5). Будем считать, что жесткая опора жидкости или цепи, включая ось, касающуюся точки подвеса O , не имеет массы.
Обратите внимание, что силы, возникающие в углах квадратного колеса, заставляющие циркулирующую цепь или элементы жидкости менять направление, являются внутренними силами с отражательной симметрией. Поэтому ими можно пренебречь при описании глобальной динамики системы.
2.2. Предварительные
Во-первых, мы суммируем силы, действующие на материальную точку, которая неподвижна или движется по горизонтальной и вращающейся платформе.Также учитываем силы, действующие на саму платформу. Если вертикальное ускорение отсутствует, сила тяжести G , действующая на материальную точку, и поддерживающая сила, действующая от опоры обратно на материальную точку, компенсируются (см. Дополнительные рисунки 10 и 11).
В лабораторной (инерциальной) системе отсчета присутствуют только реальные силы. Материальная точка ускоряется (удерживается на круговой орбите) центростремительной силой F CP . Пара действие-противодействие центростремительной силы будет обозначаться как реактивная центральная сила , R C . Эта сила представляет собой действие ускоряющегося тела на платформу.
Пара действие-противодействие центростремительной силы будет обозначаться как реактивная центральная сила , R C . Эта сила представляет собой действие ускоряющегося тела на платформу.
В неинерционной вращающейся системе отсчета , прикрепленной к платформе, силы, действующие на тело, компенсируются. Центробежная сила, F CF , представляет собой фиктивную силу, действующую на тело, не имеющую пары действие-противодействие.Это компенсируется реальной ограничивающей силой T CF , также называемой центральной силой , которая тянет тело к центру. Пара действие-противодействие T CF , действующая на платформу, представляет собой реактивную центральную силу R C .
Если материальная точка не закреплена на вращающейся платформе, а вынуждена совершать прямолинейное равномерное движение относительно платформы, динамику удобно описывать из неинерциальной вращающейся системы отсчета. В этой системе отсчета на тело действуют две силы инерции, а именно центробежная, F CF , и сила Кориолиса, F COR . Эти инерционные силы уравновешиваются реальными ограничивающими силами, обозначаемыми как T CF и T COR . Противодействием этих реальных сил, действующих на платформу, являются реактивная центральная сила R C и реактивная сила Кориолиса R COR .Сумму этих двух сил можно обозначить как реактивную силу R .
В этой системе отсчета на тело действуют две силы инерции, а именно центробежная, F CF , и сила Кориолиса, F COR . Эти инерционные силы уравновешиваются реальными ограничивающими силами, обозначаемыми как T CF и T COR . Противодействием этих реальных сил, действующих на платформу, являются реактивная центральная сила R C и реактивная сила Кориолиса R COR .Сумму этих двух сил можно обозначить как реактивную силу R .
В неинерционной сопутствующей системе отсчета , прикрепленной к неосевой точке волчка или к элементу циркулирующей массы квадратного колеса, фиктивные центробежные силы F CF , их « нейтрализующие” реальные силы связи T CF , а также пары действие-противодействие R C присутствуют. Обратите внимание, что величина этих сил не такая, как для вращающейся (прецессирующей) системы отсчета.
Обратите внимание, что величина этих сил не такая, как для вращающейся (прецессирующей) системы отсчета.
Таблица 1 предлагает обзор интерпретаций сил, действующих на систему отсчета, и углового момента системы квадратных колес, зависящей от системы отсчета. В этой таблице отдельно отмечены силы, действующие на элементы жидкости или цепи, а также действующие на опору. Обратите внимание, что результирующая сила (включая силы, присутствующие в точке поворота (подвески) O ) и результирующий крутящий момент, действующие на опору, должны равняться нулю, поскольку сама опора считается невесомой.
Таблица 1 . Силы и законы сохранения в различных системах отсчета.
2.3. Инерциальная система отсчета, интуитивная обработка
Концептуально инерциальная система отсчета позволяет простейшее интуитивное объяснение гироскопической прецессии. Можно провести простую обработку путем вычисления вклада крутящих моментов, действующих на опору. Поскольку опора считается безмассовой, действующий на нее суммарный крутящий момент должен равен нулю.
Поскольку опора считается безмассовой, действующий на нее суммарный крутящий момент должен равен нулю.
Рассмотрим изогнутое квадратное колесо с радиусом кривизны H , равным длине присоединенной к нему оси (см. рис. 2).Исследуем конфигурацию с угловым моментом вершины, направленной наружу. Как упоминалось ранее, в этой статье мы рассматриваем только простой случай, когда ось симметрии волчка образует прямой угол с вертикалью (ϑ = π/2). Поэтому цепь/жидкость в квадратном колесе циркулирует так, что в верхнем сегменте ее абсолютная скорость (измеренная в лабораторной системе отсчета) уменьшается, а в нижнем увеличивается из-за прецессии, отмеченной ω p .
Центростремительные силы, удерживающие цепь или жидкость на криволинейной траектории, имеют большую величину в нижнем и меньшую величину в верхнем участке жидкости или цепи. Соответственно центральная реактивная сила, действующая наружу на нижний опорный сегмент, также будет иметь большую величину, чем сила, действующая также наружу на верхний сегмент (см. рис. 3). Следовательно, на опору будут действовать два внешних момента: один Н G , возникающий от веса цепи или жидкости, а другой Н R С 2 , поднимается двумя реактивными центральными силами, имеющими разную величину и действующими на верхний и нижний квадратные сегменты колеса.
рис. 3). Следовательно, на опору будут действовать два внешних момента: один Н G , возникающий от веса цепи или жидкости, а другой Н R С 2 , поднимается двумя реактивными центральными силами, имеющими разную величину и действующими на верхний и нижний квадратные сегменты колеса.
Рисунок 3 . (в цвете онлайн) Модель изогнутого квадратного колеса, вид из лабораторной (инерциальной) системы отсчета (см. раздел 2.3). (A) Ось длиной H прецессирует в горизонтальной плоскости с угловой частотой ω p . Скорости элементов массы цепи/жидкости, измеренные от лабораторной рамы (зеленые стрелки), имеют меньшую величину в верхнем сегменте (где скорость элементов цепи/жидкости вычитается из скорости окружающей опоры) и большую величину в нижний сегмент (где эти скорости складываются). (B) Ограничивающие силы действуют на элементы цепи/жидкости (черные сплошные линии), в то время как реактивные силы действуют на опору (зеленые пунктирные линии).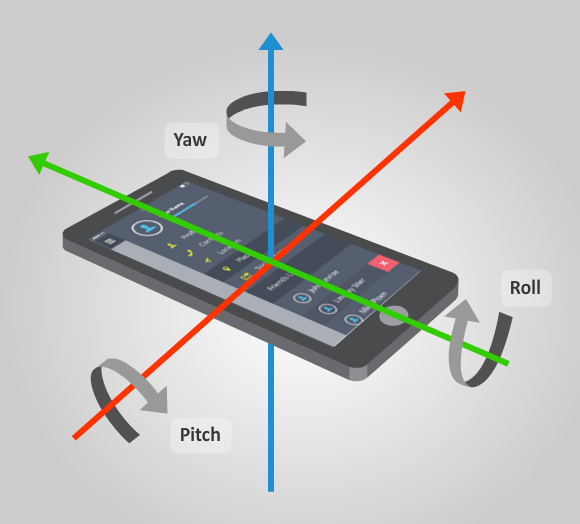 Обратите внимание на меньшую величину сил, действующих в верхнем сегменте. Синие стрелки представляют скорости цепи/жидкости, измеренные от прецессирующей рамы, которые одинаковы вокруг опоры. Обозначение сил (см. раздел 2.2): F CP – центростремительные, R C – реактивные центральные.Пара сил R C действует на опору и создает «подъемный» момент, уравновешивающий гравитационный.
Обратите внимание на меньшую величину сил, действующих в верхнем сегменте. Синие стрелки представляют скорости цепи/жидкости, измеренные от прецессирующей рамы, которые одинаковы вокруг опоры. Обозначение сил (см. раздел 2.2): F CP – центростремительные, R C – реактивные центральные.Пара сил R C действует на опору и создает «подъемный» момент, уравновешивающий гравитационный.
Пара реактивных центральных сил будет оказывать крутящий момент на O, который может уравновесить крутящий момент веса. Легко показать, что боковые сегменты квадратного колеса не вносят вклад в «подъемный» крутящий момент . В этом суть гироскопического эффекта, сформулированного в инерциальной системе отсчета
. Обратите внимание, что модель квадратного колеса также обеспечивает интуитивное понимание последовательности событий, происходящих, когда волчок, подвешенный на конце оси, освобождается. При падении на вертикальных участках возникнут пары сил, которые приведут к кратковременному угловому ускорению вокруг вертикали и инициируется прецессия.
При падении на вертикальных участках возникнут пары сил, которые приведут к кратковременному угловому ускорению вокруг вертикали и инициируется прецессия.
2.4. Инерциальная система отсчета, аналитическая обработка
Простая аналитическая обработка проблемы из инерциальной системы отсчета допускается моделью плоского квадратного колеса (рис. 4C). Мы рассматриваем только случай, когда угол нутации прямой, т. е. ϑ = π/2. Условия равновесия рассчитываются с учетом сил и моментов, действующих на опору.Результатом расчета является угловая частота прецессии.
Рисунок 4 . (в цвете онлайн) Плоская квадратная модель колеса тяжелого волчка в гравитационном поле с ускорением g , вид из лабораторной (инерциальной) системы отсчета (см. раздел 2.3). Абсолютные значения скоростей цепи/жидкости на горизонтальных участках относительно квадратного колеса отмечены синим цветом. (A,B) Центростремительные силы, F CP , действующие на жидкость или цепь в середине горизонтальных сегментов, отмеченных сплошными черными линиями, реактивные центральные силы, R C , действующие на соответствующие опорные сегменты, отмечены зелеными пунктирными линиями. Обратите внимание, что в зависимости от соотношения ω p и v они могут указывать в одном и том же или в противоположных направлениях (см. Также дополнительный рисунок 1). (C) Эскиз для расчета моментов, возникающих в симметричных точках, отмеченных r вверх и r low (см. уравнения 2, 3).
Обратите внимание, что в зависимости от соотношения ω p и v они могут указывать в одном и том же или в противоположных направлениях (см. Также дополнительный рисунок 1). (C) Эскиз для расчета моментов, возникающих в симметричных точках, отмеченных r вверх и r low (см. уравнения 2, 3).
Для скорости, ускорения и расстояния, измеренных в инерциальной (лабораторной) системе отсчета, используется «лабораторный» индекс.Обратите внимание, что простые v обозначают скорость жидкости/цепи, измеренную от прецессирующей системы отсчета.
Скорость, vlabup/low, и центростремительное ускорение, alabup/low, элемента массы цепи/жидкости, дм , в верхнем и нижнем сегментах в положениях r вверх / низ = H + δ ± h , если смотреть из лабораторного кадра, то vlabup/low=ωp×rup/low±v, а центростремительные ускорения равны
alabup/low=ωp×vlabup/low+ddt|lab(±v)=ωp×(ωp×rup/low) +2ωp×(±v) . (2)
(2)Впредь, когда знаки ± (или ∓) появляются в формулах, относящихся как к верхнему, так и к нижнему сегменту колеса, они должны ассоциироваться по порядку, т. е. + к верхнему, – к нижнему (или наоборот). Здесь мы воспользовались тем, что скорость изменения скорости потока v , «привязанная» к прецессирующему колесу, равна:
ddt|labv=ωp×v , (3)направлен наружу вдоль оси квадратного колеса.
Сила, удерживающая элемент массы на его траектории, равна dFCPup/low=dm alabup/low, а сила, действующая от элемента массы на опору, имеет вид dRCup/low=-dFCPup/low (см. рисунки 4A,B).Момент реактивных сил, действующий на элементы цепной/жидкостной массы массой дм , расположенные симметрично на верхнем и нижнем опорных сегментах, выражается как dNRCup/low=-dm·rup/low×alabup/low. Так как симметрия квадрата приводит к сокращению вкладов через δ , то dNRCup/low=-dm·(±h)×[2ωp×(±v)]=-2dm·h×(ωp×v) , который не зависит от положения на горизонтальных отрезках. Наконец, общий крутящий момент, действующий на опору, полученный путем интегрирования по двум горизонтальным сегментам, равен Н R С = − м · ч × (
Наконец, общий крутящий момент, действующий на опору, полученный путем интегрирования по двум горизонтальным сегментам, равен Н R С = − м · ч × (
4 ω
× v ).Этот крутящий момент указывает в направлении, противоположном направлению гравитационного крутящего момента Н G = м Н × г . Состояние для динамического равновесия поддержки N G Здесь упомянем, что поучительной может быть и альтернативная интерпретация сил в инерциальной системе отсчета, основанная на принципе Даламбера.Отметим также, что для «наклонной» конфигурации, когда ϑ≠π/2, вычисления становятся утомительными, но некоторые выводы подытожены в дополнительном разделе I. D.
D.
2.5. «Сопутствующая» (или «жидкая/цепная») система отсчета
В этом подходе мы вычисляем силы и моменты, действующие на верхний и нижний квадратные сегменты колеса от систем отсчета, движущихся вместе с циркулирующей цепью или жидкостью (для случая, когда угол нутации прямой, т. е. ϑ = π/2 ). Условие равновесия требует, чтобы чистый крутящий момент, действующий на жидкость или цепь, равнялся Н G + Н dev =0, где N 9010 dev2 увеличивается на 2 крутящий момент 2 на 2 пара центробежных сил в верхнем и нижнем квадратных сегментах колеса соответственно.Угловую частоту прецессии можно получить сразу, как и раньше. Модель плоского квадратного колеса позволяет получить аналитическое решение, ведущее к результатам, идентичным представленным в разделе 2.4. Каждый элемент циркулирующей массы (жидкость/цепь) будет иметь связанную систему отсчета, в которой элемент массы находится в состоянии покоя. Эти отдельные сопутствующие системы отсчета имеют разное расстояние и ориентацию по отношению к оси прецессии. Центробежные силы, а также соответствующие реактивные центральные силы должны рассчитываться для всех этих систем отсчета отдельно.Это усложняет расчет чистого крутящего момента отклонения.
Эти отдельные сопутствующие системы отсчета имеют разное расстояние и ориентацию по отношению к оси прецессии. Центробежные силы, а также соответствующие реактивные центральные силы должны рассчитываться для всех этих систем отсчета отдельно.Это усложняет расчет чистого крутящего момента отклонения.
В этом случае, хотя мы должны согласиться с приближением. Более интуитивно понятно применить модель изогнутого квадратного колеса [21, 57] (рис. 2C). Эта круговая установка облегчает расчет отдельных центробежных сил. Однако для оценки чистого крутящего момента мы выполняем аппроксимацию ч ≪ ч . В этом случае при суммировании элементарных центробежных сил, возникающих в верхнем и нижнем сегментах, считаем их параллельными друг другу и оси изогнутого квадратного колеса (рис. 5).
Рисунок 5 . (в цвете онлайн) Соответствующие силы в модели изогнутого квадратного колеса, рассматриваемые из сопутствующей системы отсчета, силы элементов цепи/жидкости, движущихся в верхнем и нижнем горизонтальных сегментах квадратного колеса (см. раздел 2.5). Обозначение сил (см. номенклатуру в разделе 2.2): F CF , центробежная сила; T CF центральная сила, обе действуют на жидкость или цепь; R C , реактивная центральная сила, действующая на опору.
раздел 2.5). Обозначение сил (см. номенклатуру в разделе 2.2): F CF , центробежная сила; T CF центральная сила, обе действуют на жидкость или цепь; R C , реактивная центральная сила, действующая на опору.
Угловые скорости отдельных систем отсчета в изогнутых верхнем и нижнем сегментах составляют Если ч ≪ Н , то соответствующая составляющая реактивных центральных (и центробежных) сил принимает вид FCFup/low≈(m/4)(v∓ωpH)2/H. Вертикальные сегменты жидкости или цепи не будут способствовать отклонению крутящего момента. После добавления вклада от обоих горизонтальных сегментов суммарный крутящий момент отклонения будет равен N dev ≈ mhvω p .Поскольку условие равновесия читается как N dev + N G = 0, это приводит к условию динамического равновесия, выражаемому также уравнением (4).
2.6. Прецессия системы отсчета
Особенно полезно определить крутящий момент в системе отсчета, прецессирующей вместе с центром масс плоского квадратного колеса (см. рис. 6). В этом кадре скорости элементов цепи/жидкости в сегментах колеса будут следовать прямым траекториям с постоянной скоростью.Вследствие этого, помимо центробежных сил, будут возникать и силы Кориолиса. Равновесие устанавливается, когда исчезает суммарный крутящий момент, действующий на жидкость или цепь, то есть Н dev + Н G = 0. Как мы увидим, только силы Кориолиса в верхнем и нижние сегменты будут способствовать крутящему моменту отклонения.
Рисунок 6 . (в цвете онлайн) Соответствующие силы в модели плоского квадратного колеса в прецессирующей системе отсчета (привязанной к оси квадратного колеса).Красные пунктирные линии обозначают силы инерции, действующие на жидкость/цепь, а зеленые пунктирные линии — реактивные силы, действующие на опору. (A) Более низкая скорость потока, когда центробежная сила преобладает над силой Кориолиса, что приводит к направленной наружу чистой силе инерции. (B) Более высокая скорость потока, когда сила Кориолиса преобладает над центробежной силой, и результатом является направленная внутрь результирующая сила инерции. Обозначение сил (см. номенклатуру в п. 2.2): F CF – центробежная, F COR – кориолисова, R – 2 реактивная (см.6).
(A) Более низкая скорость потока, когда центробежная сила преобладает над силой Кориолиса, что приводит к направленной наружу чистой силе инерции. (B) Более высокая скорость потока, когда сила Кориолиса преобладает над центробежной силой, и результатом является направленная внутрь результирующая сила инерции. Обозначение сил (см. номенклатуру в п. 2.2): F CF – центробежная, F COR – кориолисова, R – 2 реактивная (см.6).
В случае плоского квадратного колеса с углом нутации ϑ = π/2 боковые и горизонтальные сегменты колеса имеют симметричное расположение. Так как центробежные силы не зависят от скорости, их моменты сокращаются. Следовательно, вклад в момент отклонения будут вносить только силы Кориолиса. Величина их на верхнем и нижнем сегментах одинакова, но они направлены в противоположные стороны. Обратите внимание, что результирующая реактивная сила, возникающая на этих сегментах, также может быть направлена радиально внутрь или наружу, в зависимости от относительной величины силы Кориолиса и центробежной силы.
Для вертикальных сегментов силы Кориолиса равны нулю, поскольку скорости цепи/жидкости параллельны оси вращения, ω p . В верхнем и нижнем сегментах имеем v ⊥ ω p и
FCORup/low=±m4(2ωp×v)=∓m2ωpven ,, где v — скорость потока в нижнем сегменте, а e n — единичный вектор, направленный от точки вращения к центру колеса.Отклоняющий крутящий момент, действующий на точку подвеса O , будет, таким образом, равен
, где e k = e n × e z является ортогональной осью симметрии. Мы получаем, без какого-либо приближения, условие равновесия, выраженное уравнением (4).
Прецессирующая система отсчета позволяет с некоторым приближением анализировать и «наклонный» (ϑ≠π/2) случай.Поскольку расчеты утомительны, отметим лишь два важных вывода. Во-первых, точка приложения равнодействующей центробежных сил уже не будет центром квадратного колеса. Во-вторых, неожиданно, цепь/жидкость, движущаяся в косых квадратных сегментах колеса, будет , а не способствовать девиационному моменту, противодействующему гравитационному. Это открытие позволяет построить «волчок», состоящий только из горизонтальных квадратных сегментов колеса с текущим в нем газом или жидкостью.Дополнительный рисунок 3 показывает схематическую структуру и функционирование устройства, которое демонстрирует подъемный момент сил, возникающих в горизонтальных сегментах.
Во-первых, точка приложения равнодействующей центробежных сил уже не будет центром квадратного колеса. Во-вторых, неожиданно, цепь/жидкость, движущаяся в косых квадратных сегментах колеса, будет , а не способствовать девиационному моменту, противодействующему гравитационному. Это открытие позволяет построить «волчок», состоящий только из горизонтальных квадратных сегментов колеса с текущим в нем газом или жидкостью.Дополнительный рисунок 3 показывает схематическую структуру и функционирование устройства, которое демонстрирует подъемный момент сил, возникающих в горизонтальных сегментах.
2.7. Включая электромагнитные взаимодействия
Особое значение имеет прецессия тел, имеющих, кроме углового момента, дополнительный магнитный момент: взаимодействие магнитного момента с внешним магнитным полем также будет давать вклад в момент. Следовательно, прецессия будет изменена по сравнению с чисто гравитационным случаем.
Далее мы исследуем обобщенную модель квадратного колеса, участвующую как в гравитационном, так и в электромагнитном взаимодействии. Наша модель состоит из квадратного колеса, в котором цепной поток жидкости со скоростью v несет дополнительный электрический ток I . Эта структура помещена в однородное магнитное B и гравитационное g поля (см. рис. 7).
Наша модель состоит из квадратного колеса, в котором цепной поток жидкости со скоростью v несет дополнительный электрический ток I . Эта структура помещена в однородное магнитное B и гравитационное g поля (см. рис. 7).
Рисунок 7 . (в цвете онлайн) Модель квадратного колеса, в которой цепь/поток жидкости со скоростью v несет дополнительный электрический ток I .Система помещена в комбинированное магнитное B и гравитационное g поля и исследована с помощью прецессии системы отсчета с ω p . Помимо сил Кориолиса F COR силы Лоренца F LOR также способствуют устранению гравитационного момента (см. раздел 2.7).
Мы предполагаем, что при переходе к системе отсчета, вращающейся (прецессирующей) с ω p сила Лоренца не изменится (релятивистские эффекты пренебрегаем) [58]. Расчеты основаны на формальном подобии выражения силы Кориолиса и силы Лоренца [59, 60].
Расчеты основаны на формальном подобии выражения силы Кориолиса и силы Лоренца [59, 60].
Сила Кориолиса, действующая на элемент цепи/жидкости, читается как d F COR = −2· дм · ω p x магнитных элементов во внешнем магнитном поле, Поддерживаются силы Лоренца D F LOR = I · D L × B , где D L представляет собой длину текущего элемента.Следовательно, сумма сил Лоренца, действующих на верхний и нижний квадратные сегменты колеса, будет равна FLORup/low=∓2hIBen (см. рис. 7). Их крутящий момент, оказывающий на точке подвески O может быть выражен как N LOR = 2 (2 Hib ) H E ⊥ = μ B E ⊥ , где μ = 4 h 2 I = AI — магнитный момент цепи, а A — ее площадь.
Если пренебречь нутацией, динамическое равновесие устанавливается, когда магнитный момент, девиация и гравитационный момент компенсируют друг друга, то есть 4h3IB+mωpvh-mgH=0, что в итоге приводит к
ωp=mgH-4h3IBmvh=NG-μBLs=NG-NLORLs, где N G — гравитационный момент. Заметим, что в случае, когда μ B = mgH , магнитный и гравитационный моменты могут компенсировать друг друга даже в отсутствие углового момента и прецессии.
3. Заключение
В этой статье мы количественно определили модель квадратного колеса волчки. Хотя было несколько попыток найти интуитивное, основанное на силе объяснение явления прецессии, эти подходы не являются одновременно простыми, количественными и интуитивными [7, 8, 47, 48, 51, 52]. Круглые вершины не позволяют проводить легкие расчеты, гантели чрезмерно упрощены, а первая, забытая статья о модели квадратного колеса не давала никакой количественной оценки.
Предлагаемая модель состоит из тяжелой цепи или жидкости, которая без трения циркулирует по замкнутому контуру, определяемому трубой квадратной формы, и поэтому возникнет угловой момент. Эта модель позволяет объяснить и количественно описать гироскопическую прецессию с помощью простых сил, удерживающих вершину «против силы тяжести». Эти силы интерпретировались в лабораторных (инерционных), а также в двух типах или вращающихся (неинерциальных) системах отсчета. Наш подход более интуитивен, чем классическое объяснение, основанное на уравнении Ньютона-Эйлера об изменении углового момента. Мы обсуждали и расширенную модель, в которой поток несет электрический ток и помимо гравитационного присутствует внешнее магнитное поле.Эти размышления способствуют лучшему и более интуитивному пониманию сложной, но интригующей проблемы прецессии тяжелых волчков, которая является основой для понимания различных явлений, начиная от механических гироскопов и заканчивая магнитным резонансом. Обратите внимание, что варианты модели квадратного колеса также могут применяться для интуитивного объяснения динамики свободных вершин (см. Дополнительные разделы II.I и J).
Эта модель позволяет объяснить и количественно описать гироскопическую прецессию с помощью простых сил, удерживающих вершину «против силы тяжести». Эти силы интерпретировались в лабораторных (инерционных), а также в двух типах или вращающихся (неинерциальных) системах отсчета. Наш подход более интуитивен, чем классическое объяснение, основанное на уравнении Ньютона-Эйлера об изменении углового момента. Мы обсуждали и расширенную модель, в которой поток несет электрический ток и помимо гравитационного присутствует внешнее магнитное поле.Эти размышления способствуют лучшему и более интуитивному пониманию сложной, но интригующей проблемы прецессии тяжелых волчков, которая является основой для понимания различных явлений, начиная от механических гироскопов и заканчивая магнитным резонансом. Обратите внимание, что варианты модели квадратного колеса также могут применяться для интуитивного объяснения динамики свободных вершин (см. Дополнительные разделы II.I и J).
Вклад авторов
PH пришел к идее квадратного колеса, сделал первоначальную версию расчетов, подготовил рисунки, упомянутые патенты, численное моделирование и в равной степени внес свой вклад в написание статьи. ZL усовершенствовал расчеты, выполнил расчеты в дополнительных материалах и в равной степени внес свой вклад в написание статьи.
ZL усовершенствовал расчеты, выполнил расчеты в дополнительных материалах и в равной степени внес свой вклад в написание статьи.
Финансирование
ZL поддерживается грантом COFUND-FLAGERA II-CORTICITY.
Заявление о конфликте интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Благодарности
Мы в долгу перед А.Яковац, Сз. Хорват, Р. Немет, Гий. Лакос, Гай. Давиду, Г. Дьёрдьи, Л. Орошу, П. Гнедигу и Г. Домокосу за полезные обсуждения, а Cs. András, J. Tellmann, S. Krueger-Lebus, T. Lessinnes, S. Bächtold, S. Habermacher, J. Spring, I. Jalsovszky и A. Málnási-Csizmadia за помощь в работе. А. Яковак и Г. Дьёрдьи предоставили существенные идеи для подготовки рисунка 1С и объяснения в сопутствующей системе отсчета. Эта работа была поддержана Фондом Domus Hungarica. Настоящий научный вклад посвящен 650-летию основания Печского университета в Венгрии.
Дополнительный материал
Дополнительный материал к этой статье можно найти в Интернете по адресу: https://www.frontiersin.org/articles/10.3389/fphy.2019.00005/full#supplementary-material
.Ссылки
1. Симони К. Культурная история физики. Бока-Ратон, Флорида: CRC Press (2012).
Академия Google
2. Арнольд И.В. Математические методы классической механики. Нью-Йорк, штат Нью-Йорк: Спрингер (1978).
3.Борелли А. Угловой момент между физикой и математикой. В: Schlote KH, Schneider M, редакторы. Математика встречается с физикой. Франкфурт: Verlag Harri Deutsch (2011). стр. 395–440.
5. Коэн Р.Дж. Еще раз о типпе. Am J Phys. (1977) 45 : 12–7.
Академия Google
6. Чжу Л.Ю. Fun Rigid Body Dynamics. Пекин: Издательство о высшем образовании (2008 г.).
7. Морин Д. Введение в классическую механику с задачами и решениями . Кембридж: Издательство Кембриджского университета (2007).
Кембридж: Издательство Кембриджского университета (2007).
Академия Google
8. Клеппнер Д., Коленков Р. Введение в механику . Кембридж: Издательство Кембриджского университета (2014).
Академия Google
10. Хэнсон Л. Необходима ли квантовая механика для понимания магнитного резонанса? Concepts Magn Reson A. (2008) 32 : 329–40. doi: 10.1002/cmr.a.20123
Полнотекстовая перекрестная ссылка | Академия Google
11. Магнитные моменты, взаимодействующие с магнитными полями.TeachSpin Inc. Доступно на сайте: www.teachspin.com
12. Брехер К. Топология: крутящий момент о вершинах. В: Bridges Seoul Converence Proceedings (2014). стр. 51–8.
Академия Google
13. Тевари А. Динамика атмосферы и космического полета . Бостон, Массачусетс: Спрингер-Биркхаузер (2007).
Академия Google
14. Дехант В., Мэтьюз П.М. Прецессия, нутация и колебание Земли . Кембридж: Издательство Кембриджского университета (2015).
Кембридж: Издательство Кембриджского университета (2015).
20. Лазарян А., Ефроимский М. Неупругая диссипация в свободно вращающемся теле. Приложение к выравниванию космической пыли. Месяц Noti R Astr Soc. (1999) 303 : 673–684.
Академия Google
21. Яковак А. Частное сообщение . Будапешт (2013).
22. Берри М.В., Шукла П. Медленное многообразие и угол Ханнея в волчке. Евр. J физ. (2011) 32 : 115–27. дои: 10.1088/0143-0807/32/1/011
Полнотекстовая перекрестная ссылка | Академия Google
23.Виттенбург Дж. Динамика многотельных систем . Берлин: Спрингер (2008).
Академия Google
24. Драйцлер Р., Людде К. Теоретическая механика . Берлин: Спрингер (2011).
Академия Google
29. Ландау Л., Лифшиц Э.М. Механика (Том 1. Курс теоретической физики) . Оксфорд: Пергамон Пресс (1969).
Академия Google
30. Киббл Т., Беркшир Ф. Классическая механика . Лондон: Imperial College Press (2004).
Киббл Т., Беркшир Ф. Классическая механика . Лондон: Imperial College Press (2004).
Академия Google
31. Баррьентос М., Перес А., Ранада А.Ф. Слабый хаос в асимметричном тяжелом волчке Eur J Phys. (1995) 16 : 106–12.
Академия Google
34. Wilson HB, Turcoette LH, Halpern D. Расширенные математические и механические приложения с использованием MATLAB . Бока-Ратон, Флорида: Чепмен и Холл (2003).
Академия Google
35. Гандер В., Гребичек Дж. Решение задач научных вычислений с использованием Maple и MATLAB .Берлин: Спрингер (2004).
Академия Google
39. Гольдштейн Х., Пул Ч., Сафко Дж. Классическая механика . Сан-Франциско, Калифорния: Аддисон-Уэсли (2001).
Академия Google
40. Chouaieb N. Задача Кирхгофа о винтовых решениях однородных стержней и их свойства устойчивости. Тезе 2717, EPFL, Лозанна (2003 г.).
42. Слышал ВБ. Механика твердого тела: математика, физика и приложения . Вайнхайм: Wiley-VCH (2005).
Слышал ВБ. Механика твердого тела: математика, физика и приложения . Вайнхайм: Wiley-VCH (2005).
Академия Google
43. Лоуден Д.Ф. Эллиптические функции и приложения . Нью-Йорк, штат Нью-Йорк: Спрингер (1989).
Академия Google
44. Кляйн Ф., Зоммерфельд А. Theory of the Top , Vol. I. Бостон, Массачусетс: Биркхойзер (2008).
Академия Google
45. Скарборо Дж.Б. Теория гироскопа и приложения. Нью-Йорк, штат Нью-Йорк: Издательство Interscience (1958).
Академия Google
47.Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Рединг, Массачусетс: Аддисон-Уэсли (1963).
48. Баркер Э. Элементарный анализ гироскопа. Am J Phys. (1960) 28 : 808–10.
Академия Google
50. Снайдер Дж.Л. Гироскопическая прецессия. Am J Phys. (1965) 33 :847.
Академия Google
51. Усубаматов Р. , Харун А., Фидзван М., Хамзас А. Тайна гироскопа раскрыта. IJAMAE (2014) 1 : 62–7. дои: 10.15242/IJAMAE.E1113506
, Харун А., Фидзван М., Хамзас А. Тайна гироскопа раскрыта. IJAMAE (2014) 1 : 62–7. дои: 10.15242/IJAMAE.E1113506
Полнотекстовая перекрестная ссылка | Академия Google
52. Руд П. Действие равно противодействию – даже в гироскопах. Am J Phys. (1945) 13 : 175–7.
Академия Google
53. Ханц П. Частное сообщение . Клуж-Напока / Коложвар (1993). прежняя, неопубликованная версия этой статьи, отправленная Am. Дж. Физ (2007).
54. Roth W. Гироскопический расходомер US2865201 (1958).
56. Ханц П., Лазар З.И. Устройство для иллюстрации сил, возникающих во время прецессии потоком жидкости во вращающихся трубах . Заявка на патент Венгрии P1800079 (2018 г.).
57. Дьёрдьи Г. Частное сообщение . Будапешт (2013).
59. Susskind L, Hrabowski G. Теоретический минимум. Нью-Йорк, штат Нью-Йорк: Basic Books (2013).
60. Перселл Э., Морин Д. Электричество и магнетизм. Кембридж: Издательство Кембриджского университета (2013).
Перселл Э., Морин Д. Электричество и магнетизм. Кембридж: Издательство Кембриджского университета (2013).
Физика «эффекта антигравитации» гироскопа
Физика гироскопических эффектов более сложна, чем представлена в существующих математических моделях. Эффекты, представляемые этими моделями, не соответствуют реальным силам, действующим на гироскопические устройства. Новые исследования в этой области показали, что на гироскоп действует система инерционных моментов, создаваемых вращающейся массой вращающихся объектов. Действия системы сил инерции подтверждены практическими испытаниями движений гироскопа с одной боковой опорой.Действие момента внешней нагрузки на гироскоп с одной боковой опорой показывает, что движение гироскопа вверх ошибочно называют эффектом «антигравитации». Движение гироскопа вверх является результатом крутящего момента прецессии вокруг его горизонтальной оси. Новизна настоящей работы связана с математическими моделями движения гироскопов вверх и вниз под действием внешнего крутящего момента вокруг вертикальной оси. Это аналитическое исследование описывает физику восходящего движения гироскопов и подтверждает, что гироскопы не обладают свойством антигравитации.
Это аналитическое исследование описывает физику восходящего движения гироскопов и подтверждает, что гироскопы не обладают свойством антигравитации.
1. Введение
Прикладная теория гироскопов возникла в основном в ХХ веке в связи с широким применением и усилением вращения многочисленных вращающихся объектов в технике [1–4]. Свойства гироскопа используются во многих инженерных расчетах, связанных с вращающимися деталями в аэрокосмической, судостроительной и других отраслях промышленности, гироскопическим эффектам посвящено множество публикаций [5, 6]. Фундаментальные учебники и публикации по классической механике описывают гироскопические эффекты в эйлеровом члене изменения углового момента [7–9].Тем не менее предыдущие аналитические подходы основаны на нескольких предположениях и упрощениях, которые приводят к теоретической неопределенности в отношении гироскопических эффектов [10, 11]. Математические модели свойств гироскопов в публикациях не соответствуют практическим применениям гироскопических устройств [12–15]. Все вращающиеся объекты подвижных механизмов проявляют гироскопические эффекты, которые должны рассчитываться инженерными методами. Исходя из этого, исследователи придумали искусственные термины, такие как гироскопические эффекты и пары гироскопов, и установили неинерционные, негравитационные свойства, противоречащие принципам физики.
Физика гироскопических эффектов более сложна, чем представлено в литературе. Внешний вращающий момент, приложенный к гироскопу, создает систему восьми инерционных моментов, создаваемых центробежной, общей инерционной и кориолисовой силами, а также изменением углового момента вращающегося ротора. Действия системы инерционных моментов вокруг осей гироскопа взаимосвязаны и проявляют все необъяснимые ранее гироскопические свойства. На сегодняшний день физико-математические модели инерционных моментов гироскопов хорошо описаны и прошли валидацию [16–20].Однако новый аналитический подход все еще имеет некоторые математические ошибки. В некоторых публикациях отмечается неточность математических моделей при рассмотрении моментов инерции, действующих на гироскоп [20]. В технике несколько моментов нагрузки гироскопических устройств могут действовать в разных направлениях вокруг их осей вращения. Взаимосвязанное действие внутренних и внешних моментов нагрузки на гироскоп представляет собой решаемую научно-техническую задачу. Новизна настоящей работы описывает точную математическую модель движения гироскопа вверх под действием внешнего крутящего момента и объясняет физику гироскопического эффекта, который ошибочно называют свойством «антигравитации».
В технике несколько моментов нагрузки гироскопических устройств могут действовать в разных направлениях вокруг их осей вращения. Взаимосвязанное действие внутренних и внешних моментов нагрузки на гироскоп представляет собой решаемую научно-техническую задачу. Новизна настоящей работы описывает точную математическую модель движения гироскопа вверх под действием внешнего крутящего момента и объясняет физику гироскопического эффекта, который ошибочно называют свойством «антигравитации».
2. Методология
Недавние исследования физических принципов гироскопических эффектов привели к созданию математических моделей, которые можно использовать для оценки системы сил инерции, действующих на гироскоп. Новые математические модели внутренних крутящих моментов описали новые свойства гироскопа и поведение гироскопических устройств. Воздействие внешней нагрузки на гироскоп создает моменты сопротивления и прецессии, возникающие при вращении масс-элементов вращающегося ротора.Математические модели инерционных моментов, действующих на гироскоп, представлены в ряде публикаций [16–20]. В одной публикации приведены некорректные математические модели взаимосвязи внешних и внутренних моментов, действующих на гироскоп [20]. Следует внимательно рассмотреть действие системы взаимосвязанных инерционных моментов вокруг осей гироскопа. Анализ взаимозависимой последовательности действия внешнего и инерционного моментов позволяет сформулировать физические принципы движения гироскопа.Были рассмотрены действия системы крутящих моментов и их влияние на гироскопическую стойку, и соответствующие технические данные опубликованы [20]. Математические модели движения гироскопа представлены на двух примерах действия внешнего и внутреннего моментов на гироскоп с одной боковой опорой для его горизонтального расположения. Для простоты действия сил трения на опоры и шкворень не учитываются. Две математические модели движения гироскопа дают четкое представление о физике действующих внешних и внутренних моментов.Первая математическая модель рассматривает действие моментов внешней нагрузки, описываемых как момент, действующий на гироскоп вокруг оси, и момент веса гироскопа, действующий вокруг оси против часовой стрелки.
В одной публикации приведены некорректные математические модели взаимосвязи внешних и внутренних моментов, действующих на гироскоп [20]. Следует внимательно рассмотреть действие системы взаимосвязанных инерционных моментов вокруг осей гироскопа. Анализ взаимозависимой последовательности действия внешнего и инерционного моментов позволяет сформулировать физические принципы движения гироскопа.Были рассмотрены действия системы крутящих моментов и их влияние на гироскопическую стойку, и соответствующие технические данные опубликованы [20]. Математические модели движения гироскопа представлены на двух примерах действия внешнего и внутреннего моментов на гироскоп с одной боковой опорой для его горизонтального расположения. Для простоты действия сил трения на опоры и шкворень не учитываются. Две математические модели движения гироскопа дают четкое представление о физике действующих внешних и внутренних моментов.Первая математическая модель рассматривает действие моментов внешней нагрузки, описываемых как момент, действующий на гироскоп вокруг оси, и момент веса гироскопа, действующий вокруг оси против часовой стрелки. Вторая математическая модель рассматривает внешние нагрузки, описываемые как действие момента по часовой стрелке вокруг оси и действие момента веса гироскопа против часовой стрелки вокруг оси. Эта конструктивная особенность стойки гироскопа создает уникальное сочетание действующих моментов инерции и различных движений.
Вторая математическая модель рассматривает внешние нагрузки, описываемые как действие момента по часовой стрелке вокруг оси и действие момента веса гироскопа против часовой стрелки вокруг оси. Эта конструктивная особенность стойки гироскопа создает уникальное сочетание действующих моментов инерции и различных движений.
2.1. Практический пример 1
Математическая модель движения гироскопа учитывает действие момента нагрузки вокруг оси в направлении против часовой стрелки и момента нагрузки, создаваемого весом гироскопа вокруг оси. В этих условиях действие момента внешней нагрузки порождает систему инерционных моментов, действующих вокруг осей гироскопа (рис. 1). Действие момента нагрузки создает следующие инерционные моменты:
а) Момент сопротивления, создаваемый действием центробежной силы и силы Кориолиса вокруг оси по часовой стрелке (т.е., в направлении, противоположном действию момента нагрузки )(b) Процессный момент, создаваемый общими силами инерции, и изменение углового момента вращающегося ротора возникает на оси, но действует вокруг оси по часовой стрелке (т. е. , в направлении, противоположном действию веса гироскопа). Величина момента, создаваемого грузом гироскопа, меньше величины результирующих инерционных моментов, действующих вокруг оси. Последнее () вызывает движение гироскопа вверх (с) Процессный момент вокруг оси , в свою очередь, порождает момент сопротивления центробежной и Кориолисовой сил вокруг оси .Эти моменты движутся против часовой стрелки и усиливают действие веса гироскопа
е. , в направлении, противоположном действию веса гироскопа). Величина момента, создаваемого грузом гироскопа, меньше величины результирующих инерционных моментов, действующих вокруг оси. Последнее () вызывает движение гироскопа вверх (с) Процессный момент вокруг оси , в свою очередь, порождает момент сопротивления центробежной и Кориолисовой сил вокруг оси .Эти моменты движутся против часовой стрелки и усиливают действие веса гироскопа
Действие результирующего момента вокруг оси создает момент прецессии, создаваемый общими силами инерции, и изменение углового момента, возникающее на оси, но действующее вокруг оси и добавляется к моменту сопротивления вокруг оси, что приводит к моменту сопротивления.
Действие нагрузок и изменение значений взаимосвязанных инерционных моментов, действующих вокруг двух осей.Действие внешнего момента порождает момент прецессии, который действует вокруг оси, противоположной действию веса гироскопа. Эта ситуация приводит к уменьшению величины результирующего момента инерции и момента прецессии, действующего вокруг оси . Изменения значений инерционных моментов равны, поскольку они выражают внутреннюю кинетическую энергию. Это изменение выражается коэффициентом изменения инерционных моментов вокруг одной оси и объясняется следующим выражением:
где в уравнение (1) подставлены выражения инерционных моментов [16] и момента, создаваемого грузом гироскопа.Все компоненты указаны выше.
Изменения значений инерционных моментов равны, поскольку они выражают внутреннюю кинетическую энергию. Это изменение выражается коэффициентом изменения инерционных моментов вокруг одной оси и объясняется следующим выражением:
где в уравнение (1) подставлены выражения инерционных моментов [16] и момента, создаваемого грузом гироскопа.Все компоненты указаны выше.
Коэффициент представляет уменьшение значения момента прецессии, действующего вокруг оси, при уменьшении значения момента инерции вокруг оси. Эта зависимость отражает взаимосвязь инерционных моментов, действующих вокруг двух осей. Анализ уравнения (1) приводит к следующим значениям коэффициента:
(i) Отсутствие момента нагрузки, действующего вокруг оси, означает, что коэффициент равен (т. е. нет изменения значения инерционных моментов, действующих вокруг двух осей) (ii) Действие момента нагрузки означает, что коэффициент равен (я.т. е. значения инерционных действующих моментов вокруг двух осей уменьшаются) (iii) Когда момент нагрузки равен моменту прецессии (), коэффициент равен (т. е. гироскоп не поворачивается вокруг оси, а вместо этого поворачивается вокруг оси при только действие веса гироскопа).
е. гироскоп не поворачивается вокруг оси, а вместо этого поворачивается вокруг оси при только действие веса гироскопа).
Эта особенность должна быть отражена в уравнениях движения гироскопа вокруг двух осей. Разработана математическая модель для оценки движений гироскопа, вызванных действием внешнего и внутреннего моментов.Эта модель включает поправки, основанные на взаимосвязанном действии инерционных моментов, и представлена следующими дифференциальными уравнениями Эйлера: где и – угловые скорости гироскопа вокруг осей и соответственно; , , , , , , , и – внутренние моменты, создаваемые центробежной, кориолисовой и общей силами инерции и изменением углового момента, действующего вокруг осей и , соответственно [16]. Знак (-) в уравнении (3) означает, что движение происходит по часовой стрелке.Все остальные компоненты указаны выше.
Уравнения инерционных моментов [16] и уравнение (1) подставляются в уравнения (2) и (3). Составляющие моментов, создаваемые центробежной и инерционной силами, имеющие одинаковое выражение, из уравнений (2) и (3) исключаются.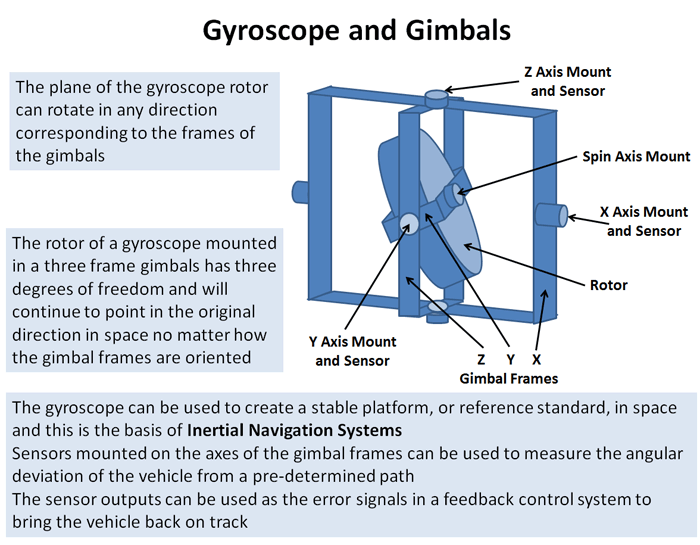 Упрощение и модификация этих уравнений аналогичны решению, представленному в рукописях [17, 18], где этот процесс подробно обоснован. Модифицированные уравнения представлены следующей системой:
где уравнение (6) представляет собой зависимость угловых скоростей гироскопа вокруг осей, которые были добавлены к уравнениям (4) и (5).Это решение представлено в рукописях [17, 18], в которых используются аналогичные аналитические подходы. Все остальные параметры указаны выше.
Упрощение и модификация этих уравнений аналогичны решению, представленному в рукописях [17, 18], где этот процесс подробно обоснован. Модифицированные уравнения представлены следующей системой:
где уравнение (6) представляет собой зависимость угловых скоростей гироскопа вокруг осей, которые были добавлены к уравнениям (4) и (5).Это решение представлено в рукописях [17, 18], в которых используются аналогичные аналитические подходы. Все остальные параметры указаны выше.
Подстановка уравнения (6) в первое уравнение (3) и преобразование дает следующее уравнение: где все компоненты указаны выше.
2.1.1. Рабочий пример
Компоненты гироскопа с одной боковой опорой перемещаются под действием моментов нагрузки и , которые создаются весом гироскопа и действуют вокруг осей и соответственно . Значение первого крутящего момента составляет половину значения крутящего момента (т. е. ). Действия крутящих моментов и движений представлены на рисунке 1. Технические данные, относящиеся к гироскопу, представлены в рукописи ([20], таблица 1). Уравнение (7) представляет собой уравнение движения гироскопа вокруг оси . Отношение угловых скоростей вокруг двух осей рассчитывается с использованием уравнения (6). Угловая скорость вокруг оси определяется следующим решением. Подставляя исходные данные гироскопа [20] и данные, представленные выше, в уравнение (7), получаем следующее уравнение:
Уравнение (8) можно упростить следующим образом:
Уравнение (10) получается путем разделения переменных для упрощения и преобразования уравнения (9):
Уравнение (11) является интегральной формой уравнения (10):
Уравнение (7) представляет собой уравнение движения гироскопа вокруг оси . Отношение угловых скоростей вокруг двух осей рассчитывается с использованием уравнения (6). Угловая скорость вокруг оси определяется следующим решением. Подставляя исходные данные гироскопа [20] и данные, представленные выше, в уравнение (7), получаем следующее уравнение:
Уравнение (8) можно упростить следующим образом:
Уравнение (10) получается путем разделения переменных для упрощения и преобразования уравнения (9):
Уравнение (11) является интегральной формой уравнения (10):
| |||||||||||||||||||||||||||||||||
Левый интеграл уравнения (11) сведен в таблицу и представлен в виде интеграла . Правый интеграл прост. Решение интегралов дает следующее уравнение: тем самым приводя к следующему:
Уравнение (13) можно преобразовать в уравнение угловой скорости для гироскопа вокруг оси:
Правая часть уравнения (14) содержит выражение , имеющее малое значение высокого порядка, при котором угловая скорость вращающегося ротора составляет около .Следовательно, этой составляющей уравнения можно пренебречь. Решение уравнения (10) дает следующее уравнение: где все компоненты указаны выше.
Угловая скорость гироскопа вокруг оси определяется скоростью вращения ротора . Подстановка в уравнения (15) и (6) дает угловые скорости гироскопа вокруг осей и :
где знак (-) в уравнении (17) означает, что прецессия гироскопа вокруг оси происходит по часовой стрелке, т. е. гироскоп движется вверх.
Крутящий момент, действующий вокруг оси, приводит к медленному вращению против часовой стрелки вокруг оси и вызывает интенсивное прецессионное вращение гироскопа вокруг оси по часовой стрелке. Гироскоп движется вверх от своего горизонтального положения. Этот эффект служит практическим доказательством отсутствия свойства антигравитации.
2.2. Практический пример 2
Математическая модель движения гироскопа рассматривается для той же стойки гироскопа и тех же технических параметров, что и в разделе 2.1, тематическое исследование 1. Разница заключается в действии момента нагрузки по часовой стрелке вокруг оси . При этом условии действия внутренних крутящих моментов и движений гироскопа следующие:
(i) Момент нагрузки создает момент сопротивления, который действует против часовой стрелки вокруг оси, и момент прецессии, который действует вокруг оси против часовой стрелки. Это совпадает с действием крутящего момента нагрузки (ii) Действие крутящего момента, создаваемого весом гироскопа, создает моменты сопротивления и прецессии.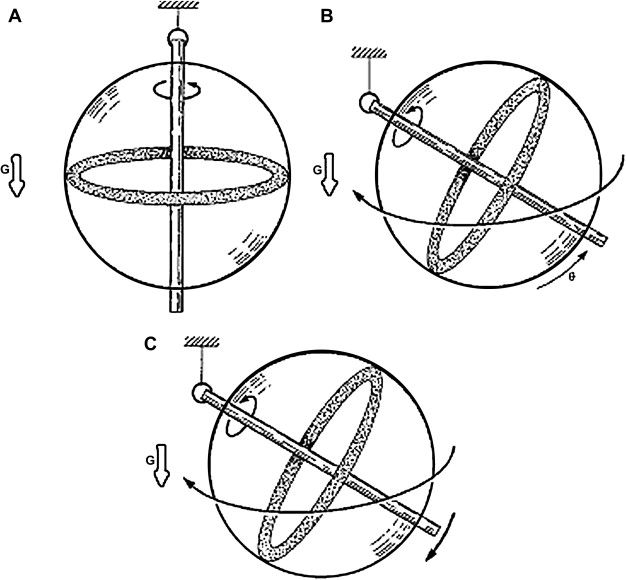 Момент сопротивления действует по часовой стрелке вокруг оси. Момент прецессии действует в направлении против часовой стрелки вокруг оси как момент
Момент сопротивления действует по часовой стрелке вокруг оси. Момент прецессии действует в направлении против часовой стрелки вокруг оси как момент
Все действующие моменты и движения гироскопа с одной боковой опорой показаны на рисунке 2.
Уравнения моментов и движений гироскопа вокруг осей и представлены следующими выражениями: где знак (-) в уравнении (18) указывает на движение по часовой стрелке. Все остальные компоненты указаны выше.
Коэффициент представляет собой пропорциональное увеличение момента прецессии вокруг оси . Коэффициент выражается как отношение суммы моментов прецессии и нагрузки к моменту прецессии, действующему вокруг оси . Выражение получается аналогично уравнению (1) и представлено следующим уравнением: где – коэффициент пропорционального увеличения величины момента прецессии, действующего вокруг оси . Все остальные параметры указаны выше.
Коэффициент обозначает увеличение момента прецессии вокруг оси или , когда значение результирующего момента вокруг оси также увеличивается. Уравнение (20) демонстрирует следующие значения коэффициента :
(i) Отсутствие момента нагрузки, действующей вокруг оси или , означает, что коэффициент (т. е. нет изменения значений инерционных моментов, действующих вокруг двух осей) (ii) Действие момента нагрузки означает, что коэффициент равен (т. е. увеличиваются значения инерционных моментов, действующих вокруг двух осей) (iii) Когда момент нагрузки веса гироскопа равен моменту прецессии (), коэффициент (i.т. е. увеличивается значение результирующего момента сопротивления, действующего вокруг оси )
Уравнение (20) демонстрирует следующие значения коэффициента :
(i) Отсутствие момента нагрузки, действующей вокруг оси или , означает, что коэффициент (т. е. нет изменения значений инерционных моментов, действующих вокруг двух осей) (ii) Действие момента нагрузки означает, что коэффициент равен (т. е. увеличиваются значения инерционных моментов, действующих вокруг двух осей) (iii) Когда момент нагрузки веса гироскопа равен моменту прецессии (), коэффициент (i.т. е. увеличивается значение результирующего момента сопротивления, действующего вокруг оси )
Уравнения для инерционных моментов, т. е. уравнения (17) и (20), подставляются в уравнения (18) и (19). Уравнения (21)–(23) упрощаются и преобразуются так же, как уравнения (4)–(6): где все параметры указаны выше.
При движении вокруг оси действующие моменты представлены совместным действием веса гироскопа с моментами прецессии и моментами сопротивления в противоположном направлении.Моменты, действующие вокруг оси, представлены действием момента нагрузки и комбинированных моментов сопротивления с моментами прецессии, действующими в противоположном направлении. Следующее решение для уравнений (21)–(23) такое же, как представлено в разделе 2.1, пример 1. Уравнение (21) можно решить, подставив определенное уравнение и используя преобразования, чтобы получить следующее уравнение:
где все компоненты указаны выше.
Следующее решение для уравнений (21)–(23) такое же, как представлено в разделе 2.1, пример 1. Уравнение (21) можно решить, подставив определенное уравнение и используя преобразования, чтобы получить следующее уравнение:
где все компоненты указаны выше.
2.2.1. Рабочий пример
Движения гироскопа с одной боковой опорой выполняются под действием вращающего момента нагрузки вокруг оси по часовой стрелке.Схема действия моментов и движений представлена на рис. 2. Уравнение (24) представляет собой уравнение движения гироскопа вокруг оси . Должны быть определены угловые скорости прецессий вокруг двух осей. Подставив исходные данные гироскопа ([20], табл. 1) в уравнение (24) и проведя преобразования, получим следующее уравнение:
Уравнение (25) упрощено. Затем выполняются шаги решения, аналогичные шагам, представленным в Разделе 2.1, Пример 1.Все комментарии, относящиеся к решениям уравнений, опущены. где знак (-) указывает на движение по часовой стрелке.
Крутящий момент, действующий вокруг оси, вызывает медленное вращение вокруг оси по часовой стрелке и интенсивное вращение гироскопа вокруг оси против часовой стрелки. Эти вращения приводят к крутящему моменту против часовой стрелки вокруг оси.
Эти вращения приводят к крутящему моменту против часовой стрелки вокруг оси.
3. Результаты и обсуждение
Математические модели гироскопических эффектов приводят к уравнениям движения гироскопа с одной боковой опорой для основного внешнего момента, действующего вокруг вертикальной оси.Модели движения гироскопа вокруг двух осей основаны на действии внешнего и внутреннего моментов, создаваемых центробежной, общей инерционной и кориолисовой силами. Они также основаны на изменении углового момента. Новый аналитический подход к задаче гироскопа демонстрирует, что действие момента внешней нагрузки вокруг вертикальной оси порождает моменты прецессии, которые поворачивают гироскоп вверх или вниз вокруг горизонтальной оси. Эти движения зависят от направления вращения вращающегося ротора.Математические модели движения гироскопа с одной боковой опорой, в которых действия внешних и внутренних моментов вокруг двух осей подтверждены наблюдениями, сделанными в ходе практических испытаний.
4. Заключение
Предыдущие математические модели гироскопических эффектов содержат множество допущений и упрощений, не подтвержденных на практике. Это новое исследование гироскопических эффектов исследует действия системы инерционных моментов, создаваемых известными инерционными силами классической механики.Математические модели движения гироскопа с одной боковой опорой и действия моментов нагрузки против и по часовой стрелке вокруг вертикальной оси объясняют движение гироскопа вверх и вниз. Движение гироскопа вверх не является свойством антигравитации, как когда-то считалось, а является результатом действия момента прецессии, создаваемого моментом нагрузки. Величина момента прецессии больше, чем величина момента, создаваемого грузом гироскопа. Аналитические модели движения гироскопа вверх и вниз четко описывают физику таких гироскопических эффектов.
Номенклатура
| : | Ускорение силы тяжести |
| : | основание натурального логарифма |
| : | Индекс для осей или |
| : | Момент инерции массы диска ротора в |
| : | момент инерции масс гироскопа вокруг оси |
| : | Расстояние между гироскоп центра масс и одной боковой поддержки |
| : | Длина гироскопа компонента |
| : | Масса вращающихся компонентов | : | Внешний радиус ротора | 91 441: | радиус гироскопа компонента | 91 441: | нагрузки крутящего момента, генерируемого веса гироскопа | 91 441: | Нагрузка крутящий момент к оси |
| : | Генерируемый крутящий момент изменением углового момента, центробежной, кориолисовой и инерционной сил, соответственно, и действующих вокруг оси |
| : | сопротивления и момента прецессии соответственно, действующих вокруг оси |
| : | |
| Вес гироскоп | |
| : | Угол наклона прядильной оси |
| : | Коэффициент изменения стоимости внутренних крутящих моментов |
| : | угловая скорость вращения ротора |
| : | Угловая скорость прецессии вокруг оси . |
Доступность данных
Данные, использованные для поддержки результатов этого исследования, можно получить у соответствующего автора по запросу.
Конфликт интересов
Автор заявляет об отсутствии конфликта интересов.
Благодарности
Работа выполнена при поддержке Кыргызского государственного технического университета им. И. Раззакова.
Гироскопический крутящий момент – обзор
2.5 Собранные уравнения движения
Уравнение Лагранжа (2.1.7) записывается с обобщенными силами в правой части. В первых четырех из следующих уравнений член линейного ускорения v˙ был заменен его нелинейным аналогом ab, определенным в уравнении. (2.1.5). Они отличаются нелинейным членом ω×v. Нелинейные эффекты более полно обсуждаются в главах 3 и 4. На данном этапе достаточно знать, что эти проблемы можно решить, добавив нелинейные члены (индекс NL ) в правую часть. Нелинейные члены обычно слишком малы, чтобы иметь значение для двигателя и уравнений изгиба.
Собранное описание динамики движения автомобиля состоит из пяти основных групп уравнений. Эти уравнения моделируют поступательное движение и вращение твердого тела, движение двигателей и выплескивающихся компонентов топлива относительно корпуса, а также изгиб планера.
Трансляция (2.4.4)
(2.5.1)mTab-sTD×ω˙−sEb×ω˙Eb+∑jmsjδ¨sj=f+fNL
Вращение (2.4.8)
(2.5.2) sTD×ab+ITDω˙+ITWDω˙Eb+∑jmsjrsj×δ¨sj=g+gNL
Двигатель (2.4.25)
(2.5.3)sEb×ab+ITWDTω˙+IEbω˙Eb+∑cEFiη¨i=gEb
Slosh (2.4.13)
(2.5.4)msj(ab−rsj×ω˙+δ ¨sj+∑ψjiη¨i)=fsjNL
Изгиб (2.4.17)
(2.5.5)cEFiTω˙Eb+∑jmsjψjiTδ¨sj+mBiη¨i=fBi
является скаляром, а не вектором. Это обычно вычисляется следующим образом, используя уравнение. (2.2.24).
(2.5.6)fBi=−mBi(ΩBi2ηi+2ζBiΩBiη˙i)+∑n(ψniTfn+σniTgn)
Термины RHS определяются следующим образом.Величины f и g представляют собой сумму всех сил и моментов соответственно, приложенных к ракете, включая силы тяги и аэродинамические силы. За исключением нелинейных сил и моментов fNL и gNL, внутренние, например выплескивающие, силы исключаются, поскольку они возникают неявно через члены ускорения выплескивания на левой стороне (2.5.5).
За исключением нелинейных сил и моментов fNL и gNL, внутренние, например выплескивающие, силы исключаются, поскольку они возникают неявно через члены ускорения выплескивания на левой стороне (2.5.5).
Величина gEb представляет собой сумму всех внешних крутящих моментов двигателя относительно точки подвеса, включая крутящие моменты привода, крутящие моменты аэродинамической нагрузки, крутящий момент несоосности тяги, эффекты топливопровода, гироскопические крутящие моменты из-за вращающихся турбомашин и так далее.Величина fsj представляет собой сумму всех сил, действующих на выплескивающуюся массу j .
Если используется модель пружины с выплескиванием, уравнение переноса системы и уравнение двигателя являются единственными уравнениями, для которых необходимо рассматривать систему координат, отличную от системы координат тела. Уравнение переноса иногда выражается в инерциальной системе отсчета. Уравнение двигателя иногда выражается в рамке двигателя. Это причины индекса b на ab, ωEb, gEb и т. д.Для последних двух переменных, когда этот индекс опускается, подразумевается, что эти переменные находятся в фрейме механизма, т. е. индекс E сам по себе означает две вещи: это переменная механизма, и она выражается в рама двигателя. Как говорилось ранее, надо понимать, что все остальное ( ω , δsj и т.д.) находится в корпусе каркаса.
д.Для последних двух переменных, когда этот индекс опускается, подразумевается, что эти переменные находятся в фрейме механизма, т. е. индекс E сам по себе означает две вещи: это переменная механизма, и она выражается в рама двигателя. Как говорилось ранее, надо понимать, что все остальное ( ω , δsj и т.д.) находится в корпусе каркаса.
Массовая матрица для заданного движения двигателя
Движение двигателя может считаться заданным или не заданным.Фраза «заданное движение двигателя» означает, что ωEb и его производная по времени являются внешними переменными, которые вводятся в динамические уравнения. Для моделирования это потребовало бы, чтобы динамика TVC вычислялась в отдельном модуле с отдельным набором переменных состояния. Альтернативой является включение движения двигателя βEb как часть вектора состояния.
Для возможности адаптации анализа к различным ситуациям вводятся дополнительные обозначения. Переменные с тильдой могут быть переопределены по мере необходимости для различных предположений модели. Для анализа, в котором можно пренебречь всеми нелинейными силами и моментами и не задавать движение двигателя, следует, что f˜=f, g˜=g, g˜Eb=gEb и т. д. С другой стороны, если транспортное средство скорость вращения вокруг любой оси велика, возможно, потребуется включить нелинейные члены. Затем эти величины будут выражены как f˜=f+fNL, g˜=g+gNL, g˜Eb=gEb+gEb,NL и т. д.
Для анализа, в котором можно пренебречь всеми нелинейными силами и моментами и не задавать движение двигателя, следует, что f˜=f, g˜=g, g˜Eb=gEb и т. д. С другой стороны, если транспортное средство скорость вращения вокруг любой оси велика, возможно, потребуется включить нелинейные члены. Затем эти величины будут выражены как f˜=f+fNL, g˜=g+gNL, g˜Eb=gEb+gEb,NL и т. д.
Для заданного движения двигателя уравнение двигателя удаляется из приведенного выше набора. Все уравнения, кроме уравнений выплескивания, имеют члены с переменной ωEb, которые смещены в правую часть.Таким образом, силы и крутящие моменты системы равны fsj,NL
(2.5.10)f˜Bi=fBi+fBi,presc
Заданные силы и крутящие моменты двигателя, здесь с нижним индексом presc, могут быть получены из (2.5.1)–(2.5.5) простым отрицание любого члена, в котором появляется ω˙Eb, и включение его в правую часть динамического уравнения. Таким образом,
(2.5.11)fpresc=sEb×ω˙Eb
(2.5.12)gpresc=-ITWDω˙Eb
(2.5.13)fBi,presc=-cEFiTω˙Eb
Обратите внимание, что не существует предписанного члена движения двигателя, который вносит вклад в выражение обобщенной силы выплескивания. уравнения (2.5.1) — (2.5.5) можно собрать в большое матричное уравнение. Для заданного движения двигателя уравнение. (2.5.3) исключается. Полезно определить 1 как единичную матрицу 3×3. Также полезно определить нулевую матрицу 3×3
(2.5.14)O≡[000]
, где
(2.5.15)0=[000]T,
нулевой вектор.
Собранные уравнения системы могут быть записаны в матричной форме как
(2.5.16)Mx¨=F.
Для автомобиля с топливными баками N и гибкими режимами M вектор ускорения определяется выражением
(2.5.17)x¨=[abTω˙Tδ¨s1Tδ¨s2T…δ¨sNTη¨1η¨2 …η¨M]T
, а вектор F формируется из правых частей уравнений (2.5.1), (2.5.2), (2.5.4) и (2.5.5);
(2.5.18)F=[f˜Tg˜Tf˜s1Tf˜s2T…f˜sNTf˜B1f˜B2…f˜BM]T.
Массовая матрица определяется формулой.(2.5.19). Вектор состояния (2.5.17) можно использовать в качестве ориентира, помогающего понять, сколько строк и столбцов представлено в этой матрице. В частности, каждый режим имеет только одну строку и один столбец. Например, если рассматриваемая ракета не имеет выплескивающегося топлива и имеет только одну гибкую моду, матрица масс будет 7 на 7.
Матрица масс с включенным движением двигателя
Используется предположение, что движение двигателя задано во многих системах управления и часто является хорошей отправной точкой для проектирования системы управления.Первоначальный анализ основан на предположении, что система TVC очень жесткая; то есть резонансы двигателей с их замкнутыми контурами позиционирования находятся на более высоких собственных частотах, чем частоты управления и значимые глобальные структурные моды. Это допущение может косвенным образом повлиять на конструкцию системы TVC, чтобы увеличить ее пропускную способность и усилить опору двигателя и конструкцию крепления исполнительного механизма («резервную»).
Для окончательной проверки конструкции может потребоваться признать тот факт, что как жесткое, так и упругое движение точки подвеса будут влиять на результирующий угол подвеса двигателя.Обычно по мере того, как структурная масса распределяется и обменивается во время проектирования транспортного средства, программа транспортного средства одновременно дорабатывается, чтобы включать необходимый анализ и испытания для поддержки подробного моделирования динамики двигателя. Детали такого моделирования и тестирования рассматриваются в главе 6.
Включение уравнения двигателя выполняется путем первоначальной установки предписанных сил движения в уравнениях. (2.5.7) через (2.5.10) к нулю. Нелинейные крутящие моменты двигателя обычно очень малы, и их также можно установить равными нулю.В двигателе экв. (2.5.3), g˜E=gE.
Отсутствует прямое влияние выплескивания на двигатель (уравнение (2.5.4)), а также воздействие выплескивания на двигатель. В то время как двигатели и выплескивание связаны косвенно через твердое тело и эластичность, эта связь обычно невелика. Основной интерес представляет сцепление двигателя и гибкость. Чтобы подчеркнуть это, рассмотрим ракету без выплескивающегося топлива. Для ракеты с модами М уравнения. (2.5.1), (2.5.2), (2.5.3) и (2.5.5) могут быть объединены в одно матричное уравнение, заданное формулой (2.5.20).
Для ракеты с выплескиванием топливных масс в эту систему уравнений несложно вставить строки и столбцы выплескивания, фигурирующие в (2.5.19). Кроме того, обычно желательно, если двигатели выровнены по оси x корпуса, применить ограничение βEx=0 (отсутствие вращения двигателя вокруг оси x ). Приблизительно это можно сделать, удалив соответствующую строку и столбец для вращения двигателя x .В разделе 2.7 ниже представлен более формальный математический подход, который применяется к аналогичной проблеме усечения выплескивания.
Если задано движение двигателя, модель TVC включает инерцию двигателя и обеспечивает углы подвеса двигателя, угловые скорости и угловые ускорения в зависимости от заданных входных данных. Если движение двигателя не задано, модель TVC необходимо модифицировать таким образом, чтобы обеспечить крутящие моменты gEy и gEz относительно точки подвеса при заданных значениях углов подвеса и команд угла подвеса.Инерция двигателя включена в уравнения системы и исключена из модели TVC.
Как правило, наиболее точным способом решения набора динамических уравнений является одновременное решение всех уравнений. Предписанный подход к движению двигателя является отходом от этого идеала, поскольку он означает, что уравнения для движения двигателя решаются отдельно от уравнений для остальной динамики. С точки зрения этой оставшейся динамики движение двигателя запаздывает на один шаг. Этот поэтапный подход к решению может потребовать меньшего временного шага для достижения численной стабильности.
Подход, который является промежуточным между предписанным и не предписанным, состоит в том, чтобы рассматривать двигатель, как предписано в уравнениях системы, но добавлять внешние крутящие моменты в отдельную модель TVC, которые представляют эффекты движения точки карданного подвеса. уравнение (2.5.3) можно переставить следующим образом:
(2.5.21)ω˙Eb=IEb−1[gEb−(sEb×ab+ITWDTω˙+∑cEFiη¨i)]
Это выражение подставляется в Модель TVC для вычисления ускорения двигателя. Термины в скобках представляют крутящие моменты двигателя из-за движения точки подвеса.Включение этих крутящих моментов повышает точность решения, но по-прежнему необходимо интегрировать динамическое движение отдельно от движения TVC, поэтому численные проблемы, описанные выше, останутся. 2
Гироскоп вики | TheReaderWiki
Гироскоп в действии. Обратите внимание на свободу вращения по всем трем осям. Ротор будет поддерживать направление своей оси вращения независимо от ориентации внешней рамы.Гироскоп (от древнегреческого γῦρος gûros , «круг» и σκοπέω skopéō , «смотреть») представляет собой устройство, используемое для измерения или поддержания ориентации и угловой скорости. [1] [2] Это прялка или диск, в котором ось вращения (ось вращения) может сама принимать любую ориентацию. При вращении ориентация этой оси не зависит от наклона или вращения крепления в соответствии с законом сохранения углового момента.
Также существуют гироскопы, основанные на других принципах работы, такие как гироскопы MEMS с микрочипом, используемые в электронных устройствах (иногда называемые гирометрами ), твердотельные кольцевые лазеры, волоконно-оптические гироскопы и чрезвычайно чувствительный квантовый гироскоп. [3]
Гироскопы применяются в инерциальных навигационных системах, например, в телескопе Хаббл или внутри стального корпуса подводной лодки. Из-за своей точности гироскопы также используются в гиротеодолитах для сохранения направления при разработке туннелей. [4] Гироскопы могут использоваться для создания гирокомпасов, которые дополняют или заменяют магнитные компасы (на кораблях, самолетах и космических кораблях, транспортных средствах в целом), для обеспечения устойчивости (велосипеды, мотоциклы и корабли) или используются как часть инерциальная система наведения.
Гироскопы MEMS популярны в некоторых устройствах бытовой электроники, таких как смартфоны.
Описание и схема
Схема гироскопа. Стрелки реакции вокруг выходной оси (синие) соответствуют силам, приложенным к входной оси (зеленые), и наоборот.Гироскоп представляет собой прибор, состоящий из колеса, закрепленного на двух или трех шарнирах, обеспечивающих поворотные опоры, позволяющие колесу вращаться вокруг одной оси. Набор из трех шарниров, один из которых установлен на другом с ортогональными осями поворота, может использоваться, чтобы позволить колесу, установленному на самом внутреннем шарнире, иметь ориентацию, не зависящую от ориентации в пространстве его опоры.
В случае гироскопа с двумя карданами внешний кардан, представляющий собой раму гироскопа, устанавливается с возможностью поворота вокруг оси в своей плоскости, определяемой опорой. Этот внешний шарнир обладает одной степенью свободы вращения, а его ось не имеет ни одной. Второй карданный шарнир, внутренний карданный вал, установлен в раме гироскопа (внешний карданный вал) с возможностью поворота вокруг оси в своей собственной плоскости, которая всегда перпендикулярна оси вращения рамы гироскопа (внешнего карданный вал). Этот внутренний подвес имеет две степени свободы вращения.
Ось прялки определяет ось вращения. Ротор вынужден вращаться вокруг оси, которая всегда перпендикулярна оси внутреннего карданного подвеса. Таким образом, ротор обладает тремя степенями свободы вращения, а его ось — двумя. Колесо реагирует на силу, приложенную к входной оси, силой реакции на выходную ось.
Поведение гироскопа легче всего оценить, рассмотрев переднее колесо велосипеда. Если колесо отклоняется от вертикали так, что верхняя часть колеса смещается влево, передний обод колеса также поворачивается влево.Другими словами, вращение на одной оси вращающегося колеса производит вращение на третьей оси.
Маховик гироскопа будет вращаться или сопротивляться вокруг выходной оси в зависимости от того, имеют ли выходные подвесы свободную или фиксированную конфигурацию. Примерами некоторых устройств со свободным выходом карданного подвеса могут быть опорные гироскопы ориентации, используемые для определения или измерения углов ориентации тангажа, крена и рыскания в космическом корабле или самолете.
Анимация гироскопа в действииЦентр тяжести ротора может находиться в фиксированном положении.Ротор одновременно вращается вокруг одной оси и способен колебаться вокруг двух других осей, и он может свободно вращаться в любом направлении вокруг фиксированной точки (за исключением собственного сопротивления, вызванного вращением ротора). Некоторые гироскопы имеют механические эквиваленты, заменяющие один или несколько элементов. Например, вращающийся ротор может быть подвешен в жидкости, а не установлен на шарнирах. Гироскоп управляющего момента (CMG) является примером устройства с фиксированным выходом и подвесом, которое используется на космических кораблях для удержания или поддержания желаемого угла наклона или направления наведения с использованием силы гироскопического сопротивления.
В некоторых особых случаях внешний карданный вал (или его эквивалент) можно не использовать, чтобы ротор имел только две степени свободы. В других случаях центр тяжести ротора может быть смещен относительно оси колебаний и, таким образом, центр тяжести ротора и центр подвески ротора могут не совпадать.
История
По сути, гироскоп представляет собой волчок, совмещенный с парой подвесов. Топы были изобретены во многих разных цивилизациях, включая классическую Грецию, Рим и Китай. [5] Большинство из них не использовались в качестве инструментов.
Первый известный прибор, похожий на гироскоп («Вращающееся зеркало» или «Зеркало Серсона»), был изобретен Джоном Серсоном в 1743 году. Он использовался в качестве уровня для определения горизонта в условиях тумана или тумана.
Первый инструмент, больше похожий на настоящий гироскоп, был сделан Иоганном Боненбергером из Германии, который впервые написал об этом в 1817 году. Сначала он назвал его «Машина». [6] [7] [8] В основе машины Боненбергера лежал вращающийся массивный шар. [9] В 1832 году американец Уолтер Р. Джонсон разработал аналогичное устройство, основанное на вращающемся диске. [10] [11] Французский математик Пьер-Симон Лаплас, работавший в Политехнической школе в Париже, рекомендовал машину для использования в качестве учебного пособия, и таким образом она привлекла внимание Леона Фуко. [12] В 1852 году Фуко использовал его в эксперименте, связанном с вращением Земли. [13] [14] Именно Фуко дал устройству его современное название, в эксперименте, чтобы увидеть (греч. skopeein , видеть) вращение Земли (греч. gyros , круг или вращение), [15] , который был виден за 8-10 минут до того, как трение замедлило вращающийся ротор.
В 1860-х годах появление электродвигателей позволило гироскопу вращаться бесконечно; это привело к созданию первого прототипа индикатора курса и более сложного устройства – гирокомпаса. Первый функциональный гирокомпас был запатентован в 1904 году немецким изобретателем Германом Аншютц-Кемпфе. [16] Позже в том же году американец Элмер Сперри разработал свой собственный дизайн, и вскоре другие страны осознали военное значение изобретения – в эпоху, когда военно-морская доблесть была наиболее важным мерилом военной мощи – и создали свой собственный гироскоп. отрасли.Компания Sperry Gyroscope быстро расширилась, чтобы поставлять стабилизаторы для самолетов и кораблей, и другие разработчики гироскопов последовали ее примеру. [17]
В 1917 году компания Chandler Company из Индианаполиса создала «гироскоп Чендлера», игрушечный гироскоп со шнурком и пьедесталом. Чендлер продолжал производить игрушки, пока компания не была куплена TEDCO Inc. в 1982 году. Игрушка Чендлер до сих пор производится TEDCO. [18]
В первые несколько десятилетий 20-го века другие изобретатели пытались (безуспешно) использовать гироскопы в качестве основы для ранних навигационных систем типа «черный ящик», создавая стабильную платформу, с которой можно было бы выполнять точные измерения ускорения (в чтобы обойти необходимость наблюдения за звездами для расчета положения).Подобные принципы были позже использованы при разработке инерциальных навигационных систем для баллистических ракет. [19]
Во время Второй мировой войны гироскоп стал основным компонентом самолетов и зенитных прицелов. [20] После войны гонка за миниатюризацией гироскопов для управляемых ракет и систем навигации оружия привела к разработке и производству так называемых миниатюрных гироскопов , которые весили менее 3 унций (85 г) и имели диаметр примерно 1 дюйм (2.{-7}} дюйма (2,5 нм).
Трехосевые гироскопы на основе МЭМС также используются в портативных электронных устройствах, таких как планшеты, смартфоны [23] , [24] и смарт-часы. [25] Это дополнение к возможности определения ускорения по трем осям, доступной на устройствах предыдущих поколений. Вместе эти датчики обеспечивают 6-компонентное обнаружение движения; акселерометры для перемещения по осям X, Y и Z и гироскопы для измерения степени и скорости вращения в пространстве (крен, тангаж и рыскание).Некоторые устройства [26] [27] дополнительно включают магнитометр для обеспечения абсолютных угловых измерений относительно магнитного поля Земли. Более новые инерциальные измерительные устройства на основе МЭМС включают до девяти осей измерения в одном корпусе интегральной схемы, обеспечивая недорогое и широко доступное измерение движения. [28]
Принципы гироскопии
Все вращающиеся объекты обладают гироскопическими свойствами. Основными свойствами, которыми может обладать объект при любом гироскопическом движении, являются жесткость в пространстве и прецессия.
Жесткость в космосе
Жесткость в космосе описывает принцип, согласно которому гироскоп остается в фиксированном положении на плоскости, в которой он вращается, не подвергаясь влиянию вращения Земли. Например, велосипедное колесо.
Прецессия
Простой случай прецессии, также известный как устойчивая прецессия, может быть описан следующим соотношением с моментом:
∑ М Икс знак равно − я ф ′ 2 грех θ потому что θ + я г ф ′ грех θ ( ф ′ потому что θ + ψ ′ ) {\ displaystyle \ sum M_ {x} = – I {\ phi ‘} ^ {2} \ sin \ theta \ cos \ theta + I_ {z} \ phi ‘\ sin \ theta (\ phi ‘\ cos \ theta + \psi ‘)}
где ф ′ {\ Displaystyle \ фи ‘} представляет прецессию, ψ ′ {\ Displaystyle \ фунтов на квадратный дюйм ‘} представлен спином, θ {\ Displaystyle \ тета} – угол нутации, а я {\ Displaystyle я} представляет инерцию вдоль соответствующей оси.Это соотношение справедливо только в том случае, когда Момент по осям Y и Z равен 0.
Уравнение можно еще сократить, заметив, что угловая скорость по оси Z равна сумме Прецессии и Вращения: ю г знак равно ф ′ потому что θ + ψ ′ {\ Displaystyle \ омега _ {г} = \ фи ‘\ соз \ тета + \ psi ‘} , Где ю г {\ Displaystyle \ омега _ {г}} представляет собой угловую скорость вдоль оси z.
∑ М Икс знак равно − я ψ ′ 2 грех θ потому что θ + я г ψ ′ ( грех θ ) ю г {\ displaystyle \ sum M_ {x} = – I {\ psi ‘} ^ {2} \ sin \ theta \ cos \ theta + I_ {z} \ psi ‘(\ sin \ theta) \ omega _ {z}}
или
∑ М Икс знак равно ψ ′ грех θ ( я г ю г − я ψ ′ потому что θ ) {\ displaystyle \ sum M_ {x} = \ psi ‘\ sin \ theta (I_ {z} \ omega _ {z} -I \ psi ‘\ cos \ theta)} [29]
Гироскопическая прецессия вызвана крутящим моментом.Описывается как скорость изменения углового момента и угловой скорости, создаваемая одним и тем же приложенным крутящим моментом. Это физическое явление приводит к кажущимся невозможными динамическим явлениям. Например, волчок. Этот гироскопический процесс используется во многих аэрокосмических условиях, таких как самолеты и вертолеты, чтобы помочь им принять желаемую ориентацию.
Современное использование
Steadicam
Установка Steadicam использовалась во время съемок фильма «Возвращение джедая» в сочетании с двумя гироскопами для дополнительной стабилизации для съемки фоновых пластин для погони на спидербайке.Изобретатель стедикама Гаррет Браун управлял съемкой, идя по лесу секвойи, управляя камерой со скоростью один кадр в секунду. При проецировании со скоростью 24 кадра в секунду создавалось впечатление полета по воздуху с опасной скоростью. [30] [31]
Указатель курса
Указатель курса или гироскоп направления имеет ось вращения, установленную горизонтально и направленную на север. В отличие от магнитного компаса, он не ищет север. Например, при использовании в авиалайнере он будет медленно отклоняться от севера, и его необходимо будет периодически переориентировать, используя в качестве ориентира магнитный компас.
Гирокомпас
В отличие от гироскопа или указателя направления, гирокомпас указывает на север. Он обнаруживает вращение Земли вокруг своей оси и ищет истинный север, а не магнитный север. Гирокомпасы обычно имеют встроенное демпфирование для предотвращения перерегулирования при повторной калибровке из-за внезапного движения.
Акселерометр
Путем определения ускорения объекта и интегрирования по времени можно рассчитать скорость объекта.Интегрируя снова, положение может быть определено. Простейший акселерометр представляет собой свободно перемещающийся в горизонтальном направлении груз, прикрепленный к пружине, и устройство для измерения натяжения пружины. Это можно улучшить, введя противодействующую силу, чтобы оттолкнуть вес назад, и измерить силу, необходимую для предотвращения перемещения веса. Более сложная конструкция состоит из гироскопа с грузом на одной из осей. Устройство будет реагировать на силу, создаваемую весом при его ускорении, путем интегрирования этой силы для получения скорости.
Варианты
Гиростат
Гиростат состоит из массивного маховика, спрятанного в прочном корпусе. [34] [35] Его поведение на столе или с различными режимами подвески или опоры служит иллюстрацией любопытного обращения обычных законов статического равновесия из-за гиростатического поведения внутреннего невидимого маховика при вращении быстро. Первый гиростат был разработан лордом Кельвином, чтобы проиллюстрировать более сложное состояние движения вращающегося тела, когда оно свободно перемещается в горизонтальной плоскости, как волчок на тротуаре или велосипед на дороге.Кельвин также использовал гиростаты для разработки механических теорий упругости материи и эфира. [36] В современной механике сплошных сред существует множество таких моделей, основанных на идеях лорда Кельвина. Они представляют собой особый тип теорий Коссера (впервые предложенных Эженом Коссера и Франсуа Коссера), которые можно использовать для описания искусственно созданных интеллектуальных материалов, а также других сложных сред. Одна из них, так называемая среда Кельвина, имеет те же уравнения, что и магнитные изоляторы вблизи состояния магнитного насыщения в приближении квазимагнетостатики. [37]
В настоящее время концепция гиростата используется при проектировании систем ориентации орбитальных космических аппаратов и спутников. [38] Например, космическая станция «Мир» имела три пары внутренних маховиков, известных как гиродины или гироскопы управляющего момента . [39]
В физике существует несколько систем, динамические уравнения которых напоминают уравнения движения гиростата. [40] Примеры включают твердое тело с полостью, заполненной невязкой, несжимаемой однородной жидкостью, [41] статическая равновесная конфигурация напряженного упругого стержня в теории эластики, [42] поляризационная динамика световой импульс, распространяющийся через нелинейную среду, [43] система Лоренца в теории хаоса, [44] и движение иона в масс-спектрометре с ловушкой Пеннинга. [45]
Гироскоп МЭМС
Гироскоп микроэлектромеханических систем (МЭМС) представляет собой миниатюрный гироскоп, используемый в электронных устройствах. Он использует идею маятника Фуко и использует вибрирующий элемент. Этот тип гироскопа был впервые использован в военных целях, но с тех пор все чаще используется в коммерческих целях. [46]
HRG
Полусферический резонаторный гироскоп (HRG), также называемый гироскопом типа «рюмка» [ противоречивый ] или грибовидный гироскоп, использует тонкую твердотельную полусферическую оболочку, закрепленную на толстый ствол.Эта оболочка приводится в изгибной резонанс электростатическими силами, создаваемыми электродами, которые наносятся непосредственно на отдельные структуры из плавленого кварца, окружающие оболочку. Гироскопический эффект получается из инерционного свойства изгибных стоячих волн.
VSG или CVG
Гироскоп с вибрирующей структурой (VSG), также называемый вибрационным гироскопом Кориолиса (CVG), [47] использует резонатор, изготовленный из различных металлических сплавов.Он занимает промежуточное положение между малоточным и недорогим МЭМС-гироскопом и более точным и дорогим волоконно-оптическим гироскопом. Параметры точности повышаются за счет использования материалов с низким собственным демпфированием, вакуумирования резонатора и цифровой электроники для уменьшения температурно-зависимого дрейфа и нестабильности управляющих сигналов. [48]
Высококачественные резонаторы типа «рюмка» используются для точных датчиков, таких как HRG. [49]
DTG
Динамически настраиваемый гироскоп (DTG) представляет собой ротор, подвешенный на универсальном шарнире с изгибными шарнирами. [50] Жесткость пружины на изгиб не зависит от скорости вращения. Однако динамическая инерция (от эффекта гироскопической реакции) карданного подвеса обеспечивает отрицательную жесткость пружины, пропорциональную квадрату скорости вращения (Хоу и Савет, 1964; Лоуренс, 1998). Следовательно, при определенной скорости, называемой скоростью настройки, два момента компенсируют друг друга, освобождая ротор от крутящего момента, что является необходимым условием идеального гироскопа.
Кольцевой лазерный гироскоп
Кольцевой лазерный гироскоп основан на эффекте Саньяка для измерения вращения путем измерения смещающейся интерференционной картины луча, разделенного на две половины, когда две половины движутся по кольцу в противоположных направлениях.
Когда Boeing 757-200 поступил в эксплуатацию в 1983 году, он был оснащен первым подходящим кольцевым лазерным гироскопом. На разработку этого гироскопа ушло много лет, и экспериментальные модели претерпели множество изменений, прежде чем инженеры и менеджеры компаний Honeywell и Boeing сочли его готовым к производству. Это был результат конкуренции с механическими гироскопами, которые продолжали совершенствоваться. Причина, по которой Honeywell из всех компаний выбрала разработку лазерного гироскопа, заключалась в том, что они были единственными, у кого не было успешной линейки механических гироскопов, поэтому они не могли конкурировать сами с собой.Первая проблема, которую им пришлось решить, заключалась в том, что при вращении лазерных гироскопов ниже определенного минимума вообще нельзя было обнаружить из-за проблемы, называемой «захватом», когда два луча действуют как связанные осцилляторы и тянут частоты друг друга к сближению. и, следовательно, нулевой выход. Решение заключалось в том, чтобы быстро встряхнуть гироскоп, чтобы он никогда не зафиксировался. Как это ни парадоксально, слишком регулярное движение дизеринга приводило к накоплению коротких периодов блокировки, когда устройство находилось в состоянии покоя в крайних точках своего трясущегося движения.Это было вылечено путем применения случайного белого шума к вибрации. Материал блока также был изменен с кварца на новую стеклокерамику Cer-Vit производства Owens Corning из-за утечек гелия. [51]
Волоконно-оптический гироскоп
Волоконно-оптический гироскоп также использует интерференцию света для обнаружения механического вращения. Две половины разделенного луча движутся в противоположных направлениях по витку оптоволоконного кабеля длиной до 5 км. Как и кольцевой лазерный гироскоп, он использует эффект Саньяка. [52]
Момент Лондона
Гироскоп момента Лондона основан на квантово-механическом явлении, согласно которому вращающийся сверхпроводник создает магнитное поле, ось которого точно совпадает с осью вращения гироскопического ротора. Магнитометр определяет ориентацию генерируемого поля, которое интерполируется для определения оси вращения. Гироскопы этого типа могут быть чрезвычайно точными и стабильными. Например, те, которые использовались в эксперименте Gravity Probe B, измеряли изменения в ориентации оси вращения гироскопа до значения лучше 0.5 миллисекунд дуги (1,4 × 10 90 721 −7 90 724 градуса, или около 2,4 × 10 90 721 −9 90 724 радиана) в течение одного года. [53] Это эквивалентно угловому разделению шириной с человеческий волос, если смотреть с расстояния 32 километра (20 миль). [54]
Гироскоп GP-B состоит из почти идеальной сферической вращающейся массы из плавленого кварца, которая служит диэлектрической опорой для тонкого слоя ниобиевого сверхпроводящего материала. Чтобы устранить трение, присутствующее в обычных подшипниках, узел ротора центрируется электрическим полем от шести электродов.После первоначального раскрутки струей гелия, которая доводит ротор до 4000 об/мин, полированный корпус гироскопа вакуумируется до сверхвысокого вакуума, чтобы еще больше уменьшить сопротивление ротора. При условии, что электроника подвески остается под напряжением, исключительная вращательная симметрия, отсутствие трения и низкое сопротивление позволят угловому моменту ротора поддерживать его вращение в течение примерно 15 000 лет. [55]
Для мониторинга гироскопа используется чувствительный СКВИД постоянного тока, который может различать изменения размером от одного кванта, или около 2 × 10 −15 Вб.Прецессия или наклон в ориентации ротора вызывает смещение магнитного поля лондонского момента относительно корпуса. Движущееся поле проходит через сверхпроводящую петлю датчика, закрепленную на корпусе, индуцируя слабый электрический ток. Ток создает напряжение на шунтирующем сопротивлении, которое преобразуется в сферические координаты микропроцессором. Система предназначена для минимизации крутящего момента Лоренца на роторе. [56] [57]
Другие примеры
Вертолеты
Несущий винт вертолета действует как гироскоп.На его движение влияет принцип гироскопической прецессии, согласно которому сила, приложенная к вращающемуся объекту, будет иметь максимальную реакцию примерно через 90 градусов. Реакция может отличаться от 90 градусов, когда действуют более сильные силы. [58] Чтобы изменить направление, вертолеты должны отрегулировать угол тангажа и угол атаки. [59]
Gyro X
Прототип автомобиля, созданный Алексом Тремулисом и Томасом Саммерсом в 1967 году. Автомобиль использует гироскопическую прецессию для движения на двух колесах.Узел, состоящий из маховика, установленного в карданном корпусе под капотом автомобиля, выполнял роль большого гироскопа. Маховик вращался с помощью гидравлических насосов, создающих гироскопический эффект на транспортном средстве. Прецессионный поршень отвечал за вращение гироскопа для изменения направления прецессионной силы, чтобы противодействовать любым силам, вызывающим дисбаланс транспортного средства. Единственный в своем роде прототип сейчас находится в автомобильном музее Лейна в Нэшвилле, штат Теннесси. [60]
Бытовая электроника
Модуль цифрового гироскопа, подключенный к плате Arduino Uno.Помимо использования в компасе, самолетах, компьютерных манипуляторах и т. д., гироскопы были внедрены в бытовую электронику. Первое использование или применение гироскопа в бытовой электронике было популяризировано Стивом Джобсом в Apple iPhone.
Поскольку гироскоп позволяет рассчитывать ориентацию и вращение, дизайнеры внедрили его в современные технологии. Интеграция гироскопа позволила более точно распознавать движение в трехмерном пространстве, чем предыдущий одинокий акселерометр в ряде смартфонов. Гироскопы в бытовой электронике часто сочетаются с акселерометрами (датчиками ускорения) для более надежного определения направления и движения.Примеры таких приложений включают такие смартфоны, как Samsung Galaxy Note 4, [61] HTC Titan, [62] Nexus 5, iPhone 5s, [63] , Nokia 808 PureView [64] и Sony Xperia, периферийные устройства игровых консолей, такие как контроллер PlayStation 3 и пульт Wii Remote, а также наборы виртуальной реальности, такие как Oculus Rift. [65]
Nintendo интегрировала гироскоп в контроллер Wii Remote консоли Wii с помощью дополнительного оборудования под названием «Wii MotionPlus». [66] Он также включен в контроллеры 3DS, Wii U GamePad и Nintendo Switch Joy-Con, которые обнаруживают движение при повороте и встряхивании.
Круизные лайнеры используют гироскопы для выравнивания чувствительных к движению устройств, таких как самовыравнивающиеся бильярдные столы. [67]
Гироскоп с маховиком с электроприводом, вставленный в велосипедное колесо, продается как альтернатива тренировочным колесам. [68] Некоторые функции телефонов Android, такие как PhotoSphere или 360 Camera, а также использование VR-гаджета не работают без датчика гироскопа в телефоне. [69]
См. также
КАК ЭТО РАБОТАЕТ; Гироскопы, которые не вращаются, облегчают парение
Пилот по-прежнему несет ответственность за управление машиной вдали от мебели, растений, деревьев и других людей. Программистам, написавшим управляющее программное обеспечение для Draganflyer, нужно было сбалансировать стабильность машины с быстродействием. Слишком большая помощь со стороны компьютера приводит к очень спокойному устройству, которое имеет тенденцию оставаться на одном месте. Слишком мало помощи, и требуется мастер, чтобы манипулировать ею.
«Это Уловка-22», — сказал мистер Драган. «Чем устойчивее вертолет, тем он менее маневренный. Есть компромисс, и эта модель все еще довольно сложная. Следующей нашей модификацией является добавление сверхлегкого режима. Мы обязательно установим на него еще несколько гироскопов, и он будет парить сам.”
Гироскопическая помощь позволяет пилотам моделей вертолетов выполнять трюки, которые раньше были невозможны. «Без гироскопов нынешнего поколения большинство людей не могли бы летать назад или выполнять маневры вбок», — сказал он.— сказал Хилленбранд. ”Теперь многие люди могут делать петли вбок, назад, со скоростью 60 миль в час”.
Некоторых это даже не устраивает. Рохелио Лозано, робототехник из Национального центра научных исследований во Франции, сказал, что он перепрограммировал свой Draganflyer так, чтобы он взлетал, парил на высоте около 15 дюймов над землей и приземлялся без какого-либо вмешательства человека.
Он использует встроенные гироскопы, но чтобы компенсировать любой дрейф, он добавил дополнительный датчик, который измеряет ориентацию относительно антенны.
Драганфлаер продается за 749 долларов, что делает его дорогой игрушкой. Таким образом, г-н Драган также предлагает устройство агентам по недвижимости и спецназу полицейского управления, которым могут понадобиться аэрофотоснимки. Миниатюрную видеокамеру можно установить на устройство за 200 долларов. Компания также производит более крупную и более дорогую модель, которая продается военным для использования в целях наблюдения.
Эти цены должны продолжать падать, сказал г-н Драган. «Всего несколько лет назад эти пьезогироскопы стоили тысячи долларов за штуку.Так как цены на комплектующие падают, цена этих машин падает до точки, где в конечном итоге они будут ниже 99 долларов.”
Что такое гироскоп и как он работает? – СидмартинБио
Что такое гироскоп и как он работает?
Гироскоп представляет собой прибор, состоящий из колеса, закрепленного на двух или трех шарнирах, обеспечивающих поворотные опоры, позволяющие колесу вращаться вокруг одной оси. Колесо реагирует на силу, приложенную к входной оси, силой реакции на выходную ось.
Что такое гироскоп в телефоне?
Акселерометр и гироскоп Акселерометры в мобильных телефонах используются для определения ориентации телефона. Гироскоп, или сокращенно гироскоп, добавляет дополнительное измерение к информации, предоставляемой акселерометром, отслеживая вращение или поворот.
Что такое гироскоп в PUBG?
Гироскоп в PUBG помогает мобильным игрокам перемещаться в стороны и вверх-вниз, не используя большой палец или пальцы для перемещения игрока по экрану вручную.Итак, в игре используется датчик гироскопа, который оптимизирует ориентацию экрана с физическим движением мобильного телефона.
Как работает гироскоп на корабле?
гирокомпас, навигационный прибор, в котором используется гироскоп с постоянным приводом для точного определения направления истинного (географического) севера. Он работает, ища равновесное направление под совместным воздействием силы гравитации и суточного вращения Земли.
Важен ли гироскоп в телефоне?
Гироскоп сообщает вашему телефону, когда вы поворачиваетесь, когда вы не перемещаетесь на несколько метров в том же направлении, поэтому он заставляет GPS быстрее определять направления, например, когда вы делаете разворот, ваше приложение GPS немедленно покажет, что вы поворачиваетесь, он очень часто используется в 3D-играх, что позволяет узнать, двигались ли вы …
Насколько важен гироскоп в мобильной версии?
Датчик гироскопа отвечает за автоповорот экрана и отображение на экране всякий раз, когда телефон поворачивается.Гироскоп способен обеспечить точное движение внутри функциональности приложения. Это позволяет пользователю выполнять большинство задач с движением самого устройства.
Как работает гироскоп в мобильном телефоне?
В современных смартфонах используется своего рода гироскоп, состоящий из крошечной вибрирующей пластины на чипе. Когда ориентация телефона меняется, эта вибрирующая пластина толкается силами Кориолиса, которые воздействуют на движущиеся объекты при их вращении.
Используют ли профессиональные игроки гироскоп?
Не все профессионалы используют гироскоп, и это ваш личный выбор.Если вы можете контролировать цель вашего устройства с помощью гироскопа, сделайте это во что бы то ни стало. Но если нет, лучше держаться подальше от него или попрактиковаться в его использовании.
Где на корабле находится гироскоп?
Гирокомпас обычно располагается на рулевой рубке как можно ближе к центру крена, тангажа и рыскания корабля, что сводит к минимуму ошибки, вызванные движением корабля.
Что такое гироскоп и для чего он используется?
В самолете будет использоваться гироскоп, помогающий определять скорость вращения вокруг оси крена самолета.Когда самолет катится, гироскоп будет измерять ненулевые значения до тех пор, пока платформа не выровняется, после чего он будет считывать нулевое значение, указывающее направление «вниз».
Что такое гироскоп и как он работает?
Гироскоп. Гироскоп — это устройство, используемое для измерения или поддержания углового положения. Он работает, используя принципы углового момента. Гироскоп состоит из вращающегося колеса или диска, а также (в некоторых случаях) многих других движущихся частей. Он помогает в навигации и играет роль в таких вещах, как гирокомпас и искусственный горизонт.
Каков принцип работы гироскопа?
Гироскоп представляет собой вращающуюся массу, работающую по принципу «жесткости в пространстве». Это означает, что когда гироскоп вращается, он имеет тенденцию оставаться на своем месте и сопротивляется перемещению.

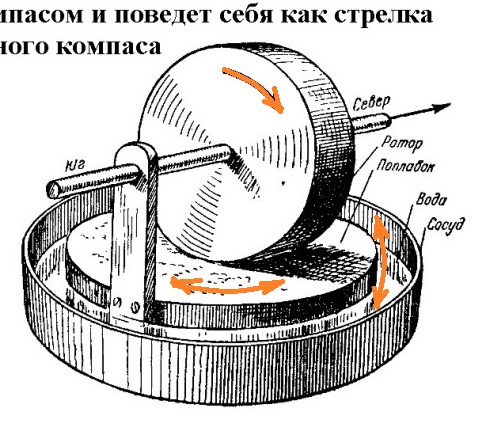

 259
259