Решение системы уравнений в Mathcad
Первоначально рассмотрим СЛАУ в Mathcad. Для их решения может использоваться блок given …find() или специальная функция lsolve(). Применение блока given …find() предопределяет необходимость задания начальных значений искомых переменных. Далее после ключевого слова given описывается СЛАУ и с помощью find() находится решение. Следует указать, что в том случае, когда СЛАУ в Mathcad имеет бесконечное множество решений блок given …find() дает конкретный результат, что несомненно следует отнести к недостаткам. В случае отсутствия решения будет выдано сообщение “Matrix is singular. Cannot compute its inversу – Матрица сингулярная. Нельзя вычислить эту инверсию”.
Применение функции lsolve( ) позволяет избежать этого недостатка.
Пример решения СЛАУ:
Для решения системы нелинейных уравнений используются два блока: given…find() и given…minerr (). Так как система нелинейных уравнений может иметь несколько решений, то полученные результаты зависят от начальных значений искомых переменных. В обоих случаях получаются приближенные решения, для которых рекомендуется делать проверку. Обычно в Mathcad требуется, чтобы количество уравнений было равно количеству искомых переменных, но в некоторых случаях, когда с точки зрения классической математики может быть получено точное решение и при меньшем количестве уравнений, данное условие может быть нарушено. На листинге представлены примеры использования блоков 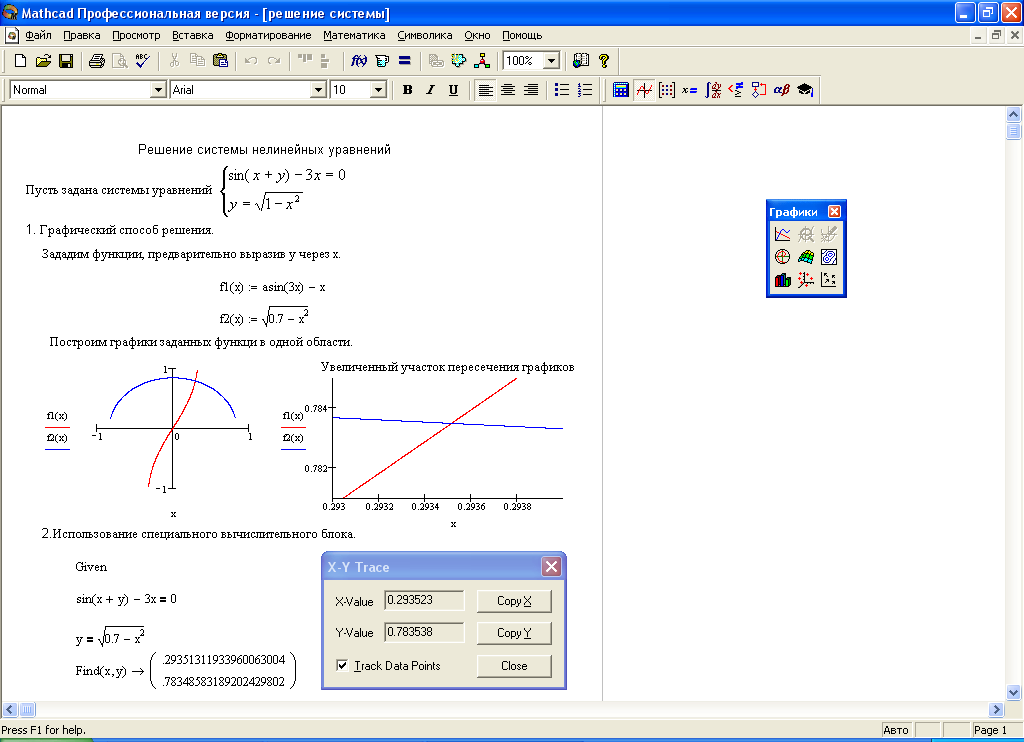
Решение уравнений и систем уравнений
Вычисление корней численными методами включает два основных этапа:
· отделение корней;
· уточнение корней до заданной точности.
Рассмотрим эти два этапа подробно.
Отделение корней нелинейного уравнения
Учитывая легкость построения графиков функций в MathCAD, в дальнейшем будет использоваться графический метод отделения корней.
Пример. Дано алгебраическое уравнение
.
Определить интервалы локализации корней этого уравнения.
Пример. Дано алгебраическое уравнение
.
Определить интервалы локализации корней этого уравнения.
На рисунке приведен график функции , построенный в MathCAD. Видно, что в качестве интервала изоляции можно принять интервал . Однако уравнение имеет три корня.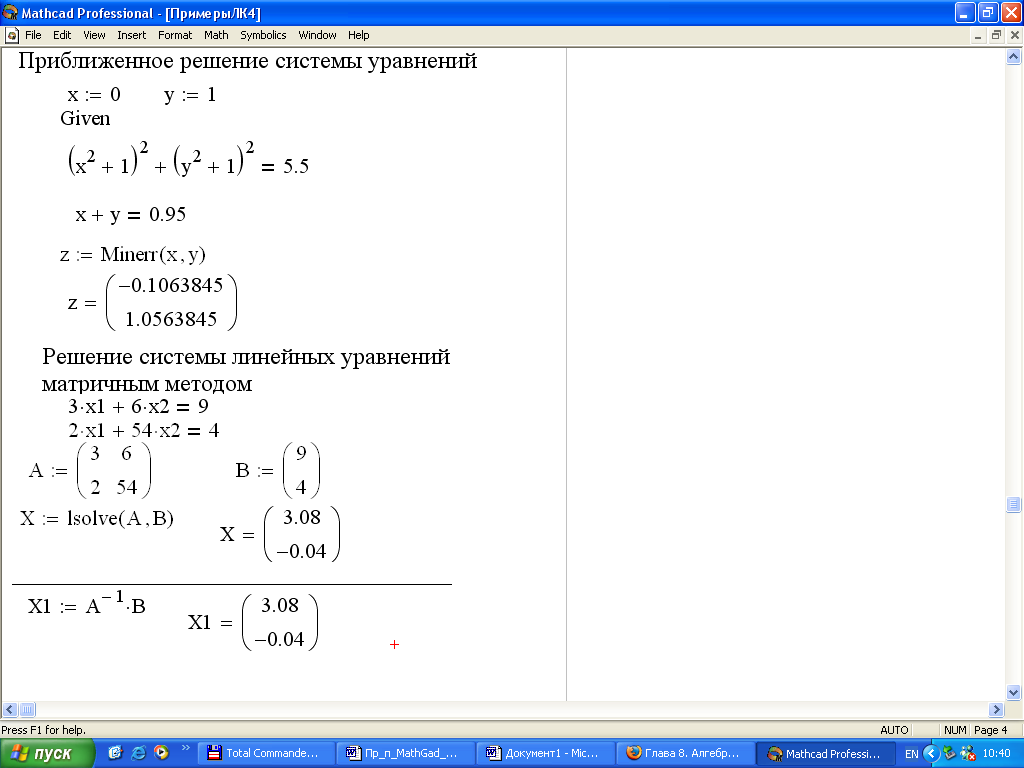 Следовательно, можно сделать вывод о наличии еще двух комплексных корней. ¨
Следовательно, можно сделать вывод о наличии еще двух комплексных корней. ¨
Уточнение корней нелинейного уравнения
Для уточнения корня используются специальные вычислительные методы такие, как метод деления отрезка пополам, метод хорд, метод касательных (метод Ньютона) и многие другие.
Функция root. В MathCAD для уточнения корней любого нелинейного уравнения (не обязательно только алгебраического) введена функция root, которая может иметь два или четыре аргумента, т.е. или , где – имя функции или арифметическое выражение, соответствующее решаемому нелинейному уравнению, – скалярная переменная, относительно которой решается уравнение, – границы интервала локализации корня.
Пример. Используя функцию , найти все три корня уравнения , включая и два комплексных.
Заметим, что для вычисления всех трех корней использовался прием понижения порядка алгебраического уравнения, рассмотренный в п. 8.1.1. ¨
8.1.1. ¨
Функция root с двумя аргументами требует задания (до обращения к функции) переменной начального значения корня из интервала локализации.
Пример 8.1.5. Используя функцию root, вычислить изменения корня нелинейного уравнения при изменении коэффициента а от 1 до 10 с шагом 1.
Функция polyroots. Для вычисления всех корней алгебраического уравнения порядка (не выше 5) рекомендуется использовать функцию polyroots. Обращение к этой функции имеет вид polyroots(v), где v – вектор, состоящий из n +1 проекций, равных коэффициентам алгебраического уравнения, т.е. . Эта функция не требует проведения процедуры локализации корней.
Пример. Используя функцию polyroots, найти все три корня уравнения , включая и два комплексных
Блок Given. При уточнении корня нелинейного уравнения можно использовать специальный вычислительный блок Given, имеющий следующую структуру:
При уточнении корня нелинейного уравнения можно использовать специальный вычислительный блок Given, имеющий следующую структуру:
Решаемое уравнение задается в виде равенства, в котором используется «жирный» знак равно, вводимый с палитры ЛОГИЧЕСКИЙ.
Ограничения содержат равенства или неравенства, которым должен удовлетворять искомый корень.
Функция Find уточняет корень уравнения, вызов этой функции имеет вид Find(x), где x – переменная, по которой уточняется корень. Если корня уравнения на заданном интервале не существует, то следует вызвать функцию Minerr(x), которая возвращает приближенное значение корня.
Для выбора алгоритма уточнения корня необходимо щелкнуть правой кнопкой мыши на имени функции Find(x) и в появившемся контекстном меню (см.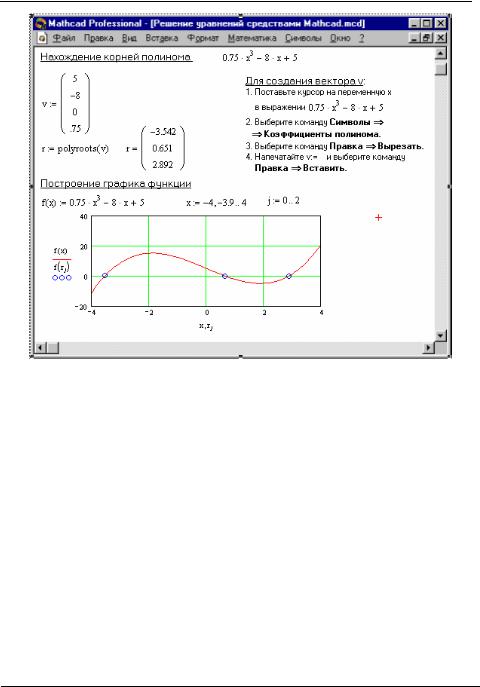 рисунок) выбрать подходящий алгоритм.
рисунок) выбрать подходящий алгоритм.
Аналогично можно задать алгоритм решения и для функции Minerr(x).
Использование численных методов в функциях Find(x), Minerr(x) требует перед блоком Given задать начальные значения переменным, по которым осуществляется поиск корней уравнения.
Пример. Используя блок Given, вычислите корень уравнения в интервале отделения .
В зависимости от того, какие функции входят в систему уравнений, можно выделить два класса систем:
· алгебраические системы уравнений;
· трансцендентные системы уравнений.
Среди алгебраических систем уравнений особое место занимают системы линейных алгебраических уравнений (СЛАУ).
Системы линейных алгебраических уравнений
Системой линейных алгебраических уравнений (СЛАУ) называется система вида:
В матричном виде систему можно записать как
,
где – матрица размерности , – вектор с проекциями.
Для вычисления решения СЛАУ следует использовать функцию lsolve, обращение к которой имеет вид: lsolve(А,b), где А – матрица системы, – вектор правой части.
Решение систем нелинейных уравнений
MathCAD дает возможность находить решение системы уравнений численными методами, при этом максимальное число уравнений в MathCAD2001i доведено до 200.
Для решения системы уравнений необходимо выполнить следующие этапы.
Задание начального приближения для всех неизвестных, входящих в систему уравнений. При небольшом числе неизвестных этот этап можно выполнить графически, как показано в примере.
Пример. Дана система уравнений:
Определить начальные приближения для решений этой системы.
Видно, что система имеет два решения: для первого решения в качестве начального приближения может быть принята точка (-2, 2), а для второго решения – точка (5, 20).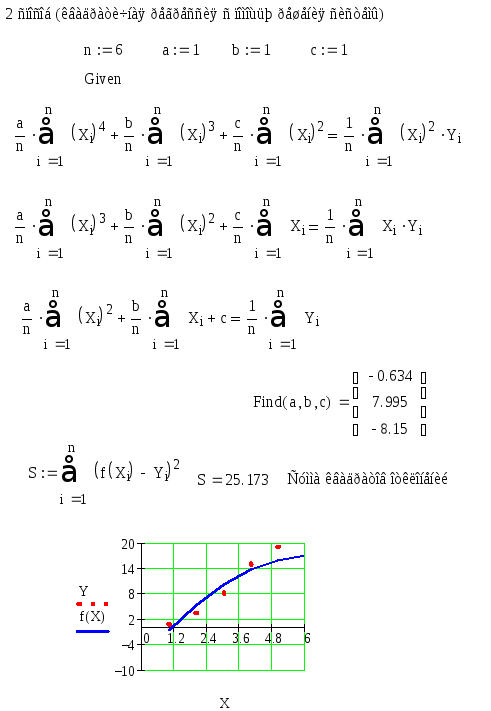 ¨
¨
Вычисление решения системы уравнений с заданной точностью. Для этого используется уже известный вычислительный блок Given.
Функция Find вычисляет решение системы уравнений с заданной точностью, и вызов этой функции имеет вид Find(x), где x – список переменных, по которым ищется решение. Начальные значения этим переменным задаются в блоке < Начальные условия >. Число аргументов функции должно быть равно числу неизвестных.
Следующие выражения недопустимы внутри блока решения:
· ограничения со знаком ¹;
· дискретная переменная или выражения, содержащие дискретную переменную в любой форме;
· блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find (или Minerr).
Пример. Используя блок Given, вычислить все решения системы предыдущего примера. Выполнить проверку найденных решений.
Выполнить проверку найденных решений.
Пример. Используя функцию , вычислите решение системы уравнений
MATHCAD 14: Основные сервисы и технологии
Главная / Математика / MATHCAD 14: Основные сервисы и технологии / Тест 4Номер 1
Какая из приведенных функций не может быть использования для решения уравнений
Ответ:
 (1) root() 
 (2) lsolve() 
 (3) Find() 
 CreateMesh() 
Номер 2
Какая переменная отвечает за точность вычислений корней уравнения функцией root() ?Ответ:
 (1) ORIGIN 
 (2) TOL 
 
 (4) аргумент функции 
Номер 3
Для численного решения уравнения с использованием функции root() необходимо задать:Ответ:
 (1) границы отрезка, где находится корень  
 (2) начальное приближение корня 
 (3) ничего не требуется 
 (4) максимальное значение функции уравнения 
Упражнение 2:
Номер 1
Решение системы уравнений с помощью блока given find дает решение:
Ответ:
 (1) приближенное 
 (2) минимальное  
 (3) точное  
 (4) максимальное 
Номер 2
Какой знак равенства в уравнениях используется в блоке решения Given Find:
Ответ:
 
 (2) == 
 (3) = 
 (4)  
Номер 3
Решение системы уравнений с помощью блока given minerr дает решение:
Ответ:
 
 (2) приближенное  
 (3) минимальное  
 (4) максимальное 
Упражнение 3:
Номер 1
Сколько корней имеет уравнение
Ответ:
 (1)
 (2) 2 
 (3) 3 
 (4) 4 
Номер 2
Какими способами можно получить решение уравнения :
Ответ:
 (1) используя root()  
 (2) используя given Find())  
 (3) используя функцию lsolver()  
 (4) используя оператор solver 
Номер 3
Выбрать правильное решение уравнения :
Ответ:
 (1)
 (2) (5. 01; 10.8) 
01; 10.8) 
 (3) (3.05;13) 
 (4) (0,1;12) 
Упражнение 4:
Номер 1
При численном нахождении корней полинома n степени с помощью функции Polyroots()Ответ:
 (1) вектор коэффициентов длиной n  
 (2) вектор коэффициентов длиной n+1 
 (3) вектор коэффициентов длиной n-1 
 (4) начальное приближение 
Номер 2
Какими способами можно получить решение уравнения :
Ответ:
 (1) +используя функцию root()  
 (2) +используя блок given Find())  
 (3) +используя функцию Polyroots() 
 (4) используя функцию lsolver() 
 (5) +используя оператор solver 
Номер 3
Выбрать действительный корень уравнения :
Ответ:
 (1) (-0. 819) 
819) 
 (2) (-1.819) 
 (3) (0.819) 
 (4) (2.819) 
Упражнение 5:
Номер 1
Система уравнений имеет вид Сколько корней имеет система.
Ответ:
 (1) 1 
 (2) 2 
 (3) 3 
 (4) 4 
Номер 2
Какими способами можно получить решение системы уравнений
Ответ:
 (1) используя функцию root()  
 (2) используя блок given Find())  
 (3) используя функцию Polyroots() 
 (4) используя функцию lsolver() 
Номер 3
Какие решения являются корнями системы уравнений?
Ответ:
 (1) (-0,53; 0. 26) 
26) 
 (2) (1,89; 2.1) 
 (3) (1.71; 0.78) 
 (4) (6.53; 8.73) 
Упражнение 6:
Номер 1
Система уравнений имеет вид Сколько корней имеет система.
Ответ:
 (1) 1 
 (2) 2 
 (3) 3 
 (4) 4 
Номер 2
Какими способами можно получить решение системы уравнений:
Ответ:
 (1) используя функцию root()  
 (2) используя блок given Find())  
 (3) используя функцию Polyroots() 
 (4) используя функцию lsolver() 
Номер 3
Какие решения являются корнями системы уравнений?
Ответ:
 (1) (-1,67; 5. 70) 
70) 
 (2) (1,56; 4.91) 
 (3) (5.53; 10.26) 
 (4) (0.15; 1.02) 
Номер 2
Сколько способов существует в MathCad для решения системы линейных алгебраических уравнений
Ответ:
 (1) 1 
 (2) 2 
 (3) 3 
 (4) 4 
Номер 3
Матрица A имеет вид , матрица .Выбрать правильное решение уравнения
Ответ:
 (1) (4; 2.93; 2.71) 
 (2) (3; 1.93; 1.71) 
 (3) (2; 0.93; 0.71) 
 (4) (1; -0.93;- 0.71) 
Упражнение 8:
Номер 1
Для решения задач оптимизации используются блоки:
Ответ:
 (1) given maximize 
 (2) given miniimize 
 (3) given find 
 (4) given solver 
Номер 2
В задаче оптимизации начальные значения неизвестных параметров вводятся с использованием знака:
Ответ:
 (1) := 
 (2) = 
 (3) = 
 (4)  
Номер 3
В задаче оптимизации оптимизируемая функция вводится с использованием знака:
Ответ:
 (1) := 
 (2) = 
 (3) = 
 (4)  
Упражнение 9:
Номер 1
Решение задачи оптимизации MathCad представляет в виде:
Ответ:
 (1) вектора 
 (2) числа (чисел) 
 (3) функции 
 (4) экстремального значения функции 
Номер 2
Максимальное значение функции при условии равно
Ответ:
 (1) 40 
 (2) 60 
 (3) 50 
 (4) 70 
Номер 3
Значения x и y, для которых функция имеет максимум при условии , равны
Ответ:
 (1) (1 ; 0. 4) 
4) 
 (2) (0.9 ; 3) 
 (3) (0.9 ;0.4) 
 (4) (0.7 ; 0.5) 
Упражнение 10:
Номер 1
Задачи оптимизации решаются методами :
Ответ:
 (1) математической статистики 
 (2) линейного программирования 
 (3) математического анализа 
 (4) решения дифференциальных уравнений  
Номер 2
Для решения задач оптимизации необходимо задать:
Ответ:
 (1) начальные значения неизвестных параметров  
 (2) начальное значение оптимизируемой функции  
 (3) ограничения для неизвестных параметров 
 (4) вид оптимизируемой функции  
Номер 3
Для решения задач оптимизации можно использовать встроенные функции MathCad:
Ответ:
 (1) maximize 
 (2) miniimize 
 (3) root() 
 (4) lsolver() 
Mathcad 14: “pattern match exception” при решении уравнения с большим количеством неизвестных
Я пытаюсь решить уравнение с 5 неизвестными в Mathcad 14.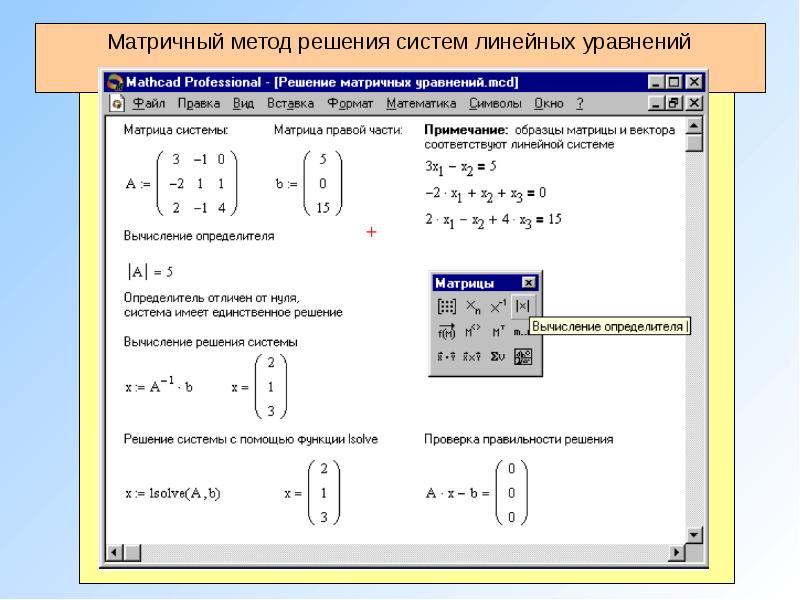 Мои уравнения выглядят так:
Мои уравнения выглядят так:
Given
0 = e
1 = d
0 = c
-1 = 81a + 27b + 9c + 3d + e
0 = 108a + 27b + 6c + d
Find(a,b,c,d,e)
Find (a, b, c, d, e) помечается красным цветом и говорит “pattern match exception”. В чем же проблема?
exception match equation mathcadПоделиться Источник user3158254 12 января 2014 в 18:28
1 ответ
- Найти объявление переменной в Mathcad
Есть ли способ быстро найти, где переменная была первоначально определена/объявлена в Mathcad. Я работаю в довольно большом Mathcad (150 страниц печатаются). Я увижу уравнение, которое использует переменные, объявленные в предыдущих разделах, однако я не могу использовать Edit->Find, поскольку…
- Импорт переменных из mathcad в excel
У меня есть программа mathcad с тысячами переменных.
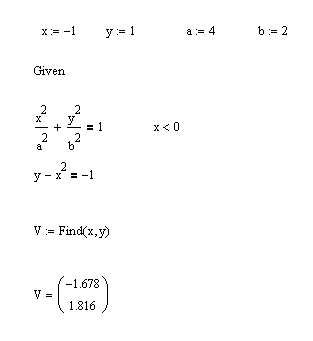 Есть ли способ использовать Python или Visual Basic для циклического перебора всех переменных в моей программе mathcad, а затем присвоить им и их значениям электронную таблицу excel? Метод python предпочтительнее, так как я никогда не…
Есть ли способ использовать Python или Visual Basic для циклического перебора всех переменных в моей программе mathcad, а затем присвоить им и их значениям электронную таблицу excel? Метод python предпочтительнее, так как я никогда не…
1
В mathcad вам нужно сделать что-то подобное:
c:=0
d:=1
e:=0
a:=1
b:=1
Given
81*a + 27*b + 9*c + 3*d + e = -1
108*a + 27*b + 6*c + d = 0
Find(a,b,c,d,e) = (0,0,0,0,-1)
Теперь, что я сделал здесь, чтобы определить переменные BEFORE в блоке решения (Given…Find), вы должны дать начальные значения, которые, по вашему мнению, близки к решению, которое вам нужно, чтобы итерация прошла успешно.
Советы: чтобы получить знак равенства в блоке решения, используйте ctrl и’=’. Если вы хотите решить для 5 неизвестных, вам нужно 5 уравнений, исходный пост выглядел так, как будто вы знали 3 переменные и искали a и b, в этом случае вы сделаете следующее:
c:=0
d:=1
e:=0
a:=1
b:=1
Given
81*a + 27*b + 9*c + 3*d + e = -1
108*a + 27*b + 6*c + d = 0
Find(a,b) = (0. 111,-0.481)
111,-0.481)
Это удерживало c, d и e до их исходных значений и повторялось для решения только для a и b.
Надеюсь, это поможет.
Поделиться Big Bream 29 января 2014 в 10:41
Похожие вопросы:
Два Неизвестных 3 Уравнения
У меня есть 3 эквалайзера и 2 неизвестных Hb и Hbo2, они выглядят так: Bxy = AB * HB + AB * Hbo2 Rxy = AR * HB + AR * Hbo2 Gxy = AG * HB + AG * Hbo2 Теперь я пытаюсь использовать матричный метод,…
Приложение с большим количеством изображений
У меня есть приложение с большим количеством картинок (сотни), на данный момент я помещаю их все в Bundle, но теперь приложение уже занимает почти 50 МБ. Существуют ли какие-либо другие методы,…
Как написать частные производные в Mathcad
Я использую Mathcad 14, и я хотел бы знать, можно ли писать частные производные в Mathcad. На палитре исчисления мы просто имеем нормальный производный символ.
На палитре исчисления мы просто имеем нормальный производный символ.
Найти объявление переменной в Mathcad
Есть ли способ быстро найти, где переменная была первоначально определена/объявлена в Mathcad. Я работаю в довольно большом Mathcad (150 страниц печатаются). Я увижу уравнение, которое использует…
Импорт переменных из mathcad в excel
У меня есть программа mathcad с тысячами переменных. Есть ли способ использовать Python или Visual Basic для циклического перебора всех переменных в моей программе mathcad, а затем присвоить им и их…
Решение уравнений с большим количеством неизвестных, чем уравнения
Я пытаюсь найти неизвестные из нескольких уравнений, но есть больше неизвестных, чем количество уравнений. Код примерно такой: syms x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13 x14 x15 x16 x17 eqn1 =…
Найти целочисленные решения для набора уравнений с большим количеством неизвестных, чем уравнения
Я пытаюсь построить систему, для которой мне нужно найти решение набора линейных уравнений с (гораздо) большим количеством переменных, чем уравнения.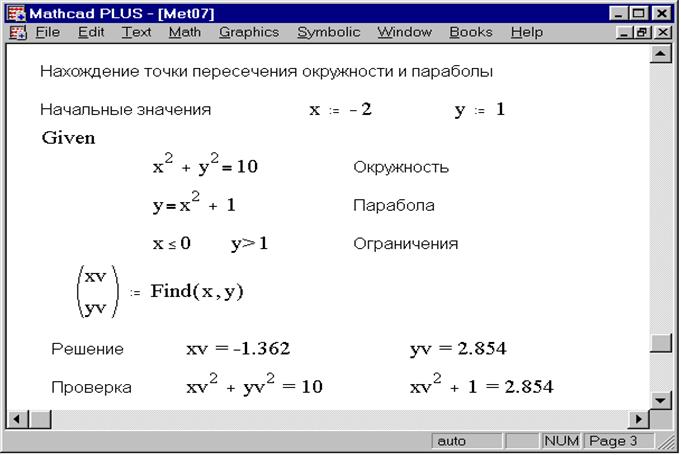 Проблема сводится к следующему: Представьте себе…
Проблема сводится к следующему: Представьте себе…
Решайте уравнения с комбинациями и для петель
У меня есть уравнения с несколькими неизвестными и диапазон чисел: eq1 = (x + 5 + y) # ans = 15 no_range = [1..5] Я знаю, что могу решить уравнение, проверив все возможные комбинации: solved = False…
vpasolve больше неизвестных, чем уравнений = > нет решений
У меня есть 3 уравнения и 4 неизвестных, которые я хочу решить. Конечно, есть решения, но vpasolve не возвращает ни одного, если я опускаюсь до 3 эквалайзеров и 3 неизвестных, это работает хорошо. Я…
Подсчет количества уравнений в моделях с соединителями
В настоящее время я оцениваю Dymola 2020 для построения модели солнечной электростанции, но я борюсь с количеством уравнений в моделях, которые используют пользовательский разъем. Вот этот код:…
Уравнения в Mathcad
Практически в каждой лабораторной работе либо курсовом проекте можно столкнуться с необходимостью решения сложного уровня с одной неизвестной.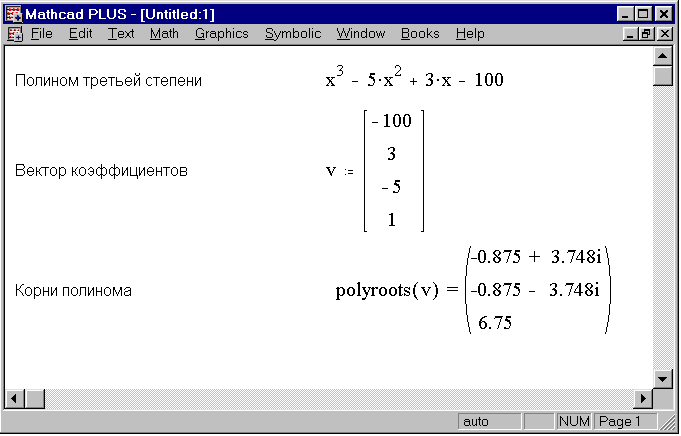 Тратить по несколько десятков минут на нудные вычисления, в ходе коих можно допустить ошибку, не хочется.
Оптимальный вариант – воспользоваться специальной математической утилитой, способной дать ответ быстро и корректно. Решение системы уравнений в маткаде можно осуществить двумя основными вариантами: в символьном и численном виде.
Тратить по несколько десятков минут на нудные вычисления, в ходе коих можно допустить ошибку, не хочется.
Оптимальный вариант – воспользоваться специальной математической утилитой, способной дать ответ быстро и корректно. Решение системы уравнений в маткаде можно осуществить двумя основными вариантами: в символьном и численном виде.
Способ первый: применение системы вычислений Given-Find.
Самый широко применяемый и легкий вариат нахождения решений уравнений и неравенств в алегебре. В рабочем поле программы записывается служебная команда Given. Она позволяет задействовать программные модули mathcad, которые необходимы для поиска ответа на уравнение. Состоят такие модули из различных численных методов решений. После этого записывается само уравнение путем набора с применением символа «равно». Найти его можно на панели Boolean (Булева алгебра).
Затем записывается команда Find(x), в которой х – искомая переменная. При помощи данной команды и выводят результат. Ее также можно присвоить определенной переменной с целью дальнейшего использования в вычислениях. Чтобы получить решение, после Find(x) вставляют символ «=» либо «→».
Чтобы получить решение, после Find(x) вставляют символ «=» либо «→».
При помощи программы MathCad можно вычислить как символьный, так и численный корень. Чтобы получить численный вариант ответа, нужно ввести все приведенные в уравнении переменные, в том числе и искомую. Для MathCad определение нужной переменной – это начальное приближение ответа. Так как численный способ имеет определенные особенности, в самом начале работы необходимо определить начальное приближение, потому что без него ответ уравнения найти не получится. Отсутствие корня либо его некорректное значение нередко становится последствием неправильного задания начального приближения. Но ответа может не быть вообще, так как само уравнение может не иметь корней.
Если решение уравнения требуется в символьном виде, то задавать все значения параметров и начальное приближение не обязательно. В таком случае вводится само уравнение в программу через оператора Find(x), после чего ставится «→». Будут задействованы немного другие функции MathCad, которые преобразовывают и упрощают выражения.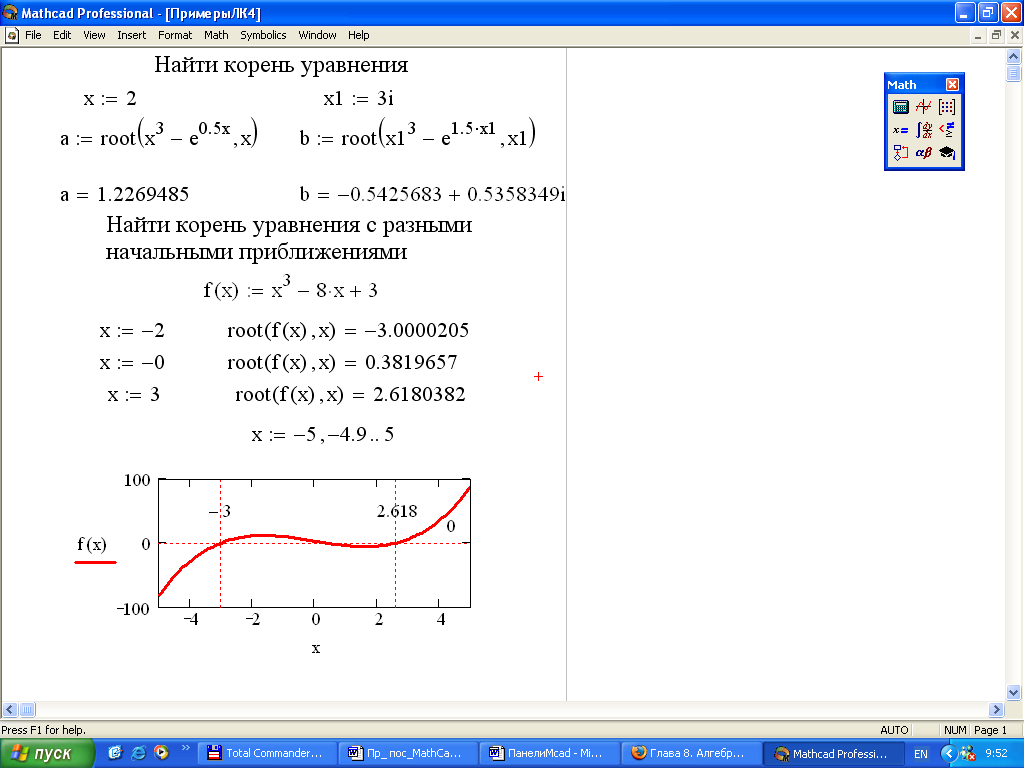 Ответом также будет определенное выражение.
Стоит сразу отметить, что программа может найти решение не каждого уравнения, так что ее возможности весьма ограниченны.
Ответом также будет определенное выражение.
Стоит сразу отметить, что программа может найти решение не каждого уравнения, так что ее возможности весьма ограниченны.
Способ второй: использование метода solve.
Данный метод, по сути, ничем не отличается от вышеописанного, так как корень уравнения находится аналогичным образом. Отличается только оформление: уравнение вносится в программу посредством операторов Find и Given. На панели Symbol после записи уравнения нажимается клавиша solve, через запятую задается нужная переменная, после чего выдается ответ путем нажатия на «→».
Нередко при помощи второго способа можно найти корень уравнения, который не удалось получить первым способом.
Скачать MathcadФункция polyroots в mathcad
Для нахождения корней полинома в MathCAD предназначена специальная функция polyroots (v). Она находит как действительные, так и комплексные корни полинома n-ой степени, коэффициенты которого хранятся в массиве v длиной n+1. Параметром данной функции является вектор-столбец коэффициентов полинома v.
Параметром данной функции является вектор-столбец коэффициентов полинома v.
Пример использования функции polyroots показан на рисунке 3.1.4. При решении задачи надо правильно формировать вектор-столбец коэффициентов полинома v, записывая в него значения коэффициентов, начиная коэффициентов при х в нулевой степени.
Решение систем уравнений
Системы уравнений в MathCAD решаются в следующем порядке:
1. Находится приближенное решение системы уравнений. Приближенное решение удобнее всего найти графически;
2. Записывается директива Given, и после нее записываются уравнения системы. Следует помнить, что вместо знака “равно” при записи уравнений используется знак “логическое равенство”, который набирается как + .
3. Записывается любое выражение, использующее функцию Find. Параметрами данной функции являются все переменные, входящие в систему. Функция возвращает вектор-столбец решений системы.
Рисунок 3.1.4 – Нахождение корней полинома при помощи функции
Пример 3.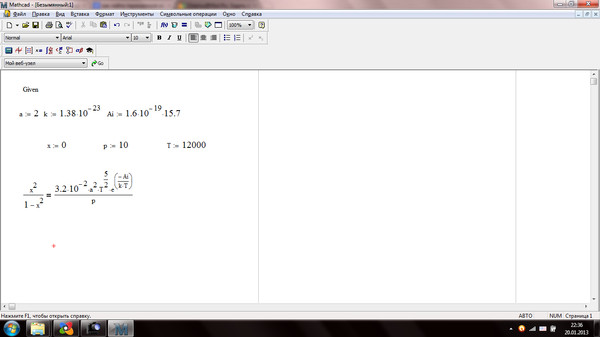 3 Найти решение системы уравнений
3 Найти решение системы уравнений
.
Процесс решения данной системы уравнений показан на рисунке 3.2.1
В результате функция Find вернула вектор-столбец и . Это значит, что решением системы уравнений являются значения и .
Символьное решение уравнений, неравенств и систем уравнений
Для символьного решения уравнений и неравенств надо выполнить следующее:
1. Вставить в рабочий лист структуру solve c панели инструментов Simbolic.
2. Ввести данные: слева – уравнение или неравенство, справа – переменную, относительно которой требуется его разрешить.
3. Щёлкнуть вне области решения, чтобы получить результат.
Рисунок 3.2.1 – Пример решения системы уравнений
При символьном решении уравнений и неравенств следует вводить знаки =, , находящиеся на панели инструментов Boolean.
При символьном решении системы уравнений после Find надо ввести с панели инструментов Simbolic.
Пример символьного решения уравнений, неравенств и систем уравнений показан на рисунке 3. 3.1
3.1
Рисунок 3.3.1 – пример символьного решения уравнения, неравенства
и системы уравнений
Некоторые возможности MathCAD
В этом разделе приводятся краткие сведения о возможностях MathCAD, которые могут быть полезны в процессе обучения.
Комплексные числа в MathCAD
MathCAD Воспринимает комплексные числа в форме a+bi, где a и b – вещественные числа. Комплексные числа можно вводить, или получать в результате вычислений. При вводе мнимые числа заканчиваются символом i или j. Нельзя использовать i или j сами по себе для обозначения мнимой единицы, во избежание смешения с именами переменных. Для ввода мнимой единицы следует напечатать 1i или 1j. При выходе из поля ввода единица не будет отображаться. Можно использовать j вместо i, если это удобнее. Чтобы MathCAD показывал нужный вам символ (i или j), выберите «Формат числа» из меню «Математика», нажмите на кнопку «Глобальный» и переключите «Мн.ед.» на i или j.
MathCAD содержит следующие операторы и функции для работы с комплексными числами:
Re(z) – вещественная часть z.
Im(z) – мнимая часть z.
arg(z) – угол в комплексной плоскости между вещественной осью и z. Результат заключён между π и –π.
– модуль z. Чтобы записать модуль выражения, заключите его в выделяющую рамку и нажмите клавишу с вертикальной чертой «|».
– Комплексно сопряжённое к z= a+bi , то есть a-bi. Чтобы применить к выражению этот оператор, выделите его и нажмите клавишу двойные кавычки «”».
При использовании в комплексной области многие функции являются многозначными. Для многозначной функции MathCAD возвращает значение, составляющее на комплексной плоскости самый малый положительный угол с положительным направлением действительной оси, то есть главное значение.
Рисунок 3.4.1 – Комплексные числа в MathCAD
На рисунке 3.4.1 показан пример использования возможностей MathCADпри работе с комплексными числами.
Последнее изменение этой страницы: 2016-12-28; Нарушение авторского права страницы
Решение уравнений с помощью функции root(f(x),x)
Способы решения уравнений в MathCAD
Форматирование трехмерных графиков
Для форматирования графика необходимо дважды щелкнуть по области построения — появится окно форматирования с несколькими вкладками: Appearance,General,Axes,Lighting,Title,Backplanes,Special, Advanced, Quick Plot Data.
Назначение вкладки Quick Plot Data было рассмотрено выше.
Вкладка Appearance позволяет менять внешний вид графика. Поле Fill Options позволяет изменить параметры заливки, поле Line Option — параметры линий, Point Options — параметры точек.
Во вкладке General (общие) в группе View можно выбрать углы поворота изображенной поверхности вокруг всех трех осей; в группе Display asможно поменять тип графика.
Во вкладке Lighting (освещение) можно управлять освещением, установив флажок Enable Lighting (включить освещение) и переключатель On(включить). Одна из 6-ти возможных схем освещения выбирается в списке Lighting scheme(схема освещения).
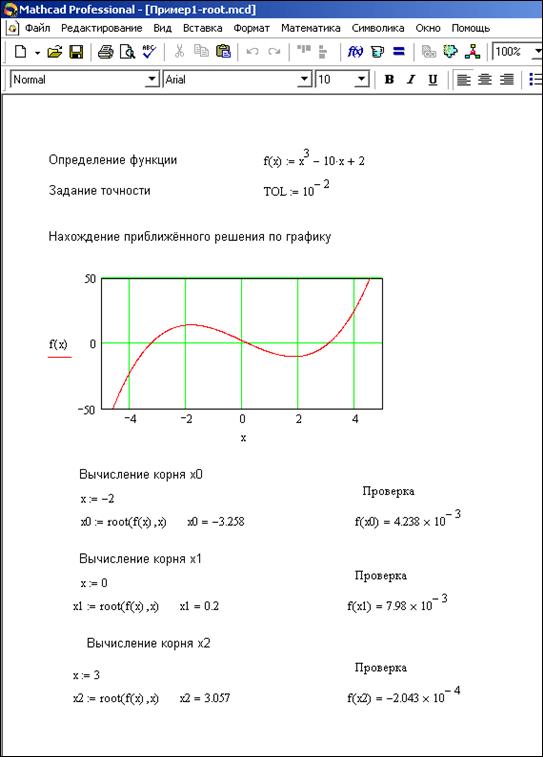
В данном разделе мы узнаем, каким образом в системе MathCAD решаются простейшие уравнения вида F(x) = 0. Решить уравнение аналитически — значит найти все его корни, т.е. такие числа, при подстановке которых в исходное уравнение получим верное равенство. Решить уравнение графически — значит найти точки пересечения графика функции с осью ОХ.
Для решений уравнения с одним неизвестным вида F(x) = 0 существует специальная функция
root(f(x),x),
где f(x) — выражение, равное нулю;
Эта функция возвращает с заданной точностью значение переменной, при котором выражение f(x) равно 0.
Внимание.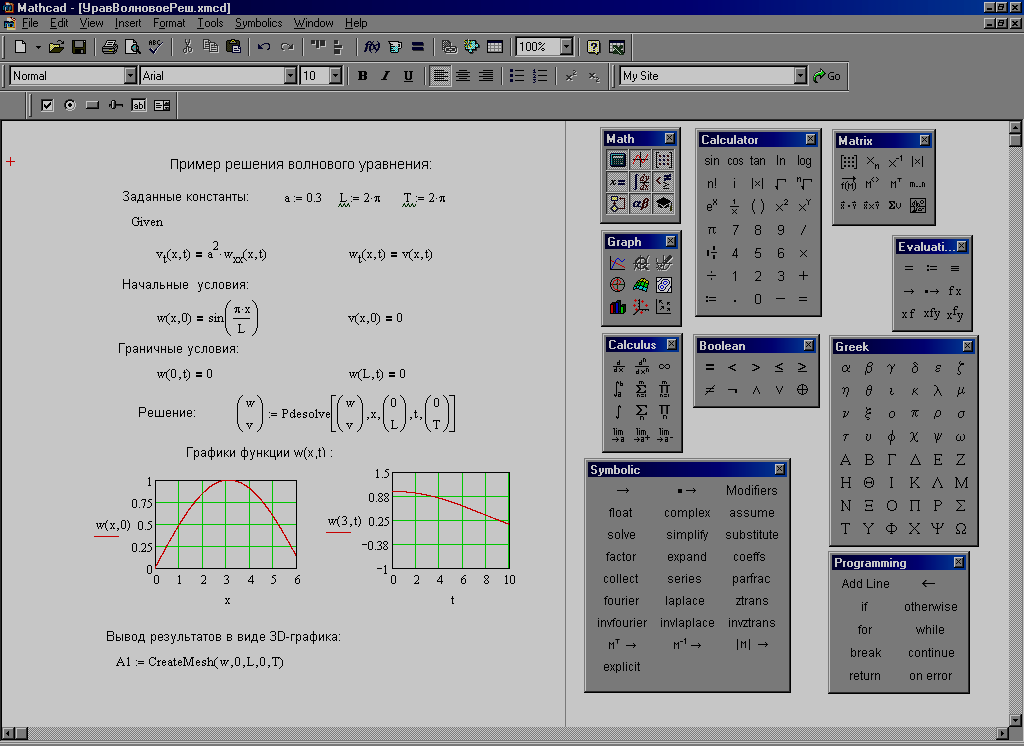 Если правая часть уравнения ¹0, то необходимо привести его к нормальному виду (перенести все в левую часть).
Если правая часть уравнения ¹0, то необходимо привести его к нормальному виду (перенести все в левую часть).
Перед использованием функции rootнеобходимо задать аргументу х начальное приближение. Если корней несколько, то для отыскания каждого корня необходимо задавать свое начальное приближение.
Внимание. Перед решением желательно построить график функции, чтобы проверить, есть ли корни (пересекает ли график ось Ох), и если есть, то сколько. Начальное приближение можно выбрать по графику поближе к точке пересечения.
Пример. Решение уравнения с помощью функции root представлено на рисунке 3.1. Перед тем как приступить к решению в системе MathCAD, в уравнении все перенесем в левую часть. Уравнение примет вид: .
Рис. 3.1. Решение уравнения при помощи функции root
Для одновременного нахождения всех корней полинома используют функцию Polyroots(v),где v — вектор коэффициентов полинома, начиная со свободного члена.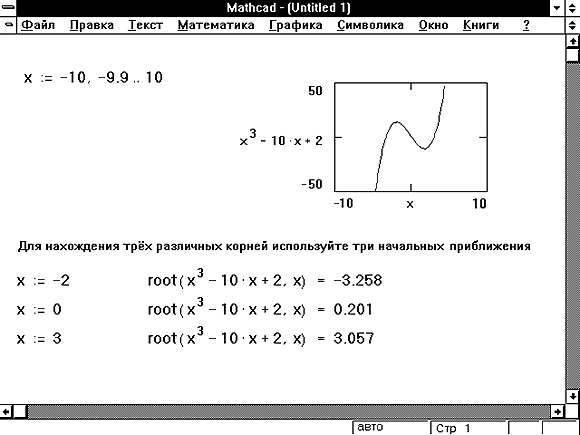 Нулевые коэффициенты опускать нельзя.В отличие от функции root функция Polyroots не требует начального приближения.
Нулевые коэффициенты опускать нельзя.В отличие от функции root функция Polyroots не требует начального приближения.
Пример. Решение уравнения с помощью функции polyroots представлено на рисунке 3.2.
Рис. 3.2. Решение уравнения с помощью функции polyroots
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась – это был конец пары: “Что-то тут концом пахнет”. 8526 – | 8113 – или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Для решения одного уравнения с одним неизвестным используется функция root. Аргументами этой функции являются выражение и переменная, входящая в выражение. Ищется значение переменной, при котором выражение обращается в ноль. Функция возвращает значение переменной, которое обращает выражение в ноль.
| root( f(z), z) | Возвращает значение z, при котором выражение или функция f(z) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр. |
Первый аргумент есть либо функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения.
Второй аргумент — имя переменной, которое используется в выражении. Это та переменная, варьируя которую Mathcad будет пытаться обратить выражение в ноль. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.
Рассмотрим пример, как найти a — решение уравнения e x = x 3 .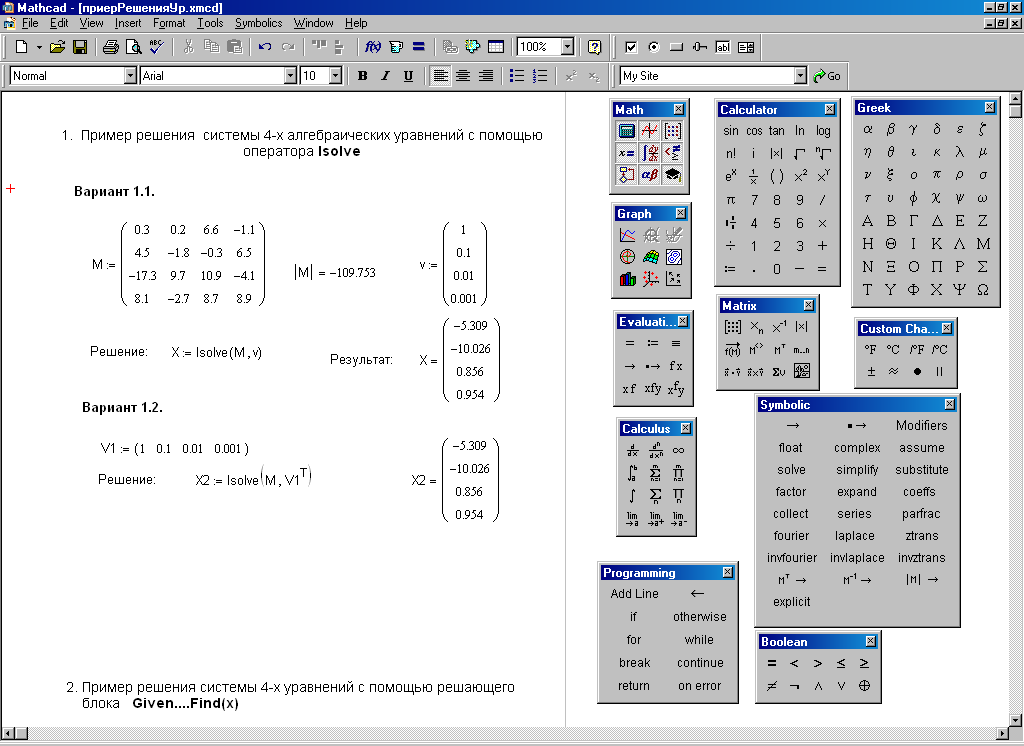 x[Space],x).
x[Space],x).
- Напечатайте a=, чтобы увидеть значение корня.
При использовании функции root имейте в виду следующее:
- Удостоверьтесь, что переменной присвоено начальное значение до начала использования функции root.
- Для выражения с несколькими корнями, например x 2 – 1 = 0, начальное значение определяет корень, который будет найден Mathcad. На Рисунке 1 приведен пример, в котором функция root возвращает различные значения, каждое из которых зависит от начального приближения.
- Mathcad позволяет находить как комплексные, так и вещественные корни. Для поиска комплексного корня следует взять в качестве начального приближения комплексное число.
- Задача решения уравнения вида f(x) = g(x) эквивалентна задаче поиска корня выражения f(x) – g(x) =0. Для этого функция root может быть использована следующим образом:
Функция root предназначена для решения одного уравнения с одним неизвестным.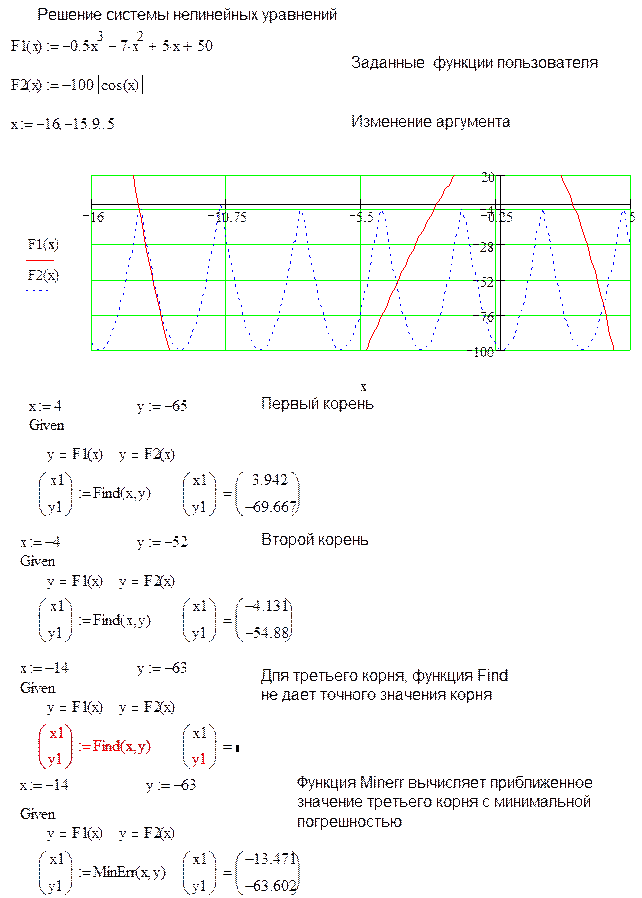 Для решения систем уравнений используйте методику, описанную в следующем разделе “Системы уравнений”. Для символьного решения уравнений или нахождения точного численного решения уравнения в терминах элементарных функций выберите Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.
Для решения систем уравнений используйте методику, описанную в следующем разделе “Системы уравнений”. Для символьного решения уравнений или нахождения точного численного решения уравнения в терминах элементарных функций выберите Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.
Рисунок 1: Использование графика и функции root для поиска корней уравнения.
Что делать, когда функция root не сходится
Mathcad в функции root использует для поиска корня метод секущей. Начальное значение, присвоенное переменной x, становится первым приближением к искомому корню. Когда значение выражения f(x) при очередном приближении становится меньше значения встроенной переменной TOL, корень считается найденным, и функция root возвращает результат.
Если после многих итераций Mathcad не может найти подходящего приближения, то появляется сообщение об ошибке “отсутствует сходимость”.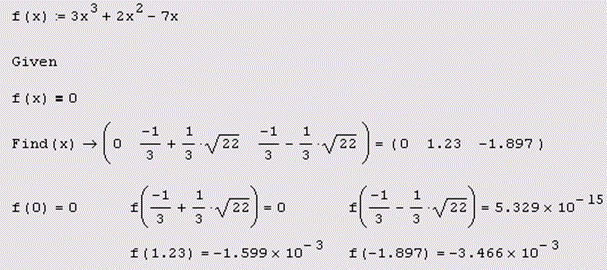 Эта ошибка может быть вызвана следующими причинами:
Эта ошибка может быть вызвана следующими причинами:
- Уравнение не имеет корней.
- Корни уравнения расположены далеко от начального приближения.
- Выражение имеет локальные максимумы или минимумы между начальным приближением и корнями.
- Выражение имеет разрывы между начальным приближением и корнями.
- Выражение имеет комплексный корень, но начальное приближение было вещественным (или наоборот).
Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x)=0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее функция root будет сходиться к точному значению. roots;using plots to find
Некоторые советы по использованию функции root
В этом разделе приведены несколько советов по использованию функции root:
- Для изменения точности, с которой функция root ищет корень, можно изменить значение встроенной переменной TOL.
 Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, функция root будет сходиться медленнее, но ответ будет более точен. Чтобы изменить значение TOL в определенной точке рабочего документа, используйте определение вида TOL := 0.01. Чтобы изменить значение TOL для всего рабочего документа, выберите из меню Математика команду Встроенные переменные и введите подходящее значение в поле TOL. Нажав “OK”, выберите из меню Математика команду Пересчитать всё, чтобы обновить все вычисления в рабочем документе с использованием нового значения переменной TOL.
Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, функция root будет сходиться медленнее, но ответ будет более точен. Чтобы изменить значение TOL в определенной точке рабочего документа, используйте определение вида TOL := 0.01. Чтобы изменить значение TOL для всего рабочего документа, выберите из меню Математика команду Встроенные переменные и введите подходящее значение в поле TOL. Нажав “OK”, выберите из меню Математика команду Пересчитать всё, чтобы обновить все вычисления в рабочем документе с использованием нового значения переменной TOL. - Если уравнение имеет несколько корней, пробуйте использовать различные начальные приближения, чтобы найти их. Использование графика функции полезно для нахождения числа корней выражения, их расположения и определения подходящих начальных приближений. Рисунок 1 показывает пример. Если два корня расположены близко друг от друга, можно уменьшить TOL, чтобы различить их.
- Если f(x) имеет малый наклон около искомого корня, функция может сходиться к значению r, отстоящему от корня достаточно далеко . В таких случаях для нахождения более точного значения корня необходимо уменьшить значение TOL. Другой вариант заключается в замене уравнения f(x)=0 на g(x)=0, где
Решение уравнений с параметром
Предположим, что нужно решать уравнение многократно при изменении одного из параметров этого уравнения. Например, пусть требуется решить уравнение для нескольких различных значений параметра a. Самый простой способ состоит в определении функции
Например, пусть требуется решить уравнение для нескольких различных значений параметра a. Самый простой способ состоит в определении функции
Чтобы решить уравнение для конкретного значения параметра a, присвойте значение параметру a и начальное значение переменной x как аргументам этой функции. Затем найдите искомое значение корня, вводя выражение f(a,x)=.
Рисунок 2 показывает пример того, как такая функция может использоваться для нахождения корней исследуемого уравнения при различных значениях параметра. Обратите внимание, что, хотя начальное значение x непосредственно входит в определение функции, нет необходимости определять его в другом месте рабочего документа.
Рисунок 2: Определение функции пользователя с функцией root.
Нахождение корней полинома
Для нахождения корней выражения, имеющего вид
лучше использовать функцию polyroots, нежели root. В отличие от функции root, функция polyroots не требует начального приближения. Кроме того, функция polyroots возвращает сразу все корни, как вещественные, так и комплексные. На Рисунках 3 и 4 приведены примеры использования функции polyroots.
Кроме того, функция polyroots возвращает сразу все корни, как вещественные, так и комплексные. На Рисунках 3 и 4 приведены примеры использования функции polyroots.
| polyroots(v) | Возвращает корни полинома степени . Коэффициенты полинома находятся в векторе v длины n+1. Возвращает вектор длины n, состоящий из корней полинома. |
Функция polyroots всегда возвращает значения корней полинома, найденные численно. Чтобы находить корни символьно, используйте команду Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.
Рисунок 3: Использование функции polyroots для решения задачи, изображенной на Рисунке 1.
Рисунок 4: Использование функции polyroots для поиска корней полинома.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
MathCAD — это просто! Часть 4.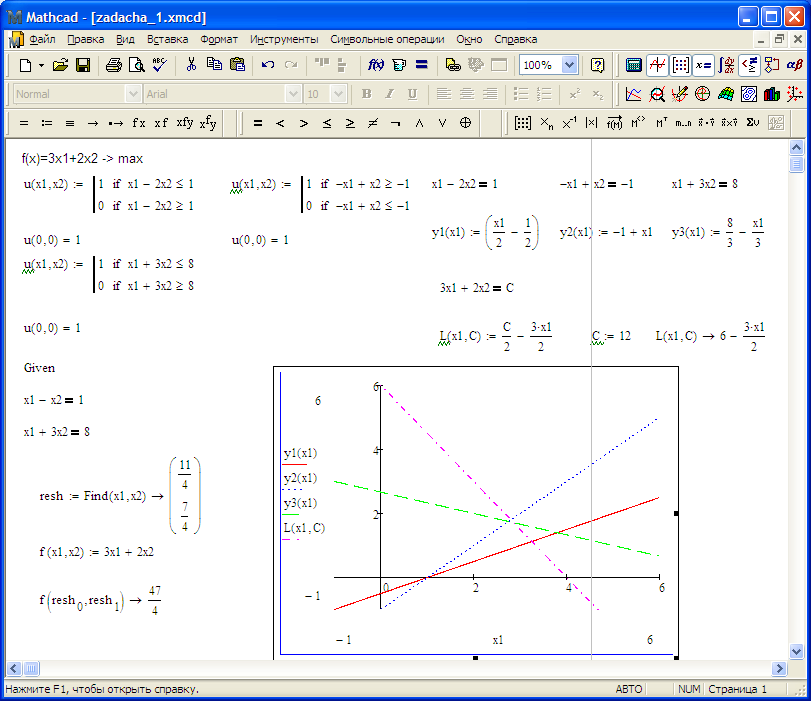 Системы линейных алгебраических уравнений
Системы линейных алгебраических уравнений
Итак, мы с вами продолжаем изучать MathCAD — самую дружелюбную к пользователю математическую среду из существующих в настоящее время. Пока мы занимались тем, что изучали способы решения уравнений — трансцендентных и алгебраических, и теперь вы знаете, как их решать с помощью MathCAD’а в общем виде или численно. Как вы могли убедиться из материала третьей части, численное решение уравнений — не такая простая задача, как может показаться с первого взгляда, однако и не такая сложная, если построить график уравнения. Но просто уравнения — это, согласитесь, довольно скучно, потому что в жизни, как правило, уравнения по одиночке не встречаются. Поэтому сегодня мы перейдем к более сложной, а значит, и более интересной, теме — попробуем решать системы уравнений. Я сказал “попробуем”? Простите, пожалуйста — я, наверное, оговорился. Конечно, не попробуем, а научимся — потому что благодаря MathCAD’у можно быть уверенным в том, что подобные попытки увенчаются успехом. Готовы? Ну что же, тогда вперед.
Готовы? Ну что же, тогда вперед.Решение систем с помощью функции lsolve
Системы уравнений многие просто-таки ненавидят еще со школы — прямо как русскую литературу. Что ж, школа может привить отвращение ко многим вещам, которые без нее могли бы оказаться гораздо более интересными. Как и любая обязаловка, она убивает романтику изучения чего-то нового. Но теперь, когда вас никто не заставляет изучать решение систем уравнений, вы можете взглянуть на них с совершенно новой для себя стороны. И поможет в этом, конечно же, MathCAD.
Для обозначения систем линейных алгебраических уравнений у математиков есть своя аббревиатура — СЛАУ. Ее используют намного чаще, чем полное название, что, в общем-то, вполне естественно — эта аббревиатура и произносима легко, и не перекрывается с другими математическими аббревиатурами. Так что и мы с вами тоже будем ее применять. СЛАУ называется система уравнений следующего вида:
k11x1 + k12x2 + … + k1nxn + l1 = 0
k12x1 + k22x2 + … + k2nxn + l2 = 0
…
kn1x1 + kn2x2 + … + knnxn + ln = 0
Здесь kij и li — какие-то числовые константы, называемые, соответственно, коэффициентами и свободными членами уравнений, а xj — переменные. Такие уравнения обычно записывают также с помощью матриц:
Такие уравнения обычно записывают также с помощью матриц:
KX + L = 0
Итак, для начала давайте посмотрим, каким именно образом в MathCAD’е нужно задавать матрицы. Для этого на панели инструментов Matrix нажмите кнопку Matrix or Vector, а в появившемся окне задайте количество столбцов и строк в матрице. Мы с вами попробуем решать для начала СЛАУ из четырех уравнений, и, соответственно, нам нужна будет матрица размером четыре на четыре элемента.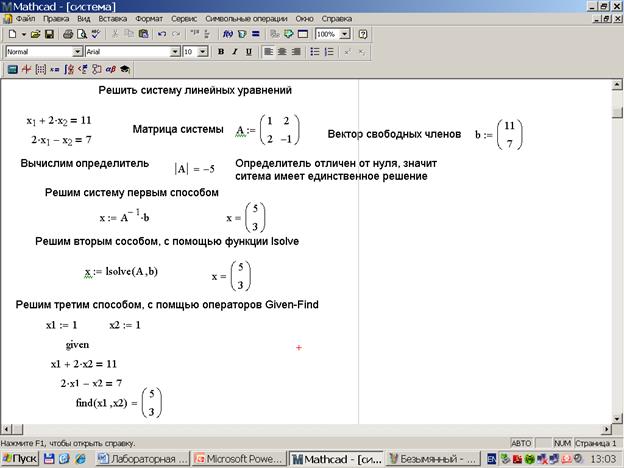 Только, поскольку мы будем присваивать значение, записанное в этой матрице, переменной, обозначающей матрицу коэффициентов, то сначала лучше записать “K_:=”, а потом уже вставлять матрицу. Обратите внимание на то, что мы будем обозначать матрицу не просто буквой К, а еще добавлять подчеркивание. Делается это специально для того, чтобы не переобозначать встроенные переменные среды MathCAD. Аналогичным образом теперь нужно задать вектор свободных членов — только его размер уже будет не 4х4, а 1х4. Для решения СЛАУ после того, как мы ввели коэффициенты (вы можете ввести их произвольно, а можете
Только, поскольку мы будем присваивать значение, записанное в этой матрице, переменной, обозначающей матрицу коэффициентов, то сначала лучше записать “K_:=”, а потом уже вставлять матрицу. Обратите внимание на то, что мы будем обозначать матрицу не просто буквой К, а еще добавлять подчеркивание. Делается это специально для того, чтобы не переобозначать встроенные переменные среды MathCAD. Аналогичным образом теперь нужно задать вектор свободных членов — только его размер уже будет не 4х4, а 1х4. Для решения СЛАУ после того, как мы ввели коэффициенты (вы можете ввести их произвольно, а можете
воспользоваться теми, которые приведены на скриншоте — с ними цифры в ответе получаются довольно ровными и красивыми), нужно для решения СЛАУ использовать функцию lsolve. У нее есть два параметра: первый — это матрица коэффициентов уравнений, а второй — вектор свободных членов. То есть для получения результата нам нужно написать:
lsolve(K_, L_) =

С помощью функции lsolve можно получать и аналитические решения СЛАУ. Давайте попробуем заменить одно из чисел в матрице коэффициентов на букву — например, “а”. Функция lsolve сразу выдаст ошибку, но не нужно этого пугаться — нужно просто заменить знак равенства на стрелку (ее можно найти на панели инструментов Symbolic или же записать комбинацией клавиш Ctrl + .). Дело в том, что знак “равно” в MathCAD’е используется для численных вычислений, а стрелка — для символьных, то есть при решении систем уравнений в общем виде нужно применять именно стрелку.
Решение с помощью solve
В общем-то, решать такую систему можно было бы и используя уже знакомый нам с вами оператор solve. Для этого достаточно записать уравнения в виде матрицы, а затем применить к ней оператор solve точно так же, как если бы мы с вами решали не целую систему, а всего лишь одно- единственное уравнение. “Записать уравнения в виде матрицы” в данном случае означает не запись матричного уравнения KX + L = 0, а просто запись в каждой строке одностолбцовой матрицы (т.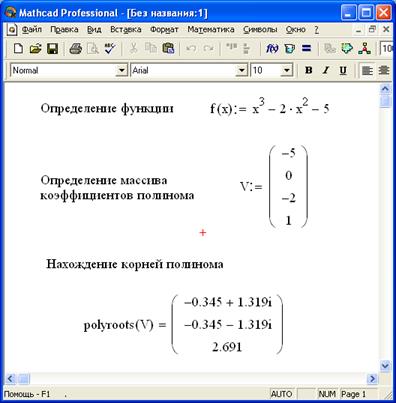 е. вектор-столбца) одного уравнения из системы. Напомню на всякий случай, что оператор solve находится на панели Symbolic, а для записи знака равенства нужно использовать не просто клавишу “=”, а ее комбинацию с клавишей Ctrl. Еще хочу добавить, что в данном случае, как, впрочем, и во многих других, которые мы с вами уже обговорили, это может вполне успешно использоваться для получения не только символьных, но и для численных решений.Решение СЛАУ с помощью solve поначалу кажется не таким уж привлекательным, однако, по сути, оно ничем не отличается от использования функции lsolve. Например, если вы замените какой-нибудь из числовых коэффициентов в одном из уравнений на букву, чтобы получить аналитическое решение, solve справится с этим точно так же быстро и хорошо, как и функция lsolve. Так что, в общем-то, выбор при решении СЛАУ в пользу функции lsolve или в пользу оператора solve — дело скорее вкуса, причем вкуса в плане записи самой системы уравнений, а не оператора или функции, у которых, в общем-то, даже названия очень и очень похожи.
е. вектор-столбца) одного уравнения из системы. Напомню на всякий случай, что оператор solve находится на панели Symbolic, а для записи знака равенства нужно использовать не просто клавишу “=”, а ее комбинацию с клавишей Ctrl. Еще хочу добавить, что в данном случае, как, впрочем, и во многих других, которые мы с вами уже обговорили, это может вполне успешно использоваться для получения не только символьных, но и для численных решений.Решение СЛАУ с помощью solve поначалу кажется не таким уж привлекательным, однако, по сути, оно ничем не отличается от использования функции lsolve. Например, если вы замените какой-нибудь из числовых коэффициентов в одном из уравнений на букву, чтобы получить аналитическое решение, solve справится с этим точно так же быстро и хорошо, как и функция lsolve. Так что, в общем-то, выбор при решении СЛАУ в пользу функции lsolve или в пользу оператора solve — дело скорее вкуса, причем вкуса в плане записи самой системы уравнений, а не оператора или функции, у которых, в общем-то, даже названия очень и очень похожи. Пожалуй, один из немногих случаев, когда все же предпочтительнее использовать именно оператор solve — это когда уравнений у нас больше, чем неизвестных, содержащихся в них. В этом случае матрица системы будет выглядеть не так, как хотелось бы, а вот с solve все будет нормально. Даже если решение найти не удастся, solve любезно об этом сообщит. Аналогичным образом можно попытаться решить СЛАУ и в том случае, когда соотношение между уравнениями и неизвестными, напротив, не в пользу уравнений (правда, как говорится, не с разгромным счетом, а то решение заведомо найти не удастся). Но даже в случае, когда мы пытаемся решить систему с тремя уравнениями и четырьмя неизвестными, оставив после solve только две из них, у нас это далеко не всегда может получиться — в этом вы можете убедиться воочию.
Пожалуй, один из немногих случаев, когда все же предпочтительнее использовать именно оператор solve — это когда уравнений у нас больше, чем неизвестных, содержащихся в них. В этом случае матрица системы будет выглядеть не так, как хотелось бы, а вот с solve все будет нормально. Даже если решение найти не удастся, solve любезно об этом сообщит. Аналогичным образом можно попытаться решить СЛАУ и в том случае, когда соотношение между уравнениями и неизвестными, напротив, не в пользу уравнений (правда, как говорится, не с разгромным счетом, а то решение заведомо найти не удастся). Но даже в случае, когда мы пытаемся решить систему с тремя уравнениями и четырьмя неизвестными, оставив после solve только две из них, у нас это далеко не всегда может получиться — в этом вы можете убедиться воочию.Численное решение СЛАУ
Что ж, давайте теперь посмотрим, как решать СЛАУ с использованием численных методов их решения. Это тоже вовсе не так сложно, как может с самого начала показаться, поскольку MathCAD имеет в своем арсенале ряд средств и на этот случай. Как и в случае с одиночными уравнениями, сначала нужно задать начальное приближение (на то оно и начальное, чтобы задавать его сначала). Только, поскольку переменная у нас теперь не одна, а их несколько, то и начальное приближение необходимо будет задать для каждой из них. В тех случаях, когда переменных в СЛАУ много, это будет совсем не просто. После того, как вы задали начальные приближения для каждой из нужных переменных, запишите сами уравнения — только сделайте это так, чтобы их и начальные приближения разделяло специальное слово “Given” (оно, конечно же, в рабочей области MathCAD’а должно быть записано безо всяких кавычек). После того, как вы записали начальные приближения, слово “Given” и сами уравнения, можно смело воспользоваться функцией find, которая найдет точные значения решений системы. Поскольку в СЛАУ каждая из переменных в итоге будет иметь только одно значение, над подбором максимально точного начального приближения можно особо и не страдать — в конечном итоге в случае СЛАУ оно скорее просто формальность, нежели реальная необходимость, и, как вы сами имели возможность убедиться, есть методы, которые прекрасно решают СЛАУ и без него.
Как и в случае с одиночными уравнениями, сначала нужно задать начальное приближение (на то оно и начальное, чтобы задавать его сначала). Только, поскольку переменная у нас теперь не одна, а их несколько, то и начальное приближение необходимо будет задать для каждой из них. В тех случаях, когда переменных в СЛАУ много, это будет совсем не просто. После того, как вы задали начальные приближения для каждой из нужных переменных, запишите сами уравнения — только сделайте это так, чтобы их и начальные приближения разделяло специальное слово “Given” (оно, конечно же, в рабочей области MathCAD’а должно быть записано безо всяких кавычек). После того, как вы записали начальные приближения, слово “Given” и сами уравнения, можно смело воспользоваться функцией find, которая найдет точные значения решений системы. Поскольку в СЛАУ каждая из переменных в итоге будет иметь только одно значение, над подбором максимально точного начального приближения можно особо и не страдать — в конечном итоге в случае СЛАУ оно скорее просто формальность, нежели реальная необходимость, и, как вы сами имели возможность убедиться, есть методы, которые прекрасно решают СЛАУ и без него.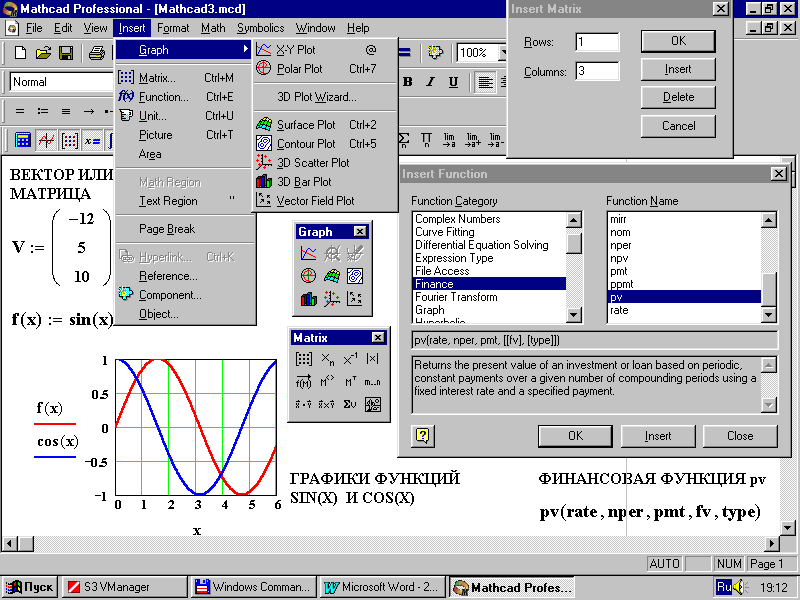
Теперь, когда вы знаете уже столько разных способов решения СЛАУ, вполне логично было бы задаться вопросом: а какой из них лучше при прочих равных условиях? В литературе, как правило, рекомендуется использовать функции lsolve или find, дающие точность до 15 знаков после запятой — однако на самом деле, учитывая тот факт, что такая точность бывает нужна не так уж часто, данным советом можно пренебречь, потому что точность решения системы намного больше зависит от нее самой, нежели от используемого метода ее решения в MathCAD’е. Так что используйте пока что смело тот, который показался вам наиболее удобным, а о погрешностях при решении СЛАУ мы с вами еще поговорим, но только, пожалуй, немного попозже.
Компьютерная газета. Статья была опубликована в номере 16 за 2008 год в рубрике soft
Mathcad системы уравнений | Cl-Box
Дек 04
Программа Mathcad обеспечивает возможность численного и символьного решения систем уравнений. Один из методов решения систем уравнения в Mathcad это метод с использованием команд Дано и Найдите . Давайте подробнее разберем как это сделать.
Один из методов решения систем уравнения в Mathcad это метод с использованием команд Дано и Найдите . Давайте подробнее разберем как это сделать.
Численное решение систем уравнений в Mathcad
Для примера рассмотрим задачу:
- Для начала надо задать начальные значения для всех неизвестных, т.к. блок Дано – Найти использует для решения численный метод (итерационный метод).
- Далее ввести команду Дано (можно с помощью клавиатуры, либо воспользоваться булевым оператором)
- Теперь вводим уравнения. Обратите внимание, что знак «=» ставится не как «определение» или «вычисление», а вводится как «Ctrl» + «=» и знак выделяется жирным.
mathcad система условий
- Теперь вводим оператор Найти после чего программа выдает нам результат.

Как видим, правильный ответ будет под номером 4.
Символьное решение систем уравнений в Mathcad
Чтобы решить систему символьно, будем использовать те же операторы, только некоторые различия в воде. Т.к. нам не нужно конкретное значение, то и начальные значения вводить не нужно.Возьмем для рассмотрения пример:
- Повторяем действия из пунктов 2 и 3 предыдущего примера, вводим команду, используя данные уравнения «Ctrl» + «=»
- Теперь вводим оператор Find, вводим переменные (x, y), чтобы произвести вычисления символьно нужно нажать «Ctrl» + «. »(Клавиша Ctrl и клавиша точки на латинской раскладке) после чего кликаем мышкой вне блока решения и программа производит расчет.
стр.S. К сожалению, программа решает не все примеры, связано это со сложностями расчета.
автор: Admin
Оставьте свой отзыв
Решение систем и систем
Вычисление корней численными методами включает два основных этапа:
· отделение корней;
· уточнение корней до заданной точности.
Рассмотрим эти два этапа подробно.
Отделение корней нелинейного уравнения
Учитывая легкость построения графиков функций в MathCAD, в дальнейшем будет использоваться графический метод отделения корней.
Пример. Дано алгебраическое уравнение
.
Определить интервалы локализации корней этого уравнения.
Пример. Дано алгебраическое уравнение
.
Определить интервалы локализации корней этого уравнения.
На рисунке приведен график функции , построенный в MathCAD. Видно, что в интервала изоляции можно использовать интервал . Однако уравнение имеет три корня. Следовательно, можно сделать вывод о наличии еще двух комплексных корней. ¨
Уточнение корней нелинейного уравнения
Для уточнения корня используются специальные вычислительные методы, как метод деления отрезка пополам, метод хорд, метод касательных (метод Ньютона) и многие другие.
Функция корень . В MathCAD для уточнения корней любого нелинейного уравнения (не обязательно алгебраического) введена функция root , которая может иметь два или четыре аргумента, т.е. или , где – имя функции или арифметическое выражение, соответствующее решаемому нелинейному уравнению переменная, – скалярная переменная, относительно которой решается уравнение, – границы интервала локализации корня.
Пример. Используя функцию , найти все три корня уравнения , включая и два комплексных.
Заметим, что для вычислений всех трех корней использовался прием понижения порядка алгебраического уравнения, рассмотренный в п. 8.1.1. ¨
Функция корневого с двумя аргументами требует задания начального значения корня из интервала локализации.
Пример 8.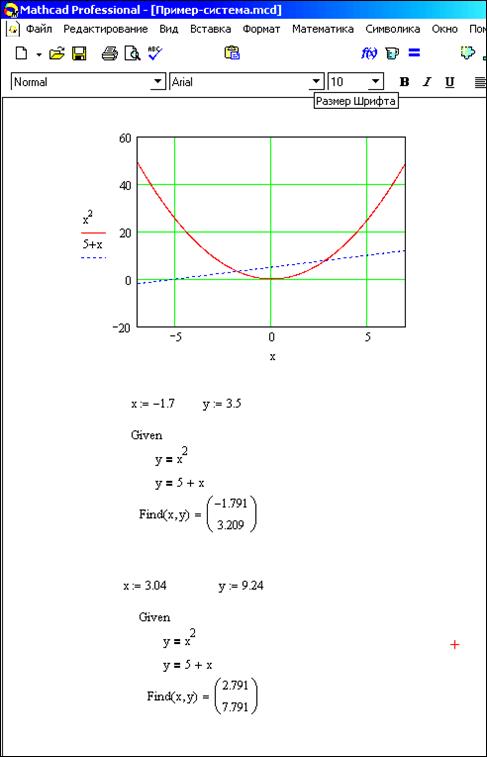 1.5. Используя функцию root , вычислить корня нелинейного уравнения при изменении коэффициента а от 1 до 10 с шагом 1.
1.5. Используя функцию root , вычислить корня нелинейного уравнения при изменении коэффициента а от 1 до 10 с шагом 1.
polyroots Функция Функция . Для вычислений всех корней алгебраического уравнения порядка (не выше 5) рекомендуется использовать функцию polyroots . Обращение к этой функции имеет вид polyroots (v) , где v – вектор, состоящий из n +1 проекций, равных коэффициентов алгебраического уравнения, т.е. . Эта функция не требует проведения процедуры локализации корней.
Пример. Используя функцию polyroots , найти все три корня уравнения , включая и два комплексных
Блок Дано . При уточнении корня нелинейного уравнения можно использовать специальный вычислительный Дано , имеющий текущую структуру:
Решенное уравнение задается в виде равенства, в котором используется «жирный блок» знак равно, вводимый с палитры ЛОГИЧЕСКИЙ.
Ограничения содержат равенства или неравенства, которым удовлетворяет искомый корень.
Функция которой Найти уточняет корень уравнения, вызов этой функции имеет вид Найти ( x ), где x – , где x – корень.Если корня уравнения на заданном интервале не существует, то следует вызвать функцию Minerr ( x ), которое возвращает приближенное значение корня.
Для выбора алгоритма уточнения корня необходимо щелкнуть правой кнопкой мыши на имя функции Найдите ( x ) и в появившемся контекстном меню (см. Рисунок) выбрать подходящий.
Аналогично можно задать алгоритм решения и для функций Minerr ( x ).
Использование численных методов в функциях Find ( x ), Minerr ( x ) переменные требует перед блоком1 , по которому осуществляется поиск корней уравнения.
Пример. Используя блок Дано , вычислите корень уравнения в интервале отделения .
В зависимости от того, какие функции входят в систему, можно выделить два класса систем:
· алгебраические системы уравнений;
· трансцендентные системы уравнений.
Среди алгебраических систем особое место занимают системы линейных алгебраических уравнений (СЛАУ).
Системы линейных алгебраических соотношений
Системой линейных алгебраических уравнений (СЛАУ) называется система вида:
В матричном виде можно записать как
901 – матрица размерности , – вектор с проекциями. Для вычислений решения СЛАУ следует использовать функцию lsolve , обращение к которой имеет вид: lsolve (А, b ), где А – матрица системы, – вектор правой части .
Решение системных уравнений
MathCAD дает возможность находить решение системы численных методов, при этом максимальное число уравнений в MathCAD2001i доведено до 200.
Для решения системы выполнить следующие этапы.
Задание начального приближения для всех неизвестных, входящих в систему уравнений. Приомом числе неизвестных этапов можно выполнить графически, как показано в примере.
Пример. Дана система соотношений:
Определить начальные приближения для этой системы.
Видно, что система имеет два решения: для первого решения в качестве начального приближения может быть принята точка (-2, 2), а для второго решения – точка (5, 20).¨
Вычисление решений системы с точностью до . Для этого используется уже известный вычислительный блок Дано .
Функция Найти вычисляет решение системы уравнений с заданной точностью, и вызов этой функции имеет вид Найти ( x ), где x – список связанных, по которому ищется решение ищется решение . Начальные значения этим переменным задаются в блоке <Начальные условия>. Число аргументов функции функции быть неизвестных.
Начальные значения этим переменным задаются в блоке <Начальные условия>. Число аргументов функции функции быть неизвестных.
Следующие выражения недопустимы внутри блока решения:
· ограничения со знаком ¹;
· дискретная переменная или выражение, дискретную переменную в любой форме;
· блоки решения не могут быть вложены друг в друга, блок может иметь только одно слово Дано и имя функции Найдите (или Minerr ).
Пример. Используя блок Дано , вычислить все решения системы предыдущего примера. Выполнить проверку найденных решений.
Пример. Используя функцию , вычислите решение системы уравнений
Решение уравнений в MathCad 13, 14, 15 наерах. Методы Given
Для решений в Mathcad можно использовать двумя способами:
Использование метода Задано – Найти :
Это наиболее распространенный способ решения обычных алгебраических уравнений.
Затем указывается начальное приближение для искомой альтернативы. Это нужно для увеличения скорости и точности решения уравнения. Если начальное приближение не задать, то mathcad по умолчанию примет его равным нулю
Рис. 1.Ввод данных в поле mathcadДалее вводится уравнение. Его можно записать в явном или неявном виде. Само уравнение набирается с клавиатуры вручную с использованием панели Calculator . Из этой панели можно взять основные математические операции: дроби, тригонометрию, факториалы и прочее. Уравнение нужно записывать с использованием логического символа “ровно”. На панели Boolean он выделен жирным шрифтом (см. Рис. 2)
Рис. 2. Панели Boolean и Calculator После уравнения вводится функция Find (x) (где х – переменная). Это функция, которая возвращает результат. Значение функции Find (x) можно использовать какой-либо альтернативный символ “: = ” и использовать ее далее в расчетах.
Это функция, которая возвращает результат. Значение функции Find (x) можно использовать какой-либо альтернативный символ “: = ” и использовать ее далее в расчетах.
Для достижения результата, после Find (x) следует поставить символ “ → ” либо “ = ” из панели Evaluation (см. Рис. 3). Причем, если вы используете символ “ → “, то mathcad определит все уравнения корни и сформирует матрицу результатов. Но если вы используете символ “ = “, то mathcad выведет единственный корень, который был наиболее близок к начальному приближению.Так что, если вы не знаете сколько корней имеет уравнение, то лучше использовать стрелочку
Рис. 3. Панель «Оценка»В зависимости от сложности уравнения через определенное время MathCad выведет результат. На рис.4 можно рассмотреть синтаксис и различие результатов выводимых mathcad. Обратите внимание, что выводимые результаты и того же уравнения различны
Рис. 4. Результат численного решения уравнения Mathcad позволяет решать уравнение в символьном виде . Например, если мы заменим все числовые константы на неизвестные параметры и решим уравнение относительно x , то результат выведется в символьном виде (см. Рис. 5). Причем, обратите внимание, что в данном случае вводить начальное приближение и мы должны использовать символ “ → ” для вывода результата
Например, если мы заменим все числовые константы на неизвестные параметры и решим уравнение относительно x , то результат выведется в символьном виде (см. Рис. 5). Причем, обратите внимание, что в данном случае вводить начальное приближение и мы должны использовать символ “ → ” для вывода результата
Использование метода Решить :
Этот метод отличается от выше рассмотренного синтаксисом.На свободном поле вводим уравнение с использованием логического символа «ровно» из панели Boolean . После ввода уравнения, не смещая курсор ввода, на панели Символическое нажимаем кнопку решить (см. Рис. 6)
Рис. 6. Панель символическаяЗатем ставим запятую и вводим переменную, относительно которой нужно уравнение (в нашем случае это x ). Нажимаем Enter на клавиатуре и смотрим результат (см. Рис. 7)
Рис. 7. Результат решения уравнения методом Решить
7. Результат решения уравнения методом РешитьОбратите внимание, что подходит метод как для численного так и для символьного представления результатов
Как показывает моя личная инженерная практика, иногда не удается решить уравнения с помощью Given – Find , но получается в Solve . При этом, к сожалению, метод Solve не очень удобен для далнейшего использования результатов решения уравнения
Mathcad find переменная не определена
MathCad | ANSYS CFX | MS Office
Поиск по сайту
Выбор языка
Решение вопросов в MathCad
Часто в курсовом проекте, либо в лабораторной работе встает вопрос о решении какого-либо сложного большого уравнения с одним неизвестным.Не всегда хочется тратить 10 – 20 минут на рутинные преобразования в процессе которых, велика вероятность допущения ошибки. Целно использует математическую программу (в данном случае MathCad), которая быстро и правильно дать ответ. Мы рассмотрим пример использования двух способов решения, причем как в числах так и в символьном виде.
Мы рассмотрим пример использования двух способов решения, причем как в числах так и в символьном виде.
Способ №1: использование вычислительного блока Дано – Найти :
Это наиболее распространенный способ решения обычных алгебраических уравнений.Он достаточно прост. В рабочем поле записываем первое слово Дано . Это служебное слово. Оно “подключает модули” программные mathcad , необходимые для решения уравнения. Эти модули в своем составе содержат основные численные методы решения: метод бисекции, простые итерации и пр. Далее пишется наше уравнение в любом – явном или неявном виде. Само уравнение набирается с использованием клавиатуры с использованием логического символа “равно”. На панельке Boolean (Булева алгебра) он выделен жирным шрифтом (см.рис. 1).
Рис. 1. Панель “Булевая алгебра”
Далее пишется слово Find (x) (где х – переменная). Это функция, которая и получает ответ. Функцию Find (x) можно использовать в расчетах. Для достижения результата, после Find (x) следует поставить символ “→” либо “=” (см. Рис. 2).
Функцию Find (x) можно использовать в расчетах. Для достижения результата, после Find (x) следует поставить символ “→” либо “=” (см. Рис. 2).
Рис. 2. Панель “Вычисления”
В зависимости от сложности уравнения через некоторое время MathCad выведет результат.
Возможности MathCad позволяют определить корень как в представленном виде (т. Е. Результаты решения уравнения представляет собой число) так и в символьном (результат – выражение). Для численного определения корня необходимо задать (определить) ВСЕ переменные входящие в уравнение и даже искомую переменную . MathCad воспринимает задание искомой как начальное приближение корня . Крайне важно задаться начальным приближением, поскольку без него корень уравнения могут быть исправлены.Нужно отметить, что некорректное задание начального приближения часто бывает неверного результата либо его отсутствия вообще.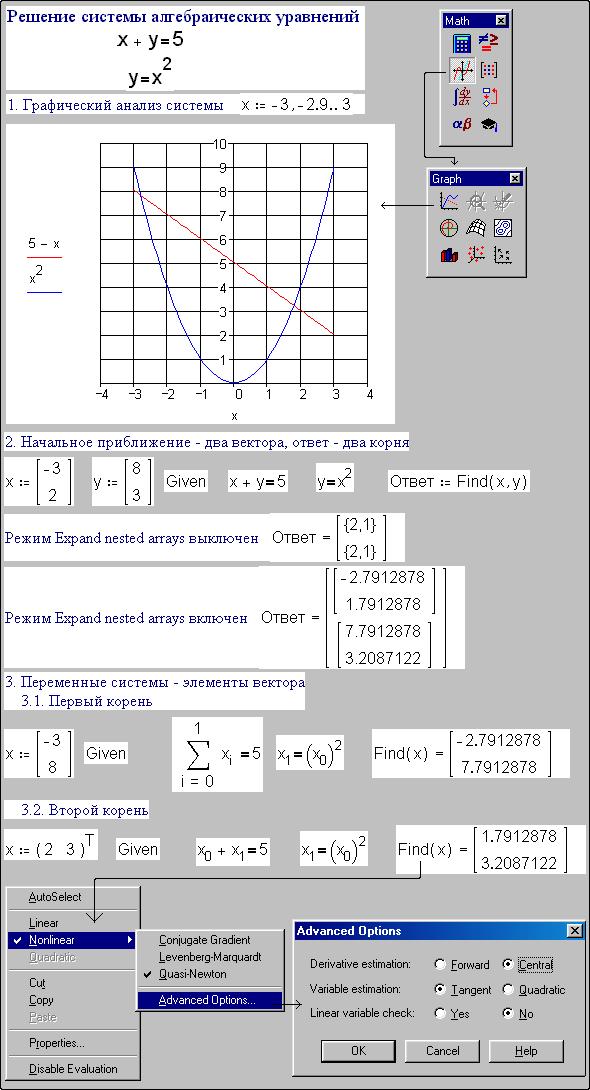 Но не стоит забывать также и о том, что корня может не быть, потому что само уравнение его не имеет.
Но не стоит забывать также и о том, что корня может не быть, потому что само уравнение его не имеет.
В том случае, если необходимо решить уравнение относительно какого-либо в символьном виде , то нет необходимости требаться значениями всех входящих в уравнение параметров и начальным приближением изменения.В этом случае поставить интеграцию (также через “жирное равно”) и после оператора Найдите (x) “→”. При этом будут работать уже другие функции MathCad , которые заточены под символьное преобразование и упрощение выражений. Результатом решения будет выражение. Стоит отметить, что MathCad сможет записать решение далеко не всякого уравнения. В этом смысле его возможности ограничены.
Для подтверждения и закрепления выше сказанного, Вам предлагается познакомиться с примерами решений уравнений как в численном так и в символьном виде.
Пример №1. Решение уравнений в MathCad с помощью блока Given Find численно: Скачать
Пример №2. Решение уравнений в MathCad с помощью блока Given Найти символьно: Скачать
Решение уравнений в MathCad с помощью блока Given Найти символьно: Скачать
Способ №2: Применение метода решить:
Этот метод по существу не отличается от рассмотренного выше, поскольку процедура нахождения корня аналогична. Разница лишь в оформлении. В этом случае наше уравнение записывается без операторов Дано и Найдите .После ввода уравнения на панели Символическое нажимаем кнопку решать (см. Рис. 3), определяем через запятую искомую переменную, жмем “→” и получаем ответ.
Рис. 3. Панель “Символьные”
Иногда, то что не получается найти с помощью Given Find получается в solution .
Пример №3. Решение уравнений в MathCad с помощью решения: Скачать
РЕШЕНИЕ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ
4 Решение системы и систем средств Mathcad
Система Mathcad широкими широкими возможными решениями систем.
Функция root, блоки Дано… Найти, Дано… Minerr
В ходе численного решения обычно выделяют два этапа:
- отделение корней – определение интервала нахождения каждого корня или приблизительного значения корня. В системе Mathcad наиболее наглядным будет отделение корней уравнения графическим способом;
- уточнение корней – на численного значения корня с вершиной.
Точность нахождения корня устанавливается с помощью системной модели TOL (Допуск сходимости – Допуск сходимости), которая по умолчанию равна 10 -3.Чем меньше значение TOL, тем точнее, вообще говоря, находится корень уравнения. Однако оптимальным является TOL = 10 -5. Переопределить значение TOL можно в окне математических свойств документа Параметры Math на вкладке Встроенные переменные ( Встроенные переменные ) или присваиванием, например, TOL: = 0.0001.
Для решения одного уравнения с одной неизвестной встроенная функция root , которая в общем виде задается
корень (f (x), x, [a, b])
и возвращает значение переменной x , при которой функция f ( x ) обращается в ноль. Параметры функции root :
Параметры функции root :
- f ( x ) – функция левой части уравнения f (x) = 0;
- x – переменная, относительно которой требуется уравнение;
- a , b (необязательные) – действительные числа, такие что a -1 слева: A -1 Ax = A -1 b . Учитывая, что A -1 A , вектор-столбец решений системы можно искать в виде
Этот прием используется в Mathcad так:
- задается матрица коэффициентов при неизвестных системы A ;
- задается столбец свободных пар ; b ;
- вводится формула для нахождения решения системы X: = A -1 b ;
- выводится вектор решений системы X =.
Кроме того, пакет Mathcad имеет встроенную функцию
lsolve (A, b),
возвращающую вектор-столбец решений системы линейных алгебраических уравнений. Аргументами функции lsolve имеют матрица коэффициентов при неизвестных системы и столбец свободных членов. Порядок решения аналогичен рассмотренному, но вместо формулы X: = A -1 b используется X: = lsolve (A, b) .
Аргументами функции lsolve имеют матрица коэффициентов при неизвестных системы и столбец свободных членов. Порядок решения аналогичен рассмотренному, но вместо формулы X: = A -1 b используется X: = lsolve (A, b) .
Реализовать широко известный метод Гаусса решения систем линейных соотношений позволяет встроенная функция rref ( M ), возвращающая ступенчатая матрица M .Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.
Решение системы линейных уравнений можно осуществить с помощью блоков Дано… Дано, Дано… Minerr . При этом неизвестным системы задается произвольное начальное приближение, проверка необязательна.
Порядок выполнения лабораторной работы
- Загрузить Mathcad Пуск / Все программы / Mathsoft Apps / Mathcad ( Пуск / Все программы / Mathsoft Apps / Mathcad ).
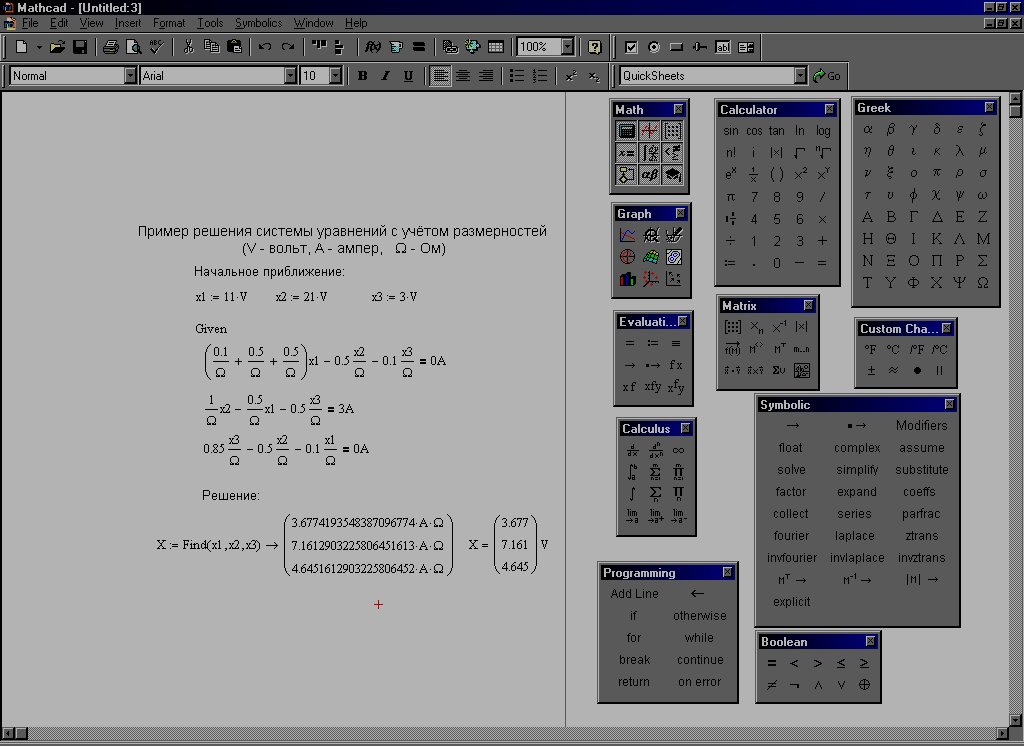
- Сохранить в личной папке на диске z: новый документ с именем ФИО1, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы ( Ctrl + S ).
- Вставить текстовую область Вставить / Текстовая область ( Вставка / Область текста ) и выполнить в поле документа текст:
Лабораторная работа № 4
Решение вопросов и систем в Mathcad.
- В новой текстовой области фамилию, имя, отчество, учебный шифр и номер варианта.
- Выполнить задание 1.
Задание 1. Решить уравнение.
Решение .
Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.
Определим функцию f ( x ), равную левую части данного уравнения, когда правая равна нулю:
Зададим ранжированную переменную x в некотором диапазоне с мелким шагом, например:
Вставим в документ графическую область.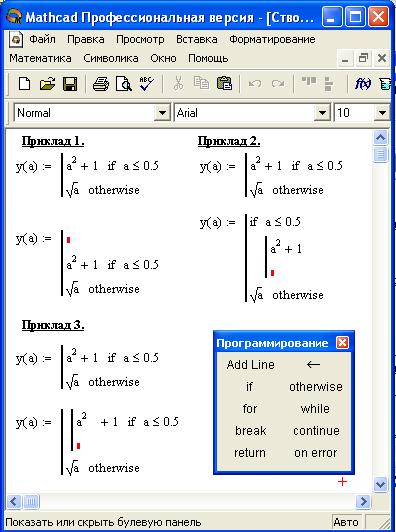 Для этого выберем дважды пиктограмму с изображением сначала на панели Math ( Математика ), затем на палитре графиков График или выполним из главного меню последовательности команд Insert / Graph / XY Plot ( Вставка / График / XY Зависимость ).
Для этого выберем дважды пиктограмму с изображением сначала на панели Math ( Математика ), затем на палитре графиков График или выполним из главного меню последовательности команд Insert / Graph / XY Plot ( Вставка / График / XY Зависимость ).
Снизу по оси абсцисс наберем x , а сбоку по оси ординат введем f ( x) .
Для появления графика щелкнем левой клавишей мыши вне графической области.
Отформатируем график функции f ( x ). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Формат ( Формат ). Установим пересечение осей графика ( Crossed – Только оси ), добавимательные линии по координатным осям ( линий сетки – Вспомогательные линии ). Отменим при этом автосетку ( Autogrid – Автосетка ) и установим количество линий сетки, равное 10.
Для подтверждения внесенных изменений нажмем последовательных Apply ( Применить ) и ОК .
После указанных преобразований графика функции f (x) будет выглядеть следующим образом:
Из графика функции f (x) видно, что уравнение имеет три корня, которые равны: x1 ≈ -1; x2 ≈ 1; х3 ≈ 2,5.
Этап отделения корней завершен.
Уточним теперь корни уравнения с помощью функции root .
Присвоим начальное приближение x и укажем точность поиска корня:
Уточним заданное приближение к значению корня с помощью функций root:
Выполним проверка, подтверждающую, что первая корень найден с заявленной точностью:
Начальное приближение можно не задавать при использовании в качестве аргументов root отрезка нахождения корня, например, второй корень можно уточнить:
Задание 2. Решить уравнение.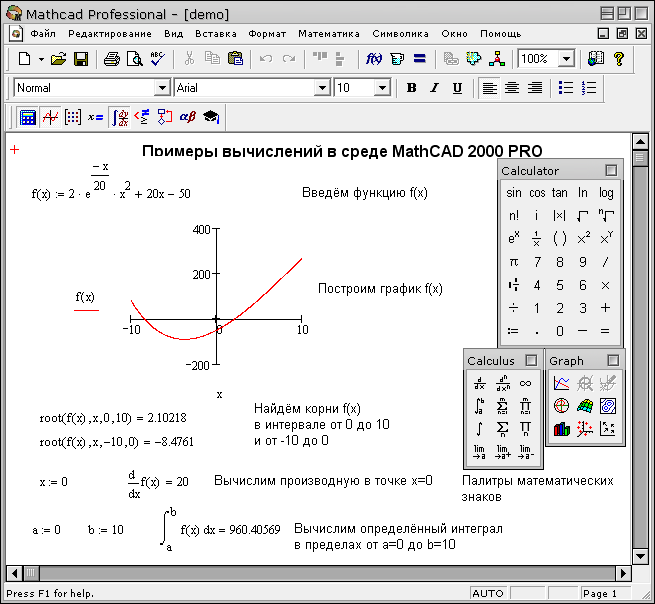
Решение .
Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x :
Выберем из главного меню Символика / Полиномиальные коэффициенты ( Символика / Коэффициенты полинома ). Появившийся вектор коэффициентов полинома выделил целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать на панели инструментов Форматирование ( Форматирование ) или комбинацию клавиш Ctrl + X .
Напечатаем v: = и вставим вектор из буфера обмена, используя кнопку Вставить на панели инструментов или комбинацию клавиш Ctrl + V .
Для достижения результата напечатаем polyroots (v) = :
Задание 3. Решить систему линейных условий Сделать проверку.
Решение.
1-й способ. Использование блока Дано… Найдите .
Зададим всем неизвестным, входящим в систему, произвольные начальные приближения, например:
Напечатаем слово Дано .Установим визир ниже и наберем уравнения системы, каждый в своем блоке. Используем при этом логический знак равенства (Ctrl + =) .
После ввода системы напечатаем X: = Найти ( x , y , z ) и получим решение системы в виде вектора, состоящего из трех элементов:
Сделаем проверку, подставив полученные значения неизвестных в уравнения системы, например, следующим образом
После знака «=» в каждой строке должен быть получен результат равный или равный правой части системы.В данном примере системная переменная ORIGIN = 1.
2-й способ. Использование блока Дано… Minerr .
Порядок решения системы этим способом аналогичен порядку использования блока Дано… Найдите и представлен вместе с проверкой:
3-й способ. Решение системы линейных уравнений матричным способом.
Решение системы линейных уравнений матричным способом.
Создадим матрицу А , состоящую из коэффициентов при неизвестных системы.Для этого напечатаем A: =, вызовем окно создания массивов ( Ctrl + M ). Число строк ( рядов ) и столбцов ( столбцов ) матрицы данной системы равно 3. Заполним пустые места матрицы коэффициентами при неизвестных системах, как показано ниже:
Зададим вектор b Бесплатные функции системы. Сначала напечатаем b : =, затем вставим шаблон матрицы ( Ctrl + M ), где количество строк ( строк ) равно 3, а количество столбцов ( столбцов ) равно 1.Заполним его:
Решим системным способом по формуле
Решим систему с помощью функций lsolve:
Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение A · X, которое должно совпасть с вектором-столбцом свободных b :
программирование mathcad скалярный трехмерный
Функция Найти (Найти) работает в ключевой связке с ключевым словом Данное (Дано). Конструкция Given – Найти расчетную методику, основанную на поиске корня вблизи точки начального приближения, заданной пользователем.
Конструкция Given – Найти расчетную методику, основанную на поиске корня вблизи точки начального приближения, заданной пользователем.
Если задано уравнение f (x) = 0, то его можно решить следующим образом с помощью блока Дано – Найти:
– задать начальное приближение
– служебное слово
- – записать уравнение, используя знак боулево равно
- – написать функцию найти с неизвестной переменной в качестве роли
В результате после вывода выведен найденный корень.
Если существует несколько корней, то их можно найти, меняя начальное приближение х0 на близкое к искомому корню.
В Mathcad можно писать программы двух видов
- 1) в виде скриптов (последовательность команд)
- 2) в настоящих программ с входными и выходными ограничениями.
Mathcad – система компьютерной алгебры из класса системного проектирования, ориентированная на подготовку интерактивных документов с вы0числениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы.
Mathcad был задуман и написан Алленом Раздовом из Массачусетского технологического института (MIT).
Mathcad имеет интуитивный и простой для использования интерфейс пользователя. Для ввода формул и данных можно использовать как клавиатуру, так и специальные панели инструментов.
Работа осуществляется в пределах рабочего листа, на котором уравнения и неограниченно, в противовес текстовой записи в языках программирования. При создании документов-приложений используется принцип WYSIWYG («Что видишь, то и получаешь» – «что видишь, то и получаешь»).
, несмотря на то, что эта программа в основном ориентирована на пользователей-непрограммистов, Mathcad также используется в сложных проектах, чтобы визуализировать результаты математического моделирования, путем использования распределенных вычислений и языков программирования. Mathcad часто используется в крупных инженерных сетях, где большое значение имеет трассируемость и соответствие стандартам.
Mathcad достаточно удобно использовать для обучения, вычислений и инженерных расчетов.Открытая архитектура приложения объединяет технологии поддержки .NET и XML легко интегрировать Mathcad практически в любые ИТ-структуры и инженерные приложения. Есть возможность создания электронных книг (электронная книга).
Программа решений для мобильных операторов и встроенных функций различных технических задач. Программа позволяет выполнять численные и символьные вычисления, выполнять операции с скалярными величинами, векторми и матрицами, автоматически переводить одни единицы измерения в другие.
MATHCAD 14: Основные сервисы и технологии
Главная / Математика / MATHCAD 14: Основные сервисы и технологии / Тест 4 Упражнение 1:Номер 1
Использование приведенных функций решений
Ответ:
& nbsp (1) корень () & nbsp
& nbsp (2) lsolve () & nbsp
& nbsp (3) Найти () & nbsp
& nbsp (4) CreateMesh () & nbsp
Номер 2
Какая переменная отвечает за точность вычислений корней функция root () ? Ответ:
& nbsp (1) ORIGIN & nbsp
& nbsp (2) TOL & nbsp
& nbsp (3) начальное приближение & nbsp
& nbsp (4) аргумент функции & nbsp
Номер 3
Для численного решения уравнения с использованием функций root () необходимо задать: Ответ:
& nbsp (1) границы отрезка, где находится корень & nbsp
& nbsp (2) начальное приближение корня & nbsp
& nbsp (3) ничего не требуется & nbsp
& nbsp (4) максимальное значение функции уравнения & nbsp
Упражнение 2:
Номер 1
Решение системы уравнений с помощью блока данного найти дает решение:
Ответ:
& nbsp (1) приближенное & nbsp
& nbsp (2) минимальное & nbsp
& nbsp (3) точное & nbsp
& nbsp (4) максимальное & nbsp
Номер 2
Какой знак равенства в уравнениях используется в блоке решения Дано Находка:
Ответ:
& nbsp (1) : = & nbsp
& nbsp (2) == & nbsp
& nbsp (3) = & nbsp
& nbsp (4) & nbsp
Номер 3
Решение системы уравнений с помощью блока данного майнера дает решение:
Ответ:
& nbsp (1) точное & nbsp
& nbsp (2) приближенное & nbsp
& nbsp (3) минимальное & nbsp
& nbsp (4) максимальное & nbsp
Упражнение 3:
Номер 1
Сколько корней имеет уравнение
Ответ:
& nbsp (1) 1 & nbsp
& nbsp (2) 2 & nbsp
& nbsp (3) 3 & nbsp
& nbsp (4) 4 & nbsp
Номер 2
Какими способами можно получить решение уравнения:
Ответ:
& nbsp (1) с использованием root () & nbsp
& nbsp (2) , используя Find ()) & nbsp
& nbsp (3) с использованием функции lsolver () & nbsp
& nbsp (4) с помощью оператора solver & nbsp
Номер 3
Выбрать правильное решение уравнения:
Ответ:
& nbsp (1) (4; 12) & nbsp
& nbsp (2) (5.01; 10.8) & nbsp
& nbsp (3) (3,05; 13) & nbsp
& nbsp (4) (0,1; 12) & nbsp
Упражнение 4:
Номер 1
При численном представлении корней полинома в степени с помощью функций Polyroots () : аргумент функции является Ответ:
& nbsp (1) вектор длины длины n & nbsp
& nbsp (2) вектор длины длины n + 1 & nbsp
& nbsp (3) вектор длины длины n-1 & nbsp
& nbsp (4) начальное приближение & nbsp
Номер 2
Какими способами можно получить решение уравнения:
Ответ:
& nbsp (1) + используя функцию root () & nbsp
& nbsp (2) + используя данный блок Find ()) & nbsp
& nbsp (3) + используя функцию Polyroots () & nbsp
& nbsp (4) с использованием функции lsolver () & nbsp
& nbsp (5) + используя оператор solver & nbsp
Номер 3
Выбрать действительный корень уравнения:
Ответ:
& nbsp (1) (-0.819) & nbsp
& nbsp (2) (-1,819) & nbsp
& nbsp (3) (0,819) & nbsp
& nbsp (4) (2,819) & nbsp
Упражнение 5:
Номер 1
Система условий имеет вид Сколько корней имеет система.
Ответ:
& nbsp (1) 1 & nbsp
& nbsp (2) 2 & nbsp
& nbsp (3) 3 & nbsp
& nbsp (4) 4 & nbsp
Номер 2
Какими способами можно получить решение системы
Ответ:
& nbsp (1) с использованием функции root () & nbsp
& nbsp (2) используя данный блок Find ()) & nbsp
& nbsp (3) с использованием функции Polyroots () & nbsp
& nbsp (4) с использованием функции lsolver () & nbsp
Номер 3
Какие решения являются корнями системы уравнений?
Ответ:
& nbsp (1) (-0,53; 0.26) & nbsp
& nbsp (2) (1,89; 2,1) & nbsp
& nbsp (3) (1,71; 0,78) & nbsp
& nbsp (4) (6,53; 8,73) & nbsp
Упражнение 6:
Номер 1
Система условий имеет вид Сколько корней имеет система.
Ответ:
& nbsp (1) 1 & nbsp
& nbsp (2) 2 & nbsp
& nbsp (3) 3 & nbsp
& nbsp (4) 4 & nbsp
Номер 2
Какими способами можно получить решение системы:
Ответ:
& nbsp (1) с использованием функции root () & nbsp
& nbsp (2) используя данный блок Find ()) & nbsp
& nbsp (3) с использованием функции Polyroots () & nbsp
& nbsp (4) с использованием функции lsolver () & nbsp
Номер 3
Какие решения являются корнями системы уравнений?
Ответ:
& nbsp (1) (-1,67; 5.70) & nbsp
& nbsp (2) (1,56; 4,91) & nbsp
& nbsp (3) (5,53; 10,26) & nbsp
& nbsp (4) (0,15; 1,02) & nbsp
Номер 2
Сколько способов существует в MathCad для решения системы линейных алгебраических уравнений
Ответ:
& nbsp (1) 1 & nbsp
& nbsp (2) 2 & nbsp
& nbsp (3) 3 & nbsp
& nbsp (4) 4 & nbsp
Номер 3
Матрица A имеет вид, матрица.Выбрать правильное решение уравнения
Ответ:
& nbsp (1) (4; 2,93; 2,71) & nbsp
& nbsp (2) (3; 1,93; 1,71) & nbsp
& nbsp (3) (2; 0,93; 0,71) & nbsp
& nbsp (4) (1; -0.93; – 0,71) & nbsp
Упражнение 8:
Номер 1
Для решения задач оптимизации используются блоки:
Ответ:
& nbsp (1) задано максимизировать & nbsp
& nbsp (2) с учетом miniimize & nbsp
& nbsp (3) данная находка & nbsp
& nbsp (4) данный решатель & nbsp
Номер 2
В задаче оптимизации начальные значения неизвестных параметров вводятся с использованием знака:
Ответ:
& nbsp (1) : = & nbsp
& nbsp (2) = & nbsp
& nbsp (3) = & nbsp
& nbsp (4) & nbsp
Номер 3
Задаче оптимизации оптимизируемая функция вводится с использованием знака:
Ответ:
& nbsp (1) : = & nbsp
& nbsp (2) = & nbsp
& nbsp (3) = & nbsp
& nbsp (4) & nbsp
Упражнение 9:
Номер 1
Решение задачи оптимизации MathCad представляет в виде:
Ответ:
& nbsp (1) вектора & nbsp
& nbsp (2) число (числа) & nbsp
& nbsp (3) функции & nbsp
& nbsp (4) экстремального значения функции & nbsp
Номер 2
Максимальное значение функции при условии равно
Ответ:
& nbsp (1) 40 & nbsp
& nbsp (2) 60 & nbsp
& nbsp (3) 50 & nbsp
& nbsp (4) 70 & nbsp
Номер 3
Значения x и y, для которых функция имеет максимум при условии, равны
Ответ:
& nbsp (1) (1; 0.4) & nbsp
& nbsp (2) (0,9; 3) & nbsp
& nbsp (3) (0,9; 0,4) & nbsp
& nbsp (4) (0,7; 0,5) & nbsp
Упражнение 10:
Номер 1
Задачи оптимизации решаются методами:
Ответ:
& nbsp (1) математической статистики & nbsp
& nbsp (2) линейного программирования & nbsp
& nbsp (3) математического анализа & nbsp
& nbsp (4) решения различных уравнений & nbsp
Номер 2
Для решения задач оптимизации необходимо задать:
Ответ:
& nbsp (1) начальные значения неизвестных параметров & nbsp
& nbsp (2) начальное значение оптимизируемой функции & nbsp
& nbsp (3) для ограничения неизвестных параметров & nbsp
& nbsp (4) вид оптимизируемой функции & nbsp
Номер 3
Для решения задач оптимизации можно использовать встроенные функции MathCad:
Ответ:
& nbsp (1) увеличить & nbsp
& nbsp (2) miniimize & nbsp
& nbsp (3) корень () & nbsp
& nbsp (4) lsolver () & nbsp
«Платформа языковых школ» НГАСУ (Сибстрин) приглашает желающих изучать иностранные языки! В Институте международной деятельности НГАСУ (Сибстрин) открылась «Платформа языковых школ».Открыт набор всех программ для обучения иностранным языкам разного уровня: английский немецкий испанский С 15 февраля начинается работа групп. Выбери свой курс! Успей записаться в свою группу! Регистрация на курс https://forms.gle/ygaJPcSBP5E91N8Q8 Подробная информация или в ИМД главный корпус НГАСУ (Сибстрин), к. 223, Тел. (383) 266-16-64 с 10.00 до 17.00 (пн-пт). Электронная почта [email protected] Тел ./: Whatsapp: 8 (993) 016 74 64 Инна Михайловна. |
Стартовал прием заявок на Региональный конкурс – выставку детских творческих работ НГАСУ (Сибстрин) Ежегодно на базе Новосибирского государственного архитектурно-строительного университета (Сибстрин) проводится региональный конкурс – выставка детских творческих работ по рисунку «Традиции академической школы живописи, рисунка и композиции». В Конкурсе могут принимать участие, обучающиеся в образовательных учреждениях детей всех типов и видов, в возрасте от 10 до 18 лет.Возраст участников определяется на момент подачи заявки. Заявки на Конкурс подаются в оргкомитет с 20 января до 20 февраля 2021 года включительно. |
Режим работы университета в весеннем семестре 2021 года Уважаемые преподаватели, студенты, сотрудники университета! В соответствии с рекомендациями Министерства науки и высшего образования Российской Федерации, рекомендации Роспотребнадзора по профилактике новой коронавирусной инфекции в образовательных организациях высшего образования принято решение по реализации образовательного процесса в весеннем семестре 2021 года.С 1 по 7 февраля 2021 года учебный процесс будет осуществляться в дистанционном формате в соответствии с расписанием. С 8 февраля 2021 года университет возвращается к традиционному формату обучения. Учебный процесс по образовательным программам очной формы обучения будет реализовываться в смешанном формате: для основного потока студентов очно, и с использованием дистанционных технологий для студентов, находящихся за пределами РФ и не имеющей возможности вернуться в Новосибирск. |

