Построение графиков онлайн на миллиметровке. Строим график функций онлайн
К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?
Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.
Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.
Grafikus.ru
Grafikus.ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.
Вот неполный перечень заданий, с которыми этот сервис успешно справляется:
- Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т. д.
- Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
- Черчение 2D-графиков в полярных координатах.
- Построение 3D-поверхностей простых функций.
- Построение 3D-поверхностей параметрических функций.
Готовый результат открывается в отдельном окне. Пользователю доступны опции скачивания, печати и копирования ссылки на него. Для последнего придется авторизоваться на сервисе через кнопки соцсетей.
Координатная плоскость Grafikus.ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.
Самая сильная сторона Grafikus.ru — возможность построения 3D-графиков. В остальном он работает не хуже и не лучше, чем ресурсы-аналоги.
Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат – значения функции у = f (х) .
Графиком функции
Другими словами, график функции y = f (х) – это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .
На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 – 2х .
Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости).
С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
Например, для функции f(х) = х 2 – 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.
График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 – 2х принимает положительные значения при х и при х > 2 , отрицательные – при 0 наименьшее значение функция у = х 2 – 2х принимает при х = 1 .
Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно – с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу
Таблица выглядит следующим образом:
Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).
Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.
Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:
Соответствующие пять точек показаны на рис. 48.
На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.
Для обоснования своего утверждения рассмотрим функцию
.
Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.
Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом.
Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.
График функции у = |f(x)|.
Нередко приходится строить график функции
Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси
Пример 2. Построить график функции у = |х|.
Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).
Пример 3 . Построить график функции y = |x 2 – 2x|.
Сначала построим график функции y = x 2 – 2x. График этой функции – парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции
График функции y = f(x) + g(x)
Рассмотрим задачу построения графика функции y = f(x) + g(x). если заданы графики функций y = f(x) и y = g(x) .
если заданы графики функций y = f(x) и y = g(x) .
Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).
Пусть точки
 е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)
Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .
При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.
Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
Давайте разберемся, что же это за алгоритмы.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2 , изображен пунктиром).
2. Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.
(рис. 3) .
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4) .
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7) .
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8) .
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.
a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.
2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.
3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.
4) Окончательный график изображен на рисунке (рис. 11) .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.
Что такое график функций
Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .
Сервисы для построения графиков функций онлайн
Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.
Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.
Инструкция:
- Введите ваше уравнение в поле после знака «=».
- Нажмите кнопку «Построить график» .
Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.
Инструкция:
- Выберите необходимый способ задания графика.
- Введите уравнение.
- Задайте интервал.
- Нажмите кнопку «Построить» .
Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.
Инструкция:
- Найдите в списке необходимую вам функцию.
- Щелкните на нее левой кнопкой мыши
- При необходимости введите коэффициенты в поле «Функция:» .
- Нажмите кнопку «Построить» .
В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.
Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).
Инструкция:
- В левом столбце кликните правой кнопкой мыши по свободной строке.
- В нижнем левом углу нажмите на значок клавиатуры.
- На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
- График строится в реальном времени.
Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.
Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
Правила построения графиков – Лабораторный практикум
Все для эксперимента… > Обработка результатов эксперимента > Правила построения графиков
|
Graph Paper
Поделиться в PinterestPinterestПоделиться в FacebookFacebookПоделиться в PocketPocketПоделиться в TwitterTwitterПоделиться в EmailEmailПоделиться в FlipboardFlipboardРабочие листы
Печатные формы
Головоломки
Футболки
Математика
Бесплатно!
Основные математические рабочие листы
Рабочие листы с дробями
Словесные задачи
Другие рабочие листы
Измерения и преобразования
Образцы и головоломки
Раскраска по номерам
Праздники и сезоны
Раннее обучение
Печатные формы
Калькуляторы
Рабочие листы по математике по классам
Новости рабочих листов, бумага для крафтинга, бумага для рисования и графические задачи ландшафтный дизайн, архитектура или просто рисование.
 Все стили графической бумаги включают дюймовые и сантиметровые варианты. Все эти PDF-файлы предназначены для печати на бумаге размером 8,5 x 11 дюймов и могут служить шаблонами для других проектов.
Все стили графической бумаги включают дюймовые и сантиметровые варианты. Все эти PDF-файлы предназначены для печати на бумаге размером 8,5 x 11 дюймов и могут служить шаблонами для других проектов.Обычная миллиметровка
8 миллиметровок для печати
Чистая стандартная и метрическая миллиметровка (или «сетчатая бумага») различных размеров. Стандартные размеры: сетки 1/4, 1/5, 1/8 и 1/10 (4 сетки на дюйм, 5 сеток на дюйм, 8 сеток на дюйм и 10 сеток на дюйм соответственно). Метрические размеры – сетки 10 мм, 5 мм, 2,5 мм и 2 мм.
Обычная миллиметровая бумага
Инженерная миллиметровая бумага
8 Миллиметровая бумага для печати
Техническая миллиметровка в стандартном и метрическом масштабе, где интервалы на миллиметровке выделены для создания групп графических единиц с основными линиями, появляющимися через каждые четыре или пять делений в зависимости от масштаба. Стандартные размеры сетки 1/4′, 1/5′, 1/8′ и 1/10′. Метрические размеры с сеткой 10 мм, 5 мм, 2,5 мм и 2 мм. Шкала может немного отличаться из-за различий в принтерах.
Метрические размеры с сеткой 10 мм, 5 мм, 2,5 мм и 2 мм. Шкала может немного отличаться из-за различий в принтерах.
Инженерная миллиметровка
Печатная миллиметровка с блоком имен
24 Миллиметровая бумага для печати
Эта обычная миллиметровка для печати содержит блок имени и даты в верхней части страницы, что делает ее идеальной для домашних заданий.
Печатная миллиметровка с блоком имен
Координатные плоскости
84 Координатные плоскости для печати PDF-файлы
Нажмите здесь, чтобы увидеть пустые координатные плоскости, включая варианты с метками на оси или на краю сетки, а также версии с Метки квадрантов. Вы можете найти полные четырехквадрантные координатные плоскости, а также пустые одноквадрантные координатные плоскости в настройках макетов для решения нескольких домашних задач на одной странице.
Координатная плоскость для печати
Точечная бумага
32 Миллиметровая бумага Печатные материалы
Точечная бумага для печати представляет собой более легкий вариант стандартной миллиметровой бумаги. Он обеспечивает минимальное количество поддержки страницы, чтобы аккуратно выровнять ваши рисунки и уравнения, и вы можете использовать столько места, сколько вам нужно, чтобы создать координатную плоскость, график или другую структуру именно там, где вы хотите, на странице. Здесь есть полностью пустые страницы для печати в формате 8,5 x 11 дюймов, а также листы задач, предварительно настроенные с пространством для одного, двух, четырех или шести макетов.
Он обеспечивает минимальное количество поддержки страницы, чтобы аккуратно выровнять ваши рисунки и уравнения, и вы можете использовать столько места, сколько вам нужно, чтобы создать координатную плоскость, график или другую структуру именно там, где вы хотите, на странице. Здесь есть полностью пустые страницы для печати в формате 8,5 x 11 дюймов, а также листы задач, предварительно настроенные с пространством для одного, двух, четырех или шести макетов.
Бумага с точками
Бумага с большими точками
8 миллиметровок для печати
Эта версия чистой точечной бумаги имеет немного более крупные точки, чем версии с высоким разрешением в наборах выше. Если вам не нужна такая высокая точность, как на точечной бумаге выше, или вашему зрению просто нужен перерыв, попробуйте эти PDF-файлы для печати…
Изометрическая точечная бумага для печати отлично подходит для рисования… изоморфов? На самом деле, изометрическая точечная бумага отлично подходит для трехмерного рисования, перспективной визуализации или альтернативной визуализации обычных двухмерных графиков. Это может быть ваша сверхдешевая CAD-система, если вы умеете рисовать карандашом!
Это может быть ваша сверхдешевая CAD-система, если вы умеете рисовать карандашом!
Бумага с изометрическими точками
Бумага с точками для печати
Хотя технически это не миллиметровая бумага, вы также найдете на этой странице чистую бумагу с точками для печати. Бумага с точками имеет те же метрические и обычные размеры, что и миллиметровка, и есть варианты с очень мелкими точками или точками немного большего размера (и их легче увидеть), в зависимости от того, что вам нужно.
Точечная бумага с мелкими точками может быть полезна, если вы хотите, чтобы точки визуально «исчезали» на расстоянии, поэтому они могут быть очень полезны для создания графика или иллюстрации, где вы не хотите, чтобы сетка была явной часть фона.
Помимо обычной бумаги с декартовыми точками, бумага с изометрическими точками на этой странице является отличным инструментом для создания трехмерных эскизов или творческой работы над геометрическими узорами.
Что можно делать с миллиметровой бумагой
Существует множество учебных занятий, для которых можно использовать миллиметровую бумагу. Наиболее очевидным применением миллиметровой бумаги является построение графиков, но многие люди также предпочитают миллиметровую бумагу для практики рукописного ввода, поскольку вертикальные ячейки могут помочь обеспечить правильное расстояние между буквами. В крайнем случае, миллиметровка может служить заменой линейки для проведения измерений. Миллиметровая бумага также полезна для рисования, и многие архитектурные проекты могут быть концептуализированы или даже завершены с помощью простой миллиметровки. Миллиметровая бумага также является отличным способом поэкспериментировать с расстановкой мебели в комнатах, расстановкой растений в ландшафтном дизайне. Многие разработчики программного обеспечения также начинают с макетов дизайна приложений или пользовательских интерфейсов, набрасывая их на миллиметровой бумаге… Я знаю, что делаю! Вы обнаружите, что миллиметровка также является отличным способом выкладывать узоры для поделок, таких как вышивка, вышивка крестом или другие подобные действия по созданию узоров. И не забывайте, задолго до того, как появился MineCraft, было множество удивительных игр с ручкой и бумагой, в которые можно играть (и часто нужно играть) на миллиметровой бумаге. Dots and box — одна из таких игр, но вы найдете множество других, включая традиционные фавориты, такие как Battleship или Connect Four.
И не забывайте, задолго до того, как появился MineCraft, было множество удивительных игр с ручкой и бумагой, в которые можно играть (и часто нужно играть) на миллиметровой бумаге. Dots and box — одна из таких игр, но вы найдете множество других, включая традиционные фавориты, такие как Battleship или Connect Four.
Если вы художник или начинающий художник, миллиметровка может стать полезным инструментом для развития ваших навыков. Зентанглинг — одна из таких форм искусства, для которой миллиметровка особенно хорошо подходит из-за развития структурированных узоров. Независимо от того, как вы научитесь выражать себя, вы обнаружите, что миллиметровка — полезный способ отточить свое художественное мастерство.
Координатная плоскость
Поделиться в PinterestPinterestПоделиться в FacebookFacebookПоделиться в PocketPocketПоделиться в TwitterTwitterПоделиться в электронной почтеEmailПоделиться в FlipboardFlipboardРабочие листы
Печатные формы
Головоломки
Футболки
Математические рабочие листы
Go Ad Free!
Основные рабочие листы по математике
Фракционный рабочие листы
Проблемы с словесными.
 Рабочие листы к 9 классу0015
Рабочие листы к 9 классу0015Worksheet News
Пустые координатные плоскости на этой странице включают варианты с метками либо на оси, либо на краю сетки, а также версии с метками квадрантов. Вы можете найти полные 4-квадрантные координатные плоскости, а также пустые 1-квадрантные координатные плоскости в настройках макетов для решения нескольких домашних задач на одной странице.
Метки квадрантов координатной плоскости
8 Рабочие листы координатной плоскости
Эти координатные плоскости, которые можно распечатать, имеют каждый квадрант, помеченный более светлым фоновым текстом в сетке. Запутались со всеми этими римскими цифрами I, II, II, IV? Вы узнаете, где они.
Метки квадрантов координатной плоскости
Пустые рабочие страницы координатной плоскости
28 рабочих листов координатной плоскости
Распечатайте эти пустые страницы координат с именами и блоками дат, когда у вас есть уравнения для построения графиков для домашнего задания! Домашнее задание, которое вы сдаете на уроке геометрии или алгебры, будет выглядеть академически проницательным.
Пустые рабочие страницы координатной плоскости
Координатная плоскость без меток
8 Рабочие листы координатной плоскости
Пригодные для печати координатные плоскости в дюймах и метрических единицах разных размеров, отлично подходят для построения диаграмм рассеяния, построения уравнений, геометрических задач или других подобных математических задач. Это полные четырехквадрантные координатные плоскости, пустые без нумерации осей. Вспомните урок геометрии в 7-м классе? Это страница графической бумаги для вас. Стандартные размеры сетки 1/4 дюйма, 1/5 дюйма, 1/8 дюйма и 1/10 дюйма. Метрические размеры с сеткой 1 сантиметр, 5 миллиметров, 2,5 миллиметра и 2 миллиметра.
Координатная плоскость без меток
Координатная плоскость с маркированной осью
8 Рабочие листы координатной плоскости
Координатные плоскости в дюймах и метрических единицах различных размеров для печати, отлично подходят для построения уравнений, геометрических задач или других подобных математических задач. Это полные четырехквадрантные графики. Эти координатные плоскости имеют метки непосредственно вдоль оси x и оси y.
Это полные четырехквадрантные графики. Эти координатные плоскости имеют метки непосредственно вдоль оси x и оси y.
Координатная плоскость с помеченной осью
Координатная плоскость с помеченными ребрами
8 Рабочие листы координатных плоскостей
Координатные плоскости различных размеров в дюймах и метрических единицах, пригодные для печати, отлично подходят для построения уравнений, геометрических задач или других подобных математических задач. Это полные четырехквадрантные графики. Эти координатные плоскости имеют метки осей x и y вдоль внешнего края страницы.
Координатная плоскость с помеченными ребрами
Координатная плоскость Квадрант 1
24 Координатная плоскость Рабочие листы
Эта распечатываемая координатная плоскость с показанным только квадрантом 1 отлично подходит для ознакомления с графическими упражнениями в 3-м, 4-м или 5-м классе или в любое время до того, как будут введены отрицательные числа.
Координатная плоскость Квадрант 1
Печатные пустые страницы координатных плоскостей
Коллекция координатных плоскостей PDF для печати на этой странице содержит ряд различных макетов, которые должны соответствовать потребностям большинства классов средней и старшей школы по алгебре. Координатные плоскости имеют размеры в обычных или метрических единицах, как и чистая миллиметровка на сайте.
Существуют версии координатной плоскости с метками осей и без них, а также версии, в которых номера квадрантов отображаются светлым текстом на фоне каждого квадранта. Существуют также версии координатной плоскости с метками на краях, а не на каждой оси, что иногда может немного упростить графические уравнения.
Что такое квадранты координатной плоскости?
Поскольку координатная плоскость естественным образом делится осями x и y, она создает четыре прямоугольные области, называемые квадрантами. Каждый квадрант соответствует области, содержащей точки с одинаковым положительным или отрицательным знаком.


 Чтобы различать линии, можно одну проводить сплошной, другую –
пунктирной, третью – штрихпунктирной и т.п. Допустимо выделять линии различным цветом. Вовсе не обязательно, чтобы в точке пересечения осей было начало координат 0:0). По каждой из осей можно отображать только интервалы измерения исследуемых величин.
Чтобы различать линии, можно одну проводить сплошной, другую –
пунктирной, третью – штрихпунктирной и т.п. Допустимо выделять линии различным цветом. Вовсе не обязательно, чтобы в точке пересечения осей было начало координат 0:0). По каждой из осей можно отображать только интервалы измерения исследуемых величин.
 д.), либо делается сравнение предсказаний теории с результатами эксперимента.
д.), либо делается сравнение предсказаний теории с результатами эксперимента.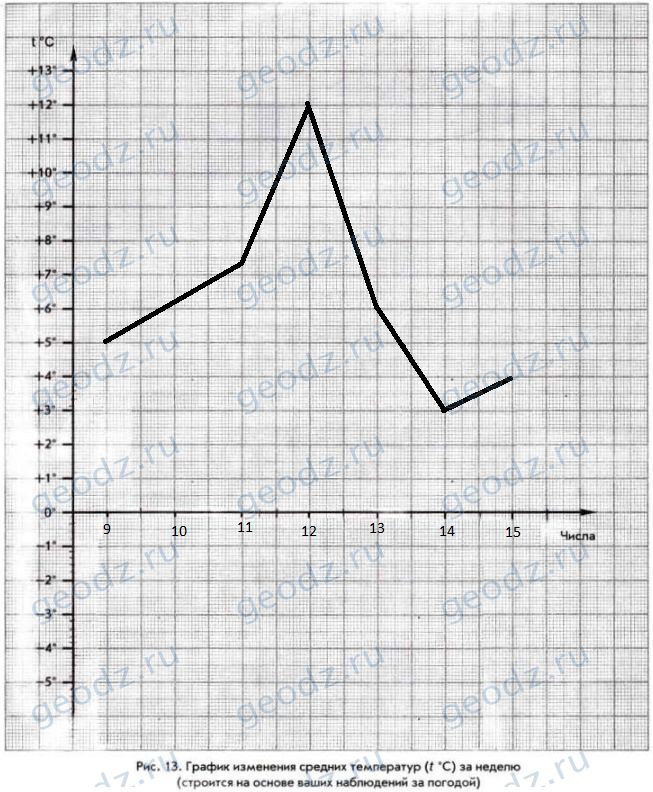 На графике в этом случае изображается кривая, полученная со средним значением параметра, и полоса, ограниченная двумя расчетными кривыми для максимального и минимального значений параметра.
На графике в этом случае изображается кривая, полученная со средним значением параметра, и полоса, ограниченная двумя расчетными кривыми для максимального и минимального значений параметра.