| 3. Сформулируйте вопросы по
графикам? (Запись вопросов на доске) |
1. Способы представления
функции(словесный, аналитический – формулой,
табличный, графический). 2. Что такое график? (graphikos – начертательный(греч), чертёж наглядно что-то изображающий, это линия, построенная определённым образом в определённой системе координат). 3. График и график функции – это равнозначные понятия? Какое является более общим? (График функции – это линия, дающая цельное представление о характере изменения функции по мере изменения аргумента, каждому значению х соответствует одно и только одно значение y.) 4. К чему относятся диаграммы? (Диаграммы – к
графикам, например, диаграмма состояния,
диаграмма растяжения материала. 5. Зачем нужны графики? Как вы представляете параболу? Формулой? Линией? Значениями? (Наглядность, информативность, график-это своеобразная фотография функции.) 6. Какие требования мы предъявляем к графику? Что входит в понятие графика? (Оси координат, их обозначение, единицы измерения, масштаб, точки, название.) 7. Всегда ли вы встречаете числовые значения? (График без числовых значений называется эскизным.) 8. Какие графики встречаются в физике? (Графики движения, скорости, ускорения, изопроцессов, ВАХ….) 9. Может ли график иметь сразу несколько названий? (Изотерма, гипербола, график изотермического сжатия.) 10.Как графики используется в физике? (Результаты
эксперимента, сравнение теории и практики,
чтение, определение величин заданных явно и
неявно, решение задач. |
4. Очень часто графическое решение легче, чем аналитическое. Докажем на примере двух задач. | Решение задач: Задача 1. От движущегося поезда отцепляют последний вагон. Поезд продолжает двигаться с той же скоростью. Сравните пути, пройденные поездом и вагоном к моменту остановки вагона. Ускорение вагона можно считать постоянным. Аналитическое решение. t – время движения; Графическое решение Задача 2. Поезд прошел между станциями путь s=17 км со
средней скоростью vср = 60 км/ч. Решение: S = (t + (t – t S = vсрt t = S/vср=17/60 V= |
1. На рисунке представлена зависимость
координаты центра шара, подвешенного на пружине,
от времени. Период колебаний равен:
2.
3. На рисунке показан процесс изменения состояния идеального газа. Внешние силы совершили над газом работу, равную 5·104 Дж. Какое количество теплоты отдает газ в этом процессе? Ответ выразите в килоджоулях (кДж). Ответ: _______________. 4.
10 моль идеального одноатомного газа охладили,
уменьшив давление в 3 раза. Затем газ нагрели до
первоначальной температуры 300 К (см. |
Графики движения по физике. Равноускоренное движение. Закон равноускоренного движения
Для построения этого графика на оси абсцисс откладывают время движения, а на оси ординат – скорость (проекцию скорости) тела. В равноускоренном движении скорость тела с течением времени изменяется. Если тело движется вдоль оси О х, зависимость его скорости от времени выражается формулами
v x =v 0x +a x t и v x =at (при v 0x = 0).
Из этих формул видно, что зависимость v х от t линейная, следовательно, графиком скорости является прямая линия. Если тело движется с некоторой начальной скоростью, эта прямая пересекает ось ординат в точке v 0x . Если же начальная скорость тела равна нулю, график скорости проходит через начало координат.
Графики скорости прямолинейного равноускоренного движения изображены на рис. 9. На этом рисунке графики 1 и 2 соответствуют движению с положительной проекцией ускорения на ось О х (скорость увеличивается), а график 3 соответствует движению с отрицательной проекцией ускорения (скорость уменьшается). График 2 соответствует движению без начальной скорости, а графики 1 и 3 – движению с начальной скоростью v ox . Угол наклона a графика к оси абсцисс зависит от ускорения движения тела. Как видно из рис. 10 и формулы (1.10),
График 2 соответствует движению без начальной скорости, а графики 1 и 3 – движению с начальной скоростью v ox . Угол наклона a графика к оси абсцисс зависит от ускорения движения тела. Как видно из рис. 10 и формулы (1.10),
tg=(v x -v 0x)/t=a x .
По графикам скорости можно определить путь, пройденный телом за промежуток времени t. Для этого определим площадь трапеции и треугольника, закрашенных на рис. 11.
В выбранном масштабе одно основание трапеции численно равно модулю проекции начальной скорости v 0x тела, а другое ее основание – модулю прокции его скорости v х в момент времени t. Высота трапеции численно равна длительности промежутка времени t. Площадь трапеции
Использовав формулу (1.11), после преобразований находим, что площадь трапеции
S=v 0x t+at 2 /2.
путь, пройденный в прямолинейном равноускоренном движении с начальной скоростью, численно равен площади трапеции, ограниченной графиком скорости, осями координат и ординатой, соответствующей значению скорости тела в момент времени t.
В выбранном масштабе высота треугольника (рис. 11,б) численно равна модулю проекции скорости v х тела в момент времени t, а основание треугольника численно равно длительности промежутка времени t. Площадь треугольника S=v x t/2.
Использовав формулу 1.12, после преобразований находим, что площадь треугольника
Правая часть последнего равенства представляет собой выражение, определяющее путь, пройденный телом. Следовательно, путь, пройденный в прямолинейном равноускоренном движении без начальной скорости, численно равен площади треугольника, ограниченного графиком скорости, осью абсцисс и ординатой, соответствующей скорости тела в момент времени t.
Вопросы.
1. Запишите формулу, по которой можно рассчитать проекцию вектора мгновенной скорости прямолинейного равноускоренного движения, если известны: а) проекция вектора начальной скорости и проекция вектора ускорения; б) проекция вектора ускорения при том, что начальная скорость равна нулю.
2. Что представляет собой график проекции вектора скорости равноускоренного движения при начальной скорости: а) равной нулю; б) не равной нулю?
3. Чем сходны и чем отличаются друг от друга движения, графики которых представлены на рисунках 11 и 12?
В обоих случаях движение происходит с ускорением, однако в первом случае ускорение положительно, а во-втором отрицательно.
Упражнения.
1. Хоккеист слегка ударил клюшкой по шайбе, придав ей скорость 2 м/с. Чему будет равна скорость шайбы через 4 с после удара, если в результате трения о лёд она движется с ускорением 0,25 м/с 2 ?
2. Лыжник съезжает с горы из состояния покоя с ускорением, равным 0,2 м/с 2 . Через какой промежуток времени его скорость возрастёт до 2 м/с?
3. В одних и тех же координатных осях постройте графики проекции вектора скорости (на ось Х, сонаправленную с вектором начальной скорости) при прямолинейном равноускоренном движении для случаев: а) v ox = 1м/с, a x = 0,5 м/с 2 ; б) v ox = 1м/с, a x = 1 м/с 2 ; в) v ox = 2 м/с, a x = 1 м/с 2 .
Масштаб во всех случаях одинаков: 1см- 1м/с; 1см – 1с.
4. В одних и тех же координатных осях постройте графики проекции вектора скорости (на ось Х, сонаправленную с вектором начальной скорости) при прямолинейном равноускоренном движении для случаев: а) v ox = 4,5 м/с, a x = -1,5 м/с 2 ; б) v ox = 3 м/с, a x = -1 м/с 2
Масштаб выберите сами.
5. На рисунке 13 представлены графики зависимости модуля вектора скорости от времени при прямолинейном движении двух тел. С каким по модулю ускорением движется тело I? тело II?
Равномерное прямолинейное движение – это частный случай неравномерного движения.
Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.
V cp = s / t
– это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:
Проекция вектора скорости на ось ОХ:
V x = x’
это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).
– это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:
Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:
Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:
V x = v 0x ± a x t
Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).
Рис. 1.15. Зависимость ускорения тела от времени.
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).
Рис. 1.16. Зависимость скорости тела от времени.
График зависимости скорости от времени (рис. 1.16) показывает, что
При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).
Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:
0a = v 0 bc = v
Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:
В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).
График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.
Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.
Рис. 1.18. Зависимость перемещения тела от времени.
Скорость тела в данный момент времени t 1 равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:
Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:
Поможет нам вывести формулу для проекции перемещения:
Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то будет выглядеть следующим образом:
Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При а x
При а x
На данном уроке мы с вами рассмотрим важную характеристику неравномерного движения – ускорение. Кроме того, мы рассмотрим неравномерное движение с постоянным ускорением. Такое движение еще называется равноускоренным или равнозамедленным. Наконец, мы поговорим о том, как графически изображать зависимости скорости тела от времени при равноускоренном движении.
Домашнее задание
Решив задачи к данному уроку, вы сможете подготовиться к вопросам 1 ГИА и вопросам А1, А2 ЕГЭ.
1. Задачи 48, 50, 52, 54 сб. задач А.П. Рымкевич, изд. 10.
2. Запишите зависимости скорости от времени и нарисуйте графики зависимости скорости тела от времени для случаев, изображенных на рис. 1, случаи б) и г). Отметьте на графиках точки поворота, если такие есть.
3. Рассмотрите следующие вопросы и ответы на них:
Вопрос. Является ли ускорение свободного падения ускорением, согласно данному выше определению?
Ответ. Конечно, является.
Ускорение свободного падения – это ускорение тела, которое свободно падает с некоторой высоты (сопротивлением воздуха нужно пренебречь).
Вопрос. Что произойдет, если ускорение тела будет направлено перпендикулярно скорости движения тела?
Ответ. Тело будет двигаться равномерно по окружности.
Вопрос. Можно ли вычислять тангенс угла наклона, воспользовавшись транспортиром и калькулятором?
Ответ. Нет! Потому что полученное таким образом ускорение будет безразмерным, а размерность ускорения, как мы показали ранее, должно иметь размерность м/с 2 .
Вопрос. Что можно сказать о движении, если график зависимости скорости от времени не является прямой?
Ответ. Можно сказать, что ускорение этого тела меняется со временем. Такое движение не будет являться равноускоренным.
Рисунок 1. Графики равномерного движения. Автор24 – интернет-биржа студенческих работ
Простейшим видом движения является равномерное движение. Его можно зафиксировать тогда, когда ускорение тела в любой момент времени будет равно нулю. Другими словами, равномерное движение представляют в виде определенного идеального положения тела, когда его скорость будет одной и той же в любой момент времени. При прохождении тела равных промежутков расстояния за одинаковые промежутки времени движение приобретает признаки равномерного прямолинейного передвижения. В реальной жизни подобные характеристики практически не встречаются.
Его можно зафиксировать тогда, когда ускорение тела в любой момент времени будет равно нулю. Другими словами, равномерное движение представляют в виде определенного идеального положения тела, когда его скорость будет одной и той же в любой момент времени. При прохождении тела равных промежутков расстояния за одинаковые промежутки времени движение приобретает признаки равномерного прямолинейного передвижения. В реальной жизни подобные характеристики практически не встречаются.
Определение 1
Путь – длина траектории, по которой в течение определенного промежутка времени двигалось конкретное тело.
Определение 2
Перемещение – расстояние между начальной и конечной точкой траектории движения тела.
Путь и перемещение – это разные понятия, так как путь является скалярной величиной, а перемещение – векторной величиной. При этом модуль вектора перемещения равняется отрезку, соединяющего начальную и конечную точку траектории движения тела.
Скорость равномерного движения
Определение 3
Скоростью равномерного движения называют модуль вектора, который вычисляется по определенной формуле. Она гласит, что вектор будет равен отношению пути, который пройден телом, ко времени, затраченному на его прохождение.
Она гласит, что вектор будет равен отношению пути, который пройден телом, ко времени, затраченному на его прохождение.
При равномерном движении совпадает направление вектора скорости с направлением движения. Это правило необходимо учитывать при построении графика равномерного движения. Перемещение и путь при подобном движении будут иметь одинаковые значения.
К равномерному движению относят также состояние покоя. В этом случае тело проходит равные расстояния за одинаковые временные промежутки. В состоянии покоя все значения будут равны нулю. При равномерном движении пройденный путь складывается из следующих составных показателей:
- начальной координаты;
- произведения скорости тела на время движения.
Графики равномерного движения
При построении графика равномерного движения с изменением скорости во времени получится прямая, которая будет проходить параллельно линии оси абсцисс. Площадь получившегося прямоугольника равняется длине пути, который пройден телом за конкретное время. То есть площадь прямоугольника будет равна произведению всех его сторон.
То есть площадь прямоугольника будет равна произведению всех его сторон.
После построения графика зависимости пройденного пути от времени, вычисляют скорость, с которой двигалось тело. В этом случае график имеет прямую линию, которая проведена из начала координат. Необходимым значением модуля вектора скорости станет тангенс угла наклона прямой по отношению к оси абсцисс. При составлении графика равномерного движения ось абсцисс является осью времени. Сильный наклон графика говорит о том, что скорость тела большая.
В физике используются следующие обозначения равномерного движения:
Оно показывает неизменность скорости, которая выражена в виде константы.
Равномерное движение проходит по:
- криволинейной траектории;
- прямолинейной траектории.
Равномерное движение описывают по формуле:
В такой формуле $s$ – этот путь, который прошло тело от начальной точки отсчета, $t$ – время тела в пути, а $s_0$ – значение пути в начальный момент времени.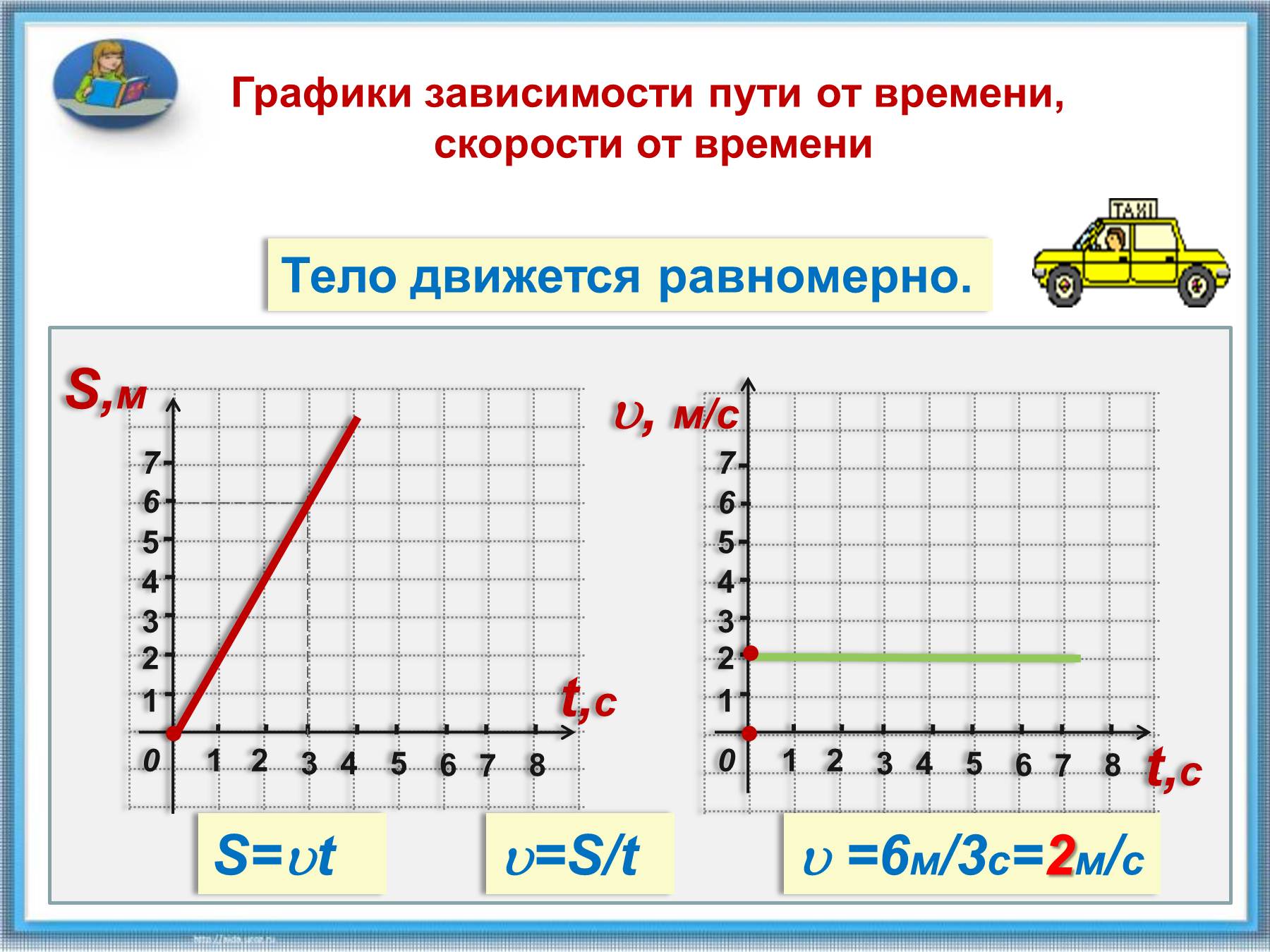
Прямолинейное движение
Замечание 1
Движение называют прямолинейным, если оно происходит по прямой линии.
Траектория прямолинейного движения – прямая линия. При скорости равномерного движения нет зависимости от времени, так как и в любой точке траектории она направлена аналогично перемещению тела. Иными словами, вектор перемещения совпадает по направлению с вектором скорости. Средняя скорость в любой промежуток времени равна мгновенной скорости.
Cкорость равномерного прямолинейного движения показывает значение перемещения материальной точки за единицу времени.
При таком движении полное ускорение выражается по формуле:
В международной системе измерений единицей ускорения является ускорение, при котором скорость тела за каждую секунду изменяется на 1 метр.
Равнопеременное движение
Частным случаем неравномерного движения тела является равномерное прямолинейное движение.
Равнопеременное движение представляет собой такое движение, когда скорость материальной точки изменяется одинаково за любые равные промежутки времени. Ускорение тела при равнопеременном движении остается на неизменном уровне по направлению и по модулю.
Ускорение тела при равнопеременном движении остается на неизменном уровне по направлению и по модулю.
Равнопеременное движение бывает двух видов: равноускоренным и равнозамедленным.
Движение тела или материальной точки с положительным ускорением считается равноускоренным. При таком способе движения оно может совершать разгон с ускорением на неизменном уровне.
Движение тела с отрицательным ускорением называют равнозамедленным. При подобном виде движения тело замедляется на равномерном уровне.
Среднюю скорость переменного движения возможно определить делением перемещения тела на время, в течение которого это перемещение совершалось. Единицей измерения средней скорости является м/с.
Мгновенная скорость и ускорение
Скорость тела или материальной точки называют мгновенной, если она есть в конкретный момент времени или в заданной точке траектории движения. Это значение называют предельным, поскольку к нему стремится средняя скорость тела при бесконечном уменьшении промежутка времени.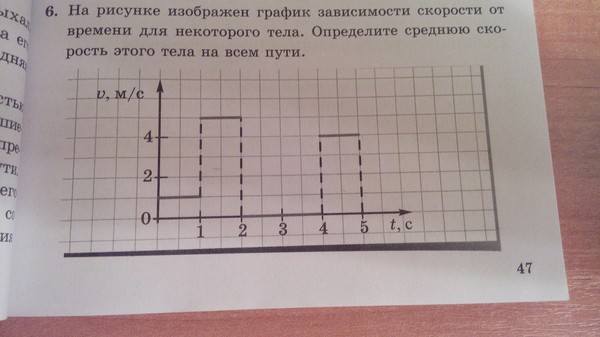 Его обозначают $Δt$.
Его обозначают $Δt$.
Мгновенная скорость выражается по следующей формуле:
Величина, которая определяет изменения в наборе скорости тела, называется ускорением. Это предельные значения величины и к ней стремится изменения скорости при бесконечном уменьшении промежутка времени $Δt$.
Перемещение при равномерном прямолинейном движении рассчитывается по формуле:
Величина $υx$ – проекция скорости на ось Х.
Отсюда следует, что закон равномерного прямолинейного движения имеет следующий вид:
В начальный момент времени $xo = 0$, поэтому остальные значения приобретают вид.
Помогите начертить график по физике ax (t) , vx (t) , sx (t) , x (t) . Не понимаю что нужно
Перевести в систему си l= 46 мм l= 34 дм S= 51 см2 S= 89 км2
1 нужен пожалуйста быстрее (казахская физика)
Ребят срочно помогите решить лабораторку пожалуйста Даю 50 баллов
1. Какая энергия называется внутренней? 2. Каким образом можно изменить внутреннюю энергию тела? 3. О чем говорит первый закон термодинамики? 4. Почем
… у работа и количество теплоты являются мерой изменения внутренней энергии? •5. Объясните, почему работа газа по изменению его объема отличается от работы внешней силы, действующей на поршень, знаком и не отличается по модуло? 6. Почему иногда подпрыгивает крышка чайника, когда в нем кипит вода? *7. В цилиндре под поршнем находится газ. В каком случае для на гревания этого газа до определенной температуры потребуется меньше энергии, когда поршень закреплен или когда он подвижен? Почему? *8. Справедлив ли закон сохранения энергии для тела, упавшего в песок с некоторой высоты? *9. Выполняется ли закон сохранения энергии при падении камня в воде? •10. Что произойдет, если в цилиндр с поршнем положить кусочек ваты, пропитанной спиртом, и резко вдвинуть поршень в цилиндр? Объясните. *11. Молоток нагревается, когда им бьют по наковальне и когда он лежит на солнце. Как вы думаете, почему?
О чем говорит первый закон термодинамики? 4. Почем
… у работа и количество теплоты являются мерой изменения внутренней энергии? •5. Объясните, почему работа газа по изменению его объема отличается от работы внешней силы, действующей на поршень, знаком и не отличается по модуло? 6. Почему иногда подпрыгивает крышка чайника, когда в нем кипит вода? *7. В цилиндре под поршнем находится газ. В каком случае для на гревания этого газа до определенной температуры потребуется меньше энергии, когда поршень закреплен или когда он подвижен? Почему? *8. Справедлив ли закон сохранения энергии для тела, упавшего в песок с некоторой высоты? *9. Выполняется ли закон сохранения энергии при падении камня в воде? •10. Что произойдет, если в цилиндр с поршнем положить кусочек ваты, пропитанной спиртом, и резко вдвинуть поршень в цилиндр? Объясните. *11. Молоток нагревается, когда им бьют по наковальне и когда он лежит на солнце. Как вы думаете, почему?
Серебряный брусок массой 3 кг нагрели от 60°С и расплавили. На сколько при этом увеличилась внутренняя энергия бруска?
На сколько при этом увеличилась внутренняя энергия бруска?
Виготовлений солдатик масою 20 г охолонув від 232°С до 32°С передавши навколишнім тілам 0,92кДж теплоты.З якого матеріала виготовлений солдатик?Народ … срочно дам 20 балов!!!!!!!!!!!!
Два екскурсійних автобуси зі школярами повинні були відправитись на екскурсію до Умані, але один із автобусів затримався із відправленням. Коли цей а … втобус виїхав у путь, перший автобус знаходився вже на відстані 20 км від Білої Церкви. За інтервал часу, протягом якого автобус, що запізнився, проїхав відрізок шляху у 20 км, перший автобус проїхав 16 км. Таким чином, на проходження кожного кілометра другий автобус витрачав на 12с менше, ніж пе, әший. На якій відстані від місця відправлення другий автобус зміг наздогнати перший? Чому дорівнювали швидкості автобусів?
ребят, прошу срочно
Скільки енергії витратили на нагрівання води масою 0,75кг від 20 до 100 і подальшого утворення пари массою250г відповідь у кДж
ОЧЕНЬ СРОЧНО!!! НЕ МОГУ ПОНЯТЬ, КАК РЕШИТЬ, А РАБОТУ УЖЕ НУЖНО СДАВАТЬ, ПОМОГИТЕ, УМОЛЯЮ И прошу, с объяснением, т.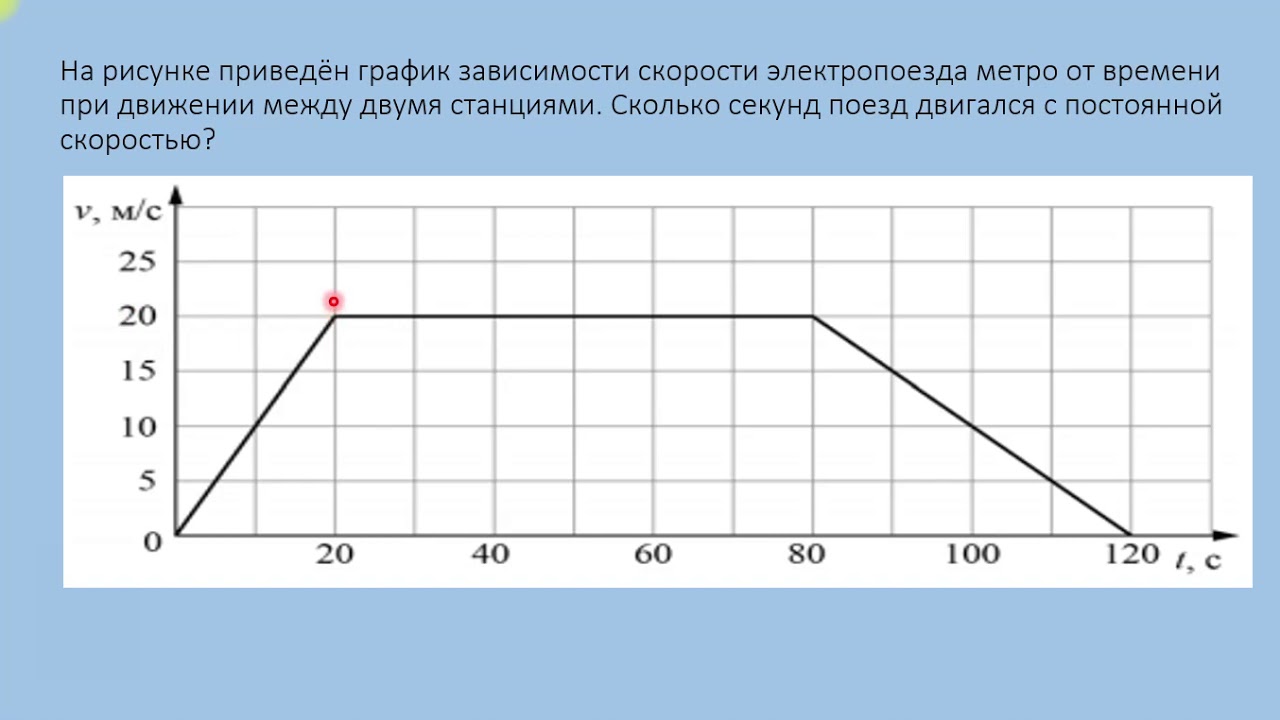 е. решение задачи с помощью сравне
… ния двух формул, как обычно делают в школах прошу, помогите
е. решение задачи с помощью сравне
… ния двух формул, как обычно делают в школах прошу, помогите
Задания по физике: Графики изопроцессов
Задания по физике: Графики изопроцессов |
Пример задания по теме “Графики изопроцессов.” |
Вариант 10- 6.
Показать материал полностью и распечатать.
При трудностях чтения смените кодировку в броузере: Вид > Кодировка > Кириллица (Windiws)
Карточки этого задания можно использовать дважды.
Первый раз по ним мы учимся определять по графикам изопроцессы, считывать значения величин и, используя полученные данные, перестраивать графики из одних осей координат в другие. При этом предполагается, что такие величины, как масса газа и его химический состав не меняются. Основное задание ученику здесь звучит так: “Найдите по данному графику значения основных параметров газа (p, V, T) в каждой точке графика. Постройте графики данных вам процессов в осях координат p(V), p(T) и V(T). Дайте название каждого изопроцесса на этих графиках”.
При этом предполагается, что такие величины, как масса газа и его химический состав не меняются. Основное задание ученику здесь звучит так: “Найдите по данному графику значения основных параметров газа (p, V, T) в каждой точке графика. Постройте графики данных вам процессов в осях координат p(V), p(T) и V(T). Дайте название каждого изопроцесса на этих графиках”.
Поскольку на карточке имеются избыточные данные, например, химический состав газа, для сильного ученика мы имеем возможность сформулировать дополнительные задания. В отдельных случаях можно дать отдельное задание повышенной сложности, например, на диаграмме p(V) начертите график процесса в виде окружности и пустьна нем ученик определит точки максимума и минимума для каждого из трех параметров p, V, T. А можно пойти и дальше, перестроить эту окружность в другие оси координат.
Использование внесистемных единиц тоже часть нашей задумки. Здесь мы показываем пример, когда переходить к системе единиц СИ
нерационально, только затрудняет процесс вычислений и все. Расчет в технических единицах много проще. Разумеется, если вы даете дополнительные задания по карточкам, например, найти количество вещества в данном примере, переход к системе СИ обязателен, что вашему ученику должно быть по силам. Рациональность действий должна часто звучать на ваших уроках и она касается не только приемов решения задач, но и других аспектов деятельности ученика.
Ответы в такого рода заданиях учащиеся сдают нам в виде таблицы; в этом случае проверить решение не составляет труда. Можно эту процедуру доверить и самим учащимся. Учительское время и силы – это золотой запас, не тратье его понапрасну!
Ответы к задачам 10 – 6.
| Карточка | 10 – 6 – 1 | 10 – 6 – 2 | 10 – 6 – 3 | 10 – 6 – 4 | 10 – 6 – 5 | 10 – 6 – 6 | 10 – 6 – 7 | 10 – 6 – 8 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Точка графика | A | B | C | A | B | C | A | B | C | A | B | C | A | B | C | A | B | C | A | B | C | A | B | C |
| Давление, p (атм) | 2 | 8 | 2 | 6 | 15 | 15 | 5 | 1 | 1 | 3 | 9 | 9 | 22,5 | 7,5 | 7,5 | 3 | 3 | 8 | 7 | 8 | 4 | 5 | 12,5 | 5 |
| Объем, V (л) | 1 | 1 | 4 | 9 | 3,6 | 9 | 2 | 10 | 2 | 30 | 30 | 10 | 1 | 3 | 1 | 80 | 30 | 30 | 18 | 9 | 9 | 4 | 4 | 10 |
| Температура, Т (К) | 150 | 600 | 600 | 200 | 200 | 500 | 300 | 300 | 60 | 200 | 600 | 200 | 900 | 900 | 300 | 800 | 300 | 800 | 400 | 400 | 200 | 200 | 500 | 500 |
Второй
раз мы используем эти карточки при изучении термодинамики. Задание такое: “Определить на каждом из участков данных вам графиков изопроцессов характер поведения основных параметров газа (p, V, T) – возрастание, убывание, неизменность. Определить знаки (+, -, 0) основных термодинамических величин A’,Q, ΔU”. В этом задании мы актуализируем в сознании учеников основные зависимости величин в термодинамике. Работа не такая простая, как кажется на первый взгляд. Так на карточках, где дана диаграмма в осях p(V) неочевидно поведение температуры, от которой в свою очередь зависит поведение внутренней энергии. Количество теплоты – величина не определяемая по поведению одного из параметров, требуется обратиться к первому закону термодинамики для определения характера ее поведения и пр.
Работа с такими карточками позволяет организовать шаталовское “многократное повторение материала” и показать эрдниевскую “диалектику взаимосвязи и взаимозависимости величин”. Малозаметные вещи… Про стену мы тоже говорим “кирпичная”, но главное-то в ней – связующий цемент.
Графики, таблицы, матрицы мы активно используем в своей работе. Они намного информативнее уравнений. Одновременное видение большой совокупности данных неизбежно рождает желание к их сравнению и анализу, часто даже на подсознательном уровне. Подсознательном… А ведь в этом ничего дурного нет. Наоборот, перенесение в область подсознания часть работы мозга – вот еще мало используемый резерв для снижения нагрузки учащихся. Пусть ум занимается не всей работой, а только той ее частью, которая подсознанию недоступна в виду ее сложности.
| Карточка | 10 – 6 – 1 | 10 – 6 – 2 | 10 – 6 – 3 | 10 – 6 – 4 | 10 – 6 – 5 | 10 – 6 – 6 | 10 – 6 – 7 | 10 – 6 – 8 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Участок графика | AB | BC | CA | AB | BC | CA | AB | BC | CA | AB | BC | CA | AB | BC | CA | AB | BC | CA | AB | BC | CA | AB | BC | CA |
| Поведение давления | ↑ | ↓ | = | ↑ | = | ↓ | ↓ | = | ↑ | ↑ | = | ↓ | ↓ | = | ↑ | = | ↑ | ↓ | ↑ | ↓ | = | ↑ | ↓ | = |
| Поведение объема | = | ↑ | ↓ | ↓ | ↑ | = | ↑ | ↓ | = | = | ↓ | ↑ | ↑ | ↓ | = | ↓ | = | ↑ | ↓ | = | ↑ | = | ↑ | ↓ |
| Поведение температуры | ↑ | = | ↓ | = | ↑ | ↓ | = | ↓ | ↑ | ↑ | ↓ | = | = | ↓ | ↑ | ↓ | ↑ | = | = | ↓ | ↑ | ↑ | = | ↓ |
| Знак работы газа | 0 | + | – | – | + | 0 | + | – | 0 | 0 | – | + | + | – | 0 | – | 0 | + | – | 0 | + | 0 | + | – |
| Знак количества теплоты | + | + | – | – | + | – | + | – | + | + | – | + | + | – | + | – | + | + | – | – | + | + | + | – |
| Знак изменения внутренней энергии | + | 0 | – | 0 | + | – | 0 | – | + | + | – | 0 | 0 | – | + | – | + | 0 | 0 | – | + | + | 0 | – |
Графики важнейших функций и их преобразования – Математика – Теория, тесты, формулы и задачи
На этой странице представлены графики важнейших функций, изучаемых в школьном курсе математики. Также представлены примеры преобразования этих графиков в различных типичных ситуациях (рассмотрены случаи когда графики смешаются вдоль осей, симметрично отражаются относительно различных осей). Представлен также вид некоторых графиков функций с модулями. Знание того, как выглядят графики основных математических функций, а также того, как они преобразовываются в различных ситуациях, может очень помочь при решении различных сложных задач на экзаменах.
Изучать графики основных функций и их преобразования онлайн:
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
- Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Графики. Часть третья | Кинематика | Физика
График зависимости ускорения тела от времени не пользуется таким же почетом и уважением, как ранее изученные нами графики движения. Тем не менее давайте поговорим и о нем.
В отличие от предыдущих графиков, график зависимости ускорения от времени не дает какой-то существенной информации о движении тела. Мы не можем сказать, куда двигался объект и насколько быстро он двигался. Даже нельзя сказать, ускорялся он или, наоборот, замедлялся, потому что это зависит не только от знака ускорения, но и от знака начальной скорости, а он нам неизвестен.
Но какую же все-таки информацию можно получить из данного графика? Во-первых, мы можем сказать, чему было равно изменение скорости.
Вспомним формулу для расчета ускорения и выразим из нее \varDelta{\vec{v}}:
\vec{a}=\dfrac{\varDelta{\vec{v}}}{\varDelta{t}}\rArr\varDelta{\vec{v}}=\vec{a}\varDelta{t}
Теперь обратимся к нашему рисунку. Скорее всего, вы уже заметили, что площадь прямоугольника, находящегося на отрезке от нулевой до второй секунды, численно совпадает с изменением скорости за это время:
S_\Box=\textcolor{#E20606}{ab}=\lvert\vec{a}\rvert\varDelta{t}=\lvert\varDelta{\vec{v}}\rvert
Если тело движется равнопеременно, то есть с постоянным ускорением, мы можем найти изменение его скорости через график зависимости ускорения от времени.3
|
Графики движения – Резюме – Гипертекст по физике
- … падающие
- графики движения
- кинематические вычисления…
© 1998–2021 Гленн Элерт
Автор, иллюстратор, веб-мастер
Нет условий постоянный.
- Механика
- Кинематика
- Движение
- Расстояние и перемещение
- Скорость и скорость
- Разгон
- Уравнения движения
- Свободное падение
- Графики движения
- Кинематика и расчет
- Кинематика в двух измерениях
- Снаряды
- Параметрические уравнения
- Dynamics I: Force
- Силы
- Сила и масса
- Действие-реакция
- Масса
- Динамика
- Статика
- Трение
- Силы в двух измерениях
- Центростремительная сила
- Кодовые рамки
- Энергия
- Работа
- Энергия
- Кинетическая энергия
- Потенциальная энергия
- Сохранение энергии
- Мощность
- Простые станки
- Dynamics II: Импульс
- Импульс и импульс
- Сохранение импульса
- Импульс и энергия
- Импульс в двух измерениях
- Вращательное движение
- Кинематика вращения
- Инерция вращения
- Вращательная динамика
- Вращательная статика
- Угловой момент
- Энергия вращения
- Прокат
- Вращение в двух измерениях
- Сила Кориолиса
- Планетарное движение
- Геоцентризм
- Гелиоцентризм
- Вселенская гравитация
- Орбитальная механика I
- Гравитационная потенциальная энергия
- Орбитальная механика II
- Плотность вытянутых тел
- Периодическое движение
- Пружины
- Простой генератор гармоник
- Маятники
- Резонанс
- Эластичность
- Жидкости
- Плотность
- Давление
- Плавучесть
- Расход жидкости
- Вязкость
- Аэродинамическое сопротивление
- Режимы потока
- Кинематика
- Теплофизика
- Тепло и температура
- Температура
- Тепловое расширение
- Атомная природа материи
- Закон о газе
- Кинетико-молекулярная теория
- Фазы
- Калориметрия
- Явное тепло
- Скрытое тепло
- Химическая потенциальная энергия
- Теплопередача
- Проводимость
- Конвекция
- Радиация
- Термодинамика
- Тепло и работа
- Диаграммы давление-объем
- Двигатели
- Холодильники
- Энергия и энтропия
- Абсолютный ноль
- Тепло и температура
- Волны и оптика
- Волновые явления
- Природа волн
- Периодические волны
- Интерференция и суперпозиция
- Интерфейсы и барьеры
- Звук
- Природа звука
- Интенсивность
- Эффект Доплера (звук)
- Ударные волны
- Дифракция и интерференция (звук)
- Стоячие волны
- ударов
- Музыка и шум
- Физическая оптика
- Природа света
- Поляризация
- Эффект Доплера (свет)
- Черенковское излучение
- Дифракция и интерференция (свет)
- Тонкопленочная интерференция
- Цвет
- Геометрическая оптика
- Отражение
- Преломление
- Зеркала сферические
- Сферические линзы
- Аберрация
- Волновые явления
- Электричество и магнетизм
- Электростатика
- Электрический заряд
- Закон Кулона
- Электрическое поле
- Электрический потенциал
- Закон Гаусса
- Проводников
- Электростатические приложения
- Конденсаторы
- Диэлектрики
- Батареи
- Электрический ток
- Электрический ток
- Электрическое сопротивление
- Электроэнергия
- цепей постоянного тока
- Резисторы в цепях
- Батареи в цепях
- Конденсаторы в цепях
- Правила Кирхгофа
- Магнитостатика
- Магнетизм
- Электромагнетизм
- Закон Ампера
- Электромагнитная сила
- Магнитодинамика
- Электромагнитная индукция
- Закон Фарадея
- Закон Ленца
- Индуктивность
- Цепи переменного тока
- Переменный ток
- RC-цепи
- Цепи RL
- LC контуры
- Электромагнитные волны
- Уравнения Максвелла
- Электромагнитные волны
- Электромагнитный спектр
- Электростатика
- Современная физика
- Относительность
- Пространство-время
- Масса-энергия
- Общая теория относительности
- Quanta
- Излучение черного тела
- Фотоэффект
- Рентгеновские снимки
- Антиматерия
- Волновая механика
- Волны материи
- Атомарные модели
- Полупроводники
- Конденсированное вещество
- Ядерная физика
- Изотопы
- Радиоактивный распад
- Период полураспада
- Энергия связи
- Деление
- Fusion
- Нуклеосинтез
- Ядерное оружие
- Радиобиология
- Физика элементарных частиц
- Квантовая электродинамика
- Квантовая хромодинамика
- Квантовая динамика вкуса
- Стандартная модель
- Помимо стандартной модели
- Относительность
- Фундаменты
- шт.
- Международная система единиц
- Гауссова система единиц
- Англо-американская система единиц
- Разные единицы
- Время
- Преобразование единиц
- Измерение
- значащие цифры
- По порядку величины
- Графики
- Графическое представление данных
- Линейная регрессия
- Подгонка по кривой
- Исчисление
- Векторы
- Тригонометрия
- Сложение и вычитание векторов
- Векторное разрешение и компоненты
- Умножение вектора
- ссылку
- Специальные символы
- Часто используемые уравнения
- Физические константы
- Астрономические данные
- Периодическая таблица элементов
- Люди в физике
- шт.
- Назад дело
- Предисловие
- Об этой книге
- Связаться с автором
- гленнелерт.нас
- Behance
- Твиттер
- YouTube
- Аффилированные сайты
- hypertextbook.com
- midwoodscience.org
- Предисловие
Чтение физики в графике
В науках мы часто изображаем отношения на графике. Мы выбрали отвертку в качестве нашего значка для чтения физики с графика, поскольку отвертка часто – это то, что вам нужно, чтобы что-то открыть, чтобы посмотреть, что внутри, что заставляет это работать.
Когда вы учитесь создавать графики в математических классах, вы часто показываете график функции – отношения между двумя переменными (обычно $ x $ и $ y $), и это почти конец. Но в науке мы строим графики многих функций и взаимосвязей, поэтому часто у нас есть много различных графиков , представляющих одну и ту же физическую ситуацию .
В результате графики могут дать вам несколько представлений одной и той же ситуации. Каждый график подчеркивает разные аспекты происходящего.Это как взять реальный объект и смотреть на него под разными углами, вращать, переворачивать и смотреть на него при разном освещении.
Рассмотрение ситуации с использованием различных графиков помогает лучше понять происходящее, сделать его более последовательным и осмысленным.
Совместное чтение графиков с инструментом истории особенно полезно, чтобы увидеть, как и какие части физической истории нам рассказывает график. Графики могут быть ценным инструментом, помогающим анализировать и разобраться в сложной ситуации.
Вот несколько советов, как сохранить четкость и безупречность графического инструмента:
- Тщательно рисуйте графики
- Обозначьте свои топоры
- Помните, как строить и читать отдельные точки
- Используйте профессиональные условные обозначения
- Научитесь считывать уклоны и площади с графика
Тщательно рисуйте графики
Когда вы работаете над заданной физической задачей, вас часто просят «нарисовать график». По моему опыту, многие студенты рассматривают это как конец, а не начало – что-то, что инструктор просил их сделать, чтобы они хотели его завершить.Но часто инструктор просит вас нарисовать график как часть построения сложных и богатых рассуждений о физической ситуации. Когда вы рисуете топоры, старайтесь делать их прямыми и перпендикулярными. Нарисуйте линии графика, чтобы правильно представить основные черты проблемы: где максимумы и минимумы? Где график пересекает ось? Какие части графика прямые, а какие изогнутые?
Вам не нужно вытаскивать линейку и транспортир каждый раз, когда вы хотите нарисовать график, чтобы помочь вам что-то понять, но будьте осторожны, рисуя достаточно прямые линии, делая прямые углы похожими на прямые, и равномерно и надлежащим образом размечая масштаб. .(Конечно, если вы создаете график для совместного использования, вы действительно хотите использовать линейку, транспортир или графическую программу!)
Дело в том, что некоторые закономерности в физической ситуации НАМНОГО легче уловить, когда вы видите их на графике или другом визуальном представлении. На тщательно нарисованном графике искомый паттерн может просто выскочить на вас. В неряшливом его будет сложно найти, а рисование графика будет просто еще одной утомительной задачей, а не способом решения.
Тщательно нарисованный график – ценный инструмент, который поможет вам понять физическую ситуацию.
Обозначьте свои топоры
В математике вы часто имеете дело только с одним графиком вида $ y = f (x) $. Были две связанные переменные – $ x $ и $ y $. Даже на уроках естествознания вам часто показывали или создавали для себя один график, представляющий взаимосвязь или набор данных. Поэтому было нормально называть горизонтальную ось «осью x», а вертикальную ось – «осью y».
В этом классе это доставит вам массу неприятностей. В этом классе мы часто будем использовать несколько графиков разных вещей одновременно, чтобы описать физическую ситуацию.Возможно, вы изображаете горизонтальное смещение объекта как функцию времени. В этом случае горизонтальное смещение может быть вертикальной осью, а время – горизонтальной осью. Тогда вы могли бы сказать такие запутанные предложения, как «У нас есть x на оси y и t на оси x». И вы, возможно, пытаетесь одновременно сравнить графики x vs t, v vs t, a vs t, F vs t, F vs x и т. Д. (См., Например, липкие тележки ДОБАВИТЬ ССЫЛКУ.)
Итак, мы назовем традиционную «ось x» горизонтальной осью , а традиционную «ось y» – вертикальной осью. (Настоящие технические термины для них – «абсцисса» и «ордината» соответственно. Мы НЕ будем использовать эти термины.) Чтобы графы, которые вы рисуете, были полезными инструментами, не забудьте пометить оси!
У нас будет так много графиков для одной и той же ситуации, что отсутствие маркировки осей приведет вас в полное замешательство! (Кроме того, по словам Рэндала Манро, невыполнение этого может повредить личным отношениям.)
Рэндалл Манро, xkcd.com/833/
Вспомните, как строить и читать отдельные точки
Помните, что каждая точка на графике показывает взаимосвязь между двумя переменными.Например, если мы строим график скорости ($ v $) как функцию времени ($ t $), чтобы построить скорость 5,0 м / с за время 7,5 с, мы идем вдоль оси времени до 7,5 и нарисуем перпендикулярно прямо вверх (пунктирная линия). Затем идем по оси скорости до 5 и проводим перпендикуляр (пунктирная линия). Место их пересечения – это точка на графике, которая представляет $ (v, t) $ = (5 м / с, 7,5 с). Конечно, если у нас есть точка на кривой, мы можем запустить эту процедуру в обратном направлении, чтобы найти координаты точки на кривой.
Хотя это может показаться очевидным, я видел, как студенты снова и снова не обращались к этим знаниям, когда их просили нарисовать или прочитать график. Конечно, для этого необходимо аккуратно нарисовать перпендикуляры и разметить шкалы.
Используйте профессиональные соглашения (или соглашения классов)
Есть два соглашения для графиков, которые могут вызвать путаницу:
Наконечники стрел
По какой-то причине несколько десятилетий назад школьное преподавание математики приняло традицию рисовать наконечники стрел на концах осей, чтобы указать, что они продолжаются вечно.Иногда это соглашение распространялось на кривые, которые представляли функции – стрелки рисовались на концах кривой, чтобы указать, что это продолжается вечно. Если вы приобрели эту привычку, пожалуйста, избавьтесь от нее. Для этого есть три причины:
- В профессиональном соглашении, используемом в научных публикациях, , а не , не использует стрелки на концах осей или графиков.
- Многие из наших функций (и даже наши координаты) не продолжаются вечно, а представляют только ограниченный диапазон переменных.
- В этом классе мы хотим использовать другое соглашение, чтобы подчеркнуть нечто иное, чем «продолжается вечно»: знаки (а именно, какое направление имеет положительный знак, поскольку направления часто будут важны).
Наше соглашение о классе будет заключаться в том, чтобы использовать стрелки ТОЛЬКО, когда мы хотим подчеркнуть, что сторона оси представляет положительную сторону.
Знаки
Некоторым студентам сложно научиться обращаться со знаками. В этом классе мы используем знаки, чтобы указывать направления и различать изменения в различных величинах, отделяя прибыль от убытков.Иногда, когда мы строим график, мы хотим подчеркнуть, какое направление является положительным направлением на нашей оси. Хотя обычно они будут располагаться «вверх и вправо», мы узнаем, что мы можем свободно выбирать наши оси и что иногда удобно выбирать их под углом или вверх ногами. Иногда мы будем помещать стрелку на положительном конце оси (никогда на отрицательном конце!), Чтобы напомнить вам, в каком направлении находится +. Ищите это! (Когда вы начнете создавать графики для опубликованных статей или профессиональных презентаций, вы воспользуетесь профессиональным соглашением и полностью откажетесь от стрелок.)
Научитесь считывать уклоны и площади с графика
В своем классе исчисления вы узнаете, что производная функции представлена наклоном ее графика, а интеграл функции представлен областью под ее графиком. В этом классе мы будем использовать наклоны и области на графиках как мощные инструменты для связи, например, положения, скорости и ускорения или потенциальной энергии и силы. Ознакомьтесь с дополнениями в конце этой статьи, чтобы узнать подробности.
Джо Редиш 27.12.17
Как нарисовать наиболее подходящую линию в физике
Введение в построение графиков и линий наилучшего соответствия
В этом руководстве мы объясняем важность научных графиков в физике и объясняем, как правильно рисовать научные графики, включая наиболее подходящие линии.Это действительно важный физический навык, и вам необходимо овладеть им, если вы хотите успешно сдать следующий практический экзамен по физике.
В этой статье мы обсуждаем:
Научные графики
Что такое научные графики?
График – это визуальное представление взаимосвязи между двумя переменными: x (независимая переменная) и y (зависимая переменная).
Графики позволяют легко определять тенденции в данных, которые вы собрали и которые можно проанализировать для выполнения вычислений или измерений, связанных с достижением цели эксперимента.
Как нарисовать научный график
| Шаг | Действие | Деталь |
| 1 | Определите переменные |
|
| 2 | Определите диапазон переменной |
|
| 3 | Определите масштаб | Определите масштаб (числовое значение для каждого квадрата или деления), который лучше всего соответствует диапазону каждой переменной.|
| 4 | Номер и обозначение каждой оси |
|
| 5 | Постройте точки данных |
|
| 6 | Нарисуйте график | Определите тенденцию или взаимосвязь между независимыми и зависимыми переменными. |
| 7 | Дайте описательный заголовок |
|
В 11 и 12 годах физики тенденции, которые вы будете исследовать, в основном линейны или могут быть преобразованы в линейные графики, и, следовательно, вам потребуется нарисовать линию наилучшего соответствия .
Рисование линии наилучшего вписывания
Ниже показан пример правильно проведенной линии наилучшего вписывания вместе с неправильной:
Как нарисовать линию наилучшего вписывания
Чтобы нарисовать линию наилучшего вписывания, учтите следующее:
- Выбросы следует игнорировать.
- Линия должна отражать тенденцию в данных, т.е. она должна лучше всего совпадать с большинством данных и меньше – с точками данных, которые отличаются от большинства.
- Линия должна быть сбалансирована, т.е. на обоих концах линии должны быть точки выше и ниже линии.
- НЕ заставляйте линию проходить через какие-либо определенные точки данных или проходить через ноль. Цель линии наилучшего соответствия – выявить тенденцию всех данных.
Почему нам нужно провести линию наилучшего соответствия?
Основными причинами проведения линии наилучшего соответствия являются:
- Уменьшить влияние как систематической, так и случайной ошибки и, таким образом, сделать эксперимент более точным и надежным.
- Найдите и используйте градиент линии наилучшего соответствия, чтобы определить неизвестное в эксперименте. Обычно определение этого неизвестного каким-то образом направлено на достижение цели
Каким образом линия наилучшего соответствия уменьшает экспериментальные ошибки?
Рисуя линию наилучшего соответствия, мы ищем наиболее сильную тенденцию в данных и, таким образом, уменьшаем влияние случайных ошибок.Если затем мы используем градиент линии наилучшего соответствия, мы смотрим на различия в значениях, а не на абсолютные значения, что уменьшает или устраняет влияние систематических ошибок.
На графиках ниже показаны четыре примера с разными типами ошибок и без ошибок:
- Идеальные данные без ошибок
- Случайная ошибка
- Случайная ошибка с выбросом
- Случайные и систематические ошибки
Градиент представляет результат эксперимента и должно иметь значение 1, поэтому уравнение линии будет \ (y = x \).
Как использование линии наилучшего соответствия уменьшает экспериментальные ошибки?
Использование графика дает такие же или лучшие результаты, чем расчет непосредственно по точкам данных с последующим усреднением, как показано в таблице ниже.
| Типы присутствующих ошибок | Результат, полученный из градиента линии наилучшего соответствия | Результат, полученный в результате расчета с использованием всех точек данных и их усреднения |
| Идеальные данные – ошибок нет | 1.00 | 1.00 |
| Случайная ошибка | 1.04 | 1.04 |
| Случайная ошибка с выбросом | 1.04 | 1.07 |
| Случайные и систематические ошибки | 9 1.01 | 1.01 | Из таблицы видно, что:


 )
)
 Виток провода находится в магнитном поле,
перпендикулярном плоскости витка, и своими
концами замкнут на амперметр. Магнитная индукция
поля меняется с течением времени согласно
графику на рисунке. В какой промежуток времени
амперметр покажет наличие электрического тока в
витке:
Виток провода находится в магнитном поле,
перпендикулярном плоскости витка, и своими
концами замкнут на амперметр. Магнитная индукция
поля меняется с течением времени согласно
графику на рисунке. В какой промежуток времени
амперметр покажет наличие электрического тока в
витке: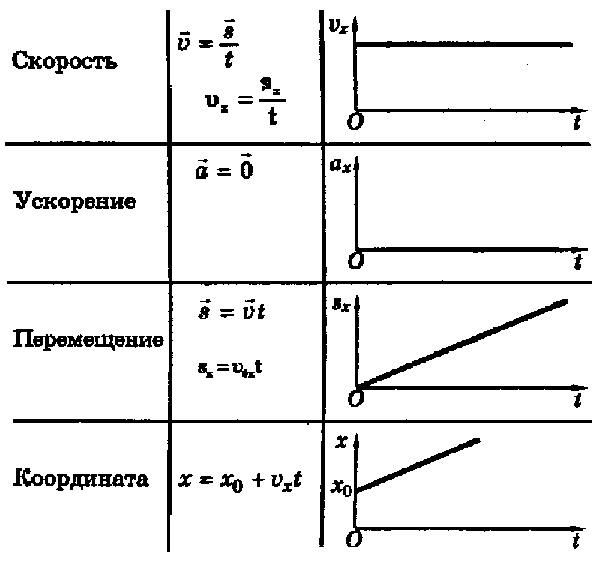 рисунок).
Какое количество теплоты сообщено газу на
участке 2 – 3?
рисунок).
Какое количество теплоты сообщено газу на
участке 2 – 3? Ускорение свободного падения – это ускорение тела, которое свободно падает с некоторой высоты (сопротивлением воздуха нужно пренебречь).
Ускорение свободного падения – это ускорение тела, которое свободно падает с некоторой высоты (сопротивлением воздуха нужно пренебречь).